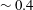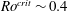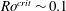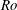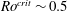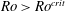1 Introduction
The morphology of the flow in Earth’s outer core and its magnetic field are thought to be intimately related. Columnar flow outside the tangent cylinder (the imaginary cylinder which circumscribes the inner core and is aligned with the rotation axis) usually results in a predominantly dipolar field, as evidenced from geodynamo simulations (Roberts & King Reference Roberts and King2013). The convection columns assume the form of alternating cyclones and anti-cyclones, and carry a large degree of helicity
$h=\boldsymbol{u}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{u})$
(where
$\boldsymbol{u}$
is the velocity field) (Sreenivasan & Jones Reference Sreenivasan and Jones2011).
1.1 An observed dipole–multipole transition in numerical dynamos
Simulations attempting to mimic the geodynamo have been surprisingly successful, in the sense that many of the published simulations produce large-scale magnetic fields which are predominantly dipolar. However, a remarkably abrupt transition between dipolar and multi-polar dynamos has been observed in many numerical datasets of spherical shell magnetohydrodynamic (MHD) convection, that appears to be robust with respect to boundary conditions or the source of convection.
This was initially reported by Kutzner & Christensen (Reference Kutzner and Christensen2002) for convection driven dynamos in a spherical shell. In these numerical experiments the Ekman number is
$Ek=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D6FA}L^{2}=10^{-3}{-}10^{-4}$
while the largest Rayleigh number is
$Ra=40Ra_{c}$
, where
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of the fluid,
$\unicode[STIX]{x1D734}=\unicode[STIX]{x1D6FA}\boldsymbol{e}_{z}$
is the rotation rate,
$L$
is the shell thickness and
$Ra_{c}$
is the critical Rayleigh number at which hydrodynamic convection first appears. Two distinct regimes of convection and magnetic field configuration were observed. When the buoyant forcing is supercritical but relatively weak, there is stable columnar convection, the magnetic field has a large dipolarity (as defined below), and there are no polarity reversals. However, when the convection is forced more strongly – for the same Ekman number – the flow becomes strongly three-dimensional and the dipole quickly breaks down. Thermal and compositional convection were considered in this work, with a variety of boundary conditions, and no dependence was found on the type of convective driving.
With a suite of numerical experiments, Christensen & Aubert (Reference Christensen and Aubert2006) showed that the transition persists for more highly forced simulations. They made the link to a local Rossby number defined as
$Ro_{\bar{n}}=Ro(\bar{n}/\unicode[STIX]{x03C0})$
, where the global scale Rossby number is
$Ro=u/2\unicode[STIX]{x1D6FA}L$
and
$\bar{n}$
is the mean spherical harmonic degree in the time-averaged kinetic energy spectrum (which is a dimensionless wavelength on spherical surfaces). The local Rossby number attempts to measure the ratio of inertial to Coriolis forces at the scale of the columnar convection. Stable columnar convection and dipolar magnetic fields were found for
$Ro_{\bar{n}}\lesssim 0.1$
, whereas columnarity is lost and multi-polar fields dominate for
$Ro_{\bar{n}}\gtrsim 0.1$
.
For a series of MHD and purely hydrodynamic spherical shell simulations (driven by a temperature difference), Soderlund, King & Aurnou (Reference Soderlund, King and Aurnou2012) (see also the corrigendum, Soderlund, King & Aurnou Reference Soderlund, King and Aurnou2014) observe a similar transition at
$Ro_{\bar{k}}=Ro(\bar{k}/\unicode[STIX]{x03C0})\sim 0.1$
. Here
$\bar{k}=(\bar{n}^{2}+\bar{m}^{2})^{1/2}$
, where
$\bar{m}$
is the mean spherical harmonic order in the time-averaged kinetic energy spectrum. The transition at
$Ro_{\bar{k}}\sim 0.1$
occurs when there is a reduction in the helicity of the flow. The change in helicity is found to be independent of magnetic field strength, suggesting that there is a purely hydrodynamic mechanism behind the transition in flow structure and hence, magnetic field morphology. Further, the three-dimensional convection observed for the more strongly forced simulations approximately follows the non-rotating, non-magnetic, turbulent convection scaling
$Re\sim Ra^{1/2}$
(Sano, Wu & Libchaber Reference Sano, Wu and Libchaber1989), suggesting that in this regime rotation and magnetic fields do not strongly influence the flow.
Using given values of
$Re$
,
$Ek$
and
$\bar{k}$
(Soderlund et al.
Reference Soderlund, King and Aurnou2012), we have calculated the local Rossby number for this dataset. Figure 1(a) shows the local Rossby number dependence of dipolarity
$f_{d}$
, the ratio of the energy in the dipole coefficients of the magnetic field to the energy in the full magnetic spectrum at the outer boundary. Also shown is the average relative axial helicity
$|h_{r}^{z}|$
(using the corrected data from Soderlund et al.
Reference Soderlund, King and Aurnou2014). This is calculated as
$\langle u_{z}\unicode[STIX]{x1D714}_{z}\rangle /(\langle |u_{z}|^{2}\rangle \langle |\unicode[STIX]{x1D714}_{z}|^{2}\rangle )^{1/2}$
, where the angle brackets denote averaging over a hemisphere, as the helicity distribution tends to be antisymmetric across the equatorial plane (figure 3
b). An abrupt decrease in the average relative axial helicity is found to correlate well with the loss of dipolarity of the magnetic field. The decrease in axial helicity is attributed to increases in thermal forcing, which causes the flow to lose its columnar structure, as measured by the columnarity (defined below).
It is noted in Soderlund et al. (Reference Soderlund, King and Aurnou2012) that the columnarity of the flow decreases less sharply than the dipolarity and axial helicity (figure 1
b), however, there remains a clear correlation between all three measures. Besides, the columnarity measure introduced by Soderlund et al. (Reference Soderlund, King and Aurnou2012) is somewhat arbitrary, and their regime boundary between columnar and non-columnar flow is chosen on a visual basis. Moreover, they calculate the dipolarity of the magnetic field as a ratio of the energy in the dipole components to the full magnetic spectrum, where authors in the past have only integrated to a degree of
$n=12$
(Christensen & Aubert Reference Christensen and Aubert2006). This choice will weakly affect the value of dipolarity for strongly dipolar magnetic fields (with a steep magnetic spectrum). However, once small magnetic scales are excited in the multi-polar dynamos (with a broader magnetic spectrum), this choice will exaggerate the decrease in dipolarity. Given these concerns, we conjecture that the transition in flow and magnetic field morphology are closely linked, and we seek an explanation for the correlation between columnarity, relative helicity and dipolarity.
So as the forcing is increased, inertia becomes more significant in the force balance. The length scale at which inertial effects are in contention with the effects of global rotation shifts into the energy-containing scales. This causes a loss of columnar structures and flow helicity, which results in the dipole collapse (Christensen & Aubert Reference Christensen and Aubert2006; Soderlund et al. Reference Soderlund, King and Aurnou2012; Dormy, Oruba & Petitdemange Reference Dormy, Oruba and Petitdemange2018). This paper addresses the question: what mechanism causes the transition from columnar to three-dimensional flow?
Figure 1. Data from Soderlund et al. (Reference Soderlund, King and Aurnou2012, Reference Soderlund, King and Aurnou2014) as a function of local Rossby number. The symbol for each quantity is shown above the corresponding axis label. (a) Dipolarity and relative axial helicity. (b) Columnarity and relative axial helicity.
Flow in Earth’s core is often characterised by
$Ro=u/2\unicode[STIX]{x1D6FA}\ell \approx 10^{-6}{-}10^{-3}$
, using the estimates
$\ell \sim 1{-}10^{3}$
km and
$u\sim 2\times 10^{-4}~\text{ms}^{-1}$
(Jackson, Jonkers & Walker Reference Jackson, Jonkers and Walker2000). Now it is observed in the purely hydrodynamic literature that inertial waves can propagate when
$Ro\lesssim 0.1$
(Baqui & Davidson Reference Baqui and Davidson2015; Sreenivasan & Davidson Reference Sreenivasan and Davidson2008; Yarom & Sharon Reference Yarom and Sharon2014). Moreover, such waves are responsible for the initial formation of columnar vortices in a rapidly rotating fluid (Staplehurst, Davidson & Dalziel Reference Staplehurst, Davidson and Dalziel2008; Ranjan & Davidson Reference Ranjan and Davidson2014). It might be expected, therefore, that at all conceivable scales in Earth’s outer core, columnar structures will be sustained by inertial waves (or some magnetically modified version of inertial waves, see Bardsley & Davidson Reference Bardsley and Davidson2017).
Despite these low Rossby number estimates, some authors have suggested the geodynamo lies close to the transition at
$Ro_{\bar{n}}\sim 0.1$
(Olson & Christensen Reference Olson and Christensen2006), in an attempt to explain geomagnetic excursions and reversals. For dynamos driven by compositional convection, Driscoll & Olson (Reference Driscoll and Olson2009) observe a reduction in dipolarity at
$Ro_{\bar{n}}\sim 0.1$
, which coincides with the onset of magnetic polarity reversals. However, for this style of convection, the decrease in dipolarity is much less abrupt. An alternate mechanism for polarity reversals was recently observed by Sheyko, Finlay & Jackson (Reference Sheyko, Finlay and Jackson2016), with a more Earth-like dynamo model. They find periodic reversals consistent with the propagation of dynamo waves, in which
$Ro_{\bar{n}}=0.06$
, contradicting the previously established regime boundary.
1.2 A transition in inertial wave propagation and in rotating turbulence
Modern studies into rotating turbulence reveal a similar transition in axially elongated flow structures. Numerical simulations of a vortical eddy, with characteristic velocity
$u$
and length scale
$\ell$
, subject to background rotation
$\unicode[STIX]{x1D6FA}$
(Sreenivasan & Davidson Reference Sreenivasan and Davidson2008) show that for
$Ro=u/2\unicode[STIX]{x1D6FA}\ell \lesssim 0.5$
the eddy rapidly elongates along the rotation axis. This behaviour is attributed to inertial wave packets propagating along the axis. However, for
$Ro\gtrsim 1$
the eddy spreads radially under the action of its own centrifugal force, with no preferential axial growth. These Rossby number limits differ slightly for different eddies, with lower (higher) bounds for anticyclonic (cyclonic) eddies, although this asymmetry is not the subject of the current work.
Experiments of inhomogeneous rotating turbulence at
$Ro\sim O(1)$
show that, on time scales of the order
$\unicode[STIX]{x1D6FA}^{-1}$
, columnar structure formation may be a result of inertial wave propagation (Davidson, Staplehurst & Dalziel Reference Davidson, Staplehurst and Dalziel2006). In a follow-up study (Staplehurst et al.
Reference Staplehurst, Davidson and Dalziel2008), this result is extended to homogeneous turbulence with a further set of experiments where turbulence was generated at
$Ro\sim 1$
and left to decay. As the energy decays, and interestingly as
$Ro$
drops below
${\sim}0.4$
, columnar structures are seen to emerge, whose axial growth is monitored by two-point vorticity correlations. The linear axial growth seen in the experiments is consistent with columnar structure formation by inertial wave propagation.
In purely hydrodynamic direct numerical simulations (DNS) of decaying, statistically homogeneous, rotating turbulence, a number of authors have observed a similar change in flow morphology with varying Rossby number. For example, Baqui & Davidson (Reference Baqui and Davidson2015) performed DNS with an initial Rossby number of
$O(1)$
, defined as
$Ro=u_{\bot }/2\unicode[STIX]{x1D6FA}\ell _{\bot }$
, where
$u_{\bot }$
is the root mean square (r.m.s.) perpendicular velocity and
$\ell _{\bot }$
is the integral length scale perpendicular to the rotation axis. The turbulence is unforced and so the kinetic energy rapidly decays, thus causing the Rossby number to fall. At the time when
$Ro\sim 0.4$
, there is a rapid growth of the length scale parallel to the rotation vector
$\ell _{\Vert }$
, which is linear and is characterised by
$\ell _{\Vert }\sim \ell _{\bot }\unicode[STIX]{x1D6FA}t$
. In contrast, the perpendicular length scale
$\ell _{\bot }$
remains approximately constant for the duration of the simulations. The linear increase in
$\ell _{\Vert }$
is explained by internal inertial wave propagation. Note that the axial extension observed here occurs on a time scale much shorter than the nonlinear time scale.
In buoyantly forced rotating turbulence we may expect inertial waves to be continually launched at the scale of the forcing, provided the Rossby number based on this length scale is small enough. Inertial waves are helical waves (see the next section), and they are an important source of helicity in a rotating fluid. Dallas & Tobias (Reference Dallas and Tobias2016) find that for a sufficiently time-independent random forcing, large amounts of relative helicity may be generated in a rotating fluid. For
$Ro\lesssim 0.2$
, defined using the forcing modes, they find a bifurcation to a state of non-zero helicity whereas for larger values of
$Ro\gtrsim 0.2$
there is an abrupt drop to zero helicity. Here several simulations are spread across a large range of
$Ro$
, so any transition cannot be tied to some critical
$Ro$
value. Even so, the Rossby number dependence of helicity is markedly abrupt.
In this paper we attempt to bridge the gap between the transition in hydrodynamic rotating turbulence and the dipolar–multipolar dynamo transition. We conjecture that the difference between the dynamo transition (local) Rossby number
$Ro^{crit}\approx 0.1$
and the rotating turbulence
$Ro^{crit}\sim 0.2{-}0.6$
is merely one of definition, i.e. which length scale is used; this will be discussed further in § 6.
1.3 Inertial waves dispersed from a localised energy source
Columnar flow structures spanning much of the core are a robust feature of most geodynamo simulations with rapid rotation. These are often interpreted in terms of boundary-driven columnar eigenmodes, i.e. steady solutions of a boundary-value problem in a rotating, internally heated spherical shell (Busse Reference Busse1975); although this relies on weak supercriticality. Convection in Earth’s outer core, on the other hand, is expected to be highly supercritical, where we expect
$Ra/Ra_{c}\sim 10^{6}$
(Gubbins Reference Gubbins2001). This necessitates an alternate mechanism to explain the columnar structure formation.
An alternative source of columnar structures in a system where the velocity and buoyancy fields are highly time dependent, are internally driven inertial waves (Davidson & Ranjan Reference Davidson and Ranjan2015). Inertial waves have the dispersion relation and group velocity
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D71B}=\pm \frac{2(\boldsymbol{k}\boldsymbol{\cdot }\unicode[STIX]{x1D734})}{k}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{c}_{g}=\pm \frac{2[k^{2}\unicode[STIX]{x1D734}-(\boldsymbol{k}\boldsymbol{\cdot }\unicode[STIX]{x1D734})\boldsymbol{k}]}{k^{3}}, & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{k}$
is the wavevector and
$k=|\boldsymbol{k}|$
. The wave frequency
$0\leqslant \unicode[STIX]{x1D71B}\leqslant 2\unicode[STIX]{x1D6FA}$
does not depend on
$k$
, but rather on the degree to which
$\boldsymbol{k}$
and
$\unicode[STIX]{x1D734}$
are aligned. Evidently when
$\boldsymbol{k}$
and
$\unicode[STIX]{x1D734}$
are nearly perpendicular the waves have low frequencies. From the group velocity (1.2), it is clear that low-frequency waves with
$\boldsymbol{k}$
perpendicular to
$\unicode[STIX]{x1D734}$
propagate energy along the rotation axis, and with the highest allowable speed
$c_{g}=\pm 2\unicode[STIX]{x1D6FA}/k$
. Crucially, it follows that all the energy in the two-dimensional disk of wavevectors with
$\boldsymbol{k}$
perpendicular to
$\unicode[STIX]{x1D734}$
is ‘folded up’ into axially propagating energy, whereas energy at some remote off-axis position is only associated with one wavevector. This explains the robust channelling of energy from a localised source along the rotation axis in a rapidly rotating fluid (see Davidson Reference Davidson2013, § 3.3.2). (For an alternative argument, based on angular momentum considerations, see Davidson et al. (Reference Davidson, Staplehurst and Dalziel2006).)
Figure 2. Isosurfaces of
$u_{z}^{2}$
coloured by helicity at (a)
$\unicode[STIX]{x1D6FA}t=2$
and (b)
$\unicode[STIX]{x1D6FA}t=10$
from Davidson & Ranjan (Reference Davidson and Ranjan2015). The axis of rotation points upwards and the axis labels are grid point numbers.
Figure 3. (a) Azimuthally (
$\unicode[STIX]{x1D719}$
) averaged
$\unicode[STIX]{x2202}T/\unicode[STIX]{x2202}\unicode[STIX]{x1D719}$
(in spherical coordinates) from a moderately forced geodynamo simulation (Ranjan et al.
Reference Ranjan, Davidson, Christensen and Wicht2018), the heat flux is concentrated in the equatorial regions. (b)
$\unicode[STIX]{x1D719}$
-averaged helicity from the same simulation. (c) The buoyant cloud initial condition and the spatial extent of the box in our simulations.
An excellent diagnostic for inertial waves emitted from a localised source is relative helicity
$h_{r}=h/|\boldsymbol{u}||\unicode[STIX]{x1D74E}|$
, the normalised point-wise correlation between velocity and vorticity. The reason for this is that inertial wave packets segregate helicity such that it is negative (positive) above (below) their source. This property extends beyond monochromatic waves to wave packets as shown by Davidson & Ranjan (Reference Davidson and Ranjan2015), where for a localised source at low-
$Ro$
, they observed a clear segregation of helicity above and below the source (figure 2). Another characteristic of low-frequency inertial wave packets is that they propagate energy at a constant speed
${\sim}2\unicode[STIX]{x1D6FA}/k_{\bot }$
, and tend to retain their value of
$k_{\bot }=(k_{x}^{2}+k_{y}^{2})^{1/2}$
. So as a wave packet elongates along the rotation axis, its transverse length scale remains constant. Internally driven inertial waves have recently been identified in a moderately supercritical dynamo simulation (Ranjan et al.
Reference Ranjan, Davidson, Christensen and Wicht2018), in which the ‘local’ Rossby number (as defined in Christensen & Aubert (Reference Christensen and Aubert2006)) is 0.08. These waves are thought to be important for sustaining columnar structures and for helicity transport in planetary cores (see figures 2 and 3
b). Further, when preferentially agitated near the equatorial plane, inertial wave packets yield a helicity distribution which could maintain an
$\unicode[STIX]{x1D6FC}^{2}$
dynamo (Davidson & Ranjan Reference Davidson and Ranjan2015, Reference Davidson and Ranjan2018). On this basis, Davidson (Reference Davidson2016) proposed and tested the hypothesis that the transition from dipolar to multipolar fields in the numerical dynamos was triggered by the suppression of inertial waves at the critical threshold
$Ro\sim 0.4$
. The results, while consistent with the hypothesis, were not entirely conclusive.
In a series of hydrodynamic and dynamo simulations, Garcia, Oruba & Dormy (Reference Garcia, Oruba and Dormy2017) observe that the equatorial symmetry of the flow is a key indicator for the dipolar–multipolar transition. Interestingly, a high degree of flow symmetry is associated with the picture outlined by Davidson (Reference Davidson2016), in the rapidly rotating regime. As the Rossby number is increased, and the system passes the critical threshold
$Ro\sim 0.4$
, a reduction in flow symmetry is expected. Thus, the relation of the dynamo transition to the symmetry of the velocity field is not inconsistent with Davidson’s hypothesis.
2 Numerical simulations with a buoyant source
Due to the extensive evidence that the transition from columnar structures to strongly three-dimensional flow is primarily hydrodynamic in origin (see § 1), we run numerical experiments of a non-conducting rotating fluid. The computational domain is Cartesian, and has dimensions
$-3L_{BOX}\leqslant z\leqslant 3L_{BOX}$
, and
$-L_{BOX}\leqslant x,y\leqslant L_{BOX}$
. The Boussinesq approximation is used, just as it is in most spherical shell simulations that have an equatorially biased buoyancy flux (Olson, Christensen & Glatzmaier Reference Olson, Christensen and Glatzmaier1999; Sakuraba & Roberts Reference Sakuraba and Roberts2009; Schaeffer et al.
Reference Schaeffer, Jault, Nataf and Fournier2017; Ranjan et al.
Reference Ranjan, Davidson, Christensen and Wicht2018) (see figure 3
a). The buoyancy initial condition is a vertically localised field of buoyant anomalies, a distribution which is inspired by the buoyancy field seen in these simulations. Gravity is in the
$y$
-direction, mimicking equatorial regions outside the tangent cylinder (see figure 3
a), and initially the velocity field is set to zero. The initial buoyancy field is composed of a random sea of buoyant blobs, with uniformly distributed sizes in the range
$\bar{\unicode[STIX]{x1D6FF}}/2<\unicode[STIX]{x1D6FF}<3\bar{\unicode[STIX]{x1D6FF}}/2$
and confined to
$|z|<3\bar{\unicode[STIX]{x1D6FF}}$
. Here
$z=0$
is the mid-plane of the box and
$\bar{\unicode[STIX]{x1D6FF}}\approx L_{BOX}/25$
is the characteristic radius of a constituent buoyant blob, each of which is spherical and has a density profile which is Gaussian. This results in a random buoyancy field with roughly 30 features in the horizontal directions (see figure 3
c).
We use the pseudo-spectral code of Yeung & Zhou (Reference Yeung and Zhou1998), where the equations solved are
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}\boldsymbol{u}+(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}+2\unicode[STIX]{x1D6FA}(\boldsymbol{e}_{z}\times \boldsymbol{u})=-\unicode[STIX]{x1D735}p+c\text{g}\boldsymbol{e}_{y}+\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}c+(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})c=\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FB}^{2}c, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0, & \displaystyle\end{eqnarray}$$
where the specific pressure
$p$
is reduced by the centrifugal acceleration,
$c=\unicode[STIX]{x1D70C}^{\prime }/\unicode[STIX]{x1D70C}_{0}$
is the dimensionless density perturbation,
$Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}=1$
and
$g$
is the uniform gravitational acceleration. Boundary conditions are periodic in all directions so we stop the simulations before any columnar structures breach the top/bottom of the box. Spatial resolution is such that there are 256 Fourier modes in the horizontal directions and 768 in the axial direction. De-aliasing is done by phase shifting and spherical truncation, after which the maximum wavenumber resolved is
$k_{\text{max}}$
. Time advancement is carried out with a Runge–Kutta order-2 predictor–corrector with an adaptive time step, the diffusive terms are treated exactly and the Courant–Friedrichs–Lewy (CFL) number is kept in the range 0.05–0.1. Incompressibility (2.3) is maintained through a projection method in spectral space.
Six simulations of varying Rossby number are performed (R1–R6), as documented in table 1, with R1 having the lowest Rossby number and R6 the highest. As the simulations are inhomogeneous, we calculate the r.m.s. velocity in the mid-plane of the box, where
$u_{rms}$
is highest in magnitude (see figure 4). For R1,
$u_{rms}$
initially rises due to the conversion of potential energy contained in the buoyant cloud to kinetic energy of the flow. As expected, inertial waves begin to propagate away from the buoyant cloud (see § 3), and the r.m.s. velocity saturates at the point when the flux of wave energy balances the energy conversion rate. For R3–6 however, the picture is different:
$u_{rms}$
rises by the same process and waves carry energy away from the buoyant region, but now there is a decrease due to dissipation. For R1 we take the typical r.m.s. velocity as the saturated value
$u_{rms}=0.023~\text{m}~\text{s}^{-1}$
, the kinematic viscosity is
$\unicode[STIX]{x1D708}=10^{-4}~\text{m}^{2}~\text{s}^{-1}$
, which gives a Reynolds number
$Re=u_{rms}\bar{\unicode[STIX]{x1D6FF}}/\unicode[STIX]{x1D708}\approx 30$
. The ‘saturated’ value we take for R2–6 is
$u_{rms}\approx 0.20~\text{m}~\text{s}^{-1}$
. This is the value where
$u_{rms}$
flattens off at large
$\unicode[STIX]{x1D6FA}t$
, which yields
$Re\approx 250$
.
Figure 4. Root mean square velocity in the mid-plane. Symbols are defined in table 1.
Table 1. Parameters for all runs. Subscripts
$b$
and
$w$
denote the buoyancy/turbulence region and the wave region respectively.
To investigate the effect of nonlinear inertial forces on wave dispersion, we increase the Rossby number by increasing the amplitude of the buoyancy source, which increases the peak value of
$u_{rms}$
(figure 4). The Ekman number is kept low at all times. If we balance the inertial and buoyancy terms in the curl of (2.1), we find a characteristic velocity based on the initial buoyancy field is
$v_{0}=(c_{rms}^{0}\text{g}\bar{\unicode[STIX]{x1D6FF}})^{1/2}$
. However this procedure is only valid for runs R2–6, as it is in these runs that inertia substantially effects the solution. We find it convenient to introduce two different Rossby numbers, one based on the initial (prescribed) buoyancy field and one based on the observed r.m.s. velocity in the saturated state,
$$\begin{eqnarray}\tilde{Ro}=\frac{v_{0}}{2\unicode[STIX]{x1D6FA}\bar{\unicode[STIX]{x1D6FF}}},\quad \overline{Ro}=\frac{u_{rms}}{2\unicode[STIX]{x1D6FA}\ell _{\bot }},\end{eqnarray}$$
(
$\tilde{Ro}$
defined for R2–6 only). Here
$\ell _{\bot }$
is the perpendicular integral scale of the flow which is of order
$\bar{\unicode[STIX]{x1D6FF}}$
(see § 3). A summary of the runs is presented in table 1, where the Ekman number
$\tilde{Ek}=\unicode[STIX]{x1D708}/2\unicode[STIX]{x1D6FA}\bar{\unicode[STIX]{x1D6FF}}^{2}$
is defined using prescribed quantities.
The
$\overline{Ro}$
values in table 1 are averages in time and space in the saturated state, the spatial averages are computed in separate regions of space: the ‘buoyancy/turbulence’
$b$
and ‘wave’
$w$
regions (defined in § 3). We note
$\overline{Ro}_{w}$
is similar to
$\tilde{Ro}$
, whereas
$\overline{Ro}_{b}$
tends to be larger due to a higher kinetic energy and smaller integral length scales. These diagnostics show the general trend of increasing Rossby number from R1–6, however we will explore later how the length scales and
$Ro$
evolve with time, and vary with height above/below the initial buoyant cloud.
Inertial wave packets are emitted at early times, and carry away a fraction of the energy of the buoyant cloud. We may expect the Rossby numbers in the waves to be smaller than those in the buoyancy/turbulence region, and this is true for R1–6.
3 Flow morphology
3.1 Isosurfaces
Figure 5. Isosurfaces of axial vorticity for runs R2, R4 and R6 at 5 % of the maximum value: dark purple is positive
$\unicode[STIX]{x1D714}_{z}$
, light yellow is negative
$\unicode[STIX]{x1D714}_{z}$
. The solid white horizontal lines indicate the extent of the wave packets
$-z_{w}$
and
$z_{w}$
, and the dashed white lines bound the buoyancy/turbulence region
$(-z_{b},z_{b})$
.
Figure 6. Vorticity isosurfaces at 5 % of the maximum value, coloured by relative helicity for runs R1, R3 and R5. The white dashed lines show the extent of the buoyancy/turbulence region
$-z_{b}$
to
$z_{b}$
, the solid white lines show the extent of the wave field
$-z_{w}$
and
$z_{w}$
.
The transition between columnar structures and disorganised flow can qualitatively be seen through isosurfaces of the velocity or vorticity fields. Here we show images of the axial vorticity
$\unicode[STIX]{x1D714}_{z}$
(figure 5) and the vorticity field
$|\unicode[STIX]{x1D74E}|$
coloured by relative helicity (figure 6). Columnar cyclone/anti-cyclone pairs (see figure 5) propagate away from the buoyant cloud (see also Davidson & Ranjan Reference Davidson and Ranjan2015), akin to the flow structures seen in dynamo simulations (Sreenivasan & Jones Reference Sreenivasan and Jones2011). Here inertial wave packets are launched for all simulations R1–6. These are the axially propagating and extending features evident in figure 5. This is confirmed by figure 6, as helicity is segregated into a pattern which is negative (positive) in the upper (lower) part of the box, a fundamental characteristic of inertial waves (see § 1). As expected from the group velocity relation for low-frequency inertial waves (1.2), ‘wider’ features advance faster, and this is seen in figures 5 and 6. For larger
$Ro$
, the buoyancy field advects and diffuses more as the waves are launched (see figure 7), leading to wave packets with a larger width, and
$c_{g}$
, from R2 to R6. As gravity is along
$y$
, for R2–6 the columnar structures lean over slightly, increasingly with larger
$Ro$
. This is due to horizontal movement in the buoyancy field, similar to the inclined columns reported by Hide, Ibbetson & Lighthill (Reference Hide, Ibbetson and Lighthill1968) and Lighthill (Reference Lighthill1970).
A striking feature for runs R3–6 is a region about the mid-plane of the box where the flow appears increasingly small scale and disordered. This turbulence is forced by the buoyancy field, is vertically localised (in the buoyancy/turbulence region), and is most easily seen in figure 6 for runs R3 and R5. It is characterised by a broadband velocity field (see below), increased energy in the small scales, and a more complex helicity distribution (i.e. not clearly segregated either side of the mid-plane). We introduce
$z_{b}(t)$
and
$z_{w}(t)$
as measures of the spatial extent of the buoyancy/turbulence region and the wave field, respectively. The buoyancy/turbulence zone,
$-z_{b}\rightarrow z_{b}$
, is defined as the height where the horizontally averaged buoyancy falls to 5 % of its maximum value. This is a robust choice as the buoyancy field is advected by the turbulence generated near the mid-plane of the box. Analogously, the extent of the wave field
$z_{w}$
is defined as the point where the horizontally averaged velocity magnitude falls to 5 % of its maximum value. The dashed white lines in figures 5 and 6 show the extent of the buoyancy/turbulence region, and the solid white lines indicate the extent of the wave field.
Figure 7 shows the buoyancy field in the mid-plane of the box at
$\unicode[STIX]{x1D6FA}t=10$
for runs R1, R3 and R6. The buoyancy field in R1 has advected a negligible amount, as expected at low-
$Ro$
, and there is little diffusion owing to the small Ekman number. However, for R3 and R6 there is a significant amount of advection and small scales are excited by the turbulence (see § 3.2), and these small scales are preferentially diffusive.
Figure 7. Buoyancy field in the mid-plane at
$\unicode[STIX]{x1D6FA}t=10$
for runs R1, R3 and R6, darker colours are higher magnitude.
3.2 Perpendicular spectra
Columnar structures formed by inertial wave propagation retain the perpendicular length scale of their source (Davidson Reference Davidson2013), for example the diameter of the buoyant blob or eddy from which the wave packet is launched. This can be seen through the group velocity of a low-frequency inertial wave packet
$c_{g}=2\unicode[STIX]{x1D6FA}/k_{\bot }$
, packets with a larger perpendicular length scale
$\ell _{\bot }$
(smaller
$k_{\bot }$
) travel faster than packets with a smaller
$\ell _{\bot }$
(larger
$k_{\bot }$
). Also, as we saw in the previous section, when the forcing is increased and the rotation weakened, we observe a disordered region about the mid-plane of the box where the flow is clearly more strongly three-dimensional. We expect the Rossby number in this turbulent region to be greater than the Rossby number of the waves launched initially, and we are interested in mapping the transition in space and time from wave dynamics, characterised by a columnar morphology, to incoherent turbulence.
To quantify these claims we compute perpendicular energy spectra as
$$\begin{eqnarray}E_{\bot }(k_{\bot })=\unicode[STIX]{x03C0}k_{\bot }\displaystyle \int \unicode[STIX]{x1D6F7}_{ii}(k_{\bot },k_{z})\,\text{d}k_{z},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6F7}_{ij}$
is the spectral tensor. These spectra typically peak at
$\unicode[STIX]{x03C0}/\ell _{\bot }$
, where
$\ell _{\bot }$
is the perpendicular integral scale of the flow (see § 3.4). To the right of the peak of
$E_{\bot }(k_{\bot })$
, we interpret
$E_{\bot }(k_{\bot })\,\text{d}k_{\bot }$
as the perpendicular kinetic energy within the wavenumber range
$k_{\bot }\rightarrow k_{\bot }+\text{d}k_{\bot }$
.
Figure 8. Perpendicular spectra (normalised by their integral) in the mid-plane for
$1\leqslant \unicode[STIX]{x1D6FA}t\leqslant 10$
(see legend), for runs R3 and R5. The black dashed line is the perpendicular spectrum of the initial buoyancy field.
Figure 9. Dissipation in the mid-plane as a function of
$\unicode[STIX]{x1D6FA}t$
and
$t$
respectively for runs R2–6. Symbols are defined in table 1.
Perpendicular spectra (normalised by their integral) in the mid-plane of the box for runs R3 and R5 are shown in figure 8, for
$1\leqslant \unicode[STIX]{x1D6FA}t\leqslant 10$
. The dashed line shows the perpendicular spectrum of the initial buoyancy field, calculated analogously to the perpendicular velocity spectra. At
$\unicode[STIX]{x1D6FA}t=1$
,
$E_{\bot }$
lies almost on top of the initial buoyancy spectrum, however the velocity field rapidly becomes broadband for both R3 and R5. It is in this sense that we characterise the flow as turbulent. We only present the spectra for R3 and R5 here for brevity, however these are representative of R2–6 (see figure 11).
It is of interest to compare
$E_{\bot }(k_{\bot })$
for R1–6. However if we hypothesise that the flow evolving in the buoyancy/turbulence region cares little about rotation, then making comparisons at the same
$\unicode[STIX]{x1D6FA}t$
might not be appropriate. So, we need an appropriate time to examine flow features and spectra in the mid-plane. Previous studies have shown that the peak of dissipation is a suitable time to compare turbulent quantities (Mininni & Pouquet Reference Mininni and Pouquet2009a
; Sahoo, Perlekar & Pandit Reference Sahoo, Perlekar and Pandit2011). The dissipation is defined
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D708}\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}$
where
$\unicode[STIX]{x1D61A}_{ij}$
is the rate of strain tensor, this may be written in terms of the enstrophy and a divergence (Davidson Reference Davidson2013)
$$\begin{eqnarray}\unicode[STIX]{x1D716}=\unicode[STIX]{x1D708}|\unicode[STIX]{x1D74E}|^{2}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }[{\sim}].\end{eqnarray}$$
A common proxy for the dissipation, which we will term the dissipation here unless stated otherwise is
$$\begin{eqnarray}\unicode[STIX]{x1D716}\approx \unicode[STIX]{x1D708}|\unicode[STIX]{x1D74E}|^{2}.\end{eqnarray}$$
This is averaged over the mid-plane of the box (for runs R2–6) and shown in figure 9. It is also useful to non-dimensionalise time with a nonlinear time scale, defined here as
$\unicode[STIX]{x1D70F}_{_{NL}}=\ell _{\bot }/u_{rms}$
and shown in figure 10 for the mid-plane of the box. In this figure the pale red stripe indicates the range of
$t/\unicode[STIX]{x1D70F}_{_{NL}}$
where the peak of dissipation lies. It is evident from figures 9 and 10 that the runs at higher
$\tilde{Ro}$
have had more time to advect and dissipate energy for the same
$\unicode[STIX]{x1D6FA}t$
. Therefore the turbulence in the buoyancy region becomes more developed in our simulations for larger
$\tilde{Ro}$
.
Figure 10. Value of
$t/\unicode[STIX]{x1D70F}_{_{NL}}$
in the mid-plane as a function of
$\unicode[STIX]{x1D6FA}t$
and
$t$
respectively for runs R1–6. The red shaded band indicates the range of
$t/\unicode[STIX]{x1D70F}_{_{NL}}$
where the peak of dissipation lies. Symbols are defined in table 1.
Figure 11. Perpendicular spectra (normalised by their integral) in the mid-plane at (a)
$\unicode[STIX]{x1D6FA}t=2$
, (b)
$\unicode[STIX]{x1D6FA}t=4$
, (c) the peak of dissipation –
$\unicode[STIX]{x1D70F}_{peak}$
and (d) at the end of the simulation,
$\unicode[STIX]{x1D6FA}t=20$
, for runs R1–6. The black dashed line is the perpendicular spectrum of the initial buoyancy field.
Runs with higher
$\tilde{Ro}$
transition to turbulence at smaller
$\unicode[STIX]{x1D6FA}t$
. However for R3–6 the dynamics is similar. Figure 11 shows perpendicular spectra for all runs at 4 distinct times: (a)
$\unicode[STIX]{x1D6FA}t=2$
, (b)
$\unicode[STIX]{x1D6FA}t=4$
, (c)
$t=\unicode[STIX]{x1D70F}_{peak}$
and (d)
$\unicode[STIX]{x1D6FA}t=20$
(the end of the simulation). At
$\unicode[STIX]{x1D6FA}t=2$
, the spectra for R1 and R2 are very close to the initial buoyancy spectrum whereas those for R5 and R6 have already begun to become broadband. As time progresses, at
$\unicode[STIX]{x1D6FA}t=4$
the spectra for R3–6 are all broadband indicating the transition to turbulence. The spectra for runs R2–6 are all very similar at the peak of dissipation
$t=\unicode[STIX]{x1D70F}_{peak}$
, and the curves are all at their most broadband point at this time. This suggests
$\unicode[STIX]{x1D70F}_{peak}$
is an objective time to compare runs R2–6. At the end of the runs,
$\unicode[STIX]{x1D6FA}t=20$
, the tails of the spectra for R3–6 have begun to fall back down, due to small-scale viscous dissipation.
3.3 Columnarity
Figure 12. Plane-averaged columnarity in the buoyancy/turbulence region and in the wave region. Four curves (a) are labelled with the corresponding
$\overline{Ro}_{b}$
value, and the dashed line is the time-averaged columnarity from the non-rotating run
$\dagger$
(see table 2). Symbols are defined in table 1.
We define the columnarity of the flow as in Ranjan et al. (Reference Ranjan, Davidson, Christensen and Wicht2018) (similar to Soderlund et al. (Reference Soderlund, King and Aurnou2012))
$$\begin{eqnarray}C(x,y)=\sqrt{\frac{\langle \unicode[STIX]{x1D714}_{z}\rangle _{z}^{2}}{\langle \unicode[STIX]{x1D714}_{z}^{2}\rangle _{z}}},\end{eqnarray}$$
where
$\langle {\sim}\rangle _{z}$
denotes averaging along
$z$
. From the above expression the mean quantity
$\langle C\rangle _{\bot }$
can be derived by averaging in the transverse plane. Figure 12 shows the columnarity
$\langle C\rangle _{\bot }$
computed in the buoyancy/turbulent region and in the wave region for runs R1–6 and
$5\leqslant \unicode[STIX]{x1D6FA}t\leqslant 20$
(for
$\unicode[STIX]{x1D6FA}t<5$
it is difficult to separate the two regions, although they are clearly identifiable at later times). For R1, we calculate
$\langle C\rangle _{\bot }^{b}$
in the region
$|z|<3\bar{\unicode[STIX]{x1D6FF}}$
as there is no turbulence and the buoyancy field only fractionally evolves. The buoyancy region and the wave region have very high columnarity for R1. This reflects the fact that inertial waves are free to propagate with ease at low Rossby number and the perpendicular length scales in the source region remain narrowly distributed about
$\bar{\unicode[STIX]{x1D6FF}}$
. Columnarity in the buoyancy/turbulence region for R2–6 decreases rapidly with increasing
$\overline{Ro}_{b}$
. Interestingly, the time-averaged columnarity
$\overline{\langle C\rangle _{\bot }^{b}}$
(see table 2) drops below 0.5 as
$\overline{Ro}_{b}$
becomes greater than 0.4 (table 1) (the transition value observed in rotating turbulence experiments, above which inertial waves cease to propagate). The dashed line on the
$\langle C\rangle _{\bot }^{b}$
plot is the time-averaged columnarity from a non-rotating run with the same initial conditions as R2–6 (see run
$\dagger$
, table 2). The time average for run
$\dagger$
is taken over the same period of simulated time
$t$
as for R6. This shows that the columnarity of the flow in the buoyancy/turbulence region for larger values of
$\overline{Ro}_{b}$
is approaching the non-rotating value of 0.29. This is reflected in the time averages
$\overline{\langle C\rangle _{\bot }^{b}}$
in table 2.
The columnarity in the wave field,
$\langle C\rangle _{\bot }^{w}$
, is calculated in a layer with a thickness of
$4\bar{\unicode[STIX]{x1D6FF}}$
that moves at the wave speed
${\sim}2\unicode[STIX]{x1D6FA}\bar{\unicode[STIX]{x1D6FF}}$
. For all runs, the wave columnarity is high, as shown by the time-averaged values
$\overline{\langle C\rangle _{\bot }^{w}}$
in table 2. This is supported by the columnar structures seen in the vorticity isosurfaces shown in figures 5 and 6.
Table 2. Time-averaged perpendicular length scale and columnarity in the buoyancy/turbulence region and in the wave region, and average relative helicity in the bottom half of the box. Run
$\dagger$
is a double resolution non-rotating run with the same initial conditions as R2–6.
3.4 Length scales
A common method of measuring length scales in turbulence experiments is to integrate the two-point autocorrelations of velocity components, yielding a characteristic length of the region within which eddies are correlated. We are interested in the temporal change of the length scales parallel and perpendicular to the rotation vector, as it is well known that in rotating turbulence these two length scales behave in very different ways (Staplehurst et al.
Reference Staplehurst, Davidson and Dalziel2008). Consider a cloud of homogeneous non-rotating turbulence, to which we suddenly apply constant rapid rotation. We would like to monitor any growth of the axial length scale due to the propagation of inertial wave packets. Now inertial waves transfer information by the coordination of phase, for example
$\unicode[STIX]{x1D71B}t$
in the ansatz
${\sim}\exp [\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}-\unicode[STIX]{x1D71B}t]$
(Greenspan Reference Greenspan1968). However, autocorrelations are almost completely devoid of phase information by their very construction (Bracewell Reference Bracewell1986), and it follows that we cannot expect to retrieve information relating to inertial wave propagation from classical integral scale measurements (Staplehurst et al.
Reference Staplehurst, Davidson and Dalziel2008).
For these reasons, we do not compute axial integral length scales using autocorrelations. We can, however, visually monitor the axial growth of velocity structures (see figure 5), and the helicity distribution (figure 6) and this reinforces our conclusion that the axial growth is due to inertial wave packets. This is verified by the time-evolution of the plane-averaged r.m.s. velocities. Figure 13 shows
$u_{rms}$
averaged over each perpendicular plane for
$2\leqslant \unicode[STIX]{x1D6FA}t\leqslant 20$
, the energy spreads to larger
$z/\bar{\unicode[STIX]{x1D6FF}}$
with
$\unicode[STIX]{x1D6FA}t$
. We show the same quantity in figure 14, but now the height is normalised by
$\unicode[STIX]{x1D6FA}t$
, there is a satisfactory collapse of these data particularly within the wave field.
Figure 13. Plane-averaged r.m.s. velocity for
$2\leqslant \unicode[STIX]{x1D6FA}t\leqslant 20$
.
Figure 14. As in figure 13, but now the left ordinate is normalised by
$\unicode[STIX]{x1D6FA}t$
.
The length scale which is important for the launching of wave packets, and to be used in the definition of
$Ro$
, is the length scale normal to the rotation axis. This perpendicular scale is often computed as (Mininni, Alexakis & Pouquet Reference Mininni, Alexakis and Pouquet2009; Mininni & Pouquet Reference Mininni and Pouquet2009b
; Sahoo et al.
Reference Sahoo, Perlekar and Pandit2011)
$$\begin{eqnarray}\ell _{\bot }=\frac{\unicode[STIX]{x03C0}\displaystyle \int k_{\bot }^{-1}E_{\bot }(k_{\bot })\,\text{d}k_{\bot }}{\displaystyle \int E_{\bot }(k_{\bot })\,\text{d}k_{\bot }},\end{eqnarray}$$
where
$E_{\bot }(k_{\bot })$
are perpendicular spectra (see § 3.2). Applied to a sinusoidal field with single wavenumber
$k$
, this gives
$\ell _{\bot }=\unicode[STIX]{x03C0}/k$
, and for a sea of Gaussian eddies of size
$\unicode[STIX]{x1D6FF}$
,
$\ell _{\bot }\approx \unicode[STIX]{x1D6FF}$
.
Figure 15 shows
$\ell _{\bot }/\bar{\unicode[STIX]{x1D6FF}}$
as a function of
$z/\bar{\unicode[STIX]{x1D6FF}}$
for times
$2\leqslant \unicode[STIX]{x1D6FA}t\leqslant 20$
. For all runs the shape of
$\ell _{\bot }/\bar{\unicode[STIX]{x1D6FF}}$
is very similar at
$\unicode[STIX]{x1D6FA}t=2$
. For R1, the perpendicular scale within the buoyant cloud quickly settles at a value of
$\ell _{\bot }/\unicode[STIX]{x1D6FF}\approx 1.1$
. For R2 however, we see the length scale in the buoyancy/turbulence region reduces, with a minimum of
$\ell _{\bot }/\unicode[STIX]{x1D6FF}\approx 0.55$
. There is a similar decrease in the perpendicular length scale for runs R3–6, although the dissipation of small-scale energy allows
$\ell _{\bot }/\unicode[STIX]{x1D6FF}$
to increase at later times in these runs. We interpret this reduction of the perpendicular length scale within the buoyancy/turbulence region in terms of the excitation of small-scale turbulence (see § 3.2). Interestingly, the minima of
$\ell _{\bot }(z=0)$
for R3–6 roughly coincide with the peaks of dissipation seen in figure 9.
The temporal decline of
$\ell _{\bot }/\unicode[STIX]{x1D6FF}$
in the wave field for all runs is expected. On inspection of the group velocity relation for low-frequency inertial wave packets, we see that energy launched with a larger perpendicular length scale travels faster, and that
$c_{g}\sim \unicode[STIX]{x1D6FA}\ell _{\bot }^{0}$
where the superscript 0 denotes
$\ell _{\bot }$
at the launch time. So, at a given
$z$
, the wave packets that arrive first are the broadest, and as time progresses narrower wave packets arrive.
Figure 15. The perpendicular length scale for
$2\leqslant \unicode[STIX]{x1D6FA}t\leqslant 20$
.
4 Helicity
Figure 16. Relative helicity at
$\unicode[STIX]{x1D6FA}t=16$
in the plane
$z=3\bar{\unicode[STIX]{x1D6FF}}$
for runs R1, R3 and R6.
The isosurfaces of vorticity coloured by relative helicity (see figure 6) show that for all runs the helicity in the wave field is segregated negative (positive) in the upper (lower) part of the box. However, for runs R2–6 the helicity distribution in the buoyancy/turbulence region is more complex. The turbulence in this region suggests that inertial waves are no longer the dominant feature of the flow, therefore we may expect less segregation of helicity.
Figure 16 shows the relative helicity
$h_{r}=\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D74E}/|\boldsymbol{u}||\unicode[STIX]{x1D74E}|$
at
$\unicode[STIX]{x1D6FA}t=16$
for runs R1, R3 and R6 in the plane
$z=3\bar{\unicode[STIX]{x1D6FF}}$
, at the upper edge of the initial buoyant cloud. For R1,
$h_{r}$
is almost entirely negative, indicating a high degree of helicity segregation. However, at larger
$\tilde{Ro}$
the helicity is progressively less segregated, due to the advancement of the turbulence to larger
$|z|/\bar{\unicode[STIX]{x1D6FF}}$
. This is clear from the approximate probability density function (PDF) of relative helicity at the same height
$z=3\bar{\unicode[STIX]{x1D6FF}}$
and the same time
$\unicode[STIX]{x1D6FA}t=16$
(see figure 17). For R1 the p.d.f. peaks at
$h_{r}=-0.64$
and has a large positive skewness of 1.6. The p.d.f.s for R2–6 are progressively less skewed, for R6 the skewness has reduced to 0.8.
Figure 17. Approximate probability density function (p.d.f.) of relative helicity
$h_{r}$
at
$z=3\bar{\unicode[STIX]{x1D6FF}}$
and
$\unicode[STIX]{x1D6FA}t=16$
.
5 Transition Rossby number
Figure 18. Rossby number (colour scale) based on
$\ell _{\bot }$
for
$|z|<10\bar{\unicode[STIX]{x1D6FF}}$
and
$1\leqslant \unicode[STIX]{x1D6FA}t\leqslant 20$
, the green contours are labelled by their value of
$Ro$
. The dashed white vertical lines indicate the time corresponding to the peak of dissipation, and the roughly horizontal dashed white lines show the extent of the buoyancy/turbulence region,
$-z_{b}$
and
$z_{b}$
.
Figure 19. (a–c) Comparison of the extent of the buoyancy/turbulence region
$z_{b}/\bar{\unicode[STIX]{x1D6FF}}$
and the contour height for
$Ro=0.3,\,0.4,\,0.5$
respectively (see green contours figure 18) for runs R2–6. The dashed lines show the linear best fit. (d) The correlation coefficient and slope for values of
$0.2\leqslant Ro\leqslant 0.6$
, the grey dot marks a slope of 1.
Just as we can look at the perpendicular length scale through height and time, we can now examine
$Ro=u_{rms}/2\unicode[STIX]{x1D6FA}\ell _{\bot }$
. This quantity is derived from plane-averaged velocities and perpendicular length scales (§ 3.4), so it depends on
$z/\bar{\unicode[STIX]{x1D6FF}}$
and time. Figure 18 shows the spatio-temporal variation of this Rossby number, indicated by the colour scale, for
$1\leqslant \unicode[STIX]{x1D6FA}t\leqslant 20$
and
$|z|<10\bar{\unicode[STIX]{x1D6FF}}$
, including green contours labelled by their
$Ro$
value. For R1 (not shown), at low-
$Ro$
, there is no turbulent region, and
$Ro<0.03$
everywhere at all times. This is expected as we are firmly in the linear regime and figure 6 (R1) shows no signs of transition to turbulence. As the initial buoyant perturbations are increased, there is a region in the centre of the box where
$Ro\gtrsim 0.4$
, this is highlighted by the
$Ro$
contours. This is mimicked by the turbulent region we see in figures 5 and 6 in the centre of the box. The vertical white dashed lines mark the peak of dissipation in the mid-plane
$\unicode[STIX]{x1D70F}_{peak}$
for each run (see § 3.2), this time approximately intersects the maximum
$Ro$
value for R2–6. The white dashed lines running from left to right show the buoyancy/turbulence region
$\pm z_{b}$
. Apart from early times, where
$\pm z_{b}$
marks the initial cloud size, these lines approximately follow the
$Ro$
contours shown,
$Ro=0.3,\,0.4,\,0.5$
. The value of the
$Ro$
contour which lies closest to
$\pm z_{b}$
increases slightly from R3–6, but is always in the range
$0.3\leqslant Ro\leqslant 0.5$
. This suggests that the buoyancy/turbulence region is approximately bounded by some critical
$Ro^{crit}$
value, within which rotation is not dominant and negligible energy is transported by inertial waves.
If we compare the extent of the cloud of turbulence
$z_{b}/\bar{\unicode[STIX]{x1D6FF}}$
with the height of the
$Ro=0.4$
contour at each time
$1\leqslant \unicode[STIX]{x1D6FA}t\leqslant 20$
for R2–6, we can see how good a match this is. Figure 19(a–c) compares
$z_{b}/\bar{\unicode[STIX]{x1D6FF}}$
with the height of three sets of
$Ro$
contours,
$Ro=0.3,\,0.4,\,0.5$
. Clearly for all three there is a positive correlation, and (a,c) are scattered slightly more than (b), the comparison at
$Ro=0.4$
. Note that here we are looking not only for minimal scatter, but for a one-to-one correspondence: i.e. a linear relationship with a slope of unity. Therefore, we have computed the correlation coefficient between
$z_{b}/\bar{\unicode[STIX]{x1D6FF}}$
and the contour heights, and the slope of the best linear fit for
$0.2\leqslant Ro\leqslant 0.6$
, to find the critical
$Ro$
that best fits these data (see figure 19
d). The correlation coefficient is greater than 0.9 for
$0.25\leqslant Ro\leqslant 0.48$
, and peaks at
$Ro=0.39$
. There is a drop to a correlation coefficient of 0.5 at
$Ro=0.6$
and this continues to decrease for larger Rossby numbers. The slope of the fit is always positive in the range
$0.2\leqslant Ro\leqslant 0.6$
, however the value at slope one is
$Ro=0.43$
. So if we give roughly equal weight to all
$0.25\lesssim Ro\lesssim 0.48$
based on the large positive correlation coefficient, then the optimum is
$Ro^{crit}\sim 0.4$
. This is supported by the visual comparison in figure 18. It is remarkable how close this critical value of
$Ro$
is compared with those found in the laboratory experiments of Staplehurst et al. (Reference Staplehurst, Davidson and Dalziel2008).
6 Discussion
In all the simulations presented here, low-frequency inertial waves are emitted from the buoyant cloud at early times, creating columnar cyclone/anti-cyclone pairs aligned with the rotation axis. The wave field is maintained at low-
$Ro$
, and the columnar vortices extend linearly towards the top/bottom of the box. We note that the simulations stop before the wave field (at low-
$Ro$
) has had sufficient time for nonlinear interactions to take place. For runs R2–6, with a larger initial buoyancy perturbation, we find that a region in the vertical centre of the box becomes turbulent. We have shown that the Rossby number,
$Ro$
, holds larger values within this turbulent region due to the combined effects of an increased r.m.s. velocity (figure 4), and a reduction in the perpendicular integral length scale (figure 15). We find that this turbulent region is approximately bounded by a critical
$Ro$
contour with the value
$Ro^{crit}\sim 0.4$
.
The critical Rossby number we find,
$Ro^{crit}\sim 0.4$
is consistent with earlier estimates from rotating turbulence (Sreenivasan & Davidson Reference Sreenivasan and Davidson2008; Staplehurst et al.
Reference Staplehurst, Davidson and Dalziel2008; Baqui & Davidson Reference Baqui and Davidson2015). This may be due to the similar practices used in this paper and by the turbulence community to estimate flow length scales. The transition seen here is similar to the transition observed in the dynamo simulations of Soderlund et al. (Reference Soderlund, King and Aurnou2012) (§ 1), where a critical Rossby number of 0.1 is reported. This Rossby number is defined using the mean spherical harmonic degree in the time-averaged kinetic energy spectrum
$\bar{n}$
, as detailed in § 1. The discrepancy between the value found here (and in rotating turbulence experiments), and the value observed across dynamo simulations (Kutzner & Christensen Reference Kutzner and Christensen2002; Christensen & Aubert Reference Christensen and Aubert2006; Soderlund et al.
Reference Soderlund, King and Aurnou2012,
$Ro^{crit}\sim 0.1$
), is likely caused by the definition of the length scale used in the local
$Ro$
.
The local Rossby number defined by Christensen & Aubert (Reference Christensen and Aubert2006) (and often used since) attempts to express the ratio of inertial to Coriolis forces at the scale of the convection. The dimensionless length scale here is defined as
$\ell _{\bar{n}}=\unicode[STIX]{x03C0}/\bar{n}$
. The calculation to acquire this length scale involves radial averaging, so it does not take radial variations into account. Indeed, as the kinetic energy spectra do not fall off rapidly, this length scale is not found to characterise flow transitions (Schaeffer et al.
Reference Schaeffer, Jault, Nataf and Fournier2017). Furthermore, the kinetic energy spectrum as a function of degree happens to be rotationally invariant, requiring that
$\ell _{\bar{n}}$
is an isotropic length scale with respect to spherical surfaces. Now experiments and numerical simulations of rapidly rotating convection have revealed that the resulting flow is highly anisotropic, namely columnar and at lower Ekman numbers, sheet-like, with
$\ell _{\unicode[STIX]{x1D719}}<\ell _{\unicode[STIX]{x1D703}}$
(Sumita & Olson Reference Sumita and Olson2000; Kageyama, Miyagoshi & Sato Reference Kageyama, Miyagoshi and Sato2008). Therefore the length scale, related to
$\ell _{\bar{n}}$
, often used by geodynamo modellers to calculate the local Rossby number is most likely larger than the perpendicular integral length scale – the crucial column width or blob size.
For a series of dynamos, Dormy et al. (Reference Dormy, Oruba and Petitdemange2018) calculated the vorticity length scale
$\ell _{\unicode[STIX]{x1D714}}^{2}=\langle \boldsymbol{u}^{2}\rangle /\langle \unicode[STIX]{x1D74E}^{2}\rangle$
(introduced in Oruba & Dormy Reference Oruba and Dormy2014), where the angle brackets denote time and volume averages. For the helical columnar convection exhibited in these simulations, we have the kinematic statement
$\unicode[STIX]{x1D735}\times \boldsymbol{u}\sim u_{rms}/\ell _{\bot }$
(Davidson Reference Davidson2014), so that
$\ell _{\unicode[STIX]{x1D714}}$
is predominantly a measure of the column width. Also reported in this paper are the values of
$\ell _{\bar{n}}$
, so for this dynamo dataset we may consider the relationship between these two length scales, as depicted in figure 20. There is an approximately linear relationship with
$\ell _{\bar{n}}\sim 5\ell _{\unicode[STIX]{x1D714}}$
, indicated by the dashed line. The shaded area is bounded by the lines
$\ell _{\bar{n}}\sim 4\ell _{\unicode[STIX]{x1D714}}$
and
$\ell _{\bar{n}}\sim 6\ell _{\unicode[STIX]{x1D714}}$
, to illustrate the sensitivity of the gradient of the fit. We return to the rotating turbulence estimate of the critical Rossby number
$Ro^{crit}\sim 0.4$
, and the transition in dynamo simulations which occurs at
$Ro_{\bar{n}}\sim 0.1$
, based on
$\ell _{\bar{n}}$
. Clearly this discrepancy of a factor of roughly 4 may be explained by the relationship shown in figure 20, where a factor of 5 is fits these data best. Indeed, Oruba & Dormy (Reference Oruba and Dormy2014) find that when the local Rossby number is based on this vorticity length, the transition between dipolar and multi-polar dynamos lies closer to 1.
Crucially, in the rotating turbulence experiments and simulations
$Ro\sim 0.4$
has been identified as the point where inertial waves stop propagating. Moreover, the source of columnar structures in these studies is shown to be inertial wave propagation (Davidson et al.
Reference Davidson, Staplehurst and Dalziel2006; Staplehurst et al.
Reference Staplehurst, Davidson and Dalziel2008; Baqui & Davidson Reference Baqui and Davidson2015). This is corroborated by the results presented here for buoyancy-driven rotating flows.
We have also shown for a set of dynamo simulations, that an appropriately defined convective-scale Rossby number of
$Ro\approx 0.5$
separates the two regimes of columnar and more three-dimensional convection. We suggest this cannot be a coincidence, and that columnar structures in dynamo simulations are sustained by the continual emission of inertial waves, originating from the buoyancy field (Davidson & Ranjan Reference Davidson and Ranjan2015; Ranjan et al.
Reference Ranjan, Davidson, Christensen and Wicht2018). In addition, the loss of helical columnar convection when the forcing is increased ubiquitously leads to the collapse of the dipole field. We thus propose a purely hydrodynamic mechanism based on fast time scale inertial wave propagation for the transition in flow structure and in turn, the inescapable dipole collapse.
Figure 20. The vorticity length scale
$\ell _{\unicode[STIX]{x1D714}}$
plotted against
$\ell _{\bar{n}}$
for a dataset from Dormy et al. (Reference Dormy, Oruba and Petitdemange2018). The shaded region is bounded by the lines
$\ell _{\bar{n}}=4\ell _{\unicode[STIX]{x1D714}}$
and
$\ell _{\bar{n}}=6\ell _{\unicode[STIX]{x1D714}}$
, and the dashed black line is
$\ell _{\bar{n}}=5\ell _{\unicode[STIX]{x1D714}}$
.
The Prandtl number
$Pr=1$
for all these simulations, however the thermal Prandtl number is expected to be closer to
$0.1$
in Earth’s outer core, and the compositional Prandtl number of
${\sim}100$
. Further, it is not known what fraction of the convective forcing is thermal or compositional, with estimates ranging from
$50/50$
thermal/compositional to 80 % compositional (Roberts & King Reference Roberts and King2013). Therefore, investigations into the effect of varying
$Pr$
within the codensity formulation, or in so-called ‘double-diffusive convection’ (Bouffard et al.
Reference Bouffard, Labrosse, Choblet, Fournier, Aubert and Tackley2017) on columnar structure formation may shed light on more realistic planetary core turbulence. For example, in the infinite Lewis number (the ratio of the thermal and compositional diffusivities) limit, buoyant plumes have a very thin filamentary structure and hence a small
$\ell _{\bot }$
.
We have neglected the magnetic field from the outset, motivated by results from previous work (Kutzner & Christensen Reference Kutzner and Christensen2002; Christensen & Aubert Reference Christensen and Aubert2006; Soderlund et al.
Reference Soderlund, King and Aurnou2012), however in Earth’s core magnetic energy should be much greater than kinetic. Moreover, dissipation is expected to be almost entirely ohmic, and the presence of a large-scale field will cause anisotropy in velocity structures. Therefore, even though the mechanism for the transition is believed to be hydrodynamic in origin, the energy and length scales involved will be modified by the magnetic field. For example, ohmic dissipation will stunt and morph magnetically modified helical waves from columnar structures into platelets, introducing another degree of anisotropy into the system. The combined decrease in both kinetic energy and (perpendicular) length scale will have an unpredictable effect on the local
$Ro$
. Under the influence of a magnetic field, the properties of inertial waves are modified, the resulting waves are termed magnetic-Coriolis waves (Bardsley & Davidson Reference Bardsley and Davidson2016, Reference Bardsley and Davidson2017) (within which magnetostrophic waves are a subset). These magnetically modified waves have a slower group velocity, with intermediate waves travelling roughly half as fast as pure inertial waves, and magnetostrophic waves are much slower. However, all such classes of waves segregate helicity in the same way as inertial waves.
Acknowledgements
This work was completed during a PhD studentship sponsored by the Leverhulme trust UK, grant no. RPG-2015-195/RG77943. The authors thank A. Ranjan and O. Bardsley for their helpful comments, and P. K. Yeung for sharing his DNS code. We also thank four anonymous referees for their constructive comments that helped improve the manuscript. The computations were performed on the high performance computing facilities, CSD3, at Cambridge University.
