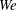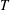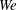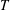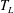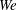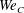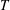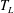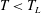1. Introduction
The transition to splashing, i.e. the disintegration of liquid droplets impacting solid surfaces, has been the subject of numerous studies ever since researchers were able to observe the impact process by high-speed imaging (Worthington Reference Worthington1876; Levin & Hobbs Reference Levin and Hobbs1971; Rein Reference Rein1993; Yarin & Weiss Reference Yarin and Weiss1995; Yarin Reference Yarin2006). Although the splashing mechanism has not been fully understood, it was experimentally found by Xu, Zhang & Nagel (Reference Xu, Zhang and Nagel2005) that the pressure of the ambient air is a key factor in the splashing process at room temperature, among others such as the liquid properties (Driscoll, Stevens & Nagel Reference Driscoll, Stevens and Nagel2010; Palacios et al. Reference Palacios, Hernández, Gómez, Zanzi and López2013; Stevens Reference Stevens2014), the droplet’s kinetic energy (Yarin & Weiss Reference Yarin and Weiss1995; Thoroddsen & Sakakibara Reference Thoroddsen and Sakakibara1998; Roisman, Rioboo & Tropea Reference Roisman, Rioboo and Tropea2002; Visser et al. Reference Visser, Tagawa, Sun and Lohse2012, Reference Visser, Frommhold, Wildeman, Mettin, Lohse and Sun2015) and the properties of the surface (Mundo, Sommerfeld & Tropea Reference Mundo, Sommerfeld and Tropea1995; Lembach et al. Reference Lembach, Tan, Roisman, Gambaryan-Roisman, Zhang, Tropea and Yarin2010; Tsai et al. Reference Tsai, Hendrix, Dijkstra, Shui and Lohse2011; Latka et al. Reference Latka, Strandburg-Peshkin, Driscoll, Stevens and Nagel2012; van der Veen et al. Reference van der Veen, Hendrix, Tran, Sun, Tsai and Lohse2014). In particular, the air layer under the droplet was thought to be responsible for splashing (Mandre, Mani & Brenner Reference Mandre, Mani and Brenner2009; Mani, Mandre & Brenner Reference Mani, Mandre and Brenner2010; Mandre & Brenner Reference Mandre and Brenner2011; Bouwhuis et al. Reference Bouwhuis, van der Veen, Tran, Keij, Winkels, Peters, van der Meer, Sun, Snoeijer and Lohse2012; Kolinski et al. Reference Kolinski, Rubinstein, Mandre, Brenner, Weitz and Mahadevan2012), but more recently it was suggested that rather than the gas under the whole droplet, the gas at the edge of the lamella plays a role in the transition to splashing (Riboux & Gordillo Reference Riboux and Gordillo2014, Reference Riboux and Gordillo2015), finding good agreement with the experimental data for isothermal impact at room temperature.
Another transition that has received much attention is the dynamic Leidenfrost transition for droplets impacting heated surfaces (Inada et al. Reference Inada, Miyasaka, Sakamoto and Hojo1988; Yao & Cai Reference Yao and Cai1988; Chandra & Avedisian Reference Chandra and Avedisian1991; Bernardin, Stebbins & Mudawar Reference Bernardin, Stebbins and Mudawar1997; Wang, Lin & Chen Reference Wang, Lin and Chen2000; Sinha-Ray, Zhang & Yarin Reference Sinha-Ray, Zhang and Yarin2011; Weickgenannt et al. Reference Weickgenannt, Zhang, Sinha-Ray, Roisman, Gambaryan-Roisman, Tropea and Yarin2011; Tran et al. Reference Tran, Staat, Prosperetti, Sun and Lohse2012, Reference Tran, Staat, Susarrey-Arce, Foertsch, van Houselt, Gardeniers, Prosperetti, Lohse and Sun2013; Quéré Reference Quéré2013; Nair et al. Reference Nair, Staat, Tran, van Houselt, Prosperetti, Lohse and Sun2014; Khavari et al. Reference Khavari, Sun, Lohse and Tran2015; Shirota et al. Reference Shirota, van Limbeek, Sun, Prosperetti and Lohse2015). When impacting a heated surface, the droplet either makes contact with the surface and boils violently or it is separated from the substrate by a layer of its own vapour for the entire duration of the impact process, the latter being the Leidenfrost state. The lowest surface temperature for which this lasting vapour layer exists is defined as the dynamic Leidenfrost temperature (Tran et al. Reference Tran, Staat, Prosperetti, Sun and Lohse2012).
What both the transition to splashing and the Leidenfrost transition have in common is that the role of the gas phase between the droplet and the substrate is very relevant. Additionally, both transitions are crucially important in numerous technological and industrial applications; so it is of fundamental and also of practical interest to understand how the transition to splashing depends on the surface temperature and the kinetic energy of the droplet.
The experimental determination of the transition to the Leidenfrost regime is particularly challenging. The distinction of droplet behaviour across the transition has normally relied on high-speed recording of the impact from side or top-angle views. In particular, the appearance of ejected droplets has been used as a criterion by many authors (Inada et al. Reference Inada, Miyasaka, Sakamoto and Hojo1988; Yao & Cai Reference Yao and Cai1988; Chandra & Avedisian Reference Chandra and Avedisian1991; Bernardin et al. Reference Bernardin, Stebbins and Mudawar1997; Wang et al. Reference Wang, Lin and Chen2000; Tran et al. Reference Tran, Staat, Prosperetti, Sun and Lohse2012, Reference Tran, Staat, Susarrey-Arce, Foertsch, van Houselt, Gardeniers, Prosperetti, Lohse and Sun2013; Nair et al. Reference Nair, Staat, Tran, van Houselt, Prosperetti, Lohse and Sun2014) to exclude the Leidenfrost state, with the assumption that then there must exist a liquid/surface contact, leading to the disintegration of the droplet. Conversely, it is assumed that a droplet is in the Leidenfrost state when there are no signs of boiling (e.g. vapour bubbles or ejected droplets). However, it is not necessarily true that any liquid/solid contact during impact must produce vapour bubbles or ejected droplets, so this way of classifying impact behaviour might be unreliable. As the existence of a complete vapour layer between the impacting droplet and the solid surface demarcates the Leidenfrost regime from the contact boiling or transition regimes (Khavari et al. Reference Khavari, Sun, Lohse and Tran2015; Shirota et al. Reference Shirota, van Limbeek, Sun, Prosperetti and Lohse2015), the most accurate means of determining the transition temperature is to measure the vapour layer directly.
In this paper, we present a method based on interferometric high-speed imaging to quantify the Leidenfrost transition temperature in a wide parameter regime. We explore the behaviour of droplets impacting heated surfaces across different regimes separated by the transition to splashing and the transition to the Leidenfrost state.
2. Experimental set-up
Figure 1 shows the schematics of the experimental set-up that allows us to observe and distinguish the different regimes of the droplets impacting the heated surfaces. We let ethanol droplets (density
![]() ${\it\rho}=789~\text{kg}~\text{m}^{-3}$
, surface tension
${\it\rho}=789~\text{kg}~\text{m}^{-3}$
, surface tension
![]() ${\it\sigma}=22~\text{mN}~\text{m}^{-1}$
, viscosity
${\it\sigma}=22~\text{mN}~\text{m}^{-1}$
, viscosity
![]() ${\it\mu}=1.1~\text{mPa}~\text{s}$
and boiling temperature
${\it\mu}=1.1~\text{mPa}~\text{s}$
and boiling temperature
![]() $T_{b}=78\,^{\circ }\text{C}$
) fall on a polished sapphire plate (Goodfellow Cambridge Ltd) from a height
$T_{b}=78\,^{\circ }\text{C}$
) fall on a polished sapphire plate (Goodfellow Cambridge Ltd) from a height
![]() $h$
. By adjusting
$h$
. By adjusting
![]() $h$
, the velocity
$h$
, the velocity
![]() $U$
of the droplet immediately before impacting the surface can be varied between 0.5 and
$U$
of the droplet immediately before impacting the surface can be varied between 0.5 and
![]() $5~\text{m}~\text{s}^{-1}$
. The droplets are generated by gently pushing the liquid out of a syringe with a syringe pump (PHD 22∕2000, Harvard Apparatus), through a tube to a flat-tip, stainless steel needle (19 gauge, Hamilton Co.). The droplet forms at the tip of the needle and detaches when its weight overcomes the surface tension at the needle’s tip. The pump is set at a sufficiently low flow rate (
$5~\text{m}~\text{s}^{-1}$
. The droplets are generated by gently pushing the liquid out of a syringe with a syringe pump (PHD 22∕2000, Harvard Apparatus), through a tube to a flat-tip, stainless steel needle (19 gauge, Hamilton Co.). The droplet forms at the tip of the needle and detaches when its weight overcomes the surface tension at the needle’s tip. The pump is set at a sufficiently low flow rate (
![]() $0.05~\text{ml}~\text{min}^{-1}$
) to ensure that the droplet detachment is only due to gravity. As a result, all the droplets in our study have a uniform diameter
$0.05~\text{ml}~\text{min}^{-1}$
) to ensure that the droplet detachment is only due to gravity. As a result, all the droplets in our study have a uniform diameter
![]() $D=2.5\pm 0.1~\text{mm}$
.
$D=2.5\pm 0.1~\text{mm}$
.

Figure 1. Schematics of the experimental set-up, where a droplet of diameter
![]() $D$
falls with velocity
$D$
falls with velocity
![]() $U$
on a sapphire plate P, which is placed on a temperature-controlled brass holder H. The impact is recorded by synchronized high-speed cameras from the side (SA1.1) and from the bottom (SA-X). Interferometric bottom-view recording of the impact is achieved by laser illumination from the bottom and a half-mirror M.
$U$
on a sapphire plate P, which is placed on a temperature-controlled brass holder H. The impact is recorded by synchronized high-speed cameras from the side (SA1.1) and from the bottom (SA-X). Interferometric bottom-view recording of the impact is achieved by laser illumination from the bottom and a half-mirror M.
The sapphire plate is heated by placing it on a brass holder (see figure 1 for the schematics), which radially embeds six cartridge heaters and a temperature probe (Omega Inc.). The surface temperature
![]() $T$
of the sapphire plate can be varied between room temperature and
$T$
of the sapphire plate can be varied between room temperature and
![]() $500\,^{\circ }\text{C}$
and is measured independently with a surface temperature probe (N-141K, Anritsu) for each experiment. The brass holder has a hole in the centre that, together with the transparent sapphire plate, allows for bottom-view recordings of the impacting droplets.
$500\,^{\circ }\text{C}$
and is measured independently with a surface temperature probe (N-141K, Anritsu) for each experiment. The brass holder has a hole in the centre that, together with the transparent sapphire plate, allows for bottom-view recordings of the impacting droplets.
To study the impact behaviours of droplets, we use two high-speed cameras (Fastcam SA1.1 & SA-X, Photron) to make synchronized recordings of the impact events from the side and the bottom. From the side-view recordings, the droplet diameter
![]() $D$
and velocity
$D$
and velocity
![]() $U$
immediately before impact are measured. To obtain interferometric recordings of the impact from the bottom, we use a continuous wave laser (iFlex-Gemini, Qioptic) as illuminating light (see figure 1). As long as the liquid is separated from the sapphire surface by a small distance, light reflected from the top surface of the sapphire plate and from the bottom surface of the droplet causes interference patterns, which consist of dark and bright fringes, that can be recorded by the high-speed camera via a half-mirror and a microscope of long working distance. In contrast, the area over which the liquid touches the surface appears dark in the recordings, because most of the light escapes through the liquid/solid interface. Based on this distinct difference, we can identify, without ambiguity, whether an impacting droplet is in the film boiling regime, in the contact boiling regime or in a transitional regime. Thus, the interferometric recording offers a unique tool to accurately determine the temperature
$U$
immediately before impact are measured. To obtain interferometric recordings of the impact from the bottom, we use a continuous wave laser (iFlex-Gemini, Qioptic) as illuminating light (see figure 1). As long as the liquid is separated from the sapphire surface by a small distance, light reflected from the top surface of the sapphire plate and from the bottom surface of the droplet causes interference patterns, which consist of dark and bright fringes, that can be recorded by the high-speed camera via a half-mirror and a microscope of long working distance. In contrast, the area over which the liquid touches the surface appears dark in the recordings, because most of the light escapes through the liquid/solid interface. Based on this distinct difference, we can identify, without ambiguity, whether an impacting droplet is in the film boiling regime, in the contact boiling regime or in a transitional regime. Thus, the interferometric recording offers a unique tool to accurately determine the temperature
![]() $T_{L}$
beyond which the impact is in the Leidenfrost regime, i.e. the droplet makes no contact with the plate during the entire impact (Tran et al.
Reference Tran, Staat, Prosperetti, Sun and Lohse2012).
$T_{L}$
beyond which the impact is in the Leidenfrost regime, i.e. the droplet makes no contact with the plate during the entire impact (Tran et al.
Reference Tran, Staat, Prosperetti, Sun and Lohse2012).
3. Experimental observations
We investigate the droplet behaviour while varying two control parameters: the surface temperature (
![]() $20\,^{\circ }\text{C}\leqslant T\leqslant 500\,^{\circ }\text{C}$
) and the impact velocity (
$20\,^{\circ }\text{C}\leqslant T\leqslant 500\,^{\circ }\text{C}$
) and the impact velocity (
![]() $0.5~\text{m}~\text{s}^{-1}\leqslant U\leqslant 5.0~\text{m}~\text{s}^{-1}$
). The impact velocity is expressed in dimensionless form as Weber number
$0.5~\text{m}~\text{s}^{-1}\leqslant U\leqslant 5.0~\text{m}~\text{s}^{-1}$
). The impact velocity is expressed in dimensionless form as Weber number
![]() $\mathit{We}={\it\rho}DU^{2}/{\it\sigma}$
(
$\mathit{We}={\it\rho}DU^{2}/{\it\sigma}$
(
![]() $100\leqslant \mathit{We}\leqslant 1500$
), which measures the kinetic energy of the droplet in comparison to its surface energy. For fixed temperature, there is a critical Weber number
$100\leqslant \mathit{We}\leqslant 1500$
), which measures the kinetic energy of the droplet in comparison to its surface energy. For fixed temperature, there is a critical Weber number
![]() $\mathit{We}_{C}$
beyond which the impacting droplet makes a splash, i.e. disintegrates into smaller droplets during the spreading phase (Levin & Hobbs Reference Levin and Hobbs1971; Mundo et al.
Reference Mundo, Sommerfeld and Tropea1995; Xu et al.
Reference Xu, Zhang and Nagel2005; Palacios et al.
Reference Palacios, Hernández, Gómez, Zanzi and López2013; Riboux & Gordillo Reference Riboux and Gordillo2014). On the other hand, for each Weber number there is also a corresponding Leidenfrost temperature
$\mathit{We}_{C}$
beyond which the impacting droplet makes a splash, i.e. disintegrates into smaller droplets during the spreading phase (Levin & Hobbs Reference Levin and Hobbs1971; Mundo et al.
Reference Mundo, Sommerfeld and Tropea1995; Xu et al.
Reference Xu, Zhang and Nagel2005; Palacios et al.
Reference Palacios, Hernández, Gómez, Zanzi and López2013; Riboux & Gordillo Reference Riboux and Gordillo2014). On the other hand, for each Weber number there is also a corresponding Leidenfrost temperature
![]() $T_{L}$
. Hence, these two transitions naturally impose four typical behaviours of the impacting droplets in the
$T_{L}$
. Hence, these two transitions naturally impose four typical behaviours of the impacting droplets in the
![]() $\mathit{We}$
–
$\mathit{We}$
–
![]() $T$
phase space: contact and no splashing (deposition regime), contact and splashing (contact–splash regime), neither contact nor splashing (bounce regime) and finally no contact, but splashing (film–splash regime).
$T$
phase space: contact and no splashing (deposition regime), contact and splashing (contact–splash regime), neither contact nor splashing (bounce regime) and finally no contact, but splashing (film–splash regime).

Figure 2. Typical sequences of ethanol droplets with diameter
![]() $D=2.5~$
mm impacting a sapphire plate for varying Weber number
$D=2.5~$
mm impacting a sapphire plate for varying Weber number
![]() $\mathit{We}$
and surface temperature
$\mathit{We}$
and surface temperature
![]() $T$
. All sequences have synchronized side-view and interferometric bottom-view recordings; the scale bars indicate
$T$
. All sequences have synchronized side-view and interferometric bottom-view recordings; the scale bars indicate
![]() $2~$
mm. (a) Deposition is observed for
$2~$
mm. (a) Deposition is observed for
![]() $\mathit{We}=86$
and
$\mathit{We}=86$
and
![]() $T=150\,^{\circ }\text{C}$
. Dark areas in the bottom view indicate contact, as does the spray of small droplets due to boiling at the solid/liquid interface in the side view. (b) For the same temperature but a higher impact velocity (
$T=150\,^{\circ }\text{C}$
. Dark areas in the bottom view indicate contact, as does the spray of small droplets due to boiling at the solid/liquid interface in the side view. (b) For the same temperature but a higher impact velocity (
![]() $\mathit{We}=1156$
) the droplet makes a contact–splash. (c) At low impact velocity (
$\mathit{We}=1156$
) the droplet makes a contact–splash. (c) At low impact velocity (
![]() $\mathit{We}=85$
) and higher temperature (
$\mathit{We}=85$
) and higher temperature (
![]() $T=200\,^{\circ }\text{C}$
) the droplet bounces off the surface. The interference pattern in the bottom view indicates that there is a lasting vapour film under the droplet during impact. (d) Now for the same temperature, but with high impact velocity (
$T=200\,^{\circ }\text{C}$
) the droplet bounces off the surface. The interference pattern in the bottom view indicates that there is a lasting vapour film under the droplet during impact. (d) Now for the same temperature, but with high impact velocity (
![]() $\mathit{We}=1190$
), a film–splash is observed.
$\mathit{We}=1190$
), a film–splash is observed.
In the deposition regime, in which the temperature and the Weber number are relatively low, the impacting droplets are deposited on the surface and boiled at the same time, as exemplified in figure 2(a). In this regime, the formation of vapour bubbles is clearly seen from the bottom view – the bubbles create dry patches on the surface which appear brighter in the bottom view, as opposed to the wetted areas that appear darker. The ejection of small droplets seen from the side view is clearly a result of the bursting of the vapour bubbles next to the surface. All the impacts in this regime are shown as (blue) diamonds in the
![]() $\mathit{We}$
–
$\mathit{We}$
–
![]() $T$
phase diagram (figure 3).
$T$
phase diagram (figure 3).
When increasing the Weber number, while keeping the temperature under
![]() $T_{L}$
, the behaviour of impacting droplets undergoes a transition to the contact–splash regime in which either a liquid sheet or smaller droplets are ejected from the lamella as a result of the high liquid inertia during the spreading phase of the impact. Note that there are two different mechanisms for the ejection of secondary droplets from the main droplet. One mechanism is associated with the impact itself (defined as splashing), while the other is connected with the boiling process at the liquid/solid interface (contact boiling). The former happens at the very early stage of impact (e.g. at
$T_{L}$
, the behaviour of impacting droplets undergoes a transition to the contact–splash regime in which either a liquid sheet or smaller droplets are ejected from the lamella as a result of the high liquid inertia during the spreading phase of the impact. Note that there are two different mechanisms for the ejection of secondary droplets from the main droplet. One mechanism is associated with the impact itself (defined as splashing), while the other is connected with the boiling process at the liquid/solid interface (contact boiling). The former happens at the very early stage of impact (e.g. at
![]() $0.1~$
ms in figure 2
b) and originates from the expanding lamella, whereas the latter happens at a much later time (e.g. at
$0.1~$
ms in figure 2
b) and originates from the expanding lamella, whereas the latter happens at a much later time (e.g. at
![]() $2.7~$
ms in figure 2
b) and originates upwards from the middle of the liquid puddle, due to bursting of vapour bubbles at the solid/liquid interface. We are thereby able to accurately distinguish the impacts in the contact–splash regime from those in the deposition regime. All of the impacts in the contact–splash regime are collected and shown as orange squares in figure 3.
$2.7~$
ms in figure 2
b) and originates upwards from the middle of the liquid puddle, due to bursting of vapour bubbles at the solid/liquid interface. We are thereby able to accurately distinguish the impacts in the contact–splash regime from those in the deposition regime. All of the impacts in the contact–splash regime are collected and shown as orange squares in figure 3.
Once the surface temperature is above the Leidenfrost temperature, the droplet and the surface are separated by a thin vapour film during the entire impact time. At a small Weber number, an impacting droplet spreads and rebounds from the surface as if the surface were superhydrophobic. Figure 2(c) shows such a bouncing droplet for
![]() $T=200\,^{\circ }\text{C}$
and
$T=200\,^{\circ }\text{C}$
and
![]() $\mathit{We}=85$
. From the bottom view it is evident that there is no contact between the droplet and surface, as an interference pattern is observed for the entire impact duration, indicating a lasting vapour film. This regime is referred to as the bounce regime and is shown with (green) circles in figure 3.
$\mathit{We}=85$
. From the bottom view it is evident that there is no contact between the droplet and surface, as an interference pattern is observed for the entire impact duration, indicating a lasting vapour film. This regime is referred to as the bounce regime and is shown with (green) circles in figure 3.

Figure 3. Phase diagram of the outcome of the impact of an ethanol droplet on a sapphire plate with varying surface temperature and Weber number. Four regimes are identified from the high-speed recordings: deposition (blue diamonds), bounce (green circles), contact–splash (orange squares) and film–splash (red triangles). The thin solid line indicates the dynamic Leidenfrost temperature
![]() $T_{L}$
, the dashed line is a guide to the eye for the transition Weber number
$T_{L}$
, the dashed line is a guide to the eye for the transition Weber number
![]() $\mathit{We}_{C}$
between regimes (c) and (d) and the thick solid line indicates the transition Weber number between regimes (a) and (b) as predicted by the model explained in § 4.
$\mathit{We}_{C}$
between regimes (c) and (d) and the thick solid line indicates the transition Weber number between regimes (a) and (b) as predicted by the model explained in § 4.
With increasing impact velocity, while still keeping the surface temperature above
![]() $T_{L}$
, the impact behaviour undergoes a transition to the film–splash regime. Figure 2(d) shows a series of representative images of an impacting droplet in this regime. Side-view measurements show that the droplet makes a splash at
$T_{L}$
, the impact behaviour undergoes a transition to the film–splash regime. Figure 2(d) shows a series of representative images of an impacting droplet in this regime. Side-view measurements show that the droplet makes a splash at
![]() $0.1~$
ms. The interference pattern observed in the bottom-view recording during the entire impact process indicates that there is indeed a vapour film that separates the liquid and the surface. In the phase diagram shown in figure 3, this regime corresponds to the region with red triangles.
$0.1~$
ms. The interference pattern observed in the bottom-view recording during the entire impact process indicates that there is indeed a vapour film that separates the liquid and the surface. In the phase diagram shown in figure 3, this regime corresponds to the region with red triangles.
By identifying the characteristic behaviours of all experiments, out of the
![]() $\mathit{We}$
–
$\mathit{We}$
–
![]() $T$
parameter space we obtain the phase diagram for impacting ethanol droplets on a sapphire plate. The four well-separated regions correspond to the four aforementioned behaviours. Notably, the Leidenfrost transition marked by a dashed line, which separates the contact boiling regimes (deposition and contact–splash) and the film boiling regimes (bounce and film–splash), shows little dependence on the Weber number and can be approximated as
$T$
parameter space we obtain the phase diagram for impacting ethanol droplets on a sapphire plate. The four well-separated regions correspond to the four aforementioned behaviours. Notably, the Leidenfrost transition marked by a dashed line, which separates the contact boiling regimes (deposition and contact–splash) and the film boiling regimes (bounce and film–splash), shows little dependence on the Weber number and can be approximated as
![]() $T_{L}\approx 165\,^{\circ }\text{C}$
. This result is consistent with the value of
$T_{L}\approx 165\,^{\circ }\text{C}$
. This result is consistent with the value of
![]() $T_{L}$
for ethanol on a smooth aluminium surface that was reported previously by Wang et al. (Reference Wang, Lin and Chen2000). Note that the insensitive dependence of
$T_{L}$
for ethanol on a smooth aluminium surface that was reported previously by Wang et al. (Reference Wang, Lin and Chen2000). Note that the insensitive dependence of
![]() $T_{L}$
on
$T_{L}$
on
![]() $\mathit{We}$
found here is not inconsistent with the recently found, stronger dependence of
$\mathit{We}$
found here is not inconsistent with the recently found, stronger dependence of
![]() $T_{L}$
on
$T_{L}$
on
![]() $\mathit{We}$
for water (Tran et al.
Reference Tran, Staat, Prosperetti, Sun and Lohse2012), because of the difference both in the working liquid and in the ranges of Weber number investigated: in our present study, the Weber number ranges from 100 to 1500, whereas in Tran et al. (Reference Tran, Staat, Prosperetti, Sun and Lohse2012), it ranged from 0.5 to 600. Nevertheless, this insensitivity of
$\mathit{We}$
for water (Tran et al.
Reference Tran, Staat, Prosperetti, Sun and Lohse2012), because of the difference both in the working liquid and in the ranges of Weber number investigated: in our present study, the Weber number ranges from 100 to 1500, whereas in Tran et al. (Reference Tran, Staat, Prosperetti, Sun and Lohse2012), it ranged from 0.5 to 600. Nevertheless, this insensitivity of
![]() $T_{L}$
on
$T_{L}$
on
![]() $\mathit{We}$
in the case of ethanol on sapphire is intriguing and deserves further studies for other combinations of materials.
$\mathit{We}$
in the case of ethanol on sapphire is intriguing and deserves further studies for other combinations of materials.
In contrast to the, at most, weak dependence of
![]() $T_{L}$
on
$T_{L}$
on
![]() $\mathit{We}$
, the critical Weber number
$\mathit{We}$
, the critical Weber number
![]() $\mathit{We}_{C}$
, at which the transition to splashing occurs, is a strongly non-monotonic function of
$\mathit{We}_{C}$
, at which the transition to splashing occurs, is a strongly non-monotonic function of
![]() $T$
. In the contact boiling regime, the transition to splashing separates the deposition regime from the contact–splash regime. The transition starts at
$T$
. In the contact boiling regime, the transition to splashing separates the deposition regime from the contact–splash regime. The transition starts at
![]() $T=20\,^{\circ }\text{C}$
and
$T=20\,^{\circ }\text{C}$
and
![]() $\mathit{We}_{C}=350$
, which agrees with the previously reported value of the transition to splashing of ethanol droplets impacting a smooth surface at room temperature (Palacios et al.
Reference Palacios, Hernández, Gómez, Zanzi and López2013). As the temperature increases,
$\mathit{We}_{C}=350$
, which agrees with the previously reported value of the transition to splashing of ethanol droplets impacting a smooth surface at room temperature (Palacios et al.
Reference Palacios, Hernández, Gómez, Zanzi and López2013). As the temperature increases,
![]() $\mathit{We}_{C}$
also increases until it reaches
$\mathit{We}_{C}$
also increases until it reaches
![]() $\mathit{We}=850$
at a temperature close to
$\mathit{We}=850$
at a temperature close to
![]() $T_{L}$
. This is striking because it shows that splashing is considerably suppressed (from
$T_{L}$
. This is striking because it shows that splashing is considerably suppressed (from
![]() $\mathit{We}_{C}=350$
to
$\mathit{We}_{C}=350$
to
![]() $\mathit{We}_{C}=850$
) as the surface temperature increases, though both surface tension and viscosity decrease with increasing temperature.
$\mathit{We}_{C}=850$
) as the surface temperature increases, though both surface tension and viscosity decrease with increasing temperature.
As the surface temperature is increased beyond
![]() $T_{L}$
,
$T_{L}$
,
![]() $\mathit{We}_{C}$
suddenly drops to a very small value
$\mathit{We}_{C}$
suddenly drops to a very small value
![]() $\mathit{We}_{C}=110$
and only increases weakly to
$\mathit{We}_{C}=110$
and only increases weakly to
![]() $\mathit{We}_{C}=200$
when the surface temperature reaches
$\mathit{We}_{C}=200$
when the surface temperature reaches
![]() $T=450\,^{\circ }\text{C}$
in this regime. Thus, the transition to splashing is not only discontinuous at
$T=450\,^{\circ }\text{C}$
in this regime. Thus, the transition to splashing is not only discontinuous at
![]() $T_{L}$
but also exhibits distinctively different behaviours in the film boiling and the contact boiling regimes.
$T_{L}$
but also exhibits distinctively different behaviours in the film boiling and the contact boiling regimes.
To the best of our knowledge, the splash transition of a drop on a heated plate below
![]() $T_{L}$
has not been reported previously, but the splash transition in the Leidenfrost state was reported by Wachters & Westerling (Reference Wachters and Westerling1966) (
$T_{L}$
has not been reported previously, but the splash transition in the Leidenfrost state was reported by Wachters & Westerling (Reference Wachters and Westerling1966) (
![]() $\mathit{We}_{C}=80$
for various liquids) and by Biance, Pirat & Ybert (Reference Biance, Pirat and Ybert2011) (
$\mathit{We}_{C}=80$
for various liquids) and by Biance, Pirat & Ybert (Reference Biance, Pirat and Ybert2011) (
![]() $\mathit{We}_{C}=300$
–
$\mathit{We}_{C}=300$
–
![]() $360$
, various liquids). Although all studies show a weak temperature dependence, the results differ, so clearly the Weber number and plate temperature are not the only relevant control parameters for splashing in the film boiling regime.
$360$
, various liquids). Although all studies show a weak temperature dependence, the results differ, so clearly the Weber number and plate temperature are not the only relevant control parameters for splashing in the film boiling regime.
4. Modelling the contact–splash transition
To explain the experimental observations in the preceding section, we make use of the theory by Riboux & Gordillo (Reference Riboux and Gordillo2014, Reference Riboux and Gordillo2015). The first step of this theory to describe the disintegration of the droplet during the initial phase after impact is to determine the ejection time
![]() $t_{e}$
, i.e. the instant at which the lamella is first ejected. This time follows from the momentum balance (Riboux & Gordillo Reference Riboux and Gordillo2014, equation (1))
$t_{e}$
, i.e. the instant at which the lamella is first ejected. This time follows from the momentum balance (Riboux & Gordillo Reference Riboux and Gordillo2014, equation (1))
with the Reynolds number
![]() $Re={\it\rho}UR/{\it\mu}$
, the Ohnesorge number
$Re={\it\rho}UR/{\it\mu}$
, the Ohnesorge number
![]() $\mathit{Oh}={\it\mu}/\sqrt{{\it\rho}R{\it\sigma}}$
and the drop radius
$\mathit{Oh}={\it\mu}/\sqrt{{\it\rho}R{\it\sigma}}$
and the drop radius
![]() $R=D/2$
. The constants
$R=D/2$
. The constants
![]() $c_{1}\simeq \sqrt{3}/2$
and
$c_{1}\simeq \sqrt{3}/2$
and
![]() $c^{2}=1.2$
are adjusted to describe the experiments of Riboux & Gordillo (Reference Riboux and Gordillo2014). Once
$c^{2}=1.2$
are adjusted to describe the experiments of Riboux & Gordillo (Reference Riboux and Gordillo2014). Once
![]() $t_{e}$
is calculated, the initial thickness of the edge of the lamella and its initial tangential velocity are determined as
$t_{e}$
is calculated, the initial thickness of the edge of the lamella and its initial tangential velocity are determined as
![]() $h_{t}(t_{e})\propto t_{e}^{3/2}$
and
$h_{t}(t_{e})\propto t_{e}^{3/2}$
and
![]() $v_{t}(t_{e})\propto t_{e}^{-1/2}$
, respectively (Riboux & Gordillo Reference Riboux and Gordillo2014). Here, the lower case variables indicate the dimensionless quantities constructed using
$v_{t}(t_{e})\propto t_{e}^{-1/2}$
, respectively (Riboux & Gordillo Reference Riboux and Gordillo2014). Here, the lower case variables indicate the dimensionless quantities constructed using
![]() $R$
,
$R$
,
![]() $U$
and
$U$
and
![]() $R/U$
as the characteristic scales of length, velocity and time.
$R/U$
as the characteristic scales of length, velocity and time.
For times larger than
![]() $t_{e}$
, the edge of the lamella experiences a vertical lift force
$t_{e}$
, the edge of the lamella experiences a vertical lift force
![]() $F_{L}$
per unit length given by the addition of the classical aerodynamic lift force and the projection in the vertical direction of the lubrication force exerted by the gas beneath the lamella (Riboux & Gordillo Reference Riboux and Gordillo2014, equation (2)),
$F_{L}$
per unit length given by the addition of the classical aerodynamic lift force and the projection in the vertical direction of the lubrication force exerted by the gas beneath the lamella (Riboux & Gordillo Reference Riboux and Gordillo2014, equation (2)),
where the subscript
![]() $g$
represents gas quantities,
$g$
represents gas quantities,
![]() $K_{u}\simeq 0.3$
is a constant determined numerically and
$K_{u}\simeq 0.3$
is a constant determined numerically and
![]() $K_{l}$
depends logarithmically on the ratio
$K_{l}$
depends logarithmically on the ratio
![]() ${\it\lambda}/(Rh_{t})$
, with
${\it\lambda}/(Rh_{t})$
, with
![]() ${\it\lambda}$
the mean free path of gas molecules. In Riboux & Gordillo (Reference Riboux and Gordillo2014) it is found that the critical lift force, above which the droplet disintegrates into smaller droplets, is given by
${\it\lambda}$
the mean free path of gas molecules. In Riboux & Gordillo (Reference Riboux and Gordillo2014) it is found that the critical lift force, above which the droplet disintegrates into smaller droplets, is given by
from which the critical impact velocity or, equivalently,
![]() $\mathit{We}_{C}$
is calculated using (4.2) (see Riboux & Gordillo (Reference Riboux and Gordillo2014) for details).
$\mathit{We}_{C}$
is calculated using (4.2) (see Riboux & Gordillo (Reference Riboux and Gordillo2014) for details).

Figure 4. (a) Sketch of the lamella for an instant of time larger than
![]() $t_{e}$
, illustrating the different regions in the flow and the temperature field deduced from the thermal boundary layer thicknesses. In the figure, blue and red represent low and high temperatures, respectively. Before the ethanol drop touches the plate, the drop is at room temperature
$t_{e}$
, illustrating the different regions in the flow and the temperature field deduced from the thermal boundary layer thicknesses. In the figure, blue and red represent low and high temperatures, respectively. Before the ethanol drop touches the plate, the drop is at room temperature
![]() $T_{l}\approx 20\,^{\circ }\text{C}$
, while the surrounding air is at
$T_{l}\approx 20\,^{\circ }\text{C}$
, while the surrounding air is at
![]() $20\,^{\circ }\text{C}\leqslant T_{g}\leqslant T$
. After impact, a small spatial region in the liquid heats up to a temperature
$20\,^{\circ }\text{C}\leqslant T_{g}\leqslant T$
. After impact, a small spatial region in the liquid heats up to a temperature
![]() $T$
and part of the gas surrounding the drop cools down to
$T$
and part of the gas surrounding the drop cools down to
![]() $T_{l}$
. The widths of the regions where the liquid is heated up and the gas is cooled down are characterized by the thicknesses of their respective thermal boundary layers
$T_{l}$
. The widths of the regions where the liquid is heated up and the gas is cooled down are characterized by the thicknesses of their respective thermal boundary layers
![]() ${\it\Delta}$
and
${\it\Delta}$
and
![]() ${\it\Delta}_{g}$
. (b) Relative widths of the liquid and gas thermal boundary layers calculated using (4.4). The differences in the widths of the thermal boundary layers depicted in this figure are caused by the disparate values of the Prandtl numbers,
${\it\Delta}_{g}$
. (b) Relative widths of the liquid and gas thermal boundary layers calculated using (4.4). The differences in the widths of the thermal boundary layers depicted in this figure are caused by the disparate values of the Prandtl numbers,
![]() $Pr\gtrsim 10$
for ethanol and
$Pr\gtrsim 10$
for ethanol and
![]() $Pr_{g}(T)\simeq 0.7$
for air.
$Pr_{g}(T)\simeq 0.7$
for air.
In order to make use of the splash criterion given by (4.3) and check whether the experimental observations in § 3 can be explained using the framework developed in Riboux & Gordillo (Reference Riboux and Gordillo2014), it is mandatory to use the correct temperature-dependent physical properties of the two fluids involved in the splashing process. Before the drop touches the substrate, the liquid is at room temperature
![]() $T_{l}\approx 20\,^{\circ }\text{C}$
and the gas temperature is
$T_{l}\approx 20\,^{\circ }\text{C}$
and the gas temperature is
![]() $20\,^{\circ }\text{C}\leqslant T_{g}\leqslant T$
. However, as soon as the drop impacts the substrate, the liquid heats up and the gas cools down in the regions characterized by their respective thermal boundary layer thicknesses,
$20\,^{\circ }\text{C}\leqslant T_{g}\leqslant T$
. However, as soon as the drop impacts the substrate, the liquid heats up and the gas cools down in the regions characterized by their respective thermal boundary layer thicknesses,
![]() ${\it\Delta}$
and
${\it\Delta}$
and
![]() ${\it\Delta}_{g}$
(sketched in figure 4
a). To estimate both thicknesses, note first that the liquid particles feeding the lamella come from the region located to the right of the dashed line sketched in figure 4(a), which ends at the relative stagnation point present in the flow when the velocity field is described in a frame of reference moving at the wetting velocity
${\it\Delta}_{g}$
(sketched in figure 4
a). To estimate both thicknesses, note first that the liquid particles feeding the lamella come from the region located to the right of the dashed line sketched in figure 4(a), which ends at the relative stagnation point present in the flow when the velocity field is described in a frame of reference moving at the wetting velocity
![]() $\sqrt{3/t}/2$
(Riboux & Gordillo Reference Riboux and Gordillo2014, Reference Riboux and Gordillo2015). Since the relative stagnation point is located at a distance from the root of the lamella proportional to its thickness,
$\sqrt{3/t}/2$
(Riboux & Gordillo Reference Riboux and Gordillo2014, Reference Riboux and Gordillo2015). Since the relative stagnation point is located at a distance from the root of the lamella proportional to its thickness,
![]() $Rh_{t}\propto Rt^{3/2}$
, and the liquid velocity feeding the liquid sheet is
$Rh_{t}\propto Rt^{3/2}$
, and the liquid velocity feeding the liquid sheet is
![]() $Uv_{t}\propto Ut^{-1/2}$
, the characteristic residence time of the fluid particles entering the lamella is
$Uv_{t}\propto Ut^{-1/2}$
, the characteristic residence time of the fluid particles entering the lamella is
![]() $Rh_{t}(t_{e})/(Uv_{t}(t_{e}))$
, which coincides with the characteristic residence time of the gas particles flowing around the edge of the liquid sheet (Riboux & Gordillo Reference Riboux and Gordillo2014, Reference Riboux and Gordillo2015). Therefore, the ratios of the thicknesses of the thermal boundary layers and the thickness of the lamella at the ejection instant,
$Rh_{t}(t_{e})/(Uv_{t}(t_{e}))$
, which coincides with the characteristic residence time of the gas particles flowing around the edge of the liquid sheet (Riboux & Gordillo Reference Riboux and Gordillo2014, Reference Riboux and Gordillo2015). Therefore, the ratios of the thicknesses of the thermal boundary layers and the thickness of the lamella at the ejection instant,
![]() $Rh_{t}(t_{e})$
, are given by
$Rh_{t}(t_{e})$
, are given by
with
![]() $Pr(T)$
and
$Pr(T)$
and
![]() $Pr_{g}(T)$
the temperature-dependent values of the Prandtl numbers for ethanol and air, respectively. Figure 4(b), where the ratios in (4.4) are represented, reveals that just a small region of the ethanol droplet in contact with the wall heats up to the temperature
$Pr_{g}(T)$
the temperature-dependent values of the Prandtl numbers for ethanol and air, respectively. Figure 4(b), where the ratios in (4.4) are represented, reveals that just a small region of the ethanol droplet in contact with the wall heats up to the temperature
![]() $T$
and, therefore, most of the liquid flowing into the lamella is at room temperature. The width of the gas thermal boundary layer is, however, comparable to the width of the liquid sheet, as is sketched in figure 4(a). Consequently, most of the air located in between the lamella and the wall cools down to the temperature of the liquid, with the exception of the region closest to the substrate, where the air keeps its initial temperature
$T$
and, therefore, most of the liquid flowing into the lamella is at room temperature. The width of the gas thermal boundary layer is, however, comparable to the width of the liquid sheet, as is sketched in figure 4(a). Consequently, most of the air located in between the lamella and the wall cools down to the temperature of the liquid, with the exception of the region closest to the substrate, where the air keeps its initial temperature
![]() $T$
.
$T$
.
Taking this all into consideration, the term representing the viscous deceleration of the tip of the lamella in the momentum balance (4.1) is calculated using the following expression for the liquid viscosity:
with
![]() $a_{0}=5.8942\times 10^{-1}$
,
$a_{0}=5.8942\times 10^{-1}$
,
![]() $a_{1}=-2.2540\times 10^{-2}$
,
$a_{1}=-2.2540\times 10^{-2}$
,
![]() $a_{2}=1.0283\times 10^{-4}$
,
$a_{2}=1.0283\times 10^{-4}$
,
![]() $a_{3}=-8.8574\times 10^{-7}$
,
$a_{3}=-8.8574\times 10^{-7}$
,
![]() $a_{4}=4.7884\times 10^{-9}$
,
$a_{4}=4.7884\times 10^{-9}$
,
![]() $a_{5}=-9.7493\times 10^{-12}$
and
$a_{5}=-9.7493\times 10^{-12}$
and
![]() $T$
in degrees Celsius (Vargaftik Reference Vargaftik1975). Because most of the liquid feeding the lamella keeps its initial temperature, the liquid density and the interfacial tension coefficient in (4.1) and (4.3) are evaluated at room temperature. The expressions for the air density and the mean free path of gas molecules in (4.2) depend on the wall temperature as
$T$
in degrees Celsius (Vargaftik Reference Vargaftik1975). Because most of the liquid feeding the lamella keeps its initial temperature, the liquid density and the interfacial tension coefficient in (4.1) and (4.3) are evaluated at room temperature. The expressions for the air density and the mean free path of gas molecules in (4.2) depend on the wall temperature as
![]() ${\it\rho}_{g}=10^{5}/(287\times T)$
kg m
${\it\rho}_{g}=10^{5}/(287\times T)$
kg m
![]() $^{-3}$
and
$^{-3}$
and
![]() ${\it\lambda}=68\times 10^{-9}\times T/293$
m, with the temperature in kelvin. However, since the gas located beneath the lamella cools down to the ethanol temperature, the value of the gas viscosity in (4.2) is evaluated at room temperature,
${\it\lambda}=68\times 10^{-9}\times T/293$
m, with the temperature in kelvin. However, since the gas located beneath the lamella cools down to the ethanol temperature, the value of the gas viscosity in (4.2) is evaluated at room temperature,
![]() ${\it\mu}_{g}=1.86\times 10^{-5}~\text{Pa}~\text{s}$
. We now employ (4.3) using the expressions for the physical properties of both the ethanol and the air as detailed above, finding that the calculated critical velocity for splashing is in quantitative agreement with experiments, as figure 3 shows.
${\it\mu}_{g}=1.86\times 10^{-5}~\text{Pa}~\text{s}$
. We now employ (4.3) using the expressions for the physical properties of both the ethanol and the air as detailed above, finding that the calculated critical velocity for splashing is in quantitative agreement with experiments, as figure 3 shows.
Recent work by Liu, Tan & Xu (Reference Liu, Tan and Xu2015) shows that when the thickness of the lamella is equal to the fastest growing wavelength of a Kelvin—Helmholtz type instability, a droplet will splash. As this model does not give a prediction based on the impact parameters of either the lamella thickness or the fastest growing wavelength, we cannot use this model to predict the critical Weber number for our experiments. With the somewhat older, but very similar model by Xu et al. (Reference Xu, Zhang and Nagel2005) we were able to fit a splash threshold to our experiments. However, the fitting parameter reported by Xu et al. (Reference Xu, Zhang and Nagel2005), a universal 0.45, is not in accord with our experiments. The best fit of that model to our data is with a fitting parameter of 0.8, including the experiments at room temperature.
5. Conclusions
In conclusion, we have investigated the splashing and Leidenfrost transitions for ethanol droplets impacting a temperature-controlled sapphire plate. We have identified four different regimes in the explored
![]() $\mathit{We}$
–
$\mathit{We}$
–
![]() $T$
phase space: deposition, contact–splash, bounce and film–splash. While the dynamic Leidenfrost transition temperature
$T$
phase space: deposition, contact–splash, bounce and film–splash. While the dynamic Leidenfrost transition temperature
![]() $T_{L}$
shows little dependence on
$T_{L}$
shows little dependence on
![]() $\mathit{We}$
, the transition to splashing shows a strong and non-monotonic dependence on
$\mathit{We}$
, the transition to splashing shows a strong and non-monotonic dependence on
![]() $T$
. By incorporating the temperature dependence of the physical properties in the theory by Riboux & Gordillo (Reference Riboux and Gordillo2014, Reference Riboux and Gordillo2015), we can quantitatively explain the splashing transition for surface temperatures below
$T$
. By incorporating the temperature dependence of the physical properties in the theory by Riboux & Gordillo (Reference Riboux and Gordillo2014, Reference Riboux and Gordillo2015), we can quantitatively explain the splashing transition for surface temperatures below
![]() $T_{L}$
. The splashing transition for droplets in the Leidenfrost state remains the subject of future research.
$T_{L}$
. The splashing transition for droplets in the Leidenfrost state remains the subject of future research.
Acknowledgements
This study was financially supported by a European Research Council (ERC) advanced grant and the Spanish MINECO under Project DPI2014-59292-C3-2-P, partly financed through European funds.