1 Introduction
Turbulence is a widespread complex phenomenon influencing the behaviour of a large variety of natural and engineering systems. Flow in a channel (Sano & Tamai Reference Sano and Tamai2016), ocean mixing (Moum et al. Reference Moum, Perlin, Nash and Mcphaden2013) and the explosion of a rotating massive star (Mösta et al. Reference Mösta, Ott, Radice, Roberts, Schnetter and Haas2015) are three examples of very different phenomena characterized by turbulent dynamics involving chaotic fluctuations of the physical properties and sharing the same basic properties. The atmosphere itself, up to a hundred metres from the Earth’s surface, is characterized by a turbulent, chaotic motion, deep knowledge and accurate modelling of which may have tremendous implications for improving meteorological and climatological predictions (Marusic, Mathis & Hutchins Reference Marusic, Mathis and Hutchins2010). Yet, achieving a thorough comprehension of the dynamics of wall-bounded turbulent flow remains a formidable challenge since turbulence appears in a variety of different states and patterns competing with the ordered laminar state (Barkley et al. Reference Barkley, Song, Mukund, Lemoult, Avila and Hof2015).
To determine low-order models for the onset of this chaotic motion from a laminar regime, recent studies have turned the attention to the dynamics of large-scale structures, neglecting the random small-scale motion: two main examples are the direct percolation model recently provided by Lemoult et al. (Reference Lemoult, Shi, Avila, Jalikop, Avila and Hof2016), and the front propagation scenario by Barkley et al. (Reference Barkley, Song, Mukund, Lemoult, Avila and Hof2015), explaining the coexistence of turbulent patterns competing with the laminar state in the transitional regime.
Even when the flow reaches a fully developed turbulent regime, it remains characterized by small-scale chaotic fluctuations as well as coherent structures, i.e. fluid motions highly correlated over both space and time (Panton Reference Panton2001), with characteristic wavelengths and lifetimes. From a dynamical point of view, this coherent motion carries a much larger momentum than the chaotic motion at small scales; thus, a careful characterization of such structures bears an enormous potential for modelling and controlling the self-sustained turbulence dynamics.
The first evidence of coherent motion in turbulent flows dates back to the sixties, when Kline et al. (Reference Kline, Reynold, Schraub and Rundstander1967) ran a series of experiments in a boundary-layer flow, observing ‘surprisingly well-organized spatially and temporally dependent motions’ in the form of streaks. These streaks populate the region close to the wall, the buffer layer representing the inner region, with an average spanwise spacing
$\unicode[STIX]{x1D706}_{z}^{+}\approx 100$
(where the superscript
$^{+}$
indicates variables expressed in inner units, non-dimensionalized by the viscous length scale
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
,
$\unicode[STIX]{x1D708}$
being the kinematic viscosity and
$u_{\unicode[STIX]{x1D70F}}$
the friction velocity).
Such streaky structures are continuously regenerated in a cycle based on the lift-up mechanism that does not depend on the outer flow, making them a robust, long-living feature of the inner layer (Hamilton, Kim & Waleffe Reference Hamilton, Kim and Waleffe1995; Waleffe Reference Waleffe1997; Jiménez & Pinelli Reference Jiménez and Pinelli1999). Concerning this regeneration cycle, a strong consensus has been achieved in the last years about the self-sustained process theorized by Hamilton et al. (Reference Hamilton, Kim and Waleffe1995) and Waleffe (Reference Waleffe1997). Grounding on modal and non-modal instability analysis, these authors conjectured a cyclic process composed of the following three steps: (i) streamwise streaks originate from weak streamwise vortices, due to the inherently non-modal lift-up process; (ii) saturating nonlinearly, they become prone to secondary instability; and (iii) the consequent streak oscillations recreate streamwise vorticity by nonlinear interactions, leading back to the first step. Such a self-sustained process can explain the robustness of oscillating streaky structures observed in transitional and turbulent flows. The extension of this theory led to the discovery of self-sustained exact coherent structures (Waleffe Reference Waleffe1998; Faisst & Eckhardt Reference Faisst and Eckhardt2003; Hof et al. Reference Hof, van Doorne, Westerweel, Nieuwstadt, Faisst, Eckhardt, Wedin, Kerswell and Waleffe2004), which are steady, periodic or chaotic states of the phase space with few unstable directions, that populate the chaotic saddle representing wall turbulence at low Reynolds numbers (Waleffe Reference Waleffe1998; Faisst & Eckhardt Reference Faisst and Eckhardt2003; Hof et al. Reference Hof, van Doorne, Westerweel, Nieuwstadt, Faisst, Eckhardt, Wedin, Kerswell and Waleffe2004).
Moreover, it has been also observed (Tomkins & Adrian Reference Tomkins and Adrian2003; Adrian Reference Adrian2007) that large-scale coherent structures populate the outer region of wall-bounded turbulent flows, with average spanwise length
$\unicode[STIX]{x1D706}_{z}\approx O(h)$
(
$h$
being the outer length scale, for instance the half-height of a channel flow or the boundary-layer thickness of the flow over a flat plate). These large-scale structures have the form of packets of hairpin vortices (Adrian Reference Adrian2007) or large-scale oscillating streaks (Tomkins & Adrian Reference Tomkins and Adrian2003). Hwang & Cossu (Reference Hwang and Cossu2010b
) have recently shown that large-scale streaky structures remain self-sustained even when small-scale motion is artificially damped. This numerical observation has been supported by the results of a linear transient growth analysis of perturbations of a mean turbulent velocity profile, showing that large-scale streamwise streaks can be amplified by a coherent lift-up effect, without the need of smaller-scale structures to sustain this growth (Cossu, Pujals & Depardon Reference Cossu, Pujals and Depardon2009; Pujals et al.
Reference Pujals, García-Villalba, Cossu and Depardon2009; Hwang & Cossu Reference Hwang and Cossu2010a
).
These results suggest a scenario based on self-sustained cycles acting at different spatial scales from the inner to the outer scale. Nevertheless, this is only a part of the complex dynamics of wall turbulence, in which inner and outer scale structures are found to influence each other, as recently shown by Hwang et al. (Reference Hwang, Lee, Sung and Zaki2016), who observed a close interaction between large-scale coherent structures and near-wall small-scale streaks. In fact, the coexistence of separate cycles at different scales does not explain the spatial and temporal intermittency of large-scale velocity fluctuations and their possible interaction with inner scale structures (Jiménez Reference Jiménez1999; Hwang et al. Reference Hwang, Lee, Sung and Zaki2016), neither the existence of the high-energy bursting events, inherently short lived and intermittent (Jiménez et al. Reference Jiménez, Kawahara, Simens, Nagata and Shiba2005), recurrently observed in wall-bounded turbulent flows.
Bursting events are dynamically very important since they carry approximately 80 % of the Reynolds stress production (Panton Reference Panton2001), accounting for a large part of the energy transported through the flow. To characterize these vigorous events, quadrant analysis of time series data has been used, showing a sequence of Q2 (
$u<0$
,
$v>0$
) events called ejections (i.e. slow fluid carried up by a positive wall-normal motion), suddenly followed by rather longer Q4 (
$u>0$
,
$v<0$
) events known as sweeps (high-speed fluid pushed down towards the wall) (Bogard & Tiederman Reference Bogard and Tiederman1986). Very recently, using a filtered and over-damped large-eddy simulation, Hwang & Bengana (Reference Hwang and Bengana2016) observed the occurrence of bursting events for isolated attached eddies of different size, the related spanwise length scale ranging between
$\unicode[STIX]{x1D706}_{z}^{+}\approx 100$
and
$\unicode[STIX]{x1D706}_{z}\approx 1.5h$
. Therefore, these energy oscillations are inherently present in the coherent motion of a fully turbulent flow even when small-scale fluctuations are damped out.
However, despite the robustness of bursts and their main features are now well recognized, their origin is still not clear. Some authors have linked them to the secondary instability of streaks; others, to the appearance of hairpin-shaped vortical structures (Moin & Kim Reference Moin and Kim1985), which can regenerate into packets populating the outer region of the flow (Robinson Reference Robinson1991), in the same way as streaks populate the buffer layer. Recently, Jiménez has investigated by a linear analysis the role of the Orr mechanism in the bursting phenomenon (Jiménez Reference Jiménez2013, Reference Jiménez2015), showing that large-scale modes of the wall-normal velocity in a turbulent minimal channel are well described by transient Orr bursts only at short times (of order
$0.15h/u_{\unicode[STIX]{x1D70F}}$
), whereas at longer times nonlinearity becomes relevant.
This work aims at providing a thorough view of energetic structures in wall-bounded turbulent flow, explaining the recurrence of bursting events as an interaction between streaky and vortical structures at different scales. The final goal is to investigate whether the formation of transient coherent structures inducing bursting events in a wall-bounded turbulent flow is governed by an energy maximization process on a suitable time scale. As bursts are short-lived and highly energetic, we use a transient growth approach in a nonlinear framework in order to unravel which kind of flow structures are able to trigger rapid events with a strong energy growth in a canonical wall-bounded turbulent flow such as the channel flow. In the same way as a linear transient growth analysis on a mean turbulent profile could explain the linear growth of streaky structures in turbulent flows (Butler & Farrell Reference Butler and Farrell1993; Pujals et al. Reference Pujals, García-Villalba, Cossu and Depardon2009), a nonlinear approach is a suitable way for studying the energetic transient events characterized by ejections and sweeps. With respect to the recent linear analysis provided by Jiménez (Reference Jiménez2013, Reference Jiménez2015), we take into account nonlinear interactions since the time horizon of the optimization analysis is larger than the linear time interval limit indicated by Jiménez (Reference Jiménez2015).
The paper is organized as follows: in the second section we define the problem and describe the employed numerical methodology; in the third section the main features of the nonlinear optimal coherent structures and their time evolution are discussed; and in the last section, some conclusions are provided. The details of the derivation of the governing equations are provided in the Appendix.
2 Problem formulation
This work provides the analysis of turbulent channel flow at friction Reynolds number
$Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}h/\unicode[STIX]{x1D708}=180$
;
$u_{\unicode[STIX]{x1D70F}}$
,
$h$
, and
$\unicode[STIX]{x1D708}$
being the friction velocity, the half-height of the channel and the kinematic viscosity, respectively. Since two scalings of the variables are employed, variables expressed in inner units (normalized using
$u_{\unicode[STIX]{x1D70F}}$
and viscous length scale,
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
) are indicated with the superscript
$^{+}$
, whereas variables without any superscript are scaled in outer units (normalized using the centreline velocity
$U_{c}$
and
$h$
). Incompressible flow is computed by solving the Navier–Stokes equations (NS) in a box having streamwise, wall-normal and spanwise dimensions equal to
$l_{x}=4\unicode[STIX]{x03C0},l_{y}=2,l_{z}=2\unicode[STIX]{x03C0}$
, respectively. No-slip boundary conditions for the three velocity components are imposed at the walls, whereas periodicity is prescribed in the streamwise and spanwise directions.
The nonlinear evolution of perturbations of the mean turbulent velocity profile is computed by solving the following system of equations (
$\widetilde{NS}$
):
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}\tilde{\boldsymbol{u}}}{\unicode[STIX]{x2202}t}=-\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\tilde{\boldsymbol{u}}-\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{U}-\boldsymbol{U}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\tilde{\boldsymbol{u}}-\unicode[STIX]{x1D735}\tilde{p}+\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}\widetilde{\boldsymbol{u}}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D749},\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\tilde{\boldsymbol{u}}=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
$\widetilde{\boldsymbol{u}}=(\widetilde{u},\widetilde{v},\widetilde{w})^{\text{T}}$
and
$\tilde{p}$
represent the velocity and pressure perturbations, respectively, which are composed of a coherent and a fluctuating part;
$\boldsymbol{U}$
is the mean turbulent flow velocity profile;
$\unicode[STIX]{x1D749}$
is the Reynolds stress tensor forcing the mean turbulent velocity profile (see (A 2) in the Appendix); and
$Re=U_{c}h/\unicode[STIX]{x1D708}$
. The Reynolds stress tensor is computed a priori by direct numerical simulation (DNS) of the fully turbulent flow. Details of the derivation of (2.1) are provided in the Appendix.
Using (2.1), we look for perturbations capable of inducing a peak of kinetic energy in a finite time
$T$
. Thus, we maximize the kinetic energy growth at time
$T$
,
$G(T)=E(T)/E(0)$
, where
$$\begin{eqnarray}E(t)=\{\tilde{\boldsymbol{u}}(t),\tilde{\boldsymbol{u}}(t)\}=\int _{V}(\widetilde{u}^{2}+\widetilde{v}^{2}+\widetilde{w}^{2})(t)\,\text{d}V,\end{eqnarray}$$
and
$V$
is the volume of the computational domain. The energy gain
$G(T)$
is maximized using a Lagrange multiplier approach, the initial energy
$E_{0}$
, equations (2.1) and the incompressibility condition being imposed as constraints using the Lagrange multipliers or adjoint variables
$(\widetilde{\boldsymbol{u}}^{\dagger },p^{\dagger },\unicode[STIX]{x1D706})$
, as follows:
$$\begin{eqnarray}\mathfrak{L}=\frac{E(T)}{E(0)}-\int _{0}^{T}\{\widetilde{\boldsymbol{u}}^{\dagger },\widetilde{NS}\}\,\text{d}t-\int _{0}^{T}\{\widetilde{p}^{\dagger },(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\widetilde{\boldsymbol{u}})\}\,\text{d}t-\unicode[STIX]{x1D706}\left(\frac{E(0)}{E_{0}}-1\right).\end{eqnarray}$$
Deriving the functional
$\mathfrak{L}$
with respect to the variables
$\widetilde{\boldsymbol{u}},\tilde{p}$
, one obtains the following adjoint equations:
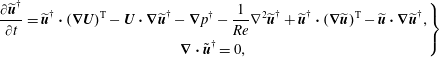$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}\widetilde{\boldsymbol{u}}^{\dagger }}{\unicode[STIX]{x2202}t}=\widetilde{\boldsymbol{u}}^{\dagger }\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\boldsymbol{U})^{\text{T}}-\boldsymbol{U}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\widetilde{\boldsymbol{u}}^{\dagger }-\unicode[STIX]{x1D735}p^{\dagger }-\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}\widetilde{\boldsymbol{u}}^{\dagger }+\widetilde{\boldsymbol{u}}^{\dagger }\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\widetilde{\boldsymbol{u}})^{\text{T}}-\widetilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\widetilde{\boldsymbol{u}}^{\dagger },\\ \unicode[STIX]{x1D735}\boldsymbol{\cdot }\tilde{\boldsymbol{u}}^{\dagger }=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
as well as the gradient of
$\mathfrak{L}$
with respect to the initial perturbation, which has to be nullified in order to maximize the given
$\mathfrak{L}$
. Following previous works focusing on nonlinear optimal perturbations of laminar base flows (see Cherubini et al.
Reference Cherubini, De Palma, Robinet and Bottaro2010; Pringle, Willis & Kerswell Reference Pringle, Willis and Kerswell2012; Rabin, Caulfield & Kerswell Reference Rabin, Caulfield and Kerswell2012; Cherubini & De Palma Reference Cherubini and De Palma2013; Duguet et al.
Reference Duguet, Monokrousos, Brandt and Henningson2013; Cherubini, De Palma & Robinet Reference Cherubini, De Palma and Robinet2015), the optimization problem is solved by direct-adjoint iterations coupled with a gradient rotation algorithm (Foures, Caulfield & Schmid Reference Foures, Caulfield and Schmid2013; Farano et al.
Reference Farano, Cherubini, Robinet and De Palma2016). Computations are performed using the spectral-element code Nek5000 (Fischer, Lottes & Kerkemeir Reference Fischer, Lottes and Kerkemeir2008), with Legendre polynomial reconstruction of degree 7 and second-order accurate Runge–Kutta time integration (Deville, Fischer & Mund Reference Deville, Fischer and Mund2002). The iterative procedure is stopped when the relative variation between two successive direct-adjoint loops,
$e=(G^{n}-G^{n-1})/G^{n}$
is smaller than
$10^{-7}$
,
$n$
being the iteration number. Depending on the selected target time, 40–80 direct-adjoint iterations are needed for reaching convergence for one set of parameters, each optimization needing an overall computational time of 100.000–800.000 hours on an IBM cluster Intel ES 4650.
The flow parameters are chosen according to the DNS of turbulent channel flow performed by Kim, Moin & Moser (Reference Kim, Moin and Moser1987) for
$Re_{\unicode[STIX]{x1D70F}}=180$
. The computational domain is discretized by 24, 20 and 20 elements in the
$x$
,
$y$
and
$z$
spatial directions, respectively, obtaining a total number of grid points equal to
$192\times 160\times 160$
. For this setting we obtain approximately the values of
$\unicode[STIX]{x0394}x^{+}\approx 12$
,
$\unicode[STIX]{x0394}z^{+}\approx 7$
,
$\unicode[STIX]{x0394}y_{max}^{+}\approx 4.4$
and
$\unicode[STIX]{x0394}y_{min}^{+}\approx 0.05$
, similar to those used by Kim et al. (Reference Kim, Moin and Moser1987). DNS has been run for approximately 13 time units (
$tu_{\unicode[STIX]{x1D70F}}/h$
) in order to evaluate the mean flow and the Reynolds stress tensor. The fully turbulent flow obtained by DNS has been validated by comparing the mean flow and the Reynolds shear stress with the results of Kim et al. (Reference Kim, Moin and Moser1987), finding a very good agreement (see the Appendix for details). Furthermore, the direct-adjoint routine has been validated by computing linear optimal perturbations following the approach by Pujals et al. (Reference Pujals, García-Villalba, Cossu and Depardon2009), who performed a local stability analysis by considering a monochromatic sinusoidal coherent perturbation in
$x$
and
$z$
. Although we perform a global analysis, where
$\tilde{\boldsymbol{u}}$
depends on the three spatial coordinates without any constraint, in the linear limit we have been able to reproduce the maximum energy amplification, the associated time as well as the shape of the optimal perturbations with their wavelength, found by a local linear optimization using the approach of Pujals et al. (Reference Pujals, García-Villalba, Cossu and Depardon2009). This result validates our direct-adjoint procedure at least in the linear limit. Finally, the nonlinear optimization approach has been validated in the laminar case with the results of Farano et al. (Reference Farano, Cherubini, Robinet and De Palma2015).
3 Results
3.1 Optimal perturbations
Nonlinear optimal structures have been computed for
$Re_{\unicode[STIX]{x1D70F}}=180$
and for different target times,
$T$
, which is a crucial independent parameter for the optimization procedure. For such a moderate value of the Reynolds number, there is not a clear spatial scale separation among the flow structures. However, structures with different scales and dynamics may be found in the inner and outer region (Chen et al.
Reference Chen, Hussain, Pei and She2014). The lifetime of coherent structures populating the flow can be employed as the target time to select the scale of the structures to be optimized. Butler & Farrell (Reference Butler and Farrell1993) have chosen as representative of the time scale of coherent structures the eddy turnover time defined as the ratio between the turbulent kinetic energy and the dissipation rate,
$k/\unicode[STIX]{x1D716}$
. In particular, they consider the value of the eddy turnover time at
$y^{+}\approx 20$
(resulting in
$T^{+}=80$
for
$Re_{\unicode[STIX]{x1D70F}}=180$
), finding optimal small-amplitude disturbances having the shape of low- and high-speed streaks with the inner typical spanwise spacing
$\unicode[STIX]{x1D706}_{z}^{+}=110$
. Here, we employ the same criterion, choosing the inner optimization time
$T_{in}^{+}=80$
, (
$T_{in}=8.16$
) approximately corresponding to one eddy turnover time evaluated in the buffer layer at
$y^{+}=19$
(Butler & Farrell Reference Butler and Farrell1993); and the outer optimization time
$T_{out}^{+}=305$
(
$T_{out}=31.12$
), corresponding approximately to one eddy turnover time at the centreline of the channel, consistent with that used by Pujals et al. (Reference Pujals, García-Villalba, Cossu and Depardon2009) for higher Reynolds numbers.
Figure 1. Shape of the optimal perturbation for
$T_{in}^{+}=80$
and
$E_{0}=10^{-2}$
at (a)
$t^{+}=0$
and (b)
$t^{+}=T_{in}^{+}$
: isosurface of negative streamwise velocity (green, (a)
$\tilde{u} =-0.025$
, (b)
$\tilde{u} =-0.18$
) and
$Q$
-criterion ((a)
$Q=10^{-6}$
, (b)
$Q=2\times 10^{-6}$
) coloured by the value of the streamwise vorticity (positive blue, negative red).
3.1.1 Optimal perturbations at the inner time scale
The resulting optimal finite-amplitude disturbance obtained for
$T_{in}^{+}$
and
$E_{0}=10^{-2}$
is shown in figure 1 at
$t^{+}=0$
(a) and
$t^{+}=T_{in}^{+}$
(b). The initial optimal perturbation consists of alternated inclined streamwise vortices (red and blue), flanking localized regions of streamwise velocity strong defects (green). Whereas, at
$T_{in}^{+}$
, the optimal disturbance consists of highly modulated streaks having a typical spanwise spacing of
$\unicode[STIX]{x1D706}_{z}^{+}\approx 113$
, surrounded by positive and negative streamwise vortices, with a spanwise spacing of
$\unicode[STIX]{x1D706}_{z}^{+}\approx 56$
; this is a typical value recovered for vortex spacing in turbulent channel flow (Panton Reference Panton2001). These nonlinear optimal streaks and vortices appear much more similar to the oscillating coherent streaky structures observed in turbulent flows than the idealized linear optimal perturbations presenting a perfect streamwise alignment (Butler & Farrell Reference Butler and Farrell1993; Pujals et al.
Reference Pujals, García-Villalba, Cossu and Depardon2009). Moreover, they are localized in space in a spot-like fashion, instead of occupying homogeneously the whole computational domain like the linear optimal ones. These nonlinear optimal structures well represent the self-sustained turbulence wall cycle: linearly growing streaks saturate and oscillate due to secondary instability, regenerating new localized quasi-streamwise vortices by nonlinear coupling. Linear optimizations are able to describe only the first step of this cycle, whereas a nonlinear approach can capture all of the elements of the cycle. Notice that a very similar optimal structure has been recovered for smaller target times, made by oscillating coherent streaks and vortices at the walls, having smaller wavelength (for instance,
$\unicode[STIX]{x1D706}_{z}^{+}\approx 65$
for
$T^{+}=21.94$
) but a very similar spot-like spatial localization. However, as already known (Jiménez & Moin Reference Jiménez and Moin1991), these streaks are not self-sustained. In fact, we have verified that the time evolution of these optimal small structures beyond the target time leads to their decay. Concerning the influence of
$E_{0}$
, we have observed that the optimal disturbances keep a similar structure as long as the initial energy is sufficiently high to trigger nonlinear effects.
The results obtained for the inner time scale are in good agreement with the well-assessed streaky structures observed near the wall by several authors by experimental and numerical techniques (Kline et al. Reference Kline, Reynold, Schraub and Rundstander1967; Panton Reference Panton2001); therefore, such results can be considered a successful validation of the proposed approach.
Figure 2. Shape of the optimal perturbation for
$T_{out}^{+}=305$
and
$E_{0}=10^{-2}$
at (a)
$t^{+}=0$
and (b)
$t^{+}=T_{out}^{+}$
: isosurface of negative streamwise velocity (green, (a)
$\tilde{u} =-0.016$
, (b)
$\tilde{u} =-0.3$
) and
$Q$
-criterion ((a)
$Q=0.045$
, (b)
$Q=0.15$
) coloured by the value of the streamwise vorticity (positive blue, negative red).
Figure 3. Shape of the optimal perturbation for
$T_{out}^{+}=305$
and
$E_{0}=10^{-2}$
at
$t^{+}=T_{out}^{+}$
: isosurface of negative streamwise velocity (green) (a,b); isosurface of
$Q$
-criterion coloured by contours of streamwise vorticity (positive blue, negative red) (b). The isosurface values are the same as in figure 2(b). Small solid circles indicate small hairpin vortices, big dashed circles indicate big hairpin vortices.
Figure 4. Outer optimal perturbation obtained for
$T_{out}^{+}=305$
and
$E_{0}=10^{-2}$
: isosurfaces of the
$Q$
-criterion (green) and isocontours of streamwise velocity (blue negative, red positive) on the planes
$z^{+}=860$
and
$z^{+}=320$
. The isosurfaces values are the same as in figure 2(b).
3.1.2 Optimal perturbations at the outer time scale
Increasing the target time to the outer time scale
$T_{out}^{+}$
, the optimization algorithm provides a different flow structure, as shown in figure 2, at
$t^{+}=0$
(a) and
$t^{+}=T_{out}^{+}$
(b). The initial optimal perturbation is strongly localized in space and is characterized by alternated streamwise vortices (red and blue) near the wall and localized patches of streamwise velocity perturbations in the outer region. At
$t^{+}=T_{out}^{+}$
this initial perturbation turns into a much more complex structure, mostly composed of packets of hairpin vortices on top of highly oscillating streamwise streaks. In particular, strong vortical structures are observed at two different scales. The small-scale structures are not symmetric and have spanwise length
$\unicode[STIX]{x1D706}_{z}^{+}\approx 100$
(consistent with the observations of Zhou et al. (Reference Zhou, Adrian, Balachandar and Kendall1999)). They are placed on top of the low-speed streaks, apparently as a result of their sinuous instability, as shown in the solid circles in figure 3. On the other hand, the largest vortical structures in the dashed circles have a clear symmetric hairpin shape, with typical wavelengths
$\unicode[STIX]{x1D706}_{z}\approx 2h$
and
$\unicode[STIX]{x1D706}_{x}\approx 2.5h$
, consistent with the observations of turbulent bulges and packets of hairpin of length
${\approx}2h$
(Adrian Reference Adrian2007) and with the dimensions of the largest attached eddy computed using large-eddy simulation by Hwang & Bengana (Reference Hwang and Bengana2016). As one can observe in figure 3, these hairpin vortices originate from the merging of the streamwise vortical structures flanking two distinct low-speed streaks (Adrian Reference Adrian2007), which are modulated quasi-symmetrically with respect to a streamwise axis passing between them. Large-scale low-speed streaks, with
$\unicode[STIX]{x1D706}_{z}\approx 2.2h$
and
$\unicode[STIX]{x1D706}_{x}\approx 5h$
are also induced between the legs of these large hairpin structures; these streaks can be observed in figure 4 in a
$z$
-constant plane passing through the head of two large hairpin vortices (blue contours in the plane at
$z^{+}=860$
for low-speed large-scale streaks). However, the streaks with higher intensity are those close to the wall, as shown by the blue contours in the
$z^{+}=320$
plane. These features recall those found for packets of hairpin vortices described by Adrian (Reference Adrian2007), who observed that the larger the packets, the weaker the backward-induced flow, due to the larger distance of the side vortices from the centre of the hairpin loop. The same author also conjectured that the passage of hairpin packets can explain the occurrence of multiple second- and fourth-quadrant events typical of turbulent bursts.
Figure 5. Logarithm of the PDF of the streamwise and wall-normal velocity for the outer optimal structures at
$t=T_{out}$
(a,c,e) and for the fully turbulent flow (b,d,f) at different constant
$y^{+}$
-planes:
$y^{+}=10$
,
$y^{+}=50$
,
$y^{+}=100$
, (a–f).
3.1.3 Probability density function analysis
Thus, we wonder whether this optimal perturbation characterized by a very complex shape, optimizing the energy at the outer spatial scale, might be a possible candidate for explaining the onset of transient recurrent bursts on top of the long-living oscillating streaks. To investigate whether ejections and sweeps could characterize the dynamics of the nonlinear optimal structure, indicating a strong correlation with bursting events, we have computed the probability density function (PDF) of the streamwise and wall-normal velocity disturbance at different wall-normal positions for the optimal perturbation at
$t^{+}=T_{out}^{+}$
. Figure 5 shows, for
$y^{+}=10,50,100$
(a,c,e), that the PDF is concentrated in the second and fourth quadrants of the
$\tilde{u} {-}\tilde{v}$
plane, indicating the prevalence of ejection and sweep events, exactly as in a strong bursting event. Going from the buffer to the outer region, the strongest contribution to the Reynolds stress slightly moves towards the sweeps region, suggesting a mechanism of energy redistribution from the outer to the wall region by means of sweep events (Jiménez Reference Jiménez1999). This PDF has been compared with that extracted from the DNS of the turbulent flow, shown in the right column of figure 5 for corresponding wall-normal positions. The two set of PDF distributions are very similar, although the data in the left column are obtained by using only the perturbation at a given time, whereas the results in the right column are computed from the statistics of the DNS. On the other hand, the PDF of the inner optimal perturbation (not shown) is quite similar to that extracted from the DNS only at
$y^{+}=10$
,
$\tilde{u}$
and
$\tilde{v}$
rapidly fading away towards the centre of the channel. This indicates that, while the inner optimal disturbance is representative of the self-sustained wall cycle, the outer nonlinear optimal disturbance is representative of bursting events populating the fully turbulent channel flow.
Figure 6. Sketch of the flow topologies associated with different regions of the
$Q{-}R$
plane,
$Q$
and
$R$
being the second and third invariant of the velocity gradient tensor, and
$D=(27/4)R^{2}+Q^{3}$
(Blackburn, Mansour & Cantwell Reference Blackburn, Mansour and Cantwell1996).
Figure 7. Logarithm of the PDF of the non-dimensional second (
$Q^{\ast }$
) and third (
$R^{\ast }$
) invariant of the velocity gradient tensor, for the outer optimal structures at
$t=T_{out}$
(a,c,e) and for the fully turbulent flow (b,d,f) at different constant
$y^{+}$
-plane (a–f:
$y^{+}=10,50,100$
). Notice that
$Q^{\ast }=Q/Q_{w}$
and
$R^{\ast }=R/Q_{w}^{3/2}$
,
$Q_{w}$
being the second invariant of the antisymmetric part of the velocity gradient tensor averaged on each
$y^{+}$
-constant plane.
3.1.4 Topology analysis
The outer optimal disturbance has been found to show the same typical features of a bursting event. However, one may wonder whether its complex structure is well representative of the vortical disturbances observed in fully turbulent conditions. In order to answer to this question, we have compared the main vorticity features of the optimal structures with those of the fully turbulent flow (Blackburn et al.
Reference Blackburn, Mansour and Cantwell1996). Chong, Perry & Cantwell (Reference Chong, Perry and Cantwell1990) proposed a topological analysis of vortical flow structures based on the first three invariants of the velocity gradient tensor, here referred to as
$P$
,
$Q$
and
$R$
, respectively. Incompressible flows being restrained to the
$P=0$
space, the flow topologies that can be found in the channel flow considered here can be classified depending on the values of
$Q$
and
$R$
. With reference to figure 6, flow structures which fall in the upper region of the
$Q{-}R$
plane are called stable (left) or unstable (right) focus topologies, representing vortex stretching or compression, respectively; whereas, in the lower region of the plane, stable (left) and unstable (right) node/saddle/saddle topologies are found. The shapes of the local flow field corresponding to these topologies are sketched in figure 6. As described by Blackburn et al. (Reference Blackburn, Mansour and Cantwell1996), for a turbulent channel flow, moving from the wall to the centreline of the channel, the PDF of
$Q$
and
$R$
will vary, indicating the different structures found at different wall-normal positions in the flow. Figure 7 provides the PDF of
$Q$
and
$R$
for the outer optimal disturbance (a,c,e) and for the DNS of the corresponding turbulent flow (b,d,f) at
$y^{+}=10,50,100$
. One can notice that in both cases, close to the wall, the PDFs are rather uniformly distributed among all quadrants of the
$Q{-}R$
plane. On the other hand, towards the centreline of the channel, the dominant structures are tube-like, shaped as those sketched in figure 6 above the line
$D=0$
. Moreover, the PDFs spread mostly in the second and fourth quadrants, indicating a predominance of stable focus/stretching and unstable node/saddle/saddle topologies. As discussed by Blackburn et al. (Reference Blackburn, Mansour and Cantwell1996) for the case of turbulent channel flow, stable focus/stretching topologies appear to provide a link between the inner and outer regions of the flow, with structures originating in the viscous sublayer and extending towards the outer region, mostly associated with hairpin or horseshoe shapes. The presence of hairpin vortices in the outer optimal disturbance and the fact that its
$Q{-}R$
topology distribution reproduces well that of the corresponding fully turbulent flow may indicate the presence of those structures in fully turbulent conditions, at least for the moderate value of the Reynolds number used here. On the other hand, the inner optimal disturbance, which does not show hairpin vortices, is characterized by a different topology distribution, without any clear preference for the stable focus/stretching and the unstable node/saddle/saddle topologies, with the vortices rapidly fading away far from the wall (not shown). Therefore, the similarity of the outer optimal flow topology with that of the fully turbulent flow suggests that these structures are well representative of the vortical dynamics of a turbulent channel flow from the wall towards the centreline of the channel.
Table 1. Wavelength and corresponding wall-normal position of the peaks of the premultiplied energy density spectrum shown in figure 8.
Figure 8. Logarithm of the premultiplied power spectrum versus the wall-normal distance
$y^{+}$
for the DNS (shaded contours), inner optimal solution (blue isolines) and outer optimal solution (black isolines) at target time. The symbols X and O indicate the maximum value for the inner and outer peak, respectively. The green dotted line joining the inner and outer energy peak provides the scaling laws
$y^{+}=c(k_{x,z}^{+})^{-1}$
, with slopes (a)
$c=0.0921$
, (b)
$c=0.4608$
, (c)
$c=0.6970$
, (d)
$c=0.1028$
, (e)
$c=0.1439$
, (f)
$c=0.1287$
.
3.1.5 Spectrum analysis
We have found that the outer optimal disturbance reproduces well the vortical topology of the corresponding turbulent channel flow; now, we want to investigate whether the size of these vortices and their main wavelengths might be representative of the broadband spectrum of wavelengths typical of turbulent flows. At this purpose, we have extracted the streamwise and spanwise premultiplied energy density spectra from the nonlinear optimal disturbances at
$T_{in}^{+}$
and
$T_{out}^{+}$
, and compared them with the same spectra extracted from the DNS of the corresponding fully developed turbulent flow. Figure 8 provides the premultiplied spectrum distributions along the wall-normal direction obtained from the DNS (shaded contours) and from the optimal disturbances at
$T_{in}^{+}$
(light blue isolines) and at
$T_{out}^{+}$
(black isolines). The spanwise (a,c,e) and streamwise (b,d,f) spectra have been obtained for energy densities computed on the basis of the streamwise (a,b), wall-normal (c,d) and spanwise (e,f) components of velocity,
$\hat{E}_{uu}$
,
$\hat{E}_{vv}$
and
$\hat{E}_{ww}$
, respectively. The X and the O symbols mark the peak values of the energy density spectrum for the inner and the outer optimal structures, respectively. Such peak values are also provided in table 1. For the inner optimal structure, the energy peak is found for
$\unicode[STIX]{x1D706}_{z}^{+}=113.8$
, rather close to the wall (
$y^{+}$
ranging from 10 to 29 depending on the considered energy density), providing the typical spanwise spacing of streaks (Kline et al.
Reference Kline, Reynold, Schraub and Rundstander1967). Concerning the streamwise wavelength, the energy peak is at
$\unicode[STIX]{x1D706}_{x}^{+}=189.4$
, corresponding to the wavelength of the strong wiggling of the streaks due to the presence of streamwise vortices flanking them. However, looking at all of the streamwise spectra (right column), one can notice a secondary peak at
$k_{x}^{+}\approx 0.0058$
, corresponding to a secondary wavelength,
$\unicode[STIX]{x1D706}_{x}^{+}\approx 1082.7$
, close to the typical streamwise wavelength of streaks in fully turbulent conditions (Kline et al.
Reference Kline, Reynold, Schraub and Rundstander1967), and roughly corresponding to the wavelength of the spot-like localization of the optimal structures characterizing the inner optimal perturbation. Nevertheless, for this inner optimal structure, both the streamwise and spanwise spectra appear very narrow, including only a small portion of the broadband range of wavenumbers found by the DNS (compare the light blue isolines with the shaded isocontours). On the other hand, the spectra computed for the outer optimal have energy peaks at larger wavelengths in
$x$
and
$z$
, with
$\unicode[STIX]{x1D706}_{x}^{+}=757.5$
well reproducing the peak value found by DNS in the
$\hat{E}_{uu}$
spectrum, probably corresponding to the streak streamwise spacing found in the outer optimal disturbance. Moreover, the outer optimal perturbation spectra are almost overlapped with those extracted from the DNS (compare the black isolines with the shaded contours), indicating that the optimal structure computed for
$T_{out}^{+}$
is well representative of the turbulent motion in the same flow condition.
Concerning the typical wavelength of the coherent structures in fully turbulent flow, the attached eddy theory of Townsend (Reference Townsend1980) suggests that the size of the typical eddies in a turbulent shear flow scales with the wall-normal direction, the smallest-eddy dimension scaling with inner units (
$l^{+}$
), and the largest-eddy dimension scaling with outer units, in both streamwise and spanwise directions. In order to verify whether this hypothesis is valid also for the optimal structures found here, we have considered the energy peaks of the premultiplied energy spectra, marked in figure 8 by X and O for the inner and outer optimal disturbance, respectively. Tracing a straight line between these two peaks (green dashed line), we can infer a scaling of the form
$y^{+}\propto \unicode[STIX]{x1D706}_{x,z}^{+}$
(
$y^{+}\propto ({k^{+}}_{x,z})^{-1}$
), as conjectured by Townsend (Reference Townsend1980). Concerning the scaling coefficients, provided in the caption of figure 8, we have obtained values very close to those available in the literature for all components of the energy (Hoyas & Jiménez Reference Hoyas and Jiménez2006; Hwang Reference Hwang2015). Thus, the scaling laws extracted on the basis of the inner and outer energy peaks reproduce well the scalings found in fully turbulent flows. However, we must remark that at the considered moderate Reynolds number a distinct scale separation in the streamwise direction is not established yet, data at higher Reynolds numbers being needed for confirming the results (del Álamo & Jiménez Reference del Álamo and Jiménez2003).
3.2 Time evolution of the outer optimal perturbation
3.2.1 Production and dissipation analysis
The optimal structure arising at the outer time scale is structurally rather complex and the mechanisms leading to a strong energy growth cannot be simply related to a large-scale cycle similar to that characterizing the inner scale (Hwang & Cossu Reference Hwang and Cossu2010b
). Insight into the energy growth mechanisms can be gained by considering the time evolution of the energy density of the structures. Scalar multiplication of (2.1) by
$\tilde{\boldsymbol{u}}$
provides the following Reynolds–Orr equation (Schmid & Henningson Reference Schmid and Henningson2012) for the disturbance:
$$\begin{eqnarray}\frac{1}{2}\frac{\unicode[STIX]{x2202}E}{\unicode[STIX]{x2202}t}=\int _{V}\underbrace{-\tilde{\boldsymbol{u}}\boldsymbol{\cdot }(\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{U})}_{P}\,\text{d}V-\int _{V}\underbrace{\frac{1}{Re}\unicode[STIX]{x1D735}\tilde{\boldsymbol{u}}\boldsymbol{ : }\unicode[STIX]{x1D735}\tilde{\boldsymbol{u}}}_{D}\,\text{d}V+\int _{V}\underbrace{\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{\cdot }\overbrace{(\overline{\tilde{\boldsymbol{u}}\tilde{\boldsymbol{u}}})}^{\unicode[STIX]{x1D70F}}}_{P_{\unicode[STIX]{x1D70F}}}\,\text{d}V,\end{eqnarray}$$
where
$P(x,y,z,t)$
is the energy production,
$D(x,y,z,t)$
is the energy dissipation and
$P_{\unicode[STIX]{x1D70F}}(x,y,z,t)$
is the contribution of the Reynolds stress to the production. Figure 9(a) shows the time evolution of these three terms integrated over the whole computational domain, denoted hereafter as
$P_{V}$
,
$D_{V}$
and
${P_{\unicode[STIX]{x1D70F}}}_{V}$
. First of all, the strong energy peak, followed by an increase of the dissipation
$D_{V}$
, confirms that the transient evolution of this optimal structure can be interpreted as a strong energy burst, which is then dissipated in time reaching a dissipation peak at
$t^{+}\approx 3T_{out}^{+}$
. Such a time interval is in agreement with the large-scale temporal oscillation observed by Hwang & Bengana (Reference Hwang and Bengana2016) for the largest attached eddy and recognized as a bursting event by Flores & Jimenez (Reference Flores and Jimenez2010). One can notice the non-negligible contribution of the term
${P_{\unicode[STIX]{x1D70F}}}_{V}$
in the early time evolution of the perturbation, except at very small times, when the main production mechanism is the Orr mechanism (Orr Reference Orr1907), as inferred by analysing the time evolution of the optimal structures provided in § 3.2.2. This points out the important role of the Reynolds stress in the dynamics of the perturbation. It is noteworthy that this result is in agreement with the analysis of Jiménez (Reference Jiménez2015) who estimates that the effect of the linear energy growth due to the Orr mechanism is dominant for
$\overline{t}=t^{+}/Re_{\unicode[STIX]{x1D70F}}<0.15$
. In our case,
$\overline{t}_{Orr}\approx 0.136$
and
$\overline{T}_{out}=T_{out}^{+}/Re_{\unicode[STIX]{x1D70F}}=1.694$
, therefore, the linear limit is less than one-tenth of the target time. Figure 9(a) shows that in the first part of the bursting event a strong linear growth can be observed followed by a larger nonlinear growth till
$t^{+}=2T_{out}^{+}$
. In particular, the contribution of the Reynolds stresses increases till
$t^{+}\approx T_{out}^{+}$
and becomes negligible for
$t^{+}>2T_{out}^{+}$
. In fact, the term
${P_{\unicode[STIX]{x1D70F}}}_{V}$
reaches its maximum approximately at the target time, when the generation of the largest hairpin vortices is completed, and then it decays in time, leading to the establishment of featureless turbulence. This behaviour can be better observed in figure 9(b) providing the projection of the time evolution of the perturbation onto a production–dissipation plane. Starting close to the origin, the trajectory reaches the peak of the total production
$P_{V}+{P_{\unicode[STIX]{x1D70F}}}_{V}$
due to the successive increase of
${P_{\unicode[STIX]{x1D70F}}}_{V}$
and
$P_{V}$
, before starting to oscillate around the point
$P_{V}\approx D_{V}\approx 0.35$
, representing the turbulent self-sustained state.
Figure 9. (a) Time evolution of the energy
$E$
(red), production
$P_{V}$
(blue), Reynolds stress production
${P_{\unicode[STIX]{x1D70F}}}_{V}$
(cyan), and dissipation
$D_{V}$
(green). (b) Trajectories in the plane
$D_{V}-P_{V}$
of the production
$P_{V}$
, Reynolds stress production
${P_{\unicode[STIX]{x1D70F}}}_{V}$
, and total production
${P_{Tot}}_{V}=P_{V}+{P_{\unicode[STIX]{x1D70F}}}_{V}$
. The time interval between symbols is equal to
$\unicode[STIX]{x0394}t^{+}=24.5$
.
Figure 10. (a) Time evolution of the net local energy production, given by the difference between the production and dissipation at each
$y^{+}$
(shaded contours), and of the wall-normal energy flux (isolines for
$\unicode[STIX]{x1D6F7}^{+}=1,2,3,4$
, from the outermost to the innermost contour) for the outer optimal structure. (b) Net local energy production (red dashed line) and wall-normal flux (black solid line) versus
$y^{+}$
, extracted at
$t^{+}=2T_{out}^{+}$
, showing a production peak in the inner zone (
$y^{+}\approx 20$
), whereas the outer region is characterized by a weak dissipation.
In order to analyse the energy production and dissipation mechanisms, we evaluate the energy exchange in the wall-normal direction by expressing the Reynolds–Orr equation using the Cartesian notation (Jiménez Reference Jiménez1999):
$$\begin{eqnarray}\left(\unicode[STIX]{x2202}_{t}+U_{j}\unicode[STIX]{x2202}_{j}-\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}\right)\frac{\tilde{u} _{i}\tilde{u} _{i}}{2}+\unicode[STIX]{x2202}_{j}\left(\tilde{u} _{j}\left(\tilde{p}+\frac{\tilde{u} _{i}\tilde{u} _{i}}{2}\right)\right)=-\tilde{u} _{i}\tilde{u} _{j}\unicode[STIX]{x2202}_{j}U_{i}-\frac{1}{Re}(\unicode[STIX]{x2202}_{j}\tilde{u} _{i})^{2}+\tilde{u} _{i}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D70F}_{ij}.\end{eqnarray}$$
Integrating this equation in the streamwise and spanwise direction, we obtain an equation for the wall-normal transport of energy, allowing one to identify the last term on the left-hand side as the wall-normal energy flux,
$\unicode[STIX]{x1D6F7}=\tilde{v}[\tilde{p}+(\tilde{u} ^{2}+\tilde{v}^{2}+\tilde{w}^{2})/2]$
, and the first two terms on the right-hand side as the production and dissipation terms (whose integral counterparts are denoted as
$P_{x,z}$
and
$D_{x,z}$
, respectively). The net energy production at a given
$y^{+}$
-constant plane, provided by the difference
$P_{x,z}-D_{x,z}$
, is plotted versus time in figure 10(a) (shaded contours). As found for fully developed turbulent flows at comparable values of
$Re_{\unicode[STIX]{x1D70F}}$
(Jiménez Reference Jiménez1999), the net production of turbulent energy (red contours) is well localized at the inner scale (
$y^{+}\approx 20$
) and extends to the outer layer for times smaller than the target time indicating that both inner and outer structures contribute to the perturbation energy increase. The isolines for positive wall-normal energy flux (
$\unicode[STIX]{x1D6F7}^{+}=1,2,3,4$
) are provided in figure 10(a), clearly indicating an outward flux of energy towards the centre of the channel for
$t^{+}\approx T_{out}^{+}$
, corresponding to the formation of the hairpin vortex. Whereas, at the centre of the channel, dissipation is found to exceed production, and the flux continuously decreases becoming slightly negative, as one can observe in figure 10(b), showing the excess of local energy production and the wall-normal flux extracted at
$t^{+}=2T_{out}^{+}$
. This indicates the presence of a coherent inverse-cascade process (Jiménez Reference Jiménez1999) typical of moderate values of
$Re_{\unicode[STIX]{x1D70F}}$
, in which energy is transferred from the inner scales at the wall, i.e. the streaks, to large-scale dissipating structures in the outer layer, the hairpin vortices. Notice that at the considered value of
$Re_{\unicode[STIX]{x1D70F}}$
, when fully turbulent flow is achieved, no energy production is observed far from the wall, whereas at larger values of
$Re_{\unicode[STIX]{x1D70F}}$
a (weaker) production peak is observed also at the outer scale (see Lee & Moser Reference Lee and Moser2015). The large-scale dissipating hairpin structures will eventually breakdown, transferring the energy to incoherent small-scale fluctuations, closing the loop. This wall-normal energy transfer occurring in a short time is thus linked to the occurrence of a transient energy peak which appears in the form of a rapid ejection (positive wall-normal velocity
$\tilde{v}$
) followed by a longer sweep (negative
$\tilde{v}$
), similar to a typical bursting event.
Figure 11. Snapshots of the time evolution of the outer optimal structures: isosurfaces of
$Q$
-criterion coloured by the wall-normal distance
$y^{+}$
.
3.2.2 Analysis of the flow structures
To further characterize the dynamics of the outer nonlinear optimal perturbation, we analyse its time evolution. Figure 11 provides
$10$
snapshots of the perturbation (
$Q$
-criterion isosurfaces, coloured by the wall-normal distance), from
$t^{+}=0$
to
$t^{+}=431$
. The initial perturbation is localized in the three space directions and is composed of two packets of thin counter-rotating vortices showing a spanwise symmetry, placed at
$y^{+}\approx 20$
(as indicated by the colours in figure 11
a). Even if the optimization is based on the outer time scale, the core of the vortical structures at initial time appears to be in the inner region, the main part of the energy of the spanwise and wall-normal velocity being located at
$y^{+}\approx 10{-}40$
(whereas at
$t^{+}=T_{out}^{+}$
the energy peak is at
$y^{+}>36$
or
$y>0.2$
, as provided in table 1). Whereas, the streamwise velocity perturbation is located far away from the wall at
$y^{+}\approx 60$
(at
$t^{+}=0$
). In figure 11(b) one can observe the typical downstream tilting due to the Orr mechanism (Orr Reference Orr1907). This initial phase of the energy growth agrees with the linear analysis of Jiménez (Reference Jiménez2015) who demonstrates that for very short times (
$\overline{t}=t^{+}/Re_{\unicode[STIX]{x1D70F}}<0.15$
) the energy growth due to the Orr mechanism is dominant. Following the evolution of the perturbation, we can notice that the vortices tend to be lifted up from the wall towards the centre of the channel, developing structures of increasing size in an inverse cascade from small to large scales (Jiménez Reference Jiménez1999). Concerning the vortical dynamics, one can observe the formation of new vortices aligned with the initial ones along modulated streamwise streaks (see figure 11
c,d). These vortices are lifted in the wall-normal direction, creating symmetric or non-symmetric arches on top of the negative streaks at the wall (Wang, Huang & Xu Reference Wang, Huang and Xu2015), as one can observe in figure 11(d,e). Once the small-scale hairpin and cane vortices have been created, some of them further grow and lift in the outer region, merging with the nearest vortices in large-scale symmetric hairpin vortices whose head is placed between two streamwise streaks at the wall (Adrian, Balachandar & Lin Reference Adrian, Balachandar and Lin2001), as shown in figure 11(f,g), generating a new weaker large-scale negative streak between the hairpin legs. Once the structures have reached their maximum spatial growth, corresponding approximately to the energy peak in figure 9(a), the structures begin to break down, starting an energy cascade from the large scales towards the small ones, closing the loop (figure 11
h,i,j).
Figure 12. (Left) Sketch of the main steps of the dynamics of the outer optimal perturbation based on the snapshots (right) extracted at (a)
$t^{+}=49$
, (b)
$t^{+}=123$
, (c)
$t^{+}=147.5$
, (d)
$t^{+}=294$
, (e)
$t^{+}=172,196.5$
, (f)
$t^{+}=221$
. Isosurfaces of negative streamwise velocity (green) and
$Q$
-criterion coloured by the values of streamwise vorticity (blue for positive, red for negative).
Figure 12 summarizes the main steps of the time evolution of the outer optimal perturbation: we conjecture it is representative of a bursting event which transfers the energy from small- to large-scale structures, and then back towards small-scale perturbations. The left panel provides a sketch of the main steps of the evolution shown by seven successive snapshots on the right panel, for
$t^{+}=49,123,147.5,172,196.5,221,294$
, respectively. An initial perturbation leading to a bursting event is originated by two flanking pairs of small counter-rotating vortices (red and blue isosurfaces at the bottom left angle of both panels), which are the first elements of the wall self-sustained cycle (Waleffe Reference Waleffe1997). These vortices initially increase their energy by the Orr mechanism and then generate low-speed streaks by the lift-up mechanism (Landahl Reference Landahl1980) (green isosurfaces, step (b)). These streaks increase their amplitude, and exhibit secondary sinuous or varicose instability (Andersson et al.
Reference Andersson, Brandt, Bottaro and Henningson2001). As a result, the initial streamwise vortices bend over the streak at the point where the instability is triggered, forming arch-shaped structures (Schoppa & Hussain Reference Schoppa and Hussain2002; Wang et al.
Reference Wang, Huang and Xu2015) (step c). Being very close to each other and continuously lifting in the wall-normal direction, two of these non-symmetric arch-shaped vortical structures merge together, generating a large symmetric hairpin structure (blue and red isosurfaces, step d). This large-scale hairpin vortex increases in size up to the centreline of the channel and then begins to break down dissipating the energy; instead, the non-symmetric small-scale vortices on top of the streaks may induce inflectional instabilities on the instantaneous velocity profile. In particular, strong low-speed streaks may induce an inflection point in the
$x{-}y$
plane, triggering a Kelvin–Helmholtz-type instability producing spanwise vorticity, such as the arch of the hairpin vortices, but also inflection points in the
$x{-}z$
plane, producing wall-normal vorticity (Heist, Hanratty & Na Reference Heist, Hanratty and Na2000). The tilting of the wall-normal vorticity by the mean velocity profile induces streamwise vortices of opposite sign with respect to the initial one (step e), as discussed by Heist et al. (Reference Heist, Hanratty and Na2000). This new counter-rotating vortex flanks the initial one, being able to create a new low-speed streak by the lift-up mechanism (step f), and the loop can restart again from the small-scale structures towards the large-scale ones. Concerning the time scales typical of this loop, the complete formation of the small arch vortices participating to the self-sustained cycle takes approximately
$\unicode[STIX]{x0394}t^{+}\approx 150$
time units (see figure 11
c–i) as in Wang et al. (Reference Wang, Huang and Xu2015), whereas the complete formation of the train of large-scale hairpin vortices takes approximately
$\unicode[STIX]{x0394}t^{+}\approx 300$
time units, which corresponds approximately to the target time
$T^{+}$
, similarly to the observations of Zhou et al. (Reference Zhou, Adrian, Balachandar and Kendall1999) where the hairpin packets have spacing approximately equal to
$\unicode[STIX]{x1D706}_{x}^{+}\approx 450$
(see figure 3). Notice that the self-sustained cycle mainly involves streaks and vortices close to the wall, but it transiently induces large-scale hairpin vortices as a by-product of its evolution. These large vortical structures have the role of realizing an inverse energy cascade reaching the outer scale and dissipating the stored energy towards smaller scales, allowing a new wall cycle to be established. It appears thus that the large-scale hairpin vortices observed in the nonlinear optimal disturbance do not directly participate into the self-sustained cycle, but they are transient dynamical features which ensure the occurrence of energy peaks and subsequent dissipation typical of bursting events.
4 Conclusion
It is known that, behind its chaotic dynamics, turbulent flow is populated by coherent structures, i.e. flow motions highly correlated over both space and time, carrying a large part of the flow momentum. In the present study, for the first time, a recently developed nonlinear optimization technique based on Lagrange multipliers is employed to unravel the dynamics of such structures.
In particular, a nonlinear transient growth analysis has been performed to study which kind of coherent structures are able to trigger rapid events with a strong energy growth, similar to bursting events, in a canonical wall-bounded turbulent flow such as the channel flow. The optimization procedure, focusing on the dynamics of finite-amplitude disturbances, provides different nonlinear optimal structures depending on the chosen time scale for the energy growth.
For an inner time scale, corresponding approximately to one eddy turnover time evaluated in the buffer layer at
$y^{+}=19$
(the superscript
$^{+}$
indicating variables expressed in inner units), nonlinear optimal structures consist of highly modulated streaks having a typical spanwise spacing
$\unicode[STIX]{x1D706}_{z}^{+}\approx 113$
, surrounded by positive and negative streamwise vortices, with a spanwise spacing
$\unicode[STIX]{x1D706}_{z}^{+}\approx 56$
. These nonlinear optimal structures, localized in space in a spot-like fashion, well represent the self-sustained cycle of turbulence at the wall: linearly growing streaks saturate and oscillate due to secondary instability, regenerating new localized quasi-streamwise vortices by nonlinear coupling.
For the outer time scale, corresponding approximately to one eddy turnover time at the centreline of the channel, a much more complex optimal structure is observed, mostly composed of packets of hairpin vortices on top of highly oscillating streamwise streaks. In particular, strong vortical and streaky structures are observed at different spatial scales, ranging from the wall to the outer layer. The probability density function of the velocity disturbance characterizing such an outer optimal is concentrated in the second and fourth quadrants of the streamwise versus wall-normal velocity plane. This indicates the prevalence of ejection and sweep events, as happens in a strong bursting event. Moreover, we show that the outer most energetic structure well describes the wavenumber spectrum, the vortical topology, and the production–dissipation wall-normal distribution typical of turbulent flows at moderate Reynolds numbers. Whereas, the inner optimal structure includes only a small portion of the broadband range of wavenumbers and vortical topologies found at different wall-normal positions by a direct numerical simulations of the fully turbulent flow. The analysis of the distribution of the most energetic wavelengths in the wall-normal direction for the inner and outer optimal disturbances shows that the optimal structures computed here scale in size accordingly to the attached eddy theory of Townsend (Reference Townsend1980). In particular, the spatial scaling laws extracted on the basis of the inner and outer energy peaks reproduce well the scalings found in fully turbulent flows.
Finally, a careful analysis of the time evolution of the optimal flow structures has been performed, providing the dynamics of the initial perturbations leading to a bursting event. An optimal bursting event is originated by two flanking pairs of small counter-rotating vortices at the wall, the basic elements of the wall self-sustained cycle; due to the Orr and lift-up mechanisms, these vortices are able to generate strong low-speed streaks, which exhibit secondary sinuous or varicose instability; as a result, the initial streamwise vortices bend over the streak at the point where the instability is triggered, forming arch-shaped structures which lift in the wall-normal direction and merge together, generating large symmetric hairpin structures; the large-scale hairpin vortices increase in size up to the centreline of the channel and then breakdown dissipating the energy; instead, the small-scale vortices on top of the wall streaks are bent and tilted by the mean flow, leading back to the creation of a pair of streamwise vortices, restarting the cycle. Thus, the self-sustained cycle at the wall appears to be the main source of energy of the bursting event, which transiently induces large-scale hairpin vortices as a by-product; these large vortical structures have the role of realizing an inverse energy cascade reaching the outer scale and eventually dissipating the stored energy towards smaller scales, allowing a new wall cycle to develop. This implies that hairpin vortices, even if inherently transient coherent structures (see Eitel-Amor et al. Reference Eitel-Amor, Örlü, Schlatter and Flores2015), are robust features of turbulent channel flows, at least at moderate friction Reynolds numbers, arising as a result of a strong nonlinear instability that repeats in time as a by-product of the self-sustained wall cycle.
These results show that, despite the main source of turbulent energy being located close to the wall and sustained by the wall cycle (Waleffe Reference Waleffe1997), for moderate values of
$Re_{\unicode[STIX]{x1D70F}}$
the turbulent motion is characterized by a complex energy transfer which involves inner and outer scales.
In conclusion, this study provides an explanation for the recurrence of energy bursts revealing that they correspond to optimal energy flow structures embedded in the fully turbulent flow. These optimal structures reproduce well the spatial spectra as well as the probability density function of the velocity typically measured in turbulent flows, recovering the mechanism of direct-inverse energy cascade. These results represent an important step towards understanding the dynamics of turbulence and paves the way to new nonlinear techniques to manipulate and control the self-sustained turbulence dynamics. A further challenge will be to extend this analysis to larger values of
$Re_{\unicode[STIX]{x1D70F}}$
, for which a clear scale separation is observed in the spatial spectra and a second peak of energy production exists at the outer scale. This will allow to model the inner–outer interaction under different operating conditions, aiming at understanding the universal mechanisms underlying the turbulent coherent motion. Moreover, further work will aim at exploring the optimal dynamics of coherent structures for other types of turbulent flows such as the boundary-layer flow.
Acknowledgements
This work was granted access to HPC resources of IDRIS under allocation
$x20162a6362$
made by GENCI (Grand Equipement National de Calcul Intensif). The authors would like to thank J.-C. Loiseau for his contribution to the implementation of the optimization algorithm in the code Nek5000 and the anonymous referees for their valuable suggestions. The authors also wish to acknowledge the computational resources of the PrInCE project (grant PONa3-00372–CUP D91D11000100007) at Politecnico di Bari.
Appendix
In order to derive the equations governing the dynamics of perturbations of the mean turbulent velocity profile in a plane channel flow, we employ a Reynolds decomposition approach similar to that used by Eitel-Amor et al. (Reference Eitel-Amor, Örlü, Schlatter and Flores2015). The instantaneous flow vector
$\boldsymbol{q}=[\boldsymbol{u},p]^{\text{T}}$
, where
$\boldsymbol{u}$
is the velocity vector and
$p$
is the pressure, is decomposed into a mean flow component
$\boldsymbol{Q}=[U,0,0,P]^{\text{T}}$
and a disturbance
$\tilde{\boldsymbol{q}}=[\tilde{u} ,\tilde{v},\tilde{w},\tilde{p}]^{\text{T}}$
:
$$\begin{eqnarray}\boldsymbol{q}(x,y,z,t)=\boldsymbol{Q}(y)+\tilde{\boldsymbol{q}}(x,y,z,t).\end{eqnarray}$$
Injecting this decomposition in the NS equations and averaging over a long time, the following Reynolds-averaged NS equations are obtained:
$$\begin{eqnarray}\boldsymbol{U}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{U}=-\unicode[STIX]{x1D735}P+\frac{1}{Re}\unicode[STIX]{x0394}\boldsymbol{U}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\overline{\tilde{\boldsymbol{u}}\tilde{\boldsymbol{u}}},\end{eqnarray}$$
$\overline{\bullet }$
denoting long-time averaging. Subtracting the time-averaged equations (A 2) from the NS equations provides the following final formulation for the dynamics of the disturbances:
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}\tilde{\boldsymbol{u}}}{\unicode[STIX]{x2202}t}+\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\tilde{\boldsymbol{u}}+\boldsymbol{U}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\tilde{\boldsymbol{u}}+\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{U}=-\unicode[STIX]{x1D735}\tilde{p}+\frac{1}{Re}\unicode[STIX]{x0394}\tilde{\boldsymbol{u}}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\overline{\tilde{\boldsymbol{u}}\tilde{\boldsymbol{u}}},\\ \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\tilde{\boldsymbol{u}}=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
$Re=U_{c}h/\unicode[STIX]{x1D708}$
,
$U_{c}$
indicating the steady centreline velocity magnitude in the plane channel. The last term of the momentum equation is the divergence of the Reynolds stress tensor
$\unicode[STIX]{x1D749}=\overline{\tilde{\boldsymbol{u}}\tilde{\boldsymbol{u}}}$
forcing the mean turbulent velocity profile (see (A 2)).
Figure 13. (a) Mean velocity profile
$U^{+}$
versus the wall-normal coordinate
$y^{+}$
(blue thick lines) obtained by the present DNS (solid) compared with the results of Kim et al. (Reference Kim, Moin and Moser1987) (dashed). The black thin lines are the linear (solid) and logarithmic (dashed) profiles. (b) Root-mean-square of
$\tilde{u}$
(red),
$\tilde{v}$
(blue),
$\tilde{w}$
(green) and Reynolds shear stress
$\overline{\tilde{u} \tilde{v}}$
(black) normalized by the wall shear velocity, versus
$y^{+}$
obtained by the present DNS (solid) compared with the results of Kim et al. (Reference Kim, Moin and Moser1987) (dashed).
This term appears when the perturbative formulation employs a base flow
$\boldsymbol{U}$
which is not a solution of the steady Navier–Stokes equations. Reynolds stresses need to be known or modelled for closing the governing equations: in this work we compute them a priori by a DNS of the fully developed turbulent flow. For this purpose, firstly, the mean flow velocity
$\boldsymbol{U}$
is computed by DNS averaging the instantaneous velocity over a long time interval and over the two homogeneous directions, obtaining the velocity profile shown in figure 13(a) (solid thick line), which is compared to the mean flow computed by Kim et al. (Reference Kim, Moin and Moser1987) (dashed thick line). Then, subtracting the computed mean flow from the instantaneous velocity field, we obtain the perturbation
$\tilde{\boldsymbol{u}}$
, which contains both coherent and fluctuating parts of the disturbances. The product
$\tilde{\boldsymbol{u}}\tilde{\boldsymbol{u}}$
is averaged in time and over the two homogeneous directions. Figure 13(b) provides the root-mean-square of
$\tilde{u}$
,
$\tilde{v}$
,
$\tilde{w}$
, as well as the Reynolds shear stress
$\overline{\tilde{u} \tilde{v}}$
(solid lines) extracted from the DNS, showing an excellent agreement with the same quantities computed by Kim et al. (Reference Kim, Moin and Moser1987) (dashed line). Based on these data, we achieve a direct evaluation of the Reynolds stress tensor
$\unicode[STIX]{x1D749}=\overline{\tilde{\boldsymbol{u}}\tilde{\boldsymbol{u}}}$
, whose divergence is shown in figure 14(a) (the three solid lines showing the
$x$
,
$y$
and
$z$
components of
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D749}$
versus the wall-normal coordinate
$y^{+}$
). The computed Reynolds stress tensor is employed as a forcing term in (2.1) for the optimization process, providing the inner and outer optimal perturbations. As a consistency check, it is also worth verifying that the computed optimal perturbations satisfy the long-time constraint implicitly imposed by forcing the NS equations with the Reynolds stress tensor. In figure 14(b) one can observe the time evolution of the energy of
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }[\tilde{\boldsymbol{u}}\tilde{\boldsymbol{u}}]$
,
$\tilde{\boldsymbol{u}}$
being the inner (green line) or the outer (red line) optimal perturbation, and
$[\boldsymbol{\cdot }]$
denoting the spatial average in the
$y$
-constant planes. It appears that, after a short transient, the energy of this term oscillates around the energy of
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D749}$
, confirming the consistency of the proposed approach.
Figure 14. (a) Streamwise (red), wall-normal (blue) and spanwise (green) components of the divergence of the Reynolds stress tensor
$\unicode[STIX]{x1D749}$
versus
$y^{+}$
obtained by the present DNS. (b) Energy of
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }[\tilde{\boldsymbol{u}}\tilde{\boldsymbol{u}}]$
(where
$[\bullet ]$
denotes the spatial average in the
$y$
-constant planes) for the outer (red line) and inner (green line) optimal perturbations versus time; the dashed line indicates the energy of
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D749}$
.
It is noteworthy that these equations are not suitable for a linear stability analysis; in fact,
$\tilde{\boldsymbol{u}}$
cannot be considered infinitesimal, since it contains both the coherent (
$\hat{\boldsymbol{u}}$
) and fluctuating (
$\boldsymbol{u}^{\prime }$
) part of the disturbances, the latter being non-zero in a turbulent flow. Whereas, previous linear instability approaches such as those used by Pujals et al. (Reference Pujals, García-Villalba, Cossu and Depardon2009), Cossu et al. (Reference Cossu, Pujals and Depardon2009) and Hwang & Cossu (Reference Hwang and Cossu2010a
) used a triple decomposition approach (see Reynolds & Hussain Reference Reynolds and Hussain1972) where
$\boldsymbol{u}=\boldsymbol{U}+\hat{\boldsymbol{u}}+\boldsymbol{u}^{\prime }$
, optimizing only the coherent part of the perturbation. However, the model used in these works cannot be easily extended to a nonlinear framework, since it neglects the long-time average of the nonlinear coherent perturbation term
$\overline{\hat{\boldsymbol{u}}\hat{\boldsymbol{u}}}$
, an hypothesis that cannot be extended to the case of finite-amplitude perturbations, where this term should be large (see also Viola et al.
Reference Viola, Iungo, Camarri, Port-Agel and Gallaire2014).
Finally, it is worth pointing out that, using a triple decomposition approach, an equation formally equivalent to (A 3) for the coherent part of the perturbation can be derived under the assumption that the variance of the probability distribution of the fluctuating part of the perturbation is small with respect to the Reynolds stress tensor
$\unicode[STIX]{x1D749}$
, so that the phase average of the fluctuating nonlinear term
$\langle \boldsymbol{u}^{\prime }\boldsymbol{u}^{\prime }\rangle$
can be neglected.
