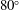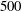1 Introduction
Long flexible bodies with bluff cross-section and exposed to flowing fluid are common in nature (e.g. plants and trees in wind) but also in engineering applications, for example, the slender offshore structures (risers, cables) immersed in ocean currents. The flow-induced vibrations (FIV) that often occur in this context lead to amplified drag forces and increased fatigue damage. Due to their impact on the structures, FIV have been the object of a number of studies, as collected in Blevins (Reference Blevins1990), Naudascher & Rockwell (Reference Naudascher and Rockwell1994) and Païdoussis, Price & de Langre (Reference Païdoussis, Price and de Langre2010). Vortex-induced vibrations (VIV) are a type of FIV which involves a mechanism of synchronization between the body response and the vortex formation in its wake. The present work focuses on the onset of the VIV regime when a slender flexible structure is placed at a large inclination angle in the current, a configuration frequently encountered in real physical systems.
The fundamentals of VIV have been well documented for a cylinder whose axis in quiescent fluid is perpendicular to the oncoming flow (normal incidence case), the body being either rigid and elastically mounted (King, Prosser & Johns Reference King, Prosser and Johns1973; Bearman Reference Bearman1984, Reference Bearman2011; Naudascher Reference Naudascher1987; Mittal & Tezduyar Reference Mittal and Tezduyar1992; Hover, Techet & Triantafyllou Reference Hover, Techet and Triantafyllou1998; Okajima, Kosugi & Nakamura Reference Okajima, Kosugi and Nakamura2002; Sarpkaya Reference Sarpkaya2004; Williamson & Govardhan Reference Williamson and Govardhan2004; Klamo, Leonard & Roshko Reference Klamo, Leonard and Roshko2006; Leontini, Thompson & Hourigan Reference Leontini, Thompson and Hourigan2006; Benaroya & Gabbai Reference Benaroya and Gabbai2008; Lucor & Triantafyllou Reference Lucor and Triantafyllou2008; Dahl et al. Reference Dahl, Hover, Triantafyllou and Oakley2010; Navrose & Mittal Reference Mittal2013; Cagney & Balabani Reference Cagney and Balabani2014; Konstantinidis Reference Konstantinidis2014) or flexible (Chaplin et al. Reference Chaplin, Bearman, Huera-Huarte and Pattenden2005; Trim et al. Reference Trim, Braaten, Lie and Tognarelli2005; Lie & Kaasen Reference Lie and Kaasen2006; Lucor, Mukundan & Triantafyllou Reference Lucor, Mukundan and Triantafyllou2006; Huera-Huarte & Bearman Reference Huera-Huarte and Bearman2009, Reference Huera-Huarte and Bearman2014; Vandiver, Jaiswal & Jhingran Reference Vandiver, Jaiswal and Jhingran2009; Bourguet, Karniadakis & Triantafyllou Reference Bourguet, Karniadakis and Triantafyllou2011a ; Bourguet et al. Reference Bourguet, Modarres-Sadeghi, Karniadakis and Triantafyllou2011b ; Modarres-Sadeghi et al. Reference Modarres-Sadeghi, Chasparis, Triantafyllou, Tognarelli and Beynet2011; Bourguet, Lucor & Triantafyllou Reference Bourguet, Lucor and Triantafyllou2012; Bourguet, Karniadakis & Triantafyllou Reference Bourguet, Karniadakis and Triantafyllou2013a ,Reference Bourguet, Karniadakis and Triantafyllou b ). VIV naturally appear both in the cross-flow direction and in the in-line direction, i.e. the direction aligned with the current in the normal incidence case. The typical amplitudes of vibration are of the order of one body diameter in the cross-flow direction and of lower magnitude in the in-line direction. The phenomenon of wake–body synchronization associated with VIV is referred to as lock-in and characterized by the coincidence of the frequency of vortex formation and the frequency of structural oscillation. VIV generally start to develop close to the Strouhal frequency, viz. the vortex shedding frequency downstream of a fixed rigid body. Under lock-in, the vortex shedding frequency can substantially deviate from the Strouhal frequency and the vibration frequency can depart from the structure natural frequency. For a long flexible body, VIV may involve several structural frequencies and wavelengths in each direction.
VIV of rigid and flexible cylinders also develop when the structure is inclined in the current (King Reference King1977; Lucor & Karniadakis Reference Lucor and Karniadakis2003; Franzini et al.
Reference Franzini, Gonçalves, Meneghini and Fujarra2013; Jain & Modarres-Sadeghi Reference Jain and Modarres-Sadeghi2013; Bourguet, Karniadakis & Triantafyllou Reference Bourguet, Karniadakis and Triantafyllou2015; Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015). The angle of inclination (
![]() $\unicode[STIX]{x1D6FC}$
) is defined as the angle between the oncoming flow direction and the plane perpendicular to the cylinder axis in quiescent fluid, i.e.
$\unicode[STIX]{x1D6FC}$
) is defined as the angle between the oncoming flow direction and the plane perpendicular to the cylinder axis in quiescent fluid, i.e.
![]() $\unicode[STIX]{x1D6FC}=0^{\circ }$
corresponds to the normal incidence configuration. The influence of body inclination on the system behaviour was quantified in the above mentioned studies, especially by assessing the validity of the independence principle (IP). The IP, which was also thoroughly analysed in the case of inclined rigid cylinders, either fixed or forced to oscillate (Van Atta Reference Van Atta1968; Ramberg Reference Ramberg1983; Thakur, Liu & Marshall Reference Thakur, Liu and Marshall2004; Zhao, Cheng & Zhou Reference Zhao, Cheng and Zhou2009; Willden & Guerbi Reference Willden and Guerbi2010), assumes that the flow dynamics is determined by the component of the oncoming flow perpendicular to the cylinder and that the component aligned with the cylinder axis, the axial component, has a negligible impact. As a result, the IP states that the system behaviours in the inclined and normal configurations should match once the physical quantities (e.g. fluid forces, vortex shedding and body oscillation frequencies) are normalized by the velocity magnitude of the inflow normal component. The IP is usually valid for
$\unicode[STIX]{x1D6FC}=0^{\circ }$
corresponds to the normal incidence configuration. The influence of body inclination on the system behaviour was quantified in the above mentioned studies, especially by assessing the validity of the independence principle (IP). The IP, which was also thoroughly analysed in the case of inclined rigid cylinders, either fixed or forced to oscillate (Van Atta Reference Van Atta1968; Ramberg Reference Ramberg1983; Thakur, Liu & Marshall Reference Thakur, Liu and Marshall2004; Zhao, Cheng & Zhou Reference Zhao, Cheng and Zhou2009; Willden & Guerbi Reference Willden and Guerbi2010), assumes that the flow dynamics is determined by the component of the oncoming flow perpendicular to the cylinder and that the component aligned with the cylinder axis, the axial component, has a negligible impact. As a result, the IP states that the system behaviours in the inclined and normal configurations should match once the physical quantities (e.g. fluid forces, vortex shedding and body oscillation frequencies) are normalized by the velocity magnitude of the inflow normal component. The IP is usually valid for
![]() $\unicode[STIX]{x1D6FC}<40^{\circ }$
for both fixed and oscillating cylinders and it was found to provide an accurate prediction of the structural responses and fluid forces for an inclined flexible cylinder subjected to VIV up to
$\unicode[STIX]{x1D6FC}<40^{\circ }$
for both fixed and oscillating cylinders and it was found to provide an accurate prediction of the structural responses and fluid forces for an inclined flexible cylinder subjected to VIV up to
![]() $\unicode[STIX]{x1D6FC}=60^{\circ }$
(Bourguet et al.
Reference Bourguet, Karniadakis and Triantafyllou2015). At larger inclination angles, the IP generally fails.
$\unicode[STIX]{x1D6FC}=60^{\circ }$
(Bourguet et al.
Reference Bourguet, Karniadakis and Triantafyllou2015). At larger inclination angles, the IP generally fails.

Figure 1. Instantaneous isosurfaces of the non-dimensional spanwise vorticity (
![]() $\unicode[STIX]{x1D714}_{z}=\pm 0.4$
), for (a) a large value of the tension (
$\unicode[STIX]{x1D714}_{z}=\pm 0.4$
), for (a) a large value of the tension (
![]() $T=4975$
,
$T=4975$
,
![]() $U^{\star }=3.47$
) for which no vibration develops and (b) a lower value of the tension (
$U^{\star }=3.47$
) for which no vibration develops and (b) a lower value of the tension (
![]() $T=1791$
,
$T=1791$
,
![]() $U^{\star }=5.79$
) leading to large-amplitude VIV. Arrows represent the oncoming flow. Part of the computational domain is shown.
$U^{\star }=5.79$
) leading to large-amplitude VIV. Arrows represent the oncoming flow. Part of the computational domain is shown.
Some aspects of the flow–structure system behaviour in the case of slender deformable bodies placed at large inclination angles have been described in a previous work concerning a flexible cylinder at
![]() $\unicode[STIX]{x1D6FC}=80^{\circ }$
(Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015). VIV of amplitudes comparable to those observed at normal incidence were reported and it was shown that the occurrence of the lock-in condition is accompanied by a profound reorganization of the wake. This reorganization is illustrated in figure 1 which represents instantaneous flow visualizations downstream of a flexible cylinder at
$\unicode[STIX]{x1D6FC}=80^{\circ }$
(Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015). VIV of amplitudes comparable to those observed at normal incidence were reported and it was shown that the occurrence of the lock-in condition is accompanied by a profound reorganization of the wake. This reorganization is illustrated in figure 1 which represents instantaneous flow visualizations downstream of a flexible cylinder at
![]() $\unicode[STIX]{x1D6FC}=80^{\circ }$
and a Reynolds number (
$\unicode[STIX]{x1D6FC}=80^{\circ }$
and a Reynolds number (
![]() $Re$
) equal to 500, based on the oncoming flow velocity magnitude and cylinder diameter. In figure 1(a) a large tension is applied to the cylinder and no vibration develops while in figure 1(b) a lower value of the tension is considered and the cylinder exhibits VIV with peak amplitudes of approximately
$Re$
) equal to 500, based on the oncoming flow velocity magnitude and cylinder diameter. In figure 1(a) a large tension is applied to the cylinder and no vibration develops while in figure 1(b) a lower value of the tension is considered and the cylinder exhibits VIV with peak amplitudes of approximately
![]() $0.7$
body diameters and an excited structural wavelength equal to twice the cylinder length (i.e. first structural mode) in the cross-flow direction. In the absence of vibration, the spanwise vortex rows forming downstream of the cylinder are not parallel to its axis. Such oblique vortex shedding, also observed for fixed rigid cylinders (Ramberg Reference Ramberg1983; Thakur et al.
Reference Thakur, Liu and Marshall2004; Willden & Guerbi Reference Willden and Guerbi2010), is not captured by the IP. It can be noted that the obliquely shed vortices are not perpendicular to the oncoming flow and the shedding angle remains lower than the inclination angle, as also reported in previous works (e.g. Lucor & Karniadakis Reference Lucor and Karniadakis2003). In contrast, the vortex rows forming in the wake of the vibrating cylinder under the lock-in condition are parallel to its axis, in spite of the large inclination angle (figure 1
b); the vortex shedding frequency is reduced by a factor larger than
$0.7$
body diameters and an excited structural wavelength equal to twice the cylinder length (i.e. first structural mode) in the cross-flow direction. In the absence of vibration, the spanwise vortex rows forming downstream of the cylinder are not parallel to its axis. Such oblique vortex shedding, also observed for fixed rigid cylinders (Ramberg Reference Ramberg1983; Thakur et al.
Reference Thakur, Liu and Marshall2004; Willden & Guerbi Reference Willden and Guerbi2010), is not captured by the IP. It can be noted that the obliquely shed vortices are not perpendicular to the oncoming flow and the shedding angle remains lower than the inclination angle, as also reported in previous works (e.g. Lucor & Karniadakis Reference Lucor and Karniadakis2003). In contrast, the vortex rows forming in the wake of the vibrating cylinder under the lock-in condition are parallel to its axis, in spite of the large inclination angle (figure 1
b); the vortex shedding frequency is reduced by a factor larger than
![]() $3.5$
compared to the stationary cylinder case. Enhancement of parallel shedding when the body oscillates had previously been noted for rigid cylinders (Lucor & Karniadakis Reference Lucor and Karniadakis2003; Jain & Modarres-Sadeghi Reference Jain and Modarres-Sadeghi2013). Parallel shedding does not ensure validity of the IP. For example in the present case the IP leads to an erroneous prediction of fluid force distributions along the span (Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015). When the tension is further reduced, VIV persist and may involve lower structural wavelengths.
$3.5$
compared to the stationary cylinder case. Enhancement of parallel shedding when the body oscillates had previously been noted for rigid cylinders (Lucor & Karniadakis Reference Lucor and Karniadakis2003; Jain & Modarres-Sadeghi Reference Jain and Modarres-Sadeghi2013). Parallel shedding does not ensure validity of the IP. For example in the present case the IP leads to an erroneous prediction of fluid force distributions along the span (Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015). When the tension is further reduced, VIV persist and may involve lower structural wavelengths.
In the above mentioned study, focus was placed on the fully developed, large-amplitude VIV of the inclined flexible cylinder. The onset of the free vibration regime remains to be investigated. More precisely, the intermediate states of the flow–structure system leading from the configuration depicted in figure 1(a) (no vibration) to the configuration illustrated in figure 1(b) (large-amplitude VIV) are still unexplored and the transition scenario, including the reorientation of the vortex rows and the modification of the flow frequency content, needs to be clarified. In a previous work concerning a rigid cylinder inclined in flow, Willden & Guerbi (Reference Willden and Guerbi2010) showed that when the body, placed at
![]() $\unicode[STIX]{x1D6FC}=80^{\circ }$
, is forced to oscillate transversely at a moderate amplitude (
$\unicode[STIX]{x1D6FC}=80^{\circ }$
, is forced to oscillate transversely at a moderate amplitude (
![]() $0.3$
diameters), the wake exhibits a mixed pattern composed of a combination of obliquely shed vortices and perpendicular braid-like vortical structures; this wake pattern was found to be associated with a slight positive energy transfer from the flow to the moving cylinder. The question arises whether flow-induced responses of the flexible cylinder start to develop under such mixed wake patterns. The connection between the spatio-temporal properties of the mixed wake patterns and body oscillations is another aspect to elucidate.
$0.3$
diameters), the wake exhibits a mixed pattern composed of a combination of obliquely shed vortices and perpendicular braid-like vortical structures; this wake pattern was found to be associated with a slight positive energy transfer from the flow to the moving cylinder. The question arises whether flow-induced responses of the flexible cylinder start to develop under such mixed wake patterns. The connection between the spatio-temporal properties of the mixed wake patterns and body oscillations is another aspect to elucidate.
These elements are addressed in the present work which aims at clarifying the onset of the responses of the flexible cylinder at large inclination angle and the concomitant alteration of fluid forcing, at shedding light on the mechanisms of flow reorganization, with the emergence of wake–body synchronization, and at quantifying the deviation from the IP in this context. On the basis of direct numerical simulation results, a combined analysis of the coupled flow–structure system behaviour is reported for a tension-dominated flexible cylinder at
![]() $\unicode[STIX]{x1D6FC}=80^{\circ }$
, over a range of tensions leading from no vibration to large-amplitude VIV. The structural parameters and the Reynolds number, equal to
$\unicode[STIX]{x1D6FC}=80^{\circ }$
, over a range of tensions leading from no vibration to large-amplitude VIV. The structural parameters and the Reynolds number, equal to
![]() $500$
, are selected in reference to the previously mentioned work concerning the fully developed VIV regime.
$500$
, are selected in reference to the previously mentioned work concerning the fully developed VIV regime.
The paper is organized as follows. The physical model and the numerical method are presented in § 2. The structural vibrations are described in § 3. The flow patterns downstream of the flexible cylinder and their link with the cylinder responses are investigated in § 4. The fluid forces are examined in § 5. The main findings of this work are summarized in § 6.
2 Formulation and numerical method
The flow–structure system is illustrated in figure 1. It is similar to that considered in a previous work concerning the VIV of a flexible cylinder at large inclination angle (Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015) except that, in the present study, higher values of the tension are selected.
The uniform oncoming flow of velocity magnitude
![]() $U$
is parallel to the (
$U$
is parallel to the (
![]() $x,z$
) plane. The cylinder has a circular cross-section and a length (
$x,z$
) plane. The cylinder has a circular cross-section and a length (
![]() $L$
) to diameter (
$L$
) to diameter (
![]() $D$
) aspect ratio
$D$
) aspect ratio
![]() $L/D=50$
. It is pinned at both ends, aligned with the
$L/D=50$
. It is pinned at both ends, aligned with the
![]() $z$
axis in the absence of deformation (fluid at rest) and free to oscillate in the in-line (
$z$
axis in the absence of deformation (fluid at rest) and free to oscillate in the in-line (
![]() $x$
axis) and cross-flow (
$x$
axis) and cross-flow (
![]() $y$
axis) directions. The cylinder inclination angle
$y$
axis) directions. The cylinder inclination angle
![]() $\unicode[STIX]{x1D6FC}$
, i.e. angle between the inflow velocity and the
$\unicode[STIX]{x1D6FC}$
, i.e. angle between the inflow velocity and the
![]() $x$
axis, is set to
$x$
axis, is set to
![]() $80^{\circ }$
. The axial component of the oncoming flow designates the component parallel to the
$80^{\circ }$
. The axial component of the oncoming flow designates the component parallel to the
![]() $z$
axis and the normal component refers to the component aligned with the
$z$
axis and the normal component refers to the component aligned with the
![]() $x$
axis. The velocity magnitude of the inflow normal component is
$x$
axis. The velocity magnitude of the inflow normal component is
![]() $U_{n}=U\cos (\unicode[STIX]{x1D6FC})$
. The Reynolds number based on
$U_{n}=U\cos (\unicode[STIX]{x1D6FC})$
. The Reynolds number based on
![]() $U$
and
$U$
and
![]() $D$
,
$D$
,
![]() $Re=\unicode[STIX]{x1D70C}_{f}UD/\unicode[STIX]{x1D707}$
, where
$Re=\unicode[STIX]{x1D70C}_{f}UD/\unicode[STIX]{x1D707}$
, where
![]() $\unicode[STIX]{x1D70C}_{f}$
and
$\unicode[STIX]{x1D70C}_{f}$
and
![]() $\unicode[STIX]{x1D707}$
denote the fluid density and viscosity, is set to 500. The Reynolds number associated with
$\unicode[STIX]{x1D707}$
denote the fluid density and viscosity, is set to 500. The Reynolds number associated with
![]() $U_{n}$
is
$U_{n}$
is
![]() $Re_{n}=Re\cos (\unicode[STIX]{x1D6FC})=86.8$
.
$Re_{n}=Re\cos (\unicode[STIX]{x1D6FC})=86.8$
.
The physical variables are non-dimensionalized by
![]() $\unicode[STIX]{x1D70C}_{f}$
,
$\unicode[STIX]{x1D70C}_{f}$
,
![]() $D$
and
$D$
and
![]() $U_{n}$
;
$U_{n}$
;
![]() $U_{n}$
is preferred to
$U_{n}$
is preferred to
![]() $U$
as reference velocity magnitude for more clarity in the comparison with the normal incidence case and assessment of the IP validity. The structure/fluid mass ratio is defined as
$U$
as reference velocity magnitude for more clarity in the comparison with the normal incidence case and assessment of the IP validity. The structure/fluid mass ratio is defined as
![]() $m=\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}D^{2}$
where
$m=\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}D^{2}$
where
![]() $\unicode[STIX]{x1D70C}_{c}$
is the body mass per unit length. The structural tension and damping are designated by
$\unicode[STIX]{x1D70C}_{c}$
is the body mass per unit length. The structural tension and damping are designated by
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D702}$
. The non-dimensional tension is defined as
$\unicode[STIX]{x1D702}$
. The non-dimensional tension is defined as
![]() $T=\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70C}_{f}D^{2}U_{n}^{2}$
and the non-dimensional damping as
$T=\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70C}_{f}D^{2}U_{n}^{2}$
and the non-dimensional damping as
![]() $K=\unicode[STIX]{x1D702}/\unicode[STIX]{x1D70C}_{f}DU_{n}$
. The displacements of the cylinder in the in-line and cross-flow directions, non-dimensionalized by
$K=\unicode[STIX]{x1D702}/\unicode[STIX]{x1D70C}_{f}DU_{n}$
. The displacements of the cylinder in the in-line and cross-flow directions, non-dimensionalized by
![]() $D$
, are denoted by
$D$
, are denoted by
![]() $\unicode[STIX]{x1D701}_{x}$
and
$\unicode[STIX]{x1D701}_{x}$
and
![]() $\unicode[STIX]{x1D701}_{y}$
. The in-line and cross-flow sectional force coefficients are defined as
$\unicode[STIX]{x1D701}_{y}$
. The in-line and cross-flow sectional force coefficients are defined as
![]() $C_{x}=2F_{x}/\unicode[STIX]{x1D70C}_{f}DU_{n}^{2}$
and
$C_{x}=2F_{x}/\unicode[STIX]{x1D70C}_{f}DU_{n}^{2}$
and
![]() $C_{y}=2F_{y}/\unicode[STIX]{x1D70C}_{f}DU_{n}^{2}$
, where
$C_{y}=2F_{y}/\unicode[STIX]{x1D70C}_{f}DU_{n}^{2}$
, where
![]() $F_{x}$
and
$F_{x}$
and
![]() $F_{y}$
are the dimensional, in-line and cross-flow sectional fluid forces. The body dynamics is governed by forced vibrating string equations which can be expressed as follows, in non-dimensional formulation:
$F_{y}$
are the dimensional, in-line and cross-flow sectional fluid forces. The body dynamics is governed by forced vibrating string equations which can be expressed as follows, in non-dimensional formulation:
where
![]() $^{\cdot }$
and
$^{\cdot }$
and
![]() $^{\prime }$
denote the time and space derivatives.
$^{\prime }$
denote the time and space derivatives.
The mass ratio and structural damping are set to the same values as in the previously mentioned work,
![]() $m=6$
and
$m=6$
and
![]() $K=0$
. Different values of the tension are considered;
$K=0$
. Different values of the tension are considered;
![]() $T$
ranges from
$T$
ranges from
![]() $240\,004$
to
$240\,004$
to
![]() $1791$
, versus
$1791$
, versus
![]() $T\leqslant 1791$
in the previous study. As shown in the following, this range of
$T\leqslant 1791$
in the previous study. As shown in the following, this range of
![]() $T$
allows to capture the emergence of the VIV phenomenon.
$T$
allows to capture the emergence of the VIV phenomenon.
The non-dimensional natural frequency associated with the non-dimensional structural wavelength
![]() $2L/nD$
, i.e. corresponding to the
$2L/nD$
, i.e. corresponding to the
![]() $n$
th sine Fourier mode defined as
$n$
th sine Fourier mode defined as
![]() $\sin (\unicode[STIX]{x03C0}nzD/L)$
, is obtained via the dispersion relation
$\sin (\unicode[STIX]{x03C0}nzD/L)$
, is obtained via the dispersion relation
![]() $f_{nat}(2L/nD)=nD/2L\sqrt{T/m}$
, in vacuum. By analogy with the case of an elastically mounted rigid cylinder, a reduced velocity is defined as the inverse of the non-dimensional, fundamental natural frequency (
$f_{nat}(2L/nD)=nD/2L\sqrt{T/m}$
, in vacuum. By analogy with the case of an elastically mounted rigid cylinder, a reduced velocity is defined as the inverse of the non-dimensional, fundamental natural frequency (
![]() $n=1$
):
$n=1$
):
The selected values of
![]() $T$
correspond to reduced velocities
$T$
correspond to reduced velocities
![]() $U^{\star }$
ranging from 0.5 to 5.79, versus
$U^{\star }$
ranging from 0.5 to 5.79, versus
![]() $U^{\star }\geqslant 5.79$
in the previous study.
$U^{\star }\geqslant 5.79$
in the previous study.
A normal incidence case (
![]() $\unicode[STIX]{x1D6FC}=0^{\circ }$
,
$\unicode[STIX]{x1D6FC}=0^{\circ }$
,
![]() $U=U_{n}$
,
$U=U_{n}$
,
![]() $Re=Re_{n}$
) is also considered. In this case, the Reynolds number may be either kept the same as the Reynolds number based on
$Re=Re_{n}$
) is also considered. In this case, the Reynolds number may be either kept the same as the Reynolds number based on
![]() $U$
in the inclined body case, i.e.
$U$
in the inclined body case, i.e.
![]() $Re=500$
, or scaled to match the Reynolds number based on
$Re=500$
, or scaled to match the Reynolds number based on
![]() $U_{n}$
in the inclined body case, i.e.
$U_{n}$
in the inclined body case, i.e.
![]() $Re=86.8$
; both values of the Reynolds number are examined here.
$Re=86.8$
; both values of the Reynolds number are examined here.
The flow past the cylinder is predicted using direct numerical simulation of the three-dimensional incompressible Navier–Stokes equations. The coupled flow–structure system is solved by the parallelized code Nektar which is based on the spectral/
![]() $hp$
element method (Karniadakis & Sherwin Reference Karniadakis and Sherwin1999). The version of the code employs a Jacobi–Galerkin formulation in the (
$hp$
element method (Karniadakis & Sherwin Reference Karniadakis and Sherwin1999). The version of the code employs a Jacobi–Galerkin formulation in the (
![]() $x,y$
) plane and a Fourier expansion in the spanwise (
$x,y$
) plane and a Fourier expansion in the spanwise (
![]() $z$
) direction. A boundary-fitted coordinate formulation is used to take into account the body unsteady deformation. Details concerning the numerical method and its validation have been reported in Newman & Karniadakis (Reference Newman and Karniadakis1997) and Evangelinos & Karniadakis (Reference Evangelinos and Karniadakis1999) for similar systems. The computational domain (
$z$
) direction. A boundary-fitted coordinate formulation is used to take into account the body unsteady deformation. Details concerning the numerical method and its validation have been reported in Newman & Karniadakis (Reference Newman and Karniadakis1997) and Evangelinos & Karniadakis (Reference Evangelinos and Karniadakis1999) for similar systems. The computational domain (
![]() $50D$
downstream and
$50D$
downstream and
![]() $20D$
in front, above, and below the cylinder), boundary conditions (no-slip condition on the cylinder surface, flow periodicity on the side boundaries) and discretization (
$20D$
in front, above, and below the cylinder), boundary conditions (no-slip condition on the cylinder surface, flow periodicity on the side boundaries) and discretization (
![]() $2175$
elements with polynomial order
$2175$
elements with polynomial order
![]() $p=7$
in the (
$p=7$
in the (
![]() $x,y$
) plane and
$x,y$
) plane and
![]() $512$
complex Fourier modes in the
$512$
complex Fourier modes in the
![]() $z$
direction) are the same as in Bourguet et al. (Reference Bourguet, Karniadakis and Triantafyllou2011a
, Reference Bourguet, Karniadakis and Triantafyllou2015), Bourguet & Triantafyllou (Reference Bourguet and Triantafyllou2015). The analysis is based on time series of more than
$z$
direction) are the same as in Bourguet et al. (Reference Bourguet, Karniadakis and Triantafyllou2011a
, Reference Bourguet, Karniadakis and Triantafyllou2015), Bourguet & Triantafyllou (Reference Bourguet and Triantafyllou2015). The analysis is based on time series of more than
![]() $200$
non-dimensional time units (based on
$200$
non-dimensional time units (based on
![]() $U_{n}$
). Convergence of each simulation is established by monitoring the mean and root mean square (r.m.s.) values of the fluid force coefficients and body displacements.
$U_{n}$
). Convergence of each simulation is established by monitoring the mean and root mean square (r.m.s.) values of the fluid force coefficients and body displacements.
3 Structural responses
A description of the body responses at the onset of the free-vibration regime is reported in this section and the validity of the IP is examined.
The inclined flexible cylinder exhibits free oscillations in both directions for
![]() $U^{\star }\geqslant 3.86$
. Selected time series of the in-line and cross-flow displacements, non-dimensionalized by
$U^{\star }\geqslant 3.86$
. Selected time series of the in-line and cross-flow displacements, non-dimensionalized by
![]() $D$
, are plotted along the span in figure 2(a–d), for two values of the reduced velocity: the lowest value at which the cylinder is found to vibrate (
$D$
, are plotted along the span in figure 2(a–d), for two values of the reduced velocity: the lowest value at which the cylinder is found to vibrate (
![]() $U^{\star }=3.86$
, figure 2
a,b) and the largest value studied in the present work (
$U^{\star }=3.86$
, figure 2
a,b) and the largest value studied in the present work (
![]() $U^{\star }=5.79$
, figure 2
c,d); the latter case corresponds to the configuration illustrated in figure 1(b). As for the other physical variables, the non-dimensionalization of the time
$U^{\star }=5.79$
, figure 2
c,d); the latter case corresponds to the configuration illustrated in figure 1(b). As for the other physical variables, the non-dimensionalization of the time
![]() $t$
considered in these plots is based on
$t$
considered in these plots is based on
![]() $U_{n}$
. The spanwise evolutions of the r.m.s. values of the non-dimensional in-line and cross-flow displacements are plotted in figure 2(e,f). In this figure and in the following, the fluctuation (denoted by
$U_{n}$
. The spanwise evolutions of the r.m.s. values of the non-dimensional in-line and cross-flow displacements are plotted in figure 2(e,f). In this figure and in the following, the fluctuation (denoted by
![]() $\tilde{\phantom{a}}$
) of the in-line response about the time-averaged position of the body is considered.
$\tilde{\phantom{a}}$
) of the in-line response about the time-averaged position of the body is considered.

Figure 2. (a–d) Selected time series of the structural responses along the span, for (a,b)
![]() $U^{\star }=3.86$
and (c,d)
$U^{\star }=3.86$
and (c,d)
![]() $U^{\star }=5.79$
: (a,c) in-line displacement fluctuation, (b,d) cross-flow displacement. (e) The r.m.s. value of the in-line displacement fluctuation and (f) the r.m.s. value of the cross-flow displacement, along the span, over a range of reduced velocities. The displacements are non-dimensionalized by the cylinder diameter.
$U^{\star }=5.79$
: (a,c) in-line displacement fluctuation, (b,d) cross-flow displacement. (e) The r.m.s. value of the in-line displacement fluctuation and (f) the r.m.s. value of the cross-flow displacement, along the span, over a range of reduced velocities. The displacements are non-dimensionalized by the cylinder diameter.
The vibration amplitudes continuously increase with the reduced velocity and the values reached in the higher range of
![]() $U^{\star }$
are comparable to those reported in previous studies concerning flexible cylinder VIV at normal incidence (Trim et al.
Reference Trim, Braaten, Lie and Tognarelli2005; Huera-Huarte & Bearman Reference Huera-Huarte and Bearman2009; Bourguet et al.
Reference Bourguet, Karniadakis and Triantafyllou2011a
); as also observed in these studies, the oscillation amplitudes are lower in the in-line direction than in the cross-flow direction.
$U^{\star }$
are comparable to those reported in previous studies concerning flexible cylinder VIV at normal incidence (Trim et al.
Reference Trim, Braaten, Lie and Tognarelli2005; Huera-Huarte & Bearman Reference Huera-Huarte and Bearman2009; Bourguet et al.
Reference Bourguet, Karniadakis and Triantafyllou2011a
); as also observed in these studies, the oscillation amplitudes are lower in the in-line direction than in the cross-flow direction.
In each direction, the structural response may present a slight asymmetry about the midspan point. For example in the in-line direction, the amplitudes reached on the first half (
![]() $z<25$
) and the second half (
$z<25$
) and the second half (
![]() $z>25$
) of the body generally differ (figure 2
e). Such asymmetry arises naturally, even for symmetrical systems (e.g. flexible cylinder at normal incidence in uniform flow; Trim et al. (Reference Trim, Braaten, Lie and Tognarelli2005)). For an inclined flexible cylinder, a source of asymmetry in the system behaviour has been identified in prior works (Bourguet et al.
Reference Bourguet, Karniadakis and Triantafyllou2015; Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015): the time-averaged in-line curvature of the cylinder induces a spanwise shear of the inflow velocity profiles locally normal and parallel to the body. In the present case, the small time-averaged in-line displacement, which remains lower than 0.4 % of the body length, results in a limited but non-negligible shear of the local inflow profiles, which may contribute to the slight asymmetry of the responses about the midspan point.
$z>25$
) of the body generally differ (figure 2
e). Such asymmetry arises naturally, even for symmetrical systems (e.g. flexible cylinder at normal incidence in uniform flow; Trim et al. (Reference Trim, Braaten, Lie and Tognarelli2005)). For an inclined flexible cylinder, a source of asymmetry in the system behaviour has been identified in prior works (Bourguet et al.
Reference Bourguet, Karniadakis and Triantafyllou2015; Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015): the time-averaged in-line curvature of the cylinder induces a spanwise shear of the inflow velocity profiles locally normal and parallel to the body. In the present case, the small time-averaged in-line displacement, which remains lower than 0.4 % of the body length, results in a limited but non-negligible shear of the local inflow profiles, which may contribute to the slight asymmetry of the responses about the midspan point.
The inclined cylinder oscillations are regular and dominated by a single frequency and a single structural wavelength in each direction. A ratio of
![]() $2$
can be established between the in-line and cross-flow vibration frequencies, as usually observed at normal incidence. Over the range of
$2$
can be established between the in-line and cross-flow vibration frequencies, as usually observed at normal incidence. Over the range of
![]() $U^{\star }$
studied, the dominant wavelengths are
$U^{\star }$
studied, the dominant wavelengths are
![]() $2L/D$
in the cross-flow direction and
$2L/D$
in the cross-flow direction and
![]() $L/D$
in the in-line direction, which correspond to the first and second sine Fourier modes of the structure, respectively; the linear dispersion relation and the frequency ratio of
$L/D$
in the in-line direction, which correspond to the first and second sine Fourier modes of the structure, respectively; the linear dispersion relation and the frequency ratio of
![]() $2$
suggest such ratio between the excited wavelengths.
$2$
suggest such ratio between the excited wavelengths.

Figure 3. (a) Maximum in-line displacement fluctuation, (b) maximum cross-flow displacement and (c) normalized cross-flow vibration frequency, as functions of the reduced velocity. The displacements are non-dimensionalized by the cylinder diameter. Some normal incidence case results are reported for comparison purposes (white and black symbols). In (c), the normalized Strouhal frequencies are indicated by a dashed-dotted line in the inclined body case and by dashed lines for both values of
![]() $Re$
in the normal incidence case.
$Re$
in the normal incidence case.
As shown in figure 2, the inclined body starts to oscillate for approximately
![]() $U^{\star }=4$
. For a better visualization of the emergence of the free-vibration regime, the maximum amplitudes of the non-dimensional in-line and cross-flow responses and the normalized cross-flow response frequency are plotted as functions of the reduced velocity in figure 3. The normalized response frequencies are defined as
$U^{\star }=4$
. For a better visualization of the emergence of the free-vibration regime, the maximum amplitudes of the non-dimensional in-line and cross-flow responses and the normalized cross-flow response frequency are plotted as functions of the reduced velocity in figure 3. The normalized response frequencies are defined as
![]() $f_{\{x,y\}}^{\star }=f_{\{x,y\}}/f_{nat}(2L/D)=f_{\{x,y\}}U^{\star }$
where
$f_{\{x,y\}}^{\star }=f_{\{x,y\}}/f_{nat}(2L/D)=f_{\{x,y\}}U^{\star }$
where
![]() $f_{\{x,y\}}$
are the non-dimensional vibration frequencies; it is recalled that
$f_{\{x,y\}}$
are the non-dimensional vibration frequencies; it is recalled that
![]() $f_{nat}(2L/D)$
designates the non-dimensional, fundamental natural frequency. Because of the ratio of
$f_{nat}(2L/D)$
designates the non-dimensional, fundamental natural frequency. Because of the ratio of
![]() $2$
noted between the in-line and cross-flow response frequencies, only the cross-flow frequency is reported (
$2$
noted between the in-line and cross-flow response frequencies, only the cross-flow frequency is reported (
![]() $f_{x}^{\star }=2f_{y}^{\star }$
). In order to quantify the impact of the inflow axial component and assess the IP validity, the results obtained in the normal incidence case, for
$f_{x}^{\star }=2f_{y}^{\star }$
). In order to quantify the impact of the inflow axial component and assess the IP validity, the results obtained in the normal incidence case, for
![]() $U^{\star }\in \{3.86,4.96,5.79\}$
, are also presented in figure 3. As previously mentioned, two values of the Reynolds number are considered at normal incidence:
$U^{\star }\in \{3.86,4.96,5.79\}$
, are also presented in figure 3. As previously mentioned, two values of the Reynolds number are considered at normal incidence:
![]() $Re=500$
and
$Re=500$
and
![]() $Re=86.8$
, which correspond to the values of
$Re=86.8$
, which correspond to the values of
![]() $Re$
and
$Re$
and
![]() $Re_{n}$
in the inclined body case.
$Re_{n}$
in the inclined body case.
Regardless of the Reynolds number value selected in the normal incidence case, the inclined body responses can clearly deviate from those observed at
![]() $\unicode[STIX]{x1D6FC}=0^{\circ }$
. For example, application of the IP would lead to a significant underestimation of the in-line oscillation amplitude. Within the range of
$\unicode[STIX]{x1D6FC}=0^{\circ }$
. For example, application of the IP would lead to a significant underestimation of the in-line oscillation amplitude. Within the range of
![]() $U^{\star }$
investigated, the vibration frequency of the inclined cylinder remains lower than the natural frequency (
$U^{\star }$
investigated, the vibration frequency of the inclined cylinder remains lower than the natural frequency (
![]() $f_{y}^{\star }<0$
); this is also the case for the cylinder placed at normal incidence. It should be mentioned that the response frequency also departs from the natural frequency modified to take into account of the immersion of the body in fluid:
$f_{y}^{\star }<0$
); this is also the case for the cylinder placed at normal incidence. It should be mentioned that the response frequency also departs from the natural frequency modified to take into account of the immersion of the body in fluid:
![]() $f_{nat}^{mod}=\sqrt{m/(m+C_{m}\unicode[STIX]{x03C0}/4)}~f_{nat}\approx 0.94~f_{nat}$
, with the added mass coefficient
$f_{nat}^{mod}=\sqrt{m/(m+C_{m}\unicode[STIX]{x03C0}/4)}~f_{nat}\approx 0.94~f_{nat}$
, with the added mass coefficient
![]() $C_{m}=1$
. Such deviation from the natural frequency is a common phenomenon for cylinders freely vibrating in flow which may be connected to the variability of the effective added mass (e.g. Bourguet et al.
Reference Bourguet, Karniadakis and Triantafyllou2011a
).
$C_{m}=1$
. Such deviation from the natural frequency is a common phenomenon for cylinders freely vibrating in flow which may be connected to the variability of the effective added mass (e.g. Bourguet et al.
Reference Bourguet, Karniadakis and Triantafyllou2011a
).
In figure 3(c), the normalized Strouhal frequencies (
![]() $StU^{\star }$
, with
$StU^{\star }$
, with
![]() $St$
the Strouhal frequency defined as the shedding frequency downstream of a fixed rigid cylinder non-dimensionalized by
$St$
the Strouhal frequency defined as the shedding frequency downstream of a fixed rigid cylinder non-dimensionalized by
![]() $U_{n}$
and
$U_{n}$
and
![]() $D$
) are indicated by a dashed-dotted line in the inclined body case (
$D$
) are indicated by a dashed-dotted line in the inclined body case (
![]() $St=0.593$
) and by dashed lines for both values of
$St=0.593$
) and by dashed lines for both values of
![]() $Re$
in the normal incidence case (
$Re$
in the normal incidence case (
![]() $St=0.208$
at
$St=0.208$
at
![]() $Re~=500$
and
$Re~=500$
and
![]() $St=0.159$
at
$St=0.159$
at
![]() $Re~=86.8$
); the values of
$Re~=86.8$
); the values of
![]() $St$
are issued from a previous study (Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015). As shown in this prior work, the large difference in the Strouhal frequencies between the normal incidence case and the inclined cylinder case coincides with distinct orientations of the spanwise vortex rows which are parallel to the body axis at
$St$
are issued from a previous study (Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015). As shown in this prior work, the large difference in the Strouhal frequencies between the normal incidence case and the inclined cylinder case coincides with distinct orientations of the spanwise vortex rows which are parallel to the body axis at
![]() $\unicode[STIX]{x1D6FC}=0^{\circ }$
and slanted at
$\unicode[STIX]{x1D6FC}=0^{\circ }$
and slanted at
![]() $\unicode[STIX]{x1D6FC}=80^{\circ }$
. At normal incidence, the structural responses emerge spontaneously at a frequency relatively close to the Strouhal frequency, as generally reported for VIV (Williamson & Govardhan Reference Williamson and Govardhan2004). In contrast, the inclined cylinder starts to vibrate at a frequency substantially lower than the shedding frequency observed for a fixed rigid cylinder at
$\unicode[STIX]{x1D6FC}=80^{\circ }$
. At normal incidence, the structural responses emerge spontaneously at a frequency relatively close to the Strouhal frequency, as generally reported for VIV (Williamson & Govardhan Reference Williamson and Govardhan2004). In contrast, the inclined cylinder starts to vibrate at a frequency substantially lower than the shedding frequency observed for a fixed rigid cylinder at
![]() $\unicode[STIX]{x1D6FC}=80^{\circ }$
: at
$\unicode[STIX]{x1D6FC}=80^{\circ }$
: at
![]() $U^{\star }=3.86$
,
$U^{\star }=3.86$
,
![]() $f_{y}=0.230$
while
$f_{y}=0.230$
while
![]() $St=0.593$
. The response frequency of the inclined body at the onset of vibration is actually closer to the values of
$St=0.593$
. The response frequency of the inclined body at the onset of vibration is actually closer to the values of
![]() $St$
at
$St$
at
![]() $\unicode[STIX]{x1D6FC}=0^{\circ }$
.
$\unicode[STIX]{x1D6FC}=0^{\circ }$
.
The proximity between the frequency at which the inclined cylinder starts to oscillate and the Strouhal frequency reported at normal incidence (under parallel shedding) suggests that the vibration onset could be accompanied by the appearance of a parallel component in the wake; this new component would combine with the oblique component naturally occurring (at a higher frequency) in the absence of oscillation. The question of the flow reorganization associated with the development of the structural responses is clarified in the next section.
4 Flow patterns
The transition scenario in the wake of the inclined cylinder at the onset of its free vibrations is investigated in this section. Special attention is paid to the synchronization between the body motion and the flow unsteadiness, and its connection with the alteration of the vortex shedding pattern occurring in the absence of vibration.

Figure 4. Same as figure 1, for (a)
![]() $U^{\star }=3.86$
, (b)
$U^{\star }=3.86$
, (b)
![]() $U^{\star }=4.13$
,(c)
$U^{\star }=4.13$
,(c)
![]() $U^{\star }=4.51$
and (d)
$U^{\star }=4.51$
and (d)
![]() $U^{\star }=4.96$
.
$U^{\star }=4.96$
.
The flow patterns associated with the emergence of the structural responses reported in § 3, are illustrated in figure 4. They represent the intermediate states of the wake between the stationary body case, characterized by an oblique vortex shedding pattern, and the large-amplitude VIV regime accompanied by parallel shedding, as depicted in figure 1. The wake downstream of the stationary flexible cylinder (
![]() $U^{\star }=3.47$
, figure 1
a) is similar to the wake previously observed in the case of a fixed rigid cylinder (Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015). The two configurations only differ by a very small in-line bending of the flexible cylinder (lower than 0.1 % of the length), which has no influence on the flow pattern; in particular the angle of shedding is equal to
$U^{\star }=3.47$
, figure 1
a) is similar to the wake previously observed in the case of a fixed rigid cylinder (Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015). The two configurations only differ by a very small in-line bending of the flexible cylinder (lower than 0.1 % of the length), which has no influence on the flow pattern; in particular the angle of shedding is equal to
![]() $66^{\circ }$
approximately, in both cases. The regular pattern encountered for
$66^{\circ }$
approximately, in both cases. The regular pattern encountered for
![]() $U^{\star }=3.86$
may be described as obliquely shed vortices interconnected by secondary braid-like structures (figure 4
a); it resembles the mixed pattern reported by Willden & Guerbi (Reference Willden and Guerbi2010) for a rigid cylinder subjected to a forced transverse oscillation of moderate amplitude. Even if the patterns occurring for the other values of
$U^{\star }=3.86$
may be described as obliquely shed vortices interconnected by secondary braid-like structures (figure 4
a); it resembles the mixed pattern reported by Willden & Guerbi (Reference Willden and Guerbi2010) for a rigid cylinder subjected to a forced transverse oscillation of moderate amplitude. Even if the patterns occurring for the other values of
![]() $U^{\star }$
in figure 4 appear to be less regular, a brief overview of the instantaneous wake structures seems to corroborate the above hypothesis concerning the combination of oblique and parallel flow components.
$U^{\star }$
in figure 4 appear to be less regular, a brief overview of the instantaneous wake structures seems to corroborate the above hypothesis concerning the combination of oblique and parallel flow components.
The flow reorganization process is analysed in two steps. In § 4.1, focus is first placed on the wake patterns developing for
![]() $U^{\star }=3.86$
, i.e. the lowest value at which the body oscillates; the spatio-temporal properties of the flow are studied through proper orthogonal decomposition (POD). Then, in § 4.2, the investigation is extended to the other values of
$U^{\star }=3.86$
, i.e. the lowest value at which the body oscillates; the spatio-temporal properties of the flow are studied through proper orthogonal decomposition (POD). Then, in § 4.2, the investigation is extended to the other values of
![]() $U^{\star }$
and a global vision of the transition scenario is presented, on the basis of spectral analysis.
$U^{\star }$
and a global vision of the transition scenario is presented, on the basis of spectral analysis.
4.1 POD analysis of the wake for
 $U^{\star }=3.86$
$U^{\star }=3.86$
POD is often employed to capture the dominant features of the flow by a low number of basis functions or modes, which can be used to elaborate reduced-order models (Berkooz, Holmes & Lumley Reference Berkooz, Holmes and Lumley1993; Ma & Karniadakis Reference Ma and Karniadakis2002; Noack et al.
Reference Noack, Afanasiev, Morzynski, Tadmor and Thiele2003). It may be an efficient tool to identify the main elements of wake unsteadiness and connect them to spatial patterns of the flow (e.g. Bourguet, Braza & Dervieux Reference Bourguet, Braza and Dervieux2007). It should be mentioned that the POD basis functions do not directly represent vortices but shed light on the underlying structure of the flow. Here, POD is applied to the non-dimensional spanwise vorticity
![]() $\unicode[STIX]{x1D714}_{z}$
in order to track the appearance of a flow component associated with body oscillation. The case
$\unicode[STIX]{x1D714}_{z}$
in order to track the appearance of a flow component associated with body oscillation. The case
![]() $U^{\star }=3.86$
is considered; it is characterized by low vibration amplitudes,
$U^{\star }=3.86$
is considered; it is characterized by low vibration amplitudes,
![]() $0.15D$
and
$0.15D$
and
![]() $0.002D$
in the cross-flow and in-line directions, respectively. The fluctuating part of
$0.002D$
in the cross-flow and in-line directions, respectively. The fluctuating part of
![]() $\unicode[STIX]{x1D714}_{z}$
can be approximated by the following expansion:
$\unicode[STIX]{x1D714}_{z}$
can be approximated by the following expansion:
where the
![]() $N_{POD}$
spatial basis functions
$N_{POD}$
spatial basis functions
![]() $\unicode[STIX]{x1D6F7}_{i}$
and time coefficients
$\unicode[STIX]{x1D6F7}_{i}$
and time coefficients
![]() $a_{i}$
are determined via the ‘snapshot-POD’ approach (Sirovich Reference Sirovich1987). The two-point time correlation tensor used to compute the POD functions is based on
$a_{i}$
are determined via the ‘snapshot-POD’ approach (Sirovich Reference Sirovich1987). The two-point time correlation tensor used to compute the POD functions is based on
![]() $N_{S}=200$
snapshots of
$N_{S}=200$
snapshots of
![]() $\unicode[STIX]{x1D714}_{z}$
, collected over
$\unicode[STIX]{x1D714}_{z}$
, collected over
![]() $4$
cycles of cross-flow oscillation. The weight of the
$4$
cycles of cross-flow oscillation. The weight of the
![]() $i$
th POD mode in expansion (4.1), also referred to as statistical content, is quantified by the magnitude of the corresponding eigenvalue
$i$
th POD mode in expansion (4.1), also referred to as statistical content, is quantified by the magnitude of the corresponding eigenvalue
![]() $\unicode[STIX]{x1D709}_{i}$
of the correlation tensor, and
$\unicode[STIX]{x1D709}_{i}$
of the correlation tensor, and
![]() $\overline{a_{i}a_{j}}=\unicode[STIX]{x1D709}_{i}\unicode[STIX]{x1D6FF}_{ij}$
, where
$\overline{a_{i}a_{j}}=\unicode[STIX]{x1D709}_{i}\unicode[STIX]{x1D6FF}_{ij}$
, where
![]() $\overline{\phantom{a}}$
designates the time-averaging operator and
$\overline{\phantom{a}}$
designates the time-averaging operator and
![]() $\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker symbol. In (4.1), the POD modes are ordered by decreasing weight. The relative weight of the first
$\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker symbol. In (4.1), the POD modes are ordered by decreasing weight. The relative weight of the first
![]() $10$
POD modes is plotted in figure 5(a). The first
$10$
POD modes is plotted in figure 5(a). The first
![]() $4$
modes, which capture 35 % of flow unsteadiness, are pairwise coupled and highlight two different components of the flow. Within each pair (modes
$4$
modes, which capture 35 % of flow unsteadiness, are pairwise coupled and highlight two different components of the flow. Within each pair (modes
![]() $1$
and
$1$
and
![]() $2$
; modes
$2$
; modes
![]() $3$
and
$3$
and
![]() $4$
), the modes exhibit comparable features. The first and third modes are selected to illustrate the distinct properties of the first two pairs. The times series of the coefficients
$4$
), the modes exhibit comparable features. The first and third modes are selected to illustrate the distinct properties of the first two pairs. The times series of the coefficients
![]() $a_{1}$
and
$a_{1}$
and
![]() $a_{3}$
are plotted in figure 5(b); for comparison purposes, the evolution of the body non-dimensional cross-flow displacement at midspan is also reported. The associated basis functions,
$a_{3}$
are plotted in figure 5(b); for comparison purposes, the evolution of the body non-dimensional cross-flow displacement at midspan is also reported. The associated basis functions,
![]() $\unicode[STIX]{x1D6F7}_{1}$
and
$\unicode[STIX]{x1D6F7}_{1}$
and
![]() $\unicode[STIX]{x1D6F7}_{3}$
, are represented in figure 5(c,d).
$\unicode[STIX]{x1D6F7}_{3}$
, are represented in figure 5(c,d).

Figure 5. POD analysis of the wake based on the non-dimensional spanwise vorticity, for
![]() $U^{\star }=3.86$
: (a) relative weight of the first
$U^{\star }=3.86$
: (a) relative weight of the first
![]() $10$
POD modes; (b) time series of the first and third POD coefficients (left axis) and non-dimensional cross-flow displacement of the cylinder at midspan (right axis); (c) and (d) spatial patterns of the first and third POD modes (isosurfaces associated with arbitrary positive and negative values). In (c,d), arrows represent the oncoming flow; part of the computational domain is shown.
$10$
POD modes; (b) time series of the first and third POD coefficients (left axis) and non-dimensional cross-flow displacement of the cylinder at midspan (right axis); (c) and (d) spatial patterns of the first and third POD modes (isosurfaces associated with arbitrary positive and negative values). In (c,d), arrows represent the oncoming flow; part of the computational domain is shown.
The first mode oscillates at a much higher frequency than the body; its frequency is approximately
![]() $2.6$
times larger than the cross-flow vibration frequency and appears to be close to the vortex shedding frequency identified for a fixed rigid cylinder (
$2.6$
times larger than the cross-flow vibration frequency and appears to be close to the vortex shedding frequency identified for a fixed rigid cylinder (
![]() $St=0.593$
). This mode is associated with a slanted spatial pattern which resembles the oblique vortex shedding pattern, previously described for a fixed rigid cylinder at this inclination angle (Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015) and visualized in figure 1(a) for a stationary flexible cylinder. The angle of the straight slanted structures observed in the wake (
$St=0.593$
). This mode is associated with a slanted spatial pattern which resembles the oblique vortex shedding pattern, previously described for a fixed rigid cylinder at this inclination angle (Bourguet & Triantafyllou Reference Bourguet and Triantafyllou2015) and visualized in figure 1(a) for a stationary flexible cylinder. The angle of the straight slanted structures observed in the wake (
![]() $66^{\circ }$
approximately) is similar to the shedding angle in the stationary body case; as previously noted, this angle is lower than the inclination angle and the slanted structures are not perpendicular to the oncoming flow. In contrast, the third mode is found to oscillate at the vibration frequency; it thus occurs at a frequency that is incommensurable with the first mode frequency. The corresponding spatial function is composed of straight structures that are parallel to the cylinder axis, with no significant trace of the large inclination angle.
$66^{\circ }$
approximately) is similar to the shedding angle in the stationary body case; as previously noted, this angle is lower than the inclination angle and the slanted structures are not perpendicular to the oncoming flow. In contrast, the third mode is found to oscillate at the vibration frequency; it thus occurs at a frequency that is incommensurable with the first mode frequency. The corresponding spatial function is composed of straight structures that are parallel to the cylinder axis, with no significant trace of the large inclination angle.
Therefore, the first POD modes show that two principal components combine in the wake of the vibrating cylinder: (i) a high-frequency oblique component, represented by the first pair of modes, that relates to the slanted wake pattern observed in the absence of vibration, and (ii) a low-frequency parallel component, represented by the second pair of modes, and associated with the emergence of a synchronization mechanism between the body motion and the flow, i.e. the lock-in condition.
It is recalled that the first
![]() $4$
modes only capture a part of the flow unsteadiness and that higher modes are required to obtain a full representation of the wake. However, the footprints of the two incommensurable components described above are clearly visible in the instantaneous flow plotted in figure 4(a): the global orientation of the vortex rows can be connected to the oblique pattern of
$4$
modes only capture a part of the flow unsteadiness and that higher modes are required to obtain a full representation of the wake. However, the footprints of the two incommensurable components described above are clearly visible in the instantaneous flow plotted in figure 4(a): the global orientation of the vortex rows can be connected to the oblique pattern of
![]() $\unicode[STIX]{x1D6F7}_{1}$
while the in-line spacing between the secondary braid-like vortices (
$\unicode[STIX]{x1D6F7}_{1}$
while the in-line spacing between the secondary braid-like vortices (
![]() $4.5D$
approximately) matches the distance between the adjacent structures of
$4.5D$
approximately) matches the distance between the adjacent structures of
![]() $\unicode[STIX]{x1D6F7}_{3}$
. In the present case where the cylinder exhibits vibrations of low amplitudes, the wake is still dominated by the high-frequency oblique component, as shown by the much larger contribution of the first pair of modes (figure 5
a). The evolution of the underlying components of the flow, when the vibration amplitudes increase, is examined in the following.
$\unicode[STIX]{x1D6F7}_{3}$
. In the present case where the cylinder exhibits vibrations of low amplitudes, the wake is still dominated by the high-frequency oblique component, as shown by the much larger contribution of the first pair of modes (figure 5
a). The evolution of the underlying components of the flow, when the vibration amplitudes increase, is examined in the following.
4.2 Scenario of flow reorganization
The analysis of wake unsteadiness is extended to the other values of
![]() $U^{\star }$
in order to explore the alteration of the flow associated with the development of the free structural responses. The investigation relies on a spectral analysis, based on Fourier transform, of the non-dimensional cross-flow component of flow velocity (
$U^{\star }$
in order to explore the alteration of the flow associated with the development of the free structural responses. The investigation relies on a spectral analysis, based on Fourier transform, of the non-dimensional cross-flow component of flow velocity (
![]() $v$
), along a line parallel to the
$v$
), along a line parallel to the
![]() $z$
axis and located
$z$
axis and located
![]() $10D$
downstream of the cylinder. In the context of a parametrical study where several values of
$10D$
downstream of the cylinder. In the context of a parametrical study where several values of
![]() $U^{\star }$
are considered, this approach is preferred to the POD technique employed in § 4.1; it directly provides a description of the wake frequency content for each case and allows a more systematic, frequency-based, identification of the flow components. Instead, POD requires an individual monitoring of each mode and does not necessarily lead to a clear distinction between flow components, especially for wake patterns that are less regular than those studied in § 4.1, e.g. the time evolution of a POD mode may involve several frequencies. For strictly periodic flows, direct connections exist between POD and Fourier expansions (Berkooz et al.
Reference Berkooz, Holmes and Lumley1993).
$U^{\star }$
are considered, this approach is preferred to the POD technique employed in § 4.1; it directly provides a description of the wake frequency content for each case and allows a more systematic, frequency-based, identification of the flow components. Instead, POD requires an individual monitoring of each mode and does not necessarily lead to a clear distinction between flow components, especially for wake patterns that are less regular than those studied in § 4.1, e.g. the time evolution of a POD mode may involve several frequencies. For strictly periodic flows, direct connections exist between POD and Fourier expansions (Berkooz et al.
Reference Berkooz, Holmes and Lumley1993).

Figure 6. Selected time series of the non-dimensional cross-flow component of flow velocity along the span,
![]() $10D$
downstream of the cylinder, for (a)
$10D$
downstream of the cylinder, for (a)
![]() $U^{\star }=3.47$
, (b)
$U^{\star }=3.47$
, (b)
![]() $U^{\star }=3.86$
, (c)
$U^{\star }=3.86$
, (c)
![]() $U^{\star }=4.13$
, (d)
$U^{\star }=4.13$
, (d)
![]() $U^{\star }=4.51$
, (e)
$U^{\star }=4.51$
, (e)
![]() $U^{\star }=4.96$
and (f)
$U^{\star }=4.96$
and (f)
![]() $U^{\star }=5.79$
.
$U^{\star }=5.79$
.
Selected time series of
![]() $v$
are plotted in figure 6, for six values of the reduced velocity ranging from
$v$
are plotted in figure 6, for six values of the reduced velocity ranging from
![]() $U^{\star }=3.47$
to
$U^{\star }=3.47$
to
![]() $U^{\star }=5.79$
, i.e. from no vibration to large-amplitude VIV, as shown in § 3. The oblique and parallel shedding patterns associated with the two extreme cases can be clearly identified in these plots, while mixed patterns develop in all the intermediate cases. The flow velocity can be approximated as follows, using
$U^{\star }=5.79$
, i.e. from no vibration to large-amplitude VIV, as shown in § 3. The oblique and parallel shedding patterns associated with the two extreme cases can be clearly identified in these plots, while mixed patterns develop in all the intermediate cases. The flow velocity can be approximated as follows, using
![]() $N_{F}+1$
temporal Fourier modes:
$N_{F}+1$
temporal Fourier modes:
where
![]() $f_{j}=j/{\mathcal{T}}$
and
$f_{j}=j/{\mathcal{T}}$
and
![]() ${\mathcal{T}}$
is the non-dimensional sampling period. Each complex coefficient
${\mathcal{T}}$
is the non-dimensional sampling period. Each complex coefficient
![]() $\hat{v}_{j}$
is written in terms of its modulus
$\hat{v}_{j}$
is written in terms of its modulus
![]() $|\hat{v}_{j}|$
, referred to as spectral amplitude in the following, and its spatial phase
$|\hat{v}_{j}|$
, referred to as spectral amplitude in the following, and its spatial phase
![]() $\unicode[STIX]{x1D6F9}_{j}$
.
$\unicode[STIX]{x1D6F9}_{j}$
.

Figure 7. Span-averaged value of the spectral amplitude of the non-dimensional transverse flow velocity,
![]() $10D$
downstream of the cylinder, as a function of the non-dimensional frequency, over a range of reduced velocities. The non-dimensional cross-flow vibration frequency is indicated by a blue dashed-dotted line. The area of large spectral amplitudes occurring close to the Strouhal frequency (
$10D$
downstream of the cylinder, as a function of the non-dimensional frequency, over a range of reduced velocities. The non-dimensional cross-flow vibration frequency is indicated by a blue dashed-dotted line. The area of large spectral amplitudes occurring close to the Strouhal frequency (
![]() $St=0.593$
) is delimited by red dashed lines and coloured in red.
$St=0.593$
) is delimited by red dashed lines and coloured in red.
The span-averaged value (denoted by
![]() $\langle \,\rangle$
) of
$\langle \,\rangle$
) of
![]() $v$
spectral amplitude is plotted as a function of the frequency (non-dimensionalized by
$v$
spectral amplitude is plotted as a function of the frequency (non-dimensionalized by
![]() $U_{n}$
) in figure 7, for the six cases considered in figure 6. In the absence of vibration (
$U_{n}$
) in figure 7, for the six cases considered in figure 6. In the absence of vibration (
![]() $U^{\star }=3.47$
), the wake is dominated by a single component which occurs at a high frequency that matches the Strouhal frequency reported in the fixed rigid cylinder case (
$U^{\star }=3.47$
), the wake is dominated by a single component which occurs at a high frequency that matches the Strouhal frequency reported in the fixed rigid cylinder case (
![]() $St=0.593$
; Bourguet & Triantafyllou (Reference Bourguet and Triantafyllou2015)). For
$St=0.593$
; Bourguet & Triantafyllou (Reference Bourguet and Triantafyllou2015)). For
![]() $U^{\star }=5.79$
, in the fully developed VIV regime, the wake is also dominated by a single component, but the corresponding peak appears at a much lower frequency that coincides with the cross-flow vibration frequency. In the intermediate cases (
$U^{\star }=5.79$
, in the fully developed VIV regime, the wake is also dominated by a single component, but the corresponding peak appears at a much lower frequency that coincides with the cross-flow vibration frequency. In the intermediate cases (
![]() $3.86\leqslant U^{\star }\leqslant 4.96$
), as suggested by POD analysis in § 4.1, two significant spectral contributions can be noted: at the cross-flow vibration frequency (blue dashed-dotted line) and around the Strouhal frequency (area delimited by red dashed lines and coloured in red). The dominant component occurring close to the Strouhal frequency, i.e. the largest peak in the red area, and the component emerging at the cross-flow vibration frequency are further investigated in the following. These two principal components of the flow are referred to as high-frequency (HF) component and low-frequency (LF) component, respectively. Due to its proximity with the frequency of vortex shedding in the fixed rigid body case, the HF component is also referred to as Strouhal component, while the LF component, which relates to the wake–body synchronization phenomenon is also referred to as lock-in component. In general, the frequencies of the two components are incommensurable and the secondary peaks of lower amplitudes that may arise in the spectra appear at frequencies which are linear combinations of these two frequencies.
$3.86\leqslant U^{\star }\leqslant 4.96$
), as suggested by POD analysis in § 4.1, two significant spectral contributions can be noted: at the cross-flow vibration frequency (blue dashed-dotted line) and around the Strouhal frequency (area delimited by red dashed lines and coloured in red). The dominant component occurring close to the Strouhal frequency, i.e. the largest peak in the red area, and the component emerging at the cross-flow vibration frequency are further investigated in the following. These two principal components of the flow are referred to as high-frequency (HF) component and low-frequency (LF) component, respectively. Due to its proximity with the frequency of vortex shedding in the fixed rigid body case, the HF component is also referred to as Strouhal component, while the LF component, which relates to the wake–body synchronization phenomenon is also referred to as lock-in component. In general, the frequencies of the two components are incommensurable and the secondary peaks of lower amplitudes that may arise in the spectra appear at frequencies which are linear combinations of these two frequencies.

Figure 8. Spanwise evolution of the spatial phases associated with the Strouhal (HF) and lock-in (LF) components of the transverse flow velocity and with the dominant component of the cross-flow motion of the cylinder. No vibration is observed for
![]() $U^{\star }=3.47$
(a). A single component appears in the flow velocity spectrum for
$U^{\star }=3.47$
(a). A single component appears in the flow velocity spectrum for
![]() $U^{\star }=3.47$
(a) and
$U^{\star }=3.47$
(a) and
![]() $U^{\star }=5.79$
(f).
$U^{\star }=5.79$
(f).
The spanwise evolutions of the spatial phases
![]() $\unicode[STIX]{x1D6F9}_{j}$
, associated with the Strouhal (HF) and lock-in (LF) components of the flow (for
$\unicode[STIX]{x1D6F9}_{j}$
, associated with the Strouhal (HF) and lock-in (LF) components of the flow (for
![]() $j>0$
) are plotted in figure 8, for each value of
$j>0$
) are plotted in figure 8, for each value of
![]() $U^{\star }$
. The two extreme cases exhibit a single component in the flow velocity spectrum and thus a single spatial phase appears in the corresponding plots. For comparison purposes, the spatial phase of the dominant component of the cross-flow displacement, obtained by considering a Fourier expansion of
$U^{\star }$
. The two extreme cases exhibit a single component in the flow velocity spectrum and thus a single spatial phase appears in the corresponding plots. For comparison purposes, the spatial phase of the dominant component of the cross-flow displacement, obtained by considering a Fourier expansion of
![]() $\unicode[STIX]{x1D701}_{y}$
similar to (4.2), is also plotted. The frequencies of the different spectral components are specified in the plot legends. The spatial phase of the Strouhal component of the flow presents comparable trends in the stationary and vibrating body cases: it continuously decreases along the span, following an evolution close to linear, which indicates that the high-frequency peak is associated with an oblique spatial structure of the flow. In the absence of other component (stationary body), it corresponds to an oblique orientation of the vortex rows, which is visualized in figure 1(a). The low-frequency peak of the flow spectrum (lock-in component), which occurs at the body vibration frequency, exhibits a spatial phase that remains close to constant along the span, similarly to the spatial phase of the body response. This peak is thus associated with a parallel spatial structure of the flow, which corresponds to a parallel vortex shedding pattern when it is the only significant component (figure 1
b). As a result, the connection of the Strouhal and lock-in components with oblique and parallel spatial structures of the flow, identified for
$\unicode[STIX]{x1D701}_{y}$
similar to (4.2), is also plotted. The frequencies of the different spectral components are specified in the plot legends. The spatial phase of the Strouhal component of the flow presents comparable trends in the stationary and vibrating body cases: it continuously decreases along the span, following an evolution close to linear, which indicates that the high-frequency peak is associated with an oblique spatial structure of the flow. In the absence of other component (stationary body), it corresponds to an oblique orientation of the vortex rows, which is visualized in figure 1(a). The low-frequency peak of the flow spectrum (lock-in component), which occurs at the body vibration frequency, exhibits a spatial phase that remains close to constant along the span, similarly to the spatial phase of the body response. This peak is thus associated with a parallel spatial structure of the flow, which corresponds to a parallel vortex shedding pattern when it is the only significant component (figure 1
b). As a result, the connection of the Strouhal and lock-in components with oblique and parallel spatial structures of the flow, identified for
![]() $U^{\star }=3.86$
through POD analysis (§ 4.1), can be generalized to the entire range of
$U^{\star }=3.86$
through POD analysis (§ 4.1), can be generalized to the entire range of
![]() $U^{\star }$
investigated.
$U^{\star }$
investigated.
In order to quantify the relative contributions of the two principal flow components as the free vibrations develop, the magnitudes of the corresponding peaks in figure 7 are plotted as functions of
![]() $U^{\star }$
in figure 9(a), and as functions of the maximum non-dimensional cross-flow displacement of the cylinder in figure 9(b). As also shown in § 4.1 via POD, the flow is dominated by the Strouhal (HF) component for
$U^{\star }$
in figure 9(a), and as functions of the maximum non-dimensional cross-flow displacement of the cylinder in figure 9(b). As also shown in § 4.1 via POD, the flow is dominated by the Strouhal (HF) component for
![]() $U^{\star }=3.86$
. The contribution of this component regularly decreases as
$U^{\star }=3.86$
. The contribution of this component regularly decreases as
![]() $U^{\star }$
and the vibration amplitude increase, while the contribution of the lock-in (LF) component continuously increases and becomes predominant for
$U^{\star }$
and the vibration amplitude increase, while the contribution of the lock-in (LF) component continuously increases and becomes predominant for
![]() $U^{\star }\geqslant 4.96$
.
$U^{\star }\geqslant 4.96$
.

Figure 9. Magnitudes of the peaks associated with the Strouhal (HF) and lock-in (LF) components of the non-dimensional transverse flow velocity in figure 7, as functions of the (a) reduced velocity and (b) maximum non-dimensional cross-flow displacement.
This analysis shows that the high-frequency oblique component of the flow that relates to the stationary body configuration, the Strouhal component, persists beyond the onset of free vibrations, which occur at a much lower and incommensurable frequency. It also shows that the vibration onset is associated with the appearance of a novel flow component, synchronized with body motion and characterized by a parallel spatial pattern, the lock-in component. The Strouhal and lock-in components coexist over a range of
![]() $U^{\star }$
, with variable contributions, which results in a variety of mixed flow patterns. The transition from oblique to parallel shedding pattern, that accompanies the amplification of the structural responses, is driven by the opposite trends of these two component contributions: the simultaneous decrease of the Strouhal component magnitude and increase of the lock-in component magnitude.
$U^{\star }$
, with variable contributions, which results in a variety of mixed flow patterns. The transition from oblique to parallel shedding pattern, that accompanies the amplification of the structural responses, is driven by the opposite trends of these two component contributions: the simultaneous decrease of the Strouhal component magnitude and increase of the lock-in component magnitude.
In the range of
![]() $U^{\star }$
associated with the emergence of the free vibrations and the above-described transition of the flow patterns, the fluid forces also undergo a major reconfiguration; this aspect is addressed in the next section.
$U^{\star }$
associated with the emergence of the free vibrations and the above-described transition of the flow patterns, the fluid forces also undergo a major reconfiguration; this aspect is addressed in the next section.
5 Fluid forces
The forces exerted by the fluid on the flexible cylinder are examined in this section. The objective is not to report a thorough description of the forcing but to emphasize some dominant features related to the onset of the free-vibration regime. The force statistics are presented first, in order to quantify the departure from the static body case and from the IP. The span-averaged values of the time-averaged in-line force coefficient and of the r.m.s. values of both force coefficients are plotted in figure 10 as functions of the reduced velocity; in figure 10(b) the fluctuation of the in-line force coefficient about its time-averaged value is considered. It is recalled that the forces are non-dimensionalized by
![]() $U_{n}$
. For comparison purposes, the normal incidence results for
$U_{n}$
. For comparison purposes, the normal incidence results for
![]() $Re=500$
and
$Re=500$
and
![]() $Re=86.8$
are also plotted. The statistics obtained for a fixed rigid cylinder, in the inclined body case and in the normal incidence cases are indicated by horizontal lines in these plots.
$Re=86.8$
are also plotted. The statistics obtained for a fixed rigid cylinder, in the inclined body case and in the normal incidence cases are indicated by horizontal lines in these plots.

Figure 10. Span-averaged values of the (a) time-averaged in-line force coefficient, (b) r.m.s. in-line force coefficient fluctuation and (c) r.m.s. cross-flow force coefficient, as functions of the reduced velocity. Some normal incidence case results are reported for comparison purposes (white and black symbols). The values obtained for a fixed rigid cylinder, in the inclined body case and in the normal incidence case for
![]() $Re=500$
and
$Re=500$
and
![]() $Re=86.8$
, are indicated by plain, dashed and dashed-dotted lines, respectively.
$Re=86.8$
, are indicated by plain, dashed and dashed-dotted lines, respectively.

Figure 11. Span-averaged value of the spectral amplitude of the cross-flow force coefficient as a function of the non-dimensional frequency, over a range of reduced velocities. The non-dimensional cross-flow vibration frequency is indicated by a blue dashed-dotted line. The area delimited by red dashed lines is the same as in figure 7; it denotes the area of large spectral amplitudes of the transverse flow velocity occurring close to the Strouhal frequency.
In the absence of vibration, the statistics of the force coefficients applied on the inclined flexible cylinder are similar to those reported for a fixed rigid body, i.e. the very small in-line bending of the stationary flexible cylinder has no significant influence. Substantial deviations are observed when the body starts to oscillate (
![]() $U^{\star }\geqslant 3.86$
). As shown in prior works concerning rigid and flexible cylinders, inclined or placed at normal incidence (e.g. Newman & Karniadakis Reference Newman and Karniadakis1997; Carberry, Sheridan & Rockwell Reference Carberry, Sheridan and Rockwell2005; Franzini et al.
Reference Franzini, Gonçalves, Meneghini and Fujarra2013; Bourguet et al.
Reference Bourguet, Karniadakis and Triantafyllou2015), body oscillation may be accompanied by a large amplification of the force fluctuations and mean in-line force. It can be noted that over the range of
$U^{\star }\geqslant 3.86$
). As shown in prior works concerning rigid and flexible cylinders, inclined or placed at normal incidence (e.g. Newman & Karniadakis Reference Newman and Karniadakis1997; Carberry, Sheridan & Rockwell Reference Carberry, Sheridan and Rockwell2005; Franzini et al.
Reference Franzini, Gonçalves, Meneghini and Fujarra2013; Bourguet et al.
Reference Bourguet, Karniadakis and Triantafyllou2015), body oscillation may be accompanied by a large amplification of the force fluctuations and mean in-line force. It can be noted that over the range of
![]() $U^{\star }$
investigated, the trends of the force statistics are not monotonic, contrary to those observed for the vibration amplitudes (figure 3
a,b). In particular, a slight reduction of the mean in-line force occurs as the body starts to vibrate, before a substantial increase for
$U^{\star }$
investigated, the trends of the force statistics are not monotonic, contrary to those observed for the vibration amplitudes (figure 3
a,b). In particular, a slight reduction of the mean in-line force occurs as the body starts to vibrate, before a substantial increase for
![]() $U^{\star }\geqslant 4.96$
. The statistics of the force coefficients may considerably differ between the inclined and normal incidence cases. As also reported based on the structural responses in § 3, the IP does not apply to the present physical system.
$U^{\star }\geqslant 4.96$
. The statistics of the force coefficients may considerably differ between the inclined and normal incidence cases. As also reported based on the structural responses in § 3, the IP does not apply to the present physical system.
The spectral content of fluid forcing is investigated in the following. The analysis focuses on the cross-flow force but comparable observations can be made for the in-line force. The cross-flow force coefficient
![]() $C_{y}$
is approximated by a Fourier expansion similar to (4.2), and the span-averaged value of its spectral amplitude is plotted as a function of the non-dimensional frequency in figure 11, for the six values of
$C_{y}$
is approximated by a Fourier expansion similar to (4.2), and the span-averaged value of its spectral amplitude is plotted as a function of the non-dimensional frequency in figure 11, for the six values of
![]() $U^{\star }$
considered in figure 7. The non-dimensional cross-flow vibration frequency is indicated by a blue dashed-dotted line and the area delimited by red dashed lines around the Strouhal frequency is the same as in figure 7. The two principal components of fluid forcing that can be identified in the spectra, peak at the same frequencies as the HF and LF components of the flow described in § 4. The onset of body oscillation is associated with the appearance of a force component at the vibration frequency. Over a range of
$U^{\star }$
considered in figure 7. The non-dimensional cross-flow vibration frequency is indicated by a blue dashed-dotted line and the area delimited by red dashed lines around the Strouhal frequency is the same as in figure 7. The two principal components of fluid forcing that can be identified in the spectra, peak at the same frequencies as the HF and LF components of the flow described in § 4. The onset of body oscillation is associated with the appearance of a force component at the vibration frequency. Over a range of
![]() $U^{\star }$
, this low-frequency force component combines with a higher-frequency peak, which already exists in the absence of vibration and corresponds to the Strouhal component of the flow.
$U^{\star }$
, this low-frequency force component combines with a higher-frequency peak, which already exists in the absence of vibration and corresponds to the Strouhal component of the flow.
The spanwise trends of the spatial phases of the force components are similar to those noted for
![]() $v$
(figure 8): the phase of the high-frequency component linearly decreases along the span while the phase of the low-frequency component remains close to the phase of the cylinder response.
$v$
(figure 8): the phase of the high-frequency component linearly decreases along the span while the phase of the low-frequency component remains close to the phase of the cylinder response.
The magnitudes of the peaks associated with the two principal components of fluid forcing are represented as functions of
![]() $U^{\star }$
in figure 12(a), and as functions of the maximum non-dimensional cross-flow displacement in figure 12(b). These plots emphasize the continuous decrease of the high-frequency component contribution as
$U^{\star }$
in figure 12(a), and as functions of the maximum non-dimensional cross-flow displacement in figure 12(b). These plots emphasize the continuous decrease of the high-frequency component contribution as
![]() $U^{\star }$
and the motion amplitude increase, which can be related to the decreasing magnitude of the Strouhal component of the flow, while the low-frequency component becomes predominant.
$U^{\star }$
and the motion amplitude increase, which can be related to the decreasing magnitude of the Strouhal component of the flow, while the low-frequency component becomes predominant.

Figure 12. Magnitudes of the peaks associated with the high- and low-frequency components of the cross-flow force coefficient in figure 11, as functions of the (a) reduced velocity and (b) maximum non-dimensional cross-flow displacement.
This brief analysis highlights the alteration of fluid forcing as the VIV regime develops and pinpoints some connections with the flow patterns.
6 Conclusion
The onset of the VIV regime of a flexible cylinder inclined at
![]() $80^{\circ }$
within a uniform current at
$80^{\circ }$
within a uniform current at
![]() $Re=500$
, has been studied on the basis of direct numerical simulation results. The flexible cylinder was modelled as a tension-dominated structure and a reduced velocity
$Re=500$
, has been studied on the basis of direct numerical simulation results. The flexible cylinder was modelled as a tension-dominated structure and a reduced velocity
![]() $U^{\star }$
was defined as the inverse of the fundamental natural frequency, non-dimensionalized by the body diameter and the velocity magnitude of the inflow normal component. In the absence of vibration, the wake of the inclined cylinder exhibits a slanted vortex shedding pattern. In contrast and in spite of the large inclination angle, the vortices are shed parallel to the body once the fully developed VIV regime is reached. In order to bridge the gap between these two extreme configurations, explore the scenario of flow reorganization and clarify the properties of fluid forcing when the free vibrations emerge, a range of reduced velocities was studied by varying the tension applied to the cylinder.
$U^{\star }$
was defined as the inverse of the fundamental natural frequency, non-dimensionalized by the body diameter and the velocity magnitude of the inflow normal component. In the absence of vibration, the wake of the inclined cylinder exhibits a slanted vortex shedding pattern. In contrast and in spite of the large inclination angle, the vortices are shed parallel to the body once the fully developed VIV regime is reached. In order to bridge the gap between these two extreme configurations, explore the scenario of flow reorganization and clarify the properties of fluid forcing when the free vibrations emerge, a range of reduced velocities was studied by varying the tension applied to the cylinder.
Additional simulations in the normal incidence case confirmed that the independence principle, which states that the flow–structure system behaviour is determined by the normal inflow component, does not apply at such large inclination angle.
The inclined cylinder starts to vibrate spontaneously in the in-line and cross-flow directions at a reduced velocity close to
![]() $4$
. Contrary to the normal incidence case, the inclined body vibrations arise far from the Strouhal frequency, i.e. the vortex shedding frequency downstream of a fixed rigid cylinder. Within the parameter space investigated, the in-line and cross-flow responses of the inclined flexible cylinder involve spatial wavelengths corresponding to the second and first structural modes respectively, with a frequency ratio of
$4$
. Contrary to the normal incidence case, the inclined body vibrations arise far from the Strouhal frequency, i.e. the vortex shedding frequency downstream of a fixed rigid cylinder. Within the parameter space investigated, the in-line and cross-flow responses of the inclined flexible cylinder involve spatial wavelengths corresponding to the second and first structural modes respectively, with a frequency ratio of
![]() $2$
, and the vibration amplitudes increase continuously with
$2$
, and the vibration amplitudes increase continuously with
![]() $U^{\star }$
.
$U^{\star }$
.
The trace of the stationary body wake is found to persist beyond the vibration onset: the flow may still exhibit an oblique component that relates to the slanted shedding pattern observed in the absence of structural response; this component which occurs close to the Strouhal frequency, at a high and incommensurable frequency compared to the vibration frequency, is referred to as Strouhal component. Over a range of
![]() $U^{\star }$
, the Strouhal component coexists with a second dominant component of the flow, the lock-in component, which is synchronized with body motion and characterized by a parallel spatial pattern. The combination of the Strouhal and lock-in components, with variable magnitudes, leads to a range of mixed wake patterns. It is shown that the amplification of the structural responses with
$U^{\star }$
, the Strouhal component coexists with a second dominant component of the flow, the lock-in component, which is synchronized with body motion and characterized by a parallel spatial pattern. The combination of the Strouhal and lock-in components, with variable magnitudes, leads to a range of mixed wake patterns. It is shown that the amplification of the structural responses with
![]() $U^{\star }$
is accompanied by a simultaneous decrease of the Strouhal component contribution and increase of the lock-in component contribution. The opposite trends of these two flow components drive the transition from the oblique to the parallel shedding pattern. The parallel shedding pattern observed in the fully developed VIV regime thus corresponds to the final stage of this transition process where any trace of the stationary body wake, associated with the Strouhal component, has vanished and the flow dynamics is entirely governed by wake–body synchronization, i.e. the lock-in component.
$U^{\star }$
is accompanied by a simultaneous decrease of the Strouhal component contribution and increase of the lock-in component contribution. The opposite trends of these two flow components drive the transition from the oblique to the parallel shedding pattern. The parallel shedding pattern observed in the fully developed VIV regime thus corresponds to the final stage of this transition process where any trace of the stationary body wake, associated with the Strouhal component, has vanished and the flow dynamics is entirely governed by wake–body synchronization, i.e. the lock-in component.
The development of the VIV regime is also accompanied by a profound alteration of fluid forcing, with the emergence of a novel component synchronized with body oscillation and the progressive disappearance of the high-frequency component related to the Strouhal component of the flow.
Acknowledgements
This work was performed using HPC resources from CALMIP (grants 2015-P1248 and 2016-P1248) and GENCI (grants x20152a7184 and c20162a7184).