1 Introduction
The nature of wing-tip vortices is an important topic of investigation due their prevalence in all forms of flight. Comprehensive reviews of previous investigations are given by Spalart (Reference Spalart1998), Crouch (Reference Crouch2005) and Savas (Reference Savas2005). Additional insight into the unsteady nature of trailing vortices is provided by Green & Acosta (Reference Green and Acosta1991).
The unsteady evolution of a vortex from a wing or control surface subjected to controlled motion, in absence of a downstream follower wing, has been addressed in a wide range of investigations. Distributions of velocity, vorticity and circulation of a tip vortex from a pitching wing were characterized by Ramaprian & Zheng (Reference Ramaprian and Zheng1998) using laser Doppler velocimetry and Chang & Park (Reference Chang and Park2000) using triple-hot-film probe measurements. Birch & Lee (Reference Birch and Lee2005) investigated the effect of perturbation frequency on the three-dimensional flow structure of a tip vortex behind a pitching wing for attached flow, light stall and deep stall oscillations using a triple-hot-wire probe. Gerontakos & Lee (Reference Gerontakos and Lee2006) employed an actuated trailing-edge flap, across the entire wingspan, on a pitching wing in order to alter the structure of the wing-tip vortex. Panagakos & Lee (Reference Panagakos and Lee2006) and Lee (Reference Lee2007) measured the effectiveness of an oscillating trailing-edge tab to control the strength of a tip vortex from a pitching wing using triple-hot-wire probe measurements. Experimental investigations of the flow structure along plunging wings at high angles of attack have been carried out by Cleaver et al. (Reference Cleaver, Wang, Gursul and Visbal2011) and Calderon et al. (Reference Calderon, Wang, Gursul and Visbal2013) using particle image velocimetry and volumetric particle image velocimetry, respectively. More recently, Fishman, Wolfinger & Rockwell (Reference Fishman, Wolfinger and Rockwell2017) determined the structure of a trailing vortex from a wing undergoing unsteady motion; the unidirectional undulation of the vortex gave rise to enhanced azimuthal vorticity when the swirl ratio became less than the critical value established by the Leibowich & Stewartson (Reference Leibowich and Stewartson1983).
Recently, Garmann & Visbal (Reference Garmann and Visbal2016a ), Garmann & Visbal (Reference Garmann and Visbal2016b ) and Garmann & Visbal (Reference Garmann and Visbal2017) have employed high-fidelity computations to investigate the flow structure of a tip vortex from a wing undergoing small amplitude, heaving oscillations. The effect of oscillation frequency and amplitude was examined with emphasis on the formation of the vortex along the wing tip. Oscillation of the wing induced large fluctuations of the vortex core structure along the wing tip which persisted downstream into the wake. Enhanced separation and stretching along the wing tip occurred as a result of such fluctuations. This separation of the vortex from the wing is associated with the formation of spiralling substructures around the periphery of the vortex, which also persists into the wake. The vertical amplitude of the vortex trajectory was shown to increase considerably with increasing streamwise distance. Moreover, the vortex trajectory developed spanwise excursions that also increased in amplitude with streamwise distance. The rate at which the vertical and spanwise excursions increased depended on the parameters of the wing oscillation; namely, oscillations with the higher frequency and amplitude produced more rapid amplification.
Self-induced unsteadiness of a vortex impinging on an aerodynamic surface can give rise to unsteady pressure fluctuations, resulting in unsteady loading and potential vibration of the surface. This phenomenon is demonstrated in the vortex interaction with a wing addressed by Barnes, Visbal & Huang (Reference Barnes, Visbal and Huang2016), with a blade investigated by Bhagwat, Caradonna & Ramasamy (Reference Bhagwat, Caradonna and Ramasamy2015) and with a fin characterized by Washburn, Jenkins & Ferman (Reference Washburn, Jenkins and Ferman1993). Rockwell (Reference Rockwell1998) has reviewed the literature characterizing the relationship between vortex impingement on a body and the induced loading. A further aspect of this class of flows is that a tip vortex impinging on a wing can yield enhanced aerodynamic performance, as shown by Hummel (Reference Hummel1983). Detailed insight into the physics of a steady vortex impinging on a wing and the associated enhancement of the lift to drag ratio, as well as buffeting of the wing surface, are given by Barnes, Visbal & Gordnier (Reference Barnes, Visbal and Gordnier2015) and Garmann & Visbal (Reference Garmann and Visbal2015) and their previous works cited therein.
The unsteady characteristics of the incident tip vortex play an important role in the physics of its interaction with an aerodynamic surface. The consequence of large-scale unsteadiness has been investigated by Garmann & Visbal (Reference Garmann and Visbal2014); they characterized the interaction of an unsteady, wandering vortex with a downstream wing using high-fidelity computations. Large amplitude sinusoidal motion in the spanwise direction was imposed on the incident vortex to simulate self-induced wandering. It was shown that the vortex developed orbital motion as it approached the wing. That is, vertical excursions of the vortex trajectory developed despite the imposed lateral motion of the vortex. This induced orbital motion strongly influenced the flow structure of the interaction and subsequently the unsteady loading experienced by the follower wing. These findings emphasize the importance of characterizing the unsteadiness of the incident vortex.
Theoretical investigations of an isolated vortex subjected to infinitesimal perturbations or finite amplitude forcing provide a basis for interpretation of the present experiments. Leibowich & Stewartson (Reference Leibowich and Stewartson1983) addressed the stability of
$a$
, Batchelor (Reference Batchelor1964) (columnar), vortex with respect to three-dimensional perturbations. Their theory employed asymptotic instability analysis that led to a stability criterion related to the swirl ratio
$q$
of the vortex, which relates the peak swirl (azimuthal) velocity and the axial velocity deficit. They showed that for small values of
$q$
, the vortex is unstable with respect to azimuthal wavenumbers.
Viola, Arratia & Gallaire (Reference Viola, Arratia and Gallaire2016) summarize more recent, related investigations, and in their own study, employ direct numerical simulation, along with theoretically based approaches, to examine the effects of harmonic forcing of a globally stable, non-parallel Batchelor vortex for extreme cases of initially infinitesimal and finite amplitude levels of forcing. The forcing acted on all three velocity components. The modal structure of the vortex was found to be a strong function of the forcing frequency and, furthermore, influenced by the amplitude of the forcing.
Another class of theoretical approaches involves the effects of self-induction. The analyses of Hama & Nuntant (Reference Hama and Nuntant1961), Hama (Reference Hama1962) and Hama (Reference Hama1963) employed this approach for a curved vortex filament, and described the temporal evolution of a vortex subjected to an initial perturbation. Their analyses demonstrate that the self-induction effects occur as a result of induced velocity, which is most prominent in the region with the largest curvature along a curved vortex. Moreover, the induced motion acts in the opposite direction to that of the circulation of the vortex.
The foregoing investigations have provided valuable insight into the structure of a perturbed trailing (tip) vortex. However, a number of issues remain unresolved and lead to experimental characterization via global imaging of the unsteady flow structure of a perturbed trailing vortex from a wing subjected to small amplitude periodic motion in the heaving mode. The present investigation focuses on the following unexplored aspects: (i) the effect of dimensionless oscillation frequency on the distributions of axial vorticity, azimuthal vorticity and axial velocity deficit; (ii) characterization of the nature of the vortex trajectory including the development of orbital motion and its evolution in the streamwise direction; (iii) the interrelationship between the onset of orbital motion and patterns of axial vorticity, azimuthal vorticity and axial velocity deficit; and (iv) the connection between the foregoing aspects and the time-dependent variation of the swirl ratio. These concepts are addressed via volumetric and cross-sectional representations of the vortex structure acquired from stereo particle image velocimetry (SPIV) in conjunction with three-dimensional reconstruction techniques.
2 Experimental system and techniques
Figure 1. (a) Schematic of stereo particle image velocimetry system. (b) Schematic of wing oscillation mechanism (not to scale). (c) Model of test section and experimental system.
Figure 2. (a) Plan and side view schematics of wing. (b) Motion profile of wing.
Experiments were performed in a large-scale, recirculating water channel in the fluids laboratory at Lehigh University. The main test section of the facility is 594 mm in depth and 613 mm in width. Flow conditioners, which include a series of honeycomb meshes and fine screens, are arranged upstream of the test section and are utilized to achieve a turbulence intensity less than 0.3 %. In the present experiments, the free-stream velocity was maintained at
$U_{\infty }=152.4~\text{mm}~\text{s}^{-1}$
which yields a chord based Reynolds number
$Re_{C}=U_{\infty }C/\unicode[STIX]{x1D708}=15\,200$
, where
$C$
is the chord of the wing and
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of water.
A stereoscopic particle image velocimetry system was utilized to determine the flow structure of a trailing vortex from a wing undergoing continuous heaving motion subjected to different oscillation frequencies. A schematic of the system is given in figure 1(a). A laser sheet oriented in the spanwise, or lateral, direction, in conjunction with two charged coupled device (CCD) cameras, are used to capture the three-dimensional velocity field at successive crossflow planes. Cameras are arranged in an angular displacement configuration and employ the Scheimpflug condition. According to Prasad (Reference Prasad2000), this condition requires that the object plane, image plane and lens plane be coplanar in order to ensure uniform focus across the image plane. In order to minimize the effects of refraction, two Plexiglass prisms filled with distilled water are positioned on the channel walls and arranged such that the camera axis is perpendicular to the incident face of the prism. Lastly, the blockage ratio of the wing with respect to the cross-sectional area of the channel, taking into account the maximum amplitude of excursion of the wing motion, is 0.01 or 1 %, which is well within the acceptable range for quality wind tunnel tests, as described by West & Apelt (Reference West and Apelt1982).
A schematic of the wing oscillation mechanism is indicated in figure 1(b). It employs a computer-controlled motor that drives a scotch-yoke mechanism that is attached to the vertically oriented sting of the wing. The sting is affixed to the centre of the wing and also fastened to a sliding bar coupled to a vertically oriented traverse. A connecting rod is used to link the sliding bar to a wheel that is attached to the motor. This mechanism converts the linear motion to rotational motion. An encoder attached to the motor is used to determine the position of the wing.
Figure 1(c) is a rendered model of the test section that includes the SPIV system, the wing perturbation mechanism and the wing positioning system. The laser head is positioned underneath the channel and the laser sheet is oriented in the spanwise direction. The wing positioning system consists of several motors with encoders that allow for precise positioning of the wing in all three directions. This system also provides controlled perturbation of the wing. In order to capture images at successive planes in the streamwise direction, the motion control system is translated along a rail system that extends the length of the channel.
Figure 2(a) shows plan and side view schematics of the experimental system. The model of the wing is a rectangular flat plate of aspect ratio
$AR=2$
, with a chord
$C=102~\text{mm}$
and span
$b=203~\text{mm}$
. The thickness of the wing
$t=1.6~\text{mm}$
and the corner radius
$r_{c}=0.5~\text{mm}$
. The wing is fixed at an angle of attack
$\unicode[STIX]{x1D6FC}_{o}=6^{\circ }$
and is subjected to continuous heaving motion in the vertical direction as indicated in the side view schematic. Figure 2(b) depicts the sinusoidal displacement amplitude
$A(\unicode[STIX]{x1D6F7})$
of the wing as a function of phase angle
$\unicode[STIX]{x1D6F7}$
. The oscillation cycle consists of the downstroke of the wing which occurs between
$\unicode[STIX]{x1D6F7}=0$
to
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x03C0}$
and the upstroke between
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x03C0}$
to
$\unicode[STIX]{x1D6F7}=2\unicode[STIX]{x03C0}$
.
Three frequencies of motion were employed in the present experiments. The non-dimensional Strouhal numbers, indicated in figure 2(b), are
$St_{C}=fC/U_{\infty }=0.08$
, 0.25 and 0.67. These values of Strouhal number correspond respectively values of wavelength
$\unicode[STIX]{x1D706}/C=U_{\infty }/fC=12$
, 4 and 1.5 or
$\unicode[STIX]{x1D706}/d_{o}=120$
, 40 and 15 where
$d_{o}$
is the diameter of the vortex from a stationary wing. The vortex diameter
$d_{o}$
is defined as twice the vortex radius
$r_{o}$
, where
$r_{o}$
is the circumferentially averaged radial location of the maximum value of swirl velocity
$(u_{\unicode[STIX]{x1D703}})_{max}$
. The displacement amplitude of the wing motion in all cases is
$A_{o}/C=0.03$
or
$A_{o}/d_{o}=0.3$
. The extreme values of Strouhal number represent the limiting frequencies of the motor control system. Preliminary diagnostics showed that the lowest value yielded unidirectional undulation of the vortex with no change in amplitude in the streamwise direction, thereby serving as a reference case. This lowest frequency falls below the lower limit where disturbance amplification occurs in the theoretical and computational investigations of Viola et al. (Reference Viola, Arratia and Gallaire2016). Moreover, the moderate and highest values
$St_{C}$
correspond to large amplification of the nonlinearly perturbed vortex, in accord with the findings of Viola et al. (Reference Viola, Arratia and Gallaire2016). These studies employ a vortex whose base flow Reynolds number
$Re_{D}=667$
in which the vortex diameter
$D$
is the characteristic length; the swirl parameter
$q=-0.5$
and the wake parameter
$a=-1.5$
. Additionally, the opposite tip vortex was investigated at all Strouhal numbers and the vortex behaviour was symmetrical to the opposite tip vortex in all cases. Namely, the differences in peak values of axial vorticity and velocity of the two vortices were within experimental error and the trajectories of orbital motion, or lack thereof, were symmetrical.
The water is seeded with
$11~\unicode[STIX]{x03BC}\text{m}$
metallic coated hollow plastic spheres which have a density of
$1.958~\text{g}~\text{cm}^{-3}$
. A dual pulsed Nd:YAG laser system is utilized to generate a laser sheet of 1.5 mm thickness which illuminates the particles. Each of the CCD cameras used to capture the particle images contains an array of 1600 pixels
$\times$
1192 pixels. Insight 4G was employed to process the particle images. Interrogation windows of 32 pixels
$\times$
32 pixels are used and contain 15–20 particle images. A 50 % overlap between camera frames is utilized and the particle images are processed using a frame-to-frame cross-correlation technique. The effective resolution of the SPIV system employed is
$14.92~\text{pixels}~\text{mm}^{-1}$
. Uncertainty analysis of the in-plane velocity measurements was performed using the procedure described in Adrian & Westerweel (Reference Adrian and Westerweel2011). The calculations yielded an in-plane velocity random error
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x0394}V}$
that is 2.2 % of the free-stream velocity. Lawson & Wu (Reference Lawson and Wu1997) provides a relationship between the in-plane and out-of-plane errors which yielded an out-of-plane random velocity error
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x0394}U}$
that is 2.6 % of the free-stream velocity.
During experiments, the laser sheet was oriented in the cross-flow direction, as previously indicated. Images were acquired at the following selected planes:
$x^{\prime }/C=0$
, 0.5, 1, 2, 3, 4 and 5; these values correspond to the distance downstream of the trailing edge of the wing, where
$x^{\prime }/C=0$
is the trailing edge. A phase-referencing technique was employed, which grouped together images taken at a given vertical position of the wing; this process provided phase-averaged images. Instantaneous vortex centres were made coincident before performing phase-averaged calculations, to eliminate the effects of meandering. Time-average calculations were also performed. That is, averages were taken over the entire oscillation cycle. For these calculations, instantaneous images were also re-centred before taking the average. This procedure is well established and accepted, as described in detail by del Pino et al. (Reference del Pino, Parras, Felli and Fernandez-Feria2011). Volumetric reconstruction was performed utilizing in-house software in conjunction with the phase-averaged images.
3 Unsteady vortex structure
3.1 Time-averaged axial and azimuthal profiles
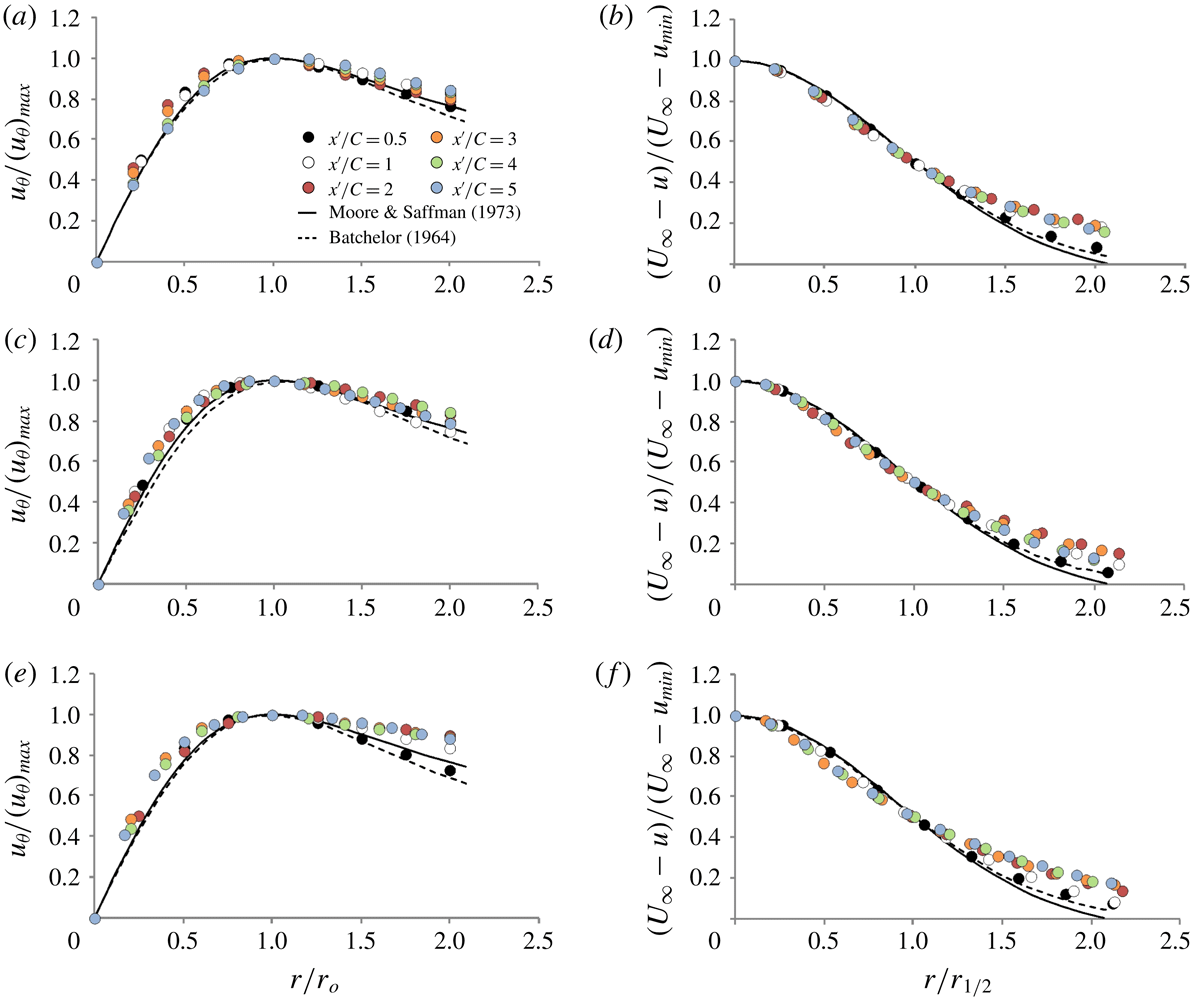
Figure 3. Comparison of time-averaged, normalized azimuthal velocity
$u_{\unicode[STIX]{x1D703}}/(u_{\unicode[STIX]{x1D703}})_{max}$
profiles as functions of vortex radius
$r_{o}$
(a,c,d) and time-averaged, normalized axial velocity deficit
$(U_{\infty }-u)/(U_{\infty }-u_{min})$
as functions of the radial half-width of the vortex
$r_{1/2}$
(b,d,f) at Strouhal number (a,b)
$St_{C}=0.08$
, (c,d)
$St_{C}=0.25$
and (e,f)
$St_{C}=0.67$
at the streamwise locations
$x^{\prime }/C$
indicated. Theoretical distributions from Batchelor (Reference Batchelor1964) and Moore & Saffman (Reference Moore and Saffman1973) are included for reference.
Figure 3 shows time-averaged profiles of azimuthal velocity
$u_{\unicode[STIX]{x1D703}}/(u_{\unicode[STIX]{x1D703}})_{max}$
as a function of radius
$r_{o}$
; and axial velocity deficit
$(U_{\infty }-u)/(U_{\infty }-u_{min})$
as functions of the radial half-width
$r_{1/2}$
. These profiles are shown at (a,b)
$St_{C}=0.08$
, (c,d)
$St_{C}=0.25$
and (e,f)
$St_{C}=0.67$
. The vortex radius
$r_{o}$
is defined as the radial location where maximum azimuthal velocity
$(u_{\unicode[STIX]{x1D703}})_{max}$
occurs and the radial half-width
$r_{1/2}$
is defined as the location where the axial velocity deficit is half its maximum value. Profiles are given for the streamwise locations
$x^{\prime }/C=0.5$
, 1, 2, 3, 4 and 5. For each case, the radial distributions were circumferentially averaged. The equation for the Batchelor (Reference Batchelor1964) vortex was used to determine the best fit to the foregoing data. To fit the data, a nonlinear least squares method was used. These bet-fit profiles at
$x^{\prime }/C=1$
are plotted for comparison for each case. Moreover, the values of the swirl parameter
$q$
and the wake parameter
$a$
that provide the best-fit at the streamwise location
$x^{\prime }/C=1$
are as follows. At
$St_{C}=0.08$
,
$a=5.22$
and
$q=1.66$
; at
$St_{C}=0.25$
,
$a=4.92$
and
$q=1.53$
; and at
$St_{C}=0.67$
,
$a=4.88$
and
$q=1.5$
. In addition to these fits corresponding to the Batchelor vortex, theoretical distributions of Moore & Saffman (Reference Moore and Saffman1973) for
$n=0.7$
are also included in figure 3.
Overall, the time-averaged, normalized distributions of azimuthal and axial velocity for the three cases are in general agreement with each other at
$x^{\prime }/C=0.5$
and agree well with the profiles of the unperturbed vortex, shown in Fishman et al. (Reference Fishman, Wolfinger and Rockwell2017). Moreover, they compare well with the theoretical distributions of Moore & Saffman (Reference Moore and Saffman1973) at
$x^{\prime }/C=0.5$
, despite the unsteady fluctuations. With increasing streamwise distance, however, departures from the theoretical profiles of Batchelor (Reference Batchelor1964) and Moore & Saffman (Reference Moore and Saffman1973) occur for all values of Strouhal number. In the azimuthal velocity profiles, the departures occur at the outer periphery of the vortex, in the region extending from
$r/r_{o}=1.5$
to
$r/r_{o}=2$
, where elevated values of azimuthal velocity, relative to the theoretical profiles, are evident and are most pronounced at
$St_{C}=0.67$
. There are similar departures from theoretical profiles of axial velocity deficit, in the form of elevated values of the data, at the outer periphery of the vortex for streamwise distances greater than
$x^{\prime }/C=0.5$
.
The foregoing departures of data for the azimuthal and axial velocity are likely due to the large variations of the scale and magnitude these velocity components during the oscillation cycle. The variation of the axial velocity deficit of the vortex, especially at larger streamwise distances, is directly evident in figure 6(a,b), shown subsequently. Since the large variations of the azimuthal velocity and the velocity deficit are associated with nonlinear effects, the resultant averaged, normalized profiles are distorted relative to those corresponding to either an unperturbed vortex or a vortex perturbed at small amplitude.
3.2 Initial state of vortex at trailing edge
Figure 4. Cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
and axial velocity deficit
$1-u/U_{\infty }$
as functions of phase angle
$\unicode[STIX]{x1D6F7}$
at each Strouhal number
$St_{C}$
at the streamwise location
$x^{\prime }/C=0$
.
Figure 5. Streamline patterns at phase angles
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6F7}=5\unicode[STIX]{x03C0}/4$
at each Strouhal number
$St_{C}$
at the streamwise location
$x^{\prime }/C=0$
.
Figure 4 shows cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
(red) and axial velocity deficit
$1-u/U_{\infty }$
(blue) as functions of phase angle
$\unicode[STIX]{x1D6F7}$
for each value of Strouhal number
$St_{C}$
. These images were taken at the trailing edge of the wing and are viewed looking upstream along the axis of the vortex. The darkest blue, wedge-like region of axial velocity deficit near the bottom of each image corresponds to the horizontal wake at the trailing edge. For the low Strouhal number,
$St_{C}=0.08$
, the vortex exhibits mild fluctuations of magnitude and spatial extent, or scale, of axial vorticity and axial velocity deficit during the oscillation cycle. The structure of the axial velocity deficit during the downstroke,
$\unicode[STIX]{x1D6F7}=0$
to
$3\unicode[STIX]{x03C0}/4$
, is nearly symmetrical to that of the upstroke,
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x03C0}$
to
$7\unicode[STIX]{x03C0}/4$
. This is not the case for axial vorticity; that is, an increase in level of axial vorticity is evident from
$\unicode[STIX]{x1D6F7}=0$
to
$3\unicode[STIX]{x03C0}/4$
, in comparison to that of
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x03C0}$
to
$7\unicode[STIX]{x03C0}/4$
. For the moderate Strouhal number
$St_{C}=0.25$
, pronounced variations of the magnitude and scale of both the axial vorticity and axial velocity deficit are evident during the oscillation cycle. Enhanced levels of axial vorticity occur during the downstroke and attenuated levels are apparent during the upstroke. Regarding the axial velocity deficit, enhanced levels occur during the downstroke and attenuate during the upstroke. For the highest Strouhal number,
$St_{C}=0.67$
, contours of both axial vorticity and axial velocity deficit are highly distorted along the wing surface from
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x03C0}/4$
to
$3\unicode[STIX]{x03C0}/4$
. This distortion is not present at the lower values of Strouhal number, i.e.
$St_{C}=0.08$
and 0.25. At
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x03C0}$
, the vortex is positioned well above the wing surface and has initiated its recovery towards circular concentrations of axial vorticity and axial velocity deficit. In contrast to the aforementioned cases at lower frequencies, the vortex exhibits lateral motion in addition to the vertical excursion which arises from the prescribed vertical heaving motion of the wing. This is evident from comparison of the location of the vortex centre relative to the tip of the wing at different values of phase angle. Specifically, from
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x03C0}$
to
$\unicode[STIX]{x1D6F7}=7\unicode[STIX]{x03C0}/4$
the vortex centre location moves further outboard and then back inboard from
$\unicode[STIX]{x1D6F7}=0$
to
$\unicode[STIX]{x1D6F7}=3\unicode[STIX]{x03C0}/4$
. The consequence of these simultaneous lateral and vertical excursions is a small amplitude orbital motion at the trailing edge of the wing, which is present only at the highest value of Strouhal number.
Figure 5 shows streamline patterns at the trailing edge of the wing,
$x^{\prime }/C=0$
, for all three values of Strouhal number
$St_{C}$
. Two phase angles,
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6F7}=5\unicode[STIX]{x03C0}/4$
, are indicated for each case. The vortex is centred in all images. Corresponding images of axial vorticity and axial velocity deficit are previously given in figure 4. In the first row of images of figure 5, corresponding to
$St_{C}=0.08$
, the streamline patterns spiral inwards towards a central focus, which corresponds to the centre of the vortex. The dark region near the centre of the vortex, corresponding to densely packed streamlines, is approximately circular. This is the case at both phase angles. Similar streamline patterns are observed at
$St_{C}=0.25$
. As previously indicated in figure 4, at
$St_{C}=0.08$
and
$St_{C}=0.25$
, patterns of axial vorticity and axial velocity deficit are undistorted, circular concentrations. The fact that the streamlines at both frequencies spiral inward makes the focus stable and indicates that the vortex is being stretched in the axial direction, in accord with the interpretation of Perry & Chong (Reference Perry and Chong2000). Moreover, at both of these frequencies, the vortex trajectory during the oscillation cycle is entirely unidirectional (in the vertical direction) and the formation of the vortex is not inhibited by the motion of the wing.
Figure 6. Cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
, axial velocity deficit
$1-u/U_{\infty }$
and azimuthal vorticity
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}C/U_{\infty }$
as functions of phase angle
$\unicode[STIX]{x1D6F7}$
at each Strouhal number
$St_{C}$
at the streamwise locations (a)
$x^{\prime }/C=0.5$
and (b)
$x^{\prime }/C=2$
.
At
$St_{C}=0.67$
, the streamline patterns spiral inwards towards a central focus at
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x03C0}/4$
. The non-circular (elongated) dark regions of densely packed streamlines near the centre of the vortex coincide with the elongated patterns of axial vorticity and axial velocity deficit along the surface of the wing as indicated in figure 4. However, the streamline topology at
$\unicode[STIX]{x1D6F7}=5\unicode[STIX]{x03C0}/4$
has undergone a fundamental transformation relative to that at lower values of Strouhal number. It consists of streamlines spiralling inwards towards a central focus at the centre of the vortex; they emanate from a limit cycle. The streamlines that spiral outwards from this limit cycle merge along a secondary limit cycle. This pattern differs from the classical streamline pattern of vortex roll up and indicates a change in the mechanism of vortex formation in the vicinity of the wing. It arises when there is a detectable phase shift between the vortex formation and the motion of the wing. This phase shift is associated with small amplitude lateral motion of the forming vortex, which represents the onset of orbital motion.
3.3 Sectional patterns of axial vorticity, axial velocity deficit and azimuthal vorticity
Figure 6(a,b) shows rows of images representing cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
(top), axial velocity deficit
$1-u/U_{\infty }$
(middle) and azimuthal vorticity
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}C/U_{\infty }$
(bottom) as functions of phase angle
$\unicode[STIX]{x1D6F7}$
. Three different Strouhal numbers
$St_{C}$
are represented at the streamwise locations
$x^{\prime }/C=0.5$
and
$x^{\prime }/C=2$
. At the low Strouhal number,
$St_{C}=0.08$
, the vortex exhibits similar characteristics as it does at the trailing edge of the wing. That is, mild variations of magnitude and spatial extent, or scale, of axial vorticity and axial velocity deficit occur. Azimuthal vorticity is detectable at all values of phase angle, but is most prevalent when the axial velocity deficit has the largest magnitude and scale; for example, from
$\unicode[STIX]{x1D6F7}=3\unicode[STIX]{x03C0}/2$
to
$\unicode[STIX]{x03C0}/4$
at
$x^{\prime }/C=0.5$
and
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x03C0}/2$
to
$\unicode[STIX]{x03C0}$
at
$x^{\prime }/C=2$
. That is, the enhanced axial velocity deficit means a steeper gradient in the radial direction, in conjunction with high-level azimuthal vorticity.
At the moderate Strouhal number,
$St_{C}=0.25$
, represented by the middle set of images in each figure, considerable variations of the magnitude and scale of axial vorticity and axial velocity deficit are evident over the oscillation cycle. Pronounced regions of azimuthal vorticity are evident in conjunction with regions of enhanced axial velocity deficit. At the high Strouhal number,
$St_{C}=0.67$
, corresponding to the bottom set of images, substantial variations of axial vorticity and axial velocity deficit occur. Similar to the lower values of Strouhal number, enhanced levels of azimuthal vorticity coincide with regions of enhanced axial velocity deficit. The scale of the concentration of axial velocity deficit is much larger than that of axial vorticity at both the moderate and high Strouhal numbers, in contrast to the patterns at low Strouhal number. The foregoing observations are consistent at all streamwise locations explored in this investigation.
In summary, clearly defined azimuthal vorticity occurs in conjunction with regions of enhanced axial velocity deficit during the oscillation cycle across all streamwise distances and for all oscillation frequencies imparted by the wing motion. This observation is consistent with that first described by Fishman et al. (Reference Fishman, Wolfinger and Rockwell2017) at a single frequency. The present findings indicate a universal occurrence extending over a range of
$St_{C}=0.08$
, 0.25 and 0.67, corresponding to ratios of wavelength
$\unicode[STIX]{x1D706}$
to vortex diameter
$d_{o}$
of
$\unicode[STIX]{x1D706}/d_{o}=120$
, 40 and 15. Moreover, these observations are consistent with the criterion described by Fishman et al. (Reference Fishman, Wolfinger and Rockwell2017), whereby pronounced azimuthal vorticity is evident when the swirl ratio
$q<\sqrt{2}$
during the oscillation cycle. The swirl ratio is defined as
$q=\unicode[STIX]{x1D6E4}/2\unicode[STIX]{x03C0}r\unicode[STIX]{x0394}u=1.567V_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x0394}u$
, where
$V_{\unicode[STIX]{x1D703}}$
is the maximum azimuthal velocity and
$\unicode[STIX]{x0394}u$
is the peak axial velocity deficit of the vortex, as indicated by Jacquin & Pantano (Reference Jacquin and Pantano2002). In turn, this finding is in accord with the onset of amplified azimuthal modes of the convective instability of the Batchelor vortex described by Leibowich & Stewartson (Reference Leibowich and Stewartson1983). Although the swirl ratio criterion described by Leibowich & Stewartson (Reference Leibowich and Stewartson1983) was developed from a parallel (columnar) Batchelor vortex, there is strong correspondence between it and the prominent physics of the present perturbed vortices. Figure 6(a,b) indicates, however, important distinctions of the vortex response that are frequency dependent.
3.4 Volumetric representations of flow structure – axial vorticity, axial velocity deficit and azimuthal vorticity
Figure 7. Temporal volumes of cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
(above) and azimuthal vorticity
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}C/U_{\infty }$
(below) superposed on iso-surfaces of axial velocity deficit
$1-u/U_{\infty }$
at each Strouhal number
$St_{C}$
at the streamwise locations (a)
$x^{\prime }/C=0.5$
and (b)
$x^{\prime }/C=2$
.
Figure 7(a) shows temporal volumes of cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
and azimuthal vorticity
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}C/U_{\infty }$
superposed on an iso-surface (blue) of axial velocity deficit
$1-u/U_{\infty }$
at the streamwise location
$x^{\prime }/C=0.5$
. At each value of Strouhal number
$St_{C}$
, the top and bottom images show, respectively, sectional contours of
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}C/U_{\infty }$
. Images are shown from an angled side view as indicated in the schematic. Linear interpolation between data planes is utilized in the construction of these temporal volumes. At the low Strouhal number
$St_{C}=0.08$
, a small diameter region of high-level axial velocity deficit penetrates the cross-sectional contours of axial vorticity over a portion of the oscillation cycle. The existence of the iso-surface of velocity deficit coincides with occurrence of detectable azimuthal vorticity along the top portion of the vortex. At the moderate Strouhal number
$St_{C}=0.25$
, the region of axial velocity deficit is relatively large compared to that at the low Strouhal number. Furthermore, slices of enhanced azimuthal vorticity are evident only in the region where axial velocity deficit is present. These features are also apparent at the high Strouhal number,
$St_{C}=0.67$
. The iso-surface of axial velocity deficit is largest in this case and is again accompanied by enhanced levels of azimuthal vorticity. Larger fluctuations in axial vorticity with increasing Strouhal number are evident.
Figure 8. Temporal volumes of cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
superposed on iso-surfaces of axial velocity deficit
$1-u/U_{\infty }$
at streamwise distances
$x^{\prime }/C=0.5$
, 3 and 5. Strouhal number is
$St_{C}=0.08$
.
Figure 9. Temporal volumes of cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
superposed on iso-surfaces of axial velocity deficit
$1-u/U_{\infty }$
at streamwise distances (a)
$~x^{\prime }/C=0.5$
, 1 and 2, and (b)
$x^{\prime }/C=3$
, 4 and 5. Strouhal number is
$St_{C}=0.25$
.
Figure 10. Temporal volumes of cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
superposed on iso-surfaces of axial velocity deficit
$1-u/U_{\infty }$
at streamwise distances (a)
$x^{\prime }/C=0.5$
and 1, and (b)
$x^{\prime }/C=2$
and 3. Strouhal number is
$St_{C}=0.67$
.
Figure 7(b) shows the equivalent temporal volumes at the streamwise location
$x^{\prime }/C=2$
. The format of the image layout is the same as that of figure 7(a). At all three frequencies, the previously established relationship is apparent. That is, the region of axial velocity deficit coincides with enhanced levels of azimuthal vorticity. At
$St_{C}=0.08$
, a narrowly confined region of high level axial velocity deficit occurs. On the other hand, it is clear that at
$St_{C}=0.25$
and 0.67, large-scale regions of high-level axial velocity deficit arise.
An important aspect of the tip vortex from an oscillating wing is whether its response takes the form of a unidirectional undulation or an orbital motion. Figures 8–10 show the interrelationship between axial vorticity, axial velocity deficit and curvature of the undulating vortex. Figure 8 shows, at the low Strouhal number,
$St_{C}=0.08$
, temporal volumes of cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
(red) overlaying iso-surfaces of axial velocity deficit
$1-u/U_{\infty }$
(blue) for streamwise distances
$x^{\prime }/C=0.5$
, 3 and 5. The schematic indicates the perspectives for the angled side and plan views.
In figure 8, at
$x^{\prime }/C=0.5$
, close to the trailing edge of the wing, it is evident that enhanced levels of axial velocity deficit
$1-u/U_{\infty }$
are present only over a portion of the cycle. This is clear in both the side and plan views. The side view shows this deficit, represented by the blue iso-surface, which occurs in the centre of the vortex at the onset of the change in vortex curvature. That is, the vortex begins to slope downward at
$\unicode[STIX]{x1D6F7}=0$
, in conjunction with occurrence of the iso-surface of axial velocity deficit. This iso-surface is attenuated where the vortex begins to slope upward. With increasing streamwise distance, from
$x^{\prime }/C=0.5$
to
$x^{\prime }/C=3$
, the spatial extent of the axial velocity deficit is greatly attenuated and there is a discernible phase shift in its temporal location relative to that of
$x^{\prime }/C=0.5$
. This is due to the phase velocity of the disturbed vortex, which is of the order of the free-stream velocity. At large streamwise distances,
$x^{\prime }/C=5$
, there is no detectable level of this high-level axial velocity deficit. As evident in the side view images, there is no discernible change in the amplitude of the vertical excursion of the concentrations of axial vorticity at increasing values of streamwise distance
$x^{\prime }/C$
. Moreover, the plan view images show that there is no lateral excursion of the vortex for all streamwise locations.
Figure 9(a,b) show, at the moderate Strouhal number
$St_{C}=0.25$
, temporal volumes of cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
superposed on iso-surfaces of axial velocity deficit
$1-u/U_{\infty }$
. At
$x^{\prime }/C=0.5$
, high-level axial velocity deficit occurs in the vortex core during a majority of the cycle. The concentration of axial velocity deficit is evident at all streamwise distances; however, it extends over a smaller number of phases of the oscillation cycle with increasing values of
$x^{\prime }/C$
. At a given value of
$x^{\prime }/C$
, the formation of this iso-surface of axial velocity deficit coincides with a change of curvature of the vortex, and the attenuation of the iso-surface corresponds to another change of curvature. Primarily, it forms along the downward sloping portion of the vortex and is attenuated on the upward sloping portion. This is consistent with the state of the vortex at the trailing edge of the wing as shown in figure 4. That is, higher magnitude axial velocity deficit, as well as axial vorticity, is present along the downward deflection of the vortex trajectory. At
$x^{\prime }/C=1$
, in the side view, at
$\unicode[STIX]{x1D6F7}=0$
the slices of axial vorticity initially slope upward. As these slices begin to slope downward, formation of enhanced axial velocity deficit is apparent. The change in curvature, that is, where the vortex changes from sloping upwards to sloping downwards, occurs in conjunction with the formation of enhanced axial velocity deficit. On the other hand, as the cross-sectional slices of axial vorticity slope upwards, the high-level axial velocity deficit is attenuated. These changes in curvature are also associated with variations of the magnitude and spatial extent of axial vorticity, whereby an increase of the scale of axial vorticity coincides with enhanced axial velocity deficit. In figure 9(b), at
$x^{\prime }/C=5$
, these same characteristics hold. Although the spatial extent of the region of enhanced axial velocity deficit is attenuated, it still forms along the downward sloping portion of the vortex albeit slightly after the change in curvature. It is no longer present where the axial vorticity slices begin sloping upward, as is consistent with previous observations. In the plan view, lateral excursion of the axial vorticity slices is evident. These excursions can be seen as deviations from the original unidirectional trajectory and occur at the onset and attenuation of the axial velocity deficit. Viewing these vertical and lateral excursions together indicates an elliptical pattern in the vortex trajectory.
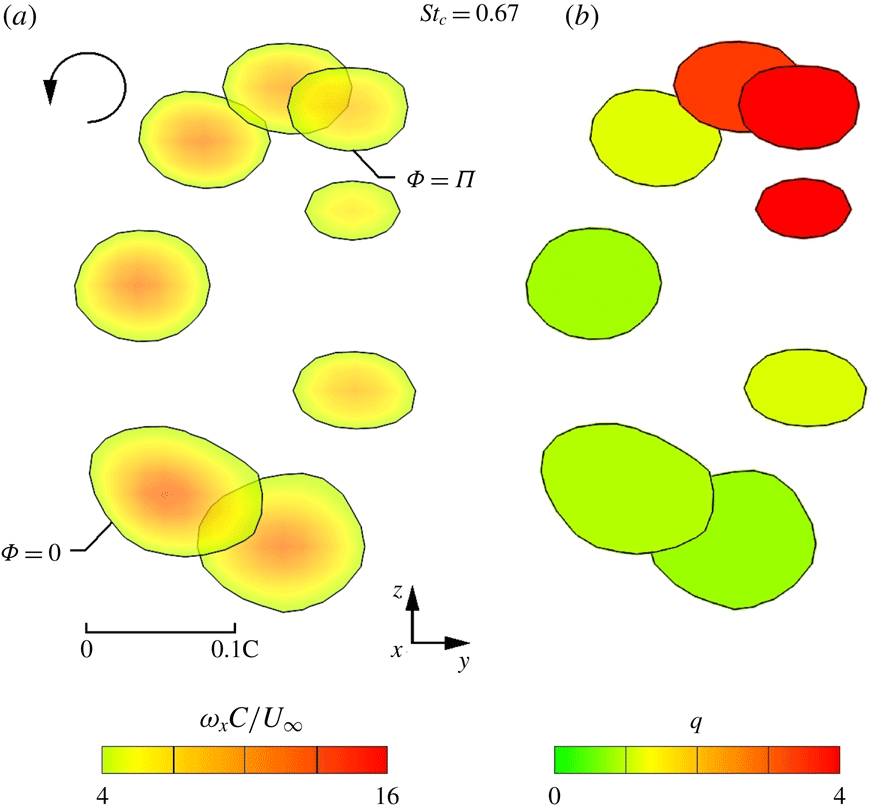
Figure 10(a,b), at the high Strouhal number
$St_{C}=0.67$
, indicates substantial deviations from unidirectional undulation of the vortex. The vortex structure and its evolution in the downstream direction are dramatically affected. Large excursions in the vertical and lateral directions are evident across all streamwise distances in figure 10(a,b) and their amplitudes are significantly amplified with increasing
$x^{\prime }/C$
. Additionally, this perturbation produces a large diameter iso-surface of axial velocity deficit that encloses the slices of axial vorticity; this observation is present at all streamwise distances. That is, a large-scale region of decelerated axial flow occurs, in contrast to aforementioned cases at lower frequencies, shown in figures 8 and 9 where the iso-surface of enhanced axial velocity deficit is embedded within the central region of the volume of axial vorticity slices. Furthermore, the formation of axial velocity deficit again occurs along the downward sloping portion of the slices of axial vorticity and is attenuated along the upward sloping portion of slices of axial vorticity. Lateral excursions of the vortex trajectory, which are evident in the plan view, depict a similar relationship.
3.5 Evolution of vortex trajectory
Figure 11. Time sequence of cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
viewed in the upstream direction at each Strouhal number
$St_{C}$
at streamwise distances (a)
$x^{\prime }/C=0.5$
, 1 and 2, and (b)
$x^{\prime }/C=3$
, 4 and 5. (c) Plots of vertical
$A_{z}/C$
and lateral
$A_{y}/C$
amplitude of the vortex motion for three Strouhal numbers
$St_{C}$
as functions of streamwise distance
$x^{\prime }/C$
.
Figure 12. Time sequence of cross-sectional slices of (a) axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
and (b) swirl ratio
$q$
viewed in the upstream direction at Strouhal number
$St_{C}=0.67$
at the streamwise location
$x^{\prime }/C=3$
.
Figure 11(a,b) indicates the degree of departure from a unidirectional undulation of the vortex via images that show the time sequence of cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
viewed in the upstream direction, such that all instantaneous slices are superposed during the oscillation cycle. For
$St_{C}=0.25$
and
$St_{C}=0.67$
, arrows are given to indicate the sense of rotation of the in-plane orbital motion.
At
$x^{\prime }/C=0.5$
in figure 11(a), the trajectory of the vortex at Strouhal numbers
$St_{C}=0.08$
and
$St_{C}=0.25$
is unidirectional and solely in the vertical direction. However, at
$St_{C}=0.25$
, the vortex experiences larger fluctuations in scale. At
$St_{C}=0.67$
, orbital motion of the vortex trajectory is clearly present and accompanied by large variations in scale. At
$x^{\prime }/C=1$
, there is relatively little change in the nature of the vortex trajectory for all three values of Strouhal number. At
$x^{\prime }/C=2$
, little change of the trajectory occurs, although attenuation of the magnitude of axial vorticity is apparent at
$St_{C}=0.08$
. The development of lateral motion of the vortex is evident at
$St_{C}=0.25$
; simultaneously, a small increase in the vertical amplitude of motion occurs. At
$St_{C}=0.67$
, there is a significant increase in the amplitude of the vortex trajectory at
$x^{\prime }/C=2$
, in both vertical and lateral directions. This observation is accompanied by severe changes in the magnitude and spatial extent of axial vorticity.
In figure 11(b), the trajectory of the vortex at
$St_{C}=0.08$
does not change significantly for the streamwise distances
$x^{\prime }/C=3$
, 4 and 5. At
$St_{C}=0.25$
, the amplitudes of the vertical and lateral excursions increase incrementally from
$x^{\prime }/C=3$
–5, such that detectable orbital motion occurs. The motion of the vortex in this case is in the opposite sense to that of the axial vorticity; that is, it is oriented in the clockwise direction. At
$St_{C}=0.67$
, the trajectory of the vortex does not change significantly over the streamwise locations
$x^{\prime }/C=3$
to 5. That is, the amplitudes in both the vertical and lateral direction remain relatively unchanged. In this case, the motion of the vortex is in the same sense as that of axial vorticity; that is, it is in the counterclockwise direction.
In essence, the three different Strouhal numbers
$St_{C}$
yield distinctly different classes of response, i.e. trajectories. At the Strouhal number
$St_{C}=0.08$
, the vortex excursion begins and remains solely in the vertical direction and its amplitude does not change with streamwise distance. At the moderate Strouhal number
$St_{C}=0.25$
, the vortex excursion is initially unidirectional in the vertical direction, but develops a lateral component with increasing streamwise distance, resulting in orbital motion in the clockwise direction. Additionally, the direction of winding in the spatial direction is opposite to its winding in time; that is, the vortex winds in the counterclockwise direction in space. At the high frequency
$St_{C}=0.67$
, the initial motion of the vortex is in both the vertical and lateral directions; that is, orbital motion is present and is oriented in the counterclockwise direction. At
$St_{C}=0.67$
, the vortex winds in the opposite, clockwise, direction in space. Moreover, the amplitudes of the excursion in the vertical direction increase by nearly an order of magnitude along the streamwise extent of the vortex. At
$St_{C}=0.67$
, as described in conjunction with figures 4 and 5, the formation of the vortex at the trailing edge is associated with lateral perturbations that are 4 % of the chord of the wing (40 % of the effective diameter of the vortex) and arise from a phase lag of the vortex formation relative to the wing motion, which does not exist for lower oscillation frequencies of the wing. This initial motion of the vortex is the genesis of a well-defined orbital motion that undergoes large amplitude amplification with streamwise distance.
Figure 11(c) shows plots of vertical
$A_{z}/C$
and lateral
$A_{y}/C$
amplitude for the three Strouhal numbers
$St_{C}$
as functions of streamwise distance
$x^{\prime }/C$
. At
$St_{C}=0.08$
the motion is entirely vertical with no significant increase in amplitude with streamwise distance. At
$St_{C}=0.25$
, the motion is initially vertical and its amplitude gradually increases until saturation is reached; simultaneously a lateral component of motion becomes more prevalent. At
$St_{C}=0.67$
, the vertical motion increases in amplitude with streamwise distance up to the location where saturation is attained, while the lateral motion remains significantly large at all streamwise locations. Saturation of the vertical amplitude of undulation occurs between
$x^{\prime }/C=3$
and 5 for the largest value of
$St_{C}$
and between
$x^{\prime }/C=4$
and 5 for the moderate value of
$St_{C}$
. Amplitude saturation, which is due to the onset of nonlinear effects, is an inherent feature of unstable flows that may be linearly unstable in their initial region of development. Such flows include perturbed trailing vortices, as described in the theoretical and computational investigation of Viola et al. (Reference Viola, Arratia and Gallaire2016). In a more general sense, the onset of nonlinear saturation is evident in experimental investigations of free shear flows, for example, the case of a perturbed mixing layer investigated by Freymuth (Reference Freymuth1966).
In order to clarify the role of the swirl ratio
$q$
during orbital motion of the vortex, figure 12 shows patterns of the vortex trajectory for the case
$St_{C}=0.67$
at the streamwise location
$x^{\prime }/C=3$
. It indicates the time sequence of cross-sectional slices of axial vorticity and, in addition, the lowest-level contour of axial vorticity filled with a colour that corresponds to the value of swirl ratio. The values of phase angle
$\unicode[STIX]{x1D6F7}$
correspond to specific instants during the cycle of the wing oscillation. A clear relationship between axial vorticity, swirl ratio and changes in vortex trajectory is evident. Most notably, changes in the direction of the vortex motion are evident where the swirl ratio reaches maximum (red) and minimum (green) values. Additionally, maximum values of swirl ratio are attained in conjunction with the attenuation of axial vorticity. This indicates that the axial velocity deficit is the dominant parameter in the swirl ratio and the predominant cause of short-wave instability. Conversely, minimum values of swirl ratio are attained in conjunction with increased strength of axial vorticity.
3.6 Volumetric representations of flow structure – axial vorticity, axial velocity deficit and swirl ratio
Figure 13. Cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
coloured according to magnitude of swirl ratio
$q$
superposed on iso-surfaces of (blue) axial velocity deficit
$1-u/U_{\infty }$
at each Strouhal number
$St_{C}$
at streamwise distances (a)
$x^{\prime }/C=0.5$
and (b)
$x^{\prime }/C=3$
.
Figure 13(a) shows temporal volumes of cross-sectional slices of axial vorticity
$\unicode[STIX]{x1D714}_{x}C/U_{\infty }$
coloured by swirl ratio
$q$
with overlaying iso-surfaces of axial velocity deficit
$1-u/U_{\infty }$
at a streamwise distance
$x^{\prime }/C=0.5$
. Each Strouhal number
$St_{C}$
is depicted in both side and plan view orientations as indicated in the schematic. At
$St_{C}=0.08$
, the swirl ratio does not vary significantly with respect to phase angle
$\unicode[STIX]{x1D6F7}$
and the trajectory of the vortex is solely in the vertical direction, as previously indicated. Higher values of swirl ratio are attained in regions where there is no significant axial velocity deficit. In general, the time sequence of axial vorticity slices slopes downward with increasing swirl ratio, and slopes upward with increasing swirl ratio. At
$St_{C}=0.25$
, a similar relationship between vortex curvature and swirl ratio is evident, whereby changes in vortex curvature coincide with regions of minimum and maximum values of swirl ratio. Moreover, in this case, larger fluctuations in swirl ratio are apparent, relative to those at
$St_{C}=0.08$
. The most pronounced changes in curvature and swirl ratio are apparent at the highest dimensionless frequency
$St_{C}=0.67$
. The magnitude of
$q$
, represented by the red contours, greatly exceeds the maximum colour bar value of 4, and can reach upwards of 20. In the side view, the cross-sectional slices slope downwards with decreasing values of swirl ratio and the formation of the axial velocity deficit occurs. When the cross-sectional slices slope upward, the value of swirl ratio increases, in conjunction with attenuation of the axial velocity deficit. In the plan view, the vortex deflects upwards (representing a lateral deflection in the actual flow) where high-level swirl ratio occurs. A pronounced change in curvature is evident at the onset of the enhanced axial velocity deficit which corresponds to a drastic decrease in swirl ratio. Interestingly,
$q$
has large values at different phases of the oscillation cycle at each Strouhal number. Large
$q$
does not necessarily occur at the largest curvature. For example, at
$St_{C}=0.67$
,
$q$
is high when the vortex is bending down and low when bending upward. At
$St_{C}=0.08$
, the opposite is true.
Figure 13(b) shows similar representations as figure 13(a), but at a streamwise distance
$x^{\prime }/C=3$
. At
$St_{C}=0.08$
, the swirl ratio does not vary significantly with respect to phase angle and the trajectory of the vortex is solely in the vertical direction, as previously shown at
$x^{\prime }/C=0.5$
in figure 13(a). Again, higher values of swirl ratio are attained in regions where there is no significant axial velocity deficit. At
$St_{C}=0.25$
, it is clear that changes in swirl ratio corresponding to changes in curvature. That is, in the side view, increasing swirl ratio coincides with upward sloping cross-sectional slices. Conversely, decreasing values of swirl ratio coincide with downward sloping cross-sectional slices, in conjunction with the onset of axial velocity deficit. These observations are consistent with the plan and side view temporal volumes at,
$St_{C}=0.67$
where remarkably large deflections occur. For the foregoing observations, it is important to note that, for each Strouhal number, the flow structure is preserved at locations downstream of the trailing edge of the wing. That is, the changes in curvature in relation to swirl ratio are consistent at each streamwise location.
4 Conclusions
This investigation focuses on the unsteady structure of a trailing vortex from a wing undergoing small amplitude heaving motion. Space–time images acquired via stereo particle image velocimetry show the effect of Strouhal number
$St_{C}$
(dimensionless frequency) on the response of the vortex in relation to the onset of its orbital motion. Low, moderate and high Strouhal numbers correspond respectively to values of
$St_{C}=0.08$
, 0.25 and 0.67. The amplitude
$A_{o}$
of the wing motion is approximately two orders of magnitude smaller than the chord. Over this range of Strouhal number, the vortex trajectory exhibits markedly different trajectories. Nevertheless, there are a number of generic physical mechanisms of the perturbed vortex that can be interpreted in terms of space–time representations of axial and azimuthal vorticity, axial velocity deficit and swirl ratio.
At low Strouhal number, the amplitude of the unidirectional excursion of the vortex remains essentially constant with streamwise distance and has a magnitude of the order of the amplitude of the wing oscillation. At moderate Strouhal number, the initial region of the vortex motion is unidirectional, but at larger streamwise distance, excursions of the vortex occur orthogonal to its initial unidirectional motion, thereby giving rise to an elliptical orbital trajectory that acts in the opposite direction to that of the circulation of the vortex. Hama & Nuntant (Reference Hama and Nuntant1961), Hama (Reference Hama1962) and Hama (Reference Hama1963) demonstrate that self-induction effects occur in accord with induced velocity, which is most prominent in the region with the largest curvature along a curved vortex and likely influence this development in association with the other vortex dynamics. At the high Strouhal number, the amplitude of the vortex undulation increases by nearly an order of magnitude with streamwise distance, with respect to the imposed perturbation, and pronounced orbital motion of the vortex has the same sense as the vortex circulation at all streamwise distances. The genesis of orbital motion is small amplitude lateral motion of the forming vortex at the trailing edge of the wing during its controlled vertical motion; moreover, the phase shift of the vortex development relative to the wing motion is altered with respect to that at lower values of Strouhal number. In both of the cases where orbital motion occurs, the region of axial velocity deficit is large compared to the region of axial vorticity. In general, a combination of the foregoing mechanisms is present in the onset of orbital motion in these cases.
Irrespective of the value of the Strouhal number or the streamwise location along the vortex, several generic physical mechanisms occur along an undulating vortex. A change in vortex curvature coincides with the onset of an enhanced axial velocity deficit in the central region of the vortex; a subsequent change in curvature occurs when this elevated deficit is attenuated. These changes are evident at the trailing edge of the wing and are consistent at all streamwise distances in accord with strengthening and weakening of the vortex. Furthermore, changes in vortex curvature, or deflection, are similarly correlated with extreme values of axial vorticity and swirl ratio, as well as with the onset and attenuation of pronounced azimuthal vorticity. Onset of pronounced azimuthal vorticity coincides with regions of enhanced axial velocity deficit at the trailing edge of the wing and at all streamwise distances for all frequencies. It consistently occurs when the swirl ratio
$q<\sqrt{2}$
, in accord with onset of convective instability of azimuthal modes Leibowich & Stewartson (Reference Leibowich and Stewartson1983). The degree to which the value of swirl ratio varies during the undulation cycle of the vortex is directly related to the excitation frequency; that is, higher frequencies produce larger variations.
Acknowledgement
This investigation was supported by the AFOSR under grant FA9550-14-1-0166, monitored by Dr D. Smith.
