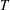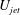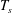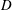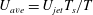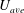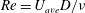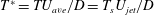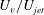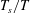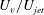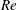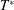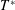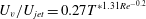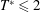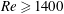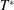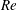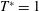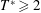1 Introduction
Periodically generated vortex rings are regularly observed in nature, e.g. animal propulsion (Colin & Costello Reference Colin and Costello2002; Dabiri et al.
Reference Dabiri, Colin, Costello and Gharib2005; Krieg & Mohseni Reference Krieg and Mohseni2015) and cardiovascular flows (Salsac et al.
Reference Salsac, Sparks, Chomaz and Lasheras2006; Kheradvar et al.
Reference Kheradvar, Houle, Pedrizzetti, Tonti, Belcik, Ashraf, Lindner, Gharib and Sahn2010; Gopalakrishnan, Pier & Biesheuvel Reference Gopalakrishnan, Pier and Biesheuvel2014). Many studies have focused on isolated vortex rings, instead of periodically generated ones, to identify the main parameters governing their physics. Glezer (Reference Glezer1988) utilized two non-dimensional parameters (Reynolds number and non-dimensional stroke time) to build a transition map to predict if a vortex ring would be turbulent upon formation or not. Gharib, Rambod & Shariff (Reference Gharib, Rambod and Shariff1998) proposed a non-dimensional time, called the formation time and defined as the ratio of the stroke length to the diameter of the cylinder (
$L/D$
), to govern the optimum formation of a vortex ring. The circulation of vortex rings grows until a formation time of approximately 4, referred to as the formation number, after which the ring cannot grow due to energetic constraints and forms trailing vortices. How these parameters, e.g. Reynolds number or formation time, affect the propagation of a vortex ring, nevertheless, is still not well quantified.
Several studies have discussed the propagation of isolated vortex rings. For short times after the formation of vortex rings, Didden (Reference Didden1979) experimentally showed that the non-dimensional axial locations of vortex core centres for two relatively low Reynolds numbers are proportional to non-dimensional time powered by 1.5. He also suggested similar scaling law with a different power for the radial location of vortex core centres and observed a linear increase in total circulation during most of the formation process, all of which were later verified numerically by Nitsche & Krasny (Reference Nitsche and Krasny1994) and James & Madnia (Reference James and Madnia1996), separately. Baird (Reference Baird1977) experimentally showed that for sufficiently large orifice diameters, the velocity of the vortex ring near the formation region is approximately half of the jet mean velocity for high Reynolds numbers, which was later verified by a formula suggested by Mohseni (Reference Mohseni2006). Baird (Reference Baird1977) also concluded that the jet injection time interval (formation time) does not affect the vortex ring velocity. However, later, Sullivan et al. (Reference Sullivan, Niemela, Hershberger, Bolster and Donnelly2008), by an empirical method, showed that the vortex core velocity is approximated by 0.3 of the piston velocity. Saffman (Reference Saffman1970) derived an equation for the velocity of a thin vortex ring in viscous flows, where the effect of viscosity is to slow down the ring after a long time. He assumed circular cores for the vortex rings, which is not a valid assumption for cases with high formation times. In this equation, similar to the classical Kelvin formula for circular vortex rings (Lamb Reference Lamb1932), the diameter and circulation of the vortex ring are required to calculate its velocity. His work was later extended by Fukumoto & Moffatt (Reference Fukumoto and Moffatt2000) to a higher-order asymptotic formula, which accounts for core deformations at high Reynolds numbers; however, this formula needs several numerical integrations. Maxworthy (Reference Maxworthy1972) experimentally studied the slowing of vortex rings and showed that the propagation velocity of a stable laminar vortex ring decays exponentially with the distance from the origin and varies as
$1/t$
, where
$t$
is time, for long times. Gan & Nickels (Reference Gan and Nickels2010) showed that a similarity theory holds for isolated vortex rings at two high Reynolds numbers. Based on the above review, most studies consider isolated vortex rings to propagate at constant speed except during early formation (Didden Reference Didden1979) or decay after long times (Maxworthy Reference Maxworthy1972). Nevertheless, how the constant speed is affected by the Reynolds number or formation time is not well described yet. In addition, the interaction between vortices for a periodically generated train of vortices may change the velocity of the vortex cores (Anderson Reference Anderson1955).
Several studies have investigated the propagation of periodically generated rings. Aydemir, Worth & Dawson (Reference Aydemir, Worth and Dawson2012) studied vortex rings for periodically initiated and terminated jets, and showed that the spacing between consecutive rings depends on both the frequency and amplitude of the inflow waveform. Krueger (Reference Krueger2010) found that by decreasing the period of the inflow, the velocity of vortex rings reduces and approaches the velocity of an isolated vortex ring. Schram & Riethmuller (Reference Schram and Riethmuller2002) studied the interaction of the leading and trailing vortex rings with each other and divided this into three stages. They showed that during the last stage, the trailing vortex rolls over the leading one, which leads to an increased vortex core velocity. Zaman & Hussain (Reference Zaman and Hussain1980) reported two distinct modes under which vortex ring pairing occurs: the ‘shear layer mode’ for cases with certain values of the Strouhal number based on the initial shear layer momentum thickness and the ‘jet column mode’ for cases with specific values of the Strouhal number based on jet diameter. They also observed that vortex pairing occurs regularly in space and time at low Reynold numbers, but less regularly at higher Reynolds numbers. Asgharzadeh & Borazjani (Reference Asgharzadeh and Borazjani2016) showed that the propagation of vortex rings in aneurysms increases with increasing Reynolds number and decreasing Womersley number. However, a general formula that can quantitatively describe the changes in the propagation of vortex rings as a function of the governing parameters, such as Reynolds number, formation time, etc. has yet to be reported.
The purpose of this study is to find a scaling law for time tracking of core centres of vortex rings. Such a relation for periodically generated vortex rings, which accounts for all the potentially important parameters, i.e. Reynolds number, period (formation time) and stroke ratio of the waveform, is missing in the literature, to the best of the knowledge of the authors. To do so, we carry out numerical simulations of vortex rings in a tank using our framework described in § 2.1. We discuss the simulated test cases in § 2.2 and validate our framework for capturing the propagation speed of vortex rings in § 2.3. We present the dynamics of the periodic vortex rings in § 3.1 and the latter’s propagation in § 3.2. Then, we discuss the proposed scaling law and compare it against available experimental measurements in § 4.
2 Methods
2.1 Governing equations and the numerical method
The governing equations are the three-dimensional, unsteady, incompressible Navier–Stokes equations. The system of equations is solved using the curvilinear immersed boundary method (Ge & Sotiropoulos Reference Ge and Sotiropoulos2007). In this method, a curvilinear grid is employed to serve as the background fluid mesh and an unstructured triangular mesh to discretize the immersed body. For the nodes in the immediate vicinity of the immersed body, the velocity field is reconstructed by interpolating along the local normal to the boundary, which is shown to be second-order accurate (Gilmanov & Sotiropoulos Reference Gilmanov and Sotiropoulos2005). The nodes inside immersed bodies are identified as solid nodes using a ray-tracing algorithm (Borazjani, Ge & Sotiropoulos Reference Borazjani, Ge and Sotiropoulos2008).
The governing equations are discretized on a hybrid staggered/non-staggered grid using a second-order accurate scheme and integrated in time using a fractional step method, which requires the solution of the nonlinear momentum equations and a pressure-Poisson equation. The implicit momentum equations are solved using Newton–Krylov method (NKM) with an approximate diagonal analytical Jacobian (Asgharzadeh & Borazjani Reference Asgharzadeh and Borazjani2017). A flexible generalized minimal residual (FGMRES) solver with multigrid preconditioner is employed for the Poisson equation (Ge & Sotiropoulos Reference Ge and Sotiropoulos2007).
The method has been validated and applied to a wide range of flow problems (Le, Borazjani & Sotiropoulos Reference Le, Borazjani and Sotiropoulos2010; Le et al.
Reference Le, Borazjani, Kang and Sotiropoulos2011; Borazjani Reference Borazjani2013; Borazjani & Daghooghi Reference Borazjani and Daghooghi2013; Borazjani et al.
Reference Borazjani, Ge, Le and Sotiropoulos2013; Daghooghi & Borazjani Reference Daghooghi and Borazjani2015b
). For high Reynolds number (e.g.
$Re_{jet}=$
$10\,000$
and
$23\,000$
) flows, a large-eddy simulation (LES) method with a dynamic Smagorinsky subgrid-scale model is employed to model turbulence. The LES method with an immersed boundary has been validated and applied to high Reynolds number flows in previous publications (e.g. see Daghooghi & Borazjani Reference Daghooghi and Borazjani2015a
; Bottom et al.
Reference Bottom, Borazjani, Blevins and Lauder2016). To show that the method can capture the propagation of vortex rings, it is further validated against vortex ring experiments in § 2.3.
Figure 1. (a) Three-dimensional view of the domain with generated vortex rings in green and a cross-section of the fluid mesh over the tank and (b) different inflow velocity waveforms for different test cases. Only every fourth grid point is shown in (a) for better illustration.
2.2 Simulated test cases and computational details
All test cases have been carried out in a set-up similar to that of Webster & Longmire (Reference Webster and Longmire1998). It consists of a square tank of size
$5.5D\times 5.5D\times 10.5D$
to which a circular cylinder of diameter
$D=72.8~\text{mm}$
and length
$2D$
is attached, as shown in figure 1(a). Note that for cases with high Reynolds numbers, the length of the domain was extended to
$19D$
to achieve a better convergence. The flow enters the domain through the cylinder, which is placed as an immersed boundary, and leaves it through the boundary across the cylinder as outflow. The no-slip condition is applied on the side walls and the wall behind the cylinder. The vortex rings are generated by a pulsed jet with period
$T$
as an inflow at the inlet of the cylinder with a profile whose magnitude varies in time according to figure 1(b). These waveforms are adopted from Webster & Longmire (Reference Webster and Longmire1998) to form a jet pulse for duration
$T_{s}$
(stroke time) and a nominal speed of
$U_{jet}$
. There is no flow between pulses. Three different ratios of
$T_{s}/T$
are considered for the inflow velocity (
$u$
) waveform (see figure 1
b). The characteristic length scale is the diameter of cylinder
$D$
. Because of the step-like inflow waveform (figure 1
b), the average velocity in each cycle is:
$$\begin{eqnarray}U_{ave}=\frac{1}{T}\int _{0}^{T}u\,\text{d}t=\frac{U_{jet}T_{s}}{T}.\end{eqnarray}$$
The computational grid consists of
$225\times 225\times 301$
nodes in the
$X$
,
$Y$
and
$Z$
directions, respectively. Due to longer domain for cases with high Reynolds numbers,
$433$
nodes were utilized in the
$Z$
direction. The region of interest is a
$1.1D\times 1.1D\times 4D$
cuboid with a uniform spacing of
$0.01D\times 0.01D\times 0.02D$
, which starts from the exit of the cylinder and is symmetric relative to the mid-plane. The grid was stretched from the cuboid to the outer edges of the computational domain using a hyperbolic tangent function as shown schematically in figure 1(a). For temporal discretization, a non-dimensional time step size (
$\triangle tU_{jet}/D$
) of 0.005 is considered for all the test cases. Therefore, the Courant number for all of the simulations is 0.5.
Table 1. Characteristics of test cases:
$Re_{ave}$
, average Reynolds number;
$Re_{jet}$
, jet Reynolds number;
$T_{ave}^{\ast }$
, average non-dimensional period;
$T_{jet}^{\ast }$
, jet non-dimensional period;
$T_{s}/T$
, stroke to period ratio;
$\unicode[STIX]{x1D6FC}$
, Womersley number;
$(U_{v}/U_{jet})_{FI}$
, vortex velocity to jet velocity ratio for the approach with ring formation included (FI);
$(U_{v}/U_{jet})_{FE}$
, vortex velocity to jet velocity ratio for the approach with ring formation excluded (FE); and
$((U_{1}-U_{v})/U_{v})_{FI}$
, relative velocity difference between first and quasi-steady vortex rings for the approach with ring formation included (FI).
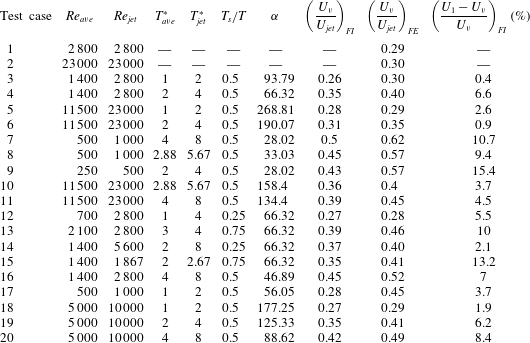
In this study, 18 periodic cases have been simulated for a range of average Reynolds numbers (
$Re_{ave}=U_{ave}D/\unicode[STIX]{x1D708}$
, where
$\unicode[STIX]{x1D708}$
is the kinematic viscosity), average non-dimensional periods (
$T_{ave}^{\ast }=TU_{ave}/D$
) and
$T_{s}/T$
, which are tabulated in table 1, accompanied by their related jet Reynolds numbers (
$Re_{jet}=U_{jet}D/\unicode[STIX]{x1D708}$
), jet non-dimensional periods (
$T_{jet}^{\ast }=TU_{jet}/D$
) and Womersley numbers (
$\unicode[STIX]{x1D6FC}=D\sqrt{2\unicode[STIX]{x03C0}/T\unicode[STIX]{x1D708}}$
). For biological flows, the Reynolds number is typically between 50 and 4000 (Colin & Costello Reference Colin and Costello2002; Gopalakrishnan et al.
Reference Gopalakrishnan, Pier and Biesheuvel2014). The Reynolds number in engineering applications is relatively higher, e.g. around 10 000 for underwater robots that employ vortex ring thrusters (Krieg & Mohseni Reference Krieg and Mohseni2008). Therefore, a range of
$Re_{ave}$
from 250 to 11 500 has been investigated here (table 1). Note that average non-dimensional period
$T_{ave}^{\ast }$
is equivalent to the formation time (
$T_{s}U_{jet}/D=L/D$
, where
$L$
is the stroke length) because
$U_{ave}T=U_{jet}T_{s}$
according to (2.1). For a broad range of flow conditions, the formation number is approximately 4 (Gharib et al.
Reference Gharib, Rambod and Shariff1998). Consequently, a range of
$T_{ave}^{\ast }$
from 1 to 4 has been investigated here (table 1). Three stroke ratios
$T_{s}/T$
of 0.25, 0.5 and 0.75 are also investigated (table 1).
2.3 Vortex detection and validation
We have validated our method against experimental data of Webster & Longmire (Reference Webster and Longmire1998) by simulating their exact set-up (test cases 1 and 2 in table 1). It is noted that these test cases are non-periodic, in contrast to the rest of the test cases (3 to 20). For numerical simulations (including those in § 3), the location of vortex ring core centres were detected by plotting the out-of-plane vorticity field on the mid-plane of the domain and locating the points with maximum vorticity magnitude similar to what is done in experiments. The location of the vortex core centres (
$S$
) were measured with respect to the edge of the cylinder, as shown in figure 1(a). For test cases 1 and 2, the vortex cores were tracked after
$tU_{jet}/D=1$
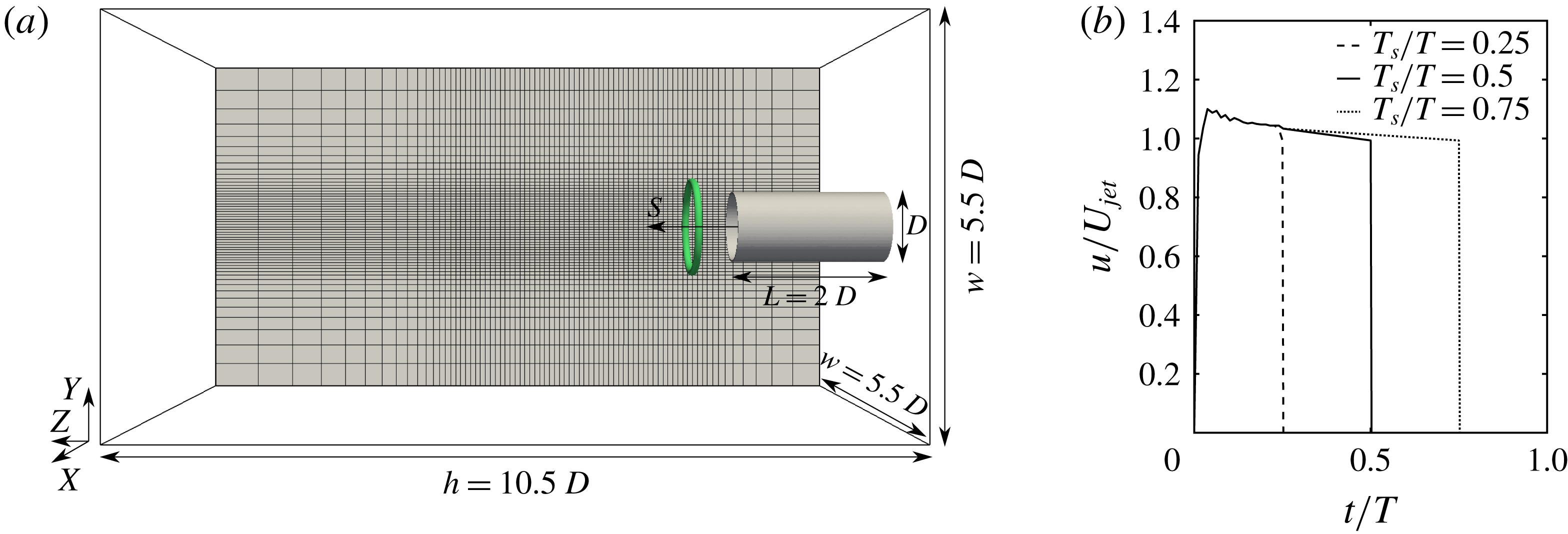
, when the ring is fully formed and detached, similar to the experiments (Webster & Longmire Reference Webster and Longmire1998). This is better demonstrated in figure 2, which shows the out-of-plane vorticity contours and velocity vectors for case 1 at three time instants. The plus sign denotes the location of highest vorticity, i.e. the vortex core centre. The results are in good agreement with the visualizations of Webster & Longmire (Reference Webster and Longmire1998). In figure 2, the thick green lines depict the vortex core boundaries identified by the Burgers’ vortex model.
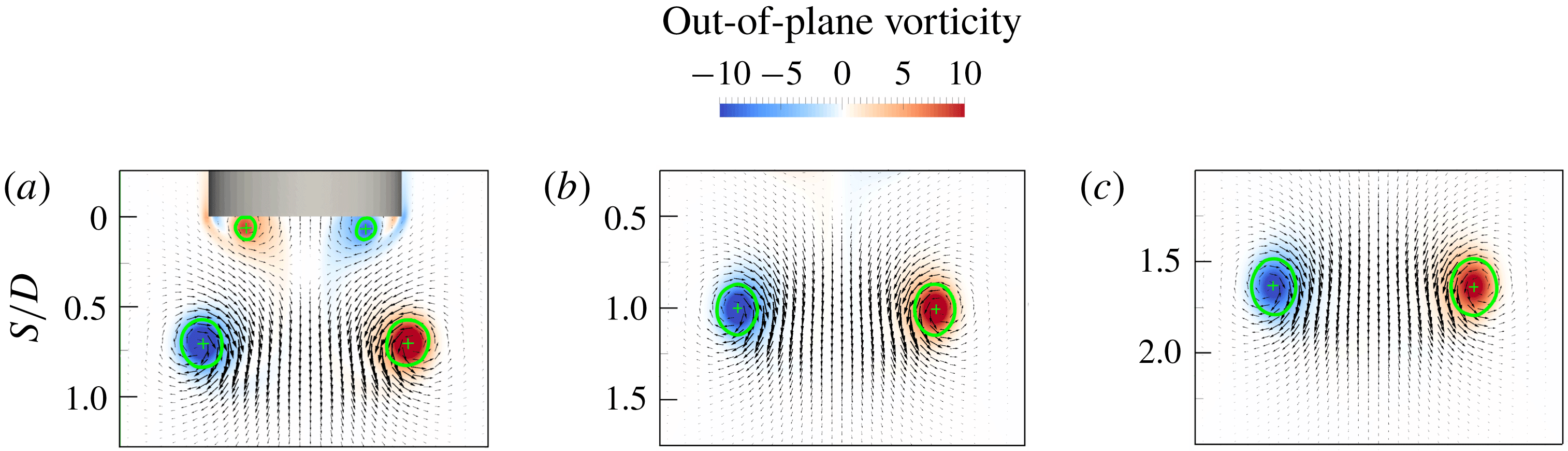
Figure 2. Out-of-plane vorticity contours and velocity vectors for test case 1 at times (a)
$tU_{jet}/D=2.62$
, (b)
$tU_{jet}/D=3.68$
and (c)
$tU_{jet}/D=5.8$
. The thick green lines and plus signs depict vortex ring core boundaries and their centres, respectively.
The Burgers’ vortex model is the exact solution of the Navier–Stokes equations for a steady viscous vortex where the stretching and viscous effects are in balance (Davidson Reference Davidson2015); therefore, the total variation of enstrophy,
$\unicode[STIX]{x1D6FA}=(\unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{i})/2$
, is zero, where
$\unicode[STIX]{x1D714}_{i}$
is the
$i$
th component of vorticity. The total variation of enstrophy for an incompressible flow with constant viscosity is (Taveira et al.
Reference Taveira, Diogo, Lopes and da Silva2013):
$$\begin{eqnarray}\frac{\text{D}\unicode[STIX]{x1D6FA}}{\text{D}t}=\unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{j}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}+\frac{1}{Re}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x2202}x_{j}\unicode[STIX]{x2202}x_{j}}-\frac{1}{Re}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}_{i}}{\unicode[STIX]{x2202}x_{j}}.\end{eqnarray}$$
Based on the Burgers model, the vortex centre is located at the peak vorticity while the boundaries of vortex cores are defined as the locations around the core centre at which the ratio of vorticity magnitude to peak vorticity equals to
$e^{-1}$
(Burgers Reference Burgers1948; Jahanbakhshi, Vaghefi & Madnia Reference Jahanbakhshi, Vaghefi and Madnia2015). The probability density functions (PDFs) of the absolute value of the total variation of enstrophy are concentrated around zero for all the test cases at different time instants. Consequently, the stretching and viscous effects are in balance. This justifies using Burgers’ model for detecting vortical structures in this study.
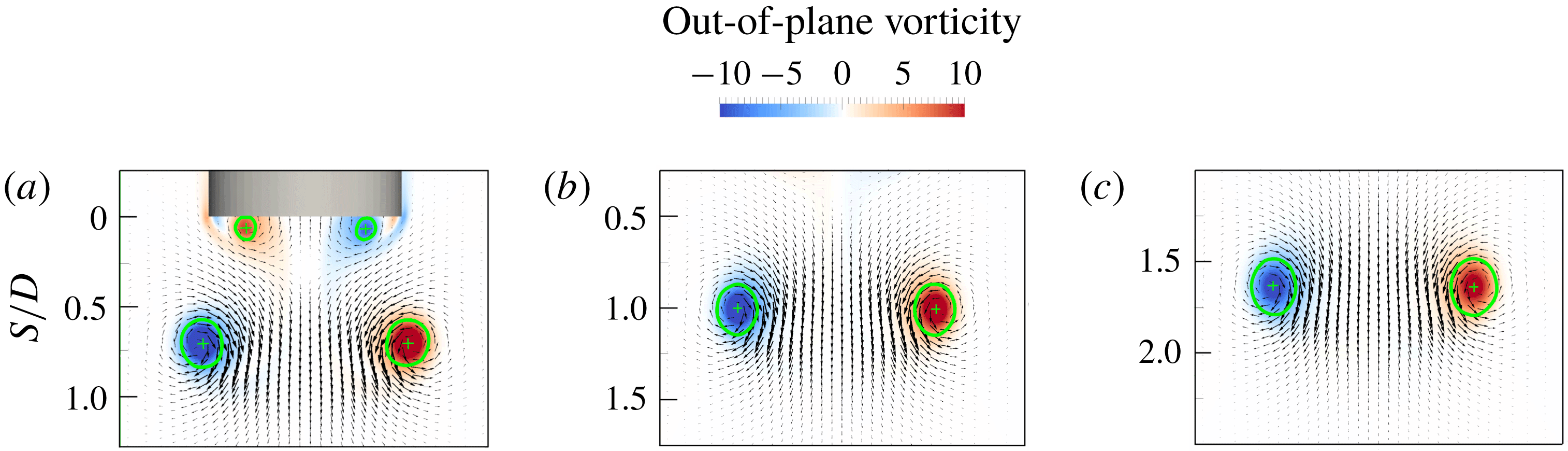
Figure 3. Comparisons of vortex core centre locations of simulations on grids 1 and 2 with 15 and 54 million grid points, respectively, against experimental data (Webster & Longmire Reference Webster and Longmire1998): (a)
$Re_{jet}=2800$
(case 1) and (b)
$Re_{jet}=23\,000$
(case 2).
The vortex core centre locations for experimental data were extracted from the velocity field and flow visualization figures reported in Webster & Longmire (Reference Webster and Longmire1998) using WebPlotDigitizer software. The time histories of the location of the vortex ring core centres are shown in figure 3. The numerical results follow the experimental ones closely for both low
$Re_{jet}=2800$
simulations (figure 3
a) and high
$Re_{jet}=23\,000$
using LES (figure 3
b). The experimental results for the first case (figure 3
a) show an upward curvature, which is not observed in the numerical results for case 2, and might be due to our approximation of the core centres from the reported figures because such an increase in velocity is not expected after the rings are fully formed. In fact, the propagation speed is expected to slightly decay for long times (Sullivan et al.
Reference Sullivan, Niemela, Hershberger, Bolster and Donnelly2008). To rule out that this is due to the resolution of our grid, a grid dependency study was also performed for case 1 (see figure 3
a) with a finer grid, labelled grid 2, with 54 million grid points, against the original grid, labelled grid 1, with 15 million grid points. The resolution of grid 2 is twice that of grid 1 in the region of interest. As can be observed in figure 3, the core centre locations of grid 1 are within 4 % of those of grid 2 and show the same trend, i.e. the results are independent of the grid resolution.
3 Results
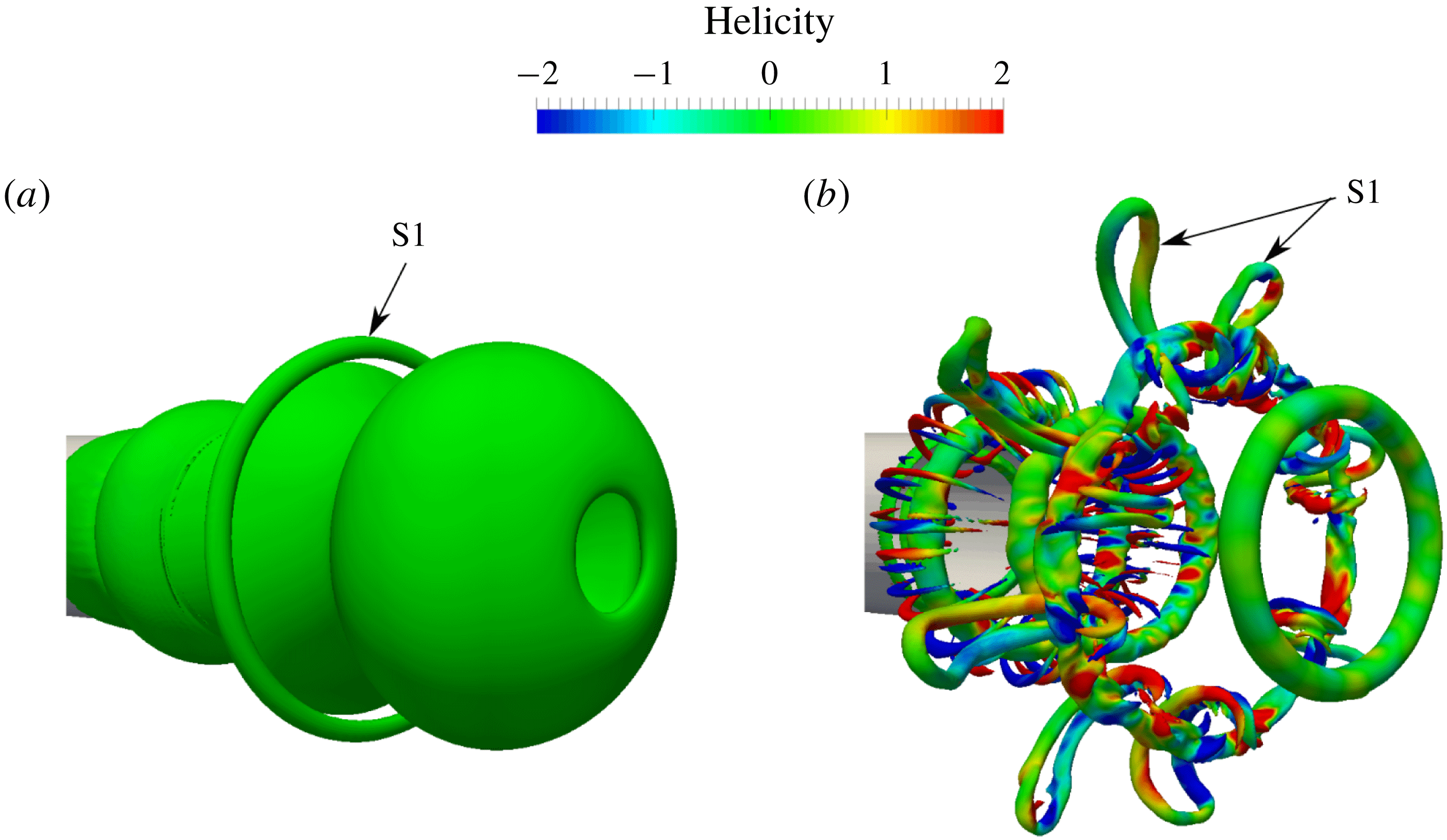
3.1 Vortex dynamics of periodic rings
The dynamics of vortex rings in a periodic set-up is an interesting phenomenon. In order to study the interaction of vortex rings, the isosurfaces of vorticity magnitude
$|\unicode[STIX]{x1D714}|$
coloured with helicity density contours (Moffatt Reference Moffatt1969) are presented in figures 4–7. Here, we describe the interaction of vortex rings in the transient regime until the periodic state is reached for case 3, and then discuss the effects of non-dimensional period and
$Re$
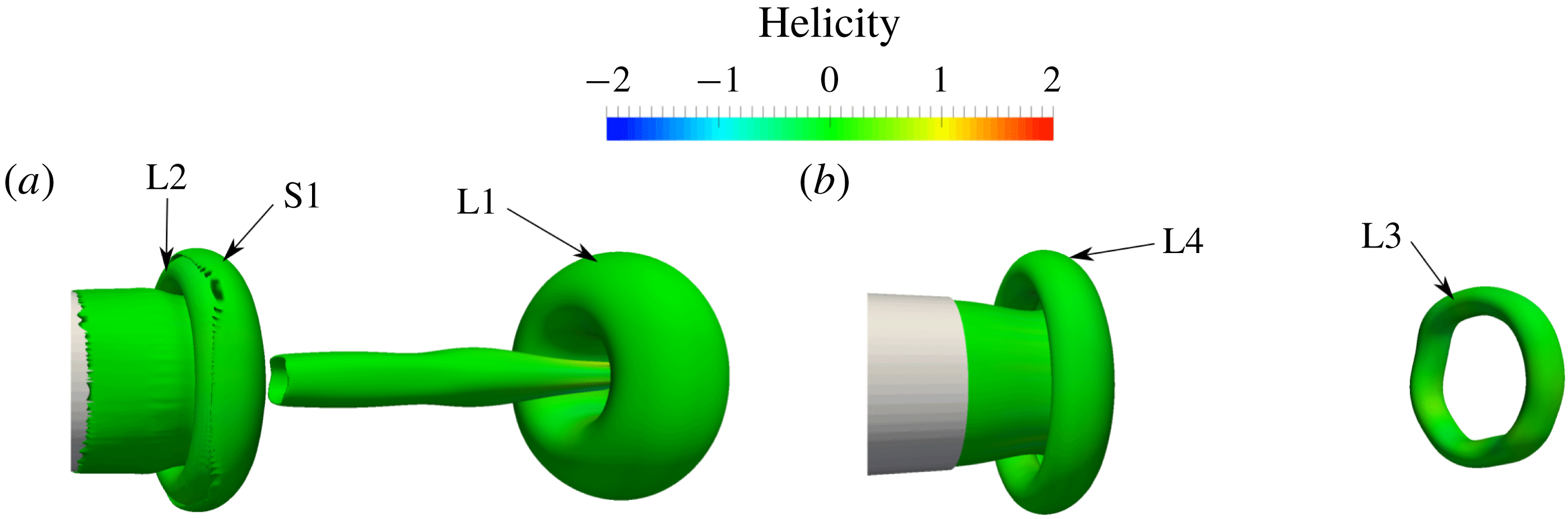
. Figure 4(a) shows that the velocity induction by the first leading vortex (L1) over the first stopping vortex (S1) toward its centre reduces its diameter and causes it to go through L1. Note that the second leading vortex (L2) has higher translational velocity relative to the other vortex rings. While S1 goes through L1, L2 gets closer to them and induces a velocity, which increases their diameter. Again, the velocity induction by L1 causes the engulfment of the L2 (figure 4
b) and consequently, L2 induces some backward velocity over S1, pushing it to the back of L1. The close interaction of S1 with the stronger vortex L1 creates wavy structures on the weaker vortex S1 which leads to Tsi–Widnall instability (figure 4
c) (Allen & Auvity Reference Allen and Auvity2002).
Figure 4. Vortex rings for case 3 (
$Re_{ave}=1400,T_{ave}^{\ast }=1$
) at times (a)
$t/T=2$
, (b)
$t/T=2.65$
, (c)
$t/T=3.75$
, (d)
$t/T=4.5$
, (e)
$t/T=5$
and (f)
$t/T=8$
visualized by plotting the
$|\unicode[STIX]{x1D714}|=4$
isosurface of vorticity magnitude and coloured by helicity density contours. Movies of the isosurface of vorticity magnitude coloured by helicity density contours and out-of-plane vorticity on mid-plane for this test case are provided in movies 1 and 2 of the supplementary material available at https://doi.org/10.1017/jfm.2018.529, respectively.
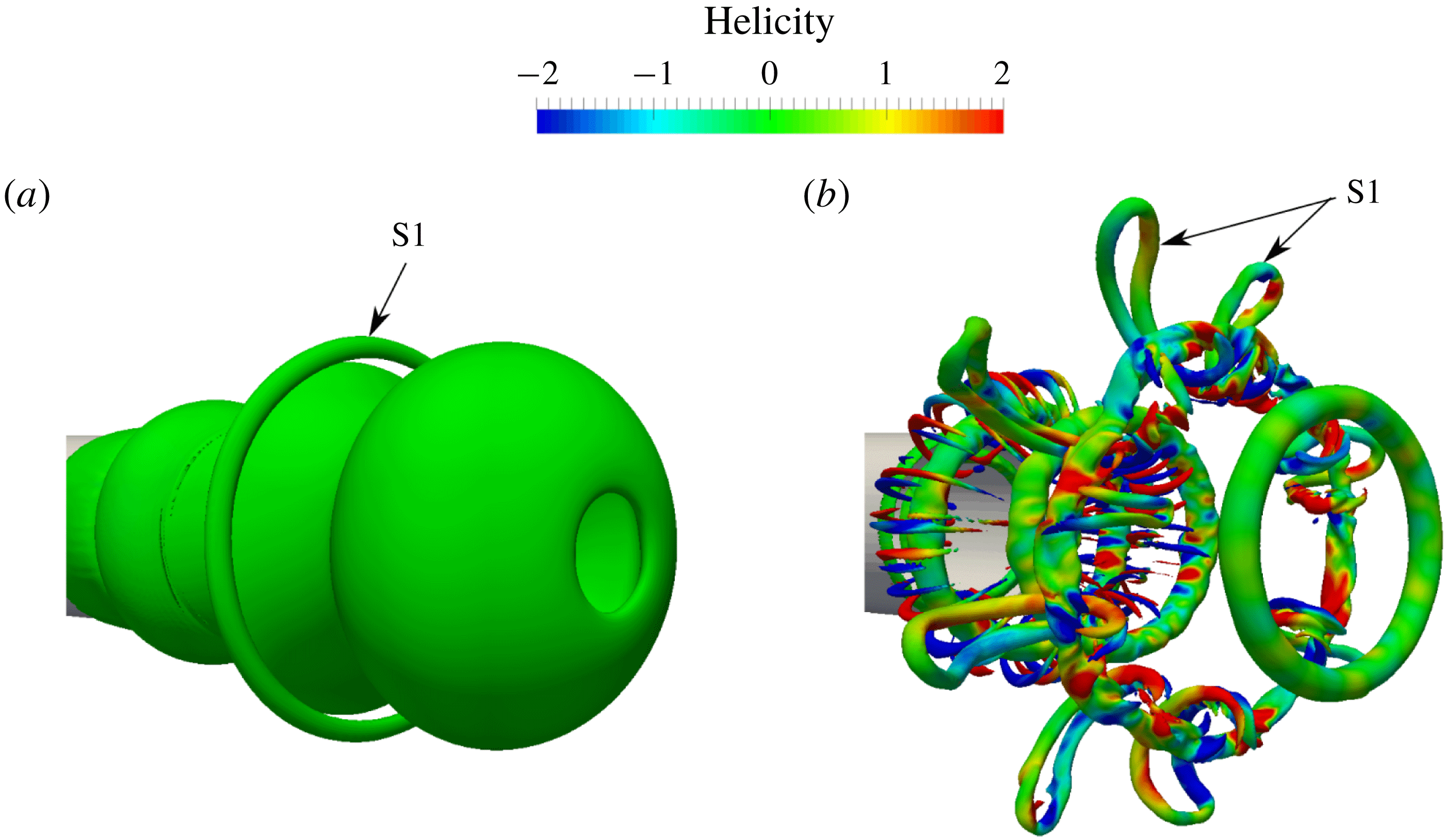
Figure 5. Effect of
$Re$
on the shape of the first stopping vortex ring (S1) at time
$t/T=3.75$
: (a) case 17 with
$Re_{ave}=500$
and (b) case 5 with
$Re_{ave}=11\,500$
, visualized by plotting the
$|\unicode[STIX]{x1D714}|=1$
and
$|\unicode[STIX]{x1D714}|=9$
isosurfaces of vorticity magnitude for (a) and (b), respectively and coloured by helicity density contours.
$T_{ave}^{\ast }=1$
for both cases.
The shapes of Tsi–Widnall instabilities are
$Re$
dependent (Saffman Reference Saffman1978). Figure 5 shows the shape of S1 for a lower
$Re_{ave}=500$
and a higher
$Re_{ave}=11\,500$
at time
$t/T=3.75$
. For the one with lower
$Re_{ave}$
, S1 is completely circular (figure 5
a), but by increasing
$Re_{ave}$
, instabilities appear and intensify (figure 5
b). For
$Re_{ave}=1400$
, L1 and S1 are not connected (figure 4
c); however, by increasing
$Re_{ave}$
, S1 ties around L1 (figure 5
b).
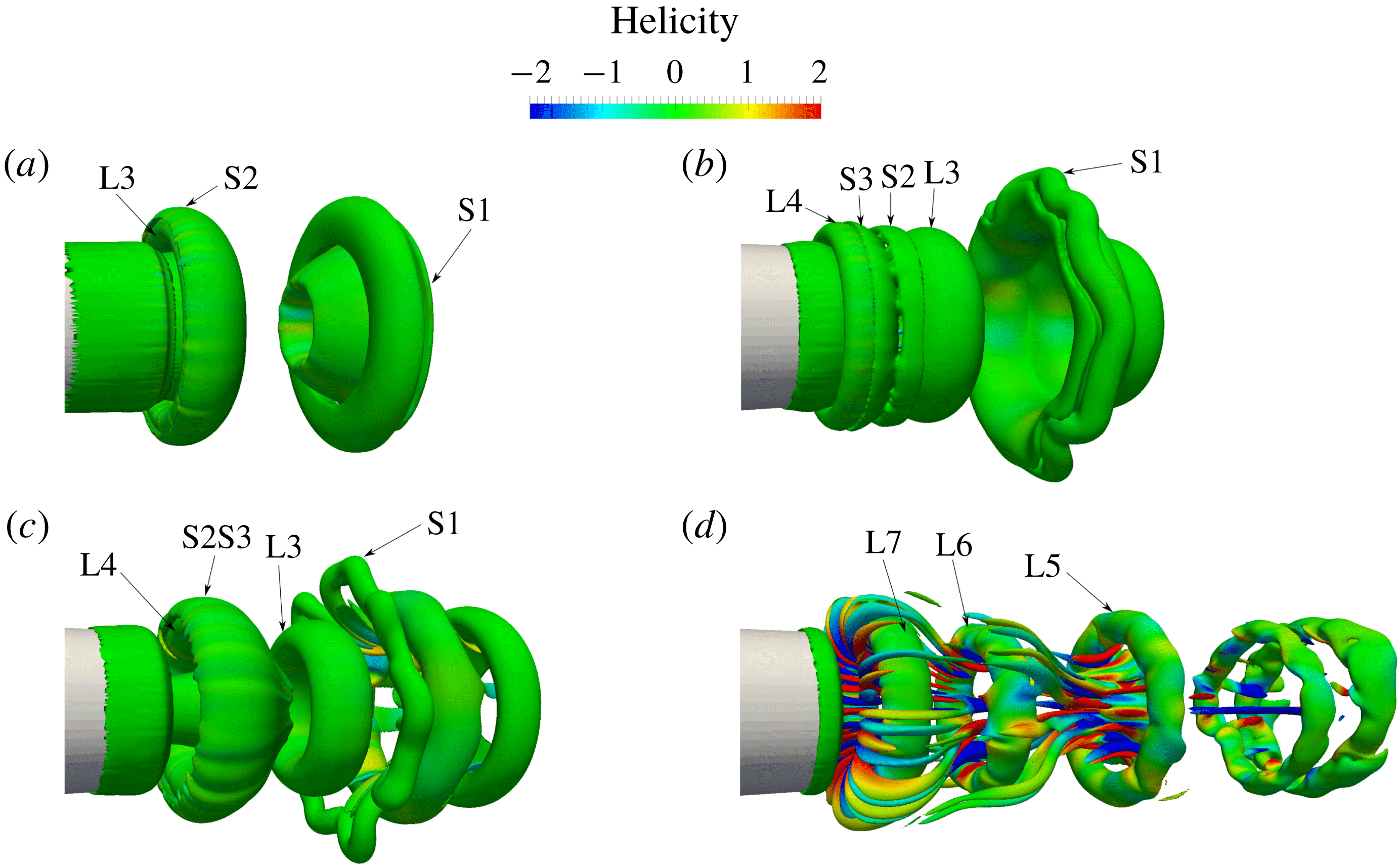
As shown in figure 4(d), the breakdown of S1 spreads the instabilities throughout the domain, distorting the two closest leading vortices (L1 and the third leading vortex (L3)). Figure 4(e) shows the hairpin vortices generated upstream around the fifth leading vortex (L5), which are indeed the stopping vortices disturbed by the instabilities. In order to study the interaction of stopping vortices, isosurfaces of vorticity with a lower magnitude are illustrated in figure 6 for the same test case, as stopping vortices are weaker than the leading vortices. Figure 6(a) shows the perfect tubular second stopping vortex (S2) that surrounds L3. As L3 moves forward, S2 and the third stopping vortex (S3) get closer (figure 6 b) and merge together – see the resultant vortex (S2S3) in figure 6(c). However, later, by the breakdown of S1 and the spread of instabilities, the stopping vortex rings lose their tubular shape and turn into hairpin vortices (figures 4 f and 6 d).
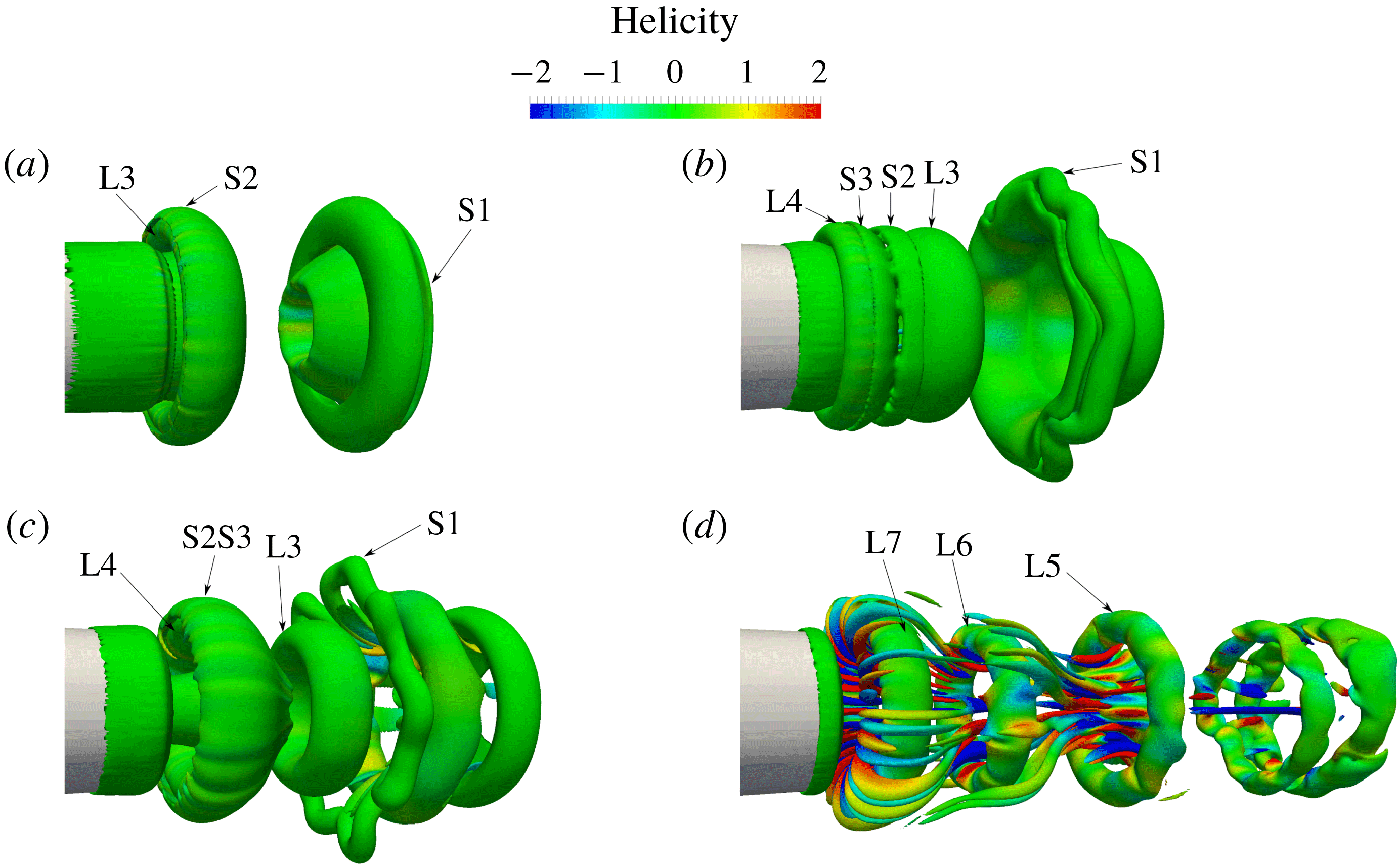
Figure 6. Stopping vortex rings for case 3 at times (a)
$t/T=2.5$
, (b)
$t/T=3.25$
, (c)
$t/T=3.85$
and (d)
$t/T=6.9$
visualized by plotting
$|\unicode[STIX]{x1D714}|=1$
,
$|\unicode[STIX]{x1D714}|=2$
and
$|\unicode[STIX]{x1D714}|=4$
isosurfaces of vorticity magnitude for (b,c), (a) and (d), respectively and coloured by helicity density contours.
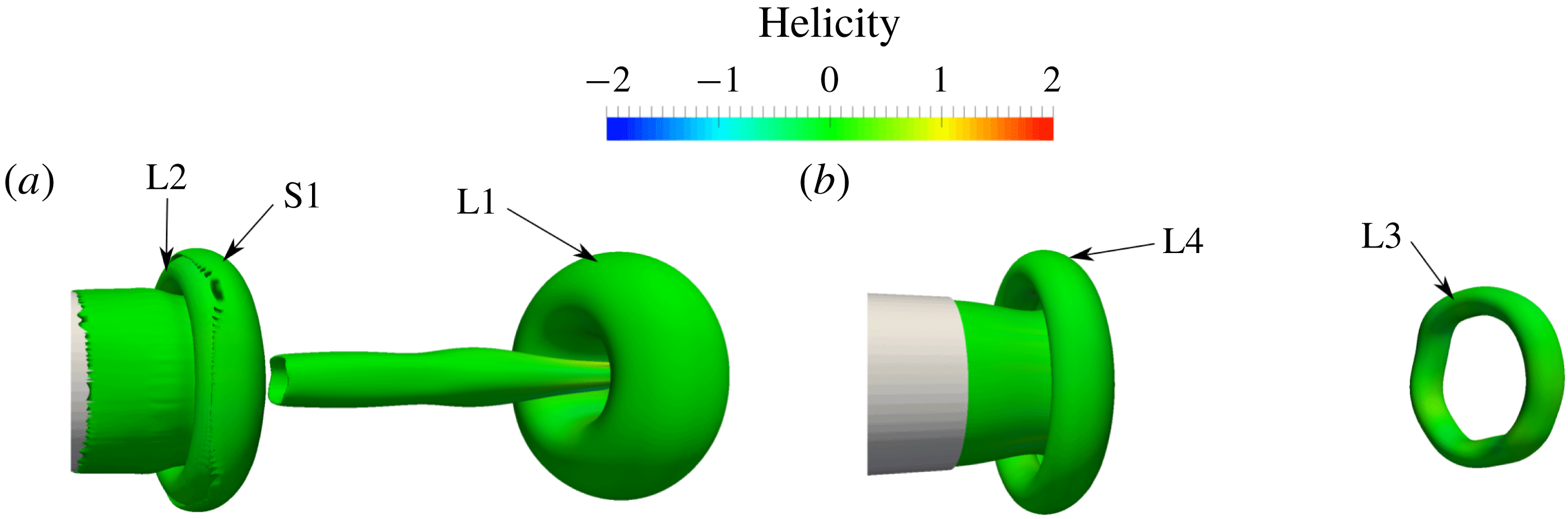
Figure 7. Vortex rings for case 16 (
$Re_{ave}=1400,T_{ave}^{\ast }=4$
) at times (a)
$t/T=2.25$
and (b)
$t/T=6.5$
, visualized by plotting
$|\unicode[STIX]{x1D714}|=0.7$
and
$|\unicode[STIX]{x1D714}|=5$
isosurfaces of vorticity magnitude, respectively and coloured by helicity density contours. The rings remain tubular at high
$T_{ave}^{\ast }$
.
The breakdown of S1 and the consequent effects over other stopping vortices was not observed for lower
$Re_{ave}=500$
. In addition, for higher
$Re_{ave}=11\,500$
, S2 and S3 turn into hairpin vortices before the breakdown of S1, as observed in figure 5(b), which might be because of the existence of immediate instabilities for vortex rings at high Reynolds numbers (Maxworthy Reference Maxworthy1972). Increasing
$T_{ave}^{\ast }$
causes S1 to surround L2, rather than L1, and to dissipate quickly without any breakdown – see figure 7(a) for test case 16. This simplifies the flow dynamics and makes reaching the quasi-steady state faster. Therefore, the stopping vortices for later periods remain tubular and the leading vortices show the same behaviour as previous periods. This is illustrated in figure 7(b) without the stopping vortices because of their very low vorticity magnitude. Note that the low vorticity long tubular structure that is located between
$L1$
and
$L2$
in figure 7(a) is the trailing jet (Gharib et al.
Reference Gharib, Rambod and Shariff1998) which is generated because of the relatively large formation time (
$T_{s}U_{jet}/D=4$
) for test case 16. These structures are also present in the quasi-steady state, but not observed in figure 7(b) because of their low vorticity magnitude.
In summary, there are two scenarios for stopping vortices after reaching the quasi-steady state. For cases with
$T_{ave}^{\ast }\leqslant 2$
and
$Re_{ave}\geqslant 1400$
, the leading vortices are surrounded by hairpin vortices which are actually the deformed precedent stopping vortices – similar to figure 6(d). By decreasing
$Re_{ave}$
or increasing
$T_{ave}^{\ast }$
, the stopping vortices surrounding the leading ones remain weak and intact (figure 7
b).
All our test cases reached quasi-steady (cyclic) state and show two distinct interaction patterns (figure 8): (a) the cases that show vortex pairing at short
$T_{ave}^{\ast }=1$
; and (b) the ones that do not pair and form a train of rings at high
$T_{ave}^{\ast }\geqslant 2$
. For cases with short
$T_{ave}^{\ast }=1$
, the quasi-steady flow field consists of three different zones. Zone 1 is defined as the distance propagated by a quasi-steady ring in a one period time interval staring from the edge of the cylinder. Here, the rings form, detach and propagate in the domain (see vortex ring L16 in figure 8
a). Zone 2, which starts from the end of zone 1 and extends approximately 4 to 5 times the length of zone 1, is where the quasi-steady vortex rings pair up and merge together (vortex rings L15, L14 and L12L13 in figure 8
a). This phenomenon starts with the acceleration of one of the rings and reduction in its diameter due to velocity inductions. In figure 8(a), the first pair of rings (L15 and L14) at the beginning of zone 2 shows the onset of the pairing process. It is clear that the stretched core of one of the vortex rings (L15) ties around the circular one (L14). The second vortex ring at the end of zone 2 in the same figure (L12L13) is indeed two vortex rings after the pairing process. Zone 3, which is located after the end of zone 2, is where the vortex rings become unstable and break down. Since this zone is mostly located at low-resolution part of the computational grid, the exact location of zone 3 may not be accurate. The approximate locations of these zones are shown in figure 8(a) for case 3 which shows the pairing process. Our results are consistent with the requirements for vortex pairing of Zaman & Hussain (Reference Zaman and Hussain1980). The
$T_{ave}^{\ast }=1$
for this flow pattern is within the bounds of Strouhal number (
$St_{D}=D/U_{ave}T=0.85$
; equivalent to
$T_{ave}^{\ast }=1/St_{D}=1.18$
) reported by Zaman & Hussain (Reference Zaman and Hussain1980) for the ‘jet column mode’ of vortex pairing. Additionally, their measured pairing location (
$S/D=1.75$
) is placed in our zone 2 for this flow pattern.
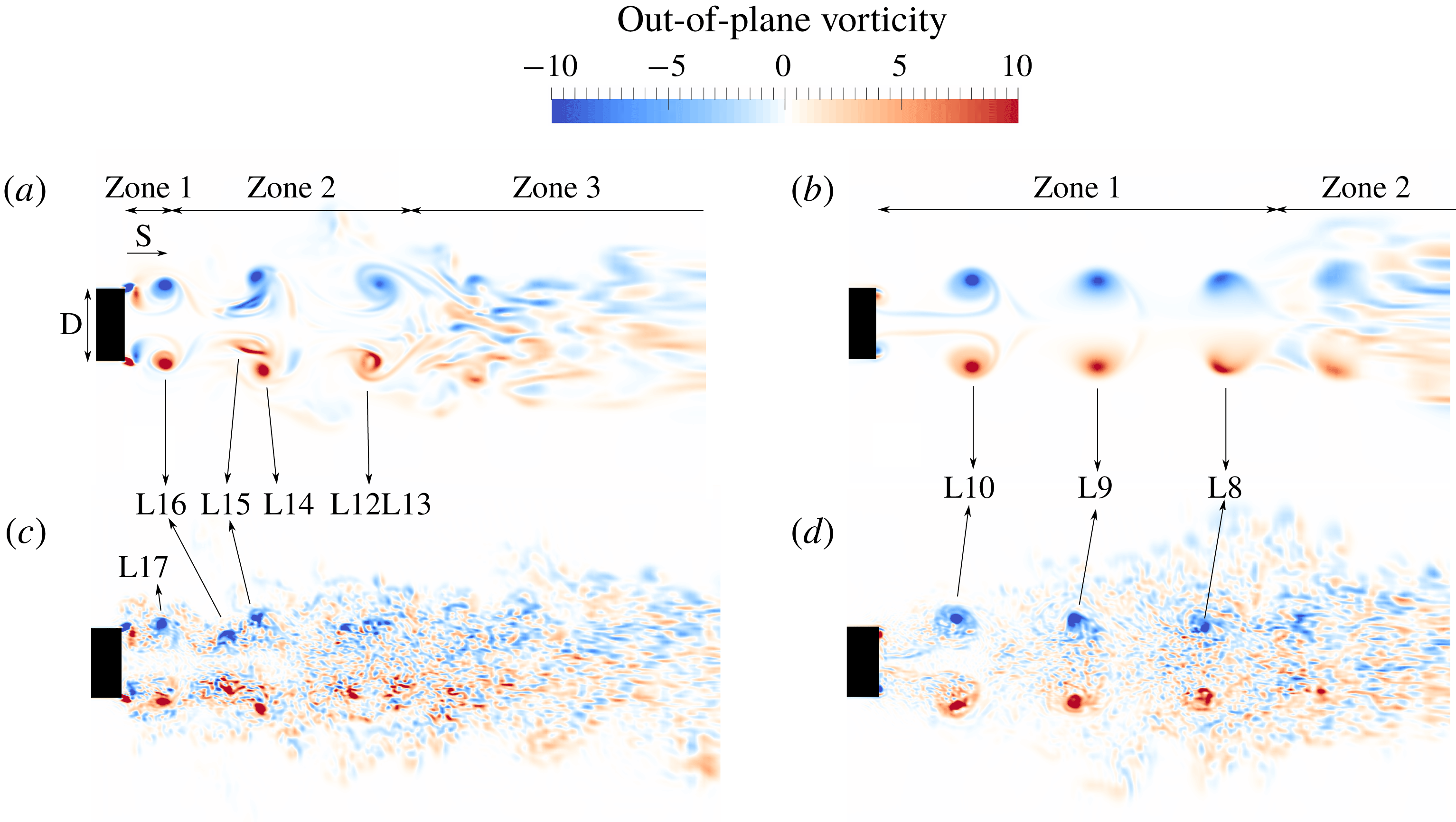
Figure 8. Out-of-plane vorticity contours of two distinct quasi-steady flow patterns for (a) case 3 (
$Re_{ave}=1400$
,
$T_{ave}^{\ast }=1$
), (b) case 4 (
$Re_{ave}=1400$
,
$T_{ave}^{\ast }=2$
), (c) case 5 (
$Re_{ave}=11\,500$
,
$T_{ave}^{\ast }=1$
) and (d) case 6 (
$Re_{ave}=11\,500$
,
$T_{ave}^{\ast }=2$
). See the movies of these flow patterns (a to d) in movies 3, 4, 5 and 6 of the supplementary material, respectively.
For cases with longer
$T_{ave}^{\ast }\geqslant 2$
, the flow pattern includes only two zones. Zone 1, similar to the first zone of the previous pattern, is where the vortex rings develop, pinch off and propagate (see vortex rings L10, L9 and L8 in figure 8
b). However, for this pattern, the length of zone 1 is relatively higher (equivalent to the distance a quasi-steady ring travels in 3 to 4 periods). For these cases, the vortex rings do not pair up after reaching quasi-steady state, due to the relatively higher distance between the rings. However, vortex rings become unstable and break out just after the end of zone 1. We called this part of the domain zone 2 for this pattern. Figure 8(b) illustrates this flow pattern for case 4.
Figures 8(c) and 8(d) show flow patterns for cases 5 and 6, respectively. Comparing these figures with figure 8(a,b), shows that increasing the Reynolds number does not affect the quasi-steady flow patterns. However, it destabilizes the pairing process (Zaman & Hussain Reference Zaman and Hussain1980) in zone 2 for the first flow pattern which delays the reaching of quasi-steady state.
It is clear that vortex interaction in zone 2 of the first flow pattern could affect the cyclic state of zone 1. However, the interaction of vortices in zone 2 (the pairing process) follows a distinct pattern which is cyclic itself – see the movies of out-of-plane vorticity on the mid-plane during quasi-steady state for cases 3 and 5 in movies 3 and 5 of the supplementary materials. There are still some small cycle-to-cycle variations in zone 1 because of the vortex interactions in zone 2. We quantified such variations by defining a 2 % threshold for the difference in the trajectory of a vortex ring in zone 1 with respect to the previous ring in that zone. In this study, all of the test cases reached the cyclic state before the analysis of their propagation. Our results show that cases with the second flow pattern, i.e. without vortex pairing in zone 2, reach a cyclic state in 3 to 4 cycles, irrespective of their
$Re_{ave}$
. However, it takes more cycles for cases with the first flow pattern to reach a cyclic state due to vortex pairing in zone 2. Since a high
$Re_{ave}$
destabilizes the vortex pairing process (Zaman & Hussain Reference Zaman and Hussain1980), increasing
$Re_{ave}$
for these cases makes reaching the cyclic state take even longer.
3.2 Propagation of vortex rings
In this section, the time histories of the location of the vortex rings are presented for all periodic test cases. Since the simulations are started from at rest condition, the propagation of the vortex rings should reach quasi-steady state. The number of periods required to reach quasi-steady state varied between 4 and 9 for different test cases. As mentioned before, the flow is considered to be quasi-steady if the change in time history of the location of a vortex ring with respect to its previous ring is less than 2 % during the first period after the formation of those vortices. In this study, we tracked vortex rings for a time interval of
$T$
for all the periodic test cases to make sure that they remain in the fine region of our grid. Additionally, the aforementioned pairing phenomenon in zone 2 for cases with low
$T_{ave}^{\ast }$
(figure 8
a,c) causes one of the rings to expand and accelerate and the other to shrink and decelerate when they get closer. Therefore, the propagation is only tracked in zone 1 before the paring process. For the cases without pairing, tracking the vortex rings for a longer time does not affect our conclusions.
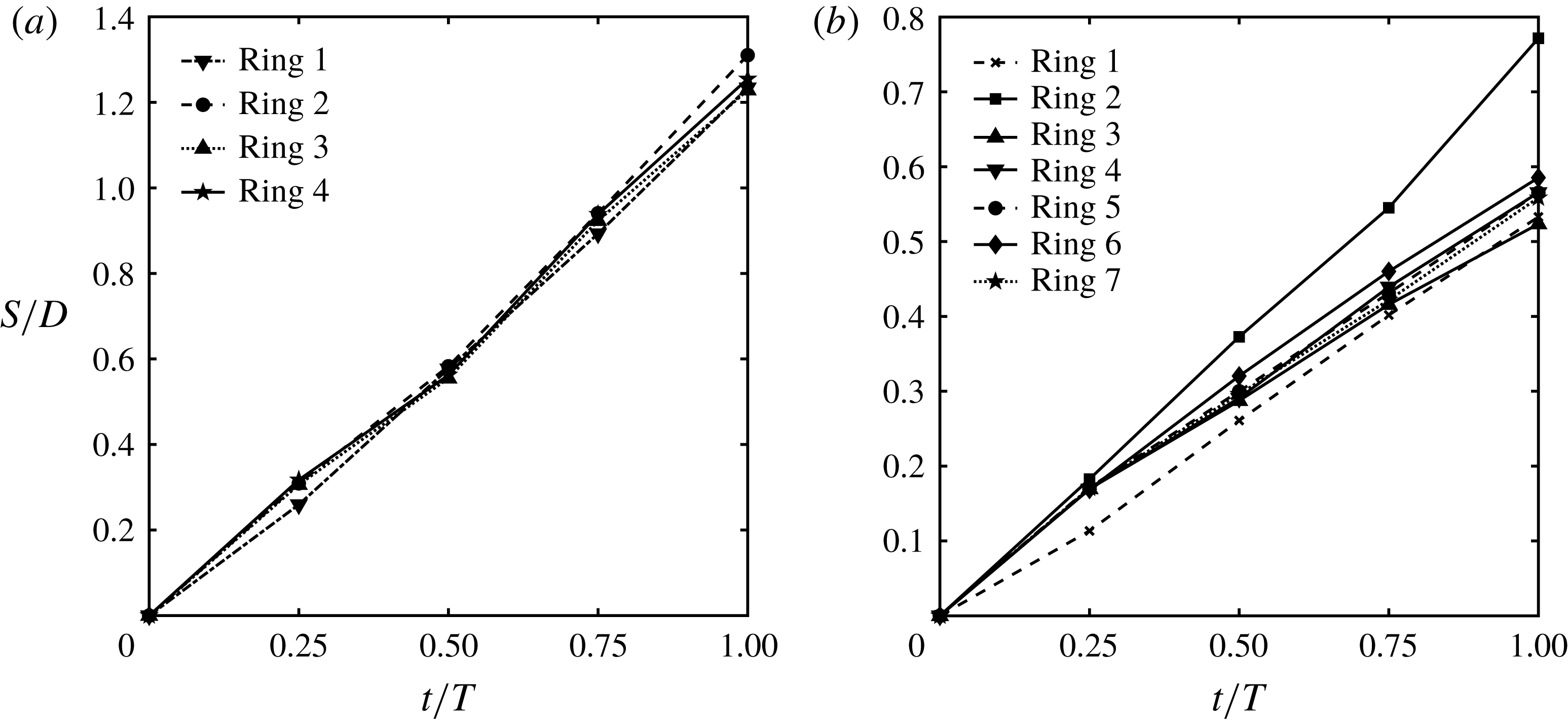
Figure 9. Location of vortex rings until reaching quasi-steady condition for test cases (a) 6 and (b) 5, travelled in one period. The movies for these cases are provided in movies 7 and 8 of the supplementary material, respectively.
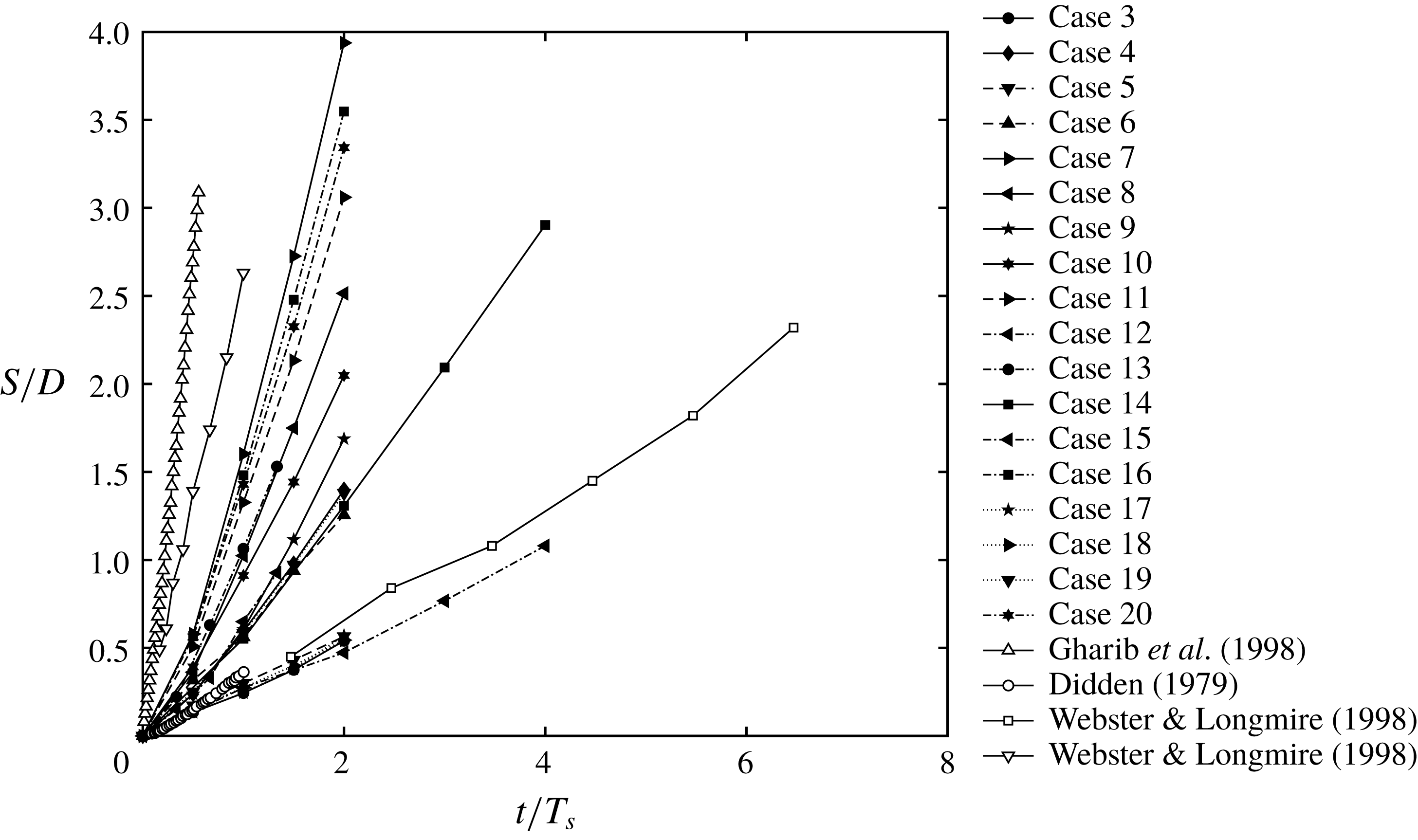
Figure 10. The location of vortex ring core centres of different numerical and experimental test cases.
Reaching the quasi-steady state is shown for test case 6 in figure 9(a). For cases with high
$T_{ave}^{\ast }$
like this case, the interaction of the vortices is negligible for a few periods after the formation of a vortex and, consequently, the propagation of vortex cores becomes quasi-steady after only 4 periods. Note that even small differences in the ring’s velocity before reaching the quasi-steady state can lead to a high level of interactions after several periods, e.g. ring 2 is engulfed by ring 1 in case 6 after four periods, as can be observed in Movie 7 in the supplementary materials, even though it is only slightly faster than ring 1 (figure 9
a). However, for these test cases, as the flow reaches quasi-steady state, a train of vortices is formed (figure 8
d). For cases with shorter
$T_{ave}^{\ast }$
, the interaction between the vortex rings plays an important role during the first periods after the formation of a vortex and it takes longer to reach the quasi-steady state – see figure 9(b) for case 5.
Figure 10 shows the locations of the vortex rings for all periodic test cases during quasi-steady state accompanied by experimental data. It should be noted that all the experimental data are non-periodic. Therefore, we used the stroke time
$T_{s}$
, instead of period
$T$
, to normalize time. The data of Gharib et al. (Reference Gharib, Rambod and Shariff1998) are for
$Re=6000$
and a formation time (
$T_{s}U_{jet}/D$
) of 14.5, which is equivalent to
$T_{ave}^{\ast }$
. The two sets of data for Webster & Longmire (Reference Webster and Longmire1998) are the same as those discussed in § 2.3 with a formation time of 1. The data of Didden (Reference Didden1979) are for
$Re=2300$
and a formation time of 1.4. As mentioned in § 1, Didden (Reference Didden1979) reported an exponential trend for the time history of the locations of vortex core centres; however, figure 10 shows that after reaching the quasi-steady state, all of the test cases, including the data of Didden (Reference Didden1979), can be approximated as linear with an R-squared, a statistical measure of how well the fitted regression line approximates the real data points (Devore Reference Devore2011), of greater than 0.97.
By dividing the slope of the lines in figure 10 by their corresponding
$T_{ave}^{\ast }$
and taking into account the relation between
$U_{jet}$
and
$U_{ave}$
(2.1), the propagation velocity of vortex rings
$U_{v}/U_{jet}$
(
$U_{v}=S/t$
) is calculated. It can be observed that the slopes are not the same for different cases and show a wide spread (figure 10). The effect of different parameters on the vortex ring velocity will be further discussed in the next section.
The slopes are calculated using two approaches: (i) calculating the slope from the core centres tracked only after the ring is fully formed and detached from the cylinder, i.e. ring formation excluded (FE) similar to Sullivan et al. (Reference Sullivan, Niemela, Hershberger, Bolster and Donnelly2008); and (ii) calculating the slope from all core centres tracked starting from the jet inflow initiation, i.e. ring formation included (FI). There are several methods in the literature for detecting the pinch-off process, e.g. using the trailing pressure maximum (Lawson & Dawson Reference Lawson and Dawson2013; Schlueter-Kuck & Dabiri Reference Schlueter-Kuck and Dabiri2016). We used Burgers’ model, as discussed in § 2.3, to detect the core boundaries and considered vortex rings pinched off when their boundaries completely disconnected from the cylinder. Including the formation process only slightly decreases the accuracy (R-squared value) of the linear fit, and it can still be considered linear for the duration presented here as observed in figure 10.
Propagation velocity
$U_{v}/U_{jet}$
for both of the above approaches are tabulated in table 1. It can be observed that including the vortex formation process decreases the computed velocity because of two reasons: (i) the rings propagate slightly slower during the formation process and their speed increases as they are formed in short times after their initiation (Didden Reference Didden1979); and (ii) tracking for a period and excluding vortex formation extends the tracking to the next inflow cycle. The next inflow cycle pushes the vortex under study forwards, causes its velocity to slightly increase compared to the approach which includes the formation process. Note that based on our results, similar to the experimental results of Maxworthy (Reference Maxworthy1977), the formation process is strongly
$Re$
dependent. Our results show that the formation process takes from approximately
$T/4$
(for cases with
$Re_{ave}>500$
) up to
$3T/4$
(for cases with
$Re_{ave}\leqslant 500$
) after the inflow initiation for quasi-steady vortex rings. Different durations of the formation process make it difficult to use the FE approach to find an empirical relation for vortex propagation as a function of time because the
$t=0$
at which the vortex is detached varies depending on the formation process. In contrast, the
$t=0$
in the approach which includes the formation process is defined based on the inflow (figure 1
b) and does not depend on
$Re_{ave}$
,
$T_{ave}^{\ast }$
or other parameters, i.e. it is suitable for finding an empirical relation for vortex propagation
$S/D$
with time
$t/T_{s}$
(figure 10).
For the approach which includes the formation process, the velocity of the first vortex (
$U_{1}$
) can be considered the velocity of an isolated vortex before the second vortex ring appears, i.e. for
$t/T<1$
. The difference between
$U_{1}$
and the quasi-steady one (
$U_{v}$
) are reported in table 1 for the approach which includes the formation process. The other approach shows the same trend. Based on the results, the difference varies between less than 1 % for case 3 and approximately 15 % for case 9. For the lowest
$T_{ave}^{\ast }=1$
, the difference varies between approximately 1 and 6 %. However, for the highest
$T_{ave}^{\ast }=4$
, it changes between approximately 5 and 11 % depending on
$Re_{ave}$
.
4 Discussion
The vortex core velocity is a function of these dimensional parameters:
$$\begin{eqnarray}U_{v}=F(U_{ave},U_{jet},T,T_{s},D,\unicode[STIX]{x1D708}),\end{eqnarray}$$
where
$F$
is a function that relates
$U_{v}$
to the other variables. One possible arrangement of non-dimensional parameters is
$U_{v}/U_{jet}=F(Re,T^{\ast },T_{s}/T,U_{ave}/U_{jet})$
. Considering the relation
$U_{ave}/U_{jet}=T_{s}/T$
(see § 2.2), two of the non-dimensional groups are equivalent. Consequently, we can eliminate
$U_{ave}/U_{jet}$
:
$$\begin{eqnarray}\frac{U_{v}}{U_{jet}}=F\left(Re,T^{\ast },\frac{T_{s}}{T}\right).\end{eqnarray}$$
$Re$
and
$T^{\ast }$
in (4.2) could be defined using either the average or jet velocity. Our results (figure 11
a) show that by choosing the average velocity in the definition of Reynolds number and the non-dimensional period and keeping both fixed, different values of
$T_{s}/T$
does not affect the vortex ring velocity substantially for both formation process excluded and included approaches; however, using the jet velocity results in different vortex ring velocities (figure 11
a). Based on linear fits to the points in figure 11(a), using
$U_{jet}$
in the definition of
$Re$
and
$T^{\ast }$
gives slopes of 0.35 and 0.25 for the formation process excluded and included approaches, respectively. On the other hand, using the average velocity gives slopes as small as 0.03 for both approaches. Note that
$Re$
can also be defined based on initial circulation of the vortex ring and be approximated as
$Re_{\unicode[STIX]{x1D706}}=U_{jet}^{2}T_{s}/2\unicode[STIX]{x1D708}$
(Gan & Nickels Reference Gan and Nickels2010). By using this definition of
$Re$
and
$T_{jet}^{\ast }$
or
$T_{ave}^{\ast }$
, the vortex ring velocity shows dependency on the stroke ratio. Based on our results, for a fixed
$Re_{\unicode[STIX]{x1D706}}=1400$
and
$T_{ave}^{\ast }=1$
, changing
$T_{s}/T$
from 0.75 to 0.5 increases
$U_{v}/U_{jet}$
by 21 % and 26 % for the formation excluded and included approaches, respectively. On the other hand, by keeping
$Re_{\unicode[STIX]{x1D706}}=5600$
and
$T_{jet}^{\ast }=8$
and changing
$T_{s}/T$
from 0.25 to 0.5,
$U_{v}/U_{jet}$
increases by 30 % and 23 % for formation excluded and included approaches, respectively. Therefore, we choose to define
$Re$
and
$T^{\ast }$
based on
$U_{ave}$
to have
$U_{v}/U_{jet}$
be approximately independent of
$T_{s}/T$
, i.e. a simpler scaling law
$U_{v}/U_{jet}\approx F(Re_{ave},T_{ave}^{\ast })$
. Note that this result is limited to waveforms illustrated in figure 1(b). Hereafter,
$Re$
=
$Re_{ave}$
and
$T^{\ast }$
=
$T_{ave}^{\ast }$
for simplicity.
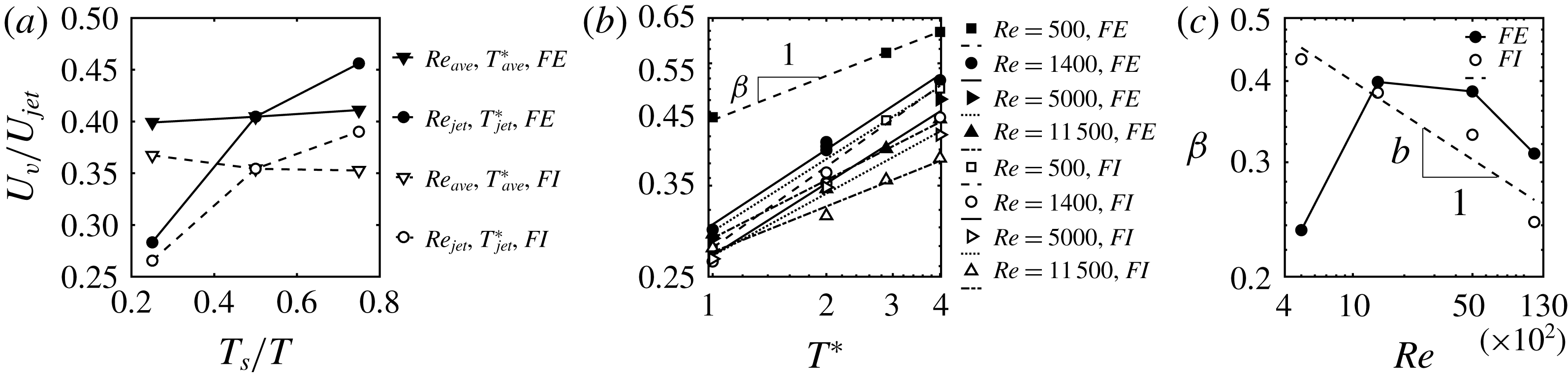
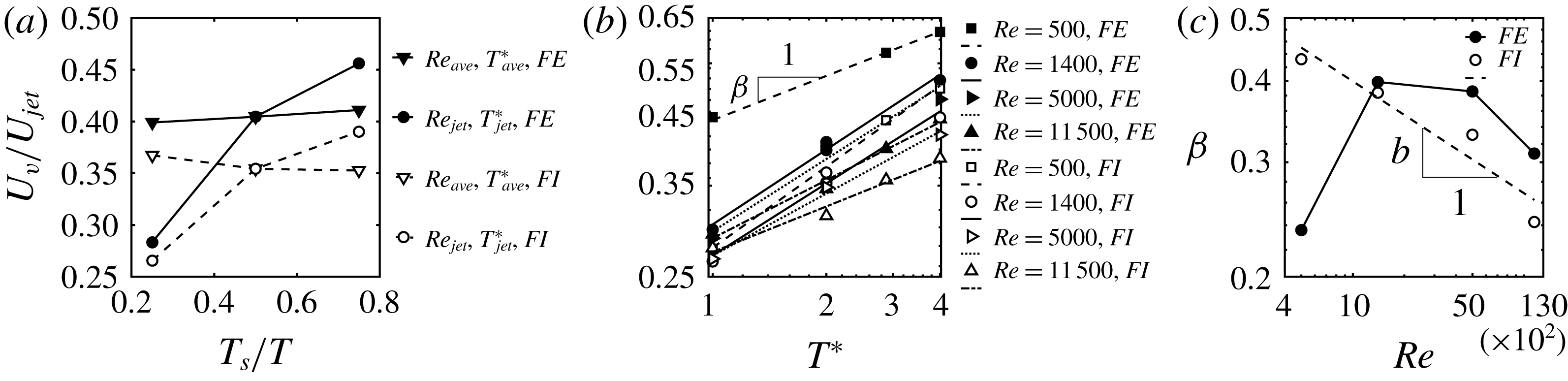
Figure 11. Vortex core velocity analysis with both ring formation excluded (FE) and ring formation included (FI): (a) the effect of
$T_{s}/T$
on vortex ring velocity for fixed
$Re$
and
$T^{\ast }$
, which are defined based on the average or jet inflow velocity, (b) the vortex velocity versus non-dimensional period for different
$Re$
on a log–log scale and (c) the slopes of the lines in (b) for relevant
$Re$
on a log–log scale.
We investigate how
$U_{v}/U_{jet}$
scales with
$Re$
and
$T^{\ast }$
by plotting
$U_{v}/U_{jet}$
versus
$T^{\ast }$
for different Reynolds numbers on a log–log scale (see figure 11
b). These lines with an R-squared greater than 0.97, closely represent lines with slope
$\unicode[STIX]{x1D6FD}$
on a log–log scale, i.e. a power law with exponent
$\unicode[STIX]{x1D6FD}$
and coefficient
$c$
(
$U_{v}/U_{jet}=cT^{\ast \unicode[STIX]{x1D6FD}}$
). Figure 11(b) shows that for a fixed non-dimensional period, the ratio of
$U_{v}/U_{jet}$
reduces by increasing the Reynolds number, e.g. it goes from 0.5 to 0.39 by increasing
$Re$
from 500 to 11 500 at
$T^{\ast }=4$
for the approach which includes the formation process. It can also be observed that for a fixed
$Re$
, increasing the
$T^{\ast }$
would increase
$U_{v}/U_{jet}$
, which is consistent with the results of Krueger (Reference Krueger2010) (see his figure 4b), e.g.
$U_{v}/U_{jet}$
changes from 0.28 to 0.5 by increasing
$T^{\ast }$
from 1 to 4 at
$Re=500$
when the formation process is included. Based on the above results,
$U_{v}/U_{jet}$
is more sensitive to
$T^{\ast }$
than
$Re$
. Note that
$T^{\ast }$
here is equivalent to formation time (Gharib et al.
Reference Gharib, Rambod and Shariff1998) as discussed in § 2.2.
We plot the exponent of the power law (
$\unicode[STIX]{x1D6FD}$
) as a function of their
$Re$
on a log–log scale (see figure 11
c). It is clear that the functional form of
$\unicode[STIX]{x1D6FD}$
depends on the velocity calculation approach. The results for the approach which includes the formation process with a relatively high accuracy, R-squared approximately 0.92, can be approximated by a line of slope
$b$
, i.e. a power law with exponent
$b$
(
$\unicode[STIX]{x1D6FD}=aRe^{b}$
). Consequently:
$$\begin{eqnarray}\frac{U_{v}}{U_{jet}}=cT^{\ast aRe^{b}},\end{eqnarray}$$
where,
$a=1.31$
,
$b=-0.2$
and
$c=0.27$
based on all of the lines in figure 11(b,c) when the formation process is included. It is interesting that the limit of (4.3) for very high
$Re$
, provides the vortex ring velocity as 0.27 of
$U_{jet}$
, which is consistent with empirical results of Sullivan et al. (Reference Sullivan, Niemela, Hershberger, Bolster and Donnelly2008). As shown in figure 11(c), the approach which excludes the formation process has the same trend as the other approach until
$Re=1400$
, i.e.
$\unicode[STIX]{x1D6FD}$
increases as
$Re$
decreases, but for the low
$Re=500$
the trend does not continue probably because of the large duration of formation process (
$3T/4$
) compared to higher
$Re$
cases (
$T/4$
). This approach is problematic because the reference time (
$t=0$
) to initiate the tracking and finding of a relation varies from case to case as the time required for the formation of the rings varies with
$Re$
– see the discussion at the end of the previous section. This makes the approach which includes the formation process a better candidate for an empirical relation for the location
$S/D$
as a function of time (figure 10) as the time in this approach is clearly defined based on the flow pulse at the inflow (
$t=0$
coincides with the start of the inflow in each period). Nevertheless, because
$\unicode[STIX]{x1D6FD}$
does not vary much with
$Re$
, we can approximate
$\unicode[STIX]{x1D6FD}$
as a constant, i.e.
$\unicode[STIX]{x1D6FD}\approx 0.3$
for the approach that excludes the formation process. This will provide us an approximation which is independent of
$Re$
, which we will investigate as well.
Considering that the translational velocity of the vortex ring is the displacement of its core centre in the streamwise direction over the required time, we can take
$S=U_{v}t$
. By dividing both sides of this equation by
$D$
and multiplying the right-hand side to
$U_{ave}T/U_{jet}T_{s}$
, which is equal to unity, we get:
$$\begin{eqnarray}\frac{S}{D}=\frac{U_{v}}{U_{jet}}\frac{U_{ave}T}{DT_{s}}t.\end{eqnarray}$$
Now, by substituting non-dimensional period
$T^{\ast }=U_{ave}T/D$
, equation (4.4) becomes:
$$\begin{eqnarray}\frac{S}{D}=\frac{U_{v}}{U_{jet}}T^{\ast }\frac{t}{T_{s}}.\end{eqnarray}$$
By substituting
$U_{v}/U_{jet}$
from (4.3), one can obtain:
$$\begin{eqnarray}\frac{S}{D}=(0.27T^{\ast 1+1.31Re^{-0.2}})\frac{t}{T_{s}}.\end{eqnarray}$$
This equation provides a scaling law for the location of vortex ring core centres at different Reynolds numbers and non-dimensional periods (formation times). Substituting
$T^{\ast }$
based on its relation with the Reynolds and Womersley numbers (
$T^{\ast }=2\unicode[STIX]{x03C0}Re/\unicode[STIX]{x1D6FC}^{2}$
), equation (4.6) is written in terms of Womersley and Reynolds numbers:
$$\begin{eqnarray}\frac{S}{D}=\left[0.27\left(\frac{2\unicode[STIX]{x03C0}Re}{\unicode[STIX]{x1D6FC}^{2}}\right)^{1+1.31Re^{-0.2}}\right]\frac{t}{T_{s}}.\end{eqnarray}$$
We see that if the Womersley number is kept constant, contrary to when
$T^{\ast }$
is kept constant (4.6), increasing
$Re$
will increase vortex propagation. Also, by fixing
$Re$
and increasing Womersley number, vortex propagation decreases as predicted by Asgharzadeh & Borazjani (Reference Asgharzadeh and Borazjani2016).
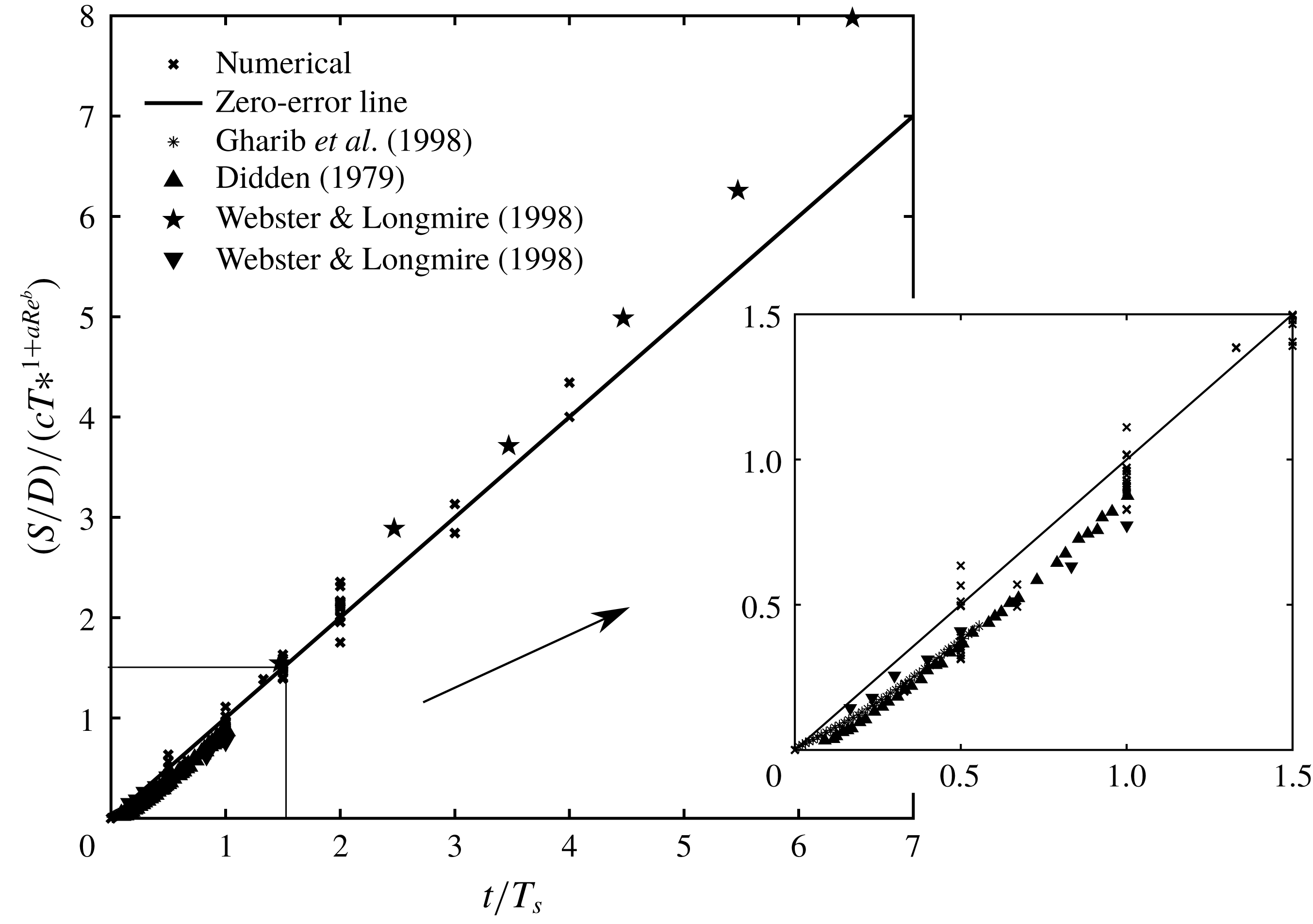
Figure 12. Location of vortex ring core centres after scaling for numerical and experimental test cases.
To see if the proposed relation (4.6) can scale the data of figure 10,
$S/D$
scaled with (4.6) is plotted against
$t/T_{s}$
in figure 12. In this figure, equation (4.6) is a line with slope one (zero error line). The proposed relation not only collapses the numerical data of figure 10 around the zero error line, but also the scattered experimental data (shown more closely in the inset of figure 12), which were not part of the curve fitting process (4.3). This is probably due to the fact that the quasi-steady velocity of the vortex ring is close (maximum 15 % difference) to the velocity of the initial (isolated) one as discussed in the previous section. Note that we did not check this scaling for closely spaced rings which interact even after reaching the quasi-steady condition. In fact, this might be another reason that the proposed scaling for periodically generated rings works for isolated ones as well. In the scaling of the experimental data, which are non-periodic, formation time (
$T_{s}U_{jet}/D$
) is used which is equivalent to
$T^{\ast }$
here. Therefore, the above scaling can be used for non-periodic rings as well by using the formation time in place of
$T^{\ast }$
.
It is interesting to observe that the experimental data for non-periodic rings (except
$\star$
Webster & Longmire (Reference Webster and Longmire1998)) fall below the zero error line as observed in figure 12. It seems that during the early formation of the vortex (
$t/T_{s}<0.25$
) the isolated rings propagate slower relative to the zero error line, but after they are fully formed, their trajectory follows almost the same slope as the zero error line. The slower speed of isolated rings during the formation process has been previously observed (Didden Reference Didden1979). The data for our periodic rings fall both above and below the line. We have observed that the periodic rings are also slightly slower during the formation process, but it is overshadowed by the effect of
$Re$
and
$T^{\ast }$
on the propagation of periodic rings. As we discussed for figure 11(b), the propagation speed is more sensitive to
$T^{\ast }$
than
$Re$
. Removing
$Re$
from the equation by considering the limit of
$Re\rightarrow \infty$
, equation (4.6) simplifies to
$S/D=(0.27T^{\ast })t/T_{s}$
which shows a noticeable degradation in the collapse of data (R-squared
$=$
0.88). Considering a constant
$\unicode[STIX]{x1D6FD}\approx 0.3$
(not
$\unicode[STIX]{x1D6FD}=aRe^{b}$
) for (4.3) and substituting into (4.5) provides another formulation for
$S/D=(0.27T^{\ast 1.3})t/T_{s}$
that is independent of
$Re$
. This formulation collapses the data (R-squared
$=$
0.97) almost as well as (4.6) (R-squared
$=$
0.98). The underlying reason is the small variation of
$\unicode[STIX]{x1D6FD}$
(
$0.24<\unicode[STIX]{x1D6FD}<0.43$
) for the range of
$Re$
of our test cases – see figure 11(c). Although including
$Re$
does not seem to be necessary for the range of
$Re$
tested here, such an approximation might not work well for very high
$Re$
(
$Re\gg 10\,000$
cases, which were not investigated here due to their high computational cost). In addition, it is clear from figure 11(b) that the increase of
$Re$
at a constant
$T^{\ast }$
decreases the propagation speed, i.e. excluding
$Re$
from the equation reduces the accuracy.
5 Conclusion
Based on different test cases for a range of Reynolds numbers, non-dimensional periods and stroke ratios (
$T_{s}/T$
), an empirical relation (4.6) for the location of periodically generated vortex rings is proposed. This equation not only scales the numerical results but also collapses the results of experiments for non-periodic rings (figures 10 and 12). Based on our results, the number of cycles needed to reach the periodic state is controlled by
$T_{ave}^{\ast }$
. For cases with short
$T_{ave}^{\ast }=1$
, it takes more cycles to reach quasi-steady (cyclic) state because of the pairing process downstream of the newly generated ring. The stability of this process for these test cases is affected by
$Re_{ave}$
. Our observations in the cyclic state show that for low
$T_{ave}^{\ast }\leqslant 2$
and high
$Re_{ave}\geqslant 1400$
, the stopping vortices deform into hairpin vortices and envelop the leading ones. However, by increasing
$T_{ave}^{\ast }$
or decreasing
$Re_{ave}$
, the original form of the stopping vortices are maintained. The results show that the periodic vortex ring velocity is close to the velocity of an isolated one (maximum 15 % difference). Based on our results, the vortex velocity
$U_{v}/U_{jet}$
becomes independent of the stroke ratio when the average velocity is used in definition of Reynolds number and non-dimensional period. In this way, vortex ring velocity becomes only a function of the Reynolds number and non-dimensional period. The vortex ring velocity is more sensitive to non-dimensional period (formation time) than the Reynolds number, and depends on them according to a power law (4.3). The results show that for a fixed non-dimensional period, vortex ring velocity decreases by increasing the Reynolds number. However, if the Womersley number is kept constant (instead of the non-dimensional period) then the vortex ring velocity increases by increasing the Reynolds number (4.7). On the other hand, keeping the Reynolds number fixed and reducing the non-dimensional period (increasing the Womersley number) decreases the vortex ring velocity.
Acknowledgements
This work was supported by AHA grant 13SDG17220022, NIH grant R03EB014860 and the Center of Computational Research (CCR) of University at Buffalo. We thank the anonymous referees whose comments has improved this paper.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2018.529.
