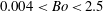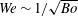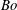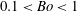1 Introduction
Collapse of small bubbles at liquid surfaces is a ubiquitous phenomenon in nature. It is a fascinating fundamental problem because of the interconnection between capillary, gravity and viscous forces. The bubble breakup process at a free surface and the subsequent jetting was visualised first by Woodcock et al. (Reference Woodcock, Kientzler, Arons and Blanchard1953) using high-speed photographic techniques who identified the following three stages: (i) the retraction and fragmentation of the top thin film, (ii) the collapse of the unstable cavity formed due to the absence of the thin film and (iii) formation and breakup of the jet. Kientzler et al. (Reference Kientzler, Arons, Blanchard and Woodcock1954) conducted experiments with a range of bubble sizes and found that the bubble collapse time decreases with decreasing bubble size. For small bubbles of radii less than 3 mm, the complete process till jetting occurs in a time of the order of
$10^{2}$
–
$10^{3}~\unicode[STIX]{x03BC}\text{s}$
with jet velocities of the order of
$1~\text{m}~\text{s}^{-1}$
to more than
$10~\text{m}~\text{s}^{-1}$
, when viscous damping can be neglected. This phenomenon is of importance in ocean–atmosphere exchange where micro-sized aerosol drops are generated by the fragmentation of the thin film, followed by larger droplets due to the jet breakup, which are still one order of magnitude less than the bubble radius; both these drops contribute to the sea–air exchange (Blanchard Reference Blanchard1963; MacIntyre Reference MacIntyre1972; Spiel Reference Spiel1995; Lhuissier & Villermaux Reference Lhuissier and Villermaux2012). In carbonated beverages such as sparkling wine, small bubbles are desired because the aerosols created by their collapse enhances the aroma (Liger-Belair, Seon & Antkowiak Reference Liger-Belair, Seon and Antkowiak2012). The aerosol generation by bubble bursting is found to be the mechanism behind the distinctive odour (petrichor) after the first rain (Joung & Buie Reference Joung and Buie2015). Bubble bursting at a compound interface, such as the interface formed after oil spill at the ocean surface, can lead to reverse mass transport of free surface materials into the bulk of the liquid (Feng et al.
Reference Feng, Roché, Vigolo, Arnaudov, Stoyanov, Gurkov, Tsutsumanova and Stone2014). In bio-reactors, bursting of free surface bubbles can cause mass scale bacterial cell destruction around aeration sites (Boulton-Stone & Blake Reference Boulton-Stone and Blake1993). In recent studies Shakhova et al. (Reference Shakhova, Semiletov, Leifer, Sergienko, Salyuk, Kosmach, Chernykh, Stubbs, Nicolsky and Tumskoy2014) found that thawing of the subsea Arctic permafrost in East Siberia releases methane, a greenhouse gas, and the transfer of this gas to the atmosphere is mediated by bubbles and their subsequent bursting at the ocean surface. The study reveals that bubbles, during stormy times, enhance the methane flux transfer from ocean to atmosphere. For all these reasons, this problem has received considerable attention so far.
A first attempt to understand the physics behind jetting from free surface bubble collapse was made by MacIntyre (Reference MacIntyre1972), who conducted experiments with dyed bubbles, and proposed a boundary layer flow along the bubble cavity which causes a stagnation pressure at the bottom of the cavity, causing jet formation. The bubble collapse at an air–water interface was first simulated numerically by Boulton-Stone & Blake (Reference Boulton-Stone and Blake1993) (herein after BSB) for a range of bubble radii
$0.5~\text{mm}<R<3~\text{mm}$
who then estimated the resulting jet velocities. Spiel (Reference Spiel1995) measured the velocities of the first drops from air bubbles bursting at a water surface and proposed an empirical exponential dependence of jet velocity on
$R$
. A more comprehensive analysis of the scaling of jet velocities (
$U_{j}$
) was done by Duchemin et al. (Reference Duchemin, Popinet, Josserand and Zaleski2002), who performed direct numerical simulations for a wide range of sizes
$1.4~\unicode[STIX]{x03BC}\text{m}<R<20~\text{mm}$
of air bubbles in water; they showed that
$U_{j}/U_{\unicode[STIX]{x1D707}}\sim (R/R_{\unicode[STIX]{x1D707}})^{-1/2}$
, where
$U_{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D707}$
and
$R_{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D707}^{2}/\unicode[STIX]{x1D70C}\unicode[STIX]{x1D70E}$
are the viscous–capillary velocity and length scales, with
$\unicode[STIX]{x1D70C}$
being the liquid density,
$\unicode[STIX]{x1D70E}$
the liquid–gas surface tension and
$\unicode[STIX]{x1D707}$
the dynamic viscosity. However, this dependence of
$U_{j}$
on
$R$
is not supported by the experimental results of Spiel (Reference Spiel1995) nor the numerical simulations of BSB which are closer to
$U_{j}\sim 1/R$
(Krishnan, Puthenveettil & Hopfinger Reference Krishnan, Puthenveettil, Hopfinger, Bai, Wang and Fang2012).
In order to answer this question of the dependence of jet velocity on bubble radius, and of the effects of viscosity and gravity on jet formation, experiments in other more viscous fluids and/or fluids of lower surface tension were needed. Such results, with different fluids, have recently been reported by Krishnan et al. (Reference Krishnan, Puthenveettil, Hopfinger, Bai, Wang and Fang2012) and Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014). Krishnan et al. (Reference Krishnan, Puthenveettil, Hopfinger, Bai, Wang and Fang2012) showed that, indeed, the viscous–capillary scaling (
$U_{j}\sim 1/\sqrt{R}$
) suggested by Duchemin et al. (Reference Duchemin, Popinet, Josserand and Zaleski2002) cannot collapse the experimental data, which displayed a
$1/R$
variation for an intermediate range of
$R$
. Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) showed that the gravity–capillary scaling,
$We\propto Bo^{-1/2}$
, (
$U_{j}\sim 1/R$
), collapse the data reasonably well for 0.007
${<}Bo<$
1, where the jet Weber number
$We=\unicode[STIX]{x1D70C}U_{j}^{2}R/\unicode[STIX]{x1D70E}$
and the Bond number
$Bo=\unicode[STIX]{x1D70C}gR^{2}/\unicode[STIX]{x1D70E}$
, with
$g$
being the acceleration due to gravity. However, as we show in this paper, such a scaling is unlikely to hold for
$Bo<0.1$
and
$Bo>$
1. Our data (see Krishnan et al.
Reference Krishnan, Puthenveettil, Hopfinger, Bai, Wang and Fang2012) can also be approximated by a
$Bo^{-1/2}$
dependence of
$We$
, but only for
$0.1<Bo<1$
, beyond which there are deviations from such a power law, as indicated also by the results of Spiel (Reference Spiel1995) and BSB. In Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014), viscous effects were expressed as a dependence of
$We\sqrt{Bo}$
on Morton number,
$Mo=Bo~Oh^{4}$
, where the Ohnesorge number
$Oh=\unicode[STIX]{x1D707}/\sqrt{\unicode[STIX]{x1D70C}R\unicode[STIX]{x1D70E}}$
. However, the extremely small values of
$Mo$
in their scaling (
$10^{-9}<Mo<10^{-6}$
) indicate the inadequacy of such a viscous scaling. These issues called for further experiments and a search for the appropriate
$Bo$
dependence of the jet
$We$
and the possible limits of the
$We\sim 1/\sqrt{Bo}$
‘power law’; the scaling of viscous effects also needed re-examination.
In this paper we show that the
$Bo$
dependence of the jet
$We$
is closely related to the square of the dimensionless cavity depth, which implies that there is no simple power-law scaling as proposed by Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014). We further show that the viscous damping effects are well captured by the Ohnesorge number, for which critical values for capillary wave damping, dominant viscous damping, the absence of jet breakup and the absence of jetting are given.
2 Experimental conditions
The experiments were conducted in a transparent acrylic tank of
$3.5\times 5~\text{cm}^{2}$
cross-sectional area and in a glass tank of
$5\times 5~\text{cm}^{2}$
cross-sectional area. The tanks were fixed on a levelling board and were filled up to the brim to avoid meniscus effects. We use distilled water and glycerol–water mixtures of 48 %, 55 %, 68 % and 72 % glycerine concentration (herein after referred to as GW48, GW55, GW68 and GW72). In addition to these fluids, we have used 2-propanol and ethanol for the measurement of static parameters of the bubble, the properties of all these fluids are given in table 1. Gas bubbles in the range of equivalent spherical radii
$0.17~\text{mm}<R<4.1~\text{mm}$
were produced by pumping air into glass capillary tubes of different sizes using a syringe pump operated at a constant discharge rate. The flow rate in the capillaries were selected so that the bubble detachment was within the periodic dripping regime described by Clanet & Lasheras (Reference Clanet and Lasheras1999) and the periodic bubbling regime of Oguz & Prosperetti (Reference Oguz and Prosperetti1993). Care was taken to avoid crowding and merging of bubbles at the free surface. Capillaries were carefully fixed in the same alignment throughout the experiments to avoid variations in bubble sizes (Doshi et al.
Reference Doshi, Cohen, Zhang, Siegel, Howell, Basaran and Nagel2003). The liquids were changed after each run to minimise surface contamination.
Table 1. Properties of the fluids, the range of radii of the bubbles and the range of dimensionless numbers used in the experiments.
$Bo=\unicode[STIX]{x1D70C}gR^{2}/\unicode[STIX]{x1D70E}$
,
$Oh=\unicode[STIX]{x1D707}/\sqrt{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70C}R}$
,
$Re=\unicode[STIX]{x1D70C}U_{j}R/\unicode[STIX]{x1D707}$
.
The rising bubbles, which are almost elliptical in shape, were photographed to determine the bubble volumes, from which the equivalent spherical radii
$R$
were calculated. The bubble stays at the free surface for a short time after its initial oscillations had died down and then bursts, giving rise to a vertical or nearly vertical jet. This time of stay for the smallest bubble of our experimentation (water,
$Bo=4.2\times 10^{-3}$
,
$Oh=9\times 10^{-3}$
) was 91 ms. The time of stay increased to more than 1 s with increasing
$Bo$
, i.e. beyond
$Bo=0.1$
, in water and glycerol–water mixtures. Since the bubbles do not break during their initial oscillations, possibly since the upper film is replenished, the bursting happens from a static configuration. This bursting process and the jet emergence from the free surface were captured by a high-speed camera (La Vision ProHS for frames per second (fps)
${\leqslant}19\,000$
and Photron SA4 for fps
${\leqslant}100\,000$
) using high intensity light emitting diode (LED) back lighting. The jet velocity was measured by tracking the tip of the jet in successive images, before the jet breaks up into drops. The image acquisition rates met the condition that
$t_{i}<1/|\text{d}U_{j}/\text{d}z|$
, where
$t_{i}=1~\text{fps}^{-1}$
. The spatial resolution was such that
$\unicode[STIX]{x0394}Z_{i}<U_{j}~t_{e}$
, where
$\unicode[STIX]{x0394}Z_{i}$
is the size of each pixel and
$t_{e}$
is the exposure time. The lowest and highest resolution for the imaging were
$27~\unicode[STIX]{x03BC}\text{m}~\text{pix}^{-1}$
and
$3.4~\unicode[STIX]{x03BC}\text{m}~\text{pix}^{-1}$
. The corresponding jet diameters were 1.3 mm and 0.03 mm respectively; the jets were hence well resolved in our images. For glycerol–water mixtures, the viscosity values are less sensitive to changes in temperature at
$30\,^{\circ }\text{C}$
than at
$20\,^{\circ }\text{C}$
; i.e.
$(\unicode[STIX]{x2202}\unicode[STIX]{x1D707}/\unicode[STIX]{x2202}T)_{20\,^{\circ }\text{C}}>(\unicode[STIX]{x2202}\unicode[STIX]{x1D707}/\unicode[STIX]{x2202}T)_{30\,^{\circ }\text{C}}$
. Hence, in regimes where viscosity of the jet is strongly dependent on viscosity (or
$Oh$
), especially when sharp changes in velocity are expected with change in
$Oh$
, as at
$Oh=0.037$
, where the viscous cutoff occurs, we conducted experiments at
$30\,^{\circ }\text{C}$
so that small changes from the set temperatures do not change the viscosity much. The experiments were conducted in a temperature controlled laboratory after the temperature stabilised to the set values of
$20\,^{\circ }\text{C}$
or
$30\,^{\circ }\text{C}$
.
3 Jet velocity scaling
A typical bubble collapse sequence is shown in figure 1 for a bubble of
$R=2.15~\text{mm}$
in water. Time evolution of the jets for the same and other conditions are shown in figures 15 and 16 in appendix B. Note that there are precursor capillary waves ahead of the kink caused by the change of the curvature of the bubble boundary from convex to concave, as seen in panels (f)–(k) in figure 1. The group velocity of these waves is equal to the kink velocity as is observed ahead of the crest of steep water waves (Perlin, Lin & Ting Reference Perlin, Lin and Ting1993). These dispersive capillary waves cause perturbations and hence weaken the jet velocity, either through a weakening of the pressure impulse at the base or by bubble pinch off. In the coalescence of larger bubbles, bubble pinch off is a frequent phenomenon (Zhang & Thoroddsen Reference Zhang and Thoroddsen2008; Zhang et al.
Reference Zhang, Thoraval, Thoroddsen and Taborek2015); we, however, observe bubble pinch off only at one low
$Bo$
in water. With decreasing bubble size or with increasing viscosity, these capillary waves are progressively damped, giving rise to an increase in jet velocity. The question of capillary wave damping and its effect on jet velocity will be examined in § 3.2.1; we focus first on the question of the origin of gravity effects on jet velocity.
Figure 1. The bursting sequence of a bubble of radius
$R=2.15~\text{mm}$
,
$Bo=0.63$
,
$Oh=0.00255$
in water. Each panel, from (a–p), is separated by
$0.25$
ms. Panels (p), (q) and (q), (r) are separated by 0.5 ms and 1.3 ms respectively. The whole process up to jet emergence at the free surface took 4.5 ms. The lines in panels (a) and (r) are 1 mm in length. A supplementary movie showing the sequence of bursting is available at https://doi.org/10.1017/jfm.2017.214.
3.1 Gravity effects
Figure 2 shows the variation of the square of the dimensionless jet velocity
$(U_{j}/U_{c})^{2}=We$
, with the square of the dimensionless radius
$(R/R_{c})^{2}=Bo$
, where the capillary velocity,
$U_{c}=\sqrt{\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}R}$
and the capillary radius,
$R_{c}=\sqrt{\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}g}$
. The water data of Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) are included in figure 2 for comparison and their results with glycerine–water solutions of 4.4–6.2 times the water viscosity are indicated by the dotted line. It is clear from figure 2 that the data of Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) show a good correlation of
$We$
with
$Bo^{-1/2}$
(
$1/R$
variation) as shown by the dashed line, corresponding to
$$\begin{eqnarray}We=55~Bo^{-1/2}\end{eqnarray}$$
covering the whole range of
$Bo$
considered. At a first view, our experimental results also seem to support a
$1/R$
variation of the jet velocity except when viscous effects become important on the bubble scale, as is in the case of GW68 and GW72. However, there is a deviation in our data from the
$1/R$
behaviour when
$Bo>1$
. Furthermore, there is also a deviation of
$We$
from the
$Bo^{-1/2}$
dependence when
$Bo<0.1$
, with the trend of
$We$
becoming independent of
$Bo$
. In fact, we show later that even in the intermediate range
$0.1<Bo<1$
, the
$Bo^{-1/2}$
scaling is only a good approximation and a continually varying power of
$Bo$
fits the present data, as well as that of BSB, better. The jet velocities of Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) in glycerine–water solutions of 4.4–6.2 times the water viscosity are larger with respect to that in water by approximately a factor of
$2$
; we do not observe such a large velocity increase in our jet velocity measurements using GW48. We also note from figure 2 that
$We$
values at the same
$Bo$
first increase with increase in viscosity (see water and GW48 (
$30\,^{\circ }\text{C}$
)) and then decrease monotonically with a further increase in viscosity. When capillary waves are damped due to increase in viscosity or decrease in bubble radius, the bubble boundary is smoother and this may lead to a higher impulse at the bubble base and hence a higher jet velocity; we discuss this viscosity effect in § 3.2.1.
Figure 2. Weber number of the emerging jet velocities as a function of the Bond number. ▵, Water; ▴, GW48 (
$30\,^{\circ }\text{C}$
); ▹, GW48 (
$20\,^{\circ }\text{C}$
); ▫, GW55; *, GW68; ♢, GW72;
$\times$
, the jet velocities of Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) for water; – –,
$We=55Bo^{-1/2}$
;
$\ldots \,$
, the jet velocities of Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) for glycerine–water solutions of viscosities 4.4 mPa s–6.2 mPa s.
The question is, what is the reason for the gravity (or
$Bo$
) dependence of jet Weber number and why should there be a
$Bo^{-1/2}$
dependence? It is well known that the jet velocity resulting from cavity collapse related with stationary surface gravity waves depends on the cavity depth or the last wave amplitude (Zeff et al.
Reference Zeff, Kleber, Fineberg and Lathrop2000; Das & Hopfinger Reference Das and Hopfinger2008). We expect a similar association between the jet velocity and the bubble cavity depth in the case of bubble collapse. In bubble collapse, the cavity depth is determined by the balance between gravity and surface tension forces, as will be shown below.
3.1.1 Dimensionless cavity depth
The cavity depth
$Z_{c}$
is defined as the depth of the base of the bubble from the free, undisturbed, liquid surface (figure 3
a). A theoretical expression of
$Z_{c}$
can easily be obtained when neglecting bubble deformation. To leading order,
$$\begin{eqnarray}Z_{c}=2R-h_{c},\end{eqnarray}$$
where
$h_{c}$
is the height of the top of the bubble from the free surface (see figure 3
a). Assuming symmetry at the point of inflection of the bubble surface at the rim gives,
$$\begin{eqnarray}h_{c}=2\unicode[STIX]{x1D702},\end{eqnarray}$$
where
$\unicode[STIX]{x1D702}=h_{c}-h_{r}$
is the height of the bubble cap above the rim, with
$h_{r}$
being the height of the rim from the free surface. Figure 3(b) shows
$h_{c}/h_{r}=h_{c}/\unicode[STIX]{x1D702}$
, plotted against
$Bo$
in the range
$10^{-1}<Bo<3$
. The measured values are close to
$h_{c}/h_{r}=~h_{c}/\unicode[STIX]{x1D702}=2$
, hence the validity of the assumptions leading to (3.3) is supported by experiments. The relatively large experimental error is due to the very small values of
$h_{r}$
and
$h_{c}$
.
Figure 3. (a) Schematic of the static bubble shape; (b)
$h_{c}/h_{r}$
as a function of
$Bo$
. ▵, Water; ▹, GW48 (
$20\,^{\circ }\text{C}$
); ▴, GW48 (
$30\,^{\circ }\text{C}$
); *, GW68; ♢, GW72; ◃, ethanol;
$+$
, 2-propanol; —,
$h_{c}/h_{r}=2$
.
For a spherical bubble, from geometry,
$$\begin{eqnarray}\unicode[STIX]{x1D702}=R-\sqrt{R^{2}-R_{r}^{2}},\end{eqnarray}$$
where
$R_{r}$
is the radius of the rim (figure 3
a). From the force balance,
$F_{B}=F_{\unicode[STIX]{x1D70E}}$
, where the buoyancy force,
$F_{B}=\unicode[STIX]{x1D70C}g(4/3)\unicode[STIX]{x03C0}R^{3}(1-\unicode[STIX]{x1D702}^{2}(3-\unicode[STIX]{x1D702}/R)/4R^{2})$
and the surface tension force,
$F_{\unicode[STIX]{x1D70E}}=(2\unicode[STIX]{x1D70E}/R)\unicode[STIX]{x03C0}R_{r}^{2}$
, we get
$$\begin{eqnarray}\frac{R_{r}}{R}=\sqrt{\frac{2}{3}Bo\left(1-\frac{\unicode[STIX]{x1D702}^{2}}{4R^{2}}\left(3-\frac{\unicode[STIX]{x1D702}}{R}\right)\right)}.\end{eqnarray}$$
When
$Bo\leqslant 1$
,
$\unicode[STIX]{x1D702}/R\leqslant 0.4$
, so the term
$\unicode[STIX]{x1D702}^{2}(3-\unicode[STIX]{x1D702}/R)/4R^{2}\leqslant 0.1$
, which can be neglected to first order, resulting in,
$$\begin{eqnarray}\frac{R_{r}}{R}=\sqrt{\frac{2}{3}Bo},\end{eqnarray}$$
which when substituted in (3.4) gives,
$$\begin{eqnarray}\unicode[STIX]{x1D702}=R\left(1-\sqrt{1-\frac{2}{3}Bo}\right).\end{eqnarray}$$
Using (3.7) in (3.3), we get from (3.2),
$$\begin{eqnarray}\frac{Z_{c}}{R}=2\sqrt{1-\frac{2}{3}Bo}.\end{eqnarray}$$
Figure 4 shows the square of the experimental
$(Z_{ce}/R)^{2}$
and the square of the theoretical dimensionless cavity depths
$(Z_{c}/R)^{2}$
, calculated from (3.8), as a function of
$Bo$
. Note that we plot
$(Z_{c}/R)^{2}$
rather than
$Z_{c}/R$
because the Weber number also has the square of velocity. It is seen that in the range
$0.1<Bo<1$
, the experimental
$(Z_{ce}/R)$
can be fitted by
$(Z_{ce}/R)^{2}\sim Bo^{-1/2}$
, which is the same approximate dependence of
$We$
on
$Bo$
seen in figure 2. In figure 2, when
$Bo$
is large,
$Bo>1$
, the jet velocity starts to decrease and at
$Bo=2.25$
,
$R=4.08~\text{mm}$
in water,
$We$
deviates considerably from the
$Bo^{-1/2}$
correlation. The experimental
$(Z_{ce}/R)^{2}$
in figure 4 shows a similar deviation from the approximate power law
$Bo^{-1/2}$
. The theoretical
$(Z_{c}/R)^{2}$
has a steeper fall off with
$Bo$
than the experimental
$(Z_{ce}/R)^{2}$
because when
$Bo>1$
, the limit of validity of (3.8) is approached. When
$Bo\rightarrow 0$
the theoretical cavity depth (3.8) tends to the asymptotic limit of
$2R$
and is practically independent of
$Bo$
when
$Bo<0.1$
because for
$Bo=0.1$
,
$Z_{c}/R=1.93$
and for
$Bo=0.01$
,
$Z_{c}/R=1.99$
, which is only a 3 % variation. We can therefore assume that when
$Bo<0.1$
,
$Z_{c}/R$
is nearly invariant. On the other hand, between
$Bo=0.1$
(
$Z_{c}/R=1.93$
) and
$Bo=1$
(
$Z_{c}/R=1.15$
) gravity has a large effect on the cavity depth.
Figure 4. Square of the dimensionless cavity depth of the bubble as a function of the Bond number. ▵, Water; ▹, GW48 (
$20\,^{\circ }\text{C}$
); ▴, GW48 (
$30\,^{\circ }\text{C}$
); *, GW68; ♢, GW72; ◃, ethanol;
$+$
, 2-propanol; – –,
$1.32Bo^{-1/2}$
; –.–,
$(Z_{c}/R)^{2}=4~(1-2/3~Bo)$
; —,
$(Z_{cd}/R)^{2}=4(\sqrt{1-2/3Bo}-0.17~Bo^{0.8})^{2}$
.
The bubble deformation is negligible up to
$Bo\approx 0.1$
and remains small up to
$Bo\approx 3/2$
, with the deformation varying from approximately 4 % to 15 % of
$R$
as
$Bo$
increases from
$0.1$
to
$1$
. Although these deformations are relatively small, this seems to affect the cavity depth sufficiently when
$Bo<1$
to make the theoretical depths (3.8) deviate noticeably from the experiments, as can be seen in figure 4 when
$Bo<1$
.
$Z_{c}/R$
given by (3.8) can be corrected for these small deformations by assuming an oblate spheroid shape of the bubble. The expression for such a corrected cavity depth is
$Z_{cd}/R\approx 2((R/R_{m})^{2}-1+\sqrt{1-(2/3)~Bo})$
, where
$R_{m}$
is the measured horizontal radius at the equator, approximated by
$(R/R_{m})^{2}~\approx 1-0.17~Bo^{0.8}$
, to get,
$$\begin{eqnarray}\frac{Z_{cd}}{R}=2\left(\sqrt{1-\frac{2}{3}Bo}-0.17Bo^{0.8}\right).\end{eqnarray}$$
As shown by the continuous line in figure 4, we obtain a better match of
$(Z_{cd}/R)^{2}$
versus
$Bo$
obtained from (3.9) with the experimental variation of
$(Z_{ce}/R)^{2}$
versus
$Bo$
, compared to that obtained by (3.8).
3.1.2 Cavity depth model for gravity effects
Gravity effects can be best demonstrated with data from one fluid alone rather than data from different viscosity fluids as in figure 2. Figure 5 shows the experimental jet velocities for water plotted in terms of
$We$
versus
$Bo$
, along with the data from BSB, the drop velocities measured by Spiel (Reference Spiel1995), the jet velocity measured from the images of Kientzler et al. (Reference Kientzler, Arons, Blanchard and Woodcock1954) and the jet velocity data of Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014). The continuous line is
$$\begin{eqnarray}We=62.5\left(\frac{Z_{cd}}{R}\right)^{2}\end{eqnarray}$$
while the dashed line is (3.1). The following three regimes can be identified in figure 5.
-
(i)
$Bo<0.1$
: at these low
$Bo$
numbers the theoretical cavity depth varies only by 3 % from
$Bo=0$
to 0.1 (see figure 4) and according to the cavity depth model (3.10),
$We$
should also asymptote to a constant value, as shown by the solid line in figure 5. Our data and those of BSB tend to asymptote toward such a constant value of
$We$
rather than to increasing
$We$
with decreasing
$Bo$
, following a
$Bo^{-1/2}$
law, given by Ghabache et al. The deviation of our data from the cavity depth model (3.10), seen as a slight increase in
$We$
with decreasing
$Bo$
, for
$Bo<0.1$
is due to capillary wave damping. As we discuss in § 3.2.1, (figure 9), if the Weber number is corrected for this damping, it is practically a constant for
$Bo<0.1$
. -
(ii)
$Bo>1$
: in this range there is no doubt a clear deviation of our
$We$
data from the
$Bo^{-1/2}$
trend. This is because the cavity depth decreases more rapidly with
$Bo$
than
$Bo^{-1/2}$
and there is also larger bubble deformation for
$Bo>1$
. -
(iii) Intermediate range
$0.1<Bo<1$
: in this range, the data of Ghabache et al. are well fitted by
$Bo^{-1/2}$
whereas the present results and those of BSB deviate noticeably from this power law and closely follow the cavity depth model (3.10). For
$0.06<Bo<0.15$
Spiel’s results follow
$We\sim Bo^{-1/2}$
but deviate from this power law when
$Bo$
increases. Spiel measured the first drop velocities and not the jet tip velocities when the jet emerges from the free surface; the values of the drop velocities are different from the unbroken jet tip velocities. Figure 6 shows the measured jet velocities at increasing heights as time increases, culminating in the first drop velocity due to jet fragmentation at some height. We see that at moderate
$Bo$
(
$0.2\leqslant Bo\leqslant 0.63$
) there is a 30 %–60 % reduction in drop velocity compared to the jet velocity at the free surface. This reduction in drop velocities increases with increasing
$Bo$
since jets from larger
$Bo$
bubbles fragment farther away from the free surface (figure 15). This decrease in drop velocities at moderate
$Bo$
is the reason why Spiel’s data are lower than the solid curve from the cavity model in figure 5.
Figure 5. Variation of jet Weber number with Bond number in water. ▵, Present experiments;
$\star$
, BSB; ♢, drop velocities of Spiel (Reference Spiel1995);
$\blacksquare$
, Kientzler et al. (Reference Kientzler, Arons, Blanchard and Woodcock1954); —,
$We=62.5~(Z_{cd}/R)^{2}$
; – –,
$We=55~Bo^{-1/2}$
;
$\times$
, jet velocities of Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) for water.
Figure 6. Variation of the jet
$We$
with the dimensionless time for bubbles of different
$Bo$
in water. ♢,
$Bo=0.2$
; ▫,
$Bo=0.3$
; ○,
$Bo=0.49$
; ▵,
$Bo=0.63$
. Unfragmented jet velocities are shown by hollow symbols while the velocities of the first drop after jet fragmentation are shown by filled symbols. The cubic polynomial fits, show the progression of velocities with time of each jet.
Based on the above considerations, it can be concluded that the present experimental data for water and the BSB data, when considered over the whole range of
$Bo$
, show better agreement with (3.10) than with (3.1). This agreement implies that the jet velocity scales as
$U_{j}\sim (Z_{cd}/R)~U_{c}$
, the gravity effects in jet velocity comes purely from the gravity effects in the cavity depth. This scaling can also be demonstrated by measuring the jet velocity from the vertical retraction of cavity, as shown in appendix A. It is shown in appendix A that the time taken by the jet to travel the distance of cavity depth is independent of gravity effects, implying that the gravity effects in jet velocity comes only from the gravity dependence of static cavity depths. As we show later in § 3.2, this conclusion is further strengthened when the experimental
$We$
, compensated for capillary wave damping is plotted verses
$Bo$
(see figure 9).
It could be argued that the dynamic cavity depth when the singular collapse commences (figure 1
m) is of importance and not the static depth just after the surface film disintegration (figure 1
c). An estimate of the change in cavity depth during the time of bubble collapse
$t_{bc}\approx 0.3~t_{c}$
(Krishnan & Puthenveettil Reference Krishnan and Puthenveettil2015), where the capillary time
$t_{c}=R\sqrt{\unicode[STIX]{x1D70C}R/\unicode[STIX]{x1D70E}}$
, is obtained by evaluating the upward bubble displacement
$\unicode[STIX]{x0394}z=gt_{bc}^{2}/2$
to get,
$$\begin{eqnarray}\unicode[STIX]{x0394}z/R\approx 4.5\times 10^{-2}Bo,\end{eqnarray}$$
which is negligible when
$Bo<1$
. Any decrease in cavity depth would hence have to be due to capillary forces caused by the curvature of the bubble base; our experiments show that this is small for small bubble sizes.
Figure 7. Variation of the dimensionless jet velocity with the dimensionless bubble radius for low
$Bo$
. The velocities and radii are normalised by the viscous capillary scales: ▵, water; ▴, GW48 (
$30\,^{\circ }\text{C}$
); ▹, GW48 (
$20\,^{\circ }\text{C}$
); ▫, GW55; *, GW68; ♢, GW72; ○, jet velocities of Duchemin et al. (Reference Duchemin, Popinet, Josserand and Zaleski2002) for water;
$\times$
, jet velocities of Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) for water; —,
$16(R/R_{\unicode[STIX]{x1D707}})^{-1/2}$
; –.–, the viscous cutoff at
$R/R_{\unicode[STIX]{x1D707}}=Oh^{-2}\simeq 730$
; – –, the vertical dashed lines demarcate the
$Bo<0.1$
data on the left with the
$Bo>0.1$
data on the right for water (W), GW48 and GW55. Viscous–capillary scaling is seen for
$Bo<0.1$
part of each data set.
The proposed scaling law for gravitational effects on jet velocity, namely
$We\sim (Z_{cd}/R)^{2}$
, where
$Z_{cd}/R$
is given by (3.9), implies that the jet
$We$
becomes practically independent of
$Bo$
at
$Bo<0.1$
. Hence at these low Bond numbers the viscous–capillary scaling of Duchemin et al. (Reference Duchemin, Popinet, Josserand and Zaleski2002) should be appropriate. As shown in figure 7, the data closely follow the relation
$$\begin{eqnarray}\frac{U_{j}}{U_{\unicode[STIX]{x1D707}}}=16\left(\frac{R}{R_{\unicode[STIX]{x1D707}}}\right)^{-1/2},\end{eqnarray}$$
i.e.
$Ca=16~Oh$
for
$Bo<0.1$
where the capillary number
$Ca=\unicode[STIX]{x1D707}U_{j}/\unicode[STIX]{x1D70E}$
. This power-law variation of jet velocity gives
$U_{j}=16~U_{c}$
or
$We=(U_{j}/U_{c})^{2}\simeq ~250$
as seen in figure 5 for
$Bo<0.1$
. The data of Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) however show a
$We\sim Bo^{-1/2}$
scaling for their whole range of
$Bo$
,
$0.007<Bo<1$
. The relation (3.12) implies that
$U_{j}\sim 1/\sqrt{R}$
(Duchemin et al.
Reference Duchemin, Popinet, Josserand and Zaleski2002). Curiously their data deviate from the
$R^{-1/2}$
scaling when
$R/R_{\unicode[STIX]{x1D707}}<5\times 10^{3}$
, which is not observed in the present experiments. The data of Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) show a
$We\sim Bo^{-1/2}$
scaling for their whole range of
$Bo$
,
$0.007<Bo<1$
.
3.2 Viscosity effects
Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) expressed the viscosity dependence of jet velocity by plotting
$We\sqrt{Bo}$
in terms of Morton number
$Mo=Oh^{4}Bo$
, a dimensionless number that contains gravity. However, there is no physical reason as to why gravity should be important in viscous damping of capillary-driven flows. Gravity determines the cavity depth and shape, but once formed, the collapse, after film rupture, is surface tension driven; as indicated above, the change in cavity depth in the bubble collapse time due to gravity is negligibly small when
$Bo$
is of order of one or less. The importance of viscous effects on capillary-driven flows is therefore expressed by an Ohnesorge number which is the ratio of viscous to capillary forces. The Ohnesorge number can also be interpreted in terms of a Reynolds number
$Re_{c}=1/Oh$
, where
$Re_{c}=\unicode[STIX]{x1D70C}U_{c}R/\unicode[STIX]{x1D707}$
. Viscosity enters the jet velocity scaling in two ways: (1) through damping of the capillary waves which merge at the bubble base and weaken the pressure impulse and (2) through direct viscous damping of the jet formation and dynamics; we discuss both these effects below.
3.2.1 Capillary wave damping
Figure 8 shows the damping of capillary waves on the collapsing cavity surface with increase in
$Oh$
. Figure 8(a,b) is a bubble collapse sequence of a moderate
$Bo$
water bubble (
$Bo=0.63$
) with
$Oh=0.0026$
. Here, in the wave train preceding the kink, two wavelengths
$\unicode[STIX]{x1D706}_{1}\approx 0.36R$
and
$\unicode[STIX]{x1D706}_{2}\approx 0.17R$
can be clearly identified, with faster, shorter waves being practically damped. The wave train group velocity is
$C_{g}=3/2\sqrt{\unicode[STIX]{x1D70E}~k/\unicode[STIX]{x1D70C}}\simeq 3/2\sqrt{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}_{1}}\approx 6U_{c}$
which corresponds to the measured speed of the kink. Figure 8(c,d) is a collapsing sequence of a smaller water bubble (
$Bo=3\times 10^{-2}$
) with a relatively larger
$Oh=0.0055$
which shows only wavelength
$\unicode[STIX]{x1D706}_{1}$
clearly; the shortest wave (
$\unicode[STIX]{x1D706}_{2}$
) is nearly damped. Figure 8(e,f) shows the capillary waves in GW48 (
$30\,^{\circ }\text{C}$
) bubble with
$Oh=0.0139$
in which the longer wave (
$\unicode[STIX]{x1D706}_{1}$
) alone moves ahead of the kink, with the amplitude noticeably decreased. As can be seen in figure 8(g,h), a further increase in
$Oh$
from
$0.0139$
to
$0.0225$
results in complete damping of the capillary waves on the cavity surface.
The amplitude
$\unicode[STIX]{x1D6FC}$
of capillary waves falls off exponentially in the form
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{0}\text{e}^{-\unicode[STIX]{x1D705}t}$
with the damping rate
$\unicode[STIX]{x1D705}=8\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D707}/\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}^{2}$
. In the collapse time
$t_{bc}\approx 0.3t_{c}$
(Krishnan & Puthenveettil Reference Krishnan and Puthenveettil2015), the decrease in capillary wave amplitude is then given by
$$\begin{eqnarray}\ln \left(\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FC}_{0}}\right)\approx -24\left(\frac{R}{\unicode[STIX]{x1D706}}\right)^{2}Oh.\end{eqnarray}$$
Figure 8. Progressive damping of capillary waves with increase in
$Oh$
, shown in image pairs from (a) to (h). Collapsing sequence, (a,b) water,
$Oh=0.0026$
(
$Bo=0.63$
); (c,d) water,
$Oh=0.0055$
(
$Bo=3\times 10^{-2}$
); (e,f) GW48 (
$30\,^{\circ }\text{C}$
),
$Oh=0.0139$
(
$Bo=0.17$
); (g,h) GW55,
$Oh=0.0225$
(
$Bo=0.47$
). In each image pair, images are separated by
$741$
,
$100$
,
$148$
and 375 ms, respectively. The lines in (a,b) 1 mm, (c,d) 0.2 mm, (e,f) 0.5 mm, (g,h) 0.5 mm.
Capillary waves can be considered completely absent when
$\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FC}_{0}=\text{e}^{-n}$
with
$n\approx 4$
. Equation (3.13) with
$n=4$
then implies that capillary waves with wavelength less than
$\unicode[STIX]{x1D706}/R\approx 0.17$
are absent at a value of
$Oh\approx 0.0048$
(see figure 8
a–d). Similarly, capillary waves of wavelength
$\unicode[STIX]{x1D706}/R\approx 0.36$
will be absent at
$Oh\approx 0.022$
(see figure 8
e–h). We can hence infer that capillary waves are progressively damped as
$Oh$
increases and there is an increase in jet velocity up to about
$Oh\approx 0.02$
due to this damping.
For given fluid properties,
$Oh$
increases with decreasing bubble radius, resulting in a corresponding decrease in
$Bo$
. We saw in figure 5 that with decreasing
$Bo$
when
$Bo<0.1$
, the jet
$We$
increases, deviating from the cavity model (3.10) and this is due to increasing capillary wave damping. If we assume that the radius at the bottom of the cavity increases by a factor
$R/\unicode[STIX]{x1D706}$
, given by (3.13), due to the presence of capillary waves, then
$We$
has to be compensated by
$\sqrt{Oh}$
to account for capillary wave damping. As shown in figure 9,
$We/Oh^{1/2}$
is practically a constant for the experimental data for
$Bo<0.1$
and matches well with the cavity depth model. The
$We$
of Spiel is also practically independent of
$Bo$
when
$Bo<0.06$
in figure 9. Even Ghabache’s data could be considered to be following our cavity depth model in figure 9 for
$Bo<0.1$
. Unfortunately, Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) have no measurements at smaller
$Bo$
, say at a
$Bo$
of
$0.003$
for a clearer verification.
Figure 9. Variation of the Weber number compensated for capillary wave damping with
$Bo$
. Symbols are the same as in figure 5. – –,
$WeOh^{-1/2}=830Bo^{-1/2}$
; —,
$WeOh^{-1/2}=900(Z_{cd}/R)^{2}$
.
Figure 10. Normalised
$We$
, uncompensated and compensated for capillary wave damping,
$We/(Z_{cd}/R)^{2}\times 10^{3}$
and
$We/((Z_{cd}/R)^{2}Oh^{1/2})$
, as functions of
$Oh$
. ▵, Water; ▴, GW48 (
$30\,^{\circ }\text{C}$
); ▹, GW48 (
$20\,^{\circ }\text{C}$
); ▫, GW55; *, GW68; ♢, GW72;
$\times$
, water data of Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014); – –,
$We/(Z_{cd}/R)^{2}=70$
; –.–,
$We/((Z_{cd}/R)^{2}Oh^{1/2})=900$
; —,
$We/((Z_{cd}/R)^{2}Oh^{1/2})=8.3\times 10^{-9}Oh^{-7.3}-0.17$
;
$\ldots \,$
, the vertical dotted line represents
$Oh_{c}=0.037$
.
In figure 10, we now plot
$We/(Z_{cd}/R)^{2}$
as a function of Ohnesorge number,
$Oh$
. There is a small region of decreasing
$We/(Z_{cd}/R)^{2}$
with increasing
$Oh$
at
$Oh<0.003$
, which is an artefact of the deviation of the theoretical cavity depth (3.9) from the experimental values at large
$Bo$
(see figure 4). When
$Oh<Oh_{c}\simeq 0.037$
, except in the range of
$0.02<Oh<Oh_{c}$
, the data sets of water and GW48 indicate an increase of
$We/(Z_{cd}/R)^{2}$
with
$Oh$
in figure 10. As mentioned above, this increase of
$We/(Z_{cd}/R)^{2}$
with
$Oh$
occurs because capillary waves are more and more damped as
$Oh$
increases, leading to a smoother cavity and hence a stronger pressure impulse. Hence we plot the compensated
$We$
, namely
$We/((Z_{cd}/R)^{2}Oh^{1/2})$
, in figure 10 as a function of
$Oh$
. This rescaling collapse the present water and GW48 data reasonably well to a nearly constant value of compensated
$We$
. The increase in compensated
$We$
with decrease in
$Oh$
at
$Oh<0.003$
(large
$Bo$
) still persists, being an outcome of (3.9) being valid only till
$Bo\approx 1$
.
3.2.2 Direct viscous damping of jet
It is seen that when
$Oh>Oh_{c}\simeq 0.037$
there is a rapid decrease in jet velocity. This is because when
$Oh>Oh_{c}$
the Reynolds number on the bubble scale falls below
$10^{2}$
, viscous effects become important on the bubble scale and the jet velocity decreases rapidly with increasing
$Oh$
. Note that
$Oh_{c}=0.037$
corresponds to
$R/R_{\unicode[STIX]{x1D707}}=Oh^{-2}\simeq 730$
in figure 7, below which the jet velocity drops off rapidly in agreement with the numerical simulations of Duchemin et al. (Reference Duchemin, Popinet, Josserand and Zaleski2002). Corresponding to
$Oh_{c}$
, we can estimate a critical Bond number
$Bo_{c}=\unicode[STIX]{x1D707}^{4}g/(0.037)^{4}\unicode[STIX]{x1D70E}^{3}\unicode[STIX]{x1D70C}$
, which is
$1.5\times 10^{-5}$
in water, beyond the range of our experiments. For higher viscosity fluids like GW68 and GW72,
$Bo_{c}=0.3$
and
$Bo_{c}=1.28$
respectively, which can be seen in figure 2, where a rapid drop of
$We$
occurs for
$Bo<Bo_{c}$
. In figure 10, we have empirically fitted this viscous regime by
$We/((Z_{cd}/R)^{2}Oh^{1/2})=8.3\times 10^{-9}Oh^{-7.3}-0.17$
. This critical value of
$Oh$
above which the jet velocity decreases rapidly corresponds to the value proposed by Walls, Henaux & Bird (Reference Walls, Henaux and Bird2015) as a critical value beyond which the jet does not breakup into drops. Figure 11 shows images of jets for different
$Oh$
values. It is seen that for conditions of figure 11(d),
$Oh=0.05>Oh_{c}$
, for instance, there is no breakup of the jet into drops (figure 16
d), whereas breakup occurs for lower values of
$Oh$
(figure 11
a,b). In figure 11(c) there is no breakup either, even though
$Oh<Oh_{c}$
(see figure 15(a) for full sequence of jet evolution). This is because the corresponding
$Bo$
is large, as discussed below in § 3.2.3. Furthermore, we find that no jet emerges when
$Oh=Oh^{\ast }\simeq 0.1$
, a value larger than the value of
$Oh^{\ast }=0.052$
proposed by San Lee et al. (Reference San Lee, Weon, Park, Je, Fezzaa and Lee2011); the difference could possibly arise from the small liquid layer depth (of the order of
$R$
) in their experiments.
Figure 11. Images of jets for different combinations of
$Bo$
and
$Oh$
to show the effect of gravity and viscosity: (a) and (b) are at approximately the same
$Bo$
, but (b) has a much larger
$Oh$
, still less than
$Oh=0.02$
; (a) and (c) are at the same
$Oh<0.02$
, but (c) has a much larger
$Bo$
; (a) and (d) have approximately the same
$Bo$
, but (d) has a much larger
$Oh>Oh_{c}=0.037$
. (a) Bubble of
$R=2.15$
mm in water,
$Bo=0.629$
,
$Oh=2.55\times 10^{-3}$
; (b)
$R=2$
mm in GW48 (
$30\,^{\circ }\text{C}$
),
$Bo=0.646$
,
$Oh=10\times 10^{-3}$
; (c)
$R=4.08$
mm in water,
$Bo=2.25$
,
$Oh=1.85\times 10^{-3}$
; (d)
$R=1.46$
mm in GW72,
$Bo=0.39$
,
$Oh=4.9\times 10^{-2}$
. The lines in (a,b,d) are 1 mm in length. The grid size in (c) is 1 mm.
Figure 10 clearly indicates the existence of an intermediary regime in the range
$0.02<Oh<Oh_{c}$
where the compensated Weber number for GW48 (
$20\,^{\circ }\text{C}$
), GW55 and GW68 falls below the nearly constant value observed when
$Oh<0.02$
. This reduction in jet velocity is most likely due to a viscous effect on the jet scale expressed here by the jet Reynolds number
$Re=\unicode[STIX]{x1D70C}U_{j}R/\unicode[STIX]{x1D707}$
that decreases from approximately
$10^{3}$
in the case of GW48 to
$10^{2}$
for GW55 (see table 1). For the latter experiment, when
$Re$
is defined with the jet radius instead the bubble radius, it is well below
$10^{2}$
.
3.2.3 Large Bond number effects
At very large
$Bo$
numbers, the ascending velocity of the bubble due to the buoyancy force approaches the bubble collapse velocity due to the capillary force. An estimate of
$Bo$
for no jet formation can be obtained from (3.11) by using
$\unicode[STIX]{x0394}z\approx 0.5~R$
during the collapse time to obtain
$Bo\approx 12$
. Walls et al. (Reference Walls, Henaux and Bird2015) indicate that there is still jet formation at
$Bo\approx$
5 (bubble in water) but no breakup into drops. As seen in figure 11(c), our experiments also show no drop formation for a
$R=4.08~\text{mm}$
bubble in water at
$Bo=2.25$
. Hence we expect that at
$Bo\approx 10$
no jet will be formed.
4 Conclusions
The first main novel result from the present work is that the dependence of the dimensionless jet velocity, expressed in terms of the Weber number (
$We$
), on the Bond number (
$Bo$
) is determined by the dimensionless cavity depth. The variation of the square of the dimensionless cavity depth
$(Z_{cd}/R)^{2}$
of the bubble with the Bond number is of the same form as that of
$We$
with
$Bo$
(compare figures 4, 5 and 9), which is not a power law. In a limited range of Bond number values,
$0.1<Bo<1$
, this dependence can however be approximated as
$Bo^{-1/2}$
as was proposed by Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014). When
$Bo<0.1$
the cavity depth approaches the asymptotic limit of
$Z_{c}/R\simeq 2$
and is practically independent of
$Bo$
; the viscous–capillary scaling of Duchemin et al. (Reference Duchemin, Popinet, Josserand and Zaleski2002) is then appropriate (figure 7). In the large Bond number limit (
$Bo>1$
) the cavity depth decreases rapidly and so does the jet velocity or
$We$
. Bubble deformation also becomes important at these large
$Bo$
numbers. No approximate power law for
$We$
in terms of
$Bo$
exists when
$Bo>1$
.
The second important conclusion is that viscosity effects are best expressed in terms of Ohnesorge number (
$Oh=$
viscous/capillary forces), which is usual for capillary-driven flows. Jet formation is strongly affected by viscosity when
$Oh>Oh_{c}\simeq 0.037$
with the jet formation being completely inhibited when
$Oh=Oh^{\ast }\simeq 0.1$
. In the range
$Oh<0.02$
an increasing viscosity can increase the jet velocity through capillary wave damping; the present experiments suggest that
$We$
is proportional to
$\sqrt{Oh}$
in this regime. In the intermediate range
$0.02<Oh<Oh_{c}$
jet velocities are lower because of low jet Reynolds number. When
$Oh>Oh_{c}$
the Reynolds number is also small on the bubble scale.
While the present results are in overall agreement with those of Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014), we point out important differences which exist at small Bond numbers (
$Bo<0.1$
) and large Bond numbers (
$Bo>1$
). These differences occur due to the variation of the cavity depth with
$Bo$
, which deviates from the approximate
$Bo^{-1/2}$
power law at small and large
$Bo$
. In addition, we bring out the complex effects of viscosity, which result in three regimes, the first in which viscosity affects the jet dynamics at large
$Oh$
, the second in which it affects only the jet formation and finally the third regime in which viscosity affects the jet velocity through capillary wave damping.
Acknowledgements
We are grateful to Professor M. Panchagnula, Department of Applied Mechanics, IIT Madras, for allowing us to use the high-speed photographic facility in his lab. We gratefully acknowledge the usage of equipments acquired under the grant SR/FST/ETII-017/2003 from DST, Government of India for this study.
Supplementary movie
Supplementary movie is available at https://doi.org/10.1017/jfm.2017.214.
Figure 12. (a) Static bubble of
$R=2.15~\text{mm}$
in water; (b) the conical cavity just before jet formation in the same bubble; (c) the shape contours extracted from (a) to (b) are superposed together to show the displacement of the bottom of the cavity.
Figure 13. (a) Variation of the difference between the static cavity depth
$Z_{ce}$
and the cavity depth just before jet formation from a conical cavity
$\widetilde{Z}_{ce}$
,
$D_{n}=Z_{ce}-\widetilde{Z}_{ce}$
, in dimensionless form with
$Bo$
for water. ▵, Water; —,
$D_{n}/Z_{ce}=0.143$
. (b) Variation of the time of cavity retraction measured from the conical shape of the cavity to the jet emergence at the free surface, in dimensionless form, with
$Bo$
. —,
$t_{j}/t_{c}=0.11$
.
Figure 14. Comparison of the jet Weber number measured by two methods plotted against
$Bo$
. ▵,
$We$
based on jet velocity at free surface;
$\bullet$
,
$We_{jc}$
based on jet velocity measured as
$U_{jc}=\widetilde{Z}_{ce}/t_{j}$
, where
$t_{j}=0.11t_{c}$
from figure 13(b) and
$\widetilde{Z}_{ce}=0.86~Z_{ce}$
; – –,
$We=55~Bo^{-1/2}$
; —,
$We=62.5(Z_{cd}/R)^{2}$
.
Appendix A. Jet velocity–cavity depth relation
The relation of jet velocity with cavity depth can also be demonstrated by considering that the jet velocity is given by
$$\begin{eqnarray}U_{jc}=\widetilde{Z}_{ce}/t_{j},\end{eqnarray}$$
where
$t_{j}$
is the time measured from the beginning of vertical retraction of the conically shaped cavity (figure 1
m) to jet emergence at the free surface (just before figure 1
q) and
$\widetilde{Z}_{ce}$
is the cavity depth at the instant when the conically shaped cavity starts to retract vertically (see figure 12
c). In writing equation (A 1), it is assumed that the jet velocity inside the cavity is constant and that the impulse at the conical cavity bottom occurs in a time short compared with
$t_{j}$
. As shown in figure 13(a),
$\widetilde{Z}_{ce}$
is found to be directly proportional to
$Z_{ce}$
with no additional dependence on
$Bo$
so that,
$$\begin{eqnarray}\widetilde{Z}_{ce}=C_{1}Z_{ce},\end{eqnarray}$$
where, from measurements in water,
$C_{1}=0.86$
. The measured values of
$t_{j}$
scale with the capillary time,
$t_{c}=\sqrt{\unicode[STIX]{x1D70C}R^{3}/\unicode[STIX]{x1D70E}}$
as,
$$\begin{eqnarray}t_{j}=C_{2}t_{c}.\end{eqnarray}$$
Figure 13(b) shows that in the intermediate range of
$Bo$
, where viscous damping of capillary waves are not significant,
$C_{2}=0.11$
, but at lower
$Bo$
values, corresponding to larger values of
$Oh$
,
$C_{2}$
is likely to be lower. We however were not able to measure at these low
$Bo$
and therefore took the same value of
$C_{2}$
, knowing that this would underestimate
$U_{j}$
. Substituting (A 2) and (A 3) in (A 1) leads to
$$\begin{eqnarray}We_{jc}=60.7~(Z_{ce}/R)^{2},\end{eqnarray}$$
where
$We_{jc}$
is the Weber number based on
$U_{jc}$
. The expression for
$We_{jc}$
(A 4) has the same functional dependence as (3.10) and is quite close to (3.10) shown in figure 5. Figure 14 compares
$We_{jc}$
determined from measured
$\widetilde{Z}_{ce}$
and
$t_{j}$
with
$We$
determined from jet velocity measurements close to the free surface; there is a close agreement between the two. The slightly lower values of
$We_{jc}$
are due to the neglect of the initial acceleration of the jet in estimating
$U_{jc}$
since
$U_{jc}$
is an average velocity measurement over
$\widetilde{Z}_{ce}$
. Hence, since the time taken for the jet to travel a distance
$\widetilde{Z}_{ce}$
– proportional to the cavity depth – scales as the capillary time
$t_{c}$
, independent of gravity effects, the gravity effects in jet velocity can only come from the gravity effects on the cavity depth.
Figure 15. Time evolution of the structure of the jet in water. Panels (a–d) are arranged in the order of decreasing
$Bo$
from the largest to the smallest
$Bo$
of present experiments (
$4.2\times 10^{-3}\leqslant Bo\leqslant 2.25$
). Time is marked on each image. (a)
$R=4.08~\text{mm}$
(
$Bo=2.25$
,
$Oh=1.85\times 10^{-3}$
). The grid size in the image is 1 mm.
$d_{j}/R\approx 0.32$
. (b)
$R=2.15~\text{mm}$
(
$Bo=0.63$
,
$Oh=2.55\times 10^{-3}$
). The line in image is 1 mm.
$d_{j}/R\approx 0.24$
. (c)
$R=0.71~\text{mm}$
(
$Bo=0.069$
,
$Oh=4.5\times 10^{-3}$
). The line in image is 0.2 mm.
$d_{j}/R\approx 0.25$
. (d)
$R=0.175~\text{mm}$
(
$Bo=0.0042$
,
$Oh=9\times 10^{-3}$
). The line in image is 0.1 mm.
$d_{j}/R\approx 0.17$
.
Figure 16. Time evolution of the structure of the jet with increasing
$Oh$
in different glycerine water solutions. Panels (a–d) are arranged in increasing order of
$Oh$
from
$Oh=1.39\times 10^{-2}$
in (a) of GW48 (
$30\,^{\circ }\text{C}$
) to
$Oh=4.9\times 10^{-2}$
in (d) of GW72. Time is marked on each image. (a)
$R=1.04~\text{mm}$
(
$Bo$
= 0.17,
$Oh=1.39\times 10^{-2}$
) in GW48 (
$30\,^{\circ }\text{C}$
). The line in image is 0.5 mm.
$d_{j}/R\approx 0.09$
. (b)
$R=0.81~\text{mm}$
(
$Bo=0.11$
,
$Oh=2.21\times 10^{-2}$
) in GW48 (
$20\,^{\circ }\text{C}$
). The line in image is 0.5 mm.
$d_{j}/R\approx 0.04$
. (c)
$R=0.71~\text{mm}$
(
$Bo=0.084$
,
$Oh=3.44\times 10^{-2}$
) in GW55. The line in image is 0.5 mm.
$d_{j}/R\approx 0.14$
. (d)
$R=1.52~\text{mm}$
(
$Bo=0.42$
,
$Oh=4.9\times 10^{-2}$
) in GW72. Grid size is 1 mm.
$d_{j}/R\approx 0.3$
.
Appendix B. Time evolution of jets
Figure 15(a–d) shows the time sequence of the evolution of jets and their breakup into drops with decreasing
$Bo$
and increasing
$Oh$
, while
$Oh<0.02$
. Among these panels, figure 15(b) shows a more detailed sequence of jet evolution for
$R=2.15~\text{mm}$
in water as a continuation of figure 1. The other panels, figures 15(a,c) and 15(d) show the jet evolution issuing from collapsing bubbles in water for different
$Bo$
and
$Oh$
values. Qualitatively, it is seen that with decreasing
$Bo$
and increasing
$Oh$
the jet velocity increases, as long as
$Oh<0.02$
, in agreement with figure 10. The jet diameter (
$d_{j}$
) is measured near the free surface when the jet just emerges. At large
$Bo$
, here at
$Bo=2.25$
(figure 15
a), there is no jet breakup into drops, with the scaled jet diameter being
$d_{j}/R\approx 0.32$
. When
$Bo=0.63$
, figure 15(b),
$d_{j}/R\approx 0.24$
and one drop is formed from the jet tip. In figure 15(c),
$Bo=0.069$
the jet fragments into three droplets and
$d_{j}/R\approx 0.25$
. A further reduction in
$Bo$
, i.e.
$Bo=4.2\times 10^{-3}$
, results in a thinner jet (
$d_{j}/R\approx 0.17$
) and the entire jet gets pinched off from the surface in addition to the initial droplets shedding from the jet tip as shown in figure 15(d).
The jet size is directly related with the bubble size as seen in figure 15(a–d). However, the damping of capillary waves causes further reduction in jet size (Ghabache et al.
Reference Ghabache, Antkowiak, Josserand and Séon2014) as could be seen in figure 15(d). This effect of damping on the jet size could be made clear by the jet behaviour in the glycerine–water solutions shown in figure 16, which shows the jet sequence with increasing
$Oh$
. Figure 16(a) shows a jet from a slightly larger bubble (
$R=1.04~\text{mm}$
,
$Bo=0.17$
,
$Oh=0.0139$
) compared with the jet in figure 15(c) (
$R=0.71~\text{mm}$
,
$Bo=0.069$
,
$Oh=0.0045$
). The jet in figure 16(a) has a smaller diameter (
$d_{j}/R\approx 0.09$
) than the jet in figure 15(c) (
$d_{j}/R\approx 0.25$
) due to much larger
$Oh$
. Both undergo drop shedding from the jet tip (three drops) but in figure 16(a) the entire jet gets pinched off from the free surface as in figure 15(d) (
$d_{j}/R\approx 0.17$
). In figure 16(b,c) jet evolution sequences for bubbles of approximately the same
$Bo$
values (
$Bo\approx 0.1$
) are shown, however, the dimensionless jet diameters are
$d_{j}/R\approx 0.04$
in figure 16(b) and
$0.14$
in figure 16(c). Only one drop is shed from the jet tip in figure 16(b,c) as viscosity effects become important. The jet is pinched off from its base in figure 16(b) as in figures 15(d) and 16(a). With increase in
$Oh$
from
$Oh=2.21\times 10^{-2}$
(figure 16
b) to
$Oh=4.9\times 10^{-2}$
(figure 16
d), the drop pinch off is fully stopped, as discussed in § 3.2 and the jet size is increased (
$d_{j}/R\approx 0.3$
).
