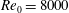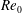1 Introduction
There has been considerable attention to the study of turbulent jet flows since these are known as the basic building block shear flows that are of substantial theoretical interest, and closely linked to the study of turbulence. One of the great theoretical efforts has been to identify the relevant scaling parameters with the aid of experimental and numerical data that enable the turbulence community to model turbulence quantities in flows that are experienced in real life. Indeed, self-similarity analysis is known as an important analytical tool to obtain scaling parameters in turbulent shear flows. The traditional concept of self-similarity, or self-preservation, which assumes that the flow scales with single velocity and length scales, has been extensively used to describe the spatial and temporal evolution of turbulence quantities. It is known that the classical scaling parameters (based on a self-preservation analysis) for turbulent shear flows were first identified by Townsend (Reference Townsend1956, Reference Townsend1976). He also proposed the idea of a ‘universal’ self-similar solution, which indicates that such a solution is unique and independent of initial conditions. For example, according to Townsend’s formulation, for a turbulent jet flow to be self-similar, the terms in the equations of motion must be of the form
$$\begin{eqnarray}\overline{U}_{i}=U_{s}\,f_{i}(x_{2}/L_{s}),\end{eqnarray}$$
and
$$\begin{eqnarray}\unicode[STIX]{x1D619}_{ij}^{0}=U_{s}^{2}g_{ij}(x_{2}/L_{s}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D619}_{ij}^{0}=\overline{u_{i}u_{j}}$
(please note that for the sake of clarity, we denote the stress tensors with the superscript ‘0’ throughout this paper. The specific purpose for this choosing will be discussed in more detail in the subsequent section). Here,
$U_{s}$
is defined as a velocity scale and
$L_{s}$
is a length scale for the self-similarity of the mean velocities
$\overline{U}_{i}$
and Reynolds stresses
$\unicode[STIX]{x1D619}_{ij}^{0}$
, where
$f_{i}$
and
$g_{ij}$
are the dimensionless self-similar functions and only depend on
$x_{2}/L_{s}$
, where
$x_{2}$
represents the cross-stream direction. In a temporally evolving flow,
$U_{s}$
and
$L_{s}$
depend only on time
$t$
, while they are functions of the streamwise distance
$x_{1}$
in a spatially evolving flow. Following Townsend, the similarity of the mean momentum and turbulent energy equations for spatially and temporally developing turbulent jets has been investigated in several works (e.g. Bradbury Reference Bradbury1965; Heskestad Reference Heskestad1965; Gutmark & Wygnanski Reference Gutmark and Wygnanski1976; Antonia, Satyaprakash & Hussain Reference Antonia, Satyaprakash and Hussain1980; Panchapakesan & Lumley Reference Panchapakesan and Lumley1993; Burattini, Antonia & Danaila Reference Burattini, Antonia and Danaila2005). For turbulent plane jets (similar to round jets and wakes), the empirical observation has been that the profiles of
$\overline{U}_{1}$
and
$\unicode[STIX]{x1D619}_{ij}^{0}$
become self-similar or at least close to a self-similar form (i.e. independent of
$x_{1}$
in a spatially evolving jet and independent of
$t$
in a temporally evolving jet) when the similarity variables are
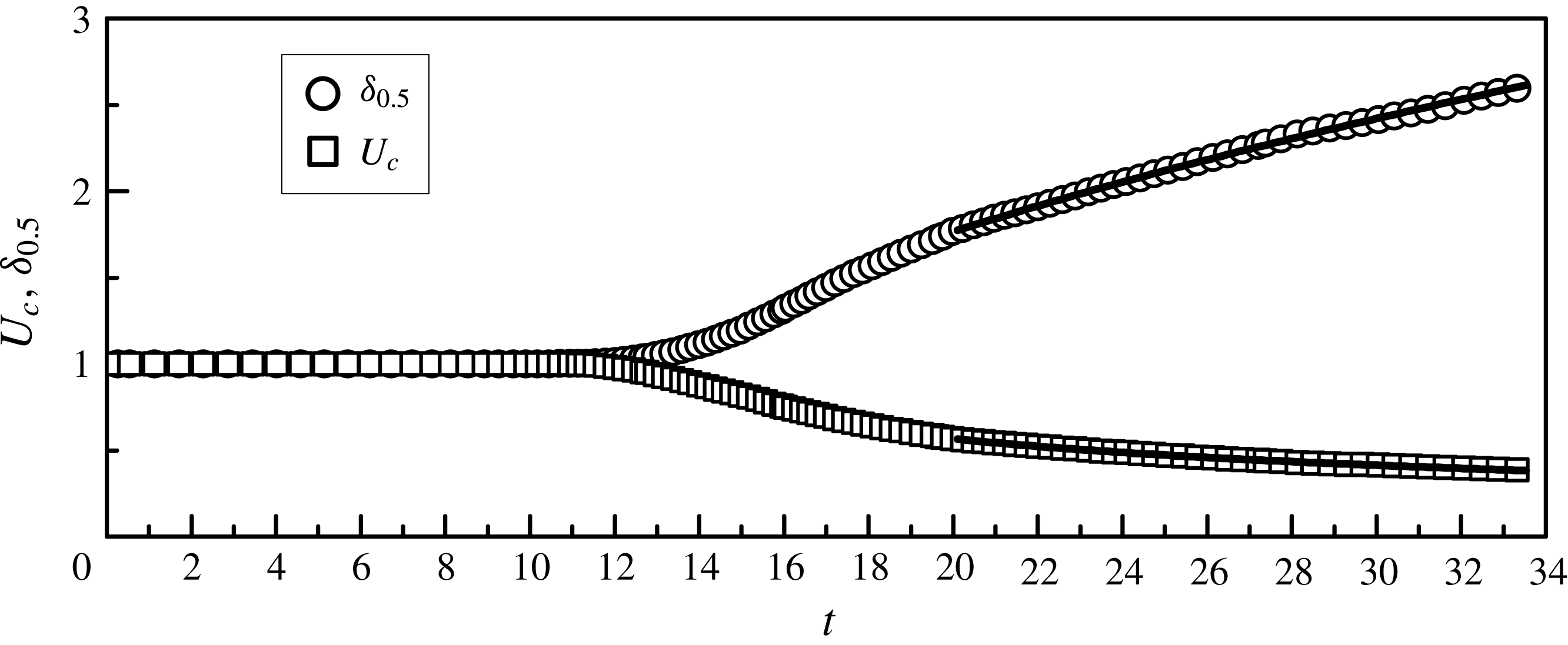
$L_{s}=\unicode[STIX]{x1D6FF}_{0.5}$
and
$U_{s}=U_{c}$
, where
$U_{c}$
is the mean streamwise velocity along the jet centreline and
$\unicode[STIX]{x1D6FF}_{0.5}$
is the jet half-width (which is defined as the location along
$x_{2}$
at which the mean jet velocity is equal to half of the local maximum mean velocity relative to the centreline).
Since introducing of the classical scaling, there has been however experimental and numerical evidence to strongly reconcile with that. For example, there has been significant scatter in the shape of the self-similar profiles of the same turbulence quantities in turbulent jet data from different investigations (e.g. the jet spread and decay rates and location of the virtual origin, etc.) (e.g. Bradbury Reference Bradbury1965; Heskestad Reference Heskestad1965; Gutmark & Wygnanski Reference Gutmark and Wygnanski1976; Antonia et al.
Reference Antonia, Satyaprakash and Hussain1980). These differences in jet flows, as well as experimental and numerical evidence in other types of turbulent flows, led George (Reference George, George and Arndt1989, Reference George1992) to suggest that the self-similarity is not universal as proposed by Townsend (Reference Townsend1956), but depends on the initial conditions. George (Reference George, George and Arndt1989) has also proposed a new approach, known as equilibrium similarity analysis, to determine the similarity scales from statistical equations such as the Reynolds stress transport equations. The role of initial conditions in turbulent flows is now well accepted as confirmed in many experimental and numerical investigations (e.g. Xu & Antonia Reference Xu and Antonia2002; George & Davidson Reference George and Davidson2004; Sadeghi & Pollard Reference Sadeghi and Pollard2012; Sadeghi, Lavoie & Pollard Reference Sadeghi, Lavoie and Pollard2014). In a recent work, George (Reference George2012) reviewed the consequence of his approach on shear flows and concluded that the theoretical conclusions from equilibrium similarity considerations are the same for wakes and jets. He noted that mean velocity profiles from different source conditions collapse when plotted using the centreline velocity
$U_{c}$
, and any appropriate width defined from the profile itself, such as the half-width
$\unicode[STIX]{x1D6FF}_{0.5}$
(similar to Townsend’s formulation), while the Reynolds stress profiles from different source conditions collapse when normalized using
$U_{c}^{2}\,\text{d}\unicode[STIX]{x1D6FF}_{0.5}/\text{d}x_{1}$
, and there is no reason to expect any of the other statistical properties from different sources to collapse at all (unlike Townsend’s predications). In view of a temporally evolving flow case, Moser, Roger & Ewing (Reference Moser, Roger and Ewing1998) and Ewing et al. (Reference Ewing, Frohnapfel, Pedersen, George and Westerweel2007) have extended George’s equilibrium analysis to governing equations for one and two-point correlations of velocity fluctuations in a temporally evolving wake. Interesting enough, they showed that single-point velocity moments have equilibrium similarity solutions of the form similar to Townsend’s results (i.e.
$f_{1}(x_{2}/\unicode[STIX]{x1D6FF}_{0.5})=\unicode[STIX]{x0394}U_{1}/U_{c}(t)$
and
$g_{ij}(x_{2}/\unicode[STIX]{x1D6FF}_{0.5})=\unicode[STIX]{x1D619}_{ij}^{0}/U_{c}(t)^{2}$
, where
$U_{c}(t)\propto (t-t_{0})^{-0.5}$
).
The other significant weakness of the classical scaling has been the fact that although experimental and numerical data usually show a satisfactory self-preservation in the mean velocity profiles, the higher moments of the velocity deviate often from a complete similarity. This issue still stands even when using the scaling parameters from the equilibrium analysis (e.g. Moser et al.
Reference Moser, Roger and Ewing1998). This has been more and less related to the insufficient distance or time to achieve the self-similarity, finite Reynolds number and initial conditions, although without providing strong theoretical evidence. For example, Sadeghi, Lavoie & Pollard (Reference Sadeghi, Lavoie and Pollard2015, Reference Sadeghi, Lavoie and Pollard2016, Reference Sadeghi, Lavoie and Pollard2018) recently investigated the axial evolution of
$\unicode[STIX]{x1D619}_{ii}^{0}$
, and subsequently the ratios
$\unicode[STIX]{x1D619}_{ij}^{0}/U_{c}^{2}$
for data from several turbulent round jets for a variety of Reynolds numbers,
$11\,000\leqslant Re_{D}\leqslant 184\,000$
, over a large range of
$10\leqslant x_{1}/D\leqslant 90$
(
$D$
is the jet diameter). It was found that
$\unicode[STIX]{x1D619}_{ij}^{0}\propto (x_{1}-x_{0})^{m}$
with
$-1.89\leqslant m\leqslant -1.78$
. Therefore, as
$U_{c}^{2}\propto (x_{1}-x_{0})^{-2}$
in this flow,
$\unicode[STIX]{x1D619}_{ij}^{0}$
has not been properly scaled with both the classical and equilibrium scaling parameters. Therefore, a serious question has arisen about a proper scaling for the higher moments of the velocity in these shear flows.
Although, the equilibrium similarity analysis has been applied with a great impact on resolving the failure of the classical scaling, the lack of a general solution for the self-similarity is still notable in the literature, especially for higher-moment quantities. Therefore, it is the main aim of this paper to use a more general technique based on Lie symmetry group analysis to formally derive the similarity of the first and second moments of the velocity for a temporally evolving jet, which can be considered as a key to revisiting the scaling laws in shear flows. An important feature that marks the Lie group approach as recognizably different from the typical self-similarity approaches is that it provides a fundamental framework for the utilization of systematic procedures leading to the integration of differential equations, to the determination of invariant solutions (similarity solutions) of initial and boundary value problems. However, the common approaches to self-similarity analysis are using an a priori set of similarity scales for all of the statistical moments in the transport equations.
Symmetry analysis of a system of differential equations based on continuous transformation groups was introduced by Sophus Lie in the nineteenth century to unify and extend various specialized methods for solving differential equations. Symmetry groups, or simply symmetries, are invariant transformations which do not alter the structural form of the equations under investigation. The profound application of Lie groups can be noted in various areas of mathematics, physics or even recently in turbulence. The groups of translations, rotations and scalings are some typical examples of such groups. Here, we briefly introduce the basic ideas of symmetries and invariant solutions while a detailed description of this method can be found in several other textbooks and papers such as Bluman (Reference Bluman1990), Hydon (Reference Hydon2000) and Bluman, Cheviakov & Anco (Reference Bluman, Cheviakov and Anco2010).
If a system of partial differential equations is given as follows:
$$\begin{eqnarray}\boldsymbol{F}(\boldsymbol{x},\boldsymbol{y},\boldsymbol{y}^{(1)},\boldsymbol{y}^{(2)},\ldots )=0,\end{eqnarray}$$
where
$\boldsymbol{x}$
is the set of independent variables,
$\boldsymbol{y}$
is the set of dependent variables and
$\boldsymbol{y}^{(n)}$
refers to the set of all
$n$
th-order derivatives of
$\boldsymbol{y}$
with respect to
$\boldsymbol{x}$
, then the variable transformation
$$\begin{eqnarray}\boldsymbol{x}^{\ast }=\unicode[STIX]{x1D753}(\boldsymbol{x},\boldsymbol{y}),\quad \boldsymbol{y}^{\ast }=\unicode[STIX]{x1D74D}(\boldsymbol{x},\boldsymbol{y})\end{eqnarray}$$
is called a symmetry transformation of (1.3) if
$$\begin{eqnarray}\boldsymbol{F}(\boldsymbol{x},\boldsymbol{y},\boldsymbol{y}^{(1)},\boldsymbol{y}^{(2)},\ldots )=0,\quad \Leftrightarrow \quad \boldsymbol{F}(\boldsymbol{x}^{\ast },\boldsymbol{y}^{\ast },\boldsymbol{y}^{\ast (1)},\boldsymbol{y}^{\ast (2)},\ldots )=0\end{eqnarray}$$
holds. In other words, the transformation (1.4) does not alter the functional form of the differential equation (1.3), and, hence, the transformation is also referred to as a form invariant transformation. Further, as an immediate result we can find that a symmetry maps a solution to a new solution. Now, let us confine ourselves to transformations, which depend on an arbitrary, continuous parameter
$\unicode[STIX]{x1D700}\in \mathbb{R}$
of the form
$$\begin{eqnarray}\boldsymbol{x}^{\ast }=\unicode[STIX]{x1D753}(\boldsymbol{x},\boldsymbol{y};\unicode[STIX]{x1D700}),\quad \boldsymbol{y}^{\ast }=\unicode[STIX]{x1D74D}(\boldsymbol{x},\boldsymbol{y};\unicode[STIX]{x1D700}).\end{eqnarray}$$
If we further imply group properties and a certain smoothness with respect to
$\boldsymbol{x}$
,
$\boldsymbol{y}$
and
$\unicode[STIX]{x1D716}$
, these symmetries constitute continuous transformation groups called Lie groups, which allow the construction of a broad set of analytic solutions to differential equations. Furthermore, and without loss of generality, it is assumed that the unitary transformation corresponds to
$\unicode[STIX]{x1D700}=0$
$$\begin{eqnarray}\boldsymbol{x}^{\ast }=\unicode[STIX]{x1D753}(\boldsymbol{x},\boldsymbol{y};\unicode[STIX]{x1D700}=0)=\boldsymbol{x},\quad \boldsymbol{y}^{\ast }=\unicode[STIX]{x1D74D}(\boldsymbol{x},\boldsymbol{y};\unicode[STIX]{x1D700}=0)=\boldsymbol{y}.\end{eqnarray}$$
Considering the latter and recollecting that the transformation rules for
$\unicode[STIX]{x1D753}$
and
$\unicode[STIX]{x1D74D}$
are sufficiently smooth and thus invertible so that a Taylor expansion about
$\unicode[STIX]{x1D700}=0$
can be done
$$\begin{eqnarray}\boldsymbol{x}^{\ast }=\left.\unicode[STIX]{x1D753}(\boldsymbol{x},\boldsymbol{y};\unicode[STIX]{x1D700}=0)+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D753}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}}\right|_{\unicode[STIX]{x1D700}=0}\unicode[STIX]{x1D700}+O(\unicode[STIX]{x1D700}^{2}),\quad \boldsymbol{y}^{\ast }=\left.\unicode[STIX]{x1D74D}(\boldsymbol{x},\boldsymbol{y};\unicode[STIX]{x1D700}=0)+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D74D}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}}\right|_{\unicode[STIX]{x1D700}=0}\unicode[STIX]{x1D700}+O(\unicode[STIX]{x1D700}^{2}).\end{eqnarray}$$
The first term on each of the right-hand sides can be replaced by (1.7) and terms of order
$O(\unicode[STIX]{x1D700})$
are formally replaced by
$\unicode[STIX]{x1D743}$
and
$\boldsymbol{\unicode[STIX]{x1D702}}$
:
$$\begin{eqnarray}\boldsymbol{x}^{\ast }=\boldsymbol{x}+\unicode[STIX]{x1D743}(\boldsymbol{x},\boldsymbol{y})\unicode[STIX]{x1D700}+O(\unicode[STIX]{x1D700}^{2}),\quad \boldsymbol{y}^{\ast }=\boldsymbol{y}+\boldsymbol{\unicode[STIX]{x1D702}}(\boldsymbol{x},\boldsymbol{y})\unicode[STIX]{x1D700}+O(\unicode[STIX]{x1D700}^{2}).\end{eqnarray}$$
The crucial implication of Lie’s first theorem states that knowing the ‘infinitesimals’
$\unicode[STIX]{x1D743}$
and
$\boldsymbol{\unicode[STIX]{x1D702}}$
in (1.8) uniquely determines the ‘global’ form of the group transformation, i.e. (1.6). If the infinitesimal of a transformation is given, its global form can be determined by integrating the first-order system using Lie’s first theorem
$$\begin{eqnarray}\frac{\text{d}\boldsymbol{x}^{\ast }(\unicode[STIX]{x1D700})}{\text{d}\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D743}(\boldsymbol{x}^{\ast }(\unicode[STIX]{x1D700}),\boldsymbol{y}^{\ast }(\unicode[STIX]{x1D700})),\quad \frac{\text{d}\boldsymbol{y}^{\ast }(\unicode[STIX]{x1D700})}{\text{d}\unicode[STIX]{x1D700}}=\boldsymbol{\unicode[STIX]{x1D702}}(\boldsymbol{x}^{\ast }(\unicode[STIX]{x1D700}),\boldsymbol{y}^{\ast }(\unicode[STIX]{x1D700})),\end{eqnarray}$$
with initial conditions:
$$\begin{eqnarray}\unicode[STIX]{x1D700}=0:\quad \boldsymbol{x}^{\ast }(\unicode[STIX]{x1D700})=\boldsymbol{x}\quad \text{and}\quad \boldsymbol{y}^{\ast }(\unicode[STIX]{x1D700})=\boldsymbol{y}.\end{eqnarray}$$
A main advantage of Lie groups is that their derivation is algorithmic, therefore, these groups (and explicit solutions constructed from them) can be found using computational methods. Once the symmetry groups of a system of differential equations are obtained, a large number of different schemes becomes available to analyse the system. For example, new solutions can be constructed from old solutions using symmetry groups or it is possible to determine which type of equations admit a given group of symmetry.
In the context of fluid mechanics and turbulence, once the symmetries are obtained, they can be used to construct self-similar solutions of the corresponding flow, although in group theory these are usually named invariant solutions. Here, we briefly introduce the definition of a group invariant solution (for more details, see e.g. Hydon Reference Hydon2000; Bluman et al.
Reference Bluman, Cheviakov and Anco2010). We define
$\boldsymbol{y}=\unicode[STIX]{x1D723}(\boldsymbol{x})$
as an invariant solution of a differential equation if:
(i)
$\boldsymbol{y}-\unicode[STIX]{x1D723}(\boldsymbol{x})$
is an invariant function with respect to the operator
$X$
, (1.12)where$$\begin{eqnarray}X[\,\boldsymbol{y}-\unicode[STIX]{x1D723}(\boldsymbol{x})]=0\quad \text{with }\boldsymbol{y}=\unicode[STIX]{x1D723}(\boldsymbol{x}),\end{eqnarray}$$
$X$
is given by (1.13)$$\begin{eqnarray}X=\unicode[STIX]{x1D709}_{i}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{i}}+\unicode[STIX]{x1D702}_{j}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y_{j}},\end{eqnarray}$$
(ii)
$\boldsymbol{y}=\unicode[STIX]{x1D723}(\boldsymbol{x})$
is a solution of a differential equation (
$\boldsymbol{F}=0$
).
Differentiating out (1.12), we obtain the hyperbolic system
$$\begin{eqnarray}\unicode[STIX]{x1D709}_{k}(\boldsymbol{x},\unicode[STIX]{x1D723})\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}_{l}}{\unicode[STIX]{x2202}x_{k}}=\unicode[STIX]{x1D702}_{l}(\boldsymbol{x},\unicode[STIX]{x1D723})\end{eqnarray}$$
to be solved by the method of characteristics, which finally leads to the characteristic condition
$$\begin{eqnarray}\frac{\text{d}x_{1}}{\unicode[STIX]{x1D709}_{1}(\boldsymbol{x},\boldsymbol{y})}=\frac{\text{d}x_{2}}{\unicode[STIX]{x1D709}_{2}(\boldsymbol{x},\boldsymbol{y})}=\cdots =\frac{\text{d}x_{m}}{\unicode[STIX]{x1D709}_{m}(\boldsymbol{x},\boldsymbol{y})}=\frac{\text{d}y_{1}}{\unicode[STIX]{x1D702}_{1}(\boldsymbol{x},\boldsymbol{y})}=\frac{\text{d}y_{2}}{\unicode[STIX]{x1D702}_{2}(\boldsymbol{x},\boldsymbol{y})}=\cdots =\frac{\text{d}y_{m}}{\unicode[STIX]{x1D702}_{n}(\boldsymbol{x},\boldsymbol{y})},\end{eqnarray}$$
where
$\unicode[STIX]{x1D723}$
has been replaced by
$\boldsymbol{y}$
. The latter is usually referred to an invariant surface condition. The system has
$m+n-1$
solutions which are regarded as new variables. This suggests taking the
$m-1$
solutions of the
$m$
equations on the left-hand side, or, more precisely the constants of integration as new independent variables, and to equate the
$n$
expressions on the right-hand side with any one of the
$m$
expressions on the left-hand side give the dependent variables.
The application of Lie symmetry group theory in turbulence has been developed by Oberlack and his co-authors in a series of papers (see e.g. Oberlack Reference Oberlack2001; Oberlack & Rosteck Reference Oberlack and Rosteck2010; Avsarkisov, Oberlack & Hoyas Reference Avsarkisov, Oberlack and Hoyas2014; Waclawczyk et al. Reference Waclawczyk, Staffolani, Oberlack, Rosteck, Wilczek and Friedrich2014; Oberlack et al. Reference Oberlack, Waclawczyk, Rosteck and Avsarkisov2015). For example, they have studied the turbulent channel and other canonical wall-bounded flows using Lie symmetry theory by investigating the infinite series of two-point correlation (TPC) and multi-point correlation (MPC) equations. The symmetry analysis of these equations together with the application of an invariant surface condition have enabled them to derive a variety of classical and new scaling laws in turbulence as the exact solutions of a symmetry invariant type of TPC and MPC.
In the present research, we employ the Lie symmetry method to the mean momentum and TPC equations as the fundamental basis to finding scaling laws. This is the first study to consider the application of symmetry in a turbulent jet flow, known as a complex type of shear flow (in which more than one independent variable is present). As a consequence of the current analytical work, we propose new scaling laws (self-similar solutions) for the mean flow and second moments of the velocity for plane jets. The results of direct numerical simulations (DNSs) are used to validate the new scaling laws. The DNS is based on a high-order method that allows for the computation of both small-scale and large-scale quantities with high accuracy (Gauding et al. Reference Gauding, Goebbert, Hasse and Peters2015).
This paper is organized as follows. The governing equations required for the symmetry analysis of a temporally evolving plane jet are given in § 2. In § 3, we present the theoretical (Lie symmetry) analysis of the governing equations for the current flow and derive new scaling laws. The DNS details and verification of scaling laws are presented in § 4. Finally, the summary and conclusions are drawn in § 5.
2 The equations governing mean flow and TPC
In the present study, the mathematical theory of Lie group analysis is applied to equations for the mean momentum and two-point correlation function of velocity. First, we consider the governing equations for an incompressible turbulent flow, i.e. continuity and mean momentum equations, which are given by
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\overline{U}_{k}}{\unicode[STIX]{x2202}x_{k}}=0\end{eqnarray}$$
and
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\overline{U}_{i}}{\unicode[STIX]{x2202}t}+\overline{U}_{k}\frac{\unicode[STIX]{x2202}\overline{U}_{i}}{\unicode[STIX]{x2202}x_{k}}=-\frac{\unicode[STIX]{x2202}\overline{P}}{\unicode[STIX]{x2202}x_{i}}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D619}_{ik}^{0}}{\unicode[STIX]{x2202}x_{k}}+\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}^{2}\overline{U}_{i}}{\unicode[STIX]{x2202}x_{k}\unicode[STIX]{x2202}x_{k}},\quad i=1,2,3,\end{eqnarray}$$
where
$\overline{U}_{i}$
and
$\overline{P}$
are respectively the mean velocity and mean pressure normalized by the density, and
$\unicode[STIX]{x1D619}_{ik}^{0}=\overline{u_{i}u_{k}}$
is the Reynolds stress tensor, which all are functions of time (
$t$
) and direction (
$x_{i}$
) (note, here overbar signifies the average. Also for simplicity, explicit dependencies on
$t$
and
$x_{i}$
are removed throughout this paper, unless there is an ambiguity). A temporally evolving plane jet is considered statistically homogeneous in the mean flow and lateral directions (
$x_{1}$
and
$x_{3}$
respectively) and spreads in the inhomogeneous direction
$x_{2}$
over time
$t$
. A schematic of the simulated temporally evolving plane jet is shown in figure 1. Therefore, while (2.1) vanishes, the equation for the mean momentum (2.2) reduces to
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\overline{U}_{1}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D619}_{12}^{0}}{\unicode[STIX]{x2202}x_{2}}-\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}^{2}\overline{U}_{1}}{\unicode[STIX]{x2202}x_{2}^{2}}=0,\end{eqnarray}$$
where
$\unicode[STIX]{x1D619}_{12}^{0}=\overline{u_{1}u_{2}}$
, where
$u_{1}$
and
$u_{2}$
are the streamwise (
$x_{1}$
) and cross-stream (
$x_{2}$
) velocity fluctuations respectively. By integrating (2.3) across the cross-stream (
$x_{2}$
) and given that
$\overline{U}_{1}$
and
$\unicode[STIX]{x1D619}_{12}^{0}$
vanish for
$x_{2}\rightarrow \pm \infty$
, it is also confirmed that
$$\begin{eqnarray}I=\int _{-\infty }^{\infty }\overline{U}_{1}(x_{2},t)\,\text{d}x_{2}=\text{const.},\end{eqnarray}$$
is a global (integral) invariant, which will be used as an important constraint in the subsequent analysis.
Figure 1. A schematic of a temporally evolving plane jet.
Now, we turn our attention to the equations for TPC and MPC. The concept of TPC and MPC of a fluctuating velocity has become an important analytical tool in turbulence since it was first established in Keller & Friedmann (Reference Keller, Friedmann, Biezeno and Burgers1924). They assumed that all correlation equations of orders higher than two are negligible. However, later, all higher correlations were taken into account from various theoretical considerations (e.g. Hinze Reference Hinze1959). Perhaps, the significance of MPCs can be considered twofold: they deliver additional information on the turbulence statistics such as length scale, and also in every higher-moment equation, only one additional unclosed tensor appears. In view of symmetries, it has been shown that a general symmetry analysis of the MPC equations results in additional symmetries compared to only those which are implied by the Navier–Stokes equations (Oberlack & Rosteck Reference Oberlack and Rosteck2010, Reference Oberlack and Rosteck2011; Avsarkisov et al. Reference Avsarkisov, Oberlack and Hoyas2014). These symmetries are denoted statistical symmetries and they have no direct counterpart in the Navier–Stokes equations. Subsequently, they play an important role in the understanding of the scaling of the higher moments of velocity. In the present paper, we only consider the TPC. The TPC of the fluctuating velocities in its most general form reads
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{D}\unicode[STIX]{x1D619}_{ij}}{\text{D}t}+\unicode[STIX]{x1D619}_{kj}\frac{\unicode[STIX]{x2202}\overline{U}_{i}(\boldsymbol{x},t)}{\unicode[STIX]{x2202}x_{k}}+\unicode[STIX]{x1D619}_{ik}\left.\frac{\unicode[STIX]{x2202}\overline{U}_{j}(\boldsymbol{x},t)}{\unicode[STIX]{x2202}x_{k}}\right|_{\boldsymbol{x}+\boldsymbol{r}}+[\overline{U}_{k}(\boldsymbol{x}+\boldsymbol{r},t)-\overline{U}_{k}(\boldsymbol{x},t)]\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D619}_{ij}}{\unicode[STIX]{x2202}r_{k}}+\frac{\unicode[STIX]{x2202}\overline{pu_{j}}}{\unicode[STIX]{x2202}x_{i}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\unicode[STIX]{x2202}\overline{pu_{j}}}{\unicode[STIX]{x2202}r_{i}}+\frac{\unicode[STIX]{x2202}\overline{u_{i}p}}{\unicode[STIX]{x2202}r_{j}}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D619}_{(ik)j}}{\unicode[STIX]{x2202}x_{k}}-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r_{k}}[\unicode[STIX]{x1D619}_{(ik)j}-\unicode[STIX]{x1D619}_{i(jk)}]\nonumber\\ \displaystyle & & \displaystyle \quad -\,\unicode[STIX]{x1D708}\left[\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D619}_{ij}}{\unicode[STIX]{x2202}x_{k}^{2}}-2\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D619}_{ij}}{\unicode[STIX]{x2202}x_{k}\unicode[STIX]{x2202}r_{k}}+2\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D619}_{ij}}{\unicode[STIX]{x2202}r_{k}\unicode[STIX]{x2202}r_{k}}\right]=0,\end{eqnarray}$$
where correlation vectors and tensors are defined as
$\unicode[STIX]{x1D619}_{ij}=\overline{u_{i}(\boldsymbol{x},t)u_{j}(\boldsymbol{x}+\boldsymbol{r},t)}$
,
$\overline{pu_{j}}=\overline{p(\boldsymbol{x},t)u_{j}(\boldsymbol{x}+\boldsymbol{r},t)}$
$\overline{u_{i}p}=\overline{u_{i}(\boldsymbol{x},t)p(\boldsymbol{x}+\boldsymbol{r},t)}$
,
$\unicode[STIX]{x1D619}_{(ik)j}=\overline{u_{i}(\boldsymbol{x},t)u_{k}(\boldsymbol{x},t)u_{j}(\boldsymbol{x}+\boldsymbol{r},t)}$
,
$\unicode[STIX]{x1D619}_{i(jk)}=\overline{u_{i}(\boldsymbol{x},t)u_{k}(\boldsymbol{x}+\boldsymbol{r},t)u_{j}(\boldsymbol{x}+\boldsymbol{r},t)}$
and
$\text{D}\unicode[STIX]{x1D619}_{ij}/\text{D}t=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t+\overline{U}_{k}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{k}))$
is the mean substantial derivative (
$u$
and
$p$
are the fluctuating components of the velocity and pressure). Furthermore, for the TPC of the fluctuating velocities, the continuity equations take the form (see, e.g. Oberlack & Rosteck Reference Oberlack and Rosteck2010)
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D619}_{ij}}{\unicode[STIX]{x2202}x_{i}}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D619}_{ij}}{\unicode[STIX]{x2202}r_{i}}=0,\quad \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D619}_{ij}}{\unicode[STIX]{x2202}r_{j}}=0,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\overline{pu_{i}}}{\unicode[STIX]{x2202}r_{i}}=0,\quad \frac{\unicode[STIX]{x2202}\overline{pu_{j}}}{\unicode[STIX]{x2202}x_{j}}-\frac{\unicode[STIX]{x2202}\overline{pu_{j}}}{\unicode[STIX]{x2202}r_{j}}=0,\end{eqnarray}$$
and
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D619}_{i(jk)}}{\unicode[STIX]{x2202}x_{i}}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D619}_{i(jk)}}{\unicode[STIX]{x2202}r_{i}}=0,\quad \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D619}_{(ik)j}}{\unicode[STIX]{x2202}r_{j}}=0.\end{eqnarray}$$
This approach is subsequently referred to as the
$\unicode[STIX]{x1D619}$
-approach. Here,
$\boldsymbol{x}$
and
$\boldsymbol{r}$
are coordinates in the physical and correlation spaces, respectively. At
$\boldsymbol{r}\rightarrow 0$
, the two-point correlation tensor
$\unicode[STIX]{x1D619}_{ij}$
reduces to the Reynolds stress tensor
$\unicode[STIX]{x1D619}_{ij}^{0}$
, i.e.
$$\begin{eqnarray}\unicode[STIX]{x1D619}_{ij}(\boldsymbol{x},\boldsymbol{r}=0,t)=\unicode[STIX]{x1D619}_{ij}^{0}(\boldsymbol{x},t)=\overline{u_{i}u_{j}}(\boldsymbol{x},t).\end{eqnarray}$$
The superscript ‘
$0$
’ denotes that tensor
$\unicode[STIX]{x1D619}_{ij}^{0}$
provides a surrogate limit
$\boldsymbol{r}\rightarrow 0$
of the two-point correlation tensor
$\unicode[STIX]{x1D619}_{ij}$
.
It is worth mentioning that higher-order MPC equations have a similar form to (2.5) and may be taken from Oberlack & Rosteck (Reference Oberlack and Rosteck2010). For a temporally evolving jet, the equations for TPC (2.5) reduce to
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D619}_{ij}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D6FF}_{i1}\unicode[STIX]{x1D619}_{2j}\frac{\unicode[STIX]{x2202}\overline{U}_{1}}{\unicode[STIX]{x2202}x_{2}}+\unicode[STIX]{x1D6FF}_{j1}\unicode[STIX]{x1D619}_{i2}\left.\frac{\unicode[STIX]{x2202}\overline{U}_{1}}{\unicode[STIX]{x2202}x_{2}}\right|_{(x_{2}+r_{2})}+[\overline{U}_{1}(x_{2}+r_{2},t)-\overline{U}_{1}(x_{2},t)]\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D619}_{ij}}{\unicode[STIX]{x2202}r_{1}}+\unicode[STIX]{x1D6FF}_{i2}\frac{\unicode[STIX]{x2202}\overline{pu_{j}}}{\unicode[STIX]{x2202}x_{2}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\unicode[STIX]{x2202}\overline{pu_{j}}}{\unicode[STIX]{x2202}r_{i}}+\frac{\unicode[STIX]{x2202}\overline{u_{i}p}}{\unicode[STIX]{x2202}r_{j}}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D619}_{(i2)j}}{\unicode[STIX]{x2202}x_{2}}-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r_{k}}[\unicode[STIX]{x1D619}_{(ik)j}-\unicode[STIX]{x1D619}_{i(jk)}]\nonumber\\ \displaystyle & & \displaystyle \quad -\,\unicode[STIX]{x1D708}\left[\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D619}_{ij}}{\unicode[STIX]{x2202}x_{2}^{2}}-2\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D619}_{ij}}{\unicode[STIX]{x2202}x_{2}\unicode[STIX]{x2202}r_{2}}+2\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D619}_{ij}}{\unicode[STIX]{x2202}r_{k}\unicode[STIX]{x2202}r_{k}}\right]=0,\end{eqnarray}$$
since
$\overline{U}_{2}=\overline{U}_{3}=0$
and
$\unicode[STIX]{x2202}\overline{(\quad )}/\unicode[STIX]{x2202}x_{1}=\unicode[STIX]{x2202}\overline{(\quad )}/\unicode[STIX]{x2202}x_{3}=0$
.
Although an advantage of the TPC equations for the fluctuating velocity (2.5) is their straightforward relation to the Reynolds stress components, the key disadvantage is the nonlinearity of the system of differential equations (2.5), which complicates further analysis concerning Lie-point symmetries. As such, we adopt another set of two-point equations based on the instantaneous velocities, also known as the
$\unicode[STIX]{x1D60F}$
-approach, so that the corresponding two-point correlation is defined by
$$\begin{eqnarray}\unicode[STIX]{x1D60F}_{ij}=\overline{U_{i}(\boldsymbol{x},t)U_{j}(\boldsymbol{x}+\boldsymbol{r},t)}.\end{eqnarray}$$
We also define the tensor
$\unicode[STIX]{x1D60F}_{ij}^{0}$
as the limit
$\boldsymbol{r}\rightarrow 0$
of the two-point correlation tensor
$\unicode[STIX]{x1D60F}_{ij}$
, i.e.
$$\begin{eqnarray}\unicode[STIX]{x1D60F}_{ij}(\boldsymbol{x},\boldsymbol{r}=0,t)=\unicode[STIX]{x1D60F}_{ij}^{0}(\boldsymbol{x},t)=\overline{U_{i}U_{j}}(\boldsymbol{x},t),\end{eqnarray}$$
where the superscript ‘
$0$
’ is again an indication of the limit
$\boldsymbol{r}\rightarrow 0$
of a two-point correlation tensor,
$\unicode[STIX]{x1D60F}_{ij}$
. The
$\unicode[STIX]{x1D60F}$
-approach, which was first introduced by Oberlack & Rosteck (Reference Oberlack and Rosteck2010, Reference Oberlack and Rosteck2011), results in a linear set of equations fully equivalent to (2.5), which is more suited for the analysis. Oberlack & Rosteck (Reference Oberlack and Rosteck2010) showed that the terms in the equations from the
$\unicode[STIX]{x1D60F}$
-approach can be directly related to the classical TPC for the fluctuating velocity, which simply allows us to change tensors from one approach to another. For example, in the case of the second moments, the following relation exists
$$\begin{eqnarray}\unicode[STIX]{x1D60F}_{ij}(\boldsymbol{x},\boldsymbol{r},t)=\unicode[STIX]{x1D619}_{ij}(\boldsymbol{x},\boldsymbol{r},t)+\overline{U}_{i}(\boldsymbol{x},t)\overline{U}_{j}(\boldsymbol{x}+\boldsymbol{r},t).\end{eqnarray}$$
As in this paper, we mainly focus on up to the second moments of the velocity, the relation (2.13) is the most applicable transformation between tensors, although a very general form of the tensor transformation for all terms can be found in Oberlack & Rosteck (Reference Oberlack and Rosteck2010). For a time evolving plane jet, the equations for two-point correlations of the instantaneous velocity, the
$\unicode[STIX]{x1D60F}$
-approach, are given by
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D60F}_{ij}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D6FF}_{i2}\frac{\unicode[STIX]{x2202}\overline{PU_{j}}}{\unicode[STIX]{x2202}x_{2}}-\frac{\unicode[STIX]{x2202}\overline{PU_{j}}}{\unicode[STIX]{x2202}r_{i}}+\frac{\unicode[STIX]{x2202}\overline{U_{i}P}}{\unicode[STIX]{x2202}r_{j}}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D60F}_{(i2)j}}{\unicode[STIX]{x2202}x_{2}}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D60F}_{(ik)j}}{\unicode[STIX]{x2202}r_{k}}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D60F}_{i(jk)}}{\unicode[STIX]{x2202}r_{k}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\unicode[STIX]{x1D708}\left[\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D60F}_{ij}}{\unicode[STIX]{x2202}x_{2}^{2}}-2\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D60F}_{ij}}{\unicode[STIX]{x2202}x_{2}\unicode[STIX]{x2202}r_{2}}+2\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D60F}_{ij}}{\unicode[STIX]{x2202}r_{k}\unicode[STIX]{x2202}r_{k}}\right]=0,\end{eqnarray}$$
where
$\overline{PU_{j}}=\overline{P(\boldsymbol{x},t)U_{j}(\boldsymbol{x}+\boldsymbol{r},t)}$
,
$\overline{U_{i}P}=\overline{U_{i}(\boldsymbol{x},t)P(\boldsymbol{x}+\boldsymbol{r},t)}$
,
$\unicode[STIX]{x1D60F}_{(ik)j}=$
$\overline{U_{i}(\boldsymbol{x},t)U_{k}(\boldsymbol{x},t)U_{j}(\boldsymbol{x}+\boldsymbol{r},t)}$
,
$\unicode[STIX]{x1D60F}_{i(jk)}=\overline{U_{i}(\boldsymbol{x},t)U_{k}(\boldsymbol{x}+\boldsymbol{r},t)U_{j}(\boldsymbol{x}+\boldsymbol{r},t)}$
. Here, we also need to mention that the momentum equation (2.3) keeps the same form in both the
$\unicode[STIX]{x1D619}$
- and
$\unicode[STIX]{x1D60F}$
-approaches in a temporally evolving plane jet, because of the vanishing velocity
$\overline{U}_{2}$
, and reads
$$\begin{eqnarray}\unicode[STIX]{x1D619}_{12}^{0}=\unicode[STIX]{x1D60F}_{12}^{0}=\overline{u_{1}u_{2}}(x_{2},t).\end{eqnarray}$$
For the TPC of the instantaneous velocities, the continuity equations in this flow reduce to
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D60F}_{2j}}{\unicode[STIX]{x2202}x_{2}}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D60F}_{ij}}{\unicode[STIX]{x2202}r_{i}}=0,\quad \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D60F}_{ij}}{\unicode[STIX]{x2202}r_{j}}=0,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\overline{PU_{i}}}{\unicode[STIX]{x2202}r_{i}}=0,\quad \frac{\unicode[STIX]{x2202}\overline{PU_{2}}}{\unicode[STIX]{x2202}x_{2}}-\frac{\unicode[STIX]{x2202}\overline{PU_{i}}}{\unicode[STIX]{x2202}r_{i}}=0,\end{eqnarray}$$
and
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D60F}_{2(jk)}}{\unicode[STIX]{x2202}x_{2}}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D60F}_{i(jk)}}{\unicode[STIX]{x2202}r_{i}}=0,\quad \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D60F}_{(ik)j}}{\unicode[STIX]{x2202}r_{j}}=0.\end{eqnarray}$$
In the present research, we apply Lie symmetry analysis to (2.3) and (2.14), while additionally considering the continuity equations for TPC (2.16)–(2.18). We further consider the relation (2.15), and at a late phase, the global invariant
$I$
in (2.4) in the current analysis. However, as the classical formulation based on the mean and the fluctuations is more well known in the field of turbulence, we will finally write the scaling laws in this notation.
At this stage, a brief discussion is required regarding the aforementioned TPC equations before they are investigated by the Lie symmetry approach. Here, these equations are considered in a large Reynolds number asymptotic, so that the viscous terms will be neglected. Constructing scaling laws for finite Reynolds number flows using the assumption of infinite Reynolds number (and subsequently neglecting viscosity) has been a common approach in the literature. For example, Townsend (Reference Townsend1956), George (Reference George, George and Arndt1989, Reference George1992), George & Castillo (Reference George and Castillo1997) and Talluru et al. (Reference Talluru, Djenidi, Kamruzzaman and Antonia2016) used this assumption to derive the scaling laws of the governing equations. In the context of symmetry, Oberlack has widely shown that the Euler equations (
$\unicode[STIX]{x1D708}=0$
) admit one more scaling group compared to the Navier–Stokes equations (e.g. Oberlack Reference Oberlack2000). Therefore, we assume that the Reynolds number tends to infinity so that the viscous terms in the two-point correlation equation may be neglected. The basis for this assumption is the fact that, to leading order only, viscosity has a negligible effect on ‘large-scale motion’ as
$Re\rightarrow \infty$
. On the other hand, it is argued that the convective terms play a negligible role in the equations for small-scale motions. So, viscosity only affects the small scales of
$O(\unicode[STIX]{x1D702})$
, where
$\unicode[STIX]{x1D702}$
is Kolmogorov length scale.
In order to distinguish between viscosity-dominated small-scale and large-scale motions, an asymptotic expansion was introduced in Oberlack (Reference Oberlack2002) and Oberlack & Guenther (Reference Oberlack and Guenther2003): the idea was initiated from the matched asymptotic expansion for locally isotropic turbulence in the correlation space. Therein the two sets of equations for the large- and small-scale motions were derived. In the former (outer layer in correlation space (
$r$
-space)), we have TPC equations with
$\unicode[STIX]{x1D708}=0$
, i.e. the TPC equations for the large-scale motions of turbulence, which are correlated over much larger separations than at small scales. Further, it was shown that by taking the one-point limit
$\boldsymbol{r}=0$
within the inviscid TPC, an error only of order
$O(Re^{-1/2})$
is made, which becomes negligibly small if the Reynolds number is large enough, i.e.
$$\begin{eqnarray}\unicode[STIX]{x1D619}_{ij}(\boldsymbol{x},\boldsymbol{r}=0,t)=\unicode[STIX]{x1D619}_{ij}^{0}(\boldsymbol{x},t)-O(Re^{-1/2}).\end{eqnarray}$$
Note that only large-scale quantities, such as the mean velocity or the Reynolds stresses, can therefore be determined in the subsequent analysis. Small-scale quantities such as dissipation can formally be obtained from the large-scale quantities or the self-similarity analysis of the small-scale motions. It is worth noting that we have also conducted the symmetry analysis for the full TPC equations while keeping the viscosity (not shown in the present paper). In this case, we arrive at self-similar solutions, which are fully consistent with the obtained solutions for the case (
$\unicode[STIX]{x1D708}=0$
), however, in less general forms. Also, we currently devote ourselves only to generating invariant scaling laws for the mean velocity and Reynolds stresses, and therefore, the
$r$
-dependency of the terms is skipped. These terms are indeed more common and applicable in the turbulence community and appear in a variety of textbooks and papers. As such, we first establish their self-similar forms, and consider the
$r$
-dependency (two-point correlation functions) in more detail in our future work (please note that we however present the general solutions for the two-point correlation functions in appendix C).
3 Lie group analysis and new scaling laws
In this paper, Lie symmetry analysis is used to find symmetry transformations of (2.3) and (2.14), and, in turn, group invariant (self-similar) solutions (scaling laws). The current theoretical analysis is considered in conjugation with numerical data to develop scaling laws. In the current section, Lie’s symmetry analysis is described and the corresponding numerical validation is provided in the next section. It should be mentioned that here, an abbreviated version of the analytical approach is presented, while for further mathematical details, the reader is referred to the appendixes. Here, we divide Lie’s symmetry procedure into two steps. First, the symmetry transformations are determined. Second, the symmetries are used to achieve self-similarity solutions. As already indicated in § 1, the derivation of symmetry groups has an algorithmic nature (which is an important advantage of this approach). Thus, a variety of computational tools is available to find continuous symmetry groups for essentially every differential equations. In the present work, a Lie software package ‘DESOLV-II’ developed by Vu, Gefferson & Carminati (Reference Vu, Gefferson and Carminati2012), was used to perform the symmetry analysis. The DESOLV-II is a Maple based module, which enables us to find all local symmetries of a system of ordinary differential equations (ODEs) or partial differential equations (PDEs). In particular, it computes the system of determining equations for the infinitesimals
$\unicode[STIX]{x1D709}(x,y)$
and
$\unicode[STIX]{x1D702}(x,y)$
(see (1.9)), which is adequate for the purpose of the present work. It should be mentioned that all results were double checked by another Maple based Lie software package (GeM) developed by Cheviakov (Reference Cheviakov2007).
In the first step, the infinitesimal generators
$\unicode[STIX]{x1D709}$
for the independent variables of
$t$
and
$x_{2}$
and
$\unicode[STIX]{x1D702}$
for the dependent variables are determined by applying the Lie symmetry method to (2.3) and (2.14), which are given in appendix A. It should be noted that the infinitesimals for the mean velocity and the Reynolds stresses as the dependent variables are only considered and compared with the DNS data in the main body of this manuscript. These are indeed the most applicable parameters in the turbulence community which have been investigated widely. It is obvious that (2.14) also contains the pressure–velocity correlation and the triple-velocity correlation, which are important, although often computationally very expensive. However, we have calculated the infinitesimals for the dependent variables of the pressure–velocity correlation and the triple-velocity correlation, and constructed the scaling laws for these parameters, which are listed fully in appendices A and B.
In the second part, once the desired symmetries of the base equations are obtained in infinitesimal form (i.e.
$\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D702}$
are known, see appendix A), the symmetry invariant (self-similar) solutions can be computed using the invariant surface condition (1.15). As such, the condition for symmetry invariant solutions reads
$$\begin{eqnarray}\displaystyle \frac{\text{d}t}{F_{1}(t)} & = & \displaystyle \frac{\text{d}x_{2}}{F_{2}(t)x_{2}+F_{3}(t)}=\frac{\text{d}\overline{U}_{1}}{a_{1}\overline{U}_{1}-F_{2}(t)\overline{U}_{1}+a_{U_{1}}}\nonumber\\ \displaystyle & = & \displaystyle \frac{\text{d}\unicode[STIX]{x1D60F}_{11}^{0}}{a_{1}\unicode[STIX]{x1D60F}_{11}^{0}-{\displaystyle \frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}}\unicode[STIX]{x1D60F}_{11}^{0}+a_{\unicode[STIX]{x1D60F}_{11}}}\nonumber\\ \displaystyle & = & \displaystyle \frac{\text{d}\unicode[STIX]{x1D60F}_{22}^{0}}{a_{1}\unicode[STIX]{x1D60F}_{22}^{0}-{\displaystyle \frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}}\unicode[STIX]{x1D60F}_{22}^{0}+a_{\unicode[STIX]{x1D60F}_{22}}}\nonumber\\ \displaystyle & = & \displaystyle \frac{\text{d}\unicode[STIX]{x1D60F}_{33}^{0}}{a_{1}\unicode[STIX]{x1D60F}_{33}^{0}-{\displaystyle \frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}}\unicode[STIX]{x1D60F}_{33}^{0}+a_{\unicode[STIX]{x1D60F}_{33}}}\nonumber\\ \displaystyle & = & \displaystyle \frac{\text{d}\unicode[STIX]{x1D60F}_{12}^{0}}{{\displaystyle \frac{\unicode[STIX]{x2202}F_{2}(t)}{\unicode[STIX]{x2202}t}}\overline{U}_{1}x_{2}+a_{1}\unicode[STIX]{x1D60F}_{12}^{0}-{\displaystyle \frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}}\unicode[STIX]{x1D60F}_{12}^{0}+F_{3}(t)\overline{U}_{1}+a_{\unicode[STIX]{x1D60F}_{12}}},\end{eqnarray}$$
where, the constants
$a_{i}$
represent group parameters, while
$F_{i}(t)$
are free functions of time, yet to be determined from DNS. The tensor
$\unicode[STIX]{x1D60F}_{ij}^{0}$
is simply related to the classical Reynolds stresses tensor
$\unicode[STIX]{x1D619}_{ij}^{0}$
by (2.13), while considering
$\boldsymbol{r}=0$
. As such, for a temporally evolving jet,
$\unicode[STIX]{x1D60F}_{ij}^{0}$
and
$\unicode[STIX]{x1D619}_{ij}^{0}$
are related as follows
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D60F}_{11}^{0}=\unicode[STIX]{x1D619}_{11}^{0}+\overline{U}_{1}^{2}(x_{2},t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D60F}_{22}^{0}=\unicode[STIX]{x1D619}_{22}^{0}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D60F}_{33}^{0}=\unicode[STIX]{x1D619}_{33}^{0}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D60F}_{12}^{0}=\unicode[STIX]{x1D619}_{12}^{0}. & \displaystyle\end{eqnarray}$$
Integration of (3.1) leads to a set of invariants (the constants of integration) which are taken as the new independent and dependent variables. Without loss of generality, the time-dependent translation symmetry in space (
$F_{3}(t)$
) may be neglected in the following analysis. First, we consider the first and second terms in (3.1). Integration of these terms results in the following invariant:
$$\begin{eqnarray}\tilde{x}_{2}=\frac{x_{2}}{\exp \left(\displaystyle \int \frac{F_{2}(t)}{F_{1}(t)}\,\text{d}t\right)}.\end{eqnarray}$$
Here (and also appearing later), the variables marked with ‘
$^{{\sim}}$
’ are constants of integration of the invariant surface condition (3.1) or in other words the invariants of the system. These variables are in fact considered as the new (similarity) variables of the system (2.3) and (2.14). Similarly, integration of the first and third terms gives
$$\begin{eqnarray}\tilde{U} _{1}(\tilde{x}_{2})=\frac{\overline{U}_{1}-a_{U_{1}}F(t)}{\exp \left(\displaystyle \int -\frac{F_{2}(t)-a_{1}}{F_{1}(t)}\,\text{d}t\right)},\end{eqnarray}$$
where
$F(t)$
is a lengthy function of
$F_{1}(t)$
,
$F_{2}(t)$
,
$a_{1}$
, which is not shown here for the sake of brevity. If we replace (3.6) and (3.7) in (2.4), it immediately follows that the scaling symmetry implied by
$a_{1}$
and translation symmetry implied by
$a_{U_{1}}$
(see (A 3) in appendix A) with respect to
$\overline{U}_{1}$
break and give
$a_{1}=a_{U_{1}}=0$
. Therefore (3.7) reduces to
$$\begin{eqnarray}\tilde{U} _{1}(\tilde{x}_{2})=\frac{\overline{U}_{1}}{\exp \left(\displaystyle \int -\frac{F_{2}(t)}{F_{1}(t)}\,\text{d}t\right)}.\end{eqnarray}$$
The above derived similarity solutions from the symmetry analysis (3.6) and (3.8) simply indicate that
$x_{2}$
and
$\overline{U}_{1}$
can be scaled with the same general function of time, i.e.
$\tilde{x_{2}}=x_{2}G(t)$
and
$\tilde{U} _{1}(\tilde{x}_{2})=\overline{U}_{1}/G(t)$
, where
$G(t)$
is
$$\begin{eqnarray}G(t)=\exp \left(\displaystyle \int -\frac{F_{2}(t)}{F_{1}(t)}\,\text{d}t\right).\end{eqnarray}$$
An important observation here is that these solutions seem to be generalized forms of the classical scalings, where the unique time-dependent length and velocity scales (such as jet half-width and the mean centreline velocity) are used for the self-similarity of the mean flow. In other words, they reduce to the classical scalings if
$G(t)\propto U_{s}(t)\propto L_{s}^{-1}(t)$
(see (1.1) and § 1 for the classical scaling arguments).
While (3.6) and (3.8) are purely derived by Lie symmetry analysis, to date there is no procedure known from first principles that determines the free functions. They allow a certain degree of freedom and, hence, the influence of initial conditions may be involved. Hence, we need some additional assumptions to carry out the analysis. In particular, we assume that
$G(t)$
follows a power-law function of time, i.e.
$$\begin{eqnarray}G(t)\propto (t-t_{0})^{n},\end{eqnarray}$$
where
$n$
is the power-law exponent and
$t_{0}$
is the virtual origin. As will be shown later in this paper, the DNS data confirm that this assumption is satisfied. Replacing (3.10) in (3.9) further leads to the following relation:
$$\begin{eqnarray}\frac{F_{2}(t)}{F_{1}(t)}=-\frac{n}{t-t_{0}}.\end{eqnarray}$$
Employing the aforementioned assumptions and integrating the remaining terms in (3.1) leads to a set of new invariants, which are introduced as novel scaling laws for the present flow (please see a detailed derivation in appendix B). These invariants are as follows:
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{\unicode[STIX]{x1D619}}_{12}^{0}(\tilde{x}_{2})=\left[\unicode[STIX]{x1D619}_{12}^{0}+\left(\frac{n\overline{U}_{1}x_{2}}{t-t_{0}}\right)\right]F_{1}(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{\unicode[STIX]{x1D619}}_{11}^{0}(\tilde{x}_{2})=-(\unicode[STIX]{x1D619}_{11}^{0}+\overline{U}_{1}^{2})F_{1}(t)+a_{\unicode[STIX]{x1D60F}_{11}}t, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{\unicode[STIX]{x1D619}}_{22}^{0}(\tilde{x}_{2})=-\unicode[STIX]{x1D619}_{22}^{0}F_{1}(t)+a_{\unicode[STIX]{x1D60F}_{22}}t, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{\unicode[STIX]{x1D619}}_{33}^{0}(\tilde{x}_{2})=-\unicode[STIX]{x1D619}_{33}^{0}F_{1}(t)+a_{\unicode[STIX]{x1D60F}_{33}}t. & \displaystyle\end{eqnarray}$$
Here
$a_{\unicode[STIX]{x1D60F}_{ii}}$
are indeed independent constants related to the symmetry group parameters (see (A 4)–(A 6)), which need to be estimated from numerical or experimental data.
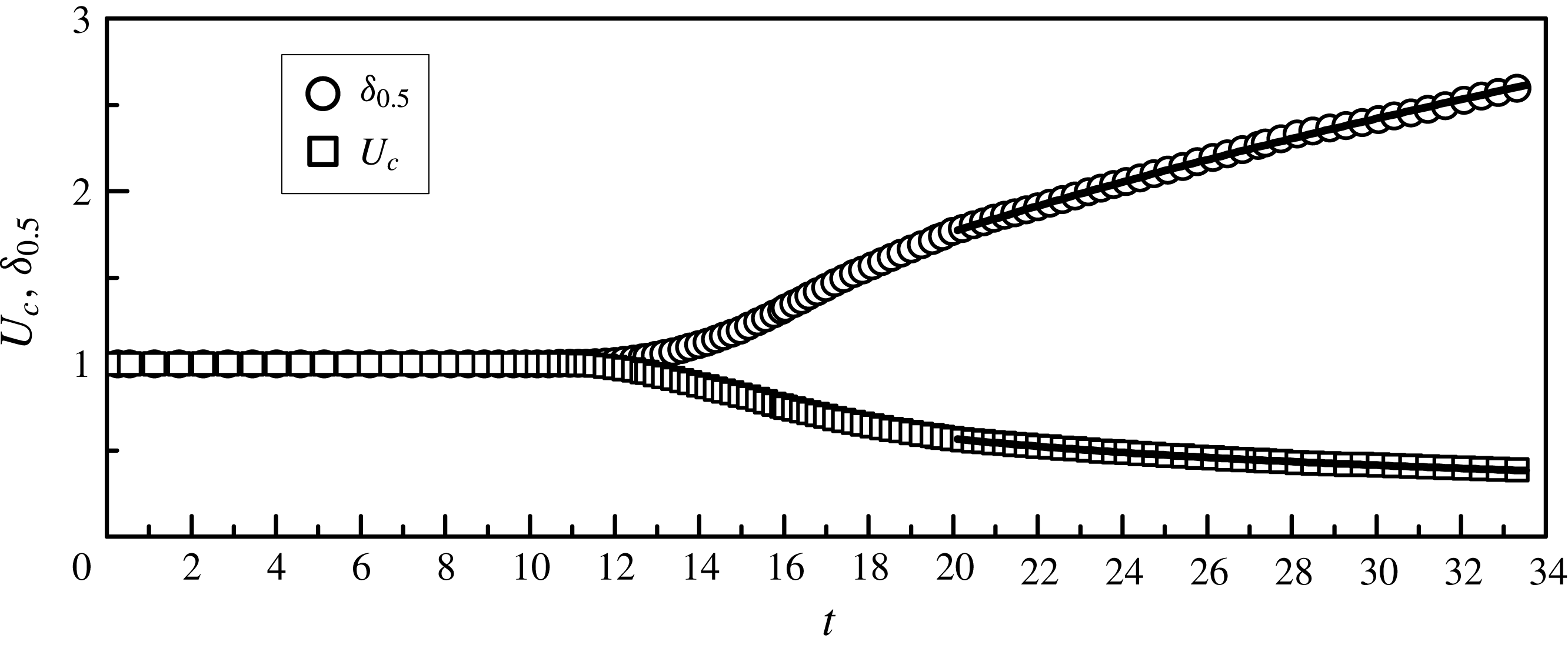
Relations (3.12)–(3.15) are the new self-similar solutions for certain combinations of the parameters (
$x_{2},\overline{U}_{1}$
and
$\unicode[STIX]{x1D619}_{ij}^{0}$
) contained in them. They clearly have different structures compared to the classical formulation for Reynolds stresses detailed in (1.2). For example, an interesting observation here is that the scaling law for
$\unicode[STIX]{x1D619}_{12}^{0}$
also contains
$\overline{U}_{1}$
and
$x_{2}$
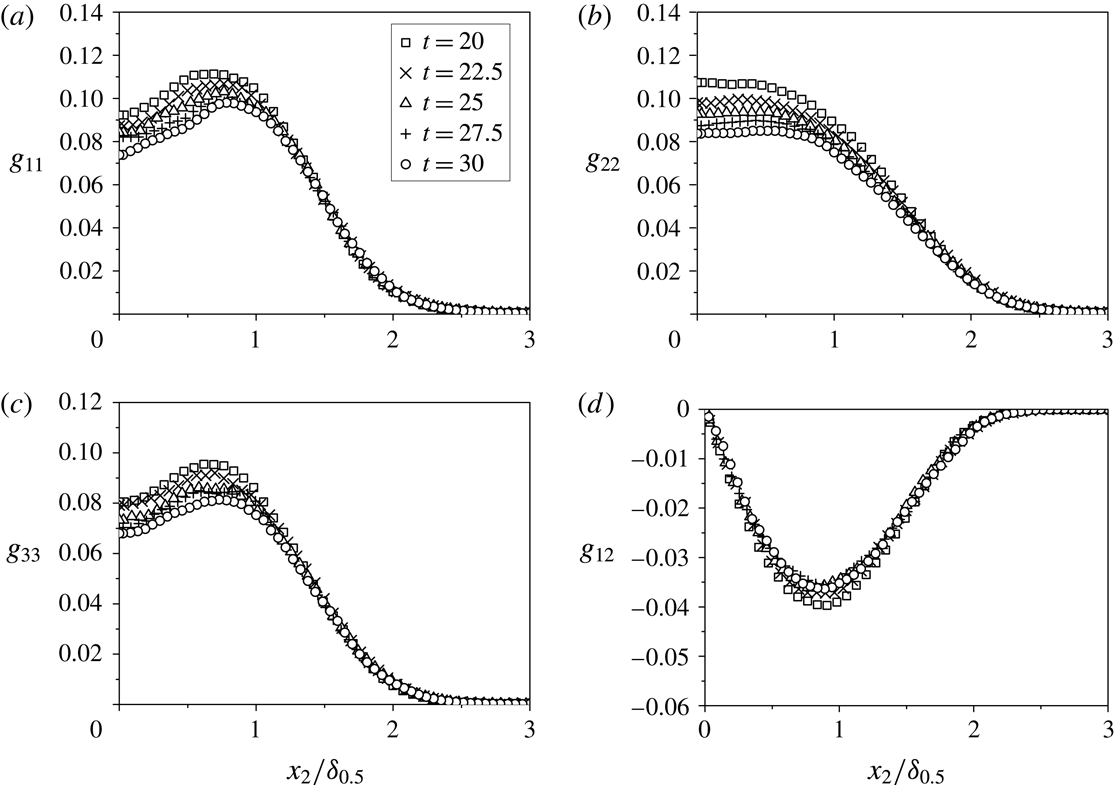
, which is clearly a different structure compared to the classical scaling which only relies on the single scaling parameters. This indeed shows the power and generality of Lie symmetry analysis as such a similarity solution, constructed based on a combination of parameters, is allowed. A physical interpretation of this mathematical observation is that a Reynolds stress term such as
$\unicode[STIX]{x1D619}_{12}^{0}$
alone may not scale. However, if it is a particular case that
$\unicode[STIX]{x1D619}_{12}^{0}$
alone scales, this can only happen when the term containing
$\overline{U}_{1}$
and
$x_{2}$
(
$n\overline{U}_{1}x_{2}/t-t_{0}$
) also scales separately.
The other notable consequence of the current symmetry analysis is that we arrive at general forms for the normal Reynolds stresses, consist of both the free function of time and the free constants
$a_{\unicode[STIX]{x1D60F}_{ii}}$
, which represent different symmetry group parameters. In fact, the constants
$a_{\unicode[STIX]{x1D60F}_{ii}}$
are parts of new symmetries extracted ‘only’ from the TPC and MPC equations, which admit a much larger set of symmetries, as identified in Oberlack & Rosteck (Reference Oberlack and Rosteck2010, Reference Oberlack and Rosteck2011) and named statistical symmetries. As shown by Oberlack & Rosteck (Reference Oberlack and Rosteck2010) and Oberlack et al. (Reference Oberlack, Waclawczyk, Rosteck and Avsarkisov2015), this statistical group, symmetry in the correlation/moment space, is one of the key ingredients for constructing scaling laws in different types of turbulent flows such as the logarithmic law of the wall, which in fact constitutes a solution of the infinite set of MPC equations. It is interesting to note that in a recent work, Djenidi & Antonia (Reference Djenidi and Antonia2015), through a self-preservation analysis based on the transport equation of the second-order longitudinal velocity structure function in decaying homogeneous isotropic turbulence (HIT), justified on the physical interpretation of this statistical group and commented that it represents the energy of the motions whose scales are excluded from the self-preservation range of scales at the initial time (even though it seems that they were not aware that this parameter is from the family of new statistical symmetry groups). Further, they suggested that there is a clear link between initial conditions and this symmetry (e.g.
$a_{\unicode[STIX]{x1D60F}_{ii}}$
), and one can expect that
$a_{\unicode[STIX]{x1D60F}_{ii}}=0$
when the effect of initial conditions becomes negligible or the decay time is very large. While Djenidi & Antonia (Reference Djenidi and Antonia2015) noted that the available direct numerical simulation (DNS) data of three-dimensional periodic box turbulence cover a relatively short decay time, their examination of the grid turbulence data revealed the existence of such a constant even though it exhibited a small value.
The present theoretical results are tested against the new DNS data obtained in a temporally evolving jet in the next section.
4 DNS and validation of scaling laws
4.1 Numerical scheme and DNS details
A direct numerical simulation (DNS) of a temporally evolving turbulent plane jet flow was performed as described in Gampert et al. (Reference Gampert, Boschung, Hennig, Gauding and Peters2014) and Gauding et al. (Reference Gauding, Goebbert, Hasse and Peters2015). A detailed description of the set-up of the simulation and a validation of the results are provided by Hunger, Gauding & Hasse (Reference Hunger, Gauding and Hasse2016). In the following, the main features of the DNS are summarized. The DNS solves the Navier–Stokes equations for an incompressible flow and was carried out on the supercomputer JUQUEEN at the research centre Juelich (Germany) using a hybrid MPI/OpenMP parallelization. The nonlinear term of the momentum equation is formulated in skew–symmetric form to reduce aliasing errors. Spatial derivatives are computed by a sixth-order implicit finite difference scheme (Lele Reference Lele1992). Temporal integration is performed by a low storage, fourth-order Runge–Kutta scheme and the Poisson equation is solved in the spectral space by employing a Helmholtz equation. The computational domain has periodic boundary conditions in streamwise
$x_{1}$
- and spanwise
$x_{3}$
-directions, while free-slip boundary conditions are used in the cross-wise
$x_{2}$
-direction. The flow is statistically homogeneous in the
$x_{1}$
–
$x_{3}$
planes. Statistics are averaged over these planes and depend only on time
$t$
and the cross-wise coordinate
$x_{2}$
. The non-dimensional size of the domain is
$L_{x_{1}}=6\unicode[STIX]{x03C0}$
,
$L_{x_{3}}=6\unicode[STIX]{x03C0}$
and
$L_{x_{2}}=12.5$
, discretized by
$2816\times 2816\times 1500$
$\backsimeq 1.2\times 10^{10}$
grid points. The size of the domain is large compared to the integral scales of the jet to reduce confinement effects. A uniform equidistant mesh is used for the inner part of the domain, while the outer part is slightly coarsened towards the cross-wise boundaries. The DNS is well resolved, since the grid width is smaller than or equal to the Kolmogorov length scale. The Navier–Stokes equations are solved in non-dimensional form and read
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}U_{k}}{\unicode[STIX]{x2202}x_{k}}=0\end{eqnarray}$$
and
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}U_{i}}{\unicode[STIX]{x2202}t}+U_{k}\frac{\unicode[STIX]{x2202}U_{i}}{\unicode[STIX]{x2202}x_{k}}=-\frac{\unicode[STIX]{x2202}P}{\unicode[STIX]{x2202}x_{i}}+\frac{1}{\mathit{Re}_{0}}\frac{\unicode[STIX]{x2202}^{2}U_{i}}{\unicode[STIX]{x2202}x_{k}\unicode[STIX]{x2202}x_{k}},\quad i=1,2,3.\end{eqnarray}$$
For non-dimensionalization the initial centreline velocity
$\overline{U}_{1}(0)$
and the initial jet thickness
$\unicode[STIX]{x1D6FF}_{0.5}(0)$
are used. The initial Reynolds number is defined as
$\mathit{Re}_{0}=\overline{U}_{1}(0)\unicode[STIX]{x1D6FF}_{0.5}(0)/\unicode[STIX]{x1D708}$
and equals 8000.
An appropriate initialization of the DNS is important. The initial velocity profile is composed of two mirrored hyperbolic–tangent mean profiles, with delta-correlated fluctuations with an intensity of 5 % superimposed. The delta-correlated fluctuations facilitate a natural transition to fully developed turbulence without forcing a specific length scale. A similar approach was used by Antonio & Fabrizio (Reference Antonio and Fabrizio2012) for the DNS of a turbulent shear layer.
4.2 Validation of the new scaling laws
In this subsection, the scaling laws derived in § 3 are validated against the DNS data of the temporally evolving jet. In addition, as it is instructive to compare them with the classical scaling laws, these are also provided.
In order to apply the classical similarity analysis to the simulated jet, the velocity scale
$U_{s}$
and the length
$L_{s}$
(see (1.1) and (1.2)) may be chosen from a variety of possible scales. Here, we choose the maximum magnitude of the mean velocity
$\overline{U}_{1}$
on the centreline (
$U_{c}$
) and the jet half-width
$\unicode[STIX]{x1D6FF}_{0.5}$
as the relevant scales, which in the literature are the most common parameters used for
$U_{s}$
and
$L_{s}$
respectively. As
$U_{c}$
and
$\unicode[STIX]{x1D6FF}_{0.5}$
are solely time-dependent functions, they are equivalent to the terms in the denominators of the relations (3.6) and (3.8), i.e.
$$\begin{eqnarray}G(t)^{-1}\propto \unicode[STIX]{x1D6FF}_{0.5}(t),\end{eqnarray}$$
and
$$\begin{eqnarray}G(t)\propto U_{c}(t),\end{eqnarray}$$
which confirms
$$\begin{eqnarray}U_{c}(t)\propto \frac{1}{\unicode[STIX]{x1D6FF}_{0.5}(t)}.\end{eqnarray}$$
Displayed in figure 2 is the temporal evolution of
$U_{c}$
and
$\unicode[STIX]{x1D6FF}_{0.5}$
. These quantities are found to closely follow a power-law behaviour for
$20\lesssim t\lesssim 34$
as:
$$\begin{eqnarray}\displaystyle & U_{c}(t)=A(t-t_{0})^{-0.5}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D6FF}_{0.5}(t)=B(t-t_{0})^{0.5}, & \displaystyle\end{eqnarray}$$
where
$A=1.91$
,
$B=0.524$
and
$t_{0}=8.64$
were fitted to the DNS data. The profiles of
$\overline{U}_{1}$
normalized by
$\unicode[STIX]{x1D6FF}_{0.5}(t)$
and
$U_{c}(t)$
at several selected time steps within
$20\lesssim t\lesssim 30$
are plotted in figure 3. As expected, these profiles show an excellent collapse of the mean flow. It is important to note that although it is identified that the classical scaling parameters for the mean velocity match within the present general solution of Lie symmetry analysis, one may still find other (time-dependent) functions
$F_{1}(t)$
and
$F_{2}(t)$
to be relevant parameters for the self-similarity of the mean profiles. In fact, the appearance of free functions such as
$F_{i}(t)$
, in the group parameters, is an important finding of the current analysis. These functions, which are possibly linked to the initial conditions, have also been detected by performing symmetry analysis on isotropic turbulence (Khabirov & Unal Reference Khabirov and Unal2002a
,Reference Khabirov and Unal
b
). Interestingly, it can be observed that the previously obtained decay laws, such as the exponential decay and the power-law decay of the energy (e.g. George & Wang Reference George and Wang2009; Oberlack & Zieleniewicz Reference Oberlack and Zieleniewicz2013), are recovered from different functional forms for
$F_{i}(t)$
. In addition, the analysis permits the possibility of combining the decay laws in time for the turbulence kinetic energy that is yet to be verified by DNS. We also note that other possible functional forms are permitted for
$F_{1}(t)$
and
$F_{2}(t)$
, for which even the transition region of turbulent plane jets is covered. This could be a potential interest for future investigations to study which general functions may be used for the collapse of profiles in the transition region where the classical scaling variables might fail.
Figure 3. The mean velocity
$\overline{U}_{1}$
normalized by
$\unicode[STIX]{x1D6FF}_{0.5}(t)$
and
$U_{c}(t)$
.
Next, the Reynolds stress components are considered, which are the main interest of this work in terms of the symmetry analysis. First, the Reynolds stress components
$\unicode[STIX]{x1D619}_{ij}^{0}\equiv \overline{u_{i}u_{j}}$
, for
$ij=11,22,33,12$
, are normalized by the classical scaling parameters, which read
$g_{ij}(x_{2}/\unicode[STIX]{x1D6FF}_{0.5})=\unicode[STIX]{x1D619}_{ij}^{0}/U_{c}^{2}$
, and which are respectively presented for
$ij=11$
, 22, 33, 12 in figure 4(a–d) for
$20\lesssim t\lesssim 30$
. As can be observed, only the profiles of the Reynolds shear stress
$\unicode[STIX]{x1D619}_{12}^{0}$
show a satisfactory collapse for different
$t$
. However, the Reynolds normal stresses,
$\unicode[STIX]{x1D619}_{11}^{0}$
,
$\unicode[STIX]{x1D619}_{22}^{0}$
,
$\unicode[STIX]{x1D619}_{33}^{0}$
significantly deviate from the similarity using the classical scaling. The departure from the self-similarity is more obvious near the centre region, where the Reynolds normal stresses are not properly scaled with
$U_{c}^{2}$
. It is apparent that for the classical scaling to hold at the centreline, the following scaling would be necessary:
$\unicode[STIX]{x1D619}_{11}^{0}(x_{2}=0)\propto \unicode[STIX]{x1D619}_{22}^{0}(x_{2}=0)\propto \unicode[STIX]{x1D619}_{33}^{0}(x_{2}=0)\propto U_{c}^{2}$
. However, it has been widely noted that the ratio of the Reynolds normal stresses and the square of the mean velocity along the centreline of jet flows significantly deviates from the equivalence during the decay, which leads to failure of the classical scaling, see e.g. Sadeghi et al. (Reference Sadeghi, Lavoie and Pollard2015).
Figure 4. The Reynolds stresses
$\unicode[STIX]{x1D619}_{ij}^{0}$
normalized by
$U_{c}$
and
$\unicode[STIX]{x1D6FF}_{0.5}$
, according to the classical scaling relation (1.2).
We turn our attention to the new derived self-similar relations (3.12)–(3.15). According to (3.12), the term
$\unicode[STIX]{x1D619}_{12}^{0}+n\overline{U}_{1}x_{2}/(t-t_{0})$
is scaled with
$F_{1}(t)$
(see appendix B). This term is a function of
$\tilde{x}_{2}$
$(x_{2}/\unicode[STIX]{x1D6FF}_{0.5})$
and is presented in figure 5 for a variety of different
$t$
. Here,
$n$
and
$t_{0}$
are taken from the power-law fit details for
$U_{c}$
(
$n=-0.5$
and
$t_{0}=8.64$
). As
$F_{1}(t)$
is simply the scale, which grows with time, it can be estimated from the values of
$\unicode[STIX]{x1D619}_{12}^{0}+n\overline{U}_{1}x_{2}/(t-t_{0})$
at similar
$\tilde{x}_{2}$
. Here,
$F_{1}(t)$
is estimated from the peak value of this function for
$20\lesssim t\lesssim 30$
, which turns out to closely follow a linear law,
$$\begin{eqnarray}F_{1}(t)=D(t-t_{0}),\end{eqnarray}$$
with
$D=-7.57$
(see figure 5). The self-similar variable
$\tilde{\unicode[STIX]{x1D619}}_{12}^{0}(\tilde{x}_{2})$
(3.12) is then presented in figure 6 for different
$t$
obtained from the DNS. As can be seen, the data exhibit a very good collapse, confirming the accuracy of (3.12) derived from Lie symmetry analysis. Further, replacing the obtained solution for
$F_{1}(t)$
(4.8) into (3.11), the following behaviour is adopted for
$F_{2}(t)$
$$\begin{eqnarray}F_{2}(t)=-Dn,\end{eqnarray}$$
where
$n=-1/2$
.
Figure 5. The temporal variation of
$\unicode[STIX]{x1D619}_{12}^{0}+n\overline{U}_{1}x_{2}/(t-t_{0})$
. The dashed line is the peak location of the profiles. The inset is the temporal evolution of
$F_{1}(t)$
.
Figure 6. The self-similar solution (3.12) compared to the DNS data.
Finally, we test the validation of other self-similar solutions (3.13)–(3.15) obtained from the current theory using the DNS data of the jet. As noted, the relations (3.13)–(3.15) contain the free function of time
$F_{1}(t)$
and constants
$a_{\unicode[STIX]{x1D60F}_{ii}}$
(which represent different translation group parameters), that cannot be obtained using Lie group analysis alone. Therefore, if these relations are accurately derived, these constants can be estimated by employing the numerical results. As previously noted, the matching of (3.12) and DNS data allows a linear solution for
$F_{1}(t)$
(4.8). As such, we can first substitute (4.8) in (3.13)–(3.15), which gives
$$\begin{eqnarray}\displaystyle & \tilde{\unicode[STIX]{x1D619}}_{11}^{0}(\tilde{x}_{2})=-D(\unicode[STIX]{x1D619}_{11}^{0}+\overline{U}_{1}^{2})(t-t_{0})+a_{\unicode[STIX]{x1D60F}_{11}}t, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \tilde{\unicode[STIX]{x1D619}}_{22}^{0}(\tilde{x}_{2})=-D\unicode[STIX]{x1D619}_{22}^{0}(t-t_{0})+a_{\unicode[STIX]{x1D60F}_{22}}t, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \tilde{\unicode[STIX]{x1D619}}_{33}^{0}(\tilde{x}_{2})=-D\unicode[STIX]{x1D619}_{33}^{0}(t-t_{0})+a_{\unicode[STIX]{x1D60F}_{33}}t. & \displaystyle\end{eqnarray}$$
The DNS data are then fitted to (4.10)–(4.12) and presented in figure 7. The parameters from fitting the scaling laws to the data are listed in table 1. Typical measures of the quality of the fit, including the residual sum of squares (RSS) and
$\text{R}^{2}$
values, are also listed in table 1. It is found that the best collapse of the data occurs when
$a_{\unicode[STIX]{x1D60F}_{11}}=0.0383$
,
$a_{\unicode[STIX]{x1D60F}_{22}}=0.070$
and
$a_{\unicode[STIX]{x1D60F}_{33}}=0.0453$
. In order to have an idea about how fast the quality of the fit degrades as the
$a_{\unicode[STIX]{x1D60F}_{ii}}$
are changed, the parameters of the quality for a variety of different imposed
$a_{\unicode[STIX]{x1D60F}_{ii}}$
are measured and listed in table 1. A perfect match between the DNS and scaling laws supports the relations (3.13)–(3.15) and the assumptions employed for their derivation.
It is worth mentioning that it seems that the existence of these new symmetries for the normal Reynolds stresses has been observed in the past, but due to lack of a strong theoretical evidence, they have not been recognized. For example, in a study based on the simulation of a time-dependent plane wake, Ghosal & Rogers (Reference Ghosal and Rogers1997) observed that all the mean velocity profiles and the Reynolds shear stress could be collapsed together using an identical scaling, but the Reynolds normal stresses were distinct for each set of initial conditions (this point was also highlighted in George Reference George2012). In addition, as the Reynolds stress profiles have almost similar shapes and vary monotonically in time, one can expect that some values for
$a_{\unicode[STIX]{x1D60F}_{11}}$
,
$a_{\unicode[STIX]{x1D60F}_{22}}$
and
$a_{\unicode[STIX]{x1D60F}_{33}}$
or other general power-law forms for
$F_{1}(t)$
may eventually exist that will collapse the data. Such a possibility has been proposed in the past (e.g. George Reference George, George and Arndt1989) such that a Reynolds stress profile, which cannot collapse using the square of the velocity scale
$U_{s}^{2}$
, may collapse from its own values. However, such normalization can be rarely found in the literature, indeed due to lack of a strong theoretical evidence. Within the present work, we develop a theoretical basis using a Lie symmetry group that predicts such behaviour for the flow evolution, as an exact solution of the two- and multi-point correlation equations, which can be an important key in ‘filling the gaps’ of our understanding of self-similarity.
Table 1. List of parameters in relation (3.13)–(3.15) fitted to the present DNS data. RSS is the residual sum of squares,
$\text{R}^{2}$
is a measure of goodness of the fit.
As a final remark, some discussion is required about the possible effects of initial conditions on the observed scaling laws. In particular, an important question is whether the observed scaling laws depend on the initial conditions or not. As noted in § 1, over the past three decades, serious questions have been raised about the possibility of the self-preservation solutions’ (and subsequently turbulence scaling laws) dependence on the initial conditions in turbulent flows. George (Reference George, George and Arndt1989, Reference George1992), who was the first to seriously raise the issue of initial conditions dependence of the self-preservation solutions, noted that there is no a priori reason to eliminate the influence of the initial conditions from the outset. This claim, however, seems to be in contradiction with the universal similarity solutions. The existence of the large scatter in numerical and experimental data in different types of turbulent flows has acknowledged George’s suggestion, even though there has not been a formal way of including the initial conditions explicitly in an analysis. The effects of the initial conditions on the turbulence scaling laws, which are a direct consequence of the similarity analysis, have been also among the potential and debatable topics of interests to the turbulence community.
For example, the decay of the turbulent kinetic energy in homogeneous and isotropic turbulence has been wieldy discussed, in particular, whether it is universal or not. In different works, George (Reference George, George and Arndt1989, Reference George1992, Reference George2012) have shown that it is possible to predict the existence of both the exponential decay and the power-law decay of the turbulent kinetic energy, both being highly dependent on initial conditions. Using Lie symmetry group analysis, Oberlack & Zieleniewicz (Reference Oberlack and Zieleniewicz2013) have successfully recovered all possible existing decay laws, including those derived by George, relating them to the symmetry group scaling parameters. Further, their results confirm the dependence of the scaling-law parameters (such as the decay exponent) on the initial conditions, which is felt through the symmetry group parameters. As noted in the conclusion section of Oberlack & Zieleniewicz (Reference Oberlack and Zieleniewicz2013), an important unanswered question is that ‘which scaling parameter is related to a given initial condition?’ This is similar to the statement in George (Reference George2012) that ‘unfortunately, our theoretical understanding of how initial conditions can persist has progressed less rapidly than our recognition that they do’. In the present context of turbulent jets, the parameters of the scaling laws are shown to be related to both the symmetry group parameters (
$a_{\unicode[STIX]{x1D60F}_{ij}}$
in (3.1)) and free functions of time (
$F_{i}(t)$
), which are most likely connected to the initial conditions. For example, as previously noted, Djenidi & Antonia (Reference Djenidi and Antonia2015) suggested that the initial conditions and the constants repressing the new symmetries (e.g.
$a_{\unicode[STIX]{x1D60F}_{ii}}$
) are directly linked together, and in fact, a relatively large decay time may be required for these constants to become non-negligible or a case where the initial conditions are not influential. We should point out that, however, that how these parameters react to different initial conditions is a subtle goal and warrants further consideration.
5 Summary and conclusions
In the present paper, Lie symmetry analysis was applied to a system of differential equations consisting of the mean momentum and two-point correlation equations of a temporally evolving plane jet. After calculating the necessary symmetries (in infinitesimal forms), they were used to derive new scaling laws and find self-similar (invariant) solutions for the given system of equations. A DNS of the turbulent plane jet flow was also performed to validate the theoretical findings.
Lie symmetry analysis revealed a general form for the self-similarity of the mean velocity which was consistent with the classical scaling-law type. It was found that the classical length and velocity scales, such as the maximum mean velocity and the jet half-width, could be specific functions of this general solution derived based on the symmetry analysis. This may suggest that many of the classical similarity type solutions, e.g. for the turbulent free-shear flows, are based on statistical symmetries, although in the original derivation, some type of ansatz functions were used and, hence, the underlying symmetries are hidden. For example, the traditional approach (e.g. Townsend Reference Townsend1956) to similarity analysis is to use an a priori set of scales, in which it is assumed that the velocity profiles in the flow can be resealed using these single scales. However, it was shown that existence of such scales is not simply an a priori choice, but is a direct consequence of the symmetry analysis. Though, it should be noted that the similarity approach introduced by George (Reference George, George and Arndt1989, Reference George1992), which is based on ‘arbitrary’ scales, is more general and closer to the outcome of the present Lie group approach.
The current analysis further led us to derive, for the first time, four self-similar solutions for the Reynolds stress terms. In contrast to the classical scaling for the second moments of the velocity, these self-similar solutions were constructed such that they contained a combination of the Reynolds stress components, mean velocity,
$x_{2}$
-direction and arbitrary constants related to the scaling group parameters. The DNS data exhibit a perfect collapse with the obtained scaling laws.
This study opens the door to a re-investigation of the scaling laws in turbulent flows. Although the current scaling laws were derived and validated for a temporally evolving plane jet, they are expected to be verified for some other types of flows. For instance, as the governing equations for the temporal mixing layer and plane wakes reduce to those as the present flow, the relations (3.12)–(3.15) can be validated in these flows (simply by replacing
$\overline{U}_{1}$
with the deficit velocity). The new self-similar solutions from the symmetry analysis for temporally evolving flows can be also applied to spatially evolving flows after imposing similar assumptions. For example, if the wake deficit velocity is small compared to the uniform flow and both spatially and temporally evolving flows are viewed from a reference frame moving with the free stream and the downstream position and time are related by
$x=U_{\infty }t$
, the mean and turbulent statistics of a temporally evolving flow (jet or wake) agree well with those in the spatially evolving wake by using transformation.
Acknowledgements
H.S. acknowledges the financial support of the Alexander von Humboldt Foundation. Additionally, the authors gratefully acknowledge the computing time granted on the supercomputer JUQUEEN at Forschungszentrum Juelich by the John von Neumann Institute for Computing (NIC).
Appendix A. List of infinitesimals
The relevant infinitesimals used in (3.1) calculated by DESOLV-II to (2.3) and (2.14) (after imposing
$\boldsymbol{r}=0$
) are
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D709}_{t}=F_{1}(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D709}_{x_{2}}=F_{2}(t)x_{2}+F_{3}(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{\overline{U}_{1}}=a_{1}\overline{U}_{1}-F_{2}(t)\overline{U}_{1}+a_{U_{1}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D60F}_{11}^{0}}=a_{1}\unicode[STIX]{x1D60F}_{11}^{0}-\frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D60F}_{11}^{0}+a_{\unicode[STIX]{x1D60F}_{11}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D60F}_{22}^{0}}=a_{1}\unicode[STIX]{x1D60F}_{22}^{0}-\frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D60F}_{22}^{0}+a_{\unicode[STIX]{x1D60F}_{22}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D60F}_{33}^{0}}=a_{1}\unicode[STIX]{x1D60F}_{33}^{0}-\frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D60F}_{33}^{0}+a_{\unicode[STIX]{x1D60F}_{33}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D60F}_{12}^{0}}=\frac{\unicode[STIX]{x2202}F_{2}(t)}{\unicode[STIX]{x2202}t}\overline{U}_{1}x_{2}+a_{1}\unicode[STIX]{x1D60F}_{12}^{0}-\frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D60F}_{12}^{0}+F_{3}(t)\overline{U}_{1}+a_{\unicode[STIX]{x1D60F}_{12}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D60F}_{ikj}^{0}}=a_{1}\unicode[STIX]{x1D60F}_{ikj}^{0}-2\frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D60F}_{ikj}^{0}+F_{2}(t)\unicode[STIX]{x1D60F}_{ikj}^{0}+a_{\unicode[STIX]{x1D60F}_{ikj}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D60F}_{ijk}^{0}}=a_{1}\unicode[STIX]{x1D60F}_{ijk}^{0}-2\frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}\unicode[STIX]{x1D60F}_{ijk}^{0}+F_{2}(t)\unicode[STIX]{x1D60F}_{ijk}^{0}+a_{\unicode[STIX]{x1D60F}_{ijk}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{\overline{PU_{j}}^{0}}=a_{1}\overline{PU_{j}}^{0}-2\frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}\overline{PU_{j}}^{0}+F_{2}(t)\overline{PU_{j}}^{0}+a_{PU_{j}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{\overline{U_{i}P}^{0}}=a_{1}\overline{U_{i}P}^{0}-2\frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}\overline{U_{i}P}^{0}+F_{2}(t)\overline{U_{i}P}^{0}+a_{U_{i}P}, & \displaystyle\end{eqnarray}$$
where,
$a_{i}$
and
$F_{i}(t)$
are respectively arbitrary constants and free functions of time.
Appendix B. Derivation of the invariant solutions
In this section, a detailed derivation of (3.12)–(3.15) as the invariants of (3.1) are provided. First, we consider the first and last terms in (3.1), which, after imposing the symmetry breaking of the scaling of
$\overline{U}_{1}$
(
$a_{1}=0$
), neglecting the translation symmetry in space (
$F_{3}(t)$
) and the translation symmetry
$a_{U_{1}}$
and replacing
$U_{1}x_{2}$
by
$\tilde{U} _{1}\tilde{x}_{2}$
(3.6) and (3.8), gives
$$\begin{eqnarray}\frac{\text{d}t}{F_{1}(t)}=\frac{\text{d}\unicode[STIX]{x1D60F}_{12}^{0}}{{\displaystyle \frac{\unicode[STIX]{x2202}F_{2}(t)}{\unicode[STIX]{x2202}t}}\tilde{U} _{1}\tilde{x}_{2}-{\displaystyle \frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}}\unicode[STIX]{x1D60F}_{12}^{0}+a_{\unicode[STIX]{x1D60F}_{12}}}.\end{eqnarray}$$
Integrating of (B 1) gives
$$\begin{eqnarray}\tilde{\unicode[STIX]{x1D619}}_{12}^{0}(\tilde{x}_{2})=F_{1}(t)\unicode[STIX]{x1D60F}_{12}^{0}(x_{2},t)-\tilde{U} _{1}\tilde{x}_{2}F_{2}(t)-a_{\unicode[STIX]{x1D60F}_{12}}t,\end{eqnarray}$$
where
$\tilde{\unicode[STIX]{x1D619}}_{12}^{0}(\tilde{x}_{2})$
is the constant of integration of the invariant surface condition (B 1), which, as before, is taken as a new self-similar variable. Replacing (3.5), (3.6), (3.8) and (3.11) in (B 2), gives
$$\begin{eqnarray}\tilde{\unicode[STIX]{x1D619}}_{12}^{0}(\tilde{x}_{2})=\left[\unicode[STIX]{x1D619}_{12}^{0}(x_{2},t)+\left(\frac{n\overline{U}_{1}(x_{2},t)x_{2}}{t-t_{0}}\right)\right]F_{1}(t)-a_{\unicode[STIX]{x1D60F}_{12}}t.\end{eqnarray}$$
At this point, we find it straightforward to let
$a_{\unicode[STIX]{x1D60F}_{12}}=0$
. This is based on a typical observation along the jet centreline that the shear Reynolds stress
$\unicode[STIX]{x1D619}_{12}^{0}$
is zero at every
$t$
(this has been also confirmed by the current DNS data). As such, equation (B 3) is only valid on the centreline when
$a_{\unicode[STIX]{x1D60F}_{12}}=0$
. Therefore, equation (B 3) reduces to
$$\begin{eqnarray}\tilde{\unicode[STIX]{x1D619}}_{12}^{0}(\tilde{x}_{2})=\left[\unicode[STIX]{x1D619}_{12}^{0}(x_{2},t)+\left(\frac{n\overline{U}_{1}(x_{2},t)x_{2}}{t-t_{0}}\right)\right]F_{1}(t),\end{eqnarray}$$
which is presented as (3.12) in § 3 and validated against DNS data in § 4. Further, if we replace
$F_{1}(t)$
with (4.8), we arrive at
$$\begin{eqnarray}\tilde{\unicode[STIX]{x1D619}}_{12}^{0}(\tilde{x}_{2})=\left[\unicode[STIX]{x1D619}_{12}^{0}(x_{2},t)+\left(\frac{n\overline{U}_{1}(x_{2},t)x_{2}}{t-t_{0}}\right)\right][D(t-t_{0})].\end{eqnarray}$$
By implementing the obtained solutions for
$\unicode[STIX]{x1D619}_{12}^{0}$
(B 5),
$\overline{U}_{1}$
(3.8) and
$x_{2}$
(3.6) into (2.3), it is straightforward to show that all the time-dependent terms are cancelled out and a reduced form for the mean momentum equation only depending on
$\tilde{x}_{2}$
can be obtained as follows:
$$\begin{eqnarray}k_{1}\tilde{U} _{1}(\tilde{x}_{2})+k_{2}\tilde{x}_{2}\frac{\unicode[STIX]{x2202}\tilde{U} _{1}(\tilde{x}_{2})}{\unicode[STIX]{x2202}\tilde{x}_{2}}+k_{3}\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D619}}_{12}^{0}(\tilde{x}_{2})}{\unicode[STIX]{x2202}\tilde{x}_{2}}+k_{4}\frac{\unicode[STIX]{x2202}^{2}\tilde{U} _{1}(\tilde{x}_{2})}{\unicode[STIX]{x2202}\tilde{x}_{2}^{2}}=0,\end{eqnarray}$$
where
$k_{i}$
are constants.
Now, we consider the first term in (3.1) together with those terms containing
$\unicode[STIX]{x1D60F}_{11}^{0},\unicode[STIX]{x1D60F}_{22}^{0}$
and
$\unicode[STIX]{x1D60F}_{33}^{0}$
:
$$\begin{eqnarray}\displaystyle \frac{\text{d}t}{F_{1}(t)} & = & \displaystyle \frac{\text{d}\unicode[STIX]{x1D60F}_{11}^{0}}{a_{1}\unicode[STIX]{x1D60F}_{11}^{0}-{\displaystyle \frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}}\unicode[STIX]{x1D60F}_{11}^{0}+a_{\unicode[STIX]{x1D60F}_{11}}}\nonumber\\ \displaystyle & = & \displaystyle \frac{\text{d}\unicode[STIX]{x1D60F}_{22}^{0}}{a_{1}\unicode[STIX]{x1D60F}_{22}^{0}-{\displaystyle \frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}}\unicode[STIX]{x1D60F}_{22}^{0}+a_{\unicode[STIX]{x1D60F}_{22}}}\nonumber\\ \displaystyle & = & \displaystyle \frac{\text{d}\unicode[STIX]{x1D60F}_{33}^{0}}{a_{1}\unicode[STIX]{x1D60F}_{33}^{0}-{\displaystyle \frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}}\unicode[STIX]{x1D60F}_{33}^{0}+a_{\unicode[STIX]{x1D60F}_{33}}}.\end{eqnarray}$$
After replacing
$a_{1}=0$
, one can obtain the following scaling laws for
$\unicode[STIX]{x1D60F}_{11}^{0}$
,
$\unicode[STIX]{x1D60F}_{22}^{0}$
and
$\unicode[STIX]{x1D60F}_{33}^{0}$
$$\begin{eqnarray}\displaystyle & \tilde{\unicode[STIX]{x1D619}}_{11}^{0}(\tilde{x}_{2})=-\unicode[STIX]{x1D60F}_{11}^{0}(x_{2},t)F_{1}(t)+a_{\unicode[STIX]{x1D60F}_{11}}t, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \tilde{\unicode[STIX]{x1D619}}_{22}^{0}(\tilde{x}_{2})=-\unicode[STIX]{x1D60F}_{22}^{0}(x_{2},t)F_{1}(t)+a_{\unicode[STIX]{x1D60F}_{22}}t, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \tilde{\unicode[STIX]{x1D619}}_{33}^{0}(\tilde{x}_{2})=-\unicode[STIX]{x1D60F}_{33}^{0}(x_{2},t)F_{1}(t)+a_{\unicode[STIX]{x1D60F}_{33}}t, & \displaystyle\end{eqnarray}$$
which after replacing (3.2)–(3.4), they read
$$\begin{eqnarray}\displaystyle & \tilde{\unicode[STIX]{x1D619}}_{11}^{0}(\tilde{x}_{2})=-(\unicode[STIX]{x1D619}_{11}^{0}(x_{2},t)+\overline{U}_{1}^{2}(x_{2},t))F_{1}(t)+a_{\unicode[STIX]{x1D60F}_{11}}t, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \tilde{\unicode[STIX]{x1D619}}_{22}^{0}(\tilde{x}_{2})=-\unicode[STIX]{x1D619}_{22}^{0}(x_{2},t)F_{1}(t)+a_{\unicode[STIX]{x1D60F}_{22}}t, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \tilde{\unicode[STIX]{x1D619}}_{33}^{0}(\tilde{x}_{2})=-\unicode[STIX]{x1D619}_{33}^{0}(x_{2},t)F_{1}(t)+a_{\unicode[STIX]{x1D60F}_{33}}t. & \displaystyle\end{eqnarray}$$
These equations are presented as the new self-similar relations in § 3. Here,
$a_{i}$
are constants (and as shown related to the new symmetry group parameters), which can be estimated from DNS or experimental data.
Additionally, the invariant solutions for the pressure–velocity correlation and the triple-velocity correlation terms are constructed and presented. The condition for symmetry invariant solutions of the pressure–velocity correlation and the triple-velocity correlation quantities, after replacing
$a_{1}=0$
, reads
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{\text{d}t}{F_{1}(t)}} & = & \displaystyle {\displaystyle \frac{\text{d}\unicode[STIX]{x1D60F}_{ikj}^{0}}{-2{\displaystyle \frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}}\unicode[STIX]{x1D60F}_{ikj}^{0}+F_{2}(t)\unicode[STIX]{x1D60F}_{ikj}^{0}+a_{\unicode[STIX]{x1D60F}_{ikj}}}}\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{\text{d}\unicode[STIX]{x1D60F}_{ijk}^{0}}{-2{\displaystyle \frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}}\unicode[STIX]{x1D60F}_{ijk}^{0}+F_{2}(t)\unicode[STIX]{x1D60F}_{ijk}^{0}+a_{\unicode[STIX]{x1D60F}_{ijk}}}}\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{\text{d}\overline{PU_{j}}^{0}}{-2{\displaystyle \frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}}\overline{PU_{j}}^{0}+F_{2}(t)\overline{PU_{j}}^{0}+a_{PU_{j}}}}\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{\text{d}\overline{U_{i}P}^{0}}{-2{\displaystyle \frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}}\overline{U_{i}P}^{0}+F_{2}(t)\overline{U_{i}P}^{0}+a_{U_{i}P}}}.\end{eqnarray}$$
By integrating of (B 14) and performing some manipulation, the following solutions are obtained
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D60F}_{ikj}^{0}(x_{2},t)=\left(a_{\unicode[STIX]{x1D60F}_{ikj}}\displaystyle \int {\displaystyle \frac{\exp (C(t))}{F_{1}(t)}}\,\text{d}t+\tilde{\unicode[STIX]{x1D60F}}_{ikj}^{0}(\tilde{x}_{2})\right)\exp (-C(t)), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D60F}_{ijk}^{0}(x_{2},t)=\left(a_{\unicode[STIX]{x1D60F}_{ijk}}\displaystyle \int {\displaystyle \frac{\exp (C(t))}{F_{1}(t)}}\,\text{d}t+\tilde{\unicode[STIX]{x1D60F}}_{ijk}^{0}(\tilde{x}_{2})\right)\exp (-C(t)), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{PU_{j}}^{0}(x_{2},t)=\left(a_{PU_{j}}\displaystyle \int {\displaystyle \frac{\exp (C(t))}{F_{1}(t)}}\,\text{d}t+\widetilde{\overline{PU_{j}}}^{0}(\tilde{x}_{2})\right)\exp (-C(t)), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{U_{i}P}^{0}(x_{2},t)=\left(a_{U_{i}P}\displaystyle \int {\displaystyle \frac{\exp (C(t))}{F_{1}(t)}}\,\text{d}t+\widetilde{\overline{U_{i}P}}^{0}(\tilde{x}_{2})\right)\exp (-C(t)), & \displaystyle\end{eqnarray}$$
where
$$\begin{eqnarray}C(t)=\int {\displaystyle \frac{-F_{2}(t)+2{\displaystyle \frac{\unicode[STIX]{x2202}F_{1}(t)}{\unicode[STIX]{x2202}t}}}{F_{1}(t)}}\,\text{d}t.\end{eqnarray}$$
As before, the variables marked with ‘
$^{{\sim}}$
’ are the constants of integration of the invariant surface condition (B 14), or the new self-similar variable. Further, we can simplify these relations by replacing
$F_{1}(t)$
(4.8) and
$F_{2}(t)$
(4.9) to achieve the following similarity solutions:
$$\begin{eqnarray}\displaystyle & \tilde{\unicode[STIX]{x1D60F}}_{ikj}^{0}(\tilde{x}_{2}) & \displaystyle =-\unicode[STIX]{x1D60F}_{ikj}^{0}(x_{2},t)D(t-t_{0})^{3/2}+{\textstyle \frac{2}{3}}a_{\unicode[STIX]{x1D60F}_{ikj}}(t-t_{0})^{3/2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \tilde{\unicode[STIX]{x1D60F}}_{ijk}^{0}(\tilde{x}_{2}) & \displaystyle =-\unicode[STIX]{x1D60F}_{ijk}^{0}(x_{2},t)D(t-t_{0})^{3/2}+{\textstyle \frac{2}{3}}a_{\unicode[STIX]{x1D60F}_{ijk}}(t-t_{0})^{3/2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \widetilde{\overline{PU_{j}}}^{0}(\tilde{x}_{2}) & \displaystyle =-\overline{PU_{j}}^{0}(x_{2},t)D(t-t_{0})^{3/2}+{\textstyle \frac{2}{3}}a_{PU_{j}}(t-t_{0})^{3/2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \widetilde{\overline{U_{i}P}}^{0}(\tilde{x}_{2}) & \displaystyle =-\overline{U_{i}P}^{0}(x_{2},t)D(t-t_{0})^{3/2}+{\textstyle \frac{2}{3}}a_{U_{i}P}(t-t_{0})^{3/2}.\end{eqnarray}$$
Finally, it should be pointed out that the tensors
$\unicode[STIX]{x1D60F}_{ikj}^{0}(x_{2},t)$
,
$\unicode[STIX]{x1D60F}_{ijk}^{0}(x_{2},t)$
,
$\overline{PU_{j}}^{0}(x_{2},t)$
,
$\overline{U_{i}P}^{0}(x_{2},t)$
are indeed related to the classical pressure–velocity correlation and the triple-velocity correlation tensors by using the following transformations (please see Oberlack & Rosteck Reference Oberlack and Rosteck2010) for the details of the tensor transformation between instantaneous and fluctuating approaches), e.g.
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D60F}_{ijk}^{0}(x_{2},t) & = & \displaystyle \unicode[STIX]{x1D619}_{ijk}^{0}(x_{2},t)+\unicode[STIX]{x1D619}_{ik}^{0}(x_{2},t)\overline{U}_{j}(x_{2},t)+\unicode[STIX]{x1D619}_{ij}^{0}(x_{2},t)\overline{U}_{k}(x_{2},t)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D619}_{jk}^{0}(x_{2},t)\overline{U}_{i}(x_{2},t)+\overline{U}_{i}(x_{2},t)\overline{U}_{k}(x_{2},t)\overline{U}_{j}(x_{2},t),\end{eqnarray}$$
$$\begin{eqnarray}\overline{PU_{j}}^{0}(x_{2},t)=\overline{pu_{j}}^{0}(x_{2},t)+\overline{P}(x_{2},t)\,\overline{U}_{j}(x_{2},t).\end{eqnarray}$$
Appendix C. The reduced form of the TPC equation
In this appendix, we examine if the similarity solutions obtained from the symmetry analysis can satisfy the TPC equation, or in other words, whether they bring this equation into a reduced self-similar form (here we only consider the base equation for the current analysis, the equation (2.14)). In the case of two point, and in full analogy, we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D60F}_{ij}(x_{2},\boldsymbol{r},t)={\displaystyle \frac{-[\tilde{\unicode[STIX]{x1D619}}_{ij}(\tilde{x}_{2},\tilde{\boldsymbol{r}})-a_{\unicode[STIX]{x1D60F}_{ij}}t]}{F_{1}(t)}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D60F}_{(ik)j}(x_{2},\boldsymbol{r},t)=\left(a_{\unicode[STIX]{x1D60F}_{(ik)j}}\displaystyle \int {\displaystyle \frac{\exp (C(t))}{F_{1}(t)}}\,\text{d}t+\tilde{H}_{(ik)j}(\tilde{x}_{2},\tilde{\boldsymbol{r}})\right)\exp (-C(t)), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D60F}_{i(jk)}(x_{2},\boldsymbol{r},t)=\left(a_{\unicode[STIX]{x1D60F}_{i(jk)}}\displaystyle \int {\displaystyle \frac{\exp (C(t))}{F_{1}(t)}}\,\text{d}t+\tilde{H}_{i(jk)}(\tilde{x}_{2},\tilde{\boldsymbol{r}})\right)\exp (-C(t)), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{PU_{j}}(x_{2},\boldsymbol{r},t)=\left(a_{PU_{j}}\displaystyle \int {\displaystyle \frac{\exp (C(t))}{F_{1}(t)}}\,\text{d}t+\widetilde{\overline{PU_{j}}}(\tilde{x}_{2},\tilde{\boldsymbol{r}})\right)\exp (-C(t)), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{U_{i}P}(x_{2},\boldsymbol{r},t)=\left(a_{U_{i}P}\displaystyle \int {\displaystyle \frac{\exp (C(t))}{F_{1}(t)}}\,\text{d}t+\widetilde{\overline{U_{i}P}}(\tilde{x}_{2},\tilde{\boldsymbol{r}})\right)\exp (-C(t)), & \displaystyle\end{eqnarray}$$
where
$K(t)$
is the relation (B 19) and
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{x}_{2}={\displaystyle \frac{x_{2}}{\exp \left(\displaystyle \int {\displaystyle \frac{F_{2}(t)}{F_{1}(t)}}\,\text{d}t\right)}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{r}_{1}={\displaystyle \frac{r_{1}}{\exp \left(\displaystyle \int {\displaystyle \frac{F_{2}(t)}{F_{1}(t)}}\,\text{d}t\right)}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{r}_{2}={\displaystyle \frac{r_{2}}{\exp \left(\displaystyle \int {\displaystyle \frac{F_{2}(t)}{F_{1}(t)}}\,\text{d}t\right)}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{r}_{3}={\displaystyle \frac{r_{3}}{\exp \left(\displaystyle \int {\displaystyle \frac{F_{2}(t)}{F_{1}(t)}}\,\text{d}t\right)}}. & \displaystyle\end{eqnarray}$$
Implementing
$F_{1}(t)$
(4.8) and
$F_{2}(t)$
(4.9) into (C 1)–(C 9) gives
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D60F}_{ij}(x_{2},\boldsymbol{r},t)={\displaystyle \frac{-[\tilde{\unicode[STIX]{x1D619}}_{ij}(\tilde{x}_{2},\tilde{\boldsymbol{r}})-a_{\unicode[STIX]{x1D60F}_{ij}}t]}{D(t-t_{0})}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D60F}_{(ik)j}(x_{2},\boldsymbol{r},t)={\displaystyle \frac{-[\tilde{\unicode[STIX]{x1D619}}_{(ik)j}(\tilde{x}_{2},\tilde{\boldsymbol{r}})-{\textstyle \frac{2}{3}}a_{\unicode[STIX]{x1D60F}_{(ik)j}}(t-t_{0})^{3/2}]}{D(t-t_{0})^{3/2}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D60F}_{i(jk)}(x_{2},\boldsymbol{r},t)={\displaystyle \frac{-[\tilde{\unicode[STIX]{x1D619}}_{i(jk)}(\tilde{x}_{2},\tilde{\boldsymbol{r}})-{\textstyle \frac{2}{3}}a_{\unicode[STIX]{x1D60F}_{i(jk)}}(t-t_{0})^{3/2}]}{D(t-t_{0})^{3/2}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{PU_{j}}(x_{2},\boldsymbol{r},t)={\displaystyle \frac{-[\widetilde{\overline{PU_{j}}}(\tilde{x}_{2},\tilde{\boldsymbol{r}})-{\textstyle \frac{2}{3}}a_{PU_{j}}(t-t_{0})^{3/2}]}{D(t-t_{0})^{3/2}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \overline{U_{i}P}(x_{2},\boldsymbol{r},t)={\displaystyle \frac{-[\widetilde{\overline{U_{i}P}}(\tilde{x}_{2},\tilde{\boldsymbol{r}})-{\textstyle \frac{2}{3}}a_{U_{i}P}(t-t_{0})^{3/2}]}{D(t-t_{0})^{3/2}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{x}_{2}={\displaystyle \frac{x_{2}}{(t-t_{0})^{1/2}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{r}_{1}={\displaystyle \frac{r_{1}}{(t-t_{0})^{1/2}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{r}_{2}={\displaystyle \frac{r_{2}}{(t-t_{0})^{1/2}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{r}_{3}={\displaystyle \frac{r_{3}}{(t-t_{0})^{1/2}}}. & \displaystyle\end{eqnarray}$$
Substituting the proposed similarity solutions into the governing equation (2.14) yields the following reduced (self-similar) form of the TPC equation (as the time-dependent portion of each term is similar and can be simply cancelled out throughout the equation)
$$\begin{eqnarray}\displaystyle & & \displaystyle \tilde{\unicode[STIX]{x1D619}}_{ij}-b_{1}\left(\tilde{r}_{1}{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D619}}_{ij}}{\unicode[STIX]{x2202}\tilde{r}_{1}}}+\tilde{r}_{2}{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D619}}_{ij}}{\unicode[STIX]{x2202}\tilde{r}_{2}}}+\tilde{r}_{3}{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D619}}_{ij}}{\unicode[STIX]{x2202}\tilde{r}_{3}}}+\tilde{x}_{2}{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D619}}_{ij}}{\unicode[STIX]{x2202}\tilde{x}_{2}}}\right)+b_{2}\left(\unicode[STIX]{x1D6FF}_{i2}{\displaystyle \frac{\unicode[STIX]{x2202}\widetilde{\overline{PU_{j}}}}{\unicode[STIX]{x2202}\tilde{x}_{2}}}-{\displaystyle \frac{\unicode[STIX]{x2202}\widetilde{\overline{PU_{j}}}}{\unicode[STIX]{x2202}\tilde{r}_{i}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\widetilde{\overline{U_{i}P}}}{\unicode[STIX]{x2202}\tilde{r}_{j}}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad +\,b_{3}\left({\displaystyle \frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D619}}_{(i2)j}}{\unicode[STIX]{x2202}\tilde{x}_{2}}}-{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D619}}_{(i1)j}}{\unicode[STIX]{x2202}\tilde{r}_{1}}}-{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D619}}_{(i2)j}}{\unicode[STIX]{x2202}\tilde{r}_{2}}}-{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D619}}_{(i3)j}}{\unicode[STIX]{x2202}\tilde{r}_{3}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D619}}_{i(j1)}}{\unicode[STIX]{x2202}\tilde{r}_{1}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D619}}_{i(j2)}}{\unicode[STIX]{x2202}\tilde{r}_{2}}}+{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D619}}_{i(j3)}}{\unicode[STIX]{x2202}\tilde{r}_{3}}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\unicode[STIX]{x1D708}b_{4}\left[{\displaystyle \frac{\unicode[STIX]{x2202}^{2}\tilde{\unicode[STIX]{x1D619}}_{ij}}{\unicode[STIX]{x2202}\tilde{x}_{2}^{2}}}-2{\displaystyle \frac{\unicode[STIX]{x2202}^{2}\tilde{\unicode[STIX]{x1D619}}_{ij}}{\unicode[STIX]{x2202}\tilde{x}_{2}\unicode[STIX]{x2202}\tilde{r}_{2}}}+2{\displaystyle \frac{\unicode[STIX]{x2202}^{2}\tilde{\unicode[STIX]{x1D619}}_{ij}}{\unicode[STIX]{x2202}\tilde{r}_{1}\unicode[STIX]{x2202}\tilde{r}_{1}}}+2{\displaystyle \frac{\unicode[STIX]{x2202}^{2}\tilde{\unicode[STIX]{x1D619}}_{ij}}{\unicode[STIX]{x2202}\tilde{r}_{2}\unicode[STIX]{x2202}\tilde{r}_{2}}}+2{\displaystyle \frac{\unicode[STIX]{x2202}^{2}\tilde{\unicode[STIX]{x1D619}}_{ij}}{\unicode[STIX]{x2202}\tilde{r}_{3}\unicode[STIX]{x2202}\tilde{r}_{3}}}\right],\end{eqnarray}$$
where
$b_{k}$
are constants.
