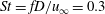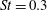1. Introduction
High speed jets in crossflows (JIC) are central to a variety of applications. In scramjet engine combustors, sonic jets of fuel are injected into a supersonic crossflow of air, where the efficient mixing of fuel and air is critical to the supersonic combustion. Accurate estimation and detailed physical understanding of the turbulent mixing mechanisms are therefore important to combustor design. Supersonic jets are used for attitude or roll control on atmospheric flight vehicles. The supersonic jet plumes reorient upon encountering the crossflowing free stream and travel downstream, where the jet and the induced flows can interact with aerodynamic control surfaces. Here, understanding the turbulent characteristics in the far field of the jet is of importance.
Past work on high speed jets in crossflow are summarized in the review paper by Mahesh (Reference Mahesh2013). Several early studies of thrust vector control using high speed transverse jets have been performed, where the induced pressure fields on the surfaces were measured to determine the change in the total thrust (e.g. Morkovin, Pierce & Craven Reference Morkovin, Pierce and Craven1952; McAulay & Pavli Reference McAulay and Pavli1960; Cubbison, Anderson & Ward Reference Cubbison, Anderson and Ward1961; Walker, Stone & Shandor Reference Walker, Stone and Shandor1963; Zukoski & Spaid Reference Zukoski and Spaid1964). Most recent studies are motivated by the application of high speed jets in crossflow to supersonic combustion (e.g. Gruber et al. Reference Gruber, Nejad, Chen and Dutton1997; Santiago & Dutton Reference Santiago and Dutton1997; Vanlerberghe et al. Reference Vanlerberghe, Santiago, Dutton and Lucht2000; Ben-Yakar, Mungal & Hanson Reference Ben-Yakar, Mungal and Hanson2006; Lazar, Elliott & Glumac Reference Lazar, Elliott and Glumac2010). A variety of methods have been used to study high speed jets in crossflow, such as Schlieren photography (e.g. Morkovin et al. Reference Morkovin, Pierce and Craven1952; Santiago & Dutton Reference Santiago and Dutton1997), planar Mie-scattering (Gruber, Nejadt & Chen Reference Gruber, Nejadt and Chen1995; Gruber et al. Reference Gruber, Nejad, Chen and Dutton1997), laser Doppler velocimetry (e.g. Santiago & Dutton Reference Santiago and Dutton1997), laser-induced fluorescence (McDaniel & Graves Reference McDaniel and Graves1986; McMillin, Seitzman & Hanson Reference McMillin, Seitzman and Hanson1994; Ben-Yakar et al. Reference Ben-Yakar, Mungal and Hanson2006) and particle image velocimetry (PIV) (Beresh, Henfling & Erven Reference Beresh, Henfling and Erven2002; Beresh et al. Reference Beresh, Erven, Henfling and Spillers2005a ,Reference Beresh, Erven, Henfling and Spillers b , Reference Beresh, Henfling, Erven and Spillers2006). Because of the complexity of this type of flow, detailed flow measurements are very difficult. Flow visualization has therefore been used to study the jet penetration, mixing and overall flow structure in high speed jets in crossflow, and some shock and vortical structures have been identified. A three-dimensional bow shock and a separation region form in front of the jet due to the blockage of the supersonic crossflow by the transverse jet. The separation region lifts the crossflow boundary layer and creates a ‘ramp’, which further induces a separation shock (e.g. Gruber et al. Reference Gruber, Nejadt and Chen1995; Santiago & Dutton Reference Santiago and Dutton1997) ahead of the bow shock. An inclined barrel shock and Mach disk form at the periphery of the high speed jet plume as the jet exits the nozzle, expands and interacts with the crossflow. The typical vortical structures in high speed jets in crossflow are identified similarly to low speed jets in crossflow, which include: the near-field jet shear layer vortices, the downstream wake vortices, the horseshoe vortices wrapping around the jet column and the counter-rotating vortex pair (CVP) in the far field. As noted by Fric & Roshko (Reference Fric and Roshko1994), the former two types of vortices are unsteady and can be observed in the instantaneous flow field; while the latter two are usually observed and defined in the mean, though they also have unsteady components.
Jet penetration in high speed crossflow has been studied by numerous researchers (e.g. Schetz & Billig Reference Schetz and Billig1966; McDaniel & Graves Reference McDaniel and Graves1986; Rothstein & Wantuck Reference Rothstein and Wantuck1992; Papamoschou & Hubbard Reference Papamoschou and Hubbard1993; Gruber et al. Reference Gruber, Nejad, Chen and Dutton1997; Ben-Yakar et al. Reference Ben-Yakar, Mungal and Hanson2006). The jet–crossflow momentum flux ratio,
is recognized as the parameter that has the dominant effect on the jet penetration. Here, the subscript
![]() $j$
denotes the jet exit condition, while the subscript
$j$
denotes the jet exit condition, while the subscript
![]() $\infty$
marks the quantities of the crossflow. Compared to the widely used
$\infty$
marks the quantities of the crossflow. Compared to the widely used
![]() $rD$
scaling (where
$rD$
scaling (where
![]() $D$
is the diameter of the nozzle at the jet exit) in incompressible jets in crossflow,
$D$
is the diameter of the nozzle at the jet exit) in incompressible jets in crossflow,
![]() $JD$
scaling appears to scale high speed jet trajectories best (e.g. Beresh et al.
Reference Beresh, Erven, Henfling and Spillers2005a
). Here,
$JD$
scaling appears to scale high speed jet trajectories best (e.g. Beresh et al.
Reference Beresh, Erven, Henfling and Spillers2005a
). Here,
![]() $r$
is the jet–crossflow velocity ratio. In most of the experimental studies, power or logarithm functions with adjustable coefficients are used to fit the experimental data. However, it is shown (§ 6) that these coefficients differ significantly between different studies, and the trajectory data from different studies show a large level of scatter even with
$r$
is the jet–crossflow velocity ratio. In most of the experimental studies, power or logarithm functions with adjustable coefficients are used to fit the experimental data. However, it is shown (§ 6) that these coefficients differ significantly between different studies, and the trajectory data from different studies show a large level of scatter even with
![]() $JD$
scaling. Papamoschou & Hubbard (Reference Papamoschou and Hubbard1993) studied the effect of crossflow Mach number and jet exit Mach number on the jet penetration for
$JD$
scaling. Papamoschou & Hubbard (Reference Papamoschou and Hubbard1993) studied the effect of crossflow Mach number and jet exit Mach number on the jet penetration for
![]() $M_{j}=1$
–3.5,
$M_{j}=1$
–3.5,
![]() $M_{\infty }=2$
–3 and
$M_{\infty }=2$
–3 and
![]() $J=1.7$
–8. They pointed out that, due to (1.1), the effect of Mach number cannot be evaluated unambiguously while keeping other quantities such as the jet–crossflow momentum flux ratio and pressure ratio constant. Their study showed that the jet penetration increases slightly with the crossflow Mach number while keeping
$J=1.7$
–8. They pointed out that, due to (1.1), the effect of Mach number cannot be evaluated unambiguously while keeping other quantities such as the jet–crossflow momentum flux ratio and pressure ratio constant. Their study showed that the jet penetration increases slightly with the crossflow Mach number while keeping
![]() $J$
constant. Also Ben-Yakar et al. (Reference Ben-Yakar, Mungal and Hanson2006) found in their experiments of hydrogen and ethylene transverse jets (
$J$
constant. Also Ben-Yakar et al. (Reference Ben-Yakar, Mungal and Hanson2006) found in their experiments of hydrogen and ethylene transverse jets (
![]() $M_{j}=1$
,
$M_{j}=1$
,
![]() $M_{\infty }=3.38$
and
$M_{\infty }=3.38$
and
![]() $J=1.4$
) that molecular weight also plays a role in jet penetration. Obviously, there are factors other than
$J=1.4$
) that molecular weight also plays a role in jet penetration. Obviously, there are factors other than
![]() $J$
that affect the jet penetration, which must be considered to yield better scaling laws for the jet trajectories.
$J$
that affect the jet penetration, which must be considered to yield better scaling laws for the jet trajectories.
Among the previous experimental studies, Santiago & Dutton (Reference Santiago and Dutton1997)’s and Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
,Reference Beresh, Erven, Henfling and Spillers
b
, Reference Beresh, Henfling, Erven and Spillers2006)’s works provide relatively more quantitative data. Santiago & Dutton (Reference Santiago and Dutton1997) measured the detailed velocity field induced by a sonic jet injected into a Mach 1.6 supersonic crossflow on the symmetric plane and cross-planes at
![]() $J=1.7$
. Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
,Reference Beresh, Erven, Henfling and Spillers
b
, Reference Beresh, Henfling, Erven and Spillers2006) carried out a series of experiments on over-expanded supersonic jets injected into subsonic crossflow for
$J=1.7$
. Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
,Reference Beresh, Erven, Henfling and Spillers
b
, Reference Beresh, Henfling, Erven and Spillers2006) carried out a series of experiments on over-expanded supersonic jets injected into subsonic crossflow for
![]() $M_{j}=3.73$
,
$M_{j}=3.73$
,
![]() $M_{\infty }=0.5$
–0.8 and
$M_{\infty }=0.5$
–0.8 and
![]() $J=2.8$
–10.2. Based on seven different flow configurations, Beresh et al. studied the influence of free-stream Mach number and that of jet–crossflow momentum flux ratio on the penetration of the jet, the turbulent characteristics in the far field downstream of the jet and the scaling of counter-rotating vortex pairs (CVP) at cross-planes. A number of numerical simulations were performed to compare to Santiago & Dutton (Reference Santiago and Dutton1997)’s work (e.g. Génin & Menon Reference Génin and Menon2010; Kawai & Lele Reference Kawai and Lele2010; Peterson & Candler Reference Peterson and Candler2010; Rana, Thornber & Drikakis Reference Rana, Thornber and Drikakis2011). Peterson & Candler (Reference Peterson and Candler2010) used detached eddy simulation (DES) and compared mean velocity and second-order quantities with the experiments of Santiago & Dutton (Reference Santiago and Dutton1997) and obtained reasonable agreement. Génin & Menon (Reference Génin and Menon2010) made detailed comparisons with experiments and also studied the effect of
$J=2.8$
–10.2. Based on seven different flow configurations, Beresh et al. studied the influence of free-stream Mach number and that of jet–crossflow momentum flux ratio on the penetration of the jet, the turbulent characteristics in the far field downstream of the jet and the scaling of counter-rotating vortex pairs (CVP) at cross-planes. A number of numerical simulations were performed to compare to Santiago & Dutton (Reference Santiago and Dutton1997)’s work (e.g. Génin & Menon Reference Génin and Menon2010; Kawai & Lele Reference Kawai and Lele2010; Peterson & Candler Reference Peterson and Candler2010; Rana, Thornber & Drikakis Reference Rana, Thornber and Drikakis2011). Peterson & Candler (Reference Peterson and Candler2010) used detached eddy simulation (DES) and compared mean velocity and second-order quantities with the experiments of Santiago & Dutton (Reference Santiago and Dutton1997) and obtained reasonable agreement. Génin & Menon (Reference Génin and Menon2010) made detailed comparisons with experiments and also studied the effect of
![]() $J$
(1.73, 5.2). They note that Kelvin–Helmholz instabilities occur in the windward side of the jet. They identify dominant vortical features in the flow and find that the windward vortex pair is more pronounced at higher
$J$
(1.73, 5.2). They note that Kelvin–Helmholz instabilities occur in the windward side of the jet. They identify dominant vortical features in the flow and find that the windward vortex pair is more pronounced at higher
![]() $J$
.
$J$
.
Kawai & Lele (Reference Kawai and Lele2010) use an implicit-LES method and obtain good agreement with experiments of Santiago & Dutton (Reference Santiago and Dutton1997), although, their Reynolds number is lower than that of the experiments. Along with a detailed qualitative description of the flow, they also study the effect of laminar and turbulent inflow on the turbulent statistics. They observe that as the vortices interact with the complex system of shocks, an acoustic wave is generated and propagates upstream causing a high unsteady oscillation of the bow shock upstream of the jet. Using a passive scalar solution, they find that the turbulent boundary layer causes enhanced mixing of the jet fluid when compared to a laminar boundary layer due to interaction of the turbulent structures in the boundary layer. They report temporal spectra at a few locations and find that the vortex formation and shock deformation occurs at an
![]() $St=fD/u_{\infty }$
of 0.2 for the laminar inflow and 0.5–0.6 for the turbulent inflow, although they note that no clear peak is obtained for the turbulent inflow case.
$St=fD/u_{\infty }$
of 0.2 for the laminar inflow and 0.5–0.6 for the turbulent inflow, although they note that no clear peak is obtained for the turbulent inflow case.
For the supersonic jet in subsonic crossflow, Arunajatesan (Reference Arunajatesan2012) and Arunajatesan & McWherter-Payne (Reference Arunajatesan and McWherter-Payne2013) use RANS and DES methods respectively to evaluate its capability to predict such complex flows by comparing to the experiments of Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a ), among others. Arunajatesan & McWherter-Payne (Reference Arunajatesan and McWherter-Payne2013) note that the DES model was sensitive to transition from RANS to LES and to the mesh used. Chai & Mahesh (Reference Chai and Mahesh2010, Reference Chai and Mahesh2011) performed LES of a supersonic jet in subsonic crossflow. They compared their results to the experiments of Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a ) and report the effect of laminar and turbulent crossflows on the mean flowfield.
Dynamic mode decomposition (DMD), also referred to as Koopman modes, have been used (Rowley et al. Reference Rowley, Mezic, Bagheri, Schlatter and Henningson2009; Schmid Reference Schmid2010) to study the dynamics of fluid flows to identify dominant frequencies and their corresponding spatial features for complex flows. This is analogous to a three-dimensional Fourier transform of the entire flowfield and has been used to identify dominant flow features for a low speed jet in crossflow by Rowley et al. (Reference Rowley, Mezic, Bagheri, Schlatter and Henningson2009), a supersonic screeching jet by Jovanovic, Schmid & Nichols (Reference Jovanovic, Schmid and Nichols2014) and axisymmetric jets using PIV data by Schmid et al. (Reference Schmid, Li, Juniper and Pust2011).
In the current study, we perform LES of both a sonic jet injected into a supersonic crossflow and a supersonic jet injected into a subsonic crossflow, where the flow conditions are compared to the experiments of Santiago & Dutton (Reference Santiago and Dutton1997) and Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a ,Reference Beresh, Erven, Henfling and Spillers b , Reference Beresh, Henfling, Erven and Spillers2006), respectively. The present work explores the detailed flow physics of high speed jets in crossflow, and studies the jet penetration and the dynamics of coherent vortical structures by examining their frequencies. Temporal spectra from LES and DMD of the flowfield are used to identify dominant flow features. A modification to the Schetz & Billig (Reference Schetz and Billig1966) theory is proposed to predict jet trajectory due to wide scatter with existing correlations.
This paper is organized as follows. The details of the algorithm are discussed in § 2. The simulation conditions, description of the computational grid and turbulent inflow generator are discussed in § 3. A qualitative description of the instantaneous and mean flowfield is presented in § 4. Section 5 validates the current simulations by comparing to experimental data. A modification of the Schetz & Billig (Reference Schetz and Billig1966) theory for predicting jet trajectory is discussed in § 6. Temporal spectra are reported in § 7 to identify dominant frequencies in the flow and finally dynamic mode decomposition of the pressure field is performed in § 8 to identify dominant flow features and their corresponding frequencies. Note that unless otherwise explicitly stated, all figures shown in the subsequent sections correspond to the finest grids used in the simulations (A3 and B2 for the sonic and supersonic injections, respectively).
2. Algorithm
The spatially filtered compressible Navier–Stokes equations for an ideal gas are solved in conservative form:
In (2.2) and (2.3),
![]() ${\it\tau}_{ij}$
and
${\it\tau}_{ij}$
and
![]() $q_{j}$
are the sub-grid scale (SGS) stress and SGS heat flux defined as
$q_{j}$
are the sub-grid scale (SGS) stress and SGS heat flux defined as
where
![]() $|\unicode[STIX]{x1D64E}|=\sqrt{2\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}}$
, and
$|\unicode[STIX]{x1D64E}|=\sqrt{2\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}}$
, and
![]() $C_{s}$
,
$C_{s}$
,
![]() $C_{I}$
,
$C_{I}$
,
![]() $Pr_{T}$
are model coefficients that are determined dynamically by the Germano identity (Germano et al.
Reference Germano, Piomelli, Moin and Cabot1991).
$Pr_{T}$
are model coefficients that are determined dynamically by the Germano identity (Germano et al.
Reference Germano, Piomelli, Moin and Cabot1991).
The above equations are solved using an algorithm developed for unstructured grids by Park & Mahesh (Reference Park and Mahesh2007). The algorithm employs a least-square method for flux reconstruction on faces of control volumes (CV), which has better spectral resolution than the fourth order central difference scheme at high wavenumbers, is more accurate than a simple symmetric reconstruction and more stable than a standard least-square reconstruction. A viscous flux splitting technique is applied, which ensures that the dominant incompressible component only depends on the nearest neighbours and is therefore more accurate at high wavenumbers, and devoid of odd–even decoupling. The algorithm uses a shock-capturing scheme that was originally proposed by Yee, Sandham & Djomehri (Reference Yee, Sandham and Djomehri1999) for structured meshes and was extended by Park & Mahesh (Reference Park and Mahesh2007) to unstructured meshes, and further localized to reduce unnecessary numerical dissipation. The shock-capturing is implemented in a predictor–corrector form. The predictor step (base scheme) is symmetric and non-dissipative, and is designed to accurately represent broadband turbulence; while the corrector step is a characteristic-based filter that is active only in the vicinity of discontinuities. Time advancement is performed using an explicit second-order Adams–Bashforth scheme. Therefore, the overall scheme avoids unnecessary numerical dissipation. Park & Mahesh (Reference Park and Mahesh2007) describe this methodology in detail, including a validation study using shock/vortex interaction, shock tube problem, two-dimensional mixing layer and homogeneous turbulence. The methodology has also been shown to perform well in various complex flows with physical features relevant to the current simulations. These include supersonic boundary layer transition due to a discrete roughness element (Iyer & Mahesh Reference Iyer and Mahesh2013) and distributed roughness (Muppidi & Mahesh Reference Muppidi and Mahesh2012), and LES of decaying isotropic turbulence and shock/turbulence interaction (Chai & Mahesh Reference Chai and Mahesh2012). The numerical method was also used to study supersonic transition to turbulence by blowing and suction at Mach 2.25 in Muppidi & Mahesh (Reference Muppidi and Mahesh2010) and shock/turbulence interaction at Mach 2.9 in a compression corner in Muppidi & Mahesh (Reference Muppidi and Mahesh2011). The LES methodology used in the current work (DSM) has been validated by Chai & Mahesh (Reference Chai and Mahesh2012) for decaying isotropic turbulence and normal shock-turbulence interaction. It has also been validated for the supersonic turbulent boundary layers used in the current work.
3. Simulation details
3.1. Problem statement
The current study considers two of the most common regimes of high-speed jets in crossflow: a sonic jet injected into a supersonic crossflow, and a supersonic jet injected into a subsonic crossflow. Figure 1 shows a schematic of the important flow features for the two regimes studied. For a sonic jet in a supersonic crossflow, the flowfield is dominated by a complex system of shocks; bow shock, barrel shock and Mach disk as shown in figure 1(a). The supersonic jet flow on the other hand resembles a low speed jet in crossflow with the exception of the presence of a shock at the jet exit as seen in figure 1(b). The flow conditions are listed in table 1 and are based on the experiments of Santiago & Dutton (Reference Santiago and Dutton1997) and Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
,Reference Beresh, Erven, Henfling and Spillers
b
, Reference Beresh, Henfling, Erven and Spillers2006), respectively. For sonic injection, the free-stream Mach number is
![]() $M_{\infty }=1.6$
and the Reynolds number based on the free-stream velocity and jet diameter
$M_{\infty }=1.6$
and the Reynolds number based on the free-stream velocity and jet diameter
![]() $D$
is
$D$
is
![]() $Re_{D}=5.9\times 10^{4}$
. The density and pressure ratio between the nozzle chamber and crossflow are
$Re_{D}=5.9\times 10^{4}$
. The density and pressure ratio between the nozzle chamber and crossflow are
![]() ${\it\rho}_{0j}/{\it\rho}_{\infty }=5.5$
and
${\it\rho}_{0j}/{\it\rho}_{\infty }=5.5$
and
![]() $p_{0j}/p_{\infty }=8.4$
, which results in a jet-to-crossflow momentum flux ratio of
$p_{0j}/p_{\infty }=8.4$
, which results in a jet-to-crossflow momentum flux ratio of
![]() $J=1.7$
. The boundary layer thickness,
$J=1.7$
. The boundary layer thickness,
![]() ${\it\delta}_{99}/D=0.775$
, is matched at
${\it\delta}_{99}/D=0.775$
, is matched at
![]() $x/D=-5$
(where
$x/D=-5$
(where
![]() $x/D$
is the streamwise coordinate scaled by the jet exit diameter, as shown in figure 2). The jet exit diameter (
$x/D$
is the streamwise coordinate scaled by the jet exit diameter, as shown in figure 2). The jet exit diameter (
![]() $D$
) is 4 mm. The stagnation pressure of the jet (
$D$
) is 4 mm. The stagnation pressure of the jet (
![]() $P_{0j}$
) is 476 kPa, the stagnation temperature of the jet (
$P_{0j}$
) is 476 kPa, the stagnation temperature of the jet (
![]() $T_{0j}$
) is 295 K and the free-stream velocity (
$T_{0j}$
) is 295 K and the free-stream velocity (
![]() $u_{\infty }$
) is
$u_{\infty }$
) is
![]() $446~\text{m}~\text{s}^{-1}$
. For supersonic injection, the free-stream Mach number is
$446~\text{m}~\text{s}^{-1}$
. For supersonic injection, the free-stream Mach number is
![]() $M_{\infty }=0.8$
, the nominal jet exit Mach number is
$M_{\infty }=0.8$
, the nominal jet exit Mach number is
![]() $M_{j}=3.73$
, the jet–crossflow momentum flux ratio is
$M_{j}=3.73$
, the jet–crossflow momentum flux ratio is
![]() $J=10.2$
and the density, pressure and temperature ratio between the nozzle chamber and crossflow are
$J=10.2$
and the density, pressure and temperature ratio between the nozzle chamber and crossflow are
![]() ${\it\rho}_{0j}/{\it\rho}_{\infty }=47.1$
,
${\it\rho}_{0j}/{\it\rho}_{\infty }=47.1$
,
![]() $p_{0j}/p_{\infty }=49.1$
and
$p_{0j}/p_{\infty }=49.1$
and
![]() $T_{0j}/T_{\infty }=1.05$
, respectively. The jet exit diameter (
$T_{0j}/T_{\infty }=1.05$
, respectively. The jet exit diameter (
![]() $D$
) is 9.53 mm. The nominal stagnation pressure of the jet (
$D$
) is 9.53 mm. The nominal stagnation pressure of the jet (
![]() $P_{0j}$
) is 4.96 MPa and the crossflow free-stream velocity
$P_{0j}$
) is 4.96 MPa and the crossflow free-stream velocity
![]() $u_{\infty }$
is
$u_{\infty }$
is
![]() $286~\text{m}~\text{s}^{-1}$
. The Reynolds number is
$286~\text{m}~\text{s}^{-1}$
. The Reynolds number is
![]() $Re_{D}=3.1\times 10^{4}$
based on free-stream conditions and the jet diameter is
$Re_{D}=3.1\times 10^{4}$
based on free-stream conditions and the jet diameter is
![]() $D$
. The boundary layer thickness,
$D$
. The boundary layer thickness,
![]() ${\it\delta}_{99}/D=1.553$
, is matched at
${\it\delta}_{99}/D=1.553$
, is matched at
![]() $x/D=26.65$
in absence of the transverse jet. Both laminar and turbulent crossflow boundary layers have been considered for each regime. The only difference between the laminar and turbulent inflow simulations, apart from the grid, is the inflow profile of the boundary layer (laminar versus turbulent) so as to match the boundary layer thickness at
$x/D=26.65$
in absence of the transverse jet. Both laminar and turbulent crossflow boundary layers have been considered for each regime. The only difference between the laminar and turbulent inflow simulations, apart from the grid, is the inflow profile of the boundary layer (laminar versus turbulent) so as to match the boundary layer thickness at
![]() $x/D=-5$
for the sonic jet and
$x/D=-5$
for the sonic jet and
![]() $x/D=26.6$
for the supersonic jet whose value is obtained from the respective experiments. The laminar boundary layer is not tripped in the simulations and therefore remains laminar upstream of the jet.
$x/D=26.6$
for the supersonic jet whose value is obtained from the respective experiments. The laminar boundary layer is not tripped in the simulations and therefore remains laminar upstream of the jet.

Figure 1. Figure showing a schematic of a jet in crossflow for the two flow configurations studied in this paper: (a) sonic jet in supersonic crossflow from Ben-Yakar et al. (Reference Ben-Yakar, Mungal and Hanson2006) and (b) supersonic jet in a subsonic crossflow from Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a ).

Figure 2. Computational mesh for sonic jet in supersonic crossflow corresponding to
![]() $A3$
(see table 2).
$A3$
(see table 2).
Table 1. Table listing the simulation parameters for the sonic and supersonic jet flows.
![]() $M_{j}$
is at the jet exit.
$M_{j}$
is at the jet exit.

Note that, in the experiments, the Reynolds numbers are
![]() $Re_{D}=2.4\times 10^{5}$
and
$Re_{D}=2.4\times 10^{5}$
and
![]() $Re_{D}=1.9\times 10^{5}$
for the sonic and supersonic injection. In the current simulations, the Reynolds number is
$Re_{D}=1.9\times 10^{5}$
for the sonic and supersonic injection. In the current simulations, the Reynolds number is
![]() $1/4$
and
$1/4$
and
![]() $1/6$
of the experiments due to computational cost, which is still high. This results in
$1/6$
of the experiments due to computational cost, which is still high. This results in
![]() $Re_{{\it\theta}}\approx 4500$
in the crossflow turbulent boundary layer; so that the crossflow turbulent boundary layer can be reasonably resolved by the current LES without wall models. Note that for the sonic injection, Kawai & Lele (Reference Kawai and Lele2010) used an
$Re_{{\it\theta}}\approx 4500$
in the crossflow turbulent boundary layer; so that the crossflow turbulent boundary layer can be reasonably resolved by the current LES without wall models. Note that for the sonic injection, Kawai & Lele (Reference Kawai and Lele2010) used an
![]() $Re_{D}=2.4\times 10^{4}$
in their LES (
$Re_{D}=2.4\times 10^{4}$
in their LES (
![]() $1/10$
of the experimental value) and obtained reasonable agreement of mean quantities with the experiment. Therefore it is assumed that the reduction of Reynolds numbers should not much affect the overall flow structure and mean flow quantities for the sonic jet in supersonic crossflow.
$1/10$
of the experimental value) and obtained reasonable agreement of mean quantities with the experiment. Therefore it is assumed that the reduction of Reynolds numbers should not much affect the overall flow structure and mean flow quantities for the sonic jet in supersonic crossflow.
3.2. Computational mesh and boundary conditions
Figure 2 shows the computational mesh and domain for the simulation of sonic jet in supersonic crossflow. Note that the origin of the coordinates is set at the centre of jet exit, and the computational domain extends
![]() $40D\times 20D\times 30D$
in the axial, wall-normal and spanwise directions (
$40D\times 20D\times 30D$
in the axial, wall-normal and spanwise directions (
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
), respectively. Preliminary computations showed that a domain of this size is large enough that the confinement effects of the boundary are absent. No-slip and adiabatic boundary conditions are imposed on the walls of the flat plate and the nozzle. An absorbing sponge boundary condition wherein the term
$z$
), respectively. Preliminary computations showed that a domain of this size is large enough that the confinement effects of the boundary are absent. No-slip and adiabatic boundary conditions are imposed on the walls of the flat plate and the nozzle. An absorbing sponge boundary condition wherein the term
![]() $-{\it\sigma}(q-q_{ref})$
is added to the governing equations, (
$-{\it\sigma}(q-q_{ref})$
is added to the governing equations, (
![]() $q_{ref}$
being the laminar reference solution), is applied at the inflow, top and side walls and outflow boundaries to minimize reflections. At the jet inlet, the experimental chamber pressure and density are specified so that the desired Mach number and thermodynamic conditions are achieved at the jet exit in the absence of crossflow. A tanh vertical velocity profile is imposed which satisfies the continuity and no-slip wall boundary conditions. At the inlet of the crossflow, either a laminar boundary layer profile or a realistic turbulent boundary layer is imposed. The turbulent boundary layer inflow is briefly discussed in § 3.3.
$q_{ref}$
being the laminar reference solution), is applied at the inflow, top and side walls and outflow boundaries to minimize reflections. At the jet inlet, the experimental chamber pressure and density are specified so that the desired Mach number and thermodynamic conditions are achieved at the jet exit in the absence of crossflow. A tanh vertical velocity profile is imposed which satisfies the continuity and no-slip wall boundary conditions. At the inlet of the crossflow, either a laminar boundary layer profile or a realistic turbulent boundary layer is imposed. The turbulent boundary layer inflow is briefly discussed in § 3.3.
Figure 3 shows the computational mesh for the simulation of supersonic jet in subsonic crossflow. In this simulation, the penetration of the jet is
![]() $1/3$
of the height of experimental apparatus. For a fair comparison, the computational domain has almost the same dimension as the wind tunnel test section to account for confinement effects of the wind tunnel walls. The computational domain extends
$1/3$
of the height of experimental apparatus. For a fair comparison, the computational domain has almost the same dimension as the wind tunnel test section to account for confinement effects of the wind tunnel walls. The computational domain extends
![]() $100D\times 32D\times 32D$
in the axial (
$100D\times 32D\times 32D$
in the axial (
![]() $x$
), wall-normal (
$x$
), wall-normal (
![]() $y$
) and spanwise (
$y$
) and spanwise (
![]() $z$
) directions, respectively, and the origin of the coordinates is again set to be the centre of the jet exit. Accordingly, adiabatic slip boundary conditions are specified for the side and top walls; while the boundary conditions for the walls of the flat plate, nozzle, jet inlet and inflow are set similar to those for sonic injection. An absorbing boundary condition is applied at the jet inflow and the outflow is placed at 80
$z$
) directions, respectively, and the origin of the coordinates is again set to be the centre of the jet exit. Accordingly, adiabatic slip boundary conditions are specified for the side and top walls; while the boundary conditions for the walls of the flat plate, nozzle, jet inlet and inflow are set similar to those for sonic injection. An absorbing boundary condition is applied at the jet inflow and the outflow is placed at 80
![]() $D$
from the jet exit, with the grid progressively coarsened towards the outflow to minimize the effect of the zero-gradient boundary condition. Figure 4 depicts the shape of the entire nozzle used in the simulation and the grid for the nozzle.
$D$
from the jet exit, with the grid progressively coarsened towards the outflow to minimize the effect of the zero-gradient boundary condition. Figure 4 depicts the shape of the entire nozzle used in the simulation and the grid for the nozzle.

Figure 3. Computational mesh for supersonic jet in subsonic crossflow corresponding to
![]() $B2$
(see table 2).
$B2$
(see table 2).

Figure 4. Figure showing the shape of the jet nozzle used for (a) sonic jet (
![]() $A3$
) and (b) supersonic jet (
$A3$
) and (b) supersonic jet (
![]() $B2$
).
$B2$
).
Table 2. Summary of grids used in the simulations.

Since the sonic jet turns and becomes horizontal closer to the wall as compared to the supersonic jet (due to a lower velocity ratio), the grid is made coarse at around
![]() $y/D\approx 5$
while the grid is relatively fine for a larger distance in
$y/D\approx 5$
while the grid is relatively fine for a larger distance in
![]() $y$
for the supersonic jet owing to its higher velocity ratio. Also, since the crossflow is supersonic for the sonic jet injection with its characteristic waves moving away from the jet, the outflow is placed closer to the jet at a distance of
$y$
for the supersonic jet owing to its higher velocity ratio. Also, since the crossflow is supersonic for the sonic jet injection with its characteristic waves moving away from the jet, the outflow is placed closer to the jet at a distance of
![]() $x/D=30$
as opposed to
$x/D=30$
as opposed to
![]() $x/D=80$
for the subsonic crossflow.
$x/D=80$
for the subsonic crossflow.
As shown in figures 2 and 3, the computational mesh is unstructured and consists of hexahedral elements only. The grids used in this study are described in table 2. Three grids were used for the sonic jet (
![]() $A1$
,
$A1$
,
![]() $A2$
and
$A2$
and
![]() $A3$
) while two grids were used for the supersonic jet (
$A3$
) while two grids were used for the supersonic jet (
![]() $B1$
and
$B1$
and
![]() $B2$
). Fine grids are used at critical regions such as the surface of the flat plate, the nozzle wall and the near field of the jet. The grids are then stretched quickly outside of those regions. The resolution is finest near the jet exit wall, where the grid spacing is
$B2$
). Fine grids are used at critical regions such as the surface of the flat plate, the nozzle wall and the near field of the jet. The grids are then stretched quickly outside of those regions. The resolution is finest near the jet exit wall, where the grid spacing is
![]() ${\it\Delta}_{r}\approx 0.01D$
in the radial direction,
${\it\Delta}_{r}\approx 0.01D$
in the radial direction,
![]() ${\it\Delta}_{{\it\theta}}\approx 0.03D$
in the azimuthal direction and
${\it\Delta}_{{\it\theta}}\approx 0.03D$
in the azimuthal direction and
![]() ${\it\Delta}_{y}\approx 0.01D$
in the
${\it\Delta}_{y}\approx 0.01D$
in the
![]() $y$
-direction for cases
$y$
-direction for cases
![]() $A1$
and
$A1$
and
![]() $B1$
(laminar crossflow boundary layer). When the crossflow boundary layer is turbulent (case
$B1$
(laminar crossflow boundary layer). When the crossflow boundary layer is turbulent (case
![]() $A2$
and
$A2$
and
![]() $B2$
),
$B2$
),
![]() ${\it\Delta}_{r}$
and
${\it\Delta}_{r}$
and
![]() ${\it\Delta}_{{\it\theta}}$
spacings are similar to those used in cases
${\it\Delta}_{{\it\theta}}$
spacings are similar to those used in cases
![]() $A1$
and
$A1$
and
![]() $B2$
, but
$B2$
, but
![]() ${\it\Delta}_{y}$
is refined within the crossflow boundary layer to capture the smaller scales, resulting in a
${\it\Delta}_{y}$
is refined within the crossflow boundary layer to capture the smaller scales, resulting in a
![]() ${\it\Delta}_{y,wall}\approx 0.001D$
. Within the turbulent boundary layer,
${\it\Delta}_{y,wall}\approx 0.001D$
. Within the turbulent boundary layer,
![]() ${\it\Delta}_{x}\approx 0.03D$
,
${\it\Delta}_{x}\approx 0.03D$
,
![]() ${\it\Delta}_{y}^{(1)}\approx 0.001D$
and
${\it\Delta}_{y}^{(1)}\approx 0.001D$
and
![]() ${\it\Delta}_{z}\approx 0.02D$
for the sonic injection, and
${\it\Delta}_{z}\approx 0.02D$
for the sonic injection, and
![]() ${\it\Delta}_{x}\approx 0.045D$
,
${\it\Delta}_{x}\approx 0.045D$
,
![]() ${\it\Delta}_{y}^{(1)}\approx 0.0015D$
and
${\it\Delta}_{y}^{(1)}\approx 0.0015D$
and
![]() ${\it\Delta}_{z}\approx 0.03D$
for the supersonic injection, resulting in viscous wall spacings of
${\it\Delta}_{z}\approx 0.03D$
for the supersonic injection, resulting in viscous wall spacings of
![]() ${\it\Delta}_{x}^{+}\approx 30$
,
${\it\Delta}_{x}^{+}\approx 30$
,
![]() ${\it\Delta}_{y}^{+(1)}\approx 1$
and
${\it\Delta}_{y}^{+(1)}\approx 1$
and
![]() ${\it\Delta}_{z}^{+}\approx 20$
for both cases. Here, the superscript ‘(1)’ denotes the first grid point above the wall of the flat plate. At this grid resolution, the crossflow boundary layers can be reasonably well captured before they interact with the transverse jet (figure 6). In the case of
${\it\Delta}_{z}^{+}\approx 20$
for both cases. Here, the superscript ‘(1)’ denotes the first grid point above the wall of the flat plate. At this grid resolution, the crossflow boundary layers can be reasonably well captured before they interact with the transverse jet (figure 6). In the case of
![]() $A3$
, the grid resolution within the inflow boundary is similar to that in case
$A3$
, the grid resolution within the inflow boundary is similar to that in case
![]() $A2$
, but the jet near field is substantially refined. For example, near the jet exit wall, the grid spacings are
$A2$
, but the jet near field is substantially refined. For example, near the jet exit wall, the grid spacings are
![]() ${\it\Delta}_{r}\approx 0.001D$
,
${\it\Delta}_{r}\approx 0.001D$
,
![]() ${\it\Delta}_{{\it\theta}}\approx 0.015D$
and
${\it\Delta}_{{\it\theta}}\approx 0.015D$
and
![]() ${\it\Delta}_{y}\approx 0.0005D$
, respectively. The largest grid spacing is of order
${\it\Delta}_{y}\approx 0.0005D$
, respectively. The largest grid spacing is of order
![]() ${\it\Delta}_{r}\approx 1D$
, as observed in figures 2 and 3. The resulting sizes of the computational meshes are listed in table 1 for each case. When a laminar crossflow boundary layer is used, the computational meshes have approximately 13 million and 15 million control volumes for sonic and supersonic injection, respectively. With a turbulent crossflow boundary layer, a relatively coarse mesh with 25 million volumes was used at first for the sonic injection, which is then refined to 75 million to evaluate the effect of grid resolution. For the supersonic injection, the simulation with a turbulent crossflow boundary layer uses around 27 million grid points.
${\it\Delta}_{r}\approx 1D$
, as observed in figures 2 and 3. The resulting sizes of the computational meshes are listed in table 1 for each case. When a laminar crossflow boundary layer is used, the computational meshes have approximately 13 million and 15 million control volumes for sonic and supersonic injection, respectively. With a turbulent crossflow boundary layer, a relatively coarse mesh with 25 million volumes was used at first for the sonic injection, which is then refined to 75 million to evaluate the effect of grid resolution. For the supersonic injection, the simulation with a turbulent crossflow boundary layer uses around 27 million grid points.
The time advancement was explicit, and the computational time step is
![]() $0.001D/U_{\infty }$
for cases
$0.001D/U_{\infty }$
for cases
![]() $A1$
and
$A1$
and
![]() $B1$
;
$B1$
;
![]() $0.0001D/U_{\infty }$
for cases
$0.0001D/U_{\infty }$
for cases
![]() $A2$
and
$A2$
and
![]() $B2$
; and
$B2$
; and
![]() $0.00001D/U_{\infty }$
for case
$0.00001D/U_{\infty }$
for case
![]() $A3$
. The fine grid simulations are initialized with preliminary simulations of corresponding cases, where a good representation of the flow field had been obtained. The simulations are advanced for
$A3$
. The fine grid simulations are initialized with preliminary simulations of corresponding cases, where a good representation of the flow field had been obtained. The simulations are advanced for
![]() $40D/U_{\infty }$
and
$40D/U_{\infty }$
and
![]() $100D/U_{\infty }$
units of time for the sonic and supersonic injection, respectively, to allow any transients to exit the domain before computing time-averaged statistics. The flow statistics are then collected for more than
$100D/U_{\infty }$
units of time for the sonic and supersonic injection, respectively, to allow any transients to exit the domain before computing time-averaged statistics. The flow statistics are then collected for more than
![]() $80D/U_{\infty }$
and
$80D/U_{\infty }$
and
![]() $200D/U_{\infty }$
non-dimensional time units, respectively to achieve acceptable convergence.
$200D/U_{\infty }$
non-dimensional time units, respectively to achieve acceptable convergence.
3.3. Turbulent inflow generator
The inflow turbulent data is generated from a separate simulation of boundary layer transition (shown in figure 5). A periodic blowing and suction velocity perturbation is applied in a small region at the wall to transition the flow to turbulence, similar to Pirozzoli, Grasso & Gatski (Reference Pirozzoli, Grasso and Gatski2004) and Muppidi & Mahesh (Reference Muppidi and Mahesh2010). The inflow generator operates under the same flow conditions (Reynolds number and Mach number) as the simulation of jets in crossflow. The inflow data are then extracted at a location where the boundary layer thickness matches the experimental condition and are stored temporally. The stored inflow data are then read by the simulation of jets in crossflow. Figure 6 shows the profiles of the mean streamwise velocity and turbulent intensities extracted at
![]() $x/D=5$
upstream of the jet exit in the absence of the jet for the
$x/D=5$
upstream of the jet exit in the absence of the jet for the
![]() $M_{\infty }=1.6$
crossflow of the sonic jet simulation. Reasonable agreement can be observed between the simulation of turbulent boundary layer with the proposed inflow generator and available DNS/experiment results.
$M_{\infty }=1.6$
crossflow of the sonic jet simulation. Reasonable agreement can be observed between the simulation of turbulent boundary layer with the proposed inflow generator and available DNS/experiment results.

Figure 5. Schematic of turbulent inflow generator.

Figure 6. Mean velocity profiles of turbulent inflow boundary layer (
![]() $M_{\infty }=1.6$
) for the sonic jet injection are compared to Pirozzoli et al. (Reference Pirozzoli, Grasso and Gatski2004) (a) and turbulent intensity profiles are compared to Elena, Lacharme & Gaviglio (Reference Elena, Lacharme and Gaviglio1985).
$M_{\infty }=1.6$
) for the sonic jet injection are compared to Pirozzoli et al. (Reference Pirozzoli, Grasso and Gatski2004) (a) and turbulent intensity profiles are compared to Elena, Lacharme & Gaviglio (Reference Elena, Lacharme and Gaviglio1985).
4. Qualitative flow description
4.1. Instantaneous flow features
4.1.1. Sonic jet in supersonic crossflow

Figure 7. 3-D view of instantaneous density gradient magnitude contours on the symmetry plane (showing shocks and compression waves) and horizontal plane close to the wall (showing the effect of the jet on the incoming turbulent features) for the sonic jet in supersonic crossflow (
![]() $A3$
).
$A3$
).

Figure 8. Isocontours of
![]() $Q$
-criterion coloured by streamwise velocity (
$Q$
-criterion coloured by streamwise velocity (
![]() $u$
) depicting the instantaneous vortical flow features for the sonic jet (
$u$
) depicting the instantaneous vortical flow features for the sonic jet (
![]() $A3$
).
$A3$
).
Figure 7 shows contours of density gradient magnitude on the central and horizontal planes. The supersonic crossflow travels from left to right and contains a fully developed turbulent boundary layer. It sees the transverse jet as an obstacle, and responds by forming of a bow shock and a recirculation region in front of the jet. The recirculation region further induces a family of compression waves that merge into a ‘separation shock’. The separation shock and bow shock form a
![]() ${\it\lambda}$
shape. Exiting the orifice, the sonic jet tries to penetrate and expand, and sets up an inclined barrel shock and Mach disk on its periphery. On the windward side of the jet, the shear layer rolls up into vortices which detach from the jet boundary and are shed downstream. Coherent flow structures are observed downstream of the jet after the jet/crossflow interaction. These coherent vortices appear to be the Kelvin–Helmholtz vortices that originate from two shear layers. One is the shear layer between the jet fluid that passes through the Mach disk and the windward barrel shock; and the other is due to the velocity difference between the jet fluid that passes through the Mach disk and the ambient crossflow.
${\it\lambda}$
shape. Exiting the orifice, the sonic jet tries to penetrate and expand, and sets up an inclined barrel shock and Mach disk on its periphery. On the windward side of the jet, the shear layer rolls up into vortices which detach from the jet boundary and are shed downstream. Coherent flow structures are observed downstream of the jet after the jet/crossflow interaction. These coherent vortices appear to be the Kelvin–Helmholtz vortices that originate from two shear layers. One is the shear layer between the jet fluid that passes through the Mach disk and the windward barrel shock; and the other is due to the velocity difference between the jet fluid that passes through the Mach disk and the ambient crossflow.
Figure 8 shows the isosurface of the second invariant of the velocity gradient tensor (
![]() $Q$
-criterion) coloured by the streamwise velocity (
$Q$
-criterion) coloured by the streamwise velocity (
![]() $u$
), which visualizes the instantaneous vortical flow features. The flow is highly unsteady, and composed of turbulent eddies of different sizes. Thin longitudinal vortices shed from the jet upstream shear layer are clearly visible. Also observed are hairpin shaped vortices close to the wall downstream of the jet, which are characteristic of turbulent boundary layers. Figure 9(a) shows the side view of the
$u$
), which visualizes the instantaneous vortical flow features. The flow is highly unsteady, and composed of turbulent eddies of different sizes. Thin longitudinal vortices shed from the jet upstream shear layer are clearly visible. Also observed are hairpin shaped vortices close to the wall downstream of the jet, which are characteristic of turbulent boundary layers. Figure 9(a) shows the side view of the
![]() $Q$
-criterion in figure 8, but coloured by temperature. Figure 9(b) is an image from the experiment of New, Lim & Luo (Reference New, Lim and Luo2003), which shows a low speed transverse jet with jet–crossflow velocity ratio
$Q$
-criterion in figure 8, but coloured by temperature. Figure 9(b) is an image from the experiment of New, Lim & Luo (Reference New, Lim and Luo2003), which shows a low speed transverse jet with jet–crossflow velocity ratio
![]() $r=1.0$
. It is interesting to note the qualitative similarity between figures 9(a) and 9(b). It shows that the longitudinal vortices in figure 8 are actually part of the shear layer vortex ‘ring’, which connects the ‘shed’ shear layer vortices in figure 7 with the jet plume.
$r=1.0$
. It is interesting to note the qualitative similarity between figures 9(a) and 9(b). It shows that the longitudinal vortices in figure 8 are actually part of the shear layer vortex ‘ring’, which connects the ‘shed’ shear layer vortices in figure 7 with the jet plume.

Figure 9. (a) Side view of isosurface of
![]() $Q$
-criteria for the sonic jet (
$Q$
-criteria for the sonic jet (
![]() $A3$
) (b) image from the low-speed experiments of New et al. (Reference New, Lim and Luo2003).
$A3$
) (b) image from the low-speed experiments of New et al. (Reference New, Lim and Luo2003).

Figure 10. Isocontours of
![]() $Q$
-criterion coloured by streamwise velocity (
$Q$
-criterion coloured by streamwise velocity (
![]() $u$
) depicting the instantaneous vortical flow features for the supersonic jet (
$u$
) depicting the instantaneous vortical flow features for the supersonic jet (
![]() $B2$
).
$B2$
).
4.1.2. Supersonic jet in subsonic crossflow
Figure 10 shows the isosurface of the
![]() $Q$
-criterion coloured by streamwise velocity (
$Q$
-criterion coloured by streamwise velocity (
![]() $u$
) for the supersonic injection. Coherent roll up of the shear layer is observed. Two trains of shear layer roll up vortices appear to be present, one due to the leading edge jet shear layer and the other due to the downstream shear layer. Also observed are wake vortices which connect the vortices to the jet shear layer vortices which have also been observed at low speed by Fric & Roshko (Reference Fric and Roshko1994) and Smith & Mungal (Reference Smith and Mungal1998), among others. In the near wall region downstream of the jet, the wall vortices are stronger when compared to the turbulent wall vortices away from the jet, possibly owing to the interaction with the wake vortices. Note that the jet plume specified in figure 1 is not observed in our simulations. Instead, we observe leading edge roll up of the jet shear layer resulting in the shedding of discrete vortices, as observed in figure 10.
$u$
) for the supersonic injection. Coherent roll up of the shear layer is observed. Two trains of shear layer roll up vortices appear to be present, one due to the leading edge jet shear layer and the other due to the downstream shear layer. Also observed are wake vortices which connect the vortices to the jet shear layer vortices which have also been observed at low speed by Fric & Roshko (Reference Fric and Roshko1994) and Smith & Mungal (Reference Smith and Mungal1998), among others. In the near wall region downstream of the jet, the wall vortices are stronger when compared to the turbulent wall vortices away from the jet, possibly owing to the interaction with the wake vortices. Note that the jet plume specified in figure 1 is not observed in our simulations. Instead, we observe leading edge roll up of the jet shear layer resulting in the shedding of discrete vortices, as observed in figure 10.

Figure 11. Figure showing (a) instantaneous divergence contours and (b) instantaneous spanwise vorticity contours in the symmetry plane for the supersonic jet (
![]() $B2$
).
$B2$
).
Figure 11 shows the instantaneous divergence contours (a) and spanwise vorticity contours (b) in the symmetry plane. The divergence contours show the shocks produced as the jet exits the nozzle. The vorticity contours show the coherent roll up of the leading edge jet shear layer. Also seen are vortical features corresponding to the shedding near the downstream jet shear layer and near wall vortices. No significant vortical activity is observed near the shocks, which appear confined within the jet. Thus, the effect of shocks on this flow configuration is not as prominent as for sonic jet injection.
Figure 12 shows the instantaneous contours of eddy viscosity normalized by molecular viscosity on the symmetrical plane for sonic injection and supersonic injection, respectively. In DSM, eddy viscosity and eddy conductivity are defined as

Figure 12. Instantaneous distribution of eddy viscosity for (a) sonic injection (
![]() $A3$
) and (b) supersonic injection (
$A3$
) and (b) supersonic injection (
![]() $B2$
).
$B2$
).
4.2. Mean flow features
4.2.1. Sonic jet in supersonic crossflow
Figure 13 shows the 3-D perspective of the mean flow field of the sonic jet in supersonic crossflow; where the central plane shows mean pressure contours, the near-wall horizontal plane shows mean Mach number contours and the streamwise velocity contours are shown on the downstream cross-plane. The in-plane streamlines are superposed on the central- and cross-planes to show the flow patterns and vortical structures. Extremely high pressure regions are observed behind the bow shock, and at the near wall region upstream of the jet, which sets up an adverse gradient near the wall. The adverse pressure gradient causes the crossflow boundary layer to separate, which further induces the separation shock in front of and above the major separation bubble. The crossflow accelerates and expands when it travels around the jet, followed by a decrease in pressure (central plane). The Mach number contour on the horizontal plane shows that, when traveling around the jet, the crossflow accelerates to supersonic speeds even very near the wall. Downstream of the jet, the pressure is extremely low, which induces reverse flow near the wall. The jet expands and accelerates as it exits the nozzle exit and encounters the crossflowing free stream, forming an inclined barrel shock and Mach disk on its periphery. The streamlines show that the jet bends quickly towards the crossflow direction after it passes through the windward side barrel shock and the Mach disk. A source point is observed downstream of the jet on the central plane, which has also been observed in studies of incompressible jets in crossflow (e.g. Muppidi & Mahesh Reference Muppidi and Mahesh2005, Reference Muppidi and Mahesh2008). This originates from the reattachment of the crossflow after it travels around the jet. The streamlines on the downstream cross-plane show the CVP, as well as another counter-rotating vortex pair near the wall. The CVP is perceived as the dominant mean flow structure downstream of the jet.

Figure 13. 3-D perspective of the mean flow field of sonic injection (
![]() $A3$
).
$A3$
).
4.2.2. Supersonic jet in subsonic crossflow
Figure 14 shows the 3-D perspective of the mean flow field of the supersonic jet in subsonic crossflow. The central plane and horizontal plane show Mach number contours, and the cross-plane shows the streamwise velocity contours. Surface streamlines are plotted to show the in-plane fluid motions. Similar to the sonic jet in supersonic crossflow, upstream and downstream recirculation regions are observed, as well as the CVP in the far field. Downstream of the jet, a source point is also observed on the central plane. The Mach number contours on the near-wall horizontal plane show that the subsonic crossflow accelerates to supersonic speeds as it travels around the jet. The central plane shows very different shock structure from the sonic injection case. All the shocks are confined to the jet, and the crossflow appears to be devoid of shocks. As stated in § 4.1, there is no bow shock and separation shock when the crossflow is subsonic. The shapes of the barrel shock and Mach disk are very different from the sonic injection, due to different jet exit condition and jet-to-crossflow momentum flux ratio. There are approximately three discernible jet cells, as indicated in figure 14, which represent alternate regions of expansion and contraction of the jet along its trajectory. Also, the strength of the jet cells decay as the jet evolves. Note that near the first jet contraction region, the downstream fluid appears to be aggressively engulfed, and the streamlines show abrupt turning towards the jet in that region. The downstream streamlines show how the crossflow is entrained by the jet. Immediately downstream of the shock, the streamlines indicate the early stage of the formation of the CVP. The upstream hovering vortex and downstream separation bubble are also observed in this case. However, the sizes of these vortices are very small compared to those in the sonic injection case or the jet diameter.

Figure 14. 3-D perspective of mean flow field of supersonic injection (
![]() $B2$
) superposed by surface and volume streamlines.
$B2$
) superposed by surface and volume streamlines.

Figure 15. Contour of wall skin friction coefficient for the sonic jet in supersonic crossflow (
![]() $A3$
).
$A3$
).

Figure 16. Contour of wall skin friction coefficient for the supersonic jet in subsonic crossflow (
![]() $B2$
).
$B2$
).
4.2.3. Wall skin friction
Figures 15 and 16 show the contours of skin friction coefficients (
![]() $C_{f}$
) on the wall for the sonic and supersonic jet flows, respectively.
$C_{f}$
) on the wall for the sonic and supersonic jet flows, respectively.
![]() $C_{f}$
is calculated from the gradient of near wall tangential velocity component (
$C_{f}$
is calculated from the gradient of near wall tangential velocity component (
![]() $u_{t}$
), i.e.
$u_{t}$
), i.e.
![]() $C_{f}={\it\mu}_{w}(\partial u_{t}/\partial y)|_{w}/{\it\rho}_{\infty }u_{\infty }^{2}$
, where
$C_{f}={\it\mu}_{w}(\partial u_{t}/\partial y)|_{w}/{\it\rho}_{\infty }u_{\infty }^{2}$
, where
![]() ${\it\mu}_{w}$
is the viscosity near the wall. As the boundary layer approaches the jet, the skin friction first decreases because of the separation region in front of the jet. Immediately upstream of the jet the flow is almost stagnant, which results in a region of low skin friction. The supersonic case (figure 16) shows similar behaviour in front of the jet, but has less changes in skin friction than that in the sonic injection case. On the sides of the jet for both cases, extremely high levels of skin friction are observed, which is due to the acceleration of the crossflow bypassing the jet. Downstream of the jets, figures 15 and 16 show very different behaviours. While the
${\it\mu}_{w}$
is the viscosity near the wall. As the boundary layer approaches the jet, the skin friction first decreases because of the separation region in front of the jet. Immediately upstream of the jet the flow is almost stagnant, which results in a region of low skin friction. The supersonic case (figure 16) shows similar behaviour in front of the jet, but has less changes in skin friction than that in the sonic injection case. On the sides of the jet for both cases, extremely high levels of skin friction are observed, which is due to the acceleration of the crossflow bypassing the jet. Downstream of the jets, figures 15 and 16 show very different behaviours. While the
![]() $C_{f}$
contours have a maxima/minima on either side of the symmetry plane for the sonic jet flow, the maxima/minima exist on the symmetry plane for the supersonic jet flow, demonstrating a significant difference in the wake characteristics of the flow. Also, a region of high
$C_{f}$
contours have a maxima/minima on either side of the symmetry plane for the sonic jet flow, the maxima/minima exist on the symmetry plane for the supersonic jet flow, demonstrating a significant difference in the wake characteristics of the flow. Also, a region of high
![]() $C_{f}$
is observed downstream of the jet at
$C_{f}$
is observed downstream of the jet at
![]() $x\approx 4$
for the sonic jet and is absent for the supersonic jet flow.
$x\approx 4$
for the sonic jet and is absent for the supersonic jet flow.
5. Comparison to experiments
5.1. Sonic jet in supersonic crossflow
Figure 17 compares the contours of mean Mach number and streamwise velocity on the central (
![]() $z/D=0$
) plane from the different simulation cases in table 1 to the experimental results. The most obvious difference between the simulation using a laminar crossflow boundary layer (case
$z/D=0$
) plane from the different simulation cases in table 1 to the experimental results. The most obvious difference between the simulation using a laminar crossflow boundary layer (case
![]() $A1$
) and the other simulations (cases
$A1$
) and the other simulations (cases
![]() $A2$
and
$A2$
and
![]() $A3$
) or the experiment is the Mach number distribution within the crossflow boundary layer. Other than this, all of the simulation results are qualitatively similar to the experimental results. Close observation shows that the shape and inclined angle of the barrel shock are better predicted by simulations using a turbulent crossflow boundary layer. Since the boundary layer thickness for both the laminar and turbulent inflows are matched (
$A3$
) or the experiment is the Mach number distribution within the crossflow boundary layer. Other than this, all of the simulation results are qualitatively similar to the experimental results. Close observation shows that the shape and inclined angle of the barrel shock are better predicted by simulations using a turbulent crossflow boundary layer. Since the boundary layer thickness for both the laminar and turbulent inflows are matched (
![]() ${\it\delta}_{99}/D=0.775$
at
${\it\delta}_{99}/D=0.775$
at
![]() $x/D=-5$
), the location of the sonic line would be closer to the wall for the turbulent inflow which could be responsible for the differences in the mean Mach number contours. This trend continues after grid refinement (case
$x/D=-5$
), the location of the sonic line would be closer to the wall for the turbulent inflow which could be responsible for the differences in the mean Mach number contours. This trend continues after grid refinement (case
![]() $A3$
), where both the barrel shock and Mach disk are much better resolved.
$A3$
), where both the barrel shock and Mach disk are much better resolved.

Figure 17. Time-averaged Mach number contours (a,c,e,g) and u velocity contours (b,d,f,h) on the central plane for the sonic jet in supersonic crossflow where, (a,b) case
![]() $A1$
, (c,d) case
$A1$
, (c,d) case
![]() $A2$
, (e,f) case
$A2$
, (e,f) case
![]() $A3$
, (g,h) experiments of Santiago & Dutton (Reference Santiago and Dutton1997).
$A3$
, (g,h) experiments of Santiago & Dutton (Reference Santiago and Dutton1997).
Quantitatively, the streamwise and vertical velocity profiles are extracted at four different downstream locations on the central plane in figure 18. Note that there are more experimental data at
![]() $x/D=3$
and
$x/D=3$
and
![]() $x/D=5$
, which are plotted together to indicate the uncertainty of the experiment. Overall, the simulation results show reasonable agreement with the experimental data, and using turbulent inflow improves the agreement, especially in the far field. Some discrepancies are observed near the wall in the near field of the jet. Santiago & Dutton (Reference Santiago and Dutton1997) note that their resolution in the near wall region is inadequate for this flow, and they do not observe the downstream recirculation region as observed by other studies (e.g. Gruber et al.
Reference Gruber, Nejadt and Chen1995; Everett & Morris Reference Everett and Morris1998). The downstream recirculation shown in figure 17 indicates that at locations
$x/D=5$
, which are plotted together to indicate the uncertainty of the experiment. Overall, the simulation results show reasonable agreement with the experimental data, and using turbulent inflow improves the agreement, especially in the far field. Some discrepancies are observed near the wall in the near field of the jet. Santiago & Dutton (Reference Santiago and Dutton1997) note that their resolution in the near wall region is inadequate for this flow, and they do not observe the downstream recirculation region as observed by other studies (e.g. Gruber et al.
Reference Gruber, Nejadt and Chen1995; Everett & Morris Reference Everett and Morris1998). The downstream recirculation shown in figure 17 indicates that at locations
![]() $x/D=1$
and
$x/D=1$
and
![]() $x/D=2$
the near wall region should have downwash vertical velocity and a relatively smaller mean streamwise velocity, as shown by the velocity profiles in the current simulations. Also, it is expected that the turbulent inflow boundary layer yields higher velocity gradients near the wall. The velocity profiles predicted from the fine grid simulation are close to those from the coarse grid simulation. However, the improvement owing to better grid resolution can be noticed from both the time-averaged quantities (figure 17) and the instantaneous flow field (§ 4.1) where finer vortical structures can only be resolved with better grid resolution. Kawai & Lele (Reference Kawai and Lele2010) observed very similar behaviour when they compared their simulation results with the experiments and during their refinement of the computational mesh. Their simulation results on the finest mesh (27.3 million) with turbulent crossflow boundary layer are shown by the hollow symbols in figure 18, which are very close to the current LES. Note that in the current study, the Reynolds number is approximately
$x/D=2$
the near wall region should have downwash vertical velocity and a relatively smaller mean streamwise velocity, as shown by the velocity profiles in the current simulations. Also, it is expected that the turbulent inflow boundary layer yields higher velocity gradients near the wall. The velocity profiles predicted from the fine grid simulation are close to those from the coarse grid simulation. However, the improvement owing to better grid resolution can be noticed from both the time-averaged quantities (figure 17) and the instantaneous flow field (§ 4.1) where finer vortical structures can only be resolved with better grid resolution. Kawai & Lele (Reference Kawai and Lele2010) observed very similar behaviour when they compared their simulation results with the experiments and during their refinement of the computational mesh. Their simulation results on the finest mesh (27.3 million) with turbulent crossflow boundary layer are shown by the hollow symbols in figure 18, which are very close to the current LES. Note that in the current study, the Reynolds number is approximately
![]() $2.5$
times higher than that used in Kawai & Lele (Reference Kawai and Lele2010).
$2.5$
times higher than that used in Kawai & Lele (Reference Kawai and Lele2010).

Figure 18. Comparisons of (a–d) streamwise and (e–h) wall-normal velocities between simulation and experiment for the sonic jet in supersonic crossflow at jet downstream locations
![]() $x/D=2,3,4,5$
. Solid lines: fine grid simulation (
$x/D=2,3,4,5$
. Solid lines: fine grid simulation (
![]() $A3$
); green dash-dot-dot lines: coarse grid simulation (
$A3$
); green dash-dot-dot lines: coarse grid simulation (
![]() $A2$
); blue dashed lines: simulation using laminar crossflow boundary layer (
$A2$
); blue dashed lines: simulation using laminar crossflow boundary layer (
![]() $A1$
); filled symbols: experiments of Santiago & Dutton (Reference Santiago and Dutton1997); hollow symbols: LES of Kawai & Lele (Reference Kawai and Lele2010).
$A1$
); filled symbols: experiments of Santiago & Dutton (Reference Santiago and Dutton1997); hollow symbols: LES of Kawai & Lele (Reference Kawai and Lele2010).

Figure 19. Comparisons of turbulent intensities for the sonic jet in supersonic crossflow, (a–d)
![]() $\overline{v^{\prime }v^{\prime }}/U_{\infty }^{2}$
and (e–h)
$\overline{v^{\prime }v^{\prime }}/U_{\infty }^{2}$
and (e–h)
![]() $\overline{-u^{\prime }v^{\prime }}/U_{\infty }^{2}$
, between simulation and experiment at jet downstream locations
$\overline{-u^{\prime }v^{\prime }}/U_{\infty }^{2}$
, between simulation and experiment at jet downstream locations
![]() $x/D=2,3,4,5$
. Solid lines: simulation (
$x/D=2,3,4,5$
. Solid lines: simulation (
![]() $A3$
); filled symbols: experiments of Santiago & Dutton (Reference Santiago and Dutton1997); hollow symbols: LES of Kawai & Lele (Reference Kawai and Lele2010).
$A3$
); filled symbols: experiments of Santiago & Dutton (Reference Santiago and Dutton1997); hollow symbols: LES of Kawai & Lele (Reference Kawai and Lele2010).
Figure 19 compares the resolved turbulent intensity profiles between the simulation using a turbulent boundary layer and the experiment. The LES results of Kawai & Lele (Reference Kawai and Lele2010) are plotted at available locations for comparison. Overall, reasonable agreement is observed with the experiment. While the vertical velocity intensities (
![]() $\overline{v^{\prime }v^{\prime }}/U_{\infty }^{2}$
) are overpredicted compared to experiments at
$\overline{v^{\prime }v^{\prime }}/U_{\infty }^{2}$
) are overpredicted compared to experiments at
![]() $x/D=2$
and 3, the same is underpredicted at
$x/D=2$
and 3, the same is underpredicted at
![]() $x/D=5$
. Note that a similar trend is also observed in the computations of Génin & Menon (Reference Génin and Menon2010). The agreement for
$x/D=5$
. Note that a similar trend is also observed in the computations of Génin & Menon (Reference Génin and Menon2010). The agreement for
![]() $\overline{-u^{\prime }v^{\prime }}/U_{\infty }^{2}$
is better except at
$\overline{-u^{\prime }v^{\prime }}/U_{\infty }^{2}$
is better except at
![]() $x/D=5$
. Some of the differences could be attributed to the uncertainties in the experimental measurements, the state of the boundary layer upstream of the jet (which is assumed to be a fully developed turbulent boundary layer in the simulations) and the lower Reynolds number used in the simulations.
$x/D=5$
. Some of the differences could be attributed to the uncertainties in the experimental measurements, the state of the boundary layer upstream of the jet (which is assumed to be a fully developed turbulent boundary layer in the simulations) and the lower Reynolds number used in the simulations.
5.2. Supersonic jet in subsonic crossflow
Figure 20 compares the time-averaged streamwise and vertical velocity fields with the experimental result. The vertical velocity fields predicted by the simulations show very good agreement with the experiment. Using turbulent inflow improves the agreement of
![]() $u$
-velocity with the experiment as compared to laminar inflow. The
$u$
-velocity with the experiment as compared to laminar inflow. The
![]() $u$
-velocity deficit is highest at the location of the jet core while the peak of
$u$
-velocity deficit is highest at the location of the jet core while the peak of
![]() $v$
-velocity marks the height of the CVP which induces the
$v$
-velocity marks the height of the CVP which induces the
![]() $v$
-velocity component on the symmetry plane. Note that the peaks of the
$v$
-velocity component on the symmetry plane. Note that the peaks of the
![]() $u$
-velocity deficit are located higher than those of the
$u$
-velocity deficit are located higher than those of the
![]() $v$
-velocity, because the kidney shaped CVP is below the jet core region.
$v$
-velocity, because the kidney shaped CVP is below the jet core region.

Figure 20. Time-averaged u velocity contour (a,c,e) and
![]() $v$
velocity contour (b,d,f) on central plane for the supersonic jet in subsonic crossflow. (a,b), laminar inflow (
$v$
velocity contour (b,d,f) on central plane for the supersonic jet in subsonic crossflow. (a,b), laminar inflow (
![]() $B1$
); (c,d), experiments of Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
); (e,f), turbulent inflow (
$B1$
); (c,d), experiments of Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
); (e,f), turbulent inflow (
![]() $B2$
).
$B2$
).

Figure 21. Comparisons of (a–e) streamwise velocity and (f–j) wall-normal velocity profiles between simulation and experiments of Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005b
) for the supersonic jet in subsonic crossflow at jet downstream locations
![]() $x/D=21$
, 26.2, 31.5, 36.7, 42.0. lines
$x/D=21$
, 26.2, 31.5, 36.7, 42.0. lines
![]() $=$
simulations (
$=$
simulations (
![]() $B1,B2$
), symbols
$B1,B2$
), symbols
![]() $=$
experiment ((a)
$=$
experiment ((a)
![]() $x/d_{j}=21.0$
, (b)
$x/d_{j}=21.0$
, (b)
![]() $x/d_{j}=26.2$
, (c)
$x/d_{j}=26.2$
, (c)
![]() $x/d_{j}=31.5$
, (d)
$x/d_{j}=31.5$
, (d)
![]() $x/d_{j}=36.7$
, (e)
$x/d_{j}=36.7$
, (e)
![]() $x/d_{j}=42.0$
, (f)
$x/d_{j}=42.0$
, (f)
![]() $x/d_{i}=21.0$
, (g)
$x/d_{i}=21.0$
, (g)
![]() $x/d_{i}=26.2$
, (h)
$x/d_{i}=26.2$
, (h)
![]() $x/d_{i}=31.5$
, (i)
$x/d_{i}=31.5$
, (i)
![]() $x/d_{i}=36.7$
, (j)
$x/d_{i}=36.7$
, (j)
![]() $x/d_{i}=42.0$
).
$x/d_{i}=42.0$
).

Figure 22. Comparisons of Reynolds stress (a–e)
![]() $\overline{v^{\prime }v^{\prime }}/U_{\infty }^{2}$
and (f–j)
$\overline{v^{\prime }v^{\prime }}/U_{\infty }^{2}$
and (f–j)
![]() $\overline{-u^{\prime }v^{\prime }}/U_{\infty }^{2}$
between simulation and experiments of Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005b
) for the supersonic jet in subsonic crossflow at jet downstream locations
$\overline{-u^{\prime }v^{\prime }}/U_{\infty }^{2}$
between simulation and experiments of Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005b
) for the supersonic jet in subsonic crossflow at jet downstream locations
![]() $x/D=21$
, 26.2, 31.5, 36.7, 42.0. lines = simulation case
$x/D=21$
, 26.2, 31.5, 36.7, 42.0. lines = simulation case
![]() $B2$
, symbols
$B2$
, symbols
![]() $=$
experiment ((a)
$=$
experiment ((a)
![]() $x/d_{j}=21.0$
, (b)
$x/d_{j}=21.0$
, (b)
![]() $x/d_{j}=26.2$
, (c)
$x/d_{j}=26.2$
, (c)
![]() $x/d_{j}=31.5$
, (d)
$x/d_{j}=31.5$
, (d)
![]() $x/d_{j}=36.7$
, (e)
$x/d_{j}=36.7$
, (e)
![]() $x/d_{j}=42.0$
, (f)
$x/d_{j}=42.0$
, (f)
![]() $x/d_{i}=21.0$
, (g)
$x/d_{i}=21.0$
, (g)
![]() $x/d_{i}=26.2$
, (h)
$x/d_{i}=26.2$
, (h)
![]() $x/d_{i}=31.5$
, (i)
$x/d_{i}=31.5$
, (i)
![]() $x/d_{i}=36.7$
, (j)
$x/d_{i}=36.7$
, (j)
![]() $x/d_{i}=42.0$
).
$x/d_{i}=42.0$
).

Figure 23. Comparisons of contours of (a) streamline velocity and (b) turbulent kinetic energy on the cross-plane at
![]() $x/D=33.8$
downstream of the jet for the supersonic jet in subsonic crossflow. The in-plane velocity vector fields are superposed on each contour. In each figure, the left half is the experimental result of Beresh et al. (Reference Beresh, Henfling, Erven and Spillers2006), and the right half is from the current LES (
$x/D=33.8$
downstream of the jet for the supersonic jet in subsonic crossflow. The in-plane velocity vector fields are superposed on each contour. In each figure, the left half is the experimental result of Beresh et al. (Reference Beresh, Henfling, Erven and Spillers2006), and the right half is from the current LES (
![]() $B2$
).
$B2$
).
Quantitatively, the mean velocity profiles are extracted at five different locations downstream of the jet, as shown in figure 21. Consistent with figure 20, the peak of the streamwise velocity deficit using laminar inflow spreads wider than the experiment result at each location, which is improved by using turbulent inflow, especially in the far field. In terms of the vertical velocity, the simulation using turbulent inflow shows very good agreement with the experiment, while using laminar inflow overpredicts the trajectory of the jet defined by the location of peak
![]() $v$
. This is reasonable, because the laminar boundary layer has less momentum near the wall, which makes it easier to be penetrated (Muppidi & Mahesh Reference Muppidi and Mahesh2005).
$v$
. This is reasonable, because the laminar boundary layer has less momentum near the wall, which makes it easier to be penetrated (Muppidi & Mahesh Reference Muppidi and Mahesh2005).
Figure 22 shows the intensity profiles at the five downstream locations in figure 21. When compared to the experiment, the agreement is very good. At
![]() $x/D=21.0$
, the simulation overpredicts the turbulent intensities slightly. At
$x/D=21.0$
, the simulation overpredicts the turbulent intensities slightly. At
![]() $x/D=42.0$
near the wall, a locally high level of
$x/D=42.0$
near the wall, a locally high level of
![]() $\overline{v^{\prime }v^{\prime }}$
is observed in the experiment but not in the simulation. Observed from the distribution of
$\overline{v^{\prime }v^{\prime }}$
is observed in the experiment but not in the simulation. Observed from the distribution of
![]() $\overline{v^{\prime }v^{\prime }}$
near the wall at other locations, it is likely that the near-wall
$\overline{v^{\prime }v^{\prime }}$
near the wall at other locations, it is likely that the near-wall
![]() $\overline{v^{\prime }v^{\prime }}$
level decreases along the streamwise direction. Therefore, it does not appear to be physical for this locally high
$\overline{v^{\prime }v^{\prime }}$
level decreases along the streamwise direction. Therefore, it does not appear to be physical for this locally high
![]() $\overline{v^{\prime }v^{\prime }}$
to occur near the wall at
$\overline{v^{\prime }v^{\prime }}$
to occur near the wall at
![]() $x/D=42.0$
. Figures 23(a) and 23(b) compare the mean streamwise velocity and turbulent kinetic energy field with the experiment respectively on the cross-plane at
$x/D=42.0$
. Figures 23(a) and 23(b) compare the mean streamwise velocity and turbulent kinetic energy field with the experiment respectively on the cross-plane at
![]() $x/D=33.8$
. Since the flow is symmetric about the span, only half of the domain is shown in the figure. In-plane velocity vector fields are superposed on each figure to show the CVP. The vector fields and contours both show good agreement with experiment. The observed agreement with experiment for both mean and intensities is very encouraging considering that they are evaluated far downstream (
$x/D=33.8$
. Since the flow is symmetric about the span, only half of the domain is shown in the figure. In-plane velocity vector fields are superposed on each figure to show the CVP. The vector fields and contours both show good agreement with experiment. The observed agreement with experiment for both mean and intensities is very encouraging considering that they are evaluated far downstream (
![]() $x/D>20$
).
$x/D>20$
).
5.2.1. Wall pressure distribution
Figure 24 shows the distribution of the pressure and pressure coefficient
![]() $C_{p}$
for sonic injection (
$C_{p}$
for sonic injection (
![]() $a$
) and supersonic injection (
$a$
) and supersonic injection (
![]() $b$
), respectively, where
$b$
), respectively, where
![]() $C_{p}=(p-p_{\infty })/(({\it\rho}_{\infty }u_{\infty }^{2})/2)$
. The symbols are from the experiments of Everett & Morris (Reference Everett and Morris1998) and Beresh et al. (Reference Beresh, Henfling and Erven2002), respectively. For sonic injection, it is observed that the maximum pressure downstream of the jet is at
$C_{p}=(p-p_{\infty })/(({\it\rho}_{\infty }u_{\infty }^{2})/2)$
. The symbols are from the experiments of Everett & Morris (Reference Everett and Morris1998) and Beresh et al. (Reference Beresh, Henfling and Erven2002), respectively. For sonic injection, it is observed that the maximum pressure downstream of the jet is at
![]() $x/D\approx 4.0$
on the centre line. The supersonic injection does not have similar pressure variation downstream of the jet, as shown in figure 24(b). Overall, reasonable agreement is observed between the experiment and current simulations.
$x/D\approx 4.0$
on the centre line. The supersonic injection does not have similar pressure variation downstream of the jet, as shown in figure 24(b). Overall, reasonable agreement is observed between the experiment and current simulations.

Figure 24. Mean wall pressure distribution along central line: (a) sonic jet (
![]() $A3$
) and (b) supersonic jet (
$A3$
) and (b) supersonic jet (
![]() $B2$
). The symbols are from the experiments of Everett & Morris (Reference Everett and Morris1998) and Beresh et al. (Reference Beresh, Henfling and Erven2002), respectively.
$B2$
). The symbols are from the experiments of Everett & Morris (Reference Everett and Morris1998) and Beresh et al. (Reference Beresh, Henfling and Erven2002), respectively.
6. Jet trajectory
6.1. Comparison with available data
Multiple definitions of jet trajectory exist; e.g. the local velocity maxima (Kamotani & Greber Reference Kamotani and Greber1972; Beresh et al. Reference Beresh, Erven, Henfling and Spillers2005a ) or the local scalar concentration maxima (Gruber et al. Reference Gruber, Nejad, Chen and Dutton1997; Smith & Mungal Reference Smith and Mungal1998; Ben-Yakar et al. Reference Ben-Yakar, Mungal and Hanson2006). However, both concentration and velocity have multiple local maxima (Kamotani & Greber Reference Kamotani and Greber1972; Yuan & Street Reference Yuan and Street1998), which makes the automatic determination of jet trajectory difficult. Similar to Muppidi & Mahesh (Reference Muppidi and Mahesh2005), this paper defines the trajectory as the streamline originating from the centre of the jet exit (centre streamline) on the time-averaged symmetry plane, which describes the path taken by the jet fluid more accurately and is more feasible in simulations.
Table 3. Coefficients for laws of jet trajectory.


Figure 25. Comparison of jet trajectory scaled with
![]() $J$
with available data for sonic (
$J$
with available data for sonic (
![]() $A3$
) and supersonic jet (
$A3$
) and supersonic jet (
![]() $B2$
).
$B2$
).
The trajectories of the high speed jets in crossflow have been investigated by a substantial number of studies, all of which show that the jet-to-crossflow momentum flux ratio,
![]() $J$
, is the dominant parameter that affects the jet trajectories. Generally, past work fits the jet trajectory data using a power law of form
$J$
, is the dominant parameter that affects the jet trajectories. Generally, past work fits the jet trajectory data using a power law of form
or a log law of form
Here,
![]() $a$
,
$a$
,
![]() $b$
and
$b$
and
![]() $c$
are coefficients that yield the best fit of the related experimental data listed in table 3, taken from Mahesh (Reference Mahesh2013), which shows the scatter in the values of these coefficients from different studies. Figure 25 shows the jet trajectories in the current simulations, where the
$c$
are coefficients that yield the best fit of the related experimental data listed in table 3, taken from Mahesh (Reference Mahesh2013), which shows the scatter in the values of these coefficients from different studies. Figure 25 shows the jet trajectories in the current simulations, where the
![]() $x$
and
$x$
and
![]() $y$
coordinates are normalized by
$y$
coordinates are normalized by
![]() $JD$
. The experimental data of Gruber et al. (Reference Gruber, Nejad, Chen and Dutton1997) and the empirical correlations from the studies of Rothstein & Wantuck (Reference Rothstein and Wantuck1992) and McDaniel & Graves (Reference McDaniel and Graves1986) are plotted together for comparison. It appears that the jet trajectory in the current simulation of sonic jet in supersonic crossflow agrees the best with the experiments of Gruber et al. (Reference Gruber, Nejad, Chen and Dutton1997). Given the scatter in the coefficients, it is not surprising to see in figure 25 that the
$JD$
. The experimental data of Gruber et al. (Reference Gruber, Nejad, Chen and Dutton1997) and the empirical correlations from the studies of Rothstein & Wantuck (Reference Rothstein and Wantuck1992) and McDaniel & Graves (Reference McDaniel and Graves1986) are plotted together for comparison. It appears that the jet trajectory in the current simulation of sonic jet in supersonic crossflow agrees the best with the experiments of Gruber et al. (Reference Gruber, Nejad, Chen and Dutton1997). Given the scatter in the coefficients, it is not surprising to see in figure 25 that the
![]() $JD$
scaling does not collapse various experimental and simulation data, and the jet trajectories under different flow conditions differ significantly from each other. Also, changing the scaling law to the widely used relation in incompressible flows (e.g.
$JD$
scaling does not collapse various experimental and simulation data, and the jet trajectories under different flow conditions differ significantly from each other. Also, changing the scaling law to the widely used relation in incompressible flows (e.g.
![]() $\sqrt{J}D$
) increases this scatter (not shown).
$\sqrt{J}D$
) increases this scatter (not shown).

Figure 26. Figure showing: (a) trajectories of supersonic transverse jet (
![]() $B2$
) by different definitions: solid: centre streamline; dash-dot-dot: maximum loci of streamwise velocity deficit; dashed: maximum loci of vertical velocity. Symbols are experimental data from Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
). (b) Comparison of jet trajectory for the supersonic jet (
$B2$
) by different definitions: solid: centre streamline; dash-dot-dot: maximum loci of streamwise velocity deficit; dashed: maximum loci of vertical velocity. Symbols are experimental data from Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
). (b) Comparison of jet trajectory for the supersonic jet (
![]() $B2$
) with Papamoschou & Hubbard (Reference Papamoschou and Hubbard1993).
$B2$
) with Papamoschou & Hubbard (Reference Papamoschou and Hubbard1993).
The trajectories in the far field of Mach
![]() $3.7$
supersonic injection has also been studied by Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
), where they defined the jet trajectories using the loci of maximum streamwise velocity deficit and vertical velocity, which are shown as the symbols
$3.7$
supersonic injection has also been studied by Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
), where they defined the jet trajectories using the loci of maximum streamwise velocity deficit and vertical velocity, which are shown as the symbols
![]() $\Box$
and ♢ respectively in figure 26(a). The curves therein correspond to trajectories calculated from the current simulation. It is shown that the trajectory defined by the loci of the maximum streamwise velocity deficit is higher than that defined by the loci of maximum vertical velocity, while both definitions yield lower jet trajectories than the definition based on the centre streamline. The agreement between the current simulation and the experiment is very good for both definitions of trajectories used in Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
). Figure 26(b) compares jet trajectory from the supersonic jet simulation with the experimental results of Papamoschou & Hubbard (Reference Papamoschou and Hubbard1993), where the momentum flux ratio is 8.9, jet Mach number varies between 1 and 4.3 and the free-stream Mach number (
$\Box$
and ♢ respectively in figure 26(a). The curves therein correspond to trajectories calculated from the current simulation. It is shown that the trajectory defined by the loci of the maximum streamwise velocity deficit is higher than that defined by the loci of maximum vertical velocity, while both definitions yield lower jet trajectories than the definition based on the centre streamline. The agreement between the current simulation and the experiment is very good for both definitions of trajectories used in Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
). Figure 26(b) compares jet trajectory from the supersonic jet simulation with the experimental results of Papamoschou & Hubbard (Reference Papamoschou and Hubbard1993), where the momentum flux ratio is 8.9, jet Mach number varies between 1 and 4.3 and the free-stream Mach number (
![]() $M_{\infty }$
) is 2 and 3. Both the crossflow and the jet have very different flow conditions, but the trajectories are close to each other, which indicates that the jet-to-crossflow momentum flux ratio
$M_{\infty }$
) is 2 and 3. Both the crossflow and the jet have very different flow conditions, but the trajectories are close to each other, which indicates that the jet-to-crossflow momentum flux ratio
![]() $J$
is the dominant parameter that determines the jet penetration. Papamoschou & Hubbard (Reference Papamoschou and Hubbard1993) found that increasing the crossflow Mach number produces an increase in the jet penetration. This is due to the stronger bow shock produced by the supersonic crossflow which reduces the streamwise velocity and increases vertical velocity of the crossflow downstream of the shock, allowing a higher penetration of the jet. Thus, the jet penetration is lower in our simulation due to a subsonic crossflow.
$J$
is the dominant parameter that determines the jet penetration. Papamoschou & Hubbard (Reference Papamoschou and Hubbard1993) found that increasing the crossflow Mach number produces an increase in the jet penetration. This is due to the stronger bow shock produced by the supersonic crossflow which reduces the streamwise velocity and increases vertical velocity of the crossflow downstream of the shock, allowing a higher penetration of the jet. Thus, the jet penetration is lower in our simulation due to a subsonic crossflow.
6.2. Prediction of jet trajectory using a modified Schetz & Billig (Reference Schetz and Billig1966) theory
Schetz & Billig (Reference Schetz and Billig1966) analysed the force balance of a jet segment along the jet normal and axial directions for a sonic jet in a supersonic crossflow (
![]() $M_{\infty }=2.1$
–2.7) at
$M_{\infty }=2.1$
–2.7) at
![]() $J=4.75$
–10, and derived a differential equation that can be used to predict the jet trajectory:
$J=4.75$
–10, and derived a differential equation that can be used to predict the jet trajectory:
where
![]() $\bar{s}=s/d$
, and
$\bar{s}=s/d$
, and
![]() $C_{D}$
is a drag coefficient determined by
$C_{D}$
is a drag coefficient determined by
The jet trajectory can be obtained by integrating (6.3) from
![]() ${\rm\pi}/2$
to
${\rm\pi}/2$
to
![]() $0$
. Schetz & Billig (Reference Schetz and Billig1966) further assume that
$0$
. Schetz & Billig (Reference Schetz and Billig1966) further assume that
![]() ${\it\rho}$
does not change along the jet, i.e.
${\it\rho}$
does not change along the jet, i.e.
![]() ${\it\rho}\equiv {\it\rho}_{j}$
. Finally, the trajectory derived from (6.3) is applied after the Mach disk, before which the jet is assumed to be a vertical straight line. Schetz & Billig (Reference Schetz and Billig1966)’s method was applied to low speed jets in crossflow and compared to the experiments of Abramovich (Reference Abramovich1963). The agreement was good for the case with
${\it\rho}\equiv {\it\rho}_{j}$
. Finally, the trajectory derived from (6.3) is applied after the Mach disk, before which the jet is assumed to be a vertical straight line. Schetz & Billig (Reference Schetz and Billig1966)’s method was applied to low speed jets in crossflow and compared to the experiments of Abramovich (Reference Abramovich1963). The agreement was good for the case with
![]() $J=4.75$
, while a relatively big discrepancy was observed when
$J=4.75$
, while a relatively big discrepancy was observed when
![]() $J=16.35$
. In the present study, we apply (6.3) after the intersection of the centre streamline and windward barrel shock since the jet deviates from the vertical direction rapidly only after this intersection. Figure 27(a) shows that the jet trajectory for the sonic jet from Schetz & Billig (Reference Schetz and Billig1966)’s theory, underpredicts the jet penetration. While the assumption of
$J=16.35$
. In the present study, we apply (6.3) after the intersection of the centre streamline and windward barrel shock since the jet deviates from the vertical direction rapidly only after this intersection. Figure 27(a) shows that the jet trajectory for the sonic jet from Schetz & Billig (Reference Schetz and Billig1966)’s theory, underpredicts the jet penetration. While the assumption of
![]() ${\it\rho}\equiv {\it\rho}_{j}$
along the jet maybe good enough for low speed jets in crossflow, it is not true for high speed transverse jets (dashed line in figure 27
a). Therefore, the density variation along the jet must be taken into account.
${\it\rho}\equiv {\it\rho}_{j}$
along the jet maybe good enough for low speed jets in crossflow, it is not true for high speed transverse jets (dashed line in figure 27
a). Therefore, the density variation along the jet must be taken into account.

Figure 27. Prediction of jet trajectory using modified theory of Schetz & Billig (Reference Schetz and Billig1966). For sonic jet (
![]() $a,A3$
) and supersonic jet (
$a,A3$
) and supersonic jet (
![]() $b,B2$
).
$b,B2$
).
The trajectory of transverse jets depend largely on the momentum flux ratio, (
![]() $J$
). At low speeds, the trajectories can depend not just on
$J$
). At low speeds, the trajectories can depend not just on
![]() $J$
but also on the velocity profile of the jet and the boundary layer thickness (Muppidi & Mahesh Reference Muppidi and Mahesh2005). At high speeds, the jet is typically unadapted and its exit state can be significantly different from that inside the nozzle. Similarly, the crossflow can be significantly modified by features like the bow shock before interacting with the jet. As a result, the local values of
$J$
but also on the velocity profile of the jet and the boundary layer thickness (Muppidi & Mahesh Reference Muppidi and Mahesh2005). At high speeds, the jet is typically unadapted and its exit state can be significantly different from that inside the nozzle. Similarly, the crossflow can be significantly modified by features like the bow shock before interacting with the jet. As a result, the local values of
![]() $J$
for high speed transverse jets can be significantly different from estimations based on the flow inside the nozzle and the free stream. If these changes can be approximated, then conventional scaling laws might still be reasonable. We define an effective density ratio:
$J$
for high speed transverse jets can be significantly different from estimations based on the flow inside the nozzle and the free stream. If these changes can be approximated, then conventional scaling laws might still be reasonable. We define an effective density ratio:
![]() $({\it\rho}/{\it\rho}_{j})^{eff}={\it\rho}_{f}/{\it\rho}_{b}$
. Here,
$({\it\rho}/{\it\rho}_{j})^{eff}={\it\rho}_{f}/{\it\rho}_{b}$
. Here,
![]() ${\it\rho}_{b}$
is the density of the jet immediately behind the barrel shock, which is the effective jet exit where the jet actually sees the crossflow; and
${\it\rho}_{b}$
is the density of the jet immediately behind the barrel shock, which is the effective jet exit where the jet actually sees the crossflow; and
![]() ${\it\rho}_{f}$
is the average density far downstream of the jet. The jet density variation in figure 27 shows that
${\it\rho}_{f}$
is the average density far downstream of the jet. The jet density variation in figure 27 shows that
![]() ${\it\rho}_{b}\approx 1.6$
and
${\it\rho}_{b}\approx 1.6$
and
![]() ${\it\rho}_{f}\approx 0.8$
, which results in
${\it\rho}_{f}\approx 0.8$
, which results in
![]() $({\it\rho}/{\it\rho}_{j})^{eff}\approx 0.5$
. Using this effective density ratio, (6.3) predicts the trajectory marked by dash-dotted curve in figure 27(b), which is much closer to the simulation result. Further, we note that after interaction with the barrel shock, the centre streamline turns suddenly by approximately
$({\it\rho}/{\it\rho}_{j})^{eff}\approx 0.5$
. Using this effective density ratio, (6.3) predicts the trajectory marked by dash-dotted curve in figure 27(b), which is much closer to the simulation result. Further, we note that after interaction with the barrel shock, the centre streamline turns suddenly by approximately
![]() $10^{\circ }$
(top right insert in figure 27
b). Therefore, (6.3) should be integrated from
$10^{\circ }$
(top right insert in figure 27
b). Therefore, (6.3) should be integrated from
![]() $80^{\circ }$
instead of
$80^{\circ }$
instead of
![]() $90^{\circ }$
. This yields the long-dashed curve in figure 27(b), which shows very good agreement with the current LES result, especially in the near field.
$90^{\circ }$
. This yields the long-dashed curve in figure 27(b), which shows very good agreement with the current LES result, especially in the near field.
We apply the same methodology to the supersonic injection and the predicted trajectory by the proposed modification to Schetz’s method is shown in figure 27(b). In this case,
![]() ${\it\rho}_{b}\approx 3.6$
and
${\it\rho}_{b}\approx 3.6$
and
![]() ${\it\rho}_{f}\approx 1$
, which results in
${\it\rho}_{f}\approx 1$
, which results in
![]() $({\it\rho}/{\it\rho}_{j})^{eff}\approx 0.2778$
; and the integration of (6.3) starts from
$({\it\rho}/{\it\rho}_{j})^{eff}\approx 0.2778$
; and the integration of (6.3) starts from
![]() $90^{\circ }$
based on the observation that the streamline turns by a negligible angle after the barrel shock, which turns back when entering the second jet cell. The agreement is very good up to
$90^{\circ }$
based on the observation that the streamline turns by a negligible angle after the barrel shock, which turns back when entering the second jet cell. The agreement is very good up to
![]() $x/D=6$
. It is encouraging that the modified Schetz’s analysis can accurately yield the trajectory of the transverse jet in the near field, though it is based on a number of assumptions (Schetz & Billig Reference Schetz and Billig1966) and requires the knowledge of density behind the barrel shock which is obtained a posteriori from the simulations.
$x/D=6$
. It is encouraging that the modified Schetz’s analysis can accurately yield the trajectory of the transverse jet in the near field, though it is based on a number of assumptions (Schetz & Billig Reference Schetz and Billig1966) and requires the knowledge of density behind the barrel shock which is obtained a posteriori from the simulations.
7. Temporal spectra
Probes were placed at various different locations in the flow and frequency spectra of pressure, velocity and density were obtained. The frequency is non-dimensionalized with
![]() $u_{\infty }$
and
$u_{\infty }$
and
![]() $D$
, to yield a Strouhal number,
$D$
, to yield a Strouhal number,
![]() $St=fD/u_{\infty }$
. A global length scale (
$St=fD/u_{\infty }$
. A global length scale (
![]() $D$
) is chosen as opposed to a local length scale since the probes were placed at various different flow features such as shocks, shear layer and boundary layer to see if the same frequency is excited in different regions of the flow.
$D$
) is chosen as opposed to a local length scale since the probes were placed at various different flow features such as shocks, shear layer and boundary layer to see if the same frequency is excited in different regions of the flow.
7.1. Sonic jet

Figure 28. Figure showing temporal spectra taken at various locations in the flowfield as indicated in the figure for the sonic jet in supersonic crossflow (
![]() $A3$
). Mean temperature contours are shown in the symmetry and wall-parallel planes.
$A3$
). Mean temperature contours are shown in the symmetry and wall-parallel planes.
Figure 28 shows the temporal spectra of pressure, vertical velocity (
![]() $v$
) and density (
$v$
) and density (
![]() ${\it\rho}$
) at various locations in the flow along with the temperature contours in the symmetry plane and a near wall plane depicting the exact locations at which the spectra are reported. In the upstream bow shock region, the pressure spectra indicate that
${\it\rho}$
) at various locations in the flow along with the temperature contours in the symmetry plane and a near wall plane depicting the exact locations at which the spectra are reported. In the upstream bow shock region, the pressure spectra indicate that
![]() $St=0.2$
–0.3 is dominant, with the
$St=0.2$
–0.3 is dominant, with the
![]() $St$
decreasing with increasing distance from the jet. The vertical velocity spectra at the barrel shock and upstream shear layer also show a peak at
$St$
decreasing with increasing distance from the jet. The vertical velocity spectra at the barrel shock and upstream shear layer also show a peak at
![]() $St=0.3$
. In the Mach disk region, peaks at
$St=0.3$
. In the Mach disk region, peaks at
![]() $St=0.1$
–0.4 are observed.
$St=0.1$
–0.4 are observed.
Downstream of the jet, along the jet trajectory, we again observe a dominant frequency of
![]() $St=0.3$
. In the near wall region, the pressure spectra show that the flow is broadband without any clear peak, due to the location of the probe being within the turbulent boundary layer. Overall, it can be seen that at different regions upstream and downstream of the jet, an
$St=0.3$
. In the near wall region, the pressure spectra show that the flow is broadband without any clear peak, due to the location of the probe being within the turbulent boundary layer. Overall, it can be seen that at different regions upstream and downstream of the jet, an
![]() $St=0.3$
mode is dominant suggesting that the flow system oscillates with a single global frequency. To better understand the spatial flow features that oscillate with this dominant
$St=0.3$
mode is dominant suggesting that the flow system oscillates with a single global frequency. To better understand the spatial flow features that oscillate with this dominant
![]() $St=0.3$
, and to see if this frequency is globally dominant, we perform dynamic mode decomposition of the pressure field in the following section.
$St=0.3$
, and to see if this frequency is globally dominant, we perform dynamic mode decomposition of the pressure field in the following section.
7.2. Supersonic jet
Figure 29 shows the pressure and
![]() $w$
velocity spectra at various different locations, as indicated in the figure. Along the leading edge shear layer,
$w$
velocity spectra at various different locations, as indicated in the figure. Along the leading edge shear layer,
![]() $St=1$
is observed to be dominant. This frequency corresponds to the leading edge shear layer roll up and extends to large distances from the jet exit along the leading edge jet shear layer. Further along the trajectory, it can be seen that the flow becomes more broadband as the coherent shear layer vortices observed in figure 10 break down into finer scales and become more turbulent. In the region between the jet and the wall, downstream of the jet,
$St=1$
is observed to be dominant. This frequency corresponds to the leading edge shear layer roll up and extends to large distances from the jet exit along the leading edge jet shear layer. Further along the trajectory, it can be seen that the flow becomes more broadband as the coherent shear layer vortices observed in figure 10 break down into finer scales and become more turbulent. In the region between the jet and the wall, downstream of the jet,
![]() $w$
velocity spectra show a peak at
$w$
velocity spectra show a peak at
![]() $St=0.3$
, which could correspond to the trailing vortices seen in figure 10.
$St=0.3$
, which could correspond to the trailing vortices seen in figure 10.

Figure 29. Figure showing temporal spectra taken at various locations in the flowfield as indicated in the figure for the supersonic jet in subsonic crossflow (
![]() $B2$
). Mean temperature contours are shown in the symmetry and wall-parallel planes.
$B2$
). Mean temperature contours are shown in the symmetry and wall-parallel planes.
Downstream of the jet in the near wall region, the spectra appears broadband suggesting that the turbulent boundary layer is not significantly altered by the jet interaction. Pressure spectra at the trailing edge of the jet show a dominant frequency of
![]() $St=30$
, although, the unsteadiness is orders of magnitude smaller than that observed in the leading edge shear layer. However, no trace of this frequency is seen elsewhere in the flow. Overall, it can be observed that the flow does not oscillate with a single global frequency like the sonic jet flow. A dominant
$St=30$
, although, the unsteadiness is orders of magnitude smaller than that observed in the leading edge shear layer. However, no trace of this frequency is seen elsewhere in the flow. Overall, it can be observed that the flow does not oscillate with a single global frequency like the sonic jet flow. A dominant
![]() $St=1$
is observed along the leading edge of the jet shear layer. Note that no data of the spectra is available from the experimental studies of Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
,Reference Beresh, Erven, Henfling and Spillers
b
).
$St=1$
is observed along the leading edge of the jet shear layer. Note that no data of the spectra is available from the experimental studies of Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a
,Reference Beresh, Erven, Henfling and Spillers
b
).
8. Dynamic mode decomposition
We perform dynamic mode decomposition (also referred to as Koopman mode decomposition) of the three-dimensional pressure field. We store snapshots of the pressure field at each spatial location to perform the decomposition which identifies the dominant frequencies in the entire flowfield along with the corresponding spatial modes for each frequency. Rowley et al. (Reference Rowley, Mezic, Bagheri, Schlatter and Henningson2009) and Schmid (Reference Schmid2010) discuss theoretical and implementation details of the decomposition. The algorithm was validated for the flow past a cylinder at
![]() $Re=60$
, 100 and 200, where the frequency of the most energetic mode shows very good agreement with the frequency obtained from the variation of drag on the cylinder.
$Re=60$
, 100 and 200, where the frequency of the most energetic mode shows very good agreement with the frequency obtained from the variation of drag on the cylinder.
The DMD analysis provides insight into the frequencies that are globally dominant in the entire flowfield (as opposed to a few locations given by temporal spectra) and whether or not a global oscillation is present in the flowfield. For each dominant frequency, the corresponding spatial mode yields the regions in the flow which are oscillating at that frequency. This information is not obtained from temporal spectra at a few probe points.
8.1. DMD of sonic jet

Figure 30. Figure showing results from the dynamic mode decomposition of the pressure field for the sonic jet in supersonic crossflow: (a) energy variation with Strouhal number (
![]() $St=fD/u_{\infty }$
), (b) isocontour of pressure of the most dominant mode, (c–d) symmetry plane pressure and spanwise vorticity contour of the most dominant mode.
$St=fD/u_{\infty }$
), (b) isocontour of pressure of the most dominant mode, (c–d) symmetry plane pressure and spanwise vorticity contour of the most dominant mode.
DMD of the entire three-dimensional pressure field was performed using 124 snapshots with a temporal spacing of
![]() ${\rm\Delta}t=0.1D/u_{\infty }$
. Figure 30(a) shows the variation of energy with
${\rm\Delta}t=0.1D/u_{\infty }$
. Figure 30(a) shows the variation of energy with
![]() $St$
and it is observed that
$St$
and it is observed that
![]() $St=0.3$
mode has the highest energy, indicating that the mode is global in nature. This is consistent with the observations of point spectra of pressure in § 7, where
$St=0.3$
mode has the highest energy, indicating that the mode is global in nature. This is consistent with the observations of point spectra of pressure in § 7, where
![]() $St=0.3$
was dominant at various different regions of the flowfield. Isocontours of pressure of the
$St=0.3$
was dominant at various different regions of the flowfield. Isocontours of pressure of the
![]() $St=0.3$
DMD mode are shown in figure 30(b), where regions of positive and negative pressure are shown. It can be seen that the
$St=0.3$
DMD mode are shown in figure 30(b), where regions of positive and negative pressure are shown. It can be seen that the
![]() $St=0.3$
mode is most dominant in the region upstream of the barrel shock. To better understand the dominant
$St=0.3$
mode is most dominant in the region upstream of the barrel shock. To better understand the dominant
![]() $St=0.3$
mode, symmetry plane contours of the pressure field are shown in figure 30(c). The pressure contour shows that the mode extends from the barrel shock region up to the bow shock upstream of the jet. This is consistent with the observations of Kawai & Lele (Reference Kawai and Lele2010) who show that an acoustic wave is generated at the barrel shock which travels upstream and interacts with the bow shock, giving rise to unsteady oscillations. The pressure contours also indicate significant contribution from the coherent vortices downstream of the jet. Animation (not shown) of figure 7 shows highly coherent vortices being shed as the barrel shock oscillates. This behaviour is unique to the sonic jet and is not observed for the supersonic case. The combination of barrel shock oscillation and coherent vortical shedding manifests as a global mode.
$St=0.3$
mode, symmetry plane contours of the pressure field are shown in figure 30(c). The pressure contour shows that the mode extends from the barrel shock region up to the bow shock upstream of the jet. This is consistent with the observations of Kawai & Lele (Reference Kawai and Lele2010) who show that an acoustic wave is generated at the barrel shock which travels upstream and interacts with the bow shock, giving rise to unsteady oscillations. The pressure contours also indicate significant contribution from the coherent vortices downstream of the jet. Animation (not shown) of figure 7 shows highly coherent vortices being shed as the barrel shock oscillates. This behaviour is unique to the sonic jet and is not observed for the supersonic case. The combination of barrel shock oscillation and coherent vortical shedding manifests as a global mode.
Based on the results from the DMD of the pressure field, the velocity field is reconstructed for the
![]() $St=0.3$
mode and the spanwise vorticity in the symmetry plane is shown in figure 30(d). It can be seen that vortices are shed both upstream and downstream of the jet, as also seen in figure 7. The upstream jet shear layer contains vorticity from the jet boundary layer which is shed into discrete vortices due to the unsteady perturbation from the barrel shock. The upstream shedding takes place immediately at the jet exit, while the downstream shedding takes place further downstream of the jet. The downstream shear layer of the jet appears to shed at the intersection of the shear layer with the Mach disk. Due to the large scale oscillation of the barrel shock, the Mach disk also oscillates with the same frequency, causing the downstream shear layer to shed at the same frequency. This coupling between the oscillation of the shocks with the shear layer shedding makes high-speed jets in crossflow different from low-speed roll up of the shear layer, although it is interesting to note the similarity in vortical features between low and high-speed flows in figure 9.
$St=0.3$
mode and the spanwise vorticity in the symmetry plane is shown in figure 30(d). It can be seen that vortices are shed both upstream and downstream of the jet, as also seen in figure 7. The upstream jet shear layer contains vorticity from the jet boundary layer which is shed into discrete vortices due to the unsteady perturbation from the barrel shock. The upstream shedding takes place immediately at the jet exit, while the downstream shedding takes place further downstream of the jet. The downstream shear layer of the jet appears to shed at the intersection of the shear layer with the Mach disk. Due to the large scale oscillation of the barrel shock, the Mach disk also oscillates with the same frequency, causing the downstream shear layer to shed at the same frequency. This coupling between the oscillation of the shocks with the shear layer shedding makes high-speed jets in crossflow different from low-speed roll up of the shear layer, although it is interesting to note the similarity in vortical features between low and high-speed flows in figure 9.

Figure 31. Figure showing instantaneous spanwise vorticity contours (a) and mean turbulent kinetic energy (TKE) (b) in the symmetry plane from the simulation.
Figure 31(a) shows the instantaneous spanwise vorticity contours from the simulation. The shedding of vortices is clearly seen in the figure. Coherent vortex roll up of positive spanwise vorticity is seen which is shed from the upstream (windward) shear layer. Vortices are also observed emanating from the interaction of the downstream shear layer with the Mach disk. Figure 31(b) shows contours of the resolved turbulent kinetic energy (TKE) to depict the regions of maximum unsteadiness in the flow. It can be seen that TKE is highest upstream of the jet, and in two regions downstream of the jet. The upstream and the top-downstream region correspond to the locations at which vortices are shed. The high TKE region downstream of the jet located closer to the wall corresponds to an unsteady shear layer which periodically sheds vortices and interacts with the wall vortices as seen from the animation of figure 7.

Figure 32. Figure showing results from the dynamic mode decomposition of the pressure field for the supersonic jet in subsonic crossflow: (a) energy variation with Strouhal number (
![]() $St=fD/u_{\infty }$
), (b) isocontour of pressure of the
$St=fD/u_{\infty }$
), (b) isocontour of pressure of the
![]() $St=1$
shear layer mode, (c,d) symmetry plane pressure and spanwise vorticity contour of the
$St=1$
shear layer mode, (c,d) symmetry plane pressure and spanwise vorticity contour of the
![]() $St=1$
shear-layer mode.
$St=1$
shear-layer mode.
8.2. DMD of supersonic jet
DMD of the entire three-dimensional pressure field was performed using 150 snapshots with a temporal spacing of
![]() ${\rm\Delta}t=0.1D/u_{\infty }$
. Figure 32(a) shows the variation of energy with
${\rm\Delta}t=0.1D/u_{\infty }$
. Figure 32(a) shows the variation of energy with
![]() $St$
and it is observed that multiple frequencies are dominant without a single peak as observed for the sonic jet. This is consistent with the observations of point spectra in § 7 where different frequencies were dominant in different regions of the flowfield. Probes placed along the upstream shear layer showed that
$St$
and it is observed that multiple frequencies are dominant without a single peak as observed for the sonic jet. This is consistent with the observations of point spectra in § 7 where different frequencies were dominant in different regions of the flowfield. Probes placed along the upstream shear layer showed that
![]() $St=1$
mode was dominant. A local peak in the energy in figure 32(a) is also observed at
$St=1$
mode was dominant. A local peak in the energy in figure 32(a) is also observed at
![]() $St=1$
. Isocontours of pressure of the
$St=1$
. Isocontours of pressure of the
![]() $St=1$
DMD mode are shown in figure 32(b). Coherent shear layer roll up is observed similar to a low speed flow. Symmetry plane pressure contours of the
$St=1$
DMD mode are shown in figure 32(b). Coherent shear layer roll up is observed similar to a low speed flow. Symmetry plane pressure contours of the
![]() $St=1$
DMD mode are shown in figure 32(c). It can be observed that the pressure unsteadiness occurs in the upstream shear layer and in the wake of the jet. It is interesting to note that the pressure unsteadiness is dominant in the upstream shear layer roll up region and not in the region of shocks indicating that the shocks do not have a significant impact on the shedding for this flow. This is in contrast to the sonic jet flow where the shock-induced unsteadiness affects the shear layer shedding. Spanwise vorticity contours of the
$St=1$
DMD mode are shown in figure 32(c). It can be observed that the pressure unsteadiness occurs in the upstream shear layer and in the wake of the jet. It is interesting to note that the pressure unsteadiness is dominant in the upstream shear layer roll up region and not in the region of shocks indicating that the shocks do not have a significant impact on the shedding for this flow. This is in contrast to the sonic jet flow where the shock-induced unsteadiness affects the shear layer shedding. Spanwise vorticity contours of the
![]() $St=1$
mode in figure 32(d) show that it is dominant in the upstream and downstream shear layers, and in the wake of the jet giving rise to trailing vortices.
$St=1$
mode in figure 32(d) show that it is dominant in the upstream and downstream shear layers, and in the wake of the jet giving rise to trailing vortices.

Figure 33. Figure showing results from the dynamic mode decomposition of the pressure field for the supersonic jet in subsonic crossflow: (a) isocontour of pressure of the
![]() $St=0.43$
mode and (b) symmetry plane spanwise vorticity contour of the
$St=0.43$
mode and (b) symmetry plane spanwise vorticity contour of the
![]() $St=0.43$
mode.
$St=0.43$
mode.
Figure 32(a) showed that multiple frequencies were dominant for this flow. Hence, we also examine the
![]() $St=0.43$
mode (figure 33
a) which has a local peak and higher energy than the
$St=0.43$
mode (figure 33
a) which has a local peak and higher energy than the
![]() $St=1$
mode. This mode appears to be dominant downstream of the jet and further along the jet trajectory when compared to the
$St=1$
mode. This mode appears to be dominant downstream of the jet and further along the jet trajectory when compared to the
![]() $St=1$
mode. From figure 10, two trains of shear layer vortices were observed corresponding to the roll up of the upstream and downstream shear layers. Symmetry plane contours of the
$St=1$
mode. From figure 10, two trains of shear layer vortices were observed corresponding to the roll up of the upstream and downstream shear layers. Symmetry plane contours of the
![]() $St=0.43$
mode show that it is initially dominant in the downstream shear layer and also interacts with the wall vortices. The pressure isocontour in figure 33(a) shows that, closer to the jet, the vortices extend all the way up to the wall. Such behaviour is reminiscent of low-speed transverse jets. This difference in the dynamics of the near-field wake reflects in the differences in mean
$St=0.43$
mode show that it is initially dominant in the downstream shear layer and also interacts with the wall vortices. The pressure isocontour in figure 33(a) shows that, closer to the jet, the vortices extend all the way up to the wall. Such behaviour is reminiscent of low-speed transverse jets. This difference in the dynamics of the near-field wake reflects in the differences in mean
![]() $C_{f}$
observed in § 4.2.3.
$C_{f}$
observed in § 4.2.3.
Results from temporal spectra and DMD reveal that a global oscillation was present for the sonic jet case and absent for the supersonic jet case. The spatial DMD mode corresponding to the global frequency of
![]() $St=0.3$
shows that the maximum oscillation in the pressure lies in the region between the bow shock and the barrel shock (figure 30
b,c) and is caused by the oscillation of the barrel shock (which is confirmed from animations of the instantaneous density gradient contours in figure 7). Also, the spatial vorticity DMD mode corresponding to
$St=0.3$
shows that the maximum oscillation in the pressure lies in the region between the bow shock and the barrel shock (figure 30
b,c) and is caused by the oscillation of the barrel shock (which is confirmed from animations of the instantaneous density gradient contours in figure 7). Also, the spatial vorticity DMD mode corresponding to
![]() $St=0.3$
shows that coherent vortex shedding occurs at the same frequency for the sonic jet. However, for the supersonic jet case, due to the subsonic nature of the crossflow boundary layer, both the bow shock upstream of the jet and the barrel shock are absent. The subsonic nature of the crossflow for the supersonic jet case allows it to adjust to the presence of the oncoming jet due to the propagation of information in the direction opposite to the crossflow, thus preventing the formation of strong shocks close to the leading edge of the jet exit. Thus, no global oscillation is observed for the supersonic jet in subsonic crossflow. Instead, a leading edge shear layer roll up occurs for the supersonic jet as observed from the spatial DMD flowfield in figure 32(b). Barrel shock oscillation modifies the axial pressure gradient experienced by the nozzle boundary layer at the leading edge of the nozzle. The adverse pressure gradient increases as the barrel shock moves closer and decreases as it moves away. The away motion of the barrel shock impulsively accelerates fluid at the leading edge of the nozzle resulting in coherent shedding. The supersonic jet case has no barrel shock and hence does not display this behaviour.
$St=0.3$
shows that coherent vortex shedding occurs at the same frequency for the sonic jet. However, for the supersonic jet case, due to the subsonic nature of the crossflow boundary layer, both the bow shock upstream of the jet and the barrel shock are absent. The subsonic nature of the crossflow for the supersonic jet case allows it to adjust to the presence of the oncoming jet due to the propagation of information in the direction opposite to the crossflow, thus preventing the formation of strong shocks close to the leading edge of the jet exit. Thus, no global oscillation is observed for the supersonic jet in subsonic crossflow. Instead, a leading edge shear layer roll up occurs for the supersonic jet as observed from the spatial DMD flowfield in figure 32(b). Barrel shock oscillation modifies the axial pressure gradient experienced by the nozzle boundary layer at the leading edge of the nozzle. The adverse pressure gradient increases as the barrel shock moves closer and decreases as it moves away. The away motion of the barrel shock impulsively accelerates fluid at the leading edge of the nozzle resulting in coherent shedding. The supersonic jet case has no barrel shock and hence does not display this behaviour.
9. Summary
LES of high-speed jets in crossflow have been performed for: (i) a sonic jet injected into a supersonic crossflow based on the experimental conditions of Santiago & Dutton (Reference Santiago and Dutton1997) and (ii) a supersonic jet injected into a subsonic crossflow based on the experimental conditions of Beresh et al. (Reference Beresh, Erven, Henfling and Spillers2005a ,Reference Beresh, Erven, Henfling and Spillers b ). Comparison of mean velocity and second-order quantities with experiment show good agreement. Both laminar and turbulent boundary layers at the inflow were reported in the quantitative comparisons and it was found that the turbulent inflow agreed better with the experiments. Qualitative flow features are discussed. The sonic jet in supersonic crossflow is characterized by a complex system of shocks which are unsteady and interact with the jet shear layers. The supersonic jet in subsonic crossflow, however, qualitatively looks more like a low-speed jet in crossflow. There is no direct evidence of the effect of the shock produced by the jet on the shedding of the shear layers.
A modification to Schetz & Billig (Reference Schetz and Billig1966)’s theory is proposed which yields good predictions of the jet trajectories for the current simulations in the near field. Temporal spectra at various locations in the flow are reported. It was found that
![]() $St=0.3$
was dominant at various regions in the flow for the sonic injection, which indicated that the flow had a global oscillation frequency associated with it. However, for the supersonic injection, no such dominant frequency was present throughout the flow. It was seen that
$St=0.3$
was dominant at various regions in the flow for the sonic injection, which indicated that the flow had a global oscillation frequency associated with it. However, for the supersonic injection, no such dominant frequency was present throughout the flow. It was seen that
![]() $St=1$
was dominant along the leading edge of the jet shear layer. DMD of the three-dimensional pressure field was performed to examine the dominant frequencies and their corresponding spatial locations in the flow. For the sonic injection, a clear peak at
$St=1$
was dominant along the leading edge of the jet shear layer. DMD of the three-dimensional pressure field was performed to examine the dominant frequencies and their corresponding spatial locations in the flow. For the sonic injection, a clear peak at
![]() $St=0.3$
was observed, consistent with the temporal spectra, thus confirming that the flow system oscillated with a global frequency. The mode was most dominant near the barrel shock region and extended up to the upstream bow shock. This mode was also associated with the shedding of vortices from the leading and trailing edge shear layers. For the supersonic injection, no single peak was found in the DMD spectrum, with multiple frequencies being dominant. A local peak was observed at
$St=0.3$
was observed, consistent with the temporal spectra, thus confirming that the flow system oscillated with a global frequency. The mode was most dominant near the barrel shock region and extended up to the upstream bow shock. This mode was also associated with the shedding of vortices from the leading and trailing edge shear layers. For the supersonic injection, no single peak was found in the DMD spectrum, with multiple frequencies being dominant. A local peak was observed at
![]() $St=1$
and it was observed that this mode corresponded to the shear layer roll up of the leading edge shear layer, consistent with the observations from the temporal spectra.
$St=1$
and it was observed that this mode corresponded to the shear layer roll up of the leading edge shear layer, consistent with the observations from the temporal spectra.
Acknowledgement
This work is supported by the National Science Foundation under grant CTS-0828162. Computer time for the simulations was provided by Minnesota Supercomputing Institute (MSI), National Institute for Computational Sciences (NICS) and Texas Advanced Computing Center (TACC). The authors would like to thank Professor Santiago and Dr Beresh for providing data from their experimental studies.