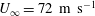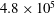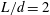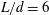1. Introduction
The interaction between the turbulent wake and other bodies has attracted much attention in recent decades because of its obvious importance in a wide range of applications (e.g. Ljungkrona, Norberg & Sunden Reference Ljungkrona, Norberg and Sunden1991; Mahir & Rockwell Reference Mahir and Rockwell1996; Zdravkovich Reference Zdravkovich2003; Munekata et al. Reference Munekata, Koshiishi, Yoshikawa and Ohba2008). These researchers used a cylinder to create a turbulent wake which interacted with another cylinder or an airfoil downstream, and mainly focused on the flow features in the interaction region such as the vortex shedding suppressing and flow patterns. Moreover, the body-wake interaction involves some important and complicated phenomena related to the Kármán-street and wake impingement, such as noise radiation and fluid resonant oscillation (e.g. Boudet, Grosjean & Jacob Reference Boudet, Grosjean and Jacob2005; Munekata et al. Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006; Jiang, Li & Zhou Reference Jiang, Li and Zhou2011; Hutcheson & Brooks Reference Hutcheson and Brooks2012). However, the physical mechanisms dictating these phenomena are still unclear and are of great interest for further detailed studies.
The wake of a circular cylinder has been extensively studied by Zdravkovich (Reference Zdravkovich1997), who summarized the different states of flow for smooth cylinders in a uniform flow according to: laminar, transition-in-wake, subcritical (transition to turbulence in the free shear layer), critical (transition to turbulence in the boundary layer) and fully turbulent. The subcritical, critical and turbulent states of flow are of most interest for body-wake interaction studies due to the Reynolds number range it encompasses. The range of Reynolds numbers based on the cylinder diameter and the incoming velocity of the uniform flow are
$(350{-}400)<\mathit{Re}<(10^{5}{-}2\times 10^{5})$
and
$(10^{5}{-}2\times 10^{5})<\mathit{Re}$
for the subcritical and critical states, respectively. The required Reynolds number is still unknown at present for the activation of a fully turbulent state of flow. The Reynolds number is expected to be the dominant parameter to determine the flow state for the smooth cylinders in a uniform flow, however, the structure of the flow may be significantly changed and transitions can occur at relatively lower values of
$\mathit{Re}$
if surface roughness or free stream turbulence are introduced. The noise radiation from the turbulent wake of a cylinder has been well recognized and carefully examined by Schlinker, Fink & Amiet (Reference Schlinker, Fink and Amiet1976). They observed that the radiation noise may decrease sharply in amplitude following an increase in Reynolds number.
Two cylinders in tandem is a common configuration for the study of body-wake interactions having important implications for flow-induced vibration and noise generation. Representative applications include heat exchanger tubes, adjacent tall buildings, bundled transmission lines and the piles of offshore platforms (Mahir & Rockwell Reference Mahir and Rockwell1996). The characteristics of the flow around this configuration has been comprehensively reviewed by Zdravkovich (Reference Zdravkovich1977), who has shown that vortex formation in the inter-cylindrical region is not present until the non-dimensional distance is longer than approximately four diameters. According to the inter-cylindrical distance, Zdravkovich (Reference Zdravkovich2003) has categorized the different possible flow regimes associated with the wake interference as follows: (i) a single vortex street formed by the cylinder upstream; (ii) a shear layer separated from the cylinder upstream reattaches intermittently onto the cylinder downstream, and vortex shedding occurs only from the downstream cylinder; (iii) vortex shedding from the cylinder downstream and intermittent vortex shedding from the cylinder upstream; (iv) vortex streets from the upstream and downstream cylinders synchronized in phase and frequency; and (v) uncoupled vortex streets take place behind both cylinders. Based on the experimental measurements on the flow interactions for tandem cylinders, Ljungkrona et al. (Reference Ljungkrona, Norberg and Sunden1991) concluded that there was no significant vortex action between the cylinders when the non-dimensional distance is less than 3.4–3.8 diameters. The flow feature in the inter-cylindrical region was also investigated by Mahir & Rockwell (Reference Mahir and Rockwell1996), who found an absence of vortex shedding for small inter-cylinder distance. Moreover, some other researchers (e.g. Fitzpatrick Reference Fitzpatrick2003; King & Pfizenmaier Reference King and Pfizenmaier2009) studied the influence of inter-cylindrical distance and rod diameter on the Strouhal numbers and sound pressure levels (SPLs). Recently, Hutcheson & Brooks (Reference Hutcheson and Brooks2012) have performed extensive acoustic measurements on multiple rod configurations to study the effect of Reynolds number, free stream turbulence and wake interference on the radiated noise.
The rod–airfoil configuration is another benchmark model for the study of body-wake interactions. A rod in this configuration is embedded upstream of the airfoil, so the turbulent wake is formed and convects downstream, which then impinges onto the airfoil and partly splits at the leading edge. Numerous studies have been performed to examine the flow characteristics for the rod–airfoil configuration including flow patterns altering, noise radiation suppressing and the fluid resonant oscillations due to the interval between the cylinder and the airfoil varying or the attack angle of the airfoil changing. Few studies however appear to have investigated the forces and turbulent fluctuations, moreover, these studies (e.g. Boudet et al. Reference Boudet, Grosjean and Jacob2005; Caraeni, Dai & Caraeni Reference Caraeni, Dai and Caraeni2007) examined the two features for the rod–airfoil configuration at a fixed interval. Munekata et al. (Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006) performed experimental measurements on the rod–airfoil configuration to investigate the effects of the interval between the cylinder and the airfoil on the characteristics of the aerodynamic sound. They found that vortex shedding from the cylinder upstream is suppressed for a short enough interval, and that simultaneously, the interaction between the turbulent wake from the cylinder upstream and the airfoil downstream is weakened and the level of noise radiation due to the interaction is correspondingly decreased. They observed the fluids resonant oscillations when the interval is varied. Munekata et al. (Reference Munekata, Koshiishi, Yoshikawa and Ohba2008) further investigated the effects of the attack angle of the airfoil located downstream on the characteristics of the aerodynamic sound and wake structure at a given interval between the cylinder and the airfoil. It was found that the SPL decreases with increasing attack angle of the airfoil because of the diffusive wake structure caused by the blocking effect of the airfoil. Jacob et al. (Reference Jacob, Boudet, Casalino and Michard2005) conducted a measurement of the interaction flow field of the rod/NACA0012 airfoil configuration, and also obtained the far field noise spectra which showed that the body-wake interaction is mainly responsible for the radiation of noise. Their experimental results provide a detailed database for the validation of the numerical simulation. More recently, Li et al. (Reference Li, Wang, Chen and Li2014) investigated experimentally the body-wake interaction noise radiated from the rod–airfoil configuration. They mainly focused on the noise control concept and found that the noise radiated is suppressed by two control methods including ‘air blowing’ on the upstream rod and a soft-vane leading edge on the airfoil.
The rod–airfoil case has also been investigated widely by numerical approaches, such as the Reynolds-averaged Navier–Stokes method (RANS) (e.g. Casalino, Jacob & Roger Reference Casalino, Jacob and Roger2003; Jacob et al. Reference Jacob, Boudet, Casalino and Michard2005), the large eddy simulation method (LES) (e.g. Casalino et al. Reference Casalino, Jacob and Roger2003; Magagnato, Sorgüven & Gabi Reference Magagnato, Sorgüven and Gabi2003; Boudet et al. Reference Boudet, Grosjean and Jacob2005; Jacob et al. Reference Jacob, Boudet, Casalino and Michard2005; Greschner et al. Reference Greschner, Thiele, Jacob and Casalino2008; Agrawal & Sharma Reference Agrawal and Sharma2014; Giret et al. Reference Giret, Sengissen, Moreau, Sanjosé and Jouhaud2015) and the detached eddy simulation method (DES) (e.g. Creschner et al. Reference Creschner, Thiele, Casalino and Jacob2004; Caraeni et al. Reference Caraeni, Dai and Caraeni2007; Gerolymos & Vallet Reference Gerolymos and Vallet2007; Greschner et al. Reference Greschner, Thiele, Jacob and Casalino2008). However, reliable results are not obtained using RANS in these papers. Jiang et al. (Reference Jiang, Li and Zhou2011) investigated interaction phenomena for a rod–airfoil configuration with different cylinder positions and attack angles of the airfoil using an experimental method and RANS. In their study, significant differences became apparent when the numerical noise spectra were compared to the experimental data. This behaviour may be explained by the fact that it is difficult for RANS to resolve the strong unsteady phenomena resulting from the impingement of the turbulent wake and the airfoil, which is mainly responsible for the noise radiation. Daude et al. (Reference Daude, Berland, Emmert, Lafon, Crouzet and Bailly2012) performed a LES on the prediction of noise radiation from a rod–airfoil configuration, and observed a good agreement between the numerical and experimental results.
In this paper, a LES technique is utilized to simulate the flow over a rod–airfoil configuration and to investigate the body-wake interactions within the flow field. The purpose is to achieve an improved understanding of some of the fundamental phenomena associated with this flow, including force varying regulation, flow structures and flow patterns in the interaction region, turbulent fluctuations and their suppression and noise radiation. Special attention is given to the fluid resonant oscillation caused by the varying interval between the cylinder upstream and airfoil downstream.
This paper is organized as follows. The mathematical formulation and numerical methods are presented in § 2. The computational overview and validation are described in § 3. Detailed results got body-wake flow interaction over a rod–airfoil configuration are then given in § 4 and the concluding remarks are given in § 5.
2. Mathematical formulation and numerical methods
2.1. Governing equations
The governing equations are the three-dimensional compressible Navier–Stokes equations in computational coordinates, these equations may be written
$$\begin{eqnarray}\frac{\partial \widetilde{U}}{\partial t}+\frac{\partial \widetilde{E}}{\partial {\it\xi}}+\frac{\partial \widetilde{F}}{\partial {\it\eta}}+\frac{\partial \widetilde{G}}{\partial {\it\zeta}}=\frac{1}{\mathit{Re}}\left(\frac{\partial \widetilde{E}_{v}}{\partial {\it\xi}}+\frac{\partial \widetilde{F}_{v}}{\partial {\it\eta}}+\frac{\partial \widetilde{G}_{v}}{\partial {\it\zeta}}\right),\end{eqnarray}$$
where,
$$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}}\displaystyle \widetilde{U}\!\!\! & = & \!\!\!U/J,\\ \displaystyle \widetilde{E}\!\!\! & = & \!\!\!({\it\xi}_{t}U+{\it\xi}_{x}E+{\it\xi}_{y}F+{\it\xi}_{z}G)/J,\quad \widetilde{E}_{v}=({\it\xi}_{x}E_{v}+{\it\xi}_{y}F_{v}+{\it\xi}_{z}G_{v})/J,\\ \displaystyle \widetilde{F}\!\!\! & = & \!\!\!({\it\eta}_{t}U+{\it\eta}_{x}E+{\it\eta}_{y}F+{\it\eta}_{z}G)/J,\quad \widetilde{F}_{v}=({\it\eta}_{x}E_{v}+{\it\eta}_{y}F_{v}+{\it\eta}_{z}G_{v})/J,\\ \displaystyle \widetilde{G}\!\!\! & = & \!\!\!({\it\zeta}_{t}U+{\it\zeta}_{x}E+{\it\zeta}_{y}F+{\it\zeta}_{z}G)/J,\quad \widetilde{G}_{v}=({\it\zeta}_{x}E_{v}+{\it\zeta}_{y}F_{v}+{\it\zeta}_{z}G_{v})/J.\end{array}\right\}\end{eqnarray}$$
The details of the governing equations (2.1) are given in Jiang et al. (Reference Jiang, Mao, Deng and Liu2014a
),
$J$
is the Jacobian of the grid transformation,
${\it\xi}_{t},{\it\xi}_{x},{\it\xi}_{y},{\it\xi}_{z},{\it\eta}_{t},{\it\eta}_{x},{\it\eta}_{y},{\it\eta}_{z},{\it\zeta}_{t},{\it\zeta}_{x},{\it\zeta}_{y}$
and
${\it\zeta}_{z}$
are grid derivatives. The grid metric derivatives have a conservative form of
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \tilde{{\it\xi}_{x}}={\it\xi}_{x}/J=(y_{{\it\eta}}z)_{{\it\zeta}}-(y_{{\it\zeta}}z)_{{\it\eta}},\quad \tilde{{\it\xi}_{y}}={\it\xi}_{y}/J=(z_{{\it\eta}}x)_{{\it\zeta}}-(z_{{\it\zeta}}x)_{{\it\eta}},\\ \tilde{{\it\xi}_{z}}={\it\xi}_{z}/J=(x_{{\it\eta}}y)_{{\it\zeta}}-(x_{{\it\zeta}}y)_{{\it\eta}},\\ \displaystyle \tilde{{\it\eta}_{x}}={\it\eta}_{x}/J=(y_{{\it\zeta}}z)_{{\it\xi}}-(y_{{\it\xi}}z)_{{\it\zeta}},\quad \tilde{{\it\eta}_{y}}={\it\eta}_{y}/J=(z_{{\it\zeta}}x)_{{\it\xi}}-(z_{{\it\xi}}x)_{{\it\zeta}},\\ \tilde{{\it\eta}_{z}}={\it\eta}_{z}/J=(x_{{\it\zeta}}y)_{{\it\xi}}-(x_{{\it\xi}}y)_{{\it\zeta}},\\ \displaystyle \tilde{{\it\zeta}_{x}}={\it\zeta}_{x}/J=(y_{{\it\xi}}z)_{{\it\eta}}-(y_{{\it\eta}}z)_{{\it\xi}},\quad \tilde{{\it\zeta}_{y}}={\it\zeta}_{y}/J=(z_{{\it\xi}}x)_{{\it\eta}}-(z_{{\it\eta}}x)_{{\it\xi}},\\ \tilde{{\it\zeta}_{z}}={\it\zeta}_{z}/J=(x_{{\it\xi}}y)_{{\it\eta}}-(x_{{\it\eta}}y)_{{\it\xi}}.\end{array}\right\}\end{eqnarray}$$
Large eddy simulation is employed in the present study for turbulence closure. In a standard compressible LES, the governing equations are filtered using a grid-filtering function and Favre-averaged variables are introduced, the small-scale structures are left unresolved and are accounted for by a subgrid scale (SGS) turbulence model (Xu, Chen & Lu Reference Xu, Chen and Lu2010). In this work, however, an alternative approach is employed where the truncation error of the high-order discretization itself is used to model the effects of the unresolved scales and is referred to as a HILES (Jiang et al. Reference Jiang, Mao, Deng and Liu2014a ). The concept of this approach is the same as that of the monotone integrated LES (MILES) proposed by Boris et al. (Reference Boris, Grinstein, Oran and Kolbe1992), and a new seventh-order hybrid cell-edge and cell-node dissipative compact scheme (HDCS-E8T7) is used (Deng et al. Reference Deng, Jiang, Mao, Liu and Tu2013b ) for spatial discretization in the HILES.
Numerous high-order schemes have been adopted for implicit LES, e.g. the high-order monotone upstream-centered schemes for conservation laws (MUSCL) (Van Leer Reference Van Leer1977) employed by Thornber & Drikakis (Reference Thornber and Drikakis2008) and Hahn et al. (Reference Hahn, Drikakis, Youngs and Williams2011), the high-order weighted essentially non-oscillatory schemes (WENO) (Jiang & Shu Reference Jiang and Shu1996) employed by Drikakis et al. (Reference Drikakis, Hahn, Mosedale and Thornber2009) and the cell-node type central compact scheme (CCSN) (Lele Reference Lele1992) employed by Visbal & Rizzetta (Reference Visbal and Rizzetta2002). Compared with the MUSCL and WENO schemes, the present HDCS-E8T7 is a linear scheme without nonlinear mechanics capturing the discontinuities, and is expected to have a higher resolution for the same order of accuracy. Moreover, the HDCS-E8T7 is a dissipative scheme with inherent dissipation and the filter operations for the CCSN are not needed.
2.2. Numerical procedure
The temporal integration for solving the governing equations (2.1) is performed using a dual time stepping approach (John & Jameson Reference John and Jameson2002) with Newton-like subiterations (Gordnier & Visbal Reference Gordnier and Visbal1993). The convective and viscous terms are discretized by the HDCS-E8T7, which employs the concept of the dissipative compact scheme (DCS) (Deng, Maekawa & Shen Reference Deng, Maekawa and Shen1996) for simulating subsonic flow on a complex geometry. Although some aeroacoustic benchmark problems have been simulated successfully by the DCS, applications of this scheme on complex grids may pose serious problems (Deng et al. Reference Deng, Mao, Tu, Liu and Zhang2011). The HDCS-E8T7 has demonstrated a promising ability in solving complex flow problems because the surface conservation law (SCL) is satisfied, which will be further discussed in § 2.3. For the convenience of understanding our high-order strategy in the present study, details of the HDCS-E8T7 will be given in the following.
Considering discretization of the convective terms,
$$\begin{eqnarray}\frac{\partial \widetilde{U}}{\partial t}+\frac{\partial \widetilde{E}}{\partial {\it\xi}}+\frac{\partial \widetilde{F}}{\partial {\it\eta}}+\frac{\partial \widetilde{G}}{\partial {\it\zeta}}=0,\end{eqnarray}$$
and their semi-discrete approximation,
$$\begin{eqnarray}\frac{\partial \widetilde{U}}{\partial t}=-{\it\delta}_{\text{I}}^{{\it\xi}}\widetilde{E}-{\it\delta}_{\text{I}}^{{\it\eta}}\widetilde{F}-{\it\delta}_{\text{I}}^{{\it\zeta}}\widetilde{G}.\end{eqnarray}$$
The discretization
${\it\delta}_{\text{I}}^{{\it\xi}}$
,
${\it\delta}_{\text{I}}^{{\it\eta}}$
and
${\it\delta}_{\text{I}}^{{\it\zeta}}$
are the same, thus we only give the discretization in the
${\it\xi}$
direction. The
${\it\delta}_{\text{I}}^{{\it\xi}}$
of the HDCS-E8T7 is
$$\begin{eqnarray}\displaystyle {\it\delta}_{\text{I}}^{{\it\xi}}\widetilde{E}_{j} & = & \displaystyle \frac{256}{175h}(\hat{E}_{j+1/2}-\hat{E}_{j-1/2})-\frac{1}{4h}(\widetilde{E}_{j+1}-\widetilde{E}_{j-1})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{100h}(\widetilde{E}_{j+2}-\widetilde{E}_{j-2})-\frac{1}{2100h}(\widetilde{E}_{j+3}-\widetilde{E}_{j-3}),\end{eqnarray}$$
where,
$\hat{E}_{j\pm 1/2}=\widetilde{E}(\hat{U} _{j\pm 1/2},\hat{{\it\xi}}_{x,j\pm 1/2},\hat{{\it\xi}}_{y,j\pm 1/2},\hat{{\it\xi}}_{z,j\pm 1/2})$
and
$\widetilde{E}_{j+m}=\widetilde{E}(\hat{U} _{j+m},\hat{{\it\xi}}_{x,j+m},\hat{{\it\xi}}_{y,j+m},\hat{{\it\xi}}_{z,j+m})$
are the fluxes at the cell edges and the cell nodes, respectively. The numerical flux
$\hat{E}_{j\pm 1/2}$
is evaluated by the variables at the cell edges,
$$\begin{eqnarray}\hat{E}_{j\pm 1/2}=\widetilde{E}\left(\hat{U} _{j\pm 1/2}^{L},\hat{U} _{j\pm 1/2}^{R},\hat{{\it\xi}}_{x,j\pm 1/2},\hat{{\it\xi}}_{y,j\pm 1/2},\hat{{\it\xi}}_{z,j\pm 1/2}\right),\end{eqnarray}$$
where,
$\hat{U} _{j\pm 1/2}^{L},\hat{U} _{j\pm 1/2}^{R}$
are variables at the cell edge.
$$\begin{eqnarray}\displaystyle & & \displaystyle {\textstyle \frac{5}{14}}(1-{\it\alpha})\hat{U} _{j-1/2}^{L}+\hat{U} _{j+1/2}^{L}+{\textstyle \frac{5}{14}}(1+{\it\alpha})\hat{U} _{j+3/2}^{L}\nonumber\\ \displaystyle & & \displaystyle \quad ={\textstyle \frac{25}{32}}(U_{j+1}+U_{j})+{\textstyle \frac{5}{64}}(U_{j+2}+U_{j-1})-{\textstyle \frac{1}{448}}(U_{j+3}+U_{j-2})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,{\it\alpha}\left[{\textstyle \frac{25}{64}}(U_{j+1}-U_{j})+{\textstyle \frac{15}{128}}(U_{j+2}-U_{j-1})-{\textstyle \frac{5}{896}}(U_{j+3}-U_{j-2})\right],\end{eqnarray}$$
where
${\it\alpha}<0$
is the dissipative parameter to control dissipation in the HDCS-E8T7. The corresponding
$\hat{U} _{j+1/2}^{R}$
can be obtained easily by setting
${\it\alpha}>0$
. In figure 1, the modified wavenumber
${\it\omega}^{\ast }$
of the HDCS-E8T7 with different dissipative parameters is compared with that of the eighth-order central compact scheme (CCSN-8) proposed by Lele (Reference Lele1992). According to the discussion given by Lele (Reference Lele1992), the real part of
${\it\omega}^{\ast }$
, namely,
${\it\omega}_{r}^{\ast }$
denotes the resolution power of a scheme, and the imaginary part of
${\it\omega}^{\ast }$
, namely,
${\it\omega}_{i}^{\ast }$
denotes the dissipation intensity of a scheme. It can be seen that the dissipative parameter
${\it\alpha}$
has effect on the resolution power of the HDCS-E8T7, but it has no influence on the order of the truncation error of the HDCS-E8T7 according to Taylor series expansion (Deng et al.
Reference Deng, Jiang, Mao, Liu, Li and Tu2015). If a proper dissipative parameter is chosen, the resolution power of the HDCS-E8T7 can be higher than that of the CCSN-8. In order to obtain fine resolution power, the HDCS-E8T7 has been optimized by following the concept of dispersion-relation-preserving (DRP) (Tam & Webb Reference Tam and Webb1993) and adjusting the value of
${\it\alpha}$
. The optimized dissipative parameter is equal to 0.3 (Deng et al.
Reference Deng, Jiang, Mao, Liu, Li and Tu2015), which will be adopted in this paper.
Figure 1. Modified wavenumber of the HDCS-E8T7.
Seven-point stencil is used by the HDCS-E8T7, thus three levels of boundary and near-boundary schemes are required. The details of the boundary and near boundary schemes are given by Jiang et al. (Reference Jiang, Mao, Deng and Liu2014a
). For computation of the viscous terms, the primitive variables,
$u,v,w,T$
, are first differentiated to form the components of the stress tensor and the heat flux vector. The viscous flux derivatives are then computed by a second application of the HDCS-E8T7.
2.3. Calculation of the grid metric derivatives
According to the study of Deng et al. (Reference Deng, Mao, Tu, Liu and Zhang2011), the SCL is always satisfied on uniform meshes, however this may not be so on curvilinear meshes. If the SCL has not been satisfied, numerical instabilities and even computing collapse may occur on complex curvilinear grids during numerical simulation. To aid in ensuring that the SCL is satisfied, the CCSNs have been successfully applied to various flow simulations by Visbal & Gaitonde (Reference Visbal and Gaitonde2002) and Rizzetta, Visbal & Morgan (Reference Rizzetta, Visbal and Morgan2008) on complex grids. In this section, we will discuss the calculation of the grid metric derivatives according to the principle of satisfying the SCL on curvilinear meshes. The grid metric derivatives of governing equations (2.1) have a conservative form of
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \tilde{{\it\xi}_{x}}={\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\eta}}y)z)-{\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\zeta}}y)z),\quad \tilde{{\it\xi}_{y}}={\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\eta}}z)x)-{\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\zeta}}z)x),\\ \displaystyle \tilde{{\it\xi}_{z}}={\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\eta}}x)y)-{\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\zeta}}x)y),\\ \displaystyle \tilde{{\it\eta}_{x}}={\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\zeta}}y)z)-{\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\xi}}y)z),\quad \tilde{{\it\eta}_{y}}={\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\zeta}}z)x)-{\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\xi}}z)x),\\ \displaystyle \tilde{{\it\eta}_{z}}={\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\zeta}}x)y)-{\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\xi}}x)y),\\ \displaystyle \tilde{{\it\zeta}_{x}}={\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\xi}}y)z)-{\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\eta}}y)z),\quad \tilde{{\it\zeta}_{y}}={\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\xi}}z)x)-{\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\eta}}z)x),\\ \displaystyle \tilde{{\it\zeta}_{z}}={\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\xi}}x)y)-{\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\eta}}x)y),\end{array}\right\}\end{eqnarray}$$
where
${\it\delta}_{\text{II}}^{{\it\xi}},{\it\delta}_{\text{II}}^{{\it\eta}},{\it\delta}_{\text{II}}^{{\it\zeta}}$
and
${\it\delta}_{\text{III}}^{{\it\xi}},{\it\delta}_{\text{III}}^{{\it\eta}},{\it\delta}_{\text{III}}^{{\it\zeta}}$
are numerical derivative operators used for the metric calculations in the
${\it\xi},{\it\eta}$
and
${\it\zeta}$
coordinate directions, respectively. For applications on curvilinear meshes, a finite difference scheme should satisfy the SCL which means
$I_{x}=I_{y}=I_{z}=0$
(Deng et al.
Reference Deng, Mao, Tu, Liu and Zhang2011),
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}I_{x}={\it\delta}_{\text{I}}^{{\it\xi}}(\tilde{{\it\xi}_{x}})+{\it\delta}_{\text{I}}^{{\it\eta}}(\tilde{{\it\eta}_{x}})+{\it\delta}_{\text{I}}^{{\it\zeta}}(\tilde{{\it\zeta}_{x}}),\\ I_{y}={\it\delta}_{\text{I}}^{{\it\xi}}(\tilde{{\it\xi}_{y}})+{\it\delta}_{\text{I}}^{{\it\eta}}(\tilde{{\it\eta}_{y}})+{\it\delta}_{\text{I}}^{{\it\zeta}}(\tilde{{\it\zeta}_{y}}),\\ I_{z}={\it\delta}_{\text{I}}^{{\it\xi}}(\tilde{{\it\xi}_{z}})+{\it\delta}_{\text{I}}^{{\it\eta}}(\tilde{{\it\eta}_{z}})+{\it\delta}_{\text{I}}^{{\it\zeta}}(\tilde{{\it\zeta}_{z}}).\end{array}\right\}\end{eqnarray}$$
In order to fulfill the SCL, the grid metrics should be calculated with a conservative form by the same schemes used for flux derivative calculations, i.e.
${\it\delta}_{\text{I}}={\it\delta}_{\text{II}}$
, to implement the conservative metric method (CMM) (Deng et al.
Reference Deng, Mao, Tu, Liu and Zhang2011). It has been proved that the CMM can be easily applied in high-order schemes if the difference operator
${\it\delta}_{\text{I}}$
of flux derivatives is not split, while it is difficult to apply in schemes where the
${\it\delta}_{\text{I}}$
is split into two upwind operators as
${\it\delta}_{\text{I}}^{+}$
and
${\it\delta}_{\text{I}}^{-}$
. Although the inner-level difference operators
${\it\delta}_{\text{III}}$
in the conservative metrics have no effect on the SCL, the constraint
${\it\delta}_{\text{III}}={\it\delta}_{\text{II}}$
is recommended by Deng et al. (Reference Deng, Mao, Tu, Liu and Zhang2011). More recently, the constraint
${\it\delta}_{\text{III}}={\it\delta}_{\text{II}}$
has been explained from a geometry viewpoint using a symmetrical conservative metric method (SCMM) (Deng et al.
Reference Deng, Min, Mao, Liu, Tu and Zhang2013a
), which can evidently increase the numerical accuracy on irregular grids. The SCMM needs symmetrical conservative metrics, which can be written as follows,
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\tilde{{\it\xi}_{x}}={\textstyle \frac{1}{2}}\left({\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\eta}}y)z)-{\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\zeta}}y)z)+{\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\zeta}}z)y)-{\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\eta}}z)y)\right),\\ \tilde{{\it\xi}_{y}}={\textstyle \frac{1}{2}}\left({\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\eta}}z)x)-{\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\zeta}}z)x)+{\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\zeta}}x)z)-{\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\eta}}x)z)\right),\\ \tilde{{\it\xi}_{z}}={\textstyle \frac{1}{2}}\left({\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\eta}}x)y)-{\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\zeta}}x)y)+{\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\zeta}}y)x)-{\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\eta}}y)x)\right),\\ \tilde{{\it\eta}_{x}}={\textstyle \frac{1}{2}}\left({\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\zeta}}y)z)-{\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\xi}}y)z)+{\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\xi}}z)y)-{\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\zeta}}z)y)\right),\\ \tilde{{\it\eta}_{y}}={\textstyle \frac{1}{2}}\left({\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\zeta}}z)x)-{\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\xi}}z)x)+{\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\xi}}x)z)-{\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\zeta}}x)z)\right),\\ \tilde{{\it\eta}_{z}}={\textstyle \frac{1}{2}}\left({\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\zeta}}x)y)-{\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\xi}}x)y)+{\it\delta}_{\text{II}}^{{\it\zeta}}(({\it\delta}_{\text{III}}^{{\it\xi}}y)x)-{\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\zeta}}y)x)\right),\\ \tilde{{\it\zeta}_{x}}={\textstyle \frac{1}{2}}\left({\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\xi}}y)z)-{\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\eta}}y)z)+{\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\eta}}z)y)-{\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\xi}}z)y)\right),\\ \tilde{{\it\zeta}_{y}}={\textstyle \frac{1}{2}}\left({\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\xi}}z)x)-{\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\eta}}z)x)+{\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\eta}}x)z)-{\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\xi}}x)z)\right),\\ \tilde{{\it\zeta}_{z}}={\textstyle \frac{1}{2}}\left({\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\xi}}x)y)-{\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\eta}}x)y)+{\it\delta}_{\text{II}}^{{\it\xi}}(({\it\delta}_{\text{III}}^{{\it\eta}}y)x)-{\it\delta}_{\text{II}}^{{\it\eta}}(({\it\delta}_{\text{III}}^{{\it\xi}}y)x)\right).\end{array}\right\}\end{eqnarray}$$
The randomized grids and a grid around wingtip are used by Deng et al. (Reference Deng, Min, Mao, Liu, Tu and Zhang2013a
) to show the improvement of the SCMM over the CMM. These grids are representative of the configuration considered in this study, thus the SCMM is a better choice for the present investigation. To eliminate the SCL errors on a curvilinear mesh, here we calculate the grid metrics with the symmetrical conservative form (2.11) by the same schemes as used for flux derivative calculations, i.e.
${\it\delta}_{\text{I}}={\it\delta}_{\text{II}}={\it\delta}_{\text{III}}$
, to implement the SCMM (Deng et al.
Reference Deng, Min, Mao, Liu, Tu and Zhang2013a
).
3. Computational overview and validation
3.1. Computational overview
We consider the rod–airfoil configuration to numerically investigate the interaction between bodies and the turbulent wake. An experiment for this configuration was carried out in the large anechoic wind tunnel at Ècole Centrale de Lyon (ECL) (Jacob et al.
Reference Jacob, Boudet, Casalino and Michard2005). A sketch of the configuration is shown in figure 2. A NACA0012 airfoil of chord
$c=0.1~\text{m}$
is located one chord downstream of a cylinder (diameter:
$d=0.01~\text{m}$
). This configuration is placed in a uniform airflow with the incoming flow conditions
$U_{\infty }=72~\text{m}~\text{s}^{-1},T_{\infty }=293~\text{K}$
, and
${\it\rho}_{\infty }=1.2~\text{kg}~\text{m}^{-3}$
. The Reynolds number based on the rod diameter and the airfoil chord are
$\mathit{Re}_{d}=4.8\times 10^{4}$
and
$\mathit{Re}_{c}=4.8\times 10^{5}$
, respectively. For comparison, a sketch of locations in the measurement (Jacob et al.
Reference Jacob, Boudet, Casalino and Michard2005) is also shown in figure 2.
Figure 2. Schematic diagram of rod–airfoil configuration for the numerical simulation and experimental measurement. Here, the solid dots A and B denote the pressure probe locations in the present simulation, the point C is the far-field acoustic monitoring location in the experiment (Jacob et al. Reference Jacob, Boudet, Casalino and Michard2005), lines D, E and F represent the locations of the particle image velocimetry (PIV) measurement (Jacob et al. Reference Jacob, Boudet, Casalino and Michard2005).
In order to investigate the interaction phenomena in the rod–airfoil configuration, the simulations are performed with the changing interval
$L$
between the cylinder and the airfoil. The incoming flow conditions for the experiment of Jacob et al. (Reference Jacob, Boudet, Casalino and Michard2005) are adopted for the present simulations. Five cases with
$L/d=2$
, 4, 6, 8 and 10 are performed to reveal the body-wake interaction phenomena within the rod–airfoil configuration. The simulation for a single cylinder is also carried out under the same incoming flow conditions as the rod–airfoil configuration to present the interaction phenomena.
In this rod–airfoil configuration, the rod wake that impinges the airfoil contains both periodic and broadband turbulent disturbances. For the simulation of turbulent flow, which is largely responsibile for the noise radiated by this rod–airfoil configuration, the HILES (Jiang et al. Reference Jiang, Mao, Deng and Liu2014a ) based on the HDCS-E8T7 scheme is employed. The far-field noise is calculated by applying the Ffowcs-Williams and Hawking (FW-H) aeroacoustic analogy (Lyrintzis Reference Lyrintzis2003) to the FW-H integration surface, and no volume integration is performed.
The grid topology is carefully designed to ensure computation accuracy. For the rod–airfoil configuration with
$L/d=10$
, figure 3 outlines the computational domain, which contains approximately 16 000 000 grid points. The meshes used for the simulation of the five cases have a similar topology, though the grid points are slightly different from each other. Considering the case of
$L/d=10$
, grid stretching is employed to increase the grid resolution near the body surface and in the interference region, ensuring that there are 481 nodes located in the streamwise direction between the rod upstream and the airfoil downstream. The minimum size of the grid in the wall-normal direction is
$1.0\times 10^{-5}$
(normalized by the reference length
$L_{ref}=0.1~\text{m}$
). The rod and the airfoil surfaces are meshed with 241 and 1081 circumferential points respectively, at each spanwise location, and with 45 points along the span. The spanwise grid is divided uniformly, and the spanwise length is chosen as
$3d$
. On the airfoil, the grid density is characterized by:
${\rm\Delta}x^{+}<90$
(
${<}20$
for
$x/c<0.1$
, i.e. in the leading edge region),
${\rm\Delta}y^{+}=0.24$
and
${\rm\Delta}z^{+}=161.8$
, where
${\rm\Delta}x^{+}$
,
${\rm\Delta}y^{+}$
and
${\rm\Delta}z^{+}$
are the near wall mesh spacing tangent to wall, normal to the wall and spanwise, in wall units, respectively. Wall units are defined in terms of the time-averaged friction velocity at the middle of airfoil upper surface. The expansion ratio is set to 1.05 for the first 121 mesh layers from the rod and airfoil surfaces. The mesh resolution on the FW-H surface can be described as
${\rm\Delta}x/L_{ref}<0.03$
and
${\rm\Delta}y/L_{ref}<0.02$
. Outside the FW-H surface, the mesh is then slightly coarsened using a stretching ratio of 1.1 until the sponge zone is met, where the stretching ratio is 1.02.
Figure 3. Sectional view of the computational mesh in the central plane. (a) Mesh global view and location of the FW-H surface (red solid line). (b) Zoom-in on the rod. (c) Zoom-in on the airfoil leading edge.
To justify the choice of the spanwise length, the two-point correlations are calculated in terms of the formulation (Pirozzoli, Grasso & Gatski Reference Pirozzoli, Grasso and Gatski2004). Figure 4 shows the two-point correlations
$R_{{\it\alpha}{\it\alpha}}(r_{z})$
for the case of
$L/d=10$
in the spanwise direction, i.e.
$z$
direction, where
${\it\alpha}$
represents the fluctuations of any one of the velocity components
$u_{i}$
(or
$u$
,
$v$
and
$w$
). The correlations decay towards zero which means that the two-point correlations are sufficiently decorrelated over a distance
$1.5d$
. This ensures that the spanwise computational domain is sufficiently wide not to inhibit the turbulence dynamics.
Figure 4. Distributions of the two-point correlations of the velocity components in the spanwise direction for the case with
$L/d=10$
at
$y/c=0$
and (a)
$x/c=-0.96$
and (b)
$x/c=-0.87$
.
At the outer boundary, far-field boundary conditions based on the LODI approximation (Poinsot & Lele Reference Poinsot and Lele1992) and sponge technique (Daniel Reference Daniel2006) are adopted. The no-slip condition is invoked on the rod and airfoil surfaces, together with fifth-order accurate approximations for an adiabatic wall and zero normal pressure gradient. At the spanwise boundaries, periodicity condition is applied. The non-dimensional time step for the present simulations is
${\rm\Delta}t=0.001c/U_{\infty }$
with
$U_{\infty }$
being the incoming velocity, corresponding to a physical time of
${\rm\Delta}t=1.389\times 10^{-6}~\text{s}$
. The time to eliminate initial transients is chosen as
$100d/U_{\infty }$
and is very similar to that commonly used in simulations of the flow past a straight circular cylinder (Gallardo, Andersson & Pettersen Reference Gallardo, Andersson and Pettersen2014). The flow statistics are collected for 20 000 time steps, corresponding either to a physical time of
$T=0.02778~\text{s}$
or to 20 flow-over times from the leading edge to the trailing edge of the airfoil. The sampling time is chosen to obtain statistically meaningful turbulence properties in a temporal averaging operation. We took samples every time step, and the sampling frequencies in the present simulations are 720 kHz. For periodic boundaries in the spanwise directions, flow statistics are averaged in the
$z$
direction.
3.2. Validation
To validate the present simulation, we compare the numerical results with the experimental measurements (Jacob et al.
Reference Jacob, Boudet, Casalino and Michard2005). Figure 5 shows the mean velocity normalized by the incoming velocity at two locations
$x/c=-0.255$
and
$x/c=0.25$
. At the location
$x/c=-0.255$
, the mean streamwise velocity
$x/c=-0.87$
near the center-line is underpredicted (the maximal relative error is 7.5 %), which is consistent with the overprediction (the maximal relative error is 9.7 %) of the mean streamwise velocity near the wall at location
$x/c=0.25$
, since the flow predicted moves more slowly between the rod and airfoil. A similar phenomenon is observed from the LES prediction of Boudet et al. (Reference Boudet, Grosjean and Jacob2005). Moreover, as shown in figure 6, the predicted profiles of the root-mean-square (r.m.s.) value of streamwise fluctuating velocity at the two locations
$x/c=-0.255$
and
$x/c=0.25$
have good agreement with those from the experimental data. This seems to indicate that the turbulence intensities are well predicted.
Figure 5. Spanwise averaged mean streamwise velocity distributions at locations
$x/c=-0.255$
(a) and
$x/c=0.25$
(b).
Figure 6. Spanwise averaged r.m.s. value of the fluctuating velocity distributions at locations
$x/c=-0.255$
(a) and
$x/c=0.25$
(b).
For the location closer to the cylinder, i.e.
$x/c=-0.87$
, figure 7 the mean streamwise velocity and r.m.s. value of streamwise fluctuating velocity compared with the corresponding data from the experimental measurements (Jacob et al.
Reference Jacob, Boudet, Casalino and Michard2005) and the LES prediction of Agrawal & Sharma (Reference Agrawal and Sharma2014). The present simulation provides similar mean streamwise velocities in comparison with the LES results of Agrawal & Sharma (Reference Agrawal and Sharma2014). Although both the experimental and numerical results exhibit the wake velocity deficit, i.e. the mean streamwise velocity is at a minimum on the center-line, a very large discrepancy in the mean velocity is observed. Agrawal & Sharma (Reference Agrawal and Sharma2014) are suspicious of the experimental mean velocity data at
$x/c=-0.87$
because the velocity deficit in the wake is expected to reduce with distance away from the rod (Agrawal & Sharma Reference Agrawal and Sharma2014; Giret et al.
Reference Giret, Sengissen, Moreau, Sanjosé and Jouhaud2015). This behaviour can be identified from the present simulation by comparing the mean streamwise velocity at
$x/c=-0.255$
(see figure 5) with at
$x/c=-0.87$
(see figure 7), however, the experimental data show the velocity deficit increasing with downstream distance. Compared with the experimental data, the r.m.s. value of streamwise fluctuating velocity is overpredicted. Yet, the two numerical solutions are close to each other, with relatively obvious differences near the center-line, indicating that a relatively higher level of streamwise fluctuating velocity is predicted by the present simulation near the center-line at
$x/c=-0.87$
. Since different methods and meshes are adopted, a dispersion of the numerical fluctuating velocity can be observed near the center-line (Giret et al.
Reference Giret, Sengissen, Moreau, Sanjosé and Jouhaud2015).
Figure 7. Spanwise averaged distributions at locations
$x/c=-0.87$
for mean streamwise velocity (a) and r.m.s. value of the fluctuating velocity (b).
Other evidence demonstrating the reliability of the present simulation is the resolved energy spectrum behind the cylinder, which is given in figure 8. The resolved scales appear to reach an inertial subrange reasonably close to a
$\mathit{St}^{-5/3}$
scaling (Xu et al.
Reference Xu, Chen and Lu2010).
$\mathit{St}$
is the characteristic Strouhal number defined as
$\mathit{St}=fd/U_{\infty }$
with
$f$
being the frequency. The illustrated slope indicates that the turbulence spectrum is captured reliably. The capability of the present numerical method for resolving energy spectra has been demonstrated in the previous study (Jiang et al.
Reference Jiang, Mao, Deng and Liu2014a
).
Figure 8. Resolved energy spectrum behind the cylinder at the location
$x=-6.5d$
,
$y=0,z=1.5d$
.
Figure 9 shows the SPL spectra at the location
$(x=0.68~\text{m},y=1.74~\text{m})$
calculated from the pressure fluctuations on the FW-H integration surface. The peak frequency is predicted quite well. Furthermore, the broadband spectrum is also fairly well described around the peak frequency. However, the spectrum at high frequencies is overpredicted, which is similar to LES results of Boudet et al. (Reference Boudet, Grosjean and Jacob2005). A possible explanation given by Boudet et al. (Reference Boudet, Grosjean and Jacob2005) for this phenomenon is that the dipole cancellation of some quadrupole terms may be momentarily ineffective, which could lead to more efficient sources. Nevertheless, a good broadband sound is predicted. It can be seen that the peak frequency in figure 9 is almost identical to the primary shedding frequency of the cylinder, which will be calculated from the power spectral densities (PSD) of the time-dependent lift coefficient in figure 13. This behaviour shows that the shedding vortex from the cylinder plays a dominant role in the flow over the rod–airfoil configuration.
Figure 9. The SPL spectra at the location
$(x=0.68~\text{m},y=1.74~\text{m})$
calculated from the pressure perturbations on the FW-H integration surface.
The present high-order numerical strategy has been applied successfully to simulate a wide range of turbulent cases such as transition and turbulence decay in the Taylor–Green vortex (Jiang et al. Reference Jiang, Mao, Deng and Liu2014a ), channel flow (Jiang et al. Reference Jiang, Mao, Deng and Liu2015), subsonic flow over a circular cylinder (Jiang et al. Reference Jiang, Mao, Deng and Liu2013) and a three-dimensional delta wing (Deng et al. Reference Deng, Jiang, Mao, Liu and Tu2013b ), stall characteristic of flow past a thin airfoil (Jiang et al. Reference Jiang, Mao, Deng and Liu2014a ) and noise radiation from a jet nozzle (Jiang et al. Reference Jiang, Mao, Deng, Liu and Yan2014b ; Mao et al. Reference Mao, Jiang, Deng and Liu2016). We have carefully examined the numerical strategy used in this study and have verified that the numerical solutions are reliable.
4. Results and discussion
4.1. Force behaviours
4.1.1. Surface pressure and friction
The behaviour of the forces exerted on the bodies, which are contributed by the pressure and viscous shear stress, is an important issue associated with the interaction between the body and turbulent wake. An illustration of the force behaviour of the rod–airfoil configuration is given by the distribution of the mean pressure on the surface of the cylinder and airfoil, shown in figure 10(a,b), respectively. As shown in figure 10(a), the airfoil behind the cylinder leads to the pressure increase in the base range of the cylinder. When the distance between the airfoil and the cylinder continues to increase, the influence of the airfoil is weakened correspondingly on the surface pressure distributions of the cylinder, and gradually converges to the distribution on the single cylinder. Moreover, in figure 10(a), the present mean pressure distributions on the surface of the cylinder are compared with the experimental results of Apelt & West (Reference Apelt and West1975), and those of Szepessy & Bearman (Reference Szepessy and Bearman1992) to complement the verification of the present simulation. The present distributions from the simulation of the single cylinder demonstrate that the angular position (70°) for the mean pressure minimum is very close to that of the experimental measurement of Szepessy & Bearman (Reference Szepessy and Bearman1992). Although the present mean pressure distributions in the base region provide an unsatisfactory comparison with the experimental data, a significant dispersion of the experimental results is observed.
Figure 10. The calculated mean pressure distributions compared with the experimental data and LES results: (a) on the surface of the cylinder, (b) on the surface of the airfoil. Here, the experimental data from Apelt & West (Reference Apelt and West1975) and Szepessy & Bearman (Reference Szepessy and Bearman1992) are measured for the circular cylinder with
$\mathit{Re}_{d}=4\times 10^{4}$
; the experimental data from ECL (Jacob et al.
Reference Jacob, Boudet, Casalino and Michard2005) and the LES results of Giret et al. (Reference Giret, Sengissen, Moreau, Sanjosé and Jouhaud2015) are obtained for the rod–airfoil configuration with
$L/d=10$
.
As shown in figure 10, the pressure distributions with
$L/d=2$
are obviously different from the others. This behaviour is related to the flow phenomena of the separated shear layers from the upstream cylinder impinging onto the leading edge of the airfoil. The main separated vortices impact the leading edge of the airfoil directly, and von Kármán vortex shedding is suppressed, which will be discussed in detail in § 4.2. The increasing
$L$
, followed by the weakening interaction between the turbulent wake and airfoil, is also consistent with the pressure distributions on the airfoil surface tending to be identical. In figure 10(b), the present mean pressure distributions on the airfoil surface are also compared with the experimental data from ECL (Jacob et al.
Reference Jacob, Boudet, Casalino and Michard2005) and the LES results of Giret et al. (Reference Giret, Sengissen, Moreau, Sanjosé and Jouhaud2015). It can be seen that the calculated solutions for the rod–airfoil configuration with
$L/d=10$
are very close to the LES results of Giret et al. (Reference Giret, Sengissen, Moreau, Sanjosé and Jouhaud2015), however, a large gap between the numerical results displayed and the experimental data can be seen. According to the discussion of Giret et al. (Reference Giret, Sengissen, Moreau, Sanjosé and Jouhaud2015), the experimental dip is most likely caused by a curvature discontinuity in the mockup leading-edge region.
Continuing the investigation of the skin friction, figure 11(a) shows the present skin friction distributions on the cylinder, together with the experimental data of Achenbach (Reference Achenbach1968) and the LES results of Giret et al. (Reference Giret, Sengissen, Moreau, Sanjosé and Jouhaud2015). It shows that the skin friction increases continuously from the stagnation point until the maximum value is obtained at the location near
${\it\theta}=45^{\circ }$
, this trend then reverses, and it finally achieves a zero or negligible negative value near
${\it\theta}=80^{\circ }$
where the flow is separated. The positive skin friction occurs obviously in the attached flow region and drops quickly at the mean separation location. Moreover, the absolute value of the skin friction observed in the attached flow region is usually much higher than that in the separated region. Although the calculated skin friction maximum of the single cylinder is underpredicted, with a relative error of 11 %. It can be seen that the present simulations for the single cylinder and the rod–airfoil configuration with
$L/d\geqslant 4$
provide similar shapes and maximum positions, as well as mean separation positions, in comparison with the experimental data of Achenbach (Reference Achenbach1968) and the LES results of Giret et al. (Reference Giret, Sengissen, Moreau, Sanjosé and Jouhaud2015). For the case of
$L/d=2$
, however, the peak skin friction is lower in the present simulations, furthermore, the mean separation in this case is earlier than in the other cases.
Figure 11. Mean skin friction distributions on the surface of bodies: (a) cylinder and (b) airfoil. Here, the calculated distributions on the surface of the cylinder are compared with the experimental data of Achenbach (Reference Achenbach1968) for the circular cylinder with
$\mathit{Re}_{d}=10^{5}$
and the LES results of Giret et al. (Reference Giret, Sengissen, Moreau, Sanjosé and Jouhaud2015) for the rod–airfoil configuration with
$L/d=10$
; moreover, the mean skin friction in this figure is non-dimensional according to the formulation given by Achenbach (Reference Achenbach1968).
To clearly demonstrate the effect of the distance
$L$
on the skin friction of the airfoil, figure 11(b) shows the mean friction distributions on the airfoil surface. It is not surprising to see that the distributions are highly distinguishable at the leading edge with
$L/d=2$
. A similar phenomenon is also identified in the surface pressure distributions shown in figure 10(b). The distinguishable distributions, i.e. the negative mean friction values observed in figure 11(b) are caused by the large separated region in the rod–airfoil configuration with
$L/d=2$
, which is in figure 14. The main vortex separated from the cylinder with negative
$z$
-vorticity entrains the boundary layer and causes early separation at the leading edge with
$L/d=2$
. With increment of the distance
$L$
, the skin friction tends to be indistinguishable. When
$L/d\geqslant 4$
, the skin friction reaches its maximum value at the leading edge, and then drops quickly, furthermore, the maximum skin friction increases as the distance
$L$
is enlarged. This behaviour may correspond to the phenomenon of the influence of the turbulent wake on the airfoil fading gradually as the distance
$L$
increases.
Table 1. The mean and fluctuating integral force for the single cylinder and rod–airfoil system. (a) The calculated mean and fluctuating integral force on the single cylinder compared with experimental data and other numerical results. Here,
$\langle C_{D}\rangle _{t}$
represents the time-averaged drag coefficient,
$\langle C_{L}\rangle _{t}$
denotes the time-averaged lift coefficient and
$C_{Lrms}$
is the r.m.s. of the lift coefficient,
$\mathit{St}$
of the present study is calculated from the figure 13. (b) The force behaviour of the rod–airfoil configuration. Here,
$\langle C_{D\text{-}rod}\rangle _{t}$
represents the time-averaged drag coefficient on the cylinder, as well as
$\langle C_{D\text{-}tol}\rangle _{t}$
,
$\langle C_{L\text{-}tol}\rangle _{t}$
and
$C_{Lrms\text{-}tol}$
are the time-averaged drag coefficient, the time-averaged lift coefficient and the r.m.s. of the lift coefficient for the whole configuration, respectively.
4.1.2. Mean and fluctuating integral force
To assess quantitatively the integral force on the rod–airfoil system, table 1(a) lists the calculated mean and fluctuating integral force on the single cylinder compared with the experimental data and other numerical results, while table 1(b) lists the force behaviour of the rod–airfoil system. There is, in general, a considerable scattering in the results of the force on the cylinder surface, the present solutions however are in good agreement with the experimental data of Szepessy & Bearman (Reference Szepessy and Bearman1992). As the Reynolds number considered here is
$O(10^{5})$
, the pressure force plays a dominant role in the total forces on the cylinder, additionally, the pressure increases in the base region as the distance
$L$
is shortened (see figure 10
a), therefore we can see in table 1(b) that the mean drag of the cylinder falls as the airfoil approaches the cylinder. The drag varys on the whole rod–airfoil system, as shown in table 1(b). The regulation of the drag varying of the is same as that of the cylinder in the configuration when the distance
$L$
increases.
Under the circumstances, it is obvious that the drag of cylinder plays a dominant role in the total drag of the rod–airfoil configuration.
As shown in table 1(b), the mean lift of the rod–airfoil system almost vanishes, however, the instability feature of this configuration can be investigated by the r.m.s. value of the lift fluctuation
$C_{Lrms\text{-}tol}$
. When
$L/d=2$
, the value of
$C_{Lrms\text{-}tol}$
is the lowest of all the five rod–airfoil configurations, and even less than that of a single cylinder, see table 1(a). This demonstrates that the lift fluctuation can be suppressed if the distance
$L$
is very short. According to the analysis above, the total forces are dominated by the surface pressure and it is natural to investigate the lift fluctuation by examining the pressure oscillation on the body surface. Figure 12 shows the distributions of r.m.s. value of the pressure fluctuation on the cylinder and airfoil. The pressure fluctuation on the rod–airfoil configuration with
$L/d=2$
is suppressed, which is consistent with the least lift fluctuation shown in table 1(b). Moreover, it is interesting to find that a hump is shown in the distributions of the pressure fluctuations on the airfoil between
$x/c=0.4$
and 0.8 (see figure 12
b). A similar shape can be observed from the typical vortex-blade interactions in counter-rotating open rotors (e.g. Roger & Carazo Reference Roger and Carazo2010; Carazo, Roger & Omais Reference Carazo, Roger and Omais2011).
Figure 12. Root-mean-square value of pressure fluctuation on the surface of bodies: (a) cylinder and (b) airfoil.
The PSD of the time-dependent lift coefficient of the rod–airfoil and cylinder are shown in figure 13. As exhibited in this figure, the smallest peak value corresponding to the least lift fluctuation given in table 1(b) is obtained by the configuration with
$L/d=2$
. Usually, the force fluctuation on a cylinder is associated with vortex shedding in the wake (e.g. Oertel & Affiliation Reference Oertel and Affiliation1990; Owen & Bearman Reference Owen and Bearman2001), and the power spectral density of the cylinder in figure 13 can be used to identify the frequency of vortex shedding (Xu et al.
Reference Xu, Chen and Lu2010). The primary frequency corresponding to the highest peak for the single cylinder is approximately 0.2. For the configurations with
$L/d\geqslant 4$
, it is interesting to find that the peak value in figure 13 periodically increases and decreases with the distance
$L$
increasing. This behaviour is most likely caused by the fluid resonant oscillations, which will be discussed in § 4.3.2. Furthermore, the
$\mathit{St}$
corresponding to the peak value increases with increments in the distance
$L$
. This feature can be reasonably related to the higher-base-pressure distribution on the cylinder with the shorter distance
$L$
in figure 10(a), and the vortex shedding suppression in the interaction region of
$L/d=2$
, which will be discussed in § 4.2.
Figure 13. Profiles of power spectral density of time-dependent lift coefficient on the rod–airfoil and cylinder. Here, the time-dependent lift coefficients are collected every 10 time steps in the last 20 000 time steps for all the cases.
Based on the above analysis, the force on the surface of the rod–airfoil configuration is affected by the distance
$L$
. In particular, the force is obviously different when
$L/d=2$
. The differences involving surface pressure and friction lead to the reduction of mean and fluctuating forces for the flow past the rod–airfoil configuration. The distance
$L$
may also have an effect on the flow structures and we thus pay more attention to the relevant flow characteristics in the next section.
4.2. Flow structures and turbulent fluctuations
Despite the complexity associated with a turbulent wake and two bodies, the dynamics of the flow in the present cases are largely determined by the interaction in the region between the cylinder and airfoil. In this section, we investigate the flow features in the interference region by first looking into the flow structures based on the time-averaged quantities. Then, the interference flow patterns are discussed using the instantaneous quantities. Finally, based on the statistical quantities, we will proceed to study the turbulent fluctuations and their suppression.
4.2.1. Mean flow structures in the interference region
We investigate the mean flow structures by first examining the vorticity consisting of the streamwise
${\it\omega}_{x}$
, vertical
${\it\omega}_{y}$
and spanwise
${\it\omega}_{z}$
vorticity. The time-averaged
${\it\omega}_{y}$
becomes zero because of the periodic boundary condition applied in the spanwise direction. The increasing vertical gradients of the streamwise
$u$
and spanwise
$w$
velocity, together with the gradients of vertical velocity
$v$
in the horizontal
$(x,z)$
-plane, give rise to a streamwise
${\it\omega}_{x}$
and spanwise
${\it\omega}_{z}$
vorticity. It is important to note that these two quantities will appear in the instantaneous turbulent flow field, but in the present cases, the time-averaged quantity
${\it\omega}_{x}$
is negligible compared with that of
${\it\omega}_{z}$
.
Time-averaged spanwise vorticity
${\it\omega}_{z\text{-}mean}$
together with the corresponding streamlines projected onto the
$(x,y)$
-plane in the interference region for
$L/d=2$
and
$L/d=4$
are shown in figure 14. Clearly, two counter-rotating vortices evolve along the axis of the cylinder. The mean streamlines are symmetric about the horizontal center-line, whereas the
${\it\omega}_{z\text{-}mean}$
contours exhibit an antisymmetry. Visualizations of the flow field in the interference region have revealed that at short enough distances, the Kármán-street type of shedding is replaced by a non-shedding mode (see e.g. Munekata et al.
Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006), with two counter-rotating vortices with opposite circulation connecting to each side of the leading edge of the airfoil. In the non-shedding mode, the negative mean friction values are observed at the leading edge (see figure 11
b) due to the main vortex separated from the cylinder with a negative
$z$
-vorticity connecting to the airfoil. Kármán-street shedding is also observed in the other three cases. Two patterns which will be further discussed in § 4.2.2 are then outlined: Kármán-street shedding for the long distances and Kármán-street suppressing for the short distances.
Figure 14. Time-averaged spanwise vorticity and streamlines in the interaction region taken from the flow field with
$U_{\propto }=72~\text{m}~\text{s}^{-1}$
,
$Re_{d}=4.8\times 10^{4}$
,
$L/d=2$
(a) and
$L/d=4$
(b).
Due to the fact that counter-rotating vortices are connected to the airfoil, the distributions of
${\it\omega}_{z\text{-}mean}$
for
$L/d=2$
are evidently different from those of other cases at the leading edge of the airfoil. This also explains why the distributions of pressure and friction, shown in figures 10(b) and 11(b) respectively, are obviously distinguishable on the surface of the airfoil for
$L/d=2$
. When the cylinder is set away from the airfoil, the counter-rotating vortices with opposite circulation emanate from each side of the cylinder and do not touch the airfoil. The interaction is relatively weak between the turbulent wake and airfoil, reasonably related to the fact that the distributions of mean friction tend to be identical on the surface of the cylinder (see figure 11
a) and the leading edge of the airfoil (see figure 11
b).
Figure 15(a) shows the contours of time-averaged streamwise velocity
$u_{m}$
in the interference region, where the counter-rotating vortices connecting with the leading edge of airfoil lead to negligible or negative values of
$u_{m}$
for the case of
$L/d=2$
; the flow behind the counter-rotating vortices is accelerated until it impinges on the leading edge of airfoil for the cases with
$L/d\geqslant 4$
(the other three cases are not shown in figure 15
a). The phenomena exhibited in this figure can be explained by the fact that in this interaction region, the flow is the result of two tendencies. The influence of the airfoil on the steady flow tends to accelerate it, whilst the counter-rotating vortices are connected with the leading edge of airfoil due to the approaching cylinder, which tends to slow the flow down.
Figure 15. Contours of time-averaged velocity taken from the flow field with
$U_{\propto }=72~\text{m}~\text{s}^{-1}$
,
$Re_{d}=4.8\times 10^{4}$
,
$L/d=2$
(a,c) and
$L/d=4$
(b,d). (a,b) Streamwise component
$u_{m}$
; (c,d) vertical component
$v_{m}$
, here solid lines denote positive values and dashed lines negative ones.
Figure 16. The r.m.s. value of streamwise velocity taken from the flow field with
$U_{\propto }=72~\text{m}~\text{s}^{-1}$
,
$Re_{d}=4.8\times 10^{4}$
,
$L/d=2$
(a) and
$L/d=4$
(b).
In figure 15(b), we plot the contours of time-averaged vertical velocity
$v_{m}$
for
$L/d=2$
and
$L/d=4$
. It can be seen that the positive
$v_{m}$
presents below the leading edge of the airfoil with
$L/d=2$
, and the negative one is observed above. However, the contrary distribution is shown in this region with
$L/d=4$
. When the incoming flow approaches the upper part of the leading edge of the airfoil with
$L/d=2$
, it experiences the downdraft depicted by the contours of
$v_{m}$
(see also the streamlines in figure 14), which produces negative horizontal gradients in
$v_{m}$
in this region, thereby giving rise to the negative
${\it\omega}_{z\text{-}mean}$
. The positive one however is generated symmetrically about the center-line, as illustrated by the contours of
${\it\omega}_{z\text{-}mean}$
in figure 14.
Finally, the contours of r.m.s. value of streamwise velocity
$u_{rms}$
are plotted in figure 16 for
$L/d=2$
and
$L/d=4$
. It can be seen that the
$u_{rms}$
values of
$L/d=2$
behind the cylinder and near the central line
$y=0$
are much lower than those of
$L/d=4$
. This phenomenon is consistent with the fact that the non-shedding mode is observed in the rod–airfoil configuration with
$L/d=2$
, and the negligible or negative
$u_{m}$
generated in the interaction region (see figure 15
a) is caused by the main separated vortices connecting to the airfoil (see figure 14) in this case. It is expected that the turbulent fluctuations in the interaction region of
$L/d=4$
are much more intensive than those of
$L/d=2$
, and the underlying reason will be further discussed in § 4.2.3 for the generation of lower-level turbulent fluctuations in the rod–airfoil configuration with
$L/d=2$
.
Figure 17. Vortical structures by iso-surface of the
$Q$
-criterion (
$Q=1000$
). The instantaneous vertical velocity
$v$
at the symmetry
$x,z$
-plane
$(y=0)$
is included to highlight the alternating pattern of the main vortices. (a) Taken from the flow field with
$U_{\propto }=72~\text{m}~\text{s}^{-1}$
,
$Re_{d}=4.8\times 10^{4}$
,
$L/d=2$
; (b)
$L/d=4$
; (c)
$L/d=6$
; (d)
$L/d=8$
; (e)
$L/d=10$
.
4.2.2. Instantaneous flow structures and interference flow patterns
Figure 17 shows instantaneous snapshots of the flow field depicted by iso-surface of the
$Q$
criterion (Jeong & Hussain Reference Jeong and Hussain1995)
$$\begin{eqnarray}Q=({\it\Omega}_{ij}{\it\Omega}_{ij}+\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij})/2,\end{eqnarray}$$
where
${\it\Omega}_{ij}=(u_{i,j}-u_{j,i})/2$
and
$\unicode[STIX]{x1D61A}_{ij}=(u_{i,j}+u_{j,i})/2$
are the antisymmetric and the symmetric components of the curl of the velocity, respectively. A positive value of
$Q$
represents the regions in which the rotation exceeds the strain. It should be recalled that the criterion (4.1) is only applied to the resolved scales obtained by the HILES and that the vortical structures could be different if the whole flow field is considered. It can be seen that the vortices in the rod wake impinge onto the airfoil, and then partly split at the leading edge. The flow topology exhibits two different patterns in the interaction region depicted by figure 17. The first one observed in this region with
$L/d=2$
includes only the primary vortical structures, roughly oriented along the axis of the cylinder. These primary structures originate from the rolling-up of the detached shear layers at each side of the cylinder. The other one presented by the rod–airfoil configuration with
$L/d=4,6,8$
and 10 comprises both the primary vortical structures and also secondary vortical structures, exhibiting a wide range of scales and orientations. These secondary structures come from the Kármán-street vortex shedding. For rod–airfoil configurations, Munekata et al. (Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006) also observed two flow patterns. In the first, the Kármán-street is not generated for a short enough distance
$L$
, whereas in the other, the Kármán vortex is steadily generated for a long distance
$L$
. Based on this observation, the authors suggested that changing the distance
$L$
led to the flow pattern altering. In figure 17, the instantaneous vertical velocity
$v$
, highlighting the alternating pattern of the main vortices, indicates that two flow patterns exist in the present study, supporting the observation made by Munekata et al. (Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006) who observed the pattern dependence of the interference flow on the distance
$L$
.
Figure 18. Juxtapositional view of the unsteady spanwise vorticity
${\it\omega}_{z}$
of vertical
$(x,y)$
-planes taken from the flow field of five rod–airfoil configurations at the central slice
$z=0.015~\text{m}$
of the computational domain.
Based on the discussion above, a possible categorization for the flow patterns associated with the interference region is given as follow: (i) for
$L/d\leqq 2$
, there is the Kármán-street suppressing mode. The eddies propagate downstream without being shed in this mode. In the present study, the Kármán-street is not generated by the free shear layers separated from the upstream cylinder in the interference region with
$L/d=2$
; (ii) for
$L/d\geqslant 4$
, Kármán-street occurs. This is classified as the Kármán-street shedding mode and occurs in the present study at
$L/d=4,6,8$
and 10. As the Reynolds number considered here is large enough, the eddies arise from the rolling-up of the shear layers at an almost fixed position and the vortex shedding then occurs when one eddy becomes strong enough to cut the opposite eddy from the supply of the circulation from the shear layer (Zdravkovich Reference Zdravkovich1997), furthermore, the distance
$L$
is too long to suppress the vortex shedding in the interaction region; (iii) for
$2<L/d<4$
, the altering mode may exist. This flow pattern is not observed in the present study, however, it has been reported by Munekata et al. (Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006) that the two flow patterns, i.e. Kármán-street shedding mode and Kármán-street suppressing mode alternate at aperiodic time intervals when
$L/d=3.1$
.
A different illustration of the instantaneous flow structures in the interaction region is given by the snapshots of the spanwise vorticity
${\it\omega}_{z}$
in the
$(x,y)$
-plane, shown in figure 18. This component of the vorticity complements the
$Q$
-iso-surfaces by enabling the visualization of the shear layers that detach from both sides of the cylinder and their further roll-up to form primary vortices, as well as the turbulent wake impinging onto the airfoil and then partly splitting at the leading edge. In the latter process, the turbulent wake containing Kármán-street shedding is clearly seen in all the vertical planes in figure 18, with the exception for the case of
$L/d=2$
, suggesting that with reducing distance
$L$
, the shear layer is less susceptible to rolling up.
In figure 18, the four vorticity planes with
$L/d\geqslant 4$
exhibit in the interaction region a clear Kármán-street shedding. Due to entrainment of free stream fluid, this turbulent wake expands as it evolves downstream until it hits the leading edge of the airfoil. For
$L/d=2$
, however, the Kármán-street shedding in the interaction region seems to be suppressed due to the short distance
$L$
. These observations suggest that vortex shedding in the present cases is influenced by the distance
$L$
between the two bodies. It is obvious that the wake from the cylinder upstream is blocked by the airfoil downstream. The blocking effect is minor for long distances between the two bodies, but becomes more evident at short distances, which may lead to the base pressure rising abnormally on the cylinder upstream (see figure 10
a). It is natural to assume that the blocking effect takes main responsibility for the Kármán-street suppression in the rod–airfoil configuration.
4.2.3. Turbulent fluctuations and their suppression
The turbulent fluctuations around a body are closely associated with the fluctuating forces exerted on it (Wu, Lu & Zhuang Reference Wu, Lu and Zhuang2007). To describe the turbulent fluctuations around the rod–airfoil configurations, the iso-contours of spanwise averaged mean value of turbulent-kinetic-energy (TKE), i.e.
$\text{TKE}_{m}$
, are shown in figure 19. The
$\text{TKE}_{m}$
is relatively smaller in the region around the airfoil with
$L/d=2$
. This feature leads to correspondingly lower fluctuating surface pressure (see figure 12
b). Moreover, the suppression of the turbulent fluctuations is also observed in the interaction region.
Figure 19. The iso-contours of spanwise averaged mean value of TKE. (a) taken from the flow field with
$L/d=2$
; (b)
$L/d=4$
; (c)
$L/d=6$
; (d)
$L/d=8$
; (e)
$L/d=10$
.
Additionally, the profiles of
$\text{TKE}_{m}$
in the interaction region along the line of symmetry of the cylinder are shown in figure 20. From the distribution behind the cylinder with
$L/d=2$
, the
$\text{TKE}_{m}$
is significantly lower in the range of approximately
$x/c<0.1$
, and increases gradually because of the development of primary vortical structures, reaching a peak value in the range of approximately
$x/c=0.15$
. It then falls as the wake propagates downstream, finally undergoing a severe jump and gaining a maximal value since the vortices in turbulent wake impinge onto the airfoil and partly split at the leading edge. It is expected in figure 20 that the reduction and jump are also present in the distributions of
$\text{TKE}_{m}$
from the flow fields with
$L/d=4,6,8,10$
. However, it may be noted that in these distributions, the maximal value of
$\text{TKE}_{m}$
is not observed after the significant jump, but is exhibited at the first peak. This difference indicates that the suppression is associated with the primary vortical structures.
Figure 20. Profiles of
$\text{TKE}_{m}$
in the interaction region along the symmetry line of the cylinder.
To understand the characteristics relating to the suppression of turbulent fluctuations of the rod–airfoil configuration with
$L/d=2$
, we analyse the underlying reason for the generation of higher-level turbulent fluctuations in the other four cases. As shown in figure 17, for the configuration with
$L/d=4,6,8,10$
, the vortex shedding occurs when one eddy becomes strong enough to cut the opposite eddy off from the supply of the circulation from the shear layer, and the formed vortex is released into the wake. The flow structures appear to be stronger in the vortex formation region which corresponds approximately to the location of the primary vortex. This observation is consistent with numerical simulation of a turbulent wake behind a curved circular cylinder (Gallardo et al.
Reference Gallardo, Andersson and Pettersen2014), and correspondingly, the maximal value of turbulent fluctuations is present at this location (see figure 20). Further downstream, but before the airfoil, the size of the structures tends to increase as their concentration decreases, this behaviour is related to the varying of
$\text{TKE}_{m}$
in figure 20 which goes down until the blocking effect is met, also consistent with the report of Mansy, Yang & Williams (Reference Mansy, Yang and Williams1994) that the amplification of the larger scales and attenuation of the smaller scales occur as the wake propagates downstream. The shedding wake containing massive turbulent fluctuations requires impingement onto the airfoil to create the second peak of turbulent fluctuations. The larger before the impact the
$\text{TKE}_{m}$
is, the higher the second peak is, as shown in figure 20. It is clear that the primary vortex shedding and the shedding wake impingement onto the airfoil play a dominant role in the production of turbulent fluctuations. However, for the case of
$L/d=2$
, primary vortex shedding is suppressed, correspondingly, the intensity of impingement is weakened, resulting in a significant suppression of the turbulent fluctuations.
4.3. Acoustic analysis and fluid resonant oscillation
4.3.1. Acoustic analysis
From the preceding analysis of the flow structures and turbulent fluctuations, it is reasonably well understood that the distance
$L$
plays an important role in the flow features relevant to the flow pattern altering and the turbulent fluctuations being suppressed. The flow features are closely associated with the noise radiation. We further analyse the influence of distance
$L$
on the noise radiation.
For rod–airfoil configurations with
$L/d=6$
and
$L/d=8$
, figure 21 shows the comparison between the overall SPLs (OASPLs) calculated directly from the HILES solutions and provided by the FW-H analogy to complement the verification with respect to the acoustics outcome. The OASPLs on the line
$y=0.4~\text{m}$
are chosen to ensure the mesh resolution is fine enough for the HILES with the HDCS-E8T7 capturing the acoustic noise. Although small differences are observed between the two results, the same varying trend of the OASPLs is predicted by the two methods. In the following, we will apply the FW-H analogy to discuss the acoustic behaviour in the far-field.
Figure 21. Comparison between the OASPLs calculated directly from the HILES solutions and provided by the FW-H analogy on the line
$y=0.4~\text{m}$
for the configuration with
$L/d=6$
and
$L/d=8$
.
Figure 22. Directivities for the OASPL of the rod–airfoil configurations at
$1.85~\text{m}$
. Here, the location for the observation angle 0 is
$x=1.85~\text{m},y=0$
.
Figure 23. The SPL spectra at the location
$(x=0.68~\text{m},y=1.74~\text{m})$
for all the five rod–airfoil configurations.
In order to show the dominant noise radiation directions of different configurations, figure 22 plots the directivities of OASPL at
$1.85~\text{m}$
for all five rod–airfoil configurations. It is clear that the dominant noise radiation directions are between the observation angles of 60° and 90°. For a further investigation of the noise radiation in the dominant radiation direction, figure 23 shows the SPL spectra at the location
$(x=0.68~\text{m},y=1.74~\text{m})$
, i.e. the observation angle 70° for all the five rod–airfoil configurations. Although a relatively narrow range around the peak frequency of the noise spectra is presented in this figure, it is clearly observed that the noise spectra is separated into two different types. The first one is a broadband noise without a manifestly distinguishable peak, which is radiated by the rod–airfoil configuration with
$L/d=2$
. The second type is present when
$L/d\geqslant 4$
. With a dominant peak, the broadband noise and the tonal noise are exhibited simultaneously in this type. Moreover, the levels of the peaks in the second type are much higher than that in the first, which is not surprising since the noise radiation in the far-field is closely associated with the flow features in the near-field. As reported by Boudet et al. (Reference Boudet, Grosjean and Jacob2005), the interaction between the wake from the cylinder upstream and the airfoil downstream is mainly responsibile for the noise radiation of the rod–airfoil configuration. In particular, the spectrum of a single cylinder may be approximately 10 dB lower than that of the rod–airfoil system (Jacob et al.
Reference Jacob, Boudet, Casalino and Michard2005), which is also supported by the observation of Munekata et al. (Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006). Based on the discussion of flow features above, vortex shedding is suppressed for a very short distance
$L/d=2$
, leading to significant suppression of the pressure fluctuations and the turbulent fluctuations, as well as the weakening of the impingement intensity. Thus, the lower levels of noise are observed for the rod–airfoil configuration with
$L/d=2$
.
To exhibit the influence of the distance
$L$
on the peak frequency of the radiative noise, a peak Strouhal number,
$\mathit{St}_{p}$
, is analysed as performed by Munekata et al. (Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006) and is defined as
$\mathit{St}_{p}=f_{p}d/U_{\infty }$
, where
$f_{p}$
represent the peak frequency given in figure 23. Quantitatively, compared with the primary frequency of the vortex shedding behind a single cylinder, represented by the
$\mathit{St}$
which is calculated from the PSD of the time-dependent lift coefficient (see figure 13), the
$\mathit{St}_{p}$
s of all the rod–airfoil configurations are linked to form a line are and plotted in figure 24 with a exception of the case of
$L/d=2$
, in which there is no manifestly distinguishable peak frequency. The
$\mathit{St}_{p}$
increases with the distance
$L$
increasing, finally approaching the primary frequency of the single cylinder, supporting the observation made by Munekata et al. (Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006) who observed the peak frequency dependence of the noise radiation on
$L/d$
. This feature may be reasonably related to the higher-base-pressure distribution on the cylinder with shorter distance
$L$
in figure 10(a), and vortex shedding suppressing in the interaction region in figure 17.
Figure 24. Effect of
$L/d$
on
$\mathit{St}$
based on peak frequency.
4.3.2. Fluid resonant oscillation
The fluid resonant oscillation within the flow interaction between the turbulent wake from a cylinder and the bodies have been observed in previous studies (e.g. Mochizuki et al.
Reference Mochizuki, Kiya, Suzuki and Arai1994). This feature is usually associated with the impingement of the turbulent wake onto the surface of the body and a feedback loop system (e.g. Mochizuki et al.
Reference Mochizuki, Kiya, Suzuki and Arai1994; Fitzpatrick Reference Fitzpatrick2003; Munekata et al.
Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006). The fluid resonant oscillation means that the vortex generation in the rod–airfoil configuration is promoted by the acoustic field induced from the wake interference between the shedding vortex behind the cylinder upstream and the airfoil downstream (Munekata et al.
Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006). In the quantitative observation made by Munekata et al. (Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006), it was found that the peak SPL depended on
$L/d$
, and increases and decreases periodically, relating to the fluid resonant oscillation. Mochizuki et al. (Reference Mochizuki, Kiya, Suzuki and Arai1994) also observed the fluid resonant oscillation in the configuration of two circular cylinders in tandem, and these authors proposed a model to describe the feedback loop system as illustrated in figure 25. According to this feedback model (Mochizuki et al.
Reference Mochizuki, Kiya, Suzuki and Arai1994), the feedback frequency
$f_{f}$
, defined by the inverse of time taken to feed back for one loop, and is described by the following equation:
$$\begin{eqnarray}f_{f}=\frac{1}{L_{f}/U_{c}+L_{f}/c},\end{eqnarray}$$
where
$L_{f}$
represents the characteristic length of feedback loop,
$U_{c}$
is the convective velocity of shedding vortex and
$c$
is the speed of sound. If the constraint
$f_{p}=nf_{f}$
is satisfied, the effect of fluid resonant oscillation becomes stronger. Here,
$n$
is a positive integer.
Figure 25. Schematic diagram of feedback system for fluid resonant oscillation.
Figure 26. The peak SPL and OASPL for the second type of noise spectra.
As shown in figure 23, there are two types of noise spectra due to the varying of the distance
$L$
. The first one is caused by the flow features related to vortex shedding suppression in the interaction region. Regarding the second one, although a similar dominant peak is present in this type of noise spectra, the value of the dominant peak varies periodically. To show this varying regularity clearly, figure 26 plots the peak SPL and OASPL for the second type of noise spectra exhibited in figure 23. The periodic increasing and decreasing of the peak SPL and OASPL are clearly exhibited in this figure and are similar to the phenomenon of fluid resonant oscillation observed by Munekata et al. (Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006). It should be noted that the regulation of the peak SPL from all the five rod–airfoil configurations in the dominant noise radiation directions, i.e. between an observation angle of 60° and 90° is similar to that at the observation angle of 70°, however, in the other directions, this regulation is not observed.
Based on the above analysis, we suggest that fluid resonant oscillation is observed in the present study. To further describe the fluid resonant oscillation, the feedback model (4.2) is adopted to analyse this phenomenon. The characteristic length
$L_{f}$
in (4.2) is reasonably well given by the horizontal distance between the leading edge and the mean separation location on the cylinder surface, corresponding to the resolved skin friction stress vanishing (Munekata et al.
Reference Munekata, Kawahara, Udo, Yoshikawa and Ohba2006), and can be determined from the figure 11(a). The values of
$L_{f}$
are listed in table 2 for
$L/d=4,6,8$
and 10, respectively.
Table 2. The corresponding parameters of the feedback model for fluid resonant oscillation.
We here deal with the convective velocity of the shedding vortex, which is used in the feedback model of the fluid resonant oscillation. Two-point cross-correlation of the unsteady pressure can be used to quantitatively determine the propagation speed of the pressure disturbances along a given path (Xu et al.
Reference Xu, Chen and Lu2010). A covariance coefficient
$C_{ij}$
for two pressure signals
$p_{i}(t)$
and
$p_{j}(t)$
with time delay
${\it\tau}$
can be defined as
$$\begin{eqnarray}C_{ij}({\it\tau})=\frac{\left\langle (p_{i}(t)-\langle p_{i}\rangle _{t})(p_{j}(t-{\it\tau})-\langle p_{j}\rangle _{t})\right\rangle _{t}}{\left\langle (p_{i}(t)-\langle p_{i}\rangle _{t})^{2}(p_{j}(t)-\langle p_{j}\rangle _{t})^{2}\right\rangle _{t}},\end{eqnarray}$$
where
$\langle ~\rangle _{t}$
denotes time average. Within the interaction region, the cross-correlation analysis is conducted for probes A and B shown in figure 25 and the results are given in figure 27. Positive time delays are obtained, indicating that the pressure disturbances within the interaction region propagate downstream toward the airfoil leading edge. The convective velocity of the shedding vortex
$U_{c}$
can then be calculated by dividing the horizontal distances between the neighbouring probes by the time delays between the peaks of the corresponding cross-correlations. Due to the differences of the grid point distributions, the horizontal distances between the probes A and B, i.e.
$L_{AB}$
may be different. For
$L/d=4$
,
$L/d=6$
,
$L/d=8$
and
$L/d=10$
, the values of
$L_{AB}$
are listed in table 2, where the corresponding speed
$U_{c}$
and the calculated feedback frequency
$f_{f}$
are also presented.
Figure 27. Cross-correlation of the downstream propagating pressure waves for (a)
$L/d=4$
; (b)
$L/d=6$
; (c)
$L/d=8$
and (d)
$L/d=10$
.
Figure 28 shows the relation between
$f_{p}$
and
$f_{f}$
for the four different interaction distances. When
$L/d=6$
and 10, the exhibited data are periodically close to the solid lines, which means that the effect of fluid resonant oscillation becomes stronger. This behaviour corresponds to the periodic change of the peak SPL and OASPL shown in figure 26. We recognize the limitations of the simplified analysis of the fluid resonant oscillation based on the feedback model; nevertheless, the results obtained from the model are of help in understanding the physical mechanism of the fluid resonant oscillation involved in this flow.
Figure 28. The relation between
$f_{p}$
and
$f_{f}$
for the four different interaction distances. Here, the solid lines mean the equation of resonant condition.
5. Concluding remarks
Numerical investigation on body-wake interaction was carried out by means of the HILES for flow over five rod–airfoil configurations with the incoming velocity
$U_{\infty }=72~\text{m}~\text{s}^{-1}$
, a Reynolds number based on the airfoil chord
$4.8\times 10^{5}$
and interaction distances
$L/d=2$
, 4, 6, 8 and 10. Due to the varying of the distance
$L$
, two flow patterns have been observed associated with the interference region, i.e. the Kármán-street suppressing mode for
$L/d=2$
and the Kármán-street shedding mode for
$L/d=4,6,8$
and 10 in the present study.
In the Kármán-street suppressing mode, the flow in the interaction region has two opposite tendencies: the influence of the airfoil on the steady flow is to accelerate it; the counter-rotating vortices connecting with the leading edge of airfoil tend to slow the flow down. Moreover, the forces exerted on the bodies, the flow structures and turbulent fluctuations as well as the noise radiation are closely associated with each other. Due to the blocking effect, the base pressure rises abnormally on the cylinder upstream, furthermore, the high base pressure leads to that von Kármán vortex shedding suppression in the region between the cylinder upstream and the airfoil downstream, correspondingly, the intensity of impingement is weakened, resulting in the significant suppression of the turbulent fluctuations and the pressure fluctuations. The obviously lower levels of noise are observed for this rod–airfoil configuration because of the significant suppression of the pressure fluctuations and the turbulent fluctuations, as well as the weakening of the impingement intensity.
In the Kármán-street shedding mode, vortex shedding occurs, and the distance
$L$
is too long to suppress the vortex shedding in the interaction region. Large velocity fluctuations and turbulent fluctuations are generated by the primary vortex shedding and the shedding wake impinging onto the airfoil. The broadband noise and tonal noise with a dominant peak are exhibited simultaneously in the SPL spectra. The value of the dominant peak varies periodically in the dominant noise radiation directions, which is recognized as a phenomenon caused by the fluid resonant oscillation within the flow interaction between the turbulent wake and the bodies. Based on the feedback model proposed by Mochizuki et al. (Reference Mochizuki, Kiya, Suzuki and Arai1994) and the pressure signal in the flow field, the fluid resonant oscillation has been further investigated, and it is confirmed that the effect of fluid resonant oscillation becomes stronger when
$L/d=6$
and 10, corresponding to the periodic change of the peak SPL and OASPL observed in the present study.
Due to the lack of data for further analysis, it cannot be determined that there is a transitional flow pattern before the Kármán-street shedding mode and after the Kármán-street suppressing mode. It would have required further simulations to reveal the flow pattern for the interaction distance
$2<L/d<4$
. Even if the hump of the pressure fluctuation distributions on the airfoil is recognized as a typical phenomenon caused by body-wake interaction, more efforts are required to clarify the effect of the body-wake interaction on the airfoil. In addition, further investigations are expected to show the sensitivity of the solution to the grid resolution and the FW-H surface type, location and shape.
Acknowledgements
The authors are very grateful to the anonymous referees for their significant and detailed comments as well as very helpful suggestions made by Professor L. P. Zhang in China Aerodynamics Research and Development Center. This study was supported by the National Natural Science Foundation of China (grant nos 11372342 and 11202226).
