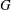1. Introduction
Thermoacoustic oscillations occur due to feedback between heat release rate fluctuations and acoustic pressure fluctuations in confined spaces. The mechanisms that cause unsteady heat release rate fluctuations are described in Lieuwen (Reference Lieuwen2012). In gas turbine combustion systems, the acoustics can be treated linearly, even for acoustic velocity fluctuations comparable to the mean flow velocity, because the perturbation Mach number remains small (Dowling Reference Dowling1997). In such thermoacoustic systems, therefore, the behaviour of the flame’s heat release rate is the dominant source of nonlinearity.
The onset of thermoacoustic oscillations is well understood using linear theories, but the subsequent nonlinear behaviour is poorly understood. Nonlinear thermoacoustics may be analysed in either the frequency or time domains. Most studies of nonlinear thermoacoustics are in the frequency domain. These studies assume a priori that the oscillations are periodic, with a dominant frequency and a fixed amplitude (Poinsot & Candel Reference Poinsot and Candel1988; Dowling Reference Dowling1997; Noiray et al. Reference Noiray, Durox, Schuller and Candel2008). Recent experiments, however, reveal that even simple thermoacoustic systems exhibit nonlinear behaviour that can be far more elaborate than period-1 limit cycle oscillations (Kabiraj et al. Reference Kabiraj, Saurabh, Wahi and Sujith2012; Kabiraj & Sujith Reference Kabiraj and Sujith2012a ,Reference Kabiraj and Sujith b ). By varying a control parameter in their thermoacoustic system, consisting of an axisymmetric laminar conical flame in a duct, Kabiraj et al. show that the system undergoes several bifurcations resulting in quasi-periodic, frequency-locked or period-k, and chaotic oscillations (Kabiraj & Sujith Reference Kabiraj and Sujith2012a ). Experiments in large industrial-scale thermoacoustic systems by Gotoda et al. (Reference Gotoda, Nikimoto, Miyano and Tachibana2011, Reference Gotoda, Amano, Miyano, Ikawa, Maki and Tachibana2012, Reference Gotoda, Shinoda, Kobayashi, Okuno and Tachibana2014) show that, as the equivalence ratio increases, the thermoacoustic behaviour undergoes a transition from stochastic fluctuations to periodic oscillations through low-dimensional chaotic oscillations, revealing similarly elaborate nonlinear behaviour.
A few studies of nonlinear thermoacoustics are in the time domain. These studies do not assume a priori that the system reaches period-1 oscillations (Culick Reference Culick1971; Margolis Reference Margolis1993; Sterling Reference Sterling1993; Jahnke & Culick Reference Jahnke and Culick1994; Lei & Turan Reference Lei and Turan2009; Stow & Dowling Reference Stow and Dowling2009). These studies show that the influence of harmonics and the interaction between different modes can be modelled with the time-domain approach. Some recent studies use approaches from dynamical systems theory to extract information about thermoacoustic oscillations in turbulent environments that is beyond the reach of conventional approaches (Nair & Sujith Reference Nair and Sujith2013; Nair et al. Reference Nair, Thampi, Karuppusamy, Gopalan and Sujith2013). Many of these studies, however, are limited by the assumption that the unsteady heat release rate is a simple, often polynomial, function of the pressure or velocity fluctuations. This assumption is unrealistic because the heat release rate of flames depends not only on the instantaneous acoustic pressure or velocity, but also on the integrated effect of historical values (Hemchandra & Lieuwen Reference Hemchandra and Lieuwen2010). Therefore, simple analytical descriptions of heat release rate that do not account for memory effects cannot capture the complexities of unsteady flame dynamics.
In this study, therefore, we combine a more realistic flame model with simple duct acoustics and do not assume a priori that the system reaches a period-1 oscillation. The system consists of a slot-stabilized two-dimensional premixed flame in an open duct. We study the nonlinear behaviour using numerical simulations of the coupled nonlinear dynamical system in the time domain. This thermoacoustic system resembles the system that has recently been investigated experimentally by Kabiraj et al. but differs in that we use a two-dimensional slot-stabilized flame and not an axisymmetric one (Kabiraj & Sujith Reference Kabiraj and Sujith2012a ). The aims of this study are: (i) to use techniques and well-established results from dynamical systems theory and nonlinear time-series analysis to characterize the nonlinear behaviour of this system, and (ii) to use instantaneous flame images of the different types of oscillation to interpret the elaborate nonlinear behaviour of this system.
In § 2 we describe the nonlinear kinematic model of the premixed flame, which is based on the
$G$
-equation, and the acoustics, which are governed by linearized momentum and energy equations. In § 3 we identify the bifurcations of this system due to variations of: (i) the flame position in the duct, which changes the amplitude and the frequency content of the acoustic perturbations at the flame, (ii) the length of the duct, which changes the natural acoustic frequencies of the system, and (iii) the mean flow velocity, which changes the flame geometry. We also examine the influence that the number of coupled acoustic modes has on these bifurcations. In § 4 we show instantaneous flame images of different types of oscillation and examine the flame wrinkling and pinch-off behaviour of each type of oscillation. In § 5 we characterize the states of the system using power spectra, phase portraits, Poincaré sections and correlation dimensions. In § 6 we highlight the role of unstable attractors in the trajectory of the system from its initial condition to its final stable state. In § 7 we identify two routes to chaos seen in this system: the period-doubling route and the Ruelle–Takens–Newhouse route. We show the sequence of steps in these routes to chaos using Poincaré sections and power spectra and we find the maximal Lyapunov exponents of the final chaotic states. In § 8 we discuss the implications of this elaborate nonlinear behaviour for the prediction of thermoacoustic oscillations.
2. The models and their governing equations
2.1. Model for the acoustics
In this study we consider a duct of length
$L_{0}$
open at both ends with a two-dimensional slot-stabilized laminar premixed flame located at a distance
$\tilde{x}_{f}$
from one end. Figure 1 shows a diagram of the system. The ratio of the area of the slot burner to the cross-sectional area of the duct,
${\it\alpha}$
, is taken to be 0.2. The base flow velocity is
${\tilde{u}}_{0}$
, the pressure is
$\tilde{p}_{0}$
and a constant mean density assumption is invoked, so that the mean density,
$\tilde{{\it\rho}}_{0}$
, and speed of sound in the unburnt mixture,
$\tilde{c}_{0}$
, remain constant everywhere in the duct. The Mach number,
$M\equiv {\tilde{u}}_{0}/\tilde{c}_{0}$
, is assumed to be small, and therefore nonlinear effects in the acoustics are negligible (Dowling Reference Dowling1997). The acoustics can be treated linearly even for large acoustic velocity fluctuations because the perturbation Mach number remains small (Dowling Reference Dowling1997). We assume that the flame length is small compared to the wavelengths of the duct’s acoustic modes. The governing equations in dimensional and non-dimensional form have been described in detail in previous studies that have used the same acoustic model (Matveev Reference Matveev2003; Balasubramanian & Sujith Reference Balasubramanian and Sujith2008; Juniper Reference Juniper2011; Subramanian & Sujith Reference Subramanian and Sujith2011; Kashinath, Hemchandra & Juniper Reference Kashinath, Hemchandra and Juniper2013a
,Reference Kashinath, Hemchandra and Juniper
b
).
Figure 1. Diagram of the two-dimensional slot-stabilized premixed flame in a duct. Here
$L_{0}$
is the length of the duct,
$\tilde{x}_{f}$
is the flame position along the duct,
${\it\alpha}=0.2$
is the fraction of the duct cross-sectional area occupied by the burner and the flow is from left to right.
The dimensional governing equations for the acoustic perturbations are the momentum and energy equations,
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{{\it\rho}}_{0}\frac{\partial {\tilde{u}}}{\partial \tilde{t}}+\frac{\partial \tilde{p}}{\partial \tilde{x}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial \tilde{p}}{\partial \tilde{t}}+{\it\gamma}\tilde{p}_{0}\frac{\partial {\tilde{u}}}{\partial \tilde{x}}+{\it\zeta}\frac{\tilde{c}_{0}}{L_{0}}\tilde{p}-({\it\gamma}-1)\tilde{\dot{Q}}\,{\it\delta}(\tilde{x}-\tilde{x}_{f})=0, & \displaystyle\end{eqnarray}$$
$\tilde{\dot{Q}}$
, which is applied at the flame’s position by multiplying
$\tilde{\dot{Q}}$
by the dimensional Dirac delta distribution
$\tilde{{\it\delta}}(\tilde{x}-\tilde{x}_{f})$
. The acoustic damping is represented by
${\it\zeta}$
, and the model for this is described later.
The above equations may be non-dimensionalized using
${\tilde{u}}_{0}$
,
$\tilde{p}_{0}{\it\gamma}M$
,
$L_{0}$
and
$L_{0}/\tilde{c}_{0}$
for speed, pressure, length and time, respectively. The dimensionless governing equations are
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial u}{\partial t}+\frac{\partial p}{\partial x}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial p}{\partial t}+\frac{\partial u}{\partial x}+{\it\zeta}p-{\it\beta}\dot{Q}\,{\it\delta}_{D}(x-x_{f})=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\beta}\equiv \frac{({\it\gamma}-1)\tilde{\dot{Q}}_{0}{\it\alpha}}{{\it\gamma}\tilde{p_{0}}\tilde{u_{0}}},\quad \dot{Q}\equiv \frac{\tilde{\dot{Q}}}{\tilde{\dot{Q_{0}}}},\end{eqnarray}$$
where
${\it\beta}\dot{Q}$
is the non-dimensional heat release rate perturbation, which encapsulates all relevant information about the flame, base velocity and ambient conditions.
The heat release rate is averaged over the cross-sectional area of the duct, and the ratio of the area of the base of the flame to the cross-sectional area of the duct,
${\it\alpha}$
, is assumed to be
$0.2$
in this paper.
For the open duct examined here, the pressure perturbations and gradient of velocity perturbations are both set to zero at the ends of the tube,
$$\begin{eqnarray}\displaystyle [p]_{x=0}=[p]_{x=1}=0,\quad \left[\frac{\partial u}{\partial x}\right]_{x=0}=\left[\frac{\partial u}{\partial x}\right]_{x=1}=0.\end{eqnarray}$$
These boundary conditions are enforced by choosing basis sets that match these boundary conditions and satisfy the dimensionless momentum equation (2.3),
$$\begin{eqnarray}u(x,t)=\mathop{\sum }_{j=1}^{N}{\it\eta}_{j}(t)\cos (j{\rm\pi}x),\quad p(x,t)=-\mathop{\sum }_{j=1}^{N}\frac{\dot{{\it\eta}}_{j}(t)}{j{\rm\pi}}\sin (j{\rm\pi}x).\end{eqnarray}$$
The governing equations are discretized using this Galerkin discretization with orthogonal basis vectors and integrated over the domain to reduce them to a system of ordinary differential equations.
In this formulation, for the sake of simplicity, we have not accounted for the effect of the temperature change across the flame on the acoustic mode shapes and frequencies. This has two important implications: (i) the eigenfrequencies of the duct are multiples of the fundamental acoustic duct mode, and hence excitation of these modes by a nonlinear heat release rate is amplified because the higher harmonics of the heat release rate overlap perfectly with the eigenmodes, and (ii) quantitative comparisons with experiments are not possible.
The acoustic damping due to radiation at the open ends of the duct and due to losses in the viscous and thermal boundary layers is modelled using correlations developed by Matveev (Reference Matveev2003) from models in Landau & Lifshitz (Reference Landau and Lifshitz1959). In this model, the acoustic damping,
${\it\zeta}$
, is dealt with by assigning damping parameters,
${\it\zeta}_{j}$
, to each mode, where
${\it\zeta}_{j}=c_{1}\,j^{2}+c_{2}\,j^{1/2}$
. Note that
$c_{1}$
and
$c_{2}$
are functions of the duct geometry and hence the fundamental acoustic frequency. Therefore higher frequencies are more heavily damped than lower frequencies.
2.2. Reduced-order model of the premixed flame: the
$G$
-equation
The flame is described by a kinematic model using a level set approach, also known as the
$G$
-equation model in combustion (Williams Reference Williams and Buckmaster1985, pp. 97–131). This model has been shown to capture the major nonlinearities in premixed flame dynamics (Dowling Reference Dowling1999; Lieuwen Reference Lieuwen2005) and has been used widely in low-order models of thermoacoustic systems with premixed flames (Dowling Reference Dowling1999; Graham & Dowling Reference Graham and Dowling2011; Subramanian & Sujith Reference Subramanian and Sujith2011). The principal assumptions of the model are that: (i) the flame is a thin surface separating unburnt reactants from burnt products; (ii) the influence of gas expansion across the flame front is negligible.
Assumption (i) requires that the flame front has length scales that are small compared to the flow and acoustic scales, and is valid in this study. Furthermore, this assumption is also valid in the wrinkled and corrugated flamelet regimes of turbulent combustion, which may be encountered in technical devices. This assumption allows for the flame to be tracked using the
$G$
-equation, which for the present two-dimensional case can be written as (Williams Reference Williams and Buckmaster1985, pp. 97–131)
$$\begin{eqnarray}\frac{\partial G}{\partial \tilde{t}}+{\tilde{U}}\frac{\partial G}{\partial \tilde{x}}+\tilde{V}\frac{\partial G}{\partial {\tilde{y}}}=s_{L}\sqrt{\left(\frac{\partial G}{\partial \tilde{x}}\right)^{2}+\left(\frac{\partial G}{\partial {\tilde{y}}}\right)^{2}},\end{eqnarray}$$
where tildes denote dimensional values,
$G(\tilde{x},{\tilde{y}},\tilde{t})$
is a time-varying function that is negative in the unburnt gas, positive in the burnt gas and zero on the flame surface,
${\tilde{U}}$
and
$\tilde{V}$
are the instantaneous velocities along the
$x$
and
$y$
directions, respectively, and
$s_{L}$
is the flame speed. In this paper the equivalence ratio is uniform,
${\it\phi}=0.85$
, and curvature and flame-stretch effects are ignored, so the flame speed,
$s_{L}=0.32\ \text{m}\ \text{s}^{-1}$
, is also uniform.
Assumption (ii) allows for the velocity field to be independently specified, neglecting the effect of the heat release on the flow field. This is strictly valid in the limit of small temperature change across the flame and implies that the flame does not modify the velocity field. Preetham & Lieuwen (Reference Preetham and Lieuwen2004) show that this assumption is valid when the amplitude of flow perturbations is below that needed for parametric instability. The amplitude range where this holds decreases when the temperature ratio across the flame increases. In this study, this assumption is consistent with the Galerkin method, which neglects the influence of the temperature change across the flame on the acoustics. Therefore, as mentioned earlier, quantitative comparisons with experiments are not possible, but these simplifications allow the flame to be modelled with a much smaller system than would be required for fully resolved computational fluid dynamics.
Equation (2.8) can be rewritten in terms of non-dimensional parameters,
$x^{\ast }=\tilde{x}/L_{f}$
,
$y^{\ast }={\tilde{y}}/R,\ u^{\ast }={\tilde{U}}/{\tilde{u}}_{0},\ v^{\ast }=\tilde{V}/{\tilde{u}}_{0}$
and
$t^{\ast }=\tilde{t}{\tilde{u}}_{0}/L_{f}$
, as
$$\begin{eqnarray}\frac{\partial G}{\partial t^{\ast }}+u^{\ast }\frac{\partial G}{\partial x^{\ast }}+{\it\beta}_{f}v^{\ast }\frac{\partial G}{\partial y^{\ast }}=\left(\frac{s_{L}}{{\tilde{u}}_{0}}\right)\sqrt{\left(\frac{\partial G}{\partial x^{\ast }}\right)^{2}+{\it\beta}_{f}^{2}\left(\frac{\partial G}{\partial y^{\ast }}\right)^{2}},\end{eqnarray}$$
where
$L_{f}$
is the nominal flame height, i.e. the height of the steady flame ignoring stretch effects,
$R$
is the half-width of the burner and
${\it\beta}_{f}$
is the flame aspect ratio,
$L_{f}/R$
.
The calculation of the heat release rate and the numerical techniques used are described in detail in our previous studies (Kashinath et al. Reference Kashinath, Hemchandra and Juniper2013a ,Reference Kashinath, Hemchandra and Juniper b ).
2.3. Reduced-order model of the perturbation velocity field
Studies of acoustically forced premixed flames have shown that acoustic waves induce velocity perturbations at the base of the flame (Boyer & Quinard Reference Boyer and Quinard1990; Baillot, Durox & Prud’homme Reference Baillot, Durox and Prud’homme1992). These velocity perturbations then travel along the flame, distorting its surface and causing flame area fluctuations that result in unsteady heat release rate oscillations. For this reason, the perturbation velocity is modelled as a travelling wave that originates at the burner lip (Ducruix, Durox & Candel Reference Ducruix, Durox and Candel2000; Preetham, Hemchandra & Lieuwen Reference Preetham and Lieuwen2008; Kashinath et al. Reference Kashinath, Hemchandra and Juniper2013b ). Experiments on laminar premixed flames (Boyer & Quinard Reference Boyer and Quinard1990; Baillot et al. Reference Baillot, Durox and Prud’homme1992; Durox, Schuller & Candel Reference Durox, Schuller and Candel2005; Birbaud, Durox & Candel Reference Birbaud, Durox and Candel2006; Kornilov, Schreel & de Goey Reference Kornilov, Schreel and de Goey2007; Karimi et al. Reference Karimi, Brear, Jin and Monty2009; Shanbhogue et al. Reference Shanbhogue, Shin, Hemchandra, Plaks and Lieuwen2009) and turbulent premixed flames (Shin et al. Reference Shin, Plaks, Lieuwen, Mondragon, Brown and McDonell2011; O’Connor & Lieuwen Reference O’Connor and Lieuwen2012), and direct numerical simulations (DNS) in our previous work (Kashinath et al. Reference Kashinath, Hemchandra and Juniper2013b ), have shown that the phase speed of these velocity perturbations is not equal to the mean flow velocity. It is a function of the forcing frequency but is independent of the forcing amplitude. Furthermore, we found that for a slot-stabilized two-dimensional premixed flame it is usually less than the mean flow velocity in the range of frequencies relevant to thermoacoustic oscillations (Kashinath et al. Reference Kashinath, Hemchandra and Juniper2013b ). This is accounted for in our models as described below.
The acoustic perturbations in this study are non-harmonic and we cannot use a frequency-dependent phase speed because these frequencies are not known a priori. For this reason we assume a constant phase speed, for which the non-dimensional streamwise perturbation velocity field is found by solving the one-dimensional advection equation,
$$\begin{eqnarray}\frac{\partial u}{\partial t}+\frac{U_{c}}{U_{0}}\frac{\partial u}{\partial x}=0.\end{eqnarray}$$
The phase speed of velocity perturbations,
$U_{c}$
, is equal to
$0.9U_{0}$
, and was chosen based on our previous work using DNS (Kashinath et al.
Reference Kashinath, Hemchandra and Juniper2013b
). In our previous work we have shown that
$U_{c}$
has a strong effect on the nonlinear behaviour of the thermoacoustic system and that subcritical bifurcations are more likely to exist for
$U_{0}>U_{c}$
than for
$U_{0}=U_{c}$
(Kashinath et al.
Reference Kashinath, Hemchandra and Juniper2013a
,Reference Kashinath, Hemchandra and Juniper
b
). The boundary condition is that the perturbation at the burner lip equals the acoustic velocity at the flame position,
$u(x_{burner},t)=u_{acoustic}(x_{f},t)$
. Therefore the axial velocity at any point in the flame domain is the delayed acoustic velocity at the burner lip, with a delay equal to the time taken for the travelling wave to propagate from the burner to that point.
As in our previous work (Kashinath et al. Reference Kashinath, Hemchandra and Juniper2013a ,Reference Kashinath, Hemchandra and Juniper b ), we solve the continuity equation within the flame domain to find the transverse velocity perturbation field,
$$\begin{eqnarray}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0.\end{eqnarray}$$
We have chosen to anchor the base of the flame to the burner lip, which simulates the case with a hot burner lip. Recent experiments on a self-excited ducted premixed flame show that flame lift-off occurs at large velocity fluctuation amplitudes and can lead to elaborate nonlinear behaviour such as intermittency, ultimately leading to flame blow-out (Kabiraj & Sujith Reference Kabiraj and Sujith2012b
). This cannot be captured in our model. Furthermore, because we assume symmetry and simulate only one half of the flame, asymmetric flame behaviour cannot be simulated. Flashback, however, is allowed, using the boundary condition proposed by Dowling (Reference Dowling1999) and implemented in the level set solver by Waugh (Reference Waugh2013). We have neglected the influence of curvature on the flame speed in this study, but this has been included in a continuation analysis of a similar thermoacoustic system by Waugh (Reference Waugh2013). Neglecting the influence of curvature on the flame speed leads to sharp cusps on the flame surface but allows faster computations because curvature is a second-order quantity that requires a much smaller time step for numerical stability. For premixed flames with constant flame speed, the heat release rate is proportional to the flame surface area, which is calculated as in previous studies (Hemchandra Reference Hemchandra2012; Kashinath et al.
Reference Kashinath, Hemchandra and Juniper2013a
,Reference Kashinath, Hemchandra and Juniper
b
). The simple velocity model and boundary conditions we use here result in an unsteady heat release rate whose mean is less than the steady heat release rate of the unperturbed flame, which is unphysical. This is a well-known feature of the
$G$
-equation approach (Oberlack & Cheviakov Reference Oberlack and Cheviakov2010). The thermoacoustic oscillations are not affected by the mean of the heat release rate but only by its rate of change. So this simple model is retained.
The evolution equations of the coupled nonlinear system, i.e. the
$G$
-equation, the acoustic equations and perturbation velocity equations (2.10) and (2.11), are solved simultaneously using a weighted essentially non-oscillatory (WENO) fifth-order scheme in space (Jiang & Peng Reference Jiang and Peng2000) with a third-order total variation diminishing (TVD) Runge–Kutta scheme (Gottlieb & Shu Reference Gottlieb and Shu1998) in time. The non-dimensionalized spatial and temporal resolution in all the simulations are
$5\times 10^{-3}$
and
$1\times 10^{-3}$
, respectively, with a uniform mesh spacing in both spatial directions. For the
$G$
-equation computations, the local level set method is used to achieve a significant reduction in computational cost (Peng Reference Peng1999) and is solved using LSGEN2D, a general level set method solver, developed by Hemchandra (Hemchandra Reference Hemchandra2009; Shreekrishna, Hemchandra & Lieuwen Reference Shreekrishna and Lieuwen2010) with extensions and modifications by Waugh (Reference Waugh2013).
Figure 2. Instantaneous images of the flame during a period-1 limit cycle oscillation, mean equivalence ratio
${\it\phi}=0.85$
, ratio of flame height to flame radius
$L_{f}/R={\it\beta}_{f}=5$
. Note the formation of sharp cusps towards the products and flame pinch-off, which are characteristics of premixed flames seen in experiments (Baillot et al.
Reference Baillot, Durox and Prud’homme1992; Ducruix et al.
Reference Ducruix, Durox and Candel2000; Durox et al.
Reference Durox, Schuller and Candel2005; Birbaud et al.
Reference Birbaud, Durox and Candel2006; Karimi et al.
Reference Karimi, Brear, Jin and Monty2009).
Figure 2 shows instantaneous flame images over one cycle of a period-1 limit cycle. Sharp cusps form towards the products and pockets of flame pinch-off, which are characteristics of premixed flames and the main sources of their nonlinearity in heat release rate. The same characteristics are seen in experiments (Baillot et al. Reference Baillot, Durox and Prud’homme1992; Ducruix et al. Reference Ducruix, Durox and Candel2000; Karimi et al. Reference Karimi, Brear, Jin and Monty2009).
3. Bifurcation analyses
A bifurcation diagram shows the changes in the nature of solutions to the governing equations as a control parameter changes. The governing equations of the coupled nonlinear dynamical system are marched forward in time starting from the steady unperturbed state until the system reaches its stable state. At a particular value of the control parameter, the points on these bifurcation diagrams are the peaks and troughs of the time series of acoustic velocity at the flame position, i.e.
$u_{f}=u(x_{f})$
, after the system reaches its stable state. Therefore, a period-1 oscillation has two points (one peak and one trough), a period-2 oscillation has four points, a period-k oscillation has
$2k$
points, and quasi-periodic and chaotic oscillations have an infinite number of points bounded within a range of
$u_{f}$
. In practice, the number of points for quasi-periodic and chaotic oscillations depends on the length of the time series. In the diagrams that follow, we show only the stable states. The unstable states are shown separately later. We choose
$u_{f}$
, the acoustic velocity at
$x_{f}$
, as the relevant physical quantity on these diagrams for two reasons: (i) it is the perturbation velocity at the burner exit and is often measured in experiments Durox et al. (Reference Durox, Schuller and Candel2005), and (ii) it perturbs the base of the flame, creating flame wrinkles that travel along the flame, which play an important role in the behaviour of the unsteady heat release rate.
3.1. Control parameter: flame position,
$x_{f}$
Figure 3 shows the bifurcation diagram, with the flame position,
$x_{f}$
, as the control parameter. The flame position influences how the flame affects the acoustics, and how the acoustics affects the flame. This is because the contribution of each mode to the acoustic velocity is
${\it\eta}_{j}\cos (j{\rm\pi}x_{f})$
, and the contribution of the heat release to each mode is
${\it\beta}\dot{Q}\sin (j{\rm\pi}x_{f})$
, where
${\it\eta}_{j}$
is the velocity amplitude of the
$j$
th mode and
${\it\beta}$
encapsulates all relevant information about the steady flame, base velocity and ambient conditions.
Figure 3. Bifurcation diagram with flame position,
$x_{f}$
, as the control parameter keeping all other parameters constant:
${\it\phi}_{mean}=0.85$
,
${\it\beta}_{f}=L_{f}/R=7$
, ratio of combustion to acoustic time scales
$L_{f}/ML_{0}=2.2$
. The
$u_{f}$
values are the peaks and troughs of the time series once the system has settled to its ultimate stable state. One set of points is obtained by increasing
$x_{f}$
starting from the stable state at the previous
$x_{f}$
. The other set of points is obtained by decreasing
$x_{f}$
. The different colours represent the most dominant acoustic mode in the power spectrum of the oscillation: mode 1 is shown in grey (red online), mode 2 in dark grey (blue online), mode 3 in black (black online) and mode 4 in very light grey (green online). Some branches end abruptly because the state becomes unstable. The sequence of bifurcations are explained in the text. This chart shows that the system can have a stable fixed point (labelled FP), stable period-1 oscillations (labelled P1), period-2 oscillations (labelled P2), frequency-locked or period-k oscillations (labelled FL), quasi-periodic oscillations (labelled QP) and chaotic oscillations (labelled CH) depending on
$x_{f}$
and initial conditions. There are several bistable regions, hence mode switching and hysteresis are possible.
The initial condition for the simulation at a new flame position is the final stable state of the previous flame position. This diagram is constructed using two sets of time-marching simulations, one by increasing
$x_{f}$
and the other by decreasing
$x_{f}$
, in order to find hysteresis in the system. The different colours represent the most dominant acoustic mode in the power spectrum of the oscillation: mode 1 is shown in light grey (red online), mode 2 in dark grey (blue online), mode 3 in black (black online) and mode 4 in very light grey (green online). This diagram shows only the stable states of the system, so some branches of solutions end abruptly when the state becomes unstable. A complete bifurcation diagram contains both stable and unstable states. The unstable states for a few cases are shown separately later.
The sequence of bifurcations from right to left (decreasing
$x_{f}$
) are: a subcritical Hopf from a stable fixed point to an unstable period-1 oscillation at
$x_{f}=0.48$
; a fold from an unstable to a stable period-1 oscillation (mode 1) at
$x_{f}=0.487$
; and a supercritical Neimark–Sacker bifurcation to quasi-periodic oscillations at
$x_{f}=0.438$
. This branch of states (mode 1) loses stability at
$x_{f}=0.42$
. A second stable branch with a dominant frequency near that of mode 2 begins at a fold bifurcation to period-1 oscillation at
$x_{f}=0.456$
. This branch has a supercritical Neimark–Sacker bifurcation to quasi-periodic oscillations at
$x_{f}=0.434$
. In the narrow band of
$0.415<x_{f}<0.422$
on the mode-2 branch, the system has period-k states, seen as just a few points on the diagram, as against many points in the quasi-periodic case. For
$0.347<x_{f}<0.415$
the system has quasi-periodic oscillations and this branch goes to a period-1 oscillation via a supercritical Neimark–Sacker bifurcation at
$x_{f}=0.347$
. The system undergoes a subcritical period-doubling bifurcation followed by a fold bifurcation at
$x_{f}=0.311$
to period-2 oscillations, which lose stability at
$x_{f}=0.289$
where the period-2 branch ends abruptly.
Similar features are noticed for lower values of
$x_{f}$
. Between
$x_{f}=0.03$
and
$0.1$
and between
$x_{f}=0.27$
and
$0.295$
there exist bands of chaos. For sizable intervals of
$x_{f}$
, at least two stable attractors coexist and the final state reached by the system therefore depends on the initial conditions. This shows that hysteresis and mode switching are possible in these bistable regions. A mode switch is an abrupt change in the oscillatory state of the system due to an external perturbation that is strong enough to shift the system from one basin of attraction into another. Mode switching does not involve a change in any control parameter. It is usually caused by noise, but can also be brought about by a coherent and carefully designed perturbation.
3.2. Solution dependence on number of modes used in the discretization
The number of Galerkin modes,
$N_{g}$
, used in the discretization of the acoustic equations affects the solutions to the governing equations of the coupled system. When there is more than one Galerkin mode, the heat release rate excites all the modes and each mode in turn affects the heat release rate via the velocity perturbation field. This couples the individual ordinary differential equations for each mode, resulting in a non-harmonic acoustic waveform and more complex behaviour than that in the single-mode case.
Figure 4. Bifurcation diagrams with flame position,
$x_{f}$
, as control parameter with different numbers of Galerkin modes,
$N_{g}$
, in the discretization: (a)
$N_{g}=1$
, (b)
$N_{g}=2$
, (c)
$N_{g}=3$
, (d)
$N_{g}=5$
, (e)
$N_{g}=10$
, ( f)
$N_{g}=19$
, (g)
$N_{g}=20$
and (h)
$N_{g}=21$
. All other parameters are kept constant:
${\it\beta}_{f}=L_{f}/R=7$
, ratio of combustion to acoustic time scales
$L_{f}/ML_{0}=2.2$
. At a given value of
$x_{f}$
the points on the diagrams are the peaks and troughs of the velocity time-series data once the system has reached a stable state. (a) For
$N_{g}=1$
the system always reaches a period-1 limit cycle. As the number of modes is increased, even though the higher modes are more heavily damped, modal interactions result in non-harmonic states such as period-2, period-k and quasi-periodic states. Further, the maximum amplitudes of oscillations are significantly higher than the single-mode case (a). ( f–h) Comparison of these panels shows that the solutions are nearly independent of the discretization when
$N_{g}$
is sufficiently large.
Figure 4 shows bifurcation diagrams with flame position,
$x_{f}$
, as control parameter using different numbers of Galerkin modes,
$N_{g}$
. Figure 4(a) shows that, when there is just one mode, the system is either stable or reaches a period-1 limit cycle. The maximum oscillation amplitude occurs at
$x_{f}=0.25$
and is about one-half of the mean flow velocity. In a previous study we have shown that period-1 limit cycles obtained in the frequency domain using a flame describing function (FDF) approach are the same as those obtained in the time domain using a single mode in the discretization (Kashinath et al.
Reference Kashinath, Hemchandra and Juniper2013a
). This is because the FDF approach assumes harmonic velocity and pressure signals and ignores the influence of the higher harmonics of the heat release rate on the acoustic velocity and pressure, as is the case when only one mode is used for the discretization. Therefore figure 4(a) is similar to the result obtained when the FDF approach is used.
We emphasize that the FDF approach we refer to here, and that is used in Kashinath et al. (Reference Kashinath, Hemchandra and Juniper2013a ), neglects the influence of the temperature change across the flame on the acoustic eigenfrequencies and eigenmode shapes. This, however, is not the same as the FDF approach as described by Noiray et al. (Reference Noiray, Durox, Schuller and Candel2008) and typically used in experiments because the influence of temperature change on the thermoacoustic eigenmodes is taken into account in their calculations.
Figure 4(b–h) shows that, as the number of modes is increased, period-2, quasi-periodic and chaotic oscillations appear. Similar behaviour is seen in numerical simulations of a thermoacoustic system by Subramanian et al. (Reference Subramanian, Mariappan, Sujith and Wahi2010) and Subramanian (Reference Subramanian2011). Furthermore, the peak amplitudes of oscillations are significantly higher than the single-mode case. This shows that, even though the amplitudes of oscillations in the higher modes are smaller than in the first mode, they have a strong effect on the amplitude of heat release rate oscillations, and therefore on the nature of solutions of the governing equations.
These figures also show that the location of the Hopf point depends on the number of modes in the discretization. This is because assuming a harmonic velocity or pressure signal (as done in a single-mode analysis) implies that all other modes are forced to be inactive and cannot contribute to the instability. The Routh–Hurwitz stability criterion from control theory shows how stability criteria depend on the order of the system, which in this system depends on the number of degrees of freedom in the acoustics.
Figure 4( f–h), at
$N_{g}=19$
, 20 and 21, shows that the solutions are nearly independent of the discretization when
$N_{g}$
is sufficiently large. Therefore we use 20 modes for this study.
In the time domain, only three to five modes are necessary to capture most of the elaborate features seen in the case with 20 modes (figure 4 g). In the frequency domain, however, it is difficult to extend the FDF approach to include the effect of interactions between modes. Furthermore, a single-mode system cannot be used to simulate mode switching because during switching the system oscillates at two or more frequencies. Simulating mode switching, multi-periodic and aperiodic behaviour requires many multi-input multi-output describing functions, which can only be calculated by forcing the flame at many different combinations of frequencies and amplitudes simultaneously (Balachandran, Dowling & Mastorakos Reference Balachandran, Dowling and Mastorakos2008; Moeck & Paschereit Reference Moeck and Paschereit2012; Boudy et al. Reference Boudy, Durox, Schuller and Candel2013). This becomes prohibitively expensive even for a small number of modes.
3.3. Control parameter: flame geometry,
$L_{f}/R$
Figure 5 shows the bifurcation diagram with the flame aspect ratio (the ratio of the flame height to the flame radius,
${\it\beta}_{f}=L_{f}/R$
) as the control parameter at four flame positions, (a)
$x_{f}=0.1$
, (b)
$x_{f}=0.2$
, (c)
$x_{f}=0.3$
and (d)
$x_{f}=0.4$
. The range of
${\it\beta}_{f}$
is 1–10, which corresponds to mean flow velocities in the range of
$0.5{-}3.5\ \text{m}\ \text{s}^{-1}$
. This range is realistic because laminar premixed flames with
${\it\phi}_{mean}=0.85$
tend to either flash back or blow off for mean flow velocities outside this range. In all cases the initial condition is the steady unperturbed flame. Parameter
${\it\beta}_{f}$
is varied by changing the mean flow velocity
$U_{0}$
keeping the equivalence ratio and flame speed constant.
Figure 5. Bifurcation diagrams with flame aspect ratio,
${\it\beta}_{f}=L_{f}/R$
, as control parameter at flame positions (a)
$x_{f}=0.1$
, (b)
$x_{f}=0.2$
, (c)
$x_{f}=0.3$
and (d)
$x_{f}=0.4$
. Here
${\it\beta}_{f}$
is varied by changing the mean flow velocity
$U_{0}$
but keeping the equivalence ratio and flame speed constant. In all cases the initial condition is the steady unperturbed flame. Firstly, we see that periodic oscillations are not necessarily the preferred stable states; quasi-periodic and chaotic oscillations are seen over significant parameter ranges. Secondly, chaotic oscillations are seen in all cases at low aspect ratios.
In all cases, when
${\it\beta}_{f}$
is decreased below 3, the system has chaotic oscillations. The route to chaos here is the Ruelle–Takens–Newhouse route and is described in detail in § 7. The system tends to chaos at low flame aspect ratios because short flames have stronger nonlinearities than long flames (Lieuwen Reference Lieuwen2005), which results in cusp formation on the flame surface at much lower oscillation amplitudes for short flames than for long flames. Therefore flame geometry plays a crucial role in the nonlinear dynamics of premixed flames, as shown by Lieuwen (Reference Lieuwen2005), using the analytical expression for the heat release rate in the flame tracking equation, which is derived from the
$G$
-equation. Lieuwen showed that this expression can be simplified to a linear function of velocity for long flames, but is a nonlinear function for short flames.
3.4. Control parameter: duct length,
$L_{0}$
Figure 6 shows the bifurcation diagram with the non-dimensional fundamental frequency of the duct,
$L_{f}/ML_{0}$
, as the control parameter at two flame positions, (a)
$x_{f}=0.07$
and (b)
$x_{f}=0.4$
. In all the simulations the initial condition is the steady unperturbed flame. The fundamental frequency of the duct is varied by changing its length,
$L_{0}$
, keeping all other parameters constant.
Figure 6. Bifurcation diagrams with non-dimensional fundamental frequency of the duct
$(L_{f}/ML_{0})$
as control parameter at positions (a)
$x_{f}=0.07$
and (b)
$x_{f}=0.4$
. The non-dimensional frequency is varied by changing the duct length
$L_{0}$
but keeping all other parameters constant. Note that the ratio of combustion to acoustic time scales,
$L_{f}/ML_{0}$
, varies when
$L_{0}$
changes. In all cases the steady-state flame position is used as the initial condition for the simulation.
In figure 6(a) and (b), the system has period-1 oscillations when the duct is short, i.e. its fundamental acoustic frequency is high, but has more elaborate oscillatory behaviour when the duct is long, i.e. its fundamental acoustic frequency is low. In this range of frequencies the flame response remains fairly constant (Kashinath et al.
Reference Kashinath, Hemchandra and Juniper2013b
). The damping due to acoustic radiation scales as the square of the frequency; therefore, higher modes in short ducts are more heavily damped than those in long ducts. Hence systems with short ducts, i.e. high
$L_{f}/ML_{0}$
, tend to behave like single-mode systems.
While the nonlinear characteristics of the
$G$
-equation are amplitude-dependent and the generation of higher harmonics is larger at larger amplitudes of oscillation, the bifurcation diagrams presented in this section show that the bifurcations leading to quasi-periodic and chaotic behaviour occur even at small or moderate amplitudes – for example, in figure 3 a Neimark–Sacker bifurcation occurs at
$x_{f}=0.02$
and
$u_{f}\approx 0.1$
, and in figure 6(a) chaos is seen in the range
$1.9<L_{f}/ML_{0}<2.2$
and
$u_{f}<0.2$
. This is because the flame dynamics and generation of higher harmonics is only half the story, while the receptivity of the higher (or lower) acoustic modes is the other half. The receptivity of the acoustics is a strong function of the geometry of the duct and the flame position. Therefore, bifurcation phenomena and elaborate nonlinear behaviour are possible even if the oscillation amplitude and generation of higher harmonics is small, provided the higher (or lower) acoustic modes are very receptive. Since both of these aspects contribute to the bifurcations and macro-system behaviour, we cannot, in this study, comment on a direct relationship between the macro-system behaviour and the amplitude dependence of the driving nonlinear characteristics of the
$G$
-equation.
4. Instantaneous flame images
Figure 7 shows images of the flame during different types of oscillation, namely (a) period-1, (b) period-2, (c) quasi-periodic, (d) period-k and (e) chaotic. Fifteen temporally equispaced images are shown for each case, spanning three cycles of the dominant frequency. Snapshots (a1–5), (a6–10) and (a11–15) are identical, showing that the oscillation is period-1. Snapshots (b1–5) have sharper cusps and larger pinch-off pockets than (b6–10). However, (b11–15) are the same as (b1–5), showing that the oscillation is period-2. Snapshots (c1–5), (c6–10) and (c11–15) are similar but not identical, with a gradual shift in flame shapes, showing a low-frequency modulation of the dominant mode of oscillation. In case (d) the behaviour is similar to the quasi-periodic case in (c), but the low-frequency modulation is at exactly one-fifth of the dominant frequency; therefore the cycle repeats itself after every 25 snapshots (not shown here). In case (e) each cycle is different. The cusps on the flame surface are of different shapes and sizes, and the intervals between pinch-off events are irregular, showing that the oscillation is chaotic.
Figure 7. Instantaneous flame images of the self-excited flame for different types of oscillation: (a) period-1 oscillation at
$x_{f}=0.435$
(mode-2 branch); (b) period-2 oscillation at
$x_{f}=0.3$
; (c) quasi-periodic oscillation at
$x_{f}=0.4$
; (d) period-k oscillation at
$x_{f}=0.286$
; and (e) chaotic oscillation at
$x_{f}=0.4$
. For panels (a–d) all other parameters are the same as in figure 8, while panel (e) has the same parameters as figure 11(e). Fifteen images are shown for each case spanning three cycles of the dominant frequency.
These images show that, while the basic flame dynamics, such as cusp formation, advection of wrinkles along the flame and pinch-off at the tip, remain the same in all cases, clear differences exist in the shape of the cusps and the instants when they are formed at the base of the flame. This is because the acoustic velocity at the flame position, which creates wrinkles by perturbing the base of the flame, are subtly different for different types of oscillation. For example, in the period-2 case, the acoustic velocity in one cycle has a smaller amplitude than in the other; therefore the cusp formed on the flame surface and the pocket that pinches off in the first cycle are smaller than the corresponding features in the second cycle. This shows that the nonlinear behaviour of the flame depends very sensitively on the way the flame surface deforms, because the flame surface deformation greatly affects the heat release rate, which in turn depends very sensitively on the velocity perturbation at the inlet plane.
The formation of cusps, their advection along the flame surface, their destruction by flame propagation normal to itself, pinch-off and rapid burning of pockets of reactants generate a heat release rate that is a highly nonlinear function of velocity perturbations. Section 3.2 showed that, within an acoustic model of the duct, several modes are required to capture the influence of this highly nonlinear unsteady heat release rate on the acoustics and the interactions between the acoustic modes via the unsteady heat release rate. Both of these are required to simulate the rich dynamics seen in experiments.
In summary, we find that the topological features of the flame wrinkling reflect some features of the macro-system behaviour, but that we cannot say that one causes the other. Recent work by Waugh (Reference Waugh2013) on matrix-free continuation of limit cycles and their bifurcations shows how Floquet modes can be used to isolate the coupled flame–acoustic motions that cause bifurcations of limit cycles.
5. Nonlinear time-series analyses
This section describes the nonlinear time-series analysis of the data obtained from simulating the self-excited system.
Figure 8. Time series of velocity and heat release rate for the different types of oscillation corresponding to different flame positions of figure 3: (a) period-1 oscillation at
$x_{f}=0.45$
; (b) period-2 oscillation at
$x_{f}=0.3$
; (c) quasi-periodic oscillation at
$x_{f}=0.4$
; (d) period-k oscillation at
$x_{f}=0.286$
; and (e) chaotic oscillation at
$x_{f}=0.046$
.
5.1. Nonlinear time series
Figure 8 shows the time series of the acoustic velocity at the flame position normalized by the mean flow velocity,
$U_{0}$
, and the heat release rate normalized by the mean heat release,
$\dot{Q}_{0}$
, for five flame positions in figure 3: (a)
$x_{f}=0.45$
, (b)
$x_{f}=0.3$
, (c)
$x_{f}=0.4$
, (d)
$x_{f}=0.286$
and (e)
$x_{f}=0.046$
. These are obtained by time marching from the steady unperturbed flame. In all cases the system is linearly unstable, so perturbations grow exponentially before nonlinear effects dominate.
In figure 8(a) the system is first attracted towards an unstable period-1 oscillatory state (
$30<t<60$
) before being repelled from it and is then attracted to a period-1 attractor (
$180<t$
). The velocity and heat release rate oscillations are periodic but not harmonic. In figure 8(b) the system is first attracted towards an unstable quasi-periodic state (
$20<t<40$
) before being repelled from it and is then attracted to a period-2 attractor (
$120<t$
). In figure 8(c) the system tends towards a quasi-periodic attractor (
$80<t$
). In figure 8(d) the system is first attracted towards an unstable quasi-periodic oscillatory state (
$15<t<35$
) before being repelled from it and finally tending towards a period-5 attractor (
$50<t$
). In figure 8(e) the system tends towards a chaotic attractor (
$50<t$
). The different attractors are characterized more precisely in subsequent sections.
5.2. Power spectra
Power spectra of the different time series in figure 8 are obtained using MATLAB’s pwelch command, which computes the power spectral density of a time series using Welch’s overlapped segment averaging spectral estimation algorithm. This is applied on 300 non-dimensional time units after the system has reached its stable state.
Figure 9. Power spectra of velocity (labelled 1) and heat release rate (labelled 2) for the different types of oscillation corresponding to different flame positions of figure 3: (a) period-1 oscillation at
$x_{f}=0.45$
; (b) period-2 oscillation at
$x_{f}=0.3$
; (c) quasi-periodic oscillation at
$x_{f}=0.4$
; (d) period-5 oscillation at
$x_{f}=0.286$
; and (e) chaotic oscillation at
$x_{f}=0.046$
. The power spectral density is on a logarithmic scale.
Figure 9 shows power spectra of the velocity at the flame position on the left (column 1) and heat release rate on the right (column 2). Figure 9(a) shows that spectra of period-1 oscillations have a dominant frequency and its higher harmonics because the signal is not sinusoidal. Figure 9(b) shows that spectra of period-2 oscillations have a dominant peak and a second peak at exactly half the frequency, and their higher harmonics. Figure 9(c) shows that spectra of quasi-periodic oscillations have several frequencies. In these spectra only two frequencies, however, are independent and incommensurate while all the others are linear combinations of the two independent frequencies. These combinations arise due to nonlinear interactions between the two independent frequencies. Figure 9(d) shows the spectra of period-5 oscillations, which resemble figure 9(c). The two independent frequencies in this case, however, are commensurate with each other. As in figure 9(c), combinations of the two frequencies arise due to nonlinear interactions between the two independent frequencies. Figure 9(e) shows that spectra of chaotic oscillations are generally broadband with peaks at frequencies that are close to some of the acoustic frequencies of the duct. The broadband part of the spectrum is at least 10 dB higher than the noise levels in figure 9(a)–(d).
5.3. Phase space reconstruction and Poincaré sections
A phase space diagram is reconstructed from the time series. The first zero crossing of the autocorrelation function was used to find an optimal time delay, and Takens’ embedding theorem was used to reconstruct the phase space. Three embedding dimensions were sufficient to represent the dynamics of the system. Figure 10 shows the phase portraits and Poincaré sections of the velocity (on the left) and heat release rate (on the right) for the oscillations in figures 8 and 9.
Figure 10. Phase portraits and Poincaré sections of velocity and heat release rate for the different types of oscillation corresponding to different flame positions of figure 3: (a) period-1 limit cycle oscillation at
$x_{f}=0.45$
; (b) period-2 oscillation at
$x_{f}=0.3$
; (c) quasi-periodic oscillation at
$x_{f}=0.4$
; (d) period-k oscillation at
$x_{f}=0.286$
; and (e) chaotic oscillation at
$x_{f}=0.046$
.
Figure 10 shows that periodic oscillations (or limit cycles), i.e. panels (a), (b) and (d), are closed loops in phase space. A period-1 oscillation, panel (a), is a single loop, a period-2 oscillation, panel (b), is a double loop, and a period-k oscillation, panel (d), is a
$k$
-loop, where
$k$
is the least common integer multiple of the two commensurate frequencies that characterize the oscillation. Their corresponding Poincaré sections, which are planes perpendicular to the attractors in phase space, have two points, four points or 2
$k$
points. Figure 10(c) shows that quasi-periodic oscillations are tori in phase space: in this case 2-tori because the oscillations have two incommensurate frequencies. On a quasi-periodic attractor, the torus is ergodic. Figure 10(e) shows that chaotic oscillations have complex topology in phase space and in the Poincaré section, because the corresponding strange attractors are highly folded fractal structures. This type of oscillation is characterized more precisely using correlation dimensions, which are described next.
Phase portraits and Poincaré sections represent the different types of oscillation distinctly. They are more useful than simply examining time series or power spectra because the well-defined topological structure of attractors can be used to obtain quantitative information about the nonlinear behaviour of the system, even in the case of noisy experimental data (Kabiraj & Sujith Reference Kabiraj and Sujith2012b ).
5.4. Correlation dimensions
The correlation dimension measures the number of active degrees of freedom in a dynamical system and is used to determine the nature of an attractor. We use the algorithm of Grassberger & Procaccia (Reference Grassberger and Procaccia1983) implemented in the online package TISEAN by Hegger, Kantz & Schreiber (Reference Hegger, Kantz and Schreiber1999), with up to seven embedding dimensions. Figure 11 shows the correlation sum (left) and its local slope (middle) as functions of the Euclidean distance in phase space. In the right column is the correlation dimension, defined as the average slope over the range of radii where the slope remains approximately constant, as a function of the embedding dimension. For periodic oscillations (a, b and d), the correlation dimension and hence the number of active degrees of freedom is unity. For quasi-periodic oscillations (c) it is two, and for chaotic oscillations (e) it is not an integer, in this case
$1.7\pm 0.15$
.
Figure 11. The correlation sum
$C(m,R)$
(left column) and its local slope
$D_{c}(m,R)=\partial \,\log C(m,R)/\partial \,\log R$
(middle column), as functions of the Euclidean distance
$R/R_{max}$
, for an embedding dimension up to
$m=7$
. The right column shows the correlation dimension defined as the average slope
$\overline{D_{c}(m,R)}=\overline{\partial \,\log C(m,R)/\partial \,\log R}$
over the range of radii where the slope remains fairly constant, as a function of the embedding dimension
$m$
. Panels (a–e) correspond to period-1, period-2, quasi-periodic, period-k and chaotic oscillations of figure 8.
The self-similar scaling region over which the correlation dimension is determined may be small when the correlation sum is a strong function of the magnification, as in case (e), where the average is found over
$0.1<R/R_{max}<0.6$
(Li & Juniper Reference Li and Juniper2013). In figure 11(a–d), however, self-similar scaling regions exist over almost two orders of magnitude, and these ranges are used to determine the correlation dimensions. The local slope of the correlation sum does not converge at very small or very large scales, indicating an absence of self-similarity at these scales. This is because, at very small scales, the dynamics are dominated by noise and, at very large scales, the self-similarity is disrupted by the finite scale of the attractor, which acts as a macroscopic cutoff filter (Kantz & Schreiber Reference Kantz and Schreiber2000).
We note here that, since the algorithm of Grassberger & Procaccia (Reference Grassberger and Procaccia1983), there have been more sophisticated algorithms that deal with noisy time series. Although one of the main applications of this algorithm is to distinguish between stochastic and deterministically chaotic time series, there are several criteria that the time series needs to satisfy for proper use of this method. Its limitations when applied to experimental data are due to experimental noise, finiteness of number of data points, non-stationarity and intermittency effects, and due to the uncertainties involved in the extrapolation of the slope to zero radius. Many of these issues are discussed in a review article by Theiler (Reference Theiler1990), and alternative methods for extracting the underlying nonlinear dynamics from noisy experimental data are discussed in Kantz & Schreiber (Reference Kantz and Schreiber2000).
6. The role of unstable attractors
An unstable attractor is a special class of measure attractor (Milnor Reference Milnor1985). Trajectories in the neighbourhood of unstable attractors are attracted towards them in some directions but repelled in others (Ashwin & Timme Reference Ashwin and Timme2005). Unstable solutions divide the phase space into basins of attraction. Identifying the unstable attractors of a dynamical system helps predict the mechanisms or pathways for a system to transition from one attractor to another. They are especially useful in noise-induced transition mechanisms such as triggering, as shown by Waugh & Juniper (Reference Waugh and Juniper2011).
Figure 12. The time series, phase portraits and Poincaré sections of trajectories starting from the steady base state to the ultimate stable state with one or more intermediate states: (a)
$x_{f}=0.480$
, (b)
$x_{f}=0.420$
, (c)
$x_{f}=0.347$
and (d)
$x_{f}=0.2651$
. For panels (a–c)
$L_{f}/ML_{0}=2.2$
and for panel (d)
$L_{f}/ML_{0}=2.0$
. The windows of the time series that are used to extract the phase portraits are shown as coloured patches. Intermediate states are shown in dark grey (red online) and light grey (green online), and the final stable state is shown in grey (blue online). These intermediate states play an important role in the mechanism of transition from one attractor to another (Waugh & Juniper Reference Waugh and Juniper2011).
The advantage of this numerical approach is that we can see how the system passes in the vicinity of unstable attractors as it moves towards a stable attractor. This has been shown in thermoacoustics only for an unstable period-1 attractor (Juniper Reference Juniper2011). It has not been shown, however, for more elaborate unstable attractors. It is, however, well known in hydrodynamics (Eckhardt et al. Reference Eckhardt, Schneider, Hof and Westerweel2007). Figures 12 and 13 show the time series, phase portraits and Poincaré sections, starting from the steady base state evolving to the ultimate stable state, via intermediate states. These intermediate states lie in the neighbourhood of the unstable attractors of the system.
Figure 13. A continuation of the previous figure, showing the intermediate states in the time evolution of the self-excited system: (a)
$x_{f}=0.295$
,
$L_{f}/ML_{0}=2.2$
; (b)
$x_{f}=0.2862$
,
$L_{f}/ML_{0}=2.0$
; (c)
$x_{f}=0.066$
,
$L_{f}/ML_{0}=2.2$
; and (d)
$x_{f}=0.063$
,
$L_{f}/ML_{0}=2.2$
. The windows of the time series that are used to extract the phase portraits are shown as coloured patches. Intermediate states are shown in dark grey (red online) and light grey (green online), and the ultimate stable state is shown in grey (blue online).
The phase portraits and Poincaré sections are used to identify these unstable attractors. In figure 12(a), the system is first attracted towards an unstable period-1 limit cycle (dark grey; red online) and then repelled from it towards a stable period-1 limit cycle of larger amplitude (grey; blue online). In figure 12(b) the system is attracted towards an unstable period-1 limit cycle on the same branch of unstable limit cycles as in panel (a), then it is repelled from it and attracted towards a second unstable quasi-periodic period state (light grey; green online), then it is repelled from this state and ultimately it tends towards another stable quasi-periodic state (grey; blue online). In figure 12(c) the system is strongly attracted from its steady base state towards a quasi-periodic state (dark grey; red online) and then repelled from it and finally tends towards a stable period-1 limit cycle (grey; blue online). In figure 12(d) the system is attracted towards an unstable period-1 limit cycle (dark grey; red online) of large amplitude before it is repelled from it towards its ultimate quasi-periodic state (grey; blue online).
In figure 13(a) there exist two intermediate unstable states. The first two are quasi-periodic (dark grey and light grey; red and green online) and the third state is a period-2 limit cycle (grey; blue online). In figure 13(b–d) some of the intermediate states are chaotic.
These figures show clearly that the system has several unstable attractors. This makes the trajectory of the system elaborate. Such elaborate behaviour has recently been observed in plane Couette flow (Gibson, Halcrow & Cvitanović Reference Gibson, Halcrow and Cvitanović2009). Gibson et al. (Reference Gibson, Halcrow and Cvitanović2009) mention that, once a system’s invariant solutions have been determined, the next step is to determine how the system dynamics interconnects the neighbourhoods of these invariant solutions. The unstable attractors of a system play a pivotal role in these interconnections.
7. Routes to chaos
If a nonlinear system exhibits chaotic dynamics, it is natural to ask how this chaotic behaviour emerges as a parameter is varied. By the early 1980s, three routes to chaos in nonlinear dynamical systems had been discovered: the period-doubling, Ruelle–Takens–Newhouse and intermittency routes (Eckmann Reference Eckmann1981). Since then, several more routes have been discovered (Ott Reference Ott2002). We have identified two routes to chaos in this study: the period-doubling and the Ruelle–Takens–Newhouse routes.
7.1. Period-doubling route
Feigenbaum in 1978 discovered a route to chaos via a cascade of period-doubling bifurcations and identified a self-similar structure of the bifurcation diagram (Argyris, Faust & Haase Reference Argyris, Faust and Haase1993). Period-doubling transitions have been observed in electrical circuits, population dynamics and convective flows, for example in experiments on Rayleigh–Bénard convection (Gollub & Benson Reference Gollub and Benson1980; Libchaber Reference Libchaber1987).
Figure 14. The period-doubling route to chaos observed in the
$x_{f}$
range of 0.285–0.31 (
$L_{f}/ML_{0}=2.0$
). (a) Bifurcation diagram constructed using the troughs of the time series of velocity perturbations at the flame position,
$u_{f}$
. A series of period-doubling bifurcations occur at
$x_{f}=0.307$
(period 1–2),
$x_{f}=0.301$
(period 2–4) and
$x_{f}=0.296$
(period 4–8). (b) Power spectra of velocity at the flame showing the emergence of subharmonics (panel 2,
$f/2$
; 3,
$f/4$
; 4,
$f/8$
) at the above-mentioned values of
$x_{f}$
, finally leading to chaotic oscillations at
$x_{f}=0.288$
in panel 5. The power spectral density (PSD) is on a logarithmic scale.
Figure 14 shows the period-doubling cascade as the flame position is changed. In figure 14(a) is the bifurcation diagram and in figure 14(b) are the power spectra at the flame location just after each period-doubling bifurcation. The first period-doubling bifurcation from period-1 to period-2 oscillations is subcritical (the unstable branch is not shown here). The arrows at
$x_{f}=0.308$
show that the transition to period-2 oscillations is abrupt. The subsequent bifurcations occur at
$x_{f}=0.301$
(period 2–4) and
$x_{f}=0.296$
(period 4–8) and are supercritical. The power spectra show the introduction of the first subharmonic of the lowest frequency at each period-doubling bifurcation, ultimately leading to chaotic oscillations with a broadband spectrum and a few peaks at
$x_{f}=0.2861$
. The length of the time series used to obtain these spectra is 300 non-dimensional units; therefore the subharmonics below
$f/8$
were not well resolved. Furthermore, the lengths along the parameter axis (
$x$
axis) between subsequent period-doubling bifurcations decreases rapidly, and this makes resolving higher period-
$2^{k}$
bifurcations difficult. The characteristics of the strange attractor at
$x_{f}=0.2861$
will be discussed in § 7.3.
7.2. Ruelle–Takens–Newhouse route
Figure 15. The Ruelle–Takens–Newhouse route to chaos observed in the
$L_{f}/ML_{0}$
range of 1.88–2.15 (
$x_{f}=0.4$
). Panels (a–l) show the Poincaré sections of phase portraits of the final state of the system at each operating point (varying
$L_{f}/ML_{0}$
). The stable quasi-periodic state (2-torus) in panel (a) develops corrugations on its surface due to stretching and folding (see panels (c–f)). This is followed by torus breakdown (see panels (g–i)) to chaos (panels (j–l)).
Ruelle & Takens (Reference Ruelle and Takens1971) proposed a theory that challenged the mechanism of turbulence generation proposed by Landau, which required an infinite number of Hopf bifurcations. This mechanism was improved and came to be known as the Ruelle–Takens–Newhouse route to chaos (Newhouse, Ruelle & Takens Reference Newhouse, Ruelle and Takens1978; Bergé et al. Reference Bergé, Pomeau, Vidal and Tuckerman1986). They proved that three successive Hopf bifurcations, producing three independent frequencies, generate a 3-torus that can become unstable and be replaced by a strange attractor (Eckmann Reference Eckmann1981). The time-dependent behaviour is not quasi-periodic with three frequencies, but is distinctly chaotic. They, however, did not predict how and when the strange attractor close to the 3-torus comes into being. Sometimes the 3-torus can lead to a period-k periodic state before the transition to chaos. The exact sequence of steps in this route is still debated (Thompson & Stewart Reference Thompson and Stewart2002). The Ruelle–Takens–Newhouse route, however, is similar to but not the same as another route to chaos directly from a 2-torus to a period-k state to chaos, without a third frequency, called the phase-locked transition (Bergé et al. Reference Bergé, Pomeau, Vidal and Tuckerman1986).
Figure 16. The Ruelle–Takens–Newhouse route to chaos observed in the
$L_{f}/ML_{0}$
range of 1.88–2.15 (
$x_{f}=0.4$
). Panels (a–l) show the power spectra of the velocity at the flame position for these states (corresponding to the same panels in figure 15). The power spectral density is on a logarithmic scale. This route to chaos is characterized by the emergence of a third frequency (marked
$f_{3}$
in panels ( f–h)) that is incommensurate with the two frequencies of the quasi-periodic state (marked
$f_{1}$
and
$f_{2}$
in panel (a)).
The Ruelle–Takens–Newhouse route to chaos has been observed in hydrodynamic systems: Rayleigh–Bénard convection (Gollub & Benson Reference Gollub and Benson1980; McLaughlin & Orszag Reference McLaughlin and Orszag1982), circular Couette flow (Gollub & Swinney Reference Gollub and Swinney1975; Fenstermacher, Swinney & Gollub Reference Fenstermacher, Swinney and Gollub1979) and DNS of converging–diverging channel flow (Guzman & Amon Reference Guzman and Amon1994, Reference Guzman and Amon1996). Recently this has also been observed in experiments in thermoacoustics by Kabiraj et al. (Reference Kabiraj, Saurabh, Wahi and Sujith2012).
Figure 15 shows the Ruelle–Takens–Newhouse route as the natural acoustic frequency of the duct,
$L_{f}/ML_{0}$
, is changed by varying the length of the duct,
$L_{0}$
. The Poincaré sections show that the quasi-periodic state (2-torus) in figure 15(a) develops corrugations on its surface (figure 15(c–f)) as it undergoes a secondary Hopf bifurcation to a 3-torus. The wrinkling of the surface of the attractor followed by the breakdown of the torus (figure 15(g–i)) is characteristic of the twofold operation of stretching and folding that ultimately leads to a strange attractor (Bergé et al.
Reference Bergé, Pomeau, Vidal and Tuckerman1986). The states shown in figure 15(k) and (l) are chaotic. The power spectra of acoustic velocity at the flame position in figure 16 show the emergence of a third frequency (figure 16( f–h)) that is incommensurate with the two frequencies of the quasi-periodic state (marked
$f_{1}$
and
$f_{2}$
in figure 16
a). This is a characteristic of the Ruelle–Takens–Newhouse route to chaos.
7.3. Characterizing chaos
Chaotic oscillations are characterized by non-integer correlation dimensions and positive maximal Lyapunov exponents. Figure 17 shows the correlation sum and its local slope as functions of the Euclidean distance, and the correlation dimension as a function of embedding dimension, for chaotic oscillations: (a) at the end of the period-doubling cascade (figure 14
b5) and (b) at the end of the Ruelle–Takens–Newhouse route to chaos (figure 15
l). The correlation dimension in panel (a) is
$2.7\pm 0.2$
and in panel (b) is
$3.6\pm 0.15$
, which are not integers. Therefore the oscillations are chaotic. Non-integer dimensions represent geometrical objects that show structure on all scales and quantifies the self-similarity of strange attractors (Kantz & Schreiber Reference Kantz and Schreiber2000).
Figure 18 shows the average divergence of trajectories of neighbouring points in phase space as a function of temporal separation. This is found using the algorithm by Kantz (Reference Kantz1994), available online in the TISEAN package (Hegger et al.
Reference Hegger, Kantz and Schreiber1999). For reliable convergence we use up to eight embedding dimensions. In figure 18(a) and (b) a linear trend is seen at temporal separation between 1 and 7, and the dashed line shows a linear fit to this trend. The slope of the linear fit gives the maximal Lyapunov exponent, which is
$0.078\pm 0.03$
in panel (a) and
$0.15\pm 0.01$
in panel (b). Note that these values are small because the non-dimensional temporal separation is used in the calculation. For a system with fundamental acoustic frequency at 100 Hz, the corresponding dimensionalized values for the Lyapunov exponents are
$2.57\pm 0.97\ \text{s}^{-1}$
in panel (a) and
$4.95\pm 0.33\ \text{s}^{-1}$
in panel (b). The exponent is positive in both cases, confirming that the oscillations are chaotic. All motions on a strange attractor are unstable. The maximal Lyapunov exponent measures the instability of chaotic solutions, i.e. rate of divergence of neighbouring trajectories in the strange attractor (Kantz & Schreiber Reference Kantz and Schreiber2000). Hence it measures the ‘strength of chaos’.
Figure 17. The correlation sum
$C(m,R)$
(left column) and its local slope
$D_{c}(m,R)=\partial \,\log C(m,R)/\partial \,\log R$
(middle column) as functions of the Euclidean distance
$R/R_{max}$
, for an embedding dimension up to
$m=7$
. The right column shows the correlation dimension defined as the average slope
$\overline{D_{c}(m,R)}=\overline{\partial \,\log C(m,R)/\partial \,\log R}$
, over the range of radii where the slope remains fairly constant, as a function of the embedding dimension
$m$
. (a) Chaotic oscillations in the period-doubling route to chaos, figure 14(b5). (b) Chaotic oscillations in the Ruelle–Takens–Newhouse route to chaos, figure 15(l).
Figure 18. The average divergence of trajectories
$S({\rm\Delta}n)$
as a function of temporal separation for an embedding dimension up to
$m=8$
for the chaotic oscillations in (a) the period-doubling route to chaos (figure 14
b5) and (b) the Ruelle–Takens–Newhouse route to chaos (figure 15
l). The local slope of the linear region gives the maximal Lyapunov exponent and this is shown as a dashed line.
8. Conclusions
In this study a reduced-order model of a ducted premixed flame is simulated and analysed using techniques from nonlinear time-series analysis and dynamical systems theory.
The bifurcations of this system for three control parameters are examined: (i) the flame position in the duct, (ii) the flame aspect ratio and (iii) the length of duct. Depending on the flame position in the duct, the system has not only period-1 oscillations but also period-2, period-k, quasi-periodic and chaotic oscillations. The transitions to these types of oscillation are via Hopf, Neimark–Sacker and period-doubling bifurcations. Some of these bifurcations are subcritical, so the state that the system reaches changes abruptly even with a smooth change in the control parameter. In certain regions of control parameter space, more than one stable state exists, and the state reached depends on the initial conditions. Therefore, there is hysteresis and so mode switching is possible. Varying the flame aspect ratio shows that chaotic oscillations are more likely in systems with short flames than with long flames because they have sharper cusps at lower amplitudes of oscillation. Varying the duct length shows that quasi-periodic and chaotic oscillations are more likely in systems with long ducts, whereas period-1 limit cycles are more likely in systems with short ducts. This is because short ducts have high natural acoustic frequencies and their higher acoustic modes are strongly damped. This shows that parameters that affect either the flame or the acoustics can influence the system’s nonlinear behaviour.
The influence of the number of coupled acoustic modes on the bifurcations and nonlinear behaviour of the system is analysed. It is shown that, when there is only one mode in the acoustics, which is similar to a frequency-domain analysis assuming harmonic oscillations, the system is either stable or has period-1 oscillations. Furthermore, the oscillation amplitude is under-predicted in large regions of parameter space and the bifurcations and multi-stability seen in the multi-modal case are not captured. The heat release rate is highly nonlinear but, because the acoustic velocity and pressure are assumed to be harmonic, the higher and subharmonics of the heat release rate cannot interact with acoustics. The multi-modal simulations show rich behaviour because (i) the highly nonlinear unsteady heat release rate can excite several modes simultaneously, which results in nonharmonic velocity perturbations that, in turn, cause elaborate flame wrinkling, and (ii) more than one mode may be linearly unstable and the energy transfer between them due to nonlinear interactions affects the transient and steady-state behaviour of the system.
Instantaneous flame images show the influence of cusp formation, their advection along the flame surface, their destruction by flame propagation normal to itself, and pinch-off and rapid burning of pockets of reactants in generating a heat release rate that is a highly nonlinear function of velocity perturbations. Furthermore, within an acoustic model of the duct, it is shown that several modes are required to capture the influence of this highly nonlinear unsteady heat release rate on the acoustics and the interactions between the acoustic modes via the unsteady heat release rate. Both of these are required to simulate the rich dynamics seen in experiments. Instantaneous flame images also reveal that the wrinkles on the flame surface and the pinch-off of flame pockets are regular for periodic oscillations, while they are irregular and have multiple time and length scales for aperiodic oscillations. This is because the magnitude and shape of the acoustic velocity at the flame position, which creates wrinkles by perturbing the flame surface, are different for different types of oscillation. For example, in the period-2 case, the acoustic velocity perturbation in one cycle has a smaller amplitude than in the other; therefore, the cusp formed on the flame surface and the pocket that pinches off in the first cycle are smaller than the corresponding features in the second cycle. The source of nonlinearity is the flame, but such nonharmonic velocity waveforms are possible because the acoustics responds at several frequencies. Our model captures this behaviour because it consists of several coupled nonlinear oscillators that are simultaneously excited by a highly nonlinear unsteady heat release rate from a realistic flame model.
The transient and steady-state behaviours of the system are analysed using power spectra of time series, phase portraits reconstructed from time series and Poincaré sections of phase portraits and by calculating correlation dimensions of the different attractors of the system. They show that the trajectory of the system from the steady base state to its ultimate oscillatory state is elaborate and involves transient attraction and repulsion by one or more unstable attractors before the system tends towards a stable state. Therefore, the unstable attractors strongly influence the system’s pathways.
Bifurcation diagrams and Poincaré sections are used to establish two routes to chaos in this system: the period-doubling route and the Ruelle–Takens–Newhouse route. These are corroborated by analyses of the power spectra of the acoustic velocity. The system tends towards strange attractors via these routes, and these attractors are characterized by computing their correlation dimensions and maximal Lyapunov exponents. These routes to chaos have been observed in experiments on a similar thermoacoustic system (Kabiraj et al. Reference Kabiraj, Saurabh, Wahi and Sujith2012).
Despite using a simple acoustic model that does not account for the temperature change across the flame, we find that this model captures much of the elaborate behaviour seen in experiments, where more realistic effects such as temperature changes, three-dimensional flow behaviour and area changes are all present (Gotoda et al. Reference Gotoda, Nikimoto, Miyano and Tachibana2011, Reference Gotoda, Amano, Miyano, Ikawa, Maki and Tachibana2012; Kabiraj et al. Reference Kabiraj, Saurabh, Wahi and Sujith2012; Kabiraj & Sujith Reference Kabiraj and Sujith2012a ,Reference Kabiraj and Sujith b ). This provides confidence that the elaborate nonlinear dynamics seen here is not because of the configuration chosen in this study. Furthermore, the power spectra of the quasi-periodic and chaotic states sometimes show strong response at frequencies that are not aligned with the frequencies of eigenmodes, which suggests that there is more to the underlying nonlinear dynamics than just perfect spectral overlap between the higher harmonics of the heat release rate and eigenmodes of the duct.
The methods from dynamical systems theory illustrated in this study are superior to both frequency-domain approaches commonly used in nonlinear thermoacoustics and time-domain approaches with simple flame models used in previous studies. This study complements recent experiments on a ducted laminar premixed flame through the detailed analysis of a reduced-order model of a similar system, with approximately 5000 degrees of freedom, that behaves qualitatively similarly. This system behaves similarly to low-dimensional chaotic dynamical systems, and several techniques from nonlinear time-series analyses and dynamical systems theory have proved useful in characterizing and interpreting its behaviour. Time-series analysis is computationally expensive because it requires simulations that contain many cycles. It is a powerful way, however, to obtain quantitative information about aperiodic oscillations. The next step is to apply continuation analysis, because it is a fast and efficient way to find periodic oscillations and their bifurcations over a large parameter space relatively quickly. This has been shown to be successful for a similar system in recent work by Waugh (Reference Waugh2013).
Finally, we note that the influence of turbulent fluctuations, which may be modelled as high-dimensional stochastic noise as a first approximation, tends to smooth out sharp flame features in the ensemble average even when the instantaneous flame surface itself is highly wrinkled (Shin & Lieuwen Reference Shin and Lieuwen2013). In a thermoacoustic system, however, the instantaneous flame shape is tightly coupled to the macro-system’s behaviour. Because the system is nonlinear, the ensemble-averaged dynamics of the fully coupled thermoacoustic system can be very different from the ensemble-averaged flame dynamics coupled to the acoustics. In nonlinear systems, noise can greatly modify the deterministic dynamics and the effect of stochastic forcing on coupled nonlinear systems can be elaborate: (i) noise can shift bifurcations in parameter space; (ii) noise can trigger transitions between attractors in multi-stable regimes; (iii) noise can stabilize unstable states and create new stable states that have no deterministic counterpart; (iv) noise can also stabilize unstable periodic orbits of chaotic attractors, making the system’s behaviour ordered in regions where the deterministic (noise-free) system is chaotic; and (v) noise can cause stochastic phase locking (or stochastic resonance), which depends on the amplitude and time scales of the noise and the inherent dynamics of the system. This can trigger behaviour that is absent in the noise-free system and even enhance the response of a nonlinear system to external signals (Longtin Reference Longtin2003). Given the non-trivial effects of stochastic noise on nonlinear dynamical systems, detailed simulations of a coupled fully nonlinear thermoacoustic system with stochastic forcing terms are needed to understand the effect of stochastic noise on nonlinear thermoacoustic oscillations.
Acknowledgements
This work was supported through funding from the European Research Council via the project ALORS 2590620, from the EPSRC and Rolls Royce via the Dorothy Hodgkin Postgraduate Award and from the IMechE.
