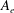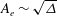1. Introduction
During the last two decades, a vertically vibrated box of granular material has become a prototype to study pattern formation (Douady, Fauve & Laroche Reference Douady, Fauve and Laroche1989; Gallas, Herrmann & Sokolowski Reference Gallas, Herrmann and Sokolowski1992; Park & Behringer Reference Park and Behringer1992; Luding et al.
Reference Luding, Clement, Blumen, Rajchenbach and Duran1994; Pöschel & Herrmann Reference Pöschel and Herrmann1995; Aoki et al.
Reference Aoki, Akiyoma, Maki and Watanabe1996; Knight et al.
Reference Knight, Ehrichs, Kuperman, Flint, Jaeger and Nagel1996; Umbanhower, Melo & Swinney Reference Umbanhower, Melo and Swinney1996; Bizon et al.
Reference Bizon, Shattuck, Swift, McCormick and Swinney1998; Shinbrot & Muzzio Reference Shinbrot and Muzzio1998; Wildman, Huntley & Parker Reference Wildman, Huntley and Parker2001; Alam, Trujillo & Herrmann Reference Alam, Trujillo and Herrmann2006; Eshuis et al.
Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007). However, the earliest works on this topic date back to Chladni (Reference Chladni1787) and Faraday (Reference Faraday1831). Chladni (Reference Chladni1787) observed in his pioneering experiment that when granular particles are slowly deposited on a vibrating surface, particles collect into heaps containing convective cells within them. Faraday (Reference Faraday1831) discovered various types of surface wave patterns in a shallow layer of vibrating grains. Recent experiments (Eshuis et al.
Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007) in a deep bed have uncovered various types of patterns depending on the shaking intensity (i.e. the dimensionless acceleration of shaking scaled by gravitational acceleration,
![]() ${\it\Gamma}$
in (2.6)) and the layer height (
${\it\Gamma}$
in (2.6)) and the layer height (
![]() $F$
) at rest. For
$F$
) at rest. For
![]() ${\it\Gamma}\leqslant 1$
the granular bed moves like a solid bed without getting detached from the bottom plate since the input energy is smaller than the potential energy of the particles, and this gives birth to a bouncing-bed state at
${\it\Gamma}\leqslant 1$
the granular bed moves like a solid bed without getting detached from the bottom plate since the input energy is smaller than the potential energy of the particles, and this gives birth to a bouncing-bed state at
![]() ${\it\Gamma}>1$
in which the particles move collectively with the sinusoidal motion of the shaker. The bouncing bed becomes unstable beyond a critical value of
${\it\Gamma}>1$
in which the particles move collectively with the sinusoidal motion of the shaker. The bouncing bed becomes unstable beyond a critical value of
![]() ${\it\Gamma}\approx 5$
, giving rise to a period-2 or
${\it\Gamma}\approx 5$
, giving rise to a period-2 or
![]() $f_{s}/2$
(where
$f_{s}/2$
(where
![]() $f_{s}$
is the frequency of the shaker) subharmonic wave via a period-doubling bifurcation (Douady et al.
Reference Douady, Fauve and Laroche1989; Eshuis et al.
Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007). Higher-order (period-4, i.e.
$f_{s}$
is the frequency of the shaker) subharmonic wave via a period-doubling bifurcation (Douady et al.
Reference Douady, Fauve and Laroche1989; Eshuis et al.
Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007). Higher-order (period-4, i.e.
![]() $f_{s}/4$
) subharmonic waves (Aoki et al.
Reference Aoki, Akiyoma, Maki and Watanabe1996; Ansari & Alam Reference Ansari, Alam, Yu, Dong, Yang and Luding2013) have also been discovered; other related patterns are Faraday waves and oscillons (Umbanhower et al.
Reference Umbanhower, Melo and Swinney1996), clustering (Olafsen & Urbach Reference Olafsen and Urbach1998), heaping (Clément, Duran & Rajchenbach Reference Clément, Duran and Rajchenbach1992), density inversion (Lan & Rosato Reference Lan and Rosato1997) or the granular Leidenfrost state (Meerson, Pöschel & Bromberg Reference Meerson, Pöschel and Bromberg2003; Eshuis et al.
Reference Eshuis, van der Weele, van der Meer and Lohse2005) and convection (Wildman et al.
Reference Wildman, Huntley and Parker2001; Eshuis et al.
Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007).
$f_{s}/4$
) subharmonic waves (Aoki et al.
Reference Aoki, Akiyoma, Maki and Watanabe1996; Ansari & Alam Reference Ansari, Alam, Yu, Dong, Yang and Luding2013) have also been discovered; other related patterns are Faraday waves and oscillons (Umbanhower et al.
Reference Umbanhower, Melo and Swinney1996), clustering (Olafsen & Urbach Reference Olafsen and Urbach1998), heaping (Clément, Duran & Rajchenbach Reference Clément, Duran and Rajchenbach1992), density inversion (Lan & Rosato Reference Lan and Rosato1997) or the granular Leidenfrost state (Meerson, Pöschel & Bromberg Reference Meerson, Pöschel and Bromberg2003; Eshuis et al.
Reference Eshuis, van der Weele, van der Meer and Lohse2005) and convection (Wildman et al.
Reference Wildman, Huntley and Parker2001; Eshuis et al.
Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007).
Focusing on the phenomenon of granular convection, we note that there are two types of convection in a vibrofluidized granular bed: (i) boundary-driven convection (Gallas et al. Reference Gallas, Herrmann and Sokolowski1992; Luding et al. Reference Luding, Clement, Blumen, Rajchenbach and Duran1994; Knight et al. Reference Knight, Ehrichs, Kuperman, Flint, Jaeger and Nagel1996) which occurs at low shaking intensities and (ii) buoyancy-driven convection (Ramirez, Risso & Cordero Reference Ramirez, Risso and Cordero2000; Wildman et al. Reference Wildman, Huntley and Parker2001; Eshuis et al. Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007, Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010; Viswanathan et al. Reference Viswanathan, Sheikh, Wildman and Huntley2011) at strong shaking. The latter type of convection was first reported by Ramirez et al. (Reference Ramirez, Risso and Cordero2000) in molecular dynamics simulations of inelastic hard disks in a box with top and bottom thermal walls that were maintained at different granular temperatures. The resulting flow patterns with convective cells show a striking resemblance to those in classical Rayleigh–Bénard convection (Chandrashekar Reference Chandrashekar1961) for a fluid heated from below. The experimental work of Wildman et al. (Reference Wildman, Huntley and Parker2001) on harmonically shaken particles in a cylinder (with open top) showed strong evidence of buoyancy-induced convection, although the walls might have played some role in these experiments.
The unequivocal experimental verification of buoyancy-induced granular convection was demonstrated by Eshuis et al. (Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007). They carried out a set of careful experiments on harmonically shaken particles in a quasi-2D box by varying the particle loading (
![]() $F$
, (2.3)) and the shaking strength (
$F$
, (2.3)) and the shaking strength (
![]() $S$
, (2.5)), leading to a complete phase diagram in the (
$S$
, (2.5)), leading to a complete phase diagram in the (
![]() $F,S$
)-plane. They observed a transition from a density-inverted state to the ‘granular’ Leidenfrost state, which is an extreme case of density inversion (where a solid-like dense region coexists with a dilute granular gas underneath it), at sufficiently strong shaking acceleration/intensity (
$F,S$
)-plane. They observed a transition from a density-inverted state to the ‘granular’ Leidenfrost state, which is an extreme case of density inversion (where a solid-like dense region coexists with a dilute granular gas underneath it), at sufficiently strong shaking acceleration/intensity (
![]() ${\it\Gamma}>10$
). It may be noted that such a Leidenfrost state (‘floating’ clusters) had earlier been predicted (Meerson et al.
Reference Meerson, Pöschel and Bromberg2003) by both a granular hydrodynamic model and molecular dynamics simulations. Eshuis et al. (Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007) found that the Leidenfrost state becomes unstable at very strong shaking intensity (
${\it\Gamma}>10$
). It may be noted that such a Leidenfrost state (‘floating’ clusters) had earlier been predicted (Meerson et al.
Reference Meerson, Pöschel and Bromberg2003) by both a granular hydrodynamic model and molecular dynamics simulations. Eshuis et al. (Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007) found that the Leidenfrost state becomes unstable at very strong shaking intensity (
![]() ${\it\Gamma}>20$
), leading to recirculating rolls. They also discovered the appearance of multiple rolls, provided the length of the box is sufficiently large, thus making the analogy with classical Rayleigh–Bénard convection transparent. Multiple convection rolls were predicted earlier in two-dimensional particle dynamics simulations by (Bizon et al.
Reference Bizon, Shattuck, Swift, McCormick and Swinney1998; Sunthar & Kumaran Reference Sunthar and Kumaran2001). Such buoyancy-induced granular convection must be contrasted with boundary-driven convection (which occurs at much lower values of
${\it\Gamma}>20$
), leading to recirculating rolls. They also discovered the appearance of multiple rolls, provided the length of the box is sufficiently large, thus making the analogy with classical Rayleigh–Bénard convection transparent. Multiple convection rolls were predicted earlier in two-dimensional particle dynamics simulations by (Bizon et al.
Reference Bizon, Shattuck, Swift, McCormick and Swinney1998; Sunthar & Kumaran Reference Sunthar and Kumaran2001). Such buoyancy-induced granular convection must be contrasted with boundary-driven convection (which occurs at much lower values of
![]() ${\it\Gamma}<5$
in a small-aspect-ratio box), which is primarily driven by friction at two side walls (Gallas et al.
Reference Gallas, Herrmann and Sokolowski1992; Luding et al.
Reference Luding, Clement, Blumen, Rajchenbach and Duran1994; Pöschel & Herrmann Reference Pöschel and Herrmann1995; Knight et al.
Reference Knight, Ehrichs, Kuperman, Flint, Jaeger and Nagel1996). Unlike in a classical fluid, where convection is governed by the competing effects of buoyancy versus viscous and thermal diffusion only, the patterns formed through granular convection are crucially dependent also on inelastic dissipation.
${\it\Gamma}<5$
in a small-aspect-ratio box), which is primarily driven by friction at two side walls (Gallas et al.
Reference Gallas, Herrmann and Sokolowski1992; Luding et al.
Reference Luding, Clement, Blumen, Rajchenbach and Duran1994; Pöschel & Herrmann Reference Pöschel and Herrmann1995; Knight et al.
Reference Knight, Ehrichs, Kuperman, Flint, Jaeger and Nagel1996). Unlike in a classical fluid, where convection is governed by the competing effects of buoyancy versus viscous and thermal diffusion only, the patterns formed through granular convection are crucially dependent also on inelastic dissipation.
To prove the above analogy with classical Rayleigh–Bénard convection from a theoretical viewpoint, a linear stability analysis of granular hydrodynamic equations was carried out by Eshuis et al. (Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010). This theory predicted that the Leidenfrost state becomes unstable above a critical shaking strength, resulting in convective patterns, as found in experiments and simulations. The critical shaking strength for the transition from the Leidenfrost state to convection for various numbers of particle layers has been determined (Eshuis et al. Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010, Reference Eshuis, van der Weele, Alam, van Gerner, van der Höf, Kuipers, Luding, van der Meer and Lohse2013), leading to a phase diagram showing the critical shaking strength as a function of particle loading (the number of particle layers at rest). Most importantly, the theoretical results for the onset of convection were found to agree quantitatively with experiment and particle simulation (with one fitting parameter). Another crucial finding of the linear stability theory is that the pattern wavelength increases linearly with increasing shaking strength, which also agrees qualitatively with experiments and simulations.
Similar linear stability analyses of granular convection had been carried out before by other researchers (Hayakawa, Yue & Hong Reference Hayakawa, Yue and Hong1995; Khain & Meerson Reference Khain and Meerson2003). Hayakawa et al. (Reference Hayakawa, Yue and Hong1995) predicted that the appearance of convective rolls is due to an instability of the bouncing-bed solution. Their linear stability analysis is based on a hydrodynamic-like traffic model of dense granular materials, in which the equation for the granular temperature is enslaved. Khain & Meerson (Reference Khain and Meerson2003) performed a linear stability analysis of a dilute granular gas under differential heating with a kinetic-theory-based hydrodynamic model. They predicted the onset of steady convection rolls as an instability of a density-inverted state in the dilute regime. The latter theoretical work is in agreement with the particle dynamics simulations of Ramirez et al. (Reference Ramirez, Risso and Cordero2000) and Paolotti et al. (Reference Paolotti, Barrat, Marconi and Puglisi2004). Direct numerical simulations of continuum equations revealed the complex role of side walls, friction and shaking intensity on convection (Bourzutschky & Miller Reference Bourzutschky and Miller1995; Ohtsuki & Ohsawa Reference Ohtsuki and Ohsawa2003) and related patterns (Carrillo, Pöschel & Saluena Reference Carrillo, Pöschel and Saluena2007) in a two-dimensional vibrated bed.
Going beyond linear stability, it is interesting to ask whether the granular convection rolls (Eshuis et al. Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007, Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010) that are born due to an instability of the Leidenfrost state are stable or not. What is the behaviour of these rolls when disturbed with finite-amplitude perturbations? While the onset of supercritical instabilities can be predicted accurately by linear stability analyses, a nonlinear theory is required if the amplitude of disturbance becomes finite. More importantly, the possibility of subcritical instabilities, leading to a bistable behaviour, can be dealt with only by nonlinear analyses. In any case, the bifurcation scenario, supercritical or subcritical, can be analysed from the well-known Landau equation which has been rigorously derived from hydrodynamic equations (Shukla & Alam Reference Shukla and Alam2009, Reference Shukla and Alam2011a ,Reference Shukla and Alam b ; Alam & Shukla Reference Alam and Shukla2013) for granular shear flow.
In this paper, we follow the recent works of Shukla & Alam (Reference Shukla and Alam2009, Reference Shukla and Alam2011a ,Reference Shukla and Alam b ) to derive the Landau equation for a vibrofluidized bed with a quasi-steady assumption (§ 2.1) for the base state. The hydrodynamic balance equations, the adopted constitutive model and its possible range of validity are discussed in § 2.2. The dimensionless balance equations are written down in § 2.3, and the density-inverted base state (Leidenfrost state) is analysed in § 2.4. The adjoint linear stability problem is formulated in § 3.1, and the nonlinear stability analysis is briefly described in § 3.2. The first Landau coefficient and the nonlinear equilibrium solutions are quantified in § 4.1. The spectral-based computational algorithm to calculate the equilibrium solutions is briefly outlined in § 4.2. The numerical results for equilibrium patterns and the bifurcation scenario are discussed in § 5.1. At quadratic order in the perturbation amplitude, we uncovered 2:1 resonance phenomena as discussed in § 5.1.1. A brief qualitative comparison of patterns obtained from nonlinear theory and experiments is made in § 5.2. The robustness of our predicted results is assessed with a specific focus on identifying the effects of the bulk viscosity, the shear work and the Prandtl number in § 6.1 and that of different free-surface boundary conditions in § 6.2. The range of validity and the limitations of the present nonlinear analysis are discussed in § 6.3. The conclusions are given in § 7.
2. Problem description and governing equations
2.1. Physical set-up, control parameters and assumptions for the theoretical analysis
Figure 1 shows the problem under consideration: a quasi-two-dimensional box of length
![]() $L_{x}$
and depth
$L_{x}$
and depth
![]() $D$
(of a few particle diameters) with open top (the height of the box is large enough that no particles will escape under shaking) which is partially filled with spheres of diameter
$D$
(of a few particle diameters) with open top (the height of the box is large enough that no particles will escape under shaking) which is partially filled with spheres of diameter
![]() $d$
having a material density of
$d$
having a material density of
![]() ${\it\rho}_{p}$
and mass
${\it\rho}_{p}$
and mass
![]() $m={\it\rho}_{p}{\rm\pi}d^{3}/6$
. This box of particles is vibrated vertically with a sine wave:
$m={\it\rho}_{p}{\rm\pi}d^{3}/6$
. This box of particles is vibrated vertically with a sine wave:
where
![]() $a_{s}$
and
$a_{s}$
and
![]() $f_{s}$
are the amplitude and frequency of shaking, respectively. The energy injected per particle over one shaking period (
$f_{s}$
are the amplitude and frequency of shaking, respectively. The energy injected per particle over one shaking period (
![]() ${\it\tau}_{s}=1/f_{s}$
) is
${\it\tau}_{s}=1/f_{s}$
) is
where
![]() $v_{s}=\text{d}y_{s}/\text{d}t=2{\rm\pi}f_{s}a_{s}\cos (2{\rm\pi}f_{s}t)$
is the translation velocity of the shaker.
$v_{s}=\text{d}y_{s}/\text{d}t=2{\rm\pi}f_{s}a_{s}\cos (2{\rm\pi}f_{s}t)$
is the translation velocity of the shaker.

Figure 1. Schematic diagram of a harmonically shaken box of particles. This is an ‘open-top’ quasi-2D box of horizontal length
![]() $L_{x}$
and a depth
$L_{x}$
and a depth
![]() $D$
of a few particle diameters.
$D$
of a few particle diameters.
Four dimensionless control parameters are needed to describe this system: (i) the particle loading parameter or the number of particle layers at rest,
where
![]() $N_{p}=(L_{x}/d)\times (D/d)\times (h_{0}/d)$
is the total number of particles, with
$N_{p}=(L_{x}/d)\times (D/d)\times (h_{0}/d)$
is the total number of particles, with
![]() $h_{0}=Fd$
being the height of the granular bed at rest; (ii) the shaking strength,
$h_{0}=Fd$
being the height of the granular bed at rest; (ii) the shaking strength,
which is a ratio of the kinetic energy injected to the system (
![]() $T_{p}N_{p}$
) and the potential energy associated with all particles (
$T_{p}N_{p}$
) and the potential energy associated with all particles (
![]() $mgdN_{p}$
); (iii) the normal restitution coefficient
$mgdN_{p}$
); (iii) the normal restitution coefficient
![]() $e$
and (iv) the length of the box
$e$
and (iv) the length of the box
![]() $L_{x}/d$
. The shaking strength (2.4) can also be re-expressed as
$L_{x}/d$
. The shaking strength (2.4) can also be re-expressed as
where
is the dimensionless shaking acceleration, called the shaking intensity, and
![]() $g$
is the acceleration due to gravity.
$g$
is the acceleration due to gravity.
For the stability analysis below, the quasi-2D box in figure 1 is assumed to be two-dimensional (i.e. to have no variations along the depth) with periodic boundary conditions along the
![]() $x$
-direction. We further assume that the granular Leidenfrost state (see § 2.4) can be characterized by a ‘quasi-steady’ state, wherein we specify a constant temperature (2.2) at the base plate which is calculated over one shaking period. (The temperature perturbation being zero at the base follows from the above mean-field approximation, see § 3.1.) A detailed energy balance at the base can yield accurate boundary conditions (Hui et al.
Reference Hui, Haff, Ungar and Jackson1984; Jenkins & Richman Reference Jenkins and Richman1986; Rao & Nott Reference Rao and Nott2008) at the expense of making the present nonlinear analysis complicated. As it is the first nonlinear analysis of granular convection phenomena, the present work is rather focused on identifying the nonlinear equilibrium solutions by employing the hydrodynamic model (§ 2.2 and § 2.3) and boundary conditions with identical assumptions to those in the previous linear analysis of the same problem (Eshuis et al.
Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010, Reference Eshuis, van der Weele, Alam, van Gerner, van der Höf, Kuipers, Luding, van der Meer and Lohse2013). The effect of different forms of base boundary conditions on the present results can be taken up in a future work.
$x$
-direction. We further assume that the granular Leidenfrost state (see § 2.4) can be characterized by a ‘quasi-steady’ state, wherein we specify a constant temperature (2.2) at the base plate which is calculated over one shaking period. (The temperature perturbation being zero at the base follows from the above mean-field approximation, see § 3.1.) A detailed energy balance at the base can yield accurate boundary conditions (Hui et al.
Reference Hui, Haff, Ungar and Jackson1984; Jenkins & Richman Reference Jenkins and Richman1986; Rao & Nott Reference Rao and Nott2008) at the expense of making the present nonlinear analysis complicated. As it is the first nonlinear analysis of granular convection phenomena, the present work is rather focused on identifying the nonlinear equilibrium solutions by employing the hydrodynamic model (§ 2.2 and § 2.3) and boundary conditions with identical assumptions to those in the previous linear analysis of the same problem (Eshuis et al.
Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010, Reference Eshuis, van der Weele, Alam, van Gerner, van der Höf, Kuipers, Luding, van der Meer and Lohse2013). The effect of different forms of base boundary conditions on the present results can be taken up in a future work.
2.2. Balance equations and constitutive relations
We use a Navier–Stokes-order hydrodynamic model for which the balance equations for mass, momentum and granular energy are (Jenkins & Richman Reference Jenkins and Richman1985a ; Sela & Goldhirsch Reference Sela and Goldhirsch1998):
is the deviatoric part of the deformation rate tensor. Here,
![]() $p$
,
$p$
,
![]() ${\it\mu}$
,
${\it\mu}$
,
![]() ${\it\zeta}$
and
${\it\zeta}$
and
![]() ${\it\kappa}$
are the pressure, shear viscosity, bulk viscosity and thermal conductivity, respectively. In many recent works, instead of the standard Fourier law (2.11), a generalized Fourier law is adopted in which a density-gradient-dependent term (
${\it\kappa}$
are the pressure, shear viscosity, bulk viscosity and thermal conductivity, respectively. In many recent works, instead of the standard Fourier law (2.11), a generalized Fourier law is adopted in which a density-gradient-dependent term (
![]() $=-{\it\kappa}_{h}\boldsymbol{{\rm\nabla}}n$
, where
$=-{\it\kappa}_{h}\boldsymbol{{\rm\nabla}}n$
, where
![]() ${\it\kappa}_{h}$
is the Dufour coefficient) is considered (Sela & Goldhirsch Reference Sela and Goldhirsch1998; Brilliantov & Pöschel Reference Brilliantov and Pöschel2004), although a recent work (Almazan et al.
Reference Almazan, Carrillo, Saluena, Garzo and Pöschel2013) on the dynamics of a vibrated bed has confirmed that the incorporation of this term can lead to a temperature maximum far away from the bottom plate in contradiction to experimental and simulation results. It may be noted that this Dufour term is of order
${\it\kappa}_{h}$
is the Dufour coefficient) is considered (Sela & Goldhirsch Reference Sela and Goldhirsch1998; Brilliantov & Pöschel Reference Brilliantov and Pöschel2004), although a recent work (Almazan et al.
Reference Almazan, Carrillo, Saluena, Garzo and Pöschel2013) on the dynamics of a vibrated bed has confirmed that the incorporation of this term can lead to a temperature maximum far away from the bottom plate in contradiction to experimental and simulation results. It may be noted that this Dufour term is of order
![]() $O({\it\epsilon}^{3})$
(where
$O({\it\epsilon}^{3})$
(where
![]() ${\it\epsilon}=\sqrt{(1-e^{2})}$
is the degree of inelasticity), as demonstrated by Sela & Goldhirsch (Reference Sela and Goldhirsch1998), and hence does not belong to the Navier–Stokes order
${\it\epsilon}=\sqrt{(1-e^{2})}$
is the degree of inelasticity), as demonstrated by Sela & Goldhirsch (Reference Sela and Goldhirsch1998), and hence does not belong to the Navier–Stokes order
![]() $O({\it\epsilon}^{2})$
.
$O({\it\epsilon}^{2})$
.
As long as we restrict our consideration to the Navier–Stokes-order description, the balance equations (2.7)–(2.9) and flux relations (2.10)–(2.11) are general and no assumptions have been made up to this point. Next, we need constitutive relations for
![]() $p$
,
$p$
,
![]() ${\it\mu}$
,
${\it\mu}$
,
![]() ${\it\zeta}$
,
${\it\zeta}$
,
![]() ${\it\kappa}$
and
${\it\kappa}$
and
![]() $\mathscr{D}$
for which different models are available (Goldhirsch Reference Goldhirsch2003). In this paper, we have chosen the following constitutive relations used by Eshuis et al. (Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010, Reference Eshuis, van der Weele, Alam, van Gerner, van der Höf, Kuipers, Luding, van der Meer and Lohse2013):
$\mathscr{D}$
for which different models are available (Goldhirsch Reference Goldhirsch2003). In this paper, we have chosen the following constitutive relations used by Eshuis et al. (Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010, Reference Eshuis, van der Weele, Alam, van Gerner, van der Höf, Kuipers, Luding, van der Meer and Lohse2013):
 $$\begin{eqnarray}\left.\begin{array}{@{}cll@{}}p(n,T)\, & =\, & nT\left(\displaystyle \frac{n_{c}+n}{n_{c}-n}\right),\quad \text{with }n_{c}=\displaystyle \frac{2}{\sqrt{3}d^{2}},\\ \mathscr{D}(n,T)\, & =\, & \displaystyle \frac{(1-e^{2})}{{\it\gamma}_{c}l}nT\sqrt{\frac{T}{m}},\quad \text{with }{\it\gamma}_{c}=2.26,\\ {\it\kappa}(n,T)\, & =\, & \displaystyle \frac{n({\it\alpha}l+d)^{2}}{l}\sqrt{\frac{T}{m}},\quad \text{with }{\it\alpha}=0.6,\\ {\it\mu}(n,T)\, & =\, & m\;\mathit{Pr}\;{\it\kappa}(n,T),\\ {\it\zeta}(n,T)\, & =\, & 0,\end{array}\!\right\},\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}cll@{}}p(n,T)\, & =\, & nT\left(\displaystyle \frac{n_{c}+n}{n_{c}-n}\right),\quad \text{with }n_{c}=\displaystyle \frac{2}{\sqrt{3}d^{2}},\\ \mathscr{D}(n,T)\, & =\, & \displaystyle \frac{(1-e^{2})}{{\it\gamma}_{c}l}nT\sqrt{\frac{T}{m}},\quad \text{with }{\it\gamma}_{c}=2.26,\\ {\it\kappa}(n,T)\, & =\, & \displaystyle \frac{n({\it\alpha}l+d)^{2}}{l}\sqrt{\frac{T}{m}},\quad \text{with }{\it\alpha}=0.6,\\ {\it\mu}(n,T)\, & =\, & m\;\mathit{Pr}\;{\it\kappa}(n,T),\\ {\it\zeta}(n,T)\, & =\, & 0,\end{array}\!\right\},\end{eqnarray}$$
where
![]() $n_{c}=2/\sqrt{3}d^{2}$
is the number density of a triangular-packed crystal,
$n_{c}=2/\sqrt{3}d^{2}$
is the number density of a triangular-packed crystal,
![]() $e$
is the coefficient of restitution and
$e$
is the coefficient of restitution and
![]() $l$
is the mean free path (Grossman, Zhou & Ben-Naim Reference Grossman, Zhou and Ben-Naim1997):
$l$
is the mean free path (Grossman, Zhou & Ben-Naim Reference Grossman, Zhou and Ben-Naim1997):
with
![]() ${\it\alpha}_{1}=1-\sqrt{3/8}$
. It should be noted that the expression of shear viscosity is taken to be proportional to the thermal conductivity, with the coefficient of proportionality being dubbed the ‘effective’ Prandtl number (
${\it\alpha}_{1}=1-\sqrt{3/8}$
. It should be noted that the expression of shear viscosity is taken to be proportional to the thermal conductivity, with the coefficient of proportionality being dubbed the ‘effective’ Prandtl number (
![]() $\mathit{Pr}$
); the numerical value of
$\mathit{Pr}$
); the numerical value of
![]() $Pr=1.7$
was used by Eshuis et al. (Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010), which yielded good agreement between the linear stability predictions and experiments. For a dense gas, the Prandtl number (
$Pr=1.7$
was used by Eshuis et al. (Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010), which yielded good agreement between the linear stability predictions and experiments. For a dense gas, the Prandtl number (
![]() $\mathit{Pr}$
) is no longer a constant but should be a function of the density; the effect of such a density-dependent Prandtl number is probed in § 6.1. We have set the bulk viscosity to zero (
$\mathit{Pr}$
) is no longer a constant but should be a function of the density; the effect of such a density-dependent Prandtl number is probed in § 6.1. We have set the bulk viscosity to zero (
![]() ${\it\zeta}=0$
), and its impact on stability results is assessed in § 6.1. Of course, the constitutive model (2.13) is based on heuristic arguments (Haff Reference Haff1983; Grossman et al.
Reference Grossman, Zhou and Ben-Naim1997) but is expected to be valid for nearly elastic particles (
${\it\zeta}=0$
), and its impact on stability results is assessed in § 6.1. Of course, the constitutive model (2.13) is based on heuristic arguments (Haff Reference Haff1983; Grossman et al.
Reference Grossman, Zhou and Ben-Naim1997) but is expected to be valid for nearly elastic particles (
![]() $e\sim 1$
) for a wide range of density, as we discuss below.
$e\sim 1$
) for a wide range of density, as we discuss below.
Grossman et al. (Reference Grossman, Zhou and Ben-Naim1997) derived the expressions for
![]() $p$
,
$p$
,
![]() ${\it\kappa}$
and
${\it\kappa}$
and
![]() $\mathscr{D}$
by employing free-volume arguments in the dense limit and subsequently using interpolations with the respective constitutive relations in the dilute limit. These interpolations include two order-one fitting parameters
$\mathscr{D}$
by employing free-volume arguments in the dense limit and subsequently using interpolations with the respective constitutive relations in the dilute limit. These interpolations include two order-one fitting parameters
![]() ${\it\gamma}_{c}$
and
${\it\gamma}_{c}$
and
![]() ${\it\alpha}$
that were obtained by matching the theoretical profiles for density and granular temperature in a thermally driven granular gas between two walls (with zero gravity) with those obtained from molecular dynamics simulations. The predicted density profile had a large density variation ranging from a dilute granular gas near one wall to a high-density cluster at the other end. Later on, the same constitutive relations were used by Meerson et al. (Reference Meerson, Pöschel and Bromberg2003) and Eshuis et al. (Reference Eshuis, van der Weele, van der Meer and Lohse2005) to predict the granular Leidenfrost state, which also consists of an extreme density contrast, with a dense cluster floating over a dilute gas under vertical vibration with gravity. Moreover, the linear stability analysis of the granular Leidenfrost state with (2.13) yielded quantitative agreement for the onset of convection instability with both experiments and simulations with just one fitting parameter (
${\it\alpha}$
that were obtained by matching the theoretical profiles for density and granular temperature in a thermally driven granular gas between two walls (with zero gravity) with those obtained from molecular dynamics simulations. The predicted density profile had a large density variation ranging from a dilute granular gas near one wall to a high-density cluster at the other end. Later on, the same constitutive relations were used by Meerson et al. (Reference Meerson, Pöschel and Bromberg2003) and Eshuis et al. (Reference Eshuis, van der Weele, van der Meer and Lohse2005) to predict the granular Leidenfrost state, which also consists of an extreme density contrast, with a dense cluster floating over a dilute gas under vertical vibration with gravity. Moreover, the linear stability analysis of the granular Leidenfrost state with (2.13) yielded quantitative agreement for the onset of convection instability with both experiments and simulations with just one fitting parameter (
![]() $Pr$
), and hence the constitutive relations (2.13) are likely to be valid for a wide range of density spanning from the dilute to the dense regimes. This motivated us to continue with the same constitutive model to analyse the nonlinear stability of the granular Leidenfrost state.
$Pr$
), and hence the constitutive relations (2.13) are likely to be valid for a wide range of density spanning from the dilute to the dense regimes. This motivated us to continue with the same constitutive model to analyse the nonlinear stability of the granular Leidenfrost state.
Given that the simplified constitutive model (2.13) works well for linear stability predictions, the goal of the present paper is to ascertain the nonlinear saturation of the same linear instability modes when one takes into account finite-amplitude perturbations. To establish the sensitivity of our nonlinear stability predictions (§ 5) on the adopted constitutive relations, we will assess the effects of (i) the bulk viscosity (
![]() ${\it\zeta}\neq 0$
), (ii) the viscous dissipation or the shear work and (iii) a density-dependent Prandtl number in § 6.1 of this paper. Moreover, the different boundary conditions at the free surface and their possible effects are discussed in § 6.2. A detailed parametric study with a different set of constitutive relations (Jenkins & Richman Reference Jenkins and Richman1985a
; Sela & Goldhirsch Reference Sela and Goldhirsch1998; Garzo, Santos & Montanero Reference Garzo, Santos and Montanero2007) is, however, beyond the scope of the present work. In this regard, we would like to remind the readers that the different forms of constitutive relations (at Navier–Stokes order) do not qualitatively affect the onset of instabilities, as demonstrated previously for various types of granular flow: (i) plane shear flow (Alam & Nott Reference Alam and Nott1998; Alam et al.
Reference Alam, Arakeri, Nott, Goddard and Herrmann2005; Gayen & Alam Reference Gayen and Alam2006; Alam, Shukla & Luding Reference Alam, Shukla and Luding2008; Alam & Shukla Reference Alam and Shukla2012), (ii) Poiseuille flow (Alam, Chikkadi & Gupta Reference Alam, Chikkadi and Gupta2009) and (iii) inclined Chute flow (Forterre & Pouliquen Reference Forterre and Pouliquen2002; Woodhouse & Hogg Reference Woodhouse and Hogg2010). Going beyond the Navier–Stokes order, it might be worthwhile to carry out a comparative study for both linear and nonlinear stability of granular convection using a non-Newtonian constitutive model (Saha & Alam Reference Saha and Alam2014).
${\it\zeta}\neq 0$
), (ii) the viscous dissipation or the shear work and (iii) a density-dependent Prandtl number in § 6.1 of this paper. Moreover, the different boundary conditions at the free surface and their possible effects are discussed in § 6.2. A detailed parametric study with a different set of constitutive relations (Jenkins & Richman Reference Jenkins and Richman1985a
; Sela & Goldhirsch Reference Sela and Goldhirsch1998; Garzo, Santos & Montanero Reference Garzo, Santos and Montanero2007) is, however, beyond the scope of the present work. In this regard, we would like to remind the readers that the different forms of constitutive relations (at Navier–Stokes order) do not qualitatively affect the onset of instabilities, as demonstrated previously for various types of granular flow: (i) plane shear flow (Alam & Nott Reference Alam and Nott1998; Alam et al.
Reference Alam, Arakeri, Nott, Goddard and Herrmann2005; Gayen & Alam Reference Gayen and Alam2006; Alam, Shukla & Luding Reference Alam, Shukla and Luding2008; Alam & Shukla Reference Alam and Shukla2012), (ii) Poiseuille flow (Alam, Chikkadi & Gupta Reference Alam, Chikkadi and Gupta2009) and (iii) inclined Chute flow (Forterre & Pouliquen Reference Forterre and Pouliquen2002; Woodhouse & Hogg Reference Woodhouse and Hogg2010). Going beyond the Navier–Stokes order, it might be worthwhile to carry out a comparative study for both linear and nonlinear stability of granular convection using a non-Newtonian constitutive model (Saha & Alam Reference Saha and Alam2014).
2.3. Dimensionless forms of the balance equations and constitutive relations
For non-dimensionalization, we use the maximum number density (
![]() $n_{R}=n_{c}$
) as the reference scale for
$n_{R}=n_{c}$
) as the reference scale for
![]() $n(\boldsymbol{x},t)$
, the granular temperature at the bottom plate as the reference temperature (
$n(\boldsymbol{x},t)$
, the granular temperature at the bottom plate as the reference temperature (
![]() $T_{R}=T_{p}$
), the particle diameter as the reference length (
$T_{R}=T_{p}$
), the particle diameter as the reference length (
![]() $L_{R}=d$
),
$L_{R}=d$
),
![]() $U_{R}=\sqrt{T_{p}/m}$
as the reference velocity and
$U_{R}=\sqrt{T_{p}/m}$
as the reference velocity and
![]() $t_{R}=L_{R}/U_{R}$
as the reference time:
$t_{R}=L_{R}/U_{R}$
as the reference time:
and from here onwards all equations and symbols are written in dimensionless forms. The dimensionless balance equations for the number density,
![]() $x$
-momentum,
$x$
-momentum,
![]() $y$
-momentum and granular energy, respectively, are
$y$
-momentum and granular energy, respectively, are
 $$\begin{eqnarray}\displaystyle n\left[\frac{\partial }{\partial t}+u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}\right]u & = & \displaystyle -\frac{\partial p}{\partial x}+\frac{\partial }{\partial x}\left[2{\it\mu}\frac{\partial u}{\partial x}+{\it\lambda}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\partial }{\partial y}\left[{\it\mu}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n\left[\frac{\partial }{\partial t}+u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}\right]u & = & \displaystyle -\frac{\partial p}{\partial x}+\frac{\partial }{\partial x}\left[2{\it\mu}\frac{\partial u}{\partial x}+{\it\lambda}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\partial }{\partial y}\left[{\it\mu}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle n\left[\frac{\partial }{\partial t}+u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}\right]v & = & \displaystyle \frac{n}{S}-\frac{\partial p}{\partial y}+\frac{\partial }{\partial y}\left[2{\it\mu}\frac{\partial v}{\partial y}+{\it\lambda}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\partial }{\partial x}\left[{\it\mu}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n\left[\frac{\partial }{\partial t}+u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}\right]v & = & \displaystyle \frac{n}{S}-\frac{\partial p}{\partial y}+\frac{\partial }{\partial y}\left[2{\it\mu}\frac{\partial v}{\partial y}+{\it\lambda}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\partial }{\partial x}\left[{\it\mu}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\right],\end{eqnarray}$$
The dimensionless forms of the transport coefficients are
![]() $p(n,T)=f_{1}(n)T$
,
$p(n,T)=f_{1}(n)T$
,
![]() ${\it\mu}(n,T)=f_{2}(n)T^{1/2}$
,
${\it\mu}(n,T)=f_{2}(n)T^{1/2}$
,
![]() ${\it\lambda}(n,T)={\it\zeta}(n,T)-{\it\mu}(n,T)\equiv -{\it\mu}(n,T)$
,
${\it\lambda}(n,T)={\it\zeta}(n,T)-{\it\mu}(n,T)\equiv -{\it\mu}(n,T)$
,
![]() ${\it\kappa}(n,T)=f_{4}(n)T^{1/2}$
and
${\it\kappa}(n,T)=f_{4}(n)T^{1/2}$
and
![]() $\mathscr{D}(n,T)=f_{5}(n)T^{3/2}$
, where
$\mathscr{D}(n,T)=f_{5}(n)T^{3/2}$
, where
![]() $f_{i}(n)$
are dimensionless functions of the number density defined as
$f_{i}(n)$
are dimensionless functions of the number density defined as
and
![]() $l(n)={\it\alpha}_{0}(n^{-1}-1)/(1-{\it\alpha}_{1}n)$
is the dimensionless mean free path, with
$l(n)={\it\alpha}_{0}(n^{-1}-1)/(1-{\it\alpha}_{1}n)$
is the dimensionless mean free path, with
![]() ${\it\alpha}_{0}=\sqrt{3/32}$
and
${\it\alpha}_{0}=\sqrt{3/32}$
and
![]() ${\it\alpha}_{1}=1-\sqrt{3/8}$
. In (2.18),
${\it\alpha}_{1}=1-\sqrt{3/8}$
. In (2.18),
![]() $S$
is the scaled granular temperature at the bottom plate,
$S$
is the scaled granular temperature at the bottom plate,
which is the same as the shaking strength as defined in (2.5). The last term on the right-hand side of (2.19),
represents viscous dissipation (or shear work), which was set to zero in the previous linear stability analysis (Eshuis et al. Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010, Reference Eshuis, van der Weele, Alam, van Gerner, van der Höf, Kuipers, Luding, van der Meer and Lohse2013) but is retained in the present nonlinear analysis. The importance of this term on nonlinear stability will be assessed in § 6.
2.4. Base state: granular Leidenfrost state
The quiescent base state is assumed to be steady and one-dimensional with no variation along the horizontal (
![]() $x$
) direction:
$x$
) direction:
On substituting (2.23) into the hydrodynamic equations, (2.16)–(2.19), we obtain the following equations for the base state:
where
![]() $F=h_{0}/d$
is the number of particle layers at rest (2.3) and
$F=h_{0}/d$
is the number of particle layers at rest (2.3) and
is the effective height of the expanded fluidized bed (Jackson Reference Jackson2000; Rao & Nott Reference Rao and Nott2008). It should be noted that the bed height
![]() $H$
is not a constant, rather it depends on the shaking strength
$H$
is not a constant, rather it depends on the shaking strength
![]() $S$
for specified values of
$S$
for specified values of
![]() $F=h_{0}/d=H_{0}$
(i.e. the bed height at rest) and the restitution coefficient (
$F=h_{0}/d=H_{0}$
(i.e. the bed height at rest) and the restitution coefficient (
![]() $e$
). Since
$e$
). Since
![]() $S$
is a measure of the injected energy, a larger value of
$S$
is a measure of the injected energy, a larger value of
![]() $S$
would imply a larger expansion of the granular bed and hence a larger value of
$S$
would imply a larger expansion of the granular bed and hence a larger value of
![]() $H$
, satisfying the constraint (2.26) of particle number-density conservation. The base-state equations (2.24), (2.25) with boundary conditions are solved numerically using the Runge–Kutta method. For all numerical calculations, we varied the bed height (
$H$
, satisfying the constraint (2.26) of particle number-density conservation. The base-state equations (2.24), (2.25) with boundary conditions are solved numerically using the Runge–Kutta method. For all numerical calculations, we varied the bed height (
![]() $H$
, (2.27)), depending on
$H$
, (2.27)), depending on
![]() $S$
, so as to compute the base state accurately such that the constraint (2.26) is satisfied within an error of
$S$
, so as to compute the base state accurately such that the constraint (2.26) is satisfied within an error of
![]() $O(10^{-6})$
.
$O(10^{-6})$
.

Figure 2. Profiles of the density (blue solid line) and temperature (red dashed line) of the Leidenfrost base state for
![]() $e=0.9$
and
$e=0.9$
and
![]() $(F,S)=$
(a) (6, 100) and (b) (6, 400). (c) Density profiles in semilog scale for different values of
$(F,S)=$
(a) (6, 100) and (b) (6, 400). (c) Density profiles in semilog scale for different values of
![]() $S$
for an initial bed height of
$S$
for an initial bed height of
![]() $F=6$
. (d) Effect of the initial bed height
$F=6$
. (d) Effect of the initial bed height
![]() $F$
on the density profiles at
$F$
on the density profiles at
![]() $S=100$
; see the text for a description of three regions (I–III) in the density profile for
$S=100$
; see the text for a description of three regions (I–III) in the density profile for
![]() $F=16$
.
$F=16$
.
Figure 2(a,b) show the base-state density (blue solid line) and granular temperature (red dashed line) profiles for two sets of parameters
![]() $(F,S)=(6,100)$
and (6, 400). It is clear that the density profile has a maximum at some vertical location away from the bottom plate, but the corresponding granular temperature decreases monotonically with increasing height. It should be noted that the bed expands (i.e.
$(F,S)=(6,100)$
and (6, 400). It is clear that the density profile has a maximum at some vertical location away from the bottom plate, but the corresponding granular temperature decreases monotonically with increasing height. It should be noted that the bed expands (i.e.
![]() $H$
, (2.27), increases) with increasing shaking strength
$H$
, (2.27), increases) with increasing shaking strength
![]() $S$
, see figure 2(a,b) for
$S$
, see figure 2(a,b) for
![]() $S=100$
and 400, respectively. A comparison of density profiles in the semilog scale for different values of
$S=100$
and 400, respectively. A comparison of density profiles in the semilog scale for different values of
![]() $S$
in figure 2(c) clarifies the existence of a ‘ballistic’ dilute layer at the top of the bed in which the density decreases exponentially with height. The latter observation follows from the dilute limit of (2.24):
$S$
in figure 2(c) clarifies the existence of a ‘ballistic’ dilute layer at the top of the bed in which the density decreases exponentially with height. The latter observation follows from the dilute limit of (2.24):
which holds for large
![]() $y\gg F$
, where
$y\gg F$
, where
![]() $T_{b}$
is the average granular temperature in the ballistic layer. It should be noted that the density is very low at the top of the bed, with particles undergoing only ballistic motion there, but the corresponding temperature variation is much smaller (see figure 2
a), and can be approximated by its average value (
$T_{b}$
is the average granular temperature in the ballistic layer. It should be noted that the density is very low at the top of the bed, with particles undergoing only ballistic motion there, but the corresponding temperature variation is much smaller (see figure 2
a), and can be approximated by its average value (
![]() $T_{b}$
) at the leading order.
$T_{b}$
) at the leading order.
For the same injected energy (
![]() $S=100$
) as in figure 2(a) but with increasing particle loading (
$S=100$
) as in figure 2(a) but with increasing particle loading (
![]() $F$
), the effective height of the bed (
$F$
), the effective height of the bed (
![]() $H$
) decreases, as is evident from a comparison of the density profiles in figure 2(d) for
$H$
) decreases, as is evident from a comparison of the density profiles in figure 2(d) for
![]() $F=6$
, 10 and 16. In all cases the density at the top of the bed decreases exponentially with height, but the thickness of this ‘ballistic’ layer decreases sharply with increasing
$F=6$
, 10 and 16. In all cases the density at the top of the bed decreases exponentially with height, but the thickness of this ‘ballistic’ layer decreases sharply with increasing
![]() $F$
. It should be noted that the maximum density in the ‘levitated’ dense layer and the density within the collisional dilute layer (beneath the dense layer) increase with increasing
$F$
. It should be noted that the maximum density in the ‘levitated’ dense layer and the density within the collisional dilute layer (beneath the dense layer) increase with increasing
![]() $F$
, leading to a more compact bed at the same energy input. Referring to the case of
$F$
, leading to a more compact bed at the same energy input. Referring to the case of
![]() $F=16$
(the red curve in figure 2
d), we identify three distinct regions in the density profile marked by I, II and III, respectively: (I) a ‘collisional’ dilute layer near the vibrating plate, (II) a ‘levitated’ dense layer at some intermediate height and (III) a ‘ballistic’ dilute layer at the top of the bed. This is the so-called granular Leidenfrost state (Eshuis et al.
Reference Eshuis, van der Weele, van der Meer and Lohse2005), or the floating cluster (Meerson et al.
Reference Meerson, Pöschel and Bromberg2003). It is clear from figures 2(c,d) that the extents of the above three regions depend on both the particle loading (
$F=16$
(the red curve in figure 2
d), we identify three distinct regions in the density profile marked by I, II and III, respectively: (I) a ‘collisional’ dilute layer near the vibrating plate, (II) a ‘levitated’ dense layer at some intermediate height and (III) a ‘ballistic’ dilute layer at the top of the bed. This is the so-called granular Leidenfrost state (Eshuis et al.
Reference Eshuis, van der Weele, van der Meer and Lohse2005), or the floating cluster (Meerson et al.
Reference Meerson, Pöschel and Bromberg2003). It is clear from figures 2(c,d) that the extents of the above three regions depend on both the particle loading (
![]() $F$
) and the shaking strength (
$F$
) and the shaking strength (
![]() $S$
). As stated before, the present work is focused on the nonlinear stability of these density-inverted base states, with the goal of ascertaining the resulting nonlinear patterns of granular convection.
$S$
). As stated before, the present work is focused on the nonlinear stability of these density-inverted base states, with the goal of ascertaining the resulting nonlinear patterns of granular convection.
3. Nonlinear stability and Landau equation
We have followed the recent works of Shukla & Alam (Reference Shukla and Alam2011b ) and Alam & Shukla (Reference Alam and Shukla2013) on the amplitude expansion method (Stuart Reference Stuart1960; Watson Reference Watson1960; Reynolds & Potter Reference Reynolds and Potter1967) to formulate the nonlinear stability problem for a vibrofluidized granular bed. The equivalence of this method with the centre manifold reduction method has been demonstrated by Shukla & Alam (Reference Shukla and Alam2009) in the context of granular Couette flow. The key features of the amplitude expansion method are (i) that the perturbation of finite amplitude can be expanded in terms of its amplitude, (ii) that the Landau equation is valid and (iii) the separation of two time scales associated with the period of perturbation and the linear growth rate. The adjoint linear stability problem is formulated in § 3.1, followed by a brief description of the amplitude expansion method and Landau equation in § 3.2.
3.1. Linear and adjoint eigenvalue problems
To analyse the stability of the Leidenfrost state, we superimpose a finite-amplitude perturbation on the static base state,
 $$\begin{eqnarray}\left.\begin{array}{@{}l@{}}n(x,y,t)=n^{0}(y)+n^{\prime }(x,y,t)\\ T(x,y,t)=T^{0}(y)+T^{\prime }(x,y,t)\\ (u,v)(x,y,t)=(u^{\prime },v^{\prime })(x,y,t)\end{array}\!\!\right\},\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}n(x,y,t)=n^{0}(y)+n^{\prime }(x,y,t)\\ T(x,y,t)=T^{0}(y)+T^{\prime }(x,y,t)\\ (u,v)(x,y,t)=(u^{\prime },v^{\prime })(x,y,t)\end{array}\!\!\right\},\end{eqnarray}$$
where the superscripts zero and prime denote the base-state and disturbance quantities, respectively. By substituting (3.1) into (2.16)–(2.19) and subtracting the base flow (2.24), (2.25), we obtain the nonlinear evolution equations for the disturbance vector
![]() $\boldsymbol{X}=(n^{\prime },u^{\prime },v^{\prime },T^{\prime })^{\text{T}}$
:
$\boldsymbol{X}=(n^{\prime },u^{\prime },v^{\prime },T^{\prime })^{\text{T}}$
:
where
![]() $\mathscr{L}=[l_{ij}]$
is the linear operator (appendix A) and
$\mathscr{L}=[l_{ij}]$
is the linear operator (appendix A) and
![]() $\mathscr{N}_{2}$
and
$\mathscr{N}_{2}$
and
![]() $\mathscr{N}_{3}$
are the quadratic and cubic nonlinear terms (appendix B), respectively.
$\mathscr{N}_{3}$
are the quadratic and cubic nonlinear terms (appendix B), respectively.
The boundary conditions are taken as
where the boundary operators
![]() $\mathscr{B}_{0}$
and
$\mathscr{B}_{0}$
and
![]() $\mathscr{B}_{H}$
are linear as defined by
$\mathscr{B}_{H}$
are linear as defined by
 $$\begin{eqnarray}\mathscr{B}_{0}=\left(\begin{array}{@{}cccc@{}}0 & 0 & 0 & 0\\ 0 & \frac{\displaystyle \partial }{\displaystyle \partial y} & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right)\quad \text{and}\quad \mathscr{B}_{H}=\left(\begin{array}{@{}cccc@{}}0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{B}_{0}=\left(\begin{array}{@{}cccc@{}}0 & 0 & 0 & 0\\ 0 & \frac{\displaystyle \partial }{\displaystyle \partial y} & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right)\quad \text{and}\quad \mathscr{B}_{H}=\left(\begin{array}{@{}cccc@{}}0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right).\end{eqnarray}$$
It should be noted that we have approximated the semi-infinite domain
![]() $y\in (0,\infty )$
by a truncated finite domain
$y\in (0,\infty )$
by a truncated finite domain
![]() $y\in (0,H)$
as in the calculation of our base state. It should be recalled from § 2.4 that the domain height
$y\in (0,H)$
as in the calculation of our base state. It should be recalled from § 2.4 that the domain height
![]() $H$
(2.27) is chosen so as to satisfy the particle conservation constraint (2.26) to an accuracy of
$H$
(2.27) is chosen so as to satisfy the particle conservation constraint (2.26) to an accuracy of
![]() $O(10^{-6})$
. We would like to emphasize here that such a representation of an infinite domain by a truncated domain is quite common in a variety of free shear layers (Lakkaraju & Alam Reference Lakkaraju and Alam2007) as well as in granular flows (Forterre & Pouliquen Reference Forterre and Pouliquen2002) – this has advantages from the viewpoint of numerical implementation too (Canuto et al.
Reference Canuto, Hussaini, Quarteroni and Zang1988), see § 4.2. In (3.4), the temperature perturbation being zero at
$O(10^{-6})$
. We would like to emphasize here that such a representation of an infinite domain by a truncated domain is quite common in a variety of free shear layers (Lakkaraju & Alam Reference Lakkaraju and Alam2007) as well as in granular flows (Forterre & Pouliquen Reference Forterre and Pouliquen2002) – this has advantages from the viewpoint of numerical implementation too (Canuto et al.
Reference Canuto, Hussaini, Quarteroni and Zang1988), see § 4.2. In (3.4), the temperature perturbation being zero at
![]() $y=0$
follows from our mean-field approximation of a constant temperature at the base, as discussed in § 2.1. It should be noted that these boundary conditions (3.4) were also used by Eshuis et al. (Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010, Reference Eshuis, van der Weele, Alam, van Gerner, van der Höf, Kuipers, Luding, van der Meer and Lohse2013) for the linear stability analysis of the same problem. We shall show in § 6.2 that changing the free-surface boundary conditions on (i) the perturbation temperature (e.g. a zero heat-flux condition,
$y=0$
follows from our mean-field approximation of a constant temperature at the base, as discussed in § 2.1. It should be noted that these boundary conditions (3.4) were also used by Eshuis et al. (Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010, Reference Eshuis, van der Weele, Alam, van Gerner, van der Höf, Kuipers, Luding, van der Meer and Lohse2013) for the linear stability analysis of the same problem. We shall show in § 6.2 that changing the free-surface boundary conditions on (i) the perturbation temperature (e.g. a zero heat-flux condition,
![]() $\partial T^{\prime }/\partial y=0$
, at
$\partial T^{\prime }/\partial y=0$
, at
![]() $y=H$
) and (ii) the perturbation velocities does not noticeably affect our predictions on the nonlinear stability of the present problem.
$y=H$
) and (ii) the perturbation velocities does not noticeably affect our predictions on the nonlinear stability of the present problem.
The linear stability problem is obtained by neglecting the nonlinear terms in the disturbance equations (3.2):
Since the linear operator and the boundary conditions are translation invariant in
![]() $x$
and time, we can seek a normal-mode solution
$x$
and time, we can seek a normal-mode solution
where
![]() $\widehat{\boldsymbol{X}}$
and
$\widehat{\boldsymbol{X}}$
and
![]() $c$
denote the complex eigenfunction and eigenvalue, respectively, and
$c$
denote the complex eigenfunction and eigenvalue, respectively, and
![]() $k_{x}$
is the real streamwise wavenumber. By substituting (3.6) into (3.5) and (3.3) we obtain an eigenvalue problem
$k_{x}$
is the real streamwise wavenumber. By substituting (3.6) into (3.5) and (3.3) we obtain an eigenvalue problem
where
![]() $\unicode[STIX]{x1D647}=\mathscr{L}(\partial /\partial x\rightarrow \text{i}k_{x},\partial /\partial y\rightarrow \text{d}/\text{d}y,\dots )$
is the complex-valued linear differential operator, and the boundary operators transform as
$\unicode[STIX]{x1D647}=\mathscr{L}(\partial /\partial x\rightarrow \text{i}k_{x},\partial /\partial y\rightarrow \text{d}/\text{d}y,\dots )$
is the complex-valued linear differential operator, and the boundary operators transform as
![]() $B_{0}=\mathscr{B}_{0}(\partial /\partial y\rightarrow \text{d}/\text{d}y)$
and
$B_{0}=\mathscr{B}_{0}(\partial /\partial y\rightarrow \text{d}/\text{d}y)$
and
![]() $B_{H}=\mathscr{B}_{H}$
. For the temporal development of perturbations (3.6), the flow is said to be stable, unstable or neutrally stable if the real part of any eigenvalue is negative, positive or zero (
$B_{H}=\mathscr{B}_{H}$
. For the temporal development of perturbations (3.6), the flow is said to be stable, unstable or neutrally stable if the real part of any eigenvalue is negative, positive or zero (
![]() $\text{Re}(c)<0,>0,=0$
), respectively.
$\text{Re}(c)<0,>0,=0$
), respectively.
Since the linear stability operator is not self-adjoint, we need to formulate the adjoint eigenvalue problem whose solution is needed to compute the Landau coefficients (§ 3.2). The adjoint operator,
![]() $\unicode[STIX]{x1D647}^{\dagger }$
, for the linear stability problem is defined via
$\unicode[STIX]{x1D647}^{\dagger }$
, for the linear stability problem is defined via
where the following definition of the inner product is adopted:
Here,
![]() $\boldsymbol{X}_{1}(y)$
and
$\boldsymbol{X}_{1}(y)$
and
![]() $\boldsymbol{X}_{2}(y)$
are two complex-valued vector functions, and the ‘tilde’ on a quantity denotes its complex conjugate. The explicit forms of
$\boldsymbol{X}_{2}(y)$
are two complex-valued vector functions, and the ‘tilde’ on a quantity denotes its complex conjugate. The explicit forms of
![]() $\unicode[STIX]{x1D647}^{\dagger }$
and the corresponding boundary conditions are determined from (3.8) via integration by parts. The adjoint eigenvalue problem can be written as
$\unicode[STIX]{x1D647}^{\dagger }$
and the corresponding boundary conditions are determined from (3.8) via integration by parts. The adjoint eigenvalue problem can be written as
where
![]() $\widehat{\boldsymbol{X}}^{\dagger }=(\widehat{n}^{\dagger },\widehat{u}^{\dagger },\widehat{v}^{\dagger },\widehat{T}^{\dagger })$
is the adjoint eigenfunction, with associated boundary conditions
$\widehat{\boldsymbol{X}}^{\dagger }=(\widehat{n}^{\dagger },\widehat{u}^{\dagger },\widehat{v}^{\dagger },\widehat{T}^{\dagger })$
is the adjoint eigenfunction, with associated boundary conditions
The elements of
![]() $\unicode[STIX]{x1D647}^{\dagger }$
are given in appendix A.
$\unicode[STIX]{x1D647}^{\dagger }$
are given in appendix A.
3.2. Amplitude expansion method and Landau equation
The normal-mode ansatz of linear stability (3.6) can be rewritten as
where
![]() $\text{e}^{at}$
accounts for the temporal variation of an infinitesimal disturbance. However, due to the finite size of the disturbances, a single mode interacts with itself and produces its harmonics which distort the base flow. Consequently, the perturbation amplitude can no longer be defined by the exponential term
$\text{e}^{at}$
accounts for the temporal variation of an infinitesimal disturbance. However, due to the finite size of the disturbances, a single mode interacts with itself and produces its harmonics which distort the base flow. Consequently, the perturbation amplitude can no longer be defined by the exponential term
![]() $\text{e}^{at}$
and the frequency of perturbation would also depend on its amplitude. Thus, the disturbance can be expressed as
$\text{e}^{at}$
and the frequency of perturbation would also depend on its amplitude. Thus, the disturbance can be expressed as
where the second term is the complex conjugate (denoted by tilde) of the first term. Here,
![]() $A$
is the real amplitude of the perturbation,
$A$
is the real amplitude of the perturbation,
![]() ${\it\theta}$
is the cycle of the fundamental wave and the summation is taken over all positive integers
${\it\theta}$
is the cycle of the fundamental wave and the summation is taken over all positive integers
![]() $k\geqslant 0$
. We require that the nonlinear problem at
$k\geqslant 0$
. We require that the nonlinear problem at
![]() $O(A)$
must reduce to the linear stability problem with an exponential growth of amplitude, i.e.
$O(A)$
must reduce to the linear stability problem with an exponential growth of amplitude, i.e.
![]() $A\rightarrow \text{e}^{at}$
for infinitesimal perturbations. Further, at
$A\rightarrow \text{e}^{at}$
for infinitesimal perturbations. Further, at
![]() $O(A^{2})$
we have only two choices: (i) the interaction of two linear modes giving the second harmonic and (ii) the interaction of the fundamental with its conjugate producing a distortion of the base flow. The above considerations suggest that the disturbance amplitude in (3.13) can be written in the form of a power series in amplitude,
$O(A^{2})$
we have only two choices: (i) the interaction of two linear modes giving the second harmonic and (ii) the interaction of the fundamental with its conjugate producing a distortion of the base flow. The above considerations suggest that the disturbance amplitude in (3.13) can be written in the form of a power series in amplitude,
where the superscripts
![]() $k$
and
$k$
and
![]() $m$
on
$m$
on
![]() $\boldsymbol{X}^{[k;m]}(y)$
are related to the Fourier mode and the order of the perturbation amplitude, respectively (Shukla & Alam Reference Shukla and Alam2011b
; Alam & Shukla Reference Alam and Shukla2013). For example,
$\boldsymbol{X}^{[k;m]}(y)$
are related to the Fourier mode and the order of the perturbation amplitude, respectively (Shukla & Alam Reference Shukla and Alam2011b
; Alam & Shukla Reference Alam and Shukla2013). For example,
![]() $[k;m]=[1;1]$
refers to the linear/fundamental mode which is of order
$[k;m]=[1;1]$
refers to the linear/fundamental mode which is of order
![]() $O(A)$
,
$O(A)$
,
![]() $[2;2]$
is the second harmonic which is of order
$[2;2]$
is the second harmonic which is of order
![]() $O(A^{2})$
,
$O(A^{2})$
,
![]() $[0;2]$
is the distortion of the base state at order
$[0;2]$
is the distortion of the base state at order
![]() $O(A^{2})$
,
$O(A^{2})$
,
![]() $[1;3]$
is the distortion of the fundamental mode at order
$[1;3]$
is the distortion of the fundamental mode at order
![]() $O(A^{3})$
, and so on.
$O(A^{3})$
, and so on.
To deal with the time-dependent terms of the disturbance equations we assume that the amplitude of the perturbation evolves according to the Landau equation (Shukla & Alam Reference Shukla and Alam2011b ; Alam & Shukla Reference Alam and Shukla2013),
and the associated frequency
![]() ${\it\omega}={\it\omega}(A)$
evolves as
${\it\omega}={\it\omega}(A)$
evolves as
In (3.15),
![]() $a^{(0)}$
and
$a^{(0)}$
and
![]() $a^{(2)}$
are the linear growth rate and the real part of the first Landau coefficient, respectively. It should be noted that in the limiting case of ‘infinitesimal-amplitude’ perturbations (
$a^{(2)}$
are the linear growth rate and the real part of the first Landau coefficient, respectively. It should be noted that in the limiting case of ‘infinitesimal-amplitude’ perturbations (
![]() $A\rightarrow 0$
) the nonlinear terms in (3.15) and (3.16) can be neglected, resulting in
$A\rightarrow 0$
) the nonlinear terms in (3.15) and (3.16) can be neglected, resulting in
which corresponds to the well-known ansatz of exponential growth in the linear stability analysis. We note in passing that the general validity of the Landau equation (3.15), (3.16) to predict nonlinear instabilities has been demonstrated for granular shear flow by deriving the same equation using an altogether different method (centre manifold reduction; Shukla & Alam Reference Shukla and Alam2009).
By substituting (3.14)–(3.16) into the disturbance equations and separating the powers of the amplitude, we obtain the following system of differential equations:
where
![]() $\unicode[STIX]{x1D647}_{km}$
and
$\unicode[STIX]{x1D647}_{km}$
and
![]() $\unicode[STIX]{x1D647}_{k}$
are the linear operators and
$\unicode[STIX]{x1D647}_{k}$
are the linear operators and
![]() $\boldsymbol{G}_{km}$
is a vector representing the sum of linear and nonlinear terms, as given by
$\boldsymbol{G}_{km}$
is a vector representing the sum of linear and nonlinear terms, as given by
are the Landau coefficients,
![]() ${\it\delta}_{k1}$
is the Kronecker delta and
${\it\delta}_{k1}$
is the Kronecker delta and
![]() $\boldsymbol{X}^{[1;1]}$
is the linear eigenfunction.
$\boldsymbol{X}^{[1;1]}$
is the linear eigenfunction.
In the weakly nonlinear regime of small growth rates,
![]() $a^{(0)}\sim 0$
, the Landau coefficients (3.21) are determined from the solvability condition of (3.18) at odd orders (
$a^{(0)}\sim 0$
, the Landau coefficients (3.21) are determined from the solvability condition of (3.18) at odd orders (
![]() $m=3,5,\dots$
):
$m=3,5,\dots$
):
 $$\begin{eqnarray}c^{(m-1)}=a^{(m-1)}+\text{i}b^{(m-1)}=\frac{\langle \widehat{\boldsymbol{X}}^{\dagger },\boldsymbol{G}_{1m}\rangle }{\langle \widehat{\boldsymbol{X}}^{\dagger },\boldsymbol{X}^{[1,1]}\rangle }=\frac{\displaystyle \int _{0}^{H}\tilde{\widehat{\boldsymbol{X}}^{\dagger }}\boldsymbol{G}_{1m}\text{d}y}{\displaystyle \int _{0}^{H}\tilde{\widehat{\boldsymbol{X}}^{\dagger }}\boldsymbol{X}^{[1;1]}\text{d}y},\end{eqnarray}$$
$$\begin{eqnarray}c^{(m-1)}=a^{(m-1)}+\text{i}b^{(m-1)}=\frac{\langle \widehat{\boldsymbol{X}}^{\dagger },\boldsymbol{G}_{1m}\rangle }{\langle \widehat{\boldsymbol{X}}^{\dagger },\boldsymbol{X}^{[1,1]}\rangle }=\frac{\displaystyle \int _{0}^{H}\tilde{\widehat{\boldsymbol{X}}^{\dagger }}\boldsymbol{G}_{1m}\text{d}y}{\displaystyle \int _{0}^{H}\tilde{\widehat{\boldsymbol{X}}^{\dagger }}\boldsymbol{X}^{[1;1]}\text{d}y},\end{eqnarray}$$
where
![]() $\widehat{\boldsymbol{X}}^{\dagger }$
is the adjoint eigenfunction as defined in (3.10). Knowing the Landau coefficients, the systems of equations (3.18) at different order
$\widehat{\boldsymbol{X}}^{\dagger }$
is the adjoint eigenfunction as defined in (3.10). Knowing the Landau coefficients, the systems of equations (3.18) at different order
![]() $O(A^{m})$
can be solved sequentially for any Fourier mode (
$O(A^{m})$
can be solved sequentially for any Fourier mode (
![]() $k=1,2,\dots$
); see § 4.2 for the related numerical procedure.
$k=1,2,\dots$
); see § 4.2 for the related numerical procedure.
4. Equilibrium solution and numerical method
4.1. First Landau coefficient and equilibrium solution
The nonlinear equilibrium/stationary solutions
![]() $A(t)=A_{e}$
of the Landau equation (3.15) are calculated by substituting
$A(t)=A_{e}$
of the Landau equation (3.15) are calculated by substituting
![]() $\text{d}A/\text{d}t=0$
. At cubic order
$\text{d}A/\text{d}t=0$
. At cubic order
![]() $O(A^{3})$
, we obtain the trivial solution
$O(A^{3})$
, we obtain the trivial solution
![]() $A_{e}=0$
, representing the base flow, and two nontrivial solutions
$A_{e}=0$
, representing the base flow, and two nontrivial solutions
where
![]() $a^{(0)}$
and
$a^{(0)}$
and
![]() $a^{(2)}$
are the growth rate and the real part of the first Landau coefficient, respectively. The non-zero solutions exist if
$a^{(2)}$
are the growth rate and the real part of the first Landau coefficient, respectively. The non-zero solutions exist if
![]() $a^{(0)}$
and
$a^{(0)}$
and
![]() $a^{(2)}$
have opposite signs. Depending on the sign of
$a^{(2)}$
have opposite signs. Depending on the sign of
![]() $a^{(0)}$
and
$a^{(0)}$
and
![]() $a^{(2)}$
, two types of bifurcations can be classified: subcritical bifurcation (
$a^{(2)}$
, two types of bifurcations can be classified: subcritical bifurcation (
![]() $a^{(0)}<0$
and
$a^{(0)}<0$
and
![]() $a^{(2)}>0$
) for which the base flow is linearly stable and supercritical bifurcation (
$a^{(2)}>0$
) for which the base flow is linearly stable and supercritical bifurcation (
![]() $a^{(0)}>0$
and
$a^{(0)}>0$
and
![]() $a^{(2)}<0$
) for linearly unstable flows. The phase equation (3.16) provides information on whether the bifurcation is stationary (
$a^{(2)}<0$
) for linearly unstable flows. The phase equation (3.16) provides information on whether the bifurcation is stationary (
![]() $b^{(0)}={\it\omega}=0$
) or oscillatory (
$b^{(0)}={\it\omega}=0$
) or oscillatory (
![]() $b^{(0)}={\it\omega}\neq 0$
), corresponding to pitchfork and Hopf bifurcations, respectively. It may be noted that the cubic Landau equation does not yield any stable equilibrium solution for the subcritical case.
$b^{(0)}={\it\omega}\neq 0$
), corresponding to pitchfork and Hopf bifurcations, respectively. It may be noted that the cubic Landau equation does not yield any stable equilibrium solution for the subcritical case.
The finite-amplitude equilibrium solution for perturbation flow fields (number density, velocity and granular temperature) at cubic order
![]() $O(A^{3})$
can be written as
$O(A^{3})$
can be written as
 $$\begin{eqnarray}\displaystyle \boldsymbol{X}(x,y,t,A_{e}) & = & \displaystyle A_{e}^{2}\boldsymbol{X}^{[0;2]}+\left[\left(A_{e}\boldsymbol{X}^{[1;1]}\text{e}^{\text{i}{\it\theta}}+A_{e}^{2}\boldsymbol{X}^{[2;2]}\text{e}^{2\text{i}{\it\theta}}+A_{e}^{3}\boldsymbol{X}^{[1;3]}\text{e}^{\text{i}{\it\theta}}+A_{e}^{3}\boldsymbol{X}^{[3;3]}\text{e}^{3\text{i}{\it\theta}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\left(A_{e}\tilde{\boldsymbol{X}}^{[1;1]}\text{e}^{-\text{i}{\it\theta}}+A_{e}^{2}\tilde{\boldsymbol{X}}^{[2;2]}\text{e}^{-2\text{i}{\it\theta}}+A_{e}^{3}\tilde{\boldsymbol{X}}^{[1;3]}\text{e}^{-\text{i}{\it\theta}}\!+A_{e}^{3}\tilde{\boldsymbol{X}}^{[3;3]}\text{e}^{-3\text{i}{\it\theta}}\right)\!\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{X}(x,y,t,A_{e}) & = & \displaystyle A_{e}^{2}\boldsymbol{X}^{[0;2]}+\left[\left(A_{e}\boldsymbol{X}^{[1;1]}\text{e}^{\text{i}{\it\theta}}+A_{e}^{2}\boldsymbol{X}^{[2;2]}\text{e}^{2\text{i}{\it\theta}}+A_{e}^{3}\boldsymbol{X}^{[1;3]}\text{e}^{\text{i}{\it\theta}}+A_{e}^{3}\boldsymbol{X}^{[3;3]}\text{e}^{3\text{i}{\it\theta}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\left(A_{e}\tilde{\boldsymbol{X}}^{[1;1]}\text{e}^{-\text{i}{\it\theta}}+A_{e}^{2}\tilde{\boldsymbol{X}}^{[2;2]}\text{e}^{-2\text{i}{\it\theta}}+A_{e}^{3}\tilde{\boldsymbol{X}}^{[1;3]}\text{e}^{-\text{i}{\it\theta}}\!+A_{e}^{3}\tilde{\boldsymbol{X}}^{[3;3]}\text{e}^{-3\text{i}{\it\theta}}\right)\!\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \boldsymbol{X}(x,y,A_{e}) & = & \displaystyle 2A_{e}\left[\boldsymbol{X}_{r}^{[1;1]}\cos 2{\rm\pi}(x/{\it\lambda}_{x})-\boldsymbol{X}_{i}^{[1;1]}\sin 2{\rm\pi}(x/{\it\lambda}_{x})\right]+A_{e}^{2}\boldsymbol{X}^{[0;2]}\nonumber\\ \displaystyle & & \displaystyle +\;2A_{e}^{2}\left[\boldsymbol{X}_{r}^{[2;2]}\cos 4{\rm\pi}(x/{\it\lambda}_{x})-\boldsymbol{X}_{i}^{[2;2]}\sin 4{\rm\pi}(x/{\it\lambda}_{x})\right]\nonumber\\ \displaystyle & & \displaystyle +\;2A_{e}^{3}\left[\boldsymbol{X}_{r}^{[1;3]}\cos 2{\rm\pi}(x/{\it\lambda}_{x})-\boldsymbol{X}_{i}^{[1;3]}\sin 2{\rm\pi}(x/{\it\lambda}_{x})\right]\nonumber\\ \displaystyle & & \displaystyle +\;2A_{e}^{3}\left[\boldsymbol{X}_{r}^{[3;3]}\cos 6{\rm\pi}(x/{\it\lambda}_{x})-\boldsymbol{X}_{i}^{[3;3]}\sin 6{\rm\pi}(x/{\it\lambda}_{x})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{X}(x,y,A_{e}) & = & \displaystyle 2A_{e}\left[\boldsymbol{X}_{r}^{[1;1]}\cos 2{\rm\pi}(x/{\it\lambda}_{x})-\boldsymbol{X}_{i}^{[1;1]}\sin 2{\rm\pi}(x/{\it\lambda}_{x})\right]+A_{e}^{2}\boldsymbol{X}^{[0;2]}\nonumber\\ \displaystyle & & \displaystyle +\;2A_{e}^{2}\left[\boldsymbol{X}_{r}^{[2;2]}\cos 4{\rm\pi}(x/{\it\lambda}_{x})-\boldsymbol{X}_{i}^{[2;2]}\sin 4{\rm\pi}(x/{\it\lambda}_{x})\right]\nonumber\\ \displaystyle & & \displaystyle +\;2A_{e}^{3}\left[\boldsymbol{X}_{r}^{[1;3]}\cos 2{\rm\pi}(x/{\it\lambda}_{x})-\boldsymbol{X}_{i}^{[1;3]}\sin 2{\rm\pi}(x/{\it\lambda}_{x})\right]\nonumber\\ \displaystyle & & \displaystyle +\;2A_{e}^{3}\left[\boldsymbol{X}_{r}^{[3;3]}\cos 6{\rm\pi}(x/{\it\lambda}_{x})-\boldsymbol{X}_{i}^{[3;3]}\sin 6{\rm\pi}(x/{\it\lambda}_{x})\right].\end{eqnarray}$$
Addition of (4.2) to the base-state solution (
![]() $\boldsymbol{X}^{0}$
) yields the nonlinear solution for flow fields:
$\boldsymbol{X}^{0}$
) yields the nonlinear solution for flow fields:
While presenting results in § 5.1 we will compare the above nonlinear solution with its linear counterpart
which involves only the fundamental mode scaled by its equilibrium amplitude.
4.2. Spectral-based numerical method
To determine the equilibrium amplitude (4.1) and the associated nonlinear pattern (4.3), the differential equations (3.18) for different Fourier modes (
![]() $k=1,2,3,\dots$
) at different orders in the perturbation amplitude
$k=1,2,3,\dots$
) at different orders in the perturbation amplitude
![]() $O(A^{m})$
must be solved, along with the first Landau coefficient (3.22). These equations are solved numerically by employing the spectral collocation scheme (Canuto et al.
Reference Canuto, Hussaini, Quarteroni and Zang1988), the details of which can be found in Shukla & Alam (Reference Shukla and Alam2011a
,Reference Shukla and Alam
b
) and Alam & Shukla (Reference Alam and Shukla2013). For the sake of completeness of the present paper, we briefly recall the salient features of our numerical scheme.
$O(A^{m})$
must be solved, along with the first Landau coefficient (3.22). These equations are solved numerically by employing the spectral collocation scheme (Canuto et al.
Reference Canuto, Hussaini, Quarteroni and Zang1988), the details of which can be found in Shukla & Alam (Reference Shukla and Alam2011a
,Reference Shukla and Alam
b
) and Alam & Shukla (Reference Alam and Shukla2013). For the sake of completeness of the present paper, we briefly recall the salient features of our numerical scheme.
At
![]() $O(A)$
we need to solve the linear stability equations in the form of the following generalized differential eigenvalue problem (put
$O(A)$
we need to solve the linear stability equations in the form of the following generalized differential eigenvalue problem (put
![]() $k=m=1$
into (3.18)):
$k=m=1$
into (3.18)):
along with homogeneous boundary conditions:
The four ordinary differential equations in (4.6) are discretized along the
![]() $y$
-direction by implementing the staggered-grid spectral collocation scheme (Alam & Nott Reference Alam and Nott1998; Alam & Shukla Reference Alam and Shukla2013) which uses
$y$
-direction by implementing the staggered-grid spectral collocation scheme (Alam & Nott Reference Alam and Nott1998; Alam & Shukla Reference Alam and Shukla2013) which uses
![]() $M$
th order Chebyshev polynomials as basis functions. More specifically, while the mass balance equation is collocated at Gauss points (which are the zeros of the Chebyshev polynomials), the momentum and granular energy equations are collocated at Gauss–Lobatto points (which are the extrema of the Chebyshev polynomials). Since the Gauss points do not include the two boundary points, there is no need to impose any ‘artificial’ boundary condition for density (Alam & Nott Reference Alam and Nott1998); such ‘artificial’ boundary conditions are, however, needed when all equations are collocated at Gauss–Lobatto points, resulting in one spurious eigenvalue. We use a transformation
$M$
th order Chebyshev polynomials as basis functions. More specifically, while the mass balance equation is collocated at Gauss points (which are the zeros of the Chebyshev polynomials), the momentum and granular energy equations are collocated at Gauss–Lobatto points (which are the extrema of the Chebyshev polynomials). Since the Gauss points do not include the two boundary points, there is no need to impose any ‘artificial’ boundary condition for density (Alam & Nott Reference Alam and Nott1998); such ‘artificial’ boundary conditions are, however, needed when all equations are collocated at Gauss–Lobatto points, resulting in one spurious eigenvalue. We use a transformation
to transfer the variables from the physical grid
![]() $y\in (0,H)$
to the spectral grid
$y\in (0,H)$
to the spectral grid
![]() ${\it\xi}\in (-1,1)$
. Upon implementing the spectral discretization of the derivative, the differential eigenvalue problem (4.6) is transformed into a generalized matrix eigenvalue problem:
${\it\xi}\in (-1,1)$
. Upon implementing the spectral discretization of the derivative, the differential eigenvalue problem (4.6) is transformed into a generalized matrix eigenvalue problem:
where
![]() $\unicode[STIX]{x1D63C}$
and
$\unicode[STIX]{x1D63C}$
and
![]() $\unicode[STIX]{x1D63D}=\unicode[STIX]{x1D644}$
are square matrices of order
$\unicode[STIX]{x1D63D}=\unicode[STIX]{x1D644}$
are square matrices of order
![]() $(4M+3)$
, with
$(4M+3)$
, with
![]() $M$
being the degree of the Chebyshev polynomial. Equation (4.9) has been solved by the QZ-algorithm of MATLAB software, yielding all eigenvalues
$M$
being the degree of the Chebyshev polynomial. Equation (4.9) has been solved by the QZ-algorithm of MATLAB software, yielding all eigenvalues
![]() $c^{(0)}$
and associated ‘discrete’ linear eigenfunctions
$c^{(0)}$
and associated ‘discrete’ linear eigenfunctions
![]() $\boldsymbol{X}^{[1;1]}=(n^{[1;1]},u^{[1;1]},v^{[1;1]},T^{[1;1]})$
. The same numerical procedure is followed to solve the adjoint eigenvalue problem (3.10), (3.11), yielding the adjoint eigenfunctions
$\boldsymbol{X}^{[1;1]}=(n^{[1;1]},u^{[1;1]},v^{[1;1]},T^{[1;1]})$
. The same numerical procedure is followed to solve the adjoint eigenvalue problem (3.10), (3.11), yielding the adjoint eigenfunctions
![]() $\hat{\boldsymbol{X}}^{\dagger }=(\hat{n}^{\dagger },{\hat{u}}^{\dagger },\hat{v}^{\dagger },\hat{T}^{\dagger })$
and related eigenvalues.
$\hat{\boldsymbol{X}}^{\dagger }=(\hat{n}^{\dagger },{\hat{u}}^{\dagger },\hat{v}^{\dagger },\hat{T}^{\dagger })$
and related eigenvalues.
The general form of equations for
![]() $k\neq 1$
and
$k\neq 1$
and
![]() $m\geqslant k$
(namely (3.18)) can be written as
$m\geqslant k$
(namely (3.18)) can be written as
![]() $\unicode[STIX]{x1D647}_{km}\boldsymbol{X}^{[k;m]}=\boldsymbol{G}_{km}$
, which at
$\unicode[STIX]{x1D647}_{km}\boldsymbol{X}^{[k;m]}=\boldsymbol{G}_{km}$
, which at
![]() $O(A^{2})$
leads to two equations:
$O(A^{2})$
leads to two equations:
where
![]() $\boldsymbol{X}$
is the discrete version of the respective modal amplitude function (
$\boldsymbol{X}$
is the discrete version of the respective modal amplitude function (
![]() $\boldsymbol{X}^{[0;2]}$
or
$\boldsymbol{X}^{[0;2]}$
or
![]() $\boldsymbol{X}^{[2;2]}$
). To deal with the dense, nearly ill-conditioned coefficient matrix
$\boldsymbol{X}^{[2;2]}$
). To deal with the dense, nearly ill-conditioned coefficient matrix
![]() $\unicode[STIX]{x1D63C}$
, we have employed the singular-value decomposition (Golub & van Loan Reference Golub and van Loan1989) to solve (4.12).
$\unicode[STIX]{x1D63C}$
, we have employed the singular-value decomposition (Golub & van Loan Reference Golub and van Loan1989) to solve (4.12).
All the above information is needed to calculate the first Landau coefficient from (3.22) which involves the ratio of two definite integrals:
 $$\begin{eqnarray}c^{(2)}=a^{(2)}+\text{i}b^{(2)}=\frac{\displaystyle \int _{0}^{H}\tilde{\widehat{\boldsymbol{X}}^{\dagger }}\boldsymbol{G}_{13}\text{d}y}{\displaystyle \int _{0}^{H}\tilde{\widehat{\boldsymbol{X}}^{\dagger }}\boldsymbol{X}^{[1;1]}\text{d}y}.\end{eqnarray}$$
$$\begin{eqnarray}c^{(2)}=a^{(2)}+\text{i}b^{(2)}=\frac{\displaystyle \int _{0}^{H}\tilde{\widehat{\boldsymbol{X}}^{\dagger }}\boldsymbol{G}_{13}\text{d}y}{\displaystyle \int _{0}^{H}\tilde{\widehat{\boldsymbol{X}}^{\dagger }}\boldsymbol{X}^{[1;1]}\text{d}y}.\end{eqnarray}$$
To achieve spectral accuracy and superior convergence, these integrals are evaluated using a Gauss–Chebyshev quadrature formula (Shukla & Alam Reference Shukla and Alam2011a
; Alam & Shukla Reference Alam and Shukla2013) which uses a Chebyshev polynomial as an interpolating polynomial. Having calculated
![]() $c^{(2)}$
from (4.13), we need to solve the equations for (i) the distortion to the fundamental mode (put
$c^{(2)}$
from (4.13), we need to solve the equations for (i) the distortion to the fundamental mode (put
![]() $k=1$
and
$k=1$
and
![]() $m=3$
into (3.18)) and (ii) the third harmonic (put
$m=3$
into (3.18)) and (ii) the third harmonic (put
![]() $k=3=m$
into (3.18)):
$k=3=m$
into (3.18)):
Before presenting results on nonlinear stability, we need to validate the numerical solution of the adjoint stability problem. It should be noted that the eigenvalues of the adjoint operator (3.10) are complex conjugates of those of the linear stability operator (3.7). To check this, we show the variation of the real part of the least stable eigenvalue (
![]() $c^{(0)}=a^{(0)}+\text{i}b^{(0)}$
) of linear (circles) and adjoint (stars) operators with wavenumber for two values of
$c^{(0)}=a^{(0)}+\text{i}b^{(0)}$
) of linear (circles) and adjoint (stars) operators with wavenumber for two values of
![]() $(F,S)=(6,100)$
and (16, 400) in figures 3(a) and (b), respectively; it should be noted that the imaginary part of the eigenvalue is identically zero (
$(F,S)=(6,100)$
and (16, 400) in figures 3(a) and (b), respectively; it should be noted that the imaginary part of the eigenvalue is identically zero (
![]() $b^{(0)}=0$
) for both cases, implying that the instability is stationary. It is clear from these figures that the numerically obtained linear and adjoint eigenvalues overlap with each other, which, in turn, validates the adjoint stability problem (3.10), (3.11).
$b^{(0)}=0$
) for both cases, implying that the instability is stationary. It is clear from these figures that the numerically obtained linear and adjoint eigenvalues overlap with each other, which, in turn, validates the adjoint stability problem (3.10), (3.11).

Figure 3. Variation of the real part of the least stable mode of linear (circles) and adjoint (stars) eigenvalues with wavenumber (
![]() $k_{x}$
) for (
$k_{x}$
) for (
![]() $F,S$
) (a)
$F,S$
) (a)
![]() $=(6,100)$
and (b)
$=(6,100)$
and (b)
![]() $=(16,400)$
, with
$=(16,400)$
, with
![]() $e=0.9$
.
$e=0.9$
.
To check the convergence of the numerical method with respect to the degree of the Chebyshev polynomial (i.e. the number of collocation points
![]() $M$
), the variation of the growth rate (
$M$
), the variation of the growth rate (
![]() $a^{(0)}$
) with
$a^{(0)}$
) with
![]() $k_{x}$
, with other parameters being the same as in figure 3(a), is shown in figure 4; the stars, triangles and circles denote results for collocation points of
$k_{x}$
, with other parameters being the same as in figure 3(a), is shown in figure 4; the stars, triangles and circles denote results for collocation points of
![]() $M=20$
, 50 and 100, respectively. It is seen that the growth rates are well matched for
$M=20$
, 50 and 100, respectively. It is seen that the growth rates are well matched for
![]() $M=50$
and 100; we have also verified that a similar agreement holds for the first Landau coefficient (not shown) too. Therefore, for all results presented in this paper the degree of the Chebyshev polynomial (
$M=50$
and 100; we have also verified that a similar agreement holds for the first Landau coefficient (not shown) too. Therefore, for all results presented in this paper the degree of the Chebyshev polynomial (
![]() $M$
) is fixed to 50.
$M$
) is fixed to 50.

Figure 4. The effect of the number of collocation points (
![]() $M$
) on the least stable mode. Parameter values are the same as in figure 3(a).
$M$
) on the least stable mode. Parameter values are the same as in figure 3(a).
5. Nonlinear convection and bifurcation scenario
Figure 5 displays the phase diagram obtained from the experiments of Eshuis et al. (Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010) for the onset of convection from the Leidenfrost state: the convection rolls appear when the shaking strength
![]() $S$
exceeds a minimum/critical value for a specified layer depth (particle loading)
$S$
exceeds a minimum/critical value for a specified layer depth (particle loading)
![]() $F$
, and the value of this critical
$F$
, and the value of this critical
![]() $S$
increases with increasing particle loading. It is clear from figure 5 that the experiment (symbols), the simulation (filled symbols) and the linear stability theory (solid line) agree well. We have analysed the nonlinear results for three values of the layer depth (
$S$
increases with increasing particle loading. It is clear from figure 5 that the experiment (symbols), the simulation (filled symbols) and the linear stability theory (solid line) agree well. We have analysed the nonlinear results for three values of the layer depth (
![]() $F=6$
, 10 and 16) over a range of shaking strengths (
$F=6$
, 10 and 16) over a range of shaking strengths (
![]() $S\in (50,800)$
) to cover the full experimental phase diagram (
$S\in (50,800)$
) to cover the full experimental phase diagram (
![]() $F\in (5,16)$
) in figure 5. The theoretical predictions look similar at any
$F\in (5,16)$
) in figure 5. The theoretical predictions look similar at any
![]() $F$
, and hence the detailed results will be presented only for
$F$
, and hence the detailed results will be presented only for
![]() $F=6$
in § 5.1. A qualitative comparison of the predicted nonlinear patterns with experimental results in a similar set-up is made in § 5.2.
$F=6$
in § 5.1. A qualitative comparison of the predicted nonlinear patterns with experimental results in a similar set-up is made in § 5.2.

Figure 5. Phase diagram in the (
![]() $F,S$
)-plane showing the results from experiment, simulation and linear stability theory, adapted from Eshuis et al. (Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010). The open and solid symbols represent experimental and simulation data, respectively, and the line represents the linear stability prediction.
$F,S$
)-plane showing the results from experiment, simulation and linear stability theory, adapted from Eshuis et al. (Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010). The open and solid symbols represent experimental and simulation data, respectively, and the line represents the linear stability prediction.
5.1. Numerical results: from ‘full’ convection to a state of ‘floating’ convection
The variation of the real part of the first Landau coefficient
![]() $a^{(2)}$
(denoted by stars) with wavenumber
$a^{(2)}$
(denoted by stars) with wavenumber
![]() $k_{x}$
, along with the corresponding variation of the growth rate
$k_{x}$
, along with the corresponding variation of the growth rate
![]() $a^{(0)}$
(circles) of the least stable mode, is shown in figure 6(a). The layer depth at rest is set to
$a^{(0)}$
(circles) of the least stable mode, is shown in figure 6(a). The layer depth at rest is set to
![]() $F=6$
and the shaking strength to
$F=6$
and the shaking strength to
![]() $S=100$
, with the restitution coefficient being
$S=100$
, with the restitution coefficient being
![]() $e=0.9$
(which is appropriate for glass balls). For this problem, we have verified that the instabilities are stationary, i.e.
$e=0.9$
(which is appropriate for glass balls). For this problem, we have verified that the instabilities are stationary, i.e.
![]() $b^{(0)}=b^{(2)}=0$
, leading to a stationary/pitchfork bifurcation from the underlying density-inverted Leidenfrost state. It is seen that
$b^{(0)}=b^{(2)}=0$
, leading to a stationary/pitchfork bifurcation from the underlying density-inverted Leidenfrost state. It is seen that
![]() $a^{(2)}<0$
for two ranges of
$a^{(2)}<0$
for two ranges of
![]() $k_{x}$
over which the Leidenfrost state is linearly unstable (
$k_{x}$
over which the Leidenfrost state is linearly unstable (
![]() $a^{(0)}>0$
): (i) small wavenumbers of
$a^{(0)}>0$
): (i) small wavenumbers of
![]() $k_{x}\in (0.0366,0.0535)$
and (ii) moderate wavenumbers of
$k_{x}\in (0.0366,0.0535)$
and (ii) moderate wavenumbers of
![]() $k_{x}\in (0.0703,0.1748)$
. Therefore, the flow admits supercritical pitchfork bifurcations for the above two ranges of
$k_{x}\in (0.0703,0.1748)$
. Therefore, the flow admits supercritical pitchfork bifurcations for the above two ranges of
![]() $k_{x}$
. The corresponding variation of the nonlinear equilibrium amplitude
$k_{x}$
. The corresponding variation of the nonlinear equilibrium amplitude
![]() $A_{e}$
(see (4.1)) is displayed in figure 6(b), confirming the existence of
$A_{e}$
(see (4.1)) is displayed in figure 6(b), confirming the existence of
![]() $A_{e}$
over the above two ranges of
$A_{e}$
over the above two ranges of
![]() $k_{x}$
. It is seen that
$k_{x}$
. It is seen that
![]() $A_{e}$
increases from both the lower and upper bifurcation points, located at
$A_{e}$
increases from both the lower and upper bifurcation points, located at
![]() $k_{xl}\approx 0.0366$
and
$k_{xl}\approx 0.0366$
and
![]() $k_{xu}\approx 0.1748$
, respectively; it should be noted further in figure 6(b) that the equilibrium solution emanating from
$k_{xu}\approx 0.1748$
, respectively; it should be noted further in figure 6(b) that the equilibrium solution emanating from
![]() $k_{xl}$
terminates at
$k_{xl}$
terminates at
![]() $k_{x}\approx 0.0535$
. Figure 6(a) confirms that there is a small window of wavenumbers
$k_{x}\approx 0.0535$
. Figure 6(a) confirms that there is a small window of wavenumbers
![]() $k_{x}\in (0.0535,0.07)$
over which
$k_{x}\in (0.0535,0.07)$
over which
![]() $a^{(0)}>0$
but
$a^{(0)}>0$
but
![]() $a^{(2)}>0$
, and hence the equilibrium solutions (4.1) do not exist there; the vertical line in figure 6(b) corresponds to the location
$a^{(2)}>0$
, and hence the equilibrium solutions (4.1) do not exist there; the vertical line in figure 6(b) corresponds to the location
![]() $k_{x}\approx 0.0703\equiv k_{d}$
at which
$k_{x}\approx 0.0703\equiv k_{d}$
at which
![]() $a^{(2)}=0$
(see figure 6
a), and hence the equilibrium amplitude diverges at
$a^{(2)}=0$
(see figure 6
a), and hence the equilibrium amplitude diverges at
![]() $k_{x}=k_{d}$
.
$k_{x}=k_{d}$
.

Figure 6. Variations of (a) the growth rate of the least stable mode
![]() $a^{(0)}$
(circles) and the real part of the first Landau coefficient
$a^{(0)}$
(circles) and the real part of the first Landau coefficient
![]() $a^{(2)}$
(stars) with wavenumber
$a^{(2)}$
(stars) with wavenumber
![]() $k_{x}$
for a shaking strength of
$k_{x}$
for a shaking strength of
![]() $S=100$
. (b) Variation of the equilibrium amplitude
$S=100$
. (b) Variation of the equilibrium amplitude
![]() $A_{e}$
with
$A_{e}$
with
![]() $k_{x}$
; see the text for details. The number of particle layers at rest is
$k_{x}$
; see the text for details. The number of particle layers at rest is
![]() $F=h_{0}/d=6$
and the restitution coefficient is
$F=h_{0}/d=6$
and the restitution coefficient is
![]() $e=0.9$
.
$e=0.9$
.
Figure 6(a) shows that the first Landau coefficient
![]() $a^{(2)}$
undergoes a sign reversal at a wavenumber of
$a^{(2)}$
undergoes a sign reversal at a wavenumber of
![]() $k_{x}\approx 0.0535\equiv k_{r}$
at which
$k_{x}\approx 0.0535\equiv k_{r}$
at which
![]() $a^{(2)}\rightarrow \pm \infty$
(i.e. a jump discontinuity), and an equilibrium solution does not exist at this location. The former is, in fact, a signature of resonance, as we discuss below.
$a^{(2)}\rightarrow \pm \infty$
(i.e. a jump discontinuity), and an equilibrium solution does not exist at this location. The former is, in fact, a signature of resonance, as we discuss below.
5.1.1. Nonlinear resonance at quadratic order
In the context of the nonlinear stability of granular plane Couette flow, Shukla & Alam (Reference Shukla and Alam2011b
) first identified two types of nonlinear resonance: (i) the mean-flow resonance and (ii) the 2:1 resonance. They traced the origin of both resonances to the modal equations at the quadratic order
![]() $O(A^{2})$
. Let us rewrite these equations for the distortion to the mean flow (
$O(A^{2})$
. Let us rewrite these equations for the distortion to the mean flow (
![]() $\boldsymbol{X}^{[0;2]}$
) and the second harmonic (
$\boldsymbol{X}^{[0;2]}$
) and the second harmonic (
![]() $\boldsymbol{X}^{[2;2]}$
):
$\boldsymbol{X}^{[2;2]}$
):
The system (5.1) has a solution iff
![]() $2a^{(0)}$
is not any of the eigenvalues of the linear problem at zero wavenumber, otherwise
$2a^{(0)}$
is not any of the eigenvalues of the linear problem at zero wavenumber, otherwise
![]() $\unicode[STIX]{x1D647}_{02}$
is singular and the solution
$\unicode[STIX]{x1D647}_{02}$
is singular and the solution
![]() $X^{[0;2]}$
blows up – this is dubbed mean-flow resonance since the underlying linear mode interacts with the mean flow. The condition for mean-flow resonance can be written as
$X^{[0;2]}$
blows up – this is dubbed mean-flow resonance since the underlying linear mode interacts with the mean flow. The condition for mean-flow resonance can be written as
where
![]() $j_{1}$
and
$j_{1}$
and
![]() $j_{2}$
refer to two different modes (note that there are a finite number of modes
$j_{2}$
refer to two different modes (note that there are a finite number of modes
![]() $(4M+3)$
, where
$(4M+3)$
, where
![]() $M$
is the number of collocation points). Similarly, the system of inhomogeneous equations (5.2) is solvable iff
$M$
is the number of collocation points). Similarly, the system of inhomogeneous equations (5.2) is solvable iff
![]() $2c^{(0)}$
is not equal to any of the eigenvalues of the linear problem with wavenumber
$2c^{(0)}$
is not equal to any of the eigenvalues of the linear problem with wavenumber
![]() $2k_{x}$
. For this case too, the solution
$2k_{x}$
. For this case too, the solution
![]() $X^{[2;2]}$
blows up due to the singularity of
$X^{[2;2]}$
blows up due to the singularity of
![]() $\unicode[STIX]{x1D647}_{22}$
– this is dubbed 2:1 resonance to highlight the underlying wavenumber ratio of two interacting linear modes. The condition for 2:1 resonance can be written as
$\unicode[STIX]{x1D647}_{22}$
– this is dubbed 2:1 resonance to highlight the underlying wavenumber ratio of two interacting linear modes. The condition for 2:1 resonance can be written as
for two modes
![]() $j_{1}$
and
$j_{1}$
and
![]() $j_{2}$
. The consequence of satisfying either of the above two resonance conditions at some location
$j_{2}$
. The consequence of satisfying either of the above two resonance conditions at some location
![]() $k_{x}$
is that the first Landau coefficient (4.13),
$k_{x}$
is that the first Landau coefficient (4.13),
is undefined at the same location since the integrand
![]() $\boldsymbol{G}_{13}(\cdot )$
is a linear function of
$\boldsymbol{G}_{13}(\cdot )$
is a linear function of
![]() $\boldsymbol{X}^{[0;2]}$
and
$\boldsymbol{X}^{[0;2]}$
and
![]() $\boldsymbol{X}^{[2;2]}$
, which diverge due to (5.5a,b
) and (5.6), respectively.
$\boldsymbol{X}^{[2;2]}$
, which diverge due to (5.5a,b
) and (5.6), respectively.
The existence of mean-flow resonance (5.5a,b
) was demonstrated in granular plane Couette flow (Shukla & Alam Reference Shukla and Alam2011a
,Reference Shukla and Alam
b
, Reference Shukla and Alam2013), but no evidence of 2:1 resonance (5.6) was found. For the present case of granular convection, figure 7 confirms that the condition (5.6) is satisfied since the growth rate curve for the least stable mode (which is real, i.e.
![]() $c^{(0)}(k_{x})\equiv a^{(0)}(k_{x})$
) intersects the curve for the growth rate of a mode
$c^{(0)}(k_{x})\equiv a^{(0)}(k_{x})$
) intersects the curve for the growth rate of a mode
![]() $a^{(0)}(2k_{x})/2$
(having twice the wavenumber) at
$a^{(0)}(2k_{x})/2$
(having twice the wavenumber) at
![]() $k_{x}\approx 0.0535=k_{r}$
(the subscript
$k_{x}\approx 0.0535=k_{r}$
(the subscript
![]() $r$
referring to the resonance location). This is responsible for the jump discontinuity of the first Landau coefficient
$r$
referring to the resonance location). This is responsible for the jump discontinuity of the first Landau coefficient
![]() $a^{(2)}$
in figure 6(a) at the same location. Therefore, the occurrence of the 2:1 resonance is responsible for the discontinuities in the first Landau coefficient and the equilibrium amplitudes in figure 6.
$a^{(2)}$
in figure 6(a) at the same location. Therefore, the occurrence of the 2:1 resonance is responsible for the discontinuities in the first Landau coefficient and the equilibrium amplitudes in figure 6.
The above nonlinear resonances are part and parcel of our single-mode analysis as elaborated by Shukla & Alam (Reference Shukla and Alam2011a ,Reference Shukla and Alam b , Reference Shukla and Alam2013) and Alam & Shukla (Reference Alam and Shukla2012, Reference Alam and Shukla2013) in various contexts of granular plane Couette flow. This has important implications on the validity of the present nonlinear analysis: the single-mode analysis is not valid at resonance points and, therefore, resonant mode interactions must be taken into account to obtain equilibrium amplitude near such resonance points. The related theory, in terms of coupled Landau equations, is complicated, but has recently been developed for plane Couette flow (Alam & Shukla 2014, unpublished). These issues are discussed later in § 6.3.
Although we have identified a plethora of such 2:1 resonances in the present vibrated-bed problem mostly at smaller values of the wavenumber
![]() $k_{x}<0.1$
, we will not elaborate on them further in this paper, except for mentioning their occurrence whenever there is such a jump discontinuity on the variation of
$k_{x}<0.1$
, we will not elaborate on them further in this paper, except for mentioning their occurrence whenever there is such a jump discontinuity on the variation of
![]() $a^{(2)}$
with any control parameter. In the rest of the paper we will largely focus on nonlinear results at moderate-to-large values of
$a^{(2)}$
with any control parameter. In the rest of the paper we will largely focus on nonlinear results at moderate-to-large values of
![]() $k_{x}$
.
$k_{x}$
.
5.1.2. Nonlinear convection patterns and their dependence on wavenumber
For parameter values as in figure 6(a) with
![]() $k_{x}=0.16$
, the linear (4.5) and nonlinear (4.4) solutions for the velocity and number-density fields in the (
$k_{x}=0.16$
, the linear (4.5) and nonlinear (4.4) solutions for the velocity and number-density fields in the (
![]() $x/d,y/d$
)-plane are displayed in the first and second rows of figure 8, respectively. (It should be noted that the wavenumber
$x/d,y/d$
)-plane are displayed in the first and second rows of figure 8, respectively. (It should be noted that the wavenumber
![]() $k_{x}=0.16$
corresponds to a wavelength of
$k_{x}=0.16$
corresponds to a wavelength of
![]() ${\it\lambda}_{x}/d\approx 39.25$
, and hence a box of length
${\it\lambda}_{x}/d\approx 39.25$
, and hence a box of length
![]() $L_{x}/d\equiv {\it\lambda}_{x}/d=40$
can accommodate one wavelength of pattern, i.e. a pair of rolls.) In the grey scale the white and black denote minimum and maximum density, respectively. Two pairs of convection rolls are observed in the velocity-vector maps (
$L_{x}/d\equiv {\it\lambda}_{x}/d=40$
can accommodate one wavelength of pattern, i.e. a pair of rolls.) In the grey scale the white and black denote minimum and maximum density, respectively. Two pairs of convection rolls are observed in the velocity-vector maps (
![]() $u,v$
) in figures 8(a,c). It should be noted that both the linear and nonlinear velocity patterns look similar; however, the structural features of the nonlinear density profile in figure 8(d) appear to be more modulated, especially at small scales, compared with its linear counterpart in figure 8(b).
$u,v$
) in figures 8(a,c). It should be noted that both the linear and nonlinear velocity patterns look similar; however, the structural features of the nonlinear density profile in figure 8(d) appear to be more modulated, especially at small scales, compared with its linear counterpart in figure 8(b).

Figure 9. Linear patterns (4.5) for (a) the velocity-vector and (b) the density fields in the (
![]() $x/d,y/d$
)-plane for
$x/d,y/d$
)-plane for
![]() $F=6$
,
$F=6$
,
![]() $S=100$
,
$S=100$
,
![]() $e=0.9$
and
$e=0.9$
and
![]() $k_{x}=0.037$
. Panels (c) and (d) are the corresponding nonlinear patterns (4.4). Panels (e) and (f) are the analogues of (c) and (d) for a higher wavenumber,
$k_{x}=0.037$
. Panels (c) and (d) are the corresponding nonlinear patterns (4.4). Panels (e) and (f) are the analogues of (c) and (d) for a higher wavenumber,
![]() $k_{x}=0.038$
.
$k_{x}=0.038$
.
Figures 9(a–d) are analogues of figures 8(a–d) for a wavenumber of
![]() $k_{x}=0.037$
(i.e.
$k_{x}=0.037$
(i.e.
![]() ${\it\lambda}_{x}/d=169.81$
). The corresponding equilibrium solutions are due to the small hump (around
${\it\lambda}_{x}/d=169.81$
). The corresponding equilibrium solutions are due to the small hump (around
![]() $k_{x}\sim 0.045$
) in the inset of figure 6(b). The linear and nonlinear velocity and density solutions look very similar for this parameter combination since the nearest bifurcation point (
$k_{x}\sim 0.045$
) in the inset of figure 6(b). The linear and nonlinear velocity and density solutions look very similar for this parameter combination since the nearest bifurcation point (
![]() $k_{c}=k_{xl}\approx 0.036$
) is located close by. In fact, the effects of nonlinearities become more pronounced as we move away from the critical point – this is evident from (e–f) in figure 9 for which
$k_{c}=k_{xl}\approx 0.036$
) is located close by. In fact, the effects of nonlinearities become more pronounced as we move away from the critical point – this is evident from (e–f) in figure 9 for which
![]() $k_{x}=0.038$
(i.e.
$k_{x}=0.038$
(i.e.
![]() ${\it\lambda}_{x}/d=165.35$
). It should be noticed that the density field in panel (
${\it\lambda}_{x}/d=165.35$
). It should be noticed that the density field in panel (
![]() $f$
) is more modulated compared with that in panel (
$f$
) is more modulated compared with that in panel (
![]() $d$
) along with a larger density variation. The related patterns of granular temperature can be anticipated from the density maps since they are inversely correlated (a higher/lower density corresponds to a lower/higher temperature, respectively), and hence are not displayed.
$d$
) along with a larger density variation. The related patterns of granular temperature can be anticipated from the density maps since they are inversely correlated (a higher/lower density corresponds to a lower/higher temperature, respectively), and hence are not displayed.
5.1.3. Nonlinear equilibrium solutions at different
 $S$
and the scaling laws
$S$
and the scaling laws
Nonlinear solutions exist at other values of the shaking strength
![]() $S$
, as it is evident from figure 10 which shows the variation of
$S$
, as it is evident from figure 10 which shows the variation of
![]() $A_{e}$
with
$A_{e}$
with
![]() $k_{x}$
for
$k_{x}$
for
![]() $S=50$
, 100, 200, 400, 600 and 800; all these solutions are steady since the underlying linear mode is stationary for each case and they originate via pitchfork bifurcations. As explained earlier with reference to figure 6, the flow is unstable for a range of
$S=50$
, 100, 200, 400, 600 and 800; all these solutions are steady since the underlying linear mode is stationary for each case and they originate via pitchfork bifurcations. As explained earlier with reference to figure 6, the flow is unstable for a range of
![]() $k_{x}\in (k_{xl},k_{xu})$
– there are two bifurcation points located at
$k_{x}\in (k_{xl},k_{xu})$
– there are two bifurcation points located at
![]() $k_{xl}$
and
$k_{xl}$
and
![]() $k_{xu}$
for each
$k_{xu}$
for each
![]() $S$
. The equilibrium solutions displayed in figure 10 emanate from the upper bifurcation point at
$S$
. The equilibrium solutions displayed in figure 10 emanate from the upper bifurcation point at
![]() $k_{xu}>0.17$
; the stationary solutions also bifurcate from the lower bifurcation point
$k_{xu}>0.17$
; the stationary solutions also bifurcate from the lower bifurcation point
![]() $k_{xl}<0.05$
(not shown) over a very narrow range of wavenumbers, similar to the small hump of equilibrium solutions in figure 6(b). For each
$k_{xl}<0.05$
(not shown) over a very narrow range of wavenumbers, similar to the small hump of equilibrium solutions in figure 6(b). For each
![]() $S$
in figure 10, we found the occurrence of 2:1 resonance near
$S$
in figure 10, we found the occurrence of 2:1 resonance near
![]() $k_{x}\sim k_{xl}$
, as explained in figure 7. These technical details are omitted for the sake of brevity. The inset of figure 10 displays the variation of
$k_{x}\sim k_{xl}$
, as explained in figure 7. These technical details are omitted for the sake of brevity. The inset of figure 10 displays the variation of
![]() $A_{e}$
with the distance from the bifurcation point
$A_{e}$
with the distance from the bifurcation point
![]() ${\rm\Delta}k=(k_{xu}-k_{x})$
, denoted by the solid line. The superimposed dashed line represents
${\rm\Delta}k=(k_{xu}-k_{x})$
, denoted by the solid line. The superimposed dashed line represents
which confirms that the square-root scaling holds near the bifurcation point. The scaling law (5.8) follows from the cubic-order Landau equation (3.15) since both the growth rate
![]() $a^{(0)}(k_{x},S,F)$
and the first Landau coefficient
$a^{(0)}(k_{x},S,F)$
and the first Landau coefficient
![]() $a^{(2)}(k_{x},S,F)$
can be expanded in Taylor series around the bifurcation point
$a^{(2)}(k_{x},S,F)$
can be expanded in Taylor series around the bifurcation point
![]() $(k_{x},S,F)=(k_{c},S_{c},F_{c})$
, resulting in
$(k_{x},S,F)=(k_{c},S_{c},F_{c})$
, resulting in
![]() $A_{e}=\sqrt{-a^{(0)}/a^{(2)}}\sim \sqrt{{\rm\Delta}k}$
to the leading order.
$A_{e}=\sqrt{-a^{(0)}/a^{(2)}}\sim \sqrt{{\rm\Delta}k}$
to the leading order.

Figure 10. Bifurcation diagrams in the
![]() $(k_{x},A_{e})$
-plane for various values of
$(k_{x},A_{e})$
-plane for various values of
![]() $S=50$
, 100, 400, 600 and 800. The inset shows the variation of
$S=50$
, 100, 400, 600 and 800. The inset shows the variation of
![]() $A_{e}$
with
$A_{e}$
with
![]() ${\rm\Delta}k=(k_{xu}-k_{x})$
(denoted by the solid line) and the square-root scaling with
${\rm\Delta}k=(k_{xu}-k_{x})$
(denoted by the solid line) and the square-root scaling with
![]() ${\rm\Delta}k$
(denoted by the dashed line) near the bifurcation point
${\rm\Delta}k$
(denoted by the dashed line) near the bifurcation point
![]() $k_{xu}\sim 0.175$
for
$k_{xu}\sim 0.175$
for
![]() $S=100$
.
$S=100$
.

Figure 11. (a) Bifurcation diagram in the
![]() $(A_{e},S)$
-plane for
$(A_{e},S)$
-plane for
![]() $k_{x}=0.16$
; the squares represent the numerical solution and the solid line is the best fit for the data points. The inset displays a zoom of the main panel near the bifurcation point in logarithmic scale; the dashed line represents a slope of
$k_{x}=0.16$
; the squares represent the numerical solution and the solid line is the best fit for the data points. The inset displays a zoom of the main panel near the bifurcation point in logarithmic scale; the dashed line represents a slope of
![]() ${\textstyle \frac{1}{2}}$
and the solid line (of slope 0.506) is a fit to these data. (b) Variations of
${\textstyle \frac{1}{2}}$
and the solid line (of slope 0.506) is a fit to these data. (b) Variations of
![]() $a^{(0)}$
(circles) and
$a^{(0)}$
(circles) and
![]() $a^{(2)}$
(stars) with
$a^{(2)}$
(stars) with
![]() $S$
; the inset shows a zoomed part of the main panel near the bifurcation point. The solid lines are fits to respective data. Other parameters are as in figure 10.
$S$
; the inset shows a zoomed part of the main panel near the bifurcation point. The solid lines are fits to respective data. Other parameters are as in figure 10.
A closer look at figure 10 indicates that the equilibrium amplitude
![]() $A_{e}$
has a non-monotonic dependence on the shaking strength
$A_{e}$
has a non-monotonic dependence on the shaking strength
![]() $S$
at a given wavenumber
$S$
at a given wavenumber
![]() $k_{x}$
. This is further clarified in the main panel of figure 11(a), with the wavenumber being set to
$k_{x}$
. This is further clarified in the main panel of figure 11(a), with the wavenumber being set to
![]() $k_{x}=0.16$
and the other parameters as in figure 10. It is seen that
$k_{x}=0.16$
and the other parameters as in figure 10. It is seen that
![]() $A_{e}$
increases sharply from zero at the bifurcation point, attains a maximum value at some value of
$A_{e}$
increases sharply from zero at the bifurcation point, attains a maximum value at some value of
![]() $S$
(
$S$
(
![]() ${\sim}150$
) and then decreases with further increase of
${\sim}150$
) and then decreases with further increase of
![]() $S$
. Figure 11(b) displays the corresponding variations of the growth rate of the least stable mode
$S$
. Figure 11(b) displays the corresponding variations of the growth rate of the least stable mode
![]() $a^{(0)}$
and the first Landau coefficient
$a^{(0)}$
and the first Landau coefficient
![]() $a^{(2)}$
with
$a^{(2)}$
with
![]() $S$
– both vary non-monotonically with
$S$
– both vary non-monotonically with
![]() $S$
. As in previous cases, the least stable mode is stationary and hence the first Landau coefficient is real, resulting in pitchfork bifurcations. The inset of figure 11(b) locates the corresponding bifurcation point
$S$
. As in previous cases, the least stable mode is stationary and hence the first Landau coefficient is real, resulting in pitchfork bifurcations. The inset of figure 11(b) locates the corresponding bifurcation point
![]() $S=S_{c}\approx 64.23$
, marked by the intersection of dashed lines passing through
$S=S_{c}\approx 64.23$
, marked by the intersection of dashed lines passing through
![]() $a^{(0)}=0$
. A zoomed part of figure 11(a) near the bifurcation point is re-plotted in terms of the distance from the bifurcation point
$a^{(0)}=0$
. A zoomed part of figure 11(a) near the bifurcation point is re-plotted in terms of the distance from the bifurcation point
![]() $(S-S_{c})$
as an inset in the logarithmic scale. The superimposed dashed line, having a slope of ‘
$(S-S_{c})$
as an inset in the logarithmic scale. The superimposed dashed line, having a slope of ‘
![]() ${\textstyle \frac{1}{2}}$
’, in this inset confirms that the square-root scaling,
${\textstyle \frac{1}{2}}$
’, in this inset confirms that the square-root scaling,
![]() $A_{e}\sim \sqrt{S-S_{c}}$
, holds close to the bifurcation point. The inset of figure 11(b) further substantiates the above finding since the growth rate (
$A_{e}\sim \sqrt{S-S_{c}}$
, holds close to the bifurcation point. The inset of figure 11(b) further substantiates the above finding since the growth rate (
![]() $a^{(0)}$
) increases linearly with
$a^{(0)}$
) increases linearly with
![]() $S$
but the Landau coefficient (
$S$
but the Landau coefficient (
![]() $a^{(2)}$
) remains almost constant near the bifurcation point, resulting in
$a^{(2)}$
) remains almost constant near the bifurcation point, resulting in
for small values of
![]() ${\rm\Delta}S=(S-S_{c})$
. On the whole, the insets of figures 10 and 11(a) confirm that both scaling laws ((5.8) and (5.9)) are valid but only for a narrow range [
${\rm\Delta}S=(S-S_{c})$
. On the whole, the insets of figures 10 and 11(a) confirm that both scaling laws ((5.8) and (5.9)) are valid but only for a narrow range [
![]() ${\rm\Delta}S/S_{c}\ll 1$
and
${\rm\Delta}S/S_{c}\ll 1$
and
![]() ${\rm\Delta}k/k_{c}\ll 1$
] around the bifurcation point, which is expected for a multi-dimensional bifurcation problem such as this.
${\rm\Delta}k/k_{c}\ll 1$
] around the bifurcation point, which is expected for a multi-dimensional bifurcation problem such as this.
5.1.4. What happens for very strong shaking? Towards a state of floating convection?
Collectively, figures 11(a,b) confirmed that the growth rate of the least stable mode decays slowly with increasing
![]() $S$
and seems to remain finite at large enough
$S$
and seems to remain finite at large enough
![]() $S$
; the equilibrium amplitude remains finite too at large
$S$
; the equilibrium amplitude remains finite too at large
![]() $S$
. An important issue is what happens to granular convection if the shaking strength is very large – does it give rise to a state of granular gas?
$S$
. An important issue is what happens to granular convection if the shaking strength is very large – does it give rise to a state of granular gas?
Figure 12 is an analogue of the nonlinear patterns in figures 8(c,d) (for
![]() $S=100$
) but for higher shaking strengths of
$S=100$
) but for higher shaking strengths of
![]() $S=200$
(a,b), 400 (c,d) and 800 (e,f). As in the case of
$S=200$
(a,b), 400 (c,d) and 800 (e,f). As in the case of
![]() $S=100$
, two pairs of convection rolls are observed within the same container of length
$S=100$
, two pairs of convection rolls are observed within the same container of length
![]() $L_{x}/d\approx 80$
. Interestingly, the centres of the convection rolls are shifted to the top of the container with increasing
$L_{x}/d\approx 80$
. Interestingly, the centres of the convection rolls are shifted to the top of the container with increasing
![]() $S$
, see figures 12(a,c,e); this is expected since the granular material is lifted to a higher elevation with higher injected energy (
$S$
, see figures 12(a,c,e); this is expected since the granular material is lifted to a higher elevation with higher injected energy (
![]() $S$
). It is noteworthy that the centres of the vortices appear to be correlated with the density maxima, as observed in these figures. At large enough shaking (
$S$
). It is noteworthy that the centres of the vortices appear to be correlated with the density maxima, as observed in these figures. At large enough shaking (
![]() $S=800$
, 12(e,f)), there is hardly any motion in the bottom of the container and the density is low there, representing a conduction state of a granular gas. Therefore, the patterns in figures 12(c,e) can be conceived of as a state of floating convection riding over a conduction state.
$S=800$
, 12(e,f)), there is hardly any motion in the bottom of the container and the density is low there, representing a conduction state of a granular gas. Therefore, the patterns in figures 12(c,e) can be conceived of as a state of floating convection riding over a conduction state.

Figure 12. The effect of the shaking strength (
![]() $S$
) on the nonlinear patterns of (a,c,e) velocity (
$S$
) on the nonlinear patterns of (a,c,e) velocity (
![]() $u^{\prime },v^{\prime }$
) and (b,d,f) density for
$u^{\prime },v^{\prime }$
) and (b,d,f) density for
![]() $F=6$
and
$F=6$
and
![]() $k_{x}=0.16$
. The shaking strength is (a,b)
$k_{x}=0.16$
. The shaking strength is (a,b)
![]() $S=200$
, (c,d) 400 and (e,f) 800.
$S=200$
, (c,d) 400 and (e,f) 800.
To characterize the convection rolls in figure 12 in terms of their strength, let us calculate the velocity circulation, defined as
The integration is carried out over a square box of size
![]() $2{\it\lambda}_{x}/5$
centred around the centre of the vortex. The variation of
$2{\it\lambda}_{x}/5$
centred around the centre of the vortex. The variation of
![]() $C$
with shaking strength
$C$
with shaking strength
![]() $S$
is shown in figure 13. It should be noted that the circulation
$S$
is shown in figure 13. It should be noted that the circulation
![]() $C$
is zero in the Leidenfrost/conduction state and becomes non-zero at the onset of convection,
$C$
is zero in the Leidenfrost/conduction state and becomes non-zero at the onset of convection,
![]() $S\geqslant S_{c}(F)$
. It is clear from figure 13 that the strength of convection (measured in terms of circulation) is maximum at some intermediate value of
$S\geqslant S_{c}(F)$
. It is clear from figure 13 that the strength of convection (measured in terms of circulation) is maximum at some intermediate value of
![]() $S$
and then diminishes sharply with further increase in
$S$
and then diminishes sharply with further increase in
![]() $S$
. This suggests that the convection would be hard to detect at very large
$S$
. This suggests that the convection would be hard to detect at very large
![]() $S$
. This conclusion is further reinforced by the fact that the centres of the vortices move towards the top surface with increasing
$S$
. This conclusion is further reinforced by the fact that the centres of the vortices move towards the top surface with increasing
![]() $S$
(see figures 12
a,c,e) and the remaining material in the bulk has almost zero velocity, implying a conduction state of the granular gas in the bulk. The latter finding clearly indicates that the granular convection is likely to degenerate into the conduction state of a granular gas if the shaking strength is strong enough. This conclusion is in tune with the experimental observations of Eshuis et al. (Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007).
$S$
(see figures 12
a,c,e) and the remaining material in the bulk has almost zero velocity, implying a conduction state of the granular gas in the bulk. The latter finding clearly indicates that the granular convection is likely to degenerate into the conduction state of a granular gas if the shaking strength is strong enough. This conclusion is in tune with the experimental observations of Eshuis et al. (Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007).

Figure 13. Variation of the velocity circulation with shaking strength for
![]() $k_{x}=0.16$
. The circles represent data points and the solid line is a best fit. Other parameters are as in figure 6.
$k_{x}=0.16$
. The circles represent data points and the solid line is a best fit. Other parameters are as in figure 6.
5.2. Qualitative comparison of patterns with experiments
A limited set of experiments has been conducted for a specific case for which a transition from the Leidenfrost state to convection is known (Eshuis et al.
Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007) to occur. The primary purpose of these experiments is to make a qualitative comparison with the nonlinear predictions and to highlight the underlying differences, if any, between experiment and theory. The experimental set-up and method, similar to those of Eshuis et al. (Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007), are detailed in Ansari & Alam (Reference Ansari, Alam, Yu, Dong, Yang and Luding2013). The monodisperse spherical glass balls (diameter
![]() $d=1.0$
mm, with a standard deviation of less than 5 %; see the snapshot in figure 14(a) to have an idea about the size uniformity of these balls) are filled into a quasi-two-dimensional rectangular Plexiglas container of length
$d=1.0$
mm, with a standard deviation of less than 5 %; see the snapshot in figure 14(a) to have an idea about the size uniformity of these balls) are filled into a quasi-two-dimensional rectangular Plexiglas container of length
![]() $L_{x}/d=80$
and depth
$L_{x}/d=80$
and depth
![]() $D/d=5.5$
(see figure 1), with an open top. This glass-ball-filled container is mounted on an electromagnetic shaker and is shaken harmonically, (2.1), along the vertical direction. The initial layer depth is set to
$D/d=5.5$
(see figure 1), with an open top. This glass-ball-filled container is mounted on an electromagnetic shaker and is shaken harmonically, (2.1), along the vertical direction. The initial layer depth is set to
![]() $F=6$
and the shaking amplitude to
$F=6$
and the shaking amplitude to
![]() $a_{s}/d=3$
; the shaking strength (2.4) is varied by varying the frequency of the shaker,
$a_{s}/d=3$
; the shaking strength (2.4) is varied by varying the frequency of the shaker,
![]() $f_{s}$
, at a rate of
$f_{s}$
, at a rate of
![]() $0.01\ \text{Hz s}^{-1}$
.
$0.01\ \text{Hz s}^{-1}$
.

Figure 14. (a) A raw snapshot of particles undergoing convective motion in experiments with parameter values of
![]() $F=6$
,
$F=6$
,
![]() $S=120$
,
$S=120$
,
![]() $a_{s}/d=3$
and
$a_{s}/d=3$
and
![]() $L_{x}/d=80$
. Instantaneous (spatially) coarse-grained maps of (b) velocity vectors and (c) density.
$L_{x}/d=80$
. Instantaneous (spatially) coarse-grained maps of (b) velocity vectors and (c) density.
When the shaking strength is increased from the Leidenfrost regime, a convection pattern with counter-rotating rolls emerges, as shown in the raw snapshot of particles in figure 14(a); the value of the shaking strength is
![]() $S=120$
. The corresponding velocity-vector map is displayed in figure 14(b), which shows four counter-rotating rolls. The pictures such as in panel (a) were captured with a high-speed camera at a framing rate of 1000 fps (frames per second) and were subsequently analysed with the aid of PIV (particle image velocimetry) software (Ansari & Alam Reference Ansari, Alam, Yu, Dong, Yang and Luding2013). It should be noted that panel (b) represents an instantaneous velocity map implying that we have not made any temporal averaging but only spatial averaging with a variable spatial box of
$S=120$
. The corresponding velocity-vector map is displayed in figure 14(b), which shows four counter-rotating rolls. The pictures such as in panel (a) were captured with a high-speed camera at a framing rate of 1000 fps (frames per second) and were subsequently analysed with the aid of PIV (particle image velocimetry) software (Ansari & Alam Reference Ansari, Alam, Yu, Dong, Yang and Luding2013). It should be noted that panel (b) represents an instantaneous velocity map implying that we have not made any temporal averaging but only spatial averaging with a variable spatial box of
![]() $16\ \text{pixels}\times 16\ \text{pixels}$
to
$16\ \text{pixels}\times 16\ \text{pixels}$
to
![]() $64\ \text{pixels}\times 64\ \text{pixels}$
. (Approximately 10 pixels corresponds to one particle diameter
$64\ \text{pixels}\times 64\ \text{pixels}$
. (Approximately 10 pixels corresponds to one particle diameter
![]() $d=1\ \text{mm}$
.) The analogue of figure 14 for a higher shaking strength of
$d=1\ \text{mm}$
.) The analogue of figure 14 for a higher shaking strength of
![]() $S=150$
is displayed in figure 15; it should be noted that the velocity vectors are superimposed on the raw image in figure 15(a).
$S=150$
is displayed in figure 15; it should be noted that the velocity vectors are superimposed on the raw image in figure 15(a).

Figure 15. The same as figure 14 but for
![]() $S=150$
. In panel (a) the raw image and the PIV velocity vectors are superimposed.
$S=150$
. In panel (a) the raw image and the PIV velocity vectors are superimposed.
In addition to calculating the PIV velocity field, the coarse-grained density map has been obtained from the digitized version of the particle snapshots by calculating an ‘effective’ density field in terms of the average light intensity over a box of
![]() $10\ \text{pixels}\times 10$
pixels. This is displayed in figures 14(c) and 15(b) which represent the instantaneous spatially averaged density field at
$10\ \text{pixels}\times 10$
pixels. This is displayed in figures 14(c) and 15(b) which represent the instantaneous spatially averaged density field at
![]() $S=120$
and 150, respectively. In each case, a Gaussian filter with a width of
$S=120$
and 150, respectively. In each case, a Gaussian filter with a width of
![]() $2{\it\sigma}$
(
$2{\it\sigma}$
(
![]() ${\it\sigma}$
is the standard deviation) was used to smoothen the density field. It is seen in figure 14(c) that there is a band of dense particle clusters around a vertical height of
${\it\sigma}$
is the standard deviation) was used to smoothen the density field. It is seen in figure 14(c) that there is a band of dense particle clusters around a vertical height of
![]() $y/d\approx 6.5$
, punctuated by dilute regions. On comparing figure 14(c) with its raw image in (a), we find that the particles shoot up through these relatively dilute regions. Once the Leidenfrost state becomes unstable at a critical shaking strength (
$y/d\approx 6.5$
, punctuated by dilute regions. On comparing figure 14(c) with its raw image in (a), we find that the particles shoot up through these relatively dilute regions. Once the Leidenfrost state becomes unstable at a critical shaking strength (
![]() $S=S_{c}(F)$
), the particles shoot up through the dense bed, creating relatively dilute channels at different horizontal locations, and rain down on two sides of each channel, thus creating two dense clusters at a lower elevation as well as two counter-rotating rolls. A comparison of figures 14(c) and 15(b) indicates that increasing the shaking strength results in a more modulated density field, with the row of dense clusters being located at a relatively higher elevation (
$S=S_{c}(F)$
), the particles shoot up through the dense bed, creating relatively dilute channels at different horizontal locations, and rain down on two sides of each channel, thus creating two dense clusters at a lower elevation as well as two counter-rotating rolls. A comparison of figures 14(c) and 15(b) indicates that increasing the shaking strength results in a more modulated density field, with the row of dense clusters being located at a relatively higher elevation (
![]() $y/d\approx 9$
in figure 15
c), as expected.
$y/d\approx 9$
in figure 15
c), as expected.
For parameter values as in the experiments of figure 14, the theoretical nonlinear patterns of velocity and number density are shown in figures 16(a) and (b), respectively. The length of the box has been chosen such that it fits four counter-rotating rolls (i.e.
![]() $L_{x}/d=2{\it\lambda}_{x}/d=4{\rm\pi}/k_{x}\approx 78.5$
), as in the experiments of figure 14(b). The theoretical density pattern in (b) looks only qualitatively similar (with respect to large-scale features) to that in the experiments in figure 14(c); the latter pattern appears to be more tenuous, having complicated small-scale features. More importantly, the dense particle clusters are located at a much higher level in theory than in experiments. (Similar observations can be made from a comparison between figures 15 and 17 at
$L_{x}/d=2{\it\lambda}_{x}/d=4{\rm\pi}/k_{x}\approx 78.5$
), as in the experiments of figure 14(b). The theoretical density pattern in (b) looks only qualitatively similar (with respect to large-scale features) to that in the experiments in figure 14(c); the latter pattern appears to be more tenuous, having complicated small-scale features. More importantly, the dense particle clusters are located at a much higher level in theory than in experiments. (Similar observations can be made from a comparison between figures 15 and 17 at
![]() $S=150$
.) The latter quantitative discrepancy between theory and experiment may be improved partially by relaxing the theoretical assumption of zero energy loss at the front and back walls of the quasi-2D container, which is assumed to be periodic in the lateral directions. This energy loss will reduce the overall energy input to the vibrating grains and can therefore be tied with a lower value of the ‘effective’ shaking strength (
$S=150$
.) The latter quantitative discrepancy between theory and experiment may be improved partially by relaxing the theoretical assumption of zero energy loss at the front and back walls of the quasi-2D container, which is assumed to be periodic in the lateral directions. This energy loss will reduce the overall energy input to the vibrating grains and can therefore be tied with a lower value of the ‘effective’ shaking strength (
![]() $S$
), which corresponds to the dense layer being located at a relatively lower height (see figure 2
c). A comparison between figures 16(b) and 17(b) for
$S$
), which corresponds to the dense layer being located at a relatively lower height (see figure 2
c). A comparison between figures 16(b) and 17(b) for
![]() $S=120$
and 150, respectively, supports the above conclusion on the location of the dense layer. In any case, the quantitative discrepancies between theory and experiment provide enough impetus to relook at (i) the underlying assumptions, (ii) the missing ingredients and (iii) the phenomenological parameters in the constitutive relations of the hydrodynamic model. Additional experiments with an exhaustive analysis are recommended for a future work.
$S=120$
and 150, respectively, supports the above conclusion on the location of the dense layer. In any case, the quantitative discrepancies between theory and experiment provide enough impetus to relook at (i) the underlying assumptions, (ii) the missing ingredients and (iii) the phenomenological parameters in the constitutive relations of the hydrodynamic model. Additional experiments with an exhaustive analysis are recommended for a future work.

Figure 16. Theoretical predictions of nonlinear patterns for (a) the velocity and (b) the density fields in the (
![]() $x,y$
)-plane for
$x,y$
)-plane for
![]() $F=6$
,
$F=6$
,
![]() $S=120$
and
$S=120$
and
![]() $k_{x}=0.16$
. The restitution coefficient for glass beads is taken to be
$k_{x}=0.16$
. The restitution coefficient for glass beads is taken to be
![]() $e=0.9$
.
$e=0.9$
.

Figure 17. The same as figure 16 but for
![]() $S=150$
.
$S=150$
.
6. Discussion: effects of different constitutive relations and boundary conditions
6.1. Effects of bulk viscosity, Prandtl number and shear work
So far, all results have been presented by setting the bulk viscosity (
![]() ${\it\zeta}=0$
) to zero in the constitutive model (2.13). To understand the effects of ‘non-zero’ bulk viscosity on the nonlinear results presented in § 5, we consider two expressions for the dimensionless bulk viscosity:
${\it\zeta}=0$
) to zero in the constitutive model (2.13). To understand the effects of ‘non-zero’ bulk viscosity on the nonlinear results presented in § 5, we consider two expressions for the dimensionless bulk viscosity:

Figure 19. (a) The density dependence of the ‘effective’ Prandtl number for a dense gas of elastically colliding hard spheres; the circles represent the exact expression obtained from the kinetic theory (see text for details) and the solid line is a polynomial fit (6.3). (b) The effect of a density-dependent Prandtl number (6.3) on the variations of
![]() $a^{(0)}$
(circles),
$a^{(0)}$
(circles),
![]() $a^{(2)}$
(stars) and
$a^{(2)}$
(stars) and
![]() $A_{e}$
(inset) with wavenumber
$A_{e}$
(inset) with wavenumber
![]() $k_{x}$
. Other parameters are the same as in figure 6.
$k_{x}$
. Other parameters are the same as in figure 6.
As elaborated in § 2.2, the shear viscosity (
![]() ${\it\mu}$
) was taken proportional to the thermal conductivity (2.13), with a constant value for the ‘effective’ Prandtl number (
${\it\mu}$
) was taken proportional to the thermal conductivity (2.13), with a constant value for the ‘effective’ Prandtl number (
![]() $Pr=1.7$
), which provided a good match (Eshuis et al.
Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010) for the critical value of the shaking strength
$Pr=1.7$
), which provided a good match (Eshuis et al.
Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010) for the critical value of the shaking strength
![]() $S$
at the onset of convection (see figure 5). However, the Prandtl number should depend on the density as expected from the kinetic theory of dense gases. By employing the explicit expressions of the shear viscosity and the thermal conductivity for nearly elastic (
$S$
at the onset of convection (see figure 5). However, the Prandtl number should depend on the density as expected from the kinetic theory of dense gases. By employing the explicit expressions of the shear viscosity and the thermal conductivity for nearly elastic (
![]() $e\sim 1$
) spheres (Jenkins & Richman Reference Jenkins and Richman1985a
,Reference Jenkins and Richman
b
), we have obtained an expression for the Prandtl number which is well fitted via a ninth-degree polynomial in
$e\sim 1$
) spheres (Jenkins & Richman Reference Jenkins and Richman1985a
,Reference Jenkins and Richman
b
), we have obtained an expression for the Prandtl number which is well fitted via a ninth-degree polynomial in
![]() ${\it\phi}$
(volume fraction of particles):
${\it\phi}$
(volume fraction of particles):
This is shown in figure 19(a) – the Prandtl number is almost constant near the dense limit, but decreases to a minimum at some intermediate density (
![]() ${\it\phi}\sim 0.2$
) and sharply increases thereafter, reaching its dilute limit. It should be noted that in figure 19(a) we have kept the average Prandtl number as 1.7, denoted by the dashed line, as in all results presented in § 5. The stability results with (6.3) are displayed in figure 19(b) and the results are marginally affected in comparison with figure 6 which was calculated with a constant
${\it\phi}\sim 0.2$
) and sharply increases thereafter, reaching its dilute limit. It should be noted that in figure 19(a) we have kept the average Prandtl number as 1.7, denoted by the dashed line, as in all results presented in § 5. The stability results with (6.3) are displayed in figure 19(b) and the results are marginally affected in comparison with figure 6 which was calculated with a constant
![]() $Pr=1.7$
. For example, the maximum growth rate is slightly larger for variable
$Pr=1.7$
. For example, the maximum growth rate is slightly larger for variable
![]() $\mathit{Pr}$
; the upper and lower critical points are shifted to
$\mathit{Pr}$
; the upper and lower critical points are shifted to
![]() $k_{xu}\approx 0.179$
and
$k_{xu}\approx 0.179$
and
![]() $k_{xl}\approx 0.0351$
(in contrast to
$k_{xl}\approx 0.0351$
(in contrast to
![]() $k_{xu}\approx 0.175$
and
$k_{xu}\approx 0.175$
and
![]() $k_{xl}\approx 0.0365$
for constant
$k_{xl}\approx 0.0365$
for constant
![]() $\mathit{Pr}$
), respectively; the locations of 2:1 resonance and
$\mathit{Pr}$
), respectively; the locations of 2:1 resonance and
![]() $a^{(2)}=0$
(i.e. diverging amplitude) are shifted to
$a^{(2)}=0$
(i.e. diverging amplitude) are shifted to
![]() $k_{r}\approx 0.0531$
and
$k_{r}\approx 0.0531$
and
![]() $k_{d}\approx 0.0671$
, (in contrast to
$k_{d}\approx 0.0671$
, (in contrast to
![]() $k_{r}\approx 0.0535$
and
$k_{r}\approx 0.0535$
and
![]() $k_{d}\approx 0.0703$
for constant
$k_{d}\approx 0.0703$
for constant
![]() $\mathit{Pr}$
), respectively. Another functional form for (6.3) was also tested (which holds for hard disks), but the results remain almost identical to figure 19(b). We have further verified that decreasing the average Prandtl number (say, to
$\mathit{Pr}$
), respectively. Another functional form for (6.3) was also tested (which holds for hard disks), but the results remain almost identical to figure 19(b). We have further verified that decreasing the average Prandtl number (say, to
![]() $Pr_{av}=1$
, with or without density variation) does not qualitatively change our results, but the growth rate of the least stable mode as well as the range of
$Pr_{av}=1$
, with or without density variation) does not qualitatively change our results, but the growth rate of the least stable mode as well as the range of
![]() $k_{x}$
over which the instability occurs increases with decreasing
$k_{x}$
over which the instability occurs increases with decreasing
![]() $Pr_{av}$
. The latter observations (not shown) are expected since the effective shear viscosity (
$Pr_{av}$
. The latter observations (not shown) are expected since the effective shear viscosity (
![]() ${\it\mu}\propto Pr{\it\kappa}$
) decreases with decreasing
${\it\mu}\propto Pr{\it\kappa}$
) decreases with decreasing
![]() $Pr_{av}$
, leading to more destabilization of the unstable mode. These results are omitted for the sake of brevity.
$Pr_{av}$
, leading to more destabilization of the unstable mode. These results are omitted for the sake of brevity.
In most stability works on classical Rayleigh–Bénard convection as well as in other free convection flows (e.g. thermal plumes), it is often assumed that the shear work or the viscous dissipation term (
![]() ${\it\Phi}_{vis}$
as in (2.22)) in the energy equation (2.19) is negligible (Gebhart et al.
Reference Gebhart, Jaluria, Mahajan and Sammakia1988; Lakkaraju & Alam Reference Lakkaraju and Alam2007). This was also assumed to hold for granular convection in previous linear stability analysis (Eshuis et al.
Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010). As mentioned in § 2, we have retained this term in our nonlinear analysis and the results presented so far refer to non-zero shear work. To check the ansatz of Eshuis et al. (Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010, Reference Eshuis, van der Weele, Alam, van Gerner, van der Höf, Kuipers, Luding, van der Meer and Lohse2013), we have repeated the calculations of figure 6 by setting the shear work to zero, and the results are shown in figure 20. A comparison of figures 6(a,b) and 20 confirms that there are no qualitative changes to either linear or nonlinear stability predictions irrespective of whether
${\it\Phi}_{vis}$
as in (2.22)) in the energy equation (2.19) is negligible (Gebhart et al.
Reference Gebhart, Jaluria, Mahajan and Sammakia1988; Lakkaraju & Alam Reference Lakkaraju and Alam2007). This was also assumed to hold for granular convection in previous linear stability analysis (Eshuis et al.
Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010). As mentioned in § 2, we have retained this term in our nonlinear analysis and the results presented so far refer to non-zero shear work. To check the ansatz of Eshuis et al. (Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010, Reference Eshuis, van der Weele, Alam, van Gerner, van der Höf, Kuipers, Luding, van der Meer and Lohse2013), we have repeated the calculations of figure 6 by setting the shear work to zero, and the results are shown in figure 20. A comparison of figures 6(a,b) and 20 confirms that there are no qualitative changes to either linear or nonlinear stability predictions irrespective of whether
![]() ${\it\Phi}_{vis}=0$
or
${\it\Phi}_{vis}=0$
or
![]() ${\it\Phi}_{vis}\neq 0$
. There exist minor quantitative differences, however; for example, the Landau coefficient
${\it\Phi}_{vis}\neq 0$
. There exist minor quantitative differences, however; for example, the Landau coefficient
![]() $a^{(2)}$
is slightly smaller (near the upper critical point
$a^{(2)}$
is slightly smaller (near the upper critical point
![]() $k_{x}\sim 0.17$
) with
$k_{x}\sim 0.17$
) with
![]() ${\it\Phi}_{vis}=0$
.
${\it\Phi}_{vis}=0$
.
6.2. Effects of free-surface boundary conditions
In all results presented so far, we have used Dirichlet conditions at the free surface, i.e. the perturbation temperature and velocities are zero (
![]() $T^{\prime }=0=u^{\prime }=v^{\prime }$
). This follows from the expectation that the perturbations decay exponentially with height such that
$T^{\prime }=0=u^{\prime }=v^{\prime }$
). This follows from the expectation that the perturbations decay exponentially with height such that
hold at
![]() $y=H$
. The above boundary conditions are equivalent to imposing Dirichlet conditions,
$y=H$
. The above boundary conditions are equivalent to imposing Dirichlet conditions,
![]() $(u^{\prime },v^{\prime },T^{\prime })\sim \exp (-k_{x}H)$
, at
$(u^{\prime },v^{\prime },T^{\prime })\sim \exp (-k_{x}H)$
, at
![]() $y=H$
. In fact, this decaying solution can be obtained by analysing the asymptotic behaviour of the linear stability equations at
$y=H$
. In fact, this decaying solution can be obtained by analysing the asymptotic behaviour of the linear stability equations at
![]() $y\rightarrow \infty$
as in the work of Forterre & Pouliquen (Reference Forterre and Pouliquen2002) on inclined chute flow – we omit the related details. Instead of Dirichlet conditions, one can also impose the Neumann conditions,
$y\rightarrow \infty$
as in the work of Forterre & Pouliquen (Reference Forterre and Pouliquen2002) on inclined chute flow – we omit the related details. Instead of Dirichlet conditions, one can also impose the Neumann conditions,
at the free surface
![]() $y=H$
. The linear stability calculations of figure 3(a) are repeated with the above two boundary conditions and the results are shown in figure 21(a). The triangles and circles represent (6.4) and (6.5), respectively, and the pluses represent results with
$y=H$
. The linear stability calculations of figure 3(a) are repeated with the above two boundary conditions and the results are shown in figure 21(a). The triangles and circles represent (6.4) and (6.5), respectively, and the pluses represent results with
![]() $T^{\prime }=0=u^{\prime }=v^{\prime }$
at
$T^{\prime }=0=u^{\prime }=v^{\prime }$
at
![]() $y=H$
as in figure 3(a). As expected, the growth rates of the least stable modes for the boundary conditions (6.4) almost overlap with those for
$y=H$
as in figure 3(a). As expected, the growth rates of the least stable modes for the boundary conditions (6.4) almost overlap with those for
![]() $T^{\prime }=0=u^{\prime }=v^{\prime }$
. However, the Neumann boundary conditions (6.5) yield slightly larger growth rates for the modes around
$T^{\prime }=0=u^{\prime }=v^{\prime }$
. However, the Neumann boundary conditions (6.5) yield slightly larger growth rates for the modes around
![]() $k_{x}=0.1$
. It is noteworthy that the overall features, including the range of
$k_{x}=0.1$
. It is noteworthy that the overall features, including the range of
![]() $k_{x}$
over which the flow is unstable (
$k_{x}$
over which the flow is unstable (
![]() $a^{(0)}>0$
), remain virtually unchanged irrespective of the choice among the above three free-surface boundary conditions.
$a^{(0)}>0$
), remain virtually unchanged irrespective of the choice among the above three free-surface boundary conditions.

Figure 21. (a) The effect of different free-surface boundary conditions on the growth rate of the least stable mode. (b) The effect of the zero heat-flux boundary condition on the variations of
![]() $a^{(0)}$
(circles),
$a^{(0)}$
(circles),
![]() $a^{(2)}$
(stars) and
$a^{(2)}$
(stars) and
![]() $A_{e}$
(inset) with
$A_{e}$
(inset) with
![]() $k_{x}$
, see text for details. Other parameters are as in figure 6.
$k_{x}$
, see text for details. Other parameters are as in figure 6.
For the base-state calculations in § 2.4, the zero heat-flux boundary condition was used at the free surface; therefore, we checked our nonlinear stability calculations of figure 6(a) with
![]() $\text{d}T^{\prime }/\text{d}y(y=H)=0$
by keeping the remaining boundary conditions the same. For this case, the adjoint boundary conditions at the free surface (3.11) need to be changed to
$\text{d}T^{\prime }/\text{d}y(y=H)=0$
by keeping the remaining boundary conditions the same. For this case, the adjoint boundary conditions at the free surface (3.11) need to be changed to
The results are shown in figure 21(b), with other parameters as in figure 6. It is clear that there are minor changes in the wavenumber variations of (i) the first Landau coefficient
![]() $a^{(2)}$
, (ii) the location of the resonance point (marked by the sign reversal of
$a^{(2)}$
, (ii) the location of the resonance point (marked by the sign reversal of
![]() $a^{(2)}$
) and (iii) the equilibrium amplitude
$a^{(2)}$
) and (iii) the equilibrium amplitude
![]() $A_{e}$
. These observations hold even if we use the boundary conditions (6.4). Therefore, our nonlinear results presented in § 5 are robust with respect to the choice of free-surface boundary conditions.
$A_{e}$
. These observations hold even if we use the boundary conditions (6.4). Therefore, our nonlinear results presented in § 5 are robust with respect to the choice of free-surface boundary conditions.
6.3. Range of validity of the present nonlinear analysis
In the above we have presented the nonlinear equilibrium amplitudes of the unstable modes for a large range of control parameters (
![]() $k_{x}$
and
$k_{x}$
and
![]() $S$
) based on the first Landau coefficient. As elaborated previously (Shukla & Alam Reference Shukla and Alam2011a
,Reference Shukla and Alam
b
, Reference Shukla and Alam2013; Alam & Shukla Reference Alam and Shukla2013), readers are again reminded that the present nonlinear results may not be valid far away from the bifurcation point since the radius of convergence of the Stuart–Landau series (3.15), (3.16) cannot be inferred from just one Landau coefficient. This requires the calculation of higher-order Landau coefficients, which is beyond the scope of the present paper.
$S$
) based on the first Landau coefficient. As elaborated previously (Shukla & Alam Reference Shukla and Alam2011a
,Reference Shukla and Alam
b
, Reference Shukla and Alam2013; Alam & Shukla Reference Alam and Shukla2013), readers are again reminded that the present nonlinear results may not be valid far away from the bifurcation point since the radius of convergence of the Stuart–Landau series (3.15), (3.16) cannot be inferred from just one Landau coefficient. This requires the calculation of higher-order Landau coefficients, which is beyond the scope of the present paper.
Another related issue is the occurrences of nonlinear resonance phenomena, namely, the mean-flow and 2:1 resonances as discussed in § 5.1.1. This also puts restrictions on the range of validity of our nonlinear analysis: the present single-mode analysis is not valid at resonance points (Shukla & Alam Reference Shukla and Alam2011b ). The resonant mode interactions, in terms of coupled Landau equations, must be developed to obtain equilibrium amplitude near such singular points, and this too is beyond the scope of the present paper.
Ideally, one should choose a simple base flow (such as uniform shear flow) to address the convergence issues. The second Landau coefficient was calculated recently by Shukla & Alam (Reference Shukla and Alam2013) for the vorticity-banding modes in plane Couette flow. They found that the cubic- and quintic-order solutions for the equilibrium amplitude match with each other near the bifurcation point. They further showed that the quintic terms have a stabilizing effect far away from the supercritical bifurcation point in the sense that the equilibrium amplitude (far away from the critical point) decreases with the addition of the second Landau coefficient. The latter is good news since this implies that the radius of convergence is not small, at least for the specific case of plane Couette flow. For the present problem as well, we need to calculate a few higher-order Landau coefficients to check the convergence of the Stuart–Landau series in the future; however, it might take years of concerted effort to resolve this issue.
7. Summary and conclusions
We have investigated the nonlinear convection phenomena in strongly shaken granular matter using a Landau-type order-parameter theory which has been derived from Navier–Stokes-order hydrodynamic equations via a weakly nonlinear analysis (Shukla & Alam Reference Shukla and Alam2009, Reference Shukla and Alam2011a
,Reference Shukla and Alam
b
; Alam & Shukla Reference Alam and Shukla2012; Shukla & Alam Reference Shukla and Alam2013; Alam & Shukla Reference Alam and Shukla2013). The hydrodynamic model and the constitutive relations are the same as in the previous linear stability analysis (Eshuis et al.
Reference Eshuis, van der Meer, Alam, van Gerner, van der Weele and Lohse2010, Reference Eshuis, van der Weele, Alam, van Gerner, van der Höf, Kuipers, Luding, van der Meer and Lohse2013) of the same problem, except that the shear-work term in the energy equation is now retained in all calculations; moreover, the robustness of both linear and nonlinear stability predictions was checked with respect to changes in some constitutive relations: (i) the bulk viscosity (
![]() ${\it\zeta}\neq 0$
), (ii) a density-dependent Prandtl number (
${\it\zeta}\neq 0$
), (ii) a density-dependent Prandtl number (
![]() $Pr({\it\phi})\neq Pr_{av}$
) and (iii) the viscous dissipation or the shear work (
$Pr({\it\phi})\neq Pr_{av}$
) and (iii) the viscous dissipation or the shear work (
![]() ${\it\Phi}_{vis}=0$
).
${\it\Phi}_{vis}=0$
).
The base state was calculated under a quasi-steady assumption by specifying an effective granular temperature at the vibrating plate which took care of the effects of harmonic shaking of the granular bed in a mean-field sense – increasing the shaking strength is equivalent to increasing this temperature. The base-state temperature decreased monotonically with height, but the density profile consisted of three distinct layers: (i) a ‘collisional’ dilute layer near the vibrating plate, (ii) a ‘levitated’ dense layer at some intermediate height and (iii) a ‘ballistic’ dilute layer at the top of the bed. This density-inverted state is also called the granular Leidenfrost state (Eshuis et al. Reference Eshuis, van der Weele, van der Meer and Lohse2005); its nonlinear stability, resulting in convective motions, was investigated in this paper. The goal of the present work was to ascertain whether the predictions of linear theory hold when nonlinearities are taken into account; in particular, (i) the issue of supercritical/subcritical pitchfork bifurcation and (ii) the possibility of subcritical Hopf bifurcation, as well as (iii) the state of this driven system at large enough shaking strength, can be addressed only via a nonlinear theory.
The adjoint linear stability problem was formulated taking into account appropriate boundary conditions, and the nonlinearities up to cubic order in the perturbation amplitude were retained in the nonlinear analysis. The leading-order nonlinear contribution to the Landau equation was provided by the first Landau coefficient which was calculated from the solvability condition (at cubic order) in terms of the adjoint eigenfunction, the fundamental mode, the second harmonic and the base-flow distortion mode. A spectral-based numerical method was used to calculate all modal eigenfunctions along with first Landau coefficient, leading to nonlinear solutions for hydrodynamic fields. The numerically obtained solutions were analysed for a range of parameters in terms of the wavenumber (
![]() $k_{x}$
) and the shaking strength (
$k_{x}$
) and the shaking strength (
![]() $S$
) for specified values of the particle loading (
$S$
) for specified values of the particle loading (
![]() $F$
).
$F$
).
Our nonlinear theory confirmed that the onset of granular convection results from a supercritical pitchfork bifurcation of the underlying density-inverted state which is linearly unstable for a range of wavenumbers (
![]() $k_{x}\in (k_{xl},k_{xu})$
) for specified values of the particle loading (
$k_{x}\in (k_{xl},k_{xu})$
) for specified values of the particle loading (
![]() $F$
) and the shaking strength (
$F$
) and the shaking strength (
![]() $S$
). More specifically, the supercritical stationary solutions were found to exist for two ranges of wavenumbers (
$S$
). More specifically, the supercritical stationary solutions were found to exist for two ranges of wavenumbers (
![]() $(k_{xl},k_{r})$
and
$(k_{xl},k_{r})$
and
![]() $(k_{d},k_{xu})$
, figure 6
b), originating from lower and upper bifurcation points located at
$(k_{d},k_{xu})$
, figure 6
b), originating from lower and upper bifurcation points located at
![]() $k_{xl}$
and
$k_{xl}$
and
![]() $k_{xu}$
, respectively, for given
$k_{xu}$
, respectively, for given
![]() $F$
and
$F$
and
![]() $S$
; at
$S$
; at
![]() $k_{x}=k_{d}$
the equilibrium amplitude
$k_{x}=k_{d}$
the equilibrium amplitude
![]() $A_{e}$
(
$A_{e}$
(
![]() $=\sqrt{(-a^{(0)}/a^{(2)})}$
) diverges since
$=\sqrt{(-a^{(0)}/a^{(2)})}$
) diverges since
![]() $a^{(2)}=0$
and is hence undefined. The nonlinear solutions near the lower bifurcation point (
$a^{(2)}=0$
and is hence undefined. The nonlinear solutions near the lower bifurcation point (
![]() $k_{xl}$
) were terminated at some value of
$k_{xl}$
) were terminated at some value of
![]() $k_{x}=k_{r}$
(close to
$k_{x}=k_{r}$
(close to
![]() $k_{xl}$
) due to the occurrence of a 2:1 resonance (§ 5.1.1). The latter phenomenon was shown to be tied to a resonant interaction (5.6) between the linear unstable mode and its second harmonic, with their wavenumbers and growth rates being in the ratio of 2:1. The telltale signature of such quadratic-order modal resonances is a jump discontinuity (figure 6
a) in the variation of the first Landau coefficient
$k_{xl}$
) due to the occurrence of a 2:1 resonance (§ 5.1.1). The latter phenomenon was shown to be tied to a resonant interaction (5.6) between the linear unstable mode and its second harmonic, with their wavenumbers and growth rates being in the ratio of 2:1. The telltale signature of such quadratic-order modal resonances is a jump discontinuity (figure 6
a) in the variation of the first Landau coefficient
![]() $c^{(2)}$
at the resonance point. For all case studies, we found no subcritical finite-amplitude solutions for the experimentally accessible range of parameters (Eshuis et al.
Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007). This conclusion is similar to that of classical Rayleigh–Bénard convection for which the primary bifurcation is also a supercritical pitchfork bifurcation, which implies that the system behaves continuously at the onset of convection instability, giving rise to well-defined steady convective patterns.
$c^{(2)}$
at the resonance point. For all case studies, we found no subcritical finite-amplitude solutions for the experimentally accessible range of parameters (Eshuis et al.
Reference Eshuis, van der Weele, van der Meer, Bos and Lohse2007). This conclusion is similar to that of classical Rayleigh–Bénard convection for which the primary bifurcation is also a supercritical pitchfork bifurcation, which implies that the system behaves continuously at the onset of convection instability, giving rise to well-defined steady convective patterns.
The linear and nonlinear patterns of the density and velocity fields were compared with each other, and we found that the nonlinear patterns could differ markedly from the linear patterns if the distance from the critical point was large. Close to the bifurcation point, the equilibrium amplitude (
![]() $A_{e}$
) was found to follow a square-root scaling law,
$A_{e}$
) was found to follow a square-root scaling law,
![]() $A_{e}\sim \sqrt{{\it\Delta}}$
, with the distance (
$A_{e}\sim \sqrt{{\it\Delta}}$
, with the distance (
![]() ${\it\Delta}=|k_{x}-k_{xc}|$
or
${\it\Delta}=|k_{x}-k_{xc}|$
or
![]() $(S-S_{c})$
) from the bifurcation point. The range of validity of this square-root scaling was shown to be very small, as expected for a multi-dimensional bifurcation problem. We showed that non-zero values of the bulk viscosity (
$(S-S_{c})$
) from the bifurcation point. The range of validity of this square-root scaling was shown to be very small, as expected for a multi-dimensional bifurcation problem. We showed that non-zero values of the bulk viscosity (
![]() ${\it\zeta}=0$
or
${\it\zeta}=0$
or
![]() $\neq 0$
) and the shear work (
$\neq 0$
) and the shear work (
![]() ${\it\Phi}_{vis}=0$
or
${\it\Phi}_{vis}=0$
or
![]() $\neq 0$
), as well as different types of free-surface boundary conditions, do not noticeably affect our predictions on (i) the least stable mode, (ii) the first Landau coefficient and (iii) the nonlinear equilibrium amplitudes. Furthermore, a density-dependent Prandtl number was also used and the effects were found to be marginal. All these sensitivity analyses confirmed that our predicted nonlinear results are robust.
$\neq 0$
), as well as different types of free-surface boundary conditions, do not noticeably affect our predictions on (i) the least stable mode, (ii) the first Landau coefficient and (iii) the nonlinear equilibrium amplitudes. Furthermore, a density-dependent Prandtl number was also used and the effects were found to be marginal. All these sensitivity analyses confirmed that our predicted nonlinear results are robust.
Our theory predicted that the nonlinear equilibrium amplitude for an unstable mode at a given wavenumber
![]() $k_{x}$
(which is inversely proportional to the length of the box) varies non-monotonically with the shaking strength (
$k_{x}$
(which is inversely proportional to the length of the box) varies non-monotonically with the shaking strength (
![]() $S$
) at any particle loading. The strength of the resulting convection (measured in terms of velocity circulation) was also found to be non-monotonic: the circulation is maximum at some intermediate value of
$S$
) at any particle loading. The strength of the resulting convection (measured in terms of velocity circulation) was also found to be non-monotonic: the circulation is maximum at some intermediate value of
![]() $S$
, with its strength diminishing with further increase of
$S$
, with its strength diminishing with further increase of
![]() $S$
. At very large values of
$S$
. At very large values of
![]() $S$
, the particles near the top surface undergo a weak convective motion, and the rest of the particles have nearly zero velocities, implying a conduction state of a granular gas in the lower portion of the granular bed, the height of which increases with increasing
$S$
, the particles near the top surface undergo a weak convective motion, and the rest of the particles have nearly zero velocities, implying a conduction state of a granular gas in the lower portion of the granular bed, the height of which increases with increasing
![]() $S$
. Therefore, we conclude that the convection is likely to give way to a conduction state of the granular gas at very large values of
$S$
. Therefore, we conclude that the convection is likely to give way to a conduction state of the granular gas at very large values of
![]() $S$
if the experiments are performed by keeping the length (
$S$
if the experiments are performed by keeping the length (
![]() $L_{x}/d$
) of the container fixed.
$L_{x}/d$
) of the container fixed.
A qualitative comparison of the predicted nonlinear patterns of the velocity and density fields was made with a limited set of experiments in a similar set-up. Although the large-scale features of the experimental patterns looked similar to those of the nonlinear solutions, there were two important differences between experiment and theory with respect to (i) the small-scale structures and (ii) the locations of the particle clusters. We speculate that the latter issue could be resolved partially by incorporating the additional energy losses due to the front and back walls of the vibrated box, resulting in an effective shaking strength that is lower than the actual energy input through the shaker. Other related issues for improvement would be the simplified boundary conditions at the bottom plate as well as the quasi-steady assumption (Ansari & Alam Reference Ansari and Alam2014) regarding the base state. On theoretical fronts alone, the present work is worthy of further study to explore the exotic consequences of
![]() $m:n$
resonance (§ 5.1.1), a proper analysis of which is likely to engender additional complications (Alam & Shukla 2014, unpublished). It might also be worthwhile to investigate the stability of the finite-amplitude nonlinear solutions to understand the secondary/tertiary bifurcation scenario (Alam et al.
Reference Alam, Arakeri, Nott, Goddard and Herrmann2005) in granular convection as well as in other granular flows.
$m:n$
resonance (§ 5.1.1), a proper analysis of which is likely to engender additional complications (Alam & Shukla 2014, unpublished). It might also be worthwhile to investigate the stability of the finite-amplitude nonlinear solutions to understand the secondary/tertiary bifurcation scenario (Alam et al.
Reference Alam, Arakeri, Nott, Goddard and Herrmann2005) in granular convection as well as in other granular flows.
Acknowledgements
M.A. acknowledges funding support from the Department of Atomic Energy, Government of India through a research grant (DAE/MA/4265; DAE-SRC Outstanding Research Investigator Project 2010–2015). We thank Mr Ronak Gupta for help to prepare figure 19(a).
Appendix A. Elements of the linear and adjoint stability operators
The elements of the linear stability operator,
![]() $\mathscr{L}=\{l_{ij}\}$
, and its adjoint operator,
$\mathscr{L}=\{l_{ij}\}$
, and its adjoint operator,
![]() $\mathscr{L}^{\dagger }=\{l_{ij}^{\dagger }\}$
, are as follows:
$\mathscr{L}^{\dagger }=\{l_{ij}^{\dagger }\}$
, are as follows:
 $$\begin{eqnarray}\left.\begin{array}{@{}l@{}}l_{11}=0,\quad l_{12}=-n^{0}\displaystyle \frac{\partial }{\partial x},\quad l_{13}=-\left(\displaystyle n_{y}^{0}+n^{0}\frac{\partial }{\partial y}\right),\quad l_{14}=0,\\ l_{21}=\displaystyle -\frac{p_{n}^{0}}{n^{0}}\frac{\partial }{\partial x},\quad l_{22}=\frac{1}{n^{0}}\left[(2{\it\mu}^{0}+{\it\lambda}^{0})\frac{\partial ^{2}}{\partial x^{2}}+{\it\mu}_{y}^{0}\frac{\partial }{\partial y}+{\it\mu}^{0}\frac{\partial ^{2}}{\partial y^{2}}\right],\\ l_{23}=\displaystyle \frac{1}{n^{0}}\left[{\it\mu}_{y}^{0}\frac{\partial }{\partial x}+({\it\mu}^{0}+{\it\lambda}^{0})\frac{\partial ^{2}}{\partial x\partial y}\right],\quad l_{24}=-\frac{p_{T}^{0}}{n^{0}}\frac{\partial }{\partial x},\\ l_{31}=\displaystyle -\frac{1}{n^{0}}\left(\frac{1}{S}+p_{ny}^{0}+p_{n}^{0}\frac{\partial }{\partial y}\right),\\ l_{32}=\displaystyle \frac{1}{n^{0}}\left[{\it\lambda}_{y}^{0}\frac{\partial }{\partial x}+({\it\lambda}^{0}+{\it\mu}^{0})\frac{\partial ^{2}}{\partial x\partial y}\right],\\ l_{33}=\displaystyle \frac{1}{n^{0}}\left[{\it\mu}^{0}\frac{\partial ^{2}}{\partial x^{2}}+(2{\it\mu}_{y}^{0}+{\it\lambda}_{y}^{0})\frac{\partial }{\partial y}+(2{\it\mu}^{0}+{\it\lambda}^{0})\frac{\partial ^{2}}{\partial y^{2}}\right],\\ l_{34}=\displaystyle -\frac{1}{n^{0}}\left(p_{Ty}^{0}+p_{T}^{0}\frac{\partial }{\partial y}\right),\\ l_{41}=\displaystyle \frac{1}{n^{0}}\left[T_{y}^{0}{\it\kappa}_{ny}^{0}+T_{y}^{0}{\it\kappa}_{n}^{0}\frac{\partial }{\partial y}+{\it\kappa}_{n}^{0}T_{yy}^{0}-\mathscr{D}_{n}^{0}\right],\\ l_{42}=\displaystyle -\frac{p^{0}}{n^{0}}\frac{\partial }{\partial x},\quad l_{43}=-T_{y}^{0}-\frac{p^{0}}{n^{0}}\frac{\partial }{\partial y},\\ l_{44}=\displaystyle \frac{1}{n^{0}}\left[{\it\kappa}^{0}\frac{\partial ^{2}}{\partial x^{2}}+\left(T_{y}^{0}{\it\kappa}_{Ty}^{0}+{\it\kappa}_{T}^{0}T_{yy}^{0}\right)+\left({\it\kappa}_{y}^{0}+T_{y}^{0}{\it\kappa}_{T}^{0}\right)\frac{\partial }{\partial y}+{\it\kappa}^{0}\frac{\partial ^{2}}{\partial y^{2}}-\mathscr{D}_{T}^{0}\right],\end{array}\!\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}l_{11}=0,\quad l_{12}=-n^{0}\displaystyle \frac{\partial }{\partial x},\quad l_{13}=-\left(\displaystyle n_{y}^{0}+n^{0}\frac{\partial }{\partial y}\right),\quad l_{14}=0,\\ l_{21}=\displaystyle -\frac{p_{n}^{0}}{n^{0}}\frac{\partial }{\partial x},\quad l_{22}=\frac{1}{n^{0}}\left[(2{\it\mu}^{0}+{\it\lambda}^{0})\frac{\partial ^{2}}{\partial x^{2}}+{\it\mu}_{y}^{0}\frac{\partial }{\partial y}+{\it\mu}^{0}\frac{\partial ^{2}}{\partial y^{2}}\right],\\ l_{23}=\displaystyle \frac{1}{n^{0}}\left[{\it\mu}_{y}^{0}\frac{\partial }{\partial x}+({\it\mu}^{0}+{\it\lambda}^{0})\frac{\partial ^{2}}{\partial x\partial y}\right],\quad l_{24}=-\frac{p_{T}^{0}}{n^{0}}\frac{\partial }{\partial x},\\ l_{31}=\displaystyle -\frac{1}{n^{0}}\left(\frac{1}{S}+p_{ny}^{0}+p_{n}^{0}\frac{\partial }{\partial y}\right),\\ l_{32}=\displaystyle \frac{1}{n^{0}}\left[{\it\lambda}_{y}^{0}\frac{\partial }{\partial x}+({\it\lambda}^{0}+{\it\mu}^{0})\frac{\partial ^{2}}{\partial x\partial y}\right],\\ l_{33}=\displaystyle \frac{1}{n^{0}}\left[{\it\mu}^{0}\frac{\partial ^{2}}{\partial x^{2}}+(2{\it\mu}_{y}^{0}+{\it\lambda}_{y}^{0})\frac{\partial }{\partial y}+(2{\it\mu}^{0}+{\it\lambda}^{0})\frac{\partial ^{2}}{\partial y^{2}}\right],\\ l_{34}=\displaystyle -\frac{1}{n^{0}}\left(p_{Ty}^{0}+p_{T}^{0}\frac{\partial }{\partial y}\right),\\ l_{41}=\displaystyle \frac{1}{n^{0}}\left[T_{y}^{0}{\it\kappa}_{ny}^{0}+T_{y}^{0}{\it\kappa}_{n}^{0}\frac{\partial }{\partial y}+{\it\kappa}_{n}^{0}T_{yy}^{0}-\mathscr{D}_{n}^{0}\right],\\ l_{42}=\displaystyle -\frac{p^{0}}{n^{0}}\frac{\partial }{\partial x},\quad l_{43}=-T_{y}^{0}-\frac{p^{0}}{n^{0}}\frac{\partial }{\partial y},\\ l_{44}=\displaystyle \frac{1}{n^{0}}\left[{\it\kappa}^{0}\frac{\partial ^{2}}{\partial x^{2}}+\left(T_{y}^{0}{\it\kappa}_{Ty}^{0}+{\it\kappa}_{T}^{0}T_{yy}^{0}\right)+\left({\it\kappa}_{y}^{0}+T_{y}^{0}{\it\kappa}_{T}^{0}\right)\frac{\partial }{\partial y}+{\it\kappa}^{0}\frac{\partial ^{2}}{\partial y^{2}}-\mathscr{D}_{T}^{0}\right],\end{array}\!\right\}\end{eqnarray}$$
 $$\begin{eqnarray}\left.\begin{array}{@{}lcl@{}}l_{11}^{\dagger }\, & =\, & 0,\quad l_{12}^{\dagger }=\displaystyle \frac{p_{n}^{0}}{n^{0}}\frac{\partial }{\partial x},\\ l_{13}^{\dagger }\, & =\, & \displaystyle -\frac{1}{n^{0}S}+\frac{p_{n}^{0}}{(n^{0})^{2}}\left(n^{0}\frac{\partial }{\partial y}-n_{y}^{0}\right),\quad l_{14}^{\dagger }=\displaystyle \frac{-\mathscr{D}_{n}^{0}}{n^{0}}+\frac{{\it\kappa}_{n}^{0}T_{y}^{0}}{(n^{0})^{2}}\left(n_{y}^{0}-n^{0}\frac{\partial }{\partial y}\right),\\ l_{21}^{\dagger }\, & =\, & \displaystyle n^{0}\frac{\partial }{\partial x},\\ l_{22}^{\dagger }\, & =\, & \displaystyle \frac{(2{\it\mu}^{0}+{\it\lambda}^{0})}{n^{0}}\frac{\partial ^{2}}{\partial x^{2}}+\frac{1}{(n^{0})^{2}}\left[\vphantom{\frac{2n_{y}^{0^{2}}{\it\mu}^{0}}{n^{0}}}-{\it\mu}_{y}^{0}n_{y}^{0}-{\it\mu}^{0}n_{yy}^{0}\right.\\ \, & \, & \left.+\,\displaystyle (n^{0}{\it\mu}_{y}^{0}-2n_{y}^{0}{\it\mu}^{0})\frac{\partial }{\partial y}+n^{0}{\it\mu}^{0}\frac{\partial ^{2}}{\partial y^{2}}+\frac{2n_{y}^{0^{2}}{\it\mu}^{0}}{n^{0}}\right],\\ l_{23}^{\dagger }\, & =\, & \displaystyle \frac{1}{(n^{0})^{2}}\left[({\it\mu}^{0}+{\it\lambda}^{0})\left(n^{0}\frac{\partial }{\partial y}-n_{y}^{0}\right)\frac{\partial }{\partial x}+n^{0}{\it\mu}_{y}^{0}\frac{\partial }{\partial x}\right],\quad l_{24}^{\dagger }=\displaystyle \frac{p^{0}}{n^{0}}\frac{\partial }{\partial x},\\ l_{31}^{\dagger }\, & =\, & \displaystyle -n_{y}^{0}+n^{0}\frac{\partial }{\partial y},\\ l_{32}^{\dagger }\, & =\, & \displaystyle \frac{1}{(n^{0})^{2}}\left[({\it\mu}^{0}+{\it\lambda}^{0})\left(n^{0}\frac{\partial }{\partial y}-n_{y}^{0}\right)\frac{\partial }{\partial x}+n^{0}{\it\lambda}_{y}^{0}\frac{\partial }{\partial x}\right],\\ l_{33}^{\dagger }\, & =\, & \displaystyle \frac{{\it\mu}^{0}}{n^{0}}\frac{\partial ^{2}}{\partial x^{2}}+\frac{1}{(n^{0})^{2}}\left[\vphantom{\frac{2n_{y}^{0^{2}}(2{\it\mu}^{0}+{\it\lambda}^{0})}{n^{0}}}\displaystyle -(2{\it\mu}_{y}^{0}+{\it\lambda}_{y}^{0})n_{y}^{0}-(2{\it\mu}^{0}+{\it\lambda}^{0})n_{yy}^{0}+\left\{n^{0}(2{\it\mu}_{y}^{0}+{\it\lambda}_{y}^{0})\right.\right.\\ \, & \, & \left.\left.\displaystyle -\;2n_{y}^{0}(2{\it\mu}^{0}+{\it\lambda}^{0})\right\}\displaystyle \frac{\partial }{\partial y}+n^{0}(2{\it\mu}^{0}+{\it\lambda}^{0})\displaystyle \frac{\partial ^{2}}{\partial y^{2}}+\frac{2n_{y}^{0^{2}}(2{\it\mu}^{0}+{\it\lambda}^{0})}{n^{0}}\right],\\ l_{34}^{\dagger }\, & =\, & \displaystyle -T_{y}^{0}+\frac{1}{(n^{0})^{2}}\left[p^{0}\left(n^{0}\frac{\partial }{\partial y}-n_{y}^{0}\right)+n^{0}p_{y}^{0}\right],\\ l_{41}^{\dagger }\, & =\, & \displaystyle 0,\quad l_{42}^{\dagger }=\frac{p_{T}^{0}}{n^{0}}\frac{\partial }{\partial x},\quad l_{43}^{\dagger }=\frac{p_{T}^{0}}{(n^{0})^{2}}\left(n^{0}\frac{\partial }{\partial y}-n_{y}^{0}\right),\\ l_{44}^{\dagger }\, & =\, & \displaystyle \frac{1}{n^{0}}\left[{\it\kappa}^{0}\frac{\partial ^{2}}{\partial x^{2}}-\mathscr{D}_{T}^{0}\right]+\frac{1}{(n^{0})^{2}}\left[\vphantom{\frac{2(n_{y}^{0})^{2}{\it\kappa}^{0}}{n^{0}}}n^{0}{\it\kappa}_{y}\frac{\partial }{\partial y}-n^{0}T_{y}^{0}{\it\kappa}_{T}^{0}\frac{\partial }{\partial y}+n_{y}^{0}T_{y}^{0}{\it\kappa}_{T}^{0}\right.\\ \, & \, & \left.\displaystyle +\;n^{0}{\it\kappa}^{0}\frac{\partial ^{2}}{\partial y^{2}}-2n_{y}^{0}{\it\kappa}^{0}\frac{\partial }{\partial y}-n_{yy}^{0}{\it\kappa}^{0}-n_{y}^{0}{\it\kappa}_{y}^{0}+\frac{2(n_{y}^{0})^{2}{\it\kappa}^{0}}{n^{0}}\right].\end{array}\!\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}lcl@{}}l_{11}^{\dagger }\, & =\, & 0,\quad l_{12}^{\dagger }=\displaystyle \frac{p_{n}^{0}}{n^{0}}\frac{\partial }{\partial x},\\ l_{13}^{\dagger }\, & =\, & \displaystyle -\frac{1}{n^{0}S}+\frac{p_{n}^{0}}{(n^{0})^{2}}\left(n^{0}\frac{\partial }{\partial y}-n_{y}^{0}\right),\quad l_{14}^{\dagger }=\displaystyle \frac{-\mathscr{D}_{n}^{0}}{n^{0}}+\frac{{\it\kappa}_{n}^{0}T_{y}^{0}}{(n^{0})^{2}}\left(n_{y}^{0}-n^{0}\frac{\partial }{\partial y}\right),\\ l_{21}^{\dagger }\, & =\, & \displaystyle n^{0}\frac{\partial }{\partial x},\\ l_{22}^{\dagger }\, & =\, & \displaystyle \frac{(2{\it\mu}^{0}+{\it\lambda}^{0})}{n^{0}}\frac{\partial ^{2}}{\partial x^{2}}+\frac{1}{(n^{0})^{2}}\left[\vphantom{\frac{2n_{y}^{0^{2}}{\it\mu}^{0}}{n^{0}}}-{\it\mu}_{y}^{0}n_{y}^{0}-{\it\mu}^{0}n_{yy}^{0}\right.\\ \, & \, & \left.+\,\displaystyle (n^{0}{\it\mu}_{y}^{0}-2n_{y}^{0}{\it\mu}^{0})\frac{\partial }{\partial y}+n^{0}{\it\mu}^{0}\frac{\partial ^{2}}{\partial y^{2}}+\frac{2n_{y}^{0^{2}}{\it\mu}^{0}}{n^{0}}\right],\\ l_{23}^{\dagger }\, & =\, & \displaystyle \frac{1}{(n^{0})^{2}}\left[({\it\mu}^{0}+{\it\lambda}^{0})\left(n^{0}\frac{\partial }{\partial y}-n_{y}^{0}\right)\frac{\partial }{\partial x}+n^{0}{\it\mu}_{y}^{0}\frac{\partial }{\partial x}\right],\quad l_{24}^{\dagger }=\displaystyle \frac{p^{0}}{n^{0}}\frac{\partial }{\partial x},\\ l_{31}^{\dagger }\, & =\, & \displaystyle -n_{y}^{0}+n^{0}\frac{\partial }{\partial y},\\ l_{32}^{\dagger }\, & =\, & \displaystyle \frac{1}{(n^{0})^{2}}\left[({\it\mu}^{0}+{\it\lambda}^{0})\left(n^{0}\frac{\partial }{\partial y}-n_{y}^{0}\right)\frac{\partial }{\partial x}+n^{0}{\it\lambda}_{y}^{0}\frac{\partial }{\partial x}\right],\\ l_{33}^{\dagger }\, & =\, & \displaystyle \frac{{\it\mu}^{0}}{n^{0}}\frac{\partial ^{2}}{\partial x^{2}}+\frac{1}{(n^{0})^{2}}\left[\vphantom{\frac{2n_{y}^{0^{2}}(2{\it\mu}^{0}+{\it\lambda}^{0})}{n^{0}}}\displaystyle -(2{\it\mu}_{y}^{0}+{\it\lambda}_{y}^{0})n_{y}^{0}-(2{\it\mu}^{0}+{\it\lambda}^{0})n_{yy}^{0}+\left\{n^{0}(2{\it\mu}_{y}^{0}+{\it\lambda}_{y}^{0})\right.\right.\\ \, & \, & \left.\left.\displaystyle -\;2n_{y}^{0}(2{\it\mu}^{0}+{\it\lambda}^{0})\right\}\displaystyle \frac{\partial }{\partial y}+n^{0}(2{\it\mu}^{0}+{\it\lambda}^{0})\displaystyle \frac{\partial ^{2}}{\partial y^{2}}+\frac{2n_{y}^{0^{2}}(2{\it\mu}^{0}+{\it\lambda}^{0})}{n^{0}}\right],\\ l_{34}^{\dagger }\, & =\, & \displaystyle -T_{y}^{0}+\frac{1}{(n^{0})^{2}}\left[p^{0}\left(n^{0}\frac{\partial }{\partial y}-n_{y}^{0}\right)+n^{0}p_{y}^{0}\right],\\ l_{41}^{\dagger }\, & =\, & \displaystyle 0,\quad l_{42}^{\dagger }=\frac{p_{T}^{0}}{n^{0}}\frac{\partial }{\partial x},\quad l_{43}^{\dagger }=\frac{p_{T}^{0}}{(n^{0})^{2}}\left(n^{0}\frac{\partial }{\partial y}-n_{y}^{0}\right),\\ l_{44}^{\dagger }\, & =\, & \displaystyle \frac{1}{n^{0}}\left[{\it\kappa}^{0}\frac{\partial ^{2}}{\partial x^{2}}-\mathscr{D}_{T}^{0}\right]+\frac{1}{(n^{0})^{2}}\left[\vphantom{\frac{2(n_{y}^{0})^{2}{\it\kappa}^{0}}{n^{0}}}n^{0}{\it\kappa}_{y}\frac{\partial }{\partial y}-n^{0}T_{y}^{0}{\it\kappa}_{T}^{0}\frac{\partial }{\partial y}+n_{y}^{0}T_{y}^{0}{\it\kappa}_{T}^{0}\right.\\ \, & \, & \left.\displaystyle +\;n^{0}{\it\kappa}^{0}\frac{\partial ^{2}}{\partial y^{2}}-2n_{y}^{0}{\it\kappa}^{0}\frac{\partial }{\partial y}-n_{yy}^{0}{\it\kappa}^{0}-n_{y}^{0}{\it\kappa}_{y}^{0}+\frac{2(n_{y}^{0})^{2}{\it\kappa}^{0}}{n^{0}}\right].\end{array}\!\right\}\end{eqnarray}$$
Appendix B. Quadratic (
 $\mathscr{N}_{2}$
) and cubic (
$\mathscr{N}_{2}$
) and cubic (
 $\mathscr{N}_{3}$
) nonlinear terms
$\mathscr{N}_{3}$
) nonlinear terms
The quadratic (
![]() $\mathscr{N}_{2}^{(j)}$
) and cubic order (
$\mathscr{N}_{2}^{(j)}$
) and cubic order (
![]() $\mathscr{N}_{3}^{(j)}$
) nonlinear terms in the perturbation equation (3.2) are given below. It should be noted that the superscripts 1–4 refer to terms in the mass,
$\mathscr{N}_{3}^{(j)}$
) nonlinear terms in the perturbation equation (3.2) are given below. It should be noted that the superscripts 1–4 refer to terms in the mass,
![]() $x$
-momentum,
$x$
-momentum,
![]() $y$
-momentum and energy balance equations, respectively.
$y$
-momentum and energy balance equations, respectively.
 $$\begin{eqnarray}\displaystyle \mathscr{N}_{2}^{(2)} & = & \displaystyle -\frac{1}{n^{0}}\left[n^{0}(\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})u^{\prime }+n^{\prime }\left(\frac{\partial u^{\prime }}{\partial t}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\;\frac{1}{n^{0}}\left[-\left(p_{nn}^{0}n^{\prime }\frac{\partial n^{\prime }}{\partial x}+p_{TT}^{0}T^{\prime }\frac{\partial T^{\prime }}{\partial x}+p_{nT}^{0}n^{\prime }\frac{\partial T^{\prime }}{\partial x}+p_{nT}^{0}T^{\prime }\frac{\partial n^{\prime }}{\partial x}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\;2\left({\it\mu}_{n}^{0}n^{\prime }+{\it\mu}_{T}^{0}T^{\prime }\right)\frac{\partial ^{2}u^{\prime }}{\partial x^{2}}+2\left({\it\mu}_{n}^{0}\frac{\partial n^{\prime }}{\partial x}+{\it\mu}_{T}^{0}\frac{\partial T^{\prime }}{\partial x}\right)\frac{\partial u^{\prime }}{\partial x}+({\it\lambda}_{n}^{0}n^{\prime }+{\it\lambda}_{T}^{0}T^{\prime })\nonumber\\ \displaystyle & & \displaystyle \times \;\frac{\partial (\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })}{\partial x}+\left({\it\lambda}_{n}^{0}\frac{\partial n^{\prime }}{\partial x}+{\it\lambda}_{T}^{0}\frac{\partial T^{\prime }}{\partial x}\right)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })+({\it\mu}_{n}^{0}n^{\prime }+{\it\mu}_{T}^{0}T^{\prime })\frac{\partial }{\partial y}\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\nonumber\\ \displaystyle & & \displaystyle \left.+\;\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\left({\it\mu}_{ny}^{0}n^{\prime }+{\it\mu}_{n}^{0}\frac{\partial n^{\prime }}{\partial y}+{\it\mu}_{Ty}^{0}T^{\prime }+{\it\mu}_{T}^{0}\frac{\partial T^{\prime }}{\partial y}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{N}_{2}^{(2)} & = & \displaystyle -\frac{1}{n^{0}}\left[n^{0}(\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})u^{\prime }+n^{\prime }\left(\frac{\partial u^{\prime }}{\partial t}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\;\frac{1}{n^{0}}\left[-\left(p_{nn}^{0}n^{\prime }\frac{\partial n^{\prime }}{\partial x}+p_{TT}^{0}T^{\prime }\frac{\partial T^{\prime }}{\partial x}+p_{nT}^{0}n^{\prime }\frac{\partial T^{\prime }}{\partial x}+p_{nT}^{0}T^{\prime }\frac{\partial n^{\prime }}{\partial x}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\;2\left({\it\mu}_{n}^{0}n^{\prime }+{\it\mu}_{T}^{0}T^{\prime }\right)\frac{\partial ^{2}u^{\prime }}{\partial x^{2}}+2\left({\it\mu}_{n}^{0}\frac{\partial n^{\prime }}{\partial x}+{\it\mu}_{T}^{0}\frac{\partial T^{\prime }}{\partial x}\right)\frac{\partial u^{\prime }}{\partial x}+({\it\lambda}_{n}^{0}n^{\prime }+{\it\lambda}_{T}^{0}T^{\prime })\nonumber\\ \displaystyle & & \displaystyle \times \;\frac{\partial (\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })}{\partial x}+\left({\it\lambda}_{n}^{0}\frac{\partial n^{\prime }}{\partial x}+{\it\lambda}_{T}^{0}\frac{\partial T^{\prime }}{\partial x}\right)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })+({\it\mu}_{n}^{0}n^{\prime }+{\it\mu}_{T}^{0}T^{\prime })\frac{\partial }{\partial y}\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\nonumber\\ \displaystyle & & \displaystyle \left.+\;\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\left({\it\mu}_{ny}^{0}n^{\prime }+{\it\mu}_{n}^{0}\frac{\partial n^{\prime }}{\partial y}+{\it\mu}_{Ty}^{0}T^{\prime }+{\it\mu}_{T}^{0}\frac{\partial T^{\prime }}{\partial y}\right)\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathscr{N}_{3}^{(2)} & = & \displaystyle -\frac{1}{n^{0}}n^{\prime }(\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})u^{\prime }+\frac{1}{n^{0}}\left[-\frac{\partial }{\partial x}\left(\frac{1}{6}p_{nnn}^{0}n^{^{\prime }3}+\frac{1}{6}p_{TTT}^{0}T^{^{\prime }3}+\frac{1}{2}p_{nnT}^{0}n^{^{\prime }2}T^{\prime }\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\;\frac{1}{2}p_{nTT}^{0}n^{\prime }T^{^{\prime }2}\right)+2\left(\frac{1}{2}{\it\mu}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}T^{^{\prime }2}+{\it\mu}_{nT}^{0}n^{\prime }T^{\prime }\right)\frac{\partial ^{2}u^{\prime }}{\partial x^{2}}\nonumber\\ \displaystyle & & \displaystyle +\;2\frac{\partial }{\partial x}\left(\frac{1}{2}{\it\mu}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}T^{^{\prime }2}+{\it\mu}_{nT}^{0}n^{\prime }T^{\prime }\right)\frac{\partial u^{\prime }}{\partial x}\nonumber\\ \displaystyle & & \displaystyle +\;\left(\frac{1}{2}{\it\lambda}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\lambda}_{TT}^{0}T^{^{\prime }2}+{\it\lambda}_{nT}^{0}n^{\prime }T^{\prime }\right)\frac{\partial (\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })}{\partial x}\,\,\,\,\nonumber\\ \displaystyle & & \displaystyle +\;\frac{\partial }{\partial x}\left(\frac{1}{2}{\it\lambda}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\lambda}_{TT}^{0}T^{^{\prime }2}+{\it\lambda}_{nT}^{0}n^{\prime }T^{\prime }\right)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\;\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\left(\frac{1}{2}{\it\mu}_{nny}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{nn}^{0}\frac{\partial n^{^{\prime }2}}{\partial y}+\frac{1}{2}{\it\mu}_{TTy}^{0}T^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}\frac{\partial T^{^{\prime }2}}{\partial y}+{\it\mu}_{nTy}^{0}n^{\prime }T^{\prime }\right.\left.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.+\;{\it\mu}_{nT}^{0}\frac{\partial n^{\prime }T^{\prime }}{\partial y}\right)+\left(\frac{1}{2}{\it\mu}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{^{\prime }2}T^{^{\prime }2}+{\it\mu}_{nT}n^{\prime }T^{\prime }\right)\frac{\partial }{\partial y}\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{N}_{3}^{(2)} & = & \displaystyle -\frac{1}{n^{0}}n^{\prime }(\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})u^{\prime }+\frac{1}{n^{0}}\left[-\frac{\partial }{\partial x}\left(\frac{1}{6}p_{nnn}^{0}n^{^{\prime }3}+\frac{1}{6}p_{TTT}^{0}T^{^{\prime }3}+\frac{1}{2}p_{nnT}^{0}n^{^{\prime }2}T^{\prime }\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\;\frac{1}{2}p_{nTT}^{0}n^{\prime }T^{^{\prime }2}\right)+2\left(\frac{1}{2}{\it\mu}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}T^{^{\prime }2}+{\it\mu}_{nT}^{0}n^{\prime }T^{\prime }\right)\frac{\partial ^{2}u^{\prime }}{\partial x^{2}}\nonumber\\ \displaystyle & & \displaystyle +\;2\frac{\partial }{\partial x}\left(\frac{1}{2}{\it\mu}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}T^{^{\prime }2}+{\it\mu}_{nT}^{0}n^{\prime }T^{\prime }\right)\frac{\partial u^{\prime }}{\partial x}\nonumber\\ \displaystyle & & \displaystyle +\;\left(\frac{1}{2}{\it\lambda}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\lambda}_{TT}^{0}T^{^{\prime }2}+{\it\lambda}_{nT}^{0}n^{\prime }T^{\prime }\right)\frac{\partial (\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })}{\partial x}\,\,\,\,\nonumber\\ \displaystyle & & \displaystyle +\;\frac{\partial }{\partial x}\left(\frac{1}{2}{\it\lambda}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\lambda}_{TT}^{0}T^{^{\prime }2}+{\it\lambda}_{nT}^{0}n^{\prime }T^{\prime }\right)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\;\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\left(\frac{1}{2}{\it\mu}_{nny}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{nn}^{0}\frac{\partial n^{^{\prime }2}}{\partial y}+\frac{1}{2}{\it\mu}_{TTy}^{0}T^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}\frac{\partial T^{^{\prime }2}}{\partial y}+{\it\mu}_{nTy}^{0}n^{\prime }T^{\prime }\right.\left.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.+\;{\it\mu}_{nT}^{0}\frac{\partial n^{\prime }T^{\prime }}{\partial y}\right)+\left(\frac{1}{2}{\it\mu}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{^{\prime }2}T^{^{\prime }2}+{\it\mu}_{nT}n^{\prime }T^{\prime }\right)\frac{\partial }{\partial y}\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathscr{N}_{2}^{(3)} & = & \displaystyle -\frac{1}{n^{0}}\left[n^{0}(\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})v^{\prime }+n^{\prime }\frac{\partial v^{\prime }}{\partial t}\right]\nonumber\\ \displaystyle & & \displaystyle +\;\frac{1}{n^{0}}\left[-\left(\frac{1}{2}p_{nny}^{0}n^{^{\prime }2}+\frac{1}{2}p_{nn}^{0}\frac{\partial n^{^{\prime }2}}{\partial y}+\frac{1}{2}p_{TTy}^{0}T^{^{\prime }2}+\frac{1}{2}p_{TT}^{0}\frac{\partial T^{^{\prime }2}}{\partial y}+p_{nTy}^{0}n^{\prime }T^{\prime }+p_{nT}^{0}\frac{\partial n^{\prime }T^{\prime }}{\partial y}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\;2\left({\it\mu}_{n}^{0}n^{\prime }+{\it\mu}_{T}^{0}T^{\prime }\right)\frac{\partial ^{2}v^{\prime }}{\partial y^{2}}+2\left({\it\mu}_{ny}^{0}n^{\prime }+{\it\mu}_{n}^{0}\frac{\partial n^{\prime }}{\partial y}+{\it\mu}_{Ty}^{0}T^{\prime }+{\it\mu}_{T}^{0}\frac{\partial T^{\prime }}{\partial y}\right)\frac{\partial v^{\prime }}{\partial y}\nonumber\\ \displaystyle & & \displaystyle +\;\left({\it\lambda}_{n}^{0}n^{\prime }+{\it\lambda}_{T}^{0}T^{\prime }\right)\frac{\partial (\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })}{\partial y}+\left({\it\lambda}_{ny}^{0}n^{\prime }+{\it\lambda}_{n}^{0}\frac{\partial n^{\prime }}{\partial y}+{\it\lambda}_{Ty}^{0}T^{\prime }+{\it\lambda}_{T}^{0}\frac{\partial T^{\prime }}{\partial y}\right)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\;({\it\mu}_{n}^{0}n^{\prime }+{\it\mu}_{T}^{0}T^{\prime })\frac{\partial }{\partial x}\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)+\left.\left({\it\mu}_{n}^{0}\frac{\partial n^{\prime }}{\partial x}+{\it\mu}_{T}^{0}\frac{\partial T^{\prime }}{\partial x}\right)\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{N}_{2}^{(3)} & = & \displaystyle -\frac{1}{n^{0}}\left[n^{0}(\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})v^{\prime }+n^{\prime }\frac{\partial v^{\prime }}{\partial t}\right]\nonumber\\ \displaystyle & & \displaystyle +\;\frac{1}{n^{0}}\left[-\left(\frac{1}{2}p_{nny}^{0}n^{^{\prime }2}+\frac{1}{2}p_{nn}^{0}\frac{\partial n^{^{\prime }2}}{\partial y}+\frac{1}{2}p_{TTy}^{0}T^{^{\prime }2}+\frac{1}{2}p_{TT}^{0}\frac{\partial T^{^{\prime }2}}{\partial y}+p_{nTy}^{0}n^{\prime }T^{\prime }+p_{nT}^{0}\frac{\partial n^{\prime }T^{\prime }}{\partial y}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\;2\left({\it\mu}_{n}^{0}n^{\prime }+{\it\mu}_{T}^{0}T^{\prime }\right)\frac{\partial ^{2}v^{\prime }}{\partial y^{2}}+2\left({\it\mu}_{ny}^{0}n^{\prime }+{\it\mu}_{n}^{0}\frac{\partial n^{\prime }}{\partial y}+{\it\mu}_{Ty}^{0}T^{\prime }+{\it\mu}_{T}^{0}\frac{\partial T^{\prime }}{\partial y}\right)\frac{\partial v^{\prime }}{\partial y}\nonumber\\ \displaystyle & & \displaystyle +\;\left({\it\lambda}_{n}^{0}n^{\prime }+{\it\lambda}_{T}^{0}T^{\prime }\right)\frac{\partial (\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })}{\partial y}+\left({\it\lambda}_{ny}^{0}n^{\prime }+{\it\lambda}_{n}^{0}\frac{\partial n^{\prime }}{\partial y}+{\it\lambda}_{Ty}^{0}T^{\prime }+{\it\lambda}_{T}^{0}\frac{\partial T^{\prime }}{\partial y}\right)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\;({\it\mu}_{n}^{0}n^{\prime }+{\it\mu}_{T}^{0}T^{\prime })\frac{\partial }{\partial x}\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)+\left.\left({\it\mu}_{n}^{0}\frac{\partial n^{\prime }}{\partial x}+{\it\mu}_{T}^{0}\frac{\partial T^{\prime }}{\partial x}\right)\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathscr{N}_{3}^{(3)} & = & \displaystyle -\frac{1}{n^{0}}n^{\prime }(\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})v^{\prime }+\frac{1}{n^{0}}\left[-\left(\frac{1}{6}p_{nnny}^{0}n^{^{\prime }3}+\frac{1}{6}p_{nnn}^{0}\frac{\partial n^{^{\prime }3}}{\partial y}+\frac{1}{6}p_{TTTy}^{0}T^{^{\prime }3}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\;\frac{1}{6}p_{TTT}^{0}\frac{\partial T^{^{\prime }3}}{\partial y}+\frac{1}{2}p_{nnTy}^{0}n^{^{\prime }2}T^{\prime }+\frac{1}{2}p_{nnT}^{0}\frac{\partial n^{^{\prime }2}T^{\prime }}{\partial y}+\frac{1}{2}p_{nTTy}^{0}n^{\prime }T^{^{\prime }2}+\frac{1}{2}p_{nTT}^{0}\frac{\partial n^{\prime }T^{^{\prime }2}}{\partial y}\right)\nonumber\\ \displaystyle & & \displaystyle +\;2\left(\frac{1}{2}{\it\mu}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}T^{^{\prime }2}+{\it\mu}_{nT}^{0}n^{\prime }T^{\prime }\right)\frac{\partial ^{2}v^{\prime }}{\partial y^{2}}\nonumber\\ \displaystyle & & \displaystyle +\;2\frac{\partial v^{\prime }}{\partial y}\left(\frac{1}{2}{\it\mu}_{nny}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{nn}^{0}\frac{\partial n^{^{\prime }2}}{\partial y}+\frac{1}{2}{\it\mu}_{TTy}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}\frac{\partial T^{^{\prime }2}}{\partial y}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\;{\it\mu}_{nTy}^{0}n^{\prime }T^{\prime }+{\it\mu}_{nT}^{0}\frac{\partial n^{\prime }T^{\prime }}{\partial y}\right)+\left(\frac{1}{2}{\it\lambda}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\lambda}_{TT}^{0}T^{^{\prime }2}+{\it\lambda}_{nT}^{0}n^{\prime }T^{\prime }\right)\frac{\partial (\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })}{\partial y}\nonumber\\ \displaystyle & & \displaystyle +\;(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })\left(\frac{1}{2}{\it\lambda}_{nny}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\lambda}_{nn}^{0}\frac{\partial n^{^{\prime }2}}{\partial y}+\frac{1}{2}{\it\lambda}_{TTy}^{0}T^{^{\prime }2}+\frac{1}{2}{\it\lambda}_{TT}^{0}\frac{\partial T^{^{\prime }2}}{\partial y}+{\it\lambda}_{nTy}^{0}n^{\prime }T^{\prime }\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\;{\it\lambda}_{nT}^{0}\frac{\partial n^{\prime }T^{\prime }}{\partial y}\right)+\left(\frac{1}{2}{\it\mu}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}T^{^{\prime }2}+{\it\mu}_{nT}^{0}n^{\prime }T^{\prime }\right)\frac{\partial }{\partial x}\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\nonumber\\ \displaystyle & & \displaystyle \left.+\;\frac{\partial }{\partial x}\left(\frac{1}{2}{\it\mu}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}T^{^{\prime }2}+{\it\mu}_{nT}^{0}n^{\prime }T^{\prime }\right)\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{N}_{3}^{(3)} & = & \displaystyle -\frac{1}{n^{0}}n^{\prime }(\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})v^{\prime }+\frac{1}{n^{0}}\left[-\left(\frac{1}{6}p_{nnny}^{0}n^{^{\prime }3}+\frac{1}{6}p_{nnn}^{0}\frac{\partial n^{^{\prime }3}}{\partial y}+\frac{1}{6}p_{TTTy}^{0}T^{^{\prime }3}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\;\frac{1}{6}p_{TTT}^{0}\frac{\partial T^{^{\prime }3}}{\partial y}+\frac{1}{2}p_{nnTy}^{0}n^{^{\prime }2}T^{\prime }+\frac{1}{2}p_{nnT}^{0}\frac{\partial n^{^{\prime }2}T^{\prime }}{\partial y}+\frac{1}{2}p_{nTTy}^{0}n^{\prime }T^{^{\prime }2}+\frac{1}{2}p_{nTT}^{0}\frac{\partial n^{\prime }T^{^{\prime }2}}{\partial y}\right)\nonumber\\ \displaystyle & & \displaystyle +\;2\left(\frac{1}{2}{\it\mu}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}T^{^{\prime }2}+{\it\mu}_{nT}^{0}n^{\prime }T^{\prime }\right)\frac{\partial ^{2}v^{\prime }}{\partial y^{2}}\nonumber\\ \displaystyle & & \displaystyle +\;2\frac{\partial v^{\prime }}{\partial y}\left(\frac{1}{2}{\it\mu}_{nny}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{nn}^{0}\frac{\partial n^{^{\prime }2}}{\partial y}+\frac{1}{2}{\it\mu}_{TTy}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}\frac{\partial T^{^{\prime }2}}{\partial y}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\;{\it\mu}_{nTy}^{0}n^{\prime }T^{\prime }+{\it\mu}_{nT}^{0}\frac{\partial n^{\prime }T^{\prime }}{\partial y}\right)+\left(\frac{1}{2}{\it\lambda}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\lambda}_{TT}^{0}T^{^{\prime }2}+{\it\lambda}_{nT}^{0}n^{\prime }T^{\prime }\right)\frac{\partial (\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })}{\partial y}\nonumber\\ \displaystyle & & \displaystyle +\;(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })\left(\frac{1}{2}{\it\lambda}_{nny}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\lambda}_{nn}^{0}\frac{\partial n^{^{\prime }2}}{\partial y}+\frac{1}{2}{\it\lambda}_{TTy}^{0}T^{^{\prime }2}+\frac{1}{2}{\it\lambda}_{TT}^{0}\frac{\partial T^{^{\prime }2}}{\partial y}+{\it\lambda}_{nTy}^{0}n^{\prime }T^{\prime }\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\;{\it\lambda}_{nT}^{0}\frac{\partial n^{\prime }T^{\prime }}{\partial y}\right)+\left(\frac{1}{2}{\it\mu}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}T^{^{\prime }2}+{\it\mu}_{nT}^{0}n^{\prime }T^{\prime }\right)\frac{\partial }{\partial x}\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\nonumber\\ \displaystyle & & \displaystyle \left.+\;\frac{\partial }{\partial x}\left(\frac{1}{2}{\it\mu}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\mu}_{TT}^{0}T^{^{\prime }2}+{\it\mu}_{nT}^{0}n^{\prime }T^{\prime }\right)\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathscr{N}_{2}^{(4)} & = & \displaystyle -\frac{1}{n^{0}}\left[n^{0}(\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})T^{\prime }+n^{\prime }\left(\frac{\partial T^{\prime }}{\partial t}+T_{y}^{0}v^{\prime }\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\;\frac{1}{n^{0}}\left[\frac{\partial T^{\prime }}{\partial x}\left({\it\kappa}_{n}^{0}\frac{\partial n^{\prime }}{\partial x}+{\it\kappa}_{T}^{0}\frac{\partial T^{\prime }}{\partial x}\right)+\frac{\partial ^{2}T^{\prime }}{\partial x^{2}}\left({\it\kappa}_{n}^{0}n^{\prime }+{\it\kappa}_{T}^{0}T^{\prime }\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\;T_{y}^{0}\left(\frac{1}{2}{\it\kappa}_{nny}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{nn}^{0}\frac{\partial n^{^{\prime }2}}{\partial y}+\frac{1}{2}{\it\kappa}_{TTy}^{0}T^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{TT}^{0}\frac{\partial T^{^{\prime }2}}{\partial y}\right.\nonumber\\ \displaystyle & & \displaystyle +\;\left.{\it\kappa}_{nTy}^{0}n^{\prime }T^{\prime }+{\it\kappa}_{nT}^{0}\frac{\partial n^{\prime }T^{\prime }}{\partial y}\right)+T_{yy}^{0}\left(\frac{1}{2}{\it\kappa}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{TT}^{0}T^{^{\prime }2}+{\it\kappa}_{nT}^{0}n^{\prime }T^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle +\;\frac{\partial T^{\prime }}{\partial y}\left({\it\kappa}_{ny}^{0}n^{\prime }+{\it\kappa}_{n}^{0}\frac{\partial n^{\prime }}{\partial y}+{\it\kappa}_{Ty}^{0}T^{\prime }+{\it\kappa}_{T}^{0}\frac{\partial T^{\prime }}{\partial y}\right)+\frac{\partial ^{2}T^{\prime }}{\partial y^{2}}\left({\it\kappa}_{n}^{0}n^{\prime }+{\it\kappa}_{T}^{0}T^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle -\;(p_{n}^{0}n^{\prime }+p_{T}^{0}T^{\prime })(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })+2{\it\mu}^{0}\left\{\left(\frac{\partial u^{\prime }}{\partial x}\right)^{2}+\left(\frac{\partial v^{\prime }}{\partial y}\right)^{2}+\frac{1}{2}\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)^{2}\!\right\}\nonumber\\ \displaystyle & & \displaystyle \left.+\;{\it\lambda}^{0}(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })^{2}-\left(\frac{1}{2}\mathscr{D}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}\mathscr{D}_{TT}^{0}T^{^{\prime }2}+\mathscr{D}_{nT}^{0}n^{\prime }T^{\prime }\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{N}_{2}^{(4)} & = & \displaystyle -\frac{1}{n^{0}}\left[n^{0}(\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})T^{\prime }+n^{\prime }\left(\frac{\partial T^{\prime }}{\partial t}+T_{y}^{0}v^{\prime }\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\;\frac{1}{n^{0}}\left[\frac{\partial T^{\prime }}{\partial x}\left({\it\kappa}_{n}^{0}\frac{\partial n^{\prime }}{\partial x}+{\it\kappa}_{T}^{0}\frac{\partial T^{\prime }}{\partial x}\right)+\frac{\partial ^{2}T^{\prime }}{\partial x^{2}}\left({\it\kappa}_{n}^{0}n^{\prime }+{\it\kappa}_{T}^{0}T^{\prime }\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\;T_{y}^{0}\left(\frac{1}{2}{\it\kappa}_{nny}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{nn}^{0}\frac{\partial n^{^{\prime }2}}{\partial y}+\frac{1}{2}{\it\kappa}_{TTy}^{0}T^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{TT}^{0}\frac{\partial T^{^{\prime }2}}{\partial y}\right.\nonumber\\ \displaystyle & & \displaystyle +\;\left.{\it\kappa}_{nTy}^{0}n^{\prime }T^{\prime }+{\it\kappa}_{nT}^{0}\frac{\partial n^{\prime }T^{\prime }}{\partial y}\right)+T_{yy}^{0}\left(\frac{1}{2}{\it\kappa}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{TT}^{0}T^{^{\prime }2}+{\it\kappa}_{nT}^{0}n^{\prime }T^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle +\;\frac{\partial T^{\prime }}{\partial y}\left({\it\kappa}_{ny}^{0}n^{\prime }+{\it\kappa}_{n}^{0}\frac{\partial n^{\prime }}{\partial y}+{\it\kappa}_{Ty}^{0}T^{\prime }+{\it\kappa}_{T}^{0}\frac{\partial T^{\prime }}{\partial y}\right)+\frac{\partial ^{2}T^{\prime }}{\partial y^{2}}\left({\it\kappa}_{n}^{0}n^{\prime }+{\it\kappa}_{T}^{0}T^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle -\;(p_{n}^{0}n^{\prime }+p_{T}^{0}T^{\prime })(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })+2{\it\mu}^{0}\left\{\left(\frac{\partial u^{\prime }}{\partial x}\right)^{2}+\left(\frac{\partial v^{\prime }}{\partial y}\right)^{2}+\frac{1}{2}\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)^{2}\!\right\}\nonumber\\ \displaystyle & & \displaystyle \left.+\;{\it\lambda}^{0}(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })^{2}-\left(\frac{1}{2}\mathscr{D}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}\mathscr{D}_{TT}^{0}T^{^{\prime }2}+\mathscr{D}_{nT}^{0}n^{\prime }T^{\prime }\right)\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathscr{N}_{3}^{(4)} & = & \displaystyle -\frac{1}{n^{0}}\;n^{\prime }(\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})T^{\prime }+\;\frac{1}{n^{0}}\left[\frac{\partial T^{\prime }}{\partial x}\frac{\partial }{\partial x}\left(\frac{1}{2}{\it\kappa}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{TT}^{0}T^{^{\prime }2}+{\it\kappa}_{nT}^{0}n^{\prime }T^{\prime }\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\;\frac{\partial ^{2}T^{\prime }}{\partial x^{2}}\left(\frac{1}{2}{\it\kappa}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{TT}^{0}T^{^{\prime }2}+{\it\kappa}_{nT}^{0}n^{\prime }T^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle +\;T_{y}^{0}\left(\frac{1}{6}{\it\kappa}_{nnny}^{0}n^{^{\prime }3}+\frac{1}{6}{\it\kappa}_{nnn}^{0}\frac{\partial n^{^{\prime }3}}{\partial y}+\frac{1}{6}{\it\kappa}_{TTTy}^{0}T^{^{\prime }3}+\frac{1}{6}{\it\kappa}_{TTT}^{0}\frac{\partial T^{^{\prime }3}}{\partial y}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\;\frac{1}{2}{\it\kappa}_{nnTy}^{0}n^{^{\prime }2}T^{\prime }+\frac{1}{2}{\it\kappa}_{nnT}^{0}\frac{\partial n^{^{\prime }2}T^{\prime }}{\partial y}+\frac{1}{2}{\it\kappa}_{nTTy}^{0}n^{\prime }T^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{nTT}^{0}\frac{\partial nT^{^{\prime }2}}{\partial y}\right)\nonumber\\ \displaystyle & & \displaystyle +\;T_{yy}^{0}\left(\frac{1}{6}{\it\kappa}_{nnn}^{0}n^{^{\prime }3}+\frac{1}{6}{\it\kappa}_{nTT}^{0}T^{^{\prime }3}+\frac{1}{2}{\it\kappa}_{nnT}^{0}n^{^{\prime }2}T^{\prime }+\frac{1}{2}{\it\kappa}_{nTT}^{0}n^{\prime }T^{^{\prime }2}\right)\nonumber\\ \displaystyle & & \displaystyle +\;\frac{\partial T^{\prime }}{\partial y}\left(\frac{1}{2}{\it\kappa}_{nny}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{nn}^{0}\frac{\partial n^{^{\prime }2}}{\partial y}+\frac{1}{2}{\it\kappa}_{TTy}^{0}T^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{TT}^{0}\frac{\partial T^{^{\prime }2}}{\partial y}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\;{\it\kappa}_{nTy}^{0}n^{\prime }T^{\prime }+{\it\kappa}_{nT}^{0}\frac{\partial n^{\prime }T^{\prime }}{\partial y}\right)+\frac{\partial ^{2}T^{\prime }}{\partial y^{2}}\left(\frac{1}{2}{\it\kappa}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{TT}^{0}T^{^{\prime }2}+{\it\kappa}_{nT}^{0}n^{\prime }T^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle -\;\left(\frac{1}{2}p_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}p_{TT}^{0}T^{^{\prime }2}+p_{nT}^{0}n^{\prime }T^{\prime }\right)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\;2({\it\mu}_{n}^{0}n^{\prime }+{\it\mu}_{T}^{0}T^{\prime })\left\{\!\left(\frac{\partial u^{\prime }}{\partial x}\right)^{2}+\left(\frac{\partial v^{\prime }}{\partial y}\right)^{2}+\frac{1}{2}\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)^{2}\!\right\}\nonumber\\ \displaystyle & & \displaystyle +\;\left({\it\lambda}_{n}^{0}n^{\prime }+{\it\lambda}_{T}^{0}T^{\prime }\right)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })^{2}\nonumber\\ \displaystyle & & \displaystyle \left.-\;\left(\frac{1}{6}\mathscr{D}_{nnn}^{0}n^{^{\prime }3}+\frac{1}{6}\mathscr{D}_{TTT}^{0}T^{^{\prime }3}+\frac{1}{2}\mathscr{D}_{nnT}^{0}n^{^{\prime }2}T^{\prime }+\frac{1}{2}\mathscr{D}_{nTT}^{0}n^{\prime }T^{^{\prime }2}\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{N}_{3}^{(4)} & = & \displaystyle -\frac{1}{n^{0}}\;n^{\prime }(\boldsymbol{u}^{\prime }\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})T^{\prime }+\;\frac{1}{n^{0}}\left[\frac{\partial T^{\prime }}{\partial x}\frac{\partial }{\partial x}\left(\frac{1}{2}{\it\kappa}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{TT}^{0}T^{^{\prime }2}+{\it\kappa}_{nT}^{0}n^{\prime }T^{\prime }\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\;\frac{\partial ^{2}T^{\prime }}{\partial x^{2}}\left(\frac{1}{2}{\it\kappa}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{TT}^{0}T^{^{\prime }2}+{\it\kappa}_{nT}^{0}n^{\prime }T^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle +\;T_{y}^{0}\left(\frac{1}{6}{\it\kappa}_{nnny}^{0}n^{^{\prime }3}+\frac{1}{6}{\it\kappa}_{nnn}^{0}\frac{\partial n^{^{\prime }3}}{\partial y}+\frac{1}{6}{\it\kappa}_{TTTy}^{0}T^{^{\prime }3}+\frac{1}{6}{\it\kappa}_{TTT}^{0}\frac{\partial T^{^{\prime }3}}{\partial y}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\;\frac{1}{2}{\it\kappa}_{nnTy}^{0}n^{^{\prime }2}T^{\prime }+\frac{1}{2}{\it\kappa}_{nnT}^{0}\frac{\partial n^{^{\prime }2}T^{\prime }}{\partial y}+\frac{1}{2}{\it\kappa}_{nTTy}^{0}n^{\prime }T^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{nTT}^{0}\frac{\partial nT^{^{\prime }2}}{\partial y}\right)\nonumber\\ \displaystyle & & \displaystyle +\;T_{yy}^{0}\left(\frac{1}{6}{\it\kappa}_{nnn}^{0}n^{^{\prime }3}+\frac{1}{6}{\it\kappa}_{nTT}^{0}T^{^{\prime }3}+\frac{1}{2}{\it\kappa}_{nnT}^{0}n^{^{\prime }2}T^{\prime }+\frac{1}{2}{\it\kappa}_{nTT}^{0}n^{\prime }T^{^{\prime }2}\right)\nonumber\\ \displaystyle & & \displaystyle +\;\frac{\partial T^{\prime }}{\partial y}\left(\frac{1}{2}{\it\kappa}_{nny}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{nn}^{0}\frac{\partial n^{^{\prime }2}}{\partial y}+\frac{1}{2}{\it\kappa}_{TTy}^{0}T^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{TT}^{0}\frac{\partial T^{^{\prime }2}}{\partial y}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\;{\it\kappa}_{nTy}^{0}n^{\prime }T^{\prime }+{\it\kappa}_{nT}^{0}\frac{\partial n^{\prime }T^{\prime }}{\partial y}\right)+\frac{\partial ^{2}T^{\prime }}{\partial y^{2}}\left(\frac{1}{2}{\it\kappa}_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}{\it\kappa}_{TT}^{0}T^{^{\prime }2}+{\it\kappa}_{nT}^{0}n^{\prime }T^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle -\;\left(\frac{1}{2}p_{nn}^{0}n^{^{\prime }2}+\frac{1}{2}p_{TT}^{0}T^{^{\prime }2}+p_{nT}^{0}n^{\prime }T^{\prime }\right)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\;2({\it\mu}_{n}^{0}n^{\prime }+{\it\mu}_{T}^{0}T^{\prime })\left\{\!\left(\frac{\partial u^{\prime }}{\partial x}\right)^{2}+\left(\frac{\partial v^{\prime }}{\partial y}\right)^{2}+\frac{1}{2}\left(\frac{\partial u^{\prime }}{\partial y}+\frac{\partial v^{\prime }}{\partial x}\right)^{2}\!\right\}\nonumber\\ \displaystyle & & \displaystyle +\;\left({\it\lambda}_{n}^{0}n^{\prime }+{\it\lambda}_{T}^{0}T^{\prime }\right)(\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}^{\prime })^{2}\nonumber\\ \displaystyle & & \displaystyle \left.-\;\left(\frac{1}{6}\mathscr{D}_{nnn}^{0}n^{^{\prime }3}+\frac{1}{6}\mathscr{D}_{TTT}^{0}T^{^{\prime }3}+\frac{1}{2}\mathscr{D}_{nnT}^{0}n^{^{\prime }2}T^{\prime }+\frac{1}{2}\mathscr{D}_{nTT}^{0}n^{\prime }T^{^{\prime }2}\right)\right].\end{eqnarray}$$