1. Introduction
The nature of the incompressible flow past a two-dimensional symmetric bluff body changes with the Reynolds number, and ranges from a symmetric steady state to the chaotic and unsteady turbulent regime, depending on the relative importance of inertial and viscous forces. A complete description of the flow, therefore, includes the knowledge of the critical Reynolds numbers at which the flow changes regime, i.e. the Reynolds number corresponding to the first onset of the several instabilities the flow undergoes. For this type of flow, the Reynolds number usually employed is based on the body thickness 
$D$ and on the free-stream velocity 
$U_\infty$ as length and velocity scales, and is thus defined as 
$Re = U_\infty D / \nu$, where 
$\nu$ is the kinematic viscosity. These scales, however, can not always be best suited to describe the physics of the problem at hand, and alternative choices might be more appropriate to predict the onset of a new regime. Ideally, one would want the critical value of the associated Reynolds number to be the same for bodies with different cross-sectional shape, as long as the physics remains the same.
When the Reynolds number is large enough, the flow past a symmetric two-dimensional bluff body undergoes a first two-dimensional instability – known as primary instability – which usually corresponds to a Hopf bifurcation from the symmetric steady state towards a time-periodic non-symmetric state characterised by vortex shedding (Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987; Monkewitz, Huerre & Chomaz Reference Monkewitz, Huerre and Chomaz1993; Noack & Eckelmann Reference Noack and Eckelmann1994). While the instability mechanism is ostensibly the same for bodies of different shape, the critical Reynolds number 
$Re_c$ bears a significant dependence on the geometry and flow configuration. Several numerical studies and experiments found that, for a circular cylinder, the onset of the primary instability occurs at 
$Re=Re_c \approx 47$ (Williamson Reference Williamson1996; Giannetti & Luchini Reference Giannetti and Luchini2007; Marquet, Sipp & Jacquin Reference Marquet, Sipp and Jacquin2008). Jackson (Reference Jackson1987) studied the onset of the primary instability for ellipses, flat plates and triangles varying the aspect ratio 
${A{\kern-4pt}R} =L/D$, where 
$L$ and 
$D$ are the streamwise and maximum cross-stream dimensions of the bodies, and the incidence angle. He reported 
$Re_c \approx 27.7$ for a normal flat plate, 
$Re_c \approx 76.7$ for an ellipse parallel to the incoming flow with 
${A{\kern-4pt}R} =2$, and 
$Re_c \approx 36$ for an equilateral triangle oriented towards the flow. For all these geometries, a large increase of 
$Re_c$ with 
${A{\kern-4pt}R}$ was observed. Thompson et al. (Reference Thompson, Radi, Rao, Sheridan and Hourigan2014) studied the wake past elliptic cylinders ranging from a normal flat plate to the circular cylinder, finding a monotonic increase of 
$Re_c$, from 
$Re_c \approx 31.6$ to 
$Re_c \approx 47.2$. Park & Yang (Reference Park and Yang2016) determined how the primary instability is affected by rounding the four corners of a square cylinder, exploring shapes between the square cylinder with sharp edges and the circular cylinder. The onset of the primary instability was found to change non-monotonically with the corner curvature; the most stable configuration is intermediate between the circular and square cylinders and has 
$Re_c \approx 47.3$. More recently, we have studied the primary instability of the flow past rectangular cylinders by varying the aspect ratio in the range 
$0.25 \le {A{\kern-4pt}R} \le 30$, and by rounding the leading-edge and/or trailing-edge corners (Chiarini, Quadrio & Auteri Reference Chiarini, Quadrio and Auteri2021). Results indicated that 
$Re_c$ increases monotonically with 
${A{\kern-4pt}R}$ from 
$Re_c \approx 34.2$ to 
$Re_c \approx 140$; its dependence on the corner curvature is non-monotonic and changes with 
${A{\kern-4pt}R}$.
The large variability of 
$Re_c$ suggests that 
$D$ and 
$U_\infty$ might not be the most appropriate length and velocity scales to describe the primary Hopf bifurcation and to predict its onset. In fact, in Chiarini et al. (Reference Chiarini, Quadrio and Auteri2021) we have shown that the length of the separation bubble in the wake and the largest reverse-flow speed measured in it are more suitable scales, for rectangular cylinders: the former dictates the spatial extent of the absolute instability pocket (Chomaz Reference Chomaz2005), while the latter directly impacts the local amplification of the unstable wave packets (Hammond & Redekopp Reference Hammond and Redekopp1997). For rectangular cylinders, the associated Reynolds number evaluated at criticality was found to be (nearly) independent of the aspect ratio and its variation to be one order of magnitude lower than that of the conventional Reynolds number based on 
$D$ and 
$U_{\infty }$. After all, the body thickness 
$D$ is not always the proper length scale to describe the flow past bluff bodies also at larger Reynolds numbers. For example, Mat Ali, Doolan & Wheatley (Reference Mat Ali, Doolan and Wheatley2011) observed that the half-width wake thickness (Pope Reference Pope2000) is more appropriate for predicting the Strouhal number of the unsteady flow past a square cylinder with a splitter plate. In contrast, several authors observed that the cylinder length 
$L$ is the proper length scale for describing the periodic flow past elongated rectangular cylinders at intermediate Reynolds numbers (see for example Okajima Reference Okajima1982; Chiarini, Quadrio & Auteri Reference Chiarini, Quadrio and Auteri2022) and that the Strouhal number based on it has an almost stepwise dependence on 
${A{\kern-4pt}R}$ due to the interaction of the impinging-shear-layer instability with the trailing-edge vortex shedding (Hourigan, Thompson & Tan Reference Hourigan, Thompson and Tan2001).
In this work, we assess the generality of the scaling presented in Chiarini et al. (Reference Chiarini, Quadrio and Auteri2021) for the primary Hopf bifurcation, by considering four different geometries (triangle, rectangle, ellipse and diamond) that yield a steady base flow with different features due to the different placement of the corners (or lack thereof). For each geometry, the aspect ratio is varied in the range 
$1 \le {A{\kern-4pt}R} \le 8$. We also show that the new scaling works pretty well for small asymmetries of the flow and when other wake-related length scales are used, provided that they are a measure of the spatial extent of the separation bubble. The work is organised as follows. After this introduction, the numerical approach is described in § 2. The results are presented in § 3 and the validity of the proposed scaling is addressed in § 4. Finally, some concluding remarks are drawn is § 5.
2. Methods
The incompressible flow over two-dimensional cylinders of different cross-sectional shape with aspect ratio 
$1 \le {A{\kern-4pt}R} \le 8$ is considered. Figure 1 shows the geometries and the notation. A Cartesian coordinate system with origin placed at the leading edge of the cylinders is used, with the 
$x$ and 
$y$ axes denoting the streamwise and vertical directions, respectively. The cylinders have length 
$L$ and maximum thickness 
$D$ and are placed in a uniform flow with velocity 
$U_\infty$ with their symmetry axes aligned with the free-stream velocity. The computational domain extends for 
$-25 \le x/D \le 75$ and 
$-40 \le y/D \le 40$ in the two directions corresponding to 
$L_x=100D$ and 
$L_y=80D$; it has been shown (Chiarini et al. Reference Chiarini, Quadrio and Auteri2021) that these dimensions are adequate to investigate the onset of the primary instability of the flow past bluff bodies with aspect ratio up to 
${A{\kern-4pt}R} =30$. The Reynolds number is based on 
$U_\infty$ and 
$D$ and is thus defined as 
$Re=U_\infty D / \nu$.
Figure 1. Sketch of the computational domain with the geometry of the triangular, rectangular, elliptical and diamond cylinders.
To obtain the base flow, the two-dimensional version of the steady Navier–Stokes equations is solved using Newton's iterations. The spatial discretisation is based on a finite-element formulation using quadratic elements (
$P_2$) and linear elements (
$P_1$) for velocity and pressure, respectively. The numerical method has been implemented in the non-commercial software FreeFem++ (Hecht Reference Hecht2012) and has been previously used and validated (Chiarini et al. Reference Chiarini, Quadrio and Auteri2021). For each configuration, a computational mesh that is perfectly symmetric with respect to the 
$y=0$ axis is used, to avoid the introduction of spurious asymmetries in the flow. The number and distribution of the triangular elements has been chosen to properly refine the region around the cylinders, by paying specific attention to the near-corner regions and to the wake. The number of triangles varies between 
$60 \times 10^3$ and 
$90 \times 10^3$ depending on the body shape and aspect ratio.
The global stability analysis of the flow is carried out by solving the eigenvalue problem stemming from the Navier–Stokes equations linearised with respect to the steady base flow. The solution is obtained by the implicitly-restarted Arnoldi iterative algorithm implemented in the ARPACK package (Lehoucq, Sorensen & Yang Reference Lehoucq, Sorensen and Yang1998). When only one eigenvalue is required, a simple shift-invert method (Saad Reference Saad2011) is used.
3. Results
3.1. Base flow
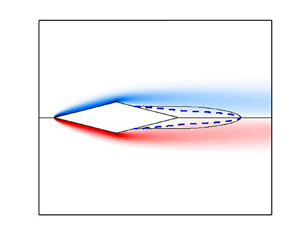
The steady base flow for the four geometries considered in this work is shown in figure 2 for 
${A{\kern-4pt}R} =4$ at a Reynolds number corresponding to the onset of the primary instability, i.e. 
$Re=68.8$, 
$Re=89.1$, 
$Re=140.1$ and 
$Re=151.1$ for the triangle, rectangle, ellipse and diamond, respectively. Being a pseudoscalar, the spatial distribution of the non-zero vorticity component 
$\omega _z=\partial V/\partial x - \partial U / \partial y$, where U and V are the x and y component of the baseflow velocity, respectively, is antisymmetric with respect to the 
$y=0$ axis, with the largest values observed in the fore part of the cylinders. Two shear layers displaying vorticity of opposite sign separate from the rear part of each cylinder, delimiting a symmetric separation bubble. For all cases, the vorticity is maximum at the leading edge; for triangles, rectangles and diamonds, the peak is localised near the sharp corners, while for ellipses, which lack corners, the peak is smeared. A second localised and weaker peak is observed near the sharp trailing-edge corners only for triangles and rectangles. In contrast, for ellipses and diamonds, the vorticity map features a wide region with large values extending from the leading-edge stagnation point to the point where the shear layers detach. For triangles, rectangles and diamonds, the point where the boundary layer separates is geometrically fixed at the trailing-edge, leading-edge and top/bottom corners, respectively. For ellipses, instead, the separation point changes with 
$Re$ and 
${A{\kern-4pt}R}$. On the other hand, for rectangles and triangles, the streamline delimiting the separation bubble originates at the trailing-edge corners at all 
${A{\kern-4pt}R}$, while for ellipses and diamonds, its origin depends on 
$Re$ and 
${A{\kern-4pt}R}$.
Figure 2. Base flow for the triangular (a), rectangular (b), elliptical (c) and diamond (d) cylinders for 
${A{\kern-4pt}R} =4$ at 
$Re=Re_c$. Streamlines are plotted on top of a vorticity map 
$\omega _z$, with the symmetric blue-to-red colourmap in the range 
$-10 \le \omega _z \le 10$. The blue dashed line is for 
$U=0$.
Figure 3 plots pressure maps. Unlike vorticity, pressure is symmetric with respect to the 
$y=0$ axis. For all geometries, the largest values are reached at the leading-edge stagnation point, as expected, while the lowest values are observed close to the point where the shear layers separate, i.e. after the trailing-edge corners for triangles, just after the leading-edge corners for rectangles, after the top/bottom corners for diamonds and upstream of the position of maximum thickness for ellipses. As expected, the positive peak of the pressure is more intense for the rectangular and elliptic cylinders as their leading edge is blunt. The pressure distribution over the cylinder largely depends on the cylinder geometry. For triangles, starting from the leading edge and moving downstream, the pressure progressively decreases and eventually reaches its minimum at the trailing-edge corners: the pressure gradient is favourable everywhere. For rectangles, instead, the longitudinal sides feature an adverse pressure gradient as the minimum of the pressure is placed just after the leading-edge corners. The ellipses and diamonds show a different distribution, with a favourable pressure gradient in the fore part of the cylinder followed by an adverse pressure gradient in the aft part.
Figure 3. As figure 2, but for the pressure field 
$P$. The blue-to-red symmetric colourmap is in the range 
$-0.5 \le P \le 0.5$.
3.2. Neutral curve
Figure 4(a) plots how the critical Reynolds number 
$Re_c$ of the primary instability, consisting in the Hopf bifurcation that produces the von Kármán wake for all cases, varies with 
${A{\kern-4pt}R}$ for the four shapes. For validation purpose, table 1 reports the results of our calculations for some geometries together with those from other references in literature and shows that they compare pretty well. The slight discrepancy for the triangular cylinder with respect to the critical values reported in literature may be probably ascribed to the different calculation methods adopted. For all cases, 
$Re_c$ increases with 
${A{\kern-4pt}R}$: an increase of the aspect ratio leads to stabilisation regardless of the cylinder geometry. Indeed, by increasing 
${A{\kern-4pt}R}$, the pockets of instability placed on the two sides of the separation bubble move downstream with respect to the point where the flow separates, so that the two shear layers that produce the instability become thicker in the instability region. This results in an increased diffusion of the shear layers and, therefore, in a weaker instability or, equivalently, in an increase of 
$Re_c$, as already observed by Chiarini et al. (Reference Chiarini, Quadrio and Auteri2021) for rectangles.
Figure 4. Dependence of 
$Re_c$ (a) and 
$\widehat {Re}_c=(U_{rev} \ell _r /\nu )|_c$ (b) on 
${A{\kern-4pt}R}$ and on the cylinder geometry.
Table 1. Comparison of 
$Re_c$ for some geometries with results from literature.
For triangles and rectangles, the function 
$Re_c({A{\kern-4pt}R} )$ increases with decreasing rate, reaching a value that is larger for the latter geometry, being 
$Re_c(8) \approx 90$ for triangles and 
$Re_c(8) \approx 120$ for rectangles. For triangles, the trend is accurately described by a power law. For triangles, this increasing trend is also related to the changes of the pressure distribution over the longitudinal sides. By plotting the pressure over a line just above or below the triangles, the favourable pressure gradient is seen to slightly decrease as 
${A{\kern-4pt}R}$ increases. This contributes to a weaker blockage, highlighted by the decrease of the maximum speed above/below the trailing-edge corners, and to less intense shear layers detaching from the trailing edge, therefore resulting in a weaker instability. On the other hand, for ellipses and diamonds, 
$Re_c$ increases faster than linearly with 
${A{\kern-4pt}R}$, with diamonds showing the fastest rate of change. Quantitatively, for ellipses and diamonds, 
$Re_c$ respectively increases from 
$Re_c \approx 46.5$ and 
$Re_c \approx 39.1$ for 
${A{\kern-4pt}R} =1$ to 
$Re_c \approx 310$ and 
$Re_c \approx 540$ for 
${A{\kern-4pt}R} = 8$. For ellipses, the curve seems to approach an oblique asymptote that instead is not observed for diamonds. For these geometries, as for triangles, the increase of 
$Re_c$ appears to be ascribed to a combination of the two effects discussed above, notwithstanding the variable position of the separation point. The superlinear growth observed for diamonds shows that the flow progressively approaches that past a flat plate as 
${A{\kern-4pt}R}$ increases, since the separation point moves downstream and the vertical size of the separation bubble decreases.
4. A new scaling
Chiarini et al. (Reference Chiarini, Quadrio and Auteri2021) observed that, for rectangular cylinders, the absolute value of the largest reverse-flow speed within the separation bubble (
$U_{rev}$) and the length (
$\ell _r$) of the bubble itself are the most important scales in the first Hopf bifurcation. They also verified that the associated Reynolds number 
$\widehat {Re}= U_{rev} \ell _r / \nu$ predicts fairly well the onset of the instability being nearly independent on 
${A{\kern-4pt}R}$. In this section, we show that this result is quite general and holds for two-dimensional cylinders of different shapes for which the primary instability corresponds to a Hopf bifurcation producing the von Kármán wake.
4.1. The reverse-flow speed
The largest reverse-flow speed 
$U_{rev}$ has a strong impact on the growth rate of the unstable mode (Hammond & Redekopp Reference Hammond and Redekopp1997). Figure 5(b) shows how this quantity changes with 
${A{\kern-4pt}R}$ at 
$Re=Re_c$. In all cases, 
$U_{rev}$ decreases to approach a horizontal asymptote for 
${A{\kern-4pt}R} \rightarrow \infty$, because the instability mechanism becomes less intense for increasing 
${A{\kern-4pt}R}$, consistently with the increase of 
$Re_c$ shown in figure 4(a). For small 
${A{\kern-4pt}R}$, 
$U_{rev}$ is maximum for triangles and minimum for rectangles: the opposite happens for 
$\ell _r$. Interestingly, the largest decrease of 
$|U_{rev}|$ for large 
${A{\kern-4pt}R}$ is observed for ellipses and diamonds: as 
${A{\kern-4pt}R}$ ranges from 
${A{\kern-4pt}R} =1$ to 
${A{\kern-4pt}R} =8$, 
$|U_{rev}|$ drops by 
$69\,\%$ and 
$74\,\%$ for diamonds and ellipses and by approximately 
$42\,\%$ and 
$53\,\%$ for rectangles and triangles. This is consistent with the largest increase of 
$Re_c$ observed for diamonds and ellipses in figure 4(a).
Figure 5. Effect of 
${A{\kern-4pt}R}$ on the length of the separation bubble 
$\ell _r$ (a) and on magnitude of the largest reverse-flow speed 
$U_{rev}$ (b).
The reverse-flow speed is relevant for two reasons: firstly, because the flow speed outside the recirculation bubble is approximately constant, increasing 
$U_{rev}$ increases the strength of the shear layer and therefore the amplification of the disturbances; secondly, increasing 
$U_{rev}$ increases the feedback due to recirculation – the stronger the feedback, the stronger the instability.
4.2. The length of the separation bubble
Figure 5(a) shows how the length of the separation bubble changes with 
${A{\kern-4pt}R}$ at 
$Re=Re_c$. The distance between the trailing edge of the cylinder and the stagnation point that closes the separation bubble, 
$\ell _r$, is found to generally decrease with 
${A{\kern-4pt}R}$. This decreasing trend is explained by the same phenomena responsible for the increase of 
$Re_c$, namely the increasing diffusion of the separated shear layers and the weakening pressure gradient over the longitudinal sides. For rectangles, 
$\ell _r$ is non-monotonic for small 
${A{\kern-4pt}R}$, due to the interaction of the shear layers separating from the leading-edge with the trailing-edge corners (Chiarini et al. Reference Chiarini, Quadrio and Auteri2021). For triangles, 
$\ell _r$ first decreases and reaches its minimum for 
${A{\kern-4pt}R} =5$ and then slightly increases again. This (small) increase of 
$\ell _r$ is due to the slight enlargement of the streamlines at the trailing-edge corners, where the shear layers separate, associated with the progressive increase of the boundary-layer thickness. For small 
${A{\kern-4pt}R}$, this effect is not appreciated, as the phenomena yielding the aforementioned decreasing trend dominate.
The size of the separation bubble is important in the onset of instability, since it is directly related to the size of the absolute instability region; the larger this region, the more unstable the flow.
4.3. The new scaling
Figure 4 plots the evolution of 
$\widehat {Re}_c=(U_{rev} \ell _r / \nu )|_c$ with 
${A{\kern-4pt}R}$, i.e. 
$\widehat {Re}$ evaluated at the onset of the primary instability, and compares it with changes of 
$Re_c$. For all geometries, the relative variation of 
$\widehat {Re}_c$ with 
${A{\kern-4pt}R}$ is much smaller than that of 
$Re_c$, and the values of 
$\widehat {Re}$ at criticality collapse quite neatly on an average value of 
$\widehat {Re}_c \approx 20$, the minimum value being 
$\widehat {Re}_c \approx 14$ for the diamond with 
${A{\kern-4pt}R} =8$ and the largest value being 
$\widehat {Re}_c \approx 35$ for the ellipse with 
${A{\kern-4pt}R} =1$. The collapse is not perfect, yet the relative variation is almost one order of magnitude less with the present scaling than with the standard form of the Reynolds number, whose minimum and maximum values are 
$Re_c \approx 39$ and 
$Re \approx 530$ for the diamond with 
${A{\kern-4pt}R} =1$ and 
${A{\kern-4pt}R} =8$, respectively. It is worth noting that the proposed scaling works quite well up to the highest 
${A{\kern-4pt}R}$ tested for all shapes. Indeed, the value of 
$\widehat {Re}_c$ seems to start deviating for the diamond cylinders at the largest 
${A{\kern-4pt}R}$ only. This is consistent with the fact that, as observed in § 3.2, in the diamond case as 
${A{\kern-4pt}R}$ increases the base flow approaches that past a flat plate that displays an instability of a different nature, for which this scaling does not work.
The newly defined 
$\widehat {Re}$, based on the magnitude of the largest reverse-flow speed 
$U_{rev}$ and on the length of the separation bubble 
$\ell _r$, is far more capable than that based on the free-stream velocity 
$U_\infty$ and cylinder thickness 
$D$ to predict the onset of the primary instability for the steady flow past symmetric two-dimensional bluff bodies. The implied scaling is not trivial, since 
$\ell _r$ and 
$U_{rev}$ depend on 
${A{\kern-4pt}R}$ quite differently for the considered geometries. It allows one to determine if the flow is linearly unstable to two-dimensional perturbations with rather good accuracy by just evaluating 
$U_{rev}$ and 
$\ell _r$ and examining whether 
$\widehat {Re}$ is larger or lower than 
$\widehat {Re}_c \approx 20$. Computing 
$\widehat {Re}$ only requires the knowledge of the base flow, whose computational cost is much smaller than that of a linear stability analysis.
4.4. Other wake-related length scales
In this section, we show that the new scaling works well when other wake-related length scales are used instead of 
$\ell _r$, provided that they are a measure of the spatial extent of the separation bubble. We keep considering 
$U_{rev}$ as the velocity scale and, following the idea that this instability is promoted by the base-flow shear layer along the dividing streamline of the body, we consider four different length scales that are a measure of the width of the separation bubble. The new length scales are the width of both the dividing streamline (
$d_{r,1}$) and the 
$U=0$ line (
$d_{r,2}$) at the streamwise position corresponding to the location of 
$U_{rev}$, and the vertical distance between the maxima of the two structural sensitivity pockets (
$d_{r,3}$) (Giannetti & Luchini Reference Giannetti and Luchini2007). Based on these length scales, we define the following Reynolds numbers:
\begin{equation} \widehat{Re}_c^{d,1}= \frac{U_{rev} d_{r,1}}{\nu}, \quad \widehat{Re}_c^{d,2}= \frac{U_{rev} d_{r,2}}{\nu}, \quad \text{and} \quad \widehat{Re}_c^{d,3}= \frac{U_{rev} d_{r,3}}{\nu}. \end{equation} Figure 6 shows that at criticality all the new proposed Reynolds numbers collapse pretty well for all the aspect ratios and the geometries considered. For all cases, the maximum variation from the average value is within 
$75\,\%$, that is, by far smaller than the maximum variation of 
$Re_c$ that is 
${\approx }290\,\%$. This is expected as all these length scales are a good measure of the spatial extent of the separation bubble, as witnessed by their dependence on both 
${A{\kern-4pt}R}$ and the body shape that is qualitatively the same to that shown for 
$\ell _r$ in figure 5. Among the different proposed Reynolds numbers, those based on the width of the dividing streamline (
$d_{r,1}$) and of the reverse-flow region (
$d_{r,2}$) show the best collapse, and their maximum relative variation is within 
$40\,\%$.
4.5. Flow asymmetry
Figure 7 deals with the robustness of the proposed scaling on asymmetries of the flow. For all the four geometries, we have fixed the aspect ratio to 
${A{\kern-4pt}R} =5$ and repeated the calculations by changing the incidence angle in the range 
$0\,^\circ \le \alpha \le 8^\circ$. For all geometries but for the triangle, an increase of 
$\alpha$ leads to a monotonic decrease of 
$Re_c$ that goes from 
$Re_c=98.8,183.3,207.0$ for 
$\alpha =0^\circ$ to 
$Re_c=50.6,115.1,167.1$ for 
$\alpha =8^\circ$ for the rectangular, elliptical and diamond cylinders, respectively. For the triangular cylinder, instead, 
$Re_c$ only marginally changes in the considered range of incidence angles, as observed by Jackson (Reference Jackson1987) for the 
${A{\kern-4pt}R} =1$ case. Figure 7(b) shows that the proposed scaling is robust to moderate asymmetries of the flow. Indeed, in this range of 
$\alpha$, the variation of 
$\widehat {Re}_c$ is much smaller than that of 
$Re_c$ and its values collapse quite well for all the body shapes: the average value is 
$\widehat {Re}_c=19.48$, while the minimum and maximum values are 
$\widehat {Re}_c=17.32$ and 
$\widehat {Re}_c=28.69$ for the triangle at 
$\alpha =1^\circ$ and the diamond at 
$\alpha =8^\circ$, respectively.
Figure 7. Dependence of 
$Re_c$ (a) and 
$\widehat {Re}_c=(U_{rev} \ell _r /\nu )|_c$ (b) on the incidence angle 
$\alpha$ and on the cylinder geometry for aspect ratio 
${A{\kern-4pt}R} =5$.
5. Conclusion
Depending on the Reynolds number, the incompressible flow past symmetric two-dimensional bluff bodies ranges from a symmetric steady state to the turbulent regime. For this class of flows, 
$Re$ is usually defined with the cross-stream size of the body 
$D$ and the free-stream velocity 
$U_\infty$ as 
$Re=U_{\infty }D / \nu$. When 
$Re$ is large enough, i.e. 
$Re>Re_c$, the flow undergoes a first two-dimensional instability, the primary instability, usually corresponding to a Hopf bifurcation leading to a time-periodic flow with vortex shedding. Although the physical mechanism behind the primary Hopf instability remains the same, the numerical value of 
$Re_c$ strongly varies when the cross-section and the aspect ratio of the body are varied (Jackson Reference Jackson1987). In this work, an alternative scaling has been proposed for the prediction of the primary Hopf instability, where the length of the separation bubble 
$\ell _r$ and the largest reverse-flow speed within it are the length and velocity scales, respectively. The appropriateness of these scales descends from their direct link to the local amplification of the unstable wave packets, and to the extension of the absolute instability region (Hammond & Redekopp Reference Hammond and Redekopp1997; Chomaz Reference Chomaz2005). At criticality, the associated Reynolds number 
$\widehat {Re}=U_{rev} \ell _r / \nu$ has been shown to collapse quite nicely across geometries and aspect ratios: its relative variation is one order of magnitude smaller than that of the conventional 
$Re_c$. Hence, this scaling, although still not ideal, is far more appropriate for predicting the onset of the primary instability than that based on 
$D$ and 
$U_\infty$. Moreover, we have shown that this scaling is robust to small asymmetries of the flow and that it works well even if other wake-related length scales are used, provided that they are a measure of the spatial extent of the separation bubble.
This observation has a significant theoretical value, inasmuch as it sheds new light on the instability mechanism leading to the von Kármán vortex street. Moreover, there is practical value in the ability to readily estimate whether the two-dimensional steady flow past a bluff body is absolutely unstable to two-dimensional perturbations by avoiding a computationally expensive stability analysis.
Funding
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Declaration of interests
The authors report no conflict of interest.
