3.1. Scalar dissipation rate

The scalar dissipation rate can be used to examine the rate of molecular mixing and is also the key parameter in many models for turbulent non-premixed combustion. Some experimental and theoretical studies have shown that if the scalar dissipation is close to the ignition or extinction limits, dissipation effects can play an important role in determining the stabilisation location (Peters & Williams Reference Peters and Williams1983; Namazian et al. Reference Namazian, Schefer and Kelly1988; Müller et al. Reference Müller, Breitbach and Peters1994; Pitsch & Fedotov Reference Pitsch and Fedotov2000). The non-dimensional scalar dissipation rate is defined as

3.2. Normalised flame index

The flame index (FI) representing the degree of mixedness was proposed by Yamashita, Shimada & Takeno (Reference Yamashita, Shimada and Takeno1996) to distinguish premixed from non-premixed flames. They defined the FI as a cosine of oxidiser and fuel gradient,

Domingo, Vervisch & Bray (Reference Domingo, Vervisch and Bray2002), Bray, Domingo & Vervisch (Reference Bray, Domingo and Vervisch2005), Domingo, Vervisch & Réveillon (Reference Domingo, Vervisch and Réveillon2005) and Knudsen & Pitsch (Reference Knudsen and Pitsch2012) have used a normalised flame index (NFI), defined as

In areas that are burning (i.e. having a non-negligible reaction rate), the NFI can be used to determine the combustion mode. When the fuel and oxidiser gradients are aligned, this term is positive and indicates the presence of a premixed flame, while when these gradients are not aligned, the NFI will be negative, indicating the presence of a non-premixed flame.

To verify that the NFI can distinguish between premixed and non-premixed burning in this spatially developing flame, a steady laminar triple-flame case was run with the same chemistry parameters as the 3D DNS. Figure 7(a) shows the reaction rate of the product in the resulting triple-flame structure, with isolines of product mass fraction and mixture fraction overlaid for reference, while figure 7(b) shows the local NFI overlaid with the same isolines. It may be noted that the NFI successfully captures the leading premixed flame, which in this example has both lean and rich branches, and the trailing diffusion flame.

Figure 7. For a steady laminar triple flame with the same chemistry parameters as the DNS: (a) the reaction rate of the product in a laminar triple flame and (b) the NFI. In both plots, dashed curved lines show product mass-fraction isolines of 0.05, 0.1 and 0.2 while the solid lines show the stoichiometric mixture fraction and the mixture fraction $Z_{ms}$ 0.07.

3.3. Edge-flame identification and velocity

As stated in the introduction, one of the main objectives here is to analyse the edge-flame velocity. To achieve this, we first need to identify the flame base. Different approaches have been used for this purpose. In experimental studies of hydrocarbon flames, commencement of chemiluminescence of $\text{CH}^{\ast }$ (Su et al. Reference Su, Sun and Mungal2006), CH PLIF (Watson et al. Reference Watson, Lyons, Donbar and Carter2000; Hult et al. Reference Hult, Meier, Meier, Harvey and Kaminski2005; Noda et al. Reference Noda, Mori, Hongo and Nishioka2005; Lyons et al. Reference Lyons, Watson, Carter and Donbar2007) or OH PLIF (Boxx et al. Reference Boxx, Heeger, Gordon, Böhm, Aigner, Dreizler and Meier2009a ,Reference Boxx, Heeger, Gordon, Böhm, Dreizler and Meier b ; Gordon et al. Reference Gordon, Boxx, Carter, Dreizler and Meier2012) has frequently been used as the flame-base marker. The excited $\text{CH}^{\ast }$ radical is short-lived and thought to mark the instantaneous reaction zone (Su et al. Reference Su, Sun and Mungal2006). These locations coincide with high heat release rate.

In DNS of premixed flames, the high-heat-release region is often marked by a critical value of a reacting scalar (Echekki & Chen Reference Echekki and Chen1998; Im & Chen Reference Im and Chen1999; Tanahashi, Fujimura & Miyauchi Reference Tanahashi, Fujimura and Miyauchi2000; Im & Chen Reference Im and Chen2001; Chakraborty & Cant Reference Chakraborty and Cant2004; Hawkes & Chen Reference Hawkes and Chen2004, Reference Hawkes and Chen2006; Chen et al. Reference Chen, Hawkes, Sankaran, Mason and Im2006; Sankaran et al. Reference Sankaran, Hawkes, Chen, Lu and Law2006; Hawkes et al. Reference Hawkes, Sankaran, Sutherland and Chen2007c ). In our case, a more involved approach is needed since we wish to separate the edges from the region downstream. Following earlier studies of extinction and reignition (Pantano Reference Pantano2004; Hawkes, Sankaran & Chen Reference Hawkes, Sankaran and Chen2007a ,Reference Hawkes, Sankaran and Chen b ), we therefore select an edge-flame marker that is the intersection of a mixture-fraction isosurface and a product mass-fraction isosurface.

To select the mixture-fraction isovalue, it was first assumed that the leading edge would be found at the mixture fraction having the highest laminar flame speed, $Z_{ms}$ , which is slightly rich of stoichiometric (0.07 in this study, i.e.  $1.2Z_{st}$ ). To select the product mass-fraction isosurface, a 1D simulation of a laminar premixed flame having the same flame parameters as the turbulent lifted flame was performed. The product mass fraction corresponding to the location of the maximum heat release rate was obtained from this simulation. The obtained value of $Y_{p}$ was 0.2. To provide an example, these choices of mixture-fraction and product mass-fraction isosurfaces are marked on for the steady laminar triple flame shown in figure 7(a). It may be observed that the chosen parameters mark the peak reaction point at the leading edge of the flame quite well. Furthermore, a sensitivity study of the key results of these choices is presented in appendix B.

To extract the intersecting contour, the isosurface of the mixture fraction was triangulated with a parallel implementation of the marching-cubes algorithm. The edges of the resulting triangles were then searched for intersections with the product mass-fraction isosurface, and the intersection location was linearly estimated based on the vertex values of the product mass fraction. Quantities were then linearly interpolated to the intersection locations. It was verified that the mixture fraction and product mass fraction interpolated to the edge flames returned the expected values to typically within 1 %. The resulting edge-flame regions from the turbulent flame DNS were then extensively visualised and compared with locations of high heat release. It was found that the leading edge flame as identified visually from the reaction rate always remained very close to the intersection of the two isosurfaces.

Flame edges defined in this way can move by three mechanisms: flow, motion relative to the flow of the product mass-fraction isosurface and motion relative to the flow of the mixture-fraction isosurface. Although the velocity tangential to the flame edge could be arbitrarily specified, we take it to be equal to the flow velocity, following previous works on flame surface evolution (Pope Reference Pope1988) and on the tracking of extinction holes (Pantano Reference Pantano2004).

To determine the edge motion, we first need a coordinate system, which we take to be moving with the flow velocity. Referring to figure 8, we define a tangent vector to the mixture-fraction isosurfaces which points along the flame edge. The vector $\boldsymbol{T}_{1}$ is normal to both the normal to the mixture-fraction isosurface $\boldsymbol{N}_{Z}$ (pointing towards the oxidiser) and to the normal to the product mass-fraction isosurface $\boldsymbol{N}_{Y_{p}}$ (pointing towards the reactants). Next, we define another vector $\boldsymbol{T}_{2}$ which is also tangential to the mixture-fraction isosurface but normal to $\boldsymbol{T}_{1}$ , and pointing towards the reactants. It is readily shown that these quantities are given by

Figure 8. The various normal and tangential vectors at the flame base: (a) schematic and (b) examples (the red–yellow surfaces are the product mass-fraction isosurfaces, the blue surfaces are the mixture-fraction isosurfaces and the solid black line is the identified edge flame).

Figure 9 now shows a schematic, in the plane containing both $\boldsymbol{N}_{Z}$ and $\boldsymbol{N}_{Y_{p}}$ , of the edge-flame motion during an infinitesimal interval of time ${\it\delta}t$ . Because the chosen coordinate system moves with the local flow velocity, only the motion of the isosurfaces relative to the flow need be considered. During this time interval, the mixture-fraction isosurface is displaced by $S_{Z}\boldsymbol{N}_{Z}{\it\delta}t$ , while the $Y_{p}=Y_{p}^{\ast }$ isosurface is displaced by $S_{d}\boldsymbol{N}_{Y_{p}}{\it\delta}t$ , where the displacement speeds are given by (Gibson, Ashurst & Kerstein Reference Gibson, Ashurst and Kerstein1988; Pope Reference Pope1988; Echekki & Chen Reference Echekki and Chen1998)

where ${\it\mu}$ is the dynamic viscosity. We denote the overall displacement of the edge point $\boldsymbol{V}_{e}{\it\delta}t$ and break this down into the orthonormal coordinates $\boldsymbol{N}_{Z}$ and $\boldsymbol{T}_{2}$ as

where $S_{e}=\boldsymbol{V}_{e}\boldsymbol{\cdot }\boldsymbol{T}_{2}$ is the projection of $\boldsymbol{V}_{e}$ into the plane of the mixture-fraction isosurface and needs to be determined. Dividing by ${\it\delta}t$ , and taking the dot product of (3.9) with $\boldsymbol{N}_{Y_{p}}$ , it can be shown (noting that $\boldsymbol{V}_{e}\boldsymbol{\cdot }\boldsymbol{N}_{Y_{p}}=S_{d}$ and using (3.8)) that

where $k$ is the inner product of the normal vectors $\boldsymbol{N}_{Y_{p}}\boldsymbol{\cdot }\boldsymbol{N}_{Z}$ .

Figure 9. Schematic of edge-flame propagation along the mixture-fraction isosurface: (a) instantaneous vectors and indicative flame edge; (b) propagation of the edge point over an infinitesimal time interval ${\it\delta}t$ .

Although the presentation here is slightly different, we have verified that the final result is the same edge speed as used first by Pantano (Reference Pantano2004) to study extinction holes and later by Hawkes et al. (Reference Hawkes, Sankaran and Chen2007a ,Reference Hawkes, Sankaran and Chen b ) to study extinction and reignition, and also by Chakraborty & Mastorakos (Reference Chakraborty and Mastorakos2008) to study ignitions.

3.4. Out-of-plane motion

Many experimental investigations of lifted flames have used laser-based planar measurements (for example Wohl, Kapp & Gazley Reference Wohl, Kapp and Gazley1949; Vanquickenborne & van Tiggelen Reference Vanquickenborne and van Tiggelen1966; Kalghatgi Reference Kalghatgi1984; Namazian et al. Reference Namazian, Schefer and Kelly1988; Miake-Lye & Hammer Reference Miake-Lye and Hammer1989; Pitts Reference Pitts1989; Takahashi & Schmoll Reference Takahashi and Schmoll1991; Schefer et al. Reference Schefer, Namazian, Filtopoulos and Kelly1994a ,Reference Schefer, Namazian and Kelly b ; Muniz & Mungal Reference Muniz and Mungal1997; Schefer Reference Schefer1997a ,Reference Schefer b ; Hasselbrink & Mungal Reference Hasselbrink and Mungal1998; Kelman, Eltobaji & Masri Reference Kelman, Eltobaji and Masri1998; Schefer & Goix Reference Schefer and Goix1998; Tacke et al. Reference Tacke, Geyer, Hassel and Janicka1998; Takahashi, John Schmoll & Katta Reference Takahashi, John Schmoll and Katta1998; Brown, Watson & Lyons Reference Brown, Watson and Lyons1999; Watson et al. Reference Watson, Lyons, Donbar and Carter1999, Reference Watson, Lyons, Donbar and Carter2000, Reference Watson, Lyons, Carter and Donbar2002, Reference Watson, Lyons, Donbar and Carter2003; Han & Mungal Reference Han and Mungal2000; Maurey et al. Reference Maurey, Cessou, Lecordier and Stepowski2000; Baillot & Demare Reference Baillot and Demare2002; Mansour Reference Mansour2003, Reference Mansour2004; Noda et al. Reference Noda, Mori, Hongo and Nishioka2005), and therefore there have been numerous questions raised about out-of-plane motion and its potential role in flame stabilisation. Out-of-plane motion of the flame is the consequence of two effects: flow motion and flame propagation. The out-of-plane flow velocity has recently become accessible in cinema PIV experiments (e.g. Lyons et al. Reference Lyons, Watson, Carter and Donbar2007; Boxx et al. Reference Boxx, Heeger, Gordon, Böhm, Aigner, Dreizler and Meier2009a ,Reference Boxx, Heeger, Gordon, Böhm, Dreizler and Meier b ; Gordon et al. Reference Gordon, Boxx, Carter, Dreizler and Meier2012; Boxx, Meier & Carter Reference Boxx, Meier and Carter2014). The flame propagation component in the out-of-plane direction is, however, not available experimentally, and while out-of-plane flow can be measured, the flame orientation is unknown in the out-of-plane direction such that its effect is unknown. However, when DNS is used the three-dimensional (3D) flow field and the flame propagation are simultaneously available for such an analysis.

Consider an infinitesimally small flame-edge segment $\text{d}s(t)$ which is moving in the out-of-plane (spanwise, $z$ ) direction in a time ${\it\delta}t$ to its new location $\text{d}s(t+{\it\delta}t)$ . Over this period the point $P(t)$ intersecting the $x{-}y$ observation plane moves to location $P(t+{\it\delta}t)$ causing an apparent in-plane motion unless the flame edge happens to be oriented normal to the $x{-}y$ plane. (It also moves in the $x{-}y$ plane due to flow and propagation in that plane, but here we adopt a coordinate system that follows that motion in order to simplify the discussion.) Figure 10 shows a schematic of this concept. It is readily observed that the observed flow speed (or flame propagation speed) in the plane is obtained by projecting the $z$ component of the flow velocity (or relative flame propagation velocity) into the $\boldsymbol{T}_{1}$ direction, then projecting the result into the $x{-}y$ plane. We denote the apparent flow velocity by $(\boldsymbol{U}_{z})_{x}$ and the apparent flame propagation by $(V_{e,z})_{x}$ (in the $x$ direction here). It is readily shown that these velocities are given by

and

Figure 10. Schematic of the displacement of the edge in the transverse and streamwise directions caused by out-of-plane motion.

4.1. General flame structure

A volume rendering of the logarithm of the scalar dissipation rate normalised by the laminar flame time scale (blue/white) and reaction rate (red/orange) is presented in figure 11. Before reading further, the interested reader may consult an animation of the vorticity magnitude (blue/white) and reaction rate (red/orange) which is presented in the online supplementary movie to this paper available at http://dx.doi.org/10.1017/jfm.2015.334. This animation is quite instructive to gain an overall picture of the flame.

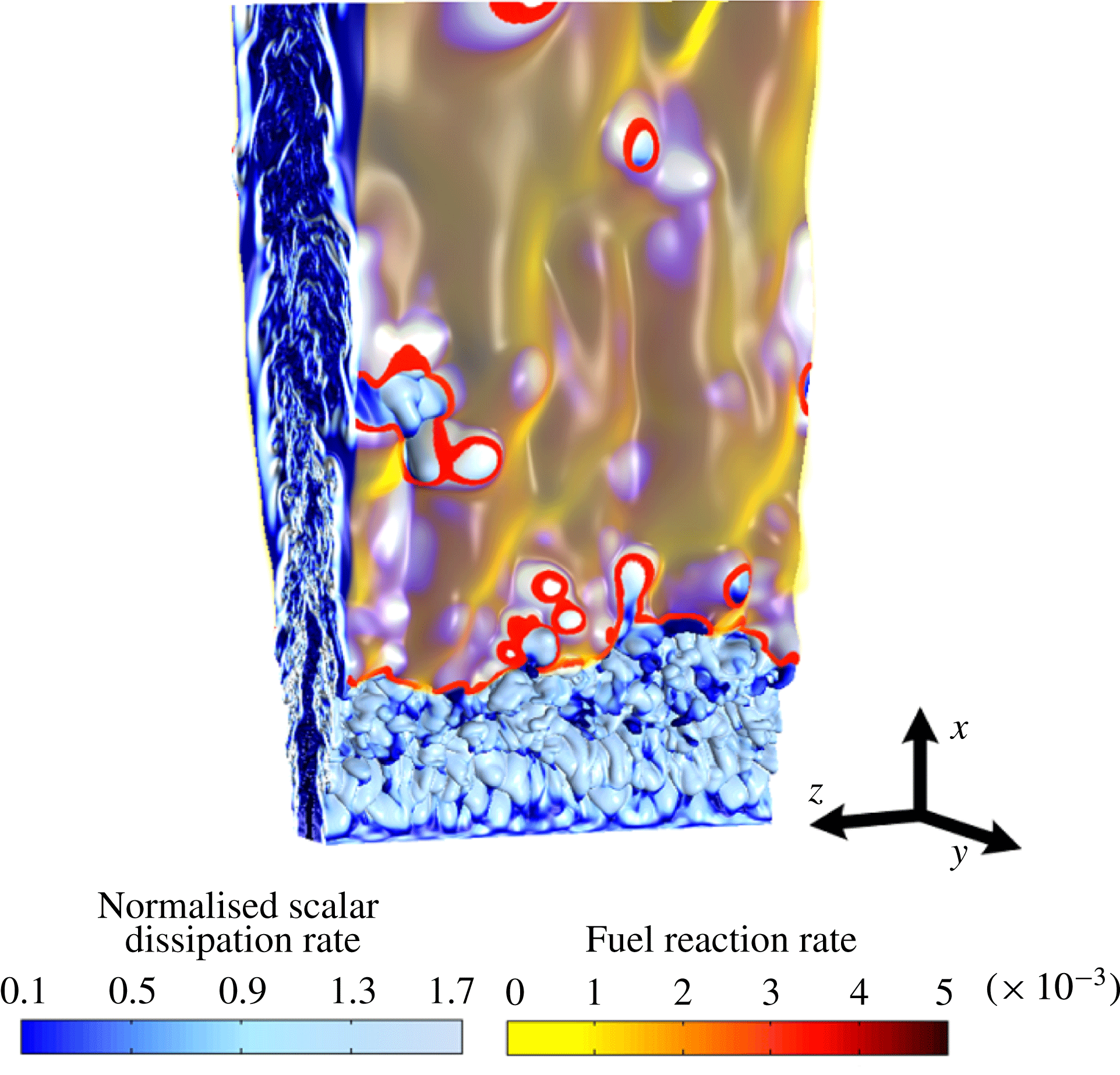
Figure 11. Three-dimensional volume rendering of the logarithm of the scalar dissipation rate (blue/white) and reaction rate (red/orange). (Only the region $x<14$ is shown.) Rendering generated by Dr Hongfeng Yu, using techniques described in Yu, Wang & Ma (Reference Yu, Wang and Ma2008); see also Akiba et al. (Reference Akiba, Ma, Chen and Hawkes2007).

It may be observed in figure 11 that the flame has a complex structure which has features that are qualitatively similar to experimental observations of lifted flames (Schefer et al. Reference Schefer, Namazian and Kelly1994b ; Schefer Reference Schefer1997a ; Schefer & Goix Reference Schefer and Goix1998; Han & Mungal Reference Han and Mungal2000; Watson et al. Reference Watson, Lyons, Donbar and Carter2000; Hult et al. Reference Hult, Meier, Meier, Harvey and Kaminski2005; Joedicke et al. Reference Joedicke, Peters and Mansour2005; Boxx et al. Reference Boxx, Heeger, Gordon, Böhm, Aigner, Dreizler and Meier2009a ,Reference Boxx, Heeger, Gordon, Böhm, Dreizler and Meier b ). Because the stoichiometric mixture fraction is small (0.055), the flame is found at the edge of the highly turbulent inner core of the jet. Heat release noticeably damps turbulence in the outer region.

Unlike the DNS of lifted hydrogen flames reported by Mizobuchi et al. (Reference Mizobuchi, Tachibana, Shinio, Ogawa and Takeno2002, Reference Mizobuchi, Shinio, Ogawa and Takeno2005), we do not observe a vigorous rich premixed flame core. We believe that this difference is because hydrogen burns much more vigorously than hydrocarbons in rich mixtures. The mixture-fraction dependence of the burning velocity is built into the present model by the mixture-fraction-dependent activation energy. Similarly, we also did not observe any diffusion flame islands on the lean side that were observed by Mizobuchi et al. (Reference Mizobuchi, Tachibana, Shinio, Ogawa and Takeno2002, Reference Mizobuchi, Shinio, Ogawa and Takeno2005). The ‘islands’ noted by Mizobuchi et al. were regions of high hydrogen consumption rate which had a negative NFI, suggesting diffusion flame burning. Once again this might have been a hydrogen-specific feature since much of the hydrogen fuel was being consumed in the rich premixed branch, leaving little to be consumed in the diffusion flame. The authors note, however, that another reason for the observed differences is the larger lifted height observed in the Mizobuchi cases, which allowed a wider flammable region to form upstream of the lifted flame location. It is also possible, though considered unlikely by the authors, that the specific one-step mechanism adopted here can explain the differences between the two studies.

To further elaborate this essential difference between hydrocarbon and hydrogen lifted flames, figure 12 shows an isosurface of product reaction rate coloured by the NFI. It may be readily observed that the leading edges are premixed, followed by a trailing diffusion flame, which is mostly connected. Notably, there is not an extensive inner region of premixed flames, unlike in the case of hydrogen (Mizobuchi et al. Reference Mizobuchi, Tachibana, Shinio, Ogawa and Takeno2002, Reference Mizobuchi, Shinio, Ogawa and Takeno2005). Flame holes can be observed as the regions downstream of the leading edge, where high values of the NFI indicate a locally premixed edge. (Other holes are observed without being surrounded by premixed edges, but these are still diffusion flames, which just have a lower reaction rate than the chosen threshold.)

Figure 12. The reaction rate isosurface of fuel, $|\dot{{\it\omega}}_{F}|=0.001$ , coloured by the NFI.

Returning to the discussion of figure 11, the leading flame edges at the base of the flame are highly convoluted. Consistent with many experimental observations of lifted flames (Schefer et al. Reference Schefer, Namazian and Kelly1994b ; Schefer Reference Schefer1997a ; Schefer & Goix Reference Schefer and Goix1998; Han & Mungal Reference Han and Mungal2000; Watson et al. Reference Watson, Lyons, Donbar and Carter2000; Hult et al. Reference Hult, Meier, Meier, Harvey and Kaminski2005; Joedicke et al. Reference Joedicke, Peters and Mansour2005; Boxx et al. Reference Boxx, Heeger, Gordon, Böhm, Aigner, Dreizler and Meier2009a ,Reference Boxx, Heeger, Gordon, Böhm, Dreizler and Meier b ), the leading edges do not typically exhibit a tribrachial structure. This lack of three distinct branches has been previously explained to result from mixture-fraction gradients ahead of the flame being too large to support distinct lean and rich branches (Stårner et al. Reference Stårner, Bilger, Frank, Marran and Long1996). Occasionally, when the flame was found in a low-strain-rate region, we did observe a short or weak rich premixed branch, but a distinct lean branch was never observed.

The reaction rate is locally higher at the flame edges than further downstream, which is consistent with the existence of a premixed leading edge flame. It is also noted that in the present case, the premixed flame edges are quite narrow and of the order of the laminar flame thickness, which implies that the premixed edge flames are quite unlike a flat turbulent premixed flame with lateral dimensions much larger than the laminar flame thickness; i.e. at this lifted height, the premixed flame theory of stabilisation is ruled out, a fact that has already been noted by others, e.g. see the discussion in Lawn (Reference Lawn2009). In the authors’ interpretation of the premixed flame theory, as opposed to the edge-flame theory, the leading premixed flame has a lateral width that is significantly larger than the laminar flame thickness. In contrast, in the authors’ interpretation, the traditional edge-flame concept is only applicable if the lateral width is the order of at most a few laminar flame thicknesses.

There is a proliferation of flame holes, not observed in earlier DNS studies of lifted flames (Mizobuchi et al. Reference Mizobuchi, Tachibana, Shinio, Ogawa and Takeno2002, Reference Mizobuchi, Shinio, Ogawa and Takeno2005; Yoo et al. Reference Yoo, Sankaran and Chen2009, Reference Yoo, Richardson, Sankaran and Chen2011). In the case of Mizobuchi et al. (Reference Mizobuchi, Tachibana, Shinio, Ogawa and Takeno2002, Reference Mizobuchi, Shinio, Ogawa and Takeno2005), conversely to our situation, isolated burning islands in a mostly non-burning stoichiometric surface were observed rather than holes in a mostly connected burning surface. As will be presented in more detail shortly, these holes originate by two different mechanisms. Some of the holes are generated by flame propagation at the leading edge while others are caused by local flame extinction. Both kinds of holes can either grow or shrink and disappear as they go downstream. They can also merge with other holes and/or split into multiple holes. The existence of extinction holes suggests that in this flame (which has a relatively low lifted height) the critical scalar dissipation rate can be locally exceeded, which suggests that extinction can moderate the stabilisation process (Lyons et al. Reference Lyons, Watson, Carter and Donbar2007).

We do not, however, observe any unconnected regions of high reaction rate ahead of the leading edge. All regions ahead of the leading edge are connected, even though in a 2D streamwise–transverse plane they may appear as unconnected flame elements. (Although one still image cannot show this, the supplementary animations certainly do.) Nor do we observe any transport of hot products or even large-scale folding of the flame into upstream unburned regions. The lack of any unconnected regions or large-scale folding of the flame to upstream unburned regions therefore rules out, for the present flame, a stabilisation mechanism supported only by upstream turbulent transport. In an early theory, Broadwell et al. (Reference Broadwell, Dahm and Mungal1985) proposed that lateral ejection of hot products and later re-entrainment into the jet could support stabilisation of the flame at a given location, but nonetheless it seems to the present authors that some upstream transport mechanism would be needed in this theory to balance the oncoming flow once the flame is re-entrained into the high-streamwise-velocity region, and thus the present results seem to rule out this early theory.

The stabilisation mechanism is evidently far from being laminar in its overall structure. The large degree of convolution of the flame edge implies that it can consume stoichiometric reactants at a much greater rate than in a laminar flame (which would present a single straight line here), similar to how increased surface area causes the turbulent burning velocity to be larger than the laminar one in premixed flames. (It should be noted that, similar to a turbulent premixed flame, the existence of locally laminar structures is, however, not ruled out.) Another way of thinking about this in a planar picture of the flame is that out-of-plane motion can lead to additional upstream transport, i.e. that flames can propagate laterally around high-velocity regions in large eddies eventually leading to additional upstream propagation. Later in the article we will show that this mechanism is very significant in some regions of the flame.

It may be observed that the leading edge structure qualitatively seems to be convoluted on the scale of large eddies. The role of large eddies can also be qualitatively observed in the animation in the supplementary material. Later in the article we will present evidence that large eddies definitely do play a role in the stabilisation.

4.2. Scalar dissipation and hole formation

As mentioned earlier, some of the observed holes in the reaction sheet are a consequence of local extinctions which occur when high-scalar-dissipation-rate structures, with scalar dissipation rate comparable to the quenching limit, occur near the mixture-fraction isosurface. The scalar dissipation is a key parameter in many modelling frameworks, and some stabilisation theories have been developed on the critical scalar dissipation concept (Peters & Williams Reference Peters and Williams1983; Müller et al. Reference Müller, Breitbach and Peters1994). To assess this theory and the qualitative observations in figure 11, instantaneous scatter plots of conditional normalised scalar dissipation rate on the mixture-fraction isosurface with the maximum laminar flame speed coloured by the product mass fraction at $t_{j}=11.55$ are presented in figure 13(a).

Figure 13. (a) Scatter plot of the logarithm of the scalar dissipation rate conditioned on the mixture-fraction isosurface $Z=0.07$ versus the distance from the nozzle and coloured by the product mass fraction for $t_{j}=11.55$ . (b) Scatter plot of the product mass fraction versus the logarithm of the scalar dissipation for $6.5<x<7.5$ .

There are a couple of interesting features to be noted in this figure. Both the scalar dissipation rate and its fluctuations are high upstream of the flame base. The high value of the logarithm of the normalised scalar dissipation rate ( $\log _{10}({\it\chi}{\it\delta}_{L}/S_{L})$ ) is more than unity, and as expected it decays in the streamwise direction. It is noticeably lower in the burning regions of the flame starting at approximately $x/H\approx 3$ (as indicated by high product mass fractions) than in the upstream non-burning regions (as indicated by low product mass fractions). It may be noted that the highest dissipation rate regions correspond to the locations of holes (indicated by regions downstream of the lifted height but having a low product mass fraction). Connections between the scalar dissipation rate and local extinctions have been noted in several other DNS studies, e.g. Pantano (Reference Pantano2004), Hawkes et al. (Reference Hawkes, Sankaran and Chen2007b ) and Karami et al. (Reference Karami, Talei, Hawkes and Chatakonda2013), and in other models that can resolve such effects, e.g. Sen, Hawkes & Menon (Reference Sen, Hawkes and Menon2010) and Punati et al. (Reference Punati, Sutherland, Kerstein, Hawkes and Chen2011). This is confirmed in figure 13(b), which shows the product mass fraction on the same isosurface versus the scalar dissipation, conditioned on the locations $6.5<x<7.5$ . Some regions of lower dissipation rate are also noted in holes. These are probably in holes that are reigniting, but also may be holes that are formed by another mechanism which is discussed below.

The structure of the observed holes is now identified and discussed in more detail using 3D visualisations. Figure 14 shows the same variables as figure 11 during the formation and reignition of an extinction hole. As shown in figure 14, the hole is formed in a region of high scalar dissipation rate which bulges out towards the oxidiser side. This appears to be connected with the passage of a large eddy. The hole is revealed to be significantly curved in the out-of-plane direction such that the high-scalar-dissipation region and thus the extinction hole has approximately similar streamwise and spanwise extents. As the large eddy passes, the scalar dissipation rate relaxes and the hole reignites.

Figure 14. Three-dimensional view of the creation and shrinking of an extinction hole. The same variables as in figure 11 are shown.

Figure 15. Three-dimensional time sequence of hole creation, showing the same variables as in figure 11.

The formation of a different type of hole is examined in figure 15. It is observed that initially there is a local downstream motion of the flame around a large eddy. This causes a horseshoe-like edge-flame structure to arise. In the subsequent frames the flame comes together in the upstream region, finally reconnecting to form a flame hole, which is termed here as an ‘inclusion hole’. If observed in a 2D $x{-}y$ plane, this would be seen as the appearance of an upstream island. The convergence of the flames on either side towards the reconnection point implies that flame propagation, and not simply out-of-plane advection, must be involved in the appearance of the upstream island in this case. Thus, the present work demonstrates two distinct mechanisms of hole formation, and a connection of the appearance of some upstream islands (as observed in a plane) with the formation of an inclusion hole. Importantly, both of these mechanisms generate mixture-fraction conditional fluctuations of temperature and species, which may be important to represent from a modelling perspective. In planar experimental measurements it is impossible to definitely determine which mechanism causes the observed holes, because holes can be created by out-of-plane motion of reacting regions into the plane or by out-of-plane motion of non-reacting regions into the plane. However, a very recent study by Boxx et al. (Reference Boxx, Meier and Carter2014) used a combination of OH PLIF and line-of-sight OH* chemiluminescence to suggest that there can be very significant out-of-plane flame-edge wrinkling, such that apparently observed in-plane holes are actually not holes but are connected to the main leading edge of the flame, which is consistent with our observations in this DNS.

4.3. Time evolution of the flame base

To demonstrate some key features of the motion of flame edges, and to relate these features to previously observed experimental measurements in 2D planes, this section considers observations of the edge-flame motion at an arbitrarily selected plane at $z=0$ . Where it results in significant effects, out-of-plane motion of the flame is also considered.

A time series of the most upstream flame-edge location is presented in figure 16 at the $z=0$ plane. The flame edge was identified as the intersection of mixture-fraction and product mass-fraction isosurfaces as discussed in § 3.3, and when more than one such location appeared in a plane, the most upstream was selected. The mean stabilisation point is $3.2H$ in the streamwise direction. Fluctuations of the order of the jet width can occur in the streamwise direction. The mean transverse location is $-1.2H$ . The maximum level of fluctuations is less than $0.5H$ in the transverse direction.

Figure 16. Temporal evolution of (a) the streamwise location and (b) the transverse location at the most upstream flame edge on the plane $z=0$ .

Several different events involving upstream and downstream motion are noted in figure 16. At times there is smooth downstream ( $P_{1},P_{3}$ ) and upstream ( $P_{2}$ ) motion, but also at times there are sudden jumps in the lifted height ( $P_{5}$ ). According to the literature, the upstream jumps are expected to be related to out-of-plane motion (Lyons et al. Reference Lyons, Watson, Carter and Donbar2007; Boxx et al. Reference Boxx, Heeger, Gordon, Böhm, Aigner, Dreizler and Meier2009a ,Reference Boxx, Heeger, Gordon, Böhm, Dreizler and Meier b ; Gordon et al. Reference Gordon, Boxx, Carter, Dreizler and Meier2012) or conceivably to the appearance of isolated islands (Broadwell et al. Reference Broadwell, Dahm and Mungal1985; Mizobuchi et al. Reference Mizobuchi, Tachibana, Shinio, Ogawa and Takeno2002, Reference Mizobuchi, Shinio, Ogawa and Takeno2005). Sudden downstream motions of the flame base are also observed. Examples of different flame motion scenarios marked in figure 16 are now discussed in more detail, whereas the probability of their occurrence is discussed in a later section of the paper.

Figure 17. Time evolution of the flame base in the plane $z=0$ during the time period $P_{1}$ , exhibiting smooth downstream motion when the apparent streamwise velocity and streamwise component of the edge velocity are positive. (a) The reaction rate on a colour scale, with vorticity contours in blue and red solid lines marking the flammability limits (laminar flame speed less than 5 % of maximum 1D laminar flame speed). (b) The logarithm of the scalar dissipation rate. (c) The apparent flow and propagation velocity vector components. In all panels the black solid line marks the product mass fraction of 0.2 while the dashed line is the mixture fraction of 0.07.

Figure 17 presents, for the time period $P_{1}$ , (a) contours of the reaction rate and vorticity magnitude, (b) contours of the logarithm of the normalised scalar dissipation rate and (c) the streamwise and transverse vector components of the apparent flow and edge-flame propagation velocities at the flame-base location. The black solid line represents the product mass fraction of 0.2 and the dashed line corresponds to the mixture fraction of 0.07, which has the maximum laminar flame speed. (Recall that the intersection of these isosurfaces defines the ‘flame edge’. It may be noted that they do indeed provide a good marker in the forthcoming figures.) The two red solid lines in figure 17(a) indicate the flammability limits. The lower and upper flammability limits of methane are ${\it\phi}=0.46$ and 1.64 respectively (Dahoe & De Goey Reference Dahoe and De Goey2003). These limits correspond to the laminar flame speed being less than approximately 5 % of the maximum laminar flame speed. The time sequences are presented from left to right. The fuel and oxidiser are on the left- and right-hand sides respectively. As can be seen, at times $t_{j}=11.49$ and 11.55 large eddies squeeze the flammable region (figure 17(a), marked as $A_{P1}$ ). This results in a comet-shaped flame front as marked by $B_{P1}$ in figure 17(a). As shown in figure 17(b), the scalar dissipation rate is also high at the flame base (marked as $C_{P1}$ ). In this case, the dissipation rate is high enough to cause a positive apparent propagation velocity, i.e. a negative relative flame speed, noting that the flame normal is pointing towards the negative streamwise direction. In the next two time sequences, $t_{j}=11.64$ and 11.70, there is no large structure in the vicinity of the flame base and the scalar dissipation begins to relax, leading to less negative relative flame speeds by $t_{j}=11.76$ . As a result, the flame speed becomes positive again and approximately balances the flow (figure 17 c).

Figure 17(c) also presents the apparent transverse propagation and flow velocities by orange and dark blue horizontal vectors respectively. It shows that the flame propagates relative to the flow towards the region of leaner mixtures and is dominant over the entrainment flow directing the flame towards the region of richer mixtures. It is noted that at times $t_{j}=11.70$ and 11.76 (as can be seen in figure 17 a) a small and weak reaction zone appears upstream of the flame base which is caused by out-of-plane motion. This effect will be analysed in more detail later in this section.

During the time period $P_{2}$ , a case of upstream propagation is presented in figure 18. Once again, the same parameters as in figure 17 are shown. As shown in figure 18(a), at time $t_{j}=15.63$ the flammable region is wide, approximately twice as wide as the laminar flame thickness. There are no large eddies containing vortical fluid around the flame base to disturb the propagation process. The absence of such structures also allows the existence of a rich premixed wing. The scalar dissipation rate is low in a large region upstream of the flame base. All of these conditions are favourable for flame propagation, and as a result the upstream propagation speed of the flame is strong, as shown in figure 18(c). Due to the subsequent passage of a large eddy, the thickness of the flammable region decreases and the scalar dissipation rate increases, which leads to the upstream propagation speed decreasing. At approximately $t_{j}=15.87$ the dissipation rate relaxes and the upstream flame propagation speed increases again.

Figure 18. Time evolution of the flame base on the plane $z=0$ for a case involving a smooth upstream propagation during period $P_{2}$ . (a) The reaction rate on a colour scale, with vorticity contours in blue and the red solid lines marking the flammability limits. (b) The logarithm of the scalar dissipation rate. (c) The apparent flow and propagation velocity vector components. In all panels the black solid line marks the product mass fraction of 0.2 while the dashed line is the mixture fraction of 0.07.

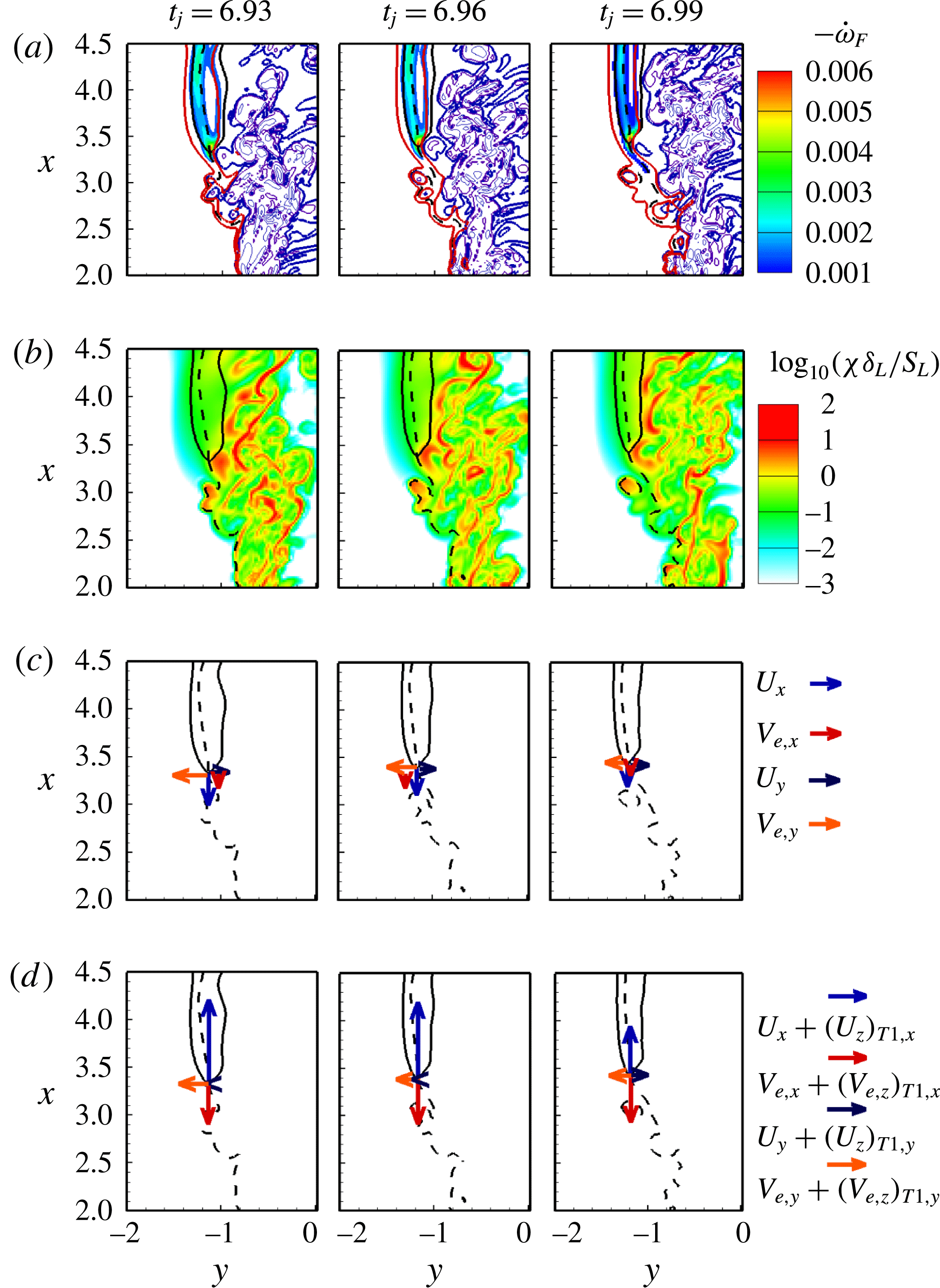
Figure 19. Time evolution of the flame base at the plane $z=0$ for a case of smooth downstream motion during time period $P_{3}$ when the apparent streamwise velocity and streamwise component of the edge velocity are negative. (a) The reaction rate on a colour scale, with the contours of vorticity magnitude in blue and the red solid lines marking the flammability limits. (b) The logarithm of the scalar dissipation rate. (c) The streamwise and transverse flow and edge propagation velocity vector components. (d) The apparent flow and propagation velocity vector components. In all panels the black solid line marks the product mass fraction of 0.2 while the dashed line is the mixture fraction of 0.07.

Figure 20. Temporal snapshots during the event $P_{4}$ involving the appearance of a hook shape. (a) Contours of the reaction rate on a colour scale, with vorticity contours in blue. (b) Contours of the logarithm of scalar dissipation. (c) Flow and flame propagation velocity vector components. In all panels the black solid line marks the product mass fraction of 0.2 while the dashed line is the mixture fraction of 0.07.

The time period $P_{3}$ shown in figure 16 is considered now. Figure 19(a,b) presents the same variables as previously shown in figure 17(a,b). Figure 19(c) shows the in-plane flow and edge-flame propagation velocities and figure 19(d) shows the apparent flow and flame propagation velocities with the out-of-plane component included. In contrast to the previous downstream motion shown in figure 17, this case features a much wider flammable region (with a weak rich premixed branch being evident) and a lower scalar dissipation rate, and as a result the flame speed is positive, which according to the in-plane picture would lead to an upstream propagation, since the flow velocity is also in the upstream direction. However, when the out-of-plane components are added in, the picture is rather different. While the upstream flame propagation is stronger with the inclusion of the out-of-plane propagation, inclusion of the $z$ component of the flow velocity results in an even larger downstream apparent velocity, thus demonstrating that out-of-plane motion definitely needs to be considered in the overall picture.

Before moving on, it is remarked that we also observed nearly every other combination of different components (flow/flame and in-plane/out-of-plane) being dominant. The above cases were selected only to provide some examples, and should not be interpreted as the statistically most significant situations. The statistically averaged picture is discussed later in the article.

Figure 20 shows an example that involves a large transverse velocity resulting in the creation of a hook structure (time period $P_{4}$ in figure 16). The variables shown are once again the same as in figure 17. At $t_{j}=14.94$ the flame initially has a fairly unconvoluted structure which is propagating towards the fuel side. At the second time instant shown a large turbulent eddy bulges out towards the oxidiser side, which may be observed at the point marked ‘ $A_{P4}$ ’, where the high-vorticity region impinges onto the flame from the oxidiser side. At the same time, a large entrainment flow is occurring at the base. The coupling of the bulging turbulent eddy and the entraining flow causes an anticlockwise rotation of the flame and distorts it into a ‘hook’ structure. Such hook structures have been observed frequently in experimental measurements of lifted flames (for instance figure 7 in Kelman et al. (Reference Kelman, Eltobaji and Masri1998), figure 3(a) in Schefer et al. (Reference Schefer, Namazian and Kelly1994b ), figures 3(f) and 4(a) in Watson et al. (Reference Watson, Lyons, Donbar and Carter2000), figure 4 in Upatnieks, Driscoll & Ceccio (Reference Upatnieks, Driscoll and Ceccio2002), figure 5 in Boxx et al. (Reference Boxx, Heeger, Gordon, Böhm, Aigner, Dreizler and Meier2009a ), figure 4 in Boxx et al. (Reference Boxx, Heeger, Gordon, Böhm, Dreizler and Meier2009b ) and figure 3 in Gordon et al. (Reference Gordon, Boxx, Carter, Dreizler and Meier2012)) and are confirmed by the present DNS. The role played by large eddies in the creation of these structures supports the schematic of Kelman et al. (Reference Kelman, Eltobaji and Masri1998), and is consistent with experimental measurements by Upatnieks et al. (Reference Upatnieks, Driscoll and Ceccio2002, Reference Upatnieks, Driscoll, Rasmussen and Ceccio2004) and Boxx et al. (Reference Boxx, Heeger, Gordon, Böhm, Aigner, Dreizler and Meier2009a ,Reference Boxx, Heeger, Gordon, Böhm, Dreizler and Meier b ). In the example shown here, the large eddy is even strong enough to cause an extinction hole above the leading edge location.

These upstream and downstream motions of the edge flame at the $z=0$ plane suggest that the edge flames might go through a cyclic motion. Therefore, the trajectories of the edge flames for the time periods when no island is observed in the $z=0$ plane will reveal this. Three different examples of cyclic motions are presented in figure 21. However, as this analysis is limited to the $z=0$ plane, excluding the out-of-plane jumps, more investigation on the overall behaviour of the flame base is needed. This will be discussed in more detail in the forthcoming sections.

Figure 21. Instantaneous trajectory of the flame base at the plane $z=0.0$ .

The appearance of flame islands upstream of the main flame has been observed in many experimental studies of lifted flames (Upatnieks et al. Reference Upatnieks, Driscoll and Ceccio2002; Lyons et al. Reference Lyons, Watson, Carter and Donbar2007; Boxx et al. Reference Boxx, Heeger, Gordon, Böhm, Aigner, Dreizler and Meier2009a ,Reference Boxx, Heeger, Gordon, Böhm, Dreizler and Meier b , Reference Boxx, Meier and Carter2014; Gordon et al. Reference Gordon, Boxx, Carter, Dreizler and Meier2012). The laser-based diagnostic techniques used in these studies rely on measurements in 2D sheets. To analyse the effect of the out-of-plane motion on flame stabilisation, access to both the out-of-plane flow and the flame propagation velocities is necessary, which has not yet been demonstrated experimentally. However, DNS provides the full 3D data, which allows for a detailed examination of the out-of-plane flame motion. In this section, an example of the appearance of a flame island near the flame base is presented. The effects of flow and flame propagation are also investigated.

Figure 22 shows the contour plots of the out-of-plane (spanwise) flow velocity. At $t_{j}=14.13$ a small island appears in a region where the out-of-plane velocity is positive. This island (marked as $A_{P5}$ ) grows rapidly, as can be seen in the next time, $t_{j}=14.28$ and 14.31. At $t_{j}=14.34$ the island disappears. The appearance of islands in the observation plane has been reported in many experimental studies of lifted flames (Upatnieks et al. Reference Upatnieks, Driscoll and Ceccio2002; Lyons et al. Reference Lyons, Watson, Carter and Donbar2007; Boxx et al. Reference Boxx, Heeger, Gordon, Böhm, Aigner, Dreizler and Meier2009a ,Reference Boxx, Heeger, Gordon, Böhm, Dreizler and Meier b , Reference Boxx, Meier and Carter2014; Gordon et al. Reference Gordon, Boxx, Carter, Dreizler and Meier2012); however, the inaccessible third dimension in the experiments has limited investigations of the physical reasons for the observed islands. It has been suggested that islands can result from either propagation or convective motion of the flame edge from the negative $z$ direction. To examine this hypothesis, the $x{-}z$ plane view of the flame base is presented in figure 23. Shown here, the flame base is a continuous structure and there is no disconnected pocket of product or reaction zone upstream of the flame base. Instead, the island is observed in the $x{-}y$ plane due to contortion and motion of the edge. (We also reiterate at this point that we never observed any disconnected upstream islands in the 3D animations of this case.) In figure 23, the flame base is also coloured by (a) spanwise velocity and (b) spanwise edge base propagation. At $t_{j}=14.13$ , while the out-of-plane velocity is positive, the out-of-plane propagation exceeds the flow and is in the opposite direction, leading to the flame island actually appearing from the opposite side as suggested by the flow alone. Eventually, the out-of-plane flow reverses and both components promote growth of the island in the $x{-}y$ plane. We also observed cases of the opposite scenario, and cases when the flow and flame velocities were aligned and not aligned. However, overall, the results certainly suggest that flame propagation in the out-of-plane direction cannot be ignored. Planned future work will quantify in an averaged sense the role of out-of-plane flow and flame propagation on the appearance of upstream islands, as well as quantifying other out-of-plane effects in an effort to better understand the existing very substantial body of experimental work based on in-plane measurements.

Figure 22. Time evolution of the flame base at plane $z=0.0$ with a sudden upstream jump in the lifted height: (a) out-of-plane flow velocity and (b) scalar dissipation rate (the black solid line in all panels marks a product mass fraction of 0.2 and the dashed line marks a mixture fraction of 0.07).

Figure 23. The $x{-}z$ plane view of the out-of-plane motion of the flame base corresponding to the appearance of an island in figure 22 with the flame base coloured by (a) spanwise and (b) edge-flame velocity.

4.4. Statistics of the flame base

This section now seeks to address quantitatively the dynamics of the flame-base region (conditional on $x/H<4.5$ ) and the turbulent flow/flame-edge interaction by studying the flow and flame velocities conditional on the instantaneous edge-flame locations. The reader is reminded that the flame base is a 3D convoluted line, i.e. all $z$ planes are considered, and that the procedure for extracting this convoluted line from the 3D data and mapping different quantities onto it was discussed in § 3.3.

Figures 24(a) and 24(b) present the probability density functions (PDFs) of the streamwise and transverse locations of the instantaneous edge-flame locations, whereas figure 24(c) shows the joint PDF of the streamwise and transverse location of the edge-flame locations. The solid black line in figure 24(c) is the temporally and spatially Favre-averaged mixture fraction, equal to 0.07 (which as explained earlier has the maximum laminar flame speed). The time-averaged location of the flame base is $3.2H$ and $1.2H$ in streamwise and transverse directions respectively, while the most likely stabilisation location is found at $x=2.8$ and $y=1.1$ . The PDFs of the streamwise and transverse locations of the flame base (figure 24 a,b) show a wide distribution of the PDFs around the time-averaged values, which is caused by the turbulence–flame interaction at the leading edge. Figure 24(c) shows that the flame base moves on the periphery of the jet with a higher probability of being located close to the averaged mixture fraction corresponding to the maximum laminar flame speed, $Z_{ms}=0.07$ . The same observation was reported in previous experimental studies (Muniz & Mungal Reference Muniz and Mungal1997; Hasselbrink & Mungal Reference Hasselbrink and Mungal1998; Joedicke et al. Reference Joedicke, Peters and Mansour2005).

Figure 24. Locations of the flame. (a) The PDF of the streamwise location of the instantaneous edge-flame locations. (b) The PDF of the transverse location of instantaneous edge-flame locations. (c) The joint PDF of the streamwise and transverse locations. The solid line is the temporal and spatial Favre-averaged mixture fraction, equal to 0.07, and the dashed lines are the temporal and spatial Favre-averaged mixture fractions corresponding to the flammability limits.

It is noted that the present finding differs from some experimental studies which determined that the average of the most upstream high-temperature location (the leading point) is found in on-average lean regions, e.g. Mansour (Reference Mansour2003, Reference Mansour2004) and Chung (Reference Chung2007). A possible reason for the differences between these experiments and the other group of experimental results (Kelman et al. Reference Kelman, Eltobaji and Masri1998; Upatnieks et al. Reference Upatnieks, Driscoll and Ceccio2002; Joedicke et al. Reference Joedicke, Peters and Mansour2005; Su et al. Reference Su, Sun and Mungal2006) supporting our DNS is that the true flame stabilisation location corresponding to the beginning of large reaction rates may lie radially inside and downstream of the most upstream high-temperature region. For the present DNS featuring a low lifted height, the flammable region is quite narrow, as shown in figure 24(c), such that differences between the location of the leading point and the stabilisation location (as judged by reaction rates) are insignificant and burning always occurs close to the on-average stoichiometric contour. In contrast, at larger lifted heights, such as those reported in Su et al. (Reference Su, Sun and Mungal2006), the region of flammable mixture fractions is larger and thus the leading point can potentially be different from the true flame stabilisation location.

The joint PDF of the flame-base location represents a similar shape to the scatter plots of the flame-base location presented by the experimental lifted slot-jet flames studied in Boxx et al. (Reference Boxx, Meier and Carter2014), even though the present conditions are somewhat different, having a much lower coflow velocity and a lower density ratio between the fuel and oxidiser jets.

Figure 25(a,b) presents the joint PDF of streamwise and transverse locations of the flame base on the right and left sides of the slot jet. A correlation may be expected if large Kelvin–Helmholtz structures exist at the flame base; however, these structures have been broken down into small eddies around $2H$ upstream of the flame base; as such, no correlation exists between these parameters.

Figure 25. The joint PDFs of (a) the transverse locations and (b) the streamwise locations of the edge flames on the right and left sides of the slot jet.

The velocity statistics are now examined. Figure 26 shows in (a–c) the PDFs of the streamwise, transverse and spanwise velocities conditioned on the instantaneous edge-flame locations, in (d–f) the joint PDFs of the streamwise, transverse and spanwise velocities conditioned on the streamwise location of the flame base and in (g–i) the joint PDFs of the streamwise, transverse and spanwise velocities conditioned on the transverse location of the flame base. All velocities are normalised by the laminar flame speed of a flat premixed flame.

Figure 26. Flow velocities conditioned on instantaneous flame-edge locations. (a–c) The PDFs of the different components. (d–f) The joint PDFs of the flow velocity components and the streamwise location of the edge-flame locations, and the mean velocities conditional on the streamwise location. (g–i) The joint PDFs of the flow velocity components and transverse locations and velocity means conditional on the transverse location.

We first discuss the PDFs considering the ensemble over all flame-edge locations having $x<4.5$ , shown in figure 26(a–c). The streamwise flow velocity has a mean of $2.5S_{L}$ with fluctuations from $-12S_{L}$ to $20S_{L}$ . Before discussing some comparisons of the present results with experimental observations, it is important to caveat these comparisons in that the locations at which we observe the velocities are within the inner reaction layer of the flame (since this is where a flame displacement speed can be sensibly evaluated) while the experimental measurements are often taken at a location where very small low-boiling-point droplets evaporate (for example Su et al. (Reference Su, Sun and Mungal2006) seeded coflow with glycerol/water fog droplets and Yuen & Gülder (Reference Yuen and Gülder2013) used submicron oil as seeding particles), which is likely to be slightly further upstream. Alternatively, where a flame marker based on OH or CH PLIF has been employed, the velocity measurements are deliberately offset towards the upstream locations (Hasselbrink & Mungal Reference Hasselbrink and Mungal1998; Upatnieks et al. Reference Upatnieks, Driscoll and Ceccio2002, Reference Upatnieks, Driscoll, Rasmussen and Ceccio2004; Gordon et al. Reference Gordon, Boxx, Carter, Dreizler and Meier2012). Proceeding with this caveat in mind, experimental observations of a $\text{CH}_{4}$ lifted flame by Muniz & Mungal (Reference Muniz and Mungal1997) showed that the mean streamwise flow velocity conditioned on flame-base locations for different flow conditions ranges from 2.1 to $2.4S_{L}$ , which is close to our observation for the mean velocity. Similarly low mean streamwise velocity conditioned on flame-base locations was also reported in other experimental studies of $\text{CH}_{4}$ lifted flames (Hasselbrink & Mungal Reference Hasselbrink and Mungal1998; Upatnieks et al. Reference Upatnieks, Driscoll and Ceccio2002, Reference Upatnieks, Driscoll, Rasmussen and Ceccio2004; Su et al. Reference Su, Sun and Mungal2006).

The most probable streamwise velocity is very close to zero, but the PDF is positively skewed, thus resulting in a positive mean velocity. These observations are very consistent with experimental observations at low lifted heights discussed in Su et al. (Reference Su, Sun and Mungal2006). Interestingly, there is a significant probability, 34 %, of observing negative streamwise velocity, suggesting a local deceleration, an observation also noted in Upatnieks et al. (Reference Upatnieks, Driscoll and Ceccio2002, Reference Upatnieks, Driscoll, Rasmussen and Ceccio2004) and Su et al. (Reference Su, Sun and Mungal2006). At this point, the reader is reminded that the statistics are conditioned on a particular mixture-fraction isosurface. While it is well known that the mean streamwise velocity and mean mixture fraction are connected in jet flows, the present results show that even once conditioned on mixture fraction, fluctuations of velocity are still significant, and, importantly, locally upstream velocities can be observed, a point that will be revisited later in more depth.

Turning now to the transverse velocity, it is noted that the mean of the transverse velocity is $-5S_{L}$ , with just 10 % possibility of being positive. The statistics of the transverse velocity therefore demonstrate a strong role of the entrainment at this lifted height. Experimental measurements of radial velocities support a role for entrainment in lifted flames (Han & Mungal Reference Han and Mungal2000). The PDF is also slightly negatively skewed.

Finally, the spanwise velocity has a nearly Gaussian distribution with zero mean, as expected in a homogeneous direction.

Figure 27. Absolute flame velocity components conditioned on the edge-flame locations (including both flow and flame propagation velocities). (a–c) The PDFs of the components. (d–f) Contour plots of the joint PDFs of the net velocity components and streamwise location of the flame edge and the streamwise conditional mean net velocities. (g–i) The joint PDFs of the net velocity components and transverse location and corresponding conditional means.

Moving on to the statistics conditioned on the streamwise distance shown in figure 26(d–f), it is observed that the conditional mean of the streamwise velocity is positive and of the order of a few $S_{L}$ , and weakly decays with downstream distance. The fluctuations are significant and decay more significantly than the mean with downstream distance. The entrainment flow in the transverse direction generally decays with downstream distance, as expected, and its fluctuations also decay strongly. While the mean spanwise velocity remains zero, its fluctuations are large at lower streamwise stations, suggesting that it can still play a role in the stabilisation mechanism.

Considering the dependence of the velocities on the transverse distance in figure 26(g–i), the picture becomes more complicated. The flame-edge-conditioned streamwise velocity is very high towards the centre of the jet, greatly exceeding $S_{L}$ , suggesting that the flame must move downstream in that region. However, on observing the trend for the transverse velocity, a confusing feature is observed. There is an overall positive correlation of the transverse velocity with the transverse position, such that the highest negative streamwise velocities tend to occur on average when $y$ is smallest. As such, it is unclear from this picture how the flame can escape from regions of low $y$ where, on average, streamwise velocities would then push the flame downstream and transverse velocities push it further inwards.

The effect of flame propagation is now factored in. Figure 27(a–c) shows the PDFs of the absolute velocities (flow plus relative propagation) in the streamwise, transverse and spanwise directions respectively. Considering first the streamwise component in figure 27(a), it is noted that compared with the previous PDF of the flow velocity in figure 26(a), the mean is now nearly zero, due to reduced probabilities of high positive velocities (downstream motion) and increased probabilities of negative velocities (upstream motion). The positive skewness is also visibly reduced. Compared with the PDF of the transverse flow velocity in figure 26(b), the net transverse velocity shown in 27(b) is shifted towards positive values such that the mean and most likely values are close to zero. The spanwise net velocity component is unremarkably different from that of the flow velocity, except that it exhibits similar fluctuation levels relative to the other velocity components.

We now turn to the means and PDFs conditional on streamwise distance shown in figure 27(d–f). Before discussing the more interesting streamwise and transverse components, we simply note that the spanwise net velocity component is not remarkable other than by having fluctuations that are significant relative to the other components, similar to the situation with the flow velocity only.

Here, figure 27(d) shows that the streamwise flow velocity on average balances the streamwise upstream flame propagation in the most probable regions of flame stabilisation. This demonstrates that the flame is stabilised by edge-flame propagation, which is a major result of the paper. It may be noted that there is some lack of balance in the downstream regions starting from approximately $x\approx 3.5$ . This is probably connected with flame holes which are move further downstream before they are annihilated. Another point to be noted in figure 27(d) is that the net velocity fluctuations are somewhat smaller than the flow velocity fluctuations in figure 26(d), suggesting that the flame speed tends to be negatively correlated with the flow speed.

Moving on to the transverse net velocity conditional on streamwise distance shown in figure 27(e), it is noted that while the conditional mean of the flow velocity plus flame propagation velocity is smaller than it was for the flow velocity alone, it still does not balance in the upstream region, where on average the flame is entrained into the jet core.

Similarly, while the streamwise net velocity conditioned on transverse distance shown in figure 27(g) has a greatly reduced conditional mean, which is close to zero at larger $y$ values, it is still positive towards the core of the jet. Finally, the transverse net velocity conditioned on transverse distance shown in figure 27(h) still cannot explain how on average the flame edges escape from the inner core of the jet, since the average velocity is negative there. Interestingly, the average propagation velocity is also now somewhat positive for large $y$ locations, suggesting outwards on average movement at large $y$ , which seems paradoxical.

To explain these apparently counterintuitive results, we now present the 2D picture. To better understand the dynamic motion of the flame base, the flame-base velocities are doubly conditioned on streamwise and transverse locations of the instantaneous edge-flame locations. Figure 28 presents (a) the streamwise velocity, (b) the transverse velocity, (c) the streamwise edge propagation velocity and (d) the transverse edge propagation velocity conditionally averaged on the streamwise and transverse instantaneous location of the flame base. The notation $\langle \cdots |(x,y)\rangle$ represents the averaged quantity doubly conditional on streamwise and transverse locations of the edge flames.

Figure 28. The following quantities, conditionally averaged on both streamwise and transverse locations of the instantaneous flame base: (a) streamwise flow velocity, (b) transverse flow velocity, (c) the streamwise edge propagation velocity, (d) the transverse edge propagation velocity, (e) the net streamwise velocity and (f) the net transverse velocity (the solid line is the temporally and spatially Favre-averaged mixture fraction, equal to 0.07).

The picture that now emerges is much clearer. In what follows, we will show that the flame tends, on average, to move sequentially around its mean location in a clockwise manner. First, considering the mean streamwise velocity in figure 28(a), it tends towards being upstream movement on the lean side and downstream on the rich side. We remark that here when we discuss the rich/lean side at this point in the article we mean the on-average rich/lean side, but note that by construction the edge flames are always located on a particular mixture-fraction isosurface. In the transverse velocity, shown in figure 28(b), there is a tendency towards a strong entraining flow at low streamwise locations and a much smaller transverse (but still negative) flow at larger $x$ values.

Flame propagation velocities also play key roles. The streamwise flame propagation velocity, shown in figure 28(c), tends mostly to counteract the streamwise flow, being generally positive on the lean side (i.e. the local flame speed is negative, leading to downstream relative motion, suggesting an influence of high scalar dissipation values in some locations) and generally large and negative on the rich side (i.e. leading to upstream relative motion). The transverse flame propagation velocity, shown in figure 28(d), similarly seems to counteract the flow velocity in very rich mixtures and towards lower lifted heights. However, it does seem to play a key role towards longer lifted heights, as it causes the flame to propagate outwards despite the small inwards flow velocity.

The net streamwise and spanwise velocities are finally shown in figure 28(e,f). Now the proposed clockwise rotation is apparent. While there are obviously large fluctuations around the averaged picture, an indicative cycle could start from the 3 o’clock location, around $x\approx 3.3$ and $y\approx 1.4$ , where the flame moves downwards and inwards. At 6 o’clock, around $x\approx 2.3$ and $y\approx 1.0$ , the flame is being strongly entrained into the jet, where it reaches a region of high streamwise velocity that exceeds the flame propagation speed, pushing it downstream again. In principle the flame would then need to move through 9 o’clock ( $x\approx 3.3$ and $y\approx 1.0$ ) then 12 o’clock to complete a cycle. Indeed, it can be observed that there is an outwards motion near 1 o’clock, round $x\approx 4.2$ and $y\approx 1.6$ . It is proposed that this motion is connected with the passage of large eddies, a point that will be elaborated later. However, this 2D picture still does not fully explain things, since the mean transverse velocity remains negative on the entire lean side, and hence the outwards motion through 9 o’clock and 12 o’clock is not supported by this analysis. To reinforce this, the mean velocity vectors are shown in figure 29. While the mean vectors clearly suggest a rotating pattern, they seem to suggest that there is no way for flame edges to escape the high-streamwise-velocity and negative-transverse-velocity regions on the lean side.

Figure 29. The conditional average on both streamwise and transverse locations of the instantaneous relative velocity vectors conditionally averaged on streamwise and transverse location of the flames (the solid line is the temporally and spatially Favre-averaged mixture fraction, equal to 0.07).

Figure 30. The following quantities, conditionally averaged on both streamwise and transverse locations of the instantaneous flame base: (a) streamwise flow velocity with the out-of-plane component added, (b) transverse flow velocity with the out-of-plane component added, (c) the streamwise edge propagation velocity with the out-of-plane component added, (d) the transverse edge propagation velocity with the out-of-plane component added, (e) the net streamwise velocity with the out-of-plane component added, (f) the net transverse velocity with the out-of-plane component added and (g) the vectors of the relative velocity with the out-of-plane component added conditionally averaged on streamwise and transverse location of the flames (the solid line is the temporally and spatially Favre-averaged mixture fraction, equal to 0.07).

At this point, out-of-plane motion needs to be invoked. While the mean out-of-plane velocities are obviously zero, they can be correlated with the flame-edge orientation to create a non-zero effect in this 2D picture. Figure 30(a,b) now shows the flow velocities with the out-of-plane component also considered. The out-of-plane component has little effect for the streamwise direction but noticeably reduces the magnitude of the inward transverse velocities on the lean side. Figure 30(c,d) shows the net relative flame propagation velocities in the streamwise and transverse directions respectively, with the out-of-plane components added in. On comparing these with the earlier figure 28 showing the in-plane components only, it may be observed that the out-of-plane flame propagation essentially tends to amplify the flame propagation effect. Of particular note in the transverse velocity is that it amplifies the positive velocity on the lean side. The resulting net velocities including both the flow and flame velocities and both in-plane and out-of-plane components are shown in figure 30(e,f). As can be seen, while the streamwise component has a similar structure to the earlier discussion when out-of-plane motion was not considered, the transverse component is now much more consistent with an overall clockwise rotation, being consistently negative at low $y$ values and consistently positive at higher values. Finally, the implied vectors are shown in figure 30(g), clearly showing a nearly complete clockwise rotation around the region of the most likely stabilisation point.

There is one caveat that needs to be mentioned. The flame edges that are located further downstream than $x\approx 3.5$ tend to continue to move downstream. It is suggested here that these are due mainly to the flame holes, both extinction and inclusion holes, which were not conditioned out of this analysis. It is also suggested that these are advected and eventually heal up at some location downstream. Further investigation of the evolution of the holes is left for future work. Finally, we refer interested readers to a sensitivity study of the key results of this section to the chosen mixture-fraction and product mass-fraction isosurfaces presented in appendix B.

4.5. Transport budget analysis

To complement the analysis of the instantaneous flame structures as performed in the previous sections, terms involved in the transport equations of the product mass fraction are analysed from a different time- and space-averaged standpoint. Following an earlier similar analysis of a lifted flame in a hot coflow (Gordon et al. Reference Gordon, Masri, Pope and Goldin2007), we attempt to identify the roles played, on average, by chemical reaction, mean convection and turbulent and molecular transport.

First, to provide some essential background, the average velocity field close to the flame base will be discussed. Earlier, in § 4.4, it was noted that locally upstream flows were observed around the flame base. As this was an initially unexpected feature it is investigated in more detail. In figure 31, the colour contours represent the Favre-averaged product mass fraction, the dashed line is $Z_{ms}$ and the solid black and red lines are $Y_{p}$ of 0.01 and 0.05 respectively. Velocity vectors, magnified by a factor of 5.0 in the region of $|y|>1.0H$ , are shown to emphasise the flow structure. The Favre mean of a variable ${\it\phi}$ is defined as $\widetilde{{\it\phi}}=\overline{{\it\rho}{\it\phi}}/\bar{{\it\rho}}$ , where ${\it\rho}$ is the density and an overbar denotes an ensemble average. The ensemble averages are computed as simultaneous temporal and spanwise direction means,

where $N_{t}$ is the number of data sets over which the average is computed. Upstream of the flame in the region $0{-}1.5H$ , a conventional entrainment flow is observed. However, around the flame base on the lean side, a negative axial velocity may be noted. Lateral entrainment flow towards the jet in the outer regions is a well-known consequence of jet spreading and mass continuity, e.g. Pope (Reference Pope2000). It is also obvious that the flow has to diverge around a local heat releasing region, for example as observed around triple flames (Ruetsch et al. Reference Ruetsch, Vervisch and Liñán1995), and as in the well-known hydrodynamic Darrieus–Landau instability mechanism (Landau Reference Landau1944). Given that the heat releasing region has a large extent downstream of the flame base, the only region where the entrainment flow can diverge is back towards to the nozzle. In our simulations, the coflow velocity is very small ( $0.002\boldsymbol{U}_{j}$ ), so this leads to a locally negative velocity. This result is not without experimental support – a PIV-based study by Su et al. (Reference Su, Sun and Mungal2006) found that for small lifted heights ( ${<}12D$ ), as is the case here, streamwise mean velocities lower than the coflow were observed. The present work shows that this is due to entrainment flow. It is important to note, however, that this observed feature of averaged upstream streamwise flow is almost certainly only possible at low lifted heights, which may be observed, for example, in the measurements of Su et al. (Reference Su, Sun and Mungal2006). The role of flow divergence and deceleration around the flame edge was also reported by Upatnieks et al. (Reference Upatnieks, Driscoll and Ceccio2002, Reference Upatnieks, Driscoll, Rasmussen and Ceccio2004); however, an on-average negative flow was not observed, consistent with expectations at the much larger lifted heights in those experiments. Furthermore, the average analysis is presented in appendix A.

Figure 31. Contours of product mass fraction with velocity vectors overlaid (the solid black and red lines are $\widetilde{Y}_{p}=0.01$ and 0.05 respectively and the black dashed line is $\widetilde{Z}_{ms}$ ).

The terms in the transport equation for the Favre average of the instantaneous product mass fraction, $Y_{p}$ , are defined in table 2, where $\boldsymbol{U}_{x}$ and $\boldsymbol{U}_{y}$ are the instantaneous streamwise and transverse velocities respectively. Figure 32 shows the terms in table 2 on a colour scale. For reference, the Favre-mean mixture fraction of 0.07 and the product mass fraction of 0.01 are also represented as dashed and solid black lines respectively. As expected, the reaction rate (RR) is a strong positive term centred on the stoichiometric region. The reaction rate term is contributed both from edge flames and the trailing diffusion flames. Convection in the streamwise direction (CX) is strongly negative in most regions but slightly positive on the outer edge of the flame base, which corresponds to the locally negative streamwise velocities that were observed in figure 31. The effects of the entrainment flow are strong and clearly observed in the convective term in the transverse direction (CY). There are a few experimental works that have discussed entrainment in lifted flames (Han & Mungal Reference Han and Mungal2000; Su et al. Reference Su, Sun and Mungal2006; Boxx et al. Reference Boxx, Heeger, Gordon, Böhm, Dreizler and Meier2009b ). The present DNS shows it to be significant, at least at this lifted height. The turbulent transport in the streamwise direction (TTX) is weaker than other terms; however, it has a positive contribution on the rich side which corresponds to gradient transport of products from downstream locations in the upstream direction. However, its contribution on the lean side is small, but negative over most regions of the flame, which corresponds to countergradient transport. The transition from gradient transport on the rich side to countergradient transport on the lean side is probably due to the decreasing turbulence intensity going from the jet core to the outer region. As discussed by Veynante et al. (Reference Veynante, Trouvé, Bray and Mantel1997), such a transition with turbulence intensity also occurs in fully premixed turbulent flames.

Figure 32. Contours of the reaction, convection, diffusion and turbulent transport terms (the solid line is $\widetilde{Y}_{p}=0.01$ and the dashed line is $\widetilde{Z}_{ms}$ ).

Figure 33. Different regions in the vicinity of the flame base.

A similar transition is observed in the transverse direction. In the inner turbulent core on the rich side, the transport is clearly out of the high product region and into the core. On the other hand, on the lean side, the transport term is once again negative, corresponding to countergradient diffusion, though it makes only a small contribution here relative to other terms. This countergradient transport may be connected with heat release, but may also be connected with intermittent entrainment-driven eddies which cause the hook-shaped structure noted earlier in figure 20, and appear to be involved.

Laminar diffusion is a relatively smaller term in all regions except for the reaction zone.

The balance between these different terms is now discussed. This depends on the location within the flame, so for the sake of brevity in the next part of the discussion, the right branch of the lifted flame will be discussed, and to make the analysis more precise, the flame base is categorised into five distinguishable regions as shown in figure 33 and described as follows.

Region A is the starting point to understand the stabilisation mechanism in this particular flame. Region A is on the lean side and upstream of the $Y_{p}=0.01$ contour. A transverse cut through this region at a location upstream of the flame at $x=2.2$ is shown in figure 34(a). In this region, the streamwise convection (towards the jet exit), turbulent transport and laminar diffusion all play a similar role and promote upstream flame transport. These are balanced by the transverse mean and turbulent convection terms, which both transport the flame into the jet core. It should be noted that the role of these terms is consistent with the role of upstream transport played on the lean side in the instantaneous picture, and transverse transport into the jet core. The effect of propagation at this very farthest upstream region only involves the laminar diffusion part.

Region B is the region upstream of the flame base and on the rich side. The transport budgets in this region can be seen on the left side of the stoichiometric line in figure 34(a). In this region there is a balance of three terms: streamwise convection balances streamwise turbulent transport, and both mean and turbulent convection in the transverse direction, which as discussed with respect to region A, transports hot products from the lean to the rich side. In a flat turbulent premixed flame, one would expect the balance to be between convection and turbulent transport in this region – but in this lifted jet flame the entrainment flow complicates this situation and makes the stabilisation mechanism fundamentally 2D.

Region C is inside the stoichiometric contour and outside of the contour of $\widetilde{Y}_{p}=0.01$ . The indicative transverse cut in this region, at $x=3.6$ , is shown in figure 34(b). In this region there is a straightforward balance of transverse turbulent gradient transport and downstream convection.

Region D is inside the stoichiometric contour, downstream of the isoline of $Y_{p}=0.01$ , and within the region of high reaction rates. Figure 34(b) presents a transverse cut through this region at $x=3.6$ . On the lean side of $y=1$ there is a complex balance between reaction rate, the effect of entrainment CY and gradient turbulent transport in the streamwise direction, which are all positive terms, balancing streamwise mean convection and gradient turbulent transport in the transverse direction. Here, the effects of propagation, which in the instantaneous picture tends to balance flow in this region, would be observable indirectly via the reaction rate term. However, in this averaged picture the diffusion flame also contributes.

Region E is the final region and it is inside the stoichiometric contour, downstream of the isoline of $Y_{p}=0.01$ , and on the rich side of the region of high reaction rates. Figure 34(b) presents a transverse cut through this region at $x=3.6$ . In Region E the laminar diffusion and reaction rate are positive terms that balance the incoming entrainment flow in the transverse direction, which is a similar balance to that expected on the lean side of a counterflow diffusion flame.

Figure 34. The convection, diffusion, turbulent transport and reaction budgets at different streamwise locations (the blue and red dashed lines are $Z_{ms}$ and $Y_{p}=0.01$ respectively).

In summary, the transport budgets show that the stabilisation mechanism is fundamentally 2D, as opposed to being dominated by transport in either the streamwise or transverse direction alone. Region A is stabilised by upstream transport balanced against transverse transport into region B; region B is stabilised by transport from region A and upstream; in region C there is a simple balance of downstream convection and transverse turbulent transport from the flame region; and finally in region D transverse transport out of the flame and downstream convection balance reaction and upstream transport. The 2D structure of this balance seems to be consistent with the instantaneous picture, with instantaneous flame edges (and the trailing diffusion flames) essentially moving around between these regions in a cyclic clockwise motion. Because averaging was performed in the third direction, it is, however, impossible to assess any out-of-plane effect in this framework. We simply state that its effect is embedded within the reaction term, i.e. the existence of high-reaction-rate regions in high-average-velocity regions is supported by the ability of flames to locally circumvent high-streamwise-velocity eddies by flows and flame propagation in the spanwise direction.