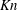1 Introduction
Thermophoresis is defined as the migration of a microscale particle in a fluid as a response to a temperature gradient within the fluid. The thermophoretic force was first observed by Tyndall (Reference Tyndall1870), who noticed a zone free of dust surrounding a heated surface. The thermophoresis is driven by stresses that arise from temperature gradients and thermal diffusion, discussed by Maxwell (Reference Maxwell1879) in relation to the Crookes radiometer. It was not until decades later that Epstein (Reference Epstein1929) incorporated Maxwell’s work into a theory for the thermophoretic force on a spherical particle suspended in a gas with a thermal gradient. The force acting on a particle is linearly dependent on the magnitude of the thermal gradient and is a product of differential bombardment of gas molecules impacting the particle. Molecules impacting from the warmer side of the gradient have higher average kinetic energy than those impacting from the cooler direction, leading to positive thermophoresis being defined in the direction opposite to the thermal gradient, from hot to cold. However, certain conditions can lead to a reversal of the direction of force production, known as negative thermophoresis, which will be the main focus of this work. The reversal of thermophoretic force was first observed qualitatively by Crookes (Reference Crookes1874), but has not yet been shown with quantitative results experimentally.
Thermophoresis plays an important role in an array of fields that inherently or necessarily deal with gases in the flow regime transitional from free-molecular to continuum. It is extensively used for aerosol sampling in combustion research, for microcontamination control in the semiconductor industry, in commercial precipitators, for the manufacturing of optical fibres in vapour deposition processes, and many more. The importance of the phenomenon explains the fact that thermophoresis has been studied extensively over the last decades.
The vast majority of research on thermophoresis is related to the impact of thermal gradients in a fluid surrounding a spherical particle in the flow regimes ranging from the free-molecular to continuum. Theoretical analyses exist for the near-continuum flow (Epstein Reference Epstein1929) as well as the free-molecular to weakly collisional flow (Waldmann Reference Waldmann1959), with attempts to extend from either of the asymptotic solutions to the transitional regime with limited success. Computational analysis, ideally, would be based on the full Boltzmann equation, but the complex nonlinear nature of this equation makes such an analysis prohibitively expensive even for modern parallel computers. Nonetheless, a number of simpler computational approaches, such as those based on the linearization of the Boltzmann equation (Loyalka Reference Loyalka1971; Sone & Aoki Reference Sone and Aoki1983), integral solutions of the Bhatnagar–Gross–Krook (BGK) model (Onishi Reference Onishi1972; Yamamoto & Ishihara Reference Yamamoto and Ishihara1988; Beresnev & Chernyak Reference Beresnev and Chernyak1995) and 13-moment equations (Cercignani Reference Cercignani1975), provide quantitative and reliable information. The theoretical and early computational analyses predict a bell-shaped thermophoretic force profile as a function of gas density (and thus Knudsen number). First, there is an increasing force as gas density increases from the free-molecular regime, with the force acting opposite to the direction of the temperature gradient (from hot to cold) and dominated by the molecular mass flux. With further increase in gas density, the force peaks at a Knudsen number
$Kn$
between 1 and 0.1, as intermolecular collisions have a pronounced detrimental effect. Finally, further increase in density leads to a decreasing force, which is asymptotic at zero when the flow regime approaches continuum.
Interestingly, many numerical (but not analytic) approaches predict the existence of negative thermophoresis, where the force not only goes to zero but reverses direction to act on an object from cold to hot as the Knudsen number decreases to a near-continuum regime. Negative thermophoresis is only expected when the particle has a thermal conductivity much higher than that of the fluid; very conductive particles may start to move from a cold area to a warmer one when the Knudsen number becomes less than
${\sim}$
0.1. Currently there is no experimental confirmation or refutation of the existence of negative thermophoretic force, in part because data on thermophoretic forces, typically scarce, do not extend to
$Kn<0.1$
(Li & Davis Reference Li and Davis1995). Please note that all Knudsen numbers presented in this work are calculated using the hard-sphere collision model as described in Sharipov (Reference Sharipov2015).
Uncertainties related to the direction and magnitude of thermophoretic forces, as well as the physical reasons behind them, are the primary motivation for this work. A single macroscale particle is used here, similar to Selden et al. (Reference Selden, Ngalande, Gimelshein, Gimelshein and Ketsdever2009a ,Reference Selden, Ngalande, Gimelshein, Muntz, Alexeenko and Ketsdever b ) and Ketsdever et al. (Reference Ketsdever, Gimelshein, Gimelshein and Selden2012), along with a completely different approach to the force characterization, based on force measurements using a nanonewton thrust stand (nNTS). The primary benefit of such an approach is its accuracy: the force can now be examined in a quantitative manner for the entire range of flow regimes from free-molecular to continuum. The work has two main objectives. First, the impact of a heated wall on a particle with high thermal conductivity is studied experimentally and numerically. The numerical modelling is based on an accurate solution of the ellipsoidal statistical (ES) model kinetic equation for varying flow conditions matching the experimental work aimed at the detailed examination of the shear and pressure mechanisms controlling the negative thermophoretic force. Second, the impact of a linear thermal gradient, established between two parallel walls, on the same particle is examined for a gas flow regime ranging from the near-free-molecular to the near-continuum. The influence of walls is minimal in this case, thus providing estimates of thermophoretic forces on a free floating particle (Knudsen number scaling may be used to evaluate microscale particles).
The possibility of the existence of thermophoretic force acting in the direction of the temperature gradient (cold to hot) was first noted by Dwyer (Reference Dwyer1967) while obtaining a higher-order solution based on the linearized 13-moment theory. The solution predicted reversal of thermophoretic force at low Knudsen numbers for a particle of high thermal conductivity. The term ‘negative thermophoresis’ was first put forth later by Sone (Reference Sone1972). Sone & Aoki (Reference Sone and Aoki1977, Reference Sone, Aoki and Fisher1981) derived an asymptotic solution for thermophoretic force up to the third order in the small Knudsen number case based on the BGK model of the Boltzmann equation. This solution predicts negative thermophoresis for infinite particle thermal conductivity at small Knudsen numbers. Later, Sone & Aoki (Reference Sone and Aoki1983) derived a solution of the BGK equation for an infinite particle thermal conductivity using a variational method. This new solution predicts negative thermophoresis for
$Kn=0{-}0.2$
with a magnitude of reversed thermophoretic force as no more than 4 % of the Waldmann free-molecular limit.
More recent solutions of the BGK model of the Boltzmann equation (Yamamoto & Ishihara Reference Yamamoto and Ishihara1988; Loyalka Reference Loyalka1992) also indicate the possibility of existence of negative thermophoretic force for a finite but large particle thermal conductivity. Loyalka (Reference Loyalka1992) cautioned that negative thermophoresis may be an artifact arising from the approximations made in the BGK model. Though Loyalka solved the linearized Boltzmann equation directly for hard-sphere molecules, it is not clear whether negative thermophoresis exists for the hard-sphere model, as numerical factors limited the gas density to Knudsen numbers greater than 1. More recently, Takata, Aoki & Sone (Reference Takata, Aoki, Sone, Weaver and Shizgal1994) were able to carry out computations for the hard-sphere model down to
$Kn\approx 0.096$
for an infinite particle thermal conductivity and a numerical scheme different from Loyalka (Reference Loyalka1992). No reversal in the direction of thermophoretic force was found. A preliminary computation at
$Kn=0.019$
found a very small negative thermophoretic force, but it was unclear whether this was a manifestation of numerical error. In summary, it remains unclear whether the reversal of thermophoretic force as predicted by numerical models is a physical phenomenon or an artifact of the models of the Boltzmann equation.
2 Theory
2.1 Waldmann limit of thermophoretic force
An expression for the thermophoretic force on a particle suspended in a gas with the Chapman–Enskog molecular velocity distribution was derived by Waldmann (Reference Waldmann1959) and Bakanov & Deryagin (Reference Bakanov and Deryagin1959) independently, under the condition that the particle size is much smaller than the gas mean free path, as
$$\begin{eqnarray}\displaystyle F=-k\left(\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}z}\right)\left(\frac{\unicode[STIX]{x03C0}R_{p}^{2}}{c_{0}}\right)\left(\frac{16}{15\sqrt{\unicode[STIX]{x03C0}}}\right)\!. & & \displaystyle\end{eqnarray}$$
This expression represents the maximum thermophoretic force production limit on a spherical particle for a given thermal gradient in the fluid. Here,
$k$
is the particle thermal conductivity,
$R_{p}$
is the particle radius and
$c_{0}$
is the most probable speed of a molecule,
$$\begin{eqnarray}\displaystyle c_{0}=\sqrt{2k_{B}T/m}, & & \displaystyle\end{eqnarray}$$
where
$k_{B}$
is Boltzmann’s constant,
$T$
is the average temperature near the sphere and
$m$
is the molecular mass.
Figure 1 depicts the direction of positive
$z$
, temperature gradient and thermophoretic force production, where
$T_{1}$
and
$T_{2}$
represent hot and cold, respectively. Note that
$z$
and the temperature gradient are positive from cold to hot, and thermophoretic force is positive from hot to cold.
Figure 1. Depiction of positive
$z$
direction, temperature gradient and thermophoretic force production.
2.2 Two half-range Maxwellian distribution limit of thermophoretic force
As the pressure of the system decreases, the mean free path of the gas molecules increases to the point that it can be assumed that the flow is one-dimensional (1D) in the
$z$
direction, where the molecules moving in the positive and negative
$z$
directions correspond to half-range Maxwellian distributions at
$T_{1}$
and
$T_{2}$
. The heat flux for this situation can be described as
$$\begin{eqnarray}\displaystyle q=-(mnc_{0}^{3})\left[\left(\frac{1}{\unicode[STIX]{x03C0}^{1/2}}\right)\left(\frac{T_{2}^{1/2}-T_{1}^{1/2}}{T^{1/2}}\right)\right]\!, & & \displaystyle\end{eqnarray}$$
where temperature
$T=(T_{1}T_{2})^{1/2}$
and number density
$n=n_{1}+n_{2}$
. The application of Green’s theorem for a motionless sphere with
$\unicode[STIX]{x1D6FC}_{p}=1$
, where
$\unicode[STIX]{x1D6FC}_{p}$
is the fraction of diffusely reflected molecules, on the force and heat transfer functions as described by Gallis, Torczynski & Rader (Reference Gallis, Torczynski and Rader2001) yields
$$\begin{eqnarray}\displaystyle F=-(mnc_{0}^{2}\unicode[STIX]{x03C0}R_{p}^{2})\left[\frac{3}{4}\left(\frac{T_{2}^{1/2}-T_{1}^{1/2}}{T_{1}^{1/2}+T_{2}^{1/2}}\right)\right]\!. & & \displaystyle\end{eqnarray}$$
The expression above for thermophoretic force agrees with the small-temperature-difference limit of the free-molecular expression of Phillips (Reference Phillips1972). The force expression above can be simply modified to incorporate a form including heat flux, as described by equation (2.3):
$$\begin{eqnarray}\displaystyle F=\left(\frac{q\unicode[STIX]{x03C0}R_{p}^{2}}{c_{0}}\right)\left[\left(\frac{3\unicode[STIX]{x03C0}^{1/2}}{8}\right)\left(\frac{2T^{1/2}}{T_{1}^{1/2}+T_{2}^{1/2}}\right)\right]\!. & & \displaystyle\end{eqnarray}$$
Comparing the Waldmann and the two half-range Maxwellian limits of thermophoretic force, it is worth noting that the former is not a function of gas pressure and the latter is linearly related to the number density of the surrounding gas. This distinction is an artifact of the small particle size assumption, which quickly breaks down as the particle-diameter-based Knudsen number decreases below unity.
3 Experimental set-up
3.1 Vacuum environment
Force measurements are taken within a cylindrical vacuum chamber with a 1.2 m diameter and length of 2 m. The chamber is pumped by two turbopumps, which are each backed by a mechanical pump. Pressure measurements are taken using a baratron, which can read pressures from 13.3 Pa down to 0.013 Pa, with argon used as the carrier gas. An nNTS, which is described in detail by Jamison, Ketsdever & Muntz (Reference Jamison, Ketsdever and Muntz2002), is used to suspend and measure force upon the test particle. The nNTS is a torsional system that measures force through rotational displacement about a central pivot point. Flexural springs with a known spring constant are located at the pivot point. The displacement of the stand is measured using a linear variable differential transformer (LVDT). The nNTS is housed in a vacuum extension off the side of the main chamber, which allows the test particle to be suspended directly in the centre of the chamber either near the single wall or between the pair of walls as described below and depicted in figure 2. The test particle utilized is a copper sphere with a diameter of 5.1 cm, and the carrier gas is argon.
3.2 Single-wall configuration
The initial single-wall orientation places a 61 cm
$\times$
61 cm
$\times$
0.9 cm copper plate within the chamber normal to the long axis of the cylinder. This plate is temperature-driven above the ambient temperature within the chamber using a heat exchanger on the back side of the plate. Water is used as the working fluid for driving the plate temperature and is controlled by a Neslab CFT-33 water chiller. The plate is placed in the centre of the chamber at a fixed distance of 1.0 cm from the test particle, which is centred on the front surface with care to limit heat transfer from the heated wall to the nNTS. The temperature of the wall is characterized using 12 thermocouples distributed across the front (i.e. facing the test particle) surface. The temperature of the surface varies by no more than
$\pm$
1 K. Following the thermal characterization of the plate, the thermocouples at the centre of the plate are removed to minimize interference in the force measurements. Six thermocouples remain around the perimeter of the wall to monitor the temperature during testing.
Figure 2. Schematic of single-wall set-up.
The single-wall set-up is tested at pressures ranging from 0.2 to 4.2 Pa, with temperatures ranging from 5 to 16 K above the ambient chamber temperature. For this orientation, the temperature difference is taken to be the difference between the ambient temperature of the chamber (assumed to be the temperature of the test particle) and the front surface of the copper plate. Owing to the geometry, there is no individual length scale for calculating temperature gradient.
3.3 Dual-wall configuration
The dual-wall set-up utilizes the same chamber and vacuum components as the single-plate orientation, with an added second 61 cm
$\times$
61 cm
$\times$
0.9 cm copper plate parallel to the first placed on the opposite side of the test particle with a plate separation of 40 cm. The particle is placed in the middle between the two plates, where the temperature gradient is uniform, thus replicating conditions typical in microscale particle transport. A diagram of the dual-wall configuration and an image of the test particle are shown in figure 3. The heated plate in the single-wall orientation is now temperature-driven by a Neslab LT-50DD recirculating bath, which both heats and chills water to establish a temperature gradient both above and below the ambient chamber temperature. The second plate is allowed to remain at the ambient temperature of the chamber, while three thermocouple readings are taken around the perimeter of the plate. Owing to radiative heat transfer, the thermally driven plate raises or lowers the temperature of the ambient plate at a rate of approximately 1 K per hour. This effect is minimized by raising or lowering the temperature of the water passing through the heat exchanger between tests to maintain a desired temperature gradient.
The dual-wall orientation was tested for a temperature gradient of
$35~\text{K}~\text{m}^{-1}$
over a pressure range of 0.015–10 Pa, and then for temperature gradients of
$15~\text{K}~\text{m}^{-1}$
and
$25~\text{K}~\text{m}^{-1}$
from 0.1 Pa to 4.0 Pa. The 35, 25 and
$15~\text{K}~\text{m}^{-1}$
temperature gradients correspond to temperature differences between the driven and ambient plates of 14.3, 10 and 6 K, respectively, with a wall separation of 40 cm for all data runs. Force measurements are taken for a copper sphere with a thermal conductivity of
$401~\text{W}~\text{m}^{-1}~\text{K}^{-1}$
.
Figure 3. Schematic of dual-wall configuration.
3.4 Data taking procedure
Before testing, the nNTS is calibrated using an electrostatic comb calibration system (ESCCS). This method of calibration utilizes metallic combs to apply a known force to the nNTS while measuring the deflection using the LVDT. The stand is calibrated for a range of forces encompassing the expected forces during testing. A linear relationship is found between force and stand displacement. Before taking force measurements, the chamber is pumped down to
$10^{-3}$
Pa to establish a zero-force condition. Next, argon is introduced into the chamber and allowed to reach a desired steady-state pressure. The steady-state displacement of the nNTS is used to determine the force on the test particle with the calibration relationship determined before testing. After the measurement is taken, the argon is evacuated from the chamber to return to base pressure to re-establish the zero-force condition. Lastly, the two zero-force conditions are compared to determine if there needs to be any correction for drift in the measurement process. This procedure is repeated for a total of three data measurements per test pressure to ensure accurate force measurement.
3.5 Error analysis
The error shown on all presented force measurements represents one standard deviation of the data points taken. In cases where measurements are added to or removed from each other, individual error measurements are summed, which is true for data presented in which the arm effect is removed. Though the sum of standard deviation error constitutes the error shown, there are multiple errors associated with force measurement. Signal noise in error measurement is measured to be 50 nN, which is 2 % of force measurements but ignored as the error is smaller than the presented standard deviation error. There is also discretization error in measurements of the LVDT, with a readout of
$\pm$
10 V on a 24-bit measurement translating to tens of nanonewtons of resolution.
Two more sources of error arise from the force calibration method for the thrust stand. The first is force measurement error when determining the electrostatic comb attraction as a function of squared voltage potential applied across the combs. The mass balance on which the force differences are measured has a published error of 0.001 g, which translates to 1 % of calibration force measurement. Second, the error associated with assuming a linear relation of voltage squared to stand displacement when calibrating has a consistent
$R^{2}$
value of 1 from day to day before data taking. If the
$R^{2}$
values were not consistently 1,
$R^{2}$
error can add to overall measurement error.
For simplicity, all force measurements will be given with error bars equalling one standard deviation of each measurement if the error is greater than the size of the symbols used to represent the data. The standard deviation error value is greater than the sum of each of the measurement errors discussed here and calculated for each individual measurement.
4 Numerical approach
The maximum thermophoretic force on a sphere is expected at a diameter-based Knudsen number,
$Kn$
, of the order of 1, while the reversal of direction of force is numerically estimated (Young Reference Young2011) to occur for
$Kn\sim 0.1$
. Therefore, a kinetic approach is to be used based on the solution of either the Boltzmann equation or one of its models. Previous studies of thermophoretic flows, with few exceptions, have used model kinetic equations (BGK) or a moment method based on the integration of a model kinetic equation, to obtain equations for different moments of the velocity distribution function. In this work, a direct solution of the ES-BGK equation is obtained. Note that the use of the direct simulation Monte Carlo (DSMC) method to statistically solve the full Boltzmann equation is impracticable for the problem under consideration (and nearly impossible for all but the largest Knudsen numbers), since the thermophoretic force amounts to only a fraction of 1 % of the pressure force on an equivalent area, which is further complicated by slow convergence of the flow over time. In all numerical simulations, a kinetic solver SMOKE (Wadsworth et al.
Reference Wadsworth, Gimelshein, Gimelshein, Wysong and Abe2008) is used. SMOKE is a parallel two-dimensional (2D)/axisymmetric finite volume solver based on conservative numerical schemes developed in Mieussens (Reference Mieussens2000). A second-order spatial discretization is applied along with an implicit time integration. Two computational set-ups have been used: an axially symmetric and a 2D one. In both cases, argon gas was modelled.
In the axially symmetric configuration, the computational domain mimics the single-wall experimental set-up and is 1.3 m long and 0.5 m high. The spatial grid consists of 38 000 cells. The velocity grid convergence was studied, and it was found that
$(14,8,18)$
points in
$(x,r,\unicode[STIX]{x1D703})$
directions were sufficient to achieve better than 5 % accuracy of thermophoretic force calculation for diameter-based Knudsen numbers higher than 1. For
$Kn$
between 0.2 and 1, the velocity grid consisting of
$(18,12,18)$
points was used to achieve grid convergence better than 5 %. Note that similar velocity grid resolution was used in Selden et al. (Reference Selden, Ngalande, Gimelshein, Gimelshein and Ketsdever2009a
), where numerical analysis of spatial and velocity grid convergence was conducted. Computations for lower Knudsen numbers required at least a week on a 32-processor computer, and achieving numerical convergence for
$Kn<0.2$
was found to be problematic. In all computations, the diffuse model with complete energy and momentum accommodation is used for gas–surface interaction, and axial symmetry is applied at
$Y=0$
. For calculations with the plate heated, the temperature of the plate (the left boundary) was set to
$T=313$
K; for calculations with the plate cooled, the temperature of the plate was set to 273 K. To match the experiments, the sphere diameter and distance from the thermally driven plate were 0.0508 m and 0.01 m, respectively.
Table 1. Computed thermophoretic force for heated and cooled plates in planar geometry.
Two primary reasons were identified for slow temporal and velocity grid convergence: a large computational domain as compared to the sphere; and the axial symmetry of the flow. The numerical analysis has shown that using a smaller, and planar, geometry allows for an orders-of-magnitude reduction in computational time. The 2D computational domain was 0.125 m
$\times$
0.1 m. For the numerical set-up to resemble the single-wall experiment, a circular geometry (a cylinder) was used with a diameter of 0.0508 m, with a distance to the thermally driven plate of 0.01 m. The plate was first heated to 313 K, and then cooled to 273 K; the temperature of the cylinder and upper and right walls was 293 K. The velocity grid convergence study was conducted, and the velocity grid of
$(24,24,24)$
was selected that provided better than 3 % force convergence. For a more in-depth description of the numerical approach, please see Ventura et al. (Reference Ventura, Gimelshein, Gimelshein and Ketsdever2013) and Selden et al. (Reference Selden, Ngalande, Gimelshein, Gimelshein and Ketsdever2009a
).
Lastly, the 1D version of the DSMC code SMILE (Ivanov et al. Reference Ivanov, Markelov, Gimelshein, Mishina, Krylov and Grechko1998) was used to evaluate the temperature profile between two parallel plates at different gas pressures. In the computations, the variable soft-sphere model was used for intermolecular collisions, and the diffuse reflection with full momentum and energy accommodation was assumed at the walls. The number of simulated molecules and cells were five million and one million, respectively. The computations were run long enough to reduce the statistical scatter to less than 0.1 %. The temperature gradient at the centre between the two plates was then determined.
5 Results and discussion
5.1 Single-wall configuration
Quantitative measurements of force production on a sphere suspended near the thermally driven plate matched the qualitative assessment published by Crookes (Reference Crookes1874). A heated thermally driven wall pushed the test sphere away from the wall at near-vacuum (
${<}$
1.0 Pa) conditions and towards the wall at higher pressures. Numerical results show a matching trend in both the planar and axisymmetric configurations described in the previous section. Complete details pertaining to the numerical results are given in Ventura et al. (Reference Ventura, Ketsdever, Webb, Alexeenko, Gimelshein, Gimelshein, Mareschal and Santos2012).
In order to analyse total thermophoretic force production on the cylindrical surface in the planar model and the spherical surface in the axisymmetric model, it is necessary to look at not only the pressure on the surface but also the sum of the shear force acting in the direction normal to the thermally driven wall. The total thermophoretic force on the cylindrical surface is given in table 1 for a range of Knudsen numbers. Table 1 also provides the separated pressure
$F_{p}$
and shear
$F_{s}$
force contributions. The shear force is always positive and mostly increases with gas pressure. Generally, the hot-to-cold direction of the shear force is related to the asymmetry in the velocity distribution function of molecules colliding with the cylinder and not the minimal bulk flow motion induced by thermal creep. Unlike the shear force, the overall pressure force changes sign from positive at large Knudsen numbers to negative at small Knudsen numbers. Since the pressure force increases more rapidly than the shear force, the total force becomes negative at
$Kn\approx 0.05$
. This is consistent with previous findings (Young Reference Young2011), where a solution to 13-moment equations was obtained for a sphere exposed to a temperature gradient in a gas.
Table 1 also presents the results for a cold plate. The forces were found to be close to symmetric with respect to the force axis to the hot plate results. Both numerical set-ups show negative thermophoresis in the reversal of the total force direction at small Knudsen numbers. The total forces for the 2D case are depicted in figure 4(a). Similar to the published predictions within Zheng (Reference Zheng2002) and Young (Reference Young2011), the maximum positive thermophoretic force is observed at a Knudsen number of approximately 0.3. The gradients of the force profile at
$F=0$
indicate that the negative thermophoretic force maximum will be of the same order as the positive thermophoretic force. This differs greatly from the predictions of Sone & Aoki (Reference Sone and Aoki1983), which place negative thermophoretic force no greater than 4 % of the Waldmann limit of thermophoretic force described previously. Although some of the difference may be attributed to different numerical approaches used, the primary reason is believed to be the proximity of the heated (or cooled) wall in the present configuration.
Figure 4. Computed thermophoretic force on a sphere near a heated and cooled plate in a planar geometry (a) and comparison of numerical and experimental force on a sphere near a heated plate in a cylindrical chamber (b).
Table 2. Computed thermophoretic forces for the axisymmetric geometry.
The second numerical configuration, an axisymmetric flow over a sphere, fairly closely reproduces the single-wall experimental configuration and, by extension, the original Crookes qualitative experiment. The shear and pressure contributions to the force are given in table 2. The pressure force initially increases with pressure, as for
$Kn>10$
the intermolecular collisions play a relatively small role, and the force is nearly proportional to the gas pressure. Similar to the 2D case, there is a maximum in the pressure force at
$Kn\approx 0.3$
, which then starts to decrease (the free-molecular mechanism become less important than Maxwell forces). Calculations are not presented for
$Kn<0.2$
, as the computational time becomes prohibitive (to a large extent due to longer transient times), but the slope of the pressure force implies that it may become negative for Knudsen numbers less than 0.1. The shear force increases monotonically with pressure. Table 2 also presents a comparison of the computed and analytic free-molecular values of thermophoretic force, which shows a reasonable agreement considering that the set-up used in the calculations differs from the ideal case assumed for the derivation of the free-molecular force limit.
While it proves extremely difficult to model the single-wall experimental set-up for pressures larger than 1 Pa with a fully kinetic approach, measurement were found considerably easier to perform for pressures of 0.1 Pa and higher, as force measurements at lower values are visibly contaminated by outgassing, and the error bars represent the maximum error seen for this specific experimental dataset. There is a range of pressures around maximum force production where both experiment and computation are relatively straightforward, and the force comparison for these pressures is presented in figure 4(b). It can be seen that the agreement between the numerical and experimental results is reasonable. Also, figure 4(b) clearly shows the existence of negative thermophoresis. The magnitude of this negative thermophoretic force at a Knudsen number of 0.02 is of the same order of magnitude as the peak of the positive force.
5.2 Dual-wall configuration
Owing to the transitional Knudsen nature of the thermophoretic force production pressure range, it cannot be assumed that the temperature profile between the two thermally driven walls is linear. Instead, the profile is steep near the walls and nearly zero directly between the walls. As the pressure of the system increases, the temperature profile between the walls approaches the linear relation expected. In order to estimate an accurate local temperature gradient, a simple 1D DSMC calculation is performed to determine the temperature profile between the two walls as a function of pressure. Figure 5 depicts the estimated temperature profile between the thermally driven walls as a function of pressure. The 1D DSMC model consists of the two thermally driven walls with a separation of 0.4 m and temperatures of 300 and 315 K for the cold and hot walls, respectively. The thermal accommodation coefficient between the simulated argon gas molecules and the wall boundaries is set at 0.9. The study does not include the test particle geometry.
Figure 5. Temperature profile as a function of pressure.
While the impact of the arm on thermophoretic force in the single-wall configuration is negligible, it has to be taken into consideration in the double-wall set-up. To this end, measurements are also taken while no test particle is on the nNTS arm to determine the force exerted by the gas on the arm alone (that arm force is calibrated out in post-processing). The resulting thermophoretic force on the spherical particle is shown in figure 6 for a Knudsen number ranging from 0.01 to 10. The Waldmann limit is calculated based on the estimated local temperature gradient near the spherical particle determined by the 1D DSMC data presented in figure 5. Note that any error bars on the data provided that are smaller than the symbols used are left out for readability.
The top axis of figure 6 represents the pressure range at which data were taken while the bottom axis is the corresponding Knudsen number. As the Knudsen number decreases from 10, the thermophoretic force increases because there are more gas molecules colliding with the test particle – this effect is dominant until the forces reach maximum at a Knudsen number of approximately 0.3. As the Knudsen number continues to increase, intermolecular collisions reduce the net momentum transfer to the test particle to the point that force production drops off. Rather than an asymptotic trend towards zero, the force crosses the zero line and a region of negative thermophoretic force production is observed around a Knudsen number of 0.03, with a maximum negative thermophoretic force of the order of 7 % of the maximum positive force and 5 % of the Waldmann limit. This trend closely follows the numerical prediction of Sone & Aoki (Reference Sone and Aoki1983), which is represented by the dash-dotted line. Note that the prediction of Sone & Aoki is not independent of Knudsen number, but is the maximum predicted value for negative thermophoretic force production. Table 3 depicts the maximum positive and negative thermophoretic forces for the thermally driven plate either heated or cooled to establish a
$35~\text{K}~\text{m}^{-1}$
temperature gradient around the test particle.
Table 3. Maximum positive and negative thermophoretic force production on a spherical test particle for heated and cooled thermally driven plate.
Figure 6. Plot of thermophoretic force production on copper test particle suspended in a
$35~\text{K}~\text{m}^{-1}$
temperature gradient.
It can be seen that, at high Knudsen numbers, the thermophoretic force on the test particle is 50 % or less of the two half-range Maxwellian prediction. This is due to the thermal gradient near the sphere significantly decreasing as the Knudsen number increases. The Waldmann limit as a function of Knudsen number is based on the estimated local temperature gradient near the sphere. It can be seen at the peak force production that the Waldmann prediction is below the measured force production, which is due to the simple 1D DSMC prediction not having the spherical geometry present. The lack of the geometry in the simple simulation leads to a better estimate of the temperature profile between the thermally driven walls, but not an exact value.
6 Conclusions
Thrust stand measurements of thermophoretic force on a 5 cm spherical particle are conducted for a Knudsen number ranging from 0.01 to 10. The primary focus of the work is the experimental validation of earlier theoretical predictions of negative thermophoresis – a phenomenon where the force acts in the direction of the temperature gradient. Two flow scenarios are considered: a particle in the vicinity of the wall, where the temperature gradient decreases with increasing distance from the wall, and a particle in a flow with a uniform temperature gradient.
In the first case, the experimental study was complemented by numerical modelling based on the solution of the ES-BGK kinetic equation. The computations are performed for an axisymmetric configuration that closely follows the experimental set-up, as well as for a 2D configuration. The numerical predictions match the measured thermophoretic force for the range of pressures where both computation and experiment were possible. Relatively large negative thermophoretic force is observed experimentally, with maximum values approaching those of the positive thermophoretic force.
In the second case, with a particle suspended between two walls in a nearly constant temperature gradient, the positive thermophoretic force increases by a factor of 10 as compared to the close-wall case, while the negative thermophoretic force is approximately the same. In the Knudsen number range from 10 to 1, the experimental measurements of positive thermophoretic force production are 50 % or less of the two half-range Maxwellian prediction. The maximum negative force is observed at a Knudsen number of approximately 0.03. This maximum is 5 % of the Waldmann limit for positive thermophoretic force, which matches the 4 % prediction of Sone & Aoki (Reference Sone and Aoki1983), and 7 % of the maximum measured positive thermophoretic force.
