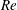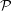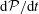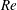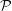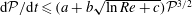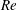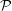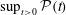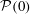1 Introduction
Energy methods are among the most popular techniques used in the mathematical analysis of evolutionary partial differential equations. At their core these methods rely on the existence of bounds for a norm
![]() ${\mathcal{Q}}$
– an ‘energy’ that is not necessarily related to a physical energy – that provides relevant information about the magnitude and regularity (smoothness) of solutions. The idea is to derive bounds on the growth rate
${\mathcal{Q}}$
– an ‘energy’ that is not necessarily related to a physical energy – that provides relevant information about the magnitude and regularity (smoothness) of solutions. The idea is to derive bounds on the growth rate
![]() $\text{d}{\mathcal{Q}}/\text{d}t$
from the equations of motion utilizing rigorous functional estimates and, given initial data with finite norm
$\text{d}{\mathcal{Q}}/\text{d}t$
from the equations of motion utilizing rigorous functional estimates and, given initial data with finite norm
![]() ${\mathcal{Q}}(0)$
, to subsequently control
${\mathcal{Q}}(0)$
, to subsequently control
![]() ${\mathcal{Q}}(t)$
for
${\mathcal{Q}}(t)$
for
![]() $t>0$
via methods of ordinary differential (in)equations. In some cases this kind of energy analysis can establish that
$t>0$
via methods of ordinary differential (in)equations. In some cases this kind of energy analysis can establish that
![]() ${\mathcal{Q}}(t)$
remains finite – sometimes even uniformly bounded – for all
${\mathcal{Q}}(t)$
remains finite – sometimes even uniformly bounded – for all
![]() $t>0$
, while in others it can only show that
$t>0$
, while in others it can only show that
![]() ${\mathcal{Q}}(t)$
is finite for all time if
${\mathcal{Q}}(t)$
is finite for all time if
![]() ${\mathcal{Q}}(0)$
is sufficiently small. And in some situations all that can be proved is that
${\mathcal{Q}}(0)$
is sufficiently small. And in some situations all that can be proved is that
![]() ${\mathcal{Q}}(t)<\infty$
during a finite time interval whose length depends on
${\mathcal{Q}}(t)<\infty$
during a finite time interval whose length depends on
![]() ${\mathcal{Q}}(0)$
. Among the many well-known examples amenable to such analysis are the incompressible Navier–Stokes equations.
${\mathcal{Q}}(0)$
. Among the many well-known examples amenable to such analysis are the incompressible Navier–Stokes equations.
In the case of unforced flows on the d-dimensional torus (
![]() $\mathbb{T}^{d}$
), for example, the
$\mathbb{T}^{d}$
), for example, the
![]() $L^{2}$
norm of the velocity vector field – proportional to the square root of the kinetic energy – decays monotonically due to viscous dissipation so it is bounded uniformly in time by its initial value. Other norms may grow, however, and their amplification reflects aspects of the cascade processes that characterize much of the complexity of nonlinear fluid mechanics.
$L^{2}$
norm of the velocity vector field – proportional to the square root of the kinetic energy – decays monotonically due to viscous dissipation so it is bounded uniformly in time by its initial value. Other norms may grow, however, and their amplification reflects aspects of the cascade processes that characterize much of the complexity of nonlinear fluid mechanics.
In
![]() $d=3$
spatial dimensions the enstrophy – the square of the
$d=3$
spatial dimensions the enstrophy – the square of the
![]() $H^{1}$
semi-norm of the velocity, which is the same as the
$H^{1}$
semi-norm of the velocity, which is the same as the
![]() $L^{2}$
norm squared of the vorticity – can be amplified by vortex stretching. Analysis establishes that the growth rate of enstrophy is a bounded function of the enstrophy, but the resulting differential (in)equations only ensure that the enstrophy remains bounded forever if the initial data are sufficiently small – in particular if the product of the initial kinetic energy and enstrophy is sufficiently small (see e.g. Doering Reference Doering2009). That is, the possibility of finite-time singularities is not ruled out by energy analysis. The enstrophy corresponds to a particularly relevant norm in this problem because limits on the
$L^{2}$
norm squared of the vorticity – can be amplified by vortex stretching. Analysis establishes that the growth rate of enstrophy is a bounded function of the enstrophy, but the resulting differential (in)equations only ensure that the enstrophy remains bounded forever if the initial data are sufficiently small – in particular if the product of the initial kinetic energy and enstrophy is sufficiently small (see e.g. Doering Reference Doering2009). That is, the possibility of finite-time singularities is not ruled out by energy analysis. The enstrophy corresponds to a particularly relevant norm in this problem because limits on the
![]() $H^{1}$
semi-norm of the velocity can be ‘bootstrapped’ to bounds on norms of higher derivatives, establishing infinite differentiability of the solutions while the enstrophy remains finite. On the other hand, divergent upper bounds on enstrophy do not guarantee divergent solutions and no ‘blow-up’ has been demonstrated to date. Hence the question of long-time existence of smooth solutions of the three-dimensional (3D) incompressible Navier–Stokes equations remains one of the grand challenges for mathematical physics.
$H^{1}$
semi-norm of the velocity can be ‘bootstrapped’ to bounds on norms of higher derivatives, establishing infinite differentiability of the solutions while the enstrophy remains finite. On the other hand, divergent upper bounds on enstrophy do not guarantee divergent solutions and no ‘blow-up’ has been demonstrated to date. Hence the question of long-time existence of smooth solutions of the three-dimensional (3D) incompressible Navier–Stokes equations remains one of the grand challenges for mathematical physics.
Much more is known about solutions of the two-dimensional (2D) Navier–Stokes equations. In the case of unforced flows on
![]() $\mathbb{T}^{2}$
, both the
$\mathbb{T}^{2}$
, both the
![]() $L^{2}$
norm and the
$L^{2}$
norm and the
![]() $H^{1}$
semi-norm of solutions (i.e. both the kinetic energy and the enstrophy) decay monotonically in time, while the
$H^{1}$
semi-norm of solutions (i.e. both the kinetic energy and the enstrophy) decay monotonically in time, while the
![]() $H^{2}$
semi-norm of the velocity field – which is equal to the
$H^{2}$
semi-norm of the velocity field – which is equal to the
![]() $H^{1}$
semi-norm of the pseudo-scalar vorticity field, the square of which is known as the palinstrophy – can be amplified by a vorticity gradient stretching mechanism. Energy methods can be used to show that the palinstrophy of solutions of 2D incompressible Navier–Stokes equations remains finite for all time and there are no potential finite-time singularities. Indeed, even in the case of forced incompressible flows on
$H^{1}$
semi-norm of the pseudo-scalar vorticity field, the square of which is known as the palinstrophy – can be amplified by a vorticity gradient stretching mechanism. Energy methods can be used to show that the palinstrophy of solutions of 2D incompressible Navier–Stokes equations remains finite for all time and there are no potential finite-time singularities. Indeed, even in the case of forced incompressible flows on
![]() $\mathbb{T}^{2}$
, energy methods have been used by Dascaliuc, Foias & Jolly (Reference Dascaliuc, Foias and Jolly2010) to construct semi-integral curves which bound the projection of the global attractor of the 2D Navier–Stokes equations in the plane spanned by enstrophy and palinstrophy, ensuring that the average palinstrophy of solutions remains bounded. This type of energy analysis has also been used by Tran & Dritschel (Reference Tran and Dritschel2006) to study enstrophy dissipation in the inviscid limit of the 2D Navier–Stokes equations.
$\mathbb{T}^{2}$
, energy methods have been used by Dascaliuc, Foias & Jolly (Reference Dascaliuc, Foias and Jolly2010) to construct semi-integral curves which bound the projection of the global attractor of the 2D Navier–Stokes equations in the plane spanned by enstrophy and palinstrophy, ensuring that the average palinstrophy of solutions remains bounded. This type of energy analysis has also been used by Tran & Dritschel (Reference Tran and Dritschel2006) to study enstrophy dissipation in the inviscid limit of the 2D Navier–Stokes equations.
In this paper we investigate the quantitative accuracy of palinstrophy amplification bounds in order to evaluate the practical predictive power of energy method analysis. We consider the incompressible 2D Navier–Stokes equation, written here as an evolution equation for the vorticity
![]() $\unicode[STIX]{x1D714}$
, on spatial domain
$\unicode[STIX]{x1D714}$
, on spatial domain
![]() $\unicode[STIX]{x1D6FA}=\mathbb{T}^{2}$
(the
$\unicode[STIX]{x1D6FA}=\mathbb{T}^{2}$
(the
![]() $L\times L$
square with periodic boundary conditions):
$L\times L$
square with periodic boundary conditions):
where
![]() $\boldsymbol{u}$
is the velocity field,
$\boldsymbol{u}$
is the velocity field,
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity, and the velocity and the vorticity are related via
$\unicode[STIX]{x1D708}$
is the kinematic viscosity, and the velocity and the vorticity are related via
with
![]() $\unicode[STIX]{x1D735}^{\bot }=[\unicode[STIX]{x2202}_{x_{2}},-\unicode[STIX]{x2202}_{x_{1}}]$
. We are interested in the time evolution of the energy, enstrophy and palinstrophy defined here, respectively, as
$\unicode[STIX]{x1D735}^{\bot }=[\unicode[STIX]{x2202}_{x_{2}},-\unicode[STIX]{x2202}_{x_{1}}]$
. We are interested in the time evolution of the energy, enstrophy and palinstrophy defined here, respectively, as
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{P}}\{\boldsymbol{u}(\cdot ,t)\}=\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x0394}\boldsymbol{u}(\cdot ,t)|^{2}\,\text{d}\unicode[STIX]{x1D6FA}=\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D735}^{\bot }\unicode[STIX]{x1D714}(\cdot ,t)|^{2}\,\text{d}\unicode[STIX]{x1D6FA} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \quad =\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D714}(\cdot ,t)|^{2}\,\text{d}\unicode[STIX]{x1D6FA}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{P}}\{\boldsymbol{u}(\cdot ,t)\}=\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x0394}\boldsymbol{u}(\cdot ,t)|^{2}\,\text{d}\unicode[STIX]{x1D6FA}=\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D735}^{\bot }\unicode[STIX]{x1D714}(\cdot ,t)|^{2}\,\text{d}\unicode[STIX]{x1D6FA} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \quad =\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D714}(\cdot ,t)|^{2}\,\text{d}\unicode[STIX]{x1D6FA}. & \displaystyle\end{eqnarray}$$
The temporal evolution of
![]() ${\mathcal{K}}$
,
${\mathcal{K}}$
,
![]() ${\mathcal{E}}$
and
${\mathcal{E}}$
and
![]() ${\mathcal{P}}$
is given by
${\mathcal{P}}$
is given by
We are focused on the question of the sharpness of rigorous analytic bounds on the instantaneous and finite-time growth of palinstrophy, the only quantity from (1.3) with non-monotonic temporal dynamics. This is of interest because the functional analysis techniques used to derive the estimates rely only on the structure of the palinstrophy growth rate functional and fundamental relations between norms and not specifically on the physics associated with the problem at hand, making this study relevant to other partial differential equations.
Dimensional analysis requires that bounds on the instantaneous rate of palinstrophy generation,
![]() ${\mathcal{R}}\{\boldsymbol{u}(\cdot ,t)\}=\text{d}{\mathcal{P}}/\text{d}t$
, as a function of the instantaneous energy, enstrophy, palinstrophy, viscosity
${\mathcal{R}}\{\boldsymbol{u}(\cdot ,t)\}=\text{d}{\mathcal{P}}/\text{d}t$
, as a function of the instantaneous energy, enstrophy, palinstrophy, viscosity
![]() $\unicode[STIX]{x1D708}$
and domain length scale
$\unicode[STIX]{x1D708}$
and domain length scale
![]() $L$
– if such bounds exist at all – must be of the form
$L$
– if such bounds exist at all – must be of the form
where the prefactor
![]() $\unicode[STIX]{x1D6E4}$
is a dimensionless function of dimensionless combinations of the energy, enstrophy, palinstrophy, viscosity and system size. An estimate of this form (1.5) will be declared sharp if and only if
$\unicode[STIX]{x1D6E4}$
is a dimensionless function of dimensionless combinations of the energy, enstrophy, palinstrophy, viscosity and system size. An estimate of this form (1.5) will be declared sharp if and only if
where the maximum is over the set
![]() ${\mathcal{S}}$
of all spatially periodic divergence-free vector fields with energy, enstrophy and palinstrophy values
${\mathcal{S}}$
of all spatially periodic divergence-free vector fields with energy, enstrophy and palinstrophy values
![]() ${\mathcal{K}}$
,
${\mathcal{K}}$
,
![]() ${\mathcal{E}}$
and
${\mathcal{E}}$
and
![]() ${\mathcal{P}}$
on the
${\mathcal{P}}$
on the
![]() $L\times L$
square. Thus the sharpness of such estimates can be addressed by solving the constrained optimization problem
$L\times L$
square. Thus the sharpness of such estimates can be addressed by solving the constrained optimization problem
where the constraint manifold
![]() ${\mathcal{S}}$
can be interpreted as the intersection (in infinite-dimensional space) of spheres of given radius measured in different norms.
${\mathcal{S}}$
can be interpreted as the intersection (in infinite-dimensional space) of spheres of given radius measured in different norms.
Given the anisotropic nature of the constraint manifold, it is desirable to seek bounds and to test estimates with the fewest possible number of parameters in the prefactor
![]() $\unicode[STIX]{x1D6E4}$
. Moreover, if we are interested in estimates that could conceivably make sense in the infinite volume limit, i.e. if we seek optimizing flow structures and bounds that are independent of the domain scale
$\unicode[STIX]{x1D6E4}$
. Moreover, if we are interested in estimates that could conceivably make sense in the infinite volume limit, i.e. if we seek optimizing flow structures and bounds that are independent of the domain scale
![]() $L$
, then the prefactor can only be a function of the dimensionless combinations
$L$
, then the prefactor can only be a function of the dimensionless combinations
![]() ${\mathcal{K}}^{1/2}/\unicode[STIX]{x1D708}$
– a ratio that is naturally referred to as the Reynolds number
${\mathcal{K}}^{1/2}/\unicode[STIX]{x1D708}$
– a ratio that is naturally referred to as the Reynolds number
![]() $Re$
– and
$Re$
– and
![]() $({\mathcal{K}}{\mathcal{P}})^{1/2}/{\mathcal{E}}$
. If we further assume an
$({\mathcal{K}}{\mathcal{P}})^{1/2}/{\mathcal{E}}$
. If we further assume an
![]() $L$
-independent estimate for
$L$
-independent estimate for
![]() ${\mathcal{R}}\{\boldsymbol{u}(\cdot ,t)\}$
whose large palinstrophy behaviour is dominated non-trivially by the leading
${\mathcal{R}}\{\boldsymbol{u}(\cdot ,t)\}$
whose large palinstrophy behaviour is dominated non-trivially by the leading
![]() ${\mathcal{P}}^{3/2}$
in (1.5), then the asymptotic prefactor can be a function of
${\mathcal{P}}^{3/2}$
in (1.5), then the asymptotic prefactor can be a function of
![]() $Re$
alone. That is, the prefactor would be of the form
$Re$
alone. That is, the prefactor would be of the form
![]() $\unicode[STIX]{x1D6E4}({\mathcal{K}},{\mathcal{E}},{\mathcal{P}},\unicode[STIX]{x1D708},L)=\unicode[STIX]{x1D6FE}(Re)$
. In fact there are rigorous upper bounds on the palinstrophy generation rate of the form
$\unicode[STIX]{x1D6E4}({\mathcal{K}},{\mathcal{E}},{\mathcal{P}},\unicode[STIX]{x1D708},L)=\unicode[STIX]{x1D6FE}(Re)$
. In fact there are rigorous upper bounds on the palinstrophy generation rate of the form
![]() ${\mathcal{R}}\leqslant \unicode[STIX]{x1D6FE}(Re)\,{\mathcal{P}}^{3/2}$
. Ayala & Protas (Reference Ayala and Protas2014a
) proved that
${\mathcal{R}}\leqslant \unicode[STIX]{x1D6FE}(Re)\,{\mathcal{P}}^{3/2}$
. Ayala & Protas (Reference Ayala and Protas2014a
) proved that
![]() ${\mathcal{R}}\lesssim Re\,{\mathcal{P}}^{3/2}$
and computed optimal vector fields indicating that the
${\mathcal{R}}\lesssim Re\,{\mathcal{P}}^{3/2}$
and computed optimal vector fields indicating that the
![]() $3/2$
exponent for
$3/2$
exponent for
![]() ${\mathcal{P}}$
is sharp but that the
${\mathcal{P}}$
is sharp but that the
![]() $O(Re)$
prefactor is not sharp.
$O(Re)$
prefactor is not sharp.
In this work we assess the sharpness of the improved estimate
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\text{d}{\mathcal{P}}}{\text{d}t}={\mathcal{R}}\{\boldsymbol{u}\}\leqslant \left(a+b\sqrt{\ln Re+c}\right){\mathcal{P}}^{3/2}\\ \displaystyle \text{with}\quad a=0,\quad b=\sqrt{2\unicode[STIX]{x03C0}},\quad c=-\ln \left(\frac{2}{\sqrt{\unicode[STIX]{x03C0}}}\right),\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\text{d}{\mathcal{P}}}{\text{d}t}={\mathcal{R}}\{\boldsymbol{u}\}\leqslant \left(a+b\sqrt{\ln Re+c}\right){\mathcal{P}}^{3/2}\\ \displaystyle \text{with}\quad a=0,\quad b=\sqrt{2\unicode[STIX]{x03C0}},\quad c=-\ln \left(\frac{2}{\sqrt{\unicode[STIX]{x03C0}}}\right),\end{array}\right\}\end{eqnarray}$$
derived in § A.1, for sufficiently large
![]() $Re$
and
$Re$
and
![]() ${\mathcal{P}}$
. Estimate (1.8) falls in the category of power-law estimates of the form
${\mathcal{P}}$
. Estimate (1.8) falls in the category of power-law estimates of the form
![]() $\text{d}{\mathcal{P}}/\text{d}t\leqslant \unicode[STIX]{x1D6E4}{\mathcal{P}}^{\unicode[STIX]{x1D6FC}}$
available in the literature, e.g. equation (2.6) in Tran & Dritschel (Reference Tran and Dritschel2006) and equation (6.6) in Dascaliuc et al. (Reference Dascaliuc, Foias and Jolly2010), with the difference being the functional form of the prefactor
$\text{d}{\mathcal{P}}/\text{d}t\leqslant \unicode[STIX]{x1D6E4}{\mathcal{P}}^{\unicode[STIX]{x1D6FC}}$
available in the literature, e.g. equation (2.6) in Tran & Dritschel (Reference Tran and Dritschel2006) and equation (6.6) in Dascaliuc et al. (Reference Dascaliuc, Foias and Jolly2010), with the difference being the functional form of the prefactor
![]() $\unicode[STIX]{x1D6E4}$
and the exponent
$\unicode[STIX]{x1D6E4}$
and the exponent
![]() $\unicode[STIX]{x1D6FC}$
. In this paper, we demonstrate (i) the sharpness of the upper bound (1.8) and (ii) the extent to which the Navier–Stokes flow starting from instantaneously optimal fields
$\unicode[STIX]{x1D6FC}$
. In this paper, we demonstrate (i) the sharpness of the upper bound (1.8) and (ii) the extent to which the Navier–Stokes flow starting from instantaneously optimal fields
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{S}}}$
saturates the corresponding finite-time estimates for palinstrophy amplification
$\widetilde{\boldsymbol{u}}_{{\mathcal{S}}}$
saturates the corresponding finite-time estimates for palinstrophy amplification
and
That the prefactors
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D713}$
depend on
$\unicode[STIX]{x1D713}$
depend on
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\unicode[STIX]{x1D708}$
only via the (initial) Reynolds number
$\unicode[STIX]{x1D708}$
only via the (initial) Reynolds number
![]() $Re_{0}={\mathcal{K}}^{1/2}(0)/\unicode[STIX]{x1D708}$
implies in particular that the peak palinstrophy amplification factor depends on the viscosity only through its appearance in the explicit function
$Re_{0}={\mathcal{K}}^{1/2}(0)/\unicode[STIX]{x1D708}$
implies in particular that the peak palinstrophy amplification factor depends on the viscosity only through its appearance in the explicit function
![]() $\unicode[STIX]{x1D713}(Re_{0})$
. We note, however, that our study does not indicate that our estimate for
$\unicode[STIX]{x1D713}(Re_{0})$
. We note, however, that our study does not indicate that our estimate for
![]() $\unicode[STIX]{x1D713}(Re)$
is sharp with respect to its Reynolds-number dependence.
$\unicode[STIX]{x1D713}(Re)$
is sharp with respect to its Reynolds-number dependence.
The remainder of this paper is as follows. The instantaneous growth of palinstrophy and structure of the optimal vector fields is reviewed in § 2. Finite-time growth and maximal amplification of palinstrophy is studied in § 3. Section 4 contains a discussion of the results along with a conclusion and closing remarks. Detailed derivation (from elementary first principles) of the improved analytic estimate (1.8) can be found in appendix A.
2 Instantaneously optimal growth of palinstrophy
Given the dependence of analytic estimate (1.8) on palinstrophy
![]() ${\mathcal{P}}$
and Reynolds number
${\mathcal{P}}$
and Reynolds number
![]() $Re={\mathcal{K}}^{1/2}/\unicode[STIX]{x1D708}$
, the sharpness of the estimate is addressed by numerically solving the constrained optimization problem for the objective functional
$Re={\mathcal{K}}^{1/2}/\unicode[STIX]{x1D708}$
, the sharpness of the estimate is addressed by numerically solving the constrained optimization problem for the objective functional
![]() ${\mathcal{R}}$
defined in (1.4):
${\mathcal{R}}$
defined in (1.4):
where
In order to investigate the asymptotic behaviour of
![]() ${\mathcal{R}}$
as
${\mathcal{R}}$
as
![]() ${\mathcal{P}}_{0}\rightarrow \infty$
, (2.1) is solved numerically for a wide range of values of the energy
${\mathcal{P}}_{0}\rightarrow \infty$
, (2.1) is solved numerically for a wide range of values of the energy
![]() ${\mathcal{K}}_{0}\in [1,100]$
and some choices of
${\mathcal{K}}_{0}\in [1,100]$
and some choices of
![]() ${\mathcal{P}}_{0}\gg {\mathcal{K}}_{0}/C_{P}^{2}$
, where
${\mathcal{P}}_{0}\gg {\mathcal{K}}_{0}/C_{P}^{2}$
, where
![]() $C_{P}=1/(2\unicode[STIX]{x03C0})^{2}$
is the Poincaré constant for the unit 2D torus. We compute with the numerical value
$C_{P}=1/(2\unicode[STIX]{x03C0})^{2}$
is the Poincaré constant for the unit 2D torus. We compute with the numerical value
![]() $\unicode[STIX]{x1D708}=10^{-3}$
for the kinematic viscosity, kept constant in all computations, allowing us to probe the dependence of the optimal rate of growth of palinstrophy for values of the Reynolds number in the range
$\unicode[STIX]{x1D708}=10^{-3}$
for the kinematic viscosity, kept constant in all computations, allowing us to probe the dependence of the optimal rate of growth of palinstrophy for values of the Reynolds number in the range
![]() $Re_{0}\in [10^{3},10^{4}]$
. For a given value of
$Re_{0}\in [10^{3},10^{4}]$
. For a given value of
![]() $Re_{0}$
, the value of
$Re_{0}$
, the value of
![]() ${\mathcal{P}}_{0}$
defining the constraint manifold
${\mathcal{P}}_{0}$
defining the constraint manifold
![]() ${\mathcal{S}}_{{\mathcal{K}}_{0},{\mathcal{P}}_{0}}$
is chosen so that the optimal vorticity field
${\mathcal{S}}_{{\mathcal{K}}_{0},{\mathcal{P}}_{0}}$
is chosen so that the optimal vorticity field
![]() $\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
of the optimal vector field
$\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
of the optimal vector field
![]() $\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}=\text{argmax}\,{\mathcal{R}}(\boldsymbol{u})$
is sufficiently localized in the computational domain, allowing for the effect of boundaries to be neglected. A family of optimal fields parametrized by their palinstrophy is then constructed by rescaling the optimal field
$\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}=\text{argmax}\,{\mathcal{R}}(\boldsymbol{u})$
is sufficiently localized in the computational domain, allowing for the effect of boundaries to be neglected. A family of optimal fields parametrized by their palinstrophy is then constructed by rescaling the optimal field
![]() $\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
using the self-similar approach described in appendix B. Details of the numerical methods for the variational problem (2.1) can be found in the work of Ayala & Protas (Reference Ayala and Protas2014a
).
$\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
using the self-similar approach described in appendix B. Details of the numerical methods for the variational problem (2.1) can be found in the work of Ayala & Protas (Reference Ayala and Protas2014a
).
Figures 1(a) and 1(b) show the optimal vorticity fields
![]() $\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
corresponding to values of Reynolds number
$\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
corresponding to values of Reynolds number
![]() $Re_{0}=10^{3}$
and
$Re_{0}=10^{3}$
and
![]() $Re_{0}=10^{4}$
, respectively, for a fixed value of palinstrophy
$Re_{0}=10^{4}$
, respectively, for a fixed value of palinstrophy
![]() ${\mathcal{P}}_{0}=10^{8}$
. In each case, the optimal vorticity field consists of a vortex quadrupole of finite area and a localized region of strong vorticity responsible for the extreme growth of palinstrophy. The size of the optimal vortical structure, relative to the size of the domain
${\mathcal{P}}_{0}=10^{8}$
. In each case, the optimal vorticity field consists of a vortex quadrupole of finite area and a localized region of strong vorticity responsible for the extreme growth of palinstrophy. The size of the optimal vortical structure, relative to the size of the domain
![]() $\unicode[STIX]{x1D6FA}$
, has a positive correlation with the Reynolds number. A thorough discussion of the properties of the optimal vorticity fields, and their corresponding time evolution under 2D Navier–Stokes dynamics, can be found in Ayala & Protas (Reference Ayala and Protas2014a
,Reference Ayala and Protas
b
).
$\unicode[STIX]{x1D6FA}$
, has a positive correlation with the Reynolds number. A thorough discussion of the properties of the optimal vorticity fields, and their corresponding time evolution under 2D Navier–Stokes dynamics, can be found in Ayala & Protas (Reference Ayala and Protas2014a
,Reference Ayala and Protas
b
).

Figure 1. Optimal vorticity field
![]() $\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
corresponding to
$\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
corresponding to
![]() ${\mathcal{P}}_{0}=10^{8}$
and values of Reynolds number (a)
${\mathcal{P}}_{0}=10^{8}$
and values of Reynolds number (a)
![]() $Re_{0}=10^{3}$
and (b)
$Re_{0}=10^{3}$
and (b)
![]() $Re_{0}=10^{4}$
. Streamlines corresponding to selected level sets of the streamfunction
$Re_{0}=10^{4}$
. Streamlines corresponding to selected level sets of the streamfunction
![]() $\unicode[STIX]{x1D713}=-\unicode[STIX]{x0394}^{-1}\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
are shown for reference.
$\unicode[STIX]{x1D713}=-\unicode[STIX]{x0394}^{-1}\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
are shown for reference.
To verify the power-law nature of the optimal instantaneous rate of production of palinstrophy and assess the sharpness of estimate (1.8) with respect to the predicted behaviour
![]() $\text{d}{\mathcal{P}}/\text{d}t\sim {\mathcal{P}}^{3/2}$
, figure 2 shows the dependence on
$\text{d}{\mathcal{P}}/\text{d}t\sim {\mathcal{P}}^{3/2}$
, figure 2 shows the dependence on
![]() ${\mathcal{P}}_{0}$
of the compensated optimal rate of growth of palinstrophy,
${\mathcal{P}}_{0}$
of the compensated optimal rate of growth of palinstrophy,
for different values of Reynolds number in the interval
![]() $Re_{0}\in [10^{3},10^{4}]$
. The data shown here are an extension of the results reported by Ayala & Protas (Reference Ayala and Protas2014a
). To focus our discussion, we only include the portion of the data where a clear power-law behaviour for
$Re_{0}\in [10^{3},10^{4}]$
. The data shown here are an extension of the results reported by Ayala & Protas (Reference Ayala and Protas2014a
). To focus our discussion, we only include the portion of the data where a clear power-law behaviour for
![]() ${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}})$
is observed, corresponding to values of palinstrophy much larger than the Poincaré limit
${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}})$
is observed, corresponding to values of palinstrophy much larger than the Poincaré limit
![]() ${\mathcal{P}}_{0}\rightarrow (\unicode[STIX]{x1D708}Re_{0}/C_{P})^{2}$
. As expected from the fact that estimate (1.8) is sharp with respect to the exponent
${\mathcal{P}}_{0}\rightarrow (\unicode[STIX]{x1D708}Re_{0}/C_{P})^{2}$
. As expected from the fact that estimate (1.8) is sharp with respect to the exponent
![]() $\unicode[STIX]{x1D6FC}=3/2$
, figure 2 shows that the compensated optimal rate of growth of palinstrophy
$\unicode[STIX]{x1D6FC}=3/2$
, figure 2 shows that the compensated optimal rate of growth of palinstrophy
![]() $\widetilde{{\mathcal{R}}}_{Re_{0},{\mathcal{P}}_{0}}$
, which corresponds to the prefactor
$\widetilde{{\mathcal{R}}}_{Re_{0},{\mathcal{P}}_{0}}$
, which corresponds to the prefactor
![]() $\unicode[STIX]{x1D6FE}(Re)$
, is indeed independent of palinstrophy in the limit
$\unicode[STIX]{x1D6FE}(Re)$
, is indeed independent of palinstrophy in the limit
![]() ${\mathcal{P}}_{0}\rightarrow \infty$
.
${\mathcal{P}}_{0}\rightarrow \infty$
.
On the other hand, to assess the sharpness of estimate (1.8) with respect to the prefactor
figures 3(a) and 3(b) show the dependence of the optimal rate of growth of palinstrophy
![]() ${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}})$
on
${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}})$
on
![]() $\ln Re_{0}$
and of the compensated optimal rate of growth of palinstrophy
$\ln Re_{0}$
and of the compensated optimal rate of growth of palinstrophy
![]() $\widetilde{{\mathcal{R}}}_{Re_{0},{\mathcal{P}}_{0}}$
on
$\widetilde{{\mathcal{R}}}_{Re_{0},{\mathcal{P}}_{0}}$
on
![]() $\ln Re_{0}$
, respectively, for three different values of palinstrophy,
$\ln Re_{0}$
, respectively, for three different values of palinstrophy,
![]() ${\mathcal{P}}_{0}=4.6\times 10^{7}$
,
${\mathcal{P}}_{0}=4.6\times 10^{7}$
,
![]() ${\mathcal{P}}_{0}=6.8\times 10^{7}$
and
${\mathcal{P}}_{0}=6.8\times 10^{7}$
and
![]() ${\mathcal{P}}_{0}=10^{8}$
. It can be observed in figure 3(b) that all data points collapse onto a single curve of the form
${\mathcal{P}}_{0}=10^{8}$
. It can be observed in figure 3(b) that all data points collapse onto a single curve of the form
with fitted parameters
shown in the figure as a red dashed curve. The values of
![]() $\tilde{a}$
,
$\tilde{a}$
,
![]() $\tilde{b}$
and
$\tilde{b}$
and
![]() $\tilde{c}$
are obtained by averaging over
$\tilde{c}$
are obtained by averaging over
![]() ${\mathcal{P}}_{0}$
the values of
${\mathcal{P}}_{0}$
the values of
![]() $a_{{\mathcal{P}}_{0}}$
,
$a_{{\mathcal{P}}_{0}}$
,
![]() $b_{{\mathcal{P}}_{0}}$
and
$b_{{\mathcal{P}}_{0}}$
and
![]() $c_{{\mathcal{P}}_{0}}$
corresponding to the parameters that provide the least-squares fit of the data to a model of the same form as estimate (1.8). Although the values of the fitted parameters
$c_{{\mathcal{P}}_{0}}$
corresponding to the parameters that provide the least-squares fit of the data to a model of the same form as estimate (1.8). Although the values of the fitted parameters
![]() $\tilde{a}$
,
$\tilde{a}$
,
![]() $\tilde{b}$
and
$\tilde{b}$
and
![]() $\tilde{c}$
differ from the corresponding values in estimate (1.8), the fundamental dependence of
$\tilde{c}$
differ from the corresponding values in estimate (1.8), the fundamental dependence of
![]() $\unicode[STIX]{x1D6FE}(Re)$
on
$\unicode[STIX]{x1D6FE}(Re)$
on
![]() $Re$
is correctly captured by the behaviour of
$Re$
is correctly captured by the behaviour of
![]() $\unicode[STIX]{x1D6FE}(Re_{0})=\widetilde{{\mathcal{R}}}_{Re_{0},{\mathcal{P}}_{0}}$
, providing positive evidence for the sharpness of estimate (1.8) with respect to the prefactor
$\unicode[STIX]{x1D6FE}(Re_{0})=\widetilde{{\mathcal{R}}}_{Re_{0},{\mathcal{P}}_{0}}$
, providing positive evidence for the sharpness of estimate (1.8) with respect to the prefactor
![]() $\unicode[STIX]{x1D6FE}(Re)$
. To summarize, the information presented in figures 2 and 3(a,b) indicates that the estimate
$\unicode[STIX]{x1D6FE}(Re)$
. To summarize, the information presented in figures 2 and 3(a,b) indicates that the estimate
is indeed sharp with respect to both the exponent
![]() $\unicode[STIX]{x1D6FC}=3/2$
and the functional form of the prefactor
$\unicode[STIX]{x1D6FC}=3/2$
and the functional form of the prefactor
![]() $\unicode[STIX]{x1D6FE}(Re)=a+b\sqrt{\ln Re+c}$
.
$\unicode[STIX]{x1D6FE}(Re)=a+b\sqrt{\ln Re+c}$
.

Figure 2. Compensated optimal instantaneous rate of growth of palinstrophy
![]() $\widetilde{{\mathcal{R}}}_{Re_{0},{\mathcal{P}}_{0}}={\mathcal{P}}_{0}^{-3/2}{\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{K}}_{0},{\mathcal{P}}_{0}})$
as a function of
$\widetilde{{\mathcal{R}}}_{Re_{0},{\mathcal{P}}_{0}}={\mathcal{P}}_{0}^{-3/2}{\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{K}}_{0},{\mathcal{P}}_{0}})$
as a function of
![]() ${\mathcal{P}}_{0}$
, for values of Reynolds number
${\mathcal{P}}_{0}$
, for values of Reynolds number
![]() $Re_{0}\in [10^{3},10^{4}]$
. The arrow indicates the direction of increasing
$Re_{0}\in [10^{3},10^{4}]$
. The arrow indicates the direction of increasing
![]() $Re_{0}$
.
$Re_{0}$
.

Figure 3. (a) Optimal rate of growth of palinstrophy,
![]() ${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{K}}_{0},{\mathcal{P}}_{0}})$
, as a function of
${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{K}}_{0},{\mathcal{P}}_{0}})$
, as a function of
![]() $\ln Re_{0}$
, for values of palinstrophy
$\ln Re_{0}$
, for values of palinstrophy
![]() ${\mathcal{P}}_{0}=4.6\times 10^{7}$
(blue stars),
${\mathcal{P}}_{0}=4.6\times 10^{7}$
(blue stars),
![]() ${\mathcal{P}}_{0}=6.8\times 10^{7}$
(red diamonds) and
${\mathcal{P}}_{0}=6.8\times 10^{7}$
(red diamonds) and
![]() ${\mathcal{P}}_{0}=10^{8}$
(black circles). (b) Compensated optimal rate of growth of palinstrophy,
${\mathcal{P}}_{0}=10^{8}$
(black circles). (b) Compensated optimal rate of growth of palinstrophy,
![]() ${\mathcal{P}}_{0}^{-3/2}{\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{K}}_{0},{\mathcal{P}}_{0}})$
, as a function of
${\mathcal{P}}_{0}^{-3/2}{\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{K}}_{0},{\mathcal{P}}_{0}})$
, as a function of
![]() $\ln Re_{0}$
, for the same values of palinstrophy as in (a). All curves collapse onto a single ‘universal’ curve of the form
$\ln Re_{0}$
, for the same values of palinstrophy as in (a). All curves collapse onto a single ‘universal’ curve of the form
![]() $\tilde{a}+\tilde{b}\sqrt{\ln Re_{0}+\tilde{c}}$
, with
$\tilde{a}+\tilde{b}\sqrt{\ln Re_{0}+\tilde{c}}$
, with
![]() $\tilde{a}=-0.093$
,
$\tilde{a}=-0.093$
,
![]() $\tilde{b}=0.128$
and
$\tilde{b}=0.128$
and
![]() $\tilde{c}=-4.38$
, shown as a red dashed curve.
$\tilde{c}=-4.38$
, shown as a red dashed curve.

Figure 4. Rescaled compensated spectral density
![]() $(|\boldsymbol{k}|/\unicode[STIX]{x1D706}_{0})^{2}S(|\boldsymbol{k}|/\unicode[STIX]{x1D706}_{0})$
, for
$(|\boldsymbol{k}|/\unicode[STIX]{x1D706}_{0})^{2}S(|\boldsymbol{k}|/\unicode[STIX]{x1D706}_{0})$
, for
![]() $\unicode[STIX]{x1D706}_{0}$
defined in (2.10), corresponding to
$\unicode[STIX]{x1D706}_{0}$
defined in (2.10), corresponding to
![]() $Re=10^{3}$
and palinstrophy values
$Re=10^{3}$
and palinstrophy values
![]() ${\mathcal{P}}_{0}=1.71\times 10^{6}$
,
${\mathcal{P}}_{0}=1.71\times 10^{6}$
,
![]() ${\mathcal{P}}_{0}=1.71\times 10^{7}$
and
${\mathcal{P}}_{0}=1.71\times 10^{7}$
and
![]() ${\mathcal{P}}_{0}=1.71\times 10^{8}$
. All curves collapse onto a ‘universal’ spectral density. The parameters
${\mathcal{P}}_{0}=1.71\times 10^{8}$
. All curves collapse onto a ‘universal’ spectral density. The parameters
![]() $P_{1}\approx 0.86$
and
$P_{1}\approx 0.86$
and
![]() $P_{2}\approx 1.88$
defining the Novikov phase diagram are shown as vertical lines.
$P_{2}\approx 1.88$
defining the Novikov phase diagram are shown as vertical lines.
To complete our analysis of the optimal instantaneous growth of palinstrophy, we now look at the structure of the spectrum of the optimal fields
![]() $\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
. A key step in the derivation of estimate (1.8) (see § A.1) is the choice of cut-off wavenumbers
$\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
. A key step in the derivation of estimate (1.8) (see § A.1) is the choice of cut-off wavenumbers
![]() $\unicode[STIX]{x1D6EC}_{1}$
and
$\unicode[STIX]{x1D6EC}_{1}$
and
![]() $\unicode[STIX]{x1D6EC}_{2}$
that define the sets
$\unicode[STIX]{x1D6EC}_{2}$
that define the sets
![]() $\{|\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{1}\}$
,
$\{|\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{1}\}$
,
![]() $\{\unicode[STIX]{x1D6EC}_{1}<|\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{2}\}$
and
$\{\unicode[STIX]{x1D6EC}_{1}<|\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{2}\}$
and
![]() $\{|\boldsymbol{k}|>\unicode[STIX]{x1D6EC}_{2}\}$
in wavenumber space, where
$\{|\boldsymbol{k}|>\unicode[STIX]{x1D6EC}_{2}\}$
in wavenumber space, where
![]() $\sum |\boldsymbol{k}||\widehat{u}(\boldsymbol{k})|$
displays different behaviour. As discussed in the appendix,
$\sum |\boldsymbol{k}||\widehat{u}(\boldsymbol{k})|$
displays different behaviour. As discussed in the appendix,
![]() $\unicode[STIX]{x1D6EC}_{1}$
and
$\unicode[STIX]{x1D6EC}_{1}$
and
![]() $\unicode[STIX]{x1D6EC}_{2}$
depend on
$\unicode[STIX]{x1D6EC}_{2}$
depend on
![]() ${\mathcal{K}}$
,
${\mathcal{K}}$
,
![]() ${\mathcal{P}}$
and
${\mathcal{P}}$
and
![]() $\unicode[STIX]{x1D708}$
as
$\unicode[STIX]{x1D708}$
as
where
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
are dimensionless parameters. Figure 4 shows the rescaled compensated spectral density
$c_{2}$
are dimensionless parameters. Figure 4 shows the rescaled compensated spectral density
![]() $(|\boldsymbol{k}|/\unicode[STIX]{x1D706}_{0})^{2}\,S(|\boldsymbol{k}|/\unicode[STIX]{x1D706}_{0})$
corresponding to the optimal fields
$(|\boldsymbol{k}|/\unicode[STIX]{x1D706}_{0})^{2}\,S(|\boldsymbol{k}|/\unicode[STIX]{x1D706}_{0})$
corresponding to the optimal fields
![]() $\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
for
$\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
for
![]() $Re=10^{3}$
and palinstrophy values
$Re=10^{3}$
and palinstrophy values
![]() ${\mathcal{P}}_{0}=1.71\times 10^{6}$
,
${\mathcal{P}}_{0}=1.71\times 10^{6}$
,
![]() ${\mathcal{P}}_{0}=1.71\times 10^{7}$
and
${\mathcal{P}}_{0}=1.71\times 10^{7}$
and
![]() ${\mathcal{P}}_{0}=1.71\times 10^{8}$
. The spectral density
${\mathcal{P}}_{0}=1.71\times 10^{8}$
. The spectral density
![]() $S(|\boldsymbol{k}|)$
is computed as
$S(|\boldsymbol{k}|)$
is computed as
and the scaling factor
![]() $\unicode[STIX]{x1D706}_{0}$
is given by
$\unicode[STIX]{x1D706}_{0}$
is given by
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}^{2}=\frac{\displaystyle \int _{0}^{\infty }|\boldsymbol{k}|^{2}S(|\boldsymbol{k}|)\,\text{d}|\boldsymbol{k}|}{\displaystyle \int _{0}^{\infty }S(|\boldsymbol{k}|)\,\text{d}|\boldsymbol{k}|}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{0}^{2}=\frac{\displaystyle \int _{0}^{\infty }|\boldsymbol{k}|^{2}S(|\boldsymbol{k}|)\,\text{d}|\boldsymbol{k}|}{\displaystyle \int _{0}^{\infty }S(|\boldsymbol{k}|)\,\text{d}|\boldsymbol{k}|}.\end{eqnarray}$$
The two wavenumbers
![]() $\unicode[STIX]{x1D706}_{1}$
and
$\unicode[STIX]{x1D706}_{1}$
and
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FA}}$
, computed as
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FA}}$
, computed as
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{1}=\frac{\displaystyle \int _{0}^{\infty }|\boldsymbol{k}|S(|\boldsymbol{k}|)\,\text{d}|\boldsymbol{k}|}{\displaystyle \int _{0}^{\infty }S(|\boldsymbol{k}|)\,\text{d}|\boldsymbol{k}|}\quad \text{and}\quad \unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FA}}=\frac{\displaystyle \int _{0}^{\infty }|\boldsymbol{k}|^{3}S(|\boldsymbol{k}|)\,\text{d}|\boldsymbol{k}|}{\displaystyle \int _{0}^{\infty }|\boldsymbol{k}|^{2}S(|\boldsymbol{k}|)\,\text{d}|\boldsymbol{k}|},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{1}=\frac{\displaystyle \int _{0}^{\infty }|\boldsymbol{k}|S(|\boldsymbol{k}|)\,\text{d}|\boldsymbol{k}|}{\displaystyle \int _{0}^{\infty }S(|\boldsymbol{k}|)\,\text{d}|\boldsymbol{k}|}\quad \text{and}\quad \unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FA}}=\frac{\displaystyle \int _{0}^{\infty }|\boldsymbol{k}|^{3}S(|\boldsymbol{k}|)\,\text{d}|\boldsymbol{k}|}{\displaystyle \int _{0}^{\infty }|\boldsymbol{k}|^{2}S(|\boldsymbol{k}|)\,\text{d}|\boldsymbol{k}|},\end{eqnarray}$$
define, along with the scaling factor
![]() $\unicode[STIX]{x1D706}_{0}$
, the Novikov phase diagram of the flow (Santangelo, Benzi & Legras Reference Santangelo, Benzi and Legras1989) in terms of the dimensionless parameters
$\unicode[STIX]{x1D706}_{0}$
, the Novikov phase diagram of the flow (Santangelo, Benzi & Legras Reference Santangelo, Benzi and Legras1989) in terms of the dimensionless parameters
which satisfy
and are shown in figure 4 as vertical lines located at
![]() $P_{1}\approx 0.86$
and
$P_{1}\approx 0.86$
and
![]() $P_{2}\approx 1.88$
. The parameter
$P_{2}\approx 1.88$
. The parameter
![]() $P_{1}$
corresponds to the location of the first local maximum of the compensated spectral density
$P_{1}$
corresponds to the location of the first local maximum of the compensated spectral density
![]() $|\boldsymbol{k}|^{2}S(|\boldsymbol{k}|)$
. As expected from the self-similar construction of the optimal fields
$|\boldsymbol{k}|^{2}S(|\boldsymbol{k}|)$
. As expected from the self-similar construction of the optimal fields
![]() $\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
, the rescaled compensated spectral densities collapse onto a single ‘universal’ spectral density, confirming the scale-invariant nature of
$\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
, the rescaled compensated spectral densities collapse onto a single ‘universal’ spectral density, confirming the scale-invariant nature of
![]() $\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
.
$\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
.
3 Finite-time growth of palinstrophy
We now focus our attention on the growth of palinstrophy
![]() ${\mathcal{P}}$
over finite time. Time integration of the sharp instantaneous estimate (1.8) and neglect of the time dependence of
${\mathcal{P}}$
over finite time. Time integration of the sharp instantaneous estimate (1.8) and neglect of the time dependence of
![]() $Re$
leads to the finite-time estimates
$Re$
leads to the finite-time estimates
and
where the prefactor
![]() $\unicode[STIX]{x1D713}(Re_{0})$
depends exclusively on the initial Reynolds number
$\unicode[STIX]{x1D713}(Re_{0})$
depends exclusively on the initial Reynolds number
![]() $Re_{0}={\mathcal{K}}^{1/2}(0)/\unicode[STIX]{x1D708}$
, and the values of
$Re_{0}={\mathcal{K}}^{1/2}(0)/\unicode[STIX]{x1D708}$
, and the values of
![]() $a$
,
$a$
,
![]() $b$
and
$b$
and
![]() $c$
are given in (2.5) and obtained by the fitting procedure described in § 2. Note that although estimate (3.1) is time-dependent, it can still be used to determine to what extent the fields saturating a sharp instantaneous estimate produce time-dependent flows which also saturate a time-dependent estimate. Also note that while (3.2) is an a priori estimate in the form of a power law which has been obtained from a sharp instantaneous estimate, there is no guarantee that it will be sharp with respect to either the exponent or the prefactor in the power law. The derivation of estimates (3.1) and (3.2) can be found in § A.2.
$c$
are given in (2.5) and obtained by the fitting procedure described in § 2. Note that although estimate (3.1) is time-dependent, it can still be used to determine to what extent the fields saturating a sharp instantaneous estimate produce time-dependent flows which also saturate a time-dependent estimate. Also note that while (3.2) is an a priori estimate in the form of a power law which has been obtained from a sharp instantaneous estimate, there is no guarantee that it will be sharp with respect to either the exponent or the prefactor in the power law. The derivation of estimates (3.1) and (3.2) can be found in § A.2.
In order to assess the sharpness of the finite-time estimates (3.1) and (3.2), we numerically solve the Cauchy problem (1.1a-c
) using the instantaneously optimal vorticity fields
![]() $\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
as initial condition, and carefully monitor the time evolution of different diagnostics, e.g.
$\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
as initial condition, and carefully monitor the time evolution of different diagnostics, e.g.
![]() ${\mathcal{K}}(t)$
,
${\mathcal{K}}(t)$
,
![]() ${\mathcal{E}}(t)$
and
${\mathcal{E}}(t)$
and
![]() ${\mathcal{P}}(t)$
, for sufficiently long times. Time integration is performed using an adaptive Runge–Kutta scheme of order 4, and spatial discretization is performed using a pseudo-spectral Fourier–Galerkin method, with the standard ‘
${\mathcal{P}}(t)$
, for sufficiently long times. Time integration is performed using an adaptive Runge–Kutta scheme of order 4, and spatial discretization is performed using a pseudo-spectral Fourier–Galerkin method, with the standard ‘
![]() $2/3$
’ dealiasing rule. The resolution is increased accordingly, ranging from
$2/3$
’ dealiasing rule. The resolution is increased accordingly, ranging from
![]() $512^{2}$
for low-
$512^{2}$
for low-
![]() $Re_{0}$
, low-
$Re_{0}$
, low-
![]() ${\mathcal{P}}_{0}$
simulations, to
${\mathcal{P}}_{0}$
simulations, to
![]() $4096^{2}$
for high-
$4096^{2}$
for high-
![]() $Re_{0}$
, high-
$Re_{0}$
, high-
![]() ${\mathcal{P}}_{0}$
simulations. We refer the reader to the work by Ayala & Protas (Reference Ayala and Protas2014b
) for a thorough discussion of the time evolution of the instantaneously optimal vorticity
${\mathcal{P}}_{0}$
simulations. We refer the reader to the work by Ayala & Protas (Reference Ayala and Protas2014b
) for a thorough discussion of the time evolution of the instantaneously optimal vorticity
![]() $\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
.
$\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
.
The sharpness of the pointwise estimate (3.1) can be studied by considering the functions
and comparing their behaviour as functions of time. For this, consider the characteristic time scale
![]() $t_{max}$
and the characteristic palinstrophy scale
$t_{max}$
and the characteristic palinstrophy scale
![]() $\unicode[STIX]{x1D70C}$
defined as
$\unicode[STIX]{x1D70C}$
defined as
and the rescaled diagnostics
and
With these definitions, the pointwise estimate (3.1) simply reads
![]() $f(\unicode[STIX]{x1D70F})\leqslant g(\unicode[STIX]{x1D70F})$
. Figure 5 shows the dependence of
$f(\unicode[STIX]{x1D70F})\leqslant g(\unicode[STIX]{x1D70F})$
. Figure 5 shows the dependence of
![]() $f$
and
$f$
and
![]() $g$
on the rescaled time
$g$
on the rescaled time
![]() $\unicode[STIX]{x1D70F}=t/t_{max}$
, corresponding to different values of
$\unicode[STIX]{x1D70F}=t/t_{max}$
, corresponding to different values of
![]() $Re\in [10^{3},10^{4}]$
and
$Re\in [10^{3},10^{4}]$
and
![]() ${\mathcal{P}}_{0}\in [1.7\times 10^{6},1.7\times 10^{9}]$
. As expected from the fact that the initial condition is constructed in a self-similar manner, all data collapse onto single ‘universal’ curves for
${\mathcal{P}}_{0}\in [1.7\times 10^{6},1.7\times 10^{9}]$
. As expected from the fact that the initial condition is constructed in a self-similar manner, all data collapse onto single ‘universal’ curves for
![]() $f$
and
$f$
and
![]() $g$
. The data indicate that estimate (3.1) is saturated only over a short interval, as expected from the fact that the fields are optimal only in an instantaneous sense, and the optimal growth of palinstrophy can be sustained only over this short interval.
$g$
. The data indicate that estimate (3.1) is saturated only over a short interval, as expected from the fact that the fields are optimal only in an instantaneous sense, and the optimal growth of palinstrophy can be sustained only over this short interval.

Figure 5. Rescaled diagnostics
![]() $f(\unicode[STIX]{x1D70F})$
(black solid lines) and
$f(\unicode[STIX]{x1D70F})$
(black solid lines) and
![]() $g(\unicode[STIX]{x1D70F})$
(blue dashed lines) for different values of
$g(\unicode[STIX]{x1D70F})$
(blue dashed lines) for different values of
![]() ${\mathcal{P}}_{0}$
and
${\mathcal{P}}_{0}$
and
![]() $Re_{0}$
. All data collapse onto a ‘universal’ pair of curves.
$Re_{0}$
. All data collapse onto a ‘universal’ pair of curves.
On the other hand, it follows from estimate (3.1) that
Figure 6(a) shows the dependence of
![]() $Q_{max}$
on
$Q_{max}$
on
![]() $Re_{0}$
, for values of palinstrophy in the range
$Re_{0}$
, for values of palinstrophy in the range
![]() ${\mathcal{P}}_{0}\in [10^{6},10^{9}]$
. The curve
${\mathcal{P}}_{0}\in [10^{6},10^{9}]$
. The curve
![]() $\unicode[STIX]{x1D6FE}(Re_{0})=\tilde{a}+\tilde{b}\sqrt{\ln Re_{0}+\tilde{c}}$
, with
$\unicode[STIX]{x1D6FE}(Re_{0})=\tilde{a}+\tilde{b}\sqrt{\ln Re_{0}+\tilde{c}}$
, with
![]() $\tilde{a}$
,
$\tilde{a}$
,
![]() $\tilde{b}$
and
$\tilde{b}$
and
![]() $\tilde{c}$
given in (2.5), is included for reference as a red dashed curve. It can be observed from figure 6(a) that, although estimate (3.1) is saturated only over a short time interval, the dependence of the finite-time growth of palinstrophy on
$\tilde{c}$
given in (2.5), is included for reference as a red dashed curve. It can be observed from figure 6(a) that, although estimate (3.1) is saturated only over a short time interval, the dependence of the finite-time growth of palinstrophy on
![]() $Re_{0}$
, when compensated by the enstrophy dissipation occurring at the maximum palinstrophy time, has a behaviour similar to that predicted by estimate (3.7).
$Re_{0}$
, when compensated by the enstrophy dissipation occurring at the maximum palinstrophy time, has a behaviour similar to that predicted by estimate (3.7).
Figure 6(b) shows the dependence on
![]() ${\mathcal{P}}(0)$
of the normalized maximum palinstrophy
${\mathcal{P}}(0)$
of the normalized maximum palinstrophy
obtained from the time evolution of the optimal vorticity
![]() $\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
, for fixed
$\widetilde{\unicode[STIX]{x1D714}}_{Re_{0},{\mathcal{P}}_{0}}$
, for fixed
![]() $Re_{0}$
. As expected from estimate (3.2), the data indicate that
$Re_{0}$
. As expected from estimate (3.2), the data indicate that
![]() ${\mathcal{P}}_{max}$
is independent of
${\mathcal{P}}_{max}$
is independent of
![]() ${\mathcal{P}}(0)$
, with its value depending only on the initial Reynolds number
${\mathcal{P}}(0)$
, with its value depending only on the initial Reynolds number
![]() $Re_{0}$
. These results provide compelling evidence supporting the sharpness of the a priori finite-time estimate (3.2) with respect to
$Re_{0}$
. These results provide compelling evidence supporting the sharpness of the a priori finite-time estimate (3.2) with respect to
![]() ${\mathcal{P}}(0)$
.
${\mathcal{P}}(0)$
.

Figure 6. (a) The quantity
![]() $Q_{max}$
, defined in (3.7), as a function of
$Q_{max}$
, defined in (3.7), as a function of
![]() $\ln Re_{0}$
. The prefactor
$\ln Re_{0}$
. The prefactor
![]() $C_{Re_{0}}=\tilde{a}+\tilde{b}\sqrt{\tilde{c}+\ln Re_{0}}$
, with
$C_{Re_{0}}=\tilde{a}+\tilde{b}\sqrt{\tilde{c}+\ln Re_{0}}$
, with
![]() $\tilde{a}$
,
$\tilde{a}$
,
![]() $\tilde{b}$
and
$\tilde{b}$
and
![]() $\tilde{c}$
from (2.5), is shown as a red dashed line. (b) Compensated maximum palinstrophy,
$\tilde{c}$
from (2.5), is shown as a red dashed line. (b) Compensated maximum palinstrophy,
![]() ${\mathcal{P}}_{max}={\mathcal{P}}_{0}^{-1}\max _{t>0}{\mathcal{P}}(t)$
, as a function of
${\mathcal{P}}_{max}={\mathcal{P}}_{0}^{-1}\max _{t>0}{\mathcal{P}}(t)$
, as a function of
![]() ${\mathcal{P}}_{0}$
, for different values of Reynolds number
${\mathcal{P}}_{0}$
, for different values of Reynolds number
![]() $Re_{0}\in [10^{3},10^{4}]$
.
$Re_{0}\in [10^{3},10^{4}]$
.
4 Discussion and conclusion
We have presented numerical confirmation that the rigorous analytic estimate
is sharp in its behaviour with respect to both the palinstrophy
![]() ${\mathcal{P}}$
and the Reynolds number
${\mathcal{P}}$
and the Reynolds number
![]() $Re$
. The power-law dependence on
$Re$
. The power-law dependence on
![]() ${\mathcal{P}}$
is predicted by the self-similar analysis from appendix B and confirmed by the data shown in figure 2, where the normalized optimal rate of growth of palinstrophy
${\mathcal{P}}$
is predicted by the self-similar analysis from appendix B and confirmed by the data shown in figure 2, where the normalized optimal rate of growth of palinstrophy
![]() ${\mathcal{P}}_{0}^{-3/2}{\mathcal{R}}(\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}})$
is plotted against
${\mathcal{P}}_{0}^{-3/2}{\mathcal{R}}(\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}})$
is plotted against
![]() ${\mathcal{P}}_{0}$
. Similarly, the dependence of
${\mathcal{P}}_{0}$
. Similarly, the dependence of
![]() ${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}})$
on
${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}})$
on
![]() $Re_{0}$
is correctly captured by the estimate, although the constants
$Re_{0}$
is correctly captured by the estimate, although the constants
![]() $\tilde{a},~\tilde{b}$
and
$\tilde{a},~\tilde{b}$
and
![]() $\tilde{c}$
that fit the optimal rate of growth in the least-squares sense differ from the analytic values given in § A.1. More careful analysis might give better constants, but it is important to note that the approach used to construct the optimal fields only ensures that solutions to (2.1) are local maximizers: there is no guarantee that they are global maximizers of
$\tilde{c}$
that fit the optimal rate of growth in the least-squares sense differ from the analytic values given in § A.1. More careful analysis might give better constants, but it is important to note that the approach used to construct the optimal fields only ensures that solutions to (2.1) are local maximizers: there is no guarantee that they are global maximizers of
![]() ${\mathcal{R}}$
. However, the best one can hope for in the search for any other maximizers is to improve the value of the constants
${\mathcal{R}}$
. However, the best one can hope for in the search for any other maximizers is to improve the value of the constants
![]() $\tilde{a}$
,
$\tilde{a}$
,
![]() $\tilde{b}$
and
$\tilde{b}$
and
![]() $\tilde{c}$
so that optimal instantaneous production of palinstrophy matches that given by the analytic estimate.
$\tilde{c}$
so that optimal instantaneous production of palinstrophy matches that given by the analytic estimate.
Regarding the finite-time growth of palinstrophy, we have provided evidence supporting the sharpness of the a priori estimate
with respect to the initial palinstrophy
![]() ${\mathcal{P}}(0)$
. For this, we have used the instantaneously optimal fields
${\mathcal{P}}(0)$
. For this, we have used the instantaneously optimal fields
![]() $\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
as initial condition in the 2D incompressible Navier–Stokes equation, and carefully monitored the time evolution of palinstrophy. The sharpness with respect to the prefactor
$\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
as initial condition in the 2D incompressible Navier–Stokes equation, and carefully monitored the time evolution of palinstrophy. The sharpness with respect to the prefactor
![]() $\unicode[STIX]{x1D713}(Re_{0})$
, on the other hand, is a more subtle issue, and instead we looked at the pointwise estimate
$\unicode[STIX]{x1D713}(Re_{0})$
, on the other hand, is a more subtle issue, and instead we looked at the pointwise estimate
This time-dependent estimate was found to be saturated by the instantaneously optimal fields
![]() $\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
only over a short time window, resulting in a sub-optimal dependence of the normalized maximum growth of palinstrophy on
$\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
only over a short time window, resulting in a sub-optimal dependence of the normalized maximum growth of palinstrophy on
![]() $Re_{0}$
. This does not mean, however, that the estimate is not sharp, as the fields
$Re_{0}$
. This does not mean, however, that the estimate is not sharp, as the fields
![]() $\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
are optimal only at time
$\widetilde{\boldsymbol{u}}_{Re_{0},{\mathcal{P}}_{0}}$
are optimal only at time
![]() $t=0$
. A better assessment of the sharpness of the pointwise estimate (3.1) could be performed by solving the finite-time optimization problem:
$t=0$
. A better assessment of the sharpness of the pointwise estimate (3.1) could be performed by solving the finite-time optimization problem:
with the constraint manifold
![]() ${\mathcal{S}}$
including only the fields that are solutions to the 2D incompressible Navier–Stokes equation defined on the interval
${\mathcal{S}}$
including only the fields that are solutions to the 2D incompressible Navier–Stokes equation defined on the interval
![]() $(0,T)$
. This finite-time optimization approach was used by Ayala & Protas (Reference Ayala and Protas2011) to study the maximum finite-time growth of enstrophy of solutions to the one-dimensional Burgers equation, with the results confirmed analytically by Pelinovsky (Reference Pelinovsky2012).
$(0,T)$
. This finite-time optimization approach was used by Ayala & Protas (Reference Ayala and Protas2011) to study the maximum finite-time growth of enstrophy of solutions to the one-dimensional Burgers equation, with the results confirmed analytically by Pelinovsky (Reference Pelinovsky2012).
To summarize, the results presented in this paper indicate that it is possible to saturate a priori finite-time estimates using fields that saturate instantaneous estimates. Time-dependent estimates, on the other hand, are saturated only over short time intervals, rendering the finite-time growth of palinstrophy obtained from instantaneously optimal fields suboptimal. This implies that in the context of the 3D Navier–Stokes equation, for which no a priori finite-time estimates for the growth of enstrophy are available and only time-dependent estimates exist, the search for solenoidal fields that are optimal for the growth of enstrophy, the key quantity controlling the regularity of solutions in 3D, must be performed following a finite-time optimization approach where the Navier–Stokes equation is included as part of the constraint, similar to the approach described in (4.4). Although computationally intensive, this task is within reach with current available resources and it is also left as an open question for subsequent work.
Acknowledgements
The authors are extremely grateful to F. Otto for useful suggestions and discussions leading to the results presented in this paper. The paper itself was substantially improved with the help of the referees’ comments and recommendations. This research was supported in part by a NSF Award PHY-1205219, a 2014 Simons Foundation Fellowship in Theoretical Physics, NSF Award DMS-1515161, and a 2016 John Simon Guggenheim Foundation Fellowship in Applied Mathematics.
Appendix A. Estimates for the growth of palinstrophy
A.1 Instantaneous growth of palinstrophy
From (1.4), the instantaneous rate of growth of palinstrophy
![]() $\text{d}{\mathcal{P}}/\text{d}t$
is defined as
$\text{d}{\mathcal{P}}/\text{d}t$
is defined as
with
![]() $\boldsymbol{u}\boldsymbol{ : }\unicode[STIX]{x1D6FA}\rightarrow \mathbb{R}^{2}$
such that
$\boldsymbol{u}\boldsymbol{ : }\unicode[STIX]{x1D6FA}\rightarrow \mathbb{R}^{2}$
such that
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0$
, and
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0$
, and
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x2202}_{1}u_{2}-\unicode[STIX]{x2202}_{2}u_{1}$
. As the quadratic form induced by
$\unicode[STIX]{x1D714}=\unicode[STIX]{x2202}_{1}u_{2}-\unicode[STIX]{x2202}_{2}u_{1}$
. As the quadratic form induced by
![]() $\unicode[STIX]{x1D735}\boldsymbol{u}$
only depends on its symmetric part
$\unicode[STIX]{x1D735}\boldsymbol{u}$
only depends on its symmetric part
![]() $(\unicode[STIX]{x1D735}\boldsymbol{u})_{S}:=(\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}})/2$
and is bounded by its spectral norm
$(\unicode[STIX]{x1D735}\boldsymbol{u})_{S}:=(\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}})/2$
and is bounded by its spectral norm
![]() $|(\unicode[STIX]{x1D735}\boldsymbol{u})_{S}|_{\unicode[STIX]{x1D70E}}:=\max \{|\unicode[STIX]{x1D706}_{1}|,|\unicode[STIX]{x1D706}_{2}|\}$
, with
$|(\unicode[STIX]{x1D735}\boldsymbol{u})_{S}|_{\unicode[STIX]{x1D70E}}:=\max \{|\unicode[STIX]{x1D706}_{1}|,|\unicode[STIX]{x1D706}_{2}|\}$
, with
![]() $\unicode[STIX]{x1D706}_{1}$
and
$\unicode[STIX]{x1D706}_{1}$
and
![]() $\unicode[STIX]{x1D706}_{2}$
being the two real eigenvalues of
$\unicode[STIX]{x1D706}_{2}$
being the two real eigenvalues of
![]() $(\unicode[STIX]{x1D735}\boldsymbol{u})_{S}$
, it follows that
$(\unicode[STIX]{x1D735}\boldsymbol{u})_{S}$
, it follows that
 $$\begin{eqnarray}\displaystyle \frac{\text{d}{\mathcal{P}}}{\text{d}t}(\boldsymbol{u}) & {\leqslant} & \displaystyle -\unicode[STIX]{x1D708}\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}^{2}+\Vert (\unicode[STIX]{x1D735}\boldsymbol{u})_{S}\Vert _{\unicode[STIX]{x1D70E},\infty }\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D714}|^{2}\,\text{d}\unicode[STIX]{x1D6FA}\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D708}\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}^{2}+2\Vert (\unicode[STIX]{x1D735}\boldsymbol{u})_{S}\Vert _{\unicode[STIX]{x1D70E},\infty }{\mathcal{P}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}{\mathcal{P}}}{\text{d}t}(\boldsymbol{u}) & {\leqslant} & \displaystyle -\unicode[STIX]{x1D708}\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}^{2}+\Vert (\unicode[STIX]{x1D735}\boldsymbol{u})_{S}\Vert _{\unicode[STIX]{x1D70E},\infty }\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D714}|^{2}\,\text{d}\unicode[STIX]{x1D6FA}\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D708}\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}^{2}+2\Vert (\unicode[STIX]{x1D735}\boldsymbol{u})_{S}\Vert _{\unicode[STIX]{x1D70E},\infty }{\mathcal{P}}.\end{eqnarray}$$
For
![]() $\unicode[STIX]{x1D6FA}$
a square of side
$\unicode[STIX]{x1D6FA}$
a square of side
![]() $L$
endowed with periodic boundary conditions, it follows that a function
$L$
endowed with periodic boundary conditions, it follows that a function
![]() $u:\unicode[STIX]{x1D6FA}\rightarrow \mathbb{R}$
and its gradient
$u:\unicode[STIX]{x1D6FA}\rightarrow \mathbb{R}$
and its gradient
![]() $\unicode[STIX]{x1D735}u$
admit a Fourier representation of the form
$\unicode[STIX]{x1D735}u$
admit a Fourier representation of the form
where
![]() $\mathbb{Z}_{0}=(2\unicode[STIX]{x03C0}/L)(\mathbb{Z}\times \mathbb{Z})$
. In Fourier space, the incompressibility condition
$\mathbb{Z}_{0}=(2\unicode[STIX]{x03C0}/L)(\mathbb{Z}\times \mathbb{Z})$
. In Fourier space, the incompressibility condition
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0$
takes the form
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0$
takes the form
![]() $\boldsymbol{k}\boldsymbol{\cdot }\widehat{\boldsymbol{u}}(\boldsymbol{k})=0$
for each
$\boldsymbol{k}\boldsymbol{\cdot }\widehat{\boldsymbol{u}}(\boldsymbol{k})=0$
for each
![]() $\boldsymbol{k}\in \mathbb{Z}_{0}\setminus \{0\}$
, which implies that
$\boldsymbol{k}\in \mathbb{Z}_{0}\setminus \{0\}$
, which implies that
![]() $\widehat{\boldsymbol{u}}(\boldsymbol{k})\in \mathbb{C}\boldsymbol{k}^{\bot }$
with
$\widehat{\boldsymbol{u}}(\boldsymbol{k})\in \mathbb{C}\boldsymbol{k}^{\bot }$
with
![]() $\boldsymbol{k}^{\bot }=(-k_{2},k_{1})$
. Together with the fact that the matrix
$\boldsymbol{k}^{\bot }=(-k_{2},k_{1})$
. Together with the fact that the matrix
![]() $(\boldsymbol{k}\otimes \boldsymbol{k}^{\bot }+\boldsymbol{k}^{\bot }\otimes \boldsymbol{k})/2$
has eigenvalues
$(\boldsymbol{k}\otimes \boldsymbol{k}^{\bot }+\boldsymbol{k}^{\bot }\otimes \boldsymbol{k})/2$
has eigenvalues
![]() $-(1/2)|\boldsymbol{k}|^{2}$
and
$-(1/2)|\boldsymbol{k}|^{2}$
and
![]() $(1/2)|\boldsymbol{k}|^{2}$
, we get the somewhat crude estimate
$(1/2)|\boldsymbol{k}|^{2}$
, we get the somewhat crude estimate
Grouping the wavenumbers into small, intermediate and high frequencies gives
where the cut-off wavenumbers
![]() $\unicode[STIX]{x1D6EC}_{1}$
and
$\unicode[STIX]{x1D6EC}_{1}$
and
![]() $\unicode[STIX]{x1D6EC}_{2}$
are yet to be determined. Each term on the right-hand side of the last inequality can be upper-bounded using the Cauchy–Schwarz inequality as
$\unicode[STIX]{x1D6EC}_{2}$
are yet to be determined. Each term on the right-hand side of the last inequality can be upper-bounded using the Cauchy–Schwarz inequality as
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{|\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{1}}|\boldsymbol{k}||\hat{\boldsymbol{u}}(\boldsymbol{k})| & {\leqslant} & \displaystyle \left(\mathop{\sum }_{|\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{1}}|\boldsymbol{k}|^{2}\right)^{1/2}\left(\mathop{\sum }_{|\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{1}}|\hat{\boldsymbol{u}}(\boldsymbol{k})|^{2}\right)^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \left(2\unicode[STIX]{x03C0}\int _{0}^{\unicode[STIX]{x1D6EC}_{1}}k^{3}\,\text{d}k\right)^{1/2}\left(2{\mathcal{K}}\right)^{1/2}=\sqrt{\unicode[STIX]{x03C0}}\unicode[STIX]{x1D6EC}_{1}^{2}{\mathcal{K}}^{1/2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{|\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{1}}|\boldsymbol{k}||\hat{\boldsymbol{u}}(\boldsymbol{k})| & {\leqslant} & \displaystyle \left(\mathop{\sum }_{|\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{1}}|\boldsymbol{k}|^{2}\right)^{1/2}\left(\mathop{\sum }_{|\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{1}}|\hat{\boldsymbol{u}}(\boldsymbol{k})|^{2}\right)^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \left(2\unicode[STIX]{x03C0}\int _{0}^{\unicode[STIX]{x1D6EC}_{1}}k^{3}\,\text{d}k\right)^{1/2}\left(2{\mathcal{K}}\right)^{1/2}=\sqrt{\unicode[STIX]{x03C0}}\unicode[STIX]{x1D6EC}_{1}^{2}{\mathcal{K}}^{1/2},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6EC}_{1}\leqslant |\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{2}}|\boldsymbol{k}||\hat{\boldsymbol{u}}(\boldsymbol{k})| & {\leqslant} & \displaystyle \left(\mathop{\sum }_{\unicode[STIX]{x1D6EC}_{1}\leqslant |\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{2}}\frac{1}{|\boldsymbol{k}|^{2}}\right)^{1/2}\left(\mathop{\sum }_{\unicode[STIX]{x1D6EC}_{1}\leqslant |\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{2}}|\boldsymbol{k}|^{4}|\hat{\boldsymbol{u}}(\boldsymbol{k})|^{2}\right)^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \left(2\unicode[STIX]{x03C0}\int _{\unicode[STIX]{x1D6EC}_{1}}^{\unicode[STIX]{x1D6EC}_{2}}\frac{\text{d}k}{k}\right)^{1/2}\left(2{\mathcal{P}}\right)^{1/2}=2\sqrt{\unicode[STIX]{x03C0}}\sqrt{\ln \left(\frac{\unicode[STIX]{x1D6EC}_{2}}{\unicode[STIX]{x1D6EC}_{1}}\right)}\,{\mathcal{P}}^{1/2}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6EC}_{1}\leqslant |\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{2}}|\boldsymbol{k}||\hat{\boldsymbol{u}}(\boldsymbol{k})| & {\leqslant} & \displaystyle \left(\mathop{\sum }_{\unicode[STIX]{x1D6EC}_{1}\leqslant |\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{2}}\frac{1}{|\boldsymbol{k}|^{2}}\right)^{1/2}\left(\mathop{\sum }_{\unicode[STIX]{x1D6EC}_{1}\leqslant |\boldsymbol{k}|\leqslant \unicode[STIX]{x1D6EC}_{2}}|\boldsymbol{k}|^{4}|\hat{\boldsymbol{u}}(\boldsymbol{k})|^{2}\right)^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \left(2\unicode[STIX]{x03C0}\int _{\unicode[STIX]{x1D6EC}_{1}}^{\unicode[STIX]{x1D6EC}_{2}}\frac{\text{d}k}{k}\right)^{1/2}\left(2{\mathcal{P}}\right)^{1/2}=2\sqrt{\unicode[STIX]{x03C0}}\sqrt{\ln \left(\frac{\unicode[STIX]{x1D6EC}_{2}}{\unicode[STIX]{x1D6EC}_{1}}\right)}\,{\mathcal{P}}^{1/2}\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{|\boldsymbol{k}|\geqslant \unicode[STIX]{x1D6EC}_{2}}|\boldsymbol{k}||\hat{\boldsymbol{u}}(\boldsymbol{k})| & {\leqslant} & \displaystyle \left(\mathop{\sum }_{|\boldsymbol{k}|\geqslant \unicode[STIX]{x1D6EC}_{2}}\frac{1}{|\boldsymbol{k}|^{4}}\right)^{1/2}\left(\mathop{\sum }_{|\boldsymbol{k}|\geqslant \unicode[STIX]{x1D6EC}_{2}}|\boldsymbol{k}|^{6}|\hat{\boldsymbol{u}}(\boldsymbol{k})|^{2}\right)^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \left(2\unicode[STIX]{x03C0}\int _{\unicode[STIX]{x1D6EC}_{2}}^{\infty }\frac{\text{d}k}{k^{3}}\right)^{1/2}\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}=\frac{\sqrt{\unicode[STIX]{x03C0}}}{\unicode[STIX]{x1D6EC}_{2}}\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{|\boldsymbol{k}|\geqslant \unicode[STIX]{x1D6EC}_{2}}|\boldsymbol{k}||\hat{\boldsymbol{u}}(\boldsymbol{k})| & {\leqslant} & \displaystyle \left(\mathop{\sum }_{|\boldsymbol{k}|\geqslant \unicode[STIX]{x1D6EC}_{2}}\frac{1}{|\boldsymbol{k}|^{4}}\right)^{1/2}\left(\mathop{\sum }_{|\boldsymbol{k}|\geqslant \unicode[STIX]{x1D6EC}_{2}}|\boldsymbol{k}|^{6}|\hat{\boldsymbol{u}}(\boldsymbol{k})|^{2}\right)^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \left(2\unicode[STIX]{x03C0}\int _{\unicode[STIX]{x1D6EC}_{2}}^{\infty }\frac{\text{d}k}{k^{3}}\right)^{1/2}\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}=\frac{\sqrt{\unicode[STIX]{x03C0}}}{\unicode[STIX]{x1D6EC}_{2}}\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}.\end{eqnarray}$$
Therefore, the estimate for
![]() $\Vert (\unicode[STIX]{x1D735}\boldsymbol{u})_{S}\Vert _{\unicode[STIX]{x1D70E},\infty }$
reads
$\Vert (\unicode[STIX]{x1D735}\boldsymbol{u})_{S}\Vert _{\unicode[STIX]{x1D70E},\infty }$
reads
with the estimate in (A 2) leading to
The sum
![]() $-\unicode[STIX]{x1D708}\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}^{2}+2\sqrt{\unicode[STIX]{x03C0}}\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}{\mathcal{P}}/\unicode[STIX]{x1D6EC}_{2}$
of the first and last terms in the last inequality is maximal when
$-\unicode[STIX]{x1D708}\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}^{2}+2\sqrt{\unicode[STIX]{x03C0}}\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}{\mathcal{P}}/\unicode[STIX]{x1D6EC}_{2}$
of the first and last terms in the last inequality is maximal when
![]() $\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}=\sqrt{\unicode[STIX]{x03C0}}{\mathcal{P}}/(2\unicode[STIX]{x1D708}\unicode[STIX]{x1D6EC}_{2})$
, attaining a maximum value of
$\Vert \unicode[STIX]{x0394}\unicode[STIX]{x1D714}\Vert _{2}=\sqrt{\unicode[STIX]{x03C0}}{\mathcal{P}}/(2\unicode[STIX]{x1D708}\unicode[STIX]{x1D6EC}_{2})$
, attaining a maximum value of
![]() $\unicode[STIX]{x03C0}{\mathcal{P}}^{2}/(4\unicode[STIX]{x1D708}\unicode[STIX]{x1D6EC}_{2}^{2})$
. Thus, the estimate for
$\unicode[STIX]{x03C0}{\mathcal{P}}^{2}/(4\unicode[STIX]{x1D708}\unicode[STIX]{x1D6EC}_{2}^{2})$
. Thus, the estimate for
![]() $\text{d}{\mathcal{P}}/\text{d}t$
reads
$\text{d}{\mathcal{P}}/\text{d}t$
reads
 $$\begin{eqnarray}\displaystyle \frac{\text{d}{\mathcal{P}}}{\text{d}t}(\boldsymbol{u}) & {\leqslant} & \displaystyle \frac{\unicode[STIX]{x03C0}}{4}\frac{{\mathcal{P}}^{2}}{\unicode[STIX]{x1D708}\unicode[STIX]{x1D6EC}_{2}^{2}}+\sqrt{\unicode[STIX]{x03C0}}\,\unicode[STIX]{x1D6EC}_{1}^{2}\,{\mathcal{K}}^{1/2}{\mathcal{P}}+2\sqrt{\unicode[STIX]{x03C0}}\sqrt{\ln \left(\frac{\unicode[STIX]{x1D6EC}_{2}}{\unicode[STIX]{x1D6EC}_{1}}\right)}\,{\mathcal{P}}^{3/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \left(\frac{\unicode[STIX]{x03C0}}{4}\frac{{\mathcal{P}}^{1/2}}{\unicode[STIX]{x1D708}\unicode[STIX]{x1D6EC}_{2}^{2}}+\sqrt{\unicode[STIX]{x03C0}}\,\frac{\unicode[STIX]{x1D6EC}_{1}^{2}{\mathcal{K}}^{1/2}}{{\mathcal{P}}^{1/2}}+2\sqrt{\unicode[STIX]{x03C0}}\sqrt{\ln \left(\frac{\unicode[STIX]{x1D6EC}_{2}}{\unicode[STIX]{x1D6EC}_{1}}\right)}\right){\mathcal{P}}^{3/2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}{\mathcal{P}}}{\text{d}t}(\boldsymbol{u}) & {\leqslant} & \displaystyle \frac{\unicode[STIX]{x03C0}}{4}\frac{{\mathcal{P}}^{2}}{\unicode[STIX]{x1D708}\unicode[STIX]{x1D6EC}_{2}^{2}}+\sqrt{\unicode[STIX]{x03C0}}\,\unicode[STIX]{x1D6EC}_{1}^{2}\,{\mathcal{K}}^{1/2}{\mathcal{P}}+2\sqrt{\unicode[STIX]{x03C0}}\sqrt{\ln \left(\frac{\unicode[STIX]{x1D6EC}_{2}}{\unicode[STIX]{x1D6EC}_{1}}\right)}\,{\mathcal{P}}^{3/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \left(\frac{\unicode[STIX]{x03C0}}{4}\frac{{\mathcal{P}}^{1/2}}{\unicode[STIX]{x1D708}\unicode[STIX]{x1D6EC}_{2}^{2}}+\sqrt{\unicode[STIX]{x03C0}}\,\frac{\unicode[STIX]{x1D6EC}_{1}^{2}{\mathcal{K}}^{1/2}}{{\mathcal{P}}^{1/2}}+2\sqrt{\unicode[STIX]{x03C0}}\sqrt{\ln \left(\frac{\unicode[STIX]{x1D6EC}_{2}}{\unicode[STIX]{x1D6EC}_{1}}\right)}\right){\mathcal{P}}^{3/2}.\end{eqnarray}$$
The cut-off wavenumbers
![]() $\unicode[STIX]{x1D6EC}_{1}$
and
$\unicode[STIX]{x1D6EC}_{1}$
and
![]() $\unicode[STIX]{x1D6EC}_{2}$
can be chosen so that
$\unicode[STIX]{x1D6EC}_{2}$
can be chosen so that
for
![]() $a$
and
$a$
and
![]() $b$
positive dimensionless numbers. For this choice of
$b$
positive dimensionless numbers. For this choice of
![]() $\unicode[STIX]{x1D6EC}_{1}$
and
$\unicode[STIX]{x1D6EC}_{1}$
and
![]() $\unicode[STIX]{x1D6EC}_{2}$
, and the introduction of the dimensionless parameter
$\unicode[STIX]{x1D6EC}_{2}$
, and the introduction of the dimensionless parameter
![]() $Re={\mathcal{K}}^{1/2}/\unicode[STIX]{x1D708}$
, the estimate becomes
$Re={\mathcal{K}}^{1/2}/\unicode[STIX]{x1D708}$
, the estimate becomes
For sufficiently large
![]() $Re$
, the prefactor
$Re$
, the prefactor
![]() $g(a,b)$
in the power-law estimate from (A 13) is minimized when
$g(a,b)$
in the power-law estimate from (A 13) is minimized when
![]() $\unicode[STIX]{x2202}g/\unicode[STIX]{x2202}a=0$
and
$\unicode[STIX]{x2202}g/\unicode[STIX]{x2202}a=0$
and
![]() $\unicode[STIX]{x2202}g/\unicode[STIX]{x2202}b=0$
, i.e. the optimal values
$\unicode[STIX]{x2202}g/\unicode[STIX]{x2202}b=0$
, i.e. the optimal values
![]() $(\tilde{a},\tilde{b})$
satisfy
$(\tilde{a},\tilde{b})$
satisfy
It follows that
![]() $\tilde{a}=(\sqrt{\unicode[STIX]{x03C0}}/4)\,\tilde{b}$
, with the minimum value
$\tilde{a}=(\sqrt{\unicode[STIX]{x03C0}}/4)\,\tilde{b}$
, with the minimum value
![]() $g(\tilde{a},\tilde{b})$
given by
$g(\tilde{a},\tilde{b})$
given by
where QI denotes the first quadrant in the
![]() $(a,b)$
plane, and
$(a,b)$
plane, and
![]() $z_{1}=-1/(2\tilde{a}^{2})$
is the smaller of the two solutions of the transcendental equation
$z_{1}=-1/(2\tilde{a}^{2})$
is the smaller of the two solutions of the transcendental equation
For values of
![]() $Re$
satisfying
$Re$
satisfying
![]() $Re>2\text{e}/\sqrt{\unicode[STIX]{x03C0}}$
, the two solutions to (A 16) are given by
$Re>2\text{e}/\sqrt{\unicode[STIX]{x03C0}}$
, the two solutions to (A 16) are given by
where
![]() $W_{k}$
is the
$W_{k}$
is the
![]() $k$
-branch of the Lambert
$k$
-branch of the Lambert
![]() $W$
function. The asymptotic expansion for
$W$
function. The asymptotic expansion for
![]() $W_{-1}$
is given by (Corless et al.
Reference Corless, Gonnet, Hare, Jeffrey and Knuth1996)
$W_{-1}$
is given by (Corless et al.
Reference Corless, Gonnet, Hare, Jeffrey and Knuth1996)
from which it follows that, for sufficiently large
![]() $Re\geqslant 2/\sqrt{\unicode[STIX]{x03C0}}$
,
$Re\geqslant 2/\sqrt{\unicode[STIX]{x03C0}}$
,
Hence, to leading order in the variable
![]() $\ln Re-\ln (2/\sqrt{\unicode[STIX]{x03C0}})$
, the optimal prefactor
$\ln Re-\ln (2/\sqrt{\unicode[STIX]{x03C0}})$
, the optimal prefactor
![]() $g(\tilde{a},\tilde{b})$
from (A 15) has the form
$g(\tilde{a},\tilde{b})$
from (A 15) has the form
giving the estimate for
![]() $\text{d}{\mathcal{P}}/\text{d}t$
as
$\text{d}{\mathcal{P}}/\text{d}t$
as
A.2 Finite-time growth of palinstrophy
To obtain an a priori estimate for the finite-time growth of palinstrophy, we use the energy dissipation equation (1.4a
), leading to
![]() ${\mathcal{K}}(t)\leqslant {\mathcal{K}}(0)$
for all
${\mathcal{K}}(t)\leqslant {\mathcal{K}}(0)$
for all
![]() $t>0$
and, since
$t>0$
and, since
![]() $Re={\mathcal{K}}^{1/2}/\unicode[STIX]{x1D708}$
,
$Re={\mathcal{K}}^{1/2}/\unicode[STIX]{x1D708}$
,
![]() $Re(t)\leqslant Re(0)=Re_{0}$
. It should be noted that estimate (A 21) holds only for values of Reynolds number
$Re(t)\leqslant Re(0)=Re_{0}$
. It should be noted that estimate (A 21) holds only for values of Reynolds number
![]() $Re\geqslant 2/\sqrt{\unicode[STIX]{x03C0}}$
; thus we expect the estimate to be valid only in the time interval where this constraint is satisfied. Using time integration of (A 21) gives
$Re\geqslant 2/\sqrt{\unicode[STIX]{x03C0}}$
; thus we expect the estimate to be valid only in the time interval where this constraint is satisfied. Using time integration of (A 21) gives
 $$\begin{eqnarray}\displaystyle \frac{\text{d}{\mathcal{P}}}{\text{d}t} & {\leqslant} & \displaystyle \left(a+b\sqrt{\ln Re_{0}+c}\right){\mathcal{P}}^{3/2}\quad \Longrightarrow \nonumber\\ \displaystyle \int _{{\mathcal{P}}(0)}^{{\mathcal{P}}(t)}{\mathcal{P}}^{-1/2}\,\text{d}{\mathcal{P}} & {\leqslant} & \displaystyle \left(a+b\sqrt{\ln Re_{0}+c}\right)\int _{0}^{t}{\mathcal{P}}(s)\,\text{d}s\quad \Longrightarrow \nonumber\\ \displaystyle {\mathcal{P}}^{1/2}(t)-{\mathcal{P}}^{1/2}(0) & {\leqslant} & \displaystyle \left(a+b\sqrt{\ln Re_{0}+c}\right)\left(\frac{{\mathcal{E}}(0)-{\mathcal{E}}(t)}{4\unicode[STIX]{x1D708}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}{\mathcal{P}}}{\text{d}t} & {\leqslant} & \displaystyle \left(a+b\sqrt{\ln Re_{0}+c}\right){\mathcal{P}}^{3/2}\quad \Longrightarrow \nonumber\\ \displaystyle \int _{{\mathcal{P}}(0)}^{{\mathcal{P}}(t)}{\mathcal{P}}^{-1/2}\,\text{d}{\mathcal{P}} & {\leqslant} & \displaystyle \left(a+b\sqrt{\ln Re_{0}+c}\right)\int _{0}^{t}{\mathcal{P}}(s)\,\text{d}s\quad \Longrightarrow \nonumber\\ \displaystyle {\mathcal{P}}^{1/2}(t)-{\mathcal{P}}^{1/2}(0) & {\leqslant} & \displaystyle \left(a+b\sqrt{\ln Re_{0}+c}\right)\left(\frac{{\mathcal{E}}(0)-{\mathcal{E}}(t)}{4\unicode[STIX]{x1D708}}\right),\end{eqnarray}$$
where time integration of the enstrophy dissipation equation (1.4b
) has been used. Although (A 23) is not an a priori estimate, i.e. given exclusively in terms of the initial data, it can still be used to determine to what extent sharp instantaneous estimates lead to sharp finite-time estimates. To obtain an a priori estimate for the maximum finite-time growth of palinstrophy, one can use the fact that
![]() ${\mathcal{E}}(t)\leqslant {\mathcal{E}}(0)$
for all
${\mathcal{E}}(t)\leqslant {\mathcal{E}}(0)$
for all
![]() $t>0$
, which follows from the enstrophy dissipation equation (1.4b
), along with the estimate
$t>0$
, which follows from the enstrophy dissipation equation (1.4b
), along with the estimate
![]() ${\mathcal{E}}\leqslant {\mathcal{K}}^{1/2}{\mathcal{P}}^{1/2}$
leading to
${\mathcal{E}}\leqslant {\mathcal{K}}^{1/2}{\mathcal{P}}^{1/2}$
leading to
which gives the a priori finite-time estimate
where the prefactor
![]() $C_{Re_{0}}$
depends exclusively on the initial Reynolds number
$C_{Re_{0}}$
depends exclusively on the initial Reynolds number
![]() $Re_{0}={\mathcal{K}}^{1/2}(0)/\unicode[STIX]{x1D708}$
, and
$Re_{0}={\mathcal{K}}^{1/2}(0)/\unicode[STIX]{x1D708}$
, and
Appendix B. Self-similar optimal fields
As discussed in § 2, we are interested in finding incompressible fields maximizing the instantaneous production of palinstrophy
![]() $\text{d}{\mathcal{P}}/\text{d}t$
. That is, we are solving the optimization problem
$\text{d}{\mathcal{P}}/\text{d}t$
. That is, we are solving the optimization problem
Optimization problem (B 1) is equivalent to problem (2.1), except that it has been written in terms of the vorticity
![]() $\unicode[STIX]{x1D714}$
instead of the velocity field
$\unicode[STIX]{x1D714}$
instead of the velocity field
![]() $\boldsymbol{u}$
. The energy, palinstrophy and objective functionals are given in terms of
$\boldsymbol{u}$
. The energy, palinstrophy and objective functionals are given in terms of
![]() $\unicode[STIX]{x1D714}$
as
$\unicode[STIX]{x1D714}$
as
The first-order optimality condition, i.e. the Euler–Lagrange equation for problem (B 1), reads
where
![]() $\unicode[STIX]{x1D706}_{{\mathcal{K}}}$
and
$\unicode[STIX]{x1D706}_{{\mathcal{K}}}$
and
![]() $\unicode[STIX]{x1D706}_{{\mathcal{P}}}$
are the Lagrange multipliers associated with the constraints defining the manifold
$\unicode[STIX]{x1D706}_{{\mathcal{P}}}$
are the Lagrange multipliers associated with the constraints defining the manifold
![]() ${\mathcal{S}}_{{\mathcal{K}}_{0},{\mathcal{P}}_{0}}$
, and the corresponding variations of the functionals
${\mathcal{S}}_{{\mathcal{K}}_{0},{\mathcal{P}}_{0}}$
, and the corresponding variations of the functionals
![]() ${\mathcal{R}}$
,
${\mathcal{R}}$
,
![]() ${\mathcal{K}}$
and
${\mathcal{K}}$
and
![]() ${\mathcal{P}}$
with respect to variations in
${\mathcal{P}}$
with respect to variations in
![]() $\unicode[STIX]{x1D714}$
are given by
$\unicode[STIX]{x1D714}$
are given by
with
![]() $\unicode[STIX]{x1D713}^{\ast }$
representing the Lagrange multiplier associated with the state equation (B 3) and obtained as the solution to the elliptic problem
$\unicode[STIX]{x1D713}^{\ast }$
representing the Lagrange multiplier associated with the state equation (B 3) and obtained as the solution to the elliptic problem
Evidence supporting the existence of optimal vorticity fields
![]() $\tilde{\unicode[STIX]{x1D714}}_{{\mathcal{K}}_{0},{\mathcal{P}}_{0}}$
, which, for fixed energy
$\tilde{\unicode[STIX]{x1D714}}_{{\mathcal{K}}_{0},{\mathcal{P}}_{0}}$
, which, for fixed energy
![]() ${\mathcal{K}}_{0}$
, vary in a self-similar manner with
${\mathcal{K}}_{0}$
, vary in a self-similar manner with
![]() ${\mathcal{P}}_{0}$
, was presented by Ayala & Protas (Reference Ayala and Protas2014a
). With this numerical evidence in mind, we look for fields
${\mathcal{P}}_{0}$
, was presented by Ayala & Protas (Reference Ayala and Protas2014a
). With this numerical evidence in mind, we look for fields
![]() $\unicode[STIX]{x1D714}_{{\mathcal{P}}_{0}}$
,
$\unicode[STIX]{x1D714}_{{\mathcal{P}}_{0}}$
,
![]() $\unicode[STIX]{x1D713}_{{\mathcal{P}}_{0}}$
and
$\unicode[STIX]{x1D713}_{{\mathcal{P}}_{0}}$
and
![]() $\unicode[STIX]{x1D713}_{{\mathcal{P}}_{0}}^{\ast }$
, satisfying (B 4) and subject to the constraints
$\unicode[STIX]{x1D713}_{{\mathcal{P}}_{0}}^{\ast }$
, satisfying (B 4) and subject to the constraints
![]() ${\mathcal{K}}(\unicode[STIX]{x1D714}_{{\mathcal{P}}_{0}})={\mathcal{K}}_{0}$
and
${\mathcal{K}}(\unicode[STIX]{x1D714}_{{\mathcal{P}}_{0}})={\mathcal{K}}_{0}$
and
![]() ${\mathcal{P}}(\unicode[STIX]{x1D714}_{{\mathcal{P}}_{0}})={\mathcal{P}}_{0}$
, of the form
${\mathcal{P}}(\unicode[STIX]{x1D714}_{{\mathcal{P}}_{0}})={\mathcal{P}}_{0}$
, of the form
for some real parameters
![]() $\unicode[STIX]{x1D6FC},~\unicode[STIX]{x1D6FD},~\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FC},~\unicode[STIX]{x1D6FD},~\unicode[STIX]{x1D6FE}$
and
![]() $q$
, and some functions
$q$
, and some functions
![]() $\unicode[STIX]{x1D6F7}$
,
$\unicode[STIX]{x1D6F7}$
,
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6F9}^{\ast }$
independent of
$\unicode[STIX]{x1D6F9}^{\ast }$
independent of
![]() ${\mathcal{P}}_{0}$
. Using these ansätze and the rescaled spatial variables
${\mathcal{P}}_{0}$
. Using these ansätze and the rescaled spatial variables
![]() $\boldsymbol{y}={\mathcal{P}}_{0}^{q}\boldsymbol{x}$
, it follows that
$\boldsymbol{y}={\mathcal{P}}_{0}^{q}\boldsymbol{x}$
, it follows that
where
![]() $\unicode[STIX]{x1D706}_{1}$
and
$\unicode[STIX]{x1D706}_{1}$
and
![]() $\unicode[STIX]{x1D706}_{2}$
are the Lagrange multipliers corresponding to the constraints
$\unicode[STIX]{x1D706}_{2}$
are the Lagrange multipliers corresponding to the constraints
The objective functional can thus be evaluated for
![]() $\unicode[STIX]{x1D714}_{{\mathcal{P}}_{0}}$
, yielding
$\unicode[STIX]{x1D714}_{{\mathcal{P}}_{0}}$
, yielding
in agreement with the observed optimal instantaneous growth, and in line with the power-law behaviour predicted by estimate (1.8). The dependence of the prefactor
on the ratio
![]() ${\mathcal{K}}_{0}^{1/2}/\unicode[STIX]{x1D708}$
is the main subject of study of the present work.
${\mathcal{K}}_{0}^{1/2}/\unicode[STIX]{x1D708}$
is the main subject of study of the present work.