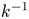1. Introduction
Despite the debate on its precise form, the logarithmic profile for mean velocity has been understood as the most fundamental feature of wall-bounded turbulence (von Kármán Reference von Kármán1930). The attached eddy hypothesis of Townsend (Reference Townsend1956, Reference Townsend1976) was built upon this feature and states the possible existence of energy-containing motions, the size of which is proportional to their distance from the wall (i.e. attached eddies) (see also Hwang & Lee Reference Hwang and Lee2020, for the theoretical basis of the hypothesis). Townsend (Reference Townsend1956, Reference Townsend1976) subsequently introduced a generic form of the second-order statistical moments of the individual energy-containing eddies under the assumption that they behave ‘inviscidly’ as in a Biot–Savart model in the region close to the wall: i.e. a slip boundary condition is considered for the wall-parallel velocity components, while the no-penetration condition is imposed on the wall-normal velocity. He then showed that linear superposition of the second-order statistical moments subject to constant Reynolds shear stress leads to
where ![]() $u'$ is the streamwise turbulent velocity fluctuation,
$u'$ is the streamwise turbulent velocity fluctuation, ![]() $u_\tau$ is the friction velocity,
$u_\tau$ is the friction velocity, ![]() $z$ is the wall-normal coordinate,
$z$ is the wall-normal coordinate, ![]() $\delta$ is the outer length scale (e.g. half height of channel, radius of pipe and thickness of boundary layer),
$\delta$ is the outer length scale (e.g. half height of channel, radius of pipe and thickness of boundary layer), ![]() $A$ is the Townsend–Perry constant and
$A$ is the Townsend–Perry constant and ![]() $B$ is a constant. Several important refinements of the original theory of Townsend (Reference Townsend1956, Reference Townsend1976) were subsequently made. These include: (1) the description of the logarithmic mean velocity in terms of the mean vorticity of individual attached eddies (e.g. Perry & Chong Reference Perry and Chong1982; Perry, Henbest & Chong Reference Perry, Henbest and Chong1986); (2) the prescription of a more realistic statistical form of the individual attached eddy (Perry & Chong Reference Perry and Chong1982; Perry et al. Reference Perry, Henbest and Chong1986; Woodcock & Marusic Reference Woodcock and Marusic2015); (3) relating the physical-space model of Townsend (Reference Townsend1956, Reference Townsend1976) to
$B$ is a constant. Several important refinements of the original theory of Townsend (Reference Townsend1956, Reference Townsend1976) were subsequently made. These include: (1) the description of the logarithmic mean velocity in terms of the mean vorticity of individual attached eddies (e.g. Perry & Chong Reference Perry and Chong1982; Perry, Henbest & Chong Reference Perry, Henbest and Chong1986); (2) the prescription of a more realistic statistical form of the individual attached eddy (Perry & Chong Reference Perry and Chong1982; Perry et al. Reference Perry, Henbest and Chong1986; Woodcock & Marusic Reference Woodcock and Marusic2015); (3) relating the physical-space model of Townsend (Reference Townsend1956, Reference Townsend1976) to ![]() $k^{-1}$ behaviour in velocity spectra (
$k^{-1}$ behaviour in velocity spectra (![]() $k$ is the spatial wavenumber in a wall-parallel direction) (Perry & Chong Reference Perry and Chong1982; Perry et al. Reference Perry, Henbest and Chong1986); (4) the empirical extensions to the near-wall region (Marusic & Kunkel Reference Marusic and Kunkel2003); and (5) the generalisation of (1.1) for higher-order turbulence statistics (Meneveau & Marusic Reference Meneveau and Marusic2013).
$k$ is the spatial wavenumber in a wall-parallel direction) (Perry & Chong Reference Perry and Chong1982; Perry et al. Reference Perry, Henbest and Chong1986); (4) the empirical extensions to the near-wall region (Marusic & Kunkel Reference Marusic and Kunkel2003); and (5) the generalisation of (1.1) for higher-order turbulence statistics (Meneveau & Marusic Reference Meneveau and Marusic2013).
Over the past two decades, a substantial amount of evidence supporting the attached eddy hypothesis and related models has emerged (see also Marusic & Monty Reference Marusic and Monty2019). For example, laboratory experiments and numerical simulations have repeatedly confirmed that (1.1) is indeed a first approximation to the streamwise and spanwise turbulence intensities in the logarithmic layer (Jiménez & Hoyas Reference Jiménez and Hoyas2008; Hultmark et al. Reference Hultmark, Vallikivi, Bailey and Smits2012; Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013; Lee & Moser Reference Lee and Moser2015; Baars & Marusic Reference Baars and Marusic2020b). The existence and the statistical structure of self-similar energy-containing motions in the logarithmic layer have also been reported with various types of eddy-extraction techniques (del Álamo et al. Reference del Álamo, Jiménez, Zandonade and Moser2006; Hwang & Cossu Reference Hwang and Cossu2011; Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014; Hwang Reference Hwang2015; Hellstöm, Marusic & Smits Reference Hellstöm, Marusic and Smits2016; Hwang & Bengana Reference Hwang and Bengana2016; Hwang & Sung Reference Hwang and Sung2018; Cheng et al. Reference Cheng, Li, Lozano-Durán and Liu2019; Baars & Marusic Reference Baars and Marusic2020a). Finally, mathematical analyses of the Navier–Stokes equations have consistently revealed that the key feature of the logarithmic layer is self-similarity with the distance from the wall, which underpins the scaling of the mean, linear and nonlinear dynamics (del Álamo & Jiménez Reference del Álamo and Jiménez2006; Hwang & Cossu Reference Hwang and Cossu2010; Klewicki Reference Klewicki2013; Moarref et al. Reference Moarref, Sharma, Tropp and McKeon2013; Hwang Reference Hwang2016; Hwang, Willis & Cossu Reference Hwang, Willis and Cossu2016; McKeon Reference McKeon2017; Eckhardt & Zammert Reference Eckhardt and Zammert2018; Doohan, Willis & Hwang Reference Doohan, Willis and Hwang2019; McKeon Reference McKeon2019; Vadarevu et al. Reference Vadarevu, Symon, Illingworth and Marusic2019; Yang, Willis & Hwang Reference Yang, Willis and Hwang2019; Hwang & Eckhardt Reference Hwang and Eckhardt2020; Hwang & Lee Reference Hwang and Lee2020; Skouloudis & Hwang Reference Skouloudis and Hwang2021).
Despite the growing evidence, the description of velocity spectra in terms of the attached eddy models still remains unsettled. In the earliest work (Perry & Chong Reference Perry and Chong1982; Perry et al. Reference Perry, Henbest and Chong1986), it was proposed that the existence of a ![]() $k^{-1}$ spectrum with the intensity of
$k^{-1}$ spectrum with the intensity of ![]() $A$ in (1.1) would be consistent with the logarithmic wall-normal dependence of streamwise turbulence intensity (see also § 2.1). In particular, the inviscid theory of Perry et al. (Reference Perry, Henbest and Chong1986) showed that such a
$A$ in (1.1) would be consistent with the logarithmic wall-normal dependence of streamwise turbulence intensity (see also § 2.1). In particular, the inviscid theory of Perry et al. (Reference Perry, Henbest and Chong1986) showed that such a ![]() $k^{-1}$ spectrum would emerge in the region where the spectrum is expected to scale simultaneously in
$k^{-1}$ spectrum would emerge in the region where the spectrum is expected to scale simultaneously in ![]() $z$ and
$z$ and ![]() $\delta$. However, early measurements from the Princeton Superpipe did not show a clearly discerned
$\delta$. However, early measurements from the Princeton Superpipe did not show a clearly discerned ![]() $k^{-1}$ spectrum, and this was subsequently postulated as a consequence of ‘incomplete similarity’ by arguing that the simultaneous scaling with
$k^{-1}$ spectrum, and this was subsequently postulated as a consequence of ‘incomplete similarity’ by arguing that the simultaneous scaling with ![]() $z$ and
$z$ and ![]() $\delta$ may not be possible (Morrison et al. Reference Morrison, Jiang, McKeon and Smits2001, Reference Morrison, McKeon, Jiang and Smits2004). It was later suggested that a well-developed
$\delta$ may not be possible (Morrison et al. Reference Morrison, Jiang, McKeon and Smits2001, Reference Morrison, McKeon, Jiang and Smits2004). It was later suggested that a well-developed ![]() $k^{-1}$ spectrum could appear in the location closer to the wall (Nickels et al. Reference Nickels, Marusic, Hafez and Chong2005), although the proposed location is too close to the wall to directly relate to (1.1), which typically appears in the upper logarithmic layer (Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013; Vallikivi, Hultmark & Smits Reference Vallikivi, Hultmark and Smits2015; Vassilicos et al. Reference Vassilicos, Laval, Foucaut and Stanislas2015), i.e.
$k^{-1}$ spectrum could appear in the location closer to the wall (Nickels et al. Reference Nickels, Marusic, Hafez and Chong2005), although the proposed location is too close to the wall to directly relate to (1.1), which typically appears in the upper logarithmic layer (Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013; Vallikivi, Hultmark & Smits Reference Vallikivi, Hultmark and Smits2015; Vassilicos et al. Reference Vassilicos, Laval, Foucaut and Stanislas2015), i.e. ![]() $O(Re_{\tau }^{-1/2}) \lesssim y/\delta \lesssim 0.15$ (
$O(Re_{\tau }^{-1/2}) \lesssim y/\delta \lesssim 0.15$ (![]() $Re_{\tau }=u_\tau \delta /\nu$ is the friction Reynolds number, where
$Re_{\tau }=u_\tau \delta /\nu$ is the friction Reynolds number, where ![]() $\nu$ is the kinematic viscosity) or the layer just above the ‘mesolayer’ (Afzal Reference Afzal1982; Sreenivasan & Sahay Reference Sreenivasan and Sahay1997; Wei et al. Reference Wei, Fife, Klewicki and Mcmurtry2005; Klewicki Reference Klewicki2013). Furthermore, it was recently suggested that a well-visible
$\nu$ is the kinematic viscosity) or the layer just above the ‘mesolayer’ (Afzal Reference Afzal1982; Sreenivasan & Sahay Reference Sreenivasan and Sahay1997; Wei et al. Reference Wei, Fife, Klewicki and Mcmurtry2005; Klewicki Reference Klewicki2013). Furthermore, it was recently suggested that a well-visible ![]() $k^{-1}$ spectrum responsible for (1.1) might appear at least for
$k^{-1}$ spectrum responsible for (1.1) might appear at least for ![]() $Re_\tau \gtrsim 8 \times 10^4$ (Samie et al. Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018; Baars & Marusic Reference Baars and Marusic2020a). In this respect, it should finally be mentioned that an alternative form of
$Re_\tau \gtrsim 8 \times 10^4$ (Samie et al. Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018; Baars & Marusic Reference Baars and Marusic2020a). In this respect, it should finally be mentioned that an alternative form of ![]() $k^{-1}$ spectrum was also recently proposed by Srinath et al. (Reference Srinath, Vassilicos, Cuvier, Laval, Stanislas and Foucaut2018) based on a space-filling argument of energy-containing motions, although their model does not necessarily rely on the existence of self-similar energy-containing motions (i.e. attached eddy hypothesis).
$k^{-1}$ spectrum was also recently proposed by Srinath et al. (Reference Srinath, Vassilicos, Cuvier, Laval, Stanislas and Foucaut2018) based on a space-filling argument of energy-containing motions, although their model does not necessarily rely on the existence of self-similar energy-containing motions (i.e. attached eddy hypothesis).
The objective of the present study is to propose a spectrum-based attached eddy model that integrates the seemingly inconsistent observations listed above into a single framework. To this end, we revisit the spectrum-based attached eddy model of Perry et al. (Reference Perry, Henbest and Chong1986), which is based on the work of Perry & Abel (Reference Perry and Abel1977). We re-examine the underlying assumptions in the model with the high-fidelity experimental data from Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018). We subsequently extend the model for small but finite ![]() $z/\delta$ and finite Reynolds number, so that its application becomes directly suitable to the location where (1.1) has been observed (layer I in figure 2). The examination reveals that, in general, the intensity of the spectrum for
$z/\delta$ and finite Reynolds number, so that its application becomes directly suitable to the location where (1.1) has been observed (layer I in figure 2). The examination reveals that, in general, the intensity of the spectrum for ![]() $1/\delta \ll k \ll 1/z$ must vary with the wall-normal direction at
$1/\delta \ll k \ll 1/z$ must vary with the wall-normal direction at ![]() $O(z/\delta )$ without assuming a well-developed
$O(z/\delta )$ without assuming a well-developed ![]() $k^{-1}$ spectrum. The presence of such a complicated spectrum in the absence of a
$k^{-1}$ spectrum. The presence of such a complicated spectrum in the absence of a ![]() $k^{-1}$ spectrum is, however, found not to affect the form of streamwise turbulence intensity in (1.1) significantly – indeed, the Townsend–Perry constant
$k^{-1}$ spectrum is, however, found not to affect the form of streamwise turbulence intensity in (1.1) significantly – indeed, the Townsend–Perry constant ![]() $A$ is found to be only weakly dependent on the Reynolds number due to viscous wall effects. The theoretical framework is further extended to the mesolayer (layer II in figure 2), and a near-wall correction is subsequently proposed. The theoretical developments made in the present study are validated with the high-fidelity experimental data of Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018).
$A$ is found to be only weakly dependent on the Reynolds number due to viscous wall effects. The theoretical framework is further extended to the mesolayer (layer II in figure 2), and a near-wall correction is subsequently proposed. The theoretical developments made in the present study are validated with the high-fidelity experimental data of Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018).
2. Background
2.1. The original model
We first revisit the original spectrum-based attached eddy model of Perry et al. (Reference Perry, Henbest and Chong1986), focusing on the streamwise velocity in a turbulent boundary layer, the thickness of which is given by ![]() $\delta$. The modelling efforts start with the streamwise turbulence intensity given in terms of the power-spectral density:
$\delta$. The modelling efforts start with the streamwise turbulence intensity given in terms of the power-spectral density:
where ![]() $\varPhi _{uu}(k_x,z)$ is the power-spectral density of streamwise velocity at each wall-normal location
$\varPhi _{uu}(k_x,z)$ is the power-spectral density of streamwise velocity at each wall-normal location ![]() $z$, and
$z$, and ![]() $k_x$ is the streamwise wavenumber. As in Townsend (Reference Townsend1976), only the flow above the thin viscous sublayer was considered, assuming that the flow is inviscid with finite slip velocity at the boundary. Under this assumption, the power-spectral density
$k_x$ is the streamwise wavenumber. As in Townsend (Reference Townsend1976), only the flow above the thin viscous sublayer was considered, assuming that the flow is inviscid with finite slip velocity at the boundary. Under this assumption, the power-spectral density ![]() $\varPhi _{uu}$ is expected to be a function of
$\varPhi _{uu}$ is expected to be a function of ![]() $u_\tau$,
$u_\tau$, ![]() $k_x$,
$k_x$, ![]() $z$ and
$z$ and ![]() $\delta$. Further to this,
$\delta$. Further to this, ![]() $z\ll \delta$ was assumed, given the wall-normal location of interest (i.e. the logarithmic layer).
$z\ll \delta$ was assumed, given the wall-normal location of interest (i.e. the logarithmic layer).
Under the two assumptions (i.e. ![]() $Re_\tau \rightarrow \infty$ and
$Re_\tau \rightarrow \infty$ and ![]() $z\ll \delta$), the model yields a power-spectral density of streamwise velocity schematically depicted in figure 1. At a given wall-normal location
$z\ll \delta$), the model yields a power-spectral density of streamwise velocity schematically depicted in figure 1. At a given wall-normal location ![]() $z\ll \delta$, energy-containing eddies of outer scale would contribute to the wavenumbers of
$z\ll \delta$, energy-containing eddies of outer scale would contribute to the wavenumbers of ![]() $k_x \sim O(1/\delta )$ through their inactive component (Perry & Abel Reference Perry and Abel1977; Perry et al. Reference Perry, Henbest and Chong1986). In this range of wavenumbers, the assumption of
$k_x \sim O(1/\delta )$ through their inactive component (Perry & Abel Reference Perry and Abel1977; Perry et al. Reference Perry, Henbest and Chong1986). In this range of wavenumbers, the assumption of ![]() $z\ll \delta$ implies that the power-spectral density can further be assumed to be independent of
$z\ll \delta$ implies that the power-spectral density can further be assumed to be independent of ![]() $z/\delta$. Using (2.1), the power-spectral density for
$z/\delta$. Using (2.1), the power-spectral density for ![]() $k_x \sim O(1/\delta )$ is then given by
$k_x \sim O(1/\delta )$ is then given by
The premultiplied power-spectral density is subsequently written as
as sketched in the ![]() $\delta$-scaling region of figure 1. For the wavenumbers of
$\delta$-scaling region of figure 1. For the wavenumbers of ![]() $k_x \sim O(1/z)$, the power-spectral density would not be a function of
$k_x \sim O(1/z)$, the power-spectral density would not be a function of ![]() $\delta$, as only eddies scaling in
$\delta$, as only eddies scaling in ![]() $z$ would contribute to these wavenumbers. Therefore, at
$z$ would contribute to these wavenumbers. Therefore, at ![]() $z\ll \delta$, the power-spectral density for
$z\ll \delta$, the power-spectral density for ![]() $k_x \sim O(1/z)$ becomes
$k_x \sim O(1/z)$ becomes
and the corresponding premultiplied power-spectral density is
This is sketched in the ![]() $z$-scaling region in figure 1. The power spectrum for very high
$z$-scaling region in figure 1. The power spectrum for very high ![]() $k_x$ should obviously be related to the energy cascade (the Kolmogrov scaling region in figure 1). Therefore it follows the scaling of inertial subrange (
$k_x$ should obviously be related to the energy cascade (the Kolmogrov scaling region in figure 1). Therefore it follows the scaling of inertial subrange (![]() $k_x^{-5/3}$ spectrum) and the dissipation at the Kolmogorov length scale
$k_x^{-5/3}$ spectrum) and the dissipation at the Kolmogorov length scale ![]() $\eta$ (Perry et al. Reference Perry, Henbest and Chong1986). The details of this part of the spectrum will not, however, be pursued here because its contribution to turbulence intensity would be small.
$\eta$ (Perry et al. Reference Perry, Henbest and Chong1986). The details of this part of the spectrum will not, however, be pursued here because its contribution to turbulence intensity would be small.

Figure 1. A schematic diagram of the streamwise velocity spectrum for the attached eddy model of Perry et al. (Reference Perry, Henbest and Chong1986). Here, the overlap region (i.e. inertial subrange) between ![]() $z$-scaling and dissipation (Kolmogorov) scaling and the dissipation scaling region are merged into a single region for simplicity (see text). Note that this is only a conceptual sketch introduced to explain the model of Perry et al. (Reference Perry, Henbest and Chong1986). Therefore it does not necessarily reflect the experimentally measured spectrum of streamwise velocity, especially when the Reynolds number is not sufficiently high.
$z$-scaling and dissipation (Kolmogorov) scaling and the dissipation scaling region are merged into a single region for simplicity (see text). Note that this is only a conceptual sketch introduced to explain the model of Perry et al. (Reference Perry, Henbest and Chong1986). Therefore it does not necessarily reflect the experimentally measured spectrum of streamwise velocity, especially when the Reynolds number is not sufficiently high.
We now consider the wavenumber region of ![]() $1/\delta \ll k_x \ll 1/z$ (the overlap region in figure 1). In this region, it was argued that both of the scalings in (2.2b) and (2.3b) would simultaneously be valid. Here, note that
$1/\delta \ll k_x \ll 1/z$ (the overlap region in figure 1). In this region, it was argued that both of the scalings in (2.2b) and (2.3b) would simultaneously be valid. Here, note that ![]() $h_1$ in (2.2b) is a function of only
$h_1$ in (2.2b) is a function of only ![]() $k_x \delta$, while
$k_x \delta$, while ![]() $h_2$ in (2.3b) is a function of
$h_2$ in (2.3b) is a function of ![]() $k_x z$. Therefore matching between (2.2b) and (2.3b) leads to
$k_x z$. Therefore matching between (2.2b) and (2.3b) leads to
where ![]() $A$ is a constant independent of both
$A$ is a constant independent of both ![]() $k_x z$ and
$k_x z$ and ![]() $k_x \delta$, resulting in the following power spectrum:
$k_x \delta$, resulting in the following power spectrum:
Using (2.1), (2.2b), (2.3b) and (2.5), the streamwise turbulence intensity, which is the area below the curve for the power-spectral density in figure 1, is obtained as
 $$\begin{align} \frac{\overline{u^\prime u^\prime}}{u_\tau^2} &= \int_{-\infty}^\infty \frac{k_x\, \varPhi_{uu}(k_x;z)}{u_\tau^2}\,\mathrm{d}(\ln k_x) = \int_{\ln (a/\delta)}^{\ln (b/z)} \frac{k_x\, \varPhi_{uu}(k_x)}{u_\tau^2}\,\mathrm{d}(\ln k_x)+C(z;Re_\tau)\nonumber\\ &={-}A\ln\left(\frac{z}{\delta}\right)+B(z;Re_\tau), \end{align}$$
$$\begin{align} \frac{\overline{u^\prime u^\prime}}{u_\tau^2} &= \int_{-\infty}^\infty \frac{k_x\, \varPhi_{uu}(k_x;z)}{u_\tau^2}\,\mathrm{d}(\ln k_x) = \int_{\ln (a/\delta)}^{\ln (b/z)} \frac{k_x\, \varPhi_{uu}(k_x)}{u_\tau^2}\,\mathrm{d}(\ln k_x)+C(z;Re_\tau)\nonumber\\ &={-}A\ln\left(\frac{z}{\delta}\right)+B(z;Re_\tau), \end{align}$$
where ![]() $a$ and
$a$ and ![]() $b$ are the constants defining the wavenumber boundaries of the
$b$ are the constants defining the wavenumber boundaries of the ![]() $k_x^{-1}$ region (blue-shaded region in figure 1) and
$k_x^{-1}$ region (blue-shaded region in figure 1) and
 \begin{equation} C\left(z;Re_\tau\right)=\frac{\overline{u^\prime u^\prime}}{u_\tau^2}-\int_{\ln (a/\delta)}^{\ln(b/z)} \frac{k_x\, \varPhi_{uu}(k_x)}{u_\tau^2}\,\mathrm{d}(\ln k_x). \end{equation}
\begin{equation} C\left(z;Re_\tau\right)=\frac{\overline{u^\prime u^\prime}}{u_\tau^2}-\int_{\ln (a/\delta)}^{\ln(b/z)} \frac{k_x\, \varPhi_{uu}(k_x)}{u_\tau^2}\,\mathrm{d}(\ln k_x). \end{equation}
Here, ![]() $C(z;Re_\tau )$ depicts the contribution from the remainder of the latter integral in (2.6a), and it should be a weak function of
$C(z;Re_\tau )$ depicts the contribution from the remainder of the latter integral in (2.6a), and it should be a weak function of ![]() $z$ and
$z$ and ![]() $Re_\tau$ due to the small contribution made from the Kolmogorov-scaling part of the spectrum. (Note that under the original assumptions of Perry et al. (Reference Perry, Henbest and Chong1986), the contribution from the outer-scaling part for
$Re_\tau$ due to the small contribution made from the Kolmogorov-scaling part of the spectrum. (Note that under the original assumptions of Perry et al. (Reference Perry, Henbest and Chong1986), the contribution from the outer-scaling part for ![]() $k_x \leq a/\delta$ to
$k_x \leq a/\delta$ to ![]() $C(z;Re_\tau )$ does not depend on
$C(z;Re_\tau )$ does not depend on ![]() $z$ and
$z$ and ![]() $Re_\tau$; see (2.2a).) If this contribution is ignored, then
$Re_\tau$; see (2.2a).) If this contribution is ignored, then ![]() $B$ and
$B$ and ![]() $C$ become constants, leading (2.6a) to be identical to (1.1) from Townsend (Reference Townsend1976). We note that (1.1) in Townsend (Reference Townsend1976) was obtained by ignoring the contribution from small-scale eddies for energy cascade and dissipation. Therefore the two models by Townsend (Reference Townsend1976) and by Perry et al. (Reference Perry, Henbest and Chong1986), the former of which was built in physical space and the latter in spectral space, become consistent.
$C$ become constants, leading (2.6a) to be identical to (1.1) from Townsend (Reference Townsend1976). We note that (1.1) in Townsend (Reference Townsend1976) was obtained by ignoring the contribution from small-scale eddies for energy cascade and dissipation. Therefore the two models by Townsend (Reference Townsend1976) and by Perry et al. (Reference Perry, Henbest and Chong1986), the former of which was built in physical space and the latter in spectral space, become consistent.
2.2. Scaling of streamwise velocity spectra
Now we examine the spectrum-based attached eddy model of Perry et al. (Reference Perry, Henbest and Chong1986) using the experimental data from Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018). These data were taken from the high Reynolds number boundary layer wind tunnel located at the University of Melbourne. The boundary-layer thickness ![]() $\delta$ and friction velocity
$\delta$ and friction velocity ![]() $u_\tau$ were estimated by fitting the measured experimental data to a composite law of the wall/wake curve in Chauhan, Monkewitz & Nagib (Reference Chauhan, Monkewitz and Nagib2010). Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018) compared their estimates for
$u_\tau$ were estimated by fitting the measured experimental data to a composite law of the wall/wake curve in Chauhan, Monkewitz & Nagib (Reference Chauhan, Monkewitz and Nagib2010). Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018) compared their estimates for ![]() $u_\tau$ from the composite fit to those measured directly by Baars et al. (Reference Baars, Squire, Talluru, Abbassi, Hutchins and Marusic2016) with a floating element drag balance, in the same facility, and matched
$u_\tau$ from the composite fit to those measured directly by Baars et al. (Reference Baars, Squire, Talluru, Abbassi, Hutchins and Marusic2016) with a floating element drag balance, in the same facility, and matched ![]() $x$ and
$x$ and ![]() $U_\infty$ (free-stream velocity) to the two highest Reynolds numbers of Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018), finding agreement to within
$U_\infty$ (free-stream velocity) to the two highest Reynolds numbers of Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018), finding agreement to within ![]() $\pm 1$% The near-wall region is fully resolved using the nanoscale thermal anemometry probes (NSTAPs) (Vallikivi & Smits Reference Vallikivi and Smits2014). The Reynolds numbers considered are
$\pm 1$% The near-wall region is fully resolved using the nanoscale thermal anemometry probes (NSTAPs) (Vallikivi & Smits Reference Vallikivi and Smits2014). The Reynolds numbers considered are ![]() $Re_\tau =6123,10\,100,14\,680,19\,680$. For further details on the experiment, the reader may refer to Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018).
$Re_\tau =6123,10\,100,14\,680,19\,680$. For further details on the experiment, the reader may refer to Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018).
Figure 2 shows the contours of the premultiplied streamwise power-spectral density of streamwise velocity at ![]() $Re_\tau =19\,680$, in which the two red straight lines indicate
$Re_\tau =19\,680$, in which the two red straight lines indicate ![]() $\lambda _x=z$ and
$\lambda _x=z$ and ![]() $\lambda _x=10\delta$. We first define the conventional logarithmic layer with a relatively conservative limit:
$\lambda _x=10\delta$. We first define the conventional logarithmic layer with a relatively conservative limit: ![]() $z \in [z_{i},z_o]$ where
$z \in [z_{i},z_o]$ where ![]() $z_i^+=200$ and
$z_i^+=200$ and ![]() $z_o=0.1\delta$ (the superscript
$z_o=0.1\delta$ (the superscript ![]() $^+$ denotes the normalisation with
$^+$ denotes the normalisation with ![]() $\delta _\nu (=\nu /u_\tau )$ and
$\delta _\nu (=\nu /u_\tau )$ and ![]() $u_\tau$). As was proposed previously (Afzal Reference Afzal1982; Sreenivasan & Sahay Reference Sreenivasan and Sahay1997; Wei et al. Reference Wei, Fife, Klewicki and Mcmurtry2005; Klewicki Reference Klewicki2013), the logarithmic layer may be partitioned further into two sublayers with the boundary at
$u_\tau$). As was proposed previously (Afzal Reference Afzal1982; Sreenivasan & Sahay Reference Sreenivasan and Sahay1997; Wei et al. Reference Wei, Fife, Klewicki and Mcmurtry2005; Klewicki Reference Klewicki2013), the logarithmic layer may be partitioned further into two sublayers with the boundary at ![]() $z_m^+=3.6 Re_\tau ^{1/2}$: i.e. layer I for
$z_m^+=3.6 Re_\tau ^{1/2}$: i.e. layer I for ![]() $z \in [z_{m},z_o]$, and layer II for
$z \in [z_{m},z_o]$, and layer II for ![]() $z \in [z_{i},z_m]$. Here, we note that the location of
$z \in [z_{i},z_m]$. Here, we note that the location of ![]() $z_m$ is a little below the empirical wall-normal location of the outer peak in the spectra (
$z_m$ is a little below the empirical wall-normal location of the outer peak in the spectra (![]() $z_m^+=3.9 Re_\tau ^{1/2}$) proposed by Mathis, Hutchins & Marusic (Reference Mathis, Hutchins and Marusic2009).
$z_m^+=3.9 Re_\tau ^{1/2}$) proposed by Mathis, Hutchins & Marusic (Reference Mathis, Hutchins and Marusic2009).
(i) Layer I (inertial sublayer): in this layer, the inertial effect would dominate the viscous wall effect. Given the inviscid-flow assumption of Perry et al. (Reference Perry, Henbest and Chong1986), this is the location where their model is supposed to be directly applicable. Indeed, the contour lines for
 $\lambda _x \gtrsim 10\delta$ in figure 2 change little along the
$\lambda _x \gtrsim 10\delta$ in figure 2 change little along the  $z$-direction and remain mostly parallel to
$z$-direction and remain mostly parallel to  $\lambda _x=10 \delta$, indicating that (2.2b) would be a good approximation for
$\lambda _x=10 \delta$, indicating that (2.2b) would be a good approximation for  $\lambda _x \gtrsim 10\delta$. Similarly, the contour lines for
$\lambda _x \gtrsim 10\delta$. Similarly, the contour lines for  $10^{-2} \delta \leq \lambda _x \leq \delta$ are approximately parallel to
$10^{-2} \delta \leq \lambda _x \leq \delta$ are approximately parallel to  $\lambda _x=z$, consistent with (2.3b). These scaling behaviours are more precisely confirmed in figure 3 – the spectra in layer I follow the scaling of (2.2b) for
$\lambda _x=z$, consistent with (2.3b). These scaling behaviours are more precisely confirmed in figure 3 – the spectra in layer I follow the scaling of (2.2b) for  $\lambda _x \gtrsim 10 \delta$ (figure 3
$\lambda _x \gtrsim 10 \delta$ (figure 3 $a$) and they do so with (2.3b) for
$a$) and they do so with (2.3b) for  $z \lesssim \lambda _x \lesssim 10 z$ (figure 3
$z \lesssim \lambda _x \lesssim 10 z$ (figure 3 $b$). Despite the scaling behaviours being fully consistent with (2.2b) and (2.3b), the spectra in between (
$b$). Despite the scaling behaviours being fully consistent with (2.2b) and (2.3b), the spectra in between ( $10 z\leq \lambda _x \leq 10 \delta$) do not seem to exhibit a well-developed
$10 z\leq \lambda _x \leq 10 \delta$) do not seem to exhibit a well-developed  $k_x^{-1}$ behaviour. Furthermore, the values of the spectra vary non-negligibly with
$k_x^{-1}$ behaviour. Furthermore, the values of the spectra vary non-negligibly with  $z$, indicating that there is an issue in comparing (2.5) with the experimental data (e.g. Morrison et al. Reference Morrison, Jiang, McKeon and Smits2001, Reference Morrison, McKeon, Jiang and Smits2004; Rosenberg et al. Reference Rosenberg, Hultmark, Vallikivi, Bailey and Smits2013). These issues will be discussed in depth in § 3.
$z$, indicating that there is an issue in comparing (2.5) with the experimental data (e.g. Morrison et al. Reference Morrison, Jiang, McKeon and Smits2001, Reference Morrison, McKeon, Jiang and Smits2004; Rosenberg et al. Reference Rosenberg, Hultmark, Vallikivi, Bailey and Smits2013). These issues will be discussed in depth in § 3.(ii) Layer II (mesolayer): given the nature of the mean momentum balance in this layer (Afzal Reference Afzal1982; Sreenivasan & Sahay Reference Sreenivasan and Sahay1997; Wei et al. Reference Wei, Fife, Klewicki and Mcmurtry2005; Klewicki Reference Klewicki2013), the viscous wall effect would be more important than the inertial effect. In particular, the premultiplied power-spectral density for
 $\lambda _x \gtrsim 10 \delta$ appears to become weaker as
$\lambda _x \gtrsim 10 \delta$ appears to become weaker as  $z\rightarrow 0$, and the related contour lines in figure 2 are not parallel to
$z\rightarrow 0$, and the related contour lines in figure 2 are not parallel to  $\lambda _x=10 \delta$. On the contrary, the power-spectral density for
$\lambda _x=10 \delta$. On the contrary, the power-spectral density for  $10^{-2} \delta \leq \lambda _x \leq 10^{-1} \delta$ still appears to follow (2.3b), as the contour lines in figure 2 are approximately parallel to
$10^{-2} \delta \leq \lambda _x \leq 10^{-1} \delta$ still appears to follow (2.3b), as the contour lines in figure 2 are approximately parallel to  $\lambda _x=z$ (see also figure 7). This is also confirmed in figure 3 – the spectra in layer II do not precisely follow the scaling of (2.2b) for
$\lambda _x=z$ (see also figure 7). This is also confirmed in figure 3 – the spectra in layer II do not precisely follow the scaling of (2.2b) for  $\lambda _x \gtrsim 10 \delta$ (figure 3
$\lambda _x \gtrsim 10 \delta$ (figure 3 $c$), while they show a behaviour consistent with (2.3b) for
$c$), while they show a behaviour consistent with (2.3b) for  $z \lesssim \lambda _x \lesssim 10 z$ (figure 3
$z \lesssim \lambda _x \lesssim 10 z$ (figure 3 $d$). These observations will be the basis of the model for layer II in § 4, obtained by extending the one in § 3.
$d$). These observations will be the basis of the model for layer II in § 4, obtained by extending the one in § 3.

Figure 2. Premultiplied streamwise power-spectral density of streamwise velocity (![]() $k_x^+\, \varPhi _{uu}^+(z;k_x)$) at
$k_x^+\, \varPhi _{uu}^+(z;k_x)$) at ![]() $Re_\tau \simeq 19\,680$ (data from Samie et al. Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018). The contour lines are
$Re_\tau \simeq 19\,680$ (data from Samie et al. Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018). The contour lines are ![]() $k_x^+\,\varPhi _{uu}^+(z;k_x)=0.25, 0.5, 0.75,$
$k_x^+\,\varPhi _{uu}^+(z;k_x)=0.25, 0.5, 0.75,$ ![]() $1, 1.25, 1.5, 1.75, 2.0$. Here, the logarithmic layer from
$1, 1.25, 1.5, 1.75, 2.0$. Here, the logarithmic layer from ![]() $z^+= 200$ to
$z^+= 200$ to ![]() $z/\delta =0.1$ is divided into two sublayers: layer I (inertial sublayer) and layer II (mesolayer). The two red solid lines indicate
$z/\delta =0.1$ is divided into two sublayers: layer I (inertial sublayer) and layer II (mesolayer). The two red solid lines indicate ![]() $\lambda _x=z$ and
$\lambda _x=z$ and ![]() $\lambda _z=10\delta$, as labelled.
$\lambda _z=10\delta$, as labelled.

Figure 3. Premultiplied streamwise power-spectral density of streamwise velocity in ![]() $(a{,}b)$ layer I and
$(a{,}b)$ layer I and ![]() $(c{,}d)$ layer II at
$(c{,}d)$ layer II at ![]() $Re_\tau =19\,680$:
$Re_\tau =19\,680$: ![]() $(a{,}c)$
$(a{,}c)$ ![]() $\delta$-scaling, and
$\delta$-scaling, and ![]() $(b{,}d)$
$(b{,}d)$ ![]() $z$-scaling. The arrows indicate the directions of increasing
$z$-scaling. The arrows indicate the directions of increasing ![]() $z$.
$z$.
We note that the classification of the logarithmic layer into layers I and II in the present study is based on the streamwise velocity spectra, not on the mean velocity. Given the streamwise mean momentum equation for a turbulent boundary layer, the streamwise mean velocity is mostly related to the Reynolds shear stress like channel and pipe flows. However, the fluctuations of the streamwise velocity carry a substantial amount of motions that contain little Reynolds shear stress. Such motions have been referred to as ‘inactive’ motions (Townsend Reference Townsend1976), which appear to be particularly important in the region close to the wall (Hwang Reference Hwang2015, Reference Hwang2016; Cho, Hwang & Choi Reference Cho, Hwang and Choi2018; Baars & Marusic Reference Baars and Marusic2020a; Deshpande, Monty & Marusic Reference Deshpande, Monty and Marusic2020). These motions do not necessarily have strong effect on the mean velocity. Therefore the empirical scaling of ![]() $z_m^+(=3.6 Re_\tau ^{1/2})$ used here is not necessarily the same as the wall-normal location (say
$z_m^+(=3.6 Re_\tau ^{1/2})$ used here is not necessarily the same as the wall-normal location (say ![]() $z_R$) that has been used to partition the inertial sublayer and the mesolayer based on the Reynolds shear stress (i.e.
$z_R$) that has been used to partition the inertial sublayer and the mesolayer based on the Reynolds shear stress (i.e. ![]() $z_R$ is the location where the Reynolds shear stress is maximum). Indeed, an empirical value of
$z_R$ is the location where the Reynolds shear stress is maximum). Indeed, an empirical value of ![]() $z_R^+$ is given by
$z_R^+$ is given by ![]() $z_R^+=1.9 Re_\tau ^{1/2}$ (Afzal & Yajnik Reference Afzal and Yajnik1973; Afzal Reference Afzal1976, Reference Afzal1982; Sreenivasan & Sahay Reference Sreenivasan and Sahay1997; Wei et al. Reference Wei, Fife, Klewicki and Mcmurtry2005; Jiménez & Moser Reference Jiménez and Moser2007; Klewicki Reference Klewicki2013), indicating that
$z_R^+=1.9 Re_\tau ^{1/2}$ (Afzal & Yajnik Reference Afzal and Yajnik1973; Afzal Reference Afzal1976, Reference Afzal1982; Sreenivasan & Sahay Reference Sreenivasan and Sahay1997; Wei et al. Reference Wei, Fife, Klewicki and Mcmurtry2005; Jiménez & Moser Reference Jiménez and Moser2007; Klewicki Reference Klewicki2013), indicating that ![]() $z_m>z_R$. This implies that the Reynolds shear stress would slightly decrease with
$z_m>z_R$. This implies that the Reynolds shear stress would slightly decrease with ![]() $z$ in layer I and that the peak Reynolds shear stress is located in layer II.
$z$ in layer I and that the peak Reynolds shear stress is located in layer II.
3. Proposed model
We first consider layer I, where the scalings in (2.2b) and (2.3b) were found to be consistent with the experimental data. The inviscid flow assumption of Perry et al. (Reference Perry, Henbest and Chong1986) would still be applicable because the streamwise velocity is not zero at the lower boundary of layer I (![]() $z=z_m$). However, the assumption of
$z=z_m$). However, the assumption of ![]() $z\ll \delta$ needs to be dealt with more carefully, if the Reynolds number is not infinite. Indeed, even at the highest Reynolds number considered in Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018) (
$z\ll \delta$ needs to be dealt with more carefully, if the Reynolds number is not infinite. Indeed, even at the highest Reynolds number considered in Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018) (![]() $Re_\tau =19\,680$),
$Re_\tau =19\,680$), ![]() $z_m \simeq 0.025 \delta$ and
$z_m \simeq 0.025 \delta$ and ![]() $z_o=0.1 \delta$. Therefore, in layer I, the value of
$z_o=0.1 \delta$. Therefore, in layer I, the value of ![]() $z/\delta$ is not infinitesimal, but only small and finite with
$z/\delta$ is not infinitesimal, but only small and finite with ![]() $z/\delta$ varying from
$z/\delta$ varying from ![]() $O(Re_\tau ^{-1/2})$ to
$O(Re_\tau ^{-1/2})$ to ![]() $O(10^{-1})$. This implies that the assumption of
$O(10^{-1})$. This implies that the assumption of ![]() $z\ll \delta$ in Perry et al. (Reference Perry, Henbest and Chong1986) would not strictly be valid in most of layer I even at
$z\ll \delta$ in Perry et al. (Reference Perry, Henbest and Chong1986) would not strictly be valid in most of layer I even at ![]() $Re_\tau =19\,680$.
$Re_\tau =19\,680$.
3.1. Spectrum at  $1/\delta \ll k_{x} \ll 1/z$ for small and finite
$1/\delta \ll k_{x} \ll 1/z$ for small and finite  $z/\delta$
$z/\delta$
If ![]() $z/\delta$ is finite in the region of interest, then the power-spectral density for
$z/\delta$ is finite in the region of interest, then the power-spectral density for ![]() $k_x \sim O(1/\delta )$ and
$k_x \sim O(1/\delta )$ and ![]() $k_x \sim O(1/z)$ would not strictly be independent of
$k_x \sim O(1/z)$ would not strictly be independent of ![]() $z/\delta$. Such a behaviour is particularly pronounced in the region above layer I where
$z/\delta$. Such a behaviour is particularly pronounced in the region above layer I where ![]() $z/\delta$ is not small: indeed, the contour lines of the premultiplied spectra in figure 2 are not parallel to
$z/\delta$ is not small: indeed, the contour lines of the premultiplied spectra in figure 2 are not parallel to ![]() $\lambda _x=10\delta$ and
$\lambda _x=10\delta$ and ![]() $\lambda _x=z$. Therefore, without loss of generality, the premultiplied spectra in (2.2b) and (2.3b) should be replaced with
$\lambda _x=z$. Therefore, without loss of generality, the premultiplied spectra in (2.2b) and (2.3b) should be replaced with
and
respectively. Considering a ![]() $z/\delta$-dependence of the spectrum for
$z/\delta$-dependence of the spectrum for ![]() $k_x \sim O(1/\delta )$ and
$k_x \sim O(1/\delta )$ and ![]() $k_x \sim O(1/z)$ is physically more sound and offers more modelling flexibility. Indeed, (3.1a) would allow one to account for any wall-normal variation of outer-scaling structures such as superstructures/very-large-scale motions, while (3.1b) allows one to consider directly the small wall-normal variation in the
$k_x \sim O(1/z)$ is physically more sound and offers more modelling flexibility. Indeed, (3.1a) would allow one to account for any wall-normal variation of outer-scaling structures such as superstructures/very-large-scale motions, while (3.1b) allows one to consider directly the small wall-normal variation in the ![]() $z$-scaling spectrum caused by the energy cascade.
$z$-scaling spectrum caused by the energy cascade.
Now (3.1a) and (3.1b) are considered for ![]() $1/\delta \ll k_{x} \ll 1/z$. For
$1/\delta \ll k_{x} \ll 1/z$. For ![]() $1/\delta \ll k_{x} \ll 1/z$, the spectrum should satisfy
$1/\delta \ll k_{x} \ll 1/z$, the spectrum should satisfy ![]() $\tilde {h}_1(k_x \delta,{z/\delta })=\tilde {h}_2(k_x z,z/\delta )$. Here,
$\tilde {h}_1(k_x \delta,{z/\delta })=\tilde {h}_2(k_x z,z/\delta )$. Here, ![]() $k_x z$ and
$k_x z$ and ![]() $k_x \delta$ must be treated as two independent variables, because the two scaling laws in (3.1a) and (3.1b) from the Buckingham
$k_x \delta$ must be treated as two independent variables, because the two scaling laws in (3.1a) and (3.1b) from the Buckingham ![]() ${\rm \pi}$ theorem are introduced to cover different values of
${\rm \pi}$ theorem are introduced to cover different values of ![]() $k_x$ at all admissible small
$k_x$ at all admissible small ![]() $z/\delta$ (Hinch Reference Hinch1991). While this may be a useful feature to proceed further to identify the form of spectrum for
$z/\delta$ (Hinch Reference Hinch1991). While this may be a useful feature to proceed further to identify the form of spectrum for ![]() $1/\delta \ll k_{x} \ll 1/z$, here we shall write the following form of the premultiplied spectrum without loss of generality:
$1/\delta \ll k_{x} \ll 1/z$, here we shall write the following form of the premultiplied spectrum without loss of generality:
leading to
where ![]() $l_{I}$ is an appropriate length scale that can be chosen for
$l_{I}$ is an appropriate length scale that can be chosen for ![]() $z\ll l_{I} \ll \delta$ in the range of
$z\ll l_{I} \ll \delta$ in the range of ![]() $1/\delta \ll k_{x} \ll 1/z$. Here, we note that only the condition of
$1/\delta \ll k_{x} \ll 1/z$. Here, we note that only the condition of ![]() $z/\delta \rightarrow 0$ is relaxed compared to Perry et al. (Reference Perry, Henbest and Chong1986), as we are concerned with finite Reynolds number and turbulence intensity for layer I. While we assume that there is no explicit form of the spectrum available for
$z/\delta \rightarrow 0$ is relaxed compared to Perry et al. (Reference Perry, Henbest and Chong1986), as we are concerned with finite Reynolds number and turbulence intensity for layer I. While we assume that there is no explicit form of the spectrum available for ![]() $1/\delta \ll k_{x} \ll 1/z$, the form of (3.3) raises several non-trivial issues to be discussed as follows.
$1/\delta \ll k_{x} \ll 1/z$, the form of (3.3) raises several non-trivial issues to be discussed as follows.
(i) The spectrum for
 $O(1/\delta ) < k_x < O(1/z)$: while (3.3) provides a general form of the spectrum for
$O(1/\delta ) < k_x < O(1/z)$: while (3.3) provides a general form of the spectrum for  $1/\delta \ll k_x \ll 1/z$, this part of the spectrum should not be interpreted as an outcome of simultaneous ‘physical’ contribution of
$1/\delta \ll k_x \ll 1/z$, this part of the spectrum should not be interpreted as an outcome of simultaneous ‘physical’ contribution of  $\delta$- and
$\delta$- and  $z$-scaling motions, as was argued in Perry et al. (Reference Perry, Henbest and Chong1986). We note that the logarithmic wall-normal dependence of the
$z$-scaling motions, as was argued in Perry et al. (Reference Perry, Henbest and Chong1986). We note that the logarithmic wall-normal dependence of the  $u$ variance in the original theory of Townsend (Reference Townsend1976) is due to the wall-reaching inactive motions of each attached eddy, the size of which varies from
$u$ variance in the original theory of Townsend (Reference Townsend1976) is due to the wall-reaching inactive motions of each attached eddy, the size of which varies from  $O(z)$ to
$O(z)$ to  $O(\delta )$. In other words, the non-zero spectrum for
$O(\delta )$. In other words, the non-zero spectrum for  $O(1/\delta ) < k_x < O(1/z)$ should be primarily from the contribution of the inactive motions of those attached eddies, as was also directly confirmed by the recent work of Deshpande et al. (Reference Deshpande, Monty and Marusic2020).
$O(1/\delta ) < k_x < O(1/z)$ should be primarily from the contribution of the inactive motions of those attached eddies, as was also directly confirmed by the recent work of Deshpande et al. (Reference Deshpande, Monty and Marusic2020).(ii) Relation to the original model: now let us assume
 $Re_\tau \rightarrow \infty$, so that the lower boundary of layer I reaches the wall (i.e.
$Re_\tau \rightarrow \infty$, so that the lower boundary of layer I reaches the wall (i.e.  $z_m \rightarrow 0$). In this case, using the Taylor series expansion about
$z_m \rightarrow 0$). In this case, using the Taylor series expansion about  $z=0$, the premultiplied power-spectral intensity in (3.1a), (3.1b) and (3.3) can further be approximated with
(3.4a)for
$z=0$, the premultiplied power-spectral intensity in (3.1a), (3.1b) and (3.3) can further be approximated with
(3.4a)for \begin{equation} \tilde{h}_1(k_x \delta, z/\delta)=\tilde{h}_1(k_x \delta,0)+\frac{\partial \tilde{h}_1(k_x \delta, 0)}{\partial (z/\delta)}\left(\frac{z}{\delta}\right)+O\left(\frac{z^2}{\delta^2}\right) \end{equation}
\begin{equation} \tilde{h}_1(k_x \delta, z/\delta)=\tilde{h}_1(k_x \delta,0)+\frac{\partial \tilde{h}_1(k_x \delta, 0)}{\partial (z/\delta)}\left(\frac{z}{\delta}\right)+O\left(\frac{z^2}{\delta^2}\right) \end{equation} $k_x \sim O(1/\delta )$,
(3.4b)for
$k_x \sim O(1/\delta )$,
(3.4b)for \begin{equation} \tilde{h}_2(k_x z, z/\delta)=\tilde{h}_2(k_x z,0)+\frac{\partial \tilde{h}_2(k_x z,0)}{\partial (z/\delta)}\left(\frac{z}{\delta}\right)+O\left(\frac{z^2}{\delta^2}\right) \end{equation}
\begin{equation} \tilde{h}_2(k_x z, z/\delta)=\tilde{h}_2(k_x z,0)+\frac{\partial \tilde{h}_2(k_x z,0)}{\partial (z/\delta)}\left(\frac{z}{\delta}\right)+O\left(\frac{z^2}{\delta^2}\right) \end{equation} $k_x \sim O(1/z)$, and
(3.4c)for
$k_x \sim O(1/z)$, and
(3.4c)for \begin{equation} {h(k_x l_{I}, z/\delta)=h(k_x l_{I}, 0)+\frac{\partial h(k_x l_{I},0)}{\partial (z/\delta)}\left(\frac{z}{\delta}\right)+O\left(\frac{z^2}{\delta^2}\right)} \end{equation}
\begin{equation} {h(k_x l_{I}, z/\delta)=h(k_x l_{I}, 0)+\frac{\partial h(k_x l_{I},0)}{\partial (z/\delta)}\left(\frac{z}{\delta}\right)+O\left(\frac{z^2}{\delta^2}\right)} \end{equation} $1/\delta \ll k_x \ll 1/z$, respectively. If the prediction (2.5) given by Perry et al. (Reference Perry, Henbest and Chong1986) is correct, it is now expected that
$1/\delta \ll k_x \ll 1/z$, respectively. If the prediction (2.5) given by Perry et al. (Reference Perry, Henbest and Chong1986) is correct, it is now expected that  $h(k_x l_{I}, 0) \rightarrow A$ in the limit as
$h(k_x l_{I}, 0) \rightarrow A$ in the limit as  $z/\delta \rightarrow 0$. Although the detailed convergence to this possible limiting behaviour would be answered only by additional measurements at higher Reynolds numbers, it is evident that in this limit, (3.1a), (3.1b) and (3.3) become identical to (2.2b), (2.3b) and (2.5) by setting
$z/\delta \rightarrow 0$. Although the detailed convergence to this possible limiting behaviour would be answered only by additional measurements at higher Reynolds numbers, it is evident that in this limit, (3.1a), (3.1b) and (3.3) become identical to (2.2b), (2.3b) and (2.5) by setting  $\tilde {h}_1(k_x \delta, 0)=h_1(k_x \delta )$,
$\tilde {h}_1(k_x \delta, 0)=h_1(k_x \delta )$,  $\tilde {h}_2(k_x z, 0)=h_2(k_x z)$ and
$\tilde {h}_2(k_x z, 0)=h_2(k_x z)$ and  $h(k_x l_{I}, 0)=A$. This implies that the original model of Perry et al. (Reference Perry, Henbest and Chong1986) would be strictly valid in the limit as
$h(k_x l_{I}, 0)=A$. This implies that the original model of Perry et al. (Reference Perry, Henbest and Chong1986) would be strictly valid in the limit as  $z/\delta \rightarrow 0$. As such, the emergence of a well-developed
$z/\delta \rightarrow 0$. As such, the emergence of a well-developed  $k_x^{-1}$ spectrum in the sense of Perry et al. (Reference Perry, Henbest and Chong1986) might be observed only for very small
$k_x^{-1}$ spectrum in the sense of Perry et al. (Reference Perry, Henbest and Chong1986) might be observed only for very small  $z/\delta$ at extremely high Reynolds numbers, as was recently proposed by Baars & Marusic (Reference Baars and Marusic2020a). Care therefore needs to be taken in interpreting (2.5) obtained from Perry et al. (Reference Perry, Henbest and Chong1986) for the experimental data where
$z/\delta$ at extremely high Reynolds numbers, as was recently proposed by Baars & Marusic (Reference Baars and Marusic2020a). Care therefore needs to be taken in interpreting (2.5) obtained from Perry et al. (Reference Perry, Henbest and Chong1986) for the experimental data where  $z/\delta$ is not infinitesimal but small. In fact, (3.4c) indicates that the wall-normal variation of the spectral intensity for
$z/\delta$ is not infinitesimal but small. In fact, (3.4c) indicates that the wall-normal variation of the spectral intensity for  $1/\delta \ll k_x \ll 1/z$ would be of
$1/\delta \ll k_x \ll 1/z$ would be of  $O(z/\delta )$. Since
$O(z/\delta )$. Since  $z/\delta \sim O(10^{-1})$ in layer I, the premultiplied spectrum for
$z/\delta \sim O(10^{-1})$ in layer I, the premultiplied spectrum for  $O(1/\delta ) < k_x < O(1/z)$ is expected to change with
$O(1/\delta ) < k_x < O(1/z)$ is expected to change with  $z/\delta$ at least by
$z/\delta$ at least by  $O(10^{-1})$. This is exactly seen in the experimental data in figure 3 as well as in other previous papers (Morrison et al. Reference Morrison, Jiang, McKeon and Smits2001, Reference Morrison, McKeon, Jiang and Smits2004; Rosenberg et al. Reference Rosenberg, Hultmark, Vallikivi, Bailey and Smits2013), and it is due to the ‘finite
$O(10^{-1})$. This is exactly seen in the experimental data in figure 3 as well as in other previous papers (Morrison et al. Reference Morrison, Jiang, McKeon and Smits2001, Reference Morrison, McKeon, Jiang and Smits2004; Rosenberg et al. Reference Rosenberg, Hultmark, Vallikivi, Bailey and Smits2013), and it is due to the ‘finite  $z/\delta$’ of the measurement locations at finite Reynolds numbers.
$z/\delta$’ of the measurement locations at finite Reynolds numbers.(iii) Townsend–Perry constant: The general form of spectrum given by (3.3) suggests that in practice (at finite Reynolds number and finite
 $z/\delta$), the premultiplied spectrum in the absence of a well-developed
$z/\delta$), the premultiplied spectrum in the absence of a well-developed  $k_x^{-1}$ spectrum in layer I would offer little insight into the Townsend–Perry constant
$k_x^{-1}$ spectrum in layer I would offer little insight into the Townsend–Perry constant  $A$ (see (2.5)). This also implies that the log-linear behaviour of the streamwise turbulence intensity, previously reported to emerge in the form of (1.1) (e.g. Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013), is not the one expected directly from the model of Perry et al. (Reference Perry, Henbest and Chong1986), because the spectrum intensity varies with
$A$ (see (2.5)). This also implies that the log-linear behaviour of the streamwise turbulence intensity, previously reported to emerge in the form of (1.1) (e.g. Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013), is not the one expected directly from the model of Perry et al. (Reference Perry, Henbest and Chong1986), because the spectrum intensity varies with  $z/\delta$ without necessarily exhibiting a well-developed
$z/\delta$ without necessarily exhibiting a well-developed  $k_x^{-1}$ spectrum. In this respect, it is now important to understand how the logarithmic wall-normal dependence of streamwise turbulence intensity would emerge without having a
$k_x^{-1}$ spectrum. In this respect, it is now important to understand how the logarithmic wall-normal dependence of streamwise turbulence intensity would emerge without having a  $k_x^{-1}$ spectrum.
$k_x^{-1}$ spectrum.
3.2. Turbulence intensity
From the discussion given above, a schematic diagram of the premultiplied power-spectral density for the model in the present study is sketched in figure 4. This schematic diagram is also consistent with the spectra observed in figure 3 (compare figure 3 with figure 4). The primary differences from the schematic diagram in figure 1 are: (1) a non-trivial form of spectrum for ![]() $1/\delta \ll k \ll 1/z$; (2) the intensity dependent on
$1/\delta \ll k \ll 1/z$; (2) the intensity dependent on ![]() $z/\delta$ for all
$z/\delta$ for all ![]() $k_x$; (3) the spectrum with order unity intensity for
$k_x$; (3) the spectrum with order unity intensity for ![]() $k_x \in [a_{I}/\delta, b_{I}/\delta ]$ from (3.1a) and (3.1b) (red-shaded region in figure 4), where
$k_x \in [a_{I}/\delta, b_{I}/\delta ]$ from (3.1a) and (3.1b) (red-shaded region in figure 4), where ![]() $a_{I}$ and
$a_{I}$ and ![]() $b_{I}$ are
$b_{I}$ are ![]() $O(1)$ constants to be defined below. In this model, the spectrum for
$O(1)$ constants to be defined below. In this model, the spectrum for ![]() $a_{I}/\delta \leq k_x \leq b_{I}/z$ is set to take the following form without loss of generality:
$a_{I}/\delta \leq k_x \leq b_{I}/z$ is set to take the following form without loss of generality:
and ![]() $a_{I}$ and
$a_{I}$ and ![]() $b_{I}$ are given such that
$b_{I}$ are given such that
where ![]() $A_{{I},0}$ is a constant of
$A_{{I},0}$ is a constant of ![]() $O(1)$, and such that
$O(1)$, and such that ![]() $\Delta A_{{I},0}(k_x l_{I},z/\delta )(\equiv k_x\,\varPhi (k_x,z)/u_\tau ^2- A_{{I},0})$ satisfies
$\Delta A_{{I},0}(k_x l_{I},z/\delta )(\equiv k_x\,\varPhi (k_x,z)/u_\tau ^2- A_{{I},0})$ satisfies
 \begin{equation} \underbrace{\int_{\ln (a_{I}/\delta)}^{\ln (b_{I}/z)} \Delta A_{{I},0}\left(k_x l_{I},\frac{z}{\delta}\right)\mathrm{d}(\ln k_x)}_{{}\equiv A_{{I},1}(z/\delta)} \sim O\left(\frac{z}{\delta}\right). \end{equation}
\begin{equation} \underbrace{\int_{\ln (a_{I}/\delta)}^{\ln (b_{I}/z)} \Delta A_{{I},0}\left(k_x l_{I},\frac{z}{\delta}\right)\mathrm{d}(\ln k_x)}_{{}\equiv A_{{I},1}(z/\delta)} \sim O\left(\frac{z}{\delta}\right). \end{equation}
In other words, with the spectrum, ![]() $A_{{I},0}$,
$A_{{I},0}$, ![]() $a_{I}$ and
$a_{I}$ and ![]() $b_{I}$ can be chosen such that the area below the premultiplied spectrum for
$b_{I}$ can be chosen such that the area below the premultiplied spectrum for ![]() $a_{I}/\delta \leq k_x \leq b_{I}/z$ is approximated by the red-shaded region in figure 4 with an error of
$a_{I}/\delta \leq k_x \leq b_{I}/z$ is approximated by the red-shaded region in figure 4 with an error of ![]() $O(z/\delta )$. We note that such a choice of
$O(z/\delta )$. We note that such a choice of ![]() $A_{{I},0}$,
$A_{{I},0}$, ![]() $a_{I}$ and
$a_{I}$ and ![]() $b_{I}$ must always be possible, because the mean-value theorem for integrals ensures the existence of
$b_{I}$ must always be possible, because the mean-value theorem for integrals ensures the existence of ![]() $A_{{I},M}(z/\delta )$ satisfying
$A_{{I},M}(z/\delta )$ satisfying
 \begin{equation} {A}_{{I},M}(z/\delta)=\left[\ln\left(\frac{b_{{I}}}{z}\right)-\ln\left(\frac{a_{{I}}}{\delta}\right)\right]^{{-}1} \int_{\ln (a_{I}/\delta)}^{\ln (b_{I}/z)} \frac{k_x\,\varPhi_{uu}(k_x,z/\delta)}{u_\tau^2}\,\mathrm{d}(\ln k_x). \end{equation}
\begin{equation} {A}_{{I},M}(z/\delta)=\left[\ln\left(\frac{b_{{I}}}{z}\right)-\ln\left(\frac{a_{{I}}}{\delta}\right)\right]^{{-}1} \int_{\ln (a_{I}/\delta)}^{\ln (b_{I}/z)} \frac{k_x\,\varPhi_{uu}(k_x,z/\delta)}{u_\tau^2}\,\mathrm{d}(\ln k_x). \end{equation}
Here, ![]() $A_{{I},M}(z/\delta )$ can further be written such that
$A_{{I},M}(z/\delta )$ can further be written such that
where ![]() $A_{{I},1}(z/\delta )$ remains at
$A_{{I},1}(z/\delta )$ remains at ![]() $O(z/\delta )$ by applying the Taylor series expansion to
$O(z/\delta )$ by applying the Taylor series expansion to ![]() $A_{{I},M}(z/\delta )$ at any wall-normal location in layer I.
$A_{{I},M}(z/\delta )$ at any wall-normal location in layer I.

Figure 4. A schematic diagram of the proposed model in the present study for the spectra in layer I.
From (2.1) and (3.6), the streamwise turbulence intensity is now written as
 \begin{align} \frac{\overline{u^\prime u^\prime}}{u_\tau^2} &= \int_{-\infty}^\infty \frac{k_x\, \varPhi_{uu}(k_x;z)}{u_\tau^2}\,\mathrm{d}(\ln k_x) = \int_{\ln (a_{I}/\delta)}^{\ln (b_{I}/z)} \frac{k_x\,\varPhi_{uu}(k_x)}{u_\tau^2}\,\mathrm{d}(\ln k_x)+C_{{I}}(z;Re_\tau) \nonumber\\ & = \left[A_{{I},0}+A_{{I},1}\left(\frac{z}{\delta}\right)\right]\left[\ln\left(\frac{b_{{I}}}{z}\right)-\ln\left(\frac{a_{{I}}}{\delta}\right)\right]+C_{{I}}(z;Re_\tau) \nonumber\\ &={-}\left[A_{{I},0}+A_{{I},1}\left(\frac{z}{\delta}\right)\right]\ln\left(\frac{z}{\delta}\right)+B_{{I}}(z;Re_\tau), \end{align}
\begin{align} \frac{\overline{u^\prime u^\prime}}{u_\tau^2} &= \int_{-\infty}^\infty \frac{k_x\, \varPhi_{uu}(k_x;z)}{u_\tau^2}\,\mathrm{d}(\ln k_x) = \int_{\ln (a_{I}/\delta)}^{\ln (b_{I}/z)} \frac{k_x\,\varPhi_{uu}(k_x)}{u_\tau^2}\,\mathrm{d}(\ln k_x)+C_{{I}}(z;Re_\tau) \nonumber\\ & = \left[A_{{I},0}+A_{{I},1}\left(\frac{z}{\delta}\right)\right]\left[\ln\left(\frac{b_{{I}}}{z}\right)-\ln\left(\frac{a_{{I}}}{\delta}\right)\right]+C_{{I}}(z;Re_\tau) \nonumber\\ &={-}\left[A_{{I},0}+A_{{I},1}\left(\frac{z}{\delta}\right)\right]\ln\left(\frac{z}{\delta}\right)+B_{{I}}(z;Re_\tau), \end{align}where
 \begin{gather} C_{{I}}\left(z;Re_\tau\right)=\frac{\overline{u^\prime u^\prime}}{u_\tau^2}-\int_{\ln (b_{I}/\delta)}^{\ln(a_{I}/z)} \frac{k_x\,\varPhi_{uu}(k_x)}{u_\tau^2}\,\mathrm{d}(\ln k_x), \end{gather}
\begin{gather} C_{{I}}\left(z;Re_\tau\right)=\frac{\overline{u^\prime u^\prime}}{u_\tau^2}-\int_{\ln (b_{I}/\delta)}^{\ln(a_{I}/z)} \frac{k_x\,\varPhi_{uu}(k_x)}{u_\tau^2}\,\mathrm{d}(\ln k_x), \end{gather}
Here, ![]() $C_{{I}}(z;Re_\tau )$ represents the contribution of the spectrum for
$C_{{I}}(z;Re_\tau )$ represents the contribution of the spectrum for ![]() $k_x< a_{I}/\delta$ and
$k_x< a_{I}/\delta$ and ![]() $k_x>b_{I}/z$ to the turbulence intensity, and it should depend weakly on
$k_x>b_{I}/z$ to the turbulence intensity, and it should depend weakly on ![]() $z$ and
$z$ and ![]() $Re_\tau$ due to the Kolmogorov-scaling part in figure 4 and the weak
$Re_\tau$ due to the Kolmogorov-scaling part in figure 4 and the weak ![]() $(z/\delta )$-dependence of (3.4a) and (3.4b) within layer I. In (3.7a) and (3.7c), the Taylor series expansion allows
$(z/\delta )$-dependence of (3.4a) and (3.4b) within layer I. In (3.7a) and (3.7c), the Taylor series expansion allows ![]() $A_{{I},1}(z/\delta )$ to be approximated further as
$A_{{I},1}(z/\delta )$ to be approximated further as
 \begin{equation} A_{{I},1}\left(\frac{z}{\delta}\right)=A_{{I},1}\left(\frac{z_{I,m}}{\delta}\right)+\frac{\mathrm{d} A_{{I},1}}{\mathrm{d} (z/\delta)}\bigg|_{z=z_{{I},m}} \frac{(z-z_{{I},m})}{\delta} +O\left(\frac{|z-z_{{I},m}|^2}{\delta^2}\right), \end{equation}
\begin{equation} A_{{I},1}\left(\frac{z}{\delta}\right)=A_{{I},1}\left(\frac{z_{I,m}}{\delta}\right)+\frac{\mathrm{d} A_{{I},1}}{\mathrm{d} (z/\delta)}\bigg|_{z=z_{{I},m}} \frac{(z-z_{{I},m})}{\delta} +O\left(\frac{|z-z_{{I},m}|^2}{\delta^2}\right), \end{equation}
where ![]() $z_{{I},m}=\sqrt {z_m z_o}$ is chosen to be the geometric mean of
$z_{{I},m}=\sqrt {z_m z_o}$ is chosen to be the geometric mean of ![]() $z_m$ and
$z_m$ and ![]() $z_o$, so that the right-hand side of (3.8) becomes a good approximation to
$z_o$, so that the right-hand side of (3.8) becomes a good approximation to ![]() $A_{{I},1}$ over the entire layer I in the ‘logarithmic’ wall-normal coordinate. The same approximation can be applied to
$A_{{I},1}$ over the entire layer I in the ‘logarithmic’ wall-normal coordinate. The same approximation can be applied to ![]() $C_{{I}}(z;Re_\tau )$ in (3.7b). Since
$C_{{I}}(z;Re_\tau )$ in (3.7b). Since ![]() $z_{I,m}/\delta$ is a function of
$z_{I,m}/\delta$ is a function of ![]() $Re_\tau$ from
$Re_\tau$ from ![]() $z_m/\delta = 3.6 Re_\tau ^{-0.5}$, the streamwise turbulence intensity is finally given by
$z_m/\delta = 3.6 Re_\tau ^{-0.5}$, the streamwise turbulence intensity is finally given by
where ![]() $A_{{I}}(Re_\tau )=A_{{I},0}+A_{{I},1}(z_{{I},m}/\delta )$ and the error at
$A_{{I}}(Re_\tau )=A_{{I},0}+A_{{I},1}(z_{{I},m}/\delta )$ and the error at ![]() $O(z/\delta )$ stems from approximation of
$O(z/\delta )$ stems from approximation of ![]() $C_{{I}}(z;Re_\tau )$ in (3.7c) for layer I. We also note that in layer I, the Reynolds shear stress would evidently be
$C_{{I}}(z;Re_\tau )$ in (3.7c) for layer I. We also note that in layer I, the Reynolds shear stress would evidently be ![]() $-\overline {u'w'}/{u_\tau ^2}= \mathrm {const} + O(z/\delta )$, where
$-\overline {u'w'}/{u_\tau ^2}= \mathrm {const} + O(z/\delta )$, where ![]() $w'$ is the wall-normal velocity fluctuation. Therefore (3.9) is consistent with the original attached eddy model of Townsend (Reference Townsend1976) with an error of
$w'$ is the wall-normal velocity fluctuation. Therefore (3.9) is consistent with the original attached eddy model of Townsend (Reference Townsend1976) with an error of ![]() $O(z/\delta )$.
$O(z/\delta )$.
Now, the logarithmic wall-normal dependence of the streamwise turbulence intensity is retrieved in (3.9) as in the classical theories (Townsend Reference Townsend1976; Perry & Chong Reference Perry and Chong1982; Perry et al. Reference Perry, Henbest and Chong1986) with a small error at ![]() $O(z/\delta ) \sim 10^{-1}$, indicating that the classical result is indeed a reliable first approximation to the streamwise turbulence intensity in layer I. Importantly, the Townsend–Perry constant
$O(z/\delta ) \sim 10^{-1}$, indicating that the classical result is indeed a reliable first approximation to the streamwise turbulence intensity in layer I. Importantly, the Townsend–Perry constant ![]() $A_{{I}}$ in this case emerges as a function of
$A_{{I}}$ in this case emerges as a function of ![]() $Re_\tau$, and, to our knowledge, the present study provides the first rigorous derivation for this feature – it would depend weakly on
$Re_\tau$, and, to our knowledge, the present study provides the first rigorous derivation for this feature – it would depend weakly on ![]() $Re_\tau$, given
$Re_\tau$, given ![]() $A_{{I},1} \sim O(z/\delta )$ from (3.6b). We note that this is a combined consequence of (3.6b) and the nature of
$A_{{I},1} \sim O(z/\delta )$ from (3.6b). We note that this is a combined consequence of (3.6b) and the nature of ![]() $z_{m}$ (or
$z_{m}$ (or ![]() $z_{{I},m}$) depending on
$z_{{I},m}$) depending on ![]() $Re_\tau$. Since
$Re_\tau$. Since ![]() $z_{m}$ is a function of
$z_{m}$ is a function of ![]() $Re_\tau$ due to the viscous wall effect, the Reynolds-number-dependent nature of
$Re_\tau$ due to the viscous wall effect, the Reynolds-number-dependent nature of ![]() $A_{{I}}(Re_\tau )$ in (3.9) essentially originates from the role of viscosity ignored in the original theories (e.g. Townsend Reference Townsend1976; Perry & Chong Reference Perry and Chong1982; Perry et al. Reference Perry, Henbest and Chong1986). This is evident from
$A_{{I}}(Re_\tau )$ in (3.9) essentially originates from the role of viscosity ignored in the original theories (e.g. Townsend Reference Townsend1976; Perry & Chong Reference Perry and Chong1982; Perry et al. Reference Perry, Henbest and Chong1986). This is evident from ![]() $z_{m}/\delta \rightarrow 0$ in the limit as
$z_{m}/\delta \rightarrow 0$ in the limit as ![]() $Re_\tau \rightarrow \infty$: that is, the velocity slip condition (i.e. non-zero spectrum at
$Re_\tau \rightarrow \infty$: that is, the velocity slip condition (i.e. non-zero spectrum at ![]() $z=z_m$) reaches all the way down to the wall in such a limit. In this case, as
$z=z_m$) reaches all the way down to the wall in such a limit. In this case, as ![]() $z/\delta \rightarrow 0$,
$z/\delta \rightarrow 0$, ![]() $A_{{I}}$ becomes constant from (3.6b), and the error of
$A_{{I}}$ becomes constant from (3.6b), and the error of ![]() $O(z/\delta )$ in (3.9) vanishes. Therefore (3.9) consequently becomes identical to (2.6) from the original model of Perry et al. (Reference Perry, Henbest and Chong1986) in the limit as
$O(z/\delta )$ in (3.9) vanishes. Therefore (3.9) consequently becomes identical to (2.6) from the original model of Perry et al. (Reference Perry, Henbest and Chong1986) in the limit as ![]() $Re_\tau \rightarrow \infty$ and
$Re_\tau \rightarrow \infty$ and ![]() $z/\delta \rightarrow 0$.
$z/\delta \rightarrow 0$.
It should, however, be mentioned that the use of the mean-value theorem in (3.6) for the derivation of (3.9) is the key difference from that of (2.6) in Perry et al. (Reference Perry, Henbest and Chong1986). The derivation here is more general and inclusive than that in Perry et al. (Reference Perry, Henbest and Chong1986), because it does not rely on the existence of a ![]() $k_x^{-1}$ spectrum. Instead, it suggests that a more general condition for the existence of an approximate logarithmic wall-normal dependence of the streamwise turbulence intensity is the existence of the premultiplied power-spectral density of
$k_x^{-1}$ spectrum. Instead, it suggests that a more general condition for the existence of an approximate logarithmic wall-normal dependence of the streamwise turbulence intensity is the existence of the premultiplied power-spectral density of ![]() $O(1)$ for
$O(1)$ for ![]() $O(1/\delta ) \leq k_x \leq O(1/z)$ (red-shaded region in figure 4), which is entirely consistent with the experimental data in figure 3. Here, it is important to note that this behaviour essentially originates from the spectrum scalings in (3.1a) and (3.1b), the general versions of (2.2) and (2.3) for finite
$O(1/\delta ) \leq k_x \leq O(1/z)$ (red-shaded region in figure 4), which is entirely consistent with the experimental data in figure 3. Here, it is important to note that this behaviour essentially originates from the spectrum scalings in (3.1a) and (3.1b), the general versions of (2.2) and (2.3) for finite ![]() $z/\delta$, because (3.9) is simply a consequence of applying the mean-value theorem in (3.6) with them. Since (2.2) and (2.3) depict the
$z/\delta$, because (3.9) is simply a consequence of applying the mean-value theorem in (3.6) with them. Since (2.2) and (2.3) depict the ![]() $\delta$-scaling inactive motions of large eddies and the
$\delta$-scaling inactive motions of large eddies and the ![]() $z$-scaling self-similar eddies, the theoretical development here is also well within the framework of the attached eddy hypothesis. Lastly, it is worth mentioning that a more accurate description for
$z$-scaling self-similar eddies, the theoretical development here is also well within the framework of the attached eddy hypothesis. Lastly, it is worth mentioning that a more accurate description for ![]() $\Delta A_{{I},0}(z_{{I},m}/\delta )$ may well be possible from a viewpoint of scaling with
$\Delta A_{{I},0}(z_{{I},m}/\delta )$ may well be possible from a viewpoint of scaling with ![]() $Re_\tau$. The recent effort made by Vassilicos et al. (Reference Vassilicos, Laval, Foucaut and Stanislas2015) can be interpreted in such a context, as it is based on a prescribed semi-empirical description for the spectrum lying between the wavenumber ranges for (2.2b) and (2.5).
$Re_\tau$. The recent effort made by Vassilicos et al. (Reference Vassilicos, Laval, Foucaut and Stanislas2015) can be interpreted in such a context, as it is based on a prescribed semi-empirical description for the spectrum lying between the wavenumber ranges for (2.2b) and (2.5).
3.3. Determination of  $A_{I}$ and
$A_{I}$ and  $B_{I}$ from experimental data
$B_{I}$ from experimental data
While the analysis in §§ 3.1 and 3.2 provides an insight into the relationship between the power-spectral density and the streamwise turbulence intensity at finite Reynolds numbers, there is a practical issue in applying it to the data obtained from laboratory experiments and numerical simulations. This issue is related to how one would choose ![]() $A_{{I},0}$,
$A_{{I},0}$, ![]() $a_{{I}}$ and
$a_{{I}}$ and ![]() $b_{{I}}$ robustly. To this end, here we propose a simple semi-empirical modelling framework for the streamwise turbulence intensity by leveraging the mean-value theorem (3.6). We start by writing the turbulence intensity as
$b_{{I}}$ robustly. To this end, here we propose a simple semi-empirical modelling framework for the streamwise turbulence intensity by leveraging the mean-value theorem (3.6). We start by writing the turbulence intensity as
 \begin{align} \frac{\overline{u^\prime u^\prime}}{u_\tau^2} & = \int_{-\infty}^\infty \frac{k_x\, \varPhi_{uu}(z;k_x;Re_\tau)}{u_\tau^2}\,\mathrm{d}(\ln k_x) \nonumber\\ &= \left[\ln\left(\frac{b_{{I},s}}{z}\right)-\ln\left(\frac{a_{{I},s}}{\delta}\right)\right] \varPi_{I}(z;Re_\tau) \nonumber\\ &= \left[\ln\left(\frac{b_{{I},s}}{a_{{I},s}}\right)-\ln\left(\frac{z}{\delta}\right)\right] \varPi_{I}(z;Re_\tau), \end{align}
\begin{align} \frac{\overline{u^\prime u^\prime}}{u_\tau^2} & = \int_{-\infty}^\infty \frac{k_x\, \varPhi_{uu}(z;k_x;Re_\tau)}{u_\tau^2}\,\mathrm{d}(\ln k_x) \nonumber\\ &= \left[\ln\left(\frac{b_{{I},s}}{z}\right)-\ln\left(\frac{a_{{I},s}}{\delta}\right)\right] \varPi_{I}(z;Re_\tau) \nonumber\\ &= \left[\ln\left(\frac{b_{{I},s}}{a_{{I},s}}\right)-\ln\left(\frac{z}{\delta}\right)\right] \varPi_{I}(z;Re_\tau), \end{align}where
Here, ![]() $a_{{I},s}$ and
$a_{{I},s}$ and ![]() $b_{{I},s}$ are constants that play roles similar to those of
$b_{{I},s}$ are constants that play roles similar to those of ![]() $a_{{I}}$ and
$a_{{I}}$ and ![]() $b_{{I}}$ in figure 4, but their values are not necessarily the same. However, given the analysis in § 3.2, they need to be chosen from the wavenumbers of
$b_{{I}}$ in figure 4, but their values are not necessarily the same. However, given the analysis in § 3.2, they need to be chosen from the wavenumbers of ![]() $\delta$- and
$\delta$- and ![]() $z$-scaling regions of the premultiplied spectra, and have to be constant at all Reynolds numbers. While this sets out a condition for
$z$-scaling regions of the premultiplied spectra, and have to be constant at all Reynolds numbers. While this sets out a condition for ![]() $a_{{I},s}$ and
$a_{{I},s}$ and ![]() $b_{{I},s}$ to be met, it is also important to note that they cannot be chosen arbitrarily. Although (3.10) is supposed to automatically yield a streamwise turbulence intensity in the form of (3.7a) for any values of
$b_{{I},s}$ to be met, it is also important to note that they cannot be chosen arbitrarily. Although (3.10) is supposed to automatically yield a streamwise turbulence intensity in the form of (3.7a) for any values of ![]() $a_{{I},s}$ and
$a_{{I},s}$ and ![]() $b_{{I},s}$, the last line of (3.10a) implies that it has a single degree of freedom for the determination of
$b_{{I},s}$, the last line of (3.10a) implies that it has a single degree of freedom for the determination of ![]() $A_{{I}}$ and
$A_{{I}}$ and ![]() $B_{{I}}$ in (3.7a) (i.e. the value of
$B_{{I}}$ in (3.7a) (i.e. the value of ![]() $b_{{I},s}/a_{{I},s}$). Indeed, if
$b_{{I},s}/a_{{I},s}$). Indeed, if ![]() $b_{{I},s}/a_{{I},s}<1$ is chosen, then
$b_{{I},s}/a_{{I},s}<1$ is chosen, then ![]() $B_{{I}}$ in (3.7a) becomes negative from (3.10a), which would obviously be non-physical. Therefore the last condition for
$B_{{I}}$ in (3.7a) becomes negative from (3.10a), which would obviously be non-physical. Therefore the last condition for ![]() $a_{{I},s}$ and
$a_{{I},s}$ and ![]() $b_{{I},s}$ to be met is that they must be chosen such that
$b_{{I},s}$ to be met is that they must be chosen such that ![]() $\ln (b_{{I},s}/a_{{I},s})\,\varPi _{I}(z;Re_\tau )$ would represent
$\ln (b_{{I},s}/a_{{I},s})\,\varPi _{I}(z;Re_\tau )$ would represent ![]() $B_{{I}}$ in (3.7a) well, while ensuring
$B_{{I}}$ in (3.7a) well, while ensuring ![]() $b_{{I},s}/a_{{I},s}>1$.
$b_{{I},s}/a_{{I},s}>1$.
In the present study, ![]() $a_{{I},s}={\rm \pi} /5$ and
$a_{{I},s}={\rm \pi} /5$ and ![]() $b_{{I},s}=2{\rm \pi}$ are chosen so that
$b_{{I},s}=2{\rm \pi}$ are chosen so that ![]() $\lambda _{x,{I}\,a}(\equiv 2{\rm \pi} \delta /a_{{I},s})=10\delta$ and
$\lambda _{x,{I}\,a}(\equiv 2{\rm \pi} \delta /a_{{I},s})=10\delta$ and ![]() $\lambda _{x,{I}\,b}(\equiv 2{\rm \pi} z/b_{{I},s})=z$. These values are obtained by trial and error. To do so, a range of candidate values of
$\lambda _{x,{I}\,b}(\equiv 2{\rm \pi} z/b_{{I},s})=z$. These values are obtained by trial and error. To do so, a range of candidate values of ![]() $a_{{I},s}$ and
$a_{{I},s}$ and ![]() $b_{{I},s}$ are first selected from the spectra in figure 3, so that
$b_{{I},s}$ are first selected from the spectra in figure 3, so that ![]() $\lambda _{x,{I}\,a}$ and
$\lambda _{x,{I}\,a}$ and ![]() $\lambda _{x,{I}\,b}$ lie in the
$\lambda _{x,{I}\,b}$ lie in the ![]() $\delta$- and
$\delta$- and ![]() $z$-scaling regions, respectively. Indeed, figure 3 shows that the premultiplied spectra in layer I scale well with
$z$-scaling regions, respectively. Indeed, figure 3 shows that the premultiplied spectra in layer I scale well with ![]() $\delta$ for
$\delta$ for ![]() $\lambda _x\simeq \lambda _{x,{I}\,a}$, and with
$\lambda _x\simeq \lambda _{x,{I}\,a}$, and with ![]() $z$ for
$z$ for ![]() $\lambda _x\simeq \lambda _{x,{I}\,b}$, and that
$\lambda _x\simeq \lambda _{x,{I}\,b}$, and that ![]() $b_{{I},s}/a_{{I},s}>1$, consistent with the purpose of
$b_{{I},s}/a_{{I},s}>1$, consistent with the purpose of ![]() $a_{{I},s}$ and
$a_{{I},s}$ and ![]() $b_{{I},s}$ introduced here. Once this is ensured, the final values of
$b_{{I},s}$ introduced here. Once this is ensured, the final values of ![]() $a_{{I},s}$ and
$a_{{I},s}$ and ![]() $b_{{I},s}$ are determined by monitoring the form of
$b_{{I},s}$ are determined by monitoring the form of ![]() $\varPi _{I}(z)$ within the layer. If a set of sensible values is chosen, then
$\varPi _{I}(z)$ within the layer. If a set of sensible values is chosen, then ![]() $\varPi _{I}(z)$ must exhibit a plateau around
$\varPi _{I}(z)$ must exhibit a plateau around ![]() $z=z_{I,m}$ in layer I. Indeed, figure 5 demonstrates that, for the given
$z=z_{I,m}$ in layer I. Indeed, figure 5 demonstrates that, for the given ![]() $a_{{I},s}$ and
$a_{{I},s}$ and ![]() $b_{{I},s}$,
$b_{{I},s}$, ![]() $\varPi _{I}(z)$ remains approximately constant in layer I. Once
$\varPi _{I}(z)$ remains approximately constant in layer I. Once ![]() $a_{{I},s}$ and
$a_{{I},s}$ and ![]() $b_{{I},s}$ are determined, the resulting streamwise turbulence intensity is approximated around
$b_{{I},s}$ are determined, the resulting streamwise turbulence intensity is approximated around ![]() $z=z_{{I},m}$ (see also (3.9)):
$z=z_{{I},m}$ (see also (3.9)):
where
The values of ![]() $A_{{I}}(Re_\tau )$ and
$A_{{I}}(Re_\tau )$ and ![]() $B_{{I}}(Re_\tau )$ are then obtained from (3.11b) and (3.11c), respectively. In the present study, the values of
$B_{{I}}(Re_\tau )$ are then obtained from (3.11b) and (3.11c), respectively. In the present study, the values of ![]() $a_{{I},s}={\rm \pi} /5$ and
$a_{{I},s}={\rm \pi} /5$ and ![]() $b_{{I},s}=2{\rm \pi}$ are first determined at
$b_{{I},s}=2{\rm \pi}$ are first determined at ![]() $Re_\tau =19\,680$ and are subsequently used for the other Reynolds numbers. Figure 6 shows the streamwise turbulence intensity and its approximation from (3.11). With the given
$Re_\tau =19\,680$ and are subsequently used for the other Reynolds numbers. Figure 6 shows the streamwise turbulence intensity and its approximation from (3.11). With the given ![]() $a_{{I},s}$ and
$a_{{I},s}$ and ![]() $b_{{I},s}$, the proposed framework in (3.10) determines both
$b_{{I},s}$, the proposed framework in (3.10) determines both ![]() $A_{{I}}$ and
$A_{{I}}$ and ![]() $B_{{I}}$ well, so that (3.11a) becomes a good fit to the turbulence intensity in layer I at all the Reynolds numbers. The computed values of
$B_{{I}}$ well, so that (3.11a) becomes a good fit to the turbulence intensity in layer I at all the Reynolds numbers. The computed values of ![]() $A_{{I}}(Re_\tau )$ and
$A_{{I}}(Re_\tau )$ and ![]() $B_{{I}}(Re_\tau )$ are also reported in table 1 with the approximation error of the model (3.11a) in layer I. The maximum error is found to be less than about 4 % at all the Reynolds numbers considered.
$B_{{I}}(Re_\tau )$ are also reported in table 1 with the approximation error of the model (3.11a) in layer I. The maximum error is found to be less than about 4 % at all the Reynolds numbers considered.

Figure 5. ![]() $\varPi _{{I}}(z)$ (solid line) from (3.10b), and
$\varPi _{{I}}(z)$ (solid line) from (3.10b), and ![]() $A_{{I}}$ (dashed line) from (3.11b): (
$A_{{I}}$ (dashed line) from (3.11b): (![]() $a$)
$a$) ![]() $Re_{\tau }=6123$; (
$Re_{\tau }=6123$; (![]() $b$)
$b$) ![]() $Re_{\tau }= 10\,100$; (
$Re_{\tau }= 10\,100$; (![]() $c$)
$c$) ![]() $Re_{\tau }=14\,680$; (
$Re_{\tau }=14\,680$; (![]() $d$)
$d$) ![]() $Re_{\tau }=19\,680$. Here,
$Re_{\tau }=19\,680$. Here, ![]() $a_{{I},s}=2{\rm \pi}$ (
$a_{{I},s}=2{\rm \pi}$ (![]() $\lambda _{x,{I}\,a}=10$) and
$\lambda _{x,{I}\,a}=10$) and ![]() $b_{{I},s}={\rm \pi} /5$ (
$b_{{I},s}={\rm \pi} /5$ (![]() $\lambda _{x,{I}\,b}=1$).
$\lambda _{x,{I}\,b}=1$).

Figure 6. Streamwise turbulence intensity (solid line) and its approximation given by (3.11) (dashed line) in layer I: (![]() $a$)
$a$) ![]() $Re_{\tau }=6123$; (
$Re_{\tau }=6123$; (![]() $b$)
$b$) ![]() $Re_{\tau }=10\,100$; (
$Re_{\tau }=10\,100$; (![]() $c$)
$c$) ![]() $Re_{\tau }=14\,680$; (
$Re_{\tau }=14\,680$; (![]() $d$)
$d$) ![]() $Re_{\tau }=19\,680$. Here,
$Re_{\tau }=19\,680$. Here, ![]() $a_{{I},s}={\rm \pi} /5$ (
$a_{{I},s}={\rm \pi} /5$ (![]() $\lambda _{x,{I}\,a}/\delta =10$) and
$\lambda _{x,{I}\,a}/\delta =10$) and ![]() $b_{{I},s}=2{\rm \pi}$ (
$b_{{I},s}=2{\rm \pi}$ (![]() $\lambda _{x,{I}\,b}/z=1$).
$\lambda _{x,{I}\,b}/z=1$).
Table 1. The Reynolds-number dependence of ![]() $A_{I}$ and
$A_{I}$ and ![]() $B_{I}$ from (3.11) with
$B_{I}$ from (3.11) with ![]() $a_{{I},s}={\rm \pi} /5$ (
$a_{{I},s}={\rm \pi} /5$ (![]() $\lambda _{x,{I}\,a}/\delta =10$) and
$\lambda _{x,{I}\,a}/\delta =10$) and ![]() $b_{{I},s}=2{\rm \pi}$ (
$b_{{I},s}=2{\rm \pi}$ (![]() $\lambda _{x,{I}\,b}/z=1$). Here,
$\lambda _{x,{I}\,b}/z=1$). Here, ![]() $\text {Error}\equiv \max _z |\overline {u^\prime u^\prime }_{{model}}-\overline {u^\prime u^\prime }|/\overline {u^\prime u^\prime }$ for
$\text {Error}\equiv \max _z |\overline {u^\prime u^\prime }_{{model}}-\overline {u^\prime u^\prime }|/\overline {u^\prime u^\prime }$ for ![]() $z \in [z_m,z_o]$, where
$z \in [z_m,z_o]$, where ![]() $\overline {u^\prime u^\prime }_{{model}}$ is from (3.11), and it indicates the maximum error of the proposed model in layer I.
$\overline {u^\prime u^\prime }_{{model}}$ is from (3.11), and it indicates the maximum error of the proposed model in layer I.

4. Extension to layer II
4.1. Scaling of spectra
The model developed in § 3 is further extended to layer II where ![]() $z_i \leq z \leq z_m$ with
$z_i \leq z \leq z_m$ with ![]() $z_i^+=200$ and
$z_i^+=200$ and ![]() $z_m^+=3.6 Re_\tau ^{1/2}$ (
$z_m^+=3.6 Re_\tau ^{1/2}$ (![]() $z_m^+=505$ at
$z_m^+=505$ at ![]() $Re_\tau =19\,680$). In particular, here we shall take an empirical approach for the information that cannot be retrieved solely with scaling arguments. Given the importance of viscous forces in this layer, the power-spectral density should be a function of
$Re_\tau =19\,680$). In particular, here we shall take an empirical approach for the information that cannot be retrieved solely with scaling arguments. Given the importance of viscous forces in this layer, the power-spectral density should be a function of ![]() $u_\tau$,
$u_\tau$, ![]() $k_x$,
$k_x$, ![]() $z$,
$z$, ![]() $\delta$ and
$\delta$ and ![]() $\delta _\nu (\equiv \nu /u_\tau )$. Without loss of generality, the outer-scaling part of the spectrum for
$\delta _\nu (\equiv \nu /u_\tau )$. Without loss of generality, the outer-scaling part of the spectrum for ![]() $k_x \sim O(1/\delta )$ would therefore be written as a function of
$k_x \sim O(1/\delta )$ would therefore be written as a function of ![]() $z^+$ and
$z^+$ and ![]() $Re_\tau (=\delta /\delta _\nu )$ as
$Re_\tau (=\delta /\delta _\nu )$ as
with the corresponding premultiplied spectrum
Similarly, the ![]() $z$-scaling part of the spectrum is written as
$z$-scaling part of the spectrum is written as
and the premultiplied spectrum is
Here, we note that the introduction of a possible dependence on ![]() $z^+$ and
$z^+$ and ![]() $Re_\tau$ in (4.1) and (4.2) is to describe the viscous wall effect on
$Re_\tau$ in (4.1) and (4.2) is to describe the viscous wall effect on ![]() $z$- and
$z$- and ![]() $\delta$-scaling motions, the scaling and the corresponding energy balance of which were discussed in detail in Hwang (Reference Hwang2016) and Cho et al. (Reference Cho, Hwang and Choi2018) using a linear theory and numerical simulation data. While the contribution of
$\delta$-scaling motions, the scaling and the corresponding energy balance of which were discussed in detail in Hwang (Reference Hwang2016) and Cho et al. (Reference Cho, Hwang and Choi2018) using a linear theory and numerical simulation data. While the contribution of ![]() $\delta$-scaling motions is sometimes accounted for separately (Baars & Marusic Reference Baars and Marusic2020a,Reference Baars and Marusicb; Deshpande et al. Reference Deshpande, Monty and Marusic2020), here we shall consider the contributions of all the energy-containing motions simultaneously.
$\delta$-scaling motions is sometimes accounted for separately (Baars & Marusic Reference Baars and Marusic2020a,Reference Baars and Marusicb; Deshpande et al. Reference Deshpande, Monty and Marusic2020), here we shall consider the contributions of all the energy-containing motions simultaneously.
The spectra given in (4.1) and (4.2) suggest that the dependence of ![]() $h_{1,{II}}$ and
$h_{1,{II}}$ and ![]() $h_{2,{II}}$ on
$h_{2,{II}}$ on ![]() $z^+$ and
$z^+$ and ![]() $Re_\tau$ would be the major complication in extending the analysis in § 3 to layer II. Therefore, from here, we shall further proceed by empirically modelling the experimental data of Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018) in layer II. As discussed in § 2, the contour lines for
$Re_\tau$ would be the major complication in extending the analysis in § 3 to layer II. Therefore, from here, we shall further proceed by empirically modelling the experimental data of Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018) in layer II. As discussed in § 2, the contour lines for ![]() $\lambda _x\gtrsim 10 \delta$ in figure 2 are not parallel to
$\lambda _x\gtrsim 10 \delta$ in figure 2 are not parallel to ![]() $\lambda _x=10 \delta$. They rather appear to fall off approximately linearly towards the wall in the logarithmic coordinates, indicating that the outer-scaling part of the spectra would empirically follow a mixed scale of
$\lambda _x=10 \delta$. They rather appear to fall off approximately linearly towards the wall in the logarithmic coordinates, indicating that the outer-scaling part of the spectra would empirically follow a mixed scale of ![]() $\lambda _x/\delta \sim (z^+)^p$, where
$\lambda _x/\delta \sim (z^+)^p$, where ![]() $p$ is a positive number to be determined. Based on this observation, (4.1) may be written as
$p$ is a positive number to be determined. Based on this observation, (4.1) may be written as
where ![]() $\delta _{{II}}=\delta (z^+)^p$ is the empirical similarity length scale formed by
$\delta _{{II}}=\delta (z^+)^p$ is the empirical similarity length scale formed by ![]() $\delta$ and
$\delta$ and ![]() $z^+$, and the
$z^+$, and the ![]() $z/\delta _{{II}}$-dependence is introduced to admit the small deviation of the spectra in layer II similarly to the case in layer I (§ 3.1). As for the inner-scaling part of the spectra, the contour lines for
$z/\delta _{{II}}$-dependence is introduced to admit the small deviation of the spectra in layer II similarly to the case in layer I (§ 3.1). As for the inner-scaling part of the spectra, the contour lines for ![]() $10^{-2} \delta \leq \lambda _x \leq 10^{-1} \delta$ in layer II (figure 2) are still approximately parallel to
$10^{-2} \delta \leq \lambda _x \leq 10^{-1} \delta$ in layer II (figure 2) are still approximately parallel to ![]() $\lambda _x=z$. Therefore
$\lambda _x=z$. Therefore ![]() $h_{2,{II}}(k_x z,z^+)$ in (4.2) is also written as
$h_{2,{II}}(k_x z,z^+)$ in (4.2) is also written as
where ![]() $z/\delta _{{II}}$ is introduced to allow for a small variation in the wall-normal location. Figure 7 confirms that the empirical scalings in (4.3a) and (4.3b) are reasonably good: the outer-scale part of the premultiplied spectra scales well with
$z/\delta _{{II}}$ is introduced to allow for a small variation in the wall-normal location. Figure 7 confirms that the empirical scalings in (4.3a) and (4.3b) are reasonably good: the outer-scale part of the premultiplied spectra scales well with ![]() $\delta _{{II}}$ for
$\delta _{{II}}$ for ![]() $p=0.41$ obtained empirically (figure 7
$p=0.41$ obtained empirically (figure 7![]() $a$), while the inner-scaling part shows good scaling with
$a$), while the inner-scaling part shows good scaling with ![]() $z$ (figure 7
$z$ (figure 7![]() $b$).
$b$).

Figure 7. Premultiplied streamwise power-spectral density of streamwise velocity in layer II (![]() $Re_\tau = 19\,680$): (
$Re_\tau = 19\,680$): (![]() $a$)
$a$) ![]() $\delta _{{II}}$-scaling and (
$\delta _{{II}}$-scaling and (![]() $b$)
$b$) ![]() $z$-scaling. Here,
$z$-scaling. Here, ![]() $\delta _{{II}}=\delta (z^+)^p$ with
$\delta _{{II}}=\delta (z^+)^p$ with ![]() $p=0.41$.
$p=0.41$.
The form of (4.3a) and (4.3b) is now identical to that of (3.1a) and (3.1b), if ![]() $\delta$ is replaced by
$\delta$ is replaced by ![]() $\delta _{II}$. The procedure in § 3.1 can therefore be applied exactly in the same manner. Without loss of generality, this yields
$\delta _{II}$. The procedure in § 3.1 can therefore be applied exactly in the same manner. Without loss of generality, this yields
for ![]() $1/\delta _{{II}} \ll k_x \ll 1/z$ with
$1/\delta _{{II}} \ll k_x \ll 1/z$ with ![]() $z \ll l_{II} \ll \delta _{II}$, and the resulting premultiplied power-spectral density for
$z \ll l_{II} \ll \delta _{II}$, and the resulting premultiplied power-spectral density for ![]() $1/\delta _{{II}} \ll k_x \ll 1/z$ is given by
$1/\delta _{{II}} \ll k_x \ll 1/z$ is given by
Equation (4.5) suggests that a ![]() $k_x^{-1}$ spectrum would also be observed at each wall-normal location in layer II. As shown in figure 7, such a spectrum does seem to appear for
$k_x^{-1}$ spectrum would also be observed at each wall-normal location in layer II. As shown in figure 7, such a spectrum does seem to appear for ![]() $50 z \lesssim \lambda _x \lesssim 0.5 \delta _{{II}}$ in the form of a peak or a narrow plateau. It also indicates that the intensity of the
$50 z \lesssim \lambda _x \lesssim 0.5 \delta _{{II}}$ in the form of a peak or a narrow plateau. It also indicates that the intensity of the ![]() $k_x^{-1}$ spectrum would vary in the wall-normal direction by
$k_x^{-1}$ spectrum would vary in the wall-normal direction by ![]() $O(z/\delta _{II})$ in layer II. Given the definition of layer II,
$O(z/\delta _{II})$ in layer II. Given the definition of layer II, ![]() $z/\delta _{II} \sim O(10^{-2})$. Figure 7 shows that the variation of the peak intensity of each premultiplied spectrum is much smaller than that in layer I (compare with figure 3), supporting the relevance of (4.5).
$z/\delta _{II} \sim O(10^{-2})$. Figure 7 shows that the variation of the peak intensity of each premultiplied spectrum is much smaller than that in layer I (compare with figure 3), supporting the relevance of (4.5).
4.2. Turbulence intensity
Given the form of spectra shown in (4.3a), (4.3b) and (4.5), the turbulence intensity in layer II can also be obtained by applying the same procedure in § 3.2. In Appendix A, it is shown that the streamwise turbulence intensity in layer II takes the following form:
where ![]() $z_{{II},m}=\sqrt {z_i z_m}$,
$z_{{II},m}=\sqrt {z_i z_m}$, ![]() $A_{{II}}(z_{{II},m};Re_\tau )$ and
$A_{{II}}(z_{{II},m};Re_\tau )$ and ![]() $B_{{II}}(z_{{II},m};Re_\tau )$ are defined in Appendix A. Here, we note that the term with
$B_{{II}}(z_{{II},m};Re_\tau )$ are defined in Appendix A. Here, we note that the term with ![]() $z^+$ now emerges, and it incorporates the effect of the viscosity into the original attached eddy model. Also, similarly to layer I,
$z^+$ now emerges, and it incorporates the effect of the viscosity into the original attached eddy model. Also, similarly to layer I, ![]() $A_{{II}}$ and
$A_{{II}}$ and ![]() $B_{{II}}$ in (4.6) are expected to depend weakly on
$B_{{II}}$ in (4.6) are expected to depend weakly on ![]() $Re_\tau$ (see Appendix A). Lastly, following the modelling procedure for layer I in § 3.3,
$Re_\tau$ (see Appendix A). Lastly, following the modelling procedure for layer I in § 3.3, ![]() $A_{{II}}(z_{{II},m};Re_\tau )$ and
$A_{{II}}(z_{{II},m};Re_\tau )$ and ![]() $B_{{II}}(z_{{II},m};Re_\tau )$ can be semi-empirically determined, such that
$B_{{II}}(z_{{II},m};Re_\tau )$ can be semi-empirically determined, such that
where
and ![]() $a_{{II},s}$ and
$a_{{II},s}$ and ![]() $b_{{II},s}$ are the fitting constants for the model in (4.6), similarly to
$b_{{II},s}$ are the fitting constants for the model in (4.6), similarly to ![]() $a_{{I},s}$ and
$a_{{I},s}$ and ![]() $b_{{I},s}$ in § 3.3. In the present study,
$b_{{I},s}$ in § 3.3. In the present study, ![]() $a_{{II},s}=2{\rm \pi} /3$ and
$a_{{II},s}=2{\rm \pi} /3$ and ![]() $b_{{II},s}=2{\rm \pi}$ are obtained by trial and error with the experimental data for all the Reynolds numbers. The determination procedure of
$b_{{II},s}=2{\rm \pi}$ are obtained by trial and error with the experimental data for all the Reynolds numbers. The determination procedure of ![]() $a_{{II},s}=2{\rm \pi} /3$ and
$a_{{II},s}=2{\rm \pi} /3$ and ![]() $b_{{II},s}=2{\rm \pi}$ follows that in § 3.3 exactly. This leads to
$b_{{II},s}=2{\rm \pi}$ follows that in § 3.3 exactly. This leads to ![]() $\lambda _{x,II\,a}(\equiv 2{\rm \pi} \delta _{II}/a_{{II},s})=3\delta _{II}$ and
$\lambda _{x,II\,a}(\equiv 2{\rm \pi} \delta _{II}/a_{{II},s})=3\delta _{II}$ and ![]() $\lambda _{x,{I}\,b}(\equiv 2{\rm \pi} z/b_{{II},s})=z$. We note that the premultiplied spectra in layer II scale well with
$\lambda _{x,{I}\,b}(\equiv 2{\rm \pi} z/b_{{II},s})=z$. We note that the premultiplied spectra in layer II scale well with ![]() $\delta _{II}$ for
$\delta _{II}$ for ![]() $\lambda _x\simeq \lambda _{x,II\,a}$ (figure 7
$\lambda _x\simeq \lambda _{x,II\,a}$ (figure 7![]() $a$) and with
$a$) and with ![]() $z$ for
$z$ for ![]() $\lambda _x\simeq \lambda _{x,II\,b}$ (figure 7
$\lambda _x\simeq \lambda _{x,II\,b}$ (figure 7![]() $b$), serving the introduced purpose of
$b$), serving the introduced purpose of ![]() $a_{{II},s}$ and
$a_{{II},s}$ and ![]() $b_{{II},s}$. Figure 8 shows
$b_{{II},s}$. Figure 8 shows ![]() $\varPi _{II}(z)$ and the corresponding
$\varPi _{II}(z)$ and the corresponding ![]() $A_{{II}}(Re_\tau )$ determined at all the Reynolds numbers. Similar to the case of layer I,
$A_{{II}}(Re_\tau )$ determined at all the Reynolds numbers. Similar to the case of layer I, ![]() $\varPi _{II}(z)$ remains approximately constant in layer II with the given
$\varPi _{II}(z)$ remains approximately constant in layer II with the given ![]() $a_{{II},s}$ and
$a_{{II},s}$ and ![]() $b_{{II},s}$, and the resulting
$b_{{II},s}$, and the resulting ![]() $A_{{II}}(Re_\tau )$ is also found to depend weakly on the Reynolds number. The streamwise turbulence intensity and its approximation from (3.11) are shown in figure 9. For the given
$A_{{II}}(Re_\tau )$ is also found to depend weakly on the Reynolds number. The streamwise turbulence intensity and its approximation from (3.11) are shown in figure 9. For the given ![]() $a_{{II},s}$ and
$a_{{II},s}$ and ![]() $b_{{II},s}$, the model in (4.6) and (4.7) well approximates the streamwise turbulence intensity in layer II at all the Reynolds numbers. Finally, the values of
$b_{{II},s}$, the model in (4.6) and (4.7) well approximates the streamwise turbulence intensity in layer II at all the Reynolds numbers. Finally, the values of ![]() $A_{{II}}(Re_\tau )$ and
$A_{{II}}(Re_\tau )$ and ![]() $B_{{II}}(Re_\tau )$ are listed in table 2. The maximum error of the model of (4.6) remains at less than 3 %.
$B_{{II}}(Re_\tau )$ are listed in table 2. The maximum error of the model of (4.6) remains at less than 3 %.

Figure 8. ![]() $\varPi _{{II}}(z)$ (solid line) from (4.7c) and
$\varPi _{{II}}(z)$ (solid line) from (4.7c) and ![]() $A_{{II}}$ (dashed line) from (4.7a): (
$A_{{II}}$ (dashed line) from (4.7a): (![]() $a$)
$a$) ![]() $Re_{\tau }=6123$; (
$Re_{\tau }=6123$; (![]() $b$)
$b$) ![]() $Re_{\tau }=10\,100$; (
$Re_{\tau }=10\,100$; (![]() $c$)
$c$) ![]() $Re_{\tau }=14\,680$; (
$Re_{\tau }=14\,680$; (![]() $d$)
$d$) ![]() $Re_{\tau }=19\,680$. Here,
$Re_{\tau }=19\,680$. Here, ![]() $a_{{II},s}=2{\rm \pi} /3$ (
$a_{{II},s}=2{\rm \pi} /3$ (![]() $\lambda _{x,II\,a}/\delta _{{II}}=3$) and
$\lambda _{x,II\,a}/\delta _{{II}}=3$) and ![]() $b_{{II},s}=2{\rm \pi}$ (
$b_{{II},s}=2{\rm \pi}$ (![]() $\lambda _{x,II\,b}/z=1$).
$\lambda _{x,II\,b}/z=1$).

Figure 9. Streamwise turbulence intensity (solid line) and its approximation given by (4.6) (dashed line) in layer II: (![]() $a$)
$a$) ![]() $Re_{\tau }=6123$; (
$Re_{\tau }=6123$; (![]() $b$)
$b$) ![]() $Re_{\tau }=10\,100$; (
$Re_{\tau }=10\,100$; (![]() $c$)
$c$) ![]() $Re_{\tau }=14\,680$; (
$Re_{\tau }=14\,680$; (![]() $d$)
$d$) ![]() $Re_{\tau }=19\,680$. Here,
$Re_{\tau }=19\,680$. Here, ![]() $a_{{II},s}=2{\rm \pi} /3$ (
$a_{{II},s}=2{\rm \pi} /3$ (![]() $\lambda _{x,II\,a}/\delta _{{II}}=3$) and
$\lambda _{x,II\,a}/\delta _{{II}}=3$) and ![]() $b_{{II},s}=2{\rm \pi}$ (
$b_{{II},s}=2{\rm \pi}$ (![]() $\lambda _{x,II\,b}/z=1$). The streamwise turbulence intensity from model (3.11a) for layer I (dashed-dotted line) is also plotted for comparison.
$\lambda _{x,II\,b}/z=1$). The streamwise turbulence intensity from model (3.11a) for layer I (dashed-dotted line) is also plotted for comparison.
Table 2. The Reynolds-number dependence of ![]() $A_{II}$ and
$A_{II}$ and ![]() $B_{II}$ from (4.7) with
$B_{II}$ from (4.7) with ![]() $a_{{II},s}=2{\rm \pi} /3$ and
$a_{{II},s}=2{\rm \pi} /3$ and ![]() $b_{{II},s}=2{\rm \pi}$. Here,
$b_{{II},s}=2{\rm \pi}$. Here, ![]() $\mathrm {Error}=\max _z |\overline {u^\prime u^\prime }_{{model}}-\overline {u^\prime u^\prime }|/\overline {u^\prime u^\prime }$ for
$\mathrm {Error}=\max _z |\overline {u^\prime u^\prime }_{{model}}-\overline {u^\prime u^\prime }|/\overline {u^\prime u^\prime }$ for ![]() $z \in [z_i,z_m]$, where
$z \in [z_i,z_m]$, where ![]() $\overline {u^\prime u^\prime }_{{model}}$ is from (4.6), and it indicates the maximum error of the proposed model in layer II.
$\overline {u^\prime u^\prime }_{{model}}$ is from (4.6), and it indicates the maximum error of the proposed model in layer II.

5. Conclusions
In the present study, we have presented a spectrum-based attached model by generalising that of Perry et al. (Reference Perry, Henbest and Chong1986) for small but finite ![]() $z/\delta$ and for finite Reynolds numbers. In layer I (the upper logarithmic layer or inertial sublayer), the analysis showed that, without loss of generality, the intensity of the spectra should vary in the wall-normal direction considerably, consistent with the experimental data. By applying the mean-value theorem to spectra in layer I, the streamwise turbulence intensity is subsequently calculated. This revealed that the Townsend–Perry constant must be weakly dependent on Reynolds number. More importantly, it was shown that a more general condition for the approximate logarithmic wall-normal dependence of the turbulence intensity is the existence of premultiplied power-spectral intensity of
$z/\delta$ and for finite Reynolds numbers. In layer I (the upper logarithmic layer or inertial sublayer), the analysis showed that, without loss of generality, the intensity of the spectra should vary in the wall-normal direction considerably, consistent with the experimental data. By applying the mean-value theorem to spectra in layer I, the streamwise turbulence intensity is subsequently calculated. This revealed that the Townsend–Perry constant must be weakly dependent on Reynolds number. More importantly, it was shown that a more general condition for the approximate logarithmic wall-normal dependence of the turbulence intensity is the existence of premultiplied power-spectral intensity of ![]() $O(1)$ for
$O(1)$ for ![]() $1/\delta \lesssim k_x \lesssim 1/z$, and that the emergence of
$1/\delta \lesssim k_x \lesssim 1/z$, and that the emergence of ![]() $k_x^{-1}$ spectra is not a necessary condition for such a form of turbulence intensity. The analysis was further extended to layer II (the lower logarithmic layer or mesolayer), and a near-wall correction term for the turbulence intensity in this layer was subsequently proposed. Finally, the predictions of the proposed model and all the related assumptions have been carefully validated with the high-fidelity experimental data by Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018).
$k_x^{-1}$ spectra is not a necessary condition for such a form of turbulence intensity. The analysis was further extended to layer II (the lower logarithmic layer or mesolayer), and a near-wall correction term for the turbulence intensity in this layer was subsequently proposed. Finally, the predictions of the proposed model and all the related assumptions have been carefully validated with the high-fidelity experimental data by Samie et al. (Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018).
Perhaps the primary contribution of the present study would lie in addressing the two issues questioned repeatedly for a long time: (1) Would a ![]() $k_x^{-1}$ spectrum be necessary for the logarithmic wall-normal dependence of turbulence intensity? (2) Is the early observation of Morrison et al. (Reference Morrison, Jiang, McKeon and Smits2001, Reference Morrison, McKeon, Jiang and Smits2004), referred to as the ‘incomplete similarity’, inconsistent with the model of Perry et al. (Reference Perry, Henbest and Chong1986)? The present study showed that the answer to the first question is ‘no’, because the more general condition is the existence of premultiplied power-spectral intensity of
$k_x^{-1}$ spectrum be necessary for the logarithmic wall-normal dependence of turbulence intensity? (2) Is the early observation of Morrison et al. (Reference Morrison, Jiang, McKeon and Smits2001, Reference Morrison, McKeon, Jiang and Smits2004), referred to as the ‘incomplete similarity’, inconsistent with the model of Perry et al. (Reference Perry, Henbest and Chong1986)? The present study showed that the answer to the first question is ‘no’, because the more general condition is the existence of premultiplied power-spectral intensity of ![]() $O(1)$ for
$O(1)$ for ![]() $1/\delta \lesssim k_x \lesssim 1/z$. We note that this condition is also physically consistent with the notion of the attached eddy hypothesis of Townsend (Reference Townsend1976) (see the discussion in § 3.2) and is therefore inclusive of the original model of Perry et al. (Reference Perry, Henbest and Chong1986). The answer to the second question is that the discrepancy between the theoretical result of Perry et al. (Reference Perry, Henbest and Chong1986) and the observation of Morrison et al. (Reference Morrison, Jiang, McKeon and Smits2001, Reference Morrison, McKeon, Jiang and Smits2004) originates from the size of
$1/\delta \lesssim k_x \lesssim 1/z$. We note that this condition is also physically consistent with the notion of the attached eddy hypothesis of Townsend (Reference Townsend1976) (see the discussion in § 3.2) and is therefore inclusive of the original model of Perry et al. (Reference Perry, Henbest and Chong1986). The answer to the second question is that the discrepancy between the theoretical result of Perry et al. (Reference Perry, Henbest and Chong1986) and the observation of Morrison et al. (Reference Morrison, Jiang, McKeon and Smits2001, Reference Morrison, McKeon, Jiang and Smits2004) originates from the size of ![]() $z/\delta$ in the ‘idealised theoretical model’ and the ‘practical experimental measurement’: the former assumes
$z/\delta$ in the ‘idealised theoretical model’ and the ‘practical experimental measurement’: the former assumes ![]() $z/\delta \ll 1$, which strictly implies
$z/\delta \ll 1$, which strictly implies ![]() $z$ in the limit as
$z$ in the limit as ![]() $z/\delta \rightarrow 0$, whereas the latter considers small but still finite
$z/\delta \rightarrow 0$, whereas the latter considers small but still finite ![]() $z/\delta$ for a ‘practical’ reason and/or due to the ‘conventional’ definition of the logarithmic layer. Indeed, if the assumption
$z/\delta$ for a ‘practical’ reason and/or due to the ‘conventional’ definition of the logarithmic layer. Indeed, if the assumption ![]() $z/\delta \rightarrow 0$ is relaxed, then the theoretical model does exhibit a behaviour consistent with the experimental data.
$z/\delta \rightarrow 0$ is relaxed, then the theoretical model does exhibit a behaviour consistent with the experimental data.
Finally, the model proposed in this study may well be refined further by making additional modelling efforts. Such tasks include semi-empirical description of the turbulence intensity above layer I and below layer II. The Kolmogorov-scaling part of the spectrum in figure 4 can also be modelled in a more delicate manner like in the original model of Perry et al. (Reference Perry, Henbest and Chong1986). These tasks remain for future work.
Acknowledgements
We are grateful to anonymous referees who contributed to improvement of § 3.1. We are also grateful to Professor E.J. Hinch, who shared a helpful discussion on (3.2).
Funding
Y.H. gratefully acknowledges the financial support from the Engineering and Physical Science Research Council (EPSRC; EP/T009365/1) in the UK, the Leverhulme trust (RPG-2019-123) and the University of Melbourne through a visiting fellowship. N.H. and I.M. gratefully acknowledge helpful discussions with R. Deshpande and the financial support of the Australian Research Council.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Streamwise turbulence intensity in layer II
Similarly to the model for layer I in § 3.1 (figure 4), a schematic diagram of the spectrum in layer II can be sketched as shown in figure 10. Given the discussion in § 4.1, the spectrum for ![]() $a_{II}/\delta _{II} \leq k_x \leq b_{II}/z$ in layer II takes the form
$a_{II}/\delta _{II} \leq k_x \leq b_{II}/z$ in layer II takes the form
and ![]() $a_{II}$ and
$a_{II}$ and ![]() $b_{II}$ are given such that
$b_{II}$ are given such that
where ![]() $A_{{II},0}$ is a constant of
$A_{{II},0}$ is a constant of ![]() $O(1)$, and such that
$O(1)$, and such that ![]() $\Delta A_{{II},0}(k_x)(\equiv k_x \varPhi (k_x)/u_\tau ^2- A_{{II},0})$ satisfies
$\Delta A_{{II},0}(k_x)(\equiv k_x \varPhi (k_x)/u_\tau ^2- A_{{II},0})$ satisfies
 \begin{equation} \underbrace{\int_{\ln (a_{II}/\delta_{II})}^{\ln (b_{II}/z)} \Delta A_{{II},0}(k_x)\,\mathrm{d}(\ln k_x)}_{{}\equiv A_{{II},1}(z/\delta_{II})} \sim O\left(\frac{z}{\delta_{II}}\right). \end{equation}
\begin{equation} \underbrace{\int_{\ln (a_{II}/\delta_{II})}^{\ln (b_{II}/z)} \Delta A_{{II},0}(k_x)\,\mathrm{d}(\ln k_x)}_{{}\equiv A_{{II},1}(z/\delta_{II})} \sim O\left(\frac{z}{\delta_{II}}\right). \end{equation}
Like the analysis in § 3, ![]() $A_{{II},0}$,
$A_{{II},0}$, ![]() $a_{II}$ and
$a_{II}$ and ![]() $b_{II}$ here are chosen such that the area below the premultiplied spectrum for
$b_{II}$ here are chosen such that the area below the premultiplied spectrum for ![]() $a_{II}/\delta \leq k_x \leq b_{II}/z$ is approximated by the red-shaded region in figure 10 with an error of
$a_{II}/\delta \leq k_x \leq b_{II}/z$ is approximated by the red-shaded region in figure 10 with an error of ![]() $O(z/\delta _{II})$. Such a choice of
$O(z/\delta _{II})$. Such a choice of ![]() $A_{{II},0}$,
$A_{{II},0}$, ![]() $a_{II}$ and
$a_{II}$ and ![]() $b_{II}$ must always be possible, because the mean-value theorem ensures the existence of
$b_{II}$ must always be possible, because the mean-value theorem ensures the existence of ![]() ${A}_{{II},M}(z/\delta )$ such that
${A}_{{II},M}(z/\delta )$ such that
 \begin{equation} {A}_{{II},M}(z/\delta_{{II}})=\left[\ln\left(\frac{b_{{II}}}{z}\right)-\ln\left(\frac{a_{{II}}}{\delta_{{II}}}\right)\right]^{{-}1} \int_{\ln (a_{II}/\delta_{{II}})}^{\ln (b_{II}/z)} \frac{k_x\,\varPhi_{uu}(k_x;z/\delta)}{u_\tau^2}\, \mathrm{d}(\ln k_x), \end{equation}
\begin{equation} {A}_{{II},M}(z/\delta_{{II}})=\left[\ln\left(\frac{b_{{II}}}{z}\right)-\ln\left(\frac{a_{{II}}}{\delta_{{II}}}\right)\right]^{{-}1} \int_{\ln (a_{II}/\delta_{{II}})}^{\ln (b_{II}/z)} \frac{k_x\,\varPhi_{uu}(k_x;z/\delta)}{u_\tau^2}\, \mathrm{d}(\ln k_x), \end{equation}where
with ![]() $A_{{II},1}(z/\delta _{{II}})$ being of
$A_{{II},1}(z/\delta _{{II}})$ being of ![]() $O(z/\delta _{{II}})$ from the Taylor expansion of
$O(z/\delta _{{II}})$ from the Taylor expansion of ![]() $A_{{II},M}(z/\delta _{{II}})$.
$A_{{II},M}(z/\delta _{{II}})$.

Figure 10. A schematic diagram of the proposed model for the spectra in layer II.
The turbulence intensity is subsequently written as
 \begin{align} \frac{\overline{u^\prime u^\prime}}{u_\tau^2}& = \int_{-\infty}^\infty \frac{k_x\, \varPhi_{uu}(k_x;z)}{u_\tau^2}\,\mathrm{d}(\ln k_x) = \int_{\ln (a_{II}/\delta_{II})}^{\ln (b_{II}/z)} \frac{k_x\,\varPhi_{uu}(k_x)}{u_\tau^2}\,\mathrm{d}(\ln k_x)+C_{{II}}(z;Re_\tau) \nonumber\\ & =\int_{\ln (b_{II}/\delta_{II})}^{\ln (a_{II}/z)} A_{{II},0} \,\mathrm{d}(\ln k_x)+\int_{\ln (a_{II}/\delta_{II})}^{\ln (b_{II}/z)} \Delta A_{{II},0}(z/\delta_{II}) \,\mathrm{d}(\ln k_x)+C_{{II}}(z;Re_\tau) \nonumber\\ &={-}\left[A_{{II},0}+A_{{II},1}\left(\frac{z}{\delta_{II}}\right)\right]\ln\left(\frac{z}{\delta_{II}}\right)+B_{{II}}(z;Re_\tau), \end{align}
\begin{align} \frac{\overline{u^\prime u^\prime}}{u_\tau^2}& = \int_{-\infty}^\infty \frac{k_x\, \varPhi_{uu}(k_x;z)}{u_\tau^2}\,\mathrm{d}(\ln k_x) = \int_{\ln (a_{II}/\delta_{II})}^{\ln (b_{II}/z)} \frac{k_x\,\varPhi_{uu}(k_x)}{u_\tau^2}\,\mathrm{d}(\ln k_x)+C_{{II}}(z;Re_\tau) \nonumber\\ & =\int_{\ln (b_{II}/\delta_{II})}^{\ln (a_{II}/z)} A_{{II},0} \,\mathrm{d}(\ln k_x)+\int_{\ln (a_{II}/\delta_{II})}^{\ln (b_{II}/z)} \Delta A_{{II},0}(z/\delta_{II}) \,\mathrm{d}(\ln k_x)+C_{{II}}(z;Re_\tau) \nonumber\\ &={-}\left[A_{{II},0}+A_{{II},1}\left(\frac{z}{\delta_{II}}\right)\right]\ln\left(\frac{z}{\delta_{II}}\right)+B_{{II}}(z;Re_\tau), \end{align}where
 \begin{equation} C_{{II}}(z;Re_\tau)=\frac{\overline{u^\prime u^\prime}}{u_\tau^2}-\int_{\ln (a_{II}/\delta_{II})}^{\ln(b_{II}/z)} \frac{k_x\,\varPhi_{uu}(k_x)}{u_\tau^2}\,\mathrm{d}(\ln k_x), \end{equation}
\begin{equation} C_{{II}}(z;Re_\tau)=\frac{\overline{u^\prime u^\prime}}{u_\tau^2}-\int_{\ln (a_{II}/\delta_{II})}^{\ln(b_{II}/z)} \frac{k_x\,\varPhi_{uu}(k_x)}{u_\tau^2}\,\mathrm{d}(\ln k_x), \end{equation}
Here, ![]() $C_{{II}}(z;Re_\tau )$ represents the contribution of the spectrum for
$C_{{II}}(z;Re_\tau )$ represents the contribution of the spectrum for ![]() $k_x< a_{II}/\delta$ and
$k_x< a_{II}/\delta$ and ![]() $k_x>b_{II}/z$ to the turbulence intensity, and it would depend weakly on
$k_x>b_{II}/z$ to the turbulence intensity, and it would depend weakly on ![]() $z$ and
$z$ and ![]() $Re_\tau$ due to the Kolmogorov-scaling part in figure 10. The turbulence intensity is further approximated as
$Re_\tau$ due to the Kolmogorov-scaling part in figure 10. The turbulence intensity is further approximated as
where ![]() $z_{{II},m}=\sqrt {z_i z_m}$ and
$z_{{II},m}=\sqrt {z_i z_m}$ and ![]() $A_{{II}}(Re_\tau )=A_{{II},0}+A_{{II},1}(z_{{II},m}/\delta )$. Here, the approximation error of (A4) is estimated to be of
$A_{{II}}(Re_\tau )=A_{{II},0}+A_{{II},1}(z_{{II},m}/\delta )$. Here, the approximation error of (A4) is estimated to be of ![]() $O(z/\delta _{II})$. This is
$O(z/\delta _{II})$. This is ![]() $O(10^{-2})$ at
$O(10^{-2})$ at ![]() $Re_\tau =19\,680$ from the definition of layer II. However, it should be mentioned that, in practice, the approximation error of (A4) for the experimental data is expected to be considerably bigger than this, because (A4) also depends on the accuracy of the empirical relations in (4.3a) and (4.3b).
$Re_\tau =19\,680$ from the definition of layer II. However, it should be mentioned that, in practice, the approximation error of (A4) for the experimental data is expected to be considerably bigger than this, because (A4) also depends on the accuracy of the empirical relations in (4.3a) and (4.3b).