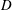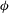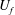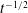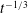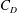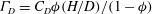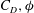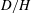1. Introduction
The study of gravity currents propagating into a porous medium, such as a channel containing an array of obstacles, is of practical importance for many geophysical and environmental applications. The obstacles increase the drag force acting on the current and provide an additional mechanism for energy dissipation. For example, snow avalanches are retarded by their interactions with long arrays of barriers, which reduce the flow speed and partially mitigate the hazard posed to built infrastructure (Hopfinger Reference Hopfinger1983; Hákonardóttir et al. Reference Hákonardóttir, Hogg, Jóhannesson, Kern and Tiefenbacher2003). Turbidity currents encounter arrays of screens that favour local sediment deposition (Oehy & Schleiss Reference Oehy and Schleiss2007). Finally, a case of considerable importance for environmental applications is when a gravitationally driven current propagates into a partially or fully vegetated channel (Tanino, Nepf & Kulis Reference Tanino, Nepf and Kulis2005; Zhang & Nepf Reference Zhang and Nepf2011). Such fluid motions are driven by differences in the temperature of water masses associated with different solar heating in emergent and submerged vegetative regions (Coates & Ferris Reference Coates and Ferris1994; Chimney, Wenkert & Pietro Reference Chimney, Wenkert and Pietro2006) or with different concentrations of phytoplankton that alter the penetration of solar radiation through the water column (Edwards, Wright & Platt Reference Edwards, Wright and Platt2004). Both effects lead to horizontal gradients of density, and these drive fluid exchange between the regions. Among other features, this exchange may be important due to the chemically distinct composition of the water masses.
In this paper, we investigate gravity currents for which the density of the fluid is determined by its temperature or salinity or other compositional component, moving through a channel filled with stationary obstacles that retard the flow. The obstacles that constitute this porous medium through which the exchange flow occurs are a staggered array of rigid horizontal cylinders of square cross-section, aligned with their axes perpendicular to the initial density gradient and the streamwise flow direction (figure 1). This porous medium is therefore characterized by the volume fraction of solids,
![]() ${\it\phi}$
, the edge length of the square cylinders,
${\it\phi}$
, the edge length of the square cylinders,
![]() $D$
, the frontal area of the cylinders per unit volume,
$D$
, the frontal area of the cylinders per unit volume,
![]() $a$
, the orientation of the cylinders and their arrangement. In the following, the edge length of the square cylinders will be referred to as the cylinder diameter. The motion is started from ‘lock-exchange’ initial conditions in which one half of the channel is filled with dense fluid and the other half is filled with less dense fluid. The channel height is denoted by
$a$
, the orientation of the cylinders and their arrangement. In the following, the edge length of the square cylinders will be referred to as the cylinder diameter. The motion is started from ‘lock-exchange’ initial conditions in which one half of the channel is filled with dense fluid and the other half is filled with less dense fluid. The channel height is denoted by
![]() $H$
. The top and bottom channel boundaries are no-slip walls. It will be shown that the structure of currents propagating through the channel differs substantially from lock-exchange flows in an unobstructed channel, for which there is much smaller dissipation (e.g. see Huppert & Simpson Reference Huppert and Simpson1980; Shin, Dalziel & Linden Reference Shin, Dalziel and Linden2004; Ungarish Reference Ungarish2009; Meiburg & Kneller Reference Meiburg and Kneller2010).
$H$
. The top and bottom channel boundaries are no-slip walls. It will be shown that the structure of currents propagating through the channel differs substantially from lock-exchange flows in an unobstructed channel, for which there is much smaller dissipation (e.g. see Huppert & Simpson Reference Huppert and Simpson1980; Shin, Dalziel & Linden Reference Shin, Dalziel and Linden2004; Ungarish Reference Ungarish2009; Meiburg & Kneller Reference Meiburg and Kneller2010).

Figure 1. Sketch of a lock-exchange flow for the case in which the relatively dense fluid initially occupies the full depth of the channel behind the lock-gate. The channel length is
![]() $L=2x_{0}$
. The gate is positioned far from the lateral endwalls of the channel (
$L=2x_{0}$
. The gate is positioned far from the lateral endwalls of the channel (
![]() $x_{0}/H\gg 1$
). Cylinders (when present) are approximately uniformly distributed within the whole volume of the channel, with their axes parallel to the spanwise (
$x_{0}/H\gg 1$
). Cylinders (when present) are approximately uniformly distributed within the whole volume of the channel, with their axes parallel to the spanwise (
![]() $z$
) direction.
$z$
) direction.
![]() $U_{f}$
denotes the front velocity of the bottom and top gravity currents.
$U_{f}$
denotes the front velocity of the bottom and top gravity currents.
Detailed measurements of the velocity, vorticity and density fields within a gravity current are seldom available from laboratory and larger-scale studies. High-resolution numerical simulations conducted with eddy-resolving techniques, however, can provide such information (e.g. Härtel, Meiburg & Necker Reference Härtel, Meiburg and Necker2000; Necker et al. Reference Necker, Härtel, Kleiser and Meiburg2002; Ooi, Constantinescu & Weber Reference Ooi, Constantinescu and Weber2009) and additionally offer a way to study the behaviour of gravity currents at conditions, such as very high Reynolds numbers, that are closer to those encountered in practical applications in geosciences and engineering (Ooi et al. Reference Ooi, Constantinescu and Weber2009). In the present investigation, the evolution of gravity currents propagating into a channel containing arrays of obstacles is studied based on 3D large eddy simulations (LES) performed using a non-dissipative Navier–Stokes solver in which the subgrid-scale terms are calculated dynamically (Pierce & Moin Reference Pierce and Moin2001). The flow past each obstacle is explicitly resolved. There is no need to include terms in the governing equations to account for the presence of the obstacles in the momentum equations, to provide a cylinder drag coefficient or to include a model for obstacle-scale generation of turbulence, as is the case for numerical models that do not resolve the flow past individual obstacles (e.g. see Jamali, Zhang & Nepf Reference Jamali, Zhang and Nepf2008; King, Tinoco & Cowen Reference King, Tinoco and Cowen2012). Instead our computations resolve the velocity field around each of the obstacles to reveal the unsteady evolution of the exchange flow. In addition to numerical simulations of the unsteady, 3D velocity and density fields, we also construct a shallow layer model of the motion (cf. Hatcher, Hogg & Woods Reference Hatcher, Hogg and Woods2000). This expresses mass conservation and the balance of momentum in terms of dependent variables averaged over the flow depth. We show that when the exchange flow has become dominated by the drag exerted by the cylinders, and inertial effects have become negligible, there exists a similarity solution for the motion (cf. Tanino et al. Reference Tanino, Nepf and Kulis2005).
When analysing the flow dynamics, it is important to recall that the cylinders are positioned with their axes horizontal and perpendicular to the axis of the channel in which the exchange flow occurs. In this configuration the results are of direct application to some arrays of barriers used to retard powder snow avalanches (Naaim-Bouvet et al.
Reference Naaim-Bouvet, Naaim, Bacher and Heiligenstein2002) and turbidity currents at the bottom of reservoirs (Oehy & Schleiss Reference Oehy and Schleiss2007). There may, however, be differences in some of the flow structures that would emerge with vertically aligned cylinders, because the predominant orientation of the vortices shed by the obstacles is different. However, as we investigate below, the major effect of the obstacles is to retard the flow, and this depends strongly on the ‘bulk’ descriptors of the porous medium, such as the volume fraction of solids,
![]() ${\it\phi}$
, and the frontal area of cylinders per unit volume,
${\it\phi}$
, and the frontal area of cylinders per unit volume,
![]() $a$
. Indeed, shallow layer models do not feature explicitly any notation of the orientation or shape of the obstacles, but instead parameterize the drag through the ‘bulk’ variables – and, as with the studies of Hatcher et al. (Reference Hatcher, Hogg and Woods2000) and Tanino et al. (Reference Tanino, Nepf and Kulis2005), it will be shown that they capture much of the flow dynamics.
$a$
. Indeed, shallow layer models do not feature explicitly any notation of the orientation or shape of the obstacles, but instead parameterize the drag through the ‘bulk’ variables – and, as with the studies of Hatcher et al. (Reference Hatcher, Hogg and Woods2000) and Tanino et al. (Reference Tanino, Nepf and Kulis2005), it will be shown that they capture much of the flow dynamics.
On release from lock-exchange initial conditions, the current accelerates relatively rapidly to reach a slumping phase in which the front velocity,
![]() $U_{f}$
, is constant. When no obstacles are present, these gravity currents continue to move with constant front velocity, provided that the hydraulic resistance associated with the boundary remains negligible, until the motion is affected by reflections from the end walls of the channel (cf. Rottman & Simpson Reference Rottman and Simpson1983; Hogg Reference Hogg2006). For flow through a porous medium with a sufficiently high volume fraction of solids, the additional drag induced by the cylinders induces deceleration long before any influence of the reflected bore on the front region is felt. The progressive action of drag initiates a transition to the self-similar drag-dominated regime in which the main forces acting on the current are due to buoyancy gradients and drag induced by the obstacles.
$U_{f}$
, is constant. When no obstacles are present, these gravity currents continue to move with constant front velocity, provided that the hydraulic resistance associated with the boundary remains negligible, until the motion is affected by reflections from the end walls of the channel (cf. Rottman & Simpson Reference Rottman and Simpson1983; Hogg Reference Hogg2006). For flow through a porous medium with a sufficiently high volume fraction of solids, the additional drag induced by the cylinders induces deceleration long before any influence of the reflected bore on the front region is felt. The progressive action of drag initiates a transition to the self-similar drag-dominated regime in which the main forces acting on the current are due to buoyancy gradients and drag induced by the obstacles.
A first important question relates to what determines the front velocity,
![]() $U_{f}$
, during the drag-dominated regime for currents generated from lock-release initial conditions. Tanino et al. (Reference Tanino, Nepf and Kulis2005) conducted experiments with an array of vertically aligned cylinders in the regime of relatively low values of the cylinder Reynolds number,
$U_{f}$
, during the drag-dominated regime for currents generated from lock-release initial conditions. Tanino et al. (Reference Tanino, Nepf and Kulis2005) conducted experiments with an array of vertically aligned cylinders in the regime of relatively low values of the cylinder Reynolds number,
![]() $\mathit{Re}_{D}\ll 1$
, where
$\mathit{Re}_{D}\ll 1$
, where
![]() $\mathit{Re}_{D}$
is defined with the mean front velocity and the cylinder diameter. In this regime where the drag developed by the cylinders is linearly proportional to the mean flow speed, they found that the front velocity varies as
$\mathit{Re}_{D}$
is defined with the mean front velocity and the cylinder diameter. In this regime where the drag developed by the cylinders is linearly proportional to the mean flow speed, they found that the front velocity varies as
![]() $t^{-1/2}$
, where
$t^{-1/2}$
, where
![]() $t$
is the time measured from the moment the lock gate is removed. Furthermore, they found that the height of the interface between the dense and less dense fluids varies approximately linearly with downstream distance between the front where the height vanishes and the lock gate. Constantinescu (Reference Constantinescu2014) reported some preliminary results and analysis of numerical simulations of these obstructed flows with the cylinders aligned horizontally as in the current study. He confirmed that when the cylinder Reynolds number is sufficiently small that the motion is viscously controlled, the front speed varies with
$t$
is the time measured from the moment the lock gate is removed. Furthermore, they found that the height of the interface between the dense and less dense fluids varies approximately linearly with downstream distance between the front where the height vanishes and the lock gate. Constantinescu (Reference Constantinescu2014) reported some preliminary results and analysis of numerical simulations of these obstructed flows with the cylinders aligned horizontally as in the current study. He confirmed that when the cylinder Reynolds number is sufficiently small that the motion is viscously controlled, the front speed varies with
![]() $t^{-1/2}$
. However, when the cylinder Reynolds number is larger, the front speed
$t^{-1/2}$
. However, when the cylinder Reynolds number is larger, the front speed
![]() $U_{f}\sim t^{-1/4}$
and the shape of the interface between the two fluids are different. It is this latter regime that is the focus of this paper, in which the behaviour of gravity currents in the quadratic drag-dominated regime is investigated over a wide range of conditions.
$U_{f}\sim t^{-1/4}$
and the shape of the interface between the two fluids are different. It is this latter regime that is the focus of this paper, in which the behaviour of gravity currents in the quadratic drag-dominated regime is investigated over a wide range of conditions.
In the present paper we extend the analysis of Constantinescu (Reference Constantinescu2014) by presenting a detailed investigation of the evolution and structure of the current and its dependence upon geometrical and flow parameters based on numerical simulations. We also examine ‘bulk’ properties such as the position of the front as a function of time, the energy budget and the total streamwise drag force. We directly estimate the mean drag coefficient of the obstacles,
![]() $C_{D}$
, during the linear and quadratic drag-dominated regimes based on the resolved flow fields around the cylinders. This is a significant advantage that arises from our numerical simulations, given that accurate experimental estimations of
$C_{D}$
, during the linear and quadratic drag-dominated regimes based on the resolved flow fields around the cylinders. This is a significant advantage that arises from our numerical simulations, given that accurate experimental estimations of
![]() $C_{D}$
for gravity currents are difficult to obtain. We also develop a new shallow layer of this density-driven motion. This reduced model is based upon the assumption that the motion is predominantly horizontal and it admits predictions that compare favourably with numerical simulations. It will be shown that the assessment of the drag force exerted by the cylinders and the associated drag coefficients are particularly important for characterizing the ensuing dynamics and for representing the motion in the ‘simplified’ shallow layer description.
$C_{D}$
for gravity currents are difficult to obtain. We also develop a new shallow layer of this density-driven motion. This reduced model is based upon the assumption that the motion is predominantly horizontal and it admits predictions that compare favourably with numerical simulations. It will be shown that the assessment of the drag force exerted by the cylinders and the associated drag coefficients are particularly important for characterizing the ensuing dynamics and for representing the motion in the ‘simplified’ shallow layer description.
The main research questions we address in this paper are as follows. (a) To what extent do the results predicted by the shallow water theory models for currents propagating into a porous channel reproduce those predicted by the 3D numerical computations? (b) How does the increase of the volume fraction of cylinders,
![]() ${\it\phi}$
, change the structure and evolution of gravity currents? (c) To what extent do other non-dimensional geometrical parameters describing the array, such as the size of the cylinders or the frontal area per unit volume, affect the evolution of the current and the temporal evolution of the total drag force induced by the cylinders? (d) Are Reynolds-number-induced scale effects important between the typical range of channel Reynolds numbers at which laboratory experiments are conducted and field-scale applications? (e) How does the drag force produced by the cylinders vary with the flow parameters? Additionally, how do these values compare with those for isolated cylinders placed in uniform incoming flow?
${\it\phi}$
, change the structure and evolution of gravity currents? (c) To what extent do other non-dimensional geometrical parameters describing the array, such as the size of the cylinders or the frontal area per unit volume, affect the evolution of the current and the temporal evolution of the total drag force induced by the cylinders? (d) Are Reynolds-number-induced scale effects important between the typical range of channel Reynolds numbers at which laboratory experiments are conducted and field-scale applications? (e) How does the drag force produced by the cylinders vary with the flow parameters? Additionally, how do these values compare with those for isolated cylinders placed in uniform incoming flow?
The paper is structured as follows. Section 2 presents the governing equations, discusses the numerical method and boundary conditions and introduces the flow and geometrical parameters of the numerical simulations. Section 3 develops a two-layer shallow model of the flow for currents that are initiated from lock-release initial conditions and derives similarity solutions for the motion in the regimes for which the cylinder Reynolds numbers are either very small or very large. Section 4 discusses how the structure of the current changes as a function of the main non-dimensional geometrical and flow parameters. Section 5 analyses how the temporal evolution of the total streamwise drag force induced by the cylinders depends on the flow and geometrical parameters that characterize the array of cylinders. Section 6 provides an estimation of the mean drag coefficient of the cylinders during the drag-dominated regime, analyses the temporal variation of the front velocity and analyses agreement with predictions based on shallow water flow theory. Section 7 discusses the temporal evolution of the energy balance. Finally, the main findings are summarized in § 8.
2. Description of the numerical model and simulations
The filtered dimensionless Navier–Stokes equations are solved along with the advection–diffusion equation for the non-dimensional scalar concentration on a non-uniform Cartesian mesh (Ooi, Constantinescu & Weber Reference Ooi, Constantinescu and Weber2007). The dimensionless filtered concentration is
![]() $C=(C^{\prime }-C_{min}^{\prime })/(C_{max}^{\prime }-C_{min}^{\prime })$
, where
$C=(C^{\prime }-C_{min}^{\prime })/(C_{max}^{\prime }-C_{min}^{\prime })$
, where
![]() $C^{\prime }$
is the concentration, and
$C^{\prime }$
is the concentration, and
![]() $C_{max}^{\prime }$
and
$C_{max}^{\prime }$
and
![]() $C_{min}^{\prime }$
represent the maximum and minimum initial concentrations in the domain. The concentrations
$C_{min}^{\prime }$
represent the maximum and minimum initial concentrations in the domain. The concentrations
![]() $C$
and
$C$
and
![]() $C^{\prime }$
are linearly related to the density of the fluid. The reduced gravity is denoted by
$C^{\prime }$
are linearly related to the density of the fluid. The reduced gravity is denoted by
![]() $g^{\prime }=g({\it\rho}_{max}-{\it\rho}_{min})/{\it\rho}_{max}$
, where
$g^{\prime }=g({\it\rho}_{max}-{\it\rho}_{min})/{\it\rho}_{max}$
, where
![]() ${\it\rho}_{max}\equiv {\it\rho}+{\rm\Delta}{\it\rho}$
and
${\it\rho}_{max}\equiv {\it\rho}+{\rm\Delta}{\it\rho}$
and
![]() ${\it\rho}_{min}\equiv {\it\rho}$
are the initial maximum (lock fluid) and minimum (ambient fluid) densities in the domain, and
${\it\rho}_{min}\equiv {\it\rho}$
are the initial maximum (lock fluid) and minimum (ambient fluid) densities in the domain, and
![]() $g$
denotes gravitational acceleration. The channel height,
$g$
denotes gravitational acceleration. The channel height,
![]() $H$
, and the buoyancy velocity,
$H$
, and the buoyancy velocity,
![]() $u_{b}=\sqrt{g^{\prime }H}$
, are used as the characteristic length and velocity scales respectively, with which the variables are non-dimensionalized and times are rendered dimensionless in terms of
$u_{b}=\sqrt{g^{\prime }H}$
, are used as the characteristic length and velocity scales respectively, with which the variables are non-dimensionalized and times are rendered dimensionless in terms of
![]() $t_{0}=H/u_{b}$
. It is assumed that the density differences are sufficiently small (
$t_{0}=H/u_{b}$
. It is assumed that the density differences are sufficiently small (
![]() ${\rm\Delta}{\it\rho}/{\it\rho}\ll 1$
) that the Boussinesq approximation may be invoked and they are only significant in the gravitational terms of the momentum equations. The subgrid-scale viscosity,
${\rm\Delta}{\it\rho}/{\it\rho}\ll 1$
) that the Boussinesq approximation may be invoked and they are only significant in the gravitational terms of the momentum equations. The subgrid-scale viscosity,
![]() ${\it\nu}_{t}$
, and subgrid-scale diffusivity,
${\it\nu}_{t}$
, and subgrid-scale diffusivity,
![]() ${\it\kappa}_{t}$
, in the filtered momentum equations and in the advection–diffusion equation for
${\it\kappa}_{t}$
, in the filtered momentum equations and in the advection–diffusion equation for
![]() $C$
are calculated using a dynamic Smagorinsky model. The equations used to evaluate
$C$
are calculated using a dynamic Smagorinsky model. The equations used to evaluate
![]() ${\it\nu}_{t}$
and
${\it\nu}_{t}$
and
![]() ${\it\kappa}_{t}$
are given in Pierce & Moin (Reference Pierce and Moin2001). The use of a dynamic model eliminates the need to specify any stratification correction in the subgrid-scale model (Kirkpatrick et al.
Reference Kirkpatrick, Ackerman, Stevens and Mansour2006; Rodi, Constantinescu & Stoesser Reference Rodi, Constantinescu and Stoesser2013). The dynamic model was found to be very successful in predicting scalar transport and mixing in turbulent flows, especially for cases where the resolved scales drive the mixing process (Rodi et al.
Reference Rodi, Constantinescu and Stoesser2013). The two parameters in the non-dimensional governing equations are the channel Reynolds number,
${\it\kappa}_{t}$
are given in Pierce & Moin (Reference Pierce and Moin2001). The use of a dynamic model eliminates the need to specify any stratification correction in the subgrid-scale model (Kirkpatrick et al.
Reference Kirkpatrick, Ackerman, Stevens and Mansour2006; Rodi, Constantinescu & Stoesser Reference Rodi, Constantinescu and Stoesser2013). The dynamic model was found to be very successful in predicting scalar transport and mixing in turbulent flows, especially for cases where the resolved scales drive the mixing process (Rodi et al.
Reference Rodi, Constantinescu and Stoesser2013). The two parameters in the non-dimensional governing equations are the channel Reynolds number,
![]() $\mathit{Re}=u_{b}H/{\it\nu}$
, and the molecular Schmidt number,
$\mathit{Re}=u_{b}H/{\it\nu}$
, and the molecular Schmidt number,
![]() $\mathit{Sc}={\it\nu}/{\it\kappa}$
, where
$\mathit{Sc}={\it\nu}/{\it\kappa}$
, where
![]() ${\it\nu}$
is the kinematic viscosity of the fluid and
${\it\nu}$
is the kinematic viscosity of the fluid and
![]() ${\it\kappa}$
is the molecular diffusivity of the dissolved species that gives rise to the density field. The coordinates in the three directions are denoted either (
${\it\kappa}$
is the molecular diffusivity of the dissolved species that gives rise to the density field. The coordinates in the three directions are denoted either (
![]() $x_{1},x_{2},x_{3}$
) in index notation or (
$x_{1},x_{2},x_{3}$
) in index notation or (
![]() $x,y,z$
). The vertical axis is
$x,y,z$
). The vertical axis is
![]() $y$
, aligned with gravitational acceleration, while the
$y$
, aligned with gravitational acceleration, while the
![]() $x$
-axis is aligned along the channel axis and the
$x$
-axis is aligned along the channel axis and the
![]() $z$
-axis is spanwise.
$z$
-axis is spanwise.
The finite-volume LES code (Pierce & Moin Reference Pierce and Moin2001; Chang & Constantinescu Reference Chang and Constantinescu2013) advances the governing equations in time using a semi-implicit iterative method that employs a staggered conservative space–time second-order-accurate discretization. A Poisson equation is solved for the pressure using a multigrid approach. All operators are discretized using central discretizations, except the convective term in the advection–diffusion equation for the concentration of the dissolved species, for which the quadratic upwind interpolation for convective kinematics (QUICK) scheme (Leonard Reference Leonard1979) is used. Despite the non-monotonic properties of the scheme that allow potentially non-physical values of the scalar to be generated in the simulation, the present code was found to predict accurately scalar transport in turbulent flow applications involving both passive and non-passive scalars (see, for example, the detailed validation for combustion applications discussed by Pierce & Moin (Reference Pierce and Moin2001, Reference Pierce and Moin2004)). Although the QUICK scheme is dissipative, for high-Reynolds-number flows the dissipation introduced by the subgrid-scale model is significant. This is the main reason why the numerical diffusion associated with the QUICK scheme in LES of scalar transport does not have a very adverse effect on the quality of the solution. Chang, Constantinescu & Park (Reference Chang, Constantinescu and Park2006, Reference Chang, Constantinescu and Park2007) discussed validation of the numerical method to predict ejection of non-buoyant and buoyant contaminants from bottom channel cavities. Ooi et al. (Reference Ooi, Constantinescu and Weber2007, Reference Ooi, Constantinescu and Weber2009) performed LES of lock-exchange intrusion currents and gravity currents propagating over a smooth flat surface. Comparison with laboratory experimental realizations showed that 3D LES accurately captured the structure of the current at different stages of its evolution. Large eddy simulation correctly predicted the change in the front speed,
![]() $U_{f}$
, with Reynolds number, Re, during the slumping phase for values up to
$U_{f}$
, with Reynolds number, Re, during the slumping phase for values up to
![]() $10^{6}$
and that
$10^{6}$
and that
![]() $U_{f}\sim t^{-1/3}$
during the buoyancy-inertia phase, in accord with analytical models of the motion (Hoult Reference Hoult1972). Gonzalez-Juez, Meiburg & Constantinescu (Reference Gonzalez-Juez, Meiburg and Constantinescu2009) and Gonzalez-Juez et al. (Reference Gonzalez-Juez, Meiburg, Tokyay and Constantinescu2010) used the same numerical model to study the changes in structure of the gravity current as it interacts with isolated obstacles mounted on a flat bed surface or situated at a small distance from the channel bed. Large eddy simulation successfully reproduced the measured time-varying drag and lift coefficients of gravity current flows impinging circular and rectangular cylinders (Ermanyuk & Gavrilov Reference Ermanyuk and Gavrilov2005a
,Reference Ermanyuk and Gavrilov
b
). Tokyay, Constantinescu & Meiburg (Reference Tokyay, Constantinescu and Meiburg2011, Reference Tokyay, Constantinescu and Meiburg2012, Reference Tokyay, Constantinescu and Meiburg2014) showed that LES predictions of vertical profiles of mean velocity and turbulent kinetic energy agreed well with experimental measurements conducted for turbulent lock-exchange gravity currents over a smooth flat surface and that the front speed variation during the drag-dominated regime was in close agreement with shallow flow theory for lock-exchange currents propagating over a rough surface.
$U_{f}\sim t^{-1/3}$
during the buoyancy-inertia phase, in accord with analytical models of the motion (Hoult Reference Hoult1972). Gonzalez-Juez, Meiburg & Constantinescu (Reference Gonzalez-Juez, Meiburg and Constantinescu2009) and Gonzalez-Juez et al. (Reference Gonzalez-Juez, Meiburg, Tokyay and Constantinescu2010) used the same numerical model to study the changes in structure of the gravity current as it interacts with isolated obstacles mounted on a flat bed surface or situated at a small distance from the channel bed. Large eddy simulation successfully reproduced the measured time-varying drag and lift coefficients of gravity current flows impinging circular and rectangular cylinders (Ermanyuk & Gavrilov Reference Ermanyuk and Gavrilov2005a
,Reference Ermanyuk and Gavrilov
b
). Tokyay, Constantinescu & Meiburg (Reference Tokyay, Constantinescu and Meiburg2011, Reference Tokyay, Constantinescu and Meiburg2012, Reference Tokyay, Constantinescu and Meiburg2014) showed that LES predictions of vertical profiles of mean velocity and turbulent kinetic energy agreed well with experimental measurements conducted for turbulent lock-exchange gravity currents over a smooth flat surface and that the front speed variation during the drag-dominated regime was in close agreement with shallow flow theory for lock-exchange currents propagating over a rough surface.
All lock-exchange simulations reported in the current study were conducted in a channel with smooth horizontal top and bottom walls and lateral vertical endwalls. The channel contained an array of square cross-section cylinders of side length
![]() $D$
. Their location was close to a regular staggered pattern in the
$D$
. Their location was close to a regular staggered pattern in the
![]() $x{-}y$
planes, but a small random displacement was applied to the initial regular pattern to reduce the regularity of the wake-to-wake interactions between neighbouring cylinders. The magnitude of the random displacement in the vertical and horizontal directions varied between
$x{-}y$
planes, but a small random displacement was applied to the initial regular pattern to reduce the regularity of the wake-to-wake interactions between neighbouring cylinders. The magnitude of the random displacement in the vertical and horizontal directions varied between
![]() $0.5D$
and
$0.5D$
and
![]() $1.0D$
. No-slip boundary conditions were employed on the velocity field at the channel walls and on the surfaces of the cylinders. The surface-normal concentration gradient was set to zero at all wall boundaries. The flow was assumed to be periodic in the spanwise direction. The time step was
$1.0D$
. No-slip boundary conditions were employed on the velocity field at the channel walls and on the surfaces of the cylinders. The surface-normal concentration gradient was set to zero at all wall boundaries. The flow was assumed to be periodic in the spanwise direction. The time step was
![]() $0.001t_{0}$
. The Schmidt number was 600, which corresponds to saline diffusion in water. Härtel et al. (Reference Härtel, Meiburg and Necker2000), Necker et al. (Reference Necker, Härtel, Kleiser and Meiburg2005) and Cantero et al. (Reference Cantero, Lee, Balachandar and Garcia2007) showed that variations in the value of the Schmidt number did not strongly alter the results in lock-exchange simulations of gravity currents as long as it was of order unity or larger. This conclusion was confirmed by Ooi et al. (Reference Ooi, Constantinescu and Weber2009) using the same code as that employed to perform the present simulations.
$0.001t_{0}$
. The Schmidt number was 600, which corresponds to saline diffusion in water. Härtel et al. (Reference Härtel, Meiburg and Necker2000), Necker et al. (Reference Necker, Härtel, Kleiser and Meiburg2005) and Cantero et al. (Reference Cantero, Lee, Balachandar and Garcia2007) showed that variations in the value of the Schmidt number did not strongly alter the results in lock-exchange simulations of gravity currents as long as it was of order unity or larger. This conclusion was confirmed by Ooi et al. (Reference Ooi, Constantinescu and Weber2009) using the same code as that employed to perform the present simulations.
The numerical runs were performed with channel Reynolds numbers, Re, in the range 100–150 000. Since a typical temperature difference between shaded and unshaded regions is just a few degrees Celsius, in a typical water depth of a few metres, it is implied that exchange flows within aquatic canopies are characterized by a Reynolds number of order
![]() $10^{4}$
. Furthermore, this Reynolds number is typical of many laboratory realizations of these flows. However, in other applications in which arrays of porous barriers are used to decelerate currents, the Reynolds number may be rather higher (e.g.
$10^{4}$
. Furthermore, this Reynolds number is typical of many laboratory realizations of these flows. However, in other applications in which arrays of porous barriers are used to decelerate currents, the Reynolds number may be rather higher (e.g.
![]() $\mathit{Re}=10^{5}{-}10^{8}$
), because the typical length scales and flow speeds are increased (see Naaim-Bouvet et al.
Reference Naaim-Bouvet, Naaim, Bacher and Heiligenstein2002; Oehy & Schleiss Reference Oehy and Schleiss2007). However, as will be shown below, the motion is retarded by the obstacles and decelerates, thus promoting the relative magnitude of viscous processes. Eventually the motion becomes fully controlled by viscous effects, and for this reason we have also conducted simulations at relatively low Reynolds numbers so that the effects of fluid turbulence are suppressed and the viscous dynamics may be analysed.
$\mathit{Re}=10^{5}{-}10^{8}$
), because the typical length scales and flow speeds are increased (see Naaim-Bouvet et al.
Reference Naaim-Bouvet, Naaim, Bacher and Heiligenstein2002; Oehy & Schleiss Reference Oehy and Schleiss2007). However, as will be shown below, the motion is retarded by the obstacles and decelerates, thus promoting the relative magnitude of viscous processes. Eventually the motion becomes fully controlled by viscous effects, and for this reason we have also conducted simulations at relatively low Reynolds numbers so that the effects of fluid turbulence are suppressed and the viscous dynamics may be analysed.
The obstructed channel is geometrically characterized by the following variables. There are
![]() $N$
square cylinders within the domain of volume
$N$
square cylinders within the domain of volume
![]() $V$
, so the volume fraction of solids is given by
$V$
, so the volume fraction of solids is given by
where
![]() $W$
is the width of the domain. The average spacing between the cylinders,
$W$
is the width of the domain. The average spacing between the cylinders,
![]() $s$
, is given by
$s$
, is given by
Finally, the frontal area of the cylinders per unit volume,
![]() $a$
, is given by
$a$
, is given by
The inverse of this quantity,
![]() $1/a$
, is a length scale characterizing the porous medium.
$1/a$
, is a length scale characterizing the porous medium.
The simulations were conducted with volume fractions of solids
![]() ${\it\phi}$
between 0 and 25 % (see table 1). Although most vegetated canopies generally have
${\it\phi}$
between 0 and 25 % (see table 1). Although most vegetated canopies generally have
![]() ${\it\phi}<8\,\%$
, there are practical applications where higher solid volume fractions can occur (Jamali et al.
Reference Jamali, Zhang and Nepf2008). For example, in the case of arrays of porous barriers used to decelerate turbidity currents advancing in reservoirs,
${\it\phi}<8\,\%$
, there are practical applications where higher solid volume fractions can occur (Jamali et al.
Reference Jamali, Zhang and Nepf2008). For example, in the case of arrays of porous barriers used to decelerate turbidity currents advancing in reservoirs,
![]() ${\it\phi}$
generally varies between 5 and 20 % and even in the case of vegetated canopies
${\it\phi}$
generally varies between 5 and 20 % and even in the case of vegetated canopies
![]() ${\it\phi}$
values as high as 45 % have been reported in mangroves with mean trunk diameters in the range
${\it\phi}$
values as high as 45 % have been reported in mangroves with mean trunk diameters in the range
![]() $D=4{-}9~\text{cm}$
(Furukawa, Wolanski & Mueller Reference Furukawa, Wolanski and Mueller1997). The range of
$D=4{-}9~\text{cm}$
(Furukawa, Wolanski & Mueller Reference Furukawa, Wolanski and Mueller1997). The range of
![]() ${\it\phi}$
in the experiments of Zhang & Nepf (Reference Zhang and Nepf2008) for currents propagating in an aquatic canopy was 0–35 %. The range of
${\it\phi}$
in the experiments of Zhang & Nepf (Reference Zhang and Nepf2008) for currents propagating in an aquatic canopy was 0–35 %. The range of
![]() $D/H$
was 0.032–0.07 in the present simulations. The average value of the cylinder Reynolds number during the quadratic drag-dominated regime,
$D/H$
was 0.032–0.07 in the present simulations. The average value of the cylinder Reynolds number during the quadratic drag-dominated regime,
![]() $\mathit{Re}_{D}$
, was between 60 and 250 for the
$\mathit{Re}_{D}$
, was between 60 and 250 for the
![]() $\mathit{Re}=15\,000$
simulation and close to 1700 for the
$\mathit{Re}=15\,000$
simulation and close to 1700 for the
![]() $\mathit{Re}=150\,000$
simulation (table 1). These values are within the range considered in the experiments of King et al. (Reference King, Tinoco and Cowen2012) conducted for steady constant-density flow in a channel containing a layer of aquatic vegetation.
$\mathit{Re}=150\,000$
simulation (table 1). These values are within the range considered in the experiments of King et al. (Reference King, Tinoco and Cowen2012) conducted for steady constant-density flow in a channel containing a layer of aquatic vegetation.
Table 1. The main parameters of the numerical simulations. As in the text,
![]() $a$
is the frontal area of the cylinders per unit volume,
$a$
is the frontal area of the cylinders per unit volume,
![]() $\mathit{Re}_{D}$
is the cylinder Reynolds number defined with
$\mathit{Re}_{D}$
is the cylinder Reynolds number defined with
![]() $D$
and the mean
$D$
and the mean
![]() $U_{f}$
after the transition to the drag-dominated regime has started,
$U_{f}$
after the transition to the drag-dominated regime has started,
![]() $N$
is the total number of cylinders,
$N$
is the total number of cylinders,
![]() $C_{D}$
is the mean total drag coefficient estimated using the instantaneous velocity fields,
$C_{D}$
is the mean total drag coefficient estimated using the instantaneous velocity fields,
![]() $C_{D}^{\prime }$
is the mean total drag coefficient estimated using
$C_{D}^{\prime }$
is the mean total drag coefficient estimated using
![]() $U_{f}(t)$
as the velocity scale and
$U_{f}(t)$
as the velocity scale and
![]() ${\it\Gamma}_{D}=C_{D}aH/(1-{\it\phi})=C_{D}({\it\phi}H/D)/(1-{\it\phi})$
is a dimensionless combined drag parameter for the region containing the cylinders.
${\it\Gamma}_{D}=C_{D}aH/(1-{\it\phi})=C_{D}({\it\phi}H/D)/(1-{\it\phi})$
is a dimensionless combined drag parameter for the region containing the cylinders.

Apart from the cylinder diameter relative to the channel depth,
![]() $D/H$
, the other non-dimensional length scale is
$D/H$
, the other non-dimensional length scale is
![]() $aH$
. All present simulations were conducted with
$aH$
. All present simulations were conducted with
![]() $aH>0.1$
(table 1) and with relative spacing,
$aH>0.1$
(table 1) and with relative spacing,
![]() $s/D$
, greater than 2. As described below, we used the simulations to estimate the drag coefficient for the array of cylinders. This is denoted
$s/D$
, greater than 2. As described below, we used the simulations to estimate the drag coefficient for the array of cylinders. This is denoted
![]() $C_{D}$
and is reported in table 1, along with a combined drag parameter for the porous medium,
$C_{D}$
and is reported in table 1, along with a combined drag parameter for the porous medium,
![]() ${\it\Gamma}_{D}=C_{D}aH/(1-{\it\phi})=C_{D}{\it\phi}(H/D)/(1-{\it\phi})$
, which was larger than 0.48 (table 1). This latter parameter represents the ratio of obstacle drag force to momentum transport and can be also thought of as a global measure of the resistance provided by the cylinders; it will be shown to play a key role in the analysis that follows (§ 3). As discussed by King et al. (Reference King, Tinoco and Cowen2012), flows with
${\it\Gamma}_{D}=C_{D}aH/(1-{\it\phi})=C_{D}{\it\phi}(H/D)/(1-{\it\phi})$
, which was larger than 0.48 (table 1). This latter parameter represents the ratio of obstacle drag force to momentum transport and can be also thought of as a global measure of the resistance provided by the cylinders; it will be shown to play a key role in the analysis that follows (§ 3). As discussed by King et al. (Reference King, Tinoco and Cowen2012), flows with
![]() ${\it\Gamma}_{D}>0.1$
and
${\it\Gamma}_{D}>0.1$
and
![]() $s/D>1$
correspond to the ‘dense flow regime’ in which the size of the wake eddies and the turbulent kinetic energy generated by the cylinders scale with
$s/D>1$
correspond to the ‘dense flow regime’ in which the size of the wake eddies and the turbulent kinetic energy generated by the cylinders scale with
![]() $D$
, and vertical gradients in the flow are fairly negligible. The range of
$D$
, and vertical gradients in the flow are fairly negligible. The range of
![]() ${\it\Gamma}_{D}$
in our simulations was 0.48–8.52, which overlaps with the values estimated by Jamali et al. (Reference Jamali, Zhang and Nepf2008) for field applications. We note that most experiments were conducted with
${\it\Gamma}_{D}$
in our simulations was 0.48–8.52, which overlaps with the values estimated by Jamali et al. (Reference Jamali, Zhang and Nepf2008) for field applications. We note that most experiments were conducted with
![]() ${\it\Gamma}_{D}<5$
, although
${\it\Gamma}_{D}<5$
, although
![]() ${\it\Gamma}_{D}$
values as high as 70 were recorded in their experiments with
${\it\Gamma}_{D}$
values as high as 70 were recorded in their experiments with
![]() ${\it\phi}=35\,\%$
.
${\it\phi}=35\,\%$
.
The computational mesh containing square cylinders was stretched in the wall-normal direction of no-slip surfaces (top and bottom walls, lateral endwalls) to resolve the near-wall flow. The grid resolution was also increased in the vicinity of the faces of the cylinders. In many of the simulations the grid spacing in these regions was approximately
![]() $0.0035H$
. Preliminary simulations were conducted for constant-density uniform flow past isolated cylinders. The grid resolution close to the isolated cylinder was the same as the one used for the cylinders within the array in the lock-exchange simulations, and the isolated cylinder simulations were conducted at comparable cylinder Reynolds numbers. The predictions of the drag coefficient for the isolated cylinder were found to be in good agreement with data in the literature (Yoon, Yang & Choi Reference Yoon, Yang and Choi2010). In most of the lock-exchange simulations, the grid contained
$0.0035H$
. Preliminary simulations were conducted for constant-density uniform flow past isolated cylinders. The grid resolution close to the isolated cylinder was the same as the one used for the cylinders within the array in the lock-exchange simulations, and the isolated cylinder simulations were conducted at comparable cylinder Reynolds numbers. The predictions of the drag coefficient for the isolated cylinder were found to be in good agreement with data in the literature (Yoon, Yang & Choi Reference Yoon, Yang and Choi2010). In most of the lock-exchange simulations, the grid contained
![]() $2400\times 200\times 48$
nodes in the streamwise (domain length
$2400\times 200\times 48$
nodes in the streamwise (domain length
![]() $12H$
), vertical (domain width
$12H$
), vertical (domain width
![]() $H$
) and spanwise (domain height
$H$
) and spanwise (domain height
![]() $H$
) directions respectively. In the simulation conducted with
$H$
) directions respectively. In the simulation conducted with
![]() $\mathit{Re}=150\,000$
(VHR_SVF12_D50), the grid was finer (
$\mathit{Re}=150\,000$
(VHR_SVF12_D50), the grid was finer (
![]() $4800\times 400\times 64$
) because of the need to sufficiently resolve the near-wall flow. In the simulation with no cylinders (HR_SVF00) in which the current advances much faster, the number of grid points in the streamwise direction was 9600 to account for the increase in the channel length to
$4800\times 400\times 64$
) because of the need to sufficiently resolve the near-wall flow. In the simulation with no cylinders (HR_SVF00) in which the current advances much faster, the number of grid points in the streamwise direction was 9600 to account for the increase in the channel length to
![]() $48H$
.
$48H$
.
Despite the fact that the arrangement of the cylinders was not exactly reflectionally symmetrical, the temporal evolution of the main variables characterizing the evolution of the currents along the bottom and top of the domain was found to be close to anti-symmetrical. This is why only the evolution of the denser bottom-propagating current forming on the right side of the lock gate in figure 1 is analysed. Typical numerical results are shown in figures 2(c) and 3. These are discussed in detail below, but first we present a shallow layer model of the motion.

Figure 2. (a) The height and (b) the depth-averaged velocity fields as a function of
![]() $x/x_{f}(t)$
for the similarity solution of a drag-dominated lock-exchange flow in the regime of high Reynolds number (
$x/x_{f}(t)$
for the similarity solution of a drag-dominated lock-exchange flow in the regime of high Reynolds number (
![]() $C_{D}=\text{const.}$
). Also plotted with symbols is the mean streamwise velocity determined from the numerical solution. (c) The scaled concentration field,
$C_{D}=\text{const.}$
). Also plotted with symbols is the mean streamwise velocity determined from the numerical solution. (c) The scaled concentration field,
![]() $C$
, as a function of downstream distance,
$C$
, as a function of downstream distance,
![]() $x$
, and height,
$x$
, and height,
![]() $z$
, when
$z$
, when
![]() $x_{f}/H=4.6$
, from the simulation with
$x_{f}/H=4.6$
, from the simulation with
![]() $\mathit{Re}=15\,000$
,
$\mathit{Re}=15\,000$
,
![]() ${\it\phi}=12\,\%$
and
${\it\phi}=12\,\%$
and
![]() $D/H=0.05$
. The dashed (blue online) and dash-dotted (red online) lines in panel (c) show the interface shape given by the analytical model,
$D/H=0.05$
. The dashed (blue online) and dash-dotted (red online) lines in panel (c) show the interface shape given by the analytical model,
![]() $h/H$
, and from the numerical simulation,
$h/H$
, and from the numerical simulation,
![]() $h_{n}/H$
, respectively. (d) The dimensionless position of the front,
$h_{n}/H$
, respectively. (d) The dimensionless position of the front,
![]() $x_{f}/H$
, as a function of dimensionless time
$x_{f}/H$
, as a function of dimensionless time
![]() $t/t_{0}$
, showing the similarity solution (dashed black line) and the results from the numerical simulation (solid pink line).
$t/t_{0}$
, showing the similarity solution (dashed black line) and the results from the numerical simulation (solid pink line).

Figure 3. Sketch of the front position,
![]() $x_{f}$
, as a function of time,
$x_{f}$
, as a function of time,
![]() $t$
, and the transitions between the various dynamical regimes for currents propagating into an obstructed channel predicted by shallow flow theory. The exponents are predicted by theory within different regimes (slumping phase, quadratic drag-dominated regime, linear drag-dominated regime). The transition times (
$t$
, and the transitions between the various dynamical regimes for currents propagating into an obstructed channel predicted by shallow flow theory. The exponents are predicted by theory within different regimes (slumping phase, quadratic drag-dominated regime, linear drag-dominated regime). The transition times (
![]() $t_{1},t_{2}$
) and locations where transition is expected to occur (
$t_{1},t_{2}$
) and locations where transition is expected to occur (
![]() $x_{1},x_{2}$
) are defined in § 3. In frame (b) the current transitions directly from the slumping phase to the linear drag-dominated regime, and this corresponds to low-Reynolds-number lock-exchange flows.
$x_{1},x_{2}$
) are defined in § 3. In frame (b) the current transitions directly from the slumping phase to the linear drag-dominated regime, and this corresponds to low-Reynolds-number lock-exchange flows.
3. Shallow water theory model
We analyse the density-driven motion to calculate the evolution of the interface between the dense and less dense fluids. We assume that mixing processes are negligible, so that the fluid density is
![]() ${\it\rho}+{\rm\Delta}{\it\rho}$
if it lies below the interface
${\it\rho}+{\rm\Delta}{\it\rho}$
if it lies below the interface
![]() $(y=h)$
or
$(y=h)$
or
![]() ${\it\rho}$
if above, and the interface evolves according to a kinematic condition. In dimensional form, mass conservation in each layer is then given by
${\it\rho}$
if above, and the interface evolves according to a kinematic condition. In dimensional form, mass conservation in each layer is then given by
The motion is analysed in a regime where the velocity is predominantly horizontal; vertical fluid accelerations are negligible and so the pressure,
![]() $p$
, adopts a locally hydrostatic balance given by
$p$
, adopts a locally hydrostatic balance given by
where
![]() $p_{T}(x)$
denotes the as yet undetermined pressure along the upper boundary
$p_{T}(x)$
denotes the as yet undetermined pressure along the upper boundary
![]() $y=H$
. Horizontal gradients of the pressure distribution drive the motion, while hydraulic resistance is provided by the array of cylinders through which the fluid flows. The drag at the boundaries of the porous domain is assumed to be much smaller than the drag due to the dispersed cylinders. The momentum balances for each layer in the Boussinesq regime are given by
$y=H$
. Horizontal gradients of the pressure distribution drive the motion, while hydraulic resistance is provided by the array of cylinders through which the fluid flows. The drag at the boundaries of the porous domain is assumed to be much smaller than the drag due to the dispersed cylinders. The momentum balances for each layer in the Boussinesq regime are given by
Following initiation from full-depth lock-release conditions, namely
![]() $h=H$
when
$h=H$
when
![]() $x<0$
and
$x<0$
and
![]() $h=0$
when
$h=0$
when
![]() $x>0$
, the dynamics governed by (3.5) and (3.6) is dominated by inertia, and the effects of drag induced by the cylinders have little effect on the motion. However, progressively the drag induced by the cylinders and the buoyancy force become the dominant terms in (3.5) and (3.6), while the inertial terms become negligible. It is insightful to employ scaling analysis to determine the temporal dependence of the velocity within the bottom layer,
$x>0$
, the dynamics governed by (3.5) and (3.6) is dominated by inertia, and the effects of drag induced by the cylinders have little effect on the motion. However, progressively the drag induced by the cylinders and the buoyancy force become the dominant terms in (3.5) and (3.6), while the inertial terms become negligible. It is insightful to employ scaling analysis to determine the temporal dependence of the velocity within the bottom layer,
![]() $u_{1}$
, and extent of the flow,
$u_{1}$
, and extent of the flow,
![]() $x_{f}$
, noting that the height of the interface
$x_{f}$
, noting that the height of the interface
![]() $h\sim H$
for the lock-release flows considered here. Thus, when drag is negligible, we find
$h\sim H$
for the lock-release flows considered here. Thus, when drag is negligible, we find
![]() $u_{1}\sim (g^{\prime }H)^{1/2}$
and
$u_{1}\sim (g^{\prime }H)^{1/2}$
and
![]() $x_{f}\sim (g^{\prime }H)^{1/2}t$
. With these dependences, we may estimate the magnitude of the inertial terms in (3.5) as
$x_{f}\sim (g^{\prime }H)^{1/2}t$
. With these dependences, we may estimate the magnitude of the inertial terms in (3.5) as
![]() $(1-{\it\phi})\partial u_{1}/\partial t\sim (1-{\it\phi})(g^{\prime }H)^{1/2}/t$
, while the drag
$(1-{\it\phi})\partial u_{1}/\partial t\sim (1-{\it\phi})(g^{\prime }H)^{1/2}/t$
, while the drag
![]() $C_{D}{\it\phi}u_{1}|u_{1}|/2D\sim C_{D}{\it\phi}g^{\prime }H/2D$
. They are thus comparable when
$C_{D}{\it\phi}u_{1}|u_{1}|/2D\sim C_{D}{\it\phi}g^{\prime }H/2D$
. They are thus comparable when
![]() $t\sim t_{1}=2(1-{\it\phi})D/[C_{D}{\it\phi}(g^{\prime }H)^{1/2}]$
and
$t\sim t_{1}=2(1-{\it\phi})D/[C_{D}{\it\phi}(g^{\prime }H)^{1/2}]$
and
![]() $x_{f}\sim x_{1}=2(1-{\it\phi})D/(C_{D}{\it\phi})$
. When
$x_{f}\sim x_{1}=2(1-{\it\phi})D/(C_{D}{\it\phi})$
. When
![]() $t\ll t_{1}$
, drag is negligible, but when
$t\ll t_{1}$
, drag is negligible, but when
![]() $t\gg t_{1}$
, drag becomes a dominant force and changes the momentum balance. Importantly, we note that the dimensional dependences of these transition length and time scales may be written as
$t\gg t_{1}$
, drag becomes a dominant force and changes the momentum balance. Importantly, we note that the dimensional dependences of these transition length and time scales may be written as
These expressions therefore reveal
![]() ${\it\Gamma}_{D}=C_{D}{\it\phi}D/[(1-{\it\phi})H]$
as the key dimensionless group of parameters that determines the onset of drag effects and their subsequent magnitude.
${\it\Gamma}_{D}=C_{D}{\it\phi}D/[(1-{\it\phi})H]$
as the key dimensionless group of parameters that determines the onset of drag effects and their subsequent magnitude.
We now examine the regime in which buoyancy and drag forces balance, noting that the momentum equations for each layer simplify to balance between the streamwise pressure gradient and the hydraulic resistance due to the cylinder (see Hatcher et al. Reference Hatcher, Hogg and Woods2000):
Then we find that the momentum balance in the lower layer may be written as
This leads to the governing equation for the interface
![]() $h(x,t)$
,
$h(x,t)$
,
where
![]() $K=2g^{\prime }D(1-{\it\phi})/[C_{D}{\it\phi}]=2u_{b}^{2}/{\it\Gamma}_{D}$
, a constant of dimensions
$K=2g^{\prime }D(1-{\it\phi})/[C_{D}{\it\phi}]=2u_{b}^{2}/{\it\Gamma}_{D}$
, a constant of dimensions
![]() $L^{2}T^{-2}$
that characterizes the mobility of the density-driven flow. We seek a similarity solution to (3.12), by writing
$L^{2}T^{-2}$
that characterizes the mobility of the density-driven flow. We seek a similarity solution to (3.12), by writing
![]() $h=HF({\it\eta})$
, with the similarity variable defined by
$h=HF({\it\eta})$
, with the similarity variable defined by
where
![]() $B$
is a dimensionless constant chosen such the interface reaches the lower boundary at
$B$
is a dimensionless constant chosen such the interface reaches the lower boundary at
![]() ${\it\eta}=1$
; this implies that
${\it\eta}=1$
; this implies that
![]() $x_{f}(t)=B(KHt^{2})^{1/3}$
. Substitution of this form into the governing equation (3.12) leads to an ordinary differential equation (ODE) for
$x_{f}(t)=B(KHt^{2})^{1/3}$
. Substitution of this form into the governing equation (3.12) leads to an ordinary differential equation (ODE) for
![]() $F({\it\eta})$
, given by
$F({\it\eta})$
, given by
subject to boundary conditions
![]() $F(0)=1/2,F(1)=0$
and
$F(0)=1/2,F(1)=0$
and
![]() $F^{\prime }(1)=-4B^{3}/9$
. The first of these boundary conditions demands that the intrusions of dense and less dense fluid are symmetric; the second defines the front to occur at
$F^{\prime }(1)=-4B^{3}/9$
. The first of these boundary conditions demands that the intrusions of dense and less dense fluid are symmetric; the second defines the front to occur at
![]() ${\it\eta}=1$
; the third is forced by the singular nature of the governing equations at
${\it\eta}=1$
; the third is forced by the singular nature of the governing equations at
![]() ${\it\eta}=1$
. This system is therefore a differential eigenvalue problem, which is solved straightforwardly using numerical techniques to evaluate the constant
${\it\eta}=1$
. This system is therefore a differential eigenvalue problem, which is solved straightforwardly using numerical techniques to evaluate the constant
![]() $B=1.162$
and to find the interface shape,
$B=1.162$
and to find the interface shape,
![]() $h/H$
(figure 2
a). Also plotted (figure 2
b) is the dimensionless velocity field in the lower layer, given by
$h/H$
(figure 2
a). Also plotted (figure 2
b) is the dimensionless velocity field in the lower layer, given by
Figure 2(c) shows the interface shape given by the analytical model superimposed on the concentration field predicted in a simulation with
![]() ${\it\phi}=12\,\%$
,
${\it\phi}=12\,\%$
,
![]() $D/H=0.05$
and
$D/H=0.05$
and
![]() $\mathit{Re}=15\,000$
. Also shown is the interface shape,
$\mathit{Re}=15\,000$
. Also shown is the interface shape,
![]() $h_{n}/H$
, calculated based on the concentration field predicted by the numerical solution, where
$h_{n}/H$
, calculated based on the concentration field predicted by the numerical solution, where
![]() $h_{n}=\int _{0}^{H}\!C\text{d}y$
. The overall agreement between the two curves in figure 2(c) is good, with the analytical solution predicting slightly lower values of the interface height,
$h_{n}=\int _{0}^{H}\!C\text{d}y$
. The overall agreement between the two curves in figure 2(c) is good, with the analytical solution predicting slightly lower values of the interface height,
![]() $h$
, over the downstream parts of the current. A similar level of agreement is observed in figure 2(b) between the numerical solution and the analytical model for the distribution of the non-dimensional mean streamwise velocity,
$h$
, over the downstream parts of the current. A similar level of agreement is observed in figure 2(b) between the numerical solution and the analytical model for the distribution of the non-dimensional mean streamwise velocity,
![]() $u_{1}/U_{f}$
. The agreement is satisfactory given that mixing is not accounted for in the analytical model. The agreement is worst close to the front of the current where mixing is especially strong. We also plot in figure 2(d) a comparison between the position of the front measured in the numerical simulations and the similarity solution (
$u_{1}/U_{f}$
. The agreement is satisfactory given that mixing is not accounted for in the analytical model. The agreement is worst close to the front of the current where mixing is especially strong. We also plot in figure 2(d) a comparison between the position of the front measured in the numerical simulations and the similarity solution (
![]() $x_{f}/H=B(2/{\it\Gamma}_{D})^{1/3}(t/t_{0})^{2/3}$
), noting that there is fair agreement between the two. In order to make this comparison and to estimate
$x_{f}/H=B(2/{\it\Gamma}_{D})^{1/3}(t/t_{0})^{2/3}$
), noting that there is fair agreement between the two. In order to make this comparison and to estimate
![]() ${\it\Gamma}_{D}$
, we have determined the drag coefficient for the array from the simulation data using the mean velocity within the bottom current as the velocity scale (more details are given in § 6).
${\it\Gamma}_{D}$
, we have determined the drag coefficient for the array from the simulation data using the mean velocity within the bottom current as the velocity scale (more details are given in § 6).
This solution is based upon the assumption that the drag exerted by the cylinders may be represented by a constant drag coefficient. Since the velocity is progressively slowing, this implies that there is a time scale,
![]() $t_{2}$
, at which the motion is no longer adequately modelled by the high-Reynolds-number representation of the drag from each cylinder. This occurs when
$t_{2}$
, at which the motion is no longer adequately modelled by the high-Reynolds-number representation of the drag from each cylinder. This occurs when
![]() $\mathit{Re}_{D}\sim 1$
, which is given when
$\mathit{Re}_{D}\sim 1$
, which is given when
The model of the motion developed above is appropriate then for
![]() $t_{1}\ll t\ll t_{2}$
, but for
$t_{1}\ll t\ll t_{2}$
, but for
![]() $t_{2}\ll t$
the governing equations are modified so that the drag is now linearly proportional to the flow speed. In this scenario the dominant balance between the hydrostatic pressure gradient and the drag is given by
$t_{2}\ll t$
the governing equations are modified so that the drag is now linearly proportional to the flow speed. In this scenario the dominant balance between the hydrostatic pressure gradient and the drag is given by
where
![]() $x_{f}(t)=(g^{\prime }H(1-{\it\phi})D^{2}t/[{\it\gamma}{\it\nu}{\it\phi}])^{1/2}$
.
$x_{f}(t)=(g^{\prime }H(1-{\it\phi})D^{2}t/[{\it\gamma}{\it\nu}{\it\phi}])^{1/2}$
.
To summarize, for these gravity currents initiated from full-depth lock-release conditions and propagating in an obstructed channel with a sufficiently high volume fraction of solids, the self-similar solution obtained based on shallow flow theory predicts (a)
![]() $U_{f}\sim t^{-1/3}$
and
$U_{f}\sim t^{-1/3}$
and
![]() $x_{f}\sim t^{2/3}$
at sufficiently high Reynolds numbers for which one can assume
$x_{f}\sim t^{2/3}$
at sufficiently high Reynolds numbers for which one can assume
![]() $C_{D}$
to be constant, and (b)
$C_{D}$
to be constant, and (b)
![]() $U_{f}\sim t^{-1/2}$
and
$U_{f}\sim t^{-1/2}$
and
![]() $x_{f}\sim t^{1/2}$
at sufficiently low Reynolds numbers where one can consider that a linear drag law (
$x_{f}\sim t^{1/2}$
at sufficiently low Reynolds numbers where one can consider that a linear drag law (
![]() $C_{D}\sim 1/\mathit{Re}_{D}$
) applies (cf. Huppert & Woods Reference Huppert and Woods1995; Tanino et al.
Reference Tanino, Nepf and Kulis2005). Furthermore, one expects currents to undergo transitions between behaviours. At very early times (
$C_{D}\sim 1/\mathit{Re}_{D}$
) applies (cf. Huppert & Woods Reference Huppert and Woods1995; Tanino et al.
Reference Tanino, Nepf and Kulis2005). Furthermore, one expects currents to undergo transitions between behaviours. At very early times (
![]() $t\ll t_{1}$
), the motion is inertia dominated, before becoming drag dominated but with the drag proportional to the square of the velocity (
$t\ll t_{1}$
), the motion is inertia dominated, before becoming drag dominated but with the drag proportional to the square of the velocity (
![]() $t_{1}\ll t\ll t_{2}$
), before entering a regime in which the drag is linearly proportional to the velocity (
$t_{1}\ll t\ll t_{2}$
), before entering a regime in which the drag is linearly proportional to the velocity (
![]() $t_{2}\ll t$
). This is illustrated in figure 3(a). It is possible that the intermediate regime of quadratic drag would not be observed (figure 3
b). This would occur if
$t_{2}\ll t$
). This is illustrated in figure 3(a). It is possible that the intermediate regime of quadratic drag would not be observed (figure 3
b). This would occur if
![]() $t_{2}\ll t_{1}$
, which corresponds to the cylinder Reynolds number being small (
$t_{2}\ll t_{1}$
, which corresponds to the cylinder Reynolds number being small (
![]() $\mathit{Re}_{D}\ll 1$
).
$\mathit{Re}_{D}\ll 1$
).
4. Structure of the gravity current
4.1. High-Reynolds-number currents
4.1.1. Effects of the solid volume fraction
This subsection analyses simulations conducted with channel Reynolds number
![]() $\mathit{Re}=15\,000$
and relative cylinder diameter
$\mathit{Re}=15\,000$
and relative cylinder diameter
![]() $D/H=0.032$
. The Reynolds number is large enough that the lock-exchange flow remains turbulent, at least close to the front of the current, until the front of the current reaches the end of the computational domain. The presence of cylinders in the channel has a large influence on mixing, especially inside the interfacial layer and in the regions close to the front.
$D/H=0.032$
. The Reynolds number is large enough that the lock-exchange flow remains turbulent, at least close to the front of the current, until the front of the current reaches the end of the computational domain. The presence of cylinders in the channel has a large influence on mixing, especially inside the interfacial layer and in the regions close to the front.
Even for channels with relatively small volume fractions of cylinders, for which the additional drag is not sufficient to trigger transition to the drag-dominated regime within the computational domain (see, for example, the simulation with
![]() ${\it\phi}=125\,\%$
, figure 4
b), the cylinders induce notable changes in the structure of the flow. For example, comparison of the concentration distributions in figures 4(a) (
${\it\phi}=125\,\%$
, figure 4
b), the cylinders induce notable changes in the structure of the flow. For example, comparison of the concentration distributions in figures 4(a) (
![]() ${\it\phi}=0\,\%$
) and 4(b) (
${\it\phi}=0\,\%$
) and 4(b) (
![]() ${\it\phi}=1.25\,\%$
) during the slumping phase shows that the interaction of the flow with the cylinders reduces the size and coherence of the large-scale interfacial Kelvin–Helmholtz (KH) billows, which continue to form due to the presence of velocity shear over a density-stratified region. However, because of the cylinders, the thickness of the interfacial layer containing mixed fluid becomes more uniform, at least at large distances from the front. Relative to the unobstructed case (
${\it\phi}=1.25\,\%$
) during the slumping phase shows that the interaction of the flow with the cylinders reduces the size and coherence of the large-scale interfacial Kelvin–Helmholtz (KH) billows, which continue to form due to the presence of velocity shear over a density-stratified region. However, because of the cylinders, the thickness of the interfacial layer containing mixed fluid becomes more uniform, at least at large distances from the front. Relative to the unobstructed case (
![]() ${\it\phi}=0\,\%$
), the width of the interfacial layer is smaller when the cylinders are present.
${\it\phi}=0\,\%$
), the width of the interfacial layer is smaller when the cylinders are present.

Figure 4. Distribution of concentration,
![]() $C$
, within a high-Reynolds-number (
$C$
, within a high-Reynolds-number (
![]() $\mathit{Re}=15\,000$
) bottom current propagating in a channel with (a)
$\mathit{Re}=15\,000$
) bottom current propagating in a channel with (a)
![]() ${\it\phi}=0\,\%$
; (b)
${\it\phi}=0\,\%$
; (b)
![]() ${\it\phi}=1.25\,\%$
,
${\it\phi}=1.25\,\%$
,
![]() $D/H=0.032$
; (c)
$D/H=0.032$
; (c)
![]() ${\it\phi}=5\,\%$
,
${\it\phi}=5\,\%$
,
![]() $D/H=0.032$
; (d)
$D/H=0.032$
; (d)
![]() ${\it\phi}=12\,\%$
,
${\it\phi}=12\,\%$
,
![]() $D/H=0.032$
. Results are compared when
$D/H=0.032$
. Results are compared when
![]() $x_{f}/H=5$
. The solid line shows the
$x_{f}/H=5$
. The solid line shows the
![]() $C=0.01$
isocontour.
$C=0.01$
isocontour.
In the simulation without cylinders (
![]() ${\it\phi}=0\,\%$
), most of the energetic large-scale eddies are situated within the interfacial layer (figure 5
a). Most of the mixing is driven by these eddies. The tail of the current beneath the interfacial layer contains a very small number of large-scale eddies. In contrast, for the case with
${\it\phi}=0\,\%$
), most of the energetic large-scale eddies are situated within the interfacial layer (figure 5
a). Most of the mixing is driven by these eddies. The tail of the current beneath the interfacial layer contains a very small number of large-scale eddies. In contrast, for the case with
![]() ${\it\phi}=1.25\,\%$
(figure 5
b) the cylinders act as a main source of large-scale turbulence within the current. Their spacing is sufficiently large that the dynamics of the separated shear layers is fairly similar to that expected for isolated cylinders in a flow that is started from rest, accelerates rapidly and then decelerates fairly slowly. Highly energetic eddies detach from the downstream ends of these shear layers and the interactions of the shear layers on the two sides of the cylinder result in the formation and shedding of larger-scale billow vortices during the time in which the incoming flow velocity is relatively large. These eddies are the main mechanism that is responsible for the increased mixing observed in the simulation with
${\it\phi}=1.25\,\%$
(figure 5
b) the cylinders act as a main source of large-scale turbulence within the current. Their spacing is sufficiently large that the dynamics of the separated shear layers is fairly similar to that expected for isolated cylinders in a flow that is started from rest, accelerates rapidly and then decelerates fairly slowly. Highly energetic eddies detach from the downstream ends of these shear layers and the interactions of the shear layers on the two sides of the cylinder result in the formation and shedding of larger-scale billow vortices during the time in which the incoming flow velocity is relatively large. These eddies are the main mechanism that is responsible for the increased mixing observed in the simulation with
![]() ${\it\phi}=1.25\,\%$
relative to that found in the simulation with
${\it\phi}=1.25\,\%$
relative to that found in the simulation with
![]() ${\it\phi}=0\,\%$
. The presence of cylinders also significantly increases mixing near the front of the current. The additional mixing induced by the cylinders explains the aforementioned differences in the distribution of the concentration/density between the
${\it\phi}=0\,\%$
. The presence of cylinders also significantly increases mixing near the front of the current. The additional mixing induced by the cylinders explains the aforementioned differences in the distribution of the concentration/density between the
![]() ${\it\phi}=0\,\%$
and
${\it\phi}=0\,\%$
and
![]() ${\it\phi}=1.25\,\%$
cases (e.g. see the concentration distributions in figure 4
a,b).
${\it\phi}=1.25\,\%$
cases (e.g. see the concentration distributions in figure 4
a,b).

Figure 5. Distribution of dimensionless vorticity magnitude,
![]() ${\it\omega}_{z}(H/u_{b})$
, within a high-Reynolds-number (
${\it\omega}_{z}(H/u_{b})$
, within a high-Reynolds-number (
![]() $\mathit{Re}=15\,000$
) current propagating in a channel with (a)
$\mathit{Re}=15\,000$
) current propagating in a channel with (a)
![]() ${\it\phi}=0\,\%$
; (b)
${\it\phi}=0\,\%$
; (b)
![]() ${\it\phi}=1.25\,\%$
,
${\it\phi}=1.25\,\%$
,
![]() $D/H=0.032$
; (c)
$D/H=0.032$
; (c)
![]() ${\it\phi}=5\,\%$
,
${\it\phi}=5\,\%$
,
![]() $D/H=0.032$
; (d)
$D/H=0.032$
; (d)
![]() ${\it\phi}=12\,\%$
,
${\it\phi}=12\,\%$
,
![]() $D/H=0.032$
. Results are compared when
$D/H=0.032$
. Results are compared when
![]() $x_{f}/H=5$
. The solid line shows the
$x_{f}/H=5$
. The solid line shows the
![]() $C=0.01$
isocontour. The rectangle in frame (d) shows the region visualized in figure 7.
$C=0.01$
isocontour. The rectangle in frame (d) shows the region visualized in figure 7.
As the solid fraction was increased to over 3 %, the current transitioned to a drag-dominated regime within the computational domain and consequently the front speed
![]() $U_{f}$
decreased with time. A clear decrease in the level of turbulence generated by the bottom no-slip boundary and by the cylinders with an increase in the solid volume fraction,
$U_{f}$
decreased with time. A clear decrease in the level of turbulence generated by the bottom no-slip boundary and by the cylinders with an increase in the solid volume fraction,
![]() ${\it\phi}$
, was observed during the later stages of the simulations. This is illustrated in figure 5 which visualizes the vortical structure of the current when
${\it\phi}$
, was observed during the later stages of the simulations. This is illustrated in figure 5 which visualizes the vortical structure of the current when
![]() $x_{f}/H\cong 5$
. Hardly any detachment of large-scale eddies from the separated shear layers is observed in the simulation with
$x_{f}/H\cong 5$
. Hardly any detachment of large-scale eddies from the separated shear layers is observed in the simulation with
![]() ${\it\phi}=12\,\%$
for the cylinders situated away from the front (figure 5
d). As the cylinder density increases, with
${\it\phi}=12\,\%$
for the cylinders situated away from the front (figure 5
d). As the cylinder density increases, with
![]() $D/H=\text{const.}$
, the interactions between the separated shear layers on the two sides of each cylinder become weaker and these interactions are different from the case of an isolated cylinder. For example, in the simulation with
$D/H=\text{const.}$
, the interactions between the separated shear layers on the two sides of each cylinder become weaker and these interactions are different from the case of an isolated cylinder. For example, in the simulation with
![]() ${\it\phi}=5\,\%$
(figure 5
c) the shear layers from one cylinder extend and interact with the cylinder situated behind it. The shedding of large-scale billows is impeded. In the simulation with
${\it\phi}=5\,\%$
(figure 5
c) the shear layers from one cylinder extend and interact with the cylinder situated behind it. The shedding of large-scale billows is impeded. In the simulation with
![]() ${\it\phi}=12\,\%$
(figure 5
d) no significant interactions between the separated shear layers are observed when
${\it\phi}=12\,\%$
(figure 5
d) no significant interactions between the separated shear layers are observed when
![]() $x_{f}/H>5$
, except for the first few cylinders behind the front. This is similar to what is observed for low-Reynolds-number currents discussed below in § 4.2. In terms of mixing, the main effect of the decrease in the energy of the eddies shed from the cylinder with increasing volume fraction
$x_{f}/H>5$
, except for the first few cylinders behind the front. This is similar to what is observed for low-Reynolds-number currents discussed below in § 4.2. In terms of mixing, the main effect of the decrease in the energy of the eddies shed from the cylinder with increasing volume fraction
![]() ${\it\phi}$
(figures 4
b–d and 5
b–d) is that mixing decreases with
${\it\phi}$
(figures 4
b–d and 5
b–d) is that mixing decreases with
![]() ${\it\phi}$
for constant
${\it\phi}$
for constant
![]() $D/H$
, once
$D/H$
, once
![]() ${\it\phi}$
becomes larger than 3 %.
${\it\phi}$
becomes larger than 3 %.
The capacity of the cylinders to generate flow unsteadiness and detachment of large-scale energetic eddies from the separated shear layers correlates with their capacity to enhance mixing. Comparison of the concentration distributions in figure 4 shows that for
![]() ${\it\phi}>3\,\%$
, no large-scale KH billows can be detected inside the interfacial layer and there is a significant decay of the size of the region containing mixed fluid behind the front with increase in the solid volume fraction. The interactions between the large-scale eddies shed from the cylinders situated in the vicinity of the bed and the bottom boundary layer become stronger as
${\it\phi}>3\,\%$
, no large-scale KH billows can be detected inside the interfacial layer and there is a significant decay of the size of the region containing mixed fluid behind the front with increase in the solid volume fraction. The interactions between the large-scale eddies shed from the cylinders situated in the vicinity of the bed and the bottom boundary layer become stronger as
![]() ${\it\phi}$
increases. Analysis of the instantaneous bed friction velocity and vorticity fields shows that some of these eddies can more than double the instantaneous bed shear stress when they approach the channel bottom. However, past a certain threshold value of the solid fraction (
${\it\phi}$
increases. Analysis of the instantaneous bed friction velocity and vorticity fields shows that some of these eddies can more than double the instantaneous bed shear stress when they approach the channel bottom. However, past a certain threshold value of the solid fraction (
![]() ${\it\phi}\cong 10\,\%$
for the series of simulations presented in figure 5), the passage of these high-vorticity eddies to the bed becomes inhibited by the presence of the cylinders.
${\it\phi}\cong 10\,\%$
for the series of simulations presented in figure 5), the passage of these high-vorticity eddies to the bed becomes inhibited by the presence of the cylinders.
In terms of the flow structure at the front, increase of the solid fraction strongly diminishes the size of the lobes and clefts of the basal current. For example, in the simulation with
![]() ${\it\phi}=1.25\,\%$
, the average size of the lobes is similar to that for the lobes forming in the case of a non-porous channel. Analysis of the results has shown that the average size of the lobes decreases by a factor larger than two as
${\it\phi}=1.25\,\%$
, the average size of the lobes is similar to that for the lobes forming in the case of a non-porous channel. Analysis of the results has shown that the average size of the lobes decreases by a factor larger than two as
![]() ${\it\phi}$
increases from 1.25 to 5 %. For
${\it\phi}$
increases from 1.25 to 5 %. For
![]() ${\it\phi}>5\,\%$
, the rate of decrease of the mean size of the lobes is much smaller than that observed between
${\it\phi}>5\,\%$
, the rate of decrease of the mean size of the lobes is much smaller than that observed between
![]() ${\it\phi}=1.25$
and 5 %.
${\it\phi}=1.25$
and 5 %.
4.1.2. Effect of cylinder size,
 $D/H$
, and frontal area,
$D/H$
, and frontal area,
 $aH$
$aH$
Up to this point we have examined the evolution and structure of the current in terms of the two parameters Re, the Reynolds number, and
![]() ${\it\phi}$
, the solid volume fraction. However, one can modify the structure of the current while keeping these two parameters constant. One way to achieve this is to increase
${\it\phi}$
, the solid volume fraction. However, one can modify the structure of the current while keeping these two parameters constant. One way to achieve this is to increase
![]() $D/H$
and, at the same time, increase the distance between the cylinders,
$D/H$
and, at the same time, increase the distance between the cylinders,
![]() $s/H$
. The effect of this variation can be inferred by comparing two simulations conducted with the same
$s/H$
. The effect of this variation can be inferred by comparing two simulations conducted with the same
![]() ${\it\phi}$
and Re (
${\it\phi}$
and Re (
![]() ${\it\phi}=12\,\%$
and
${\it\phi}=12\,\%$
and
![]() $\mathit{Re}=15\,000$
) but with different values of the cylinder diameter (
$\mathit{Re}=15\,000$
) but with different values of the cylinder diameter (
![]() $D/H=0.032$
, see figures 4
d, 5
d, and
$D/H=0.032$
, see figures 4
d, 5
d, and
![]() $D/H=0.07$
, see figure 6). As
$D/H=0.07$
, see figure 6). As
![]() ${\it\phi}$
remains the same and
${\it\phi}$
remains the same and
![]() $D/H$
increases, the frontal area
$D/H$
increases, the frontal area
![]() $aH$
decreases (table 1), which, in turn, affects the combined drag parameter
$aH$
decreases (table 1), which, in turn, affects the combined drag parameter
![]() ${\it\Gamma}_{D}=C_{D}{\it\phi}(H/D)/(1-{\it\phi})=C_{D}aH/(1-{\it\phi})$
. As
${\it\Gamma}_{D}=C_{D}{\it\phi}(H/D)/(1-{\it\phi})=C_{D}aH/(1-{\it\phi})$
. As
![]() $s/H$
and
$s/H$
and
![]() $D/H$
increase, the separated shear layers become longer, the degree of interaction between them increases and their dynamics becomes closer to that observed for isolated cylinders (e.g. contrast figures 4
d and 6
b) This is the main reason why the effect of increasing the cylinder size,
$D/H$
increase, the separated shear layers become longer, the degree of interaction between them increases and their dynamics becomes closer to that observed for isolated cylinders (e.g. contrast figures 4
d and 6
b) This is the main reason why the effect of increasing the cylinder size,
![]() $D/H$
, while keeping
$D/H$
, while keeping
![]() ${\it\phi}$
the same is to increase the mixing. Most of the increase of the volume of mixed fluid with
${\it\phi}$
the same is to increase the mixing. Most of the increase of the volume of mixed fluid with
![]() $D/H$
is due to mixing in the region situated just behind the front. The extent of this region is much smaller in the simulations with small
$D/H$
is due to mixing in the region situated just behind the front. The extent of this region is much smaller in the simulations with small
![]() $D/H$
(e.g. see the concentration distributions in figure 4
d for
$D/H$
(e.g. see the concentration distributions in figure 4
d for
![]() $D/H=0.032$
and figure 6
a for
$D/H=0.032$
and figure 6
a for
![]() $D/H=0.07$
), where the shape of the current close to the front approaches the triangular shape characteristic for low-Reynolds-number currents.
$D/H=0.07$
), where the shape of the current close to the front approaches the triangular shape characteristic for low-Reynolds-number currents.

Figure 6. Distribution of concentration
![]() $C$
(a) and dimensionless vorticity magnitude
$C$
(a) and dimensionless vorticity magnitude
![]() ${\it\omega}_{z}(H/u_{b})$
(b) within a high-Reynolds-number (
${\it\omega}_{z}(H/u_{b})$
(b) within a high-Reynolds-number (
![]() $\mathit{Re}=15\,000$
) bottom current propagating in a channel with
$\mathit{Re}=15\,000$
) bottom current propagating in a channel with
![]() ${\it\phi}=12\,\%$
containing large cylinders (
${\it\phi}=12\,\%$
containing large cylinders (
![]() $D/H=0.07$
). The solid line shows the
$D/H=0.07$
). The solid line shows the
![]() $C=0.01$
isocontour.
$C=0.01$
isocontour.
One can also examine the effects of varying the cylinder size, but keeping constant the frontal area,
![]() $aH$
. Comparison of the simulations with
$aH$
. Comparison of the simulations with
![]() ${\it\phi}=5\,\%$
,
${\it\phi}=5\,\%$
,
![]() $D/H=0.032$
(figures 4
c and 5
c) and
$D/H=0.032$
(figures 4
c and 5
c) and
![]() ${\it\phi}=12\,\%$
,
${\it\phi}=12\,\%$
,
![]() $D/H=0.07$
(figure 6) shows that increasing
$D/H=0.07$
(figure 6) shows that increasing
![]() $D/H$
while keeping the frontal area close to constant (
$D/H$
while keeping the frontal area close to constant (
![]() $aH\cong 1.6$
) increases the coherence of the KH billows and the amount of mixing in the front region. A similar effect is observed when the simulations with
$aH\cong 1.6$
) increases the coherence of the KH billows and the amount of mixing in the front region. A similar effect is observed when the simulations with
![]() ${\it\phi}=12\,\%$
,
${\it\phi}=12\,\%$
,
![]() $D/H=0.032$
and
$D/H=0.032$
and
![]() ${\it\phi}=25\,\%$
,
${\it\phi}=25\,\%$
,
![]() $D/H=0.07$
are compared, for which
$D/H=0.07$
are compared, for which
![]() $aH\cong 3.6$
. This explains why, for constant
$aH\cong 3.6$
. This explains why, for constant
![]() $aH$
, mixing increases with
$aH$
, mixing increases with
![]() ${\it\phi}$
or, equivalently, with
${\it\phi}$
or, equivalently, with
![]() $D/H$
(
$D/H$
(
![]() ${\it\phi}=aH(D/H)$
).
${\it\phi}=aH(D/H)$
).
4.1.3. Effect of the Reynolds number
In the simulation with
![]() ${\it\phi}=12\,\%$
and
${\it\phi}=12\,\%$
and
![]() $\mathit{Re}=150\,000$
, Re and
$\mathit{Re}=150\,000$
, Re and
![]() $\mathit{Re}_{D}$
are sufficiently high for the flow within the current to remain strongly turbulent in between the lock gate and the front during the whole duration of the simulation (e.g. see figure 7). The conditions in the
$\mathit{Re}_{D}$
are sufficiently high for the flow within the current to remain strongly turbulent in between the lock gate and the front during the whole duration of the simulation (e.g. see figure 7). The conditions in the
![]() $\mathit{Re}=150\,000$
simulation correspond closely to the regime for which the drag coefficient is constant, which was used to model the effect of drag force for high-Reynolds-number currents propagating into a porous medium in shallow water theory models (see Hatcher et al.
Reference Hatcher, Hogg and Woods2000; Tanino et al.
Reference Tanino, Nepf and Kulis2005, and § 3) and in models that resolve the flow within the channel and model the effect of the obstacles on the flow by adding a distributed drag-force term in the governing Navier–Stokes equations (e.g. see Jamali et al.
Reference Jamali, Zhang and Nepf2008).
$\mathit{Re}=150\,000$
simulation correspond closely to the regime for which the drag coefficient is constant, which was used to model the effect of drag force for high-Reynolds-number currents propagating into a porous medium in shallow water theory models (see Hatcher et al.
Reference Hatcher, Hogg and Woods2000; Tanino et al.
Reference Tanino, Nepf and Kulis2005, and § 3) and in models that resolve the flow within the channel and model the effect of the obstacles on the flow by adding a distributed drag-force term in the governing Navier–Stokes equations (e.g. see Jamali et al.
Reference Jamali, Zhang and Nepf2008).

Figure 7. Distribution of the dimensionless vorticity magnitude
![]() ${\it\omega}_{z}(H/u_{b})$
within a high-Reynolds-number basal current propagating in a channel with
${\it\omega}_{z}(H/u_{b})$
within a high-Reynolds-number basal current propagating in a channel with
![]() ${\it\phi}=12\,\%$
and
${\it\phi}=12\,\%$
and
![]() $D/H=0.05$
: (a)
$D/H=0.05$
: (a)
![]() $\mathit{Re}=15\,000$
; (b)
$\mathit{Re}=15\,000$
; (b)
![]() $\mathit{Re}=150\,000$
. The dashed (red online) and the solid (blue online) lines show the
$\mathit{Re}=150\,000$
. The dashed (red online) and the solid (blue online) lines show the
![]() $C=0.05$
and
$C=0.05$
and
![]() $C=0.95$
isocontours respectively. The distributions are shown in the region situated within the rectangle in figure 5(d).
$C=0.95$
isocontours respectively. The distributions are shown in the region situated within the rectangle in figure 5(d).
Figure 7 visualizes the vortical structure in the
![]() $\mathit{Re}=15\,000$
to
$\mathit{Re}=15\,000$
to
![]() $\mathit{Re}=150\,000$
simulations inside a region situated around the interface, at approximately half distance between the front and the lock-gate position (see figure 4
d). As Re increases, the fluctuations of the separated shear layers become less regular and the importance of the wake to cylinder interactions increases. The degree of three-dimensionality of the flow field and the energy of the large-scale turbulent eddies shed by the cylinders increase too. Even at large distances behind the front, the flow within the bottom current contains highly energetic turbulent eddies at
$\mathit{Re}=150\,000$
simulations inside a region situated around the interface, at approximately half distance between the front and the lock-gate position (see figure 4
d). As Re increases, the fluctuations of the separated shear layers become less regular and the importance of the wake to cylinder interactions increases. The degree of three-dimensionality of the flow field and the energy of the large-scale turbulent eddies shed by the cylinders increase too. Even at large distances behind the front, the flow within the bottom current contains highly energetic turbulent eddies at
![]() $\mathit{Re}=150\,000$
. In contrast, the vorticity fields in the
$\mathit{Re}=150\,000$
. In contrast, the vorticity fields in the
![]() $\mathit{Re}=15\,000$
case suggest an unsteady laminar flow at large distances behind the front. This is also consistent with the fact that the values of
$\mathit{Re}=15\,000$
case suggest an unsteady laminar flow at large distances behind the front. This is also consistent with the fact that the values of
![]() $\mathit{Re}_{D}$
during the later stages of the drag-dominated regime in the
$\mathit{Re}_{D}$
during the later stages of the drag-dominated regime in the
![]() $\mathit{Re}=15\,000$
case are low enough to find a laminar wake for most of the cylinders situated within the bottom current.
$\mathit{Re}=15\,000$
case are low enough to find a laminar wake for most of the cylinders situated within the bottom current.
In the
![]() $\mathit{Re}=150\,000$
case, large-scale vortical eddies detaching ‘randomly’ from the separated shear layers or being shed from the wake of one cylinder can directly interact and strongly disturb the flow around other cylinders situated in the vicinity of their trajectories. Although such interactions were also observed in the
$\mathit{Re}=150\,000$
case, large-scale vortical eddies detaching ‘randomly’ from the separated shear layers or being shed from the wake of one cylinder can directly interact and strongly disturb the flow around other cylinders situated in the vicinity of their trajectories. Although such interactions were also observed in the
![]() $\mathit{Re}=15\,000$
case, they were, for most cases, limited to the cylinders situated in the immediate vicinity of the cylinder where the detaching eddy originated and the disturbances were predominantly two-dimensional. In the
$\mathit{Re}=15\,000$
case, they were, for most cases, limited to the cylinders situated in the immediate vicinity of the cylinder where the detaching eddy originated and the disturbances were predominantly two-dimensional. In the
![]() $\mathit{Re}=150\,000$
simulation, the strong energy increase due to the 3D eddies generated by the cylinders increases the amount of mixed fluid in the region situated close to the front and over the downstream part of the interfacial layer relative to the
$\mathit{Re}=150\,000$
simulation, the strong energy increase due to the 3D eddies generated by the cylinders increases the amount of mixed fluid in the region situated close to the front and over the downstream part of the interfacial layer relative to the
![]() $\mathit{Re}=15\,000$
simulation. As Re is increased from 15 000 to 150 000, the thickness of the mixing interface, defined as the average distance between the
$\mathit{Re}=15\,000$
simulation. As Re is increased from 15 000 to 150 000, the thickness of the mixing interface, defined as the average distance between the
![]() $C=0.05$
and
$C=0.05$
and
![]() $C=0.95$
isocontours, increases by close to 30 %.
$C=0.95$
isocontours, increases by close to 30 %.
4.2. Low-Reynolds-number currents
Important differences are observed in the structure of the gravity currents between low-Reynolds-number cases (e.g.
![]() $\mathit{Re}<500$
) and high-Reynolds-number cases (
$\mathit{Re}<500$
) and high-Reynolds-number cases (
![]() $\mathit{Re}>10\,000$
). While in the former cases the flow past the cylinders remains laminar, in the latter cases the flow within the gravity current is turbulent, at least around cylinders situated close to the front.
$\mathit{Re}>10\,000$
). While in the former cases the flow past the cylinders remains laminar, in the latter cases the flow within the gravity current is turbulent, at least around cylinders situated close to the front.
In the simulations with
![]() $\mathit{Re}=100$
and 375, the interface height defined by the
$\mathit{Re}=100$
and 375, the interface height defined by the
![]() $C=0.5$
contour varies approximately linearly with the streamwise distance from the lock gate to the front (e.g. see figure 8). As the current advances, the interface rotates slowly around the midpoint (
$C=0.5$
contour varies approximately linearly with the streamwise distance from the lock gate to the front (e.g. see figure 8). As the current advances, the interface rotates slowly around the midpoint (
![]() $y/H=0.5$
) at
$y/H=0.5$
) at
![]() $x/H=0$
. This behaviour is in agreement with lock-exchange experiments (Tanino et al.
Reference Tanino, Nepf and Kulis2005) conducted for low-Reynolds-number currents propagating into a channel containing vertical circular cylinders. The thickness of the interfacial layer containing mixed fluid is almost independent of the streamwise location
$x/H=0$
. This behaviour is in agreement with lock-exchange experiments (Tanino et al.
Reference Tanino, Nepf and Kulis2005) conducted for low-Reynolds-number currents propagating into a channel containing vertical circular cylinders. The thickness of the interfacial layer containing mixed fluid is almost independent of the streamwise location
![]() $x/H$
(figure 8
a).
$x/H$
(figure 8
a).

Figure 8. Distribution of concentration
![]() $C$
(a) and dimensionless vorticity magnitude
$C$
(a) and dimensionless vorticity magnitude
![]() ${\it\omega}_{z}(H/u_{b})$
(b) within a low-Reynolds-number (
${\it\omega}_{z}(H/u_{b})$
(b) within a low-Reynolds-number (
![]() $\mathit{Re}=375$
) bottom current propagating in a channel with
$\mathit{Re}=375$
) bottom current propagating in a channel with
![]() ${\it\phi}=12\,\%$
and
${\it\phi}=12\,\%$
and
![]() $D/H=0.032$
. The solid line shows the
$D/H=0.032$
. The solid line shows the
![]() $C=0.01$
isocontour.
$C=0.01$
isocontour.
Except for the cylinders situated in the immediate vicinity of the interfacial layer, most of the amplification of the vorticity inside the bottom-propagating current is due to the flow acceleration on the sides of the cylinders (figure 8 b). Although the flow separates behind the cylinders situated close to the front, no detachment of eddies from the shear layers and no large-scale vortex shedding are observed. As a result, for low-Reynolds-number currents, the cylinders play a much less significant role in the mechanisms of mixing.
5. Total streamwise drag force
The streamwise drag force on an individual cylinder is calculated by adding the streamwise components of the pressure and viscously derived forces, and then the total drag force on the cylinders
![]() $F_{D}$
is the sum of the magnitude of these forces throughout the entire computational domain. It should be noted that because the current evolves symmetrically (to a close approximation),
$F_{D}$
is the sum of the magnitude of these forces throughout the entire computational domain. It should be noted that because the current evolves symmetrically (to a close approximation),
![]() $F_{D}/2$
is the magnitude of the force in each layer. The effects of the parameters
$F_{D}/2$
is the magnitude of the force in each layer. The effects of the parameters
![]() ${\it\phi},D/H$
,
${\it\phi},D/H$
,
![]() $aH$
and Re on the total dimensionless streamwise drag force on the cylinders,
$aH$
and Re on the total dimensionless streamwise drag force on the cylinders,
![]() $F_{D}/({\it\rho}u_{b}^{2}HW)$
, are discussed next.
$F_{D}/({\it\rho}u_{b}^{2}HW)$
, are discussed next.
The evolution of the streamwise drag
![]() $F_{D}$
for high-Reynolds-number currents (figure 9
a,b) is characterized by an initial regime in which
$F_{D}$
for high-Reynolds-number currents (figure 9
a,b) is characterized by an initial regime in which
![]() $F_{D}$
increases sharply, followed by a transient regime which is characterized by a more gradual increase of
$F_{D}$
increases sharply, followed by a transient regime which is characterized by a more gradual increase of
![]() $F_{D}$
and larger fluctuations about the mean value. The channel in the high-Reynolds-number simulations was not long enough to establish unequivocally that the flow reaches a regime in which
$F_{D}$
and larger fluctuations about the mean value. The channel in the high-Reynolds-number simulations was not long enough to establish unequivocally that the flow reaches a regime in which
![]() $F_{D}$
fluctuates around a constant value, although the data are suggestive of this behaviour.
$F_{D}$
fluctuates around a constant value, although the data are suggestive of this behaviour.

Figure 9. The total drag force acting on the cylinders,
![]() $F_{D}/({\it\rho}u_{b}^{2}HW)$
. (a) The effect of the solid volume fraction in the
$F_{D}/({\it\rho}u_{b}^{2}HW)$
. (a) The effect of the solid volume fraction in the
![]() $\mathit{Re}=15\,000$
simulations with
$\mathit{Re}=15\,000$
simulations with
![]() ${\it\phi}=1.25\,\%$
,
${\it\phi}=1.25\,\%$
,
![]() $D/H=0.032$
(light blue line L3),
$D/H=0.032$
(light blue line L3),
![]() ${\it\phi}=5\,\%$
,
${\it\phi}=5\,\%$
,
![]() $D/H=0.032$
(blue line L2) and
$D/H=0.032$
(blue line L2) and
![]() ${\it\phi}=12\,\%$
,
${\it\phi}=12\,\%$
,
![]() $D/H=0.032$
(dark grey line L1); (b) the effect of the relative cylinder size,
$D/H=0.032$
(dark grey line L1); (b) the effect of the relative cylinder size,
![]() $D/H$
, in the simulations with
$D/H$
, in the simulations with
![]() $\mathit{Re}=15\,000$
and
$\mathit{Re}=15\,000$
and
![]() ${\it\phi}=12\,\%$
and with
${\it\phi}=12\,\%$
and with
![]() $D/H=0.032$
(dark grey line L1),
$D/H=0.032$
(dark grey line L1),
![]() $D/H=0.05$
(pink line L4) and
$D/H=0.05$
(pink line L4) and
![]() $D/H=0.07$
(dark blue line L5); (c) the effects of Re in the
$D/H=0.07$
(dark blue line L5); (c) the effects of Re in the
![]() ${\it\phi}=12\,\%$
simulations with
${\it\phi}=12\,\%$
simulations with
![]() $\mathit{Re}=375$
,
$\mathit{Re}=375$
,
![]() $D/H=0.05$
(orange line L9),
$D/H=0.05$
(orange line L9),
![]() $\mathit{Re}=15\,000$
,
$\mathit{Re}=15\,000$
,
![]() $D/H=0.05$
(pink line L4) and
$D/H=0.05$
(pink line L4) and
![]() $\mathit{Re}=150\,000$
,
$\mathit{Re}=150\,000$
,
![]() $D/H=0.05$
(green line L6).
$D/H=0.05$
(green line L6).
Simulations conducted with
![]() $\mathit{Re}=15\,000$
and
$\mathit{Re}=15\,000$
and
![]() $D/H=0.032$
show that as the solid fraction increases, the distance the front propagates before the start of the transient regime for
$D/H=0.032$
show that as the solid fraction increases, the distance the front propagates before the start of the transient regime for
![]() $F_{D}$
becomes larger. At the same time, the magnitude of the fluctuations of
$F_{D}$
becomes larger. At the same time, the magnitude of the fluctuations of
![]() $F_{D}$
increases with
$F_{D}$
increases with
![]() ${\it\phi}$
. This is because, as the distance between the cylinders increases, the coherence of the eddies detaching from the separated shear layers and of the eddies shed in the wake of the cylinders increases (figure 5
b–d). The increased coherence of such eddies increases the amplitude of the larger-scale fluctuations of the forces on the cylinder from which the eddy originated and also on the cylinders situated along its path. As all simulations in figure 9(a) were conducted with identically sized cylinders, the monotonic increase of
${\it\phi}$
. This is because, as the distance between the cylinders increases, the coherence of the eddies detaching from the separated shear layers and of the eddies shed in the wake of the cylinders increases (figure 5
b–d). The increased coherence of such eddies increases the amplitude of the larger-scale fluctuations of the forces on the cylinder from which the eddy originated and also on the cylinders situated along its path. As all simulations in figure 9(a) were conducted with identically sized cylinders, the monotonic increase of
![]() $F_{D}$
with
$F_{D}$
with
![]() ${\it\phi}$
is due to the increase of the number of cylinders per unit area. Finally, the results in figure 9(a) for the simulation with
${\it\phi}$
is due to the increase of the number of cylinders per unit area. Finally, the results in figure 9(a) for the simulation with
![]() ${\it\phi}=12\,\%$
suggest that the constant-
${\it\phi}=12\,\%$
suggest that the constant-
![]() $F_{D}$
regime is reached when
$F_{D}$
regime is reached when
![]() $x_{f}/H\cong 4.5$
.
$x_{f}/H\cong 4.5$
.
The effect of increasing the cylinder size,
![]() $D/H$
, or equivalently the frontal area,
$D/H$
, or equivalently the frontal area,
![]() $aH={\it\phi}/(D/H)$
, while maintaining
$aH={\it\phi}/(D/H)$
, while maintaining
![]() ${\it\phi}$
constant is to reduce
${\it\phi}$
constant is to reduce
![]() $F_{D}$
, at least until the later stages of the transient regime when
$F_{D}$
, at least until the later stages of the transient regime when
![]() $F_{D}$
appears to approach the same constant value in the simulations conducted with
$F_{D}$
appears to approach the same constant value in the simulations conducted with
![]() $D/H=0.032$
and
$D/H=0.032$
and
![]() $D/H=0.05$
(figure 9
b). By contrast, the effect of increasing
$D/H=0.05$
(figure 9
b). By contrast, the effect of increasing
![]() ${\it\phi}$
and
${\it\phi}$
and
![]() $D/H$
while maintaining
$D/H$
while maintaining
![]() $aH$
constant does not result in significant changes in the levels of
$aH$
constant does not result in significant changes in the levels of
![]() $F_{D}$
when plotted as a function of
$F_{D}$
when plotted as a function of
![]() $x_{f}$
(e.g. compare the
$x_{f}$
(e.g. compare the
![]() $\mathit{Re}=15\,000$
cases with
$\mathit{Re}=15\,000$
cases with
![]() ${\it\phi}=5\,\%$
,
${\it\phi}=5\,\%$
,
![]() $D/H=0.032$
and with
$D/H=0.032$
and with
![]() ${\it\phi}=12\,\%$
,
${\it\phi}=12\,\%$
,
![]() $D/H=0.07$
in figure 9).
$D/H=0.07$
in figure 9).
In the simulation conducted with
![]() $\mathit{Re}=375$
, the total drag force reaches a regime where
$\mathit{Re}=375$
, the total drag force reaches a regime where
![]() $F_{D}$
is approximately constant after
$F_{D}$
is approximately constant after
![]() $t/t_{0}\cong 40$
when
$t/t_{0}\cong 40$
when
![]() $x_{f}/H\cong 3$
(figure 9
c). The drag force also becomes approximately constant in the simulation with
$x_{f}/H\cong 3$
(figure 9
c). The drag force also becomes approximately constant in the simulation with
![]() $\mathit{Re}=175$
(not shown). As no eddies separate behind the cylinders and the degree of unsteadiness of the separated shear layers is very small (figure 8
b), the amplitude of the large-scale fluctuations of
$\mathit{Re}=175$
(not shown). As no eddies separate behind the cylinders and the degree of unsteadiness of the separated shear layers is very small (figure 8
b), the amplitude of the large-scale fluctuations of
![]() $F_{D}$
in the simulation with
$F_{D}$
in the simulation with
![]() $\mathit{Re}=375$
is very small compared with those observed in the simulations with
$\mathit{Re}=375$
is very small compared with those observed in the simulations with
![]() $\mathit{Re}=15\,000$
and 150 000 conducted with the same values of
$\mathit{Re}=15\,000$
and 150 000 conducted with the same values of
![]() ${\it\phi}$
(12 %) and
${\it\phi}$
(12 %) and
![]() $D/H$
(0.05). The increase of the Reynolds number from
$D/H$
(0.05). The increase of the Reynolds number from
![]() $\mathit{Re}=15\,000$
to
$\mathit{Re}=15\,000$
to
![]() $\mathit{Re}=150\,000$
does not result in significant differences in the mean variation of
$\mathit{Re}=150\,000$
does not result in significant differences in the mean variation of
![]() $F_{D}$
with
$F_{D}$
with
![]() $x_{f}/H$
.
$x_{f}/H$
.
The shallow water theory of § 3 predicts that
![]() $F_{D}/({\it\rho}u_{b}^{2}HW)$
should become constant once a balance between drag and buoyancy develops in the later stages of the motion. If
$F_{D}/({\it\rho}u_{b}^{2}HW)$
should become constant once a balance between drag and buoyancy develops in the later stages of the motion. If
![]() $f_{D}$
is the drag force per unit volume due to the cylinders then
$f_{D}$
is the drag force per unit volume due to the cylinders then
This equation holds for both high- and low-Reynolds-number currents in which
![]() $C_{D}=\text{constant}$
and
$C_{D}=\text{constant}$
and
![]() $C_{D}\sim 1/\mathit{Re}_{D}$
respectively. We first proceed by assuming that
$C_{D}\sim 1/\mathit{Re}_{D}$
respectively. We first proceed by assuming that
![]() $\mathit{Re}_{D}\gg 1$
and so
$\mathit{Re}_{D}\gg 1$
and so
Conversely, when
![]() $\mathit{Re}_{D}\ll 1$
, we find that
$\mathit{Re}_{D}\ll 1$
, we find that
In the regime of large Reynolds number, we find that this prediction for
![]() $F_{D}$
is closely borne out by the numerical simulations in which
$F_{D}$
is closely borne out by the numerical simulations in which
![]() $F_{D}$
reaches a constant regime (e.g. the asymptotic value of
$F_{D}$
reaches a constant regime (e.g. the asymptotic value of
![]() $F_{D}/({\it\rho}u_{b}^{2}HW)$
was 0.24 in the
$F_{D}/({\it\rho}u_{b}^{2}HW)$
was 0.24 in the
![]() $\mathit{Re}=15\,000$
simulation with
$\mathit{Re}=15\,000$
simulation with
![]() ${\it\phi}=12\,\%$
and
${\it\phi}=12\,\%$
and
![]() $D/H=0.032$
, which is close to the theoretical value of 0.25). The distance travelled by the current before the constant regime is reached is expected to increase with decreasing
$D/H=0.032$
, which is close to the theoretical value of 0.25). The distance travelled by the current before the constant regime is reached is expected to increase with decreasing
![]() ${\it\phi}$
(see (3.7)). For example, the
${\it\phi}$
(see (3.7)). For example, the
![]() $\mathit{Re}=15\,000$
simulations with
$\mathit{Re}=15\,000$
simulations with
![]() ${\it\phi}<10\,\%$
are still far from reaching the constant-
${\it\phi}<10\,\%$
are still far from reaching the constant-
![]() $F_{D}$
regime by the time the current approaches the end of the channel
$F_{D}$
regime by the time the current approaches the end of the channel
![]() $(x=6H)$
. In the regime of small Reynolds numbers,
$(x=6H)$
. In the regime of small Reynolds numbers,
![]() $\mathit{Re}_{D}\ll 1$
, we find that the measured force is rather smaller than predicted (e.g.
$\mathit{Re}_{D}\ll 1$
, we find that the measured force is rather smaller than predicted (e.g.
![]() $F_{D}/({\it\rho}u_{b}^{2}HW)$
predicted in the
$F_{D}/({\it\rho}u_{b}^{2}HW)$
predicted in the
![]() $\mathit{Re}=100$
and
$\mathit{Re}=100$
and
![]() $\mathit{Re}=375$
simulations with
$\mathit{Re}=375$
simulations with
![]() ${\it\phi}=12\,\%$
is 0.22, while the theoretical value is 0.29).
${\it\phi}=12\,\%$
is 0.22, while the theoretical value is 0.29).
6. Front velocity
In this section we analyse the unsteady propagation of the front position and its parametric dependence upon the volume fraction of cylinders,
![]() ${\it\phi}$
, the channel Reynolds number Re, and the combined drag coefficient for the porous medium,
${\it\phi}$
, the channel Reynolds number Re, and the combined drag coefficient for the porous medium,
![]() ${\it\Gamma}_{D}=C_{D}aH/(1-{\it\phi})$
. These were identified as the key parameters in the shallow layer modelling of § 3 and in Jamali et al. (Reference Jamali, Zhang and Nepf2008). However, before examining these dependences, we first use the
${\it\Gamma}_{D}=C_{D}aH/(1-{\it\phi})$
. These were identified as the key parameters in the shallow layer modelling of § 3 and in Jamali et al. (Reference Jamali, Zhang and Nepf2008). However, before examining these dependences, we first use the
![]() $F_{D}$
estimated from the numerical simulations to deduce the drag coefficients of the cylinders.
$F_{D}$
estimated from the numerical simulations to deduce the drag coefficients of the cylinders.
6.1. Drag coefficient
Although it is widely acknowledged that the values of the mean drag coefficient for an array of cylinders can be different from the values for isolated cylinders of identical shape, a comprehensive description of
![]() $C_{D}$
in an array has not yet been developed (Tanino et al.
Reference Tanino, Nepf and Kulis2005). The problem is even more complex for gravity current flows in which the approaching velocity around individual cylinders is not constant in time or in space, as is the case for constant-density flow in a channel of uniform porosity.
$C_{D}$
in an array has not yet been developed (Tanino et al.
Reference Tanino, Nepf and Kulis2005). The problem is even more complex for gravity current flows in which the approaching velocity around individual cylinders is not constant in time or in space, as is the case for constant-density flow in a channel of uniform porosity.
The mean drag coefficient in the high-Reynolds-number simulations was estimated in several ways in table 1. The values of
![]() $C_{D}^{\prime }$
were estimated assuming that the front velocity
$C_{D}^{\prime }$
were estimated assuming that the front velocity
![]() $U_{f}$
is a good approximation of the mean incoming flow velocity,
$U_{f}$
is a good approximation of the mean incoming flow velocity,
![]() $U_{i}$
, in the expression for the average streamwise total (pressure and friction) drag force acting on the cylinders within the bottom current at a given moment in time (e.g.
$U_{i}$
, in the expression for the average streamwise total (pressure and friction) drag force acting on the cylinders within the bottom current at a given moment in time (e.g.
![]() $F_{D}/N_{c}=0.5{\it\rho}C_{D}^{\prime }U_{f}^{2}DW$
, where
$F_{D}/N_{c}=0.5{\it\rho}C_{D}^{\prime }U_{f}^{2}DW$
, where
![]() $N_{c}(x_{f})$
is the number of cylinders within the top and bottom currents and
$N_{c}(x_{f})$
is the number of cylinders within the top and bottom currents and
![]() $F_{D}(x_{f})$
is the total drag force on these cylinders). The main reason for computing
$F_{D}(x_{f})$
is the total drag force on these cylinders). The main reason for computing
![]() $C_{D}^{\prime }$
is that this is the definition used in experiments conducted for gravity currents advancing in a vegetated canopy, given that the only velocity easily measurable is
$C_{D}^{\prime }$
is that this is the definition used in experiments conducted for gravity currents advancing in a vegetated canopy, given that the only velocity easily measurable is
![]() $U_{f}$
(Tanino et al.
Reference Tanino, Nepf and Kulis2005; Zhang & Nepf Reference Zhang and Nepf2008). One can also try to define the drag coefficient using a physically more relevant velocity scale, similar to what is done for isolated cylinders placed in a constant-density uniform flow field. In table 1,
$U_{f}$
(Tanino et al.
Reference Tanino, Nepf and Kulis2005; Zhang & Nepf Reference Zhang and Nepf2008). One can also try to define the drag coefficient using a physically more relevant velocity scale, similar to what is done for isolated cylinders placed in a constant-density uniform flow field. In table 1,
![]() $C_{D}$
was estimated using the mean streamwise velocity within the body of the gravity current, directly calculated from the instantaneous velocity flow fields at a given time. The wake regions were eliminated when estimating the mean incoming flow velocity
$C_{D}$
was estimated using the mean streamwise velocity within the body of the gravity current, directly calculated from the instantaneous velocity flow fields at a given time. The wake regions were eliminated when estimating the mean incoming flow velocity
![]() $U_{i}$
at a given time. This is because
$U_{i}$
at a given time. This is because
![]() $U_{i}$
should be representative of ‘an average’ incoming flow velocity for the cylinders. One can see that
$U_{i}$
should be representative of ‘an average’ incoming flow velocity for the cylinders. One can see that
![]() $C_{D}^{\prime }<C_{D}$
, which is expected given that the incoming flow velocity around cylinders situated far from the front and inside the bottom current is smaller compared with that of the cylinders situated close to the front. Finally, one should note that in figure 2(d)
$C_{D}^{\prime }<C_{D}$
, which is expected given that the incoming flow velocity around cylinders situated far from the front and inside the bottom current is smaller compared with that of the cylinders situated close to the front. Finally, one should note that in figure 2(d)
![]() $U_{i}$
was estimated as the mean streamwise velocity over the whole current (including the wake regions) to make possible a direct comparison with the analytical solution. For the
$U_{i}$
was estimated as the mean streamwise velocity over the whole current (including the wake regions) to make possible a direct comparison with the analytical solution. For the
![]() $\mathit{Re}=15\,000$
simulation with
$\mathit{Re}=15\,000$
simulation with
![]() ${\it\phi}=12\,\%$
and
${\it\phi}=12\,\%$
and
![]() $D/H=0.05$
, the drag coefficient estimated using this velocity scale was approximately 3.7 times larger than
$D/H=0.05$
, the drag coefficient estimated using this velocity scale was approximately 3.7 times larger than
![]() $C_{D}$
estimated using the aforementioned procedure.
$C_{D}$
estimated using the aforementioned procedure.
One important result is that for all high-Reynolds-number simulations containing cylinders, the values of
![]() $C_{D}$
during the quadratic drag-law regime at a given front position varied by less than 10 % for
$C_{D}$
during the quadratic drag-law regime at a given front position varied by less than 10 % for
![]() $x_{f}/H>1$
. This is why only the time averaged values are quoted in table 1. The cylinder Reynolds number defined with
$x_{f}/H>1$
. This is why only the time averaged values are quoted in table 1. The cylinder Reynolds number defined with
![]() $D$
and the mean
$D$
and the mean
![]() $U_{f}$
after the transition to the drag-dominated regime has started (
$U_{f}$
after the transition to the drag-dominated regime has started (
![]() $\mathit{Re}_{D}$
in table 1) is between 60 and 1700. The experiments of Lindsey (Reference Lindsey1987) for an isolated square cylinder predict a mean drag coefficient between 1.4 and 1.5. On average, the values of
$\mathit{Re}_{D}$
in table 1) is between 60 and 1700. The experiments of Lindsey (Reference Lindsey1987) for an isolated square cylinder predict a mean drag coefficient between 1.4 and 1.5. On average, the values of
![]() $C_{D}$
in table 1
$C_{D}$
in table 1
![]() $(1.2<C_{D}<2)$
are closer to the experimental values for an isolated square cylinder compared with the values of
$(1.2<C_{D}<2)$
are closer to the experimental values for an isolated square cylinder compared with the values of
![]() $C_{D}^{\prime }$
. In the following, we will conduct our analysis based on the values of
$C_{D}^{\prime }$
. In the following, we will conduct our analysis based on the values of
![]() $C_{D}$
.
$C_{D}$
.

Figure 10. Temporal evolution of the front position,
![]() $x_{f}/H$
, of the bottom current. (a) Effect of solid volume fraction on
$x_{f}/H$
, of the bottom current. (a) Effect of solid volume fraction on
![]() $x_{f}/H(t/t_{0})$
in the
$x_{f}/H(t/t_{0})$
in the
![]() $\mathit{Re}=15\,000$
simulations with
$\mathit{Re}=15\,000$
simulations with
![]() ${\it\phi}=1.25\,\%$
,
${\it\phi}=1.25\,\%$
,
![]() $D/H=0.032$
(light blue line L2,
$D/H=0.032$
(light blue line L2,
![]() ${\it\Gamma}_{D}=0.49$
),
${\it\Gamma}_{D}=0.49$
),
![]() ${\it\phi}=5\,\%$
,
${\it\phi}=5\,\%$
,
![]() $D/H=0.032$
(blue line L3,
$D/H=0.032$
(blue line L3,
![]() ${\it\Gamma}_{D}=2.35$
),
${\it\Gamma}_{D}=2.35$
),
![]() ${\it\phi}=12\,\%$
,
${\it\phi}=12\,\%$
,
![]() $D/H=0.032$
(dark grey line L1,
$D/H=0.032$
(dark grey line L1,
![]() ${\it\Gamma}_{D}=8.5$
) and
${\it\Gamma}_{D}=8.5$
) and
![]() ${\it\phi}=25\,\%$
,
${\it\phi}=25\,\%$
,
![]() $D/H=0.07$
(green line L6,
$D/H=0.07$
(green line L6,
![]() ${\it\Gamma}_{D}=8.3$
). Also shown is the case with
${\it\Gamma}_{D}=8.3$
). Also shown is the case with
![]() $\mathit{Re}=15\,000$
and
$\mathit{Re}=15\,000$
and
![]() ${\it\phi}=0\,\%$
(red line L7). (b) Effect of the relative size of the cylinders,
${\it\phi}=0\,\%$
(red line L7). (b) Effect of the relative size of the cylinders,
![]() $D/H$
, on
$D/H$
, on
![]() $x_{f}/H(t/t_{0})$
in the
$x_{f}/H(t/t_{0})$
in the
![]() $\mathit{Re}=15\,000$
,
$\mathit{Re}=15\,000$
,
![]() ${\it\phi}=12\,\%$
simulations with
${\it\phi}=12\,\%$
simulations with
![]() $D/H=0.032$
(dark grey line L1,
$D/H=0.032$
(dark grey line L1,
![]() ${\it\Gamma}_{D}=8.5$
),
${\it\Gamma}_{D}=8.5$
),
![]() $D/H=0.05$
(pink line L4,
$D/H=0.05$
(pink line L4,
![]() ${\it\Gamma}_{D}=3.7$
) and
${\it\Gamma}_{D}=3.7$
) and
![]() $D/H=0.07$
(dark blue line L5,
$D/H=0.07$
(dark blue line L5,
![]() ${\it\Gamma}_{D}=3.5$
).
${\it\Gamma}_{D}=3.5$
).
No value is quoted for
![]() $C_{D}$
in table 1 for the simulations with
$C_{D}$
in table 1 for the simulations with
![]() $\mathit{Re}<1$
because in those cases
$\mathit{Re}<1$
because in those cases
![]() $C_{D}$
increases monotonically with
$C_{D}$
increases monotonically with
![]() $x_{f}/H$
. This result is not surprising given that for these cases, as will be discussed later, the current transitions to the linear drag-dominated regime where one expects
$x_{f}/H$
. This result is not surprising given that for these cases, as will be discussed later, the current transitions to the linear drag-dominated regime where one expects
![]() $C_{D}\sim 1/\mathit{Re}_{D}$
. The present results obtained for
$C_{D}\sim 1/\mathit{Re}_{D}$
. The present results obtained for
![]() $\mathit{Re}=100$
and
$\mathit{Re}=100$
and
![]() $\mathit{Re}=375$
show that
$\mathit{Re}=375$
show that
![]() $C_{D}\mathit{Re}_{D}={\it\gamma}$
for
$C_{D}\mathit{Re}_{D}={\it\gamma}$
for
![]() $x_{f}/H>1.5$
with
$x_{f}/H>1.5$
with
![]() ${\it\gamma}=22.5\pm 0.95$
and
${\it\gamma}=22.5\pm 0.95$
and
![]() $\mathit{Re}_{D}$
defined with
$\mathit{Re}_{D}$
defined with
![]() $U_{f}$
. However, this quoted value for
$U_{f}$
. However, this quoted value for
![]() ${\it\gamma}$
is based on only the results from two simulations and is not a universal constant; indeed, one expects that it will vary with
${\it\gamma}$
is based on only the results from two simulations and is not a universal constant; indeed, one expects that it will vary with
![]() $D/H$
,
$D/H$
,
![]() $aH$
and
$aH$
and
![]() ${\it\phi}$
for low-Reynolds-number currents. The value of
${\it\phi}$
for low-Reynolds-number currents. The value of
![]() ${\it\gamma}$
is within the range of
${\it\gamma}$
is within the range of
![]() ${\it\gamma}$
value inferred from
${\it\gamma}$
value inferred from
![]() $C_{D}=f(\mathit{Re}_{D})$
plots obtained from numerical simulations and experiments performed for isolated square cylinders for
$C_{D}=f(\mathit{Re}_{D})$
plots obtained from numerical simulations and experiments performed for isolated square cylinders for
![]() $5<\mathit{Re}_{D}<30$
(see figure 2 in Yoon et al., Reference Yoon, Yang and Choi2010).
$5<\mathit{Re}_{D}<30$
(see figure 2 in Yoon et al., Reference Yoon, Yang and Choi2010).
6.2. Effects of
 ${\it\phi}$
,
${\it\phi}$
,
 $D/H$
and
$D/H$
and
 $aH$
on the front velocity for high-Reynolds-number currents
$aH$
on the front velocity for high-Reynolds-number currents
The position of the front at each time step was determined by the spanwise-averaged location of the most downstream point situated on the
![]() $C=0.01$
isosurface. Consistent with theory and experimental observations (e.g. Shin et al.
Reference Shin, Dalziel and Linden2004), the temporal evolution of the front trajectory in figure 10(a) shows that in the simulation with no cylinders (
$C=0.01$
isosurface. Consistent with theory and experimental observations (e.g. Shin et al.
Reference Shin, Dalziel and Linden2004), the temporal evolution of the front trajectory in figure 10(a) shows that in the simulation with no cylinders (
![]() ${\it\phi}=0\,\%$
,
${\it\phi}=0\,\%$
,
![]() $\mathit{Re}=15\,000$
) the current reaches the slumping phase in which the front velocity,
$\mathit{Re}=15\,000$
) the current reaches the slumping phase in which the front velocity,
![]() $U_{f}$
, is constant a short time after the removal of the lock gate
$U_{f}$
, is constant a short time after the removal of the lock gate
![]() $(t\cong 1.5t_{0})$
. The predicted value of the front velocity
$(t\cong 1.5t_{0})$
. The predicted value of the front velocity
![]() $(U_{f}/u_{b}=0.43)$
is in excellent agreement with values inferred from experiments conducted for full-depth currents at similar Re (e.g. see Keulegan Reference Keulegan1957; Rottman & Simpson Reference Rottman and Simpson1983). Figure 10(a) also shows that the evolution of the current in the simulation with
$(U_{f}/u_{b}=0.43)$
is in excellent agreement with values inferred from experiments conducted for full-depth currents at similar Re (e.g. see Keulegan Reference Keulegan1957; Rottman & Simpson Reference Rottman and Simpson1983). Figure 10(a) also shows that the evolution of the current in the simulation with
![]() ${\it\phi}=1.25\,\%$
is qualitatively similar to the unobstructed case, the main difference being the somewhat smaller value of the front velocity (
${\it\phi}=1.25\,\%$
is qualitatively similar to the unobstructed case, the main difference being the somewhat smaller value of the front velocity (
![]() $U_{f}/u_{b}=0.39$
) during the slumping phase, due to the drag of the cylinders. It is possible that transition to a drag-dominated regime will be observed for
$U_{f}/u_{b}=0.39$
) during the slumping phase, due to the drag of the cylinders. It is possible that transition to a drag-dominated regime will be observed for
![]() ${\it\phi}=1.25\,\%$
, but that transition is not evident by the time the front approaches the end of the channel in the simulation. Once
${\it\phi}=1.25\,\%$
, but that transition is not evident by the time the front approaches the end of the channel in the simulation. Once
![]() ${\it\phi}$
becomes larger than 3 %,
${\it\phi}$
becomes larger than 3 %,
![]() $U_{f}$
starts to decay with time. The currents transition relatively quickly and relatively early on in their evolution (
$U_{f}$
starts to decay with time. The currents transition relatively quickly and relatively early on in their evolution (
![]() $t/t_{0}=2{-}5$
) to the drag-dominated regime. Empirically, we find a power-law dependence of the front position on time given by
$t/t_{0}=2{-}5$
) to the drag-dominated regime. Empirically, we find a power-law dependence of the front position on time given by
![]() $x_{f}/H\sim (t/t_{0})^{3/4}$
(figure 10), or equivalently
$x_{f}/H\sim (t/t_{0})^{3/4}$
(figure 10), or equivalently
![]() $U_{f}/u_{b}\sim (t/t_{0})^{-1/4}$
. This is not of the similarity form established above and will be discussed below.
$U_{f}/u_{b}\sim (t/t_{0})^{-1/4}$
. This is not of the similarity form established above and will be discussed below.
If the relative cylinder size,
![]() $D/H$
, is kept the same, the results in figure 10(a) (e.g. compare the results for
$D/H$
, is kept the same, the results in figure 10(a) (e.g. compare the results for
![]() ${\it\phi}=5\,\%$
and
${\it\phi}=5\,\%$
and
![]() ${\it\phi}=12\,\%$
with
${\it\phi}=12\,\%$
with
![]() $D/H=0.032$
) show that, at any given time,
$D/H=0.032$
) show that, at any given time,
![]() $x_{f}$
decreases with the increase in
$x_{f}$
decreases with the increase in
![]() ${\it\phi}$
. This result is anticipated, because the drag force,
${\it\phi}$
. This result is anticipated, because the drag force,
![]() $F_{D}$
, is roughly proportional to the number of cylinders per unit area situated inside the bottom current. Furthermore, this result is consistent with the shallow layer model, which indicates that the effects of drag are encompassed in the parameter,
$F_{D}$
, is roughly proportional to the number of cylinders per unit area situated inside the bottom current. Furthermore, this result is consistent with the shallow layer model, which indicates that the effects of drag are encompassed in the parameter,
![]() ${\it\Gamma}_{D}$
, which is an increasing function of
${\it\Gamma}_{D}$
, which is an increasing function of
![]() ${\it\phi}$
and
${\it\phi}$
and
![]() $aH$
.
$aH$
.
Figure 10(b) shows the front position as a function of time for the simulations conducted with
![]() $\mathit{Re}=15\,000$
and
$\mathit{Re}=15\,000$
and
![]() ${\it\phi}=12\,\%$
. Although all simulations exhibit transition to a drag-dominated regime with
${\it\phi}=12\,\%$
. Although all simulations exhibit transition to a drag-dominated regime with
![]() $x_{f}/H\sim (t/t_{0})^{3/4}$
, the position of the front at a given time remains a function of the cylinder size. The results show that
$x_{f}/H\sim (t/t_{0})^{3/4}$
, the position of the front at a given time remains a function of the cylinder size. The results show that
![]() $x_{f}/H$
at a given time does not increase monotonically with
$x_{f}/H$
at a given time does not increase monotonically with
![]() $D/H$
. For example, the temporal variation of
$D/H$
. For example, the temporal variation of
![]() $x_{f}/H$
is approximately the same in the simulations with
$x_{f}/H$
is approximately the same in the simulations with
![]() $D/H=0.05$
and 0.07. This means that for a given solid fraction, many small cylinders are more effective in decelerating the current than fewer larger cylinders, a result that is consistent with the shallow layer model (3.5) and (3.6). However, to justify why the evolution of the front position,
$D/H=0.05$
and 0.07. This means that for a given solid fraction, many small cylinders are more effective in decelerating the current than fewer larger cylinders, a result that is consistent with the shallow layer model (3.5) and (3.6). However, to justify why the evolution of the front position,
![]() $x_{f}/H$
, is approximately the same in the simulations with the cylinder sizes
$x_{f}/H$
, is approximately the same in the simulations with the cylinder sizes
![]() $D/H=0.05$
and 0.07 one has to consider the variation in
$D/H=0.05$
and 0.07 one has to consider the variation in
![]() $C_{D}$
with
$C_{D}$
with
![]() $D/H$
between these two cases. The increase in
$D/H$
between these two cases. The increase in
![]() $C_{D}$
with
$C_{D}$
with
![]() $D/H$
(table 1) compensates the decrease in
$D/H$
(table 1) compensates the decrease in
![]() ${\it\Gamma}_{D}$
with
${\it\Gamma}_{D}$
with
![]() $D/H$
, such that the two cases have a very close value of
$D/H$
, such that the two cases have a very close value of
![]() ${\it\Gamma}_{D}~(\cong 3.5)$
. This is a good example that shows the limitations of the common assumption that
${\it\Gamma}_{D}~(\cong 3.5)$
. This is a good example that shows the limitations of the common assumption that
![]() $C_{D}$
is only a function of
$C_{D}$
is only a function of
![]() $\mathit{Re}_{D}$
.
$\mathit{Re}_{D}$
.
The results in figure 10 clearly show that the relative speed of the current in the simulations with
![]() $\mathit{Re}=15\,000$
is mainly a function of
$\mathit{Re}=15\,000$
is mainly a function of
![]() ${\it\Gamma}_{D}$
. This is also confirmed by the results in figure 11. The temporal variation of
${\it\Gamma}_{D}$
. This is also confirmed by the results in figure 11. The temporal variation of
![]() $x_{f}/H$
with
$x_{f}/H$
with
![]() $t/t_{0}$
is replotted in figure 11(a) for the cases for which transition to the quadratic drag-dominated regime was observed in figure 10. A large spread of the curves is observed given the wide range of
$t/t_{0}$
is replotted in figure 11(a) for the cases for which transition to the quadratic drag-dominated regime was observed in figure 10. A large spread of the curves is observed given the wide range of
![]() ${\it\Gamma}_{D}$
. The similarity solution in § 3 suggests that
${\it\Gamma}_{D}$
. The similarity solution in § 3 suggests that
![]() $x_{f}/H$
is a function of the rescaled time,
$x_{f}/H$
is a function of the rescaled time,
![]() $(D(1-{\it\phi})/C_{D}{\it\phi}H)^{1/2}t/t_{0}$
. When the same data are replotted in figure 11(b) using the new scaling, the difference among the curves is reduced significantly. This result suggests that the motion is drag dominated and that the scalings developed in § 3 capture the dominant physical processes in the currents. Further confirmation of the transition from inertia- to drag-dominated behaviour can be deduced from figure 10(a,b). For example, in figure 10(b), the gravity current appears to undergo a transition in behaviour at
$(D(1-{\it\phi})/C_{D}{\it\phi}H)^{1/2}t/t_{0}$
. When the same data are replotted in figure 11(b) using the new scaling, the difference among the curves is reduced significantly. This result suggests that the motion is drag dominated and that the scalings developed in § 3 capture the dominant physical processes in the currents. Further confirmation of the transition from inertia- to drag-dominated behaviour can be deduced from figure 10(a,b). For example, in figure 10(b), the gravity current appears to undergo a transition in behaviour at
![]() $t/t_{0}\cong 1$
and
$t/t_{0}\cong 1$
and
![]() $x_{f}/H\cong 0.3$
for
$x_{f}/H\cong 0.3$
for
![]() ${\it\Gamma}_{D}=8.5$
and at
${\it\Gamma}_{D}=8.5$
and at
![]() $t/t_{0}\cong 1.8$
and
$t/t_{0}\cong 1.8$
and
![]() $x_{f}/H\cong 0.7$
for
$x_{f}/H\cong 0.7$
for
![]() ${\it\Gamma}_{D}=3.5$
. Our analysis indicated that these transitions should be inversely proportional to
${\it\Gamma}_{D}=3.5$
. Our analysis indicated that these transitions should be inversely proportional to
![]() ${\it\Gamma}_{D}$
(see (3.7)), and the estimates from the numerical simulations are broadly consistent with this scaling.
${\it\Gamma}_{D}$
(see (3.7)), and the estimates from the numerical simulations are broadly consistent with this scaling.

Figure 11. Temporal evolution of the front position,
![]() $x_{f}/H$
, of the bottom current in the
$x_{f}/H$
, of the bottom current in the
![]() $\mathit{Re}=15\,000$
simulations with
$\mathit{Re}=15\,000$
simulations with
![]() ${\it\phi}=5\,\%$
,
${\it\phi}=5\,\%$
,
![]() $D/H=0.032$
(blue line L3),
$D/H=0.032$
(blue line L3),
![]() ${\it\phi}=12\,\%$
,
${\it\phi}=12\,\%$
,
![]() $D/H=0.032$
(dark grey line L1),
$D/H=0.032$
(dark grey line L1),
![]() ${\it\phi}=12\,\%$
,
${\it\phi}=12\,\%$
,
![]() $D/H=0.05$
(pink line L4),
$D/H=0.05$
(pink line L4),
![]() ${\it\phi}=12\,\%$
,
${\it\phi}=12\,\%$
,
![]() $D/H=0.07$
(dark blue line L5) and
$D/H=0.07$
(dark blue line L5) and
![]() ${\it\phi}=25\,\%$
,
${\it\phi}=25\,\%$
,
![]() $D/H=0.07$
(green line L6). (a) Plotted against
$D/H=0.07$
(green line L6). (a) Plotted against
![]() $t/t_{0}$
; (b) plotted against
$t/t_{0}$
; (b) plotted against
![]() $(2D(1-{\it\phi})/{\it\phi}H)^{1/2}t/t_{0}$
.
$(2D(1-{\it\phi})/{\it\phi}H)^{1/2}t/t_{0}$
.
6.3. Effect of the Reynolds number on the front velocity
The front trajectories in the low-Reynolds-number simulations conducted with
![]() $\mathit{Re}=100$
and
$\mathit{Re}=100$
and
![]() $\mathit{Re}=375$
(
$\mathit{Re}=375$
(
![]() ${\it\phi}=12\,\%$
,
${\it\phi}=12\,\%$
,
![]() $D/H=0.05$
) show that the bottom current reaches a regime where
$D/H=0.05$
) show that the bottom current reaches a regime where
![]() $U_{f}$
decays with time. However, the increase of
$U_{f}$
decays with time. However, the increase of
![]() $x_{f}$
with time is slower, such that
$x_{f}$
with time is slower, such that
![]() $x_{f}/H\sim (t/t_{0})^{1/2}$
(figure 12
a). By the time the drag-dominated regime is reached
$x_{f}/H\sim (t/t_{0})^{1/2}$
(figure 12
a). By the time the drag-dominated regime is reached
![]() $(t>100t_{0})$
in the
$(t>100t_{0})$
in the
![]() $\mathit{Re}=100$
and
$\mathit{Re}=100$
and
![]() $\mathit{Re}=375$
simulations,
$\mathit{Re}=375$
simulations,
![]() $\mathit{Re}_{D}<1$
for the cylinders situated within the body of the current. This means that the flow is within the regime for which the drag is linearly proportional to the flow speed and the drag coefficient is inversely proportional to the Reynolds number,
$\mathit{Re}_{D}<1$
for the cylinders situated within the body of the current. This means that the flow is within the regime for which the drag is linearly proportional to the flow speed and the drag coefficient is inversely proportional to the Reynolds number,
![]() $\mathit{Re}_{D}$
. The evolution of the front measured in the numerical simulations of this regime of low Reynolds numbers is consistent with the shallow layer model of § 3.
$\mathit{Re}_{D}$
. The evolution of the front measured in the numerical simulations of this regime of low Reynolds numbers is consistent with the shallow layer model of § 3.

Figure 12. Effect of the Reynolds number on the temporal evolution of (a) the front position,
![]() $x_{f}/H$
and (b) the discharge of the bottom current at the lock gate (
$x_{f}/H$
and (b) the discharge of the bottom current at the lock gate (
![]() $x/H=0$
),
$x/H=0$
),
![]() $q$
, scaled by
$q$
, scaled by
![]() $q_{0}=u_{b}WH/2$
, in the
$q_{0}=u_{b}WH/2$
, in the
![]() ${\it\phi}=12\,\%$
simulations with
${\it\phi}=12\,\%$
simulations with
![]() $\mathit{Re}=100$
,
$\mathit{Re}=100$
,
![]() $D/H=0.05$
(black line L8),
$D/H=0.05$
(black line L8),
![]() $\mathit{Re}=370$
,
$\mathit{Re}=370$
,
![]() $D/H=0.05$
(orange line L9) and
$D/H=0.05$
(orange line L9) and
![]() $\mathit{Re}=15\,000$
,
$\mathit{Re}=15\,000$
,
![]() $D/H=0.032$
(dark grey line L1). Also shown is the case with
$D/H=0.032$
(dark grey line L1). Also shown is the case with
![]() $\mathit{Re}=15\,000$
and
$\mathit{Re}=15\,000$
and
![]() ${\it\phi}=0\,\%$
(red line L7). In panel (c)
${\it\phi}=0\,\%$
(red line L7). In panel (c)
![]() $q(0,t)t/[WHx_{f}(t)]$
is plotted as a function of time with the asymptotes predicted by the similarity solution in the regimes of high (dash–dotted blue line) and low (dashed red line) Reynolds numbers.
$q(0,t)t/[WHx_{f}(t)]$
is plotted as a function of time with the asymptotes predicted by the similarity solution in the regimes of high (dash–dotted blue line) and low (dashed red line) Reynolds numbers.
A further test of whether the numerical simulations are adequately represented by the similarity solutions of the shallow layer model is to evaluate the total discharge (the volume flux of fluid) at the origin,
![]() $q(x=0,t)$
, in the lower layer. We note from figure 12(b) that for both low-Reynolds-number simulations this flux decays in proportion to
$q(x=0,t)$
, in the lower layer. We note from figure 12(b) that for both low-Reynolds-number simulations this flux decays in proportion to
![]() $t^{-1/2}$
, which is again consistent with the shallow layer model. From the shallow layer model, we find that
$t^{-1/2}$
, which is again consistent with the shallow layer model. From the shallow layer model, we find that
Importantly, this ratio is independent of the parameters and equal to
![]() $(1/8)$
. We note that this is reasonably well satisfied by the data from the numerical simulations (figure 12
c), thus further confirming the applicability of the similarity solution (3.19).
$(1/8)$
. We note that this is reasonably well satisfied by the data from the numerical simulations (figure 12
c), thus further confirming the applicability of the similarity solution (3.19).
The high-Reynolds-number currents do not appear to be in complete similarity form. In the simulations, the position of the front is proportional to
![]() $t^{3/4}$
, rather than
$t^{3/4}$
, rather than
![]() $t^{2/3}$
, as given by the analytical solution. On examining the flux at the origin in the lower layer,
$t^{2/3}$
, as given by the analytical solution. On examining the flux at the origin in the lower layer,
![]() $q(x=0,t)$
(figure 12
b), we find that this decays in proportion to
$q(x=0,t)$
(figure 12
b), we find that this decays in proportion to
![]() $t^{-1/3}$
. Interestingly, this latter result is consistent with the analytical solution and perhaps indicates that the different (non-similarity) behaviour of the front position is associated with fluid dynamical features close to the front that are not represented in the current shallow layer model, whereas the similarity balance is found within the bulk. We may also examine
$t^{-1/3}$
. Interestingly, this latter result is consistent with the analytical solution and perhaps indicates that the different (non-similarity) behaviour of the front position is associated with fluid dynamical features close to the front that are not represented in the current shallow layer model, whereas the similarity balance is found within the bulk. We may also examine
![]() $q(0,t)t/[WHx_{f}(t)]$
(figure 12
c) for these currents, which is found in the shallow layer model to be given by
$q(0,t)t/[WHx_{f}(t)]$
(figure 12
c) for these currents, which is found in the shallow layer model to be given by
This ratio is a constant according to the theoretical model and there is reasonable agreement with this value in the simulations (see figure 12 c). A possible explanation for the divergence of the high-Reynolds-number cases from the similarity balance anticipated in the shallow layer model in § 3 is the neglect of mixing. We have seen that mixing is not important for low-Reynolds-number cases where most of the mixed fluid is confined to a relatively thin interfacial layer (figure 8 a). However, in the high-Reynolds-number simulations with a large solid fraction, the thickness of the interfacial layer increases significantly in the vicinity of the front (figure 4 c,d) and appreciable dilution occurs.
7. Global energy budget
For compositional gravity currents, it is convenient to form the following differential equation to relate the rates of change of the potential and kinetic energies (Necker et al. Reference Necker, Härtel, Kleiser and Meiburg2005; Ooi et al. Reference Ooi, Constantinescu and Weber2009):
In these expressions, the total kinetic energy and excess potential energy within the flow domain
![]() ${\it\Omega}$
are denoted by
${\it\Omega}$
are denoted by
![]() $E_{k}$
and
$E_{k}$
and
![]() $E_{p}$
respectively and
$E_{p}$
respectively and
![]() ${\it\varepsilon}$
is the total dissipation rate. An integral balance equation for the mechanical energy can be obtained by integrating (7.1) with time,
${\it\varepsilon}$
is the total dissipation rate. An integral balance equation for the mechanical energy can be obtained by integrating (7.1) with time,
where
![]() $E_{p0}$
is the total initial excess potential energy. The initial kinetic energy is equal to zero because the simulations are started from rest. The term
$E_{p0}$
is the total initial excess potential energy. The initial kinetic energy is equal to zero because the simulations are started from rest. The term
![]() $E_{d}=\int _{0}^{t}{\it\varepsilon}({\it\tau})\text{d}{\it\tau}$
is the time integral of the total dissipation rate. In all simulations, mechanical energy over the computational domain, expressed through (7.2), was conserved with an error of less than 0.5 % at all times.
$E_{d}=\int _{0}^{t}{\it\varepsilon}({\it\tau})\text{d}{\it\tau}$
is the time integral of the total dissipation rate. In all simulations, mechanical energy over the computational domain, expressed through (7.2), was conserved with an error of less than 0.5 % at all times.
In the simulations for obstructed channels (with
![]() ${\it\phi}>3\,\%$
), after transition to the drag-dominated regime is completed, the energy budget reduces in a good approximation to a balance between
${\it\phi}>3\,\%$
), after transition to the drag-dominated regime is completed, the energy budget reduces in a good approximation to a balance between
![]() $E_{p}$
and
$E_{p}$
and
![]() $E_{d}$
(i.e.
$E_{d}$
(i.e.
![]() $E_{k}\ll E_{p},E_{d}$
), which is consistent with the assumption that drag and buoyancy forces dominate during the drag-dominated regime. For a given channel Reynolds number, Re, and size of cylinder,
$E_{k}\ll E_{p},E_{d}$
), which is consistent with the assumption that drag and buoyancy forces dominate during the drag-dominated regime. For a given channel Reynolds number, Re, and size of cylinder,
![]() $D/H$
(e.g. for
$D/H$
(e.g. for
![]() $\mathit{Re}=15\,000$
and
$\mathit{Re}=15\,000$
and
![]() $D/H=0.032$
), the temporal variations of the global energy budget terms in (7.2) show that at any given time
$D/H=0.032$
), the temporal variations of the global energy budget terms in (7.2) show that at any given time
![]() $E_{k}$
decreases and
$E_{k}$
decreases and
![]() $E_{p}$
increases with an increase in
$E_{p}$
increases with an increase in
![]() ${\it\phi}$
(figure 13
a). The number of cylinders per unit surface area increases with
${\it\phi}$
(figure 13
a). The number of cylinders per unit surface area increases with
![]() ${\it\phi}$
, and as the total drag force and the total dissipation induced by the cylinders are proportional to the number of cylinders per unit area, the current slows down and the rate of dissipation increases.
${\it\phi}$
, and as the total drag force and the total dissipation induced by the cylinders are proportional to the number of cylinders per unit area, the current slows down and the rate of dissipation increases.

Figure 13. The effect of solid volume fraction on the variation of the excess potential energy,
![]() $E_{p}$
(dash–dot–dotted line), kinetic energy,
$E_{p}$
(dash–dot–dotted line), kinetic energy,
![]() $E_{k}$
(solid line), and integral of the total dissipation,
$E_{k}$
(solid line), and integral of the total dissipation,
![]() $E_{d}$
(dashed line), in the
$E_{d}$
(dashed line), in the
![]() $\mathit{Re}=15\,000$
simulations with
$\mathit{Re}=15\,000$
simulations with
![]() ${\it\phi}=0\,\%$
(red line L8),
${\it\phi}=0\,\%$
(red line L8),
![]() ${\it\phi}=1.25\,\%$
,
${\it\phi}=1.25\,\%$
,
![]() $D/H=0.032$
(light blue line L2),
$D/H=0.032$
(light blue line L2),
![]() ${\it\phi}=5\,\%$
,
${\it\phi}=5\,\%$
,
![]() $D/H=0.032$
(blue line L3) and
$D/H=0.032$
(blue line L3) and
![]() ${\it\phi}=12\,\%$
,
${\it\phi}=12\,\%$
,
![]() $D/H=0.032$
(dark grey line L1). Panel (a) shows the energy variation with time,
$D/H=0.032$
(dark grey line L1). Panel (a) shows the energy variation with time,
![]() $t/t_{0}$
, while panel (b) shows the variation of the energy with the front position,
$t/t_{0}$
, while panel (b) shows the variation of the energy with the front position,
![]() $x_{f}/H$
.
$x_{f}/H$
.
Consistent with the results of Ooi et al. (Reference Ooi, Constantinescu and Weber2009) for full-depth currents, the variations of the excess potential energy with time and with the front position are also close to linear during the later stages of the slumping phase in the simulation with
![]() ${\it\phi}=0\,\%$
. The decay of the excess potential energy with time is no longer linear in the simulations with
${\it\phi}=0\,\%$
. The decay of the excess potential energy with time is no longer linear in the simulations with
![]() ${\it\phi}>1.25\,\%$
. However, when the energy budget terms are plotted as a function of the front position, the variation of
${\it\phi}>1.25\,\%$
. However, when the energy budget terms are plotted as a function of the front position, the variation of
![]() $E_{p}$
with
$E_{p}$
with
![]() $x_{f}/H$
is close to linear and independent of
$x_{f}/H$
is close to linear and independent of
![]() ${\it\phi}$
, provided that the drag induced by the cylinders dominates the basal drag, a regime that is very common for the obstructed flows under consideration. At the end of this section, we use the shallow water model to justify this dependence.
${\it\phi}$
, provided that the drag induced by the cylinders dominates the basal drag, a regime that is very common for the obstructed flows under consideration. At the end of this section, we use the shallow water model to justify this dependence.
The temporal variation of the dissipation,
![]() $E_{d}$
, in the simulations with
$E_{d}$
, in the simulations with
![]() ${\it\phi}=12\,\%$
and
${\it\phi}=12\,\%$
and
![]() $\mathit{Re}=15\,000$
(figure 14
a) shows that, at any given time,
$\mathit{Re}=15\,000$
(figure 14
a) shows that, at any given time,
![]() $E_{d}$
is about the same in the simulations with
$E_{d}$
is about the same in the simulations with
![]() $D/H=0.05$
and 0.07. During the drag-dominated regime, the value of
$D/H=0.05$
and 0.07. During the drag-dominated regime, the value of
![]() $E_{d}$
is approximately 20 % smaller in the simulation with
$E_{d}$
is approximately 20 % smaller in the simulation with
![]() $D/H=0.032$
compared with the other two simulations. The main reason why at a given time
$D/H=0.032$
compared with the other two simulations. The main reason why at a given time
![]() $E_{d}(t)$
is smaller in the simulations with
$E_{d}(t)$
is smaller in the simulations with
![]() $D/H=0.032$
is because
$D/H=0.032$
is because
![]() $x_{f}$
is smaller (figure 10
b), so a smaller number of cylinders are situated within the body of the current. However, the variations of
$x_{f}$
is smaller (figure 10
b), so a smaller number of cylinders are situated within the body of the current. However, the variations of
![]() $E_{d}$
and
$E_{d}$
and
![]() $E_{p}$
as a function of
$E_{p}$
as a function of
![]() $x_{f}/H$
are approximately independent of
$x_{f}/H$
are approximately independent of
![]() $D/H$
.
$D/H$
.

Figure 14. Temporal variation of the excess potential energy,
![]() $E_{p}$
(dash–dot–dotted line), kinetic energy,
$E_{p}$
(dash–dot–dotted line), kinetic energy,
![]() $E_{k}$
(solid line), and integral of the total dissipation,
$E_{k}$
(solid line), and integral of the total dissipation,
![]() $E_{d}$
(dashed line): (a) effect of
$E_{d}$
(dashed line): (a) effect of
![]() $D/H$
in the
$D/H$
in the
![]() $\mathit{Re}=15\,000$
,
$\mathit{Re}=15\,000$
,
![]() ${\it\phi}=12\,\%$
simulations with
${\it\phi}=12\,\%$
simulations with
![]() $D/H=0.032$
(dark grey line L1),
$D/H=0.032$
(dark grey line L1),
![]() $D/H=0.05$
(pink line L4) and
$D/H=0.05$
(pink line L4) and
![]() $D/H=0.07$
(dark blue line L5); (b) effect of Re in the
$D/H=0.07$
(dark blue line L5); (b) effect of Re in the
![]() ${\it\phi}=12\,\%$
simulations with
${\it\phi}=12\,\%$
simulations with
![]() $\mathit{Re}=375$
,
$\mathit{Re}=375$
,
![]() $D/H=0.05$
(orange line L9),
$D/H=0.05$
(orange line L9),
![]() $\mathit{Re}=15\,000$
,
$\mathit{Re}=15\,000$
,
![]() $D/H=0.05$
(pink line L4) and
$D/H=0.05$
(pink line L4) and
![]() $\mathit{Re}=150\,000$
,
$\mathit{Re}=150\,000$
,
![]() $D/H=0.05$
(dark green line L10).
$D/H=0.05$
(dark green line L10).
In the case of high-Reynolds-number currents advancing in a channel with no obstacles, the front velocity increases monotonically with Re and approaches the theoretical inviscid limit,
![]() $U_{f}/u_{b}=0.5$
, at very high Reynolds numbers (see Ooi et al.
Reference Ooi, Constantinescu and Weber2009; Tokyay et al.
Reference Tokyay, Constantinescu and Meiburg2011). In contrast, in the case of high-Reynolds-number currents propagating in channels containing cylinders, the non-dimensional front velocity at a given time is not a function of
$U_{f}/u_{b}=0.5$
, at very high Reynolds numbers (see Ooi et al.
Reference Ooi, Constantinescu and Weber2009; Tokyay et al.
Reference Tokyay, Constantinescu and Meiburg2011). In contrast, in the case of high-Reynolds-number currents propagating in channels containing cylinders, the non-dimensional front velocity at a given time is not a function of
![]() $\mathit{Re}$
, provided that the current has undergone a transition to the drag-dominated regime and that the transition to this regime has completed at approximately the same non-dimensional time. For example, this is the case for the simulations (
$\mathit{Re}$
, provided that the current has undergone a transition to the drag-dominated regime and that the transition to this regime has completed at approximately the same non-dimensional time. For example, this is the case for the simulations (
![]() ${\it\phi}=15\,\%$
,
${\it\phi}=15\,\%$
,
![]() $D/H=0.05$
) with
$D/H=0.05$
) with
![]() $\mathit{Re}=150\,000$
and
$\mathit{Re}=150\,000$
and
![]() $\mathit{Re}=15\,000$
. The weak influence of Re is because the drag arises mainly from the cylinders and this is close to independent of the Reynolds number, Re, when the cylinder Reynolds number,
$\mathit{Re}=15\,000$
. The weak influence of Re is because the drag arises mainly from the cylinders and this is close to independent of the Reynolds number, Re, when the cylinder Reynolds number,
![]() $\mathit{Re}_{D}$
, is sufficiently high that the drag coefficient,
$\mathit{Re}_{D}$
, is sufficiently high that the drag coefficient,
![]() $C_{D}$
, becomes independent of
$C_{D}$
, becomes independent of
![]() $\mathit{Re}_{D}$
for most of the array.
$\mathit{Re}_{D}$
for most of the array.
A justification for the observed nearly linear variation with the front position of
![]() $E_{p}/E_{p0}$
(figure 13
b) can be given in terms of the shallow layer formulation
$E_{p}/E_{p0}$
(figure 13
b) can be given in terms of the shallow layer formulation
where
![]() $L$
is the length of the domain. This implies that
$L$
is the length of the domain. This implies that
![]() $E_{p}/E_{p0}$
must vary linearly with
$E_{p}/E_{p0}$
must vary linearly with
![]() $x_{f}/H$
. Moreover, if
$x_{f}/H$
. Moreover, if
![]() $h$
varies linearly with
$h$
varies linearly with
![]() $x$
(
$x$
(
![]() $h/H=(1-x/H)/2$
, which is a very good approximation at least for the low-Reynolds-number cases), then
$h/H=(1-x/H)/2$
, which is a very good approximation at least for the low-Reynolds-number cases), then
![]() $E_{p}/E_{p0}=1-x_{f}/18H$
. This variation of
$E_{p}/E_{p0}=1-x_{f}/18H$
. This variation of
![]() $E_{p}$
is very close to the numerical result in figure 13(b) for
$E_{p}$
is very close to the numerical result in figure 13(b) for
![]() ${\it\phi}>1.25\,\%$
. In the high-Reynolds-number cases, although not exactly linear,
${\it\phi}>1.25\,\%$
. In the high-Reynolds-number cases, although not exactly linear,
![]() $h(x)/H$
remains close to linear (e.g. figure 2
b,c). This is why the variation of
$h(x)/H$
remains close to linear (e.g. figure 2
b,c). This is why the variation of
![]() $E_{p}/E_{p0}$
with
$E_{p}/E_{p0}$
with
![]() $x_{f}/H$
remains close to linear and varies only weakly with
$x_{f}/H$
remains close to linear and varies only weakly with
![]() ${\it\phi}$
and Re for the high-Reynolds-number cases with
${\it\phi}$
and Re for the high-Reynolds-number cases with
![]() ${\it\phi}>1.25\,\%$
.
${\it\phi}>1.25\,\%$
.
8. Summary and conclusions
In this paper, Boussinesq gravity currents initiated from lock-release conditions to propagate though an array of rectangular horizontal cylinders have been investigated using 3D eddy-resolving simulations that compute the flow around individual obstacles and through a two-layer shallow water model. The simulations calculate the evolution of the dependent variables through the current; in particular, this allows the structure of the current, the drag forces and the mixing properties to be evaluated as functions of the non-dimensional parameters describing the array of cylinders. The shallow water description is a simplification of the complete dynamics, but nevertheless it is shown that the bulk dynamics of the currents may be predicted from this framework and that it is often able to reproduce the results of the simulations.
We have discussed the ways in which the size, volume fraction of the cylinders,
![]() ${\it\phi}$
, and frontal area of the cylinders per unit volume,
${\it\phi}$
, and frontal area of the cylinders per unit volume,
![]() $a$
, impact the properties of the flows. Naturally, our detailed analysis only strictly pertains to an array of horizontally aligned square cross-section cylinders that span the flow. However, some of the main trends should be expected to carry over to when the axes of the cylinders are vertical. For example, we anticipate that the coherence of the KH billows will be reduced as
$a$
, impact the properties of the flows. Naturally, our detailed analysis only strictly pertains to an array of horizontally aligned square cross-section cylinders that span the flow. However, some of the main trends should be expected to carry over to when the axes of the cylinders are vertical. For example, we anticipate that the coherence of the KH billows will be reduced as
![]() ${\it\phi}$
and
${\it\phi}$
and
![]() $aH$
increase, because this depends mainly on the shear stress across the interface, which in turn is dependent upon the magnitude of the drag measured through the combined parameter
$aH$
increase, because this depends mainly on the shear stress across the interface, which in turn is dependent upon the magnitude of the drag measured through the combined parameter
![]() ${\it\Gamma}_{D}$
. One might expect that the development of the interfacial layer will be similar for different orientations of the cylinders, provided that they remain perpendicular to the streamwise direction.
${\it\Gamma}_{D}$
. One might expect that the development of the interfacial layer will be similar for different orientations of the cylinders, provided that they remain perpendicular to the streamwise direction.
The use of LES has allowed investigation of scale effects for large-Reynolds-number currents. This is an important contribution, given the scarcity of detailed experimental data on gravity currents propagating in a porous medium at field conditions. That the temporal evolution of the bulk properties of the currents appears to be largely independent of the Reynolds number when
![]() $\mathit{Re}>10^{4}$
implies that experimental and numerical studies conducted at moderate scales may accurately represent the behaviour at much larger field scales, even if the details of the vortical structure of the current remain somewhat different.
$\mathit{Re}>10^{4}$
implies that experimental and numerical studies conducted at moderate scales may accurately represent the behaviour at much larger field scales, even if the details of the vortical structure of the current remain somewhat different.
A main advantage of eddy-resolving simulations that resolve flow past the individual obstacles is that the mean drag coefficient can be directly evaluated once an appropriate definition for the mean velocity within the array has been adopted. The results in the present work showed that if the velocity scale is chosen as the mean velocity within the current from which the wake regions are eliminated, then the predicted values of
![]() $C_{D}$
over the quadratic drag-law regime
$C_{D}$
over the quadratic drag-law regime
![]() $(1.2<C_{D}<2)$
are fairly comparable with those measured for isolated square cylinders in constant-density uniform flow. Still, for high-Reynolds-number currents these values were found to vary by up to 80 % with the geometrical characteristics of the array (
$(1.2<C_{D}<2)$
are fairly comparable with those measured for isolated square cylinders in constant-density uniform flow. Still, for high-Reynolds-number currents these values were found to vary by up to 80 % with the geometrical characteristics of the array (
![]() ${\it\phi},D/H,s/D,aH$
). Using the approach advocated in the present paper, the drag coefficient can be estimated. This eliminates the need to calibrate simpler numerical models that do not resolve the flow around individual cylinders. Moreover, the predictions of the shallow flow theory model for the temporal evolution of the front position were found to be in good agreement with the simulation results once the drag coefficient was redefined with the mean streamwise velocity within the current. Consistent with shallow water theory, the numerical simulation results confirmed that the combined drag parameter for the porous medium,
${\it\phi},D/H,s/D,aH$
). Using the approach advocated in the present paper, the drag coefficient can be estimated. This eliminates the need to calibrate simpler numerical models that do not resolve the flow around individual cylinders. Moreover, the predictions of the shallow flow theory model for the temporal evolution of the front position were found to be in good agreement with the simulation results once the drag coefficient was redefined with the mean streamwise velocity within the current. Consistent with shallow water theory, the numerical simulation results confirmed that the combined drag parameter for the porous medium,
![]() ${\it\Gamma}_{D}$
, is the key grouping of parameters that determines how fast high-Reynolds-number currents propagate through arrays of obstacles.
${\it\Gamma}_{D}$
, is the key grouping of parameters that determines how fast high-Reynolds-number currents propagate through arrays of obstacles.
An important finding of the present work was that high-Reynolds-number currents propagating through a porous medium are not exactly self-similar; that is, the velocity fields at the front and centre of the flow do not appear to exhibit the same dependences on time. We suggest that a possible explanation for this discrepancy is that the shallow layer model neglects mixing between the dense and less dense fluids. The simulations reveal that the interface is not particularly thick, but that there is significant mixing at the front of the current. Such a process is omitted from the shallow layer framework of § 3 and its inclusion remains an important outstanding challenge.
Acknowledgements
The authors gratefully acknowledge the National Center for High Performance Computing (NCHC) in Taiwan, in particular Dr W. F. Tsai, and the Transportation Research and Analysis Computing Center (TRACC) at the Argonne National Laboratory, in particular Dr S. Lottes, for providing substantial computer time. Ayse Yuksel Ozan acknowledges financial support through the Scientific and Technological Research Council of Turkey (TUBITAC) for a post-doctoral research fellowship. A.J.H. acknowledges the financial support of EPSRC (UK) under grant EP/G066353/1.