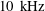1 Background and objectives

The working principle of dielectric barrier discharge (DBD) plasma actuators (PAs) has been intensively investigated in the last decade, and was recently summarized by Benard & Moreau (Reference Benard and Moreau2014), Kotsonis (Reference Kotsonis2015) and Kriegseis, Simon & Grundmann (Reference Kriegseis, Simon and Grundmann2016). Despite different overall perspectives, all three review publications emphasize the body-force distribution as being the main characteristic to understand and/or successfully predict the control mechanism of an operative PA and the effect of a discharge on a given flow scenario.

The variety of quasi-steady force-determination approaches has been contrasted by Kriegseis et al. (Reference Kriegseis, Schwarz, Tropea and Grundmann2013). More recently, Debien et al. (Reference Debien, Benard, David and Moreau2012) and Neumann et al. (Reference Neumann, Friedrich, Czarske, Kriegseis and Grundmann2013), for instance, successfully determined the phase-averaged force magnitude of a PA by means of particle image velocimetry (PIV) and laser Doppler velocimetry respectively. Moreover, based on the Navier–Stokes approach suggested by Wilke (Reference Wilke2009), the desired spatiotemporal force distribution of a PA was recently provided by Benard, Debien & Moreau (Reference Benard, Debien and Moreau2013).

Although there are several publications about the development of the volume force, there is no obvious agreement about the exact behaviour. It is widely accepted that the AC character of the operating voltage and thus the plasma discharge leads to different contributions to the force in the positive and negative half-cycles, as shown by Enloe, McHarg & McLaughlin (Reference Enloe, McHarg and McLaughlin2008) and Orlov, Font & Edelstein (Reference Orlov, Font and Edelstein2008). Most of the abovementioned investigations used a sinusoidal high-voltage signal with a frequency in the range of $1~\text{k}\text{Hz}$ to identify the phase relation of the measured volume force. Since the operating voltage was used to indicate the electric/fluid mechanical interrelation, only indirect phase information on the cause–effect relation between the discharge and the resulting force distributions was provided.

At higher operation frequencies of approximately $10~\text{k}\text{Hz}$ , lightweight high-voltage transformers can be used, allowing in-flight studies as demonstrated by Duchmann et al. (Reference Duchmann, Simon, Tropea and Grundmann2014). The investigations by Neumann et al. (Reference Neumann, Friedrich, Czarske, Kriegseis and Grundmann2013) were performed at $9.5~\text{k}\text{Hz}$ and provide the first valuable information on the phase-averaged force magnitude in this range of frequencies. However, even though promising for flight applications, to date, no investigation into the spatiotemporal force distribution has been published for such high frequencies.

The purpose of the present work, therefore, is twofold. First, phase-resolved PIV measurements are conducted at an operation frequency of $f=10~\text{k}\text{Hz}$ to provide phase-averaged velocity and force information for such fast discharge cycles. Here, the involved competition between an appropriate particle displacement and a reasonable phase resolution pushes this measurement technique to its limits. Additionally, together with the simultaneously measured discharge cyclograms (Lissajous figures), the hypothesis is tested of whether or not the temporal evolution of the discharge capacitance $C_{eff}$ (and thus the discharge intensity) is in phase with the resulting force magnitude and possibly its corresponding distribution.

2 Actuator working principle and Lissajous-figure analysis

A sketch of a DBD PA in surface discharge mode is shown in figure 1(a). Typically, the actuator consists of an upper (exposed) electrode, a dielectric and a lower (covered) electrode. The dielectric used in this experiment is made of Kapton^® ( $d=0.4~\text{m}\text{m}$ polyimide) with high permittivity. The two copper electrodes are arranged with no overlap or gap, such that the horizontal distance between $b_{1}$ and $b_{2}$ is zero. An AC voltage with a magnitude of several kilovolts is applied to the upper electrode and the lower electrode is grounded.

The resulting electric field periodically exceeds the breakdown field strength $E_{b}$ , such that air ionizes and plasma discharge occurs in both half-cycles. Accelerated by the electric field, the ions collide with the surrounding neutrals and thus impart momentum to the gas, which is commonly referred to as body or volume force. Like in the present study, experimental investigations into this force have mostly been performed in quiescent air, where the momentum transfer results in a wall jet of several metres per second magnitude.

During either half-cycle, the plasma layer gradually grows along the dielectric surface right after discharge onset ( $E\geqslant E_{b}$ ) and eventually collapses at the highest intensity right at the positive, respectively negative, peak voltage. However, even though similar at first glance, the discharges of the half-cycles show distinct differences, which were elaborated in detail, e.g., by Gibalov & Pietsch (Reference Gibalov and Pietsch2000). A streamer-like discharge comprising multiple distinct current peaks occurs during the positive half-cycle, whereas a more uniform glow discharge is maintained during the negative half-cycle. It should be noted that, similarly to the half-cycle distinction, the terms forward and backward stroke are also frequently used; see, e.g., Enloe et al. (Reference Enloe, McHarg and McLaughlin2008).

Figure 1. (a) Set-up of a DBD PA with two electrodes $b_{1}$ , $b_{2}$ and a dielectric with a thickness of $d$ . The field of view (FOV) is shown for clarity (dashed box). In addition, the electric measurement equipment is indicated. (b) Charge $Q=C_{P}V_{P}$ and operating voltage $V$ of the same DBD actuator plotted in a Lissajous figure ( $Q{-}V$ cyclogram) with characteristic capacitances $C_{0}$ and $C_{eff}$ (dashed lines). Furthermore, the acquisition points for the PIV measurements and the effective phases of the respectively determined velocity fields are emphasized.

The instantaneous discharge properties, i.e. operating voltage $V(t)$ and released charge $Q(t)=C_{P}V_{P}(t)$ , can be easily recorded by means of a high-voltage probe and across an appropriate probe capacitor respectively, which are also sketched in figure 1(a). If plotted against each other, the resulting Lissajous figure (discharge cyclogram) provides information on the consumed actuator power $P_{A}$ . Moreover, the instantaneous or phase-averaged discharge capacitance can be determined from the slope of the cyclogram according to

(2.1a,b ) $$\begin{eqnarray}C(t)=\frac{\text{d}Q(t)}{\text{d}V(t)}\quad \text{or}\quad C(\unicode[STIX]{x1D719})=\frac{\unicode[STIX]{x0394}Q(\unicode[STIX]{x1D719})}{\unicode[STIX]{x0394}V(\unicode[STIX]{x1D719})}\end{eqnarray}$$

respectively. Figure 1(b) shows the Lissajous figure for the investigated actuator, where two characteristic capacitances are indicated. The capacitance $C_{\text{0}}$ describes the pure passive (cold) capacitance of the PA, which occurs during the so-called dark periods (Manley Reference Manley1943), when no discharge is present. The effective discharge capacitance $C_{eff}$ consists of a combination of $C_{\text{0}}$ and the capacitance of the plasma itself, and thus reveals a steeper slope in the cyclogram than $C_{0}$ . One should refer to Kriegseis et al. (Reference Kriegseis, Möller, Grundmann and Tropea2011) for more details on the analysis of PA-specific discharge cyclograms.

3 Experimental procedure and PIV processing

The required velocity information for the force-determination approach is recorded with a 2D–2C PIV set-up comprising a dual-cavity Nd:YLF laser (Litron LDY303-PIV), a high-speed camera (Phantom V12, $800\times 600$ pixel resolution) and a reversely mounted Schneider-Kreuznach SKR SYMMAR 120/5.6 lens. The FOV spans $9~\text{mm}\times 6.7~\text{mm}$ in the immediate vicinity above the actuator (see figure 1 a), resulting in a resolution of approximately $88~\text{pixel}~\text{mm}^{-1}$ . To ensure a quiescent environment for the wall-jet measurements, the experiments are conduced in a plexiglass containment, which is seeded with di-ethyl-hexyl-sebacat (DEHS) tracers with a mean diameter of $d_{p}=0.9~\unicode[STIX]{x03BC}\text{m}$ . The corresponding particle response time of the tracers is determined as $\unicode[STIX]{x1D70F}_{p}=\unicode[STIX]{x1D70C}_{p}d_{p}^{2}/18\unicode[STIX]{x1D702}=2.25~\unicode[STIX]{x03BC}\text{s}$ , with $\unicode[STIX]{x1D70C}_{p}$ and $\unicode[STIX]{x1D702}$ for the DEHS density and dynamic viscosity of air respectively (see, e.g., Raffel et al. Reference Raffel, Willert, Wereley and Kompenhans2007).

The actuator is operated with a GBS Minipuls 6 at a frequency of $f=10~\text{k}\text{Hz}$ and $V_{pp}=12~\text{k}\text{V}$ (sine), which implies maximum horizontal jet velocities in the range of $u=7~\text{m}~\text{s}^{-1}$ for this actuator (see Kriegseis et al. Reference Kriegseis, Schwarz, Tropea and Grundmann2013). Accordingly, the Stokes number of the problem is determined as $Stk=\unicode[STIX]{x1D70F}_{p}u/l_{c}=1.6\times 10^{-2}$ , where $l_{c}=1~\text{m}\text{m}$ is the characteristic length scale of the problem (see, e.g., Durscher & Roy Reference Durscher and Roy2012). The operating voltage $V$ and charge probe voltage $V_{p}$ are acquired with a USB oscilloscope (Pico-Scope 4424, sample rate $1~\text{MS}~\text{s}^{-1}$ ) and directly processed with LabVIEW. Eight different phases per discharge cycle are recorded for the velocity information, which, in contrast to previous studies, are precisely adjusted to the capacitance information of the Lissajous figure; see figure 1(b). Each half-cycle is subdivided into four consecutive phases to particularly provide information during (i) the dark period at $C_{0}$ , (ii) the discharge onset/transition, (iii) the effective discharge at $C_{eff}$ and (iv) the corners of the cyclogram, where the discharge ceases.

The camera and laser are triggered and synchronized with a digital timer card (LabVIEW, NI PCI-6602), which also serves as a time base for the PA operation frequency. The PIV set-up is operated in double-frame mode at a repetition rate of $f_{cam}=3200~\text{Hz}$ , since the base clock of the NI timer card ( $f_{NI}=80~\text{M}\text{Hz}$ ) only supports discrete recording frequencies with a common factor. The laser pulse distance is accordingly set to $\unicode[STIX]{x0394}t=12.5~\unicode[STIX]{x03BC}\text{s}$ between frames, which results in a maximum particle displacement of $\unicode[STIX]{x0394}x_{max}\approx 7~\text{pixel}$ for the expected velocities. As such, it is furthermore possible to record the eight phase angles in a permutating way in only one measurement. For the given memory (8 GB) of the camera, 10 000 frames can be captured, resulting in 625 image pairs per phase angle. The phase angle of the first frame of the measurements is identified retroactively from the camera trigger and the Q-switch signal of laser cavity 1 in comparison with the discharge signals.

All image pairs are processed with commercial software (PIVTEC, PIVview), where a multigrid cross-correlation algorithm with an initial/final interrogation area (IA) size of $64\times 64/8\times 8~\text{pixel}$ is applied. To ensure statistical significance of the obtained data, a convergence study is conducted. Figure 2 shows the relative standard deviation of the velocity, $\unicode[STIX]{x1D70E}^{\ast }=\unicode[STIX]{x1D70E}_{u}/\bar{u}$ (averaged over $3\times 3$ IA), as a function of an increasing number of image pairs, where the considered images are equally distributed over the complete range of available images (per phase angle). Figure 2(a) compares the convergence properties for different characteristic locations in the wall jet. Complementarily, the convergence behaviour for all phases is additionally tested in figure 2(b) for the fully developed wall jet.

Figure 2. Statistical significance of the PIV data: convergence of the relative standard deviation $\unicode[STIX]{x1D70E}^{\ast }=\unicode[STIX]{x1D70E}_{u}/\bar{u}$ for (a) four characteristic locations of the wall jet at $\unicode[STIX]{x1D719}=0$ and (b) the fully developed wall jet $\unicode[STIX]{x2463}$ for all phase angles as indicated in figure 1(b).

Both diagrams saliently demonstrate that an order of magnitude of $10^{2}$ image pairs is sufficient to ensure statistical significance of the data. The main reason for this comparatively fast convergence is that the measurements are conducted at distinct phase angles in the cycle. The velocities of the wall jet only differ slightly if the same phase angle and therefore the same working point of the PA is used for the correlation of the image pairs. This technique makes it possible to use a small number of image pairs for the correlation – in contrast to time-averaged investigations without paying attention to the operation point in the cycle (at least an order of magnitude of $10^{3}$ image pairs in, e.g., Benard & Moreau (Reference Benard and Moreau2011) and Kriegseis et al. (Reference Kriegseis, Schwarz, Tropea and Grundmann2013)). Furthermore, the measurements are repeated three times to ensure reproducibility of the experimental results.

4 Volume-force determination

The generated horizontal volume force $f_{i}(x_{j},t)$ is determined using the two-dimensional Navier–Stokes equation (NSE) of a Newtonian incompressible fluid ( $\text{D}\unicode[STIX]{x1D70C}/\text{D}t=0$ ) with constant dynamic viscosity $\unicode[STIX]{x1D702}$ ,

(4.1) $$\begin{eqnarray}\displaystyle f_{i}=\underbrace{\vphantom{\unicode[STIX]{x1D70C}u_{j}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}}\unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}t}}_{\text{local acceleration}}+\underbrace{\unicode[STIX]{x1D70C}u_{j}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}}_{\text{convective acceleration}}-\quad \underbrace{\unicode[STIX]{x1D702}\frac{\unicode[STIX]{x2202}^{2}u_{i}}{\unicode[STIX]{x2202}x_{j}\unicode[STIX]{x2202}x_{j}}}_{\text{diffusion}}, & & \displaystyle\end{eqnarray}$$

where, furthermore, the pressure gradient is neglected as proposed (and retroactively verified) by Wilke (Reference Wilke2009). It should be noted that only $f_{x}$ is considered in the present study, since earlier studies demonstrated that the horizontal force $f_{x}$ is predominant in the problem by orders of magnitude, i.e $f_{x}\gg f_{y}$ (e.g. Benard et al. Reference Benard, Debien and Moreau2013). Further evidence for the validity of the above assumptions was provided by Dörr & Kloker (Reference Dörr and Kloker2015) based on direct numerical simulations (DNS). In their comprehensive investigation into various influential factors on the accuracy of the resulting force estimation, the above simplifications were further confirmed to be appropriate for the horizontal component in quiescent air.

The right-hand side of (4.1) comprises acceleration, convection and diffusion terms. The latter two terms can be calculated straightforwardly from the respective phase information $u_{i}(x,y,\unicode[STIX]{x1D719})$ . The phase-to-phase deviations of the first term are approximated via central differences according to

(4.2) $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}u(x,y,t)}{\unicode[STIX]{x2202}t}\approx \frac{u(x,y,\unicode[STIX]{x1D719}+\unicode[STIX]{x0394}\unicode[STIX]{x1D719})-u(x,y,\unicode[STIX]{x1D719}-\unicode[STIX]{x0394}\unicode[STIX]{x1D719})}{t(\unicode[STIX]{x1D719}+\unicode[STIX]{x0394}\unicode[STIX]{x1D719})-t(\unicode[STIX]{x1D719}-\unicode[STIX]{x0394}\unicode[STIX]{x1D719})}.\end{eqnarray}$$

It is worth mentioning that the accuracy of the acceleration term (4.2) immediately depends on the number of distinguished phases, where the latter is limited by sufficient minimum particle displacement (cf. § 3). In order to directly compare the impacts of the contributions of (4.1), the force distribution $f_{x}$ is integrated across the control volume (CV),

(4.3) $$\begin{eqnarray}\frac{F_{x}(\unicode[STIX]{x1D719})}{L}=\iint _{CV}f_{x}(x,y,\unicode[STIX]{x1D719})\,\text{d}A,\end{eqnarray}$$

and compared with all separate terms, all of which are similarly integrated across the CV. The comparison is plotted in figure 3. Obviously, the periodic contribution of local acceleration is most dominant in the diagram. The convective term is an order of magnitude weaker at almost constant values in the range of $20~\text{mN}~\text{m}^{-1}$ across all phase angles. In contrast, the contribution of the acceleration term centres around zero and therefore vanishes for a time-averaged approach.

Figure 3. Decomposition of the volume force $F_{x}$ into convective, diffusive and time-dependent parts. The error bars indicate the reproducibility based on three measurements for the overall volume force.

Scatter and/or limited reproducibility of the data is indicated as error bars in figure 3, which only reveals noticeable uncertainties for the discharge onset at $\unicode[STIX]{x1D719}=0$ and $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$ . Here, in particular, the scattered discharge of the filamentary streamer discharge of the positive half-cycle at $\unicode[STIX]{x1D719}=0$ and the variable discharge onset of the glow discharge in the negative half-cycle at $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$ result in considerable variance (cf. figure 1 b). This in turn leads to a small change of the velocity gradient $\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}t$ , causing the change in the resulting volume force.

The spatial distribution of all NSE terms is shown in figure 4 for $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$ to illustrate the respective contributions to the overall force distribution. As above, the local acceleration $\unicode[STIX]{x1D70C}\,\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}t$ is predominant over the convective acceleration $\unicode[STIX]{x1D70C}u\,\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x$ throughout the field. A closer look at the latter still reveals a positive volume force with horizontal direction in the left part of the FOV; see figure 4(b). This is due to the positive gradient $\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x$ in this part of the wall jet. The overall contribution of the diffusive (viscous) term is almost negligible: only a thin layer immediately above the dielectric has a rather mild impact on the local force distribution (cf. figures 3 and 4 c). Furthermore, the influence of shearing forces in the boundary layer further downstream results in a negative contribution to the volume force (Kriegseis et al. Reference Kriegseis, Schwarz, Tropea and Grundmann2013). As outlined above, the time-averaged force distribution is mostly dominated by the quasi-steady convective term (cf. figures 4 b,e).

Figure 4. Contribution of all NSE terms to the force distribution (phase angle $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$ is shown): (a) local acceleration $\unicode[STIX]{x1D70C}\,\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}t$ , (b) convective terms $\unicode[STIX]{x1D70C}u_{j}\,\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}$ , (c) diffusive terms $\unicode[STIX]{x1D702}\,\unicode[STIX]{x2202}^{2}u_{i}/\unicode[STIX]{x2202}x_{j}\unicode[STIX]{x2202}x_{j}$ , (d) overall volume force $f_{x}$ as the sum of all terms (a–c) according to equation (4.1). (e) The time-averaged volume force $\overline{f_{x}}$ is added for comparison purposes.

5 Interrelation of capacitance and volume force

Figure 3 already indicated a mostly negative volume force $F_{x}$ in the positive half-cycle, which then ceases right after the voltage slope changes sign at $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}/2$ . Similarly, the negative half-cycle yields largely positive forces until the voltage slope changes sign again at $\unicode[STIX]{x1D719}=3\unicode[STIX]{x03C0}/2$ . Comparison of the force histories with figure 1(b) reveals that this force breakdown coincides with collapse of the discharge in either corner of the cyclogram, where the effective discharge capacitance $C_{eff}$ falls back to the cold capacitance $C_{0}$ . In addition, figure 5 provides the volume-force distribution $f_{x}(x,y,\unicode[STIX]{x1D719})$ for all eight examined phase angles, where the positive and negative half-cycles appear in (a,c,e,g) and (b,d,f,h) respectively. The evaluated phase angles for either half-cycle are indicated at the top of the figure.

Starting from the cold capacitance $\unicode[STIX]{x1D719}=7\unicode[STIX]{x03C0}/4$ , the positive half-cycle begins at $\unicode[STIX]{x1D719}=0$ with the onset of the filamentary streamer discharge, which immediately leads to the maximum negative volume force. Due to the filamentary character of the plasma, in particular the area in the range $2~\text{m}\text{m}<x<5~\text{m}\text{m}$ massively contributes to the force (cf. also Gibalov & Pietsch Reference Gibalov and Pietsch2000). This force distribution is maintained at a slightly lower force level for the duration of the streamer discharge, which develops the effective discharge intensity $C_{eff}^{+}$ at $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}/4$ , which then collapses once the peak voltage is crossed at $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}/2$ (see also the upper right corner of the cyclogram in figure 1 b). Accordingly, the negative force domain fades away and is compensated by traces of positive force contributions, which finally cancel each other out once the discharge entirely drops during the dark period. As such, the actuator force is zero during the cold capacitance $C_{0}$ at $\unicode[STIX]{x1D719}=3\unicode[STIX]{x03C0}/4$ .

Figure 5. Volume-force distribution $f_{x}(x,y,\unicode[STIX]{x1D719})$ for all evaluated phase angles $\unicode[STIX]{x1D719}$ . The positive and negative half-cycles appear in (a,c,e,g) and (b,d,f,h) respectively, as denoted at the top of the figure; (a,b), (c,d), (e,f) and (g,h) accordingly provide the force fields during discharge onset/transition, effective discharge intensity with $C_{eff}$ , collapse of the plasma and dark period with $C_{0}$ respectively.

The more uniform glow discharge of the negative cycle starts at $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$ , where, in contrast to the streamer discharge, the positive force starts to develop immediately next to the exposed electrode and covers the area in the range $0~\text{m}\text{m}<x<3~\text{m}\text{m}$ at comparable magnitude to the positive half-cycle ( $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}$ ). During this diffusive discharge, the electrons, and more importantly the negative oxygen ions (see Boeuf, Lagmich & Pitchford Reference Boeuf, Lagmich and Pitchford2009), move from the upper exposed electrode onto the surface of the dielectric. Accordingly, both the force domain and magnitude continuously grow towards $C_{eff}^{-}$ at $\unicode[STIX]{x1D719}=5\unicode[STIX]{x03C0}/4$ . Like with the positive peak voltage ( $\unicode[STIX]{x1D719}=\unicode[STIX]{x03C0}/2$ ), the discharge similarly ceases at the negative peak voltage at $\unicode[STIX]{x1D719}=3\unicode[STIX]{x03C0}/2$ , where the plasma collapses again. Accordingly, the competition of positive and negative force contributions begins and the force magnitude drops. Finally, even though at higher magnitudes compared with $\unicode[STIX]{x1D719}=3\unicode[STIX]{x03C0}/4$ , again the positive and negative parts of the force field happen to perfectly cancel each other out during the cold capacitance $C_{0}$ at $\unicode[STIX]{x1D719}=7\unicode[STIX]{x03C0}/4$ .

To emphasize the interrelation of the actuator capacitance $C$ and the resulting force $F_{x}/L$ more saliently, both quantities are plotted atop the phase angle $\unicode[STIX]{x1D719}$ in figure 6(a). It should be noted that the capacitance has been averaged cycle-wise in the diagram and the occurrence of the characteristic capacitances, $C_{0}$ and $C_{eff}$ , is highlighted grey in the diagram.

Figure 6. Phase-averaged actuator volume force: (a) interrelation of the phase-averaged capacitance $C$ and the volume force $F_{x}$ ; note that the left ordinate starts from zero, whereas the right ordinate centres around zero; (b) comparison of normalized magnitudes $\tilde{F_{x}}(\unicode[STIX]{x1D719})=F_{x}(\unicode[STIX]{x1D719})/\text{max}|F_{x}(\unicode[STIX]{x1D719})|$ with the literature.

Most remarkably, there is no volume force $F_{x}$ during the dark periods with the cold capacitance $C_{0}$ at the two phase angles $\unicode[STIX]{x1D719}=3\unicode[STIX]{x03C0}/4$ and $\unicode[STIX]{x1D719}=7\unicode[STIX]{x03C0}/4$ . Furthermore, in accordance with the investigations of Kriegseis et al. (Reference Kriegseis, Möller, Grundmann and Tropea2011), the effective discharge capacities $C_{eff}^{-}$ and $C_{eff}^{+}$ are very similar in both half-cycles. However, it has already been demonstrated in figure 5 that the different discharge regimes nonetheless lead to significant deviations of both the force distribution $f_{x}(x,y,\unicode[STIX]{x1D719})$ and the force magnitude $F_{x}(\unicode[STIX]{x1D719})$ . The resulting difference in magnitude becomes especially obvious from direct comparison of the two half-cycles in figure 5.

Additionally, the difference in relative phase angle (per half-cycle) for the force peak demonstrates the influence of the gradual plasma growth of the glow in contrast to the fast development of the streamer discharge on the resulting force production. From the given phase resolution of the present data, a phase-angle shift of approximately $\unicode[STIX]{x0394}_{\unicode[STIX]{x1D719}}^{\pm }\approx \unicode[STIX]{x03C0}/4$ is estimated. In particular, the positive force peak of the negative half-cycle is found to perfectly coincide with the effective discharge capacitance $C_{eff}^{-}$ at $\unicode[STIX]{x1D719}=5\unicode[STIX]{x03C0}/4$ , whereas the negative peak already occurs at $\unicode[STIX]{x1D719}=0$ (thus before a fully developed $C_{eff}^{+}$ ) at approximately $50\,\%$ in strength.

The phase-averaged force magnitudes $F_{x}(\unicode[STIX]{x1D719})$ are furthermore compared with the literature in figure 6(b), where the results of equation (4.3) appear normalized according to $\tilde{F_{x}}(\unicode[STIX]{x1D719})=F_{x}(\unicode[STIX]{x1D719})/\text{max}|F_{x}(\unicode[STIX]{x1D719})|$ to account for the different geometry configurations and operating conditions of the respective PAs.

It is obvious from first glance that all studies reveal negative and positive contributions to the actuator force during the positive and negative half-cycles respectively. Moreover, the aforementioned phase-angle shift between the two half-cycles can be recognized in all of the curves of the diagram, which provides evidence for the physical significance of this shift. Interestingly, an additional (constant) phase lag of approximately $\unicode[STIX]{x03C0}/4$ between the studies in the ranges of $1~\text{k}\text{Hz}$ (Wilke Reference Wilke2009; Debien et al. Reference Debien, Benard, David and Moreau2012; Benard et al. Reference Benard, Debien and Moreau2013) and $10~\text{k}\text{Hz}$ (Neumann et al. Reference Neumann, Friedrich, Czarske, Kriegseis and Grundmann2013, present study) can be identified. On a technical note, the particle relaxation time of the DEHS tracers, $\unicode[STIX]{x1D70F}_{p}=2.25~\unicode[STIX]{x03BC}\text{s}$ , implies phase lags of $\unicode[STIX]{x0394}_{\unicode[STIX]{x1D719}}^{\unicode[STIX]{x1D70F}_{p}}\approx \unicode[STIX]{x03C0}/200$ and $\unicode[STIX]{x0394}_{\unicode[STIX]{x1D719}}^{\unicode[STIX]{x1D70F}_{p}}\approx \unicode[STIX]{x03C0}/20$ for PA operation at $1~\text{k}\text{Hz}$ and $10~\text{k}\text{Hz}$ respectively, which in either case is well below the observed phase lag. It is, therefore, hypothesized that the momentum transfer from the plasma to the surrounding air also comprises a certain (frequency-dependent) response time.

6 Concluding remarks

In agreement with the literature, the present results show that a positive volume force $F_{x}>0$ is generated by a DBD PA in the negative half-cycle during the glow discharge and a negative volume force $F_{x}<0$ is formed in the positive half-cycle during the streamer discharge. The new approach of using arbitrary phase angles across the cycle can help to drastically reduce the number of data sets needed for statistical significance. The phase-averaged force distributions $f_{x}(x,y,\unicode[STIX]{x1D719})$ provide valuable insight into the origin of the observed phase-angle shift $\unicode[STIX]{x0394}_{\unicode[STIX]{x1D719}}^{\pm }$ of the force peaks between the two half-cycles. In particular, this shift is concluded to rely on the different discharge scenarios (streamer and glow). The additional phase lag of the PA force production when operated at higher frequencies is demonstrated to not result from the finite particle response time $\unicode[STIX]{x1D70F}_{p}$ of the chosen tracers. Consequently, it is hypothesized that the plasma-to-air momentum transfer itself involves a (frequency-dependent) delay. A detailed analysis of this hypothesis is obviously beyond the scope of the present work and is foreseen to be addressed in future investigations.

Simultaneous consideration of the corresponding discharge cyclograms (Lissajous figures) uncovers the dependence of the generated volume force on the instantaneous capacitance $C(t)$ of the PA rather than the underlying operating voltage $V(t)$ . This phase distinction according to the instantaneous discharge situation provides clear formerly hidden cause–effect relations, where even the footprint of the higher discharge scatter level during discharge onset can be immediately identified in the uncertainty margin of the resulting force magnitudes. The main part of the plasma discharge at $C_{eff}$ shows the major contribution to the resulting volume force. Importantly, during dark periods, and thus passive capacitance $C_{0}$ , the overall volume force is counterbalanced to approximately zero. The periodic formation of the volume-force distribution and moreover the corresponding interrelation of the discharge and the resulting momentum transfer, as identified in the present study, can help in the design of novel and innovative control concepts in discharge-based closed-loop control applications in aerodynamics. Additionally, this new insight might serve as a basis for advanced model development of the PA source term for numerical simulations.