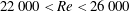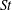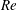1. Introduction
The wing morphology parameters thickness and camber have received much attention ever since the first aircraft were designed (e.g. Lilienthal Reference Lilienthal1889). Therefore, a substantial body of knowledge about the influence of wing morphology under steady flow conditions exists. Wing camber increases lift and the maximal lift-to-drag ratio (
$L/D$
) for wings operating both at low and at high Reynolds numbers,
$\mathit{Re}$
(Shyy et al.
Reference Shyy, Lian, Tang, Viieru and Liu2008). The aerodynamic effect of wing thickness and leading-edge radius, however, strongly depends on
$\mathit{Re}$
. High
$\mathit{Re}$
is mostly relevant for manned aviation. Here, thick wings are advantageous, since the range of acceptable angles of attack (
${\it\alpha}$
) becomes wider, and flow separation due to an unfavourable chordwise pressure gradient on the wing occurs much later than on a thin wing (Shyy et al.
Reference Shyy, Lian, Tang, Viieru and Liu2008). In contrast, low-
$\mathit{Re}$
flyers like insects, birds and bats require thin wings to operate efficiently. At low
$\mathit{Re}$
, thin wings create more lift (Kunz Reference Kunz2003) and less drag (Okamoto, Yasuda & Azuma Reference Okamoto, Yasuda and Azuma1996), which leads to a better
$L/D$
and increases performance.
As recent studies have shown, the aerodynamic mechanisms responsible for the generation of forces during bird flight deviate from the steady flow conditions that are generally assumed for airplane wings: lift-enhancing flow features have been found on the flapping wings of a hovering hummingbird (Warrick, Tobalske & Powers Reference Warrick, Tobalske and Powers2005), a robotic goose (Hubel & Tropea Reference Hubel and Tropea2010), and during the slow-speed flight of a passerine (Muijres, Johansson & Hedenstroem Reference Muijres, Johansson and Hedenstroem2012; Chang et al. Reference Chang, Ting, Su, Soong and Yang2013).
These mechanisms are similar to what has been found in insect flight: insects generate aerodynamic forces by flapping their wings with high aerodynamic angles of attack (Ellington Reference Ellington1984). Clap-and-fling, rotational lift and wake capture have been shown to increase the aerodynamic forces (for a comprehensive review, see Wang Reference Wang2005). The most prominent flow feature of both insect and bird flight is the leading-edge vortex, LEV (Ellington et al.
Reference Ellington, van den Berg, Willmott and Thomas1996; Muijres et al.
Reference Muijres, Johansson and Hedenstroem2012; Chang et al.
Reference Chang, Ting, Su, Soong and Yang2013). A LEV is a region of recirculating fluid which is closely attached to the top of the wing. It increases the force coefficients and the performance of flapping wings at low
$\mathit{Re}$
(e.g. Bomphrey et al.
Reference Bomphrey, Lawson, Harding, Taylor and Thomas2005). The LEV stability is increased by the relatively short duration of a down- or upstroke: large effective angles of attack occur only for a limited time, which reduces the amount of vorticity accumulation and therefore the size of the vortex (Wang, Birch & Dickinson Reference Wang, Birch and Dickinson2004; Bomphrey et al.
Reference Bomphrey, Lawson, Harding, Taylor and Thomas2005). Due to the partly detached nature of this robust high-lift flow system, it is uncertain whether the knowledge about wing morphology under steady flow conditions is also valid for flapping wings. Lentink & Dickinson (Reference Lentink and Dickinson2009) state that more research on the influence of airfoil shape on the LEV and force generation for wings that operate at low
$\mathit{Re}$
is highly desirable.
Some research on the influence of wing camber, thickness and leading-edge radius on wings at
$80<\mathit{Re}<10\,000$
with unsteady motion has already been completed (Dickinson & Gotz Reference Dickinson and Gotz1993; Usherwood & Ellington Reference Usherwood and Ellington2002; Altshuler, Dudley & Ellington Reference Altshuler, Dudley and Ellington2004). However, these studies focused on the net output forces created by the wings and did not consider the flow morphology. Additionally, experiments with flapping and translating wings at higher
$\mathit{Re}$
, which are more relevant for the slow-speed flapping flight of birds, have not yet been carried out.
The present study analyses the effect of airfoil shape (camber and thickness) on the four-dimensional (three-dimensional
$+$
time) flow pattern and on the circulation of flapping wings using digital particle image velocimetry (DPIV).
2. Material and methods
The flow around flapping and translating wing models was visualized in water at appropriate
$\mathit{Re}$
and flapping frequency. By combining series of two-dimensional velocity information gathered with DPIV, a full three-dimensional representation of the flow was created. These data allow an investigation of the time-resolved three-dimensional (3D) flow patterns and consequent forces or circulation and the influence of wing morphology.
2.1. Wing modelling
The wing models are based on airfoil data of a pigeon (Columba livia domestica). Bachmann (Reference Bachmann2010) provides information on the planform of the wing and on the maximum thickness of the airfoil, and Biesel, Butz & Nachtigall (Reference Biesel, Butz and Nachtigall1985) measured the position of maximum thickness, maximum camber and the position of maximum camber on a freely gliding pigeon over the full span. These data were used for generating airfoils of the 3D model wing (NACA 4-digit modified series, see table 1). The planform of the model wing – including the aspect ratio and the chord distribution over span – was simplified from the data given in Bachmann (Reference Bachmann2010). The wings were printed as a positive, then put into a box. The box was filled with liquid silicone. After drying, the printed wing was pulled out, leaving a negative form in the silicone. This form was subsequently filled with epoxy resin, yielding a transparent wing.
Figure 1. Wing model. ‘Standard wing’ (type ‘s’). Wing
$\text{length}=120~\text{mm}$
, position of spanwise
$\text{joint}=30\,\%$
of chord length. The mean chord length of the wing is 43.75 mm.
Table 1. Geometry of the standard model wing (type ‘s’).
In addition to the standard (type ‘s’) model wing (see table 1 for the airfoil data), which is based on the pigeon wing (see figure 1), four other wing models were tested in the current study: in each wing model, a single airfoil parameter was altered (see figure 2).
Figure 2. Semi-span airfoils of the five wing models that were tested. From top to bottom: no camber, high camber, standard, low thickness, high thickness.
2.2. Flow tank and kinematics
All measurements were performed in water in a recirculating flow tank with a test section of
$50~\text{cm}\times 25~\text{cm}\times 25~\text{cm}$
. A constant flow velocity (
$U_{f}$
) of
$0.46~\text{m}~\text{s}^{-1}$
was applied for all measurements. Both the excursion angle (
${\it\Phi}$
) and the geometric angle of attack (
${\it\alpha}_{geo}$
) of the wing (see figure 3) were controlled throughout the wing beat cycle (see figure 4), using a custom flapping device with two degrees of freedom. A harmonic oscillatory motion has often been observed in real birds and bats (Rosén, Spedding & Hedenstroem Reference Rosén, Spedding and Hedenstroem2004; Tian et al.
Reference Tian, Iriarte-Diaz, Middleton, Galvao, Israeli, Roemer, Sullivan, Song, Swartz and Breuer2006) and has consequently been applied to robotic birds (Hubel & Tropea Reference Hubel and Tropea2009; Ruck & Oertel Reference Ruck and Oertel2010). The flapping robot in the current study also generates a sinusoidal motion of the wing. Both the excursion angle and the geometric angle of attack are prescribed over the entire flapping cycle. The peak-to-peak flapping amplitude was set to 64°, according to what has been described for small birds (Rosén et al.
Reference Rosén, Spedding and Hedenstroem2004). As the kinematics during the upstroke differ greatly with species (Tobalske Reference Tobalske2007), the effective angle of attack during the upstroke was set for a minimum interaction with the fluid (see figure 4).
Figure 3. Definition of the geometric angle of attack (
${\it\alpha}_{geo}$
) and the excursion angle (
${\it\Phi}$
). The excursion angle is the angle between the horizontal and the wing. The geometric angle of attack is defined as the angle between the free flow and the wing chord. The effective angle of attack (see figure 4), is the angle between the wing chord and the resulting oncoming flow.
Figure 4. Kinematics of the wing. Thick line: wing excursion
${\it\Phi}$
. The wing excursion follows a sinusoidal curve with a peak-to-peak amplitude of 64°. Solid lines: geometric angle of attack. During upstroke, the geometric angle of attack is controlled so that the effective angle of attack equals zero at 75 %-span of the wing (feathering). During downstroke, the geometric angle of attack is fixed to
$0\pm 1^{\circ }$
. Dashed lines: effective angle of attack at the wing tip at the corresponding
$\mathit{St}$
. Thin vertical lines indicate the time steps where 3D flow velocity information was acquired.
$\mathit{Re}$
is calculated as
$$\begin{eqnarray}\mathit{Re}=v_{tip}\overline{c}/{\it\nu},\end{eqnarray}$$
where
$\overline{c}=\text{mean}$
chord of the wing,
${\it\nu}=\text{kinematic}$
viscosity of the fluid, and the mean wing tip velocity
$$\begin{eqnarray}v_{tip}=\sqrt{(2{\it\Phi}bf)^{2}+U_{f}^{2}},\end{eqnarray}$$
where
$b=\text{wing}$
span,
$f=\text{flapping}$
frequency.
In the experiments,
$U_{f}$
is constant and only the flapping frequency is altered to meet the target Strouhal number (
$\mathit{St}$
). As a result,
$\mathit{Re}$
is in the range of
$2.2\times 10^{4}<\mathit{Re}<2.6\times 10^{4}$
in the current study. This is in good agreement with the range reported for small and medium sized birds in slow-speed flapping flight, e.g. a thrush nightingale (
$\mathit{Re}=1.7\times 10^{4}$
, Rosén et al.
Reference Rosén, Spedding and Hedenstroem2004) and a pigeon (
$\mathit{Re}=3.9\times 10^{4}$
, Spedding, Rayner & Pennycuick Reference Spedding, Rayner and Pennycuick1984).
The dimensionless
$\mathit{St}$
relates the product of vortex shedding frequency and wake height (indicated by the wing tip amplitude, Taylor, Nudds & Thomas Reference Taylor, Nudds and Thomas2003) to the velocity of the free stream, and is calculated as
$$\begin{eqnarray}\mathit{St}=f\,A/U_{f}\end{eqnarray}$$
where
$A=$
peak-to-peak amplitude of the wing.
$\mathit{St}$
of 0.2, 0.3 and 0.4 were tested, which coincide with the relatively narrow range of
$\mathit{St}$
reported for birds (Taylor et al.
Reference Taylor, Nudds and Thomas2003). Low
$\mathit{St}$
represents fast cruising flight, and high
$\mathit{St}$
represents very slow flight and eventually near-hover flight speeds. This range of
$\mathit{St}$
corresponds to a reduced frequency (
$k=2{\rm\pi}fc/U_{f}$
) of
$0.19<k<0.38$
.
2.3. Flow field recording and analysis
Due to the highly three-dimensional flow on flapping wings, all three velocity components of the fluid in a volume of
$160~\text{mm}\times 160~\text{mm}\times 160~\text{mm}$
around the flapping wing were acquired using DPIV. A high-speed camera (A504k, Basler AG, Ahrensburg, Germany, effective
$\text{resolution}=1024~\text{pixel}\times 1024~\text{pixel}$
) was used together with a 5 W continuous wave laser (
$\text{wavelength}=532~\text{nm}$
; Snoc electronics Co., Ltd, Guangdong, China). The laser beam was conditioned using cylindrical and spherical lenses to form a light sheet with a thickness of 1.5 mm. Neutrally buoyant particles (
$\text{diameter}=57~{\rm\mu}\text{m}$
, polyamide, Intelligent Laser Applications GmbH, Jülich, Germany) were used as seeding.
A custom DPIV tool developed for this study (PIVlab v1.31, Thielicke & Stamhuis Reference Thielicke and Stamhuis2014) was used to analyse the image data. The cross-correlation was performed in three passes with decreasing window size (final window
$\text{size}=34~\text{pixel}\times 34~\text{pixel}$
with 50 % overlap), yielding
$59\times 59$
vectors per image. The DPIV data were validated; 0.18 % of the vectors in the time-resolved test volume were rejected. The velocity field was smoothed to reduce DPIV-inherent noise and missing data were interpolated in a single step using a robust penalized least squares method (Garcia Reference Garcia2010). Simulations with the DPIV code showed that the systematic (bias) error is maximally 0.025 pixels and the residual (r.m.s.) error is below 0.01 pixels (Thielicke & Stamhuis Reference Thielicke and Stamhuis2014). Along with a mean displacement of 6 pixels per image pair, as in the experiments of the present study, this gives a displacement uncertainty in the range of 0.6 %.
A stack of 59 parallel DPIV slices through the test volume was captured from two perpendicular directions (see figure 5). This procedure results in a 3D Cartesian grid with
$59\times 59\times 59$
nodes and the full
$\boldsymbol{UVW}$
velocity information at each point. The spacing between the points is 2.656 mm in all three dimensions; 205 379
$\boldsymbol{UVW}$
vectors were captured in the test volume for each time step, each
$\mathit{St}$
and each wing type.
Figure 5. Set-up of the DPIV system. The camera and the laser sheet scan through the water tunnel in the
$xy$
(a) and
$xz$
(b) planes. The arrows indicate the translation of the 2D traversing system along the
$z$
-axis (a) and along the
$y$
-axis (b).
In total, 35 time steps were captured during one beat cycle of the wing; 10 steps during the upstroke and 25 steps during the downstroke. The exposure of the camera was synchronized to the excursion of the wing; at each time step a double image with
${\rm\Delta}t=2~\text{ms}$
was captured. The highly periodic quality of the flow pattern made it possible to record data for a given stroke phase at separated wing beats. Five consecutive full beat cycles were captured for every DPIV slice, hence all data reported in this study are the
$\text{mean}\pm \text{s.d.}$
of five samples.
Qualitative analyses of the fluid dynamics require a reliable visualization technique that identifies vortical structures in three-dimensional flow. A suitable candidate for vortex visualization is the
$Q$
-criterion (e.g. Hunt, Wray & Moin Reference Hunt, Wray and Moin1988; Dubief & Delcayre Reference Dubief and Delcayre2000; Poelma, Dickson & Dickinson Reference Poelma, Dickson and Dickinson2006):
$$\begin{eqnarray}Q={\textstyle \frac{1}{2}}(|{\it\bf\Omega}|^{2}-|\unicode[STIX]{x1D64E}|^{2})\end{eqnarray}$$
where
${\it\bf\Omega}=\text{vorticity tensor}$
,
$\unicode[STIX]{x1D64E}=\text{rate-of-strain tensor}$
(Haller Reference Haller2005)
As Dubief & Delcayre (Reference Dubief and Delcayre2000) note,
$Q$
expresses the balance between local rotation rate (vorticity magnitude) and local strain rate. Regions where the vorticity magnitude exceeds the strain rate show a positive
$Q$
value and highlight vortex core structures (Lu & Shen Reference Lu and Shen2008). Particularly in the direct vicinity of a wall or a wing, the
$Q$
-criterion is supposed to perform better in terms of vortex visualization than vorticity magnitude by itself (Lu & Shen Reference Lu and Shen2008). To further support the correct identification of vortices, it was checked whether the flow follows a circular pattern either by releasing streamlines (Robinson, Kline & Spalart Reference Robinson, Kline and Spalart1989) or using line integral convolution, LIC (Cabral & Leedom Reference Cabral and Leedom1993).
2.4. Circulation estimates
To quantify the differences between the flow patterns resulting from different
$\mathit{St}$
and wing morphologies, the bound circulation was derived from the flow field. The circulation is proportional to the lift that is generated by a wing (Kutta–Joukowski theorem). This theorem has been applied to two-dimensional (e.g. Anderson Reference Anderson2007) and three-dimensional (e.g. Birch, Dickson & Dickinson Reference Birch, Dickson and Dickinson2004) steady flow conditions, yielding very good lift estimates. Although strictly appropriate only for steady flow conditions, the proportionality of circulation and lift is also reasonably well maintained in highly unsteady flows (Unal, Lin & Rockwell Reference Unal, Lin and Rockwell1997). Two methods were tested to derive the spanwise circulation (circulation around the spanwise axis)
${\it\Gamma}_{z}$
: a loop integral of the tangent velocity and an area integral of the vorticity:
$$\begin{eqnarray}{\it\Gamma}_{z}=\oint _{S_{vort}}v_{t}\text{d}S_{vort}=\int _{A_{vort}}{\it\omega}_{z}\text{d}A_{vort},\end{eqnarray}$$
where
$S_{vort}=\text{circular}$
path around the vortex core,
$v_{t}=\text{tangential}$
velocity,
$A_{vort}=\text{area}$
of the vortex core,
${\it\omega}_{z}=\text{spanwise}$
vorticity.
Several integration domains (different areas and paths) were tested. The resulting circulation estimate was remarkably consistent, and for practical reasons the area integral of vorticity was used to derive
${\it\Gamma}_{z}$
. The strength of leading-edge vortices was quantified by measuring the circulation of the LEV: the position and area of the LEV core was determined using the
$Q$
-criterion as a threshold (
$Q>600$
). Subsequently, spanwise vorticity in that area was integrated to derive the LEV circulation.
3. Results
3.1. Presence of LEVs on the ‘standard wing’
At the beginning of the downstroke, a starting vortex is shed. This vortex is linked to a weak root vortex, a strong tip vortex and to the leading-edge vortex, forming a vortex loop (see example in figure 6). At the end of each downstroke, these loops are shed and left behind in the wake, forming a series of inclined vortex loops. Due to the passive upstroke and the resulting asymmetry between up- and downstroke, an inverse Kármán vortex street, which would be typical for a thrust-producing foil with symmetric up- and downstroke (e.g. Vandenberghe, Zhan & Childress Reference Vandenberghe, Zhan and Childress2004), could not be observed.
Figure 6. Example for the 3D flow data of the ‘standard wing’ at different time steps during the downstroke;
$\mathit{St}=0.3$
. The
$Q$
-criterion (
$\text{threshold}=600$
), is used, colour coded with spanwise vorticity (vorticity around the spanwise axis), and textured with LIC.
The strength of the LEV correlates positively with
$\mathit{St}$
. The LEV is stable throughout the downstroke at
$\mathit{St}=0.2$
and 0.3 (vortices confirmed with
$Q$
-criterion/broad vorticity peak/streamlines, see example in figure 7), but not at
$\mathit{St}=0.4$
.
Figure 7. Two-dimensional confirmation of the development of an LEV. ‘Standard wing’, cross-section at 50 % span at mid-downstroke. Close to the leading edge on top of the wing, a region with elevated (clockwise) vorticity and streamlines/LIC that spiral around a focus becomes visible.
More detail on the development of the LEV is given in figure 8, which shows measurements of the cross-sectional area of the LEV at
$2/3$
span over the wingbeat cycle: as already indicated qualitatively by the 3D flow visualization, the cross-sectional area of the LEV increases substantially with
$\mathit{St}$
. At
$\mathit{St}=0.2$
, the area of the LEV peaks at about mid-downstroke, where the local flow velocity (
$U_{f}$
) and the effective angle of attack are maximal. After this peak, the LEV diameter decreases due to the gradual shedding of the vortex. At
$\mathit{St}=0.4$
, a vortex has already developed during pronation, hence before the actual downstroke starts. The following double peak in the LEV area demonstrates that the first LEV separates quickly from the wing, but a new LEV is generated after mid-downstroke. This observation is similar to the shedding and reformation of LEVs on a flapping robot simulating insect flight in a previous study (Ellington et al.
Reference Ellington, van den Berg, Willmott and Thomas1996).
Figure 8. The area of the LEV at
$2/3$
span over a wingbeat cycle. The area of the LEV is determined in a plane that is always perpendicular to the wing, where
$Q\geqslant 600$
. The size of the LEV increases with
$\mathit{St}$
.
3.2. The influence of wing morphology
3.2.1. Qualitative flow patterns
Compared to the ‘standard wing’, the vortex system stays consistent in principle for all wing types; however there are several remarkable differences concerning the LEV stability and size (see figure 9). The most striking differences will first be described on a qualitative basis; more quantitative results will be given later in this section.
Figure 9. The qualitative influence of wing morphology at 78 % of the wingbeat cycle. The
$Q$
-criterion (
$\text{threshold}=600$
), is used for visualizing vortices, colour coded with spanwise vorticity (vorticity around the spanwise axis), and textured with LIC. Weaker vortices do not appear in this illustration.
Modifications of wing thickness (thick wing ‘
$\text{t}+$
’
$=15\,\%$
thickness; standard wing ‘
$\text{s}$
’
$=7\,\%$
thickness; thin wing ‘
$\text{t}-$
’
$=3\,\%$
thickness) determine both the strength and stability of the LEV (see figure 9): at the lowest
$\mathit{St}$
, the thick wing creates a smaller LEV than the thin wing. This is less obvious for the intermediate
$\mathit{St}$
; however, the LEV on the thin wing seems to move slightly further away from the wing at the tip, indicating the onset of large-scale flow separation. At
$\mathit{St}=0.4$
, remarkable differences in the wake can be identified. Here, the thin wing creates two horse-shoe vortices at the trailing edge, indicating an unstable LEV that has been shed from the wing before. These vortices do not appear as explicitly in the wake of the thick wing.
Wing camber (highly cambered ‘
$\text{c}+$
’
$=10\,\%$
camber; standard wing ‘
$\text{s}$
’
$=5\,\%$
camber; non-cambered ‘
$\text{c}-$
’
$=0\,\%$
camber) influences the shape and size of vortices in the 3D flow field even more: at the lowest
$\mathit{St}$
, a LEV hardly appears on the highly cambered wing, in contrast to the non-cambered wing, which creates a relatively large LEV. The same trend reappears at the intermediate
$\mathit{St}$
; the LEV of the highly cambered wing stays closely attached to the wing surface, whereas the LEV of the non-cambered wing is quite distorted at the tip and moves away from the wing. In the wake of the non-cambered wing at the highest
$\mathit{St}$
, distinct horse-shoe vortices appear, again indicating an unstable LEV, similar to what has been shown for the thin wing. These vortices cannot be found in the wake of the highly cambered wing.
In summary, the qualitative visualization of the flow field reveals the following effects: a reduced wing thickness increases the size of the LEV, but decreases the stability at
$\mathit{St}=0.4$
. Increasing wing camber decreases the size of the LEV and increases vortex stability.
3.2.2. Leading-edge vortex in detail
The influence of wing morphology on the formation of an LEV was further quantified by measuring the circulation of the LEV core at
$2/3$
wing span at mid-downstroke. The circulation of the LEV increases significantly in all wing types with
$\mathit{St}$
(Lord test, significance
$\text{level}=5\,\%$
, see figure 10), indicating that the size of the LEV correlates positively with the effective angle of attack and the resulting flow velocity, which are both proportional to
$\mathit{St}$
. Camber and thickness additionally determine the strength of the LEV, as indicated earlier by the 3D visualization of the flow field: the LEV created by the thin wing is significantly stronger than the LEV on the thick wing for all except the highest
$\mathit{St}$
(see figure 10). On average, the LEV produced by the thick wing is by
$16\pm 12\,\%$
weaker. The effect of wing thickness is however not as pronounced as the effect of wing camber. The highly cambered wing creates an LEV that is on average
$30\pm 7\,\%$
weaker than the LEV created by the non-cambered wing. This effect varies only little with
$\mathit{St}$
.
Figure 10. Circulation of the LEV (dark) compared to the total bound circulation (light) for different
$\mathit{St}$
and different wing morphologies at
$2/3$
span and mid-downstroke. The effect of wing camber is more pronounced than the effect of wing thickness. The relative importance of the LEV increases with
$\mathit{St}$
. The circulation of the LEV was determined by integrating vorticity in the leading-edge region in the
$xy$
-plane, where
$Q>600$
.
Wing morphology does not only influence the strength and stability of the LEV, but also the total bound circulation, as can be seen in figure 10 (bars in light shades). The thin wing has a higher total bound circulation than the thick wing, which agrees well with the increase in the strength of the LEV. In contrast, the non-cambered wing has a lower total bound circulation, although the LEV was shown to be stronger. A possible explanation for this observation will be given in the next section.
The ratio of the LEV circulation to the total bound circulation of a wing section is indicative of the relative importance of the LEV in creating lift. The fraction of total circulation concentrated in the LEV increases with
$\mathit{St}$
from
$37\pm 9\,\%$
to
$60\pm 11\,\%$
to
$72\pm 8\,\%$
when averaged over all wing types (see figure 10). These numbers confirm that the relative contribution of the LEV to the total lift is highest for slow, near-hover flight speeds (high
$\mathit{St}$
) and significantly smaller for higher flight speed (low
$\mathit{St}$
).
3.2.3. Total bound circulation during downstroke
Further quantitative insights into the influence of wing morphology were obtained by measuring the average spanwise circulation (
$\overline{{\it\Gamma}}_{z}$
) of the full wing during downstroke (total bound circulation: this includes both the circulation of the LEV and the ‘conventional’ circulation of the wing). Here,
$\overline{{\it\Gamma}}_{z}$
increases significantly with
$\mathit{St}$
(see figure 11). The slope of this increase does not depend on wing morphology; all wing types show a similar trend. Within the range of
$\mathit{St}$
that was tested,
$\overline{{\it\Gamma}}_{z}$
increases almost by a factor of two. In addition to the effect of
$\mathit{St}$
, wing morphology also has a significant effect on the magnitude of
$\overline{{\it\Gamma}}_{z}$
: increasing wing camber increases
$\overline{{\it\Gamma}}_{z}$
(
$+19.1\pm 8.5\,\%$
with respect to the ‘standard wing’, averaged over all
$\mathit{St}$
), whereas reducing wing camber to zero greatly reduces spanwise circulation (
$-19.4\pm 4.6\,\%$
with respect to the ‘standard wing’). Modifications of wing camber have a more pronounced influence than modifications of wing thickness: the spanwise circulation on the thin wing with the sharp leading edge is slightly higher than on the ‘standard wing’ (
$+5.8\pm 2.9\,\%$
). The thick wing creates less circulation than the ‘standard wing’ (
$-7.6\pm 0.4\,\%$
).
Figure 11. Mean spanwise circulation (
$\overline{{\it\Gamma}}_{z}$
) during the downstroke for all wing types under test. The circulation increases with
$\mathit{St}$
. The highly cambered wing and the thin wing have a higher circulation than the standard wing.
Introducing wing camber increases the total bound circulation but, at the same time, it decreases the strength of the LEV. A possible explanation can be given when visualizing the sectional
${\it\Gamma}_{z}$
over the wing span of both the cambered and the non-cambered wing (see figure 12). In this figure,
${\it\Gamma}_{z}$
was normalized, so that the area under the curves always equals unity, and relative differences are emphasized. The sectional circulation is supposed to increase with span due to the positive gradient in the angle of attack and flow velocity. This trend is clearly visible only for the non-cambered wing (see figure 12). The normalization of the sectional
${\it\Gamma}_{z}$
reveals that for the highly cambered wing, the inner 50 % of the wing contribute relatively more to the generation of force. In contrast, in the non-cambered wing,
${\it\Gamma}_{z}$
peaks at about 75 % of span, clearly indicating that the generation of force is more concentrated toward the outer third of the wing where the LEV is located. Wing camber hence increases the spanwise circulation near the wing base where the effective angle of attack is small (see figure 12), but decreases the circulation at the outer 50 % of span. It was illustrated in figure 10 that this is caused by the weaker LEV on the highly cambered wing.
Figure 12. Spanwise circulation over a wing span, averaged over the duration of the downstroke and normalized with the mean
${\it\Gamma}_{z}$
during downstroke. (a)
$\mathit{St}=0.2$
, (b)
$\mathit{St}=0.3$
, (c)
$\mathit{St}=0.4$
.
4. Discussion
4.1. Flow patterns of the ‘standard wing’
The analysis of the flow around the ‘standard wing’ reveals that LEVs are generated at all
$\mathit{St}$
that were tested. Stable LEVs are created at
$0.2\leqslant \mathit{St}\leqslant 0.3$
, and several unstable LEVs dominate the flow field at
$\mathit{St}=0.4$
. The current study supports the idea that stable LEVs can also occur during the flapping flight of birds, greatly increasing the maximum attainable circulation and thereby force. Both the structure and the temporal development of these vortices are comparable to the LEVs described for insect flight (e.g. Ellington et al.
Reference Ellington, van den Berg, Willmott and Thomas1996; Liu et al.
Reference Liu, Ellington, Kawachi, Van Den Berg and Willmott1998; Birch et al.
Reference Birch, Dickson and Dickinson2004).
The contribution of the LEV to enhance aerodynamic lift seems to be generally very important on flapping wings. In the tobacco hawkmoth, the LEV is reported to contribute 13 %–65 % to total lift (Bomphrey et al.
Reference Bomphrey, Lawson, Harding, Taylor and Thomas2005). In a robotic model hawkmoth, the LEV contributes at least 65 % (van den Berg & Ellington Reference van den Berg and Ellington1997). At higher
$\mathit{Re}$
, the importance does not diminish; hummingbirds gain 15 % of lift through the LEV (Warrick et al.
Reference Warrick, Tobalske and Powers2005), and a passerine about 49 % (Muijres et al.
Reference Muijres, Johansson and Hedenstroem2012). The measurements of spanwise circulation that are given in the present study show a comparable range of contribution of the LEV to the total lift of 37 %–72 %, increasing with
$\mathit{St}$
. The circulation generated by the wings increases even when the LEV becomes progressively more unstable at
$\mathit{St}=0.4$
, which agrees with measurements of LEVs that keep on augmenting aerodynamic forces on flapping wings even when they burst (Lentink & Dickinson Reference Lentink and Dickinson2009). The results about the importance of LEVs in the ‘standard wing’ underline the fact that LEVs, even at higher
$\mathit{Re}$
, contribute substantially to the circulation, which is proportional to the lift, and they should be considered as powerful high-lift mechanism in slow-speed avian flight.
4.2. The influence of wing morphology
The net effect of wing camber and wing thickness on flapping wings is comparable to the effect in low-
$\mathit{Re}$
steady-state aerodynamics as presented in the introduction. Still, the observed net effects seem to originate from several different mechanisms in flapping wings.
4.2.1. Thickness
Changing the thickness of an airfoil has two geometric consequences: obviously, wing thickness defines the maximum section thickness of an airfoil; furthermore, wing thickness also determines the maximum leading-edge radius. The effect of maximum section thickness has been analysed by Kunz (Reference Kunz2003) in steady-state two-dimensional (2D) computations at low
$\mathit{Re}$
: when set to a positive effective angle of attack, a thick wing develops a much thicker upper-surface boundary layer at low
$\mathit{Re}$
. The low flow velocity behind the position of maximum thickness causes the airfoils to effectively ‘decamber’ (Kunz Reference Kunz2003). This explains the poor performance of thick wing sections at low
$\mathit{Re}$
under steady-state conditions. But it is questionable whether these results can be applied to flapping wings, where the fluid is mostly separated behind the position of maximum thickness.
Most of the knowledge about the leading-edge radius and the effect of sharp leading edges originates from manned aviation, e.g. delta wings that were tested at
$\mathit{Re}$
several orders of magnitude greater than in the present study. However, the influence of leading-edge radius depends strongly on
$\mathit{Re}$
(Shyy et al.
Reference Shyy, Lian, Tang, Viieru and Liu2008): under steady-state conditions, at
$\mathit{Re}>10^{6}$
, a wing with a large leading-edge radius can accept a much wider range of angles of attack than a thin wing before flow separation occurs (Shyy et al.
Reference Shyy, Lian, Tang, Viieru and Liu2008). But as
$\mathit{Re}$
decreases, the more similar the range of acceptable angles of attack becomes and hence the less important leading-edge radius becomes, until the range of acceptable angles of attack is finally equal at
$\mathit{Re}=10^{4}$
(Shyy et al.
Reference Shyy, Lian, Tang, Viieru and Liu2008). The decreasing importance of leading-edge radius at low
$\mathit{Re}$
is also supported by two-dimensional computational studies of rapidly pitching airfoils with varying leading-edge radius (Ramesh et al.
Reference Ramesh, Ke, Gopalarathnam and Edwards2012). Additional support comes from Usherwood & Ellington (Reference Usherwood and Ellington2002). Their study has shown that leading-edge radius does not significantly influence the amount of lift generated by revolving wings at low
$\mathit{Re}$
. But as that study focused on the measurements of forces, the reason for this observation could not be determined. At
$\mathit{Re}=10^{4}$
and
$\mathit{St}=0.16$
, but on a purely plunging wing, Rival et al. (Reference Rival, Kriegseis, Schaub, Widmann and Tropea2014) have shown that the leading-edge geometry (sharp versus blunt) determines the diameter of the LEV. On sharp-edged wings, slightly larger LEVs developed due to an earlier onset of the LEV growth. The measurements of the time-resolved three-dimensional flow field in the present study have shown that the somewhat increased total bound circulation that has been observed on thin flapping wings can indeed be attributed to the increase of the LEV circulation. Thickness was modified quite dramatically (3 %–15 %); nevertheless, the effect on LEV circulation (thin wing: 1 %–10 % stronger LEV than the standard wing) and also on total circulation (thin wing: 3 %–8 % higher circulation than the standard wing) is not as pronounced as expected. Therefore, sharp leading edges will generate only slightly stronger LEVs which also increases the total circulation, but the effect is much less pronounced than at higher
$\mathit{Re}$
. Further three-dimensional flow visualizations with flapping wings at
$\mathit{Re}>10^{5}$
would provide even more insight into the role of the leading-edge radius at low and high
$\mathit{Re}$
.
4.2.2. Camber
A modification of wing camber has a much more pronounced effect on the circulation: two consequences that result from the application of wing camber were identified. First, the strength of the LEV increases significantly by 33 %–61 % when wing camber is decreased (highly cambered wing versus non-cambered wing). Wing camber continues to have a strong effect on the size of the LEV even at the highest
$\mathit{St}$
, in contrast to wing thickness (see figure 10). Second, wing camber increases the total bound circulation (highly cambered versus non-cambered wing: 28 %–67 % increase in circulation). This effect is comparable to the effect of wing camber in steady-flow conditions, where an increase in camber also increases the total bound circulation (Okamoto et al.
Reference Okamoto, Yasuda and Azuma1996). The distinct effect of camber is surprising, as the role of camber in (partly) separated flow conditions, such as in the presence of an LEV, was questioned in previous studies that focused on force measurements (Dickinson & Gotz Reference Dickinson and Gotz1993; Usherwood & Ellington Reference Usherwood and Ellington2002). In the present study, it was shown that the circulation-enhancing effect of wing camber is concentrated towards the inner 50 % of the wing (see figure 12), where the effective angle of attack is relatively small, but the net flow velocity is still high, due to the velocity caused by wing translation. On a purely revolving cambered wing that mimics mid-downstroke in hovering flight as in the study of Usherwood & Ellington (Reference Usherwood and Ellington2002) however, the inner 50 % of the wing experience much lower flow velocities due to the absence of wing translation. Hence the lift-enhancing effect of camber at the inner 50 % of the wing will be much less pronounced. The present study has shown that wing camber also reduces the strength of an LEV, and therefore any gain in lift that could be achieved by additional LEV circulation. It is therefore possible that on a revolving wing with low flow velocities at the wing base, these two effects balance out, and no significant difference in net force can be measured.
The approach presented in the current study – measuring the 3D flow field around a flapping wing – is able to analyse the effect of wing camber in detail. Mapping the full flow field is necessary, as the effect of wing camber depends on spanwise position: while camber increases the conventional circulation on wing sections with relatively low effective angles of attack (the inner 50 % of the wing), it decreases the strength of LEVs on sections with high effective angles of attack (the outer 50 %) at the same time. Force measurements are not capable of distinguishing these effects.
4.2.3. Pressure distribution
The pressure distribution along the topside of an airfoil largely determines the occurrence of flow separation under steady-state conditions (e.g. Kunz Reference Kunz2003; Anderson Reference Anderson2007). If the pressure coefficient rapidly increases behind the leading edge of a wing, an adverse pressure gradient is generated. As soon as this gradient becomes too large, the kinetic energy of the fluid will not suffice to keep the fluid following the contour of the airfoil. The flow detaches at the leading edge, forming an LEV that is stable or will be shed, depending on the circumstances. The approximate pressure gradient for the different wing types was modelled with a foil-analysis program (XFOIL v6.94) and is shown in figure 13. It is shown that the non-cambered wing and the thin wing have already created such an unfavourable positive pressure gradient (the pressure increases in the flow direction) at the leading edge. This adverse pressure gradient is caused by the fluid not being gradually deflected at the leading edge. The change in direction is abrupt, creating a large positive gradient at the leading edge which promotes flow separation (Anderson Reference Anderson2007) and could explain the occurrence of large LEVs on the non-cambered wing and on the thin wing. The highly cambered wing however shows the most favourable pressure distribution for suppressing flow separation (lowest adverse pressure gradient). This is in good agreement with the results from this study even if steady-state conditions are not present. However, the fluid experiences these pressure gradients in a very short time: figure 13 shows that the highest gradients are found in the first 10 % of the chord. Along with
$U_{f}=0.46~\text{m}~\text{s}^{-1}$
(ignoring the acceleration of the fluid on top of the wing), the fluid encounters these gradients within 9.5 ms, which is short compared to the period of the flapping motion (about 1000 ms). The effect of the pressure gradient caused by the airfoil geometry therefore seems to be important also on flapping wings.
Figure 13. Gradient of the pressure coefficient at the upper surface of different wing types tested over chord
$x/c$
. 2D steady-state approximation with XFOIL,
$\mathit{Re}=20\,000$
, geometric angle of
$\text{attack}=8^{\circ }$
, viscous formulation,
$\text{NCrit}=9$
.
4.3. Implications for bird wings and conclusions
Wing geometry and wing kinematics of the flapping wing model are much less detailed than its natural counterpart. The uncomplicated design of the experiment makes it possible to draw general conclusions from the effect of wing morphology in the presence of LEVs in slow-speed flapping flight. This is important, since LEVs have been recently shown to play a key role in slow flight in birds (Muijres et al. Reference Muijres, Johansson and Hedenstroem2012; Chang et al. Reference Chang, Ting, Su, Soong and Yang2013), and more knowledge about the effect of wing morphology is needed (Lentink & Dickinson Reference Lentink and Dickinson2009). Controlled slow-speed flight is daily practice in birds, and it is one of the features that impresses most. In slow-speed flight, the wings experience relatively low flow velocities. Lift is proportional to the product of flapping frequency squared, stroke amplitude squared and force coefficients. At the same time, the maximum stroke angle, as well as the maximum flapping frequency of birds is limited due to anatomical or physiological constraints. Therefore, high force coefficients would clearly be beneficial, especially in slow flight (Lentink & Dickinson Reference Lentink and Dickinson2009). Force coefficients can be maximized by increasing the total circulation of a flapping wing, e.g. by generating LEVs.
The thickness of bird wings can easily go below 2.5 % (Friedel & Kähler Reference Friedel and Kähler2012) for the outer part of the wing (hand wing, see figure 14). In fact, thin and light hand wings will reduce inertia, and therefore reduce the inertial power necessary to accelerate the wings (Usherwood Reference Usherwood2009). But perhaps equally importantly, they will provide higher and more reliable aerodynamic forces by facilitating the development of LEVs on the hand wing. It is likely that the inner part of the wing (arm wing) and the hand wing take different roles in force generation. This has been hypothesized earlier for gliding flight (Videler, Stamhuis & Povel Reference Videler, Stamhuis and Povel2004), and the results from the present study strongly support the idea and also deliver additional evidence for slow-speed flapping flight: the hand wing has a low thickness and low camber (e.g. Biesel et al.
Reference Biesel, Butz and Nachtigall1985; Videler et al.
Reference Videler, Stamhuis and Povel2004; Videler Reference Videler2005) and experiences high angles of attack, features that the present study has shown to facilitate the formation of LEVs. The arm wing, however, seems to be optimized for fully attached flow aerodynamics: here, the effective angle of attack and the ‘local’
$\mathit{St}$
are lower, the wing is cambered and has a round leading edge; these factors hinder the development of LEVs. Camber can be actively controlled by birds (Bilo Reference Bilo1972) and e.g. a lanner falcon in free cruising flight considerably alters camber throughout the wing beat cycle (Friedel & Kähler Reference Friedel and Kähler2012). Birds may therefore use a combination of thin wings together with variable camber and wing twist to control the strength or occurrence of LEVs and therefore adapt the force coefficients and to direct the forces according to the current needs.
Figure 14. The airfoils of a typical bird wing and the definition of hand wing and arm wing.
In between the hand and the arm wing, there are several small feathers protruding from the leading edge (the alula), which could contribute to separating these two regions where different aerodynamic mechanisms dominate during slow-speed flapping flight.
The results on the effects of airfoil parameters can also contribute to understanding the wing design of bats. The thin sharp-edged membrane wing of bats (Muijres et al. Reference Muijres, Johansson, Barfield, Wolf, Spedding and Hedenstroem2008) consists, in analogy to birds, of an arm and a hand wing (Norberg Reference Norberg1990). The membrane of the arm wing (Plagiopatagium) has a higher extensibility than the other flight membranes, and is supposed to have higher camber during flight than the hand wing (Swartz et al. Reference Swartz, Groves, Kim and Walsh1996). It therefore appears likely that bat wings are optimized for generating LEVs on the hand wing (as shown by Muijres et al. Reference Muijres, Johansson, Barfield, Wolf, Spedding and Hedenstroem2008) and maintaining ‘conventional’ attached flow aerodynamics on the highly cambered arm wing, similar to what we hypothesize for birds.
Slow-speed flapping flight is only one flight mode that birds master. In normal cruising flight, it is likely that aerodynamic efficiency is maximized. That excludes the generation of large LEVs, because prominent LEVs are considered to significantly decrease the aerodynamic efficiency due to a large increase in drag (e.g. Lentink & Dickinson Reference Lentink and Dickinson2009).
It can be concluded that birds most likely rely on a wide range of aerodynamic mechanisms in flapping flight (analogous to the conclusions for the flight of insects from Srygley & Thomas Reference Srygley and Thomas2002), including force-enhancing LEVs in slow-speed flapping flight, but also aerodynamically more efficient fully attached flow in cruising flight.
5. List of symbols and abbreviations
-
${\it\alpha}$
-
Angle of attack
-
${\it\alpha}_{geo}$
-
Geometric angle of attack
-
${\it\Gamma}_{z}$
-
Circulation around the spanwise axis
-
${\it\nu}$
-
Kinematic viscosity
-
${\it\Phi}$
-
Excursion angle
-
${\it\bf\Omega}$
-
Vorticity tensor
-
${\it\omega}_{z}$
-
Vorticity around the spanwise axis
-
$2\text{D}$
-
Two-dimensional
-
$3\text{D}$
-
Three-dimensional
-
$A$
-
Peak-to-peak amplitude of the wing
-
$A_{vort}$
-
Area of the vortex core
-
$b$
-
Wing span
-
$c$
-
Chord length
-
$C_{p}$
-
Pressure coefficient
- ‘
$\text{c}-$
’
-
0 % cambered wing
- ‘
$\text{c}+$
’
-
10 % cambered wing
-
$\text{DPIV}$
-
Digital particle image velocimetry
-
$f$
-
Flapping frequency
-
$k$
-
Reduced frequency
-
$L/D$
-
Lift-to-drag ratio
-
$\text{LEV}$
-
Leading-edge vortex
-
$\text{LIC}$
-
Line integral convolution
-
$Q$
-
$Q$
-criterion
-
$\mathit{Re}$
-
Reynolds number
-
$\unicode[STIX]{x1D64E}$
-
Rate-of-strain tensor
- ‘
$\text{s}$
’
-
Standard wing
-
$S_{vort}$
-
Circular path around vortex core
-
$\mathit{St}$
-
Strouhal number
-
$t$
-
Time
-
$T$
-
Period
- ‘
$\text{t}-$
’
-
3 % thick wing
- ‘
$\text{t}+$
’
-
15 % thick wing
-
$U_{f}$
-
Free flow velocity
-
$v_{tip}$
-
Mean wing tip velocity
-
$v_{t}$
-
Tangential velocity
