1 Introduction
Orientation has a profound effect on the behaviour of non-spherical sedimenting particles influencing the rate of sedimentation, the presence or absence of horizontal drift and the scattering of light from particle suspensions. Fore–aft symmetric fibres settling in Stokes flow experience no hydrodynamic or gravitational torques and retain their initial orientations as they settle. Asymmetric fibres settling at finite Reynolds number experience competing torques due to fluid inertia, gravitational and viscous forces. Applying the finite Reynolds number slender-body theory of Khayat & Cox (Reference Khayat and Cox1989) to the case of fibres whose mass density and/or radius varies along their length, we predict a transition from vertical to oblique orientations with increasing Reynolds number or decreasing asymmetry and observe this transition in experiments. Measurement of the critical asymmetry leading to transition and the orientation of the oblique fibres provides an opportunity to quantitatively test the finite Reynolds number slender-body theory in the absence of transient effects.
Development of accurate models for the forces acting on fibres moving through fluids has long been a central problem in fluid mechanics. Stokes (Reference Stokes1851) considered the drag on an infinite cylinder in the paper in which he introduced his viscous drag law, but it was not until 60 years later with the work of Oseen (Reference Oseen1910) and Lamb (Reference Lamb1911) that an accurate model was developed. Extensive efforts to observe and model forces on cylinders with finite length developed slowly until slender-body theory was formalized by Batchelor (Reference Batchelor1970) and Cox (Reference Cox1970).
When these slender-body theories were developed, it was already known that they did not capture key features of the observed forces on fibres. They predict zero torque on a translating hydrodynamically symmetric fibre so that fibres keep their initial orientation, but it was known that fibres align with their long axes perpendicular to the fluid velocity (Lamb Reference Lamb1932; Jayaweera & Mason Reference Jayaweera and Mason1965; Batchelor Reference Batchelor1970). It was nearly twenty more years before Khayat & Cox (Reference Khayat and Cox1989) provided a calculation of forces on finite cylinders that was able to predict the inertial torque acting on fibres. Using a matched asymptotic expansion with viscous inner flow and Oseen’s approximation for the outer flow, they found that a torque producing horizontal alignment appears in the second term in the slender-body expansion.
The slow development of the theory for forces and torques on fibres was matched by slow appearance of accurate experimental measurements. It seems an easy experiment to place a fibre in a uniformly moving fluid and then measure the drag and torque. Or alternatively to drop a heavy fibre in a stationary fluid and measure the velocity and rotation toward its equilibrium orientation. One can easily observe the preferential alignment simply by dropping a small stem of grass or a plastic coffee stirrer in air. However, measurements at the low Reynolds numbers and high aspect ratios where the theory is quantitatively accurate have proven to be difficult because the inertial torques become quite small in these cases and small imperfections in the experiments can become important. Jayaweera & Mason (Reference Jayaweera and Mason1965) provide a careful set of measurements of drag coefficients for fibres and other shapes sedimenting in liquid paraffin. They have made qualitative observations about inertial torques but no measurements. Bragg, van Zuiden & Hermance (Reference Bragg, van Zuiden and Hermance1974) performed experiments that measured inertial torques and compared with a theoretical model.
There are two experimental studies that have compared their results with the theory of Khayat & Cox (Reference Khayat and Cox1989). Newsom & Bruce (Reference Newsom and Bruce1994) provide experiments on alignment and rotation of uniform graphite fibres of very high aspect ratio sedimenting in quiescent air. They use an innovative method of orientation measurement that detects transmission and absorption of polarized microwaves, and observe a dependence of torque on orientation that is consistent with the theory within the fairly large measurement uncertainties.
Recently, Lopez & Guazzelli (Reference Lopez and Guazzelli2017) performed a series of experiments in which they measured the trajectories of fibres in a cellular flow and provided systematic comparisons with several levels of models ranging from Stokes slender-body theory through the model by Khayat and Cox. They find that particle trajectories can be accurately reproduced with the Khayat and Cox model and note that the model is only quantitatively accurate at high aspect ratios. An innovation they introduce is a linearized model in which the full equations of Khayat and Cox are used to predict drag forces on parallel and perpendicular fibres while the standard mobility tensor formalism is used to interpolate the forces for angles between these two limits. This greatly simplifies the calculation of drag forces since in general the nonlinear equations must be solved iteratively to find the particle velocity at which the drag force balances the applied force.
It is important to distinguish between two different ways to consider the forces and torques on a fibre. Most of the theories, including Batchelor (Reference Batchelor1970) and Khayat & Cox (Reference Khayat and Cox1989), consider a fibre at a fixed angle of attack in a uniform flow. However, the experiments are almost all done on free fibres whose orientation with respect to their velocity and gravity can change with time in response to torques. Newsom & Bruce (Reference Newsom and Bruce1994) discuss the relevance of a quasi-steady model in which the drag forces and torques from slender-body theory for fixed fibres are combined with a viscous rotational resistance model to describe the time dependence of fibre motion. Shin, Koch & Subramanian (Reference Shin, Koch and Subramanian2006) compare this model to transient direct numerical simulations showing that it is accurate for freely settling fibres with Reynolds numbers based on a fibre half-length of order one.
One way to study inertial torques on fibres without a time dependent orientation is to produce particles with gravitational and viscous torques due to asymmetric mass distributions or shape and measure the equilibrium sedimentation orientation of these particles. An early study of asymmetric particles formed by spheres attached to fibres was performed by Jayaweera & Mason (Reference Jayaweera and Mason1966) in order to understand sedimentation of ice crystals with attached droplets. A theoretical study of the torques on a sedimenting asymmetric dumbbell formed from two different spheres was recently performed by Candelier & Mehlig (Reference Candelier and Mehlig2016). They find that for large asymmetry a dumbbell settles in a vertical orientation while for smaller asymmetry there is a stable oblique orientation.
The orientation of an isolated fibre settling in a quiescent fluid will establish the base state from which one can consider the effects of weakly turbulent flows or interparticle hydrodynamic interactions in dilute suspensions. The absence of rotation by a symmetric fibre settling in Stokes flow implies that fluid inertia and gravitational asymmetry will play a crucial role in these applications. As an example, consider the stability of a homogeneous suspension of settling non-spherical particles. Koch & Shaqfeh (Reference Koch and Shaqfeh1989) showed that hydrodynamic interactions among a suspension of initially isotropic symmetric fibres settling in Stokes flow lead to a clustering instability which has been widely observed in experiments and simulations (Guazzelli & Hinch Reference Guazzelli and Hinch2011). Shin, Koch & Subramanian (Reference Shin, Koch and Subramanian2009) demonstrated a similar instability in suspensions of settling fibres at finite Reynolds number whose initial orientations are horizontal due to inertial torques. In contrast, Goldfriend, Diamant & Witten (Reference Goldfriend, Diamant and Witten2017) predicted suppression of particle density fluctuations and the associated velocity disturbances in a system of non-spherical particles which settle vertically due to gravitational torques. Based on these studies, it is anticipated that one consequence of the orientational transition predicted in the present study could be a transition from stable to unstable sedimenting suspensions with decreasing fibre asymmetry or increasing fibre Reynolds number.
Turbulence will disrupt alignment by sedimentation. A short fibre (length smaller than the Kolmogorov length scale) responds to the local fluctuating velocity gradient in a turbulent flow by undergoing rotary motion governed by Jeffery’s equation (Jeffery Reference Jeffery1922). For a homogeneous isotropic turbulent flow, there are relationships between the initial and long-time rotational variance of neutrally buoyant fibres and the Kolmogorov shear rate (Shin & Koch Reference Shin and Koch2005; Parsa et al. Reference Parsa, Calzavarini, Toschi and Voth2012). Previous studies have considered sedimenting non-spherical particles in turbulence without inertial or gravitational torques. Siewert et al. (Reference Siewert, Kunnen, Meinke and Schröder2014) simulate sedimenting ellipsoids in turbulence and find that preferential orientation and sweeping affect sedimentation velocities. Gustavsson et al. (Reference Gustavsson, Jucha, Naso, Lévêque, Pumir and Mehlig2017) have studied orientation distributions of settling non-spherical particles in turbulence and find that turbulence creates a preferential alignment that is opposite to the stable orientation in quiescent flow. For fibres settling in a turbulent flow, the orientation behaviour is complex with turbulent velocity gradients competing with inertial torques to determine the orientation distributions (Voth & Soldati Reference Voth and Soldati2017; Kramel Reference Kramel2018).
The purposes of this paper are to provide experimental evidence for the drag forces and inertial torques acting on fibres in the presence of modest fluid inertia and to elucidate a symmetry breaking transition that occurs in the orientation of asymmetric fibres with increasing inertia or decreasing asymmetry. In § 2, we present the theoretical basis for the study. Section 2.1 reviews the predictions of Khayat & Cox (Reference Khayat and Cox1989) for symmetric fibres. In § 2.2, we show that this theory implies that asymmetric fibres undergo a sharp transition from a vertical orientation to an oblique orientation in which the inertial torque is balanced by the gravitational and viscous torques. Section 3 describes the experimental methods. Section 4 compares experimental measurements of the drag and inertial torque on symmetric fibres to the theory described in § 2.1. Section 5 provides experimental evidence for the orientational transition predicted in § 2.2.
2 Theory
Consider a slender body settling under gravity with velocity
$\boldsymbol{W}$
(see figure 1). The length of the body is
$L$
and the characteristic dimension of the cross-section is
$D$
. In § 2.1, we will first review the predictions of the leading-order slender-body theory (SBT) for Stokes flow at large aspect ratio
$\unicode[STIX]{x1D705}=L/D$
, and then present the results of the SBT of Khayat & Cox (Reference Khayat and Cox1989) which includes an Oseen approximation for fluid inertia in the outer region. (Khayat & Cox (Reference Khayat and Cox1989) define
$\unicode[STIX]{x1D705}_{KC}=D/L$
and consider
$\unicode[STIX]{x1D705}_{KC}\ll 1$
.) In § 2.2 we apply this theory to the case where the fibre radius and mass density vary along the fibre length. In § 2.3, we show via a stability analysis that asymmetric fibres exhibit a sharp transition from vertical to oblique alignment with increasing Reynolds number or decreasing asymmetry.
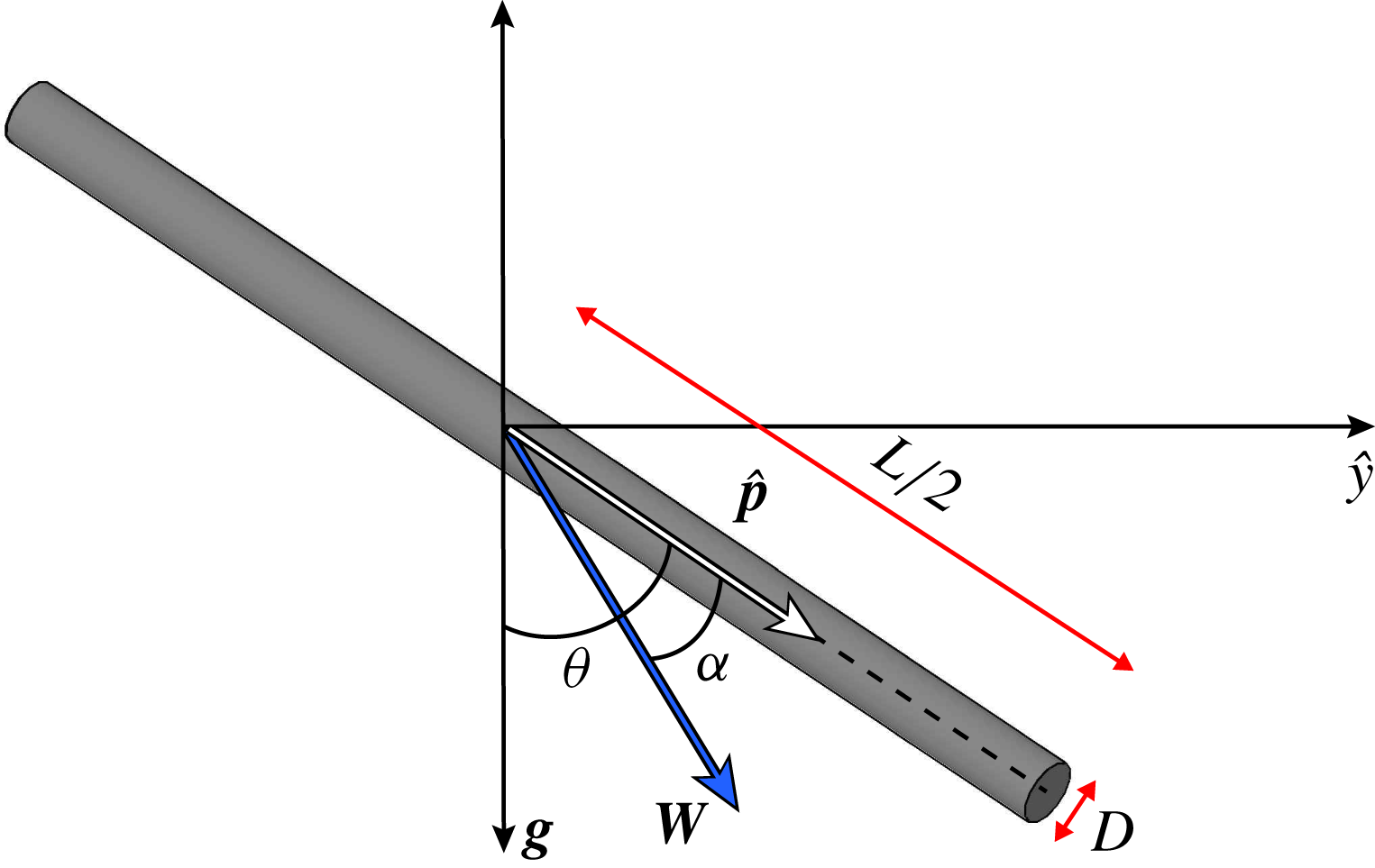
Figure 1. Schematic of a settling slender body.
$\boldsymbol{p}$
is the unit vector along the fibre axis.
$\boldsymbol{W}$
is the fibre velocity.
$\boldsymbol{g}$
is the gravitational acceleration vector.
$l=L/2$
is the half-length of the particle,
$\unicode[STIX]{x1D703}$
is the particle orientation angle and
$\unicode[STIX]{x1D6FC}$
is the angle between the sedimentation direction and the particle axis.
2.1 Forces and torques on fibres
The hydrodynamic force on a uniform cylindrical fibre obtained from Stokes slender-body theory (Batchelor Reference Batchelor1970) is to leading order at high aspect ratio
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{\boldsymbol{F}^{hydro}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}Wl}}={\displaystyle \frac{2}{\log 2\unicode[STIX]{x1D705}}}[(\cos \unicode[STIX]{x1D6FC})\boldsymbol{p}-2\;\boldsymbol{e}_{\boldsymbol{W}}], & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D707}$
is the fluid viscosity,
$\boldsymbol{p}$
the unit vector indicating the orientation of fibre axis and
$\boldsymbol{e}_{\boldsymbol{W}}=\boldsymbol{W}/W$
is the unit vector along the translation direction. From equation 2.1, we can obtain the ratio of the viscous drag due to the transverse motion to that due to the longitudinal motion to be
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{F^{\bot ,hydro}}{F^{||,hydro}}}=2, & & \displaystyle\end{eqnarray}$$
where
$F^{\bot ,hydro}=F_{z}^{hydro}(\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2)$
and
$F^{||,hydro}=F_{z}^{hydro}(\unicode[STIX]{x1D703}=0)$
. This drag anisotropy is crucial to microswimmer locomotion at low Reynolds number (Lauga & Powers Reference Lauga and Powers2009).
Khayat & Cox (Reference Khayat and Cox1989) analysed the role of fluid inertia in the motion of long slender bodies. They performed an asymptotic expansion in
$1/\log \unicode[STIX]{x1D705}$
(note the difference in perturbation expansion parameter from Batchelor (Reference Batchelor1970)) and included terms up to
$O(1/(\log \unicode[STIX]{x1D705})^{2})$
obtaining the
$Re_{l}$
-dependent force
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{\boldsymbol{F}^{hydro}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}Wl}} & = & \displaystyle {\displaystyle \frac{2}{\log \unicode[STIX]{x1D705}}}\left[(\cos \unicode[STIX]{x1D6FC})\boldsymbol{p}-2\boldsymbol{e}_{\boldsymbol{W}}\right]-\left({\displaystyle \frac{1}{\log \unicode[STIX]{x1D705}}}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\!\!\left\{2(\cos \unicode[STIX]{x1D6FC})\boldsymbol{e}_{\boldsymbol{W}}-(2-\cos \unicode[STIX]{x1D6FC}+\cos ^{2}\unicode[STIX]{x1D6FC})\boldsymbol{p}\right\}{\mathcal{C}}_{1}\right.\nonumber\\ \displaystyle & & \displaystyle -\left\{2(\cos \unicode[STIX]{x1D6FC})\boldsymbol{e}_{\boldsymbol{W}}-(2+\cos \unicode[STIX]{x1D6FC}+\cos ^{2}\unicode[STIX]{x1D6FC})\boldsymbol{p}\right\}{\mathcal{C}}_{2}\nonumber\\ \displaystyle & & \displaystyle -\,[(\cos \unicode[STIX]{x1D6FC})\boldsymbol{p}-2\boldsymbol{e}_{\boldsymbol{W}}]{\mathcal{C}}_{3}+3(\cos \unicode[STIX]{x1D6FC})\boldsymbol{p}-2\boldsymbol{e}_{\boldsymbol{W}}\nonumber\\ \displaystyle & & \displaystyle \left.+\,2\boldsymbol{e}_{\boldsymbol{W}}\boldsymbol{\cdot }\int _{-1}^{1}\boldsymbol{K}(s)\,\text{d}s+(\cos \unicode[STIX]{x1D6FC})\boldsymbol{p}\int _{-1}^{1}\log K(s)\,\text{d}s\right]+O\left({\displaystyle \frac{1}{\log \unicode[STIX]{x1D705}}}\right)^{3},\end{eqnarray}$$
where
$X=Re_{l}(1-\cos \unicode[STIX]{x1D6FC}),Y=Re_{l}(1+\cos \unicode[STIX]{x1D6FC})$
and
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{C}}_{1}={\displaystyle \frac{E_{1}(X)+\log X+\unicode[STIX]{x1D6FE}-X}{2X}} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{C}}_{2}={\displaystyle \frac{E_{1}(Y)+\log Y+\unicode[STIX]{x1D6FE}-Y}{2Y}} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{C}}_{3} & = & \displaystyle {\displaystyle \frac{1-\text{e}^{-X}}{X}}+{\displaystyle \frac{1-\text{e}^{-Y}}{Y}}+\log X+\log Y+E_{1}(X)+E_{1}(Y)\nonumber\\ \displaystyle & & \displaystyle +\,2\unicode[STIX]{x1D6FE}-2\log 4+\int _{-1}^{1}\log R_{s}\,\text{d}s.\end{eqnarray}$$
Here,
$Re_{l}=\unicode[STIX]{x1D70C}_{f}Wl/\unicode[STIX]{x1D707}$
is the Reynolds number defined based on the slender-body half-length (
$l=L/2$
),
$\unicode[STIX]{x1D6FE}=0.5772156\ldots$
is Euler’s constant and
$E_{1}(x)$
is an exponential integral function defined by
$E_{1}(x)=\int _{x}^{\infty }\text{e}^{-\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D70F}\,\text{d}\unicode[STIX]{x1D70F}$
;
$K$
is a constant scalar and
$\unicode[STIX]{x1D612}_{ij}$
a constant symmetric tensor describing the local cross-sectional shape;
$K=1$
and
$\unicode[STIX]{x1D612}_{ij}=0$
for a circular cross-section (Batchelor Reference Batchelor1970) and
$R_{s}(s)$
is the cross-sectional radius at position
$s$
. This result is valid for
$Re_{l}\ll \log \unicode[STIX]{x1D705}$
so that the third term in the expansion is small compared with the inertial contributions to the second term.
In the absence of fluid inertia, a translating body in unbounded fluid experiences no torque and will maintain its initial orientation. Fluid inertia creates a torque, which acts to rotate a fore–aft symmetric slender body toward a transverse orientation. The inertial torque calculated by Khayat & Cox (Reference Khayat and Cox1989) is
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{\boldsymbol{T}^{hydro}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}Wl^{2}}} & = & \displaystyle \left({\displaystyle \frac{1}{\log \unicode[STIX]{x1D705}}}\right)^{2}\left[\left[{\displaystyle \frac{\cos \unicode[STIX]{x1D6FC}}{X}}\left\{2+2{\displaystyle \frac{\text{e}^{-X}-1}{X}}-E_{1}(X)-\log X-\unicode[STIX]{x1D6FE}\right\}\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\,{\displaystyle \frac{\cos \unicode[STIX]{x1D6FC}}{Y}}\left\{2+2{\displaystyle \frac{\text{e}^{-Y}-1}{Y}}-E_{1}(Y)-\log Y-\unicode[STIX]{x1D6FE}\right\}\nonumber\\ \displaystyle & & \displaystyle +\,2\left\{\frac{1}{Y}\left(1+{\displaystyle \frac{\text{e}^{-Y}-1}{Y}}\right)-{\displaystyle \frac{1}{X}}\left(1+{\displaystyle \frac{\text{e}^{-X}-1}{X}}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle \left.\left.-\int _{-1}^{1}s\log R_{s}\,\text{d}s\right]\boldsymbol{p}\wedge \boldsymbol{e}_{\boldsymbol{W}}-2\boldsymbol{p}\wedge \left\{\boldsymbol{e}_{\boldsymbol{W}}\boldsymbol{\cdot }\int _{-1}^{1}s\boldsymbol{K}(s)\,\text{d}s\right\}\right]+O\left({\displaystyle \frac{1}{\log \unicode[STIX]{x1D705}}}\right)^{3}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The inertial torque vanishes for
$\unicode[STIX]{x1D6FC}=0$
and
$\unicode[STIX]{x03C0}/2$
for a slender body of uniform circular cross-section with the transverse alignment,
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/2$
, being the stable equilibrium.
2.2 Asymmetric fibres
Although Khayat & Cox (Reference Khayat and Cox1989) derived force and torque predictions (equations (2.3) and (2.7)) that allow for variations of slender-body radius along the axis, previous applications of their results have only considered fore–aft symmetric fibres. This leaves open the interesting question of how fluid inertia will influence bodies lacking fore–aft symmetry. Can we design shapes that can have lateral migration while sedimenting? For a fore–aft asymmetric body the centre of gravity does not coincide with its midpoint. The torque due to gravity about the midpoint of a sedimenting slender body is
$O(1/\log \unicode[STIX]{x1D705})$
(since the drag force balances the particle weight at
$O(1/\log \unicode[STIX]{x1D705})$
). But from (2.7), the inertial torque is
$O(Re_{l}/\log \unicode[STIX]{x1D705})^{2}$
. Thus, for most slender bodies without fore–aft symmetry, the gravitational torque will dominate the inertial torque and the body will sediment with its centreline in the vertical direction (
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D6FC}=0$
) and the centre of gravity below its midpoint as long as
$Re_{l}/\log \unicode[STIX]{x1D705}\ll 1$
. At any finite
$Re_{l}$
a fore–aft symmetric slender body (e.g. a cylinder) will sediment transversely due to the inertial torque (see figure 2
a). At
$Re_{l}=0$
, a body with asymmetry (a tapered cylinder) will always sediment with its axis aligned with gravity (see figure 2
b). The inclusion of fluid inertia induced by an asymmetric fibre introduces the possibility that a balance between gravitational and inertial torques can lead to an oblique orientation (see figure 2
c). We will consider the dynamics of two kinds of fore–aft asymmetric fibres, shown in figure 3. A cylinder of uniform circular cross-section with a centre of mass offset from its geometric centre which we will call P1 is shown in figure 3(a), and a cylinder with a step change in its radius at a point along its length which we will call P2 is shown in figure 3(b). By varying the asymmetry or the Archimedes number (which characterizes fluid inertia) we span a parameter space where the particle can transition from vertical to oblique settling orientation.
In the absence of fluid inertia (
$Re_{l}=0$
), our model particles will always have a bottom heavy alignment. For
$Re_{l}\neq 0$
, the particles also experience inertial hydrodynamic torques and the competition between inertial and gravitational torques can lead to an oblique alignment. We will show that the appearance of this oblique alignment occurs above a critical
$Re_{l}$
or below a critical degree of asymmetry via a supercritical pitch-fork bifurcation.
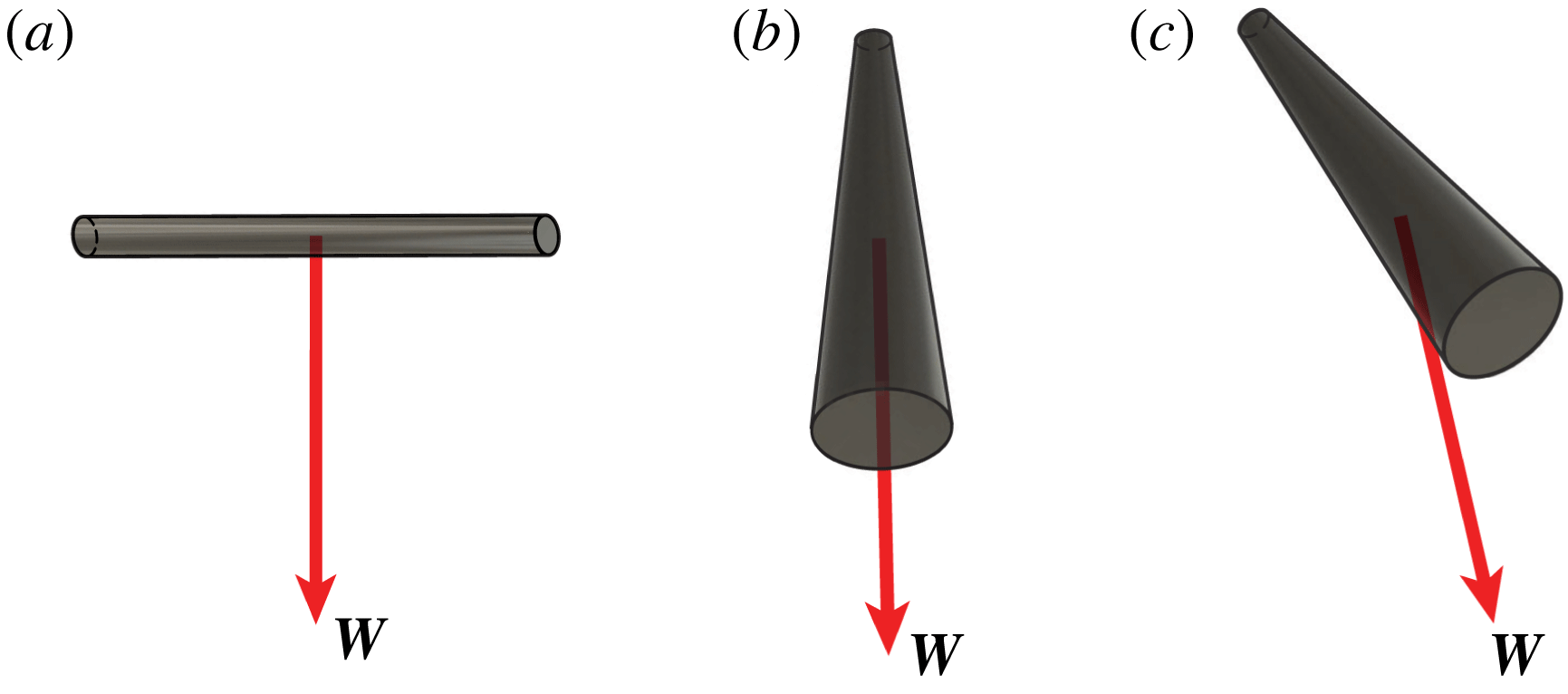
Figure 2. Equilibrium stable sedimentation orientation of (a) a fore–aft symmetric cylinder at
$Re_{l}\neq 0$
(b) a tapered cylinder at
$Re_{l}=0$
and (c) a tapered cylinder at
$Re_{l}\neq 0$
.
Figure 3. Sedimenting asymmetric fibres: (a) uniform cylinder with centre of mass offset from the midpoint which we call P1; (b) a particle consisting of two coaxial cylinders of different radii and lengths which we call P2.
The force acting on the model particles can be found from (2.3) to be
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{\boldsymbol{F}^{hydro}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}Wl\unicode[STIX]{x1D716}}} & = & \displaystyle \left[2\cos \unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D716}\left\{(3+{\mathcal{C}}_{1}+{\mathcal{C}}_{2}-{\mathcal{C}}_{3})\cos \unicode[STIX]{x1D6FC}+(2+\cos ^{2}\unicode[STIX]{x1D6FC})({\mathcal{C}}_{2}-{\mathcal{C}}_{1})\right\}\right]\boldsymbol{p}\nonumber\\ \displaystyle & & \displaystyle -\,\left[4+\unicode[STIX]{x1D716}\left\{2\cos \unicode[STIX]{x1D6FC}({\mathcal{C}}_{1}-{\mathcal{C}}_{2})+2{\mathcal{C}}_{3}-2\right\}\right]\boldsymbol{e}_{\boldsymbol{W}}\nonumber\\ \displaystyle & = & \displaystyle {\mathcal{A}}\boldsymbol{p}-{\mathcal{B}}\boldsymbol{e}_{\boldsymbol{W}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D705}=l/r$
and
$\unicode[STIX]{x1D716}=1/\log \unicode[STIX]{x1D705}$
. For particle P1 we have
$r=D/2,l=L/2$
and for P2
$r=r_{1},l=(l_{1}+l_{2})/2$
. For particle P2 the effect of fore–aft asymmetry is present in
${\mathcal{C}}_{3}$
$$\begin{eqnarray}\displaystyle {\mathcal{C}}_{3} & = & \displaystyle {\displaystyle \frac{1-\text{e}^{-X}}{X}}+{\displaystyle \frac{1-\text{e}^{-Y}}{Y}}+\log X+\log Y+E_{1}(X)+E_{1}(Y)+2\unicode[STIX]{x1D6FE}-2\log 4\nonumber\\ \displaystyle & & \displaystyle +\,\log \left[{\displaystyle \frac{4\unicode[STIX]{x1D701}}{(1+\unicode[STIX]{x1D701})^{2}}}\right]-\left({\displaystyle \frac{1-\unicode[STIX]{x1D709}}{1+\unicode[STIX]{x1D709}}}\right)\log \unicode[STIX]{x1D701},\end{eqnarray}$$
where
$\unicode[STIX]{x1D701}=r_{2}/r_{1}$
and
$\unicode[STIX]{x1D709}=l_{2}/l_{1}$
. Similarly (2.7) gives the hydrodynamic torque acting on the particle to be
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{T_{x}^{hydro}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}Wl^{2}}} & = & \displaystyle -\unicode[STIX]{x1D716}^{2}\left[{\displaystyle \frac{\cos \unicode[STIX]{x1D6FC}}{X}}\left\{2+2{\displaystyle \frac{\text{e}^{-X}-1}{X}}-E_{1}(X)-\log X-\unicode[STIX]{x1D6FE}\right\}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\cos \unicode[STIX]{x1D6FC}}{Y}\left\{2+2{\displaystyle \frac{\text{e}^{-Y}-1}{Y}}-E_{1}(Y)-\log Y-\unicode[STIX]{x1D6FE}\right\}+2\left\{{\displaystyle \frac{1}{Y}}\left(1+{\displaystyle \frac{\text{e}^{-Y}-1}{Y}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\left.{\displaystyle \frac{1}{X}}\left(1+{\displaystyle \frac{\text{e}^{-X}-1}{X}}\right)\right\}-{\displaystyle \frac{2\unicode[STIX]{x1D709}\log \unicode[STIX]{x1D701}}{(1+\unicode[STIX]{x1D709})^{2}}}\right]\sin \unicode[STIX]{x1D6FC}\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D716}^{2}{\mathcal{G}}\sin \unicode[STIX]{x1D6FC}.\end{eqnarray}$$
For particle P1, the last term is zero (
$\unicode[STIX]{x1D701}=1$
) and the hydrodynamic torque always rotates the particle toward the transverse orientation. However, for particle P2, equation (2.10) indicates that non-uniformity in the cross-section can create a non-zero Stokes torque (
$Re_{l}=0$
). At small but finite
$Re_{l}$
the torque is
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{T_{x}^{hydro}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}Wl^{2}}}\sim \unicode[STIX]{x1D716}^{2}\left[\frac{5}{6}Re_{l}\cos \unicode[STIX]{x1D6FC}+{\displaystyle \frac{2\unicode[STIX]{x1D709}\log \unicode[STIX]{x1D701}}{(1+\unicode[STIX]{x1D709})^{2}}}\right]\sin \unicode[STIX]{x1D6FC}, & & \displaystyle\end{eqnarray}$$
which indicates that the hydrodynamic torque (acting in the absence of gravitational torques) would tend to rotate the particles away from the transverse orientation for sufficiently large asymmetry. A physical situation isolating the hydrodynamic torque would occur if a neutrally buoyant particle was held in place by a pivoting pin at its centre in a uniform fluid stream. Figure 4 shows how the hydrodynamic torque (2.10) on particle P2 depends on orientation.
A freely settling particle such as those in the experiments presented in § 5 will experience forces and torques due to hydrodynamics, gravity and buoyancy effects, so that its terminal velocity and orientation will be governed by,
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{F}^{hydro}+\boldsymbol{F}^{grav}+\boldsymbol{F}^{buoy}=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{T}^{hydro}+\boldsymbol{T}^{grav}+\boldsymbol{T}^{buoy}=0. & \displaystyle\end{eqnarray}$$
Here,
$\boldsymbol{F}^{hydro}$
is given by (2.8),
$\boldsymbol{F}^{grav}=-m_{p}g\hat{z}$
, and
$\boldsymbol{F}^{buoy}=\unicode[STIX]{x1D70C}_{f}V_{p}g\hat{z}$
where
$V_{p}$
is the volume of the particle with
$V_{p}=\unicode[STIX]{x03C0}D^{2}L/4$
for P1 and
$V_{p}=\unicode[STIX]{x03C0}r_{1}^{2}l_{1}(1+\unicode[STIX]{x1D701}^{2}\unicode[STIX]{x1D709})$
for P2. The hydrodynamic torque,
$\boldsymbol{T}^{hydro}$
is given by (2.10). The gravitational torque about the midpoint is
$\boldsymbol{T}^{grav}=-mgR_{COM}\sin (\unicode[STIX]{x1D703})\hat{x}$
, where for P1 the centre of mass position,
$R_{COM}$
, is determined by the mass distribution, and for P2 the centre of mass is
$R_{COM}=l_{1}(\unicode[STIX]{x1D701}^{2}-1)\unicode[STIX]{x1D709}/(2(1+\unicode[STIX]{x1D701}^{2}\unicode[STIX]{x1D709}))$
. The buoyant torque about the midpoint is
$\boldsymbol{T}^{buoy}=0$
for P1 and
$\boldsymbol{T}^{buoy}=\unicode[STIX]{x1D70C}_{f}V_{p}\,g\,R_{COM}\sin (\unicode[STIX]{x1D703})\hat{x}$
for P2.
Figure 4. Hydrodynamic torque acting on particle P2. The cylinders are considered to be of equal length (
$\unicode[STIX]{x1D709}=1$
) while their radius ratio (
$\unicode[STIX]{x1D701}$
) is allowed to vary.
$Re_{l}=5$
.
To non-dimensionalize (2.12) and (2.13), we introduce the Archimedes number, which is the ratio of gravitational and viscous forces. We use an Archimedes number relevant to fibre sedimentation,
$$\begin{eqnarray}\displaystyle Ar={\displaystyle \frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}gV_{p}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}\unicode[STIX]{x1D716}}}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{p}-\unicode[STIX]{x1D70C}_{f}$
and
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}/\unicode[STIX]{x1D70C}_{f}$
.
Equations (2.12)–(2.13) now reduce to
$$\begin{eqnarray}\displaystyle & \displaystyle Re_{l}({\mathcal{B}}\cos (\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6FC})-{\mathcal{A}}\cos \unicode[STIX]{x1D703})=Ar & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{A}}\sin \unicode[STIX]{x1D703}-{\mathcal{B}}\sin (\unicode[STIX]{x1D703}-\unicode[STIX]{x1D6FC})=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D716}{\mathcal{G}}Re_{l}\sin \unicode[STIX]{x1D6FC}+{\displaystyle \frac{Ar}{\unicode[STIX]{x1D70C}^{\ast }}}\unicode[STIX]{x1D6FF}\sin \unicode[STIX]{x1D703}=0, & \displaystyle\end{eqnarray}$$
where
$Re_{l}=Wl/\unicode[STIX]{x1D708}$
,
$\unicode[STIX]{x1D6FF}=R_{COM}/l$
and
$\unicode[STIX]{x1D70C}^{\ast }=\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{p}$
for P1 and
$\unicode[STIX]{x1D70C}^{\ast }=1$
for P2.
${\mathcal{A}}$
and
${\mathcal{B}}$
are defined in (2.8) and
${\mathcal{G}}$
is defined in (2.10). We need to solve (2.15)–(2.17) to find the equilibrium
$\unicode[STIX]{x1D703}$
,
$\unicode[STIX]{x1D6FC}$
and
$Re_{l}$
. Combining (2.15)–(2.17) yields
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6FF}{\mathcal{B}}+\unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}^{\ast }{\mathcal{G}})\sin \unicode[STIX]{x1D6FC}=0, & & \displaystyle\end{eqnarray}$$
which clearly shows the existence of a torque equilibrium in the vertical orientation,
$\unicode[STIX]{x1D6FC}=0$
; along with the possibility of an additional equilibrium when gravitational and Stokes torques are balanced by the inertial torque,
$\unicode[STIX]{x1D6FF}{\mathcal{B}}+\unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}^{\ast }{\mathcal{G}}=0$
.
2.3 Symmetry breaking instability of the vertical orientation of asymmetric fibres
To study the stability of these equilibrium orientations we look at the total torque for small angular displacements about the
$\unicode[STIX]{x1D6FC}=0$
equilibrium orientation. From (2.18) the total torque linearized about the orientation
$\unicode[STIX]{x1D6FC}=0$
is
$$\begin{eqnarray}\displaystyle \boldsymbol{T}^{hydro}+\boldsymbol{T}^{grav}+\boldsymbol{T}^{buoy}\sim -{\displaystyle \frac{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}l\unicode[STIX]{x1D716}Re_{l}}{\unicode[STIX]{x1D70C}^{\ast }}}(\unicode[STIX]{x1D6FF}{\mathcal{B}}_{0}+\unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}^{\ast }{\mathcal{G}}_{0})\unicode[STIX]{x1D6FC}\,\hat{\boldsymbol{x}}, & & \displaystyle\end{eqnarray}$$
where expressions for
${\mathcal{B}}_{0}$
and
${\mathcal{G}}_{0}$
are given in appendix A. Here,
${\mathcal{G}}_{0}<0$
for all
$Re_{l}$
for both particles P1 and P2. For realistic fibre geometries
${\mathcal{B}}_{0}>0$
. (
${\mathcal{B}}_{0}$
changes sign for
$\unicode[STIX]{x1D716}>2(4\log 2-1-q_{1})^{-1}$
. For P1 (
$q_{1}=0$
) this translates to
$\unicode[STIX]{x1D705}\approx 2.43$
and thus would invalidate the large aspect ratio assumption of SBT;
$q_{1}<\log 4$
for all
$\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D701}$
and for particle P2 one would need size ratios of
$\unicode[STIX]{x1D709}=1,\unicode[STIX]{x1D701}=270$
for a fibre of
$\unicode[STIX]{x1D705}\approx 20$
to obtain
${\mathcal{B}}_{0}<0$
.) Since
$Re_{l}$
increases with
$Ar$
(
$Re_{l}=Ar/2$
in the Stokes drag limit of (2.15)), the total torque changes sign from a stabilizing to destabilizing one as we increase
$Ar$
for a given asymmetry
$\unicode[STIX]{x1D6FF}$
or decrease
$\unicode[STIX]{x1D6FF}$
for a given
$Ar$
. The
$\unicode[STIX]{x1D6FC}=0$
vertical configuration then becomes an unstable fixed point.
To identify the nature of the bifurcation where the system transitions from the stable fixed point of
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D703}=0$
we require a dynamical equation for the particle orientation that incorporates the resistance to particle rotation. For simplicity, we adopt the quasi-steady model of Newsom & Bruce (Reference Newsom and Bruce1994) and assume a viscous resistance to rotation obtained from Stokes flow SBT with uniform fibre radius, so that the torque balance becomes
$$\begin{eqnarray}\displaystyle \boldsymbol{T}^{hydro}+\boldsymbol{T}^{grav}+\boldsymbol{T}^{buoy}+\boldsymbol{T}^{rot}=0, & & \displaystyle\end{eqnarray}$$
where the hydrodynamic torque resisting rotation is
$$\begin{eqnarray}\displaystyle \boldsymbol{T}^{rot}=-8\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}\unicode[STIX]{x1D716}l^{3}\unicode[STIX]{x1D734}/3, & & \displaystyle\end{eqnarray}$$
and
$\unicode[STIX]{x1D734}$
is the solid-body rotation rate.
This approximation, which neglects the convection of the rotation-induced momentum disturbance by the translational motion as well as unsteady effects, may be expected to be most accurate at small to moderate
$Re_{l}$
and small asymmetry. The rotation rate (
$\unicode[STIX]{x1D6FA}$
) for a rod due to inertial torque is
$O(URe_{l}/l)$
. Thus the inertial effects due to rotation are characterized by
$Re_{\unicode[STIX]{x1D6FA}}=\unicode[STIX]{x1D6FA}l^{2}/\unicode[STIX]{x1D708}=O(Re_{l}^{2})$
. For small
$Re_{l}$
the transient effects can be neglected as they are higher-order inertia effects. Shin et al. (Reference Shin, Koch and Subramanian2006) showed using numerical simulations that the quasi-steady approximation remains valid for symmetric fibres with
$Re_{l}\approx 1$
. To analyse the stability near the transition point it is sufficient to consider the dynamical equation for the orientation at small angles
$\unicode[STIX]{x1D703}\ll 1$
. This equation, obtained by balancing the inertial, gravitational, buoyancy and rotational resistance torques, is
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{\text{d}\unicode[STIX]{x1D703}}{\text{d}t}}=-{\displaystyle \frac{3\unicode[STIX]{x1D708}Re_{l}}{4l^{2}\unicode[STIX]{x1D70C}^{\ast }}}\left({\mathcal{K}}_{2}\unicode[STIX]{x1D703}+{\mathcal{K}}_{3}\unicode[STIX]{x1D703}^{3}\right), & & \displaystyle\end{eqnarray}$$
where
${\mathcal{K}}_{2}=(\unicode[STIX]{x1D6FF}{\mathcal{B}}_{0}+\unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}^{\ast }{\mathcal{G}}_{0})\unicode[STIX]{x1D712}$
and
${\mathcal{K}}_{3}=[\unicode[STIX]{x1D6FF}({\mathcal{B}}_{2}-{\mathcal{B}}_{0})/6+\unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}^{\ast }({\mathcal{G}}_{2}-{\mathcal{G}}_{0}/6)]\unicode[STIX]{x1D712}^{3}$
. In the small angle limit,
$\unicode[STIX]{x1D6FC}=r\unicode[STIX]{x1D703}$
where
$\unicode[STIX]{x1D712}=({\mathcal{B}}_{0}-{\mathcal{A}}_{0})/{\mathcal{A}}_{0}>0$
. (For particle P2 one would need size ratios of
$\unicode[STIX]{x1D709}=1,\unicode[STIX]{x1D701}=35$
for a fibre of
$\unicode[STIX]{x1D705}\approx 20$
to obtain
$\unicode[STIX]{x1D712}<0$
.) Expressions for
${\mathcal{B}}_{2},{\mathcal{G}}_{2}$
and
${\mathcal{A}}_{2}$
are given in appendix A. The vertical configuration transitions from a stable fixed point to an unstable one when
${\mathcal{K}}_{2}$
changes sign;
${\mathcal{K}}_{3}>0$
for
$\unicode[STIX]{x1D6FF}<1.34\unicode[STIX]{x1D70C}^{\ast }$
and
${\mathcal{K}}_{2}<0$
. Thus a stable oblique orientation appears in an asymmetric fibre via a supercritical pitch-fork bifurcation.
Figure 5. Onset of oblique settling orientation for bottom heavy particles P1 and P2. Both particles have the same aspect ratio and degree of asymmetry (
$\unicode[STIX]{x1D705}=39.67$
and
$\unicode[STIX]{x1D6FF}=0.015$
).
$\unicode[STIX]{x1D70C}^{\ast }=0.31$
for P1.
Figure 5 illustrates the orientational transition for gravitationally asymmetric fibres of type P1 and P2 with
$\unicode[STIX]{x1D6FF}=0.015$
. The orientation is obtained by solving the steady state force and torque balances (equations (2.15)–(2.17)) to obtain the vertical and horizontal velocity and orientation of the freely suspended particles. The solid lines are stable and dashed lines are unstable solutions with the stability assessed using the dynamic orientational equation (2.22). The fibre remains vertical for Archimedes numbers smaller than a critical value
$Ar_{cr}=3.45$
for particle P1 and
$Ar_{cr}=0.44$
for particle P2. Two factors account for the lower value of
$Ar_{cr}$
in particles with variable radius. Firstly, the hydrodynamic torque near
$\unicode[STIX]{x1D6FC}=0$
is larger for particles with geometric asymmetry (P2) than particles with mass asymmetry (P1) (see figure 4). This is related to the fact that the
$Re_{l}=0$
hydrodynamic torque favours alignment with the large radius upward,
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}$
whereas the gravitational torque favours alignment with the large radius downward
$\unicode[STIX]{x1D6FC}=0$
. In addition, the buoyant torque,
$\boldsymbol{T}^{buoy}$
, which is present only for particle P2, acts to partially counter the gravitational torque. A supercritical pitch-fork bifurcation leads to oblique orientations above this Archimedes number. Equivalently, the bifurcation can also be observed at a critical
$\unicode[STIX]{x1D6FF}$
for fixed
$Ar$
. We illustrate this in figure 9 where we compare the theory with experiments for particles of type P1.
3 Experiments
To obtain experimental measurements of sedimentation velocity, orientation and torques on symmetric and asymmetric slender bodies, we used the set-up shown in figure 6. A Plexiglas tank 30.5 cm tall, 21 cm wide and 10.5 cm thick is filled with 50 cst silicone oil. A 1 megapixel camera records images of fibres sedimenting through the fluid at 10 or 20 frames per second. A Nila Zaila Tungsten LED light illumines a diffuser plate on the back of the tank to provide bright field imaging. In order to study effects of tank size, we created a moveable wall that restricts the smallest dimension of the tank, the thickness.
An experiment consists of holding a fibre with tweezers and fully submerging it into the fluid. The particle is released and its entire trajectory is imaged with a resolution of 250
$\unicode[STIX]{x03BC}$
m pixel
$^{-1}$
. Particles typically can be released so that they sediment with their symmetry axis nearly in the image plane, and drops that deviate from the image plane by more than few degrees are discarded. In initial experiments with lower viscosity fluid, fluid currents were a challenge. With 50 cst silicone oil and waiting at least a minute between experiments, we were not able to detect any effects of fluid currents.
Figure 6. Apparatus used in the experiments.
3.1 Fabrication of symmetric and asymmetric particles
A major challenge in these experiments is obtaining particles with adequate dimension tolerances. We found that we are able to create precision particles from glass capillary tubes filled with UV curing optical glue. This allows creation of symmetric particles by filling the entire particle and also creation of asymmetric particles of type P1 by adding bubbles to the glue on one side. We used glass capillary tubes with exterior diameter of 715
$\unicode[STIX]{x03BC}$
m and interior diameter of 500
$\unicode[STIX]{x03BC}$
m to fabricate particles with aspect ratios ranging from 20 to 100. Since the glue is transparent, some dye is needed to absorb light for bright field imaging. We had tried Rhodamine B as a fluorescent dye with dark field imaging, and concluded that the fluorescence was not effective, but Rhodamine B was a convenient absorbing dye for bright field imaging that allowed enough UV penetration to harden the glue.
Parameters for the particles we studied are given in table 1. The Reynolds number based on the diameter is in the range
$Re_{D}=WD/\unicode[STIX]{x1D708}=0.15$
to
$0.17$
. It is necessary for
$Re_{D}$
to be of this order or smaller in order to ignore inertial effects in the inner region. A calculation of the drag on an infinite cylinder that includes nonlinear inertial effects near the cylinder (Keller & Ward Reference Keller and Ward1996) is within 7 % of one that excludes such effects (see Tomotika & Aoi (Reference Tomotika and Aoi1951) and Lamb (Reference Lamb1932)) at this value of
$Re_{D}$
.
We tried many different fabrication processes before settling on glue filled glass capillaries. Early particle fabrication of symmetric and asymmetric particles with a three-dimensional (3-D) printer (Form1+ photopolymerization printer from Formlabs) allowed us to create asymmetric particles with different diameters on the two ends, type P2. However, the surface roughness was large enough to substantially affect sedimentation. An alternative technique to fabricating particles of type P2 was through machining a Teflon rod on a lathe. This process creates high surface quality, but the minimum diameter possible was 2.5 mm. At the larger Reynolds numbers of these particles, the asymmetry at the transition from horizontal to vertical is quite large. And at large asymmetries, the hydrodynamic effects of the step change in radius between the two ends become important. We finally decided to only study particles of type P1 using capillary particles because of their tight tolerances and ability to control asymmetry while still accessing Reynolds numbers at which the theory is quantitatively accurate.
Table 1. Parameters of the particles used in the experiments.
3.2 Centre of mass measurement
To calculate the centre of mass of each particle,
$R_{COM}$
, we support the particle on two razor edges and measure the force on one of the edges with a precision balance (Metter Toledo XSE105 with 0.01 mg resolution). The locations of the supporting razor edges on the particle are measured from digital images (Nikon D500 with 200 mm macro lens). With additional measurements of the length and mass of each particle, we can determine the position of the centre of mass,
$R_{COM}$
(defined as the distance from the geometric centre), and the asymmetry,
$\unicode[STIX]{x1D6FF}=R_{COM}/l$
. We fabricated 18 particles with measured asymmetries ranging from
$\unicode[STIX]{x1D6FF}=0.0003$
to
$0.074$
that are shown in figure 9. Repetition of the centre of mass measurement on the same particle flipped by 180
$^{\circ }$
shows the uncertainty in the measured
$R_{COM}$
is less than
$0.006l$
.
4 Results: symmetric fibres
Here we first present measurements of sedimentation velocity and inertial torques for symmetric fibres. We will compare with three models: the Stokes slender-body theory of (2.1), the theory of Khayat & Cox (Reference Khayat and Cox1989) in (2.8) and (2.10), and the linearization of the Khayat and Cox theory from Lopez & Guazzelli (Reference Lopez and Guazzelli2017).
4.1 Sedimentation velocity for
$\unicode[STIX]{x1D705}=20$
and
$\unicode[STIX]{x1D705}=100$
symmetric fibres
Figure 7(a) shows the measured sedimentation velocity of the symmetric
$\unicode[STIX]{x1D705}=20$
particles as a function of sedimentation angle. Both the vertical and horizontal velocities are in reasonably good agreement with all three models; however, the model from Khayat & Cox (Reference Khayat and Cox1989) as well as the linearization from Lopez & Guazzelli (Reference Lopez and Guazzelli2017) agree better than the Stokes SBT. Figure 7(b) shows the sedimentation velocities for the symmetric
$\unicode[STIX]{x1D705}=100$
particles. The
$\unicode[STIX]{x1D705}=100$
particles do not rotate quickly enough to sample all orientations in a single drop, so we used multiple drops at different initial orientations to sample the velocity as a function of orientation. Again the model from Khayat & Cox (Reference Khayat and Cox1989) and the linearization from Lopez & Guazzelli (Reference Lopez and Guazzelli2017) agree well with the measurements, but here the Stokes drag model is significantly worse. In these experiments, higher aspect ratio coincides with higher Reynolds number (
$\unicode[STIX]{x1D705}=20$
has
$Re_{l}=1.62$
and
$\unicode[STIX]{x1D705}=100$
has
$Re_{l}=8.57$
), so the more slender fibres for which
$1/\log \unicode[STIX]{x1D705}$
is smaller have larger inertial effects. Extending the Stokes SBT to include
$(1/\log \unicode[STIX]{x1D705})^{2}$
terms in the low
$Re_{l}$
limit does not significantly improve the comparison of Stokes SBT with the experimental settling velocities in figure 7, presumably because the experiments are not at sufficiently low
$Re_{l}$
. For the
$\unicode[STIX]{x1D705}=100$
particle, the condition
$Re_{l}\ll \log \unicode[STIX]{x1D705}$
is violated but the agreement of experiments and the slender-body theory that includes fluid inertia is quite good.
Figure 7. Sedimentation velocity as a function of particle orientation for symmetric fibres with (a) aspect ratio
$\unicode[STIX]{x1D705}=20$
and (b) aspect ratio
$\unicode[STIX]{x1D705}=100$
. The upper curves are the vertical velocities and the lower curves are the horizontal velocities. Symbols show measurements of three different fibres. The dot-dash red line is the Stokes slender-body theory, the dashed black line is the full model from Khayat & Cox (Reference Khayat and Cox1989), the solid black line is the linearization from Lopez & Guazzelli (Reference Lopez and Guazzelli2017).
4.2 Inertial torque for
$\unicode[STIX]{x1D705}=20$
and
$\unicode[STIX]{x1D705}=100$
symmetric fibres
Figure 8. Inertial torques as a function of fibre orientation for symmetric fibres with (a) aspect ratio
$\unicode[STIX]{x1D705}=20$
and (b) aspect ratio
$\unicode[STIX]{x1D705}=100$
. Symbols show measurements of inertial torques. The dot-dash red line is the Stokes slender-body theory, and the dashed black line is the full model from Khayat & Cox (Reference Khayat and Cox1989).
Figure 8 shows the measured inertial torque on symmetric fibres for
$\unicode[STIX]{x1D705}=20$
and
$100$
. In order to determine the inertial torque on a fibre, we experimentally measure the rotation rates of fibres and use the quasi-steady model in (2.20) and (2.21) to determine the inertial torque from the known gravitational, buoyant and rotational torques. In the figure, we show the model of Khayat & Cox (Reference Khayat and Cox1989) for the inertial torque and find that it is in good agreement with the measurements.
Shin et al. (Reference Shin, Koch and Subramanian2006) compared numerical solutions of the full Navier–Stokes equation to an Oseen approximation similar to that of Khayat & Cox (Reference Khayat and Cox1989) but allowing for the periodic boundary conditions used in the simulations. They found the theory to be quantitatively accurate for
$Re_{l}\leqslant 2$
and to underpredict the inertial torque by about 23 % at
$Re_{l}\approx 6$
. Our measured torques are somewhat smaller than the prediction for
$\unicode[STIX]{x1D705}=20$
where
$Re_{l}=1.6$
and somewhat larger for
$\unicode[STIX]{x1D705}=100$
where
$Re_{l}=8.6$
, consistent with the trend in Shin et al. (Reference Shin, Koch and Subramanian2006). (It should be noted that the simulations of Shin et al. (Reference Shin, Koch and Subramanian2006) used a line of forces so that unlike the present experiments they did not test the accuracy of the inner solution at finite
$Re_{D}$
.) However, the observed differences between the measurements and model predictions are of the same order as the reproducibility of the measurements. So, the differences between theory and experiment may be due to defects in the fibres which produce slight asymmetries. In addition, there might be deviations due to limits of the quasi-steady approximation and to non-zero
$Re_{D}$
.
Figure 9. Equilibrium settling orientation for fibres with different asymmetries,
$\unicode[STIX]{x1D6FF}$
. Black circles with error bars in (a) and (b) are the experimental data. (a) Theoretical prediction of (2.15)–(2.17) for Archimedes numbers that correspond to the minimum (dashed) and maximum (solid) density of the experimental particles. (b) Theoretical prediction of (2.15)–(2.17) for the measured density of the particle at each asymmetry.
5 Results: asymmetric fibres
We have previously discussed that settling of asymmetric fibres can result in either a vertical sedimentation orientation or an oblique orientation where the hydrodynamic torque due to fluid inertia balances the gravitational and buoyant torques. Figure 9 shows the measured equilibrium orientations of the 18 different asymmetric fibres of type P1 (mass asymmetry). There is a clear transition where particles with asymmetry in the range
$0<\unicode[STIX]{x1D6FF}<0.03$
sediment in an oblique orientation while particles with larger asymmetry sediment in a vertical orientation. The theoretical calculation in § 2 of the equilibrium orientation for particles at
$Ar=16.4$
and
$Ar=8.7$
is also shown in figure 9(a). This range of Archimedes numbers is chosen to span the minimum and maximum of the experimental particles which have different densities due to the different volume of bubbles. The experiments are consistent with the theoretical prediction of a sharp transition from oblique to vertical sedimentation. The orientation measurements are in good agreement with the theoretical prediction for
$\unicode[STIX]{x1D703}>45^{\circ }$
, while the experiments suggest a transition to vertical alignment at a slightly larger asymmetry than that predicted by the theory. Figure 9(b) compares the experiments with theoretical calculations performed for the Archimedes numbers of each individual particle.
Figure 10. Normalized fibre velocity as a function of fibre asymmetry,
$\unicode[STIX]{x1D6FF}$
. (a) The velocity component parallel to gravity. (b) The velocity component perpendicular to gravity. Black circles are the experimental data. The curves show the theoretical prediction of (2.15)–(2.17) for Archimedes numbers that correspond to the minimum (dashed) and maximum (solid) density of the experimental particles.
Figure 10 shows the normalized vertical and horizontal velocities (
$W^{\ast }=W/Ar$
) of the asymmetric fibres for which there is qualitative agreement between theory and experiments. The amplitudes of the variations in both components of the velocity are predicted well by the theory, but there is some scatter in the experimental velocities whose cause is discussed in the Appendix.
The phase boundary in
$Ar$
-
$\unicode[STIX]{x1D6FF}$
space between particles with oblique (open symbols) and vertical (closed symbols) sedimentation orientation is presented in figure 11. To obtain the phase boundary theoretically, we numerically solve (2.15)–(2.17) to obtain the solid line. We also derive an analytical approximation for the phase boundary by expanding the equilibrium equations for
$\unicode[STIX]{x1D703},\unicode[STIX]{x1D6FC}\ll 1$
. From (2.18) we then have a relation involving the asymmetry
$\unicode[STIX]{x1D6FF}$
and the transition
$Re_{l}$
. In a freely settling problem the parameters we control are the asymmetry (
$\unicode[STIX]{x1D6FF}$
) and the Archimedes number (
$Ar$
). We make one further approximation to obtain the analytical expression. We assume that during the transition, the force equilibrium in the vertical direction is dominated by the Stokes drag and the weight of the particle. This gives us
$Re_{l}\sim Ar/2$
from (2.18).
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}\sim -\left.{\displaystyle \frac{\unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}^{\ast }{\mathcal{G}}_{0}}{{\mathcal{B}}_{0}}}\right|_{Re_{l}=Ar/2}. & & \displaystyle\end{eqnarray}$$
The analytical expression (dashed line) is a good approximation of the numerical result. The quantitative agreement between theory and experiment is fairly good with the transition possibly occurring at slightly higher asymmetry in the experiments than in the theory, as might be expected based on the larger torques obtained with the full Navier–Stokes solution of Shin et al. (Reference Shin, Koch and Subramanian2006).
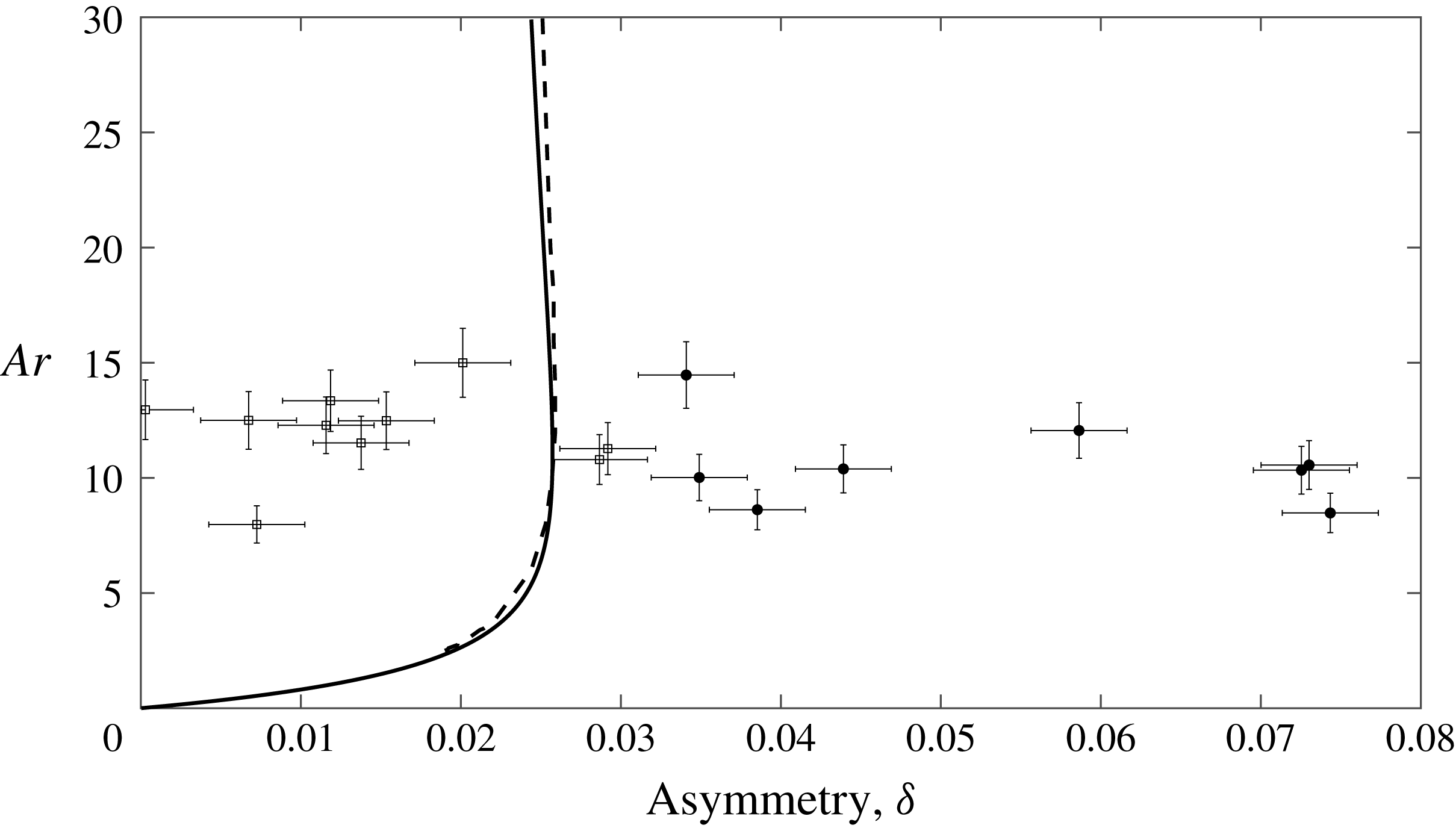
Figure 11. Phase diagram in the Archimedes asymmetry plane showing where particles sediment in oblique and vertical orientations. Experimental data with error bars are shown in the figure with filled circles for vertically settling fibres and empty squares for oblique settling ones. The solid line is the numerically obtained phase boundary whereas the dashed line is the analytical approximation (5.1).
6 Conclusions
We have presented experimental measurements to validate the predictions of Khayat & Cox (Reference Khayat and Cox1989) for the forces and torques on sedimenting slender fibres when viscous forces dominate on the fibre diameter scale while fluid inertia is important on the fibre length scale. For symmetric fibres, the forces and torques as a function of fibre orientation were inferred using a quasi-static approximation in which the inertial torque due to fibre translation is balanced by a viscous resistance to rotation. In addition, measurements of the terminal orientation of gravitationally asymmetric fibres provided a measure of the torque due to translation in the absence of transient effects. The experimental conditions were chosen to conform as closely as practically possible to the restriction of the theory to high particle aspect ratio
$\unicode[STIX]{x1D705}\gg 1$
, small inertial effects on the particle diameter scale
$Re_{D}\ll 1$
and moderate inertial effects on the fibre length scale
$Re_{l}\ll \log \unicode[STIX]{x1D705}$
while still allowing observation of deviations from Stokes SBT. The value of
$Re_{D}$
was maintained nearly constant (0.15–0.18) at values for which nonlinear inertial effects in the inner region would be modest (
${\approx}7\,\%$
). Experiments with symmetric fibres of
$\unicode[STIX]{x1D705}=20$
and
$Re_{l}=1.62$
showed good agreement with the theory of Khayat & Cox (Reference Khayat and Cox1989) and modest but measurable deviations from Stokes SBT. For longer particles with
$Re_{l}=8.57$
and
$\unicode[STIX]{x1D705}=100$
where the deviation from Stokes SBT is more dramatic, the comparison with the theory of Khayat & Cox (Reference Khayat and Cox1989) remains quite good even though the condition
$Re_{l}\ll \log \unicode[STIX]{x1D705}$
is violated.
We predicted and observed a supercritical pitch-fork bifurcation in the orientation of settling asymmetric fibres with increasing Archimedes number or decreasing particle asymmetry. At small Archimedes number
$Ar$
or large asymmetry
$\unicode[STIX]{x1D6FF}$
, the particles settle vertically. Above a critical
$Ar$
or below a critical
$\unicode[STIX]{x1D6FF}$
the particles take on stable steady oblique orientations and translate horizontally as well as vertically. Since inertia favours broadside orientation and gravitational torques favour vertical orientation, one would expect a variation in the orientation with
$Ar$
and
$\unicode[STIX]{x1D6FF}$
. This transition occurs at a critical point because the gravitational and hydrodynamic torques both go to zero in proportion to
$\unicode[STIX]{x1D6FC}$
as the particle approaches vertical alignment with coefficients that depend on
$Ar$
and
$\unicode[STIX]{x1D6FF}$
. Because the inertial torque on slender fibres is relatively modest, the transition to vertical orientation occurs at modest values of the asymmetry.
The fact that very small asymmetry can dramatically affect the sedimentation orientation of fibres has important consequences. The traditional interpretation of ice halos from clouds is that particles adopt an equilibrium orientation for symmetric particles. However, if asymmetries of just a few per cent are able to turn fibres to nearly vertical sedimentation orientations, then details about the particle shape and mass distribution will be important to particle orientation distributions.
Acknowledgements
This work was supported by the Army Research Office under grant W911NF-15-1-0205. We thank C. Etson for use of the precision balance, and B. Strickland for fabrication of the Teflon particles. We have benefited from conversations with E. Guazelli, D. Lopez, B. Mehlig, F. Lundell and S. Kramel.
Figure 12. Normalized vertical sedimentation velocities of horizontally oriented fibres of two aspect ratios as a function of tank thickness. The experimental results for
$\unicode[STIX]{x1D705}=20$
fibres with masses
$m=0.00987~\text{g}$
and
$m=0.01038~\text{g}$
are shown with crosses and right arrows respectively. The experimental results of
$\unicode[STIX]{x1D705}=100$
fibres with mass
$m=0.05344~\text{g}$
and
$m=0.04957~\text{g}$
shown with diamonds and stars, respectively. Dashed lines in both red and black represent theoretical predictions for
$\unicode[STIX]{x1D705}=20$
fibres in an infinite domain, and dashed lines in green and dark blue represent theoretical predictions for
$\unicode[STIX]{x1D705}=100$
fibres in an infinite domain.
Appendix A. Coefficients for the orientational dynamics near the transition point
The drag and torque coefficients
${\mathcal{A}},{\mathcal{B}}$
and
${\mathcal{G}}$
in (2.19) and (2.22), are expanded for
$\unicode[STIX]{x1D6FC}\ll 1$
as
${\mathcal{A}}={\mathcal{A}}_{0}+{\mathcal{A}}_{2}\unicode[STIX]{x1D6FC}^{2}$
,
${\mathcal{B}}={\mathcal{B}}_{0}+{\mathcal{B}}_{2}\unicode[STIX]{x1D6FC}^{2}$
and
${\mathcal{G}}={\mathcal{G}}_{0}+{\mathcal{G}}_{2}\unicode[STIX]{x1D6FC}^{2}$
where
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{0}=2-\unicode[STIX]{x1D716}{\displaystyle \frac{2(1-Re_{l})(E_{1}(2R)+\unicode[STIX]{x1D6FE}+\log (2Re_{l}))+e^{-2Re_{l}}+2Re_{l}(4\log (2)-q1)-1}{2Re_{l}}} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{A}}_{2}=\nonumber\\ \displaystyle & & \displaystyle \,-1+\unicode[STIX]{x1D716}{\displaystyle \frac{(1-4Re_{l})(E_{1}(2Re_{l})+\log (2Re_{l})+\unicode[STIX]{x1D6FE})+Re_{l}^{2}+(1-\text{e}^{-2Re_{l}})+4Re_{l}(4\log (2)+q1)}{8Re_{l}}}\quad \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{B}}_{0} & = & \displaystyle 4-{\displaystyle \frac{\unicode[STIX]{x1D716}}{2Re_{l}}}\big[(E_{1}(2Re_{l})+\log (2Re_{l})+\unicode[STIX]{x1D6FE}-2)(1-4Re_{l})\nonumber\\ \displaystyle & & \displaystyle +\,4Re_{l}(4\log 2-q1)-10Re_{l}+2\text{e}^{-2Re_{l}}\big]\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{B}}_{2}={\displaystyle \frac{\unicode[STIX]{x1D716}\{E_{1}(2Re_{l})+Re_{l}(3Re_{l}-8)-3\text{e}^{-2Re_{l}}+\log (2Re_{l})+\unicode[STIX]{x1D6FE}+3\}}{8Re_{l}}} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{G}}_{0}=q2-1-{\displaystyle \frac{Re_{l}\{E_{1}(2Re_{l})+\log (2Re_{l})+\unicode[STIX]{x1D6FE}-4\}-2\text{e}^{-2Re_{l}}+2}{2Re_{l}^{2}}} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{G}}_{2}={\displaystyle \frac{Re_{l}\{E_{1}(2Re_{l})+\log (2Re_{l})+\unicode[STIX]{x1D6FE}+Re_{l}^{2}+1\}-2+(3Re_{l}+2)\text{e}^{-2R}}{8Re_{l}^{2}}}, & \displaystyle\end{eqnarray}$$
where
$q1=\log [4\unicode[STIX]{x1D701}/(1+\unicode[STIX]{x1D701})^{2}]-(1-\unicode[STIX]{x1D709})/(1+\unicode[STIX]{x1D709})\log \unicode[STIX]{x1D701}$
and
$q2=-2\unicode[STIX]{x1D709}/(1+\unicode[STIX]{x1D709})^{2}\log \unicode[STIX]{x1D701}$
. For particle P1,
$q1=q2=0$
.
Appendix B. Quantifying the tank size effect
It is known that the sedimentation velocity of fibres in a finite tank of quiescent fluid can be substantially different than the case without boundaries (Jayaweera & Mason Reference Jayaweera and Mason1965). In figure 12, we show the changes in the vertical sedimentation velocity of symmetric fibres as the smallest dimension of the tank is changed. The particles sediment in a horizontal orientation with their axes perpendicular to the smallest dimension of the tank. As the tank thickness is decreased, the sedimentation velocity decreases, but the effect is fairly small. For the
$\unicode[STIX]{x1D705}=20$
fibres with
$L=14.4$
mm and
$D=0.715$
mm, there is a 9 % difference between the sedimentation velocity in a 20 mm thick tank and a 90 mm thick tank. For
$\unicode[STIX]{x1D705}=100$
fibres with
$L=72.2$
mm and
$D=0.715$
mm this difference is 16 %. The curvature suggests that the sedimentation velocity in the 90 mm tank is within a few per cent of its value in a tank of infinite size. Two factors may account for the relatively modest effects of tank size observed in the experiments. Firstly, slender bodies tend to produce a weak fluid velocity disturbance so that hydrodynamic reflections with the walls decrease with increasing aspect ratio. Secondly, inertia has the effect of producing wakes extending in the vertical direction and limiting the lateral transport of momentum near the particle position.
The comparison between the data and theoretical predictions in figure 12 as well as the data in figure 7 show that there are systematic differences of up to 10 % between the measured sedimentation velocity of different particles. These differences are bigger than is predicted by the theory for the measured masses and dimensions and are of the same order as the tank size effect. We do not currently know the cause of this variation. We suspect there may be effects from determining the volume displaced by the particles because of the slightly unreproducible shrinkage of the UV glue upon curing. There may also be effects from dust and other impurities attached to the surface of the particles. These experiments are much more delicate than we initially expected them to be, and there is need for future work on precision measurements of sedimenting fibres.
