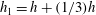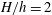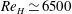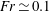1 Introduction
Characterization of the flow within and above canopies has been the subject of numerous studies in the last few decades due to its relevance in multiple industrial, atmospheric and environmental applications. In atmospheric science, for example, understanding the flow above and within plant canopies is vital to the quantification of the exchange of carbon dioxide and oxygen among other scalars (Lai et al. Reference Lai, Katul, Oren, Ellsworth and Schäfer2000). Furthermore, the interaction between the atmospheric boundary layer and urban canopies governs a multitude of processes, including pollutant transport (Belcher Reference Belcher2005) and microclimate (Souch & Grimmond Reference Souch and Grimmond2006). The physics of such interaction is further complicated by the inherent inhomogeneity of urban structures (Coceal & Belcher Reference Coceal and Belcher2004). From an environmental standpoint, aquatic vegetation regulates the kinematics and dynamics of the flow in rivers and wetlands. It supplies numerous services to the ecosystem, including the damping of water waves (Fonseca & Cahalan Reference Fonseca and Cahalan1992), providing habitat to multiple species (Hawkins et al. Reference Hawkins, Murphy, Anderson and Wilzbach1983) and enhancement of local water quality (Dennison et al. Reference Dennison, Orth, Moore, Stevenson, Carter, Kollar, Bergstorm and Batiuk1993).
The aforementioned systems share many common flow features; however, a distinction is made in the literature based on the flow confinement. Terrestrial canopies occupy a relatively small fraction of the boundary layer, whereas the flow above aquatic canopies is confined by the free surface. The former case has been studied more frequently with multiple key reviews, given by e.g. Raupach & Thom (Reference Raupach and Thom1981), Finnigan (Reference Finnigan2000) and Belcher, Harman & Finnigan (Reference Belcher, Harman and Finnigan2011). For the latter, a further distinction is made based on whether the canopy elements are fully submerged or emergent (filling the entire fluid depth or penetrating the free surface). This paper focuses on confined, submerged canopies and, from this point on, the discussion will be tailored to this case. Here, canopy density governs many aspects of the flow, including mixing and scalar transport (Poggi et al. Reference Poggi, Porporato, Ridolfi, Albertson and Katul2004; Nezu & Sanjou Reference Nezu and Sanjou2008; Tanino & Nepf Reference Tanino and Nepf2008; Chen, Jiang & Nepf Reference Chen, Jiang and Nepf2013). For dense canopies, the mean velocity profile shows an inflection near the top of the elements leading to Kelvin–Helmholtz (KH) instability (Raupach, Finnigan & Brunet Reference Raupach, Finnigan and Brunet1996). Furthermore, an obstructed shear layer that resembles a free shear layer develops and partially penetrates the canopy. The length scale of penetration has been observed to be a function of canopy density and the drag coefficient. A recent review conducted by Nepf (Reference Nepf2012) has summarized these features. The review has also identified flow phenomenon relevant to sparse submerged canopies as well as emergent ones.
The shear layer penetrates into the canopy and enhances vertical momentum transport. Based on this, Nepf & Vivoni (Reference Nepf and Vivoni2000) divided the flow into two regions: an upper region, ‘vertical exchange zone’; and a lower one, ‘longitudinal exchange zone’. The vertical exchange zone is characterized by significant turbulent transport due to the mixing layer formed above the canopy, while advection in the streamwise direction predominates within the longitudinal exchange zone. Similarly, Poggi et al. (Reference Poggi, Porporato, Ridolfi, Albertson and Katul2004) partitioned the flow into three regions based on the flow length scales. There, the topmost region resembles a rough boundary layer and exhibits similar scales. In the bottommost region, the flow is dominated by element-scale vortices (von Kármán vortices); this region extends from the bed to where the mixing layer penetrates the deepest. The middle region represents a superposition of the mixing layer and the other two regions.
In addition to categorizing the different flow regions based on turbulent transport and length scales, multiple studies investigated the turbulent structure of these flows. Poggi et al. (Reference Poggi, Porporato, Ridolfi, Albertson and Katul2004), Nezu & Sanjou (Reference Nezu and Sanjou2008) and Chen et al. (Reference Chen, Jiang and Nepf2013), among others, used quadrant analysis to quantify the relative contribution of sweep to ejection events within the different regions of the flow. These studies showed that sweeps were dominant closer to the canopy, bringing high-speed fluid into it, while ejections were dominant above the canopy. Regarding flow confinement, Nepf & Vivoni (Reference Nepf and Vivoni2000) showed that the vertical exchange zone deepens between submergence depth
![]() $H/h=1{-}2$
. Here, submergence depth is defined as the ratio of the fluid depth
$H/h=1{-}2$
. Here, submergence depth is defined as the ratio of the fluid depth
![]() $H$
to canopy height
$H$
to canopy height
![]() $h$
. However, for submergence depths 2–5, the mixing layer penetration is set by the drag coefficient and canopy density.
$h$
. However, for submergence depths 2–5, the mixing layer penetration is set by the drag coefficient and canopy density.
Moreover, recent evidence suggests a significant role of dispersive stresses for sparse canopies (Poggi et al. Reference Poggi, Porporato, Ridolfi, Albertson and Katul2004). Other recent studies include characterizing of canopy drag at different scales (e.g. Tanino & Nepf Reference Tanino and Nepf2008; Luhar & Nepf Reference Luhar and Nepf2013), flexible canopies resembling vegetation (e.g. Denny & Cowen Reference Denny, Gaylord and Cowen1997; Dijkstra & Uittenbogaard Reference Dijkstra and Uittenbogaard2010; Luhar & Nepf Reference Luhar and Nepf2011) and examining the flow adjacent to canopies (e.g. White & Nepf Reference White and Nepf2007; Rominger & Nepf Reference Rominger and Nepf2011). The majority of the previous work has focused on the flow features considering homogeneous canopies consisting of elements of equal height and cross-section. The effect of canopy element heterogeneity on the discussed flow features is far from being well understood and quantified. A recent study by Bai, Katz & Meneveau (Reference Bai, Katz and Meneveau2015) considered a canopy homogeneous in height but consisting of multiple fractal trees and used particle image velocimetry (PIV) in a refractive-index-matching channel to identify the effect of such multiscale elements on the horizontal turbulent transport within canopies. They found that fractal trees increased dispersive stresses and generated wakes that resemble their shapes.
The current work addresses important fundamental questions regarding the effect of canopy height heterogeneity on the mean flow, turbulent statistics and the features of the mixing layer. We present a well-controlled experimental study of the flow within and over two model canopies: a homogeneous one (base case) with elements of equal height, and a heterogeneous case with elements of two heights. The heterogeneous model resembles a row canopy (e.g. Weiss & Allen Reference Weiss and Allen1976; Heilman et al. Reference Heilman, McInnes, Savage, Gesch and Lascano1994; Chahine et al. Reference Chahine, Dupont, Sinfort and Brunet2014). The two models share the same density, element geometry and mean height. We use high-resolution PIV in a refractive-index-matching channel to characterize the flow within three fields of view spanning the entire canopy, allowing for the study of flow adjustment and mixing layer growth under various submergence depths. The experimental set-up is described in § 2; the experimental measurements are analysed and discussed in § 3; and the conclusions of this work are presented in § 4.
2 Experimental set-up
The flow within and above homogeneous and heterogeneous canopies was experimentally studied in a 2.5 m long, 11.25 cm wide, recirculating, refractive-index-matching (RIM), open channel. The coordinate system is defined such that
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
denote the streamwise, wall-normal and spanwise directions, with
$z$
denote the streamwise, wall-normal and spanwise directions, with
![]() $x=0$
at the canopy leading edge. The canopy models consisted of acrylic square bars with side
$x=0$
at the canopy leading edge. The canopy models consisted of acrylic square bars with side
![]() $d=6.4$
mm arranged in a staggered configuration (see figure 1
a). The elements of the homogeneous canopy had a height
$d=6.4$
mm arranged in a staggered configuration (see figure 1
a). The elements of the homogeneous canopy had a height
![]() $h=37.5$
mm; whereas the heterogeneous canopy consisted of elements with heights
$h=37.5$
mm; whereas the heterogeneous canopy consisted of elements with heights
![]() $h_{1}=h+(1/3)h=50$
mm and
$h_{1}=h+(1/3)h=50$
mm and
![]() $h_{2}=h-(1/3)h=25$
mm arranged in an alternating manner such that two rows of height
$h_{2}=h-(1/3)h=25$
mm arranged in an alternating manner such that two rows of height
![]() $h_{1}$
were followed by two rows of height
$h_{1}$
were followed by two rows of height
![]() $h_{2}$
. The average element height for the heterogeneous model was then
$h_{2}$
. The average element height for the heterogeneous model was then
![]() $\bar{h}=h=37.5$
mm, i.e. the same as that of the homogeneous case. Figure 1(b) illustrates the geometry of both canopy models and highlights the equivalence of their average element height. Both canopy models spanned the entire width of the channel, had a length
$\bar{h}=h=37.5$
mm, i.e. the same as that of the homogeneous case. Figure 1(b) illustrates the geometry of both canopy models and highlights the equivalence of their average element height. Both canopy models spanned the entire width of the channel, had a length
![]() $L=21.3h$
and were placed
$L=21.3h$
and were placed
![]() $28h$
from the inlet. The total frontal area facing the flow is equal for both canopies, resulting in a roughness density (defined as the total frontal area per bed unit area (Finnigan Reference Finnigan2000))
$28h$
from the inlet. The total frontal area facing the flow is equal for both canopies, resulting in a roughness density (defined as the total frontal area per bed unit area (Finnigan Reference Finnigan2000))
![]() $\unicode[STIX]{x1D706}_{f}=1.2$
, and categorizing the canopies as dense. The frontal area per canopy volume is
$\unicode[STIX]{x1D706}_{f}=1.2$
, and categorizing the canopies as dense. The frontal area per canopy volume is
![]() $a=n_{s}d=32~\text{m}^{-1}$
for the homogeneous canopy, whereas for the heterogeneous one
$a=n_{s}d=32~\text{m}^{-1}$
for the homogeneous canopy, whereas for the heterogeneous one
![]() $a=32~\text{m}^{-1}$
and 16 m
$a=32~\text{m}^{-1}$
and 16 m
![]() $^{-1}$
below and above
$^{-1}$
below and above
![]() $h_{2}$
. Here,
$h_{2}$
. Here,
![]() $n_{s}$
denotes the number of elements per bed unit area. The canopy solid volume fraction
$n_{s}$
denotes the number of elements per bed unit area. The canopy solid volume fraction
![]() $\unicode[STIX]{x1D719}$
(also referred to as area blockage) was set at 20 % for both models. Aqueous sodium iodide solution (
$\unicode[STIX]{x1D719}$
(also referred to as area blockage) was set at 20 % for both models. Aqueous sodium iodide solution (
![]() ${\sim}$
63 % by weight) was used as the working fluid and its refractive index was matched with that of the canopy through careful temperature control. The fluid has a density
${\sim}$
63 % by weight) was used as the working fluid and its refractive index was matched with that of the canopy through careful temperature control. The fluid has a density
![]() $\unicode[STIX]{x1D70C}_{0}=1800~\text{kg}~\text{m}^{-3}$
and a kinematic viscosity
$\unicode[STIX]{x1D70C}_{0}=1800~\text{kg}~\text{m}^{-3}$
and a kinematic viscosity
![]() $\unicode[STIX]{x1D708}=1.1\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
. Further details on the channel and the refractive-index-matching technique can be found in Blois et al. (Reference Blois, Christensen, Best, Elliot, Austin, Dutton, Bragg, Garcia and Fouke2012), Bai & Katz (Reference Bai and Katz2014) and Hamed et al. (Reference Hamed, Kamdar, Castillo and Chamorro2015). Matching the refractive index of the working fluid with that of the canopy renders it nearly invisible, allowing for unobstructed optical access. Measurements along the span of the canopy would have not been possible without this technique.
$\unicode[STIX]{x1D708}=1.1\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
. Further details on the channel and the refractive-index-matching technique can be found in Blois et al. (Reference Blois, Christensen, Best, Elliot, Austin, Dutton, Bragg, Garcia and Fouke2012), Bai & Katz (Reference Bai and Katz2014) and Hamed et al. (Reference Hamed, Kamdar, Castillo and Chamorro2015). Matching the refractive index of the working fluid with that of the canopy renders it nearly invisible, allowing for unobstructed optical access. Measurements along the span of the canopy would have not been possible without this technique.

Figure 1. Homogeneous and heterogeneous canopy models. (a) Plan view of the models with element spacing and geometry; the dashed line marks the location of the streamwise wall-normal (
![]() $x$
–
$x$
–
![]() $y$
) measurement plane. (b) Schematic highlighting the element heights for both models (
$y$
) measurement plane. (b) Schematic highlighting the element heights for both models (
![]() $h=37.5$
mm,
$h=37.5$
mm,
![]() $h_{1}=50$
mm,
$h_{1}=50$
mm,
![]() $h_{2}=25$
mm).
$h_{2}=25$
mm).
Flow field measurements were acquired at three different locations spanning the entire length of the canopy models. The measurements were made in a streamwise wall-normal (
![]() $x$
–
$x$
–
![]() $y$
) plane at the centre between canopy elements, as indicated by the dashed line in figure 1(a). This location corresponds approximately to the channel midspan and was chosen as a representative plane of the flow within the canopy. It is important to acknowledge that the flow fields presented in this paper are expected to vary laterally; however, the chosen measurement location is sufficient to provide insight into the effect of height heterogeneity on the flow turbulence. Further investigation on the lateral variations of the flows is provided in the results section through complementary wall-parallel measurements. Each model was studied under three submergence depths
$y$
) plane at the centre between canopy elements, as indicated by the dashed line in figure 1(a). This location corresponds approximately to the channel midspan and was chosen as a representative plane of the flow within the canopy. It is important to acknowledge that the flow fields presented in this paper are expected to vary laterally; however, the chosen measurement location is sufficient to provide insight into the effect of height heterogeneity on the flow turbulence. Further investigation on the lateral variations of the flows is provided in the results section through complementary wall-parallel measurements. Each model was studied under three submergence depths
![]() $H/h=2$
, 3 and 4 and turbulent, subcritical flow with Reynolds numbers
$H/h=2$
, 3 and 4 and turbulent, subcritical flow with Reynolds numbers
![]() $Re_{H}=U_{\infty }H/\unicode[STIX]{x1D708}$
and the Froude numbers
$Re_{H}=U_{\infty }H/\unicode[STIX]{x1D708}$
and the Froude numbers
![]() $Fr=U_{\infty }/\sqrt{gH}$
given in table 1. Here,
$Fr=U_{\infty }/\sqrt{gH}$
given in table 1. Here,
![]() $U_{\infty }$
denotes the incoming free-stream velocity preceding the canopy models and
$U_{\infty }$
denotes the incoming free-stream velocity preceding the canopy models and
![]() $g$
is the standard gravity. Note that
$g$
is the standard gravity. Note that
![]() $Re$
and
$Re$
and
![]() $Fr$
vary between cases predominantly due to the variation in flow depth
$Fr$
vary between cases predominantly due to the variation in flow depth
![]() $H$
and the small changes in
$H$
and the small changes in
![]() $U_{\infty }$
were not dynamically significant. The incoming boundary layer had a thickness
$U_{\infty }$
were not dynamically significant. The incoming boundary layer had a thickness
![]() $\unicode[STIX]{x1D6FF}_{99}\simeq 0.5h$
. The flow approached the fully developed condition by the end of the canopy models, allowing for the estimation of the friction velocity at the top of the canopy
$\unicode[STIX]{x1D6FF}_{99}\simeq 0.5h$
. The flow approached the fully developed condition by the end of the canopy models, allowing for the estimation of the friction velocity at the top of the canopy
![]() $u_{\unicode[STIX]{x1D70F}}=\text{max}\langle u^{\prime }v^{\prime }\rangle ^{1/2}$
. The symbol
$u_{\unicode[STIX]{x1D70F}}=\text{max}\langle u^{\prime }v^{\prime }\rangle ^{1/2}$
. The symbol
![]() $\langle \cdot \rangle$
denotes the time-averaging operator and primes denote fluctuating quantities. The roughness Reynolds number
$\langle \cdot \rangle$
denotes the time-averaging operator and primes denote fluctuating quantities. The roughness Reynolds number
![]() $Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}h/\unicode[STIX]{x1D708}$
is consequently calculated and reported in table 1 along with
$Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}h/\unicode[STIX]{x1D708}$
is consequently calculated and reported in table 1 along with
![]() $u_{\unicode[STIX]{x1D70F}}$
and other flow parameters. Using
$u_{\unicode[STIX]{x1D70F}}$
and other flow parameters. Using
![]() $\langle u^{\prime }v^{\prime }\rangle$
at the canopy height is common for the estimation of the friction velocity for homogeneous canopies (Poggi et al.
Reference Poggi, Porporato, Ridolfi, Albertson and Katul2004; Nezu & Sanjou Reference Nezu and Sanjou2008; Chen et al.
Reference Chen, Jiang and Nepf2013). For the heterogeneous canopy, the friction velocity is defined at the location of the maximum
$\langle u^{\prime }v^{\prime }\rangle$
at the canopy height is common for the estimation of the friction velocity for homogeneous canopies (Poggi et al.
Reference Poggi, Porporato, Ridolfi, Albertson and Katul2004; Nezu & Sanjou Reference Nezu and Sanjou2008; Chen et al.
Reference Chen, Jiang and Nepf2013). For the heterogeneous canopy, the friction velocity is defined at the location of the maximum
![]() $\langle u^{\prime }v^{\prime }\rangle$
at
$\langle u^{\prime }v^{\prime }\rangle$
at
![]() ${\approx}h_{1}$
. As for
${\approx}h_{1}$
. As for
![]() $Re_{\unicode[STIX]{x1D70F}}$
, the average canopy height
$Re_{\unicode[STIX]{x1D70F}}$
, the average canopy height
![]() $h$
is used as the representative length scale.
$h$
is used as the representative length scale.

Figure 2. Schematics of the experimental set-up illustrating the basic PIV components and the three streamwise wall-normal (
![]() $x$
–
$x$
–
![]() $y$
) measurement planes for the heterogeneous canopy model.
$y$
) measurement planes for the heterogeneous canopy model.
Table 1. Basic flow variables and non-dimensional parameters for the two canopy set-ups.

A planar PIV system from TSI was used for velocity field measurements in three fields of view (FOVs) spanning the entire length of the canopy models. The three FOVs (
![]() ${\sim}6h\times 2h$
,
${\sim}6h\times 2h$
,
![]() ${\sim}6h\times 3h$
and
${\sim}6h\times 3h$
and
![]() ${\sim}6h\times 4h$
) were captured by an 11 megapixel (
${\sim}6h\times 4h$
) were captured by an 11 megapixel (
![]() $4000\times 2672$
pixels), 12-bit, frame straddle, charge-coupled device (CCD) camera (see figure 2 for schematics of the experimental set-up). The working fluid was seeded with
$4000\times 2672$
pixels), 12-bit, frame straddle, charge-coupled device (CCD) camera (see figure 2 for schematics of the experimental set-up). The working fluid was seeded with
![]() $14~\unicode[STIX]{x03BC}\text{m}$
silver-coated, hollow glass spheres with a density of 1700 kg m
$14~\unicode[STIX]{x03BC}\text{m}$
silver-coated, hollow glass spheres with a density of 1700 kg m
![]() $^{-3}$
. The flow was illuminated using a 1 mm thick laser sheet supplied by a
$^{-3}$
. The flow was illuminated using a 1 mm thick laser sheet supplied by a
![]() $250~\text{mJ}~\text{pulse}^{-1}$
double-pulsed laser (Quantel). Four thousand image pairs were collected for each FOV at a frequency of 1 Hz. The image pairs were interrogated with a recursive cross-correlation method using the Insight 4G software package from TSI. The final interrogation window was
$250~\text{mJ}~\text{pulse}^{-1}$
double-pulsed laser (Quantel). Four thousand image pairs were collected for each FOV at a frequency of 1 Hz. The image pairs were interrogated with a recursive cross-correlation method using the Insight 4G software package from TSI. The final interrogation window was
![]() $16\times 16$
pixels with 50 % overlap, resulting in a final vector grid spacing
$16\times 16$
pixels with 50 % overlap, resulting in a final vector grid spacing
![]() $\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=500~\unicode[STIX]{x03BC}\text{m}$
. The same planar system and technique were used to acquire complementary measurements in a wall-parallel plane located at an elevation
$\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=500~\unicode[STIX]{x03BC}\text{m}$
. The same planar system and technique were used to acquire complementary measurements in a wall-parallel plane located at an elevation
![]() $y/h\simeq 0.6$
. The wall-parallel measurements were made within the third FOV at
$y/h\simeq 0.6$
. The wall-parallel measurements were made within the third FOV at
![]() $H/h=3$
but at a higher resolution, leading to a final vector grid spacing
$H/h=3$
but at a higher resolution, leading to a final vector grid spacing
![]() $\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}z=320$
and
$\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}z=320$
and
![]() $210~\unicode[STIX]{x03BC}\text{m}$
for the homogeneous and heterogeneous canopies. Overall, 40 000 velocity fields were collected for each canopy model.
$210~\unicode[STIX]{x03BC}\text{m}$
for the homogeneous and heterogeneous canopies. Overall, 40 000 velocity fields were collected for each canopy model.
3 Results
In this section we present the common and distinctive features of the turbulence within and above the homogeneous and heterogeneous canopies for the three submergences described in § 2. Horizontal and vertical planes as well as one-dimensional (1D) profiles of the first- and second-order turbulence statistics, quadrant analysis and snapshot proper orthogonal decomposition (POD) are used for this purpose. Owing to the extensive experimental campaign and analysis (six cases and several statistics for each one) and for brevity, we focus on the case
![]() $H/h=3$
, but note key differences with other submergence depths.
$H/h=3$
, but note key differences with other submergence depths.

Figure 3. Time-averaged streamwise velocity fields
![]() $U(x,y)/U_{\infty }$
at submergence
$U(x,y)/U_{\infty }$
at submergence
![]() $H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies. White dashed lines indicate the envelope of the canopies, and the symbol at the top left shows the free surface. The three panels correspond to the three fields of view (FOV) for the PIV.
$H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies. White dashed lines indicate the envelope of the canopies, and the symbol at the top left shows the free surface. The three panels correspond to the three fields of view (FOV) for the PIV.

Figure 4. Time-averaged streamwise velocity profiles
![]() $U(y)/U_{\infty }$
at various
$U(y)/U_{\infty }$
at various
![]() $x/h$
locations and submergences for the homogeneous (black) and heterogeneous (red) canopies: (a)
$x/h$
locations and submergences for the homogeneous (black) and heterogeneous (red) canopies: (a)
![]() $H/h=2$
; (b)
$H/h=2$
; (b)
![]() $H/h=3$
; and (c)
$H/h=3$
; and (c)
![]() $H/h=4$
.
$H/h=4$
.
3.1 Mean flow along the full length of the canopies
Time-averaged streamwise velocity contours
![]() $U(x,y)/U_{\infty }$
along the entire length of the two canopy models are illustrated in figure 3 for submergence
$U(x,y)/U_{\infty }$
along the entire length of the two canopy models are illustrated in figure 3 for submergence
![]() $H/h=3$
. In this figure and subsequent ones, the incoming velocity above the boundary layer, i.e. free-stream velocity
$H/h=3$
. In this figure and subsequent ones, the incoming velocity above the boundary layer, i.e. free-stream velocity
![]() $U_{\infty }$
, is used as a scaling quantity, and white dashed lines represent the envelope of the canopy. Both canopies induce a similar flow deceleration upstream, which extends
$U_{\infty }$
, is used as a scaling quantity, and white dashed lines represent the envelope of the canopy. Both canopies induce a similar flow deceleration upstream, which extends
![]() ${\sim}2h$
from the leading edge. However, the flow within the heterogeneous canopy exhibits a larger momentum deficit covering the area between the first two
${\sim}2h$
from the leading edge. However, the flow within the heterogeneous canopy exhibits a larger momentum deficit covering the area between the first two
![]() $h_{1}$
regions (
$h_{1}$
regions (
![]() $x/h\in [0.8,1.6]$
). The reduced velocity within the canopy leads to the formation of a shear layer that initiates at
$x/h\in [0.8,1.6]$
). The reduced velocity within the canopy leads to the formation of a shear layer that initiates at
![]() $x/h\simeq 0.4$
, downstream of the first
$x/h\simeq 0.4$
, downstream of the first
![]() $h$
and
$h$
and
![]() $h_{1}$
elements for the homogeneous and heterogeneous canopies, respectively. As in previous studies (e.g. Morse, Gardiner & Marshall Reference Morse, Gardiner and Marshall2002), the short delay in the initiation of the shear layer is probably due to the enhanced wall-normal flow near the leading edge (discussed below in the context of figures 5 and 6). The shear layer undergoes relatively rapid growth within the first FOV, followed by much reduced growth rate in the second FOV, and an approximately constant thickness at
$h_{1}$
elements for the homogeneous and heterogeneous canopies, respectively. As in previous studies (e.g. Morse, Gardiner & Marshall Reference Morse, Gardiner and Marshall2002), the short delay in the initiation of the shear layer is probably due to the enhanced wall-normal flow near the leading edge (discussed below in the context of figures 5 and 6). The shear layer undergoes relatively rapid growth within the first FOV, followed by much reduced growth rate in the second FOV, and an approximately constant thickness at
![]() $x/h\geqslant 14$
. While the bulk features of the flow in the two canopies are qualitatively similar, striking differences can be inferred from the velocity contours. The heterogeneous model triggers a more complex flow response past the leading edge and within the elements as well as a periodic distribution downstream of the first measurement region, where, as dictated by continuity, the flow experiences alternating high and low speed within
$x/h\geqslant 14$
. While the bulk features of the flow in the two canopies are qualitatively similar, striking differences can be inferred from the velocity contours. The heterogeneous model triggers a more complex flow response past the leading edge and within the elements as well as a periodic distribution downstream of the first measurement region, where, as dictated by continuity, the flow experiences alternating high and low speed within
![]() $h_{1}$
and
$h_{1}$
and
![]() $h_{2}$
heights. These periodic features are further illustrated below using 1D vertical and horizontal profiles of the mean flow.
$h_{2}$
heights. These periodic features are further illustrated below using 1D vertical and horizontal profiles of the mean flow.

Figure 5. Time-averaged streamwise velocity profiles
![]() $U(x,y=h)/U_{\infty }$
at various submergences for the homogeneous (black) and heterogeneous (red) canopies: (a)
$U(x,y=h)/U_{\infty }$
at various submergences for the homogeneous (black) and heterogeneous (red) canopies: (a)
![]() $H/h=2$
; (b)
$H/h=2$
; (b)
![]() $H/h=3$
; and (c)
$H/h=3$
; and (c)
![]() $H/h=4$
.
$H/h=4$
.

Figure 6. Time-averaged vertical velocity profiles
![]() $V(x,y=h)/U_{\infty }$
at various submergences for the homogeneous (black) and heterogeneous (red) canopies: (a)
$V(x,y=h)/U_{\infty }$
at various submergences for the homogeneous (black) and heterogeneous (red) canopies: (a)
![]() $H/h=2$
; (b)
$H/h=2$
; (b)
![]() $H/h=3$
; and (c)
$H/h=3$
; and (c)
![]() $H/h=4$
.
$H/h=4$
.
Quantitative comparison between the canopies at various submergences (
![]() $H/h=2$
, 3 and 4) is given by the 1D streamwise velocity profiles every
$H/h=2$
, 3 and 4) is given by the 1D streamwise velocity profiles every
![]() $\unicode[STIX]{x0394}x/h=0.5$
in figure 4. The
$\unicode[STIX]{x0394}x/h=0.5$
in figure 4. The
![]() $U(y)/U_{\infty }$
profiles for the two models are superimposed to aid direct comparison. In all cases, the incoming velocity profiles collapse, including the recirculation bubble upstream of the leading edge for
$U(y)/U_{\infty }$
profiles for the two models are superimposed to aid direct comparison. In all cases, the incoming velocity profiles collapse, including the recirculation bubble upstream of the leading edge for
![]() $H/h=2$
and 3. The flow within the canopies rapidly decelerates, marking an adjustment region (Belcher, Jerram & Hunt Reference Belcher, Jerram and Hunt2003; Coceal & Belcher Reference Coceal and Belcher2004; Chen et al.
Reference Chen, Jiang and Nepf2013). The spatial features of the velocity within the adjustment region are highly dependent on the local canopy geometry. As seen in figure 4, a flow deficit is formed at the canopy height
$H/h=2$
and 3. The flow within the canopies rapidly decelerates, marking an adjustment region (Belcher, Jerram & Hunt Reference Belcher, Jerram and Hunt2003; Coceal & Belcher Reference Coceal and Belcher2004; Chen et al.
Reference Chen, Jiang and Nepf2013). The spatial features of the velocity within the adjustment region are highly dependent on the local canopy geometry. As seen in figure 4, a flow deficit is formed at the canopy height
![]() $h$
at the leading edge for the homogeneous canopy. The heterogeneous model starts with two rows of height
$h$
at the leading edge for the homogeneous canopy. The heterogeneous model starts with two rows of height
![]() $h_{2}$
leading to a similar flow deficit at
$h_{2}$
leading to a similar flow deficit at
![]() $x/h=0.5$
. However, the deficit is substantially increased at the following
$x/h=0.5$
. However, the deficit is substantially increased at the following
![]() $h_{1}$
rows at
$h_{1}$
rows at
![]() $x/h=1$
. Immediately after the leading edge, large variations are observed near both
$x/h=1$
. Immediately after the leading edge, large variations are observed near both
![]() $h_{1}$
and
$h_{1}$
and
![]() $h_{2}$
, resulting in larger changes in the mean shear for the heterogeneous canopy. It is important to acknowledge that, within this adjustment region, the flow is highly three-dimensional and the complex response behind the leading edge (figure 4) is expected to vary laterally. The point here is the increased complexity of the response due to height heterogeneity. The velocity profiles in figure 4 also show the effect of the submergence and canopy geometry on the mean momentum deficit, which leads to a distinctive impact on the bulk flow over the canopies. At the lowest submergence (
$h_{2}$
, resulting in larger changes in the mean shear for the heterogeneous canopy. It is important to acknowledge that, within this adjustment region, the flow is highly three-dimensional and the complex response behind the leading edge (figure 4) is expected to vary laterally. The point here is the increased complexity of the response due to height heterogeneity. The velocity profiles in figure 4 also show the effect of the submergence and canopy geometry on the mean momentum deficit, which leads to a distinctive impact on the bulk flow over the canopies. At the lowest submergence (
![]() $H/h=2$
), the height heterogeneity leads to larger mean flow within the canopy along its entire length. This promotes mixing, which is critical for scalar transport in the region below the shear layer, i.e. in the longitudinal exchange zone defined by Nepf & Vivoni (Reference Nepf and Vivoni2000). Only for this submergence case is the boundary layer growth still significant near the free surface. The extension and characteristics of the shear layer for both models will be further discussed in § 3.2.
$H/h=2$
), the height heterogeneity leads to larger mean flow within the canopy along its entire length. This promotes mixing, which is critical for scalar transport in the region below the shear layer, i.e. in the longitudinal exchange zone defined by Nepf & Vivoni (Reference Nepf and Vivoni2000). Only for this submergence case is the boundary layer growth still significant near the free surface. The extension and characteristics of the shear layer for both models will be further discussed in § 3.2.
Belcher et al. (Reference Belcher, Jerram and Hunt2003), Coceal & Belcher (Reference Coceal and Belcher2004), Chen et al. (Reference Chen, Jiang and Nepf2013) and others have reported an exponential decay with
![]() $x$
for the streamwise
$x$
for the streamwise
![]() $U$
and vertical
$U$
and vertical
![]() $V$
velocities at the element height within the adjustment region of homogeneous canopies. A similar behaviour is observed for our homogeneous canopy across the three submergence depths, as illustrated in figures 5 and 6 for
$V$
velocities at the element height within the adjustment region of homogeneous canopies. A similar behaviour is observed for our homogeneous canopy across the three submergence depths, as illustrated in figures 5 and 6 for
![]() $U(x,y=h)/U_{\infty }$
and
$U(x,y=h)/U_{\infty }$
and
![]() $V(x,y=h)/U_{\infty }$
. The relatively large velocity variations near the leading edge represent local flow adjustment and are governed by the local geometry and the spatial distribution of the canopy elements. These variations are expected to be substantially reduced if lateral averaging was performed.
$V(x,y=h)/U_{\infty }$
. The relatively large velocity variations near the leading edge represent local flow adjustment and are governed by the local geometry and the spatial distribution of the canopy elements. These variations are expected to be substantially reduced if lateral averaging was performed.
The adjustment length
![]() $X_{D}$
for the homogeneous canopy is comparable to proposed models. Following Chen et al. (Reference Chen, Jiang and Nepf2013), we define
$X_{D}$
for the homogeneous canopy is comparable to proposed models. Following Chen et al. (Reference Chen, Jiang and Nepf2013), we define
![]() $X_{D}$
for the homogeneous case to extend from the canopy leading edge to the location where
$X_{D}$
for the homogeneous case to extend from the canopy leading edge to the location where
![]() $V(x,y=h)$
drops to 5 % of its maximum value (which occurs at
$V(x,y=h)$
drops to 5 % of its maximum value (which occurs at
![]() $x/h\simeq 0.3$
) resulting in
$x/h\simeq 0.3$
) resulting in
![]() $X_{D}=(3.0\pm 0.2)h$
for the three submergences. A model by Coceal & Belcher (Reference Coceal and Belcher2004) estimates the adjustment length as
$X_{D}=(3.0\pm 0.2)h$
for the three submergences. A model by Coceal & Belcher (Reference Coceal and Belcher2004) estimates the adjustment length as
where
![]() $L_{c}$
is the canopy drag length scale,
$L_{c}$
is the canopy drag length scale,
![]() $K=(U_{h}/u_{\unicode[STIX]{x1D70F}})(h/L_{c})$
and
$K=(U_{h}/u_{\unicode[STIX]{x1D70F}})(h/L_{c})$
and
![]() $U_{h}$
denotes the time-averaged streamwise velocity at the top of the canopy. Coceal & Belcher (Reference Coceal and Belcher2004) define
$U_{h}$
denotes the time-averaged streamwise velocity at the top of the canopy. Coceal & Belcher (Reference Coceal and Belcher2004) define
Here,
![]() $C_{D}$
is the drag coefficient. Using
$C_{D}$
is the drag coefficient. Using
![]() $C_{D}=2$
, (3.2) yields
$C_{D}=2$
, (3.2) yields
![]() $L_{c}=0.67h$
. The
$L_{c}=0.67h$
. The
![]() $C_{D}$
value is chosen following Coceal & Belcher (Reference Coceal and Belcher2004), who used
$C_{D}$
value is chosen following Coceal & Belcher (Reference Coceal and Belcher2004), who used
![]() $C_{D}=2$
for square bars with a similar density and set-up. Given this drag length scale, we obtain adjustment lengths
$C_{D}=2$
for square bars with a similar density and set-up. Given this drag length scale, we obtain adjustment lengths
![]() $X_{D}=3.8h$
,
$X_{D}=3.8h$
,
![]() $4.4h$
and
$4.4h$
and
![]() $4.3h$
for
$4.3h$
for
![]() $H/h=2$
, 3 and 4. The deviation from the measured
$H/h=2$
, 3 and 4. The deviation from the measured
![]() $X_{D}$
is probably due to the scaling coefficient in (3.1), which was proposed as a first-order approximation for unconfined urban canopies (Coceal & Belcher Reference Coceal and Belcher2004), and uncertainty in
$X_{D}$
is probably due to the scaling coefficient in (3.1), which was proposed as a first-order approximation for unconfined urban canopies (Coceal & Belcher Reference Coceal and Belcher2004), and uncertainty in
![]() $C_{D}$
. Our estimation of
$C_{D}$
. Our estimation of
![]() $X_{D}$
suggests a weak dependence on submergence depth for homogeneous canopies, supporting the finding by Chen et al. (Reference Chen, Jiang and Nepf2013). Finally, a recent formulation by Chen et al. (Reference Chen, Jiang and Nepf2013) takes into account the increase in the pressure at the canopy leading edge as follows:
$X_{D}$
suggests a weak dependence on submergence depth for homogeneous canopies, supporting the finding by Chen et al. (Reference Chen, Jiang and Nepf2013). Finally, a recent formulation by Chen et al. (Reference Chen, Jiang and Nepf2013) takes into account the increase in the pressure at the canopy leading edge as follows:
This leads to
![]() $X_{D}\approx 6.5h$
with a 5 % uncertainty due to a 20 % change in
$X_{D}\approx 6.5h$
with a 5 % uncertainty due to a 20 % change in
![]() $C_{D}$
.
$C_{D}$
.
Figures 5 and 6 also highlight the contrast in the mean flow dynamics between the homogeneous and heterogeneous canopies at the average element height
![]() $y=h$
. While in the homogeneous case the fast decay of
$y=h$
. While in the homogeneous case the fast decay of
![]() $V(x,y=h)$
is characteristic of the adjustment region, the decay in the heterogeneous case is more complex. As shown in figures 5 and 6,
$V(x,y=h)$
is characteristic of the adjustment region, the decay in the heterogeneous case is more complex. As shown in figures 5 and 6,
![]() $U(x,y=h)$
and
$U(x,y=h)$
and
![]() $V(x,y=h)$
exhibit a spatially periodic behaviour governed by the topography of the canopy; the periodicity becomes apparent within the second and third FOVs. In line with the mean streamwise velocity contours (figure 3),
$V(x,y=h)$
exhibit a spatially periodic behaviour governed by the topography of the canopy; the periodicity becomes apparent within the second and third FOVs. In line with the mean streamwise velocity contours (figure 3),
![]() $U(x,y=h)/U_{\infty }$
is larger within
$U(x,y=h)/U_{\infty }$
is larger within
![]() $h_{1}$
elements; this increase in
$h_{1}$
elements; this increase in
![]() $U(x,y=h)/U_{\infty }$
is accompanied by a decrease in
$U(x,y=h)/U_{\infty }$
is accompanied by a decrease in
![]() $V(x,y=h)/U_{\infty }$
. Figures 5 and 6 indicate that the periodic flow variations are more pronounced at the lowest submergence depth, and eventually reach a constant amplitude. In particular, the non-vanishing
$V(x,y=h)/U_{\infty }$
. Figures 5 and 6 indicate that the periodic flow variations are more pronounced at the lowest submergence depth, and eventually reach a constant amplitude. In particular, the non-vanishing
![]() $V(x,y=h)$
contrasts with the negligible counterpart in the homogeneous canopy in the region
$V(x,y=h)$
contrasts with the negligible counterpart in the homogeneous canopy in the region
![]() $x>X_{D}$
. This periodic behaviour is observed within
$x>X_{D}$
. This periodic behaviour is observed within
![]() $h_{2}<y<h_{1}$
for both
$h_{2}<y<h_{1}$
for both
![]() $U/U_{\infty }$
and
$U/U_{\infty }$
and
![]() $V/U_{\infty }$
across all submergences. As seen in figures 5 and 6, most of the flow adjustment for the heterogeneous canopy, given by the decay of the amplitude of
$V/U_{\infty }$
across all submergences. As seen in figures 5 and 6, most of the flow adjustment for the heterogeneous canopy, given by the decay of the amplitude of
![]() $U/U_{\infty }$
and
$U/U_{\infty }$
and
![]() $V/U_{\infty }$
variations, is reached at
$V/U_{\infty }$
variations, is reached at
![]() $x/h\simeq 3$
similar to the homogeneous case. The rest of the adjustment occurs within
$x/h\simeq 3$
similar to the homogeneous case. The rest of the adjustment occurs within
![]() $x/h=3$
–8, at which point the periodic variations in
$x/h=3$
–8, at which point the periodic variations in
![]() $U/U_{\infty }$
reach an approximately constant amplitude. The similarity in the length where the majority of the adjustment occurs suggests that, for engineering applications, the estimation of
$U/U_{\infty }$
reach an approximately constant amplitude. The similarity in the length where the majority of the adjustment occurs suggests that, for engineering applications, the estimation of
![]() $X_{D}$
for an equivalent homogeneous case could potentially suffice for heterogeneous canopies (under similar conditions to the one studied here).
$X_{D}$
for an equivalent homogeneous case could potentially suffice for heterogeneous canopies (under similar conditions to the one studied here).
The canopy heterogeneity induces a distinctive mean flow distribution within the canopy elements, as illustrated in figure 7. Here,
![]() $U(x,z)/U_{\infty }$
is shown within a wall-parallel plane at
$U(x,z)/U_{\infty }$
is shown within a wall-parallel plane at
![]() $y/h\simeq 0.6$
for submergence depth
$y/h\simeq 0.6$
for submergence depth
![]() $H/h=3$
and past the adjustment length (
$H/h=3$
and past the adjustment length (
![]() $x/h\in [16,18.5]$
and
$x/h\in [16,18.5]$
and
![]() $x/h\in [17,19.5]$
for the homogeneous and heterogeneous cases, respectively). Preferential spanwise flows are formed around the elements of both canopies, with significantly larger velocity in the heterogeneous case, which shows a periodic behaviour aligned with the results from the wall-normal measurements. The plane in figure 7 is located just below the top of the shorter
$x/h\in [17,19.5]$
for the homogeneous and heterogeneous cases, respectively). Preferential spanwise flows are formed around the elements of both canopies, with significantly larger velocity in the heterogeneous case, which shows a periodic behaviour aligned with the results from the wall-normal measurements. The plane in figure 7 is located just below the top of the shorter
![]() $h_{2}$
elements. While there is no flow blockage above these elements, considerable blockage is present downstream at the following longer
$h_{2}$
elements. While there is no flow blockage above these elements, considerable blockage is present downstream at the following longer
![]() $h_{1}$
elements, leading, as dictated by continuity, to the increased velocity observed in figure 7. This increased streamwise velocity around the
$h_{1}$
elements, leading, as dictated by continuity, to the increased velocity observed in figure 7. This increased streamwise velocity around the
![]() $h_{1}$
elements is expected in the region
$h_{1}$
elements is expected in the region
![]() $h_{2}<y<h_{1}$
and results in reduced mean shear at the top of the canopy
$h_{2}<y<h_{1}$
and results in reduced mean shear at the top of the canopy
![]() $(y=h_{1})$
above the longer elements in comparison with the shorter ones. This modulation of the mean shear modifies the rate of the turbulent kinetic energy production in the mixing layer above the heterogeneous canopy, as will be discussed in the following section. Along with the enhanced vertical flow in the heterogeneous canopy, the increased spanwise flow is expected to play a significant role in modulating the mixing and scalar transport especially in the longitudinal exchange zone where turbulent transport is comparatively low.
$(y=h_{1})$
above the longer elements in comparison with the shorter ones. This modulation of the mean shear modifies the rate of the turbulent kinetic energy production in the mixing layer above the heterogeneous canopy, as will be discussed in the following section. Along with the enhanced vertical flow in the heterogeneous canopy, the increased spanwise flow is expected to play a significant role in modulating the mixing and scalar transport especially in the longitudinal exchange zone where turbulent transport is comparatively low.

Figure 7. Time-averaged streamwise velocity fields
![]() $U(x,z)/U_{\infty }$
at
$U(x,z)/U_{\infty }$
at
![]() $y/h\simeq 0.6$
and
$y/h\simeq 0.6$
and
![]() $H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies; elements of height
$H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies; elements of height
![]() $h_{1}$
are shaded.
$h_{1}$
are shaded.
3.2 The turbulent kinetic energy and Reynolds shear stress

Figure 8. Turbulent kinetic energy fields
![]() $TKE=\langle u^{\prime 2}+v^{\prime 2}\rangle /2U_{\infty }^{2}$
at submergence
$TKE=\langle u^{\prime 2}+v^{\prime 2}\rangle /2U_{\infty }^{2}$
at submergence
![]() $H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies. White dashed lines indicate the envelope of the canopies, and the symbol at the top left shows the free surface.
$H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies. White dashed lines indicate the envelope of the canopies, and the symbol at the top left shows the free surface.
Height heterogeneity triggers distinctive spatial and temporal changes in the turbulence developed over and within the canopy, mainly in the mixing layer. The normalized turbulent kinetic energy
![]() $TKE=\langle u^{\prime 2}+v^{\prime 2}\rangle /2U_{\infty }^{2}$
contours are given in figure 8 for submergence
$TKE=\langle u^{\prime 2}+v^{\prime 2}\rangle /2U_{\infty }^{2}$
contours are given in figure 8 for submergence
![]() $H/h=3$
. The distribution of the
$H/h=3$
. The distribution of the
![]() $TKE$
over the heterogeneous canopy exhibits a periodic behaviour in which comparatively higher intensity is observed above the shorter
$TKE$
over the heterogeneous canopy exhibits a periodic behaviour in which comparatively higher intensity is observed above the shorter
![]() $h_{2}$
elements at the canopy height (
$h_{2}$
elements at the canopy height (
![]() $y=h_{1}$
). The 1D
$y=h_{1}$
). The 1D
![]() $TKE$
profiles for both canopies for the three submergence depths are shown in figure 9. A distinctive consequence of height heterogeneity is the enhanced
$TKE$
profiles for both canopies for the three submergence depths are shown in figure 9. A distinctive consequence of height heterogeneity is the enhanced
![]() $TKE$
along the entire canopy length for submergence
$TKE$
along the entire canopy length for submergence
![]() $H/h=2$
. A modest increase in
$H/h=2$
. A modest increase in
![]() $TKE$
is observed at submergence
$TKE$
is observed at submergence
![]() $H/h=3$
, whereas no apparent change is found for
$H/h=3$
, whereas no apparent change is found for
![]() $H/h=4$
. To investigate the trends in figures 8 and 9, the in-plane
$H/h=4$
. To investigate the trends in figures 8 and 9, the in-plane
![]() $TKE$
production rate,
$TKE$
production rate,
was analysed, but is not shown for brevity. The primary Reynolds stress
![]() $-\langle u^{\prime }v^{\prime }\rangle$
is shown and discussed below. The first term of (3.4) dominates the other terms across the two canopies and the three submergences. The higher
$-\langle u^{\prime }v^{\prime }\rangle$
is shown and discussed below. The first term of (3.4) dominates the other terms across the two canopies and the three submergences. The higher
![]() $TKE$
levels at the canopy height over the shorter
$TKE$
levels at the canopy height over the shorter
![]() $h_{2}$
elements (figure 8
b) result from a higher production rate. The enhanced production is promoted through a combination of higher Reynolds stress and larger mean shear at the canopy height over the shorter
$h_{2}$
elements (figure 8
b) result from a higher production rate. The enhanced production is promoted through a combination of higher Reynolds stress and larger mean shear at the canopy height over the shorter
![]() $h_{2}$
elements (the higher mean shear is discussed earlier in the context of figure 7). An influential role of submergence on the turbulence dynamics within and above heterogeneous canopies is suggested in figure 9. Even though the shear and turbulence development above the canopy are mostly generated locally at the flow–canopy interface, the submergence appears to contribute by modulating the mean shear distribution. The higher canopy elements produce a non-negligible blockage at the lowest submergence that enhances mean shear and, consequently,
$h_{2}$
elements (the higher mean shear is discussed earlier in the context of figure 7). An influential role of submergence on the turbulence dynamics within and above heterogeneous canopies is suggested in figure 9. Even though the shear and turbulence development above the canopy are mostly generated locally at the flow–canopy interface, the submergence appears to contribute by modulating the mean shear distribution. The higher canopy elements produce a non-negligible blockage at the lowest submergence that enhances mean shear and, consequently,
![]() $TKE$
production rate. An inspection of the maximum mean shear
$TKE$
production rate. An inspection of the maximum mean shear
![]() $\unicode[STIX]{x2202}(U/U_{\infty })/\unicode[STIX]{x2202}(y/h)$
in each vertical profile within the third measurement region indicates higher levels for
$\unicode[STIX]{x2202}(U/U_{\infty })/\unicode[STIX]{x2202}(y/h)$
in each vertical profile within the third measurement region indicates higher levels for
![]() $H/h=2$
, reaching approximately twice that for
$H/h=2$
, reaching approximately twice that for
![]() $H/h=3$
and 4 for both canopies. Furthermore, the maximum mean shear, which occurred near the top of the canopies (
$H/h=3$
and 4 for both canopies. Furthermore, the maximum mean shear, which occurred near the top of the canopies (
![]() $h$
and
$h$
and
![]() $h_{1}$
for the homogeneous and heterogeneous canopies, respectively), was consistently higher for the heterogeneous case in all submergence depths.
$h_{1}$
for the homogeneous and heterogeneous canopies, respectively), was consistently higher for the heterogeneous case in all submergence depths.

Figure 9. Turbulent kinetic energy profiles
![]() $TKE$
at (a)
$TKE$
at (a)
![]() $H/h=2$
, (b)
$H/h=2$
, (b)
![]() $H/h=3$
and (c)
$H/h=3$
and (c)
![]() $H/h=4$
. The homogeneous canopy is shown in black and the heterogeneous in red.
$H/h=4$
. The homogeneous canopy is shown in black and the heterogeneous in red.

Figure 10. Reynolds shear stress fields
![]() $-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
at submergence
$-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
at submergence
![]() $H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies. White dashed lines illustrate the envelope of the canopies, and the symbol at the top left shows the free surface. The black dashed lines indicate the penetration depths
$H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies. White dashed lines illustrate the envelope of the canopies, and the symbol at the top left shows the free surface. The black dashed lines indicate the penetration depths
![]() $\unicode[STIX]{x1D6FF}_{e}$
(3.5).
$\unicode[STIX]{x1D6FF}_{e}$
(3.5).

Figure 11. Reynolds shear stress profiles
![]() $-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
at (a)
$-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
at (a)
![]() $H/h=2$
, (b)
$H/h=2$
, (b)
![]() $H/h=3$
and (c)
$H/h=3$
and (c)
![]() $H/h=4$
. The homogeneous canopy is shown in black and the heterogeneous in red.
$H/h=4$
. The homogeneous canopy is shown in black and the heterogeneous in red.
The contours of the Reynolds shear stress
![]() $-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
for
$-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
for
![]() $H/h=3$
are shown in figure 10. The region of increased stress is a mark of the mixing layer that forms at the top of the canopy. Similar to the
$H/h=3$
are shown in figure 10. The region of increased stress is a mark of the mixing layer that forms at the top of the canopy. Similar to the
![]() $TKE$
, the heterogeneous canopy exhibits a spatially periodic distribution of
$TKE$
, the heterogeneous canopy exhibits a spatially periodic distribution of
![]() $-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
. As noted from figure 11, the profiles of the Reynolds stress appear to be shifted in the vertical direction by a distance corresponding to the element height standard deviation (
$-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
. As noted from figure 11, the profiles of the Reynolds stress appear to be shifted in the vertical direction by a distance corresponding to the element height standard deviation (
![]() $\unicode[STIX]{x1D70E}_{h}=h/3$
). Beyond the adjustment length
$\unicode[STIX]{x1D70E}_{h}=h/3$
). Beyond the adjustment length
![]() $X_{D}$
, the
$X_{D}$
, the
![]() $-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
peaks consistently occur at the top of the canopies, i.e.
$-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
peaks consistently occur at the top of the canopies, i.e.
![]() $h$
and
$h$
and
![]() $h_{1}$
for the homogeneous and heterogeneous models, respectively. This indicates that, for the purposes of modelling,
$h_{1}$
for the homogeneous and heterogeneous models, respectively. This indicates that, for the purposes of modelling,
![]() $h_{1}$
appears to be the appropriate definition for canopy height. Within the adjustment length, the behaviour of the
$h_{1}$
appears to be the appropriate definition for canopy height. Within the adjustment length, the behaviour of the
![]() $TKE$
(figures 8 and 9) and the Reynolds stress (figures 10 and 11) above and within the canopy is more complex and spatially distributed as a result of the increased three-dimensionality of the flow in this region. There, an interesting feature is the significant Reynolds stress occurring above the canopy height for both models. This behaviour corresponds to the large mean shear
$TKE$
(figures 8 and 9) and the Reynolds stress (figures 10 and 11) above and within the canopy is more complex and spatially distributed as a result of the increased three-dimensionality of the flow in this region. There, an interesting feature is the significant Reynolds stress occurring above the canopy height for both models. This behaviour corresponds to the large mean shear
![]() $\unicode[STIX]{x2202}(U/U_{\infty })/\unicode[STIX]{x2202}(y/h)$
formed due to the flow acceleration above the region where the mean shear layer initiates.
$\unicode[STIX]{x2202}(U/U_{\infty })/\unicode[STIX]{x2202}(y/h)$
formed due to the flow acceleration above the region where the mean shear layer initiates.

Figure 12. Maximum Reynolds shear stress
![]() $-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
as a function of downstream distance: (a)
$-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
as a function of downstream distance: (a)
![]() $H/h=2$
, (b)
$H/h=2$
, (b)
![]() $H/h=3$
and (c)
$H/h=3$
and (c)
![]() $H/h=4$
. Homogeneous canopy in black and heterogeneous in red.
$H/h=4$
. Homogeneous canopy in black and heterogeneous in red.
The growth of
![]() $-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
in the mixing layer beyond the adjustment length is demonstrated in figure 12, where the maximum stress within each vertical profile is shown as a function of the distance
$-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
in the mixing layer beyond the adjustment length is demonstrated in figure 12, where the maximum stress within each vertical profile is shown as a function of the distance
![]() $x/h$
. In agreement with previous studies (e.g. Belcher et al.
Reference Belcher, Jerram and Hunt2003; Chen et al.
Reference Chen, Jiang and Nepf2013), the homogeneous canopy exhibits lower turbulence intensity and turbulent stress in the adjustment region compared to further downstream. This is because the vertical advection within the adjustment region delays the initiation and growth of the mixing layer and associated vortical structures. The smaller coherent structures within the adjustment region generate weaker turbulence and Reynolds stress than is present in the fully developed mixing layer beyond the adjustment region. The maximum stress occurs near the top of the canopies (
$x/h$
. In agreement with previous studies (e.g. Belcher et al.
Reference Belcher, Jerram and Hunt2003; Chen et al.
Reference Chen, Jiang and Nepf2013), the homogeneous canopy exhibits lower turbulence intensity and turbulent stress in the adjustment region compared to further downstream. This is because the vertical advection within the adjustment region delays the initiation and growth of the mixing layer and associated vortical structures. The smaller coherent structures within the adjustment region generate weaker turbulence and Reynolds stress than is present in the fully developed mixing layer beyond the adjustment region. The maximum stress occurs near the top of the canopies (
![]() $h$
and
$h$
and
![]() $h_{1}$
for the homogeneous and heterogeneous cases, respectively), and rapidly grows within the second FOV in correspondence with the rapid growth of the mean shear layer. The growth rate is considerably reduced for
$h_{1}$
for the homogeneous and heterogeneous cases, respectively), and rapidly grows within the second FOV in correspondence with the rapid growth of the mean shear layer. The growth rate is considerably reduced for
![]() $14<x/h<20$
(
$14<x/h<20$
(
![]() $0.5~\text{m}\lesssim x\lesssim 0.75~\text{m}$
), indicating that the flow approaches the developed condition. This is in agreement with the results of Chen et al. (Reference Chen, Jiang and Nepf2013), who found the mixing layer adjustment length (where the maximum turbulent stress was reached) to be approximately 1 m for a homogeneous canopy with a roughness density
$0.5~\text{m}\lesssim x\lesssim 0.75~\text{m}$
), indicating that the flow approaches the developed condition. This is in agreement with the results of Chen et al. (Reference Chen, Jiang and Nepf2013), who found the mixing layer adjustment length (where the maximum turbulent stress was reached) to be approximately 1 m for a homogeneous canopy with a roughness density
![]() $\unicode[STIX]{x1D706}_{f}=1.36$
and similar experimental conditions. As seen in the profiles of figure 12, the heterogeneous canopy experiences larger turbulent stress (and consequently transport) for the majority of its length at submergence depths
$\unicode[STIX]{x1D706}_{f}=1.36$
and similar experimental conditions. As seen in the profiles of figure 12, the heterogeneous canopy experiences larger turbulent stress (and consequently transport) for the majority of its length at submergence depths
![]() $H/h=2$
and 3. However, both canopies exhibit similar levels for the
$H/h=2$
and 3. However, both canopies exhibit similar levels for the
![]() $H/h=4$
case.
$H/h=4$
case.
The diffusion of the generated turbulence is inferred from the evolution of the mixing layer. The thickness of the dominant portion above the canopy
![]() $\unicode[STIX]{x1D6FF}_{T}(x)/h$
is shown in figure 13, where
$\unicode[STIX]{x1D6FF}_{T}(x)/h$
is shown in figure 13, where
![]() $\unicode[STIX]{x1D6FF}_{T}$
is the height above
$\unicode[STIX]{x1D6FF}_{T}$
is the height above
![]() $h$
and
$h$
and
![]() $h_{1}$
for the homogeneous and heterogeneous canopies, respectively, at which the Reynolds stress drops to 5 % of the maximum at a given
$h_{1}$
for the homogeneous and heterogeneous canopies, respectively, at which the Reynolds stress drops to 5 % of the maximum at a given
![]() $x$
location. For the homogeneous canopy at
$x$
location. For the homogeneous canopy at
![]() $H/h=2$
,
$H/h=2$
,
![]() $\unicode[STIX]{x1D6FF}_{T}$
reached the top of the measurement region by the third FOV and thus no results are shown there. While both canopies maintain similar
$\unicode[STIX]{x1D6FF}_{T}$
reached the top of the measurement region by the third FOV and thus no results are shown there. While both canopies maintain similar
![]() $\unicode[STIX]{x1D6FF}_{T}/h$
growth rate, the mixing layer above the homogeneous canopy exhibits larger vertical extension across all submergence depths. At
$\unicode[STIX]{x1D6FF}_{T}/h$
growth rate, the mixing layer above the homogeneous canopy exhibits larger vertical extension across all submergence depths. At
![]() $H/h=2$
, the difference in this vertical extension corresponds to approximately the element height standard deviation (
$H/h=2$
, the difference in this vertical extension corresponds to approximately the element height standard deviation (
![]() $\unicode[STIX]{x1D70E}_{h}=h/3$
). However, as submergence depth increases, this difference is reduced (figure 13). The growth of the mixing layer within the canopy is more complex and has been shown to be dependent on the canopy density and drag coefficient for homogeneous canopies (Nepf Reference Nepf2012). The penetration, and consequently the total thickness, of the canopy mixing layer (estimated using the same 5 % criterion and not shown here for brevity) is significantly modulated by the topography of the heterogeneous canopy, with a more pronounced effect at low submergence depths. The penetration increases downstream of
$\unicode[STIX]{x1D70E}_{h}=h/3$
). However, as submergence depth increases, this difference is reduced (figure 13). The growth of the mixing layer within the canopy is more complex and has been shown to be dependent on the canopy density and drag coefficient for homogeneous canopies (Nepf Reference Nepf2012). The penetration, and consequently the total thickness, of the canopy mixing layer (estimated using the same 5 % criterion and not shown here for brevity) is significantly modulated by the topography of the heterogeneous canopy, with a more pronounced effect at low submergence depths. The penetration increases downstream of
![]() $h_{1}$
rows as a result of the reduced obstruction above the shorter
$h_{1}$
rows as a result of the reduced obstruction above the shorter
![]() $h_{2}$
elements. For the estimation of the mixing layer penetration, Ghisalberti (Reference Ghisalberti2009) considered the formulation
$h_{2}$
elements. For the estimation of the mixing layer penetration, Ghisalberti (Reference Ghisalberti2009) considered the formulation
based on the analysis of multiple datasets across various obstructed shear flows and showed agreement over multiple scales and systems. This formulation results in
![]() $\unicode[STIX]{x1D6FF}_{e}/h=0.14$
and
$\unicode[STIX]{x1D6FF}_{e}/h=0.14$
and
![]() $\unicode[STIX]{x1D6FF}_{e}/h=0.28$
for the homogeneous and heterogeneous canopies, respectively. Note that for the heterogeneous case
$\unicode[STIX]{x1D6FF}_{e}/h=0.28$
for the homogeneous and heterogeneous canopies, respectively. Note that for the heterogeneous case
![]() $a=16~\text{m}^{-1}$
in the penetration region
$a=16~\text{m}^{-1}$
in the penetration region
![]() $h_{2}\leqslant y\leqslant h_{1}$
. The location of the estimated
$h_{2}\leqslant y\leqslant h_{1}$
. The location of the estimated
![]() $\unicode[STIX]{x1D6FF}_{e}$
is shown in figure 10 within the third FOV with a black dashed line and evidences agreement with the experimental results in both canopies.
$\unicode[STIX]{x1D6FF}_{e}$
is shown in figure 10 within the third FOV with a black dashed line and evidences agreement with the experimental results in both canopies.

Figure 13. Extension of mixing layer
![]() $\unicode[STIX]{x1D6FF}_{T}/h$
above the homogeneous (black) and heterogeneous (red) canopies at the three submergence depths.
$\unicode[STIX]{x1D6FF}_{T}/h$
above the homogeneous (black) and heterogeneous (red) canopies at the three submergence depths.

Figure 14. An instantaneous velocity fluctuation vector field
![]() $u^{\prime }\boldsymbol{i}+v^{\prime }\boldsymbol{j}$
superimposed on the contours of
$u^{\prime }\boldsymbol{i}+v^{\prime }\boldsymbol{j}$
superimposed on the contours of
![]() $u^{\prime }/U_{\infty }$
at submergence
$u^{\prime }/U_{\infty }$
at submergence
![]() $H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies.
$H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies.

Figure 15. The ratio of the total contribution of sweep to ejection events
![]() $S_{4,2}=\sum u^{\prime }v_{4}^{\prime }\big/\sum u^{\prime }v_{2}^{\prime }$
at
$S_{4,2}=\sum u^{\prime }v_{4}^{\prime }\big/\sum u^{\prime }v_{2}^{\prime }$
at
![]() $H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies.
$H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies.
Figure 14 shows a representative instantaneous velocity fluctuation field
![]() $u^{\prime }\boldsymbol{i}+v^{\prime }\boldsymbol{j}$
, where
$u^{\prime }\boldsymbol{i}+v^{\prime }\boldsymbol{j}$
, where
![]() $\boldsymbol{i}$
and
$\boldsymbol{i}$
and
![]() $\boldsymbol{j}$
indicate the unit vectors in the streamwise and wall-normal directions, superimposed on the contours of
$\boldsymbol{j}$
indicate the unit vectors in the streamwise and wall-normal directions, superimposed on the contours of
![]() $u^{\prime }/U_{\infty }$
for
$u^{\prime }/U_{\infty }$
for
![]() $H/h=3$
. The region of intense fluctuations reaching
$H/h=3$
. The region of intense fluctuations reaching
![]() ${\sim}30\,\%$
of
${\sim}30\,\%$
of
![]() $U_{\infty }$
marks the mixing layer and, as seen in figure 14, penetrates significantly deeper below the top of the heterogeneous canopy. To further characterize these fluctuations across the entire ensemble, quadrant analysis was performed following Lu & Willmarth (Reference Lu and Willmarth1973). The events contributing to the Reynolds stress are categorized into outward interactions (quadrant 1,
$U_{\infty }$
marks the mixing layer and, as seen in figure 14, penetrates significantly deeper below the top of the heterogeneous canopy. To further characterize these fluctuations across the entire ensemble, quadrant analysis was performed following Lu & Willmarth (Reference Lu and Willmarth1973). The events contributing to the Reynolds stress are categorized into outward interactions (quadrant 1,
![]() $u^{\prime }>0,~v^{\prime }>0$
), ejections (quadrant 2,
$u^{\prime }>0,~v^{\prime }>0$
), ejections (quadrant 2,
![]() $u^{\prime }<0,~v^{\prime }>0$
), inward interactions (quadrant 3,
$u^{\prime }<0,~v^{\prime }>0$
), inward interactions (quadrant 3,
![]() $u^{\prime }<0,~v^{\prime }<0$
) and sweeps (quadrant 4,
$u^{\prime }<0,~v^{\prime }<0$
) and sweeps (quadrant 4,
![]() $u^{\prime }>0,~v^{\prime }<0$
). To quantify the relative importance of sweeps and ejections that transport high- and low-momentum fluid into and from the canopies, figure 15 shows the ratio of the total contribution of sweeps to the total contribution of ejections,
$u^{\prime }>0,~v^{\prime }<0$
). To quantify the relative importance of sweeps and ejections that transport high- and low-momentum fluid into and from the canopies, figure 15 shows the ratio of the total contribution of sweeps to the total contribution of ejections,
![]() $S_{4,2}=\sum u^{\prime }v_{4}^{\prime }\big/\sum u^{\prime }v_{2}^{\prime }$
for
$S_{4,2}=\sum u^{\prime }v_{4}^{\prime }\big/\sum u^{\prime }v_{2}^{\prime }$
for
![]() $H/h=3$
. It is common to define a threshold
$H/h=3$
. It is common to define a threshold
![]() $M$
(also referred to as hyperbolic hole) to isolate dominant events such that only events satisfying
$M$
(also referred to as hyperbolic hole) to isolate dominant events such that only events satisfying
![]() $|u^{\prime }v^{\prime }|>M|\langle u^{\prime }v^{\prime }\rangle |$
are included in
$|u^{\prime }v^{\prime }|>M|\langle u^{\prime }v^{\prime }\rangle |$
are included in
![]() $S_{4,2}$
. All events across the entire ensemble were included in the ratio
$S_{4,2}$
. All events across the entire ensemble were included in the ratio
![]() $S_{4,2}$
shown in figure 15 (i.e.
$S_{4,2}$
shown in figure 15 (i.e.
![]() $M=0$
). However, the same analysis was performed with
$M=0$
). However, the same analysis was performed with
![]() $M=3$
and it showed similar trends. As seen in figure 15, sweeps dominate near the top of both canopies while ejections dominate further away. In the heterogeneous canopy, sweeps dominate over a larger area and near the top of the
$M=3$
and it showed similar trends. As seen in figure 15, sweeps dominate near the top of both canopies while ejections dominate further away. In the heterogeneous canopy, sweeps dominate over a larger area and near the top of the
![]() $h_{1}$
and
$h_{1}$
and
![]() $h_{2}$
elements with distinctive periodicity following the topography of the canopy. In a study dedicated to characterizing the flow structure in a homogeneous canopy, Zhu, van Hout & Katz (Reference Zhu, van Hout and Katz2007) showed that sweep events entrain and push turbulent structures from the overflow into the canopy. Here in the heterogeneous case, the deeper penetration and the larger space fraction where sweep events are dominant suggest a more active exchange with the overflow within the heterogeneous canopy. Figure 15 evidences similarity across both canopies in the ejection-dominated region, which occurs the same distance above the canopy in both cases. This provides a dynamic measure showing that the impact of the heterogeneity does not extend far above the canopy. It is worth noting that additional lateral measurements are needed to ensure that the observations within the canopies in figures 14 and 15 are representative of the spanwise-averaged behaviour.
$h_{2}$
elements with distinctive periodicity following the topography of the canopy. In a study dedicated to characterizing the flow structure in a homogeneous canopy, Zhu, van Hout & Katz (Reference Zhu, van Hout and Katz2007) showed that sweep events entrain and push turbulent structures from the overflow into the canopy. Here in the heterogeneous case, the deeper penetration and the larger space fraction where sweep events are dominant suggest a more active exchange with the overflow within the heterogeneous canopy. Figure 15 evidences similarity across both canopies in the ejection-dominated region, which occurs the same distance above the canopy in both cases. This provides a dynamic measure showing that the impact of the heterogeneity does not extend far above the canopy. It is worth noting that additional lateral measurements are needed to ensure that the observations within the canopies in figures 14 and 15 are representative of the spanwise-averaged behaviour.

Figure 16. Reynolds shear stress
![]() $-\langle u^{\prime }w^{\prime }\rangle /U_{\infty }^{2}$
at
$-\langle u^{\prime }w^{\prime }\rangle /U_{\infty }^{2}$
at
![]() $y/h\simeq 0.6$
and
$y/h\simeq 0.6$
and
![]() $H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies; elements of height
$H/h=3$
for the (a) homogeneous and (b) heterogeneous canopies; elements of height
![]() $h_{1}$
are shaded.
$h_{1}$
are shaded.
Thus far we have shown that height heterogeneity manifests in enhanced transport through the mean flow and the turbulent stress
![]() $-\langle u^{\prime }v^{\prime }\rangle$
. The effect on transverse transport within the canopy is given in figure 16 where
$-\langle u^{\prime }v^{\prime }\rangle$
. The effect on transverse transport within the canopy is given in figure 16 where
![]() $-\langle u^{\prime }w^{\prime }\rangle /U_{\infty }^{2}$
is shown at
$-\langle u^{\prime }w^{\prime }\rangle /U_{\infty }^{2}$
is shown at
![]() $y/h=0.6$
. For both canopies, the transverse turbulent transport is approximately 10 % of that in the vertical direction. Compared to the homogeneous canopy, slightly lower magnitudes of
$y/h=0.6$
. For both canopies, the transverse turbulent transport is approximately 10 % of that in the vertical direction. Compared to the homogeneous canopy, slightly lower magnitudes of
![]() $-\langle u^{\prime }w^{\prime }\rangle /U_{\infty }^{2}$
are associated with the shorter
$-\langle u^{\prime }w^{\prime }\rangle /U_{\infty }^{2}$
are associated with the shorter
![]() $h_{2}$
elements while similar magnitudes but wider distributions are associated with the longer
$h_{2}$
elements while similar magnitudes but wider distributions are associated with the longer
![]() $h_{1}$
elements (in association with the higher velocity around these elements in figure 7), indicating a more complex dynamics within the heterogeneous canopy. It is noteworthy that the
$h_{1}$
elements (in association with the higher velocity around these elements in figure 7), indicating a more complex dynamics within the heterogeneous canopy. It is noteworthy that the
![]() $-\langle u^{\prime }v^{\prime }\rangle$
component of the stress (not measured in this plane) plays and important role in governing the flow dynamics within the canopy.
$-\langle u^{\prime }v^{\prime }\rangle$
component of the stress (not measured in this plane) plays and important role in governing the flow dynamics within the canopy.

Figure 17. POD modes of the streamwise velocity fluctuations
![]() $\unicode[STIX]{x1D719}_{u^{\prime }}$
for the homogeneous canopy at
$\unicode[STIX]{x1D719}_{u^{\prime }}$
for the homogeneous canopy at
![]() $H/h=3$
: (a) mode 1, (b) mode 2, (c) mode 3, (d) mode 4.
$H/h=3$
: (a) mode 1, (b) mode 2, (c) mode 3, (d) mode 4.
3.3 POD analysis
In addition to inducing vertical flows within the canopy, modifying the levels and distribution of the
![]() $TKE$
and Reynolds shear stress, and altering the extension and penetration of the canopy mixing layer, height heterogeneity has a distinctive effect on the scales and spatial features of the flow especially at low submergence depths. To gain insight into the effect of height heterogeneity on the energetic modes of the flow, snapshot POD was performed on a subset of 2000 fluctuating velocity fields for both canopies within the third field of view at
$TKE$
and Reynolds shear stress, and altering the extension and penetration of the canopy mixing layer, height heterogeneity has a distinctive effect on the scales and spatial features of the flow especially at low submergence depths. To gain insight into the effect of height heterogeneity on the energetic modes of the flow, snapshot POD was performed on a subset of 2000 fluctuating velocity fields for both canopies within the third field of view at
![]() $H/h=2$
and 3 following Sirovich (Reference Sirovich1987). For detailed information regarding POD and its implementation, the reader is referred to the work of Lumley (Reference Lumley1970), Sirovich (Reference Sirovich1987) and Berkooz, Holmes & Lumley (Reference Berkooz, Holmes and Lumley1993). Essentially, POD is used to extract the dominant spatial features of the flow by decomposing the stochastic fluctuating velocity signal
$H/h=2$
and 3 following Sirovich (Reference Sirovich1987). For detailed information regarding POD and its implementation, the reader is referred to the work of Lumley (Reference Lumley1970), Sirovich (Reference Sirovich1987) and Berkooz, Holmes & Lumley (Reference Berkooz, Holmes and Lumley1993). Essentially, POD is used to extract the dominant spatial features of the flow by decomposing the stochastic fluctuating velocity signal
![]() $\boldsymbol{u}^{\prime }(\boldsymbol{x},t)$
into a deterministic part
$\boldsymbol{u}^{\prime }(\boldsymbol{x},t)$
into a deterministic part
![]() $\unicode[STIX]{x1D753}^{n}(\boldsymbol{x})$
(POD modes) and time-dependent coefficients
$\unicode[STIX]{x1D753}^{n}(\boldsymbol{x})$
(POD modes) and time-dependent coefficients
![]() $a^{n}(t)$
as
$a^{n}(t)$
as
Here, bold symbols denote vectorial quantities and
![]() $N$
represents the number of snapshots (for this analysis
$N$
represents the number of snapshots (for this analysis
![]() $N=2000$
). The individual contribution of each mode to the total turbulent kinetic energy is given by the ratio of the eigenvalue of that mode to the sum of all
$N=2000$
). The individual contribution of each mode to the total turbulent kinetic energy is given by the ratio of the eigenvalue of that mode to the sum of all
![]() $N$
eigenvalues, i.e.
$N$
eigenvalues, i.e.
![]() $E_{n}=\unicode[STIX]{x1D706}_{n}\big/\sum _{m=1}^{N}\unicode[STIX]{x1D706}_{m}$
. Analysis of the cumulative energy convergence showed that the homogeneous case, at both submergence depths, and the heterogeneous case at
$E_{n}=\unicode[STIX]{x1D706}_{n}\big/\sum _{m=1}^{N}\unicode[STIX]{x1D706}_{m}$
. Analysis of the cumulative energy convergence showed that the homogeneous case, at both submergence depths, and the heterogeneous case at
![]() $H/h=3$
exhibit comparable energy spectra, with the first
$H/h=3$
exhibit comparable energy spectra, with the first
![]() ${\sim}20$
modes contributing 50 % of the total energy. A considerably slower convergence occurs for the heterogeneous canopy at
${\sim}20$
modes contributing 50 % of the total energy. A considerably slower convergence occurs for the heterogeneous canopy at
![]() $H/h=2$
with roughly double the number of modes contributing 50 % of the total energy, evidencing significantly richer flow dynamics.
$H/h=2$
with roughly double the number of modes contributing 50 % of the total energy, evidencing significantly richer flow dynamics.
Inspection of the first 10 streamwise POD modes
![]() $\unicode[STIX]{x1D719}_{u^{\prime }}$
indicates structural similarity across the first four modes for both canopies at both submergences. Figure 17 shows the first four streamwise velocity fluctuation modes for the homogeneous canopy at
$\unicode[STIX]{x1D719}_{u^{\prime }}$
indicates structural similarity across the first four modes for both canopies at both submergences. Figure 17 shows the first four streamwise velocity fluctuation modes for the homogeneous canopy at
![]() $H/h=3$
. In this case, these four modes contain approximately a quarter of the total energy. As shown in figure 17, the first four modes scale vertically with the canopy height
$H/h=3$
. In this case, these four modes contain approximately a quarter of the total energy. As shown in figure 17, the first four modes scale vertically with the canopy height
![]() $h$
, and are inclined at approximately
$h$
, and are inclined at approximately
![]() $15^{\circ }$
,
$15^{\circ }$
,
![]() $20^{\circ }$
,
$20^{\circ }$
,
![]() $25^{\circ }$
and
$25^{\circ }$
and
![]() $45^{\circ }$
, respectively. Significant structural differences across canopies and submergence depths are observed beyond the first four shown modes. These structures are inherently different from those of a classical free mixing layer due to the canopy obstruction and the superposition of scales discussed in Poggi et al. (Reference Poggi, Porporato, Ridolfi, Albertson and Katul2004). While the over-canopy flow is distinct from a canonical boundary layer flow due to the presence of the mixing layer and its canopy-scale turbulence, the first two modes in figure 17 exhibit structural similarity with those in the rough-wall turbulent boundary layer studied by Sen, Bhaganagar & Juttijudata (Reference Sen, Bhaganagar and Juttijudata2007). However, the ones observed here have larger inclination angles. In contrast to all other reviewed modes in both canopies, the heterogeneous case at
$45^{\circ }$
, respectively. Significant structural differences across canopies and submergence depths are observed beyond the first four shown modes. These structures are inherently different from those of a classical free mixing layer due to the canopy obstruction and the superposition of scales discussed in Poggi et al. (Reference Poggi, Porporato, Ridolfi, Albertson and Katul2004). While the over-canopy flow is distinct from a canonical boundary layer flow due to the presence of the mixing layer and its canopy-scale turbulence, the first two modes in figure 17 exhibit structural similarity with those in the rough-wall turbulent boundary layer studied by Sen, Bhaganagar & Juttijudata (Reference Sen, Bhaganagar and Juttijudata2007). However, the ones observed here have larger inclination angles. In contrast to all other reviewed modes in both canopies, the heterogeneous case at
![]() $H/h=2$
exhibited significantly inclined structures reaching from the canopy to the top of the flow domain indicative of substantial interaction between the inner- and over-canopy flows. This increased complexity along with the pronounced topography-induced periodic flows are in line with the slower convergence discussed earlier.
$H/h=2$
exhibited significantly inclined structures reaching from the canopy to the top of the flow domain indicative of substantial interaction between the inner- and over-canopy flows. This increased complexity along with the pronounced topography-induced periodic flows are in line with the slower convergence discussed earlier.
4 Conclusions
Particle image velocimetry (PIV) in a refractive-index-matching (RIM) channel was used for the examination of the effect of height heterogeneity on canopy flows. The canopy heterogeneity led to enhanced streamwise flow within the canopy at the lower submergence depths, which is especially important as the streamwise flow is essential in advecting scalars within the canopy in the region below the mixing layer. Furthermore, and in contrast with the homogeneous case, the topography of the heterogeneous canopy, which resembles a row canopy, induced spatially periodic flows with non-vanishing vertical velocity. Although the measurements are restricted to one lateral plane, the non-vanishing vertical velocity is expected to be present at other lateral locations. Moreover, height heterogeneity impacts the flow adjustment region, resulting in a comparatively more complex flow near the leading edge for the heterogeneous canopy. However, both canopies had approximately the same adjustment length.
The
![]() $TKE$
and Reynolds stress are enhanced within the heterogeneous canopy mixing layer, relative to the homogeneous canopy. Both quantities showed periodic variations associated with the topography of the canopy. The extension and penetration of the canopy mixing layer was significantly altered for the heterogeneous case with deepened penetration in proximity to the shorter elements where canopy obstruction is reduced. Furthermore, quadrant analysis showed an enhancement of sweep events near both element heights
$TKE$
and Reynolds stress are enhanced within the heterogeneous canopy mixing layer, relative to the homogeneous canopy. Both quantities showed periodic variations associated with the topography of the canopy. The extension and penetration of the canopy mixing layer was significantly altered for the heterogeneous case with deepened penetration in proximity to the shorter elements where canopy obstruction is reduced. Furthermore, quadrant analysis showed an enhancement of sweep events near both element heights
![]() $h_{1}$
and
$h_{1}$
and
![]() $h_{2}$
for the heterogeneous canopy. However, the maximum in Reynolds shear stress
$h_{2}$
for the heterogeneous canopy. However, the maximum in Reynolds shear stress
![]() $-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
occurred consistently near
$-\langle u^{\prime }v^{\prime }\rangle /U_{\infty }^{2}$
occurred consistently near
![]() $h_{1}$
indicating that this is the effective canopy height. POD analysis provided further evidence of the increased flow complexity within and above the heterogeneous canopy. The impact of heterogeneity was the most pronounced for the lowest submergence ratio (smallest
$h_{1}$
indicating that this is the effective canopy height. POD analysis provided further evidence of the increased flow complexity within and above the heterogeneous canopy. The impact of heterogeneity was the most pronounced for the lowest submergence ratio (smallest
![]() $H/h$
) and decreased with increasing submergence
$H/h$
) and decreased with increasing submergence
![]() $(H/h)$
. Further work is required to identify the limiting submergence at which the impact of heterogeneity is insignificant. Additionally, volumetric measurements are suggested to provide greater detail regarding how flow features vary across the entire span of the canopy.
$(H/h)$
. Further work is required to identify the limiting submergence at which the impact of heterogeneity is insignificant. Additionally, volumetric measurements are suggested to provide greater detail regarding how flow features vary across the entire span of the canopy.
The heterogeneous canopy exhibited higher turbulent momentum exchange at the top of the canopy, which implies higher turbulent exchange of scalars as well. This further suggests that the heterogeneous canopies experience more rapid flushing and shorter in-canopy residence time. In addition, the higher turbulent stress implies that heterogeneous canopies produce a higher contribution to channel hydraulic resistance than that of a homogeneous canopy of the same roughness density. Finally, the impact of heterogeneity on turbulence production at the canopy interface was strongly modulated by the submergence height, with heterogeneity enhancing turbulence production most at the lowest submergence depth
![]() $(H/h=2)$
.
$(H/h=2)$
.
Acknowledgements
This work was supported by the Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, as part of the start-up package of Leonardo P. Chamorro. The experiments were performed in a facility built under the National Science Foundation grant award CBET-0923106. The authors are grateful for the help of graduate student Prateek Ranjan and undergraduate student Zixu Zhang at the University of Illinois.