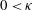1 Introduction
The study of two-dimensional vortices in a non-uniform background flow has attracted the attention of many researchers in vortex dynamics because of its overall theoretical importance and its many applications such as, for instance, flow control, geophysical flows, turbulence. To this purpose, several vortex models have been adopted, in particular point vortices, vortex patches and hollow vortices.
In the context of the detection of aircraft wakes, Moore & Saffman (Reference Moore, Saffman, Olsen, Goldburg and Rogers1971) studied the shape of finite-area vortices in a two-dimensional inviscid straining flow. They considered irrotational strain and simple shear. By modelling vortices as vortex patches, i.e. as regions with constant vorticity,
![]() $\unicode[STIX]{x1D714}=\text{const}$
, they found steady configurations with elliptical shapes. Kida (Reference Kida1981) showed analytically that the Moore & Saffman (Reference Moore, Saffman, Olsen, Goldburg and Rogers1971) solutions are particular steady cases of more general unsteady time-periodic solutions, in which, depending on the shear intensity, vortices rotate preserving their elliptical shape and varying their ellipticity. Earlier, Chaplygin and Kirchhoff had found solutions for (i) the motion of an elliptical patch of uniform vorticity in an exterior field of pure shear; (ii) the motion of a (symmetric or non-symmetric) dipolar vortex with a continuous distribution of vorticity translating steadily along a straight path; and (iii) the motion of a non-symmetric vortex dipole moving along a circular trajectory (Lamb Reference Lamb1932; Meleshko & van Heijst Reference Meleshko and van Heijst1994).
$\unicode[STIX]{x1D714}=\text{const}$
, they found steady configurations with elliptical shapes. Kida (Reference Kida1981) showed analytically that the Moore & Saffman (Reference Moore, Saffman, Olsen, Goldburg and Rogers1971) solutions are particular steady cases of more general unsteady time-periodic solutions, in which, depending on the shear intensity, vortices rotate preserving their elliptical shape and varying their ellipticity. Earlier, Chaplygin and Kirchhoff had found solutions for (i) the motion of an elliptical patch of uniform vorticity in an exterior field of pure shear; (ii) the motion of a (symmetric or non-symmetric) dipolar vortex with a continuous distribution of vorticity translating steadily along a straight path; and (iii) the motion of a non-symmetric vortex dipole moving along a circular trajectory (Lamb Reference Lamb1932; Meleshko & van Heijst Reference Meleshko and van Heijst1994).
Schecter & Dubin (Reference Schecter and Dubin2001) examined two-dimensional vortex motion in a shear flow with non-uniform vorticity. In general, a vortex travels to an extremum in the background vorticity distribution and the rate of this migration increases with the magnitude of the background vorticity gradient. They also found that a retrograde vortex, which rotates against the local shear, moves orders of magnitude faster than a prograde vortex of equal strength.
Besides the general interest in exact solutions of the Euler equations for non-trivial flows, analytical models of vortical structures in shear flows are relevant to the Earth’s atmosphere and oceans. Jupiter’s Great Red Spot is another example connected to the present study on hollow vortices: the Great Red Spot is a vortical structure that interacts with a shear flow and exhibits high vorticity in its outer region and low vorticity in its core (see Shetty, Asay-Davis & Marcus (Reference Shetty, Asay-Davis and Marcus2010), and references therein). Vorticity has also been put forward as a mechanism in the formation of the Solar system (Tanga et al. Reference Tanga, Babiano, Dubrulle and Provenzale1996).
More recently, Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012) solved a problem related to the Moore & Saffman (Reference Moore, Saffman, Olsen, Goldburg and Rogers1971) problem of vortex equilibrium in a straining flow using the hollow-vortex model that takes that the inside of the vortex to be vacuum or, equivalently, a zero-vorticity region bounded by a vortex sheet (in both cases, at steady state, a constant pressure inside the core requires a constant speed at the vortex boundary). They limited their study to the irrotational strain case and provided a closed-form analytical solution for steady configurations.
In the present study, we enrich the scenario by giving analytical solution to the problem of finding the shape a hollow vortex takes in equilibrium in a shear flow.
Zero vorticity,
![]() $\unicode[STIX]{x1D714}=0$
, means that the streamfunction
$\unicode[STIX]{x1D714}=0$
, means that the streamfunction
![]() $\unicode[STIX]{x1D713}$
is harmonic in the inside of the vortex. When the flow is steady,
$\unicode[STIX]{x1D713}$
is harmonic in the inside of the vortex. When the flow is steady,
![]() $\unicode[STIX]{x1D713}$
is constant at the boundary and, according to the maximum principle,
$\unicode[STIX]{x1D713}$
is constant at the boundary and, according to the maximum principle,
![]() $\unicode[STIX]{x1D713}$
is constant throughout the inside of the vortex. It follows that flow velocity is zero and pressure is constant in the interior. Equilibrium then requires constant flow speed along the exterior side of the bounding vortex sheet. The determination of the shape of a hollow vortex is so reduced to a free-streamline problem, whose study goes back to 19th century and Kirchhoff free-streamline theory. Birkhoff & Zarantonello (Reference Birkhoff and Zarantonello1957) and Gurevich (Reference Gurevich1966) present a broad survey of this problem. Hicks (Reference Hicks1883) and Pocklington (Reference Pocklington1895) are examples of historic solutions for hollow-vortex shapes. More recent studies on hollow vortices, based on the classical hodograph method or more innovative methods, have been produced. Among many references on the matter, one can mention, for instance, Baker, Saffman & Sheffield (Reference Baker, Saffman and Sheffield1976), Lin & Landweber (Reference Lin and Landweber1977), Crowdy & Green (Reference Crowdy and Green2011), Telib & Zannetti (Reference Telib and Zannetti2011), Crowdy, Llewellyn Smith & Freilich (Reference Crowdy, Llewellyn Smith and Freilich2012), Elcrat & Zannetti (Reference Elcrat and Zannetti2012), Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012), Zannetti & Lasagna (Reference Zannetti and Lasagna2013), Elcrat, Ferlauto & Zannetti (Reference Elcrat, Ferlauto and Zannetti2014), Green (Reference Green2015).
$\unicode[STIX]{x1D713}$
is constant throughout the inside of the vortex. It follows that flow velocity is zero and pressure is constant in the interior. Equilibrium then requires constant flow speed along the exterior side of the bounding vortex sheet. The determination of the shape of a hollow vortex is so reduced to a free-streamline problem, whose study goes back to 19th century and Kirchhoff free-streamline theory. Birkhoff & Zarantonello (Reference Birkhoff and Zarantonello1957) and Gurevich (Reference Gurevich1966) present a broad survey of this problem. Hicks (Reference Hicks1883) and Pocklington (Reference Pocklington1895) are examples of historic solutions for hollow-vortex shapes. More recent studies on hollow vortices, based on the classical hodograph method or more innovative methods, have been produced. Among many references on the matter, one can mention, for instance, Baker, Saffman & Sheffield (Reference Baker, Saffman and Sheffield1976), Lin & Landweber (Reference Lin and Landweber1977), Crowdy & Green (Reference Crowdy and Green2011), Telib & Zannetti (Reference Telib and Zannetti2011), Crowdy, Llewellyn Smith & Freilich (Reference Crowdy, Llewellyn Smith and Freilich2012), Elcrat & Zannetti (Reference Elcrat and Zannetti2012), Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012), Zannetti & Lasagna (Reference Zannetti and Lasagna2013), Elcrat, Ferlauto & Zannetti (Reference Elcrat, Ferlauto and Zannetti2014), Green (Reference Green2015).
Once the problem is non-dimensionalized, we show that the problem has one degree of freedom, i.e. the solution depends on a single non-dimensional parameter. The solutions form two separate families related to opposite or same sign of shear vorticity and vortex circulation.
When shear vorticity and vortex circulation are opposite, the solutions are analogous to and have the same flow topology as the hollow vortices in an irrotational straining flow studied by Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012). We have selected as free parameter the non-dimensional speed
![]() $\unicode[STIX]{x1D705}$
of the flow at the boundary of the vortex. As
$\unicode[STIX]{x1D705}$
of the flow at the boundary of the vortex. As
![]() $\unicode[STIX]{x1D705}\rightarrow \infty$
the solution is a point vortex. For large finite values of
$\unicode[STIX]{x1D705}\rightarrow \infty$
the solution is a point vortex. For large finite values of
![]() $\unicode[STIX]{x1D705}$
the point vortex is desingularized into a finite-area vortex. As
$\unicode[STIX]{x1D705}$
the point vortex is desingularized into a finite-area vortex. As
![]() $\unicode[STIX]{x1D705}$
decreases, the vortex area increases until a maximum area is reached and then decreases. Unlike the solution of Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012), our solution is not expressed in closed form but is obtained by a root-finding process.
$\unicode[STIX]{x1D705}$
decreases, the vortex area increases until a maximum area is reached and then decreases. Unlike the solution of Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012), our solution is not expressed in closed form but is obtained by a root-finding process.
In the family corresponding to the same sign of shear-flow vorticity and vortex circulation, the point-vortex solution is, as above, obtained for
![]() $\unicode[STIX]{x1D705}\rightarrow \infty$
. The vortex area increases monotonically as
$\unicode[STIX]{x1D705}\rightarrow \infty$
. The vortex area increases monotonically as
![]() $\unicode[STIX]{x1D705}$
decreases.
$\unicode[STIX]{x1D705}$
decreases.
The study of stability of the solutions goes beyond the scope of the present study. However the present analytical method of solution offers a tool for further studies on this important aspect of the problem, following on from, for example, the linear stability analysis described by Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012) for hollow vortices in a potential strained flow or by Crowdy et al. (Reference Crowdy, Llewellyn Smith and Freilich2012) for Pocklington’s vortex pair.
2 Hollow-vortex structure
We consider a hollow vortex in equilibrium in a two-dimensional (2-D) incompressible flow governed by the Euler equation. Then
where
![]() $\unicode[STIX]{x1D713}$
denotes the streamfunction and
$\unicode[STIX]{x1D713}$
denotes the streamfunction and
![]() $\unicode[STIX]{x1D714}$
, which is constant, the vorticity of the flow past the vortex. At infinity the flow tends to a pure shear flow, that is,
$\unicode[STIX]{x1D714}$
, which is constant, the vorticity of the flow past the vortex. At infinity the flow tends to a pure shear flow, that is,
where (
![]() $x,y$
) are Cartesian coordinates and
$x,y$
) are Cartesian coordinates and
![]() $\boldsymbol{i}$
is the unit vector along the
$\boldsymbol{i}$
is the unit vector along the
![]() $x$
-axis.
$x$
-axis.
The vorticity inside the vortex is assumed to be zero. As a consequence, the internal flow is at rest, the pressure is constant at the vortex boundary and, according to Bernoulli’s equation, the vortex boundary is a vortex sheet with constant speed
![]() $q=k$
on the external side. Steady flow and constant tangential velocity result in
$q=k$
on the external side. Steady flow and constant tangential velocity result in
where
![]() $n$
and
$n$
and
![]() $s$
are normal and tangential directions at the boundary.
$s$
are normal and tangential directions at the boundary.
This is a free-boundary problem which requires finding the vortex shape that satisfies the above conditions. For the sake of simplicity, a summary description of the solution is presented in this section while a detailed description is given in the appendices.
Briefly, the solution is obtained according to the classical conformal mapping method. Let
![]() $z=x+\text{i}y$
be the complex coordinate in the physical
$z=x+\text{i}y$
be the complex coordinate in the physical
![]() $z$
-plane of motion and
$z$
-plane of motion and
![]() $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D709}+\text{i}\unicode[STIX]{x1D702}$
the complex coordinate in a transformed
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D709}+\text{i}\unicode[STIX]{x1D702}$
the complex coordinate in a transformed
![]() $\unicode[STIX]{x1D701}$
-plane. The solution consists in finding the function
$\unicode[STIX]{x1D701}$
-plane. The solution consists in finding the function
![]() $z=z(\unicode[STIX]{x1D701})$
mapping the unit circle in the
$z=z(\unicode[STIX]{x1D701})$
mapping the unit circle in the
![]() $\unicode[STIX]{x1D701}$
-plane onto the vortex contour in the
$\unicode[STIX]{x1D701}$
-plane onto the vortex contour in the
![]() $z$
-plane.
$z$
-plane.
For flow regularity, the mapping
![]() $z(\unicode[STIX]{x1D701})$
has to be analytic outside the unit circle of the
$z(\unicode[STIX]{x1D701})$
has to be analytic outside the unit circle of the
![]() $\unicode[STIX]{x1D701}$
-plane and such that
$\unicode[STIX]{x1D701}$
-plane and such that
![]() $\lim _{\unicode[STIX]{x1D701}\rightarrow \infty }z(\unicode[STIX]{x1D701})=\infty$
and the mapping derivative
$\lim _{\unicode[STIX]{x1D701}\rightarrow \infty }z(\unicode[STIX]{x1D701})=\infty$
and the mapping derivative
![]() $\text{d}z/\text{d}\unicode[STIX]{x1D701}$
has to be analytic and different from zero. Thus,
$\text{d}z/\text{d}\unicode[STIX]{x1D701}$
has to be analytic and different from zero. Thus,
![]() $\text{d}z/\text{d}\unicode[STIX]{x1D701}$
can be expressed as
$\text{d}z/\text{d}\unicode[STIX]{x1D701}$
can be expressed as
Once the coefficients
![]() $b_{n}$
are determined by the solution process, the mapping
$b_{n}$
are determined by the solution process, the mapping
![]() $z(\unicode[STIX]{x1D701})$
is obtained by analytic integration, as shown in the appendices.
$z(\unicode[STIX]{x1D701})$
is obtained by analytic integration, as shown in the appendices.
In general, (2.1) is satisfied by the streamfunction
where the first term
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D714}}$
is the streamfunction of a pure shear flow whose constant vorticity is
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D714}}$
is the streamfunction of a pure shear flow whose constant vorticity is
![]() $\unicode[STIX]{x1D714}$
and the second term
$\unicode[STIX]{x1D714}$
and the second term
![]() $\unicode[STIX]{x1D713}_{p}$
is the streamfunction of an irrotational flow whose complex potential is
$\unicode[STIX]{x1D713}_{p}$
is the streamfunction of an irrotational flow whose complex potential is
![]() $w_{p}$
. Continuing, (2.2) is satisfied by setting
$w_{p}$
. Continuing, (2.2) is satisfied by setting
The complex potential
![]() $w_{p}(\unicode[STIX]{x1D701})$
is made up of the combination of the complex potential of a point vortex with circulation
$w_{p}(\unicode[STIX]{x1D701})$
is made up of the combination of the complex potential of a point vortex with circulation
![]() $\unicode[STIX]{x1D6FE}$
located on the origin of the
$\unicode[STIX]{x1D6FE}$
located on the origin of the
![]() $\unicode[STIX]{x1D701}$
-plane and a complex potential
$\unicode[STIX]{x1D701}$
-plane and a complex potential
![]() $G(\unicode[STIX]{x1D701})$
which is analytic for
$G(\unicode[STIX]{x1D701})$
which is analytic for
![]() $|\unicode[STIX]{x1D701}|\geqslant 1$
and is finite at infinity. Hence, in general, the latter can be written as
$|\unicode[STIX]{x1D701}|\geqslant 1$
and is finite at infinity. Hence, in general, the latter can be written as
As detailed in the appendices, for given values of vorticity
![]() $\unicode[STIX]{x1D714}$
, point-vortex circulation
$\unicode[STIX]{x1D714}$
, point-vortex circulation
![]() $\unicode[STIX]{x1D6FE}$
and vortex-contour speed
$\unicode[STIX]{x1D6FE}$
and vortex-contour speed
![]() $k$
, the coefficients
$k$
, the coefficients
![]() $b_{n}$
,
$b_{n}$
,
![]() $c_{n}$
of the above series, truncated at a suitably large value
$c_{n}$
of the above series, truncated at a suitably large value
![]() $N$
, are determined by enforcing the constraints (2.3).
$N$
, are determined by enforcing the constraints (2.3).
According to (2.5) and (2.6), Stokes’ theorem and the residue theorem, the circulation
![]() $\unicode[STIX]{x1D6E4}$
of the hollow vortex is
$\unicode[STIX]{x1D6E4}$
of the hollow vortex is
where
![]() $A_{v}$
is the vortex area and
$A_{v}$
is the vortex area and
![]() $L_{c}$
is the vortex perimeter.
$L_{c}$
is the vortex perimeter.
Let the problem be non-dimensionalized by taking the absolute value of the vorticity of the shear flow
![]() $\unicode[STIX]{x1D714}$
as reference vorticity (
$\unicode[STIX]{x1D714}$
as reference vorticity (
![]() $\unicode[STIX]{x1D714}_{ref}=|\unicode[STIX]{x1D714}|$
) and the absolute value of the vortex circulation
$\unicode[STIX]{x1D714}_{ref}=|\unicode[STIX]{x1D714}|$
) and the absolute value of the vortex circulation
![]() $\unicode[STIX]{x1D6FE}/(2\unicode[STIX]{x03C0})$
as the reference circulation
$\unicode[STIX]{x1D6FE}/(2\unicode[STIX]{x03C0})$
as the reference circulation
![]() $(\unicode[STIX]{x1D6FE}_{ref}=|\unicode[STIX]{x1D6FE}/(2\unicode[STIX]{x03C0})|)$
. The reference length and velocity become
$(\unicode[STIX]{x1D6FE}_{ref}=|\unicode[STIX]{x1D6FE}/(2\unicode[STIX]{x03C0})|)$
. The reference length and velocity become
![]() $l_{ref}=\sqrt{|\unicode[STIX]{x1D6FE}/(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D714})|}$
and
$l_{ref}=\sqrt{|\unicode[STIX]{x1D6FE}/(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D714})|}$
and
![]() $q_{ref}=\sqrt{|\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FE}/(2\unicode[STIX]{x03C0})|}$
, respectively.
$q_{ref}=\sqrt{|\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FE}/(2\unicode[STIX]{x03C0})|}$
, respectively.
The streamfunction of the non-dimensionalized problem, written as function of
![]() $\unicode[STIX]{x1D701}$
, becomes
$\unicode[STIX]{x1D701}$
, becomes
with
![]() $\unicode[STIX]{x1D6FF}=\text{sgn}(\unicode[STIX]{x1D714})$
,
$\unicode[STIX]{x1D6FF}=\text{sgn}(\unicode[STIX]{x1D714})$
,
![]() $\unicode[STIX]{x1D70F}=\text{sgn}(\unicode[STIX]{x1D6FE})$
and where
$\unicode[STIX]{x1D70F}=\text{sgn}(\unicode[STIX]{x1D6FE})$
and where
is the non-dimensional velocity at the vortex boundary. For
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
, two families of shapes are defined by varying the parameter
$\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
, two families of shapes are defined by varying the parameter
![]() $\unicode[STIX]{x1D705}$
. That is, all the solutions corresponding to given values of vorticity
$\unicode[STIX]{x1D705}$
. That is, all the solutions corresponding to given values of vorticity
![]() $\unicode[STIX]{x1D714}$
and circulation
$\unicode[STIX]{x1D714}$
and circulation
![]() $\unicode[STIX]{x1D6FE}$
can be scaled onto two family of shapes.
$\unicode[STIX]{x1D6FE}$
can be scaled onto two family of shapes.
As for Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012), the general topology of the flow can be deducted by considering the related problem of a point vortex in the same shear flow. In the physical
![]() $z$
-plane, the non-dimensionalized streamfunction for the point-vortex flow is
$z$
-plane, the non-dimensionalized streamfunction for the point-vortex flow is

Figure 1. Streamline patterns of the point-vortex solution: (a)
![]() $\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
; (b)
$\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
; (b)
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
.
Figure 1(a) shows the streamline pattern for
![]() $\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
, that is for a point vortex whose circulation is opposite to the shear vorticity. The flow has two stagnation points and a separatrix that divides a finite body of recirculating fluid entrained by the vortex from the external non-recirculating flow driven by the shear flow.
$\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
, that is for a point vortex whose circulation is opposite to the shear vorticity. The flow has two stagnation points and a separatrix that divides a finite body of recirculating fluid entrained by the vortex from the external non-recirculating flow driven by the shear flow.
Figure 1(b) shows the case of equal sign point-vortex circulation and shear vorticity (
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
). There are no stagnation points and all the streamlines are closed. Close to the point vortex the streamline shapes are near circular, while far away the shear flow makes them increasingly elongated.
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
). There are no stagnation points and all the streamlines are closed. Close to the point vortex the streamline shapes are near circular, while far away the shear flow makes them increasingly elongated.
2.1 The
 $\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
case
$\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
case

Figure 2. Hollow-vortex streamlines for
![]() $\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D705}=2$
.
$\unicode[STIX]{x1D705}=2$
.
We first consider the solutions for
![]() $\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}=-1$
for different values of
$\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}=-1$
for different values of
![]() $\unicode[STIX]{x1D705}$
. It is obvious that the
$\unicode[STIX]{x1D705}$
. It is obvious that the
![]() $\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}=1$
choice generates the same flows streaming in reversed direction.
$\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}=1$
choice generates the same flows streaming in reversed direction.
An example solution is provided by figure 2 where the flow field has been drawn for
![]() $\unicode[STIX]{x1D705}=2$
. By varying the parameter
$\unicode[STIX]{x1D705}=2$
. By varying the parameter
![]() $\unicode[STIX]{x1D705}$
, a hollow-vortex solution can be continued onto a family of vortices with different shapes and areas. Hollow-vortex shapes are displayed in figure 3(a) for given values of the non-dimensionalized speed
$\unicode[STIX]{x1D705}$
, a hollow-vortex solution can be continued onto a family of vortices with different shapes and areas. Hollow-vortex shapes are displayed in figure 3(a) for given values of the non-dimensionalized speed
![]() $\unicode[STIX]{x1D705}$
in the range
$\unicode[STIX]{x1D705}$
in the range
![]() $1.32\leqslant \unicode[STIX]{x1D705}$
. As
$1.32\leqslant \unicode[STIX]{x1D705}$
. As
![]() $\unicode[STIX]{x1D705}\rightarrow \infty$
the solution tends to a zero-area vortex, that is, to the point-vortex solution. As
$\unicode[STIX]{x1D705}\rightarrow \infty$
the solution tends to a zero-area vortex, that is, to the point-vortex solution. As
![]() $\unicode[STIX]{x1D705}$
decreases the point vortex is desingularized into more and more elongated vortices with finite area. The non-dimensional area
$\unicode[STIX]{x1D705}$
decreases the point vortex is desingularized into more and more elongated vortices with finite area. The non-dimensional area
![]() $\unicode[STIX]{x1D6FC}=A_{v}/l_{ref}^{2}$
is plotted versus
$\unicode[STIX]{x1D6FC}=A_{v}/l_{ref}^{2}$
is plotted versus
![]() $\unicode[STIX]{x1D705}$
in figure 3(b). For
$\unicode[STIX]{x1D705}$
in figure 3(b). For
![]() $\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}^{\star }\approx 1.6$
, the vortex area reaches a maximum. As
$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}^{\star }\approx 1.6$
, the vortex area reaches a maximum. As
![]() $\unicode[STIX]{x1D705}$
decreases, the shapes start to resemble those computed by Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012) for hollow vortices in a strain flow (
$\unicode[STIX]{x1D705}$
decreases, the shapes start to resemble those computed by Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012) for hollow vortices in a strain flow (
![]() $n=2$
in their notation; see their figures 2 and 3), with a limiting value for
$n=2$
in their notation; see their figures 2 and 3), with a limiting value for
![]() $\unicode[STIX]{x1D705}$
below which there is no solution as the boundary starts to self-intersect. This outcome is expected for
$\unicode[STIX]{x1D705}$
below which there is no solution as the boundary starts to self-intersect. This outcome is expected for
![]() $\unicode[STIX]{x1D705}<\unicode[STIX]{x1D705}^{\star }$
, where a decrease of speed at the vortex contour is accompanied by a decrease of the vortex area. In non-dimensional form (2.8) yields
$\unicode[STIX]{x1D705}<\unicode[STIX]{x1D705}^{\star }$
, where a decrease of speed at the vortex contour is accompanied by a decrease of the vortex area. In non-dimensional form (2.8) yields
![]() $\unicode[STIX]{x1D705}l_{c}=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FC}$
, where
$\unicode[STIX]{x1D705}l_{c}=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70F}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FC}$
, where
![]() $l_{c}$
is the non-dimensional length of the vortex contour. In the present case
$l_{c}$
is the non-dimensional length of the vortex contour. In the present case
![]() $\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D705}=-1$
and the contour length becomes
$\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D705}=-1$
and the contour length becomes
![]() $l_{c}=(2\unicode[STIX]{x03C0}-\unicode[STIX]{x1D6FC})/\unicode[STIX]{x1D705}$
. As
$l_{c}=(2\unicode[STIX]{x03C0}-\unicode[STIX]{x1D6FC})/\unicode[STIX]{x1D705}$
. As
![]() $\unicode[STIX]{x1D705}$
decreases it becomes longer and, since the vortex area is getting smaller, it will eventually self-intersect. The pinch-off happens between
$\unicode[STIX]{x1D705}$
decreases it becomes longer and, since the vortex area is getting smaller, it will eventually self-intersect. The pinch-off happens between
![]() $\unicode[STIX]{x1D705}=1.32$
and
$\unicode[STIX]{x1D705}=1.32$
and
![]() $\unicode[STIX]{x1D705}=1.31$
(the numerical procedure will produce self-intersecting shapes as
$\unicode[STIX]{x1D705}=1.31$
(the numerical procedure will produce self-intersecting shapes as
![]() $\unicode[STIX]{x1D705}$
continues to decrease). An explanation of such an agreement might be given by noticing that a shear flow can be decomposed into a strain flow plus a rigid body rotation:
$\unicode[STIX]{x1D705}$
continues to decrease). An explanation of such an agreement might be given by noticing that a shear flow can be decomposed into a strain flow plus a rigid body rotation:
![]() $\unicode[STIX]{x1D713}_{sh}=\unicode[STIX]{x1D713}_{st}+\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D714}}$
, with
$\unicode[STIX]{x1D713}_{sh}=\unicode[STIX]{x1D713}_{st}+\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D714}}$
, with
and that the streamline pattern for a hollow vortex in a strain flow has the same topology as for a
![]() $\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
hollow vortex in a shear flow (see figure 2). By taking a normalization analogous to the present one for the problem examined by Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012), that is by selecting, according to their notation, the strain factor
$\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
hollow vortex in a shear flow (see figure 2). By taking a normalization analogous to the present one for the problem examined by Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012), that is by selecting, according to their notation, the strain factor
![]() $\unicode[STIX]{x1D6FE}$
and the vortex circulation
$\unicode[STIX]{x1D6FE}$
and the vortex circulation
![]() $\unicode[STIX]{x1D6E4}$
as reference values, a non-dimensionalized speed
$\unicode[STIX]{x1D6E4}$
as reference values, a non-dimensionalized speed
![]() $\tilde{\unicode[STIX]{x1D705}}$
of the vortex contour can be defined which results in a monotonically decreasing function of the parameter
$\tilde{\unicode[STIX]{x1D705}}$
of the vortex contour can be defined which results in a monotonically decreasing function of the parameter
![]() $\unicode[STIX]{x1D707}$
used in their study. As a consequence, the behaviour of area versus
$\unicode[STIX]{x1D707}$
used in their study. As a consequence, the behaviour of area versus
![]() $\unicode[STIX]{x1D707}$
in their figure 3(b) has the same behaviour of our plot of area versus
$\unicode[STIX]{x1D707}$
in their figure 3(b) has the same behaviour of our plot of area versus
![]() $\unicode[STIX]{x1D705}$
shown by the present figure 3.
$\unicode[STIX]{x1D705}$
shown by the present figure 3.

Figure 3. Hollow vortices for
![]() $\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
. (a) Vortex shapes for
$\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
. (a) Vortex shapes for
![]() $\unicode[STIX]{x1D705}=1.4$
,
$\unicode[STIX]{x1D705}=1.4$
,
![]() $1.5$
,
$1.5$
,
![]() $1.6$
,
$1.6$
,
![]() $1.75$
,
$1.75$
,
![]() $2$
,
$2$
,
![]() $2.25$
,
$2.25$
,
![]() $2.5$
,
$2.5$
,
![]() $3$
,
$3$
,
![]() $3.5$
,
$3.5$
,
![]() $4$
; (b) non-dimensionalized vortex area versus
$4$
; (b) non-dimensionalized vortex area versus
![]() $\unicode[STIX]{x1D705}$
.
$\unicode[STIX]{x1D705}$
.

Figure 4. Streamline pattern for
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D705}=1.5$
.
$\unicode[STIX]{x1D705}=1.5$
.
2.2 The
 $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
case
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
case
Figure 4 shows the streamline pattern for
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}=1$
and for
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}=1$
and for
![]() $\unicode[STIX]{x1D705}=1.5$
. As discussed above, this solution appears as a desingularization of the point-vortex solution shown in figure 1(b). The entire flow field consists of closed streamlines and there are no stagnation points. By varying the vortex contour speed
$\unicode[STIX]{x1D705}=1.5$
. As discussed above, this solution appears as a desingularization of the point-vortex solution shown in figure 1(b). The entire flow field consists of closed streamlines and there are no stagnation points. By varying the vortex contour speed
![]() $\unicode[STIX]{x1D705}$
, the solution can be continued to vortices with different areas. Vortex shapes are drawn for given values of
$\unicode[STIX]{x1D705}$
, the solution can be continued to vortices with different areas. Vortex shapes are drawn for given values of
![]() $\unicode[STIX]{x1D705}$
in figure 5(a), the corresponding area values are plotted on figure 5(b). As
$\unicode[STIX]{x1D705}$
in figure 5(a), the corresponding area values are plotted on figure 5(b). As
![]() $\unicode[STIX]{x1D705}\rightarrow \infty$
the solution tends to a zero-area vortex, that is, to the point-vortex solution. As
$\unicode[STIX]{x1D705}\rightarrow \infty$
the solution tends to a zero-area vortex, that is, to the point-vortex solution. As
![]() $\unicode[STIX]{x1D705}$
decreases the vortex shape elongates and the area increases. The limit as
$\unicode[STIX]{x1D705}$
decreases the vortex shape elongates and the area increases. The limit as
![]() $\unicode[STIX]{x1D705}\rightarrow 0$
is an infinite stagnant strip above and below bounded by two shear flows with zero velocity at the strip boundary. This is reminiscent of the limit of the solution of Baker et al. (Reference Baker, Saffman and Sheffield1976) when the vortices in the array start to touch and the array reduces to a strip.
$\unicode[STIX]{x1D705}\rightarrow 0$
is an infinite stagnant strip above and below bounded by two shear flows with zero velocity at the strip boundary. This is reminiscent of the limit of the solution of Baker et al. (Reference Baker, Saffman and Sheffield1976) when the vortices in the array start to touch and the array reduces to a strip.

Figure 5. Hollow vortices for
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
. (a) Vortex shapes for
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
. (a) Vortex shapes for
![]() $\unicode[STIX]{x1D705}=0.75$
, 1, 1.25, 1.5, 2, 3; (b) non-dimensionalized vortex area versus
$\unicode[STIX]{x1D705}=0.75$
, 1, 1.25, 1.5, 2, 3; (b) non-dimensionalized vortex area versus
![]() $\unicode[STIX]{x1D705}$
.
$\unicode[STIX]{x1D705}$
.
3 Concluding remarks
The paper presents in detail an analytical method for determining the shape of hollow vortices in shear flows.
In a non-dimensional formulation, it is shown that the problem has one degree of freedom represented by the free choice of the non-dimensional flow speed
![]() $\unicode[STIX]{x1D705}$
at the vortex contour. For
$\unicode[STIX]{x1D705}$
at the vortex contour. For
![]() $\unicode[STIX]{x1D705}\rightarrow \infty$
the solution tends to the point-vortex flow. For finite values of
$\unicode[STIX]{x1D705}\rightarrow \infty$
the solution tends to the point-vortex flow. For finite values of
![]() $\unicode[STIX]{x1D705}$
, the solution is desingularized into finite-area vortices. The solutions form two families of shapes which correspond to vortex circulation and shear-flow vorticity having opposite sign (
$\unicode[STIX]{x1D705}$
, the solution is desingularized into finite-area vortices. The solutions form two families of shapes which correspond to vortex circulation and shear-flow vorticity having opposite sign (
![]() $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D714}<0$
) or equal sign (
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D714}<0$
) or equal sign (
![]() $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D714}>0$
).
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D714}>0$
).
For
![]() $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D714}<0$
the family of shapes resembles that described by Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012) for hollow vortices in strained potential flows. As for that family, there is a value of
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D714}<0$
the family of shapes resembles that described by Llewellyn Smith & Crowdy (Reference Llewellyn Smith and Crowdy2012) for hollow vortices in strained potential flows. As for that family, there is a value of
![]() $\unicode[STIX]{x1D705}$
for which the vortex area reaches a maximum, and there is also a minimum value of
$\unicode[STIX]{x1D705}$
for which the vortex area reaches a maximum, and there is also a minimum value of
![]() $\unicode[STIX]{x1D705}$
below which there is no solution as the vortex contour self-intersects.
$\unicode[STIX]{x1D705}$
below which there is no solution as the vortex contour self-intersects.
For
![]() $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D714}>0$
, the area of the vortex is a monotonic decreasing function of
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D714}>0$
, the area of the vortex is a monotonic decreasing function of
![]() $\unicode[STIX]{x1D705}$
. For
$\unicode[STIX]{x1D705}$
. For
![]() $\unicode[STIX]{x1D705}\rightarrow \infty$
the solution tends to the zero-area point vortex. Solutions exist for arbitrary small values of
$\unicode[STIX]{x1D705}\rightarrow \infty$
the solution tends to the zero-area point vortex. Solutions exist for arbitrary small values of
![]() $\unicode[STIX]{x1D705}$
and that for
$\unicode[STIX]{x1D705}$
and that for
![]() $\unicode[STIX]{x1D705}\rightarrow 0$
the vortex shape tends to an infinite strip.
$\unicode[STIX]{x1D705}\rightarrow 0$
the vortex shape tends to an infinite strip.
The method intrinsically looks for steady solutions, thus oscillating solutions à la Kida (Reference Kida1981) are not considered and cannot be excluded.
Acknowledgements
The authors would like to thank D. Freilich for carrying out calculations to verify the results for small values of
![]() $\unicode[STIX]{x1D705}$
.
$\unicode[STIX]{x1D705}$
.
Appendix A. Coefficient series determination
The series coefficients
![]() $b_{n}$
and
$b_{n}$
and
![]() $c_{n}$
in (2.4) and (2.7) are computed by a fixed-point iteration or zero-finding process.
$c_{n}$
in (2.4) and (2.7) are computed by a fixed-point iteration or zero-finding process.
According to (2.9) and (2.6), the complex velocity
![]() $u-\text{i}v$
, written as a function of
$u-\text{i}v$
, written as a function of
![]() $\unicode[STIX]{x1D701}$
, is
$\unicode[STIX]{x1D701}$
, is
Let
![]() $\tilde{u}$
and
$\tilde{u}$
and
![]() $\tilde{v}$
be the normal and tangential components of the flow velocity at the vortex boundary, the complex velocity
$\tilde{v}$
be the normal and tangential components of the flow velocity at the vortex boundary, the complex velocity
![]() $\tilde{u} -\text{i}\tilde{v}$
becomes
$\tilde{u} -\text{i}\tilde{v}$
becomes
We assume that
![]() $\unicode[STIX]{x1D70F}$
is positive
$\unicode[STIX]{x1D70F}$
is positive
![]() $(\unicode[STIX]{x1D70F}=1)$
, as a consequence
$(\unicode[STIX]{x1D70F}=1)$
, as a consequence
![]() $\tilde{v}$
is positive and conditions (2.3) become
$\tilde{v}$
is positive and conditions (2.3) become
![]() $\tilde{u} =0$
and
$\tilde{u} =0$
and
![]() $\tilde{v}=\unicode[STIX]{x1D705}$
, that is
$\tilde{v}=\unicode[STIX]{x1D705}$
, that is
and
Let the series (2.4), (2.7) be truncated at a suitably large value
![]() $n=N$
(in our computations we have set
$n=N$
(in our computations we have set
![]() $N=128$
). The process is started by assuming a set of values for the
$N=128$
). The process is started by assuming a set of values for the
![]() $b_{n}$
coefficients. A starting guess of
$b_{n}$
coefficients. A starting guess of
![]() $b_{n}=0$
for
$b_{n}=0$
for
![]() $n=1,\ldots ,N$
for the largest value of
$n=1,\ldots ,N$
for the largest value of
![]() $\unicode[STIX]{x1D705}$
was used, after which
$\unicode[STIX]{x1D705}$
was used, after which
![]() $\unicode[STIX]{x1D705}$
was decreased and the previous value of
$\unicode[STIX]{x1D705}$
was decreased and the previous value of
![]() $b_{n}$
was used as the starting guess. As shown below, (A 3) allows the computation of a first set of
$b_{n}$
was used as the starting guess. As shown below, (A 3) allows the computation of a first set of
![]() $c_{n}$
coefficients, then (A 4) allows the coefficients
$c_{n}$
coefficients, then (A 4) allows the coefficients
![]() $b_{n}$
to be updated. The process is repeated until the absolute maximum difference between old and new values of the coefficients
$b_{n}$
to be updated. The process is repeated until the absolute maximum difference between old and new values of the coefficients
![]() $b_{n}$
falls below a given threshold
$b_{n}$
falls below a given threshold
![]() $D$
(we set
$D$
(we set
![]() $D=10^{-10}$
). For large enough values of
$D=10^{-10}$
). For large enough values of
![]() $\unicode[STIX]{x1D705}$
(around
$\unicode[STIX]{x1D705}$
(around
![]() $1.5$
for the case
$1.5$
for the case
![]() $\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D6FF}=-\unicode[STIX]{x1D70F}$
and
![]() $1.2$
for the case
$1.2$
for the case
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
), a fixed-point iteration was used in which the new values of
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D70F}$
), a fixed-point iteration was used in which the new values of
![]() $b_{n}$
replace the old. For smaller values of
$b_{n}$
replace the old. For smaller values of
![]() $\unicode[STIX]{x1D705}$
, a multidimensional root-finding algorithm (fsolve in Matlab) is used to find zeros of the difference between old and new coefficients.
$\unicode[STIX]{x1D705}$
, a multidimensional root-finding algorithm (fsolve in Matlab) is used to find zeros of the difference between old and new coefficients.
For
![]() $|\unicode[STIX]{x1D701}|=1$
, so that
$|\unicode[STIX]{x1D701}|=1$
, so that
![]() $\unicode[STIX]{x1D701}=\text{e}^{\text{i}\unicode[STIX]{x1D711}}$
, (A 3) can be recast as
$\unicode[STIX]{x1D701}=\text{e}^{\text{i}\unicode[STIX]{x1D711}}$
, (A 3) can be recast as
with
![]() $C_{n}=-(n-1)c_{n}$
. Once old values of the right-hand side are evaluated at
$C_{n}=-(n-1)c_{n}$
. Once old values of the right-hand side are evaluated at
![]() $2N$
equispaced points of the
$2N$
equispaced points of the
![]() $\unicode[STIX]{x1D701}$
-plane unit circle, the computation of a new set of
$\unicode[STIX]{x1D701}$
-plane unit circle, the computation of a new set of
![]() $c_{n}$
(
$c_{n}$
(
![]() $n\neq 1$
) coefficients can be obtained through the discrete Fourier transform. The coefficient
$n\neq 1$
) coefficients can be obtained through the discrete Fourier transform. The coefficient
![]() $c_{1}$
is an additive constant to the potential
$c_{1}$
is an additive constant to the potential
![]() $G(\unicode[STIX]{x1D701})$
(2.7) which can be arbitrarily chosen.
$G(\unicode[STIX]{x1D701})$
(2.7) which can be arbitrarily chosen.
Then (2.4) yields
and (A 4) can be recast as
A new set of values for
![]() $b_{n}$
is obtained by the discrete Fourier transform of the right-hand side evaluated at
$b_{n}$
is obtained by the discrete Fourier transform of the right-hand side evaluated at
![]() $2N$
equispaced points of the
$2N$
equispaced points of the
![]() $\unicode[STIX]{x1D701}$
-plane unit circle by means of the old
$\unicode[STIX]{x1D701}$
-plane unit circle by means of the old
![]() $b_{n}$
values, needed to evaluate the
$b_{n}$
values, needed to evaluate the
![]() $z(\unicode[STIX]{x1D701})$
and
$z(\unicode[STIX]{x1D701})$
and
![]() $\text{d}z/\text{d}\unicode[STIX]{x1D701}$
terms, and by means of the updated
$\text{d}z/\text{d}\unicode[STIX]{x1D701}$
terms, and by means of the updated
![]() $c_{n}$
coefficients, needed to evaluate the
$c_{n}$
coefficients, needed to evaluate the
![]() $\text{d}G/\text{d}\unicode[STIX]{x1D701}$
term.
$\text{d}G/\text{d}\unicode[STIX]{x1D701}$
term.
The mapping
![]() $z(\unicode[STIX]{x1D701})$
is given by the indefinite integral
$z(\unicode[STIX]{x1D701})$
is given by the indefinite integral
![]() $z(\unicode[STIX]{x1D701})=\int (\text{d}z/\text{d}\unicode[STIX]{x1D701})\,\text{d}\unicode[STIX]{x1D701}$
, that is
$z(\unicode[STIX]{x1D701})=\int (\text{d}z/\text{d}\unicode[STIX]{x1D701})\,\text{d}\unicode[STIX]{x1D701}$
, that is
The Laurent series expansion of the integrand yields
We show below that there is a closed-form analytic relationship between the coefficients
![]() $a_{n}$
and
$a_{n}$
and
![]() $b_{n}$
having the form
$b_{n}$
having the form
![]() $a_{j}=f(b_{1},\ldots ,b_{j})$
. Since the closure condition of the vortex implies that
$a_{j}=f(b_{1},\ldots ,b_{j})$
. Since the closure condition of the vortex implies that
![]() $\oint (\text{d}z/\text{d}\unicode[STIX]{x1D701})_{|\unicode[STIX]{x1D701}|=1}\text{d}\unicode[STIX]{x1D701}=2\unicode[STIX]{x03C0}\text{i}a_{2}=0$
, the integral (A 8) is
$\oint (\text{d}z/\text{d}\unicode[STIX]{x1D701})_{|\unicode[STIX]{x1D701}|=1}\text{d}\unicode[STIX]{x1D701}=2\unicode[STIX]{x03C0}\text{i}a_{2}=0$
, the integral (A 8) is
All the solutions here found are symmetric with respect to the
![]() $x,y$
axes. As a consequence the computed
$x,y$
axes. As a consequence the computed
![]() $a_{n},b_{n}$
are all real and equal to zero for even
$a_{n},b_{n}$
are all real and equal to zero for even
![]() $n$
indexes.
$n$
indexes.
Appendix B. The
 $a_{j}=f(b_{1},\ldots ,b_{j})$
relationship
$a_{j}=f(b_{1},\ldots ,b_{j})$
relationship
We set
with
For
![]() $t=1/\unicode[STIX]{x1D701}$
, the identity (A 9) becomes
$t=1/\unicode[STIX]{x1D701}$
, the identity (A 9) becomes
The coefficients
![]() $a_{n}$
can be found as coefficients of the McLaurin series expansion or, equivalently, as residues at
$a_{n}$
can be found as coefficients of the McLaurin series expansion or, equivalently, as residues at
![]() $t=0$
of
$t=0$
of
![]() $\unicode[STIX]{x1D70E}$
, that is
$\unicode[STIX]{x1D70E}$
, that is
The first coefficient clearly is
![]() $a_{1}=\text{e}^{b_{1}}$
. The subsequent coefficients
$a_{1}=\text{e}^{b_{1}}$
. The subsequent coefficients
![]() $a_{n}$
are obtained by evaluating the right-end side of (B 4) with a recursion formula which avoids actual onerous derivations. In fact, the first derivative of
$a_{n}$
are obtained by evaluating the right-end side of (B 4) with a recursion formula which avoids actual onerous derivations. In fact, the first derivative of
![]() $\unicode[STIX]{x1D70E}$
is
$\unicode[STIX]{x1D70E}$
is
and, according to the general Leibniz rule for derivation of products, the higher-order derivatives result in
For
![]() $t=0$
, this gives
$t=0$
, this gives
![]() $(\text{d}^{j}s/\text{d}t^{j})_{t=0}=j!b_{j+1}$
, thus the values of the
$(\text{d}^{j}s/\text{d}t^{j})_{t=0}=j!b_{j+1}$
, thus the values of the
![]() $\unicode[STIX]{x1D70E}$
derivatives are given by the recursion formula
$\unicode[STIX]{x1D70E}$
derivatives are given by the recursion formula
which, according to (B 4), yields
where the starting value is
![]() $a_{1}=\text{e}^{b_{1}}$
.
$a_{1}=\text{e}^{b_{1}}$
.