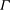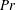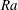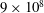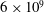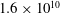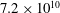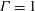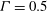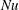1 Introduction
Thermal convection is ubiquitous in nature and in many engineering applications. Rayleigh–Bénard convection (RBC) is a model system for the study of the thermal convection problem (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010; Chillà & Schumacher Reference Chillà and Schumacher2012; Xia Reference Xia2013). Turbulent RBC has attracted a lot of interest during the last several decades, not only because of its importance in understanding the flow dynamics of buoyancy driven turbulence, but also due to its relevance to the convection phenomena occurring in geophysical and astrophysical systems (Glatzmaier et al.
Reference Glatzmaier, Coe, Hongre and Roberts1999; Busse Reference Busse1994). The Rayleigh–Bénard convection is a fluid layer between two conducting plates which is heated from below and cooled from above, maintaining a constant temperature difference
![]() $\unicode[STIX]{x0394}T$
across the fluid layer. The system is controlled by the dimensionless parameters of the Rayleigh number
$\unicode[STIX]{x0394}T$
across the fluid layer. The system is controlled by the dimensionless parameters of the Rayleigh number
![]() $Ra=\unicode[STIX]{x1D6FC}g\unicode[STIX]{x0394}TH^{3}/(\unicode[STIX]{x1D708}k)$
and the Prandtl number
$Ra=\unicode[STIX]{x1D6FC}g\unicode[STIX]{x0394}TH^{3}/(\unicode[STIX]{x1D708}k)$
and the Prandtl number
![]() $Pr=\unicode[STIX]{x1D708}/k$
, where
$Pr=\unicode[STIX]{x1D708}/k$
, where
![]() $H$
is the height (or thickness) of the fluid layer,
$H$
is the height (or thickness) of the fluid layer,
![]() $g$
is the gravitational acceleration and
$g$
is the gravitational acceleration and
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}$
and
![]() $k$
are the thermal expansion coefficient, kinematic viscosity and thermal diffusivity of the fluid. The third control parameter of the system is the geometry of the convection cell (or container), which is characterized by the aspect ratio
$k$
are the thermal expansion coefficient, kinematic viscosity and thermal diffusivity of the fluid. The third control parameter of the system is the geometry of the convection cell (or container), which is characterized by the aspect ratio
![]() $\unicode[STIX]{x1D6E4}=D/H$
, where
$\unicode[STIX]{x1D6E4}=D/H$
, where
![]() $D$
and
$D$
and
![]() $H$
are the diameter and height of the cylindrical cell (container).
$H$
are the diameter and height of the cylindrical cell (container).
For a sufficiently large temperature difference
![]() $\unicode[STIX]{x0394}T$
, thermal plumes originate from the bottom (top) boundary layers and rise (sink) due to the buoyancy force. These plumes self-organize into a large-scale circulation (LSC) that spans the size of the convection cell (Xi, Lam & Xia Reference Xi, Lam and Xia2004). The up-flow and the down-flow of the LSC are separated azimuthally by
$\unicode[STIX]{x0394}T$
, thermal plumes originate from the bottom (top) boundary layers and rise (sink) due to the buoyancy force. These plumes self-organize into a large-scale circulation (LSC) that spans the size of the convection cell (Xi, Lam & Xia Reference Xi, Lam and Xia2004). The up-flow and the down-flow of the LSC are separated azimuthally by
![]() $180^{\circ }$
. It is now generally established that the nearly vertical plane of the LSC undergoes azimuthal motion in a Brownian fashion (Sun, Xi & Xia Reference Sun, Xi and Xia2005a
; Brown, Nikolaenko & Ahlers Reference Brown, Nikolaenko and Ahlers2005; Brown & Ahlers Reference Brown and Ahlers2006a
; Xi & Xia Reference Xi and Xia2007). A fascinating feature of the LSC is that it oscillates periodically. The oscillation has two components, one is the twisting or torsional motion that the upper part and lower part of the LSC are twisting periodically (Funfschilling & Ahlers Reference Funfschilling and Ahlers2004), the other is the sloshing motion that the entire LSC displaces laterally away from the centreline of the cylindrical cell (Xi et al.
Reference Xi, Zhou, Zhou, Chan and Xia2009; Zhou et al.
Reference Zhou, Xi, Zhou, Sun and Xia2009; Brown & Ahlers Reference Brown and Ahlers2009). Most of the above mentioned features are observed in both
$180^{\circ }$
. It is now generally established that the nearly vertical plane of the LSC undergoes azimuthal motion in a Brownian fashion (Sun, Xi & Xia Reference Sun, Xi and Xia2005a
; Brown, Nikolaenko & Ahlers Reference Brown, Nikolaenko and Ahlers2005; Brown & Ahlers Reference Brown and Ahlers2006a
; Xi & Xia Reference Xi and Xia2007). A fascinating feature of the LSC is that it oscillates periodically. The oscillation has two components, one is the twisting or torsional motion that the upper part and lower part of the LSC are twisting periodically (Funfschilling & Ahlers Reference Funfschilling and Ahlers2004), the other is the sloshing motion that the entire LSC displaces laterally away from the centreline of the cylindrical cell (Xi et al.
Reference Xi, Zhou, Zhou, Chan and Xia2009; Zhou et al.
Reference Zhou, Xi, Zhou, Sun and Xia2009; Brown & Ahlers Reference Brown and Ahlers2009). Most of the above mentioned features are observed in both
![]() $\unicode[STIX]{x1D6E4}=1$
and
$\unicode[STIX]{x1D6E4}=1$
and
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells. The only differences are that in
$\unicode[STIX]{x1D6E4}=0.5$
cells. The only differences are that in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells, the LSC is more ‘fragile’, it undergoes frequent flow mode transitions from the single-roll mode to the double-roll mode (one roll on the top of the other) and back again (Xi & Xia Reference Xi and Xia2008b
; Weiss & Ahlers Reference Weiss and Ahlers2011b
), and in
$\unicode[STIX]{x1D6E4}=0.5$
cells, the LSC is more ‘fragile’, it undergoes frequent flow mode transitions from the single-roll mode to the double-roll mode (one roll on the top of the other) and back again (Xi & Xia Reference Xi and Xia2008b
; Weiss & Ahlers Reference Weiss and Ahlers2011b
), and in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells there are more cessations and reversals (Xi & Xia Reference Xi and Xia2007).
$\unicode[STIX]{x1D6E4}=0.5$
cells there are more cessations and reversals (Xi & Xia Reference Xi and Xia2007).
Later it was found that, in addition to the LSC (the dipole mode or the first mode), higher-order modes also exist. Mishra et al. (Reference Mishra, De, Verma and Eswaran2011) numerically studied the first and second modes of the convective flow and their relative weights during the cessation and reversal of the LSC (see below for explanation). Moreover, they showed the detailed flow structure of the second mode (quadrupole mode). To study the persistence of the LSC when the flow is subjected to cell rotation, cell tilting and cell changing to smaller aspect ratio, the first four Fourier modes of the convective flow and their relative weights are extracted from the azimuthal profile of velocity/temperature (Kunnen, Clercx & Geurts Reference Kunnen, Clercx and Geurts2008; Stevens, Clercx & Lohse Reference Stevens, Clercx and Lohse2011; Weiss & Ahlers Reference Weiss and Ahlers2011a
, Reference Weiss and Ahlers2013). These studies indeed identified the first and a few higher-order modes of the convective flow, and their relative weights. However the flow structure and dynamics and the
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $Ra$
dependences of the higher-order modes are still less known.
$Ra$
dependences of the higher-order modes are still less known.
Another important feature of the LSC is its cessation and reversal. The cessation is an event during which the LSC experiences a temporary halt. If after a cessation, the circulating direction of the LSC is reversed, it is a reversal of the LSC (Brown et al.
Reference Brown, Nikolaenko and Ahlers2005; Xi & Xia Reference Xi and Xia2007). The reversal phenomenon is of great importance in understanding the dynamics of turbulent flows in the Rayleigh–Bénard (RB) system (Sreenivasan, Bershadskii & Niemela Reference Sreenivasan, Bershadskii and Niemela2002; Araujo, Grossmann & Lohse Reference Araujo, Grossmann and Lohse2005; Benzi Reference Benzi2005; Verma, Ambhire & Pandey Reference Verma, Ambhire and Pandey2015), in addition, the reversal of the LSC in RB system has been found to share many similar statistical properties with reversals of the magnetic polarity of the Earth (Xi & Xia Reference Xi and Xia2007). The dynamics of the flow during the cessation/reversal is crucial for the understanding of the mechanism of these events. For two-dimensional (2-D) RB systems experiments and numerical simulations have showed that, during the reversal, the flow is not totally disorganized, instead, the LSC evolves into four small rolls, two of which reconnect and form a reversed LSC (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; Chandra & Verma Reference Chandra and Verma2011, Reference Chandra and Verma2013; Ni, Huang & Xia Reference Ni, Huang and Xia2015; Huang & Xia Reference Huang and Xia2016). For 3-D RB systems, Mishra et al. (Reference Mishra, De, Verma and Eswaran2011) were the first to notice the importance of the second-order mode during the cessation and reversal of the LSC. In their numerical simulation, they obtained the first and second Fourier modes from the vertical velocity profile near the lateral surface at the mid-plane of the
![]() $\unicode[STIX]{x1D6E4}=1$
cell at
$\unicode[STIX]{x1D6E4}=1$
cell at
![]() $Pr=0.7$
and
$Pr=0.7$
and
![]() $Ra$
from
$Ra$
from
![]() $6\times 10^{5}$
to
$6\times 10^{5}$
to
![]() $3\times 10^{7}$
. They found that the second mode experiences an increase then a decrease during a cessation and the second mode dominates the first mode during the cessation/reversal. Unfortunately, due to the fact that in
$3\times 10^{7}$
. They found that the second mode experiences an increase then a decrease during a cessation and the second mode dominates the first mode during the cessation/reversal. Unfortunately, due to the fact that in
![]() $\unicode[STIX]{x1D6E4}=1$
cells cessations/reversals are very rare (in the above mentioned numerical study only 5 cessation events were identified), the statistical properties of the higher-order modes during the cessation/reversal are not known. It has been previously found that cessations and reversals occur much more frequently in
$\unicode[STIX]{x1D6E4}=1$
cells cessations/reversals are very rare (in the above mentioned numerical study only 5 cessation events were identified), the statistical properties of the higher-order modes during the cessation/reversal are not known. It has been previously found that cessations and reversals occur much more frequently in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells (Xi & Xia Reference Xi and Xia2007). Therefore, studying the higher-order modes and their statistics in
$\unicode[STIX]{x1D6E4}=0.5$
cells (Xi & Xia Reference Xi and Xia2007). Therefore, studying the higher-order modes and their statistics in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells, especially during cessations/reversals, should shed new light on the cessation/reversal phenomenon in RB convection.
$\unicode[STIX]{x1D6E4}=0.5$
cells, especially during cessations/reversals, should shed new light on the cessation/reversal phenomenon in RB convection.
In this paper we present an experimental study of the first and a few higher-order flow modes in convection cells with aspect ratios 1 and 0.5, using both multi-temperature probe and the particle image velocimetry (PIV) methods. The amplitude and the flow structure of the first-order (or dipole) mode (also known as LSC), the second-order (or quadrupole) mode (up-flow and down-flow appear alternately and separated azimuthally by
![]() $90^{\circ }$
), the third-order (or sextupole) mode (up-flow and down-flow are separated azimuthally by
$90^{\circ }$
), the third-order (or sextupole) mode (up-flow and down-flow are separated azimuthally by
![]() $60^{\circ }$
) and the fourth-order (or octupole) mode (up-flow and down-flow are separated azimuthally by
$60^{\circ }$
) and the fourth-order (or octupole) mode (up-flow and down-flow are separated azimuthally by
![]() $45^{\circ }$
) are measured. We find that the first mode, which corresponds to the well-known LSC, dominates the flow. The second and the remaining higher-order modes are very weak. In addition, it is found that during a reversal/cessation event, the amplitude of the second, third and fourth modes experience a rapid increase followed by a decrease, which is opposite to that of the first mode – it decreases to almost zero then rebounds. We also find that during the cessation/reversal of the LSC, the second mode is the dominant one. The experiment reveals that the second mode and the remaining higher-order modes play important roles in the dynamics of the reversal/cessation of the LSC. Statistical analysis reveals that the first mode is more efficient for heat transfer. Finally we show that direct velocity measurement by PIV qualitatively confirms the flow structure of the four modes extracted from the temperature measurements.
$45^{\circ }$
) are measured. We find that the first mode, which corresponds to the well-known LSC, dominates the flow. The second and the remaining higher-order modes are very weak. In addition, it is found that during a reversal/cessation event, the amplitude of the second, third and fourth modes experience a rapid increase followed by a decrease, which is opposite to that of the first mode – it decreases to almost zero then rebounds. We also find that during the cessation/reversal of the LSC, the second mode is the dominant one. The experiment reveals that the second mode and the remaining higher-order modes play important roles in the dynamics of the reversal/cessation of the LSC. Statistical analysis reveals that the first mode is more efficient for heat transfer. Finally we show that direct velocity measurement by PIV qualitatively confirms the flow structure of the four modes extracted from the temperature measurements.
The organization of the paper is as follows. The experimental set-up and methods are introduced in § 2. In § 3 we present the main results. We summarise our findings and conclude in § 4.
2 The convection cell and experimental method
The convection cell is similar to those used in previous experiments (Xi & Xia Reference Xi and Xia2008b
), it consists of the top and the bottom plates and a Plexiglas tube of inner diameter
![]() $D=19$
cm and sidewall thickness of 5 mm. Two Plexiglas tubes with heights of 18.8 cm, 38.5 cm are used; the corresponding aspect ratios are therefore approximately 1 and 0.5. The top and bottom plates of the cell are made of 1 cm thick copper with nickel-plated surfaces. A stainless steel cover is attached to the top of the upper plate. This cover, together with the upper surface of the top copper plate, serves as a cooling chamber. Cold water is pumped to the chamber through two inlets and flows out through two outlets on the top of the chamber via a refrigerated circulator (Polyscience 9702) to remove heat from the top plate. The temperature stability of the refrigerated circulator is
$D=19$
cm and sidewall thickness of 5 mm. Two Plexiglas tubes with heights of 18.8 cm, 38.5 cm are used; the corresponding aspect ratios are therefore approximately 1 and 0.5. The top and bottom plates of the cell are made of 1 cm thick copper with nickel-plated surfaces. A stainless steel cover is attached to the top of the upper plate. This cover, together with the upper surface of the top copper plate, serves as a cooling chamber. Cold water is pumped to the chamber through two inlets and flows out through two outlets on the top of the chamber via a refrigerated circulator (Polyscience 9702) to remove heat from the top plate. The temperature stability of the refrigerated circulator is
![]() $0.01\,^{\circ }\text{C}$
. Two silicon rubber film heaters connected in series are sandwiched to the back side of the bottom plate to provide constant and uniform heating. A DC power supply Xantrex XFR 300-4 with 99.99 % long-term stability is used to provide the heating power. Two thermistors are embedded beneath the fluid-contact surface of each conducting plate to record the temperature of the plate. During the experiment, the entire cell is wrapped by several layers of Styrofoam. The experiments were all conducted under constant heating of the bottom plate while maintaining a constant temperature at the top plate. Deionized water was used as the convecting fluid. Measurements were made at the temperature difference ranging from 5.33 to
$0.01\,^{\circ }\text{C}$
. Two silicon rubber film heaters connected in series are sandwiched to the back side of the bottom plate to provide constant and uniform heating. A DC power supply Xantrex XFR 300-4 with 99.99 % long-term stability is used to provide the heating power. Two thermistors are embedded beneath the fluid-contact surface of each conducting plate to record the temperature of the plate. During the experiment, the entire cell is wrapped by several layers of Styrofoam. The experiments were all conducted under constant heating of the bottom plate while maintaining a constant temperature at the top plate. Deionized water was used as the convecting fluid. Measurements were made at the temperature difference ranging from 5.33 to
![]() $34.26\,^{\circ }\text{C}$
for
$34.26\,^{\circ }\text{C}$
for
![]() $\unicode[STIX]{x1D6E4}=1$
cell, 10.00 to
$\unicode[STIX]{x1D6E4}=1$
cell, 10.00 to
![]() $41.78\,^{\circ }\text{C}$
for
$41.78\,^{\circ }\text{C}$
for
![]() $\unicode[STIX]{x1D6E4}=0.5$
cell. The mean temperature is kept at around
$\unicode[STIX]{x1D6E4}=0.5$
cell. The mean temperature is kept at around
![]() $31\,^{\circ }\text{C}$
. The resulting values of
$31\,^{\circ }\text{C}$
. The resulting values of
![]() $Ra$
range from
$Ra$
range from
![]() $9.0\times 10^{8}$
to
$9.0\times 10^{8}$
to
![]() $6.0\times 10^{9}$
for
$6.0\times 10^{9}$
for
![]() $\unicode[STIX]{x1D6E4}=1$
geometry, and from
$\unicode[STIX]{x1D6E4}=1$
geometry, and from
![]() $1.6\times 10^{10}$
to
$1.6\times 10^{10}$
to
![]() $7.2\times 10^{10}$
for
$7.2\times 10^{10}$
for
![]() $\unicode[STIX]{x1D6E4}=0.5$
geometry; while
$\unicode[STIX]{x1D6E4}=0.5$
geometry; while
![]() $Pr$
remained within the range of 4.9–5.3. In all measurements the convection cells were levelled to within
$Pr$
remained within the range of 4.9–5.3. In all measurements the convection cells were levelled to within
![]() $0.057^{\circ }$
.
$0.057^{\circ }$
.
We use the multi-temperature-probe method to measure the orientation and the strength of the flow. Because the large-scale flow is essentially an organized motion of thermal plumes (Xi et al.
Reference Xi, Lam and Xia2004) and that when it flows up (down) along the sidewall it carries hot (cold) fluid with it. Therefore, by measuring the relative temperature differences along the perimeter of the sidewall, the azimuthal positions of the hot ascending and cold descending flows, as well as their strengths, may be obtained (Brown et al.
Reference Brown, Nikolaenko and Ahlers2005; Brown & Ahlers Reference Brown and Ahlers2006b
). The method has been described in detail elsewhere (Xi & Xia Reference Xi and Xia2008b
), basically 24 blind holes were drilled from the outside into the sidewall in such a way that they are distributed in three horizontal rows at heights
![]() $H/4$
,
$H/4$
,
![]() $H/2$
and
$H/2$
and
![]() $3H/4$
and in eight vertical columns equally spaced azimuthally around the cylinder. The end of these holes have a distance of 0.7 mm from the fluid-contact surface. Twenty-four thermistors were placed into the blind holes until they touched the bottom snugly. To ensure good thermal contact, a thin layer of thermally conductive paste was spread around the surface of the thermistors. These thermistors have a diameter of 2.5 mm with a time constant of 1 s (Omega, 44031), and were carefully calibrated individually over the temperature range of the experiment with an accuracy of
$3H/4$
and in eight vertical columns equally spaced azimuthally around the cylinder. The end of these holes have a distance of 0.7 mm from the fluid-contact surface. Twenty-four thermistors were placed into the blind holes until they touched the bottom snugly. To ensure good thermal contact, a thin layer of thermally conductive paste was spread around the surface of the thermistors. These thermistors have a diameter of 2.5 mm with a time constant of 1 s (Omega, 44031), and were carefully calibrated individually over the temperature range of the experiment with an accuracy of
![]() $0.01\,^{\circ }\text{C}$
. The thermistors were connected to a multi-channel multi-meter and their resistances were measured at a sampling frequency of 0.29 Hz, which were then converted into temperatures using the calibration curves. In previous studies, to measure the azimuthal orientation and flow strength of the LSC, the instantaneously measured temperature profile was fitted by a period-one cosine function (Cioni, Ciliberto & Sommeria Reference Cioni, Ciliberto and Sommeria1997; Brown et al.
Reference Brown, Nikolaenko and Ahlers2005; Xi & Xia Reference Xi and Xia2007). Fitting the azimuthal temperature profile to the period-one cosine function is a first-order approximation. It was later found that the measured azimuthal temperature profile does not always follow the period-one cosine function (Zhou et al.
Reference Zhou, Xi, Zhou, Sun and Xia2009; Brown & Ahlers Reference Brown and Ahlers2009; Mishra et al.
Reference Mishra, De, Verma and Eswaran2011; Stevens et al.
Reference Stevens, Clercx and Lohse2011), it should contain higher-order modes (period two, three or even higher-order components). To gain information regarding the higher-order modes, Fourier transform is applied to the azimuthal temperature profile
$0.01\,^{\circ }\text{C}$
. The thermistors were connected to a multi-channel multi-meter and their resistances were measured at a sampling frequency of 0.29 Hz, which were then converted into temperatures using the calibration curves. In previous studies, to measure the azimuthal orientation and flow strength of the LSC, the instantaneously measured temperature profile was fitted by a period-one cosine function (Cioni, Ciliberto & Sommeria Reference Cioni, Ciliberto and Sommeria1997; Brown et al.
Reference Brown, Nikolaenko and Ahlers2005; Xi & Xia Reference Xi and Xia2007). Fitting the azimuthal temperature profile to the period-one cosine function is a first-order approximation. It was later found that the measured azimuthal temperature profile does not always follow the period-one cosine function (Zhou et al.
Reference Zhou, Xi, Zhou, Sun and Xia2009; Brown & Ahlers Reference Brown and Ahlers2009; Mishra et al.
Reference Mishra, De, Verma and Eswaran2011; Stevens et al.
Reference Stevens, Clercx and Lohse2011), it should contain higher-order modes (period two, three or even higher-order components). To gain information regarding the higher-order modes, Fourier transform is applied to the azimuthal temperature profile
![]() $T(\unicode[STIX]{x1D719})$
measured at the mid-height to obtain the amplitude/strength of different Fourier modes. Since we have only eight temperature readings in the azimuthal profile, we could only obtain the first four modes of the
$T(\unicode[STIX]{x1D719})$
measured at the mid-height to obtain the amplitude/strength of different Fourier modes. Since we have only eight temperature readings in the azimuthal profile, we could only obtain the first four modes of the

Figure 1. The instantaneous azimuthal temperature profile measured at the mid-height of the convection cell by the eight temperature probes for
![]() $\unicode[STIX]{x1D6E4}=0.5$
,
$\unicode[STIX]{x1D6E4}=0.5$
,
![]() $Ra=5.7\times 10^{10}$
, at the moment when the first mode (a), the second mode (b), the third mode (c) or the fourth mode (d) is dominant, respectively.
$Ra=5.7\times 10^{10}$
, at the moment when the first mode (a), the second mode (b), the third mode (c) or the fourth mode (d) is dominant, respectively.
flow. In figure 1(a–d) we plot instantaneous azimuthal temperature profiles measured at the mid-height of the convection cell by the eight temperature probes for
![]() $\unicode[STIX]{x1D6E4}=0.5$
,
$\unicode[STIX]{x1D6E4}=0.5$
,
![]() $Ra=5.7\times 10^{10}$
, at the moment when the first mode, the second mode, the third mode and the fourth mode are dominant, respectively. The first mode (dipole mode) is the well-known single-roll large-scale circulation with size comparable to the convection cell itself, as sketched in figure 2(a). The second mode is the quadrupole mode as sketched in figure 2(b). Similarly the third mode and the fourth mode are the sextupole and the octupole modes as shown in figure 2(c,d). Applying the Fourier transform to the azimuthal temperature profile
$Ra=5.7\times 10^{10}$
, at the moment when the first mode, the second mode, the third mode and the fourth mode are dominant, respectively. The first mode (dipole mode) is the well-known single-roll large-scale circulation with size comparable to the convection cell itself, as sketched in figure 2(a). The second mode is the quadrupole mode as sketched in figure 2(b). Similarly the third mode and the fourth mode are the sextupole and the octupole modes as shown in figure 2(c,d). Applying the Fourier transform to the azimuthal temperature profile
![]() $T(\unicode[STIX]{x1D719})$
at a particular time instant would give the amplitude/strength of the first four modes:
$T(\unicode[STIX]{x1D719})$
at a particular time instant would give the amplitude/strength of the first four modes:
![]() $A_{1}$
,
$A_{1}$
,
![]() $A_{2}$
,
$A_{2}$
,
![]() $A_{3}$
and
$A_{3}$
and
![]() $A_{4}$
at that time. We repeat this process to the time trace of
$A_{4}$
at that time. We repeat this process to the time trace of
![]() $T(\unicode[STIX]{x1D719})$
, the time traces of the amplitude/strength of the four modes
$T(\unicode[STIX]{x1D719})$
, the time traces of the amplitude/strength of the four modes
![]() $A_{1}(t)$
,
$A_{1}(t)$
,
![]() $A_{2}(t)$
,
$A_{2}(t)$
,
![]() $A_{3}(t)$
and
$A_{3}(t)$
and
![]() $A_{4}(t)$
are obtained. Similarly, the time traces of the orientation of the four modes are obtained; for the sake of simplicity in this study we report the orientation
$A_{4}(t)$
are obtained. Similarly, the time traces of the orientation of the four modes are obtained; for the sake of simplicity in this study we report the orientation
![]() $\unicode[STIX]{x1D719}$
of the first mode (LSC) only. As the results from
$\unicode[STIX]{x1D719}$
of the first mode (LSC) only. As the results from
![]() $1/4$
height,
$1/4$
height,
![]() $1/2$
height and
$1/2$
height and
![]() $3/4$
height are very similar, below we only report the results from the
$3/4$
height are very similar, below we only report the results from the
![]() $1/2$
height. Our multi-thermistor method measures the flow amplitude through measurement of the temperature contrast of the hot ascending and cold descending flow structures. If the measured temperature contrasts are well above the accuracy of the thermistor, then the error of our measurements is very small. For the longest measurement the time-averaged
$1/2$
height. Our multi-thermistor method measures the flow amplitude through measurement of the temperature contrast of the hot ascending and cold descending flow structures. If the measured temperature contrasts are well above the accuracy of the thermistor, then the error of our measurements is very small. For the longest measurement the time-averaged
![]() $A_{1}$
,
$A_{1}$
,
![]() $A_{2}$
,
$A_{2}$
,
![]() $A_{3}$
,
$A_{3}$
,
![]() $A_{4}$
are
$A_{4}$
are
![]() $0.84\,^{\circ }\text{C}$
,
$0.84\,^{\circ }\text{C}$
,
![]() $0.23\,^{\circ }\text{C}$
,
$0.23\,^{\circ }\text{C}$
,
![]() $0.19\,^{\circ }\text{C}$
,
$0.19\,^{\circ }\text{C}$
,
![]() $0.06\,^{\circ }\text{C}$
, respectively, they are all well above
$0.06\,^{\circ }\text{C}$
, respectively, they are all well above
![]() $0.01\,^{\circ }\text{C}$
, thus our measurements are accurate enough.
$0.01\,^{\circ }\text{C}$
, thus our measurements are accurate enough.

Figure 2. The cartoons show the mid-height cut of (a) the first mode (dipole mode, or LSC), (b) the second mode (quadrupole mode), (c) the third mode (sextupole mode) and (d) the fourth mode (octupole mode) of the flow in the convection cell, viewed from above. Dots represent up-flow and crosses represent down-flow.

Figure 3. The ratio between the time-averaged energy contained in the
![]() $i$
th mode
$i$
th mode
![]() $\langle E_{i}\rangle$
and the time-averaged total energy of the flow
$\langle E_{i}\rangle$
and the time-averaged total energy of the flow
![]() $\langle E_{total}\rangle$
as a function of
$\langle E_{total}\rangle$
as a function of
![]() $Ra$
for
$Ra$
for
![]() $\unicode[STIX]{x1D6E4}=1$
. Inset: same as the main plot but the vertical scale is from 0 to 0.08 in order to show more clearly the relative weights of the higher-order modes.
$\unicode[STIX]{x1D6E4}=1$
. Inset: same as the main plot but the vertical scale is from 0 to 0.08 in order to show more clearly the relative weights of the higher-order modes.
3 Results and discussion
3.1 Relative weights of the different modes
We first examine the relative weights of the different flow modes. Here we follow previous studies to calculate the ratio between the time-averaged energy contained in the
![]() $i$
th Fourier mode
$i$
th Fourier mode
![]() $\langle E_{i}\rangle$
and the time-averaged total energy of the flow
$\langle E_{i}\rangle$
and the time-averaged total energy of the flow
![]() $\langle E_{total}\rangle$
for
$\langle E_{total}\rangle$
for
![]() $\unicode[STIX]{x1D6E4}=1$
, where
$\unicode[STIX]{x1D6E4}=1$
, where
![]() $\langle E_{i}\rangle =\langle {A_{i}}^{2}\rangle$
and
$\langle E_{i}\rangle =\langle {A_{i}}^{2}\rangle$
and
![]() $\langle E_{total}\rangle =\langle E_{1}\rangle +\langle E_{2}\rangle +\langle E_{3}\rangle +\langle E_{4}\rangle$
(Kunnen et al.
Reference Kunnen, Clercx and Geurts2008; Stevens et al.
Reference Stevens, Clercx and Lohse2011; Weiss & Ahlers Reference Weiss and Ahlers2011a
). The results are plotted in figure 3. It is seen from the figure that for
$\langle E_{total}\rangle =\langle E_{1}\rangle +\langle E_{2}\rangle +\langle E_{3}\rangle +\langle E_{4}\rangle$
(Kunnen et al.
Reference Kunnen, Clercx and Geurts2008; Stevens et al.
Reference Stevens, Clercx and Lohse2011; Weiss & Ahlers Reference Weiss and Ahlers2011a
). The results are plotted in figure 3. It is seen from the figure that for
![]() $\unicode[STIX]{x1D6E4}=1$
, the first mode dominates, whose energy is on average (averaged over all the
$\unicode[STIX]{x1D6E4}=1$
, the first mode dominates, whose energy is on average (averaged over all the
![]() $Ra$
) 92.0 % of the total energy of the flow. The percentage of the energy contained in first mode is increasing with
$Ra$
) 92.0 % of the total energy of the flow. The percentage of the energy contained in first mode is increasing with
![]() $Ra$
, which suggests that the LSC is stronger with increasing
$Ra$
, which suggests that the LSC is stronger with increasing
![]() $Ra$
. While the energy contained in the higher-order modes is very small, they are on average 3.7 % (second mode), 3.6 % (third mode) and 0.7 % (fourth mode) of the total energy. For
$Ra$
. While the energy contained in the higher-order modes is very small, they are on average 3.7 % (second mode), 3.6 % (third mode) and 0.7 % (fourth mode) of the total energy. For
![]() $\unicode[STIX]{x1D6E4}=0.5$
, it is seen from figure 4 that the first mode is less dominant compared to the
$\unicode[STIX]{x1D6E4}=0.5$
, it is seen from figure 4 that the first mode is less dominant compared to the
![]() $\unicode[STIX]{x1D6E4}=1$
case, but it still contains the majority (78.7 %) of the total energy of the flow on average (for all the
$\unicode[STIX]{x1D6E4}=1$
case, but it still contains the majority (78.7 %) of the total energy of the flow on average (for all the
![]() $Ra$
). The higher-order modes become stronger in this slender geometry compared to the
$Ra$
). The higher-order modes become stronger in this slender geometry compared to the
![]() $\unicode[STIX]{x1D6E4}=1$
case, they contain on average 13.7 % (the second mode), 6.5 % (the third mode) and 1.1 % (the fourth mode) of the total energy for the
$\unicode[STIX]{x1D6E4}=1$
case, they contain on average 13.7 % (the second mode), 6.5 % (the third mode) and 1.1 % (the fourth mode) of the total energy for the
![]() $Ra$
range under study. Similar to the
$Ra$
range under study. Similar to the
![]() $\unicode[STIX]{x1D6E4}=1$
case, the first mode (LSC) becomes stronger with increasing
$\unicode[STIX]{x1D6E4}=1$
case, the first mode (LSC) becomes stronger with increasing
![]() $Ra$
. The finding that the first mode is stronger with increasing
$Ra$
. The finding that the first mode is stronger with increasing
![]() $Ra$
is consistent with the results in
$Ra$
is consistent with the results in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells by Weiss & Ahlers (Reference Weiss and Ahlers2013) where they found that the percentage of the energy contained in the first mode is approximately 70 % for
$\unicode[STIX]{x1D6E4}=0.5$
cells by Weiss & Ahlers (Reference Weiss and Ahlers2013) where they found that the percentage of the energy contained in the first mode is approximately 70 % for
![]() $Ra=1.8\times 10^{10}$
and around 80 % for
$Ra=1.8\times 10^{10}$
and around 80 % for
![]() $Ra=7.2\times 10^{10}$
. The dominance of the first mode for
$Ra=7.2\times 10^{10}$
. The dominance of the first mode for
![]() $\unicode[STIX]{x1D6E4}=1$
and slightly less dominance of the first mode for
$\unicode[STIX]{x1D6E4}=1$
and slightly less dominance of the first mode for
![]() $\unicode[STIX]{x1D6E4}=0.5$
are consistent with the results from previous studies (Sun et al.
Reference Sun, Xi and Xia2005a
; Xi & Xia Reference Xi and Xia2008b
; Weiss & Ahlers Reference Weiss and Ahlers2011b
). Another way to determine the relative strength of LSC is the factor
$\unicode[STIX]{x1D6E4}=0.5$
are consistent with the results from previous studies (Sun et al.
Reference Sun, Xi and Xia2005a
; Xi & Xia Reference Xi and Xia2008b
; Weiss & Ahlers Reference Weiss and Ahlers2011b
). Another way to determine the relative strength of LSC is the factor
![]() $\bar{S_{k}}$
defined by Stevens et al. (Reference Stevens, Clercx and Lohse2011), which usually is between 0 (no LSC) and 1 (only LSC exists). Here we calculated
$\bar{S_{k}}$
defined by Stevens et al. (Reference Stevens, Clercx and Lohse2011), which usually is between 0 (no LSC) and 1 (only LSC exists). Here we calculated
![]() $\bar{S_{k}}$
for our experimental data for both
$\bar{S_{k}}$
for our experimental data for both
![]() $\unicode[STIX]{x1D6E4}=1$
and 0.5 cases. The average (over different
$\unicode[STIX]{x1D6E4}=1$
and 0.5 cases. The average (over different
![]() $Ra$
)
$Ra$
)
![]() $\bar{S_{k}}$
is 0.89 for
$\bar{S_{k}}$
is 0.89 for
![]() $\unicode[STIX]{x1D6E4}=1$
case and 0.72 for
$\unicode[STIX]{x1D6E4}=1$
case and 0.72 for
![]() $\unicode[STIX]{x1D6E4}=0.5$
case. The fact that
$\unicode[STIX]{x1D6E4}=0.5$
case. The fact that
![]() $\bar{S_{k}}$
is much larger than 0.5 for both
$\bar{S_{k}}$
is much larger than 0.5 for both
![]() $\unicode[STIX]{x1D6E4}=1$
and 0.5 cases, and
$\unicode[STIX]{x1D6E4}=1$
and 0.5 cases, and
![]() $\bar{S_{k}}$
for
$\bar{S_{k}}$
for
![]() $\unicode[STIX]{x1D6E4}=1$
case is larger than that for
$\unicode[STIX]{x1D6E4}=1$
case is larger than that for
![]() $\unicode[STIX]{x1D6E4}=0.5$
case is consistent with what we have concluded: LSC (the first mode) dominates in both
$\unicode[STIX]{x1D6E4}=0.5$
case is consistent with what we have concluded: LSC (the first mode) dominates in both
![]() $\unicode[STIX]{x1D6E4}=1$
and
$\unicode[STIX]{x1D6E4}=1$
and
![]() $\unicode[STIX]{x1D6E4}=0.5$
cases but less so for the latter case. We note however that in
$\unicode[STIX]{x1D6E4}=0.5$
cases but less so for the latter case. We note however that in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells, only for the smallest
$\unicode[STIX]{x1D6E4}=0.5$
cells, only for the smallest
![]() $Ra$
(
$Ra$
(
![]() $1.6\times 10^{10}$
),
$1.6\times 10^{10}$
),
![]() $\bar{S_{k}}$
is slightly less than 0.5, while for the other
$\bar{S_{k}}$
is slightly less than 0.5, while for the other
![]() $Ra$
,
$Ra$
,
![]() $\bar{S_{k}}$
is well above 0.7.
$\bar{S_{k}}$
is well above 0.7.

Figure 4. The ratio between the time-averaged energy contained in the
![]() $i$
th mode
$i$
th mode
![]() $\langle E_{i}\rangle$
and the time-averaged total energy of the flow
$\langle E_{i}\rangle$
and the time-averaged total energy of the flow
![]() $\langle E_{total}\rangle$
as function of
$\langle E_{total}\rangle$
as function of
![]() $Ra$
for
$Ra$
for
![]() $\unicode[STIX]{x1D6E4}=0.5$
.
$\unicode[STIX]{x1D6E4}=0.5$
.

Figure 5. An example of cessation event in
![]() $\unicode[STIX]{x1D6E4}=1$
cell at
$\unicode[STIX]{x1D6E4}=1$
cell at
![]() $Ra=5.6\times 10^{9}$
. (a) Time segment of the orientation
$Ra=5.6\times 10^{9}$
. (a) Time segment of the orientation
![]() $\unicode[STIX]{x1D719}$
of the first mode (LSC). (b) Time segments of the amplitude of the first four modes
$\unicode[STIX]{x1D719}$
of the first mode (LSC). (b) Time segments of the amplitude of the first four modes
![]() $A_{1}$
,
$A_{1}$
,
![]() $A_{2}$
,
$A_{2}$
,
![]() $A_{3}$
and
$A_{3}$
and
![]() $A_{4}$
during a cessation event. The total amplitude of the flow
$A_{4}$
during a cessation event. The total amplitude of the flow
![]() $A_{total}$
is also plotted.
$A_{total}$
is also plotted.
3.2 The behaviour of higher-order modes during a cessation/reversal
Motivated by the recent numerical study of the behaviour of the second-order mode during cessations (Mishra et al.
Reference Mishra, De, Verma and Eswaran2011), we study the behaviour of the higher-order modes during cessation/reversal events from our experimental data. We follow the previous studies by Brown et al. (Reference Brown, Nikolaenko and Ahlers2005) and ourselves (Xi & Xia Reference Xi and Xia2007) using
![]() $0.15\langle A\rangle$
as the threshold for cessation events,
$0.15\langle A\rangle$
as the threshold for cessation events,
![]() $\langle A\rangle$
is the time average of
$\langle A\rangle$
is the time average of
![]() $A$
over the entire measurement. Once
$A$
over the entire measurement. Once
![]() $A(t)$
is less than
$A(t)$
is less than
![]() $0.15\langle A\rangle$
, we go forward and backward to the local maximum
$0.15\langle A\rangle$
, we go forward and backward to the local maximum
![]() $A_{for.\,max.}$
and
$A_{for.\,max.}$
and
![]() $A_{back.\,max.}$
, these two data points are the starting and ending points of a cessation. If a cessation is accompanied by a
$A_{back.\,max.}$
, these two data points are the starting and ending points of a cessation. If a cessation is accompanied by a
![]() $180^{\circ }$
orientation change, it is a reversal of the LSC. Practically, when the orientation change is larger than
$180^{\circ }$
orientation change, it is a reversal of the LSC. Practically, when the orientation change is larger than
![]() $150^{\circ }$
, we take the cessation as a reversal. In figure 5 we plot the time segments of the orientation
$150^{\circ }$
, we take the cessation as a reversal. In figure 5 we plot the time segments of the orientation
![]() $\unicode[STIX]{x1D719}$
of the first mode (LSC), the amplitude of the first four Fourier modes:
$\unicode[STIX]{x1D719}$
of the first mode (LSC), the amplitude of the first four Fourier modes:
![]() $A_{1}$
,
$A_{1}$
,
![]() $A_{2}$
,
$A_{2}$
,
![]() $A_{3}$
and
$A_{3}$
and
![]() $A_{4}$
during a cessation event for
$A_{4}$
during a cessation event for
![]() $\unicode[STIX]{x1D6E4}=1$
and
$\unicode[STIX]{x1D6E4}=1$
and
![]() $Ra=5.6\times 10^{9}$
. By definition during the cessation event,
$Ra=5.6\times 10^{9}$
. By definition during the cessation event,
![]() $A_{1}$
drops to almost zero then rebounds. It is seen from the figure that when
$A_{1}$
drops to almost zero then rebounds. It is seen from the figure that when
![]() $A_{1}$
experiences the decrease and rebound, the second mode increases, then decreases to the level before the occurrence of the cessation. It is also found that the flow strength of the third mode
$A_{1}$
experiences the decrease and rebound, the second mode increases, then decreases to the level before the occurrence of the cessation. It is also found that the flow strength of the third mode
![]() $A_{3}$
behaves similarly as
$A_{3}$
behaves similarly as
![]() $A_{2}$
does. The flow strength of the fourth mode
$A_{2}$
does. The flow strength of the fourth mode
![]() $A_{4}$
also experiences an increase then a decrease during the cessation of the LSC, but occurs slightly ahead of the cessation. The total strength of flow
$A_{4}$
also experiences an increase then a decrease during the cessation of the LSC, but occurs slightly ahead of the cessation. The total strength of flow
![]() $A_{total}=A_{1}+A_{2}+A_{3}+A_{4}$
is also plotted in figure 5, it is found that
$A_{total}=A_{1}+A_{2}+A_{3}+A_{4}$
is also plotted in figure 5, it is found that
![]() $A_{total}$
does not drop as much as
$A_{total}$
does not drop as much as
![]() $A_{1}$
does during the cessation of the LSC, which reveals that the cessation event is only the cessation of the LSC (the first mode), not the entire flow. The increase of the second mode during a cessation is consistent with previous numerical simulation performed at
$A_{1}$
does during the cessation of the LSC, which reveals that the cessation event is only the cessation of the LSC (the first mode), not the entire flow. The increase of the second mode during a cessation is consistent with previous numerical simulation performed at
![]() $Ra=6\times 10^{5}$
,
$Ra=6\times 10^{5}$
,
![]() $Pr=0.7$
and
$Pr=0.7$
and
![]() $\unicode[STIX]{x1D6E4}=1$
(Mishra et al.
Reference Mishra, De, Verma and Eswaran2011), where they only showed the behaviour of the first and the second modes. In spite of the different
$\unicode[STIX]{x1D6E4}=1$
(Mishra et al.
Reference Mishra, De, Verma and Eswaran2011), where they only showed the behaviour of the first and the second modes. In spite of the different
![]() $Ra$
and
$Ra$
and
![]() $Pr$
, the consistency between the experiments and numerical simulation is remarkable. In figure 6 we plot the time segments of
$Pr$
, the consistency between the experiments and numerical simulation is remarkable. In figure 6 we plot the time segments of
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
![]() $A_{1}$
,
$A_{1}$
,
![]() $A_{2}$
,
$A_{2}$
,
![]() $A_{3}$
and
$A_{3}$
and
![]() $A_{4}$
during a cessation event for
$A_{4}$
during a cessation event for
![]() $\unicode[STIX]{x1D6E4}=0.5$
and
$\unicode[STIX]{x1D6E4}=0.5$
and
![]() $Ra=5.7\times 10^{10}$
. It is found that the behaviour of the higher-order modes during a cessation in
$Ra=5.7\times 10^{10}$
. It is found that the behaviour of the higher-order modes during a cessation in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cell is similar to that in the
$\unicode[STIX]{x1D6E4}=0.5$
cell is similar to that in the
![]() $\unicode[STIX]{x1D6E4}=1$
cell. Again,
$\unicode[STIX]{x1D6E4}=1$
cell. Again,
![]() $A_{total}$
does not drop as much as
$A_{total}$
does not drop as much as
![]() $A_{1}$
does during the cessation of the LSC, which reveals that in
$A_{1}$
does during the cessation of the LSC, which reveals that in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells the cessation event is not the cessation of the entire flow. In figures 7 and 8 we plot the time traces of
$\unicode[STIX]{x1D6E4}=0.5$
cells the cessation event is not the cessation of the entire flow. In figures 7 and 8 we plot the time traces of
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
![]() $A_{1}$
,
$A_{1}$
,
![]() $A_{2}$
,
$A_{2}$
,
![]() $A_{3}$
and
$A_{3}$
and
![]() $A_{4}$
during a reversal event for
$A_{4}$
during a reversal event for
![]() $\unicode[STIX]{x1D6E4}=1$
and 0.5. The behaviour of the higher-order modes during a reversal is very similar to that during a cessation.
$\unicode[STIX]{x1D6E4}=1$
and 0.5. The behaviour of the higher-order modes during a reversal is very similar to that during a cessation.

Figure 6. An example of cessation event in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cell at
$\unicode[STIX]{x1D6E4}=0.5$
cell at
![]() $Ra=5.7\times 10^{10}$
. (a) Time segment of the orientation
$Ra=5.7\times 10^{10}$
. (a) Time segment of the orientation
![]() $\unicode[STIX]{x1D719}$
of the first mode (LSC). (b) Time segments of the amplitude of the first four modes
$\unicode[STIX]{x1D719}$
of the first mode (LSC). (b) Time segments of the amplitude of the first four modes
![]() $A_{1}$
,
$A_{1}$
,
![]() $A_{2}$
,
$A_{2}$
,
![]() $A_{3}$
and
$A_{3}$
and
![]() $A_{4}$
during a cessation event. The total amplitude of the flow
$A_{4}$
during a cessation event. The total amplitude of the flow
![]() $A_{total}$
is also plotted.
$A_{total}$
is also plotted.

Figure 7. An example of reversal event in
![]() $\unicode[STIX]{x1D6E4}=1$
cell at
$\unicode[STIX]{x1D6E4}=1$
cell at
![]() $Ra=5.6\times 10^{9}$
. (a) Time segment of the orientation
$Ra=5.6\times 10^{9}$
. (a) Time segment of the orientation
![]() $\unicode[STIX]{x1D719}$
of the first mode (LSC). (b) Time segments of the amplitude of the first four modes
$\unicode[STIX]{x1D719}$
of the first mode (LSC). (b) Time segments of the amplitude of the first four modes
![]() $A_{1}$
,
$A_{1}$
,
![]() $A_{2}$
,
$A_{2}$
,
![]() $A_{3}$
and
$A_{3}$
and
![]() $A_{4}$
during a reversal event. The total amplitude of the flow
$A_{4}$
during a reversal event. The total amplitude of the flow
![]() $A_{total}$
is also plotted.
$A_{total}$
is also plotted.

Figure 8. An example of reversal event in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cell at
$\unicode[STIX]{x1D6E4}=0.5$
cell at
![]() $Ra=5.7\times 10^{10}$
. (a) Time segment of the orientation
$Ra=5.7\times 10^{10}$
. (a) Time segment of the orientation
![]() $\unicode[STIX]{x1D719}$
of the first mode (LSC). (b) Time segments of the amplitude of the first four modes
$\unicode[STIX]{x1D719}$
of the first mode (LSC). (b) Time segments of the amplitude of the first four modes
![]() $A_{1}$
,
$A_{1}$
,
![]() $A_{2}$
,
$A_{2}$
,
![]() $A_{3}$
and
$A_{3}$
and
![]() $A_{4}$
during a reversal event. The total amplitude of the flow
$A_{4}$
during a reversal event. The total amplitude of the flow
![]() $A_{total}$
is also plotted.
$A_{total}$
is also plotted.
Till now we have shown time traces of the amplitude of higher-order flow modes during cessation and reversal for both
![]() $\unicode[STIX]{x1D6E4}=1$
and
$\unicode[STIX]{x1D6E4}=1$
and
![]() $\unicode[STIX]{x1D6E4}=0.5$
cases. The common feature we can draw is that during the cessation/reversal of the LSC, the second mode and the remaining higher-order modes increase, then decrease to the level before the occurrence of the cessation/reversal. The fact that the second mode dominates during a reversal/cessation implies that, during the cessation/reversal, the single role (dipole) mode weakens and the quadrupole mode becomes stronger and takes over the first mode. Later, the dipole mode recovered and the quadrupole and the remaining higher-order modes all weaken. It is well known that in
$\unicode[STIX]{x1D6E4}=0.5$
cases. The common feature we can draw is that during the cessation/reversal of the LSC, the second mode and the remaining higher-order modes increase, then decrease to the level before the occurrence of the cessation/reversal. The fact that the second mode dominates during a reversal/cessation implies that, during the cessation/reversal, the single role (dipole) mode weakens and the quadrupole mode becomes stronger and takes over the first mode. Later, the dipole mode recovered and the quadrupole and the remaining higher-order modes all weaken. It is well known that in
![]() $\unicode[STIX]{x1D6E4}=1$
cells cessation/reversal does not occur very frequently (approximately only 1.5 times/day, see Brown et al. (Reference Brown, Nikolaenko and Ahlers2005), Xi & Xia (Reference Xi and Xia2007)), for example in a recent numerical simulation study only 5 cessations and no reversal were observed (Mishra et al.
Reference Mishra, De, Verma and Eswaran2011). The limited number of cessation/reversal events prevent one from studying its statistical properties. Previously, it was found that cessation/reversal occurs much more frequently in
$\unicode[STIX]{x1D6E4}=1$
cells cessation/reversal does not occur very frequently (approximately only 1.5 times/day, see Brown et al. (Reference Brown, Nikolaenko and Ahlers2005), Xi & Xia (Reference Xi and Xia2007)), for example in a recent numerical simulation study only 5 cessations and no reversal were observed (Mishra et al.
Reference Mishra, De, Verma and Eswaran2011). The limited number of cessation/reversal events prevent one from studying its statistical properties. Previously, it was found that cessation/reversal occurs much more frequently in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells (Xi & Xia Reference Xi and Xia2007), the large number of cessation and reversal events allows us to perform statistical analysis. We have done experiments with six different
$\unicode[STIX]{x1D6E4}=0.5$
cells (Xi & Xia Reference Xi and Xia2007), the large number of cessation and reversal events allows us to perform statistical analysis. We have done experiments with six different
![]() $Ra$
in
$Ra$
in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells, each lasting for at least two days. The longest measurement lasted for 34 days and 1855 cessations and 543 reversals were identified. In table 1 we list the number of cessations and reversals identified for each measurement. To study the relationship between the amplitudes of the different modes, we calculated the cross-correlation function between them:
$\unicode[STIX]{x1D6E4}=0.5$
cells, each lasting for at least two days. The longest measurement lasted for 34 days and 1855 cessations and 543 reversals were identified. In table 1 we list the number of cessations and reversals identified for each measurement. To study the relationship between the amplitudes of the different modes, we calculated the cross-correlation function between them:
![]() $C_{A_{i},A_{j}}(\unicode[STIX]{x1D70F})=\langle (A_{i}(t+\unicode[STIX]{x1D70F})-\langle A_{i}\rangle )(A_{j}(t)-\langle A_{j}\rangle )\rangle /(\unicode[STIX]{x1D70E}_{A_{i}}\unicode[STIX]{x1D70E}_{A_{j}})$
, where
$C_{A_{i},A_{j}}(\unicode[STIX]{x1D70F})=\langle (A_{i}(t+\unicode[STIX]{x1D70F})-\langle A_{i}\rangle )(A_{j}(t)-\langle A_{j}\rangle )\rangle /(\unicode[STIX]{x1D70E}_{A_{i}}\unicode[STIX]{x1D70E}_{A_{j}})$
, where
![]() $\unicode[STIX]{x1D70E}_{A_{i}}$
and
$\unicode[STIX]{x1D70E}_{A_{i}}$
and
![]() $\unicode[STIX]{x1D70E}_{A_{j}}$
are the standard deviations of
$\unicode[STIX]{x1D70E}_{A_{j}}$
are the standard deviations of
![]() $A_{i}$
and
$A_{i}$
and
![]() $A_{j}$
, respectively. The correlation coefficients are plotted in figure 9. We can see that
$A_{j}$
, respectively. The correlation coefficients are plotted in figure 9. We can see that
![]() $C_{A_{1},A_{2}}$
,
$C_{A_{1},A_{2}}$
,
![]() $C_{A_{1},A_{3}}$
,
$C_{A_{1},A_{3}}$
,
![]() $C_{A_{1},A_{4}}$
all show negative peaks near
$C_{A_{1},A_{4}}$
all show negative peaks near
![]() $\unicode[STIX]{x1D70F}=0$
, which implies that the amplitudes of the higher-order modes
$\unicode[STIX]{x1D70F}=0$
, which implies that the amplitudes of the higher-order modes
![]() $A_{2}$
,
$A_{2}$
,
![]() $A_{3}$
,
$A_{3}$
,
![]() $A_{4}$
are all anti-correlated with
$A_{4}$
are all anti-correlated with
![]() $A_{1}$
and the anti-correlation between
$A_{1}$
and the anti-correlation between
![]() $A_{2}$
and
$A_{2}$
and
![]() $A_{1}$
is the strongest. The results from this statistical analysis is consistent with that we have learned from the individual examples (figures 5–8): when the first mode becomes weaker, the second mode (and the other higher-order modes) becomes stronger, and vice versa. It is also noted that
$A_{1}$
is the strongest. The results from this statistical analysis is consistent with that we have learned from the individual examples (figures 5–8): when the first mode becomes weaker, the second mode (and the other higher-order modes) becomes stronger, and vice versa. It is also noted that
![]() $C_{A_{2},A_{3}}$
,
$C_{A_{2},A_{3}}$
,
![]() $C_{A_{2},A_{4}}$
,
$C_{A_{2},A_{4}}$
,
![]() $C_{A_{3},A_{4}}$
all have positive peaks near
$C_{A_{3},A_{4}}$
all have positive peaks near
![]() $\unicode[STIX]{x1D70F}=0$
, which reveals that the higher-order modes themselves are all positively correlated. Again, the positive correlation between the amplitudes of the higher-order modes are consistent with what we have learned from the individual examples (figures 5–8), i.e. when the cessation/reversal of the LSC occurs, all the higher-order modes become stronger.
$\unicode[STIX]{x1D70F}=0$
, which reveals that the higher-order modes themselves are all positively correlated. Again, the positive correlation between the amplitudes of the higher-order modes are consistent with what we have learned from the individual examples (figures 5–8), i.e. when the cessation/reversal of the LSC occurs, all the higher-order modes become stronger.

Figure 9. Cross-correlation function between the amplitudes of modes
![]() $A_{i}$
and
$A_{i}$
and
![]() $A_{j}$
as a function of time delay
$A_{j}$
as a function of time delay
![]() $\unicode[STIX]{x1D70F}$
. The data are from 34 days of measurements in a
$\unicode[STIX]{x1D70F}$
. The data are from 34 days of measurements in a
![]() $\unicode[STIX]{x1D6E4}=0.5$
cell at
$\unicode[STIX]{x1D6E4}=0.5$
cell at
![]() $Ra=5.7\times 10^{10}$
.
$Ra=5.7\times 10^{10}$
.
Table 1. The
![]() $Ra$
number, measurement time and the number of cessation/reversal events identified in the experiments for
$Ra$
number, measurement time and the number of cessation/reversal events identified in the experiments for
![]() $\unicode[STIX]{x1D6E4}=0.5$
.
$\unicode[STIX]{x1D6E4}=0.5$
.


Figure 10. (a) Ensemble-averaged time traces of amplitude of the different mode
![]() $\widetilde{A_{1}}$
,
$\widetilde{A_{1}}$
,
![]() $\widetilde{A_{2}}$
,
$\widetilde{A_{2}}$
,
![]() $\widetilde{A_{3}}$
,
$\widetilde{A_{3}}$
,
![]() $\widetilde{A_{4}}$
, the total flow amplitude
$\widetilde{A_{4}}$
, the total flow amplitude
![]() $\widetilde{A_{total}}$
and the heat transfer efficiency
$\widetilde{A_{total}}$
and the heat transfer efficiency
![]() $\widetilde{Nu}$
during cessations. (b) The same data but only
$\widetilde{Nu}$
during cessations. (b) The same data but only
![]() $\widetilde{A_{2}}$
,
$\widetilde{A_{2}}$
,
![]() $\widetilde{A_{3}}$
,
$\widetilde{A_{3}}$
,
![]() $\widetilde{A_{4}}$
are shown. The data are from the 34 days of measurements in a
$\widetilde{A_{4}}$
are shown. The data are from the 34 days of measurements in a
![]() $\unicode[STIX]{x1D6E4}=0.5$
cell at
$\unicode[STIX]{x1D6E4}=0.5$
cell at
![]() $Ra=5.7\times 10^{10}$
.
$Ra=5.7\times 10^{10}$
.

Figure 11. (a) Ensemble-averaged time traces of amplitude of the different mode
![]() $\widetilde{A_{1}}$
,
$\widetilde{A_{1}}$
,
![]() $\widetilde{A_{2}}$
,
$\widetilde{A_{2}}$
,
![]() $\widetilde{A_{3}}$
,
$\widetilde{A_{3}}$
,
![]() $\widetilde{A_{4}}$
, the total flow amplitude
$\widetilde{A_{4}}$
, the total flow amplitude
![]() $\widetilde{A_{total}}$
and the heat transfer efficiency
$\widetilde{A_{total}}$
and the heat transfer efficiency
![]() $\widetilde{Nu}$
during reversals. (b) The same data but only
$\widetilde{Nu}$
during reversals. (b) The same data but only
![]() $\widetilde{A_{2}}$
,
$\widetilde{A_{2}}$
,
![]() $\widetilde{A_{3}}$
,
$\widetilde{A_{3}}$
,
![]() $\widetilde{A_{4}}$
are shown. The data are from the 34 days of measurements in a
$\widetilde{A_{4}}$
are shown. The data are from the 34 days of measurements in a
![]() $\unicode[STIX]{x1D6E4}=0.5$
cell at
$\unicode[STIX]{x1D6E4}=0.5$
cell at
![]() $Ra=5.7\times 10^{10}$
.
$Ra=5.7\times 10^{10}$
.
Another more direct way to examine the average behaviour of the different modes during cessation/reversal is to show the ensemble-averaged time traces of different modes during the cessations/reversals. For example, to have the ensemble-averaged time trace of
![]() $A_{2}$
during cessations/reversals, we first locate the data point where the LSC is the weakest, i.e. where
$A_{2}$
during cessations/reversals, we first locate the data point where the LSC is the weakest, i.e. where
![]() $A_{1}$
is at its local minimum, during the cessation/reversal events. Then starting from this data point we go forward and backward for 40 data points, extract this 81 data point time segment of
$A_{1}$
is at its local minimum, during the cessation/reversal events. Then starting from this data point we go forward and backward for 40 data points, extract this 81 data point time segment of
![]() $A_{2}$
(corresponding to 358 s, enough to cover the mean duration time of cessation/reversal which is 60/62 s). We then average all the 1855/543 time segments of
$A_{2}$
(corresponding to 358 s, enough to cover the mean duration time of cessation/reversal which is 60/62 s). We then average all the 1855/543 time segments of
![]() $A_{2}$
(each containing a cessation/reversal) onto this 81 data points, the so-obtained averaged time trace of
$A_{2}$
(each containing a cessation/reversal) onto this 81 data points, the so-obtained averaged time trace of
![]() $A_{2}(t)$
(denoted as
$A_{2}(t)$
(denoted as
![]() $\widetilde{A_{2}}(t)$
) shows the average evolution of
$\widetilde{A_{2}}(t)$
) shows the average evolution of
![]() $A_{2}(t)$
during cessations/reversals. Similarly we obtained
$A_{2}(t)$
during cessations/reversals. Similarly we obtained
![]() $\widetilde{A_{1}}(t)$
,
$\widetilde{A_{1}}(t)$
,
![]() $\widetilde{A_{3}}(t)$
,
$\widetilde{A_{3}}(t)$
,
![]() $\widetilde{A_{4}}(t)$
,
$\widetilde{A_{4}}(t)$
,
![]() $\widetilde{A_{total}}(t)$
and
$\widetilde{A_{total}}(t)$
and
![]() $\widetilde{Nu}(t)$
(the discussion on
$\widetilde{Nu}(t)$
(the discussion on
![]() $\widetilde{Nu}(t)$
is postponed to the next section). As shown in figures 10 and 11, during cessations/reversals
$\widetilde{Nu}(t)$
is postponed to the next section). As shown in figures 10 and 11, during cessations/reversals
![]() $\widetilde{A_{2}}(t)$
experiences an increase followed by a decrease;
$\widetilde{A_{2}}(t)$
experiences an increase followed by a decrease;
![]() $\widetilde{A_{3}}(t)$
and
$\widetilde{A_{3}}(t)$
and
![]() $\widetilde{A_{4}}(t)$
also experience an increase, although very small, followed by a decrease. All these results are consistent with both the individual examples of cessations/reversals we presented in figures 5–8 and the correlation functions between
$\widetilde{A_{4}}(t)$
also experience an increase, although very small, followed by a decrease. All these results are consistent with both the individual examples of cessations/reversals we presented in figures 5–8 and the correlation functions between
![]() $A_{1}(t)$
,
$A_{1}(t)$
,
![]() $A_{2}(t)$
,
$A_{2}(t)$
,
![]() $A_{3}(t)$
and
$A_{3}(t)$
and
![]() $A_{4}(t)$
shown in figure 9. For reversals in 2-D/quasi-2-D convection systems, it is well accepted that it is the growth of corner rolls that squeeze the LSC main roll and break it, the two corner rolls then connect to form a new LSC roll in the opposite direction (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; Chandra & Verma Reference Chandra and Verma2013; Ni et al.
Reference Ni, Huang and Xia2015). For reversals in 3-D cylindrical configuration, we do not have such a detailed picture. Figure 11 tells us that cessation/reversal is not a totally random process and it is accompanied by the process of higher-order modes prevailing over the first mode. It is seen from figures 10 and 11 that during cessations/reversals
$A_{4}(t)$
shown in figure 9. For reversals in 2-D/quasi-2-D convection systems, it is well accepted that it is the growth of corner rolls that squeeze the LSC main roll and break it, the two corner rolls then connect to form a new LSC roll in the opposite direction (Sugiyama et al.
Reference Sugiyama, Ni, Stevens, Chan, Zhou, Xi, Sun, Grossmann, Xia and Lohse2010; Chandra & Verma Reference Chandra and Verma2013; Ni et al.
Reference Ni, Huang and Xia2015). For reversals in 3-D cylindrical configuration, we do not have such a detailed picture. Figure 11 tells us that cessation/reversal is not a totally random process and it is accompanied by the process of higher-order modes prevailing over the first mode. It is seen from figures 10 and 11 that during cessations/reversals
![]() $\widetilde{A_{total}}(t)$
drops by approximately 50 %, not as much as
$\widetilde{A_{total}}(t)$
drops by approximately 50 %, not as much as
![]() $\widetilde{A_{1}}(t)$
(which dropped by 80 %), which reveals that the cessation of the LSC is not the cessation of the entire flow. Although the LSC ceased, the flow energy is redistributed to the higher-order modes or the much smaller scales we are not able to measure due to the limited number of thermistors.
$\widetilde{A_{1}}(t)$
(which dropped by 80 %), which reveals that the cessation of the LSC is not the cessation of the entire flow. Although the LSC ceased, the flow energy is redistributed to the higher-order modes or the much smaller scales we are not able to measure due to the limited number of thermistors.

Figure 12. The ratio between the time-averaged flow energy of the
![]() $i$
th mode and the time-averaged total energy of the flow
$i$
th mode and the time-averaged total energy of the flow
![]() $\langle E_{i}\rangle _{ces}/\langle E_{total}\rangle _{ces}$
during cessations in
$\langle E_{i}\rangle _{ces}/\langle E_{total}\rangle _{ces}$
during cessations in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells.
$\unicode[STIX]{x1D6E4}=0.5$
cells.
From the time traces of amplitudes of the different flow modes (figures 5–8), it is seen that during the cessation/reversal the first mode is very weak and the second mode is the strongest. It is not known whether this is the case for all the cessations/reversals. To test this we calculate the time-averaged energy contained in the
![]() $i$
th mode during the cessation
$i$
th mode during the cessation
![]() $\langle E_{i}\rangle _{ces}$
. The large number of cessation/reversal events identified in our experiments allow us to do so. In figure 12 we plot the ratio between the time-averaged energy contained in the
$\langle E_{i}\rangle _{ces}$
. The large number of cessation/reversal events identified in our experiments allow us to do so. In figure 12 we plot the ratio between the time-averaged energy contained in the
![]() $i$
th mode and the total energy of the flow during cessation
$i$
th mode and the total energy of the flow during cessation
![]() $\langle E_{i}\rangle _{ces}/\langle E_{total}\rangle _{ces}$
. It is found that during the cessation, the second mode dominates, on average (averaged over all the
$\langle E_{i}\rangle _{ces}/\langle E_{total}\rangle _{ces}$
. It is found that during the cessation, the second mode dominates, on average (averaged over all the
![]() $Ra$
) it contains 51.3 % of the total flow energy, the first mode, the third mode and the fourth mode contain 21.9 %, 22.0 % and 4.8 % of the total flow energy respectively. Similarly, we plot the ratio between the time-averaged energy contained in the
$Ra$
) it contains 51.3 % of the total flow energy, the first mode, the third mode and the fourth mode contain 21.9 %, 22.0 % and 4.8 % of the total flow energy respectively. Similarly, we plot the ratio between the time-averaged energy contained in the
![]() $i$
th mode and the total energy of the flow during reversal
$i$
th mode and the total energy of the flow during reversal
![]() $\langle E_{i}\rangle _{rev}/\langle E_{total}\rangle _{rev}$
in figure 13. It is similar to the cessation case: the second mode dominates during the reversal, on average (averaged over all the
$\langle E_{i}\rangle _{rev}/\langle E_{total}\rangle _{rev}$
in figure 13. It is similar to the cessation case: the second mode dominates during the reversal, on average (averaged over all the
![]() $Ra$
) it contains 50.1 % of the total flow energy, the first mode, third mode and the fourth mode contain 22.9 %, 22.1 % and 4.9 % of the total flow energy respectively.
$Ra$
) it contains 50.1 % of the total flow energy, the first mode, third mode and the fourth mode contain 22.9 %, 22.1 % and 4.9 % of the total flow energy respectively.

Figure 13. The ratio between the time-averaged flow energy of the
![]() $i$
th mode and the time-averaged total energy of the flow
$i$
th mode and the time-averaged total energy of the flow
![]() $\langle E_{i}\rangle _{rev}/\langle E_{total}\rangle _{rev}$
during reversals in
$\langle E_{i}\rangle _{rev}/\langle E_{total}\rangle _{rev}$
during reversals in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells.
$\unicode[STIX]{x1D6E4}=0.5$
cells.
3.3 Flow mode and heat transfer
We now discuss the connections between the flow mode and the heat transfer efficiency in turbulent Rayleigh–Bénard convection. As already mentioned in § 1, a possible connection between the mean flow structure and the Nusselt number has been suggested previously by a number of studies (Roche et al.
Reference Roche, Castaing, Chabaud and Hebral2002; Chillà et al.
Reference Chillà, Rastello, Chaumat and Castaing2004; Nikolaenko et al.
Reference Nikolaenko, Brown, Funfschilling and Ahlers2005; Stringano & Verzicco Reference Stringano and Verzicco2006). Experiments indeed showed that the heat transfer efficiency depends on the internal flow mode in the turbulent RB system (Sun et al.
Reference Sun, Xi and Xia2005a
; Xi & Xia Reference Xi and Xia2008b
; Weiss & Ahlers Reference Weiss and Ahlers2011b
; Huang et al.
Reference Huang, Kaczorowski, Ni and Xia2013). A more coherent flow would produce a higher heat transfer efficiency (Huang et al.
Reference Huang, Kaczorowski, Ni and Xia2013). In this case, we would expect that the first mode, which is more coherent, should be associated with higher heat transfer efficiency. That is to say, statistically, the amplitude of the first mode should positively correlate with instantaneous Nusselt number. In the RB convection system, the Nusselt number is defined as
![]() $Nu=J_{total}/J_{conduction}$
, where
$Nu=J_{total}/J_{conduction}$
, where
![]() $J_{total}$
is the total heat flux due to pure conduction and the convective flow in the system, and
$J_{total}$
is the total heat flux due to pure conduction and the convective flow in the system, and
![]() $J_{conduction}$
is the heat flux due to pure conduction across the bottom and the top plates. As our experiment was not conducted in a thermostat box, there may exist heat leakages through the sidewall and the bottom plate. Therefore, the absolute values of the measured
$J_{conduction}$
is the heat flux due to pure conduction across the bottom and the top plates. As our experiment was not conducted in a thermostat box, there may exist heat leakages through the sidewall and the bottom plate. Therefore, the absolute values of the measured
![]() $Nu$
may suffer systematic errors at the level of a few per cent. However, because the temperatures of the top and bottom plates of the convection cell were measured simultaneously with the 24 thermistors embedded in the sidewall, we can study how the temperature difference between the top and bottom plates, hence the Nusselt number, correlates with the changes in the flow structure in the convecting fluid. We define the instantaneous Nusselt as
$Nu$
may suffer systematic errors at the level of a few per cent. However, because the temperatures of the top and bottom plates of the convection cell were measured simultaneously with the 24 thermistors embedded in the sidewall, we can study how the temperature difference between the top and bottom plates, hence the Nusselt number, correlates with the changes in the flow structure in the convecting fluid. We define the instantaneous Nusselt as
![]() $Nu(t)=JH/[\unicode[STIX]{x1D712}S\unicode[STIX]{x0394}T(t)]$
, where
$Nu(t)=JH/[\unicode[STIX]{x1D712}S\unicode[STIX]{x0394}T(t)]$
, where
![]() $J$
is the power supplied to the cell and is taken as the heat current transported by the convecting fluid,
$J$
is the power supplied to the cell and is taken as the heat current transported by the convecting fluid,
![]() $\unicode[STIX]{x1D712}$
the thermal conductivity of the fluid and
$\unicode[STIX]{x1D712}$
the thermal conductivity of the fluid and
![]() $S$
the cross-sectional area of the cell. The temperature difference
$S$
the cross-sectional area of the cell. The temperature difference
![]() $\unicode[STIX]{x0394}T(t)=T_{b}(t)-T_{t}(t)$
, where the temperatures of the bottom and top plates,
$\unicode[STIX]{x0394}T(t)=T_{b}(t)-T_{t}(t)$
, where the temperatures of the bottom and top plates,
![]() $T_{b}(t)$
and
$T_{b}(t)$
and
![]() $T_{t}(t)$
, are based on the average values of the two imbedded thermistors in each plate.
$T_{t}(t)$
, are based on the average values of the two imbedded thermistors in each plate.
Since we have measured the instantaneous
![]() $Nu$
and the amplitude of the Fourier modes of the flow simultaneously, we could study the relationship between the heat transfer efficiency and the amplitude of different modes by showing the ensemble-averaged time trace of
$Nu$
and the amplitude of the Fourier modes of the flow simultaneously, we could study the relationship between the heat transfer efficiency and the amplitude of different modes by showing the ensemble-averaged time trace of
![]() $Nu$
and the amplitudes of different modes during cessations and reversals, as shown in figures 10 and 11. It is clear that the decrease of
$Nu$
and the amplitudes of different modes during cessations and reversals, as shown in figures 10 and 11. It is clear that the decrease of
![]() $Nu$
is accompanied by a decrease of
$Nu$
is accompanied by a decrease of
![]() $A_{1}$
and an increase of
$A_{1}$
and an increase of
![]() $A_{2}$
,
$A_{2}$
,
![]() $A_{3}$
and
$A_{3}$
and
![]() $A_{4}$
, which means that the first mode, i.e. the single-roll mode, produces more efficient heat transfer on average. Two other features are readily seen from figures 10 and 11, one is that for both cessation and reversal,
$A_{4}$
, which means that the first mode, i.e. the single-roll mode, produces more efficient heat transfer on average. Two other features are readily seen from figures 10 and 11, one is that for both cessation and reversal,
![]() $Nu$
reaches its local minimum ahead of that of
$Nu$
reaches its local minimum ahead of that of
![]() $A_{1}$
, i.e. global transport is precursor of the of changes in flow dynamics. In other words, the variation of global heat transport serves to forecast the changes in the flow dynamics that are coming. The second feature is that
$A_{1}$
, i.e. global transport is precursor of the of changes in flow dynamics. In other words, the variation of global heat transport serves to forecast the changes in the flow dynamics that are coming. The second feature is that
![]() $Nu$
has a momentary overshoot above its average value during reversal, which is not seen during cessations. It was assumed previously that, after a cessation, the flow reorganizes and then can start in any of the azimuthal directions with equal probability. Therefore, reversal is just one of the possible outcomes of cessation and is dynamically not different from other cessation events. Our results here reveal that reversals can be distinguished from cessations in terms of global heat transport. It is now well understood that
$Nu$
has a momentary overshoot above its average value during reversal, which is not seen during cessations. It was assumed previously that, after a cessation, the flow reorganizes and then can start in any of the azimuthal directions with equal probability. Therefore, reversal is just one of the possible outcomes of cessation and is dynamically not different from other cessation events. Our results here reveal that reversals can be distinguished from cessations in terms of global heat transport. It is now well understood that
![]() $Nu$
will increase if either the flow or the plumes are more coherent (Xi & Xia Reference Xi and Xia2008b
; Weiss & Ahlers Reference Weiss and Ahlers2011b
; Huang et al.
Reference Huang, Kaczorowski, Ni and Xia2013). The overshoot in
$Nu$
will increase if either the flow or the plumes are more coherent (Xi & Xia Reference Xi and Xia2008b
; Weiss & Ahlers Reference Weiss and Ahlers2011b
; Huang et al.
Reference Huang, Kaczorowski, Ni and Xia2013). The overshoot in
![]() $Nu$
could be the result of either the flow or plumes becoming more coherent for that short period of time. The exact reason for the overshoot of
$Nu$
could be the result of either the flow or plumes becoming more coherent for that short period of time. The exact reason for the overshoot of
![]() $Nu$
is not known to us. It should be noted that the minimum of
$Nu$
is not known to us. It should be noted that the minimum of
![]() $Nu$
leading that of
$Nu$
leading that of
![]() $A_{1}$
for both reversal/cessation and the overshoot of
$A_{1}$
for both reversal/cessation and the overshoot of
![]() $Nu$
during reversals were also observed at other Rayleigh numbers. In a previous numerical study in 2-D convection cells it was found that
$Nu$
during reversals were also observed at other Rayleigh numbers. In a previous numerical study in 2-D convection cells it was found that
![]() $Nu$
fluctuates strongly during the reversal of the LSC. Even negative
$Nu$
fluctuates strongly during the reversal of the LSC. Even negative
![]() $Nu$
was observed at the end of the reversal process and it was suggested that the negative
$Nu$
was observed at the end of the reversal process and it was suggested that the negative
![]() $Nu$
was due to the constraints set by the geometry, which may not occur in the 3-D cylindrical geometry (Chandra & Verma Reference Chandra and Verma2013). We have not observed negative instantaneous
$Nu$
was due to the constraints set by the geometry, which may not occur in the 3-D cylindrical geometry (Chandra & Verma Reference Chandra and Verma2013). We have not observed negative instantaneous
![]() $Nu$
in our experiments.
$Nu$
in our experiments.
We could also study the relationship between the heat transfer efficiency and the amplitude of different modes by calculating their cross-correlation:
![]() $C_{Nu,A_{i}}(\unicode[STIX]{x1D70F})=\langle (Nu(t+\unicode[STIX]{x1D70F})-\langle Nu\rangle )(A_{i}(t)-\langle A_{i}\rangle )\rangle /(\unicode[STIX]{x1D70E}_{Nu}\unicode[STIX]{x1D70E}_{A_{i}})$
, where
$C_{Nu,A_{i}}(\unicode[STIX]{x1D70F})=\langle (Nu(t+\unicode[STIX]{x1D70F})-\langle Nu\rangle )(A_{i}(t)-\langle A_{i}\rangle )\rangle /(\unicode[STIX]{x1D70E}_{Nu}\unicode[STIX]{x1D70E}_{A_{i}})$
, where
![]() $\unicode[STIX]{x1D70E}_{Nu}$
and
$\unicode[STIX]{x1D70E}_{Nu}$
and
![]() $\unicode[STIX]{x1D70E}_{A_{i}}$
are the standard deviations of
$\unicode[STIX]{x1D70E}_{A_{i}}$
are the standard deviations of
![]() $Nu$
and
$Nu$
and
![]() $A_{i}$
respectively. Plotted in figure 14 are the cross-correlation functions between
$A_{i}$
respectively. Plotted in figure 14 are the cross-correlation functions between
![]() $Nu$
and the amplitude of the
$Nu$
and the amplitude of the
![]() $i$
th mode
$i$
th mode
![]() $A_{i}$
. The first thing we can see from the figure is that
$A_{i}$
. The first thing we can see from the figure is that
![]() $Nu$
is positively correlated with
$Nu$
is positively correlated with
![]() $A_{1}$
, which means that the first mode, i.e. the single-roll mode produces more efficient heat transfer on average. While the higher-order modes are negatively correlated with
$A_{1}$
, which means that the first mode, i.e. the single-roll mode produces more efficient heat transfer on average. While the higher-order modes are negatively correlated with
![]() $Nu$
. These results are consistent with results from the ensemble-averaged time traces of
$Nu$
. These results are consistent with results from the ensemble-averaged time traces of
![]() $Nu$
and amplitude of different mode shown in figures 10 and 11. We have computed the time-averaged
$Nu$
and amplitude of different mode shown in figures 10 and 11. We have computed the time-averaged
![]() $Nu$
for all the cessations, it is approximately 0.1 % lower than the time-averaged
$Nu$
for all the cessations, it is approximately 0.1 % lower than the time-averaged
![]() $Nu$
for the entire data set. As our experiment was not conducted in a thermostat box, there may exist heat leakages through the sidewall and the bottom plate. Therefore, the absolute values of the measured
$Nu$
for the entire data set. As our experiment was not conducted in a thermostat box, there may exist heat leakages through the sidewall and the bottom plate. Therefore, the absolute values of the measured
![]() $Nu$
may have a few per cent systematic errors, which is enough to prevent a detailed comparison between
$Nu$
may have a few per cent systematic errors, which is enough to prevent a detailed comparison between
![]() $Nu$
for the cessation state and the LSC state. In addition, although we have identified 1855 cessations, the total time duration of the cessation events is only approximately 3.83 % of the entire time trace, which also prevents us from having enough statistics to find an averaged
$Nu$
for the cessation state and the LSC state. In addition, although we have identified 1855 cessations, the total time duration of the cessation events is only approximately 3.83 % of the entire time trace, which also prevents us from having enough statistics to find an averaged
![]() $Nu$
during cessations.
$Nu$
during cessations.

Figure 14. Cross-correlation function between the instantaneous
![]() $Nu$
and the amplitude of the
$Nu$
and the amplitude of the
![]() $i$
th modes
$i$
th modes
![]() $A_{i}$
as a function of delay time
$A_{i}$
as a function of delay time
![]() $\unicode[STIX]{x1D70F}$
. The data are from 34 days of measurements in
$\unicode[STIX]{x1D70F}$
. The data are from 34 days of measurements in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cell at
$\unicode[STIX]{x1D6E4}=0.5$
cell at
![]() $Ra=5.7\times 10^{10}$
.
$Ra=5.7\times 10^{10}$
.

Figure 15. Snapshots of the 2-D velocity field measured by the PIV technique in a horizontal plane 1 cm below the top plate of the convection cell at
![]() $Ra=3.3\times 10^{10}$
and
$Ra=3.3\times 10^{10}$
and
![]() $\unicode[STIX]{x1D6E4}=0.5$
. The black lines with arrows are streamlines drawn to show the flow directions. The flow is dominated by the first mode (a), the second mode (b), the third mode (c) and the fourth mode (d). The last three are the velocity maps when the flow experiences a cessation. The red dash (blue solid) circles mark the position where the ascending (descending) flows are located.
$\unicode[STIX]{x1D6E4}=0.5$
. The black lines with arrows are streamlines drawn to show the flow directions. The flow is dominated by the first mode (a), the second mode (b), the third mode (c) and the fourth mode (d). The last three are the velocity maps when the flow experiences a cessation. The red dash (blue solid) circles mark the position where the ascending (descending) flows are located.
3.4 Direct PIV measurement of the higher-order modes
It is seen from our multi-temperature-probe measurements that during a cessation/reversal the first mode vanishes, while the second and the remaining higher-order modes become stronger. We have conjectured the flow structure of the higher-order modes, as shown in figure 2. A natural question is: what actually happens to the flow field? This may be answered by direct measurement of the velocity field using the PIV technique. To do this, we perform 2-D PIV measurement in a horizontal plan 1 cm below the top plate in a
![]() $\unicode[STIX]{x1D6E4}=0.5$
cell with top plate made of sapphire. Details of the cell and the PIV measurements are described in Xi, Zhou & Xia (Reference Xi, Zhou and Xia2006). The only differences are that here,
$\unicode[STIX]{x1D6E4}=0.5$
cell with top plate made of sapphire. Details of the cell and the PIV measurements are described in Xi, Zhou & Xia (Reference Xi, Zhou and Xia2006). The only differences are that here,
![]() $\unicode[STIX]{x1D6E4}$
is 0.5 and the measuring area, containing
$\unicode[STIX]{x1D6E4}$
is 0.5 and the measuring area, containing
![]() $31\times 39$
velocity vectors, covers a horizontal area of approximately
$31\times 39$
velocity vectors, covers a horizontal area of approximately
![]() $15~\text{cm}\times 19~\text{cm}$
centred at the axis of the cylindrical cell. Previously it has been shown, from the 2-D velocity map in the horizontal plane near the top plate, that the strength and the orientation of the LSC as well as its cessation/reversal can be obtained (Xi et al.
Reference Xi, Zhou and Xia2006; Xi & Xia Reference Xi and Xia2007, Reference Xi and Xia2008a
). Here, we carefully examined the velocity maps and found that, most of the time, the measured velocity map of the flow is consistent with the first mode (figure 15
a) and when cessation/reversal occurs the higher-order Fourier modes (figure 15
b–d) take over the first mode. Figure 15 shows four instantaneous 2-D horizontal velocity maps, when the flow is dominated by the first mode (dipole mode) (a), the second mode (quadrupole mode) (b), the third mode (sextupole mode) (c) and the fourth mode (octupole mode) (d). As seen in figure 15(a), the ascending flow is from the 3 o’clock direction and the descending flow is at the 9 o’clock direction (as shown by the red and blue circles), giving rise to a coherent LSC, which is the first mode sketched in figure 2(a). The velocity map similar to figure 15(a) has previously been shown in Xi & Xia (Reference Xi and Xia2007), and is shown here for comparison with the higher-order modes. In figure 15(b) the ascending flows are from approximately the 3 o’clock and the 9 o’clock directions, and the descending flow are at the 12 o’clock and 6 o’clock directions, which is consistent with the second Fourier mode sketched in figure 2(b). Similarly we found that in figure 15(c) the ascending flows are approximately from 4 o’clock, 8 o’clock and 10.5 o’clock directions, and the descending flow are roughly at 1 o’clock, 5 o’clock and 9 o’clock directions, which is qualitatively consistent with the third Fourier mode sketched in figure 2(c). And in figure 15(d) the ascending flows are from 1.5 o’clock, 3 o’clock, 8 o’clock and 9 o’clock directions, and the descending flow are at 2.5 o’clock, 5.5 o’clock, 8.5 o’clock and 12 o’clock directions, which is qualitatively consistent with the fourth Fourier mode sketched in figure 2(d). It should be noted that the temperature measurements were done at the mid-height whereas the PIV velocity measurements were performed 1 cm below the top plate. It is well known that in the convection cell, the LSC is a tilted ellipse and is twisted (Sun, Xia & Tong Reference Sun, Xia and Tong2005b
; Sun et al.
Reference Sun, Xi and Xia2005a
; Funfschilling & Ahlers Reference Funfschilling and Ahlers2004; Weiss & Ahlers Reference Weiss and Ahlers2011b
). Thus the positions of the up- and down-flow measured at the mid-height should be slightly different from those measured at 1cm below the top plate. Nevertheless the direct PIV measurements confirm qualitatively the flow structures of the higher-order modes suggested by the temperature measurements.
$15~\text{cm}\times 19~\text{cm}$
centred at the axis of the cylindrical cell. Previously it has been shown, from the 2-D velocity map in the horizontal plane near the top plate, that the strength and the orientation of the LSC as well as its cessation/reversal can be obtained (Xi et al.
Reference Xi, Zhou and Xia2006; Xi & Xia Reference Xi and Xia2007, Reference Xi and Xia2008a
). Here, we carefully examined the velocity maps and found that, most of the time, the measured velocity map of the flow is consistent with the first mode (figure 15
a) and when cessation/reversal occurs the higher-order Fourier modes (figure 15
b–d) take over the first mode. Figure 15 shows four instantaneous 2-D horizontal velocity maps, when the flow is dominated by the first mode (dipole mode) (a), the second mode (quadrupole mode) (b), the third mode (sextupole mode) (c) and the fourth mode (octupole mode) (d). As seen in figure 15(a), the ascending flow is from the 3 o’clock direction and the descending flow is at the 9 o’clock direction (as shown by the red and blue circles), giving rise to a coherent LSC, which is the first mode sketched in figure 2(a). The velocity map similar to figure 15(a) has previously been shown in Xi & Xia (Reference Xi and Xia2007), and is shown here for comparison with the higher-order modes. In figure 15(b) the ascending flows are from approximately the 3 o’clock and the 9 o’clock directions, and the descending flow are at the 12 o’clock and 6 o’clock directions, which is consistent with the second Fourier mode sketched in figure 2(b). Similarly we found that in figure 15(c) the ascending flows are approximately from 4 o’clock, 8 o’clock and 10.5 o’clock directions, and the descending flow are roughly at 1 o’clock, 5 o’clock and 9 o’clock directions, which is qualitatively consistent with the third Fourier mode sketched in figure 2(c). And in figure 15(d) the ascending flows are from 1.5 o’clock, 3 o’clock, 8 o’clock and 9 o’clock directions, and the descending flow are at 2.5 o’clock, 5.5 o’clock, 8.5 o’clock and 12 o’clock directions, which is qualitatively consistent with the fourth Fourier mode sketched in figure 2(d). It should be noted that the temperature measurements were done at the mid-height whereas the PIV velocity measurements were performed 1 cm below the top plate. It is well known that in the convection cell, the LSC is a tilted ellipse and is twisted (Sun, Xia & Tong Reference Sun, Xia and Tong2005b
; Sun et al.
Reference Sun, Xi and Xia2005a
; Funfschilling & Ahlers Reference Funfschilling and Ahlers2004; Weiss & Ahlers Reference Weiss and Ahlers2011b
). Thus the positions of the up- and down-flow measured at the mid-height should be slightly different from those measured at 1cm below the top plate. Nevertheless the direct PIV measurements confirm qualitatively the flow structures of the higher-order modes suggested by the temperature measurements.
4 Summary and conclusion
In this paper we have presented results from an experimental study of higher-order flow modes in turbulent RB convection. The experiments were performed in water-filled cylindrical cells with aspect ratio 1 and 0.5, with Rayleigh number ranging from
![]() $9.0\times 10^{8}$
to
$9.0\times 10^{8}$
to
![]() $6.0\times 10^{9}$
for the
$6.0\times 10^{9}$
for the
![]() $\unicode[STIX]{x1D6E4}=1$
geometry and from
$\unicode[STIX]{x1D6E4}=1$
geometry and from
![]() $1.6\times 10^{10}$
to
$1.6\times 10^{10}$
to
![]() $7.2\times 10^{10}$
for the
$7.2\times 10^{10}$
for the
![]() $\unicode[STIX]{x1D6E4}=0.5$
geometry respectively. The Prandtl number was kept at around 5.0. It is found that, in addition to the well-known large-scale single-roll flow (the first Fourier mode), the higher-order modes such as the quadrupole mode (the second Fourier mode), sextupole mode (the third Fourier mode) and the octupole mode (the forth Fourier mode) also exist. The directly measured velocity field using the PIV technique qualitatively confirms the existence of the four modes suggested by the temperature measurements. We found that, on average, the first mode contains 92.0 % and 78.7 % of the energy of the total flow for
$\unicode[STIX]{x1D6E4}=0.5$
geometry respectively. The Prandtl number was kept at around 5.0. It is found that, in addition to the well-known large-scale single-roll flow (the first Fourier mode), the higher-order modes such as the quadrupole mode (the second Fourier mode), sextupole mode (the third Fourier mode) and the octupole mode (the forth Fourier mode) also exist. The directly measured velocity field using the PIV technique qualitatively confirms the existence of the four modes suggested by the temperature measurements. We found that, on average, the first mode contains 92.0 % and 78.7 % of the energy of the total flow for
![]() $\unicode[STIX]{x1D6E4}=1$
and
$\unicode[STIX]{x1D6E4}=1$
and
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells, respectively. This finding confirms the dominance of the single-roll structure in
$\unicode[STIX]{x1D6E4}=0.5$
cells, respectively. This finding confirms the dominance of the single-roll structure in
![]() $\unicode[STIX]{x1D6E4}=1$
and
$\unicode[STIX]{x1D6E4}=1$
and
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells. In addition we found that in
$\unicode[STIX]{x1D6E4}=0.5$
cells. In addition we found that in
![]() $\unicode[STIX]{x1D6E4}=1$
cells the second, third, fourth modes are very weak and account for 3.7 %, 3.6 % and 0.7 % of the total flow energy. While in
$\unicode[STIX]{x1D6E4}=1$
cells the second, third, fourth modes are very weak and account for 3.7 %, 3.6 % and 0.7 % of the total flow energy. While in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells, the higher-order modes become stronger, especially the second mode, and their contributions to the total flow energy are respectively 13.7 % (the second mode), 6.5 % (the third mode) and 1.1 % (the fourth mode).
$\unicode[STIX]{x1D6E4}=0.5$
cells, the higher-order modes become stronger, especially the second mode, and their contributions to the total flow energy are respectively 13.7 % (the second mode), 6.5 % (the third mode) and 1.1 % (the fourth mode).
It is found that during a cessation/reversal the flow amplitude of the second mode increases, then decreases, which is opposite to the behaviour of the first mode – it decreases to almost zero then rebounds. The increase of the second mode during cessations/reversals was observed in a previous numerical simulation study (Mishra et al. Reference Mishra, De, Verma and Eswaran2011). Our result now provides the first experimental evidence. We in addition found that during a cessation/reversal, the third and the fourth modes also experience an increase and then a decrease in amplitude.
With a large number of measured cessation/reversal events in
![]() $\unicode[STIX]{x1D6E4}=0.5$
cells, we are able to obtain the statistical properties of the higher-order modes during a cessation/reversal. It is found that during a cessation/reversal, the second mode (quadrupole mode) dominates, which accounts for 51.3 % of the total flow energy, the first mode (dipole mode or the LSC), the third mode (sextupole mode) and the fourth mode (octupole) account for 21.9 %, 22.0 % and 4.8 % of the total flow energy respectively. Previously it was thought that during a cessation/reversal the fluid is totally disorganized or incoherent. Here we showed that although the LSC (first mode) ceased to exist, the flow still has some coherence, i.e. the second mode and the remaining higher-order ones become stronger and take over the large-scale flow. Thus the cessation of the LSC is not the cessation of the entire coherent large-scale flow. As a result the total energy of the flow
$\unicode[STIX]{x1D6E4}=0.5$
cells, we are able to obtain the statistical properties of the higher-order modes during a cessation/reversal. It is found that during a cessation/reversal, the second mode (quadrupole mode) dominates, which accounts for 51.3 % of the total flow energy, the first mode (dipole mode or the LSC), the third mode (sextupole mode) and the fourth mode (octupole) account for 21.9 %, 22.0 % and 4.8 % of the total flow energy respectively. Previously it was thought that during a cessation/reversal the fluid is totally disorganized or incoherent. Here we showed that although the LSC (first mode) ceased to exist, the flow still has some coherence, i.e. the second mode and the remaining higher-order ones become stronger and take over the large-scale flow. Thus the cessation of the LSC is not the cessation of the entire coherent large-scale flow. As a result the total energy of the flow
![]() $A_{total}$
usually does not drop as much as the LSC does during cessation/reversal. Our experimental results show conclusively for the first time in cylindrical convection cells the dynamical process of the cessation/reversal, i.e. the second mode and remaining higher-order modes prevail over the first mode temporarily, then the first mode dominates again. Recall that in 2-D convection cells the corner roll reconnection process of the reversal is also accompanied by the growth, dominance then weakening of the higher-order mode (four-roll mode). In this sense the reversal in 2-D case is consistent with our present findings in cylindrical cells, i.e. the higher-order modes prevail over the first mode during the reversal, although in quasi-2-D cells the higher-order mode (four-roll mode) is confined in the LSC plane and is thus two-dimensional, while in cylindrical cells, the higher-order modes are three-dimensional. To better understand the reversal phenomenon, both stochastic (Sreenivasan et al.
Reference Sreenivasan, Bershadskii and Niemela2002; Benzi Reference Benzi2005; Brown & Ahlers Reference Brown and Ahlers2007) and deterministic (Araujo et al.
Reference Araujo, Grossmann and Lohse2005) models are proposed. Those models consider either the imbalance between the buoyancy force and drag force on a single plume or the evolution of the LSC on the background of turbulence fluctuations. They indeed reproduced some statistical properties of the reversal/cessation events that are consistent with experimental observations. But the dynamical process of flow during the cessation/reversal, which is crucial for the understanding of the origin of the reversal/cessation, is not included in the models. Thus a quantitative study of the behaviour/evolution of the higher-order modes is necessary. Very recently Podvin & Sergent (Reference Podvin and Sergent2015) proposed a low-dimensional model for the 2-D case that included the dynamics of the different Fourier modes. With this information of the higher-orders modes, they successfully reproduced the main dynamics and time scales of reversals and cessations. Their study clearly demonstrates the importance of the higher-order modes. Thus, these higher-order modes should be included in future models of cessation/reversal of LSC in the 3-D case.
$A_{total}$
usually does not drop as much as the LSC does during cessation/reversal. Our experimental results show conclusively for the first time in cylindrical convection cells the dynamical process of the cessation/reversal, i.e. the second mode and remaining higher-order modes prevail over the first mode temporarily, then the first mode dominates again. Recall that in 2-D convection cells the corner roll reconnection process of the reversal is also accompanied by the growth, dominance then weakening of the higher-order mode (four-roll mode). In this sense the reversal in 2-D case is consistent with our present findings in cylindrical cells, i.e. the higher-order modes prevail over the first mode during the reversal, although in quasi-2-D cells the higher-order mode (four-roll mode) is confined in the LSC plane and is thus two-dimensional, while in cylindrical cells, the higher-order modes are three-dimensional. To better understand the reversal phenomenon, both stochastic (Sreenivasan et al.
Reference Sreenivasan, Bershadskii and Niemela2002; Benzi Reference Benzi2005; Brown & Ahlers Reference Brown and Ahlers2007) and deterministic (Araujo et al.
Reference Araujo, Grossmann and Lohse2005) models are proposed. Those models consider either the imbalance between the buoyancy force and drag force on a single plume or the evolution of the LSC on the background of turbulence fluctuations. They indeed reproduced some statistical properties of the reversal/cessation events that are consistent with experimental observations. But the dynamical process of flow during the cessation/reversal, which is crucial for the understanding of the origin of the reversal/cessation, is not included in the models. Thus a quantitative study of the behaviour/evolution of the higher-order modes is necessary. Very recently Podvin & Sergent (Reference Podvin and Sergent2015) proposed a low-dimensional model for the 2-D case that included the dynamics of the different Fourier modes. With this information of the higher-orders modes, they successfully reproduced the main dynamics and time scales of reversals and cessations. Their study clearly demonstrates the importance of the higher-order modes. Thus, these higher-order modes should be included in future models of cessation/reversal of LSC in the 3-D case.
We in addition measured simultaneously the instantaneous heat transfer efficiency (
![]() $Nu(t)$
) and amplitudes of the different modes and show directly that the first mode, which is more coherent, produces a higher heat transfer efficiency. It reveals that the global heat transfer is controlled by the internal flow states and a more coherent flow is able to transfer heat more efficiently. It is found that during cessation/reversal,
$Nu(t)$
) and amplitudes of the different modes and show directly that the first mode, which is more coherent, produces a higher heat transfer efficiency. It reveals that the global heat transfer is controlled by the internal flow states and a more coherent flow is able to transfer heat more efficiently. It is found that during cessation/reversal,
![]() $Nu$
reaches its local minimum ahead of that of
$Nu$
reaches its local minimum ahead of that of
![]() $A_{1}$
, i.e. global transport is precursor of the of changes in flow dynamics. It is also found that
$A_{1}$
, i.e. global transport is precursor of the of changes in flow dynamics. It is also found that
![]() $Nu$
has a momentary overshoot above its average value during reversal, which is not seen during cessations. This dynamically distinguishes reversals from cessations in terms of global transport. The overshoot in
$Nu$
has a momentary overshoot above its average value during reversal, which is not seen during cessations. This dynamically distinguishes reversals from cessations in terms of global transport. The overshoot in
![]() $Nu$
could be either the flow or plumes becoming more coherent for that short period of time. The exact reason for this is not known to us. Our results show that under nominally identical control parameters (
$Nu$
could be either the flow or plumes becoming more coherent for that short period of time. The exact reason for this is not known to us. Our results show that under nominally identical control parameters (
![]() $Ra$
,
$Ra$
,
![]() $Pr$
and
$Pr$
and
![]() $\unicode[STIX]{x1D6E4}$
) and boundary conditions, the turbulent flow can assume different internal states, and this may be detected by the global transport properties (here the instantaneous heat transfer efficiency (
$\unicode[STIX]{x1D6E4}$
) and boundary conditions, the turbulent flow can assume different internal states, and this may be detected by the global transport properties (here the instantaneous heat transfer efficiency (
![]() $Nu(t)$
). Although the difference in
$Nu(t)$
). Although the difference in
![]() $Nu$
when the flow is in different internal states is very small, this finding may provide a way to control heat transfer by manipulating the internal flow states. It also provides an example of how the global properties of a fluid system is directly linked to its internal flow states.
$Nu$
when the flow is in different internal states is very small, this finding may provide a way to control heat transfer by manipulating the internal flow states. It also provides an example of how the global properties of a fluid system is directly linked to its internal flow states.
Acknowledgement
We are grateful to the support by the National Natural Science Foundation of China (through grant no. 11472094), the Fundamental Research Funds for the Central Universities of China, the Research Grants Council of Hong Kong SAR (through grant no. 403712), the Peacock Plan of Shenzhen Municipal Government (through contract no. KQCX20130627094615415) and Fundamental Research Fund of Shenzhen Municipal Government (JCYJ20140417172417119).