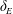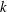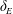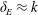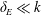1 Introduction
Rayleigh–Bénard convection (RBC), which is a representative system to study buoyancy driven flows, is the flow driven by the temperature difference,
![]() $\unicode[STIX]{x0394}T$
, between a heated horizontal plate and a parallel cooled plate a distance
$\unicode[STIX]{x0394}T$
, between a heated horizontal plate and a parallel cooled plate a distance
![]() $H$
above it. In nature, such flows invariably occur on rough boundaries, e.g. mountainous terrain for atmospheric flows and the undulating bed in the case of oceanic processes. Even in technological applications, a surface can behave as a rough wall when the boundary layer on it becomes thin at sufficiently strong buoyancy forcing. On the other hand, the effects of rotation can be prominent at geophysical scales, e.g. planetary interiors (Aurnou et al.
Reference Aurnou, Calkins, Cheng, Julien, King, Nieves, Soderlund and Stellmach2015), as well as in applications like chemical vapour deposition used to manufacture semiconductor chips. Although numerous researchers have studied the effects of rotation and of rough horizontal walls on RBC separately, leading to a better understanding of such flows, studies on the combined effects of rotation and roughness have been absent. The present work addresses this gap in our understanding by studying the impact of rough heat transfer walls on rotating RBC.
$H$
above it. In nature, such flows invariably occur on rough boundaries, e.g. mountainous terrain for atmospheric flows and the undulating bed in the case of oceanic processes. Even in technological applications, a surface can behave as a rough wall when the boundary layer on it becomes thin at sufficiently strong buoyancy forcing. On the other hand, the effects of rotation can be prominent at geophysical scales, e.g. planetary interiors (Aurnou et al.
Reference Aurnou, Calkins, Cheng, Julien, King, Nieves, Soderlund and Stellmach2015), as well as in applications like chemical vapour deposition used to manufacture semiconductor chips. Although numerous researchers have studied the effects of rotation and of rough horizontal walls on RBC separately, leading to a better understanding of such flows, studies on the combined effects of rotation and roughness have been absent. The present work addresses this gap in our understanding by studying the impact of rough heat transfer walls on rotating RBC.
The strength of the buoyancy forcing in RBC is characterized by the Rayleigh number
![]() $Ra=g\unicode[STIX]{x1D6FC}\unicode[STIX]{x0394}TH^{3}/(\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
, where
$Ra=g\unicode[STIX]{x1D6FC}\unicode[STIX]{x0394}TH^{3}/(\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
, where
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}$
and
![]() $\unicode[STIX]{x1D705}$
are the isobaric thermal expansion coefficient, kinematic viscosity and thermal diffusivity of the fluid and
$\unicode[STIX]{x1D705}$
are the isobaric thermal expansion coefficient, kinematic viscosity and thermal diffusivity of the fluid and
![]() $g$
is the gravitational acceleration. Other parameters that affect the system response are the Prandtl number
$g$
is the gravitational acceleration. Other parameters that affect the system response are the Prandtl number
![]() $Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
, the aspect ratio
$Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
, the aspect ratio
![]() $\unicode[STIX]{x1D6E4}=D/H$
and the Rossby number
$\unicode[STIX]{x1D6E4}=D/H$
and the Rossby number
![]() $Ro=\sqrt{g\unicode[STIX]{x1D6FC}\unicode[STIX]{x0394}T/H}/(2\unicode[STIX]{x1D6FA})$
, where
$Ro=\sqrt{g\unicode[STIX]{x1D6FC}\unicode[STIX]{x0394}T/H}/(2\unicode[STIX]{x1D6FA})$
, where
![]() $\unicode[STIX]{x1D6FA}$
is the angular velocity of the RBC system about an axis normal to the plates and
$\unicode[STIX]{x1D6FA}$
is the angular velocity of the RBC system about an axis normal to the plates and
![]() $D$
is the lateral dimension of the system, which, for a cylindrical geometry, is the diameter. The response of the RBC system is typically expressed in terms of the Nusselt number
$D$
is the lateral dimension of the system, which, for a cylindrical geometry, is the diameter. The response of the RBC system is typically expressed in terms of the Nusselt number
![]() $Nu=qH/(\unicode[STIX]{x0394}T\unicode[STIX]{x1D706})$
, where
$Nu=qH/(\unicode[STIX]{x0394}T\unicode[STIX]{x1D706})$
, where
![]() $q$
is the heat flux density and
$q$
is the heat flux density and
![]() $\unicode[STIX]{x1D706}$
is the thermal conductivity of the fluid. At
$\unicode[STIX]{x1D706}$
is the thermal conductivity of the fluid. At
![]() $Ra\sim 10^{9}$
and
$Ra\sim 10^{9}$
and
![]() $\unicode[STIX]{x1D6E4}=1$
, relevant to the present study, the flow in the absence of rotation is characterized by the thermal plumes emitted from the top and bottom walls. These plumes give rise to a domain-filling closed flow structure, the large-scale circulation (LSC), which in turn convects the plumes from one wall to the other (e.g. see Xi, Lam & Xia Reference Xi, Lam and Xia2004). The heat transfer in this regime is well described by the Grossmann–Lohse (GL) theory (Grossmann & Lohse Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2001, Reference Grossmann and Lohse2002), and the
$\unicode[STIX]{x1D6E4}=1$
, relevant to the present study, the flow in the absence of rotation is characterized by the thermal plumes emitted from the top and bottom walls. These plumes give rise to a domain-filling closed flow structure, the large-scale circulation (LSC), which in turn convects the plumes from one wall to the other (e.g. see Xi, Lam & Xia Reference Xi, Lam and Xia2004). The heat transfer in this regime is well described by the Grossmann–Lohse (GL) theory (Grossmann & Lohse Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2001, Reference Grossmann and Lohse2002), and the
![]() $Ra$
-dependence of
$Ra$
-dependence of
![]() $Nu$
can be approximated by
$Nu$
can be approximated by
![]() $Nu\sim Ra^{\unicode[STIX]{x1D6FE}}$
, with
$Nu\sim Ra^{\unicode[STIX]{x1D6FE}}$
, with
![]() $\unicode[STIX]{x1D6FE}\approx 0.3$
(Funfschilling et al.
Reference Funfschilling, Brown, Nikolaenko and Ahlers2005). For an overview of recent developments in RBC, see, e.g., Ahlers, Grossmann & Lohse (Reference Ahlers, Grossmann and Lohse2009).
$\unicode[STIX]{x1D6FE}\approx 0.3$
(Funfschilling et al.
Reference Funfschilling, Brown, Nikolaenko and Ahlers2005). For an overview of recent developments in RBC, see, e.g., Ahlers, Grossmann & Lohse (Reference Ahlers, Grossmann and Lohse2009).
The flow structure and
![]() $Nu$
remain largely unaffected by the Coriolis force under weak rotation, i.e. when
$Nu$
remain largely unaffected by the Coriolis force under weak rotation, i.e. when
![]() $Ro\gtrsim Ro_{c}$
(regime I). For
$Ro\gtrsim Ro_{c}$
(regime I). For
![]() $\unicode[STIX]{x1D6E4}=1$
,
$\unicode[STIX]{x1D6E4}=1$
,
![]() $Ro_{c}\approx 2.5$
(Kunnen, Clercx & Geurts Reference Kunnen, Clercx and Geurts2008; Stevens et al.
Reference Stevens, Zhong, Clercx, Ahlers and Lohse2009; Weiss et al.
Reference Weiss, Stevens, Zhong, Clercx, Lohse and Ahlers2010). For
$Ro_{c}\approx 2.5$
(Kunnen, Clercx & Geurts Reference Kunnen, Clercx and Geurts2008; Stevens et al.
Reference Stevens, Zhong, Clercx, Ahlers and Lohse2009; Weiss et al.
Reference Weiss, Stevens, Zhong, Clercx, Lohse and Ahlers2010). For
![]() $Pr\sim O(10)$
, as
$Pr\sim O(10)$
, as
![]() $Ro$
decreases below
$Ro$
decreases below
![]() $Ro_{c}$
, the LSC breaks down and the thermal plumes take the form of vertical columns of hot/cold fluid with predominantly axial vorticity emanating from the bottom/top walls. These vortical columnar plumes, which form as a result of the intensification of the cyclonic vorticity in the fluid converging into the emerging plumes, propagate deeper into the bulk flow as
$Ro_{c}$
, the LSC breaks down and the thermal plumes take the form of vertical columns of hot/cold fluid with predominantly axial vorticity emanating from the bottom/top walls. These vortical columnar plumes, which form as a result of the intensification of the cyclonic vorticity in the fluid converging into the emerging plumes, propagate deeper into the bulk flow as
![]() $Ro$
is decreased below
$Ro$
is decreased below
![]() $Ro_{c}$
(regime II), see, e.g., Kunnen, Clercx & Geurts (Reference Kunnen, Clercx and Geurts2010a
). This growth in the vertical extent of the columnar vortices is a result of the Taylor–Proudman-like phenomenon, in which axial variations in the flow are suppressed by rotation, an effect that grows stronger as
$Ro_{c}$
(regime II), see, e.g., Kunnen, Clercx & Geurts (Reference Kunnen, Clercx and Geurts2010a
). This growth in the vertical extent of the columnar vortices is a result of the Taylor–Proudman-like phenomenon, in which axial variations in the flow are suppressed by rotation, an effect that grows stronger as
![]() $Ro$
decreases. These columns draw more fluid from the Ekman boundary layers (the frictional layers on the horizontal walls in rotating flows) (Pedlosky Reference Pedlosky1987) as the radial pressure gradients associated with them are superposed on the Ekman layers. This phenomenon, commonly referred to as Ekman pumping (Rossby Reference Rossby1969; Pedlosky Reference Pedlosky1987; Vorobieff & Ecke Reference Vorobieff and Ecke2002), leads to a steady increase in
$Ro$
decreases. These columns draw more fluid from the Ekman boundary layers (the frictional layers on the horizontal walls in rotating flows) (Pedlosky Reference Pedlosky1987) as the radial pressure gradients associated with them are superposed on the Ekman layers. This phenomenon, commonly referred to as Ekman pumping (Rossby Reference Rossby1969; Pedlosky Reference Pedlosky1987; Vorobieff & Ecke Reference Vorobieff and Ecke2002), leads to a steady increase in
![]() $Nu$
until
$Nu$
until
![]() $Ro\approx 0.1$
(for
$Ro\approx 0.1$
(for
![]() $Ra\sim 10^{9}$
,
$Ra\sim 10^{9}$
,
![]() $Pr\sim 6$
and
$Pr\sim 6$
and
![]() $\unicode[STIX]{x1D6E4}=1$
, relevant to the present study), when the vortical columns span a substantial fraction of the RBC cell height. Since rotation suppresses the Rayleigh–Bénard instability (Chandrasekhar Reference Chandrasekhar1961; Rossby Reference Rossby1969), a further decrease in
$\unicode[STIX]{x1D6E4}=1$
, relevant to the present study), when the vortical columns span a substantial fraction of the RBC cell height. Since rotation suppresses the Rayleigh–Bénard instability (Chandrasekhar Reference Chandrasekhar1961; Rossby Reference Rossby1969), a further decrease in
![]() $Ro$
into regime III is characterized by a damping of the turbulence and a decrease in
$Ro$
into regime III is characterized by a damping of the turbulence and a decrease in
![]() $Nu$
(Rossby Reference Rossby1969; Kunnen, Clercx & Geurts Reference Kunnen, Clercx and Geurts2006; King et al.
Reference King, Stellmach, Noir, Hansen and Aurnou2009; Stevens et al.
Reference Stevens, Zhong, Clercx, Ahlers and Lohse2009; Kunnen, Geurts & Clercx Reference Kunnen, Geurts and Clercx2010b
; Julien et al.
Reference Julien, Knobloch, Rubio and Vasil2012; Cheng et al.
Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015).
$Nu$
(Rossby Reference Rossby1969; Kunnen, Clercx & Geurts Reference Kunnen, Clercx and Geurts2006; King et al.
Reference King, Stellmach, Noir, Hansen and Aurnou2009; Stevens et al.
Reference Stevens, Zhong, Clercx, Ahlers and Lohse2009; Kunnen, Geurts & Clercx Reference Kunnen, Geurts and Clercx2010b
; Julien et al.
Reference Julien, Knobloch, Rubio and Vasil2012; Cheng et al.
Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015).
The impact of the wall roughness on the heat transfer in non-rotating RBC is largely determined by the height of the roughness elements,
![]() $k$
, in relation to the thermal and viscous boundary layer thicknesses,
$k$
, in relation to the thermal and viscous boundary layer thicknesses,
![]() $\unicode[STIX]{x1D6FF}_{T}$
and
$\unicode[STIX]{x1D6FF}_{T}$
and
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
respectively. However, most previous studies of convection over rough walls have been performed for
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
respectively. However, most previous studies of convection over rough walls have been performed for
![]() $Pr\sim O(1{-}10)$
, for which
$Pr\sim O(1{-}10)$
, for which
![]() $\unicode[STIX]{x1D6FF}_{T}$
and
$\unicode[STIX]{x1D6FF}_{T}$
and
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
are of the same order. Perhaps hence, these studies have mostly focused on the interaction of the roughness with the thermal boundary layer, the mean thickness of which is easily estimated as
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
are of the same order. Perhaps hence, these studies have mostly focused on the interaction of the roughness with the thermal boundary layer, the mean thickness of which is easily estimated as
![]() $\unicode[STIX]{x1D6FF}_{T}\approx H/2Nu$
. Below a critical
$\unicode[STIX]{x1D6FF}_{T}\approx H/2Nu$
. Below a critical
![]() $Ra$
, the thermal boundary layer is thicker than
$Ra$
, the thermal boundary layer is thicker than
![]() $k$
, and
$k$
, and
![]() $Nu$
for the rough surface,
$Nu$
for the rough surface,
![]() $Nu_{R}$
, is similar to that for a smooth wall,
$Nu_{R}$
, is similar to that for a smooth wall,
![]() $Nu_{S}$
. As shown by Tisserand et al. (Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chilla2011),
$Nu_{S}$
. As shown by Tisserand et al. (Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chilla2011),
![]() $Nu_{R}$
can also be slightly lower than
$Nu_{R}$
can also be slightly lower than
![]() $Nu_{S}$
as the fluid inside the troughs of the roughness is near-stagnant, which results in a locally thick thermal boundary layer. As
$Nu_{S}$
as the fluid inside the troughs of the roughness is near-stagnant, which results in a locally thick thermal boundary layer. As
![]() $Ra$
increases and
$Ra$
increases and
![]() $\unicode[STIX]{x1D6FF}_{T}$
becomes smaller than
$\unicode[STIX]{x1D6FF}_{T}$
becomes smaller than
![]() $k$
, the roughness elements protrude out of the thermal boundary layer and increase the emission of plumes (Du & Tong Reference Du and Tong2000; Stringano, Pascazio & Verzicco Reference Stringano, Pascazio and Verzicco2006), and thus the heat transfer in comparison with smooth walls. For large
$k$
, the roughness elements protrude out of the thermal boundary layer and increase the emission of plumes (Du & Tong Reference Du and Tong2000; Stringano, Pascazio & Verzicco Reference Stringano, Pascazio and Verzicco2006), and thus the heat transfer in comparison with smooth walls. For large
![]() $Pr$
(
$Pr$
(
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}\gg \unicode[STIX]{x1D6FF}_{T}$
), Xie & Xia (Reference Xie and Xia2017) show that
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}\gg \unicode[STIX]{x1D6FF}_{T}$
), Xie & Xia (Reference Xie and Xia2017) show that
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
also becomes smaller than
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
also becomes smaller than
![]() $k$
at sufficiently high
$k$
at sufficiently high
![]() $Ra$
, and thus both the thermal and the viscous boundary layers are strongly perturbed by the rough wall.
$Ra$
, and thus both the thermal and the viscous boundary layers are strongly perturbed by the rough wall.
Although there exists a consensus on the effect of roughness on the magnitude of
![]() $Nu$
, its effect on
$Nu$
, its effect on
![]() $\unicode[STIX]{x1D6FE}$
seems to be unclear. Some early studies (Shen, Tong & Xia Reference Shen, Tong and Xia1996; Du & Tong Reference Du and Tong1998; Ciliberto & Laroche Reference Ciliberto and Laroche1999) report no change in
$\unicode[STIX]{x1D6FE}$
seems to be unclear. Some early studies (Shen, Tong & Xia Reference Shen, Tong and Xia1996; Du & Tong Reference Du and Tong1998; Ciliberto & Laroche Reference Ciliberto and Laroche1999) report no change in
![]() $\unicode[STIX]{x1D6FE}$
from its value for smooth plates when
$\unicode[STIX]{x1D6FE}$
from its value for smooth plates when
![]() $\unicode[STIX]{x1D6FF}_{T}<k$
, although
$\unicode[STIX]{x1D6FF}_{T}<k$
, although
![]() $Nu_{R}$
can be larger than
$Nu_{R}$
can be larger than
![]() $Nu_{S}$
by up to 80 %. However, later studies, e.g. Qiu, Xia & Tong (Reference Qiu, Xia and Tong2005) and Stringano et al. (Reference Stringano, Pascazio and Verzicco2006), have measured
$Nu_{S}$
by up to 80 %. However, later studies, e.g. Qiu, Xia & Tong (Reference Qiu, Xia and Tong2005) and Stringano et al. (Reference Stringano, Pascazio and Verzicco2006), have measured
![]() $\unicode[STIX]{x1D6FE}$
in the range 0.35–0.37. They ascribe the lower
$\unicode[STIX]{x1D6FE}$
in the range 0.35–0.37. They ascribe the lower
![]() $\unicode[STIX]{x1D6FE}$
observed in the earlier studies to the poor thermal diffusivity of the plate material (brass) used in them, which exacerbates the inherently non-isothermal character of a rough plate in an experiment. However, calculating
$\unicode[STIX]{x1D6FE}$
observed in the earlier studies to the poor thermal diffusivity of the plate material (brass) used in them, which exacerbates the inherently non-isothermal character of a rough plate in an experiment. However, calculating
![]() $Nu$
for individual plates at
$Nu$
for individual plates at
![]() $Ra\sim O(10^{12})$
, Tisserand et al. (Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chilla2011) measure
$Ra\sim O(10^{12})$
, Tisserand et al. (Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chilla2011) measure
![]() $\unicode[STIX]{x1D6FE}$
as high as 0.5 for a rough aluminium plate, which has thermal properties poorer than those of a similar copper plate. The Nusselt number for an individual plate is calculated as
$\unicode[STIX]{x1D6FE}$
as high as 0.5 for a rough aluminium plate, which has thermal properties poorer than those of a similar copper plate. The Nusselt number for an individual plate is calculated as
![]() $Nu_{p}=qH/(2|T_{p}-T_{c}|\unicode[STIX]{x1D706})$
(Tisserand et al.
Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chilla2011; Wei et al.
Reference Wei, Chan, Ni, Zhao and Xia2014), where
$Nu_{p}=qH/(2|T_{p}-T_{c}|\unicode[STIX]{x1D706})$
(Tisserand et al.
Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castaing and Chilla2011; Wei et al.
Reference Wei, Chan, Ni, Zhao and Xia2014), where
![]() $T_{p}$
and
$T_{p}$
and
![]() $T_{c}$
are the temperatures of the plate and the RBC cell centre respectively. Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014) find that, based on the boundary conditions, i.e. constant temperature or constant heat flux, and the nature of the opposite plate,
$T_{c}$
are the temperatures of the plate and the RBC cell centre respectively. Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014) find that, based on the boundary conditions, i.e. constant temperature or constant heat flux, and the nature of the opposite plate,
![]() $\unicode[STIX]{x1D6FE}$
for a rough plate can vary between 0.29 and 0.39. However, with both plates rough, they observe
$\unicode[STIX]{x1D6FE}$
for a rough plate can vary between 0.29 and 0.39. However, with both plates rough, they observe
![]() $\unicode[STIX]{x1D6FE}=0.35$
for the global
$\unicode[STIX]{x1D6FE}=0.35$
for the global
![]() $Nu$
. Xie & Xia (Reference Xie and Xia2017) show that
$Nu$
. Xie & Xia (Reference Xie and Xia2017) show that
![]() $\unicode[STIX]{x1D6FE}$
is higher in the regime
$\unicode[STIX]{x1D6FE}$
is higher in the regime
![]() $\unicode[STIX]{x1D6FF}_{T}<k<\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
than in the regime
$\unicode[STIX]{x1D6FF}_{T}<k<\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
than in the regime
![]() $k>\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
and, in qualitative agreement with the 2D simulations of Toppaladoddi, Succi & Wettlaufer (Reference Toppaladoddi, Succi and Wettlaufer2017), that
$k>\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
and, in qualitative agreement with the 2D simulations of Toppaladoddi, Succi & Wettlaufer (Reference Toppaladoddi, Succi and Wettlaufer2017), that
![]() $\unicode[STIX]{x1D6FE}$
also depends on the aspect ratio of the roughness elements.
$\unicode[STIX]{x1D6FE}$
also depends on the aspect ratio of the roughness elements.
The columnar vortices, which are presumed to be responsible for increasing the heat transfer under rotation, are intricately linked with the dynamics of the Ekman boundary layer on the horizontal surfaces. Since roughness modifies the boundary layer structure in non-rotating convection, some natural questions to ask are whether and how it affects the Ekman vortices under rotation. Although there have been prior investigations studying geostrophic turbulence (LaCasce & Brink Reference LaCasce and Brink2000) and stratified Ekman layers (see, e.g., Garrett, MacCready & Rhines Reference Garrett, MacCready and Rhines1993) on sloping boundaries, the impact of roughness on the Ekman layer and the Ekman pumping mechanism in the context of rotating natural convection has not been explored. The interaction of the effects of rotation and roughness can be important in geophysical flows. Even in technological applications, roughness effects can become relevant as the Ekman boundary layer becomes thin under strong rotation. In this study, we introduce pyramid-shaped roughness elements on the top and/or bottom walls and measure the heat transfer as a function of the rotation rate. In the next section, we describe the experimental apparatus and measurement procedures. In §§ 3 and 4, we present the results and show that, depending on the size of the roughness elements relative to the Ekman boundary layer thickness, rotation can either enhance or suppress the heat transfer in relation to that under non-rotating conditions.
2 Experimental set-up and measurement procedures
Figure 1 shows a schematic of the
![]() $\unicode[STIX]{x1D6E4}\approx 1$
cylindrical Rayleigh–Bénard cell used in this study. Only the important features of this cell are described here. For details see Kunnen et al. (Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011) and Joshi et al. (Reference Joshi, Rajaei, Kunnen and Clercx2016). The heat transfer plates with
$\unicode[STIX]{x1D6E4}\approx 1$
cylindrical Rayleigh–Bénard cell used in this study. Only the important features of this cell are described here. For details see Kunnen et al. (Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011) and Joshi et al. (Reference Joshi, Rajaei, Kunnen and Clercx2016). The heat transfer plates with
![]() $D=250$
mm are made out of solid copper blocks. Triangular grooves are machined on the surfaces of these plates, producing a square array of pyramids with height
$D=250$
mm are made out of solid copper blocks. Triangular grooves are machined on the surfaces of these plates, producing a square array of pyramids with height
![]() $k$
and a square base of side
$k$
and a square base of side
![]() $2k$
(see figure 1
b). The plates are 30 mm thick (at the base of the pyramids for rough plates). Two roughness sizes,
$2k$
(see figure 1
b). The plates are 30 mm thick (at the base of the pyramids for rough plates). Two roughness sizes,
![]() $k=1.5$
mm and 8 mm, have been used. The equivalent location of the rough surface is fixed at the mid-height of the pyramids, determining the effective height
$k=1.5$
mm and 8 mm, have been used. The equivalent location of the rough surface is fixed at the mid-height of the pyramids, determining the effective height
![]() $H_{eff}$
and the effective aspect ratio
$H_{eff}$
and the effective aspect ratio
![]() $\unicode[STIX]{x1D6E4}_{eff}$
of the RBC cell in each case. Table 1 lists the five combinations of the rough and smooth plates used, as well as
$\unicode[STIX]{x1D6E4}_{eff}$
of the RBC cell in each case. Table 1 lists the five combinations of the rough and smooth plates used, as well as
![]() $H_{eff}$
and
$H_{eff}$
and
![]() $\unicode[STIX]{x1D6E4}_{eff}$
for each case. Water is used as the working fluid. Heat is supplied to the bottom plates using ohmic heating and the top plates are cooled by recirculating water through them. A constant-temperature boundary condition is imposed at both the top and bottom plates, with temperatures
$\unicode[STIX]{x1D6E4}_{eff}$
for each case. Water is used as the working fluid. Heat is supplied to the bottom plates using ohmic heating and the top plates are cooled by recirculating water through them. A constant-temperature boundary condition is imposed at both the top and bottom plates, with temperatures
![]() $T_{t}$
and
$T_{t}$
and
![]() $T_{b}$
respectively. Five thermistors are provided in each of the plates, 0.7 mm from the wetted surface for the smooth plates and 1.0 mm from the base of the pyramids for the rough plates. The thermistors are calibrated with logarithmic polynomial fits and measure the temperature with an accuracy of
$T_{b}$
respectively. Five thermistors are provided in each of the plates, 0.7 mm from the wetted surface for the smooth plates and 1.0 mm from the base of the pyramids for the rough plates. The thermistors are calibrated with logarithmic polynomial fits and measure the temperature with an accuracy of
![]() $\pm 0.01\,^{\circ }\text{C}$
. The RBC cell is mounted on a table, the rotation rate of which can be controlled from
$\pm 0.01\,^{\circ }\text{C}$
. The RBC cell is mounted on a table, the rotation rate of which can be controlled from
![]() $\unicode[STIX]{x1D6FA}=0$
to
$\unicode[STIX]{x1D6FA}=0$
to
![]() $10~\text{rad}~\text{s}^{-1}$
with a resolution of
$10~\text{rad}~\text{s}^{-1}$
with a resolution of
![]() $0.001~\text{rad}~\text{s}^{-1}$
and a relative accuracy of 0.5 %. The maximum rotation rate used in the present study is
$0.001~\text{rad}~\text{s}^{-1}$
and a relative accuracy of 0.5 %. The maximum rotation rate used in the present study is
![]() $\unicode[STIX]{x1D6FA}=2.5~\text{rad}~\text{s}^{-1}$
, yielding a Froude number of
$\unicode[STIX]{x1D6FA}=2.5~\text{rad}~\text{s}^{-1}$
, yielding a Froude number of
![]() $Fr=\unicode[STIX]{x1D6FA}^{2}(D/2)/g=0.079$
, i.e. centrifugal effects are minor. For more details on the experimental set-up, we refer the reader to Kunnen et al. (Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011).
$Fr=\unicode[STIX]{x1D6FA}^{2}(D/2)/g=0.079$
, i.e. centrifugal effects are minor. For more details on the experimental set-up, we refer the reader to Kunnen et al. (Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011).

Figure 1. (a) Schematic of the experimental set-up: SW, cylindrical Plexiglass sidewall; CP, top and bottom copper plates; RH, heating resistors fitted into the bottom copper plate; CW, cooling water recirculating through the top copper plate; ABT, air-bleed tube which is connected to an overhead flask; SH, secondary heaters; AS, aluminium adiabatic shields; IS, insulating shields; TS, temperature sensors. The figure is not to scale. (b) Details of the roughness geometry. The figure shows the top rough plate with
![]() $k=8$
mm.
$k=8$
mm.

Figure 2. Variation of (a)
![]() $Nu$
with
$Nu$
with
![]() $Ra$
for
$Ra$
for
![]() $Ro=\infty$
, (b)
$Ro=\infty$
, (b)
![]() $Nu$
with
$Nu$
with
![]() $Ro$
and (c)
$Ro$
and (c)
![]() $Nu/Nu(Ro=\infty )$
with
$Nu/Nu(Ro=\infty )$
with
![]() $Ro$
for all
$Ro$
for all
![]() $k$
at
$k$
at
![]() $Ra=2.2\times 10^{9}$
. The nomenclature of the plate combinations is given in table 1. In (a), the straight lines represent the power law fits to the data, which result in different values of the exponent
$Ra=2.2\times 10^{9}$
. The nomenclature of the plate combinations is given in table 1. In (a), the straight lines represent the power law fits to the data, which result in different values of the exponent
![]() $\unicode[STIX]{x1D6FE}$
: dashed-dotted blue line, SS,
$\unicode[STIX]{x1D6FE}$
: dashed-dotted blue line, SS,
![]() $\unicode[STIX]{x1D6FE}=0.298$
; solid magenta line, R2S,
$\unicode[STIX]{x1D6FE}=0.298$
; solid magenta line, R2S,
![]() $\unicode[STIX]{x1D6FE}=0.297$
; solid black line, R2R2,
$\unicode[STIX]{x1D6FE}=0.297$
; solid black line, R2R2,
![]() $\unicode[STIX]{x1D6FE}=0.330$
; solid red line, R8S,
$\unicode[STIX]{x1D6FE}=0.330$
; solid red line, R8S,
![]() $\unicode[STIX]{x1D6FE}=0.302$
; solid blue line, R8R8,
$\unicode[STIX]{x1D6FE}=0.302$
; solid blue line, R8R8,
![]() $\unicode[STIX]{x1D6FE}=0.369$
.
$\unicode[STIX]{x1D6FE}=0.369$
.
Table 1. The combinations of rough and smooth plates used in the present study. The nomenclature of the various cases uses S for smooth, R for rough and a number denoting the height of the roughness element,
![]() $k$
. For example, R8S denotes an experiment using a rough top plate with
$k$
. For example, R8S denotes an experiment using a rough top plate with
![]() $k=8$
mm and a smooth bottom plate. The values of
$k=8$
mm and a smooth bottom plate. The values of
![]() $\unicode[STIX]{x1D6FE}$
in the relation
$\unicode[STIX]{x1D6FE}$
in the relation
![]() $Nu\sim Ra^{\unicode[STIX]{x1D6FE}}$
are estimated using least-squares fits to the data. The uncertainty in
$Nu\sim Ra^{\unicode[STIX]{x1D6FE}}$
are estimated using least-squares fits to the data. The uncertainty in
![]() $\unicode[STIX]{x1D6FE}$
is expressed as
$\unicode[STIX]{x1D6FE}$
is expressed as
![]() $\unicode[STIX]{x1D6FE}\pm 2\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$
, where
$\unicode[STIX]{x1D6FE}\pm 2\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$
, where
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$
is the standard error in the estimate of
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}$
is the standard error in the estimate of
![]() $\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D6FE}$
,
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{2}=(s_{\unicode[STIX]{x1D719}\unicode[STIX]{x1D719}}s_{\unicode[STIX]{x1D713}\unicode[STIX]{x1D713}}-s_{\unicode[STIX]{x1D719}\unicode[STIX]{x1D713}}^{2})/[(n-2)s_{\unicode[STIX]{x1D719}\unicode[STIX]{x1D719}}^{2}]$
,
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FE}}^{2}=(s_{\unicode[STIX]{x1D719}\unicode[STIX]{x1D719}}s_{\unicode[STIX]{x1D713}\unicode[STIX]{x1D713}}-s_{\unicode[STIX]{x1D719}\unicode[STIX]{x1D713}}^{2})/[(n-2)s_{\unicode[STIX]{x1D719}\unicode[STIX]{x1D719}}^{2}]$
,
![]() $n$
is the number of data points
$n$
is the number of data points
![]() $(Ra,Nu)$
used for the linear regression,
$(Ra,Nu)$
used for the linear regression,
![]() $\unicode[STIX]{x1D719}=\ln (Ra)$
,
$\unicode[STIX]{x1D719}=\ln (Ra)$
,
![]() $\unicode[STIX]{x1D713}=\ln (Nu)$
and
$\unicode[STIX]{x1D713}=\ln (Nu)$
and
![]() $s_{\unicode[STIX]{x1D719}\unicode[STIX]{x1D713}}=\sum _{i=1}^{n}(\unicode[STIX]{x1D719}_{i}-\bar{\unicode[STIX]{x1D719}})(\unicode[STIX]{x1D713}_{i}-\bar{\unicode[STIX]{x1D713}})$
is the covariance of
$s_{\unicode[STIX]{x1D719}\unicode[STIX]{x1D713}}=\sum _{i=1}^{n}(\unicode[STIX]{x1D719}_{i}-\bar{\unicode[STIX]{x1D719}})(\unicode[STIX]{x1D713}_{i}-\bar{\unicode[STIX]{x1D713}})$
is the covariance of
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D713}$
(Acton Reference Acton1966). An overbar denotes the sample mean for a data set.
$\unicode[STIX]{x1D713}$
(Acton Reference Acton1966). An overbar denotes the sample mean for a data set.

Data recorded at a sampling frequency of 1 Hz under steady state for longer than 6 h are used to calculate the mean quantities. The temperatures measured by the five sensors in the top (bottom) plate are averaged to calculate
![]() $T_{t}$
(
$T_{t}$
(
![]() $T_{b}$
). Fluid properties are evaluated at
$T_{b}$
). Fluid properties are evaluated at
![]() $T_{mean}=(T_{t}+T_{b})/2=24.2\pm 0.3\,^{\circ }\text{C}$
(
$T_{mean}=(T_{t}+T_{b})/2=24.2\pm 0.3\,^{\circ }\text{C}$
(
![]() $Pr=6.2$
). Heat lost from the bottom plate to the surroundings, which is less than 4 % of the input heat flux
$Pr=6.2$
). Heat lost from the bottom plate to the surroundings, which is less than 4 % of the input heat flux
![]() $Q_{I}$
at
$Q_{I}$
at
![]() $Ra=3\times 10^{8}$
and decreases to 0.2 % of
$Ra=3\times 10^{8}$
and decreases to 0.2 % of
![]() $Q_{I}$
at
$Q_{I}$
at
![]() $Ra=4.5\times 10^{9}$
, is subtracted from
$Ra=4.5\times 10^{9}$
, is subtracted from
![]() $Q_{I}$
to obtain the net heat flux density
$Q_{I}$
to obtain the net heat flux density
![]() $q$
.
$q$
.
3 Results
3.1 Effect of rough plates on heat transfer without rotation
Figure 2(a) shows the variation of
![]() $Nu$
with
$Nu$
with
![]() $Ra$
. The length of the error bars in figure 2 represents
$Ra$
. The length of the error bars in figure 2 represents
![]() $4\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D719}}$
, where
$4\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D719}}$
, where
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D719}}/\sqrt{(t_{0}/\unicode[STIX]{x1D70F}_{0})}$
is the standard error of the mean value
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D719}}/\sqrt{(t_{0}/\unicode[STIX]{x1D70F}_{0})}$
is the standard error of the mean value
![]() $\langle \unicode[STIX]{x1D719}\rangle$
of the concerned variable
$\langle \unicode[STIX]{x1D719}\rangle$
of the concerned variable
![]() $\unicode[STIX]{x1D719}$
. Here,
$\unicode[STIX]{x1D719}$
. Here,
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D719}}$
is the standard deviation of
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D719}}$
is the standard deviation of
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
![]() $t_{0}$
is the length of the time series for
$t_{0}$
is the length of the time series for
![]() $\unicode[STIX]{x1D719}(t)$
used to calculate
$\unicode[STIX]{x1D719}(t)$
used to calculate
![]() $\langle \unicode[STIX]{x1D719}\rangle$
,
$\langle \unicode[STIX]{x1D719}\rangle$
,
![]() $t$
is time and
$t$
is time and
![]() $\unicode[STIX]{x1D70F}_{0}$
is the time interval for the temporal autocorrelation of
$\unicode[STIX]{x1D70F}_{0}$
is the time interval for the temporal autocorrelation of
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
![]() $C_{\unicode[STIX]{x1D719}}(\unicode[STIX]{x1D70F})=\langle \unicode[STIX]{x1D719}(t)\unicode[STIX]{x1D719}(t+\unicode[STIX]{x1D70F})\rangle /\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D719}}^{2}$
, to decay to
$C_{\unicode[STIX]{x1D719}}(\unicode[STIX]{x1D70F})=\langle \unicode[STIX]{x1D719}(t)\unicode[STIX]{x1D719}(t+\unicode[STIX]{x1D70F})\rangle /\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D719}}^{2}$
, to decay to
![]() $1/e$
. It should be noted that in many cases the error bars are smaller than the size of the symbols.
$1/e$
. It should be noted that in many cases the error bars are smaller than the size of the symbols.
In the following discussion, different plate combinations are indicated by the corresponding subscripts to the variable (for the nomenclature, see table 1 and the caption). It should be noted that the
![]() $Ra$
range for the case SS,
$Ra$
range for the case SS,
![]() $6\times 10^{8}{-}9\times 10^{9}$
, is different from that for all the cases with rough plates, approximately
$6\times 10^{8}{-}9\times 10^{9}$
, is different from that for all the cases with rough plates, approximately
![]() $3\times 10^{8}{-}4.5\times 10^{9}$
. A least-squares fit to the data for the case SS yields
$3\times 10^{8}{-}4.5\times 10^{9}$
. A least-squares fit to the data for the case SS yields
![]() $\unicode[STIX]{x1D6FE}_{SS}=0.3$
. Both
$\unicode[STIX]{x1D6FE}_{SS}=0.3$
. Both
![]() $\unicode[STIX]{x1D6FE}_{SS}$
and
$\unicode[STIX]{x1D6FE}_{SS}$
and
![]() $Nu_{SS}$
agree well with those reported in earlier studies using smooth plates (e.g. Funfschilling et al.
Reference Funfschilling, Brown, Nikolaenko and Ahlers2005). The Nusselt number and
$Nu_{SS}$
agree well with those reported in earlier studies using smooth plates (e.g. Funfschilling et al.
Reference Funfschilling, Brown, Nikolaenko and Ahlers2005). The Nusselt number and
![]() $\unicode[STIX]{x1D6FE}$
for the case R2S are indistinguishable from those for the case SS. However, when both plates are rough,
$\unicode[STIX]{x1D6FE}$
for the case R2S are indistinguishable from those for the case SS. However, when both plates are rough,
![]() $Nu_{R2R2}$
shows slight deviations (less than 5 %) from
$Nu_{R2R2}$
shows slight deviations (less than 5 %) from
![]() $Nu_{SS}$
. The exponent
$Nu_{SS}$
. The exponent
![]() $\unicode[STIX]{x1D6FE}_{R2R2}$
is also higher, 0.33. For the cases R2S and R2R2,
$\unicode[STIX]{x1D6FE}_{R2R2}$
is also higher, 0.33. For the cases R2S and R2R2,
![]() $\unicode[STIX]{x1D6FF}_{T}\approx H/2Nu$
decreases from approximately 2.9 mm at
$\unicode[STIX]{x1D6FF}_{T}\approx H/2Nu$
decreases from approximately 2.9 mm at
![]() $Ra=2.9\times 10^{8}$
to 1.2 mm at
$Ra=2.9\times 10^{8}$
to 1.2 mm at
![]() $Ra=4.5\times 10^{9}$
. Although
$Ra=4.5\times 10^{9}$
. Although
![]() $\unicode[STIX]{x1D6FF}_{T}<k$
at the highest
$\unicode[STIX]{x1D6FF}_{T}<k$
at the highest
![]() $Ra$
, we do not observe any substantial increase in
$Ra$
, we do not observe any substantial increase in
![]() $Nu$
(less than 5 % for the case R2R2) above the case SS, perhaps because
$Nu$
(less than 5 % for the case R2R2) above the case SS, perhaps because
![]() $\unicode[STIX]{x1D6FF}_{T}$
is still only slightly smaller than
$\unicode[STIX]{x1D6FF}_{T}$
is still only slightly smaller than
![]() $k$
. Indeed, previous data with symmetrical RBC cells, e.g. from Shen et al. (Reference Shen, Tong and Xia1996), Stringano et al. (Reference Stringano, Pascazio and Verzicco2006) and Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014), appear to indicate that the increased heat transfer is manifested only when
$k$
. Indeed, previous data with symmetrical RBC cells, e.g. from Shen et al. (Reference Shen, Tong and Xia1996), Stringano et al. (Reference Stringano, Pascazio and Verzicco2006) and Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014), appear to indicate that the increased heat transfer is manifested only when
![]() $\unicode[STIX]{x1D6FF}_{T}$
becomes smaller than approximately
$\unicode[STIX]{x1D6FF}_{T}$
becomes smaller than approximately
![]() $2k/3$
.
$2k/3$
.
For the cases R8S and R8R8, the thermal boundary layer thickness is always significantly smaller (
![]() $\unicode[STIX]{x1D6FF}_{T}<2.2$
mm) than the height of the pyramid-like structures (
$\unicode[STIX]{x1D6FF}_{T}<2.2$
mm) than the height of the pyramid-like structures (
![]() $k=8$
mm). As a result,
$k=8$
mm). As a result,
![]() $Nu$
for these cases is substantially higher than that for the case SS. As expected, the heat transfer when both plates are rough (R8R8) is higher than that with only one rough plate (R8S). At
$Nu$
for these cases is substantially higher than that for the case SS. As expected, the heat transfer when both plates are rough (R8R8) is higher than that with only one rough plate (R8S). At
![]() $Ra=4.1\times 10^{9}$
,
$Ra=4.1\times 10^{9}$
,
![]() $Nu$
for the cases R8S and R8R8 is approximately 26 % (
$Nu$
for the cases R8S and R8R8 is approximately 26 % (
![]() $k/\unicode[STIX]{x1D6FF}_{T}\approx 8$
) and 80 % (
$k/\unicode[STIX]{x1D6FF}_{T}\approx 8$
) and 80 % (
![]() $k/\unicode[STIX]{x1D6FF}_{T}\approx 11$
) higher respectively than that for the case SS. The latter increase is comparable to the 76 % reported by Du & Tong (Reference Du and Tong1998) for pyramidal roughness elements at similar
$k/\unicode[STIX]{x1D6FF}_{T}\approx 11$
) higher respectively than that for the case SS. The latter increase is comparable to the 76 % reported by Du & Tong (Reference Du and Tong1998) for pyramidal roughness elements at similar
![]() $Ra$
(their data suggest
$Ra$
(their data suggest
![]() $k/\unicode[STIX]{x1D6FF}_{T}\approx 9$
). However, unlike their exponent, which maintains the same value as for the smooth case, we observe
$k/\unicode[STIX]{x1D6FF}_{T}\approx 9$
). However, unlike their exponent, which maintains the same value as for the smooth case, we observe
![]() $\unicode[STIX]{x1D6FE}_{R8R8}\approx 0.37$
. This value is close to
$\unicode[STIX]{x1D6FE}_{R8R8}\approx 0.37$
. This value is close to
![]() $\unicode[STIX]{x1D6FE}=0.35$
measured for pyramidal roughness by Qiu et al. (Reference Qiu, Xia and Tong2005) (
$\unicode[STIX]{x1D6FE}=0.35$
measured for pyramidal roughness by Qiu et al. (Reference Qiu, Xia and Tong2005) (
![]() $k/\unicode[STIX]{x1D6FF}_{T}\approx 1{-}16$
) and Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014) (
$k/\unicode[STIX]{x1D6FF}_{T}\approx 1{-}16$
) and Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014) (
![]() $k/\unicode[STIX]{x1D6FF}_{T}\approx 0.8{-}2.5$
), and agrees with
$k/\unicode[STIX]{x1D6FF}_{T}\approx 0.8{-}2.5$
), and agrees with
![]() $\unicode[STIX]{x1D6FE}=0.37$
obtained by Stringano et al. (Reference Stringano, Pascazio and Verzicco2006) from their direct numerical simulations (DNS) with axisymmetric grooves (
$\unicode[STIX]{x1D6FE}=0.37$
obtained by Stringano et al. (Reference Stringano, Pascazio and Verzicco2006) from their direct numerical simulations (DNS) with axisymmetric grooves (
![]() $k/\unicode[STIX]{x1D6FF}_{T}\approx 2{-}31$
). Stringano et al. (Reference Stringano, Pascazio and Verzicco2006) suggest that the lower exponent in Du & Tong (Reference Du and Tong1998) is the result of an interplay between the enhanced emission of plumes due to the roughness and the decrease in heat transfer due to the non-ideal brass plates. It is also clear from the above comparison that
$k/\unicode[STIX]{x1D6FF}_{T}\approx 2{-}31$
). Stringano et al. (Reference Stringano, Pascazio and Verzicco2006) suggest that the lower exponent in Du & Tong (Reference Du and Tong1998) is the result of an interplay between the enhanced emission of plumes due to the roughness and the decrease in heat transfer due to the non-ideal brass plates. It is also clear from the above comparison that
![]() $\unicode[STIX]{x1D6FE}$
is independent of
$\unicode[STIX]{x1D6FE}$
is independent of
![]() $k/\unicode[STIX]{x1D6FF}_{T}$
. It should be noted that
$k/\unicode[STIX]{x1D6FF}_{T}$
. It should be noted that
![]() $\unicode[STIX]{x1D6FE}_{R8S}$
(figure 2
a and table 1) is indistinguishable from
$\unicode[STIX]{x1D6FE}_{R8S}$
(figure 2
a and table 1) is indistinguishable from
![]() $\unicode[STIX]{x1D6FE}_{SS}=0.30$
, in line with the observations of Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014) for a similar asymmetric configuration.
$\unicode[STIX]{x1D6FE}_{SS}=0.30$
, in line with the observations of Wei et al. (Reference Wei, Chan, Ni, Zhao and Xia2014) for a similar asymmetric configuration.
To summarize the above discussion, in line with previous studies for
![]() $Pr\gtrsim 1$
, we observe no enhancement in the heat transfer when
$Pr\gtrsim 1$
, we observe no enhancement in the heat transfer when
![]() $\unicode[STIX]{x1D6FF}_{T}\gtrsim k$
. However, for
$\unicode[STIX]{x1D6FF}_{T}\gtrsim k$
. However, for
![]() $\unicode[STIX]{x1D6FF}_{T}$
smaller than
$\unicode[STIX]{x1D6FF}_{T}$
smaller than
![]() $k/4$
, a significant increase in
$k/4$
, a significant increase in
![]() $Nu$
is observed. The heat transfer enhancement with a doubly rough RBC cell is larger than that with an asymmetric cell. Although roughness increases
$Nu$
is observed. The heat transfer enhancement with a doubly rough RBC cell is larger than that with an asymmetric cell. Although roughness increases
![]() $Nu$
for sufficiently large
$Nu$
for sufficiently large
![]() $k/\unicode[STIX]{x1D6FF}_{T}$
,
$k/\unicode[STIX]{x1D6FF}_{T}$
,
![]() $\unicode[STIX]{x1D6FE}$
for the asymmetric cell is indistinguishable from that for the smooth cell, and only shows an increase when both walls are rough. For the present data,
$\unicode[STIX]{x1D6FE}$
for the asymmetric cell is indistinguishable from that for the smooth cell, and only shows an increase when both walls are rough. For the present data,
![]() $\unicode[STIX]{x1D6FE}$
is higher for larger
$\unicode[STIX]{x1D6FE}$
is higher for larger
![]() $k$
. This difference, however, may be a result of different
$k$
. This difference, however, may be a result of different
![]() $k/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
for the cases R2R2 and R8R8. According to the GL theory (Grossmann & Lohse Reference Grossmann and Lohse2001; Stevens et al.
Reference Stevens, van der Poel, Grossmann and Lohse2013b
), for
$k/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
for the cases R2R2 and R8R8. According to the GL theory (Grossmann & Lohse Reference Grossmann and Lohse2001; Stevens et al.
Reference Stevens, van der Poel, Grossmann and Lohse2013b
), for
![]() $Pr=6.2$
,
$Pr=6.2$
,
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
over a smooth wall decreases from approximately 10 mm to 5 mm as
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$
over a smooth wall decreases from approximately 10 mm to 5 mm as
![]() $Ra$
is increased from
$Ra$
is increased from
![]() $2\times 10^{8}$
to
$2\times 10^{8}$
to
![]() $5\times 10^{9}$
. Thus, the
$5\times 10^{9}$
. Thus, the
![]() $k=8$
mm roughness elements are expected to strongly perturb the viscous boundary layer, while the
$k=8$
mm roughness elements are expected to strongly perturb the viscous boundary layer, while the
![]() $k=1.5$
mm roughness elements are likely to be buried deep within it.
$k=1.5$
mm roughness elements are likely to be buried deep within it.
3.2 Effect of rough plates on heat transfer under rotation
Figure 2(b) shows the variation of
![]() $Nu$
with
$Nu$
with
![]() $Ro$
at
$Ro$
at
![]() $Ra=2.2\times 10^{9}$
. When both plates are smooth, the behaviour of
$Ra=2.2\times 10^{9}$
. When both plates are smooth, the behaviour of
![]() $Nu$
agrees well with that reported in earlier studies (e.g. Kunnen et al.
Reference Kunnen, Clercx and Geurts2006; Zhong & Ahlers Reference Zhong and Ahlers2010; Kunnen et al.
Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011; Stevens, Clercx & Lohse Reference Stevens, Clercx and Lohse2013a
): an increase in
$Nu$
agrees well with that reported in earlier studies (e.g. Kunnen et al.
Reference Kunnen, Clercx and Geurts2006; Zhong & Ahlers Reference Zhong and Ahlers2010; Kunnen et al.
Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011; Stevens, Clercx & Lohse Reference Stevens, Clercx and Lohse2013a
): an increase in
![]() $Nu$
as
$Nu$
as
![]() $Ro$
decreases below the critical value
$Ro$
decreases below the critical value
![]() $Ro_{c}\approx 2.5$
and a maximum attained at
$Ro_{c}\approx 2.5$
and a maximum attained at
![]() $Ro\approx 0.2$
, which is assumed to indicate the transition to regime III. It is evident from figure 2(b) that at all the rotation rates studied,
$Ro\approx 0.2$
, which is assumed to indicate the transition to regime III. It is evident from figure 2(b) that at all the rotation rates studied,
![]() $Nu$
for
$Nu$
for
![]() $k=8$
mm is substantially higher than that for smooth plates, while
$k=8$
mm is substantially higher than that for smooth plates, while
![]() $Nu$
for
$Nu$
for
![]() $k=1.5$
mm differs significantly from
$k=1.5$
mm differs significantly from
![]() $Nu_{SS}$
only after
$Nu_{SS}$
only after
![]() $Ro$
decreases below approximately 0.5.
$Ro$
decreases below approximately 0.5.
To better assess the above trends, the variation of
![]() $Nu/Nu(Ro=\infty )$
with
$Nu/Nu(Ro=\infty )$
with
![]() $Ro$
at
$Ro$
at
![]() $Ra=2.2\times 10^{9}$
is shown in figure 2(c). Evidently, the value of
$Ra=2.2\times 10^{9}$
is shown in figure 2(c). Evidently, the value of
![]() $Ro$
that marks the end of regime I with negligible effect of rotation, i.e.
$Ro$
that marks the end of regime I with negligible effect of rotation, i.e.
![]() $Ro_{c}\approx 2.5$
, is unchanged in the presence of the rough plates. For
$Ro_{c}\approx 2.5$
, is unchanged in the presence of the rough plates. For
![]() $k=1.5$
mm (data sets R2R2 and R2S), the trends for
$k=1.5$
mm (data sets R2R2 and R2S), the trends for
![]() $Nu/Nu(Ro=\infty )$
are qualitatively similar to those for the smooth plates, although some quantitative differences are observed. For smooth plates, the maximum value of
$Nu/Nu(Ro=\infty )$
are qualitatively similar to those for the smooth plates, although some quantitative differences are observed. For smooth plates, the maximum value of
![]() $Nu/Nu(Ro=\infty )$
is 1.11. This maximum is significantly higher in the presence of
$Nu/Nu(Ro=\infty )$
is 1.11. This maximum is significantly higher in the presence of
![]() $k=1.5$
mm roughness: 1.17 and 1.29 for the sets R2S and R2R2 respectively. Furthermore, the maxima occur at lower Rossby numbers,
$k=1.5$
mm roughness: 1.17 and 1.29 for the sets R2S and R2R2 respectively. Furthermore, the maxima occur at lower Rossby numbers,
![]() $Ro_{R2S}\approx 0.08$
and
$Ro_{R2S}\approx 0.08$
and
![]() $Ro_{R2R2}\approx 0.06$
, indicating that the regime II with enhanced heat transfer is more robust and the transition to regime III is delayed to higher rotation rates. The results for
$Ro_{R2R2}\approx 0.06$
, indicating that the regime II with enhanced heat transfer is more robust and the transition to regime III is delayed to higher rotation rates. The results for
![]() $k=8$
mm are qualitatively as well as quantitatively different from those for smooth plates. For the case R8S, the maximum value of
$k=8$
mm are qualitatively as well as quantitatively different from those for smooth plates. For the case R8S, the maximum value of
![]() $Nu/Nu(Ro=\infty )$
at
$Nu/Nu(Ro=\infty )$
at
![]() $Ro\approx 0.3$
is 1.06, which is significantly smaller than the value of 1.11 for the reference case SS. Furthermore, instead of a steady decay as
$Ro\approx 0.3$
is 1.06, which is significantly smaller than the value of 1.11 for the reference case SS. Furthermore, instead of a steady decay as
![]() $Ro$
is decreased further,
$Ro$
is decreased further,
![]() $Nu/Nu(Ro=\infty )$
shows a weak plateau at
$Nu/Nu(Ro=\infty )$
shows a weak plateau at
![]() $Ro\approx 0.1$
. However, the most significant deviations from the case SS are observed when both plates are rough. In contrast to all other cases, rotation decreases the heat transfer for the case R8R8:
$Ro\approx 0.1$
. However, the most significant deviations from the case SS are observed when both plates are rough. In contrast to all other cases, rotation decreases the heat transfer for the case R8R8:
![]() $Nu/Nu(Ro=\infty )$
is always smaller than 1 for
$Nu/Nu(Ro=\infty )$
is always smaller than 1 for
![]() $Ro\lesssim 2.5$
. After a broad plateau around
$Ro\lesssim 2.5$
. After a broad plateau around
![]() $Ro\approx 0.4$
,
$Ro\approx 0.4$
,
![]() $Nu/Nu(Ro=\infty )$
reaches a minimum at
$Nu/Nu(Ro=\infty )$
reaches a minimum at
![]() $Ro\approx 0.12$
, whereafter it increases as
$Ro\approx 0.12$
, whereafter it increases as
![]() $Ro$
is decreased further. Although one should expect the heat transfer to decay again at sufficiently high rotation rates, this trend of increase in
$Ro$
is decreased further. Although one should expect the heat transfer to decay again at sufficiently high rotation rates, this trend of increase in
![]() $Nu$
for
$Nu$
for
![]() $Ro\lesssim 0.1$
is in marked contrast to the case SS, which exhibits a suppression of heat transfer. Thus, the flow regimes observed in the reference case SS appear to be greatly modified in the presence of the
$Ro\lesssim 0.1$
is in marked contrast to the case SS, which exhibits a suppression of heat transfer. Thus, the flow regimes observed in the reference case SS appear to be greatly modified in the presence of the
![]() $k=8$
mm roughness.
$k=8$
mm roughness.
To recapitulate, although the variation of
![]() $Nu$
with
$Nu$
with
![]() $Ro$
remains qualitatively unchanged for
$Ro$
remains qualitatively unchanged for
![]() $k=1.5$
mm, the maximum of
$k=1.5$
mm, the maximum of
![]() $Nu/Nu(Ro=\infty )$
is significantly larger than that for the case SS, and regime II extends to lower
$Nu/Nu(Ro=\infty )$
is significantly larger than that for the case SS, and regime II extends to lower
![]() $Ro$
. For the asymmetric
$Ro$
. For the asymmetric
![]() $k=8$
mm case (R8S), the enhancement in
$k=8$
mm case (R8S), the enhancement in
![]() $Nu$
under rotation is significantly lower than that for SS, while for the symmetric case R8R8, rotation decreases
$Nu$
under rotation is significantly lower than that for SS, while for the symmetric case R8R8, rotation decreases
![]() $Nu$
in comparison to its value at
$Nu$
in comparison to its value at
![]() $Ro=\infty$
. In addition to the lower magnitudes,
$Ro=\infty$
. In addition to the lower magnitudes,
![]() $Nu/Nu(Ro=\infty )$
for
$Nu/Nu(Ro=\infty )$
for
![]() $k=8$
mm shows marked qualitative differences in comparison to the case SS, indicating the possibility of a different underlying flow structure.
$k=8$
mm shows marked qualitative differences in comparison to the case SS, indicating the possibility of a different underlying flow structure.
4 Discussion
It is evident from § 3 that the effect of rotation on the heat transfer depends critically on the roughness size. It should be noted that for both
![]() $k$
values, the trends for the rough–smooth combinations (R2S and R8S) are intermediate to those for the reference case SS and the respective rough–rough combinations (R2R2 and R8R8). Since we do not measure the temperature at the RBC cell centre, and the sidewall temperature may not be a good approximation to the bulk temperature at low
$k$
values, the trends for the rough–smooth combinations (R2S and R8S) are intermediate to those for the reference case SS and the respective rough–rough combinations (R2R2 and R8R8). Since we do not measure the temperature at the RBC cell centre, and the sidewall temperature may not be a good approximation to the bulk temperature at low
![]() $Ro$
(Kunnen et al.
Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011), we cannot estimate
$Ro$
(Kunnen et al.
Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011), we cannot estimate
![]() $Nu$
for the plates separately. However, to indicate the broad trends, we present the mean of
$Nu$
for the plates separately. However, to indicate the broad trends, we present the mean of
![]() $Nu/Nu(Ro=\infty )$
for the cases SS and R2R2 in figure 3(a) and that for the cases SS and R8R8 in figure 3(b). The averages of the data for the symmetric smooth and rough cases approximate very well, both qualitatively and quantitatively, the data for the corresponding asymmetric configurations. Although the agreement in the case of
$Nu/Nu(Ro=\infty )$
for the cases SS and R2R2 in figure 3(a) and that for the cases SS and R8R8 in figure 3(b). The averages of the data for the symmetric smooth and rough cases approximate very well, both qualitatively and quantitatively, the data for the corresponding asymmetric configurations. Although the agreement in the case of
![]() $k=8$
mm is not as good as for
$k=8$
mm is not as good as for
![]() $k=1.5$
mm, the overall trend for the case R8S, i.e. a non-monotonic decrease in
$k=1.5$
mm, the overall trend for the case R8S, i.e. a non-monotonic decrease in
![]() $Nu$
with decreasing
$Nu$
with decreasing
![]() $Ro$
for
$Ro$
for
![]() $0.055\lesssim Ro\lesssim 0.3$
, is very well reproduced by the average of
$0.055\lesssim Ro\lesssim 0.3$
, is very well reproduced by the average of
![]() $Nu$
for the cases SS and R8R8. This agreement suggests that in a rotating asymmetric RBC cell, each plate maintains its heat transfer characteristics, and the trend for the global
$Nu$
for the cases SS and R8R8. This agreement suggests that in a rotating asymmetric RBC cell, each plate maintains its heat transfer characteristics, and the trend for the global
![]() $Nu$
is a combination of those for
$Nu$
is a combination of those for
![]() $Nu$
for the individual plates.
$Nu$
for the individual plates.

Figure 3. Variation of
![]() $Nu/Nu(Ro=\infty )$
with
$Nu/Nu(Ro=\infty )$
with
![]() $Ro$
at
$Ro$
at
![]() $Ra=2.2\times 10^{9}$
for (a)
$Ra=2.2\times 10^{9}$
for (a)
![]() $k=1.5$
mm and (b)
$k=1.5$
mm and (b)
![]() $k=8$
mm. The variation of the Ekman boundary layer thickness
$k=8$
mm. The variation of the Ekman boundary layer thickness
![]() $\unicode[STIX]{x1D6FF}_{E}$
over a smooth wall and the characteristic horizontal length scale of the vortical columns
$\unicode[STIX]{x1D6FF}_{E}$
over a smooth wall and the characteristic horizontal length scale of the vortical columns
![]() $l=HEk^{1/3}$
(King, Stellmach & Buffett Reference King, Stellmach and Buffett2013) with
$l=HEk^{1/3}$
(King, Stellmach & Buffett Reference King, Stellmach and Buffett2013) with
![]() $Ro$
is shown in (c). In (a) and (b), the black solid lines represent the average of the data for the cases SS, and R2R2 and R8R8 respectively. In (c), the
$Ro$
is shown in (c). In (a) and (b), the black solid lines represent the average of the data for the cases SS, and R2R2 and R8R8 respectively. In (c), the
![]() $Ro$
values for all the cases differ negligibly (less than 2 %) from each other,
$Ro$
values for all the cases differ negligibly (less than 2 %) from each other,
![]() $Ro_{SS}\approx Ro_{R2R2}\approx Ro_{R8R8}$
, since
$Ro_{SS}\approx Ro_{R2R2}\approx Ro_{R8R8}$
, since
![]() $H_{eff}\approx 250$
mm for all these cases (see table 1). The vertical black dash-dotted lines denoting
$H_{eff}\approx 250$
mm for all these cases (see table 1). The vertical black dash-dotted lines denoting
![]() $Ro=0.07$
, 0.12 and 2.0, and the horizontal black dash-dotted lines denoting the lengths 8 mm and 1.5 mm are provided to aid visualization.
$Ro=0.07$
, 0.12 and 2.0, and the horizontal black dash-dotted lines denoting the lengths 8 mm and 1.5 mm are provided to aid visualization.
As discussed earlier, the heat transfer primarily depends on the interaction of the roughness with the thermal and viscous boundary layers. At
![]() $Ro\approx 2.5$
, the Prandtl–Blasius viscous boundary layer undergoes a transition to the Ekman type (Stevens et al.
Reference Stevens, Zhong, Clercx, Ahlers and Lohse2009; Rajaei et al.
Reference Rajaei, Joshi, Alards, Kunnen, Toschi and Clercx2016). Similarly to
$Ro\approx 2.5$
, the Prandtl–Blasius viscous boundary layer undergoes a transition to the Ekman type (Stevens et al.
Reference Stevens, Zhong, Clercx, Ahlers and Lohse2009; Rajaei et al.
Reference Rajaei, Joshi, Alards, Kunnen, Toschi and Clercx2016). Similarly to
![]() $Nu_{SS}$
,
$Nu_{SS}$
,
![]() $Nu_{R2R2}$
increases when
$Nu_{R2R2}$
increases when
![]() $Ro$
is decreased below 2.5 (figure 3
a) as the Ekman pumping mechanism starts to draw hot/cold fluid from the bottom/top thermal boundary layers. Figure 3(c) shows the variation of the Ekman boundary layer thickness
$Ro$
is decreased below 2.5 (figure 3
a) as the Ekman pumping mechanism starts to draw hot/cold fluid from the bottom/top thermal boundary layers. Figure 3(c) shows the variation of the Ekman boundary layer thickness
![]() $\unicode[STIX]{x1D6FF}_{E}=2.284\sqrt{\unicode[STIX]{x1D708}/\unicode[STIX]{x1D6FA}}$
(Rajaei et al.
Reference Rajaei, Joshi, Alards, Kunnen, Toschi and Clercx2016) with
$\unicode[STIX]{x1D6FF}_{E}=2.284\sqrt{\unicode[STIX]{x1D708}/\unicode[STIX]{x1D6FA}}$
(Rajaei et al.
Reference Rajaei, Joshi, Alards, Kunnen, Toschi and Clercx2016) with
![]() $Ro$
(
$Ro$
(
![]() $Ro\approx Ro_{R2R2}\approx Ro_{R8R8}$
) over a smooth wall. In the vicinity of the transition at
$Ro\approx Ro_{R2R2}\approx Ro_{R8R8}$
) over a smooth wall. In the vicinity of the transition at
![]() $Ro\approx 2.5$
,
$Ro\approx 2.5$
,
![]() $\unicode[STIX]{x1D6FF}_{E}\approx 9$
mm is significantly thicker than
$\unicode[STIX]{x1D6FF}_{E}\approx 9$
mm is significantly thicker than
![]() $k=1.5$
mm. Thus, the roughness elements are buried deep inside the Ekman layer and their effect on the heat transfer is not evident. The effect of roughness becomes significant only for
$k=1.5$
mm. Thus, the roughness elements are buried deep inside the Ekman layer and their effect on the heat transfer is not evident. The effect of roughness becomes significant only for
![]() $Ro\lesssim 0.5$
(figure 3
a) when
$Ro\lesssim 0.5$
(figure 3
a) when
![]() $\unicode[STIX]{x1D6FF}_{E}$
decreases to approximately 4 mm (figure 3
c). It should be noted that the Ekman vortices draw fluid primarily from the bulk of the boundary layer rather than the near-wall region (Stevens, Clercx & Lohse Reference Stevens, Clercx and Lohse2010). Thus, it is only when
$\unicode[STIX]{x1D6FF}_{E}$
decreases to approximately 4 mm (figure 3
c). It should be noted that the Ekman vortices draw fluid primarily from the bulk of the boundary layer rather than the near-wall region (Stevens, Clercx & Lohse Reference Stevens, Clercx and Lohse2010). Thus, it is only when
![]() $\unicode[STIX]{x1D6FF}_{E}/k$
becomes small enough that the roughness elements get exposed to a sufficiently strong radial inflow of the boundary layer fluid into the Ekman vortices. It should be noted that, as discussed in § 3.1,
$\unicode[STIX]{x1D6FF}_{E}/k$
becomes small enough that the roughness elements get exposed to a sufficiently strong radial inflow of the boundary layer fluid into the Ekman vortices. It should be noted that, as discussed in § 3.1,
![]() $\unicode[STIX]{x1D6FF}_{T}\approx k$
for
$\unicode[STIX]{x1D6FF}_{T}\approx k$
for
![]() $Ro=\infty$
at
$Ro=\infty$
at
![]() $Ra=2.2\times 10^{9}$
. Although
$Ra=2.2\times 10^{9}$
. Although
![]() $\unicode[STIX]{x1D6FF}_{T}$
can increase substantially in regime III compared with regimes I and II (Kunnen et al.
Reference Kunnen, Clercx and Geurts2006, Reference Kunnen, Geurts and Clercx2010b
, Reference Kunnen, Ostilla-Mónico, van der Poel, Verzicco and Lohse2016), it is expected to remain largely unchanged and reasonably well estimated by
$\unicode[STIX]{x1D6FF}_{T}$
can increase substantially in regime III compared with regimes I and II (Kunnen et al.
Reference Kunnen, Clercx and Geurts2006, Reference Kunnen, Geurts and Clercx2010b
, Reference Kunnen, Ostilla-Mónico, van der Poel, Verzicco and Lohse2016), it is expected to remain largely unchanged and reasonably well estimated by
![]() $\unicode[STIX]{x1D6FF}_{T}\approx H/2Nu$
in regime II (Kunnen et al.
Reference Kunnen, Clercx and Geurts2006, Reference Kunnen, Geurts and Clercx2010b
). Since
$\unicode[STIX]{x1D6FF}_{T}\approx H/2Nu$
in regime II (Kunnen et al.
Reference Kunnen, Clercx and Geurts2006, Reference Kunnen, Geurts and Clercx2010b
). Since
![]() $\unicode[STIX]{x1D6FF}_{T}\approx k$
, the radial inflow over the roughness elements is likely to generate more thermal structures from the perturbed thermal boundary layer. These structures enter the Ekman vortices and increase their heat transfer efficiency, which is reflected in the higher
$\unicode[STIX]{x1D6FF}_{T}\approx k$
, the radial inflow over the roughness elements is likely to generate more thermal structures from the perturbed thermal boundary layer. These structures enter the Ekman vortices and increase their heat transfer efficiency, which is reflected in the higher
![]() $Nu/Nu(Ro=\infty )$
for the case R2R2 in comparison with the case SS. For smooth walls, the increase in the heat transfer due to Ekman pumping is small or absent when
$Nu/Nu(Ro=\infty )$
for the case R2R2 in comparison with the case SS. For smooth walls, the increase in the heat transfer due to Ekman pumping is small or absent when
![]() $Pr\gg 1$
or
$Pr\gg 1$
or
![]() $Pr\ll 1$
(Stevens et al.
Reference Stevens, Clercx and Lohse2010). However, for the case R2R2, an increase in
$Pr\ll 1$
(Stevens et al.
Reference Stevens, Clercx and Lohse2010). However, for the case R2R2, an increase in
![]() $Nu/Nu(Ro=\infty )$
in comparison with the case SS can also be expected when
$Nu/Nu(Ro=\infty )$
in comparison with the case SS can also be expected when
![]() $\unicode[STIX]{x1D6FF}_{T}\ll k$
(
$\unicode[STIX]{x1D6FF}_{T}\ll k$
(
![]() $Pr\gg 1$
or high
$Pr\gg 1$
or high
![]() $Ra$
) due to a radial-flow-induced enhanced emission of hot/cold plumes from the thermal boundary layer at the tips of the roughness elements. On the other hand, when
$Ra$
) due to a radial-flow-induced enhanced emission of hot/cold plumes from the thermal boundary layer at the tips of the roughness elements. On the other hand, when
![]() $\unicode[STIX]{x1D6FF}_{T}\gg k$
(
$\unicode[STIX]{x1D6FF}_{T}\gg k$
(
![]() $Pr\ll 1$
or low
$Pr\ll 1$
or low
![]() $Ra$
), the enhanced emission of structures from the roughness elements may not be as effective in increasing the heat transfer efficiency due to the high thermal diffusivity of the fluid. The discussed interaction of the near-wall flow with the roughness for the case R2R2 to generate higher thermal/momentum fluctuations could be qualitatively similar to that observed in turbulent boundary layers over rough walls (Jimenez Reference Jimenez2004) and the interaction of the LSC with rough walls in non-rotating RBC (Wagner & Shishkina Reference Wagner and Shishkina2015).
$Ra$
), the enhanced emission of structures from the roughness elements may not be as effective in increasing the heat transfer efficiency due to the high thermal diffusivity of the fluid. The discussed interaction of the near-wall flow with the roughness for the case R2R2 to generate higher thermal/momentum fluctuations could be qualitatively similar to that observed in turbulent boundary layers over rough walls (Jimenez Reference Jimenez2004) and the interaction of the LSC with rough walls in non-rotating RBC (Wagner & Shishkina Reference Wagner and Shishkina2015).
The transition from regime II to regime III, indicated by the maximum of
![]() $Nu$
, is delayed to lower
$Nu$
, is delayed to lower
![]() $Ro$
in the presence of the
$Ro$
in the presence of the
![]() $k=1.5$
mm roughness (figure 3
a). For smooth walls, it is known that this transition is accompanied by an increased damping of turbulence by rotation (Boubnov & Golitsyn Reference Boubnov and Golitsyn1990; Joshi et al.
Reference Joshi, Rajaei, Kunnen and Clercx2016). Since a rough wall is expected to lead to higher turbulent fluctuations, it is not surprising that this transition is delayed to smaller
$k=1.5$
mm roughness (figure 3
a). For smooth walls, it is known that this transition is accompanied by an increased damping of turbulence by rotation (Boubnov & Golitsyn Reference Boubnov and Golitsyn1990; Joshi et al.
Reference Joshi, Rajaei, Kunnen and Clercx2016). Since a rough wall is expected to lead to higher turbulent fluctuations, it is not surprising that this transition is delayed to smaller
![]() $Ro$
in the presence of rough walls. However, it should be noted that although
$Ro$
in the presence of rough walls. However, it should be noted that although
![]() $\unicode[STIX]{x1D6FF}_{E}$
remains larger than
$\unicode[STIX]{x1D6FF}_{E}$
remains larger than
![]() $k=1.5$
mm for moderate rotation rates, it becomes equal to
$k=1.5$
mm for moderate rotation rates, it becomes equal to
![]() $k$
at
$k$
at
![]() $Ro\approx 0.07$
. Consequently, the Ekman boundary layer is strongly perturbed by the roughness, and this may lead to disruption of the Ekman pumping mechanism. This disruption explains the location
$Ro\approx 0.07$
. Consequently, the Ekman boundary layer is strongly perturbed by the roughness, and this may lead to disruption of the Ekman pumping mechanism. This disruption explains the location
![]() $Ro\approx 0.07$
of the end of regime II, after which
$Ro\approx 0.07$
of the end of regime II, after which
![]() $Nu$
decays as
$Nu$
decays as
![]() $Ro$
continues to decrease. If this is indeed the case, then the nature of the Ekman boundary layer in the vicinity of the transition, i.e. when
$Ro$
continues to decrease. If this is indeed the case, then the nature of the Ekman boundary layer in the vicinity of the transition, i.e. when
![]() $\unicode[STIX]{x1D6FF}_{E}\approx k$
, is likely to be different from its well-known structure over smooth walls. However, at sufficiently low
$\unicode[STIX]{x1D6FF}_{E}\approx k$
, is likely to be different from its well-known structure over smooth walls. However, at sufficiently low
![]() $Ro$
, when
$Ro$
, when
![]() $\unicode[STIX]{x1D6FF}_{E}\ll k$
, the faces of the pyramidal roughness elements may act like sloping boundaries. Consequently, the Ekman vortices may reappear, albeit with a slightly thicker Ekman layer
$\unicode[STIX]{x1D6FF}_{E}\ll k$
, the faces of the pyramidal roughness elements may act like sloping boundaries. Consequently, the Ekman vortices may reappear, albeit with a slightly thicker Ekman layer
![]() $\unicode[STIX]{x1D6FF}_{E,\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FF}_{E}\sqrt{\sec \unicode[STIX]{x1D6FD}}$
(Pedlosky Reference Pedlosky1987), where
$\unicode[STIX]{x1D6FF}_{E,\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FF}_{E}\sqrt{\sec \unicode[STIX]{x1D6FD}}$
(Pedlosky Reference Pedlosky1987), where
![]() $\unicode[STIX]{x1D6FD}$
is the angle the slope makes with the horizontal. In the present case,
$\unicode[STIX]{x1D6FD}$
is the angle the slope makes with the horizontal. In the present case,
![]() $\unicode[STIX]{x1D6FF}_{E,\unicode[STIX]{x1D6FD}}=1.19\unicode[STIX]{x1D6FF}_{E}$
for
$\unicode[STIX]{x1D6FF}_{E,\unicode[STIX]{x1D6FD}}=1.19\unicode[STIX]{x1D6FF}_{E}$
for
![]() $\unicode[STIX]{x1D6FD}=45^{\circ }$
. Unfortunately, the present experimental set-up cannot be operated at higher rotation rates to explore the low-
$\unicode[STIX]{x1D6FD}=45^{\circ }$
. Unfortunately, the present experimental set-up cannot be operated at higher rotation rates to explore the low-
![]() $Ro$
regime III for
$Ro$
regime III for
![]() $k=1.5$
mm.
$k=1.5$
mm.
The disruption of the Ekman pumping mechanism when
![]() $\unicode[STIX]{x1D6FF}_{E}\approx k$
and its possible re-establishment when
$\unicode[STIX]{x1D6FF}_{E}\approx k$
and its possible re-establishment when
![]() $\unicode[STIX]{x1D6FF}_{E}\ll k$
are also suggested by the data for the case R8R8. For this case,
$\unicode[STIX]{x1D6FF}_{E}\ll k$
are also suggested by the data for the case R8R8. For this case,
![]() $\unicode[STIX]{x1D6FF}_{E}$
is already equal to
$\unicode[STIX]{x1D6FF}_{E}$
is already equal to
![]() $k$
at
$k$
at
![]() $Ro\approx 2$
(figure 3
c). Consequently, there is no heat transfer enhancement due to Ekman pumping. This, perhaps combined with the turbulence suppression under rotation, leads to a slight decrease in
$Ro\approx 2$
(figure 3
c). Consequently, there is no heat transfer enhancement due to Ekman pumping. This, perhaps combined with the turbulence suppression under rotation, leads to a slight decrease in
![]() $Nu$
, approximately 2 %, for
$Nu$
, approximately 2 %, for
![]() $Ro\lesssim 2$
. The Nusselt number continues to decrease as
$Ro\lesssim 2$
. The Nusselt number continues to decrease as
![]() $Ro$
decreases, possibly due to further suppression of turbulence. It reaches a minimum at
$Ro$
decreases, possibly due to further suppression of turbulence. It reaches a minimum at
![]() $Ro\approx 0.12$
and increases again as
$Ro\approx 0.12$
and increases again as
![]() $Ro$
is reduced further. It is possible that
$Ro$
is reduced further. It is possible that
![]() $\unicode[STIX]{x1D6FF}_{E}\approx k/4$
at
$\unicode[STIX]{x1D6FF}_{E}\approx k/4$
at
![]() $Ro=0.12$
is small enough in comparison with
$Ro=0.12$
is small enough in comparison with
![]() $k$
for re-establishment of the Ekman pumping mechanism. The characteristic horizontal length scale of the vortical convection columns,
$k$
for re-establishment of the Ekman pumping mechanism. The characteristic horizontal length scale of the vortical convection columns,
![]() $l\sim HEk^{1/3}$
(King et al.
Reference King, Stellmach and Buffett2013), where
$l\sim HEk^{1/3}$
(King et al.
Reference King, Stellmach and Buffett2013), where
![]() $Ek=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D6FA}H^{2}$
is the Ekman number, is also shown in figure 3(c). At
$Ek=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D6FA}H^{2}$
is the Ekman number, is also shown in figure 3(c). At
![]() $Ro=0.12$
,
$Ro=0.12$
,
![]() $l\approx 6$
mm, i.e. slightly smaller than
$l\approx 6$
mm, i.e. slightly smaller than
![]() $k=8$
mm, which is also likely to aid this transition. However, further studies would be needed to provide strong evidence for this disruption and re-establishment of the Ekman layer. It should be noted that
$k=8$
mm, which is also likely to aid this transition. However, further studies would be needed to provide strong evidence for this disruption and re-establishment of the Ekman layer. It should be noted that
![]() $Nu$
is expected to decay again at sufficiently high rotation rates as the turbulence damping overwhelms the effect of the re-established Ekman pumping.
$Nu$
is expected to decay again at sufficiently high rotation rates as the turbulence damping overwhelms the effect of the re-established Ekman pumping.
5 Conclusion
Heat transfer measurements have been performed in rotating RBC at
![]() $Ra=2.2\times 10^{9}$
and
$Ra=2.2\times 10^{9}$
and
![]() $Pr=6.2$
in the presence of pyramid-shaped roughness elements over the horizontal plates. Our measurements in the absence of rotation agree well with those reported by other researchers. We observe that the effect of rotation on the heat transfer depends on the roughness size relative to the Ekman boundary layer thickness. The Ekman pumping mechanism remains largely unaffected by the roughness when
$Pr=6.2$
in the presence of pyramid-shaped roughness elements over the horizontal plates. Our measurements in the absence of rotation agree well with those reported by other researchers. We observe that the effect of rotation on the heat transfer depends on the roughness size relative to the Ekman boundary layer thickness. The Ekman pumping mechanism remains largely unaffected by the roughness when
![]() $\unicode[STIX]{x1D6FF}_{E}\gg k$
, as the roughness elements are buried deep inside the boundary layer. As
$\unicode[STIX]{x1D6FF}_{E}\gg k$
, as the roughness elements are buried deep inside the boundary layer. As
![]() $\unicode[STIX]{x1D6FF}_{E}$
becomes smaller, the roughness elements are exposed to the radial inflow of the fluid converging into the Ekman vortices. We believe that this interaction generates stronger momentum and temperature fluctuations, and hence leads to an increase in the heat transfer. However, when
$\unicode[STIX]{x1D6FF}_{E}$
becomes smaller, the roughness elements are exposed to the radial inflow of the fluid converging into the Ekman vortices. We believe that this interaction generates stronger momentum and temperature fluctuations, and hence leads to an increase in the heat transfer. However, when
![]() $\unicode[STIX]{x1D6FF}_{E}\approx k$
, the Ekman boundary layer is strongly perturbed by the roughness and the Ekman pumping mechanism is disrupted. It is perhaps re-established when
$\unicode[STIX]{x1D6FF}_{E}\approx k$
, the Ekman boundary layer is strongly perturbed by the roughness and the Ekman pumping mechanism is disrupted. It is perhaps re-established when
![]() $\unicode[STIX]{x1D6FF}_{E}\ll k$
, as the boundary layer flow may then be similar to that of an Ekman layer over a sloping boundary.
$\unicode[STIX]{x1D6FF}_{E}\ll k$
, as the boundary layer flow may then be similar to that of an Ekman layer over a sloping boundary.
Acknowledgement
This work is supported by the Foundation for Fundamental Research on Matter (FOM), Netherlands.