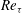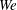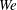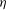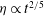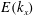1. Introduction
Waves at the air/water interface interact with turbulence, modifying the mass, momentum and energy transfer rates between the phases. These processes are crucial in many industrial applications, including condensers/evaporators and heat exchangers, where air and water usually have countercurrent flow (Bartrand, Farouk & Haas Reference Bartrand, Farouk and Haas2009; Deendarlianto et al. Reference Hohne, Lucas and Vierow2012). In such instances, predicting the evolution of the interface deformation – waves – according to the flow conditions is essential since transfer mechanisms across phases depend on the magnitude and structure of the interface deformation. However, due to the complex and very small nature of the near-interface region, the mechanisms controlling interfacial wave generation and growth in countercurrent air/water flow systems are not yet clear and still require investigation. One of the reasons is that experimental measurements near the interface, where the turbulence interacts with the waves, are extremely challenging (Thais & Magnaudet Reference Thais and Magnaudet1996). Recently, Berhanu & Falcon (Reference Berhanu and Falcon2013) used a diffusing light photography optical method combined with a fast camera and reported the full space–time resolved statistics of capillary wave turbulence at the air/water interface. However, waves were obtained by a mechanical forcing rather than by imposing a mean shear at the interface. Obtaining a description of the flow field above and below the interface is still an open issue using experimental techniques.
Direct numerical simulation (DNS) can help to provide at any given time the entire velocity/pressure fields as well as the interface deformation, ensuring a level of detail sufficient to characterize the phenomena occurring in the proximity of the interface (where experimental measurements are difficult). One of the first DNS studies on turbulence interactions across a freely deformable interface in a countercurrent air/water flow was that of Fulgosi et al. (Reference Fulgosi, Lakehal, Banerjee and De Angelis2003). The authors focused on the structure of the turbulence over the deformable interface; however, they did not characterize the process of wave generation/growth and, due to resolution constraints, they could not resolve capillary length scales. The wind-wave generation process (at low wind speed) was the objective of the DNS performed by Lin et al. (Reference Lin, Moeng, Tsai, Sullivan and Belcher2008), who remarked that wave growth is a two-stage process, initially linear and later exponential. They also found that the energy transfer from wind to waves is mainly due to turbulence-induced pressure fluctuations in the linear stage, and to wave-induced pressure fluctuations in the exponential stage. Later, Komori et al. (Reference Komori, Kurose, Iwano, Ukai and Suzuki2010) extended the analysis of Lin et al. (Reference Lin, Moeng, Tsai, Sullivan and Belcher2008), considering mass transfer phenomena across the deformable interface. They observed that the near-interface dynamics in the water side (streamwise vortices and turbulent burst) controls the transfer rates of mass and momentum across the interface.
In this work, we use DNS to analyse the process of wave generation and growth in a countercurrent air/water turbulent flow. We let the air/water interface evolve starting from flat interface conditions. The dynamics is described by three dimensionless numbers: the Reynolds number (
$\mathit{Re}_{{\it\tau}}$
, which measures the importance of inertia compared with viscosity), the Weber number (
$\mathit{We}$
, which measures the importance of inertia compared with surface tension) and the Froude number (
$\mathit{Fr}$
, which measures the importance of inertia compared with gravity). We keep
$\mathit{Re}_{{\it\tau}}$
constant and vary
$\mathit{We}$
and
$\mathit{Fr}$
. We will first consider the transient behaviour of the interface dynamics, deriving also a prediction for the initial growth of the surface elevation. Then, we will focus on the statistically steady state of the interface occurring when the pressure distribution on the interface is balanced by gravity and surface tension. Wavenumber spectra will be computed to characterize the transient and long-term structure of the interface, and compared with the predictions of wave turbulence theory (WTT) (Zakharov, Lvov & Falkovich Reference Zakharov, Lvov and Falkovich1992). Finally, the wave-induced effect on wind and current velocity profiles is briefly analysed and discussed.
2. Governing equations and numerical modelling
We consider a turbulent air–water flow, as sketched in figure 1(a). The reference geometry consists of two different domains (one for air and one for water) separated by a deformable interface. The origin of the coordinate system is located at the centre of each domain, and the
$x$
-,
$y$
- and
$z$
-axes point in the streamwise, spanwise and interface-normal directions. The air and water, which are considered to be incompressible and Newtonian, are driven by an imposed pressure gradient, and flow in opposite directions. We consider a Cartesian coordinate system where the air is placed above the water. The dimensionless continuity and Navier–Stokes equations are
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}=-\boldsymbol{{\rm\nabla}}p+\frac{1}{\mathit{Re}_{{\it\tau}}}{\rm\nabla}^{2}\boldsymbol{u}, & \displaystyle\end{eqnarray}$$
Figure 1. (a) Sketch of the computational domain. (b–d) Interface deformation and turbulent structures (contours of the magnitude of the streamline rotation vector,
${\it\Omega}$
) for
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
(simulation
$S1$
, b),
$\sqrt{\mathit{Fr}}/\mathit{We}=1.93$
(simulation
$S2$
, c) and
$\sqrt{\mathit{Fr}}/\mathit{We}=1.4$
(simulation
$S3$
, d) computed at
$t\simeq 40~\text{s}$
. The magnitude of
${\it\Omega}$
is in the range
$0<{\it\Omega}<150$
for
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
,
$0<{\it\Omega}<100$
for
$\sqrt{\mathit{Fr}}/\mathit{We}=1.93$
and
$0<{\it\Omega}<80$
for
$\sqrt{\mathit{Fr}}/\mathit{We}=1.4$
. It should be noted that the interface deformation has been magnified by a factor of 3 for
$S1$
, 25 for
$S2$
and 50 for
$S3$
.
where
$\boldsymbol{u}$
is the velocity vector and
$p$
is the pressure. Variables are made dimensionless using the half-depth of each subdomain
$h$
, the thermophysical properties of each phase (the density
${\it\rho}$
and the kinematic viscosity
${\it\nu}$
) and the corresponding shear velocity
$u_{{\it\tau}}=\sqrt{{\it\tau}_{int}/{\it\rho}}$
(
${\it\tau}_{int}$
being the shear stress at the interface). Periodic boundary conditions are employed in the streamwise and spanwise directions, whereas free-slip conditions are applied at the outer boundaries in the interface-normal direction (
$z=\pm 2h$
). At the interface, the air and water are coupled by the continuity of the velocity and of the normal/shear components of the stress tensor (dynamic boundary conditions):
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{1}{\mathit{Re}\,{\bf\tau}}(({\it\tau}_{L}-{\it\tau}_{G})\boldsymbol{\cdot }\boldsymbol{n})\boldsymbol{\cdot }\boldsymbol{n}+p_{G}-p_{L}+\frac{1}{\mathit{We}}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{n}-\frac{1}{\mathit{Fr}}{\it\eta}=0,\\ (({\it\tau}_{L}-{\it\tau}_{G})\boldsymbol{\cdot }\boldsymbol{n})\boldsymbol{\cdot }\boldsymbol{t}_{i}=0,\quad i=1,2,\\ \displaystyle \boldsymbol{u}_{G}=\frac{1}{\mathscr{R}}\boldsymbol{u}_{L},\end{array}\right\}\end{eqnarray}$$
where the subscripts
$G$
and
$L$
are for gas (air) and liquid (water) respectively,
${\bf\tau}$
is the viscous stress tensor,
${\it\eta}$
is the vertical displacement of the interface,
$\boldsymbol{n}$
and
$\boldsymbol{t}_{i}$
are the normal and the two tangential unit vectors to the interface while
$\mathscr{R}=\sqrt{{\it\rho}_{L}/{\it\rho}_{G}}$
is the square root of the density ratio. The Weber (
$\mathit{We}$
), Froude (
$\mathit{Fr}$
) and Reynolds (
$\mathit{Re}_{{\it\tau}}$
) numbers are defined as
$$\begin{eqnarray}\mathit{We}=\frac{{\it\rho}_{L}hu_{{\it\tau}L}^{2}}{{\it\gamma}},\quad \mathit{Fr}=\frac{{\it\rho}_{L}u_{{\it\tau}L}^{2}}{gh({\it\rho}_{L}-{\it\rho}_{G})},\quad \mathit{Re}_{{\it\tau}}=\frac{u_{{\it\tau}G}2h}{{\it\nu}_{G}}=\frac{u_{{\it\tau}L}2h}{{\it\nu}_{L}},\end{eqnarray}$$
where
$g$
is the acceleration due to gravity whereas
${\it\gamma}$
is the surface tension (
$u_{{\it\tau}}$
being evaluated at the beginning of the simulation).
The kinematic boundary condition for the interface is prescribed using an advection equation for the vertical elevation of the interface (boundary-fitted approach):
$$\begin{eqnarray}\frac{\partial {\it\eta}}{\partial t}+u_{x}\frac{\partial {\it\eta}}{\partial x}+u_{y}\frac{\partial {\it\eta}}{\partial y}=u_{z},\end{eqnarray}$$
where
$u_{x,y,z}$
is the air or water velocity at the interface. This equation is integrated at each time step to obtain the physical deformation of the domain. Moreover, at each time step, the deformed physical domain is transformed onto a Cartesian domain where the governing equations are solved using a pseudospectral technique which employs Fourier series in the homogeneous directions (
$x$
and
$y$
) and Chebyshev polynomials in the interface-normal direction (
$z$
) (Zonta, Marchioli & Soldati Reference Zonta, Marchioli and Soldati2012a
). In particular, the governing balance equations (equations (2.1) and (2.2)) are first separately solved in each domain, then coupled at the interface using (2.3). We employed a two-stage fractional step splitting method (Fulgosi et al.
Reference Fulgosi, Lakehal, Banerjee and De Angelis2003), where the convective terms are explicitly treated using the Adams–Bashforth scheme, while the viscous terms are discretized using the Crank–Nicolson semi-implicit scheme. Time marching is second-order accurate for the intermediate velocity and is corrected in the next step by solving the Poisson equation for the pressure. The procedures for dealiasing the solution are based on the
$2/3$
rules (see Zonta, Onorato & Soldati Reference Zonta, Onorato and Soldati2012b
; Zonta & Soldati Reference Zonta and Soldati2014 for further details).
The dimensions of the computational domain (for each phase) are
$4{\rm\pi}h\times 2{\rm\pi}h\times 2h$
, while the computational grid is made of
$256\times 128\times 129$
nodes (for each phase) in the
$x$
,
$y$
and
$z$
directions respectively. We consider an air–water turbulent flow at atmospheric pressure and at reference temperature
${\it\theta}=50\,^{\circ }\text{C}$
(common operative temperature for industrial/chemical systems). The physical properties of air and water are evaluated at this mean temperature: the square root of the density ratio is
$\mathscr{R}=29.9$
and the surface tension is
${\it\gamma}=0.0679~\text{N}~\text{m}^{-1}$
. We run three different simulations, each characterized by a specific set of dimensionless numbers and corresponding to a specific choice of the domain height
$h$
(
$h=0.045~\text{m}$
for
$S1$
,
$h=0.05~\text{m}$
for
$S2$
and
$h=0.06~\text{m}$
for
$S3$
). An overview of the simulation parameters is given in table 1.
Table 1. Wave generation in a countercurrent air–water flow: summary of the simulation parameters.
3. Results
3.1. Wave generation and growth
The dynamics of the deformable interface separating air and water currents is governed by the interaction between external forcing (pressure/velocity fluctuations and large-scale coherent structures) and restoring forces (surface tension and gravity). The interface dynamics is strongly time-dependent and can support the propagation of waves with different amplitudes and wavelengths (see figure 1
b–d for a visualization of the interaction between interface deformation and turbulence structures, visualized therein by contours of the streamline rotation vector). To characterize the time behaviour of the interface deformation, we computed the root-mean-square (r.m.s.) of the interface amplitude in time,
${\it\eta}_{rms}(t)=\langle {\it\eta}(t)^{2}\rangle ^{1/2}$
, where brackets
$\langle \cdot \rangle$
imply averaging in space. The results are shown in figure 2. We first focus on the initial stage up to
$t\simeq 6~\text{s}$
; in this stage, the growth rate of
${\it\eta}_{rms}(t)$
seems to be independent of the physical parameters of the simulations.
Figure 2. Time behaviour of the r.m.s. of the interface amplitude,
${\it\eta}_{rms}=\langle {\it\eta}(t)^{2}\rangle ^{1/2}$
, for the simulations with
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
(simulation
$S1$
, red line),
$\sqrt{\mathit{Fr}}/\mathit{We}=1.9$
(simulation
$S2$
, blue line) and
$\sqrt{\mathit{Fr}}/\mathit{We}=1.4$
(simulation
$S3$
, cyan line). The scaling law obtained by the simplified physical model (equation (3.1), thin line) and the asymptotic values predicted by (3.3) (
${\it\eta}_{rms,S}^{th}$
, right side of the figure) are also shown.
To understand this behaviour, we have developed a simple phenomenological model able to predict the growth rate of waves at the air/water interface. We consider a flat interface characterized by surface tension
${\it\gamma}$
. For this flat interface, the air/water pressure difference is
${\rm\Delta}p=0$
. The dynamics of the interface is initially triggered by vertical velocity fluctuations
$w_{l}$
in the water side. The liquid vertical velocity
$w_{l}$
corresponds to a dynamic pressure difference
${\rm\Delta}p\simeq {\it\rho}w_{l}^{2}$
which acts to deform the interface. Assuming for simplicity a locally spherical interface deformation with radius of curvature
$r$
, this air/water pressure difference can be expressed as
${\rm\Delta}p={\it\gamma}/r$
. As a consequence, we obtain
$w_{l}^{2}\propto {\it\gamma}/r$
and hence a scaling law for the liquid interface velocity
$w_{l}\propto 1/r^{1/2}$
. Large curvatures correspond to large liquid interface velocities and small curvatures correspond to small velocities.
To describe the evolution in time of the interface amplitude, we consider that the interface area
$A$
grows in time as the liquid is pushed by turbulent fluctuations towards the interface, hence
$\text{d}A/\text{d}t=hw_{l}$
(see Hoepffner, Blumenthal & Zaleski Reference Hoepffner, Blumenthal and Zaleski2011). Since
$A\propto {\it\eta}^{2}$
and considering that
$r\propto {\it\eta}$
, we get
$\text{d}{\it\eta}^{2}/\text{d}t\propto {\it\eta}^{-1/2}$
. Upon integration, we obtain
$$\begin{eqnarray}{\it\eta}\propto t^{2/5}.\end{eqnarray}$$
This behaviour is shown in figure 2, together with our DNS results. In the initial stages of the growth, the
${\it\eta}\propto t^{2/5}$
behaviour is robust and almost independent of the specific choice of the physical parameters (for
$S2$
and
$S3$
the
$t^{2/5}$
scaling is recovered starting from
$t>3~\text{s}$
). It should be noted also that the time behaviour of the wave growth observed in the present study is different from the linear law (
${\it\eta}\propto t$
) usually found in wind-driven wave generation processes (Lin et al.
Reference Lin, Moeng, Tsai, Sullivan and Belcher2008); the reason is that our configuration differs from the standard problem of wind-driven waves. The countercurrent air/water flow is characterized by the presence of two opposite boundary layers generating waves in opposite directions and producing an almost negligible streamwise surface velocity.
So far, we have considered the initial dynamics of the interface (
$t<6~\text{s}$
in figure 2). Whether the amplitude of the interface maintains a
${\it\eta}\propto t^{2/5}$
law or not depends on the interface deformability (interplay between gravity and surface tension). For
$\sqrt{\mathit{Fr}}/\mathit{We}<2$
, capillary effects always dominate, and we do not observe significant changes from the
${\it\eta}\propto t^{2/5}$
growth rate (see
$S2$
and
$S3$
in figure 2). By contrast, for
$\sqrt{\mathit{Fr}}/\mathit{We}>2$
we observe a stage of faster growth. This growth is exponential in time and is due to a resonant mechanism between the interface elevation and the wave-induced fluctuations of pressure and stress occurring for gravity waves (see Janssen Reference Janssen2004).
After a transient,
${\it\eta}_{rms}$
attains an asymptotic value, indicating a saturation for the growth of the interface amplitude (figure 2). This occurs when the hydrostatic pressure, dynamic pressure and surface tension balance:
$$\begin{eqnarray}{\rm\Delta}p_{rms}^{\prime }+\frac{1}{\mathit{We}}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }n=\frac{1}{\mathit{Fr}}{\it\eta}_{rms},\end{eqnarray}$$
where
${\rm\Delta}p_{rms}^{\prime }$
is the r.m.s. of the air/water pressure difference. Since the pressure fluctuations in the water side (
$p_{rms,L}^{\prime }$
) are larger than those in the air side,
${\rm\Delta}p_{rms}^{\prime }\simeq p_{rms,L}^{\prime }$
. Equation (3.2) can be used to roughly estimate the asymptotic value of the interface amplitude
${\it\eta}_{rms}$
. Assuming that the curvature of the interface is
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }n\simeq -{\it\eta}_{rms}$
, i.e. assuming a quasi-sinusoidal interface deformation, we obtain
$$\begin{eqnarray}{\it\eta}_{rms}\simeq \frac{\mathit{Fr}\cdot \mathit{We}}{\mathit{Fr}+\mathit{We}}p_{rms,L}^{\prime }.\end{eqnarray}$$
Equation (3.3) requires the knowledge of
$p_{rms,L}^{\prime }$
, which can be easily obtained from our simulations. The behaviour of
$p_{rms,L}^{\prime }$
as a function of the dimensionless vertical coordinate
$z^{+}=zu_{{\it\tau}}/{\it\nu}$
(interface-normal) is given in figure 3. The air/water interface is located at
$z^{+}=170$
, and the dimensionless value of
$p_{rms,L}^{\prime }$
at the interface is
$p_{rms,L}^{\prime }=3400$
for
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
(simulation
$S1$
),
$p_{rms,L}^{\prime }=240$
for
$\sqrt{\mathit{Fr}}/\mathit{We}=1.93$
(simulation
$S2$
) and
$p_{rms,L}^{\prime }=160$
for
$\sqrt{\mathit{Fr}}/\mathit{We}=1.4$
(simulation
$S3$
). Hence, our estimate for the dimensionless amplitude of the interface deformation
${\it\eta}_{rms}$
is
${\it\eta}_{rms,S1}^{th}=1\times 10^{-2}$
for
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
(simulation
$S1$
),
${\it\eta}_{rms,S2}^{th}=5.2\times 10^{-4}$
for
$\sqrt{\mathit{Fr}}/\mathit{We}=1.93$
(simulation
$S2$
) and
${\it\eta}_{rms,S3}^{th}=2\times 10^{-4}$
for
$\sqrt{\mathit{Fr}}/\mathit{We}=1.4$
(simulation
$S3$
).
Figure 3. Distribution of the pressure fluctuations,
$p_{rms,L}^{\prime }=\langle p_{L}^{\prime 2}\rangle ^{1/2}$
, in the water domain as a function of the interface-normal direction (the interface is located at
$z^{+}=zu_{{\it\tau}}/{\it\nu}=170$
) for simulations
$S1$
(
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
),
$S2$
(
$\sqrt{\mathit{Fr}}/\mathit{We}=1.93$
) and
$S3$
(
$\sqrt{\mathit{Fr}}/\mathit{We}=1.4$
).
The effect of the capillary term (
$\mathit{We}^{-1}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }n$
) turns out to be very important at the beginning of the wave generation process (see the discussion on the wave generation process in this section). It is also important in determining the structure of the interface (generation of ripples of short wavelengths, see § 3.2). However, it is less important in establishing the asymptotic value of the interface amplitude, where the leading terms of the force balance at the interface (equation (3.2)) are the dynamic pressure drop (
${\rm\Delta}p_{rms}^{\prime }$
) and the hydrostatic pressure drop (
$\mathit{Fr}^{-1}{\it\eta}_{rms}$
). Therefore, a simplified expression for the interface amplitude is
$$\begin{eqnarray}{\it\eta}_{rms,S}^{th}\simeq \mathit{Fr}\cdot p_{rms,L}^{\prime }.\end{eqnarray}$$
These results are in agreement with the amplitude of the interface deformation obtained by DNS (see the
${\it\eta}_{rms,S}^{th}$
values indicated in figure 2). We underline that the above equation cannot be used for predictions because measuring the pressure is equally difficult to measuring the surface itself. Equation (3.4) and its verification should be considered as a validation of our hypotheses on the forces acting at the free surface.
3.2. Wave spectra
The object of this section is to show the wavenumber spectra and discuss their features in the context of WTT, a statistical theory describing weakly interacting random waves.
Figure 4. Wavenumber spectra,
$E(k_{x})=\int {\it\eta}(k_{x},k_{y})\,\text{d}k_{y}$
, for simulations with
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
(simulation
$S1$
, a),
$\sqrt{\mathit{Fr}}/\mathit{We}=1.93$
(simulation
$S2$
, b) and
$\sqrt{\mathit{Fr}}/\mathit{We}=1.4$
(simulation
$S3$
, c). The insets show the temporal evolution of the energy spectrum at three different time instants (and averaged over a time window
${\rm\Delta}T=1~\text{s}$
):
$t=1~\text{s}$
, –●–;
$t=20~\text{s}$
, –▪–;
$t=40~\text{s}$
, –▴–.
Focusing on the specific case of gravity/capillary waves, WTT is based on the inviscid and irrotational equations of motion (Laplace equation with suitable boundary conditions on the free surface), which, under the hypothesis of homogeneity and weak nonlinearity, leads to an evolution equation for the wave spectrum. This equation is known as the kinetic equation. In the presence of forcing and dissipation, the kinetic equation has isotropic solutions, known as Kolmogorov–Zakharov solutions (Zakharov et al.
Reference Zakharov, Lvov and Falkovich1992), which bear similarities to the Kolmogorov solutions in fluid turbulence. In the capillary regime, the theory predicts a direct cascade of energy
$E(k)\sim k^{-15/4}$
, with
$k=\sqrt{k_{x}^{2}+k_{y}^{2}}$
. In the following, we will try to compare the theoretical predictions given by WTT with the results of our simulations in the statistically stationary regime (which can be observed for
$t>40~\text{s}$
, after the entire process of wave generation). In particular, we will compute the time-averaged (for
$t>40~\text{s}$
and using a time window of
${\rm\Delta}t\simeq 20~\text{s}$
) wavenumber spectrum
$E(k_{x})=(1/{\rm\Delta}T)\int _{t}\int _{k_{y}}E(k_{x},k_{y},t)\,\text{d}k_{y}\,\text{d}t$
. The results are shown in figure 4 as a function of the wavenumber in the streamwise direction
$k_{x}$
. The behaviour of the long-term interface (spatial) structure depends on the relative importance between turbulent fluctuations, gravity and surface tension (see Brocchini & Peregrine Reference Brocchini and Peregrine2001). The low-wavenumber region of the spectrum corresponds to the gravity regime, while the high-wavenumber region of the spectrum corresponds to the capillary regime. There is a crossover between the gravity and capillary regimes occurring at a wavenumber of
$k_{x}=k_{cap}$
. For linear waves,
$k_{cap}^{th}=2{\rm\pi}/{\it\lambda}_{cap}\simeq 300~\text{m}^{-1}$
, where we assume the capillary wavelength
${\it\lambda}_{cap}=\sqrt{4{\rm\pi}^{2}{\it\gamma}/(g{\it\rho})}\simeq 2\times 10^{-2}~\text{m}$
(see Falcon, Laroche & Fauve Reference Falcon, Laroche and Fauve2007). This value,
$k_{cap}^{th}\simeq 300~\text{m}^{-1}$
, is indicated in figure 4. Regardless of the
$\sqrt{\mathit{Fr}}/\mathit{We}$
, the wavenumber spectra exhibit for
$k\geqslant k_{cap}$
a capillary power law
$k^{-19/4}$
. It would be tempting to verify also the power law predicted by WTT when gravity is the dominant restoring force. However, within the size of our computation, this seems to not be feasible. Different interface deformations (surface roughness versus smooth waves) can be observed for different values of gravity compared with capillarity (see also the qualitative pictures in figure 1). The spectral slope in the capillary regime is consistent with that obtained theoretically from WTT when surface tension is dominant, and corresponds to the Kolmogorov–Zakharov solution of the three-wave kinetic equation (see Pushkarev & Zakharov Reference Pushkarev and Zakharov1996). Due to the directional averaging, our spectra scale as
$k_{x}^{-19/4}$
instead of
$k^{-15/4}$
. Similar power laws were observed in experiments by Wright, Budakian & Putterman (Reference Wright, Budakian and Putterman1996), Falcon et al. (Reference Falcon, Laroche and Fauve2007) and Cobelli et al. (Reference Cobelli, Przadka, Petitjeans, Lagubeau, Pagneux and Maurel2011), and more recently in simulations by Deike et al. (Reference Deike, Fuster, Berhanu and Falcon2014) and Pan & Yue (Reference Pan and Yue2014). Although WTT is developed under a number of restrictions (weak nonlinearity, homogeneity, isotropy and separation of scales between forcing and dissipation), it has already been observed (Berhanu & Falcon Reference Berhanu and Falcon2013) that some theoretical predictions can hold even if such hypotheses are not fully met. This seems to happen also in our simulations, where turbulence forces interfacial waves over a broad range of length scales (hence a sharp separation between forcing and dissipative scales is not guaranteed). The results just shown can be important in possibly clarifying the issue related to the role of viscous dissipation in the capillary wave range. In this context, we computed the ratio
${\it\alpha}/{\it\omega}$
between the linear wave propagation time
$1/{\it\omega}$
, with the angular frequency
${\it\omega}(k)=(gk+{\it\gamma}k^{3}/{\it\rho}_{L})^{1/2}$
, and the dissipative time
$1/{\it\alpha}$
, with
${\it\alpha}=2{\it\nu}k^{2}$
. For the range of wavenumbers considered here,
$10^{2}<k<10^{3}~\text{m}^{-1}$
, we obtained
$10^{-4}<{\it\alpha}/{\it\omega}<10^{-2}$
, which suggests that there is a clear time scale separation, with the linear wave propagation time being smaller compared with the dissipative time (as expected by weak turbulence theory).
To deepen our analysis, we consider the temporal evolution of the energy spectrum
$E(k_{x})$
computed for each simulation at three different time instants (
$t=1~\text{s}$
, –●–;
$t=20~\text{s}$
, –▪–;
$t=40~\text{s}$
, –▴–). The results are shown in the insets of figure 4. For
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
(figure 4
a) we observe that
$E(k_{x})$
grows in time qualitatively with a self-similar shape (Deike, Berhanu & Falcon Reference Deike, Berhanu and Falcon2013) that scales as
$k^{-19/4}$
for large
$k$
. For
$\sqrt{\mathit{Fr}}/\mathit{We}=1.93$
and
$\sqrt{\mathit{Fr}}/\mathit{We}=1.4$
(insets of figure 4
b,c) we do not observe a distinctive temporal evolution of the energy spectra: for these values of
$\sqrt{\mathit{Fr}}/\mathit{We}$
the wave dynamics is faster and at
$t=1~\text{s}$
wavenumber spectra already reach a stationary condition.
To characterize further the spatial structure of the interface, we analyse the time evolution of the energy in each wave mode during the wave generation process. In particular, we look at the instantaneous values of the wavenumber spectrum
$E(k_{x},t)=\int _{k_{y}}E(k_{x},k_{y},t)\,\text{d}k_{y}$
. Two-dimensional contour maps of
$E(k_{x},t)$
for each simulation are presented in figure 5. The time evolution of two single-wave modes, one in the gravity regime (
$\overline{k_{x}}=150~\text{m}^{-1}$
) and one in the capillary regime (
$\overline{k_{x}}=450~\text{m}^{-1}$
), is also explicitly shown for each simulation in figure 6. For
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
the growth of the gravity wave modes (
$k<200~\text{m}^{-1}$
in figure 5
a and
$\overline{k_{x}}=150~\text{m}^{-1}$
in figure 6
a) is similar to that of
${\it\eta}_{rms}$
, consisting of an initial sublinear growth (
$t<10~\text{s}$
) followed by an exponential growth (up to
$t\simeq 40$
). This behaviour is somehow visible also for wave modes in the capillary regime (
$k>300~\text{m}^{-1}$
in figure 5
a and
$\overline{k_{x}}=450~\text{m}^{-1}$
in figure 6
a). For smaller
$\sqrt{\mathit{Fr}}/\mathit{We}$
(figures 5
b,c and 6
b,c) the situation changes and the energy content of both gravity and capillary wave modes remains almost constant in time: for these values of
$\sqrt{\mathit{Fr}}/\mathit{We}$
the gravity and capillary wave modes quickly reach a statistically stationary condition characterized by a dynamical energy transfer between scales.
Figure 5. Two-dimensional contour maps of the time behaviour of the wave modes
$E(k_{x},t)$
for simulations with
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
(simulation
$S1$
, a),
$\sqrt{\mathit{Fr}}/\mathit{We}=1.93$
(simulation
$S2$
, b) and
$\sqrt{\mathit{Fr}}/\mathit{We}=1.4$
(simulation
$S3$
, c).
Figure 6. Time behaviour of
$E(\overline{k_{x}},t)$
for simulations with
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
(simulation
$S1$
, a),
$\sqrt{\mathit{Fr}}/\mathit{We}=1.93$
(simulation
$S2$
, b) and
$\sqrt{\mathit{Fr}}/\mathit{We}=1.4$
(simulation
$S3$
, c). Two different values of
$\overline{k_{x}}$
have been chosen, namely
$\overline{k_{x}}=150~\text{m}^{-1}$
and
$\overline{k_{x}}=450~\text{m}^{-1}$
.
3.3. Evolution of the wind and current velocity profiles
We finally discuss the flow modification on both the air (wind) and water (current) velocity fields due to wave–turbulence interactions. In figure 7 we show the wind (
$u^{+}=u/u_{{\it\tau}}$
) and current velocity profiles (
$u^{+}=(u-u_{I})/u_{{\it\tau}}$
, with
$u_{I}$
the interface velocity) computed at three different time instants during the transient evolution of the waves.
Figure 7. Average wind velocity profile
$u_{G}^{+}$
(a) and average current velocity profile
$u_{L}^{+}-u_{I}^{+}$
(with
$u_{I}^{+}$
the interface velocity, b) computed for simulation
$S1$
(
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
) at three different time instants (
$t=1~\text{s}$
, –●–;
$t=20~\text{s}$
, –▪–;
$t=40~\text{s}$
). Theoretical profiles describing the law of the wall (with different shifting constants) are also shown for comparison.
In particular, we chose
$t=1~\text{s}$
(–●–),
$t=20~\text{s}$
(–▪–) and
$t=40~\text{s}$
(–▴–). It should be noted that
$z^{+}=0$
represents the interface. Results are shown only for the simulation with
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
, because all the effects we wish to discuss are emphasized in this case. At the beginning of the simulations (
$t=1~\text{s}$
), when the waves are small, the wind profile (figure 7
a) collapses onto the classical law of the wall (linear-log profile):
$$\begin{eqnarray}u_{G}^{+}=\left\{\begin{array}{@{}ll@{}}z^{+}\quad \quad & \text{if}~z\leqslant 11.6,\\ 2.5\cdot \ln (z^{+})+5.5\quad \quad & \text{if}~z\geqslant 11.6,\end{array}\right.\end{eqnarray}$$
indicating that the wave-induced flow modification is weak. When the wave amplitude increases (
$t>10~\text{s}$
), there is a significant wave–turbulence interaction which produces a systematic decrease of the wind velocity (which, however, maintains the usual linear-log structure, though with a different shifting constant, i.e. 3.75 instead of 5.5). This is due to the increase of the pressure drag contributions to the total surface drag (Lin et al.
Reference Lin, Moeng, Tsai, Sullivan and Belcher2008; Grare et al.
Reference Grare, Peirson, Branger, Walker, Giovanangeli and Makin2013). We explicitly compute the time evolution of the pressure drag on the interface, for the simulation with
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
, as follows:
$$\begin{eqnarray}P_{D}=\frac{1}{L_{x}L_{y}}\int _{0}^{L_{x}}\int _{0}^{L_{y}}p_{G}\left(\frac{\partial {\it\eta}}{\partial x}+\frac{\partial {\it\eta}}{\partial y}\right)\,\text{d}x\,\text{d}y,\end{eqnarray}$$
with
$L_{x}$
and
$L_{y}$
the streamwise and spanwise extensions of the interface respectively. The pressure drag
$P_{D}$
, normalized by the reference shear stress at the interface
${\it\tau}_{int}=1.17\times 10^{-3}$
, is shown in figure 8 as a function of time. We observe that
$P_{D}/{\it\tau}_{int}$
increases rapidly during the exponential wave growth process (
$10~\text{s}<t<40~\text{s}$
, see also figure 2), and when the wave amplitude reaches a steady-state condition (
$t>40~\text{s}$
), the dimensionless pressure drag fluctuates around the average value
$P_{D}/{\it\tau}_{int}\simeq 0.1$
(shown by the dashed line in figure 8). This indicates that a significant proportion of the flow energy (
$\simeq 10\,\%$
) is lost into interface deformation. For the mean water velocity (figure 7
b), we observe that the initial current profile (
$t=1~\text{s}$
) is similar to the initial wind profile. Later, the situation changes and not all of the current profiles exhibit the usual law of the wall, suggesting the importance of orbital motions induced by large interface deformations.
Figure 8. Time evolution of the pressure drag
$P_{D}$
normalized by the reference value of the shear stress at the interface,
${\it\tau}_{int}=1.17\times 10^{-3}$
, for simulation
$S1$
(
$\sqrt{\mathit{Fr}}/\mathit{We}=2.03$
). Explicit indication of the statistically steady-state value of
$P_{D}/{\it\tau}_{int}\simeq 0.1$
is also shown (dashed line, – – –).
4. Conclusions and future development
In this work we used DNS to analyse the dynamics of a deformable interface between countercurrent air and water turbulent streams. The motion of the air/water interface was tracked employing a boundary-fitted method. At each time step, the distorted physical domain was mapped into a rectangular domain where Navier–Stokes and continuity equations were solved using a pseudospectral method. The problem can be described by three dimensionless numbers: the Reynolds number
$\mathit{Re}_{{\it\tau}}$
, the Weber number
$\mathit{We}$
and the Froude number
$\mathit{Fr}$
. We started by considering the transient behaviour of the interface dynamics. At the beginning, the growth of the interfacial wave amplitude
${\it\eta}$
is driven by surface tension and follows an
${\it\eta}\propto t^{2/5}$
law, for all the values of the physical parameters considered. Later in time, the dynamics of the interface depends on the ratio between gravity and surface tension effects, i.e. on
$\sqrt{\mathit{Fr}}/\mathit{We}$
. For
$\sqrt{\mathit{Fr}}/\mathit{We}<2$
,
${\it\eta}$
continues to evolve following an
${\it\eta}\propto t^{2/5}$
law, which indicates that surface tension remains the leading term. A simplified phenomenological model has also been derived to describe this result. For
$\sqrt{\mathit{Fr}}/\mathit{We}>2$
, we observed a faster growth rate which is probably due to gravity effects becoming more important. From a transient wave mode analysis, a similar behaviour is observed for the growth rate of the most significant modes. After the transient evolution, the interface deformation reached a statistically steady state. To characterize this statistically steady state, we computed wavenumber spectra
$E(k_{x})$
of the interface deformation, and we found a fair agreement between our results and those predicted by WTT. We finally observed that wave/turbulence interactions can produce remarkable modifications on the average wind and current velocity profiles. Further developments of this study could include surface tension gradients (air/water interface elasticity), which are of specific importance in many environmental and industrial applications (when biofilms, microlayers or contaminants are present at the air/water interface).
Acknowledgements
CINECA Supercomputing Centre (Bologna, Italy) and ISCRA Computing Initiative are gratefully acknowledged for generous allowance of computer resources. Support from PRIN under grant 2006098584 004 and from Regione Autonoma Friuli Venezia Giulia under grant PAR FSC 2007/2013 is gratefully acknowledged. F.Z. gratefully acknowledges the Department of Physics, University of Torino, for financial support under grant 234175. M.O. was supported by ONR grant no. 214N000141010991 and by MIUR grant no. PRIN 2012BFNWZ2. M.O. thanks Dr B. Giulinico for fruitful discussions.
