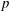1 Introduction
About half a century before the discovery of the integral invariant of velocity circulation, Cauchy (Reference Cauchy1815) found a local form of this conservation law, now called the Cauchy invariants, which constitutes the central topic of the present paper. The somewhat tortuous history of the Cauchy invariants has been documented by Frisch & Villone (Reference Frisch and Villone2014). Starting in the 1960s, the Cauchy invariants were rediscovered by application of the Noether theorem, which relates continuous invariance groups and conservation laws; at first this was done without attribution to Cauchy (Eckart Reference Eckart1960; Salmon Reference Salmon1988; Padhye & Morrison Reference Padhye and Morrison1996). But, eventually, near the end of the 20th century, proper attribution was made (Abrashkin, Zen’kovich & Yakubovich Reference Abrashkin, Zen’kovich and Yakubovich1996; Zakharov & Kuznetsov Reference Zakharov and Kuznetsov1997).
In recent years, there has been growing interest in Cauchy invariants because of the development of new applications, such as analyticity in time of fluid-particle trajectories (Frisch & Zheligovsky Reference Frisch and Zheligovsky2014; Zheligovsky & Frisch Reference Zheligovsky and Frisch2014; Rampf, Villone & Frisch Reference Rampf, Villone and Frisch2015; Besse & Frisch Reference Besse and Frisch2017, see also Constantin, Vicol & Wu Reference Constantin, Vicol and Wu2015a ; Constantin, Kukavica & Vicol Reference Constantin, Kukavica and Vicol2015b ), and the design of very accurate semi-Lagrangian numerical schemes for fluid flow (Podvigina, Zheligovsky & Frisch Reference Podvigina, Zheligovsky and Frisch2016).
Our geometric approach to the Cauchy invariants will allow us to achieve two goals. On the one hand to unify various vorticity results: as we shall see, the 3D Cauchy invariants equation, as originally formulated, the Cauchy formula relating current and initial vorticity, and Helmholtz’s result on conservation of vorticity flux may all be viewed as expressing the geometrical conservation law of vorticity. On the other hand it will allow us to extend the invariants into various directions: higher-order Cauchy invariants, magnetohydrodynamics (MHD), flow in Euclidean spaces of any dimension, and flow in curved spaces. Of course, flows of practical interest are not restricted to flat space (Kuvshinov & Schep Reference Kuvshinov and Schep1997; Marsden & Ratiu Reference Marsden and Ratiu1999). Curved spaces appear not only in General Relativistic fluid dynamics (Weinberg Reference Weinberg1972; Choquet-Bruhat Reference Choquet-Bruhat2008), but also for flows in the atmosphere and oceans of planets (Sadourny, Arakawa & Mintz Reference Sadourny, Arakawa and Mintz1968), for studies of the energy inverse cascade on negatively curved spaces (Falkovich & Gawedzki Reference Falkovich and Gawedzki2014, see also Arnold & Khesin Reference Arnold and Khesin1998, Khesin & Misiolek Reference Khesin and Misiolek2012), and also for flows on curved biological membranes (Seifert Reference Seifert1991; Ricca & Nipoti Reference Ricca and Nipoti2011; Liu & Ricca Reference Liu and Ricca2015). Moreover, recently, Gilbert & Vanneste (Reference Gilbert and Vanneste2016) have used differential geometry tools such as pullback transport to extend the generalised Lagrangian theory (GLM) of Andrews & McIntyre (Reference Andrews and McIntyre1978) to curved spaces. Hereafter, the notation 1D, 2D and 3D will refer to the usual one-, two- and three-dimensional flat (Euclidean) spaces.
For carrying out this program our key tools will be differential geometry and, to a lesser extent, variational methods.
In differential geometry we shall make use of Lie’s generalisation of advection (transport). The Lie advection of a scalar quantity is just its invariance along fluid-particle trajectories. But, here, we consider more general objects, such as vectors,
![]() $p$
-forms and tensors. For example, for our purpose, it is more convenient to consider the vorticity as a 2-form (roughly an antisymmetric second-order tensor), rather than as a vector field. These non-scalar objects live in vector spaces spanned by some basis, and Lie advection requires taking into account the distortion of the underlying vector space structure, which moves and deforms with the flow. The generalisation of the particular (material) derivative to tensors is thus the Lie derivative.
$p$
-forms and tensors. For example, for our purpose, it is more convenient to consider the vorticity as a 2-form (roughly an antisymmetric second-order tensor), rather than as a vector field. These non-scalar objects live in vector spaces spanned by some basis, and Lie advection requires taking into account the distortion of the underlying vector space structure, which moves and deforms with the flow. The generalisation of the particular (material) derivative to tensors is thus the Lie derivative.
As to variational (least-action) methods, an important advantage is that they are applicable with very little change to both flat and curved spaces, provided one uses Arnold’s formulation of ideal incompressible fluid flow as geodesics on the space SDiff of volume-preserving smooth maps (Arnold Reference Arnold1966; Arnold & Khesin Reference Arnold and Khesin1998). Since the 1950s, to derive or rediscover the Cauchy invariants equation, a frequently used approach has been via Noether’s theorem with the appropriate continuous invariance group, namely the relabelling invariance in Lagrangian coordinates. The latter can be viewed as a continuous counterpart of the permutation of Lagrangian labels if the fluids were constituted of a finite number of fluid elements; note that continuous volume-preserving transformations may be approached by such permutations (Lax Reference Lax1971; Shnirelman Reference Shnirelman1985).
The outline of the paper is as follows. Section 2 is about Lie derivatives, an extension to flow on manifolds of what is called in fluid mechanics the Lagrangian or material derivative. We then prove a very general result about Lie-advection invariance for exact
![]() $p$
-forms of order
$p$
-forms of order
![]() $p\geqslant 2$
, namely that there are generalised Cauchy invariants equations (see Theorem 1), a very concrete Lagrangian expression of Lie-advection invariance. This theorem is applicable both to linear transport theory, when the advecting velocity is prescribed, and to nonlinear (or self-consistent) transport, when the Lie-advected quantity (e.g., the vorticity) is coupled back to the velocity (e.g., through the Biot–Savart law). Contrary to most modern derivations of Cauchy invariants, our proof does not make use of Noether’s theorem. Actually, for the case of linear transport, there may not even be a suitable continuous symmetry group to ensure the existence of a Noether theorem. Section 2.4.1 is about generalised Cauchy formulae, which are actually the Hodge duals of the Cauchy invariants equations. Theorem 1 has a broad applicability, as exemplified in the subsequent sections. Section 2.5.1 is about ideal incompressible MHD. Section 2.5.2 is about adiabatic and barotropic compressible fluids. Section 2.5.3 is about barotropic ideal compressible MHD. Section 2.5.4 is about extended ideal compressible MHD. Finally, § 2.5.5 is about Tao’s recent modification of the 3D Euler equation allowing finite-time blow-up and its geometric interpretation.
$p\geqslant 2$
, namely that there are generalised Cauchy invariants equations (see Theorem 1), a very concrete Lagrangian expression of Lie-advection invariance. This theorem is applicable both to linear transport theory, when the advecting velocity is prescribed, and to nonlinear (or self-consistent) transport, when the Lie-advected quantity (e.g., the vorticity) is coupled back to the velocity (e.g., through the Biot–Savart law). Contrary to most modern derivations of Cauchy invariants, our proof does not make use of Noether’s theorem. Actually, for the case of linear transport, there may not even be a suitable continuous symmetry group to ensure the existence of a Noether theorem. Section 2.4.1 is about generalised Cauchy formulae, which are actually the Hodge duals of the Cauchy invariants equations. Theorem 1 has a broad applicability, as exemplified in the subsequent sections. Section 2.5.1 is about ideal incompressible MHD. Section 2.5.2 is about adiabatic and barotropic compressible fluids. Section 2.5.3 is about barotropic ideal compressible MHD. Section 2.5.4 is about extended ideal compressible MHD. Finally, § 2.5.5 is about Tao’s recent modification of the 3D Euler equation allowing finite-time blow-up and its geometric interpretation.
Then, in § 3, we turn to various applications in ordinary hydrodynamics. Problems of helicities for hydrodynamics and MHD and their little-studied local variants are presented in § 4. Concluding remarks and a discussion of various open problems are found in § 5. There are two sets of appendices. Appendix A gives proofs of certain technical questions, not found in the existing literature. Appendix B, ‘Differential geometry in a nutshell’, has a different purpose: it is meant to provide an interface between the fluid mechanics reader and the sometimes rather difficult literature on differential geometry. Specifically, whenever we use a concept from differential geometry that the reader may not be familiar with, e.g., a ‘pullback’, we give a soft definition in simple language in the body of the text and we refer to a suitable subsection of appendix B. There, the reader will find more precise definitions and, whenever possible, short proofs of key results, together with precise references (including sections or page numbers) to what, we believe, is particularly readable specialised literature on the topic.
2 A general result about Lie-advection and Cauchy invariants
2.1 A few words about differential geometry
In the present paper we prefer not starting with a barrage of mathematical definitions and we rather appeal to the reader’s intuition. For those hungry of precise definitions, more elaborate, but still quite elementary, material and guides to the literature are found in appendix B and its various subsections. For reasons explained in the Introduction, we feel that it is essential not to restrict our discussion to flat spaces. Otherwise we would have used a ‘half-way house’ approach where all the differential geometry is expressed in the standard language of vector operations, as done, for example in the paper of Larsson (Reference Larsson1996).
The concept of a differentiable manifold
![]() $M$
generalises to an arbitrary dimension
$M$
generalises to an arbitrary dimension
![]() $d$
that of a curve or a surface embedded in the 3D Euclidean space
$d$
that of a curve or a surface embedded in the 3D Euclidean space
![]() $\mathbb{R}^{3}$
. To achieve this in an intrinsic fashion without directly using Cartesian coordinates, the most common procedure makes use of collections of local charts, which are smooth bijections (one-to-one correspondences) with pieces of
$\mathbb{R}^{3}$
. To achieve this in an intrinsic fashion without directly using Cartesian coordinates, the most common procedure makes use of collections of local charts, which are smooth bijections (one-to-one correspondences) with pieces of
![]() $\mathbb{R}^{d}$
.
$\mathbb{R}^{d}$
.
By taking infinitesimal increments near a point
![]() $a\in M$
, one obtains tangent vectors, which are in the
$a\in M$
, one obtains tangent vectors, which are in the
![]() $d$
-dimensional tangent space
$d$
-dimensional tangent space
![]() $TM_{a}$
, a generalisation of the tangent line to a curve and the tangent plane to a surface. The union of all these tangent vectors
$TM_{a}$
, a generalisation of the tangent line to a curve and the tangent plane to a surface. The union of all these tangent vectors
 $\bigcup _{a\in M}TM_{a}$
, denoted
$\bigcup _{a\in M}TM_{a}$
, denoted
![]() $TM$
, is called the tangent bundle.
$TM$
, is called the tangent bundle.
As for ordinary vector spaces, one can define the dual of the tangent bundle, noted
![]() $T^{\ast }M$
, which can be constructed through linear forms, called 1-forms or cotangent vectors, acting on vectors of the tangent bundle
$T^{\ast }M$
, which can be constructed through linear forms, called 1-forms or cotangent vectors, acting on vectors of the tangent bundle
![]() $TM$
. The set of all these cotangent vectors is called the cotangent bundle, noted
$TM$
. The set of all these cotangent vectors is called the cotangent bundle, noted
![]() $T^{\ast }M$
. Similarly,
$T^{\ast }M$
. Similarly,
![]() $p$
-forms, where
$p$
-forms, where
![]() $p$
is an integer, are skew-symmetric
$p$
is an integer, are skew-symmetric
![]() $p$
-linear forms over the tangent bundle
$p$
-linear forms over the tangent bundle
![]() $TM$
. Note that in a flat (Euclidean) space
$TM$
. Note that in a flat (Euclidean) space
![]() $\mathbb{R}^{d}$
with coordinates
$\mathbb{R}^{d}$
with coordinates
![]() $x=\{x_{i}\}$
, where
$x=\{x_{i}\}$
, where
 $i=1,\ldots ,d$
, a 1-form is simply an expression
$i=1,\ldots ,d$
, a 1-form is simply an expression
 $\sum _{i}a_{i}(x)\,\text{d}x_{i}$
, which depends linearly on the infinitesimal increments
$\sum _{i}a_{i}(x)\,\text{d}x_{i}$
, which depends linearly on the infinitesimal increments
![]() $\text{d}x_{i}$
. It is also interesting to note that 1-forms were in common use in fluid mechanics in the works of D’Alembert, Euler and Lagrange more than a century before vectors were commonly used, say, in the lectures of Gibbs.
$\text{d}x_{i}$
. It is also interesting to note that 1-forms were in common use in fluid mechanics in the works of D’Alembert, Euler and Lagrange more than a century before vectors were commonly used, say, in the lectures of Gibbs.
An important operator on
![]() $p$
-forms is the exterior derivative,
$p$
-forms is the exterior derivative,
![]() $\text{d}$
, which linearly maps
$\text{d}$
, which linearly maps
![]() $p$
-forms to
$p$
-forms to
![]() $(p+1)$
-forms (see § B.8). An explicit definition of
$(p+1)$
-forms (see § B.8). An explicit definition of
![]() $\text{d}$
is not very helpful to build an intuitive feeling, but it is worth pointing out that the square of
$\text{d}$
is not very helpful to build an intuitive feeling, but it is worth pointing out that the square of
![]() $\text{d}$
is zero or, in words, an exact form (a form that is the exterior derivative of another one) is closed (its exterior derivative vanishes). Under certain conditions, to which we shall come back, the converse is true.
$\text{d}$
is zero or, in words, an exact form (a form that is the exterior derivative of another one) is closed (its exterior derivative vanishes). Under certain conditions, to which we shall come back, the converse is true.
2.2 Lie advection: an extension of the Lagrangian (material) derivative
In this section we present some standard mathematical concepts needed to introduce our theorem on generalised Cauchy invariants, stated in the next section. For this, we need to generalise the fluid mechanics concept of Lagrangian invariant, which applies to a scalar quantity that does not change along fluid-particle trajectories. The generalisation is called Lie-advection invariance (alternative terminologies found in the literature are ‘Lie-transport’ and ‘Lie-dragging’).
First we introduce the pullback and pushforward operations, which arise naturally when applying a change of variable, here, between Lagrangian and Eulerian coordinates at a fixed time
![]() $t$
(later, we shall let this dynamical time vary). The Lagrangian variable (initial position of the fluid particle), denoted by
$t$
(later, we shall let this dynamical time vary). The Lagrangian variable (initial position of the fluid particle), denoted by
![]() $a$
, is on a manifold
$a$
, is on a manifold
![]() $M$
(called here for concreteness Lagrangian), while the Eulerian variable (current position of the fluid particle), denoted by
$M$
(called here for concreteness Lagrangian), while the Eulerian variable (current position of the fluid particle), denoted by
![]() $x$
, is on a manifold
$x$
, is on a manifold
![]() $N$
(called here Eulerian). The sets
$N$
(called here Eulerian). The sets
![]() $M$
and
$M$
and
![]() $N$
may or may not coincide. The Lagrangian map linking
$N$
may or may not coincide. The Lagrangian map linking
![]() $a\in M$
to
$a\in M$
to
![]() $x\in N$
is defined as follows
$x\in N$
is defined as follows
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D711}:\quad M\rightarrow N\\ a\mapsto x=\unicode[STIX]{x1D711}(a).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D711}:\quad M\rightarrow N\\ a\mapsto x=\unicode[STIX]{x1D711}(a).\end{array}\right\}\end{eqnarray}$$
The change of variable
 $a\rightarrow x=\unicode[STIX]{x1D711}(a)$
induces two operations that connect objects (such as functions, vectors, forms and tensors), defined on
$a\rightarrow x=\unicode[STIX]{x1D711}(a)$
induces two operations that connect objects (such as functions, vectors, forms and tensors), defined on
![]() $M$
to corresponding ones, defined on
$M$
to corresponding ones, defined on
![]() $N$
. They are the pushforward operator, which sends objects defined on
$N$
. They are the pushforward operator, which sends objects defined on
![]() $M$
to ones defined on
$M$
to ones defined on
![]() $N$
and its inverse, the pullback operator. To define these transformations precisely, it is convenient to consider successively the cases where these operators act on real-valued functions (scalars), then on vectors, then on 1-forms, and finally on more involved objects such as
$N$
and its inverse, the pullback operator. To define these transformations precisely, it is convenient to consider successively the cases where these operators act on real-valued functions (scalars), then on vectors, then on 1-forms, and finally on more involved objects such as
![]() $p$
-forms, obtainable from the former ones by linear combinations of tensor products (see § B.2).
$p$
-forms, obtainable from the former ones by linear combinations of tensor products (see § B.2).
For the case of scalars, namely elements of
![]() ${\mathcal{F}}(M)$
, the set of real-valued smooth functions defined on
${\mathcal{F}}(M)$
, the set of real-valued smooth functions defined on
![]() $M$
, the pullback is simply a change of variable from Eulerian to Lagrangian variables and the pushforward is the converse. Specifically, the pushforward of a function
$M$
, the pullback is simply a change of variable from Eulerian to Lagrangian variables and the pushforward is the converse. Specifically, the pushforward of a function
 $f:M\rightarrow \mathbb{R}$
on
$f:M\rightarrow \mathbb{R}$
on
![]() $M$
is
$M$
is
 $\unicode[STIX]{x1D711}_{\ast }f=f\circ \unicode[STIX]{x1D711}^{-1}$
, where the symbol
$\unicode[STIX]{x1D711}_{\ast }f=f\circ \unicode[STIX]{x1D711}^{-1}$
, where the symbol
![]() $\circ$
denotes the usual composition of maps. Conversely, the pullback of a function
$\circ$
denotes the usual composition of maps. Conversely, the pullback of a function
 $f:N\rightarrow \mathbb{R}$
on
$f:N\rightarrow \mathbb{R}$
on
![]() $N$
is
$N$
is
 $\unicode[STIX]{x1D711}^{\ast }f=f\circ \unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}^{\ast }f=f\circ \unicode[STIX]{x1D711}$
.
Now, we turn to vector fields, denoted
![]() ${\mathcal{T}}_{0}^{1}(M)$
on
${\mathcal{T}}_{0}^{1}(M)$
on
![]() $M$
, a subset of the tangent bundle
$M$
, a subset of the tangent bundle
![]() $TM$
. (Why we use the notation
$TM$
. (Why we use the notation
![]() ${\mathcal{T}}_{0}^{1}(M)$
will become clear later.) At this point we cannot just make a change of variable, because the Lagrangian and the Eulerian vectors take values in different tangent spaces. But we can reinterpret tangent vectors to a manifold in terms of differentials of scalar functions defined on that manifold. To implement this, it is useful to consider a vector field
${\mathcal{T}}_{0}^{1}(M)$
will become clear later.) At this point we cannot just make a change of variable, because the Lagrangian and the Eulerian vectors take values in different tangent spaces. But we can reinterpret tangent vectors to a manifold in terms of differentials of scalar functions defined on that manifold. To implement this, it is useful to consider a vector field
![]() $X(a)$
on
$X(a)$
on
![]() $M$
as the generator of a suitable flow on
$M$
as the generator of a suitable flow on
![]() $M$
. For this, we need an auxiliary time variable, denoted
$M$
. For this, we need an auxiliary time variable, denoted
![]() $s$
, to parametrise a family of smooth maps
$s$
, to parametrise a family of smooth maps
 $\unicode[STIX]{x1D6FE}_{s}:M\rightarrow M$
. Observe that the time
$\unicode[STIX]{x1D6FE}_{s}:M\rightarrow M$
. Observe that the time
![]() $s$
is not related to the dynamical time
$s$
is not related to the dynamical time
![]() $t$
, which so far is held fixed. The maps satisfy the following equations
$t$
, which so far is held fixed. The maps satisfy the following equations
 $$\begin{eqnarray}\dot{\unicode[STIX]{x1D6FE}_{s}}:=\frac{\text{d}\unicode[STIX]{x1D6FE}_{s}}{\text{d}s}=X(\unicode[STIX]{x1D6FE}_{s}),\quad \unicode[STIX]{x1D6FE}_{0}(a)=a,\quad a\in M.\end{eqnarray}$$
$$\begin{eqnarray}\dot{\unicode[STIX]{x1D6FE}_{s}}:=\frac{\text{d}\unicode[STIX]{x1D6FE}_{s}}{\text{d}s}=X(\unicode[STIX]{x1D6FE}_{s}),\quad \unicode[STIX]{x1D6FE}_{0}(a)=a,\quad a\in M.\end{eqnarray}$$
The pushforward of the vector field
 $Y\in {\mathcal{T}}_{0}^{1}(N)$
(also called the differential of the map
$Y\in {\mathcal{T}}_{0}^{1}(N)$
(also called the differential of the map
![]() $\unicode[STIX]{x1D711}$
or the tangent map) is now defined locally at the point
$\unicode[STIX]{x1D711}$
or the tangent map) is now defined locally at the point
![]() $a\in M$
, as the linear map
$a\in M$
, as the linear map
 $\unicode[STIX]{x1D711}_{\ast }:=T_{a}\unicode[STIX]{x1D711}:TM_{a}\rightarrow TN_{\unicode[STIX]{x1D711}(a)}$
, obtained by simply identifying the resulting vector with the tangent vector to the mapped curve. This is illustrated in figure 1. Translated into equations it means that
$\unicode[STIX]{x1D711}_{\ast }:=T_{a}\unicode[STIX]{x1D711}:TM_{a}\rightarrow TN_{\unicode[STIX]{x1D711}(a)}$
, obtained by simply identifying the resulting vector with the tangent vector to the mapped curve. This is illustrated in figure 1. Translated into equations it means that
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }X=\unicode[STIX]{x1D711}_{\ast }\left.\left(\frac{\text{d}\unicode[STIX]{x1D6FE}_{s}}{\text{d}s}\right)\right|_{s=0}:=\left.\left(\frac{\text{d}}{\text{d}s}\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D6FE}_{s}\right)\right|_{s=0}=T\unicode[STIX]{x1D711}\circ X\circ \unicode[STIX]{x1D711}^{-1},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{\ast }X=\unicode[STIX]{x1D711}_{\ast }\left.\left(\frac{\text{d}\unicode[STIX]{x1D6FE}_{s}}{\text{d}s}\right)\right|_{s=0}:=\left.\left(\frac{\text{d}}{\text{d}s}\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D6FE}_{s}\right)\right|_{s=0}=T\unicode[STIX]{x1D711}\circ X\circ \unicode[STIX]{x1D711}^{-1},\end{eqnarray}$$
where
![]() $T$
denotes the tangent map and is given locally by the Jacobian matrix
$T$
denotes the tangent map and is given locally by the Jacobian matrix
 $J_{\unicode[STIX]{x1D711}}=J(\unicode[STIX]{x1D711})=\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}a$
. Recalling that
$J_{\unicode[STIX]{x1D711}}=J(\unicode[STIX]{x1D711})=\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}a$
. Recalling that
![]() $a^{i}$
denotes local coordinates on
$a^{i}$
denotes local coordinates on
![]() $M$
and
$M$
and
![]() $x^{i}$
local coordinates on
$x^{i}$
local coordinates on
![]() $N$
, in terms of these local coordinates, this formula is expressed equivalently as
$N$
, in terms of these local coordinates, this formula is expressed equivalently as
 $$\begin{eqnarray}(\unicode[STIX]{x1D711}_{\ast }X)^{i}(x)=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{i}}{\unicode[STIX]{x2202}a^{\,j}}(a)X^{j}(a)=\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{\,j}}(a)X^{j}(a).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D711}_{\ast }X)^{i}(x)=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{i}}{\unicode[STIX]{x2202}a^{\,j}}(a)X^{j}(a)=\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{\,j}}(a)X^{j}(a).\end{eqnarray}$$
To define the inverse operation, the pullback denoted
![]() $\unicode[STIX]{x1D711}^{\ast }$
, we just interchange
$\unicode[STIX]{x1D711}^{\ast }$
, we just interchange
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $\unicode[STIX]{x1D711}^{-1}$
. Thus we have
$\unicode[STIX]{x1D711}^{-1}$
. Thus we have
 $\unicode[STIX]{x1D711}_{\ast }=(\unicode[STIX]{x1D711}^{-1})^{\ast }=(\unicode[STIX]{x1D711}^{\ast })^{-1}$
and
$\unicode[STIX]{x1D711}_{\ast }=(\unicode[STIX]{x1D711}^{-1})^{\ast }=(\unicode[STIX]{x1D711}^{\ast })^{-1}$
and
 $\unicode[STIX]{x1D711}^{\ast }=(\unicode[STIX]{x1D711}^{-1})_{\ast }=(\unicode[STIX]{x1D711}_{\ast })^{-1}$
. It thus follows that the pullback of a vector field
$\unicode[STIX]{x1D711}^{\ast }=(\unicode[STIX]{x1D711}^{-1})_{\ast }=(\unicode[STIX]{x1D711}_{\ast })^{-1}$
. It thus follows that the pullback of a vector field
 $Y\in {\mathcal{T}}_{0}^{1}(N)$
on
$Y\in {\mathcal{T}}_{0}^{1}(N)$
on
![]() $N$
is
$N$
is
 $$\begin{eqnarray}\unicode[STIX]{x1D711}^{\ast }Y=(T\unicode[STIX]{x1D711})^{-1}\circ Y\circ \unicode[STIX]{x1D711},\quad \text{or componentwise}\quad (\unicode[STIX]{x1D711}^{\ast }Y)^{i}(a)=\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D711}^{-1})^{i}}{\unicode[STIX]{x2202}x^{\,j}}(x)Y^{j}(x)=\frac{\unicode[STIX]{x2202}a^{i}}{\unicode[STIX]{x2202}x^{\,j}}(x)Y^{j}(x).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}^{\ast }Y=(T\unicode[STIX]{x1D711})^{-1}\circ Y\circ \unicode[STIX]{x1D711},\quad \text{or componentwise}\quad (\unicode[STIX]{x1D711}^{\ast }Y)^{i}(a)=\frac{\unicode[STIX]{x2202}(\unicode[STIX]{x1D711}^{-1})^{i}}{\unicode[STIX]{x2202}x^{\,j}}(x)Y^{j}(x)=\frac{\unicode[STIX]{x2202}a^{i}}{\unicode[STIX]{x2202}x^{\,j}}(x)Y^{j}(x).\end{eqnarray}$$
Therefore we find that
 $\unicode[STIX]{x1D711}^{\ast }Y=(\unicode[STIX]{x1D711}^{\ast }Y)^{i}(a)(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i})=Y^{i}(x)(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x^{i})$
and
$\unicode[STIX]{x1D711}^{\ast }Y=(\unicode[STIX]{x1D711}^{\ast }Y)^{i}(a)(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i})=Y^{i}(x)(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x^{i})$
and
 $\unicode[STIX]{x1D711}_{\ast }X=(\unicode[STIX]{x1D711}_{\ast }X)^{i}(x)(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x^{i})=X^{i}(a)(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i})$
. Notice that
$\unicode[STIX]{x1D711}_{\ast }X=(\unicode[STIX]{x1D711}_{\ast }X)^{i}(x)(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x^{i})=X^{i}(a)(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i})$
. Notice that
![]() $\unicode[STIX]{x1D711}$
must be a diffeomorphism (one-to-one smooth map) in order for the pullback and pushforward operations to make sense; the only exception to this is the pullback of functions (and covariant tensors, see § B.4), since the inverse map is then not needed. Thus vector fields can only be pulled back and pushed forward by diffeomorphisms.
$\unicode[STIX]{x1D711}$
must be a diffeomorphism (one-to-one smooth map) in order for the pullback and pushforward operations to make sense; the only exception to this is the pullback of functions (and covariant tensors, see § B.4), since the inverse map is then not needed. Thus vector fields can only be pulled back and pushed forward by diffeomorphisms.

Figure 1. The curve
![]() $\unicode[STIX]{x1D6FE}_{s}$
is the integral curve of a given vector field
$\unicode[STIX]{x1D6FE}_{s}$
is the integral curve of a given vector field
![]() $X$
, while the curve
$X$
, while the curve
![]() $\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D6FE}_{s}$
is the integral curve of
$\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D6FE}_{s}$
is the integral curve of
![]() $\unicode[STIX]{x1D711}_{\ast }X$
. The pullback transformation
$\unicode[STIX]{x1D711}_{\ast }X$
. The pullback transformation
![]() $\unicode[STIX]{x1D711}^{\ast }$
is a change of variables from Eulerian to Lagrangian coordinates, while the pushforward transformation
$\unicode[STIX]{x1D711}^{\ast }$
is a change of variables from Eulerian to Lagrangian coordinates, while the pushforward transformation
![]() $\unicode[STIX]{x1D711}_{\ast }$
is a change of variables from Lagrangian to Eulerian coordinates.
$\unicode[STIX]{x1D711}_{\ast }$
is a change of variables from Lagrangian to Eulerian coordinates.
We can extend pullback and pushforward operations to linear forms on vector fields, that is 1-forms or covectors. The set of such 1-forms fields on
![]() $M$
is denoted by
$M$
is denoted by
 ${\mathcal{T}}_{1}^{0}(M)\subset T^{\ast }M$
(see §§ B.2 and B.7). In order to define the pullback of a 1-form
${\mathcal{T}}_{1}^{0}(M)\subset T^{\ast }M$
(see §§ B.2 and B.7). In order to define the pullback of a 1-form
 $\unicode[STIX]{x1D6FC}\in {\mathcal{T}}_{1}^{0}(N)$
, we introduce the linear map
$\unicode[STIX]{x1D6FC}\in {\mathcal{T}}_{1}^{0}(N)$
, we introduce the linear map
 $\unicode[STIX]{x1D711}^{\ast }:T^{\ast }N_{\unicode[STIX]{x1D711}(a)}\rightarrow T^{\ast }M_{a}$
, defined by
$\unicode[STIX]{x1D711}^{\ast }:T^{\ast }N_{\unicode[STIX]{x1D711}(a)}\rightarrow T^{\ast }M_{a}$
, defined by
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC},X\rangle :=\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D711}_{\ast }X\rangle ,\quad X\in {\mathcal{T}}_{0}^{1}(M),\quad \unicode[STIX]{x1D6FC}\in {\mathcal{T}}_{1}^{0}(N),\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC},X\rangle :=\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D711}_{\ast }X\rangle ,\quad X\in {\mathcal{T}}_{0}^{1}(M),\quad \unicode[STIX]{x1D6FC}\in {\mathcal{T}}_{1}^{0}(N),\end{eqnarray}$$
where the duality bracket
![]() $\langle \cdot ,\cdot \rangle$
is the natural pairing between the spaces
$\langle \cdot ,\cdot \rangle$
is the natural pairing between the spaces
![]() $TM_{a}$
and
$TM_{a}$
and
![]() $T^{\ast }M_{a}$
or between the spaces
$T^{\ast }M_{a}$
or between the spaces
![]() $TN_{\unicode[STIX]{x1D711}(a)}$
and
$TN_{\unicode[STIX]{x1D711}(a)}$
and
![]() $T^{\ast }N_{\unicode[STIX]{x1D711}(a)}$
. The pushforward of a 1-form
$T^{\ast }N_{\unicode[STIX]{x1D711}(a)}$
. The pushforward of a 1-form
 $\unicode[STIX]{x1D6FD}\in {\mathcal{T}}_{1}^{0}(M)$
, is defined by changing
$\unicode[STIX]{x1D6FD}\in {\mathcal{T}}_{1}^{0}(M)$
, is defined by changing
![]() $\unicode[STIX]{x1D711}$
to
$\unicode[STIX]{x1D711}$
to
![]() $\unicode[STIX]{x1D711}^{-1}$
, i.e.
$\unicode[STIX]{x1D711}^{-1}$
, i.e.
 $\unicode[STIX]{x1D711}_{\ast }:=(\unicode[STIX]{x1D711}^{-1})^{\ast }$
. In terms of local coordinates we have
$\unicode[STIX]{x1D711}_{\ast }:=(\unicode[STIX]{x1D711}^{-1})^{\ast }$
. In terms of local coordinates we have
 $$\begin{eqnarray}(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC})_{i}(a)=\frac{\unicode[STIX]{x2202}x^{\,j}}{\unicode[STIX]{x2202}a^{i}}(a)\unicode[STIX]{x1D6FC}_{j}(x),\quad (\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x1D6FD})_{i}(x)=\frac{\unicode[STIX]{x2202}a^{\,j}}{\unicode[STIX]{x2202}x^{i}}(x)\unicode[STIX]{x1D6FD}_{j}(a).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC})_{i}(a)=\frac{\unicode[STIX]{x2202}x^{\,j}}{\unicode[STIX]{x2202}a^{i}}(a)\unicode[STIX]{x1D6FC}_{j}(x),\quad (\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x1D6FD})_{i}(x)=\frac{\unicode[STIX]{x2202}a^{\,j}}{\unicode[STIX]{x2202}x^{i}}(x)\unicode[STIX]{x1D6FD}_{j}(a).\end{eqnarray}$$
Therefore we find that
 $\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC}:=(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC})_{i}(a)\,\text{d}a^{i}=\unicode[STIX]{x1D6FC}_{i}(x)\,\text{d}x^{i}$
and
$\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC}:=(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC})_{i}(a)\,\text{d}a^{i}=\unicode[STIX]{x1D6FC}_{i}(x)\,\text{d}x^{i}$
and
 $\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x1D6FD}:=(\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x1D6FD})_{i}(x)\,\text{d}x^{i}=\unicode[STIX]{x1D6FD}_{i}(a)\,\text{d}a^{i}$
.
$\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x1D6FD}:=(\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x1D6FD})_{i}(x)\,\text{d}x^{i}=\unicode[STIX]{x1D6FD}_{i}(a)\,\text{d}a^{i}$
.
Pullback and pushforward operations are easily generalised to tensor fields
 $\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
, where
$\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
, where
![]() ${\mathcal{T}}_{p}^{q}(M)$
denotes the set of
${\mathcal{T}}_{p}^{q}(M)$
denotes the set of
![]() $p$
-covariant and
$p$
-covariant and
![]() $q$
-contravariant tensor fields on
$q$
-contravariant tensor fields on
![]() $M$
. Such generalisations follow naturally since a
$M$
. Such generalisations follow naturally since a
![]() $p$
-covariant and
$p$
-covariant and
![]() $q$
-contravariant tensor can be written as linear combinations of tensor products of
$q$
-contravariant tensor can be written as linear combinations of tensor products of
![]() $p$
1-forms and
$p$
1-forms and
![]() $q$
vectors (see § B.2).
$q$
vectors (see § B.2).
In order to define the Lie derivative, we bring in the dynamical time
![]() $t$
. For this, we specialise to the case where the Lagrangian and the Eulerian points are on the same manifold (with
$t$
. For this, we specialise to the case where the Lagrangian and the Eulerian points are on the same manifold (with
![]() $N=M$
) and we consider a time-dependent vector field
$N=M$
) and we consider a time-dependent vector field
![]() $v_{t}$
, the velocity field, taken in
$v_{t}$
, the velocity field, taken in
![]() ${\mathcal{T}}_{0}^{1}(M)$
for all
${\mathcal{T}}_{0}^{1}(M)$
for all
![]() $t\geqslant 0$
. This velocity field is prescribed a priori and we do not have to specify which dynamical equation it satisfies. We define a time-dependent Lagrangian map
$t\geqslant 0$
. This velocity field is prescribed a priori and we do not have to specify which dynamical equation it satisfies. We define a time-dependent Lagrangian map
![]() $\unicode[STIX]{x1D711}_{t}$
in the usual fluid-mechanical sense as mapping the initial position of a fluid particle, following the flow, to its position at time
$\unicode[STIX]{x1D711}_{t}$
in the usual fluid-mechanical sense as mapping the initial position of a fluid particle, following the flow, to its position at time
![]() $t$
, namely as the solution of the ordinary differential equation (ODE)
$t$
, namely as the solution of the ordinary differential equation (ODE)
 $$\begin{eqnarray}\dot{\unicode[STIX]{x1D711}}_{t}=\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t}=v(t,\unicode[STIX]{x1D711}_{t}),\quad \unicode[STIX]{x1D711}_{0}=\text{Identity}.\end{eqnarray}$$
$$\begin{eqnarray}\dot{\unicode[STIX]{x1D711}}_{t}=\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t}=v(t,\unicode[STIX]{x1D711}_{t}),\quad \unicode[STIX]{x1D711}_{0}=\text{Identity}.\end{eqnarray}$$
From this equation, we also define a 2-time Lagrangian map
![]() $\unicode[STIX]{x1D711}_{t,s}$
with
$\unicode[STIX]{x1D711}_{t,s}$
with
![]() $t\geqslant 0$
and
$t\geqslant 0$
and
![]() $s\geqslant 0$
as the map from the position of a fluid particle at time
$s\geqslant 0$
as the map from the position of a fluid particle at time
![]() $s$
to its position at time
$s$
to its position at time
![]() $t$
. Allowing the time to run backwards, we do not impose
$t$
. Allowing the time to run backwards, we do not impose
![]() $t>s$
. Obviously, we have
$t>s$
. Obviously, we have
![]() $\unicode[STIX]{x1D711}_{t,0}=\unicode[STIX]{x1D711}_{t}$
. Furthermore, we obviously have the group composition rule
$\unicode[STIX]{x1D711}_{t,0}=\unicode[STIX]{x1D711}_{t}$
. Furthermore, we obviously have the group composition rule
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{t,s}=\unicode[STIX]{x1D711}_{t,\unicode[STIX]{x1D70F}}\circ \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},s}\quad \forall \,t\geqslant 0,\forall \,\unicode[STIX]{x1D70F}\geqslant 0,\forall \,s\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{t,s}=\unicode[STIX]{x1D711}_{t,\unicode[STIX]{x1D70F}}\circ \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},s}\quad \forall \,t\geqslant 0,\forall \,\unicode[STIX]{x1D70F}\geqslant 0,\forall \,s\geqslant 0.\end{eqnarray}$$
In this dynamical setting, the pullback and pushforward operations consist roughly in following a given tensor field, while taking into account the geometrical deformation of the tensor basis, along the Lagrangian flow. This will naturally lead to considering a derivative with respect to the Lagrangian flow, called the Lie derivative. The Lie derivative of a structure (for instance a vector, a 1-form or a tensor field) with respect to the time-dependent vector field
![]() $v_{t}$
measures the instantaneous rate of geometrical variation of the structure (tensor basis) as it is transported and deformed by the Lagrangian flow
$v_{t}$
measures the instantaneous rate of geometrical variation of the structure (tensor basis) as it is transported and deformed by the Lagrangian flow
![]() $\unicode[STIX]{x1D711}_{t}$
generated by
$\unicode[STIX]{x1D711}_{t}$
generated by
![]() $v_{t}$
.
$v_{t}$
.
Specifically, we first define the Lie derivative acting on a time-independent tensor field
 $\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
. To the Lagrangian map
$\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
. To the Lagrangian map
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},t}$
we associate its pullback
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},t}$
we associate its pullback
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},t}^{\ast }$
, constructed just as earlier in this section, when the dynamical time was held fixed. The Lie derivative with respect to
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},t}^{\ast }$
, constructed just as earlier in this section, when the dynamical time was held fixed. The Lie derivative with respect to
![]() $v_{t}$
is defined by
$v_{t}$
is defined by
 $$\begin{eqnarray}\unicode[STIX]{x00A3}_{v_{t}}\unicode[STIX]{x0398}:=\left.\left(\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},t}^{\ast }\unicode[STIX]{x0398}\right)\right|_{\unicode[STIX]{x1D70F}=t}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x00A3}_{v_{t}}\unicode[STIX]{x0398}:=\left.\left(\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},t}^{\ast }\unicode[STIX]{x0398}\right)\right|_{\unicode[STIX]{x1D70F}=t}.\end{eqnarray}$$
Now, we turn to a time-dependent tensor field
 $\unicode[STIX]{x0398}_{t}\in {\mathcal{T}}_{p}^{q}(M)$
and we derive the Lie-derivative theorem
$\unicode[STIX]{x0398}_{t}\in {\mathcal{T}}_{p}^{q}(M)$
and we derive the Lie-derivative theorem
![]() $\forall t\geqslant 0$
. For this, we calculate the time derivative of
$\forall t\geqslant 0$
. For this, we calculate the time derivative of
![]() $\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x0398}_{t}$
, using the product rule for derivatives and obtain
$\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x0398}_{t}$
, using the product rule for derivatives and obtain
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x0398}_{t}=\left.\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},s}^{\ast }\unicode[STIX]{x0398}_{\unicode[STIX]{x1D70F}}\right|_{\unicode[STIX]{x1D70F}=t}=\left.\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},s}^{\ast }\unicode[STIX]{x0398}_{t}\right|_{\unicode[STIX]{x1D70F}=t}+\left.\unicode[STIX]{x1D711}_{t,s}^{\ast }\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\unicode[STIX]{x0398}_{\unicode[STIX]{x1D70F}}\right|_{\unicode[STIX]{x1D70F}=t}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x0398}_{t}=\left.\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},s}^{\ast }\unicode[STIX]{x0398}_{\unicode[STIX]{x1D70F}}\right|_{\unicode[STIX]{x1D70F}=t}=\left.\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},s}^{\ast }\unicode[STIX]{x0398}_{t}\right|_{\unicode[STIX]{x1D70F}=t}+\left.\unicode[STIX]{x1D711}_{t,s}^{\ast }\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\unicode[STIX]{x0398}_{\unicode[STIX]{x1D70F}}\right|_{\unicode[STIX]{x1D70F}=t}.\end{eqnarray}$$
Then, using the group composition rule (2.9), this equation becomes
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x0398}_{t}=\left.\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},t}\circ \unicode[STIX]{x1D711}_{t,s})^{\ast }\unicode[STIX]{x0398}_{t}\right|_{\unicode[STIX]{x1D70F}=t}+\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x2202}_{t}\unicode[STIX]{x0398}_{t}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x0398}_{t}=\left.\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},t}\circ \unicode[STIX]{x1D711}_{t,s})^{\ast }\unicode[STIX]{x0398}_{t}\right|_{\unicode[STIX]{x1D70F}=t}+\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x2202}_{t}\unicode[STIX]{x0398}_{t}.\end{eqnarray}$$
Using a property for the pullback of map composition (see § B.4), namely
 $(\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713})^{\ast }=\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D711}^{\ast }$
, we obtain
$(\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713})^{\ast }=\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D711}^{\ast }$
, we obtain
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x0398}_{t}=\left.\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},t}^{\ast }\unicode[STIX]{x0398}_{t}\right|_{\unicode[STIX]{x1D70F}=t}+\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x2202}_{t}\unicode[STIX]{x0398}_{t}=\left.\unicode[STIX]{x1D711}_{t,s}^{\ast }\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},t}^{\ast }\unicode[STIX]{x0398}_{t}\right|_{\unicode[STIX]{x1D70F}=t}+\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x2202}_{t}\unicode[STIX]{x0398}_{t}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x0398}_{t}=\left.\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},t}^{\ast }\unicode[STIX]{x0398}_{t}\right|_{\unicode[STIX]{x1D70F}=t}+\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x2202}_{t}\unicode[STIX]{x0398}_{t}=\left.\unicode[STIX]{x1D711}_{t,s}^{\ast }\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F},t}^{\ast }\unicode[STIX]{x0398}_{t}\right|_{\unicode[STIX]{x1D70F}=t}+\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x2202}_{t}\unicode[STIX]{x0398}_{t}.\end{eqnarray}$$
Finally, using the definition of the Lie derivative (2.10), this equation leads to the following formula, known as the Lie-derivative theorem:
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x0398}_{t}=\unicode[STIX]{x1D711}_{t,s}^{\ast }(\unicode[STIX]{x2202}_{t}\unicode[STIX]{x0398}_{t}+\unicode[STIX]{x00A3}_{v_{t}}\unicode[STIX]{x0398}_{t}),\quad \forall t\geqslant 0,~\forall s\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t,s}^{\ast }\unicode[STIX]{x0398}_{t}=\unicode[STIX]{x1D711}_{t,s}^{\ast }(\unicode[STIX]{x2202}_{t}\unicode[STIX]{x0398}_{t}+\unicode[STIX]{x00A3}_{v_{t}}\unicode[STIX]{x0398}_{t}),\quad \forall t\geqslant 0,~\forall s\geqslant 0.\end{eqnarray}$$
In this paper, a central role will be played by tensor fields that are Lie-advection invariant (in short Lie invariant). A Lie-advection invariant tensor field
![]() $\unicode[STIX]{x0398}_{t}$
is such that its Lagrangian pullback, i.e. its pullback to time
$\unicode[STIX]{x0398}_{t}$
is such that its Lagrangian pullback, i.e. its pullback to time
![]() $t=0$
, is equal to the initial tensor field, that is
$t=0$
, is equal to the initial tensor field, that is
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x0398}_{t}=\unicode[STIX]{x0398}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x0398}_{t}=\unicode[STIX]{x0398}_{0}.\end{eqnarray}$$
In fluid mechanics terms, one then states that the tensor field
![]() $\unicode[STIX]{x0398}_{t}$
is frozen into the flow
$\unicode[STIX]{x0398}_{t}$
is frozen into the flow
![]() $\unicode[STIX]{x1D711}_{t}$
. From the Lie-derivative theorem (2.14), we immediately find that this is equivalent to having the tensor field
$\unicode[STIX]{x1D711}_{t}$
. From the Lie-derivative theorem (2.14), we immediately find that this is equivalent to having the tensor field
![]() $\unicode[STIX]{x0398}_{t}$
satisfying the equation
$\unicode[STIX]{x0398}_{t}$
satisfying the equation
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x0398}_{t}+\unicode[STIX]{x00A3}_{v_{t}}\unicode[STIX]{x0398}_{t}=0,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x0398}_{t}+\unicode[STIX]{x00A3}_{v_{t}}\unicode[STIX]{x0398}_{t}=0,\end{eqnarray}$$
which is called the Lie-advection equation. A tensor field
![]() $\unicode[STIX]{x0398}_{t}$
satisfying the Lie-advection equation (2.16) is said to be Lie-advected by the flow of
$\unicode[STIX]{x0398}_{t}$
satisfying the Lie-advection equation (2.16) is said to be Lie-advected by the flow of
![]() $v_{t}$
.
$v_{t}$
.
It is easily checked that when
![]() $\unicode[STIX]{x0398}_{t}$
is a scalar field (denoted
$\unicode[STIX]{x0398}_{t}$
is a scalar field (denoted
![]() $\unicode[STIX]{x1D703}_{t}$
) and when the manifold reduces to an Euclidean space, equation (2.16) becomes just
$\unicode[STIX]{x1D703}_{t}$
) and when the manifold reduces to an Euclidean space, equation (2.16) becomes just
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D703}_{t}+v_{t}^{i}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D703}_{t}=0,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D703}_{t}+v_{t}^{i}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D703}_{t}=0,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x2202}_{i}$
is the Eulerian derivative. Hence, in the scalar case, Lie-advection invariance of
$\unicode[STIX]{x2202}_{i}$
is the Eulerian derivative. Hence, in the scalar case, Lie-advection invariance of
![]() $\unicode[STIX]{x1D703}_{t}$
is the same as stating that
$\unicode[STIX]{x1D703}_{t}$
is the same as stating that
![]() $\unicode[STIX]{x1D703}_{t}$
is a Lagrangian (material) invariant in the usual fluid-mechanical sense. The advantage of the Lie-advection invariance formulation for higher-order objects is that, e.g., in 3D the vorticity, when considered as a 2-form, is then also Lie-advection invariant, as noticed for the first time (in 19th century language) by Helmholtz (Reference von Helmholtz1858).
$\unicode[STIX]{x1D703}_{t}$
is a Lagrangian (material) invariant in the usual fluid-mechanical sense. The advantage of the Lie-advection invariance formulation for higher-order objects is that, e.g., in 3D the vorticity, when considered as a 2-form, is then also Lie-advection invariant, as noticed for the first time (in 19th century language) by Helmholtz (Reference von Helmholtz1858).
2.3 Generalised Cauchy invariants
In this section we state a general theorem about Lie-advection invariance using differential geometry tools. The result is a natural generalisation of Cauchy invariants that arises when we consider, in an Euclidean space
![]() $\mathbb{R}^{d}$
or on a
$\mathbb{R}^{d}$
or on a
![]() $d$
-dimensional Riemannian manifold
$d$
-dimensional Riemannian manifold
![]() $(M,g)$
, a Lie-advected
$(M,g)$
, a Lie-advected
![]() $p$
-form with a crucial additional constraint of exactness (or some generalisation). We recall that a
$p$
-form with a crucial additional constraint of exactness (or some generalisation). We recall that a
![]() $d$
-dimensional Riemannian manifold
$d$
-dimensional Riemannian manifold
![]() $(M,g)$
is a differentiable manifold
$(M,g)$
is a differentiable manifold
![]() $M$
of dimension
$M$
of dimension
![]() $d$
, together with a 2-covariant tensor field, the metric tensor
$d$
, together with a 2-covariant tensor field, the metric tensor
![]() $g$
, which associates to any point
$g$
, which associates to any point
![]() $a\in M$
a 2-covariant tensor
$a\in M$
a 2-covariant tensor
![]() ${\mathcal{T}}_{2}^{0}(M)$
(see §§ B.2 and B.3). The metric tensor
${\mathcal{T}}_{2}^{0}(M)$
(see §§ B.2 and B.3). The metric tensor
![]() $g$
allows one both to define a metric on
$g$
allows one both to define a metric on
![]() $M$
for measuring distances between two points on
$M$
for measuring distances between two points on
![]() $M$
, and to define a suitable scalar product for vectors lying in a tangent space (see § B.3).
$M$
, and to define a suitable scalar product for vectors lying in a tangent space (see § B.3).
The main new result of the present section will be to show that, to each exact Lie-advected
![]() $p$
-form, corresponds a generalised Cauchy invariant. This is of course a result with applications beyond hydrodynamics, but it is not just a rewriting of Lie-advection invariance in Lagrangian coordinates: the Cauchy invariants formulation requires an additional condition other than Lie-advection invariance. The method of proving this is quite general but, of course, also applies to Euler flow in the ordinary flat 3D space. In that case, we already have the original proof of Cauchy (Reference Cauchy1815), which juggles with Eulerian and Lagrangian coordinates and thus has a flavour of pullback–pushforward argument. In addition, we have all the relatively recent derivations using Noether’s theorem in conjunction with a variational formulation of the Euler equations and the relabelling invariance (see, e.g., Salmon Reference Salmon1988). What we now present constitutes in a sense a third approach, rooted in differential geometry and allowing generalisation to a variety of hydrodynamical and MHD problems, discussed in §§ 2.5, 3 and 4.
$p$
-form, corresponds a generalised Cauchy invariant. This is of course a result with applications beyond hydrodynamics, but it is not just a rewriting of Lie-advection invariance in Lagrangian coordinates: the Cauchy invariants formulation requires an additional condition other than Lie-advection invariance. The method of proving this is quite general but, of course, also applies to Euler flow in the ordinary flat 3D space. In that case, we already have the original proof of Cauchy (Reference Cauchy1815), which juggles with Eulerian and Lagrangian coordinates and thus has a flavour of pullback–pushforward argument. In addition, we have all the relatively recent derivations using Noether’s theorem in conjunction with a variational formulation of the Euler equations and the relabelling invariance (see, e.g., Salmon Reference Salmon1988). What we now present constitutes in a sense a third approach, rooted in differential geometry and allowing generalisation to a variety of hydrodynamical and MHD problems, discussed in §§ 2.5, 3 and 4.
Let
![]() $\unicode[STIX]{x1D6FA}\subset M$
be a bounded region of the
$\unicode[STIX]{x1D6FA}\subset M$
be a bounded region of the
![]() $d$
-dimensional Riemannian manifold
$d$
-dimensional Riemannian manifold
![]() $(M,g)$
. We remind the reader that a
$(M,g)$
. We remind the reader that a
![]() $p$
-form
$p$
-form
 $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})$
is exact if it is the exterior derivative of a
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})$
is exact if it is the exterior derivative of a
![]() $(p-1)$
-form
$(p-1)$
-form
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p-1}(\unicode[STIX]{x1D6FA})$
, that is
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p-1}(\unicode[STIX]{x1D6FA})$
, that is
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}=\text{d}\unicode[STIX]{x1D6FC},\quad \unicode[STIX]{x1D6FE}\in \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA}),\quad \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p-1}(\unicode[STIX]{x1D6FA}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}=\text{d}\unicode[STIX]{x1D6FC},\quad \unicode[STIX]{x1D6FE}\in \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA}),\quad \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p-1}(\unicode[STIX]{x1D6FA}),\end{eqnarray}$$
where d denotes the exterior derivative (see § B.8). We recall that a family of
![]() $p$
-forms
$p$
-forms
 $\unicode[STIX]{x1D6FE}_{t}\in \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})$
,
$\unicode[STIX]{x1D6FE}_{t}\in \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})$
,
![]() $t>0$
, are Lie-advected by the flow of
$t>0$
, are Lie-advected by the flow of
![]() $v_{t}$
if they satisfy the Lie-advection equation
$v_{t}$
if they satisfy the Lie-advection equation
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FE}_{t}+\unicode[STIX]{x00A3}_{v_{t}}\unicode[STIX]{x1D6FE}_{t}=0,\quad \text{on}~\unicode[STIX]{x1D6FA}\subset M,~\text{with}~\unicode[STIX]{x1D6FE}_{0}~\text{given}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FE}_{t}+\unicode[STIX]{x00A3}_{v_{t}}\unicode[STIX]{x1D6FE}_{t}=0,\quad \text{on}~\unicode[STIX]{x1D6FA}\subset M,~\text{with}~\unicode[STIX]{x1D6FE}_{0}~\text{given}.\end{eqnarray}$$
Here the vector field
![]() $v_{t}$
is the generator of the Lagrangian flow
$v_{t}$
is the generator of the Lagrangian flow
![]() $\unicode[STIX]{x1D711}_{t}$
defined by (2.8).
$\unicode[STIX]{x1D711}_{t}$
defined by (2.8).
Theorem 1 (Generalised Cauchy invariants equation).
For
![]() $t>0$
, let
$t>0$
, let
 $\unicode[STIX]{x1D6FE}_{t}\in \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})$
be a time-dependent family of exact
$\unicode[STIX]{x1D6FE}_{t}\in \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})$
be a time-dependent family of exact
![]() $p$
-forms (i.e. satisfying (2.18)) that are Lie-advected (i.e. satisfy (2.19)); then we have the generalised Cauchy invariants equation
$p$
-forms (i.e. satisfying (2.18)) that are Lie-advected (i.e. satisfy (2.19)); then we have the generalised Cauchy invariants equation
 $$\begin{eqnarray}\frac{1}{(p-1)!}\,\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\,\text{d}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}}=\unicode[STIX]{x1D6FE}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{(p-1)!}\,\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\,\text{d}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}}=\unicode[STIX]{x1D6FE}_{0}.\end{eqnarray}$$
Here,
![]() $x=\unicode[STIX]{x1D711}_{t}$
denotes Eulerian coordinates and
$x=\unicode[STIX]{x1D711}_{t}$
denotes Eulerian coordinates and
![]() $\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}$
the generalised Kronecker symbol (see § B.6). Note that, henceforth, in connection with Cauchy invariants, we use the singular for ‘equation’, since in modern writing a vector or a tensor is considered a single object.
$\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}$
the generalised Kronecker symbol (see § B.6). Note that, henceforth, in connection with Cauchy invariants, we use the singular for ‘equation’, since in modern writing a vector or a tensor is considered a single object.
Proof. Since
![]() $\unicode[STIX]{x1D6FE}$
is Lie-advected, by the Lie-derivative theorem (2.14), we have
$\unicode[STIX]{x1D6FE}$
is Lie-advected, by the Lie-derivative theorem (2.14), we have
 $\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{0}$
. Then, we write
$\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{0}$
. Then, we write
![]() $\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D6FE}$
in terms of its component in the
$\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D6FE}$
in terms of its component in the
![]() $a$
-coordinates (see § B.4), to obtain
$a$
-coordinates (see § B.4), to obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{0} & = & \displaystyle \unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D6FE}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i_{1}<\cdots <i_{p}}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D6FE})_{i_{1}\ldots i_{p}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\frac{\unicode[STIX]{x2202}x^{\,j_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{\,j_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\,\unicode[STIX]{x1D6FE}_{j_{1}\ldots j_{p}}(x)\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{0} & = & \displaystyle \unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D6FE}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i_{1}<\cdots <i_{p}}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D6FE})_{i_{1}\ldots i_{p}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\frac{\unicode[STIX]{x2202}x^{\,j_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{\,j_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\,\unicode[STIX]{x1D6FE}_{j_{1}\ldots j_{p}}(x)\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}.\end{eqnarray}$$
Next, using the generalised Kronecker symbol
![]() $\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}$
, we obtain
$\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}$
, we obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE} & = & \displaystyle \text{d}\unicode[STIX]{x1D6FC}\nonumber\\ \displaystyle & = & \displaystyle \text{d}\mathop{\sum }_{i_{1}<\cdots <i_{p-1}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}(a)\wedge \text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p-1}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i_{1}<\cdots <i_{p-1}}\,\text{d}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p-1}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i_{1}<\cdots <i_{p-1}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\,\text{d}a^{k}\wedge \text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p-1}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i_{1}<\cdots <i_{p-1}}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{ki_{1}\ldots i_{p-1}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\,\text{d}a^{\,j_{1}}\wedge \cdots \wedge \text{d}a^{\,j_{p}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE} & = & \displaystyle \text{d}\unicode[STIX]{x1D6FC}\nonumber\\ \displaystyle & = & \displaystyle \text{d}\mathop{\sum }_{i_{1}<\cdots <i_{p-1}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}(a)\wedge \text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p-1}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i_{1}<\cdots <i_{p-1}}\,\text{d}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p-1}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i_{1}<\cdots <i_{p-1}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\,\text{d}a^{k}\wedge \text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p-1}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i_{1}<\cdots <i_{p-1}}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{ki_{1}\ldots i_{p-1}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\,\text{d}a^{\,j_{1}}\wedge \cdots \wedge \text{d}a^{\,j_{p}},\end{eqnarray}$$
from which we deduce
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{l_{1}\ldots l_{p}}(x)=\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{p}}^{ki_{1}\ldots i_{p-1}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x^{k}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}(x).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{l_{1}\ldots l_{p}}(x)=\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{p}}^{ki_{1}\ldots i_{p-1}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x^{k}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}(x).\end{eqnarray}$$
Substituting (2.23) into (2.21) we obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{0} & = & \displaystyle \frac{1}{p!}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{p}}^{\,j_{p}j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x^{\,j_{p}}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{p}}^{\,j_{p}j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{\,j_{p}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}(-1)^{p-1}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{p}}^{\,j_{1}\ldots j_{p}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{\,j_{p}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{0} & = & \displaystyle \frac{1}{p!}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{p}}^{\,j_{p}j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x^{\,j_{p}}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{p}}^{\,j_{p}j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{\,j_{p}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}(-1)^{p-1}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{p}}^{\,j_{1}\ldots j_{p}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{\,j_{p}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}.\end{eqnarray}$$
Using now the Laplace expansion of determinants, we may define recursively
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{p}}^{\,j_{1}\ldots j_{p}} & = & \displaystyle \left|\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FF}_{i_{1}}^{\,j_{1}} & \cdots \, & \unicode[STIX]{x1D6FF}_{i_{p}}^{\,j_{1}}\\ \vdots & \ddots & \vdots \\ \unicode[STIX]{x1D6FF}_{i_{1}}^{\,j_{p}} & \cdots \, & \unicode[STIX]{x1D6FF}_{i_{p}}^{\,j_{p}}\end{array}\right|\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=1}^{p}(-1)^{p+k}\unicode[STIX]{x1D6FF}_{i_{k}}^{\,j_{p}}\unicode[STIX]{x1D6FF}_{i_{1}\ldots \widehat{i}_{k}\ldots i_{p}}^{\,j_{1}\ldots j_{k}\ldots \widehat{j}_{p}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{p}}^{\,j_{1}\ldots j_{p}} & = & \displaystyle \left|\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FF}_{i_{1}}^{\,j_{1}} & \cdots \, & \unicode[STIX]{x1D6FF}_{i_{p}}^{\,j_{1}}\\ \vdots & \ddots & \vdots \\ \unicode[STIX]{x1D6FF}_{i_{1}}^{\,j_{p}} & \cdots \, & \unicode[STIX]{x1D6FF}_{i_{p}}^{\,j_{p}}\end{array}\right|\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k=1}^{p}(-1)^{p+k}\unicode[STIX]{x1D6FF}_{i_{k}}^{\,j_{p}}\unicode[STIX]{x1D6FF}_{i_{1}\ldots \widehat{i}_{k}\ldots i_{p}}^{\,j_{1}\ldots j_{k}\ldots \widehat{j}_{p}},\end{eqnarray}$$
where the hat indicates an omitted index in the sequence. Using (2.25), equation (2.24) becomes
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{0} & = & \displaystyle \frac{1}{p!}\mathop{\sum }_{n=1}^{p}(-1)^{n-1}\unicode[STIX]{x1D6FF}_{l_{n}}^{\,j_{p}}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \widehat{l}_{n}\ldots l_{p}}^{\,j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{\,j_{p}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\mathop{\sum }_{n=1}^{p}(-1)^{n-1}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \widehat{l}_{n}\ldots l_{p}}^{\,j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{l_{n}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\mathop{\sum }_{n=1}^{p}(-1)^{n-1}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \widehat{l}_{n}\ldots l_{p}}^{\,j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \widehat{\frac{\unicode[STIX]{x2202}x^{l_{n}}}{\unicode[STIX]{x2202}a^{i_{n}}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\unicode[STIX]{x1D6FF}_{i_{n}}^{k}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\mathop{\sum }_{n=1}^{p}(-1)^{n-1}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \widehat{l}_{n}\ldots l_{p}}^{\,j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \widehat{\frac{\unicode[STIX]{x2202}x^{l_{n}}}{\unicode[STIX]{x2202}a^{i_{n}}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{n}}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\mathop{\sum }_{n=1}^{p}(-1)^{n-1}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \widehat{l}_{n}\ldots l_{p}}^{\,j_{1}\ldots j_{p-1}}\left(\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\,\text{d}a^{i_{1}}\!\right)\wedge \cdots \wedge \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{n}}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{n}}\!\right)\wedge \cdots \wedge \left(\frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\,\text{d}a^{i_{p}}\!\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\mathop{\sum }_{n=1}^{p}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \widehat{l}_{n}\ldots l_{p}}^{\,j_{1}\ldots j_{p-1}}\,\text{d}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\wedge \text{d}x^{l_{1}}\wedge \cdots \wedge \widehat{\text{d}x^{l_{n}}}\wedge \cdots \wedge \text{d}x^{l_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{p-1}}^{\,j_{1}\ldots j_{p-1}}\,\text{d}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\wedge \text{d}x^{l_{1}}\wedge \cdots \wedge \text{d}x^{l_{p-1}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{0} & = & \displaystyle \frac{1}{p!}\mathop{\sum }_{n=1}^{p}(-1)^{n-1}\unicode[STIX]{x1D6FF}_{l_{n}}^{\,j_{p}}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \widehat{l}_{n}\ldots l_{p}}^{\,j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{\,j_{p}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\mathop{\sum }_{n=1}^{p}(-1)^{n-1}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \widehat{l}_{n}\ldots l_{p}}^{\,j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{l_{n}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\mathop{\sum }_{n=1}^{p}(-1)^{n-1}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \widehat{l}_{n}\ldots l_{p}}^{\,j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \widehat{\frac{\unicode[STIX]{x2202}x^{l_{n}}}{\unicode[STIX]{x2202}a^{i_{n}}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\unicode[STIX]{x1D6FF}_{i_{n}}^{k}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\mathop{\sum }_{n=1}^{p}(-1)^{n-1}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \widehat{l}_{n}\ldots l_{p}}^{\,j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \widehat{\frac{\unicode[STIX]{x2202}x^{l_{n}}}{\unicode[STIX]{x2202}a^{i_{n}}}}\cdots \frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{n}}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\mathop{\sum }_{n=1}^{p}(-1)^{n-1}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \widehat{l}_{n}\ldots l_{p}}^{\,j_{1}\ldots j_{p-1}}\left(\frac{\unicode[STIX]{x2202}x^{l_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\,\text{d}a^{i_{1}}\!\right)\wedge \cdots \wedge \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{n}}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\,\text{d}a^{i_{n}}\!\right)\wedge \cdots \wedge \left(\frac{\unicode[STIX]{x2202}x^{l_{p}}}{\unicode[STIX]{x2202}a^{i_{p}}}\,\text{d}a^{i_{p}}\!\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\mathop{\sum }_{n=1}^{p}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \widehat{l}_{n}\ldots l_{p}}^{\,j_{1}\ldots j_{p-1}}\,\text{d}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\wedge \text{d}x^{l_{1}}\wedge \cdots \wedge \widehat{\text{d}x^{l_{n}}}\wedge \cdots \wedge \text{d}x^{l_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{p-1}}^{\,j_{1}\ldots j_{p-1}}\,\text{d}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p-1}}\wedge \text{d}x^{l_{1}}\wedge \cdots \wedge \text{d}x^{l_{p-1}},\end{eqnarray}$$
which ends the proof. ◻
Remark 1 (Sufficient conditions for exactness of differential forms).
In Theorem 1 on the construction of generalised Cauchy invariants, we demand that the
![]() $p$
-form
$p$
-form
![]() $\unicode[STIX]{x1D6FE}$
be exact. There are several ways to obtain such an exact
$\unicode[STIX]{x1D6FE}$
be exact. There are several ways to obtain such an exact
![]() $p$
-form.
$p$
-form.
-
(i) In some problems a
 $p$
-form
$p$
-form
 $\unicode[STIX]{x1D6FE}$
appears naturally as the exterior differential of a
$\unicode[STIX]{x1D6FE}$
appears naturally as the exterior differential of a
 $(p-1)$
-form
$(p-1)$
-form
 $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p-1}(\unicode[STIX]{x1D6FA})$
, i.e.
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p-1}(\unicode[STIX]{x1D6FA})$
, i.e.
 $\unicode[STIX]{x1D6FE}=\text{d}\unicode[STIX]{x1D6FD}$
. As we will see in later sections, this is the case for the vorticity 2-form and the magnetic field 2-form.
$\unicode[STIX]{x1D6FE}=\text{d}\unicode[STIX]{x1D6FD}$
. As we will see in later sections, this is the case for the vorticity 2-form and the magnetic field 2-form. -
(ii) When
 $\unicode[STIX]{x1D6FE}_{t}$
is Lie-advected and the initial condition
$\unicode[STIX]{x1D6FE}_{t}$
is Lie-advected and the initial condition
 $\unicode[STIX]{x1D6FE}_{0}$
is exact, it follows from the commutation of the exterior derivative and the pushforward operator
$\unicode[STIX]{x1D6FE}_{0}$
is exact, it follows from the commutation of the exterior derivative and the pushforward operator
 $\unicode[STIX]{x1D711}_{t\ast }$
(see § B.8), that
$\unicode[STIX]{x1D711}_{t\ast }$
(see § B.8), that
 $\unicode[STIX]{x1D6FE}_{t}$
is exact. Indeed
$\unicode[STIX]{x1D6FE}_{t}$
is exact. Indeed
 $\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{0}$
implies that (2.27)
$\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{0}$
implies that (2.27) $$\begin{eqnarray}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D711}_{t\ast }\unicode[STIX]{x1D6FE}_{0}=\unicode[STIX]{x1D711}_{t\ast }\,\text{d}\unicode[STIX]{x1D6FC}_{0}=\text{d}(\unicode[STIX]{x1D711}_{t\ast }\unicode[STIX]{x1D6FC}_{0}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D711}_{t\ast }\unicode[STIX]{x1D6FE}_{0}=\unicode[STIX]{x1D711}_{t\ast }\,\text{d}\unicode[STIX]{x1D6FC}_{0}=\text{d}(\unicode[STIX]{x1D711}_{t\ast }\unicode[STIX]{x1D6FC}_{0}).\end{eqnarray}$$
-
(iii) Let us introduce
 $Z^{p}(M;\mathbb{R})$
, the subspace of
$Z^{p}(M;\mathbb{R})$
, the subspace of
 $\unicode[STIX]{x039B}^{p}(M)$
constituted of all closed
$\unicode[STIX]{x039B}^{p}(M)$
constituted of all closed
 $p$
-forms and
$p$
-forms and
 $B^{p}(M;\mathbb{R})$
, the subspace of
$B^{p}(M;\mathbb{R})$
, the subspace of
 $Z^{p}(M;\mathbb{R})$
constituted of all exact
$Z^{p}(M;\mathbb{R})$
constituted of all exact
 $p$
-forms. Obviously, we have
$p$
-forms. Obviously, we have
 $B^{p}(M;\mathbb{R})\subset Z^{p}(M;\mathbb{R})\subset \unicode[STIX]{x039B}^{p}(M)$
. Although
$B^{p}(M;\mathbb{R})\subset Z^{p}(M;\mathbb{R})\subset \unicode[STIX]{x039B}^{p}(M)$
. Although
 $B^{p}$
and
$B^{p}$
and
 $Z^{p}$
are infinite-dimensional, in many cases their quotient space, called the
$Z^{p}$
are infinite-dimensional, in many cases their quotient space, called the
 $p$
th cohomology vector space and noted (2.28)is finite-dimensional. For example, this is the case when
$p$
th cohomology vector space and noted (2.28)is finite-dimensional. For example, this is the case when $$\begin{eqnarray}H^{p}(M;\mathbb{R}):=\frac{Z^{p}(M;\mathbb{R})}{B^{p}(M;\mathbb{R})},\end{eqnarray}$$
$$\begin{eqnarray}H^{p}(M;\mathbb{R}):=\frac{Z^{p}(M;\mathbb{R})}{B^{p}(M;\mathbb{R})},\end{eqnarray}$$
 $M$
is a compact finite-dimensional manifold. The dimension of the vector space
$M$
is a compact finite-dimensional manifold. The dimension of the vector space
 $H^{p}$
is called the
$H^{p}$
is called the
 $p$
th Betti number, written
$p$
th Betti number, written
 $b_{p}=b_{p}(M)$
and defined by
$b_{p}=b_{p}(M)$
and defined by
 $b_{p}(M):=\text{dim}\,H^{p}(M;\mathbb{R})$
. Thus the Betti number
$b_{p}(M):=\text{dim}\,H^{p}(M;\mathbb{R})$
. Thus the Betti number
 $b_{p}(M)$
is the maximum number of closed
$b_{p}(M)$
is the maximum number of closed
 $p$
-forms on
$p$
-forms on
 $M$
, such that all linear combinations with non-vanishing coefficients are not exact. The knowledge of the Betti numbers of a given manifold
$M$
, such that all linear combinations with non-vanishing coefficients are not exact. The knowledge of the Betti numbers of a given manifold
 $M$
for
$M$
for
 $p\geqslant 1$
yields an exact quantitative answer to the question about exactness of a closed
$p\geqslant 1$
yields an exact quantitative answer to the question about exactness of a closed
 $p$
-form: (2.29)Two closed forms are equivalent or cohomologous if they differ by an exact form, and a closed
$p$
-form: (2.29)Two closed forms are equivalent or cohomologous if they differ by an exact form, and a closed $$\begin{eqnarray}\text{a closed}~p\text{-}\text{form is exact if and only if}~b_{p}(M)=0.\end{eqnarray}$$
$$\begin{eqnarray}\text{a closed}~p\text{-}\text{form is exact if and only if}~b_{p}(M)=0.\end{eqnarray}$$
 $p$
-form is exact if and only if it is cohomologous to zero. The values of the Betti numbers are related to the topological properties of the manifold
$p$
-form is exact if and only if it is cohomologous to zero. The values of the Betti numbers are related to the topological properties of the manifold
 $M$
(e.g. homology, connectedness, curvature, etc.). For more details on cohomology and homology we refer the reader to § B.13 and references therein.
$M$
(e.g. homology, connectedness, curvature, etc.). For more details on cohomology and homology we refer the reader to § B.13 and references therein.
-
(iv) By the Poincaré theorem (see, e.g., Abraham, Marsden & Ratiu (Reference Abraham, Marsden and Ratiu1998), Theorem 6.4.14), if the
 $p$
-form
$p$
-form
 $\unicode[STIX]{x1D6FE}$
is closed on
$\unicode[STIX]{x1D6FE}$
is closed on
 $\unicode[STIX]{x1D6FA}\subset M$
, i.e.
$\unicode[STIX]{x1D6FA}\subset M$
, i.e.
 $\text{d}\unicode[STIX]{x1D6FE}=0$
on
$\text{d}\unicode[STIX]{x1D6FE}=0$
on
 $\unicode[STIX]{x1D6FA}$
, then
$\unicode[STIX]{x1D6FA}$
, then
 $\unicode[STIX]{x1D6FE}$
is locally exact; that is, there exists a neighbourhood
$\unicode[STIX]{x1D6FE}$
is locally exact; that is, there exists a neighbourhood
 $U\subset \unicode[STIX]{x1D6FA}$
about each point of
$U\subset \unicode[STIX]{x1D6FA}$
about each point of
 $\unicode[STIX]{x1D6FA}$
, on which
$\unicode[STIX]{x1D6FA}$
, on which
 $\unicode[STIX]{x1D6FE}_{|_{U}}=\text{d}\unicode[STIX]{x1D6FC}$
for some
$\unicode[STIX]{x1D6FE}_{|_{U}}=\text{d}\unicode[STIX]{x1D6FC}$
for some
 $(p-1)$
-form
$(p-1)$
-form
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p-1}(U)$
. The same result holds globally on a contractible domain (Abraham et al.
Reference Abraham, Marsden and Ratiu1998, see Lemma 6.4.18). A contractible domain is roughly one in which, for any given point, the whole domain can be continuously shrunk into it (see § B.1). By the Poincaré lemma, if
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p-1}(U)$
. The same result holds globally on a contractible domain (Abraham et al.
Reference Abraham, Marsden and Ratiu1998, see Lemma 6.4.18). A contractible domain is roughly one in which, for any given point, the whole domain can be continuously shrunk into it (see § B.1). By the Poincaré lemma, if
 $M$
is a compact
$M$
is a compact
 $d$
-dimensional contractible manifold, all the Betti numbers (for
$d$
-dimensional contractible manifold, all the Betti numbers (for
 $p\geqslant 1$
) vanish, i.e.
$p\geqslant 1$
) vanish, i.e.
 $b_{1}(M)=\cdots =b_{d}(M)=0$
, and
$b_{1}(M)=\cdots =b_{d}(M)=0$
, and
 $b_{0}(M)=1$
. Contractibility is, however, an excessively strong requirement to ensure that closeness implies exactness. For differential forms of a given order
$b_{0}(M)=1$
. Contractibility is, however, an excessively strong requirement to ensure that closeness implies exactness. For differential forms of a given order
 $p$
, the vanishing of the single Betti number,
$p$
, the vanishing of the single Betti number,
 $b_{p}(M)=0$
is actually sufficient to ensure this.
$b_{p}(M)=0$
is actually sufficient to ensure this.
2.4 Alternative formulations and extensions of Theorem 1
Hereafter we discuss alternative representations of Theorem 1, which are local, such as the generalised Cauchy formula, or global, such as the integral formulation of the Cauchy invariants equations. We also give extensions of Theorem 1 for some non-exact differential forms.
2.4.1 Generalised Cauchy formula
An important operation in differential geometry is the Hodge duality, which associates to any
![]() $p$
-form a Hodge dual
$p$
-form a Hodge dual
![]() $(d-p)$
-form such that their exterior product is the fundamental metric volume
$(d-p)$
-form such that their exterior product is the fundamental metric volume
![]() $d$
-form
$d$
-form
 $\unicode[STIX]{x1D707}=\sqrt{\text{g}}\,\text{d}a^{1}\wedge \cdots \wedge \text{d}a^{d}$
, with
$\unicode[STIX]{x1D707}=\sqrt{\text{g}}\,\text{d}a^{1}\wedge \cdots \wedge \text{d}a^{d}$
, with
 $\sqrt{\text{g}}=\sqrt{\det (\text{g}_{ij})}$
(see § B.9). For example, in 3D the vorticity 2-form and the vorticity vector field (as known since the work of Helmholtz (Reference von Helmholtz1858)) are Hodge duals of each other. It is therefore of interest to rewrite the Cauchy invariants equation and its generalisations in Hodge dual form. For example, as we shall see in the next section, this will give us the Cauchy vorticity formula.
$\sqrt{\text{g}}=\sqrt{\det (\text{g}_{ij})}$
(see § B.9). For example, in 3D the vorticity 2-form and the vorticity vector field (as known since the work of Helmholtz (Reference von Helmholtz1858)) are Hodge duals of each other. It is therefore of interest to rewrite the Cauchy invariants equation and its generalisations in Hodge dual form. For example, as we shall see in the next section, this will give us the Cauchy vorticity formula.
The generalised Cauchy invariants equation (2.20) has a corresponding generalised Cauchy formula obtained by applying the Hodge dual operator, denoted
![]() $\star$
, to (2.20), that is
$\star$
, to (2.20), that is
 $$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\star (\text{d}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}})=\star \unicode[STIX]{x1D6FE}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\star (\text{d}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}})=\star \unicode[STIX]{x1D6FE}_{0}.\end{eqnarray}$$
This generalised Cauchy formula can be written in the covariant, contravariant or mixed form, by using what is known in differential geometry as the raising–lowering duality. We have already seen that the space
![]() ${\mathcal{T}}_{0}^{1}(M)$
is the vector space of 1-contravariant vector fields, while
${\mathcal{T}}_{0}^{1}(M)$
is the vector space of 1-contravariant vector fields, while
![]() ${\mathcal{T}}_{1}^{0}(M)$
, its dual, is the vector space of linear forms on
${\mathcal{T}}_{1}^{0}(M)$
, its dual, is the vector space of linear forms on
![]() ${\mathcal{T}}_{0}^{1}(M)$
, i.e. the space of 1-covariant vector fields (also called covector or 1-form fields). We then introduce the index raising operator
${\mathcal{T}}_{0}^{1}(M)$
, i.e. the space of 1-covariant vector fields (also called covector or 1-form fields). We then introduce the index raising operator
 $(\cdot )^{\sharp }:{\mathcal{T}}_{1}^{0}(M)\rightarrow {\mathcal{T}}_{0}^{1}(M)$
, which in flat space transforms the differential of a function into its gradient vector. In curved spaces
$(\cdot )^{\sharp }:{\mathcal{T}}_{1}^{0}(M)\rightarrow {\mathcal{T}}_{0}^{1}(M)$
, which in flat space transforms the differential of a function into its gradient vector. In curved spaces
![]() $\unicode[STIX]{x1D6FC}^{\sharp }$
denotes the 1-contravariant vector field obtained from the 1-form field
$\unicode[STIX]{x1D6FC}^{\sharp }$
denotes the 1-contravariant vector field obtained from the 1-form field
![]() $\unicode[STIX]{x1D6FC}$
, by using the index raising operation
$\unicode[STIX]{x1D6FC}$
, by using the index raising operation
 $\unicode[STIX]{x1D6FC}^{\sharp }=(\unicode[STIX]{x1D6FC}_{i}\,\text{d}a^{i})^{\sharp }=(\unicode[STIX]{x1D6FC}^{\sharp })^{i}\unicode[STIX]{x2202}_{i}=\text{g}^{ij}\unicode[STIX]{x1D6FC}_{j}\unicode[STIX]{x2202}_{i}$
; that is componentwise
$\unicode[STIX]{x1D6FC}^{\sharp }=(\unicode[STIX]{x1D6FC}_{i}\,\text{d}a^{i})^{\sharp }=(\unicode[STIX]{x1D6FC}^{\sharp })^{i}\unicode[STIX]{x2202}_{i}=\text{g}^{ij}\unicode[STIX]{x1D6FC}_{j}\unicode[STIX]{x2202}_{i}$
; that is componentwise
 $(\unicode[STIX]{x1D6FC}^{\sharp })^{i}=\text{g}^{ij}\unicode[STIX]{x1D6FC}_{j}$
. Conversely
$(\unicode[STIX]{x1D6FC}^{\sharp })^{i}=\text{g}^{ij}\unicode[STIX]{x1D6FC}_{j}$
. Conversely
![]() $v^{\flat }$
is the 1-form field obtained from the vector field by applying the index lowering operator
$v^{\flat }$
is the 1-form field obtained from the vector field by applying the index lowering operator
 $(\cdot )^{\flat }:{\mathcal{T}}_{0}^{1}(M)\rightarrow {\mathcal{T}}_{1}^{0}(M)$
according to the formula
$(\cdot )^{\flat }:{\mathcal{T}}_{0}^{1}(M)\rightarrow {\mathcal{T}}_{1}^{0}(M)$
according to the formula
 $v^{\flat }=(v^{i}\unicode[STIX]{x2202}_{i})^{\flat }=(v^{\flat })_{i}\,\text{d}x^{i}=\text{g}_{ij}v^{\,j}\,\text{d}x^{i}$
; componentwise, this is
$v^{\flat }=(v^{i}\unicode[STIX]{x2202}_{i})^{\flat }=(v^{\flat })_{i}\,\text{d}x^{i}=\text{g}_{ij}v^{\,j}\,\text{d}x^{i}$
; componentwise, this is
 $(v^{\flat })_{i}=\text{g}_{ij}v^{\,j}$
(see § B.3). Therefore, to obtain (2.30) in the desired formulation (covariant, contravariant or mixed form), it is required to successively apply as many times as necessary the lowering and raising operators.
$(v^{\flat })_{i}=\text{g}_{ij}v^{\,j}$
(see § B.3). Therefore, to obtain (2.30) in the desired formulation (covariant, contravariant or mixed form), it is required to successively apply as many times as necessary the lowering and raising operators.
Remark 2. We observe that the generalised Cauchy invariants equation (i.e. Theorem 1) requires only a structure of differentiable manifold, without the Riemannian structure. In contrast, the generalised Cauchy formula (2.30) requires such a Riemannian structure (see § B.3), because of the use of Hodge duality (see § B.9).
2.4.2 Space-integrated form of generalised Cauchy invariants equations
Since the generalised Cauchy invariant is an exact
![]() $p$
-form, we can apply to it what are known as the Hodge decomposition and/or the Stokes theorem. First we write the generalised Cauchy invariant as an explicit exterior differential. We have indeed
$p$
-form, we can apply to it what are known as the Hodge decomposition and/or the Stokes theorem. First we write the generalised Cauchy invariant as an explicit exterior differential. We have indeed
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\,\text{d}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\,\text{d}(\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\,\text{d}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\,\text{d}(\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}}).\end{eqnarray}$$
Since
 $\unicode[STIX]{x1D6FE}_{0}=\text{d}\unicode[STIX]{x1D6FC}_{0}$
, using the Hodge decomposition for closed forms (see § B.13), we obtain
$\unicode[STIX]{x1D6FE}_{0}=\text{d}\unicode[STIX]{x1D6FC}_{0}$
, using the Hodge decomposition for closed forms (see § B.13), we obtain
 $$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}}=\unicode[STIX]{x1D6FC}_{0}+\text{d}\unicode[STIX]{x1D6FD}+h.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}}=\unicode[STIX]{x1D6FC}_{0}+\text{d}\unicode[STIX]{x1D6FD}+h.\end{eqnarray}$$
Here, if
![]() $M$
is a compact manifold without (respectively with) boundary,
$M$
is a compact manifold without (respectively with) boundary,
![]() $\unicode[STIX]{x1D6FD}$
is an arbitrary
$\unicode[STIX]{x1D6FD}$
is an arbitrary
![]() $(p-2)$
-form (respectively normal
$(p-2)$
-form (respectively normal
![]() $(p-2)$
-form with vanishing tangential components; see next-to-last paragraph of § B.13 and references therein). In (2.32), the
$(p-2)$
-form with vanishing tangential components; see next-to-last paragraph of § B.13 and references therein). In (2.32), the
![]() $(p-1)$
-form
$(p-1)$
-form
![]() $h$
is harmonic, that is
$h$
is harmonic, that is
![]() $\text{d}h=0$
and
$\text{d}h=0$
and
![]() $\text{d}^{\star }h=0$
. Here, the operator
$\text{d}^{\star }h=0$
. Here, the operator
 $\text{d}^{\star }:\unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})\rightarrow \unicode[STIX]{x039B}^{p-1}(\unicode[STIX]{x1D6FA})$
with
$\text{d}^{\star }:\unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})\rightarrow \unicode[STIX]{x039B}^{p-1}(\unicode[STIX]{x1D6FA})$
with
![]() $p\geqslant 0$
is the exterior coderivative, obtained from the exterior derivative, but acting on the Hodge dual space (for details see § B.9). More precisely, if
$p\geqslant 0$
is the exterior coderivative, obtained from the exterior derivative, but acting on the Hodge dual space (for details see § B.9). More precisely, if
 $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})$
then we have the
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})$
then we have the
![]() $(p-1)$
-form
$(p-1)$
-form
 $\text{d}^{\star }\unicode[STIX]{x1D6FE}=(-1)^{d(p-1)+1}\star \text{d}\,\star \unicode[STIX]{x1D6FE}$
. Note that the latter looks actually more like an integration than a differentiation.
$\text{d}^{\star }\unicode[STIX]{x1D6FE}=(-1)^{d(p-1)+1}\star \text{d}\,\star \unicode[STIX]{x1D6FE}$
. Note that the latter looks actually more like an integration than a differentiation.
Now, we want to integrate this form over suitable domains, called 1-chains, 2-chains, etc. In a flat space, a 1-chain is just a finite set of 1D contours. For a general definition of
![]() $p$
-dimensional
$p$
-dimensional
![]() $p$
-chains on manifolds, see § B.12. Let
$p$
-chains on manifolds, see § B.12. Let
![]() $c$
be a
$c$
be a
![]() $(p-1)$
-chain on the manifold
$(p-1)$
-chain on the manifold
![]() $M$
. Choosing the
$M$
. Choosing the
![]() $(p-2)$
-form
$(p-2)$
-form
![]() $\unicode[STIX]{x1D6FD}$
with suitable values on the boundary
$\unicode[STIX]{x1D6FD}$
with suitable values on the boundary
![]() $\unicode[STIX]{x2202}c$
of
$\unicode[STIX]{x2202}c$
of
![]() $c$
to avoid having a boundary contribution (if a boundary is present), we obtain, using the Stokes theorem (see § B.12),
$c$
to avoid having a boundary contribution (if a boundary is present), we obtain, using the Stokes theorem (see § B.12),
 $$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\int _{c}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}}=\int _{c}\unicode[STIX]{x1D6FC}_{0}+\int _{c}h.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\int _{c}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}}=\int _{c}\unicode[STIX]{x1D6FC}_{0}+\int _{c}h.\end{eqnarray}$$
Moreover, if the Betti number
 $b_{p-1}(M)=0$
, then the second term on the right-hand side of the previous formula vanishes. Considering now a
$b_{p-1}(M)=0$
, then the second term on the right-hand side of the previous formula vanishes. Considering now a
![]() $p$
-chain
$p$
-chain
![]() $c$
, using the Stokes theorem, we obtain
$c$
, using the Stokes theorem, we obtain
 $$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\int _{\unicode[STIX]{x2202}c}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}}=\int _{\unicode[STIX]{x2202}c}\unicode[STIX]{x1D6FC}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\int _{\unicode[STIX]{x2202}c}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}\wedge \text{d}x^{\,j_{1}}\wedge \cdots \wedge \text{d}x^{\,j_{p-1}}=\int _{\unicode[STIX]{x2202}c}\unicode[STIX]{x1D6FC}_{0}.\end{eqnarray}$$
2.4.3 Generalisation to some non-exact differential forms
From Theorem 1, the following question arises naturally: can we extend the result of Theorem 1 when the
![]() $p$
-form
$p$
-form
![]() $\unicode[STIX]{x1D6FE}$
is not exact? The answer is yes under some conditions.
$\unicode[STIX]{x1D6FE}$
is not exact? The answer is yes under some conditions.
We suppose that the
![]() $p$
-form
$p$
-form
![]() $\unicode[STIX]{x1D6FE}$
of Theorem 1 can be written as
$\unicode[STIX]{x1D6FE}$
of Theorem 1 can be written as
 $\unicode[STIX]{x1D6FE}=\text{Op}\,\unicode[STIX]{x03C0}$
, where
$\unicode[STIX]{x1D6FE}=\text{Op}\,\unicode[STIX]{x03C0}$
, where
![]() $\unicode[STIX]{x03C0}$
is a
$\unicode[STIX]{x03C0}$
is a
![]() $q$
-form and the operator
$q$
-form and the operator
 $\text{Op}:\unicode[STIX]{x039B}^{q}(\unicode[STIX]{x1D6FA})\rightarrow \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})$
is a linear operator which satisfies the following conditions:
$\text{Op}:\unicode[STIX]{x039B}^{q}(\unicode[STIX]{x1D6FA})\rightarrow \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})$
is a linear operator which satisfies the following conditions:
-
(i) the commutation relation
 $[\text{Op},\unicode[STIX]{x00A3}_{v}]=0$
holds;
$[\text{Op},\unicode[STIX]{x00A3}_{v}]=0$
holds; -
(ii) the kernel of the operator
 $\text{Op}$
is such that
$\text{Op}$
is such that
 $\text{Ker}\,\text{Op}=\{\text{closed }q\text{-}\text{form, i.e.}~\unicode[STIX]{x1D705}\in \unicode[STIX]{x039B}^{q}(\unicode[STIX]{x1D6FA})\mid \text{d}\unicode[STIX]{x1D705}=0\}$
.
$\text{Ker}\,\text{Op}=\{\text{closed }q\text{-}\text{form, i.e.}~\unicode[STIX]{x1D705}\in \unicode[STIX]{x039B}^{q}(\unicode[STIX]{x1D6FA})\mid \text{d}\unicode[STIX]{x1D705}=0\}$
.
From assumption (i) the Lie-advection equation (2.19) is equivalent to
 $\text{Op}(\unicode[STIX]{x2202}_{t}\unicode[STIX]{x03C0}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x03C0})=0$
. From assumption (ii), this equation is also equivalent to
$\text{Op}(\unicode[STIX]{x2202}_{t}\unicode[STIX]{x03C0}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x03C0})=0$
. From assumption (ii), this equation is also equivalent to
 $\unicode[STIX]{x2202}_{t}\unicode[STIX]{x03C0}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x03C0}=\unicode[STIX]{x1D705}$
, with
$\unicode[STIX]{x2202}_{t}\unicode[STIX]{x03C0}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x03C0}=\unicode[STIX]{x1D705}$
, with
![]() $\unicode[STIX]{x1D705}$
a closed
$\unicode[STIX]{x1D705}$
a closed
![]() $q$
-form. Taking the exterior derivative to this equation, we obtain the equation
$q$
-form. Taking the exterior derivative to this equation, we obtain the equation
 $\unicode[STIX]{x2202}_{t}\,\text{d}\unicode[STIX]{x03C0}+\unicode[STIX]{x00A3}_{v}\,\text{d}\unicode[STIX]{x03C0}=0$
, to which we can apply Theorem 1 with
$\unicode[STIX]{x2202}_{t}\,\text{d}\unicode[STIX]{x03C0}+\unicode[STIX]{x00A3}_{v}\,\text{d}\unicode[STIX]{x03C0}=0$
, to which we can apply Theorem 1 with
 $p=q+1$
,
$p=q+1$
,
![]() $\unicode[STIX]{x1D6FE}=\text{d}\unicode[STIX]{x03C0}$
and
$\unicode[STIX]{x1D6FE}=\text{d}\unicode[STIX]{x03C0}$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}$
.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}$
.
We give now three examples. Choosing
![]() $\text{Op}\equiv \text{d}$
, the first one is obvious. The second example is
$\text{Op}\equiv \text{d}$
, the first one is obvious. The second example is
 $\text{Op}\equiv \star \text{d}:\unicode[STIX]{x039B}^{d-p-1}(\unicode[STIX]{x1D6FA})\rightarrow \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})$
. where the star denotes the Hodge dual operator. Then we have
$\text{Op}\equiv \star \text{d}:\unicode[STIX]{x039B}^{d-p-1}(\unicode[STIX]{x1D6FA})\rightarrow \unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})$
. where the star denotes the Hodge dual operator. Then we have
 $\text{Ker}\,\star \text{d}=\{\text{exact}~q\text{-}\text{form}+\text{harmonic}~q\text{-}\text{form}\}\subset \{\text{closed}~q\text{-}\text{form}\}$
, where a harmonic
$\text{Ker}\,\star \text{d}=\{\text{exact}~q\text{-}\text{form}+\text{harmonic}~q\text{-}\text{form}\}\subset \{\text{closed}~q\text{-}\text{form}\}$
, where a harmonic
![]() $q$
-form
$q$
-form
![]() $h$
satisfies
$h$
satisfies
 $\text{d}h=\text{d}^{\star }h=0$
, with
$\text{d}h=\text{d}^{\star }h=0$
, with
 $\text{d}^{\star }\equiv (-1)^{dp+1}\star \text{d}\,\star$
. In addition, the operator
$\text{d}^{\star }\equiv (-1)^{dp+1}\star \text{d}\,\star$
. In addition, the operator
![]() $\star \text{d}$
satisfies the commutation relation
$\star \text{d}$
satisfies the commutation relation
 $[\star \text{d},\unicode[STIX]{x00A3}_{v}]=0$
if and only if
$[\star \text{d},\unicode[STIX]{x00A3}_{v}]=0$
if and only if
 $[\star ,\unicode[STIX]{x00A3}_{v}]=0$
since
$[\star ,\unicode[STIX]{x00A3}_{v}]=0$
since
 $[\text{d},\unicode[STIX]{x00A3}_{v}]=0$
. Generally the Lie derivative and the Hodge star operator do not commute. When these operators do commute, i.e. when the commutation relation
$[\text{d},\unicode[STIX]{x00A3}_{v}]=0$
. Generally the Lie derivative and the Hodge star operator do not commute. When these operators do commute, i.e. when the commutation relation
 $[\text{}\unicode[STIX]{x00A3}_{v},\star ]=0$
holds we can extend Theorem 1 to forms which are the Hodge duals of exact forms. An example of such commutation relation is when the vector field
$[\text{}\unicode[STIX]{x00A3}_{v},\star ]=0$
holds we can extend Theorem 1 to forms which are the Hodge duals of exact forms. An example of such commutation relation is when the vector field
![]() $v$
generates an isometry (see § B.9). The third example is when the
$v$
generates an isometry (see § B.9). The third example is when the
![]() $p$
-form
$p$
-form
![]() $\unicode[STIX]{x1D6FE}$
is co-exact, i.e.
$\unicode[STIX]{x1D6FE}$
is co-exact, i.e.
![]() $\unicode[STIX]{x1D6FE}=\text{d}^{\star }\unicode[STIX]{x1D6FD}$
, with
$\unicode[STIX]{x1D6FE}=\text{d}^{\star }\unicode[STIX]{x1D6FD}$
, with
![]() $\unicode[STIX]{x1D6FD}$
a
$\unicode[STIX]{x1D6FD}$
a
![]() $(p+1)$
-form. Setting
$(p+1)$
-form. Setting
 $\text{Op}\equiv (-1)^{dp+1}\star \text{d}$
, we fall in the case of the second example with
$\text{Op}\equiv (-1)^{dp+1}\star \text{d}$
, we fall in the case of the second example with
 $\unicode[STIX]{x03C0}=\star \unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{d-p-1}(\unicode[STIX]{x1D6FA})$
. Of course, other interesting examples can be constructed.
$\unicode[STIX]{x03C0}=\star \unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{d-p-1}(\unicode[STIX]{x1D6FA})$
. Of course, other interesting examples can be constructed.
2.4.4 A Lagrangian Biot–Savart problem
So far, the Lie-advected
![]() $p$
-form
$p$
-form
![]() $\unicode[STIX]{x1D6FE}$
was just assumed to be expressible as the exterior derivative
$\unicode[STIX]{x1D6FE}$
was just assumed to be expressible as the exterior derivative
![]() $\text{d}\unicode[STIX]{x1D6FC}$
of a
$\text{d}\unicode[STIX]{x1D6FC}$
of a
![]() $(p-1)$
-form
$(p-1)$
-form
![]() $\unicode[STIX]{x1D6FC}$
. As we shall now see, the generalised Cauchy invariants equation (2.20), allows an inversion, which can be viewed as solving a Biot–Savart problem in Lagrangian variables: the corollary hereafter gives an explicit expression for the
$\unicode[STIX]{x1D6FC}$
. As we shall now see, the generalised Cauchy invariants equation (2.20), allows an inversion, which can be viewed as solving a Biot–Savart problem in Lagrangian variables: the corollary hereafter gives an explicit expression for the
![]() $(p-1)$
-form
$(p-1)$
-form
![]() $\unicode[STIX]{x1D6FC}$
, in which we use the notation
$\unicode[STIX]{x1D6FC}$
, in which we use the notation
 $$\begin{eqnarray}\unicode[STIX]{x0394}_{a}=\mathop{\sum }_{i=1}^{d}\unicode[STIX]{x2202}_{a^{i}}^{2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x0394}_{a}=\mathop{\sum }_{i=1}^{d}\unicode[STIX]{x2202}_{a^{i}}^{2},\end{eqnarray}$$
for the Laplacian in Lagrangian variables and
![]() $\unicode[STIX]{x0394}_{a}^{-1}$
for its formal inverse.
$\unicode[STIX]{x0394}_{a}^{-1}$
for its formal inverse.
Corollary 1 (A Lagrangian Biot–Savart problem).
Under assumptions of Theorem 1, the generalised Cauchy invariants equation (2.20) leads to
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}=\unicode[STIX]{x1D6FF}^{k\ell }\unicode[STIX]{x0394}_{a}^{-1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(\unicode[STIX]{x1D6FE}_{0\ell j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}a^{\,j_{1}}}{\unicode[STIX]{x2202}x^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{\,j_{p-1}}}{\unicode[STIX]{x2202}x^{i_{p-1}}}\right),\quad 1\leqslant i_{1}<\cdots <i_{p-1}\leqslant d.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}=\unicode[STIX]{x1D6FF}^{k\ell }\unicode[STIX]{x0394}_{a}^{-1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(\unicode[STIX]{x1D6FE}_{0\ell j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}a^{\,j_{1}}}{\unicode[STIX]{x2202}x^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{\,j_{p-1}}}{\unicode[STIX]{x2202}x^{i_{p-1}}}\right),\quad 1\leqslant i_{1}<\cdots <i_{p-1}\leqslant d.\end{eqnarray}$$
Proof. The generalised Cauchy invariants equation (2.20) gives componentwise
 $$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}}{\unicode[STIX]{x2202}a^{\ell }}\frac{\unicode[STIX]{x2202}x^{\,j_{1}}}{\unicode[STIX]{x2202}a^{l_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{\,j_{p-1}}}{\unicode[STIX]{x2202}a^{l_{p-1}}}=\unicode[STIX]{x1D6FE}_{0\ell l_{1}\ldots l_{p-1}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}}{\unicode[STIX]{x2202}a^{\ell }}\frac{\unicode[STIX]{x2202}x^{\,j_{1}}}{\unicode[STIX]{x2202}a^{l_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{\,j_{p-1}}}{\unicode[STIX]{x2202}a^{l_{p-1}}}=\unicode[STIX]{x1D6FE}_{0\ell l_{1}\ldots l_{p-1}}.\end{eqnarray}$$
Multiplying by
![]() $p-1$
suitably chosen inverse Jacobian matrices, we obtain
$p-1$
suitably chosen inverse Jacobian matrices, we obtain
 $$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}}{\unicode[STIX]{x2202}a^{\ell }}\frac{\unicode[STIX]{x2202}x^{\,j_{1}}}{\unicode[STIX]{x2202}a^{l_{1}}}\frac{\unicode[STIX]{x2202}a^{l_{1}}}{\unicode[STIX]{x2202}x^{k_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{\,j_{p-1}}}{\unicode[STIX]{x2202}a^{l_{p-1}}}\frac{\unicode[STIX]{x2202}a^{l_{p-1}}}{\unicode[STIX]{x2202}x^{k_{p-1}}}=\unicode[STIX]{x1D6FE}_{0\ell l_{1}\ldots l_{p-1}}\frac{\unicode[STIX]{x2202}a^{l_{1}}}{\unicode[STIX]{x2202}x^{k_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{l_{p-1}}}{\unicode[STIX]{x2202}x^{k_{p-1}}},\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}}{\unicode[STIX]{x2202}a^{\ell }}\frac{\unicode[STIX]{x2202}x^{\,j_{1}}}{\unicode[STIX]{x2202}a^{l_{1}}}\frac{\unicode[STIX]{x2202}a^{l_{1}}}{\unicode[STIX]{x2202}x^{k_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{\,j_{p-1}}}{\unicode[STIX]{x2202}a^{l_{p-1}}}\frac{\unicode[STIX]{x2202}a^{l_{p-1}}}{\unicode[STIX]{x2202}x^{k_{p-1}}}=\unicode[STIX]{x1D6FE}_{0\ell l_{1}\ldots l_{p-1}}\frac{\unicode[STIX]{x2202}a^{l_{1}}}{\unicode[STIX]{x2202}x^{k_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{l_{p-1}}}{\unicode[STIX]{x2202}x^{k_{p-1}}},\end{eqnarray}$$
that is
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{0\ell l_{1}\ldots l_{p-1}}\frac{\unicode[STIX]{x2202}a^{l_{1}}}{\unicode[STIX]{x2202}x^{k_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{l_{p-1}}}{\unicode[STIX]{x2202}x^{k_{p-1}}} & = & \displaystyle \frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\unicode[STIX]{x1D6FF}_{k_{1}}^{\,j_{1}}\cdots \unicode[STIX]{x1D6FF}_{k_{p-1}}^{\,j_{p-1}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}}{\unicode[STIX]{x2202}a^{\ell }}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{k_{1}\ldots k_{p-1}}^{i_{1}\ldots i_{p-1}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}}{\unicode[STIX]{x2202}a^{\ell }}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{0\ell l_{1}\ldots l_{p-1}}\frac{\unicode[STIX]{x2202}a^{l_{1}}}{\unicode[STIX]{x2202}x^{k_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{l_{p-1}}}{\unicode[STIX]{x2202}x^{k_{p-1}}} & = & \displaystyle \frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p-1}}^{i_{1}\ldots i_{p-1}}\unicode[STIX]{x1D6FF}_{k_{1}}^{\,j_{1}}\cdots \unicode[STIX]{x1D6FF}_{k_{p-1}}^{\,j_{p-1}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}}{\unicode[STIX]{x2202}a^{\ell }}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{k_{1}\ldots k_{p-1}}^{i_{1}\ldots i_{p-1}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}}{\unicode[STIX]{x2202}a^{\ell }}.\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}$
is skew-symmetric, we have
$\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}$
is skew-symmetric, we have
 $$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{k_{1}\ldots k_{p-1}}^{i_{1}\ldots i_{p-1}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}=\unicode[STIX]{x1D6FC}_{k_{1}\ldots k_{p-1}},\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{(p-1)!}\unicode[STIX]{x1D6FF}_{k_{1}\ldots k_{p-1}}^{i_{1}\ldots i_{p-1}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}=\unicode[STIX]{x1D6FC}_{k_{1}\ldots k_{p-1}},\end{eqnarray}$$
and (2.39) becomes
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}}{\unicode[STIX]{x2202}a^{\ell }}=\unicode[STIX]{x1D6FE}_{0\ell j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}a^{\,j_{1}}}{\unicode[STIX]{x2202}x^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{\,j_{p-1}}}{\unicode[STIX]{x2202}x^{i_{p-1}}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}}{\unicode[STIX]{x2202}a^{\ell }}=\unicode[STIX]{x1D6FE}_{0\ell j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}a^{\,j_{1}}}{\unicode[STIX]{x2202}x^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{\,j_{p-1}}}{\unicode[STIX]{x2202}x^{i_{p-1}}}.\end{eqnarray}$$
By application of the differential operator
 $\unicode[STIX]{x1D6FF}^{k\ell }(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{k})$
to (2.41) and summation over index
$\unicode[STIX]{x1D6FF}^{k\ell }(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{k})$
to (2.41) and summation over index
![]() $\ell$
, equation (2.41) becomes
$\ell$
, equation (2.41) becomes
 $$\begin{eqnarray}\unicode[STIX]{x0394}_{a}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}=\unicode[STIX]{x1D6FF}^{k\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(\unicode[STIX]{x1D6FE}_{0\ell j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}a^{\,j_{1}}}{\unicode[STIX]{x2202}x^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{\,j_{p-1}}}{\unicode[STIX]{x2202}x^{i_{p-1}}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x0394}_{a}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p-1}}=\unicode[STIX]{x1D6FF}^{k\ell }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(\unicode[STIX]{x1D6FE}_{0\ell j_{1}\ldots j_{p-1}}\frac{\unicode[STIX]{x2202}a^{\,j_{1}}}{\unicode[STIX]{x2202}x^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{\,j_{p-1}}}{\unicode[STIX]{x2202}x^{i_{p-1}}}\right).\end{eqnarray}$$
This equation gives (2.36) after formal inversion of the Laplacian operator
![]() $\unicode[STIX]{x0394}_{a}$
, expressed in Lagrangian variables. We observe that this inversion is reminiscent of that of the Biot–Savart law, with the left-hand side of (2.41) playing roughly the role of the curl of the
$\unicode[STIX]{x0394}_{a}$
, expressed in Lagrangian variables. We observe that this inversion is reminiscent of that of the Biot–Savart law, with the left-hand side of (2.41) playing roughly the role of the curl of the
![]() $(p-1)$
-form
$(p-1)$
-form
![]() $\unicode[STIX]{x1D6FC}$
.◻
$\unicode[STIX]{x1D6FC}$
.◻
2.5 Broad applicability of Theorem 1
Our key result, namely Theorem 1, may be viewed as a new fundamental result in linear transport theory, giving an alternative Lagrangian formulation of Lie advection for a large class of differential forms. (This was pointed out to us by Peter Constantin who made us realise that this new result in linear transport theory may be of independent interest.) Indeed there is no need to have a self-consistent coupling between the transporter (vector fields
![]() $v$
) and the transported (differential forms
$v$
) and the transported (differential forms
![]() $\unicode[STIX]{x1D6FE}$
) to obtain generalised Cauchy invariants equations. For the first time, it is here shown that Cauchy invariants equations exist for non-self-consistent linear transport. It must be pointed out that, when the Cauchy invariants were rediscovered in the 20th century, most of the time it was by making use of Noether’s theorem in the case of self-consistent nonlinear equations (Frisch & Villone Reference Frisch and Villone2014). Although Noether’s theorem is usually not available for linear transport equations, our key result shows that such generalised Cauchy invariants still do exist in linear transport theory. Consequently, our result is applicable to a large class of fluid dynamical equations that rely on Lie advection. Hereafter, we give some important examples. Some more material, dealing specifically with helicity problems in fluids and MHD, will be presented in § 4.
$\unicode[STIX]{x1D6FE}$
) to obtain generalised Cauchy invariants equations. For the first time, it is here shown that Cauchy invariants equations exist for non-self-consistent linear transport. It must be pointed out that, when the Cauchy invariants were rediscovered in the 20th century, most of the time it was by making use of Noether’s theorem in the case of self-consistent nonlinear equations (Frisch & Villone Reference Frisch and Villone2014). Although Noether’s theorem is usually not available for linear transport equations, our key result shows that such generalised Cauchy invariants still do exist in linear transport theory. Consequently, our result is applicable to a large class of fluid dynamical equations that rely on Lie advection. Hereafter, we give some important examples. Some more material, dealing specifically with helicity problems in fluids and MHD, will be presented in § 4.
2.5.1 Induction equation in ideal incompressible MHD
In incompressible ideal MHD, the magnetic flux conservation law (induction or Faraday’s equation) can be rewritten as a Lie-advection equation, provided the magnetic field is considered as a 2-form (see, e.g., Flanders Reference Flanders1963). Denoting the magnetic field 2-form by
![]() $B$
and the magnetic (vector) potential 1-form by
$B$
and the magnetic (vector) potential 1-form by
![]() $A$
, we have
$A$
, we have
and the induction equation reads
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}B+\unicode[STIX]{x00A3}_{v}B=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}B+\unicode[STIX]{x00A3}_{v}B=0.\end{eqnarray}$$
Indeed (2.44) results from the Maxwell–Faraday equation
 $\unicode[STIX]{x2202}_{t}B+\text{d}E=0$
, the Maxwell–Gauss equation
$\unicode[STIX]{x2202}_{t}B+\text{d}E=0$
, the Maxwell–Gauss equation
![]() $\text{d}B=0$
, and the (ideal) induction equation
$\text{d}B=0$
, and the (ideal) induction equation
 $E-\text{i}_{v}B=0$
, where
$E-\text{i}_{v}B=0$
, where
![]() $E$
is the dual 1-form associated to the electric (vector) field. Therefore from Theorem 1, we obtain the following Cauchy invariants equation
$E$
is the dual 1-form associated to the electric (vector) field. Therefore from Theorem 1, we obtain the following Cauchy invariants equation
 $$\begin{eqnarray}\text{d}A_{k}\wedge \text{d}x^{k}=B_{0}=\text{d}A_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\text{d}A_{k}\wedge \text{d}x^{k}=B_{0}=\text{d}A_{0}.\end{eqnarray}$$
Let us note that this equation and (2.44) can be extended to Riemannian manifolds of any dimension by keeping the same covariant form, i.e. as they stand.
We observe that (2.43) and (2.44) are known, at least for the 3D flat case (Flanders Reference Flanders1963). As to (2.45), in the flat case, it is the well-known law of conservation of magnetic flux, which is here shown to be a Cauchy-type equation.
2.5.2 Adiabatic and barotropic ideal compressible fluid
Here and in § 2.5.3 we use geometrical tools for writing fluid equations that will be discussed in more details in § 3.
An adiabatic ideal compressible fluid, with equation of state
 $p=p(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D702})$
, where the scalar
$p=p(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D702})$
, where the scalar
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\unicode[STIX]{x1D702}$
are respectively the density and the entropy, is governed by the equations
$\unicode[STIX]{x1D702}$
are respectively the density and the entropy, is governed by the equations
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}v^{\flat }+\unicode[STIX]{x00A3}_{v}v^{\flat }=-\frac{\text{d}p}{\unicode[STIX]{x1D70C}}+\frac{1}{2}\,\text{d}(v,v)_{g} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}v^{\flat }+\unicode[STIX]{x00A3}_{v}v^{\flat }=-\frac{\text{d}p}{\unicode[STIX]{x1D70C}}+\frac{1}{2}\,\text{d}(v,v)_{g} & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}\mathfrak{m}+\unicode[STIX]{x00A3}_{v}\mathfrak{m}=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}\mathfrak{m}+\unicode[STIX]{x00A3}_{v}\mathfrak{m}=0 & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D702}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D702}=0. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D702}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D702}=0. & \displaystyle\end{eqnarray}$$
Here,
![]() $\mathfrak{m}$
denotes the mass
$\mathfrak{m}$
denotes the mass
![]() $d$
-form defined by
$d$
-form defined by
 $\mathfrak{m}:=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D707}$
. Since by definition we have
$\mathfrak{m}:=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D707}$
. Since by definition we have
 $\text{div}_{\unicode[STIX]{x1D707}}v:=\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D707}$
, equation (2.47) is equivalent to
$\text{div}_{\unicode[STIX]{x1D707}}v:=\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D707}$
, equation (2.47) is equivalent to
 $\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D70C}+\text{div}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70C}v)=0$
. The Lagrangian formulation of (2.47)–(2.48) is
$\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D70C}+\text{div}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70C}v)=0$
. The Lagrangian formulation of (2.47)–(2.48) is
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{t}\circ \unicode[STIX]{x1D711}_{t}=\unicode[STIX]{x1D70C}_{0}/J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})\quad \text{and}\quad \unicode[STIX]{x1D702}_{t}\circ \unicode[STIX]{x1D711}_{t}=\unicode[STIX]{x1D702}_{0},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{t}\circ \unicode[STIX]{x1D711}_{t}=\unicode[STIX]{x1D70C}_{0}/J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})\quad \text{and}\quad \unicode[STIX]{x1D702}_{t}\circ \unicode[STIX]{x1D711}_{t}=\unicode[STIX]{x1D702}_{0},\end{eqnarray}$$
where
 $J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t}):=\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}/\unicode[STIX]{x1D707}=\sqrt{g\circ \unicode[STIX]{x1D711}_{t}}\det (\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}/\unicode[STIX]{x2202}a)$
is the Jacobian of the Lagrangian flow
$J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t}):=\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}/\unicode[STIX]{x1D707}=\sqrt{g\circ \unicode[STIX]{x1D711}_{t}}\det (\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}/\unicode[STIX]{x2202}a)$
is the Jacobian of the Lagrangian flow
![]() $\unicode[STIX]{x1D711}_{t}$
generated from the vector field
$\unicode[STIX]{x1D711}_{t}$
generated from the vector field
![]() $v$
, and
$v$
, and
 $\unicode[STIX]{x1D70C}_{0}=\unicode[STIX]{x1D70C}_{0}(a)$
and
$\unicode[STIX]{x1D70C}_{0}=\unicode[STIX]{x1D70C}_{0}(a)$
and
 $\unicode[STIX]{x1D702}_{0}=\unicode[STIX]{x1D702}_{0}(a)$
are the initial density and entropy. We now introduce the 1-form
$\unicode[STIX]{x1D702}_{0}=\unicode[STIX]{x1D702}_{0}(a)$
are the initial density and entropy. We now introduce the 1-form
![]() $\unicode[STIX]{x1D6FE}$
, with zero initial value (i.e.
$\unicode[STIX]{x1D6FE}$
, with zero initial value (i.e.
![]() $\unicode[STIX]{x1D6FE}_{0}=0$
), which satisfies the equation
$\unicode[STIX]{x1D6FE}_{0}=0$
), which satisfies the equation
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FE}=-\frac{\text{d}p}{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FE}=-\frac{\text{d}p}{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
Using the Lie-derivative theorem (2.14), integration of (2.50) yields the 1-form
![]() $\unicode[STIX]{x1D6FE}$
such that
$\unicode[STIX]{x1D6FE}$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}=-\unicode[STIX]{x1D711}_{\ast t}\int _{0}^{t}\,\text{d}\unicode[STIX]{x1D70F}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}^{\ast }\left(\frac{\text{d}p}{\unicode[STIX]{x1D70C}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}=-\unicode[STIX]{x1D711}_{\ast t}\int _{0}^{t}\,\text{d}\unicode[STIX]{x1D70F}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}^{\ast }\left(\frac{\text{d}p}{\unicode[STIX]{x1D70C}}\right).\end{eqnarray}$$
Defining the modified 1-form velocity
 $\tilde{v}^{\flat }:=v^{\flat }-\unicode[STIX]{x1D6FE}$
, and the modified 2-form vorticity
$\tilde{v}^{\flat }:=v^{\flat }-\unicode[STIX]{x1D6FE}$
, and the modified 2-form vorticity
 $\tilde{\unicode[STIX]{x1D714}}:=\text{d}\tilde{v}^{\flat }$
, from (2.46) and (2.50), we obtain
$\tilde{\unicode[STIX]{x1D714}}:=\text{d}\tilde{v}^{\flat }$
, from (2.46) and (2.50), we obtain
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\tilde{\unicode[STIX]{x1D714}}+\unicode[STIX]{x00A3}_{v}\tilde{\unicode[STIX]{x1D714}}=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\tilde{\unicode[STIX]{x1D714}}+\unicode[STIX]{x00A3}_{v}\tilde{\unicode[STIX]{x1D714}}=0.\end{eqnarray}$$
We can now apply Theorem 1 to this equation. We then obtain for (2.46) the following Lagrangian formulation
 $$\begin{eqnarray}\text{d}\tilde{v}_{k}^{\flat }\wedge \text{d}x^{k}=\unicode[STIX]{x1D714}_{0}:=\text{d}v_{0}^{\flat }.\end{eqnarray}$$
$$\begin{eqnarray}\text{d}\tilde{v}_{k}^{\flat }\wedge \text{d}x^{k}=\unicode[STIX]{x1D714}_{0}:=\text{d}v_{0}^{\flat }.\end{eqnarray}$$
Let us note that the Ertel potential vorticity 3-form
 $\text{d}v^{\flat }\wedge \text{d}\unicode[STIX]{x1D702}$
is a Lagrangian invariant since
$\text{d}v^{\flat }\wedge \text{d}\unicode[STIX]{x1D702}$
is a Lagrangian invariant since
 $(\unicode[STIX]{x2202}_{t}+\unicode[STIX]{x00A3}_{v})\,\text{d}v^{\flat }\wedge \text{d}\unicode[STIX]{x1D702}=0$
, which results from (2.46), (2.48) and the identity
$(\unicode[STIX]{x2202}_{t}+\unicode[STIX]{x00A3}_{v})\,\text{d}v^{\flat }\wedge \text{d}\unicode[STIX]{x1D702}=0$
, which results from (2.46), (2.48) and the identity
 $\text{d}p\wedge \text{d}\unicode[STIX]{x1D70C}\wedge \text{d}\unicode[STIX]{x1D702}=0$
by virtue of the dependence
$\text{d}p\wedge \text{d}\unicode[STIX]{x1D70C}\wedge \text{d}\unicode[STIX]{x1D702}=0$
by virtue of the dependence
 $p=p(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D702})$
. In three dimension,
$p=p(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D702})$
. In three dimension,
![]() $d=3$
, we can easily show that the scalar local Ertel potential vorticity
$d=3$
, we can easily show that the scalar local Ertel potential vorticity
 $\star (\text{d}v^{\flat }\wedge \text{d}\unicode[STIX]{x1D702})$
satisfies also a Lie-advection equation; thus it is also a local conserved quantity. Let us also note that in the barotropic case (Khesin & Chekanov Reference Khesin and Chekanov1989), since
$\star (\text{d}v^{\flat }\wedge \text{d}\unicode[STIX]{x1D702})$
satisfies also a Lie-advection equation; thus it is also a local conserved quantity. Let us also note that in the barotropic case (Khesin & Chekanov Reference Khesin and Chekanov1989), since
 $p=p(\unicode[STIX]{x1D70C})$
, we obtain
$p=p(\unicode[STIX]{x1D70C})$
, we obtain
 $d(\text{d}p/\unicode[STIX]{x1D70C})=0$
; thus we have
$d(\text{d}p/\unicode[STIX]{x1D70C})=0$
; thus we have
![]() $\unicode[STIX]{x1D6FE}=0$
,
$\unicode[STIX]{x1D6FE}=0$
,
![]() $\tilde{v}^{\flat }=v^{\flat }$
and
$\tilde{v}^{\flat }=v^{\flat }$
and
 $\tilde{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D714}:=\text{d}v^{\flat }$
.
$\tilde{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D714}:=\text{d}v^{\flat }$
.
2.5.3 Barotropic ideal compressible MHD
Let
![]() $b$
be the magnetic vector field,
$b$
be the magnetic vector field,
![]() $b^{\flat }$
its dual 1-form and
$b^{\flat }$
its dual 1-form and
![]() $B$
its dual 2-form. For an example of a detailed derivation of MHD models we refer to Goedbloed & Poedts (Reference Goedbloed and Poedts2004). The barotropic ideal compressible MHD, in a coordinate-free form, reads
$B$
its dual 2-form. For an example of a detailed derivation of MHD models we refer to Goedbloed & Poedts (Reference Goedbloed and Poedts2004). The barotropic ideal compressible MHD, in a coordinate-free form, reads
 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}\mathfrak{m}+\unicode[STIX]{x00A3}_{v}\mathfrak{m}=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}\mathfrak{m}+\unicode[STIX]{x00A3}_{v}\mathfrak{m}=0 & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}v^{\flat }+\unicode[STIX]{x00A3}_{v}v^{\flat }=\frac{\text{}\unicode[STIX]{x00A3}_{b}b^{\flat }-d(b,b)_{g}}{\unicode[STIX]{x1D70C}}-\text{d}\left(h-\frac{1}{2}\text{d}(v,v)_{g}\right) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}v^{\flat }+\unicode[STIX]{x00A3}_{v}v^{\flat }=\frac{\text{}\unicode[STIX]{x00A3}_{b}b^{\flat }-d(b,b)_{g}}{\unicode[STIX]{x1D70C}}-\text{d}\left(h-\frac{1}{2}\text{d}(v,v)_{g}\right) & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}B+\unicode[STIX]{x00A3}_{v}B=0. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}B+\unicode[STIX]{x00A3}_{v}B=0. & \displaystyle\end{eqnarray}$$
Here, the barotropic equation of state
 $p=p(\unicode[STIX]{x1D70C})$
is used, and the enthalpy
$p=p(\unicode[STIX]{x1D70C})$
is used, and the enthalpy
![]() $h$
is related to the pressure
$h$
is related to the pressure
![]() $p$
via the relation
$p$
via the relation
 $\text{d}h=\text{d}p/\unicode[STIX]{x1D70C}$
. In (2.55), the term
$\text{d}h=\text{d}p/\unicode[STIX]{x1D70C}$
. In (2.55), the term
 $(\text{}\unicode[STIX]{x00A3}_{b}b^{\flat }-\text{d}(b,b)_{g})/\unicode[STIX]{x1D70C}$
is the dual 1-form of the Lorentz force field. It is obtained from the Ampère law,
$(\text{}\unicode[STIX]{x00A3}_{b}b^{\flat }-\text{d}(b,b)_{g})/\unicode[STIX]{x1D70C}$
is the dual 1-form of the Lorentz force field. It is obtained from the Ampère law,
 $\text{d}\star B=\unicode[STIX]{x1D707}_{0}\,\mathfrak{j}$
, where
$\text{d}\star B=\unicode[STIX]{x1D707}_{0}\,\mathfrak{j}$
, where
![]() $\mathfrak{j}$
is the current form while
$\mathfrak{j}$
is the current form while
 $j=(\star \,\mathfrak{j})^{\sharp }=(\star \text{d}\star B)^{\sharp }/\unicode[STIX]{x1D707}_{0}$
is the current-density vector field. Indeed, in the three-dimensional case
$j=(\star \,\mathfrak{j})^{\sharp }=(\star \text{d}\star B)^{\sharp }/\unicode[STIX]{x1D707}_{0}$
is the current-density vector field. Indeed, in the three-dimensional case
![]() $d=3$
, this 1-form can be expressed as
$d=3$
, this 1-form can be expressed as
![]() $-\text{i}_{j}B/\unicode[STIX]{x1D70C}$
which is the dual 1-form of the vector field
$-\text{i}_{j}B/\unicode[STIX]{x1D70C}$
which is the dual 1-form of the vector field
![]() $j\times b/\unicode[STIX]{x1D70C}$
(Lorentz force) where the current-density vector
$j\times b/\unicode[STIX]{x1D70C}$
(Lorentz force) where the current-density vector
![]() $j$
is related to the magnetic (vector) field
$j$
is related to the magnetic (vector) field
![]() $b$
by the Ampère law
$b$
by the Ampère law
 $\unicode[STIX]{x1D707}_{0}j=\unicode[STIX]{x1D735}\times b$
(the displacement current being neglected). In the three-dimensional case
$\unicode[STIX]{x1D707}_{0}j=\unicode[STIX]{x1D735}\times b$
(the displacement current being neglected). In the three-dimensional case
![]() $d=3$
, let us note that using the relations
$d=3$
, let us note that using the relations
 $B=\text{i}_{b/\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D707}$
and
$B=\text{i}_{b/\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D707}$
and
 $[\text{}\unicode[STIX]{x00A3}_{v},\text{i}_{b/\unicode[STIX]{x1D70C}}]=\text{i}_{[v,b/\unicode[STIX]{x1D70C}]}$
(see § B.8), equation (2.56) is equivalent to
$[\text{}\unicode[STIX]{x00A3}_{v},\text{i}_{b/\unicode[STIX]{x1D70C}}]=\text{i}_{[v,b/\unicode[STIX]{x1D70C}]}$
(see § B.8), equation (2.56) is equivalent to
 $\unicode[STIX]{x2202}_{t}(b/\unicode[STIX]{x1D70C})+\unicode[STIX]{x00A3}_{v}(b/\unicode[STIX]{x1D70C})=0$
. We now introduce the 1-form
$\unicode[STIX]{x2202}_{t}(b/\unicode[STIX]{x1D70C})+\unicode[STIX]{x00A3}_{v}(b/\unicode[STIX]{x1D70C})=0$
. We now introduce the 1-form
![]() $\unicode[STIX]{x1D6FE}$
, with zero initial value (i.e.
$\unicode[STIX]{x1D6FE}$
, with zero initial value (i.e.
![]() $\unicode[STIX]{x1D6FE}_{0}=0$
), which satisfies the equation
$\unicode[STIX]{x1D6FE}_{0}=0$
), which satisfies the equation
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FE}=\frac{\text{}\unicode[STIX]{x00A3}_{b}b^{\flat }-\text{d}(b,b)_{g}}{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FE}=\frac{\text{}\unicode[STIX]{x00A3}_{b}b^{\flat }-\text{d}(b,b)_{g}}{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
Using the Lie-derivative theorem (2.14), integration of (2.57) yields the 1-form
![]() $\unicode[STIX]{x1D6FE}$
such that
$\unicode[STIX]{x1D6FE}$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D711}_{\ast t}\int _{0}^{t}\,\text{d}\unicode[STIX]{x1D70F}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}^{\ast }\left(\frac{\text{}\unicode[STIX]{x00A3}_{b}b^{\flat }-\text{d}(b,b)_{g}}{\unicode[STIX]{x1D70C}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D711}_{\ast t}\int _{0}^{t}\,\text{d}\unicode[STIX]{x1D70F}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}^{\ast }\left(\frac{\text{}\unicode[STIX]{x00A3}_{b}b^{\flat }-\text{d}(b,b)_{g}}{\unicode[STIX]{x1D70C}}\right),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D711}_{t}$
is the Lagrangian flow generated from the vector field
$\unicode[STIX]{x1D711}_{t}$
is the Lagrangian flow generated from the vector field
![]() $v$
. Defining the modified 1-form velocity
$v$
. Defining the modified 1-form velocity
 $\tilde{v}^{\flat }:=v^{\flat }-\unicode[STIX]{x1D6FE}$
, and the modified 2-form vorticity
$\tilde{v}^{\flat }:=v^{\flat }-\unicode[STIX]{x1D6FE}$
, and the modified 2-form vorticity
 $\tilde{\unicode[STIX]{x1D714}}:=\text{d}\tilde{v}^{\flat }$
, from (2.55) and (2.57), we obtain
$\tilde{\unicode[STIX]{x1D714}}:=\text{d}\tilde{v}^{\flat }$
, from (2.55) and (2.57), we obtain
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\tilde{\unicode[STIX]{x1D714}}+\unicode[STIX]{x00A3}_{v}\tilde{\unicode[STIX]{x1D714}}=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\tilde{\unicode[STIX]{x1D714}}+\unicode[STIX]{x00A3}_{v}\tilde{\unicode[STIX]{x1D714}}=0.\end{eqnarray}$$
Therefore, we can again apply Theorem 1 to (2.56) and (2.59). We then obtain for the system (2.55)–(2.56) the following Lagrangian formulation
 $$\begin{eqnarray}\text{d}\tilde{v}_{k}^{\flat }\wedge \text{d}x^{k}=\unicode[STIX]{x1D714}_{0}:=\text{d}v_{0}^{\flat },\quad \text{and}\quad \text{d}A_{k}\wedge \text{d}x^{k}=B_{0}:=\text{d}A_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\text{d}\tilde{v}_{k}^{\flat }\wedge \text{d}x^{k}=\unicode[STIX]{x1D714}_{0}:=\text{d}v_{0}^{\flat },\quad \text{and}\quad \text{d}A_{k}\wedge \text{d}x^{k}=B_{0}:=\text{d}A_{0}.\end{eqnarray}$$
Of course, the Lagrangian formulation of the equation of mass conservation (2.54) is the same as in § 2.5.2. Let us note that we can extend this formulation to adiabatic ideal compressible MHD with the equation of state
 $p=p(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D702})$
by adding to (2.54)–(2.56) the entropy equation (2.48). Let us also note that in fact there are several ways in which the full nonlinear ideal MHD equations can be recast as Lie-advection problems: for example one can use the dual 1-forms of the Elsasser (Reference Elsasser1956) variables (Marsch & Mangeney Reference Marsch and Mangeney1987).
$p=p(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D702})$
by adding to (2.54)–(2.56) the entropy equation (2.48). Let us also note that in fact there are several ways in which the full nonlinear ideal MHD equations can be recast as Lie-advection problems: for example one can use the dual 1-forms of the Elsasser (Reference Elsasser1956) variables (Marsch & Mangeney Reference Marsch and Mangeney1987).
2.5.4 Extended ideal compressible MHD
The extended MHD equations (Goedbloed & Poedts Reference Goedbloed and Poedts2004; D’Avignon, Morrison & Lingam Reference D’Avignon, Morrison and Lingam2016; Lingam, Milosevich & Morrison Reference Lingam, Milosevich and Morrison2016), in covariant form, reads
 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}\mathfrak{m}+\unicode[STIX]{x00A3}_{v}\mathfrak{m}=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}\mathfrak{m}+\unicode[STIX]{x00A3}_{v}\mathfrak{m}=0 & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}B_{\pm }+\unicode[STIX]{x00A3}_{v_{\pm }}B_{\pm }=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x2202}_{t}B_{\pm }+\unicode[STIX]{x00A3}_{v_{\pm }}B_{\pm }=0, & \displaystyle\end{eqnarray}$$
where,
 $B_{\pm }=\text{d}A_{\pm }$
,
$B_{\pm }=\text{d}A_{\pm }$
,
 $A_{\pm }=A+(d_{e}^{2}/\unicode[STIX]{x1D70C})\star \text{d}\star B+\unicode[STIX]{x1D705}_{\pm }v^{\flat }$
, and
$A_{\pm }=A+(d_{e}^{2}/\unicode[STIX]{x1D70C})\star \text{d}\star B+\unicode[STIX]{x1D705}_{\pm }v^{\flat }$
, and
 $v_{\pm }=v-\unicode[STIX]{x1D705}_{\mp }\,(\star \text{d}\star B)^{\sharp }/\unicode[STIX]{x1D70C}$
. Here, the constants
$v_{\pm }=v-\unicode[STIX]{x1D705}_{\mp }\,(\star \text{d}\star B)^{\sharp }/\unicode[STIX]{x1D70C}$
. Here, the constants
![]() $\unicode[STIX]{x1D705}_{\pm }$
are the solutions of the quadratic equation
$\unicode[STIX]{x1D705}_{\pm }$
are the solutions of the quadratic equation
 $\unicode[STIX]{x1D705}^{2}-d_{i}\unicode[STIX]{x1D705}-d_{e}^{2}=0$
, where
$\unicode[STIX]{x1D705}^{2}-d_{i}\unicode[STIX]{x1D705}-d_{e}^{2}=0$
, where
![]() $d_{i}$
and
$d_{i}$
and
![]() $d_{e}$
serve as the normalised ion and electron skin depths, respectively. In addition the variables
$d_{e}$
serve as the normalised ion and electron skin depths, respectively. In addition the variables
![]() $\mathfrak{m}$
and
$\mathfrak{m}$
and
![]() $v$
denote the total-mass form and the centre-of-mass velocity vector, respectively. As in § 2.5.1 the magnetic potential 1-form by
$v$
denote the total-mass form and the centre-of-mass velocity vector, respectively. As in § 2.5.1 the magnetic potential 1-form by
![]() $A$
is linked to the magnetic field 2-form
$A$
is linked to the magnetic field 2-form
![]() $B$
by
$B$
by
![]() $B=\text{d}A$
. Let us note that here the assumption of a barotropic equation of state was used. We can directly apply Theorem 1 to (2.62) for obtaining the following Cauchy invariants equations
$B=\text{d}A$
. Let us note that here the assumption of a barotropic equation of state was used. We can directly apply Theorem 1 to (2.62) for obtaining the following Cauchy invariants equations
 $$\begin{eqnarray}\text{d}A_{\pm k}\wedge \text{d}x_{\pm }^{k}=B_{\pm 0}:=\text{d}A_{\pm 0},\end{eqnarray}$$
$$\begin{eqnarray}\text{d}A_{\pm k}\wedge \text{d}x_{\pm }^{k}=B_{\pm 0}:=\text{d}A_{\pm 0},\end{eqnarray}$$
where
![]() $x_{\pm t}$
are the Lagrangian maps generated by the vector fields
$x_{\pm t}$
are the Lagrangian maps generated by the vector fields
![]() $v_{\pm }$
. Once again, the Lagrangian formulation of the equation of mass conservation (2.61) is the same as in § 2.5.2. When
$v_{\pm }$
. Once again, the Lagrangian formulation of the equation of mass conservation (2.61) is the same as in § 2.5.2. When
![]() $d_{e}\rightarrow 0$
, we have
$d_{e}\rightarrow 0$
, we have
![]() $\unicode[STIX]{x1D705}_{\pm }=d_{i}$
and we obtain what is called Hall MHD. When
$\unicode[STIX]{x1D705}_{\pm }=d_{i}$
and we obtain what is called Hall MHD. When
![]() $d_{i}\rightarrow 0$
, we have
$d_{i}\rightarrow 0$
, we have
 $\unicode[STIX]{x1D705}_{\pm }=\pm d_{e}$
and we obtain what is called inertial MHD. Let us note that when
$\unicode[STIX]{x1D705}_{\pm }=\pm d_{e}$
and we obtain what is called inertial MHD. Let us note that when
![]() $d_{i}\rightarrow 0$
and
$d_{i}\rightarrow 0$
and
![]() $d_{e}\rightarrow 0$
simultaneously, we obtain
$d_{e}\rightarrow 0$
simultaneously, we obtain
![]() $\unicode[STIX]{x1D705}_{\pm }=0$
and thus we do not recover the full ideal compressible MHD, since both equations (2.62) degenerate into only one equation, namely (2.56).
$\unicode[STIX]{x1D705}_{\pm }=0$
and thus we do not recover the full ideal compressible MHD, since both equations (2.62) degenerate into only one equation, namely (2.56).
2.5.5 Tao’s modification of the incompressible Euler equations in Euclidean space
The dynamics of vorticity for the case of the ordinary incompressible Euler equation will be discussed in detail in § 3, but we wish to mention that recently Tao (Reference Tao2016) has proposed an interesting modification of the incompressible Euler equations in Euclidean spaces that preserves much of its differential geometric content, but sometimes allows (proven) blow-up, that is loss of regularity in a finite time. This modification consists in keeping the Lie-advection equation for the vorticity 2-form
![]() $\unicode[STIX]{x1D714}$
, namely
$\unicode[STIX]{x1D714}$
, namely
 $(\unicode[STIX]{x2202}_{t}+\unicode[STIX]{x00A3}_{v})\,\unicode[STIX]{x1D714}=0$
, but replacing the Biot–Savart law
$(\unicode[STIX]{x2202}_{t}+\unicode[STIX]{x00A3}_{v})\,\unicode[STIX]{x1D714}=0$
, but replacing the Biot–Savart law
 $v^{\flat }=\text{d}^{\star }\unicode[STIX]{x0394}_{H}^{-1}\unicode[STIX]{x1D714}$
by the following self-consistent coupling
$v^{\flat }=\text{d}^{\star }\unicode[STIX]{x0394}_{H}^{-1}\unicode[STIX]{x1D714}$
by the following self-consistent coupling
 $v^{\flat }=\text{d}^{\star }A\unicode[STIX]{x1D714}$
. Here,
$v^{\flat }=\text{d}^{\star }A\unicode[STIX]{x1D714}$
. Here,
![]() $A$
is a linear pseudodifferential operator which is self-adjoint (like
$A$
is a linear pseudodifferential operator which is self-adjoint (like
![]() $\unicode[STIX]{x0394}_{H}^{-1}$
) and has the same degree of regularity as
$\unicode[STIX]{x0394}_{H}^{-1}$
) and has the same degree of regularity as
![]() $\unicode[STIX]{x0394}_{H}^{-1}$
. Tao (Reference Tao2016) has shown that there exist some operators
$\unicode[STIX]{x0394}_{H}^{-1}$
. Tao (Reference Tao2016) has shown that there exist some operators
![]() $A$
for which the corresponding classical solutions blow-up in finite time. Since the Lie-advection equation for the vorticity 2-form is preserved in these models, by Theorem 1, there is a corresponding generalised Cauchy invariants equation. Indeed, since
$A$
for which the corresponding classical solutions blow-up in finite time. Since the Lie-advection equation for the vorticity 2-form is preserved in these models, by Theorem 1, there is a corresponding generalised Cauchy invariants equation. Indeed, since
![]() $\unicode[STIX]{x1D714}=\text{d}v^{\flat }$
and using the modified velocity 1-form
$\unicode[STIX]{x1D714}=\text{d}v^{\flat }$
and using the modified velocity 1-form
 $u^{\flat }:=\text{d}^{\star }A\,\text{d}v^{\flat }$
, we can now define two Lagrangian maps
$u^{\flat }:=\text{d}^{\star }A\,\text{d}v^{\flat }$
, we can now define two Lagrangian maps
![]() $x_{t}$
and
$x_{t}$
and
![]() $y_{t}$
by
$y_{t}$
by
 $$\begin{eqnarray}{\dot{x}}_{t}:=\frac{\text{d}x_{t}}{\text{d}t}=u(t,x_{t})\quad \text{and}\quad {\dot{y}}_{t}:=\frac{\text{d}y_{t}}{\text{d}t}=v(t,y_{t}),\end{eqnarray}$$
$$\begin{eqnarray}{\dot{x}}_{t}:=\frac{\text{d}x_{t}}{\text{d}t}=u(t,x_{t})\quad \text{and}\quad {\dot{y}}_{t}:=\frac{\text{d}y_{t}}{\text{d}t}=v(t,y_{t}),\end{eqnarray}$$
where the vector fields
![]() $u$
and
$u$
and
![]() $v$
are linked by the relation
$v$
are linked by the relation
 $u=(\text{d}^{\star }A\,\text{d}v^{\flat })^{\sharp }$
. Recalling that in Euclidean spaces covariant and contravariant components are identical, the corresponding Cauchy invariants equation then reads
$u=(\text{d}^{\star }A\,\text{d}v^{\flat })^{\sharp }$
. Recalling that in Euclidean spaces covariant and contravariant components are identical, the corresponding Cauchy invariants equation then reads
 $$\begin{eqnarray}\text{d}{\dot{y}}_{k}\wedge \text{d}x^{k}=\unicode[STIX]{x1D714}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\text{d}{\dot{y}}_{k}\wedge \text{d}x^{k}=\unicode[STIX]{x1D714}_{0}.\end{eqnarray}$$
Remark 3 (Well-posedness: linear and nonlinear issues).
As mentioned at the beginning of § 2.5, the coupling between the
![]() $p$
-form
$p$
-form
![]() $\unicode[STIX]{x1D6FE}$
and the vector field
$\unicode[STIX]{x1D6FE}$
and the vector field
![]() $v$
, in the Lie-advection equation (2.16), could be either non-self-consistent or self-consistent. In the former case, also called passive,
$v$
, in the Lie-advection equation (2.16), could be either non-self-consistent or self-consistent. In the former case, also called passive,
![]() $v$
is prescribed at all times and there is no feedback of
$v$
is prescribed at all times and there is no feedback of
![]() $\unicode[STIX]{x1D6FE}$
on
$\unicode[STIX]{x1D6FE}$
on
![]() $v$
. In the latter case,
$v$
. In the latter case,
![]() $v$
is not prescribed (except perhaps at the initial time) and the feedback of
$v$
is not prescribed (except perhaps at the initial time) and the feedback of
![]() $\unicode[STIX]{x1D6FE}$
on
$\unicode[STIX]{x1D6FE}$
on
![]() $v$
is given by at least one additional equation linking
$v$
is given by at least one additional equation linking
![]() $v$
to
$v$
to
![]() $\unicode[STIX]{x1D6FE}$
; an instance is the full Euler equation, where the vorticity 2-form is the exterior derivative of the velocity 1-form (cf. § 3).
$\unicode[STIX]{x1D6FE}$
; an instance is the full Euler equation, where the vorticity 2-form is the exterior derivative of the velocity 1-form (cf. § 3).
In the non-self-consistent case, when the vector field
![]() $v$
is Lipschitz continuous (not necessarily divergence-free or incompressible), the associated Lagrangian flow exists globally in time (Taylor Reference Taylor1996). Therefore, equation (2.16) is well posed and has global-in-time regular solutions; thus Lie and Cauchy invariants exist globally in time too (Taylor Reference Taylor1996).
$v$
is Lipschitz continuous (not necessarily divergence-free or incompressible), the associated Lagrangian flow exists globally in time (Taylor Reference Taylor1996). Therefore, equation (2.16) is well posed and has global-in-time regular solutions; thus Lie and Cauchy invariants exist globally in time too (Taylor Reference Taylor1996).
In the self-consistent case, well-posedness of the coupled system, i.e. existence of solutions to the system constituted of (2.16) plus the additional equation linking
![]() $v$
to
$v$
to
![]() $\unicode[STIX]{x1D6FE}$
, depends of course on the specific self-consistent coupling considered.
$\unicode[STIX]{x1D6FE}$
, depends of course on the specific self-consistent coupling considered.
For example, in the case where the vector field
![]() $v$
is the velocity field given by the 3D-Euclidean incompressible Euler equations and the
$v$
is the velocity field given by the 3D-Euclidean incompressible Euler equations and the
![]() $p$
-form
$p$
-form
![]() $\unicode[STIX]{x1D714}$
is the 2-vorticity form, the self-consistent coupling is given by
$\unicode[STIX]{x1D714}$
is the 2-vorticity form, the self-consistent coupling is given by
![]() $\unicode[STIX]{x1D714}=\text{d}v^{\flat }$
(in the simplest case this means that the vorticity vector is the curl of the velocity vector). Using the Biot–Savart law, this self-consistent coupling can be rewritten as
$\unicode[STIX]{x1D714}=\text{d}v^{\flat }$
(in the simplest case this means that the vorticity vector is the curl of the velocity vector). Using the Biot–Savart law, this self-consistent coupling can be rewritten as
 $v^{\flat }=\text{d}^{\star }\unicode[STIX]{x0394}_{H}^{-1}\unicode[STIX]{x1D714}$
, where
$v^{\flat }=\text{d}^{\star }\unicode[STIX]{x0394}_{H}^{-1}\unicode[STIX]{x1D714}$
, where
![]() $\text{d}^{\star }$
is the exterior coderivative and
$\text{d}^{\star }$
is the exterior coderivative and
 $\unicode[STIX]{x0394}_{H}:=\text{d}\text{d}^{\star }+\text{d}^{\star }\text{d}$
is the Laplace–de Rham operator (see § B.13). The corresponding Cauchy problem is known to be well posed in time when the initial velocity is in Hölder or Sobolev spaces with suitable indexes of regularity. This was established in the seminal work of Lichtenstein (Reference Lichtenstein1925, Reference Lichtenstein1927) and Gyunter (Reference Gyunter1926, Reference Gyunter1934) for the case of the whole Euclidean space and, of Ebin & Marsden (Reference Ebin and Marsden1970) for the case of bounded domains. Therefore (2.16) has local-in-time regular solutions, so that Lie and Cauchy invariants exist at least for short times.
$\unicode[STIX]{x0394}_{H}:=\text{d}\text{d}^{\star }+\text{d}^{\star }\text{d}$
is the Laplace–de Rham operator (see § B.13). The corresponding Cauchy problem is known to be well posed in time when the initial velocity is in Hölder or Sobolev spaces with suitable indexes of regularity. This was established in the seminal work of Lichtenstein (Reference Lichtenstein1925, Reference Lichtenstein1927) and Gyunter (Reference Gyunter1926, Reference Gyunter1934) for the case of the whole Euclidean space and, of Ebin & Marsden (Reference Ebin and Marsden1970) for the case of bounded domains. Therefore (2.16) has local-in-time regular solutions, so that Lie and Cauchy invariants exist at least for short times.
Although the modified Euler equations of Tao (Reference Tao2016) satisfy helicity and energy (or Hamiltonian) conservation laws and possess a Kelvin circulation theorem, Tao has shown that there exist some operators
![]() $A$
for which the corresponding classical solutions blow-up in finite time. It does not mean that we can conjecture a finite-time blow-up for classical solutions of the original incompressible Euler equations (for
$A$
for which the corresponding classical solutions blow-up in finite time. It does not mean that we can conjecture a finite-time blow-up for classical solutions of the original incompressible Euler equations (for
![]() $d\geqslant 3$
), but rather that a possible absence of blow-up cannot be proved with the only properties of the Euler equations that are shared by these modified models. Although Lie-advection equation for the vorticity 2-form is preserved in these models, the Cauchy invariants equation (2.65) shows that a modification of the Biot–Savart law induces a change in the geometry of the original incompressible Euler equations. Indeed (2.65) involves two families of characteristic curves, whereas the original incompressible Euler equations deal with only one such family. In other words, on the set of incompressible vector fields we have
$d\geqslant 3$
), but rather that a possible absence of blow-up cannot be proved with the only properties of the Euler equations that are shared by these modified models. Although Lie-advection equation for the vorticity 2-form is preserved in these models, the Cauchy invariants equation (2.65) shows that a modification of the Biot–Savart law induces a change in the geometry of the original incompressible Euler equations. Indeed (2.65) involves two families of characteristic curves, whereas the original incompressible Euler equations deal with only one such family. In other words, on the set of incompressible vector fields we have
 $\text{d}^{\star }\unicode[STIX]{x0394}_{H}^{-1}\text{d}=\text{Id}$
, whereas
$\text{d}^{\star }\unicode[STIX]{x0394}_{H}^{-1}\text{d}=\text{Id}$
, whereas
 $\text{d}^{\star }A\text{d}\neq \text{Id}$
.
$\text{d}^{\star }A\text{d}\neq \text{Id}$
.
3 Vorticity and incompressible flow in hydrodynamics
In this section we apply our main result, Theorem 1, to the incompressible Euler equations on a
![]() $d$
-dimensional Riemannian manifold. This will extend to Riemannian manifolds of any dimension the notion of Cauchy invariants, first introduced by Cauchy (Reference Cauchy1815) for the three-dimensional incompressible Euler equations in ‘flat’ Euclidean spaces. First, we need to write the Euler equations in a covariant form, i.e. in terms of a 1-form
$d$
-dimensional Riemannian manifold. This will extend to Riemannian manifolds of any dimension the notion of Cauchy invariants, first introduced by Cauchy (Reference Cauchy1815) for the three-dimensional incompressible Euler equations in ‘flat’ Euclidean spaces. First, we need to write the Euler equations in a covariant form, i.e. in terms of a 1-form
![]() $v^{\flat }$
for the velocity vector field
$v^{\flat }$
for the velocity vector field
![]() $v$
; this is the aim of § 3.1. The velocity 1-form
$v$
; this is the aim of § 3.1. The velocity 1-form
![]() $v^{\flat }$
is here called the infinitesimal velocity circulation, because if we were in a flat space, we would have
$v^{\flat }$
is here called the infinitesimal velocity circulation, because if we were in a flat space, we would have
 $v^{\flat }=\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{d}\boldsymbol{x}$
. Henceforth, ordinary vectors will be denoted by bold italic font when they might otherwise be mistaken for
$v^{\flat }=\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{d}\boldsymbol{x}$
. Henceforth, ordinary vectors will be denoted by bold italic font when they might otherwise be mistaken for
![]() $p$
-forms. Then, the exterior derivative of the covariant form of the Euler equations gives a Lie-advection equation of the form (2.16) for the vorticity 2-form
$p$
-forms. Then, the exterior derivative of the covariant form of the Euler equations gives a Lie-advection equation of the form (2.16) for the vorticity 2-form
![]() $\unicode[STIX]{x1D714}$
, here called the covariant vorticity equation. Henceforth,
$\unicode[STIX]{x1D714}$
, here called the covariant vorticity equation. Henceforth,
![]() $\unicode[STIX]{x1D714}$
always denotes the vorticity 2-form and not the vorticity vector; the latter being
$\unicode[STIX]{x1D714}$
always denotes the vorticity 2-form and not the vorticity vector; the latter being
![]() $\unicode[STIX]{x1D74E}$
. In § 3.2, applying Theorem 1 to the covariant vorticity equation, we show that the Cauchy invariants equation can have different representations. In particular we show that the Cauchy invariants equation is an alternative formulation of the well-known Lie advection of the vorticity 2-form. From this point of view, the Cauchy invariant and the Cauchy vorticity formula are representations of the same conservation law, related by Hodge duality. Finally, we note that the covariant vorticity equation and the Cauchy invariants equation on a manifold have alternative derivations using variational methods in conjunction with the relabelling symmetry and Noether’s theorem.
$\unicode[STIX]{x1D74E}$
. In § 3.2, applying Theorem 1 to the covariant vorticity equation, we show that the Cauchy invariants equation can have different representations. In particular we show that the Cauchy invariants equation is an alternative formulation of the well-known Lie advection of the vorticity 2-form. From this point of view, the Cauchy invariant and the Cauchy vorticity formula are representations of the same conservation law, related by Hodge duality. Finally, we note that the covariant vorticity equation and the Cauchy invariants equation on a manifold have alternative derivations using variational methods in conjunction with the relabelling symmetry and Noether’s theorem.
3.1 Covariant formulation of the vorticity equation
In this section the vorticity will be considered as a 2-form
![]() $\unicode[STIX]{x1D714}$
. We start with the incompressible Euler equations on a
$\unicode[STIX]{x1D714}$
. We start with the incompressible Euler equations on a
![]() $d$
-dimensional Riemannian manifold
$d$
-dimensional Riemannian manifold
![]() $(M,g)$
. Written in terms of the velocity vector field
$(M,g)$
. Written in terms of the velocity vector field
![]() $v$
and of the scalar pressure field
$v$
and of the scalar pressure field
![]() $p$
, they read
$p$
, they read
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x2202}_{t}v^{i}+v^{k}\unicode[STIX]{x1D735}_{k}v^{i}=-\text{g}^{ik}\unicode[STIX]{x2202}_{k}p\quad (\text{Euler}),\\ \unicode[STIX]{x1D735}_{i}v^{i}=0\quad (\text{incompressibility condition})~x\in \unicode[STIX]{x1D6FA},t\in ]0,T\!].\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x2202}_{t}v^{i}+v^{k}\unicode[STIX]{x1D735}_{k}v^{i}=-\text{g}^{ik}\unicode[STIX]{x2202}_{k}p\quad (\text{Euler}),\\ \unicode[STIX]{x1D735}_{i}v^{i}=0\quad (\text{incompressibility condition})~x\in \unicode[STIX]{x1D6FA},t\in ]0,T\!].\end{array}\right\}\end{eqnarray}$$
Here the symbol
![]() $\unicode[STIX]{x1D735}_{k}$
denotes the covariant derivative, which can be seen as a generalisation to curved spaces of the classical partial derivative
$\unicode[STIX]{x1D735}_{k}$
denotes the covariant derivative, which can be seen as a generalisation to curved spaces of the classical partial derivative
![]() $\unicode[STIX]{x2202}_{k}$
of Euclidean spaces (for a more detailed definition, see § B.10). The geometric interpretation of the incompressible Euler equations is recalled in § A.1, while their simplest derivation is obtained from a variational formulation (least-action principle), as explained in § A.2.
$\unicode[STIX]{x2202}_{k}$
of Euclidean spaces (for a more detailed definition, see § B.10). The geometric interpretation of the incompressible Euler equations is recalled in § A.1, while their simplest derivation is obtained from a variational formulation (least-action principle), as explained in § A.2.
The Euler equations and incompressibility condition, written in the contravariant formulation (3.1), can be rewritten in the covariant formulation, i.e. in term of 1-form fields instead of vector fields. Let
![]() $v^{\flat }$
be the 1-form field obtained from the vector field by the index lowering operator
$v^{\flat }$
be the 1-form field obtained from the vector field by the index lowering operator
 $(\cdot )^{\flat }:{\mathcal{T}}_{0}^{1}(\unicode[STIX]{x1D6FA})\rightarrow {\mathcal{T}}_{1}^{0}(\unicode[STIX]{x1D6FA})$
; that is, we set
$(\cdot )^{\flat }:{\mathcal{T}}_{0}^{1}(\unicode[STIX]{x1D6FA})\rightarrow {\mathcal{T}}_{1}^{0}(\unicode[STIX]{x1D6FA})$
; that is, we set
 $v^{\flat }=(v^{i}\unicode[STIX]{x2202}_{i})^{\flat }=(v^{\flat })_{i}\,\text{d}x^{i}=\text{g}_{ij}v^{\,j}\,\text{d}x^{i}$
. Using the preservation of the metric of the Riemann–Levi-Civita connection, namely
$v^{\flat }=(v^{i}\unicode[STIX]{x2202}_{i})^{\flat }=(v^{\flat })_{i}\,\text{d}x^{i}=\text{g}_{ij}v^{\,j}\,\text{d}x^{i}$
. Using the preservation of the metric of the Riemann–Levi-Civita connection, namely
 $\unicode[STIX]{x1D735}_{k}\text{g}_{ij}=0$
, we easily find
$\unicode[STIX]{x1D735}_{k}\text{g}_{ij}=0$
, we easily find
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}v_{i}+v^{k}\unicode[STIX]{x1D735}_{k}v_{i}=-\unicode[STIX]{x2202}_{i}p,\quad x\in \unicode[STIX]{x1D6FA}\subset M,t\in ]0,T],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}v_{i}+v^{k}\unicode[STIX]{x1D735}_{k}v_{i}=-\unicode[STIX]{x2202}_{i}p,\quad x\in \unicode[STIX]{x1D6FA}\subset M,t\in ]0,T],\end{eqnarray}$$
and
 $$\begin{eqnarray}\text{g}^{ij}\unicode[STIX]{x1D735}_{i}v_{j}=0,\quad x\in \unicode[STIX]{x1D6FA},t\in ]0,T].\end{eqnarray}$$
$$\begin{eqnarray}\text{g}^{ij}\unicode[STIX]{x1D735}_{i}v_{j}=0,\quad x\in \unicode[STIX]{x1D6FA},t\in ]0,T].\end{eqnarray}$$
In compact form, equation (3.2) can be written as
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}v^{\flat }+(\unicode[STIX]{x1D735}_{v}v)^{\flat }=-\text{d}p,\quad x\in \unicode[STIX]{x1D6FA},t\in ]0,T].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}v^{\flat }+(\unicode[STIX]{x1D735}_{v}v)^{\flat }=-\text{d}p,\quad x\in \unicode[STIX]{x1D6FA},t\in ]0,T].\end{eqnarray}$$
Now we rewrite (3.4) as
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}v^{\flat }+\unicode[STIX]{x00A3}_{v}v^{\flat }+\text{d}\left(p-{\textstyle \frac{1}{2}}(v,v)_{g}\right)=0,\quad x\in \unicode[STIX]{x1D6FA},t\in ]0,T],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}v^{\flat }+\unicode[STIX]{x00A3}_{v}v^{\flat }+\text{d}\left(p-{\textstyle \frac{1}{2}}(v,v)_{g}\right)=0,\quad x\in \unicode[STIX]{x1D6FA},t\in ]0,T],\end{eqnarray}$$
an equation which differs from a Lie-advection condition for
![]() $v^{\flat }$
by just an additional exact differential (which will disappear upon application of yet another exterior differential). To obtain (3.5) we use the Cartan formula
$v^{\flat }$
by just an additional exact differential (which will disappear upon application of yet another exterior differential). To obtain (3.5) we use the Cartan formula
 $\unicode[STIX]{x00A3}_{v}v^{\flat }=\text{d}\text{i}_{v}v^{\flat }+\text{i}_{v}\,\text{d}v^{\flat }$
for the Lie derivative (§ B.8) and a rewrite of the right-hand side of the Cartan formula, precisely
$\unicode[STIX]{x00A3}_{v}v^{\flat }=\text{d}\text{i}_{v}v^{\flat }+\text{i}_{v}\,\text{d}v^{\flat }$
for the Lie derivative (§ B.8) and a rewrite of the right-hand side of the Cartan formula, precisely
 $\text{d}\text{i}_{v}v^{\flat }+\text{i}_{v}\,\text{d}v^{\flat }=(\unicode[STIX]{x1D735}_{v}v)^{\flat }+(1/2)\text{d}(v,v)_{g}$
. This is established in § A.5. In these equations
$\text{d}\text{i}_{v}v^{\flat }+\text{i}_{v}\,\text{d}v^{\flat }=(\unicode[STIX]{x1D735}_{v}v)^{\flat }+(1/2)\text{d}(v,v)_{g}$
. This is established in § A.5. In these equations
 $\text{i}_{v}:\unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})\rightarrow \unicode[STIX]{x039B}^{p-1}(\unicode[STIX]{x1D6FA})$
is the interior (or inner) product with the vector
$\text{i}_{v}:\unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})\rightarrow \unicode[STIX]{x039B}^{p-1}(\unicode[STIX]{x1D6FA})$
is the interior (or inner) product with the vector
![]() $v$
, which acts as an integration; as to
$v$
, which acts as an integration; as to
![]() $(\cdot ,\cdot )_{g}$
, it denotes the Riemannian scalar product for vector fields in
$(\cdot ,\cdot )_{g}$
, it denotes the Riemannian scalar product for vector fields in
![]() ${\mathcal{T}}_{0}^{1}(\unicode[STIX]{x1D6FA})$
, defined by
${\mathcal{T}}_{0}^{1}(\unicode[STIX]{x1D6FA})$
, defined by
 $(v,w)_{g}=\text{g}_{ij}v^{i}w^{\,j}$
(see § B.3).
$(v,w)_{g}=\text{g}_{ij}v^{i}w^{\,j}$
(see § B.3).
From a fluid-mechanical point of view, specialising to the Euclidean case, it is of interest to rewrite the Euler equations (3.5) in standard vector notation as
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\boldsymbol{v}+\unicode[STIX]{x1D735}|\boldsymbol{v}|^{2}+\unicode[STIX]{x1D74E}\times \boldsymbol{v}+\unicode[STIX]{x1D735}\left(p-\frac{|\boldsymbol{v}|^{2}}{2}\right)=0,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\boldsymbol{v}+\unicode[STIX]{x1D735}|\boldsymbol{v}|^{2}+\unicode[STIX]{x1D74E}\times \boldsymbol{v}+\unicode[STIX]{x1D735}\left(p-\frac{|\boldsymbol{v}|^{2}}{2}\right)=0,\end{eqnarray}$$
where
![]() $\times$
denotes the vector product and
$\times$
denotes the vector product and
![]() $\unicode[STIX]{x1D735}$
is the standard gradient operator in Euclidean coordinate. This has some similarity to what is known as Lamb’s form of the incompressible Euler equations, in which
$\unicode[STIX]{x1D735}$
is the standard gradient operator in Euclidean coordinate. This has some similarity to what is known as Lamb’s form of the incompressible Euler equations, in which
![]() $\unicode[STIX]{x1D74E}\times \boldsymbol{v}$
also appears. It would not be advisable to simplify (3.6) to Lamb’s form by combining the two terms involving a gradient of the local kinetic energy, because the second and third term on the left-hand side of (3.6) are both needed to obtain a Lie derivative and all the nice consequences.
$\unicode[STIX]{x1D74E}\times \boldsymbol{v}$
also appears. It would not be advisable to simplify (3.6) to Lamb’s form by combining the two terms involving a gradient of the local kinetic energy, because the second and third term on the left-hand side of (3.6) are both needed to obtain a Lie derivative and all the nice consequences.
Indeed, we can now define the vorticity 2-form as the exterior derivative of the infinitesimal velocity circulation 1-form
![]() $v^{\flat }$
, that is
$v^{\flat }$
, that is
 $$\begin{eqnarray}\unicode[STIX]{x1D714}=\text{d}v^{\flat }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}=\text{d}v^{\flat }.\end{eqnarray}$$
Taking the exterior derivative of the covariant formulation (3.5) of the Euler equations, and using the commutation relation
 $[\text{d},\unicode[STIX]{x00A3}_{v}]=0$
, we obtain
$[\text{d},\unicode[STIX]{x00A3}_{v}]=0$
, we obtain
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D714}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D714}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}=0.\end{eqnarray}$$
This establishes that the vorticity 2-form is Lie-advected, a result essentially known since Helmholtz (Reference von Helmholtz1858). In terms of the 1-form
![]() $v^{\flat }$
, the incompressibility condition
$v^{\flat }$
, the incompressibility condition
 $\unicode[STIX]{x1D735}_{i}v^{i}=0$
reads
$\unicode[STIX]{x1D735}_{i}v^{i}=0$
reads
 $\text{d}^{\star }v^{\flat }=0$
(see § B.9). Using the Hodge theorem (see § B.13), we obtain the Biot–Savart law
$\text{d}^{\star }v^{\flat }=0$
(see § B.9). Using the Hodge theorem (see § B.13), we obtain the Biot–Savart law
 $v=(\text{d}^{\star }\unicode[STIX]{x0394}_{H}^{-1}\unicode[STIX]{x1D714})^{\sharp }$
, which self-consistently expresses the velocity vector field
$v=(\text{d}^{\star }\unicode[STIX]{x0394}_{H}^{-1}\unicode[STIX]{x1D714})^{\sharp }$
, which self-consistently expresses the velocity vector field
![]() $v$
in terms of the vorticity 2-form
$v$
in terms of the vorticity 2-form
![]() $\unicode[STIX]{x1D714}$
. Indeed, using the incompressibility condition
$\unicode[STIX]{x1D714}$
. Indeed, using the incompressibility condition
 $\text{d}^{\star }v^{\flat }=0$
, we have
$\text{d}^{\star }v^{\flat }=0$
, we have
 $v=(\text{d}^{\star }\unicode[STIX]{x0394}_{H}^{-1}\unicode[STIX]{x1D714})^{\sharp }=(\unicode[STIX]{x0394}_{H}^{-1}\text{d}^{\star }\,\text{d}v^{\flat })^{\sharp }=(\unicode[STIX]{x0394}_{H}^{-1}(\text{d}^{\star }\text{d}+\text{d}\text{d}^{\star })v^{\flat })^{\sharp }=(v^{\flat })^{\sharp }=v$
.
$v=(\text{d}^{\star }\unicode[STIX]{x0394}_{H}^{-1}\unicode[STIX]{x1D714})^{\sharp }=(\unicode[STIX]{x0394}_{H}^{-1}\text{d}^{\star }\,\text{d}v^{\flat })^{\sharp }=(\unicode[STIX]{x0394}_{H}^{-1}(\text{d}^{\star }\text{d}+\text{d}\text{d}^{\star })v^{\flat })^{\sharp }=(v^{\flat })^{\sharp }=v$
.
Finally from (3.8), using the lesser known commutation relation
 $[\sharp ^{d-p}\,\star ,\unicode[STIX]{x00A3}_{v}]=0$
(with
$[\sharp ^{d-p}\,\star ,\unicode[STIX]{x00A3}_{v}]=0$
(with
![]() $p=2$
), whose proof is given in § A.6, we obtain that the vorticity vector is also Lie-advected. Here, by vorticity vector, we understand the
$p=2$
), whose proof is given in § A.6, we obtain that the vorticity vector is also Lie-advected. Here, by vorticity vector, we understand the
![]() $(d-2)$
-vector
$(d-2)$
-vector
 $\unicode[STIX]{x1D74E}:=(\star \unicode[STIX]{x1D714})^{\sharp ^{d-2}}$
(in other words a
$\unicode[STIX]{x1D74E}:=(\star \unicode[STIX]{x1D714})^{\sharp ^{d-2}}$
(in other words a
![]() $(d-2)$
-contravariant tensor). Namely, we have
$(d-2)$
-contravariant tensor). Namely, we have
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D74E}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D74E}=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D74E}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D74E}=0.\end{eqnarray}$$
Remark 4.
-
(i) An alternative derivation of the covariant vorticity equation (3.8) from the Euler equations (3.1) is to use the relabelling symmetry and Noether’s theorem (see § A.4). This derivation leads to
(3.10)from where Lie advection of the vorticity $$\begin{eqnarray}\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{0},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{0},\end{eqnarray}$$
 $\unicode[STIX]{x1D714}$
follows readily (see (2.15) and (2.16)).
$\unicode[STIX]{x1D714}$
follows readily (see (2.15) and (2.16)).
-
(ii) Let us note that in appendix B of Gilbert & Vanneste (Reference Gilbert and Vanneste2016), the authors give a variational derivation of the covariant Euler equations (3.5).
-
(iii) In § A.6, the proof of the commutation relation
 $[\sharp ^{d-p}\,\star ,\unicode[STIX]{x00A3}_{v}]=0$
is done by following an algebraic approach. A dynamical approach based on infinitesimal pullback transport and the Lie-derivative theorem could be used for an alternative proof, along the lines used in § B.9.
$[\sharp ^{d-p}\,\star ,\unicode[STIX]{x00A3}_{v}]=0$
is done by following an algebraic approach. A dynamical approach based on infinitesimal pullback transport and the Lie-derivative theorem could be used for an alternative proof, along the lines used in § B.9.
3.2 Cauchy invariants equation and Cauchy formula
We are now ready to extend to Riemannian manifolds of any dimension the Cauchy invariants equation and the Cauchy formula. We begin by observing that all assumptions of Theorem 1 are now satisfied: the vorticity 2-form
![]() $\unicode[STIX]{x1D714}=\text{d}v^{\flat }$
is exact and is Lie-advected. There from follows Corollary 2 for which we also give a direct simplified proof.
$\unicode[STIX]{x1D714}=\text{d}v^{\flat }$
is exact and is Lie-advected. There from follows Corollary 2 for which we also give a direct simplified proof.
Corollary 2 (Cauchy invariants equations on a Riemannian manifold).
Let
![]() $\unicode[STIX]{x1D711}_{t}$
be the Euler flow. We set
$\unicode[STIX]{x1D711}_{t}$
be the Euler flow. We set
![]() $x=\unicode[STIX]{x1D711}_{t}$
and
$x=\unicode[STIX]{x1D711}_{t}$
and
![]() $v=\dot{\unicode[STIX]{x1D711}}_{t}$
, with
$v=\dot{\unicode[STIX]{x1D711}}_{t}$
, with
![]() $v_{0}=\dot{\unicode[STIX]{x1D711}}_{0}$
. Then we have
$v_{0}=\dot{\unicode[STIX]{x1D711}}_{0}$
. Then we have
 $$\begin{eqnarray}\text{d}v_{k}\wedge \text{d}x^{k}=\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{0}:=\text{d}v_{0}^{\flat }.\end{eqnarray}$$
$$\begin{eqnarray}\text{d}v_{k}\wedge \text{d}x^{k}=\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{0}:=\text{d}v_{0}^{\flat }.\end{eqnarray}$$
Proof. We begin by showing that
 $\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}=\text{d}v_{k}\wedge \text{d}x^{k}$
. Indeed, we have
$\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}=\text{d}v_{k}\wedge \text{d}x^{k}$
. Indeed, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714} & = & \displaystyle (\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{ij}\,\text{d}a^{i}\wedge \,\text{d}a^{\,j}=\mathop{\sum }_{i<j}\frac{\unicode[STIX]{x2202}x^{l}}{\unicode[STIX]{x2202}a^{i}}\frac{\unicode[STIX]{x2202}x^{k}}{\unicode[STIX]{x2202}a^{\,j}}\unicode[STIX]{x1D714}_{lk}(x_{t}(a))\,\text{d}a^{i}\wedge \text{d}a^{\,j}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i<j}\frac{\unicode[STIX]{x2202}x^{l}}{\unicode[STIX]{x2202}a^{i}}\frac{\unicode[STIX]{x2202}x^{k}}{\unicode[STIX]{x2202}a^{\,j}}\left(\frac{\unicode[STIX]{x2202}v_{k}}{\unicode[STIX]{x2202}x^{l}}-\frac{\unicode[STIX]{x2202}v_{l}}{\unicode[STIX]{x2202}x^{k}}\right)\text{d}a^{i}\wedge \text{d}a^{\,j}=\mathop{\sum }_{i<j}\frac{\unicode[STIX]{x2202}v_{k}}{\unicode[STIX]{x2202}x^{l}}\left(\frac{\unicode[STIX]{x2202}x^{l}}{\unicode[STIX]{x2202}a^{i}}\frac{\unicode[STIX]{x2202}x^{k}}{\unicode[STIX]{x2202}a^{\,j}}-\frac{\unicode[STIX]{x2202}x^{l}}{\unicode[STIX]{x2202}a^{\,j}}\frac{\unicode[STIX]{x2202}x^{k}}{\unicode[STIX]{x2202}a^{i}}\right)\text{d}a^{i}\wedge \text{d}a^{\,j}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x2202}v_{k}}{\unicode[STIX]{x2202}x^{l}}\frac{\unicode[STIX]{x2202}x^{l}}{\unicode[STIX]{x2202}a^{i}}\frac{\unicode[STIX]{x2202}x^{k}}{\unicode[STIX]{x2202}a^{\,j}}\,\text{d}a^{i}\wedge \text{d}a^{\,j}=\frac{\unicode[STIX]{x2202}v_{k}}{\unicode[STIX]{x2202}a^{i}}\frac{\unicode[STIX]{x2202}x^{k}}{\unicode[STIX]{x2202}a^{\,j}}\,\text{d}a^{i}\wedge \text{d}a^{\,j}\nonumber\\ \displaystyle & = & \displaystyle \text{d}v_{k}\wedge \text{d}x^{k}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714} & = & \displaystyle (\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{ij}\,\text{d}a^{i}\wedge \,\text{d}a^{\,j}=\mathop{\sum }_{i<j}\frac{\unicode[STIX]{x2202}x^{l}}{\unicode[STIX]{x2202}a^{i}}\frac{\unicode[STIX]{x2202}x^{k}}{\unicode[STIX]{x2202}a^{\,j}}\unicode[STIX]{x1D714}_{lk}(x_{t}(a))\,\text{d}a^{i}\wedge \text{d}a^{\,j}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i<j}\frac{\unicode[STIX]{x2202}x^{l}}{\unicode[STIX]{x2202}a^{i}}\frac{\unicode[STIX]{x2202}x^{k}}{\unicode[STIX]{x2202}a^{\,j}}\left(\frac{\unicode[STIX]{x2202}v_{k}}{\unicode[STIX]{x2202}x^{l}}-\frac{\unicode[STIX]{x2202}v_{l}}{\unicode[STIX]{x2202}x^{k}}\right)\text{d}a^{i}\wedge \text{d}a^{\,j}=\mathop{\sum }_{i<j}\frac{\unicode[STIX]{x2202}v_{k}}{\unicode[STIX]{x2202}x^{l}}\left(\frac{\unicode[STIX]{x2202}x^{l}}{\unicode[STIX]{x2202}a^{i}}\frac{\unicode[STIX]{x2202}x^{k}}{\unicode[STIX]{x2202}a^{\,j}}-\frac{\unicode[STIX]{x2202}x^{l}}{\unicode[STIX]{x2202}a^{\,j}}\frac{\unicode[STIX]{x2202}x^{k}}{\unicode[STIX]{x2202}a^{i}}\right)\text{d}a^{i}\wedge \text{d}a^{\,j}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x2202}v_{k}}{\unicode[STIX]{x2202}x^{l}}\frac{\unicode[STIX]{x2202}x^{l}}{\unicode[STIX]{x2202}a^{i}}\frac{\unicode[STIX]{x2202}x^{k}}{\unicode[STIX]{x2202}a^{\,j}}\,\text{d}a^{i}\wedge \text{d}a^{\,j}=\frac{\unicode[STIX]{x2202}v_{k}}{\unicode[STIX]{x2202}a^{i}}\frac{\unicode[STIX]{x2202}x^{k}}{\unicode[STIX]{x2202}a^{\,j}}\,\text{d}a^{i}\wedge \text{d}a^{\,j}\nonumber\\ \displaystyle & = & \displaystyle \text{d}v_{k}\wedge \text{d}x^{k}.\end{eqnarray}$$
Corollary 2 follows from the covariant vorticity equation (3.8) or the conservation of the vorticity 2-form, i.e.
 $\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{0}:=\text{d}v_{0}^{\flat }$
.◻
$\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{0}:=\text{d}v_{0}^{\flat }$
.◻
Remark 5.
-
(i) (Contravariant formulation). In terms of components, the Cauchy invariants equation (3.11) reads
(3.13)The contravariant form of this equation reads $$\begin{eqnarray}\unicode[STIX]{x2202}_{k}({\dot{x}}^{i}\text{g}_{ij})\unicode[STIX]{x2202}_{l}x^{\,j}-\unicode[STIX]{x2202}_{l}({\dot{x}}^{i}\text{g}_{ij})\unicode[STIX]{x2202}_{k}x^{\,j}=\unicode[STIX]{x1D714}_{0kl},\quad 1\leqslant k<l\leqslant d.\end{eqnarray}$$
(3.14)where the
$$\begin{eqnarray}\unicode[STIX]{x2202}_{k}({\dot{x}}^{i}\text{g}_{ij})\unicode[STIX]{x2202}_{l}x^{\,j}-\unicode[STIX]{x2202}_{l}({\dot{x}}^{i}\text{g}_{ij})\unicode[STIX]{x2202}_{k}x^{\,j}=\unicode[STIX]{x1D714}_{0kl},\quad 1\leqslant k<l\leqslant d.\end{eqnarray}$$
(3.14)where the $$\begin{eqnarray}\unicode[STIX]{x1D700}^{kli_{1}\ldots i_{d-2}}\unicode[STIX]{x2202}_{k}({\dot{x}}^{i}\text{g}_{ij})\unicode[STIX]{x2202}_{l}x^{\,j}=\sqrt{\text{g}}\unicode[STIX]{x1D714}_{0}^{i_{1}\ldots i_{d-2}},\quad 1\leqslant i_{1}<\cdots <i_{d-2}\leqslant d,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}^{kli_{1}\ldots i_{d-2}}\unicode[STIX]{x2202}_{k}({\dot{x}}^{i}\text{g}_{ij})\unicode[STIX]{x2202}_{l}x^{\,j}=\sqrt{\text{g}}\unicode[STIX]{x1D714}_{0}^{i_{1}\ldots i_{d-2}},\quad 1\leqslant i_{1}<\cdots <i_{d-2}\leqslant d,\end{eqnarray}$$
 $(d-2)$
-vector
$(d-2)$
-vector
 $\unicode[STIX]{x1D74E}_{0}:=(\star \unicode[STIX]{x1D714}_{0})^{\sharp ^{d-2}}$
is defined componentwise by (3.15)
$\unicode[STIX]{x1D74E}_{0}:=(\star \unicode[STIX]{x1D714}_{0})^{\sharp ^{d-2}}$
is defined componentwise by (3.15) $$\begin{eqnarray}\unicode[STIX]{x1D714}_{0}^{i_{1}\ldots i_{d-2}}=\frac{1}{2\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{kli_{1}\ldots i_{d-2}}\unicode[STIX]{x1D714}_{0kl}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{0}^{i_{1}\ldots i_{d-2}}=\frac{1}{2\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{kli_{1}\ldots i_{d-2}}\unicode[STIX]{x1D714}_{0kl}.\end{eqnarray}$$
-
(ii) (Integrated (circulation) form of the Cauchy invariants equation). Since the Cauchy invariant may be rewritten as an exact 2-form, i.e.
(3.16)using Hodge’s decomposition, we obtain $$\begin{eqnarray}\text{d}v_{k}\wedge \text{d}x^{k}=\text{d}(v_{k}\,\text{d}x^{k}),\end{eqnarray}$$
(3.17)where
$$\begin{eqnarray}\text{d}v_{k}\wedge \text{d}x^{k}=\text{d}(v_{k}\,\text{d}x^{k}),\end{eqnarray}$$
(3.17)where $$\begin{eqnarray}v_{k}\,\text{d}x^{k}=v_{0}^{\flat }+\text{d}\unicode[STIX]{x1D713}+h,\end{eqnarray}$$
$$\begin{eqnarray}v_{k}\,\text{d}x^{k}=v_{0}^{\flat }+\text{d}\unicode[STIX]{x1D713}+h,\end{eqnarray}$$
 $\unicode[STIX]{x1D713}$
is an arbitrary 0-form (scalar function) and
$\unicode[STIX]{x1D713}$
is an arbitrary 0-form (scalar function) and
 $h$
is a harmonic 1-form. Let
$h$
is a harmonic 1-form. Let
 $c$
be a 1-chain on the manifold
$c$
be a 1-chain on the manifold
 $M$
. Choosing the function
$M$
. Choosing the function
 $\unicode[STIX]{x1D713}$
with suitable value on the boundary
$\unicode[STIX]{x1D713}$
with suitable value on the boundary
 $\unicode[STIX]{x2202}c$
(if it exists), from the Stokes theorem we obtain (3.18)Moreover if the Betti number
$\unicode[STIX]{x2202}c$
(if it exists), from the Stokes theorem we obtain (3.18)Moreover if the Betti number $$\begin{eqnarray}\int _{c}v_{k}\,\text{d}x^{k}=\int _{c}v_{0}^{\flat }+\int _{c}h.\end{eqnarray}$$
$$\begin{eqnarray}\int _{c}v_{k}\,\text{d}x^{k}=\int _{c}v_{0}^{\flat }+\int _{c}h.\end{eqnarray}$$
 $b_{1}(M)=0$
, then the second term on the right-hand side of the previous formula vanishes. Some examples for which
$b_{1}(M)=0$
, then the second term on the right-hand side of the previous formula vanishes. Some examples for which
 $b_{1}(M)=0$
are given in § B.13. Considering now a 2-chain
$b_{1}(M)=0$
are given in § B.13. Considering now a 2-chain
 $c$
, using the Stokes theorem, we obtain (3.19)This is the famous theorem of conservation of circulation, frequently ascribed to Thomson (Lord Kelvin) (Reference Thomson1869) but actually discovered by Hankel (Reference Hankel1861, see also Frisch & Villone Reference Frisch and Villone2014), using essentially the argument given above.
$c$
, using the Stokes theorem, we obtain (3.19)This is the famous theorem of conservation of circulation, frequently ascribed to Thomson (Lord Kelvin) (Reference Thomson1869) but actually discovered by Hankel (Reference Hankel1861, see also Frisch & Villone Reference Frisch and Villone2014), using essentially the argument given above. $$\begin{eqnarray}\int _{\unicode[STIX]{x2202}c}v_{k}\,\text{d}x^{k}=\int _{\unicode[STIX]{x2202}c}v_{0}^{\flat }.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\unicode[STIX]{x2202}c}v_{k}\,\text{d}x^{k}=\int _{\unicode[STIX]{x2202}c}v_{0}^{\flat }.\end{eqnarray}$$
-
(iii) (Variational derivation of the Cauchy invariants equation). The Cauchy invariants equation (3.11) on a Riemannian manifold has a variational derivation, using the relabelling symmetry and Noether’s theorem without appealing to Theorem 1 (see § A.3).
We turn now to a corollary that clarifies the relationship between the Cauchy invariants equation and the Cauchy vorticity formula, which are actually Hodge dual of each other. We refer the reader to § B.9 for detailed definition of the Hodge duality operator
 $\star :\unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})\rightarrow \unicode[STIX]{x039B}^{d-p}(\unicode[STIX]{x1D6FA})$
, which implements the already mentioned Hodge duality. Indeed, applying the Hodge dual operator to (3.11), we obtain the following.
$\star :\unicode[STIX]{x039B}^{p}(\unicode[STIX]{x1D6FA})\rightarrow \unicode[STIX]{x039B}^{d-p}(\unicode[STIX]{x1D6FA})$
, which implements the already mentioned Hodge duality. Indeed, applying the Hodge dual operator to (3.11), we obtain the following.
Corollary 3 (Cauchy vorticity formula on a Riemannian manifold).
Under the same assumptions as in Corollary 2, we have the Cauchy vorticity formula, written in general as
 $$\begin{eqnarray}\star (\text{d}v_{k}\wedge \text{d}x^{k})=\star \unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}=\star \unicode[STIX]{x1D714}_{0},\end{eqnarray}$$
$$\begin{eqnarray}\star (\text{d}v_{k}\wedge \text{d}x^{k})=\star \unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}=\star \unicode[STIX]{x1D714}_{0},\end{eqnarray}$$
and, in the case of a three-dimensional curved space, as
 $$\begin{eqnarray}\unicode[STIX]{x1D714}^{i}=\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{\,j}}\unicode[STIX]{x1D714}_{0}^{j},\quad i=1,2,3,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}^{i}=\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{\,j}}\unicode[STIX]{x1D714}_{0}^{j},\quad i=1,2,3,\end{eqnarray}$$
where the vorticity vector is defined componentwise by
 $$\begin{eqnarray}\unicode[STIX]{x1D714}^{i}=\frac{1}{2\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{ijk}\unicode[STIX]{x1D714}_{jk},\quad i=1,2,3.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}^{i}=\frac{1}{2\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{ijk}\unicode[STIX]{x1D714}_{jk},\quad i=1,2,3.\end{eqnarray}$$
Proof. Equation (3.20) is of course an immediate consequence of (3.11). To derive (3.21) in the case
![]() $d=3$
, we make use again of the index raising operator
$d=3$
, we make use again of the index raising operator
 $(\cdot )^{\sharp }:{\mathcal{T}}_{1}^{0}(M)\rightarrow {\mathcal{T}}_{0}^{1}(M)$
. In the three-dimensional curved case, equation (3.20) is an equality between 1-forms. Applying the raising operator to (3.20), we obtain an equality between (1-contravariant) vectors, given by
$(\cdot )^{\sharp }:{\mathcal{T}}_{1}^{0}(M)\rightarrow {\mathcal{T}}_{0}^{1}(M)$
. In the three-dimensional curved case, equation (3.20) is an equality between 1-forms. Applying the raising operator to (3.20), we obtain an equality between (1-contravariant) vectors, given by
 $$\begin{eqnarray}[\star (\text{d}v_{k}\wedge \text{d}x^{k})]^{\sharp }=(\star \unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})^{\sharp }=(\star \unicode[STIX]{x1D714}_{0})^{\sharp }.\end{eqnarray}$$
$$\begin{eqnarray}[\star (\text{d}v_{k}\wedge \text{d}x^{k})]^{\sharp }=(\star \unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})^{\sharp }=(\star \unicode[STIX]{x1D714}_{0})^{\sharp }.\end{eqnarray}$$
Now, we expand (3.23) and show that it is equivalent to the Cauchy formula (3.21). We set the notation
 $g_{0}=g(a)$
and
$g_{0}=g(a)$
and
 $g=g(x)$
. First, in terms of components of a 1-form, and using the inversion formula
$g=g(x)$
. First, in terms of components of a 1-form, and using the inversion formula
 $$\begin{eqnarray}\text{g}_{0}^{-1}\unicode[STIX]{x1D700}^{ijk}g_{0kn}=\unicode[STIX]{x1D700}_{lmn}g_{0}^{il}g_{0}^{\,jm},\end{eqnarray}$$
$$\begin{eqnarray}\text{g}_{0}^{-1}\unicode[STIX]{x1D700}^{ijk}g_{0kn}=\unicode[STIX]{x1D700}_{lmn}g_{0}^{il}g_{0}^{\,jm},\end{eqnarray}$$
we have
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D714}}_{0i_{1}}:=(\star \unicode[STIX]{x1D714}_{0})_{i_{1}}={\textstyle \frac{1}{2}}\sqrt{\text{g}_{0}}\unicode[STIX]{x1D700}_{i_{1}j_{1}j_{2}}\unicode[STIX]{x1D714}_{0}^{\,j_{1}j_{2}}={\textstyle \frac{1}{2}}\sqrt{\text{g}_{0}}\unicode[STIX]{x1D700}_{i_{1}j_{1}j_{2}}\text{g}_{0}^{lj_{1}}\text{g}_{0}^{mj_{2}}\unicode[STIX]{x1D714}_{0lm}={\textstyle \frac{1}{2}}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D700}^{plm}g_{0i_{1}p}\unicode[STIX]{x1D714}_{0lm}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D714}}_{0i_{1}}:=(\star \unicode[STIX]{x1D714}_{0})_{i_{1}}={\textstyle \frac{1}{2}}\sqrt{\text{g}_{0}}\unicode[STIX]{x1D700}_{i_{1}j_{1}j_{2}}\unicode[STIX]{x1D714}_{0}^{\,j_{1}j_{2}}={\textstyle \frac{1}{2}}\sqrt{\text{g}_{0}}\unicode[STIX]{x1D700}_{i_{1}j_{1}j_{2}}\text{g}_{0}^{lj_{1}}\text{g}_{0}^{mj_{2}}\unicode[STIX]{x1D714}_{0lm}={\textstyle \frac{1}{2}}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D700}^{plm}g_{0i_{1}p}\unicode[STIX]{x1D714}_{0lm}.\end{eqnarray}$$
In terms of components of a vector, we then obtain
 $$\begin{eqnarray}(\widetilde{\unicode[STIX]{x1D714}}_{0}^{\sharp })^{s}=\text{g}_{0}^{sq}\widetilde{\unicode[STIX]{x1D714}}_{0q}={\textstyle \frac{1}{2}}\text{g}_{0}^{-1/2}\text{g}_{0}^{sq}\unicode[STIX]{x1D700}^{plm}g_{0qp}\unicode[STIX]{x1D714}_{0lm}={\textstyle \frac{1}{2}}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D6FF}_{p}^{s}\unicode[STIX]{x1D700}^{plm}\unicode[STIX]{x1D714}_{0lm}={\textstyle \frac{1}{2}}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D700}^{slm}\unicode[STIX]{x1D714}_{0lm}.\end{eqnarray}$$
$$\begin{eqnarray}(\widetilde{\unicode[STIX]{x1D714}}_{0}^{\sharp })^{s}=\text{g}_{0}^{sq}\widetilde{\unicode[STIX]{x1D714}}_{0q}={\textstyle \frac{1}{2}}\text{g}_{0}^{-1/2}\text{g}_{0}^{sq}\unicode[STIX]{x1D700}^{plm}g_{0qp}\unicode[STIX]{x1D714}_{0lm}={\textstyle \frac{1}{2}}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D6FF}_{p}^{s}\unicode[STIX]{x1D700}^{plm}\unicode[STIX]{x1D714}_{0lm}={\textstyle \frac{1}{2}}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D700}^{slm}\unicode[STIX]{x1D714}_{0lm}.\end{eqnarray}$$
From the definition of the vorticity vector (3.22), we then have
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{0}^{s}=([\star \unicode[STIX]{x1D714}_{0}]^{\sharp })^{s}=\frac{1}{2\sqrt{\text{g}_{0}}}\unicode[STIX]{x1D700}^{slm}\unicode[STIX]{x1D714}_{0lm}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{0}^{s}=([\star \unicode[STIX]{x1D714}_{0}]^{\sharp })^{s}=\frac{1}{2\sqrt{\text{g}_{0}}}\unicode[STIX]{x1D700}^{slm}\unicode[STIX]{x1D714}_{0lm}.\end{eqnarray}$$
Second, in terms of components of a 1-form, we have
 $$\begin{eqnarray}\displaystyle \widetilde{\unicode[STIX]{x1D714}}_{i_{1}}:=(\star \unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{i_{1}} & = & \displaystyle {\textstyle \frac{1}{2}}\sqrt{\text{g}_{0}}\unicode[STIX]{x1D700}_{i_{1}j_{1}j_{2}}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})^{\,j_{1}j_{2}}={\textstyle \frac{1}{2}}\sqrt{\text{g}_{0}}\unicode[STIX]{x1D700}_{i_{1}j_{1}j_{2}}\text{g}_{0}^{lj_{1}}\text{g}_{0}^{mj_{2}}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{lm}\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D700}^{plm}g_{0i_{1}p}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{lm}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{\unicode[STIX]{x1D714}}_{i_{1}}:=(\star \unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{i_{1}} & = & \displaystyle {\textstyle \frac{1}{2}}\sqrt{\text{g}_{0}}\unicode[STIX]{x1D700}_{i_{1}j_{1}j_{2}}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})^{\,j_{1}j_{2}}={\textstyle \frac{1}{2}}\sqrt{\text{g}_{0}}\unicode[STIX]{x1D700}_{i_{1}j_{1}j_{2}}\text{g}_{0}^{lj_{1}}\text{g}_{0}^{mj_{2}}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{lm}\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D700}^{plm}g_{0i_{1}p}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{lm}.\end{eqnarray}$$
In terms of vector components, and using
 $\det (\unicode[STIX]{x2202}x/\unicode[STIX]{x2202}a)=\sqrt{g_{0}/g}$
, we then obtain
$\det (\unicode[STIX]{x2202}x/\unicode[STIX]{x2202}a)=\sqrt{g_{0}/g}$
, we then obtain
 $$\begin{eqnarray}\displaystyle \widetilde{\unicode[STIX]{x1D714}}^{s} & = & \displaystyle (\widetilde{\unicode[STIX]{x1D714}}^{\sharp })^{s}=\text{g}_{0}^{sq}\widetilde{\unicode[STIX]{x1D714}}_{q}=\frac{1}{2}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D700}^{plm}\text{g}_{0}^{sq}g_{0qp}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{lm}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D6FF}_{p}^{s}\unicode[STIX]{x1D700}^{plm}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{lm}=\frac{1}{2}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D700}^{slm}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{lm}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D700}^{slm}\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{l}}\frac{\unicode[STIX]{x2202}x^{\,j}}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D714}_{ij}=\frac{1}{2}\text{g}_{0}^{-1/2}\det \left(\frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}a}\right)\unicode[STIX]{x1D700}^{kij}\frac{\unicode[STIX]{x2202}a^{s}}{\unicode[STIX]{x2202}x^{k}}\unicode[STIX]{x1D714}_{ij}=\frac{\unicode[STIX]{x2202}a^{s}}{\unicode[STIX]{x2202}x^{k}}\frac{1}{2\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{kij}\unicode[STIX]{x1D714}_{ij}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x2202}a^{s}}{\unicode[STIX]{x2202}x^{k}}\unicode[STIX]{x1D714}^{k},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{\unicode[STIX]{x1D714}}^{s} & = & \displaystyle (\widetilde{\unicode[STIX]{x1D714}}^{\sharp })^{s}=\text{g}_{0}^{sq}\widetilde{\unicode[STIX]{x1D714}}_{q}=\frac{1}{2}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D700}^{plm}\text{g}_{0}^{sq}g_{0qp}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{lm}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D6FF}_{p}^{s}\unicode[STIX]{x1D700}^{plm}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{lm}=\frac{1}{2}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D700}^{slm}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714})_{lm}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\text{g}_{0}^{-1/2}\unicode[STIX]{x1D700}^{slm}\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{l}}\frac{\unicode[STIX]{x2202}x^{\,j}}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D714}_{ij}=\frac{1}{2}\text{g}_{0}^{-1/2}\det \left(\frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}a}\right)\unicode[STIX]{x1D700}^{kij}\frac{\unicode[STIX]{x2202}a^{s}}{\unicode[STIX]{x2202}x^{k}}\unicode[STIX]{x1D714}_{ij}=\frac{\unicode[STIX]{x2202}a^{s}}{\unicode[STIX]{x2202}x^{k}}\frac{1}{2\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{kij}\unicode[STIX]{x1D714}_{ij}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x2202}a^{s}}{\unicode[STIX]{x2202}x^{k}}\unicode[STIX]{x1D714}^{k},\end{eqnarray}$$
where we have used the definition of the vorticity vector (3.22). Therefore, we have
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}a^{s}}{\unicode[STIX]{x2202}x^{k}}\unicode[STIX]{x1D714}^{k}=\unicode[STIX]{x1D714}_{0}^{s},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}a^{s}}{\unicode[STIX]{x2202}x^{k}}\unicode[STIX]{x1D714}^{k}=\unicode[STIX]{x1D714}_{0}^{s},\end{eqnarray}$$
which gives (3.21) after inversion. The latter is the vector form of the Cauchy formula for a three-dimensional Riemannian manifold
![]() $(M,g)$
.◻
$(M,g)$
.◻
In dimensions
![]() $d>3$
the Cauchy vorticity formula is no more an equality in terms of 1-forms (or vectors by the lowering–raising duality) but an equality in terms of
$d>3$
the Cauchy vorticity formula is no more an equality in terms of 1-forms (or vectors by the lowering–raising duality) but an equality in terms of
![]() $(d-2)$
-forms (or
$(d-2)$
-forms (or
![]() $(d-2)$
-contravariant tensors by the lowering–raising duality). Thus for
$(d-2)$
-contravariant tensors by the lowering–raising duality). Thus for
![]() $d>3$
, there still exists a Cauchy-type formula for the vorticity, but given in general by (3.20).
$d>3$
, there still exists a Cauchy-type formula for the vorticity, but given in general by (3.20).
Specialising further, we then consider the flat 3D case and obtain the relations actually written by Cauchy (Reference Cauchy1815) in modern vector notation (Cauchy, of course, wrote them component by component).
Corollary 4 (The flat Euclidean case: Cauchy (Reference Cauchy1815)).
Let
![]() $M=\mathbb{R}^{3}$
. Then the Cauchy invariants equation reads
$M=\mathbb{R}^{3}$
. Then the Cauchy invariants equation reads
 $$\begin{eqnarray}\mathop{\sum }_{k}\unicode[STIX]{x1D735}{\dot{x}}^{k}\times \unicode[STIX]{x1D735}x^{k}=\unicode[STIX]{x1D74E}_{0},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k}\unicode[STIX]{x1D735}{\dot{x}}^{k}\times \unicode[STIX]{x1D735}x^{k}=\unicode[STIX]{x1D74E}_{0},\end{eqnarray}$$
while the Cauchy vorticity formula reads
 $$\begin{eqnarray}\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D63F}x\unicode[STIX]{x1D74E}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D63F}x\unicode[STIX]{x1D74E}_{0}.\end{eqnarray}$$
Proof. For the three-dimensional Euclidean flat space (
![]() $M=\mathbb{R}^{3}$
), we have
$M=\mathbb{R}^{3}$
), we have
![]() $\text{g}_{ij}=\unicode[STIX]{x1D6FF}_{ij}$
, so that first we obtain
$\text{g}_{ij}=\unicode[STIX]{x1D6FF}_{ij}$
, so that first we obtain
 $$\begin{eqnarray}[\star (\text{d}v_{k}\wedge \text{d}x^{k})]^{\sharp }=\mathop{\sum }_{k}\unicode[STIX]{x1D735}v^{k}\times \unicode[STIX]{x1D735}x^{k}=\mathop{\sum }_{k}\unicode[STIX]{x1D735}{\dot{x}}^{k}\times \unicode[STIX]{x1D735}x^{k},\end{eqnarray}$$
$$\begin{eqnarray}[\star (\text{d}v_{k}\wedge \text{d}x^{k})]^{\sharp }=\mathop{\sum }_{k}\unicode[STIX]{x1D735}v^{k}\times \unicode[STIX]{x1D735}x^{k}=\mathop{\sum }_{k}\unicode[STIX]{x1D735}{\dot{x}}^{k}\times \unicode[STIX]{x1D735}x^{k},\end{eqnarray}$$
and second, we obtain
 $[\star \unicode[STIX]{x1D714}_{0}]^{\sharp }=\unicode[STIX]{x1D74E}_{0}$
. Therefore we obtain the classical vector form of the Cauchy invariants found by Cauchy (Reference Cauchy1815):
$[\star \unicode[STIX]{x1D714}_{0}]^{\sharp }=\unicode[STIX]{x1D74E}_{0}$
. Therefore we obtain the classical vector form of the Cauchy invariants found by Cauchy (Reference Cauchy1815):
 $$\begin{eqnarray}\mathop{\sum }_{k}\unicode[STIX]{x1D735}{\dot{x}}^{k}\times \unicode[STIX]{x1D735}x^{k}=\unicode[STIX]{x1D74E}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k}\unicode[STIX]{x1D735}{\dot{x}}^{k}\times \unicode[STIX]{x1D735}x^{k}=\unicode[STIX]{x1D74E}_{0}.\end{eqnarray}$$
Multiplying the latter by the Jacobian matrix
![]() $\unicode[STIX]{x1D63F}x$
, and using the relation
$\unicode[STIX]{x1D63F}x$
, and using the relation
 $$\begin{eqnarray}\mathop{\sum }_{k}(\unicode[STIX]{x1D63F}x[\unicode[STIX]{x1D735}{\dot{x}}^{k}\times \unicode[STIX]{x1D735}x^{k}])^{j}=\mathop{\sum }_{k}\unicode[STIX]{x1D735}x^{j}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}{\dot{x}}^{k}\times \unicode[STIX]{x1D735}x^{k})=\unicode[STIX]{x1D714}^{\,j},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k}(\unicode[STIX]{x1D63F}x[\unicode[STIX]{x1D735}{\dot{x}}^{k}\times \unicode[STIX]{x1D735}x^{k}])^{j}=\mathop{\sum }_{k}\unicode[STIX]{x1D735}x^{j}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}{\dot{x}}^{k}\times \unicode[STIX]{x1D735}x^{k})=\unicode[STIX]{x1D714}^{\,j},\end{eqnarray}$$
we obtain
 $$\begin{eqnarray}\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D63F}x\unicode[STIX]{x1D74E}_{0},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D63F}x\unicode[STIX]{x1D74E}_{0},\end{eqnarray}$$
which is the classical vector form of the Cauchy vorticity formula. ◻
4 Local helicities in hydrodynamics and MHD
In this section we show that there are interesting instances of applications of Theorem 1 to
![]() $p$
-forms having
$p$
-forms having
![]() $p>2$
. In particular there are various local helicities. We shall not, here, discuss global (space-integrated) helicity (Moreau Reference Moreau1961; Moffatt Reference Moffatt1969). By ‘local’, we mean without spatial integration. One well-known instance is the magnetic helicity in ideal MHD flow, for which it was shown by Elsasser (Reference Elsasser1956) that it is a material-invariant. Actually, all 3D known global helicities (kinetic helicity in hydrodynamics, magnetic and cross-helicities in MHD) have local counterparts, which are Lie-advection-invariant 3-forms along fluid-particle trajectories (in fact, Hodge duals of material-invariant pseudo-scalars).
$p>2$
. In particular there are various local helicities. We shall not, here, discuss global (space-integrated) helicity (Moreau Reference Moreau1961; Moffatt Reference Moffatt1969). By ‘local’, we mean without spatial integration. One well-known instance is the magnetic helicity in ideal MHD flow, for which it was shown by Elsasser (Reference Elsasser1956) that it is a material-invariant. Actually, all 3D known global helicities (kinetic helicity in hydrodynamics, magnetic and cross-helicities in MHD) have local counterparts, which are Lie-advection-invariant 3-forms along fluid-particle trajectories (in fact, Hodge duals of material-invariant pseudo-scalars).
In what follows, we shall make repeated use of the standard result that the exterior product of a
![]() $p$
-form
$p$
-form
![]() $\unicode[STIX]{x1D714}$
and of a
$\unicode[STIX]{x1D714}$
and of a
![]() $q$
-form
$q$
-form
![]() $\unicode[STIX]{x1D6FE}$
, both of which are Lie-advected, is also Lie-advected. Indeed, we have
$\unicode[STIX]{x1D6FE}$
, both of which are Lie-advected, is also Lie-advected. Indeed, we have
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FE}=0,\quad \unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D714}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FE}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FE}=0,\quad \unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D714}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}=0.\end{eqnarray}$$
Then, using the following identity (see § B.7)
 $$\begin{eqnarray}\unicode[STIX]{x00A3}_{v}(\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714})=\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714}+\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x00A3}_{v}(\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714})=\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714}+\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714},\end{eqnarray}$$
we obtain
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}(\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714})=\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714}+\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D714}=-\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}=-\unicode[STIX]{x00A3}_{v}(\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}(\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714})=\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714}+\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D714}=-\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714}-\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}=-\unicode[STIX]{x00A3}_{v}(\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714}),\end{eqnarray}$$
which establishes the Lie advection of
![]() $\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714}$
.
$\unicode[STIX]{x1D6FE}\wedge \unicode[STIX]{x1D714}$
.
4.1 Local helicity in ideal hydrodynamics
Here we assume that
![]() $\unicode[STIX]{x1D6FA}$
is of dimension three (
$\unicode[STIX]{x1D6FA}$
is of dimension three (
![]() $d=3$
). Let us recall the covariant Euler equations (3.5), written in terms of the velocity circulation 1-form
$d=3$
). Let us recall the covariant Euler equations (3.5), written in terms of the velocity circulation 1-form
![]() $v^{\flat }$
:
$v^{\flat }$
:
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}v^{\flat }+\unicode[STIX]{x00A3}_{v}v^{\flat }=\text{d}\unicode[STIX]{x1D705}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}v^{\flat }+\unicode[STIX]{x00A3}_{v}v^{\flat }=\text{d}\unicode[STIX]{x1D705}.\end{eqnarray}$$
Here the 0-form
![]() $\unicode[STIX]{x1D705}$
, is given by
$\unicode[STIX]{x1D705}$
, is given by
 $$\begin{eqnarray}\unicode[STIX]{x1D705}:={\textstyle \frac{1}{2}}(v,v)_{g}-p\quad \text{or}\quad \unicode[STIX]{x1D705}:={\textstyle \frac{1}{2}}(v,v)_{g}-h,\quad \text{with}~\text{d}h=\text{d}p/\unicode[STIX]{x1D70C},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}:={\textstyle \frac{1}{2}}(v,v)_{g}-p\quad \text{or}\quad \unicode[STIX]{x1D705}:={\textstyle \frac{1}{2}}(v,v)_{g}-h,\quad \text{with}~\text{d}h=\text{d}p/\unicode[STIX]{x1D70C},\end{eqnarray}$$
in the incompressible case and the barotropic compressible case, respectively. Let us introduce the 0-form
![]() $\ell$
defined by the following equation
$\ell$
defined by the following equation
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\ell +\unicode[STIX]{x00A3}_{v}\ell =\unicode[STIX]{x1D705}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\ell +\unicode[STIX]{x00A3}_{v}\ell =\unicode[STIX]{x1D705}.\end{eqnarray}$$
Equation (4.6) can be integrated along the flow
![]() $\unicode[STIX]{x1D711}_{t}$
generated by the velocity vector field
$\unicode[STIX]{x1D711}_{t}$
generated by the velocity vector field
![]() $v$
, since (4.6) is equivalent to
$v$
, since (4.6) is equivalent to
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\ell \circ \unicode[STIX]{x1D711}_{t}=\unicode[STIX]{x1D705}\circ \unicode[STIX]{x1D711}_{t}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\ell \circ \unicode[STIX]{x1D711}_{t}=\unicode[STIX]{x1D705}\circ \unicode[STIX]{x1D711}_{t}.\end{eqnarray}$$
Integrating (4.6) in time, we obtain
 $$\begin{eqnarray}\ell (t,x)=\ell (0,a)+\int _{0}^{t}\unicode[STIX]{x1D705}\circ \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}\,\text{d}\unicode[STIX]{x1D70F},\end{eqnarray}$$
$$\begin{eqnarray}\ell (t,x)=\ell (0,a)+\int _{0}^{t}\unicode[STIX]{x1D705}\circ \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}\,\text{d}\unicode[STIX]{x1D70F},\end{eqnarray}$$
with the initial condition
 $\ell (0,a)=\ell _{0}(a)$
. The function
$\ell (0,a)=\ell _{0}(a)$
. The function
![]() $\ell$
appears for the first time in the work of Weber (Reference Weber1868) and might be called the Weber function. Let us introduce,
$\ell$
appears for the first time in the work of Weber (Reference Weber1868) and might be called the Weber function. Let us introduce,
![]() $u$
, the modified velocity circulation 1-form defined by
$u$
, the modified velocity circulation 1-form defined by
 $$\begin{eqnarray}u=v^{\flat }-\text{d}\ell .\end{eqnarray}$$
$$\begin{eqnarray}u=v^{\flat }-\text{d}\ell .\end{eqnarray}$$
From the definition (4.9), using (4.4)–(4.6), the 1-form
![]() $u$
satisfies
$u$
satisfies
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}u+\unicode[STIX]{x00A3}_{v}u=0,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}u+\unicode[STIX]{x00A3}_{v}u=0,\end{eqnarray}$$
and is thus Lie-advected. The 1-form
![]() $u$
appears for the first time in Clebsch (Reference Clebsch1859), where it takes the form
$u$
appears for the first time in Clebsch (Reference Clebsch1859), where it takes the form
 $u=m\,\text{d}\unicode[STIX]{x1D713}$
. Here,
$u=m\,\text{d}\unicode[STIX]{x1D713}$
. Here,
![]() $m$
and
$m$
and
![]() $\unicode[STIX]{x1D713}$
are two material invariants (Lie-advected 0-forms), now called the Clebsch variables;
$\unicode[STIX]{x1D713}$
are two material invariants (Lie-advected 0-forms), now called the Clebsch variables;
![]() $u$
might thus be called the Clebsch 1-form and the associated vector the Clebsch velocity. Of course, the vorticity 2-form
$u$
might thus be called the Clebsch 1-form and the associated vector the Clebsch velocity. Of course, the vorticity 2-form
 $\unicode[STIX]{x1D714}=\text{d}u=\text{d}v^{\flat }$
, still satisfies the Lie-advection equation
$\unicode[STIX]{x1D714}=\text{d}u=\text{d}v^{\flat }$
, still satisfies the Lie-advection equation
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D714}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D714}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}=0.\end{eqnarray}$$
From (4.10)–(4.11), we deduce that the local helicity 3-form
 $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x039B}^{3}(\unicode[STIX]{x1D6FA})$
, which is defined by
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x039B}^{3}(\unicode[STIX]{x1D6FA})$
, which is defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}=u\wedge \unicode[STIX]{x1D714}=(v^{\flat }-\text{d}\ell )\wedge \text{d}v^{\flat }=v^{\flat }\wedge \text{d}v^{\flat }-\text{d}\ell \wedge \text{d}v^{\flat },\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}=u\wedge \unicode[STIX]{x1D714}=(v^{\flat }-\text{d}\ell )\wedge \text{d}v^{\flat }=v^{\flat }\wedge \text{d}v^{\flat }-\text{d}\ell \wedge \text{d}v^{\flat },\end{eqnarray}$$
satisfies
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D70E}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D70E}=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D70E}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D70E}=0.\end{eqnarray}$$
This is a result of Oseledets (Reference Oseledets1988, where helicity is called spirality). Taking the Hodge dual of (4.13) and using the properties of the Lie derivative (see § B.5) and of the Hodge dual operator (see § B.9), we observe that the scalar local helicity
![]() $\star \unicode[STIX]{x1D70E}$
also satisfies a Lie-advection equation; thus it is also a local conserved quantity, as shown by Kuzmin (Reference Kuzmin1983) in the 3D flat space. Given that
$\star \unicode[STIX]{x1D70E}$
also satisfies a Lie-advection equation; thus it is also a local conserved quantity, as shown by Kuzmin (Reference Kuzmin1983) in the 3D flat space. Given that
![]() $\unicode[STIX]{x1D70E}$
is a 3-form in a three-dimensional space, we obviously have
$\unicode[STIX]{x1D70E}$
is a 3-form in a three-dimensional space, we obviously have
![]() $\text{d}\unicode[STIX]{x1D70E}=0$
, and thus
$\text{d}\unicode[STIX]{x1D70E}=0$
, and thus
![]() $\unicode[STIX]{x1D70E}$
is closed on
$\unicode[STIX]{x1D70E}$
is closed on
![]() $\unicode[STIX]{x1D6FA}$
. The situation is different for
$\unicode[STIX]{x1D6FA}$
. The situation is different for
![]() $d>3$
, because the 4-form
$d>3$
, because the 4-form
 $\text{d}v^{\flat }\wedge \text{d}v^{\flat }$
no longer vanishes. Indeed, the wedge product is not commutative in general (see § B.7); hence, the wedge product
$\text{d}v^{\flat }\wedge \text{d}v^{\flat }$
no longer vanishes. Indeed, the wedge product is not commutative in general (see § B.7); hence, the wedge product
![]() $\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FC}$
is identically zero only if the degree of the differential form
$\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FC}$
is identically zero only if the degree of the differential form
![]() $\unicode[STIX]{x1D6FC}$
is odd (as is the case for the cross-product of two identical vectors). Hence,
$\unicode[STIX]{x1D6FC}$
is odd (as is the case for the cross-product of two identical vectors). Hence,
![]() $\unicode[STIX]{x1D70E}$
is not closed; nevertheless, the helicity 3-form
$\unicode[STIX]{x1D70E}$
is not closed; nevertheless, the helicity 3-form
![]() $\unicode[STIX]{x1D70E}$
is still a local invariant since (4.13) remains valid on Riemannian manifolds of any dimension.
$\unicode[STIX]{x1D70E}$
is still a local invariant since (4.13) remains valid on Riemannian manifolds of any dimension.
Thus local helicity, as a Lie-advection-invariant 3-form, actually exists in any dimension
![]() $d\geqslant 3$
, although it cannot in general be associated (by Hodge duality) to a material-invariant scalar.
$d\geqslant 3$
, although it cannot in general be associated (by Hodge duality) to a material-invariant scalar.
Returning to the three-dimensional case, we now suppose that the Betti number
![]() $b_{3}=0$
(see Remark 1 and § B.13). This guarantees that the closed 3-form
$b_{3}=0$
(see Remark 1 and § B.13). This guarantees that the closed 3-form
![]() $\unicode[STIX]{x1D70E}$
is exact; that is, there exists a 2-form
$\unicode[STIX]{x1D70E}$
is exact; that is, there exists a 2-form
 $\unicode[STIX]{x03C0}\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA})$
such that
$\unicode[STIX]{x03C0}\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA})$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}=\text{d}\unicode[STIX]{x03C0},\quad \unicode[STIX]{x03C0}\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}=\text{d}\unicode[STIX]{x03C0},\quad \unicode[STIX]{x03C0}\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA}).\end{eqnarray}$$
From (4.13)–(4.14), and using Theorem 1, we obtain the following Cauchy invariants equation
 $$\begin{eqnarray}{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6FF}_{ij}^{kl}\,\text{d}\unicode[STIX]{x03C0}_{kl}\wedge \text{d}x^{i}\wedge \text{d}x^{\,j}=\unicode[STIX]{x1D70E}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6FF}_{ij}^{kl}\,\text{d}\unicode[STIX]{x03C0}_{kl}\wedge \text{d}x^{i}\wedge \text{d}x^{\,j}=\unicode[STIX]{x1D70E}_{0}.\end{eqnarray}$$
In principle
 $\unicode[STIX]{x1D70E}_{0}=u_{0}\wedge \unicode[STIX]{x1D714}_{0}=v_{0}^{\flat }\wedge \text{d}v_{0}^{\flat }-\text{d}\ell _{0}\wedge \text{d}v_{0}^{\flat }$
, but if we choose the initial condition
$\unicode[STIX]{x1D70E}_{0}=u_{0}\wedge \unicode[STIX]{x1D714}_{0}=v_{0}^{\flat }\wedge \text{d}v_{0}^{\flat }-\text{d}\ell _{0}\wedge \text{d}v_{0}^{\flat }$
, but if we choose the initial condition
![]() $\ell _{0}=0$
, we obtain
$\ell _{0}=0$
, we obtain
 $\unicode[STIX]{x1D70E}_{0}=v_{0}^{\flat }\wedge \text{d}v_{0}^{\flat }$
. As stated in Corollary 1, equation (4.15) can actually be inverted to obtain the 2-form
$\unicode[STIX]{x1D70E}_{0}=v_{0}^{\flat }\wedge \text{d}v_{0}^{\flat }$
. As stated in Corollary 1, equation (4.15) can actually be inverted to obtain the 2-form
![]() $\unicode[STIX]{x03C0}$
. In the present case, this is particularly simple: from (4.15), using the inverse Lagrangian map, one obtains componentwise
$\unicode[STIX]{x03C0}$
. In the present case, this is particularly simple: from (4.15), using the inverse Lagrangian map, one obtains componentwise
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x03C0}_{ij}}{\unicode[STIX]{x2202}a^{l}}=\unicode[STIX]{x1D70E}_{0lmn}\frac{\unicode[STIX]{x2202}a^{m}}{\unicode[STIX]{x2202}x^{i}}\frac{\unicode[STIX]{x2202}a^{n}}{\unicode[STIX]{x2202}x^{\,j}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x03C0}_{ij}}{\unicode[STIX]{x2202}a^{l}}=\unicode[STIX]{x1D70E}_{0lmn}\frac{\unicode[STIX]{x2202}a^{m}}{\unicode[STIX]{x2202}x^{i}}\frac{\unicode[STIX]{x2202}a^{n}}{\unicode[STIX]{x2202}x^{\,j}}.\end{eqnarray}$$
Taking the divergence of this equation and inverting a Laplacian, one formally obtains
 $$\begin{eqnarray}\unicode[STIX]{x03C0}_{ij}=\unicode[STIX]{x1D6FF}^{kl}\unicode[STIX]{x0394}_{a}^{-1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(\unicode[STIX]{x1D70E}_{0lmn}\frac{\unicode[STIX]{x2202}a^{m}}{\unicode[STIX]{x2202}x^{i}}\frac{\unicode[STIX]{x2202}a^{n}}{\unicode[STIX]{x2202}x^{\,j}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x03C0}_{ij}=\unicode[STIX]{x1D6FF}^{kl}\unicode[STIX]{x0394}_{a}^{-1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(\unicode[STIX]{x1D70E}_{0lmn}\frac{\unicode[STIX]{x2202}a^{m}}{\unicode[STIX]{x2202}x^{i}}\frac{\unicode[STIX]{x2202}a^{n}}{\unicode[STIX]{x2202}x^{\,j}}\right),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x0394}_{a}^{-1}$
denotes the formal inverse of the Laplacian operator
$\unicode[STIX]{x0394}_{a}^{-1}$
denotes the formal inverse of the Laplacian operator
 $\unicode[STIX]{x0394}_{a}=\sum _{i=1}^{3}\unicode[STIX]{x2202}_{a^{i}}^{2}$
in Cartesian coordinates, and
$\unicode[STIX]{x0394}_{a}=\sum _{i=1}^{3}\unicode[STIX]{x2202}_{a^{i}}^{2}$
in Cartesian coordinates, and
![]() $\unicode[STIX]{x1D6FF}^{kl}=1$
if
$\unicode[STIX]{x1D6FF}^{kl}=1$
if
![]() $k=l$
and zero otherwise.
$k=l$
and zero otherwise.
4.2 Local helicities in ideal MHD
4.2.1 Local magnetic helicity
Here we assume that
![]() $\unicode[STIX]{x1D6FA}$
is of dimension three (
$\unicode[STIX]{x1D6FA}$
is of dimension three (
![]() $d=3$
). From definition (2.43), and given that the Lie derivative and the exterior derivative commute, integration of the induction equation (2.44) leads to the following equation for the magnetic potential 1-form:
$d=3$
). From definition (2.43), and given that the Lie derivative and the exterior derivative commute, integration of the induction equation (2.44) leads to the following equation for the magnetic potential 1-form:
 $$\begin{eqnarray}\text{d}(\unicode[STIX]{x2202}_{t}A+\unicode[STIX]{x00A3}_{v}A)=0.\end{eqnarray}$$
$$\begin{eqnarray}\text{d}(\unicode[STIX]{x2202}_{t}A+\unicode[STIX]{x00A3}_{v}A)=0.\end{eqnarray}$$
Using Hodge’s decomposition for closed forms (§ B.13) and (4.18), there exists a harmonic 1-form
![]() $\mathfrak{h}$
such that
$\mathfrak{h}$
such that
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}A+\unicode[STIX]{x00A3}_{v}A=\text{d}K+\mathfrak{h},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}A+\unicode[STIX]{x00A3}_{v}A=\text{d}K+\mathfrak{h},\end{eqnarray}$$
with
![]() $K$
an arbitrary 0-form (scalar function) depending on the choice of gauge condition for the magnetic potential 1-form
$K$
an arbitrary 0-form (scalar function) depending on the choice of gauge condition for the magnetic potential 1-form
![]() $A$
. We now assume that the Betti number
$A$
. We now assume that the Betti number
![]() $b_{1}=0$
, as is the case, e.g., when the manifold is simply connected, contractible or has a positive Ricci curvature (see § B.13 and references therein). This ensures the vanishing of the harmonic 1-form
$b_{1}=0$
, as is the case, e.g., when the manifold is simply connected, contractible or has a positive Ricci curvature (see § B.13 and references therein). This ensures the vanishing of the harmonic 1-form
![]() $\mathfrak{h}$
, so that (4.19) reduces to
$\mathfrak{h}$
, so that (4.19) reduces to
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}A+\unicode[STIX]{x00A3}_{v}A=\text{d}K.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}A+\unicode[STIX]{x00A3}_{v}A=\text{d}K.\end{eqnarray}$$
We now introduce the 0-form
![]() $L$
, which is defined by the following equation
$L$
, which is defined by the following equation
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}L+\unicode[STIX]{x00A3}_{v}L=K.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}L+\unicode[STIX]{x00A3}_{v}L=K.\end{eqnarray}$$
Equation (4.21) can be integrated along the flow
![]() $\unicode[STIX]{x1D711}_{t}$
generated by the velocity vector field
$\unicode[STIX]{x1D711}_{t}$
generated by the velocity vector field
![]() $v$
, since (4.21) is equivalent to
$v$
, since (4.21) is equivalent to
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}L\circ \unicode[STIX]{x1D711}_{t}=K\circ \unicode[STIX]{x1D711}_{t}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}L\circ \unicode[STIX]{x1D711}_{t}=K\circ \unicode[STIX]{x1D711}_{t}.\end{eqnarray}$$
Integrating (4.22) in time, we obtain
 $$\begin{eqnarray}L(t,x)=L(0,a)+\int _{0}^{t}K\circ \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}\,\text{d}\unicode[STIX]{x1D70F},\end{eqnarray}$$
$$\begin{eqnarray}L(t,x)=L(0,a)+\int _{0}^{t}K\circ \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}\,\text{d}\unicode[STIX]{x1D70F},\end{eqnarray}$$
with the initial condition
 $L(0,a)=L_{0}(a)$
. We also introduce,
$L(0,a)=L_{0}(a)$
. We also introduce,
![]() ${\mathcal{A}}$
, the modified magnetic potential 1-form defined by
${\mathcal{A}}$
, the modified magnetic potential 1-form defined by
 $$\begin{eqnarray}{\mathcal{A}}=A-\text{d}L.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}=A-\text{d}L.\end{eqnarray}$$
From the definition (4.24), and using (4.20)–(4.21), the 1-form
![]() ${\mathcal{A}}$
satisfies
${\mathcal{A}}$
satisfies
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}{\mathcal{A}}+\unicode[STIX]{x00A3}_{v}{\mathcal{A}}=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}{\mathcal{A}}+\unicode[STIX]{x00A3}_{v}{\mathcal{A}}=0.\end{eqnarray}$$
From (2.44) and (4.25), we infer immediately that the magnetic helicity 3-form
 $h\in \unicode[STIX]{x039B}^{3}(\unicode[STIX]{x1D6FA})$
, which is defined by
$h\in \unicode[STIX]{x039B}^{3}(\unicode[STIX]{x1D6FA})$
, which is defined by
 $$\begin{eqnarray}h={\mathcal{A}}\wedge B={\mathcal{A}}\wedge \text{d}A=A\wedge \text{d}A-\text{d}L\wedge \text{d}A,\end{eqnarray}$$
$$\begin{eqnarray}h={\mathcal{A}}\wedge B={\mathcal{A}}\wedge \text{d}A=A\wedge \text{d}A-\text{d}L\wedge \text{d}A,\end{eqnarray}$$
satisfies
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}h+\unicode[STIX]{x00A3}_{v}h=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}h+\unicode[STIX]{x00A3}_{v}h=0.\end{eqnarray}$$
Taking the Hodge dual of (4.27) and using the properties of the Lie derivative (see § B.5) and of the Hodge dual operator (see § B.9), we observe that the scalar magnetic helicity
![]() $\star h$
also satisfies a Lie-advection equation; thus it is also a local conserved quantity, as shown first by Elsasser (Reference Elsasser1956, see also Woltjer Reference Woltjer1958) in the 3D flat space. Given that
$\star h$
also satisfies a Lie-advection equation; thus it is also a local conserved quantity, as shown first by Elsasser (Reference Elsasser1956, see also Woltjer Reference Woltjer1958) in the 3D flat space. Given that
![]() $h$
is a 3-form in a three-dimensional space, we obviously have
$h$
is a 3-form in a three-dimensional space, we obviously have
![]() $\text{d}h=0$
, and thus
$\text{d}h=0$
, and thus
![]() $h$
is closed on
$h$
is closed on
![]() $\unicode[STIX]{x1D6FA}$
. The situation is different for
$\unicode[STIX]{x1D6FA}$
. The situation is different for
![]() $d>3$
, because the 4-form
$d>3$
, because the 4-form
![]() $\text{d}A\wedge \text{d}A$
no longer vanishes; hence
$\text{d}A\wedge \text{d}A$
no longer vanishes; hence
![]() $h$
is not closed, but the magnetic helicity 3-form
$h$
is not closed, but the magnetic helicity 3-form
![]() $h$
is still a local invariant, since (4.27) remains valid on Riemannian manifolds of any dimension provided that the Betti number
$h$
is still a local invariant, since (4.27) remains valid on Riemannian manifolds of any dimension provided that the Betti number
![]() $b_{1}=0$
. Returning to the three-dimensional case, we now suppose that the Betti number
$b_{1}=0$
. Returning to the three-dimensional case, we now suppose that the Betti number
![]() $b_{3}=0$
(see Remark 1 and § B.13). This guarantees that the closed form is exact, that is there exists a 2-form
$b_{3}=0$
(see Remark 1 and § B.13). This guarantees that the closed form is exact, that is there exists a 2-form
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA})$
such that
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA})$
such that
 $$\begin{eqnarray}h=\text{d}\unicode[STIX]{x1D6FC},\quad \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA}).\end{eqnarray}$$
$$\begin{eqnarray}h=\text{d}\unicode[STIX]{x1D6FC},\quad \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA}).\end{eqnarray}$$
From (4.27)–(4.28), and using Theorem 1, we obtain yet another Cauchy invariants equation, namely
 $$\begin{eqnarray}{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6FF}_{ij}^{kl}\,\text{d}\unicode[STIX]{x1D6FC}_{kl}\wedge \text{d}x^{i}\wedge \text{d}x^{\,j}=h_{0}.\end{eqnarray}$$
$$\begin{eqnarray}{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6FF}_{ij}^{kl}\,\text{d}\unicode[STIX]{x1D6FC}_{kl}\wedge \text{d}x^{i}\wedge \text{d}x^{\,j}=h_{0}.\end{eqnarray}$$
In principle
 $h_{0}={\mathcal{A}}_{0}\wedge B_{0}=A_{0}\wedge \text{d}A_{0}-\text{d}L_{0}\wedge \text{d}A_{0}$
, but if we choose the initial condition
$h_{0}={\mathcal{A}}_{0}\wedge B_{0}=A_{0}\wedge \text{d}A_{0}-\text{d}L_{0}\wedge \text{d}A_{0}$
, but if we choose the initial condition
![]() $L_{0}=0$
, we obtain
$L_{0}=0$
, we obtain
 $h_{0}=A_{0}\wedge \text{d}A_{0}$
. Equation (4.29) can be solved, similarly to what was done in § 4.1, to obtain the 2-form
$h_{0}=A_{0}\wedge \text{d}A_{0}$
. Equation (4.29) can be solved, similarly to what was done in § 4.1, to obtain the 2-form
![]() $\unicode[STIX]{x1D6FC}$
as
$\unicode[STIX]{x1D6FC}$
as
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{ij}=\unicode[STIX]{x1D6FF}^{kl}\unicode[STIX]{x0394}_{a}^{-1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(h_{0lmn}\frac{\unicode[STIX]{x2202}a^{m}}{\unicode[STIX]{x2202}x^{i}}\frac{\unicode[STIX]{x2202}a^{n}}{\unicode[STIX]{x2202}x^{\,j}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{ij}=\unicode[STIX]{x1D6FF}^{kl}\unicode[STIX]{x0394}_{a}^{-1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(h_{0lmn}\frac{\unicode[STIX]{x2202}a^{m}}{\unicode[STIX]{x2202}x^{i}}\frac{\unicode[STIX]{x2202}a^{n}}{\unicode[STIX]{x2202}x^{\,j}}\right).\end{eqnarray}$$
4.2.2 Local cross-helicity
Here we assume that
![]() $\unicode[STIX]{x1D6FA}$
is of dimension three (
$\unicode[STIX]{x1D6FA}$
is of dimension three (
![]() $d=3$
). We define the cross-helicity 3-form
$d=3$
). We define the cross-helicity 3-form
 $\unicode[STIX]{x1D709}\in \unicode[STIX]{x039B}^{3}(\unicode[STIX]{x1D6FA})$
by
$\unicode[STIX]{x1D709}\in \unicode[STIX]{x039B}^{3}(\unicode[STIX]{x1D6FA})$
by
 $$\begin{eqnarray}\unicode[STIX]{x1D709}=u\wedge B.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}=u\wedge B.\end{eqnarray}$$
First from (2.44) and (4.10), we find that the 3-form
![]() $\unicode[STIX]{x1D709}$
satisfies
$\unicode[STIX]{x1D709}$
satisfies
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D709}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D709}=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D709}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D709}=0.\end{eqnarray}$$
Taking the Hodge dual of (4.32) and using the properties of the Lie derivative (see § B.5) and of the Hodge dual operator (see § B.9), we observe that the scalar cross-helicity
![]() $\star \unicode[STIX]{x1D709}$
also satisfies a Lie-advection equation; thus it is also a local conserved quantity, as shown by Kuzmin (Reference Kuzmin1983) for the 3D flat space. Given that
$\star \unicode[STIX]{x1D709}$
also satisfies a Lie-advection equation; thus it is also a local conserved quantity, as shown by Kuzmin (Reference Kuzmin1983) for the 3D flat space. Given that
![]() $\unicode[STIX]{x1D709}$
is a 3-form in a three-dimensional space, we obviously have
$\unicode[STIX]{x1D709}$
is a 3-form in a three-dimensional space, we obviously have
![]() $\text{d}\unicode[STIX]{x1D709}=0$
, and thus
$\text{d}\unicode[STIX]{x1D709}=0$
, and thus
![]() $\unicode[STIX]{x1D709}$
is closed on
$\unicode[STIX]{x1D709}$
is closed on
![]() $\unicode[STIX]{x1D6FA}$
. We now assume that the Betti number
$\unicode[STIX]{x1D6FA}$
. We now assume that the Betti number
![]() $b_{3}=0$
(see Remark 1 and § B.13). This guarantees that the closed 2-form
$b_{3}=0$
(see Remark 1 and § B.13). This guarantees that the closed 2-form
![]() $\unicode[STIX]{x1D709}$
is exact, that is, there exists a 2-form
$\unicode[STIX]{x1D709}$
is exact, that is, there exists a 2-form
 $\unicode[STIX]{x1D712}\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA})$
such that
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA})$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D709}=\text{d}\unicode[STIX]{x1D712},\quad \unicode[STIX]{x1D712}\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}=\text{d}\unicode[STIX]{x1D712},\quad \unicode[STIX]{x1D712}\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA}).\end{eqnarray}$$
From (4.32)–(4.33), and using Theorem 1, we obtain still another Cauchy invariants equation
 $$\begin{eqnarray}{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6FF}_{ij}^{kl}\,\text{d}\unicode[STIX]{x1D712}_{kl}\wedge \text{d}x^{i}\wedge \text{d}x^{\,j}=\unicode[STIX]{x1D709}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6FF}_{ij}^{kl}\,\text{d}\unicode[STIX]{x1D712}_{kl}\wedge \text{d}x^{i}\wedge \text{d}x^{\,j}=\unicode[STIX]{x1D709}_{0}.\end{eqnarray}$$
In principle
 $\unicode[STIX]{x1D709}_{0}=u_{0}\wedge B_{0}=v_{0}^{\flat }\wedge \text{d}A_{0}-\text{d}\ell _{0}\wedge \text{d}A_{0}$
, but if we choose the initial condition
$\unicode[STIX]{x1D709}_{0}=u_{0}\wedge B_{0}=v_{0}^{\flat }\wedge \text{d}A_{0}-\text{d}\ell _{0}\wedge \text{d}A_{0}$
, but if we choose the initial condition
![]() $\ell _{0}=0$
, then we obtain
$\ell _{0}=0$
, then we obtain
 $\unicode[STIX]{x1D709}_{0}=v_{0}^{\flat }\wedge \text{d}A_{0}$
. Equation (4.34), can be solved to find the 2-form
$\unicode[STIX]{x1D709}_{0}=v_{0}^{\flat }\wedge \text{d}A_{0}$
. Equation (4.34), can be solved to find the 2-form
![]() $\unicode[STIX]{x1D712}$
by proceeding along the same line as in § 4.1. We thus formally obtain
$\unicode[STIX]{x1D712}$
by proceeding along the same line as in § 4.1. We thus formally obtain
 $$\begin{eqnarray}\unicode[STIX]{x1D712}_{ij}=\unicode[STIX]{x1D6FF}^{kl}\unicode[STIX]{x0394}_{a}^{-1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(\unicode[STIX]{x1D709}_{0lmn}\frac{\unicode[STIX]{x2202}a^{m}}{\unicode[STIX]{x2202}x^{i}}\frac{\unicode[STIX]{x2202}a^{n}}{\unicode[STIX]{x2202}x^{\,j}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{ij}=\unicode[STIX]{x1D6FF}^{kl}\unicode[STIX]{x0394}_{a}^{-1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(\unicode[STIX]{x1D709}_{0lmn}\frac{\unicode[STIX]{x2202}a^{m}}{\unicode[STIX]{x2202}x^{i}}\frac{\unicode[STIX]{x2202}a^{n}}{\unicode[STIX]{x2202}x^{\,j}}\right).\end{eqnarray}$$
4.2.3 Local extended helicities
Here, we consider local helicities associated to the extended ideal compressible MHD equations (2.61)–(2.62) of § 2.5.4. As shown by Lingam et al. (Reference Lingam, Milosevich and Morrison2016), equations (2.62) can be rewritten in such a way that the unknowns become the magnetic potential 1-forms
![]() $A_{\pm }$
, instead of the magnetic field 2-forms
$A_{\pm }$
, instead of the magnetic field 2-forms
![]() $B_{\pm }$
, with
$B_{\pm }$
, with
 $B_{\pm }=\text{d}A_{\pm }$
and
$B_{\pm }=\text{d}A_{\pm }$
and
 $A_{\pm }:=A+(d_{e}^{2}/\unicode[STIX]{x1D70C})\star \text{d}\star B+\unicode[STIX]{x1D705}_{\pm }v^{\flat }$
. More precisely, the magnetic potential 1-forms
$A_{\pm }:=A+(d_{e}^{2}/\unicode[STIX]{x1D70C})\star \text{d}\star B+\unicode[STIX]{x1D705}_{\pm }v^{\flat }$
. More precisely, the magnetic potential 1-forms
![]() $A_{\pm }$
satisfy
$A_{\pm }$
satisfy
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}A_{\pm }+\unicode[STIX]{x00A3}_{v_{\pm }}A_{\pm }=\text{d}\unicode[STIX]{x1D713}_{\pm },\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}A_{\pm }+\unicode[STIX]{x00A3}_{v_{\pm }}A_{\pm }=\text{d}\unicode[STIX]{x1D713}_{\pm },\end{eqnarray}$$
with the earlier defined vector fields
 $v_{\pm }:=v-\unicode[STIX]{x1D705}_{\mp }\,(\star \,\text{d}\star B)^{\sharp }/\unicode[STIX]{x1D70C}$
. Explicit expressions of the 0-forms
$v_{\pm }:=v-\unicode[STIX]{x1D705}_{\mp }\,(\star \,\text{d}\star B)^{\sharp }/\unicode[STIX]{x1D70C}$
. Explicit expressions of the 0-forms
![]() $\unicode[STIX]{x1D713}_{\pm }$
are not needed here (see Lingam et al.
Reference Lingam, Milosevich and Morrison2016). Let us now introduce the 0-forms
$\unicode[STIX]{x1D713}_{\pm }$
are not needed here (see Lingam et al.
Reference Lingam, Milosevich and Morrison2016). Let us now introduce the 0-forms
![]() $L_{\pm }$
, which are defined by the following equations
$L_{\pm }$
, which are defined by the following equations
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}L_{\pm }+\unicode[STIX]{x00A3}_{v_{\pm }}L_{\pm }=\unicode[STIX]{x1D713}_{\pm },\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}L_{\pm }+\unicode[STIX]{x00A3}_{v_{\pm }}L_{\pm }=\unicode[STIX]{x1D713}_{\pm },\end{eqnarray}$$
with initial condition
 $L_{\pm }(0,a)=L_{0\,\pm }(a)$
. Equations (4.37) can be integrated along the Lagrangian flows
$L_{\pm }(0,a)=L_{0\,\pm }(a)$
. Equations (4.37) can be integrated along the Lagrangian flows
![]() $\unicode[STIX]{x1D711}_{\pm \,t}$
generated by the vector fields
$\unicode[STIX]{x1D711}_{\pm \,t}$
generated by the vector fields
![]() $v_{\pm }$
, similarly to what was done in § 4.2.1. Let us introduce,
$v_{\pm }$
, similarly to what was done in § 4.2.1. Let us introduce,
![]() ${\mathcal{A}}_{\pm }$
, the modified magnetic potential 1-forms defined by
${\mathcal{A}}_{\pm }$
, the modified magnetic potential 1-forms defined by
 $$\begin{eqnarray}{\mathcal{A}}_{\pm }=A_{\pm }-\text{d}L_{\pm }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{\pm }=A_{\pm }-\text{d}L_{\pm }.\end{eqnarray}$$
From the definition (4.38), and using (4.36)–(4.37), the 1-forms
![]() ${\mathcal{A}}_{\pm }$
satisfy
${\mathcal{A}}_{\pm }$
satisfy
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}{\mathcal{A}}_{\pm }+\unicode[STIX]{x00A3}_{v_{\pm }}{\mathcal{A}}_{\pm }=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}{\mathcal{A}}_{\pm }+\unicode[STIX]{x00A3}_{v_{\pm }}{\mathcal{A}}_{\pm }=0.\end{eqnarray}$$
From (2.62) and (4.39), we infer immediately that the extended magnetic helicity 3-forms
![]() $h_{\pm }$
, here defined by
$h_{\pm }$
, here defined by
 $$\begin{eqnarray}h_{\pm }={\mathcal{A}}_{\pm }\wedge B_{\pm }={\mathcal{A}}_{\pm }\wedge \text{d}A_{\pm }=A_{\pm }\wedge \text{d}A_{\pm }-\text{d}L_{\pm }\wedge \text{d}A_{\pm },\end{eqnarray}$$
$$\begin{eqnarray}h_{\pm }={\mathcal{A}}_{\pm }\wedge B_{\pm }={\mathcal{A}}_{\pm }\wedge \text{d}A_{\pm }=A_{\pm }\wedge \text{d}A_{\pm }-\text{d}L_{\pm }\wedge \text{d}A_{\pm },\end{eqnarray}$$
satisfy
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}h_{\pm }+\unicode[STIX]{x00A3}_{v_{\pm }}h_{\pm }=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}h_{\pm }+\unicode[STIX]{x00A3}_{v_{\pm }}h_{\pm }=0.\end{eqnarray}$$
From (4.41) we obtain that the extended magnetic helicity 3-forms
![]() $h_{\pm }$
are local invariants. By spatial integration, these local conservation laws imply also the known global conservation laws for the integrals of the 3-forms
$h_{\pm }$
are local invariants. By spatial integration, these local conservation laws imply also the known global conservation laws for the integrals of the 3-forms
 ${\mathcal{K}}_{\pm }:=A_{\pm }\wedge \text{d}A_{\pm }$
, established by Lingam et al. (Reference Lingam, Milosevich and Morrison2016). Indeed, noting that
${\mathcal{K}}_{\pm }:=A_{\pm }\wedge \text{d}A_{\pm }$
, established by Lingam et al. (Reference Lingam, Milosevich and Morrison2016). Indeed, noting that
 $h_{\pm }={\mathcal{K}}_{\pm }-\text{d}(L_{\pm }\text{d}A_{\pm })$
, using the Stokes theorem, the Lie-derivative theorem (2.14) and (4.41), we obtain, for any domain
$h_{\pm }={\mathcal{K}}_{\pm }-\text{d}(L_{\pm }\text{d}A_{\pm })$
, using the Stokes theorem, the Lie-derivative theorem (2.14) and (4.41), we obtain, for any domain
![]() $\unicode[STIX]{x1D6FA}$
,
$\unicode[STIX]{x1D6FA}$
,
 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \int _{\unicode[STIX]{x1D711}_{\pm \,t}(\unicode[STIX]{x1D6FA})}\unicode[STIX]{x2202}_{t}h_{\pm }+\unicode[STIX]{x00A3}_{v_{\pm }}h_{\pm }=\frac{\text{d}}{\text{d}t}\int _{\unicode[STIX]{x1D711}_{\pm \,t}(\unicode[STIX]{x1D6FA})}h_{\pm }\nonumber\\ \displaystyle & = & \displaystyle \frac{\text{d}}{\text{d}t}\int _{\unicode[STIX]{x1D711}_{\pm \,t}(\unicode[STIX]{x1D6FA})}{\mathcal{K}}_{\pm }+\frac{\text{d}}{\text{d}t}\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{\pm \,t}(\unicode[STIX]{x1D6FA})}L_{\pm }\,\text{d}A_{\pm }=\frac{\text{d}}{\text{d}t}\int _{\unicode[STIX]{x1D711}_{\pm \,t}(\unicode[STIX]{x1D6FA})}{\mathcal{K}}_{\pm },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \int _{\unicode[STIX]{x1D711}_{\pm \,t}(\unicode[STIX]{x1D6FA})}\unicode[STIX]{x2202}_{t}h_{\pm }+\unicode[STIX]{x00A3}_{v_{\pm }}h_{\pm }=\frac{\text{d}}{\text{d}t}\int _{\unicode[STIX]{x1D711}_{\pm \,t}(\unicode[STIX]{x1D6FA})}h_{\pm }\nonumber\\ \displaystyle & = & \displaystyle \frac{\text{d}}{\text{d}t}\int _{\unicode[STIX]{x1D711}_{\pm \,t}(\unicode[STIX]{x1D6FA})}{\mathcal{K}}_{\pm }+\frac{\text{d}}{\text{d}t}\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{\pm \,t}(\unicode[STIX]{x1D6FA})}L_{\pm }\,\text{d}A_{\pm }=\frac{\text{d}}{\text{d}t}\int _{\unicode[STIX]{x1D711}_{\pm \,t}(\unicode[STIX]{x1D6FA})}{\mathcal{K}}_{\pm },\end{eqnarray}$$
where we have supposed that the generalised vorticities
![]() $B_{\pm }$
vanish on the boundaries of
$B_{\pm }$
vanish on the boundaries of
![]() $\unicode[STIX]{x1D711}_{\pm \,t}(\unicode[STIX]{x1D6FA})$
. In the three-dimensional case
$\unicode[STIX]{x1D711}_{\pm \,t}(\unicode[STIX]{x1D6FA})$
. In the three-dimensional case
![]() $d=3$
, taking the Hodge dual of (4.41) and using the properties of the Lie derivative (see § B.5) and of the Hodge dual operator (see § B.9), we observe that the scalar extended magnetic helicities
$d=3$
, taking the Hodge dual of (4.41) and using the properties of the Lie derivative (see § B.5) and of the Hodge dual operator (see § B.9), we observe that the scalar extended magnetic helicities
![]() $\star h_{\pm }$
also satisfy Lie-advection equations; thus they are also local conserved quantities. In a three-dimensional space
$\star h_{\pm }$
also satisfy Lie-advection equations; thus they are also local conserved quantities. In a three-dimensional space
![]() $\unicode[STIX]{x1D6FA}$
, given that
$\unicode[STIX]{x1D6FA}$
, given that
 $h_{\pm }\in \unicode[STIX]{x039B}^{3}(\unicode[STIX]{x1D6FA})$
are 3-forms, we obviously have
$h_{\pm }\in \unicode[STIX]{x039B}^{3}(\unicode[STIX]{x1D6FA})$
are 3-forms, we obviously have
![]() $\text{d}h_{\pm }=0$
, and thus
$\text{d}h_{\pm }=0$
, and thus
![]() $h_{\pm }$
is closed on
$h_{\pm }$
is closed on
![]() $\unicode[STIX]{x1D6FA}$
. We now suppose that the Betti number
$\unicode[STIX]{x1D6FA}$
. We now suppose that the Betti number
![]() $b_{3}=0$
(see Remark 1 and § B.13), which guarantees that closed forms are exact. Then there exist 2-forms
$b_{3}=0$
(see Remark 1 and § B.13), which guarantees that closed forms are exact. Then there exist 2-forms
 $\unicode[STIX]{x1D6FC}_{\pm }\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA})$
such that
$\unicode[STIX]{x1D6FC}_{\pm }\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA})$
such that
 $$\begin{eqnarray}h_{\pm }=\text{d}\unicode[STIX]{x1D6FC}_{\pm },\quad \unicode[STIX]{x1D6FC}_{\pm }\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA}).\end{eqnarray}$$
$$\begin{eqnarray}h_{\pm }=\text{d}\unicode[STIX]{x1D6FC}_{\pm },\quad \unicode[STIX]{x1D6FC}_{\pm }\in \unicode[STIX]{x039B}^{2}(\unicode[STIX]{x1D6FA}).\end{eqnarray}$$
From (4.41)–(4.43), and using Theorem 1, we obtain two more Cauchy invariants equations
 $$\begin{eqnarray}{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6FF}_{ij}^{kl}\,\text{d}\unicode[STIX]{x1D6FC}_{\pm \,kl}\wedge \text{d}x_{\pm }^{i}\wedge \text{d}x_{\pm }^{\,j}=h_{\pm \,0},\end{eqnarray}$$
$$\begin{eqnarray}{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6FF}_{ij}^{kl}\,\text{d}\unicode[STIX]{x1D6FC}_{\pm \,kl}\wedge \text{d}x_{\pm }^{i}\wedge \text{d}x_{\pm }^{\,j}=h_{\pm \,0},\end{eqnarray}$$
where
![]() $x_{\pm }$
are the Lagrangian maps generated by the vector fields
$x_{\pm }$
are the Lagrangian maps generated by the vector fields
![]() $v_{\pm }$
. In principle
$v_{\pm }$
. In principle
 $h_{\pm \,0}={\mathcal{A}}_{\pm \,0}\wedge B_{\pm \,0}=A_{\pm \,0}\wedge \text{d}A_{\pm \,0}-\text{d}L_{\pm \,0}\wedge \text{d}A_{\pm \,0}$
, but if we choose the initial conditions
$h_{\pm \,0}={\mathcal{A}}_{\pm \,0}\wedge B_{\pm \,0}=A_{\pm \,0}\wedge \text{d}A_{\pm \,0}-\text{d}L_{\pm \,0}\wedge \text{d}A_{\pm \,0}$
, but if we choose the initial conditions
 $L_{\pm \,0}=0$
, we obtain
$L_{\pm \,0}=0$
, we obtain
 $h_{\pm \,0}=A_{\pm \,0}\wedge \text{d}A_{\pm \,0}={\mathcal{K}}_{\pm \,0}$
. Equations (4.44) can be solved, similarly to what was done in § 4.1, to obtain the 2-forms
$h_{\pm \,0}=A_{\pm \,0}\wedge \text{d}A_{\pm \,0}={\mathcal{K}}_{\pm \,0}$
. Equations (4.44) can be solved, similarly to what was done in § 4.1, to obtain the 2-forms
![]() $\unicode[STIX]{x1D6FC}_{\pm }$
as
$\unicode[STIX]{x1D6FC}_{\pm }$
as
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{\pm \,ij}=\unicode[STIX]{x1D6FF}^{kl}\unicode[STIX]{x0394}_{a}^{-1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(h_{\pm \,0lmn}\frac{\unicode[STIX]{x2202}a^{m}}{\unicode[STIX]{x2202}x_{\pm }^{i}}\frac{\unicode[STIX]{x2202}a^{n}}{\unicode[STIX]{x2202}x_{\pm }^{\,j}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{\pm \,ij}=\unicode[STIX]{x1D6FF}^{kl}\unicode[STIX]{x0394}_{a}^{-1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(h_{\pm \,0lmn}\frac{\unicode[STIX]{x2202}a^{m}}{\unicode[STIX]{x2202}x_{\pm }^{i}}\frac{\unicode[STIX]{x2202}a^{n}}{\unicode[STIX]{x2202}x_{\pm }^{\,j}}\right).\end{eqnarray}$$
4.3 Other high-order local invariants in hydrodynamics
Here we consider a
![]() $d$
-dimensional Riemannian manifolds
$d$
-dimensional Riemannian manifolds
![]() $(M,g)$
, with
$(M,g)$
, with
![]() $d$
an odd natural integer and
$d$
an odd natural integer and
![]() $\unicode[STIX]{x1D6FA}$
a bounded region of
$\unicode[STIX]{x1D6FA}$
a bounded region of
![]() $M$
. Again, we consider the velocity circulation 1-form
$M$
. Again, we consider the velocity circulation 1-form
![]() $u$
, which is defined by (4.9). Using the 1-form
$u$
, which is defined by (4.9). Using the 1-form
![]() $u$
, we define the
$u$
, we define the
![]() $d$
-form
$d$
-form
 $J\in \unicode[STIX]{x039B}^{d}(\unicode[STIX]{x1D6FA})$
(Serre Reference Serre1984; Gama & Frisch Reference Gama, Frisch, Proctor, Matthews and Rucklidge1993) by
$J\in \unicode[STIX]{x039B}^{d}(\unicode[STIX]{x1D6FA})$
(Serre Reference Serre1984; Gama & Frisch Reference Gama, Frisch, Proctor, Matthews and Rucklidge1993) by
 $$\begin{eqnarray}J=u\wedge (\wedge \,\text{d}u)^{(d-1)/2},\end{eqnarray}$$
$$\begin{eqnarray}J=u\wedge (\wedge \,\text{d}u)^{(d-1)/2},\end{eqnarray}$$
where
 $(\wedge \,\text{d}u)^{(d-1)/2}$
stands for
$(\wedge \,\text{d}u)^{(d-1)/2}$
stands for
 $(d-1)/2$
times the exterior product of the 2-form
$(d-1)/2$
times the exterior product of the 2-form
![]() $\text{d}u$
. It was proven by Gama & Frisch (Reference Gama, Frisch, Proctor, Matthews and Rucklidge1993) that
$\text{d}u$
. It was proven by Gama & Frisch (Reference Gama, Frisch, Proctor, Matthews and Rucklidge1993) that
![]() $J$
is Lie-advected by the velocity field
$J$
is Lie-advected by the velocity field
![]() $v$
. Indeed, first the 1-form
$v$
. Indeed, first the 1-form
![]() $u$
satisfies the Lie-advection equation (4.10). Second, taking the exterior derivative of equation (4.10) the 2-form
$u$
satisfies the Lie-advection equation (4.10). Second, taking the exterior derivative of equation (4.10) the 2-form
![]() $\text{d}u$
satisfies the same Lie-advection equation (4.10), because Lie derivative and exterior derivative commute. Therefore we obtain
$\text{d}u$
satisfies the same Lie-advection equation (4.10), because Lie derivative and exterior derivative commute. Therefore we obtain
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}J+\unicode[STIX]{x00A3}_{v}J=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}J+\unicode[STIX]{x00A3}_{v}J=0.\end{eqnarray}$$
Since
 $J\in \unicode[STIX]{x039B}^{d}(\unicode[STIX]{x1D6FA})$
, we obviously have
$J\in \unicode[STIX]{x039B}^{d}(\unicode[STIX]{x1D6FA})$
, we obviously have
![]() $\text{d}J=0$
, and thus
$\text{d}J=0$
, and thus
![]() $J$
is closed on
$J$
is closed on
![]() $\unicode[STIX]{x1D6FA}$
. We now assume again that the Betti number
$\unicode[STIX]{x1D6FA}$
. We now assume again that the Betti number
![]() $b_{p}=0$
(see Remark 1 and § B.13). This guarantees that the closed form
$b_{p}=0$
(see Remark 1 and § B.13). This guarantees that the closed form
![]() $J$
is exact; that is, there exists a
$J$
is exact; that is, there exists a
![]() $(d-1)$
-form
$(d-1)$
-form
![]() $I$
such that
$I$
such that
![]() $J=\text{d}I$
. From exactness of the
$J=\text{d}I$
. From exactness of the
![]() $d$
-form
$d$
-form
![]() $J$
and (4.46)–(4.47), using Theorem 1, we then obtain our last Cauchy invariants equation
$J$
and (4.46)–(4.47), using Theorem 1, we then obtain our last Cauchy invariants equation
 $$\begin{eqnarray}\frac{1}{(d-1)!}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{d-1}}^{\,j_{1}\ldots j_{d-1}}\,\text{d}I_{j_{1}\ldots j_{d-1}}\wedge \text{d}x^{l_{1}}\wedge \cdots \wedge \text{d}x^{l_{d-1}}=J_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{(d-1)!}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{d-1}}^{\,j_{1}\ldots j_{d-1}}\,\text{d}I_{j_{1}\ldots j_{d-1}}\wedge \text{d}x^{l_{1}}\wedge \cdots \wedge \text{d}x^{l_{d-1}}=J_{0}.\end{eqnarray}$$
In principle
 $J_{0}=u_{0}\wedge (\wedge \,\text{d}v_{0}^{\flat })^{(d-1)/2}=v_{0}^{\flat }\wedge (\wedge \,\text{d}v_{0}^{\flat })^{(d-1)/2}-\text{d}\ell _{0}\wedge (\wedge \,\text{d}v_{0}^{\flat })^{(d-1)/2}$
, but if we choose a gauge such that
$J_{0}=u_{0}\wedge (\wedge \,\text{d}v_{0}^{\flat })^{(d-1)/2}=v_{0}^{\flat }\wedge (\wedge \,\text{d}v_{0}^{\flat })^{(d-1)/2}-\text{d}\ell _{0}\wedge (\wedge \,\text{d}v_{0}^{\flat })^{(d-1)/2}$
, but if we choose a gauge such that
![]() $\ell _{0}=0$
, we obtain
$\ell _{0}=0$
, we obtain
 $J_{0}=v_{0}^{\flat }\wedge (\wedge \,\text{d}v_{0}^{\flat })^{(d-1)/2}$
. By Corollary 1, the
$J_{0}=v_{0}^{\flat }\wedge (\wedge \,\text{d}v_{0}^{\flat })^{(d-1)/2}$
. By Corollary 1, the
![]() $(d-1)$
-form
$(d-1)$
-form
![]() $I$
can be written as
$I$
can be written as
 $$\begin{eqnarray}I_{i_{1}\ldots i_{d-1}}=\unicode[STIX]{x1D6FF}^{k\ell }\unicode[STIX]{x0394}_{a}^{-1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(J_{0\ell j_{1}\ldots j_{d-1}}\frac{\unicode[STIX]{x2202}a^{\,j_{1}}}{\unicode[STIX]{x2202}x^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{\,j_{d-1}}}{\unicode[STIX]{x2202}x^{i_{d-1}}}\right).\end{eqnarray}$$
$$\begin{eqnarray}I_{i_{1}\ldots i_{d-1}}=\unicode[STIX]{x1D6FF}^{k\ell }\unicode[STIX]{x0394}_{a}^{-1}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{k}}\left(J_{0\ell j_{1}\ldots j_{d-1}}\frac{\unicode[STIX]{x2202}a^{\,j_{1}}}{\unicode[STIX]{x2202}x^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{\,j_{d-1}}}{\unicode[STIX]{x2202}x^{i_{d-1}}}\right).\end{eqnarray}$$
5 Conclusion and open problems
A key result of this paper, with all manners of applications to fluid mechanics, is Theorem 1 of § 2 on generalised Cauchy invariants equations. A straightforward instance, is the Hankel (Reference Hankel1861) proof that the Cauchy (Reference Cauchy1815) invariants are equivalent to the Helmholtz (Reference von Helmholtz1858) theorem on the Lagrangian invariance of the vorticity flux through an infinitesimal surface element. Our result is much more general, stating that any Lie-invariant and exact
![]() $p$
-form has an associated generalised Cauchy invariants equation, together with a Hodge dual formulation that generalises Cauchy’s vorticity formula. The result, when applied to suitable 3-forms, also implies various generalisations of local helicity conservation laws for Euler and MHD flow. There are several ways in which the full nonlinear ideal MHD equations (compressible or incompressible) can be recast as Lie-advection problems, leading to Cauchy invariants equations. It is however not clear at the moment if such formulations lead to interesting results on time-analyticity and numerical integration by Cauchy–Lagrange-type methods (Zheligovsky & Frisch Reference Zheligovsky and Frisch2014; Podvigina et al.
Reference Podvigina, Zheligovsky and Frisch2016). Similar questions arise for the extended MHD models discussed in § 2.5.4.
$p$
-form has an associated generalised Cauchy invariants equation, together with a Hodge dual formulation that generalises Cauchy’s vorticity formula. The result, when applied to suitable 3-forms, also implies various generalisations of local helicity conservation laws for Euler and MHD flow. There are several ways in which the full nonlinear ideal MHD equations (compressible or incompressible) can be recast as Lie-advection problems, leading to Cauchy invariants equations. It is however not clear at the moment if such formulations lead to interesting results on time-analyticity and numerical integration by Cauchy–Lagrange-type methods (Zheligovsky & Frisch Reference Zheligovsky and Frisch2014; Podvigina et al.
Reference Podvigina, Zheligovsky and Frisch2016). Similar questions arise for the extended MHD models discussed in § 2.5.4.
Cauchy-type formulations exist already for the compressible Euler–Poisson equations in both an Einstein–de Sitter universe (Zheligovsky & Frisch Reference Zheligovsky and Frisch2014, see also Ehlers & Buchert Reference Ehlers and Buchert1997) and a
![]() $\unicode[STIX]{x039B}\text{CDM}$
universe (Rampf et al.
Reference Rampf, Villone and Frisch2015). It is now clear that the results are applicable to compressible models, such as the barotropic fluid equations, and to the Euler–Poisson equations or compressible MHD for fluid plasmas.
$\unicode[STIX]{x039B}\text{CDM}$
universe (Rampf et al.
Reference Rampf, Villone and Frisch2015). It is now clear that the results are applicable to compressible models, such as the barotropic fluid equations, and to the Euler–Poisson equations or compressible MHD for fluid plasmas.
We remind the reader that problems with a Cauchy invariants formulation have potentially a number of applications. For example, we believe that Cauchy’s invariants should play an important part in understanding the regularity of classical solutions to the 3D incompressible Euler equations through the depletion phenomenon. Indeed, the Cauchy invariants involve finite sums of vector products of gradients. Individual gradients are typically growing in the course of time but the constancy of the invariants put some geometrical constraints on, for example, their alignments. This may, in due time, lead to the discovery of new estimates helping to establish 3D regularity results, possibly for all times.
We also note that the Cauchy invariants formulation for the 3D incompressible Euler equation allows constructive proofs of the regularity of Lagrangian map through recursion relations among time-Taylor coefficients. These can then in principle be implemented numerically, without being limited by the Courant–Friedrichs–Lewy condition on time steps (Podvigina et al. Reference Podvigina, Zheligovsky and Frisch2016). Given that Cauchy invariants formulation apply both to flow in Euclidean (flat) space and to flow on Riemannian curved spaces of any dimension, it is natural to ask if the constructive and numerical tools just mentioned can be extended to flow in curved spaces. This would allow us, for example, to numerically study the energy inverse cascade on negatively curved spaces, recently investigated by Falkovich & Gawedzki (Reference Falkovich and Gawedzki2014) from an analytical point of view. It would also probably help with flow in relativistic cosmology (Buchert & Ostermann Reference Buchert and Ostermann2012; Alles et al. Reference Alles, Buchert, Al Roumi and Wiegand2015).
When leaving flat space, vector quantities involving tangent spaces at two or more spatially distinct locations cannot be simply added or averaged. This problem was encountered by Gilbert & Vanneste (Reference Gilbert and Vanneste2016) in trying to handle the generalised Lagrangian mean (GLM) theory on curved spaces; they solved it by using pullback transport and optimal transport techniques. Another difficulty occurs with time-Taylor series. Time derivatives of different orders, even when they are evaluated at the same location, do live in tangent spaces of different orders and cannot be readily combined. Classical tools of differential geometry, such as the exponential map, parallel transport, Lie series or Lie transformations (Nayfeh Reference Nayfeh1973; Dragt & Finn Reference Dragt and Finn1976; Cary Reference Cary1981; Steinberg Reference Steinberg1986) could be useful to overcome this difficulty.
Finally, even in flat space, a generalised-coordinate formulation of the Cauchy invariants equation can be useful in designing Cauchy–Lagrange numerical schemes in non-Cartesian coordinates. This could help the investigation of swirling axisymmetric flow in a cylinder, for which finite-time blow-up is predicted by some numerical studies (Luo & Hou Reference Luo and Hou2014a ,Reference Luo and Hou b ). In Besse & Frisch (Reference Besse and Frisch2017) it was shown that a constructive proof of finite-time regularity, based on recursion relations adapted to wall-bounded Euler flow is available. The main difficulty is the high-precision implementation, needed to allow reliable extrapolation without getting too close to the putative blow-up time.
Acknowledgements
We are grateful to P. Constantin, B. Khesin, M. Lingam, P. J. Morrison, R. Pandit and anonymous referees for useful remarks and references. This work was supported by the VLASIX and EUROFUSION projects respectively under the grants nos ANR-13-MONU-0003-01 and EURATOM-WP15-ENR-01/IPP-01.
Appendix A. Geometric and variational developments of the incompressible Euler equations
A.1 Geometric interpretation of the incompressible Euler equations
We start by introducing briefly the notions of Lie groups and Lie algebra, which are important in the geometric view of the incompressible Euler equations. A Lie group is a differentiable manifold
![]() $G$
endowed with an associative multiplication, that is, a map
$G$
endowed with an associative multiplication, that is, a map
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}G\times G\rightarrow G\\ (\unicode[STIX]{x1D702},\unicode[STIX]{x1D70E})\mapsto \unicode[STIX]{x1D702}\unicode[STIX]{x1D70E}\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}G\times G\rightarrow G\\ (\unicode[STIX]{x1D702},\unicode[STIX]{x1D70E})\mapsto \unicode[STIX]{x1D702}\unicode[STIX]{x1D70E}\end{array}\right\}\end{eqnarray}$$
making
![]() $G$
into a group and such that
$G$
into a group and such that
 $(\unicode[STIX]{x1D70F}\unicode[STIX]{x1D702})\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D70E})$
(associativity). Moreover, there is an element
$(\unicode[STIX]{x1D70F}\unicode[STIX]{x1D702})\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D70E})$
(associativity). Moreover, there is an element
![]() $e\in G$
called the identity such that
$e\in G$
called the identity such that
 $e\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}e=\unicode[STIX]{x1D702}$
. Such multiplication mapping, as well as, the inversion mapping
$e\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}e=\unicode[STIX]{x1D702}$
. Such multiplication mapping, as well as, the inversion mapping
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}G\rightarrow G\\ \unicode[STIX]{x1D702}\mapsto \unicode[STIX]{x1D702}^{-1},\quad \text{with}~\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}^{-1}=e,\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}G\rightarrow G\\ \unicode[STIX]{x1D702}\mapsto \unicode[STIX]{x1D702}^{-1},\quad \text{with}~\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}^{-1}=e,\end{array}\right\}\end{eqnarray}$$
must be differentiable. To the Lie group
![]() $G$
, we can naturally associate the Lie algebra
$G$
, we can naturally associate the Lie algebra
![]() $\mathfrak{g}$
defined by
$\mathfrak{g}$
defined by
 $$\begin{eqnarray}\mathfrak{g}=TG_{e},\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{g}=TG_{e},\end{eqnarray}$$
i.e. the tangent vector space of
![]() $G$
at the identity
$G$
at the identity
![]() $e\in G$
. In fluid dynamics, the space
$e\in G$
. In fluid dynamics, the space
![]() $TG$
represents the Lagrangian (material) description while the space
$TG$
represents the Lagrangian (material) description while the space
![]() $\mathfrak{g}$
represents the Eulerian (spatial) description. For more details about Lie groups, Lie algebra, and their applications in physics, we refer the reader, for example, to Arnold (Reference Arnold1966), Ibragimov (Reference Ibragimov1992, Reference Ibragimov1994, Reference Ibragimov2013), Olver (Reference Olver1993), Abraham et al. (Reference Abraham, Marsden and Ratiu1998), Arnold & Khesin (Reference Arnold and Khesin1998), Duistermaat & Kolk (Reference Duistermaat and Kolk2000), Bluman & Anco (Reference Bluman and Anco2002), Fecko (Reference Fecko2006), Ivancevic & Ivancevic (Reference Ivancevic and Ivancevic2007), Holm, Schmah & Stoica (Reference Holm, Schmah and Stoica2009), Bluman, Cheviakov & Anco (Reference Bluman, Cheviakov and Anco2010) and Frankel (Reference Frankel2012).
$\mathfrak{g}$
represents the Eulerian (spatial) description. For more details about Lie groups, Lie algebra, and their applications in physics, we refer the reader, for example, to Arnold (Reference Arnold1966), Ibragimov (Reference Ibragimov1992, Reference Ibragimov1994, Reference Ibragimov2013), Olver (Reference Olver1993), Abraham et al. (Reference Abraham, Marsden and Ratiu1998), Arnold & Khesin (Reference Arnold and Khesin1998), Duistermaat & Kolk (Reference Duistermaat and Kolk2000), Bluman & Anco (Reference Bluman and Anco2002), Fecko (Reference Fecko2006), Ivancevic & Ivancevic (Reference Ivancevic and Ivancevic2007), Holm, Schmah & Stoica (Reference Holm, Schmah and Stoica2009), Bluman, Cheviakov & Anco (Reference Bluman, Cheviakov and Anco2010) and Frankel (Reference Frankel2012).
Here, the flow takes place on an oriented
![]() $d$
-dimensional Riemannian manifold
$d$
-dimensional Riemannian manifold
![]() $(M,g)$
with metric volume form
$(M,g)$
with metric volume form
 $\unicode[STIX]{x1D707}=\sqrt{\text{g}}\,\text{d}a^{1}\wedge \cdots \wedge \text{d}a^{d}\equiv \sqrt{\text{g}}\,\text{d}a$
, where
$\unicode[STIX]{x1D707}=\sqrt{\text{g}}\,\text{d}a^{1}\wedge \cdots \wedge \text{d}a^{d}\equiv \sqrt{\text{g}}\,\text{d}a$
, where
 $\sqrt{\text{g}}=\sqrt{\det (\text{g}_{ij})}$
(see § B.3). Let
$\sqrt{\text{g}}=\sqrt{\det (\text{g}_{ij})}$
(see § B.3). Let
![]() $\unicode[STIX]{x1D6FA}$
be a bounded region of
$\unicode[STIX]{x1D6FA}$
be a bounded region of
![]() $M$
. In the Arnold (Reference Arnold1966) geometric interpretation of the incompressible Euler equations, the solutions can be viewed as geodesics of the right-invariant Riemannian metric given by the kinetic energy on the infinite-dimensional group of volume-preserving diffeomorphisms. Indeed, let us define
$M$
. In the Arnold (Reference Arnold1966) geometric interpretation of the incompressible Euler equations, the solutions can be viewed as geodesics of the right-invariant Riemannian metric given by the kinetic energy on the infinite-dimensional group of volume-preserving diffeomorphisms. Indeed, let us define
 $\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
as the group of diffeomorphisms
$\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
as the group of diffeomorphisms
 $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6FA}\rightarrow \unicode[STIX]{x1D6FA}$
preserving the metric volume form
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6FA}\rightarrow \unicode[STIX]{x1D6FA}$
preserving the metric volume form
![]() $\unicode[STIX]{x1D707}$
, i.e.
$\unicode[STIX]{x1D707}$
, i.e.
 $\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}$
. Here the group multiplication is the composition mapping denoted by ‘
$\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}$
. Here the group multiplication is the composition mapping denoted by ‘
![]() $\circ$
’ and
$\circ$
’ and
![]() $\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D707}$
is the pullback of the
$\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D707}$
is the pullback of the
![]() $d$
-form
$d$
-form
![]() $\unicode[STIX]{x1D707}$
through the diffeomorphism
$\unicode[STIX]{x1D707}$
through the diffeomorphism
![]() $\unicode[STIX]{x1D711}$
. A precise definition of the action on a tensor
$\unicode[STIX]{x1D711}$
. A precise definition of the action on a tensor
![]() $\unicode[STIX]{x0398}$
of the pullback operator
$\unicode[STIX]{x0398}$
of the pullback operator
![]() $\unicode[STIX]{x1D711}^{\ast }$
is given in § B.4, but roughly speaking it consists in evaluating the tensor
$\unicode[STIX]{x1D711}^{\ast }$
is given in § B.4, but roughly speaking it consists in evaluating the tensor
![]() $\unicode[STIX]{x0398}$
at the point
$\unicode[STIX]{x0398}$
at the point
![]() $\unicode[STIX]{x1D711}(a)$
,
$\unicode[STIX]{x1D711}(a)$
,
![]() $a\in \unicode[STIX]{x1D6FA}$
(that is the right composition of
$a\in \unicode[STIX]{x1D6FA}$
(that is the right composition of
![]() $\unicode[STIX]{x0398}$
with
$\unicode[STIX]{x0398}$
with
![]() $\unicode[STIX]{x1D711}$
), while taking into account the deformation of the structure induced by the map
$\unicode[STIX]{x1D711}$
), while taking into account the deformation of the structure induced by the map
![]() $\unicode[STIX]{x1D711}$
(reminiscent of a Jacobian matrix). For the volume form
$\unicode[STIX]{x1D711}$
(reminiscent of a Jacobian matrix). For the volume form
![]() $\unicode[STIX]{x1D707}$
, the
$\unicode[STIX]{x1D707}$
, the
![]() $d$
-covariant antisymmetric tensor
$d$
-covariant antisymmetric tensor
 $$\begin{eqnarray}\unicode[STIX]{x1D707}(a)=\sqrt{g(a)}\,\text{d}a^{1}\wedge \cdots \wedge \text{d}a^{d}=\frac{1}{\text{d}!}\unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{d}}^{1\ldots d}\sqrt{g(a)}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{d}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(a)=\sqrt{g(a)}\,\text{d}a^{1}\wedge \cdots \wedge \text{d}a^{d}=\frac{1}{\text{d}!}\unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{d}}^{1\ldots d}\sqrt{g(a)}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{d}},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{d}}^{1\ldots d}$
is the generalised Kronecker symbol (see appendix B), we obtain by pullback
$\unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{d}}^{1\ldots d}$
is the generalised Kronecker symbol (see appendix B), we obtain by pullback
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D707} & = & \displaystyle \frac{1}{\text{d}!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{d}}^{1\ldots d}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{d}}}{\unicode[STIX]{x2202}a^{i_{d}}}\sqrt{g(\unicode[STIX]{x1D711}(a))}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{d}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\text{d}!}\unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{d}}^{1\ldots d}\det \left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}a}\right)\sqrt{g(\unicode[STIX]{x1D711}(a))}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{d}}\nonumber\\ \displaystyle & = & \displaystyle \det \left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}a}\right)\sqrt{g(\unicode[STIX]{x1D711}(a))}\,\text{d}a^{1}\wedge \cdots \wedge \text{d}a^{d}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D707} & = & \displaystyle \frac{1}{\text{d}!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{d}}^{1\ldots d}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{d}}}{\unicode[STIX]{x2202}a^{i_{d}}}\sqrt{g(\unicode[STIX]{x1D711}(a))}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{d}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\text{d}!}\unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{d}}^{1\ldots d}\det \left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}a}\right)\sqrt{g(\unicode[STIX]{x1D711}(a))}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{d}}\nonumber\\ \displaystyle & = & \displaystyle \det \left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}a}\right)\sqrt{g(\unicode[STIX]{x1D711}(a))}\,\text{d}a^{1}\wedge \cdots \wedge \text{d}a^{d}.\end{eqnarray}$$
 $G:=\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
is a Lie group when
$G:=\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
is a Lie group when
![]() $\unicode[STIX]{x1D6FA}$
is a compact differentiable manifold. Even if it not so, we can associate to
$\unicode[STIX]{x1D6FA}$
is a compact differentiable manifold. Even if it not so, we can associate to
![]() $G$
the Lie algebra
$G$
the Lie algebra
 $\mathfrak{g}:=TG_{e}$
consisting of all divergence-free vector fields
$\mathfrak{g}:=TG_{e}$
consisting of all divergence-free vector fields
![]() $v$
tangent to the boundary (if it is not empty), i.e. such that
$v$
tangent to the boundary (if it is not empty), i.e. such that
 $$\begin{eqnarray}\unicode[STIX]{x1D735}_{i}v^{i}=0,\quad \text{on}~\unicode[STIX]{x1D6FA},\quad \text{and}\quad (v,\unicode[STIX]{x1D708})=0,\quad \text{on}~\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D735}_{i}v^{i}=0,\quad \text{on}~\unicode[STIX]{x1D6FA},\quad \text{and}\quad (v,\unicode[STIX]{x1D708})=0,\quad \text{on}~\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D735}_{k}$
is the covariant derivative and
$\unicode[STIX]{x1D735}_{k}$
is the covariant derivative and
![]() $\unicode[STIX]{x1D708}$
denotes the unit outer normal vector at the boundary
$\unicode[STIX]{x1D708}$
denotes the unit outer normal vector at the boundary
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
. The covariant derivative
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
. The covariant derivative
![]() $\unicode[STIX]{x1D735}_{k}$
is a generalisation to curved spaces of the classical partial derivative
$\unicode[STIX]{x1D735}_{k}$
is a generalisation to curved spaces of the classical partial derivative
![]() $\unicode[STIX]{x2202}_{k}$
to Euclidean spaces (for a more detailed definition, see § B.10).
$\unicode[STIX]{x2202}_{k}$
to Euclidean spaces (for a more detailed definition, see § B.10).
In the algebra
![]() $\mathfrak{g}$
, we define the scalar product of two vector fields
$\mathfrak{g}$
, we define the scalar product of two vector fields
 $v_{1},v_{2}\in \mathfrak{g}$
, as
$v_{1},v_{2}\in \mathfrak{g}$
, as
 $$\begin{eqnarray}\langle v_{1},v_{2}\rangle _{\mathfrak{g}}=\int _{\unicode[STIX]{x1D6FA}}(v_{1},v_{2})_{g}\,\unicode[STIX]{x1D707},\end{eqnarray}$$
$$\begin{eqnarray}\langle v_{1},v_{2}\rangle _{\mathfrak{g}}=\int _{\unicode[STIX]{x1D6FA}}(v_{1},v_{2})_{g}\,\unicode[STIX]{x1D707},\end{eqnarray}$$
where the scalar product
![]() $(\cdot ,\cdot )_{g}$
, induced by the Riemannian metric
$(\cdot ,\cdot )_{g}$
, induced by the Riemannian metric
 $\text{d}s^{2}=g=\text{g}_{ij}\,\text{d}a^{i}\otimes \text{d}a^{\,j}$
, is given by
$\text{d}s^{2}=g=\text{g}_{ij}\,\text{d}a^{i}\otimes \text{d}a^{\,j}$
, is given by
 $(v,w)_{g}=\text{g}_{ij}v^{i}w^{\,j}$
,
$(v,w)_{g}=\text{g}_{ij}v^{i}w^{\,j}$
,
![]() $v$
,
$v$
,
 $w\in TM_{a}$
,
$w\in TM_{a}$
,
![]() $a\in M$
. Finally let us introduce the right translation acting on the group
$a\in M$
. Finally let us introduce the right translation acting on the group
![]() $G$
. Every element
$G$
. Every element
![]() $\unicode[STIX]{x1D711}$
of the group
$\unicode[STIX]{x1D711}$
of the group
![]() $G$
defines diffeomorphisms of the group onto itself:
$G$
defines diffeomorphisms of the group onto itself:
 $$\begin{eqnarray}R_{\unicode[STIX]{x1D711}}:G\rightarrow G,\quad R_{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}\unicode[STIX]{x1D711},\quad \forall \unicode[STIX]{x1D713}\in G.\end{eqnarray}$$
$$\begin{eqnarray}R_{\unicode[STIX]{x1D711}}:G\rightarrow G,\quad R_{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}\unicode[STIX]{x1D711},\quad \forall \unicode[STIX]{x1D713}\in G.\end{eqnarray}$$
The induced map on the tangent bundle
![]() $TG$
will be denoted by
$TG$
will be denoted by
 $$\begin{eqnarray}R_{\unicode[STIX]{x1D711}\ast }:TG_{\unicode[STIX]{x1D713}}\rightarrow TG_{\unicode[STIX]{x1D713}\unicode[STIX]{x1D711}},\quad \forall \unicode[STIX]{x1D713}\in G.\end{eqnarray}$$
$$\begin{eqnarray}R_{\unicode[STIX]{x1D711}\ast }:TG_{\unicode[STIX]{x1D713}}\rightarrow TG_{\unicode[STIX]{x1D713}\unicode[STIX]{x1D711}},\quad \forall \unicode[STIX]{x1D713}\in G.\end{eqnarray}$$
Then a Riemannian metric on the group
![]() $G$
is called right-invariant if it is preserved under all right translations
$G$
is called right-invariant if it is preserved under all right translations
![]() $R_{\unicode[STIX]{x1D711}}$
, i.e. if the derivative of the right translation carries every vector to a vector of the same length. Thus it is sufficient to give a right-invariant metric at one point of the group (for instance the identity), since the metric can be carried over to the remaining points of the group by right translations.
$R_{\unicode[STIX]{x1D711}}$
, i.e. if the derivative of the right translation carries every vector to a vector of the same length. Thus it is sufficient to give a right-invariant metric at one point of the group (for instance the identity), since the metric can be carried over to the remaining points of the group by right translations.
We now consider the flow of a uniform ideal (incompressible and non-viscous) fluid in the region
![]() $\unicode[STIX]{x1D6FA}$
. Here, and henceforth, by ‘flow’ we understand a Lagrangian map
$\unicode[STIX]{x1D6FA}$
. Here, and henceforth, by ‘flow’ we understand a Lagrangian map
 $M\ni a\rightarrow \unicode[STIX]{x1D711}_{t}(a)\in M$
, which, at this point, need not be a solution of the Euler equations. Such a flow is given by a curve
$M\ni a\rightarrow \unicode[STIX]{x1D711}_{t}(a)\in M$
, which, at this point, need not be a solution of the Euler equations. Such a flow is given by a curve
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
in the group
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
in the group
 $\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
. This means that the diffeomorphism
$\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
. This means that the diffeomorphism
![]() $\unicode[STIX]{x1D711}_{t}$
maps every particle of the fluid from the position
$\unicode[STIX]{x1D711}_{t}$
maps every particle of the fluid from the position
![]() $a$
it had at time 0 to the position
$a$
it had at time 0 to the position
![]() $x$
at time
$x$
at time
![]() $t$
.
$t$
.
If
![]() $\unicode[STIX]{x1D711}_{t}$
is to be a solution of the Euler equations then, according to the variational formulation (see, e.g., Arnold Reference Arnold1966), the curve
$\unicode[STIX]{x1D711}_{t}$
is to be a solution of the Euler equations then, according to the variational formulation (see, e.g., Arnold Reference Arnold1966), the curve
![]() $\unicode[STIX]{x1D711}_{t}$
is a geodesic of the group
$\unicode[STIX]{x1D711}_{t}$
is a geodesic of the group
 $\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
. Such a curve extremises the (Maupertuis) action defined as the time integral of the kinetic energy:
$\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
. Such a curve extremises the (Maupertuis) action defined as the time integral of the kinetic energy:
 $$\begin{eqnarray}{\mathcal{A}}_{K}:=\frac{1}{2}\int _{0}^{T}\text{d}t\langle v(t),v(t)\rangle _{\mathfrak{ g}},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{K}:=\frac{1}{2}\int _{0}^{T}\text{d}t\langle v(t),v(t)\rangle _{\mathfrak{ g}},\end{eqnarray}$$
where
![]() $v(t)$
is the Eulerian velocity vector field belonging to
$v(t)$
is the Eulerian velocity vector field belonging to
![]() $\mathfrak{g}$
. This formulation is explicitly given in Arnold (Reference Arnold1966) but was probably already known to Lagrange (Reference Lagrange1788) who never wrote it explicitly because he switched quickly from variational formulations to so-called virtual velocity formulations.
$\mathfrak{g}$
. This formulation is explicitly given in Arnold (Reference Arnold1966) but was probably already known to Lagrange (Reference Lagrange1788) who never wrote it explicitly because he switched quickly from variational formulations to so-called virtual velocity formulations.
It easily shown that the kinetic energy of the moving fluid is a right-invariant Riemannian metric on the group
 $\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
. Indeed, suppose that after time
$\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
. Indeed, suppose that after time
![]() $t$
the flow of the fluid gives a diffeomorphism
$t$
the flow of the fluid gives a diffeomorphism
![]() $\unicode[STIX]{x1D711}_{t}$
, and the velocity at this moment of time is given by the Eulerian vector field
$\unicode[STIX]{x1D711}_{t}$
, and the velocity at this moment of time is given by the Eulerian vector field
![]() $v$
. Then the diffeomorphism realised by the flow after time
$v$
. Then the diffeomorphism realised by the flow after time
![]() $t+\text{d}t$
(with
$t+\text{d}t$
(with
![]() $\text{d}t\ll 1$
) will be
$\text{d}t\ll 1$
) will be
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{t+\text{d}t}=\exp (v\,\text{d}t)\unicode[STIX]{x1D711}_{t}+o(\text{d}t),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{t+\text{d}t}=\exp (v\,\text{d}t)\unicode[STIX]{x1D711}_{t}+o(\text{d}t),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D70F}\rightarrow \exp (v\unicode[STIX]{x1D70F})$
is in one-parameter group with vector
$\unicode[STIX]{x1D70F}\rightarrow \exp (v\unicode[STIX]{x1D70F})$
is in one-parameter group with vector
![]() $v$
, i.e. the Lagrangian flow of the differential equation defined by the vector field
$v$
, i.e. the Lagrangian flow of the differential equation defined by the vector field
![]() $v$
. From (A 11) and using the definitions (A 8)–(A 9) we have
$v$
. From (A 11) and using the definitions (A 8)–(A 9) we have
 $$\begin{eqnarray}R_{{\unicode[STIX]{x1D711}_{t}}^{-1}}\left(\frac{\unicode[STIX]{x1D711}_{t+\text{d}t}-\unicode[STIX]{x1D711}_{t}}{\text{d}t}\right)=R_{{\unicode[STIX]{x1D711}_{t}}^{-1}}\left(\frac{\exp (v\,\text{d}t)-e}{\text{d}t}\right)\unicode[STIX]{x1D711}_{t}+o(1),\end{eqnarray}$$
$$\begin{eqnarray}R_{{\unicode[STIX]{x1D711}_{t}}^{-1}}\left(\frac{\unicode[STIX]{x1D711}_{t+\text{d}t}-\unicode[STIX]{x1D711}_{t}}{\text{d}t}\right)=R_{{\unicode[STIX]{x1D711}_{t}}^{-1}}\left(\frac{\exp (v\,\text{d}t)-e}{\text{d}t}\right)\unicode[STIX]{x1D711}_{t}+o(1),\end{eqnarray}$$
which, after taking the limit
![]() $\text{d}t\rightarrow 0$
, leads to
$\text{d}t\rightarrow 0$
, leads to
 $$\begin{eqnarray}v=R_{\unicode[STIX]{x1D711}_{t}^{-1}\ast }\dot{\unicode[STIX]{x1D711}}_{t}=\dot{\unicode[STIX]{x1D711}}_{t}\circ \unicode[STIX]{x1D711}_{t}^{-1}\quad \text{or}\quad \dot{\unicode[STIX]{x1D711}}_{t}=R_{\unicode[STIX]{x1D711}_{t}\ast }v=v\circ \unicode[STIX]{x1D711}_{t}.\end{eqnarray}$$
$$\begin{eqnarray}v=R_{\unicode[STIX]{x1D711}_{t}^{-1}\ast }\dot{\unicode[STIX]{x1D711}}_{t}=\dot{\unicode[STIX]{x1D711}}_{t}\circ \unicode[STIX]{x1D711}_{t}^{-1}\quad \text{or}\quad \dot{\unicode[STIX]{x1D711}}_{t}=R_{\unicode[STIX]{x1D711}_{t}\ast }v=v\circ \unicode[STIX]{x1D711}_{t}.\end{eqnarray}$$
In mathematical language the velocity field
![]() $v$
is in the algebra
$v$
is in the algebra
![]() $\mathfrak{g}$
and is obtained from the vector
$\mathfrak{g}$
and is obtained from the vector
![]() $\dot{\unicode[STIX]{x1D711}}_{t}$
, tangent to the group at the point
$\dot{\unicode[STIX]{x1D711}}_{t}$
, tangent to the group at the point
![]() $\unicode[STIX]{x1D711}_{t}$
, by right translation. In fluid-dynamics terms the vector field
$\unicode[STIX]{x1D711}_{t}$
, by right translation. In fluid-dynamics terms the vector field
 $v=v_{t}(x)$
is the Eulerian velocity field. We pass from the Lagrangian to the Eulerian description by right translations. We note that if we replace
$v=v_{t}(x)$
is the Eulerian velocity field. We pass from the Lagrangian to the Eulerian description by right translations. We note that if we replace
![]() $\unicode[STIX]{x1D711}$
by the composition
$\unicode[STIX]{x1D711}$
by the composition
![]() $\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D702}$
, for a fixed (time-independent) map
$\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D702}$
, for a fixed (time-independent) map
 $\unicode[STIX]{x1D702}\in \text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
, then
$\unicode[STIX]{x1D702}\in \text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
, then
![]() $\dot{\unicode[STIX]{x1D711}}_{t}\circ \unicode[STIX]{x1D711}_{t}^{-1}$
is independent of
$\dot{\unicode[STIX]{x1D711}}_{t}\circ \unicode[STIX]{x1D711}_{t}^{-1}$
is independent of
![]() $\unicode[STIX]{x1D702}$
. This reflects the right invariance of the Eulerian description (
$\unicode[STIX]{x1D702}$
. This reflects the right invariance of the Eulerian description (
![]() $v$
is invariant under composition of
$v$
is invariant under composition of
![]() $\unicode[STIX]{x1D711}$
by
$\unicode[STIX]{x1D711}$
by
![]() $\unicode[STIX]{x1D702}$
on the right). Therefore
$\unicode[STIX]{x1D702}$
on the right). Therefore
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
is the geodesic, on the group
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
is the geodesic, on the group
 $\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
, of the right-invariant Riemannian metric given by the quadratic form (A 7). From the Hamiltonian least-action principle we obtain the following Euler equations (A 14) in contravariant form. For the sake of completeness, details of the derivation are given in § A.2. Let
$\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
, of the right-invariant Riemannian metric given by the quadratic form (A 7). From the Hamiltonian least-action principle we obtain the following Euler equations (A 14) in contravariant form. For the sake of completeness, details of the derivation are given in § A.2. Let
![]() $v\in \mathfrak{g}$
be the velocity field defined by the right translation (A 13). Then there exists a scalar function
$v\in \mathfrak{g}$
be the velocity field defined by the right translation (A 13). Then there exists a scalar function
 $p:]0,T\!]\times \unicode[STIX]{x1D6FA}\ni (t,x)\rightarrow \mathbb{R}$
, the so-called pressure function, such that
$p:]0,T\!]\times \unicode[STIX]{x1D6FA}\ni (t,x)\rightarrow \mathbb{R}$
, the so-called pressure function, such that
![]() $(v,p)$
satisfy the following Euler equations
$(v,p)$
satisfy the following Euler equations
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{t}v^{i}+v^{k}\unicode[STIX]{x1D735}_{k}v^{i}=-\text{g}^{ik}\unicode[STIX]{x2202}_{k}p,\quad x\in \unicode[STIX]{x1D6FA},t\in ]0,T\!].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}v^{i}+v^{k}\unicode[STIX]{x1D735}_{k}v^{i}=-\text{g}^{ik}\unicode[STIX]{x2202}_{k}p,\quad x\in \unicode[STIX]{x1D6FA},t\in ]0,T\!].\end{eqnarray}$$
A.2 Derivation of the Euler equations from a least-action principle
From the discussion of § A.1, the geodesic motions
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
on
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
on
 $\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
, which correspond to the right-invariant Riemann metric defined by (A 7), are given by the extrema of the action (A 10) where
$\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
, which correspond to the right-invariant Riemann metric defined by (A 7), are given by the extrema of the action (A 10) where
 $\dot{\unicode[STIX]{x1D711}}_{t}=R_{\unicode[STIX]{x1D711}_{t}\ast }v=v(t,\unicode[STIX]{x1D711}_{t})$
, under condition
$\dot{\unicode[STIX]{x1D711}}_{t}=R_{\unicode[STIX]{x1D711}_{t}\ast }v=v(t,\unicode[STIX]{x1D711}_{t})$
, under condition
 $\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}$
. To perform the extremisation of the action (A 10) over
$\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}$
. To perform the extremisation of the action (A 10) over
 $\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
, it is convenient to impose the volume-preservation constraint
$\text{SDiff}(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D707})$
, it is convenient to impose the volume-preservation constraint
 $\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}$
through a Lagrange multiplier
$\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}$
through a Lagrange multiplier
![]() $\unicode[STIX]{x1D706}(t,a)$
by adding to the action (A 10) the term
$\unicode[STIX]{x1D706}(t,a)$
by adding to the action (A 10) the term
 $$\begin{eqnarray}{\mathcal{A}}_{I}:=\int _{0}^{T}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}-\unicode[STIX]{x1D707})\,\text{d}a\,\text{d}t.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{I}:=\int _{0}^{T}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}-\unicode[STIX]{x1D707})\,\text{d}a\,\text{d}t.\end{eqnarray}$$
We now compute the first variation of the action
 $$\begin{eqnarray}{\mathcal{A}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FA})={\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})+{\mathcal{A}}_{I}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FA}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FA})={\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})+{\mathcal{A}}_{I}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FA}).\end{eqnarray}$$
We start with
![]() $\unicode[STIX]{x1D6FF}{\mathcal{A}}_{K}$
. For its evaluation, we mainly use an integration by parts in time, the symmetry of the metric tensor
$\unicode[STIX]{x1D6FF}{\mathcal{A}}_{K}$
. For its evaluation, we mainly use an integration by parts in time, the symmetry of the metric tensor
![]() $\text{g}_{ij}$
, the definition of the covariant derivative (see § B.10), the change of variable
$\text{g}_{ij}$
, the definition of the covariant derivative (see § B.10), the change of variable
 $x=\unicode[STIX]{x1D711}_{t}(a)=\unicode[STIX]{x1D711}(t,a)$
, the equations
$x=\unicode[STIX]{x1D711}_{t}(a)=\unicode[STIX]{x1D711}(t,a)$
, the equations
 $\dot{\unicode[STIX]{x1D711}}_{t}=v(t,\unicode[STIX]{x1D711}_{t})$
and
$\dot{\unicode[STIX]{x1D711}}_{t}=v(t,\unicode[STIX]{x1D711}_{t})$
and
 $\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}$
. For the first variation of
$\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}$
. For the first variation of
![]() $\unicode[STIX]{x1D6FF}{\mathcal{A}}_{K}$
with volume preservation
$\unicode[STIX]{x1D6FF}{\mathcal{A}}_{K}$
with volume preservation
 $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{t}=\unicode[STIX]{x1D711}(t,a)$
, we then obtain
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{t}=\unicode[STIX]{x1D711}(t,a)$
, we then obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}{\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})[\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}] & = & \displaystyle \frac{1}{2}\unicode[STIX]{x1D6FF}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(x)\,\text{g}_{ij}(x)v^{i}(t,x)v^{\,j}(t,x)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\unicode[STIX]{x1D6FF}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\text{g}_{ij}(\unicode[STIX]{x1D711}(t,a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}^{i}(t,a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}^{\,j}(t,a)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x2202}_{k}\text{g}_{ij}(\unicode[STIX]{x1D711}(t,a))\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{k}(t,a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}^{i}(t,a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}^{\,j}(t,a)\nonumber\\ \displaystyle & & \displaystyle +\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\text{g}_{ij}(\unicode[STIX]{x1D711}(t,a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}^{i}(t,a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{\,j}(t,a)\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(x)\,\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{\,j}(t,\unicode[STIX]{x1D711}_{t}^{-1}(x))\left\{\vphantom{\frac{1}{2}}\!-\text{g}_{ij}(x)[\unicode[STIX]{x2202}_{t}v^{i}(t,x)+v^{k}(t,x)\unicode[STIX]{x2202}_{k}v^{i}(t,x)]\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}\unicode[STIX]{x2202}_{j}g_{ik}(x)v^{i}(t,x)v^{k}(t,x)-\unicode[STIX]{x2202}_{k}\text{g}_{ij}(x)v^{i}(t,x)v^{k}(t,x)\right\}\nonumber\\ \displaystyle & = & \displaystyle -\int _{0}^{T}\text{d}t\!\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}\,u^{\,j}\text{g}_{ij}\left\{\unicode[STIX]{x2202}_{t}v^{i}+v^{k}\unicode[STIX]{x2202}_{k}v^{i}+\frac{1}{2}g^{im}(\unicode[STIX]{x2202}_{k}g_{lm}+\unicode[STIX]{x2202}_{l}g_{km}-\unicode[STIX]{x2202}_{m}g_{lk})v^{k}v^{l}\right\}\nonumber\\ \displaystyle & = & \displaystyle -\int _{0}^{T}\text{d}t\!\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}\,u^{\,j}\text{g}_{ij}\{\unicode[STIX]{x2202}_{t}v^{i}+v^{k}\unicode[STIX]{x1D735}_{k}v^{i}\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}{\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})[\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}] & = & \displaystyle \frac{1}{2}\unicode[STIX]{x1D6FF}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(x)\,\text{g}_{ij}(x)v^{i}(t,x)v^{\,j}(t,x)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\unicode[STIX]{x1D6FF}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\text{g}_{ij}(\unicode[STIX]{x1D711}(t,a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}^{i}(t,a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}^{\,j}(t,a)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x2202}_{k}\text{g}_{ij}(\unicode[STIX]{x1D711}(t,a))\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{k}(t,a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}^{i}(t,a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}^{\,j}(t,a)\nonumber\\ \displaystyle & & \displaystyle +\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\text{g}_{ij}(\unicode[STIX]{x1D711}(t,a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}^{i}(t,a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{\,j}(t,a)\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(x)\,\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{\,j}(t,\unicode[STIX]{x1D711}_{t}^{-1}(x))\left\{\vphantom{\frac{1}{2}}\!-\text{g}_{ij}(x)[\unicode[STIX]{x2202}_{t}v^{i}(t,x)+v^{k}(t,x)\unicode[STIX]{x2202}_{k}v^{i}(t,x)]\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}\unicode[STIX]{x2202}_{j}g_{ik}(x)v^{i}(t,x)v^{k}(t,x)-\unicode[STIX]{x2202}_{k}\text{g}_{ij}(x)v^{i}(t,x)v^{k}(t,x)\right\}\nonumber\\ \displaystyle & = & \displaystyle -\int _{0}^{T}\text{d}t\!\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}\,u^{\,j}\text{g}_{ij}\left\{\unicode[STIX]{x2202}_{t}v^{i}+v^{k}\unicode[STIX]{x2202}_{k}v^{i}+\frac{1}{2}g^{im}(\unicode[STIX]{x2202}_{k}g_{lm}+\unicode[STIX]{x2202}_{l}g_{km}-\unicode[STIX]{x2202}_{m}g_{lk})v^{k}v^{l}\right\}\nonumber\\ \displaystyle & = & \displaystyle -\int _{0}^{T}\text{d}t\!\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}\,u^{\,j}\text{g}_{ij}\{\unicode[STIX]{x2202}_{t}v^{i}+v^{k}\unicode[STIX]{x1D735}_{k}v^{i}\}.\end{eqnarray}$$
Here
 $u^{\,j}(t,x)=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{\,j}(t,\unicode[STIX]{x1D711}_{t}^{-1}(x))$
and
$u^{\,j}(t,x)=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{\,j}(t,\unicode[STIX]{x1D711}_{t}^{-1}(x))$
and
![]() $\unicode[STIX]{x2202}\equiv \unicode[STIX]{x2202}_{a}$
denotes the partial derivative with respect the Lagrangian parameter
$\unicode[STIX]{x2202}\equiv \unicode[STIX]{x2202}_{a}$
denotes the partial derivative with respect the Lagrangian parameter
![]() $a$
(initial position). Next, for the first variation of
$a$
(initial position). Next, for the first variation of
![]() $\unicode[STIX]{x1D6FF}{\mathcal{A}}_{I}$
, using the definition of the volume form
$\unicode[STIX]{x1D6FF}{\mathcal{A}}_{I}$
, using the definition of the volume form
![]() $\unicode[STIX]{x1D707}$
and the following identities (see § B.6)
$\unicode[STIX]{x1D707}$
and the following identities (see § B.6)
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\det (D_{a}\unicode[STIX]{x1D711})}{\unicode[STIX]{x2202}(\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D711}^{k})}=\det (D_{a}\unicode[STIX]{x1D711})([D_{a}\unicode[STIX]{x1D711}]^{-1})_{k}^{j},\quad \unicode[STIX]{x2202}_{k}g=g\text{g}^{ij}\unicode[STIX]{x2202}_{k}\text{g}_{ij},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\det (D_{a}\unicode[STIX]{x1D711})}{\unicode[STIX]{x2202}(\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D711}^{k})}=\det (D_{a}\unicode[STIX]{x1D711})([D_{a}\unicode[STIX]{x1D711}]^{-1})_{k}^{j},\quad \unicode[STIX]{x2202}_{k}g=g\text{g}^{ij}\unicode[STIX]{x2202}_{k}\text{g}_{ij},\end{eqnarray}$$
we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}{\mathcal{A}}_{I}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FA})[\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}]\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FF}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x1D706}(t,a)\left(\sqrt{g(\unicode[STIX]{x1D711}(t,a))}\det (D_{a}\unicode[STIX]{x1D711}(t,a))-\sqrt{g(a)}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}(t,a)\left(\sqrt{g(\unicode[STIX]{x1D711}(t,a))}\det (D_{a}\unicode[STIX]{x1D711}(t,a))-\sqrt{g(a)}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x1D706}(t,a)\sqrt{g(\unicode[STIX]{x1D711}(t,a))}\det (D_{a}\unicode[STIX]{x1D711}(t,a))\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left(\frac{1}{2}\text{g}^{ij}(\unicode[STIX]{x1D711}(t,a))\unicode[STIX]{x2202}_{k}\text{g}_{ij}(\unicode[STIX]{x1D711}(t,a))\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{k}(t,a)+([D_{a}\unicode[STIX]{x1D711}(t,a)]^{-1})_{k}^{j}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{k}(t,a)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}(t,a)\left(\sqrt{g(\unicode[STIX]{x1D711}(t,a))}\det (D_{a}\unicode[STIX]{x1D711}(t,a))-\sqrt{g(a)}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(x)\,p(t,x)\left(\frac{1}{2}\text{g}^{ij}(x)\unicode[STIX]{x2202}_{k}\text{g}_{ij}(x)u^{k}(t,x)+\unicode[STIX]{x2202}_{k}u^{k}(t,x)\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}{\mathcal{A}}_{I}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FA})[\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}]\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FF}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x1D706}(t,a)\left(\sqrt{g(\unicode[STIX]{x1D711}(t,a))}\det (D_{a}\unicode[STIX]{x1D711}(t,a))-\sqrt{g(a)}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}(t,a)\left(\sqrt{g(\unicode[STIX]{x1D711}(t,a))}\det (D_{a}\unicode[STIX]{x1D711}(t,a))-\sqrt{g(a)}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x1D706}(t,a)\sqrt{g(\unicode[STIX]{x1D711}(t,a))}\det (D_{a}\unicode[STIX]{x1D711}(t,a))\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left(\frac{1}{2}\text{g}^{ij}(\unicode[STIX]{x1D711}(t,a))\unicode[STIX]{x2202}_{k}\text{g}_{ij}(\unicode[STIX]{x1D711}(t,a))\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{k}(t,a)+([D_{a}\unicode[STIX]{x1D711}(t,a)]^{-1})_{k}^{j}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}^{k}(t,a)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}(t,a)\left(\sqrt{g(\unicode[STIX]{x1D711}(t,a))}\det (D_{a}\unicode[STIX]{x1D711}(t,a))-\sqrt{g(a)}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(x)\,p(t,x)\left(\frac{1}{2}\text{g}^{ij}(x)\unicode[STIX]{x2202}_{k}\text{g}_{ij}(x)u^{k}(t,x)+\unicode[STIX]{x2202}_{k}u^{k}(t,x)\right).\end{eqnarray}$$
Here we have introduced the pressure function
![]() $p$
by setting
$p$
by setting
 $p(t,x)=\unicode[STIX]{x1D706}(t,\unicode[STIX]{x1D711}_{t}^{-1}(x))$
. Using an integration by parts in the last term of this equation, we finally obtain
$p(t,x)=\unicode[STIX]{x1D706}(t,\unicode[STIX]{x1D711}_{t}^{-1}(x))$
. Using an integration by parts in the last term of this equation, we finally obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}{\mathcal{A}}_{I}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FA})[\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}] & = & \displaystyle \int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}(t,a)\left(\sqrt{g(\unicode[STIX]{x1D711}(t,a))}\det (D_{a}\unicode[STIX]{x1D711}(t,a))-\sqrt{g(a)}\right)\nonumber\\ \displaystyle & & \displaystyle -\int _{0}^{T}\,\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(x)\,u^{k}(t,x)\unicode[STIX]{x2202}_{k}p(t,x),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}{\mathcal{A}}_{I}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FA})[\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}] & = & \displaystyle \int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}(t,a)\left(\sqrt{g(\unicode[STIX]{x1D711}(t,a))}\det (D_{a}\unicode[STIX]{x1D711}(t,a))-\sqrt{g(a)}\right)\nonumber\\ \displaystyle & & \displaystyle -\int _{0}^{T}\,\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(x)\,u^{k}(t,x)\unicode[STIX]{x2202}_{k}p(t,x),\end{eqnarray}$$
where we have used the boundary condition
 $(u,\unicode[STIX]{x1D708})=0$
on
$(u,\unicode[STIX]{x1D708})=0$
on
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
for the infinitesimal variation
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
for the infinitesimal variation
 $u(t,x)=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}(t,\unicode[STIX]{x1D711}_{t}^{-1}(x))$
. Setting the first variation
$u(t,x)=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}(t,\unicode[STIX]{x1D711}_{t}^{-1}(x))$
. Setting the first variation
![]() $\unicode[STIX]{x1D6FF}{\mathcal{A}}$
to zero, and using (A 16) and (A 17)–(A 20), we obtain the Euler equations (A 14), together with the volume-preserving condition
$\unicode[STIX]{x1D6FF}{\mathcal{A}}$
to zero, and using (A 16) and (A 17)–(A 20), we obtain the Euler equations (A 14), together with the volume-preserving condition
 $\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}$
, which is equivalent to the incompressibility condition
$\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}$
, which is equivalent to the incompressibility condition
 $\unicode[STIX]{x1D735}_{i}v^{i}=0$
for the velocity field.
$\unicode[STIX]{x1D735}_{i}v^{i}=0$
for the velocity field.
A.3 Derivation of the Cauchy invariants equation from the relabelling symmetry and a variational principle
In this appendix, from the relabelling symmetry, i.e. the invariance of the action under relabelling transformations, we recover the Cauchy invariants equation without appealing to Theorem 1. Here we follow the spirit of the proof given by Frisch & Villone (Reference Frisch and Villone2014) and references therein for the Euclidean case. The reader is also referred to this for historical discussion and description of the use of different Hamiltonian principles or least-action principles in Lagrangian coordinates. Such a strategy does not directly make use of Noether’s theorem, but is reminiscent of its proof. Before stating the result, we give the formal definition of a relabelling transformation.
Definition 1. A relabelling transformation is a map
 $\unicode[STIX]{x1D6FA}\ni a\rightarrow \unicode[STIX]{x1D702}(a)\in \unicode[STIX]{x1D6FA}$
such that
$\unicode[STIX]{x1D6FA}\ni a\rightarrow \unicode[STIX]{x1D702}(a)\in \unicode[STIX]{x1D6FA}$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D702}(a)=a+\unicode[STIX]{x1D6FF}a(a),\quad \unicode[STIX]{x1D6FF}a\in \mathfrak{g},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}(a)=a+\unicode[STIX]{x1D6FF}a(a),\quad \unicode[STIX]{x1D6FF}a\in \mathfrak{g},\end{eqnarray}$$
i.e. with
 $$\begin{eqnarray}\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}=0\quad \text{and}\quad (\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}=0\quad \text{and}\quad (\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=0.\end{eqnarray}$$
In other words the vector field
![]() $\unicode[STIX]{x1D6FF}a$
is the infinitesimal generator of a group of volume-preserving diffeomorphisms of
$\unicode[STIX]{x1D6FF}a$
is the infinitesimal generator of a group of volume-preserving diffeomorphisms of
![]() $\unicode[STIX]{x1D6FA}$
that leave the boundary
$\unicode[STIX]{x1D6FA}$
that leave the boundary
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
invariant.
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
invariant.
Theorem 2 (Cauchy invariants equation from the relabelling symmetry and variational principle).
Let
![]() $\unicode[STIX]{x1D711}_{t}$
be the Euler flow. We set
$\unicode[STIX]{x1D711}_{t}$
be the Euler flow. We set
![]() $x=\unicode[STIX]{x1D711}_{t}$
and
$x=\unicode[STIX]{x1D711}_{t}$
and
![]() $v=\dot{\unicode[STIX]{x1D711}}_{t}$
, with
$v=\dot{\unicode[STIX]{x1D711}}_{t}$
, with
![]() $v_{0}=\dot{\unicode[STIX]{x1D711}}_{0}$
. Then the invariance of the action (A 10) of § A.1 under relabelling transformations of Definition 1 implies the following Cauchy invariants conservation law:
$v_{0}=\dot{\unicode[STIX]{x1D711}}_{0}$
. Then the invariance of the action (A 10) of § A.1 under relabelling transformations of Definition 1 implies the following Cauchy invariants conservation law:
 $$\begin{eqnarray}\text{d}v_{k}\wedge \text{d}x^{k}=\unicode[STIX]{x1D714}_{0}:=\text{d}v_{0}^{\flat }.\end{eqnarray}$$
$$\begin{eqnarray}\text{d}v_{k}\wedge \text{d}x^{k}=\unicode[STIX]{x1D714}_{0}:=\text{d}v_{0}^{\flat }.\end{eqnarray}$$
Proof. The idea is first to compute the first-order variation of the action integral
 $$\begin{eqnarray}{\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})=\frac{1}{2}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})=\frac{1}{2}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a),\end{eqnarray}$$
induced by the relabelling transformations of Definition 1. The variation of
 ${\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})$
is given by
${\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})$
is given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}{\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})[\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}] & = & \displaystyle \frac{1}{2}\unicode[STIX]{x1D6FF}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x2202}_{l}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}_{t}^{l}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\nonumber\\ \displaystyle & & \displaystyle +\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}{\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})[\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}] & = & \displaystyle \frac{1}{2}\unicode[STIX]{x1D6FF}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x2202}_{l}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}_{t}^{l}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\nonumber\\ \displaystyle & & \displaystyle +\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a).\end{eqnarray}$$
The relabelling transformation of Definition 1 induces a change in the Lagrangian flow
![]() $\unicode[STIX]{x1D711}_{t}$
at time
$\unicode[STIX]{x1D711}_{t}$
at time
![]() $t$
, given by
$t$
, given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}_{t}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}}{\unicode[STIX]{x2202}a^{i}}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}^{i}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}}{\unicode[STIX]{x2202}a^{i}}\unicode[STIX]{x1D6FF}a^{i}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}_{t}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}}{\unicode[STIX]{x2202}a^{i}}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D702}^{i}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}}{\unicode[STIX]{x2202}a^{i}}\unicode[STIX]{x1D6FF}a^{i}.\end{eqnarray}$$
Substituting (A 26) in (A 25), and using the product rule, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}{\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})[\unicode[STIX]{x1D6FF}a]\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\left\{\frac{1}{2}\unicode[STIX]{x2202}_{l}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{l}(a)}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\unicode[STIX]{x1D6FF}a^{m}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\right)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\unicode[STIX]{x1D6FF}a^{n}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\left\{\frac{1}{2}\unicode[STIX]{x2202}_{l}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{l}(a)}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\unicode[STIX]{x1D6FF}a^{m}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\unicode[STIX]{x2202}_{t}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D6FF}a^{n}-\unicode[STIX]{x2202}_{t}(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x1D6FF}a^{n}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\left\{\frac{1}{2}\unicode[STIX]{x2202}_{l}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{l}(a)}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\unicode[STIX]{x1D6FF}a^{m}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\left.\unicode[STIX]{x2202}_{k}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{k}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D6FF}a^{m}-\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}^{2}\unicode[STIX]{x1D711}_{t}^{j}(a)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D6FF}a^{m}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x2202}_{t}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D6FF}a^{n}\nonumber\\ \displaystyle & & \displaystyle \quad =I_{1}+I_{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}{\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})[\unicode[STIX]{x1D6FF}a]\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\left\{\frac{1}{2}\unicode[STIX]{x2202}_{l}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{l}(a)}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\unicode[STIX]{x1D6FF}a^{m}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\right)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\unicode[STIX]{x1D6FF}a^{n}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\left\{\frac{1}{2}\unicode[STIX]{x2202}_{l}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{l}(a)}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\unicode[STIX]{x1D6FF}a^{m}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\unicode[STIX]{x2202}_{t}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D6FF}a^{n}-\unicode[STIX]{x2202}_{t}(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x1D6FF}a^{n}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\left\{\frac{1}{2}\unicode[STIX]{x2202}_{l}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{l}(a)}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\unicode[STIX]{x1D6FF}a^{m}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad -\left.\unicode[STIX]{x2202}_{k}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{k}(a)\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D6FF}a^{m}-\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\unicode[STIX]{x2202}_{t}^{2}\unicode[STIX]{x1D711}_{t}^{j}(a)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D6FF}a^{m}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad +\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x2202}_{t}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D6FF}a^{n}\nonumber\\ \displaystyle & & \displaystyle \quad =I_{1}+I_{2}.\end{eqnarray}$$
First, we show that
![]() $I_{1}=0$
. From (A 27) and using the definition of the covariant derivative, we obtain
$I_{1}=0$
. From (A 27) and using the definition of the covariant derivative, we obtain
 $$\begin{eqnarray}\displaystyle I_{1} & = & \displaystyle \int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{j}}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D6FF}a^{m}\left\{\vphantom{\frac{1}{2}}-\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})[\unicode[STIX]{x2202}_{t}v^{i}(t,\unicode[STIX]{x1D711}_{t})+v^{k}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{k}v^{i}(t,\unicode[STIX]{x1D711}_{t})]\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}\unicode[STIX]{x2202}_{j}g_{ik}(\unicode[STIX]{x1D711}_{t})v^{i}(t,\unicode[STIX]{x1D711}_{t})v^{k}(t,\unicode[STIX]{x1D711}_{t})-\unicode[STIX]{x2202}_{k}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})v^{i}(t,\unicode[STIX]{x1D711}_{t})v^{k}(t,\unicode[STIX]{x1D711}_{t})\right\}\nonumber\\ \displaystyle & = & \displaystyle -\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{j}}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D6FF}a^{m}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\left\{\vphantom{\frac{1}{2}}\unicode[STIX]{x2202}_{t}v^{i}(t,\unicode[STIX]{x1D711}_{t})+v^{k}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{k}v^{i}(t,\unicode[STIX]{x1D711}_{t})\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}g^{im}(t,\unicode[STIX]{x1D711}_{t})(\unicode[STIX]{x2202}_{k}g_{lm}(t,\unicode[STIX]{x1D711}_{t})+\unicode[STIX]{x2202}_{l}g_{km}(t,\unicode[STIX]{x1D711}_{t})-\unicode[STIX]{x2202}_{m}g_{lk}(t,\unicode[STIX]{x1D711}_{t}))v^{k}(t,\unicode[STIX]{x1D711}_{t})v^{l}(t,\unicode[STIX]{x1D711}_{t})\right\}\nonumber\\ \displaystyle & = & \displaystyle -\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{j}}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D6FF}a^{m}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\{\unicode[STIX]{x2202}_{t}v^{i}(t,\unicode[STIX]{x1D711}_{t})+v^{k}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D735}_{k}v^{i}(t,\unicode[STIX]{x1D711}_{t})\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{1} & = & \displaystyle \int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{j}}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D6FF}a^{m}\left\{\vphantom{\frac{1}{2}}-\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})[\unicode[STIX]{x2202}_{t}v^{i}(t,\unicode[STIX]{x1D711}_{t})+v^{k}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{k}v^{i}(t,\unicode[STIX]{x1D711}_{t})]\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}\unicode[STIX]{x2202}_{j}g_{ik}(\unicode[STIX]{x1D711}_{t})v^{i}(t,\unicode[STIX]{x1D711}_{t})v^{k}(t,\unicode[STIX]{x1D711}_{t})-\unicode[STIX]{x2202}_{k}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})v^{i}(t,\unicode[STIX]{x1D711}_{t})v^{k}(t,\unicode[STIX]{x1D711}_{t})\right\}\nonumber\\ \displaystyle & = & \displaystyle -\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{j}}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D6FF}a^{m}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\left\{\vphantom{\frac{1}{2}}\unicode[STIX]{x2202}_{t}v^{i}(t,\unicode[STIX]{x1D711}_{t})+v^{k}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{k}v^{i}(t,\unicode[STIX]{x1D711}_{t})\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{1}{2}g^{im}(t,\unicode[STIX]{x1D711}_{t})(\unicode[STIX]{x2202}_{k}g_{lm}(t,\unicode[STIX]{x1D711}_{t})+\unicode[STIX]{x2202}_{l}g_{km}(t,\unicode[STIX]{x1D711}_{t})-\unicode[STIX]{x2202}_{m}g_{lk}(t,\unicode[STIX]{x1D711}_{t}))v^{k}(t,\unicode[STIX]{x1D711}_{t})v^{l}(t,\unicode[STIX]{x1D711}_{t})\right\}\nonumber\\ \displaystyle & = & \displaystyle -\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{j}}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D6FF}a^{m}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\{\unicode[STIX]{x2202}_{t}v^{i}(t,\unicode[STIX]{x1D711}_{t})+v^{k}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D735}_{k}v^{i}(t,\unicode[STIX]{x1D711}_{t})\}.\end{eqnarray}$$
Using the Euler equations (A 14), the term
![]() $I_{1}$
becomes
$I_{1}$
becomes
 $$\begin{eqnarray}\displaystyle I_{1} & = & \displaystyle \int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x1D6FF}a^{m}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{j}}{\unicode[STIX]{x2202}a^{m}}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\text{g}^{ik}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{k}p(t,\unicode[STIX]{x1D711}_{t})=\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x1D6FF}a^{m}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{j}}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D6FF}_{j}^{k}\unicode[STIX]{x2202}_{k}p(t,\unicode[STIX]{x1D711}_{t})\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x1D6FF}a^{m}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{k}}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x2202}_{k}p(t,\unicode[STIX]{x1D711}_{t})=\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x1D6FF}a^{m}\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}a^{m}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{1} & = & \displaystyle \int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x1D6FF}a^{m}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{j}}{\unicode[STIX]{x2202}a^{m}}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\text{g}^{ik}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{k}p(t,\unicode[STIX]{x1D711}_{t})=\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x1D6FF}a^{m}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{j}}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x1D6FF}_{j}^{k}\unicode[STIX]{x2202}_{k}p(t,\unicode[STIX]{x1D711}_{t})\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x1D6FF}a^{m}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{k}}{\unicode[STIX]{x2202}a^{m}}\unicode[STIX]{x2202}_{k}p(t,\unicode[STIX]{x1D711}_{t})=\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x1D6FF}a^{m}\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}a^{m}}.\end{eqnarray}$$
Now, we recall that
 $\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}=g^{-1/2}\unicode[STIX]{x2202}_{i}(\sqrt{\text{g}}\unicode[STIX]{x1D6FF}a^{i})=0$
, and
$\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}=g^{-1/2}\unicode[STIX]{x2202}_{i}(\sqrt{\text{g}}\unicode[STIX]{x1D6FF}a^{i})=0$
, and
 $(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D708})=0$
. Therefore, using an integration by parts in space, the term
$(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D708})=0$
. Therefore, using an integration by parts in space, the term
![]() $I_{1}$
becomes
$I_{1}$
becomes
 $$\begin{eqnarray}I_{1}=\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x1D6FF}a^{i}\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}a^{i}}=-\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}p+\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\,\text{d}\unicode[STIX]{x1D6E4}\sqrt{g(a)}p(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=0.\end{eqnarray}$$
$$\begin{eqnarray}I_{1}=\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x1D6FF}a^{i}\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}a^{i}}=-\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}p+\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\,\text{d}\unicode[STIX]{x1D6E4}\sqrt{g(a)}p(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=0.\end{eqnarray}$$
Finally, we deal with the term
![]() $I_{2}$
defined in (A 27). For this, we use the property that
$I_{2}$
defined in (A 27). For this, we use the property that
![]() $\unicode[STIX]{x1D6FF}a\in \mathfrak{g}$
, i.e.
$\unicode[STIX]{x1D6FF}a\in \mathfrak{g}$
, i.e.
 $\unicode[STIX]{x1D735}_{n}\unicode[STIX]{x1D6FF}a^{n}=0$
and
$\unicode[STIX]{x1D735}_{n}\unicode[STIX]{x1D6FF}a^{n}=0$
and
 $(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}a^{i}\unicode[STIX]{x1D708}^{j}=0$
. Here,
$(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}a^{i}\unicode[STIX]{x1D708}^{j}=0$
. Here,
![]() $\unicode[STIX]{x1D6FF}_{ij}$
is the metric tensor of an Euclidean space with Cartesian coordinates, i.e.
$\unicode[STIX]{x1D6FF}_{ij}$
is the metric tensor of an Euclidean space with Cartesian coordinates, i.e.
![]() $\unicode[STIX]{x1D6FF}_{ij}=0$
if
$\unicode[STIX]{x1D6FF}_{ij}=0$
if
![]() $i\neq j$
and
$i\neq j$
and
![]() $\unicode[STIX]{x1D6FF}_{ij}=1$
if
$\unicode[STIX]{x1D6FF}_{ij}=1$
if
![]() $i=j$
. Such a vector
$i=j$
. Such a vector
![]() $\unicode[STIX]{x1D6FF}a$
can be constructed from a skew-symmetric 2-contravariant tensor
$\unicode[STIX]{x1D6FF}a$
can be constructed from a skew-symmetric 2-contravariant tensor
![]() $\unicode[STIX]{x1D709}^{ij}$
satisfying the following constraints:
$\unicode[STIX]{x1D709}^{ij}$
satisfying the following constraints:
 $$\begin{eqnarray}\unicode[STIX]{x1D709}^{ij}+\unicode[STIX]{x1D709}^{\,ji}=0\quad \text{on}~\unicode[STIX]{x1D6FA},\quad \unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D709}^{ik}\unicode[STIX]{x1D708}^{j}=0\quad \forall k\quad \text{on}~\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA},\quad \text{and}\quad \unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D709}^{ik}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D708}^{j}=0\quad \text{on}~\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}^{ij}+\unicode[STIX]{x1D709}^{\,ji}=0\quad \text{on}~\unicode[STIX]{x1D6FA},\quad \unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D709}^{ik}\unicode[STIX]{x1D708}^{j}=0\quad \forall k\quad \text{on}~\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA},\quad \text{and}\quad \unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D709}^{ik}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D708}^{j}=0\quad \text{on}~\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}.\end{eqnarray}$$
Indeed, if we set
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}a^{i}=\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D709}^{ij},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}a^{i}=\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D709}^{ij},\end{eqnarray}$$
then, using (A 31), we find that
 $\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}=0$
and
$\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}=0$
and
 $(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}a^{i}\unicode[STIX]{x1D708}^{j}=0$
. We observe that a skew-symmetric 2-contravariant tensor
$(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}a^{i}\unicode[STIX]{x1D708}^{j}=0$
. We observe that a skew-symmetric 2-contravariant tensor
![]() $\unicode[STIX]{x1D709}^{ij}$
satisfying
$\unicode[STIX]{x1D709}^{ij}$
satisfying
![]() $\unicode[STIX]{x1D709}_{|_{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}}^{ij}=0$
, satisfies also the boundary conditions (A 31). Using (A 31)–(A 32), the term
$\unicode[STIX]{x1D709}_{|_{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}}^{ij}=0$
, satisfies also the boundary conditions (A 31). Using (A 31)–(A 32), the term
![]() $I_{2}$
becomes
$I_{2}$
becomes
 $$\begin{eqnarray}\displaystyle I_{2} & = & \displaystyle \int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x2202}_{t}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D6FF}a^{n}\nonumber\\ \displaystyle & = & \displaystyle -\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x2202}_{k}\unicode[STIX]{x2202}_{t}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D709}^{nk}\nonumber\\ \displaystyle & & \displaystyle +\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\,\text{d}\unicode[STIX]{x1D6E4}\unicode[STIX]{x2202}_{t}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D709}^{nk}\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D6FF}_{km}\nonumber\\ \displaystyle & = & \displaystyle -\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x2202}_{t}\unicode[STIX]{x2202}_{k}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D709}^{nk}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{2} & = & \displaystyle \int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,\unicode[STIX]{x2202}_{t}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D6FF}a^{n}\nonumber\\ \displaystyle & = & \displaystyle -\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x2202}_{k}\unicode[STIX]{x2202}_{t}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D709}^{nk}\nonumber\\ \displaystyle & & \displaystyle +\int _{0}^{T}\text{d}t\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\,\text{d}\unicode[STIX]{x1D6E4}\unicode[STIX]{x2202}_{t}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D709}^{nk}\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D6FF}_{km}\nonumber\\ \displaystyle & = & \displaystyle -\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x2202}_{t}\unicode[STIX]{x2202}_{k}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D709}^{nk}.\end{eqnarray}$$
The action
 ${\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})$
should be invariant under relabelling transformations. Thus the variation of the action integral, i.e.
${\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})$
should be invariant under relabelling transformations. Thus the variation of the action integral, i.e.
![]() $\unicode[STIX]{x1D6FF}{\mathcal{A}}_{K}$
, must vanish. Therefore we have
$\unicode[STIX]{x1D6FF}{\mathcal{A}}_{K}$
, must vanish. Therefore we have
![]() $I_{2}=0$
, i.e.
$I_{2}=0$
, i.e.
 $$\begin{eqnarray}-\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x2202}_{t}\unicode[STIX]{x2202}_{k}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D709}^{nk}=0.\end{eqnarray}$$
$$\begin{eqnarray}-\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}}\,\text{d}a\,\unicode[STIX]{x2202}_{t}\unicode[STIX]{x2202}_{k}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)\unicode[STIX]{x1D709}^{nk}=0.\end{eqnarray}$$
Since the
![]() $\unicode[STIX]{x1D709}^{nk}$
’s are arbitrary, we obtain
$\unicode[STIX]{x1D709}^{nk}$
’s are arbitrary, we obtain
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x2202}_{k}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)=0,\quad \forall k,n=1,\ldots ,d.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x2202}_{k}\left(\text{g}_{ij}(\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}(a)\right)=0,\quad \forall k,n=1,\ldots ,d.\end{eqnarray}$$
Integration in time of these equations leads to
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{k}\left(v_{i}(t,\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\right)=\unicode[STIX]{x2202}_{k}v_{0n},\quad \forall k,n=1,\ldots ,d.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{k}\left(v_{i}(t,\unicode[STIX]{x1D711}_{t}(a))\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{t}^{i}(a)}{\unicode[STIX]{x2202}a^{n}}\right)=\unicode[STIX]{x2202}_{k}v_{0n},\quad \forall k,n=1,\ldots ,d.\end{eqnarray}$$
Multiplying these equalities by
 $\text{d}a^{k}\wedge \text{d}a^{n}$
and summing over the indices
$\text{d}a^{k}\wedge \text{d}a^{n}$
and summing over the indices
![]() $k$
and
$k$
and
![]() $n$
, we obtain
$n$
, we obtain
 $$\begin{eqnarray}\text{d}(v_{i}\,\text{d}x^{i})=\text{d}v_{0}^{\flat }\quad \text{i.e.}~\text{d}v_{i}\wedge \text{d}x^{i}=\unicode[STIX]{x1D714}_{0}:=\text{d}v_{0}^{\flat },\end{eqnarray}$$
$$\begin{eqnarray}\text{d}(v_{i}\,\text{d}x^{i})=\text{d}v_{0}^{\flat }\quad \text{i.e.}~\text{d}v_{i}\wedge \text{d}x^{i}=\unicode[STIX]{x1D714}_{0}:=\text{d}v_{0}^{\flat },\end{eqnarray}$$
which ends the proof. ◻
A.4 Conservation of the vorticity 2-form, directly from Noether’s theorem
As we shall now show, when Noether’s theorem is literally applied to the variational formulation of the Euler equations in conjunction with the relabelling symmetry, it does not yield the Cauchy invariants but the conservation (under pullback) of the vorticity 2-form.
For this, we introduce the Lagrangian density
![]() ${\mathcal{L}}_{K}$
associated to the action integral (A 10). Since by definition we have
${\mathcal{L}}_{K}$
associated to the action integral (A 10). Since by definition we have
 $$\begin{eqnarray}{\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})=\int _{0}^{T}\,\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,{\mathcal{L}}_{K}(a,\unicode[STIX]{x1D711},\unicode[STIX]{x2202}\unicode[STIX]{x1D711}),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{K}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FA})=\int _{0}^{T}\,\text{d}t\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}(a)\,{\mathcal{L}}_{K}(a,\unicode[STIX]{x1D711},\unicode[STIX]{x2202}\unicode[STIX]{x1D711}),\end{eqnarray}$$
then, from (A 10), we obtain
 $$\begin{eqnarray}{\mathcal{L}}_{K}(a,\unicode[STIX]{x1D711},\unicode[STIX]{x2202}\unicode[STIX]{x1D711})={\textstyle \frac{1}{2}}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}_{K}(a,\unicode[STIX]{x1D711},\unicode[STIX]{x2202}\unicode[STIX]{x1D711})={\textstyle \frac{1}{2}}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}.\end{eqnarray}$$
In this definition of the Lagrangian density,
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D711}$
denotes any first-order partial derivative of
$\unicode[STIX]{x2202}\unicode[STIX]{x1D711}$
denotes any first-order partial derivative of
![]() $\unicode[STIX]{x1D711}$
with respect to space or time variables. Let us now define the energy–momentum tensor
$\unicode[STIX]{x1D711}$
with respect to space or time variables. Let us now define the energy–momentum tensor
![]() $T_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}$
by
$T_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}$
by
 $$\begin{eqnarray}T_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}=\frac{\unicode[STIX]{x2202}{\mathcal{L}}_{K}}{\unicode[STIX]{x2202}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D6FE}})}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D6FE}}-{\mathcal{L}}_{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
$$\begin{eqnarray}T_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}=\frac{\unicode[STIX]{x2202}{\mathcal{L}}_{K}}{\unicode[STIX]{x2202}(\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D6FE}})}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D6FE}}-{\mathcal{L}}_{K}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
where the contravariant (respectively covariant) index
![]() $\unicode[STIX]{x1D6FC}$
(respectively
$\unicode[STIX]{x1D6FC}$
(respectively
![]() $\unicode[STIX]{x1D6FD}$
) denotes space–time-independent variables. The relabelling transformations, as given in Definition 1 in § A.3, lead us to choosing the following functional variations
$\unicode[STIX]{x1D6FD}$
) denotes space–time-independent variables. The relabelling transformations, as given in Definition 1 in § A.3, lead us to choosing the following functional variations
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}a,\quad \text{such that}~\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}=0,\quad \text{and}\quad (\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=0;\quad \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\equiv 0,\quad \unicode[STIX]{x1D6FF}\unicode[STIX]{x2202}\unicode[STIX]{x1D711}\equiv 0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}a,\quad \text{such that}~\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}=0,\quad \text{and}\quad (\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=0;\quad \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\equiv 0,\quad \unicode[STIX]{x1D6FF}\unicode[STIX]{x2202}\unicode[STIX]{x1D711}\equiv 0.\end{eqnarray}$$
Using these functional variations and the relabelling symmetry (i.e. invariance of the action integral (A 38) under relabelling transformations), from Noether’s theorem (Hill Reference Hill1951; Courant & Hilbert Reference Courant and Hilbert1966; Lanczos Reference Lanczos1970; Jose & Saletan Reference Jose and Saletan1998; Goldstein, Poole & Safko Reference Goldstein, Poole and Safko2001; Giaquinta & Hildebrandt Reference Giaquinta and Hildebrandt2016), we obtain the following conservation law
 $$\begin{eqnarray}\unicode[STIX]{x1D735}_{\unicode[STIX]{x1D6FC}}T^{\unicode[STIX]{x1D6FC}}=0\quad \text{where}~T^{\unicode[STIX]{x1D6FC}}=T_{i}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FF}a^{i}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D735}_{\unicode[STIX]{x1D6FC}}T^{\unicode[STIX]{x1D6FC}}=0\quad \text{where}~T^{\unicode[STIX]{x1D6FC}}=T_{i}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FF}a^{i}.\end{eqnarray}$$
More precisely, using (A 39)–(A 40) and the properties of the Euler flow
![]() $\unicode[STIX]{x1D711}_{t}$
, the components of the covariant contraction of the energy-impulsion tensor
$\unicode[STIX]{x1D711}_{t}$
, the components of the covariant contraction of the energy-impulsion tensor
![]() $T^{\unicode[STIX]{x1D6FC}}$
are
$T^{\unicode[STIX]{x1D6FC}}$
are
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle T^{t}=T_{l}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FF}a^{l}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}(\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i})}\left(\frac{1}{2}g_{mn}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{m}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{n}\right)\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x1D6FF}a^{l}=\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x1D6FF}a^{l},\\ T^{i}=-{\mathcal{L}}_{K}\unicode[STIX]{x1D6FF}a^{i}=-{\textstyle \frac{1}{2}}g_{jk}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{k}\unicode[STIX]{x1D6FF}a^{i}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle T^{t}=T_{l}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FF}a^{l}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}(\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i})}\left(\frac{1}{2}g_{mn}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{m}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{n}\right)\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x1D6FF}a^{l}=\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x1D6FF}a^{l},\\ T^{i}=-{\mathcal{L}}_{K}\unicode[STIX]{x1D6FF}a^{i}=-{\textstyle \frac{1}{2}}g_{jk}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{k}\unicode[STIX]{x1D6FF}a^{i}.\end{array}\right\}\end{eqnarray}$$
Using this equality and the boundary condition
 $(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=0$
(since
$(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=0$
(since
![]() $\unicode[STIX]{x1D6FF}a\in \mathfrak{g}$
), we obtain the boundary condition
$\unicode[STIX]{x1D6FF}a\in \mathfrak{g}$
), we obtain the boundary condition
 $(T,\unicode[STIX]{x1D708})=0$
, where
$(T,\unicode[STIX]{x1D708})=0$
, where
![]() $T$
is the vector of components
$T$
is the vector of components
![]() $T^{i}$
. Integrating the conservation law (A 42) on
$T^{i}$
. Integrating the conservation law (A 42) on
![]() $\unicode[STIX]{x1D6FA}$
and using the boundary condition
$\unicode[STIX]{x1D6FA}$
and using the boundary condition
 $(T,\unicode[STIX]{x1D708})=0$
, we obtain
$(T,\unicode[STIX]{x1D708})=0$
, we obtain
 $$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}\,\unicode[STIX]{x1D735}_{\unicode[STIX]{x1D6FC}}T^{\unicode[STIX]{x1D6FC}} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\sqrt{\text{g}}\,\unicode[STIX]{x1D735}_{\unicode[STIX]{x1D6FC}}T^{\unicode[STIX]{x1D6FC}}=\int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\unicode[STIX]{x2202}_{t}(\sqrt{\text{g}}T^{t})+\int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\unicode[STIX]{x2202}_{i}(\sqrt{\text{g}}T^{i})\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\unicode[STIX]{x2202}_{t}(\sqrt{\text{g}}T^{t})+\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\,\text{d}\unicode[STIX]{x1D6E4}\sqrt{\text{g}}\,(T,\unicode[STIX]{x1D708})=\frac{\text{d}}{\text{d}t}\int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\sqrt{\text{g}}T^{t}:=0.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D707}\,\unicode[STIX]{x1D735}_{\unicode[STIX]{x1D6FC}}T^{\unicode[STIX]{x1D6FC}} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\sqrt{\text{g}}\,\unicode[STIX]{x1D735}_{\unicode[STIX]{x1D6FC}}T^{\unicode[STIX]{x1D6FC}}=\int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\unicode[STIX]{x2202}_{t}(\sqrt{\text{g}}T^{t})+\int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\unicode[STIX]{x2202}_{i}(\sqrt{\text{g}}T^{i})\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\unicode[STIX]{x2202}_{t}(\sqrt{\text{g}}T^{t})+\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\,\text{d}\unicode[STIX]{x1D6E4}\sqrt{\text{g}}\,(T,\unicode[STIX]{x1D708})=\frac{\text{d}}{\text{d}t}\int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\sqrt{\text{g}}T^{t}:=0.\qquad\end{eqnarray}$$
We now give details of the calculation of the time-integral invariant (A 44). For this, we use the property that
![]() $\unicode[STIX]{x1D6FF}a\in \mathfrak{g}$
, i.e.
$\unicode[STIX]{x1D6FF}a\in \mathfrak{g}$
, i.e.
 $\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}=0$
and
$\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}=0$
and
 $(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}a^{i}\unicode[STIX]{x1D708}^{j}=0$
. Here,
$(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}a^{i}\unicode[STIX]{x1D708}^{j}=0$
. Here,
![]() $\unicode[STIX]{x1D6FF}_{ij}$
is the metric tensor of an Euclidean space with Cartesian coordinates, i.e.
$\unicode[STIX]{x1D6FF}_{ij}$
is the metric tensor of an Euclidean space with Cartesian coordinates, i.e.
![]() $\unicode[STIX]{x1D6FF}_{ij}=0$
if
$\unicode[STIX]{x1D6FF}_{ij}=0$
if
![]() $i\neq j$
and
$i\neq j$
and
![]() $\unicode[STIX]{x1D6FF}_{ij}=1$
if
$\unicode[STIX]{x1D6FF}_{ij}=1$
if
![]() $i=j$
. Such a vector
$i=j$
. Such a vector
![]() $\unicode[STIX]{x1D6FF}a$
can be constructed from a skew-symmetric 2-contravariant tensor
$\unicode[STIX]{x1D6FF}a$
can be constructed from a skew-symmetric 2-contravariant tensor
![]() $\unicode[STIX]{x1D709}^{ij}$
, which satisfies the following constraints
$\unicode[STIX]{x1D709}^{ij}$
, which satisfies the following constraints
 $$\begin{eqnarray}\unicode[STIX]{x1D709}^{ij}+\unicode[STIX]{x1D709}^{\,ji}=0\quad \text{on}~\unicode[STIX]{x1D6FA},\quad \unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D709}^{ik}\unicode[STIX]{x1D708}^{j}=0\quad \forall k\quad \text{on}~\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA},\quad \text{and}\quad \unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D709}^{ik}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D708}^{j}=0\quad \text{on}~\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}^{ij}+\unicode[STIX]{x1D709}^{\,ji}=0\quad \text{on}~\unicode[STIX]{x1D6FA},\quad \unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D709}^{ik}\unicode[STIX]{x1D708}^{j}=0\quad \forall k\quad \text{on}~\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA},\quad \text{and}\quad \unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D709}^{ik}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D708}^{j}=0\quad \text{on}~\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}.\end{eqnarray}$$
Indeed, if we define
![]() $\unicode[STIX]{x1D6FF}a$
by
$\unicode[STIX]{x1D6FF}a$
by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}a^{i}=\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D709}^{ij},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}a^{i}=\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D709}^{ij},\end{eqnarray}$$
then using (A 45) we obtain that
 $\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}=0$
and
$\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FF}a^{i}=0$
and
 $(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}a^{i}\unicode[STIX]{x1D708}^{j}=0$
. We note that a skew-symmetric 2-contravariant tensor
$(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D708})=\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}a^{i}\unicode[STIX]{x1D708}^{j}=0$
. We note that a skew-symmetric 2-contravariant tensor
![]() $\unicode[STIX]{x1D709}^{ij}$
, satisfying
$\unicode[STIX]{x1D709}^{ij}$
, satisfying
![]() $\unicode[STIX]{x1D709}_{|_{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}}^{ij}=0$
, also satisfies the boundary conditions (A 45). Using (A 45)–(A 46), and an integration by parts in space, the integral invariant becomes
$\unicode[STIX]{x1D709}_{|_{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}}^{ij}=0$
, also satisfies the boundary conditions (A 45). Using (A 45)–(A 46), and an integration by parts in space, the integral invariant becomes
 $$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\sqrt{\text{g}}T^{t} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\sqrt{\text{g}}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x1D6FF}a^{l}\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D709}^{kl}=\int _{\unicode[STIX]{x1D6FA}}\text{d}a\,v_{j}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D709}^{kl}\nonumber\\ \displaystyle & = & \displaystyle -\int _{\unicode[STIX]{x1D6FA}}\text{d}a\{\unicode[STIX]{x2202}_{i}v_{j}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}+v_{j}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{kl}\unicode[STIX]{x1D711}_{t}^{j}\}\unicode[STIX]{x1D709}^{kl}\nonumber\\ \displaystyle & & \displaystyle +\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\,\text{d}\unicode[STIX]{x1D6E4}v_{j}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x1D709}^{kl}\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D6FF}_{km}\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}}\text{d}a(\unicode[STIX]{x2202}_{i}v_{j}(t,\unicode[STIX]{x1D711}_{t})-\unicode[STIX]{x2202}_{j}v_{i}(t,\unicode[STIX]{x1D711}_{t}))\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x1D709}^{kl}-\int _{\unicode[STIX]{x1D6FA}}\text{d}a\,v_{j}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{kl}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x1D709}^{kl}\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}}\text{d}a(\unicode[STIX]{x2202}_{i}v_{j}(t,\unicode[STIX]{x1D711}_{t})-\unicode[STIX]{x2202}_{j}v_{i}(t,\unicode[STIX]{x1D711}_{t}))\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x1D709}^{kl}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\sqrt{\text{g}}T^{t} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\sqrt{\text{g}}\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x1D6FF}a^{l}\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\text{g}_{ij}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D709}^{kl}=\int _{\unicode[STIX]{x1D6FA}}\text{d}a\,v_{j}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D709}^{kl}\nonumber\\ \displaystyle & = & \displaystyle -\int _{\unicode[STIX]{x1D6FA}}\text{d}a\{\unicode[STIX]{x2202}_{i}v_{j}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}+v_{j}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{kl}\unicode[STIX]{x1D711}_{t}^{j}\}\unicode[STIX]{x1D709}^{kl}\nonumber\\ \displaystyle & & \displaystyle +\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\,\text{d}\unicode[STIX]{x1D6E4}v_{j}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x1D709}^{kl}\unicode[STIX]{x1D708}^{m}\unicode[STIX]{x1D6FF}_{km}\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}}\text{d}a(\unicode[STIX]{x2202}_{i}v_{j}(t,\unicode[STIX]{x1D711}_{t})-\unicode[STIX]{x2202}_{j}v_{i}(t,\unicode[STIX]{x1D711}_{t}))\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x1D709}^{kl}-\int _{\unicode[STIX]{x1D6FA}}\text{d}a\,v_{j}(t,\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x2202}_{kl}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x1D709}^{kl}\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}}\text{d}a(\unicode[STIX]{x2202}_{i}v_{j}(t,\unicode[STIX]{x1D711}_{t})-\unicode[STIX]{x2202}_{j}v_{i}(t,\unicode[STIX]{x1D711}_{t}))\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D711}_{t}^{i}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D711}_{t}^{j}\unicode[STIX]{x1D709}^{kl}.\end{eqnarray}$$
Therefore, we obtain
 $$\begin{eqnarray}\int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\unicode[STIX]{x1D709}^{kl}\,\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}_{kl}=0,\end{eqnarray}$$
$$\begin{eqnarray}\int _{\unicode[STIX]{x1D6FA}}\text{d}a\,\unicode[STIX]{x1D709}^{kl}\,\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}_{kl}=0,\end{eqnarray}$$
where we have defined the components of the vorticity 2-form
![]() $\unicode[STIX]{x1D714}_{kl}$
as
$\unicode[STIX]{x1D714}_{kl}$
as
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{kl}(t,x)=\unicode[STIX]{x2202}_{k}v_{l}(t,x)-\unicode[STIX]{x2202}_{l}v_{k}(t,x).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{kl}(t,x)=\unicode[STIX]{x2202}_{k}v_{l}(t,x)-\unicode[STIX]{x2202}_{l}v_{k}(t,x).\end{eqnarray}$$
Since the functions
![]() $\unicode[STIX]{x1D709}^{kl}$
’s are arbitrary and smooth, equality (A 48) implies
$\unicode[STIX]{x1D709}^{kl}$
’s are arbitrary and smooth, equality (A 48) implies
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}_{kl}=0,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}_{kl}=0,\end{eqnarray}$$
which implies
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{0}.\end{eqnarray}$$
Here,
 $$\begin{eqnarray}\unicode[STIX]{x1D714}(t,x)=\mathop{\sum }_{i<j}\unicode[STIX]{x1D714}_{ij}(t,x)\,\text{d}x^{i}\wedge \text{d}x^{\,j},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}(t,x)=\mathop{\sum }_{i<j}\unicode[STIX]{x1D714}_{ij}(t,x)\,\text{d}x^{i}\wedge \text{d}x^{\,j},\end{eqnarray}$$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{0}(a)=\unicode[STIX]{x1D714}(0,a)=\mathop{\sum }_{i<j}\unicode[STIX]{x1D714}_{ij}(0,a)\,\text{d}a^{i}\wedge \text{d}a^{\,j}=\mathop{\sum }_{i<j}\unicode[STIX]{x1D714}_{0ij}(a)\,\text{d}a^{i}\wedge \text{d}a^{\,j}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{0}(a)=\unicode[STIX]{x1D714}(0,a)=\mathop{\sum }_{i<j}\unicode[STIX]{x1D714}_{ij}(0,a)\,\text{d}a^{i}\wedge \text{d}a^{\,j}=\mathop{\sum }_{i<j}\unicode[STIX]{x1D714}_{0ij}(a)\,\text{d}a^{i}\wedge \text{d}a^{\,j}.\end{eqnarray}$$
Equation (A 51) establishes the invariance of the vorticity 2-form under pullback.
A.5 About Cartan’s formula
The aim of this appendix it to establish the formula
 $$\begin{eqnarray}\text{d}\text{i}_{v}v^{\flat }+\text{i}_{v}\,\text{d}v^{\flat }=(\unicode[STIX]{x1D735}_{v}v)^{\flat }+{\textstyle \frac{1}{2}}\,\text{d}(v,v)_{g}.\end{eqnarray}$$
$$\begin{eqnarray}\text{d}\text{i}_{v}v^{\flat }+\text{i}_{v}\,\text{d}v^{\flat }=(\unicode[STIX]{x1D735}_{v}v)^{\flat }+{\textstyle \frac{1}{2}}\,\text{d}(v,v)_{g}.\end{eqnarray}$$
First, using definitions of the interior product
![]() $\text{i}_{v}$
and the exterior derivative
$\text{i}_{v}$
and the exterior derivative
![]() $\text{d}$
, given in § B.8, and the symmetry of the Christoffel symbols in the definition of the covariant derivative (see § B.10), for a vector field
$\text{d}$
, given in § B.8, and the symmetry of the Christoffel symbols in the definition of the covariant derivative (see § B.10), for a vector field
 $X\in {\mathcal{T}}_{0}^{1}(M)$
and a 1-form
$X\in {\mathcal{T}}_{0}^{1}(M)$
and a 1-form
 $X\in {\mathcal{T}}_{1}^{0}(M)$
, we obtain
$X\in {\mathcal{T}}_{1}^{0}(M)$
, we obtain
 $$\begin{eqnarray}\text{i}_{X}\,\text{d}\unicode[STIX]{x1D6FC}=\text{i}_{X}\left({\textstyle \frac{1}{2}}(\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D6FC}_{j}-\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FC}_{i})\,\text{d}x^{i}\wedge \text{d}x^{\,j}\right)=X^{j}(\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D6FC}_{j})\,\text{d}x^{i}=X^{j}(\unicode[STIX]{x1D735}_{j}\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FC}_{j})\,\text{d}x^{i}.\end{eqnarray}$$
$$\begin{eqnarray}\text{i}_{X}\,\text{d}\unicode[STIX]{x1D6FC}=\text{i}_{X}\left({\textstyle \frac{1}{2}}(\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D6FC}_{j}-\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FC}_{i})\,\text{d}x^{i}\wedge \text{d}x^{\,j}\right)=X^{j}(\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D6FC}_{j})\,\text{d}x^{i}=X^{j}(\unicode[STIX]{x1D735}_{j}\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FC}_{j})\,\text{d}x^{i}.\end{eqnarray}$$
Second, using the same properties as for deriving (A 55), we obtain
 $$\begin{eqnarray}\text{d}\text{i}_{X}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x2202}_{i}(X^{j}\unicode[STIX]{x1D6FC}_{j})\,\text{d}x^{i}=\unicode[STIX]{x1D735}_{i}(X^{j}\unicode[STIX]{x1D6FC}_{j})\,\text{d}x^{i}=(X^{j}\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FC}_{j}+\unicode[STIX]{x1D6FC}_{j}\unicode[STIX]{x1D735}_{i}X^{j})\,\text{d}x^{i}.\end{eqnarray}$$
$$\begin{eqnarray}\text{d}\text{i}_{X}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x2202}_{i}(X^{j}\unicode[STIX]{x1D6FC}_{j})\,\text{d}x^{i}=\unicode[STIX]{x1D735}_{i}(X^{j}\unicode[STIX]{x1D6FC}_{j})\,\text{d}x^{i}=(X^{j}\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D6FC}_{j}+\unicode[STIX]{x1D6FC}_{j}\unicode[STIX]{x1D735}_{i}X^{j})\,\text{d}x^{i}.\end{eqnarray}$$
Adding (A 55) and (A 56), we obtain
 $$\begin{eqnarray}\text{d}\text{i}_{X}\unicode[STIX]{x1D6FC}+\text{i}_{X}\,\text{d}\unicode[STIX]{x1D6FC}=(X^{j}\unicode[STIX]{x1D735}_{j}\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\unicode[STIX]{x1D735}_{i}X^{j})\,\text{d}x^{i}=(X^{j}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\unicode[STIX]{x2202}_{i}X^{j})\,\text{d}x^{i}=\unicode[STIX]{x00A3}_{X}\unicode[STIX]{x1D6FC}.\end{eqnarray}$$
$$\begin{eqnarray}\text{d}\text{i}_{X}\unicode[STIX]{x1D6FC}+\text{i}_{X}\,\text{d}\unicode[STIX]{x1D6FC}=(X^{j}\unicode[STIX]{x1D735}_{j}\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\unicode[STIX]{x1D735}_{i}X^{j})\,\text{d}x^{i}=(X^{j}\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\unicode[STIX]{x2202}_{i}X^{j})\,\text{d}x^{i}=\unicode[STIX]{x00A3}_{X}\unicode[STIX]{x1D6FC}.\end{eqnarray}$$
Using this equation with
![]() $X=v$
and
$X=v$
and
![]() $\unicode[STIX]{x1D6FC}=v^{\flat }$
, the lowering–raising operators and the property
$\unicode[STIX]{x1D6FC}=v^{\flat }$
, the lowering–raising operators and the property
 $\unicode[STIX]{x1D735}_{i}g_{jk}=0$
, we obtain
$\unicode[STIX]{x1D735}_{i}g_{jk}=0$
, we obtain
 $$\begin{eqnarray}\displaystyle v^{\,j}\unicode[STIX]{x1D735}_{j}v_{i}^{\flat }+v_{j}^{\flat }\unicode[STIX]{x1D735}_{i}v^{\,j} & = & \displaystyle v^{\,j}\unicode[STIX]{x1D735}_{j}v_{i}^{\flat }+v^{k}g_{jk}\unicode[STIX]{x1D735}_{i}v^{\,j}=v^{\,j}\unicode[STIX]{x1D735}_{j}v_{i}^{\flat }+{\textstyle \frac{1}{2}}g_{jk}\unicode[STIX]{x1D735}_{i}(v^{\,j}v^{k})\nonumber\\ \displaystyle & = & \displaystyle v^{\,j}\unicode[STIX]{x1D735}_{j}v_{i}^{\flat }+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D735}_{i}(g_{jk}v^{\,j}v^{k})=v^{\,j}\unicode[STIX]{x1D735}_{j}v_{i}^{\flat }+{\textstyle \frac{1}{2}}\unicode[STIX]{x2202}_{i}(g_{jk}v^{\,j}v^{k}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v^{\,j}\unicode[STIX]{x1D735}_{j}v_{i}^{\flat }+v_{j}^{\flat }\unicode[STIX]{x1D735}_{i}v^{\,j} & = & \displaystyle v^{\,j}\unicode[STIX]{x1D735}_{j}v_{i}^{\flat }+v^{k}g_{jk}\unicode[STIX]{x1D735}_{i}v^{\,j}=v^{\,j}\unicode[STIX]{x1D735}_{j}v_{i}^{\flat }+{\textstyle \frac{1}{2}}g_{jk}\unicode[STIX]{x1D735}_{i}(v^{\,j}v^{k})\nonumber\\ \displaystyle & = & \displaystyle v^{\,j}\unicode[STIX]{x1D735}_{j}v_{i}^{\flat }+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D735}_{i}(g_{jk}v^{\,j}v^{k})=v^{\,j}\unicode[STIX]{x1D735}_{j}v_{i}^{\flat }+{\textstyle \frac{1}{2}}\unicode[STIX]{x2202}_{i}(g_{jk}v^{\,j}v^{k}),\end{eqnarray}$$
which re-expresses (A 54) in terms of components. For more details see, e.g., Arnold & Khesin (Reference Arnold and Khesin1998, chap. IV, pp. 202–204).
A.6 Proof of a commutation relation needed for the Lie advection of the vorticity vector
In § 3.1, to establish the Lie-advection equation for the vorticity vector, we have used a result on the commutation of the composition of the raising operator with the Hodge dual operator and the Lie derivative. Here, we give a proof of the commutation relation
 $[\sharp ^{d-p}\,\star ,\unicode[STIX]{x00A3}_{v}]=0$
with the condition
$[\sharp ^{d-p}\,\star ,\unicode[STIX]{x00A3}_{v}]=0$
with the condition
 $\unicode[STIX]{x1D735}_{i}v^{i}=0$
. We are also motivated by the observation that we were not able to find a proof in the published literature.
$\unicode[STIX]{x1D735}_{i}v^{i}=0$
. We are also motivated by the observation that we were not able to find a proof in the published literature.
Let
![]() $\unicode[STIX]{x1D714}$
be a
$\unicode[STIX]{x1D714}$
be a
![]() $p$
-form. Using the definitions of the raising operator (see § B.3) and of the Hodge dual operator (see § B.9), and recognising the determinant of the metric tensor in the following expression, we obtain
$p$
-form. Using the definitions of the raising operator (see § B.3) and of the Hodge dual operator (see § B.9), and recognising the determinant of the metric tensor in the following expression, we obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}}=([\star \unicode[STIX]{x1D714}]^{\sharp ^{d-p}})^{i_{1}\ldots i_{d-p}} & = & \displaystyle \frac{1}{p!}\sqrt{\text{g}}\unicode[STIX]{x1D700}^{\,j_{1}\ldots j_{p}l_{1}\ldots l_{d-p}}g^{\,j_{1}k_{1}}\ldots g^{\,j_{p}k_{p}}g^{i_{1}l_{1}}\ldots g^{i_{d-p}l_{d-p}}\unicode[STIX]{x1D714}_{k_{1}\ldots k_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{k_{1}\ldots k_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D714}_{k_{1}\ldots k_{p}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}}=([\star \unicode[STIX]{x1D714}]^{\sharp ^{d-p}})^{i_{1}\ldots i_{d-p}} & = & \displaystyle \frac{1}{p!}\sqrt{\text{g}}\unicode[STIX]{x1D700}^{\,j_{1}\ldots j_{p}l_{1}\ldots l_{d-p}}g^{\,j_{1}k_{1}}\ldots g^{\,j_{p}k_{p}}g^{i_{1}l_{1}}\ldots g^{i_{d-p}l_{d-p}}\unicode[STIX]{x1D714}_{k_{1}\ldots k_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{k_{1}\ldots k_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D714}_{k_{1}\ldots k_{p}}.\end{eqnarray}$$
Using definitions of the Lie derivative (see § B.7), of the raising and Hodge star operators, and using the product rule to reveal the divergence of the vector field
![]() $v$
and the term
$v$
and the term
 $\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}}$
in the next expression, we obtain
$\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}}$
in the next expression, we obtain
 $$\begin{eqnarray}\displaystyle ([\star \unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}]^{\sharp ^{d-p}})^{i_{1}\ldots i_{d-p}} & = & \displaystyle \frac{1}{p!}\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{k_{1}\ldots k_{p}i_{1}\ldots i_{d-p}}(v^{l}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D714}_{k_{1}\ldots k_{p}}+p\unicode[STIX]{x1D714}_{lk_{2}\ldots k_{p}}\unicode[STIX]{x2202}_{k_{1}}v^{l})\nonumber\\ \displaystyle & = & \displaystyle v^{l}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}}+\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}}(\unicode[STIX]{x1D735}_{l}v^{l}-\unicode[STIX]{x2202}_{l}v^{l})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{(p-1)!}\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{k_{1}\ldots k_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D714}_{lk_{2}\ldots k_{p}}\unicode[STIX]{x2202}_{k_{1}}v^{l}\nonumber\\ \displaystyle & = & \displaystyle T_{1}+\frac{1}{(p-1)!}\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{k_{1}\ldots k_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D714}_{lk_{2}\ldots k_{p}}\unicode[STIX]{x2202}_{k_{1}}v^{l}=T_{1}+T_{2}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ([\star \unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}]^{\sharp ^{d-p}})^{i_{1}\ldots i_{d-p}} & = & \displaystyle \frac{1}{p!}\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{k_{1}\ldots k_{p}i_{1}\ldots i_{d-p}}(v^{l}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D714}_{k_{1}\ldots k_{p}}+p\unicode[STIX]{x1D714}_{lk_{2}\ldots k_{p}}\unicode[STIX]{x2202}_{k_{1}}v^{l})\nonumber\\ \displaystyle & = & \displaystyle v^{l}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}}+\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}}(\unicode[STIX]{x1D735}_{l}v^{l}-\unicode[STIX]{x2202}_{l}v^{l})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{(p-1)!}\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{k_{1}\ldots k_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D714}_{lk_{2}\ldots k_{p}}\unicode[STIX]{x2202}_{k_{1}}v^{l}\nonumber\\ \displaystyle & = & \displaystyle T_{1}+\frac{1}{(p-1)!}\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x1D700}^{k_{1}\ldots k_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D714}_{lk_{2}\ldots k_{p}}\unicode[STIX]{x2202}_{k_{1}}v^{l}=T_{1}+T_{2}.\qquad\end{eqnarray}$$
Using (A 59), the antisymmetry of
![]() $\unicode[STIX]{x1D714}$
, and properties of generalised Kronecker symbols (see § B.6), we obtain
$\unicode[STIX]{x1D714}$
, and properties of generalised Kronecker symbols (see § B.6), we obtain
 $$\begin{eqnarray}\displaystyle \frac{(-1)^{p}\sqrt{\text{g}}}{(d-p)!}\unicode[STIX]{x1D700}_{i_{1}\ldots i_{d-p}j_{1}\ldots j_{p}}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}} & = & \displaystyle \frac{1}{p!(d-p)!}\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D700}^{k_{1}\ldots k_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D714}_{k_{1}\ldots k_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{k_{1}\ldots k_{p}}\unicode[STIX]{x1D714}_{k_{1}\ldots k_{p}}=\unicode[STIX]{x1D714}_{j_{1}\ldots j_{p}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{(-1)^{p}\sqrt{\text{g}}}{(d-p)!}\unicode[STIX]{x1D700}_{i_{1}\ldots i_{d-p}j_{1}\ldots j_{p}}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}} & = & \displaystyle \frac{1}{p!(d-p)!}\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D700}^{k_{1}\ldots k_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D714}_{k_{1}\ldots k_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{k_{1}\ldots k_{p}}\unicode[STIX]{x1D714}_{k_{1}\ldots k_{p}}=\unicode[STIX]{x1D714}_{j_{1}\ldots j_{p}}.\end{eqnarray}$$
Substituting (A 61) in
![]() $T_{2}$
, and using properties of generalised Kronecker symbols, we obtain
$T_{2}$
, and using properties of generalised Kronecker symbols, we obtain
 $$\begin{eqnarray}\displaystyle T_{2} & = & \displaystyle \frac{(-1)^{p}}{(p-1)!}\frac{1}{(d-p)!}\unicode[STIX]{x1D700}^{k_{1}\ldots k_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D700}_{l_{1}\ldots l_{d-p}lk_{2}\ldots k_{p}}\unicode[STIX]{x1D714}^{l_{1}\ldots l_{d-p}}\unicode[STIX]{x2202}_{k_{1}}v^{l}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(d-p)!}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{d-p}l}^{i_{1}\ldots i_{d-p}k_{1}}\unicode[STIX]{x1D714}^{l_{1}\ldots l_{d-p}}\unicode[STIX]{x2202}_{k_{1}}v^{l}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(d-p)!}\mathop{\sum }_{k=1}^{d-p+1}(-1)^{d-p+k+1}\unicode[STIX]{x1D6FF}_{l_{k}}^{k_{1}}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \hat{l}_{k}\ldots l_{d-p+1}}^{i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D714}^{l_{1}\ldots l_{d-p}}\unicode[STIX]{x2202}_{k_{1}}v^{l_{d-p+1}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{2} & = & \displaystyle \frac{(-1)^{p}}{(p-1)!}\frac{1}{(d-p)!}\unicode[STIX]{x1D700}^{k_{1}\ldots k_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D700}_{l_{1}\ldots l_{d-p}lk_{2}\ldots k_{p}}\unicode[STIX]{x1D714}^{l_{1}\ldots l_{d-p}}\unicode[STIX]{x2202}_{k_{1}}v^{l}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(d-p)!}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{d-p}l}^{i_{1}\ldots i_{d-p}k_{1}}\unicode[STIX]{x1D714}^{l_{1}\ldots l_{d-p}}\unicode[STIX]{x2202}_{k_{1}}v^{l}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{(d-p)!}\mathop{\sum }_{k=1}^{d-p+1}(-1)^{d-p+k+1}\unicode[STIX]{x1D6FF}_{l_{k}}^{k_{1}}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \hat{l}_{k}\ldots l_{d-p+1}}^{i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D714}^{l_{1}\ldots l_{d-p}}\unicode[STIX]{x2202}_{k_{1}}v^{l_{d-p+1}},\end{eqnarray}$$
where we have set
 $l_{d-p+1}:=l$
, and where the hat character
$l_{d-p+1}:=l$
, and where the hat character
![]() $\hat{\,}$
indicates an index that is omitted from the sequence. Using the antisymmetry of
$\hat{\,}$
indicates an index that is omitted from the sequence. Using the antisymmetry of
![]() $\unicode[STIX]{x1D714}$
, equation (A 62) becomes
$\unicode[STIX]{x1D714}$
, equation (A 62) becomes
 $$\begin{eqnarray}T_{2}=\unicode[STIX]{x2202}_{l}v^{l}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}}+\frac{1}{(d-p)!}\mathop{\sum }_{k=1}^{d-p}(-1)^{d-p+k+1}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \hat{l}_{k}\ldots l_{d-p}l}^{i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D714}^{l_{1}\ldots l_{d-p}}\unicode[STIX]{x2202}_{l_{k}}v^{l}=T_{21}+T_{22}.\end{eqnarray}$$
$$\begin{eqnarray}T_{2}=\unicode[STIX]{x2202}_{l}v^{l}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}}+\frac{1}{(d-p)!}\mathop{\sum }_{k=1}^{d-p}(-1)^{d-p+k+1}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \hat{l}_{k}\ldots l_{d-p}l}^{i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D714}^{l_{1}\ldots l_{d-p}}\unicode[STIX]{x2202}_{l_{k}}v^{l}=T_{21}+T_{22}.\end{eqnarray}$$
Using properties of generalised Kronecker symbols, the antisymmetry of
![]() $\unicode[STIX]{x1D714}$
, and relabelling some indices, we obtain
$\unicode[STIX]{x1D714}$
, and relabelling some indices, we obtain
 $$\begin{eqnarray}\displaystyle T_{22} & = & \displaystyle -\frac{1}{(d-p)!}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{d-p}}^{i_{1}\ldots i_{d-p}}\mathop{\sum }_{k=1}^{d-p}\unicode[STIX]{x1D714}^{l_{1}\ldots n_{k}\hat{l}_{k}\ldots l_{d-p}}\unicode[STIX]{x2202}_{n_{k}}v^{l_{k}}\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{(d-p)!}\mathop{\sum }_{k=1}^{d-p}\left((-1)^{k+1}\unicode[STIX]{x1D6FF}_{l_{1}}^{i_{k}}\unicode[STIX]{x1D6FF}_{\hat{l}_{1}l_{2}\ldots l_{d-p}}^{i_{1}\ldots \hat{i} _{k}\ldots i_{d-p}}\unicode[STIX]{x2202}_{n_{1}}v^{l_{1}}\unicode[STIX]{x1D714}^{n_{1}l_{2}\ldots l_{d-p}}+\cdots \,\right.\nonumber\\ \displaystyle & & \displaystyle +\left.(-1)^{k+d-p}\unicode[STIX]{x1D6FF}_{l_{d-p}}^{i_{k}}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \hat{l}_{d-p}}^{i_{1}\ldots \hat{i} _{k}\ldots i_{d-p}}\unicode[STIX]{x2202}_{n_{d-p}}v^{l_{d-p}}\unicode[STIX]{x1D714}^{l_{1}\ldots l_{d-p-1}n_{d-p}}\right)\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{d-p}\mathop{\sum }_{k=1}^{d-p}((-1)^{k+1}\unicode[STIX]{x2202}_{l}v^{i_{k}}\unicode[STIX]{x1D714}^{li_{1}\ldots \hat{i} _{k}\ldots i_{d-p}}+\cdots +(-1)^{k+d-p}\unicode[STIX]{x2202}_{l}v^{i_{k}}\unicode[STIX]{x1D714}^{i_{1}\ldots \hat{i} _{k}\ldots i_{d-p}l})\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x2202}_{l}v^{i_{1}}\unicode[STIX]{x1D714}^{li_{2}\ldots i_{d-p}}-\cdots -\unicode[STIX]{x2202}_{l}v^{i_{d-p}}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p-1}l}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{22} & = & \displaystyle -\frac{1}{(d-p)!}\unicode[STIX]{x1D6FF}_{l_{1}\ldots l_{d-p}}^{i_{1}\ldots i_{d-p}}\mathop{\sum }_{k=1}^{d-p}\unicode[STIX]{x1D714}^{l_{1}\ldots n_{k}\hat{l}_{k}\ldots l_{d-p}}\unicode[STIX]{x2202}_{n_{k}}v^{l_{k}}\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{(d-p)!}\mathop{\sum }_{k=1}^{d-p}\left((-1)^{k+1}\unicode[STIX]{x1D6FF}_{l_{1}}^{i_{k}}\unicode[STIX]{x1D6FF}_{\hat{l}_{1}l_{2}\ldots l_{d-p}}^{i_{1}\ldots \hat{i} _{k}\ldots i_{d-p}}\unicode[STIX]{x2202}_{n_{1}}v^{l_{1}}\unicode[STIX]{x1D714}^{n_{1}l_{2}\ldots l_{d-p}}+\cdots \,\right.\nonumber\\ \displaystyle & & \displaystyle +\left.(-1)^{k+d-p}\unicode[STIX]{x1D6FF}_{l_{d-p}}^{i_{k}}\unicode[STIX]{x1D6FF}_{l_{1}\ldots \hat{l}_{d-p}}^{i_{1}\ldots \hat{i} _{k}\ldots i_{d-p}}\unicode[STIX]{x2202}_{n_{d-p}}v^{l_{d-p}}\unicode[STIX]{x1D714}^{l_{1}\ldots l_{d-p-1}n_{d-p}}\right)\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{d-p}\mathop{\sum }_{k=1}^{d-p}((-1)^{k+1}\unicode[STIX]{x2202}_{l}v^{i_{k}}\unicode[STIX]{x1D714}^{li_{1}\ldots \hat{i} _{k}\ldots i_{d-p}}+\cdots +(-1)^{k+d-p}\unicode[STIX]{x2202}_{l}v^{i_{k}}\unicode[STIX]{x1D714}^{i_{1}\ldots \hat{i} _{k}\ldots i_{d-p}l})\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x2202}_{l}v^{i_{1}}\unicode[STIX]{x1D714}^{li_{2}\ldots i_{d-p}}-\cdots -\unicode[STIX]{x2202}_{l}v^{i_{d-p}}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p-1}l}.\end{eqnarray}$$
Finally, putting all the terms together, using the condition
 $\unicode[STIX]{x1D735}_{i}v^{i}=0$
, and remembering the definition of Lie derivative for tensors (see § B.5), we obtain
$\unicode[STIX]{x1D735}_{i}v^{i}=0$
, and remembering the definition of Lie derivative for tensors (see § B.5), we obtain
 $$\begin{eqnarray}\displaystyle ([\star \unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}]^{\sharp ^{d-p}})^{i_{1}\ldots i_{d-p}} & = & \displaystyle T_{1}+T_{2}=T_{1}+T_{21}+T_{22}\nonumber\\ \displaystyle & = & \displaystyle v^{l}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}}-\unicode[STIX]{x2202}_{l}v^{i_{1}}\unicode[STIX]{x1D714}^{li_{2}\ldots i_{d-p}}-\cdots -\unicode[STIX]{x2202}_{l}v^{i_{d-p}}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p-1}l}\nonumber\\ \displaystyle & = & \displaystyle (\text{}\unicode[STIX]{x00A3}_{v}[\star \unicode[STIX]{x1D714}]^{\sharp ^{d-p}})^{i_{1}\ldots i_{d-p}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ([\star \unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}]^{\sharp ^{d-p}})^{i_{1}\ldots i_{d-p}} & = & \displaystyle T_{1}+T_{2}=T_{1}+T_{21}+T_{22}\nonumber\\ \displaystyle & = & \displaystyle v^{l}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p}}-\unicode[STIX]{x2202}_{l}v^{i_{1}}\unicode[STIX]{x1D714}^{li_{2}\ldots i_{d-p}}-\cdots -\unicode[STIX]{x2202}_{l}v^{i_{d-p}}\unicode[STIX]{x1D714}^{i_{1}\ldots i_{d-p-1}l}\nonumber\\ \displaystyle & = & \displaystyle (\text{}\unicode[STIX]{x00A3}_{v}[\star \unicode[STIX]{x1D714}]^{\sharp ^{d-p}})^{i_{1}\ldots i_{d-p}},\end{eqnarray}$$
which ends the proof. ◻
Appendix B. Differential geometry in a nutshell
In this appendix we recall some notions of differential geometry. There exist many classical textbooks of differential geometry on manifolds, for example Helgason (Reference Helgason1962), Flanders (Reference Flanders1963), Kobayashi & Nomizu (Reference Kobayashi and Nomizu1963), Stenberg (Reference Stenberg1964), Choquet-Bruhat (Reference Choquet-Bruhat1968), Choquet-Bruhat, De Witt-Morette & Dillard-Bleick (Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977), Spivak (Reference Spivak1979), Schutz (Reference Schutz1980), de Rham (Reference De Rham1984), Arnold (Reference Arnold1989), Lovelock & Rund (Reference Lovelock and Rund1989), Abraham et al. (Reference Abraham, Marsden and Ratiu1998), Fecko (Reference Fecko2006), Frankel (Reference Frankel2012). This appendix is based on textbooks that we find pedagogical for our intended readership (Choquet-Bruhat et al. Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977; de Rham Reference De Rham1984; Abraham et al. Reference Abraham, Marsden and Ratiu1998; Arnold Reference Arnold1989; Fecko Reference Fecko2006; Frankel Reference Frankel2012), to which we give precise references.
B.1 Manifolds, tangent and cotangent bundles
A manifold is a generalisation of the notion of a smooth surface in Euclidean space. The concept of manifold has proved to be useful because they occur frequently, and not just as subsets embedded in an Euclidean space. Indeed such a generalisation, eliminating the need for a containing Euclidean space, makes the construction intrinsic to the manifold itself. Usually a differentiable (smooth) manifold
![]() $M$
of dimension
$M$
of dimension
![]() $d$
is defined through a differentiable parametric representation, called an atlas, which can be seen as a collection of charts
$d$
is defined through a differentiable parametric representation, called an atlas, which can be seen as a collection of charts
 $(U_{i},\unicode[STIX]{x1D719}_{i})_{i\in I}$
such that
$(U_{i},\unicode[STIX]{x1D719}_{i})_{i\in I}$
such that
 $M=\bigcup _{i\in I}U_{i}$
. A chart
$M=\bigcup _{i\in I}U_{i}$
. A chart
![]() $(U_{i},\unicode[STIX]{x1D719}_{i})$
is a local subset
$(U_{i},\unicode[STIX]{x1D719}_{i})$
is a local subset
![]() $U_{i}\subset M$
and local smooth bijection
$U_{i}\subset M$
and local smooth bijection
![]() $\unicode[STIX]{x1D719}_{i}$
from
$\unicode[STIX]{x1D719}_{i}$
from
![]() $U_{i}$
to an open subset of Banach space (typically
$U_{i}$
to an open subset of Banach space (typically
![]() $\mathbb{R}^{d}$
). The manifold
$\mathbb{R}^{d}$
). The manifold
![]() $M$
is then constructed by patching smoothly such objects together. For a formal definition of a differentiable manifold we refer the reader to Choquet-Bruhat et al. (Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977, § III.A.1, p. 111), Abraham et al. (Reference Abraham, Marsden and Ratiu1998, § 3.1, p. 141) and Frankel (Reference Frankel2012, § 1.2c, p. 19).
$M$
is then constructed by patching smoothly such objects together. For a formal definition of a differentiable manifold we refer the reader to Choquet-Bruhat et al. (Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977, § III.A.1, p. 111), Abraham et al. (Reference Abraham, Marsden and Ratiu1998, § 3.1, p. 141) and Frankel (Reference Frankel2012, § 1.2c, p. 19).
The set of tangent vectors to
![]() $M$
at
$M$
at
![]() $a\in M$
forms a vector space
$a\in M$
forms a vector space
![]() $TM_{a}$
. This space is called the tangent space to
$TM_{a}$
. This space is called the tangent space to
![]() $M$
at
$M$
at
![]() $a$
. The union of the tangent spaces to
$a$
. The union of the tangent spaces to
![]() $M$
at the various point of
$M$
at the various point of
![]() $M$
, i.e.
$M$
, i.e.
 $TM:=\bigcup _{a\in M}TM_{a}$
, has a natural differentiable manifold structure, the dimension of which is twice the dimension of
$TM:=\bigcup _{a\in M}TM_{a}$
, has a natural differentiable manifold structure, the dimension of which is twice the dimension of
![]() $M$
. This manifold is called the tangent bundle of
$M$
. This manifold is called the tangent bundle of
![]() $M$
and is denoted by
$M$
and is denoted by
![]() $TM$
. The mapping
$TM$
. The mapping
 $\unicode[STIX]{x03C0}:TM\rightarrow M$
, which takes a tangent vector
$\unicode[STIX]{x03C0}:TM\rightarrow M$
, which takes a tangent vector
![]() $V$
to the point
$V$
to the point
![]() $a\in M$
at which the vector is tangent to
$a\in M$
at which the vector is tangent to
![]() $M$
(i.e.
$M$
(i.e.
 $X\in TM_{a}$
), is called the natural projection. The inverse image of a point
$X\in TM_{a}$
), is called the natural projection. The inverse image of a point
![]() $a\in M$
under the natural projection, i.e.
$a\in M$
under the natural projection, i.e.
![]() $\unicode[STIX]{x03C0}^{-1}(a)$
, is the tangent space
$\unicode[STIX]{x03C0}^{-1}(a)$
, is the tangent space
![]() $TM_{a}$
. This space is called the fibre of the tangent bundle over the point
$TM_{a}$
. This space is called the fibre of the tangent bundle over the point
![]() $a$
. A vector field on
$a$
. A vector field on
![]() $M$
is a (cross-)section of
$M$
is a (cross-)section of
![]() $TM$
. A (cross-)section of a vector bundle assigns to each base point
$TM$
. A (cross-)section of a vector bundle assigns to each base point
![]() $a\in M$
a vector in the fibre
$a\in M$
a vector in the fibre
![]() $\unicode[STIX]{x03C0}^{-1}(a)$
over
$\unicode[STIX]{x03C0}^{-1}(a)$
over
![]() $a$
and the addition and scalar multiplication of sections takes place within each fibre (see, e.g., Frankel Reference Frankel2012, § 2.2, p. 48 and § III.B.3, p. 132 in Choquet-Bruhat et al.
Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977).
$a$
and the addition and scalar multiplication of sections takes place within each fibre (see, e.g., Frankel Reference Frankel2012, § 2.2, p. 48 and § III.B.3, p. 132 in Choquet-Bruhat et al.
Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977).
As for ordinary vector spaces, one can define the dual of the tangent bundle, noted
![]() $T^{\ast }M$
, which can be constructed through linear forms, called 1-forms or cotangent vectors, acting on vectors of the tangent bundle
$T^{\ast }M$
, which can be constructed through linear forms, called 1-forms or cotangent vectors, acting on vectors of the tangent bundle
![]() $TM$
. The cotangent space to
$TM$
. The cotangent space to
![]() $M$
at
$M$
at
![]() $a$
, noted
$a$
, noted
![]() $T^{\ast }M_{a}$
, is the set of all cotangent vectors to
$T^{\ast }M_{a}$
, is the set of all cotangent vectors to
![]() $M$
at
$M$
at
![]() $a$
. The cotangent bundle is the union of the cotangent spaces to the manifold
$a$
. The cotangent bundle is the union of the cotangent spaces to the manifold
![]() $M$
at all its points, that is
$M$
at all its points, that is
 $T^{\ast }M:=\bigcup _{a\in M}T^{\ast }M_{a}$
. The cotangent bundle
$T^{\ast }M:=\bigcup _{a\in M}T^{\ast }M_{a}$
. The cotangent bundle
![]() $T^{\ast }M$
has a natural differentiable manifold structure, the dimension of which is twice the dimension of
$T^{\ast }M$
has a natural differentiable manifold structure, the dimension of which is twice the dimension of
![]() $M$
.
$M$
.
Finally we introduce the notion of contractible manifolds. Let
 $c:[0,1]\rightarrow M$
be a continuous map such that
$c:[0,1]\rightarrow M$
be a continuous map such that
 $c(0)=c(1)=a\in M$
. We call
$c(0)=c(1)=a\in M$
. We call
![]() $c$
a loop in
$c$
a loop in
![]() $M$
at the point
$M$
at the point
![]() $a$
. The loop is called contractible if there is a continuous map
$a$
. The loop is called contractible if there is a continuous map
 $H:[0,1]\times [0,1]\rightarrow M$
such that
$H:[0,1]\times [0,1]\rightarrow M$
such that
 $H(t,0)=c(t)$
and
$H(t,0)=c(t)$
and
 $H(0,s)=H(1,s)=H(t,1)=a$
for all
$H(0,s)=H(1,s)=H(t,1)=a$
for all
 $t\in [0,1]$
. Indeed
$t\in [0,1]$
. Indeed
 $c_{s}(t)=H(t,s)$
has to be viewed as a family of arcs connecting
$c_{s}(t)=H(t,s)$
has to be viewed as a family of arcs connecting
![]() $c_{0}=c$
to
$c_{0}=c$
to
![]() $c_{1}$
, a constant arc. Roughly speaking, a loop is contractible when it can be shrunk continuously to the point
$c_{1}$
, a constant arc. Roughly speaking, a loop is contractible when it can be shrunk continuously to the point
![]() $a$
by loops beginning and ending at
$a$
by loops beginning and ending at
![]() $a$
. The manifold
$a$
. The manifold
![]() $M$
is contractible to a point
$M$
is contractible to a point
![]() $a$
, if every loop in
$a$
, if every loop in
![]() $M$
, which starts and ends at the point
$M$
, which starts and ends at the point
![]() $a$
is contractible. In other words the manifold
$a$
is contractible. In other words the manifold
![]() $M$
is contractible if there exists a vector field
$M$
is contractible if there exists a vector field
![]() $u$
on
$u$
on
![]() $M$
which generates a flow
$M$
which generates a flow
 $\unicode[STIX]{x1D702}_{t}:M\rightarrow M$
, with
$\unicode[STIX]{x1D702}_{t}:M\rightarrow M$
, with
 $t\in [0,1]$
, that gradually and smoothly shrinks the whole manifold
$t\in [0,1]$
, that gradually and smoothly shrinks the whole manifold
![]() $M$
to the point
$M$
to the point
![]() $a$
, i.e.
$a$
, i.e.
 $\unicode[STIX]{x1D702}_{0}=\text{Id}_{M}$
and
$\unicode[STIX]{x1D702}_{0}=\text{Id}_{M}$
and
 $\unicode[STIX]{x1D702}_{1}(x)=a$
,
$\unicode[STIX]{x1D702}_{1}(x)=a$
,
![]() $\forall x\in M$
, where the point
$\forall x\in M$
, where the point
![]() $a$
is fixed and independent of
$a$
is fixed and independent of
![]() $x$
. For more details see Abraham et al. (Reference Abraham, Marsden and Ratiu1998, § 1.6, p. 33) and Fecko (Reference Fecko2006, § 9, p. 192).
$x$
. For more details see Abraham et al. (Reference Abraham, Marsden and Ratiu1998, § 1.6, p. 33) and Fecko (Reference Fecko2006, § 9, p. 192).
B.2 Tensors
Let
![]() $\{E_{i}\}_{i\in \mathbb{N}^{\ast }}$
,
$\{E_{i}\}_{i\in \mathbb{N}^{\ast }}$
,
![]() $F$
be finite-dimensional vector spaces. Let
$F$
be finite-dimensional vector spaces. Let
 ${\mathcal{L}}^{k}(E_{1},\ldots ,E_{k};F)$
be the vector space of continuous
${\mathcal{L}}^{k}(E_{1},\ldots ,E_{k};F)$
be the vector space of continuous
![]() $k$
-multilinear maps of
$k$
-multilinear maps of
 $E_{1}\times \cdots \times E_{k}$
to
$E_{1}\times \cdots \times E_{k}$
to
![]() $F$
. The special case of the linear form on
$F$
. The special case of the linear form on
![]() $E$
, i.e.
$E$
, i.e.
 ${\mathcal{L}}(E,\mathbb{R})$
, is denoted
${\mathcal{L}}(E,\mathbb{R})$
, is denoted
![]() $E^{\ast }$
, the dual space of
$E^{\ast }$
, the dual space of
![]() $E$
. If
$E$
. If
 $\{e_{1},\ldots ,e_{d}\}$
is an ordered basis of
$\{e_{1},\ldots ,e_{d}\}$
is an ordered basis of
![]() $E$
, there is a unique ordered basis of
$E$
, there is a unique ordered basis of
![]() $E^{\ast }$
, the dual basis
$E^{\ast }$
, the dual basis
 $\{e^{1},\ldots ,e^{d}\}$
, such that
$\{e^{1},\ldots ,e^{d}\}$
, such that
 $\langle e^{\,j},e_{i}\rangle :=e^{\,j}(e_{i})=\unicode[STIX]{x1D6FF}_{i}^{j}$
, where
$\langle e^{\,j},e_{i}\rangle :=e^{\,j}(e_{i})=\unicode[STIX]{x1D6FF}_{i}^{j}$
, where
![]() $\unicode[STIX]{x1D6FF}_{i}^{j}=1$
if
$\unicode[STIX]{x1D6FF}_{i}^{j}=1$
if
![]() $i=j$
and 0 otherwise. Here
$i=j$
and 0 otherwise. Here
![]() $\langle \cdot ,\cdot \rangle$
denotes the natural pairing between
$\langle \cdot ,\cdot \rangle$
denotes the natural pairing between
![]() $E$
and
$E$
and
![]() $E^{\ast }$
. Furthermore, for each
$E^{\ast }$
. Furthermore, for each
![]() $v\in E$
,
$v\in E$
,
 $v=\langle e^{i},v\rangle e_{i}$
and for each and
$v=\langle e^{i},v\rangle e_{i}$
and for each and
![]() $\unicode[STIX]{x1D6FC}\in E^{\ast }$
,
$\unicode[STIX]{x1D6FC}\in E^{\ast }$
,
 $\unicode[STIX]{x1D6FC}=\langle \unicode[STIX]{x1D6FC},e_{i}\rangle e^{i}$
.
$\unicode[STIX]{x1D6FC}=\langle \unicode[STIX]{x1D6FC},e_{i}\rangle e^{i}$
.
For a vector space
![]() $E$
we define
$E$
we define
 $$\begin{eqnarray}\text{T}_{p}^{q}(E)={\mathcal{L}}^{q+p}(E^{\ast },\ldots ,E^{\ast },E,\ldots ,E;\mathbb{R}),\end{eqnarray}$$
$$\begin{eqnarray}\text{T}_{p}^{q}(E)={\mathcal{L}}^{q+p}(E^{\ast },\ldots ,E^{\ast },E,\ldots ,E;\mathbb{R}),\end{eqnarray}$$
(
![]() $q$
copies of
$q$
copies of
![]() $E^{\ast }$
and
$E^{\ast }$
and
![]() $p$
copies of
$p$
copies of
![]() $E$
). Elements of
$E$
). Elements of
![]() $\text{T}_{p}^{q}(E)$
are called tensors on
$\text{T}_{p}^{q}(E)$
are called tensors on
![]() $E$
, contravariant of order
$E$
, contravariant of order
![]() $q$
and covariant of order
$q$
and covariant of order
![]() $p$
; or simply of type
$p$
; or simply of type
![]() $(q,p)$
. Given
$(q,p)$
. Given
 $\unicode[STIX]{x0398}_{1}\in \text{T}_{p_{1}}^{q_{1}}(E)$
and
$\unicode[STIX]{x0398}_{1}\in \text{T}_{p_{1}}^{q_{1}}(E)$
and
 $\unicode[STIX]{x0398}_{2}\in \text{T}_{p_{2}}^{q_{2}}(E)$
, the tensor product of
$\unicode[STIX]{x0398}_{2}\in \text{T}_{p_{2}}^{q_{2}}(E)$
, the tensor product of
![]() $\unicode[STIX]{x0398}_{1}$
and
$\unicode[STIX]{x0398}_{1}$
and
![]() $\unicode[STIX]{x0398}_{2}$
is the tensor
$\unicode[STIX]{x0398}_{2}$
is the tensor
 $\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x0398}_{2}\in \text{T}_{p_{1}+p_{2}}^{q_{1}+q_{2}}(E)$
defined by
$\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x0398}_{2}\in \text{T}_{p_{1}+p_{2}}^{q_{1}+q_{2}}(E)$
defined by
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x0398}_{2})(\unicode[STIX]{x1D6FC}^{1},\ldots ,\unicode[STIX]{x1D6FC}^{q_{1}},\unicode[STIX]{x1D6FD}^{1},\ldots ,\unicode[STIX]{x1D6FD}^{q_{2}},f_{1},\ldots ,f_{p_{1}},g_{1},\ldots ,g_{p_{2}})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x0398}_{1}(\unicode[STIX]{x1D6FC}^{1},\ldots ,\unicode[STIX]{x1D6FC}^{q_{1}},f_{1},\ldots ,f_{p_{1}})\unicode[STIX]{x0398}_{2}(\unicode[STIX]{x1D6FD}^{1},\ldots ,\unicode[STIX]{x1D6FD}^{q_{2}},g_{1},\ldots ,g_{p_{2}}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x0398}_{2})(\unicode[STIX]{x1D6FC}^{1},\ldots ,\unicode[STIX]{x1D6FC}^{q_{1}},\unicode[STIX]{x1D6FD}^{1},\ldots ,\unicode[STIX]{x1D6FD}^{q_{2}},f_{1},\ldots ,f_{p_{1}},g_{1},\ldots ,g_{p_{2}})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x0398}_{1}(\unicode[STIX]{x1D6FC}^{1},\ldots ,\unicode[STIX]{x1D6FC}^{q_{1}},f_{1},\ldots ,f_{p_{1}})\unicode[STIX]{x0398}_{2}(\unicode[STIX]{x1D6FD}^{1},\ldots ,\unicode[STIX]{x1D6FD}^{q_{2}},g_{1},\ldots ,g_{p_{2}}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FC}^{\,j}$
,
$\unicode[STIX]{x1D6FC}^{\,j}$
,
![]() $\unicode[STIX]{x1D6FD}^{\,j}\in E^{\ast }$
, and
$\unicode[STIX]{x1D6FD}^{\,j}\in E^{\ast }$
, and
![]() $f_{j}$
,
$f_{j}$
,
![]() $g_{j}\in E$
. The natural basis of
$g_{j}\in E$
. The natural basis of
![]() $\text{T}_{p}^{q}(E)$
of dimension
$\text{T}_{p}^{q}(E)$
of dimension
![]() $d^{p+q}$
is given by
$d^{p+q}$
is given by
 $$\begin{eqnarray}\{e_{i_{1}}\otimes \cdots \otimes e_{i_{q}}\otimes e^{\,j_{1}}\otimes \cdots \otimes e^{\,j_{p}}\mid i_{1},\ldots ,i_{q},j_{1},\ldots j_{p}=1,\ldots ,d\}.\end{eqnarray}$$
$$\begin{eqnarray}\{e_{i_{1}}\otimes \cdots \otimes e_{i_{q}}\otimes e^{\,j_{1}}\otimes \cdots \otimes e^{\,j_{p}}\mid i_{1},\ldots ,i_{q},j_{1},\ldots j_{p}=1,\ldots ,d\}.\end{eqnarray}$$
In this basis any tensor
 $\unicode[STIX]{x0398}\in \text{T}_{p}^{q}(E)$
reads
$\unicode[STIX]{x0398}\in \text{T}_{p}^{q}(E)$
reads
 $$\begin{eqnarray}\unicode[STIX]{x0398}=\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}e_{i_{1}}\otimes \cdots \otimes e_{i_{q}}\otimes e^{\,j_{1}}\otimes \cdots \otimes e^{\,j_{p}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x0398}=\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}e_{i_{1}}\otimes \cdots \otimes e_{i_{q}}\otimes e^{\,j_{1}}\otimes \cdots \otimes e^{\,j_{p}},\end{eqnarray}$$
where the components of
![]() $\unicode[STIX]{x0398}$
are given by
$\unicode[STIX]{x0398}$
are given by
 $$\begin{eqnarray}\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1},\ldots i_{q}}=\unicode[STIX]{x0398}(e^{i_{1}},\ldots ,e^{i_{q}},e_{j_{1}},\ldots ,e_{j_{p}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1},\ldots i_{q}}=\unicode[STIX]{x0398}(e^{i_{1}},\ldots ,e^{i_{q}},e_{j_{1}},\ldots ,e_{j_{p}}).\end{eqnarray}$$
We refer to Abraham et al. (Reference Abraham, Marsden and Ratiu1998, § 5.1, p. 341) for the definition of standard operations (linear combination, contraction, contracted product, interior product, change of basis formula, tensoriality criterion, etc.) on tensors.
Let
![]() $M$
be a manifold and
$M$
be a manifold and
![]() $TM$
its tangent bundle. We call
$TM$
its tangent bundle. We call
 $\text{T}_{p}^{q}(M):=\text{T}_{p}^{q}(TM)=\bigcup _{a\in M}\text{T}_{p}^{q}(TM_{a})$
the vector bundle of tensors contravariant of order
$\text{T}_{p}^{q}(M):=\text{T}_{p}^{q}(TM)=\bigcup _{a\in M}\text{T}_{p}^{q}(TM_{a})$
the vector bundle of tensors contravariant of order
![]() $q$
and covariant of order
$q$
and covariant of order
![]() $p$
, or simply of type
$p$
, or simply of type
![]() $(q,p)$
. We identify
$(q,p)$
. We identify
![]() $\text{T}_{0}^{1}(M)$
with the tangent bundle
$\text{T}_{0}^{1}(M)$
with the tangent bundle
![]() $TM$
and call
$TM$
and call
![]() $\text{T}_{1}^{0}(M)$
the cotangent bundle of
$\text{T}_{1}^{0}(M)$
the cotangent bundle of
![]() $M$
, also denoted
$M$
, also denoted
![]() $T^{\ast }M$
(i.e. the set of linear forms on
$T^{\ast }M$
(i.e. the set of linear forms on
![]() $TM$
). The zero section of
$TM$
). The zero section of
![]() $\text{T}_{p}^{q}(M)$
is identified with
$\text{T}_{p}^{q}(M)$
is identified with
![]() $M$
. Recall that a section of a vector bundle assigns to each base point
$M$
. Recall that a section of a vector bundle assigns to each base point
![]() $a\in M$
a vector in the fibre
$a\in M$
a vector in the fibre
![]() $\unicode[STIX]{x03C0}^{-1}(a)$
over
$\unicode[STIX]{x03C0}^{-1}(a)$
over
![]() $a$
and the addition and scalar multiplication of sections takes place within each fibre. In the case of
$a$
and the addition and scalar multiplication of sections takes place within each fibre. In the case of
![]() $\text{T}_{p}^{q}(M)$
these vectors are called tensors. The
$\text{T}_{p}^{q}(M)$
these vectors are called tensors. The
![]() $\mathscr{C}^{\infty }$
sections of
$\mathscr{C}^{\infty }$
sections of
![]() $E$
are denoted by
$E$
are denoted by
![]() $\unicode[STIX]{x1D6E4}^{\infty }(E)$
. Recall that a vector field on
$\unicode[STIX]{x1D6E4}^{\infty }(E)$
. Recall that a vector field on
![]() $M$
is a
$M$
is a
![]() $\mathscr{C}^{\infty }$
section of
$\mathscr{C}^{\infty }$
section of
![]() $TM$
, i.e. an element of
$TM$
, i.e. an element of
 $\unicode[STIX]{x1D6E4}^{\infty }(TM)$
. Therefore a tensor field of type
$\unicode[STIX]{x1D6E4}^{\infty }(TM)$
. Therefore a tensor field of type
![]() $(q,p)$
on a manifold
$(q,p)$
on a manifold
![]() $M$
is a
$M$
is a
![]() $\mathscr{C}^{\infty }$
section of
$\mathscr{C}^{\infty }$
section of
![]() $\text{T}_{p}^{q}(M)$
. We denote by
$\text{T}_{p}^{q}(M)$
. We denote by
![]() ${\mathcal{T}}_{p}^{q}(M)$
the set
${\mathcal{T}}_{p}^{q}(M)$
the set
 $\unicode[STIX]{x1D6E4}^{\infty }(\text{T}_{p}^{q}(M))$
. A covector field or a differential 1-form is an element of
$\unicode[STIX]{x1D6E4}^{\infty }(\text{T}_{p}^{q}(M))$
. A covector field or a differential 1-form is an element of
![]() ${\mathcal{T}}_{1}^{0}(M)$
.
${\mathcal{T}}_{1}^{0}(M)$
.
For the tangent bundle
![]() $TM$
, a natural chart is obtained by taking the vector bundle (or tangent) map
$TM$
, a natural chart is obtained by taking the vector bundle (or tangent) map
 $T\unicode[STIX]{x1D719}:TM\rightarrow T\mathbb{R}^{d}=\mathbb{R}^{d}$
, where
$T\unicode[STIX]{x1D719}:TM\rightarrow T\mathbb{R}^{d}=\mathbb{R}^{d}$
, where
![]() $\unicode[STIX]{x1D719}$
is an admissible chart of
$\unicode[STIX]{x1D719}$
is an admissible chart of
![]() $M$
. This in turn induces a tensor bundle map
$M$
. This in turn induces a tensor bundle map
 $(T\unicode[STIX]{x1D719})_{\ast }:\text{T}_{p}^{q}(M)\rightarrow \text{T}_{p}^{q}(\mathbb{R}^{d})$
, which constitutes a natural chart on
$(T\unicode[STIX]{x1D719})_{\ast }:\text{T}_{p}^{q}(M)\rightarrow \text{T}_{p}^{q}(\mathbb{R}^{d})$
, which constitutes a natural chart on
![]() $\text{T}_{p}^{q}(M)$
. Indeed let
$\text{T}_{p}^{q}(M)$
. Indeed let
 $\unicode[STIX]{x1D719}:U\ni a\rightarrow x=\unicode[STIX]{x1D719}(a)\in U^{\prime }\subset \mathbb{R}^{d}$
a chart on
$\unicode[STIX]{x1D719}:U\ni a\rightarrow x=\unicode[STIX]{x1D719}(a)\in U^{\prime }\subset \mathbb{R}^{d}$
a chart on
![]() $M$
. Let
$M$
. Let
 $\{e_{i}\}_{1\leqslant i\leqslant d}$
(respectively
$\{e_{i}\}_{1\leqslant i\leqslant d}$
(respectively
 $\{e^{i}\}_{1\leqslant i\leqslant d}$
) be a (respectively dual) basis of
$\{e^{i}\}_{1\leqslant i\leqslant d}$
) be a (respectively dual) basis of
![]() $\mathbb{R}_{x}^{d}$
. Then
$\mathbb{R}_{x}^{d}$
. Then
 $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i}=\unicode[STIX]{x1D719}^{\ast }e_{i}=(T\unicode[STIX]{x1D719})^{-1}\circ e_{i}\circ \unicode[STIX]{x1D719}=(\unicode[STIX]{x2202}a^{\,j}/\unicode[STIX]{x2202}x^{i})e_{j}$
is a basis of
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i}=\unicode[STIX]{x1D719}^{\ast }e_{i}=(T\unicode[STIX]{x1D719})^{-1}\circ e_{i}\circ \unicode[STIX]{x1D719}=(\unicode[STIX]{x2202}a^{\,j}/\unicode[STIX]{x2202}x^{i})e_{j}$
is a basis of
![]() ${\mathcal{T}}_{0}^{1}(U)$
. The vector field
${\mathcal{T}}_{0}^{1}(U)$
. The vector field
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i}$
corresponds to the differentiation
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i}$
corresponds to the differentiation
 $f\mapsto \unicode[STIX]{x2202}f/\unicode[STIX]{x2202}a^{i}$
. In the same way the 1-forms
$f\mapsto \unicode[STIX]{x2202}f/\unicode[STIX]{x2202}a^{i}$
. In the same way the 1-forms
 $\text{d}a^{i}=\unicode[STIX]{x1D719}^{\ast }e^{i}=(\unicode[STIX]{x2202}x^{i}/\unicode[STIX]{x2202}a^{\,j})e^{\,j}$
is a basis of
$\text{d}a^{i}=\unicode[STIX]{x1D719}^{\ast }e^{i}=(\unicode[STIX]{x2202}x^{i}/\unicode[STIX]{x2202}a^{\,j})e^{\,j}$
is a basis of
![]() ${\mathcal{T}}_{1}^{0}(U)$
. Since
${\mathcal{T}}_{1}^{0}(U)$
. Since
 $$\begin{eqnarray}\langle \text{d}a^{i},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{\,j}\rangle :=\text{d}a^{i}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{\,j})=\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{l}}e^{l}\left(\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{\,j}}e_{k}\right)=\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{l}}\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{\,j}}e^{l}(e_{k})=\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{l}}\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{\,j}}\unicode[STIX]{x1D6FF}_{k}^{l}=\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}x^{\,j}}=\unicode[STIX]{x1D6FF}_{j}^{i},\end{eqnarray}$$
$$\begin{eqnarray}\langle \text{d}a^{i},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{\,j}\rangle :=\text{d}a^{i}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{\,j})=\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{l}}e^{l}\left(\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{\,j}}e_{k}\right)=\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{l}}\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{\,j}}e^{l}(e_{k})=\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{l}}\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{\,j}}\unicode[STIX]{x1D6FF}_{k}^{l}=\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}x^{\,j}}=\unicode[STIX]{x1D6FF}_{j}^{i},\end{eqnarray}$$
![]() $\{\text{d}a^{i}\}_{i}$
is the dual basis of
$\{\text{d}a^{i}\}_{i}$
is the dual basis of
![]() $\{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i}\}_{i}$
at every point of
$\{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i}\}_{i}$
at every point of
![]() $U$
. Let
$U$
. Let
 $$\begin{eqnarray}\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}=\unicode[STIX]{x0398}(\text{d}a^{i_{1}},\ldots ,\text{d}a^{i_{q}},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{\,j_{1}},\ldots ,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{\,j_{p}})\in {\mathcal{F}}(U),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}=\unicode[STIX]{x0398}(\text{d}a^{i_{1}},\ldots ,\text{d}a^{i_{q}},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{\,j_{1}},\ldots ,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{\,j_{p}})\in {\mathcal{F}}(U),\end{eqnarray}$$
where
![]() ${\mathcal{F}}(U)$
is the set of mappings from
${\mathcal{F}}(U)$
is the set of mappings from
![]() $U$
into
$U$
into
![]() $\mathbb{R}$
that are of class
$\mathbb{R}$
that are of class
![]() $\mathscr{C}^{\infty }$
. Then at every point
$\mathscr{C}^{\infty }$
. Then at every point
![]() $a$
of
$a$
of
![]() $U$
the coordinate expression of a
$U$
the coordinate expression of a
![]() $(q,p)$
-tensor field
$(q,p)$
-tensor field
 $\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
is
$\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
is
 $$\begin{eqnarray}\unicode[STIX]{x0398}_{|_{U}}=\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}(a)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{1}}}\otimes \cdots \otimes \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{q}}}\otimes \text{d}a^{\,j_{1}}\otimes \cdots \otimes \text{d}a^{\,j_{p}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x0398}_{|_{U}}=\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}(a)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{1}}}\otimes \cdots \otimes \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{q}}}\otimes \text{d}a^{\,j_{1}}\otimes \cdots \otimes \text{d}a^{\,j_{p}}.\end{eqnarray}$$
For more details see Choquet-Bruhat et al. (Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977, § III.B.1, p. 117 and § III.B.4, p. 135), Abraham et al. (Reference Abraham, Marsden and Ratiu1998, § 5.2, p. 352) and Fecko (Reference Fecko2006, § 2.5, p. 47).
B.3 Riemannian manifolds
Sometimes when dealing with manifolds it is useful to quantify geometric notions such as length, angles and volumes. All such quantities are expressed by means of the lengths of tangent vectors, that is, as the square root of a positive definite quadratic form given on every tangent space.
A Riemannian manifold is a differentiable manifold
![]() $M$
together with a differentiable 2-covariant tensor field
$M$
together with a differentiable 2-covariant tensor field
 $g\in {\mathcal{T}}_{2}^{0}(M)$
, called the metric tensor, such that: (i)
$g\in {\mathcal{T}}_{2}^{0}(M)$
, called the metric tensor, such that: (i)
![]() $g$
is symmetric, (ii) for each
$g$
is symmetric, (ii) for each
![]() $a\in M$
, the bilinear form
$a\in M$
, the bilinear form
![]() $g_{a}$
(this notation emphasises that
$g_{a}$
(this notation emphasises that
![]() $g$
is evaluated in
$g$
is evaluated in
![]() $a$
) is non-degenerate, i.e.
$a$
) is non-degenerate, i.e.
 $g_{a}(v,w)=0$
for all
$g_{a}(v,w)=0$
for all
![]() $v\in TM_{a}$
if and only if
$v\in TM_{a}$
if and only if
![]() $w=0$
. Such a manifold is said to possess a Riemannian structure. A Riemannian manifold (Riemannian structure) is called proper if
$w=0$
. Such a manifold is said to possess a Riemannian structure. A Riemannian manifold (Riemannian structure) is called proper if
![]() $g_{a}$
is a positive definite quadratic form on every tangent space, i.e.
$g_{a}$
is a positive definite quadratic form on every tangent space, i.e.
 $g_{a}(v,v)>0$
,
$g_{a}(v,v)>0$
,
 $\forall v\in TM_{a}$
,
$\forall v\in TM_{a}$
,
![]() $v\neq 0$
,
$v\neq 0$
,
![]() $a\in M$
. Otherwise the manifold is called pseudo-Riemannian or is said to possess an indefinite metric. The tensor
$a\in M$
. Otherwise the manifold is called pseudo-Riemannian or is said to possess an indefinite metric. The tensor
![]() $g$
allows one to define a metric on
$g$
allows one to define a metric on
![]() $M$
for measuring distances between two points on
$M$
for measuring distances between two points on
![]() $M$
. The Riemannian metric is given by the infinitesimal line element
$M$
. The Riemannian metric is given by the infinitesimal line element
![]() $\text{d}s^{2}$
which is defined by the metric tensor
$\text{d}s^{2}$
which is defined by the metric tensor
![]() $g$
:
$g$
:
 $$\begin{eqnarray}\text{d}s^{2}=g=\text{g}_{ij}\,\text{d}a^{i}\,\text{d}a^{\,j}=\text{g}_{ij}(a)\,\text{d}a^{i}\otimes \text{d}a^{\,j}.\end{eqnarray}$$
$$\begin{eqnarray}\text{d}s^{2}=g=\text{g}_{ij}\,\text{d}a^{i}\,\text{d}a^{\,j}=\text{g}_{ij}(a)\,\text{d}a^{i}\otimes \text{d}a^{\,j}.\end{eqnarray}$$
The tensor
![]() $g$
endows each tangent vector space
$g$
endows each tangent vector space
![]() $TM_{a}$
with an inner or scalar product,
$TM_{a}$
with an inner or scalar product,
![]() $(\cdot ,\cdot )_{g_{a}}$
called also Riemannian metric and defined by:
$(\cdot ,\cdot )_{g_{a}}$
called also Riemannian metric and defined by:
![]() $\forall a\in M$
$\forall a\in M$
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}(\cdot ,\cdot )_{g_{a}}:TM_{a}\times TM_{a}\rightarrow \mathbb{R}\\ \displaystyle \left(v=v^{i}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i}},w=w^{i}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i}}\right)\mapsto (v,w)_{g_{a}}=\text{g}_{ij}(a)v^{i}(a)w^{\,j}(a),\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}(\cdot ,\cdot )_{g_{a}}:TM_{a}\times TM_{a}\rightarrow \mathbb{R}\\ \displaystyle \left(v=v^{i}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i}},w=w^{i}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i}}\right)\mapsto (v,w)_{g_{a}}=\text{g}_{ij}(a)v^{i}(a)w^{\,j}(a),\end{array}\right\}\end{eqnarray}$$
where the notation
![]() $(\cdot ,\cdot )_{g_{a}}$
is to emphasise that the quadratic form is local, i.e. evaluated at the point
$(\cdot ,\cdot )_{g_{a}}$
is to emphasise that the quadratic form is local, i.e. evaluated at the point
![]() $a\in M$
; but most of the time it is omitted to simplify the notation into
$a\in M$
; but most of the time it is omitted to simplify the notation into
![]() $(\cdot ,\cdot )_{g}$
. The components of
$(\cdot ,\cdot )_{g}$
. The components of
![]() $g$
are differentiable on
$g$
are differentiable on
![]() $M$
and are given by
$M$
and are given by
 $$\begin{eqnarray}\text{g}_{ij}(a)=\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i}},\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{\,j}}\right)_{g_{a}}=\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{i}}\frac{\unicode[STIX]{x2202}a^{l}}{\unicode[STIX]{x2202}x^{\,j}}(e_{k},e_{l}),\end{eqnarray}$$
$$\begin{eqnarray}\text{g}_{ij}(a)=\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i}},\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{\,j}}\right)_{g_{a}}=\frac{\unicode[STIX]{x2202}a^{k}}{\unicode[STIX]{x2202}x^{i}}\frac{\unicode[STIX]{x2202}a^{l}}{\unicode[STIX]{x2202}x^{\,j}}(e_{k},e_{l}),\end{eqnarray}$$
where
![]() $(\cdot ,\cdot )$
denotes the usual scalar product in the Euclidean space, i.e. induced by the constant diagonal metric
$(\cdot ,\cdot )$
denotes the usual scalar product in the Euclidean space, i.e. induced by the constant diagonal metric
![]() $\unicode[STIX]{x1D6FF}_{ij}$
, with unity on the diagonal. Therefore, using the inner product
$\unicode[STIX]{x1D6FF}_{ij}$
, with unity on the diagonal. Therefore, using the inner product
![]() $(\cdot ,\cdot )_{g}$
, we get an isomorphism between the tangent bundle
$(\cdot ,\cdot )_{g}$
, we get an isomorphism between the tangent bundle
![]() $TM$
and the cotangent bundle
$TM$
and the cotangent bundle
![]() $T^{\ast }M$
. In particular, it induces an isomorphism of the spaces of sections, which is called the raising operator
$T^{\ast }M$
. In particular, it induces an isomorphism of the spaces of sections, which is called the raising operator
 $(\cdot )^{\sharp }:{\mathcal{T}}_{1}^{0}(M)\rightarrow {\mathcal{T}}_{0}^{1}(M)$
, with its inverse, named the lowering operator
$(\cdot )^{\sharp }:{\mathcal{T}}_{1}^{0}(M)\rightarrow {\mathcal{T}}_{0}^{1}(M)$
, with its inverse, named the lowering operator
 $(\cdot )^{\sharp }:{\mathcal{T}}_{0}^{1}(M)\rightarrow {\mathcal{T}}_{1}^{0}(M)$
. More precisely, such operators are defined by
$(\cdot )^{\sharp }:{\mathcal{T}}_{0}^{1}(M)\rightarrow {\mathcal{T}}_{1}^{0}(M)$
. More precisely, such operators are defined by
 $$\begin{eqnarray}\displaystyle & \left.\begin{array}{@{}c@{}}(\cdot )^{\sharp }:{\mathcal{T}}_{1}^{0}(M)\rightarrow {\mathcal{T}}_{0}^{1}(M)\\ \displaystyle \unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D6FC}^{\sharp }=(\unicode[STIX]{x1D6FC}_{i}\,\text{d}a^{i})^{\sharp }=(\unicode[STIX]{x1D6FC}^{\sharp })^{i}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i}},\quad (\unicode[STIX]{x1D6FC}^{\sharp })^{i}=\text{g}^{ij}\unicode[STIX]{x1D6FC}_{j},\end{array}\right\} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \left.\begin{array}{@{}c@{}}(\cdot )^{\sharp }:{\mathcal{T}}_{1}^{0}(M)\rightarrow {\mathcal{T}}_{0}^{1}(M)\\ \displaystyle \unicode[STIX]{x1D6FC}\mapsto \unicode[STIX]{x1D6FC}^{\sharp }=(\unicode[STIX]{x1D6FC}_{i}\,\text{d}a^{i})^{\sharp }=(\unicode[STIX]{x1D6FC}^{\sharp })^{i}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i}},\quad (\unicode[STIX]{x1D6FC}^{\sharp })^{i}=\text{g}^{ij}\unicode[STIX]{x1D6FC}_{j},\end{array}\right\} & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \left.\begin{array}{@{}c@{}}(\cdot )^{\flat }:{\mathcal{T}}_{0}^{1}(M)\rightarrow {\mathcal{T}}_{1}^{0}(M)\\ \displaystyle v\mapsto v^{\flat }=\left(v^{i}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i}}\right)^{\flat }=(v^{\flat })_{i}\,\text{d}a^{i},\quad (v^{\flat })_{i}=\text{g}_{ij}v^{\,j},\end{array}\right\} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \left.\begin{array}{@{}c@{}}(\cdot )^{\flat }:{\mathcal{T}}_{0}^{1}(M)\rightarrow {\mathcal{T}}_{1}^{0}(M)\\ \displaystyle v\mapsto v^{\flat }=\left(v^{i}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i}}\right)^{\flat }=(v^{\flat })_{i}\,\text{d}a^{i},\quad (v^{\flat })_{i}=\text{g}_{ij}v^{\,j},\end{array}\right\} & \displaystyle\end{eqnarray}$$
where
 $g_{ik}g^{kj}=\unicode[STIX]{x1D6FF}_{i}^{j}$
. For more details we refer the reader to Choquet-Bruhat et al. (Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977, § V.A.1, p. 285).
$g_{ik}g^{kj}=\unicode[STIX]{x1D6FF}_{i}^{j}$
. For more details we refer the reader to Choquet-Bruhat et al. (Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977, § V.A.1, p. 285).
B.4 Pullback and pushforward
Let
![]() $M$
,
$M$
,
![]() $N$
and
$N$
and
![]() $P$
be differentiable manifolds. Let
$P$
be differentiable manifolds. Let
 $\unicode[STIX]{x1D711}:M\ni a\rightarrow x=\unicode[STIX]{x1D711}(a)\in N$
and
$\unicode[STIX]{x1D711}:M\ni a\rightarrow x=\unicode[STIX]{x1D711}(a)\in N$
and
 $\unicode[STIX]{x1D713}:N\rightarrow P$
be diffeomorphisms. The pullback of
$\unicode[STIX]{x1D713}:N\rightarrow P$
be diffeomorphisms. The pullback of
 $\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{0}(N)$
by
$\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{0}(N)$
by
![]() $\unicode[STIX]{x1D711}$
is defined by
$\unicode[STIX]{x1D711}$
is defined by
 $$\begin{eqnarray}(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398})(a)(v_{1},\ldots ,v_{p})=\unicode[STIX]{x0398}(\unicode[STIX]{x1D711}(a))(T_{a}\unicode[STIX]{x1D711}(v_{1}),\ldots ,T_{a}\unicode[STIX]{x1D711}(v_{p})),\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398})(a)(v_{1},\ldots ,v_{p})=\unicode[STIX]{x0398}(\unicode[STIX]{x1D711}(a))(T_{a}\unicode[STIX]{x1D711}(v_{1}),\ldots ,T_{a}\unicode[STIX]{x1D711}(v_{p})),\end{eqnarray}$$
for all
![]() $a\in M$
, and
$a\in M$
, and
 $v_{1},\ldots ,v_{p}\in TM_{a}$
. The map
$v_{1},\ldots ,v_{p}\in TM_{a}$
. The map
 $T_{a}\unicode[STIX]{x1D711}:TM_{a}\rightarrow TN_{x=\unicode[STIX]{x1D711}(a)}$
is the tangent map of
$T_{a}\unicode[STIX]{x1D711}:TM_{a}\rightarrow TN_{x=\unicode[STIX]{x1D711}(a)}$
is the tangent map of
![]() $\unicode[STIX]{x1D711}$
at
$\unicode[STIX]{x1D711}$
at
![]() $a\in M$
, i.e. the Jacobian matrix
$a\in M$
, i.e. the Jacobian matrix
 $J_{\unicode[STIX]{x1D711}}(a)=J(\unicode[STIX]{x1D711})(a)=(\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}a)(a)$
. The pullback
$J_{\unicode[STIX]{x1D711}}(a)=J(\unicode[STIX]{x1D711})(a)=(\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}a)(a)$
. The pullback
 $\unicode[STIX]{x1D711}^{\ast }:{\mathcal{T}}_{p}^{0}(N)\rightarrow {\mathcal{T}}_{p}^{0}(M)$
is a linear isomorphism, which satisfies
$\unicode[STIX]{x1D711}^{\ast }:{\mathcal{T}}_{p}^{0}(N)\rightarrow {\mathcal{T}}_{p}^{0}(M)$
is a linear isomorphism, which satisfies
 $\unicode[STIX]{x1D711}^{\ast }(\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x0398}_{2})=(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398}_{1})\otimes (\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398}_{2})$
for any
$\unicode[STIX]{x1D711}^{\ast }(\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x0398}_{2})=(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398}_{1})\otimes (\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398}_{2})$
for any
 $\unicode[STIX]{x0398}_{1}\in {\mathcal{T}}_{p_{1}}^{0}(N)$
and
$\unicode[STIX]{x0398}_{1}\in {\mathcal{T}}_{p_{1}}^{0}(N)$
and
 $\unicode[STIX]{x0398}_{2}\in {\mathcal{T}}_{p_{2}}^{0}(N)$
. The pullback, applied to the composition of two maps,
$\unicode[STIX]{x0398}_{2}\in {\mathcal{T}}_{p_{2}}^{0}(N)$
. The pullback, applied to the composition of two maps,
![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711}$
, satisfies the following rule:
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711}$
, satisfies the following rule:
 $(\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711})^{\ast }=\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D713}^{\ast }$
. Since
$(\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711})^{\ast }=\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D713}^{\ast }$
. Since
![]() $\unicode[STIX]{x1D711}$
is a diffeomorphism,
$\unicode[STIX]{x1D711}$
is a diffeomorphism,
![]() $\unicode[STIX]{x1D711}^{\ast }$
is an isomorphism with inverse
$\unicode[STIX]{x1D711}^{\ast }$
is an isomorphism with inverse
 $(\unicode[STIX]{x1D711}^{\ast })^{-1}:=(\unicode[STIX]{x1D711}^{-1})^{\ast }$
.
$(\unicode[STIX]{x1D711}^{\ast })^{-1}:=(\unicode[STIX]{x1D711}^{-1})^{\ast }$
.
The pushforward of
 $\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
by
$\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
by
![]() $\unicode[STIX]{x1D711}$
is defined by
$\unicode[STIX]{x1D711}$
is defined by
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x0398})(x)(\unicode[STIX]{x1D6FC}^{1},\ldots ,\unicode[STIX]{x1D6FC}^{q},f_{1},\ldots ,f_{p})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x0398}(\unicode[STIX]{x1D711}^{-1}(x))(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC}^{1},\ldots ,\unicode[STIX]{x1D6FC}^{q},(T\unicode[STIX]{x1D711})^{-1}(f_{1}),\ldots ,(T\unicode[STIX]{x1D711})^{-1}(f_{p})),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x0398})(x)(\unicode[STIX]{x1D6FC}^{1},\ldots ,\unicode[STIX]{x1D6FC}^{q},f_{1},\ldots ,f_{p})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x0398}(\unicode[STIX]{x1D711}^{-1}(x))(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC}^{1},\ldots ,\unicode[STIX]{x1D6FC}^{q},(T\unicode[STIX]{x1D711})^{-1}(f_{1}),\ldots ,(T\unicode[STIX]{x1D711})^{-1}(f_{p})),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6FC}^{i}\in T^{\ast }N_{x}$
and
$\unicode[STIX]{x1D6FC}^{i}\in T^{\ast }N_{x}$
and
![]() $f_{i}\in TN_{x}$
. Using the tensor bundle map
$f_{i}\in TN_{x}$
. Using the tensor bundle map
 $(T\unicode[STIX]{x1D711})_{\ast }:\text{T}_{p}^{q}(M)\rightarrow \text{T}_{p}^{q}(N)$
, the pushforward can be written in compact form as
$(T\unicode[STIX]{x1D711})_{\ast }:\text{T}_{p}^{q}(M)\rightarrow \text{T}_{p}^{q}(N)$
, the pushforward can be written in compact form as
 $\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x0398}:=(T\unicode[STIX]{x1D711})_{\ast }\circ \unicode[STIX]{x0398}\circ \unicode[STIX]{x1D711}^{-1}$
. The pushforward
$\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x0398}:=(T\unicode[STIX]{x1D711})_{\ast }\circ \unicode[STIX]{x0398}\circ \unicode[STIX]{x1D711}^{-1}$
. The pushforward
 $\unicode[STIX]{x1D711}_{\ast }:{\mathcal{T}}_{p}^{q}(M)\rightarrow {\mathcal{T}}_{p}^{q}(N)$
is a linear isomorphism, which satisfies
$\unicode[STIX]{x1D711}_{\ast }:{\mathcal{T}}_{p}^{q}(M)\rightarrow {\mathcal{T}}_{p}^{q}(N)$
is a linear isomorphism, which satisfies
 $\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x0398}_{2})=(\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x0398}_{1})\otimes (\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x0398}_{2})$
for any
$\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x0398}_{2})=(\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x0398}_{1})\otimes (\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x0398}_{2})$
for any
 $\unicode[STIX]{x0398}_{1}\in {\mathcal{T}}_{p_{1}}^{q_{1}}(M)$
and
$\unicode[STIX]{x0398}_{1}\in {\mathcal{T}}_{p_{1}}^{q_{1}}(M)$
and
 $\unicode[STIX]{x0398}_{2}\in {\mathcal{T}}_{p_{2}}^{q_{2}}(M)$
. The pushforward of map composition verifies the following rule:
$\unicode[STIX]{x0398}_{2}\in {\mathcal{T}}_{p_{2}}^{q_{2}}(M)$
. The pushforward of map composition verifies the following rule:
 $(\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711})_{\ast }=\unicode[STIX]{x1D713}_{\ast }\unicode[STIX]{x1D711}_{\ast }$
. Since
$(\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711})_{\ast }=\unicode[STIX]{x1D713}_{\ast }\unicode[STIX]{x1D711}_{\ast }$
. Since
![]() $\unicode[STIX]{x1D711}$
is a diffeomorphism,
$\unicode[STIX]{x1D711}$
is a diffeomorphism,
![]() $\unicode[STIX]{x1D711}^{\ast }$
is an isomorphism with inverse
$\unicode[STIX]{x1D711}^{\ast }$
is an isomorphism with inverse
 $(\unicode[STIX]{x1D711}_{\ast })^{-1}:=(\unicode[STIX]{x1D711}^{-1})_{\ast }$
. The pullback of
$(\unicode[STIX]{x1D711}_{\ast })^{-1}:=(\unicode[STIX]{x1D711}^{-1})_{\ast }$
. The pullback of
 $\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(N)$
by
$\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(N)$
by
![]() $\unicode[STIX]{x1D711}$
is given by
$\unicode[STIX]{x1D711}$
is given by
 $\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398}=(\unicode[STIX]{x1D711}^{-1})_{\ast }\unicode[STIX]{x0398}$
. In other words we have
$\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398}=(\unicode[STIX]{x1D711}^{-1})_{\ast }\unicode[STIX]{x0398}$
. In other words we have
 $\unicode[STIX]{x1D711}^{\ast }=(\unicode[STIX]{x1D711}_{\ast })^{-1}=(\unicode[STIX]{x1D711}^{-1})_{\ast }$
and
$\unicode[STIX]{x1D711}^{\ast }=(\unicode[STIX]{x1D711}_{\ast })^{-1}=(\unicode[STIX]{x1D711}^{-1})_{\ast }$
and
 $\unicode[STIX]{x1D711}_{\ast }=(\unicode[STIX]{x1D711}^{\ast })^{-1}=(\unicode[STIX]{x1D711}^{-1})^{\ast }$
.
$\unicode[STIX]{x1D711}_{\ast }=(\unicode[STIX]{x1D711}^{\ast })^{-1}=(\unicode[STIX]{x1D711}^{-1})^{\ast }$
.
For finite-dimensional manifolds, pullback and pushforward can be expressed in terms of coordinates. Setting
 $m=\dim (M)$
and
$m=\dim (M)$
and
 $n=\dim (N)$
, the maps
$n=\dim (N)$
, the maps
 $x^{\,j}=\unicode[STIX]{x1D711}^{\,j}(a^{1},\ldots ,a^{m})$
, with
$x^{\,j}=\unicode[STIX]{x1D711}^{\,j}(a^{1},\ldots ,a^{m})$
, with
 $j=1,\ldots ,n$
denote the local expression of the diffeomorphism
$j=1,\ldots ,n$
denote the local expression of the diffeomorphism
 $\unicode[STIX]{x1D711}:M\rightarrow N$
relative to charts. Taking into account that the tangent map
$\unicode[STIX]{x1D711}:M\rightarrow N$
relative to charts. Taking into account that the tangent map
![]() $T\unicode[STIX]{x1D711}$
of
$T\unicode[STIX]{x1D711}$
of
![]() $\unicode[STIX]{x1D711}$
is given locally by the Jacobian matrix
$\unicode[STIX]{x1D711}$
is given locally by the Jacobian matrix
 $J_{\unicode[STIX]{x1D711}}=J(\unicode[STIX]{x1D711})=(\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}a)$
, we obtain the following coordinate expressions of the pushforward and the pullback.
$J_{\unicode[STIX]{x1D711}}=J(\unicode[STIX]{x1D711})=(\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}a)$
, we obtain the following coordinate expressions of the pushforward and the pullback.
If
 $\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
and
$\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
and
![]() $\unicode[STIX]{x1D711}$
is a diffeomorphism, the coordinates of the pushforward of
$\unicode[STIX]{x1D711}$
is a diffeomorphism, the coordinates of the pushforward of
![]() $\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x0398}$
are
$\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x0398}$
are
 $$\begin{eqnarray}(\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x0398})_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}=\left(\frac{\unicode[STIX]{x2202}x^{i_{1}}}{\unicode[STIX]{x2202}a^{k_{1}}}\circ \unicode[STIX]{x1D711}^{-1}\right)\cdots \left(\frac{\unicode[STIX]{x2202}x^{i_{q}}}{\unicode[STIX]{x2202}a^{k_{q}}}\circ \unicode[STIX]{x1D711}^{-1}\right)\frac{\unicode[STIX]{x2202}a^{l_{1}}}{\unicode[STIX]{x2202}x^{\,j_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{l_{p}}}{\unicode[STIX]{x2202}x^{\,j_{p}}}\unicode[STIX]{x0398}_{l_{1}\ldots l_{p}}^{k_{1}\ldots k_{q}}\circ \unicode[STIX]{x1D711}^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x0398})_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}=\left(\frac{\unicode[STIX]{x2202}x^{i_{1}}}{\unicode[STIX]{x2202}a^{k_{1}}}\circ \unicode[STIX]{x1D711}^{-1}\right)\cdots \left(\frac{\unicode[STIX]{x2202}x^{i_{q}}}{\unicode[STIX]{x2202}a^{k_{q}}}\circ \unicode[STIX]{x1D711}^{-1}\right)\frac{\unicode[STIX]{x2202}a^{l_{1}}}{\unicode[STIX]{x2202}x^{\,j_{1}}}\cdots \frac{\unicode[STIX]{x2202}a^{l_{p}}}{\unicode[STIX]{x2202}x^{\,j_{p}}}\unicode[STIX]{x0398}_{l_{1}\ldots l_{p}}^{k_{1}\ldots k_{q}}\circ \unicode[STIX]{x1D711}^{-1}.\end{eqnarray}$$
If
 $\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(N)$
and
$\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(N)$
and
![]() $\unicode[STIX]{x1D711}$
a diffeomorphism, the coordinates of the pullback of
$\unicode[STIX]{x1D711}$
a diffeomorphism, the coordinates of the pullback of
![]() $\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398}$
are
$\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398}$
are
 $$\begin{eqnarray}(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398})_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}=\left(\frac{\unicode[STIX]{x2202}a^{i_{1}}}{\unicode[STIX]{x2202}x^{l_{1}}}\circ \unicode[STIX]{x1D711}\right)\cdots \left(\frac{\unicode[STIX]{x2202}a^{i_{q}}}{\unicode[STIX]{x2202}a^{l_{q}}}\circ \unicode[STIX]{x1D711}\right)\frac{\unicode[STIX]{x2202}x^{k_{1}}}{\unicode[STIX]{x2202}a^{\,j_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{k_{p}}}{\unicode[STIX]{x2202}a^{\,j_{p}}}\unicode[STIX]{x0398}_{k_{1}\ldots k_{p}}^{l_{1}\ldots l_{q}}\circ \unicode[STIX]{x1D711}.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398})_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}=\left(\frac{\unicode[STIX]{x2202}a^{i_{1}}}{\unicode[STIX]{x2202}x^{l_{1}}}\circ \unicode[STIX]{x1D711}\right)\cdots \left(\frac{\unicode[STIX]{x2202}a^{i_{q}}}{\unicode[STIX]{x2202}a^{l_{q}}}\circ \unicode[STIX]{x1D711}\right)\frac{\unicode[STIX]{x2202}x^{k_{1}}}{\unicode[STIX]{x2202}a^{\,j_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{k_{p}}}{\unicode[STIX]{x2202}a^{\,j_{p}}}\unicode[STIX]{x0398}_{k_{1}\ldots k_{p}}^{l_{1}\ldots l_{q}}\circ \unicode[STIX]{x1D711}.\end{eqnarray}$$
In particular, if
 $\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{0}(N)$
the coordinates of the pullback of
$\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{0}(N)$
the coordinates of the pullback of
![]() $\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398}$
are
$\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398}$
are
 $$\begin{eqnarray}(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398})_{j_{1}\ldots j_{p}}=\frac{\unicode[STIX]{x2202}x^{k_{1}}}{\unicode[STIX]{x2202}a^{\,j_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{k_{p}}}{\unicode[STIX]{x2202}a^{\,j_{p}}}\unicode[STIX]{x0398}_{k_{1}\ldots k_{p}}\circ \unicode[STIX]{x1D711}.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398})_{j_{1}\ldots j_{p}}=\frac{\unicode[STIX]{x2202}x^{k_{1}}}{\unicode[STIX]{x2202}a^{\,j_{1}}}\cdots \frac{\unicode[STIX]{x2202}x^{k_{p}}}{\unicode[STIX]{x2202}a^{\,j_{p}}}\unicode[STIX]{x0398}_{k_{1}\ldots k_{p}}\circ \unicode[STIX]{x1D711}.\end{eqnarray}$$
If
 $v=v^{i}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i})\in {\mathcal{T}}_{0}^{1}(M)$
(respectively
$v=v^{i}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i})\in {\mathcal{T}}_{0}^{1}(M)$
(respectively
 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}\,\text{d}a^{i}\in {\mathcal{T}}_{1}^{0}(M)$
) then
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}\,\text{d}a^{i}\in {\mathcal{T}}_{1}^{0}(M)$
) then
 $\unicode[STIX]{x1D711}_{\ast }(v^{i}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i}))=v^{\,j}(\unicode[STIX]{x2202}x^{i}/\unicode[STIX]{x2202}a^{\,j})(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x^{i})$
(respectively
$\unicode[STIX]{x1D711}_{\ast }(v^{i}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i}))=v^{\,j}(\unicode[STIX]{x2202}x^{i}/\unicode[STIX]{x2202}a^{\,j})(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x^{i})$
(respectively
 $\unicode[STIX]{x1D711}^{\ast }(\unicode[STIX]{x1D6FC}_{i}\,\text{d}a^{i})=\unicode[STIX]{x1D6FC}_{j}(\unicode[STIX]{x2202}x^{\,j}/\unicode[STIX]{x2202}a^{i})\,\text{d}a^{i}$
). Therefore, using the map
$\unicode[STIX]{x1D711}^{\ast }(\unicode[STIX]{x1D6FC}_{i}\,\text{d}a^{i})=\unicode[STIX]{x1D6FC}_{j}(\unicode[STIX]{x2202}x^{\,j}/\unicode[STIX]{x2202}a^{i})\,\text{d}a^{i}$
). Therefore, using the map
 $g:N\rightarrow \mathbb{R}$
, we obtain
$g:N\rightarrow \mathbb{R}$
, we obtain
 $$\begin{eqnarray}(\unicode[STIX]{x1D711}_{\ast }v)g=\left(v^{\,j}\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{\,j}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x^{i}}\right)g=v^{\,j}\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{\,j}}\frac{\unicode[STIX]{x2202}g}{\unicode[STIX]{x2202}x^{i}}=v^{\,j}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{\,j}}g(\unicode[STIX]{x1D711}(a))=\left(v^{\,j}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{\,j}}\right)\unicode[STIX]{x1D711}^{\ast }g=v(\unicode[STIX]{x1D711}^{\ast }g).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D711}_{\ast }v)g=\left(v^{\,j}\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{\,j}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x^{i}}\right)g=v^{\,j}\frac{\unicode[STIX]{x2202}x^{i}}{\unicode[STIX]{x2202}a^{\,j}}\frac{\unicode[STIX]{x2202}g}{\unicode[STIX]{x2202}x^{i}}=v^{\,j}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{\,j}}g(\unicode[STIX]{x1D711}(a))=\left(v^{\,j}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{\,j}}\right)\unicode[STIX]{x1D711}^{\ast }g=v(\unicode[STIX]{x1D711}^{\ast }g).\end{eqnarray}$$
From the above formula we see that the pullback of covariant tensors can be defined even for maps that are not diffeomorphisms but only differentiable maps, i.e. of class
![]() $\mathscr{C}^{1}$
(see, e.g., Abraham et al.
Reference Abraham, Marsden and Ratiu1998, § 5.2, p. 355; see also § 3.1, p. 54 in Fecko Reference Fecko2006).
$\mathscr{C}^{1}$
(see, e.g., Abraham et al.
Reference Abraham, Marsden and Ratiu1998, § 5.2, p. 355; see also § 3.1, p. 54 in Fecko Reference Fecko2006).
B.5 Lie derivative
Concepts of Lie derivative and Lie advection have been presented in § 2.2, where the Lie-derivative theorem has also been stated. Here we give additional properties of the Lie differentiation process.
From an algebraic point of view, the local coordinate expression of the Lie derivative
 $\unicode[STIX]{x00A3}_{v}:{\mathcal{T}}_{p}^{q}(M)\rightarrow {\mathcal{T}}_{p}^{q}(M)$
of an arbitrary tensor
$\unicode[STIX]{x00A3}_{v}:{\mathcal{T}}_{p}^{q}(M)\rightarrow {\mathcal{T}}_{p}^{q}(M)$
of an arbitrary tensor
 $\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
is (see, e.g., Abraham et al. (Reference Abraham, Marsden and Ratiu1998), § 5.3, p. 359; see also § 4.3, p. 72 in Fecko Reference Fecko2006)
$\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
is (see, e.g., Abraham et al. (Reference Abraham, Marsden and Ratiu1998), § 5.3, p. 359; see also § 4.3, p. 72 in Fecko Reference Fecko2006)
 $$\begin{eqnarray}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x0398}=(\text{}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x0398})_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{1}}}\otimes \cdots \otimes \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{q}}}\otimes \text{d}a^{\,j_{1}}\otimes \cdots \otimes \text{d}a^{\,j_{p}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x0398}=(\text{}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x0398})_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{1}}}\otimes \cdots \otimes \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{q}}}\otimes \text{d}a^{\,j_{1}}\otimes \cdots \otimes \text{d}a^{\,j_{p}},\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle (\text{}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x0398})_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}} & = & \displaystyle v^{\ell }\unicode[STIX]{x2202}_{\ell }\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}-\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{ki_{2}\ldots i_{q}}\unicode[STIX]{x2202}_{k}v^{i_{1}}\nonumber\\ \displaystyle & & \displaystyle -\,(\text{all upper indices})+\unicode[STIX]{x0398}_{lj_{2}\ldots j_{p}}^{i_{1}\ldots i_{q}}\unicode[STIX]{x2202}_{j_{1}}v^{l}+(\text{all lower indices}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\text{}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x0398})_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}} & = & \displaystyle v^{\ell }\unicode[STIX]{x2202}_{\ell }\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}-\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{ki_{2}\ldots i_{q}}\unicode[STIX]{x2202}_{k}v^{i_{1}}\nonumber\\ \displaystyle & & \displaystyle -\,(\text{all upper indices})+\unicode[STIX]{x0398}_{lj_{2}\ldots j_{p}}^{i_{1}\ldots i_{q}}\unicode[STIX]{x2202}_{j_{1}}v^{l}+(\text{all lower indices}).\end{eqnarray}$$
Moreover the Lie derivative is a linear operator, a derivation (i.e. it satisfies the Leibniz rule):
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x00A3}_{v}(\unicode[STIX]{x1D714}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D703})=\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}+\unicode[STIX]{x1D706}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D703},\quad \unicode[STIX]{x00A3}_{v}(\unicode[STIX]{x1D714}\otimes \unicode[STIX]{x1D6FE})=\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}\otimes \unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D714}\otimes \unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FE},\\ \unicode[STIX]{x1D706}\in \mathbb{R},\quad v\in {\mathcal{T}}_{0}^{1}(M),\quad \unicode[STIX]{x1D6FE}\in {\mathcal{T}}_{s}^{r}(M),\quad \unicode[STIX]{x1D703},\unicode[STIX]{x1D714}\in {\mathcal{T}}_{p}^{q}(M).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x00A3}_{v}(\unicode[STIX]{x1D714}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D703})=\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}+\unicode[STIX]{x1D706}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D703},\quad \unicode[STIX]{x00A3}_{v}(\unicode[STIX]{x1D714}\otimes \unicode[STIX]{x1D6FE})=\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D714}\otimes \unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D714}\otimes \unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FE},\\ \unicode[STIX]{x1D706}\in \mathbb{R},\quad v\in {\mathcal{T}}_{0}^{1}(M),\quad \unicode[STIX]{x1D6FE}\in {\mathcal{T}}_{s}^{r}(M),\quad \unicode[STIX]{x1D703},\unicode[STIX]{x1D714}\in {\mathcal{T}}_{p}^{q}(M).\end{array}\right\}\end{eqnarray}$$
Furthermore, the Lie derivative is natural with respect to the pushforward and pullback by any diffeomorphism
 $\unicode[STIX]{x1D711}:M\rightarrow N$
, in the following sense
$\unicode[STIX]{x1D711}:M\rightarrow N$
, in the following sense
 $$\begin{eqnarray}{\unicode[STIX]{x1D711}_{t\ast }\unicode[STIX]{x00A3}}_{v}=\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D711}_{t\ast }v}\unicode[STIX]{x1D711}_{t\ast },\quad {\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x00A3}}_{v}=\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D711}_{t}^{\ast }v}\unicode[STIX]{x1D711}_{t}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}{\unicode[STIX]{x1D711}_{t\ast }\unicode[STIX]{x00A3}}_{v}=\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D711}_{t\ast }v}\unicode[STIX]{x1D711}_{t\ast },\quad {\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x00A3}}_{v}=\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D711}_{t}^{\ast }v}\unicode[STIX]{x1D711}_{t}^{\ast }.\end{eqnarray}$$
B.6 Permutations, generalised Kronecker symbols and determinants
The set
![]() $\mathfrak{S}_{k}$
is the permutation group on
$\mathfrak{S}_{k}$
is the permutation group on
![]() $k$
elements, which consists of all bijections
$k$
elements, which consists of all bijections
 $\unicode[STIX]{x1D70E}:\{1,\ldots ,k\}\rightarrow \{1,\ldots ,k\}$
, usually given in the form a table
$\unicode[STIX]{x1D70E}:\{1,\ldots ,k\}\rightarrow \{1,\ldots ,k\}$
, usually given in the form a table
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}1 & \ldots & k\\ \unicode[STIX]{x1D70E}(1) & \ldots & \unicode[STIX]{x1D70E}(k)\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}1 & \ldots & k\\ \unicode[STIX]{x1D70E}(1) & \ldots & \unicode[STIX]{x1D70E}(k)\end{array}\right),\end{eqnarray}$$
with the structure of a group under composition of maps. A transposition is a permutation which swaps two elements of
 $\{1,\ldots ,k\}$
. A permutation is even (respectively odd) when it can be written as the product of an even (respectively odd) number of transpositions. When a permutation is even (respectively odd)
$\{1,\ldots ,k\}$
. A permutation is even (respectively odd) when it can be written as the product of an even (respectively odd) number of transpositions. When a permutation is even (respectively odd)
 $\text{sign}\,\unicode[STIX]{x1D70E}=+1$
(respectively
$\text{sign}\,\unicode[STIX]{x1D70E}=+1$
(respectively
 $\text{sign}\,\unicode[STIX]{x1D70E}=-1$
) and
$\text{sign}\,\unicode[STIX]{x1D70E}=-1$
) and
 $\text{sign}(\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D70F})=(\text{sign}\,\unicode[STIX]{x1D70E})(\text{sign}\,\unicode[STIX]{x1D70F})$
. The dimension of
$\text{sign}(\unicode[STIX]{x1D70E}\circ \unicode[STIX]{x1D70F})=(\text{sign}\,\unicode[STIX]{x1D70E})(\text{sign}\,\unicode[STIX]{x1D70F})$
. The dimension of
![]() $\mathfrak{S}_{k}$
is
$\mathfrak{S}_{k}$
is
 $\dim (\mathfrak{S}_{k})=k!$
.
$\dim (\mathfrak{S}_{k})=k!$
.
Let
![]() $\unicode[STIX]{x1D6FF}_{ij}$
,
$\unicode[STIX]{x1D6FF}_{ij}$
,
![]() $\unicode[STIX]{x1D6FF}_{j}^{i}$
and
$\unicode[STIX]{x1D6FF}_{j}^{i}$
and
![]() $\unicode[STIX]{x1D6FF}^{ij}$
be the first Kronecker symbols defined by
$\unicode[STIX]{x1D6FF}^{ij}$
be the first Kronecker symbols defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{ij}=\unicode[STIX]{x1D6FF}_{j}^{i}=\unicode[STIX]{x1D6FF}^{ij}=\left\{\begin{array}{@{}ll@{}}0\quad & \text{if}~i\neq j\\ 1\quad & \text{if}~i=j.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{ij}=\unicode[STIX]{x1D6FF}_{j}^{i}=\unicode[STIX]{x1D6FF}^{ij}=\left\{\begin{array}{@{}ll@{}}0\quad & \text{if}~i\neq j\\ 1\quad & \text{if}~i=j.\end{array}\right.\end{eqnarray}$$
The generalised Kronecker symbol
![]() $\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}$
(also noted
$\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}$
(also noted
![]() $\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}$
) is defined by
$\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}$
) is defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}=\left\{\begin{array}{@{}ll@{}}0 & \text{if}~(i_{1}\ldots i_{p})~\text{is not a permutation of}~(j_{1}\ldots j_{p})\\ +1 & \text{if}~(i_{1}\ldots i_{p})~\text{is an even permutation of}~(j_{1}\ldots j_{p})\\ -1 & \text{if}~(i_{1}\ldots i_{p})~\text{is an odd permutation of}~(j_{1}\ldots j_{p}).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}=\left\{\begin{array}{@{}ll@{}}0 & \text{if}~(i_{1}\ldots i_{p})~\text{is not a permutation of}~(j_{1}\ldots j_{p})\\ +1 & \text{if}~(i_{1}\ldots i_{p})~\text{is an even permutation of}~(j_{1}\ldots j_{p})\\ -1 & \text{if}~(i_{1}\ldots i_{p})~\text{is an odd permutation of}~(j_{1}\ldots j_{p}).\end{array}\right.\end{eqnarray}$$
Using the Laplace expansion of determinant, the generalised Kronecker symbol
![]() $\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}$
can be recast in different forms:
$\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}$
can be recast in different forms:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{p}}^{\,j_{1}\ldots j_{p}} & = & \displaystyle \left|\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FF}_{i_{1}}^{\,j_{1}} & \ldots & \unicode[STIX]{x1D6FF}_{i_{p}}^{\,j_{1}}\\ \vdots & \ddots & \vdots \\ \unicode[STIX]{x1D6FF}_{i_{1}}^{\,j_{p}} & \ldots & \unicode[STIX]{x1D6FF}_{i_{p}}^{\,j_{p}}\end{array}\right|=\mathop{\sum }_{k=1}^{p}(-1)^{p+k}\unicode[STIX]{x1D6FF}_{i_{k}}^{\,j_{p}}\unicode[STIX]{x1D6FF}_{i_{1}\ldots \widehat{i}_{k}\ldots i_{p}}^{\,j_{1}\ldots j_{k}\ldots \widehat{j}_{p}},\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}\in \mathfrak{S}_{p}}\text{sign}(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D6FF}_{j_{\unicode[STIX]{x1D70E}(1)}}^{i_{1}}\ldots \unicode[STIX]{x1D6FF}_{j_{\unicode[STIX]{x1D70E}(p)}}^{i_{p}}=\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \mathfrak{S}_{p}}\text{sign}(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D6FF}_{j_{1}}^{i_{\unicode[STIX]{x1D70E}(1)}}\ldots \unicode[STIX]{x1D6FF}_{j_{p}}^{i_{\unicode[STIX]{x1D70E}(p)}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{p}}^{\,j_{1}\ldots j_{p}} & = & \displaystyle \left|\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FF}_{i_{1}}^{\,j_{1}} & \ldots & \unicode[STIX]{x1D6FF}_{i_{p}}^{\,j_{1}}\\ \vdots & \ddots & \vdots \\ \unicode[STIX]{x1D6FF}_{i_{1}}^{\,j_{p}} & \ldots & \unicode[STIX]{x1D6FF}_{i_{p}}^{\,j_{p}}\end{array}\right|=\mathop{\sum }_{k=1}^{p}(-1)^{p+k}\unicode[STIX]{x1D6FF}_{i_{k}}^{\,j_{p}}\unicode[STIX]{x1D6FF}_{i_{1}\ldots \widehat{i}_{k}\ldots i_{p}}^{\,j_{1}\ldots j_{k}\ldots \widehat{j}_{p}},\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}\in \mathfrak{S}_{p}}\text{sign}(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D6FF}_{j_{\unicode[STIX]{x1D70E}(1)}}^{i_{1}}\ldots \unicode[STIX]{x1D6FF}_{j_{\unicode[STIX]{x1D70E}(p)}}^{i_{p}}=\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \mathfrak{S}_{p}}\text{sign}(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D6FF}_{j_{1}}^{i_{\unicode[STIX]{x1D70E}(1)}}\ldots \unicode[STIX]{x1D6FF}_{j_{p}}^{i_{\unicode[STIX]{x1D70E}(p)}},\end{eqnarray}$$
where the hat character
![]() $\hat{~}$
indicates an index that is omitted from the sequence. Moreover, the generalised Kronecker symbol
$\hat{~}$
indicates an index that is omitted from the sequence. Moreover, the generalised Kronecker symbol
![]() $\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}$
satisfies the properties (Fecko Reference Fecko2006, § 5.6, p. 107)
$\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}$
satisfies the properties (Fecko Reference Fecko2006, § 5.6, p. 107)
 $$\begin{eqnarray}\frac{1}{p!}\unicode[STIX]{x1D6FF}_{k_{1}\ldots k_{p}}^{i_{1}\ldots i_{p}}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{k_{1}\ldots k_{p}}=\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}},\quad \text{and}\quad \unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}i_{p+1}\ldots i_{q}}^{i_{1}\ldots i_{p}i_{p+1}\ldots i_{q}}=\frac{(d-p)!}{(d-q)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{p!}\unicode[STIX]{x1D6FF}_{k_{1}\ldots k_{p}}^{i_{1}\ldots i_{p}}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{k_{1}\ldots k_{p}}=\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}},\quad \text{and}\quad \unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}i_{p+1}\ldots i_{q}}^{i_{1}\ldots i_{p}i_{p+1}\ldots i_{q}}=\frac{(d-p)!}{(d-q)!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}.\end{eqnarray}$$
We also define the second Kronecker symbols
![]() $\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}}$
and
$\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}}$
and
![]() $\unicode[STIX]{x1D700}^{i_{1}\ldots i_{p}}$
by
$\unicode[STIX]{x1D700}^{i_{1}\ldots i_{p}}$
by
 $$\begin{eqnarray}\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}}=\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{1\ldots p},\quad \unicode[STIX]{x1D700}^{i_{1}\ldots i_{p}}=\unicode[STIX]{x1D6FF}_{1\ldots p}^{i_{1}\ldots i_{p}}\quad \text{and thus}\quad \unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}=\frac{1}{(d-p)!}\unicode[STIX]{x1D700}^{i_{1}\ldots i_{p}k_{p+1}\ldots k_{d}}\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}k_{p+1}\ldots k_{d}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}}=\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{1\ldots p},\quad \unicode[STIX]{x1D700}^{i_{1}\ldots i_{p}}=\unicode[STIX]{x1D6FF}_{1\ldots p}^{i_{1}\ldots i_{p}}\quad \text{and thus}\quad \unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}=\frac{1}{(d-p)!}\unicode[STIX]{x1D700}^{i_{1}\ldots i_{p}k_{p+1}\ldots k_{d}}\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}k_{p+1}\ldots k_{d}}.\end{eqnarray}$$
Finally, let
 $d=\dim (M)$
, and
$d=\dim (M)$
, and
 $\unicode[STIX]{x1D711}:M\rightarrow M$
be of class
$\unicode[STIX]{x1D711}:M\rightarrow M$
be of class
![]() $\mathscr{C}^{1}$
. The determinant of the linear mapping (tangent map at the point
$\mathscr{C}^{1}$
. The determinant of the linear mapping (tangent map at the point
![]() $a$
)
$a$
)
 $T_{a}\unicode[STIX]{x1D711}:TM_{a}\rightarrow TM_{a}$
, is noted
$T_{a}\unicode[STIX]{x1D711}:TM_{a}\rightarrow TM_{a}$
, is noted
 $\det (T_{a}\unicode[STIX]{x1D711})=\det (\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}a)$
and is given by
$\det (T_{a}\unicode[STIX]{x1D711})=\det (\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}a)$
and is given by
 $$\begin{eqnarray}\displaystyle \det (T_{a}\unicode[STIX]{x1D711}) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}\in \mathfrak{S}_{d}}\text{sign}(\unicode[STIX]{x1D70E})\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{1}}{\unicode[STIX]{x2202}a^{\unicode[STIX]{x1D70E}(1)}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{d}}{\unicode[STIX]{x2202}a^{\unicode[STIX]{x1D70E}(d)}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}\in \mathfrak{S}_{d}}\text{sign}(\unicode[STIX]{x1D70E})\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D70E}(1)}}{\unicode[STIX]{x2202}a^{1}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D70E}(d)}}{\unicode[STIX]{x2202}a^{d}}=\unicode[STIX]{x1D700}^{i_{1}\ldots i_{d}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{1}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{d}}{\unicode[STIX]{x2202}a^{i_{d}}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D700}_{j_{1}\ldots j_{d}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{1}}}{\unicode[STIX]{x2202}a^{1}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{d}}}{\unicode[STIX]{x2202}a^{d}}=\frac{1}{d!}\unicode[STIX]{x1D700}^{i_{1}\ldots i_{d}}\unicode[STIX]{x1D700}_{i_{1}\ldots i_{d}}\det (T_{a}\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{d!}\unicode[STIX]{x1D700}^{i_{1}\ldots i_{d}}\unicode[STIX]{x1D700}_{j_{1}\ldots j_{d}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{d}}}{\unicode[STIX]{x2202}a^{i_{d}}}=\frac{1}{d!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{d}}^{i_{1}\ldots i_{d}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{d}}}{\unicode[STIX]{x2202}a^{i_{d}}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \det (T_{a}\unicode[STIX]{x1D711}) & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}\in \mathfrak{S}_{d}}\text{sign}(\unicode[STIX]{x1D70E})\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{1}}{\unicode[STIX]{x2202}a^{\unicode[STIX]{x1D70E}(1)}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{d}}{\unicode[STIX]{x2202}a^{\unicode[STIX]{x1D70E}(d)}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}\in \mathfrak{S}_{d}}\text{sign}(\unicode[STIX]{x1D70E})\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D70E}(1)}}{\unicode[STIX]{x2202}a^{1}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D70E}(d)}}{\unicode[STIX]{x2202}a^{d}}=\unicode[STIX]{x1D700}^{i_{1}\ldots i_{d}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{1}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{d}}{\unicode[STIX]{x2202}a^{i_{d}}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D700}_{j_{1}\ldots j_{d}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{1}}}{\unicode[STIX]{x2202}a^{1}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{d}}}{\unicode[STIX]{x2202}a^{d}}=\frac{1}{d!}\unicode[STIX]{x1D700}^{i_{1}\ldots i_{d}}\unicode[STIX]{x1D700}_{i_{1}\ldots i_{d}}\det (T_{a}\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{d!}\unicode[STIX]{x1D700}^{i_{1}\ldots i_{d}}\unicode[STIX]{x1D700}_{j_{1}\ldots j_{d}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{d}}}{\unicode[STIX]{x2202}a^{i_{d}}}=\frac{1}{d!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{d}}^{i_{1}\ldots i_{d}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{1}}}{\unicode[STIX]{x2202}a^{i_{1}}}\cdots \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}^{\,j_{d}}}{\unicode[STIX]{x2202}a^{i_{d}}}.\end{eqnarray}$$
The inverse matrix components of an invertible matrix
![]() $A$
is given by
$A$
is given by
 $(A^{-1})_{i}^{j}=(\det (A)^{-1})\unicode[STIX]{x0394}_{i}^{j}$
, where
$(A^{-1})_{i}^{j}=(\det (A)^{-1})\unicode[STIX]{x0394}_{i}^{j}$
, where
![]() $\unicode[STIX]{x0394}_{i}^{j}$
is the
$\unicode[STIX]{x0394}_{i}^{j}$
is the
![]() $(i,j)$
th minor, i.e. the determinant of a matrix which it is obtained from
$(i,j)$
th minor, i.e. the determinant of a matrix which it is obtained from
![]() $A$
when the
$A$
when the
![]() $i$
th row and
$i$
th row and
![]() $j$
th column are deleted. In other words we have
$j$
th column are deleted. In other words we have
 $\det (A)\unicode[STIX]{x1D6FF}_{k}^{j}=A_{i}^{j}\unicode[STIX]{x0394}_{k}^{i}=\unicode[STIX]{x0394}_{i}^{j}A_{k}^{i}$
. Therefore, we obtain
$\det (A)\unicode[STIX]{x1D6FF}_{k}^{j}=A_{i}^{j}\unicode[STIX]{x0394}_{k}^{i}=\unicode[STIX]{x0394}_{i}^{j}A_{k}^{i}$
. Therefore, we obtain
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\det (A)}{\unicode[STIX]{x2202}A_{i}^{j}}=\unicode[STIX]{x0394}_{j}^{i}=\det (A)(A^{-1})_{j}^{i}\quad \text{so that}~\text{d}(\det (A))=\det (A)\text{Tr}(A^{-1}\,\text{d}A),\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\det (A)}{\unicode[STIX]{x2202}A_{i}^{j}}=\unicode[STIX]{x0394}_{j}^{i}=\det (A)(A^{-1})_{j}^{i}\quad \text{so that}~\text{d}(\det (A))=\det (A)\text{Tr}(A^{-1}\,\text{d}A),\end{eqnarray}$$
where
![]() $\text{Tr}(A)$
denotes the trace of
$\text{Tr}(A)$
denotes the trace of
![]() $A$
, i.e.
$A$
, i.e.
![]() $\sum _{i}A_{i}^{i}$
. Now, we consider the metric tensor
$\sum _{i}A_{i}^{i}$
. Now, we consider the metric tensor
![]() $g\in {\mathcal{T}}_{2}^{0}$
which can be identified to a matrix. We define the minor
$g\in {\mathcal{T}}_{2}^{0}$
which can be identified to a matrix. We define the minor
 $a_{ij}:=g\text{g}^{ij}$
, with
$a_{ij}:=g\text{g}^{ij}$
, with
 $g=\sqrt{\det (\text{g}_{ij})}$
. It then follows that the differential of the determinant
$g=\sqrt{\det (\text{g}_{ij})}$
. It then follows that the differential of the determinant
![]() $g$
is
$g$
is
 $\text{d}g=a_{ij}\,\text{d}\text{g}_{ij}=g\text{g}^{ij}\,\text{d}\text{g}_{ij}$
. Furthermore, using partial derivatives, the differential of
$\text{d}g=a_{ij}\,\text{d}\text{g}_{ij}=g\text{g}^{ij}\,\text{d}\text{g}_{ij}$
. Furthermore, using partial derivatives, the differential of
![]() $g$
is
$g$
is
 $\text{d}g=\unicode[STIX]{x2202}_{k}g\,\text{d}a^{k}=g\text{g}^{ij}\unicode[STIX]{x2202}_{k}\text{g}_{ij}\,\text{d}a^{k}$
, from which we infer by identification that
$\text{d}g=\unicode[STIX]{x2202}_{k}g\,\text{d}a^{k}=g\text{g}^{ij}\unicode[STIX]{x2202}_{k}\text{g}_{ij}\,\text{d}a^{k}$
, from which we infer by identification that
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{k}g=g\text{g}^{ij}\unicode[STIX]{x2202}_{k}\text{g}_{ij}=-g\text{g}_{ij}\unicode[STIX]{x2202}_{k}\text{g}^{ij}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{k}g=g\text{g}^{ij}\unicode[STIX]{x2202}_{k}\text{g}_{ij}=-g\text{g}_{ij}\unicode[STIX]{x2202}_{k}\text{g}^{ij}.\end{eqnarray}$$
B.7 Exterior algebra and differential forms
Let
![]() $E$
be a finite-dimensional vector space. The space
$E$
be a finite-dimensional vector space. The space
![]() $\bigwedge ^{p}(E)$
, is the subspace of all skew-symmetric elements of
$\bigwedge ^{p}(E)$
, is the subspace of all skew-symmetric elements of
![]() ${\mathcal{L}}^{p}(E)$
or
${\mathcal{L}}^{p}(E)$
or
![]() $\text{T}_{p}^{0}(E)$
, i.e. all antisymmetric covariant
$\text{T}_{p}^{0}(E)$
, i.e. all antisymmetric covariant
![]() $p$
-tensors on
$p$
-tensors on
![]() $E$
. An element of
$E$
. An element of
![]() $\bigwedge ^{p}(E)$
is called an exterior
$\bigwedge ^{p}(E)$
is called an exterior
![]() $p$
-form. The exterior product
$p$
-form. The exterior product
![]() $\wedge$
(wedge or Grassmann product) of a
$\wedge$
(wedge or Grassmann product) of a
![]() $p$
-form and a
$p$
-form and a
![]() $q$
-form is a mapping
$q$
-form is a mapping
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \wedge :\bigwedge ^{p}(E)\times \bigwedge ^{q}(E)\rightarrow \bigwedge ^{p+q}(E)\\ (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\mapsto \unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \wedge :\bigwedge ^{p}(E)\times \bigwedge ^{q}(E)\rightarrow \bigwedge ^{p+q}(E)\\ (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\mapsto \unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD},\end{array}\right\}\end{eqnarray}$$
with
![]() $\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}$
defined by
$\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}$
defined by
 $$\begin{eqnarray}(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})(v_{1},\ldots ,v_{p+q})=\frac{1}{p!q!}\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \mathfrak{S}_{p+q}}\text{sign}(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D6FC}(v_{\unicode[STIX]{x1D70E}(1)},\ldots ,v_{\unicode[STIX]{x1D70E}(p)})\unicode[STIX]{x1D6FD}(v_{\unicode[STIX]{x1D70E}(p+1)},\ldots ,v_{\unicode[STIX]{x1D70E}(p+q)}),\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})(v_{1},\ldots ,v_{p+q})=\frac{1}{p!q!}\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \mathfrak{S}_{p+q}}\text{sign}(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D6FC}(v_{\unicode[STIX]{x1D70E}(1)},\ldots ,v_{\unicode[STIX]{x1D70E}(p)})\unicode[STIX]{x1D6FD}(v_{\unicode[STIX]{x1D70E}(p+1)},\ldots ,v_{\unicode[STIX]{x1D70E}(p+q)}),\end{eqnarray}$$
where
![]() $v_{i}\in E$
and
$v_{i}\in E$
and
![]() $\mathfrak{S}_{p}$
is the permutation group on
$\mathfrak{S}_{p}$
is the permutation group on
![]() $p$
elements. Componentwise it is defined as
$p$
elements. Componentwise it is defined as
 $$\begin{eqnarray}(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})_{i_{1}\ldots i_{p+q}}=\frac{1}{p!q!}\unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{p+q}}^{\,j_{1}\ldots j_{p}k_{1}\ldots k_{q}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p}}\unicode[STIX]{x1D6FD}_{k_{1}\ldots k_{q}}.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})_{i_{1}\ldots i_{p+q}}=\frac{1}{p!q!}\unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{p+q}}^{\,j_{1}\ldots j_{p}k_{1}\ldots k_{q}}\unicode[STIX]{x1D6FC}_{j_{1}\ldots j_{p}}\unicode[STIX]{x1D6FD}_{k_{1}\ldots k_{q}}.\end{eqnarray}$$
In particular, if
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
are 1-forms then
$\unicode[STIX]{x1D6FD}$
are 1-forms then
 $\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}\otimes \unicode[STIX]{x1D6FC}$
. It follows from the definition that the exterior product is: (i) associative
$\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FD}\otimes \unicode[STIX]{x1D6FC}$
. It follows from the definition that the exterior product is: (i) associative
 $(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})\wedge \unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FC}\wedge (\unicode[STIX]{x1D6FD}\wedge \unicode[STIX]{x1D6FE})$
; (ii) bilinear
$(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})\wedge \unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FC}\wedge (\unicode[STIX]{x1D6FD}\wedge \unicode[STIX]{x1D6FE})$
; (ii) bilinear
 $\unicode[STIX]{x1D6FC}\wedge (\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FC}\wedge (\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FE}$
and
 $\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}$
, with
$\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}$
, with
![]() $\unicode[STIX]{x1D706}\in \mathbb{R}$
; (iii) not commutative in general
$\unicode[STIX]{x1D706}\in \mathbb{R}$
; (iii) not commutative in general
 $\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}=(-1)^{pq}\unicode[STIX]{x1D6FD}\wedge \unicode[STIX]{x1D6FC}$
if
$\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}=(-1)^{pq}\unicode[STIX]{x1D6FD}\wedge \unicode[STIX]{x1D6FC}$
if
 $\unicode[STIX]{x1D6FC}\in \bigwedge ^{p}(E)$
,
$\unicode[STIX]{x1D6FC}\in \bigwedge ^{p}(E)$
,
 $\unicode[STIX]{x1D6FD}\in \bigwedge ^{q}(E)$
. From the property (iii) it follows that
$\unicode[STIX]{x1D6FD}\in \bigwedge ^{q}(E)$
. From the property (iii) it follows that
![]() $(\wedge \,\unicode[STIX]{x1D6FC})^{k}$
is identically zero if the degree of
$(\wedge \,\unicode[STIX]{x1D6FC})^{k}$
is identically zero if the degree of
![]() $\unicode[STIX]{x1D6FC}$
is odd; but not otherwise. If
$\unicode[STIX]{x1D6FC}$
is odd; but not otherwise. If
![]() $E$
is finite-dimensional with
$E$
is finite-dimensional with
 $d=\dim (E)$
, then for
$d=\dim (E)$
, then for
![]() $p>d$
,
$p>d$
,
 $\bigwedge ^{p}(E)=\{0\}$
. Indeed the only non-zero components of a totally antisymmetric covariant
$\bigwedge ^{p}(E)=\{0\}$
. Indeed the only non-zero components of a totally antisymmetric covariant
![]() $p$
-tensor are those in which all indices are different, a situation which can never exist if
$p$
-tensor are those in which all indices are different, a situation which can never exist if
![]() $p>d$
. For
$p>d$
. For
 $0<p\leqslant d$
,
$0<p\leqslant d$
,
![]() $\bigwedge ^{p}(E)$
has dimension
$\bigwedge ^{p}(E)$
has dimension
 $d!/(p!(d-p)!)$
. If
$d!/(p!(d-p)!)$
. If
 $\{e_{1},\ldots ,e_{d}\}$
is an ordered basis of
$\{e_{1},\ldots ,e_{d}\}$
is an ordered basis of
![]() $E$
and its dual basis
$E$
and its dual basis
 $\{e^{1},\ldots ,e^{d}\}$
, a basis for
$\{e^{1},\ldots ,e^{d}\}$
, a basis for
![]() $\bigwedge ^{p}(E)$
is
$\bigwedge ^{p}(E)$
is
 $$\begin{eqnarray}\{e^{i_{1}},\ldots ,e^{i_{p}}\mid 1\leqslant i_{1}<i_{2}<\cdots <i_{p}\leqslant d\}.\end{eqnarray}$$
$$\begin{eqnarray}\{e^{i_{1}},\ldots ,e^{i_{p}}\mid 1\leqslant i_{1}<i_{2}<\cdots <i_{p}\leqslant d\}.\end{eqnarray}$$
Therefore any
 $\unicode[STIX]{x1D6FC}\in \bigwedge ^{p}(E)$
, can be expanded as
$\unicode[STIX]{x1D6FC}\in \bigwedge ^{p}(E)$
, can be expanded as
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\mathop{\sum }_{i_{1}<\cdots <i_{p}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}e^{i_{1}}\wedge \cdots \wedge e^{i_{p}}=\frac{1}{p!}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}e^{i_{1}}\wedge \cdots \wedge e^{i_{p}}=\frac{1}{p!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}e^{\,j_{1}}\otimes \cdots \otimes e^{\,j_{p}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\mathop{\sum }_{i_{1}<\cdots <i_{p}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}e^{i_{1}}\wedge \cdots \wedge e^{i_{p}}=\frac{1}{p!}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}e^{i_{1}}\wedge \cdots \wedge e^{i_{p}}=\frac{1}{p!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}e^{\,j_{1}}\otimes \cdots \otimes e^{\,j_{p}}.\end{eqnarray}$$
Given the tangent vector bundle
![]() $TM$
of a manifold
$TM$
of a manifold
![]() $M$
, we can construct fiberwise the vector bundle
$M$
, we can construct fiberwise the vector bundle
![]() $\bigwedge ^{p}(M)$
of exterior differential
$\bigwedge ^{p}(M)$
of exterior differential
![]() $p$
-form on the tangent spaces of
$p$
-form on the tangent spaces of
![]() $M$
, as
$M$
, as
 $$\begin{eqnarray}\bigwedge ^{p}(M)=\bigwedge ^{p}(TM)=\mathop{\bigcup }_{a\in M}\bigwedge ^{p}(TM_{a}).\end{eqnarray}$$
$$\begin{eqnarray}\bigwedge ^{p}(M)=\bigwedge ^{p}(TM)=\mathop{\bigcup }_{a\in M}\bigwedge ^{p}(TM_{a}).\end{eqnarray}$$
The field of exterior differential
![]() $p$
-form on a manifold
$p$
-form on a manifold
![]() $M$
, denoted
$M$
, denoted
![]() $\unicode[STIX]{x039B}^{p}(M)$
, is defined as the
$\unicode[STIX]{x039B}^{p}(M)$
, is defined as the
![]() $\mathscr{C}^{\infty }$
section of
$\mathscr{C}^{\infty }$
section of
![]() $\bigwedge ^{p}(M)$
, i.e.
$\bigwedge ^{p}(M)$
, i.e.
 $\unicode[STIX]{x039B}^{p}(M)=\unicode[STIX]{x1D6E4}^{\infty }(\bigwedge ^{p}(M))$
. We have the following identifications:
$\unicode[STIX]{x039B}^{p}(M)=\unicode[STIX]{x1D6E4}^{\infty }(\bigwedge ^{p}(M))$
. We have the following identifications:
 $\unicode[STIX]{x039B}^{1}(M)={\mathcal{T}}_{1}^{0}(M)$
and
$\unicode[STIX]{x039B}^{1}(M)={\mathcal{T}}_{1}^{0}(M)$
and
 $\unicode[STIX]{x039B}^{0}(M)={\mathcal{F}}(M)$
, where
$\unicode[STIX]{x039B}^{0}(M)={\mathcal{F}}(M)$
, where
![]() ${\mathcal{F}}(M)$
is the set of mappings from
${\mathcal{F}}(M)$
is the set of mappings from
![]() $M$
into
$M$
into
![]() $\mathbb{R}$
that are of class
$\mathbb{R}$
that are of class
![]() $\mathscr{C}^{\infty }$
. As for the definition of tensors on a manifold, given
$\mathscr{C}^{\infty }$
. As for the definition of tensors on a manifold, given
![]() $(U,\unicode[STIX]{x1D719})$
, an admissible local chart on
$(U,\unicode[STIX]{x1D719})$
, an admissible local chart on
![]() $M$
, the local expression on
$M$
, the local expression on
![]() $U$
of
$U$
of
 $\unicode[STIX]{x1D6FC}\in \bigwedge ^{k}(M)$
is given by
$\unicode[STIX]{x1D6FC}\in \bigwedge ^{k}(M)$
is given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{|_{U}} & = & \displaystyle \mathop{\sum }_{i_{1}<\cdots <i_{p}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}(a)\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}=\frac{1}{p!}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}(a)\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}(a)\,\text{d}a^{\,j_{1}}\otimes \cdots \otimes \text{d}a^{\,j_{p}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{|_{U}} & = & \displaystyle \mathop{\sum }_{i_{1}<\cdots <i_{p}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}(a)\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}=\frac{1}{p!}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}(a)\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{p!}\unicode[STIX]{x1D6FF}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{p}}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}(a)\,\text{d}a^{\,j_{1}}\otimes \cdots \otimes \text{d}a^{\,j_{p}}.\end{eqnarray}$$
The differential
![]() $p$
-form is of class
$p$
-form is of class
![]() $\mathscr{C}^{k}$
, when the component maps
$\mathscr{C}^{k}$
, when the component maps
 $\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}:U\ni a\rightarrow \unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}(a)\in \mathbb{R}$
are
$\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}:U\ni a\rightarrow \unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}(a)\in \mathbb{R}$
are
![]() $k$
times continuously differentiable on
$k$
times continuously differentiable on
![]() $U$
or are differentiable functions of
$U$
or are differentiable functions of
![]() $a$
of class
$a$
of class
![]() $\mathscr{C}^{k}(U)$
.
$\mathscr{C}^{k}(U)$
.
Pullback and pushforward of
![]() $p$
-forms are just special cases of general definitions given for tensors (see § B.2) since a
$p$
-forms are just special cases of general definitions given for tensors (see § B.2) since a
![]() $p$
-form field is a totally antisymmetric covariant
$p$
-form field is a totally antisymmetric covariant
![]() $p$
-tensor field. Moreover we have the following properties. Let
$p$
-tensor field. Moreover we have the following properties. Let
 $\unicode[STIX]{x1D711}:M\rightarrow N$
be of class
$\unicode[STIX]{x1D711}:M\rightarrow N$
be of class
![]() $\mathscr{C}^{1}$
. Then
$\mathscr{C}^{1}$
. Then
 $\unicode[STIX]{x1D711}^{\ast }:\unicode[STIX]{x039B}^{k}(N)\rightarrow \unicode[STIX]{x039B}^{k}(M)$
is a homeomorphism of differential algebras, that is
$\unicode[STIX]{x1D711}^{\ast }:\unicode[STIX]{x039B}^{k}(N)\rightarrow \unicode[STIX]{x039B}^{k}(M)$
is a homeomorphism of differential algebras, that is
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D711}^{\ast }(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FD},\quad \unicode[STIX]{x1D711}^{\ast }(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FE},\\ \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x039B}^{p}(N),\quad \unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{q}(N),\quad \unicode[STIX]{x1D706}\in \mathbb{R}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D711}^{\ast }(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FD},\quad \unicode[STIX]{x1D711}^{\ast }(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FE},\\ \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x039B}^{p}(N),\quad \unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{q}(N),\quad \unicode[STIX]{x1D706}\in \mathbb{R}.\end{array}\right\}\end{eqnarray}$$
Of course similar formulae hold also for the pushforward operator when
 $\unicode[STIX]{x1D711}:M\rightarrow N$
is a diffeomorphism. The Lie derivative is a derivative on
$\unicode[STIX]{x1D711}:M\rightarrow N$
is a diffeomorphism. The Lie derivative is a derivative on
![]() $\unicode[STIX]{x039B}^{p}(M)$
, since it satisfies the Leibniz rule:
$\unicode[STIX]{x039B}^{p}(M)$
, since it satisfies the Leibniz rule:
 $$\begin{eqnarray}\unicode[STIX]{x00A3}_{v}(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})=\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FD},\quad \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M),\quad \unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{q}(M).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x00A3}_{v}(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})=\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FD},\quad \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M),\quad \unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{q}(M).\end{eqnarray}$$
From the definition of Lie derivative for tensors, the coordinate expression for the Lie derivative
 $\unicode[STIX]{x00A3}_{v}:\unicode[STIX]{x039B}^{p}(M)\rightarrow \unicode[STIX]{x039B}^{p}(M)$
of a
$\unicode[STIX]{x00A3}_{v}:\unicode[STIX]{x039B}^{p}(M)\rightarrow \unicode[STIX]{x039B}^{p}(M)$
of a
![]() $p$
-form
$p$
-form
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
 $$\begin{eqnarray}\displaystyle \text{}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FC} & = & \displaystyle \frac{1}{p!}v^{l}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{p!}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}(\unicode[STIX]{x2202}_{l}v^{i_{1}}\,\text{d}a^{l}\wedge \text{d}a^{i_{2}}\wedge \cdots \wedge \text{d}a^{i_{p}}+\cdots +\unicode[STIX]{x2202}_{l}v^{i_{p}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p-1}}\wedge \text{d}a^{l}).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FC} & = & \displaystyle \frac{1}{p!}v^{l}\unicode[STIX]{x2202}_{l}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{p!}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}(\unicode[STIX]{x2202}_{l}v^{i_{1}}\,\text{d}a^{l}\wedge \text{d}a^{i_{2}}\wedge \cdots \wedge \text{d}a^{i_{p}}+\cdots +\unicode[STIX]{x2202}_{l}v^{i_{p}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p-1}}\wedge \text{d}a^{l}).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
This can also be recast in a simpler form, which however is not antisymmetric, namely
 $$\begin{eqnarray}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FC}=\frac{1}{p!}(v^{k}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}+p\unicode[STIX]{x1D6FC}_{ki_{2}\ldots i_{p}}\unicode[STIX]{x2202}_{i_{1}}v^{k})\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FC}=\frac{1}{p!}(v^{k}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}+p\unicode[STIX]{x1D6FC}_{ki_{2}\ldots i_{p}}\unicode[STIX]{x2202}_{i_{1}}v^{k})\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}.\end{eqnarray}$$
For more details we refer the reader to Choquet-Bruhat et al. (Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977, § IV.A.1, p. 195), Abraham et al. (Reference Abraham, Marsden and Ratiu1998, § 6.1, p. 392; § 6.3, p. 417) and Fecko (Reference Fecko2006, § 5.3, p. 102).
B.8 Exterior derivative and interior product
The exterior differentiation operator
 $\text{d}:\unicode[STIX]{x039B}^{p}(M)\rightarrow \unicode[STIX]{x039B}^{p+1}(M)$
maps a
$\text{d}:\unicode[STIX]{x039B}^{p}(M)\rightarrow \unicode[STIX]{x039B}^{p+1}(M)$
maps a
![]() $p$
-form
$p$
-form
![]() $\unicode[STIX]{x1D6FC}$
of class
$\unicode[STIX]{x1D6FC}$
of class
![]() $\mathscr{C}^{k}$
into a
$\mathscr{C}^{k}$
into a
![]() $(p+1)$
-form
$(p+1)$
-form
![]() $\text{d}\unicode[STIX]{x1D6FC}$
of class
$\text{d}\unicode[STIX]{x1D6FC}$
of class
![]() $\mathscr{C}^{k-1}$
, called the exterior derivative of
$\mathscr{C}^{k-1}$
, called the exterior derivative of
![]() $\unicode[STIX]{x1D6FC}$
. The operator
$\unicode[STIX]{x1D6FC}$
. The operator
![]() $\text{d}$
is uniquely defined by the following properties:
$\text{d}$
is uniquely defined by the following properties:
-
(i)
 $\text{d}$
is linear:
$\text{d}$
is linear:
 $\text{d}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD})=\text{d}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D706}\,\text{d}\unicode[STIX]{x1D6FD}$
,
$\text{d}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD})=\text{d}\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D706}\,\text{d}\unicode[STIX]{x1D6FD}$
,
 $\unicode[STIX]{x1D706}\in \mathbb{R}$
,
$\unicode[STIX]{x1D706}\in \mathbb{R}$
,
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(M)$
;
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(M)$
; -
(ii)
 $\text{d}$
is an antiderivative; that is,
$\text{d}$
is an antiderivative; that is,
 $\text{d}$
is
$\text{d}$
is
 $\mathbb{R}$
-linear and for
$\mathbb{R}$
-linear and for
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
and
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
and
 $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{q}(M)$
,
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{q}(M)$
, $\text{d}(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})=\text{d}\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}+(-1)^{p}\unicode[STIX]{x1D6FC}\wedge \text{d}\unicode[STIX]{x1D6FD}$
(‘antiLeibniz’ product rule);
$\text{d}(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})=\text{d}\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}+(-1)^{p}\unicode[STIX]{x1D6FC}\wedge \text{d}\unicode[STIX]{x1D6FD}$
(‘antiLeibniz’ product rule); -
(iii)
 $\text{d}^{2}=\text{d}\text{d}=0$
;
$\text{d}^{2}=\text{d}\text{d}=0$
; -
(iv) if
 $f\in {\mathcal{F}}(M)$
is a 0-form, then
$f\in {\mathcal{F}}(M)$
is a 0-form, then
 $\text{d}f$
is the ordinary differential of
$\text{d}f$
is the ordinary differential of
 $f$
, i.e.
$f$
, i.e.
 $\text{d}f=\unicode[STIX]{x2202}_{i}f\,\text{d}a^{i}$
;
$\text{d}f=\unicode[STIX]{x2202}_{i}f\,\text{d}a^{i}$
; -
(v) the operation
 $\text{d}$
is local; if
$\text{d}$
is local; if
 $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
 $\unicode[STIX]{x1D6FD}$
coincide on an open set
$\unicode[STIX]{x1D6FD}$
coincide on an open set
 $U$
,
$U$
,
 $\text{d}\unicode[STIX]{x1D6FC}=\text{d}\unicode[STIX]{x1D6FD}$
on
$\text{d}\unicode[STIX]{x1D6FC}=\text{d}\unicode[STIX]{x1D6FD}$
on
 $U$
; that is, the behaviour of
$U$
; that is, the behaviour of
 $\unicode[STIX]{x1D6FC}$
outside
$\unicode[STIX]{x1D6FC}$
outside
 $U$
does not affect
$U$
does not affect
 $\text{d}\unicode[STIX]{x1D6FC}_{|_{U}}$
, i.e.
$\text{d}\unicode[STIX]{x1D6FC}_{|_{U}}$
, i.e.
 $\text{d}(\unicode[STIX]{x1D6FC}_{|_{U}})=(\text{d}\unicode[STIX]{x1D6FC})_{|_{U}}$
.
$\text{d}(\unicode[STIX]{x1D6FC}_{|_{U}})=(\text{d}\unicode[STIX]{x1D6FC})_{|_{U}}$
.
Let
 $\unicode[STIX]{x1D711}:M\rightarrow N$
be a diffeomorphism. Let
$\unicode[STIX]{x1D711}:M\rightarrow N$
be a diffeomorphism. Let
 $v\in {\mathcal{T}}_{0}^{1}(M)$
,
$v\in {\mathcal{T}}_{0}^{1}(M)$
,
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
and
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
and
 $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(N)$
. We have the properties:
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(N)$
. We have the properties:
 $$\begin{eqnarray}\unicode[STIX]{x1D711}^{\ast }(\text{d}\unicode[STIX]{x1D6FD})=\text{d}(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FD}),\quad \unicode[STIX]{x1D711}_{\ast }(\text{d}\unicode[STIX]{x1D6FC})=\text{d}(\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x1D6FC}),\quad \text{d}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x00A3}_{v}\,\text{d}\unicode[STIX]{x1D6FC}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}^{\ast }(\text{d}\unicode[STIX]{x1D6FD})=\text{d}(\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FD}),\quad \unicode[STIX]{x1D711}_{\ast }(\text{d}\unicode[STIX]{x1D6FC})=\text{d}(\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x1D6FC}),\quad \text{d}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x00A3}_{v}\,\text{d}\unicode[STIX]{x1D6FC}.\end{eqnarray}$$
The contracted multiplication or interior product (also called inner product) of a
![]() $p$
-form
$p$
-form
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
and a vector
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
and a vector
 $v\in {\mathcal{T}}_{0}^{1}(M)$
is denoted
$v\in {\mathcal{T}}_{0}^{1}(M)$
is denoted
![]() $\text{i}_{v}\unicode[STIX]{x1D6FC}$
. The operator
$\text{i}_{v}\unicode[STIX]{x1D6FC}$
. The operator
 $\text{i}_{v}:\unicode[STIX]{x039B}^{p}(M)\rightarrow \unicode[STIX]{x039B}^{p-1}(M)$
is defined as follows:
$\text{i}_{v}:\unicode[STIX]{x039B}^{p}(M)\rightarrow \unicode[STIX]{x039B}^{p-1}(M)$
is defined as follows:
-
(i)
 $\text{i}_{v}$
is an antiderivative; that is,
$\text{i}_{v}$
is an antiderivative; that is,
 $\text{i}_{v}$
is
$\text{i}_{v}$
is
 $\mathbb{R}$
-linear and for
$\mathbb{R}$
-linear and for
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
and
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
and
 $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{q}(M)$
,
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{q}(M)$
, $\text{i}_{v}(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})=(\text{i}_{v}\unicode[STIX]{x1D6FC})\wedge \unicode[STIX]{x1D6FD}+(-1)^{p}\unicode[STIX]{x1D6FC}\wedge (\text{i}_{v}\unicode[STIX]{x1D6FD})$
(‘antiLeibniz’ product rule);
$\text{i}_{v}(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD})=(\text{i}_{v}\unicode[STIX]{x1D6FC})\wedge \unicode[STIX]{x1D6FD}+(-1)^{p}\unicode[STIX]{x1D6FC}\wedge (\text{i}_{v}\unicode[STIX]{x1D6FD})$
(‘antiLeibniz’ product rule); -
(ii)
 $\text{i}_{v}f=0$
,
$\text{i}_{v}f=0$
,
 $f\in {\mathcal{F}}(M)$
;
$f\in {\mathcal{F}}(M)$
;
 $\text{i}_{v}\,\text{d}a^{i}=v^{i}$
.
$\text{i}_{v}\,\text{d}a^{i}=v^{i}$
.
Then by the ‘antiLeibniz’ rule, the coordinate expression of the interior product of a
![]() $p$
-form
$p$
-form
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
 $$\begin{eqnarray}\text{i}_{v}\unicode[STIX]{x1D6FC}=\frac{1}{(p-1)!}v^{k}\unicode[STIX]{x1D6FC}_{ki_{2}\ldots i_{p}}\,\text{d}a^{i_{2}}\wedge \cdots \wedge \text{d}a^{i_{p}}=\mathop{\sum }_{i_{1}<\cdots <i_{p-1}}v^{k}\unicode[STIX]{x1D6FC}_{ki_{1}\ldots i_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p-1}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{i}_{v}\unicode[STIX]{x1D6FC}=\frac{1}{(p-1)!}v^{k}\unicode[STIX]{x1D6FC}_{ki_{2}\ldots i_{p}}\,\text{d}a^{i_{2}}\wedge \cdots \wedge \text{d}a^{i_{p}}=\mathop{\sum }_{i_{1}<\cdots <i_{p-1}}v^{k}\unicode[STIX]{x1D6FC}_{ki_{1}\ldots i_{p-1}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p-1}}.\end{eqnarray}$$
Let
 $\unicode[STIX]{x1D711}:M\rightarrow N$
be a diffeomorphism. Let
$\unicode[STIX]{x1D711}:M\rightarrow N$
be a diffeomorphism. Let
![]() $v$
,
$v$
,
 $w\in {\mathcal{T}}_{0}^{1}(M)$
,
$w\in {\mathcal{T}}_{0}^{1}(M)$
,
 $u\in {\mathcal{T}}_{0}^{1}(N)$
,
$u\in {\mathcal{T}}_{0}^{1}(N)$
,
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
,
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
,
 $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(N)$
,
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(N)$
,
 $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x039B}^{1}(M)$
, and
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x039B}^{1}(M)$
, and
 $f\in {\mathcal{F}}(M)$
. Using the commutator notation
$f\in {\mathcal{F}}(M)$
. Using the commutator notation
 $[A,B]=AB-BA$
, we have the properties:
$[A,B]=AB-BA$
, we have the properties:
-
(i)
 $\text{i}_{v}^{2}=\text{i}_{v}\text{i}_{v}=0$
;
$\text{i}_{v}^{2}=\text{i}_{v}\text{i}_{v}=0$
; -
(ii)
 $\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FC}=\text{i}_{v}\,\text{d}\unicode[STIX]{x1D6FC}+\text{d}\text{i}_{v}\unicode[STIX]{x1D6FC}$
, (Cartan formula);
$\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FC}=\text{i}_{v}\,\text{d}\unicode[STIX]{x1D6FC}+\text{d}\text{i}_{v}\unicode[STIX]{x1D6FC}$
, (Cartan formula); -
(iii)
 $\text{i}_{fv}\unicode[STIX]{x1D6FC}=f\text{i}_{v}\unicode[STIX]{x1D6FC}=\text{i}_{v}f\unicode[STIX]{x1D6FC}$
,
$\text{i}_{fv}\unicode[STIX]{x1D6FC}=f\text{i}_{v}\unicode[STIX]{x1D6FC}=\text{i}_{v}f\unicode[STIX]{x1D6FC}$
,
 $\text{i}_{v}\,\text{d}f=\unicode[STIX]{x00A3}_{v}f$
,
$\text{i}_{v}\,\text{d}f=\unicode[STIX]{x00A3}_{v}f$
,
 $\unicode[STIX]{x00A3}_{fv}\unicode[STIX]{x1D6FC}=f\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FC}+\text{d}f\wedge \text{i}_{v}\unicode[STIX]{x1D6FC}$
;
$\unicode[STIX]{x00A3}_{fv}\unicode[STIX]{x1D6FC}=f\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D6FC}+\text{d}f\wedge \text{i}_{v}\unicode[STIX]{x1D6FC}$
; -
(iv)
 $[\text{}\unicode[STIX]{x00A3}_{v},\text{i}_{w}]\unicode[STIX]{x1D6FC}=\text{i}_{[v,w]}\unicode[STIX]{x1D6FC}$
,
$[\text{}\unicode[STIX]{x00A3}_{v},\text{i}_{w}]\unicode[STIX]{x1D6FC}=\text{i}_{[v,w]}\unicode[STIX]{x1D6FC}$
,
 $[\text{}\unicode[STIX]{x00A3}_{v},\unicode[STIX]{x00A3}_{w}]\unicode[STIX]{x1D6FC}=\unicode[STIX]{x00A3}_{[v,w]}\unicode[STIX]{x1D6FC}$
,
$[\text{}\unicode[STIX]{x00A3}_{v},\unicode[STIX]{x00A3}_{w}]\unicode[STIX]{x1D6FC}=\unicode[STIX]{x00A3}_{[v,w]}\unicode[STIX]{x1D6FC}$
,
 ${\text{i}_{v}\unicode[STIX]{x00A3}}_{v}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x00A3}_{v}\text{i}_{v}\unicode[STIX]{x1D6FC}$
,
${\text{i}_{v}\unicode[STIX]{x00A3}}_{v}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x00A3}_{v}\text{i}_{v}\unicode[STIX]{x1D6FC}$
,
 $\text{i}_{v}\text{i}_{w}\,\text{d}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x00A3}_{v}\text{i}_{w}\unicode[STIX]{x1D6FE}-\unicode[STIX]{x00A3}_{w}\text{i}_{v}\unicode[STIX]{x1D6FE}-\text{i}_{[v,w]}\unicode[STIX]{x1D6FE}$
;
$\text{i}_{v}\text{i}_{w}\,\text{d}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x00A3}_{v}\text{i}_{w}\unicode[STIX]{x1D6FE}-\unicode[STIX]{x00A3}_{w}\text{i}_{v}\unicode[STIX]{x1D6FE}-\text{i}_{[v,w]}\unicode[STIX]{x1D6FE}$
; -
(v)
 $\unicode[STIX]{x1D711}^{\ast }\text{i}_{u}\unicode[STIX]{x1D6FD}=\text{i}_{\unicode[STIX]{x1D711}^{\ast }u}\,\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D711}^{\ast }\text{i}_{u}\unicode[STIX]{x1D6FD}=\text{i}_{\unicode[STIX]{x1D711}^{\ast }u}\,\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D6FD}$
,
 $\unicode[STIX]{x1D711}_{\ast }\text{i}_{v}\unicode[STIX]{x1D6FC}=\text{i}_{\unicode[STIX]{x1D711}_{\ast }v}\,\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D711}_{\ast }\text{i}_{v}\unicode[STIX]{x1D6FC}=\text{i}_{\unicode[STIX]{x1D711}_{\ast }v}\,\unicode[STIX]{x1D711}_{\ast }\unicode[STIX]{x1D6FC}$
.
The last formula of point (iv), which expresses the exterior derivative in terms of the Lie derivative, can be extended to high-order form (see, e.g., Abraham et al. Reference Abraham, Marsden and Ratiu1998, § 6.4, p. 431). For more details about exterior derivative and interior product, we refer the reader to Choquet-Bruhat et al. (Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977, §§ IV.A.2–IV.A.4, p. 200) and Abraham et al. (Reference Abraham, Marsden and Ratiu1998, § 6.4, p. 423).
B.9 Hodge dual operator and exterior coderivative
Let
![]() $(M,g)$
be a
$(M,g)$
be a
![]() $d$
-dimensional Riemannian manifold with the volume form
$d$
-dimensional Riemannian manifold with the volume form
![]() $\unicode[STIX]{x1D707}$
. The Hodge dual operator is defined as the unique isomorphism
$\unicode[STIX]{x1D707}$
. The Hodge dual operator is defined as the unique isomorphism
 $\star :\unicode[STIX]{x039B}^{p}(M)\rightarrow \unicode[STIX]{x039B}^{d-p}(M)$
, which satisfies (see, e.g., Abraham et al.
Reference Abraham, Marsden and Ratiu1998, § 6.2, p. 411)
$\star :\unicode[STIX]{x039B}^{p}(M)\rightarrow \unicode[STIX]{x039B}^{d-p}(M)$
, which satisfies (see, e.g., Abraham et al.
Reference Abraham, Marsden and Ratiu1998, § 6.2, p. 411)
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}\wedge \star \unicode[STIX]{x1D6FD}=(\!(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\!)_{g}\,\unicode[STIX]{x1D707},\quad \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(M),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}\wedge \star \unicode[STIX]{x1D6FD}=(\!(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\!)_{g}\,\unicode[STIX]{x1D707},\quad \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(M),\end{eqnarray}$$
with
 $$\begin{eqnarray}(\!(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\!)_{g}=\frac{1}{p!}\,\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}\unicode[STIX]{x1D6FD}^{i_{1}\ldots i_{p}}=\frac{1}{p!}\,\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}\unicode[STIX]{x1D6FD}_{j_{1}\ldots j_{p}}g^{i_{1}j_{1}}\ldots g^{i_{p}j_{p}}.\end{eqnarray}$$
$$\begin{eqnarray}(\!(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\!)_{g}=\frac{1}{p!}\,\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}\unicode[STIX]{x1D6FD}^{i_{1}\ldots i_{p}}=\frac{1}{p!}\,\unicode[STIX]{x1D6FC}_{i_{1}\ldots i_{p}}\unicode[STIX]{x1D6FD}_{j_{1}\ldots j_{p}}g^{i_{1}j_{1}}\ldots g^{i_{p}j_{p}}.\end{eqnarray}$$
Using (B 46) with
 $\unicode[STIX]{x1D6FD}=\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}$
and
$\unicode[STIX]{x1D6FD}=\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}}$
and
 $\unicode[STIX]{x1D6FC}=\text{d}a^{\,j_{1}}\wedge \cdots \wedge \text{d}a^{\,j_{p}}$
, where
$\unicode[STIX]{x1D6FC}=\text{d}a^{\,j_{1}}\wedge \cdots \wedge \text{d}a^{\,j_{p}}$
, where
 $\{\,j_{1},\ldots ,j_{p}\}$
is the complementary set of indices to
$\{\,j_{1},\ldots ,j_{p}\}$
is the complementary set of indices to
 $\{\,j_{p+1},\ldots ,j_{d}\}$
, we obtain
$\{\,j_{p+1},\ldots ,j_{d}\}$
, we obtain
 $$\begin{eqnarray}\star (\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}})=\frac{1}{(d-p)!}\sqrt{\text{g}}\unicode[STIX]{x1D700}_{j_{1}\ldots j_{d}}g^{i_{1}j_{1}}\ldots g^{i_{p}j_{p}}\,\text{d}a^{\,j_{p+1}}\wedge \cdots \wedge \text{d}a^{\,j_{d}}.\end{eqnarray}$$
$$\begin{eqnarray}\star (\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{p}})=\frac{1}{(d-p)!}\sqrt{\text{g}}\unicode[STIX]{x1D700}_{j_{1}\ldots j_{d}}g^{i_{1}j_{1}}\ldots g^{i_{p}j_{p}}\,\text{d}a^{\,j_{p+1}}\wedge \cdots \wedge \text{d}a^{\,j_{d}}.\end{eqnarray}$$
Then the coordinate expression of the
![]() $(d-p)$
-form
$(d-p)$
-form
![]() $\star \unicode[STIX]{x1D6FC}$
, where
$\star \unicode[STIX]{x1D6FC}$
, where
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
, is
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
, is
 $$\begin{eqnarray}\star \unicode[STIX]{x1D6FC}=\frac{1}{(d-p)!}(\star \unicode[STIX]{x1D6FC})_{i_{1}\ldots i_{d-p}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{d-p}},\end{eqnarray}$$
$$\begin{eqnarray}\star \unicode[STIX]{x1D6FC}=\frac{1}{(d-p)!}(\star \unicode[STIX]{x1D6FC})_{i_{1}\ldots i_{d-p}}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{d-p}},\end{eqnarray}$$
with
 $$\begin{eqnarray}(\star \unicode[STIX]{x1D6FC})_{i_{1}\ldots i_{d-p}}=\frac{1}{p!}\sqrt{\text{g}}\,\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D6FC}^{\,j_{1}\ldots j_{p}}=\frac{1}{p!}\sqrt{\text{g}}\,\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}i_{1}\ldots i_{d-p}}g^{\,j_{1}k_{1}}\ldots g^{\,j_{p}k_{p}}\unicode[STIX]{x1D6FC}_{k_{1}\ldots k_{p}}.\end{eqnarray}$$
$$\begin{eqnarray}(\star \unicode[STIX]{x1D6FC})_{i_{1}\ldots i_{d-p}}=\frac{1}{p!}\sqrt{\text{g}}\,\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}i_{1}\ldots i_{d-p}}\unicode[STIX]{x1D6FC}^{\,j_{1}\ldots j_{p}}=\frac{1}{p!}\sqrt{\text{g}}\,\unicode[STIX]{x1D700}_{j_{1}\ldots j_{p}i_{1}\ldots i_{d-p}}g^{\,j_{1}k_{1}}\ldots g^{\,j_{p}k_{p}}\unicode[STIX]{x1D6FC}_{k_{1}\ldots k_{p}}.\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
 $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(M)$
. Then the Hodge dual operator satisfies
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(M)$
. Then the Hodge dual operator satisfies
 $\unicode[STIX]{x1D6FC}\wedge \star \unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}\wedge \star \unicode[STIX]{x1D6FC}=(\!(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\!)_{g}\,\unicode[STIX]{x1D707}$
,
$\unicode[STIX]{x1D6FC}\wedge \star \unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}\wedge \star \unicode[STIX]{x1D6FC}=(\!(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\!)_{g}\,\unicode[STIX]{x1D707}$
,
![]() $\star 1=\unicode[STIX]{x1D707}$
,
$\star 1=\unicode[STIX]{x1D707}$
,
![]() $\star \unicode[STIX]{x1D707}=1$
,
$\star \unicode[STIX]{x1D707}=1$
,
 $\star \star \unicode[STIX]{x1D6FC}=(-1)^{p(d-p)}\unicode[STIX]{x1D6FC}$
,
$\star \star \unicode[STIX]{x1D6FC}=(-1)^{p(d-p)}\unicode[STIX]{x1D6FC}$
,
 $(\!(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\!)_{g}=(\!(\star \unicode[STIX]{x1D6FC},\star \unicode[STIX]{x1D6FD})\!)_{g}$
. The Hodge dual is an
$(\!(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\!)_{g}=(\!(\star \unicode[STIX]{x1D6FC},\star \unicode[STIX]{x1D6FD})\!)_{g}$
. The Hodge dual is an
![]() $\mathbb{R}$
-linear operator, i.e.
$\mathbb{R}$
-linear operator, i.e.
 $\star (\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD})=\star \unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D706}\star \unicode[STIX]{x1D6FD}$
,
$\star (\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD})=\star \unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D706}\star \unicode[STIX]{x1D6FD}$
,
![]() $\unicode[STIX]{x1D706}\in \mathbb{R}$
. In particular if
$\unicode[STIX]{x1D706}\in \mathbb{R}$
. In particular if
![]() $v$
and
$v$
and
![]() $w$
are two vectors of
$w$
are two vectors of
![]() $\mathbb{R}^{3}$
, and if
$\mathbb{R}^{3}$
, and if
![]() $M=\mathbb{R}^{3}$
, then
$M=\mathbb{R}^{3}$
, then
 $v\times w=[\star (v^{\flat }\wedge w^{\flat })]^{\sharp }$
and
$v\times w=[\star (v^{\flat }\wedge w^{\flat })]^{\sharp }$
and
 $v\cdot w=\star (v^{\flat }\wedge \star w^{\flat })$
.
$v\cdot w=\star (v^{\flat }\wedge \star w^{\flat })$
.
The codifferential operator (or exterior coderivative)
 $\text{d}^{\star }:\unicode[STIX]{x039B}^{p}(M)\rightarrow \unicode[STIX]{x039B}^{p-1}(M)$
, is an
$\text{d}^{\star }:\unicode[STIX]{x039B}^{p}(M)\rightarrow \unicode[STIX]{x039B}^{p-1}(M)$
, is an
![]() $\mathbb{R}$
-linear operator which is defined by (see, e.g., Abraham et al.
Reference Abraham, Marsden and Ratiu1998, § 6.5, p. 457)
$\mathbb{R}$
-linear operator which is defined by (see, e.g., Abraham et al.
Reference Abraham, Marsden and Ratiu1998, § 6.5, p. 457)
 $$\begin{eqnarray}\text{d}^{\star }\unicode[STIX]{x1D6FC}=(-1)^{d(p-1)+1}\star \text{d}\star \unicode[STIX]{x1D6FC}.\end{eqnarray}$$
$$\begin{eqnarray}\text{d}^{\star }\unicode[STIX]{x1D6FC}=(-1)^{d(p-1)+1}\star \text{d}\star \unicode[STIX]{x1D6FC}.\end{eqnarray}$$
Since
![]() $\text{d}^{2}=0$
, then
$\text{d}^{2}=0$
, then
 $(\text{d}^{\star })^{2}=\text{d}^{\star }\circ \text{d}^{\star }=0$
.
$(\text{d}^{\star })^{2}=\text{d}^{\star }\circ \text{d}^{\star }=0$
.
Let
 $v\in {\mathcal{T}}_{0}^{1}(M)$
be a vector field on
$v\in {\mathcal{T}}_{0}^{1}(M)$
be a vector field on
![]() $M$
. Then the unique function
$M$
. Then the unique function
 $\text{div}_{\unicode[STIX]{x1D707}}v\in {\mathcal{F}}(M)$
such that
$\text{div}_{\unicode[STIX]{x1D707}}v\in {\mathcal{F}}(M)$
such that
 $$\begin{eqnarray}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D707}=:(\text{div}_{\unicode[STIX]{x1D707}}v)\unicode[STIX]{x1D707},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D707}=:(\text{div}_{\unicode[STIX]{x1D707}}v)\unicode[STIX]{x1D707},\end{eqnarray}$$
is by definition called the divergence of
![]() $v$
(see, e.g., Abraham et al.
Reference Abraham, Marsden and Ratiu1998, § 6.5, p. 455). Let
$v$
(see, e.g., Abraham et al.
Reference Abraham, Marsden and Ratiu1998, § 6.5, p. 455). Let
![]() $f$
,
$f$
,
 $h\in {\mathcal{F}}(M)$
, with
$h\in {\mathcal{F}}(M)$
, with
 $f(a)\neq 0$
,
$f(a)\neq 0$
,
![]() $\forall a\in M$
. Then we have the formula
$\forall a\in M$
. Then we have the formula
 $$\begin{eqnarray}\text{div}_{f\unicode[STIX]{x1D707}}v=\text{div}_{\unicode[STIX]{x1D707}}v+f^{-1}\text{}\unicode[STIX]{x00A3}_{v}f,\quad \text{div}_{\unicode[STIX]{x1D707}}(hv)=h\text{div}_{\unicode[STIX]{x1D707}}v+\unicode[STIX]{x00A3}_{v}h.\end{eqnarray}$$
$$\begin{eqnarray}\text{div}_{f\unicode[STIX]{x1D707}}v=\text{div}_{\unicode[STIX]{x1D707}}v+f^{-1}\text{}\unicode[STIX]{x00A3}_{v}f,\quad \text{div}_{\unicode[STIX]{x1D707}}(hv)=h\text{div}_{\unicode[STIX]{x1D707}}v+\unicode[STIX]{x00A3}_{v}h.\end{eqnarray}$$
Here, for a Riemannian manifold
![]() $(M,g)$
with an oriented chart
$(M,g)$
with an oriented chart
 $(a^{1},\ldots ,a^{d})$
on
$(a^{1},\ldots ,a^{d})$
on
![]() $M$
, the volume form
$M$
, the volume form
![]() $\unicode[STIX]{x1D707}$
is given by (see, e.g., Abraham et al.
Reference Abraham, Marsden and Ratiu1998, § 6.5, p. 457)
$\unicode[STIX]{x1D707}$
is given by (see, e.g., Abraham et al.
Reference Abraham, Marsden and Ratiu1998, § 6.5, p. 457)
 $$\begin{eqnarray}\unicode[STIX]{x1D707}(a)=\sqrt{g(a)}\,\text{d}a^{1}\wedge \cdots \wedge \text{d}a^{d}=\frac{1}{d!}\unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{d}}^{1\ldots d}\sqrt{g(a)}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{d}},\quad \text{where}~g=\det (\text{g}_{ij}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(a)=\sqrt{g(a)}\,\text{d}a^{1}\wedge \cdots \wedge \text{d}a^{d}=\frac{1}{d!}\unicode[STIX]{x1D6FF}_{i_{1}\ldots i_{d}}^{1\ldots d}\sqrt{g(a)}\,\text{d}a^{i_{1}}\wedge \cdots \wedge \text{d}a^{i_{d}},\quad \text{where}~g=\det (\text{g}_{ij}).\end{eqnarray}$$
Using the relation
 $\text{i}_{v}\unicode[STIX]{x1D707}=\star v^{\flat }$
and the Cartan formula we obtain
$\text{i}_{v}\unicode[STIX]{x1D707}=\star v^{\flat }$
and the Cartan formula we obtain
 $(\text{div}_{\unicode[STIX]{x1D707}}v)\unicode[STIX]{x1D707}:=\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D707}:=\text{d}\text{i}_{v}\unicode[STIX]{x1D707}=\text{d}\star v^{\flat }=-\star \text{d}^{\star }v^{\flat }=-(\text{d}^{\star }v^{\flat })\star 1=-(\text{d}^{\star }v^{\flat })\unicode[STIX]{x1D707}$
. Therefore
$(\text{div}_{\unicode[STIX]{x1D707}}v)\unicode[STIX]{x1D707}:=\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D707}:=\text{d}\text{i}_{v}\unicode[STIX]{x1D707}=\text{d}\star v^{\flat }=-\star \text{d}^{\star }v^{\flat }=-(\text{d}^{\star }v^{\flat })\star 1=-(\text{d}^{\star }v^{\flat })\unicode[STIX]{x1D707}$
. Therefore
 $$\begin{eqnarray}\text{div}_{\unicode[STIX]{x1D707}}v=-\text{d}^{\star }v^{\flat }=\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x2202}_{i}(\sqrt{\text{g}}v^{i}).\end{eqnarray}$$
$$\begin{eqnarray}\text{div}_{\unicode[STIX]{x1D707}}v=-\text{d}^{\star }v^{\flat }=\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x2202}_{i}(\sqrt{\text{g}}v^{i}).\end{eqnarray}$$
Let
 $\text{Op}=\text{Op}_{\unicode[STIX]{x0398}}$
be an operator that depends on a tensor field
$\text{Op}=\text{Op}_{\unicode[STIX]{x0398}}$
be an operator that depends on a tensor field
![]() $\unicode[STIX]{x0398}$
. The operator
$\unicode[STIX]{x0398}$
. The operator
![]() $\text{Op}$
is called natural with respect to the diffeomorphism
$\text{Op}$
is called natural with respect to the diffeomorphism
 $\unicode[STIX]{x1D711}:M\rightarrow N$
, if
$\unicode[STIX]{x1D711}:M\rightarrow N$
, if
 $\unicode[STIX]{x1D711}^{\ast }\text{Op}_{\unicode[STIX]{x0398}}=\text{Op}_{\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398}}\unicode[STIX]{x1D711}^{\ast }$
. Of course we have a similar definition with the pushforward operator since
$\unicode[STIX]{x1D711}^{\ast }\text{Op}_{\unicode[STIX]{x0398}}=\text{Op}_{\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x0398}}\unicode[STIX]{x1D711}^{\ast }$
. Of course we have a similar definition with the pushforward operator since
 $\unicode[STIX]{x1D711}_{\ast }=(\unicode[STIX]{x1D711}^{-1})^{\ast }$
. In the previous section, we have seen that the Lie derivative, the interior product and the exterior derivative are natural with respect to diffeomorphisms. For convenience we use now the following notation:
$\unicode[STIX]{x1D711}_{\ast }=(\unicode[STIX]{x1D711}^{-1})^{\ast }$
. In the previous section, we have seen that the Lie derivative, the interior product and the exterior derivative are natural with respect to diffeomorphisms. For convenience we use now the following notation:
![]() $\flat _{g}\equiv (\cdot )^{\flat }$
,
$\flat _{g}\equiv (\cdot )^{\flat }$
,
 $\sharp _{g}\equiv (\cdot )^{\sharp }$
,
$\sharp _{g}\equiv (\cdot )^{\sharp }$
,
![]() $\star _{g}\equiv \star$
and
$\star _{g}\equiv \star$
and
![]() $\text{d}_{g}^{\star }\equiv \text{d}^{\star }$
. All these operators are natural with respect to diffeomorphisms, i.e.
$\text{d}_{g}^{\star }\equiv \text{d}^{\star }$
. All these operators are natural with respect to diffeomorphisms, i.e.
 $$\begin{eqnarray}\unicode[STIX]{x1D711}^{\ast }\flat _{g}=\flat _{\unicode[STIX]{x1D711}^{\ast }g}\unicode[STIX]{x1D711}^{\ast },\quad \unicode[STIX]{x1D711}^{\ast }\sharp _{g}=\sharp _{\unicode[STIX]{x1D711}^{\ast }g}\unicode[STIX]{x1D711}^{\ast },\quad \unicode[STIX]{x1D711}^{\ast }\ast _{g}=\ast _{\unicode[STIX]{x1D711}^{\ast }g}\unicode[STIX]{x1D711}^{\ast },\quad \unicode[STIX]{x1D711}^{\ast }\text{d}_{g}^{\star }=\text{d}_{\unicode[STIX]{x1D711}^{\ast }g}^{\star }\unicode[STIX]{x1D711}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}^{\ast }\flat _{g}=\flat _{\unicode[STIX]{x1D711}^{\ast }g}\unicode[STIX]{x1D711}^{\ast },\quad \unicode[STIX]{x1D711}^{\ast }\sharp _{g}=\sharp _{\unicode[STIX]{x1D711}^{\ast }g}\unicode[STIX]{x1D711}^{\ast },\quad \unicode[STIX]{x1D711}^{\ast }\ast _{g}=\ast _{\unicode[STIX]{x1D711}^{\ast }g}\unicode[STIX]{x1D711}^{\ast },\quad \unicode[STIX]{x1D711}^{\ast }\text{d}_{g}^{\star }=\text{d}_{\unicode[STIX]{x1D711}^{\ast }g}^{\star }\unicode[STIX]{x1D711}^{\ast }.\end{eqnarray}$$
Let
![]() $(M,g)$
and
$(M,g)$
and
![]() $(N,h)$
be two Riemannian manifolds, and
$(N,h)$
be two Riemannian manifolds, and
 $\unicode[STIX]{x1D711}:M\rightarrow N$
a diffeomorphism. The mapping
$\unicode[STIX]{x1D711}:M\rightarrow N$
a diffeomorphism. The mapping
![]() $\unicode[STIX]{x1D711}$
is called an isometry if
$\unicode[STIX]{x1D711}$
is called an isometry if
![]() $\unicode[STIX]{x1D711}^{\star }h=g$
(see, e.g., Choquet-Bruhat et al.
Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977, § V.A.5, p. 298). If
$\unicode[STIX]{x1D711}^{\star }h=g$
(see, e.g., Choquet-Bruhat et al.
Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977, § V.A.5, p. 298). If
![]() $\unicode[STIX]{x1D711}$
is an isometry, using (B 56), we then observe that the commutators
$\unicode[STIX]{x1D711}$
is an isometry, using (B 56), we then observe that the commutators
![]() $[\unicode[STIX]{x1D711}^{\ast },\text{Op}]$
with
$[\unicode[STIX]{x1D711}^{\ast },\text{Op}]$
with
 $\text{Op}\in \{\flat ,\sharp ,\star ,\text{d}^{\star }\}$
vanish.
$\text{Op}\in \{\flat ,\sharp ,\star ,\text{d}^{\star }\}$
vanish.
Let
 $\unicode[STIX]{x1D705}\in {\mathcal{T}}_{0}^{1}(M)$
. The vector field
$\unicode[STIX]{x1D705}\in {\mathcal{T}}_{0}^{1}(M)$
. The vector field
![]() $\unicode[STIX]{x1D705}$
on
$\unicode[STIX]{x1D705}$
on
![]() $(M,g)$
is called a Killing vector field if
$(M,g)$
is called a Killing vector field if
![]() $\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D705}}g=0$
, that is it satisfies the Killing equations
$\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D705}}g=0$
, that is it satisfies the Killing equations
 $$\begin{eqnarray}(\text{}\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D705}}g)_{ij}=\unicode[STIX]{x1D705}^{k}\frac{\unicode[STIX]{x2202}\text{g}_{ij}}{\unicode[STIX]{x2202}a^{k}}+g_{kj}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}^{k}}{\unicode[STIX]{x2202}a^{i}}+g_{ik}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}^{k}}{\unicode[STIX]{x2202}a^{\,j}}=0.\end{eqnarray}$$
$$\begin{eqnarray}(\text{}\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D705}}g)_{ij}=\unicode[STIX]{x1D705}^{k}\frac{\unicode[STIX]{x2202}\text{g}_{ij}}{\unicode[STIX]{x2202}a^{k}}+g_{kj}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}^{k}}{\unicode[STIX]{x2202}a^{i}}+g_{ik}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D705}^{k}}{\unicode[STIX]{x2202}a^{\,j}}=0.\end{eqnarray}$$
Using the covariant derivative, the Killing equations (B 57) can be recast as
 $$\begin{eqnarray}(\text{}\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D705}}g)_{ij}=(\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D705}^{k})g_{kj}+(\unicode[STIX]{x1D735}_{j}\unicode[STIX]{x1D705}^{k})g_{ik}=(\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D705}_{j})+(\unicode[STIX]{x1D735}_{j}\unicode[STIX]{x1D705}_{i})=0.\end{eqnarray}$$
$$\begin{eqnarray}(\text{}\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D705}}g)_{ij}=(\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D705}^{k})g_{kj}+(\unicode[STIX]{x1D735}_{j}\unicode[STIX]{x1D705}^{k})g_{ik}=(\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D705}_{j})+(\unicode[STIX]{x1D735}_{j}\unicode[STIX]{x1D705}_{i})=0.\end{eqnarray}$$
Let us note that a Killing vector is always divergence-free, since the contraction of the 2-contravariant metric tensor
![]() $\text{g}^{ij}$
with the 2-covariant tensor appearing in (B 58) gives
$\text{g}^{ij}$
with the 2-covariant tensor appearing in (B 58) gives
 $2\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D705}^{i}=0$
. The Lie-derivative theorem (see § 2.2) implies that the vector field
$2\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x1D705}^{i}=0$
. The Lie-derivative theorem (see § 2.2) implies that the vector field
![]() $\unicode[STIX]{x1D705}$
generates a flow
$\unicode[STIX]{x1D705}$
generates a flow
 $f_{t}:M\rightarrow M$
, which leaves invariant the metric
$f_{t}:M\rightarrow M$
, which leaves invariant the metric
![]() $g$
, since
$g$
, since
![]() $f_{t}^{\ast }g=g$
. Thus the flow
$f_{t}^{\ast }g=g$
. Thus the flow
![]() $f_{t}$
, induced by the Killing vector field
$f_{t}$
, induced by the Killing vector field
![]() $\unicode[STIX]{x1D705}$
, generates a family of isometries. Since the operators
$\unicode[STIX]{x1D705}$
, generates a family of isometries. Since the operators
![]() $\flat _{g}$
,
$\flat _{g}$
,
![]() $\sharp _{g}$
,
$\sharp _{g}$
,
![]() $\star _{g}$
, and
$\star _{g}$
, and
![]() $\text{d}_{g}^{\star }$
are natural with respect to diffeomorphism we obtain
$\text{d}_{g}^{\star }$
are natural with respect to diffeomorphism we obtain
 $[f_{t}^{\ast },\text{Op}]=0$
, with
$[f_{t}^{\ast },\text{Op}]=0$
, with
 $\text{Op}\in \{\flat _{g},\sharp _{g},\star _{g},\text{d}_{g}^{\star }\}$
. Taking the derivative of
$\text{Op}\in \{\flat _{g},\sharp _{g},\star _{g},\text{d}_{g}^{\star }\}$
. Taking the derivative of
 $[f_{t}^{\ast },\text{Op}]=0$
with respect to time
$[f_{t}^{\ast },\text{Op}]=0$
with respect to time
![]() $t$
at
$t$
at
![]() $t=0$
, we obtain (see, e.g., Fecko Reference Fecko2006, § 8.3, p. 171)
$t=0$
, we obtain (see, e.g., Fecko Reference Fecko2006, § 8.3, p. 171)
 $$\begin{eqnarray}[\text{}\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D705}},\text{Op}]=0,\quad \text{Op}\in \{\flat _{g},\sharp _{g},\star _{g},\text{d}_{g}^{\star }\}.\end{eqnarray}$$
$$\begin{eqnarray}[\text{}\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D705}},\text{Op}]=0,\quad \text{Op}\in \{\flat _{g},\sharp _{g},\star _{g},\text{d}_{g}^{\star }\}.\end{eqnarray}$$
B.10 Riemannian connection and covariant derivative
The velocity vector field lies in the tangent bundle, and so the acceleration (the ‘velocity of the velocity’) lies in the tangent bundle of the tangent bundle. The acceleration of the fluid is the rate of change of the velocity vector field
![]() $v$
in the direction
$v$
in the direction
![]() $v$
of a trajectory
$v$
of a trajectory
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
(with
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
(with
 $\dot{\unicode[STIX]{x1D711}}_{t}(a)=v(t,\unicode[STIX]{x1D711}_{t}(a))$
) and is thus a special case of what is called the directional derivative. For clarity of this exposition and leaving apart physical considerations about acceleration, we assume now that the vector field
$\dot{\unicode[STIX]{x1D711}}_{t}(a)=v(t,\unicode[STIX]{x1D711}_{t}(a))$
) and is thus a special case of what is called the directional derivative. For clarity of this exposition and leaving apart physical considerations about acceleration, we assume now that the vector field
![]() $v$
is time-independent. We also consider another time-independent vector field
$v$
is time-independent. We also consider another time-independent vector field
![]() $u$
. The directional derivative of
$u$
. The directional derivative of
![]() $u$
in the direction of the vector field
$u$
in the direction of the vector field
![]() $v$
, which generates the flow
$v$
, which generates the flow
![]() $\unicode[STIX]{x1D711}_{t}$
, is noted
$\unicode[STIX]{x1D711}_{t}$
, is noted
![]() $\unicode[STIX]{x1D735}_{v}u$
and is defined by
$\unicode[STIX]{x1D735}_{v}u$
and is defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D735}_{v}u(a)=\lim _{t\rightarrow 0}\frac{{\mathcal{P}}_{\Vert }^{\ast }u(\unicode[STIX]{x1D711}_{t}(a))-u(a)}{t},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D735}_{v}u(a)=\lim _{t\rightarrow 0}\frac{{\mathcal{P}}_{\Vert }^{\ast }u(\unicode[STIX]{x1D711}_{t}(a))-u(a)}{t},\end{eqnarray}$$
where
 ${\mathcal{P}}_{\Vert }^{\ast }u(\unicode[STIX]{x1D711}_{t}(a))$
denotes a backward parallel transport of the vector
${\mathcal{P}}_{\Vert }^{\ast }u(\unicode[STIX]{x1D711}_{t}(a))$
denotes a backward parallel transport of the vector
![]() $u(\unicode[STIX]{x1D711}_{t}(a))$
. Since in an Euclidean space
$u(\unicode[STIX]{x1D711}_{t}(a))$
. Since in an Euclidean space
![]() $\mathbb{R}^{d}$
all tangent spaces are the same and identified with
$\mathbb{R}^{d}$
all tangent spaces are the same and identified with
![]() $\mathbb{R}^{d}$
, the backward parallel transport
$\mathbb{R}^{d}$
, the backward parallel transport
![]() ${\mathcal{P}}_{\Vert }^{\ast }$
is just an infinitesimal rigid translation or shift, which alters neither length nor direction of shifted vectors. However in the case of a manifold
${\mathcal{P}}_{\Vert }^{\ast }$
is just an infinitesimal rigid translation or shift, which alters neither length nor direction of shifted vectors. However in the case of a manifold
![]() $M$
, the vector
$M$
, the vector
![]() $u(\unicode[STIX]{x1D711}_{t}(a))$
belongs to the tangent space
$u(\unicode[STIX]{x1D711}_{t}(a))$
belongs to the tangent space
![]() $TM_{\unicode[STIX]{x1D711}_{t}(a)}$
, while the vector
$TM_{\unicode[STIX]{x1D711}_{t}(a)}$
, while the vector
![]() $u(a)$
belongs to
$u(a)$
belongs to
![]() $TM_{a}$
. Such vectors lie in different vector spaces and thus their difference by using rigid translation has no meaning. Therefore, on a manifold we need to introduce a rule of parallel transport (satisfying suitable requirements) as a linear mapping connecting two different tangent spaces, namely
$TM_{a}$
. Such vectors lie in different vector spaces and thus their difference by using rigid translation has no meaning. Therefore, on a manifold we need to introduce a rule of parallel transport (satisfying suitable requirements) as a linear mapping connecting two different tangent spaces, namely
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\mathcal{P}}_{\Vert ,\unicode[STIX]{x1D711},a,b}:TM_{a}\rightarrow TM_{b=\unicode[STIX]{x1D711}_{t}(a)}\\ w\mapsto {\mathcal{P}}_{\Vert ,\unicode[STIX]{x1D711},a,b}w.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\mathcal{P}}_{\Vert ,\unicode[STIX]{x1D711},a,b}:TM_{a}\rightarrow TM_{b=\unicode[STIX]{x1D711}_{t}(a)}\\ w\mapsto {\mathcal{P}}_{\Vert ,\unicode[STIX]{x1D711},a,b}w.\end{array}\right\}\end{eqnarray}$$
Note that the rule of parallel transport takes as input not only the edge point
![]() $a$
and
$a$
and
![]() $b$
, but also a path
$b$
, but also a path
![]() $\unicode[STIX]{x1D711}$
connecting them. So, if a vector field
$\unicode[STIX]{x1D711}$
connecting them. So, if a vector field
![]() $u$
is given at the point
$u$
is given at the point
![]() $a$
, in addition to a path from
$a$
, in addition to a path from
![]() $a$
to
$a$
to
![]() $b$
, the parallel transport of
$b$
, the parallel transport of
![]() $u$
is uniquely defined to the point
$u$
is uniquely defined to the point
![]() $b$
. Given another path the parallel transport is unique as well, but the resulting transported vectors may well be different. The path dependence of parallel transport is an important and typical feature, which enables one to speak about the curvature of the manifold. In fact the only situation in which all parallel transport is independent of path is when there is no curvature. In spite of this, the infinitesimal limit in (B 60) is independent of the choice of the curve, so that it may be used to define the so-called covariant derivative
$b$
. Given another path the parallel transport is unique as well, but the resulting transported vectors may well be different. The path dependence of parallel transport is an important and typical feature, which enables one to speak about the curvature of the manifold. In fact the only situation in which all parallel transport is independent of path is when there is no curvature. In spite of this, the infinitesimal limit in (B 60) is independent of the choice of the curve, so that it may be used to define the so-called covariant derivative
![]() $\unicode[STIX]{x1D735}_{w}u$
of
$\unicode[STIX]{x1D735}_{w}u$
of
![]() $u$
in the direction
$u$
in the direction
![]() $w$
, for any given vector
$w$
, for any given vector
 $w\in TM_{a}$
, since the limit does not depend on how
$w\in TM_{a}$
, since the limit does not depend on how
![]() $w$
is extended to a vector field on the whole manifold. In addition, as we shall see, covariant derivative and parallel transport can be extended to tensors. Finally, observe that the vanishing of the covariant derivative on some curve
$w$
is extended to a vector field on the whole manifold. In addition, as we shall see, covariant derivative and parallel transport can be extended to tensors. Finally, observe that the vanishing of the covariant derivative on some curve
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
amounts to stating that the vector field
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
amounts to stating that the vector field
![]() $u$
behaves as if its values along the curve
$u$
behaves as if its values along the curve
![]() $\unicode[STIX]{x1D711}_{t}$
were arising by parallel transport to the whole curve of the value taken at a particular point on the curve. Such a field along a curve is called an autoparallel field. The covariant derivative thus measures the deviation from being autoparallel. We have seen that the infinitesimal version of the parallel transport rule allows one to define a differentiation of one vector field with respect to another one; this differentiation process is called a linear connection and is noted
$\unicode[STIX]{x1D711}_{t}$
were arising by parallel transport to the whole curve of the value taken at a particular point on the curve. Such a field along a curve is called an autoparallel field. The covariant derivative thus measures the deviation from being autoparallel. We have seen that the infinitesimal version of the parallel transport rule allows one to define a differentiation of one vector field with respect to another one; this differentiation process is called a linear connection and is noted
![]() $\unicode[STIX]{x1D735}$
. In fact the role of the parallel transport and the covariant derivative can be reversed. Indeed, when it is technically feasible to perform the operation of covariant derivative, one can construct a parallel transport rule, which is simply obtained by performing the transport in such a way that the covariant derivative vanishes. This is the usual way of introducing the concept of linear connection on a manifold, which we now state formally.
$\unicode[STIX]{x1D735}$
. In fact the role of the parallel transport and the covariant derivative can be reversed. Indeed, when it is technically feasible to perform the operation of covariant derivative, one can construct a parallel transport rule, which is simply obtained by performing the transport in such a way that the covariant derivative vanishes. This is the usual way of introducing the concept of linear connection on a manifold, which we now state formally.
To each vector field
 $w\in {\mathcal{T}}_{0}^{1}(M)$
, one associates an operator
$w\in {\mathcal{T}}_{0}^{1}(M)$
, one associates an operator
![]() $\unicode[STIX]{x1D735}_{w}$
, the covariant derivative along the field
$\unicode[STIX]{x1D735}_{w}$
, the covariant derivative along the field
![]() $w$
, satisfying the following properties:
$w$
, satisfying the following properties:
-
(i) it is a linear operator on the tensor algebra, which preserves the degree
(B 62) $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D735}_{w}:{\mathcal{T}}_{p}^{q}(M)\rightarrow {\mathcal{T}}_{p}^{q}(M), & \displaystyle\end{eqnarray}$$
(B 63)
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D735}_{w}:{\mathcal{T}}_{p}^{q}(M)\rightarrow {\mathcal{T}}_{p}^{q}(M), & \displaystyle\end{eqnarray}$$
(B 63) $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D735}_{w}(\unicode[STIX]{x0398}_{1}+\unicode[STIX]{x1D706}\unicode[STIX]{x0398}_{2})=\unicode[STIX]{x1D735}_{w}\unicode[STIX]{x0398}_{1}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D735}_{w}\unicode[STIX]{x0398}_{2},\quad \unicode[STIX]{x0398}_{1},\unicode[STIX]{x0398}_{2}\in {\mathcal{T}}_{p}^{q}(M),~\unicode[STIX]{x1D706}\in \mathbb{R}; & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D735}_{w}(\unicode[STIX]{x0398}_{1}+\unicode[STIX]{x1D706}\unicode[STIX]{x0398}_{2})=\unicode[STIX]{x1D735}_{w}\unicode[STIX]{x0398}_{1}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D735}_{w}\unicode[STIX]{x0398}_{2},\quad \unicode[STIX]{x0398}_{1},\unicode[STIX]{x0398}_{2}\in {\mathcal{T}}_{p}^{q}(M),~\unicode[STIX]{x1D706}\in \mathbb{R}; & \displaystyle\end{eqnarray}$$
-
(ii) it is a derivative, i.e. it satisfies the Leibniz rule
(B 64) $$\begin{eqnarray}\unicode[STIX]{x1D735}_{w}(\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x0398}_{2})=\unicode[STIX]{x1D735}_{w}\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x0398}_{2}+\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x1D735}_{w}\unicode[STIX]{x0398}_{2},\quad \unicode[STIX]{x0398}_{1}\in {\mathcal{T}}_{p_{1}}^{q_{1}}(M),~\unicode[STIX]{x0398}_{2}\in {\mathcal{T}}_{p_{2}}^{q_{2}}(M);\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D735}_{w}(\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x0398}_{2})=\unicode[STIX]{x1D735}_{w}\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x0398}_{2}+\unicode[STIX]{x0398}_{1}\otimes \unicode[STIX]{x1D735}_{w}\unicode[STIX]{x0398}_{2},\quad \unicode[STIX]{x0398}_{1}\in {\mathcal{T}}_{p_{1}}^{q_{1}}(M),~\unicode[STIX]{x0398}_{2}\in {\mathcal{T}}_{p_{2}}^{q_{2}}(M);\end{eqnarray}$$
-
(iii) it is
 ${\mathcal{F}}$
-linear with respect to
${\mathcal{F}}$
-linear with respect to
 $w$
, i.e.
$w$
, i.e.
 $\unicode[STIX]{x1D735}_{v+\unicode[STIX]{x1D706}w}=\unicode[STIX]{x1D735}_{v}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D735}_{w}$
;
$\unicode[STIX]{x1D735}_{v+\unicode[STIX]{x1D706}w}=\unicode[STIX]{x1D735}_{v}+\unicode[STIX]{x1D706}\unicode[STIX]{x1D735}_{w}$
; -
(iv)
 $\unicode[STIX]{x1D735}_{w}f=w(f)=\unicode[STIX]{x00A3}_{w}f$
,
$\unicode[STIX]{x1D735}_{w}f=w(f)=\unicode[STIX]{x00A3}_{w}f$
,
 $\forall f\in {\mathcal{F}}(M)={\mathcal{T}}_{0}^{0}(M)$
;
$\forall f\in {\mathcal{F}}(M)={\mathcal{T}}_{0}^{0}(M)$
; -
(v)
 $\unicode[STIX]{x1D735}_{w}$
commutes with the operation of contracted multiplication.
$\unicode[STIX]{x1D735}_{w}$
commutes with the operation of contracted multiplication.
Given
![]() $(U,\unicode[STIX]{x1D719})$
an admissible local chart on a
$(U,\unicode[STIX]{x1D719})$
an admissible local chart on a
![]() $d$
-dimensional manifold
$d$
-dimensional manifold
![]() $M$
, the natural basis for
$M$
, the natural basis for
![]() ${\mathcal{T}}_{0}^{1}(U)$
is
${\mathcal{T}}_{0}^{1}(U)$
is
 $\{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a_{i}\}_{1\leqslant i\leqslant d}$
, while the natural basis for
$\{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a_{i}\}_{1\leqslant i\leqslant d}$
, while the natural basis for
![]() ${\mathcal{T}}_{1}^{0}(U)$
is the dual basis
${\mathcal{T}}_{1}^{0}(U)$
is the dual basis
 $\{\text{d}a^{i}\}_{1\leqslant i\leqslant d}$
. The covariant derivative is uniquely specified by the coefficients of linear connection
$\{\text{d}a^{i}\}_{1\leqslant i\leqslant d}$
. The covariant derivative is uniquely specified by the coefficients of linear connection
![]() $\unicode[STIX]{x1D6E4}_{jk}^{i}(a)$
with respect to the natural basis and are functions defined by
$\unicode[STIX]{x1D6E4}_{jk}^{i}(a)$
with respect to the natural basis and are functions defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x2202}_{j}=:\unicode[STIX]{x1D6E4}_{ij}^{k}\unicode[STIX]{x2202}_{k},\quad \unicode[STIX]{x1D735}_{i}\,\text{d}a^{\,j}=-\unicode[STIX]{x1D6E4}_{ki}^{j}\,\text{d}a^{k},\quad \unicode[STIX]{x1D735}_{i}:=\unicode[STIX]{x1D735}_{\unicode[STIX]{x2202}_{i}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D735}_{i}\unicode[STIX]{x2202}_{j}=:\unicode[STIX]{x1D6E4}_{ij}^{k}\unicode[STIX]{x2202}_{k},\quad \unicode[STIX]{x1D735}_{i}\,\text{d}a^{\,j}=-\unicode[STIX]{x1D6E4}_{ki}^{j}\,\text{d}a^{k},\quad \unicode[STIX]{x1D735}_{i}:=\unicode[STIX]{x1D735}_{\unicode[STIX]{x2202}_{i}},\end{eqnarray}$$
with the notation
 $\unicode[STIX]{x2202}_{i}\equiv \unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i}$
. Let us note that if
$\unicode[STIX]{x2202}_{i}\equiv \unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{i}$
. Let us note that if
 $\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
, then the covariant derivative (also called the absolute differential)
$\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
, then the covariant derivative (also called the absolute differential)
 $\unicode[STIX]{x1D735}\unicode[STIX]{x0398}=\unicode[STIX]{x1D735}_{\ell }\unicode[STIX]{x0398}\,\text{d}a^{\ell }=\unicode[STIX]{x1D735}_{\ell }\unicode[STIX]{x0398}\otimes \text{d}a^{\ell }$
is a tensor of type
$\unicode[STIX]{x1D735}\unicode[STIX]{x0398}=\unicode[STIX]{x1D735}_{\ell }\unicode[STIX]{x0398}\,\text{d}a^{\ell }=\unicode[STIX]{x1D735}_{\ell }\unicode[STIX]{x0398}\otimes \text{d}a^{\ell }$
is a tensor of type
 $(q,p+1)$
. Therefore if
$(q,p+1)$
. Therefore if
 $\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
, then
$\unicode[STIX]{x0398}\in {\mathcal{T}}_{p}^{q}(M)$
, then
 $\unicode[STIX]{x1D735}\unicode[STIX]{x0398}\in {\mathcal{T}}_{p+1}^{q}(M)$
with
$\unicode[STIX]{x1D735}\unicode[STIX]{x0398}\in {\mathcal{T}}_{p+1}^{q}(M)$
with
 $$\begin{eqnarray}\unicode[STIX]{x1D735}\unicode[STIX]{x0398}=\unicode[STIX]{x1D735}_{\ell }\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{1}}}\otimes \cdots \otimes \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{q}}}\otimes \text{d}a^{\ell }\otimes \text{d}a^{\,j_{1}}\otimes \cdots \otimes \text{d}a^{\,j_{p}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D735}\unicode[STIX]{x0398}=\unicode[STIX]{x1D735}_{\ell }\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{1}}}\otimes \cdots \otimes \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}a^{i_{q}}}\otimes \text{d}a^{\ell }\otimes \text{d}a^{\,j_{1}}\otimes \cdots \otimes \text{d}a^{\,j_{p}},\end{eqnarray}$$
with
 $$\begin{eqnarray}\unicode[STIX]{x1D735}_{\ell }\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}=\unicode[STIX]{x2202}_{\ell }\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}+\unicode[STIX]{x1D6E4}_{ik}^{i_{1}}\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{ki_{2}\ldots i_{q}}+\text{all upper indices}-\unicode[STIX]{x1D6E4}_{ij_{1}}^{l}\unicode[STIX]{x0398}_{lj_{2}\ldots j_{p}}^{i_{1}\ldots i_{q}}-\text{all lower indices}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D735}_{\ell }\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}=\unicode[STIX]{x2202}_{\ell }\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{i_{1}\ldots i_{q}}+\unicode[STIX]{x1D6E4}_{ik}^{i_{1}}\unicode[STIX]{x0398}_{j_{1}\ldots j_{p}}^{ki_{2}\ldots i_{q}}+\text{all upper indices}-\unicode[STIX]{x1D6E4}_{ij_{1}}^{l}\unicode[STIX]{x0398}_{lj_{2}\ldots j_{p}}^{i_{1}\ldots i_{q}}-\text{all lower indices}.\end{eqnarray}$$
Under a change of natural basis, resulting from a change of coordinates
 $(a^{i})_{1\leqslant i\leqslant d}\mapsto (\tilde{a}^{i}:=\tilde{a}^{i}(a))_{1\leqslant i\leqslant d}$
, the following transformation holds:
$(a^{i})_{1\leqslant i\leqslant d}\mapsto (\tilde{a}^{i}:=\tilde{a}^{i}(a))_{1\leqslant i\leqslant d}$
, the following transformation holds:
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E4}}_{jk}^{i}=\frac{\unicode[STIX]{x2202}\tilde{a}^{i}}{\unicode[STIX]{x2202}a^{l}}\frac{\unicode[STIX]{x2202}a^{m}}{\unicode[STIX]{x2202}\tilde{a}^{\,j}}\frac{\unicode[STIX]{x2202}a^{n}}{\unicode[STIX]{x2202}\tilde{a}^{k}}\unicode[STIX]{x1D6E4}_{mn}^{l}+\frac{\unicode[STIX]{x2202}\tilde{a}^{i}}{\unicode[STIX]{x2202}a^{l}}\frac{\unicode[STIX]{x2202}^{2}a^{l}}{\unicode[STIX]{x2202}\tilde{a}^{\,j}\unicode[STIX]{x2202}\tilde{a}^{k}}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E4}}_{jk}^{i}=\frac{\unicode[STIX]{x2202}\tilde{a}^{i}}{\unicode[STIX]{x2202}a^{l}}\frac{\unicode[STIX]{x2202}a^{m}}{\unicode[STIX]{x2202}\tilde{a}^{\,j}}\frac{\unicode[STIX]{x2202}a^{n}}{\unicode[STIX]{x2202}\tilde{a}^{k}}\unicode[STIX]{x1D6E4}_{mn}^{l}+\frac{\unicode[STIX]{x2202}\tilde{a}^{i}}{\unicode[STIX]{x2202}a^{l}}\frac{\unicode[STIX]{x2202}^{2}a^{l}}{\unicode[STIX]{x2202}\tilde{a}^{\,j}\unicode[STIX]{x2202}\tilde{a}^{k}}.\end{eqnarray}$$
From this expression, we observe that the coefficients of the linear connection
![]() $\unicode[STIX]{x1D6E4}_{jk}^{i}$
, called the Christoffel symbols of the second kind, are not tensors since they do not satisfy the tensoriality criterion given by the change of coordinate formula for the components of a tensor (B 16). On a
$\unicode[STIX]{x1D6E4}_{jk}^{i}$
, called the Christoffel symbols of the second kind, are not tensors since they do not satisfy the tensoriality criterion given by the change of coordinate formula for the components of a tensor (B 16). On a
![]() $\mathscr{C}^{k}$
(
$\mathscr{C}^{k}$
(
![]() $k\geqslant 2$
) manifold a connection is said to be of class
$k\geqslant 2$
) manifold a connection is said to be of class
![]() $\mathscr{C}^{r}$
if, in all charts of an atlas, the
$\mathscr{C}^{r}$
if, in all charts of an atlas, the
![]() $\unicode[STIX]{x1D6E4}_{jk}^{i}$
are of class
$\unicode[STIX]{x1D6E4}_{jk}^{i}$
are of class
![]() $\mathscr{C}^{r}$
. If
$\mathscr{C}^{r}$
. If
 $r\leqslant k-2$
the definition is coherent and does not depend on the atlas. If
$r\leqslant k-2$
the definition is coherent and does not depend on the atlas. If
![]() $\unicode[STIX]{x0398}$
is of class
$\unicode[STIX]{x0398}$
is of class
![]() $\mathscr{C}^{k-1}$
and the connection of class
$\mathscr{C}^{k-1}$
and the connection of class
![]() $\mathscr{C}^{k-2}$
, then
$\mathscr{C}^{k-2}$
, then
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x0398}$
is of class
$\unicode[STIX]{x1D735}\unicode[STIX]{x0398}$
is of class
![]() $\mathscr{C}^{k-2}$
.
$\mathscr{C}^{k-2}$
.
Let
![]() $(M,\unicode[STIX]{x1D735})$
be a manifold endowed with a linear connection,
$(M,\unicode[STIX]{x1D735})$
be a manifold endowed with a linear connection,
![]() $\unicode[STIX]{x1D735}$
the corresponding covariant derivative operator,
$\unicode[STIX]{x1D735}$
the corresponding covariant derivative operator,
![]() $t\rightarrow \unicode[STIX]{x1D6FE}_{t}$
a curve on
$t\rightarrow \unicode[STIX]{x1D6FE}_{t}$
a curve on
![]() $M$
, and
$M$
, and
 $V\in {\mathcal{T}}_{0}^{1}(M)$
. The absolute derivative of the field
$V\in {\mathcal{T}}_{0}^{1}(M)$
. The absolute derivative of the field
![]() $V$
along
$V$
along
![]() $\unicode[STIX]{x1D6FE}$
is defined as
$\unicode[STIX]{x1D6FE}$
is defined as
 $$\begin{eqnarray}\frac{\text{D}V(t)}{\text{D}t}:=\unicode[STIX]{x1D735}_{\dot{\unicode[STIX]{x1D6FE}}}V.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{D}V(t)}{\text{D}t}:=\unicode[STIX]{x1D735}_{\dot{\unicode[STIX]{x1D6FE}}}V.\end{eqnarray}$$
The vector field
![]() $V$
on
$V$
on
![]() $\unicode[STIX]{x1D6FE}$
is called autoparallel if its absolute derivative along
$\unicode[STIX]{x1D6FE}$
is called autoparallel if its absolute derivative along
![]() $\unicode[STIX]{x1D6FE}$
vanishes, i.e. if the right-hand side of (B 69) vanishes. The straight lines that result from iteration of the infinitesimal parallel transport of the velocity vector, i.e. the trajectories
$\unicode[STIX]{x1D6FE}$
vanishes, i.e. if the right-hand side of (B 69) vanishes. The straight lines that result from iteration of the infinitesimal parallel transport of the velocity vector, i.e. the trajectories
 $a\mapsto \unicode[STIX]{x1D6FE}_{t}(a)$
,
$a\mapsto \unicode[STIX]{x1D6FE}_{t}(a)$
,
![]() $a\in M$
, with zero acceleration (
$a\in M$
, with zero acceleration (
 $\unicode[STIX]{x1D735}_{\dot{\unicode[STIX]{x1D6FE}}}\dot{\unicode[STIX]{x1D6FE}}=0$
), are called the affinely parametrised geodesics on
$\unicode[STIX]{x1D735}_{\dot{\unicode[STIX]{x1D6FE}}}\dot{\unicode[STIX]{x1D6FE}}=0$
), are called the affinely parametrised geodesics on
![]() $(M,\unicode[STIX]{x1D735})$
.
$(M,\unicode[STIX]{x1D735})$
.
A fundamental object associated to a manifold
![]() $(M,\unicode[STIX]{x1D735})$
with a linear connection is the torsion operation
$(M,\unicode[STIX]{x1D735})$
with a linear connection is the torsion operation
![]() $\mathfrak{t}$
, defined by
$\mathfrak{t}$
, defined by
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\mathfrak{t}:{\mathcal{T}}_{0}^{1}(M)\times {\mathcal{T}}_{0}^{1}(M)\rightarrow {\mathcal{T}}_{0}^{1}(M)\\ (u,v)\mapsto \mathfrak{t}(u,v)=\unicode[STIX]{x1D735}_{u}\unicode[STIX]{x1D735}_{v}-\unicode[STIX]{x1D735}_{v}\unicode[STIX]{x1D735}_{u}-[u,v].\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\mathfrak{t}:{\mathcal{T}}_{0}^{1}(M)\times {\mathcal{T}}_{0}^{1}(M)\rightarrow {\mathcal{T}}_{0}^{1}(M)\\ (u,v)\mapsto \mathfrak{t}(u,v)=\unicode[STIX]{x1D735}_{u}\unicode[STIX]{x1D735}_{v}-\unicode[STIX]{x1D735}_{v}\unicode[STIX]{x1D735}_{u}-[u,v].\end{array}\right\}\end{eqnarray}$$
We observe that
![]() $\mathfrak{t}$
is antisymmetric since
$\mathfrak{t}$
is antisymmetric since
 $\mathfrak{t}(u,v)=-\mathfrak{t}(v,u)$
. The torsion tensor field
$\mathfrak{t}(u,v)=-\mathfrak{t}(v,u)$
. The torsion tensor field
 $\unicode[STIX]{x1D70F}\in {\mathcal{T}}_{2}^{1}(M)$
is defined by
$\unicode[STIX]{x1D70F}\in {\mathcal{T}}_{2}^{1}(M)$
is defined by
 $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC},u,v)=\unicode[STIX]{x1D6FC}(\mathfrak{t}(u,v))$
, for all
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC},u,v)=\unicode[STIX]{x1D6FC}(\mathfrak{t}(u,v))$
, for all
![]() $u$
,
$u$
,
 $v\in {\mathcal{T}}_{0}^{1}(M)$
and
$v\in {\mathcal{T}}_{0}^{1}(M)$
and
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{1}(M)={\mathcal{T}}_{1}^{0}(M)$
. Using the natural basis one has
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{1}(M)={\mathcal{T}}_{1}^{0}(M)$
. Using the natural basis one has
 $[\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{\,j},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{k}]=0$
, so that the components of
$[\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{\,j},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}a^{k}]=0$
, so that the components of
![]() $\unicode[STIX]{x1D70F}$
are given by
$\unicode[STIX]{x1D70F}$
are given by
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{jk}^{i}=\unicode[STIX]{x1D6E4}_{jk}^{i}-\unicode[STIX]{x1D6E4}_{kj}^{i}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{jk}^{i}=\unicode[STIX]{x1D6E4}_{jk}^{i}-\unicode[STIX]{x1D6E4}_{kj}^{i}.\end{eqnarray}$$
On a Riemannian manifold there exists a unique linear connection such that
![]() $\unicode[STIX]{x1D70F}=0$
and
$\unicode[STIX]{x1D70F}=0$
and
![]() $\unicode[STIX]{x1D735}g=0$
(i.e.
$\unicode[STIX]{x1D735}g=0$
(i.e.
 $\unicode[STIX]{x1D735}_{i}g_{jk}=\unicode[STIX]{x1D735}_{i}g^{\,jk}=0$
). Such a connection is called a Riemann–Levi-Civita (RLC) connection. The condition
$\unicode[STIX]{x1D735}_{i}g_{jk}=\unicode[STIX]{x1D735}_{i}g^{\,jk}=0$
). Such a connection is called a Riemann–Levi-Civita (RLC) connection. The condition
![]() $\unicode[STIX]{x1D70F}=0$
means that the connection
$\unicode[STIX]{x1D70F}=0$
means that the connection
![]() $\unicode[STIX]{x1D735}$
is torsion-free and thus that the Christoffel symbols are symmetric. The condition
$\unicode[STIX]{x1D735}$
is torsion-free and thus that the Christoffel symbols are symmetric. The condition
![]() $\unicode[STIX]{x1D735}g=0$
, which is equivalent to stating that
$\unicode[STIX]{x1D735}g=0$
, which is equivalent to stating that
![]() $\unicode[STIX]{x1D735}$
is a metric connection, ensures the preservation of length of vectors, which are generated by parallel transport. For an RLC connection the Christoffel symbols can be expressed in terms of the partial derivatives of the metric tensor
$\unicode[STIX]{x1D735}$
is a metric connection, ensures the preservation of length of vectors, which are generated by parallel transport. For an RLC connection the Christoffel symbols can be expressed in terms of the partial derivatives of the metric tensor
![]() $g$
:
$g$
:
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{jk}^{i}={\textstyle \frac{1}{2}}g^{il}(\unicode[STIX]{x2202}_{j}g_{kl}+\unicode[STIX]{x2202}_{k}g_{jl}-\unicode[STIX]{x2202}_{l}g_{jk}),\quad \unicode[STIX]{x1D6E4}_{jk}^{i}=\unicode[STIX]{x1D6E4}_{kj}^{i}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{jk}^{i}={\textstyle \frac{1}{2}}g^{il}(\unicode[STIX]{x2202}_{j}g_{kl}+\unicode[STIX]{x2202}_{k}g_{jl}-\unicode[STIX]{x2202}_{l}g_{jk}),\quad \unicode[STIX]{x1D6E4}_{jk}^{i}=\unicode[STIX]{x1D6E4}_{kj}^{i}.\end{eqnarray}$$
Let
 $(M,g,\unicode[STIX]{x1D735},\unicode[STIX]{x1D707})$
a Riemannian manifold endowed with a RLC connection
$(M,g,\unicode[STIX]{x1D735},\unicode[STIX]{x1D707})$
a Riemannian manifold endowed with a RLC connection
![]() $\unicode[STIX]{x1D735}$
and a volume form
$\unicode[STIX]{x1D735}$
and a volume form
![]() $\unicode[STIX]{x1D707}$
. If
$\unicode[STIX]{x1D707}$
. If
![]() $v=v^{i}\unicode[STIX]{x2202}_{i}$
, then
$v=v^{i}\unicode[STIX]{x2202}_{i}$
, then
 $$\begin{eqnarray}\text{div}_{\unicode[STIX]{x1D707}}v=\unicode[STIX]{x1D735}_{i}v^{i}=\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x2202}_{i}(\sqrt{\text{g}}v^{i}).\end{eqnarray}$$
$$\begin{eqnarray}\text{div}_{\unicode[STIX]{x1D707}}v=\unicode[STIX]{x1D735}_{i}v^{i}=\frac{1}{\sqrt{\text{g}}}\unicode[STIX]{x2202}_{i}(\sqrt{\text{g}}v^{i}).\end{eqnarray}$$
Commonly used differential operators such as the exterior derivative or the codifferential can be expressed in terms of covariant derivatives (Choquet-Bruhat et al. Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977, § V.B.4, p. 316; see also de Rham (Reference De Rham1984), chap. V, § 26, p. 106).
A detailed description of linear connections and parallel transport can be found in Choquet-Bruhat et al. (Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977, § V.B.1, p. 300) and Fecko (Reference Fecko2006, § 15.2, p. 372). We refer the reader to Choquet-Bruhat et al. (Reference Choquet-Bruhat, De Witt-Morette and Dillard-Bleick1977, § V.B.2, p. 308 and chap. V) and Fecko (Reference Fecko2006, § 15.3, p. 382 and chap. 15) for more details about RLC connections (e.g., curvature tensor).
B.11 Incompressible or divergence-free vector fields
Let
 $(M,g,\unicode[STIX]{x1D735},\unicode[STIX]{x1D707})$
be a Riemannian manifold endowed with an RLC connection
$(M,g,\unicode[STIX]{x1D735},\unicode[STIX]{x1D707})$
be a Riemannian manifold endowed with an RLC connection
![]() $\unicode[STIX]{x1D735}$
and a volume form
$\unicode[STIX]{x1D735}$
and a volume form
![]() $\unicode[STIX]{x1D707}$
. We say that a vector field
$\unicode[STIX]{x1D707}$
. We say that a vector field
 $v\in {\mathcal{T}}_{0}^{1}(M)$
is incompressible or divergence-free (with respect to
$v\in {\mathcal{T}}_{0}^{1}(M)$
is incompressible or divergence-free (with respect to
![]() $\unicode[STIX]{x1D707}$
) if
$\unicode[STIX]{x1D707}$
) if
 $\text{div}_{\unicode[STIX]{x1D707}}v=0$
. A divergence-free time-dependent smooth vector field
$\text{div}_{\unicode[STIX]{x1D707}}v=0$
. A divergence-free time-dependent smooth vector field
 $v\in {\mathcal{T}}_{0}^{1}(M)$
is the infinitesimal generator of a one-parameter family of volume-preserving smooth maps
$v\in {\mathcal{T}}_{0}^{1}(M)$
is the infinitesimal generator of a one-parameter family of volume-preserving smooth maps
 $\unicode[STIX]{x1D711}_{t}:M\rightarrow M$
, which satisfy
$\unicode[STIX]{x1D711}_{t}:M\rightarrow M$
, which satisfy
 $$\begin{eqnarray}\dot{\unicode[STIX]{x1D711}_{t}}:=\frac{\text{d}\unicode[STIX]{x1D711}_{t}}{\text{d}t}=v(t,\unicode[STIX]{x1D711}_{t}),\quad \unicode[STIX]{x1D711}_{0}=e:=\text{Identity}.\end{eqnarray}$$
$$\begin{eqnarray}\dot{\unicode[STIX]{x1D711}_{t}}:=\frac{\text{d}\unicode[STIX]{x1D711}_{t}}{\text{d}t}=v(t,\unicode[STIX]{x1D711}_{t}),\quad \unicode[STIX]{x1D711}_{0}=e:=\text{Identity}.\end{eqnarray}$$
Then
![]() $v$
is incompressible (i.e.
$v$
is incompressible (i.e.
 $\text{div}_{\unicode[STIX]{x1D707}}v=0$
) if and only if the flow
$\text{div}_{\unicode[STIX]{x1D707}}v=0$
) if and only if the flow
 $\unicode[STIX]{x1D711}_{t}:M\rightarrow M$
is volume preserving; that is the local diffeomorphism
$\unicode[STIX]{x1D711}_{t}:M\rightarrow M$
is volume preserving; that is the local diffeomorphism
 $\unicode[STIX]{x1D711}_{t}:U\rightarrow V$
is volume preserving with respect to
$\unicode[STIX]{x1D711}_{t}:U\rightarrow V$
is volume preserving with respect to
![]() $\unicode[STIX]{x1D707}_{|_{U}}$
and
$\unicode[STIX]{x1D707}_{|_{U}}$
and
![]() $\unicode[STIX]{x1D707}_{|_{V}}$
for all
$\unicode[STIX]{x1D707}_{|_{V}}$
for all
![]() $U\subset M$
. Let us introduce
$U\subset M$
. Let us introduce
![]() $J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})$
, the Jacobian of the flow
$J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})$
, the Jacobian of the flow
![]() $\unicode[STIX]{x1D711}_{t}$
with respect to the volume form
$\unicode[STIX]{x1D711}_{t}$
with respect to the volume form
![]() $\unicode[STIX]{x1D707}$
, defined by
$\unicode[STIX]{x1D707}$
, defined by
 $$\begin{eqnarray}J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})=\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D707}/\unicode[STIX]{x1D707}.\end{eqnarray}$$
$$\begin{eqnarray}J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})=\unicode[STIX]{x1D711}^{\ast }\unicode[STIX]{x1D707}/\unicode[STIX]{x1D707}.\end{eqnarray}$$
Then the time evolution of the Jacobian
![]() $J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})$
is given by the classical differential identity
$J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})$
is given by the classical differential identity
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})=J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D735}_{i}v^{i}\circ \unicode[STIX]{x1D711}_{t}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})=J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D735}_{i}v^{i}\circ \unicode[STIX]{x1D711}_{t}.\end{eqnarray}$$
From (B 76) we directly see that the volume-preserving property of the flow, in other words incompressibility,
![]() $\unicode[STIX]{x1D711}_{t}$
, i.e.
$\unicode[STIX]{x1D711}_{t}$
, i.e.
 $J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})=1$
, is equivalent – as in a flat space – to the divergence-free condition for the vector field
$J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})=1$
, is equivalent – as in a flat space – to the divergence-free condition for the vector field
![]() $v$
, i.e
$v$
, i.e
 $\unicode[STIX]{x1D735}_{i}v^{i}=0$
. The differential identity (B 76) can be easily proved from the Lie-derivative theorem (see § 2.2), which states that
$\unicode[STIX]{x1D735}_{i}v^{i}=0$
. The differential identity (B 76) can be easily proved from the Lie-derivative theorem (see § 2.2), which states that
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}=\unicode[STIX]{x1D711}_{t}^{\ast }(\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D707}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D707}),\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}=\unicode[STIX]{x1D711}_{t}^{\ast }(\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D707}+\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D707}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D707}$
is the Lie derivative of the volume form
$\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D707}$
is the Lie derivative of the volume form
![]() $\unicode[STIX]{x1D707}$
with respect to the vector field
$\unicode[STIX]{x1D707}$
with respect to the vector field
![]() $v$
. From a geometric point of view, the Lie derivative of the form
$v$
. From a geometric point of view, the Lie derivative of the form
![]() $\unicode[STIX]{x1D707}$
measures the rate of change of volume of a parallelepiped spanned by
$\unicode[STIX]{x1D707}$
measures the rate of change of volume of a parallelepiped spanned by
![]() $d$
vectors that are pushed forward by the flow
$d$
vectors that are pushed forward by the flow
![]() $\unicode[STIX]{x1D711}_{t}$
of
$\unicode[STIX]{x1D711}_{t}$
of
![]() $v$
(see § 2.2). Indeed, dividing (B 77) by
$v$
(see § 2.2). Indeed, dividing (B 77) by
![]() $\unicode[STIX]{x1D707}$
, and using the properties
$\unicode[STIX]{x1D707}$
, and using the properties
![]() $\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D707}=0$
, and
$\unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D707}=0$
, and
 $\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D707}=:(\text{div}_{\unicode[STIX]{x1D707}}v)\unicode[STIX]{x1D707}=\unicode[STIX]{x1D735}_{i}v^{i}\unicode[STIX]{x1D707}$
, we obtain
$\unicode[STIX]{x00A3}_{v}\unicode[STIX]{x1D707}=:(\text{div}_{\unicode[STIX]{x1D707}}v)\unicode[STIX]{x1D707}=\unicode[STIX]{x1D735}_{i}v^{i}\unicode[STIX]{x1D707}$
, we obtain
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})=[\unicode[STIX]{x1D711}_{t}^{\ast }(\unicode[STIX]{x1D735}_{i}v^{i}\unicode[STIX]{x1D707})]/\unicode[STIX]{x1D707}=[(\unicode[STIX]{x1D735}_{i}v^{i}\circ \unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}]/\unicode[STIX]{x1D707}=J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D735}_{i}v^{i}\circ \unicode[STIX]{x1D711}_{t}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})=[\unicode[STIX]{x1D711}_{t}^{\ast }(\unicode[STIX]{x1D735}_{i}v^{i}\unicode[STIX]{x1D707})]/\unicode[STIX]{x1D707}=[(\unicode[STIX]{x1D735}_{i}v^{i}\circ \unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D711}_{t}^{\ast }\unicode[STIX]{x1D707}]/\unicode[STIX]{x1D707}=J_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D735}_{i}v^{i}\circ \unicode[STIX]{x1D711}_{t}.\end{eqnarray}$$
B.12 Integration of differential forms and the Stokes theorem
The standard
![]() $p$
-simplex in an oriented Euclidean space
$p$
-simplex in an oriented Euclidean space
![]() $\mathbb{R}^{p}$
, is the oriented convex closed set
$\mathbb{R}^{p}$
, is the oriented convex closed set
 $\mathbb{S}_{p}=\{x\in \mathbb{R}^{p}\mid 0\leqslant x^{i}\leqslant 1,\sum _{i=1}^{p}x^{i}\leqslant 1\}$
. The vertices, which generate
$\mathbb{S}_{p}=\{x\in \mathbb{R}^{p}\mid 0\leqslant x^{i}\leqslant 1,\sum _{i=1}^{p}x^{i}\leqslant 1\}$
. The vertices, which generate
![]() $\mathbb{S}_{p}\subset \mathbb{R}^{p}$
, are the
$\mathbb{S}_{p}\subset \mathbb{R}^{p}$
, are the
![]() $p+1$
points
$p+1$
points
 $V_{0}=(0,\ldots ,0)$
,
$V_{0}=(0,\ldots ,0)$
,
 $V_{1}=(1,0\ldots ,0),\ldots ,V_{p}(0,\ldots ,0,1)$
. We shall write
$V_{1}=(1,0\ldots ,0),\ldots ,V_{p}(0,\ldots ,0,1)$
. We shall write
 $\mathbb{S}_{p}=(V_{0},\ldots ,V_{p})$
. Opposite to each vertex
$\mathbb{S}_{p}=(V_{0},\ldots ,V_{p})$
. Opposite to each vertex
![]() $V_{k}$
there is the
$V_{k}$
there is the
![]() $k$
th face of
$k$
th face of
![]() $\mathbb{S}_{p}$
, which is not a standard Euclidean simplex, sitting as it does in
$\mathbb{S}_{p}$
, which is not a standard Euclidean simplex, sitting as it does in
![]() $\mathbb{R}^{p}$
instead of
$\mathbb{R}^{p}$
instead of
![]() $\mathbb{R}^{p-1}$
. We shall rather consider it as a singular simplex in
$\mathbb{R}^{p-1}$
. We shall rather consider it as a singular simplex in
![]() $\mathbb{R}^{p}$
. In order to do this we must exhibit a specific map
$\mathbb{R}^{p}$
. In order to do this we must exhibit a specific map
 $f_{p-1}^{k}:\mathbb{S}_{p-1}\rightarrow \mathbb{S}_{p}$
given by
$f_{p-1}^{k}:\mathbb{S}_{p-1}\rightarrow \mathbb{S}_{p}$
given by
 $$\begin{eqnarray}f_{p-1}^{0}(y^{1},\ldots ,y^{\,p-1})=\left(1-\mathop{\sum }_{i=1}^{p-1}y^{i},y^{1},\ldots ,y^{\,p-1}\right),\end{eqnarray}$$
$$\begin{eqnarray}f_{p-1}^{0}(y^{1},\ldots ,y^{\,p-1})=\left(1-\mathop{\sum }_{i=1}^{p-1}y^{i},y^{1},\ldots ,y^{\,p-1}\right),\end{eqnarray}$$
and
 $$\begin{eqnarray}f_{p-1}^{k}(y^{1},\ldots ,y^{\,p-1})=(y^{1},\ldots ,y^{k-1},0,y^{k},\ldots ,y^{\,p-1}),\end{eqnarray}$$
$$\begin{eqnarray}f_{p-1}^{k}(y^{1},\ldots ,y^{\,p-1})=(y^{1},\ldots ,y^{k-1},0,y^{k},\ldots ,y^{\,p-1}),\end{eqnarray}$$
if
![]() $k\neq 0$
. A
$k\neq 0$
. A
![]() $\mathscr{C}^{m}$
-singular
$\mathscr{C}^{m}$
-singular
![]() $p$
-simplex on a
$p$
-simplex on a
![]() $\mathscr{C}^{r}$
-manifolds
$\mathscr{C}^{r}$
-manifolds
![]() $M$
,
$M$
,
 $1\leqslant m\leqslant r$
, is a
$1\leqslant m\leqslant r$
, is a
![]() $\mathscr{C}^{m}$
-map
$\mathscr{C}^{m}$
-map
 ${\mathcal{S}}_{p}:\mathbb{S}_{p}\rightarrow M$
. The points
${\mathcal{S}}_{p}:\mathbb{S}_{p}\rightarrow M$
. The points
 ${\mathcal{S}}_{p}(V_{0}),\ldots ,{\mathcal{S}}_{p}(V_{p})$
are the vertices of the singular
${\mathcal{S}}_{p}(V_{0}),\ldots ,{\mathcal{S}}_{p}(V_{p})$
are the vertices of the singular
![]() $p$
-simplex
$p$
-simplex
![]() ${\mathcal{S}}_{p}$
and the maps
${\mathcal{S}}_{p}$
and the maps
 ${\mathcal{S}}_{p}\circ f_{p-1}^{k}:\mathbb{S}_{p-1}\rightarrow M$
are called the
${\mathcal{S}}_{p}\circ f_{p-1}^{k}:\mathbb{S}_{p-1}\rightarrow M$
are called the
![]() $k$
th face of the singular
$k$
th face of the singular
![]() $p$
-simplex
$p$
-simplex
![]() ${\mathcal{S}}_{p}$
. We emphasise that there is no restriction on the rank (dimension of the image in
${\mathcal{S}}_{p}$
. We emphasise that there is no restriction on the rank (dimension of the image in
![]() $M$
) of the map
$M$
) of the map
![]() ${\mathcal{S}}_{p}$
; for example the image of
${\mathcal{S}}_{p}$
; for example the image of
![]() $\mathbb{S}_{p}$
, which is also denoted by
$\mathbb{S}_{p}$
, which is also denoted by
![]() ${\mathcal{S}}_{p}$
may be a single point in
${\mathcal{S}}_{p}$
may be a single point in
![]() $M$
. A (
$M$
. A (
![]() $\mathscr{C}^{m}$
-singular)
$\mathscr{C}^{m}$
-singular)
![]() $p$
-chain
$p$
-chain
![]() $c_{p}$
on
$c_{p}$
on
![]() $M$
is a finite linear combination with real coefficients
$M$
is a finite linear combination with real coefficients
![]() $\unicode[STIX]{x1D706}_{j}\in \mathbb{R}$
of
$\unicode[STIX]{x1D706}_{j}\in \mathbb{R}$
of
![]() $\mathscr{C}^{m}$
-singular
$\mathscr{C}^{m}$
-singular
![]() $p$
-simplexes
$p$
-simplexes
 $\{{\mathcal{S}}_{p,j}\}_{1\leqslant j\leqslant n}$
; that is
$\{{\mathcal{S}}_{p,j}\}_{1\leqslant j\leqslant n}$
; that is
 $c_{p}=\sum _{j=1}^{n}\unicode[STIX]{x1D706}_{j}{\mathcal{S}}_{p,j}$
. The boundary of a singular
$c_{p}=\sum _{j=1}^{n}\unicode[STIX]{x1D706}_{j}{\mathcal{S}}_{p,j}$
. The boundary of a singular
![]() $p$
-simplex
$p$
-simplex
![]() ${\mathcal{S}}_{p}$
is the
${\mathcal{S}}_{p}$
is the
![]() $(p-1)$
-chain
$(p-1)$
-chain
![]() $\unicode[STIX]{x2202}{\mathcal{S}}_{p}$
defined by
$\unicode[STIX]{x2202}{\mathcal{S}}_{p}$
defined by
 $$\begin{eqnarray}\unicode[STIX]{x2202}{\mathcal{S}}_{p}=\mathop{\sum }_{k=0}^{p}(-1)^{k}{\mathcal{S}}_{p}\circ f_{p-1}^{k},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}{\mathcal{S}}_{p}=\mathop{\sum }_{k=0}^{p}(-1)^{k}{\mathcal{S}}_{p}\circ f_{p-1}^{k},\end{eqnarray}$$
and that of a singular
![]() $p$
-chain is obtained by extending the operator
$p$
-chain is obtained by extending the operator
![]() $\unicode[STIX]{x2202}$
from simplexes to chains by linearity. For example, in
$\unicode[STIX]{x2202}$
from simplexes to chains by linearity. For example, in
![]() $\mathbb{R}^{2}$
the 2-simplex is a triangle
$\mathbb{R}^{2}$
the 2-simplex is a triangle
 $\mathbb{S}_{2}=(V_{0},V_{1},V_{2})$
, and its boundary is the 1-chain
$\mathbb{S}_{2}=(V_{0},V_{1},V_{2})$
, and its boundary is the 1-chain
 $\unicode[STIX]{x2202}\mathbb{S}_{2}=(V_{1},V_{2})-(V_{0},V_{2})+(V_{0},V_{1})$
. Using the relation
$\unicode[STIX]{x2202}\mathbb{S}_{2}=(V_{1},V_{2})-(V_{0},V_{2})+(V_{0},V_{1})$
. Using the relation
 $f_{p-1}^{j}\circ f_{p-2}^{j}=f_{p-2}^{i-1}\circ f_{p-2}^{i-1}$
for
$f_{p-1}^{j}\circ f_{p-2}^{j}=f_{p-2}^{i-1}\circ f_{p-2}^{i-1}$
for
![]() $j<i$
, we can verify the property
$j<i$
, we can verify the property
 $$\begin{eqnarray}\unicode[STIX]{x2202}^{2}=\unicode[STIX]{x2202}\circ \unicode[STIX]{x2202}=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}^{2}=\unicode[STIX]{x2202}\circ \unicode[STIX]{x2202}=0.\end{eqnarray}$$
The singular
![]() $p$
-simplex
$p$
-simplex
 ${\mathcal{S}}_{p}:\mathbb{S}_{p}\rightarrow M$
is the natural object over which one integrates
${\mathcal{S}}_{p}:\mathbb{S}_{p}\rightarrow M$
is the natural object over which one integrates
![]() $p$
-forms of
$p$
-forms of
![]() $M$
via the pullback
$M$
via the pullback
 $$\begin{eqnarray}\int _{{\mathcal{S}}_{p}}\unicode[STIX]{x1D6FC}=\int _{\mathbb{S}_{p}}{\mathcal{S}}_{p}^{\ast }\unicode[STIX]{x1D6FC},\quad \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M).\end{eqnarray}$$
$$\begin{eqnarray}\int _{{\mathcal{S}}_{p}}\unicode[STIX]{x1D6FC}=\int _{\mathbb{S}_{p}}{\mathcal{S}}_{p}^{\ast }\unicode[STIX]{x1D6FC},\quad \unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M).\end{eqnarray}$$
Integration of a
![]() $p$
-form over a
$p$
-form over a
![]() $p$
-chain is easily obtained by linear extension. Finally, we give the Stokes theorem on chains. If
$p$
-chain is easily obtained by linear extension. Finally, we give the Stokes theorem on chains. If
![]() $c$
is any
$c$
is any
![]() $p$
-chain and
$p$
-chain and
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p-1}(M)$
, then
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p-1}(M)$
, then
 $$\begin{eqnarray}\int _{c}\,\text{d}\unicode[STIX]{x1D6FC}=\int _{\unicode[STIX]{x2202}c}\unicode[STIX]{x1D6FC}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{c}\,\text{d}\unicode[STIX]{x1D6FC}=\int _{\unicode[STIX]{x2202}c}\unicode[STIX]{x1D6FC}.\end{eqnarray}$$
A detailed description of the Stokes theorem on chains can be found in Abraham et al. (Reference Abraham, Marsden and Ratiu1998, § 7.2C, p. 495) and Frankel (Reference Frankel2012, § 3.3, p. 110 and § 13.1, p. 333).
B.13 From local to global geometry: Betti numbers and Hodge’s generalisation of the Helmholtz decomposition
Throughout our study of hydrodynamics using a geometrical point of view, we have encountered questions that depend on the global topological structure of the space in which the flow takes place. One frequently occurring example is the need to know under what conditions a differential form that is closed (i.e. has a vanishing exterior derivative) is also exact (i.e. is the exterior derivative of some other form). Another instance has do with the generalisation of the well-known Helmholtz decomposition. The latter states that in the full 3D space, any square integrable vector field can be orthogonally decomposed into the sum of two vector fields, one being a gradient and the other one a curl. In terms of differential forms this amounts to decomposing a differential form into the sum of an exact form and of a co-exact form. Actually, the correct decomposition, called the Hodge decomposition, has sometimes a third term, which is harmonic (of vanishing Laplacian).
The appropriate tool to address such global topological issues is known as cohomology, a central subject in modern mathematics. Here we give only a glimpse of some key results that matter for the geometrical approach to fluid mechanics. The emphasis will be on Betti numbers that give necessary and sufficient conditions for a closed
![]() $p$
-form to be exact.
$p$
-form to be exact.
Let
![]() $M$
(respectively
$M$
(respectively
![]() $N$
) be a differentiable manifold of dimension
$N$
) be a differentiable manifold of dimension
![]() $d$
(respectively
$d$
(respectively
![]() $n$
). Singular
$n$
). Singular
![]() $p$
-chains have been defined in § B.12. The collection of all singular
$p$
-chains have been defined in § B.12. The collection of all singular
![]() $p$
-chains of
$p$
-chains of
![]() $M$
with coefficients in
$M$
with coefficients in
![]() $\mathbb{R}$
forms an Abelian (commutative) group, the (singular)
$\mathbb{R}$
forms an Abelian (commutative) group, the (singular)
![]() $p$
-chain group of
$p$
-chain group of
![]() $M$
with coefficients in
$M$
with coefficients in
![]() $\mathbb{R}$
, written
$\mathbb{R}$
, written
 $C_{p}(M;\mathbb{R})$
. The boundary operator
$C_{p}(M;\mathbb{R})$
. The boundary operator
![]() $\unicode[STIX]{x2202}$
defines the homomorphism
$\unicode[STIX]{x2202}$
defines the homomorphism
 $\unicode[STIX]{x2202}:C_{p}(M;\mathbb{R})\rightarrow C_{p-1}(M;\mathbb{R})$
. Given a map
$\unicode[STIX]{x2202}:C_{p}(M;\mathbb{R})\rightarrow C_{p-1}(M;\mathbb{R})$
. Given a map
 $\unicode[STIX]{x1D711}:M\rightarrow N$
we have an induced homomorphism
$\unicode[STIX]{x1D711}:M\rightarrow N$
we have an induced homomorphism
 $\unicode[STIX]{x1D711}_{\ast }:C_{p}(M;\mathbb{R})\rightarrow C_{p}(N;\mathbb{R})$
and the boundary homomorphism
$\unicode[STIX]{x1D711}_{\ast }:C_{p}(M;\mathbb{R})\rightarrow C_{p}(N;\mathbb{R})$
and the boundary homomorphism
![]() $\unicode[STIX]{x2202}$
is natural with respect to such maps, i.e.
$\unicode[STIX]{x2202}$
is natural with respect to such maps, i.e.
 $\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D711}_{\ast }=\unicode[STIX]{x1D711}_{\ast }\circ \unicode[STIX]{x2202}$
. We define a (singular)
$\unicode[STIX]{x2202}\circ \unicode[STIX]{x1D711}_{\ast }=\unicode[STIX]{x1D711}_{\ast }\circ \unicode[STIX]{x2202}$
. We define a (singular)
![]() $p$
-cycle to be a
$p$
-cycle to be a
![]() $p$
-chain
$p$
-chain
![]() $c_{p}$
whose boundary is 0. The collection of all
$c_{p}$
whose boundary is 0. The collection of all
![]() $p$
-cycles,
$p$
-cycles,
 $$\begin{eqnarray}Z_{p}(M;\mathbb{R}):=\{c_{p}\in C_{p}\mid \unicode[STIX]{x2202}c_{p}=0\}=\text{ker}\,\unicode[STIX]{x2202}:C_{p}\rightarrow C_{p-1},\end{eqnarray}$$
$$\begin{eqnarray}Z_{p}(M;\mathbb{R}):=\{c_{p}\in C_{p}\mid \unicode[STIX]{x2202}c_{p}=0\}=\text{ker}\,\unicode[STIX]{x2202}:C_{p}\rightarrow C_{p-1},\end{eqnarray}$$
that is, the kernel of the boundary homomorphism
![]() $\unicode[STIX]{x2202}$
, is a subgroup (the
$\unicode[STIX]{x2202}$
, is a subgroup (the
![]() $p$
-cycle group) of the chain group
$p$
-cycle group) of the chain group
![]() $C_{p}$
. We define a
$C_{p}$
. We define a
![]() $p$
-boundary
$p$
-boundary
![]() $\unicode[STIX]{x1D6FD}_{p}$
to be a
$\unicode[STIX]{x1D6FD}_{p}$
to be a
![]() $p$
-chain that is the boundary of some
$p$
-chain that is the boundary of some
![]() $(p+1)$
-chain. The collection of all such chains
$(p+1)$
-chain. The collection of all such chains
 $$\begin{eqnarray}B_{p}(M;\mathbb{R}):=\{\unicode[STIX]{x1D6FD}_{p}\in C_{p}\mid \unicode[STIX]{x1D6FD}_{p}=\unicode[STIX]{x2202}c_{p+1},\text{for some}~c_{p+1}\in C_{p+1}\}=\text{Im}\,\unicode[STIX]{x2202}:C_{p+1}\rightarrow C_{p},\end{eqnarray}$$
$$\begin{eqnarray}B_{p}(M;\mathbb{R}):=\{\unicode[STIX]{x1D6FD}_{p}\in C_{p}\mid \unicode[STIX]{x1D6FD}_{p}=\unicode[STIX]{x2202}c_{p+1},\text{for some}~c_{p+1}\in C_{p+1}\}=\text{Im}\,\unicode[STIX]{x2202}:C_{p+1}\rightarrow C_{p},\end{eqnarray}$$
the image or range of
![]() $\unicode[STIX]{x2202}$
, is a subgroup (the
$\unicode[STIX]{x2202}$
, is a subgroup (the
![]() $p$
-boundary group) of
$p$
-boundary group) of
![]() $C_{p}$
. In addition,
$C_{p}$
. In addition,
 $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x2202}\unicode[STIX]{x2202}c=0$
implies that
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x2202}\unicode[STIX]{x2202}c=0$
implies that
 $B_{p}\subset Z_{p}\subset C_{p}$
. When considering closed forms, we observe that boundaries contribute nothing to integrals. Thus, when integrating closed forms, we may identify two cycles if they differ by a boundary. Therefore we say that two cycles
$B_{p}\subset Z_{p}\subset C_{p}$
. When considering closed forms, we observe that boundaries contribute nothing to integrals. Thus, when integrating closed forms, we may identify two cycles if they differ by a boundary. Therefore we say that two cycles
![]() $c_{p}$
and
$c_{p}$
and
![]() $c_{p}^{\prime }$
in
$c_{p}^{\prime }$
in
 $Z_{p}(M;\mathbb{R})$
are equivalent or homologous if they differ by a boundary, that is, an element of the subgroup
$Z_{p}(M;\mathbb{R})$
are equivalent or homologous if they differ by a boundary, that is, an element of the subgroup
 $B_{p}(M;\mathbb{R})$
of
$B_{p}(M;\mathbb{R})$
of
 $Z_{p}(M;\mathbb{R})$
. The quotient group
$Z_{p}(M;\mathbb{R})$
. The quotient group
 $$\begin{eqnarray}H_{p}(M;\mathbb{R}):=\frac{Z_{p}(M;\mathbb{R})}{B_{p}(M;\mathbb{R})},\end{eqnarray}$$
$$\begin{eqnarray}H_{p}(M;\mathbb{R}):=\frac{Z_{p}(M;\mathbb{R})}{B_{p}(M;\mathbb{R})},\end{eqnarray}$$
is called the
![]() $p$
th homology group. When
$p$
th homology group. When
![]() $B_{p}$
and
$B_{p}$
and
![]() $Z_{p}$
are infinite-dimensional, in many cases
$Z_{p}$
are infinite-dimensional, in many cases
![]() $H_{p}$
is nevertheless finite-dimensional. For example, this is the case when
$H_{p}$
is nevertheless finite-dimensional. For example, this is the case when
![]() $M$
is a compact finite-dimensional manifold. The dimension of the vector space
$M$
is a compact finite-dimensional manifold. The dimension of the vector space
![]() $H_{p}$
is called the
$H_{p}$
is called the
![]() $p$
th Betti number, written
$p$
th Betti number, written
 $b_{p}=b_{p}(M)$
and defined by
$b_{p}=b_{p}(M)$
and defined by
 $$\begin{eqnarray}b_{p}(M):=\dim H_{p}(M;\mathbb{R}).\end{eqnarray}$$
$$\begin{eqnarray}b_{p}(M):=\dim H_{p}(M;\mathbb{R}).\end{eqnarray}$$
In other words,
![]() $b_{p}$
is the maximum number of
$b_{p}$
is the maximum number of
![]() $p$
-cycles on
$p$
-cycles on
![]() $M$
, such that all real linear combinations with non-vanishing coefficients are never a boundary. Since
$M$
, such that all real linear combinations with non-vanishing coefficients are never a boundary. Since
![]() $\unicode[STIX]{x1D711}_{\ast }$
commutes with the boundary homomorphism
$\unicode[STIX]{x1D711}_{\ast }$
commutes with the boundary homomorphism
![]() $\unicode[STIX]{x2202}$
, we know that
$\unicode[STIX]{x2202}$
, we know that
![]() $\unicode[STIX]{x1D711}_{\ast }$
takes cycles into cycles and boundaries into boundaries. Thus
$\unicode[STIX]{x1D711}_{\ast }$
takes cycles into cycles and boundaries into boundaries. Thus
![]() $\unicode[STIX]{x1D711}_{\ast }$
sends homology classes into homology classes, and we have an induced homomorphism
$\unicode[STIX]{x1D711}_{\ast }$
sends homology classes into homology classes, and we have an induced homomorphism
 $\unicode[STIX]{x1D711}_{\ast }:H_{p}(M;\mathbb{R})\rightarrow H_{p}(N;\mathbb{R})$
. We now give some fundamental examples. If
$\unicode[STIX]{x1D711}_{\ast }:H_{p}(M;\mathbb{R})\rightarrow H_{p}(N;\mathbb{R})$
. We now give some fundamental examples. If
![]() $M$
is compact (path-)connected (any two points of
$M$
is compact (path-)connected (any two points of
![]() $M$
can be connected by a piecewise smooth curves) then
$M$
can be connected by a piecewise smooth curves) then
 $H_{0}(M,\mathbb{R})=\mathbb{R}$
and
$H_{0}(M,\mathbb{R})=\mathbb{R}$
and
 $b_{0}(M)=1$
. If
$b_{0}(M)=1$
. If
![]() $M$
is compact but not connected, i.e. it consists of
$M$
is compact but not connected, i.e. it consists of
![]() $k$
connected pieces then
$k$
connected pieces then
 $H_{0}(M,\mathbb{R})=\mathbb{R}^{k}$
and
$H_{0}(M,\mathbb{R})=\mathbb{R}^{k}$
and
 $b_{0}(M)=k$
. If
$b_{0}(M)=k$
. If
![]() $M$
is a
$M$
is a
![]() $d$
-dimensional closed manifold (compact manifold without boundary), then
$d$
-dimensional closed manifold (compact manifold without boundary), then
 $H_{p}(M,\mathbb{R})=0$
and
$H_{p}(M,\mathbb{R})=0$
and
 $b_{p}(M)=0$
, for
$b_{p}(M)=0$
, for
![]() $p>d$
. If
$p>d$
. If
![]() $M$
is compact and simply connected (i.e. path-connected and every path between two points can be continuously transformed, staying on
$M$
is compact and simply connected (i.e. path-connected and every path between two points can be continuously transformed, staying on
![]() $M$
, into any other such path while preserving the two endpoints in question; in other words
$M$
, into any other such path while preserving the two endpoints in question; in other words
![]() $M$
is connected and every loop in
$M$
is connected and every loop in
![]() $M$
is contractible to a point) then
$M$
is contractible to a point) then
 $H_{1}(M,\mathbb{R})=0$
and
$H_{1}(M,\mathbb{R})=0$
and
 $b_{1}(M)=0$
. More examples can be found in Frankel (Reference Frankel2012, § 13.3, chap. 13, p. 347).
$b_{1}(M)=0$
. More examples can be found in Frankel (Reference Frankel2012, § 13.3, chap. 13, p. 347).
We set
 $Z^{p}(M;\mathbb{R})$
the subspace of
$Z^{p}(M;\mathbb{R})$
the subspace of
![]() $\unicode[STIX]{x039B}^{p}(M)$
constituted of all closed
$\unicode[STIX]{x039B}^{p}(M)$
constituted of all closed
![]() $p$
-forms, also called
$p$
-forms, also called
![]() $p$
-cocycles. We set
$p$
-cocycles. We set
 $B^{p}(M;\mathbb{R})$
the subspace of
$B^{p}(M;\mathbb{R})$
the subspace of
 $Z^{p}(M;\mathbb{R})$
constituted of all exact
$Z^{p}(M;\mathbb{R})$
constituted of all exact
![]() $p$
-forms, also called
$p$
-forms, also called
![]() $p$
-coboundaries. Integration allows us to associate to each closed
$p$
-coboundaries. Integration allows us to associate to each closed
![]() $p$
-form on
$p$
-form on
![]() $M$
a linear functional on
$M$
a linear functional on
![]() $p$
-cycles. This linear functional remains the same if we add to a closed
$p$
-cycles. This linear functional remains the same if we add to a closed
![]() $p$
-form an exact
$p$
-form an exact
![]() $p$
-form or if we add to a
$p$
-form or if we add to a
![]() $p$
-cycle a
$p$
-cycle a
![]() $p$
-boundary. Therefore this linear functional defines a linear transformation from the quotient space
$p$
-boundary. Therefore this linear functional defines a linear transformation from the quotient space
 $Z^{p}(M;\mathbb{R})/B^{p}(M;\mathbb{R})$
to
$Z^{p}(M;\mathbb{R})/B^{p}(M;\mathbb{R})$
to
 $H_{p}^{\ast }(M;\mathbb{R})$
that is the dual space of
$H_{p}^{\ast }(M;\mathbb{R})$
that is the dual space of
 $H_{p}(M;\mathbb{R})$
. This dual space is called the
$H_{p}(M;\mathbb{R})$
. This dual space is called the
![]() $p$
th cohomology vector space and is noted
$p$
th cohomology vector space and is noted
 $H^{p}(M;\mathbb{R})$
. Moreover, it can be shown that this linear functional is an isomorphism: this is the celebrated de Rham theorem (see, e.g., Frankel Reference Frankel2012, § 13.4, chap. 13, p. 355). Therefore we have
$H^{p}(M;\mathbb{R})$
. Moreover, it can be shown that this linear functional is an isomorphism: this is the celebrated de Rham theorem (see, e.g., Frankel Reference Frankel2012, § 13.4, chap. 13, p. 355). Therefore we have
 $$\begin{eqnarray}H^{p}(M;\mathbb{R}):=H_{p}^{\ast }(M;\mathbb{R})=\frac{Z^{p}(M;\mathbb{R})}{B^{p}(M;\mathbb{R})}.\end{eqnarray}$$
$$\begin{eqnarray}H^{p}(M;\mathbb{R}):=H_{p}^{\ast }(M;\mathbb{R})=\frac{Z^{p}(M;\mathbb{R})}{B^{p}(M;\mathbb{R})}.\end{eqnarray}$$
Two closed forms are equivalent or cohomologous if they differ by an exact form. As a consequence a closed
![]() $p$
-form is exact if and only if its integral on any
$p$
-form is exact if and only if its integral on any
![]() $p$
-cycles vanishes or if it is cohomologous to zero. Since a finite-dimensional vector space has the same dimension as its dual space, we have
$p$
-cycles vanishes or if it is cohomologous to zero. Since a finite-dimensional vector space has the same dimension as its dual space, we have
 $\dim H^{p}(M;\mathbb{R})=b_{p}(M)$
for
$\dim H^{p}(M;\mathbb{R})=b_{p}(M)$
for
![]() $M$
compact, where
$M$
compact, where
![]() $b_{p}(M)$
is the
$b_{p}(M)$
is the
![]() $p$
th Betti number. Thus
$p$
th Betti number. Thus
![]() $b_{p}(M)$
is also the maximum number of closed
$b_{p}(M)$
is also the maximum number of closed
![]() $p$
-forms on
$p$
-forms on
![]() $M$
, such that all linear combinations with non-vanishing coefficients are not exact. The knowledge of the Betti numbers of a given manifold
$M$
, such that all linear combinations with non-vanishing coefficients are not exact. The knowledge of the Betti numbers of a given manifold
![]() $M$
for
$M$
for
![]() $p\geqslant 1$
yields an exact quantitative answer to the question about exactness of a closed
$p\geqslant 1$
yields an exact quantitative answer to the question about exactness of a closed
![]() $p$
-form:
$p$
-form:
 $$\begin{eqnarray}\text{a closed}~p\text{-}\text{form is exact if and only if}~b_{p}(M)=0.\end{eqnarray}$$
$$\begin{eqnarray}\text{a closed}~p\text{-}\text{form is exact if and only if}~b_{p}(M)=0.\end{eqnarray}$$
From the Poincaré lemma (see, e.g., Abraham et al.
Reference Abraham, Marsden and Ratiu1998, Lemma 6.4.18), if
![]() $M$
is a compact
$M$
is a compact
![]() $d$
-dimensional contractible manifold (see § B.1 for the definition), all the Betti numbers
$d$
-dimensional contractible manifold (see § B.1 for the definition), all the Betti numbers
![]() $p\geqslant 1$
vanish, i.e.
$p\geqslant 1$
vanish, i.e.
 $b_{1}(M)=\cdots =b_{d}(M)=0$
, and
$b_{1}(M)=\cdots =b_{d}(M)=0$
, and
 $b_{0}(M)=1$
. Contractibility is, however, an excessively strong constraint to ensure the equivalence of closeness and exactness. For
$b_{0}(M)=1$
. Contractibility is, however, an excessively strong constraint to ensure the equivalence of closeness and exactness. For
![]() $p$
-forms of a given degree
$p$
-forms of a given degree
![]() $p$
, the vanishing of just the Betti number,
$p$
, the vanishing of just the Betti number,
![]() $b_{p}(M)$
is actually sufficient. Let us remark that from the duality between the finite-dimensional vector spaces
$b_{p}(M)$
is actually sufficient. Let us remark that from the duality between the finite-dimensional vector spaces
 $H^{p}(M;\mathbb{R})$
and
$H^{p}(M;\mathbb{R})$
and
 $H_{p}^{\ast }(M;\mathbb{R})$
exactness of
$H_{p}^{\ast }(M;\mathbb{R})$
exactness of
![]() $p$
-form can be determined from the topological properties of
$p$
-form can be determined from the topological properties of
![]() $M$
.
$M$
.
The Laplace–de Rham operator
 $\unicode[STIX]{x0394}_{H}:\unicode[STIX]{x039B}^{p}(M)\rightarrow \unicode[STIX]{x039B}^{p}(M)$
is defined by
$\unicode[STIX]{x0394}_{H}:\unicode[STIX]{x039B}^{p}(M)\rightarrow \unicode[STIX]{x039B}^{p}(M)$
is defined by
 $\unicode[STIX]{x0394}_{H}:=\text{d}\text{d}^{\star }+\text{d}^{\star }\text{d}=(\text{d}+\text{d}^{\star })(\text{d}+\text{d}^{\star })$
. A form
$\unicode[STIX]{x0394}_{H}:=\text{d}\text{d}^{\star }+\text{d}^{\star }\text{d}=(\text{d}+\text{d}^{\star })(\text{d}+\text{d}^{\star })$
. A form
![]() $\unicode[STIX]{x1D6FC}$
for which
$\unicode[STIX]{x1D6FC}$
for which
 $\unicode[STIX]{x0394}_{H}a=0$
is called harmonic. Let
$\unicode[STIX]{x0394}_{H}a=0$
is called harmonic. Let
 ${\mathcal{H}}^{p}(M):=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)\mid \unicode[STIX]{x0394}_{H}\unicode[STIX]{x1D6FC}=0\}$
denote the vector space of harmonic
${\mathcal{H}}^{p}(M):=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)\mid \unicode[STIX]{x0394}_{H}\unicode[STIX]{x1D6FC}=0\}$
denote the vector space of harmonic
![]() $p$
-forms. If
$p$
-forms. If
![]() $M$
is a closed Riemannian manifold (i.e. a compact boundaryless oriented Riemannian manifold) and
$M$
is a closed Riemannian manifold (i.e. a compact boundaryless oriented Riemannian manifold) and
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
, then
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
, then
 $\unicode[STIX]{x0394}_{H}\unicode[STIX]{x1D6FC}=0$
if and only if
$\unicode[STIX]{x0394}_{H}\unicode[STIX]{x1D6FC}=0$
if and only if
![]() $\text{d}\unicode[STIX]{x1D6FC}=0$
and
$\text{d}\unicode[STIX]{x1D6FC}=0$
and
![]() $\text{d}^{\star }\unicode[STIX]{x1D6FC}=0$
. If
$\text{d}^{\star }\unicode[STIX]{x1D6FC}=0$
. If
![]() $M$
is a compact Riemannian manifold with boundary, the condition that
$M$
is a compact Riemannian manifold with boundary, the condition that
![]() $\text{d}\unicode[STIX]{x1D6FC}=0$
and
$\text{d}\unicode[STIX]{x1D6FC}=0$
and
![]() $\text{d}^{\star }\unicode[STIX]{x1D6FC}=0$
is now stronger than
$\text{d}^{\star }\unicode[STIX]{x1D6FC}=0$
is now stronger than
 $\unicode[STIX]{x0394}_{H}\unicode[STIX]{x1D6FC}=0$
. Thus the vector space of harmonic
$\unicode[STIX]{x0394}_{H}\unicode[STIX]{x1D6FC}=0$
. Thus the vector space of harmonic
![]() $p$
-form is defined by
$p$
-form is defined by
 ${\mathcal{H}}^{p}(M)=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)\mid \text{d}\unicode[STIX]{x1D6FC}=\text{d}^{\star }\unicode[STIX]{x1D6FC}=0\}$
. The Hodge theorem (see, e.g., Frankel Reference Frankel2012, Theorem 14.28, chap. 14, p. 371; see also de Rham (Reference De Rham1984), Theorem 22, chap. V, § 1, p. 131) states that if
${\mathcal{H}}^{p}(M)=\{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)\mid \text{d}\unicode[STIX]{x1D6FC}=\text{d}^{\star }\unicode[STIX]{x1D6FC}=0\}$
. The Hodge theorem (see, e.g., Frankel Reference Frankel2012, Theorem 14.28, chap. 14, p. 371; see also de Rham (Reference De Rham1984), Theorem 22, chap. V, § 1, p. 131) states that if
![]() $M$
is a closed Riemannian manifold, then the vector space of harmonic
$M$
is a closed Riemannian manifold, then the vector space of harmonic
![]() $p$
-form is finite-dimensional and the Poisson equation
$p$
-form is finite-dimensional and the Poisson equation
 $\unicode[STIX]{x0394}_{H}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70C}$
has a solution if and only if
$\unicode[STIX]{x0394}_{H}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70C}$
has a solution if and only if
![]() $\unicode[STIX]{x1D70C}$
is orthogonal to
$\unicode[STIX]{x1D70C}$
is orthogonal to
![]() ${\mathcal{H}}^{p}(M)$
, that is
${\mathcal{H}}^{p}(M)$
, that is
 $\langle h,\unicode[STIX]{x1D70C}\rangle _{g}=0$
, for all
$\langle h,\unicode[STIX]{x1D70C}\rangle _{g}=0$
, for all
 $h\in {\mathcal{H}}^{p}(M)$
and where (see § B.9)
$h\in {\mathcal{H}}^{p}(M)$
and where (see § B.9)
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\rangle _{g}:=\int _{M}\unicode[STIX]{x1D6FC}\wedge \star \unicode[STIX]{x1D6FD}=\int _{M}(\!(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\!)_{g}\unicode[STIX]{x1D707},\quad \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(M).\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\rangle _{g}:=\int _{M}\unicode[STIX]{x1D6FC}\wedge \star \unicode[STIX]{x1D6FD}=\int _{M}(\!(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\!)_{g}\unicode[STIX]{x1D707},\quad \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(M).\end{eqnarray}$$
If
 $h_{1},h_{2},\ldots ,h_{q}$
is an orthonormal basis of
$h_{1},h_{2},\ldots ,h_{q}$
is an orthonormal basis of
![]() ${\mathcal{H}}^{p}(M)$
and
${\mathcal{H}}^{p}(M)$
and
 $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(M)$
, then
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(M)$
, then
 $\unicode[STIX]{x1D6FD}-h:=\unicode[STIX]{x1D6FD}-\sum _{i}\langle \unicode[STIX]{x1D6FD},h_{j}\rangle _{g}h_{j}$
is orthogonal to
$\unicode[STIX]{x1D6FD}-h:=\unicode[STIX]{x1D6FD}-\sum _{i}\langle \unicode[STIX]{x1D6FD},h_{j}\rangle _{g}h_{j}$
is orthogonal to
![]() ${\mathcal{H}}^{p}(M)$
and so, by Hodge’s theorem we can solve the equation
${\mathcal{H}}^{p}(M)$
and so, by Hodge’s theorem we can solve the equation
 $\unicode[STIX]{x0394}_{H}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}-h$
for
$\unicode[STIX]{x0394}_{H}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}-h$
for
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
. In other words, for any
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p}(M)$
. In other words, for any
 $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(M)$
on a closed Riemannian manifold
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p}(M)$
on a closed Riemannian manifold
![]() $M$
we can write
$M$
we can write
 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}=\text{d}(\text{d}^{\star }\unicode[STIX]{x1D6FC})+\text{d}^{\star }(\text{d}\unicode[STIX]{x1D6FC})+h.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}=\text{d}(\text{d}^{\star }\unicode[STIX]{x1D6FC})+\text{d}^{\star }(\text{d}\unicode[STIX]{x1D6FC})+h.\end{eqnarray}$$
Thus any
![]() $p$
-form
$p$
-form
![]() $\unicode[STIX]{x1D6FD}$
on a closed Riemannian manifold
$\unicode[STIX]{x1D6FD}$
on a closed Riemannian manifold
![]() $M$
can be written as the sum of an exact
$M$
can be written as the sum of an exact
![]() $p$
-form
$p$
-form
![]() $\text{d}(\text{d}^{\star }\unicode[STIX]{x1D6FC})$
, a co-exact
$\text{d}(\text{d}^{\star }\unicode[STIX]{x1D6FC})$
, a co-exact
![]() $p$
-form
$p$
-form
![]() $\text{d}^{\star }(\text{d}\unicode[STIX]{x1D6FC})$
and a harmonic
$\text{d}^{\star }(\text{d}\unicode[STIX]{x1D6FC})$
and a harmonic
![]() $p$
-form
$p$
-form
![]() $h$
. Hence, we obtain the Hodge decomposition
$h$
. Hence, we obtain the Hodge decomposition
 $$\begin{eqnarray}\unicode[STIX]{x039B}^{p}(M)=\text{d}\unicode[STIX]{x039B}^{p-1}(M)\oplus \text{d}^{\star }\unicode[STIX]{x039B}^{p+1}(M)\oplus {\mathcal{H}}^{p}(M),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x039B}^{p}(M)=\text{d}\unicode[STIX]{x039B}^{p-1}(M)\oplus \text{d}^{\star }\unicode[STIX]{x039B}^{p+1}(M)\oplus {\mathcal{H}}^{p}(M),\end{eqnarray}$$
where the three subspaces are mutually orthogonal. As already observed the Hodge decomposition generalises and extends the Helmholtz decomposition, for which the harmonic term is absent (because in
![]() $\mathbb{R}^{d}$
, the 1-cohomology
$\mathbb{R}^{d}$
, the 1-cohomology
![]() $H^{1}=0$
). In particular, from the Hodge decomposition, if
$H^{1}=0$
). In particular, from the Hodge decomposition, if
 $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p-1}(M)$
is closed on a closed manifold
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x039B}^{p-1}(M)$
is closed on a closed manifold
![]() $M$
, then
$M$
, then
 $\unicode[STIX]{x1D6FD}=\text{d}\unicode[STIX]{x1D6FC}+h$
where
$\unicode[STIX]{x1D6FD}=\text{d}\unicode[STIX]{x1D6FC}+h$
where
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p-1}(M)$
and
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x039B}^{p-1}(M)$
and
 $h\in {\mathcal{H}}^{p}(M)$
. Thus in each
$h\in {\mathcal{H}}^{p}(M)$
. Thus in each
![]() $p$
-cohomology vector space there is a unique harmonic representative, or in other words the spaces
$p$
-cohomology vector space there is a unique harmonic representative, or in other words the spaces
![]() ${\mathcal{H}}^{p}(M)$
and
${\mathcal{H}}^{p}(M)$
and
 $H^{p}(M;\mathbb{R})$
are isomorphic:
$H^{p}(M;\mathbb{R})$
are isomorphic:
 $$\begin{eqnarray}H^{p}(M;\mathbb{R})\equiv {\mathcal{H}}^{p}(M).\end{eqnarray}$$
$$\begin{eqnarray}H^{p}(M;\mathbb{R})\equiv {\mathcal{H}}^{p}(M).\end{eqnarray}$$
The Hodge theorem and decomposition have been extended to non-compact spaces by de Rham (Reference De Rham1984, see chap. V, § 32, p. 136) and to a compact Riemannian manifold with boundary (see, e.g., Abraham et al. (Reference Abraham, Marsden and Ratiu1998), § 7.5, p. 541; see also Frankel (Reference Frankel2012), § 14.3, p. 375 and references therein). In the latter case, the space of closed (respectively exact)
![]() $p$
-forms must be replaced by the space of normal
$p$
-forms must be replaced by the space of normal
![]() $p$
-forms that are closed (respectively exact). Furthermore, the space of co-closed (respectively co-exact)
$p$
-forms that are closed (respectively exact). Furthermore, the space of co-closed (respectively co-exact)
![]() $p$
-forms must be replaced by the space of co-closed (respectively co-exact) tangent
$p$
-forms must be replaced by the space of co-closed (respectively co-exact) tangent
![]() $p$
-forms (Schwarz Reference Schwarz1995). Here, ‘normal’ means with vanishing tangential components and ‘tangent’ with vanishing normal components.
$p$
-forms (Schwarz Reference Schwarz1995). Here, ‘normal’ means with vanishing tangential components and ‘tangent’ with vanishing normal components.
Finally we recall the Bochner theorem (see, e.g., Frankel Reference Frankel2012, Theorem 14.33, § 14.2, p. 374), which states that if a closed Riemannian manifold
![]() $M$
has positive Ricci curvature, then a harmonic 1-form must vanish identically, and thus
$M$
has positive Ricci curvature, then a harmonic 1-form must vanish identically, and thus
![]() $M$
has first Betti number
$M$
has first Betti number
![]() $b_{1}=0$
and 1-cohomology
$b_{1}=0$
and 1-cohomology
 $H^{1}(M,\mathbb{R})=0$
.
$H^{1}(M,\mathbb{R})=0$
.