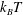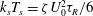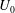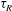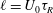1. Introduction
The behaviour of self-propelled objects such as bacteria, algae and synthetic Janus particles has become a dynamic field of research, both for the ‘swimming’ of individual particles (Lauga & Powers Reference Lauga and Powers2009) and for the collective behaviour of active suspensions (Toner, Tu & Ramaswamy Reference Toner, Tu and Ramaswamy2005). Owing to the particles’ self-motion, active matter can spontaneously phase-separate into dense and dilute regions (Cates et al. Reference Cates, Marenduzzo, Pagonabarraga and Tailleur2010; Fily & Marchetti Reference Fily and Marchetti2012; Bialké, Löwen & Speck Reference Bialké, Löwen and Speck2013; Buttinoni et al. Reference Buttinoni, Bialké, Kümmel, Löwen, Bechinger and Speck2013; Palacci et al. Reference Palacci, Sacanna, Steinberg, Pine and Chaikin2013; Stenhammar et al. Reference Stenhammar, Tiribocchi, Allen, Marenduzzo and Cates2013, Reference Stenhammar, Marenduzzo, Allen and Cates2014; Takatori, Yan & Brady Reference Takatori, Yan and Brady2014; Wysocki, Winkler & Gompper Reference Wysocki, Winkler and Gompper2014; Yang, Manning & Marchetti Reference Yang, Manning and Marchetti2014; Takatori & Brady Reference Takatori and Brady2015) and can move collectively under an orienting field (Takatori & Brady Reference Takatori and Brady2014).
Recently, the swim pressure (Takatori et al.
Reference Takatori, Yan and Brady2014; Yang et al.
Reference Yang, Manning and Marchetti2014) was introduced as a new perspective on the behaviour of active matter. The swim pressure is the pressure needed to confine active particles and is analogous to the osmotic pressure of Brownian colloids. The ‘ideal gas’ swim pressure in the dilute limit is
![]() ${\it\Pi}^{swim}=n{\it\zeta}U_{0}^{2}{\it\tau}_{R}/6$
(in 3D), where
${\it\Pi}^{swim}=n{\it\zeta}U_{0}^{2}{\it\tau}_{R}/6$
(in 3D), where
![]() $n$
is the number density of active particles,
$n$
is the number density of active particles,
![]() ${\it\zeta}$
is their drag coefficient,
${\it\zeta}$
is their drag coefficient,
![]() $U_{0}$
is the swim speed and
$U_{0}$
is the swim speed and
![]() ${\it\tau}_{R}$
is their reorientation time. The swim pressure, or stress, is defined as the moment of the swim force
${\it\tau}_{R}$
is their reorientation time. The swim pressure, or stress, is defined as the moment of the swim force
![]() $\langle {\bf\sigma}^{swim}\rangle =-n\langle \boldsymbol{x}\boldsymbol{F}^{swim}\rangle$
, where
$\langle {\bf\sigma}^{swim}\rangle =-n\langle \boldsymbol{x}\boldsymbol{F}^{swim}\rangle$
, where
![]() $\boldsymbol{F}^{swim}={\it\zeta}U_{0}\boldsymbol{q}$
, with
$\boldsymbol{F}^{swim}={\it\zeta}U_{0}\boldsymbol{q}$
, with
![]() $\boldsymbol{q}$
the orientation vector of the swimmer and
$\boldsymbol{q}$
the orientation vector of the swimmer and
![]() $\boldsymbol{x}$
its position. The ‘moment arm’ for the swim stress is the swimmer’s run length,
$\boldsymbol{x}$
its position. The ‘moment arm’ for the swim stress is the swimmer’s run length,
![]() $\ell =U_{0}{\it\tau}_{R}$
.
$\ell =U_{0}{\it\tau}_{R}$
.
The swim pressure is an average over the reorientation time
![]() ${\it\tau}_{R}$
, which implies an average over the run length
${\it\tau}_{R}$
, which implies an average over the run length
![]() $\ell$
. The swim pressure is only defined on, and applies for, lengths greater than the run length. And its use to compute forces on boundaries necessitates that the boundary or macroscopic length scale,
$\ell$
. The swim pressure is only defined on, and applies for, lengths greater than the run length. And its use to compute forces on boundaries necessitates that the boundary or macroscopic length scale,
![]() $L$
, be much larger than the run length (Yan & Brady Reference Yan and Brady2015). What happens when the length scale of interest is not large compared to the run length? Can we extend the notion of the swim pressure to such situations? Or more generally, how does the swim pressure emerge from a more microscopic description?
$L$
, be much larger than the run length (Yan & Brady Reference Yan and Brady2015). What happens when the length scale of interest is not large compared to the run length? Can we extend the notion of the swim pressure to such situations? Or more generally, how does the swim pressure emerge from a more microscopic description?
In this paper we provide such a microscopic theory and show how the swim pressure arises naturally as the characteristic macroscopic length scale becomes large compared to the run length. The theory is an extension of the well-known dynamics of passive colloidal particles to active colloidal particles, and will allow us to compute forces and torques on bodies and thus predict their motion in response to the swimmers’ activity.
2. Theory
For active colloidal particles there are three characteristic lengths: (i) the macroscopic length scale
![]() $L$
, (ii) the run length
$L$
, (ii) the run length
![]() $\ell =U_{0}{\it\tau}_{R}$
and (iii) a microscopic length
$\ell =U_{0}{\it\tau}_{R}$
and (iii) a microscopic length
![]() ${\it\delta}=\sqrt{D_{T}{\it\tau}_{R}}$
, where
${\it\delta}=\sqrt{D_{T}{\it\tau}_{R}}$
, where
![]() $D_{T}$
is the translational diffusivity of the active particles. Although in a typical application we expect
$D_{T}$
is the translational diffusivity of the active particles. Although in a typical application we expect
![]() $L>\ell \gg {\it\delta}$
, the theory we present is valid for any ratio of length scales.
$L>\ell \gg {\it\delta}$
, the theory we present is valid for any ratio of length scales.
Active Brownian particles (ABPs) are governed by the Smoluchowski equation for the probability density for finding a swimmer at
![]() $\boldsymbol{x}$
with orientation
$\boldsymbol{x}$
with orientation
![]() $\boldsymbol{q}$
:
$\boldsymbol{q}$
:
The translational and rotational fluxes are:
![]() $\boldsymbol{j}^{T}=(U_{0}\boldsymbol{q}+\boldsymbol{F}^{P}/{\it\zeta}-D_{T}\boldsymbol{{\rm\nabla}}\ln P)P$
and
$\boldsymbol{j}^{T}=(U_{0}\boldsymbol{q}+\boldsymbol{F}^{P}/{\it\zeta}-D_{T}\boldsymbol{{\rm\nabla}}\ln P)P$
and
![]() $\boldsymbol{j}^{R}=-D_{R}\boldsymbol{{\rm\nabla}}_{R}P$
, where
$\boldsymbol{j}^{R}=-D_{R}\boldsymbol{{\rm\nabla}}_{R}P$
, where
![]() $\boldsymbol{{\rm\nabla}}_{R}=\boldsymbol{q}\times \boldsymbol{{\rm\nabla}}_{\boldsymbol{q}}$
is the orientational gradient operator. For a spherical swimmer of radius
$\boldsymbol{{\rm\nabla}}_{R}=\boldsymbol{q}\times \boldsymbol{{\rm\nabla}}_{\boldsymbol{q}}$
is the orientational gradient operator. For a spherical swimmer of radius
![]() $a$
in a Newtonian solvent of viscosity
$a$
in a Newtonian solvent of viscosity
![]() ${\it\eta}$
,
${\it\eta}$
,
![]() ${\it\zeta}=6{\rm\pi}{\it\eta}a$
,
${\it\zeta}=6{\rm\pi}{\it\eta}a$
,
![]() $D_{T}=k_{B}T/{\it\zeta}=k_{B}T/6{\rm\pi}{\it\eta}a$
,
$D_{T}=k_{B}T/{\it\zeta}=k_{B}T/6{\rm\pi}{\it\eta}a$
,
![]() $D_{R}\;(=1/{\it\tau}_{R})=k_{B}T/8{\rm\pi}{\it\eta}a^{3}$
and
$D_{R}\;(=1/{\it\tau}_{R})=k_{B}T/8{\rm\pi}{\it\eta}a^{3}$
and
![]() ${\it\delta}=\sqrt{D_{T}/D_{R}}=\sqrt{4/3}a$
.
${\it\delta}=\sqrt{D_{T}/D_{R}}=\sqrt{4/3}a$
.
At a boundary surface the normal component of the translational flux must vanish,
![]() $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{j}^{T}=0$
. If there were no translational Brownian motion or boundary force (
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{j}^{T}=0$
. If there were no translational Brownian motion or boundary force (
![]() $\boldsymbol{F}^{P}=0$
), then
$\boldsymbol{F}^{P}=0$
), then
![]() $U_{0}(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{q})P=0$
, which means that either (i)
$U_{0}(\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{q})P=0$
, which means that either (i)
![]() $U_{0}=0$
or (ii)
$U_{0}=0$
or (ii)
![]() $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{q}=0$
or (iii)
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{q}=0$
or (iii)
![]() $P=0$
at the surface, none of which is true in general. It is essential to have a strong enough boundary force or translational Brownian diffusion (or both, or hydrodynamics) to prevent particle crossing. As is well known in colloidal dynamics, a hard-particle repulsive force is infinite and non-zero only at the boundary surface and the no-flux condition is satisfied via the Brownian flux.
$P=0$
at the surface, none of which is true in general. It is essential to have a strong enough boundary force or translational Brownian diffusion (or both, or hydrodynamics) to prevent particle crossing. As is well known in colloidal dynamics, a hard-particle repulsive force is infinite and non-zero only at the boundary surface and the no-flux condition is satisfied via the Brownian flux.
Rather than having a boundary force of finite range and amplitude or hydrodynamic lubrication interactions to prevent particle flux, we choose to use
![]() $D_{T}$
as this is the simplest to implement theoretically and most easily reveals the underlying physics. It is important to note that whatever means is used to prevent active particles from crossing a boundary it will introduce a microscopic length scale
$D_{T}$
as this is the simplest to implement theoretically and most easily reveals the underlying physics. It is important to note that whatever means is used to prevent active particles from crossing a boundary it will introduce a microscopic length scale
![]() ${\it\delta}$
. As we shall see, for pressures and forces,
${\it\delta}$
. As we shall see, for pressures and forces,
![]() ${\it\delta}$
will not appear in the final results. Any of the mechanisms would produce the same behaviour.
${\it\delta}$
will not appear in the final results. Any of the mechanisms would produce the same behaviour.
Indeed, Ezhilan, Alonso-Matilla & Saintillan (Reference Ezhilan, Alonso-Matilla and Saintillan2015) recently examined active particles in 2D confined between two walls without translational Brownian motion (
![]() $D_{T}\equiv 0$
) and showed that the problem could be modelled with two regions: freely swimming bulk behaviour connected to a singular surface layer of particles in contact with the walls. The action of translational Brownian motion is to spread this singular surface layer over the microscopic thickness
$D_{T}\equiv 0$
) and showed that the problem could be modelled with two regions: freely swimming bulk behaviour connected to a singular surface layer of particles in contact with the walls. The action of translational Brownian motion is to spread this singular surface layer over the microscopic thickness
![]() ${\it\delta}$
adjacent to the walls, as is standard in boundary-layer theory. Our planar 2D results are in agreement with their findings.
${\it\delta}$
adjacent to the walls, as is standard in boundary-layer theory. Our planar 2D results are in agreement with their findings.
Although we speak in terms of translational Brownian motion and forces proportional to
![]() $k_{B}T$
, this is not necessary. One can simply replace
$k_{B}T$
, this is not necessary. One can simply replace
![]() $k_{B}T$
with
$k_{B}T$
with
![]() ${\it\zeta}D_{T}$
and the results are unchanged; the translational diffusion, like the rotary diffusion
${\it\zeta}D_{T}$
and the results are unchanged; the translational diffusion, like the rotary diffusion
![]() $D_{R}$
, need not be thermal in origin. The Smoluchowski equation only requires that the random ‘Brownian’ displacements be small compared to any other length scale (e.g. the swimmer’s size).
$D_{R}$
, need not be thermal in origin. The Smoluchowski equation only requires that the random ‘Brownian’ displacements be small compared to any other length scale (e.g. the swimmer’s size).
The Smoluchowski equation applies for all length and time scales but its solution in any but the simplest situations is challenging. We need a simplified description that captures the essential physics and, more importantly, provides insight into the general behaviour and can explain phenomena without detailed calculations.
Consider a body immersed in a dilute suspension of ABPs. With
![]() $\boldsymbol{F}^{P}=0$
, the force the active colloidal particles exert on the body is given exactly by (Brady Reference Brady1993; Squires & Brady Reference Squires and Brady2005)
$\boldsymbol{F}^{P}=0$
, the force the active colloidal particles exert on the body is given exactly by (Brady Reference Brady1993; Squires & Brady Reference Squires and Brady2005)
![]() $\boldsymbol{F}=-k_{B}T\int _{S_{B}}P(\boldsymbol{x},\boldsymbol{q},t)\boldsymbol{n}\,\text{d}S$
, where
$\boldsymbol{F}=-k_{B}T\int _{S_{B}}P(\boldsymbol{x},\boldsymbol{q},t)\boldsymbol{n}\,\text{d}S$
, where
![]() $\boldsymbol{n}$
is the outer normal to the body surface as shown in figure 3. The force averaged over the orientation of the active particles is
$\boldsymbol{n}$
is the outer normal to the body surface as shown in figure 3. The force averaged over the orientation of the active particles is
where
![]() $n(\boldsymbol{x},t)\equiv \int P(\boldsymbol{x},\boldsymbol{q},t)\,\text{d}\boldsymbol{q}$
is the number density of swimmers.
$n(\boldsymbol{x},t)\equiv \int P(\boldsymbol{x},\boldsymbol{q},t)\,\text{d}\boldsymbol{q}$
is the number density of swimmers.
The conservation equations for the zeroth and first moments of the Smoluchowski equation are (Saintillan & Shelley Reference Saintillan, Shelley and Spagnolie2015)
Two remarks will help in understanding the structure of the moment equations. First, when departures from uniformity vary slowly, the
![]() $\boldsymbol{m}$
-field equation has a balance between the ‘sink’ term and the gradient in the concentration,
$\boldsymbol{m}$
-field equation has a balance between the ‘sink’ term and the gradient in the concentration,
![]() $2D_{R}\boldsymbol{m}\approx -(U_{0}\boldsymbol{{\rm\nabla}}n)/3$
, which gives a diffusive flux in the concentration field that incorporates the swim diffusivity:
$2D_{R}\boldsymbol{m}\approx -(U_{0}\boldsymbol{{\rm\nabla}}n)/3$
, which gives a diffusive flux in the concentration field that incorporates the swim diffusivity:
![]() $\boldsymbol{j}_{n}\approx -(D_{T}+(U_{0}^{2}{\it\tau}_{R})/6)\boldsymbol{{\rm\nabla}}n$
. Second, at the other extreme when variations are rapid, the
$\boldsymbol{j}_{n}\approx -(D_{T}+(U_{0}^{2}{\it\tau}_{R})/6)\boldsymbol{{\rm\nabla}}n$
. Second, at the other extreme when variations are rapid, the
![]() $\boldsymbol{m}$
-field has a natural screening length where diffusion balances the sink:
$\boldsymbol{m}$
-field has a natural screening length where diffusion balances the sink:
![]() $D_{T}{\rm\nabla}^{2}\boldsymbol{m}\approx 2D_{R}\boldsymbol{m}$
. This screening length is proportional to the microscopic length
$D_{T}{\rm\nabla}^{2}\boldsymbol{m}\approx 2D_{R}\boldsymbol{m}$
. This screening length is proportional to the microscopic length
![]() ${\it\delta}=\sqrt{D_{T}/D_{R}}$
. The screening length plays a fundamental, but unusual, role in active matter – it is essential in order to have a well-posed problem and there will be rapid variations in properties on the scale of
${\it\delta}=\sqrt{D_{T}/D_{R}}$
. The screening length plays a fundamental, but unusual, role in active matter – it is essential in order to have a well-posed problem and there will be rapid variations in properties on the scale of
![]() ${\it\delta}$
, but in the limit where
${\it\delta}$
, but in the limit where
![]() ${\it\delta}\ll \ell ,L$
, the microscopic length does not appear in the active pressure or in the forces and torques on boundaries. The athermal limit (
${\it\delta}\ll \ell ,L$
, the microscopic length does not appear in the active pressure or in the forces and torques on boundaries. The athermal limit (
![]() $D_{T}\rightarrow 0$
) is singular and
$D_{T}\rightarrow 0$
) is singular and
![]() $D_{T}$
(or
$D_{T}$
(or
![]() $k_{B}T$
) can only be set to zero after the limit is taken; the force from (2.2) will then be independent of
$k_{B}T$
) can only be set to zero after the limit is taken; the force from (2.2) will then be independent of
![]() $k_{B}T$
.
$k_{B}T$
.
3. Examples
First, we consider an infinite flat plate with normal along the
![]() $z$
-direction; there is no macroscopic length scale. The
$z$
-direction; there is no macroscopic length scale. The
![]() $n$
- and
$n$
- and
![]() $\boldsymbol{m}$
-fields are subject to no flux at
$\boldsymbol{m}$
-fields are subject to no flux at
![]() $z=0$
:
$z=0$
:
![]() $\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{j}_{n,m}=0$
and a uniform concentration and no polar order as
$\boldsymbol{n}\boldsymbol{\cdot }\boldsymbol{j}_{n,m}=0$
and a uniform concentration and no polar order as
![]() $z\rightarrow \infty$
:
$z\rightarrow \infty$
:
![]() $n\sim n^{\infty }$
and
$n\sim n^{\infty }$
and
![]() $\boldsymbol{m}\sim 0$
. The concentration and polar-order fields are simple exponentials decaying on the screening length
$\boldsymbol{m}\sim 0$
. The concentration and polar-order fields are simple exponentials decaying on the screening length
where
![]() ${\it\lambda}=\sqrt{2(1+(\ell /{\it\delta})^{2}/6)}/{\it\delta}$
is the inverse screening length.
${\it\lambda}=\sqrt{2(1+(\ell /{\it\delta})^{2}/6)}/{\it\delta}$
is the inverse screening length.
The concentration at the wall,
![]() $n(0)=n^{\infty }(1+(\ell /{\it\delta})^{2}/6)$
, is independent of the closure (which follows directly from (2.1) in 1D), always exceeds that far away and can become very large as
$n(0)=n^{\infty }(1+(\ell /{\it\delta})^{2}/6)$
, is independent of the closure (which follows directly from (2.1) in 1D), always exceeds that far away and can become very large as
![]() $\ell /{\it\delta}\rightarrow \infty$
. This ‘infinite’ concentration applies for a dilute suspension. It is not a build-up associated with a finite concentration of active particles. Rather, it is the singularity alluded to earlier that results if translational Brownian motion (or a microscopic length) is not considered. (The active particle size
$\ell /{\it\delta}\rightarrow \infty$
. This ‘infinite’ concentration applies for a dilute suspension. It is not a build-up associated with a finite concentration of active particles. Rather, it is the singularity alluded to earlier that results if translational Brownian motion (or a microscopic length) is not considered. (The active particle size
![]() $a$
must be taken into account in defining the no-flux surface
$a$
must be taken into account in defining the no-flux surface
![]() $z=0$
.)
$z=0$
.)
Even though the concentration can become arbitrarily large, the force per unit area or pressure on the wall from the microscopic force definition (2.2) is finite and independent of
![]() ${\it\delta}$
:
${\it\delta}$
:
![]() ${\it\Pi}^{W}=n(0)k_{B}T=n^{\infty }(k_{B}T+k_{s}T_{s})$
, where we have defined the swimmer’s ‘activity’
${\it\Pi}^{W}=n(0)k_{B}T=n^{\infty }(k_{B}T+k_{s}T_{s})$
, where we have defined the swimmer’s ‘activity’
![]() $k_{s}T_{s}={\it\zeta}U_{0}^{2}{\it\tau}_{R}/6=k_{B}T(\ell /{\it\delta})^{2}/6$
. We recognize the pressure on the wall as the active pressure – the sum of the osmotic pressure of Brownian particles plus the swim pressure. And note that this is true regardless of the relative magnitudes of
$k_{s}T_{s}={\it\zeta}U_{0}^{2}{\it\tau}_{R}/6=k_{B}T(\ell /{\it\delta})^{2}/6$
. We recognize the pressure on the wall as the active pressure – the sum of the osmotic pressure of Brownian particles plus the swim pressure. And note that this is true regardless of the relative magnitudes of
![]() $k_{B}T$
and
$k_{B}T$
and
![]() $k_{s}T_{s}$
(including the singular athermal limit
$k_{s}T_{s}$
(including the singular athermal limit
![]() $k_{B}T=0$
). This same independence of
$k_{B}T=0$
). This same independence of
![]() $k_{B}T$
occurs in the analogous hard-sphere rheology problem at high Péclet numbers (Brady & Morris Reference Brady and Morris1997; Squires & Brady Reference Squires and Brady2005). Also, the ratio
$k_{B}T$
occurs in the analogous hard-sphere rheology problem at high Péclet numbers (Brady & Morris Reference Brady and Morris1997; Squires & Brady Reference Squires and Brady2005). Also, the ratio
![]() $(\ell /{\it\delta})^{2}=6D^{swim}/D_{T}=U_{0}\ell /D_{T}=Pe_{\ell }$
is a Péclet number based on the run length that measures the relative importance of swimming to Brownian diffusion.
$(\ell /{\it\delta})^{2}=6D^{swim}/D_{T}=U_{0}\ell /D_{T}=Pe_{\ell }$
is a Péclet number based on the run length that measures the relative importance of swimming to Brownian diffusion.
The second problem is active Brownian particles confined between two parallel plates separated by a distance
![]() $H$
. The concentration distribution is
$H$
. The concentration distribution is
where the constant
![]() $n_{0}$
is related to the average number density of ABPs in the channel
$n_{0}$
is related to the average number density of ABPs in the channel
![]() $\langle n\rangle =\int _{0}^{H}n(z)\,\text{d}z/H$
. The concentration is identical at both walls and is the same as for a single wall with
$\langle n\rangle =\int _{0}^{H}n(z)\,\text{d}z/H$
. The concentration is identical at both walls and is the same as for a single wall with
![]() $n_{0}$
replacing
$n_{0}$
replacing
![]() $n^{\infty }$
. In the limit of large
$n^{\infty }$
. In the limit of large
![]() ${\it\lambda}H$
, corresponding to
${\it\lambda}H$
, corresponding to
![]() ${\it\delta}\ll H$
, and when
${\it\delta}\ll H$
, and when
![]() ${\it\delta}\ll \ell$
,
${\it\delta}\ll \ell$
,
![]() $n_{0}\sim \langle n\rangle [1+(\ell /H)/\sqrt{3}]^{-1}$
and the pressure at the walls becomes
$n_{0}\sim \langle n\rangle [1+(\ell /H)/\sqrt{3}]^{-1}$
and the pressure at the walls becomes
As for a single wall, the pressure is independent of the microscopic length scale
![]() ${\it\delta}$
but now depends on the ratio of the run length to the macroscopic scale
${\it\delta}$
but now depends on the ratio of the run length to the macroscopic scale
![]() $\ell /H$
. We shall see that this behaviour is generic – the influence of the run length enters as
$\ell /H$
. We shall see that this behaviour is generic – the influence of the run length enters as
![]() $\ell /L$
. In a simulation study Ray, Reichhardt & Reichhardt (Reference Ray, Reichhardt and Reichhardt2014) observed that the pressure in a channel depends on the gap spacing as predicted by (3.3) (in 2D the coefficient is
$\ell /L$
. In a simulation study Ray, Reichhardt & Reichhardt (Reference Ray, Reichhardt and Reichhardt2014) observed that the pressure in a channel depends on the gap spacing as predicted by (3.3) (in 2D the coefficient is
![]() $1/\sqrt{2}$
).
$1/\sqrt{2}$
).

Figure 1.
![]() ${\it\Pi}^{W}$
of ABPs confined between parallel walls in 2D. The inset shows the area fraction distribution
${\it\Pi}^{W}$
of ABPs confined between parallel walls in 2D. The inset shows the area fraction distribution
![]() ${\it\phi}(z)$
. Here,
${\it\phi}(z)$
. Here,
![]() $\ell =U_{0}{\it\tau}_{R}$
is the run length and
$\ell =U_{0}{\it\tau}_{R}$
is the run length and
![]() ${\it\delta}=\sqrt{D_{T}{\it\tau}_{R}}$
is the microscopic length. The swimmer’s radius is
${\it\delta}=\sqrt{D_{T}{\it\tau}_{R}}$
is the microscopic length. The swimmer’s radius is
![]() $a$
.
$a$
.
Figure 1 compares the concentration profile and pressure for a channel from the theory with results from ABP dynamic simulations (appendix A). Also shown are the theoretical predictions from closing the hierarchy at the next level including the nematic order field
![]() $\unicode[STIX]{x1D64C}$
as described in appendix B. The
$\unicode[STIX]{x1D64C}$
as described in appendix B. The
![]() $\boldsymbol{m}$
-field closure is sufficient, both qualitatively and quantitatively.
$\boldsymbol{m}$
-field closure is sufficient, both qualitatively and quantitatively.
The next problems are the concentration and pressure distribution in 3D outside and inside a sphere, and in 2D outside and inside a circle, of radius
![]() $R$
. Symmetry dictates that
$R$
. Symmetry dictates that
![]() $n(\boldsymbol{x})=n^{\infty }f(r)$
and
$n(\boldsymbol{x})=n^{\infty }f(r)$
and
![]() $\boldsymbol{m}(\boldsymbol{x})=n^{\infty }\boldsymbol{x}g(r)$
, where
$\boldsymbol{m}(\boldsymbol{x})=n^{\infty }\boldsymbol{x}g(r)$
, where
![]() $f(r)$
and
$f(r)$
and
![]() $g(r)$
are scalar functions of
$g(r)$
are scalar functions of
![]() $r$
. The exterior solution in 3D has the form of an exponentially screened concentration reminiscent of Debye screening:
$r$
. The exterior solution in 3D has the form of an exponentially screened concentration reminiscent of Debye screening:
and similarly for the
![]() $\boldsymbol{m}$
-field. In 2D Bessel functions replace the exponential:
$\boldsymbol{m}$
-field. In 2D Bessel functions replace the exponential:
where the 2D inverse screening length
![]() ${\it\lambda}^{\prime }=\sqrt{1+(\ell /{\it\delta})^{2}/2}/{\it\delta}$
,
${\it\lambda}^{\prime }=\sqrt{1+(\ell /{\it\delta})^{2}/2}/{\it\delta}$
,
![]() $\text{K}_{0,2}$
are the modified Bessel functions and
$\text{K}_{0,2}$
are the modified Bessel functions and
![]() $n_{A}^{\infty }$
is the area number density at infinity. For large
$n_{A}^{\infty }$
is the area number density at infinity. For large
![]() ${\it\lambda}^{\prime }r$
the concentration disturbance decays as
${\it\lambda}^{\prime }r$
the concentration disturbance decays as
![]() ${\sim}\text{e}^{-{\it\lambda}^{\prime }r}/\sqrt{r}$
.
${\sim}\text{e}^{-{\it\lambda}^{\prime }r}/\sqrt{r}$
.
The pressure at the sphere surface in the dual limits
![]() ${\it\delta}\ll \ell$
and
${\it\delta}\ll \ell$
and
![]() ${\it\delta}\ll R$
, but for arbitrary
${\it\delta}\ll R$
, but for arbitrary
![]() $\ell /R$
, is
$\ell /R$
, is
while for the circle
where
![]() $k_{s}T_{s}^{\prime }={\it\zeta}U_{0}^{2}{\it\tau}_{R}/2$
is the activity in 2D. We again see the effect of the finite run length entering as
$k_{s}T_{s}^{\prime }={\it\zeta}U_{0}^{2}{\it\tau}_{R}/2$
is the activity in 2D. We again see the effect of the finite run length entering as
![]() $\ell /R$
.
$\ell /R$
.
For the spherical interior problem the concentration field is given by
while for the interior problem in 2D
with
![]() $\text{I}_{0,2}$
modified Bessel functions. In the dual limits
$\text{I}_{0,2}$
modified Bessel functions. In the dual limits
![]() ${\it\delta}\ll \ell$
,
${\it\delta}\ll \ell$
,
![]() ${\it\delta}\ll R$
, the interior pressure in 2D is identical to (3.7) with
${\it\delta}\ll R$
, the interior pressure in 2D is identical to (3.7) with
![]() $\langle n_{A}\rangle$
replacing
$\langle n_{A}\rangle$
replacing
![]() $n_{A}^{\infty }$
.
$n_{A}^{\infty }$
.

Figure 2.
![]() ${\it\Pi}^{W}$
of ABPs outside and inside a circle. Legends are as in figure 1.
${\it\Pi}^{W}$
of ABPs outside and inside a circle. Legends are as in figure 1.

Figure 3. Theoretical predictions of the force on an asymmetric body in 2D with curvatures
![]() $R$
and
$R$
and
![]() $2R$
compared to ABP simulations. The symbols are simulation results and the solid lines were obtained by numerically solving for the
$2R$
compared to ABP simulations. The symbols are simulation results and the solid lines were obtained by numerically solving for the
![]() $n,\boldsymbol{m}$
fields. The force is calculated from (2.2) with body normal as
$n,\boldsymbol{m}$
fields. The force is calculated from (2.2) with body normal as
![]() $\boldsymbol{n}$
and is scaled by the bulk active pressure
$\boldsymbol{n}$
and is scaled by the bulk active pressure
![]() ${\it\Pi}^{\infty }=n(k_{B}T+k_{s}T_{s})$
.
${\it\Pi}^{\infty }=n(k_{B}T+k_{s}T_{s})$
.
Figure 2 compares the predicted results in 2D for the exterior and interior problems with ABP simulations and the next level
![]() $\unicode[STIX]{x1D64C}$
theory (by symmetry
$\unicode[STIX]{x1D64C}$
theory (by symmetry
![]() $\unicode[STIX]{x1D64C}=h(r)\unicode[STIX]{x1D644}+s(r)\boldsymbol{x}\boldsymbol{x}$
). Again, the
$\unicode[STIX]{x1D64C}=h(r)\unicode[STIX]{x1D644}+s(r)\boldsymbol{x}\boldsymbol{x}$
). Again, the
![]() $\boldsymbol{m}$
-level theory is quantitatively accurate unless
$\boldsymbol{m}$
-level theory is quantitatively accurate unless
![]() $R/{\it\delta}<5$
, which is not unexpected.
$R/{\it\delta}<5$
, which is not unexpected.
By symmetry there is no net force on a sphere or a circle in an active suspension. The Brownian osmotic pressure is independent of both
![]() ${\it\delta}$
and
${\it\delta}$
and
![]() $\ell$
(as it must be) and thus the integral of the constant Brownian osmotic pressure over the surface of any body will be zero.
$\ell$
(as it must be) and thus the integral of the constant Brownian osmotic pressure over the surface of any body will be zero.
From the examples the swim pressure has a correction due to the finite run length,
![]() ${\it\Pi}^{swim}\sim k_{s}T_{s}/[1+{\it\alpha}(\ell /R)]$
, where
${\it\Pi}^{swim}\sim k_{s}T_{s}/[1+{\it\alpha}(\ell /R)]$
, where
![]() ${\it\alpha}$
is a constant and
${\it\alpha}$
is a constant and
![]() $R$
is the curvature of the body. Thus, in the limit
$R$
is the curvature of the body. Thus, in the limit
![]() $\ell /R\ll 1$
the swim pressure is a constant at each point on the body surface and there will again be no force no matter what its shape. This is as one would expect from the pressure for a macroscopic object. Only when the run length is comparable to the local radius of curvature of a body is it possible to have a net force from the swimmers’ activity.
$\ell /R\ll 1$
the swim pressure is a constant at each point on the body surface and there will again be no force no matter what its shape. This is as one would expect from the pressure for a macroscopic object. Only when the run length is comparable to the local radius of curvature of a body is it possible to have a net force from the swimmers’ activity.
Equation (2.2) for the force applies to any body shape and for any body size. Figure 3 compares the force on an axisymmetric body in 2D determined by solving the
![]() $n,\boldsymbol{m}$
fields numerically with ABP simulations. The unsteady equations (2.3)–(2.4) were solved numerically with a standard Galerkin P2-FEM method with adaptive mesh refinement. Implicit time-stepping was used to ensure solution stability, and the solution is tracked long enough (
$n,\boldsymbol{m}$
fields numerically with ABP simulations. The unsteady equations (2.3)–(2.4) were solved numerically with a standard Galerkin P2-FEM method with adaptive mesh refinement. Implicit time-stepping was used to ensure solution stability, and the solution is tracked long enough (
![]() ${\sim}150{\it\tau}_{R}$
) to reach a steady state. The agreement is excellent. If the body were free to move, its speed would result from the balance of its Stokes drag,
${\sim}150{\it\tau}_{R}$
) to reach a steady state. The agreement is excellent. If the body were free to move, its speed would result from the balance of its Stokes drag,
![]() $-\unicode[STIX]{x1D64D}_{FU}\boldsymbol{\cdot }\boldsymbol{U}$
, with the active force, where
$-\unicode[STIX]{x1D64D}_{FU}\boldsymbol{\cdot }\boldsymbol{U}$
, with the active force, where
![]() $\unicode[STIX]{x1D64D}_{FU}$
is the hydrodynamic resistance tensor for the body. A body may also rotate if the active pressure exerts a net torque on the body, which is given by
$\unicode[STIX]{x1D64D}_{FU}$
is the hydrodynamic resistance tensor for the body. A body may also rotate if the active pressure exerts a net torque on the body, which is given by
![]() $\langle L\rangle _{\boldsymbol{q}}=-k_{B}T\oint _{S_{B}}(\boldsymbol{x}-\boldsymbol{x}_{0})\times n\boldsymbol{n}\,\text{d}S$
, where
$\langle L\rangle _{\boldsymbol{q}}=-k_{B}T\oint _{S_{B}}(\boldsymbol{x}-\boldsymbol{x}_{0})\times n\boldsymbol{n}\,\text{d}S$
, where
![]() $\boldsymbol{x}_{0}$
is the point about which the torque is taken. The angular velocity then follows from the hydrodynamic resistance tensor coupling torque and rotation,
$\boldsymbol{x}_{0}$
is the point about which the torque is taken. The angular velocity then follows from the hydrodynamic resistance tensor coupling torque and rotation,
![]() $-\unicode[STIX]{x1D64D}_{L{\it\Omega}}\boldsymbol{\cdot }{\it\bf\Omega}$
.
$-\unicode[STIX]{x1D64D}_{L{\it\Omega}}\boldsymbol{\cdot }{\it\bf\Omega}$
.
4. Discussion
From the structure of the concentration distribution and its dependence on the ratios
![]() $\ell /{\it\delta}$
and
$\ell /{\it\delta}$
and
![]() $\ell /L$
we can readily predict whether a given body will experience a net force. For example, a long thin rectangle will experience no net force or torque as the active pressures are equal on both faces. If, however, we add a side arm to create a ‘T’-shaped particle, there will be a force in the direction of the top of the ‘T’. To a first approximation at each point of the surface there will be a concentration boundary layer as in (3.1) for a flat wall and thus the active pressure will be the same at all points on the body surface. However, where the top meets the side arm, the two solutions will superimpose, giving an increased concentration in the ‘corners’ and thus a net force (and torque if the side arm is not at the midpoint). Similarly, a wedge-shaped particle will experience a force towards the point of the wedge from the overlapping of the concentration boundary layers on the inside corners. This reasoning can be continued for bodies composed of straight segments joined at angles (Fily, Baskaran & Hagan Reference Fily, Baskaran and Hagan2014). The precise magnitude of the force, of course, requires a solution of (2.3)–(2.4) for the given body geometry as done in figure 3, but the fact that there should be a force can be simply reasoned.
$\ell /L$
we can readily predict whether a given body will experience a net force. For example, a long thin rectangle will experience no net force or torque as the active pressures are equal on both faces. If, however, we add a side arm to create a ‘T’-shaped particle, there will be a force in the direction of the top of the ‘T’. To a first approximation at each point of the surface there will be a concentration boundary layer as in (3.1) for a flat wall and thus the active pressure will be the same at all points on the body surface. However, where the top meets the side arm, the two solutions will superimpose, giving an increased concentration in the ‘corners’ and thus a net force (and torque if the side arm is not at the midpoint). Similarly, a wedge-shaped particle will experience a force towards the point of the wedge from the overlapping of the concentration boundary layers on the inside corners. This reasoning can be continued for bodies composed of straight segments joined at angles (Fily, Baskaran & Hagan Reference Fily, Baskaran and Hagan2014). The precise magnitude of the force, of course, requires a solution of (2.3)–(2.4) for the given body geometry as done in figure 3, but the fact that there should be a force can be simply reasoned.
We can also reason about the interaction between two bodies through their disturbance of the concentration and polar-order fields. Two bodies will experience a depletion-like attraction due to the exclusion of active particles between them. The force can be estimated from (3.4):
![]() $\boldsymbol{F}\sim -k_{B}TV\boldsymbol{{\rm\nabla}}n$
, where
$\boldsymbol{F}\sim -k_{B}TV\boldsymbol{{\rm\nabla}}n$
, where
![]() $V$
is the volume of the first particle and the concentration gradient due to the second particle is evaluated at the centre of the first particle. When bodies are far apart the attractive force is very weak and decays exponentially with separation according to (3.4); this exponential dependence was seen in the simulations of Ray et al. (Reference Ray, Reichhardt and Reichhardt2014). Outside the screening length the concentration is undisturbed and the depletion interaction will be the same as for passive colloidal particles where the exclusion zone is geometric (Asakura & Ooswa Reference Asakura and Ooswa1954); the Brownian osmotic pressure on the exposed surfaces is replaced by the active pressure that includes the run length (3.6). Note that the exclusion occurs on the microscopic scale
$V$
is the volume of the first particle and the concentration gradient due to the second particle is evaluated at the centre of the first particle. When bodies are far apart the attractive force is very weak and decays exponentially with separation according to (3.4); this exponential dependence was seen in the simulations of Ray et al. (Reference Ray, Reichhardt and Reichhardt2014). Outside the screening length the concentration is undisturbed and the depletion interaction will be the same as for passive colloidal particles where the exclusion zone is geometric (Asakura & Ooswa Reference Asakura and Ooswa1954); the Brownian osmotic pressure on the exposed surfaces is replaced by the active pressure that includes the run length (3.6). Note that the exclusion occurs on the microscopic scale
![]() ${\it\delta}$
(or swimmer size
${\it\delta}$
(or swimmer size
![]() $a$
), not on the scale of the run length. Even when the gap between two particles is less than
$a$
), not on the scale of the run length. Even when the gap between two particles is less than
![]() $\ell$
the active particles can still access this space and exert their swim pressure.
$\ell$
the active particles can still access this space and exert their swim pressure.
In the examples we have considered there was no polar order far from the boundary, nor a gradient in the concentration of swimmers, and thus force or motion can only arise if the run length is of the order of the body size,
![]() $\ell /L\sim O(1)$
, and if the symmetry is broken by the body shape. With macroscopic polar order, which can result from an orienting field applied to the swimmers (Takatori & Brady Reference Takatori and Brady2014), even a spherical particle will experience a net force and move due to the imbalanced active pressure. We also used the simplest no-flux boundary condition on the polar-order field at the body surface, but this condition can be modified. For example, a portion of the body surface may be treated such that the active particles achieve a preferred orientation or experience a localized orienting field. Such a ‘Janus’ particle may have a net force due to a spatially varying polar-order boundary condition.
$\ell /L\sim O(1)$
, and if the symmetry is broken by the body shape. With macroscopic polar order, which can result from an orienting field applied to the swimmers (Takatori & Brady Reference Takatori and Brady2014), even a spherical particle will experience a net force and move due to the imbalanced active pressure. We also used the simplest no-flux boundary condition on the polar-order field at the body surface, but this condition can be modified. For example, a portion of the body surface may be treated such that the active particles achieve a preferred orientation or experience a localized orienting field. Such a ‘Janus’ particle may have a net force due to a spatially varying polar-order boundary condition.
Indeed, a localized boundary orienting field was used by Solon et al. (Reference Solon, Fily, Baskaran, Cates, Kafri, Kardar and Tailleur2015) to argue that the pressure of active matter is not a ‘state’ function, as the force per unit area on a wall is no longer equal to the swim pressure far from the surface. As our microscopic theory shows, this is to be expected in general: boundary curvature, the detailed flux conditions at the surface, etc. can all affect the value of the concentration at the surface and thus the force on the boundary. We showed recently (Yan & Brady Reference Yan and Brady2015) that the polar order induced by an orienting field acts like a body force on the active material, and when this ‘internal’ body force is included in the momentum balance, the force per unit area on the wall plus the integral of the internal body force is equal to the active pressure far from the surface, thus restoring the active pressure as a state function.
With an external field that tends to align the swimmers and biases their motion, for example an external torque or hydrodynamic shearing flows, the conservation equation for
![]() $\boldsymbol{m}$
now has an additional ‘sink’ term, which can be written as
$\boldsymbol{m}$
now has an additional ‘sink’ term, which can be written as
![]() $2D_{R}[\boldsymbol{m}-\boldsymbol{m}^{\infty }]$
where
$2D_{R}[\boldsymbol{m}-\boldsymbol{m}^{\infty }]$
where
![]() $\boldsymbol{m}^{\infty }$
is the polar order far from the boundary induced by the field. The equation for
$\boldsymbol{m}^{\infty }$
is the polar order far from the boundary induced by the field. The equation for
![]() $\unicode[STIX]{x1D64C}$
will have a similar
$\unicode[STIX]{x1D64C}$
will have a similar
![]() $\unicode[STIX]{x1D64C}^{\infty }$
term. One now writes conservation equations for the departures of the polar-order and nematic fields from their undisturbed values,
$\unicode[STIX]{x1D64C}^{\infty }$
term. One now writes conservation equations for the departures of the polar-order and nematic fields from their undisturbed values,
![]() $\boldsymbol{m}^{\prime }=\boldsymbol{m}-\boldsymbol{m}^{\infty }$
and
$\boldsymbol{m}^{\prime }=\boldsymbol{m}-\boldsymbol{m}^{\infty }$
and
![]() $\unicode[STIX]{x1D64C}^{\prime }=\unicode[STIX]{x1D64C}-\unicode[STIX]{x1D64C}^{\infty }$
, and then closes the disturbance equations along the lines followed here. It is not known if this simple closure proves as accurate when there is net bulk polar order.
$\unicode[STIX]{x1D64C}^{\prime }=\unicode[STIX]{x1D64C}-\unicode[STIX]{x1D64C}^{\infty }$
, and then closes the disturbance equations along the lines followed here. It is not known if this simple closure proves as accurate when there is net bulk polar order.
Since the behaviour is dominated by the rapid variations that occur on the screening length adjacent to the body surface, the situation has features in common with phoretic-like problems, and hydrodynamic fluid motion can be incorporated in a manner similar to diffusiophoresis (Anderson Reference Anderson1989; Brady Reference Brady2011; Shklyaev, Brady & Córdova-Figueroa Reference Shklyaev, Brady and Córdova-Figueroa2014).
The theory we have developed and applied for dilute active matter can be extended to higher concentrations of swimmers. The
![]() $N$
-particle Smoluchowski equation for passive Brownian particles including excluded volume and full hydrodynamic interactions is well known, as is the form of the many-body hydrodynamic swim force (Yan & Brady Reference Yan and Brady2015). Reduction to the lowest moments,
$N$
-particle Smoluchowski equation for passive Brownian particles including excluded volume and full hydrodynamic interactions is well known, as is the form of the many-body hydrodynamic swim force (Yan & Brady Reference Yan and Brady2015). Reduction to the lowest moments,
![]() $n$
and
$n$
and
![]() $\boldsymbol{m}$
, is certain to give rise to new phenomena since the swim diffusivity, which enters the flux expressions, can be a decreasing function of the swimmers’ concentration (Takatori et al.
Reference Takatori, Yan and Brady2014).
$\boldsymbol{m}$
, is certain to give rise to new phenomena since the swim diffusivity, which enters the flux expressions, can be a decreasing function of the swimmers’ concentration (Takatori et al.
Reference Takatori, Yan and Brady2014).
Acknowledgements
Discussions with S. C. Takatori and E. W. Burkholder are greatly appreciated. This work was supported by NSF grant no. CBET 1437570.
Note added in proof
After this paper was accepted we became aware of the simulation study of Smallenburg & Löwen (Reference Smallenburg and Löwen2015) for ABPs in 2D, the results of which agree with our theoretical predictions.
Appendix A. The Langevin equation and simulation
Active Brownian particles (ABPs) are governed by the overdamped Langevin equation
where
![]() $\boldsymbol{U}$
is the particle velocity,
$\boldsymbol{U}$
is the particle velocity,
![]() $\boldsymbol{F}^{P}$
is a boundary force and
$\boldsymbol{F}^{P}$
is a boundary force and
![]() $\boldsymbol{F}^{B}$
is the Brownian force responsible for the translational diffusivity
$\boldsymbol{F}^{B}$
is the Brownian force responsible for the translational diffusivity
![]() $D_{T}=k_{B}T/{\it\zeta}$
. The orientation vector
$D_{T}=k_{B}T/{\it\zeta}$
. The orientation vector
![]() $\boldsymbol{q}$
in the swim force is subject to rotational Brownian diffusion (
$\boldsymbol{q}$
in the swim force is subject to rotational Brownian diffusion (
![]() $D_{R}=1/{\it\tau}_{R}$
), and follows directly from a torque balance. For a spherical swimmer,
$D_{R}=1/{\it\tau}_{R}$
), and follows directly from a torque balance. For a spherical swimmer,
![]() ${\it\zeta}=6{\rm\pi}{\it\eta}a$
, where
${\it\zeta}=6{\rm\pi}{\it\eta}a$
, where
![]() $a$
is the swimmer’s radius and
$a$
is the swimmer’s radius and
![]() ${\it\eta}$
is the viscosity of the suspending Newtonian fluid. For Brownian reorientation,
${\it\eta}$
is the viscosity of the suspending Newtonian fluid. For Brownian reorientation,
![]() $D_{R}=k_{B}T/8{\rm\pi}{\it\eta}a^{3}$
, and the microscopic length scale
$D_{R}=k_{B}T/8{\rm\pi}{\it\eta}a^{3}$
, and the microscopic length scale
![]() ${\it\delta}=\sqrt{D_{T}/D_{R}}=\sqrt{4/3}a$
.
${\it\delta}=\sqrt{D_{T}/D_{R}}=\sqrt{4/3}a$
.
In the Brownian dynamics simulations each swimmer is a sphere of radius
![]() $a$
and the Langevin equation is integrated to track the dynamics. When a swimmer hits a boundary, it experiences a hard-particle force
$a$
and the Langevin equation is integrated to track the dynamics. When a swimmer hits a boundary, it experiences a hard-particle force
![]() $\boldsymbol{F}^{P}$
to prevent it from penetrating the boundary (following Foss & Brady (Reference Foss and Brady2000) a potential-free hard-particle force is implemented). By Newton’s Third Law the boundary experiences an opposite force
$\boldsymbol{F}^{P}$
to prevent it from penetrating the boundary (following Foss & Brady (Reference Foss and Brady2000) a potential-free hard-particle force is implemented). By Newton’s Third Law the boundary experiences an opposite force
![]() $-\boldsymbol{F}^{P}$
, and then
$-\boldsymbol{F}^{P}$
, and then
![]() ${\it\Pi}^{W}$
is calculated from the definition of the pressure:
${\it\Pi}^{W}$
is calculated from the definition of the pressure:
![]() $\sum \boldsymbol{F}^{P}/A$
in 3D or
$\sum \boldsymbol{F}^{P}/A$
in 3D or
![]() $\sum \boldsymbol{F}^{P}/L$
in 2D, where
$\sum \boldsymbol{F}^{P}/L$
in 2D, where
![]() $A$
and
$A$
and
![]() $L$
are the wall area and length, respectively.
$L$
are the wall area and length, respectively.
Swimmer–swimmer collisions are ignored because we compare the simulations with the dilute theory. Each simulation is tracked long enough to ensure that good steady-state statistics are achieved. In some cases the simulation time is as long as
![]() $3000{\it\tau}_{R}$
.
$3000{\it\tau}_{R}$
.
Appendix B. Closure of the Smoluchowski equation
As is standard (Saintillan & Shelley Reference Saintillan, Shelley and Spagnolie2015), the first few moments of the Smoluchowski equation (2.1) are
In the simplest situation of no temporal or spatial variation, a uniform concentration
![]() $n$
and no polar order
$n$
and no polar order
![]() $\boldsymbol{m}=0$
are solutions of (B 1)–(B 2), and the second moment has solution
$\boldsymbol{m}=0$
are solutions of (B 1)–(B 2), and the second moment has solution
![]() $\tilde{\unicode[STIX]{x1D64C}}=n\unicode[STIX]{x1D644}/3$
. This leads to the natural definition of the nematic order field
$\tilde{\unicode[STIX]{x1D64C}}=n\unicode[STIX]{x1D644}/3$
. This leads to the natural definition of the nematic order field
![]() $\tilde{\unicode[STIX]{x1D64C}}=\unicode[STIX]{x1D64C}+n\unicode[STIX]{x1D644}/3$
, or
$\tilde{\unicode[STIX]{x1D64C}}=\unicode[STIX]{x1D64C}+n\unicode[STIX]{x1D644}/3$
, or
![]() $\unicode[STIX]{x1D64C}(\boldsymbol{x},t)=\int (\boldsymbol{q}\boldsymbol{q}-\unicode[STIX]{x1D644}/3)P(\boldsymbol{x},\boldsymbol{q},t)\,\text{d}\boldsymbol{q}$
. The conservation equation for
$\unicode[STIX]{x1D64C}(\boldsymbol{x},t)=\int (\boldsymbol{q}\boldsymbol{q}-\unicode[STIX]{x1D644}/3)P(\boldsymbol{x},\boldsymbol{q},t)\,\text{d}\boldsymbol{q}$
. The conservation equation for
![]() $\unicode[STIX]{x1D64C}$
is
$\unicode[STIX]{x1D64C}$
is
which now does have the solution of no nematic order
![]() $\unicode[STIX]{x1D64C}=0$
in the uniform case. The flux expressions now become
$\unicode[STIX]{x1D64C}=0$
in the uniform case. The flux expressions now become
![]() $\boldsymbol{j}_{n}=U_{0}\boldsymbol{m}-D_{T}\boldsymbol{{\rm\nabla}}n$
,
$\boldsymbol{j}_{n}=U_{0}\boldsymbol{m}-D_{T}\boldsymbol{{\rm\nabla}}n$
,
![]() $\boldsymbol{j}_{m}=U_{0}\unicode[STIX]{x1D64C}+U_{0}n\unicode[STIX]{x1D644}/3-D_{T}\boldsymbol{{\rm\nabla}}\boldsymbol{m}$
and
$\boldsymbol{j}_{m}=U_{0}\unicode[STIX]{x1D64C}+U_{0}n\unicode[STIX]{x1D644}/3-D_{T}\boldsymbol{{\rm\nabla}}\boldsymbol{m}$
and
![]() $\boldsymbol{j}_{\unicode[STIX]{x1D618}}=U_{0}\tilde{\unicode[STIX]{x1D63D}}-U_{0}\boldsymbol{m}\unicode[STIX]{x1D644}/3-D_{T}\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D64C}$
.
$\boldsymbol{j}_{\unicode[STIX]{x1D618}}=U_{0}\tilde{\unicode[STIX]{x1D63D}}-U_{0}\boldsymbol{m}\unicode[STIX]{x1D644}/3-D_{T}\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D64C}$
.
We shall discuss the
![]() $\tilde{\unicode[STIX]{x1D63D}}$
-field and its closure in a moment, but we can already appreciate why closing the equations with
$\tilde{\unicode[STIX]{x1D63D}}$
-field and its closure in a moment, but we can already appreciate why closing the equations with
![]() $\unicode[STIX]{x1D64C}=0$
leads to a very good approximation as demonstrated by the results presented in the main text. First, we are not setting the second moment to zero; we are approximating the second moment with the ‘isotropic’ distribution
$\unicode[STIX]{x1D64C}=0$
leads to a very good approximation as demonstrated by the results presented in the main text. First, we are not setting the second moment to zero; we are approximating the second moment with the ‘isotropic’ distribution
![]() $\tilde{\unicode[STIX]{x1D64C}}\approx n\unicode[STIX]{x1D644}/3$
. Second, (B 4) shows that the
$\tilde{\unicode[STIX]{x1D64C}}\approx n\unicode[STIX]{x1D644}/3$
. Second, (B 4) shows that the
![]() $\unicode[STIX]{x1D64C}$
-field is screened like the
$\unicode[STIX]{x1D64C}$
-field is screened like the
![]() $\boldsymbol{m}$
-field, but with a temporal decay that is three times faster and a screening length that is a factor of
$\boldsymbol{m}$
-field, but with a temporal decay that is three times faster and a screening length that is a factor of
![]() $\sqrt{3}$
shorter. Third, as we show below, when variations are slow, like the
$\sqrt{3}$
shorter. Third, as we show below, when variations are slow, like the
![]() $\boldsymbol{m}$
-field where
$\boldsymbol{m}$
-field where
![]() $\boldsymbol{m}\sim -(U_{0}/D_{R})\boldsymbol{{\rm\nabla}}n/6$
, the nematic order goes as
$\boldsymbol{m}\sim -(U_{0}/D_{R})\boldsymbol{{\rm\nabla}}n/6$
, the nematic order goes as
![]() $\unicode[STIX]{x1D64C}\sim -(U_{0}/D_{R})\boldsymbol{{\rm\nabla}}\boldsymbol{m}\sim (U_{0}/D_{R})^{2}\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}n$
, and thus
$\unicode[STIX]{x1D64C}\sim -(U_{0}/D_{R})\boldsymbol{{\rm\nabla}}\boldsymbol{m}\sim (U_{0}/D_{R})^{2}\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}n$
, and thus
![]() $\unicode[STIX]{x1D64C}\sim O(\ell /L)^{2}n$
, which is small. Finally, for the 1D flat wall problem, the value of the concentration at the surface,
$\unicode[STIX]{x1D64C}\sim O(\ell /L)^{2}n$
, which is small. Finally, for the 1D flat wall problem, the value of the concentration at the surface,
![]() $n^{\infty }(1+(\ell /{\it\delta})^{2}/6)$
, follows directly from the full Smoluchowski equation and is independent of the closure. Thus, it is perhaps not surprising that the simple closure
$n^{\infty }(1+(\ell /{\it\delta})^{2}/6)$
, follows directly from the full Smoluchowski equation and is independent of the closure. Thus, it is perhaps not surprising that the simple closure
![]() $\unicode[STIX]{x1D64C}=0$
works very well except when the body curvature is of the order of the microscopic length
$\unicode[STIX]{x1D64C}=0$
works very well except when the body curvature is of the order of the microscopic length
![]() ${\it\delta}=\sqrt{D_{T}{\it\tau}_{R}}$
.
${\it\delta}=\sqrt{D_{T}{\it\tau}_{R}}$
.
The equation for the third moment is
where
![]() ${\it\alpha}_{ijkl}={\it\delta}_{ij}{\it\delta}_{kl}+{\it\delta}_{ik}{\it\delta}_{jl}+{\it\delta}_{il}{\it\delta}_{jk}$
is the fourth-order isotropic tensor and
${\it\alpha}_{ijkl}={\it\delta}_{ij}{\it\delta}_{kl}+{\it\delta}_{ik}{\it\delta}_{jl}+{\it\delta}_{il}{\it\delta}_{jk}$
is the fourth-order isotropic tensor and
![]() $\tilde{\unicode[STIX]{x1D63E}}=\int \boldsymbol{q}\boldsymbol{q}\boldsymbol{q}\boldsymbol{q}P(\boldsymbol{x},\boldsymbol{q})\,\text{d}\boldsymbol{q}$
is the fourth moment.
$\tilde{\unicode[STIX]{x1D63E}}=\int \boldsymbol{q}\boldsymbol{q}\boldsymbol{q}\boldsymbol{q}P(\boldsymbol{x},\boldsymbol{q})\,\text{d}\boldsymbol{q}$
is the fourth moment.
The proper ‘isotropic’
![]() $\tilde{\unicode[STIX]{x1D63D}}$
field is
$\tilde{\unicode[STIX]{x1D63D}}$
field is
![]() $\tilde{\unicode[STIX]{x1D63D}}=\unicode[STIX]{x1D63D}+({\bf\alpha}\boldsymbol{\cdot }\boldsymbol{m})/5$
, and the equation for
$\tilde{\unicode[STIX]{x1D63D}}=\unicode[STIX]{x1D63D}+({\bf\alpha}\boldsymbol{\cdot }\boldsymbol{m})/5$
, and the equation for
![]() $\unicode[STIX]{x1D63D}$
becomes
$\unicode[STIX]{x1D63D}$
becomes
In the examples where we included the nematic field
![]() $\unicode[STIX]{x1D64C}$
, we closed the equations by setting
$\unicode[STIX]{x1D64C}$
, we closed the equations by setting
![]() $\unicode[STIX]{x1D63D}=0$
, which follows from the same reasons as for setting
$\unicode[STIX]{x1D63D}=0$
, which follows from the same reasons as for setting
![]() $\unicode[STIX]{x1D64C}=0$
. With this closure the
$\unicode[STIX]{x1D64C}=0$
. With this closure the
![]() $\unicode[STIX]{x1D64C}$
-field flux is
$\unicode[STIX]{x1D64C}$
-field flux is
which was used in the examples presented in the main text. With this constitutive equation for the flux, for slow variations we see that
![]() $\unicode[STIX]{x1D64C}\sim (\ell ^{2}/135)(\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}-\unicode[STIX]{x1D644}{\rm\nabla}^{2}/3)n$
.
$\unicode[STIX]{x1D64C}\sim (\ell ^{2}/135)(\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}-\unicode[STIX]{x1D644}{\rm\nabla}^{2}/3)n$
.