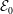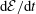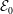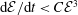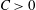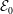1 Introduction
The objective of this investigation is to study three-dimensional (3-D) flows of viscous incompressible fluids which are constructed to exhibit extreme growth of enstrophy. It is motivated by the question of whether the solutions to the 3-D incompressible Navier–Stokes system on unbounded or periodic domains corresponding to smooth initial data may develop a singularity in finite time (Doering Reference Doering2009). By formation of a ‘singularity’ we mean the situation when some norms of the solution corresponding to smooth initial data have become unbounded after a finite time. This so-called ‘blow-up problem’ is one of the key open questions in mathematical fluid mechanics and, in fact, its importance for mathematics in general has been recognized by the Clay Mathematics Institute as one of its ‘millennium problems’ (Fefferman Reference Fefferman2000). Questions concerning global-in-time existence of smooth solutions remain open also for a number of other flow models including the 3-D Euler equations (Gibbon, Bustamante & Kerr Reference Gibbon, Bustamante and Kerr2008) and some of the ‘active scalar’ equations (Kiselev Reference Kiselev2010).
While the blow-up problem is fundamentally a question in mathematical analysis, a lot of computational studies have been carried out since the mid-1990s in order to shed light on the hydrodynamic mechanisms which might lead to singularity formation in finite time. Given that such flows evolving near the edge of regularity involve formation of very small flow structures, these computations typically require the use of state-of-the-art computational resources available at a given time. The computational studies focused on the possibility of finite-time blow-up in the 3-D Navier–Stokes and/or Euler system include (Brachet et al. Reference Brachet, Meiron, Orszag, Nickel, Morf and Frisch1983; Pumir & Siggia Reference Pumir and Siggia1990; Brachet Reference Brachet1991; Kerr Reference Kerr1993; Pelz Reference Pelz2001; Bustamante & Kerr Reference Bustamante and Kerr2008; Gibbon et al. Reference Gibbon, Bustamante and Kerr2008; Grafke et al. Reference Grafke, Homann, Dreher and Grauer2008; Ohkitani Reference Ohkitani2008; Ohkitani & Constantin Reference Ohkitani and Constantin2008; Hou Reference Hou2009; Bustamante & Brachet Reference Bustamante and Brachet2012; Orlandi, Pirozzoli & Carnevale Reference Orlandi, Pirozzoli and Carnevale2012; Orlandi et al. Reference Orlandi, Pirozzoli, Bernardini and Carnevale2014), all of which considered problems defined on domains periodic in all three dimensions. Recent investigations by Donzis et al. (Reference Donzis, Gibbon, Gupta, Kerr, Pandit and Vincenzi2013), Kerr (Reference Kerr2013b ), Gibbon et al. (Reference Gibbon, Donzis, Gupta, Kerr, Pandit and Vincenzi2014) and Kerr (Reference Kerr2013a ) focused on the time evolution of vorticity moments and compared it with the predictions derived from analysis based on rigorous bounds. We also mention the studies by Matsumoto, Bec & Frisch (Reference Matsumoto, Bec and Frisch2008) and Siegel & Caflisch (Reference Siegel and Caflisch2009), along with the references found therein, in which various complexified forms of the Euler equation were investigated. The idea of this approach is that, since the solutions to complexified equations have singularities in the complex plane, singularity formation in the real-valued problem is manifested by the collapse of the complex-plane singularities onto the real axis.
Overall, the outcome of these investigations is rather inconclusive: while for the Navier–Stokes flows most of recent computations do not offer support for finite-time blow-up, the evidence appears split in the case of the Euler system. In particular, the recent studies by Bustamante & Brachet (Reference Bustamante and Brachet2012) and Orlandi et al. (Reference Orlandi, Pirozzoli and Carnevale2012) hinted at the possibility of singularity formation in a finite time. In this connection we also mention the recent investigations by Luo & Hou (Reference Luo and Hou2014a ,Reference Luo and Hou b ) in which blow-up was observed in axisymmetric Euler flows in a bounded (tubular) domain.
A common feature of all of the aforementioned investigations was that the initial data for the Navier–Stokes or Euler system were chosen in an ad hoc manner, based on some heuristic arguments. On the other hand, in the present study we pursue a fundamentally different approach, proposed originally by Lu & Doering (Reference Lu and Doering2008) and employed also by Ayala & Protas (Reference Ayala and Protas2011, Reference Ayala and Protas2014a ,Reference Ayala and Protas b ) for a range of related problems, in which the initial condition leading to the most singular behaviour is sought systematically via solution of a suitable variational optimization problem. We carefully analyse the time evolution induced by the extreme vortex states first identified by Lu & Doering (Reference Lu and Doering2008) and compare it to the time evolution corresponding to a number of other candidate initial conditions considered in the literature (Brachet et al. Reference Brachet, Meiron, Orszag, Nickel, Morf and Frisch1983; Kerr Reference Kerr1993; Pelz Reference Pelz2001; Cichowlas & Brachet Reference Cichowlas and Brachet2005; Orlandi et al. Reference Orlandi, Pirozzoli and Carnevale2012). We demonstrate that the Taylor–Green vortex, studied in the context of the blow-up problem by Taylor & Green (Reference Taylor and Green1937), Brachet et al. (Reference Brachet, Meiron, Orszag, Nickel, Morf and Frisch1983), Brachet (Reference Brachet1991) and Cichowlas & Brachet (Reference Cichowlas and Brachet2005), is in fact a particular member of the family of extreme vortex states maximizing the instantaneous rate of enstrophy production in the limit of vanishing enstrophy. In addition, based on these findings, we identify the set of initial data, parameterized by their energy and enstrophy, for which one can a priori guarantee the global-in-time existence of smooth solutions. This result therefore offers a physically appealing interpretation of an ‘abstract’ mathematical theorem concerning global existence of classical solutions corresponding to initial data with small energy (Ladyzhenskaya Reference Ladyzhenskaya1969). We also emphasize that, in order to establish a direct link with the results of the mathematical analysis discussed below, in our investigation we follow a rather different strategy than in most of the studies referenced above. While these earlier studies relied on data from a relatively small number of simulations performed at a high (at the given time) resolution, in the present investigation we explore a broad range of cases, each of which is however computed at a more moderate resolution (or, equivalently, Reynolds number). With such an approach to the use of available computational resources, we are able to reveal trends resulting from the variation of parameters which otherwise would be hard to detect. Systematic computations conducted in this way thus allow us to probe the sharpness of the mathematical analysis relevant to the problem.
The question of regularity of solution to the Navier–Stokes system is usually addressed using ‘energy’ methods which rely on finding upper bounds (with respect to time) on certain quantities of interest, typically taken as suitable Sobolev norms of the solution. A key intermediate step is obtaining bounds on the rate of growth of the quantity of interest, a problem which can be studied using well-known methods from the theory of ordinary differential equations (ODEs). While for the Navier–Stokes system different norms of the velocity gradient or vorticity can be used to study the regularity of solutions, the use of enstrophy
![]() ${\mathcal{E}}$
(see (2.4) below) is privileged by the well-known result of Foias & Temam (Reference Foias and Temam1989), where it was established that if the uniform bound
${\mathcal{E}}$
(see (2.4) below) is privileged by the well-known result of Foias & Temam (Reference Foias and Temam1989), where it was established that if the uniform bound
holds, then the regularity of the solution
![]() $\boldsymbol{u}(t)$
is guaranteed up to time
$\boldsymbol{u}(t)$
is guaranteed up to time
![]() $T$
(to be precise, the solution remains in a suitable Gevrey class). From the computational point of view, the enstrophy
$T$
(to be precise, the solution remains in a suitable Gevrey class). From the computational point of view, the enstrophy
![]() ${\mathcal{E}}(t):={\mathcal{E}}(\boldsymbol{u}(t))$
is thus a convenient indicator of the regularity of solutions, because in the light of (1.1), singularity formation must manifest itself by the enstrophy becoming infinite.
${\mathcal{E}}(t):={\mathcal{E}}(\boldsymbol{u}(t))$
is thus a convenient indicator of the regularity of solutions, because in the light of (1.1), singularity formation must manifest itself by the enstrophy becoming infinite.
While characterization of the maximum possible finite-time growth of enstrophy in the 3-D Navier–Stokes flows is the ultimate objective of this research program, analogous questions can also be posed in the context of more tractable problems involving the 1-D Burgers equation and the 2-D Navier–Stokes equation. Although the global-in-time existence of the classical (smooth) solutions is well known for both these problems (Kreiss & Lorenz Reference Kreiss and Lorenz2004), questions concerning the sharpness of the corresponding estimates for the instantaneous and finite-time growth of various quantities are relevant, because these estimates are obtained using essentially the same methods as employed to derive their 3-D counterparts. Since in 2-D flows on unbounded or periodic domains the enstrophy may not increase (
![]() $\text{d}{\mathcal{E}}/\text{d}t\leqslant 0$
), the relevant quantity in this case is the palinstrophy
$\text{d}{\mathcal{E}}/\text{d}t\leqslant 0$
), the relevant quantity in this case is the palinstrophy
![]() ${\mathcal{P}}(\boldsymbol{u}):=1/2\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D74E}(\boldsymbol{x},t)|^{2}\,\text{d}\boldsymbol{x}$
, where
${\mathcal{P}}(\boldsymbol{u}):=1/2\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D74E}(\boldsymbol{x},t)|^{2}\,\text{d}\boldsymbol{x}$
, where
![]() $\unicode[STIX]{x1D74E}:=\unicode[STIX]{x1D735}\times \boldsymbol{u}$
is the vorticity (which reduces to a pseudo-scalar in two dimensions). Different questions concerning sharpness of estimates addressed in our research program are summarized together with the results obtained to date in table 1. We remark that the best finite-time estimate for the 1-D Burgers equation was found not to be sharp using the initial data obtained from both the instantaneous and the finite-time variational optimization problems (Ayala & Protas Reference Ayala and Protas2011). On the other hand, in two dimensions, the bounds on both the instantaneous and finite-time growth of palinstrophy were found to be sharp and, somewhat surprisingly, both estimates were realized by the same family of incompressible vector fields parameterized by energy
$\unicode[STIX]{x1D74E}:=\unicode[STIX]{x1D735}\times \boldsymbol{u}$
is the vorticity (which reduces to a pseudo-scalar in two dimensions). Different questions concerning sharpness of estimates addressed in our research program are summarized together with the results obtained to date in table 1. We remark that the best finite-time estimate for the 1-D Burgers equation was found not to be sharp using the initial data obtained from both the instantaneous and the finite-time variational optimization problems (Ayala & Protas Reference Ayala and Protas2011). On the other hand, in two dimensions, the bounds on both the instantaneous and finite-time growth of palinstrophy were found to be sharp and, somewhat surprisingly, both estimates were realized by the same family of incompressible vector fields parameterized by energy
![]() ${\mathcal{K}}$
and palinstrophy
${\mathcal{K}}$
and palinstrophy
![]() ${\mathcal{P}}$
, obtained as the solution of an instantaneous optimization problem (Ayala & Protas Reference Ayala and Protas2014a
). It is worth mentioning that while the estimate for the instantaneous rate of growth of palinstrophy
${\mathcal{P}}$
, obtained as the solution of an instantaneous optimization problem (Ayala & Protas Reference Ayala and Protas2014a
). It is worth mentioning that while the estimate for the instantaneous rate of growth of palinstrophy
![]() $\text{d}{\mathcal{P}}/\text{d}t\leqslant C{\mathcal{K}}^{1/2}{\mathcal{P}}^{3/2}/\unicode[STIX]{x1D708}$
(see table 1) was found to be sharp with respect to variations in palinstrophy, the estimate is in fact not sharp with respect to the prefactor
$\text{d}{\mathcal{P}}/\text{d}t\leqslant C{\mathcal{K}}^{1/2}{\mathcal{P}}^{3/2}/\unicode[STIX]{x1D708}$
(see table 1) was found to be sharp with respect to variations in palinstrophy, the estimate is in fact not sharp with respect to the prefactor
![]() $C_{\boldsymbol{u},\unicode[STIX]{x1D708}}={\mathcal{K}}^{1/2}/\unicode[STIX]{x1D708}$
(Ayala, Doering & Simon Reference Ayala, Doering and Simon2016), with the correct prefactor being of the form
$C_{\boldsymbol{u},\unicode[STIX]{x1D708}}={\mathcal{K}}^{1/2}/\unicode[STIX]{x1D708}$
(Ayala, Doering & Simon Reference Ayala, Doering and Simon2016), with the correct prefactor being of the form
![]() $\widetilde{C}_{\boldsymbol{u},\unicode[STIX]{x1D708}}=\sqrt{\log ({\mathcal{K}}^{1/2}/\unicode[STIX]{x1D708})}$
. We add that what distinguishes the 2-D problem, in regard to both the instantaneous and finite-time bounds, is that the right-hand side of these bounds are expressed in terms of two quantities, namely, energy
$\widetilde{C}_{\boldsymbol{u},\unicode[STIX]{x1D708}}=\sqrt{\log ({\mathcal{K}}^{1/2}/\unicode[STIX]{x1D708})}$
. We add that what distinguishes the 2-D problem, in regard to both the instantaneous and finite-time bounds, is that the right-hand side of these bounds are expressed in terms of two quantities, namely, energy
![]() ${\mathcal{K}}$
and enstrophy
${\mathcal{K}}$
and enstrophy
![]() ${\mathcal{E}}$
, in contrast to the enstrophy alone appearing in the 1-D and 3-D estimates. As a result, the 2-D instantaneous optimization problem had to be solved subject to two constraints.
${\mathcal{E}}$
, in contrast to the enstrophy alone appearing in the 1-D and 3-D estimates. As a result, the 2-D instantaneous optimization problem had to be solved subject to two constraints.
Table 1. Summary of selected estimates for the instantaneous rate of growth and the growth over finite time of enstrophy and palinstrophy in 1-D Burgers, 2-D and 3-D Navier–Stokes systems. The quantities
![]() ${\mathcal{K}}$
and
${\mathcal{K}}$
and
![]() ${\mathcal{E}}$
are defined in (2.2) and (2.4).
${\mathcal{E}}$
are defined in (2.2) and (2.4).

In the present investigation we advance the research program summarized in table 1 by assessing to what extent the finite-time growth of enstrophy predicted by the analytic estimates (2.10) and (2.14) can be actually realized by flow evolution starting from different initial conditions, including the extreme vortex states found by Lu & Doering (Reference Lu and Doering2008) to saturate the instantaneous estimate (2.9). The key finding is that, at least for the range of modest enstrophy values we considered, the growth of enstrophy corresponding to these initial data, which have the form of two colliding axisymmetric vortex rings, is rapidly depleted and there is no indication of singularity formation in finite time. Thus, should finite-time singularity be possible in the Navier–Stokes system, it is unlikely to result from initial conditions instantaneously maximizing the rate of growth of enstrophy. We also provide a comprehensive characterization of the extreme vortex states which realize estimate (2.9) together with the resulting flow evolutions.
The structure of the paper is as follows: in the next section we present analytic estimates on the instantaneous and finite-time growth of enstrophy in 3-D flows. In § 3 we formulate the variational optimization problems which will be solved to find the vortex states with the largest rate of enstrophy production and in § 4 we provide an asymptotic representation for these optimal states in the limit of vanishing enstrophy. In § 5 we present numerically computed extreme vortex states corresponding to intermediate and large enstrophy values, while in § 6 we analyse the temporal evolution corresponding to different initial data in order to compare it with the predictions of estimates (2.10) and (2.14). Our findings are discussed in § 7, whereas conclusions and outlook are deferred to § 8.
2 Bounds on the growth of enstrophy in 3-D Navier–Stokes flows
We consider the incompressible Navier–Stokes system defined on the 3-D unit cube
![]() $\unicode[STIX]{x1D6FA}=[0,1]^{3}$
with periodic boundary conditions
$\unicode[STIX]{x1D6FA}=[0,1]^{3}$
with periodic boundary conditions
where ‘
![]() $:=$
’ means ‘equal to by definition’. The enstrophy
$:=$
’ means ‘equal to by definition’. The enstrophy
![]() ${\mathcal{E}}(\boldsymbol{u})$
and its rate of growth are given by
${\mathcal{E}}(\boldsymbol{u})$
and its rate of growth are given by
For incompressible flows with periodic boundary conditions we also have the following identity (Doering & Gibbon Reference Doering and Gibbon1995)
Hence, combining (2.2)–(2.6), the energy and enstrophy satisfy the system of ordinary differential equations
A standard approach at this point is to try to upper bound
![]() $\text{d}{\mathcal{E}}/\text{d}t$
and using standard techniques of functional analysis it is possible to obtain the following well-known estimate in terms of
$\text{d}{\mathcal{E}}/\text{d}t$
and using standard techniques of functional analysis it is possible to obtain the following well-known estimate in terms of
![]() ${\mathcal{K}}$
and
${\mathcal{K}}$
and
![]() ${\mathcal{E}}$
(Doering Reference Doering2009)
${\mathcal{E}}$
(Doering Reference Doering2009)
for
![]() $c$
an absolute constant. A related estimate expressed entirely in terms of the enstrophy
$c$
an absolute constant. A related estimate expressed entirely in terms of the enstrophy
![]() ${\mathcal{E}}$
is given by
${\mathcal{E}}$
is given by
By simply integrating the differential inequality in (2.9) with respect to time we obtain the finite-time bound
 $$\begin{eqnarray}\displaystyle {\mathcal{E}}(t)\leqslant \frac{{\mathcal{E}}(0)}{\sqrt{1-\displaystyle \frac{27}{4\unicode[STIX]{x03C0}^{4}\unicode[STIX]{x1D708}^{3}}{\mathcal{E}}(0)^{2}t}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{E}}(t)\leqslant \frac{{\mathcal{E}}(0)}{\sqrt{1-\displaystyle \frac{27}{4\unicode[STIX]{x03C0}^{4}\unicode[STIX]{x1D708}^{3}}{\mathcal{E}}(0)^{2}t}}, & & \displaystyle\end{eqnarray}$$
which clearly becomes infinite at time
![]() $t_{0}=4\unicode[STIX]{x03C0}^{4}\unicode[STIX]{x1D708}^{3}/[27{\mathcal{E}}(0)^{2}]$
. Thus, based on estimate (2.10), it is not possible to establish the boundedness of the enstrophy
$t_{0}=4\unicode[STIX]{x03C0}^{4}\unicode[STIX]{x1D708}^{3}/[27{\mathcal{E}}(0)^{2}]$
. Thus, based on estimate (2.10), it is not possible to establish the boundedness of the enstrophy
![]() ${\mathcal{E}}(t)$
globally in time and hence the regularity of solutions. Therefore, the question about the finite-time singularity formation can be recast in terms of whether or not estimate (2.10) can be saturated. By this we mean the existence of initial data with enstrophy
${\mathcal{E}}(t)$
globally in time and hence the regularity of solutions. Therefore, the question about the finite-time singularity formation can be recast in terms of whether or not estimate (2.10) can be saturated. By this we mean the existence of initial data with enstrophy
![]() ${\mathcal{E}}_{0}:={\mathcal{E}}(0)>0$
such that the resulting time evolution realizes the largest growth of enstrophy
${\mathcal{E}}_{0}:={\mathcal{E}}(0)>0$
such that the resulting time evolution realizes the largest growth of enstrophy
![]() ${\mathcal{E}}(t)$
allowed by the right-hand side of estimate (2.10). A systematic search for such most singular initial data using variational optimization methods is the key theme of this study. Although different notions of sharpness of an estimate can be defined, e.g. sharpness with respect to constants or exponents in the case of estimates in the form of power laws, the precise notion of sharpness considered in this study is the following
${\mathcal{E}}(t)$
allowed by the right-hand side of estimate (2.10). A systematic search for such most singular initial data using variational optimization methods is the key theme of this study. Although different notions of sharpness of an estimate can be defined, e.g. sharpness with respect to constants or exponents in the case of estimates in the form of power laws, the precise notion of sharpness considered in this study is the following
Definition 2.1. Given a parameter
![]() $p\in \mathbb{R}$
and maps
$p\in \mathbb{R}$
and maps
![]() $f,g:\mathbb{R}\rightarrow \mathbb{R}$
, the estimate
$f,g:\mathbb{R}\rightarrow \mathbb{R}$
, the estimate
is declared sharp in the limit
![]() $p\rightarrow p_{0}\in \mathbb{R}$
if and only if
$p\rightarrow p_{0}\in \mathbb{R}$
if and only if
From this definition, the sharpness of estimates in the form
![]() $g(p)=Cp^{\unicode[STIX]{x1D6FC}}$
for some
$g(p)=Cp^{\unicode[STIX]{x1D6FC}}$
for some
![]() $C\in \mathbb{R}_{+}$
and
$C\in \mathbb{R}_{+}$
and
![]() $\unicode[STIX]{x1D6FC}\in \mathbb{R}$
can be addressed in the limit
$\unicode[STIX]{x1D6FC}\in \mathbb{R}$
can be addressed in the limit
![]() $p\rightarrow \infty$
by studying the adequacy of the exponent
$p\rightarrow \infty$
by studying the adequacy of the exponent
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
The question of sharpness of estimate (2.9) was addressed in the seminal study by Lu & Doering (Reference Lu and Doering2008), see also Lu (Reference Lu2006), who constructed a family of divergence-free velocity fields saturating this estimate. More precisely, these vector fields were parameterized by their enstrophy and for sufficiently large values of
![]() ${\mathcal{E}}$
the corresponding rate of growth
${\mathcal{E}}$
the corresponding rate of growth
![]() $\text{d}{\mathcal{E}}/\text{d}t$
was found to be proportional to
$\text{d}{\mathcal{E}}/\text{d}t$
was found to be proportional to
![]() ${\mathcal{E}}^{3}$
. Therefore, in agreement with Definition 2.1, estimate (2.9) was declared sharp up to a numerical prefactor. However, the sharpness of the instantaneous estimate alone does not allow us to conclude on the possibility of singularity formation, because for this situation to occur, a sufficiently large enstrophy growth rate would need to be sustained over a finite time window
${\mathcal{E}}^{3}$
. Therefore, in agreement with Definition 2.1, estimate (2.9) was declared sharp up to a numerical prefactor. However, the sharpness of the instantaneous estimate alone does not allow us to conclude on the possibility of singularity formation, because for this situation to occur, a sufficiently large enstrophy growth rate would need to be sustained over a finite time window
![]() $[0,t_{0})$
. In fact, assuming the instantaneous rate of growth of enstrophy in the form
$[0,t_{0})$
. In fact, assuming the instantaneous rate of growth of enstrophy in the form
![]() $\text{d}{\mathcal{E}}/\text{d}t=C{\mathcal{E}}^{\unicode[STIX]{x1D6FC}}$
for some
$\text{d}{\mathcal{E}}/\text{d}t=C{\mathcal{E}}^{\unicode[STIX]{x1D6FC}}$
for some
![]() $C>0$
, any exponent
$C>0$
, any exponent
![]() $\unicode[STIX]{x1D6FC}>2$
will produce blow-up of
$\unicode[STIX]{x1D6FC}>2$
will produce blow-up of
![]() ${\mathcal{E}}(t)$
in finite time if the rate of growth is sustained. The fact that there is no blow-up for
${\mathcal{E}}(t)$
in finite time if the rate of growth is sustained. The fact that there is no blow-up for
![]() $\unicode[STIX]{x1D6FC}\leqslant 2$
follows from Grönwall’s lemma and the fact that one factor of
$\unicode[STIX]{x1D6FC}\leqslant 2$
follows from Grönwall’s lemma and the fact that one factor of
![]() ${\mathcal{E}}$
in (2.9) can be bounded in terms of the initial energy using (2.3) as follows
${\mathcal{E}}$
in (2.9) can be bounded in terms of the initial energy using (2.3) as follows
This relation also leads to an alternative form of the estimate for the finite-time growth of enstrophy, namely
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\text{d}{\mathcal{E}}}{\text{d}t}\leqslant \frac{27}{8\unicode[STIX]{x03C0}^{4}\unicode[STIX]{x1D708}^{3}}{\mathcal{E}}^{3}\quad \Longrightarrow \\ \displaystyle \int _{{\mathcal{E}}(0)}^{{\mathcal{E}}(t)}{\mathcal{E}}^{-2}\,\text{d}{\mathcal{E}}\leqslant \frac{27}{8\unicode[STIX]{x03C0}^{4}\unicode[STIX]{x1D708}^{3}}\int _{0}^{t}{\mathcal{E}}(s)\,\text{d}s\quad \Longrightarrow \\ \displaystyle \frac{1}{{\mathcal{E}}(0)}-\frac{1}{{\mathcal{E}}(t)}\leqslant \frac{27}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D708})^{4}}[{\mathcal{K}}(0)-{\mathcal{K}}(t)],\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\text{d}{\mathcal{E}}}{\text{d}t}\leqslant \frac{27}{8\unicode[STIX]{x03C0}^{4}\unicode[STIX]{x1D708}^{3}}{\mathcal{E}}^{3}\quad \Longrightarrow \\ \displaystyle \int _{{\mathcal{E}}(0)}^{{\mathcal{E}}(t)}{\mathcal{E}}^{-2}\,\text{d}{\mathcal{E}}\leqslant \frac{27}{8\unicode[STIX]{x03C0}^{4}\unicode[STIX]{x1D708}^{3}}\int _{0}^{t}{\mathcal{E}}(s)\,\text{d}s\quad \Longrightarrow \\ \displaystyle \frac{1}{{\mathcal{E}}(0)}-\frac{1}{{\mathcal{E}}(t)}\leqslant \frac{27}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D708})^{4}}[{\mathcal{K}}(0)-{\mathcal{K}}(t)],\end{array}\right\} & & \displaystyle\end{eqnarray}$$
which is more convenient than (2.10) from the computational point of view and will be used in the present study. We note, however, that since the right-hand side of this inequality cannot be expressed entirely in terms of properties of the initial data, this is not in fact an a priori estimate. Estimate (2.14) also allows us to obtain a condition on the size of the initial data, given in terms of its energy
![]() ${\mathcal{K}}(0)$
and enstrophy
${\mathcal{K}}(0)$
and enstrophy
![]() ${\mathcal{E}}(0)$
, which guarantees that smooth solutions will exist globally in time, namely,
${\mathcal{E}}(0)$
, which guarantees that smooth solutions will exist globally in time, namely,
 $$\begin{eqnarray}\displaystyle \max _{t\geqslant 0}{\mathcal{E}}(t)\leqslant \frac{{\mathcal{E}}(0)}{1-\displaystyle \frac{27}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D708})^{4}}{\mathcal{K}}(0){\mathcal{E}}(0)} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \max _{t\geqslant 0}{\mathcal{E}}(t)\leqslant \frac{{\mathcal{E}}(0)}{1-\displaystyle \frac{27}{(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D708})^{4}}{\mathcal{K}}(0){\mathcal{E}}(0)} & & \displaystyle\end{eqnarray}$$
from which it follows that
Thus, flows with energy and enstrophy satisfying inequality (2.16) are guaranteed to be smooth for all time, in agreement with the regularity results available under the assumption of small initial data (Ladyzhenskaya Reference Ladyzhenskaya1969).
3 Instantaneously optimal growth of enstrophy
Sharpness of the instantaneous estimate (2.9), in the sense of Definition 2.1, can be probed by constructing a family of ‘extreme vortex states’
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
which, for each
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
which, for each
![]() ${\mathcal{E}}_{0}>0$
, have prescribed enstrophy
${\mathcal{E}}_{0}>0$
, have prescribed enstrophy
![]() ${\mathcal{E}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})={\mathcal{E}}_{0}$
and produce the largest possible rate of growth of enstrophy
${\mathcal{E}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})={\mathcal{E}}_{0}$
and produce the largest possible rate of growth of enstrophy
![]() ${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
. Given the form of (2.5), the fields
${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
. Given the form of (2.5), the fields
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
can be expected to exhibit (at least piecewise) smooth dependence on
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
can be expected to exhibit (at least piecewise) smooth dependence on
![]() ${\mathcal{E}}_{0}$
and we will refer to the mapping
${\mathcal{E}}_{0}$
and we will refer to the mapping
![]() ${\mathcal{E}}_{0}\longmapsto \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
as a ‘maximizing branch’. Thus, information about the sharpness of estimate (2.9) can be deduced by analysing the relation
${\mathcal{E}}_{0}\longmapsto \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
as a ‘maximizing branch’. Thus, information about the sharpness of estimate (2.9) can be deduced by analysing the relation
![]() ${\mathcal{E}}_{0}$
versus
${\mathcal{E}}_{0}$
versus
![]() ${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
obtained for a possibly broad range of enstrophy values. A maximizing branch is constructed by finding, for different values of
${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
obtained for a possibly broad range of enstrophy values. A maximizing branch is constructed by finding, for different values of
![]() ${\mathcal{E}}_{0}$
, the extreme vortex states
${\mathcal{E}}_{0}$
, the extreme vortex states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
as solutions of a variational optimization problem defined below.
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
as solutions of a variational optimization problem defined below.
Hereafter,
![]() $H^{2}(\unicode[STIX]{x1D6FA})$
will denote the Sobolev space of functions with square-integrable second derivatives endowed with the inner product (Adams & Fournier Reference Adams and Fournier2005)
$H^{2}(\unicode[STIX]{x1D6FA})$
will denote the Sobolev space of functions with square-integrable second derivatives endowed with the inner product (Adams & Fournier Reference Adams and Fournier2005)
where
![]() $\ell _{1},\ell _{2}\in \mathbb{R}_{+}$
are parameters with the meaning of length scales (the reasons for introducing these parameters in the definition of the inner product will become clear below). The inner product in the space
$\ell _{1},\ell _{2}\in \mathbb{R}_{+}$
are parameters with the meaning of length scales (the reasons for introducing these parameters in the definition of the inner product will become clear below). The inner product in the space
![]() $L_{2}(\unicode[STIX]{x1D6FA})$
is obtained from (3.1) by setting
$L_{2}(\unicode[STIX]{x1D6FA})$
is obtained from (3.1) by setting
![]() $\ell _{1}=\ell _{2}=0$
. The notation
$\ell _{1}=\ell _{2}=0$
. The notation
![]() $H_{0}^{2}(\unicode[STIX]{x1D6FA})$
will refer to the Sobolev space
$H_{0}^{2}(\unicode[STIX]{x1D6FA})$
will refer to the Sobolev space
![]() $H^{2}(\unicode[STIX]{x1D6FA})$
of functions with zero mean. For every fixed value
$H^{2}(\unicode[STIX]{x1D6FA})$
of functions with zero mean. For every fixed value
![]() ${\mathcal{E}}_{0}$
of enstrophy we will look for a divergence-free vector field
${\mathcal{E}}_{0}$
of enstrophy we will look for a divergence-free vector field
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
maximizing the objective function
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
maximizing the objective function
![]() ${\mathcal{R}}:H_{0}^{2}(\unicode[STIX]{x1D6FA})\rightarrow \mathbb{R}$
defined in (2.5). We thus have the following:
${\mathcal{R}}:H_{0}^{2}(\unicode[STIX]{x1D6FA})\rightarrow \mathbb{R}$
defined in (2.5). We thus have the following:
Problem 3.1. Given
![]() ${\mathcal{E}}_{0}\in \mathbb{R}_{+}$
and the objective functional
${\mathcal{E}}_{0}\in \mathbb{R}_{+}$
and the objective functional
![]() ${\mathcal{R}}$
from (2.5), find
${\mathcal{R}}$
from (2.5), find
which will be solved for enstrophy
![]() ${\mathcal{E}}_{0}$
spanning a broad range of values. This approach was originally proposed and investigated by Lu & Doering (Reference Lu and Doering2008). In the present study we extend and generalize these results by first showing how other fields considered in the context of the blow-up problem for both the Euler and Navier–Stokes system, namely the Taylor–Green vortex, also arise from variational Problem 3.1. We then thoroughly analyse the time evolution corresponding to our extreme vortex states and compare it with the predictions of the finite-time estimates (2.10) and (2.14). As discussed at the end of this section, some important aspects of our approach to solving Problem 3.1 are also quite different from the method adopted by Lu & Doering (Reference Lu and Doering2008).
${\mathcal{E}}_{0}$
spanning a broad range of values. This approach was originally proposed and investigated by Lu & Doering (Reference Lu and Doering2008). In the present study we extend and generalize these results by first showing how other fields considered in the context of the blow-up problem for both the Euler and Navier–Stokes system, namely the Taylor–Green vortex, also arise from variational Problem 3.1. We then thoroughly analyse the time evolution corresponding to our extreme vortex states and compare it with the predictions of the finite-time estimates (2.10) and (2.14). As discussed at the end of this section, some important aspects of our approach to solving Problem 3.1 are also quite different from the method adopted by Lu & Doering (Reference Lu and Doering2008).
The smoothness requirement in the statement of Problem 3.1 (
![]() $\boldsymbol{u}\in H_{0}^{2}(\unicode[STIX]{x1D6FA})$
) follows from the definition of the objective functional
$\boldsymbol{u}\in H_{0}^{2}(\unicode[STIX]{x1D6FA})$
) follows from the definition of the objective functional
![]() ${\mathcal{R}}$
in (2.5), where both the viscous term
${\mathcal{R}}$
in (2.5), where both the viscous term
![]() $\unicode[STIX]{x1D708}\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x0394}\boldsymbol{u}|^{2}\,\text{d}\boldsymbol{x}$
and the cubic term
$\unicode[STIX]{x1D708}\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x0394}\boldsymbol{u}|^{2}\,\text{d}\boldsymbol{x}$
and the cubic term
![]() $\int _{\unicode[STIX]{x1D6FA}}\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x0394}\boldsymbol{u}\,\text{d}\boldsymbol{x}$
contain derivatives of order up to two. The constraint manifold
$\int _{\unicode[STIX]{x1D6FA}}\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x0394}\boldsymbol{u}\,\text{d}\boldsymbol{x}$
contain derivatives of order up to two. The constraint manifold
![]() ${\mathcal{S}}_{{\mathcal{E}}_{0}}$
can be interpreted as an intersection of the manifold (a subspace)
${\mathcal{S}}_{{\mathcal{E}}_{0}}$
can be interpreted as an intersection of the manifold (a subspace)
![]() ${\mathcal{S}}_{0}\in H_{0}^{2}(\unicode[STIX]{x1D6FA})$
of divergence-free fields and the manifold
${\mathcal{S}}_{0}\in H_{0}^{2}(\unicode[STIX]{x1D6FA})$
of divergence-free fields and the manifold
![]() ${\mathcal{S}}_{{\mathcal{E}}_{0}}^{\prime }\in H_{0}^{2}(\unicode[STIX]{x1D6FA})$
of fields with prescribed enstrophy
${\mathcal{S}}_{{\mathcal{E}}_{0}}^{\prime }\in H_{0}^{2}(\unicode[STIX]{x1D6FA})$
of fields with prescribed enstrophy
![]() ${\mathcal{E}}_{0}$
. The structure of these constraint manifolds is reflected in the definition of the corresponding projections
${\mathcal{E}}_{0}$
. The structure of these constraint manifolds is reflected in the definition of the corresponding projections
![]() $\mathbb{P}_{{\mathcal{S}}}:H_{0}^{2}\rightarrow {\mathcal{S}}$
(without a subscript,
$\mathbb{P}_{{\mathcal{S}}}:H_{0}^{2}\rightarrow {\mathcal{S}}$
(without a subscript,
![]() ${\mathcal{S}}$
refers to a generic manifold) which is given for each of the two constraints as follows:
${\mathcal{S}}$
refers to a generic manifold) which is given for each of the two constraints as follows:
-
(i) (div-free)-constraint: the projection of a field
 $\boldsymbol{u}$
onto the subspace of solenoidal fields
$\boldsymbol{u}$
onto the subspace of solenoidal fields
 ${\mathcal{S}}_{0}$
is performed using the Helmholtz decomposition; accordingly, every zero-mean vector field
${\mathcal{S}}_{0}$
is performed using the Helmholtz decomposition; accordingly, every zero-mean vector field
 $\boldsymbol{u}\in H_{0}^{2}(\unicode[STIX]{x1D6FA})$
can be decomposed uniquely as (3.4)where
$\boldsymbol{u}\in H_{0}^{2}(\unicode[STIX]{x1D6FA})$
can be decomposed uniquely as (3.4)where $$\begin{eqnarray}\displaystyle \boldsymbol{u}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}+\unicode[STIX]{x1D735}\times \boldsymbol{A}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}+\unicode[STIX]{x1D735}\times \boldsymbol{A}, & & \displaystyle\end{eqnarray}$$
 $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
 $\boldsymbol{A}$
are scalar and vector potentials, respectively; it follows from the identity
$\boldsymbol{A}$
are scalar and vector potentials, respectively; it follows from the identity
 $\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{A})\equiv 0$
, valid for any sufficiently smooth vector field
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{A})\equiv 0$
, valid for any sufficiently smooth vector field
 $\boldsymbol{A}$
, that the projection
$\boldsymbol{A}$
, that the projection
 $\mathbb{P}_{{\mathcal{S}}_{0}}(\boldsymbol{u})$
is given simply by
$\mathbb{P}_{{\mathcal{S}}_{0}}(\boldsymbol{u})$
is given simply by
 $\unicode[STIX]{x1D735}\times \boldsymbol{A}$
and is therefore calculated as (3.5)where
$\unicode[STIX]{x1D735}\times \boldsymbol{A}$
and is therefore calculated as (3.5)where $$\begin{eqnarray}\displaystyle \mathbb{P}_{{\mathcal{S}}_{0}}(\boldsymbol{u})=\boldsymbol{u}-\unicode[STIX]{x1D735}[\unicode[STIX]{x1D6E5}^{-1}(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u})], & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{P}_{{\mathcal{S}}_{0}}(\boldsymbol{u})=\boldsymbol{u}-\unicode[STIX]{x1D735}[\unicode[STIX]{x1D6E5}^{-1}(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u})], & & \displaystyle\end{eqnarray}$$
 $\unicode[STIX]{x1D6E5}^{-1}$
is the inverse Laplacian associated with the periodic boundary conditions; the operator
$\unicode[STIX]{x1D6E5}^{-1}$
is the inverse Laplacian associated with the periodic boundary conditions; the operator
 $\mathbb{P}_{{\mathcal{S}}_{0}}$
is also known as the Leray–Helmholtz projector.
$\mathbb{P}_{{\mathcal{S}}_{0}}$
is also known as the Leray–Helmholtz projector.
-
(ii)
 $({\mathcal{E}}_{0})$
-constraint: the projection onto the manifold
$({\mathcal{E}}_{0})$
-constraint: the projection onto the manifold
 ${\mathcal{S}}_{{\mathcal{E}}_{0}}^{\prime }$
is calculated by the normalization (3.6)
${\mathcal{S}}_{{\mathcal{E}}_{0}}^{\prime }$
is calculated by the normalization (3.6) $$\begin{eqnarray}\displaystyle \mathbb{P}_{{\mathcal{S}}_{{\mathcal{E}}_{0}}^{\prime }}(\boldsymbol{u})=\sqrt{\frac{{\mathcal{E}}_{0}}{{\mathcal{E}}(\boldsymbol{u})}}\boldsymbol{u}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{P}_{{\mathcal{S}}_{{\mathcal{E}}_{0}}^{\prime }}(\boldsymbol{u})=\sqrt{\frac{{\mathcal{E}}_{0}}{{\mathcal{E}}(\boldsymbol{u})}}\boldsymbol{u}. & & \displaystyle\end{eqnarray}$$
Thus, composing (3.5) with (3.6), the projection onto the manifold
![]() ${\mathcal{S}}_{{\mathcal{E}}_{0}}$
defined in Problem 3.1 is constructed as
${\mathcal{S}}_{{\mathcal{E}}_{0}}$
defined in Problem 3.1 is constructed as
This approach, which was already successfully employed by Ayala & Protas (Reference Ayala and Protas2011, Reference Ayala and Protas2014a ), allows one to enforce the enstrophy constraint essentially with the machine precision.
For a given value of
![]() ${\mathcal{E}}_{0}$
, the maximizer
${\mathcal{E}}_{0}$
, the maximizer
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
can be found as
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
can be found as
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}=\lim _{n\rightarrow \infty }\boldsymbol{u}_{{\mathcal{E}}_{0}}^{(n)}$
using the following iterative procedure representing a discretization of a gradient flow projected on
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}=\lim _{n\rightarrow \infty }\boldsymbol{u}_{{\mathcal{E}}_{0}}^{(n)}$
using the following iterative procedure representing a discretization of a gradient flow projected on
![]() ${\mathcal{S}}_{{\mathcal{E}}_{0}}$
${\mathcal{S}}_{{\mathcal{E}}_{0}}$
where
![]() $\boldsymbol{u}_{{\mathcal{E}}_{0}}^{(n)}$
is an approximation of the maximizer obtained at the
$\boldsymbol{u}_{{\mathcal{E}}_{0}}^{(n)}$
is an approximation of the maximizer obtained at the
![]() $n$
th iteration,
$n$
th iteration,
![]() $\boldsymbol{u}^{0}$
is the initial guess and
$\boldsymbol{u}^{0}$
is the initial guess and
![]() $\unicode[STIX]{x1D70F}_{n}$
is the length of the step in the direction of the gradient. It is ensured that the maximizers
$\unicode[STIX]{x1D70F}_{n}$
is the length of the step in the direction of the gradient. It is ensured that the maximizers
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
obtained for different values of
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
obtained for different values of
![]() ${\mathcal{E}}_{0}$
lie on the same maximizing branch by using the continuation approach, where the maximizer
${\mathcal{E}}_{0}$
lie on the same maximizing branch by using the continuation approach, where the maximizer
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
is employed as the initial guess
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
is employed as the initial guess
![]() $\boldsymbol{u}^{0}$
to compute
$\boldsymbol{u}^{0}$
to compute
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}+\unicode[STIX]{x0394}{\mathcal{E}}}$
at the next enstrophy level for some sufficiently small
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}+\unicode[STIX]{x0394}{\mathcal{E}}}$
at the next enstrophy level for some sufficiently small
![]() $\unicode[STIX]{x0394}{\mathcal{E}}>0$
. As will be demonstrated in § 4, in the limit
$\unicode[STIX]{x0394}{\mathcal{E}}>0$
. As will be demonstrated in § 4, in the limit
![]() ${\mathcal{E}}_{0}\rightarrow 0$
optimization Problem 3.1 admits a discrete family of closed-form solutions and each of these vortex states is the limiting (initial) member
${\mathcal{E}}_{0}\rightarrow 0$
optimization Problem 3.1 admits a discrete family of closed-form solutions and each of these vortex states is the limiting (initial) member
![]() $\widetilde{\boldsymbol{u}}_{0}$
of the corresponding maximizing branch. As such, these limiting extreme vortex states are used as the initial guesses
$\widetilde{\boldsymbol{u}}_{0}$
of the corresponding maximizing branch. As such, these limiting extreme vortex states are used as the initial guesses
![]() $\boldsymbol{u}^{0}$
for the calculation of
$\boldsymbol{u}^{0}$
for the calculation of
![]() $\widetilde{\boldsymbol{u}}_{\unicode[STIX]{x0394}{\mathcal{E}}}$
, i.e. they serve as ‘seeds’ for the calculation of an entire maximizing branch (as discussed in § 7, while there exist alternatives to the continuation approach, this technique in fact results in the fastest convergence of iterations (3.8) and also ensures that all computed extreme vortex states lie on a single branch). The procedure outlined above is summarized as algorithm 1, whereas all details are presented below.
$\widetilde{\boldsymbol{u}}_{\unicode[STIX]{x0394}{\mathcal{E}}}$
, i.e. they serve as ‘seeds’ for the calculation of an entire maximizing branch (as discussed in § 7, while there exist alternatives to the continuation approach, this technique in fact results in the fastest convergence of iterations (3.8) and also ensures that all computed extreme vortex states lie on a single branch). The procedure outlined above is summarized as algorithm 1, whereas all details are presented below.

A key step of algorithm 1 is the evaluation of the gradient
![]() $\unicode[STIX]{x1D735}{\mathcal{R}}(\boldsymbol{u})$
of the objective functional
$\unicode[STIX]{x1D735}{\mathcal{R}}(\boldsymbol{u})$
of the objective functional
![]() ${\mathcal{R}}(\boldsymbol{u})$
, cf. (2.5), representing its (infinite-dimensional) sensitivity to perturbations of the velocity field
${\mathcal{R}}(\boldsymbol{u})$
, cf. (2.5), representing its (infinite-dimensional) sensitivity to perturbations of the velocity field
![]() $\boldsymbol{u}$
, and it is essential that the gradient be characterized by the required regularity, namely,
$\boldsymbol{u}$
, and it is essential that the gradient be characterized by the required regularity, namely,
![]() $\unicode[STIX]{x1D735}{\mathcal{R}}(\boldsymbol{u})\in H^{2}(\unicode[STIX]{x1D6FA})$
. This is, in fact, guaranteed by the Riesz representation theorem (Luenberger Reference Luenberger1969) applicable because the Gâteaux differential
$\unicode[STIX]{x1D735}{\mathcal{R}}(\boldsymbol{u})\in H^{2}(\unicode[STIX]{x1D6FA})$
. This is, in fact, guaranteed by the Riesz representation theorem (Luenberger Reference Luenberger1969) applicable because the Gâteaux differential
![]() ${\mathcal{R}}^{\prime }(\boldsymbol{u};\boldsymbol{\cdot }):H_{0}^{2}(\unicode[STIX]{x1D6FA})\rightarrow \mathbb{R}$
, defined as
${\mathcal{R}}^{\prime }(\boldsymbol{u};\boldsymbol{\cdot }):H_{0}^{2}(\unicode[STIX]{x1D6FA})\rightarrow \mathbb{R}$
, defined as
![]() ${\mathcal{R}}^{\prime }(\boldsymbol{u};\boldsymbol{u}^{\prime }):=\lim _{\unicode[STIX]{x1D716}\rightarrow 0}\unicode[STIX]{x1D716}^{-1}[{\mathcal{R}}(\boldsymbol{u}+\unicode[STIX]{x1D716}\boldsymbol{u}^{\prime })-{\mathcal{R}}(\boldsymbol{u})]$
for some perturbation
${\mathcal{R}}^{\prime }(\boldsymbol{u};\boldsymbol{u}^{\prime }):=\lim _{\unicode[STIX]{x1D716}\rightarrow 0}\unicode[STIX]{x1D716}^{-1}[{\mathcal{R}}(\boldsymbol{u}+\unicode[STIX]{x1D716}\boldsymbol{u}^{\prime })-{\mathcal{R}}(\boldsymbol{u})]$
for some perturbation
![]() $\boldsymbol{u}^{\prime }\in H_{0}^{2}(\unicode[STIX]{x1D6FA})$
, is a bounded linear functional on
$\boldsymbol{u}^{\prime }\in H_{0}^{2}(\unicode[STIX]{x1D6FA})$
, is a bounded linear functional on
![]() $H_{0}^{2}(\unicode[STIX]{x1D6FA})$
. The Gâteaux differential can be computed directly to give
$H_{0}^{2}(\unicode[STIX]{x1D6FA})$
. The Gâteaux differential can be computed directly to give
from which, by the Riesz representation theorem, we obtain
with the Riesz representers
![]() $\unicode[STIX]{x1D735}{\mathcal{R}}(\boldsymbol{u})$
and
$\unicode[STIX]{x1D735}{\mathcal{R}}(\boldsymbol{u})$
and
![]() $\unicode[STIX]{x1D735}^{L_{2}}{\mathcal{R}}(\boldsymbol{u})$
being the gradients computed with respect to the
$\unicode[STIX]{x1D735}^{L_{2}}{\mathcal{R}}(\boldsymbol{u})$
being the gradients computed with respect to the
![]() $H^{2}$
and
$H^{2}$
and
![]() $L_{2}$
topology, respectively, and the inner products defined in (3.1). We remark that, while the
$L_{2}$
topology, respectively, and the inner products defined in (3.1). We remark that, while the
![]() $H^{2}$
gradient is used exclusively in the actual computations, cf. (3.8), the
$H^{2}$
gradient is used exclusively in the actual computations, cf. (3.8), the
![]() $L_{2}$
gradient is computed first as an intermediate step. Identifying the Gâteaux differential (3.9) with the
$L_{2}$
gradient is computed first as an intermediate step. Identifying the Gâteaux differential (3.9) with the
![]() $L_{2}$
inner product and performing integration by parts yields
$L_{2}$
inner product and performing integration by parts yields
Similarly, identifying the Gâteaux differential (3.9) with the
![]() $H^{2}$
inner product (3.1), integrating by parts and using (3.11), we obtain the required
$H^{2}$
inner product (3.1), integrating by parts and using (3.11), we obtain the required
![]() $H^{2}$
gradient
$H^{2}$
gradient
![]() $\unicode[STIX]{x1D735}{\mathcal{R}}$
as a solution of the following elliptic boundary-value problem
$\unicode[STIX]{x1D735}{\mathcal{R}}$
as a solution of the following elliptic boundary-value problem
The gradient fields
![]() $\unicode[STIX]{x1D735}^{L_{2}}{\mathcal{R}}(\boldsymbol{u})$
and
$\unicode[STIX]{x1D735}^{L_{2}}{\mathcal{R}}(\boldsymbol{u})$
and
![]() $\unicode[STIX]{x1D735}{\mathcal{R}}(\boldsymbol{u})$
can be interpreted as infinite-dimensional sensitivities of the objective function
$\unicode[STIX]{x1D735}{\mathcal{R}}(\boldsymbol{u})$
can be interpreted as infinite-dimensional sensitivities of the objective function
![]() ${\mathcal{R}}(\boldsymbol{u})$
, cf. (2.5), with respect to perturbations of the field
${\mathcal{R}}(\boldsymbol{u})$
, cf. (2.5), with respect to perturbations of the field
![]() $\boldsymbol{u}$
. While these two gradients may point towards the same local maximizer, they represent distinct ‘directions’, since they are defined with respect to different topologies (
$\boldsymbol{u}$
. While these two gradients may point towards the same local maximizer, they represent distinct ‘directions’, since they are defined with respect to different topologies (
![]() $L_{2}$
versus
$L_{2}$
versus
![]() $H^{2}$
). As shown by Protas, Bewley & Hagen (Reference Protas, Bewley and Hagen2004), extraction of gradients in spaces of smoother functions such as
$H^{2}$
). As shown by Protas, Bewley & Hagen (Reference Protas, Bewley and Hagen2004), extraction of gradients in spaces of smoother functions such as
![]() $H^{2}(\unicode[STIX]{x1D6FA})$
can be interpreted as low-pass filtering of the
$H^{2}(\unicode[STIX]{x1D6FA})$
can be interpreted as low-pass filtering of the
![]() $L_{2}$
gradients with parameters
$L_{2}$
gradients with parameters
![]() $\ell _{1}$
and
$\ell _{1}$
and
![]() $\ell _{2}$
acting as cutoff length scales and the choice of their numerical values will be discussed in § 5.
$\ell _{2}$
acting as cutoff length scales and the choice of their numerical values will be discussed in § 5.
The step size
![]() $\unicode[STIX]{x1D70F}_{n}$
in algorithm (3.8) is computed as
$\unicode[STIX]{x1D70F}_{n}$
in algorithm (3.8) is computed as
which is done using a suitable derivative-free line-search algorithm (Ruszczyński Reference Ruszczyński2006). Equation (3.13) can be interpreted as a modification of a standard line-search method where the optimization is performed following an arc (a geodesic) lying on the constraint manifold
![]() ${\mathcal{S}}_{{\mathcal{E}}_{0}}$
, rather than a straight line. This approach was already successfully employed to solve similar problems in Ayala & Protas (Reference Ayala and Protas2011, Reference Ayala and Protas2014a
).
${\mathcal{S}}_{{\mathcal{E}}_{0}}$
, rather than a straight line. This approach was already successfully employed to solve similar problems in Ayala & Protas (Reference Ayala and Protas2011, Reference Ayala and Protas2014a
).
It ought to be emphasized here that the approach presented above in which the projections (3.5)–(3.6) and gradients (3.11)–(3.12) are obtained based on the infinite-dimensional (continuous) formulation to be discretized only at the final stage is fundamentally different from the method employed in the original study by Lu & Doering (Reference Lu and Doering2008) in which the optimization problem was solved in a fully discrete setting (the two approaches are referred to as ‘optimize-then-discretize’ and ‘discretize-then-optimize’, respectively, cf. Gunzburger Reference Gunzburger2003). A practical advantage of the continuous (‘optimize-then-discretize’) formulation used in the present work is that the expressions representing the sensitivity of the objective functional
![]() ${\mathcal{R}}$
, i.e. the gradients
${\mathcal{R}}$
, i.e. the gradients
![]() $\unicode[STIX]{x1D735}^{L_{2}}{\mathcal{R}}$
and
$\unicode[STIX]{x1D735}^{L_{2}}{\mathcal{R}}$
and
![]() $\unicode[STIX]{x1D735}{\mathcal{R}}$
, are independent of the specific discretization approach chosen to evaluate them. This should be contrasted with the discrete (‘discretize-then-optimize’) formulation, where a change of the discretization method would require rederivation of the gradient expressions. In addition, the continuous formulation allows us to strictly enforce the regularity of maximizers required in Problem 3.1. Finally and perhaps most importantly, the continuous formulation of the maximization problem makes it possible to obtain elegant closed-form solutions of the problem in the limit
$\unicode[STIX]{x1D735}{\mathcal{R}}$
, are independent of the specific discretization approach chosen to evaluate them. This should be contrasted with the discrete (‘discretize-then-optimize’) formulation, where a change of the discretization method would require rederivation of the gradient expressions. In addition, the continuous formulation allows us to strictly enforce the regularity of maximizers required in Problem 3.1. Finally and perhaps most importantly, the continuous formulation of the maximization problem makes it possible to obtain elegant closed-form solutions of the problem in the limit
![]() ${\mathcal{E}}_{0}\rightarrow 0$
, which is done in § 4 below. These analytical solutions will then be used in § 5 to guide the computation of maximizing branches by numerically solving Problem 3.1 for a broad range of
${\mathcal{E}}_{0}\rightarrow 0$
, which is done in § 4 below. These analytical solutions will then be used in § 5 to guide the computation of maximizing branches by numerically solving Problem 3.1 for a broad range of
![]() ${\mathcal{E}}_{0}$
, as outlined in algorithm 1.
${\mathcal{E}}_{0}$
, as outlined in algorithm 1.
4 Extreme vortex states in the limit
 ${\mathcal{E}}_{0}\rightarrow 0$
${\mathcal{E}}_{0}\rightarrow 0$
It is possible to find analytic solutions to Problem 3.1 in the limit
![]() ${\mathcal{E}}_{0}\rightarrow 0$
using perturbation methods. To simplify the notation, in this section we will drop the subscript
${\mathcal{E}}_{0}\rightarrow 0$
using perturbation methods. To simplify the notation, in this section we will drop the subscript
![]() ${\mathcal{E}}_{0}$
when referring to the optimal field. The Euler–Lagrange system representing the first-order optimality conditions in optimization Problem 3.1 is given by (Luenberger Reference Luenberger1969)
${\mathcal{E}}_{0}$
when referring to the optimal field. The Euler–Lagrange system representing the first-order optimality conditions in optimization Problem 3.1 is given by (Luenberger Reference Luenberger1969)
is the bilinear form from (3.11). Using the formal series expansions with
![]() $\unicode[STIX]{x1D6FC}>0$
$\unicode[STIX]{x1D6FC}>0$
Similarly, equation (4.1b ) leads to
at every order
![]() $m$
in
$m$
in
![]() ${\mathcal{E}}_{0}^{\unicode[STIX]{x1D6FC}}$
. It then follows from (4.1c
) that
${\mathcal{E}}_{0}^{\unicode[STIX]{x1D6FC}}$
. It then follows from (4.1c
) that
which, for
![]() $\unicode[STIX]{x1D6FC}\neq 0$
, forces
$\unicode[STIX]{x1D6FC}\neq 0$
, forces
![]() ${\mathcal{E}}(\boldsymbol{u}_{0})=0$
. Hence,
${\mathcal{E}}(\boldsymbol{u}_{0})=0$
. Hence,
![]() $\boldsymbol{u}_{0}\equiv 0$
,
$\boldsymbol{u}_{0}\equiv 0$
,
![]() $\unicode[STIX]{x1D6FC}=1/2$
and
$\unicode[STIX]{x1D6FC}=1/2$
and
![]() ${\mathcal{E}}(\boldsymbol{u}_{1})=1$
. The systems at orders
${\mathcal{E}}(\boldsymbol{u}_{1})=1$
. The systems at orders
![]() ${\mathcal{E}}_{0}^{1/2}$
and
${\mathcal{E}}_{0}^{1/2}$
and
![]() ${\mathcal{E}}_{0}^{1}$
are given by:
${\mathcal{E}}_{0}^{1}$
are given by:
It is worth noting that, in the light of relation (4.9), the maximum rate of growth of enstrophy in the limit of small
![]() ${\mathcal{E}}_{0}$
is in fact negative, meaning that, for sufficiently small
${\mathcal{E}}_{0}$
is in fact negative, meaning that, for sufficiently small
![]() ${\mathcal{E}}_{0}$
, the enstrophy itself is a decreasing function for all times. This observation is consistent with the small-data regularity result discussed in Introduction.
${\mathcal{E}}_{0}$
, the enstrophy itself is a decreasing function for all times. This observation is consistent with the small-data regularity result discussed in Introduction.
As regards problem (4.7) defining the triplet
![]() $\{\boldsymbol{u}_{1},q_{1},\unicode[STIX]{x1D706}_{0}\}$
, taking the divergence of (4.7a
) and using the condition
$\{\boldsymbol{u}_{1},q_{1},\unicode[STIX]{x1D706}_{0}\}$
, taking the divergence of (4.7a
) and using the condition
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{1}=0$
leads to the Laplace equation
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{1}=0$
leads to the Laplace equation
![]() $\unicode[STIX]{x0394}q_{1}=0$
in
$\unicode[STIX]{x0394}q_{1}=0$
in
![]() $\unicode[STIX]{x1D6FA}$
. Since for zero-mean functions defined on
$\unicode[STIX]{x1D6FA}$
. Since for zero-mean functions defined on
![]() $\unicode[STIX]{x1D6FA}$
,
$\unicode[STIX]{x1D6FA}$
,
![]() $\operatorname{Ker}(\unicode[STIX]{x0394})=\{0\}$
, it follows that
$\operatorname{Ker}(\unicode[STIX]{x0394})=\{0\}$
, it follows that
![]() $q_{1}\equiv 0$
and (4.7a
) is reduced to the eigenvalue problem
$q_{1}\equiv 0$
and (4.7a
) is reduced to the eigenvalue problem
with
![]() $\boldsymbol{u}_{1}$
satisfying the incompressibility condition (4.7b
). Direct calculation using (4.10) and condition (4.7c
) leads to an asymptotic expression for the objective functional in the limit of small enstrophy
$\boldsymbol{u}_{1}$
satisfying the incompressibility condition (4.7b
). Direct calculation using (4.10) and condition (4.7c
) leads to an asymptotic expression for the objective functional in the limit of small enstrophy
Solutions to the eigenvalue problem in (4.10) can be found using the Fourier expansion of
![]() $\boldsymbol{u}_{1}$
given as (with hats denoting Fourier coefficients)
$\boldsymbol{u}_{1}$
given as (with hats denoting Fourier coefficients)
where
![]() ${\mathcal{W}}\subseteq \mathbb{Z}^{3}$
is a set of wavevectors
${\mathcal{W}}\subseteq \mathbb{Z}^{3}$
is a set of wavevectors
![]() $\boldsymbol{k}$
for which
$\boldsymbol{k}$
for which
![]() $\widehat{\boldsymbol{u}}_{1}(\boldsymbol{k})\neq 0$
. The eigenvalue problem (4.10) then becomes
$\widehat{\boldsymbol{u}}_{1}(\boldsymbol{k})\neq 0$
. The eigenvalue problem (4.10) then becomes
with solutions obtained by choosing, for any
![]() $k\in \mathbb{Z}\setminus \{0\}$
, a set of wavevectors with the following structure
$k\in \mathbb{Z}\setminus \{0\}$
, a set of wavevectors with the following structure
and
![]() $\widehat{\boldsymbol{u}}_{1}(\boldsymbol{k})$
with an appropriate form satisfying the incompressibility condition
$\widehat{\boldsymbol{u}}_{1}(\boldsymbol{k})$
with an appropriate form satisfying the incompressibility condition
![]() $\widehat{\boldsymbol{u}}_{1}\boldsymbol{\cdot }\boldsymbol{k}=0$
. For the solutions to (4.10) constructed in such manner it then follows that
$\widehat{\boldsymbol{u}}_{1}\boldsymbol{\cdot }\boldsymbol{k}=0$
. For the solutions to (4.10) constructed in such manner it then follows that
![]() $\unicode[STIX]{x1D706}_{0}=2\unicode[STIX]{x1D708}(2\unicode[STIX]{x03C0})^{2}|\boldsymbol{k}|^{2}$
and the optimal asymptotic value of
$\unicode[STIX]{x1D706}_{0}=2\unicode[STIX]{x1D708}(2\unicode[STIX]{x03C0})^{2}|\boldsymbol{k}|^{2}$
and the optimal asymptotic value of
![]() ${\mathcal{R}}$
is given by
${\mathcal{R}}$
is given by
Since the fields
![]() $\boldsymbol{u}_{1}$
are real valued, their Fourier modes must satisfy
$\boldsymbol{u}_{1}$
are real valued, their Fourier modes must satisfy
![]() $\widehat{\boldsymbol{u}}_{1}(-\boldsymbol{k})=\overline{\widehat{\boldsymbol{u}}_{1}(\boldsymbol{k})}$
, where
$\widehat{\boldsymbol{u}}_{1}(-\boldsymbol{k})=\overline{\widehat{\boldsymbol{u}}_{1}(\boldsymbol{k})}$
, where
![]() $\overline{z}$
denotes the complex conjugate (c.c.) of
$\overline{z}$
denotes the complex conjugate (c.c.) of
![]() $z\in \mathbb{C}$
. Depending on the choice of
$z\in \mathbb{C}$
. Depending on the choice of
![]() ${\mathcal{W}}_{k}$
, a number of different solutions of (4.7) can be constructed and below we focus on the following three most relevant cases characterized by the largest values of
${\mathcal{W}}_{k}$
, a number of different solutions of (4.7) can be constructed and below we focus on the following three most relevant cases characterized by the largest values of
![]() ${\mathcal{R}}(\widetilde{\boldsymbol{u}})$
:
${\mathcal{R}}(\widetilde{\boldsymbol{u}})$
:
-
(i)
 ${\mathcal{W}}_{1}=\{\boldsymbol{k}_{1},\boldsymbol{k}_{2},\boldsymbol{k}_{3},-\boldsymbol{k}_{1},-\boldsymbol{k}_{2},-\boldsymbol{k}_{3}\}$
, where
${\mathcal{W}}_{1}=\{\boldsymbol{k}_{1},\boldsymbol{k}_{2},\boldsymbol{k}_{3},-\boldsymbol{k}_{1},-\boldsymbol{k}_{2},-\boldsymbol{k}_{3}\}$
, where
 $\boldsymbol{k}_{i}=\boldsymbol{e}_{i}$
,
$\boldsymbol{k}_{i}=\boldsymbol{e}_{i}$
,
 $i=1,2,3$
, is the
$i=1,2,3$
, is the
 $i$
th unit vector of the canonical basis of
$i$
th unit vector of the canonical basis of
 $\mathbb{R}^{3}$
; the most general solution can then be constructed as (4.17)with the complex-valued constant vectors
$\mathbb{R}^{3}$
; the most general solution can then be constructed as (4.17)with the complex-valued constant vectors $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{1}(\boldsymbol{x})=\boldsymbol{A}\text{e}^{2\unicode[STIX]{x03C0}\text{i}\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{B}\text{e}^{2\unicode[STIX]{x03C0}\text{i}\boldsymbol{k}_{2}\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{C}\text{e}^{2\unicode[STIX]{x03C0}\text{i}\boldsymbol{k}_{3}\boldsymbol{\cdot }\boldsymbol{x}}+\text{c.c.,} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{1}(\boldsymbol{x})=\boldsymbol{A}\text{e}^{2\unicode[STIX]{x03C0}\text{i}\boldsymbol{k}_{1}\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{B}\text{e}^{2\unicode[STIX]{x03C0}\text{i}\boldsymbol{k}_{2}\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{C}\text{e}^{2\unicode[STIX]{x03C0}\text{i}\boldsymbol{k}_{3}\boldsymbol{\cdot }\boldsymbol{x}}+\text{c.c.,} & & \displaystyle\end{eqnarray}$$
 $\boldsymbol{A}=[0,A_{2},A_{3}]$
,
$\boldsymbol{A}=[0,A_{2},A_{3}]$
,
 $\boldsymbol{B}=[B_{1},0,B_{3}]$
and
$\boldsymbol{B}=[B_{1},0,B_{3}]$
and
 $\boldsymbol{C}=[C_{1},C_{2},0]$
suitably chosen so that
$\boldsymbol{C}=[C_{1},C_{2},0]$
suitably chosen so that
 ${\mathcal{E}}(\boldsymbol{u}_{1})=1$
; hereafter we will use the values
${\mathcal{E}}(\boldsymbol{u}_{1})=1$
; hereafter we will use the values
 $A_{2}=A_{3}=\cdots =C_{2}=1/(48\unicode[STIX]{x03C0}^{2})$
; it follows that
$A_{2}=A_{3}=\cdots =C_{2}=1/(48\unicode[STIX]{x03C0}^{2})$
; it follows that
 $|\boldsymbol{k}|^{2}=1$
$|\boldsymbol{k}|^{2}=1$
 $\forall \boldsymbol{k}\in {\mathcal{W}}_{1}$
, and the optimal asymptotic value of
$\forall \boldsymbol{k}\in {\mathcal{W}}_{1}$
, and the optimal asymptotic value of
 ${\mathcal{R}}$
obtained from (4.16) is given by (4.18)
${\mathcal{R}}$
obtained from (4.16) is given by (4.18) $$\begin{eqnarray}\displaystyle {\mathcal{R}}(\widetilde{\boldsymbol{u}})\approx -8\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D708}{\mathcal{E}}_{0}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{R}}(\widetilde{\boldsymbol{u}})\approx -8\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D708}{\mathcal{E}}_{0}, & & \displaystyle\end{eqnarray}$$
-
(ii)
 ${\mathcal{W}}_{2}={\mathcal{W}}\cup (-{\mathcal{W}})$
, where
${\mathcal{W}}_{2}={\mathcal{W}}\cup (-{\mathcal{W}})$
, where
 $-{\mathcal{W}}$
denotes the set whose elements are the negatives of the elements of set
$-{\mathcal{W}}$
denotes the set whose elements are the negatives of the elements of set
 ${\mathcal{W}}$
, for
${\mathcal{W}}$
, for
 ${\mathcal{W}}=\{\boldsymbol{k}_{1}+\boldsymbol{k}_{2},\boldsymbol{k}_{1}-\boldsymbol{k}_{2},\boldsymbol{k}_{1}+\boldsymbol{k}_{3},\boldsymbol{k}_{1}-\boldsymbol{k}_{3},\boldsymbol{k}_{2}+\boldsymbol{k}_{3},\boldsymbol{k}_{2}-\boldsymbol{k}_{3}\}$
; the most general solution can be then constructed as (4.19)with the constants
${\mathcal{W}}=\{\boldsymbol{k}_{1}+\boldsymbol{k}_{2},\boldsymbol{k}_{1}-\boldsymbol{k}_{2},\boldsymbol{k}_{1}+\boldsymbol{k}_{3},\boldsymbol{k}_{1}-\boldsymbol{k}_{3},\boldsymbol{k}_{2}+\boldsymbol{k}_{3},\boldsymbol{k}_{2}-\boldsymbol{k}_{3}\}$
; the most general solution can be then constructed as (4.19)with the constants $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{1}(\boldsymbol{x}) & = & \displaystyle \boldsymbol{A}\text{e}^{2\unicode[STIX]{x03C0}i[1,1,0]\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{B}\text{e}^{2\unicode[STIX]{x03C0}i[1,-1,0]\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{C}\text{e}^{2\unicode[STIX]{x03C0}i[1,0,1]\boldsymbol{\cdot }\boldsymbol{x}}\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{D}\text{e}^{2\unicode[STIX]{x03C0}i[1,0,-1]\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{E}\text{e}^{2\unicode[STIX]{x03C0}i[0,1,1]\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{F}\text{e}^{2\unicode[STIX]{x03C0}i[0,1,-1]\boldsymbol{\cdot }\boldsymbol{x}}+\text{c.c.,}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{1}(\boldsymbol{x}) & = & \displaystyle \boldsymbol{A}\text{e}^{2\unicode[STIX]{x03C0}i[1,1,0]\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{B}\text{e}^{2\unicode[STIX]{x03C0}i[1,-1,0]\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{C}\text{e}^{2\unicode[STIX]{x03C0}i[1,0,1]\boldsymbol{\cdot }\boldsymbol{x}}\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{D}\text{e}^{2\unicode[STIX]{x03C0}i[1,0,-1]\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{E}\text{e}^{2\unicode[STIX]{x03C0}i[0,1,1]\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{F}\text{e}^{2\unicode[STIX]{x03C0}i[0,1,-1]\boldsymbol{\cdot }\boldsymbol{x}}+\text{c.c.,}\end{eqnarray}$$
 $\boldsymbol{A},\boldsymbol{B},\ldots ,\boldsymbol{F}\in \mathbb{C}^{3}$
suitably chosen so that
$\boldsymbol{A},\boldsymbol{B},\ldots ,\boldsymbol{F}\in \mathbb{C}^{3}$
suitably chosen so that
 $\boldsymbol{A}\boldsymbol{\cdot }[1,1,0]=0$
,
$\boldsymbol{A}\boldsymbol{\cdot }[1,1,0]=0$
,
 $\boldsymbol{B}\boldsymbol{\cdot }[1,-1,0]=0,\ldots ,\boldsymbol{F}\boldsymbol{\cdot }[0,1,-1]=0$
, which ensures that incompressibility condition (4.7b
) is satisfied, and that
$\boldsymbol{B}\boldsymbol{\cdot }[1,-1,0]=0,\ldots ,\boldsymbol{F}\boldsymbol{\cdot }[0,1,-1]=0$
, which ensures that incompressibility condition (4.7b
) is satisfied, and that
 ${\mathcal{E}}(\boldsymbol{u}_{1})=1$
; in this case,
${\mathcal{E}}(\boldsymbol{u}_{1})=1$
; in this case,
 $|\boldsymbol{k}|^{2}=2$
,
$|\boldsymbol{k}|^{2}=2$
,
 $\forall \boldsymbol{k}\in {\mathcal{W}}_{2}$
, and the optimal asymptotic value of
$\forall \boldsymbol{k}\in {\mathcal{W}}_{2}$
, and the optimal asymptotic value of
 ${\mathcal{R}}$
is (4.20)
${\mathcal{R}}$
is (4.20) $$\begin{eqnarray}\displaystyle {\mathcal{R}}(\widetilde{\boldsymbol{u}})\approx -16\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D708}{\mathcal{E}}_{0}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{R}}(\widetilde{\boldsymbol{u}})\approx -16\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D708}{\mathcal{E}}_{0}, & & \displaystyle\end{eqnarray}$$
-
(iii)
 ${\mathcal{W}}_{3}={\mathcal{W}}\cup (-{\mathcal{W}})$
for
${\mathcal{W}}_{3}={\mathcal{W}}\cup (-{\mathcal{W}})$
for
 ${\mathcal{W}}=\{\boldsymbol{k}_{1}+\boldsymbol{k}_{2}+\boldsymbol{k}_{3},-\boldsymbol{k}_{1}+\boldsymbol{k}_{2}+\boldsymbol{k}_{3},\boldsymbol{k}_{1}-\boldsymbol{k}_{2}+\boldsymbol{k}_{3},\boldsymbol{k}_{1}+\boldsymbol{k}_{2}-\boldsymbol{k}_{3}\}$
; the most general solution can then be constructed as (4.21)with the constants
${\mathcal{W}}=\{\boldsymbol{k}_{1}+\boldsymbol{k}_{2}+\boldsymbol{k}_{3},-\boldsymbol{k}_{1}+\boldsymbol{k}_{2}+\boldsymbol{k}_{3},\boldsymbol{k}_{1}-\boldsymbol{k}_{2}+\boldsymbol{k}_{3},\boldsymbol{k}_{1}+\boldsymbol{k}_{2}-\boldsymbol{k}_{3}\}$
; the most general solution can then be constructed as (4.21)with the constants $$\begin{eqnarray}\displaystyle \boldsymbol{u}_{1}(\boldsymbol{x}) & = & \displaystyle \boldsymbol{A}\text{e}^{2\unicode[STIX]{x03C0}i[1,1,1]\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{B}\text{e}^{2\unicode[STIX]{x03C0}i[-1,1,1]\boldsymbol{\cdot }\boldsymbol{x}}\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{C}\text{e}^{2\unicode[STIX]{x03C0}i[1,-1,1]\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{D}\text{e}^{2\unicode[STIX]{x03C0}i[1,1,-1]\boldsymbol{\cdot }\boldsymbol{x}}+\text{c.c.,}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{1}(\boldsymbol{x}) & = & \displaystyle \boldsymbol{A}\text{e}^{2\unicode[STIX]{x03C0}i[1,1,1]\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{B}\text{e}^{2\unicode[STIX]{x03C0}i[-1,1,1]\boldsymbol{\cdot }\boldsymbol{x}}\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{C}\text{e}^{2\unicode[STIX]{x03C0}i[1,-1,1]\boldsymbol{\cdot }\boldsymbol{x}}+\boldsymbol{D}\text{e}^{2\unicode[STIX]{x03C0}i[1,1,-1]\boldsymbol{\cdot }\boldsymbol{x}}+\text{c.c.,}\end{eqnarray}$$
 $\boldsymbol{A},\boldsymbol{B},\boldsymbol{C},\boldsymbol{D}\in \mathbb{C}^{3}$
suitably chosen so that
$\boldsymbol{A},\boldsymbol{B},\boldsymbol{C},\boldsymbol{D}\in \mathbb{C}^{3}$
suitably chosen so that
 $\boldsymbol{A}\boldsymbol{\cdot }[1,1,1]=0$
,
$\boldsymbol{A}\boldsymbol{\cdot }[1,1,1]=0$
,
 $\boldsymbol{B}\boldsymbol{\cdot }[-1,1,1]=0$
,
$\boldsymbol{B}\boldsymbol{\cdot }[-1,1,1]=0$
,
 $\boldsymbol{C}\boldsymbol{\cdot }[1,-1,1]=0$
and
$\boldsymbol{C}\boldsymbol{\cdot }[1,-1,1]=0$
and
 $\boldsymbol{D}\boldsymbol{\cdot }[1,1,-1]=0$
, which ensures that incompressibility condition (4.7b
) is satisfied, and that
$\boldsymbol{D}\boldsymbol{\cdot }[1,1,-1]=0$
, which ensures that incompressibility condition (4.7b
) is satisfied, and that
 ${\mathcal{E}}(\boldsymbol{u}_{1})=1$
; in this case,
${\mathcal{E}}(\boldsymbol{u}_{1})=1$
; in this case,
 $|\boldsymbol{k}|^{2}=3$
,
$|\boldsymbol{k}|^{2}=3$
,
 $\forall \boldsymbol{k}\in {\mathcal{W}}_{3}$
, and the optimal asymptotic value of
$\forall \boldsymbol{k}\in {\mathcal{W}}_{3}$
, and the optimal asymptotic value of
 ${\mathcal{R}}$
is (4.22)
${\mathcal{R}}$
is (4.22) $$\begin{eqnarray}\displaystyle {\mathcal{R}}(\widetilde{\boldsymbol{u}})\approx -24\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D708}{\mathcal{E}}_{0}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{R}}(\widetilde{\boldsymbol{u}})\approx -24\unicode[STIX]{x03C0}^{2}\unicode[STIX]{x1D708}{\mathcal{E}}_{0}. & & \displaystyle\end{eqnarray}$$
The three constructions of the extremal field
![]() $\boldsymbol{u}_{1}$
given in (4.17), (4.19) and (4.21) are all defined up to arbitrary shifts in all three directions, reflections with respect to different planes and rotations by angles which are multiples of
$\boldsymbol{u}_{1}$
given in (4.17), (4.19) and (4.21) are all defined up to arbitrary shifts in all three directions, reflections with respect to different planes and rotations by angles which are multiples of
![]() $\unicode[STIX]{x03C0}/2$
about the different axes. As a result of this non-uniqueness, there is some freedom in choosing the constants
$\unicode[STIX]{x03C0}/2$
about the different axes. As a result of this non-uniqueness, there is some freedom in choosing the constants
![]() $\boldsymbol{A},\ldots ,\boldsymbol{F}$
. Given that the optimal asymptotic value of
$\boldsymbol{A},\ldots ,\boldsymbol{F}$
. Given that the optimal asymptotic value of
![]() ${\mathcal{R}}$
depends exclusively on the wavevector magnitude
${\mathcal{R}}$
depends exclusively on the wavevector magnitude
![]() $|\boldsymbol{k}|$
, cf. (4.16), any combination of constants
$|\boldsymbol{k}|$
, cf. (4.16), any combination of constants
![]() $\boldsymbol{A},\ldots ,\boldsymbol{F}$
will produce the same optimal rate of growth of enstrophy. Thus, to fix attention, in our analysis we will set
$\boldsymbol{A},\ldots ,\boldsymbol{F}$
will produce the same optimal rate of growth of enstrophy. Thus, to fix attention, in our analysis we will set
![]() $\boldsymbol{A}=\boldsymbol{B}=\boldsymbol{C}$
in case (i),
$\boldsymbol{A}=\boldsymbol{B}=\boldsymbol{C}$
in case (i),
![]() $\boldsymbol{A}=\boldsymbol{B}=\cdots =\boldsymbol{F}$
in case (ii) and
$\boldsymbol{A}=\boldsymbol{B}=\cdots =\boldsymbol{F}$
in case (ii) and
![]() $\boldsymbol{A}=\cdots =\boldsymbol{D}$
in case (iii). With these choices, the contribution from each component of the field
$\boldsymbol{A}=\cdots =\boldsymbol{D}$
in case (iii). With these choices, the contribution from each component of the field
![]() $\boldsymbol{u}_{1}$
to the total enstrophy is the same. The maximum (i.e. least negative) value of
$\boldsymbol{u}_{1}$
to the total enstrophy is the same. The maximum (i.e. least negative) value of
![]() ${\mathcal{R}}$
can be thus obtained by choosing the smallest possible
${\mathcal{R}}$
can be thus obtained by choosing the smallest possible
![]() $|\boldsymbol{k}|^{2}$
. This maximum is achieved in case (i) with the wavevectors
$|\boldsymbol{k}|^{2}$
. This maximum is achieved in case (i) with the wavevectors
![]() $\boldsymbol{k}_{1}=[1,0,0]$
,
$\boldsymbol{k}_{1}=[1,0,0]$
,
![]() $\boldsymbol{k}_{2}=[0,1,0]$
,
$\boldsymbol{k}_{2}=[0,1,0]$
,
![]() $\boldsymbol{k}_{3}=[0,0,1]$
, and
$\boldsymbol{k}_{3}=[0,0,1]$
, and
![]() $-\boldsymbol{k}_{1}$
,
$-\boldsymbol{k}_{1}$
,
![]() $-\boldsymbol{k}_{2}$
and
$-\boldsymbol{k}_{2}$
and
![]() $-\boldsymbol{k}_{3}$
, for which
$-\boldsymbol{k}_{3}$
, for which
![]() $|\boldsymbol{k}|^{2}=1$
. Because of this maximization property, this is the field we will focus on in our analysis in §§ 5 and 6.
$|\boldsymbol{k}|^{2}=1$
. Because of this maximization property, this is the field we will focus on in our analysis in §§ 5 and 6.
The three fields constructed in (4.17), (4.19) and (4.21) are visualized in figure 1. This analysis is performed using the level sets
![]() $\unicode[STIX]{x1D6E4}_{s}(F)\subset \unicode[STIX]{x1D6FA}$
defined as
$\unicode[STIX]{x1D6E4}_{s}(F)\subset \unicode[STIX]{x1D6FA}$
defined as
for a suitable function
![]() $F:\unicode[STIX]{x1D6FA}\rightarrow \mathbb{R}$
. In figure 1(a–c) we choose
$F:\unicode[STIX]{x1D6FA}\rightarrow \mathbb{R}$
. In figure 1(a–c) we choose
![]() $F(\boldsymbol{x})=|\unicode[STIX]{x1D735}\times \boldsymbol{u}_{1}|(\boldsymbol{x})$
with
$F(\boldsymbol{x})=|\unicode[STIX]{x1D735}\times \boldsymbol{u}_{1}|(\boldsymbol{x})$
with
![]() $s=0.95\Vert \unicode[STIX]{x1D735}\times \boldsymbol{u}_{1}\Vert _{L_{\infty }}$
. To complement this information, in figure 1(d–f) we also plot the isosurfaces and cross-sectional distributions of the
$s=0.95\Vert \unicode[STIX]{x1D735}\times \boldsymbol{u}_{1}\Vert _{L_{\infty }}$
. To complement this information, in figure 1(d–f) we also plot the isosurfaces and cross-sectional distributions of the
![]() $x_{1}$
component of the field
$x_{1}$
component of the field
![]() $\boldsymbol{u}_{1}$
.
$\boldsymbol{u}_{1}$
.
The fields shown in figure 1 reveal interesting patterns involving well-defined ‘vortex cells’. More specifically, we see that in case (i), given by (4.17) and shown in figure 1(a,d), the vortex cells are staggered with respect to the orientation of the cubic domain
![]() $\unicode[STIX]{x1D6FA}$
in all three planes, whereas in case (iii), given by (4.21) and shown in figure 1(c,f), the vortex cells are aligned with the domain
$\unicode[STIX]{x1D6FA}$
in all three planes, whereas in case (iii), given by (4.21) and shown in figure 1(c,f), the vortex cells are aligned with the domain
![]() $\unicode[STIX]{x1D6FA}$
in all three planes. On the other hand, in case (ii), given by (4.19) and shown in figure 1(b,e), the vortex cells are staggered in one plane and aligned in another with the arrangement in the third plane resulting from the arrangement in the first two. These geometric properties are also reflected in the
$\unicode[STIX]{x1D6FA}$
in all three planes. On the other hand, in case (ii), given by (4.19) and shown in figure 1(b,e), the vortex cells are staggered in one plane and aligned in another with the arrangement in the third plane resulting from the arrangement in the first two. These geometric properties are also reflected in the
![]() $x_{1}$
-component of the field
$x_{1}$
-component of the field
![]() $\boldsymbol{u}_{1}$
which is independent of
$\boldsymbol{u}_{1}$
which is independent of
![]() $x_{1}$
in cases (i) and (ii), but exhibits, respectively, a staggered and aligned arrangement of the cells in the
$x_{1}$
in cases (i) and (ii), but exhibits, respectively, a staggered and aligned arrangement of the cells in the
![]() $y$
–
$y$
–
![]() $z$
plane in these two cases. In case (iii) the cells exhibit an aligned arrangement in all three planes. The geometric properties of the extreme vortex states obtained in the limit
$z$
plane in these two cases. In case (iii) the cells exhibit an aligned arrangement in all three planes. The geometric properties of the extreme vortex states obtained in the limit
![]() ${\mathcal{E}}_{0}\rightarrow 0$
are summarized in table 2. We remark that an analogous structure of the optimal fields, featuring aligned and staggered arrangements of vortex cells in the limiting case, was also discovered by Ayala & Protas (Reference Ayala and Protas2014a
) in their study of the maximum palinstrophy growth in two dimensions. While due to a smaller spatial dimension only two optimal solutions were found in that study, the one characterized by the staggered arrangement also leads to a larger (less negative) rate of palinstrophy production.
${\mathcal{E}}_{0}\rightarrow 0$
are summarized in table 2. We remark that an analogous structure of the optimal fields, featuring aligned and staggered arrangements of vortex cells in the limiting case, was also discovered by Ayala & Protas (Reference Ayala and Protas2014a
) in their study of the maximum palinstrophy growth in two dimensions. While due to a smaller spatial dimension only two optimal solutions were found in that study, the one characterized by the staggered arrangement also leads to a larger (less negative) rate of palinstrophy production.

Figure 1. Extreme vortex states obtained as solutions of the maximization of Problem 3.1 in the limit
![]() ${\mathcal{E}}_{0}\rightarrow 0$
for different choices of set
${\mathcal{E}}_{0}\rightarrow 0$
for different choices of set
![]() ${\mathcal{W}}_{k}$
, as defined in (4.15). Panels (a–c) represent the isosurfaces defined by the the relation
${\mathcal{W}}_{k}$
, as defined in (4.15). Panels (a–c) represent the isosurfaces defined by the the relation
![]() $|\unicode[STIX]{x1D735}\times \boldsymbol{u}_{1}|(\boldsymbol{x})=0.95\Vert \unicode[STIX]{x1D735}\times \boldsymbol{u}_{1}\Vert _{L_{\infty }}$
, whereas panels (d–f) depict the isosurfaces and cross-sectional distributions in the
$|\unicode[STIX]{x1D735}\times \boldsymbol{u}_{1}|(\boldsymbol{x})=0.95\Vert \unicode[STIX]{x1D735}\times \boldsymbol{u}_{1}\Vert _{L_{\infty }}$
, whereas panels (d–f) depict the isosurfaces and cross-sectional distributions in the
![]() $y$
–
$y$
–
![]() $z$
plane of the
$z$
plane of the
![]() $x_{1}$
component of the field
$x_{1}$
component of the field
![]() $\boldsymbol{u}_{1}$
. Case (i) cf. (4.17), is presented in (a,d), case (ii) cf. (4.19), in (b,e) and case (iii) cf. (4.21), in (c,f) (see also table 2).
$\boldsymbol{u}_{1}$
. Case (i) cf. (4.17), is presented in (a,d), case (ii) cf. (4.19), in (b,e) and case (iii) cf. (4.21), in (c,f) (see also table 2).
Table 2. Summary of the properties of extreme vortex states
![]() $\boldsymbol{u}_{1}$
obtained as solutions of optimization Problem 3.1 in the limit
$\boldsymbol{u}_{1}$
obtained as solutions of optimization Problem 3.1 in the limit
![]() ${\mathcal{E}}_{0}\rightarrow 0$
.
${\mathcal{E}}_{0}\rightarrow 0$
.

It is also worth mentioning that the initial data for two well-known flows, namely, the Arnold–Beltrami–Childress (ABC) flow (Majda & Bertozzi Reference Majda and Bertozzi2002) and the Taylor–Green flow (Taylor & Green Reference Taylor and Green1937), are in fact particular instances of the optimal field
![]() $\boldsymbol{u}_{1}$
corresponding to, respectively, cases (i) and (iii). Following the notation of Dombre et al. (Reference Dombre, Frisch, Greene, Hénon, Mehr and Soward1986), general ABC flows are characterized by the following velocity field
$\boldsymbol{u}_{1}$
corresponding to, respectively, cases (i) and (iii). Following the notation of Dombre et al. (Reference Dombre, Frisch, Greene, Hénon, Mehr and Soward1986), general ABC flows are characterized by the following velocity field
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}u_{1}(x_{1},x_{2},x_{3})\ & =\ & A^{\prime }\sin (2\unicode[STIX]{x03C0}x_{3})+C^{\prime }\cos (2\unicode[STIX]{x03C0}x_{2})\\ u_{2}(x_{1},x_{2},x_{3})\ & =\ & B^{\prime }\sin (2\unicode[STIX]{x03C0}x_{1})+A^{\prime }\cos (2\unicode[STIX]{x03C0}x_{3})\\ u_{3}(x_{1},x_{2},x_{3})\ & =\ & C^{\prime }\sin (2\unicode[STIX]{x03C0}x_{2})+B^{\prime }\cos (2\unicode[STIX]{x03C0}x_{1}),\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}u_{1}(x_{1},x_{2},x_{3})\ & =\ & A^{\prime }\sin (2\unicode[STIX]{x03C0}x_{3})+C^{\prime }\cos (2\unicode[STIX]{x03C0}x_{2})\\ u_{2}(x_{1},x_{2},x_{3})\ & =\ & B^{\prime }\sin (2\unicode[STIX]{x03C0}x_{1})+A^{\prime }\cos (2\unicode[STIX]{x03C0}x_{3})\\ u_{3}(x_{1},x_{2},x_{3})\ & =\ & C^{\prime }\sin (2\unicode[STIX]{x03C0}x_{2})+B^{\prime }\cos (2\unicode[STIX]{x03C0}x_{1}),\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
![]() $A^{\prime }$
,
$A^{\prime }$
,
![]() $B^{\prime }$
and
$B^{\prime }$
and
![]() $C^{\prime }$
are real constants. The vector field in (4.24) can be obtained from (4.17) by choosing
$C^{\prime }$
are real constants. The vector field in (4.24) can be obtained from (4.17) by choosing
![]() $\boldsymbol{A}=(B^{\prime }/2)[0,-i,1]$
,
$\boldsymbol{A}=(B^{\prime }/2)[0,-i,1]$
,
![]() $\boldsymbol{B}=(C^{\prime }/2)[1,0,-i]$
and
$\boldsymbol{B}=(C^{\prime }/2)[1,0,-i]$
and
![]() $\boldsymbol{C}=(A^{\prime }/2)[-i,1,0]$
. By analogy, we will refer to the state described by (4.19) as the ‘aligned ABC flow’. Likewise, the well-known Taylor–Green vortex can be obtained as a particular instance of the field
$\boldsymbol{C}=(A^{\prime }/2)[-i,1,0]$
. By analogy, we will refer to the state described by (4.19) as the ‘aligned ABC flow’. Likewise, the well-known Taylor–Green vortex can be obtained as a particular instance of the field
![]() $\boldsymbol{u}_{1}$
from (4.21) again using a suitable choice of the constants
$\boldsymbol{u}_{1}$
from (4.21) again using a suitable choice of the constants
![]() $\boldsymbol{A},\boldsymbol{B},\boldsymbol{C},\boldsymbol{D}$
. Traditionally, the velocity field
$\boldsymbol{A},\boldsymbol{B},\boldsymbol{C},\boldsymbol{D}$
. Traditionally, the velocity field
![]() $\boldsymbol{u}=[u_{1},u_{2},u_{3}]$
characterizing the Taylor–Green vortex is defined as (Brachet et al.
Reference Brachet, Meiron, Orszag, Nickel, Morf and Frisch1983)
$\boldsymbol{u}=[u_{1},u_{2},u_{3}]$
characterizing the Taylor–Green vortex is defined as (Brachet et al.
Reference Brachet, Meiron, Orszag, Nickel, Morf and Frisch1983)
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}u_{1}(x_{1},x_{2},x_{3})\ & =\ & \unicode[STIX]{x1D6FE}_{1}\sin (2\unicode[STIX]{x03C0}x_{1})\cos (2\unicode[STIX]{x03C0}x_{2})\cos (2\unicode[STIX]{x03C0}x_{3})\\ u_{2}(x_{1},x_{2},x_{3})\ & =\ & \unicode[STIX]{x1D6FE}_{2}\cos (2\unicode[STIX]{x03C0}x_{1})\sin (2\unicode[STIX]{x03C0}x_{2})\cos (2\unicode[STIX]{x03C0}x_{3})\\ u_{3}(x_{1},x_{2},x_{3})\ & =\ & \unicode[STIX]{x1D6FE}_{3}\cos (2\unicode[STIX]{x03C0}x_{1})\cos (2\unicode[STIX]{x03C0}x_{2})\sin (2\unicode[STIX]{x03C0}x_{3})\\ 0\ & =\ & \unicode[STIX]{x1D6FE}_{1}+\unicode[STIX]{x1D6FE}_{2}+\unicode[STIX]{x1D6FE}_{3},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}u_{1}(x_{1},x_{2},x_{3})\ & =\ & \unicode[STIX]{x1D6FE}_{1}\sin (2\unicode[STIX]{x03C0}x_{1})\cos (2\unicode[STIX]{x03C0}x_{2})\cos (2\unicode[STIX]{x03C0}x_{3})\\ u_{2}(x_{1},x_{2},x_{3})\ & =\ & \unicode[STIX]{x1D6FE}_{2}\cos (2\unicode[STIX]{x03C0}x_{1})\sin (2\unicode[STIX]{x03C0}x_{2})\cos (2\unicode[STIX]{x03C0}x_{3})\\ u_{3}(x_{1},x_{2},x_{3})\ & =\ & \unicode[STIX]{x1D6FE}_{3}\cos (2\unicode[STIX]{x03C0}x_{1})\cos (2\unicode[STIX]{x03C0}x_{2})\sin (2\unicode[STIX]{x03C0}x_{3})\\ 0\ & =\ & \unicode[STIX]{x1D6FE}_{1}+\unicode[STIX]{x1D6FE}_{2}+\unicode[STIX]{x1D6FE}_{3},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
for
![]() $\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D6FE}_{3}\in \mathbb{R}$
. For given values of
$\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D6FE}_{3}\in \mathbb{R}$
. For given values of
![]() $\unicode[STIX]{x1D6FE}_{1}$
,
$\unicode[STIX]{x1D6FE}_{1}$
,
![]() $\unicode[STIX]{x1D6FE}_{2}$
and
$\unicode[STIX]{x1D6FE}_{2}$
and
![]() $\unicode[STIX]{x1D6FE}_{3}$
in (4.25), the corresponding constants
$\unicode[STIX]{x1D6FE}_{3}$
in (4.25), the corresponding constants
![]() $\boldsymbol{A},\boldsymbol{B},\boldsymbol{C},\boldsymbol{D}$
in (4.21) can be found by separating them into their real and imaginary parts denoted, respectively,
$\boldsymbol{A},\boldsymbol{B},\boldsymbol{C},\boldsymbol{D}$
in (4.21) can be found by separating them into their real and imaginary parts denoted, respectively,
![]() $\boldsymbol{A}_{Re},\boldsymbol{B}_{Re},\boldsymbol{C}_{Re},\boldsymbol{D}_{Re}$
and
$\boldsymbol{A}_{Re},\boldsymbol{B}_{Re},\boldsymbol{C}_{Re},\boldsymbol{D}_{Re}$
and
![]() $\boldsymbol{A}_{Im},\boldsymbol{B}_{Im},\boldsymbol{C}_{Im},\boldsymbol{D}_{Im}$
. Then, after choosing
$\boldsymbol{A}_{Im},\boldsymbol{B}_{Im},\boldsymbol{C}_{Im},\boldsymbol{D}_{Im}$
. Then, after choosing
the imaginary parts can be determined by solving the following system of linear equations
 $$\begin{eqnarray}\displaystyle 2\left[\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3}\\ -\unicode[STIX]{x1D644}_{3} & \unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3}\\ -\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3} & \unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3}\\ -\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3} & \unicode[STIX]{x1D644}_{3}\end{array}\right]\left[\begin{array}{@{}c@{}}\boldsymbol{A}_{Im}\\ \boldsymbol{B}_{Im}\\ \boldsymbol{C}_{Im}\\ \boldsymbol{D}_{Im}\end{array}\right]=\left[\begin{array}{@{}c@{}}\mathbf{0}\\ \unicode[STIX]{x1D6FE}_{1}\boldsymbol{e}_{1}\\ \unicode[STIX]{x1D6FE}_{2}\boldsymbol{e}_{2}\\ \unicode[STIX]{x1D6FE}_{3}\boldsymbol{e}_{3}\end{array}\right], & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2\left[\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3}\\ -\unicode[STIX]{x1D644}_{3} & \unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3}\\ -\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3} & \unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3}\\ -\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3} & -\unicode[STIX]{x1D644}_{3} & \unicode[STIX]{x1D644}_{3}\end{array}\right]\left[\begin{array}{@{}c@{}}\boldsymbol{A}_{Im}\\ \boldsymbol{B}_{Im}\\ \boldsymbol{C}_{Im}\\ \boldsymbol{D}_{Im}\end{array}\right]=\left[\begin{array}{@{}c@{}}\mathbf{0}\\ \unicode[STIX]{x1D6FE}_{1}\boldsymbol{e}_{1}\\ \unicode[STIX]{x1D6FE}_{2}\boldsymbol{e}_{2}\\ \unicode[STIX]{x1D6FE}_{3}\boldsymbol{e}_{3}\end{array}\right], & & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D644}_{3}$
is the
$\unicode[STIX]{x1D644}_{3}$
is the
![]() $3\times 3$
identity matrix. The values of
$3\times 3$
identity matrix. The values of
![]() $\boldsymbol{A}_{Im},\ldots ,\boldsymbol{D}_{Im}$
are thus given by
$\boldsymbol{A}_{Im},\ldots ,\boldsymbol{D}_{Im}$
are thus given by
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\displaystyle \boldsymbol{A}_{Im}=-\frac{1}{8}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FE}_{1}\\ \unicode[STIX]{x1D6FE}_{2}\\ \unicode[STIX]{x1D6FE}_{3}\end{array}\right],\quad \boldsymbol{B}_{Im}=-\frac{1}{8}\left[\begin{array}{@{}c@{}}-\unicode[STIX]{x1D6FE}_{1}\\ \unicode[STIX]{x1D6FE}_{2}\\ \unicode[STIX]{x1D6FE}_{3}\end{array}\right],\\ \displaystyle \boldsymbol{C}_{Im}=-\frac{1}{8}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FE}_{1}\\ -\unicode[STIX]{x1D6FE}_{2}\\ \unicode[STIX]{x1D6FE}_{3}\end{array}\right],\quad \boldsymbol{D}_{Im}=-\frac{1}{8}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FE}_{1}\\ \unicode[STIX]{x1D6FE}_{2}\\ -\unicode[STIX]{x1D6FE}_{3}\end{array}\right].\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\displaystyle \boldsymbol{A}_{Im}=-\frac{1}{8}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FE}_{1}\\ \unicode[STIX]{x1D6FE}_{2}\\ \unicode[STIX]{x1D6FE}_{3}\end{array}\right],\quad \boldsymbol{B}_{Im}=-\frac{1}{8}\left[\begin{array}{@{}c@{}}-\unicode[STIX]{x1D6FE}_{1}\\ \unicode[STIX]{x1D6FE}_{2}\\ \unicode[STIX]{x1D6FE}_{3}\end{array}\right],\\ \displaystyle \boldsymbol{C}_{Im}=-\frac{1}{8}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FE}_{1}\\ -\unicode[STIX]{x1D6FE}_{2}\\ \unicode[STIX]{x1D6FE}_{3}\end{array}\right],\quad \boldsymbol{D}_{Im}=-\frac{1}{8}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FE}_{1}\\ \unicode[STIX]{x1D6FE}_{2}\\ -\unicode[STIX]{x1D6FE}_{3}\end{array}\right].\end{array} & & \displaystyle\end{eqnarray}$$
A typical choice of the parameters used in the numerical studies performed by Brachet et al. (Reference Brachet, Meiron, Orszag, Nickel, Morf and Frisch1983) and Brachet (Reference Brachet1991) is
![]() $\unicode[STIX]{x1D6FE}_{1}=-\unicode[STIX]{x1D6FE}_{2}=1$
and
$\unicode[STIX]{x1D6FE}_{1}=-\unicode[STIX]{x1D6FE}_{2}=1$
and
![]() $\unicode[STIX]{x1D6FE}_{3}=0$
.
$\unicode[STIX]{x1D6FE}_{3}=0$
.
We remark that the Taylor–Green vortex has been employed as the initial data in a number of studies aimed at triggering singular behaviour in both the Euler and Navier–Stokes systems (Taylor & Green Reference Taylor and Green1937; Brachet et al.
Reference Brachet, Meiron, Orszag, Nickel, Morf and Frisch1983; Brachet Reference Brachet1991; Bustamante & Brachet Reference Bustamante and Brachet2012). It is therefore interesting to note that it arises in the limit
![]() ${\mathcal{E}}_{0}\rightarrow 0$
as one of the extreme vortex states in the variational formulation considered in the present study. It should be emphasized, however, that out of the three optimal states identified above (see table 2), the Taylor–Green vortex is characterized by the smallest (i.e. the most negative) instantaneous rate of enstrophy production
${\mathcal{E}}_{0}\rightarrow 0$
as one of the extreme vortex states in the variational formulation considered in the present study. It should be emphasized, however, that out of the three optimal states identified above (see table 2), the Taylor–Green vortex is characterized by the smallest (i.e. the most negative) instantaneous rate of enstrophy production
![]() $\text{d}{\mathcal{E}}/\text{d}t$
. On the other hand, we are not aware of any prior studies involving ABC flows in the context of extreme behaviour and potential singularity formation. The time evolution corresponding to these states and some other initial data will be analysed in detail in § 6.
$\text{d}{\mathcal{E}}/\text{d}t$
. On the other hand, we are not aware of any prior studies involving ABC flows in the context of extreme behaviour and potential singularity formation. The time evolution corresponding to these states and some other initial data will be analysed in detail in § 6.
5 Extreme vortex states with finite
 ${\mathcal{E}}_{0}$
${\mathcal{E}}_{0}$
In this section we analyse the optimal vortex states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
obtained for finite values of the enstrophy in which we extend the results obtained in the seminal study by Lu & Doering (Reference Lu and Doering2008). As was also the case in the analogous study in two dimensions (Ayala & Protas Reference Ayala and Protas2014a
), there is a distinct branch of extreme states
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
obtained for finite values of the enstrophy in which we extend the results obtained in the seminal study by Lu & Doering (Reference Lu and Doering2008). As was also the case in the analogous study in two dimensions (Ayala & Protas Reference Ayala and Protas2014a
), there is a distinct branch of extreme states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
parameterized by the enstrophy
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
parameterized by the enstrophy
![]() ${\mathcal{E}}_{0}$
and corresponding to each of the three limiting states discussed in § 4 (cf. figure 1 and table 2). Each of these branches is computed using the continuation approach outlined in algorithm 1. As a key element of the gradient-based maximization technique (3.8), the gradient expressions (3.11)–(3.12) are approximated pseudo-spectrally using standard dealiasing of the nonlinear terms and with resolutions varying from
${\mathcal{E}}_{0}$
and corresponding to each of the three limiting states discussed in § 4 (cf. figure 1 and table 2). Each of these branches is computed using the continuation approach outlined in algorithm 1. As a key element of the gradient-based maximization technique (3.8), the gradient expressions (3.11)–(3.12) are approximated pseudo-spectrally using standard dealiasing of the nonlinear terms and with resolutions varying from
![]() $128^{3}$
in the low-enstrophy cases to
$128^{3}$
in the low-enstrophy cases to
![]() $512^{3}$
in the high-enstrophy cases, which necessitated a massively parallel implementation using the Message Passing Interface (MPI). As regards the computation of the Sobolev
$512^{3}$
in the high-enstrophy cases, which necessitated a massively parallel implementation using the Message Passing Interface (MPI). As regards the computation of the Sobolev
![]() $H^{2}$
gradients, cf. (3.12), we set
$H^{2}$
gradients, cf. (3.12), we set
![]() $\ell _{1}=0$
, whereas the second parameter
$\ell _{1}=0$
, whereas the second parameter
![]() $\ell _{2}$
was adjusted during the optimization iterations and was chosen so that
$\ell _{2}$
was adjusted during the optimization iterations and was chosen so that
![]() $\ell _{2}\in [\ell _{min},\ell _{max}]$
, where
$\ell _{2}\in [\ell _{min},\ell _{max}]$
, where
![]() $\ell _{min}$
is the length scale associated with the spatial resolution
$\ell _{min}$
is the length scale associated with the spatial resolution
![]() $N$
used for computations and
$N$
used for computations and
![]() $\ell _{max}$
is the characteristic length scale of the domain
$\ell _{max}$
is the characteristic length scale of the domain
![]() $\unicode[STIX]{x1D6FA}$
, that is,
$\unicode[STIX]{x1D6FA}$
, that is,
![]() $\ell _{min}\sim O(1/N)$
and
$\ell _{min}\sim O(1/N)$
and
![]() $\ell _{max}\sim O(1)$
. We remark that, given the equivalence of the inner products (3.1) corresponding to different values of
$\ell _{max}\sim O(1)$
. We remark that, given the equivalence of the inner products (3.1) corresponding to different values of
![]() $\ell _{1}$
and
$\ell _{1}$
and
![]() $\ell _{2}$
(as long as
$\ell _{2}$
(as long as
![]() $\ell _{2}\neq 0$
), these choices do not affect the maximizers found, but only how rapidly they are approached by iterations (3.8). For further details concerning the computational approach we refer the reader to the dissertation by Ayala (Reference Ayala2014). As was the case in the analogous 2-D problem studied by Ayala & Protas (Reference Ayala and Protas2014a
), the largest instantaneous growth of enstrophy is produced by the states with vortex cells staggered in all planes, cf. case (i) in table 2. Therefore, in our analysis we will focus exclusively on this branch of extreme vortex states which has been computed for
$\ell _{2}\neq 0$
), these choices do not affect the maximizers found, but only how rapidly they are approached by iterations (3.8). For further details concerning the computational approach we refer the reader to the dissertation by Ayala (Reference Ayala2014). As was the case in the analogous 2-D problem studied by Ayala & Protas (Reference Ayala and Protas2014a
), the largest instantaneous growth of enstrophy is produced by the states with vortex cells staggered in all planes, cf. case (i) in table 2. Therefore, in our analysis we will focus exclusively on this branch of extreme vortex states which has been computed for
![]() ${\mathcal{E}}_{0}\in [10^{-3},2\times 10^{2}]$
.
${\mathcal{E}}_{0}\in [10^{-3},2\times 10^{2}]$
.

Figure 2. (a) Maximum rate of growth of enstrophy
![]() ${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
and (b) energy of optimal states
${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
and (b) energy of optimal states
![]() ${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
as functions of
${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
as functions of
![]() ${\mathcal{E}}_{0}$
for small values of enstrophy; the dashed lines represent the asymptotic relation (4.18) (a) and the Poincaré limit
${\mathcal{E}}_{0}$
for small values of enstrophy; the dashed lines represent the asymptotic relation (4.18) (a) and the Poincaré limit
![]() ${\mathcal{K}}_{0}={\mathcal{E}}_{0}/(2\unicode[STIX]{x03C0})^{2}$
(b). (c–h) Extreme vortex states
${\mathcal{K}}_{0}={\mathcal{E}}_{0}/(2\unicode[STIX]{x03C0})^{2}$
(b). (c–h) Extreme vortex states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
obtained for the three values of enstrophy
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
obtained for the three values of enstrophy
![]() ${\mathcal{E}}_{0}$
indicated with solid symbols in (a) and (b): panels (c–e) show the isosurfaces corresponding to
${\mathcal{E}}_{0}$
indicated with solid symbols in (a) and (b): panels (c–e) show the isosurfaces corresponding to
![]() $Q(\boldsymbol{x})=1/2\Vert Q\Vert _{L_{\infty }}$
with
$Q(\boldsymbol{x})=1/2\Vert Q\Vert _{L_{\infty }}$
with
![]() $Q$
defined in (5.1), whereas panels (f–h) show the component of vorticity normal to the plane defined by
$Q$
defined in (5.1), whereas panels (f–h) show the component of vorticity normal to the plane defined by
![]() $\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{x}-\boldsymbol{x}_{0})=0$
,
$\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{x}-\boldsymbol{x}_{0})=0$
,
![]() $\boldsymbol{n}=[1,0,0]$
and
$\boldsymbol{n}=[1,0,0]$
and
![]() $\boldsymbol{x}_{0}=[1/2,1/2,1/2]$
.
$\boldsymbol{x}_{0}=[1/2,1/2,1/2]$
.

Figure 3. (a) Maximum rate of growth of enstrophy
![]() ${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
(solid line) and its cubic part
${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
(solid line) and its cubic part
![]() ${\mathcal{R}}_{cub}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
, cf. (5.3b
), (dotted line) and (b) energy of optimal states
${\mathcal{R}}_{cub}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
, cf. (5.3b
), (dotted line) and (b) energy of optimal states
![]() ${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
as functions of
${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
as functions of
![]() ${\mathcal{E}}_{0}$
for large values of enstrophy. (c–h) Extreme vortex states
${\mathcal{E}}_{0}$
for large values of enstrophy. (c–h) Extreme vortex states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
obtained for the three values of enstrophy
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
obtained for the three values of enstrophy
![]() ${\mathcal{E}}_{0}$
indicated with solid symbols in (a) and (b): panels (c–e) show the isosurfaces corresponding to
${\mathcal{E}}_{0}$
indicated with solid symbols in (a) and (b): panels (c–e) show the isosurfaces corresponding to
![]() $Q(\boldsymbol{x})=1/2\Vert Q\Vert _{L_{\infty }}$
with
$Q(\boldsymbol{x})=1/2\Vert Q\Vert _{L_{\infty }}$
with
![]() $Q$
defined in (5.1), whereas panels (f–h) show the component of vorticity normal to the plane defined by
$Q$
defined in (5.1), whereas panels (f–h) show the component of vorticity normal to the plane defined by
![]() $\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{x}-\boldsymbol{x}_{0})=0$
,
$\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{x}-\boldsymbol{x}_{0})=0$
,
![]() $\boldsymbol{n}=[1,0,-1]$
and
$\boldsymbol{n}=[1,0,-1]$
and
![]() $\boldsymbol{x}_{0}=[1/2,1/2,1/2]$
.
$\boldsymbol{x}_{0}=[1/2,1/2,1/2]$
.
The optimal instantaneous rate of growth of enstrophy
![]() ${\mathcal{R}}_{{\mathcal{E}}_{0}}={\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
and the energy of the optimal states
${\mathcal{R}}_{{\mathcal{E}}_{0}}={\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
and the energy of the optimal states
![]() ${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
are shown as functions of
${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
are shown as functions of
![]() ${\mathcal{E}}_{0}$
for small
${\mathcal{E}}_{0}$
for small
![]() ${\mathcal{E}}_{0}$
in figure 2(a,b), respectively. As indicated by the asymptotic form of
${\mathcal{E}}_{0}$
in figure 2(a,b), respectively. As indicated by the asymptotic form of
![]() ${\mathcal{R}}$
in (4.18) and the Poincaré limit
${\mathcal{R}}$
in (4.18) and the Poincaré limit
![]() ${\mathcal{K}}_{0}={\mathcal{E}}_{0}/(2\unicode[STIX]{x03C0})^{2}$
, both of which are marked in these figures, the behaviour of
${\mathcal{K}}_{0}={\mathcal{E}}_{0}/(2\unicode[STIX]{x03C0})^{2}$
, both of which are marked in these figures, the behaviour of
![]() ${\mathcal{R}}_{{\mathcal{E}}_{0}}$
and
${\mathcal{R}}_{{\mathcal{E}}_{0}}$
and
![]() ${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
as
${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
as
![]() ${\mathcal{E}}_{0}\rightarrow 0$
is correctly captured by the numerically computed optimal states. In particular, we note that
${\mathcal{E}}_{0}\rightarrow 0$
is correctly captured by the numerically computed optimal states. In particular, we note that
![]() ${\mathcal{R}}_{{\mathcal{E}}_{0}}$
is negative for
${\mathcal{R}}_{{\mathcal{E}}_{0}}$
is negative for
![]() $0\leqslant {\mathcal{E}}_{0}\lessapprox 7$
and exhibits the same trend as predicted in (4.9) for
$0\leqslant {\mathcal{E}}_{0}\lessapprox 7$
and exhibits the same trend as predicted in (4.9) for
![]() ${\mathcal{E}}_{0}\rightarrow 0$
. For larger values of
${\mathcal{E}}_{0}\rightarrow 0$
. For larger values of
![]() ${\mathcal{E}}_{0}$
the rate of growth of enstrophy becomes positive. Likewise, the asymptotic behaviour of the energy of the optimal fields does not come as a surprise since, as discussed in § 4, in the limit
${\mathcal{E}}_{0}$
the rate of growth of enstrophy becomes positive. Likewise, the asymptotic behaviour of the energy of the optimal fields does not come as a surprise since, as discussed in § 4, in the limit
![]() ${\mathcal{E}}_{0}\rightarrow 0$
the maximizers of
${\mathcal{E}}_{0}\rightarrow 0$
the maximizers of
![]() ${\mathcal{R}}$
are eigenfunctions of the Laplacian, which also happen to saturate Poincaré’s inequality.
${\mathcal{R}}$
are eigenfunctions of the Laplacian, which also happen to saturate Poincaré’s inequality.
The structure of the optimal vortex states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
is analysed next. They are visualized using (4.23) in which the vortex cores are identified as regions
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
is analysed next. They are visualized using (4.23) in which the vortex cores are identified as regions
![]() $\unicode[STIX]{x1D6F4}:=\{\unicode[STIX]{x1D6E4}_{s}(Q):s\geqslant 0\}$
for
$\unicode[STIX]{x1D6F4}:=\{\unicode[STIX]{x1D6E4}_{s}(Q):s\geqslant 0\}$
for
![]() $Q$
defined as (Davidson Reference Davidson2004)
$Q$
defined as (Davidson Reference Davidson2004)
where
![]() $\unicode[STIX]{x1D64E}$
and
$\unicode[STIX]{x1D64E}$
and
![]() $\unicode[STIX]{x1D734}$
are the symmetric and antisymmetric parts of the velocity gradient tensor
$\unicode[STIX]{x1D734}$
are the symmetric and antisymmetric parts of the velocity gradient tensor
![]() $\unicode[STIX]{x1D735}\boldsymbol{u}$
, that is,
$\unicode[STIX]{x1D735}\boldsymbol{u}$
, that is,
![]() $[\boldsymbol{S}]_{ij}=1/2(\unicode[STIX]{x2202}_{j}u_{i}+\unicode[STIX]{x2202}_{i}u_{j})$
and
$[\boldsymbol{S}]_{ij}=1/2(\unicode[STIX]{x2202}_{j}u_{i}+\unicode[STIX]{x2202}_{i}u_{j})$
and
![]() $[\unicode[STIX]{x1D734}]_{ij}=1/2(\unicode[STIX]{x2202}_{j}u_{i}-\unicode[STIX]{x2202}_{i}u_{j})$
,
$[\unicode[STIX]{x1D734}]_{ij}=1/2(\unicode[STIX]{x2202}_{j}u_{i}-\unicode[STIX]{x2202}_{i}u_{j})$
,
![]() $i,j=1,2,3$
. The quantity
$i,j=1,2,3$
. The quantity
![]() $Q$
can be interpreted as the local balance between the strain rate and the vorticity magnitude. The isosurfaces
$Q$
can be interpreted as the local balance between the strain rate and the vorticity magnitude. The isosurfaces
![]() $\unicode[STIX]{x1D6E4}_{0}(Q-0.5\Vert Q\Vert _{L_{\infty }})$
representing the optimal states
$\unicode[STIX]{x1D6E4}_{0}(Q-0.5\Vert Q\Vert _{L_{\infty }})$
representing the optimal states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
with selected values of
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
with selected values of
![]() ${\mathcal{E}}_{0}$
are shown in figure 2(c–e). For the smallest values of
${\mathcal{E}}_{0}$
are shown in figure 2(c–e). For the smallest values of
![]() ${\mathcal{E}}_{0}$
, the optimal fields exhibit a cellular structure already observed in figure 1(a). For increasing values of
${\mathcal{E}}_{0}$
, the optimal fields exhibit a cellular structure already observed in figure 1(a). For increasing values of
![]() ${\mathcal{E}}_{0}$
this cellular structure transforms into a vortex ring, as seen in figure 2(e). The component of vorticity normal to the plane
${\mathcal{E}}_{0}$
this cellular structure transforms into a vortex ring, as seen in figure 2(e). The component of vorticity normal to the plane
![]() $P_{x}=\{\boldsymbol{x}\in \unicode[STIX]{x1D6FA}:\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{x}-\boldsymbol{x}_{0})=0\}$
for
$P_{x}=\{\boldsymbol{x}\in \unicode[STIX]{x1D6FA}:\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{x}-\boldsymbol{x}_{0})=0\}$
for
![]() $\boldsymbol{n}=[1,0,0]$
and
$\boldsymbol{n}=[1,0,0]$
and
![]() $\boldsymbol{x}_{0}=[1/2,1/2,1/2]$
is shown in figure 2(f–h), where the transition from cellular structures to a localized vortex structure as enstrophy increases is evident.
$\boldsymbol{x}_{0}=[1/2,1/2,1/2]$
is shown in figure 2(f–h), where the transition from cellular structures to a localized vortex structure as enstrophy increases is evident.
The results corresponding to large values of
![]() ${\mathcal{E}}_{0}$
are shown in figure 3 with the maximum rate of growth of enstrophy
${\mathcal{E}}_{0}$
are shown in figure 3 with the maximum rate of growth of enstrophy
![]() ${\mathcal{R}}_{{\mathcal{E}}_{0}}$
plotted as a function of
${\mathcal{R}}_{{\mathcal{E}}_{0}}$
plotted as a function of
![]() ${\mathcal{E}}_{0}$
in figure 3(a). We observe that, as
${\mathcal{E}}_{0}$
in figure 3(a). We observe that, as
![]() ${\mathcal{E}}_{0}$
increases, this relation approaches a power law of the form
${\mathcal{E}}_{0}$
increases, this relation approaches a power law of the form
![]() ${\mathcal{R}}_{{\mathcal{E}}_{0}}=C_{1}^{\prime }{\mathcal{E}}_{0}^{\unicode[STIX]{x1D6FC}_{1}}$
. In order to determine the prefactor
${\mathcal{R}}_{{\mathcal{E}}_{0}}=C_{1}^{\prime }{\mathcal{E}}_{0}^{\unicode[STIX]{x1D6FC}_{1}}$
. In order to determine the prefactor
![]() $C_{1}^{\prime }$
and the exponent
$C_{1}^{\prime }$
and the exponent
![]() $\unicode[STIX]{x1D6FC}_{1}$
we perform a local least-squares fit of the power law to the actual relation
$\unicode[STIX]{x1D6FC}_{1}$
we perform a local least-squares fit of the power law to the actual relation
![]() ${\mathcal{R}}_{{\mathcal{E}}_{0}}$
versus
${\mathcal{R}}_{{\mathcal{E}}_{0}}$
versus
![]() ${\mathcal{E}}_{0}$
for increasing values of
${\mathcal{E}}_{0}$
for increasing values of
![]() ${\mathcal{E}}_{0}$
starting with
${\mathcal{E}}_{0}$
starting with
![]() ${\mathcal{E}}_{0}=20$
(this particular choice the starting value is justified below). Then, the exponent
${\mathcal{E}}_{0}=20$
(this particular choice the starting value is justified below). Then, the exponent
![]() $\unicode[STIX]{x1D6FC}_{1}$
is computed as the average of the exponents obtained from the local fits with their standard deviation providing the error bars, so that we obtain
$\unicode[STIX]{x1D6FC}_{1}$
is computed as the average of the exponents obtained from the local fits with their standard deviation providing the error bars, so that we obtain
(the same approach is also used to determine the exponents in other power-law relations detected in this study). We note that the exponent
![]() $\unicode[STIX]{x1D6FC}_{1}$
obtained in (5.2) is in fact very close to 3 which is the exponent in estimate (2.9). For the value of the viscosity coefficient used in the computations (
$\unicode[STIX]{x1D6FC}_{1}$
obtained in (5.2) is in fact very close to 3 which is the exponent in estimate (2.9). For the value of the viscosity coefficient used in the computations (
![]() $\unicode[STIX]{x1D708}=0.01$
), the constant factor
$\unicode[STIX]{x1D708}=0.01$
), the constant factor
![]() $C_{1}=27/(8\unicode[STIX]{x03C0}^{4}\unicode[STIX]{x1D708}^{3})$
in estimate (2.9) has the value
$C_{1}=27/(8\unicode[STIX]{x03C0}^{4}\unicode[STIX]{x1D708}^{3})$
in estimate (2.9) has the value
![]() $C_{1}\approx 3.465\times 10^{4}$
which is approximately seven orders of magnitude larger than
$C_{1}\approx 3.465\times 10^{4}$
which is approximately seven orders of magnitude larger than
![]() $C_{1}^{\prime }$
given in (5.2). To shed more light at the source of this discrepancy, the objective functional
$C_{1}^{\prime }$
given in (5.2). To shed more light at the source of this discrepancy, the objective functional
![]() ${\mathcal{R}}$
from (2.5) can be separated into a negative-definite viscous part
${\mathcal{R}}$
from (2.5) can be separated into a negative-definite viscous part
![]() ${\mathcal{R}}_{\unicode[STIX]{x1D708}}$
and a cubic part
${\mathcal{R}}_{\unicode[STIX]{x1D708}}$
and a cubic part
![]() ${\mathcal{R}}_{cub}$
defined as
${\mathcal{R}}_{cub}$
defined as
While the value of
![]() $C_{1}^{\prime \prime }$
is slightly larger than the value of
$C_{1}^{\prime \prime }$
is slightly larger than the value of
![]() $C_{1}^{\prime }$
in (5.2), it is still some six orders of magnitude smaller than the constant factor
$C_{1}^{\prime }$
in (5.2), it is still some six orders of magnitude smaller than the constant factor
![]() $C_{1}=27/(8\unicode[STIX]{x03C0}^{4}\unicode[STIX]{x1D708}^{3})$
from estimate (2.9). These differences notwithstanding, we may conclude that estimate (2.9) is sharp in the sense of Definition 2.1. The power laws from (5.2) and (5.4) are consistent with the results first presented by Lu (Reference Lu2006) and Lu & Doering (Reference Lu and Doering2008), where the authors reported a power law with exponent
$C_{1}=27/(8\unicode[STIX]{x03C0}^{4}\unicode[STIX]{x1D708}^{3})$
from estimate (2.9). These differences notwithstanding, we may conclude that estimate (2.9) is sharp in the sense of Definition 2.1. The power laws from (5.2) and (5.4) are consistent with the results first presented by Lu (Reference Lu2006) and Lu & Doering (Reference Lu and Doering2008), where the authors reported a power law with exponent
![]() $\unicode[STIX]{x1D6FC}_{LD}=2.99$
and a constant of proportionality
$\unicode[STIX]{x1D6FC}_{LD}=2.99$
and a constant of proportionality
![]() $C_{LD}=8.97\times 10^{-4}$
. The energy of the optimal fields
$C_{LD}=8.97\times 10^{-4}$
. The energy of the optimal fields
![]() ${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
for large values of
${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
for large values of
![]() ${\mathcal{E}}_{0}$
is shown in figure 3(b) in which we observe that the energy stops to increase at approximately
${\mathcal{E}}_{0}$
is shown in figure 3(b) in which we observe that the energy stops to increase at approximately
![]() ${\mathcal{E}}_{0}\approx 20$
. This transition justifies using
${\mathcal{E}}_{0}\approx 20$
. This transition justifies using
![]() ${\mathcal{E}}_{0}=20$
as the lower bound on the range of
${\mathcal{E}}_{0}=20$
as the lower bound on the range of
![]() ${\mathcal{E}}_{0}$
where the power laws are determined via least-square fits.
${\mathcal{E}}_{0}$
where the power laws are determined via least-square fits.
Figure 3(c–e) shows the isosurfaces
![]() $\unicode[STIX]{x1D6E4}_{0}(Q-0.5\Vert Q\Vert _{L_{\infty }})$
representing the optimal fields
$\unicode[STIX]{x1D6E4}_{0}(Q-0.5\Vert Q\Vert _{L_{\infty }})$
representing the optimal fields
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
for selected large values of
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
for selected large values of
![]() ${\mathcal{E}}_{0}$
. The formation of these localized vortex structures featuring two rings as
${\mathcal{E}}_{0}$
. The formation of these localized vortex structures featuring two rings as
![]() ${\mathcal{E}}_{0}$
increases is evident in these panels. The formation process of localized vortex structures is also visible in figure 3(f–h), where the component of vorticity normal to the plane
${\mathcal{E}}_{0}$
increases is evident in these panels. The formation process of localized vortex structures is also visible in figure 3(f–h), where the component of vorticity normal to the plane
![]() $P_{xz}=\{\boldsymbol{x}\in \unicode[STIX]{x1D6FA}:\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{x}-\boldsymbol{x}_{0})=0\}$
for
$P_{xz}=\{\boldsymbol{x}\in \unicode[STIX]{x1D6FA}:\boldsymbol{n}\boldsymbol{\cdot }(\boldsymbol{x}-\boldsymbol{x}_{0})=0\}$
for
![]() $\boldsymbol{n}=[1,0,-1]$
and
$\boldsymbol{n}=[1,0,-1]$
and
![]() $\boldsymbol{x}_{0}=[1/2,1/2,1/2]$
is shown (we note that the planes used in figures 2(c–e) and 3(c–e) have different orientations).
$\boldsymbol{x}_{0}=[1/2,1/2,1/2]$
is shown (we note that the planes used in figures 2(c–e) and 3(c–e) have different orientations).

Figure 4. (a) Maximum velocity
![]() $\Vert \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{\infty }}$
, (b) maximum vorticity
$\Vert \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{\infty }}$
, (b) maximum vorticity
![]() $\Vert \unicode[STIX]{x1D735}\times \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{\infty }}$
, (c) characteristic length scale
$\Vert \unicode[STIX]{x1D735}\times \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{\infty }}$
, (c) characteristic length scale
![]() $\unicode[STIX]{x1D6EC}$
and (d) characteristic radius
$\unicode[STIX]{x1D6EC}$
and (d) characteristic radius
![]() $R_{\unicode[STIX]{x1D6F1}}$
of the extreme vortex states as functions of
$R_{\unicode[STIX]{x1D6F1}}$
of the extreme vortex states as functions of
![]() ${\mathcal{E}}_{0}$
(all marked with blue solid lines). In all cases two distinct behaviours, corresponding to
${\mathcal{E}}_{0}$
(all marked with blue solid lines). In all cases two distinct behaviours, corresponding to
![]() ${\mathcal{E}}_{0}\rightarrow 0$
and
${\mathcal{E}}_{0}\rightarrow 0$
and
![]() ${\mathcal{E}}_{0}\rightarrow \infty$
, are evident with the corresponding approximate power laws indicated with black dashed lines.
${\mathcal{E}}_{0}\rightarrow \infty$
, are evident with the corresponding approximate power laws indicated with black dashed lines.
Next we examine the variation of different diagnostics applied to the extreme states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
as enstrophy
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
as enstrophy
![]() ${\mathcal{E}}_{0}$
increases. The maximum velocity
${\mathcal{E}}_{0}$
increases. The maximum velocity
![]() $\Vert \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{\infty }}$
and maximum vorticity
$\Vert \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{\infty }}$
and maximum vorticity
![]() $\Vert \unicode[STIX]{x1D735}\times \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{\infty }}$
of the optimal fields are shown, respectively, in figure 4(a,b) as functions of
$\Vert \unicode[STIX]{x1D735}\times \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{\infty }}$
of the optimal fields are shown, respectively, in figure 4(a,b) as functions of
![]() ${\mathcal{E}}_{0}$
. For each quantity, two distinct power laws are observed in the forms
${\mathcal{E}}_{0}$
. For each quantity, two distinct power laws are observed in the forms
and
In order to quantify the variation of the relative size of the vortex structures, we will introduce two characteristic length scales. The first one is based on the energy and enstrophy, and was defined by Doering & Gibbon (Reference Doering and Gibbon1995) as
It is therefore equivalent to the Taylor microscale
![]() $\unicode[STIX]{x1D706}^{2}=15\int _{\unicode[STIX]{x1D6FA}}|\boldsymbol{u}|^{2}\,\text{d}\boldsymbol{x}/\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D74E}|^{2}\,\text{d}\boldsymbol{x}$
used in turbulence research (Davidson Reference Davidson2004). Another length scale, better suited to the ring-like vortex structures shown in figure 3(c–e), is the average radius
$\unicode[STIX]{x1D706}^{2}=15\int _{\unicode[STIX]{x1D6FA}}|\boldsymbol{u}|^{2}\,\text{d}\boldsymbol{x}/\int _{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D74E}|^{2}\,\text{d}\boldsymbol{x}$
used in turbulence research (Davidson Reference Davidson2004). Another length scale, better suited to the ring-like vortex structures shown in figure 3(c–e), is the average radius
![]() $R_{\unicode[STIX]{x1D6F1}}$
of one of the vortex rings calculated as
$R_{\unicode[STIX]{x1D6F1}}$
of one of the vortex rings calculated as
 $$\begin{eqnarray}\displaystyle R_{\unicode[STIX]{x1D6F1}}:=\frac{\int _{\unicode[STIX]{x1D6FA}}r(\boldsymbol{x})\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6F1}}(\boldsymbol{x})\,\text{d}\boldsymbol{x}}{\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6F1}}(\boldsymbol{x})\,\text{d}\boldsymbol{x}},\quad \text{where }r(\boldsymbol{x})=|\boldsymbol{x}-\overline{\boldsymbol{x}}|,\quad \overline{\boldsymbol{x}}=\frac{\displaystyle \int _{\unicode[STIX]{x1D6FA}}\boldsymbol{x}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6F1}}(\boldsymbol{x})\,\text{d}\boldsymbol{x}}{\displaystyle \int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6F1}}(\boldsymbol{x})\,\text{d}\boldsymbol{x}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{\unicode[STIX]{x1D6F1}}:=\frac{\int _{\unicode[STIX]{x1D6FA}}r(\boldsymbol{x})\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6F1}}(\boldsymbol{x})\,\text{d}\boldsymbol{x}}{\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6F1}}(\boldsymbol{x})\,\text{d}\boldsymbol{x}},\quad \text{where }r(\boldsymbol{x})=|\boldsymbol{x}-\overline{\boldsymbol{x}}|,\quad \overline{\boldsymbol{x}}=\frac{\displaystyle \int _{\unicode[STIX]{x1D6FA}}\boldsymbol{x}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6F1}}(\boldsymbol{x})\,\text{d}\boldsymbol{x}}{\displaystyle \int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6F1}}(\boldsymbol{x})\,\text{d}\boldsymbol{x}}, & & \displaystyle\end{eqnarray}$$
and
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6F1}}$
is the characteristic function of the set
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6F1}}$
is the characteristic function of the set
In the above definition of the set
![]() $\unicode[STIX]{x1D6F1}$
, the intersection of the two regions is necessary to restrict the set
$\unicode[STIX]{x1D6F1}$
, the intersection of the two regions is necessary to restrict the set
![]() $R_{\unicode[STIX]{x1D6F1}}$
to only one of the two ring structures visible in figure 3(c–e). The quantity
$R_{\unicode[STIX]{x1D6F1}}$
to only one of the two ring structures visible in figure 3(c–e). The quantity
![]() $\overline{\boldsymbol{x}}$
can be therefore interpreted as the geometric centre of one of the vortex rings. The dependence of
$\overline{\boldsymbol{x}}$
can be therefore interpreted as the geometric centre of one of the vortex rings. The dependence of
![]() $\unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D6EC}$
and
![]() $R_{\unicode[STIX]{x1D6F1}}$
on
$R_{\unicode[STIX]{x1D6F1}}$
on
![]() ${\mathcal{E}}_{0}$
is shown in figure 4(c,d) in which the following power laws can be observed
${\mathcal{E}}_{0}$
is shown in figure 4(c,d) in which the following power laws can be observed
By comparing the error bars in the key power laws (5.2) and (5.4) with the error bars in power-law relations (5.5d–f
), (5.6d–f
), (5.10c–e
) and (5.10f–h
), we observe that there is less uncertainty in the first case, indicating that the quantities
![]() $\Vert \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{\infty }}$
,
$\Vert \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{\infty }}$
,
![]() $\Vert \unicode[STIX]{x1D735}\times \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{\infty }}$
,
$\Vert \unicode[STIX]{x1D735}\times \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{\infty }}$
,
![]() $\unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D6EC}$
and
![]() $R_{\unicode[STIX]{x1D6F1}}$
tend to be more sensitive to approximation errors than
$R_{\unicode[STIX]{x1D6F1}}$
tend to be more sensitive to approximation errors than
![]() ${\mathcal{R}}_{{\mathcal{E}}_{0}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
. Non-negligible error bars may also indicate that, due to modest enstrophy values attained in our computations, the ultimate asymptotic regime corresponding to
${\mathcal{R}}_{{\mathcal{E}}_{0}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
. Non-negligible error bars may also indicate that, due to modest enstrophy values attained in our computations, the ultimate asymptotic regime corresponding to
![]() ${\mathcal{E}}_{0}\rightarrow \infty$
has not been reached in some power laws.
${\mathcal{E}}_{0}\rightarrow \infty$
has not been reached in some power laws.
A useful aspect of employing the average ring radius
![]() $R_{\unicode[STIX]{x1D6F1}}$
as the characteristic length scale is that its observed scaling with respect to
$R_{\unicode[STIX]{x1D6F1}}$
as the characteristic length scale is that its observed scaling with respect to
![]() ${\mathcal{E}}_{0}$
can be used as an approximate indicator of the resolution
${\mathcal{E}}_{0}$
can be used as an approximate indicator of the resolution
![]() $1/N$
required to numerically solve Problem 3.1 for large values of enstrophy. From the scaling in relation (5.10f–h
), it is evident that a twofold increase in the value of
$1/N$
required to numerically solve Problem 3.1 for large values of enstrophy. From the scaling in relation (5.10f–h
), it is evident that a twofold increase in the value of
![]() ${\mathcal{E}}_{0}$
will be accompanied by a similar reduction in
${\mathcal{E}}_{0}$
will be accompanied by a similar reduction in
![]() $R_{\unicode[STIX]{x1D6F1}}$
, thus requiring an eightfold increase in the resolution (a twofold increase in each dimension). This is one of the reasons why computation of extreme vortex states
$R_{\unicode[STIX]{x1D6F1}}$
, thus requiring an eightfold increase in the resolution (a twofold increase in each dimension). This is one of the reasons why computation of extreme vortex states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
for large enstrophy values is a very challenging computational task. In particular, this relation puts a limit on the largest value of
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
for large enstrophy values is a very challenging computational task. In particular, this relation puts a limit on the largest value of
![]() ${\mathcal{E}}_{0}$
for which Problem 3.1 can be in principle solved computationally at the present moment: a value of
${\mathcal{E}}_{0}$
for which Problem 3.1 can be in principle solved computationally at the present moment: a value of
![]() ${\mathcal{E}}_{0}=2000$
, a mere order of magnitude above the largest value of
${\mathcal{E}}_{0}=2000$
, a mere order of magnitude above the largest value of
![]() ${\mathcal{E}}_{0}$
reported here, would require a resolution of
${\mathcal{E}}_{0}$
reported here, would require a resolution of
![]() $8192^{3}$
used by some of the largest Navier–Stokes simulations to date.
$8192^{3}$
used by some of the largest Navier–Stokes simulations to date.
To summarize, as the enstrophy increases from
![]() ${\mathcal{E}}_{0}\approx 0$
to
${\mathcal{E}}_{0}\approx 0$
to
![]() ${\mathcal{E}}_{0}=O(10^{2})$
, the optimal vortex states change their structure from cellular to ring-like. While with the exception of
${\mathcal{E}}_{0}=O(10^{2})$
, the optimal vortex states change their structure from cellular to ring-like. While with the exception of
![]() ${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
and
${\mathcal{R}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
and
![]() ${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
, all of the diagnostic quantities behave in a monotonous manner, the corresponding power laws change at approximately
${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
, all of the diagnostic quantities behave in a monotonous manner, the corresponding power laws change at approximately
![]() ${\mathcal{E}}_{0}\approx 20$
, the value of enstrophy which marks the transition from the cellular to the ring-like structure (cf. figure 2(e) versus 3(c)). This is also the value of enstrophy beyond which the energy
${\mathcal{E}}_{0}\approx 20$
, the value of enstrophy which marks the transition from the cellular to the ring-like structure (cf. figure 2(e) versus 3(c)). This is also the value of enstrophy beyond which the energy
![]() ${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
starts to decrease (figure 3
b). This transition also coincides with a change of the symmetry properties of the extreme vortex states
${\mathcal{K}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})$
starts to decrease (figure 3
b). This transition also coincides with a change of the symmetry properties of the extreme vortex states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
– while in the limit
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
– while in the limit
![]() ${\mathcal{E}}_{0}\rightarrow 0$
these fields feature reflection and discrete rotation symmetries (cf. § 4), for
${\mathcal{E}}_{0}\rightarrow 0$
these fields feature reflection and discrete rotation symmetries (cf. § 4), for
![]() $20\lessapprox {\mathcal{E}}_{0}\rightarrow \infty$
the optimal states are characterized by axial symmetry. The asymptotic (as
$20\lessapprox {\mathcal{E}}_{0}\rightarrow \infty$
the optimal states are characterized by axial symmetry. The asymptotic (as
![]() ${\mathcal{E}}_{0}\rightarrow \infty$
) extreme vortex states on locally maximizing branches corresponding to the aligned ABC flow and the Taylor–Green vortex (cf. table 2) are similar to the fields shown in figure 3(c–h), except for a different orientation of their symmetry axes with respect to the periodic domain
${\mathcal{E}}_{0}\rightarrow \infty$
) extreme vortex states on locally maximizing branches corresponding to the aligned ABC flow and the Taylor–Green vortex (cf. table 2) are similar to the fields shown in figure 3(c–h), except for a different orientation of their symmetry axes with respect to the periodic domain
![]() $\unicode[STIX]{x1D6FA}$
(these results are not shown here for brevity). The different power laws found here are compared to the corresponding results obtained in two dimensions in § 7. It is also worth mentioning that, as shown by Ayala & Doering (Reference Ayala and Doering2016), all power laws discussed in this section, cf. (5.2), (5.4), (5.5d–f
), (5.6d–f
) and (5.10f–h
), can be deduced rigorously using arguments based on dimensional analysis under the assumption of axisymmetry for the optimal fields
$\unicode[STIX]{x1D6FA}$
(these results are not shown here for brevity). The different power laws found here are compared to the corresponding results obtained in two dimensions in § 7. It is also worth mentioning that, as shown by Ayala & Doering (Reference Ayala and Doering2016), all power laws discussed in this section, cf. (5.2), (5.4), (5.5d–f
), (5.6d–f
) and (5.10f–h
), can be deduced rigorously using arguments based on dimensional analysis under the assumption of axisymmetry for the optimal fields
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
.
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
.
Finally, the findings of this section allow us to shed some light on the ‘small data’ result (2.16) which provides the conditions on the size of the initial data
![]() $\boldsymbol{u}_{0}$
, given in terms of its energy
$\boldsymbol{u}_{0}$
, given in terms of its energy
![]() ${\mathcal{K}}(0)$
and enstrophy
${\mathcal{K}}(0)$
and enstrophy
![]() ${\mathcal{E}}(0)$
, in the Navier–Stokes system (2.1) guaranteeing that smooth solutions exist globally in time. The power-law fits (5.2) and (5.4) allow us to sharpen condition (2.16) be replacing the constant on the right-hand side with either
${\mathcal{E}}(0)$
, in the Navier–Stokes system (2.1) guaranteeing that smooth solutions exist globally in time. The power-law fits (5.2) and (5.4) allow us to sharpen condition (2.16) be replacing the constant on the right-hand side with either
![]() $2\unicode[STIX]{x1D708}/C_{1}^{\prime }$
or
$2\unicode[STIX]{x1D708}/C_{1}^{\prime }$
or
![]() $2\unicode[STIX]{x1D708}/C_{1}^{\prime \prime }$
, so that we obtain
$2\unicode[STIX]{x1D708}/C_{1}^{\prime \prime }$
, so that we obtain
The region of the ‘phase space’
![]() $\{{\mathcal{K}},{\mathcal{E}}\}$
described by condition (5.11) is shown in white in figure 5. The grey region represents the values of
$\{{\mathcal{K}},{\mathcal{E}}\}$
described by condition (5.11) is shown in white in figure 5. The grey region represents the values of
![]() ${\mathcal{K}}(0)$
and
${\mathcal{K}}(0)$
and
![]() ${\mathcal{E}}(0)$
for which long-time existence of smooth solutions cannot be a priori guaranteed (the two shades of grey correspond to the two constants which can be used in (5.11)). Solid circles represent the different extreme states found in this section, whereas the thin curves mark the time-dependent trajectories which will be analysed in § 6. We conclude from figure 5 that the change of the properties of the optimal states
${\mathcal{E}}(0)$
for which long-time existence of smooth solutions cannot be a priori guaranteed (the two shades of grey correspond to the two constants which can be used in (5.11)). Solid circles represent the different extreme states found in this section, whereas the thin curves mark the time-dependent trajectories which will be analysed in § 6. We conclude from figure 5 that the change of the properties of the optimal states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
discussed above occurs in fact for the values of enstrophy (
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
discussed above occurs in fact for the values of enstrophy (
![]() ${\mathcal{E}}(0)\approx 20$
) for which the states
${\mathcal{E}}(0)\approx 20$
) for which the states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
are on the boundary of the region of guaranteed long-time regularity.
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
are on the boundary of the region of guaranteed long-time regularity.

Figure 5. The phase space
![]() $\{{\mathcal{K}},{\mathcal{E}}\}$
. The solid circles and triangles represent, respectively, the instantaneously optimal fields
$\{{\mathcal{K}},{\mathcal{E}}\}$
. The solid circles and triangles represent, respectively, the instantaneously optimal fields
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
and
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
and
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{K}}_{0},{\mathcal{E}}_{0}}$
, with the lines issuing from selected markers indicating the corresponding time-dependent trajectories (the optimal states
$\widetilde{\boldsymbol{u}}_{{\mathcal{K}}_{0},{\mathcal{E}}_{0}}$
, with the lines issuing from selected markers indicating the corresponding time-dependent trajectories (the optimal states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{K}}_{0},{\mathcal{E}}_{0}}$
are discussed in § 8, cf. Problem 8.1). The two lines with a negative slope represent condition (5.11) with the two different constants, whereas the line with a positive slope is the Poincaré limit
$\widetilde{\boldsymbol{u}}_{{\mathcal{K}}_{0},{\mathcal{E}}_{0}}$
are discussed in § 8, cf. Problem 8.1). The two lines with a negative slope represent condition (5.11) with the two different constants, whereas the line with a positive slope is the Poincaré limit
![]() ${\mathcal{K}}=(2\unicode[STIX]{x03C0})^{2}{\mathcal{E}}$
. The shaded areas represent regions of the phase space for which global regularity is not a priori guaranteed based on estimate (2.9) combined with fits (5.2) and (5.4).
${\mathcal{K}}=(2\unicode[STIX]{x03C0})^{2}{\mathcal{E}}$
. The shaded areas represent regions of the phase space for which global regularity is not a priori guaranteed based on estimate (2.9) combined with fits (5.2) and (5.4).
6 Time evolution of extreme vortex states
The goal of this section is to analyse the time evolution, governed by the Navier–Stokes system (2.1), with the extreme vortex states identified in § 5 used as the initial data
![]() $\boldsymbol{u}_{0}$
. In particular, we are interested in the finite-time growth of enstrophy
$\boldsymbol{u}_{0}$
. In particular, we are interested in the finite-time growth of enstrophy
![]() ${\mathcal{E}}(t)$
and how it relates to estimates (2.9), (2.14) and (2.15). We will compare these results with the growth of enstrophy obtained using other types of initial data which have also been studied in the context of the blow-up problem for both the Euler and Navier–Stokes systems, namely, the Taylor–Green vortex (Taylor & Green Reference Taylor and Green1937; Brachet et al.
Reference Brachet, Meiron, Orszag, Nickel, Morf and Frisch1983; Brachet Reference Brachet1991; Bustamante & Brachet Reference Bustamante and Brachet2012), the Kida–Pelz flow (Boratav & Pelz Reference Boratav and Pelz1994; Pelz Reference Pelz2001; Grafke et al.
Reference Grafke, Homann, Dreher and Grauer2008), colliding Lamb–Chaplygin dipoles (Orlandi et al.
Reference Orlandi, Pirozzoli and Carnevale2012) and perturbed antiparallel vortex tubes (Kerr Reference Kerr1993, Reference Kerr2013b
). Precise characterization of these different initial conditions is provided in table 3 and, for the sake of completeness, the last three states are also visualized in figure 6. We comment that, with the exception of the Taylor–Green vortex which was shown in § 4 to be a local maximizer of Problem 3.1 in the limit
${\mathcal{E}}(t)$
and how it relates to estimates (2.9), (2.14) and (2.15). We will compare these results with the growth of enstrophy obtained using other types of initial data which have also been studied in the context of the blow-up problem for both the Euler and Navier–Stokes systems, namely, the Taylor–Green vortex (Taylor & Green Reference Taylor and Green1937; Brachet et al.
Reference Brachet, Meiron, Orszag, Nickel, Morf and Frisch1983; Brachet Reference Brachet1991; Bustamante & Brachet Reference Bustamante and Brachet2012), the Kida–Pelz flow (Boratav & Pelz Reference Boratav and Pelz1994; Pelz Reference Pelz2001; Grafke et al.
Reference Grafke, Homann, Dreher and Grauer2008), colliding Lamb–Chaplygin dipoles (Orlandi et al.
Reference Orlandi, Pirozzoli and Carnevale2012) and perturbed antiparallel vortex tubes (Kerr Reference Kerr1993, Reference Kerr2013b
). Precise characterization of these different initial conditions is provided in table 3 and, for the sake of completeness, the last three states are also visualized in figure 6. We comment that, with the exception of the Taylor–Green vortex which was shown in § 4 to be a local maximizer of Problem 3.1 in the limit
![]() ${\mathcal{E}}_{0}\rightarrow 0$
, all these initial conditions were postulated based on rather ad hoc physical arguments. We also add that, in order to ensure a fair comparison, the different initial conditions listed in table 3 are rescaled to have the same enstrophy
${\mathcal{E}}_{0}\rightarrow 0$
, all these initial conditions were postulated based on rather ad hoc physical arguments. We also add that, in order to ensure a fair comparison, the different initial conditions listed in table 3 are rescaled to have the same enstrophy
![]() ${\mathcal{E}}_{0}$
, which is different from the enstrophy values used in the original studies where these initial conditions were investigated (Orlandi et al.
Reference Orlandi, Pirozzoli and Carnevale2012; Donzis et al.
Reference Donzis, Gibbon, Gupta, Kerr, Pandit and Vincenzi2013; Kerr Reference Kerr2013b
; Orlandi et al.
Reference Orlandi, Pirozzoli, Bernardini and Carnevale2014). As regards our choices of the initial enstrophy
${\mathcal{E}}_{0}$
, which is different from the enstrophy values used in the original studies where these initial conditions were investigated (Orlandi et al.
Reference Orlandi, Pirozzoli and Carnevale2012; Donzis et al.
Reference Donzis, Gibbon, Gupta, Kerr, Pandit and Vincenzi2013; Kerr Reference Kerr2013b
; Orlandi et al.
Reference Orlandi, Pirozzoli, Bernardini and Carnevale2014). As regards our choices of the initial enstrophy
![]() ${\mathcal{E}}_{0}$
, to illustrate different possible behaviours, we will consider initial data located in the two distinct regions of the phase space
${\mathcal{E}}_{0}$
, to illustrate different possible behaviours, we will consider initial data located in the two distinct regions of the phase space
![]() $\{{\mathcal{K}},{\mathcal{E}}\}$
shown in figure 5, corresponding to values of
$\{{\mathcal{K}},{\mathcal{E}}\}$
shown in figure 5, corresponding to values of
![]() ${\mathcal{K}}_{0}$
and
${\mathcal{K}}_{0}$
and
![]() ${\mathcal{E}}_{0}$
for which global regularity may or may not be a priori guaranteed according to estimates (2.15)–(2.16).
${\mathcal{E}}_{0}$
for which global regularity may or may not be a priori guaranteed according to estimates (2.15)–(2.16).
Table 3. Characterization of the different initial data used in time evolution studies in § 6.

System (2.1) is solved numerically with an approach combining a pseudo-spectral approximation of spatial derivatives with a third-order semi-implicit Runge–Kutta method (Bewley Reference Bewley2009) used to discretize the problem in time. In the evaluation of the nonlinear term dealiasing was used based on the
![]() $2/3$
rule together with the Gaussian filtering proposed by Hou & Li (Reference Hou and Li2007). Massively parallel implementation based on MPI and using the fftw routines (Frigo & Johnson Reference Frigo and Johnson2003) to perform Fourier transforms allowed us to use resolutions varying from
$2/3$
rule together with the Gaussian filtering proposed by Hou & Li (Reference Hou and Li2007). Massively parallel implementation based on MPI and using the fftw routines (Frigo & Johnson Reference Frigo and Johnson2003) to perform Fourier transforms allowed us to use resolutions varying from
![]() $256^{3}$
to
$256^{3}$
to
![]() $1024^{3}$
in the low-enstrophy and high-enstrophy cases, respectively. A number of different diagnostics were checked to ensure that all flows discussed below are well resolved. We refer the reader to the dissertation by Ayala (Reference Ayala2014) for additional details and a validation of this approach.
$1024^{3}$
in the low-enstrophy and high-enstrophy cases, respectively. A number of different diagnostics were checked to ensure that all flows discussed below are well resolved. We refer the reader to the dissertation by Ayala (Reference Ayala2014) for additional details and a validation of this approach.
The time-dependent results will be shown with respect to a normalized time defined as
![]() $\unicode[STIX]{x1D70F}:=U_{c}t/\ell _{c}$
with
$\unicode[STIX]{x1D70F}:=U_{c}t/\ell _{c}$
with
![]() $U_{c}:=\Vert \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{2}}$
and
$U_{c}:=\Vert \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}\Vert _{L_{2}}$
and
![]() $\ell _{c}=\unicode[STIX]{x1D6EC}$
(cf. (5.7)) playing the roles of the characteristic velocity and length scale. We begin by showing the time evolution of the enstrophy
$\ell _{c}=\unicode[STIX]{x1D6EC}$
(cf. (5.7)) playing the roles of the characteristic velocity and length scale. We begin by showing the time evolution of the enstrophy
![]() ${\mathcal{E}}(\unicode[STIX]{x1D70F})$
corresponding to the five different initial conditions listed in table 3 with
${\mathcal{E}}(\unicode[STIX]{x1D70F})$
corresponding to the five different initial conditions listed in table 3 with
![]() ${\mathcal{E}}_{0}=10$
and
${\mathcal{E}}_{0}=10$
and
![]() ${\mathcal{E}}_{0}=100$
in figure 7(a,b), respectively (because of the faster time scale, the time axis in the latter figure is scaled logarithmically). We see that the maximizers
${\mathcal{E}}_{0}=100$
in figure 7(a,b), respectively (because of the faster time scale, the time axis in the latter figure is scaled logarithmically). We see that the maximizers
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
of Problem 3.1 are the only initial data which triggers growth of enstrophy for these values of the initial enstrophy and, as expected, this growth is larger for
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
of Problem 3.1 are the only initial data which triggers growth of enstrophy for these values of the initial enstrophy and, as expected, this growth is larger for
![]() ${\mathcal{E}}_{0}=100$
than for
${\mathcal{E}}_{0}=100$
than for
![]() ${\mathcal{E}}_{0}=10$
. The other initial condition which exhibits some tendency for growth when
${\mathcal{E}}_{0}=10$
. The other initial condition which exhibits some tendency for growth when
![]() ${\mathcal{E}}_{0}=100$
is the Taylor–Green vortex. In all cases the enstrophy eventually decays to zero for large times.
${\mathcal{E}}_{0}=100$
is the Taylor–Green vortex. In all cases the enstrophy eventually decays to zero for large times.

Figure 6. Isosurfaces corresponding to
![]() $Q(\boldsymbol{x})=1/2\Vert Q\Vert _{L_{\infty }}$
for different initial conditions, all normalized to
$Q(\boldsymbol{x})=1/2\Vert Q\Vert _{L_{\infty }}$
for different initial conditions, all normalized to
![]() ${\mathcal{E}}_{0}=100$
: (a) Kida–Pelz flow, (b) colliding Lamb–Chaplygin dipoles and (c) perturbed antiparallel vortex tubes. Precise characterization of these different initial conditions is provided in table 3.
${\mathcal{E}}_{0}=100$
: (a) Kida–Pelz flow, (b) colliding Lamb–Chaplygin dipoles and (c) perturbed antiparallel vortex tubes. Precise characterization of these different initial conditions is provided in table 3.

Figure 7. Time evolution of enstrophy
![]() ${\mathcal{E}}(\unicode[STIX]{x1D70F})$
for the initial enstrophy (a)
${\mathcal{E}}(\unicode[STIX]{x1D70F})$
for the initial enstrophy (a)
![]() ${\mathcal{E}}_{0}=10$
and (b)
${\mathcal{E}}_{0}=10$
and (b)
![]() ${\mathcal{E}}_{0}=100$
with the initial condition
${\mathcal{E}}_{0}=100$
with the initial condition
![]() $\boldsymbol{u}_{0}$
corresponding to the instantaneous optimizer
$\boldsymbol{u}_{0}$
corresponding to the instantaneous optimizer
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
(blue solid line), the Taylor–Green vortex (red dashed-dotted line), the Kida–Pelz vortex (red dashed line), the colliding Lamb–Chaplygin dipoles (black dashed-dotted lines) and the perturbed antiparallel vortex tubes (black dashed lines). Precise characterization of these different initial conditions is provided in table 3.
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
(blue solid line), the Taylor–Green vortex (red dashed-dotted line), the Kida–Pelz vortex (red dashed line), the colliding Lamb–Chaplygin dipoles (black dashed-dotted lines) and the perturbed antiparallel vortex tubes (black dashed lines). Precise characterization of these different initial conditions is provided in table 3.
Next we examine whether the flow evolutions starting from the instantaneous maximizers
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
as the initial data saturate the finite-time estimate (2.14). We do this by defining functions
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
as the initial data saturate the finite-time estimate (2.14). We do this by defining functions

Figure 8. Evolution of functions
![]() $f(\unicode[STIX]{x1D70F})$
(blue solid lines) and
$f(\unicode[STIX]{x1D70F})$
(blue solid lines) and
![]() $g(\unicode[STIX]{x1D70F})$
(black dashed-dotted lines), cf. (6.1a,b
), for flows with the optimal initial condition
$g(\unicode[STIX]{x1D70F})$
(black dashed-dotted lines), cf. (6.1a,b
), for flows with the optimal initial condition
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
with (a)
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
with (a)
![]() ${\mathcal{E}}_{0}=10$
and (b)
${\mathcal{E}}_{0}=10$
and (b)
![]() ${\mathcal{E}}_{0}=100$
. The value
${\mathcal{E}}_{0}=100$
. The value
![]() $1/{\mathcal{E}}_{0}$
which must be attained in a hypothetical blow-up event is marked by the horizontal dashed line.
$1/{\mathcal{E}}_{0}$
which must be attained in a hypothetical blow-up event is marked by the horizontal dashed line.
We further characterize the time evolution by showing the maximum enstrophy increase
![]() $\unicode[STIX]{x1D6FF}{\mathcal{E}}:=\max _{t\geqslant 0}\{{\mathcal{E}}(t)-{\mathcal{E}}(0)\}$
and the time when the maximum is achieved
$\unicode[STIX]{x1D6FF}{\mathcal{E}}:=\max _{t\geqslant 0}\{{\mathcal{E}}(t)-{\mathcal{E}}(0)\}$
and the time when the maximum is achieved
![]() $T_{max}:=\arg \max _{t\geqslant 0}{\mathcal{E}}(t)$
as functions of
$T_{max}:=\arg \max _{t\geqslant 0}{\mathcal{E}}(t)$
as functions of
![]() ${\mathcal{E}}_{0}$
in figure 9(a,b), respectively. In both cases approximate power laws in the form
${\mathcal{E}}_{0}$
in figure 9(a,b), respectively. In both cases approximate power laws in the form
are detected in the limit
![]() ${\mathcal{E}}_{0}\rightarrow \infty$
(as regards the second result, we remark that
${\mathcal{E}}_{0}\rightarrow \infty$
(as regards the second result, we remark that
![]() $T_{max}$
is not equivalent to the time until which the enstrophy grows at the sustained rate proportional to
$T_{max}$
is not equivalent to the time until which the enstrophy grows at the sustained rate proportional to
![]() ${\mathcal{E}}_{0}^{3}$
, cf. figure 8). To complete presentation of the results, the dependence of the quantities
${\mathcal{E}}_{0}^{3}$
, cf. figure 8). To complete presentation of the results, the dependence of the quantities
on the initial enstrophy
![]() ${\mathcal{E}}_{0}$
is shown in figure 9(c,d). It is observed that both quantities approximately exhibit a power-law behaviour of the form
${\mathcal{E}}_{0}$
is shown in figure 9(c,d). It is observed that both quantities approximately exhibit a power-law behaviour of the form
![]() ${\mathcal{E}}_{0}^{-1}$
. Discussion of these results in the context of the estimates recalled in § 1 is presented in the next section.
${\mathcal{E}}_{0}^{-1}$
. Discussion of these results in the context of the estimates recalled in § 1 is presented in the next section.

Figure 9. Dependence on
![]() ${\mathcal{E}}_{0}$
of (a) the maximum enstrophy increase over finite time
${\mathcal{E}}_{0}$
of (a) the maximum enstrophy increase over finite time
![]() $\unicode[STIX]{x1D6FF}{\mathcal{E}}$
, (b) the time
$\unicode[STIX]{x1D6FF}{\mathcal{E}}$
, (b) the time
![]() $T_{max}$
when the enstrophy maximum is attained, (c) the maximum achieved by the left-hand side of estimate (2.14), cf. (6.1a
), and (d) the energy dissipation during
$T_{max}$
when the enstrophy maximum is attained, (c) the maximum achieved by the left-hand side of estimate (2.14), cf. (6.1a
), and (d) the energy dissipation during
![]() $[0,T_{max}]$
; all data correspond to the time evolution starting from the extreme vortex states
$[0,T_{max}]$
; all data correspond to the time evolution starting from the extreme vortex states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
.
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
.
7 Discussion
In this section we provide some comments about the results reported in §§ 4–6. First, we need to mention that our gradient-based approach to the solution of optimization Problem 3.1 can only yield local maximizers and, due to non-convexity of the problem, it is not possible to guarantee a priori that the maximizers found are global. To test for the possible presence of branches other than the ones found using the continuation approach described in § 3, cf. algorithm 1, we tried to find new maximizers by initializing the gradient iterations (3.8) with different initial guesses
![]() $\boldsymbol{u}^{0}$
. They were constructed as solenoidal vector fields with prescribed regularity and random structure, which was achieved by defining the Fourier coefficients of
$\boldsymbol{u}^{0}$
. They were constructed as solenoidal vector fields with prescribed regularity and random structure, which was achieved by defining the Fourier coefficients of
![]() $\boldsymbol{u}^{0}$
as
$\boldsymbol{u}^{0}$
as
![]() $\widehat{\boldsymbol{u}}^{0}(\boldsymbol{k})=F(|\boldsymbol{k}|)\text{e}^{\text{i}\unicode[STIX]{x1D719}(\boldsymbol{k})}$
with the amplitude
$\widehat{\boldsymbol{u}}^{0}(\boldsymbol{k})=F(|\boldsymbol{k}|)\text{e}^{\text{i}\unicode[STIX]{x1D719}(\boldsymbol{k})}$
with the amplitude
![]() $F(|\boldsymbol{k}|)\sim 1/|\boldsymbol{k}|^{2}$
and the phases
$F(|\boldsymbol{k}|)\sim 1/|\boldsymbol{k}|^{2}$
and the phases
![]() $\unicode[STIX]{x1D719}(\boldsymbol{k})$
chosen as random numbers uniformly distributed in
$\unicode[STIX]{x1D719}(\boldsymbol{k})$
chosen as random numbers uniformly distributed in
![]() $[0,2\unicode[STIX]{x03C0}]$
. However, in all such tests conducted for
$[0,2\unicode[STIX]{x03C0}]$
. However, in all such tests conducted for
![]() ${\mathcal{E}}_{0}=O(1)$
the gradient optimization algorithm (3.8) would always converge to maximizers
${\mathcal{E}}_{0}=O(1)$
the gradient optimization algorithm (3.8) would always converge to maximizers
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
belonging to one of the branches discussed in § 5 (modulo possible translations in the physical domain). While far from settling this issue definitely, these observations lend some credence to the conjecture that the branch identified in § 5 corresponds in fact to the global maximizers. These states appear identical to the maximizers found by Lu & Doering (Reference Lu and Doering2008) and our search has also yielded two additional branches of locally maximizing fields, although we did not capture the lower branch reported by Lu & Doering (Reference Lu and Doering2008). However, since that branch does not appear connected to any state in the limit
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
belonging to one of the branches discussed in § 5 (modulo possible translations in the physical domain). While far from settling this issue definitely, these observations lend some credence to the conjecture that the branch identified in § 5 corresponds in fact to the global maximizers. These states appear identical to the maximizers found by Lu & Doering (Reference Lu and Doering2008) and our search has also yielded two additional branches of locally maximizing fields, although we did not capture the lower branch reported by Lu & Doering (Reference Lu and Doering2008). However, since that branch does not appear connected to any state in the limit
![]() ${\mathcal{E}}_{0}\rightarrow 0$
, we speculate that it might be an artefact of the ‘discretize-then-optimize’ formulation used by Lu & Doering (Reference Lu and Doering2008), in contrast to the ‘optimize-then-discretize’ approach employed in our study which provides a more direct control over the analytic properties of the maximizers. We add that the structure of the maximizing branches found here is in fact quite similar to what was discovered by Ayala & Protas (Reference Ayala and Protas2014a
) in an analogous problem in two dimensions. Since the 2-D problem is more tractable from the computational point of view, in that case we were able to undertake a much more thorough search for other maximizers which did not however yield any solutions not associated with the main branches.
${\mathcal{E}}_{0}\rightarrow 0$
, we speculate that it might be an artefact of the ‘discretize-then-optimize’ formulation used by Lu & Doering (Reference Lu and Doering2008), in contrast to the ‘optimize-then-discretize’ approach employed in our study which provides a more direct control over the analytic properties of the maximizers. We add that the structure of the maximizing branches found here is in fact quite similar to what was discovered by Ayala & Protas (Reference Ayala and Protas2014a
) in an analogous problem in two dimensions. Since the 2-D problem is more tractable from the computational point of view, in that case we were able to undertake a much more thorough search for other maximizers which did not however yield any solutions not associated with the main branches.

Figure 10. Trajectory of the flow corresponding to the initial condition
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
with
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
with
![]() ${\mathcal{E}}_{0}=100$
in the coordinates
${\mathcal{E}}_{0}=100$
in the coordinates
![]() $\{{\mathcal{E}},\text{d}{\mathcal{E}}/\text{d}t\}$
. For comparison, in the inset the thin line represents the borderline growth at the rate
$\{{\mathcal{E}},\text{d}{\mathcal{E}}/\text{d}t\}$
. For comparison, in the inset the thin line represents the borderline growth at the rate
![]() $\text{d}{\mathcal{E}}/\text{d}t\sim {\mathcal{E}}^{2}$
.
$\text{d}{\mathcal{E}}/\text{d}t\sim {\mathcal{E}}^{2}$
.
The results reported in §§ 5 and 6 clearly exhibit two distinct behaviours, depending on whether or not global-in-time regularity can be guaranteed a priori based on estimates (2.14)–(2.16). These differences are manifested, for example, in the power laws evident in figures 4 and 9, as well as in the different behaviours of the right-hand side of estimate (2.14) with respect to time in figure 8(a,b). However, for the initial data for which global-in-time regularity cannot be ensured a priori there is no evidence of sustained growth of enstrophy strong enough to signal formation of singularity in finite time. Indeed, in figure 9(c) one sees that the quantity
![]() $\max _{t\geqslant 0}\{1/{\mathcal{E}}_{0}-1/{\mathcal{E}}(t)\}$
behaves as
$\max _{t\geqslant 0}\{1/{\mathcal{E}}_{0}-1/{\mathcal{E}}(t)\}$
behaves as
![]() $C_{1}/{\mathcal{E}}_{0}$
, where
$C_{1}/{\mathcal{E}}_{0}$
, where
![]() $C_{1}<1$
, when
$C_{1}<1$
, when
![]() ${\mathcal{E}}_{0}$
increases, revealing no tendency to approach
${\mathcal{E}}_{0}$
increases, revealing no tendency to approach
![]() $1/{\mathcal{E}}_{0}$
which is a necessary precursor of a singular behaviour (cf. discussion in § 6). To further illustrate how the rate of growth of enstrophy achieved initially by the maximizers
$1/{\mathcal{E}}_{0}$
which is a necessary precursor of a singular behaviour (cf. discussion in § 6). To further illustrate how the rate of growth of enstrophy achieved initially by the maximizers
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
is depleted in time, in figure 10 we show the flow evolution corresponding to
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
is depleted in time, in figure 10 we show the flow evolution corresponding to
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
with
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
with
![]() ${\mathcal{E}}_{0}=100$
as a trajectory in the coordinates
${\mathcal{E}}_{0}=100$
as a trajectory in the coordinates
![]() $\{{\mathcal{E}},\text{d}{\mathcal{E}}/\text{d}t\}$
. From the discussion in Introduction we know that in order for the singularity to occur in finite time, the enstrophy must grow at least at a sustained rate
$\{{\mathcal{E}},\text{d}{\mathcal{E}}/\text{d}t\}$
. From the discussion in Introduction we know that in order for the singularity to occur in finite time, the enstrophy must grow at least at a sustained rate
![]() $\text{d}{\mathcal{E}}/\text{d}t\sim {\mathcal{E}}^{\unicode[STIX]{x1D6FC}}$
for some
$\text{d}{\mathcal{E}}/\text{d}t\sim {\mathcal{E}}^{\unicode[STIX]{x1D6FC}}$
for some
![]() $\unicode[STIX]{x1D6FC}>2$
. In other words, a ‘blow-up trajectory’ will be realized only if the trajectory of the flow, expressed in
$\unicode[STIX]{x1D6FC}>2$
. In other words, a ‘blow-up trajectory’ will be realized only if the trajectory of the flow, expressed in
![]() $\{{\mathcal{E}},\text{d}{\mathcal{E}}/\text{d}t\}$
coordinates, is contained in the region
$\{{\mathcal{E}},\text{d}{\mathcal{E}}/\text{d}t\}$
coordinates, is contained in the region
![]() ${\mathcal{M}}=\{({\mathcal{E}},\text{d}{\mathcal{E}}/\text{d}t):C_{1}{\mathcal{E}}^{2}<\text{d}{\mathcal{E}}/\text{d}t\leqslant C_{2}{\mathcal{E}}^{3}\}$
, for some positive constants
${\mathcal{M}}=\{({\mathcal{E}},\text{d}{\mathcal{E}}/\text{d}t):C_{1}{\mathcal{E}}^{2}<\text{d}{\mathcal{E}}/\text{d}t\leqslant C_{2}{\mathcal{E}}^{3}\}$
, for some positive constants
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
. For the flow corresponding to the instantaneous optimizers
$C_{2}$
. For the flow corresponding to the instantaneous optimizers
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
, the initial direction of a trajectory in
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
, the initial direction of a trajectory in
![]() $\{{\mathcal{E}},\text{d}{\mathcal{E}}/\text{d}t\}$
coordinates is determined by the vector
$\{{\mathcal{E}},\text{d}{\mathcal{E}}/\text{d}t\}$
coordinates is determined by the vector
![]() $\boldsymbol{v}=[1,(\text{d}{\mathcal{R}}/\text{d}{\mathcal{E}})|_{{\mathcal{E}}_{0}}]$
and, for initial conditions
$\boldsymbol{v}=[1,(\text{d}{\mathcal{R}}/\text{d}{\mathcal{E}})|_{{\mathcal{E}}_{0}}]$
and, for initial conditions
![]() $\boldsymbol{u}_{0}$
satisfying
$\boldsymbol{u}_{0}$
satisfying
![]() ${\mathcal{R}}(\boldsymbol{u}_{0})=C{\mathcal{E}}^{3}(\boldsymbol{u}_{0})$
, it follows that
${\mathcal{R}}(\boldsymbol{u}_{0})=C{\mathcal{E}}^{3}(\boldsymbol{u}_{0})$
, it follows that
Since the optimal rate of growth is sustained only over a short interval of time, the trajectory of the flow in the
![]() $\{{\mathcal{E}},\text{d}{\mathcal{E}}/\text{d}t\}$
coordinates approaches the region
$\{{\mathcal{E}},\text{d}{\mathcal{E}}/\text{d}t\}$
coordinates approaches the region
![]() ${\mathcal{M}}$
only tangentially following the direction of the lower bound
${\mathcal{M}}$
only tangentially following the direction of the lower bound
![]() $C_{1}{\mathcal{E}}^{2}$
, and remains outside
$C_{1}{\mathcal{E}}^{2}$
, and remains outside
![]() ${\mathcal{M}}$
for all subsequent times. This behaviour is clearly seen in the inset of figure 10.
${\mathcal{M}}$
for all subsequent times. This behaviour is clearly seen in the inset of figure 10.
An interpretation of this behaviour can be proposed based on (2.7a
) from which it is clear that the evolution of the flow energy is closely related to the growth of enstrophy. In particular, if the initial energy
![]() ${\mathcal{K}}(0)$
is not sufficiently large, then its depletion due to the initial growth of enstrophy may render the flow incapable of sustaining this growth over a longer period of time. This is in fact what seems to be happening in the present problem as evidenced by the data shown in figure 5. We remark that, for a prescribed enstrophy
${\mathcal{K}}(0)$
is not sufficiently large, then its depletion due to the initial growth of enstrophy may render the flow incapable of sustaining this growth over a longer period of time. This is in fact what seems to be happening in the present problem as evidenced by the data shown in figure 5. We remark that, for a prescribed enstrophy
![]() ${\mathcal{E}}(0)$
, the flow energy cannot be increased arbitrarily as it is upper bounded by Poincaré’s inequality
${\mathcal{E}}(0)$
, the flow energy cannot be increased arbitrarily as it is upper bounded by Poincaré’s inequality
![]() ${\mathcal{K}}(0)\leqslant (2\unicode[STIX]{x03C0})^{2}{\mathcal{E}}(0)$
. This behaviour can also be understood in terms of the geometry of the extreme vortex states
${\mathcal{K}}(0)\leqslant (2\unicode[STIX]{x03C0})^{2}{\mathcal{E}}(0)$
. This behaviour can also be understood in terms of the geometry of the extreme vortex states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
. Figure 11 shows a magnification of the pair of vortex rings corresponding to the optimal field
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
. Figure 11 shows a magnification of the pair of vortex rings corresponding to the optimal field
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
with
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
with
![]() ${\mathcal{E}}_{0}=100$
. It is observed that the vorticity field
${\mathcal{E}}_{0}=100$
. It is observed that the vorticity field
![]() $\unicode[STIX]{x1D735}\times \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
inside the vortex core has an azimuthal component only which exhibits no variation in the azimuthal direction. Thus, in the limit
$\unicode[STIX]{x1D735}\times \widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
inside the vortex core has an azimuthal component only which exhibits no variation in the azimuthal direction. Thus, in the limit
![]() ${\mathcal{E}}_{0}\rightarrow \infty$
the vortex ring shrinks with respect to the domain
${\mathcal{E}}_{0}\rightarrow \infty$
the vortex ring shrinks with respect to the domain
![]() $\unicode[STIX]{x1D6FA}$
(cf. figure 4
d) and the field
$\unicode[STIX]{x1D6FA}$
(cf. figure 4
d) and the field
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
ultimately becomes axisymmetric (i.e. in this limit boundary effects vanish). At the same time, it is known that the 3-D Navier–Stokes problem on an unbounded domain and with axisymmetric initial data is globally well posed (Kim Reference Kim2003), a results which is a consequence of the celebrated theorem due to Caffarelli, Kohn & Nirenberg (Reference Caffarelli, Kohn and Nirenberg1983).
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
ultimately becomes axisymmetric (i.e. in this limit boundary effects vanish). At the same time, it is known that the 3-D Navier–Stokes problem on an unbounded domain and with axisymmetric initial data is globally well posed (Kim Reference Kim2003), a results which is a consequence of the celebrated theorem due to Caffarelli, Kohn & Nirenberg (Reference Caffarelli, Kohn and Nirenberg1983).

Figure 11. Vortex lines inside the region with the strongest vorticity in the extreme vortex state
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
with
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
with
![]() ${\mathcal{E}}_{0}=100$
. The colour coding of the vortex lines is for identification purposes only.
${\mathcal{E}}_{0}=100$
. The colour coding of the vortex lines is for identification purposes only.
We close this section by comparing the different power laws characterizing the maximizers
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
and the corresponding flow evolutions with the results obtained in analogous studies of extreme behaviour in one dimension and two dimensions (see also table 1). First, we note that the finite-time growth of enstrophy
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
and the corresponding flow evolutions with the results obtained in analogous studies of extreme behaviour in one dimension and two dimensions (see also table 1). First, we note that the finite-time growth of enstrophy
![]() $\unicode[STIX]{x1D6FF}{\mathcal{E}}$
in three dimensions, cf. figure 9(a), exhibits the same dependence on the enstrophy
$\unicode[STIX]{x1D6FF}{\mathcal{E}}$
in three dimensions, cf. figure 9(a), exhibits the same dependence on the enstrophy
![]() ${\mathcal{E}}_{0}$
of the instantaneously optimal initial data as in one dimension, i.e. is directly proportional to
${\mathcal{E}}_{0}$
of the instantaneously optimal initial data as in one dimension, i.e. is directly proportional to
![]() ${\mathcal{E}}_{0}$
in both cases (Ayala & Protas Reference Ayala and Protas2011). This is also analogous to the maximum growth of palinstrophy
${\mathcal{E}}_{0}$
in both cases (Ayala & Protas Reference Ayala and Protas2011). This is also analogous to the maximum growth of palinstrophy
![]() ${\mathcal{P}}$
in two dimensions which was found by Ayala & Protas (Reference Ayala and Protas2014a
) to scale with the palinstrophy
${\mathcal{P}}$
in two dimensions which was found by Ayala & Protas (Reference Ayala and Protas2014a
) to scale with the palinstrophy
![]() ${\mathcal{P}}_{0}$
of the initial data, when the instantaneously optimal initial condition was computed subject to one constraint only (on
${\mathcal{P}}_{0}$
of the initial data, when the instantaneously optimal initial condition was computed subject to one constraint only (on
![]() ${\mathcal{P}}_{0}$
). When the instantaneously optimal initial data were determined subject to two constraints, on
${\mathcal{P}}_{0}$
). When the instantaneously optimal initial data were determined subject to two constraints, on
![]() ${\mathcal{K}}_{0}$
and
${\mathcal{K}}_{0}$
and
![]() ${\mathcal{P}}_{0}$
, then the maximum finite-time growth of palinstrophy was found to scale with
${\mathcal{P}}_{0}$
, then the maximum finite-time growth of palinstrophy was found to scale with
![]() ${\mathcal{P}}_{0}^{3/2}$
(Ayala & Protas Reference Ayala and Protas2014b
). On the other hand, the time
${\mathcal{P}}_{0}^{3/2}$
(Ayala & Protas Reference Ayala and Protas2014b
). On the other hand, the time
![]() $T_{max}$
when the maximum enstrophy is attained, cf. figure 9(b), scales as
$T_{max}$
when the maximum enstrophy is attained, cf. figure 9(b), scales as
![]() ${\mathcal{E}}_{0}^{-2}$
, which should be contrasted with the scalings
${\mathcal{E}}_{0}^{-2}$
, which should be contrasted with the scalings
![]() ${\mathcal{E}}_{0}^{-1/2}$
and
${\mathcal{E}}_{0}^{-1/2}$
and
![]() ${\mathcal{P}}_{0}^{-1/2}$
found in the 1-D and 2-D cases, respectively. This implies that the time interval during which the extremal growth of enstrophy is sustained in three dimensions is shorter than the corresponding intervals in one dimension and two dimensions.
${\mathcal{P}}_{0}^{-1/2}$
found in the 1-D and 2-D cases, respectively. This implies that the time interval during which the extremal growth of enstrophy is sustained in three dimensions is shorter than the corresponding intervals in one dimension and two dimensions.
8 Conclusions and outlook
By constructing the initial data to exhibit the most extreme behaviour allowed for by the mathematically rigorous estimates, this study offers a fundamentally different perspective on the problem of searching for potentially singular solutions from most earlier investigations. Indeed, while the corresponding flow evolutions did not reveal any evidence for finite-time singularity formation, the initial data obtained by maximizing
![]() $\text{d}{\mathcal{E}}/\text{d}t$
produced a significantly larger growth of enstrophy in finite time than any other candidate initial conditions (cf. table 3 and figure 7). Admittedly, this observation is limited to the initial data with
$\text{d}{\mathcal{E}}/\text{d}t$
produced a significantly larger growth of enstrophy in finite time than any other candidate initial conditions (cf. table 3 and figure 7). Admittedly, this observation is limited to the initial data with
![]() ${\mathcal{E}}_{0}\leqslant 100$
, which corresponds to Reynolds numbers
${\mathcal{E}}_{0}\leqslant 100$
, which corresponds to Reynolds numbers
![]() $Re=\sqrt{{\mathcal{E}}_{0}\unicode[STIX]{x1D6EC}}/\unicode[STIX]{x1D708}\lessapprox 450$
lower than the Reynolds numbers achieved in other studies concerned with the extreme behaviour in the Navier–Stokes flows (Orlandi et al.
Reference Orlandi, Pirozzoli and Carnevale2012; Donzis et al.
Reference Donzis, Gibbon, Gupta, Kerr, Pandit and Vincenzi2013; Kerr Reference Kerr2013b
; Orlandi et al.
Reference Orlandi, Pirozzoli, Bernardini and Carnevale2014). Given that the definitions of the Reynolds numbers applicable to the various flow configurations considered in these studies were not equivalent, it is rather difficult to make a precise comparison in terms of specific numerical values, but it is clear that the largest Reynolds numbers attained in these investigations were at least an order of magnitude higher than used in the present study; for Euler flows such a comparison is obviously not possible at all. However, from the mathematical point of view, based on estimates (2.9)–(2.16), there is no clear indication that a very large initial enstrophy
$Re=\sqrt{{\mathcal{E}}_{0}\unicode[STIX]{x1D6EC}}/\unicode[STIX]{x1D708}\lessapprox 450$
lower than the Reynolds numbers achieved in other studies concerned with the extreme behaviour in the Navier–Stokes flows (Orlandi et al.
Reference Orlandi, Pirozzoli and Carnevale2012; Donzis et al.
Reference Donzis, Gibbon, Gupta, Kerr, Pandit and Vincenzi2013; Kerr Reference Kerr2013b
; Orlandi et al.
Reference Orlandi, Pirozzoli, Bernardini and Carnevale2014). Given that the definitions of the Reynolds numbers applicable to the various flow configurations considered in these studies were not equivalent, it is rather difficult to make a precise comparison in terms of specific numerical values, but it is clear that the largest Reynolds numbers attained in these investigations were at least an order of magnitude higher than used in the present study; for Euler flows such a comparison is obviously not possible at all. However, from the mathematical point of view, based on estimates (2.9)–(2.16), there is no clear indication that a very large initial enstrophy
![]() ${\mathcal{E}}_{0}$
(or, equivalently, a high Reynolds number) should be a necessary condition for singularity formation in finite time. In fact, blow-up cannot be a priori ruled out as soon as condition (2.16) is violated, which happens for all initial data lying on the grey region of the phase space in figure 5. We remark that additional results were obtained (not reported in this paper) by studying the time evolution corresponding to the optimal initial data
${\mathcal{E}}_{0}$
(or, equivalently, a high Reynolds number) should be a necessary condition for singularity formation in finite time. In fact, blow-up cannot be a priori ruled out as soon as condition (2.16) is violated, which happens for all initial data lying on the grey region of the phase space in figure 5. We remark that additional results were obtained (not reported in this paper) by studying the time evolution corresponding to the optimal initial data
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
, but using smaller values of the viscosity coefficient
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
, but using smaller values of the viscosity coefficient
![]() $\unicode[STIX]{x1D708}=10^{-3},10^{-4}$
, thereby artificially increasing the Reynolds number at the price of making the initial data suboptimal. Although these attempts did increase the amplification of enstrophy as compared to what was observed in figures 8 and 9, no signature of finite-time singularity formation could be detected either.
$\unicode[STIX]{x1D708}=10^{-3},10^{-4}$
, thereby artificially increasing the Reynolds number at the price of making the initial data suboptimal. Although these attempts did increase the amplification of enstrophy as compared to what was observed in figures 8 and 9, no signature of finite-time singularity formation could be detected either.
Our study confirmed the earlier findings of Lu & Doering (Reference Lu and Doering2008) about the sharpness of the instantaneous estimate (2.9). We also demonstrated that the finite-time estimate (2.14) is saturated by the flow evolution corresponding to the optimal initial data
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
, but only for short times, cf. figure 8, which are not long enough to trigger a singular behaviour.
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
, but only for short times, cf. figure 8, which are not long enough to trigger a singular behaviour.
In § 7 we speculated that a relatively small initial energy
![]() ${\mathcal{K}}(0)$
, cf. figure 3(b), might be the property of the extreme vortex states
${\mathcal{K}}(0)$
, cf. figure 3(b), might be the property of the extreme vortex states
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
preventing the resulting flow evolutions from sustaining a significant growth of enstrophy over long times. On the other hand, in the Introduction we showed that estimate (2.9) need not be saturated for blow-up to occur in finite time and, in fact, sustained growth at the rate
$\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}}$
preventing the resulting flow evolutions from sustaining a significant growth of enstrophy over long times. On the other hand, in the Introduction we showed that estimate (2.9) need not be saturated for blow-up to occur in finite time and, in fact, sustained growth at the rate
![]() $\text{d}{\mathcal{E}}/\text{d}t=C{\mathcal{E}}^{\unicode[STIX]{x1D6FC}}$
with any
$\text{d}{\mathcal{E}}/\text{d}t=C{\mathcal{E}}^{\unicode[STIX]{x1D6FC}}$
with any
![]() $\unicode[STIX]{x1D6FC}>2$
will also produce singularity in finite time. Thus, another strategy to construct initial data which could lead to a more sustained growth of enstrophy in finite time might be to increase its kinetic energy by allowing for a smaller instantaneous rate of growth (i.e. with an exponent
$\unicode[STIX]{x1D6FC}>2$
will also produce singularity in finite time. Thus, another strategy to construct initial data which could lead to a more sustained growth of enstrophy in finite time might be to increase its kinetic energy by allowing for a smaller instantaneous rate of growth (i.e. with an exponent
![]() $2<\unicode[STIX]{x1D6FC}\leqslant 3$
instead of
$2<\unicode[STIX]{x1D6FC}\leqslant 3$
instead of
![]() $\unicode[STIX]{x1D6FC}=3$
). This can be achieved by prescribing an additional constraint in the formulation of the variational optimization problem, resulting in
$\unicode[STIX]{x1D6FC}=3$
). This can be achieved by prescribing an additional constraint in the formulation of the variational optimization problem, resulting in
Problem 8.1.
It differs from Problem 3.1 in that the maximizers are sought at the intersection of the original constraint manifold
![]() ${\mathcal{S}}_{{\mathcal{E}}_{0}}$
and the manifold defined by the condition
${\mathcal{S}}_{{\mathcal{E}}_{0}}$
and the manifold defined by the condition
![]() ${\mathcal{K}}(\boldsymbol{u})={\mathcal{K}}_{0}$
, where
${\mathcal{K}}(\boldsymbol{u})={\mathcal{K}}_{0}$
, where
![]() ${\mathcal{K}}_{0}\leqslant (2\unicode[STIX]{x03C0})^{2}{\mathcal{E}}_{0}$
is the prescribed energy. While computation of such maximizers is more complicated, robust techniques for the solution of optimization problems of this type have been developed and were successfully used in the 2-D setting by Ayala & Protas (Reference Ayala and Protas2014a
). Preliminary results obtained in the present setting by solving Problem 8.1 for
${\mathcal{K}}_{0}\leqslant (2\unicode[STIX]{x03C0})^{2}{\mathcal{E}}_{0}$
is the prescribed energy. While computation of such maximizers is more complicated, robust techniques for the solution of optimization problems of this type have been developed and were successfully used in the 2-D setting by Ayala & Protas (Reference Ayala and Protas2014a
). Preliminary results obtained in the present setting by solving Problem 8.1 for
![]() ${\mathcal{K}}_{0}=1$
are indicated in figure 5, where we see that the flow evolutions starting from
${\mathcal{K}}_{0}=1$
are indicated in figure 5, where we see that the flow evolutions starting from
![]() $\widetilde{\boldsymbol{u}}_{{\mathcal{K}}_{0},{\mathcal{E}}_{0}}$
do not in fact produce a significant growth of enstrophy either. An alternative, and arguably more flexible approach, is to formulate this problem in terms of multiobjective optimization (Miettinen Reference Miettinen1999) in which the objective function
$\widetilde{\boldsymbol{u}}_{{\mathcal{K}}_{0},{\mathcal{E}}_{0}}$
do not in fact produce a significant growth of enstrophy either. An alternative, and arguably more flexible approach, is to formulate this problem in terms of multiobjective optimization (Miettinen Reference Miettinen1999) in which the objective function
![]() ${\mathcal{R}}(\boldsymbol{u})$
in Problem 3.1 would be replaced with
${\mathcal{R}}(\boldsymbol{u})$
in Problem 3.1 would be replaced with
where
![]() $\unicode[STIX]{x1D702}\in [0,1]$
. Solution of such a multiobjective optimization problem has the form of a ‘Pareto front’ parameterized by
$\unicode[STIX]{x1D702}\in [0,1]$
. Solution of such a multiobjective optimization problem has the form of a ‘Pareto front’ parameterized by
![]() $\unicode[STIX]{x1D702}$
. Clearly, the limits
$\unicode[STIX]{x1D702}$
. Clearly, the limits
![]() $\unicode[STIX]{x1D702}\rightarrow 1$
and
$\unicode[STIX]{x1D702}\rightarrow 1$
and
![]() $\unicode[STIX]{x1D702}\rightarrow 0$
correspond, respectively, to the extreme vortex states already found in §§ 4 and 5, and to the Poincaré limit. Another interesting possibility is to replace the energy
$\unicode[STIX]{x1D702}\rightarrow 0$
correspond, respectively, to the extreme vortex states already found in §§ 4 and 5, and to the Poincaré limit. Another interesting possibility is to replace the energy
![]() ${\mathcal{K}}(\boldsymbol{u})$
with the helicity
${\mathcal{K}}(\boldsymbol{u})$
with the helicity
![]() ${\mathcal{H}}(\boldsymbol{u}):=\int _{\unicode[STIX]{x1D6FA}}\boldsymbol{u}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{u})\,\text{d}\unicode[STIX]{x1D6FA}$
in the multiobjective formulation (8.3), as this might allow one to obtain extreme vortex states with a more complicated topology (i.e. a certain degree of ‘knottedness’). We note that all the extreme vortex states found in the present study were ‘unknotted’, i.e. were characterized by
${\mathcal{H}}(\boldsymbol{u}):=\int _{\unicode[STIX]{x1D6FA}}\boldsymbol{u}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{u})\,\text{d}\unicode[STIX]{x1D6FA}$
in the multiobjective formulation (8.3), as this might allow one to obtain extreme vortex states with a more complicated topology (i.e. a certain degree of ‘knottedness’). We note that all the extreme vortex states found in the present study were ‘unknotted’, i.e. were characterized by
![]() ${\mathcal{H}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})=0$
, as the vortex rings were in all cases disjoint (cf. figure 11).
${\mathcal{H}}(\widetilde{\boldsymbol{u}}_{{\mathcal{E}}_{0}})=0$
, as the vortex rings were in all cases disjoint (cf. figure 11).
Finally, another promising possibility to find initial data producing a larger growth of enstrophy is to solve a finite-time optimization problem of the type already studied by Ayala & Protas (Reference Ayala and Protas2011) in the context of the 1-D Burgers equation, namely
Problem 8.2.
where
![]() $T>0$
is the length of the time interval of interest and
$T>0$
is the length of the time interval of interest and
![]() $\boldsymbol{u}_{0}$
the initial data for the Navier–Stokes system (2.1). In contrast to Problems 3.1 and 8.1, solution of Problem 8.2 is more complicated as it involves flow evolution. It represents therefore a formidable computational task for the 3-D Navier–Stokes system. However, it does appear within reach given the currently available computational resources and will be studied in the near future.
$\boldsymbol{u}_{0}$
the initial data for the Navier–Stokes system (2.1). In contrast to Problems 3.1 and 8.1, solution of Problem 8.2 is more complicated as it involves flow evolution. It represents therefore a formidable computational task for the 3-D Navier–Stokes system. However, it does appear within reach given the currently available computational resources and will be studied in the near future.
Acknowledgements
The authors are indebted to C. Doering for many enlightening discussions concerning the research problems studied in this work. The authors are grateful to N. Kevlahan for making his parallel Navier–Stokes solver available, which was used to obtain the results reported in § 6. Anonymous referees provided many insightful comments which helped us improve this work. This research was funded through an Early Researcher Award (ERA) and an NSERC Discovery Grant, whereas the computational time was made available by SHARCNET under its Dedicated Resource Allocation Program. D.A. was funded in part by NSF Award DMS-1515161 at the University of Michigan and by the Institute for Pure and Applied Mathematics at UCLA.