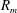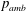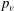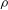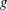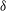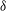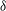1. Introduction
There exist two families of research studies on bubble dynamics. The first is relevant to microscopic cavitation bubbles where the effects of buoyancy are not of particular concern. The second family is concerned with large bubbles, such as bubbles generated by underwater explosions (UNDEX), where the effects of buoyancy are essential (Cole Reference Cole1948; Chahine et al. Reference Chahine, Frederick, Lambrecht, Harris and Mair1995; Chahine Reference Chahine1997; Klaseboer et al. Reference Klaseboer, Hung, Wang, Wang, Khoo, Boyce, Debono and Charlier2005; Hung & Hwangfu Reference Hung and Hwangfu2010).
1.1. Cavitation bubbles
Laser-generated bubbles of
$O(1)~\text{mm}$
were observed by Lauterborn & Bolle (Reference Lauterborn and Bolle1975), Lauterborn (Reference Lauterborn1982), Lauterborn & Vogel (Reference Lauterborn and Vogel1984), Lauterborn & Hentschel (Reference Lauterborn and Hentschel1985), Vogel, Lauterborn & Timm (Reference Vogel, Lauterborn and Timm1989), Ohl, Philipp & Lauterborn (Reference Ohl, Philipp and Lauterborn1995), Jin, Shaw & Emmony (Reference Jin, Shaw and Emmony1996), Shaw et al. (Reference Shaw, Jin, Schiffers and Emmony1996, Reference Shaw, Jin, Gentry and Emmony1999), Tong et al. (Reference Tong, Schiffers, Shaw, Blake and Emmony1999), Akhatov et al. (Reference Akhatov, Lindau, Topolnikov, Mettin, Vakhitova and Lauterborn2001), Brujan et al. (Reference Brujan, Nahen, Schmidt and Vogel2001, Reference Brujan, Keen, Vogel and Blake2002), Robinson et al. (Reference Robinson, Blake, Kodama, Shima and Tomita2001), Lindau & Lauterborn (Reference Lindau and Lauterborn2003), Tomita & Kodama (Reference Tomita and Kodama2003), Gonzalez-Avila et al. (Reference Gonzalez-Avila, Klaseboer, Khoo and Ohl2011) and Yang, Wang & Tan (Reference Yang, Wang and Tan2013). In these experiments, the buoyancy parameter
${\it\delta}$
, defined as
$\sqrt{{\it\rho}gR_{m}/(p_{amb}-pv)}$
in which
$R_{m}$
,
$p_{amb}$
,
$p_{v}$
,
${\it\rho}$
and
$g$
are the maximum bubble radius, ambient pressure, saturated vapour pressure, density of water and the acceleration of gravity respectively, was only
$O(0.01)$
due to the small bubble size, and buoyancy was therefore insignificant. A similar magnitude of
${\it\delta}$
appears for small spark-generated bubbles of
$O(1{-}10)~\text{mm}$
at atmospheric pressure, as observed by, for example, Shima & Nakajima (Reference Shima and Nakajima1977), Shima, Takayama & Tomita (Reference Shima, Takayama and Tomita1983), Tomita & Shima (Reference Tomita and Shima1986), Shima et al. (Reference Shima, Tomita, Gibson and Blake1989), Turangan et al. (Reference Turangan, Ong, Klaseboer and Khoo2006) and Dadvand, Khoo & Shervani-Tabar (Reference Dadvand, Khoo and Shervani-Tabar2009).
In some experimental studies, the buoyancy effects on bubble behaviours were purposely minimized. For example, free-fall apparatuses were used by Benjamin & Ellis (Reference Benjamin and Ellis1966), Blake & Gibson (Reference Blake and Gibson1981, Reference Blake and Gibson1987) and Gibson & Blake (Reference Gibson and Blake1982), where the bubble radius was as large as 20 mm but the buoyancy effect was insignificant; bubbles were also generated under microgravity conditions by Obreschkow et al. (Reference Obreschkow, Kobel, Dorsaz, De Bosset, Nicollier and Farhat2006, Reference Obreschkow, Tinguely, Dorsaz, Kobel, De Bosset and Farhat2011).
1.2. Underwater explosion bubbles
Extensive studies on UNDEX bubbles have been carried out over many decades (see, for example, Cole Reference Cole1948; Snay Reference Snay1962a ,Reference Snay b ; Krieger & Chahine Reference Krieger and Chahine2003, Reference Krieger and Chahine2005; Kan, Stuhmiller & Chan Reference Kan, Stuhmiller and Chan2005; Zhang et al. Reference Zhang, Wang, Huang and Wang2013). Underwater explosion bubbles may be subject to very large ranges of buoyancy effects depending on charge weight and depth. However, bubble dynamics in field tests associated with large amounts of explosive are difficult to optically observe or record, and the data are less available in the public literature because of confidential issues.
Most of the published papers on UNDEX bubbles that feature clear bubble images are for small amounts of explosive, for example Klaseboer et al. (Reference Klaseboer, Hung, Wang, Wang, Khoo, Boyce, Debono and Charlier2005) (10–55 g hexocire), Brett, Yiannakopoulos & van der Schaaf (Reference Brett, Yiannakopoulos and van der Schaaf2000) (0.5 kg TNT), Brett & Yiannakopolous (Reference Brett and Yiannakopolous2008) (5.3 g TNT) and Hung & Hwangfu (Reference Hung and Hwangfu2010) (1.32 g TNT equivalence). In these studies,
${\it\delta}$
was approximately within the range of 0.1–0.3. However, it is difficult to observe jet development due to opaqueness of explosion products.
1.3. Spark-generated bubbles with buoyancy effects
As commented by Chahine et al. (Reference Chahine, Frederick, Lambrecht, Harris and Mair1995), spark-generated bubbles are strong candidates for laboratory-scale models of UNDEX bubble dynamics and are, therefore, excellent sources of data for validation of simulation tools. The influence of buoyancy on the behaviour of spark bubbles is easier to observe due to the larger bubble size, especially under reduced air pressure. In Chahine (Reference Chahine1977), Hooton, Blake & Soh (Reference Hooton, Blake, Soh, Blake, Boulton-Stone and Thomas1994) and Harvey, Best & Soh (Reference Harvey, Best and Soh1996), bubbles were generated with the value of
${\it\delta}$
being approximately 0.10–0.22; these researches were concerned with the close interaction on bubbles with nearby rigid boundaries, where buoyancy is associated with secondary effects. In the works of Benjamin & Ellis (Reference Benjamin and Ellis1966), Chahine & Bovis (Reference Chahine, Bovis and Lauterborn1980), Chahine et al. (Reference Chahine, Frederick, Lambrecht, Harris and Mair1995), Best, Soh & Yu (Reference Best, Soh and Yu1996), Buogo & Cannelli (Reference Buogo and Cannelli2002) and Jayaprakash, Hsiao & Chahine (Reference Jayaprakash, Hsiao and Chahine2012), the buoyancy effects were observed for bubble jets and migration under different ambient pressures with
${\it\delta}$
ranging approximately from 0.019 to 0.215. Chahine (Reference Chahine1997) experimented on bubble behaviour near a submerged cylinder for
${\it\delta}$
up to 0.53 and provided criteria for different collapse directions.
1.4. The present work
In this paper, we carry out a systematic study of the effects of buoyancy on bubble dynamics for a large range of the buoyancy parameter,
${\it\delta}=0.034{-}0.95$
. We recorded and analysed the detailed multiple oscillation of bubbles in terms of the dimensionless buoyancy parameter and the standoff distance from a free surface or a rigid boundary. The bubbles recorded were transparent, thus the jet development and impact with the opposite bubble wall could be displayed and analysed. We also display and analyse the splitting of a bubble or bubble ring into two parts and the subsequent joining.
The remainder of the paper is organized as follows. In § 2, the experiment is illustrated, including high-speed photography and the method of generating low-pressure and discharge bubbles. The bubble dynamics in an infinite field is displayed in the range of
${\it\delta}$
from 0.034 to 0.5 in § 3, and bubble characteristics such as jet speed are analysed as functions of
${\it\delta}$
. In §§ 4 and 5, we study a bubble below a free surface for
${\it\delta}=0.07{-}0.95$
and above a rigid boundary for
${\it\delta}=0.10{-}0.53$
respectively. For both of the two configurations, the Bjerknes and buoyancy forces are in opposite directions. Three situations will be studied for each of them: (i) the Bjerknes force being dominant, (ii) the buoyancy force being dominant and (iii) the two forces being balanced. Control over the value of
${\it\delta}$
is necessary to obtain certain combinations of buoyancy and Bjerknes forces in order to acquire these scenarios, and this is done by adjusting the ambient pressure where the bubble is initiated. Finally, in § 6, this new study is summarized and the key outcomes are identified.
2. Experiment
2.1. Pressure reduction
The experiment is carried out in a cylindrical steel pressure tank with a height of 1200 mm and an inner diameter of 800 mm, as shown schematically in figure 1. The tank is channelled to an air pressure gauge and a vacuum pump. Glass windows are set on both sides of the tank for photography and illumination. The tank is partially filled with sufficiently degassed water to the depth needed, and a certain amount of air is evacuated by the pump. The air pressure inside the tank, denoted as
$p_{air}$
, is calculated by deducting the amount of pressure reduced by the pump (measured by the pressure gauge) from the air pressure outside the tank (measured by an independent barometer).
Figure 1. Experimental set-up.
2.2. Bubble generation
The bubble is initiated by Joule heating at the connect point of the electrodes by the discharge of a
$6600~{\rm\mu}\text{F}$
capacitor charged to 200 V, see figure 1. The electrodes are copper wires of 0.25 mm diameter. Upon discharge, the electrodes evaporate at the connect point, causing light emission and high temperature, thus generating a rapidly expanding bubble, referred to as a ‘discharge bubble’ in the following. Presumably, the bubble contains vapour, while electrolysis products of water and evaporated copper may also exist. From repeated observation, it is found that the centre of the bubble, before obvious migration takes place, is always located at the connect point. Therefore, this point is also referred to as the initial bubble centre.
The discharge ceases within 5 ms, but the first period of bubble oscillation can last for from 5 to over 60 ms. The period is prolonged when the air pressure is reduced. The ambient pressure
$p_{amb}$
at the bubble centre at inception is
$$\begin{eqnarray}p_{amb}=p_{air}+{\it\rho}gd,\end{eqnarray}$$
where
$p_{air}$
is the pressure of air inside the tank,
${\it\rho}$
is the density of water,
$g$
is the acceleration of gravity and
$d$
is the depth of the bubble centre at inception. The pressure due to the water depth thus becomes essential as
$p_{air}$
is low in the tank. In an infinite liquid, the maximum bubble radius (reached in the first period) is found to vary with
$p_{amb}$
but is stable and repeatable when
$p_{amb}$
is kept constant. Deviation in radius under the same
$p_{amb}$
has been found, which is likely to be caused by the uncertainties in the heating process, but fortunately in most cases the deviation is insignificant as long as the duration of the heating is similar. Therefore, a filtering process is applied according to the heating duration in order to obtain repeatable bubble sizes, leaving only the cases with durations between 2.0 and 3.0 ms to be adopted in the following. Besides, it is also reckoned that the electrodes of 0.25 mm in diameter are not likely to cause substantial influence to the bubble, and that the boundary effect from the walls of the tank should be small given the bubble diameter (approximately 150 mm at most) and the inner tank diameter (800 mm).
2.3. High-speed photography
The oscillating process of the bubble is recorded as a sequence of images with a high-speed camera (Phantom V12.1) operating at
$15\,000~\text{frames}~\text{s}^{-1}$
. The exposure time of each frame is set as
$10~{\rm\mu}\text{s}$
, which ensures the sharpness of bubble boundaries. Diffusive illumination is provided by a continuous light source and a glass diffuser at one side of the tank, opposite to the camera (see figure 1). Relatively clear images of the bubble interior are able to be captured with this set-up.
The capturing time of the last image before the copper electrodes are ignited is taken as time zero. The maximum error in time measuring equals the frame interval, approximately 0.067 ms, which is small compared with the period of bubble oscillation (typically 10–100 ms). Before bubble generation, a ruler is placed in the same vertical plane as the electrode connect point and perpendicular to the axis of the camera lens, in order to be recorded as length calibration for the captured images. Thus, spatial measurements are directly carried out on the images, and the precision is up to the actual length of a single pixel. The current set-up provides a resolution of
$3.34~\text{pixels}~\text{mm}^{-1}$
, therefore the error range in length measurement is 0.30 mm.
2.4. Parameters
The maximum radius of a bubble in an infinite fluid is defined as
$R_{m}=\sqrt{A/{\rm\pi}}$
, where
$A$
is the maximum area of the bubble on the images. The maximum radius of a bubble near a boundary is assumed as
$R_{m}$
of a bubble generated under the same
$p_{amb}$
in an infinite fluid. The radius
$R_{m}$
is used as the reference length. The pressure scale is chosen as
${\rm\Delta}p=p_{amb}-p_{v}$
;
$p_{v}$
is the saturated vapour pressure which is 2338 Pa at 20 °C. The velocity scale is
$({\rm\Delta}p/{\it\rho})^{1/2}$
and the time scale is
$R_{m}({\it\rho}/{\rm\Delta}p)^{1/2}$
. The normalization will be performed with these reference scales and the dimensionless quantities are denoted with subscript ‘
$_{\ast }$
’, unless stated otherwise.
The dimensionless distance of the bubble near a free surface,
${\it\gamma}_{f}$
, is defined as
$$\begin{eqnarray}{\it\gamma}_{f}=\frac{d_{f}}{R_{m}},\end{eqnarray}$$
where
$d_{f}$
is the distance of the bubble centroid from the free surface at inception. The dimensionless distance of the bubble near a rigid wall,
${\it\gamma}_{b}$
, is defined as
$$\begin{eqnarray}{\it\gamma}_{b}=\frac{d_{b}}{R_{m}},\end{eqnarray}$$
where
$d_{b}$
is the distance of the bubble centroid at inception from the wall.
The buoyancy parameter has been introduced as
$$\begin{eqnarray}{\it\delta}=\sqrt{{\it\rho}gR_{m}/{\rm\Delta}p}.\end{eqnarray}$$
The buoyancy parameter
${\it\delta}$
can be adjusted by changing
$p_{air}$
and the water depth
$d$
. Given a water depth of 250 mm, the average radius of the bubble is approximately 12 mm under atmospheric pressure, which yields a lower bound for
${\it\delta}$
of approximately 0.034. The experimental set-up is capable of reducing
$p_{air}$
down to 1.50 kPa; in such conditions the bubble radius reaches 55 mm and
${\it\delta}$
reaches 0.58. A larger value of
${\it\delta}$
may be obtained by further reducing
$d$
. We are thus able to provide a larger range of the buoyancy parameter
${\it\delta}$
to carry out a systematic study on the effects of buoyancy on bubble dynamics.
3. Bubble oscillation in an infinite liquid
We first consider bubble dynamics in an infinite liquid. For the first case, the ambient pressure
$p_{amb}$
at the initial centre of the bubble is 4.75 kPa. The maximum radius of the bubble,
$R_{m}$
, is 51.4 mm and the buoyancy parameter
${\it\delta}$
is calculated as 0.451.
Images of the bubble dynamics are shown in figure 2. The bubble remains approximately spherical until the end of expansion (frame 5). Then the lower bubble surface collapses faster due to buoyancy (frames 6–9) and an upward jet forms and develops rapidly (frames 9–10), penetrates the bubble and turns it into a toroidal shape (frame 10). Due to the large value of
${\it\delta}$
, the jet has a wide cross-section and forms early rather than near the end of collapse.
Figure 2. High-speed photographs of bubble oscillation in an infinite liquid with reduced air pressure,
$p_{amb}=4.75~\text{kPa}$
,
${\it\delta}=0.451$
. In this and subsequent figures, the frame number is marked at the top left corner of each frame, and the capture time (in ms) is marked in italic.
Figure 3 shows the details of jet development (frames 1–4). The jet impacts on the top of the bubble surface in frame 4. A layer of tiny bubbles appears at the impact location (frame 4). The tiny bubbles are probably generated due to instability at the interface between the jet and the bubble gas; as the jet continues to come out from the bubble top, more tiny bubbles are brought out of the toroidal bubble, see frames 6–9, and the cross-section of the toroidal bubble becomes thinner. A relatively larger cloud of tiny bubbles sits on the thin bubble ring at the end of collapse.
Figure 3. Formation and development of the jet and the completion of the first collapse phase of a bubble in an infinite liquid,
$p_{amb}=4.60~\text{kPa}$
,
${\it\delta}=0.473$
.
Returning to figure 2, the second oscillation of the bubble is depicted in frames 12–24. The ring bubble rebounds from frames 12–18. The expansion is pronounced in the upward direction and there is a major rise of the bubble’s geometry centroid. It is very interesting to notice that the cloud of tiny bubbles remains from frames 12–16, but disappears completely in frame 17. One possible reason for this is that the pressure of the large bubble becomes small enough around frame 16, and the tiny bubbles are all attracted and merged to it. From frame 18 the toroidal bubble starts to merge inside due to excessive expansion and returns to a singly connected form, since the jet inside the bubble appearing as the dark vertical shaft in frames 15–18 vanishes.
Then follows the second collapse, featured by a rapid rise of the bubble bottom which again turns into a re-entrant jet, see frames 19–24. This time the jet top is wide and flat since the bottom was flat. This is consistent with the computational result by Wang (Reference Wang2013) for bubble dynamics subject to buoyancy. As a result of this geometry, the jet impacts onto the lateral part of the contracting bubble rather than threading entirely through its interior; the bubble consequently splits into a hemispherical ‘cap’ and a torus, see frame 21. A cloud of tiny bubbles follows the jet. Both parts continue to collapse to minimum volumes in frame 24. In the third period, the cap and the torus expand with upward migration and then merge with each other. It is hard to identify through the rough bubble surface when or if the torus has regressed into a singly connected form. The cloud of tiny bubbles disappears once again when the bubble volume becomes large (frame 27).
The bubble motion features shown above are different from the free-field UNDEX bubbles in, for example, Klaseboer et al. (Reference Klaseboer, Hung, Wang, Wang, Khoo, Boyce, Debono and Charlier2005) and Hung & Hwangfu (Reference Hung and Hwangfu2010): the jet develops at an earlier stage rather than upon the completion of collapse and has a wider cross-section. This is likely to be a direct result of the large value of
${\it\delta}$
(0.451) compared with the values (0.200 and 0.119 respectively) in the two UNDEX experiments.
To verify the effects of buoyancy, two more cases are shown in figure 4, at similar
${\it\delta}$
values to the two UNDEX experiments. The bubble motion depicted in the first row of figure 4 is for
${\it\delta}=0.207$
. Compared with the case in figure 2 and 3, the bubble volume is smaller when the bubble bottom is flattened (frames 3–4) before the end of collapse, and the subsequent processes (possibly jet and toroidal bubble formation) take up a smaller portion of the first oscillation period. This has many similarities with the case in Klaseboer et al. (Reference Klaseboer, Hung, Wang, Wang, Khoo, Boyce, Debono and Charlier2005), with an UNDEX bubble in free field at
${\it\delta}=0.200$
. During the second expansion phase, a liquid jet threads through the bubble from bottom to top, appearing as the dark strip in frames 6–7.
Figure 4. Bubble oscillation in an infinite liquid for smaller
${\it\delta}$
values. First row:
$p_{amp}=9.75~\text{kPa}$
,
${\it\delta}=0.207$
; second row,
$p_{amb}=22.0~\text{kPa}$
,
${\it\delta}=0.112$
.
The bubble motion shown in the second row of figure 4 is for
${\it\delta}=0.112$
. The bubble remains spherical until shortly before the end of collapse at
$t=12.33~\text{ms}$
rather than being flattened. The jet becomes visible also in the second expansion (frame 6), but the protrusion it causes at the bubble top is sharper and more obvious than the case in the first row. The bubble behaviour including the protrusion here resembles that found with the UNDEX bubble in Hung & Hwangfu (Reference Hung and Hwangfu2010) at
${\it\delta}=0.119$
. The comparison between the bubble behaviours in figures 2–4 manifests the significant influence of the buoyancy parameter on bubble motion.
We now discuss some variation trends of some global quantities versus
${\it\delta}$
. First, the maximum jet velocity when the jet is threading through the bubble like in frames 1–4, figure 3 is measured at the jet tip. As shown in figure 5, the maximum dimensionless jet velocity
$v_{jet^{\ast }}$
decreases with
${\it\delta}$
.
Figure 5. The dimensionless maximum jet velocity
$v_{jet^{\ast }}$
versus the buoyancy parameter
${\it\delta}$
.
The dimensionless displacements of the top and bottom of a bubble surface in four cases are shown in figure 6(a). The top and bottom are defined as the highest and lowest points on the bubble surface; the dimensionless displacements are measured vertically from the initial bubble centre. Generally, the rise of the bottom is more obvious than the fall of the top in the collapse phases. In the second expansion, the top shoots upwards associated with jetting, while the bottom falls slightly but remains above zero (the initial bubble centre). More significant upward movements for the bubble top and bottom are seen for a larger buoyancy parameter, especially after the first period.
Figure 6. Time histories of (a) the dimensionless displacements of the top
$z_{top^{\ast }}$
and bottom
$z_{bttm^{\ast }}$
of a bubble surface for different
${\it\delta}$
values in an infinite liquid for the first two and a half periods and (b) the dimensionless velocity
$v_{bttm^{\ast }}$
at the bubble bottom for different values of
${\it\delta}$
.
Figure 6(b) shows the time history of the velocity of the bottom points during the first cycle of oscillation; the maximum velocity reached is smaller for larger
${\it\delta}$
values.
As shown in figure 7(a), no obvious jet is observed until the end of collapse for
${\it\delta}<0.2$
, but as
${\it\delta}$
increases, the time of jet initiation
$t_{jet^{\ast }}$
is advanced. Moreover, a bubble for larger
${\it\delta}$
exists longer in the fluid and hence is pushed further under buoyancy. Therefore, it is shown in figure 7(b) that the bubble centroid position at the end of the first oscillation becomes higher for a larger
${\it\delta}$
value. Figure 8(b) shows that the maximum radius
$R_{m2\ast }$
during the second cycle of oscillation increases with
${\it\delta}$
, implying that the energy loss at the end of collapse decreases with
${\it\delta}$
.
Figure 7. (a) The jet initiation time
$t_{jet^{\ast }}$
versus
${\it\delta}$
. Here,
$t_{jet^{\ast }}$
is the time scaled to the first period of oscillation, hence
$t_{jet^{\ast }}=1$
marks the end of collapse. The error bars mark the time span from when the bubble bottom is flattened to the time when the jet tip is first seen. (b) The displacement of the bubble centroid at the end of the first cycle,
$z_{cen^{\ast }}$
, versus
${\it\delta}$
.
Figure 8. (a) Variations of the dimensionless periods for the first three bubble oscillation cycles with
${\it\delta}$
. (b) Variations of the dimensionless second maximum radius
$R_{m2^{\ast }}$
with
${\it\delta}$
.
Figure 8(a) shows the variation of the dimensionless oscillation periods of the bubble with
${\it\delta}$
. The dimensionless first period increases to as much as 3.5 when
${\it\delta}$
falls below 0.2, and stays at approximately 2.1 when
${\it\delta}$
grows to over 0.2. This deviates from the dimensionless periods of inertial bubbles, i.e. cavitation bubbles and UNDEX bubbles, which usually approach two times the Rayleigh time (i.e. 2.18 with the current normalization) when the gravity effect is less important and become less than that when the buoyancy parameter increases. The reasons could be that, when the energy discharged is high and the ambient pressure is low, the bubble dynamics deviates from the Rayleigh–Plesset equations and heat transfer equations need to be taken into account (Gibson Reference Gibson1972).
4. Bubble collapse near a free surface
A small collapsing bubble developing a jet away from a free surface is a well-known phenomenon where the Bjerknes force dominates. Nevertheless, there are few experimental observations in the literature for a collapsing bubble with a jet towards a free surface, even though it is bound to happen when the buoyancy effect is large enough. In this section, jets are seen to develop towards or even penetrate the free surface under large
${\it\delta}$
. Moreover, special bubble behaviours are observed when the Bjerknes and buoyancy forces are balanced.
4.1. Bubble collapse with jet towards the free surface
The first case considered is for a relatively large value of
${\it\delta}$
, where
${\it\delta}=0.781$
and
${\it\gamma}_{f}=1.53$
. The bubble is initiated at a small water depth (95.8 mm) with the ambient pressure
$p_{amb}=3.24~\text{kPa}$
. It reaches a maximum radius of 62.6 mm (frame 2), thus the hydrostatic pressure at the bottom of the bubble, 3.9 kPa, is 40 % more than that at the top, 2.8 kPa. The large pressure gradient over the vertical span of the bubble results in a very early involution of the lower boundary (frame 3 and onwards), and a broad buoyancy jet forms. The jet development, the collapse and the early second expansion phase all resemble those of a bubble in an infinite fluid (compare the bubble shape in frames 2–7, figure 9 to that in frames 4–18, figure 2), but due to the existence of the free surface, the bubble top is slightly flattened and the centroid migration
$z_{cen^{\ast }}$
is smaller despite the fact that
${\it\delta}$
is larger. Numerical calculation shows that the maximum pressure occurs near the lower bubble boundary at similar
${\it\delta}$
, see Blake & Gibson (Reference Blake and Gibson1987) and Blake, Taib & Doherty (Reference Blake, Taib and Doherty1987), rather than between free surface and the bubble top.
Figure 9. Bubble motion with a jet towards a free surface for larger
${\it\delta}$
:
${\it\delta}=0.781$
,
${\it\gamma}_{f}=1.53$
.
During the second bubble expansion from frame 7, buoyancy and the jet motion contribute to the rapid upward migration of the bubble, causing a hump at the free surface; in the following collapse phase, the bubble bottom rises and lifts the entire bubble over the static water surface. After reaching a second minimum (frame 11), the bubble expands for the third time, in the form of splashing over the static water surface (frame 12).
Another case with an upward jet is illustrated in figure 10 for a relatively small value of
${\it\delta}$
, where
${\it\delta}=0.281$
and
${\it\gamma}_{f}=2.05$
. The buoyancy force prevails over the Bjerknes force again in this case. The bubble is pushed by buoyancy from below and pressed by the Bjerknes force from the free surface, and hence takes an oval shape towards the end of collapse. A high-speed liquid jet is initiated towards the free surface at the very end of collapse (frame 8); in the subsequent re-expansion, the bubble becomes toroidal with a protrusion at its upper boundary due to the jet. The jet is seen to be threading through the bubble as a dark vertical shaft inside the bubble in frame 12, with a very small cross-section. As the expansion continues, the protrusion dissolves. The bubble then goes through re-collapse and re-expansion for several cycles before finally breaking up. The current case resembles the second row in figure 3; however, here the bubble centroid migration
$z_{cen^{\ast }}$
is approximately 0.24 for
${\it\delta}=0.281$
, while in an infinite liquid
$z_{cen^{\ast }}$
should be approximately 0.4 for the same
${\it\delta}$
according to figure 7(b). This implies that the effect from the free surface is still obvious and repels the bubble.
Figure 10. Bubble motion with a jet towards a free surface for smaller
${\it\delta}$
:
${\it\delta}=0.281$
,
${\it\gamma}_{f}=2.05$
.
4.2. Bubble collapse with jet repelling from the free surface
A bubble with a relatively large value of
${\it\delta}$
still jets away from the free surface when
${\it\gamma}_{f}$
is sufficiently small. Five such cases (a–e) with
${\it\gamma}_{f}$
ranging from 0.62 to 0.97 are displayed in figures 11–12 at the same level of buoyancy,
${\it\delta}=0.40{-}0.42$
. In the first three cases, shown by figure 11,
${\it\gamma}_{f}$
is 0.62, 0.73 and 0.84 respectively. The bubble top exceeds the static water surface (see frame 1) and then forms a re-entrant jet that penetrates the bubble (frames 2–3). The jet causes a protrusion on the bubble bottom which then breaks off into an independent pulsating torus (frames 3–5). Frame 5 shows the minimum of the bubble in each case and frames 6–7 re-expansion. With the increase of
${\it\gamma}_{f}$
, the jet becomes broader and the protrusion smaller. The scenarios in figure 11 are close to that in atmospheric pressure experiments and numerical studies, see for example figure 5(a) in Pearson et al. (Reference Pearson, Cox, Blake and Otto2004) and figure 13 in Zhang & Liu (Reference Zhang and Liu2015), despite the relatively large
${\it\delta}$
and bubble sizes.
Figure 11. Bubbles with jets repelling from a free surface; seven frames are shown for each case. The value of
${\it\gamma}_{f}$
increases, being (a) 0.62, (b) 0.73 and (c) 0.84, at approximately the same value of
${\it\delta}$
between 0.40 and 0.42.
Figure 12. Bubbles with jets repelling from a free surface, with
${\it\gamma}_{f}$
increased to (d) 0.90 and (e) 0.97;
${\it\delta}$
remains within the range 0.40–0.42. Eight frames are shown for each case.
In the other two cases, shown in figure 12, the effects of the free surface are further weakened with
${\it\gamma}_{f}$
increased to 0.90 and 0.97; The jet velocity is reduced and the curvature at the jet tip becomes smaller and closer to that at the bubble bottom (frames 3–4). Therefore, when the jet impacts the bubble bottom, the protrusion as in figure 11 does not form. The toroidal bubble then collapses to a minimum (frames 5–6) and rebounds (frames 7–8).
4.3. Neutral bubble collapse
When the buoyancy and Bjerknes forces are of similar amplitudes but opposite directions, the bubble may no longer develop a jet that moves in one direction during the first collapse phase. This situation is referred to as the ‘neutral collapse’.
We noticed two types of neutral collapse behaviours for the bubble near the free surface. Figure 13 illustrates the first type, featured by bubble splitting, with a small value of
${\it\delta}$
(0.248), a medium value of
${\it\gamma}_{f}$
(1.74) and
${\it\delta}{\it\gamma}_{f}=0.432$
. The top and bottom of the bubble surface start to become more flat during the middle stage of collapse (frame 3) and the bubble then assumes an oval shape near the end of collapse (frame 4). However, at the very end of the collapse phase, violent contraction is found with the lateral part of the oval rather than the less curved top or bottom. The mechanism could be that the bubble surface with larger curvature collapses faster according to a proportional relationship between radius and Rayleigh collapse time Lauterborn (Reference Lauterborn1982). This results in the bubble splitting into two parts from its middle (frames 7–9). The liquid flowing in from sideways during the split then comes out from the top of the upper part and the bottom of the lower part; therefore a jet forms that threads through each part and causes a protrusion on the distal side of each part (frames 10–12). Later, the two parts coalesce in frames 13–15 and an integrated bubble is recovered.
Figure 13. Neutral bubble collapse with opposite jets near a free surface for smaller
${\it\delta}$
:
${\it\delta}=0.281$
,
${\it\gamma}_{f}=1.74$
,
$p_{amb}=7.42~\text{kPa}$
. Frames 6–10 are magnified to show the details.
During the subsequent collapse phase, the top and bottom parts of the bubble collapse with faster speed (frames 15–16). Presumably, two re-entrant jets are formed from both the top and the bottom and are directed towards each other, before the bubble collapses to the minimum volume (frames 16–17).
Figure 14 illustrates the second type of neutral collapse, with
${\it\delta}$
increased to 0.515 and
${\it\gamma}_{f}$
reduced to 1.17. Equilibrium between the stronger Bjerknes and buoyancy forces is achieved. Here,
$R_{m}$
reaches 53.6 mm. The proximity of the free surface causes the bubble top to repel; meanwhile, larger buoyancy pushes the bubble bottom. Therefore, the bubble assumes the shape of a red blood cell with the top and bottom surfaces becoming concave during the collapse phase (frames 5–6). In frames 6–7, the top and bottom are likely to be channelled and the bubble may turn into a ring.
Figure 14. Neutral bubble collapse with the shape of a red blood cell near a free surface for larger
${\it\delta}$
:
${\it\delta}=0.515$
,
${\it\gamma}_{f}=1.17$
,
$p_{amb}=4.32~\text{kPa}$
.
The bubble collapses to its minimum volume immediately afterwards in frame 7 and re-expands with a rough surface, see frame 8 and onwards. Subsequent collapses are no longer neutral but buoyancy is prominent, causing the bubble behaviour to resemble that of the second period in figure 2. Finally, the bubble bursts at the water surface during its third expansion (frames 13–14). Similar bubble shapes were simulated in Wang et al. (Reference Wang, Yeo, Khoo and Lam1996b ) to the end of the first collapse.
4.4. Bubble bursting at the free surface
The bubble may burst and channel to the air if initiated close enough to the free surface. With the strong buoyancy effect in the current experiment, a liquid jet is found to rise from the bubble bottom after the burst. A representative result is shown in figure 15 with the bubble initiated at a water depth of 5 mm. The liquid veneer between the bubble and the free surface is almost immediately ruptured (frame 1) after bubble initiation; a film of liquid is catapulted into the air from the circular rim where the bubble and the free surface intersect (frame 1 and onwards). The lower half of the bubble boundary continues expanding into a semispherical shape with inertia until frame 3. As the expansion continues, the liquid pressure at the bubble bottom increases due to increased water depth, and as a result, the bottom becomes flattened (frames 4–5); liquid flow then concentrates at the bottom and turns into a broad jet shooting upward (frames 6–8). The jet is conical with a round top and steadily rises with inertia to a height larger than the maximum depth of the lower bubble boundary. The formation of the jet is mainly a result of the large pressure gradient rather than the collapse of liquid, as reflected in the simulation by Boulton-Stone & Blake (Reference Boulton-Stone and Blake1993), since the bottom part of the bubble crater rises earlier than the lateral part. The jet recedes after frame 8 where a maximum height of 70.8 mm is reached.
Figure 15. Bubble bursting at a free surface for
$p_{amb}=4.75~\text{kPa}$
,
$R_{m}=37.3~\text{mm}$
and hence
${\it\gamma}_{f}=0.134$
,
${\it\delta}=0.389$
.
4.5. Criterion for jet directions
The morphologies demonstrated in the above experimental cases are summarized in figure 16, according to their
${\it\gamma}_{f}$
and
${\it\delta}$
values. Some additional cases are included in the figure, for which the images are not presented. It is clear that the cases with jets attracted to the free surface and those with jets repelled from it in the first collapse phase take up independent regions that are separated by the cases with neutral collapse (marked by crosses), such as in figures 13–14. To anticipate the position of other cases of the same kind, an exponential curve (solid line) is fitted with the existing neutral collapse cases using the least-squares method as follows:
$$\begin{eqnarray}{\it\delta}=\exp (0.33{{\it\gamma}_{f}}^{2}-2.0{\it\gamma}_{f}+1.1).\end{eqnarray}$$
The curve also suggests a criterion for jet direction. For comparison purposes the figure also provides the criterion (dashed line),
${\it\delta}{\it\gamma}_{f}\approx 0.442$
, obtained by Blake, Taib & Doherty (Reference Blake, Taib and Doherty1986) based on the point-source approximation for spherical bubbles and the method of image. The criterion of Blake et al. (Reference Blake, Taib and Doherty1986) correlates well with our criterion based on the experiments. A discrepancy is observed between them when the bubble is close to the free surface (
${\it\gamma}_{f}<1.75$
); a larger buoyancy parameter is needed for the jet to be directed towards the free surface in our criterion. This is expected, since the point-source solution and the method of image are valid only when the bubble is approximately spherical and the deformation of the free surface is small.
Figure 16. The criterion for the neutral collapse of a bubble near a free surface in terms of the buoyancy parameter
${\it\delta}$
and the dimensionless standoff
${\it\gamma}_{f}$
, obtained based on the present experimental data, compared with the criterion of Blake et al. (Reference Blake, Taib and Doherty1987). Collapse patterns: upward jet, downward jet and neutral state are displayed for the present data, the experimental data of Blake & Gibson (Reference Blake and Gibson1981), Blake et al. (Reference Blake, Taib and Doherty1987), Chahine (Reference Chahine1977), Hung & Hwangfu (Reference Hung and Hwangfu2010) and the BIM results of Wang et al. (Reference Wang, Yeo, Khoo and Lam1996b
).
Our criterion is consistent with the experiment results of Blake et al. (Reference Blake, Taib and Doherty1987). Cases with jets directed away from the free surface in the experiments of Chahine (Reference Chahine1977) and Blake & Gibson (Reference Blake and Gibson1981), as well as the UNDEX case in Hung & Hwangfu (Reference Hung and Hwangfu2010), also fit in the downward jet region. The numerical results of Wang et al. (Reference Wang, Yeo, Khoo and Lam1996a
,Reference Wang, Yeo, Khoo and Lam
b
) and Wang (Reference Wang2004) using the boundary integral method (BIM) do not agree with the criterion of Blake et al. but agree with our criterion: the near-null impulse cases in Wang et al. (Reference Wang, Yeo, Khoo and Lam1996a
) with opposite jets fall close to the neutral collapse curve in figure 16; the case (
${\it\gamma}_{f}=1$
,
${\it\delta}=0.5$
) jetting away from the free surface exceeds
${\it\delta}{\it\gamma}_{f}\approx 0.442$
but is still inside the downward jet region given by the current result.
5. Bubble dynamics above a rigid plane
In the following experiments, the bubble is initiated above a horizontal rigid wall and thus the Bjerknes force is directed opposite to the buoyancy force. Chahine (Reference Chahine1997) photographed a spark bubble splitting above a rigid wall for
${\it\gamma}_{w}<1$
and
${\it\delta}=1.51$
. We will carry out a systematic parametric study for this phenomenon in terms of the buoyancy parameter
${\it\delta}$
and dimensionless standoff distance
${\it\gamma}_{w}$
.
5.1. Bubble with jet directed away from the wall
Figure 17 demonstrates the example where the buoyancy force marginally dominates the Bjerknes attraction towards the rigid wall. The bubble is initiated at
${\it\gamma}_{w}=1.23$
. Here,
${\it\delta}$
is calculated to be 0.435, similar to that in figure 2.
Figure 17. Bubble dynamics near a rigid wall with a jet away from the wall for
${\it\delta}=0.435$
,
${\it\gamma}_{w}=1.23$
,
$p_{amb}=5.01~\text{kPa}$
.
The bubble expands approximately spherically (frames 1–2). In the collapse phase, the bottom of the bubble surface is attracted by the Bjerknes force while the rest of the bubble surface rises due to buoyancy. As a result, the bubble is deformed into a bulb shape in the early collapse phase (frame 3). In subsequent frames (3–6), the liquid at the bubble bottom becomes less retarded by the wall as the bubble migrates away; the bottom thus accelerates and involutes into a jet that is catapulted through the bubble, which can be clearly observed in frames 5–7. The faster collapse due to a larger curvature at the bubble bottom may account for the jet for being faster and narrower than in figure 2.
A toroidal bubble is formed when the jet collides with the upper bubble boundary. In the collision a portion of the bubble’s contents is dragged along with the jet, forming a protrusion above the bubble top. The protrusion then splits from the main part and becomes another toroidal bubble (see frames 8–9). This phenomenon is observed when the jet is sharp, for example in figure 11. Both toroidal bubbles continue to collapse and re-expand while migrating upwards. The lower toroidal bubble reaches the minimum volume at frame 9 and the upper one at frame 10. The two bubbles merge shortly before reaching their maximum volumes during the second expansion phase (see frames 12–13). The merged bubble continues to rise under buoyancy.
5.2. Bubble collapse onto the wall
The case with a marginal advantage of the Bjerknes force over the buoyancy force is illustrated in figure 18, with
${\it\gamma}_{w}=0.69$
,
${\it\delta}=0.281$
. The bubble collapses onto the wall at the end of collapse but some deformations are seen that are different from previous works with weak buoyancy effects.
Figure 18. Bubble collapse onto a rigid wall for
${\it\delta}=0.281$
and
${\it\gamma}_{w}=0.69$
,
$p_{amb}=7.31~\text{kPa}$
.
The bubble bottom is flattened during the middle stage of the expansion phase and is almost in contact with the rigid surface, leaving only a liquid veneer in between. In the earlier collapse phase (see frames 4–6), one may find the upper part of the bubble to lag behind when compared with results with insignificant buoyancy effects, for example figure 2(g,h) in Philipp & Lauterborn (Reference Philipp and Lauterborn1998). Therefore, the top becomes a protuberance on the bubble surface (frames 6–8). Besides, the inward flow is retarded near the wall, thus the bubble assumes a conical shape (frames 7–8). In later collapse stages, the bubble top crushes very rapidly due to its large curvature, and turns into a re-entrant jet that has a speed of over
$150~\text{m}~\text{s}^{-1}$
. This jet impacts onto the rigid wall (frames 11–13), and then splashes and corrupts the surface of the remaining part of the bubble. After that the bubble continues to collapses on the solid surface. Some remnant bubbles are left above the bubble after the crush.
5.3. Bubble split
A match of the buoyancy and Bjerknes forces is obtained in the case shown by figure 19, where
${\it\delta}=0.352$
,
${\it\gamma}_{w}=1.03$
. In the earlier collapse phase, the bottom is retarded and the bubble is prolonged (frames 4–6) similarly to the case in figure 17. However, in the later collapse phase the attraction towards the wall appears to be larger than in figure 17 and the bottom hardly rises, while the buoyancy effects are stronger than the case in figure 18 and the receding of the bubble top is less pronounced. Therefore, the whole bubble collapses in the middle and splits into two parts, see frames 7–9. The ‘tails’ of the two parts (i.e. the bottom of the upper part and the top of the lower part) recede rapidly as a result of the inward radial flow, leaving a trace of tiny bubbles along the vertical axis (see frame 10 and onwards). The fact that the ‘tails’ collapse faster than other areas of the bubble surfaces is also a result of higher local curvature. Two jets are formed subsequently associated with the two tails. The upward jet for the upper part is visible at the vertical axis of the re-expanding upper bubble in frame 17. The jet for the lower part is towards the rigid wall. The jet penetrates the lower bubble before it reaches the minimum volume and causes a protrusion on the bubble bottom, see frames 12–15. The collapse of the lower part completes in frame 16.
Figure 19. Bubble split above a rigid boundary for
${\it\delta}=0.352$
,
${\it\gamma}_{w}=1.03$
and
$p_{amb}=6.30~\text{kPa}$
.
The subsequent oscillation of the upper bubble is dominated by buoyancy, rising up and possibly forming an upward jet. However, the lower part is dominated by the Bjerknes force due to the rigid boundary. It migrates towards the wall, becomes flattened by the wall during the middle of the expansion phase and collapses to the wall subsequently.
The bubble shape in figure 19 is in good agreement with the computational results in Brujan, Pearson & Blake (Reference Brujan, Pearson and Blake2005) which had a very similar configuration (
${\it\delta}=0.352$
,
${\it\gamma}_{w}=1.0$
), however the computation stopped before the split.
5.4. Criterion for jet directions
Collapse patterns for a transient bubble above a rigid wall in terms of the buoyancy parameter
${\it\delta}$
and the dimensionless standoff
${\it\gamma}_{w}$
are displayed in figure 20 for the present data and the BIM results of Blake et al. (Reference Blake, Taib and Doherty1986), Best & Kucera (Reference Best and Kucera1992), Wang (Reference Wang1998) and Brujan et al. (Reference Brujan, Pearson and Blake2005). The behaviours are found to fall into three regions: upward jet, downward jet and neutral collapse.
Figure 20. The criterion for the neutral collapse of a bubble above a rigid boundary in terms of the buoyancy parameter
${\it\delta}$
and the dimensionless standoff
${\it\gamma}_{w}$
, obtained based on the present experimental data, compared with the criterion of Blake et al. (Reference Blake, Taib and Doherty1986). Collapse patterns of upward jet, downward jet and neutral collapse are displayed for the present data and the BIM results of Blake et al. (Reference Blake, Taib and Doherty1986), Best & Kucera (Reference Best and Kucera1992), Wang (Reference Wang1998) and Brujan et al. (Reference Brujan, Pearson and Blake2005).
The cases associated with upward jets like that in figure 17 occur in the upper-right part of the figure where either
${\it\gamma}_{w}$
or
${\it\delta}$
is large; the cases associated with downward jets like that in figure 18 occur on the lower-left side where either
${\it\delta}$
or
${\it\gamma}_{w}$
is small and
${\it\delta}<0.36$
. The neutral collapse region is between the above two regions. For larger
${\it\delta}~({\it\delta}>0.22)$
, the neutral collapse ends up with the bubble splitting into two parts; for smaller
${\it\delta}$
, the neutral collapse ends up with neither jet nor split and the bubble collapses spherically.
The splitting cases generating two parts with approximately equal volumes are marked by boxes as the ‘neutral splitting’ cases, where a balance between buoyancy and Bjerknes forces can be expected. An exponential curve (solid line) is fitted to these cases and the spherical collapse cases with the least-squares method as
$$\begin{eqnarray}{\it\delta}=\exp (0.09{{\it\gamma}_{f}}^{2}+0.9{\it\gamma}_{f}-0.2).\end{eqnarray}$$
This curve is below the dashed line representing the null impulse criterion by Blake et al. (Reference Blake, Taib and Doherty1986). Besides those mentioned in § 4.5, another explanation for this deviation may be that the bubble is slightly pushed away by the solid wall from its initial centre during expansion, so the Bjerknes effect, and hence the buoyancy required to neutralize it, is reduced.
The experimental results show good agreement with previous numerical results. The null final Kelvin impulse state cases found by Brujan et al. (Reference Brujan, Pearson and Blake2005) with the BIM are marked by dots in figure 20; they align with the current neutral splitting and spherical collapse cases. The neutral splitting bubble profile given by Brujan et al. is verified by the current experiment (figure 19). Besides, the neutral collapse cases in Best & Kucera (Reference Best and Kucera1992) marked by plus signs also appear to be close to the neutral curve of this work. Best et al. also gave BIM results for one-sided jets; these cases are found to fall into the regions of the same jet direction suggested by the current experimental results. Moreover, bulb-shaped bubbles as numerically simulated by Blake & Gibson (Reference Blake and Gibson1987) and Wang (Reference Wang1998) where either the Bjerknes or the buoyancy force marginally dominated appear close to the boundary (dotted line) between the splitting region and the jetting regions. Other experimental results from Hooton et al. (Reference Hooton, Blake, Soh, Blake, Boulton-Stone and Thomas1994) and Harvey et al. (Reference Harvey, Best and Soh1996) featuring a jet towards the rigid bottom are found in the downward jet region.
6. Summary and conclusions
This paper is concerned with bubble dynamics subject to buoyancy, which are associated with applications for underwater explosion. The bubble is produced by electric discharge in a low-pressure tank to enhance the buoyancy effects. Experiments are carried out for a bubble in an infinite field, below a free surface and above a rigid boundary.
We carried out a systematic study for a large range of
${\it\delta}$
from 0.034 to 0.95 for bubbles near boundaries by controlling the ambient pressure. The bubble in our experiment was transparent. We were thus able to display and study the jet formation, development and impact on the opposite bubble surface as well as the subsequent collapsing and rebounding of the ring bubble. We also display and analyse the split of a bubble or bubble ring into two parts and the subsequent joining. A series of new phenomena and new features observed in our experiment may be summarized as follows.
For a collapsing bubble in an infinite liquid with strong buoyancy (
${\it\delta}=0.451$
), a broad conical jet forms and turns the bubble into a toroidal shape during the middle stage. The toroidal bubble collapses into a cloud of tiny bubbles presumably due to the instability at the jet surface. The bubble breaks up during the second collapse and merges during the third expansion. With increase of
${\it\delta}$
, the dimensionless jet velocity decreases, the dimensionless maximum bubble radius during the second cycle increases, the dimensionless periods of the second and third cycles of oscillation are prolonged and the jet is initiated at an earlier stage during the collapse phase; also, the upward migration of the bubble is noticeably increased.
For a bubble oscillating near the free surface, three types of behaviour were analysed: (i) bubble collapse with a jet away from the free surface when the Bjerknes force dominates; (ii) bubble collapse with a jet towards the free surface when the buoyancy force dominates; (iii) neutral collapse without forming a one-sided jet when the buoyancy and Bjerknes forces are balanced. For case (iii), two subcases are found. One is that the bubble may split into two at the very end of collapse, each with a jet away from the original bubble centre; the other is that the bubble may involute from both top and bottom to form a red blood cell shape. The latter subcase requires larger
${\it\delta}$
. Based on our experiment, a criterion in terms of
${\it\delta}$
and
${\it\gamma}_{f}$
is provided based on the cases in (iii), and distinguishes the three types of behaviour. The criterion has a discrepancy with that of Blake et al. (Reference Blake, Taib and Doherty1986), but is more consistent with previous experimental and computational results.
For a bubble oscillating above a horizontal rigid wall, three types of behaviour were also analysed: (i) bubble collapse with a jet away from the wall when the buoyancy force is dominant; (ii) bubble collapse with a jet towards the wall when the Bjerknes force dominates; (iii) neutral collapse without forming a one-sided jet. Based on the experimental results, three regions are marked out on the
${\it\delta}{-}{\it\gamma}_{w}$
space corresponding to the three types of behaviour. Case (iii) comprises two subcases. In the first the bubble develops neither a jet nor a split, and this occurs for small
${\it\delta}$
; in the second the bubble will split into two parts at the end of collapse. We provided a criterion indicating a null Kelvin impulse state based on the
${\it\delta}$
and
${\it\gamma}_{w}$
of the cases with neither split nor jet and the cases where the bubble split into two parts with approximately the same volume.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (51222904, 51379039) and the National Program for Support of Top-notch Young Professionals. The authors are grateful for the considerable help from Dr S. P. Wang of the College of Shipbuilding Engineering, Harbin Engineering University.
