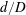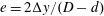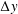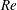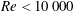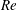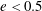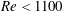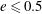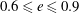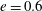1. Introduction
The present article is an extension of Choueiri & Tavoularis (Reference Choueiri and Tavoularis2014), hereafter referred to as Part 1, which contains additional details about the motivation and objectives of this work. For the present purposes, flows in eccentric annular channels are investigated as paradigms of flows in compound channels containing relatively open subchannels, inter-connected through narrow gaps; compound channels include nuclear reactor rod-bundles, double-pipe heat exchangers, inundated rivers, catheterized arteries and other technological and natural systems. Under certain conditions, flows in such channels are prone to a particular type of instability, recently termed ‘gap instability’ (Tavoularis Reference Tavoularis2011), which may lead to the formation of gap vortex streets, each consisting of pairs of staggered vortices of alternating direction forming on either side of the narrow gap, in a manner that is analogous in some ways to the von Kármán vortex street. These vortices induce strong cross-gap flow pulsations, which greatly enhance inter-subchannel mixing and cross-gap momentum, mass and heat transfer.
In Part 1, we documented in detail the gap instability and vortex generation and evolution mechanisms for a representative annular geometry and for one set of conditions. In particular, we examined flow in an annular channel with a diameter ratio of 0.50 and an eccentricity of 0.80 at a Reynolds number of 7300. While discussing these results, we elucidated the essential physical phenomena of interest, but we also acknowledged that the flow patterns in complex channels would depend on the geometry, inlet conditions and Reynolds number. The experimental determination of these effects is the objective of the work presented in this Part 2.
As far as fully developed flow in annular channels is concerned, geometry is defined by two parameters, the inner-to-outer diameter ratio
![]() $d/D$
and the eccentricity
$d/D$
and the eccentricity
![]() $e$
. In rod bundles, important geometrical parameters are the shape of the rod array, the rod pitch-to-diameter ratio
$e$
. In rod bundles, important geometrical parameters are the shape of the rod array, the rod pitch-to-diameter ratio
![]() $p/d$
and the wall pitch-to-diameter ratio
$p/d$
and the wall pitch-to-diameter ratio
![]() $w/d$
, where
$w/d$
, where
![]() $w$
is the sum of the rod diameter and the gap between the rod and an adjacent duct wall. Gap vortices in rod bundles are known to appear and form a network (Tavoularis Reference Tavoularis2011), but only for relatively small
$w$
is the sum of the rod diameter and the gap between the rod and an adjacent duct wall. Gap vortices in rod bundles are known to appear and form a network (Tavoularis Reference Tavoularis2011), but only for relatively small
![]() $p/d$
, typically
$p/d$
, typically
![]() $p/d<1.2$
(Meyer Reference Meyer2010), whereas whenever
$p/d<1.2$
(Meyer Reference Meyer2010), whereas whenever
![]() $p/d$
was sufficiently large, the effects of such vortices were not measurable (Rowe, Johnson & Knudsen Reference Rowe, Johnson and Knudsen1974; Hooper & Rehme Reference Hooper and Rehme1984; Guellouz & Tavoularis Reference Guellouz and Tavoularis2000). It is also well known that inter-subchannel mixing and heat transfer become stronger as
$p/d$
was sufficiently large, the effects of such vortices were not measurable (Rowe, Johnson & Knudsen Reference Rowe, Johnson and Knudsen1974; Hooper & Rehme Reference Hooper and Rehme1984; Guellouz & Tavoularis Reference Guellouz and Tavoularis2000). It is also well known that inter-subchannel mixing and heat transfer become stronger as
![]() $p/d$
decreases within a certain range but are weakened again when the gap size is reduced below a very small threshold (Hooper Reference Hooper1983, Reference Hooper1984; Hooper & Wood Reference Hooper and Wood1984; Rehme Reference Rehme1987, Reference Rehme1989; Baratto, Bailey & Tavoularis Reference Baratto, Bailey and Tavoularis2006; Chang & Tavoularis Reference Chang and Tavoularis2008). The frequency of cross-gap flow pulsations has also been correlated with the gap size and
$p/d$
decreases within a certain range but are weakened again when the gap size is reduced below a very small threshold (Hooper Reference Hooper1983, Reference Hooper1984; Hooper & Wood Reference Hooper and Wood1984; Rehme Reference Rehme1987, Reference Rehme1989; Baratto, Bailey & Tavoularis Reference Baratto, Bailey and Tavoularis2006; Chang & Tavoularis Reference Chang and Tavoularis2008). The frequency of cross-gap flow pulsations has also been correlated with the gap size and
![]() $p/d$
(Tapucu & Merilo Reference Tapucu and Merilo1977; Möller Reference Möller1991; Wu & Trupp Reference Wu and Trupp1993).
$p/d$
(Tapucu & Merilo Reference Tapucu and Merilo1977; Möller Reference Möller1991; Wu & Trupp Reference Wu and Trupp1993).
For a given compound channel geometry, the Reynolds number is expected to play an important role, as it affects all processes that are at work simultaneously, namely flow development starting from the channel inlet, flow instability, transition to turbulence, mixing and vortex interactions. A second factor, whose effect is intimately coupled with the Reynolds number effect, is the level and type of disturbances to the flow as it enters the channel as well as while it flows in it. By analogy with the much simpler flows in circular pipes, one would anticipate that, at least within a certain distance from the inlet and within a certain range of Reynolds numbers, flow patterns in complex channels would be largely determined by inlet conditions and Reynolds number effects. At the same time, one may also apply insight gained for pipe flows to speculate that, far from the inlet and for sufficiently large Reynolds numbers, the flow structure in complex channels may be fairly insensitive to such effects and depend only on the geometry. A conclusive resolution of these issues can only be based on reliable experimental results under well-planned conditions. Our goal is to contribute to this effort by focusing on eccentric annular channels as representative of more complex compound channels. The present work shares some goals with two previous studies in eccentric annular channels (Gosset & Tavoularis Reference Gosset and Tavoularis2006; Piot & Tavoularis Reference Piot and Tavoularis2011), but, unlike them, it is quantitative, it extends over much wider ranges of parameters and, besides the Reynolds number effect, it also addresses the inlet conditions effect.
In this article, we will examine the dependence of flow development and flow structure in eccentric annular channels on four key factors: inlet conditions, inner-to-outer diameter ratio, eccentricity and Reynolds number. To quantify this dependence, we will compare measurements of some sensitive indicators under different conditions, with the objective of isolating the influence of each of these four factors from other effects. Tests with many combinations of values of these four factors will be examined within the following ranges: three representative sets of inlet conditions, distinguished by the effectiveness of flow management in the inlet tank; three inner-to-outer diameter ratios, namely
![]() $d/D=0.25$
, 0.50 and 0.75; a full range of eccentricities, from 0 to 0.90; and Reynolds numbers from 0 to 19 000, which are expected to span the laminar, transitional and turbulent ranges. It is hoped that the present measurements and their analysis will enhance our understanding of the phenomena of gap instability and gap vortex streets in complex channels and their dependence on geometric and dynamic conditions. They are also meant to form a substantial database for the testing of analytical models and numerical investigations.
$d/D=0.25$
, 0.50 and 0.75; a full range of eccentricities, from 0 to 0.90; and Reynolds numbers from 0 to 19 000, which are expected to span the laminar, transitional and turbulent ranges. It is hoped that the present measurements and their analysis will enhance our understanding of the phenomena of gap instability and gap vortex streets in complex channels and their dependence on geometric and dynamic conditions. They are also meant to form a substantial database for the testing of analytical models and numerical investigations.

Figure 1. Sketch of the apparatus.
2. Experimental facility, instrumentation and procedures
The recirculating flow loop used in these experiments, the instrumentation used for the measurements, the measurement methodology and the measurement uncertainties have been described in Part 1, so only a summary and information unavailable in Part 1 will be presented here. Sketches showing the apparatus and the annular geometry with definitions of coordinates are presented in figures 1 and 2, respectively. The annular test section had a length of
![]() $L=1478~\text{mm}$
and consisted of two parts: an outer channel, machined and polished from acrylic blocks to a square outer surface with sides equal to 60.5 mm and a cylindrical inner surface with a diameter
$L=1478~\text{mm}$
and consisted of two parts: an outer channel, machined and polished from acrylic blocks to a square outer surface with sides equal to 60.5 mm and a cylindrical inner surface with a diameter
![]() $D=50.8~\text{mm}$
; and one of three interchangeable cores, which were cast acrylic rods with diameters
$D=50.8~\text{mm}$
; and one of three interchangeable cores, which were cast acrylic rods with diameters
![]() $d=12.7$
, 25.1 and 38.1 mm, respectively. An aqueous solution of ammonium thiocyanate (
$d=12.7$
, 25.1 and 38.1 mm, respectively. An aqueous solution of ammonium thiocyanate (
![]() $\text{NH}_{4}\text{SCN}$
), with a refractive index that matched that of the acrylic test section, was recirculated in the loop with the use of a magnetically-driven pump. When a core rod was in place, it was suspended at its two ends on horizontal traverses that were mounted inside the inlet and outlet tanks, away from the test section ends. Thus, the annular test section had three possible diameter ratio configurations, with
$\text{NH}_{4}\text{SCN}$
), with a refractive index that matched that of the acrylic test section, was recirculated in the loop with the use of a magnetically-driven pump. When a core rod was in place, it was suspended at its two ends on horizontal traverses that were mounted inside the inlet and outlet tanks, away from the test section ends. Thus, the annular test section had three possible diameter ratio configurations, with
![]() $d/D\approx 0.25$
, 0.50 and 0.75, corresponding to the hydraulic diameters
$d/D\approx 0.25$
, 0.50 and 0.75, corresponding to the hydraulic diameters
![]() $D_{h}=D-d=38.1$
, 25.7 and 12.7 mm, respectively, and dimensionless lengths
$D_{h}=D-d=38.1$
, 25.7 and 12.7 mm, respectively, and dimensionless lengths
![]() $L/D_{h}=38.8$
, 57.5 and 116.4. The eccentricity, defined as
$L/D_{h}=38.8$
, 57.5 and 116.4. The eccentricity, defined as
![]() $e=2{\rm\Delta}y/(D-d)$
, where
$e=2{\rm\Delta}y/(D-d)$
, where
![]() ${\rm\Delta}y$
is the distance between the axes of the inner and outer cylinders, was adjusted to each selected value at three positions along the test section length. The uncertainty in
${\rm\Delta}y$
is the distance between the axes of the inner and outer cylinders, was adjusted to each selected value at three positions along the test section length. The uncertainty in
![]() ${\rm\Delta}y$
was 0.5 mm, from which one can estimate the eccentricity uncertainty as 0.04. An alternative geometrical parameter is the actual gap size
${\rm\Delta}y$
was 0.5 mm, from which one can estimate the eccentricity uncertainty as 0.04. An alternative geometrical parameter is the actual gap size
![]() ${\it\delta}$
, related to the eccentricity as
${\it\delta}$
, related to the eccentricity as
![]() ${\it\delta}=(1-e)(D-d)/2$
.
${\it\delta}=(1-e)(D-d)/2$
.

Figure 2. Annular geometry with a definition of coordinates.
An important consideration in this work was the flow conditions at the inlet of the test section. To prevent the fluid that was discharged into the inlet tank from entering the test section as a high-speed jet, the inlet tank was split vertically into two parts by a divider, which also acted as an overflow and as a support for the core traversing mechanism. Fluid from the pump impinged on the divider and recirculated in the rear chamber before entering the front chamber through the overflow and through slots machined in the divider. The rear chamber was packed with a 50.8 mm thick fibrous sheet, which dampened the vortices generated by the jet impingement. The front chamber of the inlet tank was also partially or totally filled with fibrous sheets, which were stacked together and acted as flow management devices. The number of these sheets and the arrangement of sheets with different porosities could be changed in order to modify the inlet conditions. Flow uniformity and inlet turbulence suppression were further enhanced by the flow acceleration through a bell-mouth inlet.
Two types of fibrous sheets were used, one of which consisted of compacted hog’s hair, whereas the other type was synthetic and had a more cancellous structure. Unfortunately, we had no way of quantifying, or even reproducing exactly, the properties of the sheet arrangement. For this reason, we resorted to a qualitative description of inlet conditions, which is actually based on the assessment of their effects on the flow. Based on these effects, we will distinguish between three classes of inlet-tank flow management: ‘mild flow management’, for which we only used two (out of five possible) fibrous sheets of the first type; ‘moderate flow management’, for which the inlet tank was completely filled with fibrous sheets of the first type; and ‘strong flow management’, for which the inlet tank was completely filled with a combination of fibrous sheets of both types. Measurements reported in this work were collected over a period of several years, and in some of the early work documentation of the inlet conditions was of limited extent. As the flow passed through these sheets, its non-uniformity was reduced by the viscous actions and large-scale motions would tend to be broken down. At the same time, small-scale motions would be produced in the wakes of the fibres. So, overall, mild flow management would probably result in inlet flows with relatively high turbulence intensity and some remnants of slowly decaying large-scale motions, whereas strong flow management would probably result in a more uniform inlet flow with small-scale fluctuations.
Flow measurements were taken using laser Doppler velocimetry (LDV), as well as planar and stereo particle image velocimetry, but, unlike in Part 1, only LDV results are reported in the following, as they were sufficient to support the points of present interest. The uncertainty in the Reynolds number
![]() $\mathit{Re}={\it\rho}D_{h}U_{b}/{\it\mu}$
, where
$\mathit{Re}={\it\rho}D_{h}U_{b}/{\it\mu}$
, where
![]() $U_{b}$
is the bulk flow velocity,
$U_{b}$
is the bulk flow velocity,
![]() ${\it\mu}$
fluid viscosity and
${\it\mu}$
fluid viscosity and
![]() ${\it\rho}$
density, was
${\it\rho}$
density, was
![]() $\pm 6\,\%$
. The relatively high uncertainty in
$\pm 6\,\%$
. The relatively high uncertainty in
![]() $\mathit{Re}$
is attributed mainly to the high sensitivity of fluid viscosity to temperature variations and solution concentration; because of this sensitivity, the Reynolds number value was modified by even small changes in temperature. An upper bound for the Reynolds number that could be achieved in this apparatus with each test section in place was imposed by the pump’s capacity and other features of the loop and the instrumentation. For the three test sections considered in this study, which had diameter ratios
$\mathit{Re}$
is attributed mainly to the high sensitivity of fluid viscosity to temperature variations and solution concentration; because of this sensitivity, the Reynolds number value was modified by even small changes in temperature. An upper bound for the Reynolds number that could be achieved in this apparatus with each test section in place was imposed by the pump’s capacity and other features of the loop and the instrumentation. For the three test sections considered in this study, which had diameter ratios
![]() $d/D=0.25,0.50$
and 0.75, the maximum achievable Reynolds numbers were 9900, 15 500 and 19 000, respectively.
$d/D=0.25,0.50$
and 0.75, the maximum achievable Reynolds numbers were 9900, 15 500 and 19 000, respectively.
3. Issues to be investigated and investigation strategies
In Part 1, we examined in detail flow in an eccentric annular channel for a particular set of conditions, under the assumption that this was a representative case and that phenomena similar to those observed in that flow would appear under significant ranges of conditions. We identified three distinct flow regions in the considered eccentric annular channel: the entrance region, the fluctuation-growth region (FG) and the rapid-mixing region (RM). In the entrance region, fluid was diverted from the narrow gap vicinity toward the open channel and velocity fluctuations were relatively small. This region was further subdivided into two subregions: close to the inlet, there was a non-periodic entrance subregion (NE) in which there was no sign of periodic motions; and, further away, there was a periodic entrance subregion (PE), in which some periodicity was detectable. In the FG region the axial velocity at mid-gap changed from a minimum at the end of the entrance region, to a maximum at the the start of the RM region; the most prominent feature of the FG region was a rapid growth of quasi-periodic velocity fluctuations, which reached amplitudes that were a significant fraction of the bulk velocity. In the RM region, the local time-averaged velocity and the amplitude of the velocity fluctuations changed by relatively small amounts; it is in this region that the gap vortex street was fully formed.
The phenomena summarized in the previous paragraph are very complex as well being prone to be sensitive to many influences. A first step towards reaching conclusions with a broader applicability is to identify the influencing factors (or sets of conditions) that affect significantly these phenomena and over which we have some control in our experiments. The conditions that could potentially have an effect on the development and state of the flow in eccentric annular channels can be separated into two classes: geometric conditions and dynamic conditions. Geometric conditions include the diameter ratio, the eccentricity, and the length of the test section; wall roughness is another geometric condition, but it cannot be examined in this work because all test sections had smooth walls. Dynamic conditions include the Reynolds number and the inlet conditions.
For a clear illustration of the effects of each influencing factor, it is necessary to isolate each factor from other modifying and interfering factors; to do so, we need to control each type of condition independently of all others. For example, dynamic effects can be separated from geometry-related effects by comparing cases with different inlet conditions and Reynolds numbers, while keeping the diameter ratio, eccentricity and distance from the inlet fixed. Moreover, we need to define appropriate flow indicators, which will serve as quantitative criteria by which each effect will be evaluated. As discussed in Part 1, the phenomena of interest can be observed most vividly in the narrow gap centre (‘mid-gap’); therefore, much of the following discussion will be concerned with measurements at that location. Among the many flow indicators, we selected four: the time-averaged streamwise velocity
![]() $U_{z}$
, the standard deviations of the streamwise
$U_{z}$
, the standard deviations of the streamwise
![]() $u_{z}^{\prime }$
and cross-gap
$u_{z}^{\prime }$
and cross-gap
![]() $u_{x}^{\prime }$
velocity fluctuations (all non-dimensionalized by the bulk velocity
$u_{x}^{\prime }$
velocity fluctuations (all non-dimensionalized by the bulk velocity
![]() $U_{b}$
) and the frequency
$U_{b}$
) and the frequency
![]() $f$
of the cross-flow velocity fluctuation spectrum peak, expressed as a Strouhal number
$f$
of the cross-flow velocity fluctuation spectrum peak, expressed as a Strouhal number
![]() $\mathit{St}=fd/U_{b}$
.
$\mathit{St}=fd/U_{b}$
.
To avoid getting sidetracked, it is also necessary to limit the scope of the investigation to aspects that are both meaningful as well as likely to be resolved by the present experiments. The first step towards this objective is to identify a set of questions to which responses will be attempted. Among the many relevant questions that may be posed, we chose the following ones.
-
(a) For a given geometry and Reynolds number, is there a downstream distance beyond which the flow may be considered to be fully developed, namely statistically insensitive to axial position? Assuming that a fully developed state has been achieved, would it be independent of inlet conditions? Is there a value of the Reynolds number, beyond which the fully developed state would be also insensitive to
 $\mathit{Re}$
?
$\mathit{Re}$
? -
(b) Is there a critical Reynolds number
 $\mathit{Re}_{cr}$
, below which no gap instability occurs in an eccentric annular channel with a specified diameter ratio under any conditions? We need to emphasize that this
$\mathit{Re}_{cr}$
, below which no gap instability occurs in an eccentric annular channel with a specified diameter ratio under any conditions? We need to emphasize that this
 $\mathit{Re}_{cr}$
should not be confused with the synonymous property whose prediction is a main objective of linear stability analysis, as the conditions we refer to here include large disturbances of all sorts. It is an intuitive expectation, however, that such a
$\mathit{Re}_{cr}$
should not be confused with the synonymous property whose prediction is a main objective of linear stability analysis, as the conditions we refer to here include large disturbances of all sorts. It is an intuitive expectation, however, that such a
 $\mathit{Re}_{cr}$
exists, because, as
$\mathit{Re}_{cr}$
exists, because, as
 $\mathit{Re}$
decreases, viscous effects should increase in significance and eventually dampen all motions other than the basic, parallel flow. Of course, finding experimentally the value of such a
$\mathit{Re}$
decreases, viscous effects should increase in significance and eventually dampen all motions other than the basic, parallel flow. Of course, finding experimentally the value of such a
 $\mathit{Re}_{cr}$
is not an easy matter, because (i) it is impossible to impose each and every kind of disturbance to which the flow may be sensitive, and (ii) it is, in theory at least, possible for a flow that is stable within the confines of our test section to become unstable in a test section of indefinite length. These types of limitations are common to many problems in fluid mechanics; for example, it has been recognized that the Kolmogorov hypotheses, which are meant to apply to turbulent flows at arbitrarily large Reynolds numbers, cannot be disproved by any experiment which would necessarily be performed at a finite Reynolds number. Consequently, we will only seek a practical
$\mathit{Re}_{cr}$
is not an easy matter, because (i) it is impossible to impose each and every kind of disturbance to which the flow may be sensitive, and (ii) it is, in theory at least, possible for a flow that is stable within the confines of our test section to become unstable in a test section of indefinite length. These types of limitations are common to many problems in fluid mechanics; for example, it has been recognized that the Kolmogorov hypotheses, which are meant to apply to turbulent flows at arbitrarily large Reynolds numbers, cannot be disproved by any experiment which would necessarily be performed at a finite Reynolds number. Consequently, we will only seek a practical
 $\mathit{Re}_{cr}$
, namely one that corresponds to practical levels of disturbances and practical channel lengths. We believe that the present apparatus length and disturbance levels are typical of conditions encountered in industrial systems, such as nuclear reactor rod bundles.
$\mathit{Re}_{cr}$
, namely one that corresponds to practical levels of disturbances and practical channel lengths. We believe that the present apparatus length and disturbance levels are typical of conditions encountered in industrial systems, such as nuclear reactor rod bundles. -
(c) Is there a critical eccentricity
 $e_{cr}$
, below which no gap instability occurs in an eccentric annular channel with a specified diameter ratio under any conditions? The limitations that were mentioned in the previous paragraph would also apply to this question. Therefore, instead of an unconditional
$e_{cr}$
, below which no gap instability occurs in an eccentric annular channel with a specified diameter ratio under any conditions? The limitations that were mentioned in the previous paragraph would also apply to this question. Therefore, instead of an unconditional
 $e_{cr}$
, we will seek a value that applies to practical conditions.
$e_{cr}$
, we will seek a value that applies to practical conditions. -
(d) Is it possible to reconcile results for different annular channel geometries, as far as gap instability is concerned?

Figure 3. (a) Time histories of cross- and axial velocity components along the centres of the narrow gaps of annular channels with
![]() $d/D=0.50$
,
$d/D=0.50$
,
![]() $e=0.80$
,
$e=0.80$
,
![]() $\mathit{Re}=7500$
and different types of flow management (these measurements were obtained by an LDV probe that was traversed very slowly along the channel). (b) A flow state map along the channel. Crosses, circles and plus signs mark the periodic-flow entrance subregion, the FG region and the RM region.
$\mathit{Re}=7500$
and different types of flow management (these measurements were obtained by an LDV probe that was traversed very slowly along the channel). (b) A flow state map along the channel. Crosses, circles and plus signs mark the periodic-flow entrance subregion, the FG region and the RM region.
4. Effect of inlet conditions on flow development
Let us first address question (a) in § 3 by examining the effects of inlet conditions on flow development and asymptotic state for a representative case, chosen to have the same geometry and Reynolds number as the one discussed in detail in Part 1. As in Part 1, we will base our discussion upon observation of the time histories of cross-flow and axial velocities, obtained by a two-dimensional LDV probe that was traversed slowly along the channel while its measurement volume was in the centre of the narrow gap. Figure 3 shows such time histories for three types of inlet-tank flow management. This figure makes it evident that the introduction of progressively stronger flow management had the effect of prolonging the entrance region, and consequently shifting the start of the FG region towards the downstream end of the test section. In the mild and moderate flow management cases, the FG region was succeeded by the RM region, which occupied roughly
![]() $3/4$
of the test section length for the mild flow management case and
$3/4$
of the test section length for the mild flow management case and
![]() $1/4$
of it for the moderate flow management case. In contrast, in the strong flow management case, the FG region emerged only at a quarter-length distance from the exit and persisted to the exit, but the trend indicates that the RM region would have appeared in this case as well had the test section been a bit longer. Based on these observations, one may say with fair confidence that the asymptotic flow state does not depend, at least qualitatively, on the inlet conditions. Therefore, it seems acceptable to disregard the inlet condition effect when we examine measurements obtained sufficiently far downstream. Of course the evidence so far has only been based on a single geometry and Reynolds number, so it is necessary to investigate whether this conclusion has a broader validity. In the remainder of this section we will focus on cases with mild and moderate flow management, which were deemed to suffice for a general qualitative illustration of the inlet condition effects.
$1/4$
of it for the moderate flow management case. In contrast, in the strong flow management case, the FG region emerged only at a quarter-length distance from the exit and persisted to the exit, but the trend indicates that the RM region would have appeared in this case as well had the test section been a bit longer. Based on these observations, one may say with fair confidence that the asymptotic flow state does not depend, at least qualitatively, on the inlet conditions. Therefore, it seems acceptable to disregard the inlet condition effect when we examine measurements obtained sufficiently far downstream. Of course the evidence so far has only been based on a single geometry and Reynolds number, so it is necessary to investigate whether this conclusion has a broader validity. In the remainder of this section we will focus on cases with mild and moderate flow management, which were deemed to suffice for a general qualitative illustration of the inlet condition effects.
In the following, we will investigate whether asymptotic states that are qualitatively independent of inlet conditions and Reynolds number would arise for eccentric annuli with all three diameter ratios we considered. For economy of presentation, we shall limit the discussion to two sets of representative geometries: one with an eccentricity of 0.80 and another with a relative gap size
![]() ${\it\delta}/D=0.05$
, which corresponds to
${\it\delta}/D=0.05$
, which corresponds to
![]() $e=0.80$
for the case with
$e=0.80$
for the case with
![]() $d/D=0.50$
.
$d/D=0.50$
.
Figure 4 shows the variations of the four chosen flow indicators with the Reynolds number for three diameter ratios and two gap configurations. All measurements were taken in the centre of the narrow gap near the end of the test section, where the flow was most likely to be fully developed, if it ever reached that stage of development. This position corresponded to
![]() $z/D_{h}=36$
, 54, and 108 for the annuli with
$z/D_{h}=36$
, 54, and 108 for the annuli with
![]() $d/D=0.25$
, 0.50 and 0.75, respectively. The left column in this figure (a,c,e,g) is for
$d/D=0.25$
, 0.50 and 0.75, respectively. The left column in this figure (a,c,e,g) is for
![]() $e=0.80$
, while the right one (b,d,f,h) is for a gap size
$e=0.80$
, while the right one (b,d,f,h) is for a gap size
![]() ${\it\delta}/D=0.05$
. Measurements are reported for two sets of inlet conditions: mild flow management, indicated by dashed lines and hollow symbols, and moderate flow management, indicated by solid lines and filled symbols; cross-hatched or shaded areas are bounded by the loci of mild and moderate flow management points.
${\it\delta}/D=0.05$
. Measurements are reported for two sets of inlet conditions: mild flow management, indicated by dashed lines and hollow symbols, and moderate flow management, indicated by solid lines and filled symbols; cross-hatched or shaded areas are bounded by the loci of mild and moderate flow management points.

Figure 4. Reynolds number dependence of the time-averaged streamwise velocity, the standard deviations of the streamwise
![]() $u_{z}^{\prime }$
and cross-gap
$u_{z}^{\prime }$
and cross-gap
![]() $u_{x}^{\prime }$
velocity fluctuations (all non-dimensionalized by the bulk velocity) and the Strouhal number for
$u_{x}^{\prime }$
velocity fluctuations (all non-dimensionalized by the bulk velocity) and the Strouhal number for
![]() $e=0.80$
(a,c,e,g) and
$e=0.80$
(a,c,e,g) and
![]() ${\it\delta}/D=0.05$
(b,d,f,h). Solid lines and filled markers represent moderate flow management, while dashed lines and hollow markers represent mild flow management. Circular, triangular and square symbols indicate annuli with
${\it\delta}/D=0.05$
(b,d,f,h). Solid lines and filled markers represent moderate flow management, while dashed lines and hollow markers represent mild flow management. Circular, triangular and square symbols indicate annuli with
![]() $d/D=0.25,0.50$
and 0.75, respectively. Cross-hatched or shaded areas are bounded by the loci of measurements under moderate and mild flow management conditions for each diameter ratio.
$d/D=0.25,0.50$
and 0.75, respectively. Cross-hatched or shaded areas are bounded by the loci of measurements under moderate and mild flow management conditions for each diameter ratio.
A common feature observed for all cases examined is that, at low
![]() $\mathit{Re}$
, gap velocity, gap fluctuations and gap Strouhal number increased with increasing
$\mathit{Re}$
, gap velocity, gap fluctuations and gap Strouhal number increased with increasing
![]() $\mathit{Re}$
, whereas at sufficiently large
$\mathit{Re}$
, whereas at sufficiently large
![]() $\mathit{Re}$
these four parameters reached asymptotes, or showed a tendency towards such behaviour. Similar observations have been made by Lexmond, Mudde & van der Hagen (Reference Lexmond, Mudde and van der Hagen2005) and Mahmood (Reference Mahmood2011) in compound rectangular channels. This is consistent with many other flow phenomena which become weakly dependent, if at all, on
$\mathit{Re}$
these four parameters reached asymptotes, or showed a tendency towards such behaviour. Similar observations have been made by Lexmond, Mudde & van der Hagen (Reference Lexmond, Mudde and van der Hagen2005) and Mahmood (Reference Mahmood2011) in compound rectangular channels. This is consistent with many other flow phenomena which become weakly dependent, if at all, on
![]() $\mathit{Re}$
at large
$\mathit{Re}$
at large
![]() $\mathit{Re}$
and so it is not a surprise. Nevertheless, the dependence of this behaviour upon inlet conditions is unmistakable: the lower bound of
$\mathit{Re}$
and so it is not a surprise. Nevertheless, the dependence of this behaviour upon inlet conditions is unmistakable: the lower bound of
![]() $\mathit{Re}$
for quasi-asymptotic attainment of the four indicators is lower for mild flow management cases than for the corresponding moderate flow management cases. This observation conforms with our expectations: compared to moderate flow management, mild flow management allows stronger disturbances to enter the channel, which are more effective in triggering the instability and vortex generation mechanisms at relatively low
$\mathit{Re}$
for quasi-asymptotic attainment of the four indicators is lower for mild flow management cases than for the corresponding moderate flow management cases. This observation conforms with our expectations: compared to moderate flow management, mild flow management allows stronger disturbances to enter the channel, which are more effective in triggering the instability and vortex generation mechanisms at relatively low
![]() $\mathit{Re}$
. At sufficiently large
$\mathit{Re}$
. At sufficiently large
![]() $\mathit{Re}$
, however, the flow becomes sensitive to even small disturbances and so the inlet conditions have a weaker, though non-negligible, effect on the asymptotic state. The lower bound of
$\mathit{Re}$
, however, the flow becomes sensitive to even small disturbances and so the inlet conditions have a weaker, though non-negligible, effect on the asymptotic state. The lower bound of
![]() $\mathit{Re}$
for the quasi-asymptotic state depends on the geometry and the choice of flow indicator; however, in all cases considered, this bound was in the range between 7000 and 10 000, which includes the conditions of the tests presented in Part 1.
$\mathit{Re}$
for the quasi-asymptotic state depends on the geometry and the choice of flow indicator; however, in all cases considered, this bound was in the range between 7000 and 10 000, which includes the conditions of the tests presented in Part 1.
Evidence that inlet conditions have some effect on the frequency of cross-flow oscillations far from the inlet, even at relatively large Reynolds numbers, is given in figure 5, which shows values of the Strouhal number in highly eccentric annular channels with a diameter ratio of 0.50 for two sets of inlet conditions. The presented values were measured in the centre of the narrow gap at
![]() $z/D_{h}=54$
for a Reynolds number of 15 500. All other conditions being the same, one may conclude that the differences in
$z/D_{h}=54$
for a Reynolds number of 15 500. All other conditions being the same, one may conclude that the differences in
![]() $\mathit{St}$
, which are up to 20 %, would be due to differences in upstream conditions. Although both sets of results follow the same trends, it is evident that a strengthening of upstream flow management (i.e. a reduction in the level of inlet disturbances) resulted in a small, but measurable, increase in the frequency of cross-gap oscillations, especially at moderate eccentricities.
$\mathit{St}$
, which are up to 20 %, would be due to differences in upstream conditions. Although both sets of results follow the same trends, it is evident that a strengthening of upstream flow management (i.e. a reduction in the level of inlet disturbances) resulted in a small, but measurable, increase in the frequency of cross-gap oscillations, especially at moderate eccentricities.

Figure 5. Strouhal number versus eccentricity for two sets of upstream conditions;
![]() $\mathit{Re}=15\,500$
,
$\mathit{Re}=15\,500$
,
![]() $d/D=0.50$
.
$d/D=0.50$
.
5. Flow patterns for different eccentricities and Reynolds numbers
In this section, we will investigate whether the succession of flow regions identified in Part 1 and in the previous section for
![]() $d/D=0.50$
,
$d/D=0.50$
,
![]() $e=0.80$
and
$e=0.80$
and
![]() $\mathit{Re}=7300$
can also be found under different conditions. At the same time, we will attempt to provide an answer to questions (b) and (c) in § 3. To reduce the complexity of the discussion, we will first focus on the effects of eccentricity and Reynolds number for the case with
$\mathit{Re}=7300$
can also be found under different conditions. At the same time, we will attempt to provide an answer to questions (b) and (c) in § 3. To reduce the complexity of the discussion, we will first focus on the effects of eccentricity and Reynolds number for the case with
![]() $d/D=0.50$
and discuss the effect of diameter ratio in a following section. Moreover, we will initially consider mainly one type of inlet conditions, ones that were previously characterized as moderate flow management. The furthest downstream measurement location for these experiments was at
$d/D=0.50$
and discuss the effect of diameter ratio in a following section. Moreover, we will initially consider mainly one type of inlet conditions, ones that were previously characterized as moderate flow management. The furthest downstream measurement location for these experiments was at
![]() $z/D_{h}\approx 54$
and consequently only phenomena that are present within the available test section were documented. Nevertheless, in cases in which the flow structure demonstrated a well-established trend, one might speculate with some confidence on how the flow would have developed in a longer test section. Moreover, as mentioned in § 3, a specific objective of this work was to document the flow patterns not under any arbitrary conditions of disturbances and apparatus lengths, but under ‘practical’ ones.
$z/D_{h}\approx 54$
and consequently only phenomena that are present within the available test section were documented. Nevertheless, in cases in which the flow structure demonstrated a well-established trend, one might speculate with some confidence on how the flow would have developed in a longer test section. Moreover, as mentioned in § 3, a specific objective of this work was to document the flow patterns not under any arbitrary conditions of disturbances and apparatus lengths, but under ‘practical’ ones.
Figure 6 shows an array of time histories at mid-gap, measured by a slowly traversed LDV probe and obtained with moderate flow management for eccentricities in the range
![]() $0.4\leqslant e\leqslant 0.9$
and Reynolds numbers in the range
$0.4\leqslant e\leqslant 0.9$
and Reynolds numbers in the range
![]() $2100\leqslant \mathit{Re}\leqslant 15\,500$
. Similar measurements were also made for lower eccentricities and lower Reynolds numbers, but are not presented here as they mostly showed no evidence for the presence of periodic motions. Following procedures explained in Part 1, one may visually assert whether, for any given
$2100\leqslant \mathit{Re}\leqslant 15\,500$
. Similar measurements were also made for lower eccentricities and lower Reynolds numbers, but are not presented here as they mostly showed no evidence for the presence of periodic motions. Following procedures explained in Part 1, one may visually assert whether, for any given
![]() $e{-}\mathit{Re}$
combination, the flow state at the end of the channel is in the entrance region, the FG region or the RM region. To illustrate whether each flow has a quasi-periodic component or not, we have presented representative segments of local time histories at
$e{-}\mathit{Re}$
combination, the flow state at the end of the channel is in the entrance region, the FG region or the RM region. To illustrate whether each flow has a quasi-periodic component or not, we have presented representative segments of local time histories at
![]() $z/D_{h}\approx 53$
in figures 7 and 8 for the cross- and axial flow velocity components, respectively. In most cases, observation of the signal pattern makes it evident whether a flow exiting the channel was in the NE or the PE subregion of the entrance region. To increase our confidence in this assessment, the visual identification of periodicity was confirmed by inspection of power spectra (not shown here) of long time histories of the mid-gap cross-flow at
$z/D_{h}\approx 53$
in figures 7 and 8 for the cross- and axial flow velocity components, respectively. In most cases, observation of the signal pattern makes it evident whether a flow exiting the channel was in the NE or the PE subregion of the entrance region. To increase our confidence in this assessment, the visual identification of periodicity was confirmed by inspection of power spectra (not shown here) of long time histories of the mid-gap cross-flow at
![]() $z/D_{h}\approx 53$
, which clearly revealed whether they had prominent peaks or not.
$z/D_{h}\approx 53$
, which clearly revealed whether they had prominent peaks or not.

Figure 6. Time histories of cross- and axial velocity components along the centres of the narrow gaps of annular channels with
![]() $d/D=0.50$
and moderate flow management for different eccentricities and Reynolds numbers; these measurements were obtained by an LDV probe that was traversed very slowly along the channel.
$d/D=0.50$
and moderate flow management for different eccentricities and Reynolds numbers; these measurements were obtained by an LDV probe that was traversed very slowly along the channel.

Figure 7. Time histories of mid-gap cross-flow velocity in annular channels with
![]() $d/D=0.50$
and moderate flow management for different eccentricities and Reynolds numbers; these measurements were obtained by an LDV probe fixed at
$d/D=0.50$
and moderate flow management for different eccentricities and Reynolds numbers; these measurements were obtained by an LDV probe fixed at
![]() $z/D_{h}\approx 53$
.
$z/D_{h}\approx 53$
.

Figure 8. Time histories of mid-gap axial flow velocity in annular channels with
![]() $d/D=0.50$
and moderate flow management for different eccentricities and Reynolds numbers; these measurements were obtained by an LDV probe fixed at
$d/D=0.50$
and moderate flow management for different eccentricities and Reynolds numbers; these measurements were obtained by an LDV probe fixed at
![]() $z/D_{h}\approx 53$
.
$z/D_{h}\approx 53$
.
A summary of our observations concerning the states of the flows near the channel exit is shown in the form of a flow state map in figure 9. Although the presented results only extend to Reynolds numbers up to 15 500, based on figure 4 we can plausibly anticipate that the flow states would not change significantly with increasing
![]() $\mathit{Re}$
beyond that value. Of course, a question that cannot be conclusively answered by the present results is whether, and under which conditions, the flow states would change further downstream, if the channel were longer than the present one. The main observations from this map can be summarized as follows. It is noted that the values of Reynolds numbers and eccentricities cited in this discussion are not meant to be exact but indicative of magnitude.
$\mathit{Re}$
beyond that value. Of course, a question that cannot be conclusively answered by the present results is whether, and under which conditions, the flow states would change further downstream, if the channel were longer than the present one. The main observations from this map can be summarized as follows. It is noted that the values of Reynolds numbers and eccentricities cited in this discussion are not meant to be exact but indicative of magnitude.
-
(a) For
 $\mathit{Re}<1100$
, no periodicity was detectable for any eccentricity, so one may conclude that this is approximately the practical, universal, critical Reynolds number, below which all practical flows in eccentric annuli with
$\mathit{Re}<1100$
, no periodicity was detectable for any eccentricity, so one may conclude that this is approximately the practical, universal, critical Reynolds number, below which all practical flows in eccentric annuli with
 $d/D=0.50$
would be unconditionally stable as far as gap instability is concerned. This value was established with a relatively high confidence by using a wider range of measurements than the ones shown in the previous figures. Later in this section, we will discuss the dependence of the critical Reynolds number on eccentricity.
$d/D=0.50$
would be unconditionally stable as far as gap instability is concerned. This value was established with a relatively high confidence by using a wider range of measurements than the ones shown in the previous figures. Later in this section, we will discuss the dependence of the critical Reynolds number on eccentricity. -
(b) For
 $e<0.5$
, no periodicity was detectable for any Reynolds number, so one may conclude that this is approximately the practical critical eccentricity, below which flow in practical eccentric annuli with
$e<0.5$
, no periodicity was detectable for any Reynolds number, so one may conclude that this is approximately the practical critical eccentricity, below which flow in practical eccentric annuli with
 $d/D=0.50$
would be unconditionally stable as far as gap instability is concerned.
$d/D=0.50$
would be unconditionally stable as far as gap instability is concerned. -
(c) For
 $1100<\mathit{Re}<3500$
, weak periodic motions became measurable for an intermediate, narrow range of eccentricities. This indicates that the gap instability mechanism was activated under these conditions. Whether and under which conditions these motions may eventually grow to the FG stage cannot be resolved by the present results.
$1100<\mathit{Re}<3500$
, weak periodic motions became measurable for an intermediate, narrow range of eccentricities. This indicates that the gap instability mechanism was activated under these conditions. Whether and under which conditions these motions may eventually grow to the FG stage cannot be resolved by the present results. -
(d) For
 $3500<\mathit{Re}<5500$
, there is a range of eccentricities for which periodic motions reached the FG stage. This range must surely include cases that would develop to the RM stage in a longer channel.
$3500<\mathit{Re}<5500$
, there is a range of eccentricities for which periodic motions reached the FG stage. This range must surely include cases that would develop to the RM stage in a longer channel. -
(e) For the cases that had an identifiable FG region, the entrance length was rather insensitive to Reynolds number, although it varied with eccentricity.
-
(f) For
 $5500<\mathit{Re}$
, there is a range of eccentricities for which the annular flow reached the RM stage, which may be deemed to indicate the full development of the gap vortex street.
$5500<\mathit{Re}$
, there is a range of eccentricities for which the annular flow reached the RM stage, which may be deemed to indicate the full development of the gap vortex street. -
(g) For all Reynolds numbers, one may speculate that, as eccentricity approaches 1, cross-gap flows would be progressively obstructed, and they would cease altogether when the core contacts the outer channel (
 $e=1$
). The minimum eccentricity (or minimum gap size) for cross-flows to be significant would probably diminish with increasing
$e=1$
). The minimum eccentricity (or minimum gap size) for cross-flows to be significant would probably diminish with increasing
 $\mathit{Re}$
. Nevertheless, it should also be noted that the absence of cross-gap motions does not necessarily exclude the presence of instability and even vortex formation in the two mixing layers on either side of the gap.
$\mathit{Re}$
. Nevertheless, it should also be noted that the absence of cross-gap motions does not necessarily exclude the presence of instability and even vortex formation in the two mixing layers on either side of the gap.

Figure 9. Flow state map near near the exits (
![]() $z/D_{h}\approx 53$
) of eccentric annular channels with
$z/D_{h}\approx 53$
) of eccentric annular channels with
![]() $d/D=0.50$
and moderate flow management. Dashes, circles, plus signs and triangles represent measurement points within, respectively, the NE subregion, the PE subregion, the FG region and the RM region.
$d/D=0.50$
and moderate flow management. Dashes, circles, plus signs and triangles represent measurement points within, respectively, the NE subregion, the PE subregion, the FG region and the RM region.
The flow regime map in figure 9 applies to moderate inlet flow management conditions. Based on the observations made with regard to figure 3 and many other similar observations, we may assess with a fair degree of confidence that the lower bounds of the flow development regions in figure 9 would generally shift toward the left under milder inlet flow management conditions and towards the right under stronger ones.
To investigate whether suppression of cross-gap motions would affect significantly mixing in highly eccentric annular channels, we blocked completely the narrow gap along the entire length of the test-section using a 2.3 mm wide square acrylic rod. The eccentricity for this configuration was 0.75. Velocity measurements were then taken at the positions marked in figure 2 as 3, 4 and 5, which correspond to
![]() ${\it\theta}\approx 60^{\circ }$
, 90°, and 180°, for two Reynolds numbers, equal to 7000 and 13 500, respectively. Figure 10 shows two measures of mixing intensity, which are the normalized standard deviations of velocity fluctuations (‘intensities’) in the
${\it\theta}\approx 60^{\circ }$
, 90°, and 180°, for two Reynolds numbers, equal to 7000 and 13 500, respectively. Figure 10 shows two measures of mixing intensity, which are the normalized standard deviations of velocity fluctuations (‘intensities’) in the
![]() $x$
and
$x$
and
![]() $z$
directions. First of all, it is apparent that all trends shown by the measurements were consistent for both Reynolds numbers, although the intensities were somewhat lower for the higher Reynolds number, in agreement with trends in pipe flows. In the centre of the wide gap (position 5), both intensities had values that were nearly independent of the closing of the narrow gap. In contrast, intensities measured closer to the narrow gap (positions 3 and 4) decreased by large factors when the gap was closed. We further investigated the presence of quasi-periodic components in all signals by inspection of power spectra. At all positions and Reynolds numbers, the spectra in the closed-gap channel had peaks at approximately the same frequency as the one in the open-gap channel, although the peaks in the former case had a much lower amplitude and a wider bandwidth than those in the latter case. In summary, blocking the narrow gap did not eliminate the presence of periodic motions, and presumably the formation of vortex streets, but severely impeded mixing in the vicinity of the narrow gap.
$z$
directions. First of all, it is apparent that all trends shown by the measurements were consistent for both Reynolds numbers, although the intensities were somewhat lower for the higher Reynolds number, in agreement with trends in pipe flows. In the centre of the wide gap (position 5), both intensities had values that were nearly independent of the closing of the narrow gap. In contrast, intensities measured closer to the narrow gap (positions 3 and 4) decreased by large factors when the gap was closed. We further investigated the presence of quasi-periodic components in all signals by inspection of power spectra. At all positions and Reynolds numbers, the spectra in the closed-gap channel had peaks at approximately the same frequency as the one in the open-gap channel, although the peaks in the former case had a much lower amplitude and a wider bandwidth than those in the latter case. In summary, blocking the narrow gap did not eliminate the presence of periodic motions, and presumably the formation of vortex streets, but severely impeded mixing in the vicinity of the narrow gap.

Figure 10. Normalized standard deviations of velocity fluctuations at three azimuthal positions for
![]() $e\approx 0.75$
and
$e\approx 0.75$
and
![]() $z/D_{h}=54$
. Solid symbols represent the closed-gap configuration, while open ones represent the open-gap case. Circular symbols and dotted lines are for
$z/D_{h}=54$
. Solid symbols represent the closed-gap configuration, while open ones represent the open-gap case. Circular symbols and dotted lines are for
![]() $\mathit{Re}=7000$
, while square symbols and dashed lines are for
$\mathit{Re}=7000$
, while square symbols and dashed lines are for
![]() $\mathit{Re}=13\,500$
.
$\mathit{Re}=13\,500$
.
To investigate the Reynolds number dependence of flow instability in annular channels with different eccentricities, we conducted a series of specific experiments in flows with
![]() $d/D=0.50$
and moderate inlet flow management conditions. We repeated these tests for eccentricities in the range
$d/D=0.50$
and moderate inlet flow management conditions. We repeated these tests for eccentricities in the range
![]() $0\leqslant e\leqslant 0.9$
, with increments of 0.1. For each eccentricity, the tests started at a very low
$0\leqslant e\leqslant 0.9$
, with increments of 0.1. For each eccentricity, the tests started at a very low
![]() $\mathit{Re}$
, typically of the order of 100. After the flow was given sufficient time to reach stationarity, cross- and axial velocity time histories were recorded at mid-gap near the exit of the channel. Then, the flow rate was increased by a small amount (typically by
$\mathit{Re}$
, typically of the order of 100. After the flow was given sufficient time to reach stationarity, cross- and axial velocity time histories were recorded at mid-gap near the exit of the channel. Then, the flow rate was increased by a small amount (typically by
![]() $\mathit{Re}$
increments of 150 in the sensitive range) and the same type of measurements were recorded again; this was repeated until the flow rate reached the maximum capacity of the pump. The same tests were also repeated by starting at the highest obtainable flow rate and decreasing it gradually, so that we could identify possible hysteresis effects. We inspected all signals carefully and noted the conditions at which we observed a significant change in their patterns. In general, we observed two types of pattern changes, both of which were drastic, repeatable and unmistakable.
$\mathit{Re}$
increments of 150 in the sensitive range) and the same type of measurements were recorded again; this was repeated until the flow rate reached the maximum capacity of the pump. The same tests were also repeated by starting at the highest obtainable flow rate and decreasing it gradually, so that we could identify possible hysteresis effects. We inspected all signals carefully and noted the conditions at which we observed a significant change in their patterns. In general, we observed two types of pattern changes, both of which were drastic, repeatable and unmistakable.
At low eccentricities and at some critical value of
![]() $\mathit{Re}$
the velocity fluctuation level increased measurably for a small increase in
$\mathit{Re}$
the velocity fluctuation level increased measurably for a small increase in
![]() $\mathit{Re}$
, but the signals showed no evidence of periodicity. We interpreted this as an indication of transition to turbulence in the gap region and noted the Reynolds number at which this occurred as
$\mathit{Re}$
, but the signals showed no evidence of periodicity. We interpreted this as an indication of transition to turbulence in the gap region and noted the Reynolds number at which this occurred as
![]() $\mathit{Re}_{tr}$
. At high eccentricities, the cross-flow velocity signal attained a quasi-periodic waveform when the Reynolds number exceeded a value
$\mathit{Re}_{tr}$
. At high eccentricities, the cross-flow velocity signal attained a quasi-periodic waveform when the Reynolds number exceeded a value
![]() $\mathit{Re}_{cr}$
, which we interpreted as the critical Reynolds number for gap instability.
$\mathit{Re}_{cr}$
, which we interpreted as the critical Reynolds number for gap instability.
Figure 11 summarizes the values of the critical and transitional Reynolds numbers for different eccentricities. Non-periodic transition at
![]() $\mathit{Re}_{tr}\approx 6000$
was observed for the cases with
$\mathit{Re}_{tr}\approx 6000$
was observed for the cases with
![]() $0\leqslant e\leqslant 0.4$
, whereas in the case with
$0\leqslant e\leqslant 0.4$
, whereas in the case with
![]() $e=0.5$
transition to turbulence and the appearance of periodic motions appeared almost simultaneously, as though one triggered the other. It is noted that the absence of turbulence in the gap region does not necessarily exclude its presence in other parts of the channel. For eccentricities in the range
$e=0.5$
transition to turbulence and the appearance of periodic motions appeared almost simultaneously, as though one triggered the other. It is noted that the absence of turbulence in the gap region does not necessarily exclude its presence in other parts of the channel. For eccentricities in the range
![]() $0.6\leqslant e\leqslant 0.9$
, the onset of periodic motions was observed at Reynolds numbers that increased monotonically from 1100 for
$0.6\leqslant e\leqslant 0.9$
, the onset of periodic motions was observed at Reynolds numbers that increased monotonically from 1100 for
![]() $e=0.6$
to 3800 for
$e=0.6$
to 3800 for
![]() $e=0.9$
. This trend is consistent with the observations of Gosset & Tavoularis (Reference Gosset and Tavoularis2006) and Piot & Tavoularis (Reference Piot and Tavoularis2011) and demonstrates that increasing eccentricity tends to strengthen viscous forces, which in turn tend to impede cross-gap motions.
$e=0.9$
. This trend is consistent with the observations of Gosset & Tavoularis (Reference Gosset and Tavoularis2006) and Piot & Tavoularis (Reference Piot and Tavoularis2011) and demonstrates that increasing eccentricity tends to strengthen viscous forces, which in turn tend to impede cross-gap motions.

Figure 11. The effect of eccentricity on the critical Reynolds number for transition to turbulence and the critical Reynolds number for gap instability in the narrow gap. Crosses mark the conditions for the onset of transition to turbulence in the narrow gap without any discernible periodicity; plus signs mark the conditions for the onset of quasi-periodic cross-flow fluctuations in the narrow gap.
A close examination of the velocity signals revealed a wealth of interesting patterns, which in their details depended on the geometric and dynamic conditions. For example, in the PE subregion, the cross-flow signal (figure 7) had a quasi-sinusoidal waveform at relatively low Reynolds numbers, but, as
![]() $\mathit{Re}$
increased, the signal appearance tended towards a square wave shape; with further increase in
$\mathit{Re}$
increased, the signal appearance tended towards a square wave shape; with further increase in
![]() $\mathit{Re}$
, the same signal tended towards a triangular waveform. This progression indicates that, besides a fundamental oscillation mode that appears at the onset of gap instability while
$\mathit{Re}$
, the same signal tended towards a triangular waveform. This progression indicates that, besides a fundamental oscillation mode that appears at the onset of gap instability while
![]() $\mathit{Re}$
is not much larger than
$\mathit{Re}$
is not much larger than
![]() $\mathit{Re}_{cr}$
, additional modes and/or harmonics are triggered with increasing
$\mathit{Re}_{cr}$
, additional modes and/or harmonics are triggered with increasing
![]() $\mathit{Re}$
. Signal modulation at lower frequencies was also observed in some cases. Analysis of such phenomena is beyond the scope of the present work; however, further insight into the physical characteristics of annular flow during the different stages of its development can be gained by examining the supplementary movie accompanying Part 1, which shows the evolution of the cross-flow motions along the test section.
$\mathit{Re}$
. Signal modulation at lower frequencies was also observed in some cases. Analysis of such phenomena is beyond the scope of the present work; however, further insight into the physical characteristics of annular flow during the different stages of its development can be gained by examining the supplementary movie accompanying Part 1, which shows the evolution of the cross-flow motions along the test section.

Figure 12. Dependence of the time-averaged streamwise velocity, the standard deviations of the streamwise and cross-gap velocity fluctuations (all non-dimensionalized by the bulk velocity) and the Strouhal number at mid-gap near the exit of the test section (
![]() $z/D_{h}\approx 53$
) upon eccentricity (b,d,f,h) and Reynolds number (a,c,e,g); in all cases,
$z/D_{h}\approx 53$
) upon eccentricity (b,d,f,h) and Reynolds number (a,c,e,g); in all cases,
![]() $d/D=0.50$
and inlet conditions corresponded to moderate flow management.
$d/D=0.50$
and inlet conditions corresponded to moderate flow management.
6. Towards a quantification of eccentricity and Reynolds number effects
This section presents comparisons of the values of the four previously introduced flow indicators at mid-gap and near the exit of the channel for wide ranges of eccentricities and Reynolds numbers (see figure 12). To avoid complications stemming from additional geometric and dynamic effects, only cases with the same diameter ratio (0.50) and the same level of inlet flow management (moderate) were included in the comparisons. The findings of these quantitative comparisons are meant to complement the qualitative observations that were presented in previous sections. It is, of course, recognized that, among the cases for which periodic motions were detected, only a few reached a fully developed state, namely exhibited a RM region, as demonstrated in figure 9. Comparisons of values and trends for the different cases shown in figure 12 have resulted in the following main observations.
In general, and with some notable exceptions, the normalized mid-gap axial velocity decreased with increasing eccentricity and increased gradually with increasing Reynolds number. For very low eccentricities (
![]() $0\leqslant e\leqslant 0.4$
), this velocity was fairly insensitive to
$0\leqslant e\leqslant 0.4$
), this velocity was fairly insensitive to
![]() $e$
and also showed reversing trends with
$e$
and also showed reversing trends with
![]() $\mathit{Re}$
. In contrast, for very high eccentricities (
$\mathit{Re}$
. In contrast, for very high eccentricities (
![]() $0.6\leqslant e\leqslant 0.9$
) and
$0.6\leqslant e\leqslant 0.9$
) and
![]() $4700<\mathit{Re}<7500$
, the mid-gap velocity was significantly higher than values consistent with the overall decreasing trend and in some cases reached levels consistent with higher turbulence at
$4700<\mathit{Re}<7500$
, the mid-gap velocity was significantly higher than values consistent with the overall decreasing trend and in some cases reached levels consistent with higher turbulence at
![]() $\mathit{Re}=15\,500$
. The mid-gap velocity fluctuation level was fairly low and insensitive to eccentricity for
$\mathit{Re}=15\,500$
. The mid-gap velocity fluctuation level was fairly low and insensitive to eccentricity for
![]() $0\leqslant e\leqslant 0.4$
, but it both increased and became
$0\leqslant e\leqslant 0.4$
, but it both increased and became
![]() $e$
-sensitive for
$e$
-sensitive for
![]() $0.6\leqslant e\leqslant 0.9$
. The velocity fluctuation level in the low-
$0.6\leqslant e\leqslant 0.9$
. The velocity fluctuation level in the low-
![]() $e$
range was also insensitive to Reynolds number up to some
$e$
range was also insensitive to Reynolds number up to some
![]() $\mathit{Re}$
and then showed a moderate increase at some
$\mathit{Re}$
and then showed a moderate increase at some
![]() $\mathit{Re}$
in the range
$\mathit{Re}$
in the range
![]() $4700<\mathit{Re}<6100$
; this moderate increase is attributed to the onset of transition to turbulence in the gap region, rather than gap instability and related phenomena. At high eccentricities, however, the mid-gap fluctuation level increased nearly abruptly at some
$4700<\mathit{Re}<6100$
; this moderate increase is attributed to the onset of transition to turbulence in the gap region, rather than gap instability and related phenomena. At high eccentricities, however, the mid-gap fluctuation level increased nearly abruptly at some
![]() $\mathit{Re}$
-value, as a result of the flow entering the FG region. These observations support other indications that flows in the low and high
$\mathit{Re}$
-value, as a result of the flow entering the FG region. These observations support other indications that flows in the low and high
![]() $e$
-ranges belong to different classes.
$e$
-ranges belong to different classes.
In all cases with
![]() $\mathit{Re}\leqslant 7500$
that had periodic motions, the Strouhal number
$\mathit{Re}\leqslant 7500$
that had periodic motions, the Strouhal number
![]() $\mathit{St}=fd/U_{b}$
decreased measurably with increasing eccentricity. It also increased at a very slow rate with increasing Reynolds number in the range
$\mathit{St}=fd/U_{b}$
decreased measurably with increasing eccentricity. It also increased at a very slow rate with increasing Reynolds number in the range
![]() $1500\leqslant \mathit{Re}\leqslant 7500$
; at higher
$1500\leqslant \mathit{Re}\leqslant 7500$
; at higher
![]() $\mathit{Re}$
, figures 4 and 5 demonstrate that the Strouhal number tended towards asymptotic values. For
$\mathit{Re}$
, figures 4 and 5 demonstrate that the Strouhal number tended towards asymptotic values. For
![]() $\mathit{Re}=15\,500$
the Strouhal number appears to be less sensitive to eccentricity; this may be due to the increased turbulence level in the entire cross-sectional area, which tends to reduce the non-uniformity of the azimuthal velocity variation.
$\mathit{Re}=15\,500$
the Strouhal number appears to be less sensitive to eccentricity; this may be due to the increased turbulence level in the entire cross-sectional area, which tends to reduce the non-uniformity of the azimuthal velocity variation.
A related issue of interest is the dependence of the frequency of cross-flow oscillations at the gap on the relative gap size
![]() ${\it\delta}/d$
. This issue has been discussed by Chang & Tavoularis (Reference Chang and Tavoularis2008), who conducted numerical simulations of turbulent flow in a rectangular channel containing an axially aligned cylinder, focusing on the effects of relative gap size. Figure 13 summarizes some representative results of the present experiments and experimental results from previous studies. A comparison of our own results at two Reynolds numbers shows that, for a fixed
${\it\delta}/d$
. This issue has been discussed by Chang & Tavoularis (Reference Chang and Tavoularis2008), who conducted numerical simulations of turbulent flow in a rectangular channel containing an axially aligned cylinder, focusing on the effects of relative gap size. Figure 13 summarizes some representative results of the present experiments and experimental results from previous studies. A comparison of our own results at two Reynolds numbers shows that, for a fixed
![]() ${\it\delta}/d$
, an increase of
${\it\delta}/d$
, an increase of
![]() $\mathit{Re}$
from 7500 to 15 500 resulted in a significant increase in
$\mathit{Re}$
from 7500 to 15 500 resulted in a significant increase in
![]() $\mathit{St}$
, which was about 44 % on the average. Such sensitivity would presumably be diminished for
$\mathit{St}$
, which was about 44 % on the average. Such sensitivity would presumably be diminished for
![]() $\mathit{Re}>10\,000$
. A second observation, this one based on a comparison of
$\mathit{Re}>10\,000$
. A second observation, this one based on a comparison of
![]() $\mathit{St}$
at a fixed
$\mathit{St}$
at a fixed
![]() ${\it\delta}/d$
and the same
${\it\delta}/d$
and the same
![]() $\mathit{Re}$
but different inlet flow management conditions, is that a change of inlet management from moderate (case a) to strong (case b) resulted in a measurable increase in
$\mathit{Re}$
but different inlet flow management conditions, is that a change of inlet management from moderate (case a) to strong (case b) resulted in a measurable increase in
![]() $\mathit{St}$
, which was 12 % on the average. Focusing on the
$\mathit{St}$
, which was 12 % on the average. Focusing on the
![]() $\mathit{Re}=15\,500$
results alone, one may observe that
$\mathit{Re}=15\,500$
results alone, one may observe that
![]() $\mathit{St}$
was at most weakly sensitive to the relative gap size and seemed to reach a mild maximum at some intermediate value of
$\mathit{St}$
was at most weakly sensitive to the relative gap size and seemed to reach a mild maximum at some intermediate value of
![]() ${\it\delta}/d$
.
${\it\delta}/d$
.
The only other available experimental results with which we could perform direct comparisons, those by Guellouz & Tavoularis (Reference Guellouz and Tavoularis2000) for a rectangular channel containing a rod at
![]() $\mathit{Re}=108\,000$
and the ones by Baratto et al. (Reference Baratto, Bailey and Tavoularis2006) for a five-rod bundle at
$\mathit{Re}=108\,000$
and the ones by Baratto et al. (Reference Baratto, Bailey and Tavoularis2006) for a five-rod bundle at
![]() $\mathit{Re}=42\,000$
, show trends that are in general agreement with ours. The dependence of Strouhal number on the relative gap size has also been studied experimentally by Möller (Reference Möller1991) and Wu & Trupp (Reference Wu and Trupp1994); unfortunately, these authors report their results in terms of a different Strouhal number,
$\mathit{Re}=42\,000$
, show trends that are in general agreement with ours. The dependence of Strouhal number on the relative gap size has also been studied experimentally by Möller (Reference Möller1991) and Wu & Trupp (Reference Wu and Trupp1994); unfortunately, these authors report their results in terms of a different Strouhal number,
![]() $\mathit{St}_{{\it\tau}}=fd/u_{{\it\tau}}$
, which is based on the friction velocity
$\mathit{St}_{{\it\tau}}=fd/u_{{\it\tau}}$
, which is based on the friction velocity
![]() $u_{{\it\tau}}$
, and the resolution of our measurements was insufficient to determine
$u_{{\it\tau}}$
, and the resolution of our measurements was insufficient to determine
![]() $u_{{\it\tau}}$
. Möller (Reference Möller1991) considered the friction velocity at the gap, which decreases sharply with decreasing gap size and vanishes when the gap closes (Chang & Tavoularis Reference Chang and Tavoularis2008); consequently, it is not surprising that he found
$u_{{\it\tau}}$
. Möller (Reference Möller1991) considered the friction velocity at the gap, which decreases sharply with decreasing gap size and vanishes when the gap closes (Chang & Tavoularis Reference Chang and Tavoularis2008); consequently, it is not surprising that he found
![]() $\mathit{St}_{{\it\tau}}$
to be inversely proportional to the relative gap size, an observation that does not actually contradict our finding that cross-flow oscillation frequency changes little with gap size. A careful reading of the information provided by Wu & Trupp (Reference Wu and Trupp1994) in this reference and other published work of theirs indicated that they defined their
$\mathit{St}_{{\it\tau}}$
to be inversely proportional to the relative gap size, an observation that does not actually contradict our finding that cross-flow oscillation frequency changes little with gap size. A careful reading of the information provided by Wu & Trupp (Reference Wu and Trupp1994) in this reference and other published work of theirs indicated that they defined their
![]() $\mathit{St}_{{\it\tau}}$
in terms of the average, rather than the local, friction velocity; consequently, despite these authors’ claims that their
$\mathit{St}_{{\it\tau}}$
in terms of the average, rather than the local, friction velocity; consequently, despite these authors’ claims that their
![]() $\mathit{St}_{{\it\tau}}$
was inversely proportional to
$\mathit{St}_{{\it\tau}}$
was inversely proportional to
![]() ${\it\delta}/d$
, their results for the symmetric gap geometries were in fact in fair agreement with ours, as figure 13 shows. In closing, we may note that
${\it\delta}/d$
, their results for the symmetric gap geometries were in fact in fair agreement with ours, as figure 13 shows. In closing, we may note that
![]() $\mathit{St}_{{\it\tau}}$
, as defined by Möller (Reference Möller1991), is not a proper dimensionless frequency, because it contains the local friction velocity, which is extremely sensitive to geometry and flow conditions; we should also note that
$\mathit{St}_{{\it\tau}}$
, as defined by Möller (Reference Möller1991), is not a proper dimensionless frequency, because it contains the local friction velocity, which is extremely sensitive to geometry and flow conditions; we should also note that
![]() $\mathit{St}$
is not a measure of mixing efficiency in the channel and its value has no relationship to the amplitude of cross-gap velocity fluctuations, which is a true indicator of inter-subchannel mixing.
$\mathit{St}$
is not a measure of mixing efficiency in the channel and its value has no relationship to the amplitude of cross-gap velocity fluctuations, which is a true indicator of inter-subchannel mixing.

Figure 13. Variation of the Strouhal number with the dimensionless gap spacing. For the present results, (a) denotes moderate inlet management and (b) strong.
7. Attempts to quantify the effects of geometry on the flow characteristics
In this section, we will address question (d) of § 3, namely we will investigate the effect of annular geometry (i.e. the inner-to-outer diameter ratio and eccentricity) on the flow structure away form the inlet and, as much as possible, independently of Reynolds number effects. As demonstrated in a previous section, inlet effects for the three geometries considered ceased to be significant in the present test sections for
![]() $\mathit{Re}\gtrsim 7000$
, so we will only consider results in this
$\mathit{Re}\gtrsim 7000$
, so we will only consider results in this
![]() $\mathit{Re}$
-range. For a meaningful comparison of the three cases, it is necessary to compare results at the same
$\mathit{Re}$
-range. For a meaningful comparison of the three cases, it is necessary to compare results at the same
![]() $\mathit{Re}$
, which should be as large as possible. Because the highest
$\mathit{Re}$
, which should be as large as possible. Because the highest
![]() $\mathit{Re}$
that could be achieved in the channel with
$\mathit{Re}$
that could be achieved in the channel with
![]() $d/D=0.75$
was 9900, we will focus on results taken near this Reynolds number. Another concern was to isolate the effect of diameter ratio from other geometric effects. It has been amply demonstrated that the phenomena of interest in this work depend upon the relative size of the narrow gap; however, it is not clear whether it is the eccentricity, the absolute gap size or some other parameter that plays an important role. After considering various possibilities, we decided to make two sets of comparisons: first, to evaluate the diameter effect while keeping the eccentricity constant and equal to 0.80, which is the value used most extensively in Part 1 and the present article; and second, to evaluate the diameter effect while keeping the gap size
$d/D=0.75$
was 9900, we will focus on results taken near this Reynolds number. Another concern was to isolate the effect of diameter ratio from other geometric effects. It has been amply demonstrated that the phenomena of interest in this work depend upon the relative size of the narrow gap; however, it is not clear whether it is the eccentricity, the absolute gap size or some other parameter that plays an important role. After considering various possibilities, we decided to make two sets of comparisons: first, to evaluate the diameter effect while keeping the eccentricity constant and equal to 0.80, which is the value used most extensively in Part 1 and the present article; and second, to evaluate the diameter effect while keeping the gap size
![]() ${\it\delta}/D$
constant and equal to 0.05, which corresponds to
${\it\delta}/D$
constant and equal to 0.05, which corresponds to
![]() $e=0.80$
for the
$e=0.80$
for the
![]() $d/D=0.50$
case.
$d/D=0.50$
case.
Table 1 summarizes the relevant values of the chosen four flow indicators, as extracted from figure 4. It was shown previously that the dimensionless mid-gap velocity
![]() $U_{z}/U_{b}$
was affected strongly by the gap vortex street and increased considerably from the FG region to the RM region. Increasing the diameter ratio while keeping the eccentricity constant generally resulted in lower mid-gap axial velocities (figure 4
a). For the same gap size (figure 4
b),
$U_{z}/U_{b}$
was affected strongly by the gap vortex street and increased considerably from the FG region to the RM region. Increasing the diameter ratio while keeping the eccentricity constant generally resulted in lower mid-gap axial velocities (figure 4
a). For the same gap size (figure 4
b),
![]() $U_{z}/U_{b}$
for the three diameter ratios changed by lesser amounts and did not have a monotonic trend. This appears to show that
$U_{z}/U_{b}$
for the three diameter ratios changed by lesser amounts and did not have a monotonic trend. This appears to show that
![]() $U_{z}/U_{b}$
is more dependent on the gap size than on the diameter ratio within the ranges considered. The mid-gap axial flow fluctuations
$U_{z}/U_{b}$
is more dependent on the gap size than on the diameter ratio within the ranges considered. The mid-gap axial flow fluctuations
![]() $u_{z}^{\prime }/U_{b}$
appear to decrease with increasing diameter ratio, both under constant eccentricity (figure 4
c) and under constant gap size (figure 4
d). The mid-gap cross-flow fluctuations
$u_{z}^{\prime }/U_{b}$
appear to decrease with increasing diameter ratio, both under constant eccentricity (figure 4
c) and under constant gap size (figure 4
d). The mid-gap cross-flow fluctuations
![]() $u_{x}^{\prime }/U_{b}$
decrease from the case with
$u_{x}^{\prime }/U_{b}$
decrease from the case with
![]() $d/D=0.25$
to the one with
$d/D=0.25$
to the one with
![]() $d/D=0.50$
but stay about the same for the case with
$d/D=0.50$
but stay about the same for the case with
![]() $d/D=0.75$
.
$d/D=0.75$
.
Table 1. Asymptotic values of the normalized mid-gap mean axial flow velocity, normalized standard deviation of axial and cross-flow fluctuations and Strouhal number for different diameter ratios;
![]() $\mathit{Re}\approx 9300$
.
$\mathit{Re}\approx 9300$
.

An important parameter of interest in this work is the frequency of periodic motions, which was found not to change significantly along a channel with a fixed geometry at a fixed Reynolds number. To present this frequency in dimensionless form, i.e. as a Strouhal number, we need a length scale and a velocity scale. In previous discussion up to this point, we have used the inner diameter
![]() $d$
and the bulk velocity
$d$
and the bulk velocity
![]() $U_{b}$
as scales. These scales apply to the channel as a whole and may be suitable for scaling frequencies in channels with the same cross-sectional shape but different sizes or different Reynolds numbers in the asymptotic state of development. Nevertheless, the same scales are not sensitive to the channel’s internal geometry, namely the diameter ratio and eccentricity, and this explains why
$U_{b}$
as scales. These scales apply to the channel as a whole and may be suitable for scaling frequencies in channels with the same cross-sectional shape but different sizes or different Reynolds numbers in the asymptotic state of development. Nevertheless, the same scales are not sensitive to the channel’s internal geometry, namely the diameter ratio and eccentricity, and this explains why
![]() $\mathit{St}$
was found to vary with these parameters in some cases. As discussed in Part 1, gap instability originates in the mixing layers forming on either side of the gap and, consequently, frequency scaling should be based on length and velocity scales that are relevant to these mixing layers, rather than the channel as a whole. Consequently, it seems logical for one to choose a length scale that is a measure of the mixing layer thickness and a velocity scale that is a measure of the convection speed of periodic motions in the mixing layer. In a plane mixing layer, the convection speed of vortices is equal to the average velocity of the two streams, but there is no obvious choice of this scale for an eccentric annular channel. By analogy to a plane mixing layer, one could use the bulk velocity as representative of the high-velocity side of the gap mixing layer and then seek an empirical expression for the low-velocity side. In the absence of an all-encompassing theory of gap instability, we will attempt an empirical determination of both the length scale and the velocity scale, which would necessarily be valid within the ranges of measurements used for the empirical fits but whose general validity would need to be tested under a variety of geometrical conditions.
$\mathit{St}$
was found to vary with these parameters in some cases. As discussed in Part 1, gap instability originates in the mixing layers forming on either side of the gap and, consequently, frequency scaling should be based on length and velocity scales that are relevant to these mixing layers, rather than the channel as a whole. Consequently, it seems logical for one to choose a length scale that is a measure of the mixing layer thickness and a velocity scale that is a measure of the convection speed of periodic motions in the mixing layer. In a plane mixing layer, the convection speed of vortices is equal to the average velocity of the two streams, but there is no obvious choice of this scale for an eccentric annular channel. By analogy to a plane mixing layer, one could use the bulk velocity as representative of the high-velocity side of the gap mixing layer and then seek an empirical expression for the low-velocity side. In the absence of an all-encompassing theory of gap instability, we will attempt an empirical determination of both the length scale and the velocity scale, which would necessarily be valid within the ranges of measurements used for the empirical fits but whose general validity would need to be tested under a variety of geometrical conditions.
The shape of the annular geometry is defined by the diameter ratio and the eccentricity, so these parameters could be used as independent variables for scaling purposes. Instead of eccentricity, however, which is a rather complex property, it seems more straightforward to assume that the mixing layer strength would depend on the ratio of narrow and wide gap sizes
![]() ${\it\delta}/{\it\Delta}$
, which is related to eccentricity as
${\it\delta}/{\it\Delta}$
, which is related to eccentricity as
![]() ${\it\delta}/{\it\Delta}=(1-e)/(1+e)$
, such that
${\it\delta}/{\it\Delta}=(1-e)/(1+e)$
, such that
![]() ${\it\delta}/{\it\Delta}=1$
when
${\it\delta}/{\it\Delta}=1$
when
![]() $e=0$
and
$e=0$
and
![]() ${\it\delta}/{\it\Delta}=0$
when
${\it\delta}/{\it\Delta}=0$
when
![]() $e=1$
. Therefore, the mixing layer length and velocity scales can be expressed as, respectively,
$e=1$
. Therefore, the mixing layer length and velocity scales can be expressed as, respectively,
and
where
![]() ${\it\phi}_{1}((d/D),({\it\delta}/{\it\Delta}))$
and
${\it\phi}_{1}((d/D),({\it\delta}/{\it\Delta}))$
and
![]() ${\it\phi}_{2}((d/D),({\it\delta}/{\it\Delta}))$
are empirical dimensionless functions. Then, a Strouhal number of the periodic motions in eccentric annular channels may be defined in terms of mixing layer scales as
${\it\phi}_{2}((d/D),({\it\delta}/{\it\Delta}))$
are empirical dimensionless functions. Then, a Strouhal number of the periodic motions in eccentric annular channels may be defined in terms of mixing layer scales as
 $$\begin{eqnarray}\mathit{St}^{\ast }=\frac{\displaystyle fd{\it\phi}_{1}\left(\frac{d}{D},\frac{{\it\delta}}{{\it\Delta}}\right)}{\displaystyle \frac{1}{2}U_{b}\left[1+{\it\phi}_{2}\left(\frac{d}{D},\frac{{\it\delta}}{{\it\Delta}}\right)\right]}=\mathit{St}\frac{\displaystyle {\it\phi}_{1}\left(\frac{d}{D},\frac{{\it\delta}}{{\it\Delta}}\right)}{\displaystyle \frac{1}{2}\left[1+{\it\phi}_{2}\left(\frac{d}{D},\frac{{\it\delta}}{{\it\Delta}}\right)\right]}=\mathit{St}{\it\phi}\left(\frac{d}{D},\frac{{\it\delta}}{{\it\Delta}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\mathit{St}^{\ast }=\frac{\displaystyle fd{\it\phi}_{1}\left(\frac{d}{D},\frac{{\it\delta}}{{\it\Delta}}\right)}{\displaystyle \frac{1}{2}U_{b}\left[1+{\it\phi}_{2}\left(\frac{d}{D},\frac{{\it\delta}}{{\it\Delta}}\right)\right]}=\mathit{St}\frac{\displaystyle {\it\phi}_{1}\left(\frac{d}{D},\frac{{\it\delta}}{{\it\Delta}}\right)}{\displaystyle \frac{1}{2}\left[1+{\it\phi}_{2}\left(\frac{d}{D},\frac{{\it\delta}}{{\it\Delta}}\right)\right]}=\mathit{St}{\it\phi}\left(\frac{d}{D},\frac{{\it\delta}}{{\it\Delta}}\right).\end{eqnarray}$$
If the previous scaling assumption were valid, and one also took into account that the Strouhal number is insensitive to the Reynolds number for large
![]() $\mathit{Re}$
, then the value of
$\mathit{Re}$
, then the value of
![]() $\mathit{St}^{\ast }$
would have to be universal for all flows in highly eccentric annular channels at sufficiently large Reynolds numbers. For convenience, one may assume that the empirical function
$\mathit{St}^{\ast }$
would have to be universal for all flows in highly eccentric annular channels at sufficiently large Reynolds numbers. For convenience, one may assume that the empirical function
![]() ${\it\phi}$
is equal to unity for a particular geometry. If sufficient data were available for the determination of the function
${\it\phi}$
is equal to unity for a particular geometry. If sufficient data were available for the determination of the function
![]() ${\it\phi}$
, an empirical description of geometry effects upon the frequency of periodic motions would be achievable. Unfortunately, a complete set of data for all combinations of values of
${\it\phi}$
, an empirical description of geometry effects upon the frequency of periodic motions would be achievable. Unfortunately, a complete set of data for all combinations of values of
![]() $d/D$
and
$d/D$
and
![]() ${\it\delta}/{\it\Delta}$
is not available.
${\it\delta}/{\it\Delta}$
is not available.
We have put considerable effort towards establishing an empirical form for (7.3), based on the limited set of available data (see also Choueiri Reference Choueiri2014). Results of these efforts are deemed to be tentative and not validated sufficiently, so they will not be presented in detail. To assist future efforts, a summary of these results is as follows.
-
(a) With a restriction to flows with
 $\mathit{Re}>10\,000$
, (7.3) may be fitted to data to reduce the variability in the Strouhal number.
$\mathit{Re}>10\,000$
, (7.3) may be fitted to data to reduce the variability in the Strouhal number. -
(b) The function
 ${\it\phi}$
appears to be more sensitive to variations in
${\it\phi}$
appears to be more sensitive to variations in
 $d/D$
than to variations in
$d/D$
than to variations in
 $e$
; this function also depends on the upstream conditions.
$e$
; this function also depends on the upstream conditions.
The previous discussion was concerned with the peak frequency of cross-gap velocity fluctuations, which is relatively easy to measure. This frequency has been used by previous researchers as the most common indicator of quasi-periodic motions across narrow gaps. It has occasionally even appeared in empirical predictors of inter-subchannel mixing, despite the well-known fact that frequency is not a measure of the strength of such mixing but of the rate of passage of coherent structures, namely pairs of vortices in gap vortex streets. The average distance
![]() ${\it\lambda}$
between such vortex pairs, previously referred to as the wavelength of the vortex street, is related to the peak frequency as
${\it\lambda}$
between such vortex pairs, previously referred to as the wavelength of the vortex street, is related to the peak frequency as
![]() ${\it\lambda}=U_{c}/f$
, where
${\it\lambda}=U_{c}/f$
, where
![]() $U_{c}$
is the convection velocity of the coherent structures, introduced previously under the name of mixing layer velocity scale. For sufficiently large Reynolds numbers, the parameter
$U_{c}$
is the convection velocity of the coherent structures, introduced previously under the name of mixing layer velocity scale. For sufficiently large Reynolds numbers, the parameter
![]() ${\it\lambda}$
is said to be a function of geometry alone (Meyer Reference Meyer2010). In Part 1 we were able to determine the average vortex street wavelength from particle image velocimetry measurements and from frequency and convection velocity measurements for a particular geometry. Nevertheless, this procedure was quite cumbersome and time consuming and so we were unable to repeat it for other geometries. Consequently, we will delegate the scaling of vortex street wavelength to future investigations.
${\it\lambda}$
is said to be a function of geometry alone (Meyer Reference Meyer2010). In Part 1 we were able to determine the average vortex street wavelength from particle image velocimetry measurements and from frequency and convection velocity measurements for a particular geometry. Nevertheless, this procedure was quite cumbersome and time consuming and so we were unable to repeat it for other geometries. Consequently, we will delegate the scaling of vortex street wavelength to future investigations.
8. Summary and concluding remarks
In this work we identified several flow indicators that are relevant to gap instability in eccentric annular channels and examined their dependence on inlet conditions, inner-to-outer diameter ratio, eccentricity and Reynolds number. These flow indicators were the mid-gap axial flow velocity, the axial and cross-flow velocity fluctuations and the Strouhal number of the cross-flow oscillations; all were measured in the middle of the narrow gap and normalized by the bulk velocity.
Inlet conditions were found to affect the flow development, as progressively stronger flow management prolonged the entrance region and shifted the development of periodic motions and ensuing phenomena further downstream. In general, at low
![]() $\mathit{Re}$
, the four flow indicators increased with
$\mathit{Re}$
, the four flow indicators increased with
![]() $\mathit{Re}$
, at rates which were highly dependent on inlet conditions; however, at higher
$\mathit{Re}$
, at rates which were highly dependent on inlet conditions; however, at higher
![]() $\mathit{Re}$
, all these indicators approached asymptotic values which were only mildly sensitive to inlet conditions. Flows with mild inlet management (namely, with stronger inlet disturbances) reached their asymptotic states closer to the inlet than those with moderate or strong management.
$\mathit{Re}$
, all these indicators approached asymptotic values which were only mildly sensitive to inlet conditions. Flows with mild inlet management (namely, with stronger inlet disturbances) reached their asymptotic states closer to the inlet than those with moderate or strong management.
For a range of Reynolds number and eccentricity, we constructed state maps which show the various stages of flow development for a particular set of inlet conditions. It was found that, for
![]() $\mathit{Re}<1100$
or for
$\mathit{Re}<1100$
or for
![]() $e<0.5$
, no periodicity was detectable and the flow was unconditionally stable to gap instability. For
$e<0.5$
, no periodicity was detectable and the flow was unconditionally stable to gap instability. For
![]() $e\leqslant 0.5$
, transition to turbulence occurred at
$e\leqslant 0.5$
, transition to turbulence occurred at
![]() $\mathit{Re}\approx 6000$
, whereas, for
$\mathit{Re}\approx 6000$
, whereas, for
![]() $0.6\leqslant e\leqslant 0.9$
, the critical Reynolds number for the formation of periodic motions was found to increase with eccentricity from 1100 for
$0.6\leqslant e\leqslant 0.9$
, the critical Reynolds number for the formation of periodic motions was found to increase with eccentricity from 1100 for
![]() $e=0.6$
to 3800 for
$e=0.6$
to 3800 for
![]() $e=0.9$
.
$e=0.9$
.
The normalized mid-gap axial flow velocity generally decreased with increasing eccentricity, and increased asymptotically with increasing Reynolds number. The rate of increase was accelerated with the ensuing gap instability when conditions for its development were favourable. The axial and cross-flow fluctuation intensities were insensitive to eccentricity for
![]() $0\leqslant e\leqslant 0.5$
; they peaked at
$0\leqslant e\leqslant 0.5$
; they peaked at
![]() $e=0.7$
for
$e=0.7$
for
![]() $\mathit{Re}\leqslant 7500$
and at
$\mathit{Re}\leqslant 7500$
and at
![]() $e=0.9$
for
$e=0.9$
for
![]() $\mathit{Re}=15\,500$
.
$\mathit{Re}=15\,500$
.
Acknowledgements
Financial support by the Natural Sciences and Engineering Research Council of Canada and Atomic Energy of Canada Limited are gratefully acknowledged.