1 Introduction
The evaporation of water is important for the climate on Earth, body temperature control of all warm-blooded mammals and many industrial cooling processes. These varied problems involve both evaporation from a single drop and from collections of drops. The physical processes which control the evaporation of a drop on a solid substrate have been the subject of a number of recent reviews (Cazabat & Guéna Reference Cazabat and Guéna2010; Erbil Reference Erbil2012; Larson Reference Larson2014). Here we focus on two important aspects of this problem which so far have received little attention: the influence that drops inside a collection of drops have on one another and the evaporation from very large drops. We will stay inside the limit of slow evaporation, meaning that the temperature is almost constant throughout the system, and evaporation is quasi-steady.
For an evaporating drop, one would guess naively that the surface area governs the evaporation rate; however, for drops smaller than approximately a centimetre in a temperature controlled environment, detailed experiments show that the rate is proportional to the drop radius
$R$
for both pinned (Deegan et al.
Reference Deegan, Bakajin, Dupont, Huber, Nagel and Witten2000; Crafton & Black Reference Crafton and Black2004; David, Sefiane & Tadrist Reference David, Sefiane and Tadrist2007; Gelderblom et al.
Reference Gelderblom, Marin, Nair, van Houselt, Lefferts, Snoeijer and Lohse2011) and moving contact lines (Cachile, Benichou & Cazabat Reference Cachile, Benichou and Cazabat2002a
; Cachile et al.
Reference Cachile, Benichou, Poulard and Cazabat2002b
; Poulard, Benichou & Cazabat Reference Poulard, Benichou and Cazabat2003; Shahidzadeh-Bonn et al.
Reference Shahidzadeh-Bonn, Rafaï, Azouni and Bonn2006; Starov & Sefiane Reference Starov and Sefiane2009). In fact, in the regime of slow evaporation considered here, the evaporation is quasi-steady (Cazabat & Guéna Reference Cazabat and Guéna2010; Stauber, Wilson & Duffy Reference Stauber, Wilson and Duffy2015), hence evaporation rates are defined by the instantaneous drop shapes. As we will explain in more detail below, linear scaling with size results from the evaporation rate being governed by the diffusive transport through the vapour (Deegan et al.
Reference Deegan, Bakajin, Dupont, Huber, Nagel and Witten1997; Bonn et al.
Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009). The prefactor of this scaling law however depends on the shape of the drop, either through the contact angle (Gelderblom et al.
Reference Gelderblom, Marin, Nair, van Houselt, Lefferts, Snoeijer and Lohse2011; Sobac & Brutin Reference Sobac and Brutin2011) or the fact that larger drops are flattened by gravity (Cazabat & Guéna Reference Cazabat and Guéna2010).
Most of our experiments are for drops which partially wet the solid substrate. While in this case it is often observed that drops are either pinned completely (i.e. the radius is constant, (Gelderblom et al.
Reference Gelderblom, Marin, Nair, van Houselt, Lefferts, Snoeijer and Lohse2011)) or perform a stick–slip motion (Cazabat & Guéna Reference Cazabat and Guéna2010), for our systems we observe the drop radius to shrink continuously during evaporation without pinning for most substrates. We attribute this to the fact that the substrates are smooth, making the pinning force small; this is evidenced by the small contact angle hysteresis on these surfaces. A short period of pinning at the start of evaporation can however occur for a polypropylene substrate, but it does not last for more than 5 % of the duration of evaporation and does not influence the results. The avoidance of pinning means the contact angle remains almost constant, with possibly small corrections owing to evaporation. Since for small drops at constant contact angle the volume
$V$
scales as
$R^{3}$
, it follows from
$\text{d}V/\text{d}t\propto R$
that the radius scales as
$R\propto (t_{0}-t)^{1/2}$
, where
$t_{0}$
is the time at which the drop vanishes.
In this paper, we focus on the total evaporation from a drop, and explore deviations from standard scaling laws. In § 2 we calculate the diffusion-limited total evaporation from a small drop, and find linear scaling with
$R$
. Experiments with partially wetting drops show the corresponding scaling of the drop radius with time. In the next section, we show that in a small collection of drops, evaporation from an individual drop is reduced considerably compared to that from an isolated drop. This is explained by a simple, semi-quantitative, model calculation. In § 4, we measure evaporation from a spray with a wide distribution of drop sizes, and find once more that the time evolution of total evaporation is compatible with strong coupling between drops only. Finally, we consider the limit of the diffusive mechanism as drop sizes become large, extending considerably the range of drop sizes investigated previously (Kelly-Zion et al.
Reference Kelly-Zion, Pursell, Vaidya and Batra2011).
2 A single small drop
The slow evaporation of small drops is limited by diffusion (Larson Reference Larson2014). The total rate of evaporation per unit mass
$J$
equals the area of the drop multiplied by the local flux density. If
$R_{d}$
is the linear dimension of the drop (which we will define more precisely below when we calculate the evaporation rate quantitatively) the area scales as
$R_{d}^{2}$
. On the other hand, the typical length scale of the diffusive field around the drop is also set by
$R_{d}$
, so gradients, and thus the local flux of vapour, scale as
$R_{d}^{-1}$
. But this means that the total rate of evaporation is proportional to
$R_{d}^{2}/R_{d}=R_{d}$
.
We can calculate the constant of proportionality quantitatively for small drops, for which the shape is known. Small drops, for which gravity does not play an important role, have the shape of spherical caps. In this case, we can derive a formula for the total evaporation for arbitrary contact angles, simplifying the earlier treatment by Popov (Reference Popov2005). In the quasi-static limit, we have to solve Laplace’s equation
${\rm\Delta}c=0$
in the half-space above the substrate, and outside of the drop. The boundary conditions are
$c=c_{s}$
on the surface of the drop, where
$c_{s}$
is the saturation concentration, and zero flux in the plane
$z=0$
of the substrate. We start from the formula derived in Deegan et al. (Reference Deegan, Bakajin, Dupont, Huber, Nagel and Witten2000) for the concentration outside a lens-shaped drop with contact angle
${\it\theta}$
,
$0\leqslant {\it\theta}\leqslant {\rm\pi}$
:
$$\begin{eqnarray}c({\it\alpha},{\it\beta})=\sqrt{2}c_{s}\sqrt{\cosh {\it\alpha}-\cos {\it\beta}}\int _{0}^{\infty }\frac{\cosh {\it\theta}{\it\tau}\cosh (2{\rm\pi}-{\it\beta}){\it\tau}}{\cosh {\rm\pi}{\it\tau}\cosh ({\rm\pi}-{\it\theta}){\it\tau}}P_{-1/2+\text{i}{\it\tau}}(\cosh {\it\alpha})\,\text{d}{\it\tau}.\end{eqnarray}$$
Here
${\it\alpha}$
and
${\it\beta}$
are toroidal coordinates, which are related to cylindrical coordinates by the relations
$$\begin{eqnarray}r=\frac{R\sinh {\it\alpha}}{\cosh {\it\alpha}-\cos {\it\beta}},\quad z=\frac{R\sin {\it\beta}}{\cosh {\it\alpha}-\cos {\it\beta}}.\end{eqnarray}$$
In the equivalent electrostatic problem,
$J$
would be the total charge, and
$c$
the potential. Hence from the multipole expansion of the static potential (Jackson Reference Jackson1975) it follows that for large
$|\boldsymbol{r}|=\sqrt{z^{2}+r^{2}}$
,
$c$
can be expanded as:
$$\begin{eqnarray}c=\frac{J}{4{\rm\pi}D\sqrt{z^{2}+r^{2}}}+O(|\boldsymbol{r}|^{-2}),\end{eqnarray}$$
keeping only the monopole term. To calculate
$J$
we analyse the asymptotics of (2.1) for large
$|\boldsymbol{r}|$
and compare the result to (2.3). The calculation is simplified by the observation that the limit can be taken in any direction; a particular choice is to let
$z\rightarrow \infty$
as
$r=0$
, putting
${\it\alpha}=0$
in (2.1), so that
$P_{-1/2+\text{i}{\it\tau}}(\cosh {\it\alpha})=P_{-1/2+\text{i}{\it\tau}}(1)=1$
and
$z=R\sin {\it\beta}/(1-\cos {\it\beta})$
. To achieve the limit
$z\rightarrow \infty$
, we let
${\it\beta}$
approach
$2{\rm\pi}$
, since at
${\it\beta}=0$
the integral (2.1) does not converge. In this limit, the prefactor in (2.1) can be rewritten as
$$\begin{eqnarray}\sqrt{\cosh {\it\alpha}-\cos {\it\beta}}=\sqrt{1-\cos {\it\beta}}\approx \frac{\sqrt{2}R}{|z|},\end{eqnarray}$$
so that
$$\begin{eqnarray}c\approx \frac{2c_{s}R}{z}\int _{0}^{\infty }\frac{\cosh {\it\theta}{\it\tau}}{\cosh {\rm\pi}{\it\tau}\cosh ({\rm\pi}-{\it\theta}){\it\tau}}\,\text{d}{\it\tau}.\end{eqnarray}$$
Comparing to (2.3) with
$r=0$
, we find a slightly simplified, yet otherwise equivalent form of (A 8) of Popov (Reference Popov2005), taking only evaporation into the upper half-plane into account:
$$\begin{eqnarray}J=4{\rm\pi}Dc_{s}R\int _{0}^{\infty }\frac{\cosh {\it\theta}{\it\tau}}{\cosh {\rm\pi}{\it\tau}\cosh ({\rm\pi}-{\it\theta}){\it\tau}}\,\text{d}{\it\tau}.\end{eqnarray}$$
Formula (2.6) is written in terms of the contact line radius
$R$
, while the evaporation rate is really controlled by the linear dimension of the drop. In particular, for
${\it\theta}\rightarrow {\rm\pi}$
the contact line radius goes to zero for a given drop size. We therefore define
$R_{d}$
, the radius of the projection of the drop onto the substrate, as a meaningful measure of the drop size for any contact angle. It follows that
$R=R_{d}$
for
${\it\theta}\leqslant {\rm\pi}/2$
, and
$R=R_{d}\sin {\it\theta}$
for
${\rm\pi}/2<{\it\theta}\leqslant {\rm\pi}$
.
The limit
${\it\theta}\rightarrow {\rm\pi}$
requires special analysis, since the integral in (2.6) diverges, so as to keep
$J$
finite at constant
$R_{d}$
. Putting
${\it\theta}={\rm\pi}-{\it\epsilon}$
and expanding in
${\it\epsilon}$
, we can write the integrand as
$$\begin{eqnarray}\frac{\cosh ({\rm\pi}-{\it\epsilon}){\it\tau}}{\cosh {\rm\pi}{\it\tau}\cosh {\it\epsilon}{\it\tau}}=\frac{\text{e}^{-{\it\epsilon}{\it\tau}}}{\cosh {\it\epsilon}{\it\tau}}+\frac{{\it\tau}\text{e}^{-{\rm\pi}{\it\tau}}}{\cosh {\rm\pi}{\it\tau}}{\it\epsilon}+O({\it\epsilon}^{3}),\end{eqnarray}$$
and perform the integral for each term individually. This yields
$$\begin{eqnarray}J=Dc_{s}R_{d}{\rm\pi}\left[4\ln 2-\left(\frac{2\ln 2}{3}-\frac{1}{6}\right){\it\epsilon}^{2}+O({\it\epsilon}^{4})\right],\end{eqnarray}$$
the leading term of which is calculated in Smith & Barakat (Reference Smith and Barakat1975).
The other well-known limit is
${\it\theta}=0$
, a drop shaped like a two-dimensional disc. In that case one finds that in the plane
$z=0$
of the substrate (Jackson Reference Jackson1975):
$$\begin{eqnarray}j_{z}=\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{2Dc_{s}}{{\rm\pi}\sqrt{R^{2}-r^{2}}}}, & r<R,\\ 0, & r\geqslant R,\end{array}\right.\quad c=c_{s}\left\{\begin{array}{@{}ll@{}}1, & r<R,\\ {\displaystyle \frac{2}{{\rm\pi}}}\arcsin \left({\displaystyle \frac{R}{r}}\right), & r\geqslant R,\end{array}\right.\end{eqnarray}$$
where
$D$
is the diffusion constant and
$j_{z}$
the volume flux. Then the total evaporation from the drop is (Jackson Reference Jackson1975):
$$\begin{eqnarray}J=2{\rm\pi}D\int _{0}^{R}j_{z}r\,\text{d}r=4Dc_{s}R,\end{eqnarray}$$
which agrees with (2.6), since for
${\it\theta}=0$
the integral in (2.6) is evaluated as
$1/{\rm\pi}$
. Finally, for
${\it\theta}={\rm\pi}/2$
, the integral is
$1/2$
, so the total evaporation is
$J=2{\rm\pi}Dc_{s}R$
, half the value for an isolated sphere, as expected. To summarize the result for all angles, in figure 1 we plot
$J/(Dc_{s}R_{d})$
as a function of
${\it\theta}$
. Careful experiments with small partially wetting drops with pinned contact lines have confirmed the theoretical result (2.6) quantitatively over a wide range of contact angles (Gelderblom et al.
Reference Gelderblom, Marin, Nair, van Houselt, Lefferts, Snoeijer and Lohse2011).
Figure 1. The normalized evaporation rate
$J/(Dc_{s}R_{d})$
as a function of
${\it\theta}$
according to (2.6).
Figure 2. (a) Mass of a single drop of water (
$20~{\rm\mu}\text{l}$
,
${\it\theta}=94^{\circ }$
at equilibrium) on a polystyrene surface versus time. The polystyrene surface was cleaned with ethanol and water then dried with a nitrogen flow. The red power-law fit gives a power of 1.50. The measurements of the evaporation rate were made by measuring the weight of the drop as a function of time using a precision balance while simultaneously visualizing the radii using a CCD camera, all in a controlled humidity environment of
$RH=50\,\%$
and temperature
$T=21\,^{\circ }\text{C}$
. (b) Radius versus time for a
$2~{\rm\mu}\text{l}$
water drop on a superhydrophobic surface made by soot deposition followed by impregnation with a hydrophobic spray (
${\it\theta}=146^{\circ }$
at equilibrium). At very late times, the drop reaches a critical size and the water penetrates the asperities of the soot surface. At this moment, the surface changes character from superhydrophobic to relatively hydrophilic. We therefore stop taking data at this point. The red power-law fit gives a power of 0.50.
In figure 2, we present data for the evaporation of a small water drop on a partially wetting (a) and a superhydrophobic (b) surface. In both cases, and as shown explicitly in figure 2(b) for the superhydrophobic substrate, we observed the radius to decrease continuously, with no indications of contact line pinning. Since the speed of retraction is slow, as measured for example by the capillary number (Larson Reference Larson2014), the dynamic contact angle is close to its constant equilibrium value and the mode of evaporation is one of constant contact angle (Stauber et al. Reference Stauber, Wilson and Duffy2015). As is well known (Cazabat & Guéna Reference Cazabat and Guéna2010; Stauber et al. Reference Stauber, Wilson and Duffy2015), combining the evaporation rate (2.6) with the formula for the volume of a small (i.e. spherical cap-shaped) drop, one finds the drop radius to shrink like
$$\begin{eqnarray}R_{d}=\sqrt{2a}(t_{0}-t)^{1/2},\end{eqnarray}$$
where
$a$
is a constant. Clearly, the drop mass or volume then has to scale like
$V\propto (t_{0}-t)^{3/2}$
. Both scaling laws are seen to be well confirmed in figure 2, apart from at the very last stages of shrinkage.
3 Collection of monodisperse drops
To see whether there are collective effects between drops, we now compare the evaporation rate of collections of drops separated from one another by roughly their diameter with individual drops of different sizes. We consider three different cases of drop arrangements on a polystyrene surface (Petri dishes,
${\it\theta}=94^{\circ }$
at equilibrium), as shown in figure 3(a). We follow the mass of the evaporating system with a precision balance (Mettler Toledo) while visualizing the radii of the drops from above with a CCD camera (PixeLink). The polystyrene substrate was cleaned with ethanol and water before being dried with a nitrogen flow. The control of humidity is done in a climatic chamber described by Shahidzadeh & Desarnaud (Reference Shahidzadeh and Desarnaud2012). Drops are deposited gently on the substrates with a micro-pipette. The array of drops is made putting the transparent substrate on a square-patterned sheet. Case (1) is a single small drop of volume
$V_{0}$
; its evaporation rate is denoted as
$J_{V_{0}}$
. Case (2) are 10 drops of volume
$V_{0}$
, with evaporation rate
$J_{V_{0}\times 10}$
, while case (3) is a single large drop of volume
$10V_{0}$
, whose evaporation is denoted
$J_{10V_{0}}$
.
Figure 3. (a) Pictures and (b) mass as a function of time during evaporation of water drops on a polystyrene surface (
${\it\theta}=94^{\circ }$
at equilibrium,
$RH=50\,\%$
and
$T=21\,^{\circ }\text{C}$
): (1): one drop of
$10~{\rm\mu}\text{l}$
(radius
$R=1.7$
mm)
$\times$
10; (2): a collection of
$10~{\rm\mu}\text{l}$
monodisperse drops (
$R=1.7$
mm, centre-to-centre distance: 7 mm); (3): one drop of
$100~{\rm\mu}\text{l}$
,
$R=3.8$
mm. The red lines correspond to 1.5 exponent power-law fits.
In figure 3(b) we show the temporal evolution of the total mass as a function of time. In case (1) the mass has been multiplied by a factor of 10, so that the initial mass is the same in all cases. In all three cases the mass follows the same power law with exponent
$3/2$
as a single small drop. However, the prefactors are significantly different, and there is a considerable deviation near the end of the evolution for the collection of drops. Not surprisingly, the large drop takes much longer to evaporate than a single small drop and also than a collection of small drops corresponding to the same volume. If there were no interaction between the collection of small drops, the line (2) would superimpose on line (1) but the surroundings of each drop are partially saturated by the vapour from the other drops, so evaporation is slower, and hence it takes longer for the drops to evaporate, as indeed confirmed by figure 3(b).
To investigate these effects more quantitatively, we focus on the total evaporation at the beginning of the evolution (
$t=0$
). We find that
$J_{V_{0}}=2.0\times 10^{-9}~\text{kg}~\text{s}^{-1}$
, for a drop with
$R=1.7$
mm. On the other hand, the single large drop (case (3)),
$R=3.8$
mm, has a total evaporation of
$J_{10V_{0}}=5.5\times 10^{-9}~\text{kg}~\text{s}^{-1}$
. This is in reasonably good accord with the notion that the total evaporation should scale like the dominant linear dimension of the object. The large drop is bigger by a factor of 2.2, while
$J_{10V_{0}}/J_{V_{0}}=2.75$
. Exact agreement is not to be expected, since the actual shapes of the two drops are different: the size of the large drop is above the capillary length, so it starts to look like a puddle, while the smaller drop is close to a spherical cap.
To deal with a collection of drops, we would like to describe the non-uniform evaporation that takes place across it by modelling the assembly as a flat ‘superdrop’. Lacking a solution corresponding exactly to the contour of the assembly shown in figure 3(a), in a rough approximation we assume a circular arrangement having an effective radius
$R_{s}$
whose evaporation can be described by (2.9) for a drop of vanishing contact angle. The superdrop is made up of
$N$
drops of radius
$R$
whose individual rates of evaporation are described by (2.6), which we write as
$J=J_{0}Dc_{s}R$
with a constant
$J_{0}({\it\theta})$
. To calculate the total evaporation, we split the task into an ‘inner’ and an ‘outer’ problem. On the scale of the outer problem, we have an effective concentration
$c_{\mathit{eff}}(r)$
on the surface of the superdrop, with
$c\rightarrow 0$
at infinity. For
$r>R_{s}$
, the boundary condition for the outer problem is one of zero flux
$j=0$
. Inside the superdrop,
$r<R_{s}$
,
$j(r)$
can be calculated (at least in principle) by solving
${\rm\Delta}c=0$
with these boundary conditions.
On the level of the inner problem, we consider the evaporation of a small drop of radius
$R$
, kept at a concentration
$c_{s}$
, evaporating into the local environment of concentration
$c_{\mathit{eff}}(r)$
. The number density of these drops is
$N/({\rm\pi}R_{s}^{2})$
. This means that the total evaporation from an individual drop is
$$\begin{eqnarray}J_{d}=J_{0}RD(c_{s}-c_{\mathit{eff}}(r)),\end{eqnarray}$$
which translates into a density
$$\begin{eqnarray}j(r)=\frac{J_{0}NRD}{{\rm\pi}R_{s}^{2}}(c_{s}-c_{\mathit{eff}}(r)).\end{eqnarray}$$
In principle, this closes the problem, and
$j(r)$
can be computed from
$c_{\mathit{eff}}(r)$
using an integral equation (Eggers & Pismen Reference Eggers and Pismen2010). A further technical problem is that the flux formally diverges at the boundary of the superdrop, owing to the mixed boundary condition. Thus one also has to allow for the fact that the boundary is smoothed out on the scale
$R$
of an individual drop.
A full analysis of this problem would require an extensive numerical and analytical investigation, which is beyond the scope of this paper. Here, we can only pursue a rough approximation, which allows us to estimate the size of the correction that results from the drop assembly. To avoid having to solve an integral equation, we assume a constant
$c_{\mathit{eff}}$
over the superdrop (which is not true in any strict asymptotic sense) and require the fluxes to match at
$r=0$
. Then from (2.9) we have
$$\begin{eqnarray}j(0)=\frac{2Dc_{\mathit{eff}}}{{\rm\pi}R_{s}}=\frac{J_{0}NRD}{{\rm\pi}R_{s}^{2}}(c_{s}-c_{\mathit{eff}}),\end{eqnarray}$$
and this can be solved as
$$\begin{eqnarray}c_{\mathit{eff}}=\frac{J_{0}NRc_{s}}{2R_{s}+J_{0}NR}.\end{eqnarray}$$
Now we can apply (2.10) for the total evaporation to the superdrop, to obtain for the total evaporation of the arrangement of drops:
$$\begin{eqnarray}J=4Dc_{\mathit{eff}}R_{s}=\frac{2J_{0}NDc_{s}R}{1+J_{0}NR/(2R_{s})}.\end{eqnarray}$$
In the limit of large
$N$
, this means that
$J\approx 4Dc_{s}R_{s}$
, i.e. the total evaporation is determined by the radius of the superdrop. Compared to
$N$
independent drops, the rate of evaporation is reduced by a factor of
$f=2/(1+J_{0}NR/(2R_{s}))$
. Note that owing to the crudeness of our approximation this expression does not go to unity, as it should, in the very dilute limit
$R/R_{s}\rightarrow 0$
. Since the contact angle is nearly 90°, we have
$J_{0}=2{\rm\pi}$
. Estimating from figure 3(a) that
$R_{s}\approx 5R$
, and using
$N=10$
, we find a reduction by a factor of
$f\approx 0.27$
owing to collective effects. Experimentally, the collective evaporation of an arrangement of 10 drops (case (2)) is
$J_{V_{0}\times 10}=1.0\times 10^{-8}~\text{kg}~\text{s}^{-1}$
, which amounts to
$f=0.5$
.
Collective effects become weaker as the ratio of the centre-to-centre distance
$d$
, divided by the drop radius
$R$
, becomes larger. To study this effect more systematically, we measured the evaporation of smaller drops, of volume
$1~{\rm\mu}\text{l}$
(
$R=0.68$
mm) and
$2~{\rm\mu}\text{l}$
(
$R=0.86$
mm). Based on our geometrical arrangement of drops, we estimate
$R_{s}/d\approx 3/2$
. As is seen in figure 4, the agreement between theory and experiment is much improved, and is best for the smallest values of
$R/d$
.
Figure 4. Reduction of the rate of evaporation of a collection of monodisperse drops as a function of the ratio between drop radius
$R$
and the space
$d$
between drops (circles:
$1~{\rm\mu}\text{l}$
drops; triangles:
$2~{\rm\mu}\text{l}$
drops; line: theory).
Note that in our modelling we do not take into account the fact that there is greater evaporation at the edges of the superdrop. This is clear, since drops at the edges have fewer neighbours, so the atmosphere is less saturated. As a result, in the course of time, drops at the edge evaporate more quickly and disappear first. We checked that this is the case using a video recording. This is the reason that near the end of line (2) in figure 3(b) the experimental data lie above the
$3/2$
power-law fit: the outer drops have disappeared, so fewer drops imply a reduced rate of evaporation. A similar mechanism has been observed by Schäfle et al. (Reference Schäfle, Bechinger, Rinn, David and Leiderer1999), who found an instability caused by collective effects, leading to non-uniform evaporation for an initially uniform drop size distribution. As in our case, this instability starts at the boundary.
4 Evaporation of a spray of drops
In many applications, a common cooling technique is to spray water over the surface to be cooled. Spraying invariably leads to a wide size distribution of drops as seen in figure 5(a). Typically, the size distribution of drops in a spray follows a gamma distribution (Eggers & Villermaux Reference Eggers and Villermaux2008), which has a universal exponential tail. This means that small drops outnumber larger ones exponentially and the total evaporation of the ensemble will be dominated by the contribution from the smallest drops. As small drops shrink and disappear, we can expect the total evaporation to decrease according to some universal law, determined by the exponential tail.
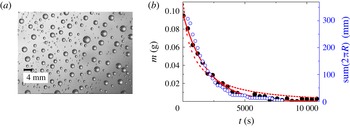
Figure 5. (a) Water drops of widely differing sizes on a polypropylene surface (
${\it\theta}\approx 90^{\circ }$
) made by spraying water using a standard agricultural spray nozzle (Teejet 11004 VS); (b) Total mass (black circles) and sum of the radii (blue circles) as a function of time during evaporation of water drops from a mica substrate. Lines are showing exponential fitting of the mass (full line for
$\text{e}^{-t}$
and dashed line for
$\text{e}^{-\sqrt{t}}$
).
The spacing between drops in the distribution is however not known: the distribution corresponds to different drop sizes with different spacing. With this in mind, we check to see if collective effects are indeed important, compared to a model without collective effects where the spacing does not come into play. To this end we calculate the total rate of evaporation
$J$
using the assumption that drops do not affect one another, keeping in mind that this is questionable, as we have seen above. We take the initial probability distribution
$p_{0}(R)$
of drop sizes
$R$
to be exponential:
$$\begin{eqnarray}p_{0}(R)=\frac{\text{e}^{-R/\overline{R}}}{\overline{R}},\end{eqnarray}$$
which is normalized to one. In the limit of non-interacting drops, the total evaporation is
$$\begin{eqnarray}J=J_{0}Dc_{s}\mathop{\sum }_{i}R_{i}\equiv J_{0}Dc_{s}N_{0}\int _{0}^{\infty }Rp(R)\,\text{d}R,\end{eqnarray}$$
where
$p(R)$
is the current distribution and
$N_{0}$
the initial number of drops. In experiment, the total mass
$M$
is measured, which is proportional to
$R^{3}$
, giving
$$\begin{eqnarray}M\propto N_{0}\int _{0}^{\infty }R^{3}p(R)\,\text{d}R.\end{eqnarray}$$
In time, the radius
$R$
of each drop changes according to (2.11), which can be written as
$$\begin{eqnarray}R_{0}=(R^{2}+2at)^{1/2},\end{eqnarray}$$
where
$R_{0}$
is the initial drop radius at
$t=0$
. The probability distribution transforms according to
$p(R)\,\text{d}R=p_{0}(R_{0})\,\text{d}R_{0}$
, and so
$$\begin{eqnarray}p(R)=p_{0}(R_{0})\frac{\text{d}R_{0}}{\text{d}R}=p_{0}(R_{0})\frac{R}{R_{0}},\end{eqnarray}$$
which together with (4.4) determines
$p(R)$
for any time
$t$
.
Using (4.5), the moments of the distribution are
$$\begin{eqnarray}\int _{0}^{\infty }p(R,t)R^{m}\,\text{d}R={\it\alpha}(\overline{R}{\it\alpha})^{m}\int _{0}^{\infty }p_{0}\left({\it\alpha}\sqrt{1+{\it\xi}^{2}}\right)\frac{{\it\xi}^{m+1}}{\sqrt{1+{\it\xi}^{2}}}\,\text{d}{\it\xi},\end{eqnarray}$$
where
$$\begin{eqnarray}{\it\alpha}=\sqrt{\frac{2at}{\overline{R}}}.\end{eqnarray}$$
Note that for
${\it\alpha}>0$
the distribution is not normalized, since drops are disappearing as their radius shrinks to zero. For the exponential distribution (4.1) one finds for the total number of drops:
$$\begin{eqnarray}N(t)=N_{0}\int _{0}^{\infty }p(R,t)\,\text{d}R=N_{0}\text{e}^{-{\it\alpha}}.\end{eqnarray}$$
Now we are in a position to compute the total evaporation or the total mass. For an exponential distribution, the integral can be calculated analytically (Gradshteyn & Ryzhik Reference Gradshteyn and Ryzhik2014), giving
$$\begin{eqnarray}\int _{0}^{\infty }R^{3}p(R,t)\,\text{d}R=\overline{R}^{3}{\it\alpha}^{4}\int _{0}^{\infty }\frac{{\it\xi}^{4}\text{e}^{-{\it\alpha}\sqrt{1+{\it\xi}^{2}}}}{\sqrt{1+{\it\xi}^{2}}}\,\text{d}{\it\xi}=3\overline{R}^{3}{\it\alpha}^{2}K_{2}({\it\alpha}),\end{eqnarray}$$
where
$K_{2}$
is a modified Bessel function of the second kind. Hence
$$\begin{eqnarray}M=M_{0}\frac{{\it\alpha}^{2}}{2}K_{2}({\it\alpha}),\end{eqnarray}$$
where
$M_{0}$
is the initial mass. For large
${\it\alpha}$
, this behaves like
$$\begin{eqnarray}M\approx M_{0}\sqrt{\frac{{\rm\pi}{\it\alpha}^{3}}{8}}\text{e}^{-{\it\alpha}},\end{eqnarray}$$
which means that the total mass scales like (up to small corrections)
$\exp (-{\it\kappa}\sqrt{t})$
, where
${\it\kappa}$
is a constant. The appearance of a stretched exponential, as opposed to the exponential tail of the original drop size distribution, comes from the evolution of the drop size distribution, driven by the square root law (2.11) for an individual drop radius.
However, in figure 5(b) one can see that the time dependence of the mass is well described by an exponential fit. The theoretical result (4.11) clearly fails, as a fit of the form
$\exp (-{\it\kappa}\sqrt{t})$
shows, and hence the assumption of an independent evolution of individual drops is not justified. For other substrates (polypropylene with
${\it\theta}\approx 90^{\circ }$
or mica with
${\it\theta}\leqslant 5^{\circ }$
) the evolution follows the same trend. Collective effects, studied in § 3 for small collections of monodisperse drops, become dominant over what would have been expected for a collection of isolated drops. This effect is so strong as to change a stretched exponential into a purely exponential behaviour, rather than merely modifying the prefactor. This is noteworthy since one would expect the highly non-uniform drop size distribution we consider to be more robust than the uniform distribution considered by Schäfle et al. (Reference Schäfle, Bechinger, Rinn, David and Leiderer1999), since evaporation is dominated by the smallest drops, which relative to their size are well separated, and more so as time goes on. This would tend to reduce collective effects. Instead, we observe that correlations introduced by the instability come to dominate the dynamics.
5 Limits of diffusion
A very large drop is nothing but a flat puddle of water, whose evaporation rate, if governed by diffusion alone, should be described by (2.10). One would expect this linear scaling with size to stop at some length scale, and eventually lead to an evaporation rate proportional to the surface area; otherwise the evaporation rate of the Atlantic ocean would be proportional to the length of its coast line! Surprisingly, previous investigations (Kelly-Zion et al. Reference Kelly-Zion, Pursell, Vaidya and Batra2011) have found a crossover (attributed to natural convection) to a different power law as function of radius, with an exponent close to 1.648.
To investigate this limit between regimes, we extended previous experiments to much greater linear dimensions. Two types of experiments were performed: (i) isolated water drops of radii between 0.6 and 60 mm on different substrates (mica, glass, polypropylene and silanized glass), which corresponds to a wide range of contact angles:
$0^{\circ }\leqslant {\it\theta}\leqslant 110^{\circ }$
and drop pinning conditions; some are repeated measurements on a single drop (‘instantaneous evaporation rate’) and (ii) cylindrical beakers filled to the rim with water, with radii between 0.75 and 400 mm. Substrates are as follows: mica cleaved just before the experiment, glass (Menzel-Glaser slides) and polypropylene cleaned with MilliQ water as well as ethanol and dried with nitrogen flow; silanized glass prepared according to Brzoska, Shahidzadeh & Rondelez (Reference Brzoska, Shahidzadeh and Rondelez1992) with Dynasylan OCTEO (Evonik) and cleaned with isopropanol left to evaporate at 70 °C. Some experiments were made with a fan perpendicular to and 10 cm away from the water interface to investigate convection effects.
In view of figure 1 one should expect a variation of the prefactor of around a factor of two, superimposed on the linear scaling for small radius. Allowing for some scatter of the data owing to this effect, all data collapse nicely onto a straight line with slope unity, up to a radius of approximately 20 mm, as seen in figure 6.
Figure 6. Rate of evaporation of water from single drops and from beakers, with and without air flow;
$u$
is the speed of the air flow, measured with a hot-wire anemometer approximately 2 cm above the evaporating system (Testo 425). The instantaneous evaporation rate – black squares – corresponds to
$J$
and
$R$
evaluated every 10 s for a single drop on a hydrophobic substrate (
${\it\theta}\approx 150^{\circ }$
).
Above that critical radius, the evaporation evolves according to the square of the radius, i.e. the flux is proportional to the surface area. We propose that above this length scale, natural convection sets in, and provides the dominant form of transport. This onset is controlled by the Rayleigh number
$$\begin{eqnarray}Ra=\frac{gR^{3}{\rm\Delta}{\it\rho}/{\it\rho}}{{\it\nu}D},\end{eqnarray}$$
with
$g=10~\text{m}~\text{s}^{-2}$
,
${\it\nu}=1.5\times 10^{-5}~\text{m}^{2}~\text{s}^{-1}$
the kinematic viscosity of air,
$D=10^{-5}~\text{m}^{2}~\text{s}^{-1}$
the diffusive coefficient and
${\rm\Delta}{\it\rho}/{\it\rho}=1\,\unicode[STIX]{x2030}$
. The usual limit of stability of convection cells for systems bounded by horizontal surfaces has a critical Rayleigh number of the order of
$10^{3}$
(Bodenschatz, Pesch & Ahlers Reference Bodenschatz, Pesch and Ahlers2000), giving a critical radius
$R_{c}\approx 25$
mm, which is consistent with the observed crossover radius. The limit size of a convection cell is the value for which the height of the cell equals the radius
$R$
of the system. If the drop is larger, the thickness of the convection layer is still set by the same length scale, so that the flux density is constant. As a result, the total flux is proportional to the area.
To further test this idea, we also measured the evaporation with a fan blowing toward the water surface. This introduces another, shorter, length scale (boundary layer thickness) into the system. As a result, the transition occurs earlier, and the rate of evaporation lies by a constant factor above that of natural convection. We suspect that the exponent of 1.648, found empirically by Kelly-Zion et al. (Reference Kelly-Zion, Pursell, Vaidya and Batra2011) (for fluids other than water), is still a reflection of the crossover between the linear and the quadratic regime.
There has been an ongoing discussion on the effect of convection on the radial shrinkage of perfectly wetting fluids, a problem distinct from the instantaneous evaporation rates considered here. While the scaling exponent for the variation of the radius as a function of the time to vanishing is close to 0.6 for water, it is close to 0.5 for most other substances (Cazabat & Guéna Reference Cazabat and Guéna2010). This difference was later attributed to convection in the vapour by Shahidzadeh-Bonn et al. (Reference Shahidzadeh-Bonn, Rafaï, Azouni and Bonn2006), taking the onset of convection to occur for
$Ra$
of order unity, rather smaller than the critical value we find here. Our new results, combined with other data on critical parameters for convection, suggests that the earlier estimate for the critical Rayleigh number is too low.
6 Conclusions
We have investigated the evaporation of drops over a wide range of length scales, in the limit that the temperature is almost uniform throughout the system – i.e. temperature gradients induced by evaporation are small. The evaporation rate only depends on the instantaneous shape of the drop, set by the drop volume and the contact angle. Very large drops resemble flat disks, which we also model by beakers filled to the rim. Experiment and theory both show linear scaling of the evaporation rate with the linear extension of the drop.
For water drops at room temperature above a radius of approximately 20 mm, the linear scaling crosses over to a quadratic scaling with the radius, making the evaporation rate proportional to the area. This is consistent with the onset of natural convection, which sets the flux of vapour per unit area. If convection is aided by a fan, the same quadratic scaling is observed, but the flux increases, and the crossover occurs at a smaller scale.
If several drops are present, separated by a distance comparable to their radius, the evaporation from a single drop is reduced significantly, owing to the saturation of the atmosphere by the other drops. Evaporation also becomes non-uniform, with drops near the border vanishing first. The size distribution within a spray of drops is strongly distorted by the interaction.
Acknowledgement
The analytical solution presented in § 2 was the subject of a third year project at the University of Bristol’s Mathematics department, done by K. Morley.
