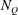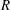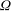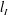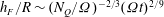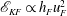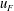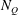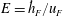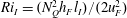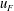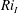1. Introduction
The interaction between shear-driven turbulence and density stratification is a key process in a wide array of geophysically relevant flows, and the ensuing vertical mixing is of central importance in understanding the flow of the world oceans (see Wunsch & Ferrari Reference Wunsch and Ferrari2004; Ivey, Winters & Koseff Reference Ivey, Winters and Koseff2008; Ferrari & Wunsch Reference Ferrari and Wunsch2009, for reviews). The dynamics of this interaction, in particular the interconnected energetics of turbulent dissipation, larger-scale ‘stirring’ and smaller-scale irreversible mixing, is extremely complex and subtle. There has been a large amount of research activity attempting to parameterise irreversible mixing in terms of larger-scale bulk measures of the flow (e.g. Linden Reference Linden1979; Fernando Reference Fernando1991; Ivey et al. Reference Ivey, Winters and Koseff2008).
Of central and ongoing interest are two inter-related questions. First, how is the kinetic energy, injected at some relatively large scale, apportioned between irreversible mixing, leading to an increase in the gravitational potential energy, and turbulent viscous dissipation; i.e. how ‘efficient’ is the mixing? Second, can the mixing in stratified flows be characterised by some relatively large-scale overturning process that tends to smear out density gradients, and hence can be considered as a diffusive process, or is it more appropriately characterised as a ‘scouring’ process that tends to maintain or indeed sharpen density gradients within a flow? These two questions are inter-related, since if the rate of increase of (global) potential energy decreases with increasing stratification, then the (local) mass flux across the interface must also decrease with increasing stratification. This implies, as originally argued by Phillips (Reference Phillips1972), that there will be a tendency of the flow to form ‘layers’ of relatively well-mixed fluid separated by thinner ‘interfaces’ of substantially stronger gradients.
Recent experimental studies of stratified Taylor–Couette flow, i.e. an annular stratified flow driven by rotation of the inner cylindrical boundary (see Woods et al. Reference Woods, Caulfield, Landel and Kuesters2010; Oglethorpe, Caulfield & Woods Reference Oglethorpe, Caulfield and Woods2013) suggest strongly that non-diffusive ‘scouring’ entrainment processes do occur, supporting a large body of previous experimental work, dating back at least to Turner (Reference Turner1968) and Kato & Phillips (Reference Kato and Phillips1969). Quite recently, Oglethorpe et al. (Reference Oglethorpe, Caulfield and Woods2013) established in stratified Taylor–Couette flow that the mixing does vary non-monotonically with stratification, and that layers do form spontaneously in an initially linearly stratified fluid. It is clearly of interest to build upon such studies to establish whether anything generic can be stated about the mixing processes that occur within stratified turbulent flows, and so it is natural to consider a range of flow geometries and forcing mechanisms.
Of specific interest, as it is perhaps more characteristic of real geophysical situations than the Taylor–Couette situation, is mixing driven primarily by vertical shear. In this case the driving mechanism in the velocity field is in direct opposition to the stabilising mechanism of the static stability. A particularly appropriate experimental flow geometry, closely related to the one originally considered by Kato & Phillips (Reference Kato and Phillips1969), is that of a stratified fluid in a cylindrical tank driven by a disc of radius
$R$
(close to the radius of the cylinder) rotating at a constant angular rotation rate
${\rm\Omega}$
at one of the boundaries. Davies et al. (Reference Davies, Guo, Boyer and Folkard1995) and Boyer, Davies & Guo (Reference Boyer, Davies and Guo1997) considered two-layer and initially linearly stratified fluid, respectively, driven by a disc just above the base of the cylinder, and observed that a well-mixed layer developed in the vicinity of the disc whose depth appeared to deepen linearly with time.
Both Davies et al. (Reference Davies, Guo, Boyer and Folkard1995) and Boyer et al. (Reference Boyer, Davies and Guo1997) argued that the potential energy production due to the local entrainment can be related linearly to the power supplied at the interface by the mobilised ‘forced’ layer. In turn, the power input is proportional to the third power of some characteristic velocity
$u_{F}^{3}$
. They further argued that this characteristic velocity should be constant in time,
$u_{F}\propto {\rm\Omega}R$
, crucially independent of the present depth of the mixed layer
$h_{F}$
. Therefore, the combination of these two arguments implied that the rate of increase of potential energy was constant in time.
In the initially two-layer case, with initial densities
${\it\rho}_{F}(0)$
and
${\it\rho}_{L}>{\it\rho}_{F}(0)$
and initial forced layer depth
$h_{F}(0)$
, conservation of mass implies straightforwardly that
$$\begin{eqnarray}g_{F}^{\prime }h_{F}=\frac{g({\it\rho}_{L}-{\it\rho}_{F}(t))h_{F}}{{\it\rho}_{0}}=C_{M},\end{eqnarray}$$
where
${\it\rho}_{0}$
is some reference density,
$g_{F}^{\prime }$
is the reduced gravity of the forced layer, and
$C_{M}$
is a constant. Furthermore, Boyer et al. (Reference Boyer, Davies and Guo1997) showed that an appropriately defined potential energy of the forced layer is proportional to
$g_{F}^{\prime }h_{F}^{2}=C_{M}h_{F}$
, and thus that the rate of change of potential energy was directly proportional to
$\text{d}h_{F}/\text{d}t$
. Therefore, they predicted that the depth of the well-mixed layer should deepen linearly in time for an initially two-layer stratification – a prediction which was supported by admittedly sparse experimental evidence. On the other hand, for the initially linearly stratified case with constant buoyancy frequency
$N_{Q}$
, as we discuss in more detail in § 3, the potential energy of the forced layer is proportional to
$N_{Q}^{2}h_{F}^{3}$
. Since they argued that the rate of increase with time of this quantity should be constant, Davies et al. (Reference Davies, Guo, Boyer and Folkard1995) predicted that
$h_{F}\propto ({\rm\Omega}t)^{1/3}$
, and they did indeed observe a decrease in the rate of change of the depth of the forced mixed layer, which is consistent with this argument, though once again there were relatively few measurements of density profiles reported.
Shravat, Cenedese & Caulfield (Reference Shravat, Cenedese and Caulfield2012) (henceforth referred to as SCC12) considered a similar two-layer flow to Boyer et al. (Reference Boyer, Davies and Guo1997), focusing on the entrainment, mixing and homogenisation of an initially two-layer stratification in a cylindrical tank, driven by a disc rotating with constant angular frequency
${\rm\Omega}$
now at the upper surface of the fluid. They observed that the depth
$h_{F}(t)$
of the forced mixed layer did not increase linearly with time, unlike the predictions of Boyer et al. (Reference Boyer, Davies and Guo1997), but rather
$h_{F}/R\sim (1+C{\rm\Omega}t)^{2/5}$
, for some empirical constant
$C$
. They showed that this scaling was consistent with a model based on the concept that the power injected into the flow by the rotating disc could not maintain constant characteristic velocities in the forced layer for sufficiently deep forced layers because this would demand an ever-increasing power both to mobilise the deepening fluid and to account for the ever-increasing viscous dissipation. Indeed, they demonstrated that the experimentally measured rate of deepening was consistent with the assumption that the kinetic energy
$\mathscr{E}_{KF}$
in the forced layer, defined as
$$\begin{eqnarray}\mathscr{E}_{KF}=\frac{1}{2}\int _{0}^{h_{F}}\!\int _{0}^{2{\rm\pi}}\!\int _{0}^{R}{\it\rho}|\boldsymbol{u}(r,{\it\theta},z,t)|^{2}r\text{d}r\text{d}{\it\theta}\text{d}z=\frac{1}{2}{\it\rho}_{L}{\rm\pi}R^{2}h_{F}u_{F}^{2},\end{eqnarray}$$
tended to a constant in time, thus making it possible to relate
$u_{F}$
to
$h_{F}$
. Central to their argument was the concept that ‘mixing’ should be considered as a two-stage process. The local ‘entrainment’ across the interface is driven by a turbulent stress due to the mobilised forced layer, which is then followed by a ‘homogenisation’ of this entrained fluid throughout the turbulent deepening forced mixed layer.
Using this inherently local entrainment model, they were able to construct a self-consistent model for deepening of the mixed layer, recovering the
$({\rm\Omega}t)^{2/5}$
scaling. This model, which they referred to as a constant-disc-power or ‘P’ model, is still based around the assumption that the characteristic turbulent velocity scale important for entrainment at the interface is proportional to the characteristic velocity scale
$u_{F}$
in the forced layer, but crucially allows for this scale to vary (and indeed decrease) with time. Considering the global energy budget of the well-mixed layer required for mobilisation and homogenisation, they argued that a constant kinetic energy
$\mathscr{E}_{KF}$
required a balance between power injected by the rotating disc, the turbulent dissipation of the entire layer, and the total power demand of both the local entrainment and the homogenisation of the fluid density throughout the forced layer. However, the constant kinetic energy scaling only emerges at later time, or equivalently for sufficiently deep forced layers, and so there were some technical difficulties in being able to run experiments of sufficiently long duration.
Furthermore, and more significantly, these two-layer experiments could shed no light on the tendency of the stratified mixing to lead to layering (or not). The conductivity-probe density measurements demonstrated that the primary interface between the well-mixed forced layer and the largely quiescent lower layer had a characteristic thickness scale
$l_{I}\sim O(1~\text{mm})$
which did not vary measurably with time. Therefore, under the hypothesis that
$\mathscr{E}_{KF}$
remains constant with time, the interfacial Richardson number,
$Ri_{I}$
, is itself a constant with time:
$$\begin{eqnarray}Ri_{I}=\frac{g_{F}^{\prime }l_{I}}{u_{F}^{2}}=\frac{g_{F}^{\prime }h_{F}l_{I}}{h_{F}u_{F}^{2}}=C_{Ri},\end{eqnarray}$$
since as already noted by Boyer et al. (Reference Boyer, Davies and Guo1997), (1.1) holds, and so
$g_{F}^{\prime }h_{F}=C_{M}$
, a constant. This constraint unfortunately makes it impossible to determine how the entrainment, and hence the mass flux local to the interface depends on
$Ri_{I}$
– a key to determining whether secondary layer formation is to be expected via the Phillips mechanism.
In the light of these observations, in this paper we consider a different flow initial condition in the same geometry as SCC12, that of an initially linearly stratified fluid as considered by Davies et al. (Reference Davies, Guo, Boyer and Folkard1995), so that we can address two primary objectives. First, we wish to verify if, analogously to the situation considered in SCC12, the assumption that the kinetic energy of the forced layer tends towards a constant, and hence that
$u_{F}\propto h_{F}^{-1/2}$
leads to a better prediction for the evolution of the mixed layer depth than the assumption of Davies et al. (Reference Davies, Guo, Boyer and Folkard1995) that
$u_{F}\propto {\rm\Omega}R$
. Secondly, we wish to explore how the local entrainment varies with the interfacial stratification, and if its variation is such that we expect layer development by the Phillips mechanism. It is important to stress that we are interested in the bulk properties of the flow at sufficiently late time, rather than the initial spin-up instabilities of the flow or the specific character of the flow in the mixed layer (see Davies et al.
Reference Davies, Guo, Boyer and Folkard1995, Munro & Davies Reference Munro and Davies2006 and Munro, Foster & Davies Reference Munro, Foster and Davies2010 for consideration of these flow dynamics). In particular, we are interested in layers which develop and persist at ‘late’ times below the primary interface due to its particular mixing dynamics, rather than ‘early’ larger-scale radially spreading intruding layers as observed by Davies et al. (Reference Davies, Guo, Boyer and Folkard1995).
To consider these two issues, the rest of the paper is organised as follows. In § 2, we describe our experimental procedure and present our observational results. By measuring large numbers of density profiles, we demonstrate that the mixed layer deepens at a rate slower than that predicted by Davies et al. (Reference Davies, Guo, Boyer and Folkard1995), thus suggesting that the assumption that
$u_{F}\propto {\rm\Omega}R$
is not appropriate for all times. Also we show that secondary layering is regularly observed, strongly suggesting that the Phillips mechanism may be occurring. In § 3, we generalise the constant-disc-power ‘P’ model presented in SCC12 with the aim of explaining the experimental findings. We demonstrate that our model is consistent with the observed dependence of the depth of the mixed layer on both time and the external parameters
${\rm\Omega}$
and
$N$
, and also that the rate of increase of potential energy is a decreasing function of
$Ri_{I}$
, consistently with the observations of robust secondary layers developing below the primary interface. Finally, in § 4, we draw our conclusions.
2. Experiments
2.1. Experimental procedure
We have conducted a series of experiments on a stratified fluid in a cylindrical tank forced at the top surface by a rotating horizontal disc, see figure 1, using the same experimental equipment as described in SCC12. We fill a cylindrical tank (30 cm height and 30 cm diameter) with fluid of a consistent height
$H=27$
cm. Using the conventional Oster double-bucket technique, we set an initial linear density stratification with a relative difference between the density at the top
${\it\rho}_{T}$
and the bottom
${\it\rho}_{B}$
of the fluid
$({\it\rho}_{B}-{\it\rho}_{T})/{\it\rho}_{T}\in (0.02,0.2)$
. We measure vertical density profiles using a conductivity probe moving vertically downwards with a speed of
$3~\text{mm}~\text{s}^{-1}$
at a sampling rate taking 100 measurements every centimetre. The profiled depth of the fluid is 20 cm, excluding regions close to the disc and to the bottom of the tank. We convert conductivity measurements into density using a calibration with a third-degree-polynomial fit. All fluid is at the (controlled) room temperature of
$20\pm 0.5\,^{\circ }\text{C}$
. Therefore, the Schmidt number for the salt-stratified water is nearly constant,
$Sc={\it\nu}/{\it\kappa}\sim 700$
, where
${\it\nu}$
is the kinematic viscosity, and
${\it\kappa}$
is the salt diffusivity.
Figure 1. A schematic of the experimental set-up showing a cylindrical tank filled with stratified fluid, forced at the surface by a rotating disc, and measured by a traversing conductivity probe from
$z=0$
(the upper surface) to
$z=-H$
(the tank base).
Following SCC12, we drive a horizontal disc (radius
$R=12$
cm) in contact with the surface of the fluid with constant angular rotation rate
${\rm\Omega}$
. Since the disc is at the top surface of the fluid, it is unfortunately only possible to measure the density profile at one radial location, and so we are unable in particular to investigate early-time transient spin-up phenomena. Furthermore, the driving disc, the cylindrical geometry, and the relatively strong density gradients (and hence refractive index variations) make optical flow measurement techniques very challenging, and so we do not conduct any particle image velocimetry. We keep the aspect ratio
$R/H$
fixed for all experiments. Thus, there are two natural control parameters for the experiments: the rotation rate
${\rm\Omega}$
and the buoyancy frequency
$N_{Q}$
defined by the initial linear stratification in the quiescent layer
$$\begin{eqnarray}{\it\rho}_{Q}(z)={\it\rho}_{T}\left(1-\frac{N_{Q}^{2}}{g}z\right),\quad N_{Q}^{2}=\frac{g({\it\rho}_{B}-{\it\rho}_{T})}{{\it\rho}_{T}H},\end{eqnarray}$$
defining the vertical coordinate
$z$
increasing upwards from
$z=-H$
at the base of the tank to
$z=0$
at the disc. The ratio of
$N_{Q}$
and
${\rm\Omega}$
defines a natural global non-dimensional parameter for the ‘profile’ Richardson number
$Ri_{P}$
defined as
$$\begin{eqnarray}Ri_{P}=N_{Q}^{2}/{\rm\Omega}^{2}.\end{eqnarray}$$
We observe that the entire column of fluid in the tank becomes well mixed over a mixing time
$T_{M}\in (1.2{-}72)\times 10^{3}~\text{s}$
. As the characteristic speed of the flow (and hence the intensity of the turbulence) depends on the disc rotation rate
${\rm\Omega}$
and its radius
$R$
, it is natural to non-dimensionalise time
$t$
and vertical distance
$z$
as
$$\begin{eqnarray}\hat{t}={\rm\Omega}t,\quad \hat{z}=\frac{z}{R}.\end{eqnarray}$$
We have analysed 20 experiments, with
$0.5~\text{s}^{-1}\leqslant N_{Q}\leqslant 1.72~\text{s}^{-1}$
and
$0.52~\text{rad}~\text{s}^{-1}\leqslant {\rm\Omega}\leqslant 3.14~\text{rad}~\text{s}^{-1}$
, resulting in
$0.14\leqslant Ri_{P}\leqslant 2.25$
(as listed in table 1). All experiments were conducted in a temperature-controlled laboratory, and to a good approximation the temperature of the experimental fluids stayed constant throughout the experiment.
Table 1. Table of experimental parameters for the 20 conducted experiments: the last two columns show the coefficients of the power-law fit for evolution of the forced mixed layer depth
$h_{F}/R=A({\rm\Omega}t)^{{\it\alpha}}$
, where
$t$
is the time from the start of the experiment.
2.2. Qualitative observations
As discussed in more detail in SCC12, the characteristic Reynolds number
$Re={\rm\Omega}R^{2}/{\it\nu}\sim O(10^{5})$
, and so a turbulent well-mixed mobilised forced layer develops near the disc, with almost homogeneous density distribution. Although there is undoubtedly a large-scale radial flow (see Davies et al.
Reference Davies, Guo, Boyer and Folkard1995, Munro & Davies Reference Munro and Davies2006, Munro et al.
Reference Munro, Foster and Davies2010 for more details), we are principally interested in the bulk later-time properties of the deepening layer. As discussed in SCC12, there is a power demand for this deepening since entrainment and homogenisation processes effectively lift the centre of mass of the water column by transporting dense fluid upward against the gravitational field. Furthermore, an increasingly strong, and noticeably sharp, density jump forms at the base of the mixed layer which effectively shields the quiescent layer underneath it from penetration and overturning by turbulent eddies. A mean azimuthal flow clearly develops due to the coherent rotation of the disc, thus creating a shear across the interface between the mobilised forced layer and the quiescent layer. We observe shear-driven overturning behaviour relatively early in an experiment when the mixed layer is relatively shallow, particularly for experiments with relatively small values of
$Ri_{P}$
, where it is reasonable to suppose that the stratification is ‘weak’ at the interface.
Figure 2. (a) Sequence of profiles of normalised density
$\hat{{\it\rho}}$
as defined in (2.4) separated in time by intervals of
${\rm\Omega}{\rm\Delta}t=4.6$
(
$Ri_{P}=0.67$
). Consecutive profiles are offset in the
$x$
-coordinate by 0.04 from each other. (b) Spatio-temporal variation of the base-10 logarithm of the normalised buoyancy frequency
$\log _{10}(N/N_{Q})$
(as defined in (2.1) and (2.5)) for the same experiment in the 3 cm below the primary interface.
However, as mentioned in the introduction, particularly when the density jump across the interface is ‘strong’ in some sense, as the turbulent eddies approach the interface they ‘scour’ dense fluid into the forced layer, and so maintain ‘sharp’ density gradients in the vicinity of the interface. Such non-diffusive scouring dynamics tends to be observed when the forced layer is sufficiently deep, particularly for larger values of
$Ri_{P}$
.
Both diffuse primary interfaces associated with overturning and sharper interfaces associated with scouring can be observed in the normalised density profile
$\hat{{\it\rho}}$
, defined as
$$\begin{eqnarray}\hat{{\it\rho}}=\frac{{\it\rho}-{\it\rho}_{T}}{{\it\rho}_{B}-{\it\rho}_{T}},\end{eqnarray}$$
and measured with the conductivity probe. Such profiles (offset by
$0.04$
for clarity) are plotted in figure 2(a) for an experiment with
$Ri_{P}=0.67$
. The thick lines mark the profiles measured at
${\rm\Omega}t=\hat{t}=0,200,400$
and
$600$
. The forced layer is very well mixed, although, consistently with the observations of SCC12 and Davies et al. (Reference Davies, Guo, Boyer and Folkard1995), the depth of the forced layer does not increase linearly with time, but rather clearly descends at a decreasing rate with time. (The unphysical offset in the top few centimetres of the profile is associated with an oscillation in the traverse when it starts to move.)
In figure 2(b), for the same experiment we plot the time evolution of the (normalised base 10) logarithm of the spatio-temporally varying buoyancy frequency
$\log _{10}[N(z,t)/N_{Q}]$
in the 3 cm below the (moving) primary interface located at
$z=-h_{F}$
, where
$$\begin{eqnarray}N^{2}(z,t)=-\frac{g}{{\it\rho}_{T}}\frac{\partial {\it\rho}}{\partial z}.\end{eqnarray}$$
We identify the primary interface location
$z=-h_{F}$
as the global (in space) maximum of this buoyancy frequency; this appears to be a robust way to identify
$h_{F}$
without ambiguity. At very early times, the primary interface is difficult to identify due to various transient effects, and so we replace the data with a black bar. At somewhat later, but still relatively early, times there is clear evidence of unstable stratification, resulting from the overturning of energetic shear-driven eddies at the base of the mixed layer. Conversely, at later times, there is both a sharper primary density interface and also long-lived secondary interfaces below the primary interface, although they exhibit complex long-time-scale dynamics, in particular through intermittent disappearance and reappearance. These secondary interfaces are also apparent in the density profiles shown in figure 2(a), for example in the highlighted profile for
$\hat{t}=400$
. We believe that these interfaces form below the primary interface, and do not appear to be associated with the radial collapse of regions of partially mixed fluid above the primary interface, which always appears to be well mixed. (Revisiting the data presented in SCC12, there is also some evidence of such secondary layers in their figure 2, and so the appearance of the secondary layers does not seem to require the quiescent layer to be linearly stratified.)
The secondary interfaces (and hence local maxima in buoyancy frequency) appear to form at a typical distance
${\sim}2$
cm below the primary interface. The location of such secondary interfaces exhibits complex dynamics, and particularly as a secondary layer gets ‘thin’ due to the continual deepening of the primary forced layer, there is non-trivial ‘coupling’ between the primary and secondary interfaces. Due to the fact that we shift the location of the primary interface to always be at zero in figure 2(b), this reduction in the depth of the secondary layer appears as an ‘upward’ migration of the secondary interface location, with the ‘coupling’ being associated with a change in the gradient of this upward migration. Interestingly, the disappearance of a secondary layer is often rapidly followed by the development of a new secondary interface and layer, as is apparent around
$\hat{t}\sim 450$
.
The primary interfacial thickness is both sharp
$l_{I}\sim O(0.1~\text{cm})$
and not apparently dependent on time in any statistically significant way, consistently with the observations of SCC12. Our observations support the hypothesis that the entrainment process at the interface over much of the flow evolution may be characterised as a ‘scouring’ process, that continually maintains a relatively sharp gradient at the interface between the two primary layers.
2.3. Quantitative analysis
Motivated by the arguments of Davies et al. (Reference Davies, Guo, Boyer and Folkard1995) and SCC12, we postulate that
$$\begin{eqnarray}{\hat{h}}_{F}=A(Ri_{P})~\hat{t}^{{\it\alpha}(Ri_{P})},\end{eqnarray}$$
where
${\hat{h}}_{F}=h/R$
is the non-dimensional forced mixed layer depth, and the premultiplying scaling factor
$A$
and the power
${\it\alpha}$
are allowed in principle to be functions of
$Ri_{P}$
. In figure 3(a), we plot
${\hat{h}}_{F}$
against non-dimensional time
$\hat{t}$
for three different typical values of
$Ri_{P}=0.3$
,
$0.52$
and
$1.09$
. A power-law approximation appears to fit each dataset well, as plotted with a solid line using the best-fit values for
${\it\alpha}(Ri_{P})$
and
$A(Ri_{P})$
listed in table 1. Two aspects are immediately apparent. First, in each case, the power-law dependence is close to
${\it\alpha}\simeq 2/9$
, as shown in the inset with a thick dashed line. Indeed, as shown in the table and figure 3(b), there is weak dependence of the power-law coefficient
${\it\alpha}$
on
$Ri_{P}$
: the mean value for all 20 experiments (as shown with a thick dashed line in figure 3
b) is
${\it\alpha}=0.229\simeq 2/9$
with a standard deviation of 0.02. The data are not consistent with the prediction of Davies et al. (Reference Davies, Guo, Boyer and Folkard1995) that
${\it\alpha}=1/3$
, as shown in the inset of figure 3(a) and in figure 3(b) with a thin dashed line. Secondly, the depth of the mixed layer increases more rapidly as
$Ri_{P}$
decreases:
$A(Ri_{P})\simeq A_{c}Ri_{P}^{-1/3}$
, where
$A_{c}=0.57$
, with
$R^{2}=0.93$
(figure 3
c).
Unlike the observations of SCC12, there is no apparent initial time offset in the data for the power-law dependence. This observation is perhaps a little surprising, since, as discussed above, the physical mechanisms of entrainment and mixing appear to change during the flow evolution from at least partially shear-driven overturning to scouring driven by impinging turbulent eddies. However, since the experimental evidence is that
${\it\alpha}<1/3$
, it appears appropriate to relax the central assumption of Davies et al. (Reference Davies, Guo, Boyer and Folkard1995), that the characteristic velocity of the forced layer
$u_{F}$
does not vary with time. Therefore, we investigate whether some generalisation of the constant-disc-power ‘P’ model discussed in SCC12 (based around the assumption that the kinetic energy of the forced layer tends towards a constant and so
$u_{F}\propto h_{F}^{-1/2}$
) may prove to be successful in describing the observed dynamics of the forced mixed layer.
Figure 3. (a) Time evolution of the non-dimensional mixed layer depth
${\hat{h}}_{F}$
for three different experiments:
$Ri_{P}=0.3$
(blue dots),
$0.52$
(green), and
$1.09$
(black); inset shows the same data on a log–log plot. (b) Best-fit values of the power-law coefficient
${\it\alpha}$
(defined in (2.6)) plotted as a function of
$Ri_{P}$
for different experiments (crosses). The lines
${\it\alpha}=2/9$
and
${\it\alpha}=1/3$
are plotted with thick and thin dashed lines respectively. (c) Log–log plot of the best-fit values of the scaling factor
$A(Ri_{P})$
(as defined in (2.6)) (crosses). The best-fit line
$A=0.57Ri_{P}^{-1/3}$
is plotted with a dashed line. Numerical values of
${\it\alpha}$
,
$A$
, and
$Ri_{P}$
are listed in table 1.
3. Mixing model
3.1. Layer properties
As a first step to developing a model for the evolution of the forced well-mixed layer, we define the reduced gravity at a given location
$z<0$
in the stratified quiescent layer as
$$\begin{eqnarray}g_{Q}^{\prime }(z)=\frac{g({\it\rho}-{\it\rho}_{T})}{{\it\rho}_{T}}=-N_{Q}^{2}\,z,\end{eqnarray}$$
using (2.1). When the forced mixed layer has depth
$h_{F}$
, the reduced gravity of the forced layer
$g_{F}^{\prime }$
, and hence the interfacial Richardson number
$Ri_{I}$
, are given by
$$\begin{eqnarray}g_{F}^{\prime }=\frac{1}{h_{F}}\int _{-h_{F}}^{0}g_{L}^{\prime }\text{d}z=\frac{N_{Q}^{2}h_{F}}{2},\quad Ri_{I}=\frac{[g_{L}^{\prime }(-h_{F})-g_{F}^{\prime }]l_{I}}{u_{F}^{2}}=\frac{N_{Q}^{2}h_{F}l_{I}}{2u_{F}^{2}},\end{eqnarray}$$
making the conventional assumptions that there is a characteristic velocity scale for the forced layer
$u_{F}$
, and that the interfacial thickness
$l_{I}$
is constant in time.
Entraining fluid across the interface increases the density in the forced mixed layer and clearly increases the potential energy of the system
$\mathscr{E}_{PF}(h_{F})$
, which we define as
$$\begin{eqnarray}\displaystyle \mathscr{E}_{PF}(h_{F}) & = & \displaystyle {\it\rho}_{T}{\rm\pi}R^{2}\int _{-h}^{0}\frac{g({\it\rho}_{F}-{\it\rho})z}{{\it\rho}_{T}}\text{d}z=\frac{{\it\rho}_{T}{\rm\pi}R^{5}N_{Q}^{2}}{12}\left(\frac{h_{F}^{3}}{R^{3}}\right)=\mathscr{E}_{PS}{\hat{h}}_{F}^{3},\end{eqnarray}$$
also defining the characteristic scale
$\mathscr{E}_{PS}$
. We now make an assumption, ‘K’, that the total kinetic energy of the forced layer (1.2) may be considered to be a constant independent of time. This was a central assumption of SCC12 consistent with their experimental data. In this flow, we assume further that this constant value of kinetic energy does not depend on the buoyancy frequency of the quiescent layer, and so
$$\begin{eqnarray}\mathscr{E}_{KF}={\textstyle \frac{1}{2}}{\it\rho}_{T}{\rm\pi}R^{2}h_{F}u_{F}^{2}=\left({\textstyle \frac{1}{2}}{\it\rho}_{T}{\rm\pi}R^{2}\right)C_{K}{\rm\Omega}^{2}R^{3},\end{eqnarray}$$
for some empirical constant
$C_{K}$
, using the Boussinesq approximation.
The key argument is that the velocity in the forced layer is fundamentally set by a balance between the forcing of the disc and the turbulent dissipation and homogenisation in the layer, and the particular properties of the quiescent layer play a much less significant role. This is a generalisation of the constant-disc-power ‘P’ model of SCC12, which assumed that there is an at least quasi-steady balance between the power input by the disc, the viscous dissipation, and the power demand for entrainment, mixing and homogenisation of the deepening forced layer. Using assumption ‘K’, it is then possible to relate
$u_{F}$
to
$h_{F}$
:
$$\begin{eqnarray}u_{F}={\rm\Omega}R\left(\frac{C_{K}}{{\hat{h}}_{F}}\right)^{1/2},\end{eqnarray}$$
crucially showing that we are assuming that
$u_{F}$
decreases as the mixed layer deepens.
It is important to stress that we do not expect this assumption to be strictly valid during the initial spin-up of the flow, i.e. in the limit as
$h_{F}\rightarrow 0$
. At such early times, we expect that the fluid will be undergoing a complicated, radially and vertically varying flow, and it may well be difficult to identify an unambiguous single characteristic velocity
$u_{F}$
of the forced layer. Indeed, at early times, we might expect the behaviour also to be consistent with the modelling assumptions of Davies et al. (Reference Davies, Guo, Boyer and Folkard1995) and Boyer et al. (Reference Boyer, Davies and Guo1997), that a characteristic velocity of the upper layer can be related linearly to the (constant) rotational velocity
${\rm\Omega}R$
of the outer edge of the rotating disc. Conversely, although we argue that assumption ‘K’ is significantly more plausible than the assumption that
$u_{F}\propto {\rm\Omega}R$
with no dependence on
$h_{F}$
, nevertheless we must remember that it is unlikely to be able to identify a single characteristic velocity
$u_{F}$
for the forced layer for all
$h_{F}$
.
3.2. Time dependence of
${\hat{h}}_{F}$
We now make a second assumption, ‘M’, which has two parts. First, following SCC12, we assume that the power
$\mathscr{P}_{I}$
locally supplied at the interface by the interfacial stress
${\it\sigma}$
is the rate of change of the work done
$\mathscr{W}$
locally at the interface by the disc forcing via the action of the turbulent flow, i.e.
$$\begin{eqnarray}\mathscr{P}_{I}=\frac{\text{d}}{\text{d}t}\mathscr{W}={\rm\pi}R^{2}u_{I}{\it\sigma}={\rm\pi}R^{2}c_{D}{\it\rho}_{T}u_{F}^{3},\end{eqnarray}$$
where
$c_{D}$
is some empirically determined drag coefficient, and
$u_{I}$
is a characteristic velocity in the immediate vicinity of the interface, which is not expected to be identical to the characteristic velocity
$u_{F}$
in the forced layer. Second, we assume that a fixed proportion
${\it\lambda}$
of this power leads to an increase of the global potential energy
$\mathscr{E}_{PF}$
of the forced layer, i.e.
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\mathscr{E}_{PF}={\it\lambda}\mathscr{P}_{I}.\end{eqnarray}$$
Although
${\it\lambda}$
may be thought of as an ‘efficiency’ of mixing in some sense, our experimental approach does not allow us either to quantify its numerical value or indeed express it in terms of more conventional measures of mixing efficiency such as the ‘flux Richardson number’
$Ri_{f}$
(the ratio of the buoyancy flux to the turbulence production rate) or the flux coefficient
${\rm\Gamma}$
(the ratio of the buoyancy flux to the turbulent dissipation rate) due to the fact that we are unable to determine quantitatively the turbulence production or dissipation rate. (See the reviews by Linden Reference Linden1979; Fernando Reference Fernando1991; Ivey et al.
Reference Ivey, Winters and Koseff2008 for further discussion of classic mixing efficiency measures.) Using (3.3), (3.5) and (3.6) the two-part assumption ‘M’ yields a straightforward differential equation for
$h_{F}$
which can be solved using the initial condition that
${\hat{h}}_{F}(0)=0$
:
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}\left[{\it\rho}_{T}{\rm\pi}R^{2}\frac{N_{Q}^{2}h_{F}^{3}}{12}\right] & = & \displaystyle {\it\lambda}c_{D}u_{F}^{3}({\it\rho}_{T}{\rm\pi}R^{2})\rightarrow {\hat{h}}_{F}=C_{K}^{3/2}\left(18{\it\phi}\left[\frac{{\rm\Omega}^{2}}{N_{Q}^{2}}\right]\hat{t}\right)^{2/9},\end{eqnarray}$$
defining
${\it\phi}={\it\lambda}c_{D}$
.
It is plausible that
${\it\phi}$
depends on some non-dimensional function of
${\rm\Omega}$
and
$N_{Q}$
, associated with some dependence of the ‘efficiency’ of the entrainment process on the developing stratification. We attempt to capture this dependence by making a third assumption, ‘E’, that the scaled entrainment parameter
$E$
, defined appropriately for this flow as
$$\begin{eqnarray}E={\dot{h}}_{F}/u_{u}\end{eqnarray}$$
(see SCC12 for further discussion), depends only on the present value of the interfacial Richardson
$Ri_{I}$
, as defined in (3.2). Using (3.5), (3.8):
$$\begin{eqnarray}\displaystyle & \displaystyle E=\frac{4{\it\phi}u_{F}^{2}}{N_{Q}^{2}h_{F}^{2}}=\frac{4{\it\phi}C_{K}{\rm\Omega}^{2}R^{3}}{N_{Q}^{2}h_{F}^{3}}={\it\phi}^{1/3}\left(\frac{2}{3}\right)^{4/3}\left(\frac{{\rm\Omega}}{N_{Q}}\right)^{2/3}\hat{t}^{-2/3}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Ri_{I}=\frac{N_{Q}^{2}h_{F}l_{I}}{2u_{F}^{2}}=\frac{N_{Q}^{2}h_{F}^{2}l_{I}}{2h_{F}u_{F}^{2}}={\it\phi}^{4/9}\left(\frac{l_{I}}{2R}\right)\frac{18^{4/9}}{C_{K}^{1/3}}\left(\frac{{\rm\Omega}}{N_{Q}}\right)^{-10/9}\hat{t}^{4/9}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}E=A_{R}Ri_{I}^{-3/2},\end{eqnarray}$$
where
$A_{R}$
is once again an empirical constant, and consistent with the previous observations of Kit, Berent & Vajda (Reference Kit, Berent and Vajda1980) in a flow with similar forcing. Since both
$E$
and
$Ri_{I}$
also depend on
${\it\phi}$
and
${\rm\Omega}/N_{Q}$
(and hence
$Ri_{P}$
), this required power-law dependence (3.11) also implies a consistency condition for
${\it\phi}$
:
$$\begin{eqnarray}{\it\phi}=\frac{A_{R}C_{K}^{1/2}}{4}\left(\frac{l_{I}}{2R}\right)^{-3/2}Ri_{P}^{-1/2}.\end{eqnarray}$$
Substituting this expression into (3.8), we obtain the final model prediction for the mixed layer depth
${\hat{h}}_{F}$
using the three key assumptions ‘K’, ‘M’, and ‘E’:
$$\begin{eqnarray}{\hat{h}}_{F}=\left(\frac{9}{2}A_{R}C_{K}^{2}\right)^{2/9}\left(\frac{2R}{l_{I}}\right)^{1/3}Ri_{P}^{-1/3}\hat{t}^{2/9}=A_{c}Ri_{P}^{-1/3}\hat{t}^{2/9}.\end{eqnarray}$$
This expression recovers precisely the observed scaling for
${\hat{h}}_{F}$
as shown in figure figure 3. Interestingly, this scaling appears to be valid for all
$h_{F}$
values we have considered, in particular for small
${\hat{h}}_{F}$
and
$\hat{t}$
, suggesting that assumption ‘K’ can be extended beyond its regime of strict applicability. Also, although we only considered one aspect ratio, with maximum values of
${\hat{h}}_{F}\simeq 2$
, there is no evidence of divergence from our model for larger values of
${\hat{h}}_{F}$
, suggesting that our central assumptions are applicable at least over this range of
${\hat{h}}_{F}$
.
3.3. Implications
Combining (3.10b
) with (3.12), the interfacial Richardson number
$Ri_{I}$
can be expressed as a function of time and
$Ri_{P}$
as defined in (2.2):
$$\begin{eqnarray}Ri_{I}=\left(\frac{9A_{R}}{2}\right)^{4/9}\left(\frac{l_{I}}{2R}\right)^{1/3}Ri_{P}^{1/3}\hat{t}^{\,4/9}.\end{eqnarray}$$
Since we now have derived scaling expressions for
${\it\phi}$
,
$u_{F}$
and
$Ri_{I}$
(and in particular
$h_{F}$
,
$u_{F}$
and
$Ri_{I}$
are all functions of
$\hat{t}$
) it is thus possible to re-express the rate of change of the flow potential energy
$\mathscr{E}_{PF}$
using (3.3) in terms of
$Ri_{I}$
and
$Ri_{P}$
:
$$\begin{eqnarray}\frac{\text{d}}{\text{d}\hat{t}}\left(\frac{\mathscr{E}_{PF}}{\mathscr{E}_{PS}}\right)=\left(3A_{R}C_{K}^{5/4}\right)\left(\frac{2R}{l_{I}}\right)^{3/4}Ri_{P}^{-1/4}Ri_{I}^{-3/4}=\left(\frac{A_{\mathscr{P}}}{Ri_{P}Ri_{I}^{3}}\right)^{1/4},\end{eqnarray}$$
defining a new empirical constant
$A_{\mathscr{P}}$
.
Therefore, within our model, the rate of increase of the (global) potential energy is predicted to be a decreasing function of the (local) interfacial Richardson number. Naturally, within this flow, increases in global potential energy are associated with the (local) mass flux across the primary interface between the well-mixed forced layer and the stratified quiescent layer. Therefore, our central assumptions and model imply that the local mass flux is also a decreasing function of the interfacial Richardson number, which is all that is required by the arguments presented by Phillips (Reference Phillips1972), and so secondary layering would be expected to occur in our flow. This too is consistent with our observations, as is apparent in figure 2, even though the modelling effort leading to (3.15) is built on a strong set of assumptions. Since the decreasing dependence of
$\text{d}\mathscr{E}_{PF}/\text{d}t$
on
$Ri_{I}$
is predicted to occur throughout the lifetime of an experiment, this particular flow geometry seems to be particularly conducive to the detailed study of the development of layers within a forced stratified turbulent flow, an issue to which we intend to return in due course.
4. Conclusions
In this paper we have described the results of a sequence of experiments designed to study turbulent entrainment, mixing and homogenisation in a shear-driven turbulent stratified flow. In particular, we have studied the increase in depth
$h_{F}$
of a surface-stress-driven mixed layer in a cylindrical tank initially filled with linearly stratified fluid. We demonstrate that the rate of increase of mixed layer depth decreases measurably with time, and furthermore that the data closely agree with the scaling
$h_{F}\propto ({\rm\Omega}/N_{Q})^{-2/3}({\rm\Omega}t)^{2/9}$
for a wide range of values of
${\rm\Omega}$
and
$N_{Q}$
. A key physical observation is that the interfacial thickness
$l_{I}$
between the forced well-mixed turbulent layer and the quiescent linearly stratified lower layer appears to be ‘scoured’, and so does not vary in a statistically significant fashion with respect to either time or
$Ri_{P}$
as defined in (2.2). Although one might expect this thickness to depend on some viscous balance within the flow, no dependence on the rotation rate
${\rm\Omega}$
(and hence the characteristic Reynolds number of the flow
$Re={\rm\Omega}^{2}R/{\it\nu}$
) is detectable; however,
$0.52~\text{rad}~\text{s}^{-1}\leqslant {\rm\Omega}\leqslant 3.14~\text{rad}~\text{s}^{-1}$
and so
$Re$
only varied by a factor of six. These observations are consistent with much previous work in a range of stratified entrainment and mixing studies (see e.g. the recent work of Oglethorpe et al.
Reference Oglethorpe, Caulfield and Woods2013), and it is an important open problem to understand the physical processes which set the thickness of interfaces between turbulent layers in stratified laboratory experiments.
We present physical and mathematical arguments to justify the observed scaling for
$h_{F}$
, and demonstrate that this scaling is consistent with three central assumptions, building on previous research. Assumption ‘M’, that the rate of the potential energy increase (due to global mixing and homogenisation throughout the deepening forced layer) is proportional to the power supplied through turbulent interfacial stresses (in turn proportional to
$u_{F}^{3}$
), builds on the arguments of Davies et al. (Reference Davies, Guo, Boyer and Folkard1995) and Boyer et al. (Reference Boyer, Davies and Guo1997). However, the central, and robust, observation that the depth
$h_{F}\propto \hat{t}^{2/9}$
appears to require that
$u_{F}$
must also vary with time, contrary to the models presented by Davies et al. (Reference Davies, Guo, Boyer and Folkard1995) and Boyer et al. (Reference Boyer, Davies and Guo1997). Building on the constant-disc-power ‘P’ model of SCC12, we make assumption ‘K’, that the kinetic energy of the forced layer tends towards a constant in time, and this constant depends on the rotation rate
${\rm\Omega}$
, but is not dependent on the stratification and hence the buoyancy frequency
$N_{Q}$
of the quiescent layer. This scaling yields the ‘correct’ observed time-dependence of
$h_{F}$
.
However, the fact that the lower layer is linearly stratified enables us to go further in modelling the interfacial entrainment dynamics, and so we make the conventional assumption (see for example the review of Fernando Reference Fernando1991), which we refer to as assumption ‘E’, that the dynamics of the entrainment depends only on the (present) value of the interfacial Richardson number
$Ri_{I}$
, as defined in (3.2). Since this in turn depends on time, assumption ‘E’ effectively imposes a consistency condition between
$h_{F}$
and
$Ri_{I}$
. As we demonstrate above, this consistency condition implies that
$h_{F}\propto Ri_{P}^{-1/3}$
, which is strongly supported by our experimental data.
Furthermore, and perhaps more interestingly, internal consistency between our model assumptions and the data also implies that the global rate of increase of potential energy, associated with local entrainment and hence mass flux across the density interface, actually decreases with the interfacial Richardson number
$Ri_{I}$
. Such an effective decrease in local mass flux with sufficiently ‘strong’ overall stratification points towards the natural development of secondary layers at the interface, due to the physical argument originally presented by Phillips (Reference Phillips1972). Such layers have been observed to develop in many different experimental situations (see the early review of Linden Reference Linden1979, and Park, Whitehead & Gnanadeskian Reference Park, Whitehead and Gnanadeskian1994, Holford & Linden Reference Holford and Linden1999, Oglethorpe et al.
Reference Oglethorpe, Caulfield and Woods2013) as well as in phenomenological models (e.g. Balmforth, Llewellyn Smith & Young Reference Balmforth, Llewellyn Smith and Young1998) that attempted to theoretically rationalise the observed layering.
This experimental geometry seems to be particularly well-suited to investigate the creation and maintenance of such dynamically generated and maintained layered density distributions. As discussed above, as the primary forced layer deepens, we observe ‘coupling’ between interfaces, leading to the disappearance of the secondary interface bounding a secondary ‘mixed’ layer, and then the re-emergence of a secondary interface and a secondary layer in new, and always deeper, regions of the initially linearly stratified quiescent layer. This experimental geometry allows the emergence, erosion and disappearance of such layers and interfaces to be observed over long time-periods (see figure 2 b), and so is an ideal test-bed to develop improvements in larger-scale parameterisations of ocean mixing (see for example Large, McWilliams & Doney Reference Large, McWilliams and Doney1994) which capture flow dynamics exhibiting spontaneous hydrodynamical layer formation due to the ‘Phillips’ mechanism. We intend to report on just such an investigation of the rich secondary layer dynamics observed in this experimental geometry in due course.
Acknowledgements
The experiments were conducted during the 2010 Geophysical Fluid Dynamics Program at Woods Hole Oceanographic Institution. Financial support from the National Science Foundation, the Office of Naval Research and Woods Hole Oceanographic Institution is gratefully acknowledged, as well as valuable technical support from A. Hansen. The research activity of C.P.C. is supported by EPSRC Programme grant EP/K034529/1 entitled ‘Mathematical Underpinnings of Stratified Turbulence’.
