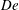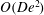1 Introduction
The Smoluchowski slip velocity is a widely used boundary condition for describing electroosmotic flows (EOFs) of Newtonian fluids in the thin electric double layer (EDL) limit (Ajdari Reference Ajdari1995, Reference Ajdari1996, Reference Ajdari2001; Stroock et al. Reference Stroock2000; Ghosal Reference Ghosal2002; Mandal et al. Reference Mandal, Ghosh, Bandopadhyay and Chakraborty2015). Application of this condition signifies that the effect of electrical body force on the fluid is replaced with a pre-specified tangential velocity at the surface (Ajdari Reference Ajdari1996), while the normal velocity remains zero. For a Newtonian fluid this slip velocity has the following expression (Hunter Reference Hunter1981; Ajdari Reference Ajdari1996; Rubinstein & Zaltzman Reference Rubinstein and Zaltzman2001; Ghosal Reference Ghosal2002; Squires & Bazant Reference Squires and Bazant2004; Yariv Reference Yariv2009; Schnitzer & Yariv Reference Schnitzer and Yariv2012c ; Mandal et al. Reference Mandal, Ghosh, Bandopadhyay and Chakraborty2015):
Here,
![]() $\boldsymbol{v}_{HS}$
denotes the Smoluchowski slip velocity,
$\boldsymbol{v}_{HS}$
denotes the Smoluchowski slip velocity,
![]() $\unicode[STIX]{x1D701}$
is the ‘zeta potential’ at the wall,
$\unicode[STIX]{x1D701}$
is the ‘zeta potential’ at the wall,
![]() $\boldsymbol{E}^{\Vert }$
is the electric field acting parallel to the EDL and
$\boldsymbol{E}^{\Vert }$
is the electric field acting parallel to the EDL and
![]() $\unicode[STIX]{x1D702}$
is the fluid viscosity. Aside from the fact that the EDL must be very thin and the surface conductance must be low (Squires & Bazant Reference Squires and Bazant2004), the above condition is quite robust and valid for a wide range of scenarios (Squires & Bazant Reference Squires and Bazant2004; Yariv Reference Yariv2009; Bahga, Vinogradova & Bazant Reference Bahga, Vinogradova and Bazant2010) (for example moderate advection strength, moderate to strong applied field etc). Most importantly, the condition (1.1) remains valid, even when the surface potential is not uniform as well as for surfaces with inherent curvatures.
$\unicode[STIX]{x1D702}$
is the fluid viscosity. Aside from the fact that the EDL must be very thin and the surface conductance must be low (Squires & Bazant Reference Squires and Bazant2004), the above condition is quite robust and valid for a wide range of scenarios (Squires & Bazant Reference Squires and Bazant2004; Yariv Reference Yariv2009; Bahga, Vinogradova & Bazant Reference Bahga, Vinogradova and Bazant2010) (for example moderate advection strength, moderate to strong applied field etc). Most importantly, the condition (1.1) remains valid, even when the surface potential is not uniform as well as for surfaces with inherent curvatures.
Despite the general nature of the above condition, one of the major short comings is that it is not an accurate description for electroosmotic slip velocity of non-Newtonian fluids. Over the past few years, the elelctrokinetically modulated flow of non-Newtonian fluids has attracted significant attention from the research community (Das & Chakraborty Reference Das and Chakraborty2006; Afonso, Alves & Pinho Reference Afonso, Alves and Pinho2009, Reference Afonso, Alves and Pinho2010, Reference Afonso, Alves and Pinho2013; Bandopadhyay, Ghosh & Chakraborty Reference Bandopadhyay, Ghosh and Chakraborty2013; Dhar, Bandopadhyay & Chakraborty Reference Dhar, Bandopadhyay and Chakraborty2013; Ng & Qi Reference Ng and Qi2014; Ghosh & Chakraborty Reference Ghosh and Chakraborty2015), for a wide gamut of reasons, including applications related to bio-fluids (Thurston & Griling Reference Thurston and Griling1978; Yeleswarapu & Kameneva Reference Yeleswarapu and Kameneva1998), as well as high-performance electrokinetic energy conversion devices (Bandopadhyay & Chakraborty Reference Bandopadhyay and Chakraborty2012; Nguyen et al. Reference Nguyen2013; Dhar, Ghosh & Chakraborty Reference Dhar, Ghosh and Chakraborty2014). Notably, bio-fluids like blood plasma (Afonso et al. Reference Afonso, Alves and Pinho2013; Brust et al. Reference Brust2013), saliva (Afonso et al. Reference Afonso, Alves and Pinho2009) etc. can be aptly characterized by non-Newtonian constitutive relationships in general and viscoelastic characteristics in particular.
It is also important to mention that while it is quite common in theoretical practice to assume spatially uniform surface potential to model electrokinetic flows and derive the pertinent slip velocities, an axially varying nature of the same, in many scenarios, appears to be a more practical proposition (Ajdari Reference Ajdari1995; Ghosal Reference Ghosal2002; Mortensen et al. Reference Mortensen2005; Brunet & Ajdari Reference Brunet and Ajdari2006; Khair & Squires Reference Khair and Squires2008; Bahga et al. Reference Bahga, Vinogradova and Bazant2010; Ng & Chu Reference Ng and Chu2011; Ghosh & Chakraborty Reference Ghosh and Chakraborty2013). This may be either attributed to unavoidable microscopic inhomogeneities associated with the microfluidic substrate (Ajdari Reference Ajdari1995, Reference Ajdari1996) or, be also an artefact of deliberate and controlled imposition of patterned surface charges in an effort to achieve certain flow characteristics (Green et al. Reference Green2002; Bahga et al. Reference Bahga, Vinogradova and Bazant2010). The fundamental fluid dynamical implication of such ‘charge modulated’ nature of the surface appears to be straightforward in the sense that the same induces a gradient in the tangential velocity component. This, in effect, gives rise to a transverse velocity component so as to satisfy the flow continuity. A combination of tangential and normal components of the flow velocity may turn out to be effective in mixing adjacent streams in an efficient manner, which is otherwise a challenging proposition in the low Reynolds number paradigm. Motivated by this consideration, various researchers (Green et al. Reference Green2002; Li et al. Reference Li2007; Ou, Moss & Rothstein Reference Ou, Moss and Rothstein2007; Chang & Yang Reference Chang and Yang2008; Chen & Cho Reference Chen and Cho2008) have explored the possibilities of employing non-uniformly charged microfluidic substrates for achieving desired functionalities.
While it is imperative that many microfluidic systems in modern applications related to medical technology must be equipped with the capability of handling complex bio-fluids, reported studies on electroosmotic transport of non-Newtonian fluids over non-uniformly charged surfaces are rather scarce (Bandopadhyay et al. Reference Bandopadhyay, Ghosh and Chakraborty2013; Ghosh & Chakraborty Reference Ghosh and Chakraborty2015; Qi & Ng Reference Qi and Ng2015a ,Reference Qi and Ng b ). A review of the literature suggests that, to the best of our knowledge, no study exists which addresses the nature of the modified Smoluchowski slip velocity for constitutively nonlinear fluids (for example, the generic second-order fluid considered in this study, typical to many practical microfluidic scenarios (Tanner Reference Tanner1966; Leal Reference Leal1975; Chan & Leal Reference Chan and Leal1979; Siddiqui & Schwarz Reference Siddiqui and Schwarz1994; Norouzi et al. Reference Norouzi2010)) in the presence of arbitrary non-uniform surface potential. Since second-order constitutive behaviour is inherently nonlinear in nature, one can infer that the relatively simple relation mentioned in (1.1) will not be valid for these fluids. Once this slip velocity at the wall (more specifically, at the edge of the EDL) is known, one can proceed towards finding the solutions for the flow in the bulk of the domain or the channel under consideration.
Here, we attempt to evaluate the modified Smoluchowski slip velocity for second-order fluids over plane surfaces in the presence of an arbitrarily varying surface potential. We assume a full three-dimensional flow field, with the external field acting in an arbitrary direction. Note that previously Yariv and coworkers (Yariv Reference Yariv2009; Yariv, Schnitzer & Frankel Reference Yariv, Schnitzer and Frankel2011; Schnitzer & Yariv Reference Schnitzer and Yariv2012a ,Reference Schnitzer and Yariv c ) have systematically derived the Smoluchowski slip velocity for spherical (Schnitzer & Yariv Reference Schnitzer and Yariv2012c ) as well as arbitrarily curved surfaces (Yariv Reference Yariv2009). These studies themselves were inspired by the work of Rubinstein and Zaltzmann (Rubinstein & Zaltzman Reference Rubinstein and Zaltzman2001; Rubinstein, Zaltzman & Lerman Reference Rubinstein, Zaltzman and Lerman2005; Zaltzman & Rubinstein Reference Zaltzman and Rubinstein2007), who rigorously studied instability-driven concentration polarization. In a series of studies (Yariv Reference Yariv2009; Yariv et al. Reference Yariv, Schnitzer and Frankel2011; Schnitzer & Yariv Reference Schnitzer and Yariv2012a ,Reference Schnitzer and Yariv b ,Reference Schnitzer and Yariv c ), Yariv and coworkers demonstrated that the most suitable method to evaluate the Smoluchowski slip velocity in a structured way was through matched asymptotic expansions (Bender & Orszag Reference Bender and Orszag1999; Leal Reference Leal2007; Nayfeh Reference Nayfeh2011). We largely follow that same mathematical framework, suitably modified for viscoelastic fluids, to derive our final results. However, the main goal of this study is to employ those well-established asymptotic tools to study the effects of polymeric stresses on the slip velocity by modelling them using a second-order constitutive relation. We reiterate that such effects have hitherto remained unexplored in the literature, wherein lies the novelty of the present work. As we later discuss, inclusion of non-Newtonian effects substantially alters the overall dynamics within the EDL, leading to a marked change in the scaling pattern of viscous stresses within the Debye layer.
We subsequently explore three specific examples of surface potential, namely, two cases of periodically patterned potentials and a step-change-like variation in the surface potential, as representative cases. In an effort to adhere to an analytical framework, we assume the surface potential to be small enough so that Debye–Hückel linearization (Ohshima Reference Ohshima2006; Ferrás et al.
Reference Ferrás2014) can be applied and further assume the Deborah number (
![]() $De$
), representing the extent of viscoelasticity, to be small enough (Bird, Armstrong & Hassager Reference Bird, Armstrong and Hassager1987) so that regular asymptotic expansions in terms of
$De$
), representing the extent of viscoelasticity, to be small enough (Bird, Armstrong & Hassager Reference Bird, Armstrong and Hassager1987) so that regular asymptotic expansions in terms of
![]() $De$
can be employed. The predictions from the asymptotic solutions are subsequently verified against independent numerical solutions for some special cases. The central finding of our analysis is a closed form description of the electroosmostic slip velocity of second-order fluids in presence of arbitrarily varying surface potentials. We further show that, in sharp contrast to Newtonian fluids, here the slip velocity in a given direction is not necessarily independent of the applied electric field in a mutually orthogonal direction.
$De$
can be employed. The predictions from the asymptotic solutions are subsequently verified against independent numerical solutions for some special cases. The central finding of our analysis is a closed form description of the electroosmostic slip velocity of second-order fluids in presence of arbitrarily varying surface potentials. We further show that, in sharp contrast to Newtonian fluids, here the slip velocity in a given direction is not necessarily independent of the applied electric field in a mutually orthogonal direction.
2 Problem formulation
2.1 System description
We consider a simple planner surface, as shown in figure 1. The origin is assumed to lie on this surface, while the
![]() $x$
and the
$x$
and the
![]() $z$
axes run parallel to the surface. The vertical axis is taken as the
$z$
axes run parallel to the surface. The vertical axis is taken as the
![]() $y$
axis. This surface bears a surface charge (
$y$
axis. This surface bears a surface charge (
![]() $\unicode[STIX]{x1D70E}^{\prime }(x^{\prime },z^{\prime })$
), which is non-uniform in nature, being an arbitrary function of
$\unicode[STIX]{x1D70E}^{\prime }(x^{\prime },z^{\prime })$
), which is non-uniform in nature, being an arbitrary function of
![]() $x$
and
$x$
and
![]() $z$
. The axis system can be chosen such that the surface charge has the simplest algebraic form. On top of the surface, a second-order fluid rests and has the following properties: viscosity
$z$
. The axis system can be chosen such that the surface charge has the simplest algebraic form. On top of the surface, a second-order fluid rests and has the following properties: viscosity
![]() $\unicode[STIX]{x1D702}$
, permittivity
$\unicode[STIX]{x1D702}$
, permittivity
![]() $\unicode[STIX]{x1D700}$
and retarded motion constants
$\unicode[STIX]{x1D700}$
and retarded motion constants
![]() $\unicode[STIX]{x1D6FC}_{1}$
and
$\unicode[STIX]{x1D6FC}_{1}$
and
![]() $b\unicode[STIX]{x1D6FC}_{1}$
. This fluid also contains electrolytes which dissociate into ions and hence form an EDL over the solid surface. The reference or, bulk density of the ions are taken to be
$b\unicode[STIX]{x1D6FC}_{1}$
. This fluid also contains electrolytes which dissociate into ions and hence form an EDL over the solid surface. The reference or, bulk density of the ions are taken to be
![]() $c_{0}^{\prime }$
. An external electric field of magnitude
$c_{0}^{\prime }$
. An external electric field of magnitude
![]() $E_{0}$
is applied parallel to the surface, which actuates EOF. We assume that this potential makes an angle
$E_{0}$
is applied parallel to the surface, which actuates EOF. We assume that this potential makes an angle
![]() $\unicode[STIX]{x1D703}$
with the
$\unicode[STIX]{x1D703}$
with the
![]() $x$
axis. We only consider a steady state EOF in the present work. Note that, the direction of the applied external field is denoted by the unit vector
$x$
axis. We only consider a steady state EOF in the present work. Note that, the direction of the applied external field is denoted by the unit vector
![]() $\hat{\boldsymbol{e}}$
, where
$\hat{\boldsymbol{e}}$
, where
![]() $\hat{\boldsymbol{e}}=\hat{\boldsymbol{e}}_{x}\cos (\unicode[STIX]{x1D703})+\hat{\boldsymbol{e}}_{z}\sin (\unicode[STIX]{x1D703})$
. Here
$\hat{\boldsymbol{e}}=\hat{\boldsymbol{e}}_{x}\cos (\unicode[STIX]{x1D703})+\hat{\boldsymbol{e}}_{z}\sin (\unicode[STIX]{x1D703})$
. Here
![]() $\hat{\boldsymbol{e}}_{x}$
and
$\hat{\boldsymbol{e}}_{x}$
and
![]() $\hat{\boldsymbol{e}}_{z}$
are unit vectors along the
$\hat{\boldsymbol{e}}_{z}$
are unit vectors along the
![]() $x$
and
$x$
and
![]() $z$
axes respectively.
$z$
axes respectively.

Figure 1. A schematic representation of the flow geometry. The origin and the axis system rest on the surface. This surface bears a non-uniform charge of the form,
![]() $\unicode[STIX]{x1D70E}^{\prime }(x^{\prime },z^{\prime })$
. An electric field of magnitude
$\unicode[STIX]{x1D70E}^{\prime }(x^{\prime },z^{\prime })$
. An electric field of magnitude
![]() $E_{0}$
(represented by the thick red line) is applied parallel to the surface in a direction
$E_{0}$
(represented by the thick red line) is applied parallel to the surface in a direction
![]() $\hat{\boldsymbol{e}}$
. This unit vector
$\hat{\boldsymbol{e}}$
. This unit vector
![]() $\hat{\boldsymbol{e}}$
makes an angle
$\hat{\boldsymbol{e}}$
makes an angle
![]() $\unicode[STIX]{x1D703}$
with the
$\unicode[STIX]{x1D703}$
with the
![]() $x$
axis. The fluid here obeys a second-order constitute relationship.
$x$
axis. The fluid here obeys a second-order constitute relationship.
Since we are interested in finding the resulting electroosmotic slip velocity, we assume the EDL thickness to be much smaller compared to the typical length scale of variation of the surface charge. This assumption is quite realistic and has been applied to a number of previously executed studies (Ajdari Reference Ajdari1996; Khair & Squires Reference Khair and Squires2008; Yariv Reference Yariv2009; Schnitzer & Yariv Reference Schnitzer and Yariv2012c
). The typical EDL thickness is given by,
![]() $\unicode[STIX]{x1D706}_{D}=\sqrt{(\unicode[STIX]{x1D700}kT)/(2\bar{z}^{2}e^{2}c_{0}^{\prime })}$
, where
$\unicode[STIX]{x1D706}_{D}=\sqrt{(\unicode[STIX]{x1D700}kT)/(2\bar{z}^{2}e^{2}c_{0}^{\prime })}$
, where
![]() $k$
is the Boltzmann constant,
$k$
is the Boltzmann constant,
![]() $T$
is the absolute temperature,
$T$
is the absolute temperature,
![]() $\bar{z}$
is the valance of the ions and
$\bar{z}$
is the valance of the ions and
![]() $e$
is the proton charge. If we assume that the length scale of variation in the surface charge is
$e$
is the proton charge. If we assume that the length scale of variation in the surface charge is
![]() $d$
, then the thin EDL limit would indicate
$d$
, then the thin EDL limit would indicate
![]() $\unicode[STIX]{x1D706}_{D}\ll d$
.
$\unicode[STIX]{x1D706}_{D}\ll d$
.
Before we move towards the detailed formulation, it is important to go through the major assumptions, apart from the thin EDL approximation as mentioned above, under which the present analysis remains valid. First, the flow is steady and the inertial effects are assumed to be negligible. Second, we assume that there are no bulk-scale imposed gradients in the salt concentration. It has been shown by a number of previous studies (Rubinstein & Zaltzman Reference Rubinstein and Zaltzman2001; Khair & Squires Reference Khair and Squires2008; Yariv Reference Yariv2009) that such gradients lead to additional flows inside the thin double layer which eventually alter the slip velocity. This additional slip velocity is sometimes referred to as chemioosmotic slip (Khair & Squires Reference Khair and Squires2008) and it drives a salt flux to make the salt concentration uniform everywhere. Third, we assume that the Dukhin number (
![]() $Du$
), which characterizes the strength of conduction within the thin EDL (Dukhin Reference Dukhin1993; Squires & Bazant Reference Squires and Bazant2004; Khair & Squires Reference Khair and Squires2008) (also referred to as the ‘surface current’), is small enough so that the conduction within the EDL may be neglected. Previously, Khair & Squires (Reference Khair and Squires2008) have shown that, if the applied external field is strong enough, it will drive an additional conduction current within the EDL which will lead to bulk concentration gradients and hence chemioosmotic slip. Such effects are neglected in the present study. In fact, Khair & Squires (Reference Khair and Squires2008), along with Yariv (Reference Yariv2009), demonstrated that in the absence of any imposed bulk-scale gradients, concentration polarization does not occur for thin EDLs provided the applied field, advection strength and the zeta potential are not too large. The final results are valid for low surface potential (usually represented by,
$Du$
), which characterizes the strength of conduction within the thin EDL (Dukhin Reference Dukhin1993; Squires & Bazant Reference Squires and Bazant2004; Khair & Squires Reference Khair and Squires2008) (also referred to as the ‘surface current’), is small enough so that the conduction within the EDL may be neglected. Previously, Khair & Squires (Reference Khair and Squires2008) have shown that, if the applied external field is strong enough, it will drive an additional conduction current within the EDL which will lead to bulk concentration gradients and hence chemioosmotic slip. Such effects are neglected in the present study. In fact, Khair & Squires (Reference Khair and Squires2008), along with Yariv (Reference Yariv2009), demonstrated that in the absence of any imposed bulk-scale gradients, concentration polarization does not occur for thin EDLs provided the applied field, advection strength and the zeta potential are not too large. The final results are valid for low surface potential (usually represented by,
![]() $\unicode[STIX]{x1D701}\leqslant 25~\text{mV}$
), in the limit,
$\unicode[STIX]{x1D701}\leqslant 25~\text{mV}$
), in the limit,
![]() $\unicode[STIX]{x1D6FF}\ll De<O(1)$
(
$\unicode[STIX]{x1D6FF}\ll De<O(1)$
(
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D706}_{D}/d$
). Finally, we note that the whole formulation breaks down, if the zeta potential is large compared to the thermal voltage (
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D706}_{D}/d$
). Finally, we note that the whole formulation breaks down, if the zeta potential is large compared to the thermal voltage (
![]() $kT/\bar{z}e$
) (Yariv Reference Yariv2009; Schnitzer & Yariv Reference Schnitzer and Yariv2012a
). The present model also fails if the applied electric field becomes asymptotically large (Schnitzer & Yariv Reference Schnitzer and Yariv2012c
). Yariv and coworkers (Schnitzer & Yariv Reference Schnitzer and Yariv2012a
,Reference Schnitzer and Yariv
c
) have previously shown that such extreme cases are often associated with nested boundary layer structures, leading to multiple distinguished limits (Bender & Orszag Reference Bender and Orszag1999). Later, we will assume that the Deborah number (
$kT/\bar{z}e$
) (Yariv Reference Yariv2009; Schnitzer & Yariv Reference Schnitzer and Yariv2012a
). The present model also fails if the applied electric field becomes asymptotically large (Schnitzer & Yariv Reference Schnitzer and Yariv2012c
). Yariv and coworkers (Schnitzer & Yariv Reference Schnitzer and Yariv2012a
,Reference Schnitzer and Yariv
c
) have previously shown that such extreme cases are often associated with nested boundary layer structures, leading to multiple distinguished limits (Bender & Orszag Reference Bender and Orszag1999). Later, we will assume that the Deborah number (
![]() $De$
) remains small enough so that a regular perturbation expansion remains possible, taking
$De$
) remains small enough so that a regular perturbation expansion remains possible, taking
![]() $De$
as the gauge function (Bird et al.
Reference Bird, Armstrong and Hassager1987).
$De$
as the gauge function (Bird et al.
Reference Bird, Armstrong and Hassager1987).
Note that, although in the present study we take a semi-infinite fluid domain, the same analysis remains valid for a channel as well. This can be attributed to the thin EDL approximation, by virtue of which, the far-field conditions would effectively represent conditions at the channel centreline. We end this subsection with a brief discussion on the possible range of values of Deborah number (
![]() $De$
). For steady flows, this number is usually defined as (Bird et al.
Reference Bird, Armstrong and Hassager1987),
$De$
). For steady flows, this number is usually defined as (Bird et al.
Reference Bird, Armstrong and Hassager1987),
![]() $De=t_{m}K$
, where
$De=t_{m}K$
, where
![]() $K$
is the characteristic strain rate and
$K$
is the characteristic strain rate and
![]() $t_{m}$
is the relaxation time (largest). In the present context, the definition becomes,
$t_{m}$
is the relaxation time (largest). In the present context, the definition becomes,
![]() $De=t_{m}u_{ref}/d$
,
$De=t_{m}u_{ref}/d$
,
![]() $u_{ref}$
being the characteristic velocity (here
$u_{ref}$
being the characteristic velocity (here
![]() $u_{ref}\sim \unicode[STIX]{x1D700}\unicode[STIX]{x1D701}_{0}^{2}/\unicode[STIX]{x1D702}d$
), while
$u_{ref}\sim \unicode[STIX]{x1D700}\unicode[STIX]{x1D701}_{0}^{2}/\unicode[STIX]{x1D702}d$
), while
![]() $t_{m}=\unicode[STIX]{x1D6FC}_{1}/\unicode[STIX]{x1D702}$
(
$t_{m}=\unicode[STIX]{x1D6FC}_{1}/\unicode[STIX]{x1D702}$
(
![]() $\unicode[STIX]{x1D6FC}_{1}$
is a material constant and
$\unicode[STIX]{x1D6FC}_{1}$
is a material constant and
![]() $\unicode[STIX]{x1D702}$
is the viscosity). For typical viscoelastic fluids,
$\unicode[STIX]{x1D702}$
is the viscosity). For typical viscoelastic fluids,
![]() $t_{m}$
has values ranging from milliseconds (ms) to seconds (s) (Ardekani et al.
Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009; Brust et al.
Reference Brust2013). As an example, Brust et al. (Reference Brust2013) have previously shown that the relaxation time for blood is of the order of 7 ms, at
$t_{m}$
has values ranging from milliseconds (ms) to seconds (s) (Ardekani et al.
Reference Ardekani, Joseph, Dunn-Rankin and Rangel2009; Brust et al.
Reference Brust2013). As an example, Brust et al. (Reference Brust2013) have previously shown that the relaxation time for blood is of the order of 7 ms, at
![]() $37\,^{\circ }\text{C}$
. Hence, for
$37\,^{\circ }\text{C}$
. Hence, for
![]() $u_{ref}\sim 10^{-4}~\text{m}~\text{s}^{-1}$
,
$u_{ref}\sim 10^{-4}~\text{m}~\text{s}^{-1}$
,
![]() $d\sim 10^{-4}{-}10^{-6}~\text{m}$
, one deduces,
$d\sim 10^{-4}{-}10^{-6}~\text{m}$
, one deduces,
![]() $De\sim O(1)-O(10^{-3})$
. However, strictly speaking, a second-order constitutive relation is not applicable for large values of the Deborah number (Bird et al.
Reference Bird, Armstrong and Hassager1987).
$De\sim O(1)-O(10^{-3})$
. However, strictly speaking, a second-order constitutive relation is not applicable for large values of the Deborah number (Bird et al.
Reference Bird, Armstrong and Hassager1987).
2.2 Governing equations
As already mentioned, we will closely follow the framework previously derived by Yariv and coworkers (Yariv Reference Yariv2009; Schnitzer & Yariv Reference Schnitzer and Yariv2012c
). To avoid repetition of the well-known equations in electrokinetics, we will directly start with the non-dimensional ones. The non-dimensionalization has been carried out following the work of Saville (Reference Saville1977) and Yariv and coworkers (Yariv Reference Yariv2009; Schnitzer & Yariv Reference Schnitzer and Yariv2012a
,Reference Schnitzer and Yariv
c
, Reference Schnitzer and Yariv2014). To this end, we first select the characteristic scales for the relevant variables. The characteristic scale of any variable
![]() $\unicode[STIX]{x1D709}$
will be denoted by
$\unicode[STIX]{x1D709}$
will be denoted by
![]() $\unicode[STIX]{x1D709}_{C}$
. As the length scale, we chose,
$\unicode[STIX]{x1D709}_{C}$
. As the length scale, we chose,
![]() $x_{C}=y_{C}=z_{C}=d$
, which is the typical scale over which the surface charge varies. For example, if the charge is periodic in nature,
$x_{C}=y_{C}=z_{C}=d$
, which is the typical scale over which the surface charge varies. For example, if the charge is periodic in nature,
![]() $d$
would be the wavelength of modulation. The potential scales as,
$d$
would be the wavelength of modulation. The potential scales as,
![]() $\unicode[STIX]{x1D713}_{C}\sim \unicode[STIX]{x1D701}_{0}$
, where
$\unicode[STIX]{x1D713}_{C}\sim \unicode[STIX]{x1D701}_{0}$
, where
![]() $\unicode[STIX]{x1D701}_{0}$
denotes the typical magnitude of surface potential. We can relate the potential
$\unicode[STIX]{x1D701}_{0}$
denotes the typical magnitude of surface potential. We can relate the potential
![]() $\unicode[STIX]{x1D701}_{0}$
with the surface charge density. If
$\unicode[STIX]{x1D701}_{0}$
with the surface charge density. If
![]() $\unicode[STIX]{x1D70E}_{c}$
is the typical order of magnitude of the surface charge, then one can define
$\unicode[STIX]{x1D70E}_{c}$
is the typical order of magnitude of the surface charge, then one can define
![]() $\unicode[STIX]{x1D701}_{0}$
as,
$\unicode[STIX]{x1D701}_{0}$
as,
![]() $\unicode[STIX]{x1D701}_{0}\sim (2kT/\bar{z}e)\sinh ^{-1}[(\bar{z}e\unicode[STIX]{x1D70E}_{c}\unicode[STIX]{x1D706}_{D})/(2\unicode[STIX]{x1D700}kT)]$
. For small values of surface charge, the foregoing relation can be linearized to
$\unicode[STIX]{x1D701}_{0}\sim (2kT/\bar{z}e)\sinh ^{-1}[(\bar{z}e\unicode[STIX]{x1D70E}_{c}\unicode[STIX]{x1D706}_{D})/(2\unicode[STIX]{x1D700}kT)]$
. For small values of surface charge, the foregoing relation can be linearized to
![]() $\unicode[STIX]{x1D701}_{0}\sim \unicode[STIX]{x1D70E}_{c}\unicode[STIX]{x1D706}_{D}/\unicode[STIX]{x1D700}$
, as previously noted by Ajdari (Reference Ajdari1996). Note that the choice of potential here is slightly different to that of Saville’s (Reference Saville1977) work, where the thermal scale was chosen as the reference value for the potential. The connection (or, equivalence) between the present choice for potential and that of the thermal scale has been discussed in more detail in appendix A.
$\unicode[STIX]{x1D701}_{0}\sim \unicode[STIX]{x1D70E}_{c}\unicode[STIX]{x1D706}_{D}/\unicode[STIX]{x1D700}$
, as previously noted by Ajdari (Reference Ajdari1996). Note that the choice of potential here is slightly different to that of Saville’s (Reference Saville1977) work, where the thermal scale was chosen as the reference value for the potential. The connection (or, equivalence) between the present choice for potential and that of the thermal scale has been discussed in more detail in appendix A.
The concentration scales as,
![]() $c_{1,C}=c_{2,C}\sim c_{0}^{\prime }$
. The velocity scales as (Saville Reference Saville1977; Yariv Reference Yariv2009),
$c_{1,C}=c_{2,C}\sim c_{0}^{\prime }$
. The velocity scales as (Saville Reference Saville1977; Yariv Reference Yariv2009),
![]() $u_{C}=v_{C}=w_{C}\sim (\unicode[STIX]{x1D700}\unicode[STIX]{x1D701}_{0}^{2}/\unicode[STIX]{x1D702}d)$
, while the stresses scale as,
$u_{C}=v_{C}=w_{C}\sim (\unicode[STIX]{x1D700}\unicode[STIX]{x1D701}_{0}^{2}/\unicode[STIX]{x1D702}d)$
, while the stresses scale as,
![]() $\unicode[STIX]{x1D70F}_{C}\sim \unicode[STIX]{x1D702}u_{C}/d$
. Finally, the pressure scales as,
$\unicode[STIX]{x1D70F}_{C}\sim \unicode[STIX]{x1D702}u_{C}/d$
. Finally, the pressure scales as,
![]() $p_{C}=\unicode[STIX]{x1D702}u_{C}/d$
. We non-dimensionalize the variables with their characteristic scales, i.e. for any variable
$p_{C}=\unicode[STIX]{x1D702}u_{C}/d$
. We non-dimensionalize the variables with their characteristic scales, i.e. for any variable
![]() $\unicode[STIX]{x1D709}^{\prime }$
it’s non-dimensional version reads,
$\unicode[STIX]{x1D709}^{\prime }$
it’s non-dimensional version reads,
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}^{\prime }/\unicode[STIX]{x1D709}_{C}$
. We further define total concentration and charge density as follows: (Mortensen et al.
Reference Mortensen2005):
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}^{\prime }/\unicode[STIX]{x1D709}_{C}$
. We further define total concentration and charge density as follows: (Mortensen et al.
Reference Mortensen2005):
![]() $\unicode[STIX]{x1D70C}=c_{1}-c_{2}$
and
$\unicode[STIX]{x1D70C}=c_{1}-c_{2}$
and
![]() $c=c_{1}+c_{2}$
. Enforcing this non-dimensionalization scheme yields the following governing equations (Saville Reference Saville1977):
$c=c_{1}+c_{2}$
. Enforcing this non-dimensionalization scheme yields the following governing equations (Saville Reference Saville1977):
First note that, in (2.1)–(2.4), the potential
![]() $\unicode[STIX]{x1D711}$
is the contribution from only the diffuse charges. The total non-dimensional potential can be written as (Bahga et al.
Reference Bahga, Vinogradova and Bazant2010),
$\unicode[STIX]{x1D711}$
is the contribution from only the diffuse charges. The total non-dimensional potential can be written as (Bahga et al.
Reference Bahga, Vinogradova and Bazant2010),
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D711}-\unicode[STIX]{x1D6FD}(\hat{\boldsymbol{e}}\boldsymbol{\cdot }\boldsymbol{r})$
. In the foregoing expression, the component
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D711}-\unicode[STIX]{x1D6FD}(\hat{\boldsymbol{e}}\boldsymbol{\cdot }\boldsymbol{r})$
. In the foregoing expression, the component
![]() $\unicode[STIX]{x1D6FD}(\hat{\boldsymbol{e}}\boldsymbol{\cdot }\boldsymbol{r})$
represents the contribution from the externally applied field. Note that the non-dimensional parameter
$\unicode[STIX]{x1D6FD}(\hat{\boldsymbol{e}}\boldsymbol{\cdot }\boldsymbol{r})$
represents the contribution from the externally applied field. Note that the non-dimensional parameter
![]() $\unicode[STIX]{x1D6FD}$
is defined as,
$\unicode[STIX]{x1D6FD}$
is defined as,
![]() $\unicode[STIX]{x1D6FD}=E_{0}d/\unicode[STIX]{x1D701}_{0}$
, which denotes the strength of the applied electric field with respect to the EDL potential. Additionally, in (2.1)–(2.2)
$\unicode[STIX]{x1D6FD}=E_{0}d/\unicode[STIX]{x1D701}_{0}$
, which denotes the strength of the applied electric field with respect to the EDL potential. Additionally, in (2.1)–(2.2)
![]() $Pe$
is the ionic Péclet number, defined as
$Pe$
is the ionic Péclet number, defined as
![]() $Pe=u_{C}d/D=\unicode[STIX]{x1D700}\unicode[STIX]{x1D701}_{0}^{2}/\unicode[STIX]{x1D702}D$
; while
$Pe=u_{C}d/D=\unicode[STIX]{x1D700}\unicode[STIX]{x1D701}_{0}^{2}/\unicode[STIX]{x1D702}D$
; while
![]() $\bar{\unicode[STIX]{x1D701}}_{0}$
is the strength of the zeta potential defined as,
$\bar{\unicode[STIX]{x1D701}}_{0}$
is the strength of the zeta potential defined as,
![]() $\bar{\unicode[STIX]{x1D701}}_{0}=\bar{z}e\unicode[STIX]{x1D701}_{0}/kT$
.
$\bar{\unicode[STIX]{x1D701}}_{0}=\bar{z}e\unicode[STIX]{x1D701}_{0}/kT$
.
In (2.4), the stress tensor for a second-order fluid is defined as (in dimensional form) (Leal Reference Leal1975; Joseph & Feng Reference Joseph and Feng1996),
![]() $\unicode[STIX]{x1D749}^{\prime }=2\unicode[STIX]{x1D702}\unicode[STIX]{x1D63C}^{\prime }+\unicode[STIX]{x1D64E}^{\prime }$
. Here
$\unicode[STIX]{x1D749}^{\prime }=2\unicode[STIX]{x1D702}\unicode[STIX]{x1D63C}^{\prime }+\unicode[STIX]{x1D64E}^{\prime }$
. Here
![]() $\unicode[STIX]{x1D63C}^{\prime }$
is the rate of strain tensor (
$\unicode[STIX]{x1D63C}^{\prime }$
is the rate of strain tensor (
![]() $=[\unicode[STIX]{x1D735}\boldsymbol{v}^{\prime }+(\unicode[STIX]{x1D735}\boldsymbol{v}^{\prime })^{\text{T}}]/2$
) and
$=[\unicode[STIX]{x1D735}\boldsymbol{v}^{\prime }+(\unicode[STIX]{x1D735}\boldsymbol{v}^{\prime })^{\text{T}}]/2$
) and
![]() $\unicode[STIX]{x1D64E}^{\prime }$
denotes the excess polymeric stresses given by,
$\unicode[STIX]{x1D64E}^{\prime }$
denotes the excess polymeric stresses given by,
![]() $\unicode[STIX]{x1D64E}^{\prime }=\unicode[STIX]{x1D6FC}_{1}(\unicode[STIX]{x1D63D}+b\unicode[STIX]{x1D63C}^{2})$
, where
$\unicode[STIX]{x1D64E}^{\prime }=\unicode[STIX]{x1D6FC}_{1}(\unicode[STIX]{x1D63D}+b\unicode[STIX]{x1D63C}^{2})$
, where
![]() $\unicode[STIX]{x1D6FC}_{1}$
and
$\unicode[STIX]{x1D6FC}_{1}$
and
![]() $b$
are material constants (Bird et al.
Reference Bird, Armstrong and Hassager1987). The tensor
$b$
are material constants (Bird et al.
Reference Bird, Armstrong and Hassager1987). The tensor
![]() $\unicode[STIX]{x1D63D}^{\prime }$
is related to the strain rate as follows (analogous to a convected derivative) (Joseph & Feng Reference Joseph and Feng1996):
$\unicode[STIX]{x1D63D}^{\prime }$
is related to the strain rate as follows (analogous to a convected derivative) (Joseph & Feng Reference Joseph and Feng1996):
![]() $\unicode[STIX]{x1D63D}^{\prime }=\unicode[STIX]{x2202}\unicode[STIX]{x1D63C}^{\prime }/\unicode[STIX]{x2202}t^{\prime }+\boldsymbol{v}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D63C}^{\prime }+\unicode[STIX]{x1D63C}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{v}^{\prime }+(\unicode[STIX]{x1D735}\boldsymbol{v}^{\prime })^{\text{T}}\boldsymbol{\cdot }\unicode[STIX]{x1D63C}^{\prime }$
. In non-dimensional form (following the aforementioned scheme), the stresses become:
$\unicode[STIX]{x1D63D}^{\prime }=\unicode[STIX]{x2202}\unicode[STIX]{x1D63C}^{\prime }/\unicode[STIX]{x2202}t^{\prime }+\boldsymbol{v}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D63C}^{\prime }+\unicode[STIX]{x1D63C}^{\prime }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{v}^{\prime }+(\unicode[STIX]{x1D735}\boldsymbol{v}^{\prime })^{\text{T}}\boldsymbol{\cdot }\unicode[STIX]{x1D63C}^{\prime }$
. In non-dimensional form (following the aforementioned scheme), the stresses become:
![]() $\unicode[STIX]{x1D749}=2\unicode[STIX]{x1D63C}+De(\unicode[STIX]{x1D64E})$
. Here
$\unicode[STIX]{x1D749}=2\unicode[STIX]{x1D63C}+De(\unicode[STIX]{x1D64E})$
. Here
![]() $De$
is the Deborah number defined as (Bird et al.
Reference Bird, Armstrong and Hassager1987),
$De$
is the Deborah number defined as (Bird et al.
Reference Bird, Armstrong and Hassager1987),
![]() $De=\unicode[STIX]{x1D6FC}_{1}u_{C}/\unicode[STIX]{x1D702}d$
. With the above considerations, the momentum equation (2.4) can be rewritten as follows:
$De=\unicode[STIX]{x1D6FC}_{1}u_{C}/\unicode[STIX]{x1D702}d$
. With the above considerations, the momentum equation (2.4) can be rewritten as follows:
Equations (2.1)–(2.5) are subject to the following boundary conditions:
In (2.6), we define (Schnitzer & Yariv Reference Schnitzer and Yariv2012c
)
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}^{\prime }\unicode[STIX]{x1D706}_{D}/\unicode[STIX]{x1D700}\unicode[STIX]{x1D701}_{0}$
. The above set of equations (2.1)–(2.7) completes the description for the EOF of second-order fluids. These are a formidable set of equations and to the best of our knowledge analytical solutions to these are not possible. However, one can look for asymptotic solutions in the thin EDL regime (
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}^{\prime }\unicode[STIX]{x1D706}_{D}/\unicode[STIX]{x1D700}\unicode[STIX]{x1D701}_{0}$
. The above set of equations (2.1)–(2.7) completes the description for the EOF of second-order fluids. These are a formidable set of equations and to the best of our knowledge analytical solutions to these are not possible. However, one can look for asymptotic solutions in the thin EDL regime (
![]() $\unicode[STIX]{x1D6FF}\ll 1$
) and small
$\unicode[STIX]{x1D6FF}\ll 1$
) and small
![]() $De$
values (
$De$
values (
![]() $De<O(1)$
). We elaborate on the asymptotic solutions in the next section.
$De<O(1)$
). We elaborate on the asymptotic solutions in the next section.
3 Asymptotic analysis for thin EDL and low
 $De$
values
$De$
values
In this section, we analyse the thin EDL limit (
![]() $\unicode[STIX]{x1D6FF}\ll 1$
), along with the assumption that
$\unicode[STIX]{x1D6FF}\ll 1$
), along with the assumption that
![]() $De<O(1)$
. A number of previous studies (Khair & Squires Reference Khair and Squires2008; Yariv Reference Yariv2009; Højgaard Olesen, Bazant & Bruus Reference Højgaard Olesen, Bazant and Bruus2010; Ghosh & Chakraborty Reference Ghosh and Chakraborty2015), most notably from Yariv and coworkers (Yariv Reference Yariv2009; Schnitzer & Yariv Reference Schnitzer and Yariv2012c
) have demonstrated that the thin EDL limit requires the application of matched asymptotic expansion (Bender & Orszag Reference Bender and Orszag1999; Nayfeh Reference Nayfeh2011). Essentially, through matched asymptotic expansion, we divide the whole domain into two (or more) layers with distinguished characteristic scaling patterns. Typically, in the EDL (the ‘inner layer’), the physical quantities show rapid variations and hence we stretch the EDL to study the dynamics within the same. On the other hand, in the bulk (the ‘outer layer’), all the quantities show slower variations, over
$De<O(1)$
. A number of previous studies (Khair & Squires Reference Khair and Squires2008; Yariv Reference Yariv2009; Højgaard Olesen, Bazant & Bruus Reference Højgaard Olesen, Bazant and Bruus2010; Ghosh & Chakraborty Reference Ghosh and Chakraborty2015), most notably from Yariv and coworkers (Yariv Reference Yariv2009; Schnitzer & Yariv Reference Schnitzer and Yariv2012c
) have demonstrated that the thin EDL limit requires the application of matched asymptotic expansion (Bender & Orszag Reference Bender and Orszag1999; Nayfeh Reference Nayfeh2011). Essentially, through matched asymptotic expansion, we divide the whole domain into two (or more) layers with distinguished characteristic scaling patterns. Typically, in the EDL (the ‘inner layer’), the physical quantities show rapid variations and hence we stretch the EDL to study the dynamics within the same. On the other hand, in the bulk (the ‘outer layer’), all the quantities show slower variations, over
![]() $O(1)$
distances. At the edge of the EDL, the variables in the EDL must be matched with their counterparts in the bulk. The singular perturbation framework employed herein closely follows that of Yariv and coworkers (Yariv Reference Yariv2009; Schnitzer & Yariv Reference Schnitzer and Yariv2012a
,Reference Schnitzer and Yariv
c
). For further details one can refer to the following works Yariv (Reference Yariv2009), Højgaard Olesen et al. (Reference Højgaard Olesen, Bazant and Bruus2010), Schnitzer & Yariv (Reference Schnitzer and Yariv2012c
). In thin EDL limit, we expand all the variables (in both the layers) in an asymptotic series of
$O(1)$
distances. At the edge of the EDL, the variables in the EDL must be matched with their counterparts in the bulk. The singular perturbation framework employed herein closely follows that of Yariv and coworkers (Yariv Reference Yariv2009; Schnitzer & Yariv Reference Schnitzer and Yariv2012a
,Reference Schnitzer and Yariv
c
). For further details one can refer to the following works Yariv (Reference Yariv2009), Højgaard Olesen et al. (Reference Højgaard Olesen, Bazant and Bruus2010), Schnitzer & Yariv (Reference Schnitzer and Yariv2012c
). In thin EDL limit, we expand all the variables (in both the layers) in an asymptotic series of
![]() $\unicode[STIX]{x1D6FF}$
as follows:
$\unicode[STIX]{x1D6FF}$
as follows:
Here,
![]() $\unicode[STIX]{x1D709}$
can represent variables like
$\unicode[STIX]{x1D709}$
can represent variables like
![]() $c$
,
$c$
,
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $u$
,
$u$
,
![]() $v$
, etc. Since our aim is to work out the modified Smoluchowski slip velocity, it would suffice to only consider the leading-order terms in the expansion (3.1) (Yariv Reference Yariv2009). Therefore, from here onwards we drop the subscript ‘0’ from all the variables since all of these would denote leading-order variables in
$v$
, etc. Since our aim is to work out the modified Smoluchowski slip velocity, it would suffice to only consider the leading-order terms in the expansion (3.1) (Yariv Reference Yariv2009). Therefore, from here onwards we drop the subscript ‘0’ from all the variables since all of these would denote leading-order variables in
![]() $\unicode[STIX]{x1D6FF}$
. In the next subsection we represent the outer layer equations, followed by inner layer equations in (3.2). This is subsequently followed by asymptotic solutions for low Deborah numbers.
$\unicode[STIX]{x1D6FF}$
. In the next subsection we represent the outer layer equations, followed by inner layer equations in (3.2). This is subsequently followed by asymptotic solutions for low Deborah numbers.
3.1 Equations in the outer layer
The leading-order outer layer equations read:
Similar equations have already been derived previously by Yariv (Reference Yariv2009), albeit for Newtonian fluids. These are subject to the far-field conditions, as mentioned in (2.7). We must also require the outer variables to match with the inner ones at the edge of the EDL. The matching conditions are discussed in the next subsection. However, based on overall charge and salt concentration balance conditions within the EDL, we can derive bulk-scale conditions for the outer layer concentration and potential to the leading order in
![]() $\unicode[STIX]{x1D6FF}$
. It can be shown (Yariv Reference Yariv2009) that the said bulk-scale conditions eventually translate to the following form, provided
$\unicode[STIX]{x1D6FF}$
. It can be shown (Yariv Reference Yariv2009) that the said bulk-scale conditions eventually translate to the following form, provided
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $Pe$
are not asymptotically large:
$Pe$
are not asymptotically large:
Taking a hint from (3.4) and in the absence of any imposed bulk-scale concentration gradients, equations (3.2) have the simple trivial solutions:
Similar solutions have previously been derived by Yariv (Reference Yariv2009) and Bazant and coworkers (Bazant, Thornton & Ajdari Reference Bazant, Thornton and Ajdari2004; Højgaard Olesen et al.
Reference Højgaard Olesen, Bazant and Bruus2010). The above solution essentially indicates that to leading order in
![]() $\unicode[STIX]{x1D6FF}$
the bulk is charge free and has uniform concentration everywhere. In light of (3.5), the outer layer momentum equations can be written in the following form:
$\unicode[STIX]{x1D6FF}$
the bulk is charge free and has uniform concentration everywhere. In light of (3.5), the outer layer momentum equations can be written in the following form:
The velocities and the pressure are subject to the matching conditions at the edge of the EDL, discussed below.
3.2 Equations in the inner layer
To derive the inner layer equations, we first need to rescale the variables. To this end, we define the following inner layer variables (rescaled for the thin EDL limit),
![]() $Y=y/\unicode[STIX]{x1D6FF}$
;
$Y=y/\unicode[STIX]{x1D6FF}$
;
![]() $X=x$
;
$X=x$
;
![]() $Z=z$
;
$Z=z$
;
![]() $U=u$
;
$U=u$
;
![]() $W=w$
;
$W=w$
;
![]() $V=v/\unicode[STIX]{x1D6FF}$
;
$V=v/\unicode[STIX]{x1D6FF}$
;
![]() $\tilde{\unicode[STIX]{x1D711}}=\unicode[STIX]{x1D711}$
;
$\tilde{\unicode[STIX]{x1D711}}=\unicode[STIX]{x1D711}$
;
![]() $\tilde{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}$
;
$\tilde{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}$
;
![]() $\tilde{c}=c$
. The pressure is rescaled as (Yariv Reference Yariv2009),
$\tilde{c}=c$
. The pressure is rescaled as (Yariv Reference Yariv2009),
![]() $P=p/\unicode[STIX]{x1D6FF}^{2}$
. The excess stresses (
$P=p/\unicode[STIX]{x1D6FF}^{2}$
. The excess stresses (
![]() $\unicode[STIX]{x1D64E}$
) are rescaled as follows:
$\unicode[STIX]{x1D64E}$
) are rescaled as follows:
![]() $\unicode[STIX]{x1D61A}_{xx}=\tilde{\unicode[STIX]{x1D61A}}_{xx}/\unicode[STIX]{x1D6FF}^{2}$
;
$\unicode[STIX]{x1D61A}_{xx}=\tilde{\unicode[STIX]{x1D61A}}_{xx}/\unicode[STIX]{x1D6FF}^{2}$
;
![]() $\unicode[STIX]{x1D61A}_{xy}=\tilde{\unicode[STIX]{x1D61A}}_{xy}/\unicode[STIX]{x1D6FF}$
;
$\unicode[STIX]{x1D61A}_{xy}=\tilde{\unicode[STIX]{x1D61A}}_{xy}/\unicode[STIX]{x1D6FF}$
;
![]() $\unicode[STIX]{x1D61A}_{xz}=\tilde{\unicode[STIX]{x1D61A}}_{xz}/\unicode[STIX]{x1D6FF}^{2}$
;
$\unicode[STIX]{x1D61A}_{xz}=\tilde{\unicode[STIX]{x1D61A}}_{xz}/\unicode[STIX]{x1D6FF}^{2}$
;
![]() $\unicode[STIX]{x1D61A}_{yz}=\tilde{\unicode[STIX]{x1D61A}}_{yz}/\unicode[STIX]{x1D6FF}$
;
$\unicode[STIX]{x1D61A}_{yz}=\tilde{\unicode[STIX]{x1D61A}}_{yz}/\unicode[STIX]{x1D6FF}$
;
![]() $\unicode[STIX]{x1D61A}_{yy}=\tilde{\unicode[STIX]{x1D61A}}_{yy}/\unicode[STIX]{x1D6FF}^{2}$
; and
$\unicode[STIX]{x1D61A}_{yy}=\tilde{\unicode[STIX]{x1D61A}}_{yy}/\unicode[STIX]{x1D6FF}^{2}$
; and
![]() $\unicode[STIX]{x1D61A}_{zz}=\tilde{\unicode[STIX]{x1D61A}}_{zz}/\unicode[STIX]{x1D6FF}^{2}$
. Note that we denote the variables in the inner layer either by uppercase letters or with a ‘tilde’ sign overhead. Similar scaling for the stresses have also been used by Saprykin, Koopmans & Kalliadasis (Reference Saprykin, Koopmans and Kalliadasis2007) for studying free surface flows of viscoelastic fluids. Previously, Yariv and coworkers (Yariv Reference Yariv2009; Schnitzer & Yariv Reference Schnitzer and Yariv2012c
), Squires and coworkers (Squires & Bazant Reference Squires and Bazant2004; Khair & Squires Reference Khair and Squires2008) and many others (Ghosh & Chakraborty Reference Ghosh and Chakraborty2015) have demonstrated that, to leading order in
$\unicode[STIX]{x1D61A}_{zz}=\tilde{\unicode[STIX]{x1D61A}}_{zz}/\unicode[STIX]{x1D6FF}^{2}$
. Note that we denote the variables in the inner layer either by uppercase letters or with a ‘tilde’ sign overhead. Similar scaling for the stresses have also been used by Saprykin, Koopmans & Kalliadasis (Reference Saprykin, Koopmans and Kalliadasis2007) for studying free surface flows of viscoelastic fluids. Previously, Yariv and coworkers (Yariv Reference Yariv2009; Schnitzer & Yariv Reference Schnitzer and Yariv2012c
), Squires and coworkers (Squires & Bazant Reference Squires and Bazant2004; Khair & Squires Reference Khair and Squires2008) and many others (Ghosh & Chakraborty Reference Ghosh and Chakraborty2015) have demonstrated that, to leading order in
![]() $\unicode[STIX]{x1D6FF}$
, the charge, concentration and the potential within the EDL are independent of the velocities (provided the assumptions stated in the previous sections are met). Hence, we can easily infer that
$\unicode[STIX]{x1D6FF}$
, the charge, concentration and the potential within the EDL are independent of the velocities (provided the assumptions stated in the previous sections are met). Hence, we can easily infer that
![]() $\tilde{\unicode[STIX]{x1D70C}}$
and
$\tilde{\unicode[STIX]{x1D70C}}$
and
![]() $\tilde{c}$
will satisfy the Boltzmann distribution, while the potential would satisfy the Poisson–Boltzmann equation (Hunter Reference Hunter1981). For a detailed derivation of the said equations, one can refer to the following works Mortensen et al. (Reference Mortensen2005), Yariv (Reference Yariv2009), Schnitzer & Yariv (Reference Schnitzer and Yariv2012c
). Previously Schnitzer & Yariv (Reference Schnitzer and Yariv2012c
) have shown that to leading order in
$\tilde{c}$
will satisfy the Boltzmann distribution, while the potential would satisfy the Poisson–Boltzmann equation (Hunter Reference Hunter1981). For a detailed derivation of the said equations, one can refer to the following works Mortensen et al. (Reference Mortensen2005), Yariv (Reference Yariv2009), Schnitzer & Yariv (Reference Schnitzer and Yariv2012c
). Previously Schnitzer & Yariv (Reference Schnitzer and Yariv2012c
) have shown that to leading order in
![]() $\unicode[STIX]{x1D6FF}$
, the ‘specified surface charge’ condition for the potential can be conveniently replaced by a ‘specified potential’ condition, which reads:
$\unicode[STIX]{x1D6FF}$
, the ‘specified surface charge’ condition for the potential can be conveniently replaced by a ‘specified potential’ condition, which reads:
![]() $\tilde{\unicode[STIX]{x1D711}}(X,Y=0,Z)=\unicode[STIX]{x1D701}(X,Z)$
, where the zeta potential
$\tilde{\unicode[STIX]{x1D711}}(X,Y=0,Z)=\unicode[STIX]{x1D701}(X,Z)$
, where the zeta potential
![]() $\unicode[STIX]{x1D701}(X,Z)$
is an arbitrary function of
$\unicode[STIX]{x1D701}(X,Z)$
is an arbitrary function of
![]() $x$
and
$x$
and
![]() $z$
. The solution for the potential reads (Schnitzer & Yariv Reference Schnitzer and Yariv2012c
):
$z$
. The solution for the potential reads (Schnitzer & Yariv Reference Schnitzer and Yariv2012c
):
The above solution remains valid beyond low values of
![]() $\bar{\unicode[STIX]{x1D701}}_{0}$
as well. For low surface potential, i.e. within the paradigm of Debye–Huckel linearization, the above equation can be simplified to:
$\bar{\unicode[STIX]{x1D701}}_{0}$
as well. For low surface potential, i.e. within the paradigm of Debye–Huckel linearization, the above equation can be simplified to:
We can now directly move on to the momentum equations inside the EDL. In presence of excess polymeric stresses, they take the following form:
These equations are subject to the following boundary conditions:
At the edge of the EDL the following matching conditions have to be satisfied (to leading order in
![]() $\unicode[STIX]{x1D6FF}$
) for the velocities and the pressure:
$\unicode[STIX]{x1D6FF}$
) for the velocities and the pressure:
The different components of the excess stress tensor (
![]() $\tilde{\unicode[STIX]{x1D61A}}_{xx}$
,
$\tilde{\unicode[STIX]{x1D61A}}_{xx}$
,
![]() $\tilde{\unicode[STIX]{x1D61A}}_{xy}\ldots$
etc.) have the following expressions, to leading order in
$\tilde{\unicode[STIX]{x1D61A}}_{xy}\ldots$
etc.) have the following expressions, to leading order in
![]() $\unicode[STIX]{x1D6FF}$
:
$\unicode[STIX]{x1D6FF}$
:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \tilde{\unicode[STIX]{x1D61A}}_{xx}=\left(1+\frac{b}{4}\right)\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\right)^{2};\quad \tilde{\unicode[STIX]{x1D61A}}_{xz}=\left(1+\frac{b}{4}\right)\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y};\\ \displaystyle \tilde{\unicode[STIX]{x1D61A}}_{yy}=\frac{b}{4}\left[\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\right)^{2}+\left(\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}\right)^{2}\right];\quad \tilde{\unicode[STIX]{x1D61A}}_{zz}=\left(1+\frac{b}{4}\right)\left(\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}\right)^{2}\\ \begin{array}{@{}rcl@{}}\displaystyle \tilde{\unicode[STIX]{x1D61A}}_{xy}\ & =\ & \displaystyle \frac{1}{2}\left(U\frac{\unicode[STIX]{x2202}^{2}U}{\unicode[STIX]{x2202}X\unicode[STIX]{x2202}Y}+V\frac{\unicode[STIX]{x2202}^{2}U}{\unicode[STIX]{x2202}Y^{2}}+W\frac{\unicode[STIX]{x2202}^{2}U}{\unicode[STIX]{x2202}Z\unicode[STIX]{x2202}Y}\right)+\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}Y}+\frac{1}{2}\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Z}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}-\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Z}\right)\\ \ & \ & \displaystyle +\,\frac{b}{4}\left\{\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Z}+\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}X}\right)\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}-2\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Z}\right\}\end{array}\\ \begin{array}{@{}rcl@{}}\displaystyle \tilde{\unicode[STIX]{x1D61A}}_{yz}\ & =\ & \displaystyle \frac{1}{2}\left(U\frac{\unicode[STIX]{x2202}^{2}W}{\unicode[STIX]{x2202}X\unicode[STIX]{x2202}Y}+V\frac{\unicode[STIX]{x2202}^{2}W}{\unicode[STIX]{x2202}Y^{2}}+W\frac{\unicode[STIX]{x2202}^{2}W}{\unicode[STIX]{x2202}Z\unicode[STIX]{x2202}Y}\right)+\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}\frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}Y}+\frac{1}{2}\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}X}-\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}X}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}\right)\\ \ & \ & \displaystyle +\,\frac{b}{4}\left\{\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Z}+\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}X}\right)\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}-2\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}X}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}\right\}.\end{array}\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \tilde{\unicode[STIX]{x1D61A}}_{xx}=\left(1+\frac{b}{4}\right)\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\right)^{2};\quad \tilde{\unicode[STIX]{x1D61A}}_{xz}=\left(1+\frac{b}{4}\right)\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y};\\ \displaystyle \tilde{\unicode[STIX]{x1D61A}}_{yy}=\frac{b}{4}\left[\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\right)^{2}+\left(\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}\right)^{2}\right];\quad \tilde{\unicode[STIX]{x1D61A}}_{zz}=\left(1+\frac{b}{4}\right)\left(\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}\right)^{2}\\ \begin{array}{@{}rcl@{}}\displaystyle \tilde{\unicode[STIX]{x1D61A}}_{xy}\ & =\ & \displaystyle \frac{1}{2}\left(U\frac{\unicode[STIX]{x2202}^{2}U}{\unicode[STIX]{x2202}X\unicode[STIX]{x2202}Y}+V\frac{\unicode[STIX]{x2202}^{2}U}{\unicode[STIX]{x2202}Y^{2}}+W\frac{\unicode[STIX]{x2202}^{2}U}{\unicode[STIX]{x2202}Z\unicode[STIX]{x2202}Y}\right)+\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}Y}+\frac{1}{2}\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Z}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}-\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Z}\right)\\ \ & \ & \displaystyle +\,\frac{b}{4}\left\{\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Z}+\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}X}\right)\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}-2\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Z}\right\}\end{array}\\ \begin{array}{@{}rcl@{}}\displaystyle \tilde{\unicode[STIX]{x1D61A}}_{yz}\ & =\ & \displaystyle \frac{1}{2}\left(U\frac{\unicode[STIX]{x2202}^{2}W}{\unicode[STIX]{x2202}X\unicode[STIX]{x2202}Y}+V\frac{\unicode[STIX]{x2202}^{2}W}{\unicode[STIX]{x2202}Y^{2}}+W\frac{\unicode[STIX]{x2202}^{2}W}{\unicode[STIX]{x2202}Z\unicode[STIX]{x2202}Y}\right)+\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}\frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}Y}+\frac{1}{2}\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}X}-\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}X}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}\right)\\ \ & \ & \displaystyle +\,\frac{b}{4}\left\{\left(\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Z}+\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}X}\right)\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}-2\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}X}\frac{\unicode[STIX]{x2202}W}{\unicode[STIX]{x2202}Y}\right\}.\end{array}\end{array}\right\}\end{eqnarray}$$
Here, we stick to the limit of
![]() $\unicode[STIX]{x1D6FD}\sim O(1)$
, as attributable to the choice of the velocity scale. The most notable feature of the scaling in the inner layer is that, for Newtonian fluids, the shear stress components vary as (non-dimensional)
$\unicode[STIX]{x1D6FD}\sim O(1)$
, as attributable to the choice of the velocity scale. The most notable feature of the scaling in the inner layer is that, for Newtonian fluids, the shear stress components vary as (non-dimensional)
![]() $\unicode[STIX]{x1D70F}_{xy}\sim \unicode[STIX]{x1D70F}_{yz}\sim O(\unicode[STIX]{x1D6FF}^{-1})$
, whereas the normal stress components scale as
$\unicode[STIX]{x1D70F}_{xy}\sim \unicode[STIX]{x1D70F}_{yz}\sim O(\unicode[STIX]{x1D6FF}^{-1})$
, whereas the normal stress components scale as
![]() $\unicode[STIX]{x1D70F}_{xx}\sim \unicode[STIX]{x1D70F}_{yy}\sim \unicode[STIX]{x1D70F}_{zz}\sim \unicode[STIX]{x1D70F}_{xz}\sim O(1)$
inside the EDL. In sharp contrast, for a second-order fluid, the normal stress components (
$\unicode[STIX]{x1D70F}_{xx}\sim \unicode[STIX]{x1D70F}_{yy}\sim \unicode[STIX]{x1D70F}_{zz}\sim \unicode[STIX]{x1D70F}_{xz}\sim O(1)$
inside the EDL. In sharp contrast, for a second-order fluid, the normal stress components (
![]() $\unicode[STIX]{x1D70F}_{xx}$
,
$\unicode[STIX]{x1D70F}_{xx}$
,
![]() $\unicode[STIX]{x1D70F}_{zz}$
, etc.) and the shear stress component
$\unicode[STIX]{x1D70F}_{zz}$
, etc.) and the shear stress component
![]() $\unicode[STIX]{x1D70F}_{xz}$
show the following variations in the inner layer,
$\unicode[STIX]{x1D70F}_{xz}$
show the following variations in the inner layer,
![]() $\unicode[STIX]{x1D70F}_{xx}\sim \unicode[STIX]{x1D70F}_{yy}\sim \unicode[STIX]{x1D70F}_{zz}\sim \unicode[STIX]{x1D70F}_{xz}\sim O(\unicode[STIX]{x1D6FF}^{-2})$
. All other stresses, i.e. the remaining shear stresses scale similarly to those of Newtonian fluids,
$\unicode[STIX]{x1D70F}_{xx}\sim \unicode[STIX]{x1D70F}_{yy}\sim \unicode[STIX]{x1D70F}_{zz}\sim \unicode[STIX]{x1D70F}_{xz}\sim O(\unicode[STIX]{x1D6FF}^{-2})$
. All other stresses, i.e. the remaining shear stresses scale similarly to those of Newtonian fluids,
![]() $\unicode[STIX]{x1D70F}_{xy}\sim \unicode[STIX]{x1D70F}_{yz}\sim O(\unicode[STIX]{x1D6FF}^{-1})$
. Therefore, the normal stresses, as well as the shear component
$\unicode[STIX]{x1D70F}_{xy}\sim \unicode[STIX]{x1D70F}_{yz}\sim O(\unicode[STIX]{x1D6FF}^{-1})$
. Therefore, the normal stresses, as well as the shear component
![]() $\unicode[STIX]{x1D70F}_{xz}$
, are asymptotically large compared to their counterparts in the bulk. This scaling pattern has been verified through comparison with numerical simulations (§ 5.1). Therefore, these stress components explicitly appear in the momentum equations within the EDL, even to leading order in
$\unicode[STIX]{x1D70F}_{xz}$
, are asymptotically large compared to their counterparts in the bulk. This scaling pattern has been verified through comparison with numerical simulations (§ 5.1). Therefore, these stress components explicitly appear in the momentum equations within the EDL, even to leading order in
![]() $\unicode[STIX]{x1D6FF}$
. We later show that the aforementioned stress components play an important role in altering the overall flow dynamics, eventually leading to anisotropic effects. This is one of the major differences between the dynamics of Newtonian and second-order fluids, within the EDL.
$\unicode[STIX]{x1D6FF}$
. We later show that the aforementioned stress components play an important role in altering the overall flow dynamics, eventually leading to anisotropic effects. This is one of the major differences between the dynamics of Newtonian and second-order fluids, within the EDL.
Finally, we note that the left-hand side of the first two conditions in (3.14) represents the slip velocity at the edge of the EDL, along the plane surface. In other words,
![]() $\lim _{Y\rightarrow \infty }U$
is the slip velocity along the
$\lim _{Y\rightarrow \infty }U$
is the slip velocity along the
![]() $x$
axis while
$x$
axis while
![]() $\lim _{Y\rightarrow \infty }W$
is the slip velocity along the
$\lim _{Y\rightarrow \infty }W$
is the slip velocity along the
![]() $z$
axis. These would furnish the bulk-scale boundary conditions for the outer layer velocities. However, the outer layer equations must also be complemented by appropriate boundary conditions along the axial directions. Fortunately, to determine the modified slip velocities we do not require any boundary conditions along the
$z$
axis. These would furnish the bulk-scale boundary conditions for the outer layer velocities. However, the outer layer equations must also be complemented by appropriate boundary conditions along the axial directions. Fortunately, to determine the modified slip velocities we do not require any boundary conditions along the
![]() $X$
and
$X$
and
![]() $Z$
axes.
$Z$
axes.
3.3 Solutions for the velocity field – Smoluchowski slip velocity
The inner layer equations of fluid motion are given by (3.9)–(3.12), subject to no-slip conditions at
![]() $Y=0$
and matching condition (3.14). The potential
$Y=0$
and matching condition (3.14). The potential
![]() $\tilde{\unicode[STIX]{x1D711}}$
is given by (3.7). Although these equations are much simpler than the full set of governing equations, they are still nonlinear in nature and hence cannot be solved exactly. Approximate solutions can however, be derived assuming
$\tilde{\unicode[STIX]{x1D711}}$
is given by (3.7). Although these equations are much simpler than the full set of governing equations, they are still nonlinear in nature and hence cannot be solved exactly. Approximate solutions can however, be derived assuming
![]() $De<O(1)$
. To this end, we expand all the flow variables in a regular asymptotic series of
$De<O(1)$
. To this end, we expand all the flow variables in a regular asymptotic series of
![]() $De$
as follows (Leal Reference Leal1975; Chan & Leal Reference Chan and Leal1979; Bird et al.
Reference Bird, Armstrong and Hassager1987):
$De$
as follows (Leal Reference Leal1975; Chan & Leal Reference Chan and Leal1979; Bird et al.
Reference Bird, Armstrong and Hassager1987):
Here we only deduce the asymptotic solutions in terms of
![]() $De$
, up to
$De$
, up to
![]() $O(De^{2})$
. Therefore, the slip velocity deduced will be correct up to
$O(De^{2})$
. Therefore, the slip velocity deduced will be correct up to
![]() $O(De^{2})$
.
$O(De^{2})$
.
3.3.1 Leading-order solutions
The leading-order equations in
![]() $De$
can be deduced from (3.9)–(3.12) quite easily. These remain same as those for Newtonian fluids. This is expected, since to leading order in
$De$
can be deduced from (3.9)–(3.12) quite easily. These remain same as those for Newtonian fluids. This is expected, since to leading order in
![]() $De$
, second-order fluids behave like Newtonian fluids. The leading-order equations read:
$De$
, second-order fluids behave like Newtonian fluids. The leading-order equations read:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle -\frac{\unicode[STIX]{x2202}P_{0}}{\unicode[STIX]{x2202}X}+\frac{\unicode[STIX]{x2202}^{2}U_{0}}{\unicode[STIX]{x2202}Y^{2}}+\frac{\unicode[STIX]{x2202}^{2}\tilde{\unicode[STIX]{x1D711}}}{\unicode[STIX]{x2202}Y^{2}}\left(\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D711}}}{\unicode[STIX]{x2202}X}-\unicode[STIX]{x1D6FD}\cos \unicode[STIX]{x1D703}\right)=0;\quad -\frac{\unicode[STIX]{x2202}P_{0}}{\unicode[STIX]{x2202}Y}+\frac{\unicode[STIX]{x2202}^{2}\tilde{\unicode[STIX]{x1D711}}}{\unicode[STIX]{x2202}Y^{2}}\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D711}}}{\unicode[STIX]{x2202}Y}=0\\ \displaystyle -\frac{\unicode[STIX]{x2202}P_{0}}{\unicode[STIX]{x2202}Z}+\frac{\unicode[STIX]{x2202}^{2}W_{0}}{\unicode[STIX]{x2202}Y^{2}}+\frac{\unicode[STIX]{x2202}^{2}\tilde{\unicode[STIX]{x1D711}}}{\unicode[STIX]{x2202}Y^{2}}\left(\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D711}}}{\unicode[STIX]{x2202}Z}-\unicode[STIX]{x1D6FD}\sin \unicode[STIX]{x1D703}\right)=0;\quad \frac{\unicode[STIX]{x2202}U_{0}}{\unicode[STIX]{x2202}X}+\frac{\unicode[STIX]{x2202}V_{0}}{\unicode[STIX]{x2202}Y}+\frac{\unicode[STIX]{x2202}W_{0}}{\unicode[STIX]{x2202}Z}=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle -\frac{\unicode[STIX]{x2202}P_{0}}{\unicode[STIX]{x2202}X}+\frac{\unicode[STIX]{x2202}^{2}U_{0}}{\unicode[STIX]{x2202}Y^{2}}+\frac{\unicode[STIX]{x2202}^{2}\tilde{\unicode[STIX]{x1D711}}}{\unicode[STIX]{x2202}Y^{2}}\left(\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D711}}}{\unicode[STIX]{x2202}X}-\unicode[STIX]{x1D6FD}\cos \unicode[STIX]{x1D703}\right)=0;\quad -\frac{\unicode[STIX]{x2202}P_{0}}{\unicode[STIX]{x2202}Y}+\frac{\unicode[STIX]{x2202}^{2}\tilde{\unicode[STIX]{x1D711}}}{\unicode[STIX]{x2202}Y^{2}}\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D711}}}{\unicode[STIX]{x2202}Y}=0\\ \displaystyle -\frac{\unicode[STIX]{x2202}P_{0}}{\unicode[STIX]{x2202}Z}+\frac{\unicode[STIX]{x2202}^{2}W_{0}}{\unicode[STIX]{x2202}Y^{2}}+\frac{\unicode[STIX]{x2202}^{2}\tilde{\unicode[STIX]{x1D711}}}{\unicode[STIX]{x2202}Y^{2}}\left(\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D711}}}{\unicode[STIX]{x2202}Z}-\unicode[STIX]{x1D6FD}\sin \unicode[STIX]{x1D703}\right)=0;\quad \frac{\unicode[STIX]{x2202}U_{0}}{\unicode[STIX]{x2202}X}+\frac{\unicode[STIX]{x2202}V_{0}}{\unicode[STIX]{x2202}Y}+\frac{\unicode[STIX]{x2202}W_{0}}{\unicode[STIX]{x2202}Z}=0.\end{array}\right\}\end{eqnarray}$$
Equation (3.17) can be solved using a general procedure that we will also follow for higher-order corrections. First we integrate the
![]() $Y$
momentum equation to deduce the pressure, which here reads,
$Y$
momentum equation to deduce the pressure, which here reads,
![]() $P_{0}=(\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}Y^{2})/2=(1/2\bar{\unicode[STIX]{x1D701}}_{0}^{2})[\cosh (\bar{\unicode[STIX]{x1D701}}_{0}\tilde{\unicode[STIX]{x1D711}})-1]$
. This pressure can be separately plugged into the
$P_{0}=(\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}Y^{2})/2=(1/2\bar{\unicode[STIX]{x1D701}}_{0}^{2})[\cosh (\bar{\unicode[STIX]{x1D701}}_{0}\tilde{\unicode[STIX]{x1D711}})-1]$
. This pressure can be separately plugged into the
![]() $X$
and
$X$
and
![]() $Z$
momentum equations and these can be subsequently integrated twice to obtain the
$Z$
momentum equations and these can be subsequently integrated twice to obtain the
![]() $X$
and
$X$
and
![]() $Z$
velocities. These velocities read:
$Z$
velocities. These velocities read:
These velocities satisfy the no-slip condition at the wall, i.e. at
![]() $Y=0$
. Further, in the limit
$Y=0$
. Further, in the limit
![]() $Y\rightarrow \infty$
,
$Y\rightarrow \infty$
,
![]() $U_{0}$
and
$U_{0}$
and
![]() $W_{0}$
both must be finite and bounded. Therefore, we must have
$W_{0}$
both must be finite and bounded. Therefore, we must have
![]() $\unicode[STIX]{x1D712}_{1}=\unicode[STIX]{x1D712}_{3}=0$
. Enforcing the no-slip boundary conditions we get,
$\unicode[STIX]{x1D712}_{1}=\unicode[STIX]{x1D712}_{3}=0$
. Enforcing the no-slip boundary conditions we get,
![]() $\unicode[STIX]{x1D712}_{2}=-\unicode[STIX]{x1D6FD}\cos (\unicode[STIX]{x1D703})\unicode[STIX]{x1D701}(X,Z)$
;
$\unicode[STIX]{x1D712}_{2}=-\unicode[STIX]{x1D6FD}\cos (\unicode[STIX]{x1D703})\unicode[STIX]{x1D701}(X,Z)$
;
![]() $\unicode[STIX]{x1D712}_{4}=-\unicode[STIX]{x1D6FD}\sin (\unicode[STIX]{x1D703})\unicode[STIX]{x1D701}(X,Z)$
. The final form of the velocities is thus:
$\unicode[STIX]{x1D712}_{4}=-\unicode[STIX]{x1D6FD}\sin (\unicode[STIX]{x1D703})\unicode[STIX]{x1D701}(X,Z)$
. The final form of the velocities is thus:
The velocities in (3.19) can now be used in the continuity equation (the last of (3.17)) to deduce the
![]() $Y$
-velocity, subject to the condition that at
$Y$
-velocity, subject to the condition that at
![]() $Y=0$
,
$Y=0$
,
![]() $V_{0}=0$
. The
$V_{0}=0$
. The
![]() $Y$
-velocity thus reads:
$Y$
-velocity thus reads:
The leading-order slip velocities in the
![]() $x$
and
$x$
and
![]() $z$
directions can be deduced respectively by evaluating the limits,
$z$
directions can be deduced respectively by evaluating the limits,
![]() $\lim _{Y\rightarrow \infty }U_{0}$
and
$\lim _{Y\rightarrow \infty }U_{0}$
and
![]() $\lim _{Y\rightarrow \infty }W_{0}$
. The slip velocities are simply:
$\lim _{Y\rightarrow \infty }W_{0}$
. The slip velocities are simply:
In (3.21),
![]() $u_{s}^{(0)}$
and
$u_{s}^{(0)}$
and
![]() $w_{s}^{(0)}$
represent leading-order slip velocities along
$w_{s}^{(0)}$
represent leading-order slip velocities along
![]() $x$
and
$x$
and
![]() $z$
directions respectively. This slip velocity can be represented in a compact vector form as follows:
$z$
directions respectively. This slip velocity can be represented in a compact vector form as follows:
We recognize that (3.22) is simply the Smoluchowski slip velocity for Newtonian fluids. We further note that this condition remains valid even when the surface potential magnitude (
![]() $\bar{\unicode[STIX]{x1D701}}_{0}$
) is not small. Other conditions for its validity are
$\bar{\unicode[STIX]{x1D701}}_{0}$
) is not small. Other conditions for its validity are
![]() $Pe\ll O(\unicode[STIX]{x1D6FF}^{-1})$
and
$Pe\ll O(\unicode[STIX]{x1D6FF}^{-1})$
and
![]() $\unicode[STIX]{x1D6FD}\ll O(\unicode[STIX]{x1D6FF}^{-1})$
, as mentioned in the previous section. Note that to leading order, the slip velocity is exactly parallel to the applied electric field, i.e. there are no cross-flow components.
$\unicode[STIX]{x1D6FD}\ll O(\unicode[STIX]{x1D6FF}^{-1})$
, as mentioned in the previous section. Note that to leading order, the slip velocity is exactly parallel to the applied electric field, i.e. there are no cross-flow components.
3.3.2 The
 $O(De)$
solutions
$O(De)$
solutions
The
![]() $O(De)$
equations are given by:
$O(De)$
equations are given by:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle -\frac{\unicode[STIX]{x2202}P_{1}}{\unicode[STIX]{x2202}X}+\frac{\unicode[STIX]{x2202}^{2}U_{1}}{\unicode[STIX]{x2202}Y^{2}}+\left(\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D61A}}_{xx}^{(0)}}{\unicode[STIX]{x2202}X}+\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D61A}}_{xy}^{(0)}}{\unicode[STIX]{x2202}Y}+\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D61A}}_{xz}^{(0)}}{\unicode[STIX]{x2202}Z}\right)=0;\quad -\frac{\unicode[STIX]{x2202}P_{1}}{\unicode[STIX]{x2202}Y}+\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D61A}}_{yy}^{(0)}}{\unicode[STIX]{x2202}Y}=0\\ \displaystyle -\frac{\unicode[STIX]{x2202}P_{1}}{\unicode[STIX]{x2202}Z}+\frac{\unicode[STIX]{x2202}^{2}W_{1}}{\unicode[STIX]{x2202}Y^{2}}+\left(\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D61A}}_{xz}^{(0)}}{\unicode[STIX]{x2202}X}+\frac{\unicode[STIX]{x2202}\tilde{S}_{zy}^{(0)}}{\unicode[STIX]{x2202}Y}+\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D61A}}_{zz}^{(0)}}{\unicode[STIX]{x2202}Z}\right)=0;\quad \frac{\unicode[STIX]{x2202}U_{1}}{\unicode[STIX]{x2202}X}+\frac{\unicode[STIX]{x2202}V_{1}}{\unicode[STIX]{x2202}Y}+\frac{\unicode[STIX]{x2202}W_{1}}{\unicode[STIX]{x2202}Z}=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle -\frac{\unicode[STIX]{x2202}P_{1}}{\unicode[STIX]{x2202}X}+\frac{\unicode[STIX]{x2202}^{2}U_{1}}{\unicode[STIX]{x2202}Y^{2}}+\left(\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D61A}}_{xx}^{(0)}}{\unicode[STIX]{x2202}X}+\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D61A}}_{xy}^{(0)}}{\unicode[STIX]{x2202}Y}+\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D61A}}_{xz}^{(0)}}{\unicode[STIX]{x2202}Z}\right)=0;\quad -\frac{\unicode[STIX]{x2202}P_{1}}{\unicode[STIX]{x2202}Y}+\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D61A}}_{yy}^{(0)}}{\unicode[STIX]{x2202}Y}=0\\ \displaystyle -\frac{\unicode[STIX]{x2202}P_{1}}{\unicode[STIX]{x2202}Z}+\frac{\unicode[STIX]{x2202}^{2}W_{1}}{\unicode[STIX]{x2202}Y^{2}}+\left(\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D61A}}_{xz}^{(0)}}{\unicode[STIX]{x2202}X}+\frac{\unicode[STIX]{x2202}\tilde{S}_{zy}^{(0)}}{\unicode[STIX]{x2202}Y}+\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D61A}}_{zz}^{(0)}}{\unicode[STIX]{x2202}Z}\right)=0;\quad \frac{\unicode[STIX]{x2202}U_{1}}{\unicode[STIX]{x2202}X}+\frac{\unicode[STIX]{x2202}V_{1}}{\unicode[STIX]{x2202}Y}+\frac{\unicode[STIX]{x2202}W_{1}}{\unicode[STIX]{x2202}Z}=0.\end{array}\right\}\end{eqnarray}$$
These are subjected to the no-slip condition at the wall and the velocities must be bounded as
![]() $Y\rightarrow \infty$
; these conditions are identical to those used for the leading-order evaluations. The excess stress components, i.e.
$Y\rightarrow \infty$
; these conditions are identical to those used for the leading-order evaluations. The excess stress components, i.e.
![]() $\tilde{\unicode[STIX]{x1D61A}}_{xx}$
,
$\tilde{\unicode[STIX]{x1D61A}}_{xx}$
,
![]() $\tilde{\unicode[STIX]{x1D61A}}_{xy}$
,
$\tilde{\unicode[STIX]{x1D61A}}_{xy}$
,
![]() $\tilde{\unicode[STIX]{x1D61A}}_{yz},\ldots$
etc. can be easily deduced from the relations given in (3.15). The solution procedure remains exactly the same as that described for the leading-order velocities, with
$\tilde{\unicode[STIX]{x1D61A}}_{yz},\ldots$
etc. can be easily deduced from the relations given in (3.15). The solution procedure remains exactly the same as that described for the leading-order velocities, with
![]() $P_{1}=\tilde{\unicode[STIX]{x1D61A}}_{yy}^{(0)}$
. We note that, at
$P_{1}=\tilde{\unicode[STIX]{x1D61A}}_{yy}^{(0)}$
. We note that, at
![]() $O(De)$
and at higher orders as well, we can continue without making any assumptions regarding the magnitude of
$O(De)$
and at higher orders as well, we can continue without making any assumptions regarding the magnitude of
![]() $\bar{\unicode[STIX]{x1D701}}_{0}$
and evaluate the velocity fields based on (3.8). However, the resulting solutions thus obtained will have extremely complicated algebraic expressions and will in general be very hard to interpret. Therefore, the approximate analytical solutions for arbitrary
$\bar{\unicode[STIX]{x1D701}}_{0}$
and evaluate the velocity fields based on (3.8). However, the resulting solutions thus obtained will have extremely complicated algebraic expressions and will in general be very hard to interpret. Therefore, the approximate analytical solutions for arbitrary
![]() $\bar{\unicode[STIX]{x1D701}}_{0}$
will be somewhat pyrrhic. Hence, to simplify the algebra, yet without sacrificing the essential physics, we now apply the low surface potential approximation, wherein,
$\bar{\unicode[STIX]{x1D701}}_{0}$
will be somewhat pyrrhic. Hence, to simplify the algebra, yet without sacrificing the essential physics, we now apply the low surface potential approximation, wherein,
![]() $\bar{\unicode[STIX]{x1D701}}_{0}\ll 1$
. Therefore, from here onwards we use (3.8) to represent the potential. The
$\bar{\unicode[STIX]{x1D701}}_{0}\ll 1$
. Therefore, from here onwards we use (3.8) to represent the potential. The
![]() $X$
and
$X$
and
![]() $Z$
velocities are then given by:
$Z$
velocities are then given by:
In (3.24),
![]() $\unicode[STIX]{x1D701}_{x}=\unicode[STIX]{x2202}\unicode[STIX]{x1D701}/\unicode[STIX]{x2202}X$
;
$\unicode[STIX]{x1D701}_{x}=\unicode[STIX]{x2202}\unicode[STIX]{x1D701}/\unicode[STIX]{x2202}X$
;
![]() $\unicode[STIX]{x1D701}_{z}=\unicode[STIX]{x2202}\unicode[STIX]{x1D701}/\unicode[STIX]{x2202}Z$
. The functions
$\unicode[STIX]{x1D701}_{z}=\unicode[STIX]{x2202}\unicode[STIX]{x1D701}/\unicode[STIX]{x2202}Z$
. The functions
![]() $F$
and
$F$
and
![]() $G$
are given by:
$G$
are given by:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}F_{x}^{(1)}=(2\cos ^{2}(\unicode[STIX]{x1D703})Y-2\cos ^{2}(\unicode[STIX]{x1D703})+b-b\cos ^{2}(\unicode[STIX]{x1D703}))\text{e}^{-Y}-b+(b+2)\cos ^{2}(\unicode[STIX]{x1D703})\\ F_{z}^{(1)}=(-b+2Y-2)\text{e}^{-Y}\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})+(b+2)\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})\\ G_{x}^{(1)}=(b+2-2Y)\text{e}^{-Y}\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})-(b+2)\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})\\ G_{z}^{(1)}=(2-2Y-b\cos ^{2}(\unicode[STIX]{x1D703})-2\cos ^{2}(\unicode[STIX]{x1D703})+2\cos ^{2}(\unicode[STIX]{x1D703})Y)\text{e}^{-Y}-2+(b+2)\cos ^{2}(\unicode[STIX]{x1D703}).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}F_{x}^{(1)}=(2\cos ^{2}(\unicode[STIX]{x1D703})Y-2\cos ^{2}(\unicode[STIX]{x1D703})+b-b\cos ^{2}(\unicode[STIX]{x1D703}))\text{e}^{-Y}-b+(b+2)\cos ^{2}(\unicode[STIX]{x1D703})\\ F_{z}^{(1)}=(-b+2Y-2)\text{e}^{-Y}\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})+(b+2)\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})\\ G_{x}^{(1)}=(b+2-2Y)\text{e}^{-Y}\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})-(b+2)\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})\\ G_{z}^{(1)}=(2-2Y-b\cos ^{2}(\unicode[STIX]{x1D703})-2\cos ^{2}(\unicode[STIX]{x1D703})+2\cos ^{2}(\unicode[STIX]{x1D703})Y)\text{e}^{-Y}-2+(b+2)\cos ^{2}(\unicode[STIX]{x1D703}).\end{array}\right\}\end{eqnarray}$$
The
![]() $Y$
-velocity can be deduced by simply plugging the expressions for
$Y$
-velocity can be deduced by simply plugging the expressions for
![]() $W_{1}$
and
$W_{1}$
and
![]() $U_{1}$
, as mentioned in (3.24), into the continuity equation and integrating once, subject to
$U_{1}$
, as mentioned in (3.24), into the continuity equation and integrating once, subject to
![]() $V_{1}(X,Y=0,Z)=0$
. However, the expression for
$V_{1}(X,Y=0,Z)=0$
. However, the expression for
![]() $V_{1}$
is algebraically complicated and hence we do not explicitly mention it here. The resulting slip velocities along the surface are:
$V_{1}$
is algebraically complicated and hence we do not explicitly mention it here. The resulting slip velocities along the surface are:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle u_{s}^{(1)}=\lim _{Y\rightarrow \infty }U_{1}={\textstyle \frac{1}{4}}\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}^{2}\{(-b+b\cos ^{2}(\unicode[STIX]{x1D703})+2\cos ^{2}(\unicode[STIX]{x1D703}))\unicode[STIX]{x1D701}_{x}+(b+2)\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})\unicode[STIX]{x1D701}_{z}\}\\ \displaystyle w_{s}^{(1)}=\lim _{Y\rightarrow \infty }W_{1}=-{\textstyle \frac{1}{4}}\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}^{2}\{(-b-2)\unicode[STIX]{x1D701}_{x}\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})-2\unicode[STIX]{x1D701}_{z}+(b+2)\unicode[STIX]{x1D701}_{z}\cos ^{2}(\unicode[STIX]{x1D703})\}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle u_{s}^{(1)}=\lim _{Y\rightarrow \infty }U_{1}={\textstyle \frac{1}{4}}\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}^{2}\{(-b+b\cos ^{2}(\unicode[STIX]{x1D703})+2\cos ^{2}(\unicode[STIX]{x1D703}))\unicode[STIX]{x1D701}_{x}+(b+2)\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})\unicode[STIX]{x1D701}_{z}\}\\ \displaystyle w_{s}^{(1)}=\lim _{Y\rightarrow \infty }W_{1}=-{\textstyle \frac{1}{4}}\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}^{2}\{(-b-2)\unicode[STIX]{x1D701}_{x}\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})-2\unicode[STIX]{x1D701}_{z}+(b+2)\unicode[STIX]{x1D701}_{z}\cos ^{2}(\unicode[STIX]{x1D703})\}.\end{array}\right\}\end{eqnarray}$$
In vector form the slip velocity is thus,
We discuss further the nature of the slip velocity in the forthcoming section (§ 4).
3.3.3 The
 $O(De^{2})$
solutions
$O(De^{2})$
solutions
The
![]() $O(De^{2})$
equations can be deduced in a similar fashion as done for the
$O(De^{2})$
equations can be deduced in a similar fashion as done for the
![]() $O(De)$
solutions. These velocities are subject the same conditions as mentioned for the previous orders. The solution procedure also remains the same as described for the
$O(De)$
solutions. These velocities are subject the same conditions as mentioned for the previous orders. The solution procedure also remains the same as described for the
![]() $O(1)$
and
$O(1)$
and
![]() $O(De)$
solutions. The solutions for
$O(De)$
solutions. The solutions for
![]() $U_{2}$
and
$U_{2}$
and
![]() $W_{2}$
thus obtained have complex algebraic forms and thus we choose not to mention them in this document for the sake of brevity. The MAPLE files containing the expressions can be made available upon request to the authors. However, we do mention the slip velocities occurring at
$W_{2}$
thus obtained have complex algebraic forms and thus we choose not to mention them in this document for the sake of brevity. The MAPLE files containing the expressions can be made available upon request to the authors. However, we do mention the slip velocities occurring at
![]() $O(De^{2})$
. These are given by:
$O(De^{2})$
. These are given by:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle u_{s}^{(2)}=\lim _{Y\rightarrow \infty }U_{2}={\textstyle \frac{1}{64}}\unicode[STIX]{x1D6FD}^{3}\unicode[STIX]{x1D701}[F_{xx}^{(2)}\unicode[STIX]{x1D701}_{xx}+F_{zz}^{(2)}\unicode[STIX]{x1D701}_{zz}+F_{xz}^{(2)}\unicode[STIX]{x1D701}_{xz}+M_{x}\unicode[STIX]{x1D701}_{x}^{2}+M_{z}\unicode[STIX]{x1D701}_{z}^{2}+M_{xz}\unicode[STIX]{x1D701}_{x}\unicode[STIX]{x1D701}_{z}]\\ \displaystyle w_{s}^{(2)}=\lim _{Y\rightarrow \infty }W_{2}={\textstyle \frac{1}{64}}\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}^{3}[G_{xx}^{(2)}\unicode[STIX]{x1D701}_{xx}+G_{zz}^{(2)}\unicode[STIX]{x1D701}_{zz}+G_{xz}^{(2)}\unicode[STIX]{x1D701}_{xz}+N_{x}\unicode[STIX]{x1D701}_{x}^{2}+N_{z}\unicode[STIX]{x1D701}_{z}^{2}+N_{xz}\unicode[STIX]{x1D701}_{x}\unicode[STIX]{x1D701}_{z}].\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle u_{s}^{(2)}=\lim _{Y\rightarrow \infty }U_{2}={\textstyle \frac{1}{64}}\unicode[STIX]{x1D6FD}^{3}\unicode[STIX]{x1D701}[F_{xx}^{(2)}\unicode[STIX]{x1D701}_{xx}+F_{zz}^{(2)}\unicode[STIX]{x1D701}_{zz}+F_{xz}^{(2)}\unicode[STIX]{x1D701}_{xz}+M_{x}\unicode[STIX]{x1D701}_{x}^{2}+M_{z}\unicode[STIX]{x1D701}_{z}^{2}+M_{xz}\unicode[STIX]{x1D701}_{x}\unicode[STIX]{x1D701}_{z}]\\ \displaystyle w_{s}^{(2)}=\lim _{Y\rightarrow \infty }W_{2}={\textstyle \frac{1}{64}}\unicode[STIX]{x1D701}\unicode[STIX]{x1D6FD}^{3}[G_{xx}^{(2)}\unicode[STIX]{x1D701}_{xx}+G_{zz}^{(2)}\unicode[STIX]{x1D701}_{zz}+G_{xz}^{(2)}\unicode[STIX]{x1D701}_{xz}+N_{x}\unicode[STIX]{x1D701}_{x}^{2}+N_{z}\unicode[STIX]{x1D701}_{z}^{2}+N_{xz}\unicode[STIX]{x1D701}_{x}\unicode[STIX]{x1D701}_{z}].\end{array}\right\}\end{eqnarray}$$
The functions
![]() $F$
,
$F$
,
![]() $G$
,
$G$
,
![]() $M$
,
$M$
,
![]() $N$
etc. have the following expressions:
$N$
etc. have the following expressions:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}F_{xx}^{(2)}=-[24\cos ^{3}(\unicode[STIX]{x1D703})-4b^{2}\cos (\unicode[STIX]{x1D703})+18\cos ^{3}(\unicode[STIX]{x1D703})b-18b\cos (\unicode[STIX]{x1D703})+4b^{2}\cos ^{3}(\unicode[STIX]{x1D703})]\unicode[STIX]{x1D701}\\ F_{zz}^{(2)}=-[24\cos (\unicode[STIX]{x1D703})-24\cos ^{3}(\unicode[STIX]{x1D703})-b^{2}\cos (\unicode[STIX]{x1D703})+6b\cos (\unicode[STIX]{x1D703})-4\cos ^{3}(\unicode[STIX]{x1D703})b^{2}-18\cos ^{3}(\unicode[STIX]{x1D703})b]\unicode[STIX]{x1D701}\\ F_{xz}^{(2)}=-[(36b+8b^{2}+48)\cos ^{2}(\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})+(b^{2}-6b)\sin (\unicode[STIX]{x1D703})]\unicode[STIX]{x1D701}\\ M_{x}=4[-8b\cos (\unicode[STIX]{x1D703})+2b^{2}\cos ^{3}(\unicode[STIX]{x1D703})+8\cos ^{3}(\unicode[STIX]{x1D703})b-2b^{2}\cos (\unicode[STIX]{x1D703})+8\cos ^{3}(\unicode[STIX]{x1D703})]\\ M_{z}=4[-8\cos ^{3}(\unicode[STIX]{x1D703})b+b^{2}\cos (\unicode[STIX]{x1D703})-2b^{2}\cos ^{3}(\unicode[STIX]{x1D703})+6b\cos (\unicode[STIX]{x1D703})-8\cos ^{3}(\unicode[STIX]{x1D703})+8\cos (\unicode[STIX]{x1D703})]\\ M_{xz}=4\sin (\unicode[STIX]{x1D703})[16b\cos ^{2}(\unicode[STIX]{x1D703})+4\cos ^{2}(\unicode[STIX]{x1D703})b^{2}-6b+16\cos ^{2}(\unicode[STIX]{x1D703})-b^{2}]\\ G_{xx}^{(2)}=-[(24+18b+4b^{2})\cos ^{2}(\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})-(12b+5b^{2})\sin (\unicode[STIX]{x1D703})]\unicode[STIX]{x1D701}\\ G_{zz}^{(2)}=-[24\sin (\unicode[STIX]{x1D703})-(24+18b+4b^{2})\cos (\unicode[STIX]{x1D703})^{2}\sin (\unicode[STIX]{x1D703})]\unicode[STIX]{x1D701}\\ G_{xz}^{(2)}=-[(9b^{2}+30b+48)\cos (\unicode[STIX]{x1D703})-(8b^{2}+36b+48)\cos ^{3}(\unicode[STIX]{x1D703})]\unicode[STIX]{x1D701}\\ N_{x}=-4[(2b^{2}+8b+8)\sin (\unicode[STIX]{x1D703})\cos ^{2}(\unicode[STIX]{x1D703})-(2b+b^{2})\sin (\unicode[STIX]{x1D703})]\\ N_{z}=-4[(-8b-2b^{2}-8)\sin (\unicode[STIX]{x1D703})\cos ^{2}(\unicode[STIX]{x1D703})+8\sin (\unicode[STIX]{x1D703})]\\ N_{xz}=4\cos (\unicode[STIX]{x1D703})[-10b+4\cos ^{2}(\unicode[STIX]{x1D703})b^{2}-3b^{2}+16b\cos ^{2}(\unicode[STIX]{x1D703})+16\cos ^{2}(\unicode[STIX]{x1D703})-16].\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}F_{xx}^{(2)}=-[24\cos ^{3}(\unicode[STIX]{x1D703})-4b^{2}\cos (\unicode[STIX]{x1D703})+18\cos ^{3}(\unicode[STIX]{x1D703})b-18b\cos (\unicode[STIX]{x1D703})+4b^{2}\cos ^{3}(\unicode[STIX]{x1D703})]\unicode[STIX]{x1D701}\\ F_{zz}^{(2)}=-[24\cos (\unicode[STIX]{x1D703})-24\cos ^{3}(\unicode[STIX]{x1D703})-b^{2}\cos (\unicode[STIX]{x1D703})+6b\cos (\unicode[STIX]{x1D703})-4\cos ^{3}(\unicode[STIX]{x1D703})b^{2}-18\cos ^{3}(\unicode[STIX]{x1D703})b]\unicode[STIX]{x1D701}\\ F_{xz}^{(2)}=-[(36b+8b^{2}+48)\cos ^{2}(\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})+(b^{2}-6b)\sin (\unicode[STIX]{x1D703})]\unicode[STIX]{x1D701}\\ M_{x}=4[-8b\cos (\unicode[STIX]{x1D703})+2b^{2}\cos ^{3}(\unicode[STIX]{x1D703})+8\cos ^{3}(\unicode[STIX]{x1D703})b-2b^{2}\cos (\unicode[STIX]{x1D703})+8\cos ^{3}(\unicode[STIX]{x1D703})]\\ M_{z}=4[-8\cos ^{3}(\unicode[STIX]{x1D703})b+b^{2}\cos (\unicode[STIX]{x1D703})-2b^{2}\cos ^{3}(\unicode[STIX]{x1D703})+6b\cos (\unicode[STIX]{x1D703})-8\cos ^{3}(\unicode[STIX]{x1D703})+8\cos (\unicode[STIX]{x1D703})]\\ M_{xz}=4\sin (\unicode[STIX]{x1D703})[16b\cos ^{2}(\unicode[STIX]{x1D703})+4\cos ^{2}(\unicode[STIX]{x1D703})b^{2}-6b+16\cos ^{2}(\unicode[STIX]{x1D703})-b^{2}]\\ G_{xx}^{(2)}=-[(24+18b+4b^{2})\cos ^{2}(\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D703})-(12b+5b^{2})\sin (\unicode[STIX]{x1D703})]\unicode[STIX]{x1D701}\\ G_{zz}^{(2)}=-[24\sin (\unicode[STIX]{x1D703})-(24+18b+4b^{2})\cos (\unicode[STIX]{x1D703})^{2}\sin (\unicode[STIX]{x1D703})]\unicode[STIX]{x1D701}\\ G_{xz}^{(2)}=-[(9b^{2}+30b+48)\cos (\unicode[STIX]{x1D703})-(8b^{2}+36b+48)\cos ^{3}(\unicode[STIX]{x1D703})]\unicode[STIX]{x1D701}\\ N_{x}=-4[(2b^{2}+8b+8)\sin (\unicode[STIX]{x1D703})\cos ^{2}(\unicode[STIX]{x1D703})-(2b+b^{2})\sin (\unicode[STIX]{x1D703})]\\ N_{z}=-4[(-8b-2b^{2}-8)\sin (\unicode[STIX]{x1D703})\cos ^{2}(\unicode[STIX]{x1D703})+8\sin (\unicode[STIX]{x1D703})]\\ N_{xz}=4\cos (\unicode[STIX]{x1D703})[-10b+4\cos ^{2}(\unicode[STIX]{x1D703})b^{2}-3b^{2}+16b\cos ^{2}(\unicode[STIX]{x1D703})+16\cos ^{2}(\unicode[STIX]{x1D703})-16].\end{array}\right\}\end{eqnarray}$$
In vector form, the slip velocity reads,
Therefore, the total slip velocity, correct up to
![]() $O(De^{2})$
, is given by:
$O(De^{2})$
, is given by:
Based on (3.31), the outer layer velocities (as mentioned in (3.6)) can be expanded in an asymptotic series of
![]() $De$
as,
$De$
as,
![]() $\boldsymbol{v}=\boldsymbol{v}_{0}+De\boldsymbol{v}_{1}+De^{2}\boldsymbol{v}_{2}+\cdots$
. The
$\boldsymbol{v}=\boldsymbol{v}_{0}+De\boldsymbol{v}_{1}+De^{2}\boldsymbol{v}_{2}+\cdots$
. The
![]() $O(De^{k})$
velocity field satisfies the equations,
$O(De^{k})$
velocity field satisfies the equations,
![]() $-\unicode[STIX]{x1D735}p_{k}+\unicode[STIX]{x1D6FB}^{2}\boldsymbol{v}_{k}+(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}^{(k-1)})=0$
;
$-\unicode[STIX]{x1D735}p_{k}+\unicode[STIX]{x1D6FB}^{2}\boldsymbol{v}_{k}+(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}^{(k-1)})=0$
;
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}_{k}=0$
, subject to the following conditions:
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}_{k}=0$
, subject to the following conditions:
![]() $\boldsymbol{v}_{k}(x,y=0,z)=\boldsymbol{v}_{s}^{(k)}(x,z)$
;
$\boldsymbol{v}_{k}(x,y=0,z)=\boldsymbol{v}_{s}^{(k)}(x,z)$
;
![]() $\boldsymbol{v}_{k}\boldsymbol{\cdot }\hat{\boldsymbol{e}}_{y}=0$
. Of course these asymptotic solutions are only valid for
$\boldsymbol{v}_{k}\boldsymbol{\cdot }\hat{\boldsymbol{e}}_{y}=0$
. Of course these asymptotic solutions are only valid for
![]() $De<O(1)$
. Note that, in (3.28),
$De<O(1)$
. Note that, in (3.28),
![]() $\unicode[STIX]{x1D701}_{xx}=\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D701}/\unicode[STIX]{x2202}X^{2}$
;
$\unicode[STIX]{x1D701}_{xx}=\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D701}/\unicode[STIX]{x2202}X^{2}$
;
![]() $\unicode[STIX]{x1D701}_{zz}=\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D701}/\unicode[STIX]{x2202}Z^{2}$
;
$\unicode[STIX]{x1D701}_{zz}=\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D701}/\unicode[STIX]{x2202}Z^{2}$
;
![]() $\unicode[STIX]{x1D701}_{xz}=\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D701}/\unicode[STIX]{x2202}X\unicode[STIX]{x2202}Z$
.
$\unicode[STIX]{x1D701}_{xz}=\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D701}/\unicode[STIX]{x2202}X\unicode[STIX]{x2202}Z$
.
4 General discussion
There are several interesting points to note from the slip velocities derived in the previous section. First, we note that the modified slip velocity is neither proportional to the surface potential nor the applied field strength (
![]() $\unicode[STIX]{x1D6FD}$
) which is in sharp contrast to the case of Newtonian fluids. Second, we note from the
$\unicode[STIX]{x1D6FD}$
) which is in sharp contrast to the case of Newtonian fluids. Second, we note from the
![]() $O(De)$
and
$O(De)$
and
![]() $O(De^{2})$
solutions that
$O(De^{2})$
solutions that
![]() $u_{s}$
(slip velocity in
$u_{s}$
(slip velocity in
![]() $x$
-direction) depends on the applied electric fields in both
$x$
-direction) depends on the applied electric fields in both
![]() $x$
and
$x$
and
![]() $z$
directions. This is attributable to the fact that both
$z$
directions. This is attributable to the fact that both
![]() $\sin \unicode[STIX]{x1D703}$
and
$\sin \unicode[STIX]{x1D703}$
and
![]() $\cos \unicode[STIX]{x1D703}$
appear in the expressions for
$\cos \unicode[STIX]{x1D703}$
appear in the expressions for
![]() $u_{s}$
at
$u_{s}$
at
![]() $O(De)$
and
$O(De)$
and
![]() $O(De^{2})$
. The same is also true for
$O(De^{2})$
. The same is also true for
![]() $w_{s}$
. Therefore, for viscoelastic fluids, the slip velocity in a given direction in general depends on the applied external fields in mutually orthogonal directions as well. This is again in sharp contrast to the cases of Newtonian fluids. Note from the
$w_{s}$
. Therefore, for viscoelastic fluids, the slip velocity in a given direction in general depends on the applied external fields in mutually orthogonal directions as well. This is again in sharp contrast to the cases of Newtonian fluids. Note from the
![]() $O(1)$
solutions that
$O(1)$
solutions that
![]() $u_{s}^{(0)}$
, which is merely the slip velocity for Newtonian fluids, is independent of
$u_{s}^{(0)}$
, which is merely the slip velocity for Newtonian fluids, is independent of
![]() $\sin \unicode[STIX]{x1D703}$
and hence the applied field in the
$\sin \unicode[STIX]{x1D703}$
and hence the applied field in the
![]() $z$
direction. We thus conclude that, for second-order fluids, the Smoluchowski slip velocity does not lie in the direction of the applied electric field.
$z$
direction. We thus conclude that, for second-order fluids, the Smoluchowski slip velocity does not lie in the direction of the applied electric field.
A natural consequence of the above discussion is that, in the absence of any electric field in the
![]() $z$
direction, a modified Smoluchowski slip velocity still exists along
$z$
direction, a modified Smoluchowski slip velocity still exists along
![]() $z$
axis. The opposite is also true for the slip velocity in
$z$
axis. The opposite is also true for the slip velocity in
![]() $x$
direction. This postulate can be easily verified, by putting
$x$
direction. This postulate can be easily verified, by putting
![]() $\sin \unicode[STIX]{x1D703}=0$
in the expression (3.31). The resulting slip velocity in the
$\sin \unicode[STIX]{x1D703}=0$
in the expression (3.31). The resulting slip velocity in the
![]() $z$
direction then reads:
$z$
direction then reads:
Analogous expressions for
![]() $u_{s}$
can also be derived, when
$u_{s}$
can also be derived, when
![]() $E_{x}=0$
or
$E_{x}=0$
or
![]() $\cos \unicode[STIX]{x1D703}=0$
. We again note that this kind of behaviour is absent for Newtonian fluids, for which the slip velocity is strictly parallel to the direction of the applied electric field. We further note that for
$\cos \unicode[STIX]{x1D703}=0$
. We again note that this kind of behaviour is absent for Newtonian fluids, for which the slip velocity is strictly parallel to the direction of the applied electric field. We further note that for
![]() $b=0$
,
$b=0$
,
![]() $w_{s}=0$
in (4.1). Therefore, the anisotropic slip velocity can be eliminated if the material constant
$w_{s}=0$
in (4.1). Therefore, the anisotropic slip velocity can be eliminated if the material constant
![]() $b=0$
. Noting that the quantity
$b=0$
. Noting that the quantity
![]() $b\unicode[STIX]{x1D6FC}_{1}$
represents the second normal stress coefficient, we can conclude from the above discussion that no anisotropic EOF is observed for second-order fluids if the normal stress coefficient in the mutually perpendicular direction to the applied electric field is zero. Another important point to note from (4.1) is that
$b\unicode[STIX]{x1D6FC}_{1}$
represents the second normal stress coefficient, we can conclude from the above discussion that no anisotropic EOF is observed for second-order fluids if the normal stress coefficient in the mutually perpendicular direction to the applied electric field is zero. Another important point to note from (4.1) is that
![]() $w_{s}=0$
if
$w_{s}=0$
if
![]() $\unicode[STIX]{x1D701}_{z}=0$
, i.e. if the surface potential is independent of the
$\unicode[STIX]{x1D701}_{z}=0$
, i.e. if the surface potential is independent of the
![]() $z$
coordinate. Such a paradigm (when
$z$
coordinate. Such a paradigm (when
![]() $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D701}(x)$
,
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D701}(x)$
,
![]() $\sin \unicode[STIX]{x1D703}=0$
), in fact results in a pure two-dimensional flow field. Note that analogous conclusions for
$\sin \unicode[STIX]{x1D703}=0$
), in fact results in a pure two-dimensional flow field. Note that analogous conclusions for
![]() $u_{s}$
remain true when
$u_{s}$
remain true when
![]() $E_{x}=0$
. Therefore, in light of the above discussion, we can conclude that nonlinear nature of the constitutive relation naturally leads to anisotropic slip velocity for second-order fluids, which is in sharp contrast to the EOF of Newtonian fluids. To the best of our knowledge, this is the first study to shed light on such anisotropic effects for EOF of second-order fluids, where the surface potential is an arbitrary function of the axial coordinates.
$E_{x}=0$
. Therefore, in light of the above discussion, we can conclude that nonlinear nature of the constitutive relation naturally leads to anisotropic slip velocity for second-order fluids, which is in sharp contrast to the EOF of Newtonian fluids. To the best of our knowledge, this is the first study to shed light on such anisotropic effects for EOF of second-order fluids, where the surface potential is an arbitrary function of the axial coordinates.
As a special case, we can look for the modified slip velocity when the flow is purely two-dimensional. Such a paradigm is realized by enforcing
![]() $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D701}(x)$
and
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D701}(x)$
and
![]() $\sin \unicode[STIX]{x1D703}=0$
, which ensures that the flow occurs in the
$\sin \unicode[STIX]{x1D703}=0$
, which ensures that the flow occurs in the
![]() $x$
and
$x$
and
![]() $y$
directions, making the
$y$
directions, making the
![]() $z$
coordinate inconsequential. The resulting slip velocity in the
$z$
coordinate inconsequential. The resulting slip velocity in the
![]() $x$
direction then becomes:
$x$
direction then becomes:
Note that one can also take the slip velocity to be along the
![]() $z$
direction and derive an equivalent expression for
$z$
direction and derive an equivalent expression for
![]() $w_{s}$
. It can be easily verified that
$w_{s}$
. It can be easily verified that
![]() $w_{s}$
and
$w_{s}$
and
![]() $u_{s}$
in (4.2) have similar expressions, with
$u_{s}$
in (4.2) have similar expressions, with
![]() $x$
-derivatives replaced by
$x$
-derivatives replaced by
![]() $z$
-derivatives. One interesting point to note from (4.2) is that the slip velocity is independent of the parameter
$z$
-derivatives. One interesting point to note from (4.2) is that the slip velocity is independent of the parameter
![]() $b$
for pure two-dimensional flows, whereas, in the case of a three-dimensional flow field the slip velocity does depend on
$b$
for pure two-dimensional flows, whereas, in the case of a three-dimensional flow field the slip velocity does depend on
![]() $b$
.
$b$
.
It can be demonstrated that the choice of the thermal scale instead of
![]() $\unicode[STIX]{x1D701}_{0}$
as the reference potential also leads to an exact equivalent result to (3.31). Other possible choices of Deborah number also lead to analogous results for the slip velocity. More elaborate discussion on the choices of potential scale, as well as
$\unicode[STIX]{x1D701}_{0}$
as the reference potential also leads to an exact equivalent result to (3.31). Other possible choices of Deborah number also lead to analogous results for the slip velocity. More elaborate discussion on the choices of potential scale, as well as
![]() $De$
, have been included in appendix A. Finally, we note that a major limitation of second-order model is that it is not strictly valid for higher values of Deborah number (
$De$
, have been included in appendix A. Finally, we note that a major limitation of second-order model is that it is not strictly valid for higher values of Deborah number (
![]() $De$
) (Bird et al.
Reference Bird, Armstrong and Hassager1987), although there are a number of studies (Griffiths, Jones & Walters Reference Griffiths, Jones and Walters1969; Bird et al.
Reference Bird, Armstrong and Hassager1987) which have employed this constitutive model beyond the range of its applicability. Of course, for larger
$De$
) (Bird et al.
Reference Bird, Armstrong and Hassager1987), although there are a number of studies (Griffiths, Jones & Walters Reference Griffiths, Jones and Walters1969; Bird et al.
Reference Bird, Armstrong and Hassager1987) which have employed this constitutive model beyond the range of its applicability. Of course, for larger
![]() $De$
values, drastic changes can be observed in the overall slip velocities. However, the present model perhaps should not be applied to such high
$De$
values, drastic changes can be observed in the overall slip velocities. However, the present model perhaps should not be applied to such high
![]() $De$
values, both because of the limitations of the constitutive model itself as well as possible divergence of the asymptotic solutions (Bender & Orszag Reference Bender and Orszag1999). However, differential constitutive models, like Oldroyd-B, upper convected Maxwell model (Bird et al.
Reference Bird, Armstrong and Hassager1987) etc. have a larger range of applicability. It can be shown (Ghosh & Chakraborty Reference Ghosh and Chakraborty2015) that the exact same scaling patterns hold for these differential models. Further, for low
$De$
values, both because of the limitations of the constitutive model itself as well as possible divergence of the asymptotic solutions (Bender & Orszag Reference Bender and Orszag1999). However, differential constitutive models, like Oldroyd-B, upper convected Maxwell model (Bird et al.
Reference Bird, Armstrong and Hassager1987) etc. have a larger range of applicability. It can be shown (Ghosh & Chakraborty Reference Ghosh and Chakraborty2015) that the exact same scaling patterns hold for these differential models. Further, for low
![]() $De$
values, the differential models and the second-order model are equivalent to a large extent (Bird et al.
Reference Bird, Armstrong and Hassager1987). Therefore, the analysis executed herein can be trivially extended to differential models with a larger range of validity. Of course, for larger values of
$De$
values, the differential models and the second-order model are equivalent to a large extent (Bird et al.
Reference Bird, Armstrong and Hassager1987). Therefore, the analysis executed herein can be trivially extended to differential models with a larger range of validity. Of course, for larger values of
![]() $De$
, one has to resort to numerical simulations. Note that the simulations can be executed on the leading-order (in
$De$
, one has to resort to numerical simulations. Note that the simulations can be executed on the leading-order (in
![]() $\unicode[STIX]{x1D6FF}$
) momentum equations within the EDL prior to application of the regular perturbation in terms of
$\unicode[STIX]{x1D6FF}$
) momentum equations within the EDL prior to application of the regular perturbation in terms of
![]() $De$
(i.e. (3.9)–(3.12)).
$De$
(i.e. (3.9)–(3.12)).
5 Representative examples
In this section, we discuss three sample cases to depict the variation in the slip velocity of a second-order fluid when the surface potential is non-uniform in nature. To this end, we first consider a periodically varying surface potential (continuously patterned zeta potential). We subsequently compare the asymptotic solutions to independent numerical simulations for the said potential distribution. We also attempt to verify the novel scaling pattern of normal stresses inside the EDL for second-order fluids by comparison with numerical results. In the second example, we consider a step-change-like variation in the potential and evaluate the resulting slip velocity. The first two examples pertain to purely two-dimensional flows, where
![]() $w=0$
throughout the domain. The final example accounts for a three-dimensional flow field, wherein the electric field has components along both the
$w=0$
throughout the domain. The final example accounts for a three-dimensional flow field, wherein the electric field has components along both the
![]() $x$
and
$x$
and
![]() $z$
axes. Moreover, the zeta potential in this example is taken as a function of both the
$z$
axes. Moreover, the zeta potential in this example is taken as a function of both the
![]() $x$
and
$x$
and
![]() $z$
coordinates.
$z$
coordinates.
5.1 Example 1: two-dimensional axially periodic potential
Consider an axially periodic potential of the form:
Here, the natural length scale of variation in the surface potential can be chosen as
![]() $d=L/2\unicode[STIX]{x03C0}$
. Therefore, application of the thin EDL approximation and evaluation of the subsequent slip velocity would require,
$d=L/2\unicode[STIX]{x03C0}$
. Therefore, application of the thin EDL approximation and evaluation of the subsequent slip velocity would require,
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D706}_{D}/d\ll 1$
. Since the flow under consideration here is two-dimensional, the slip velocity is given by (4.2). Plugging (5.1) into (4.2), we obtain:
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D706}_{D}/d\ll 1$
. Since the flow under consideration here is two-dimensional, the slip velocity is given by (4.2). Plugging (5.1) into (4.2), we obtain:
 $$\begin{eqnarray}\displaystyle u_{s} & = & \displaystyle -\unicode[STIX]{x1D6FD}(n+m\cos (x))+De\left(-{\textstyle \frac{1}{4}}m^{2}\unicode[STIX]{x1D6FD}^{2}\sin (2x)-{\textstyle \frac{1}{2}}n\unicode[STIX]{x1D6FD}^{2}m\sin (x)\right)\nonumber\\ \displaystyle & & \displaystyle +\,De^{2}\unicode[STIX]{x1D6FD}^{3}\left({\textstyle \frac{5}{8}}nm^{2}\cos (2x)+{\textstyle \frac{5}{32}}m^{3}\cos (x)+{\textstyle \frac{3}{8}}m\cos (x)n^{2}+{\textstyle \frac{1}{8}}nm^{2}+{\textstyle \frac{7}{32}}m^{3}\cos (3x)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\cdots .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{s} & = & \displaystyle -\unicode[STIX]{x1D6FD}(n+m\cos (x))+De\left(-{\textstyle \frac{1}{4}}m^{2}\unicode[STIX]{x1D6FD}^{2}\sin (2x)-{\textstyle \frac{1}{2}}n\unicode[STIX]{x1D6FD}^{2}m\sin (x)\right)\nonumber\\ \displaystyle & & \displaystyle +\,De^{2}\unicode[STIX]{x1D6FD}^{3}\left({\textstyle \frac{5}{8}}nm^{2}\cos (2x)+{\textstyle \frac{5}{32}}m^{3}\cos (x)+{\textstyle \frac{3}{8}}m\cos (x)n^{2}+{\textstyle \frac{1}{8}}nm^{2}+{\textstyle \frac{7}{32}}m^{3}\cos (3x)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\cdots .\end{eqnarray}$$
The most interesting point to note from (5.2) is that, at
![]() $O(De^{2})$
, there is an axially invariant component of the slip velocity given by
$O(De^{2})$
, there is an axially invariant component of the slip velocity given by
![]() $(1/8)nm^{2}$
. This component would alter the net throughput in a channel. For Newtonian fluids, the net throughput would only depend on
$(1/8)nm^{2}$
. This component would alter the net throughput in a channel. For Newtonian fluids, the net throughput would only depend on
![]() $n$
; however, for second-order fluids the net throughput also depends on
$n$
; however, for second-order fluids the net throughput also depends on
![]() $m$
, as evident from (5.2).
$m$
, as evident from (5.2).
Note that, if
![]() $m=0$
, i.e. if the potential is uniform along the channel, the
$m=0$
, i.e. if the potential is uniform along the channel, the
![]() $O(De)$
,
$O(De)$
,
![]() $O(De^{2})$
and consequently all higher-order contributions to the slip velocity vanish. In such cases the Smoluchowski slip velocities for second-order fluids and Newtonian fluids are identical. Figure 2 depicts the typical variation in
$O(De^{2})$
and consequently all higher-order contributions to the slip velocity vanish. In such cases the Smoluchowski slip velocities for second-order fluids and Newtonian fluids are identical. Figure 2 depicts the typical variation in
![]() $u_{s}$
as a function of
$u_{s}$
as a function of
![]() $x$
for four different values of
$x$
for four different values of
![]() $De=0$
, 0.1, 0.2 and 0.3, while we have chosen,
$De=0$
, 0.1, 0.2 and 0.3, while we have chosen,
![]() $n=0.5$
and
$n=0.5$
and
![]() $m=1$
. We observe that notable deviation from the Newtonian case (
$m=1$
. We observe that notable deviation from the Newtonian case (
![]() $De=0$
) only occurs where the potential has comparatively larger values. As we increase the value of
$De=0$
) only occurs where the potential has comparatively larger values. As we increase the value of
![]() $De$
, the slip velocity becomes somewhat asymmetric with respect to
$De$
, the slip velocity becomes somewhat asymmetric with respect to
![]() $x$
.
$x$
.

Figure 2. Variation in slip velocity (
![]() $u_{s}$
) versus
$u_{s}$
) versus
![]() $x$
, for four different values of
$x$
, for four different values of
![]() $De=0$
(Newtonian), 0.1, 0.2 and 0.3. The potential here is periodically varying along the wall, with the expression,
$De=0$
(Newtonian), 0.1, 0.2 and 0.3. The potential here is periodically varying along the wall, with the expression,
![]() $\unicode[STIX]{x1D701}^{\prime }(x^{\prime })=\unicode[STIX]{x1D701}_{0}[n+m\cos (2\unicode[STIX]{x03C0}x^{\prime }/L)]$
. Here we have taken
$\unicode[STIX]{x1D701}^{\prime }(x^{\prime })=\unicode[STIX]{x1D701}_{0}[n+m\cos (2\unicode[STIX]{x03C0}x^{\prime }/L)]$
. Here we have taken
![]() $n=0.5$
,
$n=0.5$
,
![]() $m=1$
and
$m=1$
and
![]() $\unicode[STIX]{x1D6FD}=1.5$
.
$\unicode[STIX]{x1D6FD}=1.5$
.
5.1.1 Comparison with numerical simulations
In an effort to verify the accuracy of the asymptotic approximations, we compare them with independent numerical simulations. To this end, we simulate purely two-dimensional flows where the surface potential is chosen as (5.1). Figure 3 depicts the whole set-up for the numerical simulations, including the governing equations, the boundary conditions and the mesh. The details of the domain size and number of grid points are stated in the caption. The mesh size has been made smaller near the bottom wall to capture the dynamics within the EDL. The governing equations, as shown in figure 3, are subject to the following assumptions: (i) low surface potential; (ii) low ionic Péclet number (
![]() $Pe$
) and (iii) the field strength
$Pe$
) and (iii) the field strength
![]() $\unicode[STIX]{x1D6FD}\sim O(1)$
or less. Note that here the potential can be expressed as follows:
$\unicode[STIX]{x1D6FD}\sim O(1)$
or less. Note that here the potential can be expressed as follows:
![]() $\unicode[STIX]{x1D711}=ne^{-y/\unicode[STIX]{x1D6FF}}+me^{-y/\unicode[STIX]{x1D6FF}_{1}}\cos (x)$
, where
$\unicode[STIX]{x1D711}=ne^{-y/\unicode[STIX]{x1D6FF}}+me^{-y/\unicode[STIX]{x1D6FF}_{1}}\cos (x)$
, where
![]() $\unicode[STIX]{x1D6FF}_{1}^{-1}=\sqrt{1+\unicode[STIX]{x1D6FF}^{-2}}$
. We executed the numerical simulations for the thin EDL limit, implying
$\unicode[STIX]{x1D6FF}_{1}^{-1}=\sqrt{1+\unicode[STIX]{x1D6FF}^{-2}}$
. We executed the numerical simulations for the thin EDL limit, implying
![]() $\unicode[STIX]{x1D6FF}\ll 1$
, in order to comply with the conditions of our asymptotic analysis. The simulations were performed in ANSYS FLUENT, which uses a finite volume based framework along with the SIMPLE algorithm for pressure–velocity coupling (Patankar Reference Patankar1980). A more detailed formulation for the numerical simulations along with some of the major difficulties in simulating the given system are discussed in appendix B.
$\unicode[STIX]{x1D6FF}\ll 1$
, in order to comply with the conditions of our asymptotic analysis. The simulations were performed in ANSYS FLUENT, which uses a finite volume based framework along with the SIMPLE algorithm for pressure–velocity coupling (Patankar Reference Patankar1980). A more detailed formulation for the numerical simulations along with some of the major difficulties in simulating the given system are discussed in appendix B.

Figure 3. Set-up for the numerical computation. The governing equations and the boundary conditions are presented in the set-up for comprehensiveness. The domain size is chosen as
![]() $2\unicode[STIX]{x03C0}\times 10$
ensuring lengthwise periodicity and an infinite domain along the transverse direction, as required in our analysis. We perform simulations with grid resolution
$2\unicode[STIX]{x03C0}\times 10$
ensuring lengthwise periodicity and an infinite domain along the transverse direction, as required in our analysis. We perform simulations with grid resolution
![]() $50\times 600$
. We consider non-uniformly spaced grids, and the successive ratios between two consecutive grid sizes are 1.05. The arrow shows the direction of non-uniform spacing. Note that the expressions for excess polymeric stresses
$50\times 600$
. We consider non-uniformly spaced grids, and the successive ratios between two consecutive grid sizes are 1.05. The arrow shows the direction of non-uniform spacing. Note that the expressions for excess polymeric stresses
![]() $\unicode[STIX]{x1D64E}$
have been given in § 2. Here,
$\unicode[STIX]{x1D64E}$
have been given in § 2. Here,
![]() $\unicode[STIX]{x1D6FF}=0.01$
. Other relevant details have been mentioned within the figure itself.
$\unicode[STIX]{x1D6FF}=0.01$
. Other relevant details have been mentioned within the figure itself.
Figure 4 demonstrates the comparison between numerical and analytical solutions for the slip velocity for four different values of Deborah number (
![]() $De=0.04$
, 0.08, 0.11, 0.15). Specifically, we have compared the quantity,
$De=0.04$
, 0.08, 0.11, 0.15). Specifically, we have compared the quantity,
![]() $\unicode[STIX]{x0394}u_{s}=u_{s}-u_{newt.}$
, i.e. the difference between the slip velocities of Newtonian and second-order fluids, with
$\unicode[STIX]{x0394}u_{s}=u_{s}-u_{newt.}$
, i.e. the difference between the slip velocities of Newtonian and second-order fluids, with
![]() $\unicode[STIX]{x1D6FF}=0.01$
. Note that, analytically
$\unicode[STIX]{x1D6FF}=0.01$
. Note that, analytically
![]() $\unicode[STIX]{x0394}u_{s}=De\,u_{s}^{(1)}+De^{2}u_{s}^{(2)}+\cdots$
and hence we essentially compare only the contribution from the higher-order corrections with the corresponding numerical estimates. Therefore, the present comparison is perhaps more rigorous in nature. For the numerical solutions, the slip velocity was estimated just outside the EDL, at a location
$\unicode[STIX]{x0394}u_{s}=De\,u_{s}^{(1)}+De^{2}u_{s}^{(2)}+\cdots$
and hence we essentially compare only the contribution from the higher-order corrections with the corresponding numerical estimates. Therefore, the present comparison is perhaps more rigorous in nature. For the numerical solutions, the slip velocity was estimated just outside the EDL, at a location
![]() $y=0.013$
. Values of all other relevant parameters have been stated in the caption. We note that very good comparison between numerical and analytical solutions can be observed for all values of
$y=0.013$
. Values of all other relevant parameters have been stated in the caption. We note that very good comparison between numerical and analytical solutions can be observed for all values of
![]() $De$
, which validates our analytical estimates.
$De$
, which validates our analytical estimates.

Figure 4. Comparison between numerical (marker) and analytical (lines) solutions for a periodic zeta potential for four different values of
![]() $De=0.04$
, 0.08, 0.11 and 0.15. We have compared the solutions for the quantity,
$De=0.04$
, 0.08, 0.11 and 0.15. We have compared the solutions for the quantity,
![]() $\unicode[STIX]{x0394}u_{s}=u_{s}-u_{newt.}$
, i.e. the change in the slip velocity for second-order fluids. Here,
$\unicode[STIX]{x0394}u_{s}=u_{s}-u_{newt.}$
, i.e. the change in the slip velocity for second-order fluids. Here,
![]() $u_{s}$
is the slip velocity for second-order fluids and
$u_{s}$
is the slip velocity for second-order fluids and
![]() $u_{newt.}$
is that of Newtonian fluids. Values of other parameters are as follows:
$u_{newt.}$
is that of Newtonian fluids. Values of other parameters are as follows:
![]() $\unicode[STIX]{x1D6FD}=0.5$
,
$\unicode[STIX]{x1D6FD}=0.5$
,
![]() $m=0.2$
,
$m=0.2$
,
![]() $n=0.5$
,
$n=0.5$
,
![]() $\unicode[STIX]{x1D6FF}=0.01$
. The numerical solutions have been depicted for the location
$\unicode[STIX]{x1D6FF}=0.01$
. The numerical solutions have been depicted for the location
![]() $y=0.013$
, i.e. just outside the EDL.
$y=0.013$
, i.e. just outside the EDL.
Figure 5 demonstrates the novel scaling pattern of normal stresses (as mentioned in § 3.3) inside the EDL for second-order fluids. Here, we plot the numerically evaluated normal stress component (
![]() $\unicode[STIX]{x1D70F}_{xx}$
) as a function of EDL thickness (
$\unicode[STIX]{x1D70F}_{xx}$
) as a function of EDL thickness (
![]() $\unicode[STIX]{x1D6FF}$
) for both Newtonian and second-order fluids (with
$\unicode[STIX]{x1D6FF}$
) for both Newtonian and second-order fluids (with
![]() $De=0.15$
). Simultaneously, the predicted scaling patterns have also been plotted for both of the fluids. Values of all other relevant parameters have been stated in the caption. Our scaling indicates that for second-order fluids,
$De=0.15$
). Simultaneously, the predicted scaling patterns have also been plotted for both of the fluids. Values of all other relevant parameters have been stated in the caption. Our scaling indicates that for second-order fluids,
![]() $\unicode[STIX]{x1D70F}_{xx}\sim T_{s}\unicode[STIX]{x1D6FF}^{-2}$
, where
$\unicode[STIX]{x1D70F}_{xx}\sim T_{s}\unicode[STIX]{x1D6FF}^{-2}$
, where
![]() $T_{s}$
depends on
$T_{s}$
depends on
![]() $n$
,
$n$
,
![]() $m$
,
$m$
,
![]() $\unicode[STIX]{x1D6FD}$
etc. and for Newtonian fluids,
$\unicode[STIX]{x1D6FD}$
etc. and for Newtonian fluids,
![]() $\unicode[STIX]{x1D70F}_{xx}\sim T_{n}=\text{a constant}$
, depending on
$\unicode[STIX]{x1D70F}_{xx}\sim T_{n}=\text{a constant}$
, depending on
![]() $n$
,
$n$
,
![]() $m$
,
$m$
,
![]() $\unicode[STIX]{x1D6FD}$
etc. The figure under consideration clearly verifies the said scaling and acts as another good test for the validity of the asymptotic analysis executed herein. The constants have been chosen as
$\unicode[STIX]{x1D6FD}$
etc. The figure under consideration clearly verifies the said scaling and acts as another good test for the validity of the asymptotic analysis executed herein. The constants have been chosen as
![]() $T_{s}=0.16$
and
$T_{s}=0.16$
and
![]() $T_{n}=0.1$
.
$T_{n}=0.1$
.

Figure 5. Comparison between analytical scaling (lines) and numerical solutions (markers) for the normal stress (
![]() $\unicode[STIX]{x1D70F}_{xx}$
) inside the EDL as a function of
$\unicode[STIX]{x1D70F}_{xx}$
) inside the EDL as a function of
![]() $\unicode[STIX]{x1D6FF}$
. Our analytical scaling suggests that for second-order fluids,
$\unicode[STIX]{x1D6FF}$
. Our analytical scaling suggests that for second-order fluids,
![]() $\unicode[STIX]{x1D70F}_{xx}\sim \unicode[STIX]{x1D6FF}^{-2}$
in the EDL, whereas for a Newtonian fluid,
$\unicode[STIX]{x1D70F}_{xx}\sim \unicode[STIX]{x1D6FF}^{-2}$
in the EDL, whereas for a Newtonian fluid,
![]() $\unicode[STIX]{x1D70F}_{xx}\sim \unicode[STIX]{x1D6FF}^{0}$
, i.e. has a constant value inside the EDL. The exact same trend is indeed reflected by the numerical simulations. The rest of the parameters have been taken as follows:
$\unicode[STIX]{x1D70F}_{xx}\sim \unicode[STIX]{x1D6FF}^{0}$
, i.e. has a constant value inside the EDL. The exact same trend is indeed reflected by the numerical simulations. The rest of the parameters have been taken as follows:
![]() $\unicode[STIX]{x1D6FD}=0.5$
,
$\unicode[STIX]{x1D6FD}=0.5$
,
![]() $n=0.5$
,
$n=0.5$
,
![]() $m=0.2$
.
$m=0.2$
.
5.2 Example 2: step-change-like variation in zeta potential
A step change in the zeta potential is typically represented by an abrupt discontinuous change in
![]() $\unicode[STIX]{x1D701}$
along the wall. A number of studies have previously been executed (Fu Reference Fu2003; Brotherton & Davis Reference Brotherton and Davis2004; Yariv Reference Yariv2004), which investigate the dynamics of Newtonian fluids in the presence of a step change in the surface potential. However, in reality, such abrupt changes are not likely to exist, since they would give rise to very high electric field strengths inside the solid surface. Therefore, a more likely scenario is where the potential varies smoothly over a short distance as compared to the total length of the device. Hence, if our resolution lies in the length scale of the channel/device, the sharp but continuous change in the potential would indeed be perceived as an abrupt step change.
$\unicode[STIX]{x1D701}$
along the wall. A number of studies have previously been executed (Fu Reference Fu2003; Brotherton & Davis Reference Brotherton and Davis2004; Yariv Reference Yariv2004), which investigate the dynamics of Newtonian fluids in the presence of a step change in the surface potential. However, in reality, such abrupt changes are not likely to exist, since they would give rise to very high electric field strengths inside the solid surface. Therefore, a more likely scenario is where the potential varies smoothly over a short distance as compared to the total length of the device. Hence, if our resolution lies in the length scale of the channel/device, the sharp but continuous change in the potential would indeed be perceived as an abrupt step change.
A good analogy for modelling abrupt variations in a certain variable can be found in phase-field methods (Jacqmin Reference Jacqmin1999), where the order parameter
![]() $\unicode[STIX]{x1D719}$
changes abruptly across the interface from
$\unicode[STIX]{x1D719}$
changes abruptly across the interface from
![]() $-1$
to 1. Although on the system length scale this is a step change in the value of
$-1$
to 1. Although on the system length scale this is a step change in the value of
![]() $\unicode[STIX]{x1D719}$
leading to a sharp interface, on a finer scale the interface is actually assumed to be diffuse (Yang, Li & Ding Reference Yang, Li and Ding2013) with a typical thickness
$\unicode[STIX]{x1D719}$
leading to a sharp interface, on a finer scale the interface is actually assumed to be diffuse (Yang, Li & Ding Reference Yang, Li and Ding2013) with a typical thickness
![]() $\unicode[STIX]{x1D70D}$
. Therefore, the variation in
$\unicode[STIX]{x1D70D}$
. Therefore, the variation in
![]() $\unicode[STIX]{x1D719}$
is actually assumed to be smooth and is taken to be of the form (Wang, Qian & Sheng Reference Wang, Qian and Sheng2008),
$\unicode[STIX]{x1D719}$
is actually assumed to be smooth and is taken to be of the form (Wang, Qian & Sheng Reference Wang, Qian and Sheng2008),
![]() $\unicode[STIX]{x1D719}=\tanh [(x^{\prime }-x_{0}^{\prime })/\unicode[STIX]{x1D70D}]$
, where
$\unicode[STIX]{x1D719}=\tanh [(x^{\prime }-x_{0}^{\prime })/\unicode[STIX]{x1D70D}]$
, where
![]() $x_{0}^{\prime }$
is the location of the interface. The system length scale (say
$x_{0}^{\prime }$
is the location of the interface. The system length scale (say
![]() $L$
) is much larger than the typical interface thickness
$L$
) is much larger than the typical interface thickness
![]() $\unicode[STIX]{x1D70D}$
, with the ratio of the two being termed the Cahn number (Chaudhury, Ghosh & Chakraborty Reference Chaudhury, Ghosh and Chakraborty2013). In the same spirit, here also we take a similar variation in the surface potential, assuming the potential changes from
$\unicode[STIX]{x1D70D}$
, with the ratio of the two being termed the Cahn number (Chaudhury, Ghosh & Chakraborty Reference Chaudhury, Ghosh and Chakraborty2013). In the same spirit, here also we take a similar variation in the surface potential, assuming the potential changes from
![]() $\unicode[STIX]{x1D701}_{1}^{\prime }$
to
$\unicode[STIX]{x1D701}_{1}^{\prime }$
to
![]() $\unicode[STIX]{x1D701}_{2}^{\prime }$
smoothly over a length scale of
$\unicode[STIX]{x1D701}_{2}^{\prime }$
smoothly over a length scale of
![]() $d$
. This length scale is assumed to be much smaller than the overall system length scale
$d$
. This length scale is assumed to be much smaller than the overall system length scale
![]() $L$
. However, since typical EDL thickness is very small, usually of the order of nanometres, the length scale
$L$
. However, since typical EDL thickness is very small, usually of the order of nanometres, the length scale
![]() $d$
can still be large compared to
$d$
can still be large compared to
![]() $\unicode[STIX]{x1D706}_{D}$
. Therefore, we assume that although
$\unicode[STIX]{x1D706}_{D}$
. Therefore, we assume that although
![]() $d\ll L$
, we still have
$d\ll L$
, we still have
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D706}_{D}/d\ll 1$
, so that the thin EDL approximation remains valid. Accordingly, the zeta potential is expressed as:
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D706}_{D}/d\ll 1$
, so that the thin EDL approximation remains valid. Accordingly, the zeta potential is expressed as:
We can choose
![]() $\unicode[STIX]{x1D701}_{0}=\unicode[STIX]{x1D701}_{1}^{\prime }$
and
$\unicode[STIX]{x1D701}_{0}=\unicode[STIX]{x1D701}_{1}^{\prime }$
and
![]() $d$
as the length scale of variation in the potential. The non-dimensional potential would thus read:
$d$
as the length scale of variation in the potential. The non-dimensional potential would thus read:
We further note that, similar continuous but sharp variations are also witnessed in shock waves (Kundu & Cohen Reference Kundu and Cohen2004), where the fluid properties vary continuously yet extremely rapidly over a very small length (thickness of the shock wave front) so that the change in the properties seems abrupt over a larger length scale.
Equation (5.4) can be plugged into (4.2) to obtain the slip velocity correct up to
![]() $O(De^{2})$
. Figure 6 showcases the resulting variation in
$O(De^{2})$
. Figure 6 showcases the resulting variation in
![]() $u_{s}$
versus
$u_{s}$
versus
![]() $x$
for three different values of
$x$
for three different values of
![]() $De=0$
(Newtonian), 0.2 and 0.35, while the other parameters are stated in the caption. In the inset we have depicted the variation in the surface potential as a function of axial location to represent the step-change-like variation. We again note that, similar to the previous figure, the deviations from Newtonian behaviour are only notable when the potential, and hence the velocity, have relatively high magnitude. Note that the slip velocities for second-order fluids slightly lag behind those of Newtonian fluids, as attributable to the fading memory of such fluids.
$De=0$
(Newtonian), 0.2 and 0.35, while the other parameters are stated in the caption. In the inset we have depicted the variation in the surface potential as a function of axial location to represent the step-change-like variation. We again note that, similar to the previous figure, the deviations from Newtonian behaviour are only notable when the potential, and hence the velocity, have relatively high magnitude. Note that the slip velocities for second-order fluids slightly lag behind those of Newtonian fluids, as attributable to the fading memory of such fluids.

Figure 6. Variation in slip velocity (
![]() $u_{s}$
) versus
$u_{s}$
) versus
![]() $x$
for four different values of
$x$
for four different values of
![]() $De=0$
(Newtonian), 0.2 and 0.35. The potential here mimics a step-change-like variation, given by,
$De=0$
(Newtonian), 0.2 and 0.35. The potential here mimics a step-change-like variation, given by,
![]() $\unicode[STIX]{x1D701}^{\prime }(x^{\prime })=1/2\cdot ((\unicode[STIX]{x1D701}_{1}^{\prime }+\unicode[STIX]{x1D701}_{2}^{\prime })+(\unicode[STIX]{x1D701}_{2}^{\prime }-\unicode[STIX]{x1D701}_{1}^{\prime })\cdot \tanh (x^{\prime }/d))$
. This kind of variation resembles that of a step change in the potential, from
$\unicode[STIX]{x1D701}^{\prime }(x^{\prime })=1/2\cdot ((\unicode[STIX]{x1D701}_{1}^{\prime }+\unicode[STIX]{x1D701}_{2}^{\prime })+(\unicode[STIX]{x1D701}_{2}^{\prime }-\unicode[STIX]{x1D701}_{1}^{\prime })\cdot \tanh (x^{\prime }/d))$
. This kind of variation resembles that of a step change in the potential, from
![]() $\unicode[STIX]{x1D701}_{1}$
to
$\unicode[STIX]{x1D701}_{1}$
to
![]() $\unicode[STIX]{x1D701}_{2}$
. In the inset we have shown how the potential varies along the surface. Here, we have taken
$\unicode[STIX]{x1D701}_{2}$
. In the inset we have shown how the potential varies along the surface. Here, we have taken
![]() $\unicode[STIX]{x1D701}_{2}=0.2$
and
$\unicode[STIX]{x1D701}_{2}=0.2$
and
![]() $\unicode[STIX]{x1D6FD}=1.75$
.
$\unicode[STIX]{x1D6FD}=1.75$
.
5.3 Cases of transverse flow
We take up one last example, where cases of fully three-dimensional transverse flows are investigated. To this end, we would consider a zeta potential of the following form (non-dimensional):
Clearly, this potential varies along both the
![]() $x$
and
$x$
and
![]() $z$
axes and is analogous to a ‘chess-board’ patterning. We also consider an applied electric field which has components along both the
$z$
axes and is analogous to a ‘chess-board’ patterning. We also consider an applied electric field which has components along both the
![]() $x$
and
$x$
and
![]() $z$
axes. The choices for the characteristic scales here remain the same as those in § 5.1.
$z$
axes. The choices for the characteristic scales here remain the same as those in § 5.1.

Figure 7. Vector plot of slip velocity (
![]() $\boldsymbol{v}_{s}=u_{s}\hat{\boldsymbol{e}}_{\boldsymbol{x}}+w_{s}\hat{\boldsymbol{e}}_{\boldsymbol{z}}$
) on the
$\boldsymbol{v}_{s}=u_{s}\hat{\boldsymbol{e}}_{\boldsymbol{x}}+w_{s}\hat{\boldsymbol{e}}_{\boldsymbol{z}}$
) on the
![]() $xz$
plane for an applied electric field at an angle
$xz$
plane for an applied electric field at an angle
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$
with the
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$
with the
![]() $x$
axis, denoted by the red arrow. Here, (a) is for Newtonian fluids and (b) is for second-order fluids, with
$x$
axis, denoted by the red arrow. Here, (a) is for Newtonian fluids and (b) is for second-order fluids, with
![]() $De=0.35$
,
$De=0.35$
,
![]() $b=1$
. Other parameters have the values:
$b=1$
. Other parameters have the values:
![]() $\unicode[STIX]{x1D6FD}=3$
,
$\unicode[STIX]{x1D6FD}=3$
,
![]() $m=1$
,
$m=1$
,
![]() $n=0$
. The quantities in the vector plot have been scaled with a value 1.8.
$n=0$
. The quantities in the vector plot have been scaled with a value 1.8.
Figure 7(a,b) depict the vector plot of the slip velocity (
![]() $\boldsymbol{v}_{s}=u_{s}\hat{\boldsymbol{e}}_{\boldsymbol{x}}+w_{s}\hat{\boldsymbol{e}}_{\boldsymbol{z}}$
) for Newtonian (in a) and second-order fluids (in b), with the applied field having components in both the
$\boldsymbol{v}_{s}=u_{s}\hat{\boldsymbol{e}}_{\boldsymbol{x}}+w_{s}\hat{\boldsymbol{e}}_{\boldsymbol{z}}$
) for Newtonian (in a) and second-order fluids (in b), with the applied field having components in both the
![]() $x$
and
$x$
and
![]() $z$
directions. In this figure the field (represented with the thick red arrow) acts at an angle
$z$
directions. In this figure the field (represented with the thick red arrow) acts at an angle
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$
with the
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$
with the
![]() $x$
axis. Values of all other parameters have been stated in the caption. We first note from figure 7(a) that for Newtonian fluids, the slip velocity (
$x$
axis. Values of all other parameters have been stated in the caption. We first note from figure 7(a) that for Newtonian fluids, the slip velocity (
![]() $\boldsymbol{v}_{s}$
) is perfectly aligned to, or parallel with, the applied electric field. On the other hand, figure 7(b) clearly demonstrates that for second-order fluids, the velocity is, in general, non-parallel to the applied electric field, as we discussed in § 4 (see (4.1)). Note that in a Newtonian fluid, such anisotropic effects can only come into play if bulk-scale concentration gradients are present (chemioosmotic flow (Khair & Squires Reference Khair and Squires2008; Yariv Reference Yariv2009)). However, in sharp contrast, for second-order fluids, the nonlinearity in the constitutive equations itself guarantees such ‘cross-stream’ flows, without any bulk-scale concentration gradients. The main reason for the said misalignment is the presence of secondary flows originating from
$\boldsymbol{v}_{s}$
) is perfectly aligned to, or parallel with, the applied electric field. On the other hand, figure 7(b) clearly demonstrates that for second-order fluids, the velocity is, in general, non-parallel to the applied electric field, as we discussed in § 4 (see (4.1)). Note that in a Newtonian fluid, such anisotropic effects can only come into play if bulk-scale concentration gradients are present (chemioosmotic flow (Khair & Squires Reference Khair and Squires2008; Yariv Reference Yariv2009)). However, in sharp contrast, for second-order fluids, the nonlinearity in the constitutive equations itself guarantees such ‘cross-stream’ flows, without any bulk-scale concentration gradients. The main reason for the said misalignment is the presence of secondary flows originating from
![]() $O(De)$
and
$O(De)$
and
![]() $O(De^{2})$
terms, as discussed in detail in §§ 3 and 4. On a related note, we emphasize that a series of studies by Vinogradova and coworkers (Belyaev & Vinogradova Reference Belyaev and Vinogradova2010; Feuillebois, Bazant & Vinogradova Reference Feuillebois, Bazant and Vinogradova2010; Belyaev & Vinogradova Reference Belyaev and Vinogradova2011; Vinogradova & Belyaev Reference Vinogradova and Belyaev2011; Schmieschek et al.
Reference Schmieschek2012) and others (Ghosh & Chakraborty Reference Ghosh and Chakraborty2013) have demonstrated that similar anisotropic flows for Newotnian fluids might also be generated by employing patterned slip on the channel wall in the presence of simple pressure-driven flows.
$O(De^{2})$
terms, as discussed in detail in §§ 3 and 4. On a related note, we emphasize that a series of studies by Vinogradova and coworkers (Belyaev & Vinogradova Reference Belyaev and Vinogradova2010; Feuillebois, Bazant & Vinogradova Reference Feuillebois, Bazant and Vinogradova2010; Belyaev & Vinogradova Reference Belyaev and Vinogradova2011; Vinogradova & Belyaev Reference Vinogradova and Belyaev2011; Schmieschek et al.
Reference Schmieschek2012) and others (Ghosh & Chakraborty Reference Ghosh and Chakraborty2013) have demonstrated that similar anisotropic flows for Newotnian fluids might also be generated by employing patterned slip on the channel wall in the presence of simple pressure-driven flows.
6 Conclusions
The present study focuses on the modified Smoluchowski slip velocity, pertinent to the EOF of second-order fluids over a plane surface in the presence of an arbitrary zeta potential while the applied axial field acts parallel to the plane. We first apply singular perturbation to resolve the dynamics within the EDL. The resultant equations are subsequently solved using a regular asymptotic expansion for small values of the Deborah number. Here, we have considered a fully three-dimensional flow field, wherein, the slip velocity can act in any direction. The modified slip velocity derived here is correct up to
![]() $O(De^{2})$
. As a special case, we have also derived the resulting slip velocity based on a purely two-dimensional flow. Finally, we have explored a few sample cases to showcase the effects of viscoelasticity on the slip velocity. To this end, two separate kinds of potential have been considered, first, an axially periodic potential and second, a step-change-like variation in the zeta potential. The predictions from the asymptotic analysis have been subsequently verified by comparison with independent numerical estimates.
$O(De^{2})$
. As a special case, we have also derived the resulting slip velocity based on a purely two-dimensional flow. Finally, we have explored a few sample cases to showcase the effects of viscoelasticity on the slip velocity. To this end, two separate kinds of potential have been considered, first, an axially periodic potential and second, a step-change-like variation in the zeta potential. The predictions from the asymptotic analysis have been subsequently verified by comparison with independent numerical estimates.
Several interesting conclusions can be drawn from the present study. First, we have shown that the electroosmotic slip velocity for second-order fluids is not linearly proportional to the surface potential and is inherently anisotropic in nature. This is in sharp contrast to the case of Newtonian fluids, for which the slip velocity is strictly along the direction of the applied field. Here, we have demonstrated that the slip velocity in one direction is in general dependent on the electric field strength in a mutually orthogonal direction. With regards to a periodic potential, we have deduced that the
![]() $O(De^{2})$
contribution to the slip velocity has an axially invariant component, which potentially alters the net throughput in a channel compared to Newtonian fluids.
$O(De^{2})$
contribution to the slip velocity has an axially invariant component, which potentially alters the net throughput in a channel compared to Newtonian fluids.
A number of future extensions are possible to the present analysis. The present study only concentrates on an arbitrary zeta potential in the presence of planner surfaces. One can thus look for modified slip velocities for flows over surfaces with arbitrary shapes and potential as a generalization of the above problem. Another interesting extension could be analysis of slip velocity in presence of a potential and/or applied electric field varying with time. For Newtonian fluids, the Smoluchowski slip velocity remains unaltered, irrespective of whether the variables are also functions of time, provided the time scale of variation is below a critical value. However, second-order fluids have a natural relaxation time scale of their own, which can vary over a wide range. Thus, the modified Smoluchowski slip velocity may be altered, when the externally imposed time scale has the same order of magnitude as that of the relaxation time scale of the fluid itself.
Appendix A. Discussion on the possible choices of characteristic potential and Deborah number
In the seminal work of Saville (Reference Saville1977), the potential was scaled with the thermal potential, i.e.
![]() $\unicode[STIX]{x1D713}_{T}=kT/\bar{z}e$
. Here, instead we choose a slightly different reference value for the same. This choice slightly changes the definition of ionic Péclet number (
$\unicode[STIX]{x1D713}_{T}=kT/\bar{z}e$
. Here, instead we choose a slightly different reference value for the same. This choice slightly changes the definition of ionic Péclet number (
![]() $Pe$
) and the non-dimensional field strength (
$Pe$
) and the non-dimensional field strength (
![]() $\unicode[STIX]{x1D6FD}$
). In particular, the Péclet number (
$\unicode[STIX]{x1D6FD}$
). In particular, the Péclet number (
![]() $Pe$
) in the present study can be linked to that of Saville’s work (
$Pe$
) in the present study can be linked to that of Saville’s work (
![]() $N_{p}$
) as follows,
$N_{p}$
) as follows,
![]() $Pe=\bar{\unicode[STIX]{x1D701}}_{0}^{2}N_{p}$
, where
$Pe=\bar{\unicode[STIX]{x1D701}}_{0}^{2}N_{p}$
, where
![]() $N_{p}=\unicode[STIX]{x1D700}k^{2}T^{2}/\unicode[STIX]{x1D702}D\bar{z}^{2}e^{2}$
, while the field strengths are linked as follows:
$N_{p}=\unicode[STIX]{x1D700}k^{2}T^{2}/\unicode[STIX]{x1D702}D\bar{z}^{2}e^{2}$
, while the field strengths are linked as follows:
![]() $\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}/\bar{\unicode[STIX]{x1D701}}_{0}$
,
$\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}/\bar{\unicode[STIX]{x1D701}}_{0}$
,
![]() $\tilde{\unicode[STIX]{x1D6FD}}$
being the field strength defined in Saville’s work. However, we note that for evaluating the Smoluchowski slip velocity only the leading-order equations in
$\tilde{\unicode[STIX]{x1D6FD}}$
being the field strength defined in Saville’s work. However, we note that for evaluating the Smoluchowski slip velocity only the leading-order equations in
![]() $\unicode[STIX]{x1D6FF}$
are required. At this order, charge and momentum transport are decoupled and hence the parameters
$\unicode[STIX]{x1D6FF}$
are required. At this order, charge and momentum transport are decoupled and hence the parameters
![]() $Pe$
and
$Pe$
and
![]() $\unicode[STIX]{x1D6FD}$
do not explicitly govern the potential distribution, provided they are not asymptotically large. Therefore, the choice of potential scale is not particularly important at leading order in
$\unicode[STIX]{x1D6FD}$
do not explicitly govern the potential distribution, provided they are not asymptotically large. Therefore, the choice of potential scale is not particularly important at leading order in
![]() $\unicode[STIX]{x1D6FF}$
and the two choices discussed here (i.e. the thermal scale and the characteristic potential scale taken here) eventually lead to equivalent results. Of course, if one aims to go to higher order in
$\unicode[STIX]{x1D6FF}$
and the two choices discussed here (i.e. the thermal scale and the characteristic potential scale taken here) eventually lead to equivalent results. Of course, if one aims to go to higher order in
![]() $\unicode[STIX]{x1D6FF}$
, the choice of potential should be made more carefully.
$\unicode[STIX]{x1D6FF}$
, the choice of potential should be made more carefully.
The equivalence of the two scales for the potential (i.e.
![]() $\unicode[STIX]{x1D701}_{0}$
and
$\unicode[STIX]{x1D701}_{0}$
and
![]() $kT/\bar{z}e$
) can be verified very easily in the present context, which is discussed below. Taking the choice of potential as the thermal scale, we can denote all the corresponding non-dimensional numbers such as
$kT/\bar{z}e$
) can be verified very easily in the present context, which is discussed below. Taking the choice of potential as the thermal scale, we can denote all the corresponding non-dimensional numbers such as
![]() $De$
,
$De$
,
![]() $Pe$
etc. and variables with a tilde overhead. As such the two set of non-dimensional numbers will be linked in the following way:
$Pe$
etc. and variables with a tilde overhead. As such the two set of non-dimensional numbers will be linked in the following way:
![]() $De=\bar{\unicode[STIX]{x1D701}}_{0}^{2}\tilde{D}e$
;
$De=\bar{\unicode[STIX]{x1D701}}_{0}^{2}\tilde{D}e$
;
![]() $\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}/\bar{\unicode[STIX]{x1D701}}_{0}$
;
$\unicode[STIX]{x1D6FD}=\tilde{\unicode[STIX]{x1D6FD}}/\bar{\unicode[STIX]{x1D701}}_{0}$
;
![]() $\unicode[STIX]{x1D701}=\tilde{\unicode[STIX]{x1D701}}/\bar{\unicode[STIX]{x1D701}}_{0}$
;
$\unicode[STIX]{x1D701}=\tilde{\unicode[STIX]{x1D701}}/\bar{\unicode[STIX]{x1D701}}_{0}$
;
![]() $U=\tilde{U} /\bar{\unicode[STIX]{x1D701}}_{0}^{2}$
, etc., while the characteristic velocities will be linked as follows:
$U=\tilde{U} /\bar{\unicode[STIX]{x1D701}}_{0}^{2}$
, etc., while the characteristic velocities will be linked as follows:
![]() $u_{C}=\bar{\unicode[STIX]{x1D701}}_{0}^{2}\tilde{u} _{C}$
. Now, if we assume that the typical magnitude of the surface potential is low enough, i.e.
$u_{C}=\bar{\unicode[STIX]{x1D701}}_{0}^{2}\tilde{u} _{C}$
. Now, if we assume that the typical magnitude of the surface potential is low enough, i.e.
![]() $\bar{\unicode[STIX]{x1D701}}_{0}\ll 1$
, we can expand the velocities and the potential in an asymptotic series of
$\bar{\unicode[STIX]{x1D701}}_{0}\ll 1$
, we can expand the velocities and the potential in an asymptotic series of
![]() $\bar{\unicode[STIX]{x1D701}}_{0}$
. For instance, the expansion for the velocity would read:
$\bar{\unicode[STIX]{x1D701}}_{0}$
. For instance, the expansion for the velocity would read:
Given the expansion (A 1),
![]() $\tilde{D}e$
can take arbitrary values provided it stays at
$\tilde{D}e$
can take arbitrary values provided it stays at
![]() $O(1)$
or less (as opposed to
$O(1)$
or less (as opposed to
![]() $De\ll 1$
assumed in § 3). It can then be very easily deduced that the leading-order potential is given by,
$De\ll 1$
assumed in § 3). It can then be very easily deduced that the leading-order potential is given by,
![]() $\tilde{\unicode[STIX]{x1D711}}_{0}=\unicode[STIX]{x1D701}(X,Z)\text{e}^{-Y}$
, where
$\tilde{\unicode[STIX]{x1D711}}_{0}=\unicode[STIX]{x1D701}(X,Z)\text{e}^{-Y}$
, where
![]() $\unicode[STIX]{x1D701}(X,Z)=\unicode[STIX]{x1D701}^{\prime }(x^{\prime },z^{\prime })/(kT\bar{\unicode[STIX]{x1D701}}_{0}/\bar{z}e)$
. Therefore, it is straightforward to deduce that the leading-order velocity is given by:
$\unicode[STIX]{x1D701}(X,Z)=\unicode[STIX]{x1D701}^{\prime }(x^{\prime },z^{\prime })/(kT\bar{\unicode[STIX]{x1D701}}_{0}/\bar{z}e)$
. Therefore, it is straightforward to deduce that the leading-order velocity is given by:
Analogous expression can also be given for
![]() $\tilde{W}_{0}$
. Recalling (3.19), we note that the expression for
$\tilde{W}_{0}$
. Recalling (3.19), we note that the expression for
![]() $\tilde{U} _{0}$
can be straight away derived from that of
$\tilde{U} _{0}$
can be straight away derived from that of
![]() $U_{0}$
by simply replacing
$U_{0}$
by simply replacing
![]() $\unicode[STIX]{x1D6FD}$
with
$\unicode[STIX]{x1D6FD}$
with
![]() $\tilde{\unicode[STIX]{x1D6FD}}$
. At
$\tilde{\unicode[STIX]{x1D6FD}}$
. At
![]() $O(\bar{\unicode[STIX]{x1D701}}_{0}^{2})$
, the effect of viscoelasticity comes in through the appearance of
$O(\bar{\unicode[STIX]{x1D701}}_{0}^{2})$
, the effect of viscoelasticity comes in through the appearance of
![]() $\tilde{D}e$
. By solving the
$\tilde{D}e$
. By solving the
![]() $O(\bar{\unicode[STIX]{x1D701}}_{0}^{2})$
problem based on (3.7)–(3.12), we can easily deduce that the velocities at this order can be expressed as:
$O(\bar{\unicode[STIX]{x1D701}}_{0}^{2})$
problem based on (3.7)–(3.12), we can easily deduce that the velocities at this order can be expressed as:
Here,
![]() $\breve{U}_{1}$
and
$\breve{U}_{1}$
and
![]() $\breve{W}_{1}$
have the exact same expressions as
$\breve{W}_{1}$
have the exact same expressions as
![]() $U_{1}$
and
$U_{1}$
and
![]() $W_{1}$
in (3.24), with
$W_{1}$
in (3.24), with
![]() $\unicode[STIX]{x1D6FD}$
replaced by
$\unicode[STIX]{x1D6FD}$
replaced by
![]() $\tilde{\unicode[STIX]{x1D6FD}}$
. Analogous expressions as (A 2) and (A 3) can also be derived for the velocities at
$\tilde{\unicode[STIX]{x1D6FD}}$
. Analogous expressions as (A 2) and (A 3) can also be derived for the velocities at
![]() $O(\bar{\unicode[STIX]{x1D701}}_{0}^{2})$
, although we have to note that at this order
$O(\bar{\unicode[STIX]{x1D701}}_{0}^{2})$
, although we have to note that at this order
![]() $\tilde{\unicode[STIX]{x1D711}}_{2}\neq 0$
(whereas,
$\tilde{\unicode[STIX]{x1D711}}_{2}\neq 0$
(whereas,
![]() $\tilde{\unicode[STIX]{x1D711}}_{1}=0$
). However
$\tilde{\unicode[STIX]{x1D711}}_{1}=0$
). However
![]() $\tilde{\unicode[STIX]{x1D711}}_{2}$
does not contribute to the slip velocity. Hence, following the above analysis, the modified Smoluchowski slip velocity can be written as:
$\tilde{\unicode[STIX]{x1D711}}_{2}$
does not contribute to the slip velocity. Hence, following the above analysis, the modified Smoluchowski slip velocity can be written as:
The expressions for
![]() $\tilde{\boldsymbol{v}}_{s}^{(k)}$
can be deduced from the expressions for
$\tilde{\boldsymbol{v}}_{s}^{(k)}$
can be deduced from the expressions for
![]() $\boldsymbol{v}_{s}^{(k)}$
in § 3 simply by directly replacing
$\boldsymbol{v}_{s}^{(k)}$
in § 3 simply by directly replacing
![]() $\unicode[STIX]{x1D6FD}$
with
$\unicode[STIX]{x1D6FD}$
with
![]() $\tilde{\unicode[STIX]{x1D6FD}}$
and
$\tilde{\unicode[STIX]{x1D6FD}}$
and
![]() $\unicode[STIX]{x1D701}$
with
$\unicode[STIX]{x1D701}$
with
![]() $\tilde{\unicode[STIX]{x1D701}}(=\bar{\unicode[STIX]{x1D701}}_{0}\unicode[STIX]{x1D701})$
. This shows that the two choices for potential are equivalent to leading order in
$\tilde{\unicode[STIX]{x1D701}}(=\bar{\unicode[STIX]{x1D701}}_{0}\unicode[STIX]{x1D701})$
. This shows that the two choices for potential are equivalent to leading order in
![]() $\unicode[STIX]{x1D6FF}$
. We reiterate that in (A 4),
$\unicode[STIX]{x1D6FF}$
. We reiterate that in (A 4),
![]() $\tilde{D}e=\tilde{u} _{c}\unicode[STIX]{x1D706}/d=\unicode[STIX]{x1D700}\unicode[STIX]{x1D713}_{T}^{2}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D702}d^{2}$
, where
$\tilde{D}e=\tilde{u} _{c}\unicode[STIX]{x1D706}/d=\unicode[STIX]{x1D700}\unicode[STIX]{x1D713}_{T}^{2}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D702}d^{2}$
, where
![]() $\unicode[STIX]{x1D713}_{T}=kT/\bar{z}e$
, while
$\unicode[STIX]{x1D713}_{T}=kT/\bar{z}e$
, while
![]() $\tilde{D}e$
can be
$\tilde{D}e$
can be
![]() $O(1)$
.
$O(1)$
.
In a similar fashion we can further propose that another good choice for
![]() $De$
would be based on the Smoluchowski formula, defined as follows:
$De$
would be based on the Smoluchowski formula, defined as follows:
![]() $\bar{D}e=U_{HS}\unicode[STIX]{x1D6FC}_{1}/\unicode[STIX]{x1D702}d=De\unicode[STIX]{x1D6FD}$
, where
$\bar{D}e=U_{HS}\unicode[STIX]{x1D6FC}_{1}/\unicode[STIX]{x1D702}d=De\unicode[STIX]{x1D6FD}$
, where
![]() $U_{HS}=\unicode[STIX]{x1D700}\unicode[STIX]{x1D701}_{0}E_{0}/\unicode[STIX]{x1D702}$
,
$U_{HS}=\unicode[STIX]{x1D700}\unicode[STIX]{x1D701}_{0}E_{0}/\unicode[STIX]{x1D702}$
,
![]() $\unicode[STIX]{x1D701}_{0}$
being the characteristic magnitude of the potential. Noting that
$\unicode[STIX]{x1D701}_{0}$
being the characteristic magnitude of the potential. Noting that
![]() $\tilde{\boldsymbol{v}}\sim O(\bar{\unicode[STIX]{x1D701}}_{0})$
and defining
$\tilde{\boldsymbol{v}}\sim O(\bar{\unicode[STIX]{x1D701}}_{0})$
and defining
![]() $\tilde{\boldsymbol{v}}=\bar{\unicode[STIX]{x1D701}}_{0}\bar{\boldsymbol{v}}$
and expanding in terms of
$\tilde{\boldsymbol{v}}=\bar{\unicode[STIX]{x1D701}}_{0}\bar{\boldsymbol{v}}$
and expanding in terms of
![]() $\bar{D}e$
(i.e.
$\bar{D}e$
(i.e.
![]() $\bar{\boldsymbol{v}}=\bar{\boldsymbol{v}}_{0}+\bar{D}e\bar{\boldsymbol{v}}_{1}+\cdots$
etc.), it can be deduced (following the same steps delineated in § 3 and herein) that the resulting slip velocity can be expressed as follows:
$\bar{\boldsymbol{v}}=\bar{\boldsymbol{v}}_{0}+\bar{D}e\bar{\boldsymbol{v}}_{1}+\cdots$
etc.), it can be deduced (following the same steps delineated in § 3 and herein) that the resulting slip velocity can be expressed as follows:
In (A 5), the components
![]() $\bar{\boldsymbol{v}}_{s}^{(k)}$
can be deduced by replacing
$\bar{\boldsymbol{v}}_{s}^{(k)}$
can be deduced by replacing
![]() $\tilde{\unicode[STIX]{x1D701}}$
directly with
$\tilde{\unicode[STIX]{x1D701}}$
directly with
![]() $\unicode[STIX]{x1D701}$
in the expressions for
$\unicode[STIX]{x1D701}$
in the expressions for
![]() $\tilde{\boldsymbol{v}}_{s}^{(k)}$
and hence they are independent of
$\tilde{\boldsymbol{v}}_{s}^{(k)}$
and hence they are independent of
![]() $\bar{\unicode[STIX]{x1D701}}_{0}$
. We reiterate that here the limit
$\bar{\unicode[STIX]{x1D701}}_{0}$
. We reiterate that here the limit
![]() $\bar{D}e\ll 1$
has been applied. This choice of Deborah number stems from the fact that since the velocity is actually
$\bar{D}e\ll 1$
has been applied. This choice of Deborah number stems from the fact that since the velocity is actually
![]() $O(\bar{\unicode[STIX]{x1D701}}_{0}\tilde{\unicode[STIX]{x1D6FD}})$
, the effective Deborah number is
$O(\bar{\unicode[STIX]{x1D701}}_{0}\tilde{\unicode[STIX]{x1D6FD}})$
, the effective Deborah number is
![]() $\bar{D}e=De\unicode[STIX]{x1D6FD}$
.
$\bar{D}e=De\unicode[STIX]{x1D6FD}$
.
Appendix B. Discussion on the numerical simulations in 5.1.1
The simulations have been executed for thin EDLs (
![]() $\unicode[STIX]{x1D6FF}\ll 1$
) and it was further assumed that the charges obey the Boltzmann distribution. A good reason for such an assumption is that the derivation of the slip velocity stems from the Boltzmann distribution itself (Ajdari Reference Ajdari1996; Yariv Reference Yariv2009). Hence a reasonably good agreement between the numerical and the asymptotic solutions would verify the accuracy of the asymptotic expansion in terms of
$\unicode[STIX]{x1D6FF}\ll 1$
) and it was further assumed that the charges obey the Boltzmann distribution. A good reason for such an assumption is that the derivation of the slip velocity stems from the Boltzmann distribution itself (Ajdari Reference Ajdari1996; Yariv Reference Yariv2009). Hence a reasonably good agreement between the numerical and the asymptotic solutions would verify the accuracy of the asymptotic expansion in terms of
![]() $De$
. In addition to this, the novel scaling patterns of the normal stress components for second-order fluids have also been compared with the numerical estimations in § 5.1.1.
$De$
. In addition to this, the novel scaling patterns of the normal stress components for second-order fluids have also been compared with the numerical estimations in § 5.1.1.
A simplified form, enough to verify the analytically estimated modified slip velocity, can be deduced by enforcing the following assumptions on the governing equations of § 2: (i) low surface potential,
![]() $\bar{\unicode[STIX]{x1D701}}_{0}\ll 1$
and (ii)
$\bar{\unicode[STIX]{x1D701}}_{0}\ll 1$
and (ii)
![]() $\unicode[STIX]{x1D6FD}=E_{0}d/\unicode[STIX]{x1D701}_{0}\sim O(1)$
and (iii) low ionic Péclet number,
$\unicode[STIX]{x1D6FD}=E_{0}d/\unicode[STIX]{x1D701}_{0}\sim O(1)$
and (iii) low ionic Péclet number,
![]() $Pe\ll 1$
. It can be easily verified that after applying the said approximations, the charge density and the concentration are given by:
$Pe\ll 1$
. It can be easily verified that after applying the said approximations, the charge density and the concentration are given by:
![]() $\unicode[STIX]{x1D70C}=-2\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D70C}=-2\unicode[STIX]{x1D711}$
and
![]() $c=2$
. As such, the potential then satisfies the Poisson–Boltzmann equation subject to Debye–Huckel linearization (Ajdari Reference Ajdari1996) and is given by:
$c=2$
. As such, the potential then satisfies the Poisson–Boltzmann equation subject to Debye–Huckel linearization (Ajdari Reference Ajdari1996) and is given by:
![]() $\unicode[STIX]{x1D6FF}^{-2}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}$
, subject to the boundary conditions,
$\unicode[STIX]{x1D6FF}^{-2}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}$
, subject to the boundary conditions,
![]() $\unicode[STIX]{x1D711}(x,y=0)=n+m\cos (x)$
and
$\unicode[STIX]{x1D711}(x,y=0)=n+m\cos (x)$
and
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}y\rightarrow 0$
as
$\unicode[STIX]{x2202}\unicode[STIX]{x1D711}/\unicode[STIX]{x2202}y\rightarrow 0$
as
![]() $y\rightarrow 0$
. It can be easily shown that it has the following solution:
$y\rightarrow 0$
. It can be easily shown that it has the following solution:
The momentum equation (2.4) can thus be simplified to (Ajdari Reference Ajdari1996; Yariv Reference Yariv2004):
In (B 2), the potential is given by (B 1) and
![]() $\unicode[STIX]{x1D64E}$
represents the excess polymeric stresses, which have been mentioned in § 2. Note that (B 2) has previously been used by a number of researchers (Ajdari Reference Ajdari1996; Bahga et al.
Reference Bahga, Vinogradova and Bazant2010; Ghosh & Chakraborty Reference Ghosh and Chakraborty2015) to represent a simplified version of the EOFs for various kinds of fluids. The velocities satisfy no-slip boundary condition at the wall and have vanishing gradients at the upper boundary representing the far-field conditions. This equation is solved in a rectangular domain as shown in figure 3. The details of the grid resolution have been mentioned in the caption of that figure, while the equations have also been displayed therein. In an effort to deduce the slip velocity, we have solved the governing equations for
$\unicode[STIX]{x1D64E}$
represents the excess polymeric stresses, which have been mentioned in § 2. Note that (B 2) has previously been used by a number of researchers (Ajdari Reference Ajdari1996; Bahga et al.
Reference Bahga, Vinogradova and Bazant2010; Ghosh & Chakraborty Reference Ghosh and Chakraborty2015) to represent a simplified version of the EOFs for various kinds of fluids. The velocities satisfy no-slip boundary condition at the wall and have vanishing gradients at the upper boundary representing the far-field conditions. This equation is solved in a rectangular domain as shown in figure 3. The details of the grid resolution have been mentioned in the caption of that figure, while the equations have also been displayed therein. In an effort to deduce the slip velocity, we have solved the governing equations for
![]() $\unicode[STIX]{x1D6FF}=0.01$
, which signifies a thin EDL. The convergence criteria were set as
$\unicode[STIX]{x1D6FF}=0.01$
, which signifies a thin EDL. The convergence criteria were set as
![]() $10^{-7}$
for the scaled residuals of all the variables.
$10^{-7}$
for the scaled residuals of all the variables.
One of the major challenges in simulating the EOF of a second-order fluid is that the normal stresses scale as
![]() $O(\unicode[STIX]{x1D6FF}^{-2})$
, which are asymptotically large. However, the present analysis valid in the limit
$O(\unicode[STIX]{x1D6FF}^{-2})$
, which are asymptotically large. However, the present analysis valid in the limit
![]() $\unicode[STIX]{x1D6FF}\ll De<O(1)$
. Hence, even if we choose
$\unicode[STIX]{x1D6FF}\ll De<O(1)$
. Hence, even if we choose
![]() $\unicode[STIX]{x1D6FF}=0.01$
and keep all other variables at
$\unicode[STIX]{x1D6FF}=0.01$
and keep all other variables at
![]() $O(1)$
or less, the normal stresses become
$O(1)$
or less, the normal stresses become
![]() $O(10^{4})$
, which can lead to divergent results. For smaller EDL thickness, the stresses blow up even faster. We noted that, if the parameters
$O(10^{4})$
, which can lead to divergent results. For smaller EDL thickness, the stresses blow up even faster. We noted that, if the parameters
![]() $n$
,
$n$
,
![]() $m$
and
$m$
and
![]() $\unicode[STIX]{x1D6FD}$
all are chosen to be less than unity, strong convergence can be achieved, leading to accurate results. On a related note, Bird et al. (Reference Bird, Armstrong and Hassager1987), in their seminal book on polymeric liquids, have asserted that asymptotic expansion in terms of
$\unicode[STIX]{x1D6FD}$
all are chosen to be less than unity, strong convergence can be achieved, leading to accurate results. On a related note, Bird et al. (Reference Bird, Armstrong and Hassager1987), in their seminal book on polymeric liquids, have asserted that asymptotic expansion in terms of
![]() $De$
remains a tried and tested method for second-order fluids (see chap. 6 in their book). For simpler flows without body forces, there are several available theorems (like the Tanner–Pipkin theorem, the theorem of Giesekus, etc.), see Bird et al. (Reference Bird, Armstrong and Hassager1987), which furnish exact solutions for the velocity and pressure fields of second-order fluids, once the equivalent Newtonian flow field is known.
$De$
remains a tried and tested method for second-order fluids (see chap. 6 in their book). For simpler flows without body forces, there are several available theorems (like the Tanner–Pipkin theorem, the theorem of Giesekus, etc.), see Bird et al. (Reference Bird, Armstrong and Hassager1987), which furnish exact solutions for the velocity and pressure fields of second-order fluids, once the equivalent Newtonian flow field is known.