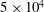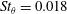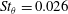1 Introduction
There has been a considerable number of studies on the effects of the initial conditions on free shear layers and jets for more than five decades. In particular, great attention has been paid to the state of the nozzle-exit boundary layer, which may vary from one experiment to another depending on the facility characteristics and on the nozzle diameter and geometry. For instance, the jets are often initially laminar in small-scale experiments, whereas they are initially turbulent in full-scale experiments. In order to make meaningful comparisons, it can therefore be necessary to trip the boundary layer in the nozzle in order to generate turbulent exit conditions, as was the case in the pioneering work of Bradshaw (Reference Bradshaw1966) and Crow & Champagne (Reference Crow and Champagne1971).
The differences obtained between initially laminar and initially turbulent shear layers and jets have been described in a long list of papers. In the laminar case, instability waves are amplified just downstream of the nozzle at a preferred momentum-thickness-based Strouhal number equal to
$St_{\unicode[STIX]{x1D703}}=0.017$
according to the linear stability analyses conducted from hyperbolic–tangent velocity profiles (Michalke Reference Michalke1984), and varying within the range
$0.009\leqslant St_{\unicode[STIX]{x1D703}}\leqslant 0.018$
in experiments (Sato Reference Sato1971; Zaman & Hussain Reference Zaman and Hussain1981; Gutmark & Ho Reference Gutmark and Ho1983). The shear layers subsequently roll up to form essentially two-dimensional vortical structures, whose interactions result in three-dimensional turbulence. The levels of velocity fluctuations rapidly increase and reach a sharp peak during that laminar–turbulent transition. In the initially turbulent case, on the contrary, they grow monotonically and very slowly from the nozzle exit (Bradshaw Reference Bradshaw1966; Hill, Jenkins & Gilbert Reference Hill, Jenkins and Gilbert1976; Hussain & Zedan Reference Hussain and Zedan1978b
; Browand & Latigo Reference Browand and Latigo1979; Husain & Hussain Reference Husain and Hussain1979). Moreover, the jet flow development is faster in the laminar case than in the turbulent case, leading to a shorter potential core and a higher rate of centreline velocity decay (Hill et al.
Reference Hill, Jenkins and Gilbert1976; Raman, Zaman & Rice Reference Raman, Zaman and Rice1989; Russ & Strykowski Reference Russ and Strykowski1993; Raman, Rice & Reshotko Reference Raman, Rice and Reshotko1994; Xu & Antonia Reference Xu and Antonia2002). The impact of the nozzle-exit boundary-layer state is also significant on jet noise sources, as reported in the review papers by Crighton (Reference Crighton1981) and Lilley (Reference Lilley and Hubbard1994). It has notably been established in Maestrello & McDaid (Reference Maestrello and McDaid1971), Zaman (Reference Zaman1985a
,Reference Zaman
b
) and Bridges & Hussain (Reference Bridges and Hussain1987) that initially laminar jets emit more noise than initially turbulent jets, and that the additional acoustic components can be attributed to the pairings of the two-dimensional vortices induced by the laminar–turbulent transition in the shear layers. After the transition, coherent, well-organized turbulent structures appear to persist, as revealed by the experiments of Brown & Roshko (Reference Brown and Roshko1974) and Wygnanski et al. (Reference Wygnanski, Oster, Fiedler and Dziomba1979). The presence of coherent structures in initially turbulent mixing layers is less obvious according to Chandrsuda et al. (Reference Chandrsuda, Mehta, Weir and Bradshaw1978), but is supported by the measurements in such flows of a peak Strouhal number of
$St_{\unicode[STIX]{x1D703}}=0.022{-}0.028$
by Drubka & Nagib (Reference Drubka and Nagib1981), Hussain & Zaman (Reference Hussain and Zaman1985) and Morris & Foss (Reference Morris and Foss2003). The reasons for these values of Strouhal number well above those obtained for initially laminar flow conditions remain however unexplained, as was noted by Ho & Huerre (Reference Ho and Huerre1984).
The issue of jet initial conditions has recently received renewed attention in the aeroacoustics community since Viswanathan (Reference Viswanathan2004) stated that the jet far-field measurements of Tanna (Reference Tanna1977) might be contaminated by spurious facility noise. In reply to this, Harper-Bourne (Reference Harper-Bourne2010) suggested that the extra components emerging at high frequencies in Tanna’s (Reference Tanna1977) sound spectra are due to laminar flow conditions at the nozzle exit. This seems to be confirmed by the experimental results obtained by Viswanathan & Clark (Reference Viswanathan and Clark2004), Zaman (Reference Zaman2012) and Karon & Ahuja (Reference Karon and Ahuja2013) for high-subsonic jets exhausting from two nozzles of different internal profiles, namely the ASME and the conical nozzles. Indeed, more noise is measured with the ASME nozzle than with the conical nozzle, that is, for highly disturbed, nominally laminar boundary layers than for turbulent boundary layers; refer to the nozzle-exit conditions of table 1. For instance, for the jet at a Mach number of 0.896 considered by Zaman (Reference Zaman2012), the sound levels with the ASME nozzle are stronger by 2–3 dB for diameter-based Strouhal numbers
$St_{D}\geqslant 0.3$
at all radiation angles, and approximately by 1 dB for lower frequencies at angles between
$60^{\circ }$
and
$90^{\circ }$
with respect to the flow direction. On the basis of flow visualizations, Zaman (Reference Zaman2017) related this to the perseverance of organized coherent structures in the shear layers of the jets issuing from the ASME nozzle. Similarly, in the experiment of Fontaine et al. (Reference Fontaine, Elliott, Austin and Freund2015) who explored the shear-layer flow properties and the noise of three initially highly disturbed jets with different nozzle-exit conditions, given in table 1, the jet from the small nozzle with a partially developed boundary layer generates 3 dB more intense sound than the two jets from the medium and large nozzles with fully turbulent boundary layers. In addition, the peak turbulence intensities a few diameters downstream of the nozzle exit are stronger for the first jet.
Table 1. Flow conditions at the nozzle exit for round jets (Zaman Reference Zaman2012; Karon & Ahuja Reference Karon and Ahuja2013; Fontaine et al. Reference Fontaine, Elliott, Austin and Freund2015; Brès et al. Reference Brès, Jordan, Jaunet, Le Rallic, Cavalieri, Towne, Lele, Colonius and Schmidt2018) and at the separation point created using a sharp edge for a turbulent boundary layer (Morris & Foss Reference Morris and Foss2003).
The relative importance of each of the nozzle-exit parameters in the above results is difficult to distinguish, because these parameters usually vary simultaneously, as illustrated in table 1. When the nozzle-exit flow conditions become turbulent, with or without boundary-layer tripping, the shape factor of the boundary-layer profile decreases. This factor, defined as
$H=\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
where
$\unicode[STIX]{x1D6FF}^{\ast }$
and
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
are the boundary-layer displacement and momentum thickness, takes values of around 2.5 for laminar profiles and 1.4 for turbulent profiles. At the same time, the boundary-layer thickness increases, and the nozzle-exit peak turbulence intensities
$u_{e}^{\prime }/u_{j}$
, where
$u_{e}^{\prime }$
and
$u_{j}$
are the maximum root mean square (r.m.s.) value of the velocity fluctuations and the jet velocity, most often grow. In some experiments, similar turbulence levels are obtained, as, for instance, in the work of Morris & Zaman (Reference Morris and Zaman2009) where values of
$u_{e}^{\prime }/u_{j}$
equal to
$6.7\,\%$
and
$7.5\,\%$
are reported for untripped and tripped jets at a diameter-based Reynolds number
$Re_{D}=3\times 10^{5}$
. It even happens that the velocity fluctuations are larger in laminar than in turbulent nozzle-exit boundary layers. Examples of this counter-intuitive tendency have been given by Raman et al. (Reference Raman, Zaman and Rice1989, Reference Raman, Rice and Reshotko1994) for tripped/untripped jets and by Zaman (Reference Zaman2012) who measured values of
$u_{e}^{\prime }/u_{j}$
around
$11\,\%$
using the ASME nozzle but around
$7\,\%$
using the conical nozzle for jets at
$2\times 10^{5}\leqslant Re_{D}\leqslant 6\times 10^{5}$
, see the values for
$Re_{D}=2.2\times 10^{5}$
in table 1. In that case, the effects of the velocity profile and those of the turbulence levels are likely to counteract each other, which may result in some confusion.
Therefore, there is clearly a need to study the influence of the nozzle-exit boundary-layer profile with all other exit parameters held constant. For this, it seems worthwhile to use unsteady compressible simulations, which have made spectacular progress over the last three decades, and now allow us to conduct investigations under controlled conditions. Large-eddy simulations (LES) have for instance been run by the first author over the last decade (Bogey & Bailly Reference Bogey and Bailly2010; Bogey, Marsden & Bailly Reference Bogey, Marsden and Bailly2011b
,Reference Bogey, Marsden and Bailly
c
, Reference Bogey, Marsden and Bailly2012a
,Reference Bogey, Marsden and Bailly
b
; Bogey & Marsden Reference Bogey and Marsden2013; Bogey Reference Bogey2018) to investigate the impact of nozzle-exit conditions on initially laminar and highly disturbed subsonic round jets. Due to limitations in computing resources, the jets had moderate Reynolds numbers
$Re_{D}$
of between
$2.5\times 10^{4}$
and
$2\times 10^{5}$
, and all exhibited laminar mean velocity profiles at the nozzle exit, in order to ensure numerical accuracy. Subsonic jets with tripped boundary layers have also been recently calculated by an increasing number of other researchers, including Lorteau, Cléro & Vuillot (Reference Lorteau, Cléro and Vuillot2015) and Zhu et al. (Reference Zhu, Pérez Arroyo, Fosso Pouangué, Sanjosé and Moreau2018), among others. Specifically concerning initially turbulent jets, the first attempts of computation have been made by Bogey, Barré & Bailly (Reference Bogey, Barré and Bailly2008) and Uzun & Hussaini (Reference Uzun and Hussaini2007). However, the grid was too coarse in the former case, while its spatial extent was limited to 4.5 diameters downstream of the nozzle in the latter. Later, Sandberg, Sandham & Suponitsky (Reference Sandberg, Sandham and Suponitsky2012) carried out a simulation of a fully turbulent pipe flow at
$Re_{D}=7500$
exiting into a coflow, and Bühler, Kleiser & Bogey (Reference Bühler, Kleiser and Bogey2014) successfully computed a jet at
$Re_{D}=18\,100$
with turbulent conditions at the exit of a pipe nozzle. None of these studies however addresses the question of the mean velocity profile. More recently, two jets at
$Re_{D}=2\times 10^{5}$
with nozzle-exit conditions roughly matching those found in experiments using the ASME and the conical nozzles have been performed by Bogey & Marsden (Reference Bogey and Marsden2016). Unfortunately, the results for the two jets are very similar, suggesting that the jet initial conditions in the simulations do not adequately reflect those in the experiments. Finally, Brès et al. (Reference Brès, Jordan, Jaunet, Le Rallic, Cavalieri, Towne, Lele, Colonius and Schmidt2018) calculated two isothermal subsonic jets at
$Re_{D}=10^{6}$
with initially laminar and turbulent nozzle-exit boundary layers, as indicated in table 1. The initially laminar jet radiates greater high-frequency noise than the initially turbulent jet, which was attributed to the fact that the instability waves in the near-nozzle region grow at different rates in the two jets.
In the present work, the influence of the nozzle-exit boundary-layer profile on high-subsonic jets is investigated by combining well-resolved large-eddy simulations and linear stability analyses for three isothermal round jets at a Mach number
$M=u_{j}/c_{a}=0.9$
and a Reynolds number
$Re_{D}=u_{j}D/\unicode[STIX]{x1D708}=5\times 10^{4}$
, where
$c_{a}$
,
$D$
and
$\unicode[STIX]{x1D708}$
are the speed of sound in the ambient medium, the jet diameter and the kinematic molecular viscosity. In order to consider the effects of the mean velocity profile alone, momentum boundary-layer thicknesses of
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\simeq 0.028r_{0}$
and peak turbulence intensities of
$u_{e}^{\prime }/u_{j}\simeq 6\,\%$
are prescribed at the exit of a pipe nozzle for all jets. The boundary-layer profiles however vary, and are laminar in the first jet and transitional (partially developed) in the two others, with shape factors
$H$
ranging between 1.71 and 2.29. The first objective will be to determine whether the flow and sound fields of the jets show significant differences, and whether these differences correspond to those usually encountered between initially laminar and initially turbulent jets, namely a faster flow development, stronger velocity fluctuations in the mixing layers and more noise in the acoustic field in the laminar case. In particular, comparisons will be made with the trends observed in the experiments of Zaman (Reference Zaman2012, Reference Zaman2017) using the ASME and the conical nozzles and of Fontaine et al. (Reference Fontaine, Elliott, Austin and Freund2015), and in the simulations of Brès et al. (Reference Brès, Jordan, Jaunet, Le Rallic, Cavalieri, Towne, Lele, Colonius and Schmidt2018). They will be mostly qualitative due to the disparities in upstream flow conditions. The second objective will be to propose an explanation for the higher noise levels expected for a laminar boundary-layer profile. For that purpose, the development of the instability waves very near the nozzle exit and during the transition from a boundary layer to a shear layer will be detailed. It will also be discussed based on the linear stability analyses conducted from the mean-flow fields, as in Fontaine et al. (Reference Fontaine, Elliott, Austin and Freund2015) and Brès et al. (Reference Brès, Jordan, Jaunet, Le Rallic, Cavalieri, Towne, Lele, Colonius and Schmidt2018). However, while the latter authors mainly focused on the amplification rates of the instability waves, the present study will specially examine the sensitivity of the unstable frequencies to the nozzle-exit velocity profile, previously noted by Drubka & Nagib (Reference Drubka and Nagib1981), Hussain & Zaman (Reference Hussain and Zaman1985) and Morris & Foss (Reference Morris and Foss2003) for shear layers, and its possible role in the discrepancies observed in the flow and sound fields of the jets.
The paper is organized as follows. The parameters of the three jets, of the large-eddy simulations, of the extrapolations of the LES acoustic near fields to the far field and of the linear stability analyses are documented in § 2. The nozzle-exit flow properties, the mixing-layer and jet flow fields and the jet acoustic fields are described in § 3. Concluding remarks are given in § 4. Finally, comparisons of the non-laminar nozzle-inlet velocity profiles imposed for two of the three jets with boundary-layer measurements are shown in appendix A, and results from a grid-refinement study are provided in appendix B.
2 Parameters
2.1 Jet definition
Three isothermal round jets at a Mach number
$M=0.9$
and a Reynolds number
$Re_{D}=5\times 10^{4}$
, referred to as jetBL, jetT1 and jetT2 in what follows, have been simulated. They originate at
$z=0$
from a pipe nozzle of radius
$r_{0}$
and length
$2r_{0}$
, whose lip is
$0.053r_{0}$
thick, into a medium at rest of temperature
$T_{a}=293~\text{K}$
and pressure
$p_{a}=10^{5}~\text{Pa}$
. At the pipe inlet, at
$z=-2r_{0}$
, different boundary-layer profiles, whose main characteristics are collected in table 2, are imposed for the axial velocity. Radial and azimuthal velocities are set to zero, pressure is equal to
$p_{a}$
and temperature is determined by a Crocco–Busemann relation.
Table 2. Shape factor
$H$
, momentum thickness
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
and 99 % velocity thickness
$\unicode[STIX]{x1D6FF}_{99}$
of the boundary-layer profile at the pipe-nozzle inlet and strength of the trip-like excitation
$\unicode[STIX]{x1D6FC}_{trip}$
.
The inlet axial velocity profiles are represented in figure 1(a). In jetBL, the profile is a Blasius laminar boundary-layer profile with a shape factor
$H=\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}=2.55$
, where the boundary-layer displacement and momentum thickness are respectively defined as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}^{\ast }=\int _{0}^{\infty }\left(1-\frac{\langle u_{z}\rangle }{\langle u_{z}\rangle (r=0)}\right)\,\text{d}r, & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}=\int _{0}^{\infty }\frac{\langle u_{z}\rangle }{\langle u_{z}\rangle (r=0)}\left(1-\frac{\langle u_{z}\rangle }{\langle u_{z}\rangle (r=0)}\right)\,\text{d}r. & & \displaystyle\end{eqnarray}$$
The Blasius profile is given by the Pohlhausen’s fourth-order polynomial approximation
$$\begin{eqnarray}\frac{u_{inlet}(r)}{u_{j}}=\left\{\begin{array}{@{}l@{}}\displaystyle \frac{(r_{0}-r)}{\unicode[STIX]{x1D6FF}_{BL}}\left[2-2\left(\frac{(r_{0}-r)}{\unicode[STIX]{x1D6FF}_{BL}}\right)^{2}+\left(\frac{r_{0}-r}{\unicode[STIX]{x1D6FF}_{BL}}\right)^{3}\right]\quad \text{if }r\geqslant r_{0}-\unicode[STIX]{x1D6FF}_{BL}\\ \displaystyle 1\quad \text{otherwise},\end{array}\right.\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FF}_{BL}$
is the boundary-layer thickness.
In jetT1 and jetT2, the inlet profiles are transitional boundary-layer profiles with
$H=1.88$
and
$1.52$
, respectively. They are derived from the turbulent profile proposed by De Chant (Reference De Chant2005), and defined as
$$\begin{eqnarray}\frac{u_{inlet}(r)}{u_{j}}=\left\{\begin{array}{@{}l@{}}\displaystyle \left(\sin \left[\frac{\unicode[STIX]{x03C0}}{2}\left(\frac{r_{0}-r}{\unicode[STIX]{x1D6FF}_{T_{i}}}\right)^{\unicode[STIX]{x1D6FD}_{i}}\right]\right)^{\unicode[STIX]{x1D6FE}_{i}}\quad \text{if }r\geqslant r_{0}-\unicode[STIX]{x1D6FF}_{T_{i}}\\ \displaystyle 1\quad \text{otherwise},\end{array}\right.\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FF}_{T_{i}}$
is the boundary-layer thickness, and the values of the exponents
$\unicode[STIX]{x1D6FD}_{i}$
and
$\unicode[STIX]{x1D6FE}_{i}$
are equal to
$\unicode[STIX]{x1D6FD}_{1}=0.464$
and
$\unicode[STIX]{x1D6FE}_{1}=1.32$
, and to
$\unicode[STIX]{x1D6FD}_{2}=0.423$
and
$\unicode[STIX]{x1D6FE}_{2}=0.82$
. Considering the strong similarities between the near-wall mean-flow statistics obtained for turbulent pipe and boundary-layer flows (Monty et al.
Reference Monty, Hutchins, Ng, Marusic and Chong2009), they have been designed to fit the experimental data provided by Schubauer & Klebanoff (Reference Schubauer and Klebanoff1955) for a flat-plate boundary layer in the region of changeover from laminar to fully turbulent conditions, as shown in appendix A.
Figure 1. Representation (a) of the axial velocity profile
$u_{inlet}$
imposed at the pipe-nozzle inlet and (b) of the peak r.m.s. values of axial velocity fluctuations
$u_{z}^{\prime }$
in the nozzle:
In the three jets, the inlet boundary-layer thicknesses are arbitrarily set to
$\unicode[STIX]{x1D6FF}_{BL}=0.25r_{0}$
in jetBL,
$\unicode[STIX]{x1D6FF}_{T_{1}}=1.043\unicode[STIX]{x1D6FF}_{BL}=0.26r_{0}$
in JetT1 and
$\unicode[STIX]{x1D6FF}_{T_{2}}=1.328\unicode[STIX]{x1D6FF}_{BL}=0.33r_{0}$
in JetT2, in order to obtain a momentum thickness of
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}=0.0288r_{0}$
in all cases. The associated 99 % velocity thicknesses
$\unicode[STIX]{x1D6FF}_{99}$
thus vary from
$0.202r_{0}$
in jetBL up to
$0.254r_{0}$
in jetT2. With respect to the experiments of Zaman (Reference Zaman2012) and Karon & Ahuja (Reference Karon and Ahuja2013), see in table 1, the boundary layers in the present jets are thicker to guarantee a high numerical accuracy, as will be discussed in § 2.3 and in appendix B. Given the jet Reynolds number of
$Re_{D}=5\times 10^{4}$
, chosen to perform very well resolved LES, this also leads to a momentum-thickness-based Reynolds number of
$Re_{\unicode[STIX]{x1D703}}=u_{j}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D708}=720$
, which is comparable to the values measured in the experiments. This is of importance because
$Re_{\unicode[STIX]{x1D703}}$
is a key parameter in developing shear layers (Hussain & Zedan Reference Hussain and Zedan1978b
; Bogey & Marsden Reference Bogey and Marsden2013).
In order to generate disturbed upstream conditions for the jets, which otherwise would initially contain negligible velocity fluctuations, the boundary layers are ‘tripped’ in the pipe using an arbitrary forcing whose parameters are determined by trial and error (Klebanoff & Diehl Reference Klebanoff and Diehl1952; Coles Reference Coles1962; Erm & Joubert Reference Erm and Joubert1991; Castillo & Johansson Reference Castillo and Johansson2012; Hutchings Reference Hutchings2012; Schlatter & Örlü Reference Schlatter and Örlü2012). In simulations, forcing devices of different kinds have been proposed. A small step can for instance be mounted on the wall inside the nozzle. Random fluctuations, synthetic turbulence or instability modes can alternatively be imposed on the flow profiles. In the present jets, the forcing procedure detailed in appendix A of Bogey et al. (Reference Bogey, Marsden and Bailly2011b
) is implemented. It consists in adding random low-level vortical disturbances uncorrelated in the azimuthal direction in the boundary layers. It has been previously used for both laminar (Bogey et al.
Reference Bogey, Marsden and Bailly2011b
, Reference Bogey, Marsden and Bailly2012a
,Reference Bogey, Marsden and Bailly
b
; Bogey & Marsden Reference Bogey and Marsden2013) and non-laminar (Bogey & Marsden Reference Bogey and Marsden2016) boundary-layer profiles. The forcing is applied at the axial position
$z=-0.95r_{0}$
and at the radial position of
$r=r_{0}-\unicode[STIX]{x1D6FF}_{BL}/2=0.875r_{0}$
in all cases. However, the forcing magnitudes are not the same, and have been adjusted after preliminary tests to obtain peak nozzle-exit turbulence intensities
$u_{e}^{\prime }/u_{j}$
of 6 % for all jets. This level is close to those measured by Zaman (Reference Zaman2012) just downstream of the conical nozzle for initially turbulent jets, refer to table 1 for instance. The values of the coefficient
$\unicode[STIX]{x1D6FC}_{trip}$
setting the maximum value of the added velocity fluctuations to
$\unicode[STIX]{x1D6FC}_{trip}u_{j}$
, hence specifying the forcing strength, are given in table 2. They are equal to 0.046, 0.0675 and 0.083 in jetBL, jetT1 and jetT2, respectively. Consequently, the lower the inlet boundary-layer shape factor, the higher the amplitude of the excitation necessary to reach
$u_{e}^{\prime }/u_{j}=6\,\%$
, This is illustrated in figure 1(b) showing the variations of the maximum r.m.s. value of axial velocity fluctuations in the pipe.
As pointed out above, there exit some discrepancies between the nozzle-exit conditions of the present jets and of the experiments of table 1 in terms of
$Re_{D}$
and ratio
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}/r_{0}$
. The higher value of
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}/r_{0}$
in the simulations, in particular, will result in lower frequencies in the shear layers just downstream of the nozzle. Thanks to the similarities in
$Re_{\unicode[STIX]{x1D703}}$
and
$u_{e}^{\prime }/u_{j}$
, the physical mechanisms at play in this zone can yet be expected to be of the same nature as those in the experiments using the ASME and conical nozzles. Performing qualitative comparisons with the trends revealed in these experiments therefore appears relevant. Quantitative comparisons with measurements for reference jets of the literature will also be made throughout the paper. They are given mainly for illustration purposes, because these jets have Reynolds numbers
$Re_{D}\simeq 10^{6}$
and certainly very thin nozzle-exit boundary layers. In addition, they are most likely initially fully turbulent, and such a case is not considered in this study. It is however hoped that on the basis of the differences obtained between jetT1 and jetT2, results for a more turbulent boundary-layer profile could be extrapolated. Finally, the experimental jets all exhaust for a convergent nozzle, leading to a pressure gradient at the nozzle exit whose effects are unclear (Zaman Reference Zaman2012), which is not taken into account in the simulations.
2.2 LES numerical methods
For the LES, the numerical framework is identical to that used in previous jet simulations (Bogey & Bailly Reference Bogey and Bailly2010; Bogey et al.
Reference Bogey, Marsden and Bailly2011b
, Reference Bogey, Marsden and Bailly2012a
,Reference Bogey, Marsden and Bailly
b
; Bogey & Marsden Reference Bogey and Marsden2013; Bogey Reference Bogey2018). They are carried out using an in-house solver of the three-dimensional filtered compressible Navier–Stokes equations in cylindrical coordinates
$(r,\unicode[STIX]{x1D703},z)$
based on low-dissipation and low-dispersion explicit schemes. The axis singularity is taken into account by the method of Mohseni & Colonius (Reference Mohseni and Colonius2000). In order to alleviate the time-step restriction near the cylindrical origin, the derivatives in the azimuthal direction around the axis are calculated at coarser resolutions than permitted by the grid (Bogey, de Cacqueray & Bailly Reference Bogey, de Cacqueray and Bailly2011a
). For the points closest to the jet axis, they are evaluated using
$16$
points, yielding an effective resolution of
$2\unicode[STIX]{x03C0}/16$
. Fourth-order eleven-point centred finite differences are used for spatial discretization, and a second-order six-stage Runge–Kutta algorithm is implemented for time integration (Bogey & Bailly Reference Bogey and Bailly2004). A sixth-order eleven-point centred filter (Bogey, de Cacqueray & Bailly Reference Bogey, de Cacqueray and Bailly2009b
) is applied explicitly to the flow variables every time step. Non-centred finite differences and filters are also used near the pipe walls and the grid boundaries (Berland et al.
Reference Berland, Bogey, Marsden and Bailly2007; Bogey & Bailly Reference Bogey and Bailly2010). At the boundaries, the radiation conditions of Tam & Dong (Reference Tam and Dong1996) are applied, with the addition at the outflow of a sponge zone combining grid stretching and Laplacian filtering (Bogey & Bailly Reference Bogey and Bailly2002). At the inflow and radial boundaries, density and pressure are also brought back close to
$p_{a}$
and
$\unicode[STIX]{x1D70C}_{a}$
every
$0.055r_{0}/c_{a}$
at rate of
$0.5\,\%$
, in order to keep the mean values of density and pressure around their ambient values without generating significant acoustic reflections. No co-flow is imposed.
Table 3. Numbers of grid points
$N_{r}$
,
$N_{\unicode[STIX]{x1D703}}$
and
$N_{z}$
, mesh spacings
$\unicode[STIX]{x0394}r$
at
$r=r_{0}$
,
$r_{0}\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x0394}z$
at
$z=0$
, extents of the physical domain
$L_{r}$
and
$L_{z}$
and simulation time
$T$
after the transient period.
In the present large-eddy simulations, the explicit filtering is employed to remove grid-to-grid oscillations, but also as a subgrid-scale high-order dissipation model in order to relax turbulent energy from scales at wavenumbers close to the grid cutoff wavenumber while leaving larger scales mostly unaffected. The performance of this LES approach has been assessed in past studies for subsonic jets, Taylor–Green vortices and turbulent channel flows (Bogey & Bailly Reference Bogey and Bailly2006, Reference Bogey and Bailly2009; Bogey et al. Reference Bogey, Marsden and Bailly2011b ; Fauconnier, Bogey & Dick Reference Fauconnier, Bogey and Dick2013; Kremer & Bogey Reference Kremer and Bogey2015), from comparisons with the solutions of direct numerical simulations and from the examination of the magnitude and the properties of the filtering dissipation in the wavenumber space.
2.3 Simulation parameters
The grid used in the present jet simulations is detailed and referred to as gridz40B in a recent grid-sensitivity study of the flow and acoustic fields of an initially highly disturbed isothermal round jet at
$M=0.9$
and
$Re_{D}=10^{5}$
(Bogey Reference Bogey2018). As indicated in table 3, it contains
$N_{r}\times N_{\unicode[STIX]{x1D703}}\times N_{z}=504\times 1024\times 2048=10^{9}$
points. It extends radially out to
$L_{r}=15r_{0}$
and axially, excluding the 100-point outflow sponge zone, down to
$L_{z}=40r_{0}$
. There are 169 points along the pipe nozzle between
$z=-2r_{0}$
and
$0$
, 96 points between
$r=0$
and
$r_{0}$
and 41 points between
$r=r_{0}-\unicode[STIX]{x1D6FF}_{BL}=0.75r_{0}$
and
$r_{0}$
. In the radial direction, the mesh spacing
$\unicode[STIX]{x0394}r$
is minimum and equal to
$0.0036r_{0}$
at
$r=r_{0}$
, and is equal to
$0.0141r_{0}$
at
$r=0$
,
$0.0148r_{0}$
at
$r=2r_{0}$
,
$0.0335r_{0}$
at
$r=4r_{0}$
and
$0.075r_{0}$
between
$r=6.25r_{0}$
and
$L_{r}$
. The latter mesh spacing leads to a diameter-based Strouhal number of
$St_{D}=f\,D/u_{j}=5.9$
for an acoustic wave discretized by five points per wavelength, where
$f$
is the frequency. In the axial direction, the mesh spacing
$\unicode[STIX]{x0394}z$
is minimum and equal to
$0.0072r_{0}$
between
$z=-r_{0}$
and
$0$
, and increases at a stretching rate of 0.103 % farther downstream to reach
$0.0127r_{0}$
at
$z=5r_{0}$
,
$0.0178r_{0}$
at
$z=10r_{0}$
,
$0.0230r_{0}$
at
$z=15r_{0}$
and
$0.0488r_{0}$
at
$z=L_{z}$
.
The quality of gridz40B has been shown in Bogey (Reference Bogey2018) for a jet at
$Re_{D}=10^{5}$
characterized, at the nozzle exit, by a laminar Blasius boundary layer of thickness
$\unicode[STIX]{x1D6FF}_{BL}=0.15r_{0}$
and a peak turbulence intensity of
$u_{e}^{\prime }/u_{j}=9\,\%$
. Therefore, it is highly likely that in the present work, the grid resolution is appropriate for jetBL at
$Re_{D}=5\times 10^{4}$
with
$\unicode[STIX]{x1D6FF}_{BL}=0.25r_{0}$
and
$u_{e}^{\prime }/u_{j}=6\,\%$
. For jetT1 and jetT2 with non-laminar boundary-layer profiles, the suitability of the grid is less obvious. In order to address this issue, the near-wall mesh spacings in the pipe expressed in wall units based on the wall friction velocity at the nozzle exit are provided in table 4. They are such that
$\unicode[STIX]{x0394}r^{+}\leqslant 2.7$
,
$(r_{0}\unicode[STIX]{x0394}\unicode[STIX]{x1D703})^{+}\leqslant 4.6$
and
$\unicode[STIX]{x0394}z^{+}\leqslant 5.4$
. The azimuthal and axial mesh spacings meet the requirements needed to compute turbulent wall-bounded flows accurately using direct numerical simulation (Kim, Moin, & Moser Reference Kim, Moin and Moser1987; Spalart Reference Spalart1988) or LES involving relaxation filtering (Gloerfelt & Berland Reference Gloerfelt and Berland2012; Kremer & Bogey Reference Kremer and Bogey2015). On the contrary, the wall-normal spacing is two or three times larger than the recommended value of
$\unicode[STIX]{x0394}r^{+}=1$
. For the simulation of an initially fully turbulent jet, refining the wall-normal region by a factor of at least three would therefore be necessary, which would increase by the same amount the computational cost due to the explicit time-integration scheme. For the initially transitional jets considered in this paper, the sensitivity to the wall-normal spacing has however been assessed in a preliminary study using two shorter grids extending axially, excluding the outflow sponge zones, only down to
$z=4r_{0}$
in order to save computational time. The coarsest of the two grids coincides with gridz40B in the boundary-layer region. The finest one is also identical to the latter in that region in the directions
$\unicode[STIX]{x1D703}$
and
$z$
, but differs in the radial direction with
$\unicode[STIX]{x0394}r/r_{0}=0.18\,\%$
, instead of
$\unicode[STIX]{x0394}r/r_{0}=0.36\,\%$
, at
$r=r_{0}$
. The tripping procedure is exactly the same in all cases, but the time step is twice as small in the LES using the finest grid because of the numerical stability condition, leading to an application of the relaxation filtering that is twice as frequent. The mean and fluctuating velocity profiles obtained at the nozzle exit using the two grids, represented in appendix B for jetT2, are superimposed. This demonstrates that the LES solutions in the pipe do not depend on the radial mesh spacing at
$r=r_{0}$
or on the relaxation filtering.
Table 4. Near-wall mesh spacings
$\unicode[STIX]{x0394}r$
,
$r_{0}\unicode[STIX]{x0394}\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x0394}z$
given in wall units based on the wall friction velocity
$u_{\unicode[STIX]{x1D70F}}$
at the nozzle exit.
In the three jet LES, the time step is defined by
$\unicode[STIX]{x0394}t=0.7\times \unicode[STIX]{x0394}r(r=r_{0})/c_{a}$
, yielding
$\unicode[STIX]{x0394}t=0.0023\times r_{0}/u_{j}$
. After a transient period of
$275r_{0}/u_{j}$
, the simulation time
$T$
, given in table 3, is equal to
$500r_{0}/u_{j}$
. During that time period, the signals of density, velocities and pressure obtained on the jet axis at
$r=0$
, on the cylindrical surfaces located at
$r=r_{0}$
and
$r=L_{r}=15r_{0}$
and in the cross-sections at
$z=-1.5r_{0}$
,
$z=0$
and
$z=L_{z}=40r_{0}$
, are recorded at a sampling frequency allowing spectra to be computed up to
$St_{D}=12.8$
. The signals obtained in the four azimuthal planes at
$\unicode[STIX]{x1D703}=0$
,
$\unicode[STIX]{x03C0}/4$
,
$\unicode[STIX]{x03C0}/2$
and
$3\unicode[STIX]{x03C0}/4$
are also stored, but at a halved frequency in order to reduce storage requirements. Finally, the Fourier coefficients estimated over the full section
$(r,z)$
for the first nine azimuthal modes for density, velocities and pressure are similarly saved. The flow and acoustic near-field statistics presented in the next sections are calculated from these recordings. They are averaged in the azimuthal direction, when possible. Time spectra are evaluated from overlapping samples of duration
$45r_{0}/u_{j}$
on the jet axis, and
$90r_{0}/u_{j}$
otherwise. In the azimuthal direction, post-processing can be performed up to the mode
$n_{\unicode[STIX]{x1D703}}=128$
, where
$n_{\unicode[STIX]{x1D703}}$
is the dimensionless azimuthal wavenumber such that
$n_{\unicode[STIX]{x1D703}}=k_{\unicode[STIX]{x1D703}}r$
.
Finally, the simulations required 200 GB of memory and have run for
$340\,000$
iterations each. They have been performed using an OpenMP-based in-house solver on single nodes with 256 GB of memory, consisting of four Intel Sandy Bridge E5-4650 8-core processors at a clock speed of 2.7 GHz or of two Intel Xeon CPU E5-2670v3 8-core processors at 2.6 GHz. The time per iteration is approximately equal to 120 s in the first case using 32 cores and to 140 s in the second case using 16 cores, leading to the consumption of 1070 and 620 CPU hours, respectively, for 1000 iterations. Therefore, a total number of the order of 1 billion computational hours has been necessary for the full study.
2.4 Linear stability analysis
Inviscid spatial stability analyses have been carried out from the mean flow fields of the jets, as was done in previous investigations (Fontaine et al.
Reference Fontaine, Elliott, Austin and Freund2015; Brès et al.
Reference Brès, Jordan, Jaunet, Le Rallic, Cavalieri, Towne, Lele, Colonius and Schmidt2018). More precisely, the compressible Rayleigh equation (Michalke Reference Michalke1984; Sabatini & Bailly Reference Sabatini and Bailly2015) has been solved for the LES profiles of mean axial velocity and mean density, locally considered parallel, from
$z=0.02r_{0}$
down to
$z=5r_{0}$
. Viscous effects are not taken into account because they are expected to be very weak at the Reynolds numbers
$Re_{\unicode[STIX]{x1D703}}\gtrsim 700$
considered in this work (Morris Reference Morris1976, Reference Morris2010). For a given axial distance
$z$
and a given Strouhal number
$St_{D}$
, the compressible Rayleigh equation is solved through a shooting technique (Morris Reference Morris2010), based on the Euler method for the integration step and on the secant method for the search of the complex wavenumber
$k_{z}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
. The integration is performed on a grid with a spatial step of
$0.0001r_{0}$
, extending from the LES grid point closest to the jet axis at
$r=0.007r_{0}$
out to
$r=5r_{0}$
. Since the present stability study is performed directly from the LES profiles, which may contain high-frequency noise in the near-nozzle region of high mean-flow gradients, the profiles and their radial derivatives are filtered using a sixth-order eleven-point centred filter (Bogey et al.
Reference Bogey, de Cacqueray and Bailly2009b
). A cubic spline interpolation is then employed to calculate the mean-flow values on the aforesaid grid. It can be noted that, in order to check the sensitivity of the results to the filtering, a tenth-order eleven-point centred filter has also been used to smooth the LES profiles of jetT2, in the case which exhibits the strongest gradients. The eigenvalues
$k_{z}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
thus obtained are identical to those calculated using the sixth-order filter.
2.5 Far-field extrapolation
The LES near-field fluctuations have been propagated to the far field using an in-house OpenMP-based solver of the isentropic linearized Euler equations (ILEE) in cylindrical coordinates, based on the same numerical methods as the LES (Bogey et al.
Reference Bogey, Barré, Juvé and Bailly2009a
; Bogey Reference Bogey2018). The extrapolations are carried out from the velocity and pressure fluctuations recorded on the cylindric surface at
$r=L_{r}=15r_{0}$
and on the axial sections at
$z=-1.5r_{0}$
and
$z=L_{z}=40r_{0}$
over a time period of
$500r_{0}/u_{j}$
during the jet simulations, at a sampling frequency corresponding to
$St_{D}=12.8$
. They aim to provide the pressure waves radiated at a distance of
$150r_{0}$
from the nozzle exit, where far-field acoustic conditions are expected to apply according to measurements (Ahuja, Tester & Tanna Reference Ahuja, Tester and Tanna1987; Viswanathan Reference Viswanathan2006), between the angles of
$\unicode[STIX]{x1D719}=15^{\circ }$
and
$165^{\circ }$
relative to the jet direction.
In practice, in order to compute separately the downstream and the upstream acoustic fields, whose magnitudes strongly vary, two far-field extrapolations are performed on two different grids, yielding results for
$15^{\circ }\leqslant \unicode[STIX]{x1D719}\leqslant 90^{\circ }$
and for
$60^{\circ }\leqslant \unicode[STIX]{x1D719}\leqslant 165^{\circ }$
, respectively. The two grids are identical in the radial and the azimuthal directions, with
$N_{r}=2058$
and
$N_{\unicode[STIX]{x1D703}}=256$
. In the direction
$r$
, they extend from
$r=2.5r_{0}$
out to
$r=151r_{0}$
with a mesh spacing of
$\unicode[STIX]{x0394}r=0.075r_{0}$
, and end with a 80-point sponge zone. In the axial direction, the two grids respectively contain
$N_{z}=2171$
and
$N_{z}=3111$
points, and extend, excluding the 80-point sponge zones implemented at the upstream and downstream boundaries, from
$z=-6r_{0}$
up to
$z=146r_{0}$
and from
$z=-146r_{0}$
up to
$z=76r_{0}$
, with a mesh spacing of
$\unicode[STIX]{x0394}z=0.075r_{0}$
. This mesh spacing, leading to a Strouhal number
$St_{D}=5.9$
for an acoustic wave discretized by five points per wavelength, is identical to that in the LES near field.
In the first computation, the LES fluctuations are imposed onto the extrapolation grid for
$-1.5r_{0}\leqslant z\leqslant L_{z}$
at
$r=L_{r}=15r_{0}$
, for
$2.5r_{0}\leqslant r\leqslant L_{r}$
at
$z=-1.5r_{0}$
and for
$7.5r_{0}\leqslant r\leqslant L_{r}$
at
$z=L_{z}=40r_{0}$
. The opening angle relative to the flow direction, with the nozzle exit as origin, is
$\unicode[STIX]{x1D719}=10^{\circ }$
, which allows most of the downstream noise components to be taken into account. In the second computation, the LES data are imposed onto the extrapolation grid as in the first one at
$z=-1.5r_{0}$
and at
$r=L_{r}=15r_{0}$
, but only for
$14r_{0}\leqslant r\leqslant L_{r}$
at
$z=L_{z}=40r_{0}$
. The opening angle is larger than in the first case in order to avoid the presence of aerodynamic disturbances (Arndt, Long & Glauser Reference Arndt, Long and Glauser1997) on the extrapolation surface, which might cause low-frequency spurious waves (Bogey & Bailly Reference Bogey and Bailly2010) in the upstream direction where noise levels are much lower than in the downstream direction.
Each ILEE computation requires 105 or 150 GB of memory depending on the grid used, and lasts during 7700 iterations. This leads to a total number approximately of 25 000 CPU hours consumed using 16-core nodes based on Intel Xeon CPU E5-2670 processors at 2.6 GHz. Finally, the far-field spectra are evaluated from the pressure signals obtained at
$150r_{0}$
from the nozzle exit during the final 6000 iterations of the computations, i.e. during nearly
$470r_{0}/u_{j}$
. Thus, for the peak Strouhal number of
$St_{D}=0.2$
emerging in the downstream direction, and for the lowest Strouhal number of
$St_{D}=0.075$
represented in § 3.4.2, the far-field signals contains 48 and 18 time periods, respectively. The statistical convergence of the results is furthermore increased by calculating the spectra using overlapping samples of duration
$90r_{0}/u_{j}$
, and by averaging in the azimuthal direction.
3 Results
3.1 Jet flow initial conditions
3.1.1 Nozzle-exit boundary-layer properties
Figure 2. Radial profiles at the nozzle exit at
$z=0$
(a) of mean axial velocity
$\langle u_{z}\rangle$
and (b) of the r.m.s. values of axial velocity fluctuations
$u_{z}^{\prime }$
:
Table 5. Nozzle-exit parameters: shape factor
$H$
, momentum thickness
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
, 99 % velocity thickness
$\unicode[STIX]{x1D6FF}_{99}$
and vorticity thickness
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}$
of the boundary-layer profile, Reynolds number
$Re_{\unicode[STIX]{x1D703}}=u_{j}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D708}$
, value
$u_{e}^{\prime }/u_{j}$
and radial position
$r_{e}$
of peak axial turbulence intensity and peak azimuthal mode
$n_{\unicode[STIX]{x1D703}}$
at
$r=r_{e}$
.
The profiles of mean and r.m.s. axial velocities calculated at the nozzle exit are presented in figure 2. Their main properties are provided in table 5. In figure 2(a), as intended, the mean velocity profiles differ significantly, and have shape factors
$H$
of 2.29 for jetBL, 1.96 for jetT1 and 1.71 for jetT2. The boundary-layer momentum thicknesses are similar, and range only from
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}=0.0299r_{0}$
for jetBL down to
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}=0.0274r_{0}$
for jetT2, leading to Reynolds numbers
$Re_{\unicode[STIX]{x1D703}}$
between
$685$
and
$747$
. From jetBL to jetT2, in addition, the 99 % velocity thickness
$\unicode[STIX]{x1D6FF}_{99}$
increases slightly and the vorticity thickness
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}=\langle u_{z}\rangle (r=0)/\max (|\unicode[STIX]{x2202}\langle u_{z}\rangle /\unicode[STIX]{x2202}r|)$
evaluated from the maximum value of velocity gradient strongly decreases from
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}=0.118r_{0}$
down to
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}=0.043r_{0}$
. The mean velocity profile for jetBL corresponds to a laminar boundary-layer profile, and, given that
$H\simeq 1.45$
is obtained (Spalart Reference Spalart1988; Erm & Joubert Reference Erm and Joubert1991; Fernholz & Finley Reference Fernholz and Finley1996; Schlatter & Örlü Reference Schlatter and Örlü2012) for fully developed boundary layers at
$Re_{\unicode[STIX]{x1D703}}=700$
, the profiles for jetT1 and jetT2 are both transitional.
In figure 2(b), the peak turbulence intensities, imposed by the boundary-layer forcing, are all close to
$u_{e}^{\prime }/u_{j}=6.1\,\%$
. They are reached roughly at the positions of the maximum velocity gradients, hence move nearer to the wall from
$r_{e}=0.935r_{0}$
for jetBL up to
$r_{e}=0.975r_{0}$
for jetT2, as reported in table 5. The radial profile of r.m.s. velocity also changes with the boundary-layer shape. In the non-laminar cases, compared to the laminar case (Zaman Reference Zaman1985a
,Reference Zaman
b
), the peak is sharper and resembles that obtained in the inner region of turbulent boundary layers (Spalart Reference Spalart1988; Schlatter & Örlü Reference Schlatter and Örlü2012) as well as that measured just downstream of the nozzle lip for such flows (Morris & Foss Reference Morris and Foss2003; Fontaine et al.
Reference Fontaine, Elliott, Austin and Freund2015).
With respect to the parameters of the inlet boundary layers in table 2, the nozzle-exit parameters in table 5 are slightly different due to the flow development in the pipe between the forcing at
$z=-0.95r_{0}$
and the exit at
$z=0$
. The boundary layer has a lower shape factor and a larger momentum thickness at the exit than at the pipe inlet for jetBL, whereas the opposite trends are observed for the two other jets.
The profiles of the skewness and kurtosis factors of the axial velocity fluctuations at
$z=0$
are depicted in figure 3. As expected, significant deviations from the values of 0 and 3 are found in the interfaces between the laminar inner-pipe region and the highly disturbed boundary layers, around
$r=0.75r_{0}$
. They are stronger, in absolute value, as the mean velocity profile has a more turbulent shape, and indicate the occurrence of intermittent bursts of low-velocity fluid. In the boundary layers, the strongest deviations are obtained for the laminar case, close to the wall as well as on the high-speed side of the boundary layers. For instance, at
$r=r_{0}-\unicode[STIX]{x1D6FF}_{94}=0.827r_{0}$
where
$\unicode[STIX]{x1D6FF}_{94}$
is the 94 % velocity boundary-layer thickness, equal to
$0.173r_{0}$
for all jets, the skewness values are of
$-0.65$
for JetBL,
$-0.43$
for JetT1 and
$-0.28$
for JetT2. This tendency is in agreement with that obtained by Zaman (Reference Zaman2017) who measured, also at
$r=r_{0}-\unicode[STIX]{x1D6FF}_{94}$
, lower values of velocity skewness for nominally laminar nozzle-exit conditions than for turbulent ones.
Figure 3. Radial profiles at the nozzle exit (a) of the skewness factor and (b) of the kurtosis factor of axial velocity fluctuations
$u_{z}^{\prime }$
:
Figure 4. Power spectral densities (PSD) of axial velocity fluctuations
$u_{z}^{\prime }$
obtained at the nozzle exit at the position
$r=r_{e}$
of peak axial turbulence intensity, as a function (a) of Strouhal number
$St_{D}$
and (b) of azimuthal mode
$n_{\unicode[STIX]{x1D703}}$
:
The properties of the jet initial disturbances are examined by computing spectra of axial velocity fluctuations at the nozzle exit in both the inner and the outer boundary-layer regions. The spectra estimated in the inner region at the position
$r=r_{e}$
of the turbulence intensity peak, i.e. between
$r_{e}=0.935r_{0}$
for jetBL and
$r_{e}=0.975r_{0}$
for jetT2, are represented as a function of the Strouhal number
$St_{D}$
in figure 4(a) and of the azimuthal mode
$n_{\unicode[STIX]{x1D703}}$
in figure 4(b). Their shapes are roughly the same in the three cases, and correspond, as was discussed in a specific note (Bogey et al.
Reference Bogey, Marsden and Bailly2011c
), to the spectral shapes encountered for turbulent wall-bounded flows because of the presence of large-scale elongated structures. As the boundary-layer profile changes from laminar to turbulent, the magnitude of the low-frequency components at
$St_{D}<0.8$
slightly strengthens in figure 4(a), which may be linked to the larger 99 % velocity thickness of the profile. Most obviously, the dominant components in figure 4(b) shift towards higher modes, resulting in peaks at
$n_{\unicode[STIX]{x1D703}}=50$
for jetBL,
$n_{\unicode[STIX]{x1D703}}=51$
for jetT1 and
$n_{\unicode[STIX]{x1D703}}=64$
for jetT2, as reported in table 5. The turbulent structures are thus spaced out by
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}=0.13r_{0}$
,
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}=0.12r_{0}$
and
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}=0.10r_{0}$
, respectively. The modification of their spatial arrangement in the azimuthal direction may be related to the increase of the velocity gradient.
The spectra evaluated in the outer boundary-layer region at
$r=r_{0}-\unicode[STIX]{x1D6FF}_{94}=0.827r_{0}$
in all cases are depicted in figure 5. Their levels are normalized by the r.m.s. values of velocity fluctuations at this position, equal to
$\langle u_{z}^{\prime 2}\rangle ^{1/2}=0.0248u_{j}$
for JetBL,
$0.0283u_{j}$
for JetT1 and
$0.0285u_{j}$
for JetT2. The spectra are very similar to each other, both in shape and in amplitude. Compared to the near-wall spectra, two important differences can be noticed. First, a significant amount of energy is contained by the components centred around a Strouhal number of
$St_{D}=3.2$
in figure 5(a), whereas a rapid collapse is observed for
$St_{D}\geqslant 1.6$
in figure 4(a). Second, the dominant mode in the azimuthal direction is
$n_{\unicode[STIX]{x1D703}}\simeq 40$
for all cases in figure 5(b), whereas it is higher, and increases for a lower boundary-layer shape factor in figure 4(b). Therefore, the turbulent structures organize differently near the wall and further away, as expected (Tomkins & Adrian Reference Tomkins and Adrian2005). Furthermore, they appear to depend on the form of the velocity profile in the first region, but not in the second one.
Figure 5. Power spectral densities of axial velocity fluctuations
$u_{z}^{\prime }$
obtained at the nozzle exit at
$r=r_{0}-\unicode[STIX]{x1D6FF}_{94}$
, as a function (a) of Strouhal number
$St_{D}$
and (b) of azimuthal mode
$n_{\unicode[STIX]{x1D703}}$
:
3.1.2 Very near-nozzle instability waves
In order to characterize the instability waves initially growing in the shear layers, an inviscid linear stability analysis is carried out following the methodology described in § 2.4 from the LES mean flow profiles at
$z=0.1r_{0}$
, corresponding to
$z\simeq 3.6\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(0)$
in terms of nozzle-exit boundary-layer momentum thickness
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(0)$
. The mean velocity profiles at this position are shown in figure 6(a). They are very similar to the nozzle-exit profiles of figure 2(a), and have momentum thicknesses only 2 % larger than the exit values reported in table 5. This persistence of the mean velocity profile is in agreement with the measurements of Morris & Foss (Reference Morris and Foss2003) downstream of a sharp corner for a turbulent boundary layer at
$Re_{\unicode[STIX]{x1D703}}=4650$
, as indicated in table 1. For the comparison, a hyperbolic–tangent velocity profile with
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}=0.0288r_{0}$
, that is the momentum thickness imposed at the pipe-nozzle inlet, is also plotted. This type of analytical profile is often used in linear stability analyses for mixing layers and jets (Michalke Reference Michalke1984), providing good predictions of the peak Strouhal number
$St_{\unicode[STIX]{x1D703}}$
for initially laminar conditions (Gutmark & Ho Reference Gutmark and Ho1983), but poor ones for initially turbulent conditions (Drubka & Nagib Reference Drubka and Nagib1981; Hussain & Zaman Reference Hussain and Zaman1985).
The instability amplification rates
$-\text{Im}(k_{z})\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
computed for the first two azimuthal modes
$n_{\unicode[STIX]{x1D703}}=0$
and
$n_{\unicode[STIX]{x1D703}}=1$
are represented in figure 6(b) as a function of the Strouhal number
$St_{\unicode[STIX]{x1D703}}$
. Their peak frequencies are gathered in table 6. The curves obtained for the two modes are superimposed, due to the value of
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}/r_{0}<1/25$
(Michalke Reference Michalke1984), with a slight predominance of the axisymmetric mode. Their sensitivity to the velocity profile is much more spectacular. For jetBL, the range of unstable frequencies is narrower and the peak growth rate is higher than those for the hyperbolic–tangent profile. Despite these discrepancies, the peak grow rates are reached at very similar Strouhal numbers, namely
$St_{\unicode[STIX]{x1D703}}=0.018$
for jetBL and
$St_{\unicode[STIX]{x1D703}}=0.017$
for the analytical profile. For the two other jets, the range of unstable frequencies broadens and the growth rates strengthen as the exit profile deviates from a laminar profile. In addition, the peak Strouhal number increases to
$St_{\unicode[STIX]{x1D703}}=0.026$
for jetT1 and to
$St_{\unicode[STIX]{x1D703}}=0.032$
for jetT2.
Figure 6. Representation (a) of the profiles of mean axial velocity
$\langle u_{z}\rangle$
at
$z=0.1r_{0}$
and (b) of the instability growth rates
$-\text{Im}(k_{z})$
obtained for the profiles using an inviscid linear stability analysis for modes
$n_{\unicode[STIX]{x1D703}}=0$
for
$n_{\unicode[STIX]{x1D703}}=1$
for 
$St_{\unicode[STIX]{x1D703}}$
; – ⋅ – ⋅ results for a two-dimensional hyperbolic–tangent velocity profile with
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}=0.0288r_{0}$
.
Table 6. Peak Strouhal numbers
$St_{D}$
,
$St_{\unicode[STIX]{x1D703}}$
,
$St_{\unicode[STIX]{x1D714}}$
and
$St^{+}$
of instability growth rates obtained using an inviscid linear stability analysis at
$z=0.1r_{0}$
.
The present changes in peak frequency at
$z=0.1r_{0}\simeq 3.6\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(0)$
depending on the boundary-layer profile are consistent with the data of the literature. For instance, the peak Strouhal numbers of
$St_{\unicode[STIX]{x1D703}}=0.022-0.028$
measured by Drubka & Nagib (Reference Drubka and Nagib1981) and Hussain & Zaman (Reference Hussain and Zaman1985) in initially turbulent mixing layers are greater than those found around
$St_{\unicode[STIX]{x1D703}}=0.013$
in initially laminar mixing layers. Closer to this study, in the experiments of Morris & Foss (Reference Morris and Foss2003), a hump emerges at
$St_{\unicode[STIX]{x1D703}}\simeq 0.06$
in the velocity spectrum acquired
$3.54\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(0)$
downstream of a sharp edge, where
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(0)$
here denotes the boundary-layer momentum thickness at the edge. Finally, the linear stability analyses performed at
$z=0.08r_{0}$
in Fontaine et al. (Reference Fontaine, Elliott, Austin and Freund2015) and at
$z=0.16r_{0}$
in Brès et al. (Reference Brès, Jordan, Jaunet, Le Rallic, Cavalieri, Towne, Lele, Colonius and Schmidt2018) for the jets reported in table 1 also reveal peak amplification rates at higher
$St_{\unicode[STIX]{x1D703}}$
for turbulent than for laminar nozzle-exit flow conditions. Indeed, while the peak Strouhal numbers emerge at
$St_{\unicode[STIX]{x1D703}}=0.012{-}0.014$
for the short-nozzle case in Fontaine et al. (Reference Fontaine, Elliott, Austin and Freund2015) and for Baseline_LES_10M in Brès et al. (Reference Brès, Jordan, Jaunet, Le Rallic, Cavalieri, Towne, Lele, Colonius and Schmidt2018), they are equal to
$St_{\unicode[STIX]{x1D703}}=0.09$
for the long-nozzle case and to
$St_{\unicode[STIX]{x1D703}}=0.024$
for BL16M_WM_Turb. Remark that the positions of
$z=0.08r_{0}$
for the long-nozzle case and of
$z=0.16r_{0}$
for BL16M_WM_Turb correspond respectively to
$z=1.9\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(0)$
and to
$z=11\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(0)$
. The variations of the peak frequencies with the axial position will be discussed later in § 3.2.3.
Figure 7. Power spectral densities of radial velocity fluctuations
$u_{r}^{\prime }$
at
$r=r_{0}$
at (a)
$z=0.1r_{0}$
, (b)
$z=0.2r_{0}$
and (c)
$z=0.4r_{0}$
, as a function of
$St_{D}$
:
$z=0.1r_{0}$
: 
Instead of the momentum thickness, the peak frequency of the instability growth rates can be related to other length scales of the velocity profiles, such as the vorticity thickness
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}$
or viscous wall units at the nozzle exit, as proposed by Morris & Foss (Reference Morris and Foss2003). The resulting Strouhal numbers
$St_{\unicode[STIX]{x1D714}}=f\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D714}}/u_{j}$
and
$St^{+}=f\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}^{2}$
are given in table 6. As the boundary-layer shape factor
$H$
decreases, the latter varies from 0.078 for jetBL down to 0.040 for jetT2, whereas the former remains very close to 0.07. Therefore, the frequency of the initial instability wave is primarily linked to the high-shear portion of the velocity profiles, as was noted by Fontaine et al. (Reference Fontaine, Elliott, Austin and Freund2015).
The spectra of radial velocity fluctuations calculated at
$r=r_{0}$
at
$z=0.1r_{0}$
,
$z=0.2r_{0}$
and
$z=0.4r_{0}$
are represented in figure 7 as a function of
$St_{D}$
. The peak diameter-based Strouhal numbers obtained from the mean-flow profiles at
$z=0.1r_{0}$
using the linear stability analysis, provided in table 6, are also indicated. For all jets, a hump appears in the spectra, centred on a frequency moving slowly towards lower frequencies in the downstream direction, as for the separating boundary layer of Morris & Foss (Reference Morris and Foss2003). The peak frequencies are in very good agreement with the linear stability results, especially in figure 7(b) for
$z=0.2r_{0}$
. Moreover, the hump rapidly grows, at a rate which is lowest for jetBL and highest for jetT2, as predicted by the instability amplification rates of figure 6(b). Therefore, for the present initially disturbed jets, the flow development very near the nozzle is driven by the instability waves examined in this section.
Figure 8. Snapshots in the
$(z,r)$
plane of vorticity norm
$|\unicode[STIX]{x1D74E}|$
for (a) jetBL, (b) jetT1 and (c) jetT2. The colour scales range from 0 up to (a,c,e)
$18u_{j}/r_{0}$
and (b,d,f)
$9u_{j}/r_{0}$
, from white to red.
3.2 Shear-layer development
3.2.1 Vorticity snapshots
Instantaneous fields of vorticity norm obtained down to
$z=3.5r_{0}$
and to
$z=12r_{0}$
are represented in figures 8(a,c,e) and 8(b,d,f), respectively. Very near the nozzle lip, in figure 8(a,c,e), the levels of vorticity are higher for jetT2 than for the two other jets due to the sharper boundary-layer profile. In that region, the turbulent structures are elongated in the downstream direction, which is characteristic of wall-bounded flows. In the radial direction, their length scales are of the order of boundary-layer thickness for jetBL, but are much smaller for jetT1 and especially for jetT2. For the latter jet, in particular, strong levels of vorticity are only found around
$r=r_{0}$
. This is the case nearly down to
$z=0.5r_{0}$
, in agreement with the persistence of the mean boundary-layer profile mentioned above. These results supports again that the initial shear-layer development is essentially related to the vorticity thickness of the velocity profile. Further away from the nozzle, the shear layers seem to roll up around
$z=1.5r_{0}$
for jetBL but earlier for jetT1 and jetT2, which is in line with the instability amplification rates of the previous section. Then, they exhibit typical features of turbulent mixing layers. Finally, in figure 8(b,d,f), the mixing layers appear to be fully developed for
$z\gtrsim 4r_{0}$
. However, they spread faster for jetBL than for the two other jets. The presence of large-scale structures resembling the coherent structures of the flow visualizations of Brown & Roshko (Reference Brown and Roshko1974) is also more obvious for the laminar boundary-layer profile than for the non-laminar profiles. Similar effects of the exit velocity profile on the organized structures in the shear layers of jets were recently revealed by the experiments of Zaman (Reference Zaman2017) using the ASME and the conical nozzles. It should be reminded that the definition of coherent structures may vary from one researcher to another. In this work, following Hussain (Reference Hussain1986) and Fieldler (Reference Fieldler1988), they refer to regions of correlated and concentrated vorticity, of size comparable to the transverse length scale of the shear layer, which are spatially isolated from each other and show similarity with the corresponding structures of the (preceding) laminar–turbulent transition.
3.2.2 Flow field properties
The variations of the shear-layer momentum thickness are represented over
$0\leqslant z\leqslant 6r_{0}$
in figure 9(a) and over
$0\leqslant z\leqslant 15r_{0}$
in figure 9(b). The spreading rates
$\text{d}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}/\text{d}z$
are also shown in figure 9(a). The differences are significant between jetBL and jetT1 with boundary-layer profiles with
$H=2.29$
and
$1.96$
, but they are rather weak between the two transitional cases with
$H=1.96$
and
$1.71$
. For
$z\leqslant 3r_{0}$
, the mixing layers develop faster for jetT1 and jetT2 than for jetBL. This can be due to the higher growth rates of the jet initial instability waves as the shape factor
$H$
decreases, highlighted in figure 6. Farther downstream, in contrast, the mixing layers spread most rapidly for jetBL, which was suggested by the vorticity fields of figure 8, but has no evident cause at first sight. In this region, a better agreement with the measurements of Fleury (Reference Fleury2006) and Castelain (Reference Castelain2006) for jets at
$M=0.9$
and
$Re_{D}\simeq 10^{6}$
, undoubtedly initially turbulent, is obtained for the jets with non-laminar boundary-layer profiles. Furthermore, for jetBL, the shear-layer spreading rate increases monotonically with the axial distance up to values around
$0.030$
at
$z=5r_{0}$
. For jetT1 and jetT2, on the contrary, they reach peak values of 0.0275 at
$z=1.3r_{0}$
and of
$0.030$
at
$z=1.5r_{0}$
, respectively, and do not exceed values of
$0.024$
for
$z\geqslant 4r_{0}$
.
Figure 9. Variations of shear-layer momentum thickness
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
for
$\text{d}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}/\text{d}z$
for 
$M=0.9$
: ♢ Fleury (Reference Fleury2006) at
$Re_{D}=7.7\times 10^{5}$
and ▫ Castelain (Reference Castelain2006) at
$Re_{D}=10^{6}$
. In order to illustrate the change of the mean-flow profiles in the region of boundary-layer/mixing-layer transition, the profiles of mean axial velocity at
$z=0.8r_{0}$
,
$1.6r_{0}$
and
$3.2r_{0}$
are provided in figure 10. The radial distances are normalized by the local shear-layer momentum thicknesses, which, however, are nearly the same in the present jets at
$z=0.8r_{0}$
and
$3.2r_{0}$
, and only vary from
$0.054r_{0}$
in jetBL up to
$0.065r_{0}$
in jetT2 at
$z=1.6r_{0}$
. At
$z=0.8r_{0}$
, corresponding to
$z=28\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(0)$
, the velocity profiles differ significantly. This is particularly the case for their high-speed portions, which still bear strong similarities with the nozzle-exit profiles. The latter result is consistent with that obtained for a turbulent boundary layer at
$z=29\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(0)$
in the experiments of Morris & Foss (Reference Morris and Foss2003). Farther away from the nozzle, the mean velocity profiles are very close to each other at
$z=1.6r_{0}$
and almost superimposed at
$z=3.2r_{0}$
, and exhibit no clear reminiscence of the boundary-layer profiles.
Figure 10. Radial profiles of mean axial velocity
$\langle u_{z}\rangle$
at (a)
$z=0.8r_{0}$
, (b)
$z=1.6r_{0}$
and (c)
$z=3.2r_{0}$
:
Figure 11. Variations of the r.m.s. values of (a) axial and (b) radial velocity fluctuations
$u_{z}^{\prime }$
and
$u_{r}^{\prime }$
at
$r=r_{0}$
:
$M=0.9$
: ♢ Fleury (Reference Fleury2006) at
$Re_{D}=7.7\times 10^{5}$
and ▫ Castelain (Reference Castelain2006) at
$Re_{D}=10^{6}$
.
Table 7. Peak turbulence intensities in the jets.
The r.m.s. values of axial and radial velocity fluctuations at
$r=r_{0}$
are displayed down to
$z=15r_{0}$
in figure 11. They follow trends which are similar to those for the mixing-layer spreading rate. Just downstream of the nozzle, they increase more rapidly for jetT1 and jetT2 than for jetBL, thus reaching peaks around
$z=r_{0}$
in the former case, but
$z=5r_{0}$
in the latter. In addition, the levels are lower for the transitional boundary-layer profiles. This is true for the peak levels in the jets, given in table 7, which are equal, for
$u_{z}^{\prime }$
and
$u_{r}^{\prime }$
for instance, to approximately
$0.157u_{j}$
and
$0.12u_{j}$
for jetT1 and jetT2, but to
$0.174u_{j}$
and
$0.131u_{j}$
for jetBL. The difference in turbulence intensity is also significant down to
$z=15r_{0}$
, which is roughly the position of the end of the jet potential core. Therefore, the effects of the exit boundary-layer profile on the turbulence in the mixing layers last far downstream of the nozzle, despite, notably, the nearly identical mean-flow profiles obtained at
$z=3.2r_{0}$
in figure 10(c). Finally, as for the shear-layer momentum thickness, the results for the jets with non-laminar mean velocity profiles better agree with the measurements of Fleury (Reference Fleury2006) and Castelain (Reference Castelain2006) than those for jetBL.
Comparisons between numerical and experimental data may only be fully relevant for identical upstream flow conditions. It can however be mentioned that in the similarity region of an axisymmetric mixing layer, initially with
$Re_{\unicode[STIX]{x1D703}}=349$
,
$u_{e}^{\prime }/u_{j}=6.18\,\%$
and
$H=2.47$
, Hussain & Zedan (Reference Hussain and Zedan1978b
) obtained a spreading rate of 0.0294 and a peak axial turbulence intensity of 16.7 %, which are both comparable to the values reached in jetBL. Moreover, the changes undergone by the mixing layers of the present jets as the nozzle-exit velocity profile deviates from a laminar profile, namely a slower growth and weaker velocity fluctuations, correspond to those observed experimentally when initially laminar shear layers are tripped and become initially turbulent (Hill et al.
Reference Hill, Jenkins and Gilbert1976; Browand & Latigo Reference Browand and Latigo1979; Husain & Hussain Reference Husain and Hussain1979). They also resemble the changes induced by increasing the exit turbulence levels only (Hussain & Zedan Reference Hussain and Zedan1978a
; Bogey et al.
Reference Bogey, Marsden and Bailly2012b
).
Finally, the skewness factors of the axial and radial velocity fluctuations at
$r=r_{0}$
are represented in figure 12. In the vicinity of the nozzle exit, in all cases, they differ appreciably from zero, which is expected at the interface between the highly disturbed shear layers and the ambient medium. Their positive values are due to the sudden eruptions of high-velocity fluid at the outer edge of the mixing layers. For jetT1 and jetT2, the skewness factors rapidly decrease, whereas they remain greater than 0.1 down to
$z=4r_{0}$
for jetBL. This can be related to the slower initial development of the shear layers in the latter case. Farther downstream, for
$z\geqslant 6r_{0}$
, the skewness factors, albeit much lower than previously, are still higher for jetBL than for the other jets. Given the links between velocity skewness and large-scale vortices in free shear flows (Yule Reference Yule1978), this result suggests the presence of stronger coherent structures in the first jet.
Figure 12. Variations of the skewness values of (a) axial and (b) radial velocity fluctuations
$u_{z}^{\prime }$
and
$u_{r}^{\prime }$
at
$r=r_{0}$
:
3.2.3 Instability waves and velocity spectra
Some results of the inviscid linear stability analysis carried out, as reported in § 2.4, from the LES mean-flow fields between
$z=0.02r_{0}$
and
$5r_{0}$
are provided in order to investigate the properties of the instability waves, and their variations in the axial direction, during the boundary-layer/mixing-layer transition and further downstream, They will help us to identify the possible cause of the differences between the shear-layer developments.
The instability amplification rates
$-\text{Im}(k_{z})\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}$
calculated for
$n_{\unicode[STIX]{x1D703}}=0$
and
$=1$
at
$z=0.1r_{0}$
,
$0.4r_{0}$
,
$0.8r_{0}$
,
$1.6r_{0}$
and
$3.2r_{0}$
are represented in figure 13 as a function of the Strouhal number
$St_{\unicode[STIX]{x1D703}}$
. The curves obtained for the two azimuthal modes are nearly superimposed on each other except for
$z=3.2r_{0}$
, where lower unstable frequencies are found for
$n_{\unicode[STIX]{x1D703}}=1$
than for
$n_{\unicode[STIX]{x1D703}}=0$
due to the mixing-layer thickness of
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}\simeq 0.1r_{0}$
at this location (Michalke Reference Michalke1984). As the distance from the nozzle exit increases, the amplification curves change appreciably in level and shape for all jets. For jetBL, the instability growth rates are lower, and the ranges of unstable frequencies broaden. However, the peak Strouhal numbers, equal to
$St_{\unicode[STIX]{x1D703}}=0.018$
at
$z=0.1r_{0}$
, do not vary much with the axial position. For jetT1 and jetT2 with non-laminar boundary-layer profiles, the changes with the distance from the nozzle are more important. The reduction of the growth rates is stronger and, above all, the peak Strouhal numbers
$St_{\unicode[STIX]{x1D703}}$
, of 0.026 for jetT1 and of 0.032 for jetT2 at
$z=0.1r_{0}$
, decrease significantly. At
$z=3.2r_{0}$
, finally, the amplification curves are the nearly the same for the three jets, which is not surprising given the very similar velocity profiles of figure 10(c).
Figure 13. Representation of the instability growth rates
$-\text{Im}(k_{z})$
obtained using an inviscid linear stability analysis at
$z=0.1r_{0}$
,
$0.4r_{0}$
,
$0.8r_{0}$
,
$1.6r_{0}$
and
$3.2r_{0}$
for ——
$n_{\unicode[STIX]{x1D703}}=0$
and
$n_{\unicode[STIX]{x1D703}}=1$
for (a) jetBL, (b) jetT1 and (c) jetT2, as a function of
$St_{\unicode[STIX]{x1D703}}$
; – – – peak frequencies at
$z=0.1r_{0}$
.
Figure 14. Axial variations of the peak Strouhal numbers (a)
$St_{\unicode[STIX]{x1D703}}$
, (b)
$St_{\unicode[STIX]{x1D714}}$
and (c)
$St_{D}$
of instability growth rates obtained for
$n_{\unicode[STIX]{x1D703}}=0$
;
$n_{\unicode[STIX]{x1D703}}=1$
. In order to highlight their variations downstream of the nozzle, the peak Strouhal numbers
$St_{\unicode[STIX]{x1D703}}$
of the instability growth rates are plotted in figure 14(a) between
$z=0.02r_{0}$
and
$3.5r_{0}$
. The values obtained for
$n_{\unicode[STIX]{x1D703}}=0$
and
$1$
are identical to each other down to
$z\simeq r_{0}$
, and then gradually diverge due to the thickening of the mixing layer, yielding
$St_{\unicode[STIX]{x1D703}}\simeq 0.018$
for
$n_{\unicode[STIX]{x1D703}}=0$
and
$St_{\unicode[STIX]{x1D703}}\simeq 0.014$
for
$n_{\unicode[STIX]{x1D703}}=1$
at
$z=3.5r_{0}$
in all cases. More interestingly, strong discrepancies appear in the vicinity of the nozzle exit between the three jets. In that region, for jetBL, the peak Strouhal numbers do not change much with the axial distance and remain close to a value of
$St_{\unicode[STIX]{x1D703}}=0.018$
corresponding roughly to the Strouhal numbers emerging farther downstream in the mixing layers. For jetT1 and jetT2, on the contrary, they rapidly decrease during the changeover from a boundary-layer profile to a mixing-layer profile, from values of the order of or higher than 0.03 at
$z=0.02r_{0}$
down to values lower than
$0.02$
at
$z\simeq 0.6r_{0}\simeq 20\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(0)$
. These variations of
$St_{\unicode[STIX]{x1D703}}$
are in very good agreement with the experimental data of Morris & Foss (Reference Morris and Foss2003) for a turbulent boundary layer.
As in the study mentioned above, a scaling with the local shear-layer vorticity thickness is applied to the peak frequencies of the instability growth rates. The resulting Strouhal numbers
$St_{\unicode[STIX]{x1D714}}$
are shown in figure 14(b) between
$z=0.02r_{0}$
and
$3.5r_{0}$
. For the present jets, they are very close to each other at any of the locations considered. This is particularly true, despite the different boundary-layer profiles, near the nozzle, where Strouhal numbers
$St_{\unicode[STIX]{x1D714}}\simeq 0.07$
are continuously found between
$z=0.02r_{0}$
and
$z\simeq 2r_{0}$
. Therefore, for a given mean flow profile, the peak frequency of the instability waves is only fixed by the maximum velocity gradient.
The variations of the most unstable Strouhal numbers
$St_{\unicode[STIX]{x1D703}}$
downstream of the nozzle do not reflect those of the most unstable frequencies because of the increase of the shear-layer momentum thickness in the axial direction. For that reason, the instability growth rates
$-\text{Im}(k_{z})r_{0}$
obtained for
$n_{\unicode[STIX]{x1D703}}=0$
and
$1$
at
$z=0.4r_{0}$
,
$0.8r_{0}$
,
$1.6r_{0}$
and
$3.2r_{0}$
are re-plotted in figure 15 as a function of the diameter-based Strouhal number
$St_{D}$
. The peak Strouhal numbers
$St_{D}$
are also represented in figure 14(c) between
$z=0.02r_{0}$
and
$z=3.5r_{0}$
. As the distance from the nozzle increases, they move to lower values due to the shear-layer thickening. During the initial stage of flow development between the nozzle exit and
$z\simeq 0.6r_{0}$
, the frequency decrease is however much more pronounced for jetT1 and jetT2 than for jetBL. In their linear stability analyses, Brès et al. (Reference Brès, Jordan, Jaunet, Le Rallic, Cavalieri, Towne, Lele, Colonius and Schmidt2018) recently noted, as in this work, that downstream of the nozzle the range of the unstable frequencies are more quickly reduced for their initially turbulent jet than for their initially laminar jet with thicker exit boundary layer. They attributed this to the fact that the instability waves in the near-nozzle region grow at a higher rate in the first jet because of the faster shear-layer spreading in this case. On the basis of the present results, this appears to be also strongly linked to the difference in peak instability frequency between laminar and non-laminar boundary-layer profiles.
Figure 15. Representation of —— the instability growth rates
$-\text{Im}(k_{z})$
at
$z=0.4r_{0}$
,
$0.8r_{0}$
,
$1.6r_{0}$
and
$3.2r_{0}$
as a function of
$St_{D}$
and of the peak frequencies at – – –
$z=0.1r_{0}$
and – ⋅ – ⋅
$0.2r_{0}$
obtained using an inviscid linear stability analysis for
$n_{\unicode[STIX]{x1D703}}=0$
for (a) jetBL, (b) jetT1 and (c) jetT2;
$n_{\unicode[STIX]{x1D703}}=1$
. The dependence of the range of the unstable frequencies on the boundary-layer profiles has substantial effects on the spatial evolution of the instability waves developing downstream of the nozzle. Examine, for instance, the peak frequencies obtained at
$z=0.1r_{0}$
in figure 15. The more non-laminar the boundary-layer profile, the earlier they leave the range of the unstable frequencies. The growth rates calculated between
$z=0.02r_{0}$
and
$3.5r_{0}$
for the peak frequencies at
$z=0.1r_{0}$
,
$0.2r_{0}$
and
$0.4r_{0}$
, chosen to cover the frequency range of the initial instability waves, are also represented in figure 16. In all cases, they sharply decrease downstream of the nozzle. However, they remain appreciable down to
$z\simeq 3.5r_{0}\simeq 125\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(0)$
in figure 16(a) for jetBL, whereas they become negligible or negative as early as
$z\simeq r_{0}\simeq 35\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}(0)$
in figure 16(b,c) for jetT1 and jetT2. As a result, the instability waves developing very near the nozzle continue to be amplified, even at a low rate, over a relatively large axial distance for the laminar boundary-layer profile, whereas they are rapidly damped for the non-laminar profiles.
Figure 16. Axial variations of the instability growth rates
$-\text{Im}(k_{z})$
obtained at the peak Strouhal numbers
$St_{D}$
at ——
$z=0.1r_{0}$
, – – –
$z=0.2r_{0}$
and – ⋅ –⋅
$z=0.4r_{0}$
for
$n_{\unicode[STIX]{x1D703}}=0$
for (a) jetBL, (b) jetT1 and (c) jetT2, normalized by the maximum growth rates at
$z=0.1r_{0}$
;
$n_{\unicode[STIX]{x1D703}}=1$
. Velocity spectra computed in the mixing layers are discussed in light of the results of the linear stability analysis. First, the spectra of radial velocity fluctuations obtained at
$r=r_{0}$
at
$z=0.8r_{0}$
,
$1.6r_{0}$
,
$3.2r_{0}$
,
$4.8r_{0}$
,
$6.4r_{0}$
and
$10r_{0}$
are represented in figure 17 as a function of the Strouhal number
$St_{D}$
, along with the peak frequencies of instability growth rates at
$z=0.1r_{0}$
. At
$z=0.8r_{0}$
, in figure 17(a), the spectra resemble those of figure 7 acquired farther upstream. They are dominated by humps associated with the initial instability waves, peaking at frequencies slightly lower than those predicted at
$z=0.1r_{0}$
due to the shear-layer thickening. As the distance from the nozzle increases, in all cases, the humps diminish and eventually vanish as turbulence develops in the mixing layers. However, for jetBL, the hump remains noticeable at
$z=4.8r_{0}$
in figure 17(d), whereas it cannot be observed at
$z=3.2r_{0}$
in figure 17(c) for jetT1 and jetT2. This discrepancy can be explained by the linear stability analysis, indicating a longer persistence of the initial instability waves for the laminar boundary layer than for the transitional ones. Farther downstream, at
$z=6.4r_{0}$
and
$10r_{0}$
in figure 17(e,f), the spectra are all broadband, but significant differences appear at low frequencies. More precisely, the levels are higher for jetBL than for jetT1 and jetT2 at
$St_{D}\lesssim 1$
. Therefore, in the jet with a laminar boundary layer, the initial instability components last over a larger distance, but also lead to stronger large-scale structures in the mixing layers after having disappeared. These results are in line with the comments on coherent structures made previously from the vorticity fields and the skewness factors at
$r=r_{0}$
, and with the visualizations of Zaman (Reference Zaman2017) for initially nominally laminar jets.
Figure 17. Power spectral densities of radial velocity fluctuations
$u_{r}^{\prime }$
at
$r=r_{0}$
at (a)
$z=0.8r_{0}$
, (b)
$z=1.6r_{0}$
, (c)
$z=3.2r_{0}$
, (d)
$z=4.8r_{0}$
, (e)
$z=6.4r_{0}$
and (f)
$z=10r_{0}$
as a function of
$St_{D}$
:
$z=0.1r_{0}$
: 
Figure 18. Power spectral densities of radial velocity fluctuations
$u_{r}^{\prime }$
at
$r=r_{0}$
at (a)
$z=0.8r_{0}$
, (b)
$z=3.2r_{0}$
and (c)
$z=10r_{0}$
, as a function of mode
$n_{\unicode[STIX]{x1D703}}$
:
In order to explore the azimuthal distribution of the flow disturbances, the spectra of radial velocity fluctuations at
$r=r_{0}$
at
$z=0.8r_{0}$
,
$3.2r_{0}$
and
$10r_{0}$
are depicted in figure 18 as a function of mode
$n_{\unicode[STIX]{x1D703}}$
. At the first location, in figure 18(a), the spectra have nearly identical shapes over the whole range of modes considered. Since the azimuthal velocity spectra at the nozzle exit are also close to each other in figures 4(b) and 5(b), the mechanisms at play between
$z=0$
and
$0.8r_{0}$
are of the same nature in the three jets. The levels are highest for jetT2 and lowest for jetBL, and for a given jet, they are maximum for the axisymmetric mode, remain strong up to modes
$n_{\unicode[STIX]{x1D703}}=3$
or 4, and then sharply decrease for higher modes. These trends are consistent with the features of the instability waves initially growing in the shear layers, namely higher amplification rates for a more turbulent nozzle-exit boundary layer, and very similar rates for the first five azimuthal modes (Brès et al.
Reference Brès, Jordan, Jaunet, Le Rallic, Cavalieri, Towne, Lele, Colonius and Schmidt2018). Farther downstream, at
$z=3.2r_{0}$
and
$10r_{0}$
in figure 18(b,c), the spectra are superimposed for
$n_{\unicode[STIX]{x1D703}}\geqslant 16$
, but the levels are higher for jetBL than for jetT1 and jetT2 at lower mode numbers. The difference in level is largest for
$n_{\unicode[STIX]{x1D703}}\leqslant 2$
at
$z=3.2r_{0}$
, which may be related to the presence of instability components at this position for jetBL, and for
$n_{\unicode[STIX]{x1D703}}\leqslant 5$
at
$z=10r_{0}$
. The intense large-scale structures in the mixing layers of jetBL revealed by the spectra of figure 17(c–f) are consequently significantly correlated in the azimuthal direction.
Finally, the spectra of radial velocity fluctuations at
$r=r_{0}$
at
$z=0.8r_{0}$
,
$3.2r_{0}$
and
$10r_{0}$
for mode
$n_{\unicode[STIX]{x1D703}}=1$
are displayed in figure 19 as a function of
$St_{D}$
. For brevity, only the results for
$n_{\unicode[STIX]{x1D703}}=1$
are reported, but those obtained for the other first azimuthal modes are very similar. As in figure 17(a,c,f), humps associated with the initial instability waves dominate at
$z=0.8r_{0}$
, the hump still appears only for jetBL at
$z=3.2r_{0}$
, and the low-frequency components are stronger for jetBL than for the other jets at
$z=10r_{0}$
. The instability waves however emerge more clearly in the present case than in the spectra computed from the full velocity fields. Compared to the broadband levels, indeed, their peak levels are more than two decades higher in figure 19(a), whereas they are 3–4 times higher in figure 17(a).
Figure 19. Power spectral densities for mode
$n_{\unicode[STIX]{x1D703}}=1$
of radial velocity fluctuations
$u_{r}^{\prime }$
at
$r=r_{0}$
at (a)
$z=0.8r_{0}$
, (b)
$z=3.2r_{0}$
and (c)
$z=10r_{0}$
, as a function of
$St_{D}$
:
$z=0.1r_{0}$
: 
3.3 Jet development
3.3.1 Vorticity snapshots
Snapshots of the vorticity norm obtained from the nozzle exit down to
$z=25r_{0}$
are provided in figure 20. Overall, they look like each other, and display, from upstream to downstream, the growth of the turbulent mixing layers, the closing of the jet potential cores and the regions of developed jet flows. Large-scale coherent structures may also be seen in the shear layers, for instance at
$z\simeq 11r_{0}$
for jetBL and at
$z\simeq 12r_{0}$
for jetT2. As the shape factor of the exit boundary-layer profile decreases, the mixing layers visibly merge later, as expected given the reduction in shear-layer spreading rate noted in previous section. As a result, the end of the potential core is located around
$z=13r_{0}$
in figure 20(a) for the laminar boundary-layer profile, but around
$z=15r_{0}$
in figure 20(c) for the transitional profile with
$H=1.71$
.
Figure 20. Snapshots in the
$(z,r)$
plane of vorticity norm
$|\unicode[STIX]{x1D74E}|$
for (a) jetBL, (b) jetT1 and (c) jetT2. The colour scale ranges from 0 up to
$5.5u_{j}/r_{0}$
, from white to red.
3.3.2 Flow field properties
The variations of the centreline mean axial velocity are presented in figure 21. In figure 21(a), as the nozzle-exit boundary-layer profile changes from laminar to turbulent, the jet flow develops more slowly. The potential core thus ends at
$z_{c}=12.4r_{0}$
for jetBL,
$14.8r_{0}$
for jetT1 and
$15.6r_{0}$
for jetT2, as indicated in table 8, where
$z_{c}$
is defined such as
$\langle u_{z}\rangle (z_{c})=0.95u_{j}$
at
$r=0$
. Even if the comparisons must be taken with care due to the moderate Reynolds number and the thick initial shear layers of the present jets, this leads to a better agreement with the measurements of Lau, Morris & Fisher (Reference Lau, Morris and Fisher1979) and Fleury et al. (Reference Fleury, Bailly, Jondeau, Michard and Juvé2008) for jets at
$M=0.9$
and
$Re_{D}\simeq 10^{6}$
plotted in the figure. Downstream of the potential core, the centreline velocity seems to decay at a similar rate in three jets. According to figure 21(b), however, the decay rate is slightly lower for jetT1 and jetT2 than for jetBL.
Figure 21. Variations of centreline mean axial velocity
$\langle u_{z}\rangle$
as a function of (a)
$z$
and (b)
$z-z_{c}$
:
$M=0.9$
:
$\circ$
Lau et al. (Reference Lau, Morris and Fisher1979) at
$Re_{D}=10^{6}$
and ♢ Fleury et al. (Reference Fleury, Bailly, Jondeau, Michard and Juvé2008) at
$Re_{D}=7.7\times 10^{5}$
.
Table 8. Axial position of the end of the potential core
$z_{c}$
and peak r.m.s. values of velocity fluctuations
$u_{z}^{\prime }$
and
$u_{r}^{\prime }$
on the jet axis.
The centreline r.m.s. values of axial velocity fluctuations are shown in figure 22(a). As for the mean-flow profiles, the differences are significant between jetBL and the two jets with transitional boundary-layer profiles, but relatively weak between the latter jets. The results are also closer to the experimental data of Lau et al. (Reference Lau, Morris and Fisher1979) and Fleury et al. (Reference Fleury, Bailly, Jondeau, Michard and Juvé2008) for these jets. The peak turbulence intensities are reached at
$z\simeq 17r_{0}$
for jetBL but later at
$z\simeq 22r_{0}$
for the two other jets, which corresponds, relative to the end of the potential core, to
$z\simeq z_{c}+5r_{0}$
and
$z_{c}+7r_{0}$
respectively. They are equal to 14.3 % for jetBL, but decrease approximately down to 13 % for the jets with non-laminar boundary-layer profiles, see also in table 8 for the radial turbulence intensities. This trend is similar to that obtained in the mixing layers down to
$z=15r_{0}$
in figure 11.
The spectra of the centreline axial velocity fluctuations at
$z=z_{c}+5r_{0}$
, i.e. roughly at the positions of the peak r.m.s. levels, are depicted in figure 22(b) as a function of
$St_{D}$
. The spectra are superimposed and follow a
$-5/3$
power law at
$St_{D}\geqslant 0.5$
, but they significantly differ and show highest levels for jetBL at lower Strouhal numbers. Therefore, stronger large-scale structures are found not only in the mixing layers, but also downstream of the potential core for the jet with a laminar boundary-layer profile. This may be the cause for the divergence in velocity decay of figure 21(b).
Figure 22. Properties of the centreline axial velocity fluctuations
$u_{z}^{\prime }$
: (a) axial variations of r.m.s. values and (b) power spectral densities at
$z=z_{c}+5r_{0}$
as a function of
$St_{D}$
for
$St_{D}^{-5/3}$
. The changes observed between the present jets with laminar and transitional exit mean velocity profiles are comparable to those obtained experimentally between untripped and tripped jets (Raman et al.
Reference Raman, Zaman and Rice1989, Reference Raman, Rice and Reshotko1994; Russ & Strykowski Reference Russ and Strykowski1993), as well as to those happening when the initial fluctuation level increases (Bogey et al.
Reference Bogey, Marsden and Bailly2012b
). In particular, in Raman et al. (Reference Raman, Zaman and Rice1989), tripped and untripped jets at
$M=0.3$
and
$Re_{D}=6\times 10^{5}$
with nozzle-exit turbulence intensities
$u_{e}^{\prime }/u_{j}\simeq 7\,\%$
and boundary-layer shape factors
$H\simeq 1.55$
and
$1.80$
, respectively, were considered. The flow development in the tripped jets is shifted by
$2r_{0}$
in the downstream direction with respect to the untripped jet, which is in line with the results of this study. However, the peak turbulence intensities on the centreline, located at
$z\simeq z_{c}+7r_{0}$
, are similar in the tripped and untripped jets, which disagrees with figure 22. The reason for this may be that the exit boundary layer of the untripped jet of Raman et al. (Reference Raman, Zaman and Rice1989) is not laminar but transitional. This may also be due to the larger boundary-layer thickness in the simulations (Bogey & Marsden Reference Bogey and Marsden2013).
3.4 Acoustic fields
3.4.1 Pressure snapshots
Snapshots of the pressure fields obtained in the LES are given in figure 23. In all cases, large-scale hydrodynamic fluctuations, classically attributed to the flow coherent structures (Arndt et al.
Reference Arndt, Long and Glauser1997), dominate within and very near the jets. Farther from the axis, sound waves emerge and propagate in the acoustic field. The waves emitted in the flow direction are strong and have long wavelengths, which is typical of the downstream subsonic jet noise component (Tam et al.
Reference Tam, Viswanathan, Ahuja and Panda2008). Those travelling in the sideline and upstream directions are weaker and have shorter wavelengths. For the three jets, the latter ones appear to be mainly generated between
$z=5r_{0}$
and
$10r_{0}$
. Their amplitudes, however, are visibly higher for jetBL in figure 23(a) than for jetT1 and jetT2 in figure 23(b,c).
Figure 23. Snapshots in the
$(z,r)$
plane of pressure fluctuations
$p-p_{a}$
for (a) jetBL, (b) jetT1 and (c) jetT2. The colour scale ranges from
$-70$
to
$70$
Pa, from blue to red.
3.4.2 Near-field and far-field pressure levels
The properties of the jet acoustic near fields are investigated from the pressure signals recorded at
$r=L_{r}=15r_{0}$
during the LES. Those of the jet far fields are characterized from the fluctuations given at 150 radii from the nozzle exit by the two ILEE computations of sound propagation described in § 2.5. In the second case, the results presented thereafter for the angles
$\unicode[STIX]{x1D719}\leqslant 60^{\circ }$
relative to the jet direction are obtained in the computation in which the LES data are imposed onto the ILEE grid for
$r\geqslant 7.5r_{0}$
at
$z=L_{z}=40r_{0}$
in order to capture most of the downstream noise components. Those for
$\unicode[STIX]{x1D719}\geqslant 60^{\circ }$
come from the computation in which the LES/ILEE coupling at
$z=L_{z}$
is carried out only for
$r\geqslant 14r_{0}$
to avoid the generation of significant spurious waves for large radiation angles where the noise levels are weak. It should be noted that the two far-field extrapolations provide nearly identical results at
$\unicode[STIX]{x1D719}=60^{\circ }$
for Strouhal numbers greater than
$St_{D}=0.075$
, demonstrating the negligible influence of the downstream extrapolation surface on the frequencies of interest. The overall sound pressure levels in this paper are all calculated by integrating the sound spectra from the Strouhal number value given above.
The noise levels obtained at
$r=15r_{0}$
between
$z=0$
and
$40r_{0}$
, and at 150 radii from the nozzle exit between
$\unicode[STIX]{x1D719}=15^{\circ }$
and
$150^{\circ }$
are represented in figure 24. For illustration purposes, the experimental data of Bogey et al. (Reference Bogey, Barré, Fleury, Bailly and Juvé2007) and Bridges & Brown (Reference Bridges and Brown2005) for isothermal jets at
$M=0.9$
and
$Re_{D}\simeq 10^{6}$
are also plotted. With respect to the simulated jets, these jets have 15–20 times higher Reynolds numbers and certainly quite different nozzle-exit conditions, including much thinner exit boundary layers, which may be the cause for the extra noise radiated by the jet of Bogey et al. (Reference Bogey, Barré, Fleury, Bailly and Juvé2007) in figure 24(a). Despite this, however, a good qualitative agreement is found with the simulation results. More importantly, for all near-field and far-field observation points, the noise levels are 2–3 dB higher for jetBL with a laminar boundary-layer profile than for the two jets with transitional profiles. In addition, the levels for jetT2 are just very slightly lower than those for jetT1. These trends are very similar to those reported for the r.m.s. values of velocity fluctuations in the jets, as expected due to the links existing between acoustic sources and turbulence intensities in subsonic jets (Zaman Reference Zaman1986).
Figure 24. Overall sound pressure levels (OASPL) obtained (a) at
$r=15r_{0}$
and (b) at a distance of
$150r_{0}$
from the nozzle exit as a function of the angle
$\unicode[STIX]{x1D719}$
relative to the jet direction:
$M=0.9$
: ▿ Bogey et al. (Reference Bogey, Barré, Fleury, Bailly and Juvé2007) at
$Re_{D}=7.9\times 10^{5}$
and ▵ Bridges & Brown (Reference Bridges and Brown2005) at
$Re_{D}=10^{6}$
. The sound pressure levels obtained at
$r=15r_{0}$
for the modes
$n_{\unicode[STIX]{x1D703}}=0$
, 1 and 2 are shown in figure 25. The levels for
$n_{\unicode[STIX]{x1D703}}=0$
are maximum at
$z=L_{z}=40r_{0}$
and sharply decrease in the upstream direction, whereas those for
$n_{\unicode[STIX]{x1D703}}=1$
and 2 reach a peak at
$z\simeq 25r_{0}$
and
$z\simeq 20r_{0}$
, respectively. These peak positions are consistent with the far-field directivities found experimentally for the first azimuthal modes. For instance, for the jet at
$M=0.6$
of Cavalieri et al. (Reference Cavalieri, Jordan, Colonius and Gervais2012), noise is strongest in the downstream direction for the axisymmetric mode and for the angles of
$\unicode[STIX]{x1D719}=30^{\circ }$
for
$n_{\unicode[STIX]{x1D703}}=1$
and of
$\unicode[STIX]{x1D719}=40^{\circ }$
for
$n_{\unicode[STIX]{x1D703}}=2$
. Here, for each mode considered, the noise levels are 2–3 dB higher for jetBL than for jetT1 and jetT2, and the levels for the last two jets do not differ appreciably, just as in figure 24 for the full pressure signals. This is in line with the resemblances of the features of the full velocity flow fields and of their first modal components in the azimuthal direction, depicted in figures 17 and 19.
Figure 25. Overall sound pressure levels obtained at
$r=15r_{0}$
for modes (a)
$n_{\unicode[STIX]{x1D703}}=0$
, (b)
$n_{\unicode[STIX]{x1D703}}=1$
and (c)
$n_{\unicode[STIX]{x1D703}}=2$
:
The pressure spectra calculated at
$r=15r_{0}$
at
$z=0$
,
$20r_{0}$
and
$40r_{0}$
are represented in figure 26 as a function of the Strouhal number
$St_{D}$
. Those evaluated in far field for the angles of
$\unicode[STIX]{x1D719}=30^{\circ }$
,
$90^{\circ }$
and
$150^{\circ }$
are provided in figure 27. When possible, the corresponding measurements of Bridges & Brown (Reference Bridges and Brown2005) and Bogey et al. (Reference Bogey, Barré, Fleury, Bailly and Juvé2007) for jets at
$Re_{D}\simeq 10^{6}$
are shown. As for the overall sound levels, they compare well with the simulation results, with a better fit for the data of Bridges & Brown (Reference Bridges and Brown2005). The spectra for the present jets have similar shapes, typical of subsonic jet noise (Mollo-Christensen, Kolpin & Martucelli Reference Mollo-Christensen, Kolpin and Martucelli1964; Tam Reference Tam1998). For small radiation angles, in figure 26(c) and figure 27(a), they are dominated by a narrow-band component centred around
$St_{D}=0.2$
. The noise levels are 2–3 dB higher for jetBL than for the two other jets for
$St_{D}\leqslant 0.3$
, but are rather close to each other for
$St_{D}\geqslant 0.6$
. This can be related to the velocity spectra of figures 17(f) and 22(b) obtained near the end of the potential core, where the downstream acoustic components originate (Panda, Seasholtz & Elam Reference Panda, Seasholtz and Elam2005; Bogey & Bailly Reference Bogey and Bailly2007; Tam et al.
Reference Tam, Viswanathan, Ahuja and Panda2008; Bogey Reference Bogey2019), which also contain stronger low-frequency components for jetBL but are superimposed at high frequencies. For large radiation angles, in figures 26(a,b) and 27(b,c), the pressure spectra are broadband. In that case, the emitted sound is louder for jetBL than for jetT1 and jetT2 not only at
$St_{D}\leqslant 0.3$
as previously, but also at higher Strouhal numbers. In particular, an increase of 1–1.5 dB is noted over
$1.2\leqslant St_{D}\leqslant 4.8$
. This most likely results from the higher turbulence intensities in the mixing layers for jetBL, in a region where the acoustic sources have a wide range of frequencies (Chu & Kaplan Reference Chu and Kaplan1976; Fisher, Harper-Bourne & Glegg Reference Fisher, Harper-Bourne and Glegg1977; Narayanan, Barber & Polak Reference Narayanan, Barber and Polak2002; Lee & Bridges Reference Lee and Bridges2005). The difference at
$St_{D}\geqslant 3.2$
is however rather surprising given the velocity spectra of figures 17 and 22, none of which exhibits stronger components at such Strouhal numbers for jetBL.
Figure 26. Sound pressure levels (SPL) obtained at
$r=15r_{0}$
at (a)
$z=0$
, (b)
$z=20r_{0}$
and (c)
$z=40r_{0}$
, as a function of
$St_{D}$
:
$M=0.9$
and
$Re_{D}=7.9\times 10^{5}$
.
Figure 27. Sound pressure levels obtained at
$150r_{0}$
from the nozzle exit for (a)
$\unicode[STIX]{x1D719}=30^{\circ }$
, (b)
$\unicode[STIX]{x1D719}=90^{\circ }$
and (c)
$\unicode[STIX]{x1D719}=150^{\circ }$
, as a function of
$St_{D}$
:
$M=0.9$
and
$Re_{D}=10^{6}$
. It is difficult to compare the present results with the experimental data available for tripped and untripped jets, because tripping usually mainly results in removing the noise generated by the vortex pairings occurring in fully laminar jets (Zaman Reference Zaman1985a
; Bridges & Hussain Reference Bridges and Hussain1987; Bogey & Bailly Reference Bogey and Bailly2010; Bogey et al.
Reference Bogey, Marsden and Bailly2012b
). Nevertheless, they bear significant similarities with the results obtained for the jets exhausting from the ASME and the conical nozzles (Viswanathan & Clark Reference Viswanathan and Clark2004; Zaman Reference Zaman2012; Karon & Ahuja Reference Karon and Ahuja2013). Indeed, approximately 2 dB more noise is emitted in the first case, which was attributed by Zaman (Reference Zaman2012) to the fact that the exit boundary layers are nominally laminar with the ASME nozzle, but turbulent with the conical nozzle. This hypothesis was further supported by Karon & Ahuja (Reference Karon and Ahuja2013) who measured lower boundary-layer shape factors for the conical nozzle and found, for instance,
$H=2.34$
in the ASME case but
$H=1.71$
in the conical case for
$M=0.4$
, as indicated in table 1. The difference in noise level between the ASME and the conical nozzles is maximum at frequencies typically one decade higher than the jet noise peak frequencies, and is stronger for
$\unicode[STIX]{x1D719}=90^{\circ }$
than for
$\unicode[STIX]{x1D719}=30^{\circ }$
. Neither of these trends are observed in this work. This may be due to the thick boundary layers in the simulations, yielding a peak Strouhal number of only
$St_{D}=1.20$
early on in the shear layers of jetBL. By making the boundary-layer/shear-layer transition happen over a distance of
$5r_{0}{-}6r_{0}$
for jetBL, the thick exit velocity profiles also allow the effects of the boundary-layer shape on the mixing-layer turbulent structures to persist, as pointed out in § 3.3.2, down to the end of the potential core, where low-frequency sound waves are radiated in the downstream direction. Thus, it can be assumed that with a thinner boundary layer, the extra noise components for the jet with a laminar nozzle-exit mean velocity profile would emerge at higher frequencies, and would be lower for small emission angles, leading to a better agreement with the ASME case.
4 Conclusion
The influence of the nozzle-exit velocity profile has been investigated for isothermal round jets at a Mach number of
$M=0.9$
and a Reynolds number of
$Re_{D}=5\times 10^{4}$
with a boundary-layer momentum thickness of 2.8 % of the jet radius and a peak turbulence intensity of 6 % at the exit of pipe nozzle. One jet with a laminar boundary-layer profile of shape factor
$H=2.29$
and two jets with transitional profiles with
$H=1.71$
and 1.96 are considered. The jet flow and sound fields computed for the laminar profile differ significantly from those for the two transitional profiles. The latter ones are very close to each other, suggesting that similar results would be obtained for a turbulent profile. In the non-laminar cases, the jets develop more slowly, the turbulence intensities are lower in the mixing layers but also just downstream of the jet potential core, and less noise is emitted in the acoustic field. Due to the sharper velocity gradient very near the nozzle, the initial shear-layer instability waves also grow more rapidly and at higher frequencies, in agreement with the predictions of a linear stability analysis performed from the simulation profiles. Compared to the peak unstable frequencies in a mixing layer of same momentum thickness, these frequencies are similar for the jet with a laminar boundary-layer profile, but greater for the two other ones. As a result, the initial instability waves persist over a larger distance in the laminar case, organizing the flow and leading to stronger large-scale structures downstream of the boundary-layer/mixing-layer transition, than in the non-laminar cases.
By combining high-fidelity computations of jets with well-controlled upstream conditions and linear stability analyses, this study suggests explanations for and connections between some flow and acoustic features of free shear flows and jets, which have been observed experimentally for years or even decades but whose reasons are still unclear. This is the case for the discrepancy in frequency of the initial instability waves between initially laminar and initially turbulent conditions. The present results show that this discrepancy is due to the fact that the most unstable frequencies near the nozzle are fixed by the maximum velocity gradient and not by the boundary-layer momentum thickness. Concerning the controversial issue of the persistence of coherent structures in turbulent mixing layers, it is found that that such structures are more likely to form for a laminar boundary-layer profile than for a non-laminar profile, because of the continuity of the peak instability-wave frequencies during the changeover from a boundary-layer to a mixing-layer profile in the first case, but of their significant decrease in the other one. Thus, it becomes easier to understand why for some nozzles such as the ASME nozzle, at the exit of which the flow is highly disturbed but the mean velocity profile is laminar, intense large-scale structures appear in the mixing layers and additional noise is measured in the acoustic field.
In this paper, in order to ensure a high numerical accuracy at a reasonable computational cost, the effects of the boundary-layer velocity profile have been investigated for a jet at a Reynolds number of
$Re_{D}=5\times 10^{4}$
with a thick boundary layer. Of course, it would be interesting to consider jets at higher Reynolds numbers with thinner boundary layers in further simulations to get closer to the conditions encountered in the laboratory-scale experiments of the literature. New experiments detailing the shear-layer turbulence properties just downstream of the nozzle for laminar and turbulent nozzle-exit velocity profiles would also be a useful complement of the present work.
Acknowledgements
This work was granted access to the HPC resources of FLMSN (Fédération Lyonnaise de Modélisation et Sciences Numériques), partner of EQUIPEX EQUIP@MESO, and of the resources of CINES (Centre Informatique National de l’Enseignement Supérieur) and IDRIS (Institut du Développement et des Ressources en Informatique Scientifique) under the allocation 2018-2a0204 made by GENCI (Grand Equipement National de Calcul Intensif). It was performed within the framework of the Labex CeLyA of Université de Lyon, within the programme ‘Investissements d’Avenir’ (ANR-10-LABX-0060/ANR-16-IDEX-0005) operated by the French National Research Agency (ANR).
Appendix A
In the simulations of jetT1 and jetT2, the axial velocity profiles T1 and T2 given by equation (2.4) with
$i=1$
and
$2$
are imposed at the pipe-nozzle inlet at
$z=-2r_{0}$
. Considering the strong similarities between the near-wall mean-flow statistics obtained for turbulent pipe and boundary-layer flows (Monty et al.
Reference Monty, Hutchins, Ng, Marusic and Chong2009), they have been designed to fit the experimental data provided by Schubauer & Klebanoff (Reference Schubauer and Klebanoff1955) for a boundary layer over a flat plate in the region of laminar–turbulent flow transition at two axial positions. For the comparison, the measured profiles and the T1 and T2 profiles are represented in figure 28 as a function of the distance to the wall as in the experiment, using the boundary-layer thicknesses of
$\unicode[STIX]{x1D6FF}_{T_{1}}=0.73$
cm and
$\unicode[STIX]{x1D6FF}_{T_{2}}=1.17$
cm in equation (2.4). In both cases, a very good agreement is observed close to the wall as well as far away from it.
Figure 28. Representation of boundary-layer mean velocity profiles measured by Schubauer & Klebanoff (Reference Schubauer and Klebanoff1955) close to the laminar–turbulent transition and of profiles given by (2.4) with
$y=r_{0}-r$
: (a) ○ measurements at
$x=1.91~\text{m}$
and —— profile T1 with
$\unicode[STIX]{x1D6FF}_{T_{1}}=0.73~\text{cm}$
, (b) ○ measurements at
$x=2.06~\text{m}$
and —— profile T2 with
$\unicode[STIX]{x1D6FF}_{T_{2}}=1.17~\text{cm}$
.
Appendix B
In a preliminary grid-sensitivity study, simulations of jetT1 and jetT2 have been performed using two grids extending in the axial direction, excluding the outflow sponge zones, only down to
$z=4r_{0}$
in order to save computational time. The coarsest of the two grids coincides with the grid used for the full jet LES, defined in table 3, in the boundary-layer region. The finest grid is identical to the coarsest one in the directions
$\unicode[STIX]{x1D703}$
and
$z$
, but differs in the radial direction with
$\unicode[STIX]{x0394}r/r_{0}=0.18\,\%$
instead of
$\unicode[STIX]{x0394}r/r_{0}=0.36\,\%$
at
$r=r_{0}$
. In the two additional LES, the tripping procedure is exactly the same as in the jet LES. In the LES using the finest grid, however, the time step is twice as small because of the numerical stability condition, leading to an application of the relaxation filtering that is twice as frequent. The flow properties obtained using the two different grids at the nozzle exit are found to be nearly identical. Consequently, they depend neither on the wall-normal spacing, nor on the explicit filtering applied to remove grid-to-grid oscillations as well as to relax subgrid-scale turbulent energy.
Figure 29. Nozzle-exit profiles (a) of mean axial velocity
$\langle u_{z}\rangle$
and (b) of turbulence intensities
$\langle u_{z}^{\prime 2}\rangle ^{1/2}/u_{j}$
, ——
$\langle u_{r}^{\prime 2}\rangle ^{1/2}/u_{j}$
, – – –
$\langle u_{\unicode[STIX]{x1D703}}^{\prime 2}\rangle ^{1/2}/u_{j}$
and – ⋅ –⋅
$\langle u_{r}^{\prime }u_{z}^{\prime }\rangle ^{1/2}/u_{j}$
obtained for jetT2 using (black)
$\unicode[STIX]{x0394}r/r_{0}=0.36\,\%$
and (grey)
$\unicode[STIX]{x0394}r/r_{0}=0.18\,\%$
at
$r=r_{0}$
.
Figure 30. Nozzle-exit profiles (a) of mean axial velocity and (b) of turbulence intensities, represented in wall units based on the wall friction velocity using the same line types as in figure 29.
By way of illustration, the nozzle-exit profiles of mean axial velocity and of turbulence intensities obtained for jetT2, that is for the jet with the sharpest boundary-layer profile, are represented in figure 29 using outer units and in figure 30 using wall units. The solutions calculated using the two grids with
$\unicode[STIX]{x0394}r/r_{0}=0.36\,\%$
and
$\unicode[STIX]{x0394}r/r_{0}=0.18\,\%$
at the wall superpose or are very close to each other.
