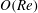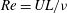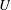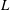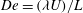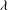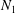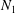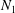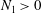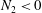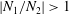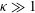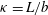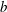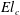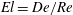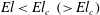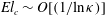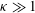1. Introduction
We examine the orientation of a sedimenting spheroid, of an arbitrary aspect ratio, under the influence of weak inertia and viscoelasticity. The orientation dynamics of a single anisotropic particle in an otherwise quiescent fluid is the first step to understanding the dynamics of a sedimenting suspension of such particles. Examples of anisotropic particle suspensions abound in both natural settings and industrial applications. Paper manufacture involves the processing of cellulose fibre suspensions in an aqueous medium, and the orientation distribution of the high-aspect-ratio fibres under flow conditions decides, in part, the characteristics of the final product. Fibre-like inclusions in a polymer matrix are known to enhance the mechanical properties of the resulting composite, and the degree of enhancement depends strongly on the fibre orientations. The latter in turn is determined by the flow conditions in the molten state. Sedimentation of anisotropic particles (or, more generally, migration under the action of a body force) is directly relevant to gravity-based concentration of naturally occurring flake-shaped mineral particles, to the settling and aggregation of large crystallites in magma chambers (Koyaguchi et al. Reference Koyaguchi, Hallworth, Huppert and Sparks1990; Schwindinger Reference Schwindinger1999), and to the determination of haematocrit by centrifugation (Caro et al. Reference Caro, Pedley, Schroter and Seed2012). Competition between the sedimentation-induced orientation drift and turbulent dispersion controls the anisotropy of the orientation distribution of ice crystals in clouds which, in turn, determines their scattering and absorption characteristics (Cho, Iribarne & Richards Reference Cho, Iribarne and Richards1981; Klett Reference Klett1995; Garrett et al. Reference Garrett, Gerber, Baumgardner, Twohy and Weinstock2003; Hogan et al. Reference Hogan, Tian, Brown, Westbrook, Heymsfield and Eastment2012). The role of clouds in the global radiative budget is well known (Ramanathan, Barkstrom & Harrison Reference Ramanathan, Barkstrom and Harrison1989).
The study of sedimenting anisotropic particles is also of immense fundamental significance. The pioneering work of Koch & Shaqfeh (Reference Koch and Shaqfeh1989) with regard to the instability of a homogeneous dilute suspension of sedimenting spheroids to number-density waves, and later experiments (Herzhaft & Guazzelli Reference Herzhaft and Guazzelli1999) and numerical simulations (Butler & Shaqfeh Reference Butler and Shaqfeh2002; Saintillan, Shaqfeh & Darve Reference Saintillan, Shaqfeh and Darve2006) of such suspensions that examine the particle–cluster dynamics in the nonlinear regime, highlight the profound differences in the nature of the number-density fluctuations in relation to those known for a stable homogeneous suspension of sedimenting spheres (Caflisch & Luke Reference Caflisch and Luke1985; Koch & Shaqfeh Reference Koch and Shaqfeh1991; Herzhaft et al. Reference Herzhaft, Hinch, Nicolai and Guazzelli1995; Tee et al. Reference Tee, Weitz, Shraiman, Mucha and Brenner2004). Recent efforts have examined the effects of microscale inertia (Shin, Koch & Subramanian Reference Shin, Koch and Subramanian2006, Reference Shin, Koch and Subramanian2009) and suspending fluid viscoelasticity (Ramanathan & Saintillan Reference Ramanathan and Saintillan2012) on the above instability. In the linear stability scenario, there is a quasisteady balance between the weak-shear-induced torque (associated with a small-amplitude velocity perturbation) and the torque acting on an isolated sedimenting particle in the absence of a shear. The resulting orientation drift, together with the migration induced by a lift force associated with the weak shearing flow, determine the stability of the homogeneous state. The original analysis of Koch and Shaqfeh, in the Stokes regime, relied on the shearing torque acting alone to produce an excess of particle orientations along the local extensional axis, and the resulting orientation drift led to an exponential growth of concentration inhomogeneities (Koch & Shaqfeh Reference Koch and Shaqfeh1989). Shin et al. (Reference Shin, Koch and Subramanian2009) show that the shifting of the orientation peak towards the plane transverse to gravity, on account of the inertial torque acting to orient particles broadside-on, together with an additional stabilizing inertial lift force, weakens the original instability. In the viscoelastic case, the lift force is destabilizing, and even a suspension of spherical particles is unstable (Ramanathan & Saintillan Reference Ramanathan and Saintillan2012). An estimate of the inertial and viscoelastic torques acting on an isolated particle would be crucial in determining the orientation drift, which, as seen above, controls stability of a dilute suspension either in presence of inertia or in a viscoelastic fluid. One expects the stability characteristics to be a sensitive function of the particle aspect ratio. This serves as an additional motivation for determining the torque on a model anisotropic particle due to inertia or viscoelasticity.
An argument based on reversibility of the Stokes equations shows that an axisymmetric particle, that is additionally fore–aft symmetric, must retain its initial orientation when sedimenting under gravity. This leads to a problem when calculating averaged properties such as the bulk sedimentation rate since the particle orientation distribution, in the Stokesian regime, is indeterminate in the absence of interparticle interactions. In this paper, we have taken the spheroidal geometry as being representative of a general axisymmetric particle. The torques on a spheroid, due to the first effects of fluid inertia and viscoelasticity, are determined as a function of its aspect ratio
![]() ${\it\kappa}=L/b$
,
${\it\kappa}=L/b$
,
![]() $L$
and
$L$
and
![]() $b$
being the semi-major and semi-minor axes, respectively. Even weak torques will have a strong cumulative effect over long times, and lead to a particle orientation distribution independent of initial conditions, eliminating the above orientational degeneracy (Leal Reference Leal1979). The analysis is largely restricted to the limit
$b$
being the semi-major and semi-minor axes, respectively. Even weak torques will have a strong cumulative effect over long times, and lead to a particle orientation distribution independent of initial conditions, eliminating the above orientational degeneracy (Leal Reference Leal1979). The analysis is largely restricted to the limit
![]() $\mathit{Re},\mathit{De}\ll 1$
, where
$\mathit{Re},\mathit{De}\ll 1$
, where
![]() $\mathit{Re}={\it\rho}UL/{\it\mu}$
and
$\mathit{Re}={\it\rho}UL/{\it\mu}$
and
![]() $\mathit{De}=U{\it\lambda}/L$
are dimensionless measures of the importance of inertia and elasticity on the scale of the particle; here,
$\mathit{De}=U{\it\lambda}/L$
are dimensionless measures of the importance of inertia and elasticity on the scale of the particle; here,
![]() $U$
is the sedimentation velocity,
$U$
is the sedimentation velocity,
![]() ${\it\nu}$
is the fluid kinematic viscosity and
${\it\nu}$
is the fluid kinematic viscosity and
![]() ${\it\lambda}$
is a representative microstructural relaxation time in the viscoelastic case. For small
${\it\lambda}$
is a representative microstructural relaxation time in the viscoelastic case. For small
![]() $\mathit{De}$
, the stress in a viscoelastic fluid may be expanded as a retarded-motion expansion, with a truncation at
$\mathit{De}$
, the stress in a viscoelastic fluid may be expanded as a retarded-motion expansion, with a truncation at
![]() $O(\mathit{De}^{n})$
yielding the constitutive equation for the
$O(\mathit{De}^{n})$
yielding the constitutive equation for the
![]() $n\text{th}$
order Rivlin–Ericksen fluid (Bird, Armstrong & Hassager Reference Bird, Armstrong and Hassager1987; Larson Reference Larson1988). The
$n\text{th}$
order Rivlin–Ericksen fluid (Bird, Armstrong & Hassager Reference Bird, Armstrong and Hassager1987; Larson Reference Larson1988). The
![]() $O(\mathit{De})$
torque may be evaluated using the leading-order departure from a Newtonian behaviour in this expansion, which corresponds to a second-order fluid. The constitutive equation for the latter is characterized by a single dimensionless parameter, denoted here by
$O(\mathit{De})$
torque may be evaluated using the leading-order departure from a Newtonian behaviour in this expansion, which corresponds to a second-order fluid. The constitutive equation for the latter is characterized by a single dimensionless parameter, denoted here by
![]() ${\it\epsilon}$
, which determines the ratio of the first (
${\it\epsilon}$
, which determines the ratio of the first (
![]() $N_{1}$
) and the second (
$N_{1}$
) and the second (
![]() $N_{2}$
) normal stress differences; specifically,
$N_{2}$
) normal stress differences; specifically,
![]() $N_{2}/N_{1}=-(1+2{\it\epsilon})/2{\it\epsilon}$
(Larson Reference Larson1988; Koch & Subramanian Reference Koch and Subramanian2006). In appendix A, we also analyse the corrections to the Stokes drag on a spheroid for small but finite
$N_{2}/N_{1}=-(1+2{\it\epsilon})/2{\it\epsilon}$
(Larson Reference Larson1988; Koch & Subramanian Reference Koch and Subramanian2006). In appendix A, we also analyse the corrections to the Stokes drag on a spheroid for small but finite
![]() $\mathit{Re}$
and
$\mathit{Re}$
and
![]() $\mathit{De}$
. As argued therein, the symmetry of the Stokes velocity field and the regular nature of the viscoelastic drag contribution implies that the leading-order correction in this case is
$\mathit{De}$
. As argued therein, the symmetry of the Stokes velocity field and the regular nature of the viscoelastic drag contribution implies that the leading-order correction in this case is
![]() $O(\mathit{De}^{2})$
rather than
$O(\mathit{De}^{2})$
rather than
![]() $O(\mathit{De})$
, and requires, in principle, a third-order fluid rheology for its calculation. A sedimenting spheroid of an arbitrary orientation is therefore analogous to a translating sphere where there is a decrease in the drag coefficient, only at
$O(\mathit{De})$
, and requires, in principle, a third-order fluid rheology for its calculation. A sedimenting spheroid of an arbitrary orientation is therefore analogous to a translating sphere where there is a decrease in the drag coefficient, only at
![]() $O(\mathit{De}^{2})$
, due to elastic effects (Caswell & Schwarz Reference Caswell and Schwarz1962; Chilcott & Rallison Reference Chilcott and Rallison1988). The aforementioned reversibility argument leads to degenerate situations even in the presence of an ambient shearing flow. Neutrally buoyant axisymmetric particles in a simple shear flow rotate along Jeffery orbits, with the distribution across orbits being determined by the initial orientation distribution in the Stokes limit (Jeffery Reference Jeffery1922). This leads to an indeterminate suspension rheology in shear, and there have been earlier efforts that examine the role of weak Brownian motion in determining the orientation distribution across Jeffery orbits (Leal & Hinch Reference Leal and Hinch1971; Hinch & Leal Reference Hinch and Leal1972). The resolution of this indeterminacy due to microscale inertia, for arbitrary aspect ratio spheroids, is examined in a companion paper (Dabade, Marath & Subramanian Reference Dabade, Marath and Subramanian2015).
$O(\mathit{De}^{2})$
, due to elastic effects (Caswell & Schwarz Reference Caswell and Schwarz1962; Chilcott & Rallison Reference Chilcott and Rallison1988). The aforementioned reversibility argument leads to degenerate situations even in the presence of an ambient shearing flow. Neutrally buoyant axisymmetric particles in a simple shear flow rotate along Jeffery orbits, with the distribution across orbits being determined by the initial orientation distribution in the Stokes limit (Jeffery Reference Jeffery1922). This leads to an indeterminate suspension rheology in shear, and there have been earlier efforts that examine the role of weak Brownian motion in determining the orientation distribution across Jeffery orbits (Leal & Hinch Reference Leal and Hinch1971; Hinch & Leal Reference Hinch and Leal1972). The resolution of this indeterminacy due to microscale inertia, for arbitrary aspect ratio spheroids, is examined in a companion paper (Dabade, Marath & Subramanian Reference Dabade, Marath and Subramanian2015).
We obtain, for the first time, analytical expressions for both the inertial and viscoelastic torques acting on prolate and oblate spheroids of an arbitrary aspect ratio. The simpler expressions for limiting cases allow comparison with earlier literature discussed below. The sedimentation problem here, and the shear flow problem in a companion paper (Dabade et al.
Reference Dabade, Marath and Subramanian2015), also serve as testing grounds for a novel spheroidal harmonics formalism, developed by Kushch and co-workers (Kushch Reference Kushch1997, Reference Kushch1998; Kushch & Sangani Reference Kushch and Sangani2000), and discussed in some detail in § 3. The motion of a sedimenting spheroid in an otherwise quiescent fluid is a classical problem in theoretical microhydrodynamics, and there have been several analytical investigations, in the Stokes regime, based on the method of singularities (Chwang & Wu Reference Chwang and Wu1974, Reference Chwang and Wu1975; Chwang Reference Chwang1975; Kim Reference Kim1985a
; Kim & Arunachalam Reference Kim and Arunachalam1987). Analytical investigations of the perturbing effects of inertia and viscoelasticity have been restricted to slender fibres or near-spheres. Cox (Reference Cox1965) found the
![]() $O(\mathit{Re})$
inertial torque acting on a spheroid of small eccentricity, and later, Khayat & Cox (Reference Khayat and Cox1989) obtained the inertial torque, for finite
$O(\mathit{Re})$
inertial torque acting on a spheroid of small eccentricity, and later, Khayat & Cox (Reference Khayat and Cox1989) obtained the inertial torque, for finite
![]() $\mathit{Re}$
, acting on a sedimenting fibre of large aspect ratio (such that
$\mathit{Re}$
, acting on a sedimenting fibre of large aspect ratio (such that
![]() $\mathit{Re}<O(\ln {\it\kappa})$
,
$\mathit{Re}<O(\ln {\it\kappa})$
,
![]() ${\it\kappa}$
being the fibre aspect ratio) using slender-body theory (Batchelor Reference Batchelor1970; Cox Reference Cox1970); a simpler derivation, based on a Fourier-space formulation of the generalized reciprocal theorem, was given by Subramanian & Koch (Reference Subramanian and Koch2005). The results obtained here are consistent with the above limiting forms. The slow sedimentation of a slender particle in a second-order fluid was first analysed by Leal (Reference Leal1975). In accordance with arguments based on tensioned streamlines (for
${\it\kappa}$
being the fibre aspect ratio) using slender-body theory (Batchelor Reference Batchelor1970; Cox Reference Cox1970); a simpler derivation, based on a Fourier-space formulation of the generalized reciprocal theorem, was given by Subramanian & Koch (Reference Subramanian and Koch2005). The results obtained here are consistent with the above limiting forms. The slow sedimentation of a slender particle in a second-order fluid was first analysed by Leal (Reference Leal1975). In accordance with arguments based on tensioned streamlines (for
![]() $N_{1}>0$
), the elastic torque acts to turn the particle into a vertical orientation. However, the
$N_{1}>0$
), the elastic torque acts to turn the particle into a vertical orientation. However, the
![]() $O(\mathit{De})$
torque from Leal’s analysis, which stabilizes the vertical orientation, remains finite even for an infinitely slender fibre (
$O(\mathit{De})$
torque from Leal’s analysis, which stabilizes the vertical orientation, remains finite even for an infinitely slender fibre (
![]() ${\it\kappa}\rightarrow \infty$
). The analysis here, and supporting scaling arguments, show that the original analysis is erroneous. The torque is logarithmically small in the limit of large aspect ratios, although the approach to zero is remarkably abrupt in character – the elastic torque begins to decrease only beyond an aspect ratio of
${\it\kappa}\rightarrow \infty$
). The analysis here, and supporting scaling arguments, show that the original analysis is erroneous. The torque is logarithmically small in the limit of large aspect ratios, although the approach to zero is remarkably abrupt in character – the elastic torque begins to decrease only beyond an aspect ratio of
![]() $O(100)$
for a general second-order fluid! The sedimentation of a general axisymmetric particle was also examined by Brunn (Reference Brunn1977). While he showed, based on symmetry arguments, the stabilization of either the vertical or horizontal orientation in a second-order fluid, as to which one of these orientations is actually stabilized was not known in the absence of a detailed calculation.
$O(100)$
for a general second-order fluid! The sedimentation of a general axisymmetric particle was also examined by Brunn (Reference Brunn1977). While he showed, based on symmetry arguments, the stabilization of either the vertical or horizontal orientation in a second-order fluid, as to which one of these orientations is actually stabilized was not known in the absence of a detailed calculation.
Apart from the above analytical results, there have been semi-analytical calculations of the torque acting on an arbitrary aspect ratio prolate spheroid. Kim (Reference Kim1986a
) examined the torque on a prolate spheroid sedimenting in a second-order fluid. More recently, Galdi et al. (Reference Galdi, Vaidya, Pokorny, Daniel and Feng2002) have determined the inertial and viscoelastic torques on a sedimenting prolate spheroid. The authors use singularity representations for the disturbance velocity fields originally developed for prolate spheroids (Chwang & Wu Reference Chwang and Wu1974, Reference Chwang and Wu1975), and later extended by Kim and co-workers to tri-axial ellipsoids (Kim Reference Kim1985a
,Reference Kim
b
, Reference Kim1986b
; Kim & Arunachalam Reference Kim and Arunachalam1987); although analytical forms of the disturbance velocity fields were used, the final torque integral in both cases was evaluated numerically. A simple analytical result was found by Kim (Reference Kim1986a
) in the co-rotational limit (
![]() ${\it\epsilon}=-1;N_{2}/N_{1}=-1/2$
) for a tri-axial ellipsoid. Galdi (Reference Galdi2000) independently obtained a similar result for a prolate spheroid in this limit via an expression that involves only the surface vorticity field. Although the co-rotational limit is unrealistic for a dilute polymer solution (typical normal stress difference ratios correspond to
${\it\epsilon}=-1;N_{2}/N_{1}=-1/2$
) for a tri-axial ellipsoid. Galdi (Reference Galdi2000) independently obtained a similar result for a prolate spheroid in this limit via an expression that involves only the surface vorticity field. Although the co-rotational limit is unrealistic for a dilute polymer solution (typical normal stress difference ratios correspond to
![]() ${\it\epsilon}$
ranging between
${\it\epsilon}$
ranging between
![]() $-0.5$
and
$-0.5$
and
![]() $-0.7$
; see Koch & Subramanian Reference Koch and Subramanian2006), it is a better approximation for other complex fluids (colloidal suspensions and emulsions) that also exhibit a second-order rheology in appropriate limits. Galdi et al. (Reference Galdi, Vaidya, Pokorny, Daniel and Feng2002) have characterized their results in terms of a critical elasticity number (
$-0.7$
; see Koch & Subramanian Reference Koch and Subramanian2006), it is a better approximation for other complex fluids (colloidal suspensions and emulsions) that also exhibit a second-order rheology in appropriate limits. Galdi et al. (Reference Galdi, Vaidya, Pokorny, Daniel and Feng2002) have characterized their results in terms of a critical elasticity number (
![]() $\mathit{El}$
), defined as the ratio
$\mathit{El}$
), defined as the ratio
![]() $\mathit{De}/\mathit{Re}$
, as a function of the aspect ratio. The numerically determined curve correctly predicts the viscoelastic torque for a slender fibre to be much greater in magnitude than the inertial torque for comparable
$\mathit{De}/\mathit{Re}$
, as a function of the aspect ratio. The numerically determined curve correctly predicts the viscoelastic torque for a slender fibre to be much greater in magnitude than the inertial torque for comparable
![]() $\mathit{De}$
and
$\mathit{De}$
and
![]() $\mathit{Re}$
. The analysis here shows that, for large
$\mathit{Re}$
. The analysis here shows that, for large
![]() ${\it\kappa}$
,
${\it\kappa}$
,
![]() $\mathit{Re}$
needs to be
$\mathit{Re}$
needs to be
![]() $O(\ln {\it\kappa})$
larger than
$O(\ln {\it\kappa})$
larger than
![]() $\mathit{De}$
for inertial effects to remain comparable. The above authors also observed an unexpected reversal in sign of the viscoelastic torque for certain ranges of
$\mathit{De}$
for inertial effects to remain comparable. The above authors also observed an unexpected reversal in sign of the viscoelastic torque for certain ranges of
![]() ${\it\epsilon}$
, and for large aspect ratios. It will be seen in § 4.2.4 that such a change in sign is due to the use of an incorrect constitutive equation for a second-order fluid. Our analysis predicts the total viscoelastic torque to have the same sign (opposite to the inertial torque) for the relevant values of
${\it\epsilon}$
, and for large aspect ratios. It will be seen in § 4.2.4 that such a change in sign is due to the use of an incorrect constitutive equation for a second-order fluid. Our analysis predicts the total viscoelastic torque to have the same sign (opposite to the inertial torque) for the relevant values of
![]() ${\it\epsilon}$
.
${\it\epsilon}$
.
The paper is structured as follows. In § 2, we use the generalized reciprocal theorem (Leal Reference Leal1979; Subramanian & Koch Reference Subramanian and Koch2005, Reference Subramanian and Koch2006) to obtain the inertial and viscoelastic contributions to the torque in terms of the disturbance velocity fields for canonical motions of a spheroid. In § 3, we discuss in detail the spheroidal harmonics formalism, originally developed for elastic composites by Kushch and co-workers (Kushch Reference Kushch1997, Reference Kushch1998; Kushch & Sangani Reference Kushch and Sangani2000; Kushch & Sevostianov Reference Kushch and Sevostianov2004), and use it to obtain the Stokes disturbance velocity fields for a translating and rotating spheroid required by the reciprocal theorem formulation. The results are developed in detail for a prolate spheroid, with those for an oblate spheroid being obtained via a simple transformation. In § 4, we first present analytical expressions for the inertial torque in § 4.1. For the viscoelastic torque, the results of relevance to dilute polymer solutions are given in § 4.2.1, while § 4.2.2 combines the inertial and viscoelastic torques, the latter for polymer solutions, in terms of a plot of the critical elasticity number (
![]() $\mathit{El}$
) as a function of the aspect ratio. Next, in § 4.2.3, we examine the slender-fibre limit in some detail, in light of earlier erroneous results, and finally, in § 4.2.4, we discuss the
$\mathit{El}$
) as a function of the aspect ratio. Next, in § 4.2.3, we examine the slender-fibre limit in some detail, in light of earlier erroneous results, and finally, in § 4.2.4, we discuss the
![]() ${\it\epsilon}$
-dependence of the elastic torque, with the emphasis being on a general second-order fluid rather than the restricted range of
${\it\epsilon}$
-dependence of the elastic torque, with the emphasis being on a general second-order fluid rather than the restricted range of
![]() ${\it\epsilon}$
that pertains to polymer solutions. In § 5, we present a discussion of the sedimentation problem outside the restrictive second-order fluid paradigm, together with some analysis, the emphasis being on large aspect ratios. Section 6 includes a summary of the main results.This is followed by a brief examination of the importance of flexibility for large-aspect-ratio fibres, and the possibility of the neutral curve being determined from a balance between fibre flexibility and fluid viscoelasticity.
${\it\epsilon}$
that pertains to polymer solutions. In § 5, we present a discussion of the sedimentation problem outside the restrictive second-order fluid paradigm, together with some analysis, the emphasis being on large aspect ratios. Section 6 includes a summary of the main results.This is followed by a brief examination of the importance of flexibility for large-aspect-ratio fibres, and the possibility of the neutral curve being determined from a balance between fibre flexibility and fluid viscoelasticity.
2. The generalized reciprocal theorem
The generalized reciprocal theorem relates the velocity and stress fields of the problem of interest,
![]() $({\bf\sigma}^{(1)},\boldsymbol{u}^{(1)})$
, and a simpler test problem,
$({\bf\sigma}^{(1)},\boldsymbol{u}^{(1)})$
, and a simpler test problem,
![]() $({\bf\sigma}^{(2)},\boldsymbol{u}^{(2)})$
, for which the solution is known. Both
$({\bf\sigma}^{(2)},\boldsymbol{u}^{(2)})$
, for which the solution is known. Both
![]() $({\bf\sigma}^{(1)},\boldsymbol{u}^{(1)})$
and
$({\bf\sigma}^{(1)},\boldsymbol{u}^{(1)})$
and
![]() $({\bf\sigma}^{(2)},\boldsymbol{u}^{(2)})$
are solutions of the flow past the same body (a spheroid in the present case), but with different boundary conditions and possibly governed by different dynamical equations (Leal Reference Leal1979; Subramanian & Koch Reference Subramanian and Koch2005, Reference Subramanian and Koch2006). Since the quantities of interest here are both the inertial and viscoelastic torques on a sedimenting spheroid,
$({\bf\sigma}^{(2)},\boldsymbol{u}^{(2)})$
are solutions of the flow past the same body (a spheroid in the present case), but with different boundary conditions and possibly governed by different dynamical equations (Leal Reference Leal1979; Subramanian & Koch Reference Subramanian and Koch2005, Reference Subramanian and Koch2006). Since the quantities of interest here are both the inertial and viscoelastic torques on a sedimenting spheroid,
![]() $({\bf\sigma}^{(1)},\boldsymbol{u}^{(1)})$
is taken to correspond to a spheroid translating in an otherwise quiescent non-Newtonian fluid, with the inertial acceleration being taken into account. The test problem,
$({\bf\sigma}^{(1)},\boldsymbol{u}^{(1)})$
is taken to correspond to a spheroid translating in an otherwise quiescent non-Newtonian fluid, with the inertial acceleration being taken into account. The test problem,
![]() $({\bf\sigma}^{(2)},\boldsymbol{u}^{(2)})$
corresponds to the inertialess rotation of a spheroid (with the same instantaneous orientation) in a Newtonian fluid at rest and about an axis transverse to its axis of symmetry. The reciprocal theorem then yields the following identity:
$({\bf\sigma}^{(2)},\boldsymbol{u}^{(2)})$
corresponds to the inertialess rotation of a spheroid (with the same instantaneous orientation) in a Newtonian fluid at rest and about an axis transverse to its axis of symmetry. The reciprocal theorem then yields the following identity:
where
![]() $\boldsymbol{n}$
is the unit normal pointing out of the fluid domain
$\boldsymbol{n}$
is the unit normal pointing out of the fluid domain
![]() $V$
. As will be seen below, the disturbance velocity fields decay sufficiently rapidly away from the particle, so the surface integrals at infinity may be neglected, and the bounding surface
$V$
. As will be seen below, the disturbance velocity fields decay sufficiently rapidly away from the particle, so the surface integrals at infinity may be neglected, and the bounding surface
![]() $S$
in the integrals in (2.1) is that of the spheroid (
$S$
in the integrals in (2.1) is that of the spheroid (
![]() $S_{p}$
).
$S_{p}$
).
The non-dimensional equations of motion and the continuity equation for the problem of interest,
![]() $({\bf\sigma}^{(1)},\boldsymbol{u}^{(1)})$
, are given by:
$({\bf\sigma}^{(1)},\boldsymbol{u}^{(1)})$
, are given by:
where the second term is the deviatoric Newtonian stress with
![]() $\boldsymbol{e}^{(1)}=(\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)}+\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)^{\dagger }})/2$
being the rate-of-strain tensor where
$\boldsymbol{e}^{(1)}=(\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)}+\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)^{\dagger }})/2$
being the rate-of-strain tensor where
![]() $\boldsymbol{{\rm\nabla}}u^{\dagger }$
refers to the transpose of the velocity gradient tensor and
$\boldsymbol{{\rm\nabla}}u^{\dagger }$
refers to the transpose of the velocity gradient tensor and
![]() ${\bf\sigma}_{NN}^{(1)}$
denotes the viscoelastic stress. The Deborah number is a dimensionless measure of viscoelasticity, being defined as
${\bf\sigma}_{NN}^{(1)}$
denotes the viscoelastic stress. The Deborah number is a dimensionless measure of viscoelasticity, being defined as
![]() $\mathit{De}=U{\it\lambda}/L$
, and may be regarded as the ratio of the intrinsic relaxation time of the microstructure to the imposed flow time scale. The present analysis is valid in the limit
$\mathit{De}=U{\it\lambda}/L$
, and may be regarded as the ratio of the intrinsic relaxation time of the microstructure to the imposed flow time scale. The present analysis is valid in the limit
![]() $\mathit{De}\ll 1$
, corresponding to slow, slowly varying flows. In this regime, the fluid rheology is governed by the retarded-motion expansion (see Bird et al.
Reference Bird, Armstrong and Hassager1987; Larson Reference Larson1988). To
$\mathit{De}\ll 1$
, corresponding to slow, slowly varying flows. In this regime, the fluid rheology is governed by the retarded-motion expansion (see Bird et al.
Reference Bird, Armstrong and Hassager1987; Larson Reference Larson1988). To
![]() $O(\mathit{De})$
, this expansion reduces to (2.6), the constitutive relation for a second-order fluid, which rigorously accounts for the first effects of viscoelasticity. With
$O(\mathit{De})$
, this expansion reduces to (2.6), the constitutive relation for a second-order fluid, which rigorously accounts for the first effects of viscoelasticity. With
![]() ${\bf\sigma}_{NN}^{(1)}$
defined as the stress in a second-order fluid (see (2.8) below), (2.6) predicts a constant shear viscosity and a quadratic shear-rate dependence of the first and second normal stress differences (
${\bf\sigma}_{NN}^{(1)}$
defined as the stress in a second-order fluid (see (2.8) below), (2.6) predicts a constant shear viscosity and a quadratic shear-rate dependence of the first and second normal stress differences (
![]() $N_{1}$
and
$N_{1}$
and
![]() $N_{2}$
) in a viscometric flow. The intrinsic relaxation time can be expressed as the ratio of the sum of normal stress coefficients to the shear viscosity (
$N_{2}$
) in a viscometric flow. The intrinsic relaxation time can be expressed as the ratio of the sum of normal stress coefficients to the shear viscosity (
![]() ${\it\lambda}=({\it\psi}_{1}+{\it\psi}_{2})/{\it\mu}$
,
${\it\lambda}=({\it\psi}_{1}+{\it\psi}_{2})/{\it\mu}$
,
![]() ${\it\psi}_{i}=N_{i}/\dot{{\it\gamma}}^{2}$
;
${\it\psi}_{i}=N_{i}/\dot{{\it\gamma}}^{2}$
;
![]() $i=1,2$
). In the original expansion, shear-thinning appears at
$i=1,2$
). In the original expansion, shear-thinning appears at
![]() $O(\mathit{De}^{2})$
, shear-rate dependence of the normal stress coefficients appears at
$O(\mathit{De}^{2})$
, shear-rate dependence of the normal stress coefficients appears at
![]() $O(\mathit{De}^{3})$
, and so on. However, the orientational degeneracy in the Stokes limit, arising from dependence on initial conditions, is already resolved at
$O(\mathit{De}^{3})$
, and so on. However, the orientational degeneracy in the Stokes limit, arising from dependence on initial conditions, is already resolved at
![]() $O(\mathit{De})$
, and these higher-order effects will not qualitatively alter the predicted behaviour for small
$O(\mathit{De})$
, and these higher-order effects will not qualitatively alter the predicted behaviour for small
![]() $\mathit{De}$
.
$\mathit{De}$
.
Using (2.6), the equations of motion, (2.2), may now be written as:
where the second-order fluid stress may be written as the sum of a co-rotational
![]() $({\bf\sigma}_{NNC}^{(1)})$
and a quadratic
$({\bf\sigma}_{NNC}^{(1)})$
and a quadratic
![]() $({\bf\sigma}_{NNQ}^{(1)})$
contribution:
$({\bf\sigma}_{NNQ}^{(1)})$
contribution:
with (Koch & Subramanian Reference Koch and Subramanian2006; Subramanian & Koch Reference Subramanian and Koch2007)
where the first term within brackets is proportional to the second-order Rivlin–Ericksen tensor, and
![]() ${\it\epsilon}_{d}=-2({\it\psi}_{1}+{\it\psi}_{2})/{\it\psi}_{1}$
. The relation between the above expression and one used in the present work may be seen from substituting
${\it\epsilon}_{d}=-2({\it\psi}_{1}+{\it\psi}_{2})/{\it\psi}_{1}$
. The relation between the above expression and one used in the present work may be seen from substituting
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)\dagger }=\boldsymbol{e}^{(1)}-{\bf\omega}^{(1)}$
and
$\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)\dagger }=\boldsymbol{e}^{(1)}-{\bf\omega}^{(1)}$
and
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)}=\boldsymbol{e}^{(1)}+{\bf\omega}^{(1)}$
, whence one finds
$\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)}=\boldsymbol{e}^{(1)}+{\bf\omega}^{(1)}$
, whence one finds
![]() ${\it\epsilon}_{d}=1/{\it\epsilon}$
.
${\it\epsilon}_{d}=1/{\it\epsilon}$
.
The test problem,
![]() $({\bf\sigma}^{(2)},\boldsymbol{u}^{(2)})$
in (2.1), is the inertialess rotation of a spheroid, with the same instantaneous orientation as in the actual problem, in an otherwise quiescent Newtonian fluid. Since the translating spheroid in the actual problem does not have a spin about its symmetry axis, the test angular velocity,
$({\bf\sigma}^{(2)},\boldsymbol{u}^{(2)})$
in (2.1), is the inertialess rotation of a spheroid, with the same instantaneous orientation as in the actual problem, in an otherwise quiescent Newtonian fluid. Since the translating spheroid in the actual problem does not have a spin about its symmetry axis, the test angular velocity,
![]() ${\it\bf\Omega}^{(2)}$
, may be chosen as being orthogonal to this axis. The equations of motion and continuity in this case are given by:
${\it\bf\Omega}^{(2)}$
, may be chosen as being orthogonal to this axis. The equations of motion and continuity in this case are given by:
Returning to the reciprocal theorem identity, equation (2.1), the second surface integral on the left-hand side in (2.1) is identically zero since the spheroid in the test problem exerts only a torque but no force. Using the boundary condition, (2.14), the first surface integral in (2.1) reduces to –
![]() $\boldsymbol{L}_{sed}\boldsymbol{\cdot }{\it\bf\Omega}^{(2)}$
,
$\boldsymbol{L}_{sed}\boldsymbol{\cdot }{\it\bf\Omega}^{(2)}$
,
![]() $\boldsymbol{L}_{sed}$
being the torque acting on the translating spheroid. Thus, (2.1) takes the form:
$\boldsymbol{L}_{sed}$
being the torque acting on the translating spheroid. Thus, (2.1) takes the form:
where
![]() $\boldsymbol{L}_{sed}$
is the non-dimensional torque measured in units of
$\boldsymbol{L}_{sed}$
is the non-dimensional torque measured in units of
![]() ${\it\mu}UL^{2}$
. It is convenient to write the inertial acceleration in terms of the disturbance velocity field, which, as will be seen in § 3, is readily expressed in terms of decaying spheroidal harmonics. Writing
${\it\mu}UL^{2}$
. It is convenient to write the inertial acceleration in terms of the disturbance velocity field, which, as will be seen in § 3, is readily expressed in terms of decaying spheroidal harmonics. Writing
![]() $\boldsymbol{u}^{(1)}=\hat{\boldsymbol{U}}+\boldsymbol{u}^{(1)^{\prime }}$
, with
$\boldsymbol{u}^{(1)}=\hat{\boldsymbol{U}}+\boldsymbol{u}^{(1)^{\prime }}$
, with
![]() $\boldsymbol{u}^{(1)^{\prime }}\rightarrow 0$
for
$\boldsymbol{u}^{(1)^{\prime }}\rightarrow 0$
for
![]() $\boldsymbol{r}\rightarrow \infty$
, we have:
$\boldsymbol{r}\rightarrow \infty$
, we have:
Noting that the velocity field in the test problem is linear in
![]() ${\it\bf\Omega}^{(2)}$
, one may write
${\it\bf\Omega}^{(2)}$
, one may write
![]() $\boldsymbol{u}^{(2)}=\unicode[STIX]{x1D650}^{(2)}\boldsymbol{\cdot }{\it\bf\Omega}^{(2)}$
, where
$\boldsymbol{u}^{(2)}=\unicode[STIX]{x1D650}^{(2)}\boldsymbol{\cdot }{\it\bf\Omega}^{(2)}$
, where
![]() $\unicode[STIX]{x1D650}^{(2)}$
is a second-order tensor dependent only on the geometry of the spheroidal particle. Apart from the constraint of being orthogonal to the spheroidal axis of symmetry,
$\unicode[STIX]{x1D650}^{(2)}$
is a second-order tensor dependent only on the geometry of the spheroidal particle. Apart from the constraint of being orthogonal to the spheroidal axis of symmetry,
![]() ${\it\bf\Omega}^{(2)}$
is arbitrary, and since there can be no torque along the symmetry axis, one obtains from (2.17):
${\it\bf\Omega}^{(2)}$
is arbitrary, and since there can be no torque along the symmetry axis, one obtains from (2.17):
The Stokesian limit leads to a zero torque, and expectedly,
![]() $\boldsymbol{L}_{sed}$
involves terms proportional to
$\boldsymbol{L}_{sed}$
involves terms proportional to
![]() $\mathit{Re}$
and
$\mathit{Re}$
and
![]() $\mathit{De}$
. Apart from the restriction to second-order-fluid rheology, (2.18) does not yet exploit the simplifications that accrue in the limit
$\mathit{De}$
. Apart from the restriction to second-order-fluid rheology, (2.18) does not yet exploit the simplifications that accrue in the limit
![]() $\mathit{De},\mathit{Re}\ll 1$
, since the integrands in (2.18) involve
$\mathit{De},\mathit{Re}\ll 1$
, since the integrands in (2.18) involve
![]() $\boldsymbol{u}^{(1)^{\prime }}$
, which requires the solution of the nonlinear equations of motion for finite
$\boldsymbol{u}^{(1)^{\prime }}$
, which requires the solution of the nonlinear equations of motion for finite
![]() $\mathit{Re}$
. If one only needs the
$\mathit{Re}$
. If one only needs the
![]() $O(\mathit{Re})$
and
$O(\mathit{Re})$
and
![]() $O(\mathit{De})$
contributions, however, one may replace
$O(\mathit{De})$
contributions, however, one may replace
![]() $\boldsymbol{u}^{(1)^{\prime }}$
by
$\boldsymbol{u}^{(1)^{\prime }}$
by
![]() $\boldsymbol{u}_{s}^{(1)}$
, where
$\boldsymbol{u}_{s}^{(1)}$
, where
![]() $\boldsymbol{u}_{s}^{(1)}$
is the disturbance velocity field due to a translating spheroid at
$\boldsymbol{u}_{s}^{(1)}$
is the disturbance velocity field due to a translating spheroid at
![]() $\mathit{Re}=\mathit{De}=0$
. To see that the
$\mathit{Re}=\mathit{De}=0$
. To see that the
![]() $\mathit{Re}$
- and
$\mathit{Re}$
- and
![]() $\mathit{De}$
-dependent terms in
$\mathit{De}$
-dependent terms in
![]() $\boldsymbol{u}^{(1)^{\prime }}$
lead only to higher-order corrections to
$\boldsymbol{u}^{(1)^{\prime }}$
lead only to higher-order corrections to
![]() $\boldsymbol{L}_{sed}$
, it is sufficient to verify that the two volume integrals in (2.18), with
$\boldsymbol{L}_{sed}$
, it is sufficient to verify that the two volume integrals in (2.18), with
![]() $\boldsymbol{u}^{(1)^{\prime }}$
replaced by
$\boldsymbol{u}^{(1)^{\prime }}$
replaced by
![]() $\boldsymbol{u}_{s}^{(1)}$
, remain convergent, and this convergence is readily illustrated using the far-field behaviour of the Stokes velocity fields. In the integrand for the inertial torque, the dominant contribution for large distances (
$\boldsymbol{u}_{s}^{(1)}$
, remain convergent, and this convergence is readily illustrated using the far-field behaviour of the Stokes velocity fields. In the integrand for the inertial torque, the dominant contribution for large distances (
![]() $r\gg O(L)$
) comes from the linearized inertial term,
$r\gg O(L)$
) comes from the linearized inertial term,
![]() $\hat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)^{\prime }}$
, corresponding to convection by the ambient flow. Since
$\hat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)^{\prime }}$
, corresponding to convection by the ambient flow. Since
![]() $\boldsymbol{u}_{s}^{(1)}\sim O(1/r)$
, this term decays as
$\boldsymbol{u}_{s}^{(1)}\sim O(1/r)$
, this term decays as
![]() $O(1/r^{2})$
, and since the disturbance velocity field due to a rotating spheroidal particle decays as
$O(1/r^{2})$
, and since the disturbance velocity field due to a rotating spheroidal particle decays as
![]() $O(1/r^{2})$
, the integrand for the inertial torque is
$O(1/r^{2})$
, the integrand for the inertial torque is
![]() $O(1/r^{4})$
, implying convergence for large
$O(1/r^{4})$
, implying convergence for large
![]() $r$
. Considering the viscoelastic torque integral, the non-Newtonian stress
$r$
. Considering the viscoelastic torque integral, the non-Newtonian stress
![]() ${\bf\sigma}_{NN}^{(1)}\sim (\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)})^{2}\sim O(1/r^{4})$
; with
${\bf\sigma}_{NN}^{(1)}\sim (\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)})^{2}\sim O(1/r^{4})$
; with
![]() $\unicode[STIX]{x1D650}^{(2)}\sim O(1/r^{2})$
,
$\unicode[STIX]{x1D650}^{(2)}\sim O(1/r^{2})$
,
![]() $\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D650}^{(2)}\sim O(1/r^{3})$
, the integrand is
$\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D650}^{(2)}\sim O(1/r^{3})$
, the integrand is
![]() $O(1/r^{7})$
and decays faster than that for the inertial torque contribution, and the resulting integral is again convergent. The convergence of the volume integrals indicates the regular nature of both the inertial and viscoelastic torque contributions. Although the elastic corrections for small
$O(1/r^{7})$
and decays faster than that for the inertial torque contribution, and the resulting integral is again convergent. The convergence of the volume integrals indicates the regular nature of both the inertial and viscoelastic torque contributions. Although the elastic corrections for small
![]() $\mathit{De}$
, based on the retarded-motion expansion, typically lead to convergent integrals, this is not the case with inertia. For instance, the well-known
$\mathit{De}$
, based on the retarded-motion expansion, typically lead to convergent integrals, this is not the case with inertia. For instance, the well-known
![]() $O(\mathit{Re})$
correction to the Stokes drag on a sphere (Leal Reference Leal1992), and more generally for any fore–aft symmetric body (including the spheroid considered here in appendix A), has a singular nature. Thus, a reciprocal theorem formulation for the drag leads to a volume integral that would be divergent on using the Stokes estimates as above, and convergence requires use of the Oseen velocity field at leading order. Physically, the inertial correction to the torque on a spheroid is dominated by the contribution from a volume of
$O(\mathit{Re})$
correction to the Stokes drag on a sphere (Leal Reference Leal1992), and more generally for any fore–aft symmetric body (including the spheroid considered here in appendix A), has a singular nature. Thus, a reciprocal theorem formulation for the drag leads to a volume integral that would be divergent on using the Stokes estimates as above, and convergence requires use of the Oseen velocity field at leading order. Physically, the inertial correction to the torque on a spheroid is dominated by the contribution from a volume of
![]() $O(L^{3})$
around it, while the corresponding correction to the force originates at distances of the order of
$O(L^{3})$
around it, while the corresponding correction to the force originates at distances of the order of
![]() $O(L\mathit{Re}^{-1})$
, the inertial screening length. In light of the above scaling estimates, one may write (2.18) in the form:
$O(L\mathit{Re}^{-1})$
, the inertial screening length. In light of the above scaling estimates, one may write (2.18) in the form:
where the subscript ‘
![]() $s$
’ denotes a Stokesian field.
$s$
’ denotes a Stokesian field.
3. The spheroidal harmonics formalism
In this section, we discuss a novel analytical framework, the vector spheroidal harmonics formalism, introduced originally by Kushch and co-workers in the context of determining the averaged properties of a composite consisting of an elastic matrix with spheroidal inclusions (Kushch Reference Kushch1997, Reference Kushch1998). The formalism applies to the case where both the matrix and the inclusions are governed by the Lame equations of linear elasticity given by:
where
![]() $\tilde{\boldsymbol{u}}$
is the displacement field and
$\tilde{\boldsymbol{u}}$
is the displacement field and
![]() ${\it\nu}$
is Poisson’s ratio. On identifying
${\it\nu}$
is Poisson’s ratio. On identifying
![]() $\tilde{\boldsymbol{u}}$
in the matrix with the velocity field, the combination
$\tilde{\boldsymbol{u}}$
in the matrix with the velocity field, the combination
![]() $(2(1-{\it\nu})/(1-2{\it\nu}))\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\tilde{\boldsymbol{u}}$
, which tends to a finite value at any point even as
$(2(1-{\it\nu})/(1-2{\it\nu}))\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\tilde{\boldsymbol{u}}$
, which tends to a finite value at any point even as
![]() ${\it\nu}\rightarrow 1/2,\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\tilde{\boldsymbol{u}}\rightarrow 0$
, with the pressure field enforcing the incompressibility constraint, and taking the limit where the moduli of the spheroidal inclusions tend to infinity, the same formalism becomes applicable to the case of hydrodynamically interacting rigid spheroidal particles immersed in a Newtonian fluid that satisfies the Stokes equations. Such an identification has already been made by Kushch and Sangani, who have used the formalism to determine the effective viscosity of a periodic array of such particles, but this has unfortunately not been published yet. In what follows, we therefore give some of the details of this formalism, mainly those relevant to the motion of a single particle, before using it to obtain the relevant disturbance velocity and stress fields.
${\it\nu}\rightarrow 1/2,\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\tilde{\boldsymbol{u}}\rightarrow 0$
, with the pressure field enforcing the incompressibility constraint, and taking the limit where the moduli of the spheroidal inclusions tend to infinity, the same formalism becomes applicable to the case of hydrodynamically interacting rigid spheroidal particles immersed in a Newtonian fluid that satisfies the Stokes equations. Such an identification has already been made by Kushch and Sangani, who have used the formalism to determine the effective viscosity of a periodic array of such particles, but this has unfortunately not been published yet. In what follows, we therefore give some of the details of this formalism, mainly those relevant to the motion of a single particle, before using it to obtain the relevant disturbance velocity and stress fields.
The formalism expresses the general solution of the Stokes equations, around an arbitrary number of spheroidal particles, as a superposition of growing and decaying partial vectorial solutions centred at each particle, and being defined in terms of a local spheroidal coordinate system aligned with the axis of symmetry of the particle under consideration. Thus, one writes the general expression for the velocity field around
![]() $N$
particles in the form:
$N$
particles in the form:
where
![]() $\boldsymbol{r}_{p}=\boldsymbol{x}-\boldsymbol{x}_{p}$
is the position vector relative to the centre (
$\boldsymbol{r}_{p}=\boldsymbol{x}-\boldsymbol{x}_{p}$
is the position vector relative to the centre (
![]() $\boldsymbol{x}_{p}$
) of the
$\boldsymbol{x}_{p}$
) of the
![]() $p$
th spheroid. The growing (regular) solutions are given by:
$p$
th spheroid. The growing (regular) solutions are given by:
 $$\begin{eqnarray}\displaystyle \boldsymbol{s}_{ts}^{(3)} & = & \displaystyle \boldsymbol{e}_{1}\{-(x-\text{i}y)\text{D}_{2}f_{t+1}^{s-1}-[{\it\xi}_{0}^{2}-1]\,\text{d}\text{D}_{1}f_{t}^{s}+(t-s+1)(t-s+2){\it\beta}_{t}f_{t+1}^{s-1}\}\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{e}_{2}\{(x+\text{i}y)\text{D}_{1}f_{t+1}^{s+1}-[{\it\xi}_{0}^{2}-1]\,\text{d}\text{D}_{2}f_{t}^{s}-(t+s+1)(t+s+2){\it\beta}_{t}f_{t+1}^{s+1}\}\nonumber\\ \displaystyle & & \displaystyle +\,\mathbf{1}_{z}[z\text{D}_{3}f_{t+1}^{s}-{\it\xi}_{0}^{2}\,\text{d}\text{D}_{3}f_{t}^{s}-C_{ts}\,f_{t+1}^{s}],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{s}_{ts}^{(3)} & = & \displaystyle \boldsymbol{e}_{1}\{-(x-\text{i}y)\text{D}_{2}f_{t+1}^{s-1}-[{\it\xi}_{0}^{2}-1]\,\text{d}\text{D}_{1}f_{t}^{s}+(t-s+1)(t-s+2){\it\beta}_{t}f_{t+1}^{s-1}\}\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{e}_{2}\{(x+\text{i}y)\text{D}_{1}f_{t+1}^{s+1}-[{\it\xi}_{0}^{2}-1]\,\text{d}\text{D}_{2}f_{t}^{s}-(t+s+1)(t+s+2){\it\beta}_{t}f_{t+1}^{s+1}\}\nonumber\\ \displaystyle & & \displaystyle +\,\mathbf{1}_{z}[z\text{D}_{3}f_{t+1}^{s}-{\it\xi}_{0}^{2}\,\text{d}\text{D}_{3}f_{t}^{s}-C_{ts}\,f_{t+1}^{s}],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \boldsymbol{S}_{ts}^{(3)} & = & \displaystyle \boldsymbol{e}_{1}\{-(x-\text{i}y)\text{D}_{2}F_{t-1}^{s-1}-[{\it\xi}_{0}^{2}-1]\,\text{d}\text{D}_{1}F_{t}^{s}+(t+s-1)(t+s){\it\beta}_{-(t+1)}F_{t-1}^{s-1}\}\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{e}_{2}\{(x+\text{i}y)\text{D}_{1}F_{t-1}^{s+1}-[{\it\xi}_{0}^{2}-1]\,\text{d}\text{D}_{2}F_{t}^{s}-(t-s-1)(t-s){\it\beta}_{-(t+1)}F_{t-1}^{s+1}\}\nonumber\\ \displaystyle & & \displaystyle +\,\mathbf{1}_{z}[z\text{D}_{3}F_{t-1}^{s}-{\it\xi}_{0}^{2}\,\text{d}\text{D}_{3}F_{t}^{s}-C_{-(t+1),s}F_{t-1}^{s}],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{S}_{ts}^{(3)} & = & \displaystyle \boldsymbol{e}_{1}\{-(x-\text{i}y)\text{D}_{2}F_{t-1}^{s-1}-[{\it\xi}_{0}^{2}-1]\,\text{d}\text{D}_{1}F_{t}^{s}+(t+s-1)(t+s){\it\beta}_{-(t+1)}F_{t-1}^{s-1}\}\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{e}_{2}\{(x+\text{i}y)\text{D}_{1}F_{t-1}^{s+1}-[{\it\xi}_{0}^{2}-1]\,\text{d}\text{D}_{2}F_{t}^{s}-(t-s-1)(t-s){\it\beta}_{-(t+1)}F_{t-1}^{s+1}\}\nonumber\\ \displaystyle & & \displaystyle +\,\mathbf{1}_{z}[z\text{D}_{3}F_{t-1}^{s}-{\it\xi}_{0}^{2}\,\text{d}\text{D}_{3}F_{t}^{s}-C_{-(t+1),s}F_{t-1}^{s}],\end{eqnarray}$$
In all of the above,
![]() $({\it\xi},{\it\eta},{\it\phi})$
denote the spheroidal coordinates. The above expressions for the partial vectorial solutions are valid for the prolate case, in which case
$({\it\xi},{\it\eta},{\it\phi})$
denote the spheroidal coordinates. The above expressions for the partial vectorial solutions are valid for the prolate case, in which case
![]() $({\it\xi},{\it\eta},{\it\phi})$
are related to the Cartesian coordinates
$({\it\xi},{\it\eta},{\it\phi})$
are related to the Cartesian coordinates
![]() $(x,y,z)$
as
$(x,y,z)$
as
![]() $x+\text{i}y=d\sqrt{{\it\xi}^{2}-1}\sqrt{1-{\it\eta}^{2}}\exp (\text{i}{\it\phi}),z=d{\it\xi}{\it\eta}$
, with
$x+\text{i}y=d\sqrt{{\it\xi}^{2}-1}\sqrt{1-{\it\eta}^{2}}\exp (\text{i}{\it\phi}),z=d{\it\xi}{\it\eta}$
, with
![]() $1\leqslant {\it\xi}\leqslant \infty ,|{\it\eta}|\leqslant 1,0\leqslant {\it\phi}<2{\rm\pi}$
. The constant-
$1\leqslant {\it\xi}\leqslant \infty ,|{\it\eta}|\leqslant 1,0\leqslant {\it\phi}<2{\rm\pi}$
. The constant-
![]() ${\it\xi}$
surfaces denote a family of confocal prolate spheroids, with the interfoci distance being equal to
${\it\xi}$
surfaces denote a family of confocal prolate spheroids, with the interfoci distance being equal to
![]() $2d$
, and
$2d$
, and
![]() ${\it\xi}_{0}$
denotes the surface of the particle.
${\it\xi}_{0}$
denotes the surface of the particle.
![]() ${\it\xi}=1$
reduces to the line segment connecting the foci, and the limit
${\it\xi}=1$
reduces to the line segment connecting the foci, and the limit
![]() ${\it\xi}_{0}\rightarrow 1$
therefore corresponds to the limit of an infinitely slender particle. The constant-
${\it\xi}_{0}\rightarrow 1$
therefore corresponds to the limit of an infinitely slender particle. The constant-
![]() ${\it\eta}$
surfaces represent a family of confocal two-sheeted hyperboloids, while the constant-
${\it\eta}$
surfaces represent a family of confocal two-sheeted hyperboloids, while the constant-
![]() ${\it\phi}$
surfaces are planes passing through the axis of symmetry. The oblate spheroidal coordinate system may be obtained by replacing
${\it\phi}$
surfaces are planes passing through the axis of symmetry. The oblate spheroidal coordinate system may be obtained by replacing
![]() ${\it\xi}$
by
${\it\xi}$
by
![]() $\text{i}\sqrt{{\it\xi}^{2}-1}$
and
$\text{i}\sqrt{{\it\xi}^{2}-1}$
and
![]() $d$
by
$d$
by
![]() $-\text{i}d$
in the above expressions for the prolate case. With this substitution, the constant-
$-\text{i}d$
in the above expressions for the prolate case. With this substitution, the constant-
![]() ${\it\xi}$
surfaces are confocal oblate spheroids with
${\it\xi}$
surfaces are confocal oblate spheroids with
![]() ${\it\xi}=1$
degenerating to the focal circle with diameter
${\it\xi}=1$
degenerating to the focal circle with diameter
![]() $2d$
, and the limit
$2d$
, and the limit
![]() ${\it\xi}_{0}\rightarrow 1$
now denotes the limit of a flat disk. The constant-
${\it\xi}_{0}\rightarrow 1$
now denotes the limit of a flat disk. The constant-
![]() ${\it\eta}$
surfaces are confocal single-sheeted hyperboloids, while the constant-
${\it\eta}$
surfaces are confocal single-sheeted hyperboloids, while the constant-
![]() ${\it\phi}$
surfaces remain planes through the symmetry axis as in the prolate case. With increasing
${\it\phi}$
surfaces remain planes through the symmetry axis as in the prolate case. With increasing
![]() ${\it\xi}$
, or decreasing
${\it\xi}$
, or decreasing
![]() $d$
, the constant
$d$
, the constant
![]() ${\it\xi}$
-surfaces, in both the prolate and oblate cases, approach a spherical shape and the constant-
${\it\xi}$
-surfaces, in both the prolate and oblate cases, approach a spherical shape and the constant-
![]() ${\it\eta}$
surfaces approach a conical geometry. The important limiting case of a spherical particle of radius
${\it\eta}$
surfaces approach a conical geometry. The important limiting case of a spherical particle of radius
![]() $a$
may therefore be obtained by taking
$a$
may therefore be obtained by taking
![]() ${\it\xi},{\it\xi}_{0}\rightarrow \infty$
,
${\it\xi},{\it\xi}_{0}\rightarrow \infty$
,
![]() $d\rightarrow 0$
, with
$d\rightarrow 0$
, with
![]() $d{\it\xi}=r$
being fixed and equal to the radial distance to the point of interest, and
$d{\it\xi}=r$
being fixed and equal to the radial distance to the point of interest, and
![]() $d{\it\xi}_{0}=a$
being the radius of the spherical particle.
$d{\it\xi}_{0}=a$
being the radius of the spherical particle.
The general superposition, (3.2), together with re-expansion formulae (addition theorems) for the partial solutions due to an arbitrary translation and rotation of the coordinate system, reduce the satisfaction of the boundary conditions at the surfaces of the rigid particles, of the form
![]() $\boldsymbol{u}(\boldsymbol{r}_{p})=\boldsymbol{U}_{p}+{\it\bf\Omega}_{p}\wedge \boldsymbol{r}_{p}$
, to an infinite system of linear equations in the unknown amplitudes
$\boldsymbol{u}(\boldsymbol{r}_{p})=\boldsymbol{U}_{p}+{\it\bf\Omega}_{p}\wedge \boldsymbol{r}_{p}$
, to an infinite system of linear equations in the unknown amplitudes
![]() $A_{ts}^{(i)(p)}$
and
$A_{ts}^{(i)(p)}$
and
![]() $a_{ts}^{(i)(p)}$
. Such an approach has been successfully applied to the case of spherical particles (Sangani & Mo Reference Sangani and Mo1994), and Kushch, in a series of earlier articles, has extended the formulation to spheroidal particles (Kushch Reference Kushch1995, Reference Kushch1997, Reference Kushch1998). The aforementioned re-expansion formulae come into play only when there are multiple interacting particles, and are therefore beyond the scope of the present paper, which deals with the orientation of a single sedimenting particle. The exterior velocity disturbance field in the domain
$a_{ts}^{(i)(p)}$
. Such an approach has been successfully applied to the case of spherical particles (Sangani & Mo Reference Sangani and Mo1994), and Kushch, in a series of earlier articles, has extended the formulation to spheroidal particles (Kushch Reference Kushch1995, Reference Kushch1997, Reference Kushch1998). The aforementioned re-expansion formulae come into play only when there are multiple interacting particles, and are therefore beyond the scope of the present paper, which deals with the orientation of a single sedimenting particle. The exterior velocity disturbance field in the domain
![]() ${\it\xi}\geqslant {\it\xi}_{0}$
around a single spheroidal particle, due to an imposed ambient flow, may be expressed in terms of the decaying partial solutions alone as:
${\it\xi}\geqslant {\it\xi}_{0}$
around a single spheroidal particle, due to an imposed ambient flow, may be expressed in terms of the decaying partial solutions alone as:
where we note from (3.6)–(3.8) that the
![]() $\boldsymbol{S}_{ts}^{(1)}$
and
$\boldsymbol{S}_{ts}^{(1)}$
and
![]() $\boldsymbol{S}_{ts}^{(2)}$
are vector harmonic functions (
$\boldsymbol{S}_{ts}^{(2)}$
are vector harmonic functions (
![]() ${\rm\nabla}^{2}\boldsymbol{S}_{ts}^{(i)}=0$
for
${\rm\nabla}^{2}\boldsymbol{S}_{ts}^{(i)}=0$
for
![]() $i=1,2$
). The
$i=1,2$
). The
![]() $\boldsymbol{S}_{ts}^{(3)}$
, which are vector biharmonic functions (
$\boldsymbol{S}_{ts}^{(3)}$
, which are vector biharmonic functions (
![]() ${\rm\nabla}^{4}\boldsymbol{S}_{ts}^{(3)}=0$
), lead to a non-trivial pressure field. We have
${\rm\nabla}^{4}\boldsymbol{S}_{ts}^{(3)}=0$
), lead to a non-trivial pressure field. We have
so the associated pressure field is
![]() $(2/d)D_{t}^{s}$
, with
$(2/d)D_{t}^{s}$
, with
![]() $D_{t}^{s}$
being a scalar harmonic given by
$D_{t}^{s}$
being a scalar harmonic given by
![]() $D_{t}^{s}=\text{d}\text{D}_{3}F_{t-1}^{s}$
, where
$D_{t}^{s}=\text{d}\text{D}_{3}F_{t-1}^{s}$
, where
![]() $\text{D}_{3}F_{t-1}^{s}=\text{D}_{1}F_{t-1}^{s+1}=-\text{D}_{2}F_{t-1}^{s-1}$
. The singular solutions in (3.9) satisfy the additional properties:
$\text{D}_{3}F_{t-1}^{s}=\text{D}_{1}F_{t-1}^{s+1}=-\text{D}_{2}F_{t-1}^{s-1}$
. The singular solutions in (3.9) satisfy the additional properties:
The structure of the spheroidal harmonics formalism developed above is similar to the well-known solution, in terms of vector spherical harmonics, given originally by Lamb (see chapter 4 of Kim & Karrila Reference Kim and Karrila1991), and that has often been used for determining the effective properties of composites with spherical inclusions (Sangani & Mo Reference Sangani and Mo1994). For the case of a single particle, not acting as a source of mass, and whose induced disturbance velocity field is required to decay for large distances, this solution is of the form:
where
![]() $\boldsymbol{x}$
is now the position vector relative to the sphere centre with
$\boldsymbol{x}$
is now the position vector relative to the sphere centre with
![]() $c_{n}=(n+3)/(2(n+1)(2n+3))$
and
$c_{n}=(n+3)/(2(n+1)(2n+3))$
and
![]() $b_{n}=-n/((n+1)(2n+3))$
. Here,
$b_{n}=-n/((n+1)(2n+3))$
. Here,
![]() $p_{n}$
,
$p_{n}$
,
![]() ${\it\chi}_{n}$
and
${\it\chi}_{n}$
and
![]() ${\it\phi}_{n}$
are (scalar) solid spherical harmonics of the
${\it\phi}_{n}$
are (scalar) solid spherical harmonics of the
![]() $n$
th order. Since, for instance,
$n$
th order. Since, for instance,
![]() $p_{-n-1}=r^{-n-1}\!\sum _{m=-n}^{n}A_{mn}Y_{n}^{m}({\it\theta},{\it\phi})=r^{-n-1}\!\sum _{m=-n}^{n}A_{mn}P_{n}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\phi}}$
, one may write (3.15) in the form:
$p_{-n-1}=r^{-n-1}\!\sum _{m=-n}^{n}A_{mn}Y_{n}^{m}({\it\theta},{\it\phi})=r^{-n-1}\!\sum _{m=-n}^{n}A_{mn}P_{n}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\phi}}$
, one may write (3.15) in the form:
where each of
![]() $p_{n,m}$
,
$p_{n,m}$
,
![]() ${\it\chi}_{n,m}$
and
${\it\chi}_{n,m}$
and
![]() ${\it\phi}_{n,m}$
are proportional to
${\it\phi}_{n,m}$
are proportional to
![]() $r^{n}P_{n}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\phi}}$
. From comparing (3.16) with (3.9) and (3.6)–(3.8), it may be seen that the terms in (3.15) involving
$r^{n}P_{n}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\phi}}$
. From comparing (3.16) with (3.9) and (3.6)–(3.8), it may be seen that the terms in (3.15) involving
![]() ${\it\chi}_{n}$
and
${\it\chi}_{n}$
and
![]() ${\it\phi}_{n}$
are harmonic, and are therefore similar to
${\it\phi}_{n}$
are harmonic, and are therefore similar to
![]() $\boldsymbol{S}_{ts}^{(1)}$
and
$\boldsymbol{S}_{ts}^{(1)}$
and
![]() $\boldsymbol{S}_{ts}^{(2)}$
, with
$\boldsymbol{S}_{ts}^{(2)}$
, with
![]() $\boldsymbol{S}_{ts}^{(1)}$
being the analogue of
$\boldsymbol{S}_{ts}^{(1)}$
being the analogue of
![]() $\boldsymbol{{\rm\nabla}}{\it\phi}_{-n-1,m}$
, since both describe decaying irrotational flow contributions. Importantly,
$\boldsymbol{{\rm\nabla}}{\it\phi}_{-n-1,m}$
, since both describe decaying irrotational flow contributions. Importantly,
![]() $\boldsymbol{S}_{ts}^{(3)}$
is the analogue of the term involving
$\boldsymbol{S}_{ts}^{(3)}$
is the analogue of the term involving
![]() $p_{n,m}$
. The latter term also satisfies the biharmonic equation and has an associated pressure field. The Kushch formalism is, in fact, a slightly more economical reformulation of the Lamb series in that the velocity disturbance of canonical flow problems are described by fewer terms in the general series given by (3.9). For example, the disturbance velocity field produced by a translating sphere has an
$p_{n,m}$
. The latter term also satisfies the biharmonic equation and has an associated pressure field. The Kushch formalism is, in fact, a slightly more economical reformulation of the Lamb series in that the velocity disturbance of canonical flow problems are described by fewer terms in the general series given by (3.9). For example, the disturbance velocity field produced by a translating sphere has an
![]() $O(1/r)$
component corresponding to the action of the point force at the sphere centre, and a more rapidly decaying
$O(1/r)$
component corresponding to the action of the point force at the sphere centre, and a more rapidly decaying
![]() $O(1/r^{3})$
irrotational component that arises from the finite size of the sphere, being equivalent to an additional (degenerate) quadrupole at the centre. For the Lamb series, this velocity field requires the term involving
$O(1/r^{3})$
irrotational component that arises from the finite size of the sphere, being equivalent to an additional (degenerate) quadrupole at the centre. For the Lamb series, this velocity field requires the term involving
![]() $p_{-2}$
that generates the Stokeslet part and the potential term proportional to
$p_{-2}$
that generates the Stokeslet part and the potential term proportional to
![]() $\boldsymbol{{\rm\nabla}}{\it\phi}_{-2}$
that generates the
$\boldsymbol{{\rm\nabla}}{\it\phi}_{-2}$
that generates the
![]() $O(1/r^{3})$
terms (Kim & Karrila Reference Kim and Karrila1991). On the other hand, as will be seen below, the entire velocity field due to a translating spheroid is contained in
$O(1/r^{3})$
terms (Kim & Karrila Reference Kim and Karrila1991). On the other hand, as will be seen below, the entire velocity field due to a translating spheroid is contained in
![]() $\boldsymbol{S}_{1s}^{(3)}$
for
$\boldsymbol{S}_{1s}^{(3)}$
for
![]() $s=1,0,-1$
(the different values of
$s=1,0,-1$
(the different values of
![]() $s$
correspond to translations along and transverse to the axis of symmetry). This additional simplification is possible owing to the addition of terms proportional to
$s$
correspond to translations along and transverse to the axis of symmetry). This additional simplification is possible owing to the addition of terms proportional to
![]() $\bar{{\it\xi}}_{0}^{2}$
in (3.8), and these terms taken together are in the form of the gradient of a scalar. This, in effect, includes the additional irrotational component of the disturbance velocity field that is needed in order to satisfy the no-slip boundary condition on the surface of the particle (
$\bar{{\it\xi}}_{0}^{2}$
in (3.8), and these terms taken together are in the form of the gradient of a scalar. This, in effect, includes the additional irrotational component of the disturbance velocity field that is needed in order to satisfy the no-slip boundary condition on the surface of the particle (
![]() ${\it\xi}={\it\xi}_{0}$
). In contrast, the Lamb series solution evidently does not involve the particle size
${\it\xi}={\it\xi}_{0}$
). In contrast, the Lamb series solution evidently does not involve the particle size
![]() $a$
. Thus, while each of the terms in (3.15) is a homogeneous function of
$a$
. Thus, while each of the terms in (3.15) is a homogeneous function of
![]() $r$
, the biharmonic component in
$r$
, the biharmonic component in
![]() $\boldsymbol{S}_{ts}^{(3)}$
in Kushch’s formalism is not a homogeneous function of
$\boldsymbol{S}_{ts}^{(3)}$
in Kushch’s formalism is not a homogeneous function of
![]() ${\it\xi}$
, at leading order, in the limit of large
${\it\xi}$
, at leading order, in the limit of large
![]() ${\it\xi}$
(with
${\it\xi}$
(with
![]() $d{\it\xi}$
finite). As will be shown in a companion paper (Dabade et al.
Reference Dabade, Marath and Subramanian2015), the above remains true even for the case of an ambient linear flow. In this case, the disturbance velocity field due to a force-free torque-free spherical particle has an
$d{\it\xi}$
finite). As will be shown in a companion paper (Dabade et al.
Reference Dabade, Marath and Subramanian2015), the above remains true even for the case of an ambient linear flow. In this case, the disturbance velocity field due to a force-free torque-free spherical particle has an
![]() $O(1/r^{2})$
part that corresponds to the stresslet singularity and an irrotational
$O(1/r^{2})$
part that corresponds to the stresslet singularity and an irrotational
![]() $O(1/r^{4})$
contribution, and these arise from the terms proportional to
$O(1/r^{4})$
contribution, and these arise from the terms proportional to
![]() $p_{-3}$
and
$p_{-3}$
and
![]() ${\it\phi}_{-3}$
, respectively, in the Lamb series. In contrast, the entire disturbance velocity field due to a spheroidal particle in an axisymmetric extensional flow aligned with the particle axis of symmetry is generated by
${\it\phi}_{-3}$
, respectively, in the Lamb series. In contrast, the entire disturbance velocity field due to a spheroidal particle in an axisymmetric extensional flow aligned with the particle axis of symmetry is generated by
![]() $\boldsymbol{S}_{2,0}^{(3)}$
. Similarly, the entire disturbance field in a planar extension, transverse to the symmetry axis, is given by a linear combination of
$\boldsymbol{S}_{2,0}^{(3)}$
. Similarly, the entire disturbance field in a planar extension, transverse to the symmetry axis, is given by a linear combination of
![]() $\boldsymbol{S}_{2,2}^{(3)}$
and
$\boldsymbol{S}_{2,2}^{(3)}$
and
![]() $\boldsymbol{S}_{2,-2}^{(3)}$
.
$\boldsymbol{S}_{2,-2}^{(3)}$
.
Having clarified the general structure of the spheroidal harmonics formalism, we construct the disturbance velocity fields that enter the reciprocal theorem formulation given in § 2. The requirement of far-field decay is already satisfied by (3.9). The satisfaction of the no-slip boundary condition on the particle surface requires expressions for the three decaying partial vectorial solutions for
![]() ${\it\xi}={\it\xi}_{0}$
, which, for the prolate spheroid, are given by:
${\it\xi}={\it\xi}_{0}$
, which, for the prolate spheroid, are given by:
 $$\begin{eqnarray}\displaystyle \boldsymbol{S}_{ts}^{(3)}|_{{\it\xi}={\it\xi}_{0}} & = & \displaystyle \boldsymbol{e}_{1}\{-(t-s+1){\it\xi}_{0}Q_{t}^{s-1}+(t+s-1)[1+(t+s){\it\beta}_{-(t+1)}]Q_{t-1}^{s-1}\}Y_{t-1}^{s-1}\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{e}_{2}\{(t-s-1){\it\xi}_{0}Q_{t}^{s+1}-(t-s-1)[1+(t-s){\it\beta}_{-(t+1)}]Q_{t-1}^{s+1}\}Y_{t-1}^{s+1}\nonumber\\ \displaystyle & & \displaystyle +\,\mathbf{1}_{z}\{-(t-s){\it\xi}_{0}Q_{t}^{s}-C_{-(t+1),s}Q_{t-1}^{s}\}Y_{t-1}^{s},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{S}_{ts}^{(3)}|_{{\it\xi}={\it\xi}_{0}} & = & \displaystyle \boldsymbol{e}_{1}\{-(t-s+1){\it\xi}_{0}Q_{t}^{s-1}+(t+s-1)[1+(t+s){\it\beta}_{-(t+1)}]Q_{t-1}^{s-1}\}Y_{t-1}^{s-1}\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{e}_{2}\{(t-s-1){\it\xi}_{0}Q_{t}^{s+1}-(t-s-1)[1+(t-s){\it\beta}_{-(t+1)}]Q_{t-1}^{s+1}\}Y_{t-1}^{s+1}\nonumber\\ \displaystyle & & \displaystyle +\,\mathbf{1}_{z}\{-(t-s){\it\xi}_{0}Q_{t}^{s}-C_{-(t+1),s}Q_{t-1}^{s}\}Y_{t-1}^{s},\end{eqnarray}$$
The simplest velocity field is that due to a spheroid rotating about its axis of symmetry. As for a rotating sphere, this field is harmonic without an associated pressure field, being proportional to
![]() $\boldsymbol{S}_{2,0}^{(2)}$
; the Lamb series for a rotating sphere gives
$\boldsymbol{S}_{2,0}^{(2)}$
; the Lamb series for a rotating sphere gives
![]() $\boldsymbol{{\rm\nabla}}\wedge (\boldsymbol{x}{\it\chi}_{-2})$
. The inertial acceleration and the non-Newtonian stress field that appear in the torque integrals in (2.19) require the disturbance velocity field due to a spheroid translating in an arbitrary orientation. The linearity of the Stokes equations imply that
$\boldsymbol{{\rm\nabla}}\wedge (\boldsymbol{x}{\it\chi}_{-2})$
. The inertial acceleration and the non-Newtonian stress field that appear in the torque integrals in (2.19) require the disturbance velocity field due to a spheroid translating in an arbitrary orientation. The linearity of the Stokes equations imply that
![]() $\boldsymbol{u}_{s}^{(1)}$
may be written as the following superposition of the axial and transverse translation fields:
$\boldsymbol{u}_{s}^{(1)}$
may be written as the following superposition of the axial and transverse translation fields:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \boldsymbol{u}_{s}^{(1)}=A_{z}(\boldsymbol{S}_{1,0}^{(3)})+A_{x}(\boldsymbol{S}_{1,1}^{(3)}-\boldsymbol{S}_{1,-1}^{(3)}),\quad \text{where}\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle A_{z}=\frac{U\cos {\it\alpha}}{({\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})+Q_{0}^{0}({\it\xi}_{0}))},\quad A_{x}=\frac{U\sin {\it\alpha}}{(3Q_{0}^{0}({\it\xi}_{0})-{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0}))}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \boldsymbol{u}_{s}^{(1)}=A_{z}(\boldsymbol{S}_{1,0}^{(3)})+A_{x}(\boldsymbol{S}_{1,1}^{(3)}-\boldsymbol{S}_{1,-1}^{(3)}),\quad \text{where}\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle A_{z}=\frac{U\cos {\it\alpha}}{({\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})+Q_{0}^{0}({\it\xi}_{0}))},\quad A_{x}=\frac{U\sin {\it\alpha}}{(3Q_{0}^{0}({\it\xi}_{0})-{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0}))}\end{eqnarray}$$
and
![]() $\boldsymbol{U}=U(\sin {\it\alpha}\mathbf{1}_{x}+\cos {\it\alpha}\mathbf{1}_{z})$
is the velocity of translation of the spheroid with
$\boldsymbol{U}=U(\sin {\it\alpha}\mathbf{1}_{x}+\cos {\it\alpha}\mathbf{1}_{z})$
is the velocity of translation of the spheroid with
![]() ${\it\alpha}$
being the angle between
${\it\alpha}$
being the angle between
![]() $\boldsymbol{U}$
and the spheroidal axis. Thus,
$\boldsymbol{U}$
and the spheroidal axis. Thus,
![]() $\boldsymbol{S}_{1,0}^{(3)}$
in (3.20) gives the disturbance velocity field for axial translation, and the particular combination
$\boldsymbol{S}_{1,0}^{(3)}$
in (3.20) gives the disturbance velocity field for axial translation, and the particular combination
![]() $\boldsymbol{S}_{1,1}^{(3)}-\boldsymbol{S}_{1,-1}^{(3)}$
corresponds to transverse translation along the
$\boldsymbol{S}_{1,1}^{(3)}-\boldsymbol{S}_{1,-1}^{(3)}$
corresponds to transverse translation along the
![]() $x$
-direction (
$x$
-direction (
![]() $\boldsymbol{S}_{1,1}^{(3)}+\boldsymbol{S}_{1,-1}^{(3)}$
gives the velocity field for
$\boldsymbol{S}_{1,1}^{(3)}+\boldsymbol{S}_{1,-1}^{(3)}$
gives the velocity field for
![]() $y$
-translation). Here, we have chosen the
$y$
-translation). Here, we have chosen the
![]() $xz$
plane as the one containing the vector
$xz$
plane as the one containing the vector
![]() $\hat{\boldsymbol{U}}$
and the unit vector along the axis of symmetry, and the torque vector is therefore perpendicular to this plane. Accordingly, the test velocity field,
$\hat{\boldsymbol{U}}$
and the unit vector along the axis of symmetry, and the torque vector is therefore perpendicular to this plane. Accordingly, the test velocity field,
![]() $\boldsymbol{u}^{(2)}$
in (2.1) corresponds to a rotation about the
$\boldsymbol{u}^{(2)}$
in (2.1) corresponds to a rotation about the
![]() $y$
-axis, and for an angular velocity with unit magnitude,
$y$
-axis, and for an angular velocity with unit magnitude,
![]() $\boldsymbol{u}_{s}^{(2)}$
is given by:
$\boldsymbol{u}_{s}^{(2)}$
is given by:
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}_{s}^{(2)}=A_{1y}(\boldsymbol{S}_{1,1}^{(2)}+\boldsymbol{S}_{1,-1}^{(2)})+A_{2y}(\boldsymbol{S}_{2,1}^{(3)}-\boldsymbol{S}_{2,-1}^{(3)}),\quad \text{where }\\ \quad \displaystyle A_{1y}=\frac{d(2{\it\xi}_{0}^{2}-1)}{(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0}))},\\ \quad \displaystyle A_{2y}=\frac{d({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0}))},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}_{s}^{(2)}=A_{1y}(\boldsymbol{S}_{1,1}^{(2)}+\boldsymbol{S}_{1,-1}^{(2)})+A_{2y}(\boldsymbol{S}_{2,1}^{(3)}-\boldsymbol{S}_{2,-1}^{(3)}),\quad \text{where }\\ \quad \displaystyle A_{1y}=\frac{d(2{\it\xi}_{0}^{2}-1)}{(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0}))},\\ \quad \displaystyle A_{2y}=\frac{d({\it\xi}_{0}Q_{1}^{1}({\it\xi}_{0})+2\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{0}({\it\xi}_{0}))}{Q_{2}^{1}({\it\xi}_{0})(2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0}))},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
and
![]() $\unicode[STIX]{x1D650}^{(2)}$
in (2.19) is given by
$\unicode[STIX]{x1D650}^{(2)}$
in (2.19) is given by
![]() $\boldsymbol{u}_{s}^{(2)}\mathbf{1}_{y}$
. Note that while the axial rotation above only involved an
$\boldsymbol{u}_{s}^{(2)}\mathbf{1}_{y}$
. Note that while the axial rotation above only involved an
![]() $\boldsymbol{S}_{ts}^{(2)}$
, the transverse rotation field also involves the
$\boldsymbol{S}_{ts}^{(2)}$
, the transverse rotation field also involves the
![]() $\boldsymbol{S}_{ts}^{(3)}$
since the rotation of a non-spherical particle leads to a non-trivial pressure field. A detailed comparison that shows the equivalence of (3.20) and (3.21) to the corresponding expressions obtained from the method of singularities (Chwang & Wu Reference Chwang and Wu1974, Reference Chwang and Wu1975) is given in appendix B.
$\boldsymbol{S}_{ts}^{(3)}$
since the rotation of a non-spherical particle leads to a non-trivial pressure field. A detailed comparison that shows the equivalence of (3.20) and (3.21) to the corresponding expressions obtained from the method of singularities (Chwang & Wu Reference Chwang and Wu1974, Reference Chwang and Wu1975) is given in appendix B.
The velocity fields given by (3.20) and (3.21) may now be used in (2.19) and, as will be seen in § 4, an integration in spheroidal coordinates yields analytical expressions for the torque on a prolate spheroid of an arbitrary aspect ratio as a function of
![]() $d$
and
$d$
and
![]() ${\it\xi}_{0}$
. The torques on an oblate spheroid may simply be obtained using
${\it\xi}_{0}$
. The torques on an oblate spheroid may simply be obtained using
![]() ${\it\xi}_{0}\leftrightarrow \text{i}\sqrt{{\it\xi}_{0}^{2}-1},d\leftrightarrow -\text{i}d$
in the corresponding prolate forms. Before moving on to the results, it is worth spending a little time discussing earlier efforts based on a different approach, the method of singularities (Leal Reference Leal1992), that also analyse the motion of spheroidal particles and the associated disturbance velocity fields for various canonical scenarios. By distributing appropriate combinations of the fundamental Stokes singularities (Stokeslets, stresslets, potential dipoles and quadrupoles) along the axis of symmetry between the foci, Chwang and Wu, in a series of articles, obtained the velocity disturbance fields due to a prolate spheroid in a variety of flows, including ambient linear and quadratic flows (Chwang & Wu Reference Chwang and Wu1974, Reference Chwang and Wu1975; Chwang Reference Chwang1975). These representations of the disturbance velocity fields, together with similar representations for the Faxen relations, have been subsequently used by Kim and co-workers (Kim Reference Kim1985a
,Reference Kim
b
, Reference Kim1986b
) to analyse the interactions between a pair of sedimenting spheroids using the method of reflections (except near contact). Kim and co-workers (Kim & Arunachalam Reference Kim and Arunachalam1987; Kim & Karrila Reference Kim and Karrila1991) generalized the singularity representations to a tri-axial ellipsoid, there being an areal distribution of fundamental singularities on the surface of a focal ellipse in this case. In the limiting case of an oblate spheroid, there is an areal distribution on a focal disk in a plane transverse to the symmetry axis. The Faxen relations for a sphere were originally generalized to the case of a tri-axial ellipsoid much earlier (Brenner Reference Brenner1966), but the resulting representations were in the form of an infinite series in terms of singularities located at the geometric centre. These have been found to be numerically intractable (Claeys & Brady Reference Claeys and Brady1993b
), and are subject to convergence problems at small separations (Kim & Arunachalam Reference Kim and Arunachalam1987). Later, Claeys and Brady have used the results of Kim and co-workers to analyse the hydrodynamic interactions between a finite number of spheroidal particles (Claeys & Brady Reference Claeys and Brady1993b
), and in an infinite suspension, both ordered (Claeys & Brady Reference Claeys and Brady1993c
) and disordered (Claeys & Brady Reference Claeys and Brady1993a
). The authors extended the idea of the Stokesian dynamics method, originally proposed for suspensions of spherical particles (Brady & Bossis Reference Brady and Bossis1988), to spheroidal particles, and the results of Kim and co-workers were used to construct the far-field mobility matrix. The aforementioned efforts of Chwang and Wu for single particles, and those of Kim and Brady for both finite and infinite systems of particles, are for prolate spheroids. Recently, Shatz (Reference Shatz2004) has shown that the Stokes disturbance fields for an oblate spheroid may still be obtained by a line distribution of the fundamental Stokes singularities as opposed to the areal distribution mentioned above. This is possible by placing the singularities along an imaginary focal length, aligned with the symmetry axis, a singularity at a point along this axis being equivalent to a singularity all along the perimeter of a (real) focal circle transverse to the axis of symmetry. The notion of an imaginary focal length mimics the transition relations between the prolate and oblate spheroidal coordinates (
${\it\xi}_{0}\leftrightarrow \text{i}\sqrt{{\it\xi}_{0}^{2}-1},d\leftrightarrow -\text{i}d$
in the corresponding prolate forms. Before moving on to the results, it is worth spending a little time discussing earlier efforts based on a different approach, the method of singularities (Leal Reference Leal1992), that also analyse the motion of spheroidal particles and the associated disturbance velocity fields for various canonical scenarios. By distributing appropriate combinations of the fundamental Stokes singularities (Stokeslets, stresslets, potential dipoles and quadrupoles) along the axis of symmetry between the foci, Chwang and Wu, in a series of articles, obtained the velocity disturbance fields due to a prolate spheroid in a variety of flows, including ambient linear and quadratic flows (Chwang & Wu Reference Chwang and Wu1974, Reference Chwang and Wu1975; Chwang Reference Chwang1975). These representations of the disturbance velocity fields, together with similar representations for the Faxen relations, have been subsequently used by Kim and co-workers (Kim Reference Kim1985a
,Reference Kim
b
, Reference Kim1986b
) to analyse the interactions between a pair of sedimenting spheroids using the method of reflections (except near contact). Kim and co-workers (Kim & Arunachalam Reference Kim and Arunachalam1987; Kim & Karrila Reference Kim and Karrila1991) generalized the singularity representations to a tri-axial ellipsoid, there being an areal distribution of fundamental singularities on the surface of a focal ellipse in this case. In the limiting case of an oblate spheroid, there is an areal distribution on a focal disk in a plane transverse to the symmetry axis. The Faxen relations for a sphere were originally generalized to the case of a tri-axial ellipsoid much earlier (Brenner Reference Brenner1966), but the resulting representations were in the form of an infinite series in terms of singularities located at the geometric centre. These have been found to be numerically intractable (Claeys & Brady Reference Claeys and Brady1993b
), and are subject to convergence problems at small separations (Kim & Arunachalam Reference Kim and Arunachalam1987). Later, Claeys and Brady have used the results of Kim and co-workers to analyse the hydrodynamic interactions between a finite number of spheroidal particles (Claeys & Brady Reference Claeys and Brady1993b
), and in an infinite suspension, both ordered (Claeys & Brady Reference Claeys and Brady1993c
) and disordered (Claeys & Brady Reference Claeys and Brady1993a
). The authors extended the idea of the Stokesian dynamics method, originally proposed for suspensions of spherical particles (Brady & Bossis Reference Brady and Bossis1988), to spheroidal particles, and the results of Kim and co-workers were used to construct the far-field mobility matrix. The aforementioned efforts of Chwang and Wu for single particles, and those of Kim and Brady for both finite and infinite systems of particles, are for prolate spheroids. Recently, Shatz (Reference Shatz2004) has shown that the Stokes disturbance fields for an oblate spheroid may still be obtained by a line distribution of the fundamental Stokes singularities as opposed to the areal distribution mentioned above. This is possible by placing the singularities along an imaginary focal length, aligned with the symmetry axis, a singularity at a point along this axis being equivalent to a singularity all along the perimeter of a (real) focal circle transverse to the axis of symmetry. The notion of an imaginary focal length mimics the transition relations between the prolate and oblate spheroidal coordinates (
![]() $d\leftrightarrow -\text{i}d$
) given earlier. From its ready applicability to prolate and oblate spheroids of an arbitrary aspect ratio, and from the ease of obtaining closed-form analytical results, the Kushch formalism presented here appears more advantageous. The singularity method yields the disturbance velocity fields in terms of integral representations which are cumbersome to handle analytically (as already noted, Kim (Reference Kim1986a
), despite using the singularity representation of the velocity field calculated the viscoelastic torque integral numerically). Although these integrals can be evaluated in closed form, the Kushch solution yields a elegant rearrangement of the resulting analytical forms in a manner that mimics the original Lamb series. For these reasons we have adopted this formalism here, and in a companion paper (Dabade et al.
Reference Dabade, Marath and Subramanian2015), to characterize the orientation dynamics of spheroidal particles in sedimentation and shearing flows.
$d\leftrightarrow -\text{i}d$
) given earlier. From its ready applicability to prolate and oblate spheroids of an arbitrary aspect ratio, and from the ease of obtaining closed-form analytical results, the Kushch formalism presented here appears more advantageous. The singularity method yields the disturbance velocity fields in terms of integral representations which are cumbersome to handle analytically (as already noted, Kim (Reference Kim1986a
), despite using the singularity representation of the velocity field calculated the viscoelastic torque integral numerically). Although these integrals can be evaluated in closed form, the Kushch solution yields a elegant rearrangement of the resulting analytical forms in a manner that mimics the original Lamb series. For these reasons we have adopted this formalism here, and in a companion paper (Dabade et al.
Reference Dabade, Marath and Subramanian2015), to characterize the orientation dynamics of spheroidal particles in sedimentation and shearing flows.
4. The torques on a sedimenting spheroid
The final expression, equation (2.19), from the generalized reciprocal theorem formulation, with the expressions (3.20) and (3.21) for the velocity fields, are used to obtain closed-form expressions for the inertial and viscoelastic torques as a function of the particle aspect ratio for both prolate and oblate spheroids. The regular nature of the torque contributions, together with symmetry arguments, imply that the inertial and viscoelastic torques, apart from being proportional to
![]() $\mathit{Re}$
and
$\mathit{Re}$
and
![]() $\mathit{De}$
, respectively, must have the general form
$\mathit{De}$
, respectively, must have the general form
![]() $F({\it\xi}_{0})\hat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{p}(\hat{\boldsymbol{U}}\wedge \boldsymbol{p})$
,
$F({\it\xi}_{0})\hat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{p}(\hat{\boldsymbol{U}}\wedge \boldsymbol{p})$
,
![]() $\boldsymbol{p}$
being the unit vector along the symmetry axis. For the viscoelastic case, there is an additional dependence on
$\boldsymbol{p}$
being the unit vector along the symmetry axis. For the viscoelastic case, there is an additional dependence on
![]() ${\it\epsilon}$
, the second-order fluid parameter, so that
${\it\epsilon}$
, the second-order fluid parameter, so that
![]() $F({\it\xi}_{0})_{visco}\equiv F({\it\xi}_{0};{\it\epsilon})_{visco}$
. Importantly, both torque contributions have an angular dependence given by
$F({\it\xi}_{0})_{visco}\equiv F({\it\xi}_{0};{\it\epsilon})_{visco}$
. Importantly, both torque contributions have an angular dependence given by
![]() $\sin 2{\it\alpha}$
,
$\sin 2{\it\alpha}$
,
![]() ${\it\alpha}$
being the angle between
${\it\alpha}$
being the angle between
![]() $\hat{\boldsymbol{U}}$
and
$\hat{\boldsymbol{U}}$
and
![]() $\boldsymbol{p}$
. The dimensional inertial (elastic) torque is given by
$\boldsymbol{p}$
. The dimensional inertial (elastic) torque is given by
![]() $\mathit{Re}(\mathit{De})F({\it\xi}_{0}){\it\mu}UL^{2}\sin {\it\alpha}\cos {\it\alpha}$
, so that the peak value is attained at
$\mathit{Re}(\mathit{De})F({\it\xi}_{0}){\it\mu}UL^{2}\sin {\it\alpha}\cos {\it\alpha}$
, so that the peak value is attained at
![]() ${\it\alpha}=45^{\circ }$
, and the torque vanishes for the longitudinal (
${\it\alpha}=45^{\circ }$
, and the torque vanishes for the longitudinal (
![]() $\hat{\boldsymbol{U}}\Vert \boldsymbol{p}$
) and transverse (
$\hat{\boldsymbol{U}}\Vert \boldsymbol{p}$
) and transverse (
![]() $\hat{\boldsymbol{U}}\bot \boldsymbol{p}$
) orientations; only one of these equilibria is stable, however. The detailed integration in spheroidal coordinates determines
$\hat{\boldsymbol{U}}\bot \boldsymbol{p}$
) orientations; only one of these equilibria is stable, however. The detailed integration in spheroidal coordinates determines
![]() $F({\it\xi}_{0})$
, which then characterizes the torque dependence on aspect ratio. From figure 1, it is seen that a torque driving a prolate spheroid towards a longside-on orientation implies a positive
$F({\it\xi}_{0})$
, which then characterizes the torque dependence on aspect ratio. From figure 1, it is seen that a torque driving a prolate spheroid towards a longside-on orientation implies a positive
![]() $F({\it\xi}_{0})$
, while an approach towards a broadside-on orientation implies a negative
$F({\it\xi}_{0})$
, while an approach towards a broadside-on orientation implies a negative
![]() $F({\it\xi}_{0})$
; the opposite is true for an oblate spheroid.
$F({\it\xi}_{0})$
; the opposite is true for an oblate spheroid.

Figure 1. The sense of the torques, and the corresponding signs of
![]() $F({\it\xi}_{0})$
for sedimenting prolate (a) and oblate (b) spheroids.
$F({\it\xi}_{0})$
for sedimenting prolate (a) and oblate (b) spheroids.
For the inertial case, it will be seen in § 4.1 that
![]() $F({\it\xi}_{0})$
has the same sign for all
$F({\it\xi}_{0})$
has the same sign for all
![]() ${\it\xi}_{0}\,{\it\epsilon}(1,\infty )$
, although it changes sign in going from a prolate to an oblate spheroid. The inertial torque favours the broadside-on configuration for both prolate and oblate spheroids. A prolate spheroid in this orientation has its
${\it\xi}_{0}\,{\it\epsilon}(1,\infty )$
, although it changes sign in going from a prolate to an oblate spheroid. The inertial torque favours the broadside-on configuration for both prolate and oblate spheroids. A prolate spheroid in this orientation has its
![]() $\boldsymbol{p}\bot \hat{\boldsymbol{U}}$
, while an oblate spheroid in the same orientation has
$\boldsymbol{p}\bot \hat{\boldsymbol{U}}$
, while an oblate spheroid in the same orientation has
![]() $\boldsymbol{p}\Vert \hat{\boldsymbol{U}}$
, this being consistent with the change in sign of
$\boldsymbol{p}\Vert \hat{\boldsymbol{U}}$
, this being consistent with the change in sign of
![]() $F({\it\xi}_{0})$
. For
$F({\it\xi}_{0})$
. For
![]() $\mathit{Re}\sim O(1)$
or larger, the broadside-on orientation arises since the wake of the front portion of the spheroid ‘shields’ the rear, which catches up with the front as a result. Although not literally true for
$\mathit{Re}\sim O(1)$
or larger, the broadside-on orientation arises since the wake of the front portion of the spheroid ‘shields’ the rear, which catches up with the front as a result. Although not literally true for
![]() $\mathit{Re}\ll 1$
, the wake now being asymptotically far away in the Oseen region, the
$\mathit{Re}\ll 1$
, the wake now being asymptotically far away in the Oseen region, the
![]() $O(\mathit{Re})$
correction to the Stokes velocity field, in the inner region, nevertheless reflects the asymmetry of the outer Oseen field. The nature of the inertial torque is generic, and occurs even when the anisotropic body is a compound object formed, for instance, as a result of two touching spheres; the tendency of the two spheres, in this configuration, to rotate onto a broadside-on orientation is well known (Fortes, Joseph & Lundgren Reference Fortes, Joseph and Lundgren1987).
$O(\mathit{Re})$
correction to the Stokes velocity field, in the inner region, nevertheless reflects the asymmetry of the outer Oseen field. The nature of the inertial torque is generic, and occurs even when the anisotropic body is a compound object formed, for instance, as a result of two touching spheres; the tendency of the two spheres, in this configuration, to rotate onto a broadside-on orientation is well known (Fortes, Joseph & Lundgren Reference Fortes, Joseph and Lundgren1987).
For the viscoelastic case, to begin with, we restrict our attention to spheroids sedimenting in polymer solutions, in which case
![]() ${\it\epsilon}$
is restricted to the narrow interval
${\it\epsilon}$
is restricted to the narrow interval
![]() $(-0.7,-0.5)$
. For these
$(-0.7,-0.5)$
. For these
![]() ${\it\epsilon}$
values, as will be in § 4.2, viscoelasticity stabilizes the longside-on orientation (
${\it\epsilon}$
values, as will be in § 4.2, viscoelasticity stabilizes the longside-on orientation (
![]() $\boldsymbol{p}\Vert \hat{\boldsymbol{U}}$
for a prolate spheroid and
$\boldsymbol{p}\Vert \hat{\boldsymbol{U}}$
for a prolate spheroid and
![]() $\boldsymbol{p}\bot \hat{\boldsymbol{U}}$
for an oblate spheroid), and this may be explained based on the well-known idea of tensioned streamlines. At the microstructural level, the first effect of a weak ambient flow (small
$\boldsymbol{p}\bot \hat{\boldsymbol{U}}$
for an oblate spheroid), and this may be explained based on the well-known idea of tensioned streamlines. At the microstructural level, the first effect of a weak ambient flow (small
![]() $\mathit{De}$
) on the suspended polymers is to stretch them, on average, along the local extensional axis, leading to an enhancement in the shear viscosity. The second-order fluid rheology denotes the first departure from such a Newtonian response and, at this order, the distribution of polymer configurations tilts away from the local extensional axis towards the flow direction on account of the rotation induced by the local vorticity. This effect is captured by the co-rotational contribution to the polymeric stress given by (2.9). The slight flow-alignment of the polymers leads to a tensile stress component along the local flow direction and, at
$\mathit{De}$
) on the suspended polymers is to stretch them, on average, along the local extensional axis, leading to an enhancement in the shear viscosity. The second-order fluid rheology denotes the first departure from such a Newtonian response and, at this order, the distribution of polymer configurations tilts away from the local extensional axis towards the flow direction on account of the rotation induced by the local vorticity. This effect is captured by the co-rotational contribution to the polymeric stress given by (2.9). The slight flow-alignment of the polymers leads to a tensile stress component along the local flow direction and, at
![]() $O(\mathit{De})$
, one may therefore regard the streamlines as being similar to stretched rubber bands. The tendency of the bent streamlines to snap straight leads to a torque on the spheroid acting to align it to a longside-on orientation. Note that the quadratic stress component depends only on the rate-of-strain tensor, and yields
$O(\mathit{De})$
, one may therefore regard the streamlines as being similar to stretched rubber bands. The tendency of the bent streamlines to snap straight leads to a torque on the spheroid acting to align it to a longside-on orientation. Note that the quadratic stress component depends only on the rate-of-strain tensor, and yields
![]() $N_{1}=0$
, implying the absence of a flow-aligned tension.
$N_{1}=0$
, implying the absence of a flow-aligned tension.
Thus, physical arguments suggest that either inertia or elasticity (when consistent with a tensioned-streamline configuration), acting in isolation on a prolate or an oblate spheroid, leads to the same equilibrium orientation for all aspect ratios. Although
![]() $F({\it\xi}_{0})$
changes sign in going from inertia to viscoelasticity, the identical angular dependence implies that inertia and elasticity, even when acting simultaneously, cannot lead to equilibrium orientations intermediate between those parallel and perpendicular to
$F({\it\xi}_{0})$
changes sign in going from inertia to viscoelasticity, the identical angular dependence implies that inertia and elasticity, even when acting simultaneously, cannot lead to equilibrium orientations intermediate between those parallel and perpendicular to
![]() $\hat{\boldsymbol{U}}$
, as observed in some earlier experiments (Joseph & Liu Reference Joseph and Liu1993; Liu & Joseph Reference Liu and Joseph1993). Intermediate equilibria are likely when one includes higher-order contributions, but these would be restricted to an asymptotically small angular interval of
$\hat{\boldsymbol{U}}$
, as observed in some earlier experiments (Joseph & Liu Reference Joseph and Liu1993; Liu & Joseph Reference Liu and Joseph1993). Intermediate equilibria are likely when one includes higher-order contributions, but these would be restricted to an asymptotically small angular interval of
![]() $O(\mathit{Re})$
or
$O(\mathit{Re})$
or
![]() $O(\mathit{De})$
in the limit
$O(\mathit{De})$
in the limit
![]() $\mathit{Re},\mathit{De}\ll 1$
. To the order considered here, therefore, depending on the ratio
$\mathit{Re},\mathit{De}\ll 1$
. To the order considered here, therefore, depending on the ratio
![]() $\mathit{De}/\mathit{Re}$
, the so-called elasticity number
$\mathit{De}/\mathit{Re}$
, the so-called elasticity number
![]() $\mathit{El}$
, either the inertial or viscoelastic torque is dominant for all orientations. The ratio of the two torques, at leading order, is given by
$\mathit{El}$
, either the inertial or viscoelastic torque is dominant for all orientations. The ratio of the two torques, at leading order, is given by
![]() $[\mathit{Re}\,F({\it\xi}_{0})_{inertia}]/[\mathit{De}\,F({\it\xi}_{0};{\it\epsilon})_{visco}]$
, and equating this to unity yields the critical curve separating the two equilibria. This neutral curve may be written in the form
$[\mathit{Re}\,F({\it\xi}_{0})_{inertia}]/[\mathit{De}\,F({\it\xi}_{0};{\it\epsilon})_{visco}]$
, and equating this to unity yields the critical curve separating the two equilibria. This neutral curve may be written in the form
![]() $\mathit{El}=\mathscr{G}({\it\xi}_{0};{\it\epsilon})$
, with
$\mathit{El}=\mathscr{G}({\it\xi}_{0};{\it\epsilon})$
, with
![]() $\mathscr{G}({\it\xi}_{0})=F({\it\xi}_{0})_{inertia}/F({\it\xi}_{0};{\it\epsilon})_{visco}$
, and would separate a region of longside-on orientation above from a broadside-on orientation below. The detailed results obtained in § 4.2.2 determine this curve as a function of the spheroid aspect ratio.
$\mathscr{G}({\it\xi}_{0})=F({\it\xi}_{0})_{inertia}/F({\it\xi}_{0};{\it\epsilon})_{visco}$
, and would separate a region of longside-on orientation above from a broadside-on orientation below. The detailed results obtained in § 4.2.2 determine this curve as a function of the spheroid aspect ratio.
The argument above, of the viscoelastic torque leading to a longside-on configuration, relies on the notion of tensioned streamlines. This in turn depends on
![]() $N_{1}$
being dominant and positive, as is true for polymer solutions. Other complex fluids in near-equilibrium scenarios have
$N_{1}$
being dominant and positive, as is true for polymer solutions. Other complex fluids in near-equilibrium scenarios have
![]() $N_{2}$
being comparable to
$N_{2}$
being comparable to
![]() $N_{1}$
, although still smaller in magnitude. An alternate scenario is where
$N_{1}$
, although still smaller in magnitude. An alternate scenario is where
![]() ${\it\epsilon}=0$
, when only the quadratic component of the polymeric stress survives, and one has an
${\it\epsilon}=0$
, when only the quadratic component of the polymeric stress survives, and one has an
![]() $N_{2}$
-dominant second-order fluid. That the effects of a non-zero
$N_{2}$
-dominant second-order fluid. That the effects of a non-zero
![]() $N_{2}$
are more subtle is known from the case of polymer solutions (Tanner Reference Tanner2000). More recently, the consequence of a dominant
$N_{2}$
are more subtle is known from the case of polymer solutions (Tanner Reference Tanner2000). More recently, the consequence of a dominant
![]() $N_{2}$
on the nature of the free-surface perturbation has been examined in the context of suspensions of non-Brownian particles (Boyer, Pouliquen & Guazzelli Reference Boyer, Pouliquen and Guazzelli2011). The observations have been explained based on the notion of tensioned vortex lines in the base-state azimuthal flow (Hinch Reference Hinch2011), although we note that such suspensions, unlike the second-order fluids considered here, are far from thermal equilibrium. Nevertheless, we consider the dependence of the viscoelastic torque on both
$N_{2}$
on the nature of the free-surface perturbation has been examined in the context of suspensions of non-Brownian particles (Boyer, Pouliquen & Guazzelli Reference Boyer, Pouliquen and Guazzelli2011). The observations have been explained based on the notion of tensioned vortex lines in the base-state azimuthal flow (Hinch Reference Hinch2011), although we note that such suspensions, unlike the second-order fluids considered here, are far from thermal equilibrium. Nevertheless, we consider the dependence of the viscoelastic torque on both
![]() ${\it\xi}_{0}$
and
${\it\xi}_{0}$
and
![]() ${\it\epsilon}$
in § 4.2.4, and show that, for
${\it\epsilon}$
in § 4.2.4, and show that, for
![]() ${\it\epsilon}\geqslant 0$
, the torque acting on a prolate spheroid does change sign for certain aspect ratios, thereby stabilizing the broadside-on orientation. Further, this change in sign appears explainable based on a tensioned vortex line configuration, although the geometry is significantly more complicated than those of the viscometric flows considered in earlier efforts (Keentok et al.
Reference Keentok, Georgescu, Sherwood and Tanner1980; Hinch Reference Hinch2011).
${\it\epsilon}\geqslant 0$
, the torque acting on a prolate spheroid does change sign for certain aspect ratios, thereby stabilizing the broadside-on orientation. Further, this change in sign appears explainable based on a tensioned vortex line configuration, although the geometry is significantly more complicated than those of the viscometric flows considered in earlier efforts (Keentok et al.
Reference Keentok, Georgescu, Sherwood and Tanner1980; Hinch Reference Hinch2011).
4.1. The inertial torque
With the spheroid eccentricity defined as
![]() $e=1/{\it\xi}_{0}$
, the shape function
$e=1/{\it\xi}_{0}$
, the shape function
![]() $F({\it\xi}_{0})$
for the inertial torque, for a prolate spheroid, is given by:
$F({\it\xi}_{0})$
for the inertial torque, for a prolate spheroid, is given by:
 $$\begin{eqnarray}\displaystyle F({\it\xi}_{0})_{inertia} & = & \displaystyle \frac{-{\rm\pi}e^{2}(420e+2240e^{3}+4249e^{5}-2152e^{7})}{315((e^{2}+1)\tanh ^{-1}e-e)^{2}((1-3e^{2})\tanh ^{-1}e-e)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\rm\pi}e^{2}(420+3360e^{2}+1890e^{4}-1470e^{6})\tanh ^{-1}e}{315((e^{2}+1)\tanh ^{-1}e-e)^{2}((1-3e^{2})\tanh ^{-1}e-e)}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{{\rm\pi}e^{2}(1260e-1995e^{3}+2730e^{5}-1995e^{7})(\tanh ^{-1}e)^{2}}{315((e^{2}+1)\tanh ^{-1}e-e)^{2}((1-3e^{2})\tanh ^{-1}e-e)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F({\it\xi}_{0})_{inertia} & = & \displaystyle \frac{-{\rm\pi}e^{2}(420e+2240e^{3}+4249e^{5}-2152e^{7})}{315((e^{2}+1)\tanh ^{-1}e-e)^{2}((1-3e^{2})\tanh ^{-1}e-e)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\rm\pi}e^{2}(420+3360e^{2}+1890e^{4}-1470e^{6})\tanh ^{-1}e}{315((e^{2}+1)\tanh ^{-1}e-e)^{2}((1-3e^{2})\tanh ^{-1}e-e)}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{{\rm\pi}e^{2}(1260e-1995e^{3}+2730e^{5}-1995e^{7})(\tanh ^{-1}e)^{2}}{315((e^{2}+1)\tanh ^{-1}e-e)^{2}((1-3e^{2})\tanh ^{-1}e-e)},\end{eqnarray}$$
and that for an oblate spheroid is given by:
 $$\begin{eqnarray}\displaystyle F({\it\xi}_{0})_{inertia} & = & \displaystyle \frac{{\rm\pi}e^{3}\sqrt{1-e^{2}}(-420+3500e^{2}-9989e^{4}+4757e^{6})}{315\sqrt{1-e^{2}}(-e\sqrt{1-e^{2}}+(1+2e^{2})\sin ^{-1}e)(e\sqrt{1-e^{2}}+(2e^{2}-1)\sin ^{-1}e)^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{210{\rm\pi}e^{2}(2-24e^{2}+69e^{4}-67e^{6}+20e^{8})\sin ^{-1}e}{315\sqrt{1-e^{2}}(-e\sqrt{1-e^{2}}+(1+2e^{2})\sin ^{-1}e)(e\sqrt{1-e^{2}}+(2e^{2}-1)\sin ^{-1}e)^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{105{\rm\pi}e^{3}(12-17e^{2}+24e^{4})(\sin ^{-1}e)^{2}}{315(-e\sqrt{1-e^{2}}+(1+2e^{2})\sin ^{-1}e)(e\sqrt{1-e^{2}}+(2e^{2}-1)\sin ^{-1}e)^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F({\it\xi}_{0})_{inertia} & = & \displaystyle \frac{{\rm\pi}e^{3}\sqrt{1-e^{2}}(-420+3500e^{2}-9989e^{4}+4757e^{6})}{315\sqrt{1-e^{2}}(-e\sqrt{1-e^{2}}+(1+2e^{2})\sin ^{-1}e)(e\sqrt{1-e^{2}}+(2e^{2}-1)\sin ^{-1}e)^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{210{\rm\pi}e^{2}(2-24e^{2}+69e^{4}-67e^{6}+20e^{8})\sin ^{-1}e}{315\sqrt{1-e^{2}}(-e\sqrt{1-e^{2}}+(1+2e^{2})\sin ^{-1}e)(e\sqrt{1-e^{2}}+(2e^{2}-1)\sin ^{-1}e)^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{105{\rm\pi}e^{3}(12-17e^{2}+24e^{4})(\sin ^{-1}e)^{2}}{315(-e\sqrt{1-e^{2}}+(1+2e^{2})\sin ^{-1}e)(e\sqrt{1-e^{2}}+(2e^{2}-1)\sin ^{-1}e)^{2}}.\end{eqnarray}$$
The analytical expressions given above, and those given later for the viscoelastic case, were obtained using the symbolic computing tool Mathematica. We have verified that the values obtained using (4.1) match those obtained earlier by Galdi et al. (Reference Galdi, Vaidya, Pokorny, Daniel and Feng2002) for a prolate spheroid. As discussed in the introduction, these authors used the singularity method (Chwang & Wu Reference Chwang and Wu1974, Reference Chwang and Wu1975) to calculate the disturbance velocity fields, and evaluated the torque integral numerically.
In the limit
![]() $e\rightarrow 0~({\it\xi}_{0}\rightarrow \infty )$
, corresponding to a spheroid of small eccentricity, (4.1) reduces to
$e\rightarrow 0~({\it\xi}_{0}\rightarrow \infty )$
, corresponding to a spheroid of small eccentricity, (4.1) reduces to
![]() $F({\it\xi}_{0})_{inertia}\approx -811{\rm\pi}/1120{\it\xi}_{0}^{2}$
, and the dimensional inertial torque for a prolate near-sphere is given by:
$F({\it\xi}_{0})_{inertia}\approx -811{\rm\pi}/1120{\it\xi}_{0}^{2}$
, and the dimensional inertial torque for a prolate near-sphere is given by:
where
![]() $\hat{\boldsymbol{l}}=\boldsymbol{p}\wedge \hat{\boldsymbol{U}}$
. Cox (Reference Cox1965) obtained
$\hat{\boldsymbol{l}}=\boldsymbol{p}\wedge \hat{\boldsymbol{U}}$
. Cox (Reference Cox1965) obtained
![]() $-\mathit{Re}(29{\rm\pi}/20){\it\delta}({\it\mu}UL^{2})\sin {\it\alpha}\cos {\it\alpha}$
from a perturbation analysis. The small parameter here,
$-\mathit{Re}(29{\rm\pi}/20){\it\delta}({\it\mu}UL^{2})\sin {\it\alpha}\cos {\it\alpha}$
from a perturbation analysis. The small parameter here,
![]() ${\it\delta}$
, is the departure from sphericity obtained from writing the equation for a small-eccentricity spheroid in the invariant form
${\it\delta}$
, is the departure from sphericity obtained from writing the equation for a small-eccentricity spheroid in the invariant form
![]() $r=a[1+{\it\delta}\{(\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{n})^{2}-1\}]$
,
$r=a[1+{\it\delta}\{(\boldsymbol{p}\boldsymbol{\cdot }\boldsymbol{n})^{2}-1\}]$
,
![]() $\boldsymbol{n}$
being the unit radial vector, and equating the major and minor axes to
$\boldsymbol{n}$
being the unit radial vector, and equating the major and minor axes to
![]() ${\it\xi}_{0}$
and
${\it\xi}_{0}$
and
![]() $({\it\xi}_{0}^{2}-1)^{1/2}\approx {\it\xi}_{0}(1-1/(2{\it\xi}_{0}^{2}))$
, respectively. It may be readily shown then that
$({\it\xi}_{0}^{2}-1)^{1/2}\approx {\it\xi}_{0}(1-1/(2{\it\xi}_{0}^{2}))$
, respectively. It may be readily shown then that
![]() $a=d{\it\xi}_{0}$
and
$a=d{\it\xi}_{0}$
and
![]() ${\it\delta}=1/(2{\it\xi}_{0}^{2})$
for the prolate case. The transformation
${\it\delta}=1/(2{\it\xi}_{0}^{2})$
for the prolate case. The transformation
![]() ${\it\xi}_{0}\leftrightarrow \text{i}({\it\xi}_{0}^{2}-1)^{1/2}$
shows that
${\it\xi}_{0}\leftrightarrow \text{i}({\it\xi}_{0}^{2}-1)^{1/2}$
shows that
![]() ${\it\delta}=-1/(2{\it\xi}_{0}^{2})$
for an oblate near-sphere; thus, the leading-order torques, in the near-sphere limit, must differ only in sign for the prolate and oblate cases. We are, however, unable to explain the puzzling difference in the analytical form of the coefficient between (4.3) and Cox’s result above; although, it must be noted that the numerical values are nearly identical (
${\it\delta}=-1/(2{\it\xi}_{0}^{2})$
for an oblate near-sphere; thus, the leading-order torques, in the near-sphere limit, must differ only in sign for the prolate and oblate cases. We are, however, unable to explain the puzzling difference in the analytical form of the coefficient between (4.3) and Cox’s result above; although, it must be noted that the numerical values are nearly identical (
![]() $29/40=0.725;811/1120\approx 0.724$
).
$29/40=0.725;811/1120\approx 0.724$
).
In the slender-fibre limit,
![]() ${\it\xi}_{0}\rightarrow 1$
, and
${\it\xi}_{0}\rightarrow 1$
, and
![]() $F({\it\xi}_{0})_{inertia}\approx -20{\rm\pi}/3[\ln ({\it\xi}_{0}-1)]^{2}$
from (4.1), the dimensional torque being given by:
$F({\it\xi}_{0})_{inertia}\approx -20{\rm\pi}/3[\ln ({\it\xi}_{0}-1)]^{2}$
from (4.1), the dimensional torque being given by:
The fibre aspect ratio is given by
![]() ${\it\kappa}={\it\xi}_{0}/({\it\xi}_{0}^{2}-1)^{1/2}\approx (1/2^{1/2})({\it\xi}_{0}-1)^{-1/2}$
, so that
${\it\kappa}={\it\xi}_{0}/({\it\xi}_{0}^{2}-1)^{1/2}\approx (1/2^{1/2})({\it\xi}_{0}-1)^{-1/2}$
, so that
![]() $\text{ln}\,{\it\kappa}\approx -\text{ln}({\it\xi}_{0}-1)/2+O(1)$
. Using this, (4.4) matches with the result obtained by Khayat and Cox, in the limit of small
$\text{ln}\,{\it\kappa}\approx -\text{ln}({\it\xi}_{0}-1)/2+O(1)$
. Using this, (4.4) matches with the result obtained by Khayat and Cox, in the limit of small
![]() $\mathit{Re}$
(Khayat & Cox Reference Khayat and Cox1989; Subramanian & Koch Reference Subramanian and Koch2005). The small-
$\mathit{Re}$
(Khayat & Cox Reference Khayat and Cox1989; Subramanian & Koch Reference Subramanian and Koch2005). The small-
![]() $\mathit{Re}$
formulation shows the regular nature of the inertial correction. The contribution to the torque integral, at leading logarithmic order, comes from a region of
$\mathit{Re}$
formulation shows the regular nature of the inertial correction. The contribution to the torque integral, at leading logarithmic order, comes from a region of
![]() $O(L^{3})$
around the fibre. From viscous slender-body theory (Batchelor Reference Batchelor1970), the disturbance velocity fields
$O(L^{3})$
around the fibre. From viscous slender-body theory (Batchelor Reference Batchelor1970), the disturbance velocity fields
![]() $\boldsymbol{u}^{(1)}$
and
$\boldsymbol{u}^{(1)}$
and
![]() $\boldsymbol{u}^{(2)}$
are known to be small, being
$\boldsymbol{u}^{(2)}$
are known to be small, being
![]() $O[\ln ({\it\xi}_{0}-1)]^{-1}$
on these length scales, and the torque integral therefore involves the linearized inertial term
$O[\ln ({\it\xi}_{0}-1)]^{-1}$
on these length scales, and the torque integral therefore involves the linearized inertial term
![]() $-\!\int (\hat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)})\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V$
at leading logarithmic order. The logarithmic smallness of the disturbance velocity field implies that the measure of inertial effects on length scales of
$-\!\int (\hat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)})\boldsymbol{\cdot }\boldsymbol{u}^{(2)}\,\text{d}V$
at leading logarithmic order. The logarithmic smallness of the disturbance velocity field implies that the measure of inertial effects on length scales of
![]() $O(L)$
is not
$O(L)$
is not
![]() $\mathit{Re}$
, but
$\mathit{Re}$
, but
![]() $\mathit{Re}[\ln ({\it\xi}_{0}-1)]^{-1}$
, and the torque arises from a linear force density of
$\mathit{Re}[\ln ({\it\xi}_{0}-1)]^{-1}$
, and the torque arises from a linear force density of
![]() $\mathit{Re}[\ln ({\it\xi}_{0}-1)]^{-2}({\it\mu}U)$
acting with a moment arm of
$\mathit{Re}[\ln ({\it\xi}_{0}-1)]^{-2}({\it\mu}U)$
acting with a moment arm of
![]() $O(L)$
. Considering the oblate case, from (4.2),
$O(L)$
. Considering the oblate case, from (4.2),
![]() $\lim _{{\it\xi}_{0}\rightarrow 1}F({\it\xi}_{0})_{inertia}=38/9-17\,216/945{\rm\pi}^{2}$
, and the finite torque on a flat disk is therefore given by:
$\lim _{{\it\xi}_{0}\rightarrow 1}F({\it\xi}_{0})_{inertia}=38/9-17\,216/945{\rm\pi}^{2}$
, and the finite torque on a flat disk is therefore given by:
Figures 2 and 3 show plots of the inertial shape function, as a function of the eccentricity
![]() $e$
, for both the prolate and oblate cases, together with the near-sphere (large
$e$
, for both the prolate and oblate cases, together with the near-sphere (large
![]() ${\it\xi}_{0}$
) and slender-fibre/flat-disk (small (
${\it\xi}_{0}$
) and slender-fibre/flat-disk (small (
![]() ${\it\xi}_{0}-1$
)) asymptotes. For the prolate case, as implied by the asymptotes above, the torque is a non-monotonic function of
${\it\xi}_{0}-1$
)) asymptotes. For the prolate case, as implied by the asymptotes above, the torque is a non-monotonic function of
![]() ${\it\xi}_{0}$
, with the peak torque, measured in units of
${\it\xi}_{0}$
, with the peak torque, measured in units of
![]() ${\it\mu}UL^{2}$
, corresponding to
${\it\mu}UL^{2}$
, corresponding to
![]() $e\approx 0.85$
(an aspect ratio of approximately 1.9). The asymptote, (4.4), obtained from leading logarithmic-order slender-body theory starts to become quantitatively accurate, (to within 20 %) only for aspect ratios in excess of a 100!. The approximation, obtained from (4.1), with the neglect of algebraically small terms alone, performs much better. For the oblate spheroid, the inertial torque is a monotonic function, and the near-sphere asymptote remains a good approximation till an eccentricity of 0.6.
$e\approx 0.85$
(an aspect ratio of approximately 1.9). The asymptote, (4.4), obtained from leading logarithmic-order slender-body theory starts to become quantitatively accurate, (to within 20 %) only for aspect ratios in excess of a 100!. The approximation, obtained from (4.1), with the neglect of algebraically small terms alone, performs much better. For the oblate spheroid, the inertial torque is a monotonic function, and the near-sphere asymptote remains a good approximation till an eccentricity of 0.6.

Figure 2. The inertial shape function for a prolate spheroid as a function of the eccentricity
![]() $e(1/{\it\xi}_{0})$
, together with near-sphere and slender fibre asymptotes. The latter include the leading logarithmic-order prediction given by (4.4), a two-term asymptote accurate to
$e(1/{\it\xi}_{0})$
, together with near-sphere and slender fibre asymptotes. The latter include the leading logarithmic-order prediction given by (4.4), a two-term asymptote accurate to
![]() $O[\ln ({\it\xi}_{0}-1)^{-3}]$
, and one that includes terms of all logarithmic orders.
$O[\ln ({\it\xi}_{0}-1)^{-3}]$
, and one that includes terms of all logarithmic orders.

Figure 3. The inertial shape function for an oblate spheroid as a function of the eccentricity
![]() $e(1/{\it\xi}_{0})$
, together with the near-sphere and flat-disk asymptotes.
$e(1/{\it\xi}_{0})$
, together with the near-sphere and flat-disk asymptotes.
4.2. The viscoelastic torque
4.2.1. The viscoelastic torque in dilute polymer solutions
The shape function for the viscoelastic torque, acting on a prolate spheroid, is given by:
 $$\begin{eqnarray}\displaystyle F({\it\xi}_{0})_{visco} & = & \displaystyle \frac{8{\rm\pi}e^{3}{\it\epsilon}(-3e-(e^{2}-3)\tanh ^{-1}e)}{(e-(e^{2}+1)\tanh ^{-1}e)((3e^{2}-1)\tanh ^{-1}e+e)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{16{\rm\pi}e^{3}({\it\epsilon}+1)(-3e^{2}+32e^{4}+(6e-26e^{3})\tanh ^{-1}e+(13e^{4}-6e^{2}-3)(\tanh ^{-1}e)^{2})}{(e-(e^{2}+1)\tanh ^{-1}e)^{2}((3e^{2}-1)\tanh ^{-1}e+e)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F({\it\xi}_{0})_{visco} & = & \displaystyle \frac{8{\rm\pi}e^{3}{\it\epsilon}(-3e-(e^{2}-3)\tanh ^{-1}e)}{(e-(e^{2}+1)\tanh ^{-1}e)((3e^{2}-1)\tanh ^{-1}e+e)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{16{\rm\pi}e^{3}({\it\epsilon}+1)(-3e^{2}+32e^{4}+(6e-26e^{3})\tanh ^{-1}e+(13e^{4}-6e^{2}-3)(\tanh ^{-1}e)^{2})}{(e-(e^{2}+1)\tanh ^{-1}e)^{2}((3e^{2}-1)\tanh ^{-1}e+e)},\end{eqnarray}$$
and that for an oblate spheroid is given by:
 $$\begin{eqnarray}\displaystyle F({\it\xi}_{0})_{visco} & = & \displaystyle \frac{-8{\rm\pi}e^{3}{\it\epsilon}(3e\sqrt{1-e^{2}}+(2e^{2}-3)\sin ^{-1}e)}{e^{2}(e^{2}-1)+2e\sqrt{1-e^{2}}(\sin ^{-1}e)+(4e^{4}-1)(\sin ^{-1}e)^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{16{\rm\pi}e^{3}(1+{\it\epsilon})(29e^{4}+3e^{2}-2e\sqrt{1-e^{2}}(10e^{2}+3)\sin ^{-1}e-(4e^{4}+12e^{2}-3)(\sin ^{-1}e)^{2})}{(e\sqrt{1-e^{2}}+(2e^{2}-1)\sin ^{-1}e)^{2}(e\sqrt{1-e^{2}}-(2e^{2}+1)\sin ^{-1}e)},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F({\it\xi}_{0})_{visco} & = & \displaystyle \frac{-8{\rm\pi}e^{3}{\it\epsilon}(3e\sqrt{1-e^{2}}+(2e^{2}-3)\sin ^{-1}e)}{e^{2}(e^{2}-1)+2e\sqrt{1-e^{2}}(\sin ^{-1}e)+(4e^{4}-1)(\sin ^{-1}e)^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{16{\rm\pi}e^{3}(1+{\it\epsilon})(29e^{4}+3e^{2}-2e\sqrt{1-e^{2}}(10e^{2}+3)\sin ^{-1}e-(4e^{4}+12e^{2}-3)(\sin ^{-1}e)^{2})}{(e\sqrt{1-e^{2}}+(2e^{2}-1)\sin ^{-1}e)^{2}(e\sqrt{1-e^{2}}-(2e^{2}+1)\sin ^{-1}e)},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where the terms proportional to
![]() ${\it\epsilon}$
and
${\it\epsilon}$
and
![]() $(1+{\it\epsilon})$
correspond, respectively, to the co-rotational and quadratic stress contributions. In this section we restrict ourselves to values of
$(1+{\it\epsilon})$
correspond, respectively, to the co-rotational and quadratic stress contributions. In this section we restrict ourselves to values of
![]() ${\it\epsilon}$
between
${\it\epsilon}$
between
![]() $-1$
and
$-1$
and
![]() $-0.5$
, which includes the range corresponding to dilute polymer solutions. For this choice of
$-0.5$
, which includes the range corresponding to dilute polymer solutions. For this choice of
![]() ${\it\epsilon}$
,
${\it\epsilon}$
,
![]() $F({\it\xi}_{0})$
, as given by (4.6), is positive for all
$F({\it\xi}_{0})$
, as given by (4.6), is positive for all
![]() ${\it\xi}_{0}$
, while that given by (4.7) is negative. The resulting sense of rotation in either case is consistent with the tensioned-streamline argument given earlier.
${\it\xi}_{0}$
, while that given by (4.7) is negative. The resulting sense of rotation in either case is consistent with the tensioned-streamline argument given earlier.
In the limit
![]() $e\rightarrow 0~({\it\xi}_{0}\rightarrow \infty )$
, expectedly,
$e\rightarrow 0~({\it\xi}_{0}\rightarrow \infty )$
, expectedly,
![]() $F({\it\xi}_{0})_{visco}\approx \pm 3{\rm\pi}{\it\epsilon}/5{\it\xi}_{0}^{2}$
from (4.6) and (4.7), so the dimensional viscoelastic torque acting on a near-sphere is given by:
$F({\it\xi}_{0})_{visco}\approx \pm 3{\rm\pi}{\it\epsilon}/5{\it\xi}_{0}^{2}$
from (4.6) and (4.7), so the dimensional viscoelastic torque acting on a near-sphere is given by:
where the plus and minus signs correspond to the oblate and prolate cases, respectively. Note that the near-sphere torque at
![]() $O({\it\xi}_{0}^{-2})$
arises from co-rotational stresses alone; quadratic stresses lead to a smaller
$O({\it\xi}_{0}^{-2})$
arises from co-rotational stresses alone; quadratic stresses lead to a smaller
![]() $O({\it\xi}_{0}^{-4})$
contribution, which therefore does not change in sign in going from the prolate to the oblate case. In the limit of a flat disk (
$O({\it\xi}_{0}^{-4})$
contribution, which therefore does not change in sign in going from the prolate to the oblate case. In the limit of a flat disk (
![]() ${\it\xi}_{0}\rightarrow 1$
), one obtains
${\it\xi}_{0}\rightarrow 1$
), one obtains
![]() $F({\it\xi}_{0})_{visco}\approx (32/3{\rm\pi}^{2})(13{\rm\pi}^{2}-128)(1+{\it\epsilon})+(16/3){\it\epsilon}$
from (4.7), with the dimensional viscoelastic torque being given by:
$F({\it\xi}_{0})_{visco}\approx (32/3{\rm\pi}^{2})(13{\rm\pi}^{2}-128)(1+{\it\epsilon})+(16/3){\it\epsilon}$
from (4.7), with the dimensional viscoelastic torque being given by:
which includes both co-rotational and quadratic terms. We are not aware of any theoretical predictions to compare (4.8) and (4.9) with.

Figure 4. The viscoelastic shape function for a prolate spheroid plotted as a function of the eccentricity
![]() $e(1/{\it\xi}_{0})$
.
$e(1/{\it\xi}_{0})$
.
Leal (Reference Leal1975) determined the torque acting on a slender fibre sedimenting in a second-order fluid to be
![]() $\lim _{{\it\xi}_{0}\rightarrow 1}L_{sed(visco)}=K\mathit{De}({\it\mu}UL^{2})\sin 2{\it\alpha}$
, where the torque coefficient
$\lim _{{\it\xi}_{0}\rightarrow 1}L_{sed(visco)}=K\mathit{De}({\it\mu}UL^{2})\sin 2{\it\alpha}$
, where the torque coefficient
![]() $K$
, in the present notation, is given by:
$K$
, in the present notation, is given by:
where
![]() $c$
is an
$c$
is an
![]() $O(1)$
constant,
$O(1)$
constant,
![]() ${\it\rho}=(x^{2}+y^{2})^{1/2}$
and
${\it\rho}=(x^{2}+y^{2})^{1/2}$
and
![]() $R(z)$
, the cross-sectional radius, characterizes the longitudinal geometry of the fibre. The precise value of
$R(z)$
, the cross-sectional radius, characterizes the longitudinal geometry of the fibre. The precise value of
![]() $c$
does not matter since, to leading order, the dominant contribution to the
$c$
does not matter since, to leading order, the dominant contribution to the
![]() ${\it\rho}$
-integral in (4.10) comes from the lower limit. With
${\it\rho}$
-integral in (4.10) comes from the lower limit. With
![]() $R(z)\sim O({\it\xi}_{0}-1)^{1/2}$
, the integral is
$R(z)\sim O({\it\xi}_{0}-1)^{1/2}$
, the integral is
![]() $O[\ln ({\it\xi}_{0}-1)^{3}]$
and independent of the longitudinal geometry at leading logarithmic order. Importantly,
$O[\ln ({\it\xi}_{0}-1)^{3}]$
and independent of the longitudinal geometry at leading logarithmic order. Importantly,
![]() $K$
is independent of the diameter
$K$
is independent of the diameter
![]() $b$
, and does not approach zero in the limit
$b$
, and does not approach zero in the limit
![]() ${\it\xi}_{0}\rightarrow 1$
, despite the surface area being vanishingly small in this limit (
${\it\xi}_{0}\rightarrow 1$
, despite the surface area being vanishingly small in this limit (
![]() $L$
finite and
$L$
finite and
![]() $b\rightarrow 0$
). This is, however, incorrect. From the exact result, equation (4.6), one obtains
$b\rightarrow 0$
). This is, however, incorrect. From the exact result, equation (4.6), one obtains
![]() $\lim _{{\it\xi}_{0}\rightarrow 1}F({\it\xi}_{0})_{visco}\approx -(16{\rm\pi}(1+{\it\epsilon}))/\ln ({\it\xi}_{0}-1)+8{\rm\pi}{\it\epsilon}/\ln ({\it\xi}_{0}-1)$
, so the dimensional viscoelastic torque for a very slender prolate spheroid is:
$\lim _{{\it\xi}_{0}\rightarrow 1}F({\it\xi}_{0})_{visco}\approx -(16{\rm\pi}(1+{\it\epsilon}))/\ln ({\it\xi}_{0}-1)+8{\rm\pi}{\it\epsilon}/\ln ({\it\xi}_{0}-1)$
, so the dimensional viscoelastic torque for a very slender prolate spheroid is:
at leading logarithmic order. Unlike (4.10), (4.11) does vanish for
![]() ${\it\xi}_{0}\rightarrow 1$
. A detailed analysis for the viscoelastic torque in the slender-fibre limit, together with supporting scaling arguments, is presented in § 4.2.3. For now, we note that the
${\it\xi}_{0}\rightarrow 1$
. A detailed analysis for the viscoelastic torque in the slender-fibre limit, together with supporting scaling arguments, is presented in § 4.2.3. For now, we note that the
![]() $O[\ln ({\it\xi}_{0}-1)]^{-1}$
scaling in (4.11) implies that
$O[\ln ({\it\xi}_{0}-1)]^{-1}$
scaling in (4.11) implies that
![]() $\lim _{{\it\xi}_{0}\rightarrow 1}(F({\it\xi}_{0})_{visco}/F({\it\xi}_{0})_{inertia})\approx \ln ({\it\xi}_{0}-1)\gg 1$
, and one must therefore have
$\lim _{{\it\xi}_{0}\rightarrow 1}(F({\it\xi}_{0})_{visco}/F({\it\xi}_{0})_{inertia})\approx \ln ({\it\xi}_{0}-1)\gg 1$
, and one must therefore have
![]() $\mathit{Re}\sim O[\ln ({\it\xi}_{0}-1)]\mathit{De}\gg \mathit{De}$
in order for a sedimenting slender fibre to adopt a broadside-on orientation due to inertia. It will be seen below (§ 4.2.2), from plots of the neutral curves, that although (4.11) is true in principle, it has an extremely restricted range of validity (in requiring unrealistically high aspect ratios).
$\mathit{Re}\sim O[\ln ({\it\xi}_{0}-1)]\mathit{De}\gg \mathit{De}$
in order for a sedimenting slender fibre to adopt a broadside-on orientation due to inertia. It will be seen below (§ 4.2.2), from plots of the neutral curves, that although (4.11) is true in principle, it has an extremely restricted range of validity (in requiring unrealistically high aspect ratios).
In figures 4 and 5, the viscoelastic shape function is plotted as a function of the eccentricity
![]() $e$
for both prolate and oblate spheroids. As pointed out already, the shape function in either case remains single-signed for the values of
$e$
for both prolate and oblate spheroids. As pointed out already, the shape function in either case remains single-signed for the values of
![]() ${\it\epsilon}$
considered (those characteristic of polymer solutions). In figure 4 the torque drops to zero, in the slender-fibre limit, in an astonishingly abrupt fashion! In order to resolve this precipitous fall for large aspect ratios, the contributions to the shape function due to the co-rotational and quadratic stresses are plotted individually for the prolate case in figure 6. It is clearly the quadratic contribution that is responsible for the near-discontinuous behaviour of the shape function for
${\it\epsilon}$
considered (those characteristic of polymer solutions). In figure 4 the torque drops to zero, in the slender-fibre limit, in an astonishingly abrupt fashion! In order to resolve this precipitous fall for large aspect ratios, the contributions to the shape function due to the co-rotational and quadratic stresses are plotted individually for the prolate case in figure 6. It is clearly the quadratic contribution that is responsible for the near-discontinuous behaviour of the shape function for
![]() ${\it\xi}_{0}\rightarrow 1$
. The variation in the co-rotational contribution is seen to be relatively gentle in comparison, although still substantially steeper than the inertial case (see figure 2). Our co-rotational torque agrees with that obtained by Galdi (Reference Galdi2000), but differs from that obtained from the general formula of Brunn (Reference Brunn1977) on using the appropriate expressions for the translational and rotational resistance functions. Also included in figure 6 are the near-sphere and slender fibre asymptotes for comparison. While the former remains a reasonable approximation till
${\it\xi}_{0}\rightarrow 1$
. The variation in the co-rotational contribution is seen to be relatively gentle in comparison, although still substantially steeper than the inertial case (see figure 2). Our co-rotational torque agrees with that obtained by Galdi (Reference Galdi2000), but differs from that obtained from the general formula of Brunn (Reference Brunn1977) on using the appropriate expressions for the translational and rotational resistance functions. Also included in figure 6 are the near-sphere and slender fibre asymptotes for comparison. While the former remains a reasonable approximation till
![]() $e\approx 0.7$
(an aspect ratio of 2), the leading logarithmic-order approximation in (4.11) is quite useless. Including an additional term, of
$e\approx 0.7$
(an aspect ratio of 2), the leading logarithmic-order approximation in (4.11) is quite useless. Including an additional term, of
![]() $O[\ln ({\it\xi}_{0}-1)]^{-2}$
, captures the non-monotonic behaviour for
$O[\ln ({\it\xi}_{0}-1)]^{-2}$
, captures the non-monotonic behaviour for
![]() ${\it\xi}_{0}$
close to 1, but loses quantitative accuracy when
${\it\xi}_{0}$
close to 1, but loses quantitative accuracy when
![]() $e=0.995$
(an aspect ratio of 10); an approximation that retains terms to all logarithmic orders performs much better. Figure 7 shows the co-rotational and quadratic torque contributions for the oblate case, together with the near-sphere and one- and two-term flat disk asymptotes. There is no major distinction between the two contributions as regards their variation with aspect ratio. There is, however, a very small interval of non-monotonicity, for the quadratic contribution, close to the flat-disk limit, so that the peak quadratic torque arises at an
$e=0.995$
(an aspect ratio of 10); an approximation that retains terms to all logarithmic orders performs much better. Figure 7 shows the co-rotational and quadratic torque contributions for the oblate case, together with the near-sphere and one- and two-term flat disk asymptotes. There is no major distinction between the two contributions as regards their variation with aspect ratio. There is, however, a very small interval of non-monotonicity, for the quadratic contribution, close to the flat-disk limit, so that the peak quadratic torque arises at an
![]() $e$
slightly smaller than unity. Importantly, the co-rotational and quadratic contributions have opposite signs for the oblate case. Thus, while the individual stress contributions still support a longside-on orientation for the prolate spheroid, for the oblate case, the quadratic contribution alone would lead to a broadside-on orientation. The dominance of the co-rotational contribution ensures that the total torque on an oblate spheroid still supports a longside-on orientation.
$e$
slightly smaller than unity. Importantly, the co-rotational and quadratic contributions have opposite signs for the oblate case. Thus, while the individual stress contributions still support a longside-on orientation for the prolate spheroid, for the oblate case, the quadratic contribution alone would lead to a broadside-on orientation. The dominance of the co-rotational contribution ensures that the total torque on an oblate spheroid still supports a longside-on orientation.

Figure 5. The viscoelastic shape function for an oblate spheroid plotted as a function of the eccentricity
![]() $e(1/{\it\xi}_{0})$
.
$e(1/{\it\xi}_{0})$
.

Figure 6. (a) Quadratic contribution to the viscoelastic shape function for a prolate spheroid as a function of eccentricity
![]() $e(1/{\it\xi}_{0})$
, together with near-sphere and slender-body asymptotes and (b) magnified version of the region close to
$e(1/{\it\xi}_{0})$
, together with near-sphere and slender-body asymptotes and (b) magnified version of the region close to
![]() ${\it\xi}_{0}=1$
. (c) Corresponding plot for the co-rotational contribution and (d) magnified version of the region close to
${\it\xi}_{0}=1$
. (c) Corresponding plot for the co-rotational contribution and (d) magnified version of the region close to
![]() ${\it\xi}_{0}=1$
.
${\it\xi}_{0}=1$
.
Galdi et al. (Reference Galdi, Vaidya, Pokorny, Daniel and Feng2002) evaluated the viscoelastic torque acting on a prolate spheroid sedimenting in a second-order fluid numerically. However, (4.6) cannot be compared with their result, since they have used an incorrect constitutive equation. The authors follow the alternate convention presented in § 4.2.4, but with
![]() ${\it\epsilon}=2({\it\psi}_{1}+{\it\psi}_{2})/|{\it\psi}_{1}|$
. As a result, the constitutive equation takes the form:
${\it\epsilon}=2({\it\psi}_{1}+{\it\psi}_{2})/|{\it\psi}_{1}|$
. As a result, the constitutive equation takes the form:
when written in terms of
![]() ${\it\psi}_{1}$
and
${\it\psi}_{1}$
and
![]() ${\it\psi}_{2}$
(
${\it\psi}_{2}$
(
![]() ${\it\psi}_{1}$
assumed to be positive). A comparison between (4.12) and the expressions (2.8)–(2.10) shows that the coefficients of the quadratic and co-rotational parts in (4.12) are incorrect. Indeed, while Galdi et al. (Reference Galdi, Vaidya, Pokorny, Daniel and Feng2002) report a change of sign for the viscoelastic torque on a prolate spheroid for
${\it\psi}_{1}$
assumed to be positive). A comparison between (4.12) and the expressions (2.8)–(2.10) shows that the coefficients of the quadratic and co-rotational parts in (4.12) are incorrect. Indeed, while Galdi et al. (Reference Galdi, Vaidya, Pokorny, Daniel and Feng2002) report a change of sign for the viscoelastic torque on a prolate spheroid for
![]() ${\it\epsilon}_{galdi}=0.7$
and 0.8, which corresponds to
${\it\epsilon}_{galdi}=0.7$
and 0.8, which corresponds to
![]() ${\it\epsilon}=-1.42$
and
${\it\epsilon}=-1.42$
and
![]() $-1.25$
respectively, in the present work, the viscoelastic torque does not change sign for these
$-1.25$
respectively, in the present work, the viscoelastic torque does not change sign for these
![]() ${\it\epsilon}$
values.
${\it\epsilon}$
values.

Figure 7. (a) Co-rotational contribution to the viscoelastic shape function for an oblate spheroid plotted as a function of the eccentricity
![]() $e(1/{\it\xi}_{0})$
, together with near-sphere and flat-disk asymptotes. (b) Corresponding plot for the quadratic stress contribution and (c) magnified section highlighting the non-monotonic dependence on aspect ratio close to
$e(1/{\it\xi}_{0})$
, together with near-sphere and flat-disk asymptotes. (b) Corresponding plot for the quadratic stress contribution and (c) magnified section highlighting the non-monotonic dependence on aspect ratio close to
![]() ${\it\xi}_{0}=1$
with a maximum at
${\it\xi}_{0}=1$
with a maximum at
![]() $e=0.9993$
.
$e=0.9993$
.
4.2.2. Neutral curve: competing inertial and viscoelastic torques
From §§ 4.1 and 4.2.1, the inertial and viscoelastic torques (for polymer solutions) are seen to act in opposite directions for both prolate and oblate spheroids. These torques are plotted together in figure 8, and a balance of the two torques must lead to a neutral curve. The latter curve is the critical value of
![]() $\mathit{El}~(=\mathit{De}/\mathit{Re})$
, given by the ratio
$\mathit{El}~(=\mathit{De}/\mathit{Re})$
, given by the ratio
![]() $F({\it\xi}_{0})_{inertia}/F({\it\xi}_{0})_{visco}$
, plotted as a function of the spheroid aspect ratio, that separates regions where the broadside-on and longside-on orientations are stable. The neutral curves may be obtained from the analytical expressions given earlier for an arbitrary aspect ratio spheroid (see (4.1), (4.2), (4.6) and (4.7)), and are plotted in figure 9 for the prolate and oblate cases, together with the asymptotes for limiting aspect ratios. It is clear, as the prolate spheroid approaches a slender fibre, that the viscoelastic torque becomes dominant. The critical elasticity number becomes asymptotically small, being
$F({\it\xi}_{0})_{inertia}/F({\it\xi}_{0})_{visco}$
, plotted as a function of the spheroid aspect ratio, that separates regions where the broadside-on and longside-on orientations are stable. The neutral curves may be obtained from the analytical expressions given earlier for an arbitrary aspect ratio spheroid (see (4.1), (4.2), (4.6) and (4.7)), and are plotted in figure 9 for the prolate and oblate cases, together with the asymptotes for limiting aspect ratios. It is clear, as the prolate spheroid approaches a slender fibre, that the viscoelastic torque becomes dominant. The critical elasticity number becomes asymptotically small, being
![]() $O[\ln ({\it\xi}_{0}-1)]^{-1}$
, and even a tiny amount of viscoelasticity is sufficient to overcome inertial forces in this limit. Thus, a sufficiently slender fibre is expected to invariably orient parallel to its direction of translation. For the oblate case,
$O[\ln ({\it\xi}_{0}-1)]^{-1}$
, and even a tiny amount of viscoelasticity is sufficient to overcome inertial forces in this limit. Thus, a sufficiently slender fibre is expected to invariably orient parallel to its direction of translation. For the oblate case,
![]() $\mathit{El}_{c}$
tends to a finite constant in the flat-disk limit, since both inertial and viscoelastic torques have finite values in this limit. Further,
$\mathit{El}_{c}$
tends to a finite constant in the flat-disk limit, since both inertial and viscoelastic torques have finite values in this limit. Further,
![]() $\mathit{El}_{c}$
also tends to a finite constant as the spheroid (prolate or oblate) tends to a sphere, since both the inertial and viscoelastic torques decay as
$\mathit{El}_{c}$
also tends to a finite constant as the spheroid (prolate or oblate) tends to a sphere, since both the inertial and viscoelastic torques decay as
![]() $O({\it\xi}_{0}^{-2})$
in the limit
$O({\it\xi}_{0}^{-2})$
in the limit
![]() ${\it\xi}_{0}\rightarrow 0$
; an exception occurs for
${\it\xi}_{0}\rightarrow 0$
; an exception occurs for
![]() ${\it\epsilon}=0$
, since the quadratic contribution to the viscoelastic torque is
${\it\epsilon}=0$
, since the quadratic contribution to the viscoelastic torque is
![]() $O({\it\xi}_{0}^{-4})$
, and
$O({\it\xi}_{0}^{-4})$
, and
![]() $\mathit{El}_{c}~(=-811/672{\it\epsilon})$
must therefore diverge as
$\mathit{El}_{c}~(=-811/672{\it\epsilon})$
must therefore diverge as
![]() ${\it\xi}_{0}^{2}$
in the near-sphere limit.
${\it\xi}_{0}^{2}$
in the near-sphere limit.

Figure 8. (a,b) Aspect-ratio dependence of the inertial and viscoelastic torques on prolate and oblate spheroids, respectively.

Figure 9. (a,b) Plot corresponding to the critical elasticity number (
![]() $\mathit{El}_{c}$
), as a function of the spheroid aspect ratio, for prolate and oblate spheroids, respectively.
$\mathit{El}_{c}$
), as a function of the spheroid aspect ratio, for prolate and oblate spheroids, respectively.
4.2.3. The viscoelastic torque on a slender fibre
Despite the restricted range of validity pointed out above, it is worth delving into the large-aspect-ratio scaling of the viscoelastic torque in some detail. On one hand, the slender-fibre limit appears more subtle for the elastic case than for the inertial case examined earlier; a more detailed examination shows the length scales that contribute dominantly to the torque and, thence, the reason why it is much larger than its inertial analogue. On the other hand, the reason why an earlier, oft-cited, analysis (Leal Reference Leal1975) turns out to be erroneous also needs an explanation. While earlier authors, including Kim (Reference Kim1986a
) and Brunn (Reference Brunn1977), have pointed to a possible error in Leal’s analysis, there has not been a detailed re-examination of the original calculation. The scaling arguments below, based on slender-body theory, show that the
![]() $O[\ln ({\it\xi}_{0}-1)]^{-1}$
torque in (4.11) can, in fact, be calculated only by including terms in the velocity fields that are algebraically small in the aspect ratio, and this remains true even for non-spheroidal geometries. Thus, slender-body theory in its usual form, one that involves expanding the relevant fields in a power series of inverse logarithms of the aspect ratio, ends up predicting only a portion of the leading-order torque for a slender spheroid, and is zero at
$O[\ln ({\it\xi}_{0}-1)]^{-1}$
torque in (4.11) can, in fact, be calculated only by including terms in the velocity fields that are algebraically small in the aspect ratio, and this remains true even for non-spheroidal geometries. Thus, slender-body theory in its usual form, one that involves expanding the relevant fields in a power series of inverse logarithms of the aspect ratio, ends up predicting only a portion of the leading-order torque for a slender spheroid, and is zero at
![]() $O[\ln ({\it\xi}_{0}-1)]^{-1}$
for a circular cylinder.
$O[\ln ({\it\xi}_{0}-1)]^{-1}$
for a circular cylinder.
Considering the viscoelastic torque integral,
![]() $\mathit{De}\!\int {\bf\sigma}_{NNs}^{(1)}:\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(2)}\,\text{d}V$
, the contribution from the outer region of
$\mathit{De}\!\int {\bf\sigma}_{NNs}^{(1)}:\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(2)}\,\text{d}V$
, the contribution from the outer region of
![]() $O(L^{3})$
around the fibre may be estimated using
$O(L^{3})$
around the fibre may be estimated using
![]() $\boldsymbol{u}^{(1)},\boldsymbol{u}^{(2)}\sim O[\ln ({\it\xi}_{0}-1)]^{-1}$
,
$\boldsymbol{u}^{(1)},\boldsymbol{u}^{(2)}\sim O[\ln ({\it\xi}_{0}-1)]^{-1}$
,
![]() ${\bf\sigma}_{NNs}^{(1)}\sim O[\ln ({\it\xi}_{0}-1)]^{-2}$
, and this leads to a torque of
${\bf\sigma}_{NNs}^{(1)}\sim O[\ln ({\it\xi}_{0}-1)]^{-2}$
, and this leads to a torque of
![]() $O(\mathit{De}[\ln ({\it\xi}_{0}-1)]^{-3})$
. On using estimates valid for the matching region, characterized by the range of length scales
$O(\mathit{De}[\ln ({\it\xi}_{0}-1)]^{-3})$
. On using estimates valid for the matching region, characterized by the range of length scales
![]() $b\ll r\ll L$
, we have
$b\ll r\ll L$
, we have
![]() $\boldsymbol{u}^{(1)},\boldsymbol{u}^{(2)}\sim [\ln ({\it\xi}_{0}-1)]^{-1}O(\ln {\it\rho})$
,
$\boldsymbol{u}^{(1)},\boldsymbol{u}^{(2)}\sim [\ln ({\it\xi}_{0}-1)]^{-1}O(\ln {\it\rho})$
,
![]() ${\bf\sigma}_{NNs}^{(1)}\sim (\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)})^{2}\sim [\ln ({\it\xi}_{0}-1)]^{-2}(1/{\it\rho}^{2})$
,
${\bf\sigma}_{NNs}^{(1)}\sim (\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)})^{2}\sim [\ln ({\it\xi}_{0}-1)]^{-2}(1/{\it\rho}^{2})$
,
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(2)}\sim [\ln ({\it\xi}_{0}-1)]^{-1}(1/{\it\rho})$
,
$\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(2)}\sim [\ln ({\it\xi}_{0}-1)]^{-1}(1/{\it\rho})$
,
![]() $\text{d}V\sim ({\it\rho}\,\text{d}{\it\rho})$
, where
$\text{d}V\sim ({\it\rho}\,\text{d}{\it\rho})$
, where
![]() ${\it\rho}~(\ll 1)$
is the non-dimensional transverse radial distance in the plane perpendicular to
${\it\rho}~(\ll 1)$
is the non-dimensional transverse radial distance in the plane perpendicular to
![]() $\boldsymbol{p}$
. As a result, the torque contribution becomes
$\boldsymbol{p}$
. As a result, the torque contribution becomes
![]() $[\ln ({\it\xi}_{0}-1)]^{-3}\!\int \!\text{d}{\it\rho}/{\it\rho}^{2}$
, which is divergent for
$[\ln ({\it\xi}_{0}-1)]^{-3}\!\int \!\text{d}{\it\rho}/{\it\rho}^{2}$
, which is divergent for
![]() ${\it\rho}\rightarrow 0$
. This algebraic divergence is cut off at a length scale of the order of the fibre diameter,
${\it\rho}\rightarrow 0$
. This algebraic divergence is cut off at a length scale of the order of the fibre diameter,
![]() ${\it\rho}\sim O({\it\xi}_{0}-1)^{1/2}$
, whence one obtains a torque scaling of
${\it\rho}\sim O({\it\xi}_{0}-1)^{1/2}$
, whence one obtains a torque scaling of
![]() $O[\ln ({\it\xi}_{0}-1)]^{-3}({\it\xi}_{0}-1)^{-1/2}$
for
$O[\ln ({\it\xi}_{0}-1)]^{-3}({\it\xi}_{0}-1)^{-1/2}$
for
![]() ${\it\xi}_{0}\rightarrow 1$
. These arguments make it clear that, unlike the inertial case, the dominant contribution to the elastic torque appears to come from a region around the fibre of
${\it\xi}_{0}\rightarrow 1$
. These arguments make it clear that, unlike the inertial case, the dominant contribution to the elastic torque appears to come from a region around the fibre of
![]() $O(b)$
, corresponding to the inner region in slender-body theory with a volume of
$O(b)$
, corresponding to the inner region in slender-body theory with a volume of
![]() $O(b^{2}L)$
(a conclusion also reached by Leal Reference Leal1975), and the dimensional viscoelastic torque based on these considerations must be
$O(b^{2}L)$
(a conclusion also reached by Leal Reference Leal1975), and the dimensional viscoelastic torque based on these considerations must be
![]() $\mathit{De}({\it\mu}UL^{2})O[\ln ({\it\xi}_{0}-1)]^{-3}({\it\xi}_{0}-1)^{-1/2}\mathscr{H}({\it\epsilon})$
, where the function
$\mathit{De}({\it\mu}UL^{2})O[\ln ({\it\xi}_{0}-1)]^{-3}({\it\xi}_{0}-1)^{-1/2}\mathscr{H}({\it\epsilon})$
, where the function
![]() $\mathscr{H}({\it\epsilon})$
is determined by the relative magnitudes of the co-rotational and quadratic contributions. In other words, naive scaling arguments suggest a torque that is not merely finite in the slender-fibre limit, as found by Leal (see (4.10)), but instead diverges linearly with increasing aspect ratio (when measured in units of
$\mathscr{H}({\it\epsilon})$
is determined by the relative magnitudes of the co-rotational and quadratic contributions. In other words, naive scaling arguments suggest a torque that is not merely finite in the slender-fibre limit, as found by Leal (see (4.10)), but instead diverges linearly with increasing aspect ratio (when measured in units of
![]() ${\it\mu}UL^{2}$
). Consistency with the logarithmic decay exhibited by the exact solution in § 4.2 evidently implies symmetry-based cancellations that make the viscoelastic contribution smaller than the expected order, and this requires a more detailed examination.
${\it\mu}UL^{2}$
). Consistency with the logarithmic decay exhibited by the exact solution in § 4.2 evidently implies symmetry-based cancellations that make the viscoelastic contribution smaller than the expected order, and this requires a more detailed examination.
In attempting an explanation for the viscoelastic torque scaling, it is convenient to consider the simpler co-rotational limit,
![]() ${\it\epsilon}=-1$
; the arguments for the more involved quadratic stress contribution are given in appendix C. As evident from (4.11), the torque scaling in the slender-fibre limit remains the same for both the co-rotational and quadratic contributions, although the range of validity is much smaller in the latter case. For
${\it\epsilon}=-1$
; the arguments for the more involved quadratic stress contribution are given in appendix C. As evident from (4.11), the torque scaling in the slender-fibre limit remains the same for both the co-rotational and quadratic contributions, although the range of validity is much smaller in the latter case. For
![]() ${\it\epsilon}=-1$
, the velocity field in the second-order fluid remains the same as that of the Newtonian fluid, the divergence of the co-rotational polymeric stress being balanced by the gradient of the Giesekus pressure field (this is always true in two dimensions on account of the Tanner–Pipkin theorem; see Bird et al.
Reference Bird, Armstrong and Hassager1987). The co-rotational torque is therefore given by the following surface integral:
${\it\epsilon}=-1$
, the velocity field in the second-order fluid remains the same as that of the Newtonian fluid, the divergence of the co-rotational polymeric stress being balanced by the gradient of the Giesekus pressure field (this is always true in two dimensions on account of the Tanner–Pipkin theorem; see Bird et al.
Reference Bird, Armstrong and Hassager1987). The co-rotational torque is therefore given by the following surface integral:
where
![]() ${\bf\sigma}_{NNC}^{(1)}$
is as defined in (2.9) and
${\bf\sigma}_{NNC}^{(1)}$
is as defined in (2.9) and
![]() $p^{G}={\it\epsilon}(\partial p_{s}/\partial t+\boldsymbol{u}_{s}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{s}+\boldsymbol{e}_{s}:\boldsymbol{e}_{s})$
is the Giesekus pressure field defined in terms of the Stokes fields; for simplicity, we have omitted the superscript 1 attached to the original problem in § 2. In a reference frame that translates with the spheroid, one has a steady scenario on account of the unchanged orientation and because
$p^{G}={\it\epsilon}(\partial p_{s}/\partial t+\boldsymbol{u}_{s}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}p_{s}+\boldsymbol{e}_{s}:\boldsymbol{e}_{s})$
is the Giesekus pressure field defined in terms of the Stokes fields; for simplicity, we have omitted the superscript 1 attached to the original problem in § 2. In a reference frame that translates with the spheroid, one has a steady scenario on account of the unchanged orientation and because
![]() $\boldsymbol{u}_{s}=0$
on the particle surface (
$\boldsymbol{u}_{s}=0$
on the particle surface (
![]() $\text{D}/\text{D}t=0$
at leading order). Thus,
$\text{D}/\text{D}t=0$
at leading order). Thus,
![]() ${\bf\sigma}_{NNC}^{(1)}=2{\it\epsilon}({\bf\omega}_{s}\boldsymbol{\cdot }\boldsymbol{e}_{s}-\boldsymbol{e}_{s}\boldsymbol{\cdot }{\bf\omega}_{s})$
and
${\bf\sigma}_{NNC}^{(1)}=2{\it\epsilon}({\bf\omega}_{s}\boldsymbol{\cdot }\boldsymbol{e}_{s}-\boldsymbol{e}_{s}\boldsymbol{\cdot }{\bf\omega}_{s})$
and
![]() $p^{G}={\it\epsilon}(\boldsymbol{e}_{s}:\boldsymbol{e}_{s})$
on the surface. Since the flow close to the surface must, locally, be a simple shear flow, one may write
$p^{G}={\it\epsilon}(\boldsymbol{e}_{s}:\boldsymbol{e}_{s})$
on the surface. Since the flow close to the surface must, locally, be a simple shear flow, one may write
![]() $\boldsymbol{u}_{s}=|\tilde{{\bf\omega}}(\boldsymbol{n})|y_{n}\boldsymbol{t}$
, where
$\boldsymbol{u}_{s}=|\tilde{{\bf\omega}}(\boldsymbol{n})|y_{n}\boldsymbol{t}$
, where
![]() $\tilde{{\bf\omega}}(\boldsymbol{n})$
denotes the surface vorticity field of the leading-order Stokes flow,
$\tilde{{\bf\omega}}(\boldsymbol{n})$
denotes the surface vorticity field of the leading-order Stokes flow,
![]() $y_{n}$
is the distance normal to the surface, and
$y_{n}$
is the distance normal to the surface, and
![]() $\boldsymbol{t}$
is the unit tangent vector along the local flow direction. As a result, one has
$\boldsymbol{t}$
is the unit tangent vector along the local flow direction. As a result, one has
![]() ${\bf\omega}_{s}=(|\tilde{{\bf\omega}}(\boldsymbol{n})|(\boldsymbol{n}\boldsymbol{t}-\boldsymbol{t}\boldsymbol{n}))/2$
,
${\bf\omega}_{s}=(|\tilde{{\bf\omega}}(\boldsymbol{n})|(\boldsymbol{n}\boldsymbol{t}-\boldsymbol{t}\boldsymbol{n}))/2$
,
![]() $\boldsymbol{e}_{s}=(2|\tilde{{\bf\omega}}(\boldsymbol{n})|(\boldsymbol{n}\boldsymbol{t}+\boldsymbol{t}\boldsymbol{n}))/2$
; therefore,
$\boldsymbol{e}_{s}=(2|\tilde{{\bf\omega}}(\boldsymbol{n})|(\boldsymbol{n}\boldsymbol{t}+\boldsymbol{t}\boldsymbol{n}))/2$
; therefore,
![]() $\boldsymbol{e}_{s}:\boldsymbol{e}_{s}=(|\tilde{{\bf\omega}}(\boldsymbol{n})|^{2})/2$
and
$\boldsymbol{e}_{s}:\boldsymbol{e}_{s}=(|\tilde{{\bf\omega}}(\boldsymbol{n})|^{2})/2$
and
![]() ${\bf\omega}_{s}\boldsymbol{\cdot }\boldsymbol{e}_{s}-\boldsymbol{e}_{s}\boldsymbol{\cdot }{\bf\omega}_{s}=(|\tilde{{\bf\omega}}(\boldsymbol{n})|^{2}(\boldsymbol{n}\boldsymbol{n}-\boldsymbol{t}\boldsymbol{t}))/2$
. Using these expressions, the co-rotational torque integral reduces to:
${\bf\omega}_{s}\boldsymbol{\cdot }\boldsymbol{e}_{s}-\boldsymbol{e}_{s}\boldsymbol{\cdot }{\bf\omega}_{s}=(|\tilde{{\bf\omega}}(\boldsymbol{n})|^{2}(\boldsymbol{n}\boldsymbol{n}-\boldsymbol{t}\boldsymbol{t}))/2$
. Using these expressions, the co-rotational torque integral reduces to:
in terms of the surface vorticity field. The much simpler expression above was first derived by Berker (Reference Berker1964), has been used by Galdi (Reference Galdi2000) to obtain the co-rotational torque in an analytical form, and forms the basis of the scaling arguments that follow. In a cylindrical coordinate system
![]() $|\tilde{{\bf\omega}}|^{2}=\tilde{{\it\omega}}_{{\it\rho}}^{2}+\tilde{{\it\omega}}_{z}^{2}+\tilde{{\it\omega}}_{{\it\phi}}^{2}$
, with the
$|\tilde{{\bf\omega}}|^{2}=\tilde{{\it\omega}}_{{\it\rho}}^{2}+\tilde{{\it\omega}}_{z}^{2}+\tilde{{\it\omega}}_{{\it\phi}}^{2}$
, with the
![]() $z$
-axis along
$z$
-axis along
![]() $\boldsymbol{p}$
. To within algebraic errors in the inverse aspect ratio,
$\boldsymbol{p}$
. To within algebraic errors in the inverse aspect ratio,
![]() $\tilde{{\it\omega}}_{{\it\phi}}$
arises from the unidirectional flow induced by the component of the fibre translation along
$\tilde{{\it\omega}}_{{\it\phi}}$
arises from the unidirectional flow induced by the component of the fibre translation along
![]() $\boldsymbol{p}$
, while
$\boldsymbol{p}$
, while
![]() $\tilde{{\it\omega}}_{z}$
is the axial component associated with the two-dimensional disturbance field induced by transverse translation. The radial component
$\tilde{{\it\omega}}_{z}$
is the axial component associated with the two-dimensional disturbance field induced by transverse translation. The radial component
![]() $\tilde{{\it\omega}}_{{\it\rho}}$
must be identically zero, to any logarithmic order, for a fibre with a circular cross-section. Note that, at leading logarithmic order, the non-zero vorticity components,
$\tilde{{\it\omega}}_{{\it\rho}}$
must be identically zero, to any logarithmic order, for a fibre with a circular cross-section. Note that, at leading logarithmic order, the non-zero vorticity components,
![]() $\tilde{{\it\omega}}_{z}$
and
$\tilde{{\it\omega}}_{z}$
and
![]() $\tilde{{\it\omega}}_{{\it\phi}}$
, are
$\tilde{{\it\omega}}_{{\it\phi}}$
, are
![]() $O[\ln ({\it\xi}_{0}-1)]^{-1}(U/b)$
on the fibre surface and, using this estimate, (4.14) gives a nominal torque scaling of
$O[\ln ({\it\xi}_{0}-1)]^{-1}(U/b)$
on the fibre surface and, using this estimate, (4.14) gives a nominal torque scaling of
![]() $\mathit{De}\,{\it\epsilon}[\ln ({\it\xi}_{0}-1)]^{-2}U^{2}/b^{2}O(Lb)\sim \mathit{De}\,{\it\epsilon}({\it\xi}_{0}-1)^{-1/2}/[\ln ({\it\xi}_{0}-1)]^{2}$
, that again diverges in the limit of a vanishing radius. Not including algebraically small contributions,
$\mathit{De}\,{\it\epsilon}[\ln ({\it\xi}_{0}-1)]^{-2}U^{2}/b^{2}O(Lb)\sim \mathit{De}\,{\it\epsilon}({\it\xi}_{0}-1)^{-1/2}/[\ln ({\it\xi}_{0}-1)]^{2}$
, that again diverges in the limit of a vanishing radius. Not including algebraically small contributions,
![]() $\boldsymbol{r}\wedge \boldsymbol{n}\approx s\boldsymbol{p}\wedge \hat{{\bf\rho}}$
,
$\boldsymbol{r}\wedge \boldsymbol{n}\approx s\boldsymbol{p}\wedge \hat{{\bf\rho}}$
,
![]() $\hat{{\bf\rho}}$
now being the unit radial vector in the transverse plane and
$\hat{{\bf\rho}}$
now being the unit radial vector in the transverse plane and
![]() $s$
the axial coordinate. The integral in (4.14) takes the form:
$s$
the axial coordinate. The integral in (4.14) takes the form:
for a slender fibre with a circular cross-section, where
![]() $\text{d}{\it\Omega}$
denotes angular integration over the unit circle. From linearity and symmetry arguments, the vorticity field due to transverse translation must have the form
$\text{d}{\it\Omega}$
denotes angular integration over the unit circle. From linearity and symmetry arguments, the vorticity field due to transverse translation must have the form
![]() $\tilde{{\bf\omega}}^{t}=\tilde{{\it\omega}}_{z}\boldsymbol{p}\sim g_{z}(s)\boldsymbol{U}^{t}\wedge \hat{{\bf\rho}}f({\it\rho})$
, where
$\tilde{{\bf\omega}}^{t}=\tilde{{\it\omega}}_{z}\boldsymbol{p}\sim g_{z}(s)\boldsymbol{U}^{t}\wedge \hat{{\bf\rho}}f({\it\rho})$
, where
![]() $\boldsymbol{U}^{t}=\boldsymbol{U}\boldsymbol{\cdot }(\boldsymbol{I}-\boldsymbol{p}\boldsymbol{p})$
,
$\boldsymbol{U}^{t}=\boldsymbol{U}\boldsymbol{\cdot }(\boldsymbol{I}-\boldsymbol{p}\boldsymbol{p})$
,
![]() $f({\it\rho})\sim 1/{\it\rho}^{2}$
and the function
$f({\it\rho})\sim 1/{\it\rho}^{2}$
and the function
![]() $g_{z}(s)$
accounts for the
$g_{z}(s)$
accounts for the
![]() $s$
-dependence of the transverse force density to all orders in
$s$
-dependence of the transverse force density to all orders in
![]() $(\ln {\it\kappa})^{-1}$
. As is known (Shaqfeh, Mackaplow & Schiek Reference Shaqfeh, Mackaplow and Schiek1994), determining the force density as a function of
$(\ln {\it\kappa})^{-1}$
. As is known (Shaqfeh, Mackaplow & Schiek Reference Shaqfeh, Mackaplow and Schiek1994), determining the force density as a function of
![]() $s$
, to all logarithmic orders, requires the solution of an integral equation. However, the present argument relies on the angular dependence of the integrand in (4.15) in the plane transverse to
$s$
, to all logarithmic orders, requires the solution of an integral equation. However, the present argument relies on the angular dependence of the integrand in (4.15) in the plane transverse to
![]() $\boldsymbol{p}$
, and the detailed
$\boldsymbol{p}$
, and the detailed
![]() $s$
-dependence of the force density is of no consequence to the angular integration in (4.15). One may now write the square of the axial vorticity field in the form
$s$
-dependence of the force density is of no consequence to the angular integration in (4.15). One may now write the square of the axial vorticity field in the form
![]() $\tilde{{\it\omega}}_{z}^{2}\sim g_{z}^{2}(s)f^{2}({\it\rho})(\boldsymbol{U}^{t}\wedge \hat{{\bf\rho}})\boldsymbol{\cdot }(\boldsymbol{U}^{t}\wedge \hat{{\bf\rho}})$
, where only the surface value of
$\tilde{{\it\omega}}_{z}^{2}\sim g_{z}^{2}(s)f^{2}({\it\rho})(\boldsymbol{U}^{t}\wedge \hat{{\bf\rho}})\boldsymbol{\cdot }(\boldsymbol{U}^{t}\wedge \hat{{\bf\rho}})$
, where only the surface value of
![]() $f({\it\rho})$
is required in (4.15). Inserting this form in (4.15),
$f({\it\rho})$
is required in (4.15). Inserting this form in (4.15),
![]() $\int \tilde{{\it\omega}}_{z}^{2}\,\text{d}{\it\Omega}$
involves the integral
$\int \tilde{{\it\omega}}_{z}^{2}\,\text{d}{\it\Omega}$
involves the integral
![]() $\int \hat{{\bf\rho}}\hat{{\bf\rho}}\hat{{\bf\rho}}\,\text{d}{\it\Omega}$
, which is, of course, identically zero, being the integral of an odd-ordered unit normal polyad. For a circular cross-section, the
$\int \hat{{\bf\rho}}\hat{{\bf\rho}}\hat{{\bf\rho}}\,\text{d}{\it\Omega}$
, which is, of course, identically zero, being the integral of an odd-ordered unit normal polyad. For a circular cross-section, the
![]() $\tilde{{\it\omega}}_{{\it\phi}}$
arising from longitudinal motion is independent of
$\tilde{{\it\omega}}_{{\it\phi}}$
arising from longitudinal motion is independent of
![]() ${\it\phi}$
, and must have a scalar pre-factor, similar to
${\it\phi}$
, and must have a scalar pre-factor, similar to
![]() $g_{z}(s)$
above, that accounts for the
$g_{z}(s)$
above, that accounts for the
![]() $s$
-dependence of the longitudinal force density. Thus, the only dependence on
$s$
-dependence of the longitudinal force density. Thus, the only dependence on
![]() $\hat{{\bf\rho}}$
for the term involving
$\hat{{\bf\rho}}$
for the term involving
![]() $\tilde{{\it\omega}}_{{\it\phi}}^{2}$
comes from the moment arm, and
$\tilde{{\it\omega}}_{{\it\phi}}^{2}$
comes from the moment arm, and
![]() $\int (\boldsymbol{p}\wedge \hat{{\bf\rho}})\tilde{{\it\omega}}_{{\it\phi}}^{2}\,\text{d}{\it\Omega}$
is therefore proportional to
$\int (\boldsymbol{p}\wedge \hat{{\bf\rho}})\tilde{{\it\omega}}_{{\it\phi}}^{2}\,\text{d}{\it\Omega}$
is therefore proportional to
![]() $\int \hat{{\bf\rho}}\,\text{d}{\it\Omega}$
, which is again zero. The trivial result arises due to the longitudinal and transverse motions of the fibre contributing to different vorticity components at any logarithmic order. This remains true for non-spheroidal shapes and for non-circular cross-sections, and thus the nominal scaling of
$\int \hat{{\bf\rho}}\,\text{d}{\it\Omega}$
, which is again zero. The trivial result arises due to the longitudinal and transverse motions of the fibre contributing to different vorticity components at any logarithmic order. This remains true for non-spheroidal shapes and for non-circular cross-sections, and thus the nominal scaling of
![]() $\mathit{De}\,{\it\epsilon}({\it\xi}_{0}-1)^{-1/2}/[\ln ({\it\xi}_{0}-1)]^{2}$
does not work even for the most general slender body.
$\mathit{De}\,{\it\epsilon}({\it\xi}_{0}-1)^{-1/2}/[\ln ({\it\xi}_{0}-1)]^{2}$
does not work even for the most general slender body.
The first non-trivial contribution to the co-rotational torque on a slender fibre, of a circular cross-section, must arise from algebraically small terms in the vorticity field and, in addition, must involve a coupling of the longitudinal and transverse motions (there can be no torque when the fibre moves along or perpendicular to its orientation). For a circular cross-section, the longitudinal translation contributes to
![]() $\tilde{{\it\omega}}_{{\it\phi}}$
alone, and the leading-order contribution will occur as the product of an algebraically small term in
$\tilde{{\it\omega}}_{{\it\phi}}$
alone, and the leading-order contribution will occur as the product of an algebraically small term in
![]() $\tilde{{\it\omega}}_{{\it\phi}}$
, of
$\tilde{{\it\omega}}_{{\it\phi}}$
, of
![]() $O({\it\xi}_{0}-1)^{1/2}$
, and the familiar
$O({\it\xi}_{0}-1)^{1/2}$
, and the familiar
![]() $O[\ln ({\it\xi}_{0}-1)]^{-1}$
slender-body term in the same vorticity component. One of these contributions may be determined from slender-body theory as the variation of the velocity field
$O[\ln ({\it\xi}_{0}-1)]^{-1}$
slender-body term in the same vorticity component. One of these contributions may be determined from slender-body theory as the variation of the velocity field
![]() $(u_{{\it\rho}}^{t},u_{{\it\phi}}^{t})$
with the axial coordinate. The velocity fields associated with the transverse motion are given by:
$(u_{{\it\rho}}^{t},u_{{\it\phi}}^{t})$
with the axial coordinate. The velocity fields associated with the transverse motion are given by:
However, the second contribution, at an algebraically small order, arises due to the axial velocity disturbance induced by transverse translation, and cannot be calculated from slender-body theory. Thus, slender-body theory to any logarithmic order can lead only to a partial torque contribution.
Including algebraically small terms in (4.15) would lead to a torque scaling of
![]() $O[\ln ({\it\xi}_{0}-1)]^{-2}$
, which, however, is still logarithmically smaller than that obtained from the exact solution (see (4.11)). The resolution of this discrepancy requires a careful expansion of the exact vorticity field for
$O[\ln ({\it\xi}_{0}-1)]^{-2}$
, which, however, is still logarithmically smaller than that obtained from the exact solution (see (4.11)). The resolution of this discrepancy requires a careful expansion of the exact vorticity field for
![]() ${\it\xi}_{0}\rightarrow 1$
. Substitution of the algebraically small contributions from this expansion in (4.15) leads, after an integration over
${\it\xi}_{0}\rightarrow 1$
. Substitution of the algebraically small contributions from this expansion in (4.15) leads, after an integration over
![]() ${\it\Omega}$
, to:
${\it\Omega}$
, to:
where
![]() $F^{l}$
and
$F^{l}$
and
![]() $F^{t}$
are, respectively, the magnitudes of the force components parallel and perpendicular to the fibre axis. For a spheroid, the non-dimensional radius
$F^{t}$
are, respectively, the magnitudes of the force components parallel and perpendicular to the fibre axis. For a spheroid, the non-dimensional radius
![]() $\hat{b}(s)\propto \sqrt{1-s^{2}}$
, which makes the integral in (4.17) logarithmically divergent at
$\hat{b}(s)\propto \sqrt{1-s^{2}}$
, which makes the integral in (4.17) logarithmically divergent at
![]() $s=\pm 1$
. This divergence will be cut off by accounting for edge effects when
$s=\pm 1$
. This divergence will be cut off by accounting for edge effects when
![]() $(1-s)\sim O({\it\xi}_{0}-1)^{1/2}$
, leading to an
$(1-s)\sim O({\it\xi}_{0}-1)^{1/2}$
, leading to an
![]() $O[\ln ({\it\xi}_{0}-1)]$
estimate for the integral, and, therefore, to the correct torque scaling of
$O[\ln ({\it\xi}_{0}-1)]$
estimate for the integral, and, therefore, to the correct torque scaling of
![]() $O[\ln ({\it\xi}_{0}-1)]^{-1}$
. Thus, the dominant contribution to the slender fibre elastic torque comes from a region intermediate between the centre and the edge of the spheroid with
$O[\ln ({\it\xi}_{0}-1)]^{-1}$
. Thus, the dominant contribution to the slender fibre elastic torque comes from a region intermediate between the centre and the edge of the spheroid with
![]() $({\it\xi}_{0}-1)^{1/2}\ll (1-s)\ll 1$
, although this is only logarithmically larger than contributions from regions where
$({\it\xi}_{0}-1)^{1/2}\ll (1-s)\ll 1$
, although this is only logarithmically larger than contributions from regions where
![]() $1-s\sim O(1)$
and
$1-s\sim O(1)$
and
![]() $O({\it\xi}_{0}-1)^{1/2}$
. It is also worth noting from (4.17) that this logarithmic divergence is not restricted to slender spheroids, and remains true for fibres with
$O({\it\xi}_{0}-1)^{1/2}$
. It is also worth noting from (4.17) that this logarithmic divergence is not restricted to slender spheroids, and remains true for fibres with
![]() $\hat{b}(s)\propto (1-s^{2})^{{\it\alpha}}$
, with
$\hat{b}(s)\propto (1-s^{2})^{{\it\alpha}}$
, with
![]() ${\it\alpha}>0$
. The torque on a slender cylinder (
${\it\alpha}>0$
. The torque on a slender cylinder (
![]() $\hat{b}(s)$
is a constant) arises solely from edge contributions.
$\hat{b}(s)$
is a constant) arises solely from edge contributions.
In summary, then, the usual slender-body theory formalism appears unable to give the complete leading-order torque for a sedimenting slender fibre, of an arbitrary cross-section, in a second-order fluid. The torque, as evaluated from the exact solution for a slender spheroid, vanishes for large aspect ratios, and the Leal (Reference Leal1975) result is likely erroneous.
4.2.4. Viscoelastic torque in other second-order fluids
Thus far, we have examined the viscoelastic torque for the second-order fluid parameter,
![]() ${\it\epsilon}=-N_{1}/(2(N_{1}+N_{2}))$
, lying between
${\it\epsilon}=-N_{1}/(2(N_{1}+N_{2}))$
, lying between
![]() $-1$
and
$-1$
and
![]() $-0.5$
. As already mentioned, this corresponds to second-order rheology emerging as the small-
$-0.5$
. As already mentioned, this corresponds to second-order rheology emerging as the small-
![]() $\mathit{De}$
limit of a polymer solution, and the narrow range of
$\mathit{De}$
limit of a polymer solution, and the narrow range of
![]() ${\it\epsilon}$
values arises due to typical magnitudes of
${\it\epsilon}$
values arises due to typical magnitudes of
![]() $N_{2}/N_{1}~(N_{2}/N_{1}=-(1+2{\it\epsilon})/(2{\it\epsilon}))$
being much smaller than unity for dilute polymer solutions. All complex fluids with an isotropic microstructure in the undeformed state exhibit second-order fluid rheology near equilibrium, where the relevant microstructural relaxation time is small in comparison to the flow time scale. Further, unlike polymeric solutions, the normal stress differences for many of these systems are comparable in magnitude. Restricting ourselves to cases where analytical expressions for the normal stress differences are available: examples of such fluids include non-dilute suspensions of Brownian spherical particles (Brady & Vicic Reference Brady and Vicic1995), dilute suspensions of Brownian spheroids (Brenner & Condiff Reference Brenner and Condiff1974), and dilute emulsions of surfactant-free (Raja, Subramanian & Koch Reference Raja, Subramanian and Koch2010), surfactant-covered (Vlahovska, Blawzdziewicz & Loewenberg Reference Vlahovska, Blawzdziewicz and Loewenberg2002) spherical drops and vesicles (Vlahovska & Garica Reference Vlahovska and Garica2007). Consideration of these examples below shows that
$N_{2}/N_{1}~(N_{2}/N_{1}=-(1+2{\it\epsilon})/(2{\it\epsilon}))$
being much smaller than unity for dilute polymer solutions. All complex fluids with an isotropic microstructure in the undeformed state exhibit second-order fluid rheology near equilibrium, where the relevant microstructural relaxation time is small in comparison to the flow time scale. Further, unlike polymeric solutions, the normal stress differences for many of these systems are comparable in magnitude. Restricting ourselves to cases where analytical expressions for the normal stress differences are available: examples of such fluids include non-dilute suspensions of Brownian spherical particles (Brady & Vicic Reference Brady and Vicic1995), dilute suspensions of Brownian spheroids (Brenner & Condiff Reference Brenner and Condiff1974), and dilute emulsions of surfactant-free (Raja, Subramanian & Koch Reference Raja, Subramanian and Koch2010), surfactant-covered (Vlahovska, Blawzdziewicz & Loewenberg Reference Vlahovska, Blawzdziewicz and Loewenberg2002) spherical drops and vesicles (Vlahovska & Garica Reference Vlahovska and Garica2007). Consideration of these examples below shows that
![]() ${\it\epsilon}$
varies over a significantly wider range when compared to polymer solutions alone. In all of these cases, however,
${\it\epsilon}$
varies over a significantly wider range when compared to polymer solutions alone. In all of these cases, however,
![]() $N_{1}$
is positive while
$N_{1}$
is positive while
![]() $N_{2}$
is negative, so that
$N_{2}$
is negative, so that
![]() ${\it\epsilon}$
remains negative as for polymer solutions. Even this restriction disappears if one includes active fluids. Suspensions of microscopic swimmers that swim on account of intrinsic extensile dipoles (so-called pushers) exhibit a negative
${\it\epsilon}$
remains negative as for polymer solutions. Even this restriction disappears if one includes active fluids. Suspensions of microscopic swimmers that swim on account of intrinsic extensile dipoles (so-called pushers) exhibit a negative
![]() $N_{1}$
in the presence of a weak shear (Saintillan Reference Saintillan2010). As noted earlier, there also exist examples of passive fluids – for instance, non-Brownian suspensions far from equilibrium (and isotropy) – that exhibit a negative
$N_{1}$
in the presence of a weak shear (Saintillan Reference Saintillan2010). As noted earlier, there also exist examples of passive fluids – for instance, non-Brownian suspensions far from equilibrium (and isotropy) – that exhibit a negative
![]() $N_{1}$
with a much larger
$N_{1}$
with a much larger
![]() $N_{2}$
of the same sign, but these do not conform to the second-order fluid paradigm. Thus, although the consequences in viscometric flow geometries have recently been examined for such fluids (Boyer et al.
Reference Boyer, Pouliquen and Guazzelli2011; Hinch Reference Hinch2011), non-viscometric situations, such as the one considered here, might be significantly more complicated. With the above, more general, notion of a second-order fluid, it is a worthwhile exercise to examine the dependence of the viscoelastic torque on spheroid aspect ratio over the entire range of
$N_{2}$
of the same sign, but these do not conform to the second-order fluid paradigm. Thus, although the consequences in viscometric flow geometries have recently been examined for such fluids (Boyer et al.
Reference Boyer, Pouliquen and Guazzelli2011; Hinch Reference Hinch2011), non-viscometric situations, such as the one considered here, might be significantly more complicated. With the above, more general, notion of a second-order fluid, it is a worthwhile exercise to examine the dependence of the viscoelastic torque on spheroid aspect ratio over the entire range of
![]() ${\it\epsilon}$
. We find below that the torque on a prolate spheroid changes sign over a certain
${\it\epsilon}$
. We find below that the torque on a prolate spheroid changes sign over a certain
![]() ${\it\epsilon}$
-interval that is a function of its aspect ratio, and this, in principle, allows for the orientation of a sedimenting anisotropic particle to act as a rheological probe.
${\it\epsilon}$
-interval that is a function of its aspect ratio, and this, in principle, allows for the orientation of a sedimenting anisotropic particle to act as a rheological probe.
To begin with, we calculate the
![]() ${\it\epsilon}$
values for the complex fluids quoted above. For a dilute suspension of Brownian spheres (of radius
${\it\epsilon}$
values for the complex fluids quoted above. For a dilute suspension of Brownian spheres (of radius
![]() $a$
), at low shear rates, the normal stress differences are
$a$
), at low shear rates, the normal stress differences are
![]() $O({\it\mu}\dot{{\it\gamma}}\mathit{Pe}{\it\phi}^{2})$
, where
$O({\it\mu}\dot{{\it\gamma}}\mathit{Pe}{\it\phi}^{2})$
, where
![]() ${\it\mu}$
is the suspending fluid viscosity,
${\it\mu}$
is the suspending fluid viscosity,
![]() $\dot{{\it\gamma}}$
the imposed shear rate and
$\dot{{\it\gamma}}$
the imposed shear rate and
![]() ${\it\phi}$
the volume fraction. The Pèclet number based on the Stokes–Einstein diffusivity,
${\it\phi}$
the volume fraction. The Pèclet number based on the Stokes–Einstein diffusivity,
![]() $\mathit{Pe}=6{\rm\pi}{\it\mu}a^{3}/kT$
, where
$\mathit{Pe}=6{\rm\pi}{\it\mu}a^{3}/kT$
, where
![]() $k$
is Boltzmann’s constant, plays the role of
$k$
is Boltzmann’s constant, plays the role of
![]() $\mathit{De}$
, so that the weak-shear regime corresponds to
$\mathit{De}$
, so that the weak-shear regime corresponds to
![]() $\mathit{Pe}\ll 1$
. At
$\mathit{Pe}\ll 1$
. At
![]() $O({\it\phi})$
, a suspension of spheres remains Newtonian, and an anisotropic microstructure requires hydrodynamic interactions. The latter accounts for the
$O({\it\phi})$
, a suspension of spheres remains Newtonian, and an anisotropic microstructure requires hydrodynamic interactions. The latter accounts for the
![]() $O({\it\phi}^{2})$
scaling and, as shown by Brady & Vicic (Reference Brady and Vicic1995), the ratio of the normal stress differences is given by:
$O({\it\phi}^{2})$
scaling and, as shown by Brady & Vicic (Reference Brady and Vicic1995), the ratio of the normal stress differences is given by:
The
![]() ${\it\epsilon}$
corresponding to (4.18) is
${\it\epsilon}$
corresponding to (4.18) is
![]() $-4.07$
. For a dilute suspension of Brownian spheroids, at low shear rates, normal stress differences arise from the anisotropic orientation distribution even in the absence of interspheroid interactions. They are
$-4.07$
. For a dilute suspension of Brownian spheroids, at low shear rates, normal stress differences arise from the anisotropic orientation distribution even in the absence of interspheroid interactions. They are
![]() $O({\it\mu}\dot{{\it\gamma}}\mathit{Pe}_{r}{\it\phi})$
, where
$O({\it\mu}\dot{{\it\gamma}}\mathit{Pe}_{r}{\it\phi})$
, where
![]() ${\it\phi}$
is again the volume fraction, and the rotary Pèclet number, defined by
${\it\phi}$
is again the volume fraction, and the rotary Pèclet number, defined by
![]() $Pe_{r}=\dot{{\it\gamma}}/D_{r}$
, is now the equivalent of
$Pe_{r}=\dot{{\it\gamma}}/D_{r}$
, is now the equivalent of
![]() $\mathit{De}$
,
$\mathit{De}$
,
![]() $D_{r}$
being the rotary diffusivity and given by
$D_{r}$
being the rotary diffusivity and given by
![]() $D_{r}=-3kT({\it\xi}_{0}-(1+{\it\xi}_{0}^{2})\cosh ^{-1}({\it\xi}_{0}/\bar{{\it\xi}_{0}}))/(16d^{3}{\rm\pi}{\it\mu}(2{\it\xi}_{0}^{2}-1))$
for a prolate spheroid, and
$D_{r}=-3kT({\it\xi}_{0}-(1+{\it\xi}_{0}^{2})\cosh ^{-1}({\it\xi}_{0}/\bar{{\it\xi}_{0}}))/(16d^{3}{\rm\pi}{\it\mu}(2{\it\xi}_{0}^{2}-1))$
for a prolate spheroid, and
![]() $D_{r}=3kT(\bar{{\it\xi}_{0}}-(-2+{\it\xi}_{0}^{2})\sec ^{-1}({\it\xi}_{0}/\bar{{\it\xi}_{0}}))/(16d^{3}{\rm\pi}{\it\mu}(2{\it\xi}_{0}^{2}-1))$
for an oblate spheroid, where
$D_{r}=3kT(\bar{{\it\xi}_{0}}-(-2+{\it\xi}_{0}^{2})\sec ^{-1}({\it\xi}_{0}/\bar{{\it\xi}_{0}}))/(16d^{3}{\rm\pi}{\it\mu}(2{\it\xi}_{0}^{2}-1))$
for an oblate spheroid, where
![]() $\bar{{\it\xi}_{0}}=\sqrt{{\it\xi}_{0}^{2}-1}$
(Brenner & Condiff Reference Brenner and Condiff1974). For
$\bar{{\it\xi}_{0}}=\sqrt{{\it\xi}_{0}^{2}-1}$
(Brenner & Condiff Reference Brenner and Condiff1974). For
![]() $\mathit{Pe}_{r}\ll 1$
, the ratio of the normal stress differences is a function of only the spheroid aspect ratio, and is given by (Brenner & Condiff Reference Brenner and Condiff1974):
$\mathit{Pe}_{r}\ll 1$
, the ratio of the normal stress differences is a function of only the spheroid aspect ratio, and is given by (Brenner & Condiff Reference Brenner and Condiff1974):
where
 $$\begin{eqnarray}\displaystyle f({\it\xi}_{0}) & = & \displaystyle -7\left(\frac{3{\it\xi}_{0}^{2}-2-3{\it\xi}_{0}\bar{{\it\xi}}_{0}^{2}\text{sech}^{-1}\displaystyle \frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}}}{\bar{{\it\xi}_{0}}^{3}}\right)\left(\frac{5{\it\xi}_{0}-3{\it\xi}_{0}^{3}}{\bar{{\it\xi}_{0}}^{4}}+3\text{sech}^{-1}\frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\left(\frac{3{\it\xi}_{0}+(1-3{\it\xi}_{0}^{2})\text{sech}^{-1}\displaystyle \frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}}}{\bar{{\it\xi}_{0}}^{2}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f({\it\xi}_{0}) & = & \displaystyle -7\left(\frac{3{\it\xi}_{0}^{2}-2-3{\it\xi}_{0}\bar{{\it\xi}}_{0}^{2}\text{sech}^{-1}\displaystyle \frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}}}{\bar{{\it\xi}_{0}}^{3}}\right)\left(\frac{5{\it\xi}_{0}-3{\it\xi}_{0}^{3}}{\bar{{\it\xi}_{0}}^{4}}+3\text{sech}^{-1}\frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\left(\frac{3{\it\xi}_{0}+(1-3{\it\xi}_{0}^{2})\text{sech}^{-1}\displaystyle \frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}}}{\bar{{\it\xi}_{0}}^{2}}\right),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle g({\it\xi}_{0}) & = & \displaystyle \frac{\displaystyle 2(3{\it\xi}_{0}^{3}+{\it\xi}_{0})^{2}-2{\it\xi}_{0}(27{\it\xi}_{0}^{6}+84{\it\xi}_{0}^{4}-149{\it\xi}_{0}^{2}+50)\text{sech}^{-1}\frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}}}{\bar{{\it\xi}_{0}}^{9}}+\left(\text{sech}^{-1}\frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}}\right)^{2},\nonumber\\ \displaystyle & & \displaystyle \times \left(\!\frac{\displaystyle 6(9{\it\xi}_{0}^{6}+59{\it\xi}_{0}^{4}-57{\it\xi}_{0}^{2}+5)-18\bar{{\it\xi}_{0}}^{2}{\it\xi}_{0}({\it\xi}_{0}^{4}+10{\it\xi}_{0}^{2}-3)\text{sech}^{-1}\frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}}}{\bar{{\it\xi}_{0}}^{7}}\!\right)\!,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g({\it\xi}_{0}) & = & \displaystyle \frac{\displaystyle 2(3{\it\xi}_{0}^{3}+{\it\xi}_{0})^{2}-2{\it\xi}_{0}(27{\it\xi}_{0}^{6}+84{\it\xi}_{0}^{4}-149{\it\xi}_{0}^{2}+50)\text{sech}^{-1}\frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}}}{\bar{{\it\xi}_{0}}^{9}}+\left(\text{sech}^{-1}\frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}}\right)^{2},\nonumber\\ \displaystyle & & \displaystyle \times \left(\!\frac{\displaystyle 6(9{\it\xi}_{0}^{6}+59{\it\xi}_{0}^{4}-57{\it\xi}_{0}^{2}+5)-18\bar{{\it\xi}_{0}}^{2}{\it\xi}_{0}({\it\xi}_{0}^{4}+10{\it\xi}_{0}^{2}-3)\text{sech}^{-1}\frac{\bar{{\it\xi}}_{0}}{{\it\xi}_{0}}}{\bar{{\it\xi}_{0}}^{7}}\!\right)\!,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle f({\it\xi}_{0}) & = & \displaystyle \left(21\bar{{\it\xi}_{0}}+7(2-3{\it\xi}_{0}^{2})\cos ^{-1}\frac{\bar{{\it\xi}_{0}}}{{\it\xi}_{0}}\right)\left(\bar{{\it\xi}_{0}}(3{\it\xi}_{0}^{2}+2)-3{\it\xi}_{0}^{4}\cos ^{-1}\frac{\bar{{\it\xi}_{0}}}{{\it\xi}_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\left(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}_{0}}{\it\xi}_{0}^{2}\cos ^{-1}\frac{\bar{{\it\xi}_{0}}}{{\it\xi}_{0}}+1\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f({\it\xi}_{0}) & = & \displaystyle \left(21\bar{{\it\xi}_{0}}+7(2-3{\it\xi}_{0}^{2})\cos ^{-1}\frac{\bar{{\it\xi}_{0}}}{{\it\xi}_{0}}\right)\left(\bar{{\it\xi}_{0}}(3{\it\xi}_{0}^{2}+2)-3{\it\xi}_{0}^{4}\cos ^{-1}\frac{\bar{{\it\xi}_{0}}}{{\it\xi}_{0}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\left(-3{\it\xi}_{0}^{2}+3\bar{{\it\xi}_{0}}{\it\xi}_{0}^{2}\cos ^{-1}\frac{\bar{{\it\xi}_{0}}}{{\it\xi}_{0}}+1\right),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle g({\it\xi}_{0}) & = & \displaystyle -18{\it\xi}_{0}^{6}+66{\it\xi}_{0}^{4}-80{\it\xi}_{0}^{2}+32+(-54{\it\xi}_{0}^{8}+516{\it\xi}_{0}^{6}-528{\it\xi}_{0}^{4}+96{\it\xi}_{0}^{2})\left(\cos ^{-1}\frac{\bar{{\it\xi}_{0}}}{{\it\xi}_{0}}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle +\,\bar{{\it\xi}_{0}}\!\!\left(\cos ^{-1}\frac{\bar{{\it\xi}_{0}}}{{\it\xi}_{0}}\right)^{3}\left(\frac{54{\it\xi}_{0}^{6}-330{\it\xi}_{0}^{4}+200{\it\xi}_{0}^{2}-24}{\left(\cos ^{-1}\displaystyle \frac{\bar{{\it\xi}_{0}}}{{\it\xi}_{0}}\right)^{2}}+(18{\it\xi}_{0}^{8}-216{\it\xi}_{0}^{6}+144{\it\xi}_{0}^{4})\right),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g({\it\xi}_{0}) & = & \displaystyle -18{\it\xi}_{0}^{6}+66{\it\xi}_{0}^{4}-80{\it\xi}_{0}^{2}+32+(-54{\it\xi}_{0}^{8}+516{\it\xi}_{0}^{6}-528{\it\xi}_{0}^{4}+96{\it\xi}_{0}^{2})\left(\cos ^{-1}\frac{\bar{{\it\xi}_{0}}}{{\it\xi}_{0}}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle +\,\bar{{\it\xi}_{0}}\!\!\left(\cos ^{-1}\frac{\bar{{\it\xi}_{0}}}{{\it\xi}_{0}}\right)^{3}\left(\frac{54{\it\xi}_{0}^{6}-330{\it\xi}_{0}^{4}+200{\it\xi}_{0}^{2}-24}{\left(\cos ^{-1}\displaystyle \frac{\bar{{\it\xi}_{0}}}{{\it\xi}_{0}}\right)^{2}}+(18{\it\xi}_{0}^{8}-216{\it\xi}_{0}^{6}+144{\it\xi}_{0}^{4})\right),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
for
![]() $\mathit{Ca}\ll 1$
. The
$\mathit{Ca}\ll 1$
. The
![]() ${\it\epsilon}$
based on (4.24) ranges from
${\it\epsilon}$
based on (4.24) ranges from
![]() $-0.90~({\it\lambda}\rightarrow 0)$
to
$-0.90~({\it\lambda}\rightarrow 0)$
to
![]() $-0.63~({\it\lambda}\rightarrow \infty )$
. Dilute emulsions with surfactant-covered spherical drops, in the presence of significant elasticity (
$-0.63~({\it\lambda}\rightarrow \infty )$
. Dilute emulsions with surfactant-covered spherical drops, in the presence of significant elasticity (
![]() $\mathit{Ma}\mathit{Ca}\sim O(1)$
) but negligible deformation (
$\mathit{Ma}\mathit{Ca}\sim O(1)$
) but negligible deformation (
![]() $\mathit{Ca}\ll 1$
), conform to the co-rotational limit (Vlahovska, Blawzdziewicz & Loewenberg Reference Vlahovska, Blawzdziewicz and Loewenberg2000; Vlahovska et al.
Reference Vlahovska, Blawzdziewicz and Loewenberg2002); here, the normal stress differences are
$\mathit{Ca}\ll 1$
), conform to the co-rotational limit (Vlahovska, Blawzdziewicz & Loewenberg Reference Vlahovska, Blawzdziewicz and Loewenberg2000; Vlahovska et al.
Reference Vlahovska, Blawzdziewicz and Loewenberg2002); here, the normal stress differences are
![]() $O({\it\mu}\dot{{\it\gamma}}{\it\phi}Ma^{-1})$
for
$O({\it\mu}\dot{{\it\gamma}}{\it\phi}Ma^{-1})$
for
![]() $Ma\gg 1$
,
$Ma\gg 1$
,
![]() $Ma$
being the Marangoni number, defined as
$Ma$
being the Marangoni number, defined as
![]() $RTc_{s}/{\it\mu}a{\it\Gamma}$
, where
$RTc_{s}/{\it\mu}a{\it\Gamma}$
, where
![]() $c_{s}$
is the equilibrium surface concentration of the adsorbed surfactants. The above remains true for a suspension of vesicles in the tank-treading regime (Vlahovska & Garica Reference Vlahovska and Garica2007).
$c_{s}$
is the equilibrium surface concentration of the adsorbed surfactants. The above remains true for a suspension of vesicles in the tank-treading regime (Vlahovska & Garica Reference Vlahovska and Garica2007).

Figure 10. Plot of
![]() $N_{1}/N_{2}$
versus
$N_{1}/N_{2}$
versus
![]() ${\it\epsilon}$
plot for different complex fluids. Here,
${\it\epsilon}$
plot for different complex fluids. Here,
![]() $N_{1}$
and
$N_{1}$
and
![]() $N_{2}$
are the first and second normal stress differences with
$N_{2}$
are the first and second normal stress differences with
![]() $N_{1}/N_{2}=-2{\it\epsilon}/(1+2{\it\epsilon})$
,
$N_{1}/N_{2}=-2{\it\epsilon}/(1+2{\it\epsilon})$
,
![]() ${\it\epsilon}$
being the second-order fluid parameter.
${\it\epsilon}$
being the second-order fluid parameter.
In all the above cases, with increasing volume fraction, the second-order fluid regime, as inferred from a low-shear plateau in the shear viscosity and the normal stress coefficients, becomes a more restricted one owing to a general slowing down of the microstructural relaxation. From numerical simulations (Loewenberg & Hinch Reference Loewenberg and Hinch1996), one observes shear-thinning of the normal stress differences, although their ratio remains comparable to that in the dilute regime. The
![]() ${\it\epsilon}$
values accessed by the aforementioned (second-order) complex fluids are summarized in figure 10, where the ratio of the normal stress differences is plotted against
${\it\epsilon}$
values accessed by the aforementioned (second-order) complex fluids are summarized in figure 10, where the ratio of the normal stress differences is plotted against
![]() ${\it\epsilon}$
.
${\it\epsilon}$
.
![]() $N_{1}$
and
$N_{1}$
and
![]() $N_{2}$
have the same sign when
$N_{2}$
have the same sign when
![]() $-0.5\leqslant {\it\epsilon}\leqslant 0$
, and have opposite signs outside this range. Further,
$-0.5\leqslant {\it\epsilon}\leqslant 0$
, and have opposite signs outside this range. Further,
![]() $|N_{1}/N_{2}|>1~({<}1)$
for
$|N_{1}/N_{2}|>1~({<}1)$
for
![]() ${\it\epsilon}<-0.5~({\it\epsilon}>0)$
. Since
${\it\epsilon}<-0.5~({\it\epsilon}>0)$
. Since
![]() $N_{2}$
becomes greater than
$N_{2}$
becomes greater than
![]() $N_{1}$
for
$N_{1}$
for
![]() ${\it\epsilon}>0$
, the sum,
${\it\epsilon}>0$
, the sum,
![]() ${\it\psi}_{1}+{\it\psi}_{2}$
, which was used to define the relaxation time
${\it\psi}_{1}+{\it\psi}_{2}$
, which was used to define the relaxation time
![]() ${\it\lambda}$
in § 2, has opposing signs in the intervals
${\it\lambda}$
in § 2, has opposing signs in the intervals
![]() ${\it\epsilon}<-0.5$
and
${\it\epsilon}<-0.5$
and
![]() ${\it\epsilon}>0$
. In order to keep
${\it\epsilon}>0$
. In order to keep
![]() $\mathit{De}$
positive despite this sign change,
$\mathit{De}$
positive despite this sign change,
![]() ${\it\lambda}$
is defined based on
${\it\lambda}$
is defined based on
![]() $|{\it\psi}_{1}+{\it\psi}_{2}|$
and, as a result, the shape functions in (4.6) and (4.7) are redefined by multiplying them with sgn
$|{\it\psi}_{1}+{\it\psi}_{2}|$
and, as a result, the shape functions in (4.6) and (4.7) are redefined by multiplying them with sgn
![]() $({\it\psi}_{1}+{\it\psi}_{2})$
. We now systematically study the variation of the viscoelastic torque with
$({\it\psi}_{1}+{\it\psi}_{2})$
. We now systematically study the variation of the viscoelastic torque with
![]() ${\it\epsilon}$
, restricting
${\it\epsilon}$
, restricting
![]() $N_{1}$
to be positive and
$N_{1}$
to be positive and
![]() $N_{2}$
to be negative. A reversal in the signs of both
$N_{2}$
to be negative. A reversal in the signs of both
![]() $N_{1}$
and
$N_{1}$
and
![]() $N_{2}$
(which can occur in an active suspension) reverses the sign of the torque, for all
$N_{2}$
(which can occur in an active suspension) reverses the sign of the torque, for all
![]() ${\it\epsilon}$
values, for both oblate and prolate spheroids.
${\it\epsilon}$
values, for both oblate and prolate spheroids.

Figure 11. Viscoelastic shape function for a prolate spheroid plotted as a function of the eccentricity
![]() $e$
and
$e$
and
![]() ${\it\epsilon}$
for (a)
${\it\epsilon}$
for (a)
![]() $N_{1}$
-dominant and (b)
$N_{1}$
-dominant and (b)
![]() $N_{2}$
-dominant fluids. (c,d) Sections at different
$N_{2}$
-dominant fluids. (c,d) Sections at different
![]() ${\it\epsilon}$
s through the plots in (a,b), respectively. The inset of (c) for
${\it\epsilon}$
s through the plots in (a,b), respectively. The inset of (c) for
![]() ${\it\epsilon}=-5$
shows the reversal of sign at really large aspect ratios, whereas for
${\it\epsilon}=-5$
shows the reversal of sign at really large aspect ratios, whereas for
![]() ${\it\epsilon}=-1$
there is no such reversal.
${\it\epsilon}=-1$
there is no such reversal.
For a prolate spheroid, unlike the range
![]() $-1<{\it\epsilon}<-0.5$
examined earlier (see figure 6), the co-rotational and quadratic torques are of opposing signs when
$-1<{\it\epsilon}<-0.5$
examined earlier (see figure 6), the co-rotational and quadratic torques are of opposing signs when
![]() ${\it\epsilon}>0$
and
${\it\epsilon}>0$
and
![]() ${\it\epsilon}<-1$
, and the final orientation depends on their relative magnitudes. To see the effect of the opposing quadratic and co-rotational torques on an arbitrary aspect ratio spheroid, the redefined viscoelastic shape function is plotted in figure 11 as a function of both
${\it\epsilon}<-1$
, and the final orientation depends on their relative magnitudes. To see the effect of the opposing quadratic and co-rotational torques on an arbitrary aspect ratio spheroid, the redefined viscoelastic shape function is plotted in figure 11 as a function of both
![]() ${\it\epsilon}$
and the eccentricity, for an
${\it\epsilon}$
and the eccentricity, for an
![]() $N_{1}$
-dominant fluid (
$N_{1}$
-dominant fluid (
![]() ${\it\epsilon}<-0.5$
) as well as an
${\it\epsilon}<-0.5$
) as well as an
![]() $N_{2}$
-dominant fluid (
$N_{2}$
-dominant fluid (
![]() ${\it\epsilon}>0$
). The different
${\it\epsilon}>0$
). The different
![]() ${\it\epsilon}$
-sections in the lower panel illustrate the change in sign of the torque. It is clear that in an
${\it\epsilon}$
-sections in the lower panel illustrate the change in sign of the torque. It is clear that in an
![]() $N_{2}$
-dominant fluid the torque favours a longside-on orientation until an order unity aspect ratio, beyond which the spheroid sediments with a broadside-on orientation. For an
$N_{2}$
-dominant fluid the torque favours a longside-on orientation until an order unity aspect ratio, beyond which the spheroid sediments with a broadside-on orientation. For an
![]() $N_{1}$
-dominant fluid, the broadside-on orientation is favoured only for really large aspect ratios of
$N_{1}$
-dominant fluid, the broadside-on orientation is favoured only for really large aspect ratios of
![]() $O(100)$
and for sufficiently negative
$O(100)$
and for sufficiently negative
![]() ${\it\epsilon}$
(see the insets for
${\it\epsilon}$
(see the insets for
![]() ${\it\epsilon}=-5$
and
${\it\epsilon}=-5$
and
![]() ${\it\epsilon}=-1$
). Thus, in the slender-fibre limit, the torque favours a broadside-on orientation for both the
${\it\epsilon}=-1$
). Thus, in the slender-fibre limit, the torque favours a broadside-on orientation for both the
![]() $N_{2}$
-dominant and the
$N_{2}$
-dominant and the
![]() $N_{1}$
-dominant fluid. From (4.11), the ratio of the quadratic and co-rotational torques is
$N_{1}$
-dominant fluid. From (4.11), the ratio of the quadratic and co-rotational torques is
![]() $2(1+{\it\epsilon})/{\it\epsilon}$
in the slender-fibre limit, implying that for
$2(1+{\it\epsilon})/{\it\epsilon}$
in the slender-fibre limit, implying that for
![]() ${\it\epsilon}<-2$
and
${\it\epsilon}<-2$
and
![]() ${\it\epsilon}>0$
, the quadratic torque imposes the broadside-on orientation, consistent with figure 11.
${\it\epsilon}>0$
, the quadratic torque imposes the broadside-on orientation, consistent with figure 11.
The tendency of the quadratic torque to stabilize the broadside-on orientation may be understood based on a tensioned vortex line argument. The surface vortex lines and (projected) streamlines are plotted for a prolate spheroid (
![]() ${\it\kappa}=5$
), centred at the origin, and sedimenting at an angle of
${\it\kappa}=5$
), centred at the origin, and sedimenting at an angle of
![]() ${\rm\pi}/4$
, in figure 13(a). The vortex lines close in on themselves and the streamlines run from the front to the rear stagnation point. The flow close to the spheroid is locally a simple shear (except at the stagnation points), this being responsible for the orthogonality of the streamlines and vortex lines. The magnitude of the vortex line tension is proportional to the magnitude of surface vorticity. The (normalized) variation of the latter, as a function of the
${\rm\pi}/4$
, in figure 13(a). The vortex lines close in on themselves and the streamlines run from the front to the rear stagnation point. The flow close to the spheroid is locally a simple shear (except at the stagnation points), this being responsible for the orthogonality of the streamlines and vortex lines. The magnitude of the vortex line tension is proportional to the magnitude of surface vorticity. The (normalized) variation of the latter, as a function of the
![]() $X$
-coordinate, is shown in figure 13(b). The portions of the vortex lines in zones 1 and 2 (the lower and upper halves of the spheroid, respectively) experience on an average a higher tension. The pull exerted by these highly tensioned zones draws the spheroid towards a broadside-on orientation.
$X$
-coordinate, is shown in figure 13(b). The portions of the vortex lines in zones 1 and 2 (the lower and upper halves of the spheroid, respectively) experience on an average a higher tension. The pull exerted by these highly tensioned zones draws the spheroid towards a broadside-on orientation.
For an oblate spheroid, the co-rotational and quadratic contributions to the torque are of opposing signs only in the range
![]() $-1\leqslant {\it\epsilon}\leqslant -0.5$
. Even in this range, however, the co-rotational torque dominates, leading to a longside-on orientation for all
$-1\leqslant {\it\epsilon}\leqslant -0.5$
. Even in this range, however, the co-rotational torque dominates, leading to a longside-on orientation for all
![]() ${\it\epsilon}$
values. This is seen from figure 12, where the viscoelastic shape function is plotted as a function of both
${\it\epsilon}$
values. This is seen from figure 12, where the viscoelastic shape function is plotted as a function of both
![]() ${\it\epsilon}$
and the eccentricity. This may also be seen from the expression for the flat disk (see (4.9)) in which case the ratio is
${\it\epsilon}$
and the eccentricity. This may also be seen from the expression for the flat disk (see (4.9)) in which case the ratio is
![]() $0.0617(1+{\it\epsilon})/{\it\epsilon}$
; the co-rotational torque dominates in this limit, leading to a longside-on orientation.
$0.0617(1+{\it\epsilon})/{\it\epsilon}$
; the co-rotational torque dominates in this limit, leading to a longside-on orientation.

Figure 12. Viscoelastic shape function for an oblate spheroid plotted as a function of the eccentricity
![]() $e$
and
$e$
and
![]() ${\it\epsilon}$
for (a)
${\it\epsilon}$
for (a)
![]() $N_{1}$
-dominant and (b)
$N_{1}$
-dominant and (b)
![]() $N_{2}$
-dominant fluids. (c,d) Sections at different
$N_{2}$
-dominant fluids. (c,d) Sections at different
![]() ${\it\epsilon}$
s through the plots in (a,b), respectively.
${\it\epsilon}$
s through the plots in (a,b), respectively.

Figure 13. (a) Surface streamlines and surface vortex lines on a prolate spheroid (
![]() ${\it\kappa}=5$
), centred at the origin, sedimenting with a velocity
${\it\kappa}=5$
), centred at the origin, sedimenting with a velocity
![]() $\boldsymbol{U}$
, which makes an angle of
$\boldsymbol{U}$
, which makes an angle of
![]() ${\rm\pi}/4$
with orientation vector
${\rm\pi}/4$
with orientation vector
![]() $\boldsymbol{p}$
. (b) Variation of the normalized magnitude along each of the vortex line. The asterisk symbols denote the points at which vortex lines crosses the symmetry plane of the spheroid.
$\boldsymbol{p}$
. (b) Variation of the normalized magnitude along each of the vortex line. The asterisk symbols denote the points at which vortex lines crosses the symmetry plane of the spheroid.
5. Viscoelastic torque on a fibre for large
 $\mathit{De}$
$\mathit{De}$
The second-order fluid regime, which underlies the analysis in the earlier sections, restricts the Deborah number to very small values. This restriction becomes particularly severe for large-aspect-ratio fibres, where the velocity gradient ranges from being
![]() $O(U/L)(\ln {\it\kappa})^{-1}$
, on length scales of
$O(U/L)(\ln {\it\kappa})^{-1}$
, on length scales of
![]() $O(L)$
, to being
$O(L)$
, to being
![]() $O(U/b)(\ln {\it\kappa})^{-1}$
close to the fibre. For such particles, the above restriction applies to the Deborah number based on the radius, implying that
$O(U/b)(\ln {\it\kappa})^{-1}$
close to the fibre. For such particles, the above restriction applies to the Deborah number based on the radius, implying that
![]() $\mathit{De}$
, as defined in § 2, must be smaller than
$\mathit{De}$
, as defined in § 2, must be smaller than
![]() $O(1/{\it\kappa})$
. Experiments carried out on sedimenting particles in polymer solutions conform neither to the stringent requirement on the relaxation time nor to the diluteness constraint in general (Leal Reference Leal1979; Chiba, Song & Horikawa Reference Chiba, Song and Horikawa1986; Cho, Cho & Park Reference Cho, Cho and Park1992; Joseph & Liu Reference Joseph and Liu1993). The observations indicate that the sense of the viscoelastic torque remains unaltered even outside of the second-order fluid regime, although a quantitative analysis would now have to account for the finite rate of microstructural relaxation even in the dilute regime. In what follows, we discuss the physical picture, along with scaling arguments and some analysis, relevant to a slender fibre sedimenting at finite
$O(1/{\it\kappa})$
. Experiments carried out on sedimenting particles in polymer solutions conform neither to the stringent requirement on the relaxation time nor to the diluteness constraint in general (Leal Reference Leal1979; Chiba, Song & Horikawa Reference Chiba, Song and Horikawa1986; Cho, Cho & Park Reference Cho, Cho and Park1992; Joseph & Liu Reference Joseph and Liu1993). The observations indicate that the sense of the viscoelastic torque remains unaltered even outside of the second-order fluid regime, although a quantitative analysis would now have to account for the finite rate of microstructural relaxation even in the dilute regime. In what follows, we discuss the physical picture, along with scaling arguments and some analysis, relevant to a slender fibre sedimenting at finite
![]() $\mathit{De}$
in a dilute polymer solution.
$\mathit{De}$
in a dilute polymer solution.
For finite
![]() $\mathit{De}$
, the stress can be modelled using the Oldroyd-B constitutive equation (Larson Reference Larson1988) and the deviatoric polymeric stress (
$\mathit{De}$
, the stress can be modelled using the Oldroyd-B constitutive equation (Larson Reference Larson1988) and the deviatoric polymeric stress (
![]() ${\bf\sigma}_{NN}$
) is governed by:
${\bf\sigma}_{NN}$
) is governed by:
where
![]() ${\it\delta}_{U}/({\it\delta}t)$
is the upper convected derivative and
${\it\delta}_{U}/({\it\delta}t)$
is the upper convected derivative and
![]() $G=nkT$
is the shear modulus (
$G=nkT$
is the shear modulus (
![]() $n$
here is the polymer number density, and the dilute regime implies that
$n$
here is the polymer number density, and the dilute regime implies that
![]() $nR_{g}^{3}\ll 1$
, with
$nR_{g}^{3}\ll 1$
, with
![]() $R_{g}$
being the characteristic size of a polymer coil). The polymer stress at any point can be obtained by inverting (5.1) along a particular streamline, leading to the following expression for the stress made non-dimensional by
$R_{g}$
being the characteristic size of a polymer coil). The polymer stress at any point can be obtained by inverting (5.1) along a particular streamline, leading to the following expression for the stress made non-dimensional by
![]() $G$
:
$G$
:
where
![]() $\unicode[STIX]{x1D60A}_{ij}^{-1}(t,t^{\prime })=(\partial x_{i}(t)/\partial r_{q}(t^{\prime }))(\partial x_{j}(t)/\partial r_{q}(t^{\prime }))$
, is the Finger tensor relating the configuration at time
$\unicode[STIX]{x1D60A}_{ij}^{-1}(t,t^{\prime })=(\partial x_{i}(t)/\partial r_{q}(t^{\prime }))(\partial x_{j}(t)/\partial r_{q}(t^{\prime }))$
, is the Finger tensor relating the configuration at time
![]() $t$
,
$t$
,
![]() $\boldsymbol{x}(t)$
, to that at an earlier time
$\boldsymbol{x}(t)$
, to that at an earlier time
![]() $t^{\prime }$
,
$t^{\prime }$
,
![]() $\boldsymbol{r}(t^{\prime })$
, and
$\boldsymbol{r}(t^{\prime })$
, and
![]() $\text{D}t^{\prime }$
denotes integration along a streamline.
$\text{D}t^{\prime }$
denotes integration along a streamline.
For a slender fibre, it is natural to consider three physically distinct regimes, depending on the ordering of the two flow time scales,
![]() $L/U$
and
$L/U$
and
![]() $b/U$
, relative to the relaxation time scale
$b/U$
, relative to the relaxation time scale
![]() ${\it\tau}$
. The second-order fluid regime, as indicated above, corresponds to
${\it\tau}$
. The second-order fluid regime, as indicated above, corresponds to
![]() ${\it\tau}\ll b/U\ll L/U$
. The other extreme, where
${\it\tau}\ll b/U\ll L/U$
. The other extreme, where
![]() ${\it\tau}\gg L/U\gg b/U$
, corresponds to
${\it\tau}\gg L/U\gg b/U$
, corresponds to
![]() $\mathit{De}\gg 1$
, when the polymer molecules do not relax as they are convected past the sedimenting fibre. In this limit, the upper convected derivative in (5.1) is dominant, and the polymer molecules are affinely deformed by the flow. The stress given by (5.2) reduces to just the Finger tensor, the response of a neo-Hookean solid (Rallison & Hinch Reference Rallison and Hinch2004). Viscous slender-body theory may now be used to estimate the contributions to the viscoelastic torque from the outer (
$\mathit{De}\gg 1$
, when the polymer molecules do not relax as they are convected past the sedimenting fibre. In this limit, the upper convected derivative in (5.1) is dominant, and the polymer molecules are affinely deformed by the flow. The stress given by (5.2) reduces to just the Finger tensor, the response of a neo-Hookean solid (Rallison & Hinch Reference Rallison and Hinch2004). Viscous slender-body theory may now be used to estimate the contributions to the viscoelastic torque from the outer (
![]() $r\sim O(L)$
) and inner (
$r\sim O(L)$
) and inner (
![]() $r\sim O(b)$
) regions. In the outer region,
$r\sim O(b)$
) regions. In the outer region,
![]() ${\bf\sigma}_{NN}\sim O(1/\text{ln}\,{\it\kappa})$
, corresponding to the strain resulting from an
${\bf\sigma}_{NN}\sim O(1/\text{ln}\,{\it\kappa})$
, corresponding to the strain resulting from an
![]() $O(1/\text{ln}\,{\it\kappa})$
velocity field acting over an
$O(1/\text{ln}\,{\it\kappa})$
velocity field acting over an
![]() $O(1)$
time interval,
$O(1)$
time interval,
![]() $\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D650}^{(2)}\sim O(1/\text{ln}\,{\it\kappa})$
,
$\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D650}^{(2)}\sim O(1/\text{ln}\,{\it\kappa})$
,
![]() $\text{d}V\sim O(1)$
, so the torque integral,
$\text{d}V\sim O(1)$
, so the torque integral,
![]() $\int \!\!{\bf\sigma}_{NN}\,:\,\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D650}^{(2)}\,\text{d}V\sim O[1/(\ln {\it\kappa})^{2}]$
. The polymer molecules spend only an
$\int \!\!{\bf\sigma}_{NN}\,:\,\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D650}^{(2)}\,\text{d}V\sim O[1/(\ln {\it\kappa})^{2}]$
. The polymer molecules spend only an
![]() $O(1/{\it\kappa})$
time in the inner region, the velocity field in this region being
$O(1/{\it\kappa})$
time in the inner region, the velocity field in this region being
![]() $O(\ln {\it\rho}/\text{ln}\,{\it\kappa})$
; thus
$O(\ln {\it\rho}/\text{ln}\,{\it\kappa})$
; thus
![]() ${\bf\sigma}_{NN}\sim O(1/({\it\kappa}{\it\rho}\ln {\it\kappa}))$
,
${\bf\sigma}_{NN}\sim O(1/({\it\kappa}{\it\rho}\ln {\it\kappa}))$
,
![]() $\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D650}^{(2)}\sim O(1/({\it\rho}\ln {\it\kappa}))$
,
$\boldsymbol{{\rm\nabla}}\unicode[STIX]{x1D650}^{(2)}\sim O(1/({\it\rho}\ln {\it\kappa}))$
,
![]() $\text{d}V\sim O({\it\rho}^{2})$
, with
$\text{d}V\sim O({\it\rho}^{2})$
, with
![]() ${\it\rho}\sim O(b)$
. The inner region contribution to the torque integral scales as
${\it\rho}\sim O(b)$
. The inner region contribution to the torque integral scales as
![]() $O[1/({\it\kappa}(\ln {\it\kappa})^{2})]$
. In contrast to the second-order fluid regime discussed in § 4.2.3, the arguments above suggest the dominance of the outer region for
$O[1/({\it\kappa}(\ln {\it\kappa})^{2})]$
. In contrast to the second-order fluid regime discussed in § 4.2.3, the arguments above suggest the dominance of the outer region for
![]() $\mathit{De}\gg 1$
. For a slender fibre, the logarithmically weak disturbance velocity field in the outer region implies that the stress at any given point may be obtained by integrating along the (straight) streamlines of the ambient uniform flow at leading logarithmic order, and this allows for a simple calculation in Fourier space. Using the convolution theorem, the volume integral for torque can be rewritten in Fourier space as:
$\mathit{De}\gg 1$
. For a slender fibre, the logarithmically weak disturbance velocity field in the outer region implies that the stress at any given point may be obtained by integrating along the (straight) streamlines of the ambient uniform flow at leading logarithmic order, and this allows for a simple calculation in Fourier space. Using the convolution theorem, the volume integral for torque can be rewritten in Fourier space as:
where the
![]() $\hat{{\bf\sigma}}_{NN}(\boldsymbol{k})$
and
$\hat{{\bf\sigma}}_{NN}(\boldsymbol{k})$
and
![]() $\hat{\boldsymbol{U}}^{(2)}\!(\boldsymbol{k})$
are the Fourier-transformed non-Newtonian stress and test velocity fields, the Fourier transform being defined by
$\hat{\boldsymbol{U}}^{(2)}\!(\boldsymbol{k})$
are the Fourier-transformed non-Newtonian stress and test velocity fields, the Fourier transform being defined by
![]() $\hat{\boldsymbol{f}}(\boldsymbol{k})=\int \!\text{e}^{-\text{i}2{\rm\pi}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}}f(\boldsymbol{r})\,\text{d}\boldsymbol{r}$
. Retaining only the material derivative on the left-hand side in (5.1), at leading order, and transforming, one obtains:
$\hat{\boldsymbol{f}}(\boldsymbol{k})=\int \!\text{e}^{-\text{i}2{\rm\pi}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}}f(\boldsymbol{r})\,\text{d}\boldsymbol{r}$
. Retaining only the material derivative on the left-hand side in (5.1), at leading order, and transforming, one obtains:
 $$\begin{eqnarray}\hat{{\it\sigma}}_{NNij}(\boldsymbol{k})=\frac{\text{i}2{\rm\pi}(k_{i}\hat{u} _{j}^{(1)}+k_{j}\hat{u} _{i}^{(1)})}{\displaystyle \frac{1}{\mathit{De}}-\text{i}2{\rm\pi}\hat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{k}},\end{eqnarray}$$
$$\begin{eqnarray}\hat{{\it\sigma}}_{NNij}(\boldsymbol{k})=\frac{\text{i}2{\rm\pi}(k_{i}\hat{u} _{j}^{(1)}+k_{j}\hat{u} _{i}^{(1)})}{\displaystyle \frac{1}{\mathit{De}}-\text{i}2{\rm\pi}\hat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{k}},\end{eqnarray}$$
where
![]() $\hat{\boldsymbol{u}}^{(1)}(\boldsymbol{k})$
is the Fourier-transformed disturbance velocity field due to a translating fibre given by (Subramanian & Koch Reference Subramanian and Koch2005):
$\hat{\boldsymbol{u}}^{(1)}(\boldsymbol{k})$
is the Fourier-transformed disturbance velocity field due to a translating fibre given by (Subramanian & Koch Reference Subramanian and Koch2005):

Figure 14. (a) Leading order non-dimensional elastic torque on a sedimenting slender fibre, as a function of the angle of inclination, for finite
![]() $\mathit{De}\gg O({\it\kappa}^{-1/2})$
. (b) A shift in the location of the peak torque, back towards
$\mathit{De}\gg O({\it\kappa}^{-1/2})$
. (b) A shift in the location of the peak torque, back towards
![]() $45^{\circ }$
, is apparent as
$45^{\circ }$
, is apparent as
![]() $\mathit{De}$
decreases.
$\mathit{De}$
decreases.
The Fourier transform of
![]() $\unicode[STIX]{x1D650}^{(2)}$
, proportional to the disturbance due to a rotating fibre, is given by (Subramanian & Koch Reference Subramanian and Koch2005):
$\unicode[STIX]{x1D650}^{(2)}$
, proportional to the disturbance due to a rotating fibre, is given by (Subramanian & Koch Reference Subramanian and Koch2005):
Here,
![]() $\text{j}_{0}$
and
$\text{j}_{0}$
and
![]() $\text{j}_{1}$
are the zeroth- and first-order spherical Bessel functions. For infinite
$\text{j}_{1}$
are the zeroth- and first-order spherical Bessel functions. For infinite
![]() $\mathit{De}$
, using (5.4)–(5.6), the Fourier-space integral in (5.3) may be interpreted in the sense of a Cauchy principal value, and its evaluation leads to the following dimensional elastic torque:
$\mathit{De}$
, using (5.4)–(5.6), the Fourier-space integral in (5.3) may be interpreted in the sense of a Cauchy principal value, and its evaluation leads to the following dimensional elastic torque:
This
![]() $O[GL^{3}/(\ln {\it\kappa})^{2}]$
torque again leads to a longside-on orientation. Although the angular dependence in (5.7) is more complicated than the simple
$O[GL^{3}/(\ln {\it\kappa})^{2}]$
torque again leads to a longside-on orientation. Although the angular dependence in (5.7) is more complicated than the simple
![]() $\sin 2{\it\alpha}$
dependence found for a second-order fluid, the torque still peaks at an angle very close to 45°. The torque integral may be evaluated numerically for finite
$\sin 2{\it\alpha}$
dependence found for a second-order fluid, the torque still peaks at an angle very close to 45°. The torque integral may be evaluated numerically for finite
![]() $\mathit{De}$
, and the calculation shows that, with decreasing
$\mathit{De}$
, and the calculation shows that, with decreasing
![]() $\mathit{De}$
, the peak torque shifts to smaller angles, as seen in figure 14. For small enough
$\mathit{De}$
, the peak torque shifts to smaller angles, as seen in figure 14. For small enough
![]() $\mathit{De}$
, it again reverts to 45°, consistent with symmetry arguments applicable to a second-order fluid approximation in the outer region. The above analysis, based on the outer region alone, fails when the dominant torque contribution shifts to the inner region. This happens when
$\mathit{De}$
, it again reverts to 45°, consistent with symmetry arguments applicable to a second-order fluid approximation in the outer region. The above analysis, based on the outer region alone, fails when the dominant torque contribution shifts to the inner region. This happens when
![]() $\mathit{De}$
reduces to
$\mathit{De}$
reduces to
![]() $O({\it\kappa}^{-1/2})$
, and relaxation effects can no longer be neglected in the inner region (note that, for
$O({\it\kappa}^{-1/2})$
, and relaxation effects can no longer be neglected in the inner region (note that, for
![]() $\mathit{De}\gg O({\it\kappa}^{-1/2})$
, the stress in the inner region is proportional to the finger tensor, as in the outer region; the second-order fluid assumption of dominant relaxation becomes uniformly valid in the entire fluid domain only at an asymptotically smaller
$\mathit{De}\gg O({\it\kappa}^{-1/2})$
, the stress in the inner region is proportional to the finger tensor, as in the outer region; the second-order fluid assumption of dominant relaxation becomes uniformly valid in the entire fluid domain only at an asymptotically smaller
![]() $\mathit{De}$
of
$\mathit{De}$
of
![]() $O(1/{\it\kappa})$
, when the leading-order torque contribution continues to come from the inner region; see § 4.2.3).
$O(1/{\it\kappa})$
, when the leading-order torque contribution continues to come from the inner region; see § 4.2.3).
Although the analysis sketched above, based on slender-body theory, gives a convergent expression for the large-
![]() $\mathit{De}$
elastic torque, that this is the total torque is not obvious. This is because the scaling arguments above, that establish the dominance of the outer region, do not account for the detailed kinematics of the flow in the vicinity of the stagnation points. For spheres, it is known that the extensional nature of the flow close to the rear stagnation point, together with the large residence time involved, leads to highly stretched polymers once
$\mathit{De}$
elastic torque, that this is the total torque is not obvious. This is because the scaling arguments above, that establish the dominance of the outer region, do not account for the detailed kinematics of the flow in the vicinity of the stagnation points. For spheres, it is known that the extensional nature of the flow close to the rear stagnation point, together with the large residence time involved, leads to highly stretched polymers once
![]() $\mathit{De}$
exceeds a value of order unity. The resulting region of stretched polymers in the vicinity of the rear stagnation streamline, the so-called ‘birefringent strand’ (Rallision & Hinch Reference Rallision and Hinch1988; Harlen Reference Harlen1990; Harlen, Rallison & Chilcott Reference Harlen, Rallison and Chilcott1990), extends for a considerably large distance downstream of the sedimenting sphere for large
$\mathit{De}$
exceeds a value of order unity. The resulting region of stretched polymers in the vicinity of the rear stagnation streamline, the so-called ‘birefringent strand’ (Rallision & Hinch Reference Rallision and Hinch1988; Harlen Reference Harlen1990; Harlen, Rallison & Chilcott Reference Harlen, Rallison and Chilcott1990), extends for a considerably large distance downstream of the sedimenting sphere for large
![]() $\mathit{De}$
. In turn, this leads to a pronounced upstream–downstream asymmetry, with the flow downstream of the sphere relaxing at a much slower rate to the ambient in an extended elastic wake (Arigo et al.
Reference Arigo, Rajagopalan, Shapley and Mckinley1995). The birefringent strand affects the drag on the sedimenting sphere for large
$\mathit{De}$
. In turn, this leads to a pronounced upstream–downstream asymmetry, with the flow downstream of the sphere relaxing at a much slower rate to the ambient in an extended elastic wake (Arigo et al.
Reference Arigo, Rajagopalan, Shapley and Mckinley1995). The birefringent strand affects the drag on the sedimenting sphere for large
![]() $\mathit{De}$
. The sphere drag initially decreases from its Stokes value with increasing
$\mathit{De}$
. The sphere drag initially decreases from its Stokes value with increasing
![]() $\mathit{De}$
(as mentioned in § 1, this is captured even within the limited framework of an ordered fluid expansion, and is related to the decrease in the polymer contribution to the shear viscosity in a Lagrangian unsteady flow), but starts to increase again beyond
$\mathit{De}$
(as mentioned in § 1, this is captured even within the limited framework of an ordered fluid expansion, and is related to the decrease in the polymer contribution to the shear viscosity in a Lagrangian unsteady flow), but starts to increase again beyond
![]() $\mathit{De}\sim O(1)$
to a value higher than the Stokes value on account of the stress boundary layer, close to the rear stagnation point, associated with the birefringent strand; although, the precise extent of drag increase depends on the polymer extensibility (McKinley Reference McKinley2002).
$\mathit{De}\sim O(1)$
to a value higher than the Stokes value on account of the stress boundary layer, close to the rear stagnation point, associated with the birefringent strand; although, the precise extent of drag increase depends on the polymer extensibility (McKinley Reference McKinley2002).
In analogy with the sphere, one therefore expects the presence of a birefringent strand behind a sedimenting slender spheroid at large
![]() $\mathit{De}$
. Unlike a sphere, the asymmetry of the stagnation point configuration for a spheroid, sedimenting in an inclined orientation, implies that there will be an additional torque contribution associated with the strand. The finite
$\mathit{De}$
. Unlike a sphere, the asymmetry of the stagnation point configuration for a spheroid, sedimenting in an inclined orientation, implies that there will be an additional torque contribution associated with the strand. The finite
![]() $\mathit{De}$
motion of a slender spheroid/fibre in a simple shear flow is simpler in this sense since, on one hand, the time-dependent orientation implies there is not enough time to build up a birefringent strand and, on the other hand, the flow relative to the fibre being an extensional flow, the stagnation points are located at the fibre midplane, implying the absence of a birefringent-strand-induced torque. Slender-body theory in this case does yield the dominant correction to the angular velocity (Harlen & Koch Reference Harlen and Koch1993). Now, the location of the stagnation point on a sedimenting spheroid must, in principle, be derived as part of the solution, but simulations of suspensions of finitely extensible nonlinear elastic (FENE) dumbbells past sedimenting particles indicate a largely unmodified velocity field in the dilute limit (Binous & Phillips Reference Binous and Phillips1993); thus, some insight may be gained by examining the stagnation points of the Stokes velocity field. For the sedimentation angle
$\mathit{De}$
motion of a slender spheroid/fibre in a simple shear flow is simpler in this sense since, on one hand, the time-dependent orientation implies there is not enough time to build up a birefringent strand and, on the other hand, the flow relative to the fibre being an extensional flow, the stagnation points are located at the fibre midplane, implying the absence of a birefringent-strand-induced torque. Slender-body theory in this case does yield the dominant correction to the angular velocity (Harlen & Koch Reference Harlen and Koch1993). Now, the location of the stagnation point on a sedimenting spheroid must, in principle, be derived as part of the solution, but simulations of suspensions of finitely extensible nonlinear elastic (FENE) dumbbells past sedimenting particles indicate a largely unmodified velocity field in the dilute limit (Binous & Phillips Reference Binous and Phillips1993); thus, some insight may be gained by examining the stagnation points of the Stokes velocity field. For the sedimentation angle
![]() ${\it\alpha}$
bounded away from 0 and
${\it\alpha}$
bounded away from 0 and
![]() ${\rm\pi}/2$
, the symmetrically located stagnation points are given by
${\rm\pi}/2$
, the symmetrically located stagnation points are given by
![]() ${\it\eta}_{s}=\pm [1-4({\it\xi}_{0}-1)\tan ^{2}{\it\alpha}]$
. For
${\it\eta}_{s}=\pm [1-4({\it\xi}_{0}-1)\tan ^{2}{\it\alpha}]$
. For
![]() ${\it\xi}_{0}\rightarrow 1$
, the rear stagnation point is located at an asymptotically small distance of
${\it\xi}_{0}\rightarrow 1$
, the rear stagnation point is located at an asymptotically small distance of
![]() $O(b/{\it\kappa})$
from the edge (
$O(b/{\it\kappa})$
from the edge (
![]() ${\it\eta}=1$
), and the flow close to this stagnation point on length scales smaller than
${\it\eta}=1$
), and the flow close to this stagnation point on length scales smaller than
![]() $O(b/{\it\kappa})$
is a nonlinear extensional flow with
$O(b/{\it\kappa})$
is a nonlinear extensional flow with
![]() $u_{{\it\xi}}\sim ({\it\xi}-{\it\xi}_{0})^{2}$
, similar to that behind a sphere on length scales smaller than its radius. Interestingly, this suggests that the largest accessible strain rate for a slender spheroid is
$u_{{\it\xi}}\sim ({\it\xi}-{\it\xi}_{0})^{2}$
, similar to that behind a sphere on length scales smaller than its radius. Interestingly, this suggests that the largest accessible strain rate for a slender spheroid is
![]() $O(U{\it\kappa}/b)$
in the vicinity of the stagnation point (and not
$O(U{\it\kappa}/b)$
in the vicinity of the stagnation point (and not
![]() $O(U/b)$
), and thus, even when
$O(U/b)$
), and thus, even when
![]() $\mathit{De}\ll O(1/{\it\kappa})$
, the second-order fluid regime described in earlier sections, there would a localized region of extended polymers in the vicinity of the rear stagnation point.
$\mathit{De}\ll O(1/{\it\kappa})$
, the second-order fluid regime described in earlier sections, there would a localized region of extended polymers in the vicinity of the rear stagnation point.
If the location of the stagnation points above is not significantly changed when
![]() $\mathit{De}\sim O(1)$
, the birefringent-strand-induced torque may be estimated as the force exerted by the strand times a moment arm of
$\mathit{De}\sim O(1)$
, the birefringent-strand-induced torque may be estimated as the force exerted by the strand times a moment arm of
![]() $O(L)$
. This force is
$O(L)$
. This force is
![]() $O({\bf\sigma}_{str}{\it\delta}^{2})$
, where
$O({\bf\sigma}_{str}{\it\delta}^{2})$
, where
![]() ${\it\delta}$
is the strand thickness and
${\it\delta}$
is the strand thickness and
![]() ${\bf\sigma}_{str}$
is the Newtonian stress within the strand of highly stretched polymers. Assuming the stress response of the strand to be analogous to a semi-dilute solution of aligned (inextensible) fibres of the same length as the fully stretched polymers (Rallision & Hinch Reference Rallision and Hinch1988), we have
${\bf\sigma}_{str}$
is the Newtonian stress within the strand of highly stretched polymers. Assuming the stress response of the strand to be analogous to a semi-dilute solution of aligned (inextensible) fibres of the same length as the fully stretched polymers (Rallision & Hinch Reference Rallision and Hinch1988), we have
![]() ${\it\sigma}\sim {\it\mu}_{p}E$
, with
${\it\sigma}\sim {\it\mu}_{p}E$
, with
![]() ${\it\mu}_{p}$
being the enhanced strand viscosity in the semi-dilute regime and
${\it\mu}_{p}$
being the enhanced strand viscosity in the semi-dilute regime and
![]() $E$
the rate of extension in the vicinity of the stagnation point. Based on the kinematics of the nonlinear extensional flow behind a sphere (Harlen Reference Harlen1990), one finds
$E$
the rate of extension in the vicinity of the stagnation point. Based on the kinematics of the nonlinear extensional flow behind a sphere (Harlen Reference Harlen1990), one finds
![]() ${\it\delta}\sim O(b/{\it\kappa}\sqrt{E_{x}})$
,
${\it\delta}\sim O(b/{\it\kappa}\sqrt{E_{x}})$
,
![]() $E_{x}$
being the ratio of the fully stretched length of the polymer to its equilibrium extension (
$E_{x}$
being the ratio of the fully stretched length of the polymer to its equilibrium extension (
![]() $R_{g}$
), and
$R_{g}$
), and
![]() $b/{\it\kappa}$
being the smallest significant geometrical length scale. The rate of extension
$b/{\it\kappa}$
being the smallest significant geometrical length scale. The rate of extension
![]() $E$
may be written as
$E$
may be written as
![]() $O(U{\it\kappa}/b)f({\it\lambda})$
, following Harlen et al. (Reference Harlen, Rallison and Chilcott1990), where the single parameter
$O(U{\it\kappa}/b)f({\it\lambda})$
, following Harlen et al. (Reference Harlen, Rallison and Chilcott1990), where the single parameter
![]() ${\it\lambda}=(({\it\mu}_{p}{\it\delta}^{2})/{\it\mu})\log [b/({\it\kappa}{\it\delta})]$
characterizes the modified velocity field outside the birefringent strand. It may be shown, based on the analysis of Harlen et al. (Reference Harlen, Rallison and Chilcott1990), that
${\it\lambda}=(({\it\mu}_{p}{\it\delta}^{2})/{\it\mu})\log [b/({\it\kappa}{\it\delta})]$
characterizes the modified velocity field outside the birefringent strand. It may be shown, based on the analysis of Harlen et al. (Reference Harlen, Rallison and Chilcott1990), that
![]() $E$
varies from
$E$
varies from
![]() $O(U{\it\kappa}/b)$
for
$O(U{\it\kappa}/b)$
for
![]() ${\it\lambda}=0$
(no strand) to
${\it\lambda}=0$
(no strand) to
![]() $O(U{\it\kappa}/b){\it\lambda}^{-1/2}$
for
$O(U{\it\kappa}/b){\it\lambda}^{-1/2}$
for
![]() ${\it\lambda}\gg 1$
. The extreme thinness of the strand in the present case implies that
${\it\lambda}\gg 1$
. The extreme thinness of the strand in the present case implies that
![]() $E\sim O(U{\it\kappa}/b)$
in the present context. Combining these estimates, the torque contribution may be written as
$E\sim O(U{\it\kappa}/b)$
in the present context. Combining these estimates, the torque contribution may be written as
![]() $\boldsymbol{L}_{str}\sim FL\sim ({\it\mu}_{p}{\it\delta}^{2})(U{\it\kappa}/b)L\sim ({\it\mu}_{p}/E_{x})(Ub/{\it\kappa})L$
. This torque evidently stabilizes a longside-on orientation since the birefringent strand at the edge of the slender spheroid is expected to ‘pull’ it onto a vertical orientation.
$\boldsymbol{L}_{str}\sim FL\sim ({\it\mu}_{p}{\it\delta}^{2})(U{\it\kappa}/b)L\sim ({\it\mu}_{p}/E_{x})(Ub/{\it\kappa})L$
. This torque evidently stabilizes a longside-on orientation since the birefringent strand at the edge of the slender spheroid is expected to ‘pull’ it onto a vertical orientation.
It is important to note that the birefringent strand above may not be the only region of highly stretched polymers. Most polymer molecules sufficiently close to the surface of the slender spheroid (at distances much smaller than
![]() $O(b)$
) would be highly stretched when they reach the rear, having travelled only a distance of
$O(b)$
) would be highly stretched when they reach the rear, having travelled only a distance of
![]() $O(b)$
along the spheroid surface. These stretched polymers would, however, move away from the spheroid before they traverse a distance of
$O(b)$
along the spheroid surface. These stretched polymers would, however, move away from the spheroid before they traverse a distance of
![]() $O(L)$
, along the surface of the spheroid, needed to reach the rear stagnation point at the edge. It is only for distances from the surface that are much smaller than
$O(L)$
, along the surface of the spheroid, needed to reach the rear stagnation point at the edge. It is only for distances from the surface that are much smaller than
![]() $O(b/{\it\kappa})$
that the normal velocity is small enough for the molecules to reach the rear stagnation point before moving away from the surface. Thus, most polymer molecules close to the spheroid go on to form a birefringent ‘sheet’ behind it, with a thickness of
$O(b/{\it\kappa})$
that the normal velocity is small enough for the molecules to reach the rear stagnation point before moving away from the surface. Thus, most polymer molecules close to the spheroid go on to form a birefringent ‘sheet’ behind it, with a thickness of
![]() $O(b/\sqrt{E_{x}})$
, having undergone stretching by the nonlinear planar extensional flow in the transverse plane of the spheroid axis. The small fraction of polymer molecules that pass close to the rear stagnation point and are stretched by the three-dimensional nonlinear extensional flow in this region go on to form the much thinner birefringent strand above, with a transverse dimension of
$O(b/\sqrt{E_{x}})$
, having undergone stretching by the nonlinear planar extensional flow in the transverse plane of the spheroid axis. The small fraction of polymer molecules that pass close to the rear stagnation point and are stretched by the three-dimensional nonlinear extensional flow in this region go on to form the much thinner birefringent strand above, with a transverse dimension of
![]() $O(b/\sqrt{E_{x}})$
. The birefringent sheet, being present all along the rear of the spheroid, does not lead to a torque and, therefore, does not enter the scaling arguments for the torque contributions above.
$O(b/\sqrt{E_{x}})$
. The birefringent sheet, being present all along the rear of the spheroid, does not lead to a torque and, therefore, does not enter the scaling arguments for the torque contributions above.
We are now in a position to compare the relative magnitudes of the torque due to the strand and that from the outer region. This ratio may be written as
![]() $\boldsymbol{L}_{outer}/\boldsymbol{L}_{str}\sim GL^{3}/(\ln {\it\kappa})^{2}[({\it\mu}_{p}/E_{x})(Ub/{\it\kappa})L]^{-1}$
. Using the known scale for the fibre suspension viscosity in the semi-dilute regime
$\boldsymbol{L}_{outer}/\boldsymbol{L}_{str}\sim GL^{3}/(\ln {\it\kappa})^{2}[({\it\mu}_{p}/E_{x})(Ub/{\it\kappa})L]^{-1}$
. Using the known scale for the fibre suspension viscosity in the semi-dilute regime
![]() ${\it\mu}_{p}\sim {\it\mu}(nR_{g}^{3})E_{x}^{3}/\text{ln}\,E_{x}$
(Batchelor Reference Batchelor1971), this ratio may be rewritten in terms of the polymer relaxation time,
${\it\mu}_{p}\sim {\it\mu}(nR_{g}^{3})E_{x}^{3}/\text{ln}\,E_{x}$
(Batchelor Reference Batchelor1971), this ratio may be rewritten in terms of the polymer relaxation time,
![]() ${\it\tau}={\it\mu}R_{g}^{3}/kT$
, as
${\it\tau}={\it\mu}R_{g}^{3}/kT$
, as
![]() $\mathit{De}^{-1}[\ln E_{x}/(\ln {\it\kappa})^{2}]~(L/b)^{2}E_{x}^{-2}$
; not withstanding logarithmic factors, the condition for the outer torque to be dominant turns out to be
$\mathit{De}^{-1}[\ln E_{x}/(\ln {\it\kappa})^{2}]~(L/b)^{2}E_{x}^{-2}$
; not withstanding logarithmic factors, the condition for the outer torque to be dominant turns out to be
![]() $\mathit{De}\ll (L/b/E_{x})^{2}$
– the aspect ratio of the spheroid must be greater than the ‘aspect ratio’ of the polymer (the aspect ratio here being defined as the ratio of the full extended length to the coil dimension). Finally, it must be mentioned that the polymer stress field that contributes to the outer torque will be set up in a time of
$\mathit{De}\ll (L/b/E_{x})^{2}$
– the aspect ratio of the spheroid must be greater than the ‘aspect ratio’ of the polymer (the aspect ratio here being defined as the ratio of the full extended length to the coil dimension). Finally, it must be mentioned that the polymer stress field that contributes to the outer torque will be set up in a time of
![]() $O(L/U)$
, but the formation of the birefringent strand in the vicinity of the stagnation point might take a significantly longer time.
$O(L/U)$
, but the formation of the birefringent strand in the vicinity of the stagnation point might take a significantly longer time.
6. Conclusions
Over the years, a large number of analytical and numerical investigations have examined the effects of inertia and elasticity on the sedimentation of anisotropic particles, with some of the early work dating back to the 1960s (Cox Reference Cox1965). The analytical investigations in particular have mainly focused on limiting cases of slender fibres and near-spheres. The comprehensive analysis given here, based on a spheroidal harmonics framework, encompasses the entire spectrum of aspect ratios for spheroidal particles. The principal results are closed-form analytical expressions for the inertial and viscoelastic torques on prolate and oblate spheroids, of an arbitrary aspect ratio, in §§ 4.1 and 4.2.1 – see (4.1), (4.2), (4.6) and (4.7). The results predict a broadside-on orientation due to inertia and a longside-on orientation due to viscoelasticity for dilute polymer solutions. The opposing inertial and viscoelastic torques have the same angular dependence, and a balance of the two leads to a neutral curve that separates broadside-on and longside-on orientations in an
![]() $\mathit{El}$
-aspect ratio plane (figure 9 in § 4.2.2). The expansion of the exact torque expressions in appropriate limits has helped reveal inconsistencies in earlier analytical work, particularly for case of the viscoelastic torque, including those of Leal (Reference Leal1975) and Galdi et al. (Reference Galdi, Vaidya, Pokorny, Daniel and Feng2002). Analysis of the viscoelastic torque surface, as a function of the aspect ratio and the second-order fluid parameter, reveals regimes of both broadside-on and longside-on orientations for a prolate spheroid, depending on the sign and magnitude of the ratio of normal stress differences (figure 11 in § 4.2.4). This may allow for a sedimenting anisotropic particle to act as rheological probe for a suspending complex fluid medium.
$\mathit{El}$
-aspect ratio plane (figure 9 in § 4.2.2). The expansion of the exact torque expressions in appropriate limits has helped reveal inconsistencies in earlier analytical work, particularly for case of the viscoelastic torque, including those of Leal (Reference Leal1975) and Galdi et al. (Reference Galdi, Vaidya, Pokorny, Daniel and Feng2002). Analysis of the viscoelastic torque surface, as a function of the aspect ratio and the second-order fluid parameter, reveals regimes of both broadside-on and longside-on orientations for a prolate spheroid, depending on the sign and magnitude of the ratio of normal stress differences (figure 11 in § 4.2.4). This may allow for a sedimenting anisotropic particle to act as rheological probe for a suspending complex fluid medium.
A salient feature of the neutral curve above is that
![]() $\mathit{El}\rightarrow 0$
for large aspect ratios owing to the inertial torque becoming vanishingly small in relation to the viscoelastic torque. For slender fibres, effects of fibre flexibility start to become important. Weak flexibility, similar to inertia, drives a slender fibre towards a horizontal orientation (Xu & Nadim Reference Xu and Nadim1994; Li et al.
Reference Li, Manikantan, Saintillan and Spagnolie2013) and, for sufficiently slender fibres, the neutral curve must result from a balance of fibre flexibility and fluid viscoelasticity. In terms of scalings, the spatially inhomogeneous force distribution resulting from a balance of gravity (
$\mathit{El}\rightarrow 0$
for large aspect ratios owing to the inertial torque becoming vanishingly small in relation to the viscoelastic torque. For slender fibres, effects of fibre flexibility start to become important. Weak flexibility, similar to inertia, drives a slender fibre towards a horizontal orientation (Xu & Nadim Reference Xu and Nadim1994; Li et al.
Reference Li, Manikantan, Saintillan and Spagnolie2013) and, for sufficiently slender fibres, the neutral curve must result from a balance of fibre flexibility and fluid viscoelasticity. In terms of scalings, the spatially inhomogeneous force distribution resulting from a balance of gravity (
![]() $F_{g}=mg$
) and a hydrodynamic drag of
$F_{g}=mg$
) and a hydrodynamic drag of
![]() $O({\it\mu}UL/\text{ln}\,{\it\kappa})$
drives a small-amplitude deformation of
$O({\it\mu}UL/\text{ln}\,{\it\kappa})$
drives a small-amplitude deformation of
![]() $O[{\it\mu}UL^{4}/(\ln {\it\kappa})EI]$
, where
$O[{\it\mu}UL^{4}/(\ln {\it\kappa})EI]$
, where
![]() $E$
is the elastic modulus of the filament and
$E$
is the elastic modulus of the filament and
![]() $I\sim O(b^{4})$
is its moment of inertia. The force per unit length of
$I\sim O(b^{4})$
is its moment of inertia. The force per unit length of
![]() $O({\it\mu}U/\text{ln}\,{\it\kappa})$
, coupled with the above deformation, leads to a torque whose magnitude,
$O({\it\mu}U/\text{ln}\,{\it\kappa})$
, coupled with the above deformation, leads to a torque whose magnitude,
![]() $L_{flex}\sim O[{\it\mu}^{2}U^{2}L^{5}/(\ln {\it\kappa})^{2}Eb^{4}]$
at leading logarithmic order. One may, in fact, determine the leading-order neutral curve, for weakly flexible spheroidal fibres, to within algebraically small errors in the aspect ratio, using the expression for the deformation-induced angular velocity calculated recently by Li et al. (Reference Li, Manikantan, Saintillan and Spagnolie2013) for such fibres. Such accuracy is necessary since, as already seen in § 4.2.3, leading logarithmic-order slender-body theory provides a very poor approximation of the exact viscoelastic torque, even for very large aspect ratios. From equation (4.25) in Li et al. (Reference Li, Manikantan, Saintillan and Spagnolie2013), use of the time scale of
$L_{flex}\sim O[{\it\mu}^{2}U^{2}L^{5}/(\ln {\it\kappa})^{2}Eb^{4}]$
at leading logarithmic order. One may, in fact, determine the leading-order neutral curve, for weakly flexible spheroidal fibres, to within algebraically small errors in the aspect ratio, using the expression for the deformation-induced angular velocity calculated recently by Li et al. (Reference Li, Manikantan, Saintillan and Spagnolie2013) for such fibres. Such accuracy is necessary since, as already seen in § 4.2.3, leading logarithmic-order slender-body theory provides a very poor approximation of the exact viscoelastic torque, even for very large aspect ratios. From equation (4.25) in Li et al. (Reference Li, Manikantan, Saintillan and Spagnolie2013), use of the time scale of
![]() $O(L^{2}{\it\mu}/F_{g})$
leads to a dimensional angular velocity given by
$O(L^{2}{\it\mu}/F_{g})$
leads to a dimensional angular velocity given by
![]() ${\it\bf\Omega}_{flex}=((3[-\ln 2-\ln ({\it\xi}_{0}-1)-7/2]F_{g})/(640{\it\beta}{\rm\pi}{\it\mu}L^{2}))(\mathbf{1}_{\boldsymbol{g}}\,\boldsymbol{\cdot }\,\boldsymbol{p})(\mathbf{1}_{\boldsymbol{g}}\wedge \boldsymbol{p})$
in the present notation, with
${\it\bf\Omega}_{flex}=((3[-\ln 2-\ln ({\it\xi}_{0}-1)-7/2]F_{g})/(640{\it\beta}{\rm\pi}{\it\mu}L^{2}))(\mathbf{1}_{\boldsymbol{g}}\,\boldsymbol{\cdot }\,\boldsymbol{p})(\mathbf{1}_{\boldsymbol{g}}\wedge \boldsymbol{p})$
in the present notation, with
![]() $\mathbf{1}_{g}$
being the unit vector along gravity. Here,
$\mathbf{1}_{g}$
being the unit vector along gravity. Here,
![]() ${\it\beta}=({\rm\pi}Eb^{4})/(4F_{g}L^{2})$
is the elastogravitational parameter with the weakly-flexible limit, strictly speaking, corresponding to
${\it\beta}=({\rm\pi}Eb^{4})/(4F_{g}L^{2})$
is the elastogravitational parameter with the weakly-flexible limit, strictly speaking, corresponding to
![]() ${\it\beta}\gg 1$
; in practice, even
${\it\beta}\gg 1$
; in practice, even
![]() ${\it\beta}=0.02$
appears to be large enough (Li et al.
Reference Li, Manikantan, Saintillan and Spagnolie2013). The flexibility-induced torque would then be
${\it\beta}=0.02$
appears to be large enough (Li et al.
Reference Li, Manikantan, Saintillan and Spagnolie2013). The flexibility-induced torque would then be
![]() $\boldsymbol{L}_{flex}={\it\bf\Omega}_{flex}[(2{\rm\pi}{\it\mu}L^{3})/3(\ln 2-\ln ({\it\xi}_{0}-1)-1)]$
, where the term in brackets is the rotational resistance function correct to all logarithmic orders. The dimensional viscoelastic and inertial torques may be written in terms of the gravitational force
$\boldsymbol{L}_{flex}={\it\bf\Omega}_{flex}[(2{\rm\pi}{\it\mu}L^{3})/3(\ln 2-\ln ({\it\xi}_{0}-1)-1)]$
, where the term in brackets is the rotational resistance function correct to all logarithmic orders. The dimensional viscoelastic and inertial torques may be written in terms of the gravitational force
![]() $F_{g}$
as
$F_{g}$
as
![]() $\boldsymbol{L}_{visco/inertia}=-(\mathit{De}_{g}/\mathit{Re}_{g})\,F_{g}L\,(1/(k_{\bot }k_{\Vert }))\,F({\it\xi}_{0})_{visco/inertia}~(\mathbf{1}_{\boldsymbol{g}}\boldsymbol{\cdot }\boldsymbol{p})(\mathbf{1}_{\boldsymbol{g}}\wedge \boldsymbol{p})$
, with
$\boldsymbol{L}_{visco/inertia}=-(\mathit{De}_{g}/\mathit{Re}_{g})\,F_{g}L\,(1/(k_{\bot }k_{\Vert }))\,F({\it\xi}_{0})_{visco/inertia}~(\mathbf{1}_{\boldsymbol{g}}\boldsymbol{\cdot }\boldsymbol{p})(\mathbf{1}_{\boldsymbol{g}}\wedge \boldsymbol{p})$
, with
![]() $F({\it\xi}_{0})_{visco}$
and
$F({\it\xi}_{0})_{visco}$
and
![]() $F({\it\xi}_{0})_{inertia}$
being given by (4.1) and (4.6), respectively. Here,
$F({\it\xi}_{0})_{inertia}$
being given by (4.1) and (4.6), respectively. Here,
![]() $\mathit{De}_{g}$
and
$\mathit{De}_{g}$
and
![]() $\mathit{Re}_{g}$
are the Deborah and Reynolds numbers defined in terms of the gravitational force,
$\mathit{Re}_{g}$
are the Deborah and Reynolds numbers defined in terms of the gravitational force,
![]() $\mathit{De}_{g}=(F_{g}{\it\tau})/({\it\mu}L^{2})$
and
$\mathit{De}_{g}=(F_{g}{\it\tau})/({\it\mu}L^{2})$
and
![]() $\mathit{Re}_{g}=({\it\rho}F_{g})/{\it\mu}^{2}$
.
$\mathit{Re}_{g}=({\it\rho}F_{g})/{\it\mu}^{2}$
.
![]() $k_{\bot }$
and
$k_{\bot }$
and
![]() $k_{\Vert }$
are the non-dimensional resistance functions for the translation of a spheroid. For the large aspect ratios of interest here, these aspect ratio functions reduce to simpler limiting forms given by
$k_{\Vert }$
are the non-dimensional resistance functions for the translation of a spheroid. For the large aspect ratios of interest here, these aspect ratio functions reduce to simpler limiting forms given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle F^{l}({\it\xi}_{0})_{visco}=\frac{8{\rm\pi}{\it\epsilon}(3+\ln ({\it\xi}_{0}-1)-\ln 2)}{-1+(\ln ({\it\xi}_{0}-1)-\ln 2)^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{8{\rm\pi}(1+{\it\epsilon})(58+2(\ln ({\it\xi}_{0}-1)-\ln 2)(10+\ln ({\it\xi}_{0}-1)-\ln 2))}{(1+\ln ({\it\xi}_{0}-1)-\ln 2)^{2}(1+\ln 2-\ln ({\it\xi}_{0}-1))},\quad \nonumber\\ \displaystyle & & \displaystyle F^{l}({\it\xi}_{0})_{inertia}=\frac{{\rm\pi}(4757-2100\ln 2+2100\ln ({\it\xi}_{0}-1))}{315(-1+\ln 2-\ln ({\it\xi}_{0}-1))^{2}(1+\ln 2-\ln ({\it\xi}_{0}-1))},\quad \nonumber\\ \displaystyle & & \displaystyle k_{\bot }^{l}=\frac{8{\rm\pi}}{1+\ln 2-\ln ({\it\xi}_{0}-1)}\quad \text{and}\quad k_{\Vert }^{l}=\frac{4{\rm\pi}}{-1+\ln 2-\ln ({\it\xi}_{0}-1)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle F^{l}({\it\xi}_{0})_{visco}=\frac{8{\rm\pi}{\it\epsilon}(3+\ln ({\it\xi}_{0}-1)-\ln 2)}{-1+(\ln ({\it\xi}_{0}-1)-\ln 2)^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{8{\rm\pi}(1+{\it\epsilon})(58+2(\ln ({\it\xi}_{0}-1)-\ln 2)(10+\ln ({\it\xi}_{0}-1)-\ln 2))}{(1+\ln ({\it\xi}_{0}-1)-\ln 2)^{2}(1+\ln 2-\ln ({\it\xi}_{0}-1))},\quad \nonumber\\ \displaystyle & & \displaystyle F^{l}({\it\xi}_{0})_{inertia}=\frac{{\rm\pi}(4757-2100\ln 2+2100\ln ({\it\xi}_{0}-1))}{315(-1+\ln 2-\ln ({\it\xi}_{0}-1))^{2}(1+\ln 2-\ln ({\it\xi}_{0}-1))},\quad \nonumber\\ \displaystyle & & \displaystyle k_{\bot }^{l}=\frac{8{\rm\pi}}{1+\ln 2-\ln ({\it\xi}_{0}-1)}\quad \text{and}\quad k_{\Vert }^{l}=\frac{4{\rm\pi}}{-1+\ln 2-\ln ({\it\xi}_{0}-1)},\end{eqnarray}$$
all of which are again accurate to all logarithmic orders. The neutral curve, defined by
![]() $\boldsymbol{L}_{visco}=\boldsymbol{L}_{flex}+\boldsymbol{L}_{inertia}$
, may therefore be written in the form:
$\boldsymbol{L}_{visco}=\boldsymbol{L}_{flex}+\boldsymbol{L}_{inertia}$
, may therefore be written in the form:
 $$\begin{eqnarray}\frac{\mathit{De}_{g}}{\mathit{Re}_{g}}=\frac{\displaystyle \frac{-F({\it\xi}_{0})_{inertia}^{l}}{k_{\bot }^{l}\,k_{\Vert }^{l}}+\frac{({\it\xi}_{0}-1)^{-2}}{\mathit{Re}_{g}{\it\beta}_{n}}\frac{(\ln ({\it\xi}_{0}-1)+\ln 2+7/2)}{320(\ln ({\it\xi}_{0}-1)-\ln 2+1)}}{\displaystyle \frac{F({\it\xi}_{0})_{visco}^{l}}{k_{\bot }^{l}\,k_{\Vert }^{l}}},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathit{De}_{g}}{\mathit{Re}_{g}}=\frac{\displaystyle \frac{-F({\it\xi}_{0})_{inertia}^{l}}{k_{\bot }^{l}\,k_{\Vert }^{l}}+\frac{({\it\xi}_{0}-1)^{-2}}{\mathit{Re}_{g}{\it\beta}_{n}}\frac{(\ln ({\it\xi}_{0}-1)+\ln 2+7/2)}{320(\ln ({\it\xi}_{0}-1)-\ln 2+1)}}{\displaystyle \frac{F({\it\xi}_{0})_{visco}^{l}}{k_{\bot }^{l}\,k_{\Vert }^{l}}},\end{eqnarray}$$
for slender flexible fibres. In addition to depending on the aspect ratio, the neutral curve is now also a function of the parameter
![]() $\mathit{Re}_{g}{\it\beta}_{n}$
that measures the relative importance of inertia and flexibility for slender fibres. Here,
$\mathit{Re}_{g}{\it\beta}_{n}$
that measures the relative importance of inertia and flexibility for slender fibres. Here,
![]() ${\it\beta}_{n}=({\rm\pi}EL^{2})/(4F_{g})$
is a nominal elastogravitational parameter based on
${\it\beta}_{n}=({\rm\pi}EL^{2})/(4F_{g})$
is a nominal elastogravitational parameter based on
![]() $L$
alone, with
$L$
alone, with
![]() ${\it\beta}={\it\beta}_{n}({\it\xi}_{0}-1)^{2}$
. The neutral curves are plotted in figure 15 for various values of
${\it\beta}={\it\beta}_{n}({\it\xi}_{0}-1)^{2}$
. The neutral curves are plotted in figure 15 for various values of
![]() $\mathit{Re}_{g}{\it\beta}_{n}$
. The limit
$\mathit{Re}_{g}{\it\beta}_{n}$
. The limit
![]() $\mathit{Re}_{g}{\it\beta}_{n}\rightarrow \infty$
corresponds, of course, to the original rigid fibre, the balance here being between inertia and viscoelasticity. For large but finite
$\mathit{Re}_{g}{\it\beta}_{n}\rightarrow \infty$
corresponds, of course, to the original rigid fibre, the balance here being between inertia and viscoelasticity. For large but finite
![]() $\mathit{Re}_{g}{\it\beta}_{n}$
, fibre flexibility causes the neutral curve to diverge at unit eccentricity. For sufficiently large
$\mathit{Re}_{g}{\it\beta}_{n}$
, fibre flexibility causes the neutral curve to diverge at unit eccentricity. For sufficiently large
![]() $\mathit{Re}_{g}{\it\beta}_{n}$
, the transition from a decrease with aspect ratio to an eventual divergence for large aspect ratios implies a transition from an inertia–viscoelasticity balance to a flexibility–viscoelasticity balance. The aspect ratios corresponding to the minima may be regarded the cross-over values. The neutral curves for flexible fibres depend on the longitudinal profile of the fibre. For cylindrical fibres, in particular, both the gravitational and hydrodynamic forces per unit length are constant at leading logarithmic order, and the flexibility-induced deformation arises from the effects of non-local hydrodynamics at
$\mathit{Re}_{g}{\it\beta}_{n}$
, the transition from a decrease with aspect ratio to an eventual divergence for large aspect ratios implies a transition from an inertia–viscoelasticity balance to a flexibility–viscoelasticity balance. The aspect ratios corresponding to the minima may be regarded the cross-over values. The neutral curves for flexible fibres depend on the longitudinal profile of the fibre. For cylindrical fibres, in particular, both the gravitational and hydrodynamic forces per unit length are constant at leading logarithmic order, and the flexibility-induced deformation arises from the effects of non-local hydrodynamics at
![]() $O(\ln {\it\kappa})^{-2}$
, leading to an asymptotically smaller torque,
$O(\ln {\it\kappa})^{-2}$
, leading to an asymptotically smaller torque,
![]() $L_{flex}\sim O[{\it\mu}^{2}U^{2}L^{5}/(\ln {\it\kappa})^{4}Eb^{4}]$
(Xu & Nadim Reference Xu and Nadim1994; Li et al.
Reference Li, Manikantan, Saintillan and Spagnolie2013). Thus, the flexibility-controlled regime along a given neutral curve will come into play only at higher aspect ratios (relative to a spheroidal fibre).
$L_{flex}\sim O[{\it\mu}^{2}U^{2}L^{5}/(\ln {\it\kappa})^{4}Eb^{4}]$
(Xu & Nadim Reference Xu and Nadim1994; Li et al.
Reference Li, Manikantan, Saintillan and Spagnolie2013). Thus, the flexibility-controlled regime along a given neutral curve will come into play only at higher aspect ratios (relative to a spheroidal fibre).

Figure 15. The neutral curves, including the effects of fibre flexibility, plotted for various values of
![]() $\mathit{Re}_{g}{\it\beta}_{n}$
. Each curve separates a longside-on orientation regime above from a broadside-on one below.
$\mathit{Re}_{g}{\it\beta}_{n}$
. Each curve separates a longside-on orientation regime above from a broadside-on one below.
Following Li et al. (Reference Li, Manikantan, Saintillan and Spagnolie2013), one may also characterize the trajectory of a fibre sedimenting under gravity in the presence of the combined effects of inertia, viscoelasticity and flexibility. In the Stokesian limit, the absence of a torque implies that the fibre drifts indefinitely in the lateral direction. A non-zero torque curtails this indefinite migration. Writing the torques as
![]() $\boldsymbol{L}_{flex/inertia/visco}=-L_{flex/inertia/visco}(\mathbf{1}_{\boldsymbol{g}}\boldsymbol{\cdot }\boldsymbol{p})$
$\boldsymbol{L}_{flex/inertia/visco}=-L_{flex/inertia/visco}(\mathbf{1}_{\boldsymbol{g}}\boldsymbol{\cdot }\boldsymbol{p})$
![]() $(\mathbf{1}_{\boldsymbol{g}}\wedge \boldsymbol{p})$
, and defining a torque coefficient as
$(\mathbf{1}_{\boldsymbol{g}}\wedge \boldsymbol{p})$
, and defining a torque coefficient as
![]() $C_{1}=(L_{visco}+L_{inertia}+L_{flex})/\!$
(
$C_{1}=(L_{visco}+L_{inertia}+L_{flex})/\!$
(
![]() $(2{\rm\pi}{\it\mu}L^{3})/3$
$(2{\rm\pi}{\it\mu}L^{3})/3$
![]() $(\ln 2-\ln ({\it\xi}_{0}-1)-1)$
), and with
$(\ln 2-\ln ({\it\xi}_{0}-1)-1)$
), and with
![]() ${\it\alpha}_{g}(t)$
being the angle between the gravity and the fibre orientation (
${\it\alpha}_{g}(t)$
being the angle between the gravity and the fibre orientation (
![]() ${\it\alpha}_{g}={\rm\pi}/2,0$
corresponding to the broadside-on and longside-on orientations respectively), one obtains:
${\it\alpha}_{g}={\rm\pi}/2,0$
corresponding to the broadside-on and longside-on orientations respectively), one obtains:
Appendix A. Effect of inertia and viscoelasticity on the drag of a sedimenting spheroid
In this section, we determine the perturbing effects of fluid inertia and viscoelasticity, on the drag acting on a sedimenting spheroid, using the generalized reciprocal theorem formulation discussed in § 2. Brenner (Reference Brenner1961) has calculated the
![]() $O(\mathit{Re})$
Oseen correction to the drag on an arbitrary particle in terms of the Stokes drag. The drag due to fluid inertia calculated here is compared with Brenner’s results, specialized to the case of a spheroid. For the drag calculation, the generalized reciprocal theorem identity, in (2.1), takes the form:
$O(\mathit{Re})$
Oseen correction to the drag on an arbitrary particle in terms of the Stokes drag. The drag due to fluid inertia calculated here is compared with Brenner’s results, specialized to the case of a spheroid. For the drag calculation, the generalized reciprocal theorem identity, in (2.1), takes the form:
where, as usual, the unit normal vector
![]() $\boldsymbol{n}$
points into the fluid domain. The first and the second integrals on the right-hand side may be used to determine the inertial drag at
$\boldsymbol{n}$
points into the fluid domain. The first and the second integrals on the right-hand side may be used to determine the inertial drag at
![]() $O(\mathit{Re})$
and viscoelastic drag at
$O(\mathit{Re})$
and viscoelastic drag at
![]() $O(\mathit{De})$
, respectively. The problem of interest is a spheroid translating with
$O(\mathit{De})$
, respectively. The problem of interest is a spheroid translating with
![]() $\hat{\boldsymbol{U}}_{1}$
in a non-Newtonian (second-order) fluid, with inertial effects being taken into account, and the test problem is the Stokes translation of the same spheroid with a velocity
$\hat{\boldsymbol{U}}_{1}$
in a non-Newtonian (second-order) fluid, with inertial effects being taken into account, and the test problem is the Stokes translation of the same spheroid with a velocity
![]() $\hat{\boldsymbol{U}}_{2}$
. In the limit
$\hat{\boldsymbol{U}}_{2}$
. In the limit
![]() $\mathit{Re},\mathit{De}\ll 1$
, one does not need to include the effects of elasticity in the disturbance velocity fields that enter the inertial integral, and vice versa, and therefore inertia and elasticity contribute additively in this limit. The two drag corrections are considered separately below.
$\mathit{Re},\mathit{De}\ll 1$
, one does not need to include the effects of elasticity in the disturbance velocity fields that enter the inertial integral, and vice versa, and therefore inertia and elasticity contribute additively in this limit. The two drag corrections are considered separately below.
A.1. Effect of viscoelasticity
Since the velocity disturbance
![]() $\boldsymbol{u}^{(1)}$
decays as
$\boldsymbol{u}^{(1)}$
decays as
![]() $O(1/r)$
in the Stokes limit, as shown in § 2, the non-Newtonian stress in the viscoelastic integral, in (A 1), must be
$O(1/r)$
in the Stokes limit, as shown in § 2, the non-Newtonian stress in the viscoelastic integral, in (A 1), must be
![]() $O(1/r^{4})$
for large
$O(1/r^{4})$
for large
![]() $r$
. The velocity field in the test problem also decays as
$r$
. The velocity field in the test problem also decays as
![]() $O(1/r)$
, so that the entire viscoelastic integrand decays as
$O(1/r)$
, so that the entire viscoelastic integrand decays as
![]() $O(1/r^{6})$
, and Stokes estimates lead to a convergent behaviour for large
$O(1/r^{6})$
, and Stokes estimates lead to a convergent behaviour for large
![]() $r$
. Note that this would remain true even at higher orders in
$r$
. Note that this would remain true even at higher orders in
![]() $\mathit{De}$
, based on estimates obtained from the retarded-motion expansion. The convergent behaviour ensures that viscoelasticity, for small
$\mathit{De}$
, based on estimates obtained from the retarded-motion expansion. The convergent behaviour ensures that viscoelasticity, for small
![]() $\mathit{De}$
, remains a regular correction, and one may use the Stokes fields to obtain the leading-order drag correction. However, the Stokes velocity fields in both test and actual problems are even functions of position (
$\mathit{De}$
, remains a regular correction, and one may use the Stokes fields to obtain the leading-order drag correction. However, the Stokes velocity fields in both test and actual problems are even functions of position (
![]() $\boldsymbol{r}$
), which makes the viscoelastic integrand an odd function of
$\boldsymbol{r}$
), which makes the viscoelastic integrand an odd function of
![]() $\boldsymbol{r}$
at
$\boldsymbol{r}$
at
![]() $O(\mathit{De})$
, and thus, despite there being a correction to the velocity (a slight downstream shift of the Stokes streamline pattern) and pressure fields at
$O(\mathit{De})$
, and thus, despite there being a correction to the velocity (a slight downstream shift of the Stokes streamline pattern) and pressure fields at
![]() $O(\mathit{De})$
, the contribution to the drag is zero at this order. At
$O(\mathit{De})$
, the contribution to the drag is zero at this order. At
![]() $O(\mathit{De}^{2})$
, the stress would be a cubic function of the velocity and even in
$O(\mathit{De}^{2})$
, the stress would be a cubic function of the velocity and even in
![]() $\boldsymbol{r}$
, leading to a non-trivial elastic correction; this would, however, require a third-order fluid rheology, which is beyond the scope of the present calculation. Note that the argument above, based on the symmetry of the Stokes fields, and that leads to the absence of an
$\boldsymbol{r}$
, leading to a non-trivial elastic correction; this would, however, require a third-order fluid rheology, which is beyond the scope of the present calculation. Note that the argument above, based on the symmetry of the Stokes fields, and that leads to the absence of an
![]() $O(\mathit{De})$
drag contribution, may also be applied to the inertial case. However, inertia has a singular character for a translating body in an unbounded domain, and, as shown below, the symmetry argument only ensures that there cannot arise an
$O(\mathit{De})$
drag contribution, may also be applied to the inertial case. However, inertia has a singular character for a translating body in an unbounded domain, and, as shown below, the symmetry argument only ensures that there cannot arise an
![]() $O(\mathit{Re})$
to the drag from the inner region where the Stokes solution provides a valid leading-order approximation.
$O(\mathit{Re})$
to the drag from the inner region where the Stokes solution provides a valid leading-order approximation.
A.2. Effect of inertia
The integrand in the inertia integral takes the form –
![]() $\hat{\boldsymbol{U}}^{(1)}\,\boldsymbol{\cdot }\,\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)}\boldsymbol{\cdot }\boldsymbol{u}^{(2)}$
for large distances, which, based on the Stokes estimates, would be
$\hat{\boldsymbol{U}}^{(1)}\,\boldsymbol{\cdot }\,\boldsymbol{{\rm\nabla}}\boldsymbol{u}^{(1)}\boldsymbol{\cdot }\boldsymbol{u}^{(2)}$
for large distances, which, based on the Stokes estimates, would be
![]() $O(1/r^{3})$
. Thus, the inertial integral appears logarithmically divergent on length scales of the order of the size of the spheroid, implying that the dominant contribution to the drag comes, in principle, from the matching region (and is
$O(1/r^{3})$
. Thus, the inertial integral appears logarithmically divergent on length scales of the order of the size of the spheroid, implying that the dominant contribution to the drag comes, in principle, from the matching region (and is
![]() $O(\mathit{Re}\ln \mathit{Re})$
) with comparable contributions from the inner and outer (
$O(\mathit{Re}\ln \mathit{Re})$
) with comparable contributions from the inner and outer (
![]() $r\sim O(\mathit{Re}^{-1})$
) regions at a logarithmically smaller order. However, the symmetry arguments detailed above, in the context of the viscoelastic drag correction, ensure that the contributions from the inner and matching regions are identically zero, and only the outer region contribution, of
$r\sim O(\mathit{Re}^{-1})$
) regions at a logarithmically smaller order. However, the symmetry arguments detailed above, in the context of the viscoelastic drag correction, ensure that the contributions from the inner and matching regions are identically zero, and only the outer region contribution, of
![]() $O(\mathit{Re})$
and governed by the Oseen equation, survives. Since this contribution comes from a region of a scale much larger than the particle size, the inertial acceleration may be replaced by the linearized form used in the scaling arguments above, and the translating spheroid may be replaced by an equivalent point force. One may then use the convolution theorem to express the inertial integral, on the right-hand side in (A 1), in terms of the Fourier-transformed disturbance fields:
$O(\mathit{Re})$
and governed by the Oseen equation, survives. Since this contribution comes from a region of a scale much larger than the particle size, the inertial acceleration may be replaced by the linearized form used in the scaling arguments above, and the translating spheroid may be replaced by an equivalent point force. One may then use the convolution theorem to express the inertial integral, on the right-hand side in (A 1), in terms of the Fourier-transformed disturbance fields:
where the Fourier transform is defined as
![]() $\hat{\boldsymbol{f}}(\boldsymbol{k})=\int \!\text{e}^{-\text{i}2{\rm\pi}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}}f(\boldsymbol{r})\,\text{d}\boldsymbol{r}$
. The Fourier-transformed disturbance velocity fields in the actual and test problems are obtained by taking Fourier transforms of the Oseen and Stokes equations, respectively, and are given by:
$\hat{\boldsymbol{f}}(\boldsymbol{k})=\int \!\text{e}^{-\text{i}2{\rm\pi}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}}f(\boldsymbol{r})\,\text{d}\boldsymbol{r}$
. The Fourier-transformed disturbance velocity fields in the actual and test problems are obtained by taking Fourier transforms of the Oseen and Stokes equations, respectively, and are given by:
The force exerted by a spheroid of eccentricity
![]() $e$
, translating in a quiescent Newtonian fluid with orientation
$e$
, translating in a quiescent Newtonian fluid with orientation
![]() $\boldsymbol{p}$
and velocity
$\boldsymbol{p}$
and velocity
![]() $\boldsymbol{U}$
is given in Kim & Karrila (Reference Kim and Karrila1991), and in units of
$\boldsymbol{U}$
is given in Kim & Karrila (Reference Kim and Karrila1991), and in units of
![]() ${\it\mu}UL$
, is given by:
${\it\mu}UL$
, is given by:
where, for a prolate spheroid,
 $$\begin{eqnarray}\displaystyle & \displaystyle X^{A}=\frac{8e^{3}}{\displaystyle 3\left(-2e+(1+e^{2})\ln \left(\frac{1+e}{1-e}\right)\right)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle X^{A}=\frac{8e^{3}}{\displaystyle 3\left(-2e+(1+e^{2})\ln \left(\frac{1+e}{1-e}\right)\right)}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle Y^{A}=\frac{16e^{3}}{\displaystyle 3\left(2e+(-1+3e^{2})\ln \left(\frac{1+e}{1-e}\right)\right)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Y^{A}=\frac{16e^{3}}{\displaystyle 3\left(2e+(-1+3e^{2})\ln \left(\frac{1+e}{1-e}\right)\right)}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle X^{A}=\frac{4e^{3}}{\displaystyle 3\left((2e^{2}-1)\cot ^{-1}\left(\frac{\sqrt{1-e^{2}}}{e}\right)+e\sqrt{1-e^{2}}\right)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle X^{A}=\frac{4e^{3}}{\displaystyle 3\left((2e^{2}-1)\cot ^{-1}\left(\frac{\sqrt{1-e^{2}}}{e}\right)+e\sqrt{1-e^{2}}\right)}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle Y^{A}=\frac{8e^{3}}{\displaystyle 3\left((2e^{2}+1)\cot ^{-1}\left(\frac{\sqrt{1-e^{2}}}{e}\right)-e\sqrt{1-e^{2}}\right)}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Y^{A}=\frac{8e^{3}}{\displaystyle 3\left((2e^{2}+1)\cot ^{-1}\left(\frac{\sqrt{1-e^{2}}}{e}\right)-e\sqrt{1-e^{2}}\right)}. & \displaystyle\end{eqnarray}$$
Equations (A 5), (A 4), (A 3) and (A 2) may now be used to rewrite (A 1), noting the fact that the first and second integrals on the left-hand side are related to the drag in the actual problem (
![]() $\boldsymbol{D}_{1}\boldsymbol{\cdot }\hat{\boldsymbol{U}}_{2}$
) and the test problem (
$\boldsymbol{D}_{1}\boldsymbol{\cdot }\hat{\boldsymbol{U}}_{2}$
) and the test problem (
![]() $-\unicode[STIX]{x1D64D}\boldsymbol{\cdot }\hat{\boldsymbol{U}}_{2}$
) respectively. One obtains:
$-\unicode[STIX]{x1D64D}\boldsymbol{\cdot }\hat{\boldsymbol{U}}_{2}$
) respectively. One obtains:
Since
![]() $\hat{\boldsymbol{U}}_{2}$
is arbitrary, the
$\hat{\boldsymbol{U}}_{2}$
is arbitrary, the
![]() $O(\mathit{Re})$
correction to the Stokes drag is given by the following Fourier-space integral:
$O(\mathit{Re})$
correction to the Stokes drag is given by the following Fourier-space integral:
The above integral is evaluated in a coordinate system aligned with
![]() $\hat{\boldsymbol{U}}_{1}$
and the result, which conforms to the general Oseen drag calculated in Brenner (Reference Brenner1961), is given by:
$\hat{\boldsymbol{U}}_{1}$
and the result, which conforms to the general Oseen drag calculated in Brenner (Reference Brenner1961), is given by:
 $$\begin{eqnarray}\displaystyle \boldsymbol{F}_{correction} & = & \displaystyle -\frac{9{\rm\pi}\mathit{Re}}{8} [(3X^{A}-(X^{A}\cos ^{2}{\it\alpha}+Y^{A}\sin ^{2}{\it\alpha}))X^{A}\boldsymbol{p}\boldsymbol{p}\nonumber\\ \displaystyle & & \displaystyle +\,(3Y^{A}-(X^{A}\cos ^{2}{\it\alpha}+Y^{A}\sin ^{2}{\it\alpha}))Y^{A}(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})\!]\boldsymbol{\cdot }\,\hat{\boldsymbol{U}}_{1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{F}_{correction} & = & \displaystyle -\frac{9{\rm\pi}\mathit{Re}}{8} [(3X^{A}-(X^{A}\cos ^{2}{\it\alpha}+Y^{A}\sin ^{2}{\it\alpha}))X^{A}\boldsymbol{p}\boldsymbol{p}\nonumber\\ \displaystyle & & \displaystyle +\,(3Y^{A}-(X^{A}\cos ^{2}{\it\alpha}+Y^{A}\sin ^{2}{\it\alpha}))Y^{A}(\unicode[STIX]{x1D644}-\boldsymbol{p}\boldsymbol{p})\!]\boldsymbol{\cdot }\,\hat{\boldsymbol{U}}_{1},\end{eqnarray}$$
where
![]() ${\it\alpha}=\cos ^{-1}(\hat{\boldsymbol{U}}_{1}\boldsymbol{\cdot }\boldsymbol{p})$
. In the limit
${\it\alpha}=\cos ^{-1}(\hat{\boldsymbol{U}}_{1}\boldsymbol{\cdot }\boldsymbol{p})$
. In the limit
![]() $e\rightarrow 0$
(sphere),
$e\rightarrow 0$
(sphere),
![]() $X^{A}$
and
$X^{A}$
and
![]() $Y^{A}$
for both prolate and oblate spheroids approach unity, giving the familiar Oseen drag for a sphere. Note that the Oseen drag does not capture the
$Y^{A}$
for both prolate and oblate spheroids approach unity, giving the familiar Oseen drag for a sphere. Note that the Oseen drag does not capture the
![]() $O(\mathit{Re})$
inertial correction when the particle is not fore–aft symmetric, since in this case there is an additional
$O(\mathit{Re})$
inertial correction when the particle is not fore–aft symmetric, since in this case there is an additional
![]() $O(\mathit{Re})$
contribution arising from the inner region, where the Oseen linearization of the inertial term is invalid.
$O(\mathit{Re})$
contribution arising from the inner region, where the Oseen linearization of the inertial term is invalid.
Appendix B. The Kushch and Chwang & Wu velocity fields
Herein, we show that the expressions for the disturbance velocity fields given in § 3, in terms of the spheroidal vector harmonic functions, are identical to those derived earlier by Chwang & Wu (Reference Chwang and Wu1974, Reference Chwang and Wu1975), Chwang (Reference Chwang1975), using the method of singularities, for a prolate spheroid of an arbitrary aspect ratio. We consider the different canonical motions of the spheroid involved in the reciprocal theorem formulation (axisymmetric and non-axisymmetric translations in the actual problem and transverse rotation in the test problem) in sequence.
(a) Axisymmetric translation:
The method of singularities yields the following expression for the disturbance velocity field due to a prolate spheroid translating along its axis, at unit velocity, in an otherwise quiescent unbounded fluid domain:
where
![]() ${\it\alpha}_{1}=\,e^{2}/[-2e+(1+e^{2})\ln ((1+e)/(1-e))]$
and
${\it\alpha}_{1}=\,e^{2}/[-2e+(1+e^{2})\ln ((1+e)/(1-e))]$
and
![]() ${\it\beta}_{1}=(1-e^{2})/(2[-2e+(1+e^{2})\ln ((1+e)/(1-e))])$
and
${\it\beta}_{1}=(1-e^{2})/(2[-2e+(1+e^{2})\ln ((1+e)/(1-e))])$
and
![]() ${\it\rho}^{2}=x^{2}+y^{2}$
. Further,
${\it\rho}^{2}=x^{2}+y^{2}$
. Further,
![]() $R_{1}^{2}=(z+d)^{2}+x^{2}+y^{2}=\,d({\it\xi}+{\it\eta})$
and
$R_{1}^{2}=(z+d)^{2}+x^{2}+y^{2}=\,d({\it\xi}+{\it\eta})$
and
![]() $R_{2}^{2}=(z-d)^{2}+x^{2}+y^{2}=\,d({\it\xi}-{\it\eta})$
. The functions
$R_{2}^{2}=(z-d)^{2}+x^{2}+y^{2}=\,d({\it\xi}-{\it\eta})$
. The functions
![]() $B_{m,n}$
are defined via the recurrence relation
$B_{m,n}$
are defined via the recurrence relation
![]() $B_{m,n}=-(d^{n-1}/(m-2))(1/R_{2}^{m-2}+(-1)^{n}/R_{1}^{m-2})+((n-1)/(m-2))B_{m-2,n-2}+zB_{m,n-1}$
. Using this relation, and the expressions for
$B_{m,n}=-(d^{n-1}/(m-2))(1/R_{2}^{m-2}+(-1)^{n}/R_{1}^{m-2})+((n-1)/(m-2))B_{m-2,n-2}+zB_{m,n-1}$
. Using this relation, and the expressions for
![]() $R_{1}$
and
$R_{1}$
and
![]() $R_{2}$
above, in terms of the spheroidal coordinates, one finds
$R_{2}$
above, in terms of the spheroidal coordinates, one finds
![]() $B_{1,0}\!=\!\ln (({\it\xi}\!+\!1)/({\it\xi}\!-\!1))$
,
$B_{1,0}\!=\!\ln (({\it\xi}\!+\!1)/({\it\xi}\!-\!1))$
,
![]() $B_{1,1}=d{\it\eta}[{\it\xi}\ln (({\it\xi}+1)/({\it\xi}-1))-2]$
and
$B_{1,1}=d{\it\eta}[{\it\xi}\ln (({\it\xi}+1)/({\it\xi}-1))-2]$
and
![]() $B_{3,0}=2{\it\xi}/(d^{2}({\it\xi}^{2}-1)({\it\xi}^{2}-{\it\eta}^{2}))$
.
$B_{3,0}=2{\it\xi}/(d^{2}({\it\xi}^{2}-1)({\it\xi}^{2}-{\it\eta}^{2}))$
.
The axial component of the disturbance field in (B 1) is given by:
Using
![]() $e=1/{\it\xi}_{0}$
, and expressing
$e=1/{\it\xi}_{0}$
, and expressing
![]() ${\it\alpha}_{1}$
and
${\it\alpha}_{1}$
and
![]() ${\it\beta}_{1}$
in terms of
${\it\beta}_{1}$
in terms of
![]() ${\it\xi}_{0}$
, one finds after some simplification:
${\it\xi}_{0}$
, one finds after some simplification:
 $$\begin{eqnarray}u_{z}^{\prime CW}=\frac{1}{\displaystyle \left[({\it\xi}_{0}^{2}+1)\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}-2{\it\xi}_{0}\right]}\left[({\it\rho}^{2}B_{3,0}-2B_{1,0})-({\it\xi}_{0}^{2}-1)\frac{\partial B_{1,1}}{\partial z}\right].\end{eqnarray}$$
$$\begin{eqnarray}u_{z}^{\prime CW}=\frac{1}{\displaystyle \left[({\it\xi}_{0}^{2}+1)\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}-2{\it\xi}_{0}\right]}\left[({\it\rho}^{2}B_{3,0}-2B_{1,0})-({\it\xi}_{0}^{2}-1)\frac{\partial B_{1,1}}{\partial z}\right].\end{eqnarray}$$
Next, using the expressions for the
![]() $B_{m,n}$
above, one may show that:
$B_{m,n}$
above, one may show that:
 $$\begin{eqnarray}u_{z}^{\prime CW}=\frac{1}{\left[\displaystyle \frac{({\it\xi}_{0}^{2}+1)}{2}\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}-{\it\xi}_{0}\right]}\left[\left\{\frac{{\it\xi}(1-{\it\eta}^{2})}{({\it\xi}^{2}-{\it\eta}^{2})}-\ln \frac{{\it\xi}+1}{{\it\xi}-1}+\frac{\partial }{\partial z}(dF_{1}^{0})\right\}-{\it\xi}_{0}^{2}\frac{\partial }{\partial z}(dF_{1}^{0})\right].\end{eqnarray}$$
$$\begin{eqnarray}u_{z}^{\prime CW}=\frac{1}{\left[\displaystyle \frac{({\it\xi}_{0}^{2}+1)}{2}\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}-{\it\xi}_{0}\right]}\left[\left\{\frac{{\it\xi}(1-{\it\eta}^{2})}{({\it\xi}^{2}-{\it\eta}^{2})}-\ln \frac{{\it\xi}+1}{{\it\xi}-1}+\frac{\partial }{\partial z}(dF_{1}^{0})\right\}-{\it\xi}_{0}^{2}\frac{\partial }{\partial z}(dF_{1}^{0})\right].\end{eqnarray}$$
One may use the fact that
![]() $\partial /\partial z\!=\!((({\it\xi}^{2}\!-\!1){\it\eta})/(d({\it\xi}^{2}\!-\!{\it\eta}^{2})))(\partial /\partial {\it\xi})\!+\!(((1-{\it\eta}^{2}){\it\xi})/(d({\it\xi}^{2}-{\it\eta}^{2})))\partial /\partial {\it\eta}$
in spheroidal coordinates to simplify the first of the
$\partial /\partial z\!=\!((({\it\xi}^{2}\!-\!1){\it\eta})/(d({\it\xi}^{2}\!-\!{\it\eta}^{2})))(\partial /\partial {\it\xi})\!+\!(((1-{\it\eta}^{2}){\it\xi})/(d({\it\xi}^{2}-{\it\eta}^{2})))\partial /\partial {\it\eta}$
in spheroidal coordinates to simplify the first of the
![]() $z$
-derivatives, and obtain:
$z$
-derivatives, and obtain:
 $$\begin{eqnarray}\displaystyle u_{z}^{\prime CW} & = & \displaystyle \frac{1}{\displaystyle \left[\frac{({\it\xi}_{0}^{2}+1)}{2}\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}-{\it\xi}_{0}\right]}\left[\left\{\frac{{\it\xi}(1-{\it\eta}^{2})}{({\it\xi}^{2}-{\it\eta}^{2})}-\ln \frac{{\it\xi}+1}{{\it\xi}-1}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.+\,\frac{({\it\xi}^{2}-1){\it\eta}^{2}}{({\it\xi}^{2}-{\it\eta}^{2})}\frac{\text{d}Q_{1}^{0}}{\text{d}{\it\xi}}+\frac{(1-{\it\eta}^{2}){\it\xi}}{({\it\xi}^{2}-{\it\eta}^{2})}Q_{1}^{0}\right\}-{\it\xi}_{0}^{2}\frac{\partial }{\partial z}(dF_{1}^{0})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{z}^{\prime CW} & = & \displaystyle \frac{1}{\displaystyle \left[\frac{({\it\xi}_{0}^{2}+1)}{2}\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}-{\it\xi}_{0}\right]}\left[\left\{\frac{{\it\xi}(1-{\it\eta}^{2})}{({\it\xi}^{2}-{\it\eta}^{2})}-\ln \frac{{\it\xi}+1}{{\it\xi}-1}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.+\,\frac{({\it\xi}^{2}-1){\it\eta}^{2}}{({\it\xi}^{2}-{\it\eta}^{2})}\frac{\text{d}Q_{1}^{0}}{\text{d}{\it\xi}}+\frac{(1-{\it\eta}^{2}){\it\xi}}{({\it\xi}^{2}-{\it\eta}^{2})}Q_{1}^{0}\right\}-{\it\xi}_{0}^{2}\frac{\partial }{\partial z}(dF_{1}^{0})\right].\end{eqnarray}$$
Now, using
![]() $Q_{1}^{0}=({\it\xi}/2)\ln (({\it\xi}+1)/({\it\xi}-1))-1={\it\xi}Q_{0}^{0}-1$
,
$Q_{1}^{0}=({\it\xi}/2)\ln (({\it\xi}+1)/({\it\xi}-1))-1={\it\xi}Q_{0}^{0}-1$
,
![]() $\text{d}Q_{1}^{0}/\text{d}{\it\xi}=Q_{0}^{0}+{\it\xi}(\text{d}Q_{1}^{0}/\text{d}{\it\xi})$
to simplify both the term within braces, and the
$\text{d}Q_{1}^{0}/\text{d}{\it\xi}=Q_{0}^{0}+{\it\xi}(\text{d}Q_{1}^{0}/\text{d}{\it\xi})$
to simplify both the term within braces, and the
![]() ${\it\xi}_{0}$
-dependent pre-factor in (B 8), and reverting to the Cartesian derivative in the
${\it\xi}_{0}$
-dependent pre-factor in (B 8), and reverting to the Cartesian derivative in the
![]() $z$
-direction, one obtains:
$z$
-direction, one obtains:
Finally, since
![]() $F_{0}^{0}({\it\xi},{\it\eta})\equiv F_{0}^{0}({\it\xi})=Q_{0}^{0}({\it\xi})$
, (B 9) can be written as:
$F_{0}^{0}({\it\xi},{\it\eta})\equiv F_{0}^{0}({\it\xi})=Q_{0}^{0}({\it\xi})$
, (B 9) can be written as:
The original expression, equation (B 1), has only a radial component in the transverse plane, which in turn is only a function of the transverse radial coordinate (
![]() ${\it\rho}$
), as must be the case for an axisymmetric field. Thus, it is sufficient to consider only one of the transverse components, the
${\it\rho}$
), as must be the case for an axisymmetric field. Thus, it is sufficient to consider only one of the transverse components, the
![]() $x$
-component, of the disturbance velocity field, which, from (B 1), is given by:
$x$
-component, of the disturbance velocity field, which, from (B 1), is given by:
Using the expressions for the
![]() $R_{i}$
in terms of the spheroidal coordinates, and rewriting
$R_{i}$
in terms of the spheroidal coordinates, and rewriting
![]() ${\it\alpha}_{1}$
and
${\it\alpha}_{1}$
and
![]() ${\it\beta}_{1}$
in terms of
${\it\beta}_{1}$
in terms of
![]() ${\it\xi}_{0}$
, one finds
${\it\xi}_{0}$
, one finds
Now,
![]() $-{\it\eta}/(d({\it\xi}^{2}-{\it\eta}^{2}))=((({\it\xi}^{2}-1){\it\eta})/(d({\it\xi}^{2}-{\it\eta}^{2})))(\text{d}Q_{0}^{0}/\text{d}{\it\xi})=\text{d}Q_{0}^{0}/\text{d}z=\text{d}F_{0}^{0}/\text{d}z$
, so that (B 12) may be written in the form:
$-{\it\eta}/(d({\it\xi}^{2}-{\it\eta}^{2}))=((({\it\xi}^{2}-1){\it\eta})/(d({\it\xi}^{2}-{\it\eta}^{2})))(\text{d}Q_{0}^{0}/\text{d}{\it\xi})=\text{d}Q_{0}^{0}/\text{d}z=\text{d}F_{0}^{0}/\text{d}z$
, so that (B 12) may be written in the form:
The expressions (B 10) and (B 13), together with the corresponding expression for
![]() $u_{y}^{\prime }$
, may be combined into the following single vector field:
$u_{y}^{\prime }$
, may be combined into the following single vector field:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle \frac{1}{[{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})+Q_{0}^{0}({\it\xi}_{0})]}\left[\vphantom{\frac{\partial F_{1}^{0}}{\partial y}}\boldsymbol{x}D_{3}F_{0}^{0}-\{F_{0}^{0}+d{\it\xi}_{0}^{2}(D_{3}F_{1}^{0})\}\mathbf{1}_{z}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,d({\it\xi}_{0}^{2}-1)\left(\mathbf{1}_{x}\frac{\partial F_{1}^{0}}{\partial x}+\mathbf{1}_{y}\frac{\partial F_{1}^{0}}{\partial y}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle \frac{1}{[{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})+Q_{0}^{0}({\it\xi}_{0})]}\left[\vphantom{\frac{\partial F_{1}^{0}}{\partial y}}\boldsymbol{x}D_{3}F_{0}^{0}-\{F_{0}^{0}+d{\it\xi}_{0}^{2}(D_{3}F_{1}^{0})\}\mathbf{1}_{z}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,d({\it\xi}_{0}^{2}-1)\left(\mathbf{1}_{x}\frac{\partial F_{1}^{0}}{\partial x}+\mathbf{1}_{y}\frac{\partial F_{1}^{0}}{\partial y}\right)\right],\end{eqnarray}$$
where
![]() $\text{D}_{3}=\partial /\partial z$
. From the spheroidal harmonics formalism, the velocity field in axial translation is given by (see (3.20)):
$\text{D}_{3}=\partial /\partial z$
. From the spheroidal harmonics formalism, the velocity field in axial translation is given by (see (3.20)):
where
![]() $\boldsymbol{S}_{1,0}^{(3)}$
, from (3.8), with
$\boldsymbol{S}_{1,0}^{(3)}$
, from (3.8), with
![]() $t=1,s=0$
, is given by:
$t=1,s=0$
, is given by:
Using the relations
![]() $\text{D}_{1}F_{0}^{1}=\text{D}_{3}F_{0}^{0}$
,
$\text{D}_{1}F_{0}^{1}=\text{D}_{3}F_{0}^{0}$
,
![]() $\text{D}_{2}F_{0}^{-1}=-\text{D}_{3}F_{0}^{0}$
, and the expressions for
$\text{D}_{2}F_{0}^{-1}=-\text{D}_{3}F_{0}^{0}$
, and the expressions for
![]() $\boldsymbol{e}_{1}$
,
$\boldsymbol{e}_{1}$
,
![]() $\boldsymbol{e}_{2}$
,
$\boldsymbol{e}_{2}$
,
![]() $\text{D}_{1}$
and
$\text{D}_{1}$
and
![]() $\text{D}_{2}$
, in terms of
$\text{D}_{2}$
, in terms of
![]() $\mathbf{1}_{x}$
,
$\mathbf{1}_{x}$
,
![]() $\mathbf{1}_{y}$
,
$\mathbf{1}_{y}$
,
![]() $\partial /\partial x$
and
$\partial /\partial x$
and
![]() $\partial /\partial y$
, the above expression, when substituted in (B 15), reduces to (B 14).
$\partial /\partial y$
, the above expression, when substituted in (B 15), reduces to (B 14).
(b) Non-axisymmetric translation:
The method of singularities yields the following expression for the disturbance velocity field due to a prolate spheroid translating perpendicular to its axis of symmetry, at unit velocity, in a quiescent unbounded fluid domain:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle -{\it\alpha}_{2}\left[B_{1,0}\mathbf{1}_{x}+x{\it\rho}B_{3,0}\mathbf{1}_{{\it\rho}}+x\left(\frac{1}{R_{2}}-\frac{1}{R_{1}}\right)\mathbf{1}_{z}\right]\nonumber\\ \displaystyle & & \displaystyle +\,{\it\beta}_{2}\boldsymbol{{\rm\nabla}}\left[x\left(\frac{z-d}{{\it\rho}^{2}}R_{1}-\frac{z+d}{{\it\rho}^{2}}R_{2}+B_{1,0}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime CW}(\boldsymbol{x}) & = & \displaystyle -{\it\alpha}_{2}\left[B_{1,0}\mathbf{1}_{x}+x{\it\rho}B_{3,0}\mathbf{1}_{{\it\rho}}+x\left(\frac{1}{R_{2}}-\frac{1}{R_{1}}\right)\mathbf{1}_{z}\right]\nonumber\\ \displaystyle & & \displaystyle +\,{\it\beta}_{2}\boldsymbol{{\rm\nabla}}\left[x\left(\frac{z-d}{{\it\rho}^{2}}R_{1}-\frac{z+d}{{\it\rho}^{2}}R_{2}+B_{1,0}\right)\right],\end{eqnarray}$$
where
![]() ${\it\alpha}_{2}=2e^{2}/[2e+(3e^{2}-1)\ln ((1+e)/(1-e))]$
and
${\it\alpha}_{2}=2e^{2}/[2e+(3e^{2}-1)\ln ((1+e)/(1-e))]$
and
![]() ${\it\beta}_{2}=(1-e^{2})/[2e+(3e^{2}-1)\ln ((1+e)/(1-e))]$
. Writing
${\it\beta}_{2}=(1-e^{2})/[2e+(3e^{2}-1)\ln ((1+e)/(1-e))]$
. Writing
![]() ${\it\alpha}_{2}$
and
${\it\alpha}_{2}$
and
![]() ${\it\beta}_{2}$
in terms of
${\it\beta}_{2}$
in terms of
![]() ${\it\xi}_{0}$
, and using
${\it\xi}_{0}$
, and using
![]() $R_{1,2}=d({\it\xi}\pm {\it\eta})$
, the individual components of the disturbance field are given by:
$R_{1,2}=d({\it\xi}\pm {\it\eta})$
, the individual components of the disturbance field are given by:
(i)
 $$\begin{eqnarray}\displaystyle u_{z}^{\prime CW} & = & \displaystyle \frac{1}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-2x\!\left(\frac{1}{R_{2}}-\frac{1}{R_{1}}\right)\!\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial z}\!\!\left(x\left\{\frac{z-d}{{\it\rho}^{2}}R_{1}-\frac{z+d}{{\it\rho}^{2}}R_{2}+B_{1,0}\right\}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{z}^{\prime CW} & = & \displaystyle \frac{1}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-2x\!\left(\frac{1}{R_{2}}-\frac{1}{R_{1}}\right)\!\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial z}\!\!\left(x\left\{\frac{z-d}{{\it\rho}^{2}}R_{1}-\frac{z+d}{{\it\rho}^{2}}R_{2}+B_{1,0}\right\}\right)\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{\cos {\it\phi}}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left[-\frac{4{\it\eta}({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}}{({\it\xi}^{2}-{\it\eta}^{2})}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial z}\!\left\{d({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}\left(-\frac{2{\it\xi}}{({\it\xi}^{2}-1)}+\ln \frac{{\it\xi}+1}{{\it\xi}-1}\right)\right\}\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{\cos {\it\phi}}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\left[-\frac{4{\it\eta}({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}}{({\it\xi}^{2}-{\it\eta}^{2})}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial z}\!\left\{d({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}\left(-\frac{2{\it\xi}}{({\it\xi}^{2}-1)}+\ln \frac{{\it\xi}+1}{{\it\xi}-1}\right)\right\}\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{4\cos {\it\phi}\,{\it\eta}(1-{\it\eta}^{2})^{1/2}}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\frac{1}{({\it\xi}^{2}-{\it\eta}^{2})({\it\xi}^{2}-1)^{1/2}}({\it\xi}_{0}^{2}-{\it\xi}^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{4\cos {\it\phi}\,{\it\eta}(1-{\it\eta}^{2})^{1/2}}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\frac{1}{({\it\xi}^{2}-{\it\eta}^{2})({\it\xi}^{2}-1)^{1/2}}({\it\xi}_{0}^{2}-{\it\xi}^{2}).\end{eqnarray}$$
(ii)
 $$\begin{eqnarray}\displaystyle u_{x}^{\prime CW} & = & \displaystyle \frac{1}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[\vphantom{\frac{\partial }{\partial x}}-2B_{1,0}-2x^{2}B_{3,0}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial x}\!\!\left(x\left\{\frac{z-d}{{\it\rho}^{2}}R_{1}-\frac{z+d}{{\it\rho}^{2}}R_{2}+B_{1,0}\right\}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{x}^{\prime CW} & = & \displaystyle \frac{1}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[\vphantom{\frac{\partial }{\partial x}}-2B_{1,0}-2x^{2}B_{3,0}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial x}\!\!\left(x\left\{\frac{z-d}{{\it\rho}^{2}}R_{1}-\frac{z+d}{{\it\rho}^{2}}R_{2}+B_{1,0}\right\}\right)\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{1}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-2\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\cos ^{2}{\it\phi}\frac{4{\it\xi}(1-{\it\eta}^{2})}{({\it\xi}^{2}-{\it\eta}^{2})}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,({\it\xi}_{0}^{2}-1)\left\{\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\frac{2{\it\xi}}{({\it\xi}^{2}-1)}+\cos ^{2}{\it\phi}\frac{4(1-{\it\eta}^{2}){\it\xi}}{({\it\xi}^{2}-1)({\it\xi}^{2}-{\it\eta}^{2})}\right\}\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{1}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-2\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\cos ^{2}{\it\phi}\frac{4{\it\xi}(1-{\it\eta}^{2})}{({\it\xi}^{2}-{\it\eta}^{2})}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,({\it\xi}_{0}^{2}-1)\left\{\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\frac{2{\it\xi}}{({\it\xi}^{2}-1)}+\cos ^{2}{\it\phi}\frac{4(1-{\it\eta}^{2}){\it\xi}}{({\it\xi}^{2}-1)({\it\xi}^{2}-{\it\eta}^{2})}\right\}\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
(iii)
 $$\begin{eqnarray}\displaystyle u_{y}^{\prime CW} & = & \displaystyle \frac{1}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[-2xyB_{3,0}+({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial y}\!\!\left(x\left\{\frac{z-d}{{\it\rho}^{2}}R_{1}-\frac{z+d}{{\it\rho}^{2}}R_{2}+B_{1,0}\right\}\right)\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{y}^{\prime CW} & = & \displaystyle \frac{1}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[-2xyB_{3,0}+({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial y}\!\!\left(x\left\{\frac{z-d}{{\it\rho}^{2}}R_{1}-\frac{z+d}{{\it\rho}^{2}}R_{2}+B_{1,0}\right\}\right)\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{1}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-\frac{4{\it\xi}(1-{\it\eta}^{2})\cos {\it\phi}\sin {\it\phi}}{({\it\xi}^{2}-{\it\eta}^{2})}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,({\it\xi}_{0}^{2}-1)({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}\cos {\it\phi}\frac{\partial }{\partial y}\!\!\left(\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\frac{2{\it\xi}}{({\it\xi}^{2}-1)}\right)\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{1}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-\frac{4{\it\xi}(1-{\it\eta}^{2})\cos {\it\phi}\sin {\it\phi}}{({\it\xi}^{2}-{\it\eta}^{2})}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,({\it\xi}_{0}^{2}-1)({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}\cos {\it\phi}\frac{\partial }{\partial y}\!\!\left(\ln \frac{{\it\xi}+1}{{\it\xi}-1}-\frac{2{\it\xi}}{({\it\xi}^{2}-1)}\right)\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{4{\it\xi}(1-{\it\eta}^{2})\cos {\it\phi}\sin {\it\phi}}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\frac{1}{({\it\xi}^{2}-{\it\eta}^{2})({\it\xi}^{2}-1)}({\it\xi}_{0}^{2}-{\it\xi}^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{4{\it\xi}(1-{\it\eta}^{2})\cos {\it\phi}\sin {\it\phi}}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\frac{1}{({\it\xi}^{2}-{\it\eta}^{2})({\it\xi}^{2}-1)}({\it\xi}_{0}^{2}-{\it\xi}^{2}).\end{eqnarray}$$
From the spheroidal harmonics formalism, the velocity field in transverse translation is given by (see (3.20)):
Again, using the expressions for
![]() $\boldsymbol{S}_{1,1}^{(3)}$
and
$\boldsymbol{S}_{1,1}^{(3)}$
and
![]() $\boldsymbol{S}_{1,-1}^{(3)}$
from (3.8), (B 26) takes the form:
$\boldsymbol{S}_{1,-1}^{(3)}$
from (3.8), (B 26) takes the form:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x}) & = & \displaystyle \frac{1}{[3Q_{0}^{0}({\it\xi}_{0})-{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})]}\!\!\left[-2\!\left(\boldsymbol{x}\frac{\partial F_{0}^{0}}{\partial x}-F_{0}^{0}\mathbf{1}_{x}\right)-\mathbf{1}_{z}d{\it\xi}_{0}^{2}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,d({\it\xi}_{0}^{2}-1)\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)\!(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x}) & = & \displaystyle \frac{1}{[3Q_{0}^{0}({\it\xi}_{0})-{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})]}\!\!\left[-2\!\left(\boldsymbol{x}\frac{\partial F_{0}^{0}}{\partial x}-F_{0}^{0}\mathbf{1}_{x}\right)-\mathbf{1}_{z}d{\it\xi}_{0}^{2}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,d({\it\xi}_{0}^{2}-1)\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)\!(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right].\end{eqnarray}$$
With the expressions for
![]() $Q_{0}^{0}$
and
$Q_{0}^{0}$
and
![]() $Q_{1}^{0}$
given earlier, we have
$Q_{1}^{0}$
given earlier, we have
![]() $3Q_{0}^{0}-{\it\xi}_{0}Q_{1}^{0}=(2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln (({\it\xi}_{0}+1)/({\it\xi}_{0}-1)))/2$
and, since
$3Q_{0}^{0}-{\it\xi}_{0}Q_{1}^{0}=(2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln (({\it\xi}_{0}+1)/({\it\xi}_{0}-1)))/2$
and, since
![]() $F_{0}^{0}=Q_{0}^{0}$
, one obtains:
$F_{0}^{0}=Q_{0}^{0}$
, one obtains:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x}) & = & \displaystyle \frac{2}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-2\!\left(\boldsymbol{x}\frac{\partial Q_{0}^{0}}{\partial x}-Q_{0}^{0}\mathbf{1}_{x}\right)-\mathbf{1}_{z}d{\it\xi}_{0}^{2}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,d({\it\xi}_{0}^{2}-1)\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)\!(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x}) & = & \displaystyle \frac{2}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-2\!\left(\boldsymbol{x}\frac{\partial Q_{0}^{0}}{\partial x}-Q_{0}^{0}\mathbf{1}_{x}\right)-\mathbf{1}_{z}d{\it\xi}_{0}^{2}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,d({\it\xi}_{0}^{2}-1)\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)\!(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right].\end{eqnarray}$$
The individual velocity components are given by:
 $$\begin{eqnarray}\displaystyle & \displaystyle u_{z}^{\prime }=\frac{2}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-2z\frac{\partial Q_{0}^{0}}{\partial x}-d{\it\xi}_{0}^{2}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u_{z}^{\prime }=\frac{2}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-2z\frac{\partial Q_{0}^{0}}{\partial x}-d{\it\xi}_{0}^{2}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right], & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle u_{x}^{\prime }=\frac{2}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-2x\left(\frac{\partial Q_{0}^{0}}{\partial x}-Q_{0}^{0}\right)-d({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial x}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right], & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u_{x}^{\prime }=\frac{2}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-2x\left(\frac{\partial Q_{0}^{0}}{\partial x}-Q_{0}^{0}\right)-d({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial x}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right], & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle u_{y}^{\prime }=\frac{2}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-2y\frac{\partial Q_{0}^{0}}{\partial x}-d({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial y}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right]. & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u_{y}^{\prime }=\frac{2}{\displaystyle \left[2{\it\xi}_{0}+(3-{\it\xi}_{0}^{2})\ln \frac{{\it\xi}_{0}+1}{{\it\xi}_{0}-1}\right]}\!\!\left[-2y\frac{\partial Q_{0}^{0}}{\partial x}-d({\it\xi}_{0}^{2}-1)\frac{\partial }{\partial y}(P_{1}^{1}Q_{1}^{1}\cos {\it\phi})\right]. & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\partial }{\partial x} & = & \displaystyle \frac{({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}({\it\xi}\cos {\it\phi})}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\xi}}-\frac{({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}({\it\eta}\cos {\it\phi})}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\eta}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\sin {\it\phi}}{d({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}}\frac{\partial }{\partial {\it\phi}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial }{\partial x} & = & \displaystyle \frac{({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}({\it\xi}\cos {\it\phi})}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\xi}}-\frac{({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}({\it\eta}\cos {\it\phi})}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\eta}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\sin {\it\phi}}{d({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}}\frac{\partial }{\partial {\it\phi}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\partial }{\partial y} & = & \displaystyle \frac{({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}({\it\xi}\sin {\it\phi})}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\xi}}-\frac{({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}({\it\eta}\sin {\it\phi})}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\eta}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\cos {\it\phi}}{d({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}}\frac{\partial }{\partial {\it\phi}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial }{\partial y} & = & \displaystyle \frac{({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}({\it\xi}\sin {\it\phi})}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\xi}}-\frac{({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}({\it\eta}\sin {\it\phi})}{d({\it\xi}^{2}-{\it\eta}^{2})}\frac{\partial }{\partial {\it\eta}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\cos {\it\phi}}{d({\it\xi}^{2}-1)^{1/2}(1-{\it\eta}^{2})^{1/2}}\frac{\partial }{\partial {\it\phi}},\end{eqnarray}$$
(c) Transverse rotation of spheroid about the minor axis:
The method of singularities yields the following expression for the disturbance velocity field due to a prolate spheroid rotating about its minor axis (
![]() $y$
-axis), at unit angular velocity, in a quiescent unbounded fluid domain:
$y$
-axis), at unit angular velocity, in a quiescent unbounded fluid domain:
where
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\it\gamma}_{3}=\frac{(1-e^{2})}{\displaystyle -2e+(1+e^{2})\ln \left(\frac{1+e}{1-e}\right)},\quad \nonumber\\ \displaystyle & & \displaystyle {\it\alpha}_{3}=2e^{2}{\it\gamma}_{3}\frac{\displaystyle -2e+\ln \left(\frac{1+e}{1-e}\right)}{\displaystyle 2e(2e^{2}-3)+3(1-e^{2})\ln \left(\frac{1+e}{1-e}\right)},\quad \nonumber\\ \displaystyle & & \displaystyle {\it\beta}_{3}=\frac{1-e^{2}}{4e^{2}}{\it\alpha}_{3},\quad {\it\gamma}_{3}^{\prime }=\frac{{\it\gamma}_{3}}{e^{2}-1},\quad \nonumber\\ \displaystyle & & \displaystyle {\it\alpha}_{3}^{\prime }=e^{2}{\it\gamma}_{3}^{\prime }\frac{\displaystyle -2e+(1-e^{2})\ln \left(\frac{1+e}{1-e}\right)}{\displaystyle 2e(2e^{2}-3)+3(1-e^{2})\ln \left(\frac{1+e}{1-e}\right)},\quad \nonumber\\ \displaystyle & & \displaystyle {\it\beta}_{3}^{\prime }=\frac{1-e^{2}}{4e^{2}}{\it\alpha}_{3}^{\prime },\quad A_{1}=zB_{3,1}-B_{3,2}\quad \text{and}\quad A_{3}=d^{2}B_{3,0}-B_{3,2}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\gamma}_{3}=\frac{(1-e^{2})}{\displaystyle -2e+(1+e^{2})\ln \left(\frac{1+e}{1-e}\right)},\quad \nonumber\\ \displaystyle & & \displaystyle {\it\alpha}_{3}=2e^{2}{\it\gamma}_{3}\frac{\displaystyle -2e+\ln \left(\frac{1+e}{1-e}\right)}{\displaystyle 2e(2e^{2}-3)+3(1-e^{2})\ln \left(\frac{1+e}{1-e}\right)},\quad \nonumber\\ \displaystyle & & \displaystyle {\it\beta}_{3}=\frac{1-e^{2}}{4e^{2}}{\it\alpha}_{3},\quad {\it\gamma}_{3}^{\prime }=\frac{{\it\gamma}_{3}}{e^{2}-1},\quad \nonumber\\ \displaystyle & & \displaystyle {\it\alpha}_{3}^{\prime }=e^{2}{\it\gamma}_{3}^{\prime }\frac{\displaystyle -2e+(1-e^{2})\ln \left(\frac{1+e}{1-e}\right)}{\displaystyle 2e(2e^{2}-3)+3(1-e^{2})\ln \left(\frac{1+e}{1-e}\right)},\quad \nonumber\\ \displaystyle & & \displaystyle {\it\beta}_{3}^{\prime }=\frac{1-e^{2}}{4e^{2}}{\it\alpha}_{3}^{\prime },\quad A_{1}=zB_{3,1}-B_{3,2}\quad \text{and}\quad A_{3}=d^{2}B_{3,0}-B_{3,2}.\qquad\end{eqnarray}$$
Writing the velocity field in terms of
![]() ${\it\xi}_{0}$
, the individual components of the disturbance field are given by:
${\it\xi}_{0}$
, the individual components of the disturbance field are given by:
(i)
 $$\begin{eqnarray}\displaystyle u_{z}^{\prime CW} & = & \displaystyle \frac{1}{2(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}x(2zB_{3,1}-2B_{3,2}+d^{2}B_{3,0}-B_{3,2})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2{\it\xi}_{0}^{2}-1}{(-2{\it\xi}_{0}+2({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}x(d^{2}B_{3,0}-B_{3,2})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\it\xi}_{0}^{2}-1}{2(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}\frac{\partial }{\partial z}(x(d^{2}B_{3,1}-B_{3,3})),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{z}^{\prime CW} & = & \displaystyle \frac{1}{2(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}x(2zB_{3,1}-2B_{3,2}+d^{2}B_{3,0}-B_{3,2})\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2{\it\xi}_{0}^{2}-1}{(-2{\it\xi}_{0}+2({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}x(d^{2}B_{3,0}-B_{3,2})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\it\xi}_{0}^{2}-1}{2(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}\frac{\partial }{\partial z}(x(d^{2}B_{3,1}-B_{3,3})),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{\displaystyle d\sqrt{1-{\it\eta}^{2}}\left(2{\it\xi}({\it\eta}^{2}+{\it\xi}^{2}+(-2-{\it\eta}^{2}+{\it\xi}^{2}){\it\xi}_{0}^{2})+({\it\eta}^{2}-{\it\xi}^{2})({\it\xi}^{2}-1)({\it\xi}_{0}^{2}+1)\ln \left(\frac{{\it\xi}+1}{{\it\xi}-1}\right)\right)\cos ({\it\phi})}{2\sqrt{{\it\xi}^{2}-1}({\it\xi}^{2}-{\it\eta}^{2})(-{\it\xi}_{0}+(1+{\it\xi}_{0}^{2})\cot \,h^{-1}({\it\xi}_{0}))}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{\displaystyle d\sqrt{1-{\it\eta}^{2}}\left(2{\it\xi}({\it\eta}^{2}+{\it\xi}^{2}+(-2-{\it\eta}^{2}+{\it\xi}^{2}){\it\xi}_{0}^{2})+({\it\eta}^{2}-{\it\xi}^{2})({\it\xi}^{2}-1)({\it\xi}_{0}^{2}+1)\ln \left(\frac{{\it\xi}+1}{{\it\xi}-1}\right)\right)\cos ({\it\phi})}{2\sqrt{{\it\xi}^{2}-1}({\it\xi}^{2}-{\it\eta}^{2})(-{\it\xi}_{0}+(1+{\it\xi}_{0}^{2})\cot \,h^{-1}({\it\xi}_{0}))}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
(ii)
 $$\begin{eqnarray}\displaystyle u_{x}^{\prime CW} & = & \displaystyle \frac{x^{2}B_{3,1}}{(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}+\frac{{\it\xi}_{0}^{2}-1}{2(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{\partial }{\partial x}(x(d^{2}B_{3,1}-B_{3,3}))+\frac{2{\it\xi}_{0}^{2}-1}{(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}B_{1,1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{x}^{\prime CW} & = & \displaystyle \frac{x^{2}B_{3,1}}{(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}+\frac{{\it\xi}_{0}^{2}-1}{2(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{\partial }{\partial x}(x(d^{2}B_{3,1}-B_{3,3}))+\frac{2{\it\xi}_{0}^{2}-1}{(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}B_{1,1},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{d{\it\eta}(1-{\it\eta}^{2})({\it\xi}^{2}-{\it\xi}_{0}^{2})\cos (2{\it\phi})}{(-{\it\xi}_{0}+(1+{\it\xi}_{0}^{2})\coth ^{-1}({\it\xi}_{0}))(-{\it\eta}^{2}+{\it\xi}^{2})({\it\xi}^{2}-1)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d{\it\eta}({\it\xi}^{2}-1)(({\it\eta}^{2}+1){\it\xi}_{0}^{2}-{\it\xi}^{2}({\it\xi}_{0}^{2}+1)+{\it\xi}({\it\xi}^{2}-\,{\it\eta}^{2})({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}))}{(-{\it\xi}_{0}+(1+{\it\xi}_{0}^{2})\coth ^{-1}({\it\xi}_{0}))(-{\it\eta}^{2}+{\it\xi}^{2})({\it\xi}^{2}-1)}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \frac{d{\it\eta}(1-{\it\eta}^{2})({\it\xi}^{2}-{\it\xi}_{0}^{2})\cos (2{\it\phi})}{(-{\it\xi}_{0}+(1+{\it\xi}_{0}^{2})\coth ^{-1}({\it\xi}_{0}))(-{\it\eta}^{2}+{\it\xi}^{2})({\it\xi}^{2}-1)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d{\it\eta}({\it\xi}^{2}-1)(({\it\eta}^{2}+1){\it\xi}_{0}^{2}-{\it\xi}^{2}({\it\xi}_{0}^{2}+1)+{\it\xi}({\it\xi}^{2}-\,{\it\eta}^{2})({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}))}{(-{\it\xi}_{0}+(1+{\it\xi}_{0}^{2})\coth ^{-1}({\it\xi}_{0}))(-{\it\eta}^{2}+{\it\xi}^{2})({\it\xi}^{2}-1)}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
(iii)
 $$\begin{eqnarray}\displaystyle u_{y}^{\prime CW} & = & \displaystyle \frac{xyB_{3,1}}{(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}+\frac{{\it\xi}_{0}^{2}-1}{2(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{\partial }{\partial y}(x(d^{2}B_{3,1}-B_{3,3})),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{y}^{\prime CW} & = & \displaystyle \frac{xyB_{3,1}}{(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}+\frac{{\it\xi}_{0}^{2}-1}{2(-{\it\xi}_{0}+({\it\xi}_{0}^{2}+1)\coth ^{-1}({\it\xi}_{0}))}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{\partial }{\partial y}(x(d^{2}B_{3,1}-B_{3,3})),\end{eqnarray}$$
and
From the spheroidal harmonics formalism, the velocity field for a rotation about the minor axis (
![]() $y$
axis) is given by (see (3.21))
$y$
axis) is given by (see (3.21))
Using the expressions for
![]() $\boldsymbol{S}_{1,1}^{(2)}$
,
$\boldsymbol{S}_{1,1}^{(2)}$
,
![]() $\boldsymbol{S}_{1,-1}^{(2)}$
,
$\boldsymbol{S}_{1,-1}^{(2)}$
,
![]() $\boldsymbol{S}_{2,1}^{(3)}$
and
$\boldsymbol{S}_{2,1}^{(3)}$
and
![]() $\boldsymbol{S}_{2,-1}^{(3)}$
from (3.7) and (3.8), (B 44) takes the form:
$\boldsymbol{S}_{2,-1}^{(3)}$
from (3.7) and (3.8), (B 44) takes the form:
 $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x}) & = & \displaystyle \frac{d(2{\it\xi}_{0}^{2}-1)}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}[2P_{1}^{0}Q_{1}^{0}\mathbf{1}_{x}+P_{1}^{1}Q_{1}^{1}\cos ({\it\phi})\mathbf{1}_{z}]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}\left[\boldsymbol{x}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin ({\it\phi}))-\frac{d{\it\xi}_{0}^{2}}{3}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\times \,\frac{\partial }{\partial z}(P_{2}^{1}Q_{2}^{1}\cos ({\it\phi}))\mathbf{1}_{z}-\frac{d({\it\xi}_{0}^{2}-1)}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\cos ({\it\phi}))\right].\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}^{\prime }(\boldsymbol{x}) & = & \displaystyle \frac{d(2{\it\xi}_{0}^{2}-1)}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}[2P_{1}^{0}Q_{1}^{0}\mathbf{1}_{x}+P_{1}^{1}Q_{1}^{1}\cos ({\it\phi})\mathbf{1}_{z}]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}\left[\boldsymbol{x}\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin ({\it\phi}))-\frac{d{\it\xi}_{0}^{2}}{3}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\times \,\frac{\partial }{\partial z}(P_{2}^{1}Q_{2}^{1}\cos ({\it\phi}))\mathbf{1}_{z}-\frac{d({\it\xi}_{0}^{2}-1)}{3}\left(\mathbf{1}_{x}\frac{\partial }{\partial x}+\mathbf{1}_{y}\frac{\partial }{\partial y}\right)(P_{2}^{1}Q_{2}^{1}\cos ({\it\phi}))\right].\qquad\end{eqnarray}$$
The individual components are given by
 $$\begin{eqnarray}\displaystyle u_{z}^{\prime } & = & \displaystyle \frac{d(2{\it\xi}_{0}^{2}-1)}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}[P_{1}^{1}Q_{1}^{1}\cos ({\it\phi})]+\frac{d}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[z\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin ({\it\phi}))-\frac{d{\it\xi}_{0}^{2}}{3}\frac{\partial }{\partial z}(P_{2}^{1}Q_{2}^{1}\cos ({\it\phi}))\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{z}^{\prime } & = & \displaystyle \frac{d(2{\it\xi}_{0}^{2}-1)}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}[P_{1}^{1}Q_{1}^{1}\cos ({\it\phi})]+\frac{d}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[z\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin ({\it\phi}))-\frac{d{\it\xi}_{0}^{2}}{3}\frac{\partial }{\partial z}(P_{2}^{1}Q_{2}^{1}\cos ({\it\phi}))\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle u_{x}^{\prime } & = & \displaystyle \frac{d(2{\it\xi}_{0}^{2}-1)}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}[2P_{1}^{0}Q_{1}^{0}]+\frac{d}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[x\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin ({\it\phi}))-\frac{d({\it\xi}_{0}^{2}-1)}{3}\frac{\partial }{\partial x}(P_{2}^{1}Q_{2}^{1}\cos ({\it\phi}))\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{x}^{\prime } & = & \displaystyle \frac{d(2{\it\xi}_{0}^{2}-1)}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}[2P_{1}^{0}Q_{1}^{0}]+\frac{d}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[x\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin ({\it\phi}))-\frac{d({\it\xi}_{0}^{2}-1)}{3}\frac{\partial }{\partial x}(P_{2}^{1}Q_{2}^{1}\cos ({\it\phi}))\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle u_{y}^{\prime } & = & \displaystyle \frac{d}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[y\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin ({\it\phi}))-\frac{d({\it\xi}_{0}^{2}-1)}{3}\frac{\partial }{\partial y}(P_{2}^{1}Q_{2}^{1}\cos ({\it\phi}))\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{y}^{\prime } & = & \displaystyle \frac{d}{2{\it\xi}_{0}Q_{1}^{0}({\it\xi}_{0})-\sqrt{{\it\xi}_{0}^{2}-1}Q_{1}^{1}({\it\xi}_{0})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[y\frac{\partial }{\partial z}(P_{1}^{1}Q_{1}^{1}\sin ({\it\phi}))-\frac{d({\it\xi}_{0}^{2}-1)}{3}\frac{\partial }{\partial y}(P_{2}^{1}Q_{2}^{1}\cos ({\it\phi}))\right].\end{eqnarray}$$
Appendix C. The aspect-ratio-scaling for the
 $O(\mathit{De})$
viscoelastic torque on a fibre sedimenting in a second-order fluid
$O(\mathit{De})$
viscoelastic torque on a fibre sedimenting in a second-order fluid
Herein, we provide the arguments leading to the
![]() $O[\ln ({\it\xi}_{0}-1)]^{-1}$
scaling for the torque associated with the quadratic terms in the second-order fluid stress (the contribution proportional to
$O[\ln ({\it\xi}_{0}-1)]^{-1}$
scaling for the torque associated with the quadratic terms in the second-order fluid stress (the contribution proportional to
![]() $(1+{\it\epsilon})$
in (2.8)). The torque integral in this case is given by:
$(1+{\it\epsilon})$
in (2.8)). The torque integral in this case is given by:
where
![]() ${\bf\sigma}_{NNQ}^{(1)}$
is defined in (2.10), and the second term involves the Newtonian stress associated with the
${\bf\sigma}_{NNQ}^{(1)}$
is defined in (2.10), and the second term involves the Newtonian stress associated with the
![]() $O(\mathit{De})$
velocity and pressure fields. Considering the first term, and splitting the rate of strain
$O(\mathit{De})$
velocity and pressure fields. Considering the first term, and splitting the rate of strain
![]() $\boldsymbol{e}_{s}$
associated with the Stokes velocity field into contributions, corresponding to the longitudinal (
$\boldsymbol{e}_{s}$
associated with the Stokes velocity field into contributions, corresponding to the longitudinal (
![]() $\boldsymbol{e}_{s}^{l}$
) and transverse (
$\boldsymbol{e}_{s}^{l}$
) and transverse (
![]() $\boldsymbol{e}_{s}^{t}$
) translation components, one may write
$\boldsymbol{e}_{s}^{t}$
) translation components, one may write
![]() ${\bf\sigma}_{NNQ}^{(1)}=4(1+{\it\epsilon})(\boldsymbol{e}_{s}^{l}+\boldsymbol{e}_{s}^{t})\boldsymbol{\cdot }(\boldsymbol{e}_{s}^{l}+\boldsymbol{e}_{s}^{t})$
. The first integral in (C 1) takes the form:
${\bf\sigma}_{NNQ}^{(1)}=4(1+{\it\epsilon})(\boldsymbol{e}_{s}^{l}+\boldsymbol{e}_{s}^{t})\boldsymbol{\cdot }(\boldsymbol{e}_{s}^{l}+\boldsymbol{e}_{s}^{t})$
. The first integral in (C 1) takes the form:
since
![]() $\boldsymbol{n}\approx \hat{{\bf\rho}}$
to within algebraic errors. Here, we have neglected the ‘self’ terms proportional to
$\boldsymbol{n}\approx \hat{{\bf\rho}}$
to within algebraic errors. Here, we have neglected the ‘self’ terms proportional to
![]() $\boldsymbol{e}^{l}\boldsymbol{\cdot }\boldsymbol{e}^{l}$
and
$\boldsymbol{e}^{l}\boldsymbol{\cdot }\boldsymbol{e}^{l}$
and
![]() $\boldsymbol{e}^{t}\boldsymbol{\cdot }\boldsymbol{e}^{t}$
for reasons already stated in § 4.2.3. Now, to within algebraic errors,
$\boldsymbol{e}^{t}\boldsymbol{\cdot }\boldsymbol{e}^{t}$
for reasons already stated in § 4.2.3. Now, to within algebraic errors,
![]() $\boldsymbol{e}^{l}\propto (U_{z}/b)(\boldsymbol{p}\hat{{\bf\rho}}+\hat{{\bf\rho}}\boldsymbol{p})$
corresponding to the unidirectional longitudinal flow
$\boldsymbol{e}^{l}\propto (U_{z}/b)(\boldsymbol{p}\hat{{\bf\rho}}+\hat{{\bf\rho}}\boldsymbol{p})$
corresponding to the unidirectional longitudinal flow
![]() $u_{z}({\it\rho})\boldsymbol{p}$
. Next, from linearity and symmetry arguments,
$u_{z}({\it\rho})\boldsymbol{p}$
. Next, from linearity and symmetry arguments,
Hence,
where we have not included the
![]() $s$
-dependence of the transverse force density. This form implies
$s$
-dependence of the transverse force density. This form implies
![]() $(\boldsymbol{e}^{l}\boldsymbol{\cdot }\boldsymbol{e}^{t}+\boldsymbol{e}^{t}\boldsymbol{\cdot }\boldsymbol{e}^{l})\boldsymbol{\cdot }\hat{{\bf\rho}}$
in (C 2) is a vector along
$(\boldsymbol{e}^{l}\boldsymbol{\cdot }\boldsymbol{e}^{t}+\boldsymbol{e}^{t}\boldsymbol{\cdot }\boldsymbol{e}^{l})\boldsymbol{\cdot }\hat{{\bf\rho}}$
in (C 2) is a vector along
![]() $\boldsymbol{p}$
, to all logarithmic orders, and the quadratic polymeric stress cannot directly contribute to a torque, via the first term in (C 1), at any logarithmic order. Since it is the divergence of this polymeric stress contribution that drives the
$\boldsymbol{p}$
, to all logarithmic orders, and the quadratic polymeric stress cannot directly contribute to a torque, via the first term in (C 1), at any logarithmic order. Since it is the divergence of this polymeric stress contribution that drives the
![]() $O(\mathit{De})$
velocity and pressure fields, an indirect contribution to the viscoelastic torque driven by the
$O(\mathit{De})$
velocity and pressure fields, an indirect contribution to the viscoelastic torque driven by the
![]() $O(\mathit{De})$
Newtonian stress appears unlikely. To show this, we start from the torque-free nature of the quadratic polymeric stress to all logarithmic orders. Written in index notation, this condition is given by:
$O(\mathit{De})$
Newtonian stress appears unlikely. To show this, we start from the torque-free nature of the quadratic polymeric stress to all logarithmic orders. Written in index notation, this condition is given by: