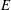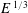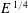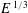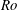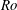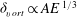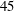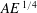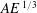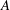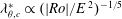1. Introduction
Rotating flows occur in a wide range of applications including industrial, geophysical and astrophysical processes. Geophysical flows in particular engender much interest due to their importance to our understanding of processes underpinning Earth’s climate and weather systems. Examples of rotating geophysical flows include hurricanes and polar vortices, which each exhibit coherent vortical structures. In such flows, a variety of polygonal configurations have been observed, with Venus’s dipolar polar vortex (e.g. Taylor et al. Reference Taylor, Beer, Chahine, Diner, Elson, Haskins, McCleese, Martonchik, Reichley and Bradley1980; Piccioni et al. Reference Piccioni, Drossart, Sanchez-Lavega, Hueso, Taylor, Wilson, Grassi, Zasova, Moriconi and Adriani2007; Luz et al. Reference Luz, Berry, Piccioni, Drossart, Politi, Wilson, Erard and Nuccilli2011) and Saturn’s hexagonal northern hemisphere polar vortex (e.g. Godfrey Reference Godfrey1988; Fletcher et al. Reference Fletcher, Irwin, Orton, Teanby, Achterberg, Bjoraker, Read, Simon-Miller, Howett, de Kok, Bowles, Calcutt, Hesman and Flasar2008; Gombosi & Ingersoll Reference Gombosi and Ingersoll2010; Sánchez-Lavega et al. Reference Sánchez-Lavega, Río-Gaztelurrutia, Hueso, Pérez-Hoyos, García-Melendo, Antuñano, Mendikoa, Rojas, Lillo and Barrado-Navascués2014) representing well-known examples. Despite our fascination with these polygonal structures, their formation and preferred azimuthal wavenumbers are still not very well understood.
The polygonal configurations found in the large-scale structures of atmospheric polar vortices have been hypothesized to be related to barotropic instability (Aguiar Reference Aguiar2008; Aguiar et al.
Reference Aguiar, Read, Wordsworth, Salter and Hiro Yamazaki2010; Montabone et al.
Reference Montabone, Wordsworth, Aguiar, Jacoby, Manfrin, Read, Castrejon-Pita, Gostiaux, Sommeria, Viboud and Didelle2010) and baroclinic instability (e.g. Godfrey & Moore Reference Godfrey and Moore1986; Read Reference Read1988; Williams Reference Williams2003; Lian & Showman Reference Lian and Showman2008). Polygonal patterns that resemble those shown by polar vortices and hurricane eyes have been created in simple confinements and studied using theoretical, experimental and numerical approaches. Studies of barotropic instability often examine the stability of the nested Stewartson layers, whose thicknesses scale with some power of the Ekman number,
![]() $\mathit{E}\,$
, as produced via differential rotation. The thicknesses of the shear layers have been shown theoretically to scale with
$\mathit{E}\,$
, as produced via differential rotation. The thicknesses of the shear layers have been shown theoretically to scale with
![]() $\mathit{E}\,^{1/3}$
and
$\mathit{E}\,^{1/3}$
and
![]() $\mathit{E}\,^{1/4}$
(Stewartson Reference Stewartson1957). The thicker layer is a depth-independent structure responsible for smoothing out the azimuthal velocity, while the thinner layer is a depth-dependent structure which serves to complete the meridional circulation induced by the Ekman layers. Provided that the differential forcing is sufficiently strong, an initially circular Stewartson layer becomes unstable, forming a chain of vortices that rearrange themselves into polygonal configurations (van de Konijnenberg et al.
Reference van de Konijnenberg, Nielsen, Juul Rasmussen and Stenum1999). With increased forcing, the number of vortices decreases through a merging process, eventually saturating to a stable polygonal pattern.
$\mathit{E}\,^{1/4}$
(Stewartson Reference Stewartson1957). The thicker layer is a depth-independent structure responsible for smoothing out the azimuthal velocity, while the thinner layer is a depth-dependent structure which serves to complete the meridional circulation induced by the Ekman layers. Provided that the differential forcing is sufficiently strong, an initially circular Stewartson layer becomes unstable, forming a chain of vortices that rearrange themselves into polygonal configurations (van de Konijnenberg et al.
Reference van de Konijnenberg, Nielsen, Juul Rasmussen and Stenum1999). With increased forcing, the number of vortices decreases through a merging process, eventually saturating to a stable polygonal pattern.
Experimental studies of differential-rotating flows have been able to establish the onset of instability and the trends of the preferred azimuthal wavenumbers with changing flow conditions (e.g. Rabaud & Couder Reference Rabaud and Couder1983; Chomaz et al.
Reference Chomaz, Rabaud, Basdevant and Couder1988; Früh & Read Reference Früh and Read1999; Bergeron et al.
Reference Bergeron, Coutsias, Lynov and Nielsen2000; Aguiar et al.
Reference Aguiar, Read, Wordsworth, Salter and Hiro Yamazaki2010). These set-ups typically involve a rotating tank, with a disk rotating differentially at the horizontal boundaries while sharing the same axis of rotation with the tank. A range of small-aspect-ratio containers (tank height to disk radius) studied by Rabaud & Couder (Reference Rabaud and Couder1983) revealed a variety of critical Reynolds numbers. This suggests that the instability onset of the flow is dependent on the aspect ratio. However, this result may be a consequence of the external Reynolds number definition used, which adopts a length scale based on the height of the tank. It was later determined by Niino & Misawa (Reference Niino and Misawa1984) that a more appropriate parameter required to describe the stability of the flow is a Reynolds number definition based on the
![]() $\mathit{E}\,^{1/4}$
Stewartson layer thickness, namely the internal Reynolds number (Früh & Read Reference Früh and Read1999). However, even with this adopted definition, the linear stability analysis results of Niino & Misawa (Reference Niino and Misawa1984) demonstrated an increase in critical internal Reynolds number and an increase in critical azimuthal wavenumber with increasing shear-layer thickness (in effect, increasing the aspect ratio or
$\mathit{E}\,^{1/4}$
Stewartson layer thickness, namely the internal Reynolds number (Früh & Read Reference Früh and Read1999). However, even with this adopted definition, the linear stability analysis results of Niino & Misawa (Reference Niino and Misawa1984) demonstrated an increase in critical internal Reynolds number and an increase in critical azimuthal wavenumber with increasing shear-layer thickness (in effect, increasing the aspect ratio or
![]() $\mathit{E}\,$
) at marginal stability.
$\mathit{E}\,$
) at marginal stability.
A review of the reported critical internal Reynolds numbers and their characteristic length scales by Vo, Montabone & Sheard (Reference Vo, Montabone and Sheard2014) demonstrated a small range of instability onset values when characterized by
![]() $\mathit{Ro}/\mathit{E}\,^{3/4}$
(proportional to the internal Reynolds number in Niino & Misawa (Reference Niino and Misawa1984)), where
$\mathit{Ro}/\mathit{E}\,^{3/4}$
(proportional to the internal Reynolds number in Niino & Misawa (Reference Niino and Misawa1984)), where
![]() $\mathit{Ro}$
is the Rossby number. Niino & Misawa (Reference Niino and Misawa1984) postulate that Stewartson layers with thickness less than approximately
$\mathit{Ro}$
is the Rossby number. Niino & Misawa (Reference Niino and Misawa1984) postulate that Stewartson layers with thickness less than approximately
![]() $4\,\%$
of their radius have stability that is insensitive to the shear-layer radius. Given the dependence of the shear-layer thickness on the enclosure height expected from Stewartson (Reference Stewartson1957), it remains unclear how robust the limiting thickness of
$4\,\%$
of their radius have stability that is insensitive to the shear-layer radius. Given the dependence of the shear-layer thickness on the enclosure height expected from Stewartson (Reference Stewartson1957), it remains unclear how robust the limiting thickness of
![]() $4\,\%$
of radius is, and how well Niino & Misawa (Reference Niino and Misawa1984) predictions for thicker shear layers (such as might be produced at higher
$4\,\%$
of radius is, and how well Niino & Misawa (Reference Niino and Misawa1984) predictions for thicker shear layers (such as might be produced at higher
![]() $\mathit{E}\,$
or in taller enclosures) hold against simulations of the full enclosure.
$\mathit{E}\,$
or in taller enclosures) hold against simulations of the full enclosure.
A large variation of aspect ratios for similar rotating flows has been explored previously, although with a different focus. For example, the stability of astrophysical disks that adopt a Keplerian rotation
![]() $({\rm\Omega}\propto r^{-3/2})$
has been studied primarily using a rotating cylindrical annulus (e.g. Hollerbach & Fournier Reference Hollerbach, Fournier, Rosner, Rüdiger and Bonanno2004; Szklarski & Rüdiger Reference Szklarski and Rüdiger2007; Liu Reference Liu2008; Avila Reference Avila2012; Gissinger, Goodman & Ji Reference Gissinger, Goodman and Ji2012; Paoletti et al.
Reference Paoletti, van Gils, Dubrulle, Sun, Lohse and Lathrop2012; Schartman et al.
Reference Schartman, Ji, Burin and Goodman2012). A problem with this configuration is that the axial boundaries have a pronounced effect on the interior flow, which causes difficulty in producing smooth Keplerian velocity profiles. Thus, the variation of aspect ratios in these studies stems from the endeavour of minimizing the influence of the end walls by separating them as much as possible. In contrast, this paper seeks to characterize the aspect ratio dependence in relation to the structure, stability and preferred azimuthal linear instability modes of the flow, not only at marginal stability, but also beyond it. This is achieved using numerical simulation and conducting linear stability analysis across a large range of flow conditions and a number of aspect ratios.
$({\rm\Omega}\propto r^{-3/2})$
has been studied primarily using a rotating cylindrical annulus (e.g. Hollerbach & Fournier Reference Hollerbach, Fournier, Rosner, Rüdiger and Bonanno2004; Szklarski & Rüdiger Reference Szklarski and Rüdiger2007; Liu Reference Liu2008; Avila Reference Avila2012; Gissinger, Goodman & Ji Reference Gissinger, Goodman and Ji2012; Paoletti et al.
Reference Paoletti, van Gils, Dubrulle, Sun, Lohse and Lathrop2012; Schartman et al.
Reference Schartman, Ji, Burin and Goodman2012). A problem with this configuration is that the axial boundaries have a pronounced effect on the interior flow, which causes difficulty in producing smooth Keplerian velocity profiles. Thus, the variation of aspect ratios in these studies stems from the endeavour of minimizing the influence of the end walls by separating them as much as possible. In contrast, this paper seeks to characterize the aspect ratio dependence in relation to the structure, stability and preferred azimuthal linear instability modes of the flow, not only at marginal stability, but also beyond it. This is achieved using numerical simulation and conducting linear stability analysis across a large range of flow conditions and a number of aspect ratios.
Another open question is concerned with the validity of the quasi-two-dimensional model implemented in previous differential-rotation studies (Chomaz et al.
Reference Chomaz, Rabaud, Basdevant and Couder1988; van de Konijnenberg et al.
Reference van de Konijnenberg, Nielsen, Juul Rasmussen and Stenum1999; Bergeron et al.
Reference Bergeron, Coutsias, Lynov and Nielsen2000; Früh & Nielsen Reference Früh and Nielsen2003) which have been useful in reinforcing the experimental results. The full three-dimensional flow has not been simulated previously due to the high computational expense that it demands; this is hence why the majority of the numerical studies have only considered quasi-two-dimensional models of the system. These models compute flow on an
![]() $r{-}{\it\theta}$
plane with no depth variation, and incorporate friction induced by the Ekman layers on the horizontal boundaries via a linear forcing term on the quasi-two-dimensional velocity field. A consequence, though, is that the
$r{-}{\it\theta}$
plane with no depth variation, and incorporate friction induced by the Ekman layers on the horizontal boundaries via a linear forcing term on the quasi-two-dimensional velocity field. A consequence, though, is that the
![]() $\mathit{E}\,^{1/3}$
Stewartson layer is not captured, and this reason has been cited as a possible explanation for the discrepancies observed between the experimental and numerical results (van de Konijnenberg et al.
Reference van de Konijnenberg, Nielsen, Juul Rasmussen and Stenum1999; Früh & Nielsen Reference Früh and Nielsen2003; Schaeffer & Cardin Reference Schaeffer and Cardin2005). The significance of the
$\mathit{E}\,^{1/3}$
Stewartson layer is not captured, and this reason has been cited as a possible explanation for the discrepancies observed between the experimental and numerical results (van de Konijnenberg et al.
Reference van de Konijnenberg, Nielsen, Juul Rasmussen and Stenum1999; Früh & Nielsen Reference Früh and Nielsen2003; Schaeffer & Cardin Reference Schaeffer and Cardin2005). The significance of the
![]() $\mathit{E}\,^{1/3}$
layer on the flow structure and its stability still remains unclear due to the lack of simulations of the full enclosure required for comparison with the quasi-two-dimensional solutions.
$\mathit{E}\,^{1/3}$
layer on the flow structure and its stability still remains unclear due to the lack of simulations of the full enclosure required for comparison with the quasi-two-dimensional solutions.
A recent numerical study by Vo et al. (Reference Vo, Montabone and Sheard2014) implemented an axisymmetric model to detail the axisymmetric flow structure and its stability for an aspect ratio of
![]() $A=2/3$
. Two primary linear instability modes were found: a low-wavenumber mode they referred to as mode I and a high-wavenumber mode referred to as mode II. The mode I instability structure exhibits a highly depth-independent chain of alternating-sign vortices within the shear layer, possessing a reflective symmetry about the mid-depth, while the mode II instability is a disturbance localized at the disk–tank interface near the horizontal boundaries. Both instability modes displayed azimuthal deformations resulting in polygonal patterns, although only mode I distorted the vertical Stewartson layer in the interior. It was proposed that the mode II instability originates from the breaking of depth independence of the flow, which occurs only at high internal Reynolds numbers. This result suggests that the mode I and mode II instabilities may be related to the instability of the
$A=2/3$
. Two primary linear instability modes were found: a low-wavenumber mode they referred to as mode I and a high-wavenumber mode referred to as mode II. The mode I instability structure exhibits a highly depth-independent chain of alternating-sign vortices within the shear layer, possessing a reflective symmetry about the mid-depth, while the mode II instability is a disturbance localized at the disk–tank interface near the horizontal boundaries. Both instability modes displayed azimuthal deformations resulting in polygonal patterns, although only mode I distorted the vertical Stewartson layer in the interior. It was proposed that the mode II instability originates from the breaking of depth independence of the flow, which occurs only at high internal Reynolds numbers. This result suggests that the mode I and mode II instabilities may be related to the instability of the
![]() $\mathit{E}\,^{1/4}$
and
$\mathit{E}\,^{1/4}$
and
![]() $\mathit{E}\,^{1/3}$
layers respectively. This paper extends the methodologies used in the Vo et al. (Reference Vo, Montabone and Sheard2014) study through the addition of quasi-two-dimensional modelling, providing for the first time a direct comparison between the axisymmetric simulation and quasi-two-dimensional modelling of Stewartson layers produced by a differential-rotation system. This work therefore serves to inform the validity and accuracy of quasi-two-dimensional models employed in previous and future studies.
$\mathit{E}\,^{1/3}$
layers respectively. This paper extends the methodologies used in the Vo et al. (Reference Vo, Montabone and Sheard2014) study through the addition of quasi-two-dimensional modelling, providing for the first time a direct comparison between the axisymmetric simulation and quasi-two-dimensional modelling of Stewartson layers produced by a differential-rotation system. This work therefore serves to inform the validity and accuracy of quasi-two-dimensional models employed in previous and future studies.
The remainder of this paper is set out as follows. The numerical methods and models used throughout this paper are detailed in § 2. Following this, the axisymmetric flow structures for a wide range of flow conditions are discussed in § 3. This entails two subsections: a comparison of results between the axisymmetric and quasi-two-dimensional models for
![]() $A=2/3$
and a comparison between various aspect ratios for the axisymmetric model only. Section 4 is structured similarly to § 3 except that it discusses the linear stability of the flow. Finally, conclusions are presented in § 5.
$A=2/3$
and a comparison between various aspect ratios for the axisymmetric model only. Section 4 is structured similarly to § 3 except that it discusses the linear stability of the flow. Finally, conclusions are presented in § 5.
2. Methodology
2.1. System description and governing parameters
The system studied in this paper follows that of Früh & Read (Reference Früh and Read1999) and Vo et al. (Reference Vo, Montabone and Sheard2014). Flow in a cylindrical tank rotating with angular speed
![]() ${\rm\Omega}$
is differentially forced at a rate of
${\rm\Omega}$
is differentially forced at a rate of
![]() ${\it\omega}$
relative to the tank by disks situated flush with the top and bottom boundaries. A schematic of this system and its key dimensions is illustrated in figure 1(a). The disk radius is half the tank radius
${\it\omega}$
relative to the tank by disks situated flush with the top and bottom boundaries. A schematic of this system and its key dimensions is illustrated in figure 1(a). The disk radius is half the tank radius
![]() $(R_{d}=R_{t}/2)$
and the aspect ratio of the shear layer is the ratio of the tank height to the disk radius,
$(R_{d}=R_{t}/2)$
and the aspect ratio of the shear layer is the ratio of the tank height to the disk radius,
![]() $A=H/R_{d}$
.
$A=H/R_{d}$
.

Figure 1. (a) A schematic diagram of the differential-rotating disk set-up under investigation. The key dimensions are the disk radius
![]() $R_{d}$
, tank radius
$R_{d}$
, tank radius
![]() $R_{t}$
and tank height
$R_{t}$
and tank height
![]() $H$
. The disks and tank rotate about the central axis (dashed line) at rates of
$H$
. The disks and tank rotate about the central axis (dashed line) at rates of
![]() ${\rm\Omega}+{\it\omega}$
and
${\rm\Omega}+{\it\omega}$
and
![]() ${\rm\Omega}$
respectively. An overlay of the spatially discretized semi-meridional
${\rm\Omega}$
respectively. An overlay of the spatially discretized semi-meridional
![]() $r$
–
$r$
–
![]() $z$
plane used to simulate axisymmetric flows in an
$z$
plane used to simulate axisymmetric flows in an
![]() $A=2/3$
enclosure is also shown. The macro elements and the coordinate system are illustrated. An inset demonstrating the high-order collocation grid within the macro elements is shown in (b). The inset domain is exact in (a) and (b). Macro elements for the (c)
$A=2/3$
enclosure is also shown. The macro elements and the coordinate system are illustrated. An inset demonstrating the high-order collocation grid within the macro elements is shown in (b). The inset domain is exact in (a) and (b). Macro elements for the (c)
![]() $A=1/6$
and (d)
$A=1/6$
and (d)
![]() $A=2$
meshes are also shown.
$A=2$
meshes are also shown.
The flow is governed by the time-dependent incompressible Navier–Stokes equations, which in an inertial frame of reference are written as
Several important non-dimensional parameters can be obtained by taking the ratios of viscous, inertial and Coriolis forces. The Rossby number,
![]() $\mathit{Ro}$
, is the ratio between the inertial and Coriolis forces, which provides a measure of rotational importance in the system. The Ekman number,
$\mathit{Ro}$
, is the ratio between the inertial and Coriolis forces, which provides a measure of rotational importance in the system. The Ekman number,
![]() $\mathit{E}\,$
, indicates an interaction between the frictional forces and the Coriolis forces in the system. These are respectively defined as
$\mathit{E}\,$
, indicates an interaction between the frictional forces and the Coriolis forces in the system. These are respectively defined as
and
where
![]() $\overline{{\rm\Omega}}={\rm\Omega}+{\it\omega}/2$
is the appropriate mean rotation rate following Früh & Read (Reference Früh and Read1999) and Aguiar (Reference Aguiar2008).
$\overline{{\rm\Omega}}={\rm\Omega}+{\it\omega}/2$
is the appropriate mean rotation rate following Früh & Read (Reference Früh and Read1999) and Aguiar (Reference Aguiar2008).
The ratio of inertial to viscous forces is represented by the Reynolds number,
where
![]() $U$
and
$U$
and
![]() $L$
represent the characteristic velocity and length scales respectively. Two Reynolds numbers have been defined in the literature for differential-rotating flows, namely the external and internal Reynolds numbers (Früh & Read Reference Früh and Read1999). These are defined using a velocity scale of
$L$
represent the characteristic velocity and length scales respectively. Two Reynolds numbers have been defined in the literature for differential-rotating flows, namely the external and internal Reynolds numbers (Früh & Read Reference Früh and Read1999). These are defined using a velocity scale of
![]() $R_{d}{\it\omega}$
and length scales of either
$R_{d}{\it\omega}$
and length scales of either
![]() $H$
or
$H$
or
![]() $(\mathit{E}\,/4)^{1/4}H$
respectively,
$(\mathit{E}\,/4)^{1/4}H$
respectively,
and
It has been established that a constant internal Reynolds number can describe the onset of a non-axisymmetric instability (e.g. Busse Reference Busse1968; Niino & Misawa Reference Niino and Misawa1984; van de Konijnenberg et al.
Reference van de Konijnenberg, Nielsen, Juul Rasmussen and Stenum1999; Früh & Nielsen Reference Früh and Nielsen2003). Additionally, Vo et al. (Reference Vo, Montabone and Sheard2014) found that by taking into consideration the various characteristic scales used to define
![]() $\mathit{Re}_{i}$
, a consistent instability onset given by
$\mathit{Re}_{i}$
, a consistent instability onset given by
![]() $|\mathit{Ro}|/\mathit{E}\,^{3/4}\approx 16$
is derived. This corresponds to
$|\mathit{Ro}|/\mathit{E}\,^{3/4}\approx 16$
is derived. This corresponds to
![]() $\mathit{Re}_{i,c}\approx 22.4$
using (2.6).
$\mathit{Re}_{i,c}\approx 22.4$
using (2.6).
2.2. Axisymmetric and quasi-two-dimensional models
The flows reported in this paper have been computed using two different approaches, namely the axisymmetric simulation of the full enclosure and quasi-two-dimensional modelling. With both approaches, the base flows are assumed to be axisymmetric and are computed on semi-meridional domains using the same numerical treatment. The governing equations and spatial domain used for axisymmetric modelling are described first, followed by a description of the quasi-two-dimensional modelling approach.
The dimensionless governing equations are obtained by scaling lengths by
![]() $R_{d}$
, velocity by
$R_{d}$
, velocity by
![]() $R_{d}{\rm\Omega}$
, time by
$R_{d}{\rm\Omega}$
, time by
![]() ${\rm\Omega}^{-1}$
and pressure by
${\rm\Omega}^{-1}$
and pressure by
![]() ${\it\rho}(R_{d}{\rm\Omega})^{2}$
. On replacing variables and operators with their dimensionless counterparts, the governing equations become
${\it\rho}(R_{d}{\rm\Omega})^{2}$
. On replacing variables and operators with their dimensionless counterparts, the governing equations become
All variables are referred to in their dimensionless forms hereafter. Evidently, there is a limited range of computable Rossby numbers that stems from the denominator in the coefficient of diffusion. That is, only simulations that satisfy
![]() $A\mathit{Ro}<1$
achieve positive diffusion. This restriction is explained by the physical behaviour expressed as
$A\mathit{Ro}<1$
achieve positive diffusion. This restriction is explained by the physical behaviour expressed as
![]() $A\mathit{Ro}\rightarrow 1$
. It can be shown that
$A\mathit{Ro}\rightarrow 1$
. It can be shown that
![]() $A\mathit{Ro}=1$
represents the limit of
$A\mathit{Ro}=1$
represents the limit of
![]() ${\it\omega}\rightarrow \infty$
for a constant
${\it\omega}\rightarrow \infty$
for a constant
![]() ${\rm\Omega}$
, and so this is a physical limit for the system (Vo et al.
Reference Vo, Montabone and Sheard2014).
${\rm\Omega}$
, and so this is a physical limit for the system (Vo et al.
Reference Vo, Montabone and Sheard2014).
The axisymmetric flow is computed on a semi-meridional domain. The spatially discretized domain for
![]() $A=2/3$
is the same as that adopted by Vo et al. (Reference Vo, Montabone and Sheard2014). The macro elements of the mesh are illustrated in figure 1(a) overlaying the schematic of the system. The mesh elements are densely populated around
$A=2/3$
is the same as that adopted by Vo et al. (Reference Vo, Montabone and Sheard2014). The macro elements of the mesh are illustrated in figure 1(a) overlaying the schematic of the system. The mesh elements are densely populated around
![]() $r=1$
and the horizontal boundaries where shear and boundary layers are expected. The high-order collocation grid implemented for the spatial discretization is shown in figure 1(b), which is a close-up of the inset from figure 1(a). The boundaries of the domain are solid, with the exception of the left boundary (dashed line), which represents the axis of rotation and symmetry. This symmetry boundary is treated as per Blackburn & Sherwin (Reference Blackburn and Sherwin2004); zero radial and azimuthal velocities are exactly enforced as Dirichlet boundary conditions, whereas a zero Neumann condition is imposed on the axial velocity. On solid boundaries, azimuthal velocity profiles are imposed where
$r=1$
and the horizontal boundaries where shear and boundary layers are expected. The high-order collocation grid implemented for the spatial discretization is shown in figure 1(b), which is a close-up of the inset from figure 1(a). The boundaries of the domain are solid, with the exception of the left boundary (dashed line), which represents the axis of rotation and symmetry. This symmetry boundary is treated as per Blackburn & Sherwin (Reference Blackburn and Sherwin2004); zero radial and azimuthal velocities are exactly enforced as Dirichlet boundary conditions, whereas a zero Neumann condition is imposed on the axial velocity. On solid boundaries, azimuthal velocity profiles are imposed where
The variation in aspect ratio is achieved by keeping
![]() $R_{d}$
(and
$R_{d}$
(and
![]() $R_{t}$
) constant while changing
$R_{t}$
) constant while changing
![]() $H$
. The same mesh properties and boundary conditions as adopted by the
$H$
. The same mesh properties and boundary conditions as adopted by the
![]() $A=2/3$
mesh apply to all values of
$A=2/3$
mesh apply to all values of
![]() $A$
investigated in this paper. The macro elements of the spatially discretized semi-meridional plane for the smallest and largest aspect ratios (
$A$
investigated in this paper. The macro elements of the spatially discretized semi-meridional plane for the smallest and largest aspect ratios (
![]() $A=1/6$
and
$A=1/6$
and
![]() $A=2$
) are portrayed in figure 1(c,d).
$A=2$
) are portrayed in figure 1(c,d).
Unlike the axisymmetric model, the quasi-two-dimensional model omits axial dependence of the flow. The Ekman friction induced from the horizontal walls in the axisymmetric model is instead captured through an external forcing term. Using the same normalization as used for (2.7), the non-dimensional quasi-two-dimensional equations are written as
Since the base flow of the quasi-two-dimensional model is also assumed to be axisymmetric (
![]() $\partial /\partial {\it\theta}=0$
), the solution becomes a one-dimensional problem in
$\partial /\partial {\it\theta}=0$
), the solution becomes a one-dimensional problem in
![]() $r$
. However, for consistency with the axisymmetric simulations, the quasi-two-dimensional simulations are computed using a modified version of the same spectral-element solver. With the numerical treatment employed in this study, the one-dimensionality is achieved by adopting a quasi-one-dimensional domain. That is, a special mesh with a small arbitrary axial extent (
$r$
. However, for consistency with the axisymmetric simulations, the quasi-two-dimensional simulations are computed using a modified version of the same spectral-element solver. With the numerical treatment employed in this study, the one-dimensionality is achieved by adopting a quasi-one-dimensional domain. That is, a special mesh with a small arbitrary axial extent (
![]() $0.01$
length units) is employed. Due to the depth-independent solutions for the quasi-two-dimensional model, this does not relate to the aspect ratio of the tank being investigated.
$0.01$
length units) is employed. Due to the depth-independent solutions for the quasi-two-dimensional model, this does not relate to the aspect ratio of the tank being investigated.
On the axis and tank sidewall, the same boundary conditions as imposed for the axisymmetric model are implemented in the quasi-two-dimensional model. Stress-free conditions comprising a Dirichlet condition of zero axial velocity and Neumann conditions of zero normal radial and azimuthal velocity gradients are imposed on the top and bottom boundaries. This approach naturally suppresses axial flow and dependence, and the addition of the forcing term to the solver achieves the desired axisymmetric quasi-two-dimensional modelling of the system for any aspect ratio. To facilitate comparison with previous investigations of the same set-up (Vo et al.
Reference Vo, Montabone and Sheard2014), an aspect ratio of
![]() $A=2/3$
is considered for the quasi-two-dimensional modelling reported in this paper.
$A=2/3$
is considered for the quasi-two-dimensional modelling reported in this paper.
The governing equations of both models are solved in cylindrical coordinates using a code adopting a nodal spectral-element discretization in space and a third-order time-integration scheme based on backward differentiation (Karniadakis, Israeli & Orszag Reference Karniadakis, Israeli and Orszag1991). Imposed upon each macro-element are Lagrangian tensor-product polynomial shape functions, for which the polynomial degree can be varied to control the spatial resolution of the domain. Gauss–Lobatto–Legendre quadrature points are used for interpolation. This formulation follows that employed by Vo et al. (Reference Vo, Montabone and Sheard2014) and has been validated in previous studies (Sheard & Ryan Reference Sheard and Ryan2007; Sheard Reference Sheard2009).
A grid independence study of the
![]() $A=2/3$
mesh used for the axisymmetric model has previously been conducted in Vo et al. (Reference Vo, Montabone and Sheard2014), which determined that an element polynomial degree
$A=2/3$
mesh used for the axisymmetric model has previously been conducted in Vo et al. (Reference Vo, Montabone and Sheard2014), which determined that an element polynomial degree
![]() $N_{p}=11$
produced small errors (
$N_{p}=11$
produced small errors (
![]() ${\it\epsilon}<O(0.1\,\%)$
) in several global flow quantities. The meshes constructed in this study for other aspect ratios adopt consistent element sizes, and hence the same polynomial degree is used for axisymmetric simulations throughout this study. A further test of grid independence was implemented for the mesh used for quasi-two-dimensional simulations, and, balancing accuracy against computational expense, it has been decided to employ
${\it\epsilon}<O(0.1\,\%)$
) in several global flow quantities. The meshes constructed in this study for other aspect ratios adopt consistent element sizes, and hence the same polynomial degree is used for axisymmetric simulations throughout this study. A further test of grid independence was implemented for the mesh used for quasi-two-dimensional simulations, and, balancing accuracy against computational expense, it has been decided to employ
![]() $N_{p}=6$
, achieving
$N_{p}=6$
, achieving
![]() ${\it\epsilon}<O(1\,\%)$
. The uncertainties expressed for power-law fits throughout this paper correspond to the standard error (estimated standard deviation) of the least-squares estimates of the coefficients and exponents arising from a linear regression of log–log data.
${\it\epsilon}<O(1\,\%)$
. The uncertainties expressed for power-law fits throughout this paper correspond to the standard error (estimated standard deviation) of the least-squares estimates of the coefficients and exponents arising from a linear regression of log–log data.
2.3. Linear stability analysis technique
The growth or decay of three-dimensional perturbations introduced into steady-state or periodic solutions of the base flow can be obtained through a linear stability analysis. The adopted method is similar to that described by Barkley & Henderson (Reference Barkley and Henderson1996), although it is formulated in cylindrical coordinates and retains the full complex form of the perturbation mode shape for azimuthal precession (Cogan, Ryan & Sheard Reference Cogan, Ryan and Sheard2011; Vo et al. Reference Vo, Montabone and Sheard2014).
The linear stability analysis formulation begins by decomposing the flow variables into the sum of the axisymmetric base flow and an arbitrarily small three-dimensional disturbance,
![]() $\boldsymbol{u}=\overline{\boldsymbol{u}}(z,r,t)+{\it\delta}\boldsymbol{u}^{\prime }(z,r,{\it\theta},t)$
, where
$\boldsymbol{u}=\overline{\boldsymbol{u}}(z,r,t)+{\it\delta}\boldsymbol{u}^{\prime }(z,r,{\it\theta},t)$
, where
![]() ${\it\delta}$
is a small positive constant. It should be noted that
${\it\delta}$
is a small positive constant. It should be noted that
![]() $\overline{\boldsymbol{u}}$
is two-dimensional and
$\overline{\boldsymbol{u}}$
is two-dimensional and
![]() $\boldsymbol{u}^{\prime }$
is three-dimensional, decomposed into individual azimuthal Fourier modes with wavenumber
$\boldsymbol{u}^{\prime }$
is three-dimensional, decomposed into individual azimuthal Fourier modes with wavenumber
![]() $k$
. Substitution of these decompositions into (2.7) and retaining terms of
$k$
. Substitution of these decompositions into (2.7) and retaining terms of
![]() $O({\it\delta})$
(terms of
$O({\it\delta})$
(terms of
![]() $O({\it\delta}^{2})$
may be neglected as they are negligible for small
$O({\it\delta}^{2})$
may be neglected as they are negligible for small
![]() $\boldsymbol{u}^{\prime }$
) yields the linearized Navier–Stokes equations,
$\boldsymbol{u}^{\prime }$
) yields the linearized Navier–Stokes equations,
is added to the right-hand side of the momentum equation. The quasi-two-dimensional perturbation
![]() $\boldsymbol{u}_{\bot }^{\prime }$
varies spatially in
$\boldsymbol{u}_{\bot }^{\prime }$
varies spatially in
![]() $r$
and
$r$
and
![]() ${\it\theta}$
. The same analysis is performed on the two sets of equations.
${\it\theta}$
. The same analysis is performed on the two sets of equations.
The linear stability analysis calculates the complex Floquet multipliers
![]() ${\it\mu}_{F}$
of the system, which correspond to the eigenvalues of a linearized evolution operator describing time integration of (2.10). The Floquet multipliers are related to the exponential growth rates of individual wavenumbers through
${\it\mu}_{F}$
of the system, which correspond to the eigenvalues of a linearized evolution operator describing time integration of (2.10). The Floquet multipliers are related to the exponential growth rates of individual wavenumbers through
where
![]() ${\it\sigma}_{R}$
denotes the real component of the growth rate and
${\it\sigma}_{R}$
denotes the real component of the growth rate and
![]() $T$
is the time interval over which the equations are integrated within the eigenmode solver. Since only the real component of the growth rate is considered here, as it is all that is required to determine the stability of the flow, the subscript ‘
$T$
is the time interval over which the equations are integrated within the eigenmode solver. Since only the real component of the growth rate is considered here, as it is all that is required to determine the stability of the flow, the subscript ‘
![]() $R$
’ is omitted hereafter. Hence, the growth rate may be evaluated through
$R$
’ is omitted hereafter. Hence, the growth rate may be evaluated through
![]() ${\it\sigma}=\log |{\it\mu}|/T$
. By definition, stable flows are characterized by
${\it\sigma}=\log |{\it\mu}|/T$
. By definition, stable flows are characterized by
![]() ${\it\sigma}<0$
while unstable flows are characterized by
${\it\sigma}<0$
while unstable flows are characterized by
![]() ${\it\sigma}>0$
. Neutral stability occurs when
${\it\sigma}>0$
. Neutral stability occurs when
![]() ${\it\sigma}=0$
(
${\it\sigma}=0$
(
![]() $|{\it\mu}|=1$
). Only the most dominant eigenvalue is sought for each wavenumber, corresponding to the mode with the largest growth rate. An implicitly restarted Arnoldi method is used to extract the leading eigenmodes of the linearized perturbation fields (Sheard Reference Sheard2011).
$|{\it\mu}|=1$
). Only the most dominant eigenvalue is sought for each wavenumber, corresponding to the mode with the largest growth rate. An implicitly restarted Arnoldi method is used to extract the leading eigenmodes of the linearized perturbation fields (Sheard Reference Sheard2011).
3. Results: axisymmetric flow
The axisymmetric flows for a wide range of flow conditions have been computed using both the axisymmetric model and the quasi-two-dimensional model. Time-evolved solutions are taken to be steady state when velocity variations are less than
![]() $10^{-12}$
between successive time steps. A comparison between the results of the two models is first described for an aspect ratio of
$10^{-12}$
between successive time steps. A comparison between the results of the two models is first described for an aspect ratio of
![]() $A=2/3$
. Following this, a section pertaining only to the axisymmetric modelling of a range of aspect ratios is presented. The flow structures, vertical shear-layer profiles and thicknesses are discussed in each section.
$A=2/3$
. Following this, a section pertaining only to the axisymmetric modelling of a range of aspect ratios is presented. The flow structures, vertical shear-layer profiles and thicknesses are discussed in each section.
3.1. Axisymmetric and quasi-two-dimensional models (
 $A=2/3$
)
$A=2/3$
)
3.1.1. Steady-state axisymmetric flow structure
A variety of steady-state solutions for
![]() $A=2/3$
have been obtained using the axisymmetric and quasi-two-dimensional models. The flow structures from the axisymmetric model for
$A=2/3$
have been obtained using the axisymmetric and quasi-two-dimensional models. The flow structures from the axisymmetric model for
![]() $A=2/3$
have been detailed previously in Vo et al. (Reference Vo, Montabone and Sheard2014). Thus, the focus here is on the comparisons between the two models. Simulations are performed for Rossby numbers in the range
$A=2/3$
have been detailed previously in Vo et al. (Reference Vo, Montabone and Sheard2014). Thus, the focus here is on the comparisons between the two models. Simulations are performed for Rossby numbers in the range
![]() $-2.0\leqslant \mathit{Ro}\leqslant 1.0$
and Ekman numbers in the range
$-2.0\leqslant \mathit{Ro}\leqslant 1.0$
and Ekman numbers in the range
![]() $3\times 10^{-5}\leqslant \mathit{E}\,\leqslant 3\times 10^{-3}$
.
$3\times 10^{-5}\leqslant \mathit{E}\,\leqslant 3\times 10^{-3}$
.

Figure 2. Structure of the axisymmetric flows visualized on the semi-meridional
![]() $r$
–
$r$
–
![]() $z$
plane. Azimuthal velocities (
$z$
plane. Azimuthal velocities (
![]() $u_{\bot {\it\theta}},u_{{\it\theta}}$
) (left) and axial vorticities (
$u_{\bot {\it\theta}},u_{{\it\theta}}$
) (left) and axial vorticities (
![]() ${\it\omega}_{\bot z},{\it\omega}_{z}$
) (right) are shown for
${\it\omega}_{\bot z},{\it\omega}_{z}$
) (right) are shown for
![]() $\mathit{E}\,=3\times 10^{-4}$
at (i)
$\mathit{E}\,=3\times 10^{-4}$
at (i)
![]() $\mathit{Ro}=0.1$
, (ii)
$\mathit{Ro}=0.1$
, (ii)
![]() $\mathit{Ro}=0.5$
, (iii)
$\mathit{Ro}=0.5$
, (iii)
![]() $\mathit{Ro}=-1.0$
and (iv)
$\mathit{Ro}=-1.0$
and (iv)
![]() $\mathit{Ro}=-2.0$
. The flow solutions from the (a) quasi-two-dimensional model and (b) axisymmetric model are shown. For the azimuthal velocity plots, equi-spaced contour levels are plotted between
$\mathit{Ro}=-2.0$
. The flow solutions from the (a) quasi-two-dimensional model and (b) axisymmetric model are shown. For the azimuthal velocity plots, equi-spaced contour levels are plotted between
![]() $\pm |2(\mathit{Ro}+{\it\omega})+{\it\omega}/\mathit{Ro}|$
, while for the axial vorticity plots, equi-spaced contour levels are plotted between
$\pm |2(\mathit{Ro}+{\it\omega})+{\it\omega}/\mathit{Ro}|$
, while for the axial vorticity plots, equi-spaced contour levels are plotted between
![]() $2\overline{{\rm\Omega}}\pm 10|{\it\omega}|$
. Dark to light shading represents low to high values, respectively, while solid and dashed contour lines identify positive and negative contour levels respectively. The domain shown represents the entire semi-meridional plane with
$2\overline{{\rm\Omega}}\pm 10|{\it\omega}|$
. Dark to light shading represents low to high values, respectively, while solid and dashed contour lines identify positive and negative contour levels respectively. The domain shown represents the entire semi-meridional plane with
![]() $0\leqslant r\leqslant 2$
for the quasi-two-dimensional model and
$0\leqslant r\leqslant 2$
for the quasi-two-dimensional model and
![]() $0\leqslant r\leqslant 2$
and
$0\leqslant r\leqslant 2$
and
![]() $0\leqslant z\leqslant 2/3$
for the axisymmetric model. The quasi-two-dimensional solutions have been stretched vertically (without loss of correctness) for visual clarity.
$0\leqslant z\leqslant 2/3$
for the axisymmetric model. The quasi-two-dimensional solutions have been stretched vertically (without loss of correctness) for visual clarity.
Figure 2 presents azimuthal velocity and axial vorticity solutions obtained from the quasi-two-dimensional model (a) and axisymmetric model (b). Flow conditions are of various
![]() $\mathit{Ro}$
for
$\mathit{Ro}$
for
![]() $\mathit{E}\,=3\times 10^{-4}$
. For visualization purposes, the one-dimensional solution is projected vertically. The
$\mathit{E}\,=3\times 10^{-4}$
. For visualization purposes, the one-dimensional solution is projected vertically. The
![]() $\mathit{Ro}$
conditions presented here are largely chosen to demonstrate the difference in the depth dependence of the flow between the two models. It should be noted that the contour levels plotted for both models at each
$\mathit{Ro}$
conditions presented here are largely chosen to demonstrate the difference in the depth dependence of the flow between the two models. It should be noted that the contour levels plotted for both models at each
![]() $\mathit{Ro}$
are the same. At
$\mathit{Ro}$
are the same. At
![]() $\mathit{Ro}=0.1$
(i), the flow from the axisymmetric model is strongly depth-independent and is reflective of that observed from the quasi-two-dimensional model. These low-
$\mathit{Ro}=0.1$
(i), the flow from the axisymmetric model is strongly depth-independent and is reflective of that observed from the quasi-two-dimensional model. These low-
![]() $\mathit{Ro}$
flows typically reveal a concentrated band of axial vorticity at
$\mathit{Ro}$
flows typically reveal a concentrated band of axial vorticity at
![]() $r=1$
which aligns with the radial location of the disk–tank interface. Indeed, the flow solutions between the two models become more similar at smaller Rossby numbers as the effects of Ekman pumping/suction become weaker (see also Vo et al.
Reference Vo, Montabone and Sheard2014, figure 3ai).
$r=1$
which aligns with the radial location of the disk–tank interface. Indeed, the flow solutions between the two models become more similar at smaller Rossby numbers as the effects of Ekman pumping/suction become weaker (see also Vo et al.
Reference Vo, Montabone and Sheard2014, figure 3ai).
At larger Rossby numbers, the stronger circulations induced by the Ekman layers are captured in the axisymmetric model and therefore the depth independence observed at lower
![]() $\mathit{Ro}$
is lost. This loss is observed at
$\mathit{Ro}$
is lost. This loss is observed at
![]() $\mathit{Ro}=0.5$
(panel ii) whereby the azimuthal velocity and axial vorticity contours are no longer parallel to the axis of rotation. The axial vorticity contours clearly depict diagonal negative-vorticity strands originating from the disk–tank interface instead of a continuous vertical shear layer. The solutions of the quasi-two-dimensional model provide a very good agreement with the interior of the axisymmetric solutions despite not simulating depth-dependent features. Quantitative comparisons are provided in § 3.1.2.
$\mathit{Ro}=0.5$
(panel ii) whereby the azimuthal velocity and axial vorticity contours are no longer parallel to the axis of rotation. The axial vorticity contours clearly depict diagonal negative-vorticity strands originating from the disk–tank interface instead of a continuous vertical shear layer. The solutions of the quasi-two-dimensional model provide a very good agreement with the interior of the axisymmetric solutions despite not simulating depth-dependent features. Quantitative comparisons are provided in § 3.1.2.
Similarly, for negative-
![]() $\mathit{Ro}$
flows, there is a transition from highly depth-independent flow to depth-dependent flow as
$\mathit{Ro}$
flows, there is a transition from highly depth-independent flow to depth-dependent flow as
![]() $|\mathit{Ro}|$
is increased. As was observed by Vo et al. (Reference Vo, Montabone and Sheard2014), negative-
$|\mathit{Ro}|$
is increased. As was observed by Vo et al. (Reference Vo, Montabone and Sheard2014), negative-
![]() $\mathit{Ro}$
flows are able to maintain depth independence at higher
$\mathit{Ro}$
flows are able to maintain depth independence at higher
![]() $|\mathit{Ro}|$
as compared with positive-
$|\mathit{Ro}|$
as compared with positive-
![]() $\mathit{Ro}$
flows. Hence, the flow at
$\mathit{Ro}$
flows. Hence, the flow at
![]() $\mathit{Ro}=-1.0$
(panel iii) in the axisymmetric model displays traits that are very similar to small positive
$\mathit{Ro}=-1.0$
(panel iii) in the axisymmetric model displays traits that are very similar to small positive
![]() $\mathit{Ro}$
. Again, the solutions of the quasi-two-dimensional model demonstrate very good agreement in the radial locations of the contour lines and their values. This is in contrast to the stronger
$\mathit{Ro}$
. Again, the solutions of the quasi-two-dimensional model demonstrate very good agreement in the radial locations of the contour lines and their values. This is in contrast to the stronger
![]() $\mathit{Ro}=-2.0$
flow (panel iv), where axial invariance is broken, although in a different manner compared with that observed in the positive-
$\mathit{Ro}=-2.0$
flow (panel iv), where axial invariance is broken, although in a different manner compared with that observed in the positive-
![]() $\mathit{Ro}$
regime. The axisymmetric model presents negative regions of vorticity on the inner side of the vertical shear layer in addition to the thin negative-vorticity boundary layer along the horizontal. The interior region occupying
$\mathit{Ro}$
regime. The axisymmetric model presents negative regions of vorticity on the inner side of the vertical shear layer in addition to the thin negative-vorticity boundary layer along the horizontal. The interior region occupying
![]() $r<1$
exhibits both positive and negative axial vorticity. However, the quasi-two-dimensional flow exhibits only negative axial vorticity for
$r<1$
exhibits both positive and negative axial vorticity. However, the quasi-two-dimensional flow exhibits only negative axial vorticity for
![]() $r<1$
.
$r<1$
.
Overall, the agreement between the two models is excellent at low
![]() $|\mathit{Ro}|$
and remains robust outside the shear layer for
$|\mathit{Ro}|$
and remains robust outside the shear layer for
![]() $|\mathit{Ro}|$
exceeding the loss of depth independence. The key difference between the two models is primarily observed in the axial vorticity contours where the vertical shear layer is broken. It has been proposed in Vo et al. (Reference Vo, Montabone and Sheard2014) that the breaking of the depth independence in the flow may be connected with the mode II linear instability. As depth independence is implicit in the quasi-two-dimensional model, the mode II instability is not expected to emerge in the linear stability analysis of the quasi-two-dimensional model. The linear stability of these flows is discussed later in § 4.1.
$|\mathit{Ro}|$
exceeding the loss of depth independence. The key difference between the two models is primarily observed in the axial vorticity contours where the vertical shear layer is broken. It has been proposed in Vo et al. (Reference Vo, Montabone and Sheard2014) that the breaking of the depth independence in the flow may be connected with the mode II linear instability. As depth independence is implicit in the quasi-two-dimensional model, the mode II instability is not expected to emerge in the linear stability analysis of the quasi-two-dimensional model. The linear stability of these flows is discussed later in § 4.1.
3.1.2. Vertical shear-layer profile and thickness

Figure 3. (a) Scaled relative azimuthal velocity and (b) scaled relative axial vorticity profiles for
![]() $\mathit{E}\,=3\times 10^{-4}$
at various
$\mathit{E}\,=3\times 10^{-4}$
at various
![]() $\mathit{Ro}$
: quasi-two-dimensional model (left); axisymmetric model (right). The relative azimuthal velocity is scaled by the non-dimensional differential-rotation rate
$\mathit{Ro}$
: quasi-two-dimensional model (left); axisymmetric model (right). The relative azimuthal velocity is scaled by the non-dimensional differential-rotation rate
![]() $u_{(\bot ){\it\theta},rel}=(2A\mathit{Ro})/(1-A\mathit{Ro})$
while the relative axial vorticity is scaled by the non-dimensional axial vorticity attributed by the differential-rotation rate
$u_{(\bot ){\it\theta},rel}=(2A\mathit{Ro})/(1-A\mathit{Ro})$
while the relative axial vorticity is scaled by the non-dimensional axial vorticity attributed by the differential-rotation rate
![]() $2u_{(\bot ){\it\theta},rel}=(4A\mathit{Ro})/(1-A\mathit{Ro})$
. The profiles have been extracted at mid-depth for the axisymmetric model. The quasi-two-dimensional solutions are
$2u_{(\bot ){\it\theta},rel}=(4A\mathit{Ro})/(1-A\mathit{Ro})$
. The profiles have been extracted at mid-depth for the axisymmetric model. The quasi-two-dimensional solutions are
![]() $z$
-independent.
$z$
-independent.
Profiles of the azimuthal velocity relative to the tank and axial vorticity have been extracted from the quasi-two-dimensional and axisymmetric models. Typical profiles of these two flow variables for
![]() $\mathit{E}\,=3\times 10^{-4}$
have been scaled and are shown in figure 3. The azimuthal velocity profiles have been scaled by the non-dimensional differential-rotation rate
$\mathit{E}\,=3\times 10^{-4}$
have been scaled and are shown in figure 3. The azimuthal velocity profiles have been scaled by the non-dimensional differential-rotation rate
![]() $2A\mathit{Ro}/(1-A\mathit{Ro})$
, while the axial vorticity profiles have been scaled by the non-dimensional axial vorticity of the differential-rotation rate
$2A\mathit{Ro}/(1-A\mathit{Ro})$
, while the axial vorticity profiles have been scaled by the non-dimensional axial vorticity of the differential-rotation rate
![]() $({\it\omega}_{(\bot )z}-2)(1-A\mathit{Ro})/(4A\mathit{Ro})$
. There is a strong similarity in the scaled relative azimuthal velocity profiles across the various Rossby numbers in both models. In fact, there is no difference in the quasi-two-dimensional flow solutions, whereas a deviation is observed at
$({\it\omega}_{(\bot )z}-2)(1-A\mathit{Ro})/(4A\mathit{Ro})$
. There is a strong similarity in the scaled relative azimuthal velocity profiles across the various Rossby numbers in both models. In fact, there is no difference in the quasi-two-dimensional flow solutions, whereas a deviation is observed at
![]() $\mathit{Ro}=0.5$
in the axisymmetric model caused by the breaking of depth independence in the flow. Despite this, the profiles are very similar between the two models for small
$\mathit{Ro}=0.5$
in the axisymmetric model caused by the breaking of depth independence in the flow. Despite this, the profiles are very similar between the two models for small
![]() $\mathit{Ro}$
, which is expected since the use of the quasi-two-dimensional model does not directly affect the azimuthal component of the flow. The collapse of the data demonstrates a flow that rotates at a relative angular rate of
$\mathit{Ro}$
, which is expected since the use of the quasi-two-dimensional model does not directly affect the azimuthal component of the flow. The collapse of the data demonstrates a flow that rotates at a relative angular rate of
![]() ${\it\omega}$
for
${\it\omega}$
for
![]() $r\lesssim 0.9$
, while the flow rotates at the tank rate
$r\lesssim 0.9$
, while the flow rotates at the tank rate
![]() ${\rm\Omega}$
for
${\rm\Omega}$
for
![]() $r\gtrsim 1.2$
. In the intermediate region, there is a transition from the disk rotation rate to the tank rotation rate, which is achieved through the
$r\gtrsim 1.2$
. In the intermediate region, there is a transition from the disk rotation rate to the tank rotation rate, which is achieved through the
![]() $\mathit{E}\,^{1/4}$
Stewartson shear layer. Indeed, the
$\mathit{E}\,^{1/4}$
Stewartson shear layer. Indeed, the
![]() $\mathit{E}\,^{1/4}$
layer functions to smooth out the azimuthal velocity (Smith Reference Smith1984; Vooren Reference Vooren1992; Schaeffer & Cardin Reference Schaeffer and Cardin2005). Furthermore, by using the appropriate scaling and adopting the azimuthal velocity profile derived by Niino & Misawa (Reference Niino and Misawa1984), a strong change over the same radial extent (
$\mathit{E}\,^{1/4}$
layer functions to smooth out the azimuthal velocity (Smith Reference Smith1984; Vooren Reference Vooren1992; Schaeffer & Cardin Reference Schaeffer and Cardin2005). Furthermore, by using the appropriate scaling and adopting the azimuthal velocity profile derived by Niino & Misawa (Reference Niino and Misawa1984), a strong change over the same radial extent (
![]() $0.9\lesssim r\lesssim 1.2$
) is demonstrated, consistent with the computed shear layer.
$0.9\lesssim r\lesssim 1.2$
) is demonstrated, consistent with the computed shear layer.
Distinct differences between the two models are seen in the profiles of the scaled axial vorticity profiles around
![]() $r=1$
(figure 3
b). A sharp change in the gradient of the profile at
$r=1$
(figure 3
b). A sharp change in the gradient of the profile at
![]() $r=1$
exists in the quasi-two-dimensional solution, which is smooth in the axisymmetric model solutions. This difference is explained by the absence of axial variation in the quasi-two-dimensional flows, which is required to capture the
$r=1$
exists in the quasi-two-dimensional solution, which is smooth in the axisymmetric model solutions. This difference is explained by the absence of axial variation in the quasi-two-dimensional flows, which is required to capture the
![]() $\mathit{E}\,^{1/3}$
layer. That is, the meridional circulation supported by the
$\mathit{E}\,^{1/3}$
layer. That is, the meridional circulation supported by the
![]() $\mathit{E}\,^{1/3}$
layer smooths out the axial vorticity in the axisymmetric model solutions. Consequently, the minimum axial vorticity value from the quasi-two-dimensional model is much lower compared with the axisymmetric model solution. Moreover, there are no differences in the scaled profiles across the range of Rossby numbers in the quasi-two-dimensional solutions, which is in contrast to the axisymmetric model solutions. Again, the depth dependence induced by the higher differential-rotation rates (high
$\mathit{E}\,^{1/3}$
layer smooths out the axial vorticity in the axisymmetric model solutions. Consequently, the minimum axial vorticity value from the quasi-two-dimensional model is much lower compared with the axisymmetric model solution. Moreover, there are no differences in the scaled profiles across the range of Rossby numbers in the quasi-two-dimensional solutions, which is in contrast to the axisymmetric model solutions. Again, the depth dependence induced by the higher differential-rotation rates (high
![]() $\mathit{Ro}$
) is the reason for the deviation seen in the
$\mathit{Ro}$
) is the reason for the deviation seen in the
![]() $\mathit{Ro}=0.5$
profile compared with the other Rossby numbers of the axisymmetric model. That is, at
$\mathit{Ro}=0.5$
profile compared with the other Rossby numbers of the axisymmetric model. That is, at
![]() $\mathit{Ro}=0.5$
the single minimum in the profile is replaced by a flattened band of weaker vorticity. The axial vorticity minima in both models suggest that the flows may be susceptible to shear instability via the Rayleigh–Kuo criterion (Rayleigh Reference Rayleigh1880; Kuo Reference Kuo1949). The Rayleigh–Kuo criterion states that the radial derivative of the absolute axial vorticity (sum of the background and relative vorticities) must change sign somewhere within the domain in order for instability to exist. This criterion is a necessary but not sufficient condition.
$\mathit{Ro}=0.5$
the single minimum in the profile is replaced by a flattened band of weaker vorticity. The axial vorticity minima in both models suggest that the flows may be susceptible to shear instability via the Rayleigh–Kuo criterion (Rayleigh Reference Rayleigh1880; Kuo Reference Kuo1949). The Rayleigh–Kuo criterion states that the radial derivative of the absolute axial vorticity (sum of the background and relative vorticities) must change sign somewhere within the domain in order for instability to exist. This criterion is a necessary but not sufficient condition.
Measurements for the
![]() $\mathit{E}\,^{1/4}$
Stewartson layer thickness were conducted using similar techniques to those performed for the axisymmetric base flows in Vo et al. (Reference Vo, Montabone and Sheard2014) (see their figure
$\mathit{E}\,^{1/4}$
Stewartson layer thickness were conducted using similar techniques to those performed for the axisymmetric base flows in Vo et al. (Reference Vo, Montabone and Sheard2014) (see their figure
![]() $5$
). The
$5$
). The
![]() $\mathit{E}\,^{1/4}$
layer thickness,
$\mathit{E}\,^{1/4}$
layer thickness,
![]() ${\it\delta}_{vel}$
, is defined as the difference in radial locations corresponding to
${\it\delta}_{vel}$
, is defined as the difference in radial locations corresponding to
![]() $(\{u_{{\it\theta}-rel}/r\}_{max}-0.15{\rm\Delta}\{u_{{\it\theta}-rel}/r\})$
and
$(\{u_{{\it\theta}-rel}/r\}_{max}-0.15{\rm\Delta}\{u_{{\it\theta}-rel}/r\})$
and
![]() $(\{u_{{\it\theta}-rel}/r\}_{min}+0.15{\rm\Delta}\{u_{{\it\theta}-rel}/r\})$
, where
$(\{u_{{\it\theta}-rel}/r\}_{min}+0.15{\rm\Delta}\{u_{{\it\theta}-rel}/r\})$
, where
![]() $u_{{\it\theta}-rel}$
represents the relative azimuthal velocity and
$u_{{\it\theta}-rel}$
represents the relative azimuthal velocity and
![]() ${\rm\Delta}\{u_{{\it\theta}-rel}/r\}$
is the difference between the maximum and minimum values of
${\rm\Delta}\{u_{{\it\theta}-rel}/r\}$
is the difference between the maximum and minimum values of
![]() $u_{{\it\theta}-rel}/r$
. Although this
$u_{{\it\theta}-rel}/r$
. Although this
![]() $15\,\%$
threshold has been chosen arbitrarily to represent the results, it has been determined that the scalings obtained using this approach are quite insensitive to the chosen threshold value. The thickness of the
$15\,\%$
threshold has been chosen arbitrarily to represent the results, it has been determined that the scalings obtained using this approach are quite insensitive to the chosen threshold value. The thickness of the
![]() $\mathit{E}\,^{1/3}$
layer,
$\mathit{E}\,^{1/3}$
layer,
![]() ${\it\delta}_{vort}$
, is defined as the difference in radial locations corresponding to maximum and minimum radial gradients of axial vorticity. The thickness of this layer is not measured for the quasi-two-dimensional solutions since the discontinuous axial vorticity profile consistently yields a zero thickness. This result is supported physically as the quasi-two-dimensional model does not compute any depth-dependent structures and is therefore unable to generate the
${\it\delta}_{vort}$
, is defined as the difference in radial locations corresponding to maximum and minimum radial gradients of axial vorticity. The thickness of this layer is not measured for the quasi-two-dimensional solutions since the discontinuous axial vorticity profile consistently yields a zero thickness. This result is supported physically as the quasi-two-dimensional model does not compute any depth-dependent structures and is therefore unable to generate the
![]() $\mathit{E}\,^{1/3}$
layer responsible for smoothing out the discontinuous vorticity.
$\mathit{E}\,^{1/3}$
layer responsible for smoothing out the discontinuous vorticity.

Figure 4. The shear-layer thickness based on the relative azimuthal velocity,
![]() ${\it\delta}_{vel}$
, as a function of
${\it\delta}_{vel}$
, as a function of
![]() $\mathit{E}\,$
for quasi-two-dimensional solutions. The data are independent of
$\mathit{E}\,$
for quasi-two-dimensional solutions. The data are independent of
![]() $|\mathit{Ro}|$
.
$|\mathit{Ro}|$
.
A power-law fit to the thickness of the
![]() $\mathit{E}\,^{1/4}$
layer against
$\mathit{E}\,^{1/4}$
layer against
![]() $\mathit{E}\,$
is determined as
$\mathit{E}\,$
is determined as
![]() ${\it\delta}_{vel}=1.26(\pm 0.02)\mathit{E}\,^{0.260\pm 0.002}$
for the quasi-two-dimensional model and is shown in figure 4. This relationship is found to be independent of
${\it\delta}_{vel}=1.26(\pm 0.02)\mathit{E}\,^{0.260\pm 0.002}$
for the quasi-two-dimensional model and is shown in figure 4. This relationship is found to be independent of
![]() $\mathit{Ro}$
. Pleasingly, this is extremely close to the relationship obtained for the axisymmetric flows with
$\mathit{Ro}$
. Pleasingly, this is extremely close to the relationship obtained for the axisymmetric flows with
![]() $A=2/3$
and very small
$A=2/3$
and very small
![]() $|\mathit{Ro}|$
, which was found to be
$|\mathit{Ro}|$
, which was found to be
![]() ${\it\delta}_{vel}=1.22(\pm 0.03)\mathit{E}\,^{0.260\pm 0.003}$
. It should be noted that Vo et al. (Reference Vo, Montabone and Sheard2014) measured the shear-layer thickness differently and hence the relationships presented here are different from those reported previously. Using their thickness measurement method, we obtain
${\it\delta}_{vel}=1.22(\pm 0.03)\mathit{E}\,^{0.260\pm 0.003}$
. It should be noted that Vo et al. (Reference Vo, Montabone and Sheard2014) measured the shear-layer thickness differently and hence the relationships presented here are different from those reported previously. Using their thickness measurement method, we obtain
![]() ${\it\delta}_{vel}=1.32(\pm 0.02)\mathit{E}\,^{0.219\pm 0.002}$
for the quasi-two-dimensional model, which is in good agreement with their reported
${\it\delta}_{vel}=1.32(\pm 0.02)\mathit{E}\,^{0.219\pm 0.002}$
for the quasi-two-dimensional model, which is in good agreement with their reported
![]() ${\it\delta}_{vel}=1.31\mathit{E}\,^{0.220}$
using an axisymmetric model. Although the quasi-two-dimensional and axisymmetric models demonstrate excellent agreement with thickness relationships at
${\it\delta}_{vel}=1.31\mathit{E}\,^{0.220}$
using an axisymmetric model. Although the quasi-two-dimensional and axisymmetric models demonstrate excellent agreement with thickness relationships at
![]() $|\mathit{Ro}|=0.005$
, the
$|\mathit{Ro}|=0.005$
, the
![]() $\mathit{Ro}$
independence of the
$\mathit{Ro}$
independence of the
![]() $\mathit{E}\,^{1/4}$
layer thickness is not observed in the axisymmetric model solutions computed here (consistent with Vo et al.
Reference Vo, Montabone and Sheard2014). This represents a key difference between the two models and suggests that the thickness of the
$\mathit{E}\,^{1/4}$
layer thickness is not observed in the axisymmetric model solutions computed here (consistent with Vo et al.
Reference Vo, Montabone and Sheard2014). This represents a key difference between the two models and suggests that the thickness of the
![]() $\mathit{E}\,^{1/4}$
Stewartson layer is modified by meridional circulations, which become stronger as
$\mathit{E}\,^{1/4}$
Stewartson layer is modified by meridional circulations, which become stronger as
![]() $|\mathit{Ro}|$
is increased, and are excluded from the quasi-two-dimensional simulations.
$|\mathit{Ro}|$
is increased, and are excluded from the quasi-two-dimensional simulations.
3.2. Variation of the aspect ratio of the axisymmetric model
The effect of varying the aspect ratio is numerically investigated by varying the height of the tank while keeping the disk radius constant in the axisymmetric model. The motivation for this originates from the theoretical definition of the Stewartson layer thickness, which scales linearly with height (i.e.
![]() ${\it\delta}_{vel}\propto (H/R_{d})\mathit{E}\,^{1/4}$
). The height of the container can be expressed through the non-dimensional aspect ratio parameter, and therefore the effect of varying
${\it\delta}_{vel}\propto (H/R_{d})\mathit{E}\,^{1/4}$
). The height of the container can be expressed through the non-dimensional aspect ratio parameter, and therefore the effect of varying
![]() $A$
in relation to the Stewartson layer can be determined. The neutral stability curves obtained by Niino & Misawa (Reference Niino and Misawa1984) in a differentially forced flow demonstrated a stabilizing effect with increasing
$A$
in relation to the Stewartson layer can be determined. The neutral stability curves obtained by Niino & Misawa (Reference Niino and Misawa1984) in a differentially forced flow demonstrated a stabilizing effect with increasing
![]() $A$
. For their idealized differential single-disk set-up, they reported that the shear layer was not influenced by the geometry provided that the ratio of the disk radius to the
$A$
. For their idealized differential single-disk set-up, they reported that the shear layer was not influenced by the geometry provided that the ratio of the disk radius to the
![]() $\mathit{E}\,^{1/4}$
theoretical thickness was greater than
$\mathit{E}\,^{1/4}$
theoretical thickness was greater than
![]() $25$
(i.e.
$25$
(i.e.
![]() ${\it\gamma}=R_{d}/(\mathit{E}\,/4)^{1/4}H>25$
). Considering the smallest and largest Ekman numbers in this study (
${\it\gamma}=R_{d}/(\mathit{E}\,/4)^{1/4}H>25$
). Considering the smallest and largest Ekman numbers in this study (
![]() $\mathit{E}\,=5\times 10^{-5}$
and
$\mathit{E}\,=5\times 10^{-5}$
and
![]() $\mathit{E}\,=3\times 10^{-3}$
respectively), the criterion of Niino & Misawa (Reference Niino and Misawa1984) gives that geometrical effects are negligible for
$\mathit{E}\,=3\times 10^{-3}$
respectively), the criterion of Niino & Misawa (Reference Niino and Misawa1984) gives that geometrical effects are negligible for
![]() $A\lesssim 0.24$
and
$A\lesssim 0.24$
and
![]() $A\lesssim 0.67$
respectively.
$A\lesssim 0.67$
respectively.
The flow structures produced at aspect ratios in the range
![]() $1/6\leqslant A\leqslant 2$
for the axisymmetric model are presented in this section. This range of aspect ratios allows us to probe the changing structure and stability characteristics of the flow in comparison with Niino & Misawa (Reference Niino and Misawa1984).
$1/6\leqslant A\leqslant 2$
for the axisymmetric model are presented in this section. This range of aspect ratios allows us to probe the changing structure and stability characteristics of the flow in comparison with Niino & Misawa (Reference Niino and Misawa1984).
3.2.1. Steady-state axisymmetric flow structure

Figure 5. Structure of the axisymmetric flows visualized on the semi-meridional
![]() $r$
–
$r$
–
![]() $z$
plane. Axial velocities,
$z$
plane. Axial velocities,
![]() $u_{z}$
(left), and axial vorticities,
$u_{z}$
(left), and axial vorticities,
![]() ${\it\omega}_{z}$
(right), are shown for
${\it\omega}_{z}$
(right), are shown for
![]() $\mathit{Ro}=0.3$
and
$\mathit{Ro}=0.3$
and
![]() $\mathit{E}\,=7\times 10^{-4}$
at
$\mathit{E}\,=7\times 10^{-4}$
at
![]() $A=1/6$
(a),
$A=1/6$
(a),
![]() $2/3$
(b),
$2/3$
(b),
![]() $4/3$
(c) and
$4/3$
(c) and
![]() $A=2$
(d). The images are to scale. For the axial velocity plots, equi-spaced contour levels are plotted between
$A=2$
(d). The images are to scale. For the axial velocity plots, equi-spaced contour levels are plotted between
![]() $\pm 0.1|\mathit{Ro}|(1+{\it\omega})$
, while the axial vorticity contour levels are as per figure 2.
$\pm 0.1|\mathit{Ro}|(1+{\it\omega})$
, while the axial vorticity contour levels are as per figure 2.
Contours of the axial velocity and axial vorticity of the axisymmetric steady-state base flows for a variety of values of
![]() $A$
at fixed
$A$
at fixed
![]() $\mathit{Ro}=0.3$
and
$\mathit{Ro}=0.3$
and
![]() $\mathit{E}\,=7\times 10^{-4}$
are illustrated in figure 5. The contours of axial velocity demonstrate a pair of meridional circulations on each horizontal boundary for all
$\mathit{E}\,=7\times 10^{-4}$
are illustrated in figure 5. The contours of axial velocity demonstrate a pair of meridional circulations on each horizontal boundary for all
![]() $A$
investigated, while the axial vorticity contours display a column of vorticity at
$A$
investigated, while the axial vorticity contours display a column of vorticity at
![]() $r=1$
. For small
$r=1$
. For small
![]() $A$
, variation of the flow is largely confined near
$A$
, variation of the flow is largely confined near
![]() $r=1$
, where the axial vorticity is strongly concentrated as a column. The meridional circulation and the vorticity column broaden as the aspect ratio is increased. This broadening effect is more clearly seen in the contours of axial velocity where at
$r=1$
, where the axial vorticity is strongly concentrated as a column. The meridional circulation and the vorticity column broaden as the aspect ratio is increased. This broadening effect is more clearly seen in the contours of axial velocity where at
![]() $A=2$
, the recirculation zones have extended to the entire radial domain. It is apparent that the axis of symmetry and the sidewalls are influencing the flow at this aspect ratio. Presumably this will act to limit the Stewartson layer scaling with
$A=2$
, the recirculation zones have extended to the entire radial domain. It is apparent that the axis of symmetry and the sidewalls are influencing the flow at this aspect ratio. Presumably this will act to limit the Stewartson layer scaling with
![]() $H$
(and
$H$
(and
![]() $A$
). Despite this, the reflective symmetry about mid-depth in the axial velocity contours is maintained throughout the entire range of
$A$
). Despite this, the reflective symmetry about mid-depth in the axial velocity contours is maintained throughout the entire range of
![]() $A$
. Although the shear layer becomes progressively weaker and thicker with increasing
$A$
. Although the shear layer becomes progressively weaker and thicker with increasing
![]() $A$
, an approximately depth-independent region still persists at large
$A$
, an approximately depth-independent region still persists at large
![]() $A$
. These characteristics are consistent through a large range of
$A$
. These characteristics are consistent through a large range of
![]() $E$
and
$E$
and
![]() $Ro$
conditions investigated here, as will be discussed in § 3.2.3.
$Ro$
conditions investigated here, as will be discussed in § 3.2.3.
3.2.2. Vertical shear-layer profile and thickness
Despite the qualitative similarities between the solutions for the various aspect ratios, the profiles of axial vorticity for the smallest and largest
![]() $A$
illustrate significant differences. The data for the axial vorticity have been extracted at mid-depth and are presented using two different scalings in figure 6(a,b). In (a), the relative axial vorticity has been scaled by
$A$
illustrate significant differences. The data for the axial vorticity have been extracted at mid-depth and are presented using two different scalings in figure 6(a,b). In (a), the relative axial vorticity has been scaled by
![]() $(4A\mathit{Ro})/(1-A\mathit{Ro})$
, which collapses the disk and tank vorticities to values of 1 and 0 respectively. This plot demonstrates a weakening of the vorticity in the shear layer and a broadening of the shear layer with increasing
$(4A\mathit{Ro})/(1-A\mathit{Ro})$
, which collapses the disk and tank vorticities to values of 1 and 0 respectively. This plot demonstrates a weakening of the vorticity in the shear layer and a broadening of the shear layer with increasing
![]() $A$
. That is, the shearing effect is less pronounced as the aspect ratio is increased. For
$A$
. That is, the shearing effect is less pronounced as the aspect ratio is increased. For
![]() $A=1/6$
, the profile strongly depicts flow adopting an axial vorticity value associated with the differential-rotation rate
$A=1/6$
, the profile strongly depicts flow adopting an axial vorticity value associated with the differential-rotation rate
![]() $(({\it\omega}_{z}-2)(1-A\mathit{Ro})/(4A\mathit{Ro})=1)$
for
$(({\it\omega}_{z}-2)(1-A\mathit{Ro})/(4A\mathit{Ro})=1)$
for
![]() $r\lesssim 0.9$
, and a value associated with the tank rotation rate
$r\lesssim 0.9$
, and a value associated with the tank rotation rate
![]() $(({\it\omega}_{z}-2)(1-A\mathit{Ro})/(4A\mathit{Ro})=0)$
for
$(({\it\omega}_{z}-2)(1-A\mathit{Ro})/(4A\mathit{Ro})=0)$
for
![]() $r\gtrsim 1.1$
. As the aspect ratio is increased, the radial extent over which the flow adopts neither 1 or 0 for
$r\gtrsim 1.1$
. As the aspect ratio is increased, the radial extent over which the flow adopts neither 1 or 0 for
![]() $({\it\omega}_{z}-2)(1-A\mathit{Ro})/(4A\mathit{Ro})$
also increases. At sufficiently high
$({\it\omega}_{z}-2)(1-A\mathit{Ro})/(4A\mathit{Ro})$
also increases. At sufficiently high
![]() $A$
, the flow begins to exhibit values less than those induced by the disk and tank. That is, there is no part of the interior exhibiting solid-body rotation with either the disk or the tank – the enclosure is confining the Stewartson layer. For example, at
$A$
, the flow begins to exhibit values less than those induced by the disk and tank. That is, there is no part of the interior exhibiting solid-body rotation with either the disk or the tank – the enclosure is confining the Stewartson layer. For example, at
![]() $A=2$
, the flow adopts approximately 88 % of the relative axial vorticity generated by the disk at
$A=2$
, the flow adopts approximately 88 % of the relative axial vorticity generated by the disk at
![]() $r=0$
and approximately 91 % of the axial vorticity generated by the tank at
$r=0$
and approximately 91 % of the axial vorticity generated by the tank at
![]() $r=2$
. The pronounced meridional circulations evident at larger
$r=2$
. The pronounced meridional circulations evident at larger
![]() $A$
may be responsible for the weakening of axial vorticity in the interior flow.
$A$
may be responsible for the weakening of axial vorticity in the interior flow.

Figure 6. Profiles of variables as a function of aspect ratio: (a) the scaled relative axial vorticity against radius; (b) the relative axial vorticity against a scaled radius; (c) the axial velocity against radius; (d) the axial velocity normalized by its respective maximum value against a scaled radius. Panels (a,b) have been extracted at
![]() $z/A=0.5$
(mid-depth) while (c,d) have been extracted at
$z/A=0.5$
(mid-depth) while (c,d) have been extracted at
![]() $z/A=0.9$
.
$z/A=0.9$
.
In panel (b), the unscaled relative axial vorticity is shown to demonstrate similarity in the radial locations of the profile minima. The radius has been scaled as
![]() $(r-1)/A$
to portray the similarity between each curve and to illustrate the diminishing radial range over which a constant vorticity value is exhibited with increasing
$(r-1)/A$
to portray the similarity between each curve and to illustrate the diminishing radial range over which a constant vorticity value is exhibited with increasing
![]() $A$
. A slight shift in the local minimum of each curve towards the tank sidewall with increasing
$A$
. A slight shift in the local minimum of each curve towards the tank sidewall with increasing
![]() $A$
can also be seen.
$A$
can also be seen.
The shift in the local minimum can be explained by the asymmetry in the recirculation on either side of the axial jet produced at the disk–tank interface, as shown in panel (c). Although it is difficult to see, the profile of
![]() $A=1/6$
is almost symmetric about the disk radius with the circulations on either side of the jet exhibiting similar strengths. However, the asymmetry becomes more pronounced with increasing aspect ratio. The asymmetry is more clearly depicted in panel (d), which is a plot of the axial velocity scaled against its respective maximum value as a function of
$A=1/6$
is almost symmetric about the disk radius with the circulations on either side of the jet exhibiting similar strengths. However, the asymmetry becomes more pronounced with increasing aspect ratio. The asymmetry is more clearly depicted in panel (d), which is a plot of the axial velocity scaled against its respective maximum value as a function of
![]() $(r-1)/A$
. The magnitude of the axial velocity is seen to increase with increasing
$(r-1)/A$
. The magnitude of the axial velocity is seen to increase with increasing
![]() $A$
for negative values of
$A$
for negative values of
![]() $(r-1)/A$
while it decreases for positive values of
$(r-1)/A$
while it decreases for positive values of
![]() $(r-1)/A$
. Thus, it appears that the jet has shifted slightly towards the tank sidewall in order to compensate for the stronger circulation displayed on the side closer to the axis of rotation.
$(r-1)/A$
. Thus, it appears that the jet has shifted slightly towards the tank sidewall in order to compensate for the stronger circulation displayed on the side closer to the axis of rotation.

Figure 7. The shear-layer thickness based on (a) the relative azimuthal velocity
![]() ${\it\delta}_{vel}$
and (b) the axial vorticity
${\it\delta}_{vel}$
and (b) the axial vorticity
![]() ${\it\delta}_{vort}$
, as a function of
${\it\delta}_{vort}$
, as a function of
![]() $A\mathit{E}\,^{1/4}$
and
$A\mathit{E}\,^{1/4}$
and
![]() $A\mathit{E}\,^{1/3}$
respectively. Data for
$A\mathit{E}\,^{1/3}$
respectively. Data for
![]() $A=1/6$
(♢),
$A=1/6$
(♢),
![]() $A=2/3$
(▫),
$A=2/3$
(▫),
![]() $A=4/3$
(▵) and
$A=4/3$
(▵) and
![]() $A=2$
(○) are shaded as a function of
$A=2$
(○) are shaded as a function of
![]() $\mathit{E}\,$
, where dark and light shading represents low and high
$\mathit{E}\,$
, where dark and light shading represents low and high
![]() $\mathit{E}\,$
respectively. The Rossby number examined is close to zero at
$\mathit{E}\,$
respectively. The Rossby number examined is close to zero at
![]() $\mathit{Ro}=0.005$
. The fitted long-dashed line is represented by
$\mathit{Ro}=0.005$
. The fitted long-dashed line is represented by
![]() ${\it\delta}_{vel}=1.71(\pm 0.02)[A\mathit{E}\,^{1/4}]^{1.00\pm 0.005}$
(a) and
${\it\delta}_{vel}=1.71(\pm 0.02)[A\mathit{E}\,^{1/4}]^{1.00\pm 0.005}$
(a) and
![]() ${\it\delta}_{vort}=2.26(\pm 0.04)[A\mathit{E}\,^{1/3}]^{0.991\pm 0.006}$
(b).
${\it\delta}_{vort}=2.26(\pm 0.04)[A\mathit{E}\,^{1/3}]^{0.991\pm 0.006}$
(b).
The measured thicknesses for
![]() ${\it\delta}_{vel}$
and
${\it\delta}_{vel}$
and
![]() ${\it\delta}_{vort}$
have been plotted against their respective theoretical scalings of
${\it\delta}_{vort}$
have been plotted against their respective theoretical scalings of
![]() $A\mathit{E}\,^{1/4}$
and
$A\mathit{E}\,^{1/4}$
and
![]() $A\mathit{E}\,^{1/3}$
in figure 7. Both shear layers demonstrate a very good agreement with the theoretical scaling, as evidenced by the highly linear relationship (power-law exponent of unity). The relationships of the fitted data (long-dashed lines) are given by
$A\mathit{E}\,^{1/3}$
in figure 7. Both shear layers demonstrate a very good agreement with the theoretical scaling, as evidenced by the highly linear relationship (power-law exponent of unity). The relationships of the fitted data (long-dashed lines) are given by
![]() ${\it\delta}_{vel}=1.71(\pm 0.02)[A\mathit{E}\,^{1/4}]^{1.00\pm 0.005}$
and
${\it\delta}_{vel}=1.71(\pm 0.02)[A\mathit{E}\,^{1/4}]^{1.00\pm 0.005}$
and
![]() ${\it\delta}_{vort}=2.26(\pm 0.04)[A\mathit{E}\,^{1/3}]^{0.991\pm 0.006}$
. Here, a unit exponent is obtained from thicknesses measured using a
${\it\delta}_{vort}=2.26(\pm 0.04)[A\mathit{E}\,^{1/3}]^{0.991\pm 0.006}$
. Here, a unit exponent is obtained from thicknesses measured using a
![]() $15\,\%$
threshold (see § 3.1.2). This scaling was almost insensitive to the arbitrary threshold used for thickness measurements; threshold values between
$15\,\%$
threshold (see § 3.1.2). This scaling was almost insensitive to the arbitrary threshold used for thickness measurements; threshold values between
![]() $5\,\%$
(achieving
$5\,\%$
(achieving
![]() $0.980\pm 0.010$
exponent) and
$0.980\pm 0.010$
exponent) and
![]() $30\,\%$
(achieving
$30\,\%$
(achieving
![]() $1.01\pm 0.005$
exponent) also demonstrated a highly linear relationship between
$1.01\pm 0.005$
exponent) also demonstrated a highly linear relationship between
![]() ${\it\delta}_{vel}$
and
${\it\delta}_{vel}$
and
![]() $A\mathit{E}\,^{1/4}$
. The small-thickness data (low
$A\mathit{E}\,^{1/4}$
. The small-thickness data (low
![]() $\mathit{E}\,$
and small
$\mathit{E}\,$
and small
![]() $A$
) align very well with the fitted line, which is in contrast to the large-thickness data points (high
$A$
) align very well with the fitted line, which is in contrast to the large-thickness data points (high
![]() $\mathit{E}\,$
and large
$\mathit{E}\,$
and large
![]() $A$
) where slight deviations from the fitted line are observed. The data begin to depart from the fitted line for
$A$
) where slight deviations from the fitted line are observed. The data begin to depart from the fitted line for
![]() $A\mathit{E}\,^{1/4}\gtrsim 0.34$
.
$A\mathit{E}\,^{1/4}\gtrsim 0.34$
.
The theoretical scaling is lost at sufficiently high
![]() $A\mathit{E}\,^{1/4}$
and
$A\mathit{E}\,^{1/4}$
and
![]() $A\mathit{E}\,^{1/3}$
due to the confining effects of the enclosure. This is more evident with the
$A\mathit{E}\,^{1/3}$
due to the confining effects of the enclosure. This is more evident with the
![]() $\mathit{E}\,^{1/4}$
layer as it is the thicker Stewartson layer. For the range of
$\mathit{E}\,^{1/4}$
layer as it is the thicker Stewartson layer. For the range of
![]() $\mathit{E}\,$
and
$\mathit{E}\,$
and
![]() $A$
investigated here, the
$A$
investigated here, the
![]() $\mathit{E}\,^{1/3}$
does not appear to be significantly affected by the confinement. These observations are supported by power-law fits of the shear-layer thicknesses as a function of
$\mathit{E}\,^{1/3}$
does not appear to be significantly affected by the confinement. These observations are supported by power-law fits of the shear-layer thicknesses as a function of
![]() $\mathit{E}\,$
alone for
$\mathit{E}\,$
alone for
![]() $1/6\leqslant A\leqslant 2$
. The exponents on
$1/6\leqslant A\leqslant 2$
. The exponents on
![]() $\mathit{E}\,$
obtained for
$\mathit{E}\,$
obtained for
![]() ${\it\delta}_{vel}$
are
${\it\delta}_{vel}$
are
![]() $0.245\pm 0.002~(A=1/6),0.260\pm 0.003~(A=2/3),0.248\pm 0.003~(A=4/3)$
and
$0.245\pm 0.002~(A=1/6),0.260\pm 0.003~(A=2/3),0.248\pm 0.003~(A=4/3)$
and
![]() $0.204\pm 0.005~(A=2)$
, deviating from the theoretical value by approximately
$0.204\pm 0.005~(A=2)$
, deviating from the theoretical value by approximately
![]() $2\,\%,4\,\%,0.8\,\%$
and
$2\,\%,4\,\%,0.8\,\%$
and
![]() $18.4\,\%$
respectively. The large deviation at
$18.4\,\%$
respectively. The large deviation at
![]() $A=2$
is due to the confinement effects of the container experienced by the thicker shear layers. However, for
$A=2$
is due to the confinement effects of the container experienced by the thicker shear layers. However, for
![]() ${\it\delta}_{vort}$
the exponents remain consistent around the theoretical value of
${\it\delta}_{vort}$
the exponents remain consistent around the theoretical value of
![]() $1/3$
, suggesting that confinement effects are not pronounced at these aspect ratios. The exponents on
$1/3$
, suggesting that confinement effects are not pronounced at these aspect ratios. The exponents on
![]() $\mathit{E}\,$
for
$\mathit{E}\,$
for
![]() ${\it\delta}_{vort}$
are given by
${\it\delta}_{vort}$
are given by
![]() $0.315\pm 0.016~(A=1/6)$
,
$0.315\pm 0.016~(A=1/6)$
,
![]() $0.310\pm 0.004~(A=2/3)$
,
$0.310\pm 0.004~(A=2/3)$
,
![]() $0.317\pm 0.002~(A=4/3)$
and
$0.317\pm 0.002~(A=4/3)$
and
![]() $0.323\pm 0.002~(A=2)$
. To further support the hypothesis that
$0.323\pm 0.002~(A=2)$
. To further support the hypothesis that
![]() ${\it\delta}_{vel}$
loses its
${\it\delta}_{vel}$
loses its
![]() $\mathit{E}\,^{1/4}$
scaling due to the thicker shear layers at high
$\mathit{E}\,^{1/4}$
scaling due to the thicker shear layers at high
![]() $\mathit{E}\,$
and
$\mathit{E}\,$
and
![]() $A=2$
, a systematic analysis was conducted whereby a set of regressions incorporating successively more points (starting from the smallest
$A=2$
, a systematic analysis was conducted whereby a set of regressions incorporating successively more points (starting from the smallest
![]() $\mathit{E}\,$
) were fitted to the power law. The data demonstrate an exponent on
$\mathit{E}\,$
) were fitted to the power law. The data demonstrate an exponent on
![]() $\mathit{E}\,$
of
$\mathit{E}\,$
of
![]() $0.255\pm 0.002$
for
$0.255\pm 0.002$
for
![]() $\mathit{E}\,\leqslant 1\times 10^{-4}$
, which gradually decreases towards
$\mathit{E}\,\leqslant 1\times 10^{-4}$
, which gradually decreases towards
![]() $0.204\pm 0.005$
(
$0.204\pm 0.005$
(
![]() $\mathit{E}\,\leqslant 3\times 10^{-3}$
) when larger
$\mathit{E}\,\leqslant 3\times 10^{-3}$
) when larger
![]() $\mathit{E}\,$
data are included. On performing the same analysis for
$\mathit{E}\,$
data are included. On performing the same analysis for
![]() $A=4/3$
, exponent values close to
$A=4/3$
, exponent values close to
![]() $1/4$
are consistently yielded, which suggests that over the range of Ekman numbers studied here, the Stewartson layers produced in
$1/4$
are consistently yielded, which suggests that over the range of Ekman numbers studied here, the Stewartson layers produced in
![]() $A\lesssim 4/3$
containers are unaffected by the confining walls.
$A\lesssim 4/3$
containers are unaffected by the confining walls.
Similarly, an independent relationship between
![]() ${\it\delta}$
and
${\it\delta}$
and
![]() $A$
can be established to determine the agreement with the theoretical definition of the Stewartson layer thickness, which has linear scaling with
$A$
can be established to determine the agreement with the theoretical definition of the Stewartson layer thickness, which has linear scaling with
![]() $A$
. Power-law fits of the data yield
$A$
. Power-law fits of the data yield
![]() ${\it\delta}_{vel}\propto A^{0.959\pm 0.036}$
and
${\it\delta}_{vel}\propto A^{0.959\pm 0.036}$
and
![]() ${\it\delta}_{vort}\propto A^{1.02\pm 0.01}$
at the largest
${\it\delta}_{vort}\propto A^{1.02\pm 0.01}$
at the largest
![]() $\mathit{E}\,=3\times 10^{-3}$
, and
$\mathit{E}\,=3\times 10^{-3}$
, and
![]() ${\it\delta}_{vel}\propto A^{1.01\pm 0.01}$
and
${\it\delta}_{vel}\propto A^{1.01\pm 0.01}$
and
![]() ${\it\delta}_{vort}\propto A^{1.04\pm 0.01}$
at the lowest
${\it\delta}_{vort}\propto A^{1.04\pm 0.01}$
at the lowest
![]() $\mathit{E}\,=5\times 10^{-5}$
. An approximate unit exponent for
$\mathit{E}\,=5\times 10^{-5}$
. An approximate unit exponent for
![]() $A$
is obtained between these two extreme
$A$
is obtained between these two extreme
![]() $\mathit{E}\,$
cases. Again,
$\mathit{E}\,$
cases. Again,
![]() ${\it\delta}_{vort}$
demonstrates excellent agreement with the theoretical scaling across all
${\it\delta}_{vort}$
demonstrates excellent agreement with the theoretical scaling across all
![]() $\mathit{E}\,$
since the thinner shear layers in this system are not significantly influenced by the confinement. In contrast, the thicker shear layers are modified by the confinement, resulting in the sub-unity exponent
$\mathit{E}\,$
since the thinner shear layers in this system are not significantly influenced by the confinement. In contrast, the thicker shear layers are modified by the confinement, resulting in the sub-unity exponent
![]() $0.959\pm 0.036$
at the largest Ekman number considered.
$0.959\pm 0.036$
at the largest Ekman number considered.
It has now been demonstrated that the theoretical relationships
![]() ${\it\delta}_{vel}\propto A\mathit{E}\,^{1/4}$
and
${\it\delta}_{vel}\propto A\mathit{E}\,^{1/4}$
and
![]() ${\it\delta}_{vort}\propto A\mathit{E}\,^{1/3}$
hold strongly throughout the majority of the explored parameter space. The slight deviations from the theoretical scalings are attributed to the confinement effects experienced by the shear layer. Additionally, the independent scalings of
${\it\delta}_{vort}\propto A\mathit{E}\,^{1/3}$
hold strongly throughout the majority of the explored parameter space. The slight deviations from the theoretical scalings are attributed to the confinement effects experienced by the shear layer. Additionally, the independent scalings of
![]() $A,\mathit{E}\,^{1/4}$
and
$A,\mathit{E}\,^{1/4}$
and
![]() $\mathit{E}\,^{1/3}$
for the shear-layer thicknesses have been recovered.
$\mathit{E}\,^{1/3}$
for the shear-layer thicknesses have been recovered.
It has been determined that increase in
![]() $\mathit{E}\,$
for a constant
$\mathit{E}\,$
for a constant
![]() $\mathit{Ro}$
yields an increasingly stable shear layer (Früh & Read Reference Früh and Read1999; Vo et al.
Reference Vo, Montabone and Sheard2014). Thus, it is expected that increase of the shear-layer thickness by increasing
$\mathit{Ro}$
yields an increasingly stable shear layer (Früh & Read Reference Früh and Read1999; Vo et al.
Reference Vo, Montabone and Sheard2014). Thus, it is expected that increase of the shear-layer thickness by increasing
![]() $A$
will also result in a more stable flow. Results of a linear stability analysis conducted on flows produced in large-aspect-ratio containers reinforce this idea and are examined later in § 4.2.
$A$
will also result in a more stable flow. Results of a linear stability analysis conducted on flows produced in large-aspect-ratio containers reinforce this idea and are examined later in § 4.2.
3.2.3. Aspect ratio dependence on the flow characterization
The height dependence of the flow structure as a function of the aspect ratio is now examined. A pair of non-dimensional parameters independent of height can be obtained from the Rossby and Ekman numbers. Substitution of
![]() $H=AR_{d}$
into the definitions of
$H=AR_{d}$
into the definitions of
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{E}\,$
((2.2) and (2.3)) and the search for a group of variables independent of height yield
$\mathit{E}\,$
((2.2) and (2.3)) and the search for a group of variables independent of height yield
The height dependence of the flow has been visually characterized into two categories as determined through contours of axial velocity. The categories and their associated axial velocity contours are shown in figure 8, with both cases belonging to the positive-
![]() $\mathit{Ro}$
regime. Category 1 demonstrates a reflective symmetry about the mid-plane while category 2 portrays a breaking of this symmetry.
$\mathit{Ro}$
regime. Category 1 demonstrates a reflective symmetry about the mid-plane while category 2 portrays a breaking of this symmetry.

Figure 8. The two types of axial velocity contours used to characterize the height dependence of the flow. Characterization is determined for steady-state axisymmetric flows. Category 1 (a) is reflectively symmetric about the mid-plane while category 2 (b) breaks the mid-plane symmetry. The flow conditions are (a)
![]() $(\mathit{Ro},\mathit{E}\,)=(9.97\times 10^{-3},2.99\times 10^{-3})$
and (b)
$(\mathit{Ro},\mathit{E}\,)=(9.97\times 10^{-3},2.99\times 10^{-3})$
and (b)
![]() $(\mathit{Ro},\mathit{E}\,)=(0.692,2.31\times 10^{-3})$
. Dark shading and dashed lines denote negative values; light shading and unbroken lines denote positive values.
$(\mathit{Ro},\mathit{E}\,)=(0.692,2.31\times 10^{-3})$
. Dark shading and dashed lines denote negative values; light shading and unbroken lines denote positive values.
The solution of the flow condition combined with the aspect ratio has been characterized as either category 1 or 2. Figure 9 shows a plot of
![]() $A\mathit{Ro}$
and
$A\mathit{Ro}$
and
![]() $\mathit{E}\,A^{2}$
and their respective category. Small-
$\mathit{E}\,A^{2}$
and their respective category. Small-
![]() $A\mathit{Ro}$
and large-
$A\mathit{Ro}$
and large-
![]() $\mathit{E}\,A^{2}$
regimes are seen to be dominated by category 1 flows. The flow transitions to category 2 with increasing
$\mathit{E}\,A^{2}$
regimes are seen to be dominated by category 1 flows. The flow transitions to category 2 with increasing
![]() $A\mathit{Ro}$
and decreasing
$A\mathit{Ro}$
and decreasing
![]() $\mathit{E}\,A^{2}$
.
$\mathit{E}\,A^{2}$
.

Figure 9. A plot of
![]() $A\mathit{Ro}$
against
$A\mathit{Ro}$
against
![]() $\mathit{E}\,A^{2}$
and its respective category as characterized in figure 8. The categories are coloured such that category 1 is represented by dark-shaded symbols (blue online) and category 2 by light-shaded symbols (yellow online). Aspect ratios of
$\mathit{E}\,A^{2}$
and its respective category as characterized in figure 8. The categories are coloured such that category 1 is represented by dark-shaded symbols (blue online) and category 2 by light-shaded symbols (yellow online). Aspect ratios of
![]() $A=1/6$
(▵),
$A=1/6$
(▵),
![]() $A=1/3$
(▿),
$A=1/3$
(▿),
![]() $A=2/3$
(▫),
$A=2/3$
(▫),
![]() $A=4/3$
(♢) and
$A=4/3$
(♢) and
![]() $A=2$
(○) are represented by different symbols. The solid line represents the transition between reflectively symmetric (category 1) and symmetry-broken (category 2) flow, which is governed by
$A=2$
(○) are represented by different symbols. The solid line represents the transition between reflectively symmetric (category 1) and symmetry-broken (category 2) flow, which is governed by
![]() $\mathit{Ro}_{c1-c2}=13.35\mathit{E}\,^{0.5}$
(
$\mathit{Ro}_{c1-c2}=13.35\mathit{E}\,^{0.5}$
(
![]() $\mathit{Re}_{\mathit{E}\,}=26.7$
). An upper bound for the transition represented by the dashed line is described by
$\mathit{Re}_{\mathit{E}\,}=26.7$
). An upper bound for the transition represented by the dashed line is described by
![]() $\mathit{Ro}_{c1-c2}=28.2\mathit{E}\,^{0.5}$
(
$\mathit{Ro}_{c1-c2}=28.2\mathit{E}\,^{0.5}$
(
![]() $\mathit{Re}_{\mathit{E}\,}=56.4$
). The shaded region bounded by the solid line and the dashed line represents a transition zone which exhibits both category 1 and category 2.
$\mathit{Re}_{\mathit{E}\,}=56.4$
). The shaded region bounded by the solid line and the dashed line represents a transition zone which exhibits both category 1 and category 2.
A transition between reflectively symmetric (category 1) and symmetry-broken flow (category 2) has been estimated. This was achieved by determining thresholds first for the appearance of category 2 flows and second for the disappearance of category 1 flows. The equation
![]() $A\mathit{Ro}_{c1-c2}=13.35(\mathit{E}\,A^{2})^{0.5}$
describes the onset of category 2 flows well and was determined by visual inspection. The relationship simplifies to
$A\mathit{Ro}_{c1-c2}=13.35(\mathit{E}\,A^{2})^{0.5}$
describes the onset of category 2 flows well and was determined by visual inspection. The relationship simplifies to
![]() $\mathit{Ro}_{c1-c2}=13.35\mathit{E}\,^{0.5}$
, which is independent of the aspect ratio, and is shown by the solid line in figure 9. Similarly, the equation
$\mathit{Ro}_{c1-c2}=13.35\mathit{E}\,^{0.5}$
, which is independent of the aspect ratio, and is shown by the solid line in figure 9. Similarly, the equation
![]() $\mathit{Ro}_{c1-c2}=28.2\mathit{E}\,^{0.5}$
was determined to describe where category 1 flows cease to appear, as is shown by the dashed line. These two relationships respectively form the lower and upper bounds of a transitional regime occupied by either category, as represented by shading in the figure. The relationships of the transitions suggest that the symmetry-breaking threshold can be described by a constant governed by
$\mathit{Ro}_{c1-c2}=28.2\mathit{E}\,^{0.5}$
was determined to describe where category 1 flows cease to appear, as is shown by the dashed line. These two relationships respectively form the lower and upper bounds of a transitional regime occupied by either category, as represented by shading in the figure. The relationships of the transitions suggest that the symmetry-breaking threshold can be described by a constant governed by
![]() $\mathit{Ro}/\sqrt{\mathit{E}\,}$
. This parameter group can be expressed in terms of the forcing parameters through
$\mathit{Ro}/\sqrt{\mathit{E}\,}$
. This parameter group can be expressed in terms of the forcing parameters through
Furthermore, the presence of
![]() $\sqrt{\mathit{E}\,}$
suggests that the breaking of reflective symmetry may scale with the Ekman layer thickness. By adopting a length scale of
$\sqrt{\mathit{E}\,}$
suggests that the breaking of reflective symmetry may scale with the Ekman layer thickness. By adopting a length scale of
![]() $L=\mathit{E}\,^{1/2}H$
and a velocity scale of
$L=\mathit{E}\,^{1/2}H$
and a velocity scale of
![]() $U=R_{d}{\it\omega}$
, a Reynolds number based on the Ekman layer thickness can be defined as
$U=R_{d}{\it\omega}$
, a Reynolds number based on the Ekman layer thickness can be defined as
Thus, combination of the threshold equations of
![]() $\mathit{Ro}_{c1-c2}=13.35\mathit{E}\,^{0.5}$
(lower bound) and
$\mathit{Ro}_{c1-c2}=13.35\mathit{E}\,^{0.5}$
(lower bound) and
![]() $\mathit{Ro}_{c1-c2}=28.2\mathit{E}\,^{0.5}$
(upper bound) with (3.4) yields constant values of
$\mathit{Ro}_{c1-c2}=28.2\mathit{E}\,^{0.5}$
(upper bound) with (3.4) yields constant values of
![]() $\mathit{Re}_{\mathit{E}\,}=26.7$
and
$\mathit{Re}_{\mathit{E}\,}=26.7$
and
![]() $\mathit{Re}_{\mathit{E}\,}=56.4$
respectively.
$\mathit{Re}_{\mathit{E}\,}=56.4$
respectively.

Figure 10. Axial velocity contours of (a)
![]() $\mathit{Ro}=-0.3$
and (b)
$\mathit{Ro}=-0.3$
and (b)
![]() $\mathit{Ro}=-2$
for
$\mathit{Ro}=-2$
for
![]() $\mathit{E}\,=3\times 10^{-4}$
. Both cases demonstrate reflective symmetry about the horizontal mid-plane. The contour levels are as per figure 5.
$\mathit{E}\,=3\times 10^{-4}$
. Both cases demonstrate reflective symmetry about the horizontal mid-plane. The contour levels are as per figure 5.
All of the axisymmetric steady-state flows in the negative-
![]() $\mathit{Ro}$
regime demonstrated reflective symmetry about the mid-plane in the axial velocity contours. The axial velocity contours for a small and large negative-
$\mathit{Ro}$
regime demonstrated reflective symmetry about the mid-plane in the axial velocity contours. The axial velocity contours for a small and large negative-
![]() $\mathit{Ro}$
flow are shown in figure 10 (also see figure 2
b iii, iv). The small-
$\mathit{Ro}$
flow are shown in figure 10 (also see figure 2
b iii, iv). The small-
![]() $\mathit{Ro}$
flow with
$\mathit{Ro}$
flow with
![]() $\mathit{Ro}=-0.3$
demonstrates Ekman pumping and suction on the horizontal boundaries which is reflectively symmetric about the mid-plane, similar to that of the small-positive-
$\mathit{Ro}=-0.3$
demonstrates Ekman pumping and suction on the horizontal boundaries which is reflectively symmetric about the mid-plane, similar to that of the small-positive-
![]() $\mathit{Ro}$
cases. Increase of
$\mathit{Ro}$
cases. Increase of
![]() $|\mathit{Ro}|$
in the negative-
$|\mathit{Ro}|$
in the negative-
![]() $\mathit{Ro}$
regime causes a deviation from this typical structure such that an extra circulation is created at the inner side of the fluid pumping and suction zone. However, this altered structure continues to exhibit reflective symmetry about the mid-plane in the axial velocity contours. Thus, in considering only axisymmetric steady-state flows, the negative-
$\mathit{Ro}$
regime causes a deviation from this typical structure such that an extra circulation is created at the inner side of the fluid pumping and suction zone. However, this altered structure continues to exhibit reflective symmetry about the mid-plane in the axial velocity contours. Thus, in considering only axisymmetric steady-state flows, the negative-
![]() $A\mathit{Ro}$
regime is characterized only by category 1 flow. In the positive-
$A\mathit{Ro}$
regime is characterized only by category 1 flow. In the positive-
![]() $A\mathit{Ro}$
regime, the flow conditions are limited by
$A\mathit{Ro}$
regime, the flow conditions are limited by
![]() $A\mathit{Ro}=1$
, which corresponds to
$A\mathit{Ro}=1$
, which corresponds to
![]() ${\it\omega}\rightarrow \infty$
. This constraint has been described in § 2.2.
${\it\omega}\rightarrow \infty$
. This constraint has been described in § 2.2.
4. Results: linear stability analysis
Following the structure of the previous section, a comparison between the axisymmetric and quasi-two-dimensional solutions for
![]() $A=2/3$
, and the solutions of the axisymmetric model for a variety of
$A=2/3$
, and the solutions of the axisymmetric model for a variety of
![]() $A$
are described separately in the following subsections.
$A$
are described separately in the following subsections.
4.1. Axisymmetric and quasi-two-dimensional models (
 $A=2/3$
)
$A=2/3$
)
The growth rates for a range of azimuthal wavenumbers were obtained throughout the parameter space for both the quasi-two-dimensional and axisymmetric models. The data identify the most unstable linear wavenumbers and the onset of instability as a function of
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{E}\,$
. Regime diagrams for both the negative- and positive-
$\mathit{E}\,$
. Regime diagrams for both the negative- and positive-
![]() $\mathit{Ro}$
regimes have been generated for the axisymmetric model with
$\mathit{Ro}$
regimes have been generated for the axisymmetric model with
![]() $A=2/3$
in Vo et al. (Reference Vo, Montabone and Sheard2014). Here, similar regime maps have been generated for the quasi-two-dimensional model with
$A=2/3$
in Vo et al. (Reference Vo, Montabone and Sheard2014). Here, similar regime maps have been generated for the quasi-two-dimensional model with
![]() $A=2/3$
. Again, the discussion in this section is focused on quasi-two-dimensional results with differences from the axisymmetric model being highlighted.
$A=2/3$
. Again, the discussion in this section is focused on quasi-two-dimensional results with differences from the axisymmetric model being highlighted.
4.1.1. Preferred azimuthal wavenumbers
The linear stability analysis determined growth rates over a wide range of azimuthal wavenumbers. Fractional peak wavenumbers and the corresponding peak growth rates were then calculated via the local maximum of a parabolic fitting of the peak and the adjacent wavenumbers (growth rate data are shown later in § 4.1.2). The analysis predicts identical preferred azimuthal wavenumbers for positive- and negative-
![]() $\mathit{Ro}$
quasi-two-dimensional flows, and therefore the most unstable wavenumber is a function of
$\mathit{Ro}$
quasi-two-dimensional flows, and therefore the most unstable wavenumber is a function of
![]() $|\mathit{Ro}|$
rather than
$|\mathit{Ro}|$
rather than
![]() $\mathit{Ro}$
itself. The regime diagram of the preferred wavenumber as a function of
$\mathit{Ro}$
itself. The regime diagram of the preferred wavenumber as a function of
![]() $|\mathit{Ro}|$
and
$|\mathit{Ro}|$
and
![]() $\mathit{E}\,$
is presented in figure 11(a). The number depicted within the contour bands on the regime diagram represents a range of fractional wavenumbers. For example, a contour band of 7 represents wavenumbers in the range
$\mathit{E}\,$
is presented in figure 11(a). The number depicted within the contour bands on the regime diagram represents a range of fractional wavenumbers. For example, a contour band of 7 represents wavenumbers in the range
![]() $6.5\leqslant k<7.5$
. Data from over 100 different flow conditions were used to produce the regime diagram. The regime diagram also includes the instability onset determined from both models for comparison.
$6.5\leqslant k<7.5$
. Data from over 100 different flow conditions were used to produce the regime diagram. The regime diagram also includes the instability onset determined from both models for comparison.

Figure 11. (a) The regime diagram of the most unstable linear wavenumber as a function of
![]() $\mathit{E}\,$
and
$\mathit{E}\,$
and
![]() $|\mathit{Ro}|$
for the quasi-two-dimensional model. The short-dashed lines represent the transition between one wavenumber and another, denoted by the labels shown within the band. The azimuthal wavenumber is associated with the mode I instability. The solid boundary lines represent the range of triangulation. The left thick-dashed boundary line represents the stability threshold, which is given by
$|\mathit{Ro}|$
for the quasi-two-dimensional model. The short-dashed lines represent the transition between one wavenumber and another, denoted by the labels shown within the band. The azimuthal wavenumber is associated with the mode I instability. The solid boundary lines represent the range of triangulation. The left thick-dashed boundary line represents the stability threshold, which is given by
![]() $|\mathit{Ro}_{c}|=18.7(\pm 0.7)\mathit{E}\,^{0.769\pm 0.005}$
(quasi-two-dimensional model) and
$|\mathit{Ro}_{c}|=18.7(\pm 0.7)\mathit{E}\,^{0.769\pm 0.005}$
(quasi-two-dimensional model) and
![]() $|\mathit{Ro}_{c}|=18.1(\pm 0.8)\mathit{E}\,^{0.767\pm 0.006}$
(axisymmetric model). These thresholds are determined using both positive- and negative-
$|\mathit{Ro}_{c}|=18.1(\pm 0.8)\mathit{E}\,^{0.767\pm 0.006}$
(axisymmetric model). These thresholds are determined using both positive- and negative-
![]() $\mathit{Ro}$
data. (b) Regression of the preferred azimuthal wavelength of the mode I instability through a plot of
$\mathit{Ro}$
data. (b) Regression of the preferred azimuthal wavelength of the mode I instability through a plot of
![]() $\log _{10}({\it\lambda}_{{\it\theta}})$
against
$\log _{10}({\it\lambda}_{{\it\theta}})$
against
![]() $\log _{10}(|\mathit{Ro}|/\mathit{E}\,^{2})$
. The data points here correspond to flow conditions of
$\log _{10}(|\mathit{Ro}|/\mathit{E}\,^{2})$
. The data points here correspond to flow conditions of
![]() $\mathit{Re}_{E}\lesssim 26.7$
from the quasi-two-dimensional solutions. The fitted lines are defined by
$\mathit{Re}_{E}\lesssim 26.7$
from the quasi-two-dimensional solutions. The fitted lines are defined by
![]() ${\it\lambda}_{{\it\theta}}=10.7(\pm 0.4)[|\mathit{Ro}|/\mathit{E}\,^{2}]^{-0.160\pm 0.002}$
(quasi-two-dimensional model) and
${\it\lambda}_{{\it\theta}}=10.7(\pm 0.4)[|\mathit{Ro}|/\mathit{E}\,^{2}]^{-0.160\pm 0.002}$
(quasi-two-dimensional model) and
![]() ${\it\lambda}_{{\it\theta}}=12.0(\pm 0.4)[|\mathit{Ro}|/\mathit{E}\,^{2}]^{-0.169\pm 0.002}$
(axisymmetric model).
${\it\lambda}_{{\it\theta}}=12.0(\pm 0.4)[|\mathit{Ro}|/\mathit{E}\,^{2}]^{-0.169\pm 0.002}$
(axisymmetric model).
The threshold line was determined by empirically fitting data points of
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{E}\,$
that correspond to zero growth rates for both positive- and negative-
$\mathit{E}\,$
that correspond to zero growth rates for both positive- and negative-
![]() $\mathit{Ro}$
flows. This yields a relationship between
$\mathit{Ro}$
flows. This yields a relationship between
![]() $|\mathit{Ro}|$
and
$|\mathit{Ro}|$
and
![]() $\mathit{E}\,$
given by
$\mathit{E}\,$
given by
The exponent of
![]() $\mathit{E}\,$
is comparable with the relationship obtained from the axisymmetric model, namely
$\mathit{E}\,$
is comparable with the relationship obtained from the axisymmetric model, namely
![]() $0.767\pm 0.006$
, and is in good agreement with the theoretical value of
$0.767\pm 0.006$
, and is in good agreement with the theoretical value of
![]() $3/4$
. This suggests that the
$3/4$
. This suggests that the
![]() $\mathit{E}\,^{1/3}$
shear layer does not significantly influence the stability of the base flow to three-dimensional disturbances, particularly at the onset of instability. Furthermore, the values of the coefficient of the Ekman number in the stability threshold relationship between the quasi-two-dimensional model and the axisymmetric simulations are comparable, namely
$\mathit{E}\,^{1/3}$
shear layer does not significantly influence the stability of the base flow to three-dimensional disturbances, particularly at the onset of instability. Furthermore, the values of the coefficient of the Ekman number in the stability threshold relationship between the quasi-two-dimensional model and the axisymmetric simulations are comparable, namely
![]() $18.7(\pm 0.7)$
and
$18.7(\pm 0.7)$
and
![]() $18.1(\pm 0.8)$
respectively.
$18.1(\pm 0.8)$
respectively.
The linear stability analysis also demonstrates an increase in preferred azimuthal wavenumber with increasing
![]() $|\mathit{Ro}|$
and decreasing
$|\mathit{Ro}|$
and decreasing
![]() $\mathit{E}\,$
. This is surprising since the preferred azimuthal wavenumber of the instability was thought to be related to the thickness of the shear layer, for which quasi-two-dimensional flows have shown no dependence on
$\mathit{E}\,$
. This is surprising since the preferred azimuthal wavenumber of the instability was thought to be related to the thickness of the shear layer, for which quasi-two-dimensional flows have shown no dependence on
![]() $\mathit{Ro}$
(§ 3.1.2). Thus, these trends depict unstable wavenumbers as being functions of both
$\mathit{Ro}$
(§ 3.1.2). Thus, these trends depict unstable wavenumbers as being functions of both
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{E}\,$
, in agreement with previous experimental studies (Früh & Read Reference Früh and Read1999; Aguiar et al.
Reference Aguiar, Read, Wordsworth, Salter and Hiro Yamazaki2010).
$\mathit{E}\,$
, in agreement with previous experimental studies (Früh & Read Reference Früh and Read1999; Aguiar et al.
Reference Aguiar, Read, Wordsworth, Salter and Hiro Yamazaki2010).
The preferred wavenumbers depict trends similar to those observed from the axisymmetric model (see Vo et al.
Reference Vo, Montabone and Sheard2014). The lines of constant wavenumber of the quasi-two-dimensional solutions in figure 11(a) illustrate comparable contour lines to those in the positive low-
![]() $\mathit{Re}_{i}$
regime and all negative-
$\mathit{Re}_{i}$
regime and all negative-
![]() $\mathit{Re}_{i}$
flows produced via axisymmetric simulations. The difference at high-
$\mathit{Re}_{i}$
flows produced via axisymmetric simulations. The difference at high-
![]() $\mathit{Re}_{i}$
flows in the positive-
$\mathit{Re}_{i}$
flows in the positive-
![]() $\mathit{Re}_{i}$
regime is due to the depth-dependent structures that arise in the axisymmetric model, which in turn encourages the growth of other instability modes (i.e. mode II). Thus, a comparison of the data associated with reflectively symmetric flows can be used to illustrate the similarities in preferred wavenumbers between the two models. From § 3.2.3, it is now known that the regime of reflectively symmetric flow is given by
$\mathit{Re}_{i}$
regime is due to the depth-dependent structures that arise in the axisymmetric model, which in turn encourages the growth of other instability modes (i.e. mode II). Thus, a comparison of the data associated with reflectively symmetric flows can be used to illustrate the similarities in preferred wavenumbers between the two models. From § 3.2.3, it is now known that the regime of reflectively symmetric flow is given by
![]() $\mathit{Re}_{\mathit{E}\,}\lesssim 26.7$
. Under this constraint, the preferred wavelength relationship is found to be
$\mathit{Re}_{\mathit{E}\,}\lesssim 26.7$
. Under this constraint, the preferred wavelength relationship is found to be
![]() ${\it\lambda}_{{\it\theta}}=12.0(\pm 0.4)[|\mathit{Ro}|/\mathit{E}\,^{2}]^{-0.169\pm 0.002}$
for the axisymmetric model, which is represented by the dashed line in figure 11(b). For the same range of
${\it\lambda}_{{\it\theta}}=12.0(\pm 0.4)[|\mathit{Ro}|/\mathit{E}\,^{2}]^{-0.169\pm 0.002}$
for the axisymmetric model, which is represented by the dashed line in figure 11(b). For the same range of
![]() $\mathit{Re}_{\mathit{E}\,}$
, the quasi-two-dimensional model provides a preferred azimuthal wavelength relationship given by
$\mathit{Re}_{\mathit{E}\,}$
, the quasi-two-dimensional model provides a preferred azimuthal wavelength relationship given by
represented by the solid line. Despite the agreement in the instability thresholds between the two models, there is a statistically significant difference between the wavelength relationships. This may be due to the wavelength relationship utilizing data throughout the entire parameter space rather than only those situated at the threshold. Vo et al. (Reference Vo, Montabone and Sheard2014) observed unstable azimuthal wavenumbers, changing its dependence from
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{E}\,$
at low
$\mathit{E}\,$
at low
![]() $\mathit{Re}_{i}$
to predominantly
$\mathit{Re}_{i}$
to predominantly
![]() $\mathit{Ro}$
at higher
$\mathit{Ro}$
at higher
![]() $\mathit{Re}_{i}$
where the mode II instability arises. Although empirical fits were performed on
$\mathit{Re}_{i}$
where the mode II instability arises. Although empirical fits were performed on
![]() $\mathit{Re}_{\mathit{E}\,}\lesssim 26.7$
, there is still evidence of the preferred wavenumber of the mode I instability differing between the quasi-two-dimensional and axisymmetric models in that regime.
$\mathit{Re}_{\mathit{E}\,}\lesssim 26.7$
, there is still evidence of the preferred wavenumber of the mode I instability differing between the quasi-two-dimensional and axisymmetric models in that regime.
The relationships of both models scale approximately with
![]() ${\it\lambda}_{{\it\theta}}\propto \mathit{E}\,^{1/3}/|\mathit{Ro}|^{1/6}$
. It was proposed by Vo et al. (Reference Vo, Montabone and Sheard2014) that the
${\it\lambda}_{{\it\theta}}\propto \mathit{E}\,^{1/3}/|\mathit{Ro}|^{1/6}$
. It was proposed by Vo et al. (Reference Vo, Montabone and Sheard2014) that the
![]() $\mathit{E}\,^{1/3}$
scale may be due to the
$\mathit{E}\,^{1/3}$
scale may be due to the
![]() $\mathit{E}\,^{1/3}$
Stewartson layer. However, since the quasi-two-dimensional model does not capture the
$\mathit{E}\,^{1/3}$
Stewartson layer. However, since the quasi-two-dimensional model does not capture the
![]() $\mathit{E}\,^{1/3}$
layer, this analysis conclusively demonstrates that the
$\mathit{E}\,^{1/3}$
layer, this analysis conclusively demonstrates that the
![]() $\mathit{E}\,^{1/3}$
scaling in the preferred wavelength is not related to the
$\mathit{E}\,^{1/3}$
scaling in the preferred wavelength is not related to the
![]() $\mathit{E}\,^{1/3}$
Stewartson layer.
$\mathit{E}\,^{1/3}$
Stewartson layer.
The linear stability analysis results thus far have illustrated very small differences between the quasi-two-dimensional and axisymmetric model solutions in terms of the preferred wavenumbers for reflectively symmetric flows and the onset of instability. To further elucidate the similarities and differences between the two models, the growth rates and the instability mode shapes are investigated in the following sections.

Figure 12. Growth rate
![]() ${\it\sigma}$
as a function of azimuthal wavenumber
${\it\sigma}$
as a function of azimuthal wavenumber
![]() $k$
for various
$k$
for various
![]() $\mathit{E}\,$
at
$\mathit{E}\,$
at
![]() $\mathit{Ro}=0.395$
from (a) the quasi-two-dimensional model and (b) the axisymmetric model. The quasi-two-dimensional solutions illustrate only the mode I instability while the axisymmetric model demonstrates modes I and II. The dashed line represents neutral stability, where points above and below symbolize unstable and stable modes respectively.
$\mathit{Ro}=0.395$
from (a) the quasi-two-dimensional model and (b) the axisymmetric model. The quasi-two-dimensional solutions illustrate only the mode I instability while the axisymmetric model demonstrates modes I and II. The dashed line represents neutral stability, where points above and below symbolize unstable and stable modes respectively.
4.1.2. Growth rates
A comparison between the linear stability analysis results obtained from the quasi-two-dimensional model and the axisymmetric model at high
![]() $\mathit{Re}_{i}$
is demonstrated in figure 12 for
$\mathit{Re}_{i}$
is demonstrated in figure 12 for
![]() $\mathit{Ro}=0.395$
at various values of
$\mathit{Ro}=0.395$
at various values of
![]() $\mathit{E}\,$
. A single instability mode is observed in the quasi-two-dimensional model solutions (figure 12
a) which is associated with the mode I instability. The absence of the mode II instability in the quasi-two-dimensional solutions supports the suggestion from Vo et al. (Reference Vo, Montabone and Sheard2014) that the origin of the mode II instability is related to depth-dependent features in the base flows. The presence of the mode II instability is illustrated in (b), which shows the growth rates predicted from the axisymmetric model for the same flow conditions as in (a). The flow is unstable to the mode II instability for
$\mathit{E}\,$
. A single instability mode is observed in the quasi-two-dimensional model solutions (figure 12
a) which is associated with the mode I instability. The absence of the mode II instability in the quasi-two-dimensional solutions supports the suggestion from Vo et al. (Reference Vo, Montabone and Sheard2014) that the origin of the mode II instability is related to depth-dependent features in the base flows. The presence of the mode II instability is illustrated in (b), which shows the growth rates predicted from the axisymmetric model for the same flow conditions as in (a). The flow is unstable to the mode II instability for
![]() $\mathit{E}\,\leqslant 9.47\times 10^{-4}$
. Although the growth rate data for
$\mathit{E}\,\leqslant 9.47\times 10^{-4}$
. Although the growth rate data for
![]() $\mathit{E}\,=1.05\times 10^{-3}$
depict a waveband for structures consistent with the mode II perturbations, the growth rates are all negative and therefore the mode II instability would not be observable at that Ekman number. The growth rates and the most unstable azimuthal wavenumber are comparable for
$\mathit{E}\,=1.05\times 10^{-3}$
depict a waveband for structures consistent with the mode II perturbations, the growth rates are all negative and therefore the mode II instability would not be observable at that Ekman number. The growth rates and the most unstable azimuthal wavenumber are comparable for
![]() $\mathit{E}\,=3.16\times 10^{-3}$
between both the axisymmetric and quasi-two-dimensional models, while the mode II instability is absent in the axisymmetric model solution. This agreement is lost at lower
$\mathit{E}\,=3.16\times 10^{-3}$
between both the axisymmetric and quasi-two-dimensional models, while the mode II instability is absent in the axisymmetric model solution. This agreement is lost at lower
![]() $\mathit{E}\,$
where the depth-dependent structures suppress the growth of the mode I instability and lower the preferred wavenumber. This is why the wavelength analysis presented in the previous section was conducted for reflectively symmetric flows only.
$\mathit{E}\,$
where the depth-dependent structures suppress the growth of the mode I instability and lower the preferred wavenumber. This is why the wavelength analysis presented in the previous section was conducted for reflectively symmetric flows only.
The qualitative trends in growth rate and preferential wavenumber are similar between the axisymmetric and quasi-two-dimensional models. That is, the growth rates of the perturbations introduced into the base flow increase with decreasing
![]() $\mathit{E}\,$
. This may be explained as follows: decreasing the Ekman number causes the Stewartson layers to become thinner, which leads to greater susceptibility to instability. Additionally, the preferred azimuthal wavenumber increases with decreasing
$\mathit{E}\,$
. This may be explained as follows: decreasing the Ekman number causes the Stewartson layers to become thinner, which leads to greater susceptibility to instability. Additionally, the preferred azimuthal wavenumber increases with decreasing
![]() $\mathit{E}\,$
provided the flow is mode I dominant. Similar trends are observed with varying Rossby number, whereby increasing
$\mathit{E}\,$
provided the flow is mode I dominant. Similar trends are observed with varying Rossby number, whereby increasing
![]() $\mathit{Ro}$
yields larger growth rates and higher preferred azimuthal wavenumbers. A clearer depiction of these trends is illustrated via the regime diagram (figure 11
a). Furthermore, it is determined that the preferred azimuthal wavenumbers between the positive- and negative-
$\mathit{Ro}$
yields larger growth rates and higher preferred azimuthal wavenumbers. A clearer depiction of these trends is illustrated via the regime diagram (figure 11
a). Furthermore, it is determined that the preferred azimuthal wavenumbers between the positive- and negative-
![]() $\mathit{Ro}$
regimes are identical for the quasi-two-dimensional model, which is in contrast to the results for the axisymmetric model (Vo et al.
Reference Vo, Montabone and Sheard2014). However, the growth rates differ between positive- and negative-
$\mathit{Ro}$
regimes are identical for the quasi-two-dimensional model, which is in contrast to the results for the axisymmetric model (Vo et al.
Reference Vo, Montabone and Sheard2014). However, the growth rates differ between positive- and negative-
![]() $\mathit{Ro}$
in the quasi-two-dimensional model despite the identical wavenumbers. The difference in growth rates between the two regimes is discussed later in § 4.1.4.
$\mathit{Ro}$
in the quasi-two-dimensional model despite the identical wavenumbers. The difference in growth rates between the two regimes is discussed later in § 4.1.4.
4.1.3. Global instability mode shapes and visualization on the horizontal plane
The profile of the growth rate as a function of azimuthal wavenumber for the quasi-two-dimensional model has revealed only one type of instability mode which is suspected to be the mode I instability. To confirm this, the dominant quasi-two-dimensional eigenvector fields are visualized in figure 13(a). The contours of axial vorticity for
![]() $k=3$
(
$k=3$
(
![]() $\mathit{Ro}=0.395$
and
$\mathit{Ro}=0.395$
and
![]() $\mathit{E}\,=3.16\times 10^{-3}$
) and
$\mathit{E}\,=3.16\times 10^{-3}$
) and
![]() $k=6$
(
$k=6$
(
![]() $\mathit{Ro}=0.395$
and
$\mathit{Ro}=0.395$
and
![]() $\mathit{E}\,=5.26\times 10^{-4}$
) are viewed in the
$\mathit{E}\,=5.26\times 10^{-4}$
) are viewed in the
![]() $r$
–
$r$
–
![]() ${\it\theta}$
plane. The growth rates for these flows have been illustrated in figure 12(a). Both
${\it\theta}$
plane. The growth rates for these flows have been illustrated in figure 12(a). Both
![]() $k=3$
and
$k=3$
and
![]() $k=6$
eigenvector fields demonstrate two rings of alternating-sign vortices bracketing the disk–tank interface (
$k=6$
eigenvector fields demonstrate two rings of alternating-sign vortices bracketing the disk–tank interface (
![]() $r=1$
). This structure is consistent with the mode I instability portrayed in the axisymmetric model solutions obtained by Vo et al. (Reference Vo, Montabone and Sheard2014) and those computed for various
$r=1$
). This structure is consistent with the mode I instability portrayed in the axisymmetric model solutions obtained by Vo et al. (Reference Vo, Montabone and Sheard2014) and those computed for various
![]() $A$
as shown later in § 4.2.2.
$A$
as shown later in § 4.2.2.

Figure 13. Dominant instability mode structures for
![]() $\mathit{Ro}=0.395$
with (a)
$\mathit{Ro}=0.395$
with (a)
![]() $\mathit{E}\,=3.16\times 10^{-3}$
(
$\mathit{E}\,=3.16\times 10^{-3}$
(
![]() $k=3$
) and (b)
$k=3$
) and (b)
![]() $\mathit{E}\,=5.26\times 10^{-4}$
(
$\mathit{E}\,=5.26\times 10^{-4}$
(
![]() $k=6$
). (i) Contours of axial vorticity of the two-dimensional perturbation field depicted on the
$k=6$
). (i) Contours of axial vorticity of the two-dimensional perturbation field depicted on the
![]() $r{-}{\it\theta}$
plane. Given the arbitrary scaling of linearized eigenvector fields, equi-spaced contour levels are plotted between
$r{-}{\it\theta}$
plane. Given the arbitrary scaling of linearized eigenvector fields, equi-spaced contour levels are plotted between
![]() $\pm (|{\it\omega}_{\bot z,min}|+|{\it\omega}_{\bot z,max}|)/2$
. (ii) A linear non-axisymmetric flow approximation constructed by superimposing the axisymmetric base flow and the leading instability mode with azimuthal wavenumber in panel (i). This flow field is not representative of the three-dimensional non-axisymmetric flow since nonlinear effects are omitted here but rather serves as a guide to the flow distortions invoked by the instability. Contours of axial vorticity are plotted, with levels as per figure 2. The orientation is such that the positive
$\pm (|{\it\omega}_{\bot z,min}|+|{\it\omega}_{\bot z,max}|)/2$
. (ii) A linear non-axisymmetric flow approximation constructed by superimposing the axisymmetric base flow and the leading instability mode with azimuthal wavenumber in panel (i). This flow field is not representative of the three-dimensional non-axisymmetric flow since nonlinear effects are omitted here but rather serves as a guide to the flow distortions invoked by the instability. Contours of axial vorticity are plotted, with levels as per figure 2. The orientation is such that the positive
![]() $\mathit{Ro}$
causes the central region to rotate counterclockwise faster than the outer region.
$\mathit{Ro}$
causes the central region to rotate counterclockwise faster than the outer region.
A visualization of the non-axisymmetric structure predicted by the linear stability analysis is obtained by superimposing the leading eigenmodes onto their respective axisymmetric base flows. Illustrations of these structures for the instability modes are shown in figure 13(ii). It is emphasized that the depictions in the
![]() $r$
–
$r$
–
![]() ${\it\theta}$
plane are not representations of the actual three-dimensional flow structure, rather they are an illustration of the linear instability mode for which the amplitudes have been arbitrarily scaled. Importantly, this type of visualization reveals the type of distortions on the base flow made capable by the most unstable azimuthal instability mode. For both
${\it\theta}$
plane are not representations of the actual three-dimensional flow structure, rather they are an illustration of the linear instability mode for which the amplitudes have been arbitrarily scaled. Importantly, this type of visualization reveals the type of distortions on the base flow made capable by the most unstable azimuthal instability mode. For both
![]() $k=3$
and
$k=3$
and
![]() $k=6$
, which belong to the mode I branch in the quasi-two-dimensional solutions, the shear layer deforms into a polygon with the number of sides corresponding to that of the unstable azimuthal wavenumber: a triangle for
$k=6$
, which belong to the mode I branch in the quasi-two-dimensional solutions, the shear layer deforms into a polygon with the number of sides corresponding to that of the unstable azimuthal wavenumber: a triangle for
![]() $k=3$
and a hexagon for
$k=3$
and a hexagon for
![]() $k=6$
. In these examples, a thin layer of axial vorticity is present and forms the border of the polygonal shape. This layer is weaker in comparison with both its interior and the surrounding flow in terms of its vorticity. These types of deformations are representative of the mode I instability and are in agreement with those obtained in the axisymmetric model. Additionally, the negative-
$k=6$
. In these examples, a thin layer of axial vorticity is present and forms the border of the polygonal shape. This layer is weaker in comparison with both its interior and the surrounding flow in terms of its vorticity. These types of deformations are representative of the mode I instability and are in agreement with those obtained in the axisymmetric model. Additionally, the negative-
![]() $\mathit{Ro}$
flows demonstrate the same type of deformations.
$\mathit{Ro}$
flows demonstrate the same type of deformations.
The perturbation fields and the superposition with their base flow have strongly demonstrated that the first unstable wavenumber branches (mode I) from both the quasi-two-dimensional and axisymmetric models are the same. It is believed that this instability mode is associated with the instability of the
![]() $\mathit{E}\,^{1/4}$
layer, responsible for the polygonal deformations in the azimuthal direction. The linear stability analysis results further reinforce the idea that the mode II instability, which was found to be localized to the disk–tank interface, is related to the
$\mathit{E}\,^{1/4}$
layer, responsible for the polygonal deformations in the azimuthal direction. The linear stability analysis results further reinforce the idea that the mode II instability, which was found to be localized to the disk–tank interface, is related to the
![]() $\mathit{E}\,^{1/3}$
layer. This suggestion arises from the coincident region between the mode II instability and the interaction of the Ekman pumping and the Stewartson layer in the axisymmetric model solutions, both of which are absent from the quasi-two-dimensional solutions.
$\mathit{E}\,^{1/3}$
layer. This suggestion arises from the coincident region between the mode II instability and the interaction of the Ekman pumping and the Stewartson layer in the axisymmetric model solutions, both of which are absent from the quasi-two-dimensional solutions.
4.1.4. Similarity in growth rates between positive and negative Rossby numbers in quasi-two-dimensional flows
It was revealed that the peak azimuthal wavenumbers between positive- and negative-
![]() $\mathit{Ro}$
regimes in the quasi-two-dimensional solutions are identical (§ 4.1.1). However, the growth rates between the two regimes are different. Thus, a relationship describing the growth rates between positive- and negative-
$\mathit{Ro}$
regimes in the quasi-two-dimensional solutions are identical (§ 4.1.1). However, the growth rates between the two regimes are different. Thus, a relationship describing the growth rates between positive- and negative-
![]() $\mathit{Ro}$
flows is sought. The growth rate as a function of the Rossby number for a particular wavenumber (
$\mathit{Ro}$
flows is sought. The growth rate as a function of the Rossby number for a particular wavenumber (
![]() $k=4$
) is illustrated in figure 14(a). An increase in
$k=4$
) is illustrated in figure 14(a). An increase in
![]() $|\mathit{Ro}|$
and decrease in
$|\mathit{Ro}|$
and decrease in
![]() $\mathit{E}\,$
achieves a larger growth rate. However, the rate of increase differs between the positive- and negative-
$\mathit{E}\,$
achieves a larger growth rate. However, the rate of increase differs between the positive- and negative-
![]() $\mathit{Ro}$
regimes. That is, in assuming that the growth rates are all positive, the curves adopt a power-law behaviour of
$\mathit{Ro}$
regimes. That is, in assuming that the growth rates are all positive, the curves adopt a power-law behaviour of
![]() ${\it\sigma}\propto \mathit{Ro}^{{\it\alpha}}$
such that
${\it\sigma}\propto \mathit{Ro}^{{\it\alpha}}$
such that
![]() ${\it\alpha}<1$
and
${\it\alpha}<1$
and
![]() ${\it\alpha}>1$
for negative and positive
${\it\alpha}>1$
for negative and positive
![]() $\mathit{Ro}$
respectively.
$\mathit{Ro}$
respectively.

Figure 14. (a) Growth rate
![]() ${\it\sigma}$
as a function of
${\it\sigma}$
as a function of
![]() $\mathit{Ro}$
for various
$\mathit{Ro}$
for various
![]() $\mathit{E}\,$
at
$\mathit{E}\,$
at
![]() $k=4$
. The dashed line represents neutral stability, where points above and below symbolize unstable and stable modes respectively. (b) The product of (
$k=4$
. The dashed line represents neutral stability, where points above and below symbolize unstable and stable modes respectively. (b) The product of (
![]() $1-A\mathit{Ro}$
) and
$1-A\mathit{Ro}$
) and
![]() ${\it\sigma}$
as a function of
${\it\sigma}$
as a function of
![]() $\mathit{Ro}$
for both the positive- and negative-
$\mathit{Ro}$
for both the positive- and negative-
![]() $\mathit{Ro}$
regimes. Each line represents a different Ekman number with
$\mathit{Ro}$
regimes. Each line represents a different Ekman number with
![]() $k=4$
. (c) A reproduction of panel (b) except that the magnitude of
$k=4$
. (c) A reproduction of panel (b) except that the magnitude of
![]() $\mathit{Ro}$
is used to demonstrate the reflective symmetry about the vertical axis between positive- and negative-
$\mathit{Ro}$
is used to demonstrate the reflective symmetry about the vertical axis between positive- and negative-
![]() $\mathit{Ro}$
data. (d) The relationship of the ratio between growth rates obtained from positive- and negative-
$\mathit{Ro}$
data. (d) The relationship of the ratio between growth rates obtained from positive- and negative-
![]() $\mathit{Ro}$
flow as a function of
$\mathit{Ro}$
flow as a function of
![]() $|\mathit{Ro}|$
. The growth rates have been computed from the quasi-two-dimensional model.
$|\mathit{Ro}|$
. The growth rates have been computed from the quasi-two-dimensional model.
It is noted that the dimensionless growth rate used here has been scaled by
![]() ${\rm\Omega}$
(as per the governing equations, § 2.2), whereas
${\rm\Omega}$
(as per the governing equations, § 2.2), whereas
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{E}\,$
have been scaled by
$\mathit{E}\,$
have been scaled by
![]() $\overline{{\rm\Omega}}$
. Therefore, a more consistent comparison of the growth rates between the positive- and negative-
$\overline{{\rm\Omega}}$
. Therefore, a more consistent comparison of the growth rates between the positive- and negative-
![]() $\mathit{Ro}$
regimes may be achieved by using a dimensionless growth rate that is scaled by
$\mathit{Ro}$
regimes may be achieved by using a dimensionless growth rate that is scaled by
![]() $\overline{{\rm\Omega}}$
. The growth rate has dimensions of the reciprocal time scale and can be written as
$\overline{{\rm\Omega}}$
. The growth rate has dimensions of the reciprocal time scale and can be written as
![]() ${\it\sigma}^{\ast }={\rm\Omega}{\it\sigma}$
. Thus, a factor of
${\it\sigma}^{\ast }={\rm\Omega}{\it\sigma}$
. Thus, a factor of
![]() ${\rm\Omega}/\overline{{\rm\Omega}}$
is required to convert the growth rate to a
${\rm\Omega}/\overline{{\rm\Omega}}$
is required to convert the growth rate to a
![]() $\overline{{\rm\Omega}}$
scaling, and can be rewritten as
$\overline{{\rm\Omega}}$
scaling, and can be rewritten as
![]() ${\rm\Omega}/\overline{{\rm\Omega}}=1-A\mathit{Ro}$
. The dimensional growth rate scaled by
${\rm\Omega}/\overline{{\rm\Omega}}=1-A\mathit{Ro}$
. The dimensional growth rate scaled by
![]() $\overline{{\rm\Omega}}$
is then given by
$\overline{{\rm\Omega}}$
is then given by
The rescaled dimensional growth rate as a function of
![]() $\mathit{Ro}$
is illustrated in figure 14(b). The growth rate data now demonstrate reflective symmetry about
$\mathit{Ro}$
is illustrated in figure 14(b). The growth rate data now demonstrate reflective symmetry about
![]() $\mathit{Ro}=0$
. This is more clearly observed in (c), which is a plot of
$\mathit{Ro}=0$
. This is more clearly observed in (c), which is a plot of
![]() $(1-A\mathit{Ro}){\it\sigma}$
as a function of
$(1-A\mathit{Ro}){\it\sigma}$
as a function of
![]() $|\mathit{Ro}|$
, with square and triangle symbols representing positive- and negative-
$|\mathit{Ro}|$
, with square and triangle symbols representing positive- and negative-
![]() $\mathit{Ro}$
data respectively. The growth rates associated with the negative- and positive-
$\mathit{Ro}$
data respectively. The growth rates associated with the negative- and positive-
![]() $\mathit{Ro}$
flows demonstrate a very strong collapse. Thus, the relationship
$\mathit{Ro}$
flows demonstrate a very strong collapse. Thus, the relationship
![]() $(1-A\mathit{Ro}){\it\sigma}_{pos\,\mathit{Ro}}=(1-A(-\mathit{Ro})){\it\sigma}_{neg\,\mathit{Ro}}$
holds true for quasi-two-dimensional flows, where
$(1-A\mathit{Ro}){\it\sigma}_{pos\,\mathit{Ro}}=(1-A(-\mathit{Ro})){\it\sigma}_{neg\,\mathit{Ro}}$
holds true for quasi-two-dimensional flows, where
![]() ${\it\sigma}_{pos\,\mathit{Ro}}$
and
${\it\sigma}_{pos\,\mathit{Ro}}$
and
![]() ${\it\sigma}_{neg\,\mathit{Ro}}$
represent the growth rates associated with positive- and negative-
${\it\sigma}_{neg\,\mathit{Ro}}$
represent the growth rates associated with positive- and negative-
![]() $\mathit{Ro}$
flows respectively. The ratio of growth rates between the two
$\mathit{Ro}$
flows respectively. The ratio of growth rates between the two
![]() $\mathit{Ro}$
regimes is thereby described by
$\mathit{Ro}$
regimes is thereby described by
Figure 14(d) is an illustration of the perfect agreement for
![]() $k=4$
. The ratio of positive- and negative-
$k=4$
. The ratio of positive- and negative-
![]() $\mathit{Ro}$
growth rates was also calculated for every azimuthal wavenumber throughout the parameter space, and the results consistently exhibited the relationship described in (4.4). Therefore, the ratio of the growth rate is independent of the azimuthal wavenumber and the Ekman number. It is interesting to note that, in the case where
$\mathit{Ro}$
growth rates was also calculated for every azimuthal wavenumber throughout the parameter space, and the results consistently exhibited the relationship described in (4.4). Therefore, the ratio of the growth rate is independent of the azimuthal wavenumber and the Ekman number. It is interesting to note that, in the case where
![]() $\mathit{Ro}>0$
, (4.4) is identical to the normalized disk speed in the positive-
$\mathit{Ro}>0$
, (4.4) is identical to the normalized disk speed in the positive-
![]() $\mathit{Ro}$
regime, which is given by
$\mathit{Ro}$
regime, which is given by
The relationship describing the growth rates between positive- and negative-
![]() $\mathit{Ro}$
regimes is not observed for the solutions of the axisymmetric model. This difference may be explained by the Ekman suction/pumping (depending on the sign and magnitude of
$\mathit{Ro}$
regimes is not observed for the solutions of the axisymmetric model. This difference may be explained by the Ekman suction/pumping (depending on the sign and magnitude of
![]() $\mathit{Ro}$
) induced by the Ekman layers in the axisymmetric model which is not captured by the quasi-two-dimensional model.
$\mathit{Ro}$
) induced by the Ekman layers in the axisymmetric model which is not captured by the quasi-two-dimensional model.
4.2. Variation of the aspect ratio of the axisymmetric model
Attention is now turned towards the linear stability analysis results obtained for the axisymmetric model at various aspect ratios. This section covers the growth rates, global instability mode shapes and aspect ratio dependence. Agreement with the linear stability analysis results of Niino & Misawa (Reference Niino and Misawa1984) is also discussed.
4.2.1. Growth rates
The growth rates for a range of azimuthal wavenumbers have been determined via a linear stability analysis performed on steady-state axisymmetric base flows for a variety of values of
![]() $A$
. In considering a single aspect ratio, the effect of varying the Rossby and Ekman numbers on the growth rate as a function of azimuthal wavenumber demonstrates the same trends as observed in the previous section (
$A$
. In considering a single aspect ratio, the effect of varying the Rossby and Ekman numbers on the growth rate as a function of azimuthal wavenumber demonstrates the same trends as observed in the previous section (
![]() $A=2/3$
). That is, increase of the Rossby number or decrease of the Ekman number invokes larger growth rates in the perturbations and causes a preference towards higher azimuthal wavenumbers.
$A=2/3$
). That is, increase of the Rossby number or decrease of the Ekman number invokes larger growth rates in the perturbations and causes a preference towards higher azimuthal wavenumbers.
Typical profiles of growth rates against wavenumber for various values of
![]() $A$
are shown in figure 15(a), with
$A$
are shown in figure 15(a), with
![]() $\mathit{Ro}=0.1$
and
$\mathit{Ro}=0.1$
and
![]() $\mathit{E}\,=7\times 10^{-4}$
. The reference aspect ratio
$\mathit{E}\,=7\times 10^{-4}$
. The reference aspect ratio
![]() $A=2/3$
described in the previous section demonstrates a single peak in the profile associated with the mode I instability, with a corresponding integer peak wavenumber of
$A=2/3$
described in the previous section demonstrates a single peak in the profile associated with the mode I instability, with a corresponding integer peak wavenumber of
![]() $k_{peak}=4$
. The mode I waveband is in the range
$k_{peak}=4$
. The mode I waveband is in the range
![]() $1\lesssim k\lesssim 9$
. By decreasing
$1\lesssim k\lesssim 9$
. By decreasing
![]() $A$
, the stability of the flow is seen to shift its preference towards higher azimuthal wavenumbers and increase its mode I waveband. For example, for
$A$
, the stability of the flow is seen to shift its preference towards higher azimuthal wavenumbers and increase its mode I waveband. For example, for
![]() $A=1/3$
the integer peak wavenumber increases to
$A=1/3$
the integer peak wavenumber increases to
![]() $k_{peak}=7$
and the waveband extends its range to
$k_{peak}=7$
and the waveband extends its range to
![]() $1\lesssim k\lesssim 18$
. In contrast, increase of the aspect ratio to
$1\lesssim k\lesssim 18$
. In contrast, increase of the aspect ratio to
![]() $A=2$
yields a smaller preferred azimuthal wavenumber (
$A=2$
yields a smaller preferred azimuthal wavenumber (
![]() $k_{peak}=2$
) with a decreased mode I waveband (
$k_{peak}=2$
) with a decreased mode I waveband (
![]() $1\lesssim k\lesssim 4$
).
$1\lesssim k\lesssim 4$
).

Figure 15. Growth rate
![]() ${\it\sigma}$
as a function of (a) the azimuthal wavenumber
${\it\sigma}$
as a function of (a) the azimuthal wavenumber
![]() $k$
and (b) the scaled azimuthal wavenumber
$k$
and (b) the scaled azimuthal wavenumber
![]() $kA$
, for
$kA$
, for
![]() $\mathit{Ro}=0.1,\mathit{E}\,=7\times 10^{-4}$
and various aspect ratios.
$\mathit{Ro}=0.1,\mathit{E}\,=7\times 10^{-4}$
and various aspect ratios.
Upon closer inspection of the growth rate profiles, it appears that the
![]() $A=4/3$
and
$A=4/3$
and
![]() $A=2$
data exhibit peak growth rates that are smaller than for the cases of
$A=2$
data exhibit peak growth rates that are smaller than for the cases of
![]() $A\leqslant 2/3$
. For this particular flow condition, the growth rates for
$A\leqslant 2/3$
. For this particular flow condition, the growth rates for
![]() $A=2$
portray a stable flow to all non-axisymmetric disturbances, with the slowest decaying wavenumber characterized by
$A=2$
portray a stable flow to all non-axisymmetric disturbances, with the slowest decaying wavenumber characterized by
![]() $k_{peak}=2$
. The negative growth rates conveyed by all wavenumbers in this case demonstrate the increased stability of the flow, which is in agreement with what was expressed in § 3.2.2, namely a thicker shear layer produced by a larger
$k_{peak}=2$
. The negative growth rates conveyed by all wavenumbers in this case demonstrate the increased stability of the flow, which is in agreement with what was expressed in § 3.2.2, namely a thicker shear layer produced by a larger
![]() $A$
results in a more stable flow. Thus, increase of the aspect ratio decreases the observed azimuthal wavenumber and growth rates. The trend of increasing
$A$
results in a more stable flow. Thus, increase of the aspect ratio decreases the observed azimuthal wavenumber and growth rates. The trend of increasing
![]() $A$
causing the flow to favour lower wavenumbers is seen not only for this flow condition but throughout the large parameter space covered. These trends further suggest that the instability associated with the Stewartson layer is weak due to the reduction of the velocity gradients across the shear layer, as was observed in the radial profiles of axial vorticity (see figure 6
a).
$A$
causing the flow to favour lower wavenumbers is seen not only for this flow condition but throughout the large parameter space covered. These trends further suggest that the instability associated with the Stewartson layer is weak due to the reduction of the velocity gradients across the shear layer, as was observed in the radial profiles of axial vorticity (see figure 6
a).
The similarity in the magnitudes of the peak growth rates for cases of
![]() $A\leqslant 2/3$
in figure 15(a) suggests that a specific flow condition has a corresponding maximum growth rate which is independent of the aspect ratio, provided that the shear layer is not greatly affected by the confinement. The theoretical shear-layer thickness
$A\leqslant 2/3$
in figure 15(a) suggests that a specific flow condition has a corresponding maximum growth rate which is independent of the aspect ratio, provided that the shear layer is not greatly affected by the confinement. The theoretical shear-layer thickness
![]() ${\it\delta}=A(\mathit{E}\,/4)^{1/4}$
suggests that the thickness is scaled with the enclosure height. If the dominant wavenumber scales with the thickness, then this suggests that the wavenumber can be rescaled by
${\it\delta}=A(\mathit{E}\,/4)^{1/4}$
suggests that the thickness is scaled with the enclosure height. If the dominant wavenumber scales with the thickness, then this suggests that the wavenumber can be rescaled by
![]() $A$
also, such that a universal collapse of the data is achieved for
$A$
also, such that a universal collapse of the data is achieved for
![]() ${\it\sigma}$
as a function of
${\it\sigma}$
as a function of
![]() $kA$
. This is illustrated in figure 15(b). The collapse for cases
$kA$
. This is illustrated in figure 15(b). The collapse for cases
![]() $A\leqslant 2/3$
demonstrates strong agreement with each other. This can be explained by the similar profiles exhibited in the scaled axial vorticity throughout the shear layer, which is the unstable part of the flow (see figure 6). This also explains why the growth rate profiles for
$A\leqslant 2/3$
demonstrates strong agreement with each other. This can be explained by the similar profiles exhibited in the scaled axial vorticity throughout the shear layer, which is the unstable part of the flow (see figure 6). This also explains why the growth rate profiles for
![]() $A=4/3$
and
$A=4/3$
and
![]() $A=2$
do not conform with the lower aspect ratios since at these aspect ratios the
$A=2$
do not conform with the lower aspect ratios since at these aspect ratios the
![]() $\mathit{E}\,^{1/4}$
Stewartson layer is affected by the confinement.
$\mathit{E}\,^{1/4}$
Stewartson layer is affected by the confinement.
4.2.2. Global instability mode shapes and visualization on the horizontal plane
The three-dimensional perturbation fields of the most unstable wavenumber have been obtained through a linear stability analysis. A comparison between the leading eigenvector fields for
![]() $\mathit{Ro}=0.1$
and
$\mathit{Ro}=0.1$
and
![]() $\mathit{E}\,=7\times 10^{-4}$
with
$\mathit{E}\,=7\times 10^{-4}$
with
![]() $A=1/6,2/3$
and 2 is portrayed in figure 16. The contours of axial vorticity for each value of
$A=1/6,2/3$
and 2 is portrayed in figure 16. The contours of axial vorticity for each value of
![]() $A$
demonstrate a strong pair of opposing axial vorticity bands at the disk–tank interface (left and middle columns), which is indicative of the mode I instability. This is in agreement with the growth rate data, which illustrate a single maximum that is representative of the mode I instability (figure 15). The
$A$
demonstrate a strong pair of opposing axial vorticity bands at the disk–tank interface (left and middle columns), which is indicative of the mode I instability. This is in agreement with the growth rate data, which illustrate a single maximum that is representative of the mode I instability (figure 15). The
![]() $r$
–
$r$
–
![]() $z$
plane of the leading perturbation field has been extracted such that the plane passes approximately through a maximum amplitude of the sinusoidal azimuthal disturbance. With increasing
$z$
plane of the leading perturbation field has been extracted such that the plane passes approximately through a maximum amplitude of the sinusoidal azimuthal disturbance. With increasing
![]() $A$
, the positive- and negative-vorticity bands are seen to increase in thickness and almost fill the entire domain for
$A$
, the positive- and negative-vorticity bands are seen to increase in thickness and almost fill the entire domain for
![]() $A=2$
. Thus, the region that is susceptible to instability increases as
$A=2$
. Thus, the region that is susceptible to instability increases as
![]() $A$
increases due to the thickening of the
$A$
increases due to the thickening of the
![]() $\mathit{E}\,^{1/4}$
shear layer.
$\mathit{E}\,^{1/4}$
shear layer.

Figure 16. Flow conditions of
![]() $(\mathit{Ro},\mathit{E}\,)=(0.1,7\times 10^{-4})$
for (a)
$(\mathit{Ro},\mathit{E}\,)=(0.1,7\times 10^{-4})$
for (a)
![]() $A=1/6,k=15$
, (b)
$A=1/6,k=15$
, (b)
![]() $A=2/3,k=4$
and (c)
$A=2/3,k=4$
and (c)
![]() $A=2,k=2$
. Left column: contours of axial vorticity of the three-dimensional perturbation field of a given azimuthal wavenumber depicted on the full meridional
$A=2,k=2$
. Left column: contours of axial vorticity of the three-dimensional perturbation field of a given azimuthal wavenumber depicted on the full meridional
![]() $r{-}z$
plane
$r{-}z$
plane
![]() $(-2\leqslant r\leqslant 2)$
. The plane has been extracted such that it passes through an approximate maximum amplitude of the sinusoidal azimuthal disturbance. Contour levels are as per figure 13. Middle column: the same as the left column except viewed in the
$(-2\leqslant r\leqslant 2)$
. The plane has been extracted such that it passes through an approximate maximum amplitude of the sinusoidal azimuthal disturbance. Contour levels are as per figure 13. Middle column: the same as the left column except viewed in the
![]() $r{-}{\it\theta}$
plane at mid-depth. Right column: the respective linear non-axisymmetric flows constructed by superimposing the axisymmetric base flow and the most unstable azimuthal linear instability wavenumber at mid-depth. Contour levels are as per figure 2.
$r{-}{\it\theta}$
plane at mid-depth. Right column: the respective linear non-axisymmetric flows constructed by superimposing the axisymmetric base flow and the most unstable azimuthal linear instability wavenumber at mid-depth. Contour levels are as per figure 2.
The perturbation field associated with the most unstable azimuthal wavenumber has been superimposed onto its respective base flow for visualization purposes. The resultant contours of axial vorticity for the different cases are illustrated in the right column of figure 16. For each wavenumber, the flow demonstrates a polygonal configuration bordering
![]() $r=1$
. Similarly to the structures obtained in
$r=1$
. Similarly to the structures obtained in
![]() $A=2/3$
, the ring of vorticity is comprised of very low vorticity surrounded by higher axial vorticity. These characteristics are consistent with the mode I instability and support the reported polygonal structures obtained experimentally in both small- and moderate-aspect-ratio containers (e.g. Rabaud & Couder Reference Rabaud and Couder1983; Chomaz et al.
Reference Chomaz, Rabaud, Basdevant and Couder1988; Früh & Read Reference Früh and Read1999; Aguiar et al.
Reference Aguiar, Read, Wordsworth, Salter and Hiro Yamazaki2010).
$A=2/3$
, the ring of vorticity is comprised of very low vorticity surrounded by higher axial vorticity. These characteristics are consistent with the mode I instability and support the reported polygonal structures obtained experimentally in both small- and moderate-aspect-ratio containers (e.g. Rabaud & Couder Reference Rabaud and Couder1983; Chomaz et al.
Reference Chomaz, Rabaud, Basdevant and Couder1988; Früh & Read Reference Früh and Read1999; Aguiar et al.
Reference Aguiar, Read, Wordsworth, Salter and Hiro Yamazaki2010).

Figure 17. (a) The regime diagram of the most unstable linear wavenumber scaled with the aspect ratio,
![]() $kA$
, as a function of
$kA$
, as a function of
![]() $\mathit{E}\,$
and positive
$\mathit{E}\,$
and positive
![]() $\mathit{Ro}$
(axisymmetric model). This plot is representative of a universal regime diagram such that the linearly predicted azimuthal wavenumber can be determined by dividing the
$\mathit{Ro}$
(axisymmetric model). This plot is representative of a universal regime diagram such that the linearly predicted azimuthal wavenumber can be determined by dividing the
![]() $kA$
value by the aspect ratio considered. The contour map is constructed using
$kA$
value by the aspect ratio considered. The contour map is constructed using
![]() $A=2/3$
data (Vo et al.
Reference Vo, Montabone and Sheard2014). The solid lines denote integer scaled wavenumbers determined from
$A=2/3$
data (Vo et al.
Reference Vo, Montabone and Sheard2014). The solid lines denote integer scaled wavenumbers determined from
![]() $A=1/6$
data while the dashed lines are those determined from
$A=1/6$
data while the dashed lines are those determined from
![]() $A=2/3$
. The left thick boundary lines represent the stability thresholds for
$A=2/3$
. The left thick boundary lines represent the stability thresholds for
![]() $A=1/6$
(solid line) and
$A=1/6$
(solid line) and
![]() $A=2/3$
(dashed line), which are given by
$A=2/3$
(dashed line), which are given by
![]() $\mathit{Ro}_{c}=16.0(\pm 1.2)\mathit{E}\,^{0.756\pm 0.010}$
(using positive data only) and
$\mathit{Ro}_{c}=16.0(\pm 1.2)\mathit{E}\,^{0.756\pm 0.010}$
(using positive data only) and
![]() $\mathit{Ro}_{c}=18.1(\pm 0.8)\mathit{E}\,^{0.767\pm 0.006}$
respectively. The wide-dotted line represents the transition from reflectively symmetric flow to symmetry-broken flow, defined as
$\mathit{Ro}_{c}=18.1(\pm 0.8)\mathit{E}\,^{0.767\pm 0.006}$
respectively. The wide-dotted line represents the transition from reflectively symmetric flow to symmetry-broken flow, defined as
![]() $\mathit{Ro}_{c1-c2}=13.4\mathit{E}\,^{0.5}$
(
$\mathit{Ro}_{c1-c2}=13.4\mathit{E}\,^{0.5}$
(
![]() $\mathit{Re}_{\mathit{E}\,}=26.7$
). (b) Regression of the preferred normalized azimuthal wavelength for flows described by
$\mathit{Re}_{\mathit{E}\,}=26.7$
). (b) Regression of the preferred normalized azimuthal wavelength for flows described by
![]() $\mathit{Re}\lesssim 26.7$
as a function of
$\mathit{Re}\lesssim 26.7$
as a function of
![]() $|\mathit{Ro}|/\mathit{E}\,^{2}$
. The normalized azimuthal wavelength is defined as
$|\mathit{Ro}|/\mathit{E}\,^{2}$
. The normalized azimuthal wavelength is defined as
![]() ${\it\lambda}_{{\it\theta}}^{\ast }=2{\rm\pi}/(kA)$
. Data for
${\it\lambda}_{{\it\theta}}^{\ast }=2{\rm\pi}/(kA)$
. Data for
![]() $A=1/6$
(▫) and
$A=1/6$
(▫) and
![]() $A=2/3$
(▵) are shown with fits described by
$A=2/3$
(▵) are shown with fits described by
![]() ${\it\lambda}_{{\it\theta}}^{\ast }=26.1(\pm 1.7)[|\mathit{Ro}|/\mathit{E}\,^{2}]^{-0.188\pm 0.005}$
and
${\it\lambda}_{{\it\theta}}^{\ast }=26.1(\pm 1.7)[|\mathit{Ro}|/\mathit{E}\,^{2}]^{-0.188\pm 0.005}$
and
![]() ${\it\lambda}_{{\it\theta}}^{\ast }=18.0(\pm 0.7)[|\mathit{Ro}|/\mathit{E}\,^{2}]^{-0.169\pm 0.002}$
respectively.
${\it\lambda}_{{\it\theta}}^{\ast }=18.0(\pm 0.7)[|\mathit{Ro}|/\mathit{E}\,^{2}]^{-0.169\pm 0.002}$
respectively.
4.2.3. Aspect ratio dependence in the axisymmetric model
A regime diagram of the most unstable wavenumber as a function of
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{E}\,$
has been generated for
$\mathit{E}\,$
has been generated for
![]() $A=1/6$
(not shown here; instead a universal regime diagram that incorporates these data is shown later in figure 17
a). The same characteristics as displayed in the regime diagram for
$A=1/6$
(not shown here; instead a universal regime diagram that incorporates these data is shown later in figure 17
a). The same characteristics as displayed in the regime diagram for
![]() $A=2/3$
(Vo et al.
Reference Vo, Montabone and Sheard2014) are seen. A wide range of unstable azimuthal wavenumbers of
$A=2/3$
(Vo et al.
Reference Vo, Montabone and Sheard2014) are seen. A wide range of unstable azimuthal wavenumbers of
![]() $7\leqslant k\leqslant 35$
was observed throughout the computed parameter space. This range is much greater than that obtained for
$7\leqslant k\leqslant 35$
was observed throughout the computed parameter space. This range is much greater than that obtained for
![]() $A=2/3$
(
$A=2/3$
(
![]() $2\leqslant k\leqslant 9$
). However, taking into consideration the aspect ratio, the scaled wavenumbers are in the range
$2\leqslant k\leqslant 9$
). However, taking into consideration the aspect ratio, the scaled wavenumbers are in the range
![]() $1\leqslant kA\leqslant 6$
for both
$1\leqslant kA\leqslant 6$
for both
![]() $A=1/6$
and
$A=1/6$
and
![]() $A=2/3$
.
$A=2/3$
.
It was established in § 4.2.1 that for a sufficiently small
![]() $A$
(
$A$
(
![]() $A\lesssim 2/3$
), the growth rate data can be universally described by scaling the azimuthal wavenumber by
$A\lesssim 2/3$
), the growth rate data can be universally described by scaling the azimuthal wavenumber by
![]() $A$
. Thus, a regime diagram of the scaled parameter
$A$
. Thus, a regime diagram of the scaled parameter
![]() $kA$
can be produced as a function of
$kA$
can be produced as a function of
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{E}\,$
. This is illustrated in figure 17(a). The contour lines of integer
$\mathit{E}\,$
. This is illustrated in figure 17(a). The contour lines of integer
![]() $kA$
values for both the
$kA$
values for both the
![]() $A=1/6$
(solid lines) and
$A=1/6$
(solid lines) and
![]() $A=2/3$
data (dashed lines) overlay the contour map. Despite the large difference in the values of
$A=2/3$
data (dashed lines) overlay the contour map. Despite the large difference in the values of
![]() $A$
, the
$A$
, the
![]() $kA$
lines for both values of
$kA$
lines for both values of
![]() $A$
portray a good alignment throughout much of the explored parameter space. This map is approximately universal as there is not a perfect agreement between the two sets of data: the linearly predicted azimuthal wavenumber can be determined by dividing the value by the aspect ratio of interest. That is, the regime diagram for
$A$
portray a good alignment throughout much of the explored parameter space. This map is approximately universal as there is not a perfect agreement between the two sets of data: the linearly predicted azimuthal wavenumber can be determined by dividing the value by the aspect ratio of interest. That is, the regime diagram for
![]() $A=2/3$
(Vo et al.
Reference Vo, Montabone and Sheard2014) (and for any other aspect ratio
$A=2/3$
(Vo et al.
Reference Vo, Montabone and Sheard2014) (and for any other aspect ratio
![]() $A\lesssim 2/3$
) can be reproduced by using figure 17(a) and multiplying the values by
$A\lesssim 2/3$
) can be reproduced by using figure 17(a) and multiplying the values by
![]() $1/A$
. The slight discrepancy between the scaled data for
$1/A$
. The slight discrepancy between the scaled data for
![]() $A=1/6$
and
$A=1/6$
and
![]() $A=2/3$
is discussed in detail later in this section.
$A=2/3$
is discussed in detail later in this section.
The preferred wavenumber trends are dependent on two regimes, namely the reflectively symmetric and symmetry-broken regimes. The transition between these two regimes is described by
![]() $\mathit{Ro}_{c1-c2}=13.4\mathit{E}\,^{0.5}$
(
$\mathit{Ro}_{c1-c2}=13.4\mathit{E}\,^{0.5}$
(
![]() $\mathit{Re}_{\mathit{E}\,}=26.7$
, § 3.2.3). The trends in both aspect ratio cases conform well to their respective regions separated by the transition threshold because the relationship itself is independent of the aspect ratio. Generally, flows in the reflectively symmetric regime (
$\mathit{Re}_{\mathit{E}\,}=26.7$
, § 3.2.3). The trends in both aspect ratio cases conform well to their respective regions separated by the transition threshold because the relationship itself is independent of the aspect ratio. Generally, flows in the reflectively symmetric regime (
![]() $\mathit{Re}_{\mathit{E}\,}<26.7$
) portray an increase in the preferred azimuthal wavenumber with either increasing
$\mathit{Re}_{\mathit{E}\,}<26.7$
) portray an increase in the preferred azimuthal wavenumber with either increasing
![]() $\mathit{Ro}$
or decreasing
$\mathit{Ro}$
or decreasing
![]() $\mathit{E}\,$
. In the symmetry-broken regime (
$\mathit{E}\,$
. In the symmetry-broken regime (
![]() $\mathit{Re}_{\mathit{E}\,}>26.7$
), the contours of preferred wavenumbers become largely independent of
$\mathit{Re}_{\mathit{E}\,}>26.7$
), the contours of preferred wavenumbers become largely independent of
![]() $\mathit{E}\,$
.
$\mathit{E}\,$
.
The instability threshold for
![]() $A=1/6$
is
$A=1/6$
is
![]() $\mathit{Ro}_{c}=16.0(\pm 1.2)\mathit{E}\,^{0.756\pm 0.010}$
, which is comparable with that obtained for
$\mathit{Ro}_{c}=16.0(\pm 1.2)\mathit{E}\,^{0.756\pm 0.010}$
, which is comparable with that obtained for
![]() $A=2/3$
(
$A=2/3$
(
![]() $\mathit{Ro}_{c}=18.1(\pm 0.8)\mathit{E}\,^{0.767\pm 0.006}$
). This is expected since the maximum growth rates associated with the mode I instability appear to have little dependence on the aspect ratio (§ 4.2.1), provided the shear layer is not affected by the container walls. In fact, the flow conditions in
$\mathit{Ro}_{c}=18.1(\pm 0.8)\mathit{E}\,^{0.767\pm 0.006}$
). This is expected since the maximum growth rates associated with the mode I instability appear to have little dependence on the aspect ratio (§ 4.2.1), provided the shear layer is not affected by the container walls. In fact, the flow conditions in
![]() $A=1/6$
demonstrated slightly higher growth rates as compared with
$A=1/6$
demonstrated slightly higher growth rates as compared with
![]() $A=2/3$
, which is probably due to the greater velocity gradients across the shear layer. Thus, the instability threshold of
$A=2/3$
, which is probably due to the greater velocity gradients across the shear layer. Thus, the instability threshold of
![]() $A=1/6$
would be more representative of a pure
$A=1/6$
would be more representative of a pure
![]() $\mathit{E}\,^{1/4}$
Stewartson layer becoming unstable. This explanation is reinforced by the exponent of
$\mathit{E}\,^{1/4}$
Stewartson layer becoming unstable. This explanation is reinforced by the exponent of
![]() $\mathit{E}\,$
demonstrating an almost identical value to the theoretical prediction of
$\mathit{E}\,$
demonstrating an almost identical value to the theoretical prediction of
![]() $3/4$
(the value
$3/4$
(the value
![]() $3/4$
lies within the error bounds of the scaling for
$3/4$
lies within the error bounds of the scaling for
![]() $A=1/6$
but not
$A=1/6$
but not
![]() $A=2/3$
). This also explains the greater deviation of the Ekman number exponent from the theoretical
$A=2/3$
). This also explains the greater deviation of the Ekman number exponent from the theoretical
![]() $3/4$
value and that predicted for
$3/4$
value and that predicted for
![]() $A=2/3$
. That is, the
$A=2/3$
. That is, the
![]() $\mathit{E}\,^{1/4}$
Stewartson layer is slightly affected by the confinement in
$\mathit{E}\,^{1/4}$
Stewartson layer is slightly affected by the confinement in
![]() $A=2/3$
and therefore the instabilities are not able to grow to the maximum potential associated with the flow conditions (characterized by
$A=2/3$
and therefore the instabilities are not able to grow to the maximum potential associated with the flow conditions (characterized by
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{E}\,$
). The instability threshold for
$\mathit{E}\,$
). The instability threshold for
![]() $A=1/6$
corresponds to
$A=1/6$
corresponds to
![]() $\mathit{Re}_{i,c}\approx 22.6$
, which importantly equates to a critical
$\mathit{Re}_{i,c}\approx 22.6$
, which importantly equates to a critical
![]() $\mathit{Ro}/\mathit{E}\,^{3/4}$
of approximately
$\mathit{Ro}/\mathit{E}\,^{3/4}$
of approximately
![]() $16$
. This critical value is the average value determined by previous studies (see table
$16$
. This critical value is the average value determined by previous studies (see table
![]() $1$
in Vo et al.
Reference Vo, Montabone and Sheard2014).
$1$
in Vo et al.
Reference Vo, Montabone and Sheard2014).
The slight differences between the scaled data for
![]() $A=1/6$
and
$A=1/6$
and
![]() $A=2/3$
can be explained by revisiting the marginal stability results of Niino & Misawa (Reference Niino and Misawa1984). They determined that the critical internal Reynolds number and critical wavenumber become constant when the ratio of the disk radius to the
$A=2/3$
can be explained by revisiting the marginal stability results of Niino & Misawa (Reference Niino and Misawa1984). They determined that the critical internal Reynolds number and critical wavenumber become constant when the ratio of the disk radius to the
![]() $\mathit{E}\,^{1/4}$
theoretical thickness is greater than 25 (i.e.
$\mathit{E}\,^{1/4}$
theoretical thickness is greater than 25 (i.e.
![]() ${\it\gamma}=R_{d}/(\mathit{E}\,/4)^{1/4}H>25$
). That is, the curvature effect becomes more negligible with decreasing
${\it\gamma}=R_{d}/(\mathit{E}\,/4)^{1/4}H>25$
). That is, the curvature effect becomes more negligible with decreasing
![]() $A$
or decreasing
$A$
or decreasing
![]() $\mathit{E}\,$
. It transpires that only the
$\mathit{E}\,$
. It transpires that only the
![]() $A=1/6$
data satisfy this condition for the entire range of Ekman numbers considered in this study (achieving
$A=1/6$
data satisfy this condition for the entire range of Ekman numbers considered in this study (achieving
![]() ${\it\gamma}\gtrsim 36$
). Thus, the results of Niino & Misawa (Reference Niino and Misawa1984) predict that the larger aspect ratios produce shear layers that are influenced by the geometry and therefore will exhibit a larger
${\it\gamma}\gtrsim 36$
). Thus, the results of Niino & Misawa (Reference Niino and Misawa1984) predict that the larger aspect ratios produce shear layers that are influenced by the geometry and therefore will exhibit a larger
![]() $\mathit{Re}_{i,c}$
and larger
$\mathit{Re}_{i,c}$
and larger
![]() $k_{c}$
.
$k_{c}$
.
It is possible to quantify the effect of non-negligible shear-layer thickness (i.e. large
![]() $A$
) on the resulting relationship between
$A$
) on the resulting relationship between
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{E}\,$
at marginal stability. Taking data from figure
$\mathit{E}\,$
at marginal stability. Taking data from figure
![]() $5$
of Niino & Misawa (Reference Niino and Misawa1984), the critical internal Reynolds number is found to fit very well to
$5$
of Niino & Misawa (Reference Niino and Misawa1984), the critical internal Reynolds number is found to fit very well to
![]() $\mathit{Re}_{i,c}=11.5+69.1{\it\gamma}^{-1.96}$
(it should be noted that their
$\mathit{Re}_{i,c}=11.5+69.1{\it\gamma}^{-1.96}$
(it should be noted that their
![]() $\mathit{Re}_{i}$
definition differs by a factor of
$\mathit{Re}_{i}$
definition differs by a factor of
![]() $1/\sqrt{2}$
from ours, see Vo et al. (Reference Vo, Montabone and Sheard2014)). The ranges of Ekman numbers (
$1/\sqrt{2}$
from ours, see Vo et al. (Reference Vo, Montabone and Sheard2014)). The ranges of Ekman numbers (
![]() $5\times 10^{-5}\leqslant \mathit{E}\,\leqslant 3\times 10^{-3}$
) and enclosure aspect ratios (
$5\times 10^{-5}\leqslant \mathit{E}\,\leqslant 3\times 10^{-3}$
) and enclosure aspect ratios (
![]() $1/6\leqslant A\leqslant 2$
) investigated here are applied to the empirical relationship to determine
$1/6\leqslant A\leqslant 2$
) investigated here are applied to the empirical relationship to determine
![]() $\mathit{Re}_{i,c}$
. Correction of the
$\mathit{Re}_{i,c}$
. Correction of the
![]() $\mathit{Re}_{i}$
prefactor and empirical fitting of power-law curves to the marginal Rossby–Ekman number pairs yield exponents for the
$\mathit{Re}_{i}$
prefactor and empirical fitting of power-law curves to the marginal Rossby–Ekman number pairs yield exponents for the
![]() $\mathit{E}\,$
in
$\mathit{E}\,$
in
![]() $\mathit{Ro}/\mathit{E}\,^{{\it\eta}}$
as provided in table 1. For negligibly thin shear layers (
$\mathit{Ro}/\mathit{E}\,^{{\it\eta}}$
as provided in table 1. For negligibly thin shear layers (
![]() $A\rightarrow 0$
),
$A\rightarrow 0$
),
![]() ${\it\eta}\rightarrow 3/4$
, which is equivalent to that obtained theoretically by Busse (Reference Busse1968). The exponent deviates from this value as
${\it\eta}\rightarrow 3/4$
, which is equivalent to that obtained theoretically by Busse (Reference Busse1968). The exponent deviates from this value as
![]() $A$
increases. As a comparison, the exponents obtained numerically (figure 17
a) and those calculated from Niino & Misawa (Reference Niino and Misawa1984) given in table 1 differ by just
$A$
increases. As a comparison, the exponents obtained numerically (figure 17
a) and those calculated from Niino & Misawa (Reference Niino and Misawa1984) given in table 1 differ by just
![]() $0.65\,\%$
and
$0.65\,\%$
and
![]() $0.16\,\%$
for
$0.16\,\%$
for
![]() $A=1/6$
and
$A=1/6$
and
![]() $A=2/3$
respectively. Furthermore, the predicted exponents in table 1 suggest that a more suitable threshold for geometry-independent shear layers is
$A=2/3$
respectively. Furthermore, the predicted exponents in table 1 suggest that a more suitable threshold for geometry-independent shear layers is
![]() ${\it\gamma}\gtrsim 45$
. This value is required to achieve an error of less than
${\it\gamma}\gtrsim 45$
. This value is required to achieve an error of less than
![]() $0.1\,\%$
when compared with the theoretical value of
$0.1\,\%$
when compared with the theoretical value of
![]() $3/4$
. This is a revised value to the
$3/4$
. This is a revised value to the
![]() ${\it\gamma}>25$
previously quoted by Niino & Misawa (Reference Niino and Misawa1984) and would align the neutral curve closer to the
${\it\gamma}>25$
previously quoted by Niino & Misawa (Reference Niino and Misawa1984) and would align the neutral curve closer to the
![]() ${\it\gamma}\rightarrow \infty$
curve illustrated in their figure 5.
${\it\gamma}\rightarrow \infty$
curve illustrated in their figure 5.
Table 1. Exponent of the Ekman number
![]() ${\it\eta}$
, for
${\it\eta}$
, for
![]() $\mathit{Ro}/\mathit{E}\,^{{\it\eta}}$
describing marginal stability for various values of
$\mathit{Ro}/\mathit{E}\,^{{\it\eta}}$
describing marginal stability for various values of
![]() $A$
based on the marginal stability analysis of Niino & Misawa (Reference Niino and Misawa1984). The deviation is calculated from
$A$
based on the marginal stability analysis of Niino & Misawa (Reference Niino and Misawa1984). The deviation is calculated from
![]() $({\it\eta}-3/4)/(3/4)$
, where
$({\it\eta}-3/4)/(3/4)$
, where
![]() $3/4$
represents the theoretical exponent value. The range of
$3/4$
represents the theoretical exponent value. The range of
![]() ${\it\gamma}$
achieved for
${\it\gamma}$
achieved for
![]() $\mathit{E}\,<3\times 10^{-3}$
and a fixed
$\mathit{E}\,<3\times 10^{-3}$
and a fixed
![]() $A$
is also displayed.
$A$
is also displayed.

Turning attention now to the preferred azimuthal wavelength, a plot of the preferred normalized azimuthal wavelength (
![]() ${\it\lambda}_{{\it\theta}}^{\ast }=2{\rm\pi}/(kA)$
) against
${\it\lambda}_{{\it\theta}}^{\ast }=2{\rm\pi}/(kA)$
) against
![]() $|\mathit{Ro}|/\mathit{E}\,^{2}$
for
$|\mathit{Ro}|/\mathit{E}\,^{2}$
for
![]() $A=1/6$
and
$A=1/6$
and
![]() $A=2/3$
is shown in figure 17(b). The data only include flow conditions of
$A=2/3$
is shown in figure 17(b). The data only include flow conditions of
![]() $\mathit{Re}_{\mathit{E}\,}\lesssim 26.7$
. Both sets of aspect ratio data demonstrate different relationships for the preferred unstable wavelengths due to the curvature effects. These relationships are given by
$\mathit{Re}_{\mathit{E}\,}\lesssim 26.7$
. Both sets of aspect ratio data demonstrate different relationships for the preferred unstable wavelengths due to the curvature effects. These relationships are given by
and
for
![]() $A=1/6$
and
$A=1/6$
and
![]() $A=2/3$
respectively. It is seen that the approximate
$A=2/3$
respectively. It is seen that the approximate
![]() $\mathit{E}\,^{1/3}$
scaling is lost for
$\mathit{E}\,^{1/3}$
scaling is lost for
![]() $A=1/6$
(
$A=1/6$
(
![]() $\propto E^{0}\cdot 376$
instead of
$\propto E^{0}\cdot 376$
instead of
![]() $\propto E^{0}\cdot 338$
). Thus, the
$\propto E^{0}\cdot 338$
). Thus, the
![]() $\mathit{E}\,^{1/3}$
scaling obtained for
$\mathit{E}\,^{1/3}$
scaling obtained for
![]() $A=2/3$
is merely coincidental, and is unrelated to the
$A=2/3$
is merely coincidental, and is unrelated to the
![]() $\mathit{E}\,^{1/3}$
layer. This confirms the earlier conjecture to this effect from the quasi-two-dimensional results described in § 4.1.1. The difference in the preferred wavelength is observed to be greatest at low
$\mathit{E}\,^{1/3}$
layer. This confirms the earlier conjecture to this effect from the quasi-two-dimensional results described in § 4.1.1. The difference in the preferred wavelength is observed to be greatest at low
![]() $|\mathit{Ro}|/\mathit{E}\,^{2}$
(predominantly large
$|\mathit{Ro}|/\mathit{E}\,^{2}$
(predominantly large
![]() $\mathit{E}\,$
), and to decrease with increasing
$\mathit{E}\,$
), and to decrease with increasing
![]() $|\mathit{Ro}|/\mathit{E}\,^{2}$
(predominantly decreasing
$|\mathit{Ro}|/\mathit{E}\,^{2}$
(predominantly decreasing
![]() $\mathit{E}\,$
) until approximately
$\mathit{E}\,$
) until approximately
![]() $\log _{10}(|\mathit{Ro}|/\mathit{E}\,^{2})=8$
. The large and small differences in preferred wavelengths at large and small
$\log _{10}(|\mathit{Ro}|/\mathit{E}\,^{2})=8$
. The large and small differences in preferred wavelengths at large and small
![]() $\mathit{E}\,$
respectively are reflected in figure 17(a) via the lines of integer
$\mathit{E}\,$
respectively are reflected in figure 17(a) via the lines of integer
![]() $kA$
. That is, the discrepancy between the lines becomes more prominent at larger
$kA$
. That is, the discrepancy between the lines becomes more prominent at larger
![]() $\mathit{E}\,$
, corresponding to thicker shear layers.
$\mathit{E}\,$
, corresponding to thicker shear layers.
The scaling for the azimuthal wavelengths at marginal stability can now be determined by substituting
![]() $\mathit{Ro}_{c}$
into the relationship for
$\mathit{Ro}_{c}$
into the relationship for
![]() ${\it\lambda}_{{\it\theta}}^{\ast }$
. Thus, at the onset of instability the scaled azimuthal wavelength is expressed in terms of
${\it\lambda}_{{\it\theta}}^{\ast }$
. Thus, at the onset of instability the scaled azimuthal wavelength is expressed in terms of
![]() $\mathit{E}\,$
only. The exponents of
$\mathit{E}\,$
only. The exponents of
![]() $\mathit{E}\,$
are calculated to be 0.234 and 0.208 for
$\mathit{E}\,$
are calculated to be 0.234 and 0.208 for
![]() $A=1/6$
and
$A=1/6$
and
![]() $A=2/3$
respectively. Linear theory in various rotating shear layers predicts that at the threshold of instability, the wavelength should scale linearly with the thickness of the shear layer (e.g. Drazin & Howard Reference Drazin and Howard1966; Niino & Misawa Reference Niino and Misawa1984; Sommeria, Meyers & Swinney Reference Sommeria, Meyers and Swinney1991). Here, this implies that
$A=2/3$
respectively. Linear theory in various rotating shear layers predicts that at the threshold of instability, the wavelength should scale linearly with the thickness of the shear layer (e.g. Drazin & Howard Reference Drazin and Howard1966; Niino & Misawa Reference Niino and Misawa1984; Sommeria, Meyers & Swinney Reference Sommeria, Meyers and Swinney1991). Here, this implies that
![]() ${\it\lambda}_{{\it\theta},c}^{\ast }\propto \mathit{E}\,^{1/4}$
. Equations (4.6) and (4.7) demonstrate that for the present system,
${\it\lambda}_{{\it\theta},c}^{\ast }\propto \mathit{E}\,^{1/4}$
. Equations (4.6) and (4.7) demonstrate that for the present system,
![]() ${\it\lambda}_{{\it\theta},c}^{\ast }\propto (|\mathit{Ro}|/\mathit{E}\,^{2})^{{\it\kappa}}$
, where the exponents are
${\it\lambda}_{{\it\theta},c}^{\ast }\propto (|\mathit{Ro}|/\mathit{E}\,^{2})^{{\it\kappa}}$
, where the exponents are
![]() ${\it\kappa}=-0.188\pm 0.005$
and
${\it\kappa}=-0.188\pm 0.005$
and
![]() ${\it\kappa}=-0.169\pm 0.002$
for
${\it\kappa}=-0.169\pm 0.002$
for
![]() $A=1/6$
and
$A=1/6$
and
![]() $A=2/3$
respectively. Substitution of the theoretical scaling
$A=2/3$
respectively. Substitution of the theoretical scaling
![]() $\mathit{Ro}_{c}\propto \mathit{E}\,^{3/4}$
for vanishingly thin shear layers (
$\mathit{Ro}_{c}\propto \mathit{E}\,^{3/4}$
for vanishingly thin shear layers (
![]() $A\rightarrow 0$
) yields
$A\rightarrow 0$
) yields
![]() ${\it\lambda}_{{\it\theta},c}^{\ast }\propto (\mathit{E}\,^{-5/4})^{{\it\kappa}}$
. Thus, an exponent of
${\it\lambda}_{{\it\theta},c}^{\ast }\propto (\mathit{E}\,^{-5/4})^{{\it\kappa}}$
. Thus, an exponent of
![]() ${\it\kappa}=-1/5$
is required for
${\it\kappa}=-1/5$
is required for
![]() ${\it\lambda}_{{\it\theta},c}^{\ast }\propto (|\mathit{Ro}|/\mathit{E}\,^{2})^{{\it\kappa}}$
to satisfy the
${\it\lambda}_{{\it\theta},c}^{\ast }\propto (|\mathit{Ro}|/\mathit{E}\,^{2})^{{\it\kappa}}$
to satisfy the
![]() $\mathit{E}\,^{1/4}$
scaling from linear theory. The empirical exponents of
$\mathit{E}\,^{1/4}$
scaling from linear theory. The empirical exponents of
![]() $-0.169\pm 0.002$
and
$-0.169\pm 0.002$
and
![]() $-0.188\pm 0.005$
are consistent with the scaling approaching the limiting
$-0.188\pm 0.005$
are consistent with the scaling approaching the limiting
![]() $-1/5$
exponent as
$-1/5$
exponent as
![]() $A\rightarrow 0$
. The fact that the exponent is not
$A\rightarrow 0$
. The fact that the exponent is not
![]() $-1/5$
at
$-1/5$
at
![]() $A=1/6$
reflects the earlier suggestion that geometry-independent shear layers are somewhat thinner than the
$A=1/6$
reflects the earlier suggestion that geometry-independent shear layers are somewhat thinner than the
![]() ${\it\gamma}>25$
threshold suggested by Niino & Misawa (Reference Niino and Misawa1984) for the parameter range considered in this study.
${\it\gamma}>25$
threshold suggested by Niino & Misawa (Reference Niino and Misawa1984) for the parameter range considered in this study.
5. Conclusions
In this paper, the axisymmetric base flow structure of a differential-rotating flow and its linear stability have been examined via axisymmetric and quasi-two-dimensional models. A direct comparison between the solutions from both models was performed to determine the validity of the models and in turn establish the importance of the role of the Stewartson
![]() $\mathit{E}\,^{1/3}$
layer on the linear stability of the flow. In addition to this, various aspect ratio containers were investigated using the axisymmetric model to study the aspect ratio dependence to reinforce the marginal stability results of Niino & Misawa (Reference Niino and Misawa1984) and further the understanding reported by Vo et al. (Reference Vo, Montabone and Sheard2014).
$\mathit{E}\,^{1/3}$
layer on the linear stability of the flow. In addition to this, various aspect ratio containers were investigated using the axisymmetric model to study the aspect ratio dependence to reinforce the marginal stability results of Niino & Misawa (Reference Niino and Misawa1984) and further the understanding reported by Vo et al. (Reference Vo, Montabone and Sheard2014).
Flows with Rossby numbers in the range
![]() $-2.0\leqslant \mathit{Ro}\leqslant 1.0$
and Ekman numbers in the range
$-2.0\leqslant \mathit{Ro}\leqslant 1.0$
and Ekman numbers in the range
![]() $5\times 10^{-5}\leqslant \mathit{E}\,\leqslant ~3\times 10^{-3}$
were investigated. The same flow features were obtained between the axisymmetric and quasi-two-dimensional models for small
$5\times 10^{-5}\leqslant \mathit{E}\,\leqslant ~3\times 10^{-3}$
were investigated. The same flow features were obtained between the axisymmetric and quasi-two-dimensional models for small
![]() $|\mathit{Ro}|$
, with differences observed at large
$|\mathit{Ro}|$
, with differences observed at large
![]() $|\mathit{Ro}|$
, where depth-dependent features become present. Both models displayed a shear layer produced at the disk–tank interface for positive- and negative-
$|\mathit{Ro}|$
, where depth-dependent features become present. Both models displayed a shear layer produced at the disk–tank interface for positive- and negative-
![]() $\mathit{Ro}$
flows. The similarity in the flows is reflected in the measured
$\mathit{Ro}$
flows. The similarity in the flows is reflected in the measured
![]() $\mathit{E}\,^{1/4}$
layer thickness whereby the axisymmetric and quasi-two-dimensional solutions yield
$\mathit{E}\,^{1/4}$
layer thickness whereby the axisymmetric and quasi-two-dimensional solutions yield
![]() ${\it\delta}_{vel}=1.22(\pm 0.03)\mathit{E}\,^{0.260\pm 0.003}$
and
${\it\delta}_{vel}=1.22(\pm 0.03)\mathit{E}\,^{0.260\pm 0.003}$
and
![]() ${\it\delta}_{vel}=1.26(\pm 0.02)\mathit{E}\,^{0.260\pm 0.002}$
respectively. It is interesting to note that the thickness relationship for the quasi-two-dimensional model is independent of
${\it\delta}_{vel}=1.26(\pm 0.02)\mathit{E}\,^{0.260\pm 0.002}$
respectively. It is interesting to note that the thickness relationship for the quasi-two-dimensional model is independent of
![]() $\mathit{Ro}$
, rather than being limited to
$\mathit{Ro}$
, rather than being limited to
![]() $\mathit{Ro}\rightarrow 0$
.
$\mathit{Ro}\rightarrow 0$
.
Despite the
![]() $\mathit{Ro}$
independence in the shear-layer thickness in quasi-two-dimensional solutions, the azimuthal wavenumber preference for the linear instability of the flow remains dependent on both
$\mathit{Ro}$
independence in the shear-layer thickness in quasi-two-dimensional solutions, the azimuthal wavenumber preference for the linear instability of the flow remains dependent on both
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{E}\,$
, similar to that illustrated by the axisymmetric model. Additionally, the quasi-two-dimensional solutions displayed identical preferred azimuthal wavenumbers between the positive- and negative-
$\mathit{E}\,$
, similar to that illustrated by the axisymmetric model. Additionally, the quasi-two-dimensional solutions displayed identical preferred azimuthal wavenumbers between the positive- and negative-
![]() $\mathit{Ro}$
regimes, which is in contrast to the axisymmetric model. Despite these differences, the onset of instability and wavenumbers at low
$\mathit{Ro}$
regimes, which is in contrast to the axisymmetric model. Despite these differences, the onset of instability and wavenumbers at low
![]() $\mathit{Re}_{i}$
were comparable between the two models. A fit of the azimuthal wavelength as a function of
$\mathit{Re}_{i}$
were comparable between the two models. A fit of the azimuthal wavelength as a function of
![]() $|\mathit{Ro}|/\mathit{E}\,^{2}$
suggested that
$|\mathit{Ro}|/\mathit{E}\,^{2}$
suggested that
![]() ${\it\lambda}_{{\it\theta}}$
scales approximately with
${\it\lambda}_{{\it\theta}}$
scales approximately with
![]() $\mathit{E}\,^{1/3}/|\mathit{Ro}|^{1/6}$
. A similar relationship was obtained for the axisymmetric model. However, it is now known that the
$\mathit{E}\,^{1/3}/|\mathit{Ro}|^{1/6}$
. A similar relationship was obtained for the axisymmetric model. However, it is now known that the
![]() $1/3$
exponent is not related to the
$1/3$
exponent is not related to the
![]() $\mathit{E}\,^{1/3}$
layer and these exponents instead are a consequence of the non-negligible shear-layer thickness leading to a deviation from the ideal marginal wavelength scaling of
$\mathit{E}\,^{1/3}$
layer and these exponents instead are a consequence of the non-negligible shear-layer thickness leading to a deviation from the ideal marginal wavelength scaling of
![]() $(|\mathit{Ro}|/\mathit{E}\,^{2})^{-1/5}$
.
$(|\mathit{Ro}|/\mathit{E}\,^{2})^{-1/5}$
.
The growth rate as a function of the wavenumber demonstrates the typical trend of increasing growth rate and corresponding azimuthal wavenumber with increasing
![]() $\mathit{Ro}$
and decreasing
$\mathit{Ro}$
and decreasing
![]() $\mathit{E}\,$
. More importantly, the quasi-two-dimensional solutions only revealed the mode I instability branch, which is associated with the pair of opposite-signed vorticity shown throughout the interior coinciding with the disk–tank radius. The superposition of the axisymmetric base flow and the perturbation field highlighted the resulting deformed structures, which were consistent with the mode I instability. The absence of the mode II instability further reinforces the argument that this instability is generated as a consequence of the breaking of depth independence in the axisymmetric base flow, as proposed by Vo et al. (Reference Vo, Montabone and Sheard2014). In general, this paper has demonstrated that the quasi-two-dimensional model is accurate in describing the onset of instability, the linearly preferred azimuthal wavenumber and the qualitative trends, as compared with the axisymmetric model.
$\mathit{E}\,$
. More importantly, the quasi-two-dimensional solutions only revealed the mode I instability branch, which is associated with the pair of opposite-signed vorticity shown throughout the interior coinciding with the disk–tank radius. The superposition of the axisymmetric base flow and the perturbation field highlighted the resulting deformed structures, which were consistent with the mode I instability. The absence of the mode II instability further reinforces the argument that this instability is generated as a consequence of the breaking of depth independence in the axisymmetric base flow, as proposed by Vo et al. (Reference Vo, Montabone and Sheard2014). In general, this paper has demonstrated that the quasi-two-dimensional model is accurate in describing the onset of instability, the linearly preferred azimuthal wavenumber and the qualitative trends, as compared with the axisymmetric model.
A closer examination of the axisymmetric model was conducted by investigating aspect ratios in the range
![]() $1/6\leqslant A\leqslant 2$
. The effect of a large-aspect-ratio container yielded a broadening of the shear layer, while a more concentrated shear layer was obtained for small-aspect-ratio containers. It was found that the thickness data deviate from the theoretical scaling with either increasing
$1/6\leqslant A\leqslant 2$
. The effect of a large-aspect-ratio container yielded a broadening of the shear layer, while a more concentrated shear layer was obtained for small-aspect-ratio containers. It was found that the thickness data deviate from the theoretical scaling with either increasing
![]() $A$
or
$A$
or
![]() $\mathit{E}\,$
due to the confinement effects. However, this was mainly evident with the thicker
$\mathit{E}\,$
due to the confinement effects. However, this was mainly evident with the thicker
![]() ${\it\delta}_{vort}$
layer at
${\it\delta}_{vort}$
layer at
![]() $A=2$
. The data deviated from the theoretical scaling for
$A=2$
. The data deviated from the theoretical scaling for
![]() $A\mathit{E}\,^{1/4}\gtrsim 0.34$
in this system. The thinner
$A\mathit{E}\,^{1/4}\gtrsim 0.34$
in this system. The thinner
![]() ${\it\delta}_{vort}$
layer consistently displayed exponents that were in agreement with theory. The effect of the aspect ratio on the structure of the flow was determined via a universal diagram governed by
${\it\delta}_{vort}$
layer consistently displayed exponents that were in agreement with theory. The effect of the aspect ratio on the structure of the flow was determined via a universal diagram governed by
![]() $\log _{10}(\mathit{E}\,A^{2})$
and
$\log _{10}(\mathit{E}\,A^{2})$
and
![]() $\log _{10}(A\mathit{Ro})$
. A transition between reflectively symmetric and symmetry-broken flows was observed, and the empirical fits of the transition lines yielded no dependence on the aspect ratio.
$\log _{10}(A\mathit{Ro})$
. A transition between reflectively symmetric and symmetry-broken flows was observed, and the empirical fits of the transition lines yielded no dependence on the aspect ratio.
The linear stability analysis of flows in various aspect ratios revealed that beyond a certain
![]() $A$
, the Stewartson
$A$
, the Stewartson
![]() $\mathit{E}\,^{1/4}$
layer becomes weaker and shifts its preference towards low azimuthal wavenumbers. In contrast, given a sufficiently small
$\mathit{E}\,^{1/4}$
layer becomes weaker and shifts its preference towards low azimuthal wavenumbers. In contrast, given a sufficiently small
![]() $A$
whereby the Stewartson layer is unhindered by the confining walls, the growth rates demonstrate a similar maximum to that obtained by
$A$
whereby the Stewartson layer is unhindered by the confining walls, the growth rates demonstrate a similar maximum to that obtained by
![]() $A=2/3$
. The threshold of instability was determined to be
$A=2/3$
. The threshold of instability was determined to be
![]() $\mathit{Ro}_{c}\propto \mathit{E}\,^{0.756\pm 0.010}$
for
$\mathit{Ro}_{c}\propto \mathit{E}\,^{0.756\pm 0.010}$
for
![]() $A=1/6$
, which is closer to the ideal scaling of
$A=1/6$
, which is closer to the ideal scaling of
![]() $\mathit{E}\,^{1/4}$
than that obtained for
$\mathit{E}\,^{1/4}$
than that obtained for
![]() $A=2/3$
(
$A=2/3$
(
![]() $\mathit{Ro}_{c}\propto \mathit{E}\,^{0.767\pm 0.006}$
). The difference in exponents is explained via an analysis of the marginal stability results obtained by Niino & Misawa (Reference Niino and Misawa1984), who suggested that curvature effects become significant below
$\mathit{Ro}_{c}\propto \mathit{E}\,^{0.767\pm 0.006}$
). The difference in exponents is explained via an analysis of the marginal stability results obtained by Niino & Misawa (Reference Niino and Misawa1984), who suggested that curvature effects become significant below
![]() ${\it\gamma}\leqslant 25$
. The results here predict
${\it\gamma}\leqslant 25$
. The results here predict
![]() ${\it\gamma}\lesssim 45$
as a more suitable threshold. Despite the slight differences realized between
${\it\gamma}\lesssim 45$
as a more suitable threshold. Despite the slight differences realized between
![]() $A=1/6$
and
$A=1/6$
and
![]() $A=2/3$
at marginal stability, the difference in preferred azimuthal wavenumber between the two aspect ratios was largely corrected by scaling the wavenumber by the aspect ratio. The universality in aspect ratio was demonstrated through a regime diagram of
$A=2/3$
at marginal stability, the difference in preferred azimuthal wavenumber between the two aspect ratios was largely corrected by scaling the wavenumber by the aspect ratio. The universality in aspect ratio was demonstrated through a regime diagram of
![]() $kA$
as a function of
$kA$
as a function of
![]() $\mathit{Ro}$
and
$\mathit{Ro}$
and
![]() $\mathit{E}\,$
for flows beyond marginal stability.
$\mathit{E}\,$
for flows beyond marginal stability.
It is noted that the results presented in this paper on the stability of the shear layer have focused on its linear evolution. The interaction between several instability modes and other nonlinear effects are likely to alter the evolution of instabilities and their ultimate azimuthal wavenumber in the saturated flow state.
Acknowledgements
This research was supported by ARC Discovery grants DP120100153 and DP150102920, high-performance computing time allocations from the National Computational Infrastructure (NCI) and the Victorian Life Sciences Computation Initiative (VLSCI), and the Monash SunGRID. T.V. was supported by an Engineering Research Living Allowance through the Faculty of Engineering, Monash University. The authors thank the anonymous referees whose comments have helped to improve the quality of this paper.