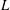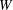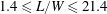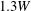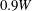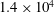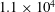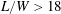1 Introduction
Many structures in our everyday life can be approximated as finite wall-mounted cylinders (FWMCs), such as skyscrapers, aircraft landing gears and submarine appendages. Given their ubiquity, understanding the flow around them is of fundamental importance. Beyond the flow structure, there has been a growing interest in the noise generated by FWMCs, which is linked with the fluctuating surface pressure caused by vortex shedding. Despite numerous studies, which have been comprehensively reviewed by Porteous, Moreau & Doolan (Reference Porteous, Moreau and Doolan2014), there is still no single model that can universally describe the wake structure of a FWMC and how it is affected by various parameters, such as its aspect ratio and the condition of the oncoming flow. The focus of this paper is to examine the role of aspect ratio in determining a square FWMC’s wake structure and the cross-stream forces acting on it, while maintaining the oncoming boundary-layer conditions.
The flow around a square FWMC is complex due to the three-dimensionality of the flow. An infinite length cylinder sheds quasi-periodic Kármán vortices uniformly across its span. For a FWMC, the wake flow is additionally influenced by the ‘junction’ and ‘free-end’ flow. Junction flow refers to the interaction of the oncoming boundary layer on the wall with that on the cylinder at their junction. A pair of counter-rotating streamwise vortices is observed on both sides of the cylinder when the junction flow is time averaged (Wang, Cao & Zhou Reference Wang, Cao and Zhou2014), which are referred to as ‘base’ or ‘junction’ vortices. These junction vortices induce upwash in a square FWMC wake, which intensifies with increasing boundary-layer thickness (Wang et al. Reference Wang, Zhou, Chan and Lam2006). Note that these junction vortices are distinct from the legs of a horseshoe vortex system, as they are formed by different flow mechanisms (Porteous et al. Reference Porteous, Moreau and Doolan2014). The free-end flow refers to downwash from the free end (or tip) of the cylinder towards the wall due to the low pressure region immediately downwind of the cylinder. Similar to junction flow, the time-averaged free-end flow typically resembles a pair of counter-rotating streamwise vortices (Etzolt & Fiedler Reference Etzolt and Fiedler1976; Kawamura et al. Reference Kawamura, Hiwada, Hibino, Mabuchi and Kumada1984; Park & Lee Reference Park and Lee2000), which are thus sometimes referred to as ‘tip’ vortices.
When both base and tip vortices are present, there are a total of four streamwise vortices downstream of the cylinder and the structure is referred to as quadrupole. In a similar fashion, the flow structure is referred to as dipole for the cases where only one vortex pair is present. However, neither tip nor base vortices form at very low aspect ratio. Instead, Sakamoto & Arie (Reference Sakamoto and Arie1983) reported arch-type (or symmetric) vortex shedding behind square FWMCs with an aspect ratio of less than two.
Figure 1. A square FWMC mounted to a flat wall with width
$W$
and span
$L$
subject to a flow with free-stream velocity
$U_{\infty }$
and an incoming boundary-layer height of
$\unicode[STIX]{x1D6FF}$
.
There are two major parameters affecting the wake structure that is formed behind a square FWMC: the aspect ratio (here expressed as
$L/W$
, where
$L$
is the length/span of the cylinder and
$W$
is its width/side length) and
$\unicode[STIX]{x1D6FF}/W$
(where
$\unicode[STIX]{x1D6FF}$
is the oncoming boundary-layer height). It should be noted that many previous studies have the boundary-layer height normalised against the cylinder length (
$\unicode[STIX]{x1D6FF}/L$
) instead. The effect of Reynolds number on the wake structure is small (Bourgeois, Sattari & Martinuzzi Reference Bourgeois, Sattari and Martinuzzi2011) and therefore is not a point of focus in this paper. In earlier studies, only the aspect ratio was considered to be the main parameter affecting the wake structure. This implies that there are critical values of aspect ratios separating the arch, dipole and quadrupole structures. However, there are conflicting reported values of critical aspect ratio, varying from
$L/W=2$
to 6, depending on boundary-layer thickness and oncoming flow turbulence (Sakamoto & Arie Reference Sakamoto and Arie1983; Kawamura et al.
Reference Kawamura, Hiwada, Hibino, Mabuchi and Kumada1984). Lee (Reference Lee1975) reported that increasing the turbulence intensity of the oncoming flow (up to 12.5 % in this study) results in a rise in the base pressure of an infinite cylinder. This was later confirmed by Tieleman & Akins (Reference Tieleman and Akins1996) for surface-mounted prisms. However, according to Drazin & Reid (Reference Drazin and Reid2004) it will not affect the large-scale vortices formed due to wake instability. For the case of a wall-mounted cube, Hearst, Gomit & Ganapathisubramani (Reference Hearst, Gomit and Ganapathisubramani2016) observed that varying the level of turbulence intensity from 0.5 to 8.9 % does not affect the stagnation point on the cylinder’s upstream face and the reattachment point of the wake.
The aforementioned arch, dipole and quadrupole wake structures refer only to time-averaged flow. The instantaneous wake structure is more complicated and three-dimensional. Studying the instantaneous structure is important to understand the intermittent nature of the vortex shedding by an FWMC. Studies as early as that by Sakamoto & Arie (Reference Sakamoto and Arie1983) reported that for a cylinder with
$L/W=7$
, the shedding alternates between symmetric and anti-symmetric shedding patterns. Bourgeois et al. (Reference Bourgeois, Sattari and Martinuzzi2011) and Hosseini, Bourgeois & Martinuzzi (Reference Hosseini, Bourgeois and Martinuzzi2013) identified the instantaneous three-dimensional structure, by phase averaging the flow structure obtained from particle image velocimetry (PIV) measurements. Performed on a cylinder with
$L/W=4$
and boundary-layer height of
$\unicode[STIX]{x1D6FF}/L=0.18$
, Bourgeois et al. (Reference Bourgeois, Sattari and Martinuzzi2011) show that a ‘half-loop’ pattern is formed for a FWMC with a dipole time-averaged wake structure. Such a structure is similar to the ‘staggered arranged’ pattern proposed by Wang & Zhou (Reference Wang and Zhou2009), in which there are two principal vortices oriented similarly to the cylinder length and they are connected by an arch-like structure near the free end. However, the half-loop structure shows an additional feature: the structures from previous shedding periods are still interlinked in a ‘braid’ pattern. Hosseini et al. (Reference Hosseini, Bourgeois and Martinuzzi2013) expanded on this study and showed that by reducing
$\unicode[STIX]{x1D6FF}/L$
while keeping the aspect ratio constant at
$L/W=8$
, the time-averaged wake structure becomes quadrupole and the associated transient wake structure has a ‘full-loop’ pattern. Based on this study, Hosseini et al. (Reference Hosseini, Bourgeois and Martinuzzi2013) questioned the practice of using aspect ratio alone to determine the wake structure of FWMCs.
Another salient feature of the vortex shedding by FWMCs is the phenomenon of cellular shedding. This refers to the division of shedding along the span of a cylinder into regions shedding at different frequencies. Although cellular shedding has been widely reported for circular FWMCs (Lee Reference Lee1997), Hosseini et al. (Reference Hosseini, Bourgeois and Martinuzzi2013) suggested that cellular shedding may not occur at all for square FWMCs. However, cellular shedding has been observed in the wake of square FWMCs by Moreau & Doolan (Reference Moreau and Doolan2013) and Porteous, Moreau & Doolan (Reference Porteous, Moreau and Doolan2017). Cellular shedding is of particular interest in this study as Moreau & Doolan (Reference Moreau and Doolan2013) suggested that dual dominant tones produced by square FWMCs with
$L/W>8.7$
are associated with two vortex shedding cells detected by analysing the wake spectra. As is the case with transition from dipole to quadrupole wake structure, the aspect ratio above which cellular shedding occurs for circular FWMCs varies between studies and is as diverse as from
$L/W=1$
to 7 (Sakamoto & Arie Reference Sakamoto and Arie1983; Okamoto & Sunabashiri Reference Okamoto and Sunabashiri1992; Lee Reference Lee1997; Sumner, Heseltine & Dansereau Reference Sumner, Heseltine and Dansereau2004).
Finally, there is the question of how the wake structure relates to the noise generated by a square FWMC. Being a virtually ubiquitous geometry, the noise emanating from FWMCs is not merely an annoyance, but also a contributor to environmental noise pollution, which is a known public health issue (Passchier-Vermeer & Passchier Reference Passchier-Vermeer and Passchier2000). An infinite length cylinder sheds quasi-periodic Kármán vortices, which results in surface pressure fluctuations on the cylinder and an associated Aeolian tone according to the relationship between the unsteady pressure and the noise as developed by Curle (Reference Curle1955). A study specific to the aeroacoustics of square FWMCs was recently presented by Porteous et al. (Reference Porteous, Moreau and Doolan2017), who performed noise measurements of cylinders with aspect ratios
$0.29\leqslant L/W\leqslant 23$
. Four shedding regimes based on the aspect ratio were identified, each emitting tonal noise with distinct characteristics. Within Regime R0, which has the lowest aspect ratio
$L/W<2$
, no tonal noise was detected. In the order of increasing aspect ratio, Regime RI (
$2<L/W<10$
), RII (
$10<L/W<18$
) and RIII (
$L/W>18$
) emit a tonal noise with one, two and three peak frequencies, respectively.
In summary, there are many models that attempt to describe the wake flow structure of a square FWMC but none is universally accepted. One such example is the ambiguity in the critical aspect ratio that marks the transition from dipole to quadrupole wake structure. While the study by Porteous et al. (Reference Porteous, Moreau and Doolan2017) provides some insight to the importance of aspect ratio, limited experimental data points leaves the three-dimensional wake flow structure to be inferred from two-dimensional flow data. The amplitude modulation of the acoustic signal observed by Porteous et al. (Reference Porteous, Moreau and Doolan2017) is thought to be related to intermittent shedding, but has not been conclusively studied.
To address these knowledge gaps, a combined numerical and experimental study has been performed to provide a better understanding of the wake flow structure formed by square FWMCs, with a focus on how it is affected by aspect ratio. Large-eddy simulations (LES) were performed for FWMCs with aspect ratios of
$L/W=1.4$
, 4.3, 10 and 18.6, and experimental results for
$L/W=1.5$
to 21.6 are presented to validate and support the findings made from the numerical simulations. In particular, this paper provides three-dimensional flow data around the cylinders and high resolution surface pressure data for cases in which the approaching boundary layer is turbulent. By inspecting the three-dimensional flow structure visualisation, a new parametric diagram is presented to show how aspect ratio and boundary-layer height determine the dipole/quadrupole pattern of the time-averaged wake flow. For the first time, evidence of intermittent and cellular shedding is presented in the form of time-history data of cylinder surface pressure and spectral proper orthogonal decomposition (SPOD).
2 Methodology
To investigate the effect of aspect ratio on the wake structure of a square FWMC, LES was performed for four different cylinders:
$L/W=1.4$
, 4.3, 10 and 18.6. The FWMC geometry and the oncoming flow conditions employed in the LES were based on the experimental study by Porteous et al. (Reference Porteous, Moreau and Doolan2017). The numerical procedure and computational domain of the LES are described in § 2.1. Mean and unsteady experimental data from Porteous et al. (Reference Porteous, Moreau and Doolan2017) were used to validate the numerical predictions in this paper. An overview of these experiments is provided in § 2.2.1 of this paper and readers are referred to the paper by Porteous et al. (Reference Porteous, Moreau and Doolan2017) for full details. New experimental results of surface pressure measurements on the cylinder are also presented. The methodology for these newer measurements is outlined in § 2.2.2. Section 2.3 lists the details of the test cases examined in this study and in § 2.4 the oncoming boundary-layer parameters in the experiment and LES are compared.
2.1 Numerical simulations
2.1.1 Large-eddy simulations
Since the velocities in this study are low, with the maximum Mach number less than 0.2, the air may be assumed to be incompressible. The filtered equations for continuity and momentum for an incompressible fluid with constant properties are
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\bar{U}_{i}}{\unicode[STIX]{x2202}x_{i}}=0,\end{eqnarray}$$
and
$$\begin{eqnarray}\unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x2202}\bar{U}_{i}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}(\bar{U}_{i}\bar{U}_{j})=-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{i}}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{ij}}{\unicode[STIX]{x2202}x_{j}}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}(\unicode[STIX]{x1D70E}_{ij}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D70C}$
is the density and
$\bar{U}$
is the filtered velocity. The stress tensor due to molecular viscosity,
$\unicode[STIX]{x1D70E}_{ij}$
, is defined by
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{ij}=\left[\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}U_{i}}{\unicode[STIX]{x2202}x_{j}}+\frac{\unicode[STIX]{x2202}U_{j}}{\unicode[STIX]{x2202}x_{i}}\right)\right]-\frac{2}{3}\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}\bar{U}_{l}}{\unicode[STIX]{x2202}\bar{x}_{l}}\unicode[STIX]{x1D6FF}_{ij}\end{eqnarray}$$
and
$\unicode[STIX]{x1D70F}_{ij}$
is the subgrid-scale stress defined by
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{ij}=\unicode[STIX]{x1D70C}\overline{U_{i}U_{j}}-\unicode[STIX]{x1D70C}\bar{U}_{i}\bar{U}_{j}.\end{eqnarray}$$
The subgrid-scale model used in the simulations was proposed by Smagorinsky (Reference Smagorinsky1964). Here, the model employs the Boussinesq hypothesis to compute subgrid-scale turbulent stresses,
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{ij}-{\textstyle \frac{1}{3}}\unicode[STIX]{x1D70F}_{kk}\unicode[STIX]{x1D6FF}_{ij}=-2\unicode[STIX]{x1D707}_{t}\bar{S}_{ij}.\end{eqnarray}$$
The rate of strain tensor,
$\bar{S}_{ij}$
, is
$$\begin{eqnarray}\bar{S}_{ij}=\frac{1}{2}\left(\frac{\unicode[STIX]{x2202}U_{i}}{\unicode[STIX]{x2202}x_{j}}+\frac{\unicode[STIX]{x2202}U_{j}}{\unicode[STIX]{x2202}x_{i}}\right)\end{eqnarray}$$
and the subgrid-scale turbulent viscosity,
$\unicode[STIX]{x1D707}_{t}$
, is modelled by
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{t}=\unicode[STIX]{x1D70C}L_{s}^{2}\unicode[STIX]{x1D6E5}^{2}|\bar{S}|,\end{eqnarray}$$
where
$L_{s}$
is the mixing length for subgrid scales and
$|\bar{S}|=\sqrt{2\bar{S}_{ij}\bar{S}_{ij}}$
.
$L_{s}$
is computed using
$$\begin{eqnarray}L_{s}=\text{min}(\unicode[STIX]{x1D705}y_{wall},C_{s}\unicode[STIX]{x1D6E5}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D705}$
is the von Kármán constant,
$y_{wall}$
is the distance to the closest wall,
$C_{s}$
is the Smagorinsky constant and the subgrid filter width,
$\unicode[STIX]{x1D6E5}$
, is defined as
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}=V^{1/3},\end{eqnarray}$$
where
$V$
is the volume of a cell in the computational domain. In this application,
$C_{s}$
is evaluated using the dynamic procedure based on the Germano identity (Germano et al.
Reference Germano, Piomelli, Moin and Cabot1991), which uses a solution proposed by Lilly (Reference Lilly1992). Details of the dynamic procedure and its implementation have been presented by Kim (Reference Kim2004). The interaction between the oncoming boundary layer formed on the wall and the boundary layer formed on the surface of the cylinder is important in the formation of the junction flow structures. As such, the flow in the boundary-layer region was resolved in the LES and no wall model was implemented.
These equations were solved with the aid of ANSYS FLUENT 17.2 finite-volume solver. The temporal discretisation scheme is advanced using a second-order implicit method and the convection term is discretised using a second-order central-differencing scheme. The SIMPLEC method (Van Doormaal & Raithby Reference Van Doormaal and Raithby1984) was used to handle the iterative process of pressure–velocity coupling. The convergence criteria at each time step were set at scaled residual of
$10^{-4}$
for the continuity equation and each directional component of the velocity, which was typically attained in less than 30 iterations per time step.
The time step size,
$\unicode[STIX]{x0394}t$
, was
$5\times 10^{-6}$
s, which corresponds to a Nyquist frequency of 100 kHz. This
$\unicode[STIX]{x0394}t$
was selected to keep the Courant–Friedrichs–Levy number along the streamwise direction,
$\text{CFL}=U_{\infty }\unicode[STIX]{x0394}t/\unicode[STIX]{x0394}x\approx 1$
around the cylinder, with
$\unicode[STIX]{x0394}x$
being the grid spacing on the surface of the cylinder along the streamwise direction. The simulation for each aspect ratio was run for a total of 16 000 time steps or 0.1 s in physical time. All time-averaged results shown in § 3 were obtained by averaging the data over the last 12 000 time steps or 0.075 s, which corresponds to 343 flow-through times across the width of the cylinders. Computations were performed on the Raijin cluster of the Australian National Computational Infrastructure (NCI) on a single computation node, which consists of 28 Intel Xeon E5-2690v4 2.6 GHz processor cores with 128 GB physical memory.
2.1.2 Boundary conditions
The oncoming free stream is simulated using a velocity inlet of
$U_{\infty }=32~\text{m}~\text{s}^{-1}$
as the boundary condition at approximately
$140W$
or 1 m upstream of the FWMC. To allow the wake to develop and avoid backflow, a pressure outlet condition of zero gauge pressure was applied
$80W$
or 0.57 m downstream of the cylinder, which corresponds to more than four times the span of the cylinder with the highest aspect ratio (
$L/W=18.6$
). A no-slip condition is applied to the mounting wall and the faces of the cylinder. Periodic boundary conditions are applied to the cross-stream boundaries of the domain, which are
$30W$
or 0.21 m apart. The boundary conditions are summarised in figure 2.
Figure 2. Schematic diagram of the computational domain. The type and value of the boundary conditions are specified.
Forced transition was necessary in this study to create a turbulent boundary layer with parameters similar to those in the experiments. To generate the turbulent boundary layer, a uniform jet injected through a 10 mm or
$1.4W$
wide slot along the wall was used, as shown in figure 2. This is akin to the boundary-layer tripping method employed by Wolf & Lele (Reference Wolf and Lele2012), except no suction is employed in this study which adds a small amount of momentum to the flow. However, due to its placement,
${\approx}100W$
upstream of the FWMC, and the large cross-section of the domain the local momentum injection is deemed to have enough time and space to dissipate into the global flow.
An inlet velocity of
$1~\text{m}~\text{s}^{-1}$
or
$U/U_{\infty }=0.03$
was applied to the slot area. The desired boundary-layer thickness, 9.1 mm, was then found to occur 1 m downstream of the main inlet of the computational domain, hence the FWMC was placed at this location. Jet velocities other than
$1~\text{m}~\text{s}^{-1}$
were also tested:
$0.5~\text{m}~\text{s}^{-1}$
,
$1.2~\text{m}~\text{s}^{-1}$
and
$1.5~\text{m}~\text{s}^{-1}$
. While higher velocities accelerate the growth, and therefore allow a smaller computational domain, using a value of
$1~\text{m}~\text{s}^{-1}$
was found to yield the profile closest to the law of the wall. Detailed parameters of the boundary-layer profile are presented in § 2.4.
2.1.3 Computational grid
Computational grids were created for four cylinders with aspect ratios of:
$L/W=1.4$
, 4.3, 10 and 18.6. A H-grid blocking scheme was employed to mesh the computational domain, with an O-grid in the immediate vicinity of the cylinder acting as an inflation layer. The total number of cells in the computational domain varies from
$12.7$
million for the lowest aspect ratio of
$L/W=1.4$
to
$27.1$
million for the highest aspect ratio of
$L/W=18.6$
. In a similar fashion, the number of elements across the span of the cylinder,
$N_{z}$
, ranges from
$N_{z}=40$
for
$L/W=1.4$
to
$N_{z}=250$
for
$L/W=18.6$
. The number of elements on the cylinder along the streamwise,
$N_{x}$
, and cross-stream,
$N_{y}$
, directions are consistently 70 for all aspect ratios. Table 3 provides a summary of these details. Based on these grid parameters, the average
$z^{+}$
value (spanwise direction) on the cylinder varies from 31 to 66 and the
$x^{+}$
value (streamwise direction) is constantly 22, which puts these simulations in the medium-to-high resolution LES regime according to the criteria by Wagner, Hüttl & Sagaut (Reference Wagner, Hüttl and Sagaut2007). The size of these spanwise elements is reduced near the wall junction and the free-end tip to properly capture the more complex flow in these regions. There are 40 elements across each side of the square cross-section, this is consistent for all aspect ratios. The
$y^{+}$
value on the surface of the wall and all sides of the cylinder is less than 2.
From the size of the computational domain shown in figure 2, the gap between the cylinder’s top surface and the top boundary is
$2L$
for the cylinder the highest aspect ratio (
$L/W=18.6$
). Behera & Saha (Reference Behera and Saha2019) performed numerical simulations of the flow past a finite wall-mounted square cylinder, where they examined three different gap heights of
$1.3L$
,
$1.7L$
and
$2.1L$
, and found that the flow field predicted in the three domains is almost identical. To confirm the domain independence in the current study, a simulation was run using a computational domain with a gap height of
$L$
. Figure 3 compares the time-averaged pressure coefficient on the back face (or ‘base’, facing downstream) obtained using the domains with
$2L$
and
$L$
. Unless stated, the pressure data herein are presented as a pressure coefficient,
$C_{p}(z,t)$
, defined as
$$\begin{eqnarray}C_{p}(z,t)=\frac{p(t)-\overline{p_{\infty }}}{0.5\unicode[STIX]{x1D70C}{U_{\infty }}^{2}},\end{eqnarray}$$
where
$p(z,t)$
is the pressure time recorded at a specific spanwise location,
$\overline{p_{\infty }}$
is the time-averaged free-stream static pressure. Although the gap height has been reduced from
$2L$
to
$L$
, the base pressure coefficient maintains a consistent profile across its span. This suggest that the minimum gap of
$2L$
employed in the simulations in this paper is sufficient to ensure domain independence. The maximum blockage of the cylinder with the highest aspect ratio of
$L/W=18.6$
is 0.6 %, which is much lower than the recommended maximum of 3 % by Tominaga et al. (Reference Tominaga, Mochida, Yoshie, Kataoka, Nozu, Yoshikawa and Shirasawa2008).
Figure 3. Time-averaged base pressure coefficient obtained from the computational domains where the gap between the cylinder top surface and the top boundary is
$L$
and
$2L$
.
Three grid resolutions were used to demonstrate grid spacing convergence, which is presented below for the aspect ratio
$L/W=4.3$
. The grid convergence index (GCI), following the method proposed by Roache (Reference Roache1997), was computed for each grid refinement to estimate the spatial discretisation errors. The refinement was focused on the immediate vicinity of the cylinder and the wake region, but with the aforementioned
$y^{+}$
values maintained in all three grids. As such, the grid refinement was not isotropic and the refinement ratio was estimated as
$\unicode[STIX]{x1D6FC}=(N_{j}/N_{j+1})^{1/3}$
, where
$N$
is the number of cells in the computational domain and subscript
$j=1,2,3$
indicates the coarse, medium and fine mesh, respectively.
The first parameter used to assess the grid convergence was the time-averaged drag force coefficient,
$\overline{C_{Fx}}$
. Force coefficient in this paper is defined as
$$\begin{eqnarray}C_{F_{i}}=\frac{F_{i}}{0.5\unicode[STIX]{x1D70C}U_{\infty }^{2}LW},\end{eqnarray}$$
where
$F_{i}$
is the force acting on the cylinder in direction
$i=x,y,z$
and the planform area is evaluated by
$LW$
. The second parameter considered here was the time-averaged velocity in the wake region. The time-averaged velocity is spatially averaged along the line formed by the intersection of the
$x/W=4$
and
$y/W=0.6$
planes. Spatially averaged velocity was preferred over single-point velocity, because of the unsteady and three-dimensional nature of the wake flow.
The results of the grid convergence study for
$L/W=4.3$
are summarised in table 1;
$\text{GCI}_{2,1}$
and
$\text{GCI}_{3,2}$
are the grid convergence indices for the coarse-to-medium and medium-to-fine refinements, respectively. The discretisation error was quantified by
$\unicode[STIX]{x1D700}$
, which is the percentage error between the value predicted by the LES with the medium resolution grid and that predicted by the Richardson extrapolation method when the grid spacing approaches zero. The
$\text{GCI}_{3,2}$
of both
$\overline{C_{Fx}}$
and
$\overline{U}$
are lower than their respective
$\text{GCI}_{2,1}$
, which indicates that the flow variables are converging to a value as the grid spacing is reduced. The spatial discretisation error for the medium grid
$\overline{C_{Fx}}$
and
$\overline{U}$
are 5.17 % and 3.34 %, respectively. The medium mesh was deemed to have a good balance between the discretisation error and the computational cost, and therefore was used to obtain the LES results. The mesh for the cylinders with
$L/W=1.4$
, 10 and 18.6 also exhibit similar convergence behaviours.
Table 1. The results of the grid convergence study for
$L/W=4.3$
, showing the grid convergence indexes and the spatial discretisation error obtained using Richardson’s extrapolation method.
The validation of the LES using experimental data is presented concurrently with the discussion of the results. Validations are available in § 3.1 for the time-averaged velocity field, §§ 3.3.1 and 3.3.2 for the cylinder surface pressure (both time evolution and time averaged) and § 3.3.3 for the frequency content of the wake velocity.
2.2 Experimental methodology
2.2.1 Hot-wire measurement
Flow-induced wake velocity measurements were taken in the University of Adelaide’s Anechoic Wind Tunnel (AWT). The air flows through an outlet with a height of 75 mm and a width of 275 mm. The flow is exhausted into an anechoic chamber with internal dimensions of
$1.4~\text{m}\times 1.4~\text{m}\times 1.6~\text{m}$
. The walls of this chamber are lined with pyramid shaped foam wedges which provide a near-anechoic environment above 250 Hz. The experiments conducted in the AWT were performed at a free-stream velocity of
$U_{\infty }=32~\text{m}~\text{s}^{-1}$
corresponding to a Reynolds number of
$Re_{W}=U_{\infty }W/\unicode[STIX]{x1D708}=1.4\times 10^{4}$
.
A test rig was designed to automatically change the aspect ratio of the square cylinder in small increments. A stepper motor is used to rotate a 300 mm threaded rod with an 8 mm pitch via a helical shaft coupling. The cylinder is driven linearly through a square hole in a flat plate made from 10 mm thick aluminium. The aluminium plate measures 150 mm in the streamwise (
$x$
) direction and 300 mm in the cross-stream (
$y$
) direction while the hole is located in the centre of the plate at a position of 43 mm downstream of jet exit plane. For the hot-wire wake surveys, the results for four different aspect ratio FWMCs are included in this paper:
$L/W=1.4$
, 4.3, 10, 18.6.
Hot-wire anemometry was used to perform a wake survey of the streamwise velocity downstream of the FWMCs. A Dantec Dynamics miniature hot-wire (model 55P16) controlled by an IFA300 Constant Temperature Anemometer system was used for the wake survey. The hot-wire is made from platinum plated tungsten, with a diameter of
$5~\unicode[STIX]{x03BC}\text{m}$
and a wire length of 1.25 mm. The measurement plane behind each aspect ratio cylinder was a grid of points that measured 50 mm in the streamwise (
$x$
) direction and the length of the cylinder in the spanwise (
$z$
) direction. The measurement plane began at approximately 0.2 mm from the trailing edge of the cylinder and 2 mm above surface of the plate. Additionally, the measurement plane was located at
$y/W=0.6$
to avoid entering the reverse flow region. The grid increments in the
$x$
and
$z$
directions were
$\unicode[STIX]{x0394}x_{hw}=\unicode[STIX]{x0394}z_{hw}=2$
mm. A hot-wire velocity record was taken at each node in the grid. A National Instruments PXI Express Chassis (Model PXIe-1082) with PXIe-4499 simultaneous sample and hold ADC cards was used to collect data from the hot-wire. These cards have built-in antialiasing low-pass filters with cutoff of DC to 0.4 of the sampling frequency. Velocity measurements were sampled at
$2^{15}$
Hz for 15 s. The complete description of the method employed for the hot-wire measurements is available in Porteous (Reference Porteous2016) and Porteous et al. (Reference Porteous, Moreau and Doolan2017).
2.2.2 Surface pressure measurements
Surface pressure measurements were performed in a wind tunnel facility at the University of New South Wales (UNSW), known as the ‘18 inch Wind Tunnel’ (18WT). The 18WT is an open-circuit, suction-type, closed-test-section wind tunnel with a working section that measures
$460~\text{mm}\times 460~\text{mm}$
and a maximum velocity of
$29~\text{m}~\text{s}^{-1}$
. Air first passes through a series of smoothing screens before entering a contraction with a contraction ratio of 5.5 and subsequently passing through the test section. The air is drawn through the wind tunnel by an 8-blade, 5.5 kW axial fan located downstream of the test section. Afterwards, the air is ejected through a vertical diffuser. The longitudinal turbulence intensity at
$15~\text{m}~\text{s}^{-1}$
(the speed for which the surface pressure and flow visualisation experiments were conducted) is approximately 0.5 %, which is comparable to the turbulence intensity measured in the AWT.
The FWMC models used for surface pressure measurements were three-dimensionally (3-D) printed out of ABS plastic using an ‘Ultimaker
$^{2}$
’ 3-D printer. Two models were printed with width of 12 mm and aspect ratio of
$L/W=4$
and 12.5. Each model was printed with a series of internal passages that ran from the base of the cylinder to a number of pressure taps located on one of the cylinder side faces. The pressure taps each had a diameter of 1 mm and the internal passages had an inner diameter of 1.5 mm. The
$L/W=4$
cylinder has eight pressure taps while the
$L/W=12.5$
FWMC has seven pressure taps. The pressure taps were evenly spaced in the spanwise direction of the cylinders and located directly in the centre of the side face, as illustrated in figure 1. The spanwise location of the pressure taps for each cylinder considered in this paper is provided in table 2. The spanwise position axis has been normalised by the total span of each cylinder, such that
$z/L=0$
is the wall junction and
$z/L=1$
is the free-end tip. The FWMCs were printed such that they could be pressed through a
$12~\text{mm}\times 12~\text{mm}$
hole located in the floor of the working section. The square hole was such that the cylinder and the hole made an interference fit. The hole was located 150 mm from the end of the contraction. The aspect ratio of each FWMC could be lowered by reducing the length of the cylinder exposed to the flow. Once an aspect ratio had been selected, the cylinder was clamped outside of the wind tunnel to prevent any movement. It should be noted that because each of the two printed FWMC models had a fixed number of pressure taps, the number of pressure taps exposed to the flow changed with variation in aspect ratio.
Table 2. The spanwise location of the pressure taps on the cylinder side faces.
The Reynolds number for experiments in the 18WT was slightly lower than AWT at
$Re_{W}=1.1\times 10^{4}$
owing to a slightly lower velocity (
$U_{\infty }=15~\text{m}~\text{s}^{-1}$
) and slightly higher cylinder width (
$W=12$
mm). According to Bourgeois et al. (Reference Bourgeois, Sattari and Martinuzzi2011), the fixed separation point on a two-dimensional (2-D) square cylinder makes the wake dynamics of the ensuing vortex street largely independent of Reynolds number. Bourgeois et al. (Reference Bourgeois, Sattari and Martinuzzi2011) also shows that the Strouhal number of vortex shedding for square FWMCs with
$L/W=4$
remains constant between
$Re_{W}=0.5\times 10^{4}$
to
$2\times 10^{4}$
. It is thus reasonable to assume that the vortex shedding process at
$Re_{W}=1.1\times 10^{4}$
and
$Re_{W}=1.4\times 10^{4}$
will be similar for the test cases studied here. Hence, the surface pressure measurements performed in the 18WT at a lower Reynolds number should be indicative of the processes occurring in the AWT at higher Reynolds numbers.
In the 18WT surface pressure measurements, the aspect ratios presented in this paper are:
$L/W=1.5$
, 4, 9.9 and 12.5. Note that these values are slightly different than the aspect ratios for AWT and LES, due to the different test rig set-up. Nonetheless, these aspect ratios were selected to be as close as possible to the those selected for the LES.
Static and fluctuating pressures were measured using a 16 channel Scanivalve digital sensor array (DSA), model number 3217/16 Px (Serial No. 10136). Each channel has a temperature compensated piezoresistive pressure sensor and measures differential pressure relative to a common reference pressure port. The module also contains a 16-bit ADC and pressures are recorded at a maximum rate of 500 samples/second/channel. The differential input pressure range of the DSA is
$\pm 2.5~\text{kPa}$
.
In this study, each pressure port in the FWMC was connected to a channel of the DSA via PVC tubing with an inner diameter of 1.53 mm and length of 600 mm. The reference pressure port was connected to a static wall pressure tap on the roof of the 18WT test section. According to the DSA calibration sheet, static readings of each channel of the DSA is accurate to within
$\pm 0.09\,\%$
of the output. The dynamic response of the pressure tubing system was estimated using the approach of Holman (Reference Holman2010). The natural frequency of the system is calculated to be approximately
$\unicode[STIX]{x1D714}_{n}=1300$
Hz while the damping ratio is approximately
$h_{damp}=0.063$
. Bendat & Piersol (Reference Bendat and Piersol2010) recommend that for systems with low damping, the frequencies of interest must be less than 20 % of the natural frequency. For the current system, this corresponds to a usable frequency range of less than 260 Hz. For the surface pressure experiments conducted in this study, the frequencies of interest where vortex shedding occurs, lie between 120 to 240 Hz depending on the aspect ratio. Thus, the system is suitable for dynamic pressure measurements in this case. The experimental error of the amplitude of the pressure measured by the Scanivalve is approximately
$\pm$
3.5 % full scale across all frequencies.
2.3 Summary of test cases
Table 3 provides a summary of the dimensions, tonal noise regime and grid sizes (where applicable) for all of the cylinders, both in the experiments and LES, presented in this paper. The total number of cells and grid resolution on the surface are shown for cylinders included in the LES. Note that the dimensions of the cylinders in the LES are based on the experiments in the AWT.
Unless otherwise stated, the coordinate system used in this paper has its origin at the junction of the FWMC, centred on the FWMC axis. The
$x$
-direction runs parallel with the free-stream flow, the
$z$
-direction runs parallel with the span of the FWMC and the
$y$
-direction runs orthogonal to both, in the cross-stream direction.
Table 3. A comparison of the dimensions of the cylinders presented in this paper. For cylinders included in the LES, key grid parameters are also included.
2.4 Wall boundary-layer characterisation
To characterise the incoming flow conditions, the wall boundary-layer profile at the cylinder location (but with the cylinder removed) was measured in both the AWT and the 18WT. Similarly, the boundary layer in the LES was measured at the position of the cylinder, in a computational domain without the cylinder. Table 4 compares the measured boundary-layer integral properties, normalised by the appropriate scale. These include the boundary-layer thickness,
$\unicode[STIX]{x1D6FF}/W$
, the friction velocity,
$u_{\unicode[STIX]{x1D70F}}/U_{\infty }$
, the parameter
$\unicode[STIX]{x1D6F1}$
(which describes the boundary layer’s streamwise pressure gradient), the displacement thickness,
$\unicode[STIX]{x1D6FF}^{\ast }/W$
, the momentum thickness,
$\unicode[STIX]{x1D703}^{\ast }/W$
, the shape factor,
$H=\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D703}^{\ast }$
, and the Reynolds number based on momentum thickness,
$Re_{\unicode[STIX]{x1D703}}=U_{\infty }\unicode[STIX]{x1D703}/\unicode[STIX]{x1D708}$
.
Table 4. A comparison of key characteristics of the incoming boundary layers.
For the AWT wall boundary layer, both the friction velocity,
$u_{\unicode[STIX]{x1D70F}}$
, and the parameter
$\unicode[STIX]{x1D6F1}$
were estimated by fitting the boundary-layer mean velocity profile to the law of the wake for turbulent boundary layers (Coles Reference Coles1956). The 18WT wall boundary layer could not be fitted to Cole’s law of the wake as the log region of the boundary layer was small. Instead the friction velocity was estimated using the traditional ‘Clauser chart’ method (Clauser Reference Clauser1954) with the value of
$\unicode[STIX]{x1D6F1}$
assumed to be 0. In the LES,
$u_{\unicode[STIX]{x1D70F}}$
was determined by fitting the log-law region of the boundary layer to the law of the wall (von Kármán Reference von Kármán1931). Table 4 shows that the integral parameters of the boundary layer in the LES reasonably replicate the boundary layer in experiments, lying between the AWT and 18WT parameters.
According to Wilcox (Reference Wilcox2006), a
$\unicode[STIX]{x1D6F1}$
value of between 0 and 0.6, as measured for all boundary-layer cases, indicates a near-zero streamwise pressure gradient. Also shown in table 4, the AWT boundary layer has a shape factor of
$H=1.6$
while the 18WT boundary layer has a shape factor of
$H=1.4$
. According to Pope (Reference Pope2000), a fully developed turbulent boundary layer has a shape factor of 1.3 while a laminar boundary layer has a shape factor of
$H=2.6$
. This indicates that in the LES and both experiments, the incoming boundary layers are in a turbulent and nearly fully developed state.
2.5 Power spectral density
Power spectral densities (PSDs) were estimated using Welch’s averaged modified periodogram method (Welch Reference Welch1967) and the values are expressed in
$\text{dB}~\text{Hz}^{-1}$
re.
$20~\unicode[STIX]{x03BC}\text{Pa}$
. The filtered time-history data from the experiments were split into 41 overlapping blocks of 240 points each. The 95 % confidence interval for each narrowband level is approximately
$\pm 1.6~\text{dB}~\text{Hz}^{-1}$
for the surface pressure PSD and
$\pm 0.6~\text{dB}~\text{Hz}^{-1}$
for the wake velocity. In these plots the ordinate axis is the height above the junction normalised by the length of the cylinder,
$z/L$
. In figure 14, the frequency resolution is significantly more coarse at
$\unicode[STIX]{x1D6E5}f=48$
Hz for LES, compared to 8 Hz for the experiments, and this is due to the much shorter sampling time of the simulations. Despite the difference in frequency resolution, the predicted spectra are in good agreement with the experimental measurements. The frequency axis in the spectral maps is expressed in Strouhal number based on the diameter of the cylinder,
$St=fW/U_{\infty }$
.
2.6 Spectral proper orthogonal decomposition
Spectral proper orthogonal decomposition (SPOD) is a method to decompose the cross-spectral density of time-resolved flow data and subsequently identify modes that each oscillate at a single frequency. While the more conventional space-only proper orthogonal decomposition (POD) only identifies modes which are spatially coherent, SPOD yields modes that are coherent in both space and time. The paper by Towne, Schmidt & Colonius (Reference Towne, Schmidt and Colonius2018) provides a good background of SPOD and how it relates to space-only POD. In this paper, SPOD was used to identify the different types of coherent flow structures along the span of the cylinder and how they are affected by a change in aspect ratio. Implementation of SPOD in this study follows the method described by Towne et al. (Reference Towne, Schmidt and Colonius2018). To perform the fast Fourier transform (FFT) in the decomposition, the time-history data from the simulations were divided into nine blocks containing 1024 data points each with 50 % overlap. This resulted in the SPOD modes being grouped in frequency bands with
$\unicode[STIX]{x0394}f\approx 98$
Hz. The flow modes with the highest energy levels were then chosen for analysis.
3 Results
Time-averaged wake velocity and turbulence intensity are first presented in § 3.1, comparing experimental results with LES to validate the numerical model; an in-depth analysis of these results is available in Porteous et al. (Reference Porteous, Moreau and Doolan2017). The validation is not limited to this section, but also in other result sections where experimental results are shown. Time-averaged wake structure results are then presented in § 3.2, by showing wake velocity maps normal to the free stream and three-dimensional flow visualisation using
$\unicode[STIX]{x1D706}_{2}$
criterion. This is followed by § 3.3, where cellular shedding behaviour is demonstrated using surface pressure fluctuations on the cylinder’s side face, wake velocity spectra and SPOD.
3.1 Time-averaged velocity
Before discussing the new results, the general flow features from the numerical prediction are validated here against published experimental measurements. Figure 4 shows the normalised time-averaged streamwise velocity,
$\bar{u}/U_{\infty }$
, comparing the numerical results with hot-wire measurements at
$x/W=4$
downstream of the cylinder, as described in § 2.2.1. The spanwise position axis has been normalised by the total span of each cylinder, such that
$z/L=0$
is the wall junction and
$z/L=1$
is the free-end tip. A local maximum in the vicinity of the junction is consistently observed for
$L/W=10$
and 18.6, which indicates the presence of a junction vortex pair. For a comprehensive discussion of these wake velocity and turbulence intensity profiles, readers are directed to the study of Porteous et al. (Reference Porteous, Moreau and Doolan2017).
Figure 4. Time-averaged spanwise profiles of
$u$
at
$x/W=4$
on the plane
$y/W=0.6$
for aspect ratios
$L/W=1.4,4.3,10$
and
$18.6$
, comparing experimental against LES data.
Figure 5. Spanwise profiles of turbulence intensity at
$x/W=4$
on the plane
$y/W=0.6$
for aspect ratios
$L/W=1.4,4.3,10$
and 18.6, comparing experimental against LES data.
Figure 6. Contour maps of the time-averaged streamwise velocity,
$\bar{u}/V_{\infty }$
, obtained from the experiments for aspect ratios: (a)
$L/W=1.4$
, (c)
$L/W=4.3$
, (e)
$L/W=10$
, (g)
$L/W=18.6$
; and also from LES: (b)
$L/W=1.4$
, (d)
$L/W=4.3$
, (f)
$L/W=10$
, (h)
$L/W=18.6$
. The contours were plotted on the hot-wire measurement plane,
$y/W=0.6$
. The boundary-layer height is indicated by the dashed line.
Figure 6 shows the normalised time-averaged velocity map measured on the
$x$
–
$z$
plane at
$y/W=0.6$
, comparing experimental and numerical results. For lower aspect ratios, the downwash penetrates deep into the wake region, which is due to the intense velocity deficit in the near-wake region. According to Wang et al. (Reference Wang, Zhou, Chan and Lam2006), the presence of the downwash implies the existence of a streamwise vortex pair immediately downstream of the free end. Downstream of the junction region (from
$x/W=2$
) for
$L/W=18.6$
, there is an accelerated flow region at about the boundary-layer height. These important features are observed in both experiments and LES. The only discrepancies occur in the immediate downstream of the cylinder (
$0.5<x/W<2$
), where the velocity deficit is consistently larger in the simulations. This may be attributed to the sensitivity of the single hot-wire to both streamwise and spanwise velocity.
Satisfactory agreement is shown for all aspect ratios, thus providing validation of the numerical model. There are still spanwise variations, which could be made smoother by including more simulation time into the time averaging. However, as shown in the comparisons with the experimental measurements throughout this paper, the general features of the flow have been reasonably captured and thus observations on the effect of aspect ratio on the wake structure may be drawn from the LES predictions.
3.2 Time-averaged wake structure
With the numerical simulations validated, the time-averaged wake will now be discussed. Many studies have observed that the time-averaged wake of a FWMC is either dipole or quadrupole in nature (Wang & Zhou Reference Wang and Zhou2009; Hosseini et al. Reference Hosseini, Bourgeois and Martinuzzi2013), but the parameters affecting the transition from one wake pattern to another have remained unclear. In this section, the effects of aspect ratio, along with boundary-layer height, on the time-averaged wake are investigated based on observations made from the current and past studies.
Figure 7 shows the contour and vector field of the time-averaged wake velocity predicted by LES on the
$y$
–
$z$
plane at
$x/W=2$
, and the blue horizontal line indicates the boundary-layer height,
$\unicode[STIX]{x1D6FF}$
. As discussed in the introduction, the parameter that determines the dipole/quadrupole nature of the time-averaged wake structure requires further investigation. In this study the boundary-layer height is kept constant, allowing the focus to be on the role of aspect ratio.
Figure 7. Contour map of the time-averaged normalised wake velocity in streamwise direction
$\overline{u}/U_{\infty }$
obtained from LES on the plane
$x/W=2$
, for FWMCs with aspect ratio: (a)
$L/W=1.4$
, R0; (b)
$L/W=4.3$
, RI; (c)
$L/W=10$
, boundary between RI and RII; (d)
$L/W=18.6$
, RIII. The dashed blue line indicates the boundary-layer height.
For an aspect ratio where the cylinder is shedding in mode R0, shown in figure 7(a) for
$L/W=1.4$
, neither a dipole nor a quadrupole wake structure is observed. This is because the boundary layer engulfs almost the entire cylinder as
$\unicode[STIX]{x1D6FF}/L=0.93$
and the free-end flow dominates the entire span (Mason & Morton Reference Mason and Morton1987), penetrating all the way to the wall (figures 6
a and 6
b). In figure 7(b), a dipole wake structure is present for
$L/W=4.3$
(RI), which has been observed previously for FWMCs at this approximate aspect ratio by Bourgeois et al. (Reference Bourgeois, Sattari and Martinuzzi2011). The major difference between
$L/W=1.4$
and 4.3 is the upwash on either side of the cylinder. By inspecting the velocity vector field, stronger upwash is observed for the higher aspect ratio of
$L/W=4.3$
, whereas for
$L/W=1.4$
the upwash is relatively weaker and the velocity is primarily directed to the centre axis of the cylinder (
$y/W=0$
).
The time-averaged wake for
$L/W=10$
, which is in transition from RI to RII, is particularly interesting as a dipole structure appears to be present but spans the entire length of the cylinder, as may be seen in figure 7(c). For the highest aspect ratio of
$L/W=18.6$
, representing RIII, the time-averaged wake structure is distinctively quadrupole in figure 7(d). The velocity vector field at the sides of the cylinder for the aspect ratios of 10 and 18.6 show qualitative similarities, with points of velocity divergence observed in the lower half of the span as indicated in figures 7(c) and 7(d). The divergence corresponds to the quadrupole structure as the flow above this point curls towards the free end thus creating a vortex pair and the flow below this point curls towards the wall junction to create a second vortex pair, hence the four poles of a quadrupole structure. This indicates that the wake structure of
$L/W=10$
is a dipole wake structure transitioning to a quadrupole. Comparing the region in
$-2<y/W<2$
, the velocity deficit in the near wake is the most intense for
$L/W=10$
, which may also be observed in figure 6. A further increase in aspect ratio shifts the dipole due to free-end flow further away from the junction, but the strength and size of the dipole is maintained. The lack of influence from free-end flow allows junction vortices to form, and thus the quadrupole pattern to develop. It also results in the velocity deficit for
$L/W=18.6$
being less intense than the lower aspect ratios.
Figure 8 shows the time-averaged flow structure of the LES results by plotting the
$\unicode[STIX]{x1D706}_{2}$
isosurface for the FWMCs with
$L/W=1.4$
to 18.6 and coloured by mean streamwise velocity
$\overline{u}$
. The
$\unicode[STIX]{x1D706}_{2}$
criterion is a known vortex core identification method, which works by evaluating the second real eigenvalue of the squared sum of the symmetric and anti-symmetric parts of the velocity gradient tensor (Jeong & Hussain Reference Jeong and Hussain1995). In general, these flow visualisations are analogous to the velocity field on the wake plane shown in figure 7.
Figure 8. Visualisation of time-averaged flow structure using the flow data from LES by plotting the isosurface of
$\unicode[STIX]{x1D706}_{2}$
criterion coloured by time-averaged streamwise velocity, for aspect ratios: (a)
$L/W=1.4$
, R0; (b)
$L/W=4.3$
, RI; (c)
$L/W=10$
, boundary between RI and RII; (d)
$L/W=18.6$
, RIII.
For
$L/W=1.4$
, the time-averaged wake exhibits an arch-type structure, where structures are shed from the entire span on both sides of the cylinder, as well as from the free end. A dipole mean wake structure is present for
$L/W=4.3$
at the immediate downstream region of the free end, characterised by the trailing vortices emanating from near the tip. For
$L/W=10$
, a dipole pattern similar to
$L/W=4.3$
is also present, but with the trailing vortices starting to form at a streamwise position further downstream. This is related to the increased vortex formation length reported by Porteous et al. (Reference Porteous, Moreau and Doolan2017) around this aspect ratio, which is due to a weak downward penetration from the free-end flow. This is corroborated by the angle of the shear layer and the more intense velocity deficit region relative to other aspect ratios shown in figure 6. For the highest aspect ratio of
$L/W=18.6$
, the time-averaged flow structure is quadrupole, with both the free end and junction vortex pairs visible in figure 8(d). As is the case for
$L/W=4.3$
and 10, the tip vortex pair is again well defined. However, the junction flow structure is relatively less defined, which indicates a discrepancy of scale between the two vortex pairs; this is also suggested in the wake flow results of figure 7. A horseshoe vortex system is also present just upstream of the junction region for all aspect ratios.
Comparing the time-averaged wake structures in figures 7 and 8 with the results of other published studies suggests that the number of poles formed is not simply dependent on aspect ratio. Instead our results reinforce the notion that the transition from a dipole to a quadrupole structure depends on both the aspect ratio and the relative thickness of the boundary layer, which has also been suggested by Hosseini et al. (Reference Hosseini, Bourgeois and Martinuzzi2013). They found that a ‘thin’ boundary layer relative to the cylinder height (
$\unicode[STIX]{x1D6FF}/L=0.09$
) results in a dipole wake structure, while a ‘thick’ one (
$\unicode[STIX]{x1D6FF}/L=0.32$
) results in a quadrupole structure; both measurements were performed on a square FWMC with an aspect ratio of
$L/W=8$
. Interestingly, for the FWMC with
$L/W=4.3$
and
$\unicode[STIX]{x1D6FF}/L=0.302$
in our study, which is comparable to their ‘thick’ boundary layer, the wake structure is clearly dipole. Conversely, for the FWMC with
$L/W=18.6$
, which has a comparably ‘thin’ boundary layer of
$\unicode[STIX]{x1D6FF}/L=0.093$
, the mean wake structure is quadrupole.
Figure 9. A parametric diagram of the transition of the time-averaged wake structure from dipole to quadrupole.
Based on these observations, a parametric diagram to predict the dipole/quadrupole mean wake structure is proposed in figure 9. It incorporates the dipole/quadrupole structure identified in this study, along with previous studies by Becker et al. (Reference Becker, Hahn, Kaltenbacher and Lerch2008), Wang & Zhou (Reference Wang and Zhou2009), Bourgeois et al. (Reference Bourgeois, Sattari and Martinuzzi2011) and Hosseini et al. (Reference Hosseini, Bourgeois and Martinuzzi2013). The diagram is based on the aspect ratio (
$L/W$
) and boundary-layer thickness relative to the diameter of the cylinder (
$\unicode[STIX]{x1D6FF}/W$
) as the parameters affecting the wake structure. Using these parameters, the FWMC cases with dipole wake structure are grouped in the bottom left corner, while those with quadrupole structure are grouped in the top right corner. Due to the limited published data on the dipole/quadrupole wake structure generated by a square FWMC, the exact transition line cannot be not definitely drawn and therefore a region where the transition occurs is given instead. As highlighted by the results of Wang & Zhou (Reference Wang and Zhou2009), the transition to quadrupole occurs much earlier at
$L/W\approx 5$
. This suggests there may be other factors affecting where exactly the transition occurs within the region, and, as such, a future parametric study is necessary to determine the true extent of the transition region.
In the case of Hosseini et al. (Reference Hosseini, Bourgeois and Martinuzzi2013), the two test cases lie on either side of the transition region due to a change in boundary-layer thickness, or transitions by moving horizontally in the model. For the study presented in this paper and that by Wang & Zhou (Reference Wang and Zhou2009), the transition occurs due to a change in aspect ratio, which results in crossing the transition region vertically in the model. Furthermore, it shows that square FWMCs in RI and RIII generate dipole and quadrupole wake structure, respectively, while the transition from dipole to quadrupole occurs during the transition from RI to RII.
3.3 Spanwise variation of vortex shedding
With the effect of aspect ratio on the time-averaged wake of a FWMC established in § 3.2, its effect on the time-dependent wake structure is explored in the following sections. Of particular interest here is the spanwise variation of the surface pressure and the wake structure, along with their spectral content.
3.3.1 Time series of cylinder side pressure
This section examines the spanwise variation over time of the pressure coefficient on the side face of the cylinder and how it is affected by a change in aspect ratio. Pressure coefficient here has been defined in (2.10). The time-series pressure data from experiment and LES were filtered using a bandpass filter inclusive of the shedding frequency, to preserve only the fluctuation due to shedding in the wake. The bandpass frequencies are between the Strouhal numbers,
$St=fW/U_{\infty }$
, of 0.05 and 0.23; this corresponds to 50 Hz and 230 Hz for the experimental data, and 100 Hz and 1000 Hz for the LES data. As
$U_{\infty }$
and
$W$
differ between the experiments (18AWT parameters) and LES (matching AWT parameters), the time scale is normalised against the time taken for the free stream to travel the length of cylinder diameter, mathematically expressed as
$tU_{\infty }/W$
.
Figure 10. The time histories of spanwise pressure coefficient measured in the experiments, for FWMCs with aspect ratios: (a)
$L/W=1.5$
, R0; (b)
$L/W=4.0$
, RI; (c)
$L/W=9.9$
, boundary between RI and RII; (d)
$L/W=12.5$
, RII.
Figure 10 presents the pressure coefficient time histories,
$C_{p}(z,t)$
obtained from the experiments for various aspect ratio FWMCs, in which the measurements were performed on the side face of the cylinder. A striking feature of the surface pressure fluctuation is the intermittency of vortex shedding. In figure 10(a,b), the amplitude modulation for the lower aspect ratios (R0 and RI) occurs at a frequency uniform across the entire span of the cylinder. The behaviour for the higher aspect ratios (RII and RIII) is different, figure 11 also shows the surface pressure on the cylinder side face, but obtained from the simulation results, which provides a higher spatial resolution of the surface pressure. The results show good qualitative agreement, with two distinct behaviours of shedding intermittency are also shown in different flow regimes (R0/RI and RII/RIII). The discrepancy in magnitude is likely due to the difference in flow parameters between the LES and 18WT facility (see table 4), small difference in aspect ratio, as well as pressure attenuation related to the frequency response of the pressure measurement tubes.
Figure 11. The time histories of spanwise pressure coefficient predicted by LES, for FWMCs with aspect ratios: (a)
$L/W=1.4$
, R0; (b)
$L/W=4.3$
, RI; (c)
$L/W=10$
, boundary between RI and RII; (d)
$L/W=18.6$
, RIII.
The time histories for R0 and RI are characterised by long periods of low amplitude fluctuations followed by bursts of high amplitude events, as may be seen in figures 10(a)–10(b). This phenomenon is known as intermittent shedding and has been observed in previous studies (Wang & Zhou Reference Wang and Zhou2009) and is also analogous to the amplitude modulation of the acoustic signal observed by Porteous et al. (Reference Porteous, Moreau and Doolan2017). Wang & Zhou (Reference Wang and Zhou2009) and, more recently, Behera & Saha (Reference Behera and Saha2019) relate this intermittent change in amplitude to the shedding alternating between anti-symmetric (high amplitude) and symmetric (low amplitude) modes. There is also spanwise variation in the strength of the shedding, which is strong near the junction but becomes slightly weaker towards the free end, as is more obviously shown for
$L/W=4.0$
. Similar patterns are predicted by the LES in figures 11(a) and 11(b), in which the modulation of the shedding strength is also present. Furthermore, shedding also occurs along the entire span of the cylinder, but is stronger towards the junction. Interestingly, the shedding for the higher aspect ratios (RII and RIII) is inherently different from the lower ones. There are now two distinct shedding regions, with the region closer to the free end shedding at a lower frequency (figures 10
c, 10
d, 11
c and 11
d).
For the higher aspect ratios (figures 10 c, 10 d, 11 c and 11 d), there are two independent shedding regions along the span of the cylinder: one in the vicinity of the free end and another covering the midspan to the junction. This behaviour is referred to as ‘cellular shedding’, which has been widely observed for circular FWMCs, but until recently its existence for square ones had been questioned. It was claimed by Hosseini et al. (Reference Hosseini, Bourgeois and Martinuzzi2013) that cellular shedding does not occur for square FWMCs, however both experimental and simulation results of this study clearly exhibit this phenomenon.
Comparing figures 10(c) and 11(c), both the measurement and LES prediction show weak shedding in the lower cell while maintaining relatively intense shedding in the upper cell. The fact that the shedding is weak over more than half of the span indicates a weak cross-stream force fluctuation and, analogously, explains the absence of tonal noise in the transition from RI to RII in the study of Porteous et al. (Reference Porteous, Moreau and Doolan2017). However, this behaviour appears to be limited to the transition from RI to RII, as the shedding is strong in both cells when the aspect ratio is further increased, as shown for
$L/W=12.5$
measured experimentally (RII, figure 10
d) and
$L/W=18.6$
predicted by LES (RIII, figure 11
d). Furthermore, the shedding in these cells is occasionally in phase and at other times out of phase, as they shed at slightly different frequencies. This observation is explored further by looking at the spectral content of the surface pressure and wake velocity in § 3.3.3.
3.3.2 Time-averaged base pressure
This section presents the time-averaged surface pressure on the back face (or ‘base’, facing downstream). While the side face pressure shown in § 3.3.1 is useful to observe cellular shedding, the base pressure provides insight into the near-wall dynamics. Figure 12 shows the time-averaged base pressure of cylinders from
$L/W=1.5$
to 18.6 expressed in
$\overline{C_{p}}$
, comparing experimental and LES data. The profiles predicted by LES are in reasonable agreement with their experimental counterparts, where the reasons for the discrepancy have been discussed in § 3.3.1. In general, higher aspect ratio results in lower
$\overline{C_{p}}$
, which indicates stronger suction in the region immediately downstream of the cylinder. Furthermore, the pressure profiles reduce towards the free end, which is a manifestation of the free-end effects and is consistent with the study of Lee (Reference Lee1997). For a very high aspect ratio of
$L/W=18.6$
, there is a low pressure region around
$z/L=0.2$
–0.4, which is attributed to accelerated flow due to the rollup of the junction flow.
Figure 12. Spanwise time-averaged pressure coefficient on the back face of cylinders with aspect ratios from
$L/W=1$
to
$L/W=18.6$
, showing both experimental and numerical results.
3.3.3 Frequency decomposition
From § 3.3.1, the vortex shedding frequency appears to shift with a change in aspect ratio and, when cellular shedding occurs, each cell sheds at a distinct frequency. To quantify this observation, the frequency content of the side face pressure and the near-wake velocity are presented in this section. Figure 13 shows spectral maps of the fluctuating surface pressure on the side face of selected aspect ratio FWMCs in experiments. This is accompanied by spectral maps of the wake velocity measured in experiments and simulations at
$x=2W$
across the cylinder span in figure 14. Figure 15 shows the wake velocity spectra for aspect ratios that do not have direct counterparts in the simulation:
$L/W=12.9$
(RII) and 21.4 (RIII), but are deemed important to understand transition to cellular shedding.
Figure 13. Spectral maps of the PSD of cylinder side face pressure fluctuations (in
$\text{dB}~\text{Hz}^{-1}$
re.
$20~\unicode[STIX]{x03BC}\text{Pa}$
) obtained from experiment, for FWMCs with aspect ratios: (a)
$L/W=1.5$
, R0; (b)
$L/W=4.0$
, RI; (c)
$L/W=9.9$
, boundary between RI and RII; (d)
$L/W=12.5$
, RII. The white portions of each map indicate portions of the FWMCs where no pressure data were taken.
Figure 14. Spectral maps of the PSD of fluctuating velocity (in
$\text{dB}~\text{Hz}^{-1}$
re.
$20~\unicode[STIX]{x03BC}\text{Pa}$
), measured along the spanwise line at
$x/W\approx 2$
. Results obtained from experiments are shown for aspect ratios: (a)
$L/W=1.4$
, R0; (c)
$L/W=4.3$
, RI; (e)
$L/W=10$
, boundary between RI and RII; (g)
$L/W=18.6$
, RIII; and results from LES: (b)
$L/W=1.4$
, R0; (d)
$L/W=4.3$
, RI; (f)
$L/W=10$
, boundary between RI and RII; (h)
$L/W=18.6$
, RIII. The red dashed line indicates boundary-layer thickness.
Figure 15. Spectral maps of the fluctuating part of wake velocity, presented as PSDs (
$\text{dB}~\text{Hz}^{-1}$
re.
$20~\unicode[STIX]{x03BC}\text{Pa}$
), measured along the spanwise line at
$x/W\approx 2$
on the hot-wire measurement plane obtained from the experiments, for FWMCs with aspect ratios: (a)
$L/W=12.9$
, RII (two cells); (b)
$L/W=21.9$
, RIII (three cells). The red dashed line indicates boundary-layer thickness.
A salient feature of the surface pressure spectral maps in figure 13 is the change in shedding behaviour when the cylinder transitions from a single cell (in figures 13
a and 13
b) in R0 and RI, to a double cell (in figure 13
d) in RII. The spectral map for
$L/W=9.9$
(figure 13
c) is on the boundary between RI and RII, so shows a very weak junction cell. This observation is consistent with the PSDs obtained from hot-wire measurements in figure 14.
The spectral map for the FWMC with
$L/W=1.5$
(R0) in figure 13(a) shows that periodicity is still detected on the surface of the cylinder, despite the fact that no Aeolian tone is detected at this aspect ratio (Porteous et al.
Reference Porteous, Moreau and Doolan2017). The energy in the signal is contained in a wide bandwidth, with the spectral energy spread over a large range of frequencies centred at
$St=0.09$
. This indicates that the signal is highly modulated. The modulation is likely caused by the deep relative immersion in the turbulent boundary layer, which contains highly turbulent flow with a wide range of flow scales at different velocities. A similar observation may be made in the wake velocity spectra of
$L/W=1.4$
shown in figures 14(a) and 14(b). Interestingly, the wake periodicity in this regime is the lower than the
$St\approx 0.1$
observed for RI to RIII.
In RI for
$L/W=4$
, shown in figure 13(b), the main vortex shedding peak is located at the junction of the cylinder and reduces in magnitude towards the free end. This is in agreement with the wake spectra for
$L/W=4.3$
shown in figures 14(c) and 14(d). Moving through RI from
$L/W=4$
to 10 (which are not shown here for brevity), vortices are shed from the entire cylinder span but with significantly lower magnitude than that of
$L/W=4$
. Eventually the trend reverses and the shedding is stronger in the vicinity of the free end. This culminates with aspect ratio
$L/W=9.9$
at the boundary between RI and RII, presented in figure 13(c), which is dominated by a peak signal at the free end and a weak junction cell can only just be observed. Unlike other aspect ratios, however, strong periodicity of the free-end cell is not reflected in the wake velocity (figures 14
e and 14
f) and instead weak fluctuations with a consistent frequency are present along almost the span of the cylinder. The low level of fluctuations results in a lack of tonal noise at these aspect ratios, as reported by Porteous et al. (Reference Porteous, Moreau and Doolan2017).
With a small increase in aspect ratio, the amplitude of the junction cell rises rapidly and for
$L/W=12.5$
(in figure 13
d), the amplitude of the junction cell exceeds that of the free-end cell. These results demonstrate that as the cylinder transitions from RI to RII the free-end cell forms first at approximately
$L/W\approx 9$
, while the formation of the junction cell is delayed until the conditions at the junction become more favourable for two-dimensional shedding. This transition is also reflected in the wake velocity spectra in figure 15(a) for
$L/W=12.9$
in RII. Here, two vortex shedding peaks are also observed: a lower frequency peak towards the free end of the cylinder beginning from
$z/L=0.5$
to 1 and a stronger peak at a higher frequency at the junction region starting from
$z/L=0$
to 0.4.
A further increase in aspect ratio into RIII leads to an additional shedding cell. As shown in figures 14(g) and 15(b), the junction cell has bifurcated into two cells: a junction cell which now only spans from
$z/L=0$
to 0.2 and a new mid-span cell spanning from
$z/L=0.2$
to 0.6. The third cell is not shown in the simulation result (figure 14
h), which is thought to be due to the lower spectral resolution of the LES.
The results presented in figures 10 to 15 demonstrate the presence of cellular shedding for square FWMCs. The change in shedding behaviour in each shedding regime is aligned with that of tonal noise generation support the hypothesis that these two phenomena are related, as proposed by Moreau & Doolan (Reference Moreau and Doolan2013) and Porteous et al. (Reference Porteous, Moreau and Doolan2017).
3.3.4 Spectral proper orthogonal decomposition
As shown in § 3.3.3, spectral maps are suitable to quantify the shedding frequency along a particular direction, but provide only limited spatial information to visualise the wake structure. The SPOD method proposed by Towne et al. (Reference Towne, Schmidt and Colonius2018) can be used for wake structure visualisation, due to its capability to identify flow structures that are both spatially and temporally coherent. This section presents the results obtained using SPOD method, that are consistent with the observations made in the preceding sections.
Figure 16 shows the energy spectra of mode 1 from a SPOD of the velocity component in the
$y$
-direction,
$v$
, obtained from LES on the plane
$y/W=0.6$
, for
$L/W=1.4$
to 18.6. Across all aspect ratios, the frequency bands which contain the most energy, indicated by the peaks, are the ones which include their respective shedding frequency identified in § 3.3.3. For
$L/W=1.4$
, the frequency bands containing the most energy are lower than those for the higher aspect ratios, which is due to the shedding for RI occurring at a lower frequency. As the aspect ratio is increased from
$L/W=4.3$
to 18.6 the energy is contained in an increasingly wider bandwidth, which is due to the cellular shedding occurring at multiple frequencies for aspect ratios in RII and RIII.
Figure 16. The energy spectra of the first mode identified by SPOD of
$v$
obtained from LES for
$L/W=1.4$
to 18.6 on the plane
$y/W=0.6$
.
Figures 17–20 show the SPOD modes of
$v$
predicted by LES on the plane
$y/W=0.6$
, to inspect the effect of aspect ratio on the spanwise coherent flow structure. Two frequency bands containing the highest energy level for a particular aspect ratio are shown in each figure, with each row showing the first three modes contained in one of these bands. Each frequency band is identified by its mid-band Strouhal number
$St_{mid}$
. The integrated energy level of each mode is indicated by
$\unicode[STIX]{x1D706}$
in each panel.
Figure 17. SPOD modes of
$v$
obtained from LES on the plane
$y/W=0.6$
for FWMC with
$L/W=1.4$
, R0. The dashed blue line indicates boundary-layer height.
Figure 18. SPOD modes of
$v$
obtained from LES on the plane
$y/W=0.6$
for FWMC with
$L/W=4.3$
, RI. The dashed blue line indicates boundary-layer height.
Figures 17 and 18 show the SPOD modes for the aspect ratios of
$L/W=1.4$
and 4.3, respectively. The modes for these aspect ratios exhibit similar behaviour; in both frequency bands shown, coherent structures are only observed in mode 1. Furthermore, the wake structure is shed uniformly across the span of the cylinder for both aspect ratios, as has been observed in § 3.3. The difference is the frequency bands containing most energy for
$L/W=4.3$
are one band higher than those for
$L/W=1.4$
. This is expected as the shedding frequency for
$L/W=4.3$
is higher than
$L/W=1.4$
, as has previously been noted in § 3.3.3.
Figure 19. SPOD modes of
$v$
obtained from LES on the plane
$y/W=0.6$
for FWMC with
$L/W=10$
, RII. The dashed blue line indicates boundary-layer height.
Figure 20. SPOD modes of
$v$
obtained from LES on the plane
$y/W=0.6$
for FWMC with
$L/W=18.6$
, RIII. The dashed blue line indicates boundary-layer height.
The modes for
$L/W=10$
are shown in figure 19. Similar to
$L/W=1.4$
and 4.3, the most energetic mode in both frequency bands shows only one coherent structure, but for
$L/W=10$
the structure is shed only across
$z/L\lessapprox 0.6$
. Furthermore, evidence of cellular shedding is present in mode 2 of both frequency bands, the free-end cell occurs at
$z/L\approx 0.75$
and the junction cell at
$z/L\approx 0.25$
. This is due to
$L/W=10$
being in the transition from a single to multi-cellular shedding.
In the decomposition for
$L/W=18.6$
shown in figure 20, shedding from all three cells is evident. In the frequency band with
$St_{mid}=0.107$
, modes 1, 2 and 3 show shedding from midspan, free-end and junction cells, respectively. In the frequency band with
$St_{mid}=0.128$
, modes 1 and 2 show midspan and junction cells, respectively, but no free-end shedding is observed. This is because midspan and junction shedding at this aspect ratio occur at
$St\approx 0.12$
(see figure 14h), which is close the boundary of the frequency bands shown. Free-end shedding, however, occurs at
$St\approx 0.095$
, which is at the lower end of frequency band
$St_{mid}=0.107$
and therefore not present in the higher frequency band. Instead, mode 3 shows a free-end/midspan combination, which occasionally occur when the two cells are in-phase as has been shown in figures 10 and 11. The structures from free-end, midspan and junction shedding cells show similarities to the coherent wake flow structures shown by Porteous et al. (Reference Porteous, Moreau and Doolan2017) to generate the first, second and third tonal noise peaks, respectively, for an FWMC in RIII.
4 Conclusions
This paper presents a study characterising the near-wake structure of square FWMCs and how it is affected by the aspect ratio of the cylinder. Large-eddy simulations have been performed for FWMCs with aspect ratios of
$L/W=1.4$
, 4.3, 10 and 18.6 to obtain comprehensive flow field data in the wake region and surface pressure fluctuations on the cylinder. Experimental measurements of FWMCs with aspect ratios of
$1.4\leqslant L/W\leqslant 21.5$
are presented to validate the LES results.
Increasing the aspect ratio while maintaining boundary-layer conditions results in the time-averaged wake structure transitioning from dipole to quadrupole. A new parametric diagram to predict the dipole/quadrupole pattern of time-averaged wake structure, which has been a much debated topic, is presented here. As both the aspect ratio (
$L/W$
) and the boundary-layer thickness relative to the cylinder width (
$\unicode[STIX]{x1D6FF}/W$
) have been found to play a role, the diagram accommodates both of these parameters. It is capable of separating dipole and quadrupole structures reported by the current and previous studies into separate regions, with a transition region between them. This parametric diagram will benefit from a comprehensive parametric study to provide a more definitive transition threshold.
Cellular shedding occurs for square FWMCs with high aspect ratios, up to three cells are present for
$L/W>18$
, as demonstrated both experimentally and numerically in this study. The spectral content of the wake velocity and the side face pressure of the cylinder reveals that each cell sheds at a distinct frequency. Consequently, for
$L/W>10$
where cellular shedding occurs, each cell sheds in phase and out of phase with each other intermittently. For the aspect ratios of
$L/W\approx 4$
and 10, the side face pressure shows significant amplitude modulation temporally and spatially in the spanwise direction. Together, these phenomena result in the tonal nature and the amplitude modulation of the noise emitted by square FWMCs. The spectral proper orthogonal decomposition technique has been shown to be a viable method in identifying the frequency of cellular shedding and visualising the associated wake structures in the near wake of FWMCs.
Acknowledgement
This research was undertaken with the assistance of resources and services from the National Computational Infrastructure (NCI), which is supported by the Australian Government.
