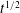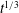1 Introduction
Recent developments in micro- and nanoscale surface patterning technology have made it possible to obtain tailored topography of solid surfaces with a wide range of wettability conditions. This has allowed the investigation of novel liquid–solid interaction behaviours, which are qualitatively different from the dynamics of liquids on smooth solid surfaces. On microtextured hydrophobic surfaces, drops roll (Mahadevan & Pomeau Reference Mahadevan and Pomeau1999; Richard & Quéré Reference Richard and Quéré1999) rather than slide (Kim, Lee & Kang Reference Kim, Lee and Kang2003). Drops bounce (Richard, Clanet & Quéré Reference Richard, Clanet and Quéré2002) or fragment (Tsai et al. Reference Tsai, Pacheco, Pirat, Lefferts and Lohse2009) upon collision with super-water-repellent surfaces depending on the impact conditions. When a drop is deposited on microdecorated hydrophilic surfaces, the liquid wicks into the gaps of protrusions; this behaviour is termed hemiwicking (Bico, Thiele & Quéré Reference Bico, Thiele and Quéré2002). Hemiwicking on a superhydrophilic surface leads to a variety of intriguing flow characteristics such as polygonal spreading (Courbin et al. Reference Courbin, Denieul, Dressaire, Roper, Ajdari and Stone2007), zippering wetting front (Kim et al. Reference Kim, Moon, Lee, Lee, Chang and Kim2011a ) and an enormous rise in the liquid film against gravity (Xiao, Enright & Wang Reference Xiao, Enright and Wang2010).
In the present study, we consider the rate of a liquid film climbing a rough hydrophilic substrate that is touching a liquid bath. The flow speed and film thickness are so small that inertia and gravity can be neglected compared to viscous resistance. The rate of hemiwicking is then determined by the balance between the driving capillary forces and resisting viscous forces. Thus, the fundamental physics does not differ from a capillarity-driven tube imbibition problem (Washburn Reference Washburn1921), and a simple scaling law can be readily constructed as Ishino et al. (Reference Ishino, Reyssat, Reyssat, Okumura and Quéré2007) explained. Because the capillary force is scaled as
![]() ${\it\gamma}a$
, where
${\it\gamma}a$
, where
![]() ${\it\gamma}$
is the liquid–gas surface tension and
${\it\gamma}$
is the liquid–gas surface tension and
![]() $a$
is the length scale that generates the capillary effect, and the viscous force is scaled as
$a$
is the length scale that generates the capillary effect, and the viscous force is scaled as
![]() ${\it\mu}L\dot{L}$
, where
${\it\mu}L\dot{L}$
, where
![]() ${\it\mu}$
is the liquid viscosity,
${\it\mu}$
is the liquid viscosity,
![]() $L$
is the imbibition distance from the source and the dot denotes the time derivative, the force balance leads to a diffusive rule for
$L$
is the imbibition distance from the source and the dot denotes the time derivative, the force balance leads to a diffusive rule for
![]() $L:L\sim (Dt)^{1/2}$
, where the dynamical coefficient
$L:L\sim (Dt)^{1/2}$
, where the dynamical coefficient
![]() $D\sim {\it\gamma}a/{\it\mu}$
. A number of studies regarding hemiwicking on superhydrophilic substrates have found that the imbibition length indeed grows like
$D\sim {\it\gamma}a/{\it\mu}$
. A number of studies regarding hemiwicking on superhydrophilic substrates have found that the imbibition length indeed grows like
![]() $t^{1/2}$
(Bico, Tordeus & Quéré Reference Bico, Tordeus and Quéré2001; Courbin et al.
Reference Courbin, Denieul, Dressaire, Roper, Ajdari and Stone2007; Ishino et al.
Reference Ishino, Reyssat, Reyssat, Okumura and Quéré2007; Srivastava et al.
Reference Srivastava, Din, Judson, MacDonald and Meinhart2010; Kim et al.
Reference Kim, Moon, Lee, Lee, Chang and Kim2011a
,Reference Kim, Moon, Lee, Mahadevan and Kim
b
).
$t^{1/2}$
(Bico, Tordeus & Quéré Reference Bico, Tordeus and Quéré2001; Courbin et al.
Reference Courbin, Denieul, Dressaire, Roper, Ajdari and Stone2007; Ishino et al.
Reference Ishino, Reyssat, Reyssat, Okumura and Quéré2007; Srivastava et al.
Reference Srivastava, Din, Judson, MacDonald and Meinhart2010; Kim et al.
Reference Kim, Moon, Lee, Lee, Chang and Kim2011a
,Reference Kim, Moon, Lee, Mahadevan and Kim
b
).
However, rough substrates cannot be described by a single geometric parameter, such as a tube with a constant radius
![]() $a$
. For example, a square array of circular micropillars should be described by the following three parameters: the height, diameter and spacing of the pillars. As a result, different forms of the dynamical coefficient have been suggested by various authors for regular micropillar arrays (Bico et al.
Reference Bico, Tordeus and Quéré2001; Courbin et al.
Reference Courbin, Denieul, Dressaire, Roper, Ajdari and Stone2007; Ishino et al.
Reference Ishino, Reyssat, Reyssat, Okumura and Quéré2007; Srivastava et al.
Reference Srivastava, Din, Judson, MacDonald and Meinhart2010; Kim et al.
Reference Kim, Moon, Lee, Mahadevan and Kim2011b
). These previously suggested forms of the dynamical coefficient only hold under limited conditions, which implies that further studies are called for to gain a general understanding of the dynamics of hemiwicking. In addition to densely spaced micropillar arrays, we consider cases where micropillars are sparse and the meniscus should travel a significant distance before encountering neighbouring pillars.
$a$
. For example, a square array of circular micropillars should be described by the following three parameters: the height, diameter and spacing of the pillars. As a result, different forms of the dynamical coefficient have been suggested by various authors for regular micropillar arrays (Bico et al.
Reference Bico, Tordeus and Quéré2001; Courbin et al.
Reference Courbin, Denieul, Dressaire, Roper, Ajdari and Stone2007; Ishino et al.
Reference Ishino, Reyssat, Reyssat, Okumura and Quéré2007; Srivastava et al.
Reference Srivastava, Din, Judson, MacDonald and Meinhart2010; Kim et al.
Reference Kim, Moon, Lee, Mahadevan and Kim2011b
). These previously suggested forms of the dynamical coefficient only hold under limited conditions, which implies that further studies are called for to gain a general understanding of the dynamics of hemiwicking. In addition to densely spaced micropillar arrays, we consider cases where micropillars are sparse and the meniscus should travel a significant distance before encountering neighbouring pillars.
In the following we begin with describing the experimental set-up and procedures. We then present scaling laws developed for hemiwicking on pillar arrays with a wide range of pillar dimensions and lattice structures. Both the macroscopic and microscopic descriptions of the propagation velocity of the wetting front are presented, and these are corroborated experimentally. Finally, we discuss the effect of the pillar density on the hemiwicking flow to find the maximum pillar spacing up to which the assumption of densely spaced pillars is valid.
2 Experiments
To fabricate rough hydrophilic substrates, we etch an Si wafer using the deep reactive ion etching process. This results in pillar arrays having various geometric parameters depending on the design of the photomask and the etching duration. The pillar arrays are coated with an Si-incorporated diamond-like carbon film using a gas mixture of benzene and silane in a radio frequency chemical vapour deposition chamber. Then, the surfaces are plasma etched with oxygen to turn them superhydrophilic owing to the hydrophilic Si–O bonds and nanoscale roughness. For more detailed process conditions, see Yi et al. (Reference Yi, Moon, Ahmded, Kim, Cha, Kim, Kim and Lee2010). As shown in figure 1(a), the individual pillars are cylindrical with height
![]() $h$
and diameter
$h$
and diameter
![]() $d$
, and are arranged with longitudinal and transverse pitches
$d$
, and are arranged with longitudinal and transverse pitches
![]() $s_{x}$
and
$s_{x}$
and
![]() $s_{y}$
, respectively. The skewness of an array is determined by the angle
$s_{y}$
, respectively. The skewness of an array is determined by the angle
![]() ${\it\alpha}$
, which can range from 0 to
${\it\alpha}$
, which can range from 0 to
![]() $\tan ^{-1}(s_{y}/s_{x})$
. See figure 1(b–e). In our experiments,
$\tan ^{-1}(s_{y}/s_{x})$
. See figure 1(b–e). In our experiments,
![]() $h$
ranges from 10 to 35
$h$
ranges from 10 to 35
![]() ${\rm\mu}\text{m}$
,
${\rm\mu}\text{m}$
,
![]() $d$
from 10 to 20
$d$
from 10 to 20
![]() ${\rm\mu}\text{m}$
,
${\rm\mu}\text{m}$
,
![]() $s_{x}$
from 12.5 to 112.5
$s_{x}$
from 12.5 to 112.5
![]() ${\rm\mu}\text{m}$
,
${\rm\mu}\text{m}$
,
![]() $s_{y}$
from 15 to 389.7
$s_{y}$
from 15 to 389.7
![]() ${\rm\mu}\text{m}$
and
${\rm\mu}\text{m}$
and
![]() ${\it\alpha}$
from 0 to
${\it\alpha}$
from 0 to
![]() $60^{\circ }$
. The roughness,
$60^{\circ }$
. The roughness,
![]() $f$
, which is defined as the ratio of the actual solid surface area to the projected area,
$f$
, which is defined as the ratio of the actual solid surface area to the projected area,
![]() $f=1+{\rm\pi}dh/(s_{x}s_{y})$
, ranges from 1.03 to 4.63.
$f=1+{\rm\pi}dh/(s_{x}s_{y})$
, ranges from 1.03 to 4.63.

Figure 1. (a) Scanning electron microscopy (SEM) image of a micropillar array of Si with geometric parameters indicated. The pitches
![]() $s_{x}$
and
$s_{x}$
and
![]() $s_{y}$
correspond to the centre-to-centre distance between neighbouring pillars. (b–e) Lattice structures with different skewness values measured according to
$s_{y}$
correspond to the centre-to-centre distance between neighbouring pillars. (b–e) Lattice structures with different skewness values measured according to
![]() ${\it\alpha}$
and longitudinal pitch
${\it\alpha}$
and longitudinal pitch
![]() $s_{x}$
. (f) Wetting of a pillar with interface propagation by the distance
$s_{x}$
. (f) Wetting of a pillar with interface propagation by the distance
![]() $s_{x}$
.
$s_{x}$
.
As reservoir liquids, we use deionized water, silicone oil, 99 wt% ethylene glycol (with 1 wt% water) and 90 wt% glycerine (with 10 wt% water). Table 1 lists their density (
![]() ${\it\rho}$
), surface tension (
${\it\rho}$
), surface tension (
![]() ${\it\gamma}$
) and viscosity (
${\it\gamma}$
) and viscosity (
![]() ${\it\mu}$
). All of the liquids completely wet the micropillar arrays, so the equilibrium contact angle of the liquids with the prepared solid surfaces is nearly zero. We use the equilibrium contact angle in the later evaluation of the surface energy. The area of the pillar arrays is measured to be
${\it\mu}$
). All of the liquids completely wet the micropillar arrays, so the equilibrium contact angle of the liquids with the prepared solid surfaces is nearly zero. We use the equilibrium contact angle in the later evaluation of the surface energy. The area of the pillar arrays is measured to be
![]() $4\times 50~\text{mm}^{2}$
, and touches the reservoir liquid vertically. The liquid film climbing the surface is recorded with a high-speed camera (Photron Fastcam SA1.1) at a frame rate of up to 500
$4\times 50~\text{mm}^{2}$
, and touches the reservoir liquid vertically. The liquid film climbing the surface is recorded with a high-speed camera (Photron Fastcam SA1.1) at a frame rate of up to 500
![]() $\text{s}^{-1}$
.
$\text{s}^{-1}$
.
Table 1. Properties of liquids used in the experiments.

While the front edge of the rising liquid film appears fairly straight when viewed from a distance, as shown in figure 2(a), close observation reveals complex advancing dynamics originating from the presence of the pillars. For rectangular arrays with
![]() ${\it\alpha}=0$
, the lateral propagation of a protruding step, or zippering, must occur before the contact line advances to the next row of pillars (Courbin et al.
Reference Courbin, Denieul, Dressaire, Roper, Ajdari and Stone2007; Kim et al.
Reference Kim, Moon, Lee, Lee, Chang and Kim2011a
), as shown in figure 2(b). On skewed arrays, as displayed in figure 2(c), the liquid film apparently radiated from each pillar drives the advance of the contact line. Below, we develop a scaling law to predict the advancing speed of the seemingly straight interface edge, and then investigate the microscopic dynamics of a liquid meniscus influenced by individual pillars.
${\it\alpha}=0$
, the lateral propagation of a protruding step, or zippering, must occur before the contact line advances to the next row of pillars (Courbin et al.
Reference Courbin, Denieul, Dressaire, Roper, Ajdari and Stone2007; Kim et al.
Reference Kim, Moon, Lee, Lee, Chang and Kim2011a
), as shown in figure 2(b). On skewed arrays, as displayed in figure 2(c), the liquid film apparently radiated from each pillar drives the advance of the contact line. Below, we develop a scaling law to predict the advancing speed of the seemingly straight interface edge, and then investigate the microscopic dynamics of a liquid meniscus influenced by individual pillars.

Figure 2. (a) Macroscopic view of the liquid rise (ethylene glycol 99 wt%) due to wicking within an array of micropillars with
![]() ${\it\alpha}=0$
and
${\it\alpha}=0$
and
![]() $\{h,d,s_{x},s_{y}\}=\{26.5,10,20,20\}$
$\{h,d,s_{x},s_{y}\}=\{26.5,10,20,20\}$
![]() ${\rm\mu}\text{m}$
. Enclosed by an ellipse at 5.0 s is a bulk protruding from the reservoir liquid. (b) Magnified view of liquid rise on a rectangular pillar array with
${\rm\mu}\text{m}$
. Enclosed by an ellipse at 5.0 s is a bulk protruding from the reservoir liquid. (b) Magnified view of liquid rise on a rectangular pillar array with
![]() ${\it\alpha}=0$
and
${\it\alpha}=0$
and
![]() $\{h,d,s_{x},s_{y}\}=\{7.2,10,40,40\}$
$\{h,d,s_{x},s_{y}\}=\{7.2,10,40,40\}$
![]() ${\rm\mu}\text{m}$
. (c) Magnified view of liquid rise on a skewed pillar array with
${\rm\mu}\text{m}$
. (c) Magnified view of liquid rise on a skewed pillar array with
![]() ${\it\alpha}=60^{\circ }$
and
${\it\alpha}=60^{\circ }$
and
![]() $\{h,d,s_{x},s_{y}\}=\{20,20,62.5,216.5\}~{\rm\mu}\text{m}$
. The liquid shown in (b,c) is water. (d) Side view of the microarray before (upper panel) and after (lower panel) liquid impregnation (ethylene glycol 99 wt%). (e) Regions I and II, which are used to evaluate the viscous friction due to the substrate.
$\{h,d,s_{x},s_{y}\}=\{20,20,62.5,216.5\}~{\rm\mu}\text{m}$
. The liquid shown in (b,c) is water. (d) Side view of the microarray before (upper panel) and after (lower panel) liquid impregnation (ethylene glycol 99 wt%). (e) Regions I and II, which are used to evaluate the viscous friction due to the substrate.
3 Macroscopic model of hemiwicking dynamics
We consider the advancing rate of a liquid film on a superhydrophilic textured substrate that touches a reservoir liquid. The film thickness is defined by the pillar height
![]() $h$
. The hydraulic diameter of a rectangular duct,
$h$
. The hydraulic diameter of a rectangular duct,
![]() $D_{h}$
, is given by
$D_{h}$
, is given by
![]() $D_{h}=2s_{y}h/(h+s_{y})$
and the ratio
$D_{h}=2s_{y}h/(h+s_{y})$
and the ratio
![]() $D_{h}/h$
ranges from 0.48 to 1.86 in our experiments. The Reynolds numbers based on
$D_{h}/h$
ranges from 0.48 to 1.86 in our experiments. The Reynolds numbers based on
![]() $h$
and
$h$
and
![]() $D_{h}$
,
$D_{h}$
,
![]() $\mathit{Re}_{h}={\it\rho}Uh/{\it\mu}$
and
$\mathit{Re}_{h}={\it\rho}Uh/{\it\mu}$
and
![]() $\mathit{Re}_{D}={\it\rho}UD_{h}/{\it\mu}$
, with
$\mathit{Re}_{D}={\it\rho}UD_{h}/{\it\mu}$
, with
![]() $U$
being the flow speed, are both
$U$
being the flow speed, are both
![]() $O(10^{-10}{-}10^{-2})$
in our experiments; thus, the inertial effect is negligible. The Bond number, defined by
$O(10^{-10}{-}10^{-2})$
in our experiments; thus, the inertial effect is negligible. The Bond number, defined by
![]() $\mathit{Bo}={\it\rho}h^{2}g/{\it\gamma}$
, with
$\mathit{Bo}={\it\rho}h^{2}g/{\it\gamma}$
, with
![]() $g$
being the gravitational acceleration, is
$g$
being the gravitational acceleration, is
![]() $O(10^{-7}{-}10^{-4})$
, implying negligible effects of gravity. The flow is driven by capillary forces at the rising front. To evaluate the driving force, we first consider a film that newly wets the area
$O(10^{-7}{-}10^{-4})$
, implying negligible effects of gravity. The flow is driven by capillary forces at the rising front. To evaluate the driving force, we first consider a film that newly wets the area
![]() $s_{x}s_{y}$
containing a single pillar, as shown in figure 1(f). By observing the side view of the liquid spreading through a forest of micropillars, as shown in figure 2(d), we find that the tops of the pillars are hardly wetted as the wet front propagates. Although we do not preclude the possibility that the top surfaces slowly become wet as the liquid meniscus climbs the pillars over a long period of time, this would hardly affect the rate of wetting that occurs at the propagation front.
$s_{x}s_{y}$
containing a single pillar, as shown in figure 1(f). By observing the side view of the liquid spreading through a forest of micropillars, as shown in figure 2(d), we find that the tops of the pillars are hardly wetted as the wet front propagates. Although we do not preclude the possibility that the top surfaces slowly become wet as the liquid meniscus climbs the pillars over a long period of time, this would hardly affect the rate of wetting that occurs at the propagation front.
The change in the surface energy as the dry surface area turns wet is given by
![]() $\text{d}E^{\prime }=(s_{x}s_{y}-({\rm\pi}/4)d^{2}){\it\gamma}+(fs_{x}s_{y}-({\rm\pi}/4)d^{2})({\it\gamma}_{SL}-{\it\gamma}_{SG})$
, where
$\text{d}E^{\prime }=(s_{x}s_{y}-({\rm\pi}/4)d^{2}){\it\gamma}+(fs_{x}s_{y}-({\rm\pi}/4)d^{2})({\it\gamma}_{SL}-{\it\gamma}_{SG})$
, where
![]() ${\it\gamma}_{SL}$
and
${\it\gamma}_{SL}$
and
![]() ${\it\gamma}_{SG}$
are the solid–liquid and solid–gas interfacial energy per unit area, respectively. At the macroscale, where the pillar diameter and pitches are negligible compared to the rise height (Kim et al.
Reference Kim, Moon, Lee, Lee, Chang and Kim2011a
), we write the change in the surface energy per unit width associated with the advance of the liquid front by
${\it\gamma}_{SG}$
are the solid–liquid and solid–gas interfacial energy per unit area, respectively. At the macroscale, where the pillar diameter and pitches are negligible compared to the rise height (Kim et al.
Reference Kim, Moon, Lee, Lee, Chang and Kim2011a
), we write the change in the surface energy per unit width associated with the advance of the liquid front by
![]() $\text{d}L$
as
$\text{d}L$
as
![]() $\text{d}E=\{{\it\gamma}[1-({\rm\pi}/4)d^{2}/(s_{x}s_{y})]+({\it\gamma}_{SL}-{\it\gamma}_{SG})[f-({\rm\pi}/4)d^{2}/(s_{x}s_{y})]\}\,\text{d}L$
. On the basis of Young’s equation,
$\text{d}E=\{{\it\gamma}[1-({\rm\pi}/4)d^{2}/(s_{x}s_{y})]+({\it\gamma}_{SL}-{\it\gamma}_{SG})[f-({\rm\pi}/4)d^{2}/(s_{x}s_{y})]\}\,\text{d}L$
. On the basis of Young’s equation,
![]() ${\it\gamma}={\it\gamma}_{SG}-{\it\gamma}_{SL}$
with a zero contact angle, we obtain
${\it\gamma}={\it\gamma}_{SG}-{\it\gamma}_{SL}$
with a zero contact angle, we obtain
![]() $\text{d}E=-{\it\gamma}(f-1)\,\text{d}L$
. The driving force per unit width can then be estimated as
$\text{d}E=-{\it\gamma}(f-1)\,\text{d}L$
. The driving force per unit width can then be estimated as
![]() $F_{d}=-\text{d}E/\text{d}L=(f-1){\it\gamma}$
.
$F_{d}=-\text{d}E/\text{d}L=(f-1){\it\gamma}$
.
The negligible effects of inertia imply that the driving force is balanced by the resisting viscous force. The viscous shear force is exerted on the liquid flow by the base and pillar side walls. We consider flow profiles in region I (before encountering pillars) and region II (between pillars) separately, as illustrated in figure 2(e). Inertialess film flows satisfying the no-slip boundary conditions at the solid surfaces and a shear-free condition at the liquid–gas interface allow us to approximate the velocity in each region as follows (figure 3):
![]() $u(y,z)=U_{m}[2(z/h)-(z/h)^{2}]$
for region I and
$u(y,z)=U_{m}[2(z/h)-(z/h)^{2}]$
for region I and
![]() $u^{\prime }(y,z)=U_{m}^{\prime }[2(z/h)-(z/h)^{2}][1-4(y/\bar{s})^{2}]$
for region II, where
$u^{\prime }(y,z)=U_{m}^{\prime }[2(z/h)-(z/h)^{2}][1-4(y/\bar{s})^{2}]$
for region II, where
![]() $U_{m}$
and
$U_{m}$
and
![]() $U_{m}^{\prime }$
are the maximum velocities in each region. Here,
$U_{m}^{\prime }$
are the maximum velocities in each region. Here,
![]() $\bar{s}$
corresponds to the wall-to-wall spacing between neighbouring pillars. The spacing starts from
$\bar{s}$
corresponds to the wall-to-wall spacing between neighbouring pillars. The spacing starts from
![]() $s_{y}$
at the inlet, shrinks to
$s_{y}$
at the inlet, shrinks to
![]() $s_{y}-d$
and grows back to
$s_{y}-d$
and grows back to
![]() $s_{y}$
at the outlet of region II. We simply determine
$s_{y}$
at the outlet of region II. We simply determine
![]() $\bar{s}$
by dividing the area of region II by the length
$\bar{s}$
by dividing the area of region II by the length
![]() $d$
. Thus,
$d$
. Thus,
![]() $\bar{s}$
can be considered as the average wall-to-wall distance:
$\bar{s}$
can be considered as the average wall-to-wall distance:
![]() $\bar{s}=(s_{y}d-{\rm\pi}d^{2}/4)/d=s_{y}-({\rm\pi}/4)d$
. The flow rates of regions I and II are respectively given by
$\bar{s}=(s_{y}d-{\rm\pi}d^{2}/4)/d=s_{y}-({\rm\pi}/4)d$
. The flow rates of regions I and II are respectively given by
The average velocity is
![]() $U=q_{1}/(s_{y}h)=(2/3)U_{m}$
in region I and
$U=q_{1}/(s_{y}h)=(2/3)U_{m}$
in region I and
![]() $U^{\prime }=q_{2}/(\bar{s}h)=(4/9)U_{m}^{\prime }$
in region II. For
$U^{\prime }=q_{2}/(\bar{s}h)=(4/9)U_{m}^{\prime }$
in region II. For
![]() $q_{1}=q_{2}$
, we find
$q_{1}=q_{2}$
, we find
![]() $U^{\prime }=(s_{y}/\bar{s})U$
.
$U^{\prime }=(s_{y}/\bar{s})U$
.

Figure 3. Velocity profiles of (a) region I and (b) region II.
Our simplified assumptions of the velocity profiles give the following scaling estimates of the shear force. The shear force exerted by the base of region I with the area
![]() $(s_{x}-d)s_{y}$
is scaled as
$(s_{x}-d)s_{y}$
is scaled as
In region II, the shear forces due to the base
![]() $F_{2,b}$
and the pillar sides
$F_{2,b}$
and the pillar sides
![]() $F_{2,s}$
are respectively scaled as
$F_{2,s}$
are respectively scaled as
The shear force acting on a unit cell with the area
![]() $s_{x}s_{y}$
encompassing regions I and II is then scaled as
$s_{x}s_{y}$
encompassing regions I and II is then scaled as
![]() $\hat{F}_{r}\sim F_{1}+F_{2,b}+F_{2,s}$
:
$\hat{F}_{r}\sim F_{1}+F_{2,b}+F_{2,s}$
:
where
![]() ${\it\epsilon}\sim s_{y}s/\bar{s}^{2}-1$
and
${\it\epsilon}\sim s_{y}s/\bar{s}^{2}-1$
and
![]() $s=s_{y}-d$
. Because
$s=s_{y}-d$
. Because
![]() ${\it\epsilon}/\{1+s/[(f-1)h]\}$
is typically smaller than 0.1 under our experimental conditions, we neglect the term involving
${\it\epsilon}/\{1+s/[(f-1)h]\}$
is typically smaller than 0.1 under our experimental conditions, we neglect the term involving
![]() ${\it\epsilon}$
when compared with the other terms in the bracket of (3.6). Then the term in the bracket reduces to
${\it\epsilon}$
when compared with the other terms in the bracket of (3.6). Then the term in the bracket reduces to
![]() $1+(f-1)h/s$
. We finally obtain the scale of the total resisting force on the liquid film of propagation distance
$1+(f-1)h/s$
. We finally obtain the scale of the total resisting force on the liquid film of propagation distance
![]() $L$
per unit width:
$L$
per unit width:
In the macroscopic model, which ignores the effects of the pillar arrangement at the propagating front, we simply take
![]() $U\approx \dot{L}$
. Balancing
$U\approx \dot{L}$
. Balancing
![]() $F_{d}$
and
$F_{d}$
and
![]() $F_{r}$
gives the speed of the hemiwicking front as
$F_{r}$
gives the speed of the hemiwicking front as
where the dimensionless coefficient
![]() ${\it\eta}$
is specified solely by the dimensions of the pillar array:
${\it\eta}$
is specified solely by the dimensions of the pillar array:
![]() ${\it\eta}=(f-1)/[1+h(f-1)/s]$
. Integrating (3.8) yields
${\it\eta}=(f-1)/[1+h(f-1)/s]$
. Integrating (3.8) yields
While a similar scaling relation that reveals the diffusive dynamics of a hemiwicking front on micropillar arrays was reported earlier (Kim et al.
Reference Kim, Moon, Lee, Lee, Chang and Kim2011a
,Reference Kim, Moon, Lee, Mahadevan and Kim
b
), here we suggest a generalized coefficient
![]() ${\it\eta}$
, which is not restricted to a case where
${\it\eta}$
, which is not restricted to a case where
![]() $h\approx s$
, as in previous works. We compare this theoretical prediction with the experimental results obtained by using various pillar arrays and different liquids, as discussed below.
$h\approx s$
, as in previous works. We compare this theoretical prediction with the experimental results obtained by using various pillar arrays and different liquids, as discussed below.
Figure 4(a) shows that the propagation distance of the wetting front increases linearly with
![]() $\sqrt{t}$
for various pillar arrays and liquids but with different slopes. We see in figure 4(b) that the current scaling law (3.9) makes all of the data collapse onto a single straight line, which validates our theory. In the plot, we scale the distance
$\sqrt{t}$
for various pillar arrays and liquids but with different slopes. We see in figure 4(b) that the current scaling law (3.9) makes all of the data collapse onto a single straight line, which validates our theory. In the plot, we scale the distance
![]() $L$
with the capillary length
$L$
with the capillary length
![]() $l_{c}=[{\it\gamma}/({\it\rho}g)]^{1/2}$
, which corresponds to the characteristic elevation of the meniscus touching a smooth hydrophilic vertical wall. Figure 4(c) displays the slopes of the best fitting straight line for each experimental condition versus
$l_{c}=[{\it\gamma}/({\it\rho}g)]^{1/2}$
, which corresponds to the characteristic elevation of the meniscus touching a smooth hydrophilic vertical wall. Figure 4(c) displays the slopes of the best fitting straight line for each experimental condition versus
![]() ${\it\eta}$
, to show that they scatter within
${\it\eta}$
, to show that they scatter within
![]() $\pm 10\,\%$
of the average value, 0.49. In the figure, we include error bars, which account for the measurement errors associated with image analysis (
$\pm 10\,\%$
of the average value, 0.49. In the figure, we include error bars, which account for the measurement errors associated with image analysis (
![]() ${\sim}\pm 1$
pixel) and the variation of pillar dimensions (
${\sim}\pm 1$
pixel) and the variation of pillar dimensions (
![]() ${\sim}\pm 1.5~{\rm\mu}\text{m}$
) that occur inevitably in fabrication. Our scaling law is seen to be valid regardless of the skewness of the pillar lattices despite differences in the microscopic shapes of the wetting front, as demonstrated in figure 2(b,c). This is consistent with our simplified estimations of the driving and resisting forces, ignoring the detailed lattice structure under the assumption that
${\sim}\pm 1.5~{\rm\mu}\text{m}$
) that occur inevitably in fabrication. Our scaling law is seen to be valid regardless of the skewness of the pillar lattices despite differences in the microscopic shapes of the wetting front, as demonstrated in figure 2(b,c). This is consistent with our simplified estimations of the driving and resisting forces, ignoring the detailed lattice structure under the assumption that
![]() $d$
,
$d$
,
![]() $s_{x}$
and
$s_{x}$
and
![]() $s_{y}$
are significantly smaller than
$s_{y}$
are significantly smaller than
![]() $L$
.
$L$
.

Figure 4. (a) Propagation distance of the wet front versus
![]() $\sqrt{t}$
. (b) The scaled wetting distance (
$\sqrt{t}$
. (b) The scaled wetting distance (
![]() $L/l_{c}$
) plotted according to the scaling law (3.9). The slope of the best fitting straight line is 0.49. (c) Slope of the best fitting lines of the data in (b) against the structural dimensionless coefficient
$L/l_{c}$
) plotted according to the scaling law (3.9). The slope of the best fitting straight line is 0.49. (c) Slope of the best fitting lines of the data in (b) against the structural dimensionless coefficient
![]() ${\it\eta}$
. (d) Experimental conditions for the symbols.
${\it\eta}$
. (d) Experimental conditions for the symbols.

Figure 5. Schematics of the meniscus propagation at the microscale the moment the meniscus reaches the top of some pillars behind the contact line: (a) densely spaced pillar array, (b) sparsely spaced pillar array.
In the skewed arrays, the pitches differ in the longitudinal (
![]() $s_{x}$
) and transverse (
$s_{x}$
) and transverse (
![]() $s_{y}$
) directions, and
$s_{y}$
) directions, and
![]() $s_{y}$
plays a more important role than
$s_{y}$
plays a more important role than
![]() $s_{x}$
in determining the viscous resisting force, as seen in (3.7). Because skewed arrays have a larger transverse pitch than square arrays for the same pillar density (e.g.
$s_{x}$
in determining the viscous resisting force, as seen in (3.7). Because skewed arrays have a larger transverse pitch than square arrays for the same pillar density (e.g.
![]() $s_{y}$
for a skewed array with
$s_{y}$
for a skewed array with
![]() ${\it\alpha}=45^{\circ }$
is
${\it\alpha}=45^{\circ }$
is
![]() $\sqrt{2}$
times larger than the pitch of the same array with
$\sqrt{2}$
times larger than the pitch of the same array with
![]() ${\it\alpha}=0$
), skewed arrays always exhibit faster wetting front propagation than square arrays. Note that
${\it\alpha}=0$
), skewed arrays always exhibit faster wetting front propagation than square arrays. Note that
![]() ${\it\eta}$
in (3.9) increases with
${\it\eta}$
in (3.9) increases with
![]() $s=s_{y}-d$
. It is then possible to design a pillar arrangement which maximizes the hemiwicking velocity for the given pillar dimensions,
$s=s_{y}-d$
. It is then possible to design a pillar arrangement which maximizes the hemiwicking velocity for the given pillar dimensions,
![]() $h$
and
$h$
and
![]() $d$
, and the roughness,
$d$
, and the roughness,
![]() $f$
. Since we need to maximize
$f$
. Since we need to maximize
![]() $s_{y}$
, we let
$s_{y}$
, we let
![]() $s_{x}=d$
, the smallest longitudinal pitch allowable, which gives the maximum transverse pitch
$s_{x}=d$
, the smallest longitudinal pitch allowable, which gives the maximum transverse pitch
![]() $s_{m}={\rm\pi}h/(f-1)$
. Then, the maximum structural coefficient is
$s_{m}={\rm\pi}h/(f-1)$
. Then, the maximum structural coefficient is
![]() ${\it\eta}_{m}=(f-1)/[1+h(f-1)/(s_{m}-d)]$
, and the maximized hemiwicking distance is written as
${\it\eta}_{m}=(f-1)/[1+h(f-1)/(s_{m}-d)]$
, and the maximized hemiwicking distance is written as
![]() $L\approx 0.49({\it\gamma}{\it\eta}_{m}h/{\it\mu})^{1/2}t^{1/2}$
, where the prefactor 0.49 is empirically obtained in figure 4(b). For instance, when the substrate conditions are such that
$L\approx 0.49({\it\gamma}{\it\eta}_{m}h/{\it\mu})^{1/2}t^{1/2}$
, where the prefactor 0.49 is empirically obtained in figure 4(b). For instance, when the substrate conditions are such that
![]() $h=26$
$h=26$
![]() ${\rm\mu}\text{m}$
,
${\rm\mu}\text{m}$
,
![]() $d=10~{\rm\mu}\text{m}$
and
$d=10~{\rm\mu}\text{m}$
and
![]() $f=2$
, the maximum structural coefficient is predicted to be 0.734 when
$f=2$
, the maximum structural coefficient is predicted to be 0.734 when
![]() $s_{y}=82~{\rm\mu}\text{m}$
and
$s_{y}=82~{\rm\mu}\text{m}$
and
![]() $s_{x}=10$
$s_{x}=10$
![]() ${\rm\mu}\text{m}$
(with
${\rm\mu}\text{m}$
(with
![]() ${\it\alpha}=0$
), which is 1.8 times higher than that of a square array with
${\it\alpha}=0$
), which is 1.8 times higher than that of a square array with
![]() $s_{x}=s_{y}=29~{\rm\mu}\text{m}$
.
$s_{x}=s_{y}=29~{\rm\mu}\text{m}$
.
In appendix A, we compare our experimental results with the previously suggested scaling laws for the hemiwicking speed, and find that those theories fail to predict all of the experimental data. It can also be shown that our scaling law (3.9) is compatible with a previous theory (Ishino et al.) in the limit where it was derived. When the gap of pillars (
![]() $s$
) is much larger than the height (
$s$
) is much larger than the height (
![]() $h$
),
$h$
),
![]() $s\gg h$
, the resisting force is dominated by the friction of the base. Thus, we get
$s\gg h$
, the resisting force is dominated by the friction of the base. Thus, we get
![]() ${\it\eta}\approx f-1$
, which reduces (3.9) to
${\it\eta}\approx f-1$
, which reduces (3.9) to
![]() $L\sim (Dt)^{1/2}$
, where
$L\sim (Dt)^{1/2}$
, where
![]() $D\sim ({\it\gamma}/{\it\mu})[dh^{2}/(s_{x}s_{y})]$
. This is consistent with the theory of Ishino et al. in the limit
$D\sim ({\it\gamma}/{\it\mu})[dh^{2}/(s_{x}s_{y})]$
. This is consistent with the theory of Ishino et al. in the limit
![]() $s\gg h$
. When the gap of pillars (
$s\gg h$
. When the gap of pillars (
![]() $s$
) is much smaller than the height (
$s$
) is much smaller than the height (
![]() $h$
),
$h$
),
![]() $s\ll h$
, the friction of the pillar sides governs the resisting force, and we get
$s\ll h$
, the friction of the pillar sides governs the resisting force, and we get
![]() ${\it\eta}\approx s/h$
, yielding
${\it\eta}\approx s/h$
, yielding
![]() $D\sim ({\it\gamma}/{\it\mu})s$
. Ishino et al. suggested
$D\sim ({\it\gamma}/{\it\mu})s$
. Ishino et al. suggested
![]() $D\sim ({\it\gamma}/{\it\mu})d[\ln (2s_{x}/d)-1.31]$
by using the theory of Hasimoto (Reference Hasimoto1959) for the flow past an array of circular cylinders. Because our micropillar arrays do not cover the cases
$D\sim ({\it\gamma}/{\it\mu})d[\ln (2s_{x}/d)-1.31]$
by using the theory of Hasimoto (Reference Hasimoto1959) for the flow past an array of circular cylinders. Because our micropillar arrays do not cover the cases
![]() $s\ll h$
, we are unable to give the range of
$s\ll h$
, we are unable to give the range of
![]() $h/s$
up to which our simplified prediction is valid. However, our scaling shares common features with that of Ishino et al. in that
$h/s$
up to which our simplified prediction is valid. However, our scaling shares common features with that of Ishino et al. in that
![]() $D$
is independent of
$D$
is independent of
![]() $h$
and increases with
$h$
and increases with
![]() $s$
. Our dynamical coefficients yield a similar plot to figure 6 of Ishino et al., which essentially demonstrates the experimental data’s independence of
$s$
. Our dynamical coefficients yield a similar plot to figure 6 of Ishino et al., which essentially demonstrates the experimental data’s independence of
![]() $h$
.
$h$
.
4 Microscopic model of hemiwicking dynamics
While the foregoing model considers the speed of the wicking front as viewed from a distance, the magnified views of the front, figure 2(b,c), lead us to consider the effects of individual pillars and their spacing on the shape and local speed of the interface. We illustrate the profiles of the liquid film at the wet front in figure 5, for both dense (a) and sparse (b) arrays. While the film climbs the hydrophilic pillar (in the
![]() $z$
-direction), the meniscus extends over the substrate surface. In the figure,
$z$
-direction), the meniscus extends over the substrate surface. In the figure,
![]() $x_{0}$
corresponds to the distance from a pillar whose top has been just reached by the climbing film (denoted by A in figure 5) to the wet front on the base. When the array is skewed by
$x_{0}$
corresponds to the distance from a pillar whose top has been just reached by the climbing film (denoted by A in figure 5) to the wet front on the base. When the array is skewed by
![]() ${\it\alpha}$
, the centre-to-centre distance
${\it\alpha}$
, the centre-to-centre distance
![]() $b$
from pillar A to the nearest pillar in the next row (pillar B) can be shown to be
$b$
from pillar A to the nearest pillar in the next row (pillar B) can be shown to be
![]() $b=\text{min}\{s_{x}/\cos {\it\alpha},[(s_{x}/\cos {\it\alpha}-s_{y}\sin {\it\alpha})^{2}+s_{y}^{2}\cos ^{2}{\it\alpha}]^{1/2}\}$
. We refer to the pillar array as dense when pillar B is located within
$b=\text{min}\{s_{x}/\cos {\it\alpha},[(s_{x}/\cos {\it\alpha}-s_{y}\sin {\it\alpha})^{2}+s_{y}^{2}\cos ^{2}{\it\alpha}]^{1/2}\}$
. We refer to the pillar array as dense when pillar B is located within
![]() $x_{0}$
from pillar A and as sparse when pillar B is located farther than
$x_{0}$
from pillar A and as sparse when pillar B is located farther than
![]() $x_{0}$
from pillar A.
$x_{0}$
from pillar A.
To find the scaling approximation of
![]() $x_{0}$
, we consider the force balance for the meniscus hanging on the pillars at the wet front. The capillary force along the pillar perimeter,
$x_{0}$
, we consider the force balance for the meniscus hanging on the pillars at the wet front. The capillary force along the pillar perimeter,
![]() $F_{c}={\rm\pi}d{\it\gamma}$
, is balanced by the force due to the pressure drop across the interface (
$F_{c}={\rm\pi}d{\it\gamma}$
, is balanced by the force due to the pressure drop across the interface (
![]() ${\rm\Delta}p$
) on the area
${\rm\Delta}p$
) on the area
![]() $s_{y}x_{0}$
, which gives
$s_{y}x_{0}$
, which gives
![]() ${\rm\Delta}p\approx {\rm\pi}d{\it\gamma}/(s_{y}x_{0})$
. The directions of the capillary and pressure forces are denoted in figure 5(b). By relating
${\rm\Delta}p\approx {\rm\pi}d{\it\gamma}/(s_{y}x_{0})$
. The directions of the capillary and pressure forces are denoted in figure 5(b). By relating
![]() ${\rm\Delta}p$
to the meniscus curvature via the Young–Laplace equation,
${\rm\Delta}p$
to the meniscus curvature via the Young–Laplace equation,
![]() ${\rm\Delta}p\approx {\it\gamma}\partial ^{2}z/\partial x^{2}\sim {\it\gamma}h/x_{0}^{2}$
, we get
${\rm\Delta}p\approx {\it\gamma}\partial ^{2}z/\partial x^{2}\sim {\it\gamma}h/x_{0}^{2}$
, we get
As noted above, we consider two different situations where the smallest pillar spacing that a meniscus needs to extend before encountering a neighbouring pillar,
![]() $b-d$
, is either less than or greater than
$b-d$
, is either less than or greater than
![]() $x_{0}$
. If
$x_{0}$
. If
![]() $b-d<x_{0}$
, the meniscus touches the next pillar before it reaches top of the previous pillar, i.e. the pillars are dense. However, the meniscus needs to keep extending on the base even after reaching the top to meet the next pillar if
$b-d<x_{0}$
, the meniscus touches the next pillar before it reaches top of the previous pillar, i.e. the pillars are dense. However, the meniscus needs to keep extending on the base even after reaching the top to meet the next pillar if
![]() $b-d>x_{0}$
, i.e. the pillars are sparse.
$b-d>x_{0}$
, i.e. the pillars are sparse.
First, we consider the wetting front propagation for
![]() $b-d<x_{0}$
, i.e. when the pillars are dense. In this case, multiple pillars are partially touched by the front meniscus, as shown in figure 5(a). If the effect of a single pillar is taken into account, the driving force per unit width is given by
$b-d<x_{0}$
, i.e. when the pillars are dense. In this case, multiple pillars are partially touched by the front meniscus, as shown in figure 5(a). If the effect of a single pillar is taken into account, the driving force per unit width is given by
![]() $-\text{d}E/\text{d}x=-(\text{d}E/\text{d}z)(\text{d}z/\text{d}x)$
, where
$-\text{d}E/\text{d}x=-(\text{d}E/\text{d}z)(\text{d}z/\text{d}x)$
, where
![]() $z$
is the direction perpendicular to the base. Here
$z$
is the direction perpendicular to the base. Here
![]() $-\text{d}E/\text{d}z$
corresponds to the capillary force (per transverse pitch
$-\text{d}E/\text{d}z$
corresponds to the capillary force (per transverse pitch
![]() $s_{y}$
) pulling the liquid upward along the pillar of diameter
$s_{y}$
) pulling the liquid upward along the pillar of diameter
![]() $d$
, so that
$d$
, so that
![]() $-\text{d}E/\text{d}z\approx {\rm\pi}{\it\gamma}d/s_{y}$
. Given the number of pillars partially touched by the meniscus per transverse pitch,
$-\text{d}E/\text{d}z\approx {\rm\pi}{\it\gamma}d/s_{y}$
. Given the number of pillars partially touched by the meniscus per transverse pitch,
![]() $n$
, we get
$n$
, we get
![]() $\text{d}z/\text{d}x\sim h/(ns_{x})$
, where
$\text{d}z/\text{d}x\sim h/(ns_{x})$
, where
![]() $ns_{x}$
approximates the length of meniscus extension. The driving force arises at multiple pillars, which gives
$ns_{x}$
approximates the length of meniscus extension. The driving force arises at multiple pillars, which gives
![]() $F_{d}=-n\,\text{d}E/\text{d}x\sim {\rm\pi}{\it\gamma}dh/(s_{x}s_{y})$
. Because
$F_{d}=-n\,\text{d}E/\text{d}x\sim {\rm\pi}{\it\gamma}dh/(s_{x}s_{y})$
. Because
![]() $f={\rm\pi}{\it\gamma}dh/(s_{x}s_{y})+1$
, we get
$f={\rm\pi}{\it\gamma}dh/(s_{x}s_{y})+1$
, we get
![]() $F_{d}\sim (f-1){\it\gamma}$
.
$F_{d}\sim (f-1){\it\gamma}$
.
Although the local advance of the interface is ‘driven’ by individual pillars at the wetting front, the liquid that wets new pillars and their neighbour must come from the liquid reservoir a distance away of
![]() $L$
. Thus, the viscous resisting force per unit width is scaled as
$L$
. Thus, the viscous resisting force per unit width is scaled as
![]() $F_{r}\sim {\it\mu}{\dot{x}}L[1/h+(f-1)/s]$
, following (3.7). Balancing the driving and resisting forces yields the scaling estimates of the microscopic advancing velocity and distance of the meniscus:
$F_{r}\sim {\it\mu}{\dot{x}}L[1/h+(f-1)/s]$
, following (3.7). Balancing the driving and resisting forces yields the scaling estimates of the microscopic advancing velocity and distance of the meniscus:
This is consistent with the result of Kim et al. (Reference Kim, Moon, Lee, Lee, Chang and Kim2011a
), a constant speed of zippering at a given distance from a liquid source (
![]() $L$
). The macroscopic front propagation is a collective consequence of microscopic wicking in the direction perpendicular to the free surface of the liquid reservoir. Then we see that (4.2) is consistent with (3.8) for macro time scales.
$L$
). The macroscopic front propagation is a collective consequence of microscopic wicking in the direction perpendicular to the free surface of the liquid reservoir. Then we see that (4.2) is consistent with (3.8) for macro time scales.
We next consider the rate of increase in
![]() $x$
for
$x$
for
![]() $b-d>x_{0}$
, i.e. when the pillars are sparse, figure 5(b). Because
$b-d>x_{0}$
, i.e. when the pillars are sparse, figure 5(b). Because
![]() $b\geqslant s_{x}$
always holds, we have
$b\geqslant s_{x}$
always holds, we have
![]() $x_{0}<s_{x}-d$
. The meniscus that touches the top of pillar must propagate further to meet the next pillar, as shown in figures 2(c) and 5(b). For
$x_{0}<s_{x}-d$
. The meniscus that touches the top of pillar must propagate further to meet the next pillar, as shown in figures 2(c) and 5(b). For
![]() $x>x_{0}$
, the driving force is given by the product of the pressure drop,
$x>x_{0}$
, the driving force is given by the product of the pressure drop,
![]() ${\it\gamma}{\it\kappa}$
, and an area
${\it\gamma}{\it\kappa}$
, and an area
![]() $s_{y}h$
, which gives the driving force per transverse pitch:
$s_{y}h$
, which gives the driving force per transverse pitch:
![]() $F_{d}\sim {\it\gamma}h{\it\kappa}$
. Here, the meniscus curvature is
$F_{d}\sim {\it\gamma}h{\it\kappa}$
. Here, the meniscus curvature is
![]() ${\it\kappa}\sim h/x^{2}$
, so that
${\it\kappa}\sim h/x^{2}$
, so that
![]() $F_{d}\sim {\it\gamma}h^{2}/x^{2}$
. The viscous resisting force is again scaled as
$F_{d}\sim {\it\gamma}h^{2}/x^{2}$
. The viscous resisting force is again scaled as
![]() $F_{r}\sim {\it\mu}{\dot{x}}L(f-1)/({\it\eta}h)$
along the same line as above. Then, balancing
$F_{r}\sim {\it\mu}{\dot{x}}L(f-1)/({\it\eta}h)$
along the same line as above. Then, balancing
![]() $F_{d}$
and
$F_{d}$
and
![]() $F_{r}$
gives the local front speed
$F_{r}$
gives the local front speed
![]() ${\dot{x}}$
as
${\dot{x}}$
as
Then, we get the scaling law for meniscus extension on sparse pillar arrays when
![]() $x>x_{0}$
:
$x>x_{0}$
:
Our analysis on the meniscus extension around individual pillars reveals that
![]() $x$
grows like
$x$
grows like
![]() $t$
for
$t$
for
![]() $x<x_{0}$
(for both dense and sparse pillars) and like
$x<x_{0}$
(for both dense and sparse pillars) and like
![]() $t^{1/3}$
for
$t^{1/3}$
for
![]() $x>x_{0}$
(for sparse pillars only). Figure 6 shows that the experimentally measured meniscus extension indeed follows the above power laws, which hold regardless of the skewness of the pillar array. This supports our unified model for the microscopic extension of the meniscus, whether it appears to laterally zip (figure 5
$x>x_{0}$
(for sparse pillars only). Figure 6 shows that the experimentally measured meniscus extension indeed follows the above power laws, which hold regardless of the skewness of the pillar array. This supports our unified model for the microscopic extension of the meniscus, whether it appears to laterally zip (figure 5
![]() $a$
) or radiate (figure 5
$a$
) or radiate (figure 5
![]() $b$
) from the pillars at the wet front. That is, the meniscus advances as it spreads on the base surface while climbing the pillars at the front regardless of the pillar arrangement.
$b$
) from the pillars at the wet front. That is, the meniscus advances as it spreads on the base surface while climbing the pillars at the front regardless of the pillar arrangement.

Figure 6. Dimensionless advancing distance of meniscus on the base,
![]() $x/x_{0}$
, versus the dimensionless elapsed time
$x/x_{0}$
, versus the dimensionless elapsed time
![]() $({\it\eta}{\it\gamma}/{\it\mu}h)t/l_{c}^{2}$
on a log–log scale for sparse arrays. The insets show linear plots of
$({\it\eta}{\it\gamma}/{\it\mu}h)t/l_{c}^{2}$
on a log–log scale for sparse arrays. The insets show linear plots of
![]() $x$
versus
$x$
versus
![]() $t$
with error bars. The liquid is water. (a) Square pillar array with
$t$
with error bars. The liquid is water. (a) Square pillar array with
![]() $\{h,d,s_{x},s_{y}\}=\{7.2,10,40,40\}~{\rm\mu}\text{m}$
and the corresponding
$\{h,d,s_{x},s_{y}\}=\{7.2,10,40,40\}~{\rm\mu}\text{m}$
and the corresponding
![]() $b=40~{\rm\mu}\text{m}$
. The distance of the meniscus from the liquid source
$b=40~{\rm\mu}\text{m}$
. The distance of the meniscus from the liquid source
![]() $L\approx 7$
mm. (b) Skewed pillar array of
$L\approx 7$
mm. (b) Skewed pillar array of
![]() ${\it\alpha}=60^{\circ }$
with
${\it\alpha}=60^{\circ }$
with
![]() $\{h,d,s_{x},s_{y}\}=\{20,20,62.5,216.5\}~{\rm\mu}\text{m}$
and the corresponding
$\{h,d,s_{x},s_{y}\}=\{20,20,62.5,216.5\}~{\rm\mu}\text{m}$
and the corresponding
![]() $b=125$
$b=125$
![]() ${\rm\mu}\text{m}$
. The distance of the meniscus from the liquid source is
${\rm\mu}\text{m}$
. The distance of the meniscus from the liquid source is
![]() $L\approx 5$
mm.
$L\approx 5$
mm.
Figure 7(a) plots the experimental data from dense and sparse pillar arrays according to the scaling law (3.9). The data from the dense arrays clearly collapse onto a single straight line, while those from the sparse arrays deviate from the master curve. Still, the macroscopic wetting distance
![]() $L$
grows like
$L$
grows like
![]() $t^{1/2}$
on the sparse arrays, which can be explained as follows. On the sparse arrays, the liquid front advances the distance
$t^{1/2}$
on the sparse arrays, which can be explained as follows. On the sparse arrays, the liquid front advances the distance
![]() $x_{0}$
at the rate given by (4.2) for the duration
$x_{0}$
at the rate given by (4.2) for the duration
![]() ${\it\tau}_{0}$
, and the rest of the distance
${\it\tau}_{0}$
, and the rest of the distance
![]() $x_{1}$
at the rate (4.4) for
$x_{1}$
at the rate (4.4) for
![]() ${\it\tau}_{1}$
before encountering the pillar in the next row:
${\it\tau}_{1}$
before encountering the pillar in the next row:
![]() $s_{x}-d=x_{0}+x_{1}$
. Now we write the average velocity in the former region
$s_{x}-d=x_{0}+x_{1}$
. Now we write the average velocity in the former region
![]() $\bar{u}_{0}=x_{0}/{\it\tau}_{0}\sim {\it\beta}/L$
with
$\bar{u}_{0}=x_{0}/{\it\tau}_{0}\sim {\it\beta}/L$
with
![]() ${\it\beta}={\it\gamma}{\it\eta}h/{\it\mu}$
. The average velocity in the latter region is given by
${\it\beta}={\it\gamma}{\it\eta}h/{\it\mu}$
. The average velocity in the latter region is given by
![]() $\bar{u}_{1}=x_{1}/{\it\tau}_{1}\sim {\it\beta}{\it\phi}/L$
, where
$\bar{u}_{1}=x_{1}/{\it\tau}_{1}\sim {\it\beta}{\it\phi}/L$
, where
![]() ${\it\phi}=h^{2}/[(f-1)\bar{x}_{1}^{2}]$
from (4.4), with
${\it\phi}=h^{2}/[(f-1)\bar{x}_{1}^{2}]$
from (4.4), with
![]() $\bar{x}_{1}$
being a value that gives the average velocity. From a macroscopic point of view,
$\bar{x}_{1}$
being a value that gives the average velocity. From a macroscopic point of view,
Because
![]() $L\dot{L}/{\it\beta}\sim {\it\zeta}$
with
$L\dot{L}/{\it\beta}\sim {\it\zeta}$
with
![]() ${\it\zeta}=(s_{x}-d)/(x_{0}+x_{1}/{\it\phi})$
being a function of only the given pillar dimensions, we get
${\it\zeta}=(s_{x}-d)/(x_{0}+x_{1}/{\it\phi})$
being a function of only the given pillar dimensions, we get
![]() $L\sim ({\it\beta}{\it\zeta}t)^{1/2}$
for sparse arrays. The dynamical coefficient is smaller than that for dense pillar arrays because
$L\sim ({\it\beta}{\it\zeta}t)^{1/2}$
for sparse arrays. The dynamical coefficient is smaller than that for dense pillar arrays because
![]() ${\it\zeta}$
involves an additional term
${\it\zeta}$
involves an additional term
![]() $x_{1}/{\it\phi}$
in the denominator. The deviation of the dynamical coefficient of sparse pillar arrays from the value of the dense arrays increases with
$x_{1}/{\it\phi}$
in the denominator. The deviation of the dynamical coefficient of sparse pillar arrays from the value of the dense arrays increases with
![]() $s_{x}$
, which accompanies an increase of
$s_{x}$
, which accompanies an increase of
![]() $x_{1}/{\it\phi}$
.
$x_{1}/{\it\phi}$
.

Figure 7. (a) Scaled wicking distance versus scaled time for dense (filled symbol) and sparse (empty symbol) pillar arrays; the experimental conditions are listed in the table. The slope of the best fitting line for the dense arrays is 0.49. The inset plots the same experimental data on the log–log scale to show that the slope is close to 0.5 for sparse and dense arrays. (b) Schematic of the wet distance growth versus time on a dense pillar array (dotted line) and sparse pillar array (solid line).
![]() $L$
grows like
$L$
grows like
![]() $t$
in blue sections, but like
$t$
in blue sections, but like
![]() $t^{1/3}$
in red sections. The wet distance propagation on the sparse array appears to follow
$t^{1/3}$
in red sections. The wet distance propagation on the sparse array appears to follow
![]() $L\sim t^{1/2}$
at the macroscale (grey broken line). (c) Regime map for the validity of the scaling law for macroscopic wicking, equation (3.9), under the dense pillar assumption. The filled and empty symbols correspond to the conditions where the dense pillar assumption is valid and invalid, respectively. All of the experimental conditions tested in this work are shown including those of (a).
$L\sim t^{1/2}$
at the macroscale (grey broken line). (c) Regime map for the validity of the scaling law for macroscopic wicking, equation (3.9), under the dense pillar assumption. The filled and empty symbols correspond to the conditions where the dense pillar assumption is valid and invalid, respectively. All of the experimental conditions tested in this work are shown including those of (a).
To aid the understanding of the reduced slope (or dynamical coefficient) in sparse arrays in a graphical manner, figure 7(b) schematically compares the wet front propagations from the liquid reservoir on dense and sparse arrays. On the dense array,
![]() $L$
grows like
$L$
grows like
![]() $t^{1/2}$
following the scaling law (3.9), which is shown by a dotted line. On the sparse array, however, the wet distance grows like
$t^{1/2}$
following the scaling law (3.9), which is shown by a dotted line. On the sparse array, however, the wet distance grows like
![]() $t$
in the vicinity of the front pillar (with a slope dependent on its distance from the reservoir
$t$
in the vicinity of the front pillar (with a slope dependent on its distance from the reservoir
![]() $L$
), but slows down when far from the pillar. The process repeats when the meniscus meets the next pillar. The deviations from the dotted line caused by such a slowdown accumulate with increasing
$L$
), but slows down when far from the pillar. The process repeats when the meniscus meets the next pillar. The deviations from the dotted line caused by such a slowdown accumulate with increasing
![]() $t$
, which allows us to discriminate the data points on sparse pillar arrays from those on dense pillar arrays in figure 7(a). We also find in figure 7(a) that the data points of the sparse pillar arrays are shifted to the right near
$t$
, which allows us to discriminate the data points on sparse pillar arrays from those on dense pillar arrays in figure 7(a). We also find in figure 7(a) that the data points of the sparse pillar arrays are shifted to the right near
![]() $t=0$
, which is partly caused by retarded wicking initiation. When the pillar arrays are sparse, the bulk, indicated by an empty ellipse in figure 2(a), first forms at the centre of the substrate and then fills the rest of the dry side area before a film flow emerges. On dense arrays, however, the film flow initiates almost immediately as the bulk emerges upon the substrate contacting the liquid reservoir.
$t=0$
, which is partly caused by retarded wicking initiation. When the pillar arrays are sparse, the bulk, indicated by an empty ellipse in figure 2(a), first forms at the centre of the substrate and then fills the rest of the dry side area before a film flow emerges. On dense arrays, however, the film flow initiates almost immediately as the bulk emerges upon the substrate contacting the liquid reservoir.
Because the slowdown of the meniscus on sparse pillar arrays is directly associated with the change in the power law of
![]() $x$
for
$x$
for
![]() $b-d>x_{0}$
, we naturally expect that the regime boundary indicating the validity of the dense pillar assumption would be represented by the ratio
$b-d>x_{0}$
, we naturally expect that the regime boundary indicating the validity of the dense pillar assumption would be represented by the ratio
![]() $(b-d)/x_{0}$
. Figure 7(c) indeed shows that the dense array and sparse array regimes are divided by a horizontal line, which corresponds to
$(b-d)/x_{0}$
. Figure 7(c) indeed shows that the dense array and sparse array regimes are divided by a horizontal line, which corresponds to
![]() $(b-d)/x_{0}\approx 1.35$
, where we used the right-hand side of (4.1) to determine a characteristic value of
$(b-d)/x_{0}\approx 1.35$
, where we used the right-hand side of (4.1) to determine a characteristic value of
![]() $x_{0}$
. Here, the filled symbols correspond to the conditions where the slope of the best fitting line lies between 0.44 and 0.54 (90 % and 110 % of the slope of the best fitting line for the filled symbols in figure 7(a), i.e. 0.49), and the empty symbols correspond to a slope of less than 0.44. The horizontal regime boundary reveals that dense and sparse arrays cannot simply be discriminated according to the ratio of the pitch to the diameter,
$x_{0}$
. Here, the filled symbols correspond to the conditions where the slope of the best fitting line lies between 0.44 and 0.54 (90 % and 110 % of the slope of the best fitting line for the filled symbols in figure 7(a), i.e. 0.49), and the empty symbols correspond to a slope of less than 0.44. The horizontal regime boundary reveals that dense and sparse arrays cannot simply be discriminated according to the ratio of the pitch to the diameter,
![]() $s_{x}/d$
. Rather, the boundary is a function of the pillar height as well as the diameter and pitch, as described by our model.
$s_{x}/d$
. Rather, the boundary is a function of the pillar height as well as the diameter and pitch, as described by our model.
5 Conclusions
We have constructed scaling laws to estimate the velocity of hemiwicking on rough substrates and experimentally corroborated them for different liquids and various arrangements of hydrophilic pillar arrays. Both the macroscopic and microscopic flow behaviours have been considered. From the former viewpoint, the wicking front appears parallel to the free surface of the reservoir regardless of the pillar arrangement. The inertia-free dynamics has been analysed by balancing the capillary forces that drive the flow and the resisting viscous shear forces. At macroscopic length scales, the distance from the reservoir to the wicking front
![]() $L$
grows like
$L$
grows like
![]() $({\it\eta}{\it\gamma}h/{\it\mu})^{1/2}t^{1/2}$
regardless of the precise arrangement of the pillars. At microscopic length scales where
$({\it\eta}{\it\gamma}h/{\it\mu})^{1/2}t^{1/2}$
regardless of the precise arrangement of the pillars. At microscopic length scales where
![]() $L$
can be effectively assumed to be a constant, the meniscus extension
$L$
can be effectively assumed to be a constant, the meniscus extension
![]() $x$
grows like
$x$
grows like
![]() $t$
in the vicinity of the front pillar. However, the microscopic meniscus extension slows down significantly with the transition of the power law from
$t$
in the vicinity of the front pillar. However, the microscopic meniscus extension slows down significantly with the transition of the power law from
![]() $x\sim t$
to
$x\sim t$
to
![]() $x\sim t^{1/3}$
while the meniscus spreads on sparse pillar arrays. We have further showed that the macroscopic diffusive behaviour of
$x\sim t^{1/3}$
while the meniscus spreads on sparse pillar arrays. We have further showed that the macroscopic diffusive behaviour of
![]() $L$
persists on sparse pillar arrays but with a smaller dynamical coefficient that for dense pillar arrays.
$L$
persists on sparse pillar arrays but with a smaller dynamical coefficient that for dense pillar arrays.

Figure 8. Experimentally measured propagation distance of wet front plotted against various scaling laws for square arrays. The scaling laws are from (a) Bico et al. (Reference Bico, Tordeus and Quéré2001), (b) Courbin et al. (Reference Courbin, Denieul, Dressaire, Roper, Ajdari and Stone2007), (c) Ishino et al. (Reference Ishino, Reyssat, Reyssat, Okumura and Quéré2007), (d) Srivastava et al. (Reference Srivastava, Din, Judson, MacDonald and Meinhart2010), (e) Kim et al. (Reference Kim, Moon, Lee, Mahadevan and Kim2011b ) and (f) the current model, equation (3.9). (g) Table of the experimental conditions.
In addition to the fact that our macroscopic scaling law explains the experimental data covering a wide range of ratios of pillar pitch to height, a remarkable advance of our theory is that the model can consider non-square and even skewed arrays. We have found that the transverse and longitudinal pitches have unequal roles for the viscous resistance, while the driving force is only dependent on an averaged geometric parameter: the roughness. This study can be used to analyse a thin film spreading on a rough hydrophilic surface, like that in mundane painting activities (Kim et al. Reference Kim, Choi, Moon, Lee, Chang, Lee and Kim2015), as well as practical applications including evaporative cooling, absorption refrigeration, paper-based microfluidics (Martinez, Phillips & Whitesides Reference Martinez, Phillips and Whitesides2008) and water harvesting from humid air (Lee & Kim Reference Lee and Kim2012).
Acknowledgements
This work was supported by the National Research Foundation of Korea (grant nos 2014023206 and 2014048162) via SNU-IAMD.
Appendix A. Comparison of experiment with previous theories
Several scaling laws have been previously suggested to model the hemiwicking speed on square arrays of micropillars. They commonly present the propagation distance of the wet front,
![]() $L$
, in the form of
$L$
, in the form of
![]() $L\sim (Dt)^{1/2}$
, where the dynamical coefficient
$L\sim (Dt)^{1/2}$
, where the dynamical coefficient
![]() $D$
is a function of
$D$
is a function of
![]() ${\it\gamma}$
,
${\it\gamma}$
,
![]() ${\it\mu}$
and geometrical parameters. We list the driving and resisting forces and
${\it\mu}$
and geometrical parameters. We list the driving and resisting forces and
![]() $D$
suggested by each reference in table 2, and compare the models with the current experimental results for square arrays in figure 8.
$D$
suggested by each reference in table 2, and compare the models with the current experimental results for square arrays in figure 8.
Table 2. Scales of driving and resisting forces and dynamical coefficients suggested in previous studies.

The limits of the previous models can be briefly summarized as follows. Bico et al. considered the viscous forces of the array base while ignoring the effects of pillar side walls. Courbin et al. excessively simplified the driving force and considered the viscous force of the pillar side only. Ishino et al. suggested a scaling law for
![]() $s\gg h$
, and the corresponding data points (empty circle, square and triangles) collapse onto a single straight line in figure 8(c). However, the other experimental data that do not correspond to the limit deviate from the line. Srivastava et al. resorted to numerical simulation results to give a power law in an empirical manner, but failed to account for all of the flow physics. Kim et al. (Reference Kim, Moon, Lee, Mahadevan and Kim2011b
) did not discriminate between regions I and II in figure 2(e), which caused errors as shown in figure 8(e).
$s\gg h$
, and the corresponding data points (empty circle, square and triangles) collapse onto a single straight line in figure 8(c). However, the other experimental data that do not correspond to the limit deviate from the line. Srivastava et al. resorted to numerical simulation results to give a power law in an empirical manner, but failed to account for all of the flow physics. Kim et al. (Reference Kim, Moon, Lee, Mahadevan and Kim2011b
) did not discriminate between regions I and II in figure 2(e), which caused errors as shown in figure 8(e).