1. Introduction
The importance of flow control for the reduction of turbulent skin-friction drag has been growing steadily over the years, because of efficiency and environmental reasons. Unfortunately, friction drag reduction of both passive (e.g. riblets) and active techniques are proportional to the fraction of the surface covered by the drag-reducing device. Moreover, in parallel flows, where most research for skin-friction drag reduction has taken place, drag is entirely due to friction. However, the practical appeal of drag reduction is limited in duct flows, where energetic efficiency can be trivially improved by enlarging the cross-section of the duct, yielding reduced energy consumption easily and at a small capital cost.
In more complex flows, aerodynamic drag includes additional contributions besides viscous friction, such as pressure drag, parasitic drag, lift-induced drag and wave drag. What ultimately matters is reducing the overall drag. The research community is beginning to explore how skin-friction reduction affects the other drag components. Banchetti, Luchini & Quadrio (Reference Banchetti, Luchini and Quadrio2020) applied spanwise forcing via streamwise-travelling waves to a channel flow with a wall-mounted bump that generates pressure drag. They found that a distributed reduction of friction favourably modifies the pressure field, improving the net energetic benefits by about 50 %. Similarly, Nguyen, Ricco & Pironti (Reference Nguyen, Ricco and Pironti2021) applied a temporally spanwise-oscillating pressure gradient to a channel flow with transverse bars at the wall, and found that pressure drag is reduced nearly as much as friction drag, although the overall net energy budget remains slightly negative.
One of the applications where drag reduction entails obvious benefits is on aircraft, where achieving aerodynamic efficiency is the key. Flow over aircraft wings features pressure gradients and shock waves, which are responsible for significant drag penalty, amenable to control through a variety of techniques (Bushnell Reference Bushnell2004), including placement of small control bumps to modify the shock (Bruce & Colliss Reference Bruce and Colliss2015), and use of oscillatory blowing to delay flow separation (Seifert et al. Reference Seifert, Bachar, Koss, Shepshelovich and Wygnanski1993). Most of these studies are experimental, or based on Reynolds-averaged Navier–Stokes (RANS) simulations. Recently, Atzori et al. (Reference Atzori, Vinuesa, Fahland, Stroh, Gatti, Frohnapfel and Schlatter2020) studied with high-fidelity large-eddy simulations (LES) the effect of uniform blowing or suction on the incompressible flow past a NACA4412 airfoil at Reynolds number (based on free-stream velocity and chord length) of 
$Re=200\,000$. They found that the wing efficiency improves up to 11 % when uniform suction is applied to the suction side, leading to friction drag increase, but pressure drag reduction. Fahland et al. (Reference Fahland, Stroh, Frohnapfel, Atzori, Vinuesa, Schlatter and Gatti2021) demonstrated the potential of blowing on the pressure side under various conditions, achieving a maximum total net drag saving of 14 %. Kornilov (Reference Kornilov2021) carried out an experimental study of blowing/suction on two-dimensional low-speed airfoils, and provided ideal estimates of the power spent for actuation. Albers & Schröder (Reference Albers and Schröder2021) studied with implicit LES the same airfoil as considered by Atzori et al. (Reference Atzori, Vinuesa, Fahland, Stroh, Gatti, Frohnapfel and Schlatter2020), but controlled the flow via spanwise-travelling waves of wall-normal deformation. They generalised their previous results based on a different wing section (Albers, Meysonnat & Schröder Reference Albers, Meysonnat and Schröder2019) and demonstrated that control alters both friction and pressure drag, thus improving the overall aerodynamic performance of the wing.
All these works have considered the flow in incompressible or subsonic regimes. However, there are reasons to suspect (see e.g. Mele, Tognaccini & Catalano (Reference Mele, Tognaccini and Catalano2016), in the context of riblets) that a further advantage of reducing skin friction on a wing resides in the ability to interact with the position and strength of the shock waves that may form in the transonic regime. A similar outcome was found by Banchetti (Reference Banchetti2020) in a preliminary stage of the present work, with a RANS study of an aircraft with spanwise forcing. Here we present the first direct numerical simulation (DNS) of the turbulent flow over an airfoil in the transonic regime, where flow control originally targeted at friction reduction is applied. Specifically, we explore the extent to which a localised control for skin-friction reduction interacts with the shock and alters the aerodynamic performance of the airfoil. The results are also extrapolated to the whole aircraft. The active control technique chosen for the study is streamwise-travelling waves of spanwise forcing (Quadrio, Ricco & Viotti Reference Quadrio, Ricco and Viotti2009), which produce large (hence easily measurable) effects and large net savings as well. Although physical actuators to implement such forcing on an airplane are currently unavailable, the general conclusions are expected to be valid for any skin-friction reduction technology, be it active or passive.
2. Methods
We study by DNS the transonic flow around the supercritical V2C airfoil (see figure 1), designed by Dassault Aviation within the European research programme TFAST. The Reynolds and Mach numbers are set to 
$Re_\infty = U_\infty c /\nu _\infty = 3 \times 10^{5}$ and 
$M_\infty =U_\infty /a_\infty =0.7$, where 
$c$ is the airfoil chord and 
$U_\infty$, 
$\nu _\infty$ and 
$a_\infty$ are the free-stream velocity, kinematic viscosity and sound speed, with 
$U_\infty$ and 
$c$ being the reference velocity and length, unless otherwise noted. The 
$x$, 
$y$ and 
$z$ axes indicate the chordwise, vertical and spanwise directions. The angle of attack is 
$\alpha =4^{\circ }$, which corresponds to the maximum aerodynamic efficiency of the profile.
Figure 1. Geometry of the V2C airfoil. Forcing is applied at 
$x_f$ (on both sides) to initiate transition; and 
$x_s$ and 
$x_e$ denote start and end of the suction-side actuated region for cases C1 (blue dashed line) and C2 (red continuous line).
The DNS code (see Memmolo, Bernardini & Pirozzoli (Reference Memmolo, Bernardini and Pirozzoli2018), for a detailed description) solves the compressible Navier–Stokes equations for a calorically perfect gas. It is based on a baseline second-order, energy-consistent finite-volume discretisation, with local activation of a third-order shock-capturing weighted essentially non-oscillatory (WENO) numerical flux, controlled by a modified Ducros sensor (Ducros et al. Reference Ducros, Ferrand, Nicoud, Weber, Darracq, Gacherieu and Poinsot1999). Time advancement uses a low-storage, third-order Runge–Kutta scheme. At the far field, characteristics-based non-reflective boundary conditions are used (Poinsot & Lele Reference Poinsot and Lele1992), whereas periodicity is enforced in the spanwise direction. Discretisation is based on a C-type mesh, with radius of 
$25c$; the outflow is placed at 
$25c$ from the trailing edge. The domain extends for 
$0.1c$ in the spanwise 
$z$ direction, to ensure decorrelation of all the flow structures on the airfoil and in the wake (Hosseini et al. Reference Hosseini, Vinuesa, Schlatter, Hanifi and Henningson2016; Zhang & Samtaney Reference Zhang and Samtaney2016). The incoming flow is laminar. As done by Schlatter & Örlü (Reference Schlatter and Örlü2012), transition to turbulence is enforced on both sides of the airfoil via a time-varying wall-normal body force located around 
$x = x_f = 0.1c$, in such a way as to minimise disturbances associated with boundary layer tripping.
Streamwise-travelling waves of spanwise velocity are applied to a portion of the suction side of the wing, according to
\begin{equation} w_w (x,t) = A f(x) \sin ( \kappa_x x - \omega t ), \end{equation}
where 
$A$ is the maximum forcing amplitude, and 
$\kappa _x$ and 
$\omega$ are the spatial and temporal frequencies of the wave. As in Yudhistira & Skote (Reference Yudhistira and Skote2011), a smoothing function 
$f(x)$ is used to raise the spanwise velocity at the initial position 
$x_s$ and then return it to zero at 
$x_e$.
Two forcing configurations are considered, hereinafter referred to as cases C1 and C2: they have been selected after a preliminary study, such that the stronger forcing scheme C2 yields flow separation past the shock wave, whereas the milder forcing scheme C1 barely does so. In both cases the actuated region starts past the tripping zone, and ends past the shock. In particular, case C1 has 
$x_s=0.3$, 
$x_e=0.78$, 
$A=0.5$, 
$\omega =11.3$ and 
$\kappa _x=161$. In C2 the actuated region starts earlier at 
$x_s=0.2$, and the forcing amplitude is larger, i.e. 
$A=0.684$. For the C2 forcing, this corresponds to 
$A^{+} \approx 6.6$, 
$\omega ^{+} \approx 0.06$ and 
$\kappa _x^{+} \approx 0.013$ after expressing quantities in viscous units computed with the average value of the friction velocity along the actuated region: this is not far from the incompressible channel flow maximum net saving, yielding about 33 % drag reduction and 20 % net power savings at a friction Reynolds number of 
$Re_\tau =200$. (Note that forcing optimisation on the wing would by itself deserve a more detailed investigation.)
Six DNS have been carried out. Four employ a baseline grid with 536 million cells and include a reference uncontrolled case, as well as C1 and C2 (the latter repeated at a different angle of attack; see later § 3.3). This mesh size is comparable to that used by Zauner, De Tullio & Sandham (Reference Zauner, De Tullio and Sandham2019) for the same profile but at the larger 
$Re_\infty =5 \times 10^{5}$. The uncontrolled and C2 cases have also been computed on a finer mesh made by 1.8 billions cells, to check grid convergence. The baseline mesh has 
$4096 \times 512 \times 256$ cells, with uniform spacing in the spanwise direction and a hyperbolic-tangent clustering in the wall-normal direction to achieve sufficient resolution close to the airfoil and in the wake. The finer mesh, including 
$6144 \times 768 \times 384$ cells, has the number of cells increased by 50 % in each coordinate direction. An a posteriori check has confirmed that requirements for a fully resolved DNS (Hosseini et al. Reference Hosseini, Vinuesa, Schlatter, Hanifi and Henningson2016), namely 
$\Delta x^{+} < 10$, 
$\Delta y^{+} < 0.5$ and 
$\Delta z^{+} < 5$, are satisfied in the near-wall region. The same authors determined that for such flow this resolution is also adequate to resolve the wake region. The simulations are advanced in time with a constant step, selected to maintain the maximum Courant–Friedrichs–Lewy number below unity. Specifically, we use 
$\Delta t= 1.5 \times 10^{-4}$ for the baseline mesh, and 
$\Delta t = 1 \times 10^{-4}$ for the fine mesh. The flow statistics are accumulated over a time interval of 
$40 c/U_\infty$, after reaching statistical equilibrium.
3. Results
3.1. Instantaneous and mean fields
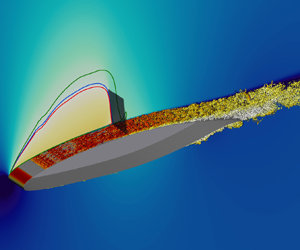
An overview of the mean and instantaneous fields in the uncontrolled case is provided by figure 2, where instantaneous vortical structures are visualised via isosurfaces of the imaginary part 
$\lambda _{ci}$ of the complex conjugate eigenvalue pair of the velocity gradient tensor (Zhou et al. Reference Zhou, Adrian, Balachandar and Kendall1999). The shock is also shown, together with the mean Mach number, in the background colour map. The three sonic lines at 
$M=1$ are shown for the reference, C1 and C2 cases. The flow becomes supersonic at the nose and remains laminar up to the tripping. The supersonic region extends up to 
$x \approx 0.5c$, where the shock wave produces an abrupt recompression. Flow control shifts the shock downstream, enlarging the supersonic region, whose streamwise and vertical dimensions increase from 
$D_x=0.47c$, 
$D_y=0.35c$ (reference), to 
$D_x=0.48c, D_y=0.36c$ (C1), and to 
$D_x=0.52c, D_y=0.42c$ (C2). The shock strength correspondingly increases, with the pressure jump measured at 
$y=0.2$ increasing from 
$\Delta p=0.121$ (reference), to 
$\Delta p=0.136$ (C1), and to 
$\Delta p=0.167$ (C2). At the same time, the maximum Mach number increases from 
$M=1.087$ (reference), to 
$M=1.093$ (C1), and to 
$M=1.116$ (C2), whereas its position is nearly unaffected, at 
$(x,y)\approx (0.39c,0.094c)$. These modifications are consistent with decreased friction over the actuated region, yielding increased supersonic speeds.
Figure 2. Instantaneous turbulent structures (uncontrolled case) visualised in terms of isosurfaces of the swirling strength (
$\lambda _{ci}=100$), and coloured with the turbulence kinetic energy 
$k$ (white-to-red colour map for 
$0 \leqslant k \leqslant 1$). The background colour map is for the mean Mach number (symmetric blue-to-red colour map for 
$0.5 \leqslant M \leqslant 1.5$). Sonic lines at 
$M=1$ are drawn for the uncontrolled (red), C1 (blue) and C2 (green) flow cases. The shock wave is shown via the grey isosurface of 
$\partial \rho / \partial x = 10$.
The development of the near-wall flow along the suction side is visualised in figure 3 for the three flow cases, where the instantaneous chordwise velocity (a proxy for the instantaneous wall friction) is shown at the first grid point off the wall. The right panels plot the mean velocity profile at 
$x/c=0.4$ and 
$x/c=0.6$, i.e. before and after the shock. The boundary layer is laminar up to the tripping location, whence a pattern of alternating low- and high-speed streaks is generated. Then, in the uncontrolled case the fluctuations undergo transient decay, and then grow further up to 
$x \approx 0.46c$, where interaction with the shock wave disrupts the streaks. Immediately past 
$x_s$, control produces visible spanwise meandering in the developing streaks and affects the transition process, so that the streaks nearly vanish at 
$x_s + 0.1c$. Past the shock, the uncontrolled case features scattered spots of backflow 
$u<0$, which are most intense in the C2 flow case, suggesting separation of the boundary layer in the mean sense.
Figure 3. Instantaneous chordwise velocity at the first grid point off the wing surface over the suction side, for uncontrolled (a), C1 (b) and C2 (c) flow cases. Red lines mark the boundaries of the actuated region, and green lines the position of the shock. The two panels on the right plot the mean velocity profile in local wall units upstream and downstream of the shock.
3.2. Wall friction and pressure
Figure 4 plots the mean friction and pressure coefficients 
$c_f=2 \tau _w/(\rho _\infty U_\infty ^{2})$ and 
$c_p=2(p_w-p_\infty )/(\rho _\infty U_\infty ^{2})$, where 
$\tau _w = \mu \hat {\boldsymbol {t}} \boldsymbol {\cdot } \partial \boldsymbol {u} / \partial n$ is the wall shear stress, with 
$\hat {\boldsymbol {t}}$ the tangential unit vector and 
$\partial / \partial n$ the derivative in the wall-normal direction. Here 
$\mu$, 
$\rho$ and 
$p_w$ are the dynamic viscosity, density and wall pressure.
Figure 4. Mean friction coefficient 
$c_f$ (a) and mean pressure coefficient 
$c_p$ (b). Symbols denote the uncontrolled and C2 cases computed on the finer mesh. Note that green and red symbols almost overlap on the pressure side.
Results from the baseline mesh (solid lines) and the finer mesh (symbols) are overlapping, and especially 
$c_p$ is very nearly mesh-independent. Only the peak of 
$c_f$, in the relatively unimportant nose region of the airfoil, is slightly under-resolved by the baseline mesh. The changes between the uncontrolled and actuated cases are, however, very well predicted on both meshes. Since the pressure side is not actuated and the flow properties are virtually unaffected, only the suction side is considered hereafter. Past the leading-edge peak, 
$c_f$ decreases rapidly in the laminar region, up to 
$x_f$, where the effect of numerical tripping is clearly visible. Further downstream, 
$c_f$ drops because of the shock wave–boundary layer interaction at 
$x \approx 0.45c$ and, after a transient increase, it slowly drops again, eventually becoming negative right upstream of the trailing edge. In the uncontrolled case, despite the negative 
$u$ fluctuations observed in the instantaneous field in figure 3, 
$c_f$ past the shock wave remains positive. In the controlled cases, forcing does its job of reducing friction in the actuated part of the wing. It is known (Quadrio & Ricco Reference Quadrio and Ricco2004; Skote Reference Skote2012) that some spatial extent is required for drag reduction to develop. Once this is accounted for, the local skin friction reduction is in line with expectations based on incompressible channel flow simulations. In both controlled cases, 
$c_f$ becomes negative past the shock wave, but negligibly so for C1, in agreement with the instantaneous visualisations of figure 3.
The pressure coefficient, after the leading-edge expansion, features a plateau that extends all the way to the near-shock region, as per the design of the airfoil. Then, in the rear part, 
$c_p$ progressively increases, and becomes nearly zero at the trailing edge. In the controlled cases, two distinct effects are observed: the compression associated with the shock wave is shifted downstream, and the leading-edge expansion intensifies. The recirculating region in the controlled cases mitigates the adverse pressure gradient near the shock, yielding a milder slope of the 
$c_p(x)$ curve. Hence the shock wave moves downstream, leading to a larger supersonic region with a higher velocity therein, and therefore to a stronger expansion in the fore part of the airfoil. Both effects are more evident in the C2 case, designed to yield stronger effects. Overall, the control modifies the 
$c_p$ distribution in a way that is consistent with a slight increase of the free-stream Mach number, but only on the suction side.
3.3. Aerodynamic forces and aircraft-level performance
The control-induced modifications to friction and pressure favourably affect lift and drag. Table 1 compares the lift and drag coefficients 
$C_l$ and 
$C_d$ of the airfoil for the uncontrolled and controlled cases. The friction and pressure contributions to the overall drag are separately accounted for, and reported as 
$C_{d,f}$ and 
$C_{d,p}$. Control reduces the friction drag by 7.3 % and 13.4 % for the C1 and C2 cases, respectively. These reductions are quite substantial, as control is applied only to about one-quarter of the airfoil surface. Naturally, friction drag reduction is larger for the C2 case, owing to its longer actuation region and stronger intensity. Pressure drag changes are instead quite different in the two cases: 
$C_{d,p}$ decreases by 2.4 % in the C1 case, and increases by 5.5 % in the C2 case. These combined changes result in reduction of the total drag in both cases, quantified as 4.5 % for C1, and as a marginal 0.8 % for C2. However, an additional crucial change is the increase of the lift coefficient. In agreement with the changes in the pressure distribution shown in figure 4, the increase of 
$C_l$ is minimal for C1 (
$+1.5\,\%$ only), but quite large for C2 (
$+11.3\,\%$). The wing efficiency, therefore, is significantly enhanced in both cases, by 6.8 % for C1, and by 13.5 % for C2.
Table 1. Lift and drag coefficients (
$C_l, C_d$) of the airfoil, and splitting of drag coefficient into friction and pressure contributions (
$C_{d,f}, C_{d,p}$), for uncontrolled, C1 and C2 flow cases. Here 
$\varDelta$ stands for relative change, and the last two columns refer to the C2 case computed for an angle of attack 
$\alpha =3.45^{\circ }$ (see text).
Increasing the wing efficiency implies that the lift required to balance the aircraft weight can be obtained at lower angle of attack, hence with lower drag penalty. To determine this contribution to drag reduction, we start by computing 
$C_l$–
$\alpha$ and 
$C_d$–
$\alpha$ maps (not shown) for the uncontrolled airfoil via auxiliary RANS simulations, using a modified version of the same flow solver with the Spalart–Allmaras turbulence model. Under the assumption that small changes of 
$\alpha$ do not alter the control-induced percentage changes of the aerodynamic forces, the new angle of attack is identified: for the C2 case, it is 
$\alpha =3.45^{\circ }$, for which an additional DNS is carried out (its results are shown in the last two columns of table 1). The lift coefficient is 
$C_l=0.730$, hence slightly less than expected, but the drag coefficient drops to 
$C_d = 0.0210$, i.e. with 15 % of drag reduction.
It is instructive to tentatively scale these figures, although with inevitable approximations, up to the full aircraft. As an example, we consider the wing–body configuration DLR-F6 defined in the Second AIAA CFD drag prediction workshop (Laflin et al. Reference Laflin, Klausmeyer, Zickuhr, Vassberg, Wahls, Morrison, Brodersen, Rakowitz, Tinoco and Godard2005), with flight conditions 
$M_\infty =0.75$ and 
$Re_\infty = 3 \times 10^{6}$. The reference lift coefficient is 
$C_L=0.5$, obtained at angle of attack 
$\alpha =0.52^{\circ }$, at the cost of 
$C_D=0.0295$. We look for the achievable drag reduction when control C2 is applied. In doing this, the following two simplifying assumptions are made: (i) the wing is responsible for the entire lift and its non-lift-induced drag is one-third of the total drag; and (ii) changes to 
$C_l$ and 
$C_d$ resulting from control are constant along the wing span, and do not change with 
$\alpha$, 
$M_\infty$ and 
$Re_\infty$, so that the values reported in table 1 apply. Using information available from https://aiaa-dpw.larc.nasa.gov/Workshop2/DPW_forces_WB_375, applying C2 control would reduce the angle of attack to 
$\alpha =0.0125^{\circ }$, thus yielding 
$C_D =0.0272$, hence with a drag reduction of approximately 8.5 %. The additional small benefit of direct skin-friction reduction leads to about 9 % reduction for the aircraft drag. It is also important to note that the actuation power required by the C2 forcing is very small. Under the assumption of actuation with unitary efficiency, it equals the power transferred to the viscous fluid by the boundary forcing. By computing its time-average value after the DNS, it is measured to be 
$5.5 \times 10^{-4} \rho _\infty U_\infty ^{3}$. Owing to the localised actuation (the actuated area is approximately one-quarter of the wing surface, and one-twelfth of the entire aircraft surface), the actuation power would thus be about 1 % of the overall power expenditure.
4. Concluding discussion
The first DNS of the controlled compressible turbulent transonic flow over a wing slab, at 
$M_\infty =0.7$ and 
$Re_\infty =3 \times 10^{5}$, has been presented. The aerodynamic performance of the wing is improved by using active spanwise wall forcing to locally reduce skin friction over a portion of the wing suction side. The forcing causes stronger expansion in the fore part and a delayed, more intense shock. This is equivalent to an increase of the Mach number on the suction side of the wing, and significantly improves the lift/drag ratio. For a constant angle of attack, the aerodynamic efficiency has been observed to increase by 13.5 % (with drag decreased by 0.8 % only). Higher aerodynamic efficiency allows the required lift to be achieved at a lower angle of attack, yielding significant reduction of the total drag, which we have quantified via DNS to be about 15 %. We have also estimated that this may lead to overall drag reduction of about 9 % for a full aircraft in cruise flight, and that the energy cost for the active control is about 
$1\,\%$ of the total power expenditure. Realising that a local friction control may yield global benefits has enormous importance in terms of both practical feasibility and cost/benefit assessment.
We close this paper by acknowledging possible limitations. First, the 
$Re_\infty$ value considered here is clearly not representative of an airplane in transonic flight, and serious design attempts should consider higher 
$Re$. Luckily, we know that skin-friction drag reduction techniques retain their effectiveness at higher 
$Re$, as brought forward by Luchini (Reference Luchini1996) and later stressed by Spalart & McLean (Reference Spalart and McLean2011). This was confirmed for spanwise forcing by Gatti & Quadrio (Reference Gatti and Quadrio2016), although the optimal wall actuation parameters may change slightly with 
$Re$. Also, available information (Yao & Hussain Reference Yao and Hussain2019) confirms that spanwise forcing is effective in the compressible regime. Second, the reported drag reduction of 9 % should by no means be taken as a maximum achievable gain. Indeed, the available forcing information for incompressible flow over a plane wall does not easily translate to aircraft in cruise conditions; moreover, the plane-channel maximum power-saving condition is most probably not optimal here. Locating where, when and how much the control should be activated is a new optimisation problem, whose solution might lead to much better performance. Above all, one should always be aware of the challenge of designing actuators capable of efficiently meeting the required specifications. The general ideas discussed here, however, retain their validity also for other schemes for friction reduction, including passive strategies, e.g. riblets, that remain the most obvious choice for applications.
All in all, we believe that considering skin-friction drag reduction as a tool and not only as a goal in flows where friction drag is not the key target for optimisation might open new avenues for a more widespread use of flow control.
Acknowledgements
Computational resources have been provided by CINECA through grant TragFoil and by HLRS through grant TuCoWi. We acknowledge F. Billard and M. Braza for providing data about the V2C airfoil.
Funding
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Declaration of interests
The authors report no conflict of interest.
