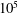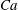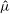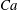1 Introduction
Multiphase turbulent flows are ubiquitous in nature and several industrial applications such as cloud formation, plankton dispersion in the sea, fuel sprays, emulsification, homogenisation and mixing in chemical reactors and drag reduction. In particular, two-phase flows which typically comprise a secondary phase dispersed into a primary carrier flow (e.g. droplets/bubbles dispersed into water or air) are prevalent in many applications involving drag reduction, heat transfer, liquid atomisation etc. Theoretical and numerical modelling of such flows is extremely challenging due to the wide range of length and time scales involved and nonlinear interaction between the dispersed and carrier phase. Among the many parameters that influence the global response and local flow dynamics of two-phase systems, the shape, deformability and orientation of a non-spherical anisotropic dispersed phase play very important roles. Understanding the dynamics of deformation and orientation of an anisotropic dispersed phase (for e.g. ellipsoidal bubbles or drops) and its dependence on the underlying local flow topology can thus be useful for optimising several industrial and engineering applications.
In this work, we study the shape and orientation statistics of neutrally buoyant, sub-Kolmogorov droplets dispersed into a turbulent Taylor–Couette (TC) flow. TC flow is one of the paradigmatic systems to study turbulence in wall-bounded systems (see Grossmann, Lohse & Sun (Reference Grossmann, Lohse and Sun2016) for a recent review). It is a geometrically simple system where the flow is driven by two independently rotating co-axial cylinders. The driving in a TC flow can be quantified using
![]() $Re_{i}=r_{i}\unicode[STIX]{x1D714}_{i}(r_{o}-r_{i})/\unicode[STIX]{x1D708}$
and
$Re_{i}=r_{i}\unicode[STIX]{x1D714}_{i}(r_{o}-r_{i})/\unicode[STIX]{x1D708}$
and
![]() $Re_{o}=r_{o}\unicode[STIX]{x1D714}_{o}(r_{o}-r_{i})/\unicode[STIX]{x1D708}$
which are the inner and outer cylinder Reynolds number, respectively (
$Re_{o}=r_{o}\unicode[STIX]{x1D714}_{o}(r_{o}-r_{i})/\unicode[STIX]{x1D708}$
which are the inner and outer cylinder Reynolds number, respectively (
![]() $r_{i}$
,
$r_{i}$
,
![]() $r_{o}$
and
$r_{o}$
and
![]() $\unicode[STIX]{x1D714}_{i}$
,
$\unicode[STIX]{x1D714}_{i}$
,
![]() $\unicode[STIX]{x1D714}_{o}$
are the radii and angular velocities of the inner and outer cylinder, respectively while
$\unicode[STIX]{x1D714}_{o}$
are the radii and angular velocities of the inner and outer cylinder, respectively while
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity of the carrier fluid). When the driving in TC flow is beyond a critical value, the flow transitions from a purely azimuthal laminar flow to a turbulent flow, during which a wide range of coherent flow patterns develop in the gap width. The various regimes that can be observed in a single-phase turbulent TC flow have been summarised by Andereck, Liu & Swinney (Reference Andereck, Liu and Swinney1986) for the low Reynolds number regime and recently extended for the highly turbulent case by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
). In the last decade, two-phase TC flow has also received massive interest due to the strong reductions in drag that can be achieved with the addition of a very small concentration of dispersed phase (
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of the carrier fluid). When the driving in TC flow is beyond a critical value, the flow transitions from a purely azimuthal laminar flow to a turbulent flow, during which a wide range of coherent flow patterns develop in the gap width. The various regimes that can be observed in a single-phase turbulent TC flow have been summarised by Andereck, Liu & Swinney (Reference Andereck, Liu and Swinney1986) for the low Reynolds number regime and recently extended for the highly turbulent case by Ostilla-Mónico et al. (Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014c
). In the last decade, two-phase TC flow has also received massive interest due to the strong reductions in drag that can be achieved with the addition of a very small concentration of dispersed phase (
![]() ${\sim}O(1)$
% of bubbles in water). Moreover, through several experimental and numerical studies in turbulent channel and TC flow, it has been shown that the deformability of the bubbles is of paramount importance to achieve strong drag reduction (Lu & Tryggvason Reference Lu and Tryggvason2008; Dabiri, Lu & Tryggvason Reference Dabiri, Lu and Tryggvason2013; van Gils et al.
Reference van Gils, Narezo Guzman, Sun and Lohse2013) while the exact physical mechanism is still unclear. It thus becomes important to understand the dynamics of deformation of a dispersed phase (for example bubbles/drops) in a turbulent carrier flow.
${\sim}O(1)$
% of bubbles in water). Moreover, through several experimental and numerical studies in turbulent channel and TC flow, it has been shown that the deformability of the bubbles is of paramount importance to achieve strong drag reduction (Lu & Tryggvason Reference Lu and Tryggvason2008; Dabiri, Lu & Tryggvason Reference Dabiri, Lu and Tryggvason2013; van Gils et al.
Reference van Gils, Narezo Guzman, Sun and Lohse2013) while the exact physical mechanism is still unclear. It thus becomes important to understand the dynamics of deformation of a dispersed phase (for example bubbles/drops) in a turbulent carrier flow.
The degree of deformation of the dispersed phase depends on many factors such as the size of the drops/bubbles, intensity of local inertial and viscous forces which tend to elongate or deform the drop from its initial spherical shape, surface tension forces which are responsible for restoring the drop back to its original spherical shape etc. (Rallison Reference Rallison1984; Stone Reference Stone1994). In his pioneering work, Taylor (Reference Taylor1932, Reference Taylor1934) was one of the first to study theoretically the deformation of a viscous drop dispersed into a carrier fluid where he showed that the shape of a deformed drop in presence of a velocity gradient depends on the viscosity ratio of the droplet to the carrier phase
![]() $\hat{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D707}_{d}/\unicode[STIX]{x1D707}_{c}$
(
$\hat{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D707}_{d}/\unicode[STIX]{x1D707}_{c}$
(
![]() $\unicode[STIX]{x1D707}_{d}$
and
$\unicode[STIX]{x1D707}_{d}$
and
![]() $\unicode[STIX]{x1D707}_{c}$
are the dynamic viscosities of the droplet and the carrier liquid respectively) and the capillary number
$\unicode[STIX]{x1D707}_{c}$
are the dynamic viscosities of the droplet and the carrier liquid respectively) and the capillary number
![]() $Ca=\unicode[STIX]{x1D707}_{c}RG/\unicode[STIX]{x1D70E}$
(
$Ca=\unicode[STIX]{x1D707}_{c}RG/\unicode[STIX]{x1D70E}$
(
![]() $R$
,
$R$
,
![]() $G$
and
$G$
and
![]() $\unicode[STIX]{x1D70E}$
are the drop radius, local shear rate and surface tension, respectively) which is the ratio of viscous to surface tension forces. In flows where the range of velocity gradients experienced by the dispersed phase is limited and deviation of the drop shape from sphericity is small, analytical solutions to compute the shape of the drop exist (Chaffey & Brenner Reference Chaffey and Brenner1967; Cox Reference Cox1969; Frankel & Acrivos Reference Frankel and Acrivos1970). However, when the flow field becomes complex and deviation from sphericity is beyond a critical value, the constitutive equations become intractable.
$\unicode[STIX]{x1D70E}$
are the drop radius, local shear rate and surface tension, respectively) which is the ratio of viscous to surface tension forces. In flows where the range of velocity gradients experienced by the dispersed phase is limited and deviation of the drop shape from sphericity is small, analytical solutions to compute the shape of the drop exist (Chaffey & Brenner Reference Chaffey and Brenner1967; Cox Reference Cox1969; Frankel & Acrivos Reference Frankel and Acrivos1970). However, when the flow field becomes complex and deviation from sphericity is beyond a critical value, the constitutive equations become intractable.
In turbulent flows, when the dispersed phase is larger than the Kolmogorov length scale, inertial forces play a primary role in deforming the drops which may eventually lead to breakup. Kolmogorov (Reference Kolmogorov1949) and Hinze (Reference Hinze1955) proposed one of the earliest models to study the process of deformation and breakup of such droplets dispersed into a turbulent carrier flow. The breakup of these droplets and its distribution in homogeneous isotropic turbulence was further investigated by Perlekar et al. (Reference Perlekar, Biferale, Sbragaglia, Srivastava and Toschi2012) using a multicomponent lattice Boltzmann method. Through Lagrangian tracking of individual droplets, these simulations showed that the local Weber number at the droplet position emerges as a crucial parameter and is strongly correlated with the degree of deformation and thus eventual breakup. A series of studies used the front-tracking approach to investigate the influence of inertial size spherical and deformable bubbles on the wall drag in a turbulent channel flow (Lu, Fernández & Tryggvason Reference Lu, Fernández and Tryggvason2005; Lu & Tryggvason Reference Lu and Tryggvason2008; Dabiri et al.
Reference Dabiri, Lu and Tryggvason2013; Tryggvason et al.
Reference Tryggvason, Dabiri, Aboulhasanzadeh and Lu2013). While the process of breakup and coalescence of the droplets cannot be modelled yet using this approach, it provides useful insight into the effect of deformability on the dynamics of bubbles much larger than the Kolmogorov scale (
![]() $d_{b}\sim 100\unicode[STIX]{x1D702}_{k}$
) in wall-bounded turbulence.
$d_{b}\sim 100\unicode[STIX]{x1D702}_{k}$
) in wall-bounded turbulence.
When the drops are smaller than Kolmogorov scale (sub-Kolmogorov), local viscous forces acting on the droplet become dominant in the deformation process thus making the capillary number (
![]() $Ca$
) relevant. In this situation Cristini et al. (Reference Cristini, Blawzdziewicz, Loewenberg and Collins2003) used the boundary integral formulation to study the deformation and breakup process of drops dispersed into an isotropic turbulent flow with
$Ca$
) relevant. In this situation Cristini et al. (Reference Cristini, Blawzdziewicz, Loewenberg and Collins2003) used the boundary integral formulation to study the deformation and breakup process of drops dispersed into an isotropic turbulent flow with
![]() $Re_{\unicode[STIX]{x1D706}}\sim 50$
(
$Re_{\unicode[STIX]{x1D706}}\sim 50$
(
![]() $\unicode[STIX]{x1D706}$
is the Taylor microscale). The process of drop deformation, elongation, neck formation and eventual breakup into satellite droplets was completely resolved and captured in these simulations. However, such fully resolved simulations come at an expense of the intensity of turbulence that can be achieved in the carrier flow field and also the number of droplets that can be simulated simultaneously.
$\unicode[STIX]{x1D706}$
is the Taylor microscale). The process of drop deformation, elongation, neck formation and eventual breakup into satellite droplets was completely resolved and captured in these simulations. However, such fully resolved simulations come at an expense of the intensity of turbulence that can be achieved in the carrier flow field and also the number of droplets that can be simulated simultaneously.
Due to the huge computational costs involved, simulating millions of fully resolved droplets or bubbles which can deform, breakup and coalesce in highly turbulent flow fields is still beyond reach (Tryggvason et al.
Reference Tryggvason, Dabiri, Aboulhasanzadeh and Lu2013). However, useful insights into such flows can still be obtained with the use of sub-grid models that can capture the motion and deformation of the dispersed phase. Instead of fully resolving the interaction between the dispersed phase and carrier phase, semi-empirical or phenomenological models can be used to track, deform, breakup or coalesce a large number of droplets or bubbles in highly turbulent environments. Such an approach has been adopted by Biferale, Meneveau & Verzicco (Reference Biferale, Meneveau and Verzicco2014), where they study the deformation and orientation statistics of approximately
![]() $10^{4}$
sub-Kolmogorov neutrally buoyant drops in homogenous isotropic turbulence. The drops were assumed to be triaxial ellipsoids and the shape and orientation of these passively advected drops was calculated using a phenomenological model proposed by Maffettone & Minale (Reference Maffettone and Minale1998). More recently, Babler et al. (Reference Babler, Biferale, Brandt, Feudel, Guseva, Lanotte, Marchioli, Picano, Sardina and Soldati2015) studied the breakup of approximately
$10^{4}$
sub-Kolmogorov neutrally buoyant drops in homogenous isotropic turbulence. The drops were assumed to be triaxial ellipsoids and the shape and orientation of these passively advected drops was calculated using a phenomenological model proposed by Maffettone & Minale (Reference Maffettone and Minale1998). More recently, Babler et al. (Reference Babler, Biferale, Brandt, Feudel, Guseva, Lanotte, Marchioli, Picano, Sardina and Soldati2015) studied the breakup of approximately
![]() $10^{5}$
colloidal aggregates in canonical set-ups like turbulent channel flow, developing boundary layer and homogenous isotropic turbulence. A similar work by Marchioli & Soldati (Reference Marchioli and Soldati2015) investigated the statistics of ductile rupture of colloidal aggregates tracked as massless particles in a turbulent channel flow. A simple criteria for aggregate breakup or rupture was adopted by both Babler et al. (Reference Babler, Biferale, Brandt, Feudel, Guseva, Lanotte, Marchioli, Picano, Sardina and Soldati2015) and Marchioli & Soldati (Reference Marchioli and Soldati2015) where the occurrence of a colloid breakup is directly related to the local hydrodynamic stress being higher than a critical threshold stress. In these studies, simulations of millions of droplets or colloidal aggregates in highly turbulent environments has been possible only due to the coupling of direct numerical simulations (DNS) of the carrier phase with a semi-empirical or phenomenological model for the deformation and breakup process. In this study we use a similar approach and couple a sub-grid deformation model along with DNS of the carrier flow to simultaneously track approximately
$10^{5}$
colloidal aggregates in canonical set-ups like turbulent channel flow, developing boundary layer and homogenous isotropic turbulence. A similar work by Marchioli & Soldati (Reference Marchioli and Soldati2015) investigated the statistics of ductile rupture of colloidal aggregates tracked as massless particles in a turbulent channel flow. A simple criteria for aggregate breakup or rupture was adopted by both Babler et al. (Reference Babler, Biferale, Brandt, Feudel, Guseva, Lanotte, Marchioli, Picano, Sardina and Soldati2015) and Marchioli & Soldati (Reference Marchioli and Soldati2015) where the occurrence of a colloid breakup is directly related to the local hydrodynamic stress being higher than a critical threshold stress. In these studies, simulations of millions of droplets or colloidal aggregates in highly turbulent environments has been possible only due to the coupling of direct numerical simulations (DNS) of the carrier phase with a semi-empirical or phenomenological model for the deformation and breakup process. In this study we use a similar approach and couple a sub-grid deformation model along with DNS of the carrier flow to simultaneously track approximately
![]() $10^{5}$
neutrally buoyant sub-Kolmogorov deformable passive drops in a turbulent TC flow.
$10^{5}$
neutrally buoyant sub-Kolmogorov deformable passive drops in a turbulent TC flow.
As mentioned previously, the driving of the TC system can induce several transitions in the flow from a purely laminar state to a fully turbulent system. In this study the outer cylinder is kept stationary (
![]() $Re_{o}=0$
) and only the inner cylinder is rotated until the system transitions into turbulence. We consider two different inner cylinder Reynolds numbers; one where there is a strong footprint of coherent structures, i.e. the Taylor rolls, and a higher
$Re_{o}=0$
) and only the inner cylinder is rotated until the system transitions into turbulence. We consider two different inner cylinder Reynolds numbers; one where there is a strong footprint of coherent structures, i.e. the Taylor rolls, and a higher
![]() $Re_{i}$
where the turbulence intensity is higher and the rolls lose their coherence. For each of these drivings, we vary the capillary number (
$Re_{i}$
where the turbulence intensity is higher and the rolls lose their coherence. For each of these drivings, we vary the capillary number (
![]() $Ca$
) and viscosity ratio (
$Ca$
) and viscosity ratio (
![]() $\hat{\unicode[STIX]{x1D707}}$
) of the droplets with the carrier fluid. The drops are treated as passive inertialess particles while the deformation and orientation of these drops is computed based on the phenomenological model proposed by Maffettone & Minale (Reference Maffettone and Minale1998) (hereafter referred to as the ‘MM’ model).
$\hat{\unicode[STIX]{x1D707}}$
) of the droplets with the carrier fluid. The drops are treated as passive inertialess particles while the deformation and orientation of these drops is computed based on the phenomenological model proposed by Maffettone & Minale (Reference Maffettone and Minale1998) (hereafter referred to as the ‘MM’ model).
This approach is similar to the one adopted by Biferale et al. (Reference Biferale, Meneveau and Verzicco2014) for drops dispersed in homogenous isotropic turbulence (HIT) and also by de Tullio et al. (Reference de Tullio, Nam, Pascazio, Balaras and Verzicco2012) to predict haemolysis by tracking several deformable red blood cells. A significant difference in this work in comparison to the work of Biferale et al. (Reference Biferale, Meneveau and Verzicco2014) is that we study the deformation of drops in a highly inhomogenous and anisotropic carrier flow (here Taylor–Couette) as opposed to a homogenous and isotropic turbulent environment. Given that TC flow is one of the paradigmatic systems in wall-bounded turbulent flows, we expect that the results from this study would have significant relevance in understanding deformation of drops in other canonical wall-bounded set-ups such as pipe flow, channel flows, convective turbulence etc. (Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2000, Reference Eckhardt, Grossmann and Lohse2007a ). In this work we consider only neutrally buoyant sub-Kolmogorov drops which we model with tracer-like zero-way coupling. Although this restricts us from studying the physics behind turbulence modification it does allow us to study the deformation dynamics of drops in a inhomogenous and anisotropic system. Additionally, in a later section we present arguments on why the tracer-like zero-way coupling is a reasonable approximation for sub-Kolmogorov neutrally buoyant drops. One open question we focus on in this work is the spatial dependence of the degree of deformation of the dispersed phase and how the shapes of the drops vary as they are transported in the flow. Are the drops more prolate or more oblate like and does the capillary number and viscosity ratio have an influence on the shape? How do these drops deform in different regions of the flow like the Taylor rolls, plume ejection and plume impact regions, respectively (Ostilla-Mónico et al. Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b )? What is the preferential direction of orientation of these drops in the boundary layers and bulk region? These are some questions we attempt to answer in this paper.
In the following section, we elaborate on the numerical schemes and methods employed to solve the equations of the carrier phase and the dispersed phase and also give a brief review on the MM model which is used to compute the deformation and orientation characteristics of the drops. In § 3 we discuss the results of our simulations where we analyse the averaged profiles of extent of deformation of the drops, probability distribution functions (p.d.f.s) of the extent of anisotropy in the dispersed phase and their orientational preferences for different
![]() $Ca$
and
$Ca$
and
![]() $\hat{\unicode[STIX]{x1D707}}$
. Finally, in § 4 we summarise the paper and give an outlook on future line of simulations.
$\hat{\unicode[STIX]{x1D707}}$
. Finally, in § 4 we summarise the paper and give an outlook on future line of simulations.
2 Governing equations and numerical details
For the carrier flow, DNS was used to solve the Navier–Stokes equations in cylindrical coordinates using a second-order accurate finite-difference scheme with fractional time stepping (Verzicco & Orlandi Reference Verzicco and Orlandi1996; van der Poel et al.
Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015). This code has already been validated and tested extensively for a wide range of parameters to study the various spatio-temporal dynamics of high Reynolds number single-phase TC turbulence for both the rotating and stationary outer cylinder cases (Ostilla-Mónico et al.
Reference Ostilla-Mónico, Stevens, Grossmann, Verzicco and Lohse2013, Reference Ostilla-Mónico, Huisman, Jannink, Van Gils, Verzicco, Grossmann, Sun and Lohse2014a
,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse
b
,Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse
c
). The code for DNS along with two-way coupled Lagrangian tracking have also been validated and used previously for studying the effect of buoyant spherical bubbles on the net drag reduction in a turbulent Taylor–Couette flow (Spandan et al.
Reference Spandan, Ostilla-Mónico, Verzicco and Lohse2016). For the purpose of this study the radius ratio and aspect ratio of the TC set-up is fixed to
![]() $\unicode[STIX]{x1D702}=r_{i}/r_{o}=0.833$
and
$\unicode[STIX]{x1D702}=r_{i}/r_{o}=0.833$
and
![]() $\unicode[STIX]{x1D6E4}=L/d=4$
, respectively. Periodic boundary conditions are employed in the azimuthal and axial directions and a non-uniform grid spacing (clipped Chebychev clustering) is employed in the wall-normal direction. Since we employ periodic boundary conditions in the axial direction, we have ensured through additional test simulations that the mean profiles and other relevant statistics discussed in § 3 are not influenced by increasing the aspect ratio (Ostilla-Mónico, Verzicco & Lohse Reference Ostilla-Mónico, Verzicco and Lohse2015; Spandan et al.
Reference Spandan, Ostilla-Mónico, Verzicco and Lohse2016).
$\unicode[STIX]{x1D6E4}=L/d=4$
, respectively. Periodic boundary conditions are employed in the azimuthal and axial directions and a non-uniform grid spacing (clipped Chebychev clustering) is employed in the wall-normal direction. Since we employ periodic boundary conditions in the axial direction, we have ensured through additional test simulations that the mean profiles and other relevant statistics discussed in § 3 are not influenced by increasing the aspect ratio (Ostilla-Mónico, Verzicco & Lohse Reference Ostilla-Mónico, Verzicco and Lohse2015; Spandan et al.
Reference Spandan, Ostilla-Mónico, Verzicco and Lohse2016).
The dispersed phase is composed of neutrally buoyant sub-Kolmogorov drops which are treated as passive tracers (Biferale et al.
Reference Biferale, Meneveau and Verzicco2014). The dispersed phase is advected based on the local velocity of the carrier phase at the exact location of each drop. Here it is important to note that the drops being treated as massless passive tracers with no back reaction on the flow is a zero-way coupled approximation in comparison to the one-way/two-way/four-way coupled approaches typically adopted in particle-laden turbulent flow studies (Elghobashi Reference Elghobashi1994). Such an approximation simplifies the problem since computing drag, lift and added mass closures for continuously deforming drops is a highly non-trivial issue and is not the focus of this study. Nonetheless, given that the dispersed phase is neutrally buoyant and sub-Kolmogorov in size (
![]() $R/\unicode[STIX]{x1D702}_{k}\sim 0.025{-}0.075$
) even during deformation, it can be argued that the behaviour of these particles/droplets is close to that of passive tracers given the extremely small particle time scales (or in other words low Stokes numbers) and minimal wake effects.
$R/\unicode[STIX]{x1D702}_{k}\sim 0.025{-}0.075$
) even during deformation, it can be argued that the behaviour of these particles/droplets is close to that of passive tracers given the extremely small particle time scales (or in other words low Stokes numbers) and minimal wake effects.
Since the dispersed phase is treated in a Lagrangian manner, the position of each droplet does not necessarily coincide with the location of grid nodes on the carrier phase mesh. This limitation is overcome with the use of a trilinear interpolation scheme to compute the velocity of the carrier phase at the exact droplet position. The droplet position is updated after every time step according to (2.1) using a second-order Runge–Kutta scheme (
![]() $\boldsymbol{v}$
is the interpolated carrier phase velocity at the droplet position and
$\boldsymbol{v}$
is the interpolated carrier phase velocity at the droplet position and
![]() $\boldsymbol{x}_{p}$
is the droplet position vector).
$\boldsymbol{x}_{p}$
is the droplet position vector).
In order to couple the tracking of the droplets with deformation, the droplets are assumed to be triaxial ellipsoids. Under this assumption, the drop shape and orientation can be easily described in the form of a second-order positive–definite symmetric tensor
![]() $\unicode[STIX]{x1D64E}$
(shape tensor). This tensor satisfies the condition
$\unicode[STIX]{x1D64E}$
(shape tensor). This tensor satisfies the condition
![]() $\unicode[STIX]{x1D64E}^{-1}\boldsymbol{ : }\boldsymbol{x}\boldsymbol{x}=1$
, where
$\unicode[STIX]{x1D64E}^{-1}\boldsymbol{ : }\boldsymbol{x}\boldsymbol{x}=1$
, where
![]() $\boldsymbol{x}$
is the position vector of any point on the ellipsoid surface relative to its origin. For any known tensor
$\boldsymbol{x}$
is the position vector of any point on the ellipsoid surface relative to its origin. For any known tensor
![]() $\unicode[STIX]{x1D64E}$
, the eigenvalues of the shape tensor give the square of the semi-axes of the ellipsoid while the eigenvectors give the orientation of the semi-axes of the ellipsoid. In case of ellipsoidal drops, the MM model proposes a phenomenological evolution equation of the shape tensor
$\unicode[STIX]{x1D64E}$
, the eigenvalues of the shape tensor give the square of the semi-axes of the ellipsoid while the eigenvectors give the orientation of the semi-axes of the ellipsoid. In case of ellipsoidal drops, the MM model proposes a phenomenological evolution equation of the shape tensor
![]() $\unicode[STIX]{x1D64E}$
based on the competing actions of drag which tends to elongate the droplet and surface tension which tends to recover the spherical shape corresponding to minimum surface energy. In dimensional form this equation reads:
$\unicode[STIX]{x1D64E}$
based on the competing actions of drag which tends to elongate the droplet and surface tension which tends to recover the spherical shape corresponding to minimum surface energy. In dimensional form this equation reads:
We now non-dimensionalise as follows:
![]() $\unicode[STIX]{x1D64E}^{\ast }=\unicode[STIX]{x1D64E}/R^{2}$
where
$\unicode[STIX]{x1D64E}^{\ast }=\unicode[STIX]{x1D64E}/R^{2}$
where
![]() $R$
is the radius of the undistorted spherical drop.
$R$
is the radius of the undistorted spherical drop.
![]() $\unicode[STIX]{x1D640}^{\ast }=\unicode[STIX]{x1D640}/G$
and
$\unicode[STIX]{x1D640}^{\ast }=\unicode[STIX]{x1D640}/G$
and
![]() $\unicode[STIX]{x1D734}^{\ast }=\unicode[STIX]{x1D734}/G$
are the non-dimensional strain rate and vorticity rate tensors;
$\unicode[STIX]{x1D734}^{\ast }=\unicode[STIX]{x1D734}/G$
are the non-dimensional strain rate and vorticity rate tensors;
![]() $\unicode[STIX]{x1D640}=0.5[\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}}]$
,
$\unicode[STIX]{x1D640}=0.5[\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}}]$
,
![]() $\unicode[STIX]{x1D734}=0.5[\unicode[STIX]{x1D735}\boldsymbol{u}-\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}}]$
and where
$\unicode[STIX]{x1D734}=0.5[\unicode[STIX]{x1D735}\boldsymbol{u}-\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}}]$
and where
![]() $G=1/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
is the inverse Kolmogorov turbulent time scale. To compute
$G=1/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
is the inverse Kolmogorov turbulent time scale. To compute
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, we use the exact relations between the driving torque and the volume-averaged dissipation in the flow as given in Eckhardt, Grossmann & Lohse (Reference Eckhardt, Grossmann and Lohse2007b
). The capillary number
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, we use the exact relations between the driving torque and the volume-averaged dissipation in the flow as given in Eckhardt, Grossmann & Lohse (Reference Eckhardt, Grossmann and Lohse2007b
). The capillary number
![]() $Ca$
which is the ratio of the viscous forces to the interfacial forces and can also be defined as the ratio of the interfacial relaxation time (
$Ca$
which is the ratio of the viscous forces to the interfacial forces and can also be defined as the ratio of the interfacial relaxation time (
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}_{c}R/\unicode[STIX]{x1D70E}$
) to the characteristic flow time (
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}_{c}R/\unicode[STIX]{x1D70E}$
) to the characteristic flow time (
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
) i.e.
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
) i.e.
![]() $Ca=\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
;
$Ca=\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
;
![]() $\unicode[STIX]{x1D707}_{c}$
is viscosity of the carrier phase and
$\unicode[STIX]{x1D707}_{c}$
is viscosity of the carrier phase and
![]() $\unicode[STIX]{x1D70E}$
the interfacial tension. Since the maximum capillary number
$\unicode[STIX]{x1D70E}$
the interfacial tension. Since the maximum capillary number
![]() $Ca$
we consider in this study is
$Ca$
we consider in this study is
![]() $Ca=0.3$
i.e.
$Ca=0.3$
i.e.
![]() $\unicode[STIX]{x1D70F}<\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, the deformation dynamics is inherently decoupled from the fluctuations in the underlying turbulent flow.
$\unicode[STIX]{x1D70F}<\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, the deformation dynamics is inherently decoupled from the fluctuations in the underlying turbulent flow.
In non-dimensional form the evolution equation for the shape tensor (
![]() $\unicode[STIX]{x1D64E}^{\ast }$
) can be written as follows:
$\unicode[STIX]{x1D64E}^{\ast }$
) can be written as follows:
Since we consider both fluids to be incompressible and with no occurrence of droplet breakup or coalescence, the volume of each droplet must be conserved. This implies that the third invariant or the determinant of the tensor
![]() $\unicode[STIX]{x1D64E}$
must be constant and the function
$\unicode[STIX]{x1D64E}$
must be constant and the function
![]() $g(\unicode[STIX]{x1D64E}^{\ast })=3\mathit{III}_{s}/\mathit{II}_{s}$
embedded into the evolution equation ensures volume conservation (
$g(\unicode[STIX]{x1D64E}^{\ast })=3\mathit{III}_{s}/\mathit{II}_{s}$
embedded into the evolution equation ensures volume conservation (
![]() $\mathit{II}_{s}$
and
$\mathit{II}_{s}$
and
![]() $\mathit{III}_{s}$
are the second and third invariant of the shape tensor, respectively). The parameters
$\mathit{III}_{s}$
are the second and third invariant of the shape tensor, respectively). The parameters
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
depend only on the viscosity ratio (
$f_{2}$
depend only on the viscosity ratio (
![]() $\hat{\unicode[STIX]{x1D707}}$
) and are chosen to make the MM model recover the asymptotic limits for small
$\hat{\unicode[STIX]{x1D707}}$
) and are chosen to make the MM model recover the asymptotic limits for small
![]() $Ca$
, viscosity ratio
$Ca$
, viscosity ratio
![]() $1/\hat{\unicode[STIX]{x1D707}}\rightarrow 1$
and
$1/\hat{\unicode[STIX]{x1D707}}\rightarrow 1$
and
![]() $\hat{\unicode[STIX]{x1D707}}=1$
and is given by Maffettone & Minale (Reference Maffettone and Minale1998) as follows:
$\hat{\unicode[STIX]{x1D707}}=1$
and is given by Maffettone & Minale (Reference Maffettone and Minale1998) as follows:
Here we briefly discuss the various factors affecting the choice of the functions
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
. The expression for
$f_{2}$
. The expression for
![]() $f_{2}$
in (2.4) under predicts the net deformation when
$f_{2}$
in (2.4) under predicts the net deformation when
![]() $Ca$
and
$Ca$
and
![]() $\hat{\unicode[STIX]{x1D707}}$
are large and this can be corrected by including an additional dependence of
$\hat{\unicode[STIX]{x1D707}}$
are large and this can be corrected by including an additional dependence of
![]() $f_{2}$
on
$f_{2}$
on
![]() $Ca$
(Maffettone & Minale Reference Maffettone and Minale1998; Biferale et al.
Reference Biferale, Meneveau and Verzicco2014). In particular, this correction becomes significant when the droplet capillary number is relatively high i.e.
$Ca$
(Maffettone & Minale Reference Maffettone and Minale1998; Biferale et al.
Reference Biferale, Meneveau and Verzicco2014). In particular, this correction becomes significant when the droplet capillary number is relatively high i.e.
![]() $Ca>0.3$
which is the upper limit of the
$Ca>0.3$
which is the upper limit of the
![]() $Ca$
chosen in our study (Maffettone & Minale Reference Maffettone and Minale1998). Additionally, when the droplet is relatively large in comparison to the gap between the shearing walls i.e.
$Ca$
chosen in our study (Maffettone & Minale Reference Maffettone and Minale1998). Additionally, when the droplet is relatively large in comparison to the gap between the shearing walls i.e.
![]() $R/h>0.15$
(
$R/h>0.15$
(
![]() $h$
is the confinement length scale) confinement effects become important and the functions
$h$
is the confinement length scale) confinement effects become important and the functions
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
also depend on
$f_{2}$
also depend on
![]() $R/h$
(Minale Reference Minale2008, Reference Minale2010; Vananroye, Van Puyvelde & Moldenaers Reference Vananroye, Van Puyvelde and Moldenaers2011). In the current study we consider only sub-Kolmogorov drops such that they see locally a linearised flow field and thus the ratio
$R/h$
(Minale Reference Minale2008, Reference Minale2010; Vananroye, Van Puyvelde & Moldenaers Reference Vananroye, Van Puyvelde and Moldenaers2011). In the current study we consider only sub-Kolmogorov drops such that they see locally a linearised flow field and thus the ratio
![]() $R/h$
(where the confinement length scale is based on the cylinder gap width) is very small i.e.
$R/h$
(where the confinement length scale is based on the cylinder gap width) is very small i.e.
![]() $R/h\sim 0.01$
in comparison to the thresh hold value of 0.15. When the drops approach the walls, the boundary layer thickness can be taken to be the confinement length scale and since we only consider sub-Kolmogorov droplets the maximum value of the confinement ratio
$R/h\sim 0.01$
in comparison to the thresh hold value of 0.15. When the drops approach the walls, the boundary layer thickness can be taken to be the confinement length scale and since we only consider sub-Kolmogorov droplets the maximum value of the confinement ratio
![]() $R/h$
based on the boundary layer thickness is 0.1. Based on the above arguments, the simplified forms of the functions
$R/h$
based on the boundary layer thickness is 0.1. Based on the above arguments, the simplified forms of the functions
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
given in (2.4) are chosen for this study.
$f_{2}$
given in (2.4) are chosen for this study.
The constitutive equation for the evolution of the shape tensor (2.3) has terms which would require the evaluation of the local strain rate and rotation rate tensor at the location of the droplet. An interpolation scheme similar to the one used for computing the velocity in (2.1) is implemented for this purpose. Analogous to the carrier phase, azimuthal and axial periodicity is adopted for the dispersed phase, i.e. when the droplets exit an azimuthal or axial boundary they are re-entered at the opposite boundary with the same velocity, shape and orientation. An ad hoc approach needs to be implemented for the interaction of a droplet with the wall. Although the droplets which are treated as passive tracers never cross the wall boundaries since the drops are tracked based on the local fluid velocity at its centre of mass the edge of a highly deformed droplet near a wall can cross the wall boundary leading to an unphysical situation. To overcome this we construct a hypothetical bounding box around a deformed droplet with the centre of mass of this box coinciding with the centre of mass of the droplet. The boundaries of this box are then used as the reference planes for modelling the elastic collision. Here it is important to note that modelling the collision between a continuously deforming droplet and a wall is an extremely challenging and interesting subject in itself. The influence of our collision approximation on the deformation statistics is discussed in detail in the next section.
The entire simulation for a single case consists of two parts. Firstly, the carrier phase is simulated without any dispersed phase until it reaches a statistically stationary state. At this point the simulation is stopped and
![]() $10^{5}$
sub-Kolmogorov spherical drops are introduced in the gap width at random positions and the simulation is allowed to continue. The trajectories and the information on the shape tensor of every droplet is recorded at a frequency of approximately 20 snapshots every
$10^{5}$
sub-Kolmogorov spherical drops are introduced in the gap width at random positions and the simulation is allowed to continue. The trajectories and the information on the shape tensor of every droplet is recorded at a frequency of approximately 20 snapshots every
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
for almost 100 full inner cylinder rotations. The complete simulation set consists of two different inner cylinder Reynolds numbers (
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
for almost 100 full inner cylinder rotations. The complete simulation set consists of two different inner cylinder Reynolds numbers (
![]() $Re_{i}=2500$
, 5000), four different capillary numbers (
$Re_{i}=2500$
, 5000), four different capillary numbers (
![]() $Ca=0.05$
, 0.1, 0.2 and 0.3) and two different viscosity ratios (
$Ca=0.05$
, 0.1, 0.2 and 0.3) and two different viscosity ratios (
![]() $\hat{\unicode[STIX]{x1D707}}=1$
and 100).
$\hat{\unicode[STIX]{x1D707}}=1$
and 100).

Figure 1. Azimuthally, axially and time-averaged radial profiles of deformation parameter (
![]() $D$
) for four different
$D$
) for four different
![]() $Ca$
; (a)
$Ca$
; (a)
![]() $Re_{i}=2500$
, (b)
$Re_{i}=2500$
, (b)
![]() $Re_{i}=5000$
. The viscosity ratio
$Re_{i}=5000$
. The viscosity ratio
![]() $\unicode[STIX]{x1D707}=1$
. The direction of the arrow indicates increasing
$\unicode[STIX]{x1D707}=1$
. The direction of the arrow indicates increasing
![]() $Ca$
. The grey shaded areas near the left and right extremes of the
$Ca$
. The grey shaded areas near the left and right extremes of the
![]() $\tilde{r}$
axis represent the inner and outer cylinder boundary layer thickness, respectively.
$\tilde{r}$
axis represent the inner and outer cylinder boundary layer thickness, respectively.
3 Results
In this section we analyse the statistics of the shape and orientation of the droplets for different Reynolds
![]() $Re_{i}$
and capillary numbers
$Re_{i}$
and capillary numbers
![]() $Ca$
while keeping the viscosity ratio fixed at
$Ca$
while keeping the viscosity ratio fixed at
![]() $\hat{\unicode[STIX]{x1D707}}=1$
. Since we consider the droplets to be triaxial ellipsoidal, we denote the lengths of the three semi-axes by
$\hat{\unicode[STIX]{x1D707}}=1$
. Since we consider the droplets to be triaxial ellipsoidal, we denote the lengths of the three semi-axes by
![]() $d_{1}$
,
$d_{1}$
,
![]() $d_{2}$
and
$d_{2}$
and
![]() $d_{3}$
(
$d_{3}$
(
![]() $d_{1}<d_{2}<d_{3}$
); i.e.
$d_{1}<d_{2}<d_{3}$
); i.e.
![]() $d_{1}$
and
$d_{1}$
and
![]() $d_{3}$
are the lengths of the minor and major semi-axes, respectively.
$d_{3}$
are the lengths of the minor and major semi-axes, respectively.
3.1 Droplet shape distribution
In order to quantify the degree of deformation in the droplet shape, we make use of a non-dimensional deformation parameter defined as
![]() $D=(d_{3}-d_{1})/(d_{3}+d_{1})$
(Taylor Reference Taylor1932, Reference Taylor1934; Guido & Villone Reference Guido and Villone1998; Maffettone & Minale Reference Maffettone and Minale1998; Guido, Minale & Maffettone Reference Guido, Minale and Maffettone2000; Biferale et al.
Reference Biferale, Meneveau and Verzicco2014). When
$D=(d_{3}-d_{1})/(d_{3}+d_{1})$
(Taylor Reference Taylor1932, Reference Taylor1934; Guido & Villone Reference Guido and Villone1998; Maffettone & Minale Reference Maffettone and Minale1998; Guido, Minale & Maffettone Reference Guido, Minale and Maffettone2000; Biferale et al.
Reference Biferale, Meneveau and Verzicco2014). When
![]() $D\sim 0$
, the droplet is close to spherical, while
$D\sim 0$
, the droplet is close to spherical, while
![]() $D\gg 0$
implies the droplet is highly deformed. In order to properly quantify the correlation between the spatial position of the droplets and the degree of deformation, we plot the radial profiles of azimuthally, axially and time-averaged deformation parameter for droplets with four different
$D\gg 0$
implies the droplet is highly deformed. In order to properly quantify the correlation between the spatial position of the droplets and the degree of deformation, we plot the radial profiles of azimuthally, axially and time-averaged deformation parameter for droplets with four different
![]() $Ca$
in figure 1. The radial positions of the drops are normalised using
$Ca$
in figure 1. The radial positions of the drops are normalised using
![]() $\tilde{r}=(r-r_{i})/(r_{o}-r_{i})$
; the drop is close to the inner cylinder when
$\tilde{r}=(r-r_{i})/(r_{o}-r_{i})$
; the drop is close to the inner cylinder when
![]() $\tilde{r}\sim 0$
and close to the outer cylinder when
$\tilde{r}\sim 0$
and close to the outer cylinder when
![]() $\tilde{r}\sim 1$
. Along with the averaged profiles we show the inner boundary layer (IBL) and outer boundary layer (OBL) thickness using grey shaded areas which have been computed following the approach described in Ostilla-Mónico et al. (Reference Ostilla-Mónico, Stevens, Grossmann, Verzicco and Lohse2013, Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b
), Spandan et al. (Reference Spandan, Ostilla-Mónico, Verzicco and Lohse2016).
$\tilde{r}\sim 1$
. Along with the averaged profiles we show the inner boundary layer (IBL) and outer boundary layer (OBL) thickness using grey shaded areas which have been computed following the approach described in Ostilla-Mónico et al. (Reference Ostilla-Mónico, Stevens, Grossmann, Verzicco and Lohse2013, Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014b
), Spandan et al. (Reference Spandan, Ostilla-Mónico, Verzicco and Lohse2016).

Figure 2. Zoomed in plot of figure 1(a). The schematic on the right shows interaction of a highly deformed drop (top) and a relatively less deformed drop (bottom) with the wall. The dotted line around each droplet shows the hypothetical bounding box constructed around each droplet. The centre of mass of a less deformed drop can approach more closely to the wall as compared to a highly deformed drop.
We can clearly observe in figure 1 that the capillary number
![]() $Ca$
has a strong influence on the mean deformation parameter
$Ca$
has a strong influence on the mean deformation parameter
![]() $D$
. As expected,
$D$
. As expected,
![]() $D$
increases with increasing
$D$
increases with increasing
![]() $Ca$
due to weakening surface tension forces. Additionally, as noted from figure 1 a clear indication of the spatial dependence of the deformation parameter
$Ca$
due to weakening surface tension forces. Additionally, as noted from figure 1 a clear indication of the spatial dependence of the deformation parameter
![]() $D$
is observed.
$D$
is observed.
![]() $D$
is higher near the boundary layers (marked by grey shaded areas) for both Reynolds numbers as compared to the bulk where it is almost three times lower. Additionally, we also find that when
$D$
is higher near the boundary layers (marked by grey shaded areas) for both Reynolds numbers as compared to the bulk where it is almost three times lower. Additionally, we also find that when
![]() $Ca=0.2$
and
$Ca=0.2$
and
![]() $Ca=0.3$
, the peak of the deformation parameter
$Ca=0.3$
, the peak of the deformation parameter
![]() $D$
lies away from the inner cylinder. To observe this deviation more clearly, in figure 2 we show a zoomed-in plot of figure 1(a) and it can be clearly seen that for
$D$
lies away from the inner cylinder. To observe this deviation more clearly, in figure 2 we show a zoomed-in plot of figure 1(a) and it can be clearly seen that for
![]() $Ca=0.2$
and
$Ca=0.2$
and
![]() $Ca=0.3$
there is a slight increase in
$Ca=0.3$
there is a slight increase in
![]() $D$
away from the wall and the occurrence of this peak moves away from the wall with increasing
$D$
away from the wall and the occurrence of this peak moves away from the wall with increasing
![]() $Ca$
. This is just a consequence of the modelling of interaction of the droplet with the wall. Since we assume elastic collision between the bounding box of a deformed droplet and the wall, the centre of mass of a highly deformed droplet lies farther away from the wall as compared to a less deformed droplet as shown in the schematic of figure 2. Indeed, this also depends on the relative orientation of the droplets with the wall and we will analyse this in detail in later sections. Through several test simulations it has been ensured that the shift in peak of
$Ca$
. This is just a consequence of the modelling of interaction of the droplet with the wall. Since we assume elastic collision between the bounding box of a deformed droplet and the wall, the centre of mass of a highly deformed droplet lies farther away from the wall as compared to a less deformed droplet as shown in the schematic of figure 2. Indeed, this also depends on the relative orientation of the droplets with the wall and we will analyse this in detail in later sections. Through several test simulations it has been ensured that the shift in peak of
![]() $D$
is indeed due to the collision and not due to any additional boundary layer dynamics (e.g. droplets modelled without any collision do not show any shift in the peak of
$D$
is indeed due to the collision and not due to any additional boundary layer dynamics (e.g. droplets modelled without any collision do not show any shift in the peak of
![]() $D$
). This argument is further strengthened in § 3.3 where we study the deformation of more viscous drops.
$D$
). This argument is further strengthened in § 3.3 where we study the deformation of more viscous drops.

Figure 3. Azimuthally, radially and time-averaged axial profiles of the deformation parameter (
![]() $D$
) for four different
$D$
) for four different
![]() $Ca$
; (a)
$Ca$
; (a)
![]() $Re_{i}=2500$
(b)
$Re_{i}=2500$
(b)
![]() $Re_{i}=5000$
. The viscosity ratio
$Re_{i}=5000$
. The viscosity ratio
![]() $\unicode[STIX]{x1D707}=1$
. The direction of the arrow indicates increasing
$\unicode[STIX]{x1D707}=1$
. The direction of the arrow indicates increasing
![]() $Ca$
(refer to figure 1 for description of the markers). Instantaneous snapshots of the azimuthal velocity of the corresponding
$Ca$
(refer to figure 1 for description of the markers). Instantaneous snapshots of the azimuthal velocity of the corresponding
![]() $Re_{i}$
are shown on the top of each plot to better visualise the plume ejections and the Taylor rolls along with a quiver plot of half the domain to show the direction of flow. The colour scale shows the instantaneous azimuthal velocity.
$Re_{i}$
are shown on the top of each plot to better visualise the plume ejections and the Taylor rolls along with a quiver plot of half the domain to show the direction of flow. The colour scale shows the instantaneous azimuthal velocity.

Figure 4. Azimuthally and time-averaged profiles of the viscous dissipation: (a) radial profiles (b) axial profiles. Net dissipation is computed as a volume and time average of local dissipation rate and is normalised using its corresponding maximum value
![]() $\hat{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}/\text{max}(\unicode[STIX]{x1D716})$
.
$\hat{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}/\text{max}(\unicode[STIX]{x1D716})$
.
Similar to figure 1 we plot axial profiles of the azimuthally, radially and time-averaged deformation parameter
![]() $D$
as a function of the normalised axial position
$D$
as a function of the normalised axial position
![]() $\tilde{z}=z/d$
for
$\tilde{z}=z/d$
for
![]() $Re_{i}=2500$
and 5000 and for different
$Re_{i}=2500$
and 5000 and for different
![]() $Ca$
in figure 3. When
$Ca$
in figure 3. When
![]() $Re_{i}=2500$
(cf. bottom panel of figure 3
a), we observe that regardless of the capillary number,
$Re_{i}=2500$
(cf. bottom panel of figure 3
a), we observe that regardless of the capillary number,
![]() $D$
is higher near the plume ejection regions of the inner cylinder i.e.
$D$
is higher near the plume ejection regions of the inner cylinder i.e.
![]() $\tilde{z}\sim 1$
and 3 (also refer to central and top panels in figure 3
a) which show an instantaneous snapshot of the carrier phase azimuthal velocity along with a quiver plot of a zoomed-in section). This is a result of relatively high strain rates stretching the ellipsoidal drops in the plume ejection region near the inner cylinder; an effect likely to be produced by the Taylor rolls which locally make the boundary layer produced by the cylinder rotation thinner or thicker. A similar observation is made even for
$\tilde{z}\sim 1$
and 3 (also refer to central and top panels in figure 3
a) which show an instantaneous snapshot of the carrier phase azimuthal velocity along with a quiver plot of a zoomed-in section). This is a result of relatively high strain rates stretching the ellipsoidal drops in the plume ejection region near the inner cylinder; an effect likely to be produced by the Taylor rolls which locally make the boundary layer produced by the cylinder rotation thinner or thicker. A similar observation is made even for
![]() $Re_{i}=5000$
in figure 3(b) where the plume ejection regions near the inner cylinder are at approximately
$Re_{i}=5000$
in figure 3(b) where the plume ejection regions near the inner cylinder are at approximately
![]() $\tilde{z}=1.75$
and 3.75. Although relatively high strain rates are observed in the plume ejection regions, the plumes themselves which extend from the inner cylinder into the bulk have a relatively lower strain rate owing to a strong azimuthal velocity component. This causes a sudden drop in
$\tilde{z}=1.75$
and 3.75. Although relatively high strain rates are observed in the plume ejection regions, the plumes themselves which extend from the inner cylinder into the bulk have a relatively lower strain rate owing to a strong azimuthal velocity component. This causes a sudden drop in
![]() $D$
at the exact axial position where the plumes extend into the bulk, an effect which is seen very clearly for
$D$
at the exact axial position where the plumes extend into the bulk, an effect which is seen very clearly for
![]() $Re_{i}=2500$
due to the more coherent nature of the plumes (figure 3
a). However, when the Reynolds number is increased the plumes are more erratic and turbulent and the sudden drop in
$Re_{i}=2500$
due to the more coherent nature of the plumes (figure 3
a). However, when the Reynolds number is increased the plumes are more erratic and turbulent and the sudden drop in
![]() $D$
gets averaged out and is not observed any more. The differences in plume structure in the bulk of the flow for both Reynolds number is clearly visible in the instantaneous snapshots of the azimuthal velocity in figure 3.
$D$
gets averaged out and is not observed any more. The differences in plume structure in the bulk of the flow for both Reynolds number is clearly visible in the instantaneous snapshots of the azimuthal velocity in figure 3.
Deformation is directly related to the strain rates experienced by the droplets. In order the further understand the correlation between the strain rates in the flow and the net deformation observed we plot the averaged profiles of normalised viscous dissipation (square of the magnitude of the strain rate) against the radial and axial position. The total dissipation per unit mass is computed as a volume and time average of the local dissipation rate (Eckhardt et al.
Reference Eckhardt, Grossmann and Lohse2007b
). After spatial averaging the net dissipation is normalised using its corresponding maximum value
![]() $\hat{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}/\text{max}(\unicode[STIX]{x1D716})$
and is plotted against the normalised radial position in figure 4(a) and the normalised axial position in figure 4(b). On comparing the averaged radial and axial profiles of the deformation parameter (figures 1 and 3) along with the normalised dissipation (figures 4(a) and (b)) a very strong correlation is observed between both quantities, thus confirming the hypothesis that high local strain rates are crucial for strong drop deformation.
$\hat{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}/\text{max}(\unicode[STIX]{x1D716})$
and is plotted against the normalised radial position in figure 4(a) and the normalised axial position in figure 4(b). On comparing the averaged radial and axial profiles of the deformation parameter (figures 1 and 3) along with the normalised dissipation (figures 4(a) and (b)) a very strong correlation is observed between both quantities, thus confirming the hypothesis that high local strain rates are crucial for strong drop deformation.
Until now we have looked at the variation of the deformation parameter
![]() $D$
with the radial and axial distance in the TC domain. Although
$D$
with the radial and axial distance in the TC domain. Although
![]() $D$
can be used to study whether the droplet is close to spherical or highly deformed, it cannot be used to distinguish between oblate (disk-like) and prolate (cigar-like) droplets. In order to make this distinction, Biferale et al. (Reference Biferale, Meneveau and Verzicco2014) used the
$D$
can be used to study whether the droplet is close to spherical or highly deformed, it cannot be used to distinguish between oblate (disk-like) and prolate (cigar-like) droplets. In order to make this distinction, Biferale et al. (Reference Biferale, Meneveau and Verzicco2014) used the
![]() $s^{\ast }$
parameter which was introduced by Lund & Rogers (Reference Lund and Rogers1994) to quantify the probability distribution of strain rate tensor eigenvalues in turbulent flows. The shapes of the droplets can also be categorised based on simple ratios of the semi-axes i.e.
$s^{\ast }$
parameter which was introduced by Lund & Rogers (Reference Lund and Rogers1994) to quantify the probability distribution of strain rate tensor eigenvalues in turbulent flows. The shapes of the droplets can also be categorised based on simple ratios of the semi-axes i.e.
![]() $d_{2}/d_{1}$
and
$d_{2}/d_{1}$
and
![]() $d_{3}/d_{1}$
(where
$d_{3}/d_{1}$
(where
![]() $d_{1}<d_{2}<d_{3}$
). When the droplet is close to spherical
$d_{1}<d_{2}<d_{3}$
). When the droplet is close to spherical
![]() $d_{2}/d_{1}\sim d_{3}/d_{1}\sim 1$
, while for deformed droplets both
$d_{2}/d_{1}\sim d_{3}/d_{1}\sim 1$
, while for deformed droplets both
![]() $d_{2}/d_{1}>1$
and
$d_{2}/d_{1}>1$
and
![]() $d_{3}/d_{1}>1$
. When the droplets are deformed they can additionally be categorised into oblate (disk-like) ellipsoids when
$d_{3}/d_{1}>1$
. When the droplets are deformed they can additionally be categorised into oblate (disk-like) ellipsoids when
![]() $d_{2}/d_{1}\sim d_{3}/d_{1}$
and prolate (cigar-like) ellipsoids when
$d_{2}/d_{1}\sim d_{3}/d_{1}$
and prolate (cigar-like) ellipsoids when
![]() $d_{2}/d_{1}\ll d_{3}/d_{1}$
.
$d_{2}/d_{1}\ll d_{3}/d_{1}$
.

Figure 5. Probability distribution function (p.d.f.) of the ratio of semi-axes (
![]() $d_{1}<d_{2}<d_{3}$
) for
$d_{1}<d_{2}<d_{3}$
) for
![]() $Re_{i}=2500$
and
$Re_{i}=2500$
and
![]() $\hat{\unicode[STIX]{x1D707}}=1$
: (a–c)
$\hat{\unicode[STIX]{x1D707}}=1$
: (a–c)
![]() $Ca=0.05$
, (d–f)
$Ca=0.05$
, (d–f)
![]() $Ca=0.2$
. The three panels for each
$Ca=0.2$
. The three panels for each
![]() $Ca$
correspond to droplets in the IBL, bulk and OBL.
$Ca$
correspond to droplets in the IBL, bulk and OBL.
In figure 5, we plot the p.d.f.s of the ratio of semi-axes (
![]() $d_{2}/d_{1}$
and
$d_{2}/d_{1}$
and
![]() $d_{3}/d_{1}$
) of droplets for two different capillary numbers
$d_{3}/d_{1}$
) of droplets for two different capillary numbers
![]() $Ca=0.05$
and 0.2 while
$Ca=0.05$
and 0.2 while
![]() $Re_{i}=2500$
and
$Re_{i}=2500$
and
![]() $\hat{\unicode[STIX]{x1D707}}=1$
. The three different panels for each capillary number correspond to the position of the droplet in the IBL, bulk region (BULK) and the OBL. When
$\hat{\unicode[STIX]{x1D707}}=1$
. The three different panels for each capillary number correspond to the position of the droplet in the IBL, bulk region (BULK) and the OBL. When
![]() $Ca=0.05$
, the droplets are almost spheroidal or in other words axis-symmetric (i.e.
$Ca=0.05$
, the droplets are almost spheroidal or in other words axis-symmetric (i.e.
![]() $d_{2}/d_{1}\sim 1$
). In the bulk, where the strain rates are relatively weaker as compared to the boundary layer region, the droplet is close to being spherical with minimum deformation (i.e.
$d_{2}/d_{1}\sim 1$
). In the bulk, where the strain rates are relatively weaker as compared to the boundary layer region, the droplet is close to being spherical with minimum deformation (i.e.
![]() $d_{2}/d_{1}\sim d_{3}/d_{1}\sim 1$
). Additionally, the p.d.f.s of
$d_{2}/d_{1}\sim d_{3}/d_{1}\sim 1$
). Additionally, the p.d.f.s of
![]() $d_{3}/d_{1}$
in the IBL and OBL have much wider tails indicating that the droplets are more prolate in comparison to the bulk region. Biferale et al. (Reference Biferale, Meneveau and Verzicco2014) found that with increasing capillary number ellipsoidal drops in homogenous isotropic turbulence tend to be more cigar-like or prolate where the major axis (
$d_{3}/d_{1}$
in the IBL and OBL have much wider tails indicating that the droplets are more prolate in comparison to the bulk region. Biferale et al. (Reference Biferale, Meneveau and Verzicco2014) found that with increasing capillary number ellipsoidal drops in homogenous isotropic turbulence tend to be more cigar-like or prolate where the major axis (
![]() $d_{3}$
) is relatively much larger than the other two axes (
$d_{3}$
) is relatively much larger than the other two axes (
![]() $d_{1}$
,
$d_{1}$
,
![]() $d_{2}$
). A similar behaviour can be observed in figure 5(d–f) when the capillary number is increased to
$d_{2}$
). A similar behaviour can be observed in figure 5(d–f) when the capillary number is increased to
![]() $Ca=0.2$
. The tails of
$Ca=0.2$
. The tails of
![]() $d_{3}/d_{1}$
become much wider in the IBL and OBL regions as compared to
$d_{3}/d_{1}$
become much wider in the IBL and OBL regions as compared to
![]() $Ca=0.05$
which is a consequence of the weaker surface tension forces for higher capillary number drops. An additional consequence is that the droplets now tend to become less spheroidal and more triaxial.
$Ca=0.05$
which is a consequence of the weaker surface tension forces for higher capillary number drops. An additional consequence is that the droplets now tend to become less spheroidal and more triaxial.

Figure 6. Probability distribution functions of the streamwise orientation of the major axis of droplets for
![]() $Ca=0.05$
and
$Ca=0.05$
and
![]() $Ca=0.2$
: (a–c)
$Ca=0.2$
: (a–c)
![]() $Re_{i}=2500$
, (b–d)
$Re_{i}=2500$
, (b–d)
![]() $Re_{i}=5000$
. The three panels for each
$Re_{i}=5000$
. The three panels for each
![]() $Re_{i}$
correspond to droplets in the IBL, bulk and the OBL.
$Re_{i}$
correspond to droplets in the IBL, bulk and the OBL.
3.2 Orientational behaviour of the drops
In addition to the shape and size of the ellipsoidal droplets, it would also be interesting to understand their orientational preference. A number of studies (Mortensen et al.
Reference Mortensen, Andersson, Gillissen and Boersma2008; Marchioli, Fantoni & Soldati Reference Marchioli, Fantoni and Soldati2010; Njobuenwu & Fairweather Reference Njobuenwu and Fairweather2015) investigating the orientation behaviour of axis-symmetric solid ellipsoidal particles in wall-bounded turbulent flows found that the major axis of the particles tend to align with the streamwise direction near the wall. Rigid rod-/fibre-like particles immersed in a isotropic turbulent flow align with the vorticity and the strain rate eigenvectors and their orientational behaviour has a strong dependence on the shape (Parsa et al.
Reference Parsa, Calzavarini, Toschi and Voth2012; Byron et al.
Reference Byron, Einarsson, Gustavsson, Voth, Mehlig and Variano2015; Ni et al.
Reference Ni, Kramel, Ouellette and Voth2015). The shape and size of solid ellipsoidal particles does not depend on their spatial position and underlying flow conditions. However, for deforming droplets the orientation dynamics can be strongly coupled to the shape evolution which would in turn depend on the local flow conditions. Biferale et al. (Reference Biferale, Meneveau and Verzicco2014) found that neutrally buoyant ellipsoidal droplets dispersed into a homogenous isotropic turbulent flow aligned with the most extensional strain rate eigendirection and the vorticity. With an increase in the capillary number
![]() $Ca$
the alignment is lost due to an increase in the interfacial relaxation time.
$Ca$
the alignment is lost due to an increase in the interfacial relaxation time.

Figure 7. Probability distribution functions of the cosine of the angle between the eigenvector of the major axis (
![]() $\boldsymbol{e}^{\mathbf{3}}$
) of the ellipsoid and three strain rate eigendirections (
$\boldsymbol{e}^{\mathbf{3}}$
) of the ellipsoid and three strain rate eigendirections (
![]() $\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{1}},\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{2}},\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{3}}$
)
$\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{1}},\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{2}},\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{3}}$
)
![]() $Re_{i}=2500~\hat{\unicode[STIX]{x1D707}}=1$
for (a–c)
$Re_{i}=2500~\hat{\unicode[STIX]{x1D707}}=1$
for (a–c)
![]() $Ca=0.05$
and (d–f)
$Ca=0.05$
and (d–f)
![]() $Ca=0.2$
.
$Ca=0.2$
.

Figure 8. Probability distribution functions of the cosine of the angle between the eigenvector of the semi-major axis (
![]() $\boldsymbol{e}^{\mathbf{3}}$
) of the ellipsoid and the vorticity (
$\boldsymbol{e}^{\mathbf{3}}$
) of the ellipsoid and the vorticity (
![]() $\unicode[STIX]{x1D734}$
)
$\unicode[STIX]{x1D734}$
)
![]() $\hat{\unicode[STIX]{x1D707}}=1$
for (a–c)
$\hat{\unicode[STIX]{x1D707}}=1$
for (a–c)
![]() $Re_{i}=2500$
and (d–f)
$Re_{i}=2500$
and (d–f)
![]() $Re_{i}=5000$
.
$Re_{i}=5000$
.
Here we describe the relative orientation of the major axis of the ellipsoidal droplets with respect to the coordinate system in the form of direction cosines of the angle between them i.e.
![]() $l=\cos \unicode[STIX]{x1D703}_{\hat{\unicode[STIX]{x1D703}}}$
,
$l=\cos \unicode[STIX]{x1D703}_{\hat{\unicode[STIX]{x1D703}}}$
,
![]() $m=\cos \unicode[STIX]{x1D703}_{\hat{r}}$
,
$m=\cos \unicode[STIX]{x1D703}_{\hat{r}}$
,
![]() $n=\cos \unicode[STIX]{x1D703}_{\hat{z}}$
, where
$n=\cos \unicode[STIX]{x1D703}_{\hat{z}}$
, where
![]() $l$
,
$l$
,
![]() $m$
,
$m$
,
![]() $n$
are the direction cosine of the orientation with
$n$
are the direction cosine of the orientation with
![]() $\hat{\unicode[STIX]{x1D703}}$
(streamwise),
$\hat{\unicode[STIX]{x1D703}}$
(streamwise),
![]() $\hat{r}$
(wall-normal) and
$\hat{r}$
(wall-normal) and
![]() $\hat{z}$
(spanwise) directions, respectively. In order to study the statistics of droplet orientation in detail, we plot the p.d.f.s of the cosine of the angle between the droplet major axis and the streamwise direction in figure 6. We observe that the droplets tend to be strongly aligned with the streamwise direction (i.e.
$\hat{z}$
(spanwise) directions, respectively. In order to study the statistics of droplet orientation in detail, we plot the p.d.f.s of the cosine of the angle between the droplet major axis and the streamwise direction in figure 6. We observe that the droplets tend to be strongly aligned with the streamwise direction (i.e.
![]() $l\sim 1.0$
) in the IBL and OBL. As can be seen from figure 6(a,d), the alignment is more pronounced in the case of
$l\sim 1.0$
) in the IBL and OBL. As can be seen from figure 6(a,d), the alignment is more pronounced in the case of
![]() $Re_{i}=2500$
as compared to
$Re_{i}=2500$
as compared to
![]() $Re_{i}=5000$
. This may be possible due to the more erratic and time-dependent nature of the boundary layer region and plume ejections from the inner cylinder in the case of
$Re_{i}=5000$
. This may be possible due to the more erratic and time-dependent nature of the boundary layer region and plume ejections from the inner cylinder in the case of
![]() $Re_{i}=5000$
as was also seen in the contour plots of figure 3(b). A similar behaviour is also seen in the case of solid ellipsoidal particles in the vicinity of a wall in a turbulent channel flow (Mortensen et al.
Reference Mortensen, Andersson, Gillissen and Boersma2008; Marchioli et al.
Reference Marchioli, Fantoni and Soldati2010; Njobuenwu & Fairweather Reference Njobuenwu and Fairweather2015). The capillary number
$Re_{i}=5000$
as was also seen in the contour plots of figure 3(b). A similar behaviour is also seen in the case of solid ellipsoidal particles in the vicinity of a wall in a turbulent channel flow (Mortensen et al.
Reference Mortensen, Andersson, Gillissen and Boersma2008; Marchioli et al.
Reference Marchioli, Fantoni and Soldati2010; Njobuenwu & Fairweather Reference Njobuenwu and Fairweather2015). The capillary number
![]() $Ca$
seems to have minimal influence on the orientational behaviour of drops suggesting that it is only dominant in the deformation process and not in the effective orientation of the drops. Since the drops are sub-Kolmogorov the drops experience uniform local flow conditions or in other words sample only the linear velocity gradients and thus the
$Ca$
seems to have minimal influence on the orientational behaviour of drops suggesting that it is only dominant in the deformation process and not in the effective orientation of the drops. Since the drops are sub-Kolmogorov the drops experience uniform local flow conditions or in other words sample only the linear velocity gradients and thus the
![]() $Ca$
number plays an important role only in deforming the droplet but not in its relative orientation especially given the fact that
$Ca$
number plays an important role only in deforming the droplet but not in its relative orientation especially given the fact that
![]() $Ca$
is computed based solely on the ratios of the stretching forces and the retracting surface tension forces. Thus, no matter how much the droplet deforms the major axis is always oriented with the streamwise direction in the boundary layers due to the strong deformation of the underlying fluid material element in the boundary layers. In the bulk, the orientation of the droplets is highly isotropic showing no specific preference in alignment with the streamwise direction which is a consequence of the efficient mixing provided by the Taylor rolls.
$Ca$
is computed based solely on the ratios of the stretching forces and the retracting surface tension forces. Thus, no matter how much the droplet deforms the major axis is always oriented with the streamwise direction in the boundary layers due to the strong deformation of the underlying fluid material element in the boundary layers. In the bulk, the orientation of the droplets is highly isotropic showing no specific preference in alignment with the streamwise direction which is a consequence of the efficient mixing provided by the Taylor rolls.
Now we look at the orientation statistics of the major axis with respect to the local strain rate eigendirections and vorticity. In figures 7 and 8 we plot the p.d.f.s of the cosine of the angle between the eigenvector of the major axis (
![]() $\boldsymbol{e}^{\mathbf{3}}$
), the three strain rate eigendirections (
$\boldsymbol{e}^{\mathbf{3}}$
), the three strain rate eigendirections (
![]() $\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{1}},\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{2}},\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{3}}$
, where
$\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{1}},\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{2}},\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{3}}$
, where
![]() $\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{1}}$
and
$\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{1}}$
and
![]() $\boldsymbol{e}_{\boldsymbol{s}}^{3}$
are the compressive and extensional strain rates, respectively) and vorticity (
$\boldsymbol{e}_{\boldsymbol{s}}^{3}$
are the compressive and extensional strain rates, respectively) and vorticity (
![]() $\unicode[STIX]{x1D74E}$
), respectively. In homogenous isotropic turbulence, Biferale et al. (Reference Biferale, Meneveau and Verzicco2014) found that the major axis of neutrally buoyant ellipsoidal droplets align with both the most extensional strain rate eigendirection and vorticity. In figures 7 and 8 we find that the preference of alignment with the strain rate eigendirections and vorticity depends again strongly on its relative spatial location.
$\unicode[STIX]{x1D74E}$
), respectively. In homogenous isotropic turbulence, Biferale et al. (Reference Biferale, Meneveau and Verzicco2014) found that the major axis of neutrally buoyant ellipsoidal droplets align with both the most extensional strain rate eigendirection and vorticity. In figures 7 and 8 we find that the preference of alignment with the strain rate eigendirections and vorticity depends again strongly on its relative spatial location.
In figure 7, we consider two different configurations with capillary numbers
![]() $Ca=0.05$
and
$Ca=0.05$
and
![]() $Ca=0.2$
for a fixed Reynolds number
$Ca=0.2$
for a fixed Reynolds number
![]() $Re_{i}=2500$
. In the boundary layer regions the ellipsoid major axis has a strong preference to align with the extensional strain rate eigendirection (here the extensional strain rate direction in the boundary layers is the azimuthal direction). In the bulk, the preference is relatively more uniform while some traces of droplets aligning with
$Re_{i}=2500$
. In the boundary layer regions the ellipsoid major axis has a strong preference to align with the extensional strain rate eigendirection (here the extensional strain rate direction in the boundary layers is the azimuthal direction). In the bulk, the preference is relatively more uniform while some traces of droplets aligning with
![]() $\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{3}}$
can still be found, an indication that there seems to be a competition between the extensional strain rates trying to align itself with the droplet major axis and the homogenising nature of the Taylor rolls. This effect is clearly seen when
$\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{3}}$
can still be found, an indication that there seems to be a competition between the extensional strain rates trying to align itself with the droplet major axis and the homogenising nature of the Taylor rolls. This effect is clearly seen when
![]() $Ca=0.2$
given the prolate nature of the droplets (cf. figure 5). While the ellipsoidal droplets tend to align with the most extensional strain rate direction in the IBL region (figure 7
a,d) they prefer to be aligned orthogonally with the vorticity (figure 8
a,d). This is different from the behaviour of solid axis-symmetric ellipsoidal particles in an isotropic turbulent flow where rod-like particles tend to align with the vorticity (Shin & Koch Reference Shin and Koch2005; Parsa et al.
Reference Parsa, Calzavarini, Toschi and Voth2012; Chevillard & Meneveau Reference Chevillard and Meneveau2013). The difference in behaviour is a consequence of the inhomogeneity and anisotropy of the carrier flow along with the ellipsoidal droplets continuously deforming based to the underlying flow conditions unlike solid ellipsoidal particles which are fixed in shape. With increase in Reynolds number
$Ca=0.2$
given the prolate nature of the droplets (cf. figure 5). While the ellipsoidal droplets tend to align with the most extensional strain rate direction in the IBL region (figure 7
a,d) they prefer to be aligned orthogonally with the vorticity (figure 8
a,d). This is different from the behaviour of solid axis-symmetric ellipsoidal particles in an isotropic turbulent flow where rod-like particles tend to align with the vorticity (Shin & Koch Reference Shin and Koch2005; Parsa et al.
Reference Parsa, Calzavarini, Toschi and Voth2012; Chevillard & Meneveau Reference Chevillard and Meneveau2013). The difference in behaviour is a consequence of the inhomogeneity and anisotropy of the carrier flow along with the ellipsoidal droplets continuously deforming based to the underlying flow conditions unlike solid ellipsoidal particles which are fixed in shape. With increase in Reynolds number
![]() $Re_{i}$
, the preference of alignment with the vorticity stays qualitatively similar. Overall, we find that the spatial position of the droplet is crucial in determining the orientational preference of the immersed droplets owing to the strong inhomogeneity and anisotropy in the field.
$Re_{i}$
, the preference of alignment with the vorticity stays qualitatively similar. Overall, we find that the spatial position of the droplet is crucial in determining the orientational preference of the immersed droplets owing to the strong inhomogeneity and anisotropy in the field.
Until now we have looked at the effect of capillary number
![]() $Ca$
and Reynolds number
$Ca$
and Reynolds number
![]() $Re_{i}$
on the droplet deformation and orientation statistics and in the next subsection we will study the effect of viscosity ratio
$Re_{i}$
on the droplet deformation and orientation statistics and in the next subsection we will study the effect of viscosity ratio
![]() $\hat{\unicode[STIX]{x1D707}}$
.
$\hat{\unicode[STIX]{x1D707}}$
.

Figure 9. Azimuthally, axially and time-averaged radial profiles of deformation parameter (
![]() $D$
) for four different
$D$
) for four different
![]() $Ca$
; (a)
$Ca$
; (a)
![]() $Re_{i}=2500$
, (b)
$Re_{i}=2500$
, (b)
![]() $Re_{i}=5000$
. The viscosity ratio is
$Re_{i}=5000$
. The viscosity ratio is
![]() $\hat{\unicode[STIX]{x1D707}}=100$
. The direction of the arrow indicates increasing
$\hat{\unicode[STIX]{x1D707}}=100$
. The direction of the arrow indicates increasing
![]() $Ca$
. The grey shaded areas near the left and right extremes of the
$Ca$
. The grey shaded areas near the left and right extremes of the
![]() $x$
-axis represent the inner and outer cylinder boundary layer thickness, respectively.
$x$
-axis represent the inner and outer cylinder boundary layer thickness, respectively.
3.3 Effect of viscosity ratio
In figure 9 we plot the averaged radial profiles of the deformation parameter
![]() $D$
for different
$D$
for different
![]() $Ca$
in a high viscosity ratio system
$Ca$
in a high viscosity ratio system
![]() $\hat{\unicode[STIX]{x1D707}}=100$
. On comparison with
$\hat{\unicode[STIX]{x1D707}}=100$
. On comparison with
![]() $\hat{\unicode[STIX]{x1D707}}=1$
(cf. figure 1) the degree of deformation is at least 5 times smaller for all capillary numbers. This behaviour can be intuitively expected as for the same strain rates the stretching is lower for more viscous drops given the additional viscous dissipation due to the internal flow in the drops. Additionally, due to the relatively smaller deformations the peaks in the deformation parameter
$\hat{\unicode[STIX]{x1D707}}=1$
(cf. figure 1) the degree of deformation is at least 5 times smaller for all capillary numbers. This behaviour can be intuitively expected as for the same strain rates the stretching is lower for more viscous drops given the additional viscous dissipation due to the internal flow in the drops. Additionally, due to the relatively smaller deformations the peaks in the deformation parameter
![]() $D$
lie close to the wall for all
$D$
lie close to the wall for all
![]() $Ca$
. While it is clear from figure 9 that there is a reduction in the overall deformation of the droplets, it would be interesting to look at the shape of the droplets as we did in figure 5; i.e. in the case of
$Ca$
. While it is clear from figure 9 that there is a reduction in the overall deformation of the droplets, it would be interesting to look at the shape of the droplets as we did in figure 5; i.e. in the case of
![]() $\hat{\unicode[STIX]{x1D707}}=1$
the droplets were more prolate (cigar-like). In figure 10 we plot the p.d.f.s of the ratio of semi-axes in the IBL, bulk region and OBL (similar to figure 5). It can be seen that the semi-axes ratios
$\hat{\unicode[STIX]{x1D707}}=1$
the droplets were more prolate (cigar-like). In figure 10 we plot the p.d.f.s of the ratio of semi-axes in the IBL, bulk region and OBL (similar to figure 5). It can be seen that the semi-axes ratios
![]() $d_{2}/d_{1}\sim d_{3}/d_{1}>1$
which is a clear indication that the droplets tend to be more oblate (disk-like) when
$d_{2}/d_{1}\sim d_{3}/d_{1}>1$
which is a clear indication that the droplets tend to be more oblate (disk-like) when
![]() $\hat{\unicode[STIX]{x1D707}}=100$
. A similar behaviour is observed when the capillary number of the drops is increased. While we found previously that the capillary number plays an important role in the degree of deformation of the droplets, here we find that the droplet shape also depends strongly on the viscosity ratio
$\hat{\unicode[STIX]{x1D707}}=100$
. A similar behaviour is observed when the capillary number of the drops is increased. While we found previously that the capillary number plays an important role in the degree of deformation of the droplets, here we find that the droplet shape also depends strongly on the viscosity ratio
![]() $\hat{\unicode[STIX]{x1D707}}$
.
$\hat{\unicode[STIX]{x1D707}}$
.

Figure 10. Probability distribution function (p.d.f.) of the ratio of semi-axes (
![]() $d_{1}<d_{2}<d_{3}$
) for
$d_{1}<d_{2}<d_{3}$
) for
![]() $Re_{i}=2500$
and
$Re_{i}=2500$
and
![]() $\hat{\unicode[STIX]{x1D707}}=100$
: (a–c)
$\hat{\unicode[STIX]{x1D707}}=100$
: (a–c)
![]() $Ca=0.05$
, (d–f)
$Ca=0.05$
, (d–f)
![]() $Ca=0.2$
.
$Ca=0.2$
.

Figure 11. Probability distribution functions of the streamwise orientation of the major axis of droplets for
![]() $Ca=0.05$
and
$Ca=0.05$
and
![]() $Ca=0.2$
and
$Ca=0.2$
and
![]() $\hat{\unicode[STIX]{x1D707}}=100$
: (a)
$\hat{\unicode[STIX]{x1D707}}=100$
: (a)
![]() $Re_{i}=2500$
, (b)
$Re_{i}=2500$
, (b)
![]() $Re_{i}=5000$
.
$Re_{i}=5000$
.

Figure 12. Probability distribution functions of the cosine of the angle between the eigenvector of the semi-major axis (
![]() $\boldsymbol{e}^{\mathbf{3}}$
) of the ellipsoid and three strain rate eigendirections (
$\boldsymbol{e}^{\mathbf{3}}$
) of the ellipsoid and three strain rate eigendirections (
![]() $\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{1}},\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{2}},\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{3}}$
)
$\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{1}},\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{2}},\boldsymbol{e}_{\boldsymbol{s}}^{\mathbf{3}}$
)
![]() $Re_{i}=2500~\hat{\unicode[STIX]{x1D707}}=100$
for (a)
$Re_{i}=2500~\hat{\unicode[STIX]{x1D707}}=100$
for (a)
![]() $Ca=0.05$
and (b)
$Ca=0.05$
and (b)
![]() $Ca=0.2$
.
$Ca=0.2$
.
In order to understand these dependencies we need to go back to the equation governing the droplet shape (i.e. (2.3)). By changing the viscosity ratio we influence the values of the parameters
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
which are calculated according to (2.4).
$f_{2}$
which are calculated according to (2.4).
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
are monotonically decreasing functions of
$f_{2}$
are monotonically decreasing functions of
![]() $\hat{\unicode[STIX]{x1D707}}$
and while the ratio
$\hat{\unicode[STIX]{x1D707}}$
and while the ratio
![]() $f_{1}/f_{2}$
is almost constant (see also figure 11 of Biferale et al. (Reference Biferale, Meneveau and Verzicco2014)),
$f_{1}/f_{2}$
is almost constant (see also figure 11 of Biferale et al. (Reference Biferale, Meneveau and Verzicco2014)),
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
decrease by up to a factor of almost 50 by increasing the viscosity ratio from
$f_{2}$
decrease by up to a factor of almost 50 by increasing the viscosity ratio from
![]() $\hat{\unicode[STIX]{x1D707}}=1$
to
$\hat{\unicode[STIX]{x1D707}}=1$
to
![]() $\hat{\unicode[STIX]{x1D707}}=100$
. This has a strong influence on the effective strengths of droplet stretching, relaxation and rotation of the ellipsoidal droplets. More importantly, in comparison to low viscosity ratio systems the influence of rotation becomes more dominant when the viscosity ratio is high (Biferale et al.
Reference Biferale, Meneveau and Verzicco2014). Additionally, reducing
$\hat{\unicode[STIX]{x1D707}}=100$
. This has a strong influence on the effective strengths of droplet stretching, relaxation and rotation of the ellipsoidal droplets. More importantly, in comparison to low viscosity ratio systems the influence of rotation becomes more dominant when the viscosity ratio is high (Biferale et al.
Reference Biferale, Meneveau and Verzicco2014). Additionally, reducing
![]() $f_{1}$
results in an increase in the effective interfacial relaxation time (i.e.
$f_{1}$
results in an increase in the effective interfacial relaxation time (i.e.
![]() $\unicode[STIX]{x1D70F}/f_{1}$
) or in other words the surface tension force acting on the ellipsoidal droplet has lesser time to adjust to the local flow conditions resulting in some highly stretched drops. The increased influence of rotation can also result in the loss of a preferential stretching axis for the ellipsoid thus resulting in more oblate or disk-like droplets.
$\unicode[STIX]{x1D70F}/f_{1}$
) or in other words the surface tension force acting on the ellipsoidal droplet has lesser time to adjust to the local flow conditions resulting in some highly stretched drops. The increased influence of rotation can also result in the loss of a preferential stretching axis for the ellipsoid thus resulting in more oblate or disk-like droplets.
Here it is important to note that the decorrelating effect of straining with rotation has been observed previously in multiple studies. Girimaji & Pope (Reference Girimaji and Pope1990) studied the evolution of infinitesimal material elements in homogeneous isotropic turbulence using DNS where they concluded that the material line elements align poorly with the straining direction due to the effect of rotation. This effect is attributed to the vorticity sweeping the material elements (in our case the axes of the ellipsoidal drop) away from the maximum strain rate direction along with the rotation of the principal strain rate axes relative to the material lines. Given that we are studying a highly inhomogeneous and anisotropic wall sheared flow, the former effect is more pronounced and is the cause of observed droplet shapes. More recently Johnson & Meneveau (Reference Johnson and Meneveau2015) calculated the Cramèr function for finite time Lyapunov exponents (FTLE) of Lagrangian particles in isotropic turbulence and by isolating the effect of the strain rate tensor they concluded that the deformation of a fluid volume is higher when the immersed particle does not rotate which resonates very well with the deformation statistics of highly viscous drops we observe in our study.
To understand the influence of rotation on the relative orientation of the drops we plot p.d.f.s of the direction cosine of the major axis with the streamwise direction in figure 11 for two different Reynolds numbers and
![]() $\hat{\unicode[STIX]{x1D707}}=100$
. It can be immediately observed that similar to
$\hat{\unicode[STIX]{x1D707}}=100$
. It can be immediately observed that similar to
![]() $\hat{\unicode[STIX]{x1D707}}=1$
the orientation is highly isotropic in the bulk region even for
$\hat{\unicode[STIX]{x1D707}}=1$
the orientation is highly isotropic in the bulk region even for
![]() $\hat{\unicode[STIX]{x1D707}}=100$
. In the IBL and OBL, while there is a tendency for the major axis to align with the streamwise direction which is similar to what we observed for
$\hat{\unicode[STIX]{x1D707}}=100$
. In the IBL and OBL, while there is a tendency for the major axis to align with the streamwise direction which is similar to what we observed for
![]() $\hat{\unicode[STIX]{x1D707}}=1$
, the distribution of the orientation for
$\hat{\unicode[STIX]{x1D707}}=1$
, the distribution of the orientation for
![]() $\hat{\unicode[STIX]{x1D707}}=100$
is more uniform than
$\hat{\unicode[STIX]{x1D707}}=100$
is more uniform than
![]() $\hat{\unicode[STIX]{x1D707}}=1$
which can be explained from earlier discussions about the increased influence of rotation. A similar behaviour is also observed in the p.d.f.s of orientation of the major axis with the eigendirections of the strain rate tensor which are shown in figure 12. In the IBL and OBL the droplets tend to align with the most extensional strain rate eigendirection which is similar to
$\hat{\unicode[STIX]{x1D707}}=1$
which can be explained from earlier discussions about the increased influence of rotation. A similar behaviour is also observed in the p.d.f.s of orientation of the major axis with the eigendirections of the strain rate tensor which are shown in figure 12. In the IBL and OBL the droplets tend to align with the most extensional strain rate eigendirection which is similar to
![]() $\hat{\unicode[STIX]{x1D707}}=1$
while the distribution is relatively more uniform. This is in contrast to the behaviour of oblate disk-like solid ellipsoids in an isotropic turbulent flow (Chevillard & Meneveau Reference Chevillard and Meneveau2013) the droplets do not tend to align orthogonally to the most contracting eigendirection. These effects are connected to the anisotropy and continuously deforming nature of the drops as discussed previously.
$\hat{\unicode[STIX]{x1D707}}=1$
while the distribution is relatively more uniform. This is in contrast to the behaviour of oblate disk-like solid ellipsoids in an isotropic turbulent flow (Chevillard & Meneveau Reference Chevillard and Meneveau2013) the droplets do not tend to align orthogonally to the most contracting eigendirection. These effects are connected to the anisotropy and continuously deforming nature of the drops as discussed previously.
From figures 7, 8 and 12 it is clear that the orientational behaviour of continuously deforming ellipsoidal droplets is completely different from that of solid axis-symmetric ellipsoids. For both viscosity ratios, the capillary number has negligible influence on the rotational behaviour of the droplets, suggesting that the droplets adjust to the underlying flow conditions regardless of the degree of deformation.
4 Summary and outlook
In this work we study the influence of capillary number
![]() $Ca$
and viscosity ratio
$Ca$
and viscosity ratio
![]() $\hat{\unicode[STIX]{x1D707}}$
on the deformation and orientation statistics of neutrally buoyant sub-Kolmogorov drops dispersed into a turbulent Taylor–Couette (TC) flow. The drops are considered to be triaxial ellipsoids which allows us to mathematically represent the surface of the drop using a symmetric second-order positive–definite tensor. By coupling the phenomenological model proposed by Maffettone & Minale (Reference Maffettone and Minale1998) for ellipsoidal drops with Lagrangian tracking and DNS for the carrier flow, we solve the time-dependent evolution equation of the shape tensor of approximately
$\hat{\unicode[STIX]{x1D707}}$
on the deformation and orientation statistics of neutrally buoyant sub-Kolmogorov drops dispersed into a turbulent Taylor–Couette (TC) flow. The drops are considered to be triaxial ellipsoids which allows us to mathematically represent the surface of the drop using a symmetric second-order positive–definite tensor. By coupling the phenomenological model proposed by Maffettone & Minale (Reference Maffettone and Minale1998) for ellipsoidal drops with Lagrangian tracking and DNS for the carrier flow, we solve the time-dependent evolution equation of the shape tensor of approximately
![]() $10^{5}$
drops dispersed into a turbulent TC flow. We find that increasing the capillary number results in large deformations of the ellipsoidal droplets due to weakening surface tension forces. Additionally, the drops deform more when they are in the inner and outer boundary layer as compared to the bulk region. Due to increased influence of rotation with increase in viscosity ratio, the droplets tend to be more oblate or disk-like as compared to more prolate or cigar-like droplets for low viscosity ratio systems. Regardless of the capillary number
$10^{5}$
drops dispersed into a turbulent TC flow. We find that increasing the capillary number results in large deformations of the ellipsoidal droplets due to weakening surface tension forces. Additionally, the drops deform more when they are in the inner and outer boundary layer as compared to the bulk region. Due to increased influence of rotation with increase in viscosity ratio, the droplets tend to be more oblate or disk-like as compared to more prolate or cigar-like droplets for low viscosity ratio systems. Regardless of the capillary number
![]() $Ca$
and viscosity ratio
$Ca$
and viscosity ratio
![]() $\hat{\unicode[STIX]{x1D707}}$
, the major axis of the drop tends to align with the streamwise direction in the inner and outer boundary layer while the orientation is highly isotropic in the bulk; a behaviour similar to solid ellipsoidal particles in a turbulent channel flow. However, the preference of orientation with the eigendirections of strain rate tensor of these drops is very different from those exhibited by axis-symmetric ellipsoids in a isotropic turbulent flow. This is a result of the continuously deforming nature of the ellipsoidal drops dispersed into a highly inhomogeneous anisotropic flow.
$\hat{\unicode[STIX]{x1D707}}$
, the major axis of the drop tends to align with the streamwise direction in the inner and outer boundary layer while the orientation is highly isotropic in the bulk; a behaviour similar to solid ellipsoidal particles in a turbulent channel flow. However, the preference of orientation with the eigendirections of strain rate tensor of these drops is very different from those exhibited by axis-symmetric ellipsoids in a isotropic turbulent flow. This is a result of the continuously deforming nature of the ellipsoidal drops dispersed into a highly inhomogeneous anisotropic flow.
In our next line of simulations we focus on tracking continuously deforming ellipsoids with relevant hydrodynamic forces acting on them along with two-way coupling onto the carrier phase which will help us understand the influence of deformability of bubbles/drops on the dynamics of the carrier phase and consequently drag reduction. However, it needs to be remembered that this involves an extremely challenging task of collecting closure relations for the various forces acting on continuously deforming small ellipsoidal bubbles/drops with a slip velocity such as drag, lift, added-mass, history force etc. (Maxey & Riley Reference Maxey and Riley1983; Eaton & Fessler Reference Eaton and Fessler1994; Elghobashi Reference Elghobashi1994; Magnaudet & Eames Reference Magnaudet and Eames2000). To explore the physics behind the experiments of van Gils et al. (Reference van Gils, Narezo Guzman, Sun and Lohse2013) where 40 % drag reduction was achieved using bubbles much larger than Kolmogorov scale, more advanced techniques such as immersed boundaries and front tracking are being implemented.
Acknowledgements
We would like to thank R. Ostilla-Mónico for various stimulating discussions during the development of the code. This work was supported by the Netherlands Center for Multiscale Catalytic Energy Conversion (MCEC), an NWO Gravitation programme funded by the Ministry of Education, Culture and Science of the government of the Netherlands and the FOM-CSER program. We acknowledge PRACE for awarding us access to FERMI based in Italy at CINECA under PRACE project number 2015133124 and NWO for granting us computational time on Cartesius cluster from the Dutch Supercomputing Consortium SURFsara.