2 The method

To study numerically the onset of convection in fluid spheres, internally heated and subject to radial gravity $\boldsymbol{g}=-{\it\gamma}\boldsymbol{r}$ , with ${\it\gamma}>0$ , we apply the Boussinesq approximation to the mass, momentum and energy equations, written in the rotating frame of reference of the sphere. We also neglect the centrifugal force since ${\it\Omega}^{2}/{\it\gamma}\ll 1$ , as happens, for instance, in the major planets, and we take constant density in the Coriolis term. In addition, we consider the radius, $r_{o}$ , of the sphere as the longitudinal scale, a viscous time scale $r_{o}^{2}/{\it\nu}$ , and ${\it\nu}^{2}/{\it\gamma}{\it\alpha}r_{o}^{4}$ as the temperature scale. The physical constants are the kinematic viscosity, ${\it\nu}$ , and the thermal expansion coefficient, ${\it\alpha}$ .

To reduce the number of equations, the velocity field is written in terms of toroidal and poloidal velocity potentials, i.e. $\boldsymbol{v}=\boldsymbol{{\rm\nabla}}\times ({\it\Psi}\boldsymbol{r})+\boldsymbol{{\rm\nabla}}\times \boldsymbol{{\rm\nabla}}\times ({\it\Phi}\boldsymbol{r})$ , and the equations are linearised around the conduction state $\boldsymbol{v}=\mathbf{0}$ and $T_{c}(r)$ , with $T_{c}(r)=T_{0}+\mathscr{S}(r_{o}^{2}-r^{2})/6{\it\kappa}$ . The constant $\mathscr{S}$ is $q/c_{p}$ , $q$ being the rate of internal heat generation per unit mass, $c_{p}$ the specific heat at constant pressure and ${\it\kappa}$ the thermal diffusivity. The equations are

(2.1) $$\begin{eqnarray}\displaystyle & \left(\partial _{t}-{\rm\nabla}^{2}\right)\mathscr{L}_{2}{\it\Psi}=2Ta^{1/2}\,\left(\partial _{{\it\varphi}}{\it\Psi}-\mathscr{Q}{\it\Phi}\right), & \displaystyle\end{eqnarray}$$

(2.2) $$\begin{eqnarray}\displaystyle & \left(\partial _{t}-{\rm\nabla}^{2}\right)\mathscr{L}_{2}{\rm\nabla}^{2}{\it\Phi}=2Ta^{1/2}\,\left(\partial _{{\it\varphi}}{\rm\nabla}^{2}{\it\Phi}+\mathscr{Q}{\it\Psi}\right)-\mathscr{L}_{2}{\it\Theta}, & \displaystyle\end{eqnarray}$$

(2.3) $$\begin{eqnarray}\displaystyle & \left({\it\sigma}\partial _{t}-{\rm\nabla}^{2}\right){\it\Theta}=Ra\mathscr{L}_{2}{\it\Phi}, & \displaystyle\end{eqnarray}$$

where ${\it\Theta}(r,{\it\theta},{\it\varphi})=T(r,{\it\theta},{\it\varphi})-T_{c}(r)$ is the temperature perturbation and $(r,{\it\theta},{\it\varphi})$ are the spherical coordinates, ${\it\theta}$ measuring the colatitude. The operators $\mathscr{L}_{2}$ and $\mathscr{Q}$ are defined as $\mathscr{L}_{2}=-r^{2}{\rm\nabla}^{2}+\partial _{r}(r^{2}\partial _{r})$ and $\mathscr{Q}=r\cos {\it\theta}{\rm\nabla}^{2}-(\mathscr{L}_{2}+r\partial r)(\cos {\it\theta}\partial r-r^{-1}\sin {\it\theta}\partial {\it\theta})$ .

The non-dimensional parameters are the internal Rayleigh, Prandtl and Taylor numbers, defined as

(2.4a−c ) $$\begin{eqnarray}\displaystyle Ra=\frac{\mathscr{S}{\it\gamma}{\it\alpha}r_{o}^{6}}{3{\it\kappa}^{2}{\it\nu}},\quad {\it\sigma}=\frac{{\it\nu}}{{\it\kappa}}\quad \text{and}\quad Ta^{1/2}=\frac{{\it\Omega}r_{o}^{2}}{{\it\nu}} & & \displaystyle\end{eqnarray}$$

respectively.

Finally, stress-free boundary conditions, ${\it\Phi}=\partial _{rr}{\it\Phi}=\partial _{r}({\it\Psi}/r)=0$ , and a perfectly conducting boundary, which means ${\it\Theta}=0$ at $r=r_{o}$ , are taken. At $r=0$ regularity conditions are enforced since a collocation method in a Gauss–Lobatto mesh of $N+1$ points is used to discretise the equations radially. Radial derivative matrices and radial differential operators are built incorporating all of these conditions.

On the sphere the equations for $\boldsymbol{X}=({\it\Phi},{\it\Psi},{\it\Theta})$ are solved by expanding the functions in spherical harmonic series up to degree $L$ , namely

(2.5) $$\begin{eqnarray}\boldsymbol{X}(r,{\it\theta},{\it\varphi},t)=\mathop{\sum }_{l=0}^{L}\mathop{\sum }_{m=-l}^{l}\boldsymbol{X}_{l}^{m}(r,t)Y_{l}^{m}({\it\theta},{\it\varphi}),\end{eqnarray}$$

with $Y_{l}^{m}({\it\theta},{\it\varphi})=P_{l}^{m}(\cos {\it\theta})\text{e}^{\text{i}m{\it\phi}}$ and $P_{l}^{m}$ being the normalised associated Legendre functions of degree $l$ and order $m$ . In this way, the system (2.1)–(2.3) decouples for each order $m$ , and systems, $\dot{\boldsymbol{X}}_{m}=\unicode[STIX]{x1D63C}_{m}\boldsymbol{X}_{m}$ , of $3(L-m+1)(N-1)$ complex ordinary differential equations are obtained.

The matrices $\unicode[STIX]{x1D63C}_{m}$ are block-tridiagonal due to the structure of $\mathscr{Q}$ , with $(L-m+1)$ rows of blocks of dimension $3(N-1)$ . The onset of convection is given by the instability of the zero solution of these systems. To find the leading spectrum of $\unicode[STIX]{x1D63C}_{m}$ (maximal real part), shift-invert preconditioners are employed. The eigenvalue problem $\unicode[STIX]{x1D63C}_{m}\boldsymbol{u}={\it\lambda}\boldsymbol{u}$ is transformed into $(\unicode[STIX]{x1D63C}_{m}-{\it\zeta}\unicode[STIX]{x1D644})^{-1}\boldsymbol{u}={\it\mu}\boldsymbol{u}$ , where ${\it\zeta}$ is a complex shift. The eigenvectors of both problems are the same, and the eigenvalues are related by ${\it\lambda}={\it\zeta}+1/{\it\mu}$ . To find the ${\it\mu}$ values of largest modulus the ARPACK package, based on Arnoldi algorithms (see Lehoucq & Sorensen Reference Lehoucq and Sorensen1996), is used. The linear systems with matrix $(\unicode[STIX]{x1D63C}_{m}-{\it\zeta}\unicode[STIX]{x1D644})$ are solved by means of an adapted LU decomposition (where LU stands for lower and upper factors). If ${\it\zeta}={\it\rho}+\text{i}{\it\omega}$ with ${\it\rho}\gtrapprox 0$ we obtain the eigenvalues ${\it\lambda}={\it\lambda}_{r}+\text{i}{\it\lambda}_{i}$ closest to $\text{i}{\it\omega}$ . A sequence of imaginary parts ${\it\omega}$ is examined, using the information from nearby calculations, to ensure that no modes close to critical are missed. For the same reason, if an azimuthal wavenumber $m_{0}$ is preferred for some value of the parameters, an interval $[m_{0}-{\rm\Delta}m,m_{0}+{\rm\Delta}m]$ is also explored, and a finer mesh of ${\it\omega}$ values is used from time to time. The critical values of the parameters are found by applying a root-finding algorithm to the equation ${\it\lambda}_{r}=0$ . For any set of parameters the truncation constants $N$ and $L$ have been taken to bound the errors below 1 %. The maximal values used for the highest $m$ were $N=80$ and $L=180$ . More detailed information on the method used can be found in Sánchez, Garcia & Net (Reference Sánchez, Garcia and Net2016).

Table 1. Comparison of the critical parameters $Ra_{c}$ , ${\it\omega}_{c}$ and $m_{c}$ , for stress-free boundary conditions with previous results of Zhang & Liao (Reference Zhang and Liao2004), and for non-slip boundary conditions with Zhang et al. (Reference Zhang, Liao and Busse2007).

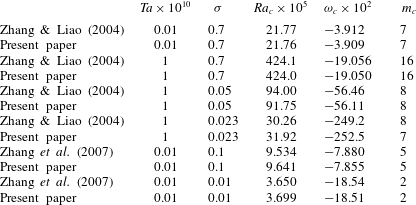
The instability of the conduction state is always via a Hopf bifurcation. It gives rise to waves travelling azimuthally when $m_{c}>0$ , and oscillations of the fluid if $m_{c}=0$ . When $m_{c}>0$ , the negative frequencies give positive drifting velocities $c=-{\it\omega}_{c}/m_{c}$ , i.e. the waves drift in the prograde direction.

First of all, our results were compared with those of Zhang & Liao (Reference Zhang and Liao2004) and Zhang et al. (Reference Zhang, Liao and Busse2007). The transformations for the critical Rayleigh number $Ra_{c}^{Z}=Ra_{c}/\sqrt{Ta}$ and the critical precession frequency ${\it\omega}_{c}^{Z}={\it\omega}_{c}/\sqrt{Ta}$ were used, to take into account the different non-dimensional scales of the authors. Some of the values checked are given in table 1. The critical parameters agree very well when $Ta=10^{8}$ , and only slight discrepancies are found for ${\it\sigma}=0.023$ . In this case the critical wavenumber is different, but the Rayleigh number for $m=8$ is $3.203\times 10^{6}$ , very close to that of our $m_{c}=7$ mode, with ${\it\omega}_{c}=-2.489\times 10^{4}$ , which agrees very well with that of Zhang & Liao (Reference Zhang and Liao2004). Moreover, both eigenfunctions are equatorially attached, so different codes and numerical truncation errors could justify the small differences.

3 Taylor number dependence

Figure 1 shows the Taylor number dependence of $Ra_{c}$ , $-{\it\omega}_{c}$ , and $m_{c}$ for ${\it\sigma}=0.01$ , representative of very low Prandtl numbers. In figure 1(a), the left axis and the magenta curve correspond to the Rayleigh parameter, while the blue curve and the right axis indicate the drifting frequency. The marginal curves are the envelope of more than 50 curves, one for each of the wavenumbers taken and shown in figure 1(b).

There are two regimes. For Taylor numbers below $6.31\times 10^{10}$ , $Ra_{c}$ increases linearly with the Taylor number, and ${\it\omega}_{c}$ goes as the square root. At higher $Ta$ , $Ra_{c}$ and ${\it\omega}_{c}$ follow potential laws different from those predicted for the asymptotic theory of large ${\it\sigma}$ . Initially, the preferred wavenumber is $m_{c}=1$ . The preference of this mode of convection is in agreement with that found by Busse & Simitev (Reference Busse and Simitev2004). Afterwards, it jumps to $m_{c}=8$ and increases monotonically following a staircase. For the Prandtl number used, the selected laws are $Ra_{c}=9635+5.879\times 10^{-5}Ta$ , ${\it\omega}_{c}=-0.175Ta^{0.500}$ if $m_{c}=1$ , and $Ra_{c}=2.85\times 10^{-3}Ta^{0.845}$ , ${\it\omega}_{c}=-1.58Ta^{0.428}$ and $m_{c}=1.71\times 10^{-2}Ta^{0.251}$ (magenta solid line) for the highest $Ta$ .

Figure 1. Critical (a) Rayleigh number (magenta) and minus the precession frequency (blue), and (b) azimuthal wavenumber versus the Taylor number.

Figure 2. Contour plots of (a–f) ${\it\Theta}$ , (g–l) $v_{{\it\varphi}}$ and (m–r) $E_{K}$ , for two solutions. (a–c, g–i, m–o) The solution for the inertial $m_{c}=1$ mode with ${\it\sigma}=0.01$ , $Ta=4.47\times 10^{10},Ra_{c}=2.60\times 10^{6}$ and ${\it\omega}_{c}=-3.71\times 10^{4}$ ; (d–f, j–l, p–r) the solution for an EA mode of $m_{c}=50$ and ${\it\sigma}=0.01$ , $Ta=7.56\times 10^{13}$ , $Ra_{c}=1.53\times 10^{9}$ and ${\it\omega}_{c}=-1.36\times 10^{6}$ . Green means zero for ${\it\Theta}$ and $v_{{\it\varphi}}$ , and blue means zero for $E_{K}$ . The dashed lines marked on each surface indicate the position where the other two projections are taken. The spherical and meridional projections almost cut the maximum values of the cells and vortices.

Figure 2(a–f) shows the contour plots of the temperature perturbation, figure 2(g–l) those of the azimuthal velocity, $v_{{\it\varphi}}$ , and figure 2(m–r) those of the kinetic energy density, $E_{K}=\Vert \boldsymbol{v}\Vert ^{2}/2$ . Each set of three panels includes projections of the fields on a spherical surface, and on the equatorial and a meridional plane. The lines marked on each surface indicate the position where the other two projections are taken. Figure 2(a–c, g–i, m–o) corresponds to the critical $m_{c}=1$ mode of convection. Figure 2(d–f, j–l, p–r) shows the critical inertial $m_{c}=50$ equatorially attached mode of convection, of the type described in Zhang (Reference Zhang1993). The size of the equatorial waveguide agrees very well with that of the inertial solutions found in that paper; consequently, due to the high wavenumber, the conduction state is stable in almost all of the body of the fluid.

The contour plots of both solutions have a symmetric ${\it\Theta}$ with respect to the equator, and $v_{{\it\varphi}}$ and $E_{K}$ have their maxima in the equatorial plane at $r=r_{o}$ . The temperature perturbation of the $m=1$ pattern fills the domain, while that of the EA modes is strongly trapped in the outer surface. In both cases most of the contribution to the kinetic energy density comes from the azimuthal velocity.

4 Prandtl number dependence

Figure 3 shows the dependence of the critical parameters on the Prandtl number for a large Taylor number. In this case four different behaviours are distinguished in the range computed. Below approximately ${\it\sigma}=6\times 10^{-6}$ , the preferred modes are axisymmetric with oscillatory frequencies almost an order of magnitude higher than that of the other inertial modes. It should be noticed that this mode of convection cannot be described as a perturbed solution of an inertial wave since it does not travel. Next, up to approximately $1.10\times 10^{-3}$ , the preferred eigenmode has constant azimuthal wavenumber $m_{c}=1$ with the pattern of convection shown before. From approximately $1.10\times 10^{-3}$ to $1.06\times 10^{-2}$ , the preferred modes are EA. In this transition the critical wavenumber jumps from 1 to 8 and then increases up to 27. Finally, near $1.06\times 10^{-2}$ , the wavenumber falls from 27 to 14 in a third transition. By increasing ${\it\sigma}$ , there is, initially, a small transition zone where the eigenfunctions retain characteristics of the EA modes in the sense that the kinetic energy density remains maximal at the equator, but the cells of convection spread to the interior of the sphere, detaching progressively from the outer surface and spiralling, but forming several humps in the interior of the spirals. These linear solutions were first described in spherical shells by Ardes, Busse & Wicht (Reference Ardes, Busse and Wicht1997). From ${\it\sigma}\approx 0.02$ , the preferred modes are already spiralling columnar and detached from the equator. Then, the wavenumber increases, making a zigzag, so from $m_{c}\gtrsim 17$ there are different preferred spiralling patterns of convection with the same azimuthal wavenumber, which differ in the radial location, width and curvature of the spirals.

Figure 3. Critical (a) Rayleigh number (magenta) and minus the precession frequency (blue), and (b) azimuthal wavenumber versus the Prandtl number.

Figure 4. Contour plots of (a–f) ${\it\Theta}$ , (g–l) $v_{{\it\varphi}}$ and (m–r) $E_{K}$ , for two solutions. (a–c, g–i, m–o) The solution for the axisymmetric mode, with $Ta=5\times 10^{12}$ , ${\it\sigma}=10^{-7}$ , $Ra_{c}=6.72\times 10^{3}$ , ${\it\omega}_{c}=-2.00\times 10^{6}$ ; (d–f, j–l, p–r) the solution for an SP mode of $m_{c}=23$ and $Ta=5\times 10^{12}$ , ${\it\sigma}=5.03\times 10^{-2}$ , $Ra_{c}=5.84\times 10^{8}$ , ${\it\omega}_{c}=-4.18\times 10^{4}$ . The projections are selected following the same criteria as in figure 2.

In this case the type of law fulfilled by the critical parameters in each interval is not always potential. When $m_{c}=1$ , while the precession frequency is constant ( $3.95\times 10^{5}$ ), the Rayleigh number follows the quadratic law $Ra_{c}=7.699\times 10^{3}+4.759\times 10^{7}{\it\sigma}+2.976\times 10^{12}{\it\sigma}^{2}$ only from ${\it\sigma}=10^{-4}$ . For the equatorially attached modes, power laws $Ra_{c}=3.98\times 10^{11}{\it\sigma}^{1.70}$ , ${\it\omega}_{c}=-2.40\times 10^{5}{\it\sigma}^{0.13}$ and $m_{c}=332.4{\it\sigma}^{0.54}$ are obtained. Finally, in the fourth interval, the critical Rayleigh number goes as $Ra_{c}=5.553\times 10^{7}+1.315\times 10^{10}{\it\sigma}-5.140\times 10^{10}{\it\sigma}^{2}$ and the precession frequency as ${\it\omega}_{c}=-1.143\times 10^{4}{\it\sigma}^{0.44}$ .

In figure 4 contour plots of the axisymmetric mode and one of the $m_{c}=23$ SP modes found are represented. They correspond to the first and last intervals of figure 3. The former has ${\it\Theta}$ and the components $v_{r}$ and $v_{{\it\varphi}}$ of the velocity field antisymmetric with respect to the equator, and $v_{{\it\theta}}$ is symmetric. This mode is described with more detail in the next section. For the latter, the symmetries of these fields are interchanged and $E_{K}$ is columnar.

5 The low-Prandtl-number limit

To illustrate what happens in the low-Prandtl-number limit and how the axisymmetric mode becomes preferred, the four lowest neutral curves at ${\it\sigma}=10^{-7}$ , i.e. those of $m=0,1,2,3$ , plus that of $m=20$ , just as an example, are represented in figure 5. Figure 5(a) shows the Rayleigh number versus ${\it\sigma}$ , and figure 5(b) shows the absolute value of the frequency. It should be noticed that the envelope of this curves does not give $Ra_{c}$ since, as was seen before, at $Ta=5\times 10^{12}$ , the $m_{c}=1$ mode is replaced by an EA mode with $m_{c}=8$ .

When a mode reaches the ${\it\sigma}$ -zero limit, $Ra^{m}$ and ${\it\omega}^{m}$ become constant. At ${\it\sigma}=10^{-2}$ the Rayleigh number of the axisymmetric mode is more than an order of magnitude higher than the critical value, but since it reaches the asymptotic limit (independence of $Ra^{m}$ with ${\it\sigma}$ ) at a lower value of ${\it\sigma}$ than the other $m$ and the slopes of $Ra^{m}$ versus ${\it\sigma}$ are similar before the limit, it becomes preferred.

Figure 5. (a) Critical Rayleigh number and (b) critical absolute value of the frequency of the modes $m=0,1,2,3$ and $20$ versus the Prandtl number.

Figure 6. Snapshots of the meridional projection of the contour plots of the preferred axisymmetric mode for ${\it\sigma}=10^{-7}$ , $Ta=5\times 10^{12}$ , $Ra_{c}=6.72\times 10^{3}$ and ${\it\omega}_{c}=-2.00\times 10^{6}$ .

Figure 6 shows a sequence of projections of the contour plots of ${\it\Theta}$ and all of the components of the velocity field, $(v_{r},v_{{\it\theta}},v_{{\it\varphi}})$ , onto a meridional plane in a period of oscillation, for ${\it\sigma}=10^{-7}$ . The axisymmetric velocity field consists of the superposition of a single vortex in the $(r,{\it\theta})$ plane, which fills the meridional section, and a transverse azimuthal circulation, antisymmetric with respect to the equator. Both components oscillate periodically in time with a phase shift of ${\rm\pi}/2$ , i.e.

(5.1) $$\begin{eqnarray}\displaystyle v_{r}(t,r,{\it\theta})\! & = & \displaystyle \!v_{r}^{0}(r,{\it\theta})\cos ({\it\omega}t+{\it\delta}),\end{eqnarray}$$

(5.2) $$\begin{eqnarray}\displaystyle v_{{\it\theta}}(t,r,{\it\theta})\! & = & \displaystyle \!v_{{\it\theta}}^{0}(r,{\it\theta})\cos ({\it\omega}t+{\it\delta}),\end{eqnarray}$$

(5.3) $$\begin{eqnarray}\displaystyle v_{{\it\varphi}}(t,r,{\it\theta})\! & = & \displaystyle \!v_{{\it\varphi}}^{0}(r,{\it\theta})\sin ({\it\omega}t+{\it\delta}),\end{eqnarray}$$

(5.4) $$\begin{eqnarray}\displaystyle {\it\Theta}(t,r,{\it\theta})\! & = & \displaystyle \!{\it\Theta}^{0}(r,{\it\theta})\cos ({\it\omega}t+{\it\delta}).\end{eqnarray}$$

The oscillation of the vortex consists of its change in amplitude and sense of rotation, maintaining its shape, and that of $v_{{\it\varphi}}$ of the alternation of the prograde and retrograde velocities between the two hemispheres. Then, its mean zonal flow integrated over an oscillation period is zero. This type of axisymmetric mode is known as torsional. Since $v_{r}$ , $v_{{\it\theta}}$ and $v_{{\it\varphi}}$ are out of phase and the maxima are of the same order, the maximum kinetic energy density is localised in the interior of the sphere and in a thin band of the surface at low latitudes when $v_{r}$ , $v_{{\it\theta}}$ have maxima, and in the surface at mid-latitudes when $v_{{\it\varphi}}$ is the dominant component.

Torsional oscillations in rapidly rotating systems were studied by Liao & Zhang (Reference Liao and Zhang2006) and Liao, Zhang & Chang (Reference Liao, Zhang and Chang2007) in a rotating annular channel uniformly heated from below. The authors developed an asymptotic theory (confirmed by numerical calculations) describing the mechanism for the excitation and maintenance of the oscillations. According to them, the Coriolis force provides the restoring force, and the heating the energy necessary to sustain the oscillations against viscous dissipation. Moreover, they demonstrate, in the range of parameters explored in the present paper ( $Ta\gg 1$ and ${\it\sigma}\ll 1$ ), that nonlinear torsional oscillations can be maintained by thermal convection at supercritical $Ra$ .

In our case, the instability giving rise to torsional modes is purely hydrodynamic, as in Liao et al. (Reference Liao, Zhang and Chang2007). The existence of azimuthal velocity in the linear regime can be easily understood by looking at (2.1)–(2.3) for the axisymmetric modes in the low-Prandtl-number limit $(\partial _{{\it\varphi}}=0,{\it\sigma}\rightarrow 0)$ , and at the expression of the velocity field in terms of the potentials, $v_{r}=-(\sin {\it\theta}\partial _{{\it\theta}{\it\theta}}^{2}{\it\Phi}+\cos {\it\theta}\partial _{{\it\theta}}{\it\Phi})/r\sin {\it\theta}$ , $v_{{\it\theta}}=\partial _{r{\it\theta}}^{2}(r{\it\Phi})/r$ and $v_{{\it\varphi}}=-\partial _{{\it\theta}}{\it\Psi}$ . Since $v_{{\it\varphi}}$ depends only on ${\it\Psi}$ , as soon as a non-zero meridional velocity field appears ( ${\it\Phi}\neq 0$ ) due to the heating, the Coriolis force generates an azimuthal velocity of different sign in each hemisphere. Moreover, at critical values of the parameters the time dependence is $\boldsymbol{X}(t,r,{\it\theta})=\exp (\text{i}{\it\omega}t)\boldsymbol{X}(r,{\it\theta})$ , so by replacing $\partial _{t}$ by $\text{i}{\it\omega}$ in the equations it is clear that there is a phase lag of ${\rm\pi}/2$ between ${\it\Phi}$ and ${\it\Psi}$ , or, which is the same, between $v_{r},v_{{\it\theta}}$ and $v_{{\it\varphi}}$ .

By considering the annulus as a polar slice of a spherical shell (where gravity is almost parallel to the rotation vector), it is possible to relate the critical parameters of both geometries. By defining $d$ as the depth of the annulus and $g$ as its constant gravity, it results that $Ta_{L}^{1/2}=(d/r_{o})^{2}Ta^{1/2}$ . The subscript $L$ means that parameters are scaled as in Liao & Zhang (Reference Liao and Zhang2006) and Liao et al. (Reference Liao, Zhang and Chang2007). They deduce that for ${\it\sigma}Ta_{L}^{1/2}=0.1$ the most unstable mode is axisymmetric and oscillatory when $Ta\gg 1$ . By estimating $d=r_{o}/10$ , the above relations give ${\it\sigma}Ta^{1/2}=10$ . Our calculations show the beginning of axisymmetric oscillations at ${\it\sigma}Ta^{1/2}\approx 13$ (see figure 3). Taking into account the inaccurate estimation, the result agrees very well with the relation found in the annulus. Moreover, the order of magnitude of the frequency of the oscillations is the same; for instance, with ${\it\omega}_{L}={\it\omega}/Ta^{1/2}$ and the values of figure 5, i.e. for $Ta=5\times 10^{12}$ and ${\it\omega}=2\times 10^{6}$ , ${\it\omega}_{L}=0.89$ , which is close to ${\it\omega}_{L}=1.4$ , given in Liao & Zhang (Reference Liao and Zhang2006) for $Ta=10^{10}$ . However, as is discussed in the conclusions, we have not been able to find preferred torsional modes for ${\it\sigma}=0.01$ at high Taylor numbers.