2.1. Direct numerical simulation

We first describe the method of our DNS. We consider the incompressible Navier–Stokes equations in a periodic cube with the side length $2{\rm \pi}$

(2.1)\begin{equation} \partial_t {\boldsymbol{u}} + ({\boldsymbol{u}}\boldsymbol{\cdot}{\boldsymbol{\nabla}}) {\boldsymbol{u}} ={-} {\boldsymbol{\nabla}} p + \nu \nabla^{2} {\boldsymbol{u}} + {\boldsymbol{F}}, \quad {\boldsymbol{\nabla}} \boldsymbol{\cdot} {\boldsymbol{u}} = 0, \end{equation}

where ${\boldsymbol {u}}, p$ and $\nu$ denote the velocity, the pressure and the kinematic viscosity. The fluid density is normalised to unity. The velocity and the pressure are functions of the spatial coordinates ${\boldsymbol {x}}$ and the time $t$.

We add a large-scale forcing, ${\boldsymbol {F}}$, to keep the system in a statistically steady state, which is expressed in the Fourier space as

(2.2)\begin{equation} \hat{{\boldsymbol{F}}}({\boldsymbol{k}}, t) =\begin{cases} \dfrac{\epsilon_{in}}{E_f} \hat{{\boldsymbol{u}}}({\boldsymbol{k}}, t), & (0 < |{\boldsymbol{k}}| \le k_f), \\ {\boldsymbol{0}}, & (\textrm{otherwise}). \end{cases} \end{equation}

Here, $\hat {{\boldsymbol {F}}}({\boldsymbol {k}}, t)$ and $\hat {{\boldsymbol {u}}}({\boldsymbol {k}}, t)$ are the Fourier modes of the forcing and of the velocity, and ${\boldsymbol {k}}$ denotes the wavevector. The forcing parameters, $\epsilon _{in}$ and $k_f$, are the energy input rate and the maximum forcing wavenumber, respectively. By $E_f$, we denote the kinetic energy in the forcing range

(2.3)\begin{equation} E_f = \sum_{\substack{{\boldsymbol{k}}\\ |{\boldsymbol{k}}| \le k_f}} \tfrac{1}{2}|\hat{{\boldsymbol{u}}}({\boldsymbol{k}}, t)|^{2}. \end{equation}

With this setting, the numerically realised energy input rate by the forcing is indeed kept constant in time. This type of forcing is often used in DNSs by various authors, including Carini & Quadrio (Reference Carini and Quadrio2010).

Numerically, we solve the forced Navier–Stokes equations in the form of the vorticity equations with the Fourier-spectral method with $N^{3}$ grid points in the cube. We mainly set $N = 512$. The aliasing error is removed by the phase shift and the isotropic truncation (setting to zero the modes in $|{\boldsymbol {k}}| \ge \sqrt {2}N/3$). We use the fourth-order Runge–Kutta scheme for the time stepping. We set the parameter values as follows: $\nu = 5.30 \times 10^{-4}$, $\epsilon _{in} = 1.00\times 10^{-1}$, $k_f = 2.50$ and the size of the time step $\Delta t = 1.87 \times 10^{-3}$. We make ten random initial velocity fields with the energy spectrum $E(k) \propto k^{4} \exp (-k^{2}/2)$ by setting identically and independently distributed Gaussian random variables to the real and imaginary parts of the incompressible velocity Fourier modes. The kinetic energy of the initial field is set to $0.50$. For each initial data set, we run the simulation for ten large-scale turnover times and the statistics are collected after that. The resultant velocity fields are regarded as being in a statistically steady state with the Taylor-scale based Reynolds number being $R_\lambda = 210$. The large-scale eddy turnover time is $\tau _{to} = \langle L(t) \rangle / (2 \langle E(t) \rangle / 3)^{1/2} = 1.80$, which is calculated with the energy, $E(t) = \sum _{{\boldsymbol {k}}} |\hat {{\boldsymbol {u}}}({\boldsymbol {k}}, t)|^{2}/ 2$, and the integral-length scale, $L(t) = (3{\rm \pi} )/(4E(t))\times \sum _{{\boldsymbol {k}}} |\hat {{\boldsymbol {u}}}({\boldsymbol {k}}, t)|^{2} / |{\boldsymbol {k}}|$. Here, $\langle \cdot \rangle$ denotes the average over time and the ensemble. The root-mean-square velocity is $u_{rms} = (2\langle E(t) \rangle /3)^{1/2} = 6.25\times 10^{-1}$. The relation between the truncation wavenumber, $k_{max} = \sqrt {2}N/3$, and the Kolmogorov dissipation length scale, $\eta = (\nu ^{3}/\langle \epsilon \rangle )^{1/4}$, is $k_{max} \eta = 1.51$. Here, $\langle \epsilon \rangle$ is the mean energy dissipation rate, which is here indeed equal to the prescribed energy input rate $\epsilon _{in}$.

2.2. Eulerian correlation and response function

Here, we start with a decomposition of the incompressible velocity Fourier modes in Eulerian coordinates, which have only two independent components. Such a decomposition becomes crucially important when we later consider the FRRs by adding random noise to the Navier–Stokes equations. We adopt the Craya–Herring decomposition defined with the reference vector chosen here as $-{\boldsymbol {e}}_z = (0, 0, -1)$, (see, e.g. Sagaut & Cambon Reference Sagaut and Cambon2008), which is

(2.4)\begin{equation} \hat{{\boldsymbol{u}}}({\boldsymbol{k}}, t) = \hat{u}_\varphi({\boldsymbol{k}}, t) {\boldsymbol{e}}_\varphi + \hat{u}_\theta({\boldsymbol{k}}, t) {\boldsymbol{e}}_\theta. \end{equation}

Here, the unit vectors are written in the spherical coordinate system as ${\boldsymbol {e}}_\varphi = (-\sin \varphi , \cos \varphi , 0)$ and ${\boldsymbol {e}}_\theta = (\cos \theta \cos \varphi , \cos \theta \sin \varphi , -\sin \theta )$ with the polar angle $\theta \, (0 \le \theta \le {\rm \pi})$ and the azimuthal angle $\varphi \, (0 \le \varphi < 2{\rm \pi} )$ of the wavevector ${\boldsymbol {k}} = k(\sin \theta \cos \varphi , \sin \theta \sin \varphi , \cos \theta )$, where $k = |{\boldsymbol {k}}|$. If ${\boldsymbol {k}}$ is aligned with the $z$-axis ($\theta = 0$ or ${\rm \pi}$), we set $\varphi = 0$.

With this decomposition we define the correlation function of the velocity Fourier modes in the Eulerian coordinates as

(2.5)\begin{equation} C_{\alpha \beta}({\boldsymbol{k}}, t \mid {\boldsymbol{q}}, s) = \langle \hat{u}_\alpha ({\boldsymbol{k}}, t) \hat{u}_\beta ({\boldsymbol{q}}, s) \rangle, \end{equation}

where the indices, $\alpha , \beta$, are either $\varphi$ or $\theta$.

In the numerical simulation, we calculate the shell average of the diagonal correlation functions

(2.6)\begin{equation} C_{\alpha \alpha}(k, t - s) = \frac{1}{N(k, k + \Delta k)} \sum_{\substack{{\boldsymbol{k}} \\ k \le |{\boldsymbol{k}}| < k + \Delta k}} C_{\alpha \alpha}({\boldsymbol{k}}, t \mid{-}{\boldsymbol{k}}, s), \end{equation}

where $N(k, k + \Delta k)$ is the number of Fourier modes lying in the annulus $k \le |{\boldsymbol {k}}| < k + \Delta k$. We set here $\Delta k = 1$. Notice that we assume isotropy in the Fourier space and a statistically steady state. We calculate the autocorrelation function of each mode, $C_{\alpha \alpha }({\boldsymbol {k}}, t\mid -{\boldsymbol {k}}, s)$, by way of the temporal Fourier modes using the Wiener–Khinchin theorem. In practice, we record the time series of the real and imaginary parts of each Fourier mode and calculate the mean of the squared modulus of the Fourier transform of the time series.

Now we define the mean linear response function of the velocity Fourier modes in Eulerian coordinates as

(2.7)\begin{equation} G_{\alpha \beta}({\boldsymbol{k}}, t \mid {\boldsymbol{q}}, s) = \left\langle \frac{\delta \hat{u}_\alpha ({\boldsymbol{k}}, t)} {\delta \hat{u}_\beta ({\boldsymbol{q}}, s)} \right\rangle. \end{equation}

In our numerical calculation of the mean linear response function, we adopt the method used for the shell model in Biferale et al. (Reference Biferale, Daumont, Lacorata and Vulpiani2001). Specifically, we take the numerical solution at time $t_0$ in the statistically steady state and consider two solutions: one starts from $\hat {{\boldsymbol {u}}}_\alpha ({\boldsymbol {q}}, t_0)$ and the other starts from a perturbed solution, $\hat {{\boldsymbol {u}}}_\alpha ({\boldsymbol {q}}, t_0) + \Delta \hat {{\boldsymbol {u}}}_\alpha ({\boldsymbol {q}}, t_0)$. We then integrate the Navier–Stokes equations starting from the two initial conditions independently. At some later time $t\, (> t_0)$, the difference between the two solutions, which is denoted by $\Delta \hat {{\boldsymbol {u}}}_\alpha ({\boldsymbol {k}}, t)$, yields one sample of the linear response function

(2.8)\begin{equation} G_{\alpha \beta}({\boldsymbol{k}}, t \mid {\boldsymbol{q}}, t_0) \sim \frac{\Delta \hat{u}_\alpha ({\boldsymbol{k}}, t)} {\Delta \hat{u}_\beta ({\boldsymbol{q}}, t_0)}, \end{equation}

provided that the difference stays so small that the evolution is essentially linear. We then take the average of the right-hand side of (2.8) over time $t_0$ and over the ensemble of several numerical solutions.

As in the correlation function, we calculate the shell average of the diagonal part of the response function,

(2.9)\begin{equation} G_{\alpha \alpha}(k, t - t_0) = \frac{1}{N(k, k + \Delta k)} \sum_{\substack{{\boldsymbol{k}} \\ k \le |{\boldsymbol{k}}| < k + \Delta k}} G_{\alpha \alpha}({\boldsymbol{k}}, t \mid{-}{\boldsymbol{k}}, t_0). \end{equation}

In the calculation of the shell average, we add the initial perturbation at time $t_0$ (the denominator in (2.8)) to all the modes in the shell. For the initial perturbation, we set only the real part: in other words, $\textrm {Im}[\Delta \hat {u}_\alpha (-{\boldsymbol {k}}, t_0)] = 0$. We set the initial perturbation, $\textrm {Re}[\Delta \hat {u}_\alpha (-{\boldsymbol {k}}, t_0)]$, to five per cent of the standard deviation of $|\hat {u}_\alpha ({\boldsymbol {k}}, t)|$ (the sign of the initial perturbation is always positive). We check that the shell-averaged response function calculated in this manner agrees well with the mode-wise response function, $G_{\alpha \alpha }({\boldsymbol {k}}, t \mid -{\boldsymbol {k}}, t_0)$, which is calculated by adding the initial perturbation only to two modes $\hat {u}(\pm {\boldsymbol {k}}, t_0)$ with ${\boldsymbol {k}}$ and $-{\boldsymbol {k}}$ being within the same shell.

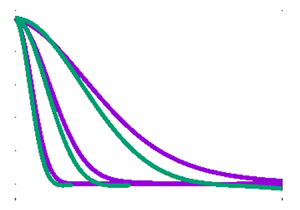
In figure 1, we show the shell-averaged correlation functions normalised with the equal-time values and the shell-averaged linear response functions for six representative wavenumbers. The wavenumbers are chosen as powers of one half times the Kolmogorov dissipation wavenumber, $k_\eta = (\langle \epsilon \rangle / \nu ^{3})^{1/4} = 160$, up to the one in the energy-containing range, $k = k_\eta 2^{-5} = 2 k_f = 5$. In figure 1 we show only the real parts of the correlation and response functions since the imaginary parts are approximately two orders of magnitude smaller than the real parts. For the shell-averaged other components, the correlation function $C_{\theta \theta }(k, t - s)$ is nearly identical to $C_{\varphi \varphi }(k, t - s)$ and the response function $G_{\theta \theta }(k, t - s)$ is nearly identical to $G_{\varphi \varphi }(k, t - s)$.

Figure 1. The shell-averaged correlation function and the shell-averaged mean linear response function of the diagonal $\varphi$-component for $k=k_\eta , k_\eta / 2, k_\eta /4$ (a) and $k = k_\eta /8, k_\eta / 16, k_\eta / 32$ (b). Notice that the correlation function is normalised with the equal-time value $C_{\varphi \varphi }(k, 0)$. Here the large-scale eddy turnover time is $\tau _{to} = 1.80$. Insets: the averaged energy spectrum with the representative wavenumbers depicted by vertical lines.

We here observe a small but measurable difference between the correlation function and the linear response function. In particular, the FDT, $C_{\varphi \varphi } \propto G_{\varphi \varphi }$, is invalid for all the representative wavenumbers spanning from the inertial range to the dissipation range. Here, we regard $k_f < k \le k_\eta / 4 = 40$ as the inertial range and $k > 40$ as the dissipation range based on the shape of the energy spectrum shown in the inset of figure 1. Another observation in figure 1 is the tendency that the response functions are generally smaller than the normalised correlation functions. We do not have an explanation of this tendency.

This breakdown of the FDT, which is as expected, is a manifestation of the fact that the velocity Fourier modes of turbulence are not described with the equilibrium statistical mechanics (Marconi et al. Reference Marconi, Puglisi, Rondoni and Vulpiani2008) regardless of the wavenumber ranges. Here, we point out an apparently contradictory fact: the probability density functions (p.d.f.s) of the real and imaginary parts of the velocity Fourier modes in all the wavenumber ranges are known to become closer to the Gaussian distribution as we increase the Reynolds number (Brun & Pumir Reference Brun and Pumir2001). In our simulation, the p.d.f.s are indeed close to Gaussian for all the six wavenumbers selected in figure 1. Those p.d.f.s are shown in Appendix E. The Gaussian distribution implies the FDT, provided that there is no correlation among different wavenumber modes. An example with correlated degrees of freedom, whose marginal p.d.f. is near Gaussian, is carefully examined by Marconi et al. (Reference Marconi, Puglisi, Rondoni and Vulpiani2008). Indeed, they showed that the example does not satisfy the FDT. The homogeneous isotropic turbulence is another example of having a Gaussian (marginal) p.d.f. not showing the FDT.

Coming back to figure 1, despite the difference between the correlation function and the linear response function, we observe that their characteristic times defined, for example, as the integral time scales, seem to be of the same order of magnitude. This point will be studied in § 4 together with the Lagrangian counterparts.

We end this section by commenting on details of the averaging of the correlation and response functions. We set the length of the temporal window for the correlation function to $1.85\tau _{to}$ for the small wavenumbers, $k = k_\eta /32, k_\eta / 16$ and $k_\eta /8$, and to $0.265\tau _{to}$ for large wavenumbers, $k = k_\eta / 4, k_\eta / 2$ and $k_\eta$. The correlation functions shown in figure 1 are given in one half of these window lengths. We take a total of 15 such windows (5 windows in 3 simulations) in the averaging for the former set of $k$ values and total 200 windows (20 windows in 10 simulations) for the latter set of $k$ values. For the linear response function, the length of the temporal window for each wavenumber is $0.833\tau _{to}, 0.331\tau _{to}, 0.164\tau _{to}$ for the set of the small wavenumbers and $0.331\tau _{to}$ for the set of the large wavenumbers. The total number of windows are 20 (20 windows in 1 simulation), 100 (50 windows in 2 simulations) and 200 (100 windows in 2 simulations) respectively for the former set of three $k$ values and 50 windows (50 windows in 1 simulation) for the latter set of three $k$ values. Now the question with this sampling is whether the means of the correlation function and the linear response function shown in figure 1 are converged or not. To check this, we decrease the number of samples to $1/3$ and compare the averages over the full sample to those over the $1/3$ sample. The difference between the averages is at most a few per cent for both the correlation function and the response function. This is the case for large wavenumbers $k_\eta /16$ and $k_\eta /32$. For other wavenumbers, the difference between the samples is smaller than a few per cent. We regard the difference as small enough and consider that the average reached convergence. This difference in the averages is less than the discrepancy between the correlation function and the response functions shown in figure 1.

2.3. FRR with random forcing

As mentioned in § 1, the linear response function cannot be written in general with the two-point correlation function. However, if the uncorrelated Gaussian noise is added to the evolution equation, we can obtain several expressions of the linear response function (FRR) in terms of certain correlation functions. Here, we consider two FRRs and compare them with the linear response function without the noise shown in the previous subsection.

For homogeneous and isotropic Navier–Stokes turbulence, one of the expressions was derived by Novikov (Reference Novikov1965) and numerically studied by Carini & Quadrio (Reference Carini and Quadrio2010). To give the precise expression, we now fix some notation. We first add the random Gaussian noise $\hat {\xi }_\alpha ({\boldsymbol {k}}, t)$ to the Navier–Stokes equations in Fourier space in addition to the large-scale forcing as

(2.10)\begin{align} \partial_t \hat{u}_\alpha({\boldsymbol{k}}, t) &= ({\boldsymbol{e}}_\alpha)_j \left(-\frac{\textrm{i}}{2}\right) P_{jlm}({\boldsymbol{k}}) \sum_{\substack{{\boldsymbol{p}}, {\boldsymbol{q}} \\ {\boldsymbol{p}} + {\boldsymbol{q}} + {\boldsymbol{k}} = {\boldsymbol{0}}}} \hat{u}_l(-{\boldsymbol{p}}, t) \hat{u}_m(-{\boldsymbol{q}}, t) - \nu k^{2} \hat{u}_\alpha({\boldsymbol{k}}, t) \nonumber\\ &\quad + \hat{F}_\alpha({\boldsymbol{k}}, t) + \hat{\xi}_\alpha({\boldsymbol{k}}, t). \end{align}

Here, we take summation over the repeated indices $j, l$ and $m$ and the index $\alpha$ denotes the Craya–Herring component $\varphi$ or $\theta$. The projection operator is $P_{jlm}({\boldsymbol {k}}) = k_m P_{jl}({\boldsymbol {k}}) + k_l P_{jm}({\boldsymbol {k}})$, where $P_{jl}({\boldsymbol {k}}) = \delta _{jl} - k_j k_l / k^{2}$ with $\delta _{jl}$ being the Kronecker delta and $k = |{\boldsymbol {k}}|$. The real and imaginary parts of the noise, $\hat {\xi }_\alpha ({\boldsymbol {k}}, t)$, are identically and independently distributed Gaussian random variables with the following mean and covariance:

(2.11)\begin{gather} \langle \hat{\xi}_\alpha({\boldsymbol{k}}, t) \rangle = 0, \end{gather}

(2.12)\begin{gather}\langle \hat{\xi}_\alpha({\boldsymbol{k}}, t) \hat{\xi}_\beta({\boldsymbol{p}}, s) \rangle = 2 \sigma^{2}(k) T \delta_{\alpha, \beta} \delta_{{\boldsymbol{k}}, -{\boldsymbol{p}}} \delta(t - s), \end{gather}

where $\sigma (k)$ is some function of $k$, $T$ is a parameter which we call ‘temperature’ in this paper for convenience and $\delta (t)$ is the Dirac delta function.

The diagonal linear response function with the noise, denoted by $G^{(T)}_{\alpha \alpha }({\boldsymbol {k}}, t\mid -{\boldsymbol {k}}, s)$, is expressed as

(2.13)\begin{equation} G^{(T)}_{\alpha \alpha}({\boldsymbol{k}}, t\mid{-}{\boldsymbol{k}}, s) = \frac{1}{2\sigma^{2}(k) T} \left\langle \hat{u}_\alpha({\boldsymbol{k}}, t) \hat{\xi}_\alpha(-{\boldsymbol{k}}, s) \right\rangle. \end{equation}

We denote the right-hand side of (2.13) as $J^{(T)}_{\alpha \alpha }({\boldsymbol {k}}, t\mid -{\boldsymbol {k}}, s)$. This is the first FRR which we consider. The value of $J^{(T)}_{\alpha \alpha }({\boldsymbol {k}}, t\mid -{\boldsymbol {k}}, s)$ at the equal time, $t - s = 0$, should be one, which is guaranteed by the variance (2.12). In Carini & Quadrio (Reference Carini and Quadrio2010), the expression (2.13) was shown numerically to be equal to the linear response function in the dissipation range without the random noise if the noise is sufficiently small.

This FRR holds in general for a randomly forced system. As the name, FRR, indicates, it gives the relation between the fluctuation (the random noise) and the response. The FRR (2.13) has been used in statistical mechanics, see for example Cugliandolo, Kurchan & Parisi (Reference Cugliandolo, Kurchan and Parisi1994), and can be obtained also from the statistical field-theoretic formalism on the linear response function, see e.g. § 10.4 of Cardy (Reference Cardy1996) or chapter 36 of Zinn-Justin (Reference Zinn-Justin2002). The theoretical basis of Carini & Quadrio (Reference Carini and Quadrio2010) is Luchini et al. (Reference Luchini, Quadrio and Zuccher2006), in which the FRR was referred to as a well-known result of signal theory. According to Marconi et al. (Reference Marconi, Puglisi, Rondoni and Vulpiani2008), this FRR, not only for the Navier–Stokes equations but also for general Langevin equations, is ascribed to Novikov (Reference Novikov1965). In this paper we call it Novikov–Carini–Quadrio FRR.

Now we move to another expression of the linear response function in terms of the two-point or multi-point correlation functions of $\hat {u}$, which was outlined in Matsumoto et al. (Reference Matsumoto, Otsuki, Ooshida, Goto and Nakahara2014). For brevity, we write the nonlinear term and the large-scale forcing as

(2.14)\begin{equation} \varLambda_\alpha({\boldsymbol{k}}, t) = ({\boldsymbol{e}}_\alpha)_j \left(-\frac{\textrm{i}}{2}\right) P_{jlm}({\boldsymbol{k}}) \sum_{\substack{{\boldsymbol{p}}, {\boldsymbol{q}} \\ {\boldsymbol{p}} + {\boldsymbol{q}} + {\boldsymbol{k}} = {\boldsymbol{0}}}} \hat{u}_l(-{\boldsymbol{p}}, t) \hat{u}_m(-{\boldsymbol{q}}, t) + \hat{F}_\alpha({\boldsymbol{k}}, t). \end{equation}

Using this $\varLambda _\alpha ({\boldsymbol {k}}, t)$, we have another expression of the diagonal response function as

(2.15)\begin{align} G^{(T)}_{\alpha \alpha}({\boldsymbol{k}}, t\mid{-}{\boldsymbol{k}}, s) &= \frac{1}{2\sigma^{2}(k) T} \left[ 2\nu k^{2} C_{\alpha \alpha}({\boldsymbol{k}}, t\mid{-}{\boldsymbol{k}}, s) -\left\{ \langle \varLambda_\alpha^{*}({\boldsymbol{k}}, t) \hat{u}_\alpha({\boldsymbol{k}}, s) \rangle\right.\right.\nonumber\\ &\quad \left.\left. + \langle \varLambda_\alpha^{*}({\boldsymbol{k}}, s) \hat{u}_\alpha({\boldsymbol{k}}, t) \rangle \right\} \right]. \end{align}

We denote the right-hand side of (2.15) as $H^{(T)}_{\alpha \alpha }({\boldsymbol {k}}, t \mid -{\boldsymbol {k}}, s)$. This form was derived by adapting the Harada–Sasa relation of the nonlinear Langevin equation in non-equilibrium steady state (Harada & Sasa Reference Harada and Sasa2005, Reference Harada and Sasa2006) to the Navier–Stokes equations with Gaussian noise (2.10). We call $H^{(T)}_{\alpha \alpha }({\boldsymbol {k}}, t \mid - {\boldsymbol {k}}, s)$ the Harada–Sasa FRR in this paper. Heuristically, the Harada–Sasa FRR can be also obtained from (2.13) by re-writing the noise $\hat {\xi }_\alpha (-{\boldsymbol {k}}, s)$ with the dissipation term, $\varLambda _\alpha ({\boldsymbol {k}}, t)$ and the time-derivative term via (2.10). We can next eliminate the time-derivative term by using the causality of the response function and the symmetry of the auto-correlation function $C_{\alpha \alpha }({\boldsymbol {k}}, t\mid -{\boldsymbol {k}}, s)$. Then, we arrive at the Harada–Sasa FRR from the Novikov–Carini–Quadrio FRR. However, the original derivation of the Harada–Sasa FRR does not depend on (2.13). A derivation of (2.15) is given in Appendix A.

Now let us observe the structure of the Harada–Sasa FRR (2.15) at the formal level. It provides a closed expression of the linear response function in terms of the second-order correlation function and many third-order correlation functions (recall that $\varLambda _\alpha ({\boldsymbol {k}}, t)$ involves the nonlinear term as given in (2.14)). In particular, the second and third terms of the FRR (2.15) describe the deviation from the FDT, $G_{\alpha \alpha } \propto C_{\alpha \alpha }$, implying that the nonlinearity is responsible for the deviation. This point will be examined later numerically. Another observation concerns the value of $H^{(T)}_{\alpha \alpha }({\boldsymbol {k}}, t \mid -{\boldsymbol {k}}, s)$ at the equal time, $t - s = 0$, which should be one. This is guaranteed by the statistical steadiness of the energy of each component of the Fourier mode, i.e. $\partial _t \langle |\hat {u}_\alpha ({\boldsymbol {k}}, t)|^{2}\rangle = 0$. More precisely, under the steadiness, the numerator on the right-hand side of (2.15) at $t = s$ is equal to the energy input by the noise, $2\sigma ^{2} T$.

The two FRRs, which are basically equivalent expressions, hold owing to the random noise. However, the noise's role in this study is not physical but just theoretical, as mentioned in § 1. Let us argue that the two FRRs are consistent with the FDT in the absolute equilibrium where the velocity Fourier modes follow the Gaussian distribution and become independent from each other. For the Harada–Sasa FRR, the triple correlation vanishes in the absolute equilibrium and hence it becomes consistent with the FDT. For the Novikov–Carini–Quadrio FRR, we consider it in the following manner. First, the absolute equilibrium for this case can be realised by the Langevin noise with a finite $T$ and $\sigma (k)=k^{1}$, as found by Forster, Nelson & Stephen (Reference Forster, Nelson and Stephen1977). Second, let us here ignore the large-scale forcing $\hat {{\boldsymbol {F}}}({\boldsymbol {k}}, t)$ for the sake of the argument. In this setting, the Navier–Stokes equations become just an Ornstein–Uhlenbeck process given by the viscous term and the noise. Then we can see that the Novikov–Carini–Quadrio FRR expression is consistent with the FDT.

Now, a question we numerically address is the same as Carini & Quadrio (Reference Carini and Quadrio2010): whether the FRRs with a sufficiently small noise amplitude $T$ are good approximations of the response function without the noise. To answer this question, we compare the shell-averaged Novikov–Carini–Quadrio FRR, $J^{(T)}_{\alpha \alpha }({\boldsymbol {k}}, t\mid -{\boldsymbol {k}}, s)$, and the Harada–Sasa FRR, $H^{(T)}_{\alpha \alpha }({\boldsymbol {k}}, t\mid -{\boldsymbol {k}}, s)$, with a small $T$ to the response function without the noise, $G_{\alpha \alpha }(k\mid t - s)$. The shell averages of the FRRs are defined in a similar fashion to (2.9). As a small amplitude, we here take the value of the temperature $T = 10^{-6}$ and $\sigma (k) = k^{-1}$ (which corresponds to the wavenumber-independent noise spectrum). With this choice, the energy spectrum is close to that of the noiseless case except for the far dissipation range as shown in figure 2. To calculate the FRRs, we solve the stochastic Navier–Stokes equations in terms of the vorticity equations in the Cartesian $xyz$ components with the same fourth-order Runge–Kutta method as in the deterministic case (we do not use a stochastic scheme). The noise is generated in the Craya–Herring components, $(\hat {\xi }_\varphi ({\boldsymbol {k}}, t), \hat {\xi }_\theta ({\boldsymbol {k}}, t))$, and then transformed to the $xyz$ components. This noise is added for all the wavenumbers in the computational (Cartesian) Fourier domain. The time-step size is $\Delta t = 1.87 \times 10^{-3}$, which is the same as in the deterministic case. In the Runge–Kutta scheme, we do not generate the random noise at the middle time $t + \Delta t / 2$ but use the same noise generated at the time $t$.

Figure 2. Comparison of energy spectra with and without the small random forcing, $\hat {{\boldsymbol {\xi }}}({\boldsymbol {k}}, t)$. Here, the noise variance parameters in (2.12) are $T = 10^{-6}$ and $\sigma (k) = k^{-1}$.

The numerical calculations of the two FRRs are done as follows. We show here only the $\varphi$ component ($\alpha = \varphi$). For $J^{(T)}_{\varphi \varphi }({\boldsymbol {k}}, t\mid -{\boldsymbol {k}}, s)$, we use the same method as Carini & Quadrio (Reference Carini and Quadrio2010), namely, calculate the correlation between $\hat {u}_\varphi ({\boldsymbol {k}}, t)$ and $\hat {\xi }_\varphi (-{\boldsymbol {k}}, s)$. The calculation of $H^{(T)}_{\varphi \varphi }({\boldsymbol {k}}, t\mid -{\boldsymbol {k}}, s)$ is done by computing the correlations involved, such as $\varLambda _\varphi ^{*}({\boldsymbol {k}}, t)$ and $\hat {u}_\varphi ({\boldsymbol {k}}, s)$ and so forth. The results are shown in figure 3. We observe that the three response functions agree well for large wavenumbers, more precisely, from the end of the inertial range to the dissipation wavenumber $k_\eta$. For smaller wavenumbers, the two expressions start to deviate from each other. While the Novikov–Carini–Quadrio expression $J^{(T)}$ keeps a better agreement with $G$, the Harada–Sasa expression $H^{(T)}$ shows sizeable deviations. By increasing the number of samples, the deviations becomes smaller, however. The worse agreement of $H^{(T)}$ has been anticipated from our previous study of the shell model (Matsumoto et al. Reference Matsumoto, Otsuki, Ooshida, Goto and Nakahara2014) since the summations in the shell-model equivalent of (2.15) caused loss of significant digits, in particular, in the inertial range. This is also the case for the Navier–Stokes case, as we will now show. The Novikov–Carini–Quadrio FRR, $J^{(T)}$, does not have such a cancellation and hence exhibits better agreement.

Figure 3. The shell-averaged Novikov–Carini–Quadrio expression of the linear response function, $J^{(T)} (k, t - s)$, the Harada–Sasa expression, $H^{(T)}(k, t - s)$, and the linear response function in the noiseless case, $G(k, t - s)$, which is the same as shown in figure 1. Here, the noise is specified by $\sigma (k) = k^{-1}$ and $T = 10^{-6}$; (a) for $k = k_\eta , k_\eta /2, k_\eta /4$, (b) for $k = k_\eta / 8, k_\eta / 16$. The Harada–Sasa expression $H^{(T)}$ for $k = k_\eta /16$ (plotted with circles) has the numerical value of $0.2$ at the origin and becomes negative for $(t - s)/\tau _{to} > 0.03$, implying that statistical convergence is not reached. Here, the $k = k_\eta /32 = 5$ case is not shown because of similar but much larger discrepancies.

To discuss the cancellation of significant digits in (2.15), we write separately the shell averages of the nonlinear and linear parts of the Harada–Sasa FRR as

(2.16)\begin{gather} L_\alpha(k, t, s) = \frac{1}{N(k, k + \Delta k)} \sum_{\substack{{\boldsymbol{k}} \\ k \le |{\boldsymbol{k}}| < k + \Delta k}} \frac{1}{2\sigma^{2}(k) T} \langle \varLambda^{*}_\alpha({\boldsymbol{k}}, t) \hat{u}_\alpha({\boldsymbol{k}}, s) \rangle, \end{gather}

(2.17)\begin{gather}D_\alpha(k, t, s) = \frac{1}{N(k, k + \Delta k)} \sum_{\substack{{\boldsymbol{k}} \\ k \le |{\boldsymbol{k}}| < k + \Delta k}} \frac{1}{\sigma^{2}(k) T} \nu k^{2} C_{\alpha \alpha}({\boldsymbol{k}}, t\mid{-} {\boldsymbol{k}}, s). \end{gather}

Here, notice that the wavenumber factors, $\sigma (k)$ and $k^{2}$, are inside the summation. This is necessary for our limited range of the wavenumbers, $k_\eta / 16 = 10 \le k \le 160 = k_\eta$ with $\Delta k = 1$. The shell-averaged Harada–Sasa FRR is given as $H^{(T)}_{\alpha \alpha }(k, t - s) = D_\alpha (k, t, s) - [L_\alpha (k, t, s) + L_\alpha (k, s, t)]$ (which is shown in figure 3). These shell-averaged parts are plotted in figure 4 for $k = k_\eta / 4$ and $k_\eta / 8$. Although the overall shapes of the triple correlations $L_\varphi (k, t, s)$ and $L_\varphi (k, s, t)$ ($t > s$) are nearly symmetrical with respect to the horizontal axis, the former is slightly larger than the latter in magnitude. The positive sign of $L_\varphi (k, t, s)$ can be a reflection of the direct energy cascade. We can now see that the cancellation is twofold: the first is in the sum $L_\varphi (k, t, s) + L_\varphi (k, s, t)$ and the second is in the subtraction of the sum from the viscous term. Roughly one significant digit is lost in each cancellation. This implies that, in order to calculate $H^{(T)}$ with the right order of magnitude, the correlations involved should be calculated with more than 3-digit accuracy. This is a demanding numerical requirement in particular for those in small wavenumbers since a very long integration time is required to make fluctuation of the average small.

Figure 4. Twofold cancellations involved in evaluation of the Harada–Sasa FRR, $H_{\varphi \varphi }^{(T)}(k, t - s) = D_\varphi (k, t - s) - [L_\varphi (k, t, s) + L_\varphi (k, s, t)]$, with $R_\lambda = 210 (k_\eta = 160)$.

Next, we consider Reynolds number effect on the Harada–Sasa FRR. With a smaller Reynolds number, $R_\lambda = 130$ with $\nu = 1.34 \times 10^{-3}$, let us show the FRR in figure 5 and the cancellations in the Harada–Sasa FRR in figure 6. In these figures, the noise is specified by $\sigma (k) = k^{-1}$ and $T = 10^{-6}$. Comparing figure 5 to figure 3(a) for the higher Reynolds number, we find that the FRR's behaviour is similar, although the agreement for the largest $k$ becomes poor for the lower Reynolds number case. We now argue that this poor agreement is due to the cancellations, which become more severe as we decrease the Reynolds number. As shown in figure 6, the twofold cancellations occur also for the lower Reynolds number case. Here, we notice in figure 6(b) that the values of $D_\varphi$ and the sum of $L_\varphi$ for $k = k_\eta /4 = 20$ around the origin ($t - s = 0$) with $R_\lambda = 130$ is approximately $100$. In contrast, the corresponding value is $55$ for $k = k_\eta / 8 = 20$ with $R_\lambda = 210$, as shown in figure 4(b). If this value at the origin is smaller, then the second cancellation, namely the loss of significant digits, becomes less severe. This gives rise to the poor agreement for $k = k_\eta / 4$ shown in figure 5. These observation suggest that, as we increase the Reynolds number, the Harada–Sasa FRR agrees better with the linear response function for small wavenumbers.

Figure 5. Same as figure 3 but with a lower Reynolds number $R_\lambda = 130\, (k_\eta = 80)$.

Figure 6. Same as figure 4 but with a lower Reynolds number $R_\lambda = 130\, (k_\eta = 80)$.

Now let us come back to the formal observation of the Harada–Sasa FRR (2.15). We previously noted that the sum of the second and third terms on the right-hand side of (2.15) is formally responsible for the deviation from the FDT. This formal observation assumes that the functional form of the sum as the time difference, $t - s$, is very much different from that of the first term in (2.15). However, this assumption is not valid, as indicated by the second cancellation. As shown in figure 4(b), the numerical data demonstrate that the functional form of the sum is quite close to that of the viscous contribution. Contrary to the formal observation of (2.15), in reality, the deviation from the FDT arises equally both from the viscous contribution and the nonlinear contributions. The viscous contribution to the deviation is not at all negligible for all of the time range. By contrast, in the shell-model study of the Harada–Sasa FRR (Matsumoto et al. Reference Matsumoto, Otsuki, Ooshida, Goto and Nakahara2014), the second cancellation was not observed. This is probably owing to the extremely small kinematic viscosity of the shell model. It is also consistent with our observation that the second cancellation for the Navier–Stokes case becomes less severe as we decrease the Reynolds number. It is then suggested that the second cancellation does not occur for the Navier–Stokes case if the Reynolds number is sufficiently large. There is one technical remark, however; when we increase the Reynolds number, we may need to adjust the noise temperature $T$ to have the same energy spectrum with $T = 0$ as we illustrated in figure 2. Another implication of the second cancellation shown in figure 4(b) is that the sum of the triple correlations, $L_\varphi (k,t,s) + L_\varphi (k, s, t)$, is very close to $D_\varphi (k, t - s)$ which is the correlation function multiplied by $\nu k^{2}$ in the whole $t - s$ domain. This suggests that this combination of the triple correlations can be well approximated with the pair correlation with a suitable constant depending on $k$, which is considered to be a kind of eddy viscosity.

Regarding the wavenumber-dependent noise amplitude $\sigma (k)$, we have considered numerically so far only one case, $\sigma (k) = k^{-1}$ with $T = 10^{-6}$. In principle, the Novikov–Carini–Quadrio FRR and the Harada–Sasa FRR hold for any $\sigma (k)$ and $T$. We now briefly mention that the FRRs hold numerically for other choices of $\sigma (k)$ and $T$. Indeed, with an arbitrary choice of $\sigma (k)$ and $T$, the corresponding numerical solution can be quite different from what we wish to simulate as turbulent flow in nature. For example, the energy spectrum may be different from the Kolmogorov spectrum $E(k) \propto k^{-5/3}$. But our focus here is to use those FRRs with the random noise to approximate the linear response function without the noise. For this purpose, given $\sigma (k)$, we expect that sufficiently small $T$ enables us to have the Eulerian velocity with the noise being statistically close to the one without the noise. It should be noticed here that, in addition to the noise, we have the large-scale forcing $\hat {{\boldsymbol {F}}}({\boldsymbol {k}}, t)$. As one variation of $k$-dependence of $\sigma (k)$, we set $\sigma (k) = k^{-2}$ with $R_\lambda = 130$. In this case, we find that $T=10^{-4}$ is small enough to have the same $E(k)$ as in the noiseless case. The FRRs for this noise behave similarly to those as depicted in figure 3.

To test the FRRs for the velocity field with $E(k) \not \propto k^{-5/3}$, an easy way is to use a suitable $\sigma (k)$ and to increase the temperature $T$. In one numerical experiment with $R_\lambda = 130$, we consider $\sigma (k) = k^{-1}$ and $T = 10^{-4}$, where the energy spectrum becomes $E(k) \propto k^{-1}$ for all the wavenumbers (if $T$ is much smaller than that value, $E(k)$ follows $k^{-5/3}$ because of the large-scale forcing $\hat {{\boldsymbol {F}}}({\boldsymbol {k}}, t)$). This spectrum $E(k) \propto k^{-1}$ is consistent with the renormalisation group analysis for $\sigma (k) = k^{-1}$, see, e.g. Frisch (Reference Frisch1996) and Sain, Manu & Pandit (Reference Sain and Pandit1998). In this non-Kolmogorov case, the directly measured linear response function $G_{\varphi \varphi }^{(T)}$ also differs from the noiseless one $G_{\varphi \varphi }$. We here also find that the Novikov–Carini–Quadrio FRR and the Harada–Sasa FRR agree well with the directly measured response function $G_{\varphi \varphi }^{(T)}$. From these examples it is now clear that those FRRs are not limited to the case characterised by the Kolmogorov spectrum.

To summarise, we conclude that the two FRRs with the sufficiently small random noise agree well with the linear response function in the deterministic setting (without the random noise) at least from the dissipation range up to the middle of the inertial range. In practice, the Novikov–Carini–Quadrio FRR, $J^{(T)}$, is numerically easier to calculate accurately than the Harada–Sasa FRR, $H^{(T)}$. The direct evaluation of the linear response function (Biferale et al. Reference Biferale, Daumont, Lacorata and Vulpiani2001) yields the least fluctuating result among the three methods, although its computational cost is high. It requires us to solve simultaneously two solutions of the Navier–Stokes equations. In principle, one solution of the Navier–Stokes equations and one solution of the linearised Navier–Stokes equations are sufficient for the direct evaluation. However, its cost is not very different from solving the two fully nonlinear equations. We show a possible theoretical use of the Novikov–Carini–Quadrio FRR in Appendix C, which is related to the subject of § 4.

The details of the averaging of the FRRs in this section are as follows. With $R_\lambda = 210$, the length of the temporal window for calculating $H^{(T)}$ and $J^{(T)}$ is $0.267\tau _{to}$ for the large wavenumbers $k = k_\eta , k_\eta / 2$ and $k_\eta / 4$. The total number of the windows is 200. In one simulation we take 20 windows consecutively. Furthermore, we repeat this for the ensemble of 10 simulations. For the small wavenumbers, $k = k_\eta / 8$ and $k_\eta / 16$, the window length is $0.667\tau _{to}$. The total number of windows is 100, which consists of 10 consecutive windows in each simulation of the ensemble. In the low Reynolds number ($R_\lambda = 130$) case shown in figures 5 and 6, the time window to calculate the FRRs is $0.554\tau _{to}$ and the total number of windows is 200. We take 100 windows consecutively in one simulation. We repeat this for the ensemble of two simulations.

3.1. Passive vector method for the Lagrangian velocity

We use Kraichnan's notation of the Lagrangian velocity, ${\boldsymbol {v}}({\boldsymbol {a}}, t_\ell \mid t_m)$, also known as the generalised velocity (Kraichnan Reference Kraichnan1965). This is the velocity of a fluid particle measured at time $t = t_m$, which is called the measuring time. This particular fluid particle passes the point whose coordinate is ${\boldsymbol {a}}$ at time $t = t_\ell$. The coordinate ${\boldsymbol {a}}$ and the time $t_\ell$ are called the Lagrangian label and the labelling time, respectively. An intuitively natural choice is $t_m \ge t_\ell$ as made in the LRA and the LDIA. In the ALHDIA the opposite choice $t_\ell \ge t_m$ was made: one lets the labelling time vary by keeping the measuring time constant. In this case, the velocity measured at the fixed time, $t_m$, is a Lagrangian invariant later in the labelling time. Therefore, we have the following passive vector equations describing the labelling-time evolution of the Lagrangian velocity:

(3.1)\begin{equation} \partial_{t_\ell} {\boldsymbol{v}}({\boldsymbol{x}}, t_\ell\mid t_m) + ({\boldsymbol{u}}({\boldsymbol{x}}, t_\ell) \boldsymbol{\cdot} {\boldsymbol{\nabla}}) {\boldsymbol{v}}({\boldsymbol{x}}, t_\ell\mid t_m) = {\boldsymbol{0}}. \end{equation}

The initial condition of the Lagrangian velocity is given by the Eulerian velocity at the measuring time.

In our numerical simulation of the statistically steady state, we set the initial Lagrangian velocity from the Eulerian velocity by ${\boldsymbol {v}}({\boldsymbol {x}}, t_m\mid t_m) = {\boldsymbol {u}}({\boldsymbol {x}}, t_m)$, we then solve the passive vector equation (3.1) and the Navier–Stokes equations (2.1) simultaneously with the same numerical method as described in § 2.1. After some long time, we reset the Lagrangian velocity to the current Eulerian velocity. Repeating this procedure, we obtain an ensemble of the Lagrangian velocity evolving in the labelling time.

It is known that this passive vector method for the Lagrangian velocity has a serious numerical difficulty due to the lack of any dissipation in (3.1), see e.g. Gotoh et al. (Reference Gotoh, Rogallo, Herring and Kraichnan1993). The difficulty is that the energy spectrum of the Lagrangian velocity, $E_v(k, t_\ell )$, starting with the same spectrum as the Eulerian one at $t_\ell = t_m$, increases quickly, especially at high wavenumbers. Hence, the truncation error of the Lagrangian velocity becomes large in a finite time. The question is, how long we can trust the Lagrangian velocity calculated with the passive vector method for a given spatial resolution? We will examine this point in the next subsection.

3.2. Lagrangian correlation and linear response function

Having obtained the Fourier coefficient of the Lagrangian velocity, $\hat {{\boldsymbol {v}}}({\boldsymbol {k}}, t_\ell \mid t_m)$, we consider the following Lagrangian correlation function:

(3.2)\begin{equation} C^{(L)}_{jn}({\boldsymbol{k}}, {\boldsymbol{q}}, t_\ell \mid t_\ell, t_m) = \langle \hat{v}_j({\boldsymbol{k}}, t_\ell \mid t_\ell) \hat{v}_n({\boldsymbol{q}}, t_\ell \mid t_m) \rangle = \langle \hat{u}_j({\boldsymbol{k}}, t_\ell) \hat{v}_n({\boldsymbol{q}}, t_\ell\mid t_m) \rangle \end{equation}

and the linear response function

(3.3)\begin{equation} G^{(L)}_{jn}({\boldsymbol{k}}, {\boldsymbol{q}}, t_\ell\mid t_\ell, t_m) = \left\langle \frac{\delta \hat{v}_j({\boldsymbol{k}}, t_\ell\mid t_\ell)} {\delta \hat{v}_n({\boldsymbol{q}}, t_\ell\mid t_m)} \right\rangle = \left\langle \frac{\delta \hat{u}_j({\boldsymbol{k}}, t_\ell)} {\delta \hat{v}_n({\boldsymbol{q}}, t_\ell\mid t_m)} \right\rangle, \end{equation}

for $t_\ell \ge t_m$. Notice that the two functions in this time ordering are the same as used in the ALHDIA. The indices, $j$ and $n$, take values $1, 2$ or $3$ which correspond to the $x$, $y$ and $z$ components, respectively. The Lagrangian velocity ceases to be solenoidal for $t_\ell > t_m$. To define the linear response function in (3.3), we adopt the notation used by Kida & Goto (Reference Kida and Goto1997). Hence, the variation is with respect to the velocity, not the infinitesimal probe force or the source term.

Let us compare the Lagrangian response function (3.3) with those Lagrangian response functions used in the DIAs. The one used in the LHDIA (Kraichnan Reference Kraichnan1965) corresponds to

(3.4)\begin{equation} G^{(L)}_{jn}({\boldsymbol{k}}, t_\ell\mid t_m; {\boldsymbol{q}}, s_\ell\mid s_m) = \left\langle \frac{\delta \hat{v}_j({\boldsymbol{k}}, t_\ell\mid t_m)} {\delta \hat{f}_n({\boldsymbol{q}}, s_\ell\mid s_m)} \right\rangle, \end{equation}

with $t_\ell \ge t_m$ and $s_\ell \ge s_m$. Hence, four time variables are involved in the LHDIA. Here, $\hat {{\boldsymbol {f}}}({\boldsymbol {q}}, s_\ell \mid s_m)$ is the Fourier mode of the infinitesimal probe force added to the right-hand side of (3.1). Another one used in the ALHDIA (Kraichnan Reference Kraichnan1965, Reference Kraichnan1966) is an abridged version of (3.4),

(3.5)\begin{equation} G^{(L)}_{jn}({\boldsymbol{k}}, t_\ell\mid t_\ell; {\boldsymbol{q}}, t_\ell\mid t_m) = \left\langle \frac{\delta \hat{v}_j({\boldsymbol{k}}, t_\ell\mid t_\ell)} {\delta \hat{f}_n({\boldsymbol{q}}, t_\ell\mid t_m)} \right\rangle, \end{equation}

where only two time variables are involved and the numerator is an equal-time velocity. This (3.5) coincides with (3.3), which we will study numerically. Yet another one used in the LRA and the LDIA is

(3.6)\begin{equation} G^{(L)}_{jn}({\boldsymbol{k}}, t_\ell\mid t_m; {\boldsymbol{q}}, t_\ell\mid t_\ell) = \left\langle \frac{\delta \hat{v}_j({\boldsymbol{k}}, t_\ell\mid t_m)} {\delta \hat{g}_n({\boldsymbol{q}}, t_\ell\mid t_\ell)} \right\rangle, \end{equation}

with $t_\ell \le t_m$ (Kaneda Reference Kaneda1981; Kida & Goto Reference Kida and Goto1997). This time ordering is different from that in the ALHDIA and our DNS study. Here, $\hat {{\boldsymbol {g}}}({\boldsymbol {q}}, t_\ell \mid t_m)$ is the infinitesimal probe force added to the right-hand side of the measuring-time evolution equation of the Lagrangian velocity (B4): see also Appendices B and D.

We now move to DNS of (3.2) and (3.3). We calculate the correlation function (3.2) from the Lagrangian velocity in the same way as the Eulerian one. Let us here write the time of the Eulerian simulation as $t$. For the direct calculation of the response function (3.3), we add a small initial perturbation $\Delta \hat {{\boldsymbol {u}}}({\boldsymbol {k}}, t_0)$ at $t = t_0$, to both the Eulerian and Lagrangian velocity fields. This ‘initial’ time $t_0$ for the perturbation becomes the measuring time for the Lagrangian velocity, namely, $t_0 = t_m$. We then consider evolution in the labelling time $t = t_\ell \, (\ge t_m)$ of the two pairs of velocity fields: the unperturbed pair, $( \hat {{\boldsymbol {u}}}({\boldsymbol {k}}, t), \hat {{\boldsymbol {v}}}({\boldsymbol {k}}, t\mid t_m))$, and the perturbed pair, $( \hat {{\boldsymbol {u}}}^{\prime } ({\boldsymbol {k}}, t), \hat {{\boldsymbol {v}}}^{\prime }({\boldsymbol {k}}, t\mid t_m))$. For the two pairs, we solve the Navier–Stokes equations (2.1) and the passive vector equations (3.1) simultaneously. More specifically, the starting condition of the perturbed pair is $\hat {{\boldsymbol {u}}}^{\prime } ({\boldsymbol {k}}, t_m) = \hat {{\boldsymbol {u}}}({\boldsymbol {k}}, t_m) + \Delta \hat {{\boldsymbol {u}}}({\boldsymbol {k}}, t_m)$ and $\hat {{\boldsymbol {v}}}^{\prime } ({\boldsymbol {k}}, t_m\mid t_m) = \hat {{\boldsymbol {u}}}^{\prime } ({\boldsymbol {k}}, t_m)$. For the unperturbed Lagrangian velocity, $\hat {{\boldsymbol {v}}}({\boldsymbol {k}}, t_m\mid t_m) = \hat {{\boldsymbol {u}}}({\boldsymbol {k}}, t_m)$. The response function at labelling time $t$ can be obtained via $[\hat {{\boldsymbol {u}}}^{\prime } ({\boldsymbol {k}}, t) - \hat {{\boldsymbol {u}}}({\boldsymbol {k}}, t)]/ [\hat {{\boldsymbol {v}}}^{\prime } ({\boldsymbol {k}}, t\mid t_m) - \hat {{\boldsymbol {v}}}({\boldsymbol {k}}, t\mid t_m)]$. We repeat this procedure to calculate the Lagrangian response function.

In figure 7, we show the shell-averaged correlation and response functions

(3.7)\begin{gather} C^{(L)}(k, t_\ell - t_m) = \frac{1}{3N(k, k + \Delta k)} \sum_{\substack{{\boldsymbol{k}} \\ k \le |{\boldsymbol{k}}| < k + \Delta k}} C^{(L)}_{jj}({\boldsymbol{k}}, -{\boldsymbol{k}}, t_\ell\mid t_\ell, t_m), \end{gather}

(3.8)\begin{gather}G^{(L)}(k, t_\ell - t_m) = \frac{1}{3N(k, k + \Delta k)} \sum_{\substack{{\boldsymbol{k}} \\ k \le |{\boldsymbol{k}}| < k + \Delta k}} G^{(L)}_{jj}({\boldsymbol{k}}, -{\boldsymbol{k}}, t_\ell\mid t_\ell, t_m). \end{gather}

Here, we take summation over the index $j$. We add the initial perturbation $\Delta \hat {u}_j({\boldsymbol {k}}, t_m)$ for all the modes within the shell $k \le |{\boldsymbol {k}}| < k + \Delta k$. The initial perturbation for each mode is set as $\Delta \hat {{\boldsymbol {u}}}({\boldsymbol {k}}, t_m) = \Delta u_0 {\boldsymbol {e}}_\varphi + \Delta u_0 {\boldsymbol {e}}_\theta$. Here, $\Delta u_0$ is a real positive number whose magnitude is five per cent of the standard deviation of $|\hat {u}_\varphi ({\boldsymbol {k}}, t)|$.

Figure 7. Shell-averaged correlation functions and linear response functions in Lagrangian coordinates for $k = k_\eta, k_\eta / 2, k_\eta / 4$ from left to right (a) and for $k = k_\eta/8, k_\eta/16, k_\eta/32$ from left to right (b). We show only the real parts since the imaginary parts are orders-of-magnitude smaller. The correlations of $k = k_\eta / 2$ and $k_\eta / 4$ are very close to each other. The increase of the correlation functions at short time is discussed in the text. The noisy behaviour of the response functions is due to lack of the statistical samples. In (b), the response functions are calculated up to around $t_\ell - t_m = 0.55\tau _{to}$.

Before discussing the results shown in figure 7, let us first consider the effect of the truncation error of the passive vector method. As shown in figure 7, it takes approximately one large-scale turnover time, which is approximately $\tau _{to} = 1.80$, for the correlation function to decrease to $20\,\%$ of the value at the origin $t_\ell - t_m = 0$ for the small wavenumber $k = k_\eta / 16$. The question is then, with the resolution $k_{max} \eta = 1.50$, whether we can trust the computed correlation function and response function up to this time lag, $t_\ell - t_m \simeq \tau _{to}$. To answer this question, we do the following resolution study. We decrease the Reynolds number to $R_\lambda = 130$ by setting the kinematic viscosity to $\nu = 1.34\times 10^{-3}$. We compute this case with two resolutions, $256^{3}$ and $512^{3}$ grid points. The two simulations yield $k_{max}\eta = 1.50$ and $3.00$, respectively. The large-scale turnover time is approximately $1.74$. We compare the correlation functions calculated with the two resolutions in figure 8. We observe that the correlation functions agree well up to approximately one large-scale turnover time. Regarding the Lagrangian response function, whose numerical calculation is costly, we further decrease the Reynolds number to $R_\lambda = 70$ ($\nu = 3.75 \times 10^{-3}$) and calculate the solutions with two resolutions, $128^{3}$ and $256^{3}$ grid points. The two simulations have $k_{max} \eta = 1.63$ and $3.26$. The large-scale turnover time is now $1.86$. The comparison of the response function is shown in figure 9. We observe that the response functions for the small wavenumbers agree well up to one turnover time. Therefore, we infer that $k_{max}\eta = 1.50$ is sufficient to study the correlation function and the response function up to one large-scale turnover time in our study. In Gotoh et al. (Reference Gotoh, Rogallo, Herring and Kraichnan1993), $k_{max}\eta = 2.0$ is recommended, however.

Figure 8. Resolution dependence of the Lagrangian correlation function for $R_\lambda = 130$. The Kolmogorov dissipation wavenumber is $k_\eta = 80$. The truncation wavenumbers of the two resolutions are $k_{max} = 120$ and $241$. The correlation functions of $k = k_\eta / 4$ and $k_\eta / 2$ are again very close, as in figure 7.

Figure 9. Resolution dependence of the Lagrangian linear response function for $R_\lambda = 70$. The Kolmogorov dissipation wavenumber is here $k_\eta = 37$ For simplicity, we take $k_\eta / 2, k_\eta / 4$ and $k_\eta / 8$ as $k = 18, 9$ and $5$, respectively. The truncation wavenumbers of the two resolutions are $k_{max} = 60$ and $120$.

Having checked that the correlation function and the response function are reliable up to $t_\ell - t_m \simeq \tau _{to}$, we now list observations from figure 7. First, the Lagrangian correlation functions decrease more slowly than the Eulerian ones, which will be analysed quantitatively in the next section. Second, the correlation functions at the equal time $t_\ell - t_m = 0$ have positive slopes (time derivatives) and hence their peaks are shifted from the origin for all the six wavenumbers shown in figure 7. For small wavenumbers, the slopes at the origin in figure 7 are hardly seen as positive, but we verify that they are positive by magnifying the figure. This positive slope at the origin is peculiar. It is caused by the asymmetry of the Lagrangian correlation function with respect to swapping the labelling and measuring times, $t_\ell$ and $t_m$, as discussed in Kraichnan (Reference Kraichnan1966) and Gotoh et al. (Reference Gotoh, Rogallo, Herring and Kraichnan1993) for the physical space. It can be shown that the slope at the origin, $\partial _{t_\ell } C_{jj}^{(L)}({\boldsymbol {k}}, -{\boldsymbol {k}}, t_\ell \mid t_\ell , t_m)$ as $t_\ell \to t_m$ (from above), is equal to $\partial _{t_\ell } \langle |\hat {{\boldsymbol {v}}}({\boldsymbol {k}}, t_\ell \mid t_m)|^{2} \rangle /2$ in the same limit. In order to observe how the Lagrangian modes change in time, we show the labelling-time evolution of the energy spectrum of the Lagrangian velocity in figure 10, which is defined as

(3.9)\begin{equation} E_v(k, t_\ell\mid t_m) = \sum_{\substack{{\boldsymbol{k}}\\ k \le |{\boldsymbol{k}}| < k + \Delta k}} \tfrac{1}{2} |\hat{{\boldsymbol{v}}}({\boldsymbol{k}}, t_\ell \mid t_m)|^{2}, \end{equation}

where $\Delta k = 1$. As shown in figure 10, the Lagrangian spectrum $E_v(k, t_\ell \mid t_m)$ for large $k \,(\sim k_\eta )$ becomes much larger than the initial spectrum that is identical to the Eulerian energy spectrum. As explained in Kraichnan (Reference Kraichnan1966) and Gotoh et al. (Reference Gotoh, Rogallo, Herring and Kraichnan1993), the spectrum $E_v(k, t_\ell \mid t_m)$ for $k \ge k_\eta$, if it is fully numerically resolved, grows toward the $k^{-1}$ spectrum by the same mechanism as the viscous–convective-range spectrum for the passive scalar. This growth corresponds to $\partial _{t_\ell } \langle |\hat {{\boldsymbol {v}}}({\boldsymbol {k}}, t_\ell \mid t_m)|^{2} \rangle > 0$ at short times for large $k$ and this implies $\partial _{t_\ell } C_{jj}^{(L)}({\boldsymbol {k}}, -{\boldsymbol {k}}, t_\ell \mid t_\ell , t_m) > 0$ for large $k$. Therefore, the Lagrangian velocity correlation of large $k$ grows at short times, as seen in figures 7(a) and 8. At the same time, the total kinetic energy of the Lagrangian velocity is conserved. To respect this conservation, the spectrum $E_v(k, t_\ell \mid t_m)$ for small $k$ decreases, as seen in figure 10. This implies that $\partial _{t_\ell } C_{jj}^{(L)}({\boldsymbol {k}}, -{\boldsymbol {k}}, t_\ell \mid t_\ell , t_m) < 0$ for small $k$ at short times. Indeed, in our simulation, for the two smallest wavenumbers, $k = 1$ and $2$, the slopes of the Lagrangian velocity correlation at the origin are negative (figure not shown).

Figure 10. Labelling-time evolution of the energy spectrum of the Lagrangian velocity with $R_\lambda = 210$. The plotted curves’ labelling times correspond to $t_\ell = t_m, t_m + 0.05\tau _{to}, t_m + 0.1 \tau _{to}, t_m + 0.2 \tau _{to}, \ldots , t_m + 1.0\tau _{to}$. We take neither temporal nor ensemble averages for each curve.

Lastly, we observe that the FDT, $C^{(L)} \propto G^{(L)}$, is violated also in Lagrangian coordinates for all the wavenumbers shown in figure 7. In the Lagrangian coordinates, the response functions are larger than the correlation functions for small wavenumbers. In the Eulerian coordinates, the opposite is true, as shown in figure 1. The same tendency as in the Lagrangian coordinates, namely $G > C$, was observed in the shell model (Matsumoto et al. Reference Matsumoto, Otsuki, Ooshida, Goto and Nakahara2014). We do not have an explanation for this tendency in Lagrangian coordinates. Comparing the present result to that of the ALHDIA, we note that the difference between the Lagrangian correlation function and the response function obtained here is much larger than that of the ALHDIA for the inertial range, which was shown in figure 2 of Kraichnan (Reference Kraichnan1966). The ALHDIA's two functions are nearly identical in the range of the vertical axis, $0.6 \le G^{(L)} \le 1.0$ and then they deviate from each other in $G^{(L)} \le 0.6$. A possible explanation for this discrepancy between ours and the ALHDIA's is a finite Reynolds number effect since the ALHDIA treated the inertial-range quantities by setting $\nu = 0$.

Let us here comment on the FRR in Lagrangian coordinates. An FRR expression of the Lagrangian response function (3.3) analogous to the Eulerian FRRs cannot be obtained by adding the Gaussian random forcing to the right-hand side of the passive vector equation (3.1) in Fourier space. This is because the Lagrangian velocity measured at $t_\ell$, which is in the numerator of (3.3), is not a solution to the passive vector equation. Instead, to obtain an FRR, we should add the Gaussian noise to the equation of the Lagrangian velocity ${\boldsymbol {v}}({\boldsymbol {a}}, t_\ell \mid s_m)$, which describes the evolution in the measuring time $s_m$ ranging from $t_m$ to $t_\ell$ (see (B4) in Appendix B). Notice that this equation is different from the passive vector equation (3.1) describing the evolution in the labelling time. Under this setting, the Novikov–Carini–Quadrio FRR and the Harada–Sasa FRR for the Lagrangian response function are obtained on a formal level, as we describe in Appendix B. Contrary to the Eulerian case, numerical computation of these Lagrangian FRRs as they are is nearly impossible since it requires evaluation of the position function (Kaneda Reference Kaneda1981). This is beyond the scope of our present study. Therefore we do not pursue numerical study of the Lagrangian FRRs here.

We end this section by describing the number of samples used in the calculation of the Lagrangian correlation functions and the response functions. The correlation functions shown in figure 7 are averaged in the following way. The length of the temporal window for calculating the correlation function is $1.67\tau _{to}$ and we take five consecutive windows from two simulations. Thus the total number of samples is 10. The response functions shown in figure 7 are averaged as follows. For the large wavenumbers, $k=k_\eta , k_\eta / 2$ and $k_\eta / 4$, the total number of samples is 20. Here, the length of the time windows are $0.333\tau _{to}, 0.333\tau _{to}$ and $0.444\tau _{to}$, respectively. We take the 20 windows consecutively in one simulation. For the small wavenumbers, $k=k_\eta / 8 , k_\eta / 16$ and $k_\eta / 32$, the total number of samples are 20, 32 and 32, respectively. The window lengths are $0.556\tau _{to}$, $0.667\tau _{to}$ and $0.667 \tau _{to}$, respectively. We place the windows consecutively in one simulation. As in the Eulerian case, we check the convergence of the correlation function and the response function by comparing the average over the full samples and some smaller samples. Here, we decrease the number of samples by $1/2$. The difference between the averages for the two sample data sets is within a few per cent for both the correlation function and the response function. In this sense, we regard that the correlation function and the response function have reached convergence.

In the resolution study, the correlation functions shown in figure 8 are averaged as follows. For the $k_{max}\eta = 1.5$ case with $256^{3}$ grid points, we take $29$ consecutive windows with the length $1.69\tau _{to}$ from one simulation. Hence, the total number of samples is $29$. For the $k_{max}\eta = 3.0$ case with $512^{3}$ grid points, we take 5 consecutive windows with the length $3.0$ from one simulation. Hence, the total number of samples is 5. Although the sample sizes differ by approximately a factor 6, good agreement is observed. In the resolution study of the response function shown in figure 9, we use $128^{3}$ and $256^{3}$ grid points. We take the windows of the following sizes, $0.430\tau _{to}, 0.538\tau _{to}, 1.08\tau _{to}$ and $1.08\tau _{to}$, for $k = k_\eta , k_\eta /2, k_\eta / 4$ and $k_\eta / 8$, respectively. The number of the windows are $30$ for $k = k_\eta , k_\eta /2$ and $60$ for $k_\eta / 4, k_\eta / 8$. The windows are placed consecutively in one simulation. This setting is the same for the two resolutions.