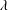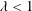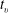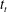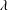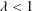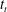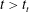1 Introduction
Liquid waste from coastal cities is often discharged into the marine environment through outfall tunnels drilled into the seabed. At the point of discharge, the (buoyant) effluent emanates from multiple diffusers and then merges together to form a single line-plume. The plume continues to rise to the sea surface if the sea water has uniform density. More desirably, density stratification may cause the plume to spread at some intermediate depth along its level of neutral buoyancy. In the coastal ocean, where ascending effluent plumes are situated, seawater can vary between states of uniform density and comparatively strong stratification. This variation has an obvious impact on the height of rise of the effluent. For example, the waste water from Boston is discharged into Massachusetts Bay, which tends to be well mixed in winter because of surface cooling and wind forcing. In summer, near-surface waters become both fresher and warmer as a result of which the plume is trapped below this light surface layer (Hunt et al. Reference Hunt, Mansfield, Mickelson, Albro, Geyer and Roberts2010).
At smaller scales, a plume in an evolving stratified environment is also relevant to naturally or hybrid ventilated buildings. Consider, for example, a building that contains internal sources of buoyancy in the form of heat-producing electrical equipment that creates vertically ascending thermal plumes. This heat is vented to the exterior environment through high-level openings. The escaping buoyant air is, in turn, replaced with cool ambient air that enters the building through low-level openings (Linden, Lane-Serff & Smeed Reference Linden, Lane-Serff and Smeed1990). An interior two-layer stratification thereby develops where, at steady state, the temperature of the buoyant upper layer matches the temperature of the plume at the interface. Any subsequent changes in the plume source conditions, for example due to an alteration of equipment operation (Bolster, Maillard & Linden Reference Bolster, Maillard and Linden2008), may lead to partial and eventual full detrainment of the plume below the ceiling.
Common to both of the above examples is vertical convection from an isolated source that yields an (ascending) plume. Plume flow in a stratified or uniform ambient was investigated quantitatively by Morton, Taylor & Turner (Reference Morton, Taylor and Turner1956), who developed a one-dimensional model to describe a statistically steady turbulent plume released from a point source into an unbounded uniform or stratified ambient. In particular, analytical solutions were found for the case of a uniform ambient. This model has since been tested and widely adapted to a variety of circumstances including effects of a finite-sized ambient (Baines & Turner Reference Baines and Turner1969; Germeles Reference Germeles1975), plumes and fountains in stratified fluids (Morton Reference Morton1959; Bloomfield & Kerr Reference Bloomfield and Kerr1998, Reference Bloomfield and Kerr2000), and line-plumes in two-layer stratified fluids (Noh, Fernando & Ching Reference Noh, Fernando and Ching1992) – see Woods (Reference Woods2010) for further details.
In one particularly relevant application, Baines & Turner (Reference Baines and Turner1969) examined the evolution of the (initially uniform) ambient density in a finite control volume containing an ascending vertical plume: the so-called filling-box model. Upon reaching the free surface, the plume fluid spread in the lateral direction to form a lighter upper layer that deepened in time. The ‘first front’, the interface between the discharged plume fluid and the original ambient, descended against the direction of the rising plume and some fraction of this discharged plume fluid was re-entrained into the plume and carried again to the free surface. Although the lighter density of the upper layer diminished the plume vertical velocity, the density difference across the first front never became so strong that the plume could not arrive at the free surface.
Numerous other studies have expanded upon the seminal work of Baines & Turner (Reference Baines and Turner1969) by considering a non-uniform ambient at the initial time. For example, Kumagai (Reference Kumagai1984) generated a dense plume through a nozzle placed at the free surface of a two-layer stratified ambient, in which the plume could not initially fall through the lower layer. The plume evolved to become a fountain below the ambient interface rising back to the interface and then spreading horizontally. Kumagai (Reference Kumagai1984) adapted the filling-box model by parameterizing the entrainment from the lower layer fluid below the interface. This so-called fountain top entrainment had the effect of progressively deepening the interface as a result of the transport of entrained lower layer fluid returning upwards. Following Kumagai (Reference Kumagai1984), Mott & Woods (Reference Mott and Woods2009) considered plume impingement from above upon an ambient interface as an intense mixing process that thickened the interface instead of deepening it. In collapsing their data, Mott & Woods (Reference Mott and Woods2009) found it helpful to introduce a parameter
$\unicode[STIX]{x1D6EC}$
, which was the ratio of the reduced gravity of the plume just above the interface with respect to the upper layer ambient to the reduced gravity associated with the upper and lower ambient layers. For
$0\leqslant \unicode[STIX]{x1D6EC}<1$
, the plume at the location of the interface was lighter than the lower layer fluid and so was expected to spread along the ambient interface. By contrast, for
$\unicode[STIX]{x1D6EC}>1$
, the plume was expected to descend into the lower layer. The values of
$\unicode[STIX]{x1D6EC}$
in the experiments of Kumagai (Reference Kumagai1984) were limited to between 0 and 0.15, while Mott & Woods (Reference Mott and Woods2009) ran experiments with a notably larger range:
$0<\unicode[STIX]{x1D6EC}<0.64$
. In both sets of experiments the plume was observed to spread along the interface, as expected. In this case the plume flow in the upper layer can be regarded, at least initially, as a filling-box process with the interface serving as a surrogate bottom boundary.
Wallace & Sheff (Reference Wallace and Sheff1987) and Kulkarni, Murphy & Manohar (Reference Kulkarni, Murphy and Manohar1993) respectively performed experiments of line-source and point-source plumes with effective values of
$\unicode[STIX]{x1D6EC}$
being less than and greater than unity. Although they did not compute this quantity explicitly, the values of
$\unicode[STIX]{x1D6EC}$
ranged from 0.19 to 2.92 in the study of Wallace & Sheff (Reference Wallace and Sheff1987) and from 0.11 to 2.76 in the study of Kulkarni et al. (Reference Kulkarni, Murphy and Manohar1993). These
$\unicode[STIX]{x1D6EC}$
values we estimate from plume theory assuming an ideal point-source and an entrainment coefficient of 0.1. In both sets of experiments the tank was sufficiently large that boundaries played an insignificant role. Wallace & Sheff (Reference Wallace and Sheff1987) and Kulkarni et al. (Reference Kulkarni, Murphy and Manohar1993) observed different evolution regimes depending upon different combinations of the experimental parameters, including the density and volume flux of the plume source, the depth of the upper layer and the densities of the upper and lower layers. If the plume density just above the interface was significantly greater than that of the lower layer (
$\unicode[STIX]{x1D6EC}\geqslant 2.92$
in the study of Wallace & Sheff (Reference Wallace and Sheff1987) and
$\unicode[STIX]{x1D6EC}\geqslant 2.25$
in the study of Kulkarni et al. (Reference Kulkarni, Murphy and Manohar1993)), all of the plume fluid penetrated through the interface. Conversely, if the density of the plume just above the interface was smaller than that of the lower layer (
$\unicode[STIX]{x1D6EC}\leqslant 0.19$
in the study of Wallace & Sheff (Reference Wallace and Sheff1987) and
$\unicode[STIX]{x1D6EC}\leqslant 0.21$
in the study of Kulkarni et al. (Reference Kulkarni, Murphy and Manohar1993)), some plume fluid nonetheless penetrated into the lower layer due to inertia. An inverted fountain was thereby formed and whatever plume fluid penetrated into the lower layer eventually flowed as an interfacial gravity current along the ambient interface. Finally, a partial penetration regime occurred if the mean density of the plume just above the interface was comparable to the lower layer density (
$\unicode[STIX]{x1D6EC}\approx 0.97$
in the study of Wallace & Sheff (Reference Wallace and Sheff1987) and
$0.86\leqslant \unicode[STIX]{x1D6EC}\leqslant 2.13$
in the study of Kulkarni et al. (Reference Kulkarni, Murphy and Manohar1993)). Because the horizontal time-averaged density distribution of a plume was non-uniform (as opposed to the uniformity assumed by the so-called ‘top-hat’ formulation) and rather varied as an approximate Gaussian distribution, the fluid in the core (periphery) of the plume was denser (lighter) than the lower layer. Thus, as the plume impinged upon the interface, part of the plume penetrated through the interface and continued to descend while the rest intruded at the interface. We refer to this phenomenon as a ‘splitting plume’.
In related work, a downslope-propagating gravity current impinging upon an interface in a two-layer ambient was examined by Wells & Wettlaufer (Reference Wells and Wettlaufer2007) and Cortés, Rueda & Wells (Reference Cortés, Rueda and Wells2014). Like Kumagai (Reference Kumagai1984) and Mott & Woods (Reference Mott and Woods2009), Wells & Wettlaufer (Reference Wells and Wettlaufer2007) determined that gravity current fluid accumulated at the interface of the two-layer fluid causing the gravity current to break through the interface after some time. Like Kulkarni et al. (Reference Kulkarni, Murphy and Manohar1993), Cortés et al. (Reference Cortés, Rueda and Wells2014) found three different regimes characterized by (i) total penetration of the gravity current through the interface, (ii) total spreading along the ambient interface or (iii) partial splitting at the interface. Cortés et al. (Reference Cortés, Rueda and Wells2014) characterized the regimes in terms of a bulk Richardson number,
$\mathit{Ri}$
, (which is effectively inversely proportional to
$\unicode[STIX]{x1D6EC}$
) and a Froude number,
$\mathit{Fr}$
, which is the ratio of the current speed to the shallow water speed based on the current height.
One of the principal limiting assumptions associated with the above studies is that the upper ambient layer is uninfluenced by external effects, being affected by the impinging plume alone. In the present investigation we extend this previous line of inquiry by examining a line-source plume that descends into a two-layer stratified ambient in which the upper layer is allowed to deepen as a consequence of surface fresh water inputs that, at least initially, are larger than the flux of fresh water out of the upper layer due to entrainment into the descending plume. The surface level is kept fixed by extracting fluid from the bottom of the lower layer at the same rate as fresh water and plume fluid are added at the top. With this set-up, we are able to observe in some experiments the transition in time from a bottom spreading plume to an interfacially splitting plume and then finally to an interfacially spreading plume. We characterize this complete life cycle in terms of relevant experimental parameters associated both with the plume and also with the ambient stratification.
The rest of the manuscript is organized as follows. In § 2, equations for the evolution of a plume in unbounded and bounded domains are reviewed. The experimental set-up is presented in § 3. Thereafter, the detailed analyses of three experiments exhibiting qualitatively different flow behaviour are considered. Section 4 also contains a summary of salient quantitative results. Finally, our discussion and conclusions are provided in § 5.
2 Theory
2.1 Equations for a line-source plume
Morton et al. (Reference Morton, Taylor and Turner1956) formulated equations to describe a statistically steady plume descending into an infinite environment. Although derived for a point-source plume, the model is readily adapted for a line-source plume geometry (Lee & Emmons Reference Lee and Emmons1961). These are the equations presented here.
The horizontal cross-section of the plume is assumed to have self-similar time-averaged horizontal profiles that scale with height. For conceptual convenience, the profiles are taken to have top-hat structure. In reality, the time-averaged structure is closer to Gaussian and it is because of this that one might expect plume-splitting behaviour, as discussed in the Introduction. However, the intent of this section is to classify when plume splitting may occur, but not to model the splitting process itself. Under the top-hat assumption, the time-averaged profiles of the vertical velocity and reduced gravity are
$$\begin{eqnarray}w(x,z)=\left\{\begin{array}{@{}ll@{}}\bar{w}(z),\quad & \text{ if }|x|\leqslant b(z),\\ 0,\quad & \text{if }|x|>b(z).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}g^{\prime }(x,z)=\left\{\begin{array}{@{}ll@{}}\bar{g}^{\prime }(z),\quad & \text{ if }|x|\leqslant b(z),\\ 0.\quad & \text{ if }|x|>b(z).\end{array}\right.\end{eqnarray}$$
Here,
$x$
is the horizontal coordinate with origin at the plume midpoint,
$z$
is the vertical coordinate whose positive direction is taken to be downward from the point-source for a descending plume,
$b(z)$
is the half-width of the line-plume,
$\bar{w}(z)$
is the mean vertical velocity of the plume and
$\bar{g}^{\prime }(z)=g\,(\bar{\unicode[STIX]{x1D70C}}(z)-\unicode[STIX]{x1D70C}_{0}(z))/\unicode[STIX]{x1D70C}_{0}(0)$
is the mean reduced gravity, in which
$g$
is gravity and
$\bar{\unicode[STIX]{x1D70C}}(z)$
and
$\unicode[STIX]{x1D70C}_{0}(z)$
are the densities of the plume and ambient, respectively, measured at elevation
$z$
. The ambient density,
$\unicode[STIX]{x1D70C}_{0}(z)$
, is taken to be smaller than the plume density, at least near the source, so that
$\bar{g}^{\prime }(z)$
is positive. At any vertical level, the volume, momentum and buoyancy fluxes per unit width of a line-plume are defined by
$$\begin{eqnarray}\displaystyle & \displaystyle Q(z)=\int _{-\infty }^{\infty }w\,\text{d}x=2\bar{w}(z)b(z), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle M(z)=\int _{-\infty }^{\infty }w^{2}\,\text{d}x=2\bar{w}^{2}(z)b(z), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F(z)=\int _{-\infty }^{\infty }wg^{\prime }\,\text{d}x=2\bar{g}^{\prime }(z)\bar{w}(z)b(z). & \displaystyle\end{eqnarray}$$
Assuming density variations between the ambient and plume are small, the Boussinesq approximation can be invoked, in which case the dynamics of an ascending plume is equivalent to that of the descending plume studied here. The system is closed by making the entrainment assumption that the horizontal inflow velocity just outside the plume due to entrainment is proportional to the mean vertical velocity of the plume at that vertical level with proportionality constant
$\unicode[STIX]{x1D6FC}$
. Reported values for the so-called entrainment coefficient differ depending on the experimental details (Lee & Emmons Reference Lee and Emmons1961; Kotsovinos Reference Kotsovinos1975; Yuana & Cox Reference Yuana and Cox1996), but it is generally agreed that for a line-plume
$\unicode[STIX]{x1D6FC}$
falls between about 0.1 and 0.16. From the conservation of volume, momentum and buoyancy for an incompressible fluid, the following respective equations can be derived for the (steady state) vertical variation of
$Q$
,
$M$
and
$F$
:
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}Q}{\text{d}z}=2\unicode[STIX]{x1D6FC}\frac{M}{Q}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}M}{\text{d}z}=\frac{FQ}{M}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}F}{\text{d}z}=-Q\frac{\text{d}g_{0}^{\prime }}{\text{d}z}. & \displaystyle\end{eqnarray}$$
Here
$g_{0}^{\prime }(z)=g(\unicode[STIX]{x1D70C}_{0}(z)-\unicode[STIX]{x1D70C}_{0}(0))/\unicode[STIX]{x1D70C}_{0}(0)$
is the reduced gravity for the ambient density relative to a characteristic density,
$\unicode[STIX]{x1D70C}_{0}(0)$
.
2.2 Solutions in a uniform ambient
For an ideal line-plume originating from an infinitesimally thin source at
$z=0$
and descending through a uniform ambient, theoretical solutions can be obtained from (2.6)–(2.8) by setting
$g_{0}^{\prime }(z)=0$
and taking the source volume and momentum fluxes to be zero. The volume, momentum and buoyancy fluxes per unit width as functions of depth are found to be
$$\begin{eqnarray}\displaystyle & \displaystyle Q(z)=\left(2\unicode[STIX]{x1D6FC}\right)^{2/3}F_{s}^{1/3}z, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle M(z)=\left(2\unicode[STIX]{x1D6FC}\right)^{1/3}F_{s}^{2/3}z, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F(z)=F_{s}, & \displaystyle\end{eqnarray}$$
where
$F_{s}$
is the source buoyancy flux per unit width. From (2.3)–(2.5), it follows that the mean reduced gravity of the plume is
$$\begin{eqnarray}\bar{g}^{\prime }(z)=\frac{F_{s}}{Q(z)}=\left(2\unicode[STIX]{x1D6FC}\right)^{-2/3}F_{s}^{2/3}z^{-1},\end{eqnarray}$$
and the half-width of the plume is
$$\begin{eqnarray}b(z)=\frac{Q^{2}(z)}{2M(z)}=\unicode[STIX]{x1D6FC}z.\end{eqnarray}$$
2.3 Filling-box theory
The above solutions apply for the case of a line-plume in a stationary unbounded ambient. Considering a descending line-source plume in a confined region, such as a rectangular tank with length
$L_{T}$
, the vertical velocity of the rising ambient return flow can be obtained from conservation of volume as
$-Q(z)/L_{T}$
. By extension, and ignoring diffusion, the ambient density evolves according to the following advection equation (Baines & Turner Reference Baines and Turner1969):
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}g_{0}^{\prime }}{\unicode[STIX]{x2202}t}=\frac{Q}{L_{T}}\frac{\unicode[STIX]{x2202}g_{0}^{\prime }}{\unicode[STIX]{x2202}z}.\end{eqnarray}$$
The filling-box model is obtained by coupling (2.14) with (2.6)–(2.8). Taking this approach, Baines & Turner (Reference Baines and Turner1969) derived an expression for the position of the first front with time,
$t$
. They assumed that the ambient density increases linearly with
$t$
in the long-time limit whereas other variables, such as the plume radius, vertical velocity and reduced gravity were time independent.
Germeles (Reference Germeles1975) extended the Baines & Turner (Reference Baines and Turner1969) model by considering non-ideal plumes and, more importantly, by developing a numerical algorithm to solve the filling-box model, in which the ambient density profile was discretized into a staircase structure. At each time step a new layer representing the discharged fluid from the plume impacting the lower boundary was added at the bottom of the profile.
The time for the entire box to be filled with discharged plume fluid, equivalent to the time required by the first front to reach the elevation of the source, is referred to as the filling-box time,
$T_{fb}$
. For an ideal line-source plume, the filling-box time is given by (Baines & Turner Reference Baines and Turner1969):
$$\begin{eqnarray}T_{fb}=\frac{L_{T}}{(2\unicode[STIX]{x1D6FC})^{2/3}F_{s}^{1/3}}.\end{eqnarray}$$
2.4 Plume incident upon an interface of a two-layer fluid
For an ideal plume falling through a two-layer stratified ambient with a lower layer having density
$\unicode[STIX]{x1D70C}_{l}$
and depth
$H_{l}$
and an upper layer having density
$\unicode[STIX]{x1D70C}_{u}$
and depth
$H_{u}$
, (2.12) gives the reduced gravity of the plume just above the interface as
$$\begin{eqnarray}\bar{g}^{\prime }(H_{u})=g\frac{\bar{\unicode[STIX]{x1D70C}}(H_{u})-\unicode[STIX]{x1D70C}_{u}}{\unicode[STIX]{x1D70C}_{u}}=\left(2\unicode[STIX]{x1D6FC}\right)^{-2/3}F_{s}^{2/3}H_{u}^{-1}.\end{eqnarray}$$
At this depth, the mean density of the plume is less than (greater than) the lower layer density if
$\bar{g}^{\prime }(H_{u})$
is less than (greater than) the reduced gravity,
$g_{ul}^{\prime }$
, based on the density contrast between the lower and upper layers where
$$\begin{eqnarray}g_{ul}^{\prime }=g\frac{\unicode[STIX]{x1D70C}_{l}-\unicode[STIX]{x1D70C}_{u}}{\unicode[STIX]{x1D70C}_{u}}.\end{eqnarray}$$
As suggested by the previous discussion, the ability of the plume to descend within the lower layer can be assessed by forming the ratio of these two quantities (Mott & Woods Reference Mott and Woods2009):
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}\equiv \frac{\bar{g}^{\prime }(H_{u})}{g_{ul}^{\prime }}=(2\unicode[STIX]{x1D6FC})^{-2/3}\frac{F_{s}^{2/3}/H_{u}}{g_{ul}^{\prime }}.\end{eqnarray}$$
If
$\unicode[STIX]{x1D6EC}>1$
, the plume can penetrate through the interface initially and will continue to do so for all time: the finite width of the domain implies that the upper layer thickness
$H_{u}$
will progressively decrease as the ambient fluid in the upper layer is entrained into the plume and carried to depth. As a result,
$\bar{g}^{\prime }(H_{u})$
and hence
$\unicode[STIX]{x1D6EC}$
will increase with time so that
$\unicode[STIX]{x1D6EC}$
is always greater than unity. On the other hand, if
$\unicode[STIX]{x1D6EC}<1$
initially, the plume will spread at the interface. Over time, the plume will therefore descend into the evolving stratified ambient in the upper layer as predicted by the filling-box theory of Baines & Turner (Reference Baines and Turner1969). This situation will persist if
$\unicode[STIX]{x1D6EC}\ll 1$
in which case the ambient interface effectively plays the role of a solid bottom boundary. However, if
$\unicode[STIX]{x1D6EC}$
is initially not too much smaller than 1, it is possible that
$\bar{g}^{\prime }(H_{u})$
will increase sufficiently as a result of the density increase of the upper layer ambient so that plume breakthrough occurs at some later time (Mott & Woods Reference Mott and Woods2009).
For a constant flux gravity current propagating downslope through the interface of a two-layer ambient, Cortés et al. (Reference Cortés, Rueda and Wells2014) argued that both the Richardson number,
$\mathit{Ri}$
, and the Froude number,
$\mathit{Fr}$
, determine whether the gravity current splits or not. They defined
$$\begin{eqnarray}\displaystyle & \displaystyle \mathit{Ri}=\left(\frac{F_{s}^{2/3}/H_{u}}{g_{ul}^{\prime }}\right)^{-1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathit{Fr}=\frac{U}{(g^{\prime }h)^{1/2}}, & \displaystyle\end{eqnarray}$$
in which
$U$
,
$g^{\prime }$
and
$h$
are the average velocity, reduced gravity and the thickness of the gravity current, respectively. From the dimensional analysis of a two-dimensional gravity current,
$F_{s}^{2/3}/H_{u}$
is proportional to the reduced gravity of the gravity current just above the interface. Accordingly,
$\mathit{Ri}$
defined by (2.19) is proportional to
$\unicode[STIX]{x1D6EC}^{-1}$
.
2.5 Filling-box flow in a two-layer ambient fluid containing an ambient source and sink
As a non-trivial extension of the flow scenario described in § 2.4, consider a case in which lower layer fluid is extracted from the bottom of the domain with a constant volume flux per unit width
$Q_{sink}$
while fluid with density
$\unicode[STIX]{x1D70C}_{u}$
is injected at the surface with constant volume flux per unit width
$Q_{u}$
, as shown in figure 1. So that the total volume in the domain remains constant (and hence the free surface stationary),
$Q_{sink}$
is chosen to equal the sum of
$Q_{u}$
and the volume flux per unit width from the line-plume source,
$Q_{s}$
. For an ideal plume,
$Q_{s}=0$
, by definition, and therefore
$Q_{sink}=Q_{u}$
.
Figure 1. Schematic of a line-plume descending through a two-layer ambient with upper layer density
$\unicode[STIX]{x1D70C}_{u}$
, upper layer depth
$H_{u}$
and lower layer density
$\unicode[STIX]{x1D70C}_{l}$
, lower layer depth
$H_{l}$
. The source density of the non-ideal plume is
$\unicode[STIX]{x1D70C}_{s}$
and its volume flux per unit width is
$Q_{s}$
. Fluid of density
$\unicode[STIX]{x1D70C}_{u}$
is also injected at a constant rate,
$Q_{u}$
, equally at either side of the domain near the surface. Meanwhile, fluid is extracted at a constant rate
$Q_{sink}=Q_{s}+Q_{u}$
equally at either side of the domain from the bottom, so that the free surface remains fixed in time.
In the absence of the plume, the interface would descend at a speed
$Q_{sink}/L_{T}$
. Conversely, in the absence of the sinking flow
$(Q_{sink}=0)$
and as a consequence of entrainment of upper layer fluid into a pure plume, the interface would rise at the (time-variable) speed
$Q(H_{u})/L_{T}$
. If
$Q_{sink}>0$
and the plume penetrates into the lower layer, carrying entrained upper layer fluid to depth, the interface would have a speed of
$\left(Q_{sink}-Q(H_{u})\right)/L_{T}$
, with a downward (upward) direction if the sign is positive (negative). The competition between these effects with
$Q_{sink}>0$
and
$Q(H_{u})>0$
are considered here specifically for the circumstance in which
$H_{u}$
is initially zero. By extension,
$H_{u}(t)$
can be expressed as
$$\begin{eqnarray}H_{u}(t)=\int _{0}^{t}\frac{Q_{sink}-Q(H_{u}(\unicode[STIX]{x1D70F}))}{L_{T}}\,\text{d}\unicode[STIX]{x1D70F}.\end{eqnarray}$$
Assuming the plume always penetrates into the lower layer, the interface deepens asymptotically to a depth
$H_{u\infty }$
, at which point the volume flux per unit width of the plume at the interface
$Q(H_{u\infty })$
is balanced by
$Q_{sink}$
. Using (2.9), the steady state upper layer thickness is predicted to be
$$\begin{eqnarray}H_{u\infty }=\frac{Q_{sink}}{(2\unicode[STIX]{x1D6FC})^{2/3}F_{s}^{1/3}}.\end{eqnarray}$$
The characteristic time for the interface to deepen to its time-independent value is
$$\begin{eqnarray}\frac{H_{u\infty }}{Q_{sink}/L_{T}}=\frac{L_{T}}{(2\unicode[STIX]{x1D6FC})^{2/3}F_{s}^{1/3}},\end{eqnarray}$$
which is just the filling-box time
$T_{fb}$
expressed in (2.15).
The steady state upper layer depth prescribed by (2.22) can only be achieved if the plume density at
$H_{u\infty }$
is greater than
$\unicode[STIX]{x1D70C}_{l}$
so that the plume continues to descend into the lower layer. Analogous to the time-dependent variable
$\unicode[STIX]{x1D6EC}$
prescribed by (2.18), we define a time-independent variable
$\unicode[STIX]{x1D706}$
by
$$\begin{eqnarray}\unicode[STIX]{x1D706}\equiv \lim _{t\rightarrow \infty }\unicode[STIX]{x1D6EC}=\frac{\bar{g}^{\prime }(H_{u\infty })}{g_{ul}^{\prime }}=\frac{F_{s}}{g_{ul}^{\prime }\,Q_{sink}}.\end{eqnarray}$$
The term
$g_{ul}^{\prime }\,Q_{sink}=g_{ul}^{\prime }\,Q(H_{u\infty })$
can be interpreted as the loss of buoyancy flux per unit width that is experienced by the plume as a consequence of traversing the interface. By extension,
$\unicode[STIX]{x1D706}^{-1}$
is the relative loss of buoyancy flux per unit width as the plume penetrates into the lower layer from the upper layer.
While Mott & Woods (Reference Mott and Woods2009) focused on cases with no sinking flow and initially with
$\unicode[STIX]{x1D6EC}<1$
, here we consider cases where
$\unicode[STIX]{x1D6EC}$
, though initially greater than unity, subsequently decreases as the sinking flow acts to increase
$H_{u}$
. Whether
$\unicode[STIX]{x1D6EC}<1$
in the long-time limit depends on the value of
$\unicode[STIX]{x1D706}$
given by (2.24), which in turn depends upon the external parameters
$F_{s}$
,
$Q_{sink}$
and
$g_{ul}^{\prime }$
, all of which are time independent by assumption. If
$\unicode[STIX]{x1D706}>1$
, the plume is predicted to descend into the lower layer for all time. By contrast if
$\unicode[STIX]{x1D706}<1$
, eventually the plume will not penetrate through the interface, and will instead spread above the lower layer. In the latter case, one anticipates a transition regime in which the plume splits, corresponding to partial outflow along the interface as
$\unicode[STIX]{x1D6EC}$
falls below a value of order unity. Once splitting begins, a positive feedback occurs whereby the upper layer deepens and further decreases
$\unicode[STIX]{x1D6EC}$
, so that eventually the plume is expected to spread entirely at the interface. These predictions are tested against laboratory experiments. Although our analysis, experimental and otherwise, is here restricted to a line-source plume, we expect the condition
$\unicode[STIX]{x1D706}=1$
likewise represents a marginal case when the plume structure takes other shapes at the source, e.g. a point, or even a distributed, source. Indeed, this is the basis for the comparisons with environmental and architectural flows that we draw in § 5.
3 Experimental set-up
Laboratory experiments were conducted in an acrylic tank with rectangular cross-section, as shown schematically in figure 2. The tank measured
$L_{T}=120~\text{cm}$
long,
$W_{T}=7.6~\text{cm}$
wide and
$H_{T}=40~\text{cm}$
deep. The tank was filled to a depth
$H=30~\text{cm}$
with salt water of density
$\unicode[STIX]{x1D70C}_{l}$
, measured with an Anton Paar DMA 4500 densitometer, having a precision of
$\pm 0.00001~\text{g}~\text{cm}^{-3}$
. The density
$\unicode[STIX]{x1D70C}_{l}$
varied between
$1.00100~\text{g}~\text{cm}^{-3}$
and
$1.02000~\text{g}~\text{cm}^{-3}$
among different experiments. A relatively thin (
${\sim}5$
cm) upper layer was established by adding fresh water dyed with green food colouring through sponge floats at both ends of the tank. Density profiles were measured by a vertically oriented microscale conductivity probe (Precision Measurement Engineering, MSCTI) having a measuring frequency of 10 Hz. This probe was connected to a vertically traversing plate located at
$x=-15~\text{cm}$
, i.e. 15 cm to the left of the plume source. The plate and probe moved downward at a speed of
$0.5~\text{cm}~\text{s}^{-1}$
. Motion control was achieved using a stepper motor (Oriental Motor, PK245-01AA) connected to a computer running LabView. Probe measurements confirmed that the initial interface thickness was approximately 1 cm.
Figure 2. Schematic diagram of the laboratory experimental set-up. The tank measured
$L_{T}=120~\text{cm}$
long,
$W_{T}=8~\text{cm}$
wide and
$H_{T}=40~\text{cm}$
deep. The upper layer of the ambient was fresh water with density
$\unicode[STIX]{x1D70C}_{u}$
and the lower layer was filled with salt water having density
$\unicode[STIX]{x1D70C}_{l}$
.
A line-source nozzle spanning the tank width was located in the middle of the tank. The nozzle, whose opening measured 0.4 cm wide by 7.1 cm long, had a T-shaped internal structure that reduced the outflow speed. A piece of coarse sponge material was attached to the opening to introduce small perturbations to the flow and thereby trigger a laminar to turbulent transition in the plume. Schematics of the nozzle can be found in appendix C of Roes (Reference Roes2014).
As shown in figure 2, the nozzle opening was always situated at the approximate mid-depth of the interface at the initial instant. Thus every experiment, regardless of the value of
$\unicode[STIX]{x1D6EC}$
, began the same way, i.e. with plume fluid falling all the way to the bottom of the tank.
Over the course of each experiment, red food colouring was periodically injected into the tubing connected to the source nozzle. At early times dye was injected every
${\sim}3~\text{min}$
including at
$t=0$
. This time interval grew to 6 min as the experiment progressed and the flow dynamics became less transient. An electroluminescent light sheet with near-uniform intensity (Electric Vinyl, Perf-Alite Electric Vinyl) was placed 20 cm behind the tank. In front of the tank at a distance of 3 m was situated a digital video camera (Panasonic HDC-HS250) that recorded experimental images with a frame rate of 30 f.p.s. Although the shortest of our experiments lasted just over 1 h, experiments were more typically run for 2 h and, in one extreme case, more than 4 h. For all experiments, digital movies were analysed by extracting one frame per second to make time-lapse movies that were then imported into Matlab.
The experiment began with the activation of two peristaltic pumps (Manostat, Carter and Newport FPU5-MT/N) that acted as a source of salt water for the plume and as a source of fresh water for the surface layer. The peristaltic pumps also extracted water from the bottom of the tank. The use of peristaltic pumps with tubing of consistent diameter, wall thickness and material type ensured that the total volume of injected fluid was equal to the volume of extracted fluid. The pumps were calibrated by measuring with a stopwatch the time required to fill a graduated cylinder to a volume of 230 ml. The constant rate of injection of fresh water,
$Q_{u}W_{T}$
, ranged from
$2.0~\text{cm}^{-3}~\text{s}^{-1}$
to
$7.1~\text{cm}^{-3}~\text{s}^{-1}$
in different experiments. Meanwhile, the source had a constant volume flux of
$Q_{s}W_{T}$
that fell between
$0.6\,\text{cm}^{3}~\text{s}^{-1}$
and
$2.0~\text{cm}^{3}~\text{s}^{-1}$
in different experiments.
The plume was generated by injecting dense salt water of density
$\unicode[STIX]{x1D70C}_{s}>\unicode[STIX]{x1D70C}_{l}$
, ranging between
$\unicode[STIX]{x1D70C}_{s}=1.0130~\text{g}~\text{cm}^{-3}$
and
$1.1102~\text{g}~\text{cm}^{-3}$
. Multiple ambient density profiles were collected during each experiment, with a single traverse taking approximately 1 min. This was sufficiently fast compared to the slowly varying ambient density, that each profile could be considered as an instantaneous measurement of the ambient density. The probe was calibrated before and after each experiment using four salt water solutions whose densities were accurately measured with the densitometer.
4 Experimental results
4.1 Qualitative results and analysis methods
Three experiments are presented here for the purpose of illustrating the range of flow behaviour that was generally observed.
A classical filling-box-type experiment is shown in figure 3. Experimental parameters correspond to experiment 22 in table 1, where the source buoyancy flux per unit width was calculated from
$$\begin{eqnarray}F_{s}=Q_{s}g\frac{\unicode[STIX]{x1D70C}_{s}-\unicode[STIX]{x1D70C}_{u}}{\unicode[STIX]{x1D70C}_{u}}.\end{eqnarray}$$
Two comments are necessary regarding (4.1). Firstly, and because the nozzle was initially located at the elevation of the ambient interface, it should be understood that the above definition for
$F_{s}$
does not apply for small
$t$
. Secondly,
$Q_{s}>0$
. To account for the finite source volume flux of the plume, the virtual source distance,
$z_{v}$
, was computed using the methodology of Hunt & Kaye (Reference Hunt and Kaye2001). For the experiments of table 1,
$z_{v}\lesssim 0.2~\text{cm}$
which is an order of magnitude smaller than the terminal upper layer thickness. Based on this observation, it is sufficient and convenient to set the elevation of the nozzle tip as the origin,
$z=0$
.
Figure 3. Snapshots from a classical filling-box-type experiment (experiment 22 in table 1), with
$\unicode[STIX]{x1D706}=1.180$
, taken at time (a) 0.7 min, (b) 3 min and (c) 60 min. For future reference, note that the upper layer thickness is measured from the base of the nozzle, not the free surface. (d) Vertical time series collected at
$x=-20~\text{cm}$
. For flow visualization purposes, red dye is injected into the plume every 3 min at the start of the experiment and every 6 min thereafter. (e) Density profiles measured at the times indicated.
Table 1. Experimental parameters. Experiments 22, 9 and 2 correspond to the experiments shown in figures 3, 4 and 6, respectively.
With
$\unicode[STIX]{x1D706}=1.180$
, the plume is expected to descend to the tank bottom for all times, a fact confirmed by figure 3(a–c). Shortly after the start of the experiment (figure 3
a) the plume arrived at the tank bottom and then spread as a gravity current until it reached the side walls. The first front (figure 3
b), which demarcates the interface between discharged plume fluid and uncontaminated lower layer fluid, ascended continuously because the plume volume flux per unit width at the first front was greater than
$Q_{sink}$
. The fluid below the first front remained continuously stratified, as indicated by the density profile collected at 4 min (figure 3
e). Thereafter the first front ascended to a terminal elevation of
$2.60\pm 0.07~\text{cm}$
, at which elevation the plume volume flux through the front was balanced by the volume flux of the sink at the tank bottom. After the upper layer reached a depth of
$0.78\pm 0.07~\text{cm}$
, the plume began to split and an interfacial gravity current was formed. As confirmed by figure 3(c), however, the depth of the resultant intermediate layer remained modest and the plume continued to fall all the way to the bottom boundary for the entire duration of the experiment, approximately an hour.
Vertical time series were constructed from the experimental video by stacking together a series of vertical slices (one pixel wide) taken at
$x=-20~\text{cm}$
from successive video frames, as shown in figure 3 (d). This panel makes clear the progressive deepening of the upper layer from 0 cm to
$0.98\pm 0.07~\text{cm}$
. The terminal depth in question may be compared with the predicted depth
$H_{u\infty }$
using (2.22). Assuming
$\unicode[STIX]{x1D6FC}=0.1$
, we predict
$H_{u\infty }=0.84\,\text{cm}$
, which is in reasonable agreement with the measured value.
Figure 4. As in figure 3, but for an experiment with
$\unicode[STIX]{x1D706}=0.791$
(experiment 9 in table 1). In panel (d), the extrapolation of the interface between the intermediate and lower layers is intersected by the
$x$
axis, from which the virtual time,
$t_{v}=11$
min can be found. In panel (e), the
$\circ$
and
$\ast$
markers indicate the measured depths of the splitting and spreading intrusions, respectively, for each applicable time. The locations denoted by ‘A’ and ‘B’ indicate the upper and lower depths, respectively, bounding the intermediate layer of fluid formed by the intrusion at
$t=82$
min.
Figure 3(e) shows density profiles taken at successive times. Profiles collected after a significant time had elapsed confirmed that the upper fresh water layer reached a terminal depth of approximately 1.0 cm, measured from the base of the plume nozzle. Below this depth the ambient consisted of a gradually thickening interface and a lower layer whose density, nearly uniform in
$z$
, increased slowly with time,
$t$
.
An experiment exhibiting a transition to an interfacially spreading plume is shown in figure 4. The experimental parameters correspond to those given for experiment 9 in table 1 and are comparable to those of experiment 22 (shown in figure 3) except that the plume source density,
$\unicode[STIX]{x1D70C}_{s}$
, is smaller by
$0.02~\text{g}~\text{cm}^{-3}$
. The smaller value of
$\unicode[STIX]{x1D70C}_{s}$
results in a decrease of
$F_{s}$
to
$5.49~\text{cm}^{3}~\text{s}^{-3}$
, and a corresponding decrease of
$\unicode[STIX]{x1D706}$
to
$0.791$
. Although
$\unicode[STIX]{x1D70C}_{s}>\unicode[STIX]{x1D70C}_{l}$
, because
$\unicode[STIX]{x1D706}$
is less than unity it is anticipated that the plume will eventually spread entirely at or above the interface of the two-layer ambient, intruding within an intermediate layer.
At early times (figure 4
a), the plume descends to the bottom as before. After
${\sim}10$
min, the plume splits at the interface to form an intrusion that propagates to
$x=-20$
cm at 10 min (figure 4
b). Later, the plume spreads entirely within this intermediate layer, as shown in figure 4(c). We refer to the process by which the intrusion evolves first from a splitting intrusion (with some plume fluid continuing to penetrate through the lower ambient layer) to a spreading intrusion (with no plume fluid falling into the lower layer) as the ‘transition’. The time
$t_{t}$
corresponds to the end of the transition process and can be estimated from movies of the experiments by noting the time at which the red fluid injected into the plume first spreads entirely above the lower layer. For the experiment shown in figure 4,
$t_{t}\simeq 35$
min with an error of
$\pm 3$
min. The end of the transition can be determined more accurately from vertical time series images (e.g. figure 4 d) by tracking the rate of descent of the interface between the intermediate and lower layers. When the transition is complete, no plume fluid penetrates all the way through the interface at the top of the lower layer. As a result, there is no fountain top entrainment that would otherwise transport lower layer fluid to the interface (Kumagai Reference Kumagai1984). If we consider the fluid below the interface as a control volume, then following transition a constant outflow from this volume due to the bottom sinks results in a steady descent of the interface at speed
$Q_{sink}/L_{T}=0.005~\text{cm}~\text{s}^{-1}$
. After locating the time-variable interface depth from the vertical time series, we find the best-fit line at later times when the interface is observed to descend at a constant speed. Separately, we fit a degree-five polynomial to the interface depth versus time plot at early times. The intersection of the best-fit line and polynomial gives
$t_{t}$
. For the experiment shown in figure 4,
$t_{t}=36\pm 1$
min. This measurement is characteristic of other experiments, i.e.
$t_{t}$
is typically of the order of tens of minutes. If no transition occurred after two hours (for most experiments), it was deemed that transition would never occur.
The time for the start of transition is also estimated from the vertical time series. From the aforementioned best-fit line to the late-time interface depth versus time, we extrapolated backward in time to find the intersection of this line with
$z=0$
, indicating the elevation of the source. This point of intersection defines a ‘virtual time’,
$t_{v}$
. For the experiment shown in figure 4,
$t_{v}=11$
min. If we imagine a similar experiment starting from
$t=t_{v}$
with
$F_{s}=0$
, so that the plume is in fact a jet, the ambient interface will descend with the constant rate
$Q_{sink}/L_{T}$
from the beginning. After time
$t_{t}-t_{v}$
the ambient interface will exactly overlap the ambient interface shown in figure 4 (d). The virtual time is therefore the time delay of the real experiment with
$F_{s}>0$
from an analogue experiment with
$F_{s}=0$
. From this point of view, we can also consider
$t_{v}$
as the approximate onset (or start) time of the transition process.
For the experiment shown in figure 4, the green-dyed upper layer deepened to a measured value of
$H_{u\infty }=0.94\pm 0.07~\text{cm}$
. This was consistent with the prediction of 0.96 cm obtained from (2.22) with
$\unicode[STIX]{x1D6FC}=0.1$
.
Although the first front moved upwards for
$t<10$
min (figure 4 d), it later moved downwards as splitting occurred because
$Q_{sink}$
exceeded the plume volume flux per unit width through the first front. After transition, when the plume stopped penetrating into the lower layer, the first front descended at the same rate,
$Q_{sink}/L_{T}$
, as the interface.
Figure 4(e) shows the density profiles measured with the conductivity probe at different times. Before the transition was complete the ambient resembled a two-layer stratification. The ambient thereafter evolved towards a three-layer profile. The intermediate layer was formed by the intrusion, whose steady state density,
$\bar{\unicode[STIX]{x1D70C}}(H_{u\infty })$
, can be estimated using (2.12). Given
$z=H_{u\infty }$
and
$Q(H_{u\infty })=Q_{sink}$
,
$$\begin{eqnarray}\bar{\unicode[STIX]{x1D70C}}(H_{u\infty })=\unicode[STIX]{x1D70C}_{u}\left(\frac{\bar{g}^{\prime }(H_{u\infty })}{g}+1\right)=\unicode[STIX]{x1D70C}_{u}\left(\frac{F_{s}}{g\,Q_{sink}}+1\right).\end{eqnarray}$$
For the experiment shown in figure 4, the mean density calculated from (4.2) is
$1.0083~\text{g}~\text{cm}^{-3}$
. We compare this prediction with measured values taken at
$t=82$
min at depths between points A and B in figure 4(e). Consistent with (4.2), the mean density of the intermediate layer is measured to be
$\unicode[STIX]{x1D70C}_{int}=1.0085\pm 0.0003~\text{g}~\text{cm}^{-3}$
. The time-variable intrusion depth can be inferred from the right-hand side of figure 4 (d) as the left-most point of the sideways parabola-like red curves that appear between the upper (green-dyed) layer and the lower layer. These intrusion depths are superimposed as symbols plotted on the density profiles in figure 4(e), showing that the intrusion descended at a level close to the middle of the near-uniform middle layer. The positions of the fronts of the first observed interfacial gravity currents are tracked at different times and are plotted in the
$x$
–
$t$
plane, as shown in figure 5. The data points satisfying
$|x|<30~\text{cm}$
are fitted with a pair of best-fit lines, whose slopes indicate the (approximately constant) initial speeds of propagation. The small difference between the speed of the leftward-propagating current,
$0.067\pm 0.002~\text{cm}~\text{s}^{-1}$
, and that of the rightward-propagating current,
$0.064\pm 0.002~\text{cm}~\text{s}^{-1}$
, may reflect a slight asymmetry in the rate of freshwater injection in the upper layer. For the experiments in which transition occurred, the average of the left and right front speeds shall be denoted by
$U_{intr}$
.
Figure 5. Intrusion front location versus time (experiment 9 in table 1). The slopes of the best-fit lines show the initial propagation speeds of the splitting intrusion in the left and right directions.
For the experiment shown in figure 6, the source density is
$\unicode[STIX]{x1D70C}_{s}=1.02697~\text{g}~\text{cm}^{-3}$
. The corresponding source buoyancy flux per unit width is
$F_{s}=2.24~\text{cm}^{3}~\text{s}^{-3}$
and
$\unicode[STIX]{x1D706}=0.320$
(see experiment 2 of table 1). Consistent with expectations, the experiment shows a faster transition compared to the experiment exhibited in figure 4. Here,
$t_{v}\simeq 2.2$
min and the transition is complete after
$t_{t}=20~\text{min}$
. Thereafter the interface descends at the same rate of
$0.005~\text{cm}~\text{s}^{-1}$
as seen for experiment 9. The density profiles are shown in figure 6(e). Following transition, a three-layer stratification evolved from a two-layer stratification as observed in the experiment shown in figure 4. From (4.2), we expect
$\bar{\unicode[STIX]{x1D70C}}(H_{u\infty })=1.0024~\text{g}~\text{cm}^{-3}$
. The mean density of the intermediate layer is calculated from the last measured profile at
$t=72$
min over the range between points A and B indicated in figure 6(e). We find that
$\unicode[STIX]{x1D70C}_{int}=1.0030\pm 0.0002~\text{g}~\text{cm}^{-3}$
, which agrees reasonably well with the predicted value.
4.2 Quantitative results
The value of the ambient fluid density measured at the deepest depth,
$z=28~\text{cm}$
, from figure 3 is plotted against time in figure 7. For sake of comparison, figure 7 also contains an analogue filling-box prediction computed using the Germeles algorithm (Germeles Reference Germeles1975). In drawing the solid curve, we have assumed an ideal plume and have applied the same source buoyancy flux but have presumed a uniform ambient having the same density as that of the lower layer from the experiment. The significant deviations between this solid curve and the experimental data points for
$t\gtrsim 500$
s affirm the non-trivial influence of the deepening upper layer and the commensurate transport of upper layer fluid to depth by the plume.
Figure 7. Ambient fluid density measured at a depth of
$z=28~\text{cm}$
for the experiment shown in figure 3. A corresponding filling-box prediction in which the upper layer is omitted is plotted as the solid line.
Figure 8. Regime diagram indicating transition versus no transition for the experiments described in table 1. Here
$\unicode[STIX]{x1D706}$
is given by (2.24) and
$g_{ul}^{\prime }=g(\unicode[STIX]{x1D70C}_{l}-\unicode[STIX]{x1D70C}_{u})/\unicode[STIX]{x1D70C}_{u}$
is the reduced gravity between the ambient upper and lower layers. Moreover,
$t_{t}$
is the end of transition time and
$T_{fb}$
is given by (2.15). The solid symbols correspond to the experiments shown in figures 3, 4 and 6, respectively, with decreasing
$\unicode[STIX]{x1D706}$
.
A series of experiments were run with a range of parameters as listed in table 1. Figure 8 shows a regime diagram indicating whether or not transition occurred; measurements are plotted in the
$g_{ul}^{\prime }$
–
$\unicode[STIX]{x1D706}$
plane. Experiments that did and did not include transition are drawn, respectively, with circles and squares. In the former case, the circle radius indicates the time,
$t_{t}$
, needed to complete the process of transition. In § 2.5, it was argued that
$\unicode[STIX]{x1D706}=1$
ought to represent a dividing line in such regime diagrams. Figure 8 confirms that this interpretation is accurate. As expected, the figure also confirms that
$t_{t}$
generally increases with
$\unicode[STIX]{x1D706}$
for
$0<\unicode[STIX]{x1D706}<1$
.
Figure 9. Non-dimensional virtual time and end of transition time versus
$\unicode[STIX]{x1D706}$
. Both times are normalized by the filling-box time
$T_{fb}=(2\unicode[STIX]{x1D6FC})^{-2/3}L_{T}F_{s}^{-1/3}$
with
$\unicode[STIX]{x1D6FC}=0.1$
.
For the experiments wherein transition occurred, figure 9 shows the values of
$t_{v}$
and
$t_{t}$
(normalized by the filling-box time,
$T_{fb}$
) plotted against
$\unicode[STIX]{x1D706}$
. For a wide range of
$g_{ul}^{\prime }$
, the data collapse well, which indicates that
$\unicode[STIX]{x1D706}$
is the appropriate parameter for characterizing the plume splitting and transition processes. Both
$t_{v}$
and
$t_{t}$
become very large compared with the filling-box time as
$\unicode[STIX]{x1D706}\rightarrow 1^{-}$
. The relative loss of the plume buoyancy flux decreases as
$\unicode[STIX]{x1D706}$
increases and thus it takes more time for the transition to initiate and to complete. To help generalize the results, figure 9 includes empirically fitted curves to the data, which have the following respective equations:
$$\begin{eqnarray}\frac{t_{v}}{T_{fb}}=(-2.16\pm 0.25)\log (1-\unicode[STIX]{x1D706}),\quad \frac{t_{t}}{T_{fb}}=(-4.63\pm 0.48)\log (1-\unicode[STIX]{x1D706}^{1/2}).\end{eqnarray}$$
Also for the experiments with transition, the mean steady state density,
$\unicode[STIX]{x1D70C}_{int}$
, of the intermediate layer is plotted against
$F_{s}/\left(g\,Q_{sink}\right)$
in figure 10. The data collapse well with the prediction of (4.2), which confirms that
$\unicode[STIX]{x1D70C}_{int}$
is independent of
$\unicode[STIX]{x1D70C}_{l}$
and the tank dimension.
Figure 10. Mean steady state density of the intermediate layer in those experiments where transition occurred. The straight line indicates the prediction of (4.2).
Images such as figure 6(b) suggest that a significant amount of plume fluid may accumulate along the interface even before transition. Because this discharged plume fluid contains solute (and, in the marine outfall scenario, aqueous pollution), it is desirable to estimate the mass of solute,
$M_{int}$
, within the intermediate layer in question at time
$t_{t}$
. This information can be gleaned from the conductivity probe data. Care is taken to discount any solute present in the (diffuse) interface at the initial time. Figure 11 plots
$M_{int}$
versus
$\unicode[STIX]{x1D706}$
where the former variable has been normalized by
$M_{total}$
, the total mass of solute supplied by the plume source over
$0\leqslant t\leqslant t_{t}$
. Before the onset of splitting, all the plume fluid falls through the lower layer. With larger
$\unicode[STIX]{x1D706}<1$
, it takes more time for splitting to initiate. Thus more plume fluid descends to the bottom boundary as a result of which
$M_{int}/M_{total}$
is less than in experiments where
$\unicode[STIX]{x1D706}$
is small and splitting occurs earlier, albeit with intermediate fluid whose density may be little larger than
$\unicode[STIX]{x1D70C}_{u}$
. When applied to the marine outfall example discussed previously, this tells us that the relative amount of pollution that can be carried to the surface will increase with
$\unicode[STIX]{x1D706}$
.
Figure 11. Ratio of the solute mass in the intermediate layer,
$M_{int}$
, at
$t_{t}$
to the total mass of solute,
$M_{total}$
, injected by the nozzle during
$0\leqslant t\leqslant t_{t}$
.
After transition, discharged plume fluid intrudes roughly in the middle of the intermediate layer as shown in figures 4 (d) and 6 (d). Of course, the intermediate layer thickens over the duration of the experiment and hence the depth at which plume fluid discharges as an intrusion descends with time. Figures such as 4 (d) and 6 (d) show that the rate of descent,
$W_{intr}$
, is approximately constant; accordingly, a unique value for
$W_{intr}$
can be calculated for each experiment in which transition occurred. In figure 12, we plot
$W_{intr}$
against
$\unicode[STIX]{x1D706}$
. Considering the symmetric geometry of the intrusion (e.g. see figures 4
c and 6
c), approximately one-half of the intrusion fluid lies below the intrusion depth, and
$W_{intr}$
is approximately
$0.5(\pm 0.1)\,Q_{sink}/L_{T}$
.
Figure 12. Descent rate,
$W_{intr}$
, of the intrusion spreading depth versus
$\unicode[STIX]{x1D706}$
.
Whereas figure 12 considers the vertical descent of the intrusions, figure 13 shows the variation of
$U_{intr}$
with
$\unicode[STIX]{x1D706}$
. Studies of intrusions often non-dimensionalize the front speed using, as a characteristic vertical length scale, the intrusion height. We find it more instructive, however, to non-dimensionalize
$U_{intr}$
with
$\unicode[STIX]{x1D6FC}F_{s}^{1/3}$
. So normalized, and although there is some scatter in the data, the front speed decreases approximately linearly with increasing
$\unicode[STIX]{x1D706}$
. The qualitative trend of the data from figure 13 can be understood by referring to figures 4(b) and 6(b), which suggest that thicker and faster advancing intrusions are associated with smaller values of
$\unicode[STIX]{x1D706}$
. Taken together, the marine outfall implication of figures 11 and 13 is as follows: with smaller
$\unicode[STIX]{x1D706}$
, more passive scalars accumulate in the vicinity of the pycnocline and their lateral transport along the pycnocline and away from the point of vertical convection is larger.
Figure 13. Normalized intrusion front speed,
$U_{intr}$
, versus
$\unicode[STIX]{x1D706}$
. In some experiments with large
$Q_{u}$
, the asymmetries in the fresh water influxes at the two ends of the tank were large and introduced large errors indicated by the comparatively long lengths of the vertical error bars.
5 Discussion and conclusions
We have examined the influence of a deepening upper layer on the behaviour of a line-source plume that falls through a two-layer stratified ambient fluid. Depending upon the relative loss of buoyancy flux of the plume at the interface, which we express using the parameter
$\unicode[STIX]{x1D706}=F_{s}/(g_{ul}^{\prime }\,Q_{sink})$
, either a bottom-propagating gravity current develops and persists (if
$\unicode[STIX]{x1D706}>1$
) or the plume splits then spreads entirely as an intrusion that propagates between the upper and lower layers (if
$\unicode[STIX]{x1D706}<1$
). During plume splitting some fraction of the plume fluid discharges once the upper layer depth surpasses a critical value. Unlike the experiments of Kumagai (Reference Kumagai1984) and Mott & Woods (Reference Mott and Woods2009), which examined the eventual breakthrough of a plume at an interface due to solute accumulation, an opposite transition process is observed in many of our laboratory experiments. Specifically, the plume evolves from total penetration to partial discharge (splitting) to complete discharge with interfacial spreading occurring in a deepening intermediate layer of approximately constant density.
Because initially a plume entrains upper layer fluid and carries it to depth, the ambient interface descends more slowly at first than it would if the source were a jet (
$F_{s}=0$
), which does not penetrate the interface. However, if a jet source flow was initiated at the virtual time
$t=t_{v}$
rather than
$t=0$
, the ambient interface would, in due course, overlap with the descending ambient interface observed in our experiments employing plumes. This is the way in which we consider
$t_{v}$
to represent the approximate onset of the transition process, and
$t_{t}$
to represent the corresponding end where no plume fluid reaches the lower layer. As shown in figure 9,
$t_{v}$
and
$t_{t}$
normalized by the filling-box time
$T_{fb}$
collapse well when plotted against
$\unicode[STIX]{x1D706}$
and both become very large as
$\unicode[STIX]{x1D706}\rightarrow 1^{-}$
.
Although our experiments are highly idealized, they can provide further insights into some important environmental flows. Consider again the outflow of aqueous pollutants in Massachusetts Bay. The outfall tunnel extends 13 km offshore and is connected to a 2 km long diffuser which is located along the seafloor. The effluent is discharged through 55 risers into the sea whose local depth is approximately 34 m. The average volume flux of the waste water from all 55 risers is
$16.0~\text{m}^{3}~\text{s}^{-1}$
and the waste water density is taken as
$1.0~\text{g}~\text{cm}^{-3}$
(Hunt et al.
Reference Hunt, Mansfield, Mickelson, Albro, Geyer and Roberts2010; Roberts et al.
Reference Roberts, Hunt, Mickelson and Tian2011). From surveys conducted in summer (Hunt et al.
Reference Hunt, Mansfield, Roberts, Albro, Geyer, Steinhauer and Mickelson2002), the stratification in Massachusetts Bay can be represented approximately as a two-layer fluid with a 10 m upper layer of density
$1.0226~\text{g}~\text{cm}^{-3}$
and a 24 m lower layer of density
$1.0245~\text{g}~\text{cm}^{-3}$
such that
$g_{ul}^{\prime }=0.018~\text{m}~\text{s}^{-2}$
. Moreover, the buoyancy flux per unit length of the diffuser is taken to be
$F_{s}=0.019~\text{m}^{3}~\text{s}^{-3}$
. Also from (2.12), the reduced gravity of the plume varies with elevation
$z$
as
$\bar{g}^{\prime }(z)=0.21~\text{m}^{2}~\text{s}^{-2}\times z^{-1}$
where
$z=0$
corresponds to the seafloor. Accordingly, the reduced gravity of the plume at the interface (
$z=24$
m) is
$0.0087~\text{m}~\text{s}^{-2}$
. From (2.18),
$\unicode[STIX]{x1D6EC}=0.48$
which signifies that the plume will be arrested below the upper layer. As winter approaches, and due to surface cooling and wind forcing, the water column becomes well mixed. The interface steadily approaches the seafloor and the ambient reduced gravity decreases. Both of these factors serve to increase
$\unicode[STIX]{x1D6EC}$
. Although the directionality of the interface advance relative to the source is opposite to that in our experiments, the present results apply because the interface vertical velocity is small. We anticipate that plume splitting should occur as
$\unicode[STIX]{x1D6EC}$
approaches unity, and complete transport of the pollutants to the free surface should occur for
$\unicode[STIX]{x1D6EC}>1$
.
Another similar, albeit inverted, example concerns the displacement ventilation of a building containing low-level and high-level vents to the exterior. We consider a ground-level heat source such as a piece of electrical equipment that generates an ideal plume having a buoyancy flux per unit width,
$F_{s}$
. The plume ascends to the ceiling at
$z=H$
and discharges its fluid to form an upper layer where the reduced gravity,
$g_{ul}^{\prime }$
, between the upper and lower ambient layers is identical to the reduced gravity of the plume
$\bar{g}^{\prime }(H)$
measured at the ceiling at
$t=0$
. Over time, the interface descends towards the source before reaching a terminal elevation,
$h$
, which is prescribed by the area of the upper and lower vents and the height of the building zone (see (2.11) of Linden et al. (Reference Linden, Lane-Serff and Smeed1990)). Applying (2.9) with
$z=h$
and (2.12) with
$z=H$
into (2.24), we find that
$\unicode[STIX]{x1D706}=H/h>1$
. Thus transition and outflow of the plume along the ambient interface cannot occur as indeed has been observed experimentally (Linden et al.
Reference Linden, Lane-Serff and Smeed1990). However, if after steady state is achieved the heat source is turned down and the outflow rate,
$Q_{sink}$
, through the high-level vent is enhanced artificially by a ratio greater than
$H/h$
, (e.g. using an extraction fan), then
$\unicode[STIX]{x1D706}$
can fall below unity. In this scenario, transition is anticipated and a three-layer stratification will develop.
In the Introduction, we presented a qualitative description for plume splitting along the ambient interface and thereby emphasized the importance of a non-uniform density distribution over the plume cross-section. Efforts to model the plume splitting analytically have been pursued; in particular, we attempted to parameterize the fraction of the plume fluid that would ‘split’ (and therefore discharge along the ambient interface) given Gaussian distributions for velocity and density. At early times when the ambient interface is sharp, the calculation is straightforward and the total volume and density of discharged fluid can readily be obtained. Complications arise, however, for larger times when the sharp ambient interface must be replaced by a zone of continuous stratification. In this latter case, the plume splitting behaviour depends on the local buoyancy frequency of the ambient as well as the local reduced gravity of the plume. Future work will aim to more satisfactorily model the time evolution of the splitting process. Ultimately, we wish to derive a parameterization of the plume-splitting process that can be straightforwardly incorporated into a filling-box model.
Acknowledgement
Funding for this study was generously provided by NSERC through the Discovery Grant and RTI programs.
