2. Numerical method

We directly simulate TC flow by solving the incompressible Navier–Stokes equations in cylindrical coordinates in a rotating frame described below

(2.1)$$\begin{gather} \frac{\partial\boldsymbol{u}}{\partial t} + \boldsymbol{u}\boldsymbol{\cdot} \boldsymbol{\nabla}{\boldsymbol{u}} + 2\boldsymbol{\varOmega}_{rf} \times \boldsymbol{u} ={-}\boldsymbol{\nabla}{p} + \nu \nabla^2{\boldsymbol{u}}, \end{gather}$$

(2.2)$$\begin{gather}\boldsymbol{\nabla} \boldsymbol{\cdot} {\boldsymbol{u}} = 0, \end{gather}$$

where $\boldsymbol {u}$ is the velocity, $\varOmega _{rf}$ the angular velocity of the rotating frame, $p$ the pressure and $t$ the time. We use a second-order energy-conserving central finite-difference scheme for the spatial discretization. Time is advanced using a third-order Runge–Kutta for the explicit terms and a second-order Crank–Nicolson scheme for the implicit treatment of the wall-normal viscous terms. The complete algorithm is described in Verzicco & Orlandi (Reference Verzicco and Orlandi1996) and van der Poel et al. (Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015). We use the open-source code AFiD, which has been parallelized using MPI directives and has been heavily validated for TC flow (Ostilla-Mónico et al. Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014).

TC flow has two non-dimensional geometrical parameters which define the system: the radius ratio $\eta =r_i/r_o$, where $r_i$ and $r_o$ are the radii of the inner and outer cylinders, respectively, and the aspect ratio $\varGamma =L/d$, where $d=r_o-r_i$ is the gap between the cylinders, and $L$ is the vertical height (or axial periodic length) of the system. In our case, we fix $\eta =0.909$, a small gap, and $\varGamma =2.33$ with axially periodic boundary conditions, which corresponds to allowing a single pair of rolls of wavelength $\lambda _{TR}/d=2.33$. While we artificially fix $\lambda _{TR}$, in real systems, the roll axial wavelength adjusts to the flow and to the endwall locations (if nearby). For the purpose of this research, we ignore this effect, and justify this in Appendix B, where we show results for a different roll wavelengths $\lambda _{TR}/d=3$, as well as for two pairs of rolls, to ensure that the results are as independent as possible from domain size effects. We find that, while the quantitative values of the results change (by less than $10\,\%$), the qualitative features of the results presented below are robust.

We simulate TC flow in the rotating frame discussed by Dubrulle et al. (Reference Dubrulle, Dauchot, Daviaud, Longaretti, Richard and Zahn2005), where the inner and outer cylinder velocities are set to $\pm \frac {1}{2}U$, with $U$ being the characteristic velocity. With this, we have two control parameters: the shear Reynolds number $Re_s=Ud/\nu$, where $\nu$ is the fluid kinematic viscosity, and the non-dimensional Coriolis parameter $R_\varOmega =2d\boldsymbol{\varOmega}_{rf}/U$. For pure inner-cylinder rotation at $u_i$ inner-cylinder velocity, we obtain $R_\varOmega =1-\eta$ and $U=2u_i/(1+\eta )$. A schematic of the system is shown in figure 1, where the azimuthal ($\theta$), radial ($r$) and axial ($z$) coordinates are indicated. For convenience, we define the non-dimensional radial coordinate $\tilde {r}=(r-r_i)/d$, the non-dimensional axial coordinate $\tilde {z}=z/d$ and the non-dimensional streamwise coordinate $\tilde {x}=r\theta /d$. Quantities are non-dimensionalized using the inner-cylinder velocity $u_i$, and the characteristic length $d$ unless stated otherwise. From here on, any quantity will be represented non-dimensionally unless stated otherwise.

We set the order of rotational symmetry in the azimuthal direction to $n_{sym}=20$ to reduce computational costs. This results in a streamwise periodic length of $2{\rm \pi}$ half-gaps in the mid-gap, such that $\tilde {x}$ is in the $(0,{\rm \pi} )$ range. This is enough to generate accurate statistics when no boundary inhomogeneities are present (Ostilla-Mónico, Verzicco & Lohse Reference Ostilla-Mónico, Verzicco and Lohse2015; Sacco et al. Reference Sacco, Verzicco and Ostilla-Mónico2019). To further prove that the results are independent of $n_{sym}$, additional simulations are provided in Appendix B. Depending on the Reynolds number, we vary the number of discretization points $N_i$ of the simulation grid. In the current study, we simulate $Re_s=7.22\times 10^2$ (steady Taylor vortex regime) with a resolution of $N_\theta \times N_r \times N_z =32 \times 64 \times 64$, $Re_s=2.28\times 10^3$ (modulated Taylor vortex regime) with $128 \times 256 \times 128$, $Re_s=10^4$ (turbulent Taylor vortex regime) with $192 \times 384 \times 256$ and $Re_s=3\times 10^4$ (turbulent Taylor vortex regime) with $384 \times 512 \times 512$. This covers everything from steady Taylor vortex flow to fully turbulent flow in the ultimate regime. A table containing all simulated cases and the resulting torque is provided in Appendix A.

The adequacy of the resolution is checked by ensuring the energy input from the cylinders matches the viscous dissipation to within $2\,\%$ (Ostilla-Mónico et al. Reference Ostilla-Mónico, van der Poel, Verzicco, Grossmann and Lohse2014). The simulations are started from initial conditions of white noise, and are run for 400 large-eddy turnover times (defined as $d/U$) to collect statistics after the transient has passed. An additional criterion for temporal convergence of the statistics is that the angular velocity transport, defined as $J_\omega (r)=r^3(\langle u_r u_\theta /r \rangle _{\theta ,z,t} - \nu \partial _r\langle u_\theta /r \rangle _{\theta ,z,t})$ (Eckhardt et al. Reference Eckhardt, Grossmann and Lohse2007) must be constant to within $2\,\%$, where $\langle \cdots \rangle _{x_i}$ denotes an averaging operator over variable $x_i$. What this expresses is that the time average of the convective and viscous parts of the torque are approximately constant at every radial coordinate. This provides a more stringent criterion than just looking at the convergence of torque, as we use a second-order statistics $(\langle u_r u_\theta /r\rangle _{\theta ,z,t})$ to ensure converge. The torque $T$ is then calculated as the radial average of $J(r)$.

In a classical TC problem, the cylinders have a homogeneous no-slip boundary condition, where the velocity of the fluid at the wall is simply the cylinder velocity. The flow is maintained by a torque applied at the cylinders $T$, which is usually non-dimensionalized in the form of the Nusselt number $Nu=T/T_{pa}$, where $T_{pa}$ is the torque for the purely azimuthal flow solution. In the current study, we alternate no-slip and free-slip boundary conditions. Free-slip boundary conditions are mathematically expressed by the combination of no penetration ($u_r=0$), and vanishing normal derivatives of the two velocity components tangential to the wall ($\partial _r u_\theta =\partial _r u_z=0$). We impose the stress-free boundary condition by setting the shear $\tau$ originating from the wall to zero at the first grid point. This is done through modifying the viscous term, which for a staggered velocity is first approximated using a finite difference of shears ($[\tau ^+-\tau ^-]/\varDelta$), and these shears are then approximated using a finite difference of velocities. The finite-difference approach of the code rapidly allows us to change between no-slip and stress-free conditions by setting $\tau ^-$ to be either zero, or to be the velocity gradient between the current velocity and the wall. More details on the code operation are provided in van der Poel et al. (Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015).

There are infinitely many geometric patterns of no-slip and free-slip conditions possible. In this study, we reduce the geometrical parameter space to only consider the four patterns shown in figure 1. We further reduce the parameter space by equally partitioning the patterned surfaces between no-slip and free-slip boundary conditions. If the repeating pattern is one-dimensional infinite stripes, it suffices to state the orientation of the stripes, and the spatial frequency to characterize it. In particular, the spatial frequency $f_j$ is the number of repeating patterns per unit gap width, and it is the inverse of the spatial period, or wavelength $\lambda _j$ of the pattern. In the case of alternating free-slip and no-slip boundary conditions in the azimuthal (streamwise) direction, the pattern wavelength is given by $\lambda _x = \hat {L}_x/f=2{\rm \pi} r_i/(dn_{sym}f)$, while for stripes that alternate in the axial (spanwise) direction (figure 3a) the pattern wavelength is $\lambda _z=\varGamma /f$. For the inclined/spiral patterns, there are two ways to calculate the effective wavelength $\lambda _\alpha$ of the pattern, as it extends in both stream- and spanwise directions. It is given by either $\lambda _x \sin (\alpha )$, or $\lambda _z\cos (\alpha )$, where $\alpha$ is the angle of inclination of the pattern with respect to the streamwise direction. These formulas become invalid in the limits of $\alpha =0$ and $\alpha ={\rm \pi} /2$, respectively. A visual can be seen in figure 10(a).

The checkerboard patterns can be quantified through two wavelengths: one in the axial direction and one in the azimuthal direction. When these are equal, we obtain a checkerboard pattern composed of repeating squares, and otherwise we obtain repeating rectangles. In the limit of one of the two wavelengths becoming infinite, we obtain either pure axial or azimuthal variations. Further visuals on how $\lambda _\alpha$ or an equivalent orientation of a checkerboard pattern can be defined are provided in figure 15(a).

3. Pure axial (spanwise) and azimuthal (streamwise) inhomogeneities

The first patterns we discuss are azimuthal and axial patterns, which can be understood as purely streamwise and purely spanwise inhomogeneous boundary conditions respectively (figure 1c,d). The case of axial (spanwise) variations is particularly interesting, because it is expected to generate the sort of Reynolds-stress imbalances that induce additional secondary flows. In addition, axial patterns are ‘frozen’ from the point of view of cylinder and, because they are invariant in time, they are easier to analyse.

We begin by showing the instantaneous velocity near the inner cylinder at $\tilde {r}\approx 0.05$ for the intermediate Reynolds number case $Re_s=2.28\times 10^3$, in the modulated Taylor vortex regime. We first focus on the homogeneous case, where we can see strong axial variation, due to the presence of the Taylor roll, as well as azimuthal patterns caused by the waviness of the roll. This azimuthal waviness is disrupted in figure 2(a,b) by the insertion of the azimuthal inhomogeneities. It is also disrupted by the insertion of axial inhomogeneities. Furthermore, the axial stratification changes character when axial patterns are introduced. There is not much evidence of turbulence, and we expect the Reynolds stresses to be weak in this case. We highlight that this Reynolds number is most similar to those which have been explored by Naim & Baig (Reference Naim and Baig2019). However, due to the small radius ratio they considered, the inner cylinder is more active in producing turbulent streaks, which explains the qualitative differences between the cases in Naim & Baig (Reference Naim and Baig2019) and our simulations.

Figure 2. Near-wall instantaneous azimuthal velocity (a) and (b) azimuthal inhomogeneity with $f_x=0.32$ and $f_x=2.55$ respectively; (c) no inhomogeneity; and (d), (e) and (f): axial inhomogeneities with $f_z=0.43$, $f_z=0.86$ and $f_z=3.43$, respectively. All results are for $Re_s=2.28 \times 10^3$. Yellow stripes correspond to stress-free zones and blue zones correspond to no-slip zones.

In the turbulent Taylor vortex regime, the picture is somewhat similar to what was analysed above. In figure 3, we show the instantaneous azimuthal velocities near the inner cylinder for $Re_s=10^4$ at $\tilde {r}\approx 0.015$ for various patterns. This value of $\tilde {r}$ roughly corresponds to $y^+=13-15$ in wall units, depending on the case, where $y^+=(r-r_i)/\delta _\nu$, $\delta _\nu$ is the viscous unit $\delta _\nu =\nu /u_\tau$, and $u_\tau$ is the frictional velocity. Near-wall turbulent streaks can be seen due to the higher Reynolds number. For the case of azimuthal variations, the influence of the pattern on the flow is minor for the lowest frequencies. The web of streaks is somewhat disrupted, but the effect is small due to the inherent elongation of streaks in the streamwise direction which bridges the gap across patterns effectively. Aside from weak signatures of the pattern, these cases do not significantly deviate from the homogeneous case shown in panel (c). This is consistent with the fact that azimuthal inhomogeneities will not generate additional spanwise gradients of Reynolds stresses which are known to induce secondary flows. Thus, as first approximation, we do not expect them to affect the Taylor rolls much.

Figure 3. Near-wall instantaneous azimuthal velocity (a) and (b) azimuthal inhomogeneity with $f_x=0.32$ and $f_x=2.55$ respectively; (c) no inhomogeneity; and (d), (e) and (f) axial inhomogeneities with $f_z=0.43$, $f_z=0.86$ and $f_z=3.43$, respectively. All results are for $Re_s=10^4$. Yellow stripes correspond to stress-free zones and blue zones correspond to no-slip zones.

Axial inhomogeneities have a larger effect on the flow structure near the walls for the lower frequencies. Parts of the flow are never forced, while other parts are always forced. The azimuthal elongation of streaks cannot adequately redistribute momentum in the axial direction, and larger changes in velocity than those seen in the homogeneous case can be observed. For the lowest frequency, the roll structure is somewhat disrupted. The pattern wavelength coincides with the roll wavelength, so the roll ‘places’ itself above the no-slip boundary, and this mitigates the overall effect the inhomogeneities have on the flow. However, for $f_z=0.86$ (figure 3e), the pattern wavelength is double the roll wavelength, and this significantly interferes with the roll formation. As the frequency is further increased, the destructive interference is weakened. For the highest frequency simulated ($f_z=3.43$, figure 3f) the axial variation is less strong even if the signature of the pattern is much more apparent than for azimuthal variations.

We continue by showing the non-dimensional torque $Nu$ for various Reynolds numbers and stripe wavelengths in figure 4(a,b). Our first observation is that the $Nu(k)$ curve is monotonic for almost all cases except for the large $Re$ cases of figure 4(b,d), to which we will return later to. Smaller pattern sizes result in higher torques even if the area ratio between no-slip and stress-free regions is kept constant at 50 % each, consistent with the existing literature (Watanabe et al. Reference Watanabe, Mamori and Fukagata2017; Naim & Baig Reference Naim and Baig2019). These results are emphasized in panels (c,d), which show the Nusselt number normalized by that obtained when the walls are fully no slip ($Nu/Nu_0$). In the case of azimuthal variations, the patterns have a small effect: except for $Re_s=3\times 10^4$, the torque drops down only to $85\,\%$ of the homogeneous value for the smallest frequencies (largest patterns) simulated. For the axial (spanwise) inhomogeneities the relative drops in torque is much larger ($\sim 30\,\%$). This finding is consistent with Watanabe et al. (Reference Watanabe, Mamori and Fukagata2017) and Naim & Baig (Reference Naim and Baig2019), who obtained the largest drop in friction for stripes aligned in the axial direction. The magnitudes of drag reduction achieved are also of the same order as those in these previous studies, in particular, with the $32\,\%$ drag reduction seen for axial patterns in Naim & Baig (Reference Naim and Baig2019).

Figure 4. (a,b) Non-dimensionalized ($Nu$) and (c,d) normalized torque ($Nu/Nu_0$, with $Nu_0$ the non-dimensionalized torque for homogeneous cylinders) at various wavelengths and Reynolds number. (a,c) Azimuthal inhomogeneities as in figure 1(c). (b,d) Axial inhomogeneities as in figure 1(d).

Increasing the frequency increases the torque, and for the smaller $Re_s$ cases with azimuthal inhomogeneities, the asymptotic value of $Nu/Nu_0 \to 1$ is reached in practice for $f_x>3$ even if only $50\,\%$ of the cylinder surface is providing the torque. This means that the local shear at these parts will be almost double the one present for the homogeneous case. For $Re_s=3\times 10^4$ the results also tend to an asymptote but at a slower rate. Our results are consistent with the numerical Rayleigh–Bénard studies by Bakhuis et al. (Reference Bakhuis, Ostilla-Mónico, Van Der Poel, Verzicco and Lohse2018), which found a similar effect on the Nusselt number: with a $50\,\%$ area coverage of conducting surface, the full heat transfer of the homogeneous case was recovered for the smallest patterns of alternating insulating and conducting surfaces.

To explore the non-monotonicity of the $Nu(\,f_z)$ curve at higher Reynolds numbers (figure 4b) we turn to the secondary flows. As mentioned in the introduction, we can expect that non-homogeneity patterns in the boundary layers generate secondary flows that interfere with the existing Taylor rolls. To corroborate this, we show the temporally and azimuthally averaged azimuthal velocities $\langle u_\theta \rangle _{\theta ,t}$ for $Re_s=10^4$ and several values of $f_z$ in figure 5 alongside the homogeneous case. Here, it is even more apparent that the pattern frequency $f_z=0.86$ has a strong impact on the rolls, because it imposes an inhomogeneity that has a wavelength of one half that of the inhomogeneity generated by a roll pair, and the Prandtl flow of the secondary type induced by the pattern has a destructive interference with the roll. Decreasing $f_z$ to one stripe pair per roll pair matches the imposed axial inhomogeneity with the natural one from the Taylor roll pair. The roll pair will then locate itself such that the ‘ejection’, or outflow region, where the outgoing streams are generated, will reside on top of the no-slip region. Conversely, increasing the frequency of the imposed axial inhomogeneity, results in the associated secondary flow being increasingly absorbed inside of the boundary layer while the roll remains unaffected.

Figure 5. Azimuthally and temporally averaged azimuthal velocity for $\eta =0.909$, $Re_s =10^4$ and axial inhomogeneities at several frequencies (a) $f_z=0.43$, (b) $f_z=0.86$, (c) $f_z=3.43$ and (d) no inhomogeneity. Yellow stripes correspond to stress-free zones and blue zones correspond to no-slip zones. (e,f) Roll amplitude normalized by the roll amplitude for the homogeneous case for azimuthal and axial variations as a function of $Re_s$ and pattern frequency.

We can quantify this disruption using the roll amplitude. We calculate this taking the temporally and azimuthally averaged radial velocity ($\langle u_r \rangle _{t,\theta }$), and computing the magnitude of the first Fourier mode in the axial direction at the mid-gap $\tilde {r}=0.5$. In figure 5(e,f) we show this amplitude $A$ normalized by the amplitude for the homogeneous case ($A_0$) as a function of Reynolds number and pattern frequency for both azimuthal and axial patterns. For the latter, we can see very clearly that, for the three higher $Re_s$, the amplitude shows a large dip for $f_z=0.86$. For the low-$Re$ case in the steady Taylor vortex regime there are no Reynolds stresses, as well as for all cases with azimuthal variations where there is no axial/spanwise imbalance, the behaviour of $A/A_0$ is monotonic, i.e. the roll amplitude increases as the pattern gets smaller.

The disruption of the roll can be distinguished from a pure boundary layer effect by examining how the axial patterns affect the behaviour of the temporally, axially and azimuthally averaged azimuthal velocity $\langle u_\theta (r_i) \rangle _{\theta ,t,z}$. Figures 6(a) and 6(b) show this for the lowest and highest $Re$ simulated. The special behaviour of the $f_z=0.86$ case seen previously vanishes, and the curves are ordered according to $f_z$ for both low and high Reynolds numbers. We can further examine this by looking at how the effective slip in the inner cylinder behaves. The effective slip velocity $U_s$ is defined as the deficit, or slip, between the inner-cylinder velocity and $\langle u_\theta (r_i) \rangle _{\theta ,t,z}$. The effective slip length $\ell$ is then calculated using the averaged azimuthal velocity gradient at the inner cylinder as $\ell =U_s/\langle \partial _r u_\theta (r_i) \rangle _{\theta ,t,z}$. These quantities are shown in figures 6(c) and 6(d) for the azimuthal variations as a function of Reynolds number and pattern frequency. Remarkably, no apparent change is observed at $f_z=0.86$ for the effective slip properties. All the curves behave monotonically, with the effective slip length, with the effective slip velocity decreasing with increasing pattern frequency. To highlight this, we show the local torque, non-dimensionalized as a Nusselt number along the axial direction at the inner cylinder for various axial inhomogeneities for $Re_s=2.28 \times 10^3$ and $Re_s=1 \times 10^4$ in the figure 7. We can first see how the presence of the roll causes even the fully no-slip case to have axial inhomogeneities, and that boundary inhomogeneities interact with this existing inhomogeneity. Furthermore, the inhomogeneities cause the average value of the torque to increase, especially at the interface between regions. The local peaks are higher for smaller pattern frequencies as the slip velocity is higher. These results highlight the crucial difference between TC and the other shear flows previously studied: the disruption coming from the boundary is able to interact with large-scale components to multiply its effects.

Figure 6. Mean azimuthal velocity along the radial gap for various pattern frequencies $f_z$ for (a) $Re_s=722$ and (b) $Re_s=3 \times 10^4$; darker colours signify higher values of $f_z$, while the dashed black line is the homogeneous case. (c) Effective slip length; and (d) effective slip velocity for all simulated cases of axial inhomogeneities.

Figure 7. Temporally and azimuthally averaged Nusselt number at the inner cylinder along the axial direction for various axial inhomogeneities $f_z$ at (a) $Re_s=2.28\times 10^3$ and (b) $Re_s=1 \times 10^4$.

To further visualize the changes that are taking place due to the axial (spanwise) pattern, we turn to the Reynolds stress. In rectangular coordinates, we can write a relatively simple equation for a time- and streamwise-averaged streamwise vorticity $\varOmega _x$ (Einstein & Li Reference Einstein and Li1958),

(3.1)\begin{align} \overline{v} \frac{\partial \varOmega_x }{\partial y} + \overline{w} \frac{\partial \varOmega_x }{\partial z} = \left( \frac{\partial^2 }{\partial y^2} - \frac{\partial^2 }{\partial z^2} \right)(-\langle \overline{v'w'} \rangle) + \frac{\partial^2 }{\partial y \partial z}( \overline{v^{\prime 2}} - \overline{w^{\prime 2}}) + \nu \left( \frac{\partial^2 \varOmega_x }{\partial z^2} + \frac{\partial^2 \varOmega_x }{\partial z^2} \right ), \end{align}

where $\overline {\phi }$ denotes the temporal- and streamwise-averaging operator, $\phi ^\prime$ are fluctuations around that mean and $\overline {\omega }_x$ is simply $\varOmega _x$, representing the secondary flow.

This equation is derived by performing a streamwise- and temporal Reynolds-averaging operation on the vorticity advection–diffusion equation

(3.2)\begin{equation} \frac{\textrm{D}\boldsymbol{\omega}}{\textrm{D}t} ={-}\boldsymbol{\omega}\boldsymbol{\cdot} \boldsymbol{\nabla}\boldsymbol{u} + \nu\nabla^2\boldsymbol{\omega}, \end{equation}

where $\boldsymbol {\omega }$ is the flow vorticity and $\textrm {D}/\textrm {D}t$ denotes a convective derivative. By using the definition of vorticity, the continuity equation and the properties of cross-derivatives, the seventeen terms originating from Reynolds stresses can be reduced to the four to which the viscid terms are added (Einstein & Li Reference Einstein and Li1958).

For TC flow, this equation becomes even more complicated because of cylindrical coordinates. The reduction to (3.1) would add many curvature terms and complicate the interpretation. Basing ourselves on the analysis by Brauckmann, Salewski & Eckhardt (Reference Brauckmann, Salewski and Eckhardt2015), we can estimate the magnitude of the curvature terms to be of the order of $R_C=(1-\eta )/\sqrt {\eta }$, which is $0.09$ in our narrow-gap and low curvature case. Hence, we keep the rectangular coordinates as they appear to us to be more useful to gain some insights, and for now we neglect the error introduced due to curvature. This essentially means taking $\varOmega _x$, i.e. the Reynolds-averaged streamwise vorticity to be equivalent to $\varOmega _\theta$, setting $v=u_r$ and $w=u_z$, and using $\langle \phi \rangle _{\theta ,t}$ for the $\overline {\phi }$ operator.

We focus on the generation of $\varOmega _x$ through spanwise gradients in shear Reynolds stresses. These types of gradients induce the secondary flows, which are known as secondary Prandtl flows of the second type (cf. $\S$1). We first show the behaviour of the $\langle u_r u_z \rangle$ Reynolds stress in figure 8, and in figure 9, we visualize $G_\varOmega =\partial ^2_z\langle u_ru_z\rangle$ near the walls. The case with no inhomogeneity shows a concentration of $G_\varOmega$ near the walls. Here, $G_\varOmega$ shows a spanwise variation which is periodic with a period equal to the rolls. This is hardly surprising as this imbalance keeps the roll stable. For the $f_z=0.43$ case, the pattern cannot impose a different period of spanwise variation of stresses, which are now increased on the no-slip surface. For the $f_z=0.86$ case is where we see a significant interference between the period imposed by the pattern, and that which stabilizes the roll – and this causes the disruption seen above. Finally, while some disruption in the $G$ pattern can be seen in the $f_z=3.43$ case, the oscillations become averaged out due to their higher frequency. This shows how the maximum roll disruption takes place: it is coupled to a disruption of the ‘natural’ period of the Reynolds stresses.

Figure 8. Azimuthally and temporally averaged Reynolds shear stress $\langle u_r u_z \rangle$ for $Re_s =3\times 10^4$ and axial inhomogeneities for (a) $f_z=0.43$, (b) $f_z=0.86$, (c) $f_z=3.43$ and (d) no inhomogeneity. Yellow stripes correspond to stress-free zones and blue zones correspond to no-slip zones.

Figure 9. Azimuthally and temporally averaged spanwise Reynolds shear stress imbalance $G_\varOmega$ for $\eta =0.909$, $Re_s =3\times 10^4$ and axial inhomogeneities at several frequencies (a) $f_z=0.43$, (b) $f_z=0.86$, (c) $f_z=3.43$ and (d) no inhomogeneity. Yellow stripes correspond to stress-free zones and blue zones correspond to no-slip zones.

4. Mixed spanwise and streamwise variations

4.1. Spiral patterns

In this subsection, we modify the one-dimensional patterns studied above by placing them at an arbitrary oblique angle to the flow. This results in spiral or oblique patterns, which resemble a barber pole and introduce chirality into the system. While, in a statistical sense, axial symmetry is recovered because every point is equally likely to be no slip or stress free as the pattern moves through the domain, axial symmetry is persistently broken in an instantaneous sense and this is known to induce spanwise (axial) velocities (Hasegawa, Frohnapfel & Kasagi Reference Hasegawa, Frohnapfel and Kasagi2011; Watanabe et al. Reference Watanabe, Mamori and Fukagata2017). This induced velocity makes spiral patterns another good candidate for affecting the rolls, as Ostilla-Mónico et al. (Reference Ostilla-Mónico, Verzicco, Grossmann and Lohse2016) observed that an axial pressure gradient that generated an axial velocity was capable of moving these structures.

We simulate oblique patterns for three (more) angles between $\theta =0^\circ$ (purely axial inhomogeneity) and $\theta =90^\circ$ (purely azimuthal inhomogeneity). A sketch that quantifies the wavelength of the underlying pattern and the speed at which it moves through the domain is provided in figure 10(a,b) respectively. In particular, in figure 10(b) we plot the relative spanwise ($v_{s,z}=-U\sin (\alpha )\cos (\alpha )/2$) and streamwise ($v_{s,x}=-U\sin ^2(\alpha )/2$) pattern velocities with respect to the domain in figure 10(b), for all possible angles of inclination. The maximum pattern velocity in the $z$ direction is attained when $\alpha =45^\circ$, and is equal to half of the cylinder speed $U/2$.

Figure 10. (a) Inclined pattern parameters; (b) velocity of the pattern in spanwise $v_{s,z}$ (solid red) and streamwise $v_{s,x}$ (dashed blue) directions for various angles of inclination. Near-wall instantaneous azimuthal velocity of inclined inhomogeneity for $Re_s=10^4$ with (c) $\alpha =36.6^{\circ }$, $f_\alpha =0.53$ and (d) $\alpha =20.4^{\circ }$, $f_\alpha =0.92$.

Intuitively, we may think that the pattern moves as the stripes do, and that by following the movement of the stripes we are following the pattern. However, what is relevant here is how the boundaries between stripes move, i.e. tracking the way the inhomogeneous direction moves, because it is the direction across which imbalances exist.

We start by visualizing the near-wall azimuthal velocities for $\alpha =36.6^{\circ }$ and $\alpha =20.4^{\circ }$ in figures 10(c) and 10(d), respectively, to show the effect of an inclined pattern on the flow. While the signatures are stronger than for purely azimuthal variations, they appear weaker than those coming from purely axial variations as the elongated streaks are able to bridge the gap between patterns. We continue by plotting the normalized torque for two Reynolds numbers considered in figure 11, in the modulated Taylor vortex regime and in the turbulent Taylor vortex regime. The large differences between the resulting torque when using axially and azimuthally oriented patterns are apparent in this representation, as they are the two limit cases of spiral patterns. Unsurprisingly, we find that, for the most part, the torques with different angles of the pattern lie between those of the azimuthal and axial patterns in a predictable, monotonic order, again consistent with Watanabe et al. (Reference Watanabe, Mamori and Fukagata2017) and Naim & Baig (Reference Naim and Baig2019).

Figure 11. Normalized torque for various $\alpha$; (a) $Re_s=7.22\times 10^2$ and (b) $Re_s=10^4$.

Before moving to the secondary flows themselves, we quantify the induced axial (spanwise) velocities by showing $\langle v_z \rangle _{\theta ,z,t}$ as a function of radius for several patterns and several Reynolds numbers in figure 12. As can be seen from the figure, it is hard to discern a simple behaviour from the plots, aside from some indications that, as $f_z\to \infty$, the induced velocities go to zero. For $\alpha =56.0^\circ$ and $f_z=1.72$ the induced velocity does not change significantly with $Re_s$, while for $\alpha =36.6^\circ$, the $Re_s$ dependence is much stronger, with $\sim 50\,\%$ variations. The only real conclusion we can make is that the patterns will induce a velocity, which is of the order of 1 %–2 % of the cylinder velocity. This coincides with the direction of the movement of pattern inhomogeneity, and not the pattern itself.

Figure 12. Mean induced axial velocity as a function of radius. (a) Varying pattern frequency $f_z$ with constant angle $\alpha =36.6^\circ$ and constant $Re_s=3\times 10^4$. (b) Varying pattern angle $\alpha$ with constant frequency $f_z=1.72$ and constant $Re_s=3\times 10^4$. (c) Varying shear Reynolds number $Re_s$ with constant $\alpha =36.6^\circ$ and constant $f_z=1.72$. (d) Varying shear Reynolds number $Re_s$ with constant $\alpha =56.0^\circ$ and constant $f_z=1.72$.

Even if the induced velocities are small, they are enough to nudge the large-scale structures. Indeed, when we examine $\langle u_\theta \rangle _{\theta ,t}$, we find that the clear signature of the rolls is absent. One such case is presented in figure 13(a), which shows $\langle u_\theta \rangle _{\theta ,t}$ for the spiral pattern $f_z=1.72$, $\alpha =36.6^{\circ }$ and $Re_s=10^4$. However, strong rolls are still present in an instantaneous velocity field. We quantify this statement by showing the auto-correlation of the radial velocity in the mid-gap along the axial direction in figure 13(b). The large-scale structures still exist as the radial velocity at the mid-point of the span is negatively correlated at the wavelength of a Taylor roll.

Figure 13. (a) Average azimuthal velocity for a pattern of inclined stripes at $Re_s=10^4$, $\alpha =36.6^{\circ }$ and $f_z=1.72$; (b) Radial velocity auto-correlation in the mid-gap along the axial direction for homogeneous TC (dashed) and $\alpha =36.6^{\circ }$, $f_z=1.72$ (solid). (c,d) Space–time diagram of the azimuthal velocity in the mid-gap for (c) homogeneous TC; and (d) $\alpha =36.6^{\circ }$ and $f_z=1.72$. Red and blue dashed lines correspond to the maximum and the minimum mid-gap average azimuthal velocities in time, respectively, predicted from the phase angle of the fundamental mode of the Fourier transform.

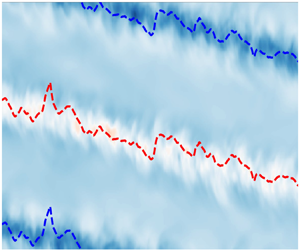
The next step is to quantify the way the rolls are moving around. To quantify the axial velocity of the rolls, we follow Sacco et al. (Reference Sacco, Verzicco and Ostilla-Mónico2019), and take the Fourier transform of the azimuthal velocity in the mid-gap. We use the phase $\phi$ of the Fourier mode which is axisymmetric and fundamental in the axial direction to find the axial displacement of the rolls, and hence their velocity $v_{roll,z} = \dot {\phi } \varGamma /(2{\rm \pi} )$. To show the effectiveness of this approach, we depict space–time diagrams of the azimuthally averaged azimuthal velocity in the mid-gap in figure 13(c,d), with the predicted location of the roll superimposed. For the first case, shown in figure 13(c), the rolls remain relatively steady, fluctuating around a fixed position. For the second case, in figure 13(d), we can see that the rolls follow the induced velocity, and are moving downwards in time at a certain velocity, instead of moving upwards following the motion of the spiral. To explain this, we return to the diagram in figure 10(b). The no-slip region is swept downwards by the incoming free-slip region, and the Reynolds-stress imbalance follows this direction of movement. We postulate that the change in inhomogeneities in the downwards direction tends to move the roll downwards along the direction of change of inhomogeneities.

In figure 14(a,c,e), we show the roll velocity $v_{roll,z}$ for various pattern frequencies and varying Reynolds number. We highlight again that the negative sign of the axial roll velocity denotes that the rolls are moving downwards in the axial direction, and not upwards, following the stripe. For all the angles of inclination of the pattern, the roll velocity is non-monotonic; it increases with pattern frequency until a maximum is reached, and then decreases as the pattern becomes smaller and its effect becomes confined to the boundary layers.

Figure 14. (a,c,e) Axial roll velocity for $Re_s=2.28 \times 10^3, 10^4, 3.00 \times 10^4$. (b,d,f) Axial roll velocity as the percentage of the spanwise pattern velocity for different angles and axial frequencies of the pattern for $Re_s=2.28 \times 10^3, 10^4, 3.00 \times 10^4$.

The rolls appear to have a certain resistance to moving because they achieve small velocities relative to those of the pattern. Indeed, the roll velocity is of the order of the induced axial velocities. It is very hard to elucidate what the functional form of $v_{roll,z}(\alpha ,f_z,Re_s)$ is. For the $Re_s$ shown, some patterns seem to be present. First, increasing the angle of inclination from $\alpha =20.4^{\circ }$ to $\alpha =36.6^{\circ }$, increases the roll velocity peak. However, if the angle of inclination further increases to $\alpha =56.0^{\circ }$, a decrease in the roll velocity peak is observed. To account for this, we show in figure 14(b,d,f) the roll velocity as a percentage of the pattern velocity in the axial direction, plotted for various pattern frequencies and angles of inclination. It can be clearly seen that, for smaller values of $\alpha$, the rolls move with a higher fraction of the geometrical velocity, even if the absolute velocities are smaller. The second noticeable thing is that there is a $f_z$ frequency for which the velocity is maximal, and further increasing or decreasing the pattern size will slow down the roll movement. While due to the limitations of our computer simulations it is impossible to do a proper $f_z$ sweep, this underlying pattern is present for almost all curves. Finally, the dependence on $Re_s$ cannot be properly elucidated. It is clear that, as $Re_s$ increases, the rolls keep on moving, in line with the presence of induced velocities for all values of $Re_s$ seen in figure 12. However, the underlying pattern is not clear. So, to summarize, these oblique patterns will generate induced velocities that move the rolls at velocities much slower than the cylinder speed, but how to optimize this velocity is unclear. Further supporting material that shows that oblique patterns induce spanwise velocities and move the rolls is provided in Appendix B for different roll wavelengths and numbers of rolls.

4.2. Checkerboard patterns

The final pattern we have studied is checkerboard patterns, as shown in figure 15(a). A schematic that defines their parameters is shown in figure 15(a). Similar to spiral patterns, these patterns are inhomogeneous in both axial (spanwise) and azimuthal (streamwise) directions, and will generate spanwise imbalances in the Reynolds stresses which can induce secondary flows. However, checkerboard patterns do not break the axial symmetry, so, in principle, we would not expect that a persistent axial velocity will result from their application, and this is indeed corroborated when looking at the statistics. Furthermore, as they move with the cylinder, the imbalances change and a symmetry is restored. Thus, their effect on the rolls is hard to guess a priori because the intermittent imbalances could modify the rolls, or the effect could be rapidly absorbed within the boundary layers.

Figure 15. (a) Checkerboard pattern parameters and (b) near-wall instantaneous azimuthal velocity of $\alpha =45^{\circ }$ square checkerboard pattern at Re _s=10⁴.

To show the effect of the pattern on the boundary layer, we present the near-wall azimuthal velocity in figure 15(b). Unlike the spiral pattern, the footprint on the flow appears to be much smaller. Indeed, the flow appears to be very similar to that generated by azimuthal inhomogeneities, where the streak elongation is able to wash away the inhomogeneities very fast. To corroborate this, we show the torque of a square checkerboard pattern (i.e. $\alpha =45^{\circ }$) for various frequencies, as shown in figure 16. The curve is monotonic, and the torque increases with increasing pattern frequency. The checkerboard case is thus not as special as the axial or spiral patterns.

Figure 16. (a) Non-dimensionalized and (b) normalized torque at various square checkerboard frequencies and Reynolds numbers.

To further analyse the square checkerboard pattern, we can compare its effect on the torque with the spiral pattern at $\alpha =36.6^{\circ }$. To do this, we also simulated a similar rectangular checkerboard pattern at $\alpha =36.6^{\circ }$. In figure 17(a), we show the normalized torques for the two checkerboard patterns considered, and the spiral case, for $Re_s=10^4$. For the lower frequencies, the spiral pattern has a much lower torque than the checkerboard patterns, whereas for the higher frequencies there is no significant difference in the torque.

Figure 17. (a) Normalized torque for different patterns: $\alpha =36.6^{\circ }$ spiral pattern (SP), $\alpha =36.6^{\circ }$ rectangle checkerboard (CB) pattern, and $\alpha =45^{\circ }$ square checkerboard for $Re_s=10^4$. (b) Normalized roll amplitude for different pattern frequencies and two types of checkerboard pattern at $Re_s=10^4$.

The absence of a large dip in the torque for small frequencies is another indication that the checkerboard pattern barely disrupts the rolls. This is further corroborated by figure 17(b), which shows the normalized roll amplitude for the two checkerboard cases studied. The values of $A/A_0$ seen for both checkerboard geometries are in line with those observed for azimuthal variations. Both azimuthal and checkerboard patterns do not significantly disrupt the rolls and induce no meaningful secondary flows, making them of low interest to our future research. Therefore, our analysis on this case is brief.

5. Summary and conclusion

Four pattern geometries of stress-free and no-slip boundary conditions have been applied on the inner cylinder of a TC system to study the effect of boundary inhomogeneities on existing pinned secondary flows (known as Taylor rolls) as well as other flow statistics. We found that the azimuthal variations do not significantly alter the rolls and reduce the torque by moderate amounts (as low as $10\,\%$ for most of the Reynolds numbers simulated) even if $50\,\%$ of the surface is patterned and not able to transmit shear. The natural elongation of streaks in the streamwise direction counters the effect of azimuthal patterns effectively. In addition, because the azimuthal pattern is moving with the cylinder, the flow will see intermittent stress-free and no-slip conditions, which restore symmetry in an average sense.

The picture is different for the axial variations. A certain portion of the cylinder is always stress free at any time, and this generates a persistent imbalance. Axial variations reduce the torque to values as low as $65\,\%$ of the homogeneous TC torque value, consistent with the low Reynolds number results found by Watanabe et al. (Reference Watanabe, Mamori and Fukagata2017) and Naim & Baig (Reference Naim and Baig2019). In addition, the $f_z=0.86$ pattern was found to generate Reynolds-stress imbalances that induce a secondary flow that destructively interferes with the rolls, and this reduces the torque beyond what is expected from just boundary layer effects analysed through effective slip lengths and velocities.

We also applied spiral variations which break axial reflection symmetries of the problem and introduce chirality. This induces a persistent axial velocity, which does not heavily modify the roll but it is able to move it around along the direction of relative pattern velocity with respect to the cylinder. For the three angles of inclination studied, there is an optimum frequency at each inclination angle for which the roll movement becomes maximum, which does not always coincide with the frequency that generates the maximum induced velocity. When normalizing the roll velocity by the relative pattern velocity, we found that the patterns with smaller angles of inclination tend to move the rolls with a higher fraction of this velocity.

The last pattern we studied was the checkerboard pattern which neither generates an induced velocity nor a persistent Reynolds-stress imbalance. Because of this, it ends up not having a significant effect on the rolls, while modifying the torque in a similar manner to the azimuthal patterns.

This study has served as confirmation that the Taylor rolls can be affected by careful patterning of the inner-cylinder boundary. Limitations of this study are primarily due to the fact that the parameter space to be explored is very large, and that we are only dealing with a narrow-gap TC system with radius ratio $\eta =0.909$ under pure inner-cylinder rotation. While this selection was advantageous to focus on Taylor rolls, as they are present even at higher $Re_s$, in order to fully comprehend the effect of boundary heterogeneity, we must further simulate radius ratios or combinations of different cylinder rotations where the rolls are not present at higher $Re_s$. Further work will also include the analysis of more realistic finite slip length patterns, which are obtainable in the laboratory.