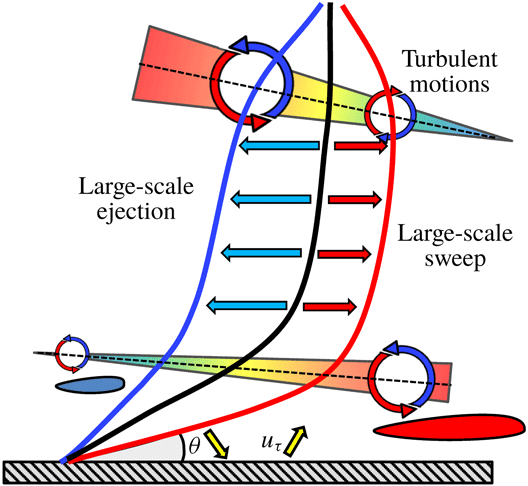
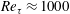1 Introduction
Any turbulent boundary layer at a moderate-to-high Reynolds number is populated with a wide spectrum of structures – ‘eddies’ – that cover a range bounded by the Kolmogorov length, at one end, and multiples of the boundary-layer thickness, at the other. With dissipative and inertial scales left aside, the dynamically important smallest-scale structures are the near-wall ‘streaks’ in the buffer region, which are separated by a mean spanwise distance of approximately 100 wall units and have a streamwise length scale of the order of 1000 wall units. Beyond the buffer region, the conventional paradigm, as described by the attached-eddy hypothesis (Townsend Reference Townsend1980; Perry, Henbest & Chong Reference Perry, Henbest and Chong1986), is one of a hierarchy of wall-attached eddies whose size grows in proportion to the wall distance. These eddies are primarily responsible for the turbulence energy and the shear stress in the log-law region, the former decaying logarithmically with the distance from the wall, in accord with the attached-eddy hypothesis.
While there is firm evidence for the validity of the principal elements of the attached-eddy hypothesis (Davidson et al.
Reference Davidson, Krogstad and Nickels2006; de Silva et al.
Reference de Silva, Marusic, Woodcock and Meneveau2015; Vassilicos et al.
Reference Vassilicos, Laval, Foucaut and Stanislas2015; Woodcock & Marusic Reference Woodcock and Marusic2015; de Giovanetti, Hwang & Choi Reference de Giovanetti, Hwang and Choi2016; Hwang & Bengana Reference Hwang and Bengana2016; Baars & Marusic Reference Baars and Marusic2018; Hwang & Sung Reference Hwang and Sung2018; Srinath et al.
Reference Srinath, Vassilicos, Cuvier, Laval, Stanislas and Foucaut2018; Marusic & Monty Reference Marusic and Monty2019), both measurements (Vassilicos et al.
Reference Vassilicos, Laval, Foucaut and Stanislas2015; Baidya et al.
Reference Baidya, Philip, Hutchins, Monty and Marusic2017; Fiorini et al.
Reference Fiorini, Bellani, Örlü, Segalini, Alfredsson and Talamelli2017; Willert et al.
Reference Willert, Soria, Stanislas, Klinner, Amili, Eisfelder, Cuvier, Bellani, Fiorini and Talamelli2017; Samie et al.
Reference Samie, Marusic, Hutchins, Fu, Fan, Hultmark and Smits2018) and simulations (Lee & Moser Reference Lee and Moser2015; Yamamoto & Tsuji Reference Yamamoto and Tsuji2018) show that the logarithmic decay of the turbulence energy does not extend over the entire log layer at friction Reynolds number values
![]() $Re_{\unicode[STIX]{x1D70F}}>1000$
, but is interrupted by a distinctive plateau region (or hump) of elevated energy in a layer centred around
$Re_{\unicode[STIX]{x1D70F}}>1000$
, but is interrupted by a distinctive plateau region (or hump) of elevated energy in a layer centred around
![]() $y^{+}\approx 3.9\sqrt{Re_{\unicode[STIX]{x1D70F}}}$
(Marusic, Mathis & Hutchins Reference Marusic, Mathis and Hutchins2010), which is associated with large-scale motions. Although Agostini & Leschziner (Reference Agostini and Leschziner2017) have provided arguments that link the plateau region to an extended interpretation of the attached-eddy hypothesis, this region is nevertheless distinctive and is not compatible with the conventional form of the hypothesis. An important aspect of this distinction is that the level of energy in the plateau is observed to rise progressively with the Reynolds number, the implication being that the large-scale structures in this region are increasingly influential, both directly through the shear stress associated with them and through their impact on, or interaction with, smaller-scale structures. Spectra of the streamwise energy as a function of the streamwise and spanwise wavelength (Del Alamo et al.
Reference Del Alamo, Jiménez, Zandonade and Moser2004; Chandran et al.
Reference Chandran, Baidya, Monty and Marusic2017) show that the energetic structures in the plateau region are separated by a spanwise distance that scales with the thickness of the boundary layer, typically
$y^{+}\approx 3.9\sqrt{Re_{\unicode[STIX]{x1D70F}}}$
(Marusic, Mathis & Hutchins Reference Marusic, Mathis and Hutchins2010), which is associated with large-scale motions. Although Agostini & Leschziner (Reference Agostini and Leschziner2017) have provided arguments that link the plateau region to an extended interpretation of the attached-eddy hypothesis, this region is nevertheless distinctive and is not compatible with the conventional form of the hypothesis. An important aspect of this distinction is that the level of energy in the plateau is observed to rise progressively with the Reynolds number, the implication being that the large-scale structures in this region are increasingly influential, both directly through the shear stress associated with them and through their impact on, or interaction with, smaller-scale structures. Spectra of the streamwise energy as a function of the streamwise and spanwise wavelength (Del Alamo et al.
Reference Del Alamo, Jiménez, Zandonade and Moser2004; Chandran et al.
Reference Chandran, Baidya, Monty and Marusic2017) show that the energetic structures in the plateau region are separated by a spanwise distance that scales with the thickness of the boundary layer, typically
![]() $0.5\unicode[STIX]{x1D6FF}$
–
$0.5\unicode[STIX]{x1D6FF}$
–
![]() $1\unicode[STIX]{x1D6FF}$
, while their length is of the order of
$1\unicode[STIX]{x1D6FF}$
, while their length is of the order of
![]() $5\unicode[STIX]{x1D6FF}$
–
$5\unicode[STIX]{x1D6FF}$
–
![]() $10\unicode[STIX]{x1D6FF}$
. Del Álamo et al. (Reference Del Álamo, Jimenez, Zandonade and Moser2006), Flores & Jiménez (Reference Flores and Jiménez2010), Mizuno & Jiménez (Reference Mizuno and Jiménez2013), Hwang & Bengana (Reference Hwang and Bengana2016) and Kevin, Monty & Hutchins (Reference Kevin, Monty and Hutchins2019) provide evidence for the proposition that these structures are quasi-autonomous, being caused, driven and sustained by processes analogous to those that sustain the near-wall streaks and thus being associated with large-scale ejections and sweeps forming quasi-streamwise vortices. There is an ongoing debate about the presence of very-large-scale structures in the outer part of the boundary layer and their contribution to the turbulence energy and the shear stress. Mathis, Hutchins & Marusic (Reference Mathis, Hutchins and Marusic2009) and Ganapathisubramani et al. (Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012), for example, claim that structures having streamwise length scales of 20 channel half-heights and longer make a material contribution to the total turbulence energy, but this is contradicted by Dennis & Nickels (Reference Dennis and Nickels2011). The contribution of these very large structures to the shear stress is likely to be marginal, as they are essentially irrotational and therefore dynamically inactive, in the sense discussed by Bradshaw (Reference Bradshaw1967), Townsend (Reference Townsend1980) and Jiménez (Reference Jiménez2013), among others.
$10\unicode[STIX]{x1D6FF}$
. Del Álamo et al. (Reference Del Álamo, Jimenez, Zandonade and Moser2006), Flores & Jiménez (Reference Flores and Jiménez2010), Mizuno & Jiménez (Reference Mizuno and Jiménez2013), Hwang & Bengana (Reference Hwang and Bengana2016) and Kevin, Monty & Hutchins (Reference Kevin, Monty and Hutchins2019) provide evidence for the proposition that these structures are quasi-autonomous, being caused, driven and sustained by processes analogous to those that sustain the near-wall streaks and thus being associated with large-scale ejections and sweeps forming quasi-streamwise vortices. There is an ongoing debate about the presence of very-large-scale structures in the outer part of the boundary layer and their contribution to the turbulence energy and the shear stress. Mathis, Hutchins & Marusic (Reference Mathis, Hutchins and Marusic2009) and Ganapathisubramani et al. (Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012), for example, claim that structures having streamwise length scales of 20 channel half-heights and longer make a material contribution to the total turbulence energy, but this is contradicted by Dennis & Nickels (Reference Dennis and Nickels2011). The contribution of these very large structures to the shear stress is likely to be marginal, as they are essentially irrotational and therefore dynamically inactive, in the sense discussed by Bradshaw (Reference Bradshaw1967), Townsend (Reference Townsend1980) and Jiménez (Reference Jiménez2013), among others.
The influence of the energetic structures on the turbulent conditions below the plateau has been the subject of numerous studies over the past two decades (Guala, Metzger & McKeon Reference Guala, Metzger and McKeon2011; Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2011; Ganapathisubramani et al. Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012; Jacobi & McKeon Reference Jacobi and McKeon2013; Talluru et al. Reference Talluru, Baidya, Hutchins and Marusic2014; Duvvuri & McKeon Reference Duvvuri and McKeon2015; Agostini, Leschziner & Gaitonde Reference Agostini, Leschziner and Gaitonde2016; Agostini & Leschziner Reference Agostini and Leschziner2016a ,Reference Agostini and Leschziner b ; Zhang & Chernyshenko Reference Zhang and Chernyshenko2016; Howland & Yang Reference Howland and Yang2018). Interest in this influence has been driven by the observations, some dating back to the late 1970s and 1980s (e.g. Brown & Thomas Reference Brown and Thomas1977; Bandyopadhyay & Hussain Reference Bandyopadhyay and Hussain1984), that the structures in this layer, interpreted as coherent regions of large-scale streamwise velocity fluctuations, exert strong ‘footprints’ on the viscosity-affected near-wall layer and also cause an amplification or an attenuation of the small-scale near-wall structures – referred to as ‘modulation’ – depending upon the sign of the streamwise velocity fluctuations in the footprints (see Agostini & Leschziner (Reference Agostini and Leschziner2016b ), for example, which contains several direct numerical simulation (DNS)-derived coloured snapshots). The large-scale fluctuations have been shown to be strongly correlated across the entire layer below the location of the large-scale motions, especially when the streamwise lag due to shear is taken into account, and this high correlation level also extends to large-scale skin-friction fluctuations (Blackwelder & Kovasznay Reference Blackwelder and Kovasznay1972; Brown & Thomas Reference Brown and Thomas1977). Both footprinting and modulation are of particular interest in the context of skin-friction control, whether active or passive, because the influence of the footprints increases, relative to the uncontrolled case, due to the fact that the control diminishes the near-wall small-scale activity that affects most directly the drag.
A key to studying and quantifying the consequences of the footprinting and modulation is a rationally defensible method for separating ‘large scales’ from ‘small scales’, the quotes intended to convey the fact that the distinction is not rigorous and depends on the manner in which the two scale ranges are defined. The separation has been effected along two main routes: the imposition of cut-off spectral filters (Bernardini & Pirozzoli Reference Bernardini and Pirozzoli2011; Mathis et al.
Reference Mathis, Marusic, Chernyshenko and Hutchins2013; Chung et al.
Reference Chung, Marusic, Monty, Vallikivi and Smits2015; Zhang & Chernyshenko Reference Zhang and Chernyshenko2016; Hwang & Sung Reference Hwang and Sung2017) and the use of empirical mode decomposition (EMD) (Agostini & Leschziner Reference Agostini and Leschziner2014; Cormier, Gatti & Frohnapfel Reference Cormier, Gatti and Frohnapfel2016), the latter preferred in the present work for reasons discussed in § 3. A third method, recently proposed by Baars, Hutchins & Marusic (Reference Baars, Hutchins and Marusic2016) in an experimental setting, is based on a coherence function, in Fourier space, between the velocity signal at the outer location at which the large-scale structures are observed and the velocity signal at any other wall-normal location. A coherence coefficient is then derived, again in Fourier space, which is used as a scaling factor to extract the coherent large-scales part from the raw signal, subject to a chosen threshold. Apart from the limitation imposed by the need to choose a specific outer location for the reference signal, the use of this approach for a spatially two-dimensional decomposition would require a coherence coefficients map in
![]() $\unicode[STIX]{x1D706}_{x}$
–
$\unicode[STIX]{x1D706}_{x}$
–
![]() $\unicode[STIX]{x1D706}_{z}$
space to be derived from spatial DNS fields. However, this task would require a very large number of temporal snapshots to be stored and processed, and it is also hindered by the fact that the spatial snapshots contain only a sparse set of large-scale structures, as the size of the simulation domain is limited by resource constraints. In contrast, the EMD is driven by the data contained in independent snapshots, and it does not, therefore, rely on their number, except insofar as the quality of the statistical convergence depends on the number of realisations included in the analysis. The EMD is also tolerant to the sparsity of large-scale structures in any one snapshot.
$\unicode[STIX]{x1D706}_{z}$
space to be derived from spatial DNS fields. However, this task would require a very large number of temporal snapshots to be stored and processed, and it is also hindered by the fact that the spatial snapshots contain only a sparse set of large-scale structures, as the size of the simulation domain is limited by resource constraints. In contrast, the EMD is driven by the data contained in independent snapshots, and it does not, therefore, rely on their number, except insofar as the quality of the statistical convergence depends on the number of realisations included in the analysis. The EMD is also tolerant to the sparsity of large-scale structures in any one snapshot.
Once the scales have been separated, their statistical properties can be studied in isolation, as can the interaction between them, of which the correlation between large-scale and small-scale motions and the characteristics of the modulation are of greatest interest. The extent to which such studies can be pursued depends greatly on the format and volume of the database available for analysis. The best foundation, by far, is the form of a temporal sequence of full-volume snapshots, which can only be derived from DNS, albeit at lower Reynolds-number values than those that can be realised in experimental flows. Experiments, mostly undertaken with hot-wire anemometry (Ganapathisubramani et al. Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012; Mathis et al. Reference Mathis, Marusic, Chernyshenko and Hutchins2013; Vallikivi, Hultmark & Smits Reference Vallikivi, Hultmark and Smits2015; Örlü et al. Reference Örlü, Fiorini, Segalini, Bellani, Talamelli and Alfredsson2017), are almost invariably restricted to time signals across the wall-normal lines, requiring the assumption of the Taylor hypothesis to infer spatial properties that evolve in the streamwise direction. Although corrections to the basic Taylor hypothesis have been proposed by Dróżdż & Elsner (Reference Dróżdż and Elsner2017) and Yang & Howland (Reference Yang and Howland2018), these do not negate the basic limitations of the method.
The quantification of the modulation has been the subject of several proposals. The classical approach, proposed by Mathis et al. (Reference Mathis, Hutchins and Marusic2011), involves the evaluation of the envelope of the small-scale signal,
![]() $Env(u_{SS})$
, obtained by low-pass filtering
$Env(u_{SS})$
, obtained by low-pass filtering
![]() $u_{SS}^{2}$
, and determining its correlation with the large-scale signal through the correlation coefficient
$u_{SS}^{2}$
, and determining its correlation with the large-scale signal through the correlation coefficient
![]() $\overline{u_{LS}Env(u_{SS})}/(\sqrt{\overline{u_{LS}u_{LS}}}\sqrt{\overline{Env(u_{SS})^{2}}})$
, with the envelope determined by means of the Hilbert transform. Among a number of interesting observations arising from the modulation correlation is that the correlation is positive below
$\overline{u_{LS}Env(u_{SS})}/(\sqrt{\overline{u_{LS}u_{LS}}}\sqrt{\overline{Env(u_{SS})^{2}}})$
, with the envelope determined by means of the Hilbert transform. Among a number of interesting observations arising from the modulation correlation is that the correlation is positive below
![]() $y^{+}\approx 150$
, while it is negative beyond this distance. This sign reversal is observed to be only weakly dependent on the Reynolds number, as shown by Mathis et al. (Reference Mathis, Hutchins and Marusic2009). There is, as yet, no consensus on the origin of this sign switch, alternative interpretations having been proposed by Jacobi & McKeon (Reference Jacobi and McKeon2013), Baars et al. (Reference Baars, Talluru, Hutchins and Marusic2015) and Zhang & Chernyshenko (Reference Zhang and Chernyshenko2016). Agostini et al. (Reference Agostini, Leschziner and Gaitonde2016) have shown that the envelope of positive small-scale fluctuation is significantly different from that of negative fluctuations, due to the skewness of the probability density function (p.d.f.) of the small-scale motions, related to the ‘splatting’/‘anti-splatting’ phenomena (Agostini & Leschziner Reference Agostini and Leschziner2014). Hence, in reality, there are two correlation coefficients. However, both feature a change in sign at
$y^{+}\approx 150$
, while it is negative beyond this distance. This sign reversal is observed to be only weakly dependent on the Reynolds number, as shown by Mathis et al. (Reference Mathis, Hutchins and Marusic2009). There is, as yet, no consensus on the origin of this sign switch, alternative interpretations having been proposed by Jacobi & McKeon (Reference Jacobi and McKeon2013), Baars et al. (Reference Baars, Talluru, Hutchins and Marusic2015) and Zhang & Chernyshenko (Reference Zhang and Chernyshenko2016). Agostini et al. (Reference Agostini, Leschziner and Gaitonde2016) have shown that the envelope of positive small-scale fluctuation is significantly different from that of negative fluctuations, due to the skewness of the probability density function (p.d.f.) of the small-scale motions, related to the ‘splatting’/‘anti-splatting’ phenomena (Agostini & Leschziner Reference Agostini and Leschziner2014). Hence, in reality, there are two correlation coefficients. However, both feature a change in sign at
![]() $y^{+}\approx 100{-}200$
. It is arguable that the lack of insight into the details of the scale-interaction processes, in general, and the correlation behaviour, in particular, is due to insufficiently searching scrutiny of available DNS data – a gap this paper aims to fill.
$y^{+}\approx 100{-}200$
. It is arguable that the lack of insight into the details of the scale-interaction processes, in general, and the correlation behaviour, in particular, is due to insufficiently searching scrutiny of available DNS data – a gap this paper aims to fill.
A tangible outcome of the studies by Marusic and collaborators is an empirical relationship that permits the statistics of the near-wall turbulence to be ‘predicted’, irrespective of the Reynolds number. The cornerstone of this relationship is a ‘universal’ small-scale signal, unaffected by large-scale motions (and thus Reynolds number), which is then modified (or corrected) by functional coefficients that vary with
![]() $y^{+}$
and premultiply the Reynolds-number-dependent large-scale outer fluctuations in the log-law region. This relationship reflects the assumption that the modulation of the streamwise turbulence energy is symmetric with respect of the sign of the large-scale motions. Agostini et al. (Reference Agostini, Leschziner and Gaitonde2016) and Agostini & Leschziner (Reference Agostini and Leschziner2016b
, Reference Agostini and Leschziner2018) show, however, that the assumption of symmetry is not correct, especially not in the presence of drag-reducing actuation, and that the physical interactions at play are more complicated than those represented by the prediction formula. Recent work by Zhang & Chernyshenko (Reference Zhang and Chernyshenko2016) has resulted in a theoretical framework, based on the assumption of quasi-steadiness, that yields results consistent with Marusic’s empirical relationship. In this respect, the availability of DNS data, including those of the writers, has been decisive in securing the success of the quasi-steady theory, the validity of which has been examined by Agostini & Leschziner (Reference Agostini and Leschziner2016a
) by reference to DNS at
$y^{+}$
and premultiply the Reynolds-number-dependent large-scale outer fluctuations in the log-law region. This relationship reflects the assumption that the modulation of the streamwise turbulence energy is symmetric with respect of the sign of the large-scale motions. Agostini et al. (Reference Agostini, Leschziner and Gaitonde2016) and Agostini & Leschziner (Reference Agostini and Leschziner2016b
, Reference Agostini and Leschziner2018) show, however, that the assumption of symmetry is not correct, especially not in the presence of drag-reducing actuation, and that the physical interactions at play are more complicated than those represented by the prediction formula. Recent work by Zhang & Chernyshenko (Reference Zhang and Chernyshenko2016) has resulted in a theoretical framework, based on the assumption of quasi-steadiness, that yields results consistent with Marusic’s empirical relationship. In this respect, the availability of DNS data, including those of the writers, has been decisive in securing the success of the quasi-steady theory, the validity of which has been examined by Agostini & Leschziner (Reference Agostini and Leschziner2016a
) by reference to DNS at
![]() $Re_{\unicode[STIX]{x1D70F}}=4200$
reported by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014).
$Re_{\unicode[STIX]{x1D70F}}=4200$
reported by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014).
The correlation coefficient and Marusic’s prediction formula, while informative, do not provide tangible statements on the impact of modulation on the skin friction. Subject to the validity of quasi-steady equilibrium and the assumption of a universal small-scale field that responds without time delay to large-scale perturbations, it does allow, at least to some extent, the effects of the large scales on the statistics of the near-wall layer to be predicted (Zhang & Chernyshenko Reference Zhang and Chernyshenko2016). To go beyond this rather limited framework, more extensive statistical analyses are required, exploiting full-volume fields. Such analyses have been pursued by Agostini & Leschziner (Reference Agostini and Leschziner2018), in the context of skin-friction reduction by means of oscillatory spanwise wall motion. These studies have led, among others, to the quantification of the contribution of different scales to the skin friction and of the dependence of the variance of the small-scale skin-friction fluctuations on the intensity and sign of the footprints, the latter shown to be exceptionally sensitive when the actuation causes the drag to reduce substantially through a drastic weakening of the near-wall streaks.
The present paper constitutes a major extension of the previous analysis by Agostini & Leschziner (Reference Agostini and Leschziner2018). The focus here is, however, on the canonical channel flow. A wide range of statistical algorithms are being brought to bear on full-volume datasets arising from the authors’ own DNS data. One focal point of the study is the interaction between large scales and small scales and, in particular, the identification of the processes driving the modulation of the small scales by the large scales. This is done through the derivation and manipulation of joint and conditional p.d.f.s, from which the dependence of small-scale streamwise and shear stresses on large-scale fluctuations is extracted. A second major facet of the present study is the quantification of the contributions of different scales to the skin friction, and of the dependence of these contributions on the sign and magnitude of the large-scale wall-shear footprints.
2 The database and statistical processing
The DNS data forming the basis of the present analysis were the subject of earlier papers by Agostini & Leschziner (Reference Agostini and Leschziner2018), which focused primarily on the physical processes associated with drag-reducing wall actuation. Therefore, only a brief statement of the main characteristics is given here.
The simulations were performed over a box of length, height and depth of
![]() $4\unicode[STIX]{x03C0}h\times 2h\times 2\unicode[STIX]{x03C0}h$
, respectively, corresponding to approximately
$4\unicode[STIX]{x03C0}h\times 2h\times 2\unicode[STIX]{x03C0}h$
, respectively, corresponding to approximately
![]() $(12\times 2\times 6)\times 10^{3}$
wall units. The box was covered with a finite-volume mesh of
$(12\times 2\times 6)\times 10^{3}$
wall units. The box was covered with a finite-volume mesh of
![]() $1056\times 528\times 1056$
$1056\times 528\times 1056$
![]() $(=589\times 10^{6})$
cells. The corresponding cell dimensions were
$(=589\times 10^{6})$
cells. The corresponding cell dimensions were
![]() $(x^{+},y_{min}^{+},y_{max}^{+},z^{+})=(12.2,0.4,7.2,6.1)$
.
$(x^{+},y_{min}^{+},y_{max}^{+},z^{+})=(12.2,0.4,7.2,6.1)$
.
The computational scheme combined a fractional-step method with fourth-order spatial discretisation, a third-order Gear-like time-marching scheme and a multigrid-based solution of the pressure-Poisson equation. All simulations were progressed with a time-marching step chosen such that the Courant–Friedrichs–Lewy number did not exceed 0.25. Field variables were stored at intervals of
![]() $\unicode[STIX]{x1D6FF}t^{+}\approx 10$
.
$\unicode[STIX]{x1D6FF}t^{+}\approx 10$
.
The adequacy of the resolution is demonstrated in Agostini, Touber & Leschziner (Reference Agostini, Touber and Leschziner2014) by means of a comparison with a simulation of the canonical channel flow over a grid of 1.2B cells, an examination of the resolved dissipation, relative to the imbalance of other terms in the turbulence-energy budget, an evaluation of the ratio of cell distances to the Kolmogorov length scale and a comparison of the energy budget for the unactuated flow with the budget reported by Moser, Kim & Mansour (Reference Moser, Kim and Mansour1999) for a Reynolds number similar to the present value.
3 Scale separation
In order to investigate the interaction between turbulent motions at different length scales, the spectrum of motions needs to be appropriately partitioned into sub-ranges, each associated with a relatively narrow band of scales. In the present work, this is achieved with the EMD (Huang et al. Reference Huang, Shen, Long, Wu, Shih, Zheng, Yen, Tung and Liu1998). The method originates from signal processing of temporally evolving functions, and the present authors have adapted it to two-dimensional spatial fields (Agostini et al. Reference Agostini, Leschziner and Gaitonde2016), exploiting it to investigate a range of scale-interaction issues for canonical and forced channel flows. The application of the method to all wall-parallel two-dimensional fields of any full-volume numerical snapshot then yields a three-dimensional scale decomposition of the turbulence field.
The EMD splits the spatial field into intrinsic mode functions, driven purely by the local characteristic scales of the turbulence field. The method requires no predetermined functional elements and involves no linear elements or loss of filter-induced energy. The number of EMD modes selected to separate the scales depends on the width of the spectrum of scales to be resolved. As the number of modes is progressively increased, starting from the raw signal, the scales of the motions captured increase and their energy declines. The mode-generation process is stopped when the residual, beyond the highest intrinsic mode function, has an insignificant energy content. An EMD mode is not a signal having a unique frequency or length scale, but one that has a narrow range of scales and is characterised by a narrow-band spectrum with a mean scale that rises with mode number
![]() $i$
. More precisely, for a fully turbulent flow, the mean frequency and the bandwidth associated with each mode double between two successive modes (Flandrin, Rilling & Goncalves Reference Flandrin, Rilling and Goncalves2004). In effect, the EMD is a ‘sifting’ process: the modes are extracted one after the other, starting at the highest frequency, so that the features (properties) of any one mode will remain unchanged whatever number of modes is used for the decomposition. The mode-specific sub-spectra for the present Reynolds number are included in figure 2 of Agostini & Leschziner (Reference Agostini and Leschziner2018).
$i$
. More precisely, for a fully turbulent flow, the mean frequency and the bandwidth associated with each mode double between two successive modes (Flandrin, Rilling & Goncalves Reference Flandrin, Rilling and Goncalves2004). In effect, the EMD is a ‘sifting’ process: the modes are extracted one after the other, starting at the highest frequency, so that the features (properties) of any one mode will remain unchanged whatever number of modes is used for the decomposition. The mode-specific sub-spectra for the present Reynolds number are included in figure 2 of Agostini & Leschziner (Reference Agostini and Leschziner2018).
The outcome of the EMD process is conveyed by figure 1. This shows the pre-multiplied spanwise spectrum for the present channel flow, decomposed into three sub-ranges and reconstructed from six EMD modes: the small-scale sub-range at the low-wavelength end consists of modes
![]() $1+2$
; the large-scale sub-range at the high-wavelength end comprises modes
$1+2$
; the large-scale sub-range at the high-wavelength end comprises modes
![]() $4+5+6$
; and the intermediate-scale sub-range consists of mode 3. The original spectrum can be recovered by summing up the modal spectra and adding to the sum contributions that represent the interaction between modes; this equality will be clarified below by reference to mode-specific normal- and shear-stress profiles.
$4+5+6$
; and the intermediate-scale sub-range consists of mode 3. The original spectrum can be recovered by summing up the modal spectra and adding to the sum contributions that represent the interaction between modes; this equality will be clarified below by reference to mode-specific normal- and shear-stress profiles.
It must be acknowledged here that the decision on how to attribute modes into ‘large scales’ and ‘small scales’ is somewhat subjective, as is also the conventional approach of imposing spectral Fourier filters to separate the scales. The present attribution is based on extensive experience by the authors in applying the EMD to several flows, reported and justified in Agostini & Leschziner (Reference Agostini and Leschziner2014, Reference Agostini and Leschziner2017, Reference Agostini and Leschziner2018). A limitation that is unavoidable in respect of the scale attribution is that the Reynolds number of the present flow is low, in which case the large-/small-scale separation, represented by the intermediate-scale sub-range, is rather tenuous. Nevertheless, it is observed that the small-scale sub-range is confined to
![]() $\unicode[STIX]{x1D706}_{z}^{+}\approx 200$
, while the large-scale sub-range starts at
$\unicode[STIX]{x1D706}_{z}^{+}\approx 200$
, while the large-scale sub-range starts at
![]() $\unicode[STIX]{x1D706}_{z}^{+}\approx 800$
and, importantly, contains the outer energetic maximum at
$\unicode[STIX]{x1D706}_{z}^{+}\approx 800$
and, importantly, contains the outer energetic maximum at
![]() $y^{+}\approx 200$
,
$y^{+}\approx 200$
,
![]() $\unicode[STIX]{x1D706}_{z}^{+}\approx 1000$
that is conventionally associated with the outer large scales that give rise to the plateau in the streamwise-energy profile.
$\unicode[STIX]{x1D706}_{z}^{+}\approx 1000$
that is conventionally associated with the outer large scales that give rise to the plateau in the streamwise-energy profile.
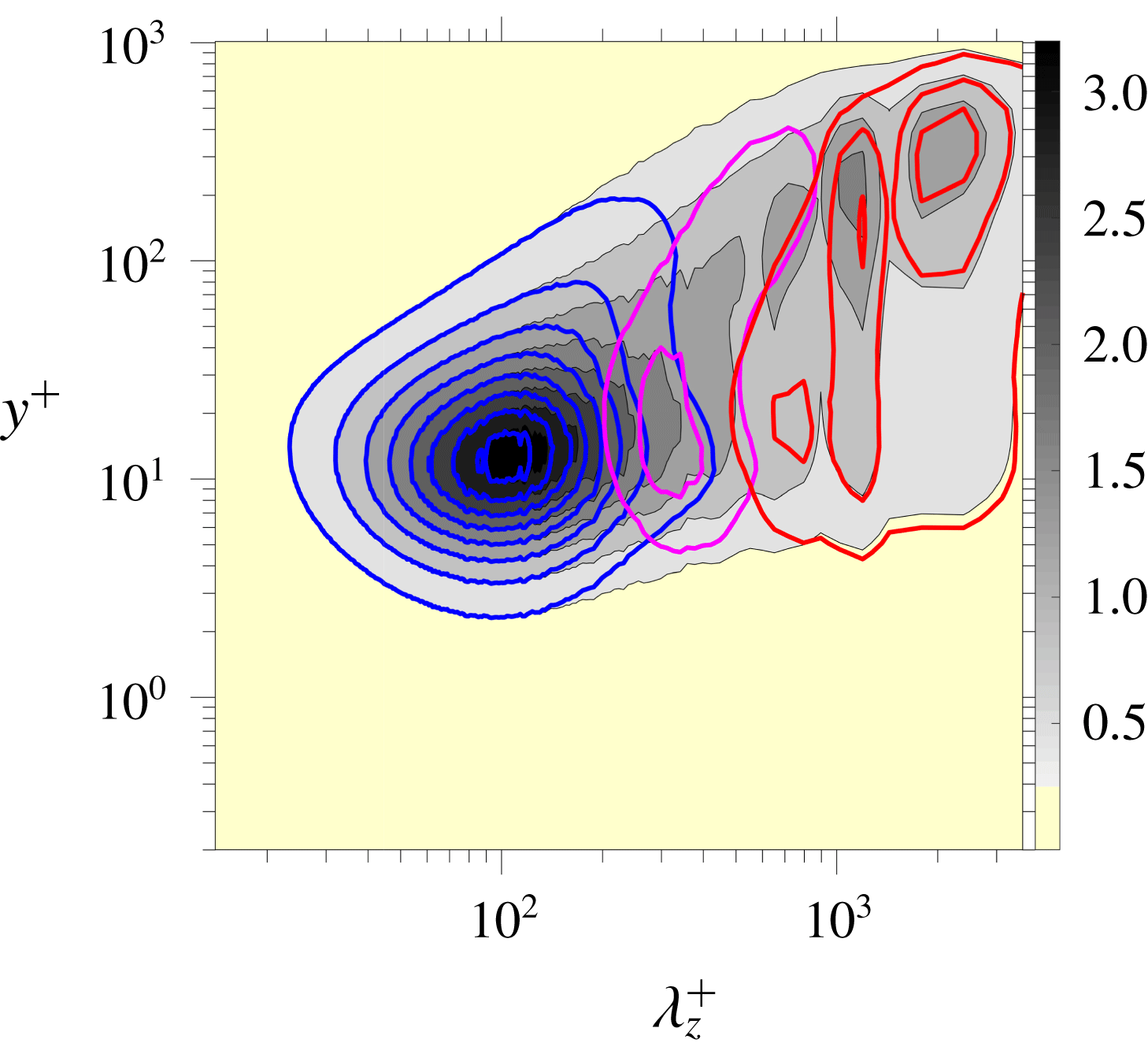
Figure 1. Premultiplied spanwise spectral maps for the streamwise turbulent fluctuations: grey contours represent the total field; blue, magenta and red iso-lines represent, respectively, sub-spectra for small-scale, intermediate-scale and large-scale fluctuations.
4 Statistical processing
With the mode decomposition effected, various statistical properties can be obtained to identify the contribution of modes to the turbulent stresses, the interactions between modes and the effect of different scales on the skin friction. These statistics were here derived from full-volume velocity fields at 150 time levels, separated by intervals of
![]() $\unicode[STIX]{x0394}tu_{\unicode[STIX]{x1D70F}}^{2}/\unicode[STIX]{x1D708}=50$
.
$\unicode[STIX]{x0394}tu_{\unicode[STIX]{x1D70F}}^{2}/\unicode[STIX]{x1D708}=50$
.
The approach taken here is to derive all statistical quantities of interest, at any wall-normal location,
![]() $y^{+}$
, from two variants of joint p.d.f.s of the form
$y^{+}$
, from two variants of joint p.d.f.s of the form
![]() $P(X_{1},\ldots ,X_{n},Y)$
and
$P(X_{1},\ldots ,X_{n},Y)$
and
![]() $P(X_{1},\ldots ,X_{n},Y)/P(Y)$
, the latter referred to as conditional p.d.f. The
$P(X_{1},\ldots ,X_{n},Y)/P(Y)$
, the latter referred to as conditional p.d.f. The
![]() $X_{i}$
arguments of the p.d.f.s are any flow variables of interest – e.g. the velocity components or EMD-derived modal constituents of the components. The argument
$X_{i}$
arguments of the p.d.f.s are any flow variables of interest – e.g. the velocity components or EMD-derived modal constituents of the components. The argument
![]() $Y$
is distinct from the others in so far as most statistics presented below are of correlations conditional on
$Y$
is distinct from the others in so far as most statistics presented below are of correlations conditional on
![]() $Y$
. A standard condition imposed on the joint p.d.f.s is
$Y$
. A standard condition imposed on the joint p.d.f.s is
Quantities derived from the joint p.d.f.s are the mean value of any variable
![]() $X_{i}$
,
$X_{i}$
,
the variance of fluctuations relative to the mean values,
![]() $x_{i}=X_{i}-\overline{X_{i}}$
, with
$x_{i}=X_{i}-\overline{X_{i}}$
, with
![]() $\overline{x_{i}}=0$
,
$\overline{x_{i}}=0$
,
and distributions of the mean and variance across the condition variable
![]() $Y$
, respectively,
$Y$
, respectively,
These derivatives thus represent the contribution of the properties in question to their respective totals within a band of
![]() $\text{d}Y$
, and their integral with respect to
$\text{d}Y$
, and their integral with respect to
![]() $Y$
then yields the property itself.
$Y$
then yields the property itself.
Figure 2 arises from the particular example
![]() $i=1$
,
$i=1$
,
![]() $j=1$
,
$j=1$
,
![]() $n=1$
,
$n=1$
,
![]() $X_{1}=U^{+}$
in (4.4) and (4.5), and
$X_{1}=U^{+}$
in (4.4) and (4.5), and
![]() $Y=Cf_{LS}$
, the large-scale skin-friction fluctuation – i.e. the local and instantaneous value associated with large-scale footprints. The distribution
$Y=Cf_{LS}$
, the large-scale skin-friction fluctuation – i.e. the local and instantaneous value associated with large-scale footprints. The distribution
![]() $\text{d}\overline{uu}^{+}/\text{d}Cf_{LS}$
at any
$\text{d}\overline{uu}^{+}/\text{d}Cf_{LS}$
at any
![]() $y^{+}$
location can be derived from (4.5) and the wall-normal profile of the streamwise stress
$y^{+}$
location can be derived from (4.5) and the wall-normal profile of the streamwise stress
![]() $\overline{uu}^{+}$
then arises upon integrating this field over
$\overline{uu}^{+}$
then arises upon integrating this field over
![]() $Cf_{LS}$
. The former field is shown in figure 2(a) and the latter profile is given in figure 2(b).
$Cf_{LS}$
. The former field is shown in figure 2(a) and the latter profile is given in figure 2(b).
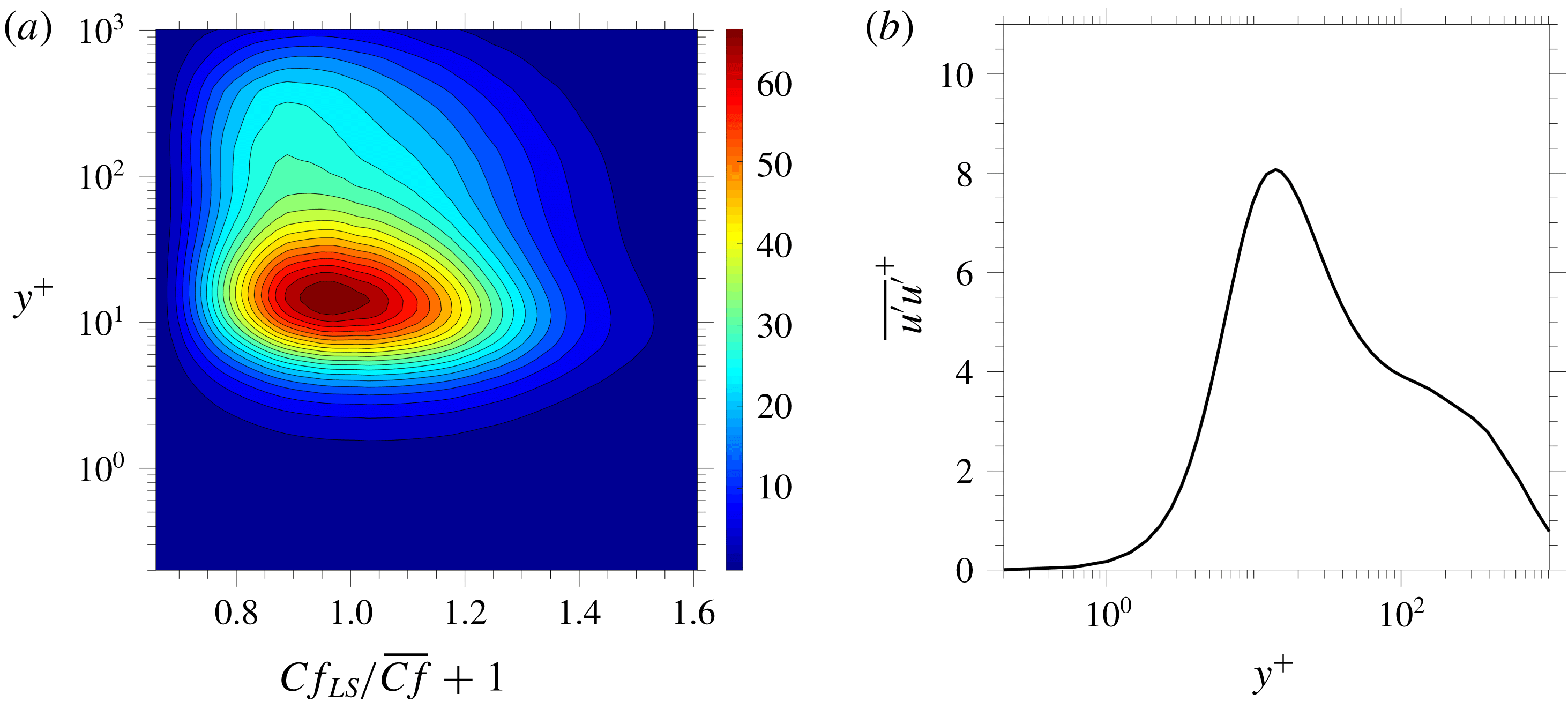
Figure 2. Properties of streamwise stress
![]() $\overline{uu}^{+}$
: (a) map of stress derivative
$\overline{uu}^{+}$
: (a) map of stress derivative
![]() $\text{d}\overline{uu}^{+}/\text{d}Cf_{LS}$
across
$\text{d}\overline{uu}^{+}/\text{d}Cf_{LS}$
across
![]() $(Cf_{LS},y^{+})$
plane (4.5); (b) wall-normal profile of the stress arising from integration of the field in map (a) with respect to
$(Cf_{LS},y^{+})$
plane (4.5); (b) wall-normal profile of the stress arising from integration of the field in map (a) with respect to
![]() $Cf_{LS}$
.
$Cf_{LS}$
.
In all statistics to follow,
![]() $Y$
is
$Y$
is
![]() $Cf_{LS}$
, the p.d.f. of which is shown in figure 3. Its asymmetric shape indicates that positive large-scale velocity fluctuations, induced by large-scale motions, are fewer in number, but more intense than negative fluctuations, which are more numerous, but weaker in intensity. The coloured tails in the p.d.f. define the regions of extreme 1.5 % positive or negative events. Some statistics to follow focus specifically on these extreme tail regions, involving the integration of (4.5) over the coloured tails only, in order to clarify the limiting states of
$Cf_{LS}$
, the p.d.f. of which is shown in figure 3. Its asymmetric shape indicates that positive large-scale velocity fluctuations, induced by large-scale motions, are fewer in number, but more intense than negative fluctuations, which are more numerous, but weaker in intensity. The coloured tails in the p.d.f. define the regions of extreme 1.5 % positive or negative events. Some statistics to follow focus specifically on these extreme tail regions, involving the integration of (4.5) over the coloured tails only, in order to clarify the limiting states of
![]() $Cf_{LS}$
-conditional correlations.
$Cf_{LS}$
-conditional correlations.

Figure 3. The p.d.f. of large-scale skin-friction fluctuations; the blue and red regions represent areas of 1.5 % extreme negative and positive events, respectively.
The map in figure 2(a), derived from
![]() $P(U^{+},Cf_{LS})$
, provides information, at any
$P(U^{+},Cf_{LS})$
, provides information, at any
![]() $y^{+}$
location, about the rate of the contribution of
$y^{+}$
location, about the rate of the contribution of
![]() $\overline{uu}^{+}$
with
$\overline{uu}^{+}$
with
![]() $Cf_{LS}$
to the total streamwise stress. Because the p.d.f. is subject to the constraint expressed by (4.1), it is not possible to gain a clear view of the variation of
$Cf_{LS}$
to the total streamwise stress. Because the p.d.f. is subject to the constraint expressed by (4.1), it is not possible to gain a clear view of the variation of
![]() $\overline{uu}^{+}$
at any condition
$\overline{uu}^{+}$
at any condition
![]() $Cf_{LS}$
relative to the mean level at this condition. This limitation can be circumvented by using the conditional p.d.f.
$Cf_{LS}$
relative to the mean level at this condition. This limitation can be circumvented by using the conditional p.d.f.
![]() $P(X_{1},\ldots ,X_{n},Y)/P(Y)$
. This then yields conditional mean values,
$P(X_{1},\ldots ,X_{n},Y)/P(Y)$
. This then yields conditional mean values,
![]() $\overline{X_{i}}|_{Y}$
, and corresponding conditional variance values,
$\overline{X_{i}}|_{Y}$
, and corresponding conditional variance values,
![]() $\overline{x_{i}x_{j}}|_{Y}$
, respectively, from
$\overline{x_{i}x_{j}}|_{Y}$
, respectively, from
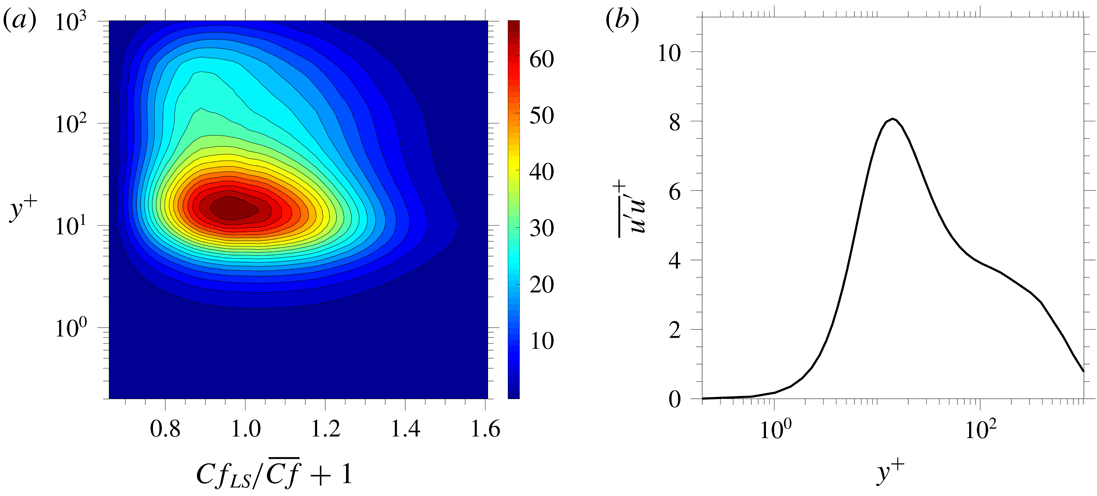
For the same example considered above in figure 2(a,b), the map of the conditional variation of the streamwise-velocity fluctuations, (
![]() $\overline{uu}^{+}|_{Cf_{LS}}$
), is shown in figure 4(a). This brings to light the fact, obscured in figure 2(a), that positive large-scale skin-friction fluctuations go hand-in-hand with an amplification of the streamwise stress in the buffer layer, associated predominantly with small-scale fluctuations, while at extreme negative skin-friction fluctuations, there is a weaker rise in the normal stress around
$\overline{uu}^{+}|_{Cf_{LS}}$
), is shown in figure 4(a). This brings to light the fact, obscured in figure 2(a), that positive large-scale skin-friction fluctuations go hand-in-hand with an amplification of the streamwise stress in the buffer layer, associated predominantly with small-scale fluctuations, while at extreme negative skin-friction fluctuations, there is a weaker rise in the normal stress around
![]() $y^{+}\approx 300$
, indicative of the increasing prominence of outer large-scale motions. An enhanced view of the above features is given in figure 4(b) by the blue and red profiles that represent, respectively, the average of the conditional streamwise stresses obtained by integrating (4.7) over the blue and red 1.5 % tails in figure 3.
$y^{+}\approx 300$
, indicative of the increasing prominence of outer large-scale motions. An enhanced view of the above features is given in figure 4(b) by the blue and red profiles that represent, respectively, the average of the conditional streamwise stresses obtained by integrating (4.7) over the blue and red 1.5 % tails in figure 3.

Figure 4. Properties of streamwise stress
![]() $\overline{uu}^{+}|_{Cf_{LS}}$
: (a) map of stress derivative
$\overline{uu}^{+}|_{Cf_{LS}}$
: (a) map of stress derivative
![]() $\overline{uu}^{+}|_{Cf_{LS}}$
across
$\overline{uu}^{+}|_{Cf_{LS}}$
across
![]() $(Cf_{LS},y^{+})$
plane (4.7); (b) wall-normal profiles of the conditional streamwise stresses obtained by integrating (4.7) over the blue and red 1.5 % tails in figure 3.
$(Cf_{LS},y^{+})$
plane (4.7); (b) wall-normal profiles of the conditional streamwise stresses obtained by integrating (4.7) over the blue and red 1.5 % tails in figure 3.
A major objective of this paper is to examine the contribution of different scales, and their interactions, to the skin friction. To this end, two previously established methods are exploited. Both are given below in two non-dimensional forms: one using outer scales and the other inner scales. The first is the Fukagata–Iwamoto–Kasagi (FIK) relationship, derived upon integrating repeatedly the one-dimensional streamwise-momentum equation for fully developed channel flow:
 $$\begin{eqnarray}\displaystyle Cf & = & \displaystyle \frac{6}{Re}+\int _{0}^{1}6\left(1-\frac{y}{h}\right)\left(\frac{-\overline{uv}}{U_{b}^{2}}\right)\text{d}\left(\frac{y}{h}\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{6}{Re}+\int _{0}^{Re_{\unicode[STIX]{x1D70F}}}\underbrace{\frac{6Re_{\unicode[STIX]{x1D70F}}}{Re^{2}}\left(1-\frac{y^{+}}{Re_{\unicode[STIX]{x1D70F}}}\right)(-\overline{uv}^{+})}_{Cf_{FIK}^{+}}\,\text{d}y^{+},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Cf & = & \displaystyle \frac{6}{Re}+\int _{0}^{1}6\left(1-\frac{y}{h}\right)\left(\frac{-\overline{uv}}{U_{b}^{2}}\right)\text{d}\left(\frac{y}{h}\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{6}{Re}+\int _{0}^{Re_{\unicode[STIX]{x1D70F}}}\underbrace{\frac{6Re_{\unicode[STIX]{x1D70F}}}{Re^{2}}\left(1-\frac{y^{+}}{Re_{\unicode[STIX]{x1D70F}}}\right)(-\overline{uv}^{+})}_{Cf_{FIK}^{+}}\,\text{d}y^{+},\end{eqnarray}$$
in which the first term, containing the bulk Reynolds number, accounts for the laminar contribution. Here,
![]() $Re=U_{b}h/\unicode[STIX]{x1D708}$
is the bulk Reynolds number and
$Re=U_{b}h/\unicode[STIX]{x1D708}$
is the bulk Reynolds number and
![]() $h$
is the channel half-height.
$h$
is the channel half-height.
An alternative relationship, proposed by Renard & Deck (Reference Renard and Deck2016) (RD), arises from energy-conservation considerations, specifically the energy that is fed into the flow to cover the viscous dissipation and the turbulence-energy generation, represented by the two respective additive terms in
 $$\begin{eqnarray}\displaystyle Cf & = & \displaystyle \int _{0}^{\unicode[STIX]{x1D6FF}}\left[\frac{2\unicode[STIX]{x1D708}}{U_{\infty }^{3}}\left(\frac{\unicode[STIX]{x2202}\overline{U}}{\unicode[STIX]{x2202}y}\right)^{2}+\frac{-2\overline{uv}}{U_{\infty }^{3}}\frac{\unicode[STIX]{x2202}\overline{U}}{\unicode[STIX]{x2202}y}\right]\text{d}y\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{Re_{\unicode[STIX]{x1D70F}}}\left[\underbrace{Cf\sqrt{\frac{Cf}{2}}\left(\frac{\unicode[STIX]{x2202}\overline{U}^{+}}{\unicode[STIX]{x2202}y^{+}}\right)^{2}}_{Cf_{a}^{+}}+\underbrace{Cf\sqrt{\frac{Cf}{2}}\left(-\overline{uv}^{+}\frac{\unicode[STIX]{x2202}\overline{U^{+}}}{\unicode[STIX]{x2202}y^{+}}\right)}_{Cf_{b}^{+}}\right]\text{d}y^{+}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Cf & = & \displaystyle \int _{0}^{\unicode[STIX]{x1D6FF}}\left[\frac{2\unicode[STIX]{x1D708}}{U_{\infty }^{3}}\left(\frac{\unicode[STIX]{x2202}\overline{U}}{\unicode[STIX]{x2202}y}\right)^{2}+\frac{-2\overline{uv}}{U_{\infty }^{3}}\frac{\unicode[STIX]{x2202}\overline{U}}{\unicode[STIX]{x2202}y}\right]\text{d}y\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{Re_{\unicode[STIX]{x1D70F}}}\left[\underbrace{Cf\sqrt{\frac{Cf}{2}}\left(\frac{\unicode[STIX]{x2202}\overline{U}^{+}}{\unicode[STIX]{x2202}y^{+}}\right)^{2}}_{Cf_{a}^{+}}+\underbrace{Cf\sqrt{\frac{Cf}{2}}\left(-\overline{uv}^{+}\frac{\unicode[STIX]{x2202}\overline{U^{+}}}{\unicode[STIX]{x2202}y^{+}}\right)}_{Cf_{b}^{+}}\right]\text{d}y^{+}.\end{eqnarray}$$
The integrand groups designated
![]() $Cf_{FIK}^{+}$
in (4.8) and
$Cf_{FIK}^{+}$
in (4.8) and
![]() $Cf_{a}^{+}$
and
$Cf_{a}^{+}$
and
![]() $Cf_{b}^{+}$
in (4.9) will be used in the analysis undertaken in §§ 7.1 and 7.2, respectively.
$Cf_{b}^{+}$
in (4.9) will be used in the analysis undertaken in §§ 7.1 and 7.2, respectively.
The two alternative expressions for the skin friction, equations (4.8) and (4.9), do not merely arise from physically different principles, but more importantly from the perspective of the present work, they allow different phenomena and interactions to be illuminated, as will emerge in §§ 7.1 and 7.2.
5 Characteristics of large-scale motions
Characteristics of the large-scale field are conveyed here in two ways. First, the level of wall-normal correlation is illustrated in figure 5. This provides a map of the two-point correlation between
![]() $Cf_{LS}$
and
$Cf_{LS}$
and
![]() $u_{LS}(y^{+})$
, with the two points separated by
$u_{LS}(y^{+})$
, with the two points separated by
![]() $y^{+}$
and the streamwise increment
$y^{+}$
and the streamwise increment
![]() $\unicode[STIX]{x0394}x$
, where
$\unicode[STIX]{x0394}x$
, where
![]() $Cf_{LS}$
is defined from the streamwise velocity fluctuation at
$Cf_{LS}$
is defined from the streamwise velocity fluctuation at
![]() $y^{+}\approx 0.2$
. The inclusion of
$y^{+}\approx 0.2$
. The inclusion of
![]() $\unicode[STIX]{x0394}x$
allows the lag in the correlation to be clarified, especially of the locus of maximum correlation.
$\unicode[STIX]{x0394}x$
allows the lag in the correlation to be clarified, especially of the locus of maximum correlation.

Figure 5. Map of two-point correlation between
![]() $Cf_{LS}$
and
$Cf_{LS}$
and
![]() $u_{LS}(y^{+})$
in the
$u_{LS}(y^{+})$
in the
![]() $(y^{+},\unicode[STIX]{x0394}x)$
plane, with
$(y^{+},\unicode[STIX]{x0394}x)$
plane, with
![]() $y=0$
the reference point.
$y=0$
the reference point.
The plot shows, in agreement with previous observations, that the large-scale motions are highly correlated across the entire near-wall layer, with the streamwise lag in the maximum correlation level increasing with
![]() $y^{+}$
. The lag at
$y^{+}$
. The lag at
![]() $y^{+}=200$
is approximately 750 wall units, and this translates to an average angle across this layer of approximately
$y^{+}=200$
is approximately 750 wall units, and this translates to an average angle across this layer of approximately
![]() $15^{\circ }$
.
$15^{\circ }$
.

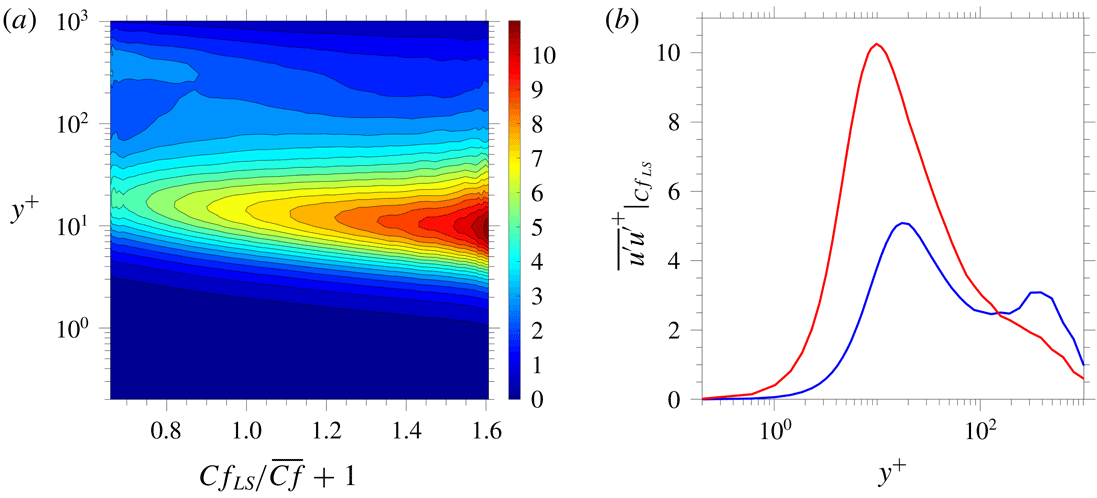
Figure 6. Conditional mean velocity: (a) map of the conditional increment in the mean velocities
![]() $(\overline{U^{\prime }}^{+}|_{Cf_{LS}}=\overline{U}^{+}|_{Cf_{LS}}-\overline{U}^{+})$
; (b) profiles of conditional mean velocity of
$(\overline{U^{\prime }}^{+}|_{Cf_{LS}}=\overline{U}^{+}|_{Cf_{LS}}-\overline{U}^{+})$
; (b) profiles of conditional mean velocity of
![]() $\overline{U}^{+}|_{Cf_{LS}}$
determined over the extreme
$\overline{U}^{+}|_{Cf_{LS}}$
determined over the extreme
![]() $\pm 1.5\,\%$
events of the tails of the p.d.f. in figure 3 and around the condition
$\pm 1.5\,\%$
events of the tails of the p.d.f. in figure 3 and around the condition
![]() $Cf_{LS}=0$
events, conveyed by the red, blue and magenta lines, respectively.
$Cf_{LS}=0$
events, conveyed by the red, blue and magenta lines, respectively.
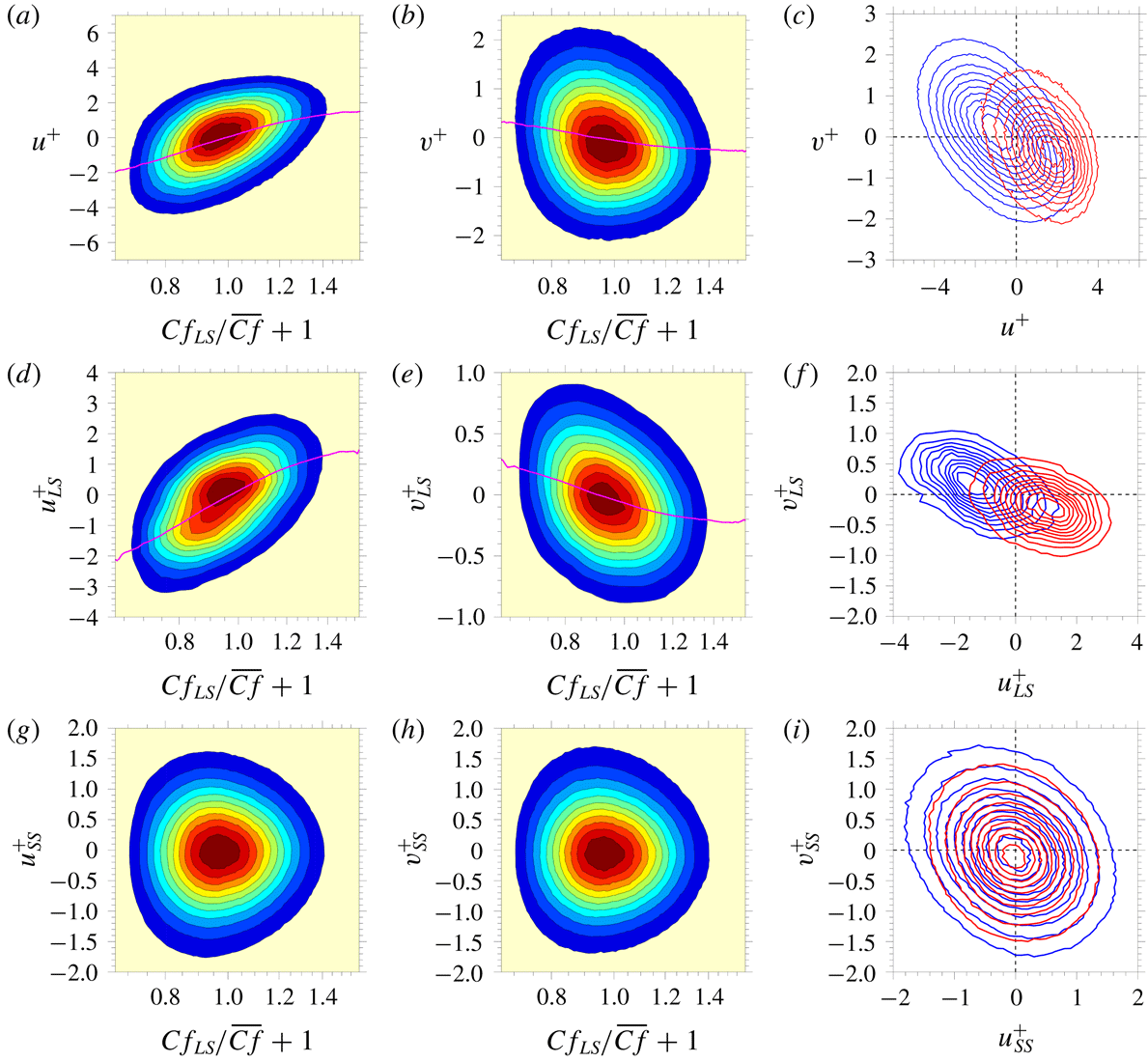
The set of plots in figure 6 provides an alternative view of the wall-normal correlation of the large-scale motions. Figure 6(a) shows the wall-normal variation of the increment between the mean velocity sampled conditionally on
![]() $Cf_{LS}$
and its average across
$Cf_{LS}$
and its average across
![]() $Cf_{LS}$
at the relevant
$Cf_{LS}$
at the relevant
![]() $y^{+}$
location – i.e.
$y^{+}$
location – i.e.
![]() $\overline{U^{\prime }}^{+}|_{Cf_{LS}}=\overline{U}^{+}|_{Cf_{LS}}-\overline{U}^{+}$
. This increment can be determined from the (
$\overline{U^{\prime }}^{+}|_{Cf_{LS}}=\overline{U}^{+}|_{Cf_{LS}}-\overline{U}^{+}$
. This increment can be determined from the (
![]() $U^{+},Cf_{LS}$
) p.d.f. using (4.6) at each wall-normal location.
$U^{+},Cf_{LS}$
) p.d.f. using (4.6) at each wall-normal location.
The map of
![]() $\overline{U^{\prime }}^{+}|_{Cf_{LS}}(y^{+})$
, shown in figure 6(a), demonstrates that negative/positive large-scale skin-friction fluctuations – generally referred to as ‘footprints’ – are strongly correlated with negative/positive large-scale velocity fluctuations, respectively, across a large section of the wall layer. As
$\overline{U^{\prime }}^{+}|_{Cf_{LS}}(y^{+})$
, shown in figure 6(a), demonstrates that negative/positive large-scale skin-friction fluctuations – generally referred to as ‘footprints’ – are strongly correlated with negative/positive large-scale velocity fluctuations, respectively, across a large section of the wall layer. As
![]() $\overline{U^{\prime }}^{+}|_{Cf_{LS}}$
tends to zero very close to the wall, the contour level declines rapidly below
$\overline{U^{\prime }}^{+}|_{Cf_{LS}}$
tends to zero very close to the wall, the contour level declines rapidly below
![]() $y^{+}<5$
. Figure 6(b) accentuates the wall-normal correlation by showing conditional mean-velocity profiles (blue and red lines) sampled across the extreme
$y^{+}<5$
. Figure 6(b) accentuates the wall-normal correlation by showing conditional mean-velocity profiles (blue and red lines) sampled across the extreme
![]() $\pm 1.5\,\%$
tails in figure 3, relative to the profile at
$\pm 1.5\,\%$
tails in figure 3, relative to the profile at
![]() $Cf_{LS}=0$
(magenta line), which is close to the
$Cf_{LS}=0$
(magenta line), which is close to the
![]() $Cf_{LS}$
-averaged overall mean velocity. A distinctive feature of the profiles, which will be the subject of the discussion of the modulation to follow below, is that the increment in the gradient of the conditional velocity profiles, relative to the overall mean, switches sign either from negative in the buffer layer to positive in the outer region, or vice versa, beyond
$Cf_{LS}$
-averaged overall mean velocity. A distinctive feature of the profiles, which will be the subject of the discussion of the modulation to follow below, is that the increment in the gradient of the conditional velocity profiles, relative to the overall mean, switches sign either from negative in the buffer layer to positive in the outer region, or vice versa, beyond
![]() $y^{+}\approx 150$
. The importance of this switch relates to a corresponding switch in shear-induced generation of fluctuations, as will become clear below.
$y^{+}\approx 150$
. The importance of this switch relates to a corresponding switch in shear-induced generation of fluctuations, as will become clear below.

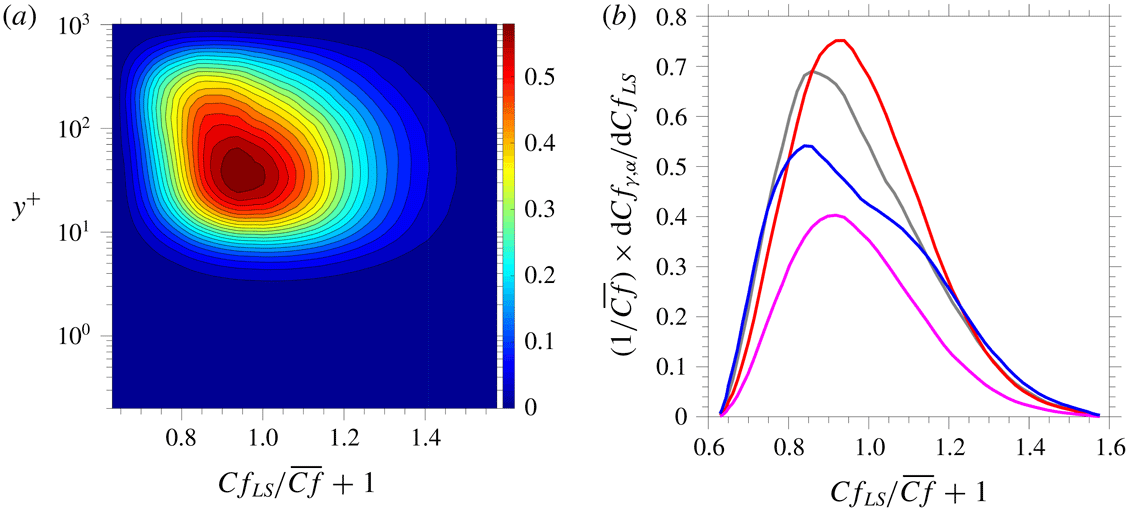
Figure 7. Contribution of large-scale turbulent stresses to the respective total levels: (a) map of
![]() $Cf_{LS}$
-wise gradient of large-scale streamwise stress
$Cf_{LS}$
-wise gradient of large-scale streamwise stress
![]() $\text{d}\overline{u_{LS}u_{LS}}^{+}/\text{d}Cf_{LS}$
; (b) map of
$\text{d}\overline{u_{LS}u_{LS}}^{+}/\text{d}Cf_{LS}$
; (b) map of
![]() $Cf_{LS}$
-wise gradient of large-scale shear stress
$Cf_{LS}$
-wise gradient of large-scale shear stress
![]() $-\text{d}\overline{u_{LS}v_{LS}}^{+}/\text{d}Cf_{LS}$
; (c) wall-normal profiles of scale-wise contributions to streamwise stress; (d) wall-normal profiles of scale-wise contributions to shear stress.
$-\text{d}\overline{u_{LS}v_{LS}}^{+}/\text{d}Cf_{LS}$
; (c) wall-normal profiles of scale-wise contributions to streamwise stress; (d) wall-normal profiles of scale-wise contributions to shear stress.
Figure 7 provides a view of the direct contribution of the outer large scales to the streamwise-normal and the shear stresses. The maps in figure 7(a,b) were obtained from the joint p.d.f.
![]() $P(U_{LS},V_{LS},Cf_{LS})$
. Figures 7(c) and 7(d) show the scale-wise contributions (small scale (SS), large scale (LS) and intermediate scale (IS)) to the streamwise stress and shear stress, respectively. Importantly, the plots include not only the primary (diagonal) components ([SS, SS]; [LS, LS]; [IS, IS]) but also the mixed-scale contributions that may be interpreted as signifying the modulation by any one larger-scale signal of a smaller-scale signal – e.g.
$P(U_{LS},V_{LS},Cf_{LS})$
. Figures 7(c) and 7(d) show the scale-wise contributions (small scale (SS), large scale (LS) and intermediate scale (IS)) to the streamwise stress and shear stress, respectively. Importantly, the plots include not only the primary (diagonal) components ([SS, SS]; [LS, LS]; [IS, IS]) but also the mixed-scale contributions that may be interpreted as signifying the modulation by any one larger-scale signal of a smaller-scale signal – e.g.
![]() $\overline{u_{LS}v_{IS}}$
may be interpreted as the large-scale motion modulating the intermediate-scale motion. The large-scale contributions in figures 7(c) and 7(d) are given by the blue lines, and these have been obtained by integrating the maps in figures 7(a) and 7(b), respectively, across
$\overline{u_{LS}v_{IS}}$
may be interpreted as the large-scale motion modulating the intermediate-scale motion. The large-scale contributions in figures 7(c) and 7(d) are given by the blue lines, and these have been obtained by integrating the maps in figures 7(a) and 7(b), respectively, across
![]() $Cf_{LS}$
.
$Cf_{LS}$
.
The contribution of the large-scale motions to the streamwise stress is fairly uniform within the range
![]() $y^{+}\approx 10{-}500$
, but features a weak maximum around
$y^{+}\approx 10{-}500$
, but features a weak maximum around
![]() $y^{+}\approx 300$
, i.e. markedly higher than the value
$y^{+}\approx 300$
, i.e. markedly higher than the value
![]() $3.9\sqrt{Re_{\unicode[STIX]{x1D70F}}}$
(
$3.9\sqrt{Re_{\unicode[STIX]{x1D70F}}}$
(
![]() ${\approx}125$
, for
${\approx}125$
, for
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
) proposed by Marusic et al. (Reference Marusic, Mathis and Hutchins2010) as the location at which the large-scale structures primarily reside. The origin of this discrepancy is not obvious. It is noted that the present Reynolds number is significantly lower than the values of the flows upon which the empirical correlation is based. Thus, the intensity of the outer motions is lower here, and the outer maximum in
$Re_{\unicode[STIX]{x1D70F}}=1000$
) proposed by Marusic et al. (Reference Marusic, Mathis and Hutchins2010) as the location at which the large-scale structures primarily reside. The origin of this discrepancy is not obvious. It is noted that the present Reynolds number is significantly lower than the values of the flows upon which the empirical correlation is based. Thus, the intensity of the outer motions is lower here, and the outer maximum in
![]() $\overline{u_{LS}u_{LS}}^{+}$
is clearly quite tenuous. However, the corresponding maximum in
$\overline{u_{LS}u_{LS}}^{+}$
is clearly quite tenuous. However, the corresponding maximum in
![]() $-\overline{u_{LS}v_{LS}}^{+}$
is more prominent, and this supports the observation that the
$-\overline{u_{LS}v_{LS}}^{+}$
is more prominent, and this supports the observation that the
![]() $y^{+}$
value that best defines the position of the large-scale structures is significantly higher than
$y^{+}$
value that best defines the position of the large-scale structures is significantly higher than
![]() $3.9\sqrt{Re_{\unicode[STIX]{x1D70F}}}$
, at least at the present Reynolds number. The uniformity in the level of
$3.9\sqrt{Re_{\unicode[STIX]{x1D70F}}}$
, at least at the present Reynolds number. The uniformity in the level of
![]() $\overline{u_{LS}u_{LS}}^{+}$
is consistent with the footprinting concept, reflected by the relatively high level of energy density across the layer
$\overline{u_{LS}u_{LS}}^{+}$
is consistent with the footprinting concept, reflected by the relatively high level of energy density across the layer
![]() $y^{+}\approx 10{-}500$
in the high-wavelength range of the spectral map in figure 1. As seen from the map in figure 7(a), the large-scale streamwise stress arises from contributions originating primarily from negative large-scale-velocity events – around
$y^{+}\approx 10{-}500$
in the high-wavelength range of the spectral map in figure 1. As seen from the map in figure 7(a), the large-scale streamwise stress arises from contributions originating primarily from negative large-scale-velocity events – around
![]() $Cf_{LS}/\overline{Cf}+1=0.85$
, in particular, close to the maximum of the skewed
$Cf_{LS}/\overline{Cf}+1=0.85$
, in particular, close to the maximum of the skewed
![]() $Cf_{LS}$
p.d.f. shown in figure 3. In the outer part,
$Cf_{LS}$
p.d.f. shown in figure 3. In the outer part,
![]() $y^{+}>100$
, the increase towards the maximum at
$y^{+}>100$
, the increase towards the maximum at
![]() $y^{+}\approx 300$
coincides with the peak in large-scale shear stress, figure 7(b), also around
$y^{+}\approx 300$
coincides with the peak in large-scale shear stress, figure 7(b), also around
![]() $Cf_{LS}=0.85$
, and this is clearly the origin of the maximum in the large-scale (blue) shear-stress profile in figure 7(d). This peak, coupled with the exceptionally high mean-velocity gradient – the blue profile in figure 6(b) – suggests that the outer peak values in both stresses are due to elevated shear-induced production. Although the large-scale shear stress is low in the buffer region, it appears that it is high enough, especially in the bulges visible around
$Cf_{LS}=0.85$
, and this is clearly the origin of the maximum in the large-scale (blue) shear-stress profile in figure 7(d). This peak, coupled with the exceptionally high mean-velocity gradient – the blue profile in figure 6(b) – suggests that the outer peak values in both stresses are due to elevated shear-induced production. Although the large-scale shear stress is low in the buffer region, it appears that it is high enough, especially in the bulges visible around
![]() $y^{+}\approx 10-20$
at
$y^{+}\approx 10-20$
at
![]() $Cf_{LS}/\overline{Cf}\approx -0.2$
and 0.3, to combine with the very high shear strain in the buffer layer to induce, by production, the elevated normal stress around
$Cf_{LS}/\overline{Cf}\approx -0.2$
and 0.3, to combine with the very high shear strain in the buffer layer to induce, by production, the elevated normal stress around
![]() $y^{+}=20$
. The peak large-scale stresses are of the order of 20 %–30 % of the respective total maxima – although, as might be expected, the local proportion is considerably larger in the outer region, around
$y^{+}=20$
. The peak large-scale stresses are of the order of 20 %–30 % of the respective total maxima – although, as might be expected, the local proportion is considerably larger in the outer region, around
![]() $y^{+}=300{-}500$
.
$y^{+}=300{-}500$
.
The effect of the shear stress on the skin friction can be quantified by means of the FIK and RD relationships, equations (4.8) and (4.9), respectively, and this will be shown below in the context of a discussion of other contributions to the skin friction. Suffice it to say here that the FIK relationship yields a large-scale contribution to the total skin friction of 24 %, which may be claimed to be remarkably high, considering the low value of the Reynolds number of the flow being examined.
6 Impact of large scales on small scales
It is well established (Guala et al.
Reference Guala, Metzger and McKeon2011; Mathis et al.
Reference Mathis, Hutchins and Marusic2011; Ganapathisubramani et al.
Reference Ganapathisubramani, Hutchins, Monty, Chung and Marusic2012; Jacobi & McKeon Reference Jacobi and McKeon2013; Talluru et al.
Reference Talluru, Baidya, Hutchins and Marusic2014; Duvvuri & McKeon Reference Duvvuri and McKeon2015; Agostini et al.
Reference Agostini, Leschziner and Gaitonde2016; Agostini & Leschziner Reference Agostini and Leschziner2016a
; Zhang & Chernyshenko Reference Zhang and Chernyshenko2016; Hwang & Sung Reference Hwang and Sung2017, among others) that the correlation between the intensity of small-scale motions and large-scale motions is positive close to the wall, but changes sign at some position beyond the buffer layer. Various physical arguments have been advanced in efforts to explain this reversal. One is based on the concept that a traverse across the flow, on any wall-normal line along which the correlation is evaluated, crosses large-scale structures that are inclined roughly at 13–18
![]() $^{\circ }$
relative to the wall. Another explanation is based on the concept that large-scale convective motions, associated with sweeps and ejections, shift the profile of small-scale streamwise stress, which features a maximum in the buffer layer, normal to the wall. Thus, depending upon whether a location is above or below the maximum, the effect of either sweeps or ejections on the incremental change in the streamwise energy at that location will be of opposite sign. However, this explanation can only apply to a reversal at a location around the buffer layer, while the reversal occurs at
$^{\circ }$
relative to the wall. Another explanation is based on the concept that large-scale convective motions, associated with sweeps and ejections, shift the profile of small-scale streamwise stress, which features a maximum in the buffer layer, normal to the wall. Thus, depending upon whether a location is above or below the maximum, the effect of either sweeps or ejections on the incremental change in the streamwise energy at that location will be of opposite sign. However, this explanation can only apply to a reversal at a location around the buffer layer, while the reversal occurs at
![]() $y^{+}>100$
. Here, a different interpretation is advanced, based on an examination of the production of small-scale fluctuations.
$y^{+}>100$
. Here, a different interpretation is advanced, based on an examination of the production of small-scale fluctuations.
The first issue examined below is the correlation between the small-scale and large-scale fluctuations,
![]() $u_{SS}$
and
$u_{SS}$
and
![]() $u_{LS}$
, respectively. This can be deduced from the set of plots in figure 8. The map of the conditional small-scale energy
$u_{LS}$
, respectively. This can be deduced from the set of plots in figure 8. The map of the conditional small-scale energy
![]() $\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}$
is plotted in figure 8(a). As expected, the contours bring to light the fact that
$\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}$
is plotted in figure 8(a). As expected, the contours bring to light the fact that
![]() $\overline{u_{SS}u_{SS}}^{+}$
reaches a maximum in the vicinity of
$\overline{u_{SS}u_{SS}}^{+}$
reaches a maximum in the vicinity of
![]() $y^{+}\approx 12$
, and that its magnitude strengthens as
$y^{+}\approx 12$
, and that its magnitude strengthens as
![]() $Cf_{LS}$
and the velocity gradient increase near the wall. Conversely,
$Cf_{LS}$
and the velocity gradient increase near the wall. Conversely,
![]() $\overline{u_{SS}u_{SS}}^{+}$
declines towards a minimum as
$\overline{u_{SS}u_{SS}}^{+}$
declines towards a minimum as
![]() $Cf_{LS}$
and the near-wall velocity gradient reduce. The level of energy amplification and attenuation – conventionally understood to be the ‘modulation’ – is accentuated in figure 8(b), which shows three profiles of
$Cf_{LS}$
and the near-wall velocity gradient reduce. The level of energy amplification and attenuation – conventionally understood to be the ‘modulation’ – is accentuated in figure 8(b), which shows three profiles of
![]() $\overline{u_{SS}u_{SS}}^{+}$
for the extreme
$\overline{u_{SS}u_{SS}}^{+}$
for the extreme
![]() $\pm 1.5\,\%$
of
$\pm 1.5\,\%$
of
![]() $Cf_{LS}$
(red and blue profiles, respectively), relative to the profile around
$Cf_{LS}$
(red and blue profiles, respectively), relative to the profile around
![]() $Cf_{LS}=0$
(magenta profile).
$Cf_{LS}=0$
(magenta profile).
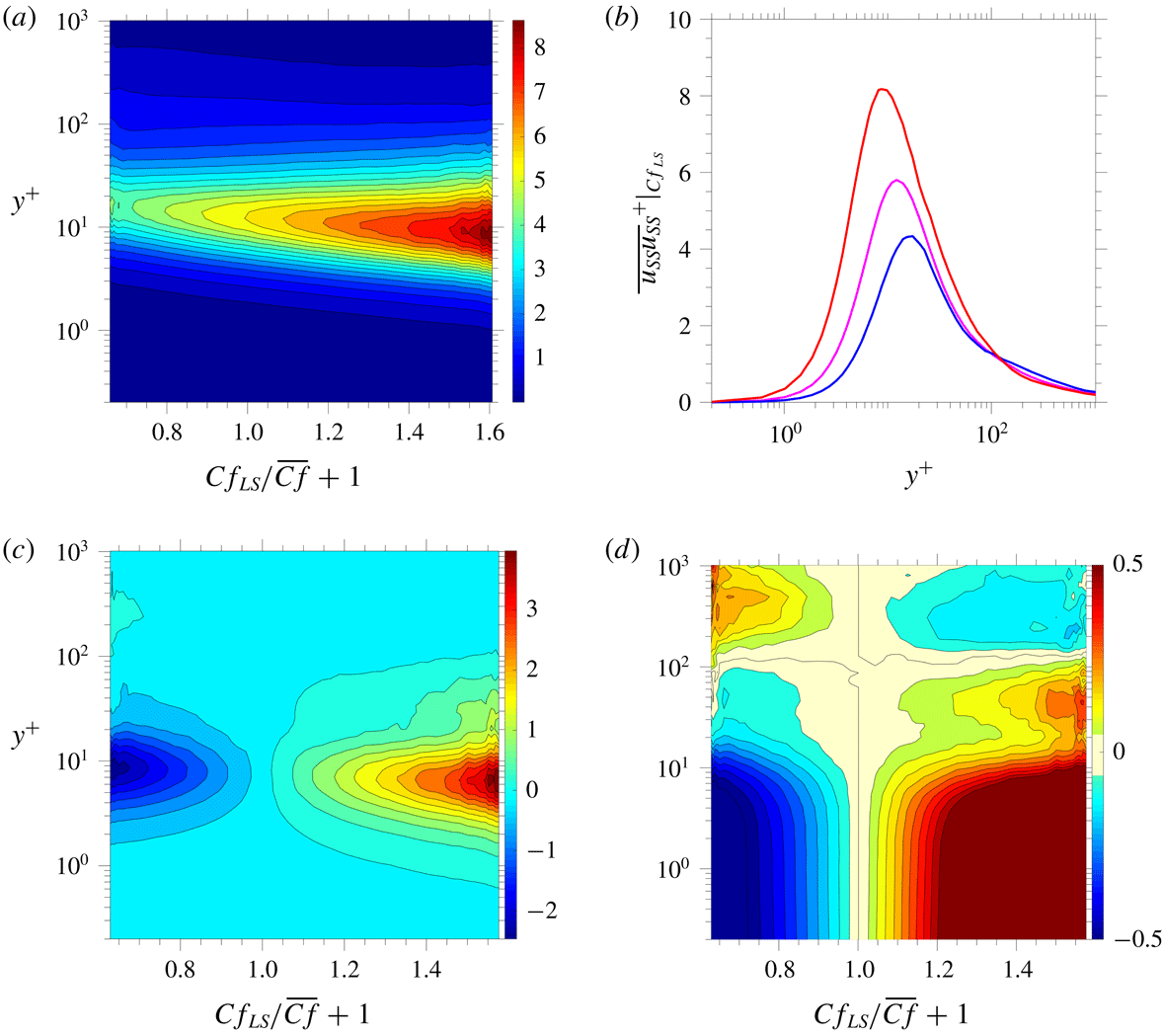
The sensitivity of the small-scale fluctuations to the footprints, shown in figure 8, also translates to a corresponding sensitivity of the small-scale skin-friction fluctuations. This is shown in figure 9 in the form of the standard deviation of the conditional small-scale skin-friction fluctuations as a function of
![]() $Cf_{LS}$
. Unsurprisingly, the intensity of the small-scale fluctuations varies substantially, with positive footprints causing a strong increase, while negative footprints result in a more modest decline, but this asymmetry is due to the fact that negative
$Cf_{LS}$
. Unsurprisingly, the intensity of the small-scale fluctuations varies substantially, with positive footprints causing a strong increase, while negative footprints result in a more modest decline, but this asymmetry is due to the fact that negative
![]() $Cf_{LS}$
footprints are weaker than positive ones. The close to linear variation, consistent with the map in figure 8(a), implies that the small-scale turbulence responds rapidly to changes in the large-scale fluctuation, thus supporting the assumption that the near-wall state complies with the quasi-steady concept. As an aside, reference is made here to Agostini & Leschziner (Reference Agostini and Leschziner2018) in which it is shown that drag-reducing actuation by spanwise wall motion renders the standard deviation of the conditional small-scale skin-friction fluctuations a highly nonlinear function of
$Cf_{LS}$
footprints are weaker than positive ones. The close to linear variation, consistent with the map in figure 8(a), implies that the small-scale turbulence responds rapidly to changes in the large-scale fluctuation, thus supporting the assumption that the near-wall state complies with the quasi-steady concept. As an aside, reference is made here to Agostini & Leschziner (Reference Agostini and Leschziner2018) in which it is shown that drag-reducing actuation by spanwise wall motion renders the standard deviation of the conditional small-scale skin-friction fluctuations a highly nonlinear function of
![]() $Cf_{LS}$
. As explained in Agostini & Leschziner (Reference Agostini and Leschziner2018), this is due to the control significantly weakening the near-wall streaks, thus increasing the impact of the outer structures, relative to the canonical case.
$Cf_{LS}$
. As explained in Agostini & Leschziner (Reference Agostini and Leschziner2018), this is due to the control significantly weakening the near-wall streaks, thus increasing the impact of the outer structures, relative to the canonical case.
The relationship between
![]() $u_{SS}$
and
$u_{SS}$
and
![]() $Cf_{LS}$
in the outer region is difficult to recognise from the map of
$Cf_{LS}$
in the outer region is difficult to recognise from the map of
![]() $\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}$
, because the magnitude of the velocity fluctuations produced within the streaky buffer layer is at least ten times higher than the fluctuations associated with small-scale structures in the outer flow. This is readily recognised from the red profile for
$\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}$
, because the magnitude of the velocity fluctuations produced within the streaky buffer layer is at least ten times higher than the fluctuations associated with small-scale structures in the outer flow. This is readily recognised from the red profile for
![]() $\overline{u_{SS}u_{SS}}^{+}$
in figure 7(c). In order to overcome this limitation, attention is focused in figures 8(c) and 8(d) on the increment
$\overline{u_{SS}u_{SS}}^{+}$
in figure 7(c). In order to overcome this limitation, attention is focused in figures 8(c) and 8(d) on the increment
![]() $(\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}-\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}=0})$
and its normalised value
$(\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}-\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}=0})$
and its normalised value
![]() $(\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}-\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}=0})/(\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}=0})$
, respectively. The former conveys the fact the negative and positive
$(\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}-\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}=0})/(\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}=0})$
, respectively. The former conveys the fact the negative and positive
![]() $Cf_{LS}$
fluctuations go hand-in-hand with, respectively, an attenuation and amplification of small-scale motions around the buffer layer – i.e. the correlation is positive. However, the map in figure 8(d) shows a reversal in correlation at approximately
$Cf_{LS}$
fluctuations go hand-in-hand with, respectively, an attenuation and amplification of small-scale motions around the buffer layer – i.e. the correlation is positive. However, the map in figure 8(d) shows a reversal in correlation at approximately
![]() $y^{+}\approx 150$
, confirming earlier observations in studies noted at the beginning of this section.
$y^{+}\approx 150$
, confirming earlier observations in studies noted at the beginning of this section.

Figure 8. Correlation of small-scale and large-scale motions: (a) map of conditional streamwise small-scale stress
![]() $\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}$
; (b) profiles of conditional streamwise small-scale stress
$\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}$
; (b) profiles of conditional streamwise small-scale stress
![]() $\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}$
averaged over the 1.5 % lowest, highest and weakest
$\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}$
averaged over the 1.5 % lowest, highest and weakest
![]() $Cf_{LS}$
events, conveyed by the blue, red and magenta lines, respectively; (c) map of increment of conditional streamwise small-scale stress
$Cf_{LS}$
events, conveyed by the blue, red and magenta lines, respectively; (c) map of increment of conditional streamwise small-scale stress
![]() $\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}-\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}=0}$
; (d) map of normalised increment of conditional streamwise small-scale stress
$\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}}-\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}=0}$
; (d) map of normalised increment of conditional streamwise small-scale stress
![]() $(\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}})/(\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}=0})-1$
.
$(\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}})/(\overline{u_{SS}u_{SS}}^{+}|_{Cf_{LS}=0})-1$
.

Figure 9. Standard deviation of small-scale skin-friction fluctuations conditional on large-scale skin-friction fluctuations.
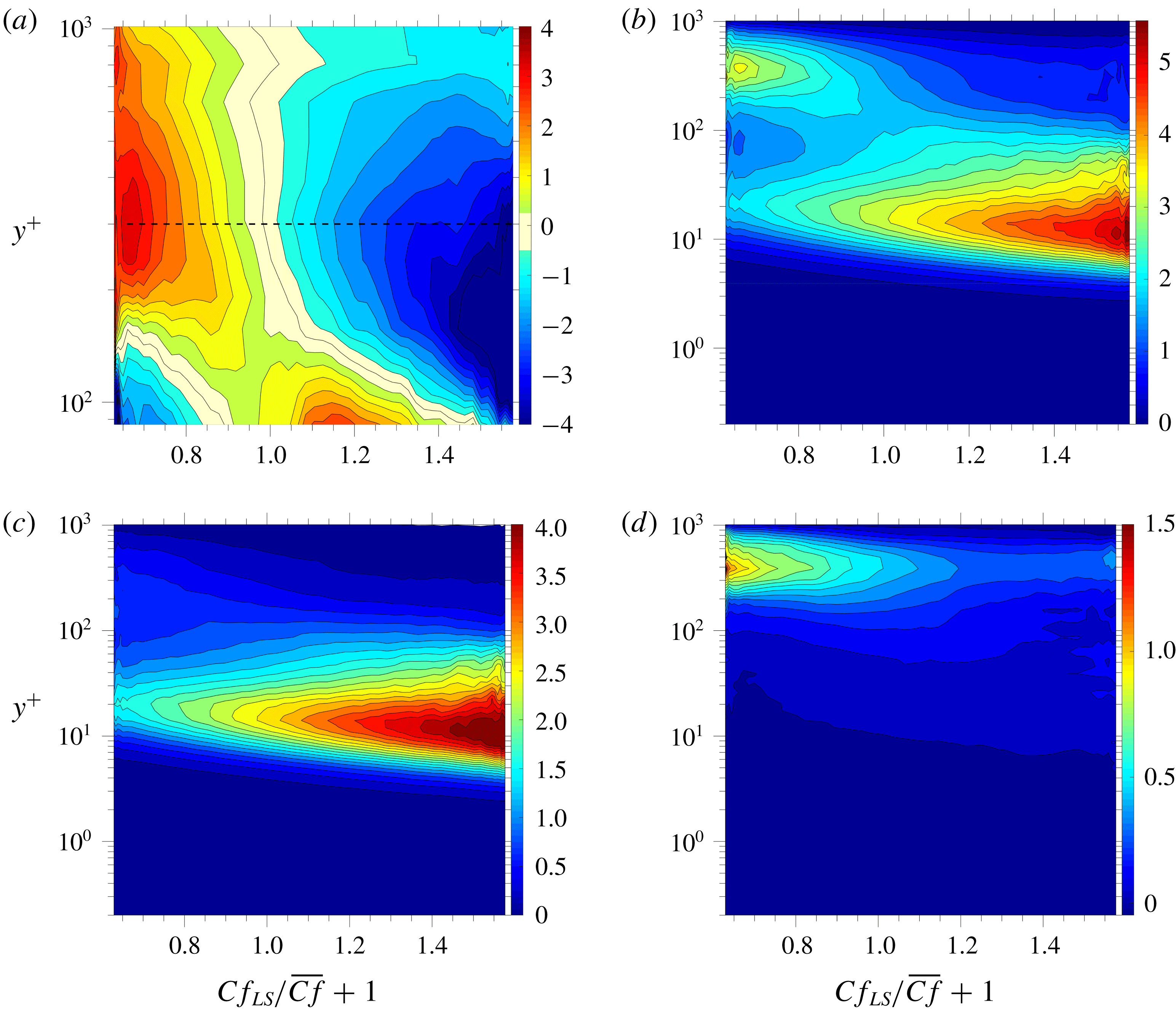
Figure 10. Alternative forms of the conditional production rates of the streamwise stress: (a) wall-normal gradient of the incremental large-scale velocity profile, conditional on
![]() $Cf_{LS}$
,
$Cf_{LS}$
,
![]() $\text{d}(\overline{U^{\prime }}^{+}|_{Cf_{LS}}-\overline{U^{\prime }}^{+}|_{Cf_{LS=0}})/\text{d}y^{+}$
; (b) production driven by the total shear stress,
$\text{d}(\overline{U^{\prime }}^{+}|_{Cf_{LS}}-\overline{U^{\prime }}^{+}|_{Cf_{LS=0}})/\text{d}y^{+}$
; (b) production driven by the total shear stress,
![]() $y^{+}\times -\overline{uv}^{+}(\text{d}\overline{U}^{+}/\text{d}y^{+})|_{Cf_{LS}}$
; (c) production driven by the small-scale shear stress,
$y^{+}\times -\overline{uv}^{+}(\text{d}\overline{U}^{+}/\text{d}y^{+})|_{Cf_{LS}}$
; (c) production driven by the small-scale shear stress,
![]() $y^{+}\times -\overline{u_{SS}v_{SS}}^{+}(\text{d}\overline{U}^{+}/\text{d}y^{+})|_{Cf_{LS}}$
; (d) production driven by the large-scale shear stress,
$y^{+}\times -\overline{u_{SS}v_{SS}}^{+}(\text{d}\overline{U}^{+}/\text{d}y^{+})|_{Cf_{LS}}$
; (d) production driven by the large-scale shear stress,
![]() $y^{+}\times -\overline{u_{LS}v_{LS}}^{+}(\text{d}\overline{U}^{+}/\text{d}y^{+})|_{Cf_{LS}}$
.
$y^{+}\times -\overline{u_{LS}v_{LS}}^{+}(\text{d}\overline{U}^{+}/\text{d}y^{+})|_{Cf_{LS}}$
.
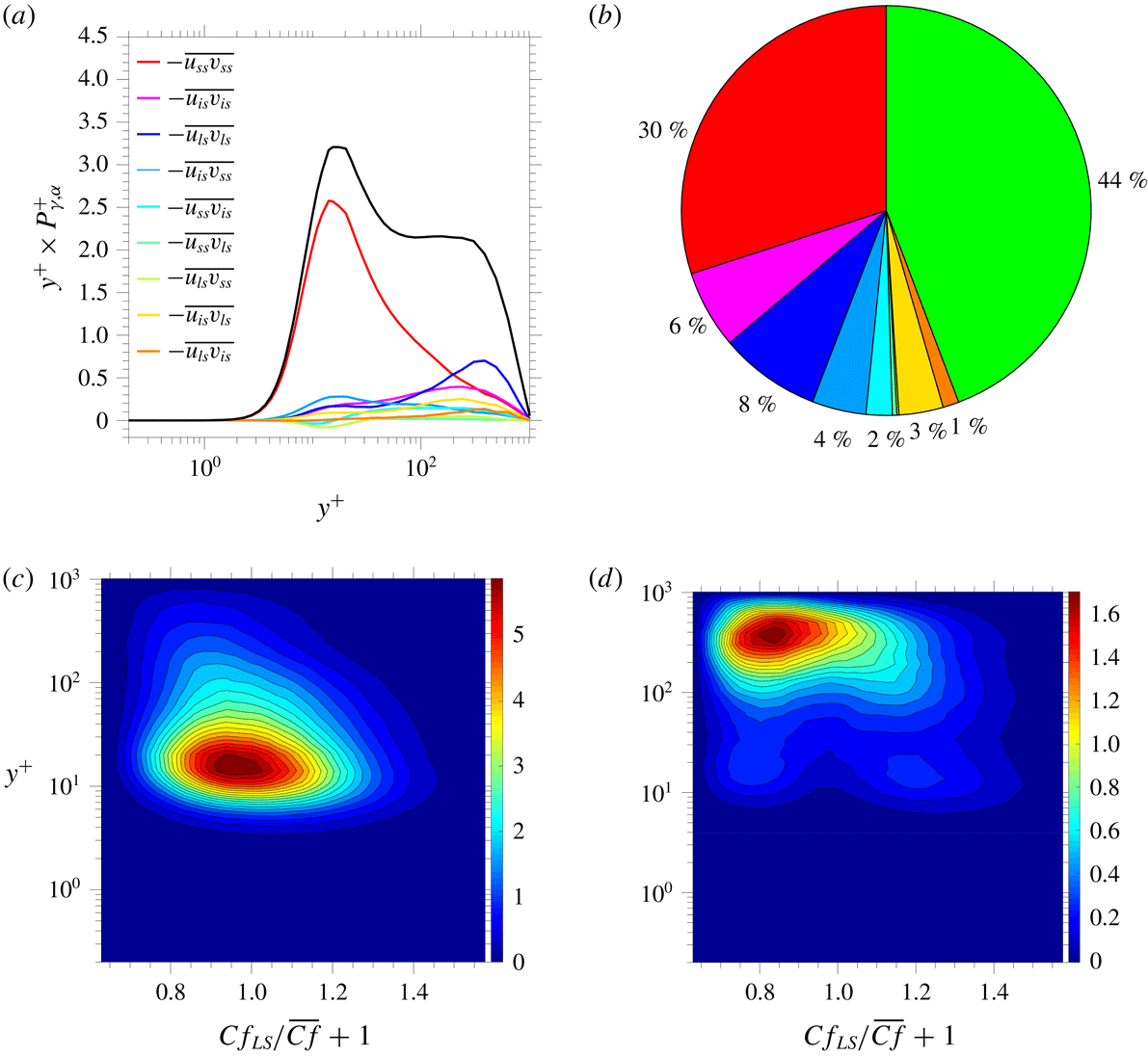
An explanation for the above reversal in correlation, alternative to previous proposals, is suggested by the results in figure 10. This shows, first, in figure 10(a), the wall-normal gradient
![]() $\text{d}\overline{U^{\prime }}^{+}|_{Cf_{LS}}/\text{d}y^{+}$
of the fields in figure 6(a) – i.e. the gradient of the incremental velocity, conditional on the large-scale skin-friction value. Purely for reasons of greater clarity, attention is restricted in this map to the range
$\text{d}\overline{U^{\prime }}^{+}|_{Cf_{LS}}/\text{d}y^{+}$
of the fields in figure 6(a) – i.e. the gradient of the incremental velocity, conditional on the large-scale skin-friction value. Purely for reasons of greater clarity, attention is restricted in this map to the range
![]() $y^{+}=80{-}1000$
. There is, self-evidently, a close similarity between this map and the map in figure 8(d). Corresponding to the variations in the gradient in figure 10(a) are variations in the production rate of the streamwise energy. Three different, conditional, forms of the production are shown in figure 10(b–d). The first is of the total production; the second is the production induced by the small-scale motion; and the third is the production associated with the large-scale motions. All three are premultiplied by
$y^{+}=80{-}1000$
. There is, self-evidently, a close similarity between this map and the map in figure 8(d). Corresponding to the variations in the gradient in figure 10(a) are variations in the production rate of the streamwise energy. Three different, conditional, forms of the production are shown in figure 10(b–d). The first is of the total production; the second is the production induced by the small-scale motion; and the third is the production associated with the large-scale motions. All three are premultiplied by
![]() $y^{+}$
, so as to compensate for the optical distortion, due to compression, that is caused by the logarithmic scale of
$y^{+}$
, so as to compensate for the optical distortion, due to compression, that is caused by the logarithmic scale of
![]() $y^{+}$
.
$y^{+}$
.
In the map of the production rate, figure 10(b), there are two regions within which maxima in the production are observed: one is close to the wall, driven by the increasing near-wall shear strain that accompanies the increased
![]() $Cf_{LS}$
level, and a second outer maximum, induced by the elevated strain in the negative range of
$Cf_{LS}$
level, and a second outer maximum, induced by the elevated strain in the negative range of
![]() $Cf_{LS}$
. This connection is thus consistent with the observation that the level of small-scale energy in the inner region is positively correlated with large-scale fluctuations, while the outer small-scale energy is negatively correlated with the outer large-scale fluctuations. Although the map in figure 10(b) shows the production of the total streamwise stress, involving the total shear stress, it is pointed out that this total is dominated, near the wall, by the small-scale component, while in the outer region the total combines similar levels of small-scale and large-scale components. This argument is given weight by the maps in figures 10(c) and 10(d), showing the production rates by the small-scale and large-scale shear stresses, respectively. The former highlights the fact that the production rate of the small-scale streamwise stress is concentrated in the buffer layer, and driven by positive large-scale fluctuations, while the large-scale production predominates in the outer part of the flow and is driven by negative large-scale motions. These causal connections are also consistent with the previous discussion of the implications of the results shown in figure 8.
$Cf_{LS}$
. This connection is thus consistent with the observation that the level of small-scale energy in the inner region is positively correlated with large-scale fluctuations, while the outer small-scale energy is negatively correlated with the outer large-scale fluctuations. Although the map in figure 10(b) shows the production of the total streamwise stress, involving the total shear stress, it is pointed out that this total is dominated, near the wall, by the small-scale component, while in the outer region the total combines similar levels of small-scale and large-scale components. This argument is given weight by the maps in figures 10(c) and 10(d), showing the production rates by the small-scale and large-scale shear stresses, respectively. The former highlights the fact that the production rate of the small-scale streamwise stress is concentrated in the buffer layer, and driven by positive large-scale fluctuations, while the large-scale production predominates in the outer part of the flow and is driven by negative large-scale motions. These causal connections are also consistent with the previous discussion of the implications of the results shown in figure 8.
As observed earlier in figure 7(d), the large-scale shear-stress contribution reaches its maximum at
![]() $y^{+}\approx 300$
. This contribution arises primarily in association with negative skin-friction fluctuations, which are positively correlated with large-scale velocity fluctuations throughout the log layer. As the turbulent shear stress is the principal driver of the skin friction, especially when its level is high in the outer layer, it is instructive to examine the conditions at
$y^{+}\approx 300$
. This contribution arises primarily in association with negative skin-friction fluctuations, which are positively correlated with large-scale velocity fluctuations throughout the log layer. As the turbulent shear stress is the principal driver of the skin friction, especially when its level is high in the outer layer, it is instructive to examine the conditions at
![]() $y^{+}\approx 300$
in greater detail. This is done in figure 11, which compares, by way of joint p.d.f.s
$y^{+}\approx 300$
in greater detail. This is done in figure 11, which compares, by way of joint p.d.f.s
![]() $P(u^{+},v^{+},Cf_{LS})$
(figure 11
a–c),
$P(u^{+},v^{+},Cf_{LS})$
(figure 11
a–c),
![]() $P(u_{LS}^{+},v_{LS}^{+},Cf_{LS})$
(figure 11
d–f) and
$P(u_{LS}^{+},v_{LS}^{+},Cf_{LS})$
(figure 11
d–f) and
![]() $P(u_{SS}^{+},v_{SS}^{+},Cf_{LS})$
(figure 11
g–i), the variations of the total, large-scale and small-scale velocity fluctuations at
$P(u_{SS}^{+},v_{SS}^{+},Cf_{LS})$
(figure 11
g–i), the variations of the total, large-scale and small-scale velocity fluctuations at
![]() $y^{+}\approx 300$
as functions of the large-scale skin-friction fluctuations
$y^{+}\approx 300$
as functions of the large-scale skin-friction fluctuations
![]() $Cf_{LS}$
. In addition, the right-most plots included in the three rows are joint p.d.f.s
$Cf_{LS}$
. In addition, the right-most plots included in the three rows are joint p.d.f.s
![]() $P(u^{+},v^{+})$
,
$P(u^{+},v^{+})$
,
![]() $P(u_{LS}^{+},v_{LS}^{+})$
and
$P(u_{LS}^{+},v_{LS}^{+})$
and
![]() $P(u_{SS}^{+},v_{SS}^{+})$
, respectively, derived from
$P(u_{SS}^{+},v_{SS}^{+})$
, respectively, derived from
![]() $P(u^{+},v^{+},Cf_{LS})$
and analogous p.d.f.s for the large-scale and small-scale fluctuations. The red and blue p.d.f. contours are conditional on events within, respectively, the extreme positive and negative 5 % tails of the
$P(u^{+},v^{+},Cf_{LS})$
and analogous p.d.f.s for the large-scale and small-scale fluctuations. The red and blue p.d.f. contours are conditional on events within, respectively, the extreme positive and negative 5 % tails of the
![]() $Cf_{LS}$
p.d.f. (figure 3), thus characterising the state of the stress field at the extreme positive and negative footprints.
$Cf_{LS}$
p.d.f. (figure 3), thus characterising the state of the stress field at the extreme positive and negative footprints.
The p.d.f.s in the top and middle rows, figure 11(a,b,d,e), contain magenta lines, which identify the average values of the respective fluctuations across the
![]() $Cf_{LS}$
range – e.g.
$Cf_{LS}$
range – e.g.
![]() $\overline{U^{\prime }}^{+}|_{Cf_{LS}}$
and
$\overline{U^{\prime }}^{+}|_{Cf_{LS}}$
and
![]() $\overline{V^{\prime }}^{+}|_{Cf_{LS}}$
in figures 11(a) and 11(b). The shape of these p.d.f.s in the upper two rows, accentuated by the magenta loci, allows the observation that negative
$\overline{V^{\prime }}^{+}|_{Cf_{LS}}$
in figures 11(a) and 11(b). The shape of these p.d.f.s in the upper two rows, accentuated by the magenta loci, allows the observation that negative
![]() $Cf_{LS}$
values are associated preferentially with negative
$Cf_{LS}$
values are associated preferentially with negative
![]() $\overline{U^{\prime }}^{+}|_{Cf_{LS}}$
and positive
$\overline{U^{\prime }}^{+}|_{Cf_{LS}}$
and positive
![]() $\overline{V^{\prime }}^{+}|_{Cf_{LS}}$
values, i.e. ejections, while positive
$\overline{V^{\prime }}^{+}|_{Cf_{LS}}$
values, i.e. ejections, while positive
![]() $Cf_{LS}$
values are accompanied preferentially by sweeping motions. This conclusion is further supported by the joint p.d.f.s for the velocity fluctuations in figure 11(c,f). The red p.d.f.s are clearly associated with large-scale sweeps, while the blue ones are associated with ejections. For large positive
$Cf_{LS}$
values are accompanied preferentially by sweeping motions. This conclusion is further supported by the joint p.d.f.s for the velocity fluctuations in figure 11(c,f). The red p.d.f.s are clearly associated with large-scale sweeps, while the blue ones are associated with ejections. For large positive
![]() $Cf_{LS}$
values, and hence also large positive
$Cf_{LS}$
values, and hence also large positive
![]() $u_{LS}^{+}$
levels in the outer region, the intensity of fluctuations is relatively low, while the reverse is observed for large negative
$u_{LS}^{+}$
levels in the outer region, the intensity of fluctuations is relatively low, while the reverse is observed for large negative
![]() $Cf_{LS}$
values. This is in accord with the large-scale shear-stress map in figure 7(b) and also with the associated production-rate map in figure 10(d). The implication of the p.d.f.s is that there exist large-scale vortical motions in the cross-flow, associated with the ejections and sweeps, and this is entirely consistent with the behaviour of large-scale velocity field shown in figure 6. The fact that the above features are broadly common to both the total and large-scale fluctuations is not surprising, as the large-scale motions exert a dominant influence on the total field at the wall-normal location considered (
$Cf_{LS}$
values. This is in accord with the large-scale shear-stress map in figure 7(b) and also with the associated production-rate map in figure 10(d). The implication of the p.d.f.s is that there exist large-scale vortical motions in the cross-flow, associated with the ejections and sweeps, and this is entirely consistent with the behaviour of large-scale velocity field shown in figure 6. The fact that the above features are broadly common to both the total and large-scale fluctuations is not surprising, as the large-scale motions exert a dominant influence on the total field at the wall-normal location considered (
![]() $y^{+}=300$
). An exception to this commonality of features relates to the marked differences in the shape of the joint velocity p.d.f.s in figure 11(c,f). The far more elongated shape in the latter p.d.f.s signifies that the structures captured by these p.d.f.s are elongated and thus characterised by a relatively low ratio
$y^{+}=300$
). An exception to this commonality of features relates to the marked differences in the shape of the joint velocity p.d.f.s in figure 11(c,f). The far more elongated shape in the latter p.d.f.s signifies that the structures captured by these p.d.f.s are elongated and thus characterised by a relatively low ratio
![]() $\overline{v_{LS}^{+2}}/\overline{u_{LS}^{+2}}$
. Indeed, the ratio of the largest to the smallest eigenvalues of the large-scale-stress matrix was found to be around 10. Consistently, an examination of the Reynolds-stress field within the stress-invariant map (not included here) revealed a distinct trend towards one-component turbulence at the location considered.
$\overline{v_{LS}^{+2}}/\overline{u_{LS}^{+2}}$
. Indeed, the ratio of the largest to the smallest eigenvalues of the large-scale-stress matrix was found to be around 10. Consistently, an examination of the Reynolds-stress field within the stress-invariant map (not included here) revealed a distinct trend towards one-component turbulence at the location considered.
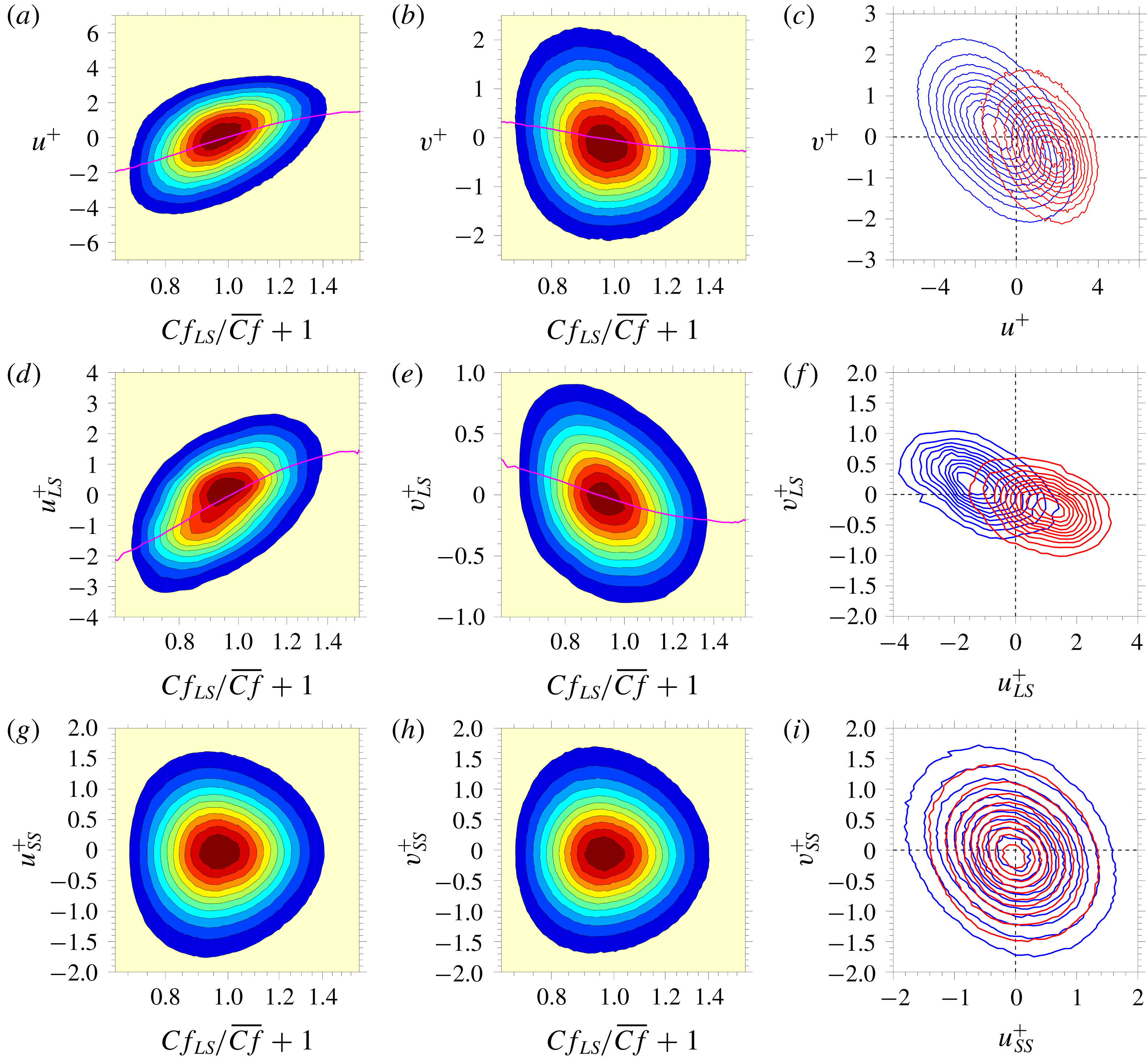
Figure 11. Probability density functions of turbulent-velocity fluctuations at
![]() $y^{+}\approx 300$
: (a) joint p.d.f.
$y^{+}\approx 300$
: (a) joint p.d.f.
![]() $P(u^{+},Cf_{LS})$
; (b) joint p.d.f.
$P(u^{+},Cf_{LS})$
; (b) joint p.d.f.
![]() $P(v^{+},Cf_{LS})$
; (c) joint p.d.f.s
$P(v^{+},Cf_{LS})$
; (c) joint p.d.f.s
![]() $P(u^{+},v^{+})$
derived from joint p.d.f.
$P(u^{+},v^{+})$
derived from joint p.d.f.
![]() $P(u^{+},v^{+},Cf_{LS})$
at the extreme positive and negative 5 % of the
$P(u^{+},v^{+},Cf_{LS})$
at the extreme positive and negative 5 % of the
![]() $Cf_{LS}$
tails; magenta lines in (a) and (b) are loci of the conditional averages
$Cf_{LS}$
tails; magenta lines in (a) and (b) are loci of the conditional averages
![]() $\overline{U^{\prime }}^{+}|_{Cf_{LS}}$
and
$\overline{U^{\prime }}^{+}|_{Cf_{LS}}$
and
![]() $\overline{V^{\prime }}^{+}|_{Cf_{LS}}$
, respectively; (d,g), (e,h) and (f,i) correspond to (a), (b) and (c), respectively, but pertain to the large-scale and small-scale fluctuations, respectively.
$\overline{V^{\prime }}^{+}|_{Cf_{LS}}$
, respectively; (d,g), (e,h) and (f,i) correspond to (a), (b) and (c), respectively, but pertain to the large-scale and small-scale fluctuations, respectively.
Probability density functions for the small-scale velocity fluctuations, corresponding to those discussed above for the large-scale fluctuations and obtained from
![]() $P(u_{SS}^{+},v_{SS}^{+},Cf_{LS})$
, are shown in figure 11(g,h,i). The plots reveal that negative large-scale fluctuations are associated with a modest increase in the level of small-scale intensity, implying a negative correlation between large-scale and small-scale fluctuations. This increase is consistent with the maps in figures 8(c) and 10(c), the former showing a weak maximum and the latter featuring a weak ridge of elevated production of small-scale intensity around
$P(u_{SS}^{+},v_{SS}^{+},Cf_{LS})$
, are shown in figure 11(g,h,i). The plots reveal that negative large-scale fluctuations are associated with a modest increase in the level of small-scale intensity, implying a negative correlation between large-scale and small-scale fluctuations. This increase is consistent with the maps in figures 8(c) and 10(c), the former showing a weak maximum and the latter featuring a weak ridge of elevated production of small-scale intensity around
![]() $y^{+}\approx 300$
for negative
$y^{+}\approx 300$
for negative
![]() $Cf_{LS}$
values. It is also consistent with the conditional profiles of small-scale streamwise stress shown in figure 8(c), which indicates a reversal in the sign, at
$Cf_{LS}$
values. It is also consistent with the conditional profiles of small-scale streamwise stress shown in figure 8(c), which indicates a reversal in the sign, at
![]() $y^{+}\approx 150$
, of the difference between the streamwise stress levels conditional on the extreme 1.5 % positive and negative
$y^{+}\approx 150$
, of the difference between the streamwise stress levels conditional on the extreme 1.5 % positive and negative
![]() $Cf_{LS}$
tails, respectively.
$Cf_{LS}$
tails, respectively.
7 Effects of scales on skin friction
This section discusses physical interactions which contribute to the skin friction. This subject is pursued by reference to (4.8) and (4.9), both of which link distributions of statistical properties across the boundary layer to the skin friction, the former derived from the
![]() $y$
-wise integrated one-dimensional momentum equation, while the latter arises from the energy principle. The present EMD scale-decomposition method allows, in both cases, the contribution of different scales to the skin friction, as well as the contribution of terms conditional on
$y$
-wise integrated one-dimensional momentum equation, while the latter arises from the energy principle. The present EMD scale-decomposition method allows, in both cases, the contribution of different scales to the skin friction, as well as the contribution of terms conditional on
![]() $Cf_{LS}$
, to be examined. This is the approach taken in the two following subsections relating, respectively, to the FIK and RD identities.
$Cf_{LS}$
, to be examined. This is the approach taken in the two following subsections relating, respectively, to the FIK and RD identities.
7.1 Analysis of the FIK relationship
Attention is directed first to the FIK identity (4.8). In order to identify scale-specific contributions to
![]() $Cf$
, the respective shear-stress fragments (
$Cf$
, the respective shear-stress fragments (
![]() $\overline{u_{\unicode[STIX]{x1D6FE}}v_{\unicode[STIX]{x1D6FC}}}^{+}$
) are injected into (4.8). The wall-normal distributions of the constituent integrands in the FIK associated with the various fragments are shown in figures 12(a) and 12(b). The only difference between the two figures is that the latter is premultiplied by
$\overline{u_{\unicode[STIX]{x1D6FE}}v_{\unicode[STIX]{x1D6FC}}}^{+}$
) are injected into (4.8). The wall-normal distributions of the constituent integrands in the FIK associated with the various fragments are shown in figures 12(a) and 12(b). The only difference between the two figures is that the latter is premultiplied by
![]() $y^{+}$
. While this scaling shifts the maxima towards larger
$y^{+}$
. While this scaling shifts the maxima towards larger
![]() $y^{+}$
values, the advantage is that the areas under the respective curves represent faithfully the contribution of the fragments to the integrand
$y^{+}$
values, the advantage is that the areas under the respective curves represent faithfully the contribution of the fragments to the integrand
![]() $Cf_{FIK}^{+}$
. The respective contributions to the total
$Cf_{FIK}^{+}$
. The respective contributions to the total
![]() $Cf$
thus arise from integrating these distributions over
$Cf$
thus arise from integrating these distributions over
![]() $y^{+}$
, and the result is shown by the pie-chart given in figure 12(c), the grey segment representing the laminar contribution. The most dominant terms, at 28 % and 24 %, are associated with small-scale and large-scale motions, respectively. The processes thus responsible for the major part of
$y^{+}$
, and the result is shown by the pie-chart given in figure 12(c), the grey segment representing the laminar contribution. The most dominant terms, at 28 % and 24 %, are associated with small-scale and large-scale motions, respectively. The processes thus responsible for the major part of
![]() $Cf$
are small-scale fluctuations, mainly in the buffer layer, and the large-scale structures, in the outer flow. The sum of the cross-terms contributes almost 30 % to the total. Of these, the cross-terms
$Cf$
are small-scale fluctuations, mainly in the buffer layer, and the large-scale structures, in the outer flow. The sum of the cross-terms contributes almost 30 % to the total. Of these, the cross-terms
![]() $\overline{u_{SS}v_{LS}}^{+}$
and
$\overline{u_{SS}v_{LS}}^{+}$
and
![]() $\overline{u_{LS}v_{SS}}^{+}$
make a weak contribution at around 3 %. The implication is that the explicit modulation of the small-scale motions by the large-scale fluctuations does not have a significant impact on the skin friction. In contrast, as shown in figure 8, the magnitude of the small-scale fluctuations varies significantly with
$\overline{u_{LS}v_{SS}}^{+}$
make a weak contribution at around 3 %. The implication is that the explicit modulation of the small-scale motions by the large-scale fluctuations does not have a significant impact on the skin friction. In contrast, as shown in figure 8, the magnitude of the small-scale fluctuations varies significantly with
![]() $Cf_{LS}$
, the implication being that the contribution of the modulation is embedded in the characteristics of the small-scale fluctuations. In fact, it is arguable, in light of the discussion in § 6, that the use of the term modulation is questionable, at least when interpreted as a direct wave-like interference between the large-scale and small-scale motions. In reality, the evidence presented in § 6 suggests that the large-scale structures modify ‘locally’ the velocity gradient and
$Cf_{LS}$
, the implication being that the contribution of the modulation is embedded in the characteristics of the small-scale fluctuations. In fact, it is arguable, in light of the discussion in § 6, that the use of the term modulation is questionable, at least when interpreted as a direct wave-like interference between the large-scale and small-scale motions. In reality, the evidence presented in § 6 suggests that the large-scale structures modify ‘locally’ the velocity gradient and
![]() $u_{\unicode[STIX]{x1D70F}}$
, thus driving the variations of small-scale fluctuations by changes to the shear-induced production of the shear stress and turbulence energy. The adverb ‘locally’ is intended to imply that the time scale associated with large-scale fluctuations and the regions affected by these fluctuations is much longer than the time scale dictating changes in the small scales, which underpins the quasi-steady theory formulated by Zhang & Chernyshenko (Reference Zhang and Chernyshenko2016).
$u_{\unicode[STIX]{x1D70F}}$
, thus driving the variations of small-scale fluctuations by changes to the shear-induced production of the shear stress and turbulence energy. The adverb ‘locally’ is intended to imply that the time scale associated with large-scale fluctuations and the regions affected by these fluctuations is much longer than the time scale dictating changes in the small scales, which underpins the quasi-steady theory formulated by Zhang & Chernyshenko (Reference Zhang and Chernyshenko2016).

Figure 12. Contribution of different scales to the skin friction via the FIK identity: (a) contribution of different shear-stress fragments to the integrand in the FIK identity; (b) same as (a), but premultiplied by
![]() $y^{+}$
; (c) contributions of different scales to
$y^{+}$
; (c) contributions of different scales to
![]() $Cf$
, the grey segment representing the viscous part, i.e. the leading term in (4.8).
$Cf$
, the grey segment representing the viscous part, i.e. the leading term in (4.8).
In order to examine the distribution of the skin friction conditional on
![]() $Cf_{LS}$
– i.e. the degree to which the friction is induced by contributions that vary with the sign and intensity of the large-scale fluctuations – a map of
$Cf_{LS}$
– i.e. the degree to which the friction is induced by contributions that vary with the sign and intensity of the large-scale fluctuations – a map of
![]() $(\text{d}\overline{uv}^{+}/\text{d}Cf_{LS})(Cf_{LS},y^{+})$
is derived from the joint p.d.f.s
$(\text{d}\overline{uv}^{+}/\text{d}Cf_{LS})(Cf_{LS},y^{+})$
is derived from the joint p.d.f.s
![]() $P(u^{+},v^{+},Cf_{LS})$
, by using (4.4) at each wall-normal location, and then by injecting the map obtained into the FIK decomposition (4.8). Figure 13(a) presents the former map. The coloured lines represent the contributions identified in the caption – i.e.
$P(u^{+},v^{+},Cf_{LS})$
, by using (4.4) at each wall-normal location, and then by injecting the map obtained into the FIK decomposition (4.8). Figure 13(a) presents the former map. The coloured lines represent the contributions identified in the caption – i.e.
![]() $\text{d}Cf_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}}/\text{d}Cf_{LS}$
. The results shown in figure 13 indicate that, while the skin friction is materially affected by all scales for both positive and negative large-scale footprints, there is a bias towards contributions from negative large-scale fluctuations in the outer region, above
$\text{d}Cf_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}}/\text{d}Cf_{LS}$
. The results shown in figure 13 indicate that, while the skin friction is materially affected by all scales for both positive and negative large-scale footprints, there is a bias towards contributions from negative large-scale fluctuations in the outer region, above
![]() $y^{+}\approx 100$
. This conforms to several results discussed earlier concerning the dominance of the large-scale stresses in association with negative
$y^{+}\approx 100$
. This conforms to several results discussed earlier concerning the dominance of the large-scale stresses in association with negative
![]() $Cf_{LS}$
values. In contrast, the main contribution at positive large-scale fluctuations originates preferentially from the buffer layer, due to the amplification of small-scale fluctuations by the footprints. However, large-scale motions also make a major contribution at large positive footprints, and this is consistent with the map in figure 7(b), which features a bulge in the large-scale shear stress at large positive
$Cf_{LS}$
values. In contrast, the main contribution at positive large-scale fluctuations originates preferentially from the buffer layer, due to the amplification of small-scale fluctuations by the footprints. However, large-scale motions also make a major contribution at large positive footprints, and this is consistent with the map in figure 7(b), which features a bulge in the large-scale shear stress at large positive
![]() $Cf_{LS}$
values. Hence, intense negative and, to a lesser extent, positive large-scale motions, which are correlated with
$Cf_{LS}$
values. Hence, intense negative and, to a lesser extent, positive large-scale motions, which are correlated with
![]() $Cf_{LS}$
-values, make significant contributions to the skin friction. Negative large-scale fluctuations tend to diminish the intensity of small-scale motions in the buffer layer, as shown in figure 8(a), giving added weight to the large-scale turbulent motions occurring in the outer region.
$Cf_{LS}$
-values, make significant contributions to the skin friction. Negative large-scale fluctuations tend to diminish the intensity of small-scale motions in the buffer layer, as shown in figure 8(a), giving added weight to the large-scale turbulent motions occurring in the outer region.

Figure 13. Conditional contributions to the skin friction via the FIK identity: (a) wall-normal distribution of the
![]() $Cf_{LS}$
-wise gradient of skin friction,
$Cf_{LS}$
-wise gradient of skin friction,
![]() $\text{d}Cf_{FIK}/\text{d}Cf_{LS}$
; (b) wall-normal-integrated
$\text{d}Cf_{FIK}/\text{d}Cf_{LS}$
; (b) wall-normal-integrated
![]() $Cf_{LS}$
-wise gradients of contributions of different scales, associated with
$Cf_{LS}$
-wise gradients of contributions of different scales, associated with
![]() $\overline{u_{\unicode[STIX]{x1D6FE}}u_{\unicode[STIX]{x1D6FC}}}$
, to
$\overline{u_{\unicode[STIX]{x1D6FE}}u_{\unicode[STIX]{x1D6FC}}}$
, to
![]() $Cf$
(i.e. the
$Cf$
(i.e. the
![]() $y^{+}$
-integral of the field in map (a)); colours of lines correspond to those in figure 12, except for the grey line, which represents the sum of all mixed-scale terms.
$y^{+}$
-integral of the field in map (a)); colours of lines correspond to those in figure 12, except for the grey line, which represents the sum of all mixed-scale terms.

Figure 14. Contributions of viscous and turbulent terms to the skin friction as derived from the RD relationship: (a) wall-normal profiles of premultiplied integrands
![]() $Cf_{a}^{+}$
(green line) and
$Cf_{a}^{+}$
(green line) and
![]() $Cf_{b}^{+}$
(grey line) in (4.9), the black line representing the sum of both fragments; (b) contribution of viscous and turbulent terms to the skin friction (i.e. integrals of
$Cf_{b}^{+}$
(grey line) in (4.9), the black line representing the sum of both fragments; (b) contribution of viscous and turbulent terms to the skin friction (i.e. integrals of
![]() $Cf_{a}^{+}$
and
$Cf_{a}^{+}$
and
![]() $Cf_{b}^{+}$
); (c) map of
$Cf_{b}^{+}$
); (c) map of
![]() $y^{+}\times \text{d}Cf_{a}^{+}/\text{d}Cf_{LS}$
; (d) map of
$y^{+}\times \text{d}Cf_{a}^{+}/\text{d}Cf_{LS}$
; (d) map of
![]() $y^{+}\times \text{d}Cf_{b}^{+}/\text{d}Cf_{LS}$
.
$y^{+}\times \text{d}Cf_{b}^{+}/\text{d}Cf_{LS}$
.
7.2 Analysis of the RD relationship
Attention is directed next to the examination of various contributions to the alternative skin-friction relation given by (4.9). Results are presented for the integrands in equation (4.9), denoted by
![]() $Cf_{a}^{+}$
and
$Cf_{a}^{+}$
and
![]() $Cf_{b}^{+}$
, which represent the local viscous dissipation and turbulence production, respectively, and also for the total skin friction
$Cf_{b}^{+}$
, which represent the local viscous dissipation and turbulence production, respectively, and also for the total skin friction
![]() $Cf$
, i.e. the sum of the
$Cf$
, i.e. the sum of the
![]() $y$
-wise integrals of
$y$
-wise integrals of
![]() $Cf_{a}^{+}$
and
$Cf_{a}^{+}$
and
![]() $Cf_{b}^{+}$
. First, figure 14(a) gives, by way of the green and grey lines, respectively, the wall-normal distributions of
$Cf_{b}^{+}$
. First, figure 14(a) gives, by way of the green and grey lines, respectively, the wall-normal distributions of
![]() $Cf_{a}^{+}$
and
$Cf_{a}^{+}$
and
![]() $Cf_{b}^{+}$
. As the profiles are plotted against
$Cf_{b}^{+}$
. As the profiles are plotted against
![]() $\log y^{+}$
, they have been premultiplied, as before, by
$\log y^{+}$
, they have been premultiplied, as before, by
![]() $y^{+}$
so that the areas below the curves give a visually correct representation of their contribution to
$y^{+}$
so that the areas below the curves give a visually correct representation of their contribution to
![]() $Cf$
. In the viscous sublayer, the turbulent production is close to zero, while the viscous term is close to constant, hence rising close to linearly in figure 14(a) to a maximum around
$Cf$
. In the viscous sublayer, the turbulent production is close to zero, while the viscous term is close to constant, hence rising close to linearly in figure 14(a) to a maximum around
![]() $y^{+}\approx 7$
, after which it drops rapidly to close to zero in the log-law region. The variation of the gradient
$y^{+}\approx 7$
, after which it drops rapidly to close to zero in the log-law region. The variation of the gradient
![]() $y^{+}\times \text{d}Cf_{a}^{+}/\text{d}Cf_{LS}$
across
$y^{+}\times \text{d}Cf_{a}^{+}/\text{d}Cf_{LS}$
across
![]() $Cf_{LS}$
, shown in figure 14(c), indicates a slight bias towards negative values of
$Cf_{LS}$
, shown in figure 14(c), indicates a slight bias towards negative values of
![]() $Cf_{LS}$
, and this reflects the fact that the viscous sublayer thickens (in absolute terms) when the negative large-scale footprints reduce the near-wall velocity and
$Cf_{LS}$
, and this reflects the fact that the viscous sublayer thickens (in absolute terms) when the negative large-scale footprints reduce the near-wall velocity and
![]() $u_{\unicode[STIX]{x1D70F}}$
. The turbulent production rises sharply from close to zero at the upper end of the viscous sublayer to reach a maximum in the buffer layer, but the premultiplication shifts this maximum to around
$u_{\unicode[STIX]{x1D70F}}$
. The turbulent production rises sharply from close to zero at the upper end of the viscous sublayer to reach a maximum in the buffer layer, but the premultiplication shifts this maximum to around
![]() $y^{+}\approx 20$
, after which the production then drops steeply to settle to a near-linear decline in the range
$y^{+}\approx 20$
, after which the production then drops steeply to settle to a near-linear decline in the range
![]() $80<y^{+}<400$
. Because the large scales at
$80<y^{+}<400$
. Because the large scales at
![]() $y^{+}\approx 300$
give rise to an increase in production, as shown in figure 10(b), it is reasonable to expect a weak second maximum in figure 14(a). However, no such maximum is present, and this must reflect the weakness of the outer large-scale production at the present low Reynolds number. On the other hand, figure 14(d) showing
$y^{+}\approx 300$
give rise to an increase in production, as shown in figure 10(b), it is reasonable to expect a weak second maximum in figure 14(a). However, no such maximum is present, and this must reflect the weakness of the outer large-scale production at the present low Reynolds number. On the other hand, figure 14(d) showing
![]() $y^{+}\times \text{d}Cf_{b}^{+}/\text{d}Cf_{LS}$
across
$y^{+}\times \text{d}Cf_{b}^{+}/\text{d}Cf_{LS}$
across
![]() $Cf_{LS}$
reveals, in accord with previous considerations (e.g. figure 7), the presence of a weak outer maximum at
$Cf_{LS}$
reveals, in accord with previous considerations (e.g. figure 7), the presence of a weak outer maximum at
![]() $y^{+}\approx 300$
,
$y^{+}\approx 300$
,
![]() $Cf_{LS}/\overline{Cf}\approx -0.15$
. It thus appears that the absence of an outer maximum in figure 14(a) is simply due the low level of the
$Cf_{LS}/\overline{Cf}\approx -0.15$
. It thus appears that the absence of an outer maximum in figure 14(a) is simply due the low level of the
![]() $Cf_{LS}$
-wise integral in the outer part of the field in figure 14(d). As previously shown by Renard & Deck (Reference Renard and Deck2016), an outer maximum does appear when the influence of the outer structures rises with increasing Reynolds number.
$Cf_{LS}$
-wise integral in the outer part of the field in figure 14(d). As previously shown by Renard & Deck (Reference Renard and Deck2016), an outer maximum does appear when the influence of the outer structures rises with increasing Reynolds number.
Figure 14(b) shows the contribution of the viscous and turbulent term (i.e. their integrals over
![]() $y^{+}$
to
$y^{+}$
to
![]() $Cf$
), the overall value being identical to that of the FIK identity. This split – 44 % and 56 %, arising from the viscous and turbulent fragment, respectively – will obviously shift progressively towards higher contributions of the turbulent fragment as the Reynolds number increases.
$Cf$
), the overall value being identical to that of the FIK identity. This split – 44 % and 56 %, arising from the viscous and turbulent fragment, respectively – will obviously shift progressively towards higher contributions of the turbulent fragment as the Reynolds number increases.

Figure 15. Contributions of scale-related turbulent shear-stress fragments to the skin friction via the RD relationship: (a) wall-normal profiles of scale-specific premultiplied production contributions to the integrand
![]() $Cf_{b}^{+}$
in (4.9), the black line representing the sum of all contributions; (b) contribution of fragments to the skin friction, segment colours corresponding to those of curves in (a), except for the large green segment which represents the viscous contribution, as in figure 14(b); (c) map of
$Cf_{b}^{+}$
in (4.9), the black line representing the sum of all contributions; (b) contribution of fragments to the skin friction, segment colours corresponding to those of curves in (a), except for the large green segment which represents the viscous contribution, as in figure 14(b); (c) map of
![]() $y^{+}\times \text{d}Cf_{b,SS}^{+}/\text{d}Cf_{LS}$
associated with the small-scale shear-stress fragment; (d) map of
$y^{+}\times \text{d}Cf_{b,SS}^{+}/\text{d}Cf_{LS}$
associated with the small-scale shear-stress fragment; (d) map of
![]() $y^{+}\times \text{d}Cf_{b,LS}^{+}/\text{d}Cf_{LS}$
associated with the large-scale shear-stress fragment.
$y^{+}\times \text{d}Cf_{b,LS}^{+}/\text{d}Cf_{LS}$
associated with the large-scale shear-stress fragment.
As done in the FIK analysis, § 7.1, it is possible to identify, here too, the production-related contribution of different fragments of the shear stress to
![]() $Cf_{b}^{+}$
and hence to
$Cf_{b}^{+}$
and hence to
![]() $Cf$
. This is done in figure 15(a), which shows the nine fragments also considered in the FIK analysis. Integrating these with respect to
$Cf$
. This is done in figure 15(a), which shows the nine fragments also considered in the FIK analysis. Integrating these with respect to
![]() $y^{+}$
then gives the segments shown in figure 15(b), which signify the respective contributions to
$y^{+}$
then gives the segments shown in figure 15(b), which signify the respective contributions to
![]() $Cf$
, alongside the contribution of the viscous term, represented by the green segment. It is important to point out that, as is the case with the stress fragments of figure 12, the sum of all fragments in figure 14 yields the total given by the black curve. The figure shows that the bulk of
$Cf$
, alongside the contribution of the viscous term, represented by the green segment. It is important to point out that, as is the case with the stress fragments of figure 12, the sum of all fragments in figure 14 yields the total given by the black curve. The figure shows that the bulk of
![]() $Cf_{b}^{+}$
is due to the small scales – namely 30 % of the total. The distribution of its premultiplied gradient
$Cf_{b}^{+}$
is due to the small scales – namely 30 % of the total. The distribution of its premultiplied gradient
![]() $y^{+}\times \text{d}Cf_{b,SS}^{+}/\text{d}Cf_{LS}$
, shown in figure 15(c), reveals a bias towards negative footprints in the outer region, and this is consistent with the enhanced small-scale production indicated by the wedge-shaped, light-blue region around
$y^{+}\times \text{d}Cf_{b,SS}^{+}/\text{d}Cf_{LS}$
, shown in figure 15(c), reveals a bias towards negative footprints in the outer region, and this is consistent with the enhanced small-scale production indicated by the wedge-shaped, light-blue region around
![]() $y^{+}\approx 300$
,
$y^{+}\approx 300$
,
![]() $Cf_{LS}/\overline{Cf}<-0.1$
in figure 10(c). In contrast, the contribution of the large scales is relatively low, at 8 %, and the map of
$Cf_{LS}/\overline{Cf}<-0.1$
in figure 10(c). In contrast, the contribution of the large scales is relatively low, at 8 %, and the map of
![]() $y^{+}\times \text{d}Cf_{b,LS}^{+}/\text{d}Cf_{LS}$
conveys the fact that this term is associated primarily with negative footprints, a feature entirely consistent with earlier results – e.g. figure 10(b,d).
$y^{+}\times \text{d}Cf_{b,LS}^{+}/\text{d}Cf_{LS}$
conveys the fact that this term is associated primarily with negative footprints, a feature entirely consistent with earlier results – e.g. figure 10(b,d).
Figure 16 finally conveys the contribution of the small-scale, large-scale and intermediate-scale contributions to the skin friction. This figure is this analogous to figure 13(b) pertaining to the FIK relationship. Here again, there is a clear bias of the large-scale contribution towards negative values of the fluctuations and thus
![]() $Cf_{LS}$
, but the relative contributions of the small and large scales differ greatly from those derived from the FIK identity.
$Cf_{LS}$
, but the relative contributions of the small and large scales differ greatly from those derived from the FIK identity.
Figure 16. Contributions of wall-normal-integrated
![]() $Cf_{LS}$
-wise gradients of different fragments, associated with
$Cf_{LS}$
-wise gradients of different fragments, associated with
![]() $\overline{u_{\unicode[STIX]{x1D6FE}}u_{\unicode[STIX]{x1D6FC}}}$
, to the skin friction via the RD relationship; red line: small-scale contribution; blue line: large-scale contribution; magenta line: intermediate-scale contribution. The red and blue lines arise, respectively, from the
$\overline{u_{\unicode[STIX]{x1D6FE}}u_{\unicode[STIX]{x1D6FC}}}$
, to the skin friction via the RD relationship; red line: small-scale contribution; blue line: large-scale contribution; magenta line: intermediate-scale contribution. The red and blue lines arise, respectively, from the
![]() $y$
-wise integration of maps (c) and (d) in figure 15.
$y$
-wise integration of maps (c) and (d) in figure 15.
The differences between the results of the FIK and RD relationships – exemplified most starkly by the juxtaposition of figures 15(b) and 12(c) – are perplexing at first sight. In particular, the contribution to
![]() $Cf$
of the large scales arising from the RD analysis is only 8 % relative to 24 % derived from the FIK analysis. However, it needs to be recognised that the two relationship express very different physical processes.
$Cf$
of the large scales arising from the RD analysis is only 8 % relative to 24 % derived from the FIK analysis. However, it needs to be recognised that the two relationship express very different physical processes.
One important difference relates to the viscous contributions. In the FIK relationship, this contribution is insignificant, as it expresses the skin friction of a laminar channel flow at the given Reynolds number. In contrast, the viscous term in the RD relationship is almost 10 times larger, as it reflects the consequences of the severe steepening of the velocity gradient at the wall by the turbulent shear stress above the viscous sublayer on the viscous dissipation, thus almost halving the contribution of the turbulent part of the RD relationship. In addition, the large-scale footprints in the viscous layer cause significant variations in the near-wall shear strain, and this indirect effect also increases the weight of the viscous contribution at the expense of the turbulent one. If attention is restricted to the turbulent contributions of the FIK and RD relationships then the proportion associated with the large scales amount to 23 % and 15 %, respectively. This difference is still large, but both figures demonstrate the importance of the large scales to the skin friction.
A second important point of difference lies in the nature of the turbulence processes represented by the turbulence-related fragments in the two relationships. Within the RD framework, the turbulent contributions characterise the energy generated by the specific turbulent shear-stress fragments in combination with the shear strain. In the case of the large-scale motions, the associated structures are elongated and characterised by substantial streamwise fluctuations and only modest cross-flow fluctuations. The relatively modest shear stress associated with these structures thus gives rise, in combination with the relatively low strain in the outer region, to relatively modest production. This is illustrated in figure 10(d), and figure 15(d) also shows that the production by the large-scale structures is largely confined to layer above
![]() $y^{+}>100$
. In the FIK identity, the contribution of the shear stress below
$y^{+}>100$
. In the FIK identity, the contribution of the shear stress below
![]() $y^{+}\approx 100$
is also modest, but its importance to
$y^{+}\approx 100$
is also modest, but its importance to
![]() $Cf$
above this distance is substantially enhanced by the much lower weight of the small-scale contributions returned by the FIK identity. The much higher level that the RD relationship yields is due to the intense shear strain favouring the production above and within the buffer layer, as conveyed by figure 15(c). In the FIK relationship, the small-scale contribution to the integrand in the layer remote from the wall is rather low, as shown in figure 12(b), and this enhances the weight of the large-scale contribution.
$Cf$
above this distance is substantially enhanced by the much lower weight of the small-scale contributions returned by the FIK identity. The much higher level that the RD relationship yields is due to the intense shear strain favouring the production above and within the buffer layer, as conveyed by figure 15(c). In the FIK relationship, the small-scale contribution to the integrand in the layer remote from the wall is rather low, as shown in figure 12(b), and this enhances the weight of the large-scale contribution.
Ultimately, it is impossible to reconcile the FIK- and RD-described scale-related contributions, and to untangle the direct production-related contribution of the large-scale motion from its indirect effects via footprinting within the RD framework. A statement that can be made is that the FIK analysis gives a more direct, force-derived, and thus more meaningful, quantification of the contribution of the large scales to the skin friction.
8 Conclusions
The goal of this study was to illuminate the mechanisms by which the large outer scales in the energy-plateau region of a wall-bounded shear layer affect the small-scale turbulence field, in general, and the wall friction statistics, in particular. This was approached by means of a rational scale-separation technique and a rigorous extraction of relevant statistical properties from joint and conditional p.d.f.s. Particular attention was devoted to identifying the dependence of the small-scale streamwise energy, shear stress and skin-friction variance on the intensity of large-scale skin-friction fluctuations – i.e. the footprints of the large-scale structures on the modulation of the small-scale field. A second major objective was to quantify the contribution of different scales to the skin friction.
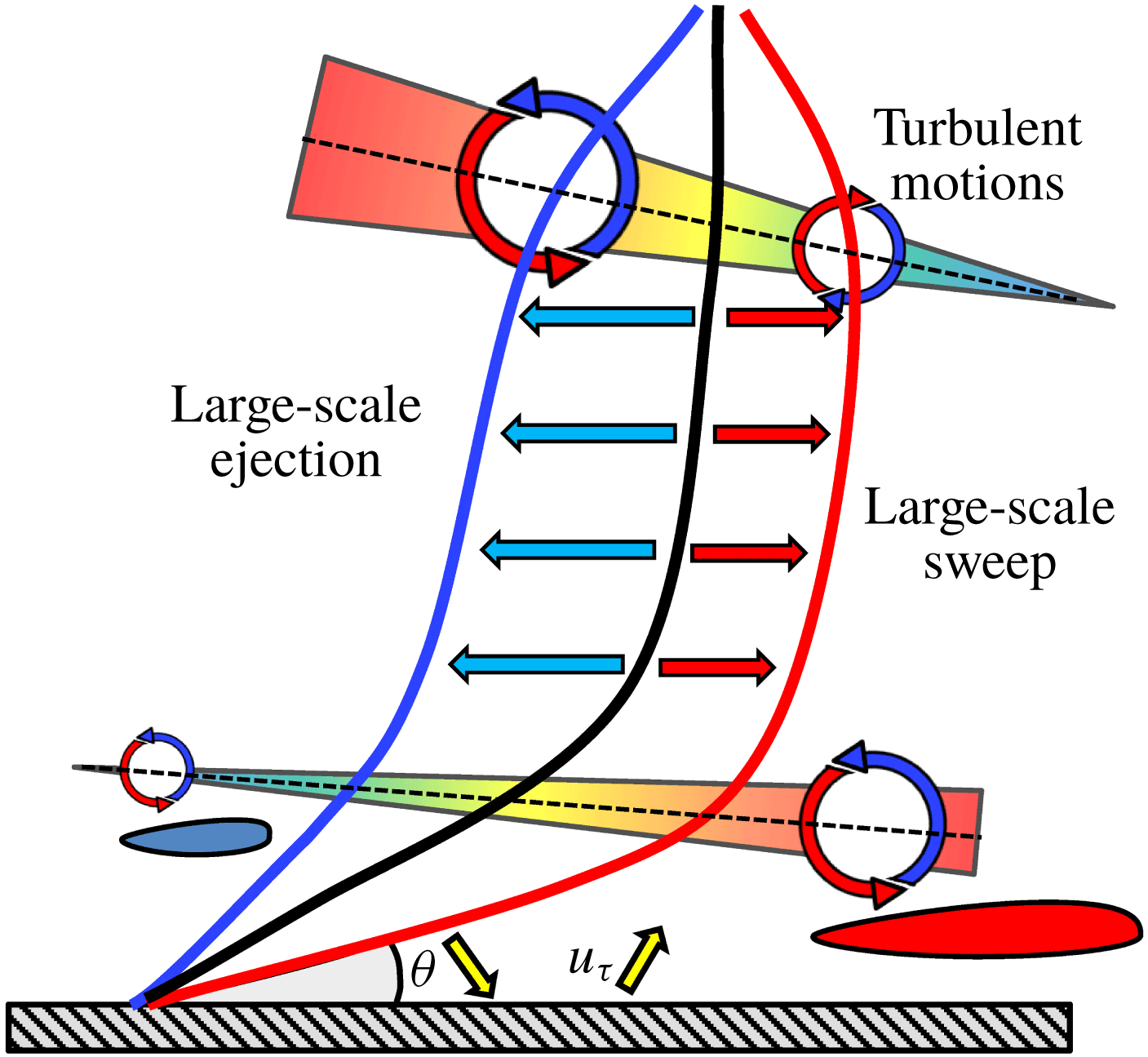
Figure 17. Conceptual schematic of the effects of large-scale fluctuations on the strain rate and consequent amplification/attenuation of near-wall and outer-layer turbulence.
The study has yielded a number statistical interactions that reinforce previous observations, but also revealed new mechanisms or explained more fully the former. The main conclusions may be summarised as follows, supported by the schematic given in figure 17:
(i) The well-established change in the sign of the correlation linking the large-scale motion with the small-scale motion at
 $y^{+}\approx 100$
is due to a reversal of shear-induced production rates. With reference to figure 17, positive large-scale fluctuations, associated with positive large-scale skin fluctuations, cause an increase of shear strain and shear production in the buffer layer, thus increasing small-scale activity. Concurrently, the shear strain in the outer region is reduced, resulting in a decline in the small-scale activity in the outer region. The reverse occurs in the presence of negative large-scale fluctuations. The variations in the velocity field are caused by large-scale sweeps and ejections, the former increasing the near-wall strain and the latter decreasing it.
$y^{+}\approx 100$
is due to a reversal of shear-induced production rates. With reference to figure 17, positive large-scale fluctuations, associated with positive large-scale skin fluctuations, cause an increase of shear strain and shear production in the buffer layer, thus increasing small-scale activity. Concurrently, the shear strain in the outer region is reduced, resulting in a decline in the small-scale activity in the outer region. The reverse occurs in the presence of negative large-scale fluctuations. The variations in the velocity field are caused by large-scale sweeps and ejections, the former increasing the near-wall strain and the latter decreasing it.(ii) The widespread use of the term ‘modulation’ suggests a direct interaction between the large-scale and small-scale fluctuations. However, in reality, the interaction is indirect, occurring via shear-strain increase and decrease in the buffer layer and consequent variations in turbulence production.
(iii) The reversal of the shear gradient in the outer region also affects the intensity of the large-scale motions by shear-induced production. Thus, negative large-scale velocity fluctuations cause an increase in the outer production and hence a rise in the large-scale turbulence intensity. In other words, the increase in the large-scale outer motions goes hand-in-hand with a decrease in turbulence in the buffer layer.
(iv) Small-scale turbulence in the buffer layer – i.e. the streak strength and the shear stress – rises close to linearly with the intensity of positive large-scale fluctuations in the velocity close to the wall and in the skin friction. The large-scale skin-friction fluctuations vary between
 $-40\,\%$
and
$-40\,\%$
and
 $+60\,\%$
relative to the mean value, causing the standard deviation of the small-scale skin friction to vary between 25 % and 65 % of the mean friction factor, the asymmetry relative to the mean value reflecting the skewness of the p.d.f. of the large-scale skin friction. These levels of fluctuations are remarkably large in view of the relatively low Reynolds number of the flow considered, and bring to light starkly the magnitude of the ‘modulation’.
$+60\,\%$
relative to the mean value, causing the standard deviation of the small-scale skin friction to vary between 25 % and 65 % of the mean friction factor, the asymmetry relative to the mean value reflecting the skewness of the p.d.f. of the large-scale skin friction. These levels of fluctuations are remarkably large in view of the relatively low Reynolds number of the flow considered, and bring to light starkly the magnitude of the ‘modulation’.(v) A quantification of the contributions of different scales to the skin friction via the FIK identity shows that the large-scale motions contribute 24 % of the drag, a level almost as high as the small-scale motions. Mixed-scale contributions arising from correlations between the large-scale and small-scale motions to shear-stress fragments are small, implying that direct ‘modulation’, used in the strict sense of the term, is small. Rather, the effect of the large scales on the small scale is indirect, as already noted, and this gives rise to an intensification of the small-scale contribution to the skin friction.
(vi) The alternative quantification via the RD identity suggests that the contribution of the large scales to the skin friction is much lower, at 8 % (or 15 % of the total turbulent part). However, this method partitions the roles of the different scales by virtue of their contribution to energy production, and it also characterises the influence of the viscous contribution by shear-strain-driven dissipation in the near-wall layer. This method of partitioning is very different from the FIK method, yielding a viscous contribution which is almost as high as the turbulent contribution, relative to only 5 % resulting from the FIK decomposition. The fact that the small-scale contribution to the drag is, proportionately, much larger than that arising from the FIK identity reflects that turbulence production by shear in the upper part of the buffer layer is the dominant contributor, relative to the modest generation in the outer region, and this suggests that the amplification of the small-scale intensity in the buffer layer by the action of the outer structures is of substantial importance, but not reflected explicitly by the contribution of the outer structures to the skin friction. Hence, the conclusion, based on heuristic arguments, is that the FIK identity gives a more realistic representation of the contribution of the large-scale structures to the skin friction.
Acknowledgements
The research reported in this paper was undertaken within the framework of the EU-China project DRAGY, grant agreement 690623. The authors acknowledge the provision of HPC resources by the UK supercomputing facility ARCHER via the UK Turbulence Consortium funded by EPSRC grant no. EP/L000261/1 as well as the CX2 facility of Imperial College London.