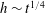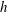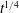1 Introduction
Liquid flows within porous media are commonly observed in our daily lives, such as in wet foods (Fisher Reference Fisher1999), paper (Kim et al. Reference Kim, Moon, Lee, Mahadevan and Kim2011), kitchen sponges (Siddique, Anderson & Bondarev Reference Siddique, Anderson and Bondarev2009) and cements (Galan, Perron & Glasser Reference Galan, Perron and Glasser2015), let alone in materials of interest in geosciences and bioengineering, e.g. soil (Yeh et al. Reference Yeh, Guzman, Srivastava and Gagnard1994), rocks (Goehring, Morris & Lin Reference Goehring, Morris and Lin2006) and scaffolds for tissue regeneration (Chung, Gamcsik & King Reference Chung, Gamcsik and King2011). Initially dry media are wetted spontaneously upon touching a liquid if the solid prefers to contact the liquid to air. An understanding of and prediction of the soaking and drying phenomena are relevant to various situations including food processing and preservation (Welti-Chanes, Velez-Ruiz & Barbosa-Canovas Reference Welti-Chanes, Velez-Ruiz and Barbosa-Cänovas2016), functional fabric design (Vasiliev Reference Vasiliev2008), landslides (Take et al. Reference Take, Bolten, Wong and Yeung2004) and building safety (Šelih, Sousa & Bremner Reference Šelih, Sousa and Bremner1994). We also note that highly absorbent sponges are finding diverse medical applications including dressing, wound healing (Kobatake, Mita & Kato Reference Kobatake, Mita and Kato2015; Lee et al. Reference Lee, Park, Kim, Kim, Moon, Mueller and Jeong2016a ) and dental treatments (Castro-Ceseña et al. Reference Castro-Ceseña, Camacho-Villegasb, Lugo-Fabresb, Novitskayac, McKittricka and Licea-Navarrob2016), where liquid imbibition dynamics plays an important role.
Here, we address a question that is seemingly so simple but has not been answered adequately yet. How fast is an initially dry cellulose (kitchen) sponge wetted when placed on a liquid bath? Darcy’s law is used in general to describe the flow of a fluid through a porous medium:
$\boldsymbol{q}=-(k/\unicode[STIX]{x1D707})\unicode[STIX]{x1D735}p$
, where
$\boldsymbol{q}$
is the flux,
$k$
is the permeability,
$\unicode[STIX]{x1D707}$
is the liquid viscosity and
$p$
is the pressure. However, one can usually obtain
$\boldsymbol{q}$
only when the pressure gradient driving the flow and the permeability of the medium are known a priori. Alternatively, the
$k$
value of a medium is inferred from the measured value of
$\boldsymbol{q}$
(Kim et al.
Reference Kim, Choi, Moon, Lee, Chang, Lee and Kim2015). When the liquid wicks into a porous medium via capillary effects and the size of the fluid conduit (such as the pore radius,
$a$
) is constant, Washburn’s equation (Bell & Cameron Reference Bell and Cameraon1906; Lucas Reference Lucas1918; Washburn Reference Washburn1921) can give the liquid velocity, leading to a rule that the wetting distance
$h$
grows like
$(\unicode[STIX]{x1D70E}at/\unicode[STIX]{x1D707})^{1/2}$
, where
$\unicode[STIX]{x1D70E}$
is the liquid–air surface tension and
$t$
is time.
When the pore size, or the channel gap, varies along the direction of the capillary flow, the scaling exponent
$\unicode[STIX]{x1D6FD}$
in the form of
$h\sim t^{\unicode[STIX]{x1D6FD}}$
deviates from
$1/2$
, being a function of the shape of the gap (Reyssat et al.
Reference Reyssat, Courbin, Reyssat and Stone2008; Gorce, Hewitt & Vella Reference Gorce, Hewitt and Vella2016). For capillary flows occurring against gravity in open geometries imposing no length scale, the curvature of the advancing liquid front may change with height, as has been observed in sharp vertical corners (Ponomarenko, Qu & Clanet Reference Ponomarenko, Quéré and Clanet2011; Weislogel Reference Weislogel2012) and walls decorated with short pillars with rounded edges (Obara & Okumura Reference Obara and Okumura2012). In both of these cases, the rise height was shown to grow like
$t^{1/3}$
rather than
$t^{1/2}$
. This non-diffusive behaviour can be simply explained as follows. The viscous flow driven by capillary pressure satisfies
$\unicode[STIX]{x1D707}{\dot{h}}/r^{2}\sim \unicode[STIX]{x1D70E}/(rh)$
. The radius of curvature of the advancing meniscus,
$r$
, varies with
$h$
when it is free to do so in such a way that the capillary and gravitational forces balance:
$r\sim \unicode[STIX]{x1D70E}/(\unicode[STIX]{x1D70C}gh)$
, with
$\unicode[STIX]{x1D70C}$
and
$g$
being the liquid density and the gravitational acceleration respectively. Then, one obtains
$h\sim [\unicode[STIX]{x1D70E}^{2}/(\unicode[STIX]{x1D70C}g\unicode[STIX]{x1D707})]^{1/3}t^{1/3}$
.
Although the theory for the rise of a liquid film on a rough surface, namely hemiwicking, is relatively well established (Ishino et al. Reference Ishino, Reyssat, Reyssat, Okumura and Quéré2007; Ponomarenko et al. Reference Ponomarenko, Quéré and Clanet2011; Obara & Okumura Reference Obara and Okumura2012; Weislogel Reference Weislogel2012; Kim et al. Reference Kim, Choi, Moon, Lee, Chang, Lee and Kim2015; Kim, Moon & Kim Reference Kim, Moon and Kim2016), the understanding of capillarity-driven wicking within bulk porous media against gravity is still far from complete. It has been reported that the power law of rise height versus time in packed glass beads deviates from that of Washburn in the late stages (Delker, Pengra & Wong Reference Delker, Pengra and Wong1996; Lago & Araujo Reference Lago and Araujo2001), but the mechanism behind the regime transition remains elusive. Idealized formulations of wicking in both homogeneous (e.g. a packed bed of spheres) and heterogeneous (e.g. fractured rocks) porous media have been proposed (Nia & Jessen Reference Nia and Jessen2015), but without experimental verification. Vella & Huppert (Reference Vella and Huppert2007) measured the capillary rise height of water in a cellulose sponge, focusing on the front of the fully saturated region, which was found to follow Washburn’s law, but no account was given of a partially saturated region.
Figure 1. Structure of a cellulose sponge. (a) Optical image of a commercial cellulose sponge. (b) Scanning electron microscopy image of a millimetric large void whose wall contains numerous microscopic voids. (c) Scanning electron microscopy image of the cellulose sheets constituting the pore wall.
Furthermore, most previous studies of capillary flows within porous media have dealt with the case where voids are surrounded by impermeable walls, including those mentioned above. When relatively large voids are fenced with microporous sheets, as observed in cellulose sponges, whose structure will be delineated below, a liquid can infiltrate into either large voids or microscale wall pores. Depending on the dominant path of the liquid, the permeability differs to a great degree. Moreover, whether the flow is driven by the capillary effects of large voids or micropores, together with different permeability, can give rise to different scaling behaviour of the rise height. Cellulose sponges provide an easily accessible platform to study this unusual flow dynamics in porous materials.
In the following, we begin by characterizing the pore structure of cellulose sponges. Then, we describe the observed results of capillary rise of non-aqueous liquids in the sponges. To rationalize the power laws obtained through the experiments, we carry out scaling analyses based on Darcy’s law. In particular, we focus on the length scales playing dominant roles in determining the permeability and curvature pressure in the two distinct regimes found through experiment.
2 Experiments
2.1 Characterization of pore structure and size
The porous medium of current interest, cellulose sponge, has a pore structure distinct from bulk porous media like glass beads, soil and rocks. The sponge is made from a mixture of shredded cellulose sheets and sodium sulphate crystals (Märtson et al. Reference Märtson, Viljanto, Hurme, Laippala and Saukko1999; Coda Reference Coda2005). The mixture, viscose, is heated to melt the crystals and drain the molten liquid away, which eventually forms ellipsoidal millimetric holes in cellulose walls with micrometric pores. Images of a commercially available hydrophilic cellulose sponge (VWR) are shown in figure 1. The voids can be largely classified into macroscale and microscale pores, the former of which are visible and the latter hardly visible to the naked eye. In addition to the optical image of the sponge, figure 1(a), we present scanning electron microscopy images of a macro void (figure 1 b) surrounded by nano-thickness sheets with micropores (figure 1 c).
To use sponges with different sized pores in capillary rise experiments, we varied the macro void size
$R$
by compressing pristine sponges of width
$w_{0}=21$
mm. The sponges were fully soaked in water, and then dried in an oven for 8 h at
$60\,^{\circ }\text{C}$
while being compressed with a metal frame of the desired width. The resulting sponge width was
$w=14$
, 10, 7 or 2.5 mm depending on the frame width. We optically measured the radius of the macro voids of the sponges to obtain the areal portions for each pore size. The detailed measurement results are given in supplementary material available at https://doi.org/10.1017/jfm.2017.165. The average radius (
$\pm$
standard deviation) of the macro pores in the sponges was such that
$R=0.72$
(
$\pm 0.30$
), 0.44 (
$\pm 0.20$
), 0.28 (
$\pm 0.12$
) and 0.19 (
$\pm 0.08$
) mm for
$w=21,14,10$
and 7 mm respectively. It turned out that
$R$
varied approximately linearly with the sponge width as
$(R-R_{1})/(R_{0}-R_{1})=(w-w_{1})/(w_{0}-w_{1})$
, where
$R_{0}$
and
$R_{1}$
are the radii of macro voids in the sponges of widths
$w_{0}$
and
$w_{1}$
respectively, as shown in the supplementary material.
We measured the distribution of microscale wall pore radius using a porosimeter (Autopore IV9500, Micrometrics) for the pristine sponge; the results are given in the supplementary material. We found that the radius of the micropores is dominantly concentrated around
$r_{0}\sim 1~\unicode[STIX]{x03BC}\text{m}$
. Moreover, measurement of the size distribution of the microscale wall pores of a highly compressed sponge (to the width of 2.5 mm from 21 mm) revealed that the radius of the micropores is still dominantly
${\sim}1$
$\unicode[STIX]{x03BC}\text{m}$
while the macro voids have been shrunk to
${\sim}10$
$\unicode[STIX]{x03BC}\text{m}$
in radius. Therefore, the size of the micropores varied insignificantly in all of the sponges used in this work.
2.2 Capillary rise experiments
To measure the rate of capillary rise, we brought a cellulose sponge into contact with a liquid reservoir and took time sequential images with a CMOS camera (Photron SA 1.1), as shown in figure 2(a). As reservoir liquids, we used 99 wt% ethylene glycol (1 wt% water), turpentine (Nghe An Container Joint Stock Company) and four kinds of silicone oil (10, 100, 350 and 1000 cSt), whose properties are listed in table 1. The vapour pressures of the liquids are very low at atmospheric conditions, so that the effects of evaporation during our capillary rise experiments can be neglected. We avoided water in this work, as it causes swelling of cellulose sponge in the course of capillary imbibition, to focus on the flow of liquid alone. Simultaneous swelling and wicking of hygroexpansive materials including cellulose sponges (Siddique et al. Reference Siddique, Anderson and Bondarev2009), paper (Reyssat & Mahadevan Reference Reyssat and Mahadevan2009; Lee et al. Reference Lee, Kim, Kim and Mahadevan2016b ) and hydrogels (Yoon et al. Reference Yoon, Cai, Suo and Hayward2010) due to water is a challenging problem worth pursuing based on the results of this work.
Figure 2. Capillary rise dynamics in a cellulose sponge. (a) Wetting front of silicone oil IV propagating against gravity with time. (b) Experimental image of silicone oil IV propagating within a horizontally situated sponge. (c) Experimentally measured rise height of different liquids in a pristine (uncompressed) sponge with time. (d) Capillary rise height in the early stages and horizontal imbibition length within sponges with different average sizes of macro voids. Inset: images of pristine and compressed sponges. (e) Symbols used in figures 2, 3 and 6.
Table 1. Liquid properties at
$23\,^{\circ }\text{C}$
.
Figure 2(c) shows the temporal evolution of the rise height,
$h$
, of the different liquids in pristine cellulose sponges. We see that
$h$
grows like
$t^{1/2}$
initially but the power law changes to
$h\sim t^{1/4}$
later. This is a result clearly distinguishable from the capillary imbibition in a horizontally situated sponge, which exhibits persistent Washburn dynamics under negligible effects of evaporation. Moreover, our result is distinct from the aforementioned non-diffusive dynamics in sharp corners (Ponomarenko et al.
Reference Ponomarenko, Quéré and Clanet2011; Weislogel Reference Weislogel2012) or rounded-edge pillar arrays (Obara & Okumura Reference Obara and Okumura2012), in that the exponent of the present power law changes from
$1/2$
to
$1/4$
rather than being a constant of
$1/3$
. We explain the physical origins of the observed power laws and derive them in the following.
3 Early stages of capillary rise
We start with the early stages where the rise height grows like
$t^{1/2}$
. This diffusive behaviour is readily explained via Darcy’s law, which is now written as
${\dot{h}}=-(k/\unicode[STIX]{x1D707})(\text{d}p/\text{d}z+\unicode[STIX]{x1D70C}g)$
. The pressure gradient is provided by the capillary action, thus
$|\text{d}p/\text{d}z|\sim (\unicode[STIX]{x1D70E}/r)/h$
. In the early stages where
$h\ll \unicode[STIX]{x1D70E}/(\unicode[STIX]{x1D70C}gr)$
, we ignore the gravitational effect, to obtain
$h{\dot{h}}\sim (k/\unicode[STIX]{x1D707})(\unicode[STIX]{x1D70E}/r)$
. Integration of this relation is possible upon identifying the permeability
$k$
and the radius of curvature of the advancing meniscus in the sponge,
$r$
. Comparison of Darcy’s law with Washburn’s equation reveals that
$k$
corresponds to the cross-sectional area of the fluid conduit in a porous medium. When both large and small voids are present, viscous liquids would preferably fill large voids due to lower frictional resistance as long as capillary actions, which are inversely proportional to the meniscus radius, are strong enough to overcome gravity. Hence, we take
$k\sim R^{2}$
and
$r\sim R$
, with
$R$
being the characteristic radius of macro voids. Then, we obtain the following scaling law for
$h$
:
$$\begin{eqnarray}h\sim \left(\frac{\unicode[STIX]{x1D70E}Rt}{\unicode[STIX]{x1D707}}\right)^{1/2}.\end{eqnarray}$$
Although this form is identical to Washburn’s equation, a remarkable feature here is that we use only the characteristic length scale of macro voids to describe the capillary rise dynamics of the heterogeneous porous media. To verify our assumption that the wicking through sponges in the early stages is dominated by capillary flows through macro voids, we measured the rise speeds of various liquids within sponges with different sizes of macro voids. The measurement results for early-stage rise heights for different liquids and sponges of varying
$R$
are plotted versus time in figure 2(c) as filled symbols. Since the theory neglects the gravitational effect, (3.1) must also hold for horizontal imbibition. Thus, we measured the imbibition length in the horizontally situated sponge as shown in figure 2(b), where a bar of uncompressed sponge touches a liquid vessel at one end. Figure 2(d) shows that the early-stage data scattered in figure 2(b) and the measurement results for horizontal imbibition are indeed collapsed onto a single straight line with a slope of
$1/2$
when plotted against
$\unicode[STIX]{x1D70E}Rt/\unicode[STIX]{x1D707}$
, consistent with our scaling law (3.1). The only difference in the vertical and horizontal imbibition is that (3.1) holds for the entire duration of horizontal wicking, unlike vertical wicking.
4 Late stages of capillary rise
To investigate the fluid flow beyond the early stages, we first compare the optical images of macro voids near the wet–dry interface in the early and late stages in figure 3(a,b). While the macro voids in the early stages are completely filled with liquid, those in the late stages are only wet in their walls and corners. We have also found that the transition from the complete filling (early) stage to the partial filling (late) stage occurs at a higher elevation for liquids with a higher surface tension, while the transition height is independent of the liquid viscosity. These observations indicate that liquid fails to fill the macro voids completely from a certain elevation due to gravitational effects. Then, the liquid menisci should hang in the corners of the macro voids, as depicted in figure 3(b), a physical picture consistent with previous studies dealing with corner flows (Ponomarenko et al.
Reference Ponomarenko, Quéré and Clanet2011; Obara & Okumura Reference Obara and Okumura2012; Weislogel Reference Weislogel2012). Since the driving curvature force and the cross-sectional area of the fluid conduit are altogether different from those of the early stages,
$k$
and
$r$
in Darcy’s law must change in the late stages.
Figure 3. Effects of gravity on liquid-filling behaviour of voids and late-stage rise dynamics. (a) Left: optical image of a sponge soaked with liquid in the early stages. Right: a schematic of a macro void completely filled with liquid. (b) Left: optical image of a sponge near its wet–dry interface in the late stages. Right: a schematic of a macro void wetted at the corner with microscale wall pores saturated with liquid. Here,
$\unicode[STIX]{x1D706}$
indicates the radius of curvature of the meniscus at the wet corner. (c) A schematic of a liquid entering microscale wall pores from a wet corner of macro voids and estimates of pressure. Here,
$p_{c}$
and
$p_{m}$
correspond to the pressures in the corner liquid and micropore respectively. (d) Liquid rise height in the late stages plotted according to the scaling law (4.1). (
$e$
) The experimentally measured liquid rise height scaled by Jurin’s height,
$h_{J}$
, of macro voids in each case. The horizontal line indicates the boundary between the early and late stages.
If the walls of the corners are impermeable (Ponomarenko et al.
Reference Ponomarenko, Quéré and Clanet2011; Obara & Okumura Reference Obara and Okumura2012; Weislogel Reference Weislogel2012), the liquid hanging in the corner is responsible for both capillary pressure (
$\unicode[STIX]{x1D70E}/r$
) and area of conduit (
$k$
), which leads to the
$t^{1/3}$
law as explained in § 1. The critical difference of the sponges from the substrates of previous studies is that the sheets surrounding the macro voids are permeable, with a number of micropores of radius
$r_{0}\sim 1$
$\unicode[STIX]{x03BC}\text{m}$
. The permeable sheets absorb liquid as it gradually wets the macro voids only in the corners. We still estimate the characteristic radius of curvature,
$\unicode[STIX]{x1D706}$
, of the wet corners of macro pores at the height
$h$
as
$\unicode[STIX]{x1D706}\sim \unicode[STIX]{x1D70E}/(\unicode[STIX]{x1D70C}gh)$
based on the balance of capillary and gravitational effects. As the pressure difference in the micropores at the rising front,
$p_{a}-p_{m}\sim \unicode[STIX]{x1D70E}/r_{0}$
, is greater than that in the corner liquid,
$p_{a}-p_{c}\sim \unicode[STIX]{x1D70E}/\unicode[STIX]{x1D706}$
, with
$p_{a}$
being the atmospheric pressure, the liquid flow can be driven from the wet corner to the wall pores; see figure 3(c). In the late stages, therefore, liquid rise is driven by capillary pressure provided by microscale wall pores, leading to
$r\sim r_{0}$
, where
$r$
is the radius of curvature responsible for the dominant driving force in Darcy’s law. Now, the remaining question is what path the liquid takes from the reservoir to the micropores at the rising front, which determines
$k$
. As depicted in figure 3(c), the dominant flow path is provided by the liquid hanging in the macro voids rather than microscale wall pores with excessively small cross-sectional area causing too much viscous dissipation. Therefore, the permeability
$k$
can be scaled as the cross-sectional area of a wet corner, which is a function of the rise height
$h$
and the compression ratio
$\unicode[STIX]{x1D716}=R/R_{0}$
, with
$R_{0}$
being the macro pore size of the pristine sponge.
Figure 4 shows a schematic of a corner of an individual macro void which is compressed by external pressure in the lateral (
$x$
) direction. We are interested in the change of fluid conduit area,
$A_{0}$
to
$A$
, while the meniscus curvature
$\unicode[STIX]{x1D706}$
is maintained. Assuming that the void size changes insignificantly in the
$y$
-direction, which is confirmed by negligible extension of the sponge in the direction perpendicular to that of pressure, we write
$R/\tan \unicode[STIX]{x1D6FC}\sim R_{0}/\tan \unicode[STIX]{x1D6FC}_{0}$
, where
$\unicode[STIX]{x1D6FC}_{0}$
and
$\unicode[STIX]{x1D6FC}$
are the corner angles of uncompressed and compressed voids respectively. Since
$A_{0}\sim \unicode[STIX]{x1D706}^{2}/\tan \unicode[STIX]{x1D6FC}_{0}$
and
$A\sim \unicode[STIX]{x1D706}^{2}/\tan \unicode[STIX]{x1D6FC}$
, we obtain
$A/A_{0}\sim \tan \unicode[STIX]{x1D6FC}_{0}/\tan \unicode[STIX]{x1D6FC}\sim R_{0}/R$
. The permeability of the uncompressed sponge is given by
$k_{0}\sim A_{0}\sim \unicode[STIX]{x1D706}^{2}$
, and thus the permeability of the compressed sponge
$k\sim A\sim \unicode[STIX]{x1D706}^{2}/\unicode[STIX]{x1D716}\sim \unicode[STIX]{x1D716}^{-1}[\unicode[STIX]{x1D70E}/(\unicode[STIX]{x1D70C}gh)]^{2}$
, where
$\unicode[STIX]{x1D716}=R/R_{0}$
is the compression ratio. The permeability decreases with the rise height because the radius of curvature of the meniscus should decrease to overcome gravity. Highly compressed sponges with a low
$\unicode[STIX]{x1D716}$
have a high
$k$
because the corner area occupied by a meniscus is larger than the wet corner area of less compressed sponges with the same meniscus curvature.
Figure 4. Deformation of a wet corner of macro voids by the external pressure in (a) the uncompressed sponge and (b) the compressed sponge. Given the same radius of the meniscus curvature
$\unicode[STIX]{x1D706}\sim \unicode[STIX]{x1D70E}/(\unicode[STIX]{x1D70C}gh)$
, the cross-sectional area of the liquid conduit increases with the compression of the macro void.
Darcy’s law, which is written as
${\dot{h}}\sim (k/\unicode[STIX]{x1D707})(\unicode[STIX]{x0394}p/h)$
, with
$\unicode[STIX]{x0394}p\sim \unicode[STIX]{x1D70E}/r_{0}$
, allows us to obtain the scaling law for
$h$
in the late stages:
$$\begin{eqnarray}h\sim \left[\frac{\unicode[STIX]{x1D70E}^{3}}{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D70C}g)^{2}\unicode[STIX]{x1D716}r_{0}}\right]^{1/4}t^{1/4}.\end{eqnarray}$$
In figure 3(d), we plot the experimentally measured rise height in the late stages according to the scaling law (4.1). The data, which are the open symbols scattered in figure 2(c), are collapsed onto a single straight line regardless of changes in
$\unicode[STIX]{x1D70E}$
,
$\unicode[STIX]{x1D707}$
,
$\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D716}$
by our theory. We further show that the flow in the late stages is indeed driven by the capillary pressure in the micropores rather than that in the wet corners of macro pores using (4.1) in the appendix. Figure 3(e) reveals that the transition height at which the power law changes from
$h\sim t^{1/2}$
(filled symbols) to
$h\sim t^{1/4}$
(empty symbols) corresponds to Jurin’s height (Jurin Reference Jurin1718) of macro voids for each sponge:
$h_{J}\sim \unicode[STIX]{x1D70E}/(\unicode[STIX]{x1D70C}gR)$
. This result confirms that liquid fails to completely fill the macro voids due to gravitational effects beyond Jurin’s height, causing a qualitative difference in the rise dynamics before and after the transition height.
5 Conclusions
Our experiments and scaling laws capture the fundamental physical picture of capillary rise within multiple-pore-sized cellulose sponges. The dominant roles of macro voids in the early stages have been identified, where the liquid can completely fill the voids. In this regime, the classical Washburn dynamics based on the macro void size holds despite the existence of micropores. The non-diffusive
$t^{1/4}$
behaviour of the rise height in the late stages, where macro voids can only be partially filled while micropores are saturated, has been uncovered and rationalized by considering corner menisci whose radius of curvature changes with the rise height.
The
$t^{1/4}$
law of the rise height arises, in contrast to the
$t^{1/3}$
law for impermeable corner flows, because the sheets surrounding the macro voids are permeable. Then, one would expect to see a transition of the power law if the walls of macro voids change from impermeable to permeable along the flow direction. One feasible scheme to achieve such an observation, depicted in figure 5, starts by impregnating a sponge with liquid 1. Although the lower part of the sponge is soaked, with its macro voids filled completely, the upper part is mainly wet in the porous sheets only. Now, one cuts the sponge and lets the upper part touch liquid 2, which is immiscible with liquid 1. Then, one would see the
$t^{1/2}$
behaviour in the very early stage, and subsequently the
$t^{1/3}$
behaviour where the walls already saturated with liquid 1 are impermeable. Finally, the power law would be
$t^{1/4}$
as liquid 2 meets dry porous, and thus permeable, walls.
Figure 5. A proposed experimental scheme to observe the transition of the power law of the rise height from
$t^{1/3}$
to
$t^{1/4}$
.
Although we have focused on a cellulose sponge due to its mundane and practical importance and characteristic pseudo-bimodal pore structures, our theoretical framework considering different scales of fluid conduit and driving curvature forces depending on the rise height should be useful for understanding capillary rise dynamics in other heterogeneous porous media. We have used only non-aqueous liquids to avoid swelling of the porous medium. However, an understanding of the imbibition of aqueous liquids in hygroexpansive porous materials, such as cellulose sponges and hydrogels, can be built upon the basis of our study. This process involves simultaneous poroelastic deformation and wicking through pores of time-varying volume, resulting in a change of power law (Siddique et al. Reference Siddique, Anderson and Bondarev2009), which is currently under investigation.
Acknowledgements
We are grateful to Professors L. Mahadevan and T. H. Choi for stimulating discussions. This work was supported by the National Research Foundation of Korea (grant nos 2015035006 and 2016901290) via SNU-IAMD.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2017.165.
Appendix. Driving pressure in the late stages
Figure 6. Capillary rise height of liquid A in a pristine sponge based on two different assumptions. Here,
$h_{m}$
and
$h_{c}$
assume that the flow is driven by the capillary pressure in micropores and in wet corners of macro voids respectively. The squares are our experimental measurement results. The rise height
$h_{p}$
corresponds to the empirical law of Obara & Okumura (Reference Obara and Okumura2012) on pillar arrays:
$h_{p}\approx 0.12[\unicode[STIX]{x1D70E}^{2}/(\unicode[STIX]{x1D70C}g\unicode[STIX]{x1D707})]^{1/3}t^{1/3}$
, where the permeability should be higher because of the simpler configuration of the flow path.
In the late stages, the dominant flow path from the reservoir to the rising front is through wet corners of macro voids instead of walls of micropores, a natural consequence to avoid excessive viscous dissipation. Here, we quantitatively show that the driving pressure is provided by the micropores rather than the corner meniscus by comparing the velocities predicted based on the two assumptions. When the flow is assumed to be driven by the capillary pressure of the micropores, its velocity is given via Darcy’s law:
${\dot{h}}\approx (\hat{k}/\unicode[STIX]{x1D707})(\unicode[STIX]{x1D70E}/r_{0})/h$
, where
$\hat{k}=C\unicode[STIX]{x1D706}^{2}$
is the value of the permeability that results in the best fitting curve of figure 3(d). Integration with respect to time gives the rise height
$h_{m}\approx 0.099[\unicode[STIX]{x1D70E}^{3}/(\unicode[STIX]{x1D707}\unicode[STIX]{x1D70C}^{2}g^{2}\unicode[STIX]{x1D716}r_{0})]^{1/4}t^{1/4}$
and the corresponding
$C=2.4\times 10^{-5}$
. If the curvature force of the wet corner is assumed to drive the flow, the velocity would be written as
${\dot{h}}\approx (\hat{k}/\unicode[STIX]{x1D707})(\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D706})/h$
, where we use the same value of
$\hat{k}=C\unicode[STIX]{x1D706}^{2}$
because the dominant flow path is still through wet corners. Then, integration yields the rise height under the assumption of corner-driven flows:
$h_{c}\approx 0.042[\unicode[STIX]{x1D70E}^{2}/(\unicode[STIX]{x1D70C}g\unicode[STIX]{x1D707})]^{1/3}t^{1/3}$
. Figure 6 plots
$h_{m}$
and
$h_{c}$
versus time for liquid A with our experimental data, revealing that the theoretically predicted velocity of the corner-driven flow cannot be as high as the actual measurement data. In the figure, we have added the result of Obara & Okumura (Reference Obara and Okumura2012), the rise height on a wall decorated with short pillars with rounded edges,
$h_{p}$
. Although ruled by
$t^{1/3}$
like
$h_{c}$
,
$h_{p}$
is higher than
$h_{c}$
as a result of its greater permeability due to the much simpler flow path configuration of pillar arrays than sponges. Overall, our quantitative comparison in figure 6 indicates that the capillary rise in a porous medium where voids are surrounded by permeable walls is promoted compared with a medium with impermeable sheets because the flow is driven by the strong capillary pressure of the microscale wall pores.
