Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-24T05:21:37.941Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounding the scalar dissipation scale for mixing flows in the presence of sources

Published online by Cambridge University Press:  28 October 2011

A. Alexakis  and
A. Tzella
A. Alexakis*
Affiliation:
Laboratoire de Physique Statistique, CNRS UMR 8550, Ecole Normale Supérieure, 24 rue Lhomond, Paris, 75005, France
A. Tzella*
Affiliation:
Laboratoire de Météorologie Dynamique, CNRS UMR 8539, Ecole Normale Supérieure, 24 rue Lhomond, Paris, 75005, France
*
†Email addresses for correspondence: alexakis@lps.ens.fr, tzella@lmd.ens.fr
†Email addresses for correspondence: alexakis@lps.ens.fr, tzella@lmd.ens.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the mixing properties of scalars stirred by spatially smooth, divergence-free flows and maintained by a steady source–sink distribution. We focus on the spatial variation of the scalar field, described by the dissipation wavenumber, 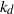, that we define as a function of the mean variance of the scalar and its gradient. We derive a set of upper bounds that for large Péclet number (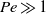) yield four distinct regimes for the scaling behaviour of 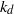, one of which corresponds to the Batchelor regime. The transition between these regimes is controlled by the value of and the ratio 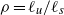, where 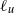and 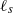are, respectively, the characteristic length scales of the velocity and source fields. A fifth regime is revealed by homogenization theory. These regimes reflect the balance between different processes: scalar injection, molecular diffusion, stirring and bulk transport from the sources to the sinks. We verify the relevance of these bounds by numerical simulations for a two-dimensional, chaotically mixing example flow and discuss their relation to previous bounds. Finally, we note some implications for three-dimensional turbulent flows.

JFM classification

Mixing: Mixing Flow Control: Mixing enhancement Mathematical Foundations: Variational methods
Type
Papers
Information
Journal of Fluid Mechanics , Volume 688 , 10 December 2011 , pp. 443 - 460
Copyright
Copyright © Cambridge University Press 2011

References

1. Antonsen, T. M. J., Fand, Z., Ott, E. & Garcia-López, E. 1996 The role of chaotic orbits in the determination of power spectra of passive scalars. Phys. Fluids 8, 3094.CrossRefGoogle Scholar
2. Aref, H. 1984 Stirring by chaotic advection. J. Fluid Mech. 143, 1.CrossRefGoogle Scholar
3. Aref, H. 2002 The development of chaotic advection. Phys. Fluids 14, 1315–1325.CrossRefGoogle Scholar
4. Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.CrossRefGoogle Scholar
5. Doering, C. R. & Thiffeault, J.-L. 2006 Multiscale mixing efficiencies for steady sources. Phys. Rev. E 74 (2).CrossRefGoogle ScholarPubMed
6. Keating, S. R., Kramer, P. R. & Smith, K. S. 2010 Homogenization and mixing measures for a replenishing passive scalar field. Phys. Fluids 22, 075105.CrossRefGoogle Scholar
7. Kramer, P. R. & Keating, S. R. 2009 Homogenization theory for a replenishing passive scalar field. Chinese Ann. Math. Ser. B 30, 631–644.CrossRefGoogle Scholar
8. Lin, Z., Bod’ová, K. & Doering, C. R. 2010 Models and measures of mixing and effective diffusion scalings. Discrete Continuous Dyn. Syst. 28, 259–274.CrossRefGoogle Scholar
9. Lin, Z., Thiffeault, J.-L. & Doering, C. R. 2011 Optimal stirring strategies for passive scalar mixing. J. Fluid Mech. 675, 465–476.CrossRefGoogle Scholar
10. Majda, A. J. & Kramer, P. R. 1999 Simplified models for turbulent diffusion: Theory, numerical modelling and physical phenomena. Phys. Rep. 314, 237–574.CrossRefGoogle Scholar
11. Ott, E. 1993 Chaos in Dynamical Systems. Cambridge University Press.Google Scholar
12. Ottino, J. M. 1989 The Kinematics of Mixing: Stretching, Chaos and Transport. Cambridge University Press.Google Scholar
13. Pierrehumbert, R. T. 1994 Tracer microstructure in the large-eddy dominated regime. Chaos Solitons Fractals 4, 1091–1110.CrossRefGoogle Scholar
14. Plasting, S. C. & Young, W. R. 2006 A bound on scalar variance for the advection–diffusion equation. J. Fluid Mech. 552, 289–298.CrossRefGoogle Scholar
15. Shaw, T. A., Thiffeault, J.-L. & Doering, C. R. 2007 Stirring up trouble: multi-scale mixing measures for steady scalar sources. Physica D 231, 143–164.CrossRefGoogle Scholar
16. Taylor, G. 1921 Diffusion by continuous movement. Proc. Lond. Math. Soc. 20, 196–212.Google Scholar
17. Thiffeault, J.-L. 2011 Using multiscale norms to quantify mixing and transport. Nonlinearity (in press).CrossRefGoogle Scholar
18. Thiffeault, J.-L., Doering, C. R. & Gibbon, J. D. 2004 A bound on mixing efficiency for the advection–diffusion equation. J. Fluid Mech. 521, 105–114.CrossRefGoogle Scholar
19. Thiffeault, J.-L. & Pavliotis, G. A. 2008 Optimizing the source distribution in fluid mixing. Physica D: Nonlinear Phenom. 237, 918–929.CrossRefGoogle Scholar