3.1 Single drops

We measure the vertical dynamics of drops of three different radii, $R=0.32$  mm, $R=0.36$  mm and $R=0.40$  mm, across the range of driving accelerations from $\unicode[STIX]{x1D6FE}=2.5g$ to $\unicode[STIX]{x1D6FE}=4.2g$ , in increments of $0.1g$ . This parameter space was chosen to focus on drops in the $(2,1)$ bouncing and walking regimes (see figure 1) in which the resonance between drop and wave assumed in the derivations of the trajectory equations of Moláček & Bush (Reference Moláček and Bush2013b ) and Oza et al. (Reference Oza, Rosales and Bush2013) is achieved.

In order to compute ${\mathcal{S}}$ and ${\mathcal{C}}$ for a given $R$ and $\unicode[STIX]{x1D6FE}$ , we used the following procedure. A high-speed camera (Phantom v5.2, macro lens, $2\times$ teleconverter, tube extension) was used to record simultaneously the motion of the drop and the bath at a frame rate of 3000 fps, corresponding to 75 frames per Faraday period, $T_{F}$ . A snapshot from one of these videos is shown in figure 2(b). The dark stripe at the top of the frame corresponds to the far edge of the bath and is out of focus due to the small depth of field of the magnifying lens. As shown in figure 2(c), this same frame can be thresholded to yield an outline of the drop’s edge, the top of which we denote by $z_{T}$ , and a horizontal line near the top of the frame, representing the vertical position of the bath’s edge, ${\mathcal{B}}$ . By thresholding each frame in the video, we obtain time series ${\mathcal{B}}(t)$ and $z_{T}(t)$ , examples of which are shown in figures 3(a,b). If a droplet was walking, it was recorded as it moved through the high-speed camera’s field of view while the overhead camera simultaneously recorded its horizontal motion.

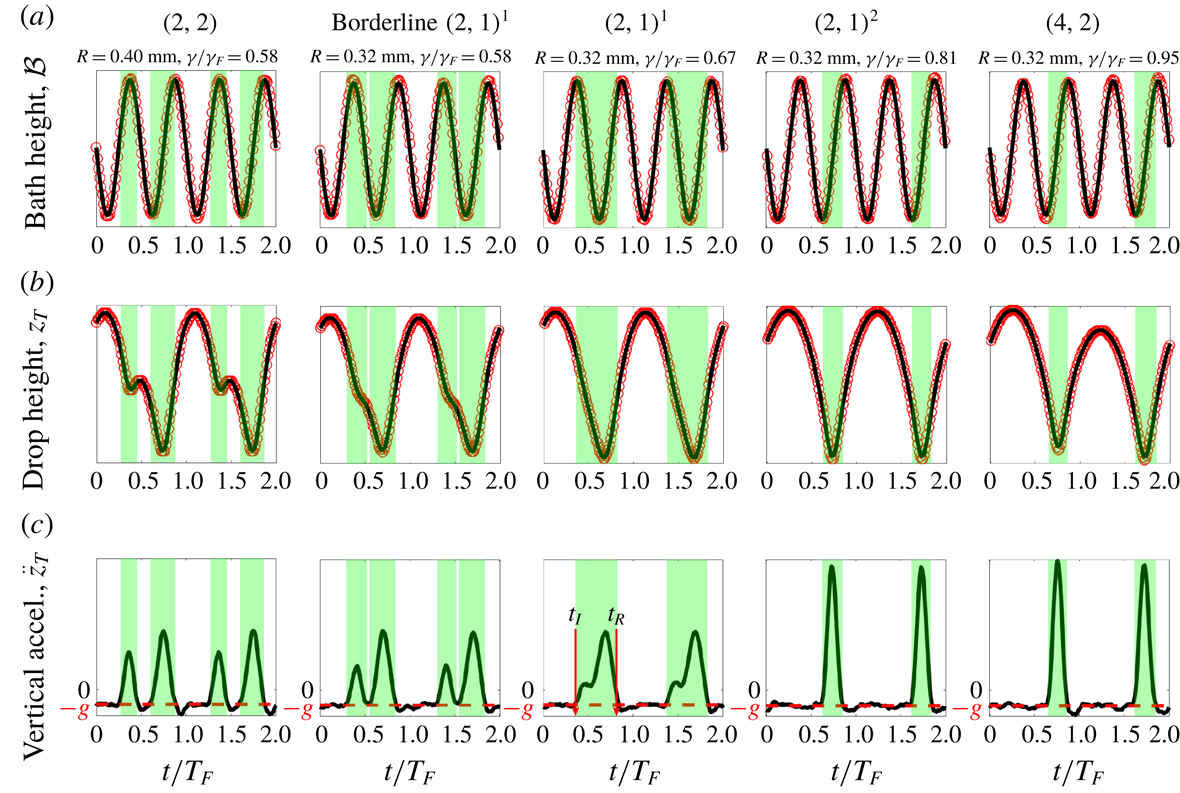
Figure 3. Examples of the time evolution of (a) the bath’s vertical position, (b) the drop’s vertical position and (c) the drop’s vertical acceleration for the five bouncing modes observed in our experiments. The Faraday period is $T_{F}=1/40$  s. The red data points in (a) and (b) are obtained by tracking the vertical position of the bath’s edge and the top of the drop respectively. For the sake of comparison, pure sinusoids with the bath’s oscillation frequency of 80 Hz are plotted with solid lines in (a). The solid lines in (b) are the result of applying the smoothing Savitzky–Golay filter to the experimental data, which are then differentiated twice to obtain the drop’s vertical acceleration reported in (c). The red dashed lines in (c) indicate the free-fall acceleration, $-g$ . Each green shaded region indicates a calculated period of contact between the drop and the bath, starting at the time of drop impact, $t_{I}$ , and ending at the time of drop release, $t_{R}$ . The vertical scales in (a) and (b) are arbitrary.

The contact force, $F_{N}(t)$ , can be computed directly from $z_{T}(t)$ . A Savitzky–Golay filter is used to compute the drop’s vertical acceleration, $\ddot{z}_{T}$ (figure 3 c). The acceleration of the top of the drop provides a good approximation to the acceleration of the drop’s centre of mass provided the drop deformation during impact is small. In our experiments, the maximum deformation observed is ${\approx}5\,\%$ of the undeformed drop diameter. The regions of constant acceleration in the time series of $\ddot{z}_{T}$ occur when the drop is in free flight, with acceleration $-g$ , while the regions of increased acceleration, shaded in green in figure 3(c), occur when the drop is in contact with the bath; $F_{N}(t)$ is then obtained by subtracting the free-fall acceleration, $-g$ , from $\ddot{z}_{T}$ and is necessarily zero when the drop is not in contact with the bath. We note that when a drop is walking in a straight line at a constant speed, the vertical position recorded by the high-speed camera will be of the form $z_{T}(t)+at+b$ , where $z_{T}(t)$ would be the vertical position recorded if the drop was bouncing in place and the linear function reflects the drop’s translation across the camera’s field of view. Since the linear function $at+b$ makes no contribution to the second derivative, the drop’s horizontal motion does not affect the computed vertical acceleration. When a drop is near the $(2,2)$ to $(2,1)^{1}$ transition, it is difficult to characterize the bouncing mode (Galeano-Rios et al. Reference Galeano-Rios, Milewski and Vanden-Broeck2017). We classify a drop as being in a ‘borderline’ $(2,1)^{1}$ mode when two distinct impacts per Faraday period are discernible by analysing $F_{N}(t)$ in figure 3(c), but the droplet does not rebound upwards between these impacts, as determined by analysing $z_{T}(t)$ in figure 3(b).

Figure 4. The dependence of (a) the phase parameter ${\mathcal{S}}$ , (b) the phase parameter ${\mathcal{C}}$ and (c) the walking speed, $u$ , on the non-dimensional driving acceleration of the bath, $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FE}_{F}$ , for single bouncing drops of size $R=0.32$  mm (red), $R=0.36$  mm (green) and $R=0.40$  mm (blue). The unfilled and filled markers indicate experimental data and denote whether the droplet is bouncing or walking, respectively. The shape of the marker denotes the experimentally observed bouncing mode: $(2,2)$ mode (*), borderline $(2,1)^{1}$ mode ( $\star$ ),  $(2,1)^{1}$ mode (▫), $(2,1)^{2}$ mode (▵), $(4,2)$ mode (○). Characteristic error bars are shown. In (a) and (b) the dotted and solid curves are the corresponding theoretical predictions (see § 4.1) and denote whether the droplet is predicted to bounce or walk, respectively. For values of $\unicode[STIX]{x1D6FE}$ where (*), ( $\star$ ) or (▫) bouncing modes were experimentally observed, the $(2,1)^{1}$ phase functions of the form given in table 2 are used for the theoretical predictions. For (▵) and (○) modes, the $(2,1)^{2}$ phase functions are used. The discontinuities in the theoretical curves occur at the $(2,1)^{1}$ to $(2,1)^{2}$ transitions. In (c), the solid and dashed lines represent, respectively, the walking speeds predicted by our variable-impact-phase trajectory equation (see § 4.1) and the constant-impact-phase trajectory equation of Oza et al. (Reference Oza, Rosales and Bush2013).

Our direct measurements of the vertical motion of both bouncing and walking droplets will be valuable in benchmarking and guiding the development of theoretical models. Our measurements of the contact times and contact forces across a range of bouncing modes (figure 3) are very similar to those predicted theoretically by the droplet impact models of Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015) and Galeano-Rios et al. (Reference Galeano-Rios, Milewski and Vanden-Broeck2017). For example, comparing figure 3c to figures 8 and 11 in Galeano-Rios et al. (Reference Galeano-Rios, Milewski and Vanden-Broeck2017) indicates that the model of Galeano-Rios et al. (Reference Galeano-Rios, Milewski and Vanden-Broeck2017) accurately captures the $(2,2)$ to $(2,1)^{1}$ to $(2,1)^{2}$ progression in bouncing modes as $\unicode[STIX]{x1D6FE}$ is increased. For a drop in the $(2,2)$ mode, as $\unicode[STIX]{x1D6FE}$ is increased progressively, the contact force during the first impact decreases relative to that during the second impact, and the time of flight between these two impacts also decreases. At the critical $\unicode[STIX]{x1D6FE}$ value at which these two initially separate impacts merge, the drop becomes a $(2,1)^{1}$ bouncer. As $\unicode[STIX]{x1D6FE}$ is further increased, the time of the drop’s release from the bath, $t_{R}$ , remains approximately constant, while the time of impact, $t_{I}$ , moves progressively closer to $t_{R}$ until the drop eventually enters a $(2,1)^{2}$ mode.

Once $F_{N}(t)$ is computed, the trapezoidal rule is used to numerically calculate ${\mathcal{S}}$ (2.2) and ${\mathcal{C}}$ (2.6). When performing the integrals, the time $t=0$ is defined such that ${\mathcal{B}}(t)=-(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}^{2})\sin (\unicode[STIX]{x1D714}t)$ . For each $R$ and $\unicode[STIX]{x1D6FE}$ , approximately 20 bounces were recorded and the phase parameters were computed for each bounce and then averaged. The standard deviation of the phase parameters before averaging is of the order of 1 %. To compute $S$ and $C$ for drops in a $(4,2)$ mode, the integrals in (2.2) and (2.6) were evaluated from $t$ to $t+2T_{F}$ . We emphasize that ${\mathcal{S}}$ and ${\mathcal{C}}$ represent average impact phases weighted by the contact force $F_{N}(t)$ . We have observed that within the $(2,1)^{2}$ mode, the times of drop impact, $t_{I}$ , and release, $t_{R}$ , from the bath may remain approximately constant as $\unicode[STIX]{x1D6FE}$ is increased. Thus, one might infer that the drop’s impact phase is independent of $\unicode[STIX]{x1D6FE}$ . However, even when $t_{I}$ and $t_{R}$ remain constant, the profile $F_{N}(t)$ for $t_{I}\leqslant t\leqslant t_{R}$ shifts as $\unicode[STIX]{x1D6FE}$ increases, resulting in changes to both ${\mathcal{S}}$ and ${\mathcal{C}}$ . Hence, knowledge of the time dependence of the contact force is critical in order to model effectively the coupling between the drop’s horizontal and vertical motion.

The dependences of ${\mathcal{S}}$ , ${\mathcal{C}}$ and the walking speed, $u$ , on $R$ and $\unicode[STIX]{x1D6FE}$ are shown in figure 4. Both ${\mathcal{S}}$ and ${\mathcal{C}}$ are seen to have two distinct trends separated by the $(2,1)^{1}$ to $(2,1)^{2}$ transition. Before this transition, both ${\mathcal{S}}$ and ${\mathcal{C}}$ increase approximately linearly with $\unicode[STIX]{x1D6FE}$ , while after the transition ${\mathcal{S}}$ saturates to a constant value of approximately 1 while ${\mathcal{C}}$ decreases monotonically.

3.2 Pairs of identical drops

Figure 5. The dependence of the inter-drop separation distance, $d$ , on the dimensionless driving acceleration, $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FE}_{F}$ , for stable, bound droplet pairs of radius $R=0.32$  mm. Circles indicate data obtained by increasing the driving acceleration and triangles indicate data obtained by lowering it again. The top-most data points indicate the instability thresholds, $\unicode[STIX]{x1D6FE}_{\ast }$ , at which the stationary pairs go unstable to horizontal motion, in a manner detailed in figure 7. A characteristic error bar is shown for an $n=1$ data point. The bouncing threshold $\unicode[STIX]{x1D6FE}_{B}$ , $(1,1)\rightarrow (2,2)$ transition, $(2,2)\rightarrow (2,1)$ transition, and walking threshold, $\unicode[STIX]{x1D6FE}_{W}$ , for a single drop of radius $R=0.32$  mm are shown for reference. The vertical ticks along the horizontal lines denoting $\unicode[STIX]{x1D6FE}_{B}$ and $\unicode[STIX]{x1D6FE}_{W}$ indicate the stable separation distances, $d_{n}$ , predicted by our theoretical model (see § 4.3).

We proceed by highlighting the critical role of bouncing phase variations on the bouncing to walking transition of identical droplet pairs. As shown by Eddi et al. (Reference Eddi, Decelle, Fort and Couder2009), droplet pairs can exist in a discrete set of bound states corresponding to each drop bouncing in a minimum of its neighbour’s wavefield. The quantized set of possible inter-drop separation distances, $d_{n}$ , is characterized by the binding number $n=\{1,3/2,2,5/2,\ldots ,\}$ , where integers and half-integers denote pairs bouncing in- and out-of-phase, respectively (Eddi et al. Reference Eddi, Decelle, Fort and Couder2009). We consider the behaviour of bouncing pairs of two different radii, $R=0.32$  mm and $R=0.40$  mm, with various binding numbers $n$ , as $\unicode[STIX]{x1D6FE}$ is increased progressively. These sizes were chosen to ensure that, close to their instability thresholds, the pairs had different vertical dynamics, specifically, the larger and smaller pairs are in $(2,1)^{1}$ and $(2,1)^{2}$ bouncing modes, respectively.

For each pair size, $\unicode[STIX]{x1D6FE}$ is set slightly above the bouncing threshold for a single drop, $\unicode[STIX]{x1D6FE}_{B}$ , and two identical drops are created that bounce in a $(1,1)$ mode. As $(1,1)$ pairs bounce with the same period as the vibrating bath they can only bounce in phase. It was possible to initialize $(1,1)$ pairs in six binding numbers $n\in [1,6]$ (see figure 5). Our findings extend the work of Eddi et al. (Reference Eddi, Decelle, Fort and Couder2009) who reported three possible $n\in [1,3]$ , for $(1,1)$ pairs. Pairs starting with a different, intermediate $d$ , spontaneously adjust their spacing to reach the closest stable $d_{n}$ . For each $(1,1)$ pair in $n\in [1,6]$ , we increased $\unicode[STIX]{x1D6FE}$ incrementally, causing the inter-drop distances to evolve as reported in figure 5, as the pairs transitioned from $(1,1)$ to $(2,1)$ bouncing modes. We note that as $\unicode[STIX]{x1D6FE}$ is increased, the bouncing phase can flip spontaneously. For example, in-phase $n=2$ and $n=4$ $(1,1)$ pairs end up as out-of-phase $n=3/2$ and $n=5/2$ $(2,1)$ pairs, respectively. The $(2,1)$ pairs ultimately go unstable to horizontal motion at $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{\ast }$ , indicated by the top-most data points in figure 5. For pairs of size $R=0.32$  mm, the instability threshold, $\unicode[STIX]{x1D6FE}_{\ast }$ , occurs above the walking threshold of a single drop, $\unicode[STIX]{x1D6FE}_{W}$ , as shown in detail in figure 7.

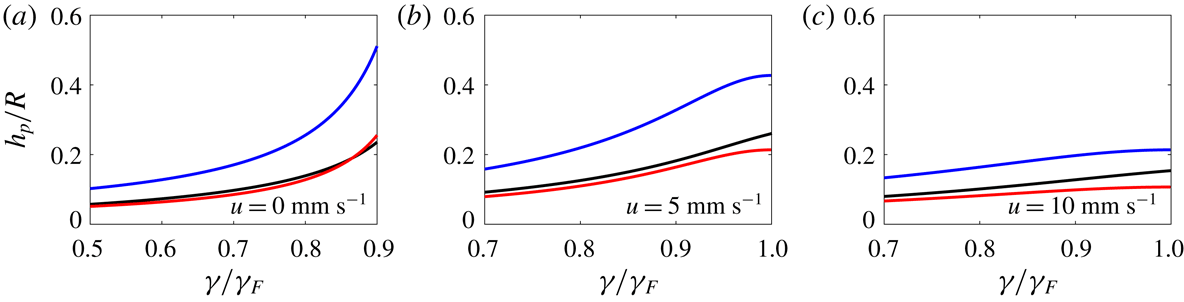
Due to the increased amplitude and spatial extent of a drop’s wavefield close to $\unicode[STIX]{x1D6FE}_{\ast }$ , $(2,1)$ pairs could be initialized with larger binding numbers $n$ that were not accessible in the vicinity of $\unicode[STIX]{x1D6FE}_{B}$ . As shown in figure 5, eleven possible $n$ were found for $(2,1)$ pairs, as compared to the six reported by Eddi et al. (Reference Eddi, Decelle, Fort and Couder2009). For each new $n$ , a $(2,1)$ pair was initialized at a driving acceleration slightly below the anticipated instability threshold, and $\unicode[STIX]{x1D6FE}$ was then increased until $\unicode[STIX]{x1D6FE}_{\ast }$ was found. For each of the eleven $(2,1)$ binding numbers $n$ , we also progressively decreased $\unicode[STIX]{x1D6FE}$ until the pairs coalesced with the bath. This progression revealed hysteresis in the dependence of $d$ on $\unicode[STIX]{x1D6FE}$ as well as the existence of additional $(1,1)$ binding numbers up to $n=11$ . These additional states were impossible to achieve by initializing the pairs in the vicinity of $\unicode[STIX]{x1D6FE}_{B}$ due to the weakness of the droplet–droplet interaction at such large $n$ and low $\unicode[STIX]{x1D6FE}$ . For drops of radius $R=0.40$  mm, the dependence of $d$ on $\unicode[STIX]{x1D6FE}$ and $n$ is very similar to that presented in figure 5, except that the instability thresholds, $\unicode[STIX]{x1D6FE}_{\ast }$ , occur below the walking threshold of an individual drop, $\unicode[STIX]{x1D6FE}_{W}$ , as shown in figure 7.

In addition to measuring the inter-drop distance $d$ , we used the technique presented in § 3.1 to measure the phase parameters ${\mathcal{S}}$ and ${\mathcal{C}}$ for drops in period-doubled $(2,1)$ pairs with binding numbers $n=1$ and $n=2$ . The results are presented in figure 6. For drops in the $(2,1)^{1}$ mode, both ${\mathcal{S}}$ and ${\mathcal{C}}$ increase with decreasing $n$ . For drops in the $(2,1)^{2}$ mode, ${\mathcal{S}}$ has saturated to 1 and does not depend strongly on $n$ , while ${\mathcal{C}}$ now decreases with decreasing $n$ . Notably, the bouncing mode transitions are different when the drops are in pairs. Specifically, the $(2,2)\rightarrow (2,1)^{1}$ , $(2,1)^{1}\rightarrow (2,1)^{2}$ , and $(2,1)^{2}\rightarrow (4,2)$ transitions occur at lower values of $\unicode[STIX]{x1D6FE}$ than for single drops, and these values decrease monotonically with decreasing $n$ .

Figure 6. The dependence of the phase parameters ${\mathcal{S}}$ and ${\mathcal{C}}$ on the non-dimensional driving acceleration, $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FE}_{F}$ , for bouncing pairs of size $R=0.32$  mm and $R=0.40$ mm with binding numbers $n=1$ (red) and $n=2$ (green). The corresponding data for a single bouncer, from figure 4(a,b), are shown for reference, in black. The shape of each data point indicates the bouncing mode: $(2,2)$ mode (*), borderline $(2,1)^{1}$ mode ( $\star$ ),  $(2,1)^{1}$ mode (▫),  $(2,1)^{2}$ mode (▵), $(4,2)$ mode (○). Characteristic error bars are shown. Data were collected up until the instability threshold, $\unicode[STIX]{x1D6FE}_{\ast }$ , at which the pair went unstable to horizontal motion. Theoretical predictions of our variable-phase model (see § 4.3) are shown for reference by solid curves.

Figure 7. The instability thresholds, $\unicode[STIX]{x1D6FE}_{\ast }$ , and type of instability for identical droplet pairs of radius $R=0.40\text{ mm}$ (blue) and $R=0.32\text{ mm}$ (red), as are in $(2,1)^{1}$ and $(2,1)^{2}$ bouncing modes, respectively. Circles denote experimental data and the squares connected by dashed lines are the theoretical predictions of the variable-phase model presented in § 4.3. Characteristic error bars are shown. Note that the experimental data for $R=0.32\text{ mm}$ correspond to the top most data points in figure 5. The instability thresholds are normalized by the walking threshold of a single drop, $\unicode[STIX]{x1D6FE}_{W}$ , as was measured to be $\unicode[STIX]{x1D6FE}_{W}\approx 0.77\unicode[STIX]{x1D6FE}_{F}$ and $\unicode[STIX]{x1D6FE}_{W}\approx 0.88\unicode[STIX]{x1D6FE}_{F}$ for drops of size $R=0.40$  mm and $R=0.32$  mm, respectively. The type of instability predicted by the theoretical model is discussed in § 4.3.

In figure 7, we show the dependence of a pair’s instability threshold, $\unicode[STIX]{x1D6FE}_{\ast }$ , on the binding number, $n$ , for the two drop sizes considered. The larger pair, of radius $R=0.40$  mm, bounces in a $(2,1)^{1}$ mode in the vicinity of $\unicode[STIX]{x1D6FE}_{\ast }$ and destabilizes below the walking threshold of an individual drop, $\unicode[STIX]{x1D6FE}_{W}$ . For all $n$ , the pair destabilizes into oscillations along the line connecting the drops, which we refer to henceforth as co-linear oscillations. An example of the onset of co-linear oscillations is shown in figure 8(a). Conversely, the smaller pair, of radius $R=0.32$  mm, bounces in a $(2,1)^{2}$ mode in the vicinity of $\unicode[STIX]{x1D6FE}_{\ast }$ and goes unstable above $\unicode[STIX]{x1D6FE}_{W}$ . For the smaller pair, the type of instability now depends on $n$ . An $n=1$ pair goes unstable to orbital motion (figure 8 b) while pairs in higher $n>1$ , go unstable to promenading states, in which the drops walk side-by-side (Borghesi et al. Reference Borghesi, Moukhtar, Labousse, Eddi, Fort and Couder2014; Arbelaiz et al. Reference Arbelaiz, Oza and Bush2018). Promenading pairs with $n=\{3/2,2,5/2\}$ move in straight lines (figure 8 c), while pairs with $n\geqslant 3$ exhibit lateral oscillations (figure 8 d). We note that for pairs of size $R=0.32$  mm, the type of instability is sensitive to small size variations between the two drops. Specifically, if the size variation is ${\gtrsim}5\,\%$ , the difference in walking thresholds between the two drops causes one drop to orbit the other, which initially remains stationary. Orbital motion then occurs at most separation distances, not just for the $n=1$ pair. As seen in figure 7, for both pair sizes, $\unicode[STIX]{x1D6FE}_{\ast }$ tends to $\unicode[STIX]{x1D6FE}_{W}$ as $n$ increases, due to the interaction between the drops decreasing with increasing $n$ .

Figure 8. Examples of the onset of instability of bound droplet pairs: (a) co-linear oscillations ( $R=0.40$  mm,  $n=3.5$ ), (b) orbiting ( $R=0.32$  mm,  $n=1$ ), (c) promenading ( $R=0.32$  mm,  $n=2$ ) and (d) promenading with lateral oscillations ( $R=0.32$  mm,  $n=5$ ). Panel (a) shows the evolution of the inter-drop distance $d$ . Panels (b–d) show trajectories of the droplets coloured according to the droplet speed.

4.1 Impact-phase variations for single drops

We proceed by calculating how ${\mathcal{S}}$ and ${\mathcal{C}}$ vary with $\unicode[STIX]{x1D6FE}$ for single bouncers and straight-line walkers, in order to compare the predictions of our theoretical models for ${\mathcal{S}}$ and ${\mathcal{C}}$ with our experimental results in figure 4. According to the trajectory equation (2.9), the following equations must be satisfied for a single drop walking in a straight line with constant speed $u$ :

(4.6a ) $$\begin{eqnarray}\bar{h}_{p}={\displaystyle \frac{AM_{e}{\mathcal{S}}(\unicode[STIX]{x1D6E4},\bar{h}_{p},\unicode[STIX]{x1D6FA})}{R\sqrt{1+\bar{u}^{2}}}},\end{eqnarray}$$

(4.6b,c ) $$\begin{eqnarray}\bar{u}=\sqrt{\unicode[STIX]{x1D719}-{\displaystyle \frac{1}{2}}(1+\sqrt{1+4\unicode[STIX]{x1D719}})},\quad \unicode[STIX]{x1D719}={\displaystyle \frac{AM_{e}\unicode[STIX]{x1D6FD}{\mathcal{S}}(\unicode[STIX]{x1D6E4},\bar{h}_{p},\unicode[STIX]{x1D6FA}){\mathcal{C}}(\unicode[STIX]{x1D6E4},\bar{h}_{p},\unicode[STIX]{x1D6FA})}{R}}.\end{eqnarray}$$

$R$

$\unicode[STIX]{x1D6FE}_{W}$

$\unicode[STIX]{x1D6FE}$

$\unicode[STIX]{x1D719}=2$

$\bar{u}=0$

$\unicode[STIX]{x1D6FE}$

$\bar{h}_{p}$

$\bar{u}=0$

$\bar{h}_{p}$

${\mathcal{S}}$

${\mathcal{C}}$

$\bar{u}$

$\bar{h}_{p}$

$\bar{h}_{p}$

${\mathcal{S}}$

${\mathcal{C}}$

In figure 4, we compare our theoretical predictions for ${\mathcal{S}}$ and ${\mathcal{C}}$ with our experimental data. For values of $\unicode[STIX]{x1D6FE}$ where $(2,2)$ and $(4,2)$ modes were experimentally observed, we used our phase relations for $(2,1)^{1}$ and $(2,1)^{2}$ modes, respectively, as an approximation. Our model is seen to capture all of the observed trends in ${\mathcal{S}}$ and ${\mathcal{C}}$ , however, there is a horizontal shift between our experimental and theoretical data for the phase parameter ${\mathcal{S}}$ in the $(2,1)^{1}$ mode. This shift is a result of slight differences in the profile of the contact force, $F_{N}(t)$ , observed experimentally and predicted theoretically by the linear spring model. In particular, ${\mathcal{S}}$ is highly sensitive to the relative heights of the two maxima in $F_{N}(t)$ in the $(2,1)^{1}$ mode seen in figure 3, while ${\mathcal{C}}$ is not.

In figure 4(c), we compare our experimental data of walking thresholds and speeds for single drops with the theoretical predictions of both the constant-impact-phase model of Oza et al. (Reference Oza, Rosales and Bush2013) and the variable-phase model developed in this study. Oza et al. (Reference Oza, Rosales and Bush2013) used a fixed value of $\sin (\unicode[STIX]{x1D6F7})/2={\mathcal{S}}{\mathcal{C}}=0.30$ , chosen to best match the dependence of the walking speed on $\unicode[STIX]{x1D6FE}$ for a drop of radius $R=0.40$  mm. As seen in figure 4(c), this assumption of constant-impact-phase results in significant discrepancies between the theoretical predictions and experimental data for other drop sizes. By capturing the dependence of ${\mathcal{S}}$ and ${\mathcal{C}}$ on $R$ and $\unicode[STIX]{x1D6FE}$ , our model is able to adequately predict the walking thresholds across a range of drop sizes, $R=0.32$ , 0.36 and 0.40 mm. We note that for a drop radius of $R=0.36$  mm, the predicted walking speed at the walking threshold is non-zero, as the walking threshold occurs at the locus of the $(2,1)^{1}$ to $(2,1)^{2}$ transition, where the phase parameters change discontinuously. We also note that the model of Oza et al. (Reference Oza, Rosales and Bush2013) significantly over-predicts the experimentally measured walking speeds as $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FE}_{F}$ approaches 1. By capturing the decrease in ${\mathcal{C}}$ with increasing $\unicode[STIX]{x1D6FE}$ in the $(2,1)^{2}$ mode, our variable-phase model is able to better capture the experimentally observed plateau in walking speeds at high memories. As shown in figure 12 in appendix A, our wave model underpredicts the local wave amplitude, $h_{p}$ , for fast walkers at high memories, compared to the model of Moláček & Bush (Reference Moláček and Bush2013b ) which is in agreement with experimental wavefield measurements. This results in the slight decrease in the theoretically predicted walking speed with increasing $\unicode[STIX]{x1D6FE}$ that is evident in figure 4(c) for a drop of radius $R=0.40$  mm.

4.2 Impact-phase variations for multiple drops

When modelling droplet–droplet interactions, it is necessary to use a wave model that accurately captures the far-field decay of the waves. Damiano et al. (Reference Damiano, Brun, Harris, Galeano-Rios and Bush2016), Tadrist et al. (Reference Tadrist, Shim, Gilet and Schlagheck2018b ) and Turton et al. (Reference Turton, Couchman and Bush2018) all proposed the inclusion of a spatio-temporal damping factor which modifies the wave kernel in (2.10) to an expression of the form $J_{0}(k_{F}|\boldsymbol{x}-\boldsymbol{x}_{p}(s)|)\exp \{-\unicode[STIX]{x1D6FC}|\boldsymbol{x}-\boldsymbol{x}_{p}(s)|^{2}/(t-s)\}$ . However, this factor is derived using a long-time asymptotic expansion that introduces an unphysical singularity in the second spatial derivative at $|\boldsymbol{x}-\boldsymbol{x}_{p}(s)|=0$ . The presence of this singularity greatly complicates a stability analysis of the trajectory equation (2.9). In order to analyse the stability of orbiting pairs, Oza et al. (Reference Oza, Siéfert, Harris, Moláček and Bush2017) modified this damping factor by setting $(t-s)\rightarrow (t-s+T_{F})$ . In their study of promenading pairs, Arbelaiz et al. (Reference Arbelaiz, Oza and Bush2018) neglected the spatio-temporal damping factor altogether. To eliminate these mathematical difficulties, in appendix B we use a quasi-static approximation to derive a purely spatial damping factor that is smooth at $|\boldsymbol{x}-\boldsymbol{x}_{p}(s)|=0$ , while remaining consistent with the spatio-temporal damping factor of Turton et al. (Reference Turton, Couchman and Bush2018) in the far field.

Based on (2.9), the equations governing a system of $N$ interacting drops are

(4.7) $$\begin{eqnarray}\unicode[STIX]{x1D705}\ddot{\bar{\boldsymbol{x}}}_{i}+\dot{\bar{\boldsymbol{x}}}_{i}=-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70E}_{i}{\mathcal{C}}_{i}\unicode[STIX]{x1D735}\bar{h}(\bar{\boldsymbol{x}}_{i},\bar{t}),\quad i=1,2,\ldots ,N,\end{eqnarray}$$

where

(4.8) $$\begin{eqnarray}\bar{h}(\bar{\boldsymbol{x}},\bar{t})={\displaystyle \frac{AM_{e}}{R}}\mathop{\sum }_{j=1}^{N}\unicode[STIX]{x1D70E}_{j}\displaystyle \displaystyle \int _{-\infty }^{\bar{t}}{\mathcal{S}}_{j}f(|\bar{\boldsymbol{x}}-\bar{\boldsymbol{x}}_{j}(\bar{s})|)\text{e}^{-(\bar{t}-\bar{s})}\,\text{d}\bar{s}\end{eqnarray}$$

and the wave kernel, with the spatial damping factor derived in appendix B, is

(4.9) $$\begin{eqnarray}f(\bar{r})=J_{0}(\bar{r})[1+(\unicode[STIX]{x1D709}K_{1}(\unicode[STIX]{x1D709}\bar{r})\bar{r}-1)\text{e}^{-\bar{r}^{-2}}],\end{eqnarray}$$

where $\unicode[STIX]{x1D709}$ is defined in table 1. As a $(2,1)$ drop can either impact the bath during the first or second cycle of the bath’s oscillation, the parameters $\unicode[STIX]{x1D70E}_{i}=\pm 1$ are chosen to describe the relative bouncing phase of the drops: $\unicode[STIX]{x1D70E}_{i}\unicode[STIX]{x1D70E}_{j}=1$ and $\unicode[STIX]{x1D70E}_{i}\unicode[STIX]{x1D70E}_{j}=-1$ indicate that drops $i$ and $j$ are bouncing in-phase and out-of-phase, respectively. The phase parameters ${\mathcal{S}}_{i}$ and ${\mathcal{C}}_{i}$ describe modulations in the bouncing phase of the $i$ th drop within a given bath cycle.

The trajectory equation (4.7) highlights two main mechanisms through which droplets interact. Firstly, the gradient of the strobed wavefield, $\unicode[STIX]{x1D735}h$ , beneath a drop is altered due to waves generated by neighbouring drops. Secondly, neighbouring drops also alter the local wave amplitude beneath a drop, $h_{p}$ , which will change the drop’s vertical dynamics and hence ${\mathcal{S}}$ and ${\mathcal{C}}$ . This second interaction mechanism is not captured by a constant phase model but can significantly affect droplet–droplet interactions as we shall demonstrate in our analysis of the stability of droplet pairs.

4.3 Stability of bound droplet pairs

We analyse the stability of a bound pair of identical droplets using the system of (4.7). Pairs will exist in stationary bound states when the right-hand sides of (4.7) are zero, corresponding to the discrete set of separation distances, $d_{n}$ , that satisfy $f^{\prime }(d_{n})=0$ . In order for a separation distance $d_{n}$ to be stable, it must correspond to each drop bouncing in a minimum of its neighbour’s wavefield (Eddi et al. Reference Eddi, Decelle, Fort and Couder2009). Thus, for drop’s bouncing in-phase $(\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}=1)$ or out-of-phase $(\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}=-1)$ , the stable separation distances correspond to the minima or maxima of $f(r)$ , respectively. In figure 5, we plot our theoretical predictions for stable values of $d_{n}$ at two values of $\unicode[STIX]{x1D6FE}$ , the bouncing threshold, $\unicode[STIX]{x1D6FE}_{B}$ , and the walking threshold, $\unicode[STIX]{x1D6FE}_{W}$ , of an individual drop. The values of $d_{n}$ are dependent on the vertical bouncing mode of the drops, as $(1,1)$ and $(2,1)$ drops excite waves of different wavelengths. Using the deep water dispersion relation for gravity–capillary waves, $\unicode[STIX]{x1D714}^{2}=gk+\unicode[STIX]{x1D70E}k^{3}/\unicode[STIX]{x1D70C}$ , we expect the wavelengths of the wavefields produced by $(1,1)$ and $(2,1)$ bouncers to be $\unicode[STIX]{x1D706}_{(1,1)}=2.86$  mm and $\unicode[STIX]{x1D706}_{(2,1)}=\unicode[STIX]{x1D706}_{F}=4.75$  mm, respectively. For the $(1,1)$ pairs in the vicinity of $\unicode[STIX]{x1D6FE}_{B}$ , our theoretical predictions for $d_{n}$ are found to be in good agreement with our experimental data, except at the high binding numbers $n=10$ and 11. This discrepancy presumably arises because the drop–drop interaction is so weak at such low $\unicode[STIX]{x1D6FE}$ and large $n$ that the drops had not fully settled into their equilibrium separation distances. For the $(2,1)$ pairs in the vicinity of $\unicode[STIX]{x1D6FE}_{W}$ , theoretical predictions are again found to be in good agreement with the experimental data, but slightly underpredict the experimental values of $d_{n}$ at small $n$ . One expects this slight discrepancy to be caused by the travelling wave fronts generated at each impact, an effect detailed by Galeano-Rios et al. (Reference Galeano-Rios, Couchman, Caldairou and Bush2018) that is not captured by the wave model (4.8).

Next, we examine how stationary $(2,1)$ bound pairs destabilize into horizontal motion as $\unicode[STIX]{x1D6FE}$ is increased. We assume that the drops start at stable positions $(x_{1},y_{1})=(0,0)$ and $(x_{2},y_{2})=(d_{n},0)$ and introduce arbitrary horizontal perturbations $x_{1}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}x_{1}$ , $y_{1}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}y_{1}$ , $x_{2}=d_{n}+\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}x_{2}$ , $y_{2}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}y_{2}$ . As shown in appendix C, substituting these perturbations into (4.7) and retaining only terms up to $O(\unicode[STIX]{x1D716})$ yields the following $12\times 12$ block diagonal, linear system:

(4.10) $$\begin{eqnarray}{\displaystyle \frac{\text{d}\unicode[STIX]{x1D64C}}{\text{d}t}}=\left[\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D63C}_{3\times 3} & \mathbf{0} & \mathbf{0} & \mathbf{0}\\ \mathbf{0} & \unicode[STIX]{x1D63D}_{3\times 3} & \mathbf{0} & \mathbf{0}\\ \mathbf{0} & \mathbf{0} & \unicode[STIX]{x1D63E}_{3\times 3} & \mathbf{0}\\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \unicode[STIX]{x1D63E}_{3\times 3}\end{array}\right]\unicode[STIX]{x1D64C},\end{eqnarray}$$

where

(4.11) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64C} & = & \displaystyle \big(\unicode[STIX]{x1D6FF}x_{1}+\unicode[STIX]{x1D6FF}x_{2},\unicode[STIX]{x1D6FF}u_{1}+\unicode[STIX]{x1D6FF}u_{2},\unicode[STIX]{x1D6FF}X_{1}+\unicode[STIX]{x1D6FF}X_{2},\unicode[STIX]{x1D6FF}x_{2}-\unicode[STIX]{x1D6FF}x_{1},\unicode[STIX]{x1D6FF}u_{2}-\unicode[STIX]{x1D6FF}u_{1},\unicode[STIX]{x1D6FF}X_{2}-\unicode[STIX]{x1D6FF}X_{1},\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}y_{1},\unicode[STIX]{x1D6FF}v_{1},\unicode[STIX]{x1D6FF}Y_{1},\unicode[STIX]{x1D6FF}y_{2},\unicode[STIX]{x1D6FF}v_{2},\unicode[STIX]{x1D6FF}Y_{2}\big),\end{eqnarray}$$

(4.12) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D63C} & = & \displaystyle \left[\begin{array}{@{}ccc@{}}0 & 1 & 0\\ -\unicode[STIX]{x1D712}-\unicode[STIX]{x1D713} & -{\displaystyle \frac{1}{\unicode[STIX]{x1D705}}} & \unicode[STIX]{x1D712}+\unicode[STIX]{x1D713}\\ 1 & 0 & -1\end{array}\right],\quad \unicode[STIX]{x1D63D}=\left[\begin{array}{@{}ccc@{}}0 & 1 & 0\\ -\unicode[STIX]{x1D712}-\unicode[STIX]{x1D713} & -{\displaystyle \frac{1}{\unicode[STIX]{x1D705}}} & \unicode[STIX]{x1D712}-\unicode[STIX]{x1D713}\\ 1 & 0 & -1\end{array}\right],\nonumber\\ \displaystyle & & \displaystyle \qquad \unicode[STIX]{x1D63E}=\left[\begin{array}{@{}ccc@{}}0 & 1 & 0\\ -\unicode[STIX]{x1D712} & -{\displaystyle \frac{1}{\unicode[STIX]{x1D705}}} & \unicode[STIX]{x1D712}\\ 1 & 0 & -1\end{array}\right],\end{eqnarray}$$

(4.13a,b ) $$\begin{eqnarray}\unicode[STIX]{x1D712}={\displaystyle \frac{AM_{e}\unicode[STIX]{x1D6FD}{\mathcal{C}}_{n}{\mathcal{S}}_{n}}{R\unicode[STIX]{x1D705}}}f^{\prime \prime }(0),\quad \unicode[STIX]{x1D713}={\displaystyle \frac{AM_{e}\unicode[STIX]{x1D6FD}{\mathcal{C}}_{n}{\mathcal{S}}_{n}}{R\unicode[STIX]{x1D705}}}\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}f^{\prime \prime }(\bar{d}_{n}).\end{eqnarray}$$

The effect of the vertical dynamics on the pair’s horizontal stability is captured by ${\mathcal{S}}_{n}$ and ${\mathcal{C}}_{n}$ , which are the values of the phase parameters for each drop in an initially horizontally static pair with separation distance $d_{n}$ . Following the same procedure as in § 4.1, ${\mathcal{S}}_{n}$ and ${\mathcal{C}}_{n}$ can be found by solving the implicit equation (4.8) for the local wave amplitude, $\bar{h}_{p}$ :

(4.14) $$\begin{eqnarray}\bar{h}_{p}={\displaystyle \frac{AM_{e}{\mathcal{S}}(\unicode[STIX]{x1D6E4},\bar{h}_{p},\unicode[STIX]{x1D6FA})}{R}}(1+\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}f(\bar{d}_{n})).\end{eqnarray}$$

Having obtained $\bar{h}_{p}$ for a given separation distance $\bar{d}_{n}$ , the corresponding values of ${\mathcal{S}}_{n}$ and ${\mathcal{C}}_{n}$ can be obtained using the relations in table 2.

In figure 6, we compare our theoretical predictions for ${\mathcal{S}}_{n}$ and ${\mathcal{C}}_{n}$ with our experimental data for pairs of radius $R=0.32$  mm and 0.40 mm with binding numbers $n=1$ and 2. Both our theoretical model and experimental data highlight important features of the phase parameters close to the pair instability thresholds. The pairs of radius $R=0.40$  mm are in a $(2,1)^{1}$ bouncing mode and both ${\mathcal{S}}_{n}$ and ${\mathcal{C}}_{n}$ increase with decreasing $n$ . Conversely, the pairs of radius $R=0.32$ mm are in a $(2,1)^{2}$ bouncing mode and while ${\mathcal{S}}$ has saturated to 1 for all $n$ , ${\mathcal{C}}$ now decreases with decreasing $n$ . We proceed by demonstrating that this subtle difference in the dependences of ${\mathcal{S}}$ and ${\mathcal{C}}$ on $n$ has a dramatic effect on a pair’s horizontal stability.

The block diagonal matrix in (4.10) indicates that there are three ways in which a pair of initially stationary drops may destabilize into horizontal motion. The sub-matrix $\unicode[STIX]{x1D63C}$ governs the stability of the quantity $\unicode[STIX]{x1D6FF}x_{1}+\unicode[STIX]{x1D6FF}x_{2}$ which corresponds to motion of the pair’s centre of mass in the $\hat{\unicode[STIX]{x1D66D}}$ -direction. All of the eigenvalues of $\unicode[STIX]{x1D63C}$ are real and one is zero, indicating that the pair is invariant to changes in the $\hat{\unicode[STIX]{x1D66D}}$ position of its centre of mass. As $\unicode[STIX]{x1D6FE}$ is increased across the instability threshold $\unicode[STIX]{x1D6FE}_{\ast }$ , the two non-zero eigenvalues switch from both being negative, to one being negative and the other positive. The resulting instability corresponds to a translation of the pair’s centre of mass in the $\hat{\boldsymbol{x}}$ -direction, where one drop follows the other while the inter-drop spacing, $d$ , remains fixed. We refer to this instability as a co-linear translation.

The sub-matrix $\unicode[STIX]{x1D63D}$ governs the stability of the quantity $\unicode[STIX]{x1D6FF}x_{2}-\unicode[STIX]{x1D6FF}x_{1}$ , which corresponds to changes in the inter-drop distance, $d$ . $\unicode[STIX]{x1D63D}$ has a real eigenvalue and a pair of complex conjugate eigenvalues. As $\unicode[STIX]{x1D6FE}$ is increased across the instability threshold $\unicode[STIX]{x1D6FE}_{\ast }$ , the real eigenvalue remains negative, while the real parts of both complex conjugate eigenvalues switch from negative to positive. The resulting instability corresponds to co-linear oscillations in the $\hat{\boldsymbol{x}}$ -direction about a fixed centre of mass.

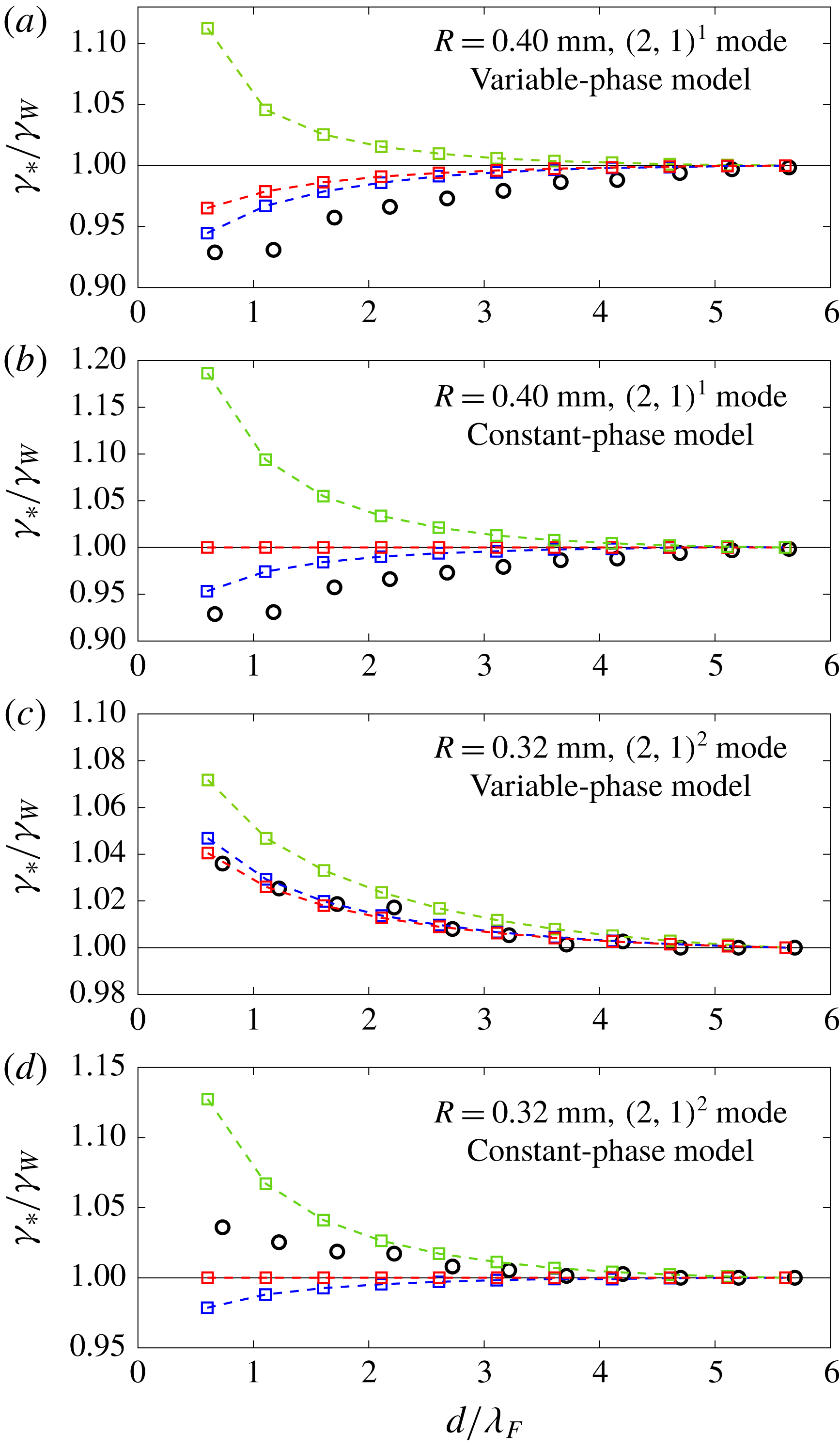
Figure 11. The theoretical instability thresholds, $\unicode[STIX]{x1D6FE}_{\ast }$ , for co-linear translations of the pair’s centre of mass (green, matrix $\unicode[STIX]{x1D63C}$ ), co-linear oscillations (blue, matrix $\unicode[STIX]{x1D63D}$ ) and transverse motion (red, matrix $\unicode[STIX]{x1D63E}$ ) as a function of the pair’s initial separation distance, $d$ . The corresponding experimental data from figure 7 are indicated by the black circles. The panels illustrate predicted thresholds for (a) $R=0.40$  mm with a variable-phase model, (b) $R=0.40$  mm with a constant-phase model, (c) $R=0.32$  mm with a variable-phase model and (d) $R=0.32$  mm with a constant-phase model. The variable- and constant-phase models correspond to predictions based on the linear system (4.10) using the phase functions ${\mathcal{S}}$ and ${\mathcal{C}}$ listed in table 2, and the constant value of the phase parameter $\sin (\unicode[STIX]{x1D6F7})/2={\mathcal{S}}{\mathcal{C}}=0.30$ used by Oza et al. (Reference Oza, Rosales and Bush2013), respectively.

The sub-matrix $\unicode[STIX]{x1D63E}$ governs each drop’s stability to perturbations in the $\hat{\boldsymbol{y}}$ -direction, which we will refer to as transverse perturbations. The onset of orbital and promenading motion are both examples of such transverse instabilities. We note that $\unicode[STIX]{x1D63E}$ is exactly the matrix obtained by Oza et al. (Reference Oza, Rosales and Bush2013) that governs the bouncing to walking transition of a single droplet. As the linear system (4.10) predicts that the transverse perturbations of each drop in a pair are independent of the motion of the neighbouring droplet, it might seem that each drop will destabilize into walking in the $\hat{\boldsymbol{y}}$ -direction at $\unicode[STIX]{x1D6FE}_{W}$ , the walking threshold of an individual droplet. However, this is not the case: although the pairs do not interact through the gradient of each other’s wavefield, they modify each other’s local wave amplitude, $h_{p}$ , as captured by the phase parameters ${\mathcal{S}}$ and ${\mathcal{C}}$ . Therefore, for transverse perturbations, the droplets interact solely through modulations in their vertical dynamics, an effect that cannot be captured by a constant-impact-phase model.

In figure 11, we present the theoretical instability thresholds, $\unicode[STIX]{x1D6FE}_{\ast }$ , for co-linear translations of the pair’s centre of mass (matrix $\unicode[STIX]{x1D63C}$ ), co-linear oscillations (matrix $\unicode[STIX]{x1D63D}$ ) and transverse motions (matrix $\unicode[STIX]{x1D63E}$ ) as a function of the pair’s initial separation distance, $d_{n}$ . We compare our experimental measurements from figure 7 to the theoretical predictions based on both our variable-impact-phase functions ${\mathcal{S}}$ and ${\mathcal{C}}$ listed in table 2, and the constant impact phase $\sin (\unicode[STIX]{x1D6F7})/2={\mathcal{S}}{\mathcal{C}}=0.30$ used by Oza et al. (Reference Oza, Rosales and Bush2013). For pairs in the $(2,1)^{2}$ mode, our variable-phase model predicts that the pairs destabilize above the walking threshold of an individual drop, $\unicode[STIX]{x1D6FE}_{W}$ , and that the most unstable motion is transverse, in agreement with our experiments. We note that for higher binding numbers $n$ , the instability thresholds for transverse motion and co-linear oscillations become progressively closer. This is consistent with our experimental observations that the promenading states begin to oscillate for $n>2.5$ . For pairs in the $(2,1)^{1}$ mode, our variable-phase model predicts that the pairs now destabilize below $\unicode[STIX]{x1D6FE}_{W}$ with the most unstable motion corresponding to co-linear oscillations, again in agreement with our experimental results.

Comparing the predictions of our variable-phase model with those of a constant-phase model makes clear that modulations in the vertical dynamics strongly affect the stability of droplet pairs. For example, a constant-phase model cannot predict the difference in behaviour between the $(2,1)^{1}$ and $(2,1)^{2}$ pairs: it predicts that both pair sizes should destabilize into co-linear oscillations below $\unicode[STIX]{x1D6FE}_{W}$ . The fact that $(2,1)^{1}$ and $(2,1)^{2}$ pairs destabilize below and above $\unicode[STIX]{x1D6FE}_{W}$ , respectively, is a direct consequence of the phase variations induced by the presence of a neighbouring drop. As the binding number, $n$ , of a pair decreases, so does the local wave amplitude beneath each drop, $h_{p}$ , as each drop sits in a deeper minimum of its neighbour’s wavefield. Based on table 2, we see that the phase parameters have opposite dependencies on $h_{p}$ for $(2,1)^{1}$ and $(2,1)^{2}$ drops. In the $(2,1)^{1}$ mode, both ${\mathcal{S}}$ and ${\mathcal{C}}$ increase with decreasing $h_{p}$ . Therefore, pairs with smaller binding numbers $n$ generate relatively large waves and receive relatively large horizontal impulses from the bath, prompting an onset of motion below $\unicode[STIX]{x1D6FE}_{W}$ . Conversely, for pairs in a $(2,1)^{2}$ mode, ${\mathcal{S}}$ has saturated to 1 while ${\mathcal{C}}$ now decreases with decreasing $h_{p}$ causing the drops to stabilize each other above $\unicode[STIX]{x1D6FE}_{W}$ .