2. Experimental approach

We consider a circular cylinder of diameter $d$, length $L$, density $\rho _c \simeq 1160\ \textrm {kg} \ \textrm {m}^{-3}$ and Young modulus $E \simeq 1$ MPa falling through quiescent water (density $\rho _f \simeq 1000\ \textrm {kg} \ \textrm {m}^{-3}$, kinematic viscosity $\nu \simeq 10^{-6}\ \textrm {m} \ \textrm {s}^{-2}$) under the influence of gravitational acceleration $g$. The problem is governed by four dimensionless parameters, including the solid-to-fluid density ratio $m^*={\rho _c}/{\rho _f}$ and the elongation ratio of the cylinder $L/d$. We next introduce the gravitational velocity $V_g=\sqrt {(m^*-1) g d}$, which was shown by Toupoint, Ern & Roig (Reference Toupoint, Ern and Roig2019) to be the relevant velocity scale for the buoyancy-driven fall of cylinders in a comparable range of control parameters. Comparing this free-fall velocity with the velocity $V_c$ associated with the bending modes of a finite-length cylinder (with a potential added-mass coefficient of 1) provides the dimensionless parameter called ‘velocity ratio’ $U^*$ accounting for the body deformability, such that

(2.1a,b)\begin{equation} U^* = \frac{V_g}{V_c} \quad \textrm{with}\quad V_c= f_0 L \quad \textrm{and} \quad f_0 = \frac{d}{L^2}\sqrt{\frac{E}{\rho_c + \rho_f}}. \end{equation}

Last, we introduce the Archimedes number $Ar$ balancing buoyancy and viscosity effects, $Ar={V_g d}/{\nu }$. Note that, once the mean fall velocity $U$ of the cylinder is determined from experiments, the Reynolds number $Re = U d/\nu$ can be defined, for comparison with the case of fixed bodies embedded in an incoming flow.

The procedure followed is to start the series of experiments with a long cylinder (typically $L \simeq 120$ mm for a cylinder with $d=1$ mm) and to gradually decrease its length by steps of $5$ mm. This results in a joint variation of $L/d$ and $U^*$, while $m^*$ and $Ar$ are kept constant. We operated two methods of release of the flexible cylinders, in order to investigate the impact of initial conditions on the cylinder behaviour and to test the robustness of the phenomenon uncovered. Both methods used immersed bodies to avoid the presence of bubbles on the body surface. The first one consisted in releasing the cylinder hold straight from both ends. The second one intended to ensure no tension of the cylinder at release, and consisted in delicately pushing with a thin long-enough plate the body lying straight on a diving-board. Both methods provided the same observations, indicating that the origin of the oscillatory deformations is not related to prestressing. In both configurations, we could not avoid a slight initial inclination of the body at release. Inclination angles relative to horizontal are in all cases less than $7^\circ$, and in most cases less than $4^\circ$. The resulting lateral drift of the body (less than $7\,\%$ of the mean vertical velocity) decreased with the progressive slipping towards horizontality of the body due to the added-mass torque (see, for instance, Ern et al. (Reference Ern, Risso, Fabre and Magnaudet2012), for a discussion on the role of this torque). Regardless of the release conditions, we observed that the deformations are robust with respect to the presence of a weak drift, as phase locking between the oscillations of the two ends of the cylinder was preserved despite path asymmetry. The inclination angle may, however, affect the amplitude of oscillation and the drag coefficient, as will be discussed later.

Recordings of the falling cylinders were performed by shadowgraphy with two synchronized scientific complementary metal-oxide-semiconductor (sCMOS) cameras, $2560 \times 2160$ pixels (px), at a frequency of $50$ Hz and placed in front of two $20\ \textrm {cm} \times 20\ \textrm {cm}$ backlight flat panels producing directional illumination. A sketch of the experimental configuration is provided in figure 1. One camera imaged a field of view of $122\ \textrm {mm} \times 103\ \textrm {mm}$ in a vertical plane (which limits the length of the cylinders), and the second camera imaged a region of $167\ \textrm {mm} \times 141\ \textrm {mm}$ in a horizontal plane thanks to a mirror inclined at $45^\circ$.

Figure 1. Sketch of the experimental set-up, showing the positions of the cameras, the measurement volume in the square-section water tank, along with a qualitative picture of the falling cylinder. Cropped binarized images from both cameras obtained by image processing are also displayed, and show the centreline of the cylinder contour (red line).

For elongated bodies such as those considered here, important distortion effects on the body shape arise with perspective vision, as the body is unavoidably inclined in an angular field of view and off-centre relative to the line of sight of the camera. To disentangle the contributions to the cylinder behaviour of the different degrees of freedom is then an awkward procedure, even for rigid bodies, which is often resolved by capturing and reprojecting two generatrices of the cylinder (Toupoint et al. Reference Toupoint, Ern and Roig2019). In the case of a deforming body, this routine can no longer be employed straightforwardly.

To solve the problem, we used telecentric lenses, which combine several advantages: magnification and spatial resolution (typically, $15.3$ px mm$^{-1}$ for the horizontal plane and $21$ px mm$^{-1}$ for the vertical one) are invariant along the depth of field (telecentricity depth), parallax is avoided, and distortion is lower than with standard lenses. Calibration is carried out by recording a fixed object of known dimensions at different locations in the cubic measurement volume, confirming the constant magnification in the field of view (variations below $0.1$ px). The analysis of body displacements and deformations in time in the vertical and horizontal planes is performed by image processing, in particular to track the mean centreline of the cylinder (figure 1).

3. General observations and results

We first consider the case of a cylinder falling with a mean vertical velocity corresponding to $Re \simeq 42$ ($d=1$ mm). For sufficiently short cylinders, no deformation is visible. The cylinder maintains a straight conformation, falling with its axis perpendicular to gravity like a rigid cylinder. For $L/d \simeq 57$, the path of the cylinder can be considered as rectilinear, since only very weak non-reproducible irregular horizontal displacements are recorded (less than $3\,\%$ of $d$), as is commonly the case in experiments with freely moving objects (see discussions in Ern et al. (Reference Ern, Risso, Fabre and Magnaudet2012) and Toupoint et al. (Reference Toupoint, Ern and Roig2019)).

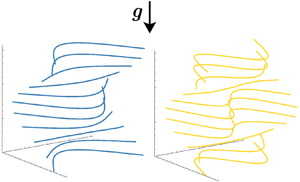
However, as the elongation ratio of the cylinder increases, a sequence of periodic deformations emerges. For $L/d$ larger than approximately $60$, a time-periodic deformation of the cylinder sets in. It is composed of one crest and two nodes, as illustrated in figure 2(a). It will be termed $M_1$ in reference to the corresponding bending mode of a beam. As $L/d$ is further increased, the amplitude of deformation grows, reaches a maximum for $L/d \simeq 70$ (value at the cylinder ends of approximately $0.66 d$ and span-averaged value of $0.3 d$), and decreases beyond. Oscillatory deformation $M_1$ is observed until $L/d \simeq 95$, featuring a displacement amplitude at the cylinder ends of $0.22 d$ and a span-averaged value of $0.15 d$. For $L/d \simeq 98$, the cylinder switches to $M_2$ (in reference to mode $2$), characterized by two crests and three nodes, as illustrated in figure 2(b). The amplitude at the cylinder ends is then $0.37 d$ (span-averaged amplitude 0.15 d). Behaviour $M_2$ is observed until $L/d \simeq 110$, which is the largest elongation ratio considered for this sequence, featuring a displacement amplitude at the cylinder ends of $0.71 d$ and a span-averaged value of $0.32d$.

Figure 2. Illustrations of the bending oscillatory deformations of a cylinder (with $d=1$ mm): (a) $M_1$ ($L/d = 70$) and (b) $M_2$ ($L/d = 110$). The left panels show three-dimensional views, with $y$ standing for the vertical coordinate. The right panels show the deformation in the horizontal ($x,z$) plane, with $x$ describing the undeformed cylinder axis and $z$ the transverse direction. The dashed black lines outline the envelope given by (3.1) with an amplitude adjusted to that of the cylinder ends in the experiments.

The bending deformations uncovered here feature several remarkable properties. First, they are restricted in a very distinctive manner to the horizontal plane, that is, perpendicular to the mean fall velocity of the body. Associated vertical displacements are considerably weaker, one or more orders of magnitude lower than those observed in the horizontal plane, and correspond to vertical velocity fluctuations less than $10\,\%$ of $U$. Such difference between horizontal and vertical oscillation magnitudes is a typical property of freely moving bodies close to the onset of an oscillatory path (see Ern et al. Reference Ern, Risso, Fabre and Magnaudet2012) as well as low-$Re$ vortex-induced vibrations observed for rigid (Singh & Mittal Reference Singh and Mittal2005) or flexible (Bourguet et al. Reference Bourguet, Karniadakis and Triantafyllou2011) cylinders.

Second, only a considerably weaker rigid-body oscillatory motion is observed here in the horizontal plane (displacement of the centre of gravity by less than $5\,\%$ of $d$, an order of magnitude comparable to that of fluctuations arising from tiny imperfections in the experiment).

The third consideration is that a significant decrease in mean fall velocity occurs when shape oscillations appear. The coloured crosses in figure 3(a) show the evolution of the Reynolds number $Re$ as the elongation ratio and the behaviour of the body vary. The periodic deformation of the body results in a loss of mean fall velocity, and therefore $Re$, of approximately 5 %–10 % for $M_1$. No significant change is then observed for $M_2$. The strength of the loss is related to the amplitude of deformation experienced by the body, the lower mean fall velocity being obtained for $L/d \simeq 70$, for which the deformation is most marked. The nearby plotted values for $L/d = 72$ and $74$ correspond to cases presenting a lateral drift of approximately $7\,\%$ and interestingly show higher mean vertical velocities than $L/d=70$, because of their weaker amplitude of oscillation. The periodic deformation experienced by the cylinder therefore results in additional drag. Drag amplification depends on the amplitude of deformation; a comparable trend was reported for vortex-induced vibrations of rigid cylinders (see e.g. Khalak & Williamson Reference Khalak and Williamson1999). This behaviour is illustrated in figure 3(b), displaying the drag coefficient associated with the mean vertical velocity of the body, $C_d = ({{\rm \pi} }/{2}) ({V_g}/{U})^2$, obtained by balancing buoyancy and mean drag. Values from Toupoint et al. (Reference Toupoint, Ern and Roig2019) for freely falling rigid cylinders with $m^* \simeq 1.16$ (black symbols) and from Vakil & Green (Reference Vakil and Green2009) for fixed rigid cylinders (dark grey cross) are also displayed, for comparison purpose.

Figure 3. (a) Reynolds number $Re$ and (b) drag coefficient $C_d$ as functions of the elongation ratio $L/d$ for $d=1$ mm (crosses) and $d=1.9$ mm (triangles): rectilinear motion $R$ (green); azimuthal rigid-body oscillatory motion AZI (orange); oscillatory deformations $M_1$ (blue) and $M_2$ (red). Values of $C_d$ for freely falling rigid cylinders with $L/d = 10$ and $20$, and $m^*\simeq 1.16$ from Toupoint et al. (Reference Toupoint, Ern and Roig2019) (black symbols) and for a fixed rigid cylinder with $L/d = 20$ from Vakil & Green (Reference Vakil and Green2009) (dark grey cross).

A step forward in the understanding of flexible-body behaviour is achieved from the analysis of the frequencies associated with the periodic deformations. Recordings were carried out on long time series (more than $20$ oscillation cycles) and frequencies could thus be determined accurately based on fast Fourier transform. The oscillatory deformations are dominated by a single frequency, except in some transition regions that will be discussed in the following. Furthermore, both cylinder ends are remarkably synchronized, displaying the same frequencies and phase difference over the whole recording.

The deformation frequency $f$ of the freely falling cylinder is plotted as a function of the elongation ratio in figure 4(a), for $M_1$ (blue crosses) and $M_2$ (red crosses). These frequencies can be compared with the natural frequencies of the bending modes $i$ of an unsupported cylinder with free ends immersed in still fluid. Using a linear Euler–Bernoulli beam model and including added-mass effects (with an added-mass coefficient equal to $1$) lead to the bending mode frequencies, $f_i = \alpha _i\,f_0$, where the constants $\alpha _i$ are related to the roots of the equation $\cosh {\beta _i} \cos {\beta _i} - 1 = 0$ by $\alpha _i = \beta _i^2 / (8{\rm \pi} )$, giving $\alpha _1 \simeq 0.890$, $\alpha _2 \simeq 2.454$, $\alpha _3 \simeq 4.811$, $\alpha _4 \simeq 7.952$, …. At a given time $t$, the corresponding deformed shape of the cylinder for mode $i$ can be expressed in the form $z_c \sin {( 2 {\rm \pi}f_i t + \phi _i)}$, where $\phi _i$ is a constant phase and the amplitude $z_c$ depends on the longitudinal coordinate $x$ along the cylinder axis as

(3.1a)\begin{gather} z_c = \cos(\beta_i x/L) + \cosh(\beta_i x/L) + K [ \sin(\beta_i x/L) + \sinh(\beta_i x/L) ] \end{gather}

(3.1b)\begin{gather}\textrm{with} \quad K = [ \sin(\beta_i) + \sinh(\beta_i) ] / [\cos(\beta_i) - \cosh(\beta_i)]. \end{gather}

Figure 4. (a) Deformation frequency $f$ of the freely falling cylinder for $M_1$ and $M_2$; natural frequencies $f_i$ (solid lines for $d=1$ mm, dashed–dotted lines for $d=1.9$ mm); frequency of AZI for $d=1.9$ mm. Crosses and triangles: same convention as in figure 3(a). Open and filled circles: $f_w$ from Williamson & Brown (Reference Williamson and Brown1998) and from Buffoni (Reference Buffoni2003), respectively. Coloured dashed ($d=1$ mm) and dotted ($d=1.9$ mm) vertical lines: values of $L/d$ corresponding to $f_i = f_w$ for mode $1$ (blue) and mode $2$ (red) according to (4.1). (b) Frequencies $f$ and $f_w$ normalized with $f_0$ as functions of the velocity ratio $U^*$. Horizontal lines: values of $\alpha _i$. Vertical lines: values of $U^*$ corresponding to those of $L/d$ in (a). (c,d) Main frequency content: (c) near the transition $T_{\text {A--1}}$ from AZI to $M_1$ for $Re \simeq 120$, $L/d \simeq 37$ (orange) and $L/d \simeq 39$ (blue); and (d) near the transition $T_{\text {1--2}}$ from $M_1$ to $M_2$ for $Re \simeq 42$, $L/d \simeq 95$ (blue) and $L/d \simeq 98$ (red).

Note that for all modes $i$ the integral of $z_c$ between $0$ and $L$ is zero, so that the position of the centre of gravity of the cylinder in this model equation does not evolve in time. The frequencies $f_i$ with $i \in \{1,2\}$ are plotted with thin dashed lines in figure 4(a) for mode $1$ (blue) and mode $2$ (red), showing the correspondence between the succession with $L/d$ of the vibrational modes $f_i$ and the experimental observations. The envelopes of the first two modes provided by (3.1) are also superposed (thick black dashed lines) on the deformed states of the cylinder determined experimentally at different times in figure 2, yielding again good agreement.

Comparing now the deformation frequency $f$ with the inertial time scale associated with the body free fall $d / U$, which is also the characteristic time scale for vortex shedding about the body, provides values of $f d / U$ varying in the range 0.105–0.140. These values are close to the Strouhal number value, $St_w = 0.105$, associated with subcritical vortex shedding downstream of a long cylinder determined by Buffoni (Reference Buffoni2003) for $Re=42$ by slightly vibrating the cylinder to trigger the flow. The wake frequencies $f_w = St_w U/ d$ extracted from Buffoni (Reference Buffoni2003) using the Reynolds numbers corresponding to each $L/d$ in our experiments are drawn with filled circles in figure 4(a); these values are close to the measured deformation frequencies. Figure 4(b) summarizes the comparison between the frequencies. The data points (blue crosses for $M_1$ and red ones for $M_2$) indicate the evolution of the body deformation frequency, $f$, normalized with the proper bending frequency of the cylinder, $f_0$, as a function of $U^*$. The wake frequencies $f_w$ (also normalized with $f_0$) obtained from Buffoni (Reference Buffoni2003) are drawn with filled circles. We can see that the deformation frequency of the freely moving cylinder is locked to the wake frequency. As $L/d$ varies, the deformation frequency departs from the natural frequencies of the cylinder, indicated by horizontal lines at $\alpha _i$. At a given stage, however, the next mode of the cylinder is excited and a frequency jump occurs, as can be seen here between $M_1$ and $M_2$. For all the $L/d$ investigated, the close agreement of the deformation frequency with the wake frequency suggests that the bending deformations observed are linked to the wake unsteadiness. Furthermore, the results indicate that the cylinder degrees of freedom in deformability allow wake instability to be triggered below the threshold for fixed rigid bodies, as the present Reynolds-number values ($Re \simeq 40$) would be subcritical in the rigid-body case (Inoue & Sakuragi Reference Inoue and Sakuragi2008). This point will be discussed further in § 4.

The second situation investigated is that of a freely falling cylinder displaying a periodic motion in association with an unsteady wake. For that purpose, a higher Reynolds number is considered, namely $Re \simeq 120$, obtained for cylinders with $d=1.9$ mm (figure 3a, triangular data points). At this $Re$, a rigid-body azimuthal oscillation (termed AZI in the following) of the flexible cylinder is observed from $L/d \simeq 21$ to $L/d \simeq 37$. It corresponds to the azimuthal oscillation reported by Toupoint et al. (Reference Toupoint, Ern and Roig2019) for rigid cylinders with $L/d = 20$, $m^* \simeq 1.16$, $Re \simeq 130$ and $Re \simeq 220$. In both cases, this rotational oscillatory motion features reproducible low-amplitude (approximately $0.2^\circ$) oscillations of the azimuthal angle of the cylinder, on top of irregular weak displacements comparable to those observed for the rectilinear path at $Re \simeq 42$. As shown in figure 4(a) (orange triangles), the AZI oscillation occurs at a frequency of approximately $4.2$ Hz. This corresponds to a Strouhal number of $0.13$, which is slightly smaller than that of the Bénard–von Kármán instability about a fixed cylinder at this $Re$, $St_w \simeq 0.17$, obtained from the relation proposed by Williamson & Brown (Reference Williamson and Brown1998). Using dye visualization, Toupoint et al. (Reference Toupoint, Ern and Roig2019) showed that the AZI motion is coupled with an unsteady wake (see their figure 17c), similar to those for fixed long cylinders referred to as ‘Type II’ by Inoue & Sakuragi (Reference Inoue and Sakuragi2008) and as ‘oblique vortex shedding’ by Williamson (Reference Williamson1989). However, for the freely moving cylinder, a periodic beating of the wake was observed near the body ends, at the oscillation frequency of the azimuthal angle, and in phase opposition between the two ends.

Now, for $L/d \simeq 39$, we observed that mode $1$ oscillatory deformations (i.e. $M_1$) set in. Behaviour $M_1$ is further observed until $L/d \simeq 57$, the largest elongation ratio that could be investigated for this cylinder. The highest amplitude of deformation is reached for $L/d \simeq 52$, with a displacement of the cylinder ends of $0.8 d$ and a span-averaged value of $0.39 d$. Note that, in this case also, higher mode responses are expected to exist. Mode $2$ deformations were in fact observed for a different cylinder having slightly smaller diameter ($d=1.8$ mm) and larger length ($L=131$ mm), i.e. $L/d \simeq 73$. This sequence of deformations shares the properties described in the previous case, in particular the significant velocity decrease and associated drop in $Re$ (figure 3a, triangular data points). The resulting increase in drag is conspicuous in figure 3(b) (triangular data points). For this case also, the proximity between the wake frequency $f_w$ determined from the expression $St_w(Re)$ proposed by Williamson & Brown (Reference Williamson and Brown1998) (open circles), the cylinder natural frequency $f_i$ (dotted curves) and the observed deformation frequency $f$ (triangular data points) is manifest in figure 4(a) and (b).

In this second situation, the oscillatory deformations supplant an oscillatory rigid-body motion (i.e. AZI). For sufficiently short flexible cylinders, vortex shedding is coupled with a rigid-body vibration of the cylinder. This corresponds to cylinder ends moving in phase opposition, a property shared with $M_2$ but conflicting with $M_1$. Deformation $M_1$ is nevertheless triggered for a slightly longer cylinder. Closer examination of the main frequency content of the body displacement near the onset of $M_1$ reveals that the transition features mixed responses: the oscillatory deformation and the rigid-body motion coexist for both $L/d \simeq 37$ and $L/d \simeq 39$, as can be seen in figure 4(c). The rigid-body motion predominates in the former case, whereas it is outweighed by the deformations in the latter, and disappears as the elongation ratio is increased further. Note that coexistence of $M_1$ and $M_2$ was not detected here in the measurements for $L/d \simeq 95$ and $L/d \simeq 98$ close to the transition $T_{\text {1--2}}$ from $M_1$ to $M_2$ for $Re \simeq 42$ (figure 4d), while superposition of deformation modes is commonly observed for a flexible cylinder held from its ends (Chaplin et al. Reference Chaplin, Bearman, Huera-Huarte and Pattenden2005; Huera-Huarte, Bangash & González Reference Huera-Huarte, Bangash and González2014).

4. Concluding remarks

We investigated experimentally the behaviour of an elongated flexible cylinder settling at moderate Reynolds number under the effect of gravity in a fluid otherwise at rest. For a given cylinder diameter, the experimental approach consisted in gradually decreasing the body length, thereby changing its natural deformation frequency without significantly impacting its mean falling velocity in the absence of deformation. Short enough cylinders behaved like rigid bodies, showing no detectable reconfiguration, and fell with their axis perpendicular to gravity. However, for longer cylinders and therefore higher velocity ratios $U^*$, the experiments brought to light the springing up of periodic oscillatory deformations of the freely falling flexible cylinders in specific parameter ranges. To the best of our knowledge, the only counterpart of this phenomenon in the literature concerns freely rising bubbles, as discussed in the introduction.

We further showed that the sequence of oscillatory deformations emerging when the cylinder length is increased involve the bending modes of an unsupported beam with free ends, each mode being associated with a natural frequency $f_i$. Besides, comparison of the deformation frequency with the vortex shedding frequency $f_w$ expected for a non-deformable cylinder at the same Reynolds number indicated that the deformations are coupled with wake unsteadiness. Flow-induced bending deformations involving mode $i$ are expected to occur during free fall when $f_i$ is close to $f_w$. The simple criterion matching bending mode natural frequency to vortex shedding frequency, $f_i = f_w$, corresponds to

(4.1)\begin{equation} L/d = \sqrt{\alpha_i/(U St_w)} ({E}/({\rho_c+\rho_f}) )^{1/4}.\end{equation}

For a cylinder of diameter $d$, this expression can be used to obtain a prediction of $L/d$ associated with mode $i$ by assuming $U=V_g$ (or $C_d={\rm \pi} /2$), which allows one to determine $Re$ and subsequently $St_w$ ($St_w \simeq 0.1$ and $0.17$ for $d=1$ and $1.9$ mm, respectively). Corresponding estimations for $L/d$ and $U^*$ are reported in figure 4(a) and (b) for modes 1 and 2 (vertical blue and red lines) and appear consistent with experimental observations. From (4.1) we can expect the occurrence of higher-order bending modes, for instance in the $d=1$ mm case for $L/d \approx 162$ ($M_3$) and $L/d \approx 208$ ($M_4$).

The experiments also revealed that the oscillatory deformations can develop for distinct flow configurations. Bending oscillations for a freely falling cylinder are here shown to appear for bodies displaying a rectilinear path with a steady wake, and for bodies displaying a rigid-body oscillatory motion coupled with an unsteady wake. In the former case, the close agreement between deformation and wake frequencies suggests that the bending deformations that replace the rectilinear fall are also related to wake unsteadiness, though the Reynolds number would be subcritical in the rigid-body case ($Re \simeq 40$). This indicates that deformability may allow wake instability to be triggered below the threshold corresponding to fixed rigid bodies. The anticipation of wake destabilization due to degrees of freedom of the body has been observed for closely related problems of fluid–body interaction. For instance, Cossu & Morino (Reference Cossu and Morino2000) and Meliga & Chomaz (Reference Meliga and Chomaz2011) investigated the global stability and the nonlinear dynamics close to the threshold of vortex-induced vibrations in the wake of a damped, spring-mounted, circular cylinder. They demonstrated the role of the natural eigenvalue of the cylinder-only system on triggering subcritical vortex shedding at low solid-to-fluid density ratios. In the case of freely moving rigid bodies having different geometries, theoretical and computational studies also revealed that the coupling between the degrees of freedom of the body and the fluid can shift the thresholds and frequencies associated with wake instability about the fixed body or in contrast give rise to different regimes of path instability (Tchoufag, Fabre & Magnaudet Reference Tchoufag, Fabre and Magnaudet2014; Mathai et al. Reference Mathai, Zhu, Sun and Lohse2017). For instance, in the limit of heavy plates, Assemat, Fabre & Magnaudet (Reference Assemat, Fabre and Magnaudet2012) found that the threshold of path instability matches that found for a fixed plate, whereas it decreases when the solid-to-fluid mass ratio decreases, while keeping Strouhal-number values comparable with those of the fixed plate. The present observations provide experimental evidence of the destabilization of a coupled solid–fluid system at a frequency characteristic of vortex shedding, and for Reynolds numbers that are subcritical in the fixed rigid-body case, with the novelty that the degrees of freedom in deformability of the body are involved here. In the second flow configuration, oscillatory bending deformations develop for bodies displaying a periodic motion coupled with an unsteady wake. Except very close to the threshold, the cylinder response to wake forcing becomes essentially a deformation, which takes over the rigid-body displacement of the body. In turn, as the displacements of the cylinder ends shift in this case from phase-opposition to in-phase motion, it leads to a change of wake structure, which still needs to be explored.

A major issue now regards the identification and characterization of the wake structures associated with the different deformation modes. The detailed interaction between the flow and the deforming body remains also to be elucidated, in connection with the different amplitudes of deformation that emerge. We are currently heading in that direction, the challenge being to be able to capture both the body and the flow structure over the two orders of magnitude of length scales involved in the problem (spanning from $d$ to $L$). At issue here is also a better understanding of the role of the cylinder free ends. As observed for freely falling deformable plates by Tam (Reference Tam2015), deformation may concentrate on the body periphery, where the flow field distribution is likely to trigger it. The degrees of freedom in translation and rotation associated with the cylinder free ends may also play a role in deformation phenomena, in the same way they enable the occurrence of oscillatory paths for finite-length rigid cylinders different from those observed for two-dimensional cylinders. As a first step to address this question, we carried out preliminary experiments with flexible rings in a comparable range of parameters. They brought to light oscillatory deformations of the ring at a nearby frequency, illustrated in figure 5; this indicates that also in a closed configuration (i.e. in the absence of end effects), the degrees of freedom in deformability of the body can be excited by the surrounding flow and can couple with it.

Figure 5. Deformation at a frequency $f \simeq 4.5$ Hz of a thin flexible ring freely falling at approximately $5$ cm s$^{-1}$ in water at rest (ring diameter $D \simeq 7$ cm, square-section width $l \simeq 1.5$ mm), corresponding to $Re \simeq 75$ (based on $l$). (a) Ring shape in the horizontal ($x, z$) plane at several times $t$. The central inset shows a sketch of the deformation with magnified displacements. The local radial displacement about the time-averaged deformation is denoted $r$, $A_r$ is the corresponding amplitude and $\theta$ is the azimuthal angle. (b) Normalized amplitude $A_r/l$ spanned along $\theta$. (c) Temporal evolutions of $r/l$ for crest points $2$ and $4$ and for node point $3$.